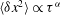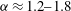1. Introduction
Turbulence is a natural state of space and laboratory plasmas. The fundamental principles to investigate developed turbulence were laid by Kolmogorov (Reference Kolmogorov1941a
,Reference Kolmogorov
b
) in the framework of a statistical description and cascading model. Turbulence in a flow usually emerges due to boundary effects. In hydrodynamic flows, the velocity shear near the flow boundary strongly affects the development of turbulence. For viscous neutral fluids (even with an arbitrarily small viscosity coefficient
![]() ${\it\nu}$
), the velocity must vanish at the flow boundary. In magnetohydrodynamics (MHD), a theoretical treatment must consider not only the material boundaries of the flow and the presence of highly dispersive modes, but also the structures (waves, eddies, etc.) formed by the magnetic and electric fields. In 1987, Zeldovich discussed the concept of turbulent flow with filamentary vortices in magnetofluids in order to explain the intermittency as a turbulence property originated from the coupling of hierarchical vortices. He also considered a hypothesis on the universality of intermittent turbulence properties on small scales.
${\it\nu}$
), the velocity must vanish at the flow boundary. In magnetohydrodynamics (MHD), a theoretical treatment must consider not only the material boundaries of the flow and the presence of highly dispersive modes, but also the structures (waves, eddies, etc.) formed by the magnetic and electric fields. In 1987, Zeldovich discussed the concept of turbulent flow with filamentary vortices in magnetofluids in order to explain the intermittency as a turbulence property originated from the coupling of hierarchical vortices. He also considered a hypothesis on the universality of intermittent turbulence properties on small scales.
Satellite observations of space plasmas provide experimental data on the turbulence properties on spatial and temporal scales that are unavailable in laboratory experiments. Studies of low-frequency MHD turbulence in the solar wind (SW) and at the outer magnetospheric boundaries with turbulent boundary layers (TBL) in the frequency range
![]() $10^{-7}~\text{Hz}<f<10~\text{Hz}$
(the plasma is to be treated as a magnetohydrodynamic fluid; as Alfven wave phenomena and reconnection phenomenon can be investigated experimentally in detail) are especially important, because such measurements turn out to be complementary to measurements available in laboratory plasma experiments.
$10^{-7}~\text{Hz}<f<10~\text{Hz}$
(the plasma is to be treated as a magnetohydrodynamic fluid; as Alfven wave phenomena and reconnection phenomenon can be investigated experimentally in detail) are especially important, because such measurements turn out to be complementary to measurements available in laboratory plasma experiments.
At the boundary of the Earth’s magnetosphere (magnetopause, MP), an external boundary layer is formed due to interaction of the collisionless SW plasma flow with the magnetospheric magnetic field (figure 1). The small scale plasma fluctuations in the SW and at the boundary of the Earth’s magnetosphere are observed to be highly turbulent (see for example: Burlaga Reference Burlaga1991; Bruno et al. Reference Bruno, Carbone, Sorriso-Valvo and Bavassano2003; Zelenyi & Milovanov Reference Zelenyi and Milovanov2004; Savin et al. Reference Savin, Skalsky, Zelenyi, Avanov, Borodkova, Klimov, Lutsenko, Panov, Romanov and Smirnov2005–Reference Savin, Amata, Budaev, Zelenyi, Kronberg, Buechner, Safrankova, Nemecek, Blecki and Kozak2014; Bruno & Carbone Reference Bruno and Carbone2013 etc.). The turbulence in the boundary of the Earth’s magnetosphere is inhomogeneous.

Figure 1. (a) The Earth’s magnetospheric plasma, a schematic of the SE streaming of the MP: 1 – magnetopause, 2 – polar cusp, 3 – dipole moment, 4 – magnetic field, 5 – plasma cloud, 6 – plasma flow, 7 – turbulent boundary layer, 8 – summer (upper half) and 9 – winter (bottom half). (b) Tokamak plasma cross-section: 1 – core, 2 – edge, 3 – scrape-off layer, 4 – divertor plasma, 5 – wall, 6 – divertor.
In laboratory experiments, plasma turbulence can be investigated depending on different driving forces, magnetic and electric field effects. This especially relates to high-temperature plasma in fusion devices (tokamaks, helical devices and stellarators, linear machines). The different magnetic topology of fusion devices gives an opportunity for the study of various magnetically confined plasmas. Confinement of thermonuclear plasma in a tokamak (toroidal magnetic volume, figure 1) is highly promising for the realization of fusion reactors. Plasma in a tokamak and other fusion devices demonstrate the properties of complex systems with self-organization (Kadomtsev Reference Kadomtsev1992). Purely diffusive transport processes cannot explain a variety of experiments in magnetically confined plasmas. Experimental observations have shown that plasma losses due to particle transport across the (via) magnetic field significantly exceed what was expected in the case of collisional diffusion only. Numerous experimental studies in fusion devices (see, e.g. Diamond et al. Reference Diamond, Itoh, Itoh and Hahm2005; Zweben et al. Reference Zweben, Boedo, Grulke, Hidalgo, LaBombard, Maqueda, Scarin and Terry2007; Budaev et al. Reference Budaev, Ohno, Masuzaki, Morisaki, Komori and Takamura2008a ,Reference Budaev, Savin, Zelenyi, Ohno, Takamura and Amata b ; Budaev, Savin & Zelenyi Reference Budaev, Savin and Zelenyi2011; Conway Reference Conway2008; Tynan, Fujisawa & McKeeb Reference Tynan, Fujisawa and McKeeb2009 etc.) show that the core and edge plasmas are highly turbulent. Strong plasma turbulence drives enhanced plasma losses due to large cross-field transport (called anomalous diffusion) above the standard collisional diffusion. Large cross-field transport induced by plasma turbulence due to fluctuations on a microscopic length scale such as the ion Larmor radius, collisionless skin depth or resistive layer width (see, e.g. Connor & Wilson Reference Connor and Wilson1994) results in the degradation of plasma confinement. There are many possible driving mechanisms in fusion devices that can lead to anomalous diffusion. Plasma turbulence models consider different types of instabilities to investigate transport properties of a 3-D pressure-gradient-driven turbulence (see, e.g. Carreras, Lynch & LaBombard Reference Carreras, Lynch and LaBombard2001a ) over a broad range of space and time scales. The underlying instabilities are resistive ballooning modes, resistive interchange modes and others. The coupling of processes on different scales is essential in a treating of the anomalous diffusion processes and of the nonlinear evolution of 3-D plasma turbulence.
The turbulence level (the ratio of the fluctuation amplitude to their mean value) and cross-field turbulent transport are increased in the edge region. It is observed in fusion devices of different scales, with various magnetic topologies (tokamaks, helical devices and others) and plasma heating. Several reasons for such turbulent level enhancement have been considered, but the dominant factor is presumably the universal behaviour of turbulent processes under the influence of boundary effects. The edge plasma region (figure 1) is characterized by substantial variations of plasma parameters and transport barriers. Edge plasma turbulence is driven by drift-wave, interchange and kinetic alvenic-type instabilities in the frequency range from
![]() ${\sim}0.1~\text{kHz}$
to
${\sim}0.1~\text{kHz}$
to
![]() ${\sim}1~\text{MHz}$
. In tokamaks, in an edge plasma with closed magnetic surfaces, the turbulence is dominated by drift waves (Scott Reference Scott2005), while in the region of open magnetic field lines (so called scrape-off-layer SOL), interchange instability is the main mechanism driving the turbulence. In edge plasmas, fluctuations of the background plasma exist in the form of long-living large-scale correlated structures Sometimes they are called blobs or coherent structures. These correlated structures were experimentally registered in the SOL of various fusion devices (see e.g. Zweben et al.
Reference Zweben, Boedo, Grulke, Hidalgo, LaBombard, Maqueda, Scarin and Terry2007).
${\sim}1~\text{MHz}$
. In tokamaks, in an edge plasma with closed magnetic surfaces, the turbulence is dominated by drift waves (Scott Reference Scott2005), while in the region of open magnetic field lines (so called scrape-off-layer SOL), interchange instability is the main mechanism driving the turbulence. In edge plasmas, fluctuations of the background plasma exist in the form of long-living large-scale correlated structures Sometimes they are called blobs or coherent structures. These correlated structures were experimentally registered in the SOL of various fusion devices (see e.g. Zweben et al.
Reference Zweben, Boedo, Grulke, Hidalgo, LaBombard, Maqueda, Scarin and Terry2007).
Typical signals of turbulent plasma fluctuations in space and laboratory plasmas are shown in figure 2. Fluctuations are self-similar and have power spectra exhibiting non-trivial frequency dependence. In the TBL near Earth’s MP and in the edges of fusion devices, plasma turbulence demonstrates a strong intermittency (see Budaev et al. Reference Budaev, Savin and Zelenyi2011) with bursty waveforms.

Figure 2. Fluctuations in space and laboratory plasmas. (a) Ion flux SPECTR-R data 2012-03-20, 12-21 UT; (b) SW ion flux, WIND data 12-03-20 12-21 UT; (c) ion flux CLUSTER 4 data 2012-03-20 13-18 UT; (d) edge plasma density in tokamak T-10.
Intermittency was first considered by Novikov & Stewart (Reference Novikov and Stewart1964), who considered it to be a local breaking of turbulence homogeneity which occurs when active regions coexist with passive (quasi-laminar) ones. It is a general belief that intermittency in hydrodynamics was observed to be a clear departure from the Kolmogorov
![]() $-5/3$
scaling exponent of the energy spectrum in various turbulence experiments at finite Reynolds numbers. The consensus is that the intermittent property of turbulence calls for a power-law of the energy spectrum having an exponent
$-5/3$
scaling exponent of the energy spectrum in various turbulence experiments at finite Reynolds numbers. The consensus is that the intermittent property of turbulence calls for a power-law of the energy spectrum having an exponent
![]() $-5/3-c$
, with an intermittency correction exponent
$-5/3-c$
, with an intermittency correction exponent
![]() $c\geqslant 0$
. The intermittency can be characterized by using statistical properties which deviate from the statistics of the Kolmogorov K41 model. In experiments, intermittency is typically observed as non-Gaussian statistical fluctuations (see discussion below).
$c\geqslant 0$
. The intermittency can be characterized by using statistical properties which deviate from the statistics of the Kolmogorov K41 model. In experiments, intermittency is typically observed as non-Gaussian statistical fluctuations (see discussion below).
The intermittency phenomenon is observed in hydrodynamics (see Frish Reference Frish1995) and in turbulent magnetized plasmas (see, e.g. review Budaev et al.
Reference Budaev, Savin and Zelenyi2011 and references therein), both with high and moderate kinetic Reynolds numbers (
![]() $\mathit{Re}$
) and magnetic Reynolds numbers (
$\mathit{Re}$
) and magnetic Reynolds numbers (
![]() $\mathit{Re}_{m}$
)
$\mathit{Re}_{m}$
)
![]() $\mathit{Re},\mathit{Re}_{m}<1000$
. Intermittency is the property responsible for anomalous plasma transport: anomalous cross-field diffusion in fusion devices and enhanced transport by intensive plasma jets from the SW through the TBL inside the geomagnetic trap of the Earth (Savin et al.
Reference Savin, Zelenyi, Amata, Budaev, Buechner, Blecki, Balikhin, Klimov, Korepanov and Kozak2010; Zelenyi et al.
Reference Zelenyi, Zastenker, Petrukovich, Chesalin, Nazarov, Prokhorenko and Larionov2013). Intermittency is observed to be a property of different variables – the plasma density, electric field, velocity, magnetic field and the particle flux both in the Earth’s TBL and in the edges of fusion devices (see Zweben et al.
Reference Zweben, Boedo, Grulke, Hidalgo, LaBombard, Maqueda, Scarin and Terry2007; Budaev et al.
Reference Budaev, Savin and Zelenyi2011).
$\mathit{Re},\mathit{Re}_{m}<1000$
. Intermittency is the property responsible for anomalous plasma transport: anomalous cross-field diffusion in fusion devices and enhanced transport by intensive plasma jets from the SW through the TBL inside the geomagnetic trap of the Earth (Savin et al.
Reference Savin, Zelenyi, Amata, Budaev, Buechner, Blecki, Balikhin, Klimov, Korepanov and Kozak2010; Zelenyi et al.
Reference Zelenyi, Zastenker, Petrukovich, Chesalin, Nazarov, Prokhorenko and Larionov2013). Intermittency is observed to be a property of different variables – the plasma density, electric field, velocity, magnetic field and the particle flux both in the Earth’s TBL and in the edges of fusion devices (see Zweben et al.
Reference Zweben, Boedo, Grulke, Hidalgo, LaBombard, Maqueda, Scarin and Terry2007; Budaev et al.
Reference Budaev, Savin and Zelenyi2011).
Consideration of interrelated phenomena in laboratory and space plasmas helps to promote the interpretation of scientific results in a broader context by sharing data, methods, knowledge, perspectives and reasoning. It is unrealistic to expect the dimensional parameters corresponding to space plasmas to be matched in the laboratory. In comparison to space plasmas, laboratory devices generate plasmas with dimensions that are too small, magnetic fields that are too big, neutral pressures that are too large and plasma densities that are too high. However, in a laboratory experiment on fusion devices, the subset of plasma turbulence parameters are observed to be relevant to a specific process which share the same phenomenological regime as the subset of analogous space parameters, even if less important parameters are mismatched (see, e.g. Koepke Reference Koepke2008a
,Reference Koepke
b
). Spatial and temporal scales in space can be vastly different from those in laboratory plasmas, but normalization by the gyroradius or the Debye length and ratios of the plasma-to-cyclotron frequency for electrons and ions allow a more relevant subset of dimensionless parameters that offer a valid link between experiments in the laboratory and plasmas in space. Regime boundaries are assigned by normalizing a dimensional parameter to an appropriate reference or scale value to make it dimensionless, and noting the values at which transitions occur in the physical behaviour or approximations. Turbulence-related problems involve interactions between flow, waves and instabilities. The treatment of this problem can be based on the similarity of the dimensionless, hydrodynamics parameters including the Euler number and the Reynolds number. The dimensionless Euler number, derived from pressure, density and velocity is defined according to
![]() $\mathit{Eu}={\it\upsilon}^{\prime }({\it\rho}^{\prime }/\mathit{p}^{\prime })^{1/2}$
, where
$\mathit{Eu}={\it\upsilon}^{\prime }({\it\rho}^{\prime }/\mathit{p}^{\prime })^{1/2}$
, where
![]() ${\it\upsilon}^{\prime }$
,
${\it\upsilon}^{\prime }$
,
![]() ${\it\rho}^{\prime }$
and
${\it\rho}^{\prime }$
and
![]() $\mathit{p}^{\prime }$
are normalized versions of the velocity, density and pressure, respectively. The dimensionless Euler number conveys the degree of similarity between the hydrodynamics in the laboratory and in a space plasma (see discussion in Ryutov et al.
Reference Ryutov, Drake, Kane, Liang, Remington and Wood-Vasey1999). For both the laboratory plasma in the edge of a fusion device, and magnetospheric plasma, the dimensionless Euler number
$\mathit{p}^{\prime }$
are normalized versions of the velocity, density and pressure, respectively. The dimensionless Euler number conveys the degree of similarity between the hydrodynamics in the laboratory and in a space plasma (see discussion in Ryutov et al.
Reference Ryutov, Drake, Kane, Liang, Remington and Wood-Vasey1999). For both the laboratory plasma in the edge of a fusion device, and magnetospheric plasma, the dimensionless Euler number
![]() $Eu$
is estimated to be in the range from
$Eu$
is estimated to be in the range from
![]() ${\sim}0.1$
to
${\sim}0.1$
to
![]() ${\sim}10$
(see Koepke Reference Koepke2008a
,Reference Koepke
b
). Although the laboratory and space values of velocity and pressures are very different, the Euler numbers for laboratory and space plasmas are the same, indicating that the hydrodynamics both in the laboratory and in space should behave similarly (see discussion in Koepke Reference Koepke2008a
,Reference Koepke
b
, Ryutov et al.
Reference Ryutov, Drake, Kane, Liang, Remington and Wood-Vasey1999. Likewise, kinetic and magnetic Reynolds numbers
${\sim}10$
(see Koepke Reference Koepke2008a
,Reference Koepke
b
). Although the laboratory and space values of velocity and pressures are very different, the Euler numbers for laboratory and space plasmas are the same, indicating that the hydrodynamics both in the laboratory and in space should behave similarly (see discussion in Koepke Reference Koepke2008a
,Reference Koepke
b
, Ryutov et al.
Reference Ryutov, Drake, Kane, Liang, Remington and Wood-Vasey1999. Likewise, kinetic and magnetic Reynolds numbers
![]() $\mathit{Re},\mathit{Re}_{m}<1000$
are similar in the magnetospheric TBL and boundary plasma in fusion devices.
$\mathit{Re},\mathit{Re}_{m}<1000$
are similar in the magnetospheric TBL and boundary plasma in fusion devices.
The driving forces of the intermittent bursts can be pressure gradients and other effects which can drive various large-scale instabilities. In space plasma, some recent experimental spacecraft observations inside the magnetosheath – MSH (see Nemecek et al. Reference Nemecek, Safrankova, Prech, Sibeck, Kokubun and Mukai1998; Savin et al. Reference Savin, Skalsky, Zelenyi, Avanov, Borodkova, Klimov, Lutsenko, Panov, Romanov and Smirnov2005, Reference Savin, Amata, Zelenyi, Lutsenko, Safrankova, Nemecek, Borodkova, Buechner, Daly and Kronberg2012, Reference Savin, Amata, Budaev, Zelenyi, Kronberg, Buechner, Safrankova, Nemecek, Blecki and Kozak2014 and references therein) revealed the presence of very fast plasma streams (supermagnetosonic plasma stream – SPS). SPS’s last up to several tens of seconds and have an extremely high pressure (several times larger than the SW pressure). SPS’s are considered to be extreme events, which can drive an intermittent turbulence at the MP TBL (Savin et al. Reference Savin, Amata, Zelenyi, Lutsenko, Safrankova, Nemecek, Borodkova, Buechner, Daly and Kronberg2012, Reference Savin, Amata, Budaev, Zelenyi, Kronberg, Buechner, Safrankova, Nemecek, Blecki and Kozak2014). In the edge SOL region of fusion devices, interchange instabilities can drive large-scale coherent structures which are observed as filaments elongated along magnetic field (see, e.g. Scott Reference Scott1997; Budaev et al. Reference Budaev, Savin and Zelenyi2011 and references therein).
There are no clear observations that density filaments may be a trigger and an origin of the intermittent nature of plasma velocity fluctuations. Moreover, experimental observations have shown a similarity of statistical characteristics of the observable variables (plasma density, velocity, electric and magnetic field fluxes). This is an argument in favour of investigating the intermittency as a phenomenon induced by these observable variables. In the treatment of the intermittency problem, driving and damping due to nonlinear coupling of small and large-scale modes should be considered.
Developed turbulence is characterized by a large number of coupled modes, a small-scale structure and random fluctuations of velocities and fields. Hence, it can be best described by statistical methods using a probability distribution function (PDF) or, equivalently, all of the moments of the distribution function which can be measured in experiments. In the simplest case, the PDF of the fluctuations amplitudes obey the Gaussian (so called normal) law. Gaussian statistics describe e.g. classical Brownian motion, in which correlations decay exponentially. To describe random processes with memory and long-range correlations, other laws can be considered (see, e.g. Guikhman & Skorokhod Reference Guikhman and Skorokhod1969).
In the literature, it is considered that the non-Gaussian distribution of turbulence velocity increments lead to a violation of the original Kolmogorov scaling
![]() $-5/3$
(see below), and in fact intermittency manifests as a non-Gaussian velocity distribution. This argument has been controversial since even in local homogeneous isotropic turbulence the velocity increments cannot be Gaussian (see discussion in Chen Reference Chen2006). Lévy flights, or anomalous diffusion processes (known in the mathematical literature as
$-5/3$
(see below), and in fact intermittency manifests as a non-Gaussian velocity distribution. This argument has been controversial since even in local homogeneous isotropic turbulence the velocity increments cannot be Gaussian (see discussion in Chen Reference Chen2006). Lévy flights, or anomalous diffusion processes (known in the mathematical literature as
![]() ${\it\alpha}$
-stable Lévy processes), can be used as a description of non-Gaussian fluctuations. They have infinite variance (except for the Gaussian case). The non-Gaussian Lévy stable distribution of the velocity difference has an algebraic decay tail and possesses scale-invariance and self-similarity properties. There are a few models which have considered intermittency (see below).
${\it\alpha}$
-stable Lévy processes), can be used as a description of non-Gaussian fluctuations. They have infinite variance (except for the Gaussian case). The non-Gaussian Lévy stable distribution of the velocity difference has an algebraic decay tail and possesses scale-invariance and self-similarity properties. There are a few models which have considered intermittency (see below).
Two-point, or higher order quantities, measured in intermittent turbulence obey non-Gaussian statistics (contrary to near-Gaussian statistics of the single-point quantities measured in homogeneous and isotropic flows). The departure of the PDF from a Gaussian shape leads to a break of the trivial self-similarity – scale invariance.
In turbulence research, analytic methods have been developed, such as the quasilinear approximation (Millionshtchikov Reference Millionshtchikov1941; Vedenov, Velikhov & Sagdeev Reference Vedenov, Velikhov and Sagdeev1961), the weak turbulence theory or direct interaction approximation (Kraichnan Reference Kraichnan1959; Kadomtsev Reference Kadomtsev1965 and other related works). However, existing analytic models are as yet incapable of providing as detailed and exact descriptions as semi-empirical cascade models based on a statistical approach. Theoretical treatments of plasma dynamics based on kinetic theory, MHD equations and Braginsky equations (Braginskii Reference Braginskii and Leontovich1965; Galeev & Sudan Reference Galeev and Sudan1983,1984) and reduced equations (see Horton Reference Horton1990; Zeiler, Drake & Rogers Reference Zeiler, Drake and Rogers1997; Diamond et al. Reference Diamond, Itoh, Itoh and Hahm2005 and references there) describe many plasma properties in space and laboratory plasmas. No theoretical models are now available (analytically and by numerical simulations) to predict the long-term behaviour of plasmas and to explain all experimental observations. This especially concerns the description of intermittent turbulence, long-range correlations and anomalous turbulent transport observed in plasmas. In analytical models, the theoretical treatments in fact consist of the renormalization of viscosity and of a random force (which obey Gaussian statistics in most of the models) in order to account for mode coupling and long-range correlations. Since this treatment is made in a mean-field approach, it cannot give a detailed description of intermittency. The intermittency results from turbulent activity; but this activity is itself not distributed homogeneously. In such a process, the distribution function is not described by exponential laws (such as a Gaussian) but it is described by power laws. The turbulence of hydrodynamic flows, plasma turbulence in laboratory devices and astrophysics are described by non-trivial algebraic, fractional stable (see (Monin & Yaglom Reference Monin and Yaglom1971, Reference Monin and Yaglom1975) and other related papers), log-normal (Kolmogorov Reference Kolmogorov1962), log-Poisson (Dubrulle Reference Dubrulle1994; She & Leveque Reference She and Leveque1994), log-Levy (Schertzer, Lovejoy & Hubert Reference Schertzer, Lovejoy, Hubert, Ern and Weiping2002) and other statistics known in probability theory (see, e.g. Guikhman & Skorokhod Reference Guikhman and Skorokhod1969).
The main hypotheses on the statistical treatment of developed turbulence were formulated by Kolmogorov (known as K41 theory). According to Richardson’s scenario (Richardson Reference Richardson1922), in a turbulent flow there is a cascade transfer of energy toward small scales, where dissipation is due to molecular friction. For fully developed isotropic turbulence, Kolmogorov suggested a constant rate of energy transfer from large to small scales in a turbulent cascade process, assuming the statistical quasi-equilibrium of turbulent fluctuations in the inertial range
![]() ${\it\eta}\ll l\ll L$
(where
${\it\eta}\ll l\ll L$
(where
![]() $L$
is energy-injection scale and
$L$
is energy-injection scale and
![]() ${\it\eta}$
is the dissipation scale), for high Reynolds numbers. It is considered that energy dissipation is averaged over a ball of size
${\it\eta}$
is the dissipation scale), for high Reynolds numbers. It is considered that energy dissipation is averaged over a ball of size
![]() $l$
,
$l$
,
![]() ${\it\varepsilon}_{l}$
, and velocity differences across a distance
${\it\varepsilon}_{l}$
, and velocity differences across a distance
![]() $l$
. Kolmogorov in the K41 model assumed that all statistically averaged moments (the
$l$
. Kolmogorov in the K41 model assumed that all statistically averaged moments (the
![]() $q$
th-order structure functions
$q$
th-order structure functions
![]() $S(q,l)\sim \langle |{\it\delta}_{l}{\it\upsilon}|^{q}\rangle$
,
$S(q,l)\sim \langle |{\it\delta}_{l}{\it\upsilon}|^{q}\rangle$
,
![]() $\langle \cdots \rangle$
in an ensemble averaging of increments
$\langle \cdots \rangle$
in an ensemble averaging of increments
![]() ${\it\delta}_{l}{\it\upsilon}={\it\upsilon}(x+l)-{\it\upsilon}(x)$
at scale
${\it\delta}_{l}{\it\upsilon}={\it\upsilon}(x+l)-{\it\upsilon}(x)$
at scale
![]() $l$
) depend only on the mean energy dissipation rate and spatial scale
$l$
) depend only on the mean energy dissipation rate and spatial scale
![]() $l$
. The scaling behaviour is
$l$
. The scaling behaviour is
with a linear functional exponent,
![]() ${\it\zeta}(q)=q/3$
.
${\it\zeta}(q)=q/3$
.
From dimensionality considerations, Kolmogorov derived the well-known scaling
![]() $E_{k}\sim k^{-5/3}$
(the five-thirds Kolmogorov–Obukhov spectrum) for the energy spectrum of developed isotropic turbulence in the inertial range. This law provides a relatively good description of the spectrum of fully developed isotropic hydrodynamic turbulence. More precise measurements of the turbulence spectrum showed that the exponent in the law
$E_{k}\sim k^{-5/3}$
(the five-thirds Kolmogorov–Obukhov spectrum) for the energy spectrum of developed isotropic turbulence in the inertial range. This law provides a relatively good description of the spectrum of fully developed isotropic hydrodynamic turbulence. More precise measurements of the turbulence spectrum showed that the exponent in the law
![]() $E_{k}\sim k^{-{\it\gamma}}$
differs from five-thirds,
$E_{k}\sim k^{-{\it\gamma}}$
differs from five-thirds,
![]() ${\it\gamma}=1.71\pm 0.02$
(see, e.g. Frish Reference Frish1995). This slight difference from five-thirds is of fundamental importance because it arises from intermittency and special statistical symmetries of the turbulent process. Experimental investigations and computer simulations of turbulent hydrodynamic flows have shown that the scaling for structure functions of high orders (
${\it\gamma}=1.71\pm 0.02$
(see, e.g. Frish Reference Frish1995). This slight difference from five-thirds is of fundamental importance because it arises from intermittency and special statistical symmetries of the turbulent process. Experimental investigations and computer simulations of turbulent hydrodynamic flows have shown that the scaling for structure functions of high orders (
![]() $q>3$
) deviates from the
$q>3$
) deviates from the
![]() $q/3$
predicted by the K41 theory; the reason is the intermittent nature of turbulence.
$q/3$
predicted by the K41 theory; the reason is the intermittent nature of turbulence.
The magnetic field in a turbulent plasma induces an anisotropy of the dynamics since field lines can easily be shifted but resist bending. In a plasma embedded in a strong magnetic field, small-scale fluctuations occur mainly in planes perpendicular to the magnetic field, making the turbulence anisotropic. Iroshnikov (Reference Iroshnikov1963) and Kraichnan (Reference Kraichnan1965) (IK model) include the influence of a magnetic field via mutual scattering of Alfvén waves triggered by velocity fluctuations. The IK fluctuations have an energy spectrum
![]() $E_{k}\sim k^{-3/2}$
. Recent results in MHD turbulence theory and 3-D numerical simulations (see, e.g. Schekochihin & Cowley (Reference Schekochihin, Cowley and Molokov2007) and references therein) cause some doubts regarding the general validity of the scaling predicted by 2-D phenomenology. It appears that the weak-turbulence Alfvén wave interaction along the local magnetic field, the basis of the IK concept, does not control the turbulent dynamics, which is instead dominated by swirling cross-field motions similar to hydrodynamic turbulence. These results illustrate that decaying turbulence is qualitatively different from its forced counterpart: in the viscous scale, the system can lose a property of 2-D dynamics. A paradigm of simplified 2-D slab models (e.g. Hasegawa & Mima Reference Hasegawa and Mima1977) and a separation of a purely parallel (shear Alfvén) dynamics from a cross-field motion (vorticity advection) is now reconsidered in MHD turbulence (Goldreich & Sridhar Reference Goldreich and Sridhar1995) as well as in laboratory edge plasma turbulence (see e.g. Scott Reference Scott1997, Reference Scott2005 and references therein). A phenomenology of ‘intermediate’ turbulence by Goldreich and Sridhar (known as the GS95 model (Goldreich & Sridhar Reference Goldreich and Sridhar1995)) was postulated as a balance between the K41 and IK energy cascades and has accounted for the local anisotropy induced by a magnetic field. The GS95 model assumes that eddies are filamentary, contrary to the spherical eddies in the IK model. In MHD turbulence theory, the GS95 model came to be used instead of the IK model.
$E_{k}\sim k^{-3/2}$
. Recent results in MHD turbulence theory and 3-D numerical simulations (see, e.g. Schekochihin & Cowley (Reference Schekochihin, Cowley and Molokov2007) and references therein) cause some doubts regarding the general validity of the scaling predicted by 2-D phenomenology. It appears that the weak-turbulence Alfvén wave interaction along the local magnetic field, the basis of the IK concept, does not control the turbulent dynamics, which is instead dominated by swirling cross-field motions similar to hydrodynamic turbulence. These results illustrate that decaying turbulence is qualitatively different from its forced counterpart: in the viscous scale, the system can lose a property of 2-D dynamics. A paradigm of simplified 2-D slab models (e.g. Hasegawa & Mima Reference Hasegawa and Mima1977) and a separation of a purely parallel (shear Alfvén) dynamics from a cross-field motion (vorticity advection) is now reconsidered in MHD turbulence (Goldreich & Sridhar Reference Goldreich and Sridhar1995) as well as in laboratory edge plasma turbulence (see e.g. Scott Reference Scott1997, Reference Scott2005 and references therein). A phenomenology of ‘intermediate’ turbulence by Goldreich and Sridhar (known as the GS95 model (Goldreich & Sridhar Reference Goldreich and Sridhar1995)) was postulated as a balance between the K41 and IK energy cascades and has accounted for the local anisotropy induced by a magnetic field. The GS95 model assumes that eddies are filamentary, contrary to the spherical eddies in the IK model. In MHD turbulence theory, the GS95 model came to be used instead of the IK model.
One of the typical features of intermittent turbulent flow (hydrodynamic and magnetohydrodynamic) is the anisotropy emerging due to the effect of the flow boundary. This anisotropy locally violates symmetries that are allowed in the flow as a whole, and conserves only those that are responsible for the turbulent cascade; it preserves scale invariance not in an infinite range, but only in a restricted range of the scales. Therefore, the intermittency and self-similarity properties are related not only and not so much to turbulence driven instability types, but rather to symmetries responsible for the scale invariance in the significantly restricted range of scales (e.g. scales of the boundary layer or wave structures in magnetofluids). Such an approach to the treatment of self-similarity properties suggests a description of experimental data in various turbulent media in the framework of a single paradigm (see, e.g. Budaev et al. Reference Budaev, Savin and Zelenyi2011).
Turbulence can possess several types of symmetries, including scale invariance symmetry. The problem of scale invariance (a self-similarity or a dilatational symmetry) is important for the study of turbulence. The symmetries are presented in the governing equations of motion. Theoretical studies predict generalized scale invariant laws associated with hidden statistical symmetries. The extended self-similarity (ESS) criterion, which was proposed phenomenologically in hydrodynamics by Benzi et al. (Reference Benzi, Ciliberto, Tripiccione, Baudet, Massaioli and Succi1993) and was later considered in the log-Poisson model of turbulence in Dubrulle (Reference Dubrulle1994) and She & Leveque (Reference She and Leveque1994), assumes a scaling of the form
![]() $S_{q}(l)\sim S_{3}(l)^{{\it\zeta}(q)/{\it\zeta}(3)}$
for an extended scale of
$S_{q}(l)\sim S_{3}(l)^{{\it\zeta}(q)/{\it\zeta}(3)}$
for an extended scale of
![]() $l\geqslant 5{\it\eta}$
. In neutral fluid turbulence, the ESS property is observed up to the dissipation scales (Benzi et al.
Reference Benzi, Ciliberto, Tripiccione, Baudet, Massaioli and Succi1993; Dubrulle Reference Dubrulle1994; Frish Reference Frish1995).
$l\geqslant 5{\it\eta}$
. In neutral fluid turbulence, the ESS property is observed up to the dissipation scales (Benzi et al.
Reference Benzi, Ciliberto, Tripiccione, Baudet, Massaioli and Succi1993; Dubrulle Reference Dubrulle1994; Frish Reference Frish1995).
Statistical self-similarity considered by the hierarchical cascade paradigm of turbulence involves (instead of exact self-similarity) random fractal construction: at each iteration the scaling of each piece is selected randomly from a set range and sub-pieces of each piece have the same distribution of sizes. Kolmogorov’s K41 model considers statistical homogeneity. Intermittency can be generated by the anisotropy in the cascade process leading to a statistical inhomogeneity and a break of the simplest scale invariance. A multiplicative cascade is used to consider an intermittency: energy is transferred from large eddies down to small scales through a cascade process (or vice-versa in inverse cascade) in which the transfer rate at a given scale is not spatially homogeneous as in the K41 theory.
The multifractal formalism (see Frish Reference Frish1995) was introduced to overcome the significant limitations of traditional approaches for the exploration of extremely variable fields (e.g. intermittency) in the context of fully-developed turbulence data analysis to account for the experimental observations of the deviation from Kolmogorov’s K41 theory. Multifractal phenomena describe the concept of different regions of an object having different fractal properties. In a stochastic multifractal field
![]() $\unicode[STIX]{x1D608}$
, the behaviour around any point is described by a local power law:
$\unicode[STIX]{x1D608}$
, the behaviour around any point is described by a local power law:
![]() $\unicode[STIX]{x1D608}(x)-\unicode[STIX]{x1D608}(x+a)\sim a^{h(x)}$
with the singularity exponent
$\unicode[STIX]{x1D608}(x)-\unicode[STIX]{x1D608}(x+a)\sim a^{h(x)}$
with the singularity exponent
![]() $h(x)$
describing the local degree of singularity or regularity around the point
$h(x)$
describing the local degree of singularity or regularity around the point
![]() $x$
. The multifractal approach provides a quantitative description of a broad range of heterogeneous phenomena including intermittency of developed turbulence (see Mandelbrot Reference Mandelbrot1982; Harte Reference Harte2001). The advantage of the multifractal approach is its ability to treat and to analyse self-similarity from the largest to the smallest scales considering the large scales to be coupled with the intermediate and small scales (see appendix A).
$x$
. The multifractal approach provides a quantitative description of a broad range of heterogeneous phenomena including intermittency of developed turbulence (see Mandelbrot Reference Mandelbrot1982; Harte Reference Harte2001). The advantage of the multifractal approach is its ability to treat and to analyse self-similarity from the largest to the smallest scales considering the large scales to be coupled with the intermediate and small scales (see appendix A).
An analysis of turbulence self-similarity (or equivalently a search for the statistical symmetries of turbulence) led to models of fully developed turbulence for hydrodynamic systems such as the log-normal Kolmogorov model (K62, Reference Kolmogorov1962), the multifractal (see Frish Reference Frish1995) and the log-Poisson (Dubrulle Reference Dubrulle1994; She & Leveque Reference She and Leveque1994) models. In the K62 model, Kolmogorov proposed to account for the local inhomogeneity of turbulence. Kolmogorov originated the similarity hypothesis (power laws) for the moments of the dissipation energy and formulated the normal law for the logarithm of the dissipation energy (the log-normal law). Later, multiplicative hierarchical cascade models such as the
![]() ${\it\beta}$
-model, the
${\it\beta}$
-model, the
![]() ${\it\alpha}$
-model and the
${\it\alpha}$
-model and the
![]() $p$
-model (see Frish Reference Frish1995) considered the energy cascading process in turbulent flows. Studies of power laws for the moments led to the development of later turbulence models including the most favourable one – the log-Poisson model (Dubrulle Reference Dubrulle1994; She & Leveque Reference She and Leveque1994).
$p$
-model (see Frish Reference Frish1995) considered the energy cascading process in turbulent flows. Studies of power laws for the moments led to the development of later turbulence models including the most favourable one – the log-Poisson model (Dubrulle Reference Dubrulle1994; She & Leveque Reference She and Leveque1994).
A generalized description of intermittent turbulence is provided by the log-Poisson model, which considers a stochastic multiplicative cascade and a log-Poisson distribution of the dissipation energy. This model makes use of a hierarchy of moment’s, the existence of limiting dissipative structures and power laws. Such characteristics agree with the most common turbulence properties observed in experiments, in particular with the ESS property. The assumptions of the log-Poisson model concern the scaling properties of structures of different intensities in a system with a relatively low Reynolds number and a limited (in the classical sense) inertial range. The ESS property accounts for boundary effects and implies that self-similarity occurs on a finite spatial and temporal scale rather than in infinite space, thereby providing a natural means of analysing viscous (dissipative) effects and the properties of limiting dissipative structures (in particular, their dimensions). For instance, the log-Poisson model of 3-D isotropic hydrodynamic turbulence assumes a filamentary geometry for singular dissipative structures (Dubrulle Reference Dubrulle1994; She & Leveque Reference She and Leveque1994). The log-Poisson model that accounts for the 2-D Iroshnikov–Kraichnan (IK) empirics describing 2-D singular dissipative structures (Carbone, Veltry & Bruno Reference Carbone, Veltry and Bruno1996; Politano, Pouquet & Carbone Reference Politano, Pouquet and Carbone1998). The ESS of the log-Poisson process establishes long-range correlations, which give rise to an anomalous process – superdiffusion. In the TBL of the Earth’s magnetosphere, this results in anomalous transport through the barrier. In edge plasma of fusion devices, this property leads to enhanced cross-field plasma losses.
All cascade models of intermittent turbulence have adjustable parameters that are difficult to determine from first principles and physical arguments and which provide enough freedom to account for the experimental data. The scaling
![]() ${\it\zeta}(q)$
of the structure functions (1.1) is helpful to validate cascade models of developed turbulence with intermittency. In hydrodynamics, experimental scaling follows the predictions of the log-Poisson model, see Frish (Reference Frish1995). In plasma turbulence, the first results were obtained in the last decade. In this review we present recent experimental results regarding self-similarity observed in space plasmas (SW and Earth’s magnetosphere) and in fusion devices. We focus on the cascade models of plasma turbulence, with intermittency and scale invariance. It helps to reveal the universality of intermittent turbulence features (both in magnetofluids and in neutral fluids) currently under discussion in the literature.
${\it\zeta}(q)$
of the structure functions (1.1) is helpful to validate cascade models of developed turbulence with intermittency. In hydrodynamics, experimental scaling follows the predictions of the log-Poisson model, see Frish (Reference Frish1995). In plasma turbulence, the first results were obtained in the last decade. In this review we present recent experimental results regarding self-similarity observed in space plasmas (SW and Earth’s magnetosphere) and in fusion devices. We focus on the cascade models of plasma turbulence, with intermittency and scale invariance. It helps to reveal the universality of intermittent turbulence features (both in magnetofluids and in neutral fluids) currently under discussion in the literature.
2. Experimental data
2.1. Measurements in space plasma
Space plasmas in the outer magnetosphere and SW have been investigated by a number of spacecraft: WIND/ACE (SW), INTERBALL-1, CLUSTER, DOUBLE STAR, GEOTAIL, POLAR, THEMIS etc. Measurements have allowed for the collection of data on the ion and electron moments (sampling rate up to 0.1–0.3 Hz), electric and magnetic fields (sampling rate 1–64 Hz) and energetic particles. Since 2011, the measurements have been made on the SPECTR-R spacecraft (Zelenyi et al.
Reference Zelenyi, Zastenker, Petrukovich, Chesalin, Nazarov, Prokhorenko and Larionov2013) at a unique orbit with high apogee
![]() ${\sim}300\,000~\text{km}$
, sliding along the magnetospheric boundaries for up to a few days. Measurements by SPECTR-R provide data regarding ion flux, density, velocity and temperature from the solarward hemisphere, with record sampling over a broad frequency range up to 32 Hz and energetic particle distributions (see e.g. Savin et al.
Reference Savin, Skalsky, Zelenyi, Avanov, Borodkova, Klimov, Lutsenko, Panov, Romanov and Smirnov2005–Reference Savin, Amata, Budaev, Zelenyi, Kronberg, Buechner, Safrankova, Nemecek, Blecki and Kozak2014, Zelenyi et al.
Reference Zelenyi, Zastenker, Petrukovich, Chesalin, Nazarov, Prokhorenko and Larionov2013 and references therein). The magnetic field (
${\sim}300\,000~\text{km}$
, sliding along the magnetospheric boundaries for up to a few days. Measurements by SPECTR-R provide data regarding ion flux, density, velocity and temperature from the solarward hemisphere, with record sampling over a broad frequency range up to 32 Hz and energetic particle distributions (see e.g. Savin et al.
Reference Savin, Skalsky, Zelenyi, Avanov, Borodkova, Klimov, Lutsenko, Panov, Romanov and Smirnov2005–Reference Savin, Amata, Budaev, Zelenyi, Kronberg, Buechner, Safrankova, Nemecek, Blecki and Kozak2014, Zelenyi et al.
Reference Zelenyi, Zastenker, Petrukovich, Chesalin, Nazarov, Prokhorenko and Larionov2013 and references therein). The magnetic field (
![]() $B$
) measurements rely on standard fluxgate magnetometers aboard scientific spacecraft (see e.g. Klimov et al.
Reference Klimov, Romanov, Amata, Blecki, Buechner, Juchniewicz, Rustenbach, Triska, Woolliscroft and Savin1997). Faraday cups of various orientation are used for the measurement of the ion flux amplitude and its direction. Faraday cups on INTERBALL-1 and SPECTR-R were used to measure the ion flux with a sampling rate up to 32 Hz, which is comparable with magnetometer data sampling, see Zelenyi et al. (Reference Zelenyi, Zastenker, Petrukovich, Chesalin, Nazarov, Prokhorenko and Larionov2013) and references therein for details. For the other spacecraft, the data are provided by ion energy spectrometers (of the ‘top hat’ type), which give
$B$
) measurements rely on standard fluxgate magnetometers aboard scientific spacecraft (see e.g. Klimov et al.
Reference Klimov, Romanov, Amata, Blecki, Buechner, Juchniewicz, Rustenbach, Triska, Woolliscroft and Savin1997). Faraday cups of various orientation are used for the measurement of the ion flux amplitude and its direction. Faraday cups on INTERBALL-1 and SPECTR-R were used to measure the ion flux with a sampling rate up to 32 Hz, which is comparable with magnetometer data sampling, see Zelenyi et al. (Reference Zelenyi, Zastenker, Petrukovich, Chesalin, Nazarov, Prokhorenko and Larionov2013) and references therein for details. For the other spacecraft, the data are provided by ion energy spectrometers (of the ‘top hat’ type), which give
![]() $n$
and
$n$
and
![]() $V$
time series with sampling rate less than 1 Hz (see e.g. Reme et al.
Reference Reme, Bosqued, Sauvaud, Cros, Dandouras, Aoustin, Martz, Médale, Rouzaud and Möbius1997). The dynamic pressure (
$V$
time series with sampling rate less than 1 Hz (see e.g. Reme et al.
Reference Reme, Bosqued, Sauvaud, Cros, Dandouras, Aoustin, Martz, Médale, Rouzaud and Möbius1997). The dynamic pressure (
![]() ${\sim}nV^{2}$
) is calculated from the measured parameters
${\sim}nV^{2}$
) is calculated from the measured parameters
![]() $n$
and
$n$
and
![]() $V$
. Signal-to-noise ratio is typically
$V$
. Signal-to-noise ratio is typically
![]() ${>}10$
for all plasma parameters measured in the outer magnetospheric space.
${>}10$
for all plasma parameters measured in the outer magnetospheric space.
The plasma in the SW and at the magnetospheric boundaries are observed to be non-equilibrium and turbulent. Significant progress in studying the SW turbulence has been achieved in recent decades (see Chang, Tam & Wu Reference Chang, Tam and Wu2004; Hnat, Chapman & Rowlands Reference Hnat, Chapman and Rowlands2005; Marsh & Tu Reference Marsh and Tu2006; Macek Reference Macek2007; Matthaeus et al.
Reference Matthaeus, Weygand, Chuychai, Dasso, Smith and Kivelson2008; Zastenker et al.
Reference Zastenker and Zelenyi2011; Alexandrova et al.
Reference Alexandrova, Saur, Lacombe, Mangeney, Mitchell, Schwartz and Robert2009; Riazantseva, Zastenker & Karavaev Reference Riazantseva, Zastenker, Karavaev and Maksmovic2010; Podesta & Gary Reference Podesta and Gary2011; Vörös Reference Vörös2011; Wicks et al.
Reference Wicks, Horbury, Chen and Schekochihin2011; Chen et al.
Reference Chen, Salem, Bonnell, Mozer and Bale2012, Reference Chen, Sorriso-Valvo, Safrankova and Nemecek2014; Dura et al.
Reference Dura, Hnat, Robinson and Dendy2012; Kiyani et al.
Reference Kiyani, Chapman, Sahraoui, Hnat, Fauvarque and Khotyaintsev2013; Zastenker et al.
Reference Zastenker, Safrankova, Nemecek, Prech, Cermak, Vaverka, Komarek, Voita, Chesalin and Karimov2013; Osman et al.
Reference Osman, Kiyani, Chapman and Hnat2014a
,Reference Osman, Matthaeus, Gosling, Greco, Servidio, Hnat, Chapman and Phan
b
; Riazantseva et al.
Reference Riazantseva, Budaev, Zelenyi, Zastenker, Pavlos, Safrankova, Nemecek, Prech and Nemec2015 and references therein). The most comprehensive study of SW turbulence properties are provided in the low-frequency range (see Bruno & Carbone Reference Bruno and Carbone2013 etc.). The majority of these papers discuss the power spectrum of the interplanetary magnetic field fluctuations. In numerous papers, it has been indicated that the slope of these spectrum nears
![]() $-5/3$
, corresponding to a Kolmogorov–Obuchov spectrum. The high-frequency magnetic field fluctuations have been well studied (see, e.g. Alexandrova et al.
Reference Alexandrova, Saur, Lacombe, Mangeney, Mitchell, Schwartz and Robert2009; Yordanova et al.
Reference Yordanova, Balogh, Noullez and von Steiger2009; Salem et al.
Reference Salem, Howes, Sundkvist, Bale, Chaston, Chen and Mozer2012 etc.). The deviation of the velocity spectra from the magnetic field spectra in the SW has been discussed (see, e.g. Borovsky Reference Borovsky2008; Salem et al.
Reference Salem, Howes, Sundkvist, Bale, Chaston, Chen and Mozer2012 etc.). The ion flux fluctuations measured on the SPECTR-R spacecraft (Riazantseva et al.
Reference Riazantseva, Budaev, Zelenyi, Zastenker, Pavlos, Safrankova, Nemecek, Prech and Nemec2015) are shown in figure 3. The SW ion flux variations obey a multiscale character, which is discussed in numerous papers (see e.g. Zelenyi & Milovanov Reference Zelenyi and Milovanov2004; Budaev et al.
Reference Budaev, Savin and Zelenyi2011; Riazantseva et al.
Reference Riazantseva, Budaev, Zelenyi, Zastenker, Pavlos, Safrankova, Nemecek, Prech and Nemec2015 and references therein).
$-5/3$
, corresponding to a Kolmogorov–Obuchov spectrum. The high-frequency magnetic field fluctuations have been well studied (see, e.g. Alexandrova et al.
Reference Alexandrova, Saur, Lacombe, Mangeney, Mitchell, Schwartz and Robert2009; Yordanova et al.
Reference Yordanova, Balogh, Noullez and von Steiger2009; Salem et al.
Reference Salem, Howes, Sundkvist, Bale, Chaston, Chen and Mozer2012 etc.). The deviation of the velocity spectra from the magnetic field spectra in the SW has been discussed (see, e.g. Borovsky Reference Borovsky2008; Salem et al.
Reference Salem, Howes, Sundkvist, Bale, Chaston, Chen and Mozer2012 etc.). The ion flux fluctuations measured on the SPECTR-R spacecraft (Riazantseva et al.
Reference Riazantseva, Budaev, Zelenyi, Zastenker, Pavlos, Safrankova, Nemecek, Prech and Nemec2015) are shown in figure 3. The SW ion flux variations obey a multiscale character, which is discussed in numerous papers (see e.g. Zelenyi & Milovanov Reference Zelenyi and Milovanov2004; Budaev et al.
Reference Budaev, Savin and Zelenyi2011; Riazantseva et al.
Reference Riazantseva, Budaev, Zelenyi, Zastenker, Pavlos, Safrankova, Nemecek, Prech and Nemec2015 and references therein).

Figure 3. (a) Typical signal of SW ion flux, BMSW measurements on SPECTR-R from 27-09-2011 23:00 to 28-09-2011 08:20 UT. (b) Power spectrum of ion flux (grey curve, black dots give average value in frequency with
![]() ${\rm\Delta}f/f\sim 20\,\%$
) in SW, SPECTR-R 28-09-2011 03:08-03:25 UT. Solid black lines show the linear approximation by power laws with power exponents of P1 and P2. Above 10 Hz the device noise becomes comparable with the signal in SW and we do not use these data for analysis.
${\rm\Delta}f/f\sim 20\,\%$
) in SW, SPECTR-R 28-09-2011 03:08-03:25 UT. Solid black lines show the linear approximation by power laws with power exponents of P1 and P2. Above 10 Hz the device noise becomes comparable with the signal in SW and we do not use these data for analysis.
![]() $F_{break}$
marks the kink frequency where the average slope changes (‘is breaking’).
$F_{break}$
marks the kink frequency where the average slope changes (‘is breaking’).
The spectrum of the ion flux fluctuations measured by SPECTR-R is shown in figure 3 (Riazantseva et al.
Reference Riazantseva, Budaev, Zelenyi, Zastenker, Pavlos, Safrankova, Nemecek, Prech and Nemec2015). A spectral kink is typically observed in frequency spectra. The kink frequency,
![]() $F_{break}$
, is close to the low hybrid one. The Doppler shift effect has been discussed to explain the kinked frequency spectrum, for example a Kolmogorov-like
$F_{break}$
, is close to the low hybrid one. The Doppler shift effect has been discussed to explain the kinked frequency spectrum, for example a Kolmogorov-like
![]() $k$
-spectrum was observed by Doppler shifts, accounting for Cluster magnetic measurement above the cusp MP (Romanov, Zelenyi & Savin Reference Romanov, Zelenyi and Savin2012).
$k$
-spectrum was observed by Doppler shifts, accounting for Cluster magnetic measurement above the cusp MP (Romanov, Zelenyi & Savin Reference Romanov, Zelenyi and Savin2012).
The distribution function of ion flux fluctuations is non-Gaussian, demonstrating heavy tails originating from the intermittent behaviour of the signal (see figure 4).

Figure 4. An example of the PDF of ion flux variations on a scale 0.1 s (solid line) and the corresponding Gaussian fit (dashed line), SPECTR-R 28-09-2011 03:08–03:25 UT.
Multi-spacecraft simultaneous measurements allow comparison of turbulence spectra in the SW and at the magnetospheric boundaries, such as bow shock (BS) and MP. The ion flux power spectra in a quiet SW (obtained by the WIND spacecraft) is compared with data obtained by SPECTR-R in the TBL, figure 5(a): maxima of the spectra (e.g. at
![]() ${\sim}0.05~\text{mHz}$
,
${\sim}0.05~\text{mHz}$
,
![]() ${\sim}0.2{-}0.3$
and
${\sim}0.2{-}0.3$
and
![]() ${\sim}0.5~\text{mHz}$
, figure 5
a) are observed in the same frequency bandwidths. This allows for consideration of a link in the processes in the SW and TBL, including a cross-magnetospheric correlation (Savin et al.
Reference Savin, Amata, Budaev, Zelenyi, Kronberg, Buechner, Safrankova, Nemecek, Blecki and Kozak2014). The spectra on figure 5(b) demonstrate rather good correspondence between BS/foreshock (most probable source region for the SPS/jets) and TBL at the magnetic obstacle boundary. The maxima in the low-frequency part and slopes in the high-frequency part of the spectra are observed downflow until the boundary of the geomagnetic tail (SPECTR-R, shadowed curve in figure 5
b, see Savin et al.
Reference Savin, Amata, Zelenyi, Budaev, Consolini, Consolini, Treumann, Lucek, Safrankova and Nemecek2008, Reference Savin, Amata, Zelenyi, Lutsenko, Safrankova, Nemecek, Borodkova, Buechner, Daly and Kronberg2012, Reference Savin, Amata, Budaev, Zelenyi, Kronberg, Buechner, Safrankova, Nemecek, Blecki and Kozak2014).
${\sim}0.5~\text{mHz}$
, figure 5
a) are observed in the same frequency bandwidths. This allows for consideration of a link in the processes in the SW and TBL, including a cross-magnetospheric correlation (Savin et al.
Reference Savin, Amata, Budaev, Zelenyi, Kronberg, Buechner, Safrankova, Nemecek, Blecki and Kozak2014). The spectra on figure 5(b) demonstrate rather good correspondence between BS/foreshock (most probable source region for the SPS/jets) and TBL at the magnetic obstacle boundary. The maxima in the low-frequency part and slopes in the high-frequency part of the spectra are observed downflow until the boundary of the geomagnetic tail (SPECTR-R, shadowed curve in figure 5
b, see Savin et al.
Reference Savin, Amata, Zelenyi, Budaev, Consolini, Consolini, Treumann, Lucek, Safrankova and Nemecek2008, Reference Savin, Amata, Zelenyi, Lutsenko, Safrankova, Nemecek, Borodkova, Buechner, Daly and Kronberg2012, Reference Savin, Amata, Budaev, Zelenyi, Kronberg, Buechner, Safrankova, Nemecek, Blecki and Kozak2014).

Figure 5. Power spectra of ion flux in SW, BS and TBL-simultaneous measurements on WIND, CLUSTER-4 and SPECTR-R on 20.03.12. (a) WIND (SW, lower curve) and SPECTR-R (TBL, upper curve), 13-21 UT, red line shows the power law fit with exponent of
![]() $-1.67$
, (vertical lines indicate local maxima); (b) Cluster-4 (SW/BS/MSH, thick violet curve) and SPECTR-R (TBL, shadowed), 13-18 UT.
$-1.67$
, (vertical lines indicate local maxima); (b) Cluster-4 (SW/BS/MSH, thick violet curve) and SPECTR-R (TBL, shadowed), 13-18 UT.
In the magnetospheric boundary layers, the plasma jets (supermagnetosonic plasma streams, SPS, being the most powerful, see e.g. Budaev et al. (Reference Budaev, Savin and Zelenyi2011), Savin et al. (Reference Savin, Amata, Zelenyi, Lutsenko, Safrankova, Nemecek, Borodkova, Buechner, Daly and Kronberg2012–Reference Savin, Amata, Budaev, Zelenyi, Kronberg, Buechner, Safrankova, Nemecek, Blecki and Kozak2014) and references therein) are observed with a highly enhanced dynamic pressure (
![]() $P_{dyn}$
). At the magnetospheric boundary downtail, these deflected SPS are mixed with the laminar plasma flow around the MP, flowing with subsonic velocity at the dayside MSH area. The SPS are seen as spikes in the pressure evolution
$P_{dyn}$
). At the magnetospheric boundary downtail, these deflected SPS are mixed with the laminar plasma flow around the MP, flowing with subsonic velocity at the dayside MSH area. The SPS are seen as spikes in the pressure evolution
![]() $P_{dyn}$
(detected by the spacecraft DOUBLE STAR, CLUSTER-4 and GEOTAIL) with an amplitude exceeding three standard deviations, see figure 6. Observations at the different locations demonstrated SPS in MSH with an average magnetosonic Mach number of 2.1. Statistics of the flux and dynamic pressure fluctuations have quite close features (Savin et al.
Reference Savin, Amata, Budaev, Zelenyi, Kronberg, Buechner, Safrankova, Nemecek, Blecki and Kozak2014).
$P_{dyn}$
(detected by the spacecraft DOUBLE STAR, CLUSTER-4 and GEOTAIL) with an amplitude exceeding three standard deviations, see figure 6. Observations at the different locations demonstrated SPS in MSH with an average magnetosonic Mach number of 2.1. Statistics of the flux and dynamic pressure fluctuations have quite close features (Savin et al.
Reference Savin, Amata, Budaev, Zelenyi, Kronberg, Buechner, Safrankova, Nemecek, Blecki and Kozak2014).

Figure 6. Plasma jets with enhanced dynamic pressure observed on 27-03-2005 (Savin et al.
Reference Savin, Amata, Budaev, Zelenyi, Kronberg, Buechner, Safrankova, Nemecek, Blecki and Kozak2014), (a–d) Dynamic pressure normalized by the SW pressure,
![]() $P_{dyn}/P_{SW}$
; obtained by DOUBLE STAR, horizontal lines show the levels of 2 and 3 standard deviations used for jet identification; – dynamic pressure
$P_{dyn}/P_{SW}$
; obtained by DOUBLE STAR, horizontal lines show the levels of 2 and 3 standard deviations used for jet identification; – dynamic pressure
![]() $P_{dyn}$
, (nP), obtained by Cluster-4; – CNO – channel of energetic particles (
$P_{dyn}$
, (nP), obtained by Cluster-4; – CNO – channel of energetic particles (
![]() ${>}274~\text{keV}$
, C
${>}274~\text{keV}$
, C
![]() $+$
, N
$+$
, N
![]() $+$
and O
$+$
and O
![]() $+$
, units – 1/(
$+$
, units – 1/(
![]() $\text{cm}^{2}$
sr s keV)) obtained by CLUSTER-4; – Dynamic pressure
$\text{cm}^{2}$
sr s keV)) obtained by CLUSTER-4; – Dynamic pressure
![]() $P_{dyn}$
, (nP), obtained by GEOTAIL.
$P_{dyn}$
, (nP), obtained by GEOTAIL.
Maxima of the power spectra (see figure 5) can be analysed by using bicoherence, which is obtained by averaging the bispectrum over statistically equivalent realizations and normalizing the result. The bicoherence measures three-wave coupling and is only large when the phase between the wave at sum frequency
![]() $Fs=Fl+Fk$
and the other two is nearly constant over a significant number of realizations. The 2-D bicoherence graph is used to detect 3-wave interactions considering the 3-wave process with sum frequency
$Fs=Fl+Fk$
and the other two is nearly constant over a significant number of realizations. The 2-D bicoherence graph is used to detect 3-wave interactions considering the 3-wave process with sum frequency
![]() $Fs$
(
$Fs$
(
![]() $Fl$
is the vertical axis of figure 7,
$Fl$
is the vertical axis of figure 7,
![]() $Fk$
is the horizontal one). The bicoherence can be computed using a (continuous) wavelet transform (WT) instead of a Fourier transform, in order to improve the statistics (see details in van Milligen et al.
Reference van Milligen, Sanchez, Estrada, Hidalgo, Brafias, Carreras and Garda1995; Savin et al.
Reference Savin, Skalsky, Zelenyi, Avanov, Borodkova, Klimov, Lutsenko, Panov, Romanov and Smirnov2005). We assume cascade signatures e.g. for the horizontal maxima in figure 7, when at the sum frequency,
$Fk$
is the horizontal one). The bicoherence can be computed using a (continuous) wavelet transform (WT) instead of a Fourier transform, in order to improve the statistics (see details in van Milligen et al.
Reference van Milligen, Sanchez, Estrada, Hidalgo, Brafias, Carreras and Garda1995; Savin et al.
Reference Savin, Skalsky, Zelenyi, Avanov, Borodkova, Klimov, Lutsenko, Panov, Romanov and Smirnov2005). We assume cascade signatures e.g. for the horizontal maxima in figure 7, when at the sum frequency,
![]() $Fs=Fl+Fk$
, the bicoherence has a comparable value with that at the starting point (
$Fs=Fl+Fk$
, the bicoherence has a comparable value with that at the starting point (
![]() $F_{1};F_{2}$
). This implies that the wave at the sum frequency interacts in its turn with the same initial mode at frequency
$F_{1};F_{2}$
). This implies that the wave at the sum frequency interacts in its turn with the same initial mode at frequency
![]() $F_{1}$
in the further 3-wave process:
$F_{1}$
in the further 3-wave process:
![]() $F_{3}=F_{1}+F_{2}$
etc.
$F_{3}=F_{1}+F_{2}$
etc.

Figure 7. Wavelet bicoherence of
![]() $P_{dyn}$
measured by DOUBLE STAR at 04-13 UT on 27-03-2005 (Savin et al.
Reference Savin, Amata, Budaev, Zelenyi, Kronberg, Buechner, Safrankova, Nemecek, Blecki and Kozak2014).
$P_{dyn}$
measured by DOUBLE STAR at 04-13 UT on 27-03-2005 (Savin et al.
Reference Savin, Amata, Budaev, Zelenyi, Kronberg, Buechner, Safrankova, Nemecek, Blecki and Kozak2014).
Figure 7 demonstrates 3-wave interactions: at the low-frequency bandwidth there are local maxima points indicating sharply defined, locked frequencies on the bicoherence graph which are the result of a coupling of several resonance modes, with frequencies suggested by the cavity and surface modes’ theories. At the high-frequency bandwidth, the bicoherence graph has no discrete maxima. Such observation allows the following scenario of the excitation mechanism to be invoked: the SW fluctuations at 0.15–10 mHz excite several boundary modes; the BS and the BS foreshock (see figure 6) are likely a source of the energy. The coupling of these resonance boundary modes leads later on to a cascade process which forms a power-law spectrum in the high-frequency bandwidth (cf. figure 5). The resonance boundary modes modulate the penetration of the SW plasma through the flank MP due to SPS impacts, and they also modulate the O
![]() $+$
ion outflow from the magnetosphere into the SW (see figure 6 and Savin et al.
Reference Savin, Amata, Budaev, Zelenyi, Kronberg, Buechner, Safrankova, Nemecek, Blecki and Kozak2014).
$+$
ion outflow from the magnetosphere into the SW (see figure 6 and Savin et al.
Reference Savin, Amata, Budaev, Zelenyi, Kronberg, Buechner, Safrankova, Nemecek, Blecki and Kozak2014).
Taylor ‘frozen-in turbulence’ hypothesis. We here note the Eulerian viewpoints of turbulence and the Taylor ‘frozen-in turbulence’ hypothesis which is usually used in plasma measurements both in space and in laboratory devices. In space, the SW speed,
![]() $V_{sw}$
is much higher than the local MHD wave speeds. We can thus consider measurements at a set of times
$V_{sw}$
is much higher than the local MHD wave speeds. We can thus consider measurements at a set of times
![]() $t_{i}$
to be at a set of locations in the plasma given by
$t_{i}$
to be at a set of locations in the plasma given by
![]() $x_{i}=x_{0}-V_{sw}t_{i}$
This approximation, known as the Taylor ‘frozen-in turbulence’ hypothesis greatly simplifies the analysis of the data. The Taylor (Reference Taylor1938) hypothesis makes an assumption that the advection contributed by the turbulent circulations themselves must be small and that therefore, the advection of a field of turbulence past a fixed point can be taken as being mainly due to the larger, energy containing scales (the mean flow). Taylor proposed his frozen-in turbulence hypothesis in terms of Eulerian mean flow. Although it is only valid when the integral scales have sufficiently high power compared with the smaller scales, this hypothesis delivered a linkage between the Eulerian and Lagrangian viewpoints of turbulence. The Taylor ‘frozen-in turbulence’ hypothesis is widely used in neutral fluid measurements. Usually experimentalists performed Eulerian measurements based on time-resolved single-point measurements. Lagrangian measurements are challenging because they involve the tracking of particle trajectories, but such measurements are not now available in plasma. For a detailed introduction to the statistical mechanics of Eulerian and Lagrangian turbulence see Monin & Yaglom (Reference Monin and Yaglom1975) and Frish (Reference Frish1995). In MHD turbulence of interplanetary plasmas, the Lagrangian information has been extracted following the Taylor hypothesis, involving the magnetic flux frozen in a wide scale range. In the Earth’s magnetosheath, the plasma flow speed can be lower than the wave speed and therefore temporal changes at the spacecraft are due to a complex combination of the plasma moving over the spacecraft, and the turbulent fluctuations propagating in the plasma frame. Taylor’s hypothesis has been used to explain, e.g. the morphologies of jets in MSH (Savin et al.
Reference Savin, Amata, Budaev, Zelenyi, Kronberg, Buechner, Safrankova, Nemecek, Blecki and Kozak2014). However, it remains a hypothesis. To describe intermittency, a problem of chaotic motion of individual fluid particles and mixing flow should be considered. To characterize the intermittency of developed turbulence in the Eulerian framework, one can consider mixing and chaotic motion (chaotic advection, when neighbouring trajectories separate exponentially fast with time) due to Lagrangian chaos phenomenon (see, e.g. Monin & Yaglom Reference Monin and Yaglom1975; Ottino Reference Ottino1989). Considering chaos in Lagrangian space, the exponential growth of separation between advected trajectories
$x_{i}=x_{0}-V_{sw}t_{i}$
This approximation, known as the Taylor ‘frozen-in turbulence’ hypothesis greatly simplifies the analysis of the data. The Taylor (Reference Taylor1938) hypothesis makes an assumption that the advection contributed by the turbulent circulations themselves must be small and that therefore, the advection of a field of turbulence past a fixed point can be taken as being mainly due to the larger, energy containing scales (the mean flow). Taylor proposed his frozen-in turbulence hypothesis in terms of Eulerian mean flow. Although it is only valid when the integral scales have sufficiently high power compared with the smaller scales, this hypothesis delivered a linkage between the Eulerian and Lagrangian viewpoints of turbulence. The Taylor ‘frozen-in turbulence’ hypothesis is widely used in neutral fluid measurements. Usually experimentalists performed Eulerian measurements based on time-resolved single-point measurements. Lagrangian measurements are challenging because they involve the tracking of particle trajectories, but such measurements are not now available in plasma. For a detailed introduction to the statistical mechanics of Eulerian and Lagrangian turbulence see Monin & Yaglom (Reference Monin and Yaglom1975) and Frish (Reference Frish1995). In MHD turbulence of interplanetary plasmas, the Lagrangian information has been extracted following the Taylor hypothesis, involving the magnetic flux frozen in a wide scale range. In the Earth’s magnetosheath, the plasma flow speed can be lower than the wave speed and therefore temporal changes at the spacecraft are due to a complex combination of the plasma moving over the spacecraft, and the turbulent fluctuations propagating in the plasma frame. Taylor’s hypothesis has been used to explain, e.g. the morphologies of jets in MSH (Savin et al.
Reference Savin, Amata, Budaev, Zelenyi, Kronberg, Buechner, Safrankova, Nemecek, Blecki and Kozak2014). However, it remains a hypothesis. To describe intermittency, a problem of chaotic motion of individual fluid particles and mixing flow should be considered. To characterize the intermittency of developed turbulence in the Eulerian framework, one can consider mixing and chaotic motion (chaotic advection, when neighbouring trajectories separate exponentially fast with time) due to Lagrangian chaos phenomenon (see, e.g. Monin & Yaglom Reference Monin and Yaglom1975; Ottino Reference Ottino1989). Considering chaos in Lagrangian space, the exponential growth of separation between advected trajectories
![]() $l(t)=l_{0}\text{e}^{{\it\lambda}t}$
in time is assumed only for a separation
$l(t)=l_{0}\text{e}^{{\it\lambda}t}$
in time is assumed only for a separation
![]() $l\ll {\it\eta}$
, where
$l\ll {\it\eta}$
, where
![]() ${\it\lambda}$
is the Lyapunov exponent,
${\it\lambda}$
is the Lyapunov exponent,
![]() ${\it\eta}$
is the characteristic scale of the smallest Eulerian structures (i.e. dissipative eddies in plasma turbulence). In isotropic homogeneous 3-D turbulence in the inertial range
${\it\eta}$
is the characteristic scale of the smallest Eulerian structures (i.e. dissipative eddies in plasma turbulence). In isotropic homogeneous 3-D turbulence in the inertial range
![]() ${\it\eta}\ll l\ll L$
the Richardson law
${\it\eta}\ll l\ll L$
the Richardson law
![]() $\langle l^{2}\rangle \sim t^{3}$
and standard diffusive regime
$\langle l^{2}\rangle \sim t^{3}$
and standard diffusive regime
![]() $\langle l^{2}\rangle \sim t$
for very large separations
$\langle l^{2}\rangle \sim t$
for very large separations
![]() $l\gg L$
are assumed. In order to treat intermittent turbulence keeping in the Eulerian framework, we may assume power law scaling
$l\gg L$
are assumed. In order to treat intermittent turbulence keeping in the Eulerian framework, we may assume power law scaling
![]() $\langle l^{2}\rangle \sim t^{h}$
(i.e. index
$\langle l^{2}\rangle \sim t^{h}$
(i.e. index
![]() $h$
may depend on a scale) being more general than Richardson’s law. Such an approach corresponds to the multifractal formalism that is a bridge between the Eulerian and Lagrangian descriptions, see, e.g. Frish (Reference Frish1995). The intermittency can be described by the multifractal formalism (see below) exploiting Eulerian measurements in space and laboratory plasmas.
$h$
may depend on a scale) being more general than Richardson’s law. Such an approach corresponds to the multifractal formalism that is a bridge between the Eulerian and Lagrangian descriptions, see, e.g. Frish (Reference Frish1995). The intermittency can be described by the multifractal formalism (see below) exploiting Eulerian measurements in space and laboratory plasmas.
2.2. Measurements in fusion devices
Plasma turbulence has been measured in many fusion devices, starting with experiments on tokamak TMP in 1956 at Kurchatov Institute (see Nedospasov Reference Nedospasov1992). Experiments are made in fusion devices with different topology of magnetic field – tokamaks, helical devices and stellarators, reversed field pinch and linear devices. Topology of the magnetic field is taken into account when MHD stability and large-scale plasma dynamics are considered. A lot of experimental evidence has been observed now that plasma in fusion devices is turbulent and level of plasma fluctuations is increased in the peripheral zone of plasma discharge. Edge plasma turbulence is intermittent with an enhanced level of turbulent flux, leading to anomalously large cross-field plasma transport (see Introduction). Thus, the edge region of the plasma in fusion devices is highly interesting for the investigation of the nature of enhanced plasma transport linked with intermittency and the self-similarity of plasma turbulence.
Experimental measurements of edge plasma parameters are reviewed in Zweben et al. (Reference Zweben, Boedo, Grulke, Hidalgo, LaBombard, Maqueda, Scarin and Terry2007) and other related papers. In such experiments, plasma dynamics is characterized typically by moderate kinetic Reynolds numbers (
![]() $\mathit{Re}\,<\,100$
) and magnetic Reynolds numbers (
$\mathit{Re}\,<\,100$
) and magnetic Reynolds numbers (
![]() $\mathit{Re}_{m}<1000$
), see Budaev et al. (Reference Budaev, Savin and Zelenyi2011).
$\mathit{Re}_{m}<1000$
), see Budaev et al. (Reference Budaev, Savin and Zelenyi2011).
The main fluctuating quantities of interest for edge plasma turbulence are the electron density
![]() $n$
, electron temperature
$n$
, electron temperature
![]() $Te$
, the electrostatic potential
$Te$
, the electrostatic potential
![]() ${\it\varphi}$
and the flow speed
${\it\varphi}$
and the flow speed
![]() $\boldsymbol{v}$
. Electric (Langmuir) probes are used to measure plasma fluctuations in magnetic fusion devices. The technique of Langmuir probes is simply to insert one or more small biased electrodes inside the plasma and then to measure the fluctuations seen by these probes. Probe signals contain a large amount of data which can be interpreted in terms of the local
$\boldsymbol{v}$
. Electric (Langmuir) probes are used to measure plasma fluctuations in magnetic fusion devices. The technique of Langmuir probes is simply to insert one or more small biased electrodes inside the plasma and then to measure the fluctuations seen by these probes. Probe signals contain a large amount of data which can be interpreted in terms of the local
![]() $n$
,
$n$
,
![]() $Te$
,
$Te$
,
![]() ${\it\varphi}$
within the frequency and length scales of
${\it\varphi}$
within the frequency and length scales of
![]() ${\sim}1~\text{kHz}{-}1~\text{MHz}$
and
${\sim}1~\text{kHz}{-}1~\text{MHz}$
and
![]() ${\sim}0.1{-}10~\text{cm}$
. The limitation of probes (with size typically 1 mm) is that they must not significantly perturb the plasma or vice versa. In practice, this allows for the investigation of plasmas with up to
${\sim}0.1{-}10~\text{cm}$
. The limitation of probes (with size typically 1 mm) is that they must not significantly perturb the plasma or vice versa. In practice, this allows for the investigation of plasmas with up to
![]() $Te\sim 100~\text{eV}$
, which is a typical condition of edge plasma in fusion devices.
$Te\sim 100~\text{eV}$
, which is a typical condition of edge plasma in fusion devices.
Accuracy of plasma parameter estimation depends on the assumptions made during probe data analysis. If the electron temperature fluctuations are neglected, the poloidal electric field
![]() $E$
and hence the radial drift
$E$
and hence the radial drift
![]() $E\times B$
velocity (cross-field) of fluctuations,
$E\times B$
velocity (cross-field) of fluctuations,
![]() $v$
, can be calculated from measurements of the potential fluctuations with two separated Langmuir probe tips. The cross-field particle transport
$v$
, can be calculated from measurements of the potential fluctuations with two separated Langmuir probe tips. The cross-field particle transport
![]() ${\it\Gamma}$
due to fluctuations can be calculated from such velocity estimation and density fluctuations with a third tip in between,
${\it\Gamma}$
due to fluctuations can be calculated from such velocity estimation and density fluctuations with a third tip in between,
![]() ${\it\Gamma}=nv$
. The calculation of electric field and the radial
${\it\Gamma}=nv$
. The calculation of electric field and the radial
![]() $E\times B$
velocity assumes that the temperature and sheath drop are identical in both tips and that the intermittent objects are larger than the separation between the tips; the last assumption is justified later using beam emission spectroscopy data (see Boedo et al.
Reference Boedo, Rudakov, Moyer, Krasheninnikov, Whyte, McKee, Tynan, Schaffer, Stangeby and West2001). In experiments, probe separation between two neighbouring probe tips is typically 3–5 mm which is sufficiently small. This separation influences the underestimation of Fourier components with wavelengths as small as twice the probe tip separation. Details on the possible errors introduced by neglect of the temperature fluctuations and finite probe tip separation is discussed by Endler (Reference Endler1999). Probe measurements of density and temperature have been successfully compared with non-perturbing measurements such as Thomson scattering (see Zweben et al.
Reference Zweben, Boedo, Grulke, Hidalgo, LaBombard, Maqueda, Scarin and Terry2007).
$E\times B$
velocity assumes that the temperature and sheath drop are identical in both tips and that the intermittent objects are larger than the separation between the tips; the last assumption is justified later using beam emission spectroscopy data (see Boedo et al.
Reference Boedo, Rudakov, Moyer, Krasheninnikov, Whyte, McKee, Tynan, Schaffer, Stangeby and West2001). In experiments, probe separation between two neighbouring probe tips is typically 3–5 mm which is sufficiently small. This separation influences the underestimation of Fourier components with wavelengths as small as twice the probe tip separation. Details on the possible errors introduced by neglect of the temperature fluctuations and finite probe tip separation is discussed by Endler (Reference Endler1999). Probe measurements of density and temperature have been successfully compared with non-perturbing measurements such as Thomson scattering (see Zweben et al.
Reference Zweben, Boedo, Grulke, Hidalgo, LaBombard, Maqueda, Scarin and Terry2007).
Numerous Langmuir probe measurements were made on tokamaks: T-10 by Vershkov, Grashin & Chankin (Reference Vershkov, Grashin and Chankin1987), D-IIID by Boedo et al. (Reference Boedo, Rudakov, Moyer, Krasheninnikov, Whyte, McKee, Tynan, Schaffer, Stangeby and West2001), TEXTOR by Huber et al. (Reference Huber, Samm, Schweer and Mertens2005), JET by Gonçalves et al. (Reference Gonçalves, Hidalgo, Silva, Pedrosa and Erents2005), Tore Supra by Antar, Counsell & Yu (Reference Antar, Counsell and Yu2003), JT-60U by Asakura et al. (Reference Asakura, Sakurai, Shimada, Koide, Hosogane and Itami2000), Asdex-U by Endler et al. (1995), MAST by Antar, Counsell & Ahn (Reference Antar, Counsell and Ahn2005), on stellarators and helical devices: LHD by Ohno et al. (Reference Ohno, Masuzaki, Miyoshi, Takamura, Budaev, Morisaki, Ohyabu and Komori2006), L-2 by Skvortsova et al. (Reference Skvortsova, Korolev, Batanov, Petrov, Sarksyan, Kharchev, Shatalin, Laskul, Pavlov and Popov2006), TJ-II by Alonso et al. (Reference Alonso, Zweben, Carvalho, de Pablo, de la Cal, Hidalgo, Klinger, van Milligen, Maqueda and Pedrosa2006), on linear machines by Carter (Reference Carter2006), Chiu & Sen (Reference Chiu and Sen2000), on reversed field pinches by Antoni et al. (Reference Antoni, Cavazzana, Desideri, Martines, Serianni and Tramontin1998), on plasma device NAGDIS-II by Ohno et al. (Reference Ohno, Budaev, Furuta, Miyoshi and Takamura2004), PISCES by Schmitz et al. (Reference Schmitz, Lehmer, Chevalier and Tynan1990) and others fusion devices. The plasma fluctuations have been experimentally observed to be highly correlated and of constant amplitude along the magnetic field lines (over more than one toroidal turn in toroidal devices). Magnetic pickup coils are used to measure magnetic field.
Typical time traces of the density
![]() $n(t)$
fluctuations measured using Langmuir probes in the edge of fusion devices are shown in figure 8. Taylor’s hypothesis was used to make analyse this experimental data.
$n(t)$
fluctuations measured using Langmuir probes in the edge of fusion devices are shown in figure 8. Taylor’s hypothesis was used to make analyse this experimental data.

Figure 8. (a) Time traces of density fluctuations (subtracted by mean value and normalized by standard deviation) in magnetized edge plasmas: the T-10 tokamak SOL plasma, NAGDIS-II attached plasma, LHD divertor plasma, JT-60U tokamak SOL plasma. (b) Typical waveform of high intensity bursts in T-10 tokamak and NAGDIS-II device. (c) Power spectrum
![]() $S(f)=|n(f)|^{2}$
of the density fluctuations. Solid line – power-law
$S(f)=|n(f)|^{2}$
of the density fluctuations. Solid line – power-law
![]() $1/f$
; dashed line – a noise level in the signal. SOL plasma, T-10 tokamak.
$1/f$
; dashed line – a noise level in the signal. SOL plasma, T-10 tokamak.
The density, electric field (i.e. cross-field velocity) and cross-field particle flux fluctuations possess a high-frequency part and the peaks of total intensity (referred to as the bursts) caused by the intermittent structures. There exist fluctuations in each burst and maxima are separated by a time greater than the auto-correlation time. The characteristic time scale of the bursts is of
![]() ${\sim}40{-}200~{\rm\mu}\text{s}$
(figure 8
b). In many experiments, several scaling ranges with respect to the frequency are typically registered in the broadened frequency spectra of density and electric field fluctuation (see example on figure 8) with no
${\sim}40{-}200~{\rm\mu}\text{s}$
(figure 8
b). In many experiments, several scaling ranges with respect to the frequency are typically registered in the broadened frequency spectra of density and electric field fluctuation (see example on figure 8) with no
![]() $1/f$
behaviour. The typical value of the scaling exponent of the power spectra in the high-frequency range above
$1/f$
behaviour. The typical value of the scaling exponent of the power spectra in the high-frequency range above
![]() ${\sim}100~\text{kHz}$
is in the range of
${\sim}100~\text{kHz}$
is in the range of
![]() ${\it\gamma}\approx 1.2{-}2.5$
. There are no monochromatic peaks in the broadened spectra. Thus, the process cannot be considered to consist of any coherent structures in isolation from the background turbulence. It should be noted that the frequency Fourier spectra of all observables (density, electric field and velocity, cross-field particle fluxes) are of decayed shape.
${\it\gamma}\approx 1.2{-}2.5$
. There are no monochromatic peaks in the broadened spectra. Thus, the process cannot be considered to consist of any coherent structures in isolation from the background turbulence. It should be noted that the frequency Fourier spectra of all observables (density, electric field and velocity, cross-field particle fluxes) are of decayed shape.
The spectrum of poloidal wavenumber,
![]() $k_{pol}$
, (integrated over all frequencies) broadens similarly to the shape of the frequency spectrum (integrated over all poloidal wavenumbers) as is expected from the Taylor hypothesis of frozen flux. In the edge plasma
$k_{pol}$
, (integrated over all frequencies) broadens similarly to the shape of the frequency spectrum (integrated over all poloidal wavenumbers) as is expected from the Taylor hypothesis of frozen flux. In the edge plasma
![]() $k_{pol}$
is in the range
$k_{pol}$
is in the range
![]() ${\sim}0.1{-}5~\text{cm}^{-1}$
, corresponding to the scaling
${\sim}0.1{-}5~\text{cm}^{-1}$
, corresponding to the scaling
![]() $\langle k_{pol}\rangle {\it\rho}_{i}\sim 0.02{-}0.1$
(
$\langle k_{pol}\rangle {\it\rho}_{i}\sim 0.02{-}0.1$
(
![]() $\langle k_{pol}\rangle$
is averaged value,
$\langle k_{pol}\rangle$
is averaged value,
![]() ${\it\rho}_{i}$
– local ion gyroradius), i.e. to the typical low-frequency turbulence range (see Zweben et al.
Reference Zweben, Boedo, Grulke, Hidalgo, LaBombard, Maqueda, Scarin and Terry2007).
${\it\rho}_{i}$
– local ion gyroradius), i.e. to the typical low-frequency turbulence range (see Zweben et al.
Reference Zweben, Boedo, Grulke, Hidalgo, LaBombard, Maqueda, Scarin and Terry2007).
Turbulence properties regarding magnetic structure and magnetic curvature were studied in tokamaks TF-2 (Budaev et al.
Reference Budaev, Bogomolov, Borovsky and Ivanov1990), T-10 (Kirnev et al.
Reference Kirnev, Budaev, Grashin, Khimchenko and Sarytchev2005), HYBTOK-II (Budaev et al.
Reference Budaev, Takamura, Kikuchi, Uesugi and Ohno2003) and the Large Helical Device (Ohno et al.
Reference Ohno, Masuzaki, Miyoshi, Takamura, Budaev, Morisaki, Ohyabu and Komori2006). Turbulent fluxes, fluctuation level and turbulent spectra were measured in these toroidal plasma discharges at outboard and inboard sides (which are of different magnetic curvature) of the torus to reveal any differences in the property regarding magnetic curvature. Intermittent fluctuations were observed both at the outboard and inboard side of a toroidal plasma; they were identical statistically. These experimental observations have demonstrated that
![]() $B\boldsymbol{{\rm\nabla}}B$
drift due to magnetic curvature is likely not a dominant effect of intermittency origin in toroidal plasmas.
$B\boldsymbol{{\rm\nabla}}B$
drift due to magnetic curvature is likely not a dominant effect of intermittency origin in toroidal plasmas.
Intermittent plasma transport. Experimental results obtained in the last two decades have shown that intermittent turbulence of plasma in the edge of tokamaks, helical devices and linear devices have similar properties independent of which device the measurements are made in (see Budaev et al.
Reference Budaev, Savin and Zelenyi2011). Cross-field plasma particle flux in the edge of fusion devices is inhomogeneous in time and space (see figure 9
a). Numerous experiments have shown that cross-field plasma transport in the edge plasma of fusion devices (tokamaks, helical and linear devices) cannot be described by classical diffusion with constant diffusion coefficient. A large fraction (up to
![]() ${\sim}50\,\%$
) of cross-field plasma flux consists of large-scale coherent structure transport. Such cross-field transport in the literature is often described by an effective diffusion coefficient that can reach a value much larger than the Bohm coefficient (up to tens of magnitude). This is called anomalous diffusion (despite the fact that the process does not look like gas diffusion). Intermittent transport (radial and poloidal) was observed using different diagnostics (see review Boedo et al.
Reference Boedo, Rudakov, Moyer, Krasheninnikov, Whyte, McKee, Tynan, Schaffer, Stangeby and West2001; D’Ippolito, Myra & Zweben Reference D’Ippolito, Myra and Zweben2011; Maqueda, Stotler & Zweben Reference Maqueda, Stotler and Zweben2011). The level of time-averaged flux originates not only from amplitudes of density and electric field fluctuations, but also a large contribution from the correlation between density
${\sim}50\,\%$
) of cross-field plasma flux consists of large-scale coherent structure transport. Such cross-field transport in the literature is often described by an effective diffusion coefficient that can reach a value much larger than the Bohm coefficient (up to tens of magnitude). This is called anomalous diffusion (despite the fact that the process does not look like gas diffusion). Intermittent transport (radial and poloidal) was observed using different diagnostics (see review Boedo et al.
Reference Boedo, Rudakov, Moyer, Krasheninnikov, Whyte, McKee, Tynan, Schaffer, Stangeby and West2001; D’Ippolito, Myra & Zweben Reference D’Ippolito, Myra and Zweben2011; Maqueda, Stotler & Zweben Reference Maqueda, Stotler and Zweben2011). The level of time-averaged flux originates not only from amplitudes of density and electric field fluctuations, but also a large contribution from the correlation between density
![]() $n(t)$
and drift velocity
$n(t)$
and drift velocity
![]() $v(t)$
(defined by electric field). The Fourier spectra of the flux is broadened. Detailed analysis of experimental data has shown the self-similarity of the plasma flux. A hierarchy of structures is seen, e.g. on the WT as tree-like structure (figure 9
b). This hierarchy of scales is evidence of fractality and long-range correlation. Such a feature is typical of a cascade process in developed turbulence and should be analysed by statistical methods.
$v(t)$
(defined by electric field). The Fourier spectra of the flux is broadened. Detailed analysis of experimental data has shown the self-similarity of the plasma flux. A hierarchy of structures is seen, e.g. on the WT as tree-like structure (figure 9
b). This hierarchy of scales is evidence of fractality and long-range correlation. Such a feature is typical of a cascade process in developed turbulence and should be analysed by statistical methods.

Figure 9. Cross-field plasma flux in the edge of the T-10 tokamak: (a) typical signal and (b) wavelet decomposition, white curve is the flux signal.
Numerous experimental evidence in edge plasmas of fusion devices have shown that the PDFs of the fluctuations (constructed as a histogram of the experimental signal – density, electric field or particle flux) are typically non-Gaussian, figure 10, and illustrate the intermittent nature of the process. Positively skewed PDFs are typically observed in the SOL and in the far-SOL region in fusion devices, e.g. on Tore Supra, Alcator C-Mod, MAST and PISCES (Antar et al. Reference Antar, Counsell and Yu2003). At the same time, a negatively skewed PDF (related to negative burst waveforms) was observed on the Large Helical Device in some edge plasma regions (Ohno et al. Reference Ohno, Masuzaki, Miyoshi, Takamura, Budaev, Morisaki, Ohyabu and Komori2006). Intermittent fluctuations (non-Gaussian PDFs) of the edge density, velocity and turbulent transport flux have been seen in many toroidal fusion devices (see Zweben et al. Reference Zweben, Boedo, Grulke, Hidalgo, LaBombard, Maqueda, Scarin and Terry2007).

Figure 10. Typical PDFs of fluctuations in edge plasma. (a) Cross-field particle flux
![]() ${\it\Gamma}$
in the T-10 tokamak SOL by solid line. Experimental data are normalized by the standard deviation
${\it\Gamma}$
in the T-10 tokamak SOL by solid line. Experimental data are normalized by the standard deviation
![]() ${\it\sigma}$
. Gaussian fits of the PDF’s are shown in dashed-dotted line, the Lorentz distribution by dashed line. (b) Evolution of the PDF’s shape with minor radius, the SOL of the T-10 tokamak LCMS at
${\it\sigma}$
. Gaussian fits of the PDF’s are shown in dashed-dotted line, the Lorentz distribution by dashed line. (b) Evolution of the PDF’s shape with minor radius, the SOL of the T-10 tokamak LCMS at
![]() $r=30~\text{cm}$
. (c) Density (blue thick dashed line) and velocity (red solid line) simultaneously measured in the same location in the T-10 tokamak SOL. Experimental data are normalized by the standard deviation value. Gaussian fits of the PDF’s are shown in dashed line.
$r=30~\text{cm}$
. (c) Density (blue thick dashed line) and velocity (red solid line) simultaneously measured in the same location in the T-10 tokamak SOL. Experimental data are normalized by the standard deviation value. Gaussian fits of the PDF’s are shown in dashed line.
It is worth stressing that both the density and velocity of the plasma fluctuations obey a non-Gaussian PDF of similar shape. This is illustrated in figure 10(c), where PDFs of density and velocity fluctuations measured by Langmuir probes in the same location (within size of 4 mm) are shown. Such observations are an argument in favour of treating turbulent transport intermittency as linked with both density and velocity intermittency.
There is no clear evidence that the PDF’s shape depends strictly on plasma parameters such as local plasma density, electron temperature, plasma gradients and particle flux value. An evolution of the PDF’s shape with minor radius is observed (see figure 10 b), e.g. from a near-Gaussian shape at LCFS to the strictly positively skewed at the far-SOL. To analyse the shape of the PDF in detail, the structure function should be investigated.
The fluctuations observed in tokamaks, helical devices and linear devices are characterized by scale-invariance (self-similarity) (see, e.g. Budaev et al.
Reference Budaev, Ohno, Masuzaki, Morisaki, Komori and Takamura2008a
,Reference Budaev, Savin, Zelenyi, Ohno, Takamura and Amata
b
). The self-similarity is illustrated by the hierarchy of scales on WT, figure 9(b). The observations of scale-invariance and power-laws are a manifestations of the fractality (self-similarity) of turbulence which can be characterised by a fractal dimension (or a set of dimensions). The fractal structure of edge plasma turbulence in fusion devices is very complicated. Depending on the accuracy of the description, different fractal indices can be used to characterize the scale invariance, such as the correlation dimension (fractal dimension) and Hurst exponent (see Hurst Reference Hurst1951; Grassberger & Procaccia Reference Grassberger and Procaccia1983). The correlation dimension of edge plasma turbulence in TEXTOR, T-10 tokamaks is in the range from
![]() ${\sim}6$
to 15 (Budaev et al.
Reference Budaev, Fuchs, Ivanov and Samm1993, Reference Budaev, Savin and Zelenyi2011). This is a relatively low fractal dimension (in comparison with infinity for ‘white noise’). The Hurst exponent for edge plasma turbulence was estimated to be of 0.6–0.8 (on tokamaks DIII-D Carreras, Lynch & Zaslavsky (Reference Carreras, Lynch and Zaslavsky2001b
), Tore Supra (Antar et al.
Reference Antar, Krasheninnikov, Devynck, Doerner, Hollmann, Boedo, Luckhardt and Conn2001), T-10 (Budaev & Khimchenko Reference Budaev and Khimchenko2007)) and demonstrates a tendency to increase toward the wall. Values
${\sim}6$
to 15 (Budaev et al.
Reference Budaev, Fuchs, Ivanov and Samm1993, Reference Budaev, Savin and Zelenyi2011). This is a relatively low fractal dimension (in comparison with infinity for ‘white noise’). The Hurst exponent for edge plasma turbulence was estimated to be of 0.6–0.8 (on tokamaks DIII-D Carreras, Lynch & Zaslavsky (Reference Carreras, Lynch and Zaslavsky2001b
), Tore Supra (Antar et al.
Reference Antar, Krasheninnikov, Devynck, Doerner, Hollmann, Boedo, Luckhardt and Conn2001), T-10 (Budaev & Khimchenko Reference Budaev and Khimchenko2007)) and demonstrates a tendency to increase toward the wall. Values
![]() $H>1/2$
corresponds to a long-range correlation and superdiffusion. The Hurst exponent describes the coarse grain structure of a fractal object. Detailed characterization is available by multifractal analysis.
$H>1/2$
corresponds to a long-range correlation and superdiffusion. The Hurst exponent describes the coarse grain structure of a fractal object. Detailed characterization is available by multifractal analysis.
3. Generalized self-similarity of plasma turbulence
3.1. Multifractal cascade process
A treatment of the turbulence problem in any analytic theory or direct numerical solution of the equations describing plasma turbulence face a fundamental problem: the cascade nature of the process, the number of degrees-of-freedom increases algebraically for increasingly small spatial scales. This is why cascade turbulence models are better suited for a description of the long range spatiotemporal scales. Within the cascade paradigm, many properties of such turbulence can be described, in particular, its multiscale and multifractal nature. By incorporating an anisotropic multiplicative cascade, it becomes possible to develop a multifractal turbulence model (see review Budaev et al. Reference Budaev, Savin and Zelenyi2011 and other related papers), i.e. to consider how the self-similarity depends on the local spatial scale.
The multifractal approach is a generalization of a self-similarity consideration in a system with rich statistical properties. It is appropriate to study both statistically homogeneous plasma turbulence (such as interplanetary SW or core tokamak plasmas) and intermittent plasma turbulence in the Earth’s magnetosphere and in edge of fusion devices. The multifractal approach is used to model a hierarchical turbulence cascade of a flow bounded by an upper limit (e.g. TBL). Such an approach reconsiders the cascade model K41 of Kolmogorov which represents a monofractal model with trivial self-similarity in the inertial range, supposing the inertial range is very large.
In the developed turbulence of incompressible fluids, Kolmogorov (Reference Kolmogorov1962) first formulated a hypothesis invoking some statistical independence in the cascading process, which led to the log-normal model for the rate of dissipation of turbulent kinetic energy. The next step of a generalization was the multifractal formalism (see Frish Reference Frish1995) proposed to quantify the boundary conditions influence on the turbulence statistical properties.
For multifractals, as far as the PDF of increments
![]() ${\it\delta}_{l}X(t)$
at different time scales
${\it\delta}_{l}X(t)$
at different time scales
![]() $l$
are concerned, reshaping from ‘quasi-Gaussian’ at large scale
$l$
are concerned, reshaping from ‘quasi-Gaussian’ at large scale
![]() $L$
(i.e. boundary scale) will occur, with fat tailed PDF’s at small scales. This transformation of the PDF’s for SW turbulence is illustrated in figure 11 where, the PDF’s for different time scales are plotted in logarithmic scale. The fat tails appear at the scale related to the ‘coarse’ time scale
$L$
(i.e. boundary scale) will occur, with fat tailed PDF’s at small scales. This transformation of the PDF’s for SW turbulence is illustrated in figure 11 where, the PDF’s for different time scales are plotted in logarithmic scale. The fat tails appear at the scale related to the ‘coarse’ time scale
![]() $L$
– a characteristics of multifractality. A typical scale for
$L$
– a characteristics of multifractality. A typical scale for
![]() $L$
is of
$L$
is of
![]() ${\sim}10{-}10^{4}~\text{s}$
for the Earth’s magnetosphere and of
${\sim}10{-}10^{4}~\text{s}$
for the Earth’s magnetosphere and of
![]() ${\sim}50{-}500~{\rm\mu}\text{s}$
for the edge plasma in fusion devices (see Budaev et al.
Reference Budaev, Savin and Zelenyi2011). The multifractality property was registered in TBL of the Earth’s magnetosphere (Budaev et al.
Reference Budaev, Savin and Zelenyi2011), in edge turbulence of tokamaks: Tore Supra (Antar et al.
Reference Antar, Krasheninnikov, Devynck, Doerner, Hollmann, Boedo, Luckhardt and Conn2001), T-10 (Budaev et al.
Reference Budaev, Ohno, Masuzaki, Morisaki, Komori and Takamura2008a
,Reference Budaev, Savin, Zelenyi, Ohno, Takamura and Amata
b
), Hybtok-II (Budaev et al.
Reference Budaev, Kikuchi, Uesugi and Takamura2004), CASTOR (Zajac et al.
Reference Zajac, Budaev, Dufkova, Nanobashvili and Weinzettl2005), TCABR (Rodrigues Neto et al.
Reference Rodrigues Neto, Guimarães-Filho, Caldas, Nascimento and Kuznetsov2008), MAST (Kono & Škorić Reference Kono and Škorić2010), JT-60U, heliotron LHD and a linear device NAGDIS-II (Budaev et al.
Reference Budaev, Ohno, Masuzaki, Morisaki, Komori and Takamura2008a
,Reference Budaev, Savin, Zelenyi, Ohno, Takamura and Amata
b
). The multifractal theory of energy transfer in the multiplicative cascade process can involve multifractal properties of the observables, see appendix A.
${\sim}50{-}500~{\rm\mu}\text{s}$
for the edge plasma in fusion devices (see Budaev et al.
Reference Budaev, Savin and Zelenyi2011). The multifractality property was registered in TBL of the Earth’s magnetosphere (Budaev et al.
Reference Budaev, Savin and Zelenyi2011), in edge turbulence of tokamaks: Tore Supra (Antar et al.
Reference Antar, Krasheninnikov, Devynck, Doerner, Hollmann, Boedo, Luckhardt and Conn2001), T-10 (Budaev et al.
Reference Budaev, Ohno, Masuzaki, Morisaki, Komori and Takamura2008a
,Reference Budaev, Savin, Zelenyi, Ohno, Takamura and Amata
b
), Hybtok-II (Budaev et al.
Reference Budaev, Kikuchi, Uesugi and Takamura2004), CASTOR (Zajac et al.
Reference Zajac, Budaev, Dufkova, Nanobashvili and Weinzettl2005), TCABR (Rodrigues Neto et al.
Reference Rodrigues Neto, Guimarães-Filho, Caldas, Nascimento and Kuznetsov2008), MAST (Kono & Škorić Reference Kono and Škorić2010), JT-60U, heliotron LHD and a linear device NAGDIS-II (Budaev et al.
Reference Budaev, Ohno, Masuzaki, Morisaki, Komori and Takamura2008a
,Reference Budaev, Savin, Zelenyi, Ohno, Takamura and Amata
b
). The multifractal theory of energy transfer in the multiplicative cascade process can involve multifractal properties of the observables, see appendix A.

Figure 11. Multifractal property of magnetized plasma, SW ion flux, SPECTR-R data, 20.03.2012 12UT. (a) Standardized estimated PDF’s of ion flux increments
![]() ${\it\delta}_{{\it\tau}}{\it\Gamma}(t)$
(normalized to its standard deviation
${\it\delta}_{{\it\tau}}{\it\Gamma}(t)$
(normalized to its standard deviation
![]() ${\it\sigma}_{{\it\Gamma}}$
) for different time scales (from top to bottom)
${\it\sigma}_{{\it\Gamma}}$
) for different time scales (from top to bottom)
![]() ${\it\tau}=0.25$
, 1, 4, 16, 64, 256, 1024, 2048, 4096, 16 384 s (from top to bottom). Plots have been arbitrary shifted for illustration. (b) Third (skewness – by circles) and fourth (flatness – by squares) moments of the increment PDFs for different time scales
${\it\tau}=0.25$
, 1, 4, 16, 64, 256, 1024, 2048, 4096, 16 384 s (from top to bottom). Plots have been arbitrary shifted for illustration. (b) Third (skewness – by circles) and fourth (flatness – by squares) moments of the increment PDFs for different time scales
![]() ${\it\tau}$
.
${\it\tau}$
.
Considering stochastic cascade models in the Eulerian framework, the intermittency can be described quantitatively in terms of a multifractal formalism that is a bridge between Eulerian and Lagrangian descriptions (see above discussion on Taylor ‘frozen-in turbulence’ hypothesis in § 2) The goal is to compute the multifractal spectra
![]() $D(h)$
starting from the equations of motion or from the experimental investigation of a turbulent process. Experimental observations of scaling
$D(h)$
starting from the equations of motion or from the experimental investigation of a turbulent process. Experimental observations of scaling
![]() ${\it\zeta}(q)$
and multifractal spectra
${\it\zeta}(q)$
and multifractal spectra
![]() $D(h)$
are crucial to understand how we can formulate the most general form of a multifractal random field which is consistent with the time and space scaling properties of the governing equations describing plasma turbulence.
$D(h)$
are crucial to understand how we can formulate the most general form of a multifractal random field which is consistent with the time and space scaling properties of the governing equations describing plasma turbulence.
A statistical description of plasma intermittency relates to the question how higher-order correlations influence the development of turbulence. In hydrodynamics, a well-known Kolmogorov (‘
![]() $4/5$
’) law relates the third-order structure function to the energy dissipation rate. Usually, it is stated with the assumptions of isotropy, homogeneity and time stationarity of the statistics of the velocity increments
$4/5$
’) law relates the third-order structure function to the energy dissipation rate. Usually, it is stated with the assumptions of isotropy, homogeneity and time stationarity of the statistics of the velocity increments
![]() ${\it\delta}_{l}{\it\upsilon}$
. Kolmogorov’s third-order law (Kolmogorov Reference Kolmogorov1941a
,Reference Kolmogorov
b
) requires that (certain) third-order moments,
${\it\delta}_{l}{\it\upsilon}$
. Kolmogorov’s third-order law (Kolmogorov Reference Kolmogorov1941a
,Reference Kolmogorov
b
) requires that (certain) third-order moments,
![]() $S(q,l)=\langle |{\it\delta}_{l}{\it\upsilon}|^{q}\rangle ,q=3$
, are non-zero and proportional to the non-zero energy flux
$S(q,l)=\langle |{\it\delta}_{l}{\it\upsilon}|^{q}\rangle ,q=3$
, are non-zero and proportional to the non-zero energy flux
![]() ${\it\varepsilon}$
,
${\it\varepsilon}$
,
Derived from the Navier–Stokes equations (NSE) (see Frish Reference Frish1995) and valid in the inertial range, assure that the third-order structure function is unaffected by intermittency. It also requires adoption of the von Kármán–Howard–Monin hypothesis (von Kármán & Howarth Reference von Kármán and Howarth1938; Monin & Yaglom Reference Monin and Yaglom1975) that the rate of energy dissipation
![]() ${\it\varepsilon}$
approaches a constant non-zero value as the Reynolds number tends to infinity. The well-known von Kármán–Howard–Monin hierarchy of equations relate the evolution of the second-order correlations to third-order ones, the evolution of the third-order correlations to fourth order ones, and so on to infinite order.
${\it\varepsilon}$
approaches a constant non-zero value as the Reynolds number tends to infinity. The well-known von Kármán–Howard–Monin hierarchy of equations relate the evolution of the second-order correlations to third-order ones, the evolution of the third-order correlations to fourth order ones, and so on to infinite order.
For turbulent MHD fluctuations exact relations for third-order structure functions and their derivatives are considered in theoretical treatments (see Basu, Naji & Pandit Reference Basu, Naji and Pandit2014 and references therein, Politano & Pouquet Reference Politano and Pouquet1998a
,Reference Politano and Pouquet
b
). It is a direct analog of the von Kármán–Howarth–Monin vector relation in anisotropic hydrodynamic turbulence. The quantities used in MHD treatment (e.g. by Politano & Pouquet Reference Politano and Pouquet1998a
,Reference Politano and Pouquet
b
) are the plus and minus Elsässer vectors,
![]() $z^{\pm }={\it\upsilon}\pm b$
, where
$z^{\pm }={\it\upsilon}\pm b$
, where
![]() $b$
is the magnetic field in Alfven speed units, and their fluctuations over vector spatial differences. On this point, Chandrasekhar (Reference Chandrasekhar1951) noticed that the Elsässer variables have an ambiguous symmetry under parity. Considering von Kármán–Howard–Monin hypothesis, the prospects of a universal description of MHD turbulence are discussed in the literature (see Wan et al.
Reference Wan, Oughton, Servidio and Matthaeus2012; Basu et al.
Reference Basu, Naji and Pandit2014). Multifractal measures are appropriate quantities for such a description.
$b$
is the magnetic field in Alfven speed units, and their fluctuations over vector spatial differences. On this point, Chandrasekhar (Reference Chandrasekhar1951) noticed that the Elsässer variables have an ambiguous symmetry under parity. Considering von Kármán–Howard–Monin hypothesis, the prospects of a universal description of MHD turbulence are discussed in the literature (see Wan et al.
Reference Wan, Oughton, Servidio and Matthaeus2012; Basu et al.
Reference Basu, Naji and Pandit2014). Multifractal measures are appropriate quantities for such a description.
Exploiting Eulerian measurements (see discussion on Taylor ‘frozen-in turbulence’ hypothesis in § 2), the scaling
![]() ${\it\zeta}(q)$
and
${\it\zeta}(q)$
and
![]() $D(h)$
are calculated from experimental time-series by using the WTMM method, which is very powerful in estimating the multifractal measures, see appendix A.
$D(h)$
are calculated from experimental time-series by using the WTMM method, which is very powerful in estimating the multifractal measures, see appendix A.
Multifractal spectra
![]() $D(h)$
estimated by the WTMM method (see appendix A) are plotted in figure 12 against the Hölder exponent
$D(h)$
estimated by the WTMM method (see appendix A) are plotted in figure 12 against the Hölder exponent
![]() $h^{\ast }=1+(h-h_{Dmax})$
(where
$h^{\ast }=1+(h-h_{Dmax})$
(where
![]() $h_{Dmax}$
is the Hölder exponent at a maximum of the
$h_{Dmax}$
is the Hölder exponent at a maximum of the
![]() $D(h)$
spectrum). In this frame, the spectra are centred around 1. The experimental signals from space and laboratory plasmas are characterized by the broadened
$D(h)$
spectrum). In this frame, the spectra are centred around 1. The experimental signals from space and laboratory plasmas are characterized by the broadened
![]() $D(h)$
spectra, being of a convex (bell-like) shape (figure 12). This is the typical shape of singularity spectra observed in multifractal fields (cf. examples in Harte Reference Harte2001). For a monofractal process, the
$D(h)$
spectra, being of a convex (bell-like) shape (figure 12). This is the typical shape of singularity spectra observed in multifractal fields (cf. examples in Harte Reference Harte2001). For a monofractal process, the
![]() $D(h)$
spectrum collapses to a point (an example is the data from SW and MSH outside the TBL in figure 12). The maximum of
$D(h)$
spectrum collapses to a point (an example is the data from SW and MSH outside the TBL in figure 12). The maximum of
![]() $D(h)$
is in the range of 0.8–1. A value close to 1 suggests that the experimental signal is singular almost everywhere. This implies that turbulent fluctuations are characterized by a rapid increase in amplitude. The broadness of the
$D(h)$
is in the range of 0.8–1. A value close to 1 suggests that the experimental signal is singular almost everywhere. This implies that turbulent fluctuations are characterized by a rapid increase in amplitude. The broadness of the
![]() $D(h)$
singularity spectrum provides a measure of multifractality (deviation from the monofractal process, i.e. K41) and lies in the range of 0.5–1.2. This range is typical for the strong intermittency observed in numerical models and experiments in fluids and plasma turbulence (see Budaev et al.
Reference Budaev, Savin and Zelenyi2011). The Hölder exponents exceed that of a Brownian signal with
$D(h)$
singularity spectrum provides a measure of multifractality (deviation from the monofractal process, i.e. K41) and lies in the range of 0.5–1.2. This range is typical for the strong intermittency observed in numerical models and experiments in fluids and plasma turbulence (see Budaev et al.
Reference Budaev, Savin and Zelenyi2011). The Hölder exponents exceed that of a Brownian signal with
![]() $h=1/3$
. A typical view of
$h=1/3$
. A typical view of
![]() $h(q)$
is shown in figure 13.
$h(q)$
is shown in figure 13.

Figure 12. Multifractal spectra
![]() $D(h)$
versus the normalized Hölder exponent
$D(h)$
versus the normalized Hölder exponent
![]() $h^{\ast }=1+(h-h_{Dmax})$
(centred around 1 by subtracting
$h^{\ast }=1+(h-h_{Dmax})$
(centred around 1 by subtracting
![]() $h_{Dmax}$
). TBL ion flux SPECTR-R data (SW SPECTR-R) 20.03.2012, magnetic field
$h_{Dmax}$
). TBL ion flux SPECTR-R data (SW SPECTR-R) 20.03.2012, magnetic field
![]() $B_{x}$
in the MSH outside the TBL (MSH
$B_{x}$
in the MSH outside the TBL (MSH
![]() $B_{x}$
) INTERBALL-I, 19.06.1998, SW ion flux WIND data 20.03.2012, the ion flux in the Earth’s magnetosphere TBL (TBL ion flux), 29.03.1996; edge plasma turbulence in tokamak T-10 (T-10 SOL), near the last closed magnetic surface (T-10 LCFS); in NAGDIS-II for attached plasma (N-II attach) and for detached plasma (N-II detach).
$B_{x}$
) INTERBALL-I, 19.06.1998, SW ion flux WIND data 20.03.2012, the ion flux in the Earth’s magnetosphere TBL (TBL ion flux), 29.03.1996; edge plasma turbulence in tokamak T-10 (T-10 SOL), near the last closed magnetic surface (T-10 LCFS); in NAGDIS-II for attached plasma (N-II attach) and for detached plasma (N-II detach).

Figure 13. Hölder exponent
![]() $h(q)$
. Density fluctuations in SOL of T-10 tokamak (T-10 SOL), magnetic field
$h(q)$
. Density fluctuations in SOL of T-10 tokamak (T-10 SOL), magnetic field
![]() $B_{x}$
in SW (SW
$B_{x}$
in SW (SW
![]() $B_{x}$
) from GEOTAIL data; ion flux in TBL (TBL ion flux) INTERBALL data 19.06.1998.
$B_{x}$
) from GEOTAIL data; ion flux in TBL (TBL ion flux) INTERBALL data 19.06.1998.
Waiting-time statistics. Another statistical approach is studying extreme events (bursts) in the signal. The waiting-time is defined as the time interval
![]() ${\rm\Delta}t$
between two consecutive maxima in a burst intensity selected above a threshold (of level crossing of a signal, e.g. of
${\rm\Delta}t$
between two consecutive maxima in a burst intensity selected above a threshold (of level crossing of a signal, e.g. of
![]() $2{-}3$
standard deviation in amplitude). The distribution
$2{-}3$
standard deviation in amplitude). The distribution
![]() $P({\rm\Delta}t)\sim ({\rm\Delta}t)^{{\it\gamma}}$
of the times are called persistence PDFs and the exponent
$P({\rm\Delta}t)\sim ({\rm\Delta}t)^{{\it\gamma}}$
of the times are called persistence PDFs and the exponent
![]() ${\it\gamma}$
is called the persistence exponent (see, e.g. Perlekar et al.
Reference Perlekar, Ray, Mitra and Pandit2011).
${\it\gamma}$
is called the persistence exponent (see, e.g. Perlekar et al.
Reference Perlekar, Ray, Mitra and Pandit2011).
Typical waiting-times series constructed from intervals between successive bursts in the signal are shown in figure 14, demonstrating intermittency and the scale hierarchy in the wavelet decomposition. Typically, the PDFs of these series are not decayed exponentially. A typical power law exponent of the PDF,
![]() $P({\rm\Delta}t)\sim ({\rm\Delta}t)^{{\it\gamma}}$
(see example in figure 15 is of
$P({\rm\Delta}t)\sim ({\rm\Delta}t)^{{\it\gamma}}$
(see example in figure 15 is of
![]() ${\it\gamma}\approx -3$
to
${\it\gamma}\approx -3$
to
![]() $-2$
, Savin et al.
Reference Savin, Budaev, Zelenyi, Amata, Lutsenko, Borodkova, Zhang, Angelopoulos, Safrankova and Nemecek2011). For the normal random process with Gaussian statistics it should be
$-2$
, Savin et al.
Reference Savin, Budaev, Zelenyi, Amata, Lutsenko, Borodkova, Zhang, Angelopoulos, Safrankova and Nemecek2011). For the normal random process with Gaussian statistics it should be
![]() ${\sim}1$
. The power law of the waiting-time PDF was observed in experiments on T-10 tokamak (Budaev et al.
Reference Budaev, Ohno, Masuzaki, Morisaki, Komori and Takamura2008a
,Reference Budaev, Savin, Zelenyi, Ohno, Takamura and Amata
b
), Large Helical Device (Ohno et al.
Reference Ohno, Masuzaki, Miyoshi, Takamura, Budaev, Morisaki, Ohyabu and Komori2006), D-IIID tokamak and other devices (Sánchez et al.
Reference Sánchez, van Milligen, Newman and Carreras2003) and in the Earth’s magnetosphere (Savin et al.
Reference Savin, Budaev, Zelenyi, Amata, Lutsenko, Borodkova, Zhang, Angelopoulos, Safrankova and Nemecek2011).
${\sim}1$
. The power law of the waiting-time PDF was observed in experiments on T-10 tokamak (Budaev et al.
Reference Budaev, Ohno, Masuzaki, Morisaki, Komori and Takamura2008a
,Reference Budaev, Savin, Zelenyi, Ohno, Takamura and Amata
b
), Large Helical Device (Ohno et al.
Reference Ohno, Masuzaki, Miyoshi, Takamura, Budaev, Morisaki, Ohyabu and Komori2006), D-IIID tokamak and other devices (Sánchez et al.
Reference Sánchez, van Milligen, Newman and Carreras2003) and in the Earth’s magnetosphere (Savin et al.
Reference Savin, Budaev, Zelenyi, Amata, Lutsenko, Borodkova, Zhang, Angelopoulos, Safrankova and Nemecek2011).

Figure 14. Intermittent waiting-time series
![]() ${\rm\Delta}t$
and its wavelet decomposition. Hierarchy of scales is observed as an evidence of fractality and long-term correlation. Cross-field flux in the SOL of T-10 tokamak.
${\rm\Delta}t$
and its wavelet decomposition. Hierarchy of scales is observed as an evidence of fractality and long-term correlation. Cross-field flux in the SOL of T-10 tokamak.

Figure 15. The PDF of waiting times for extreme events (peaks above 2 standard deviations) in log–log plot. 2 – TBL,
![]() $B_{z}$
, CLUSTER, 02.02.2003, 3 – TBL,
$B_{z}$
, CLUSTER, 02.02.2003, 3 – TBL,
![]() $nV_{z}$
, CLUSTER, 02.02.2003, 4 – TBL,
$nV_{z}$
, CLUSTER, 02.02.2003, 4 – TBL,
![]() $B_{y}$
, GEOTAIL, 16.04.1996, 18:54-20:04 UT, 6 – TBL,
$B_{y}$
, GEOTAIL, 16.04.1996, 18:54-20:04 UT, 6 – TBL,
![]() $nV$
, GEOTAIL, 16.04.1996, 18:54-20:04 UT.
$nV$
, GEOTAIL, 16.04.1996, 18:54-20:04 UT.
If the triggering of the turbulent bursts are not correlated, such a process may follow the Poisson process, and the probability density function of the waiting times,
![]() ${\rm\Delta}t$
, should be an exponential law:
${\rm\Delta}t$
, should be an exponential law:
![]() $P({\rm\Delta}t)={\it\gamma}^{-1}\text{e}^{-{\rm\Delta}t/{\it\gamma}}$
– the law of rare events. This exponential PDF is considered in the frame of self-organized criticality (SOC) hypothesis (Bak, Tang & Wiesenfeld Reference Bak, Tang and Wiesenfeld1988). However, statistical analysis shows a general lack of an exponential decay of the waiting-time PDF observed in the plasma TBLs, suggesting long-range correlation. This has raised criticism about the applicability of the simple SOC concept to the plasma TBLs.
$P({\rm\Delta}t)={\it\gamma}^{-1}\text{e}^{-{\rm\Delta}t/{\it\gamma}}$
– the law of rare events. This exponential PDF is considered in the frame of self-organized criticality (SOC) hypothesis (Bak, Tang & Wiesenfeld Reference Bak, Tang and Wiesenfeld1988). However, statistical analysis shows a general lack of an exponential decay of the waiting-time PDF observed in the plasma TBLs, suggesting long-range correlation. This has raised criticism about the applicability of the simple SOC concept to the plasma TBLs.
3.2. Generalized scale invariance
A statistical description of intermittent turbulence is available through the structure functions. The structure functions are the various order moments of the PDF of the fluctuating quantity:
![]() $S_{q}({\it\tau})=\langle |{\it\delta}_{{\it\tau}}X|^{q}\rangle$
, where
$S_{q}({\it\tau})=\langle |{\it\delta}_{{\it\tau}}X|^{q}\rangle$
, where
![]() ${\it\delta}_{{\it\tau}}X=X(t+{\it\tau})-X(t)$
,
${\it\delta}_{{\it\tau}}X=X(t+{\it\tau})-X(t)$
,
![]() $\langle \cdots \rangle$
is the ensemble average of experimental time-series
$\langle \cdots \rangle$
is the ensemble average of experimental time-series
![]() $X(t)$
. Typically, the structure functions
$X(t)$
. Typically, the structure functions
![]() $S_{q}({\it\tau})$
exhibit a saturation over some ‘coarse’ time scale (
$S_{q}({\it\tau})$
exhibit a saturation over some ‘coarse’ time scale (
![]() ${>}1~\text{s}$
in the Earth’s magnetosphere TBL and
${>}1~\text{s}$
in the Earth’s magnetosphere TBL and
![]() ${>}10~{\rm\mu}\text{s}$
in fusion devices), figure 16. The power dependence
${>}10~{\rm\mu}\text{s}$
in fusion devices), figure 16. The power dependence
![]() $S_{q}({\it\tau})\sim {\it\tau}^{{\it\zeta}(q)}$
is observed only on limited time scales. Such behaviour is typical for data from plasma TBLs. This was observed in space plasma (INTERBALL, CLUSTER, WIND, SPECTR-R, DOUBLE STAR, GEOTAIL, POLAR spacecrafts) and laboratory plasma devices (tokamaks, stellarators and linear machines), Budaev et al. (Reference Budaev, Savin and Zelenyi2011).
$S_{q}({\it\tau})\sim {\it\tau}^{{\it\zeta}(q)}$
is observed only on limited time scales. Such behaviour is typical for data from plasma TBLs. This was observed in space plasma (INTERBALL, CLUSTER, WIND, SPECTR-R, DOUBLE STAR, GEOTAIL, POLAR spacecrafts) and laboratory plasma devices (tokamaks, stellarators and linear machines), Budaev et al. (Reference Budaev, Savin and Zelenyi2011).

Figure 16. The high-order structure functions
![]() $S_{q}({\it\tau})$
of different orders (
$S_{q}({\it\tau})$
of different orders (
![]() $q=2$
, 3, 4, 5, 6, 7, 8 from bottom up) versus time scale
$q=2$
, 3, 4, 5, 6, 7, 8 from bottom up) versus time scale
![]() ${\it\tau}$
in log–log plot. (a) SW ion flux, BMSW data SPECTR-R on 28.09.2011; (b) plasma density in edge of T-10 tokamak.
${\it\tau}$
in log–log plot. (a) SW ion flux, BMSW data SPECTR-R on 28.09.2011; (b) plasma density in edge of T-10 tokamak.
Hydrodynamic turbulence (Benzi et al.
Reference Benzi, Ciliberto, Tripiccione, Baudet, Massaioli and Succi1993) in wind tunnel experiments have shown that scaling laws of the velocity increments can be extended up into a dissipative range:
![]() $S_{q}(l)$
has a power-law dependence on
$S_{q}(l)$
has a power-law dependence on
![]() $S_{3}(l)$
,
$S_{3}(l)$
,
over a range which is substantially longer (for long ranges of scale
![]() $l\geqslant 5{\it\eta}$
,
$l\geqslant 5{\it\eta}$
,
![]() ${\it\eta}$
– dissipation scale) than the scaling range obtained by plotting
${\it\eta}$
– dissipation scale) than the scaling range obtained by plotting
![]() $S_{q}(l)$
as a function of
$S_{q}(l)$
as a function of
![]() $l$
. This behaviour holds even for intermittent turbulence at a moderate Reynolds number and was named an ESS. This ESS property is observed on the broad range of scales from large to small scales including the dissipation range. The ESS corresponds to the scaling in a turbulent cascade not with respect to the usual distance, but with respect to an effective scale defined by the third-order moment of the velocity field.
$l$
. This behaviour holds even for intermittent turbulence at a moderate Reynolds number and was named an ESS. This ESS property is observed on the broad range of scales from large to small scales including the dissipation range. The ESS corresponds to the scaling in a turbulent cascade not with respect to the usual distance, but with respect to an effective scale defined by the third-order moment of the velocity field.
This phenomenological observation led to the criterion of the generalized self-similarity in the form
![]() $S_{q}(l)\sim S_{p}(l)^{{\it\zeta}(q)/{\it\zeta}(p)}$
, for any pair of structure functions. Such a property is explained in the frameworks of the log-Poisson cascade models (generalization of multifractal models) of intermittent turbulence, see below. In the general case, scaling laws
$S_{q}(l)\sim S_{p}(l)^{{\it\zeta}(q)/{\it\zeta}(p)}$
, for any pair of structure functions. Such a property is explained in the frameworks of the log-Poisson cascade models (generalization of multifractal models) of intermittent turbulence, see below. In the general case, scaling laws
![]() ${\it\zeta}(q)$
represent a nonlinear function of
${\it\zeta}(q)$
represent a nonlinear function of
![]() $q$
. So, generalized self-similarity (scale invariance) is considered to be the ESS property and nonlinear scaling laws
$q$
. So, generalized self-similarity (scale invariance) is considered to be the ESS property and nonlinear scaling laws
![]() ${\it\zeta}(q)$
describing a universal property of scale invariance in the framework of the log-Poisson cascade models (see below).
${\it\zeta}(q)$
describing a universal property of scale invariance in the framework of the log-Poisson cascade models (see below).
The ESS property is illustrated in the log–log plots: the dependence of
![]() $S_{q}({\it\tau})$
on
$S_{q}({\it\tau})$
on
![]() $S_{3}({\it\tau})$
is seen to be linear almost over up to three orders of magnitude in time (figure 17). All data from edge plasma in fusion devices (tokamaks T-10, HYBTOK-II, JT-60U, heliotron LHD, linear NAGDIS-II (Budaev et al.
Reference Budaev, Ohno, Masuzaki, Morisaki, Komori and Takamura2008a
,Reference Budaev, Savin, Zelenyi, Ohno, Takamura and Amata
b
)) and space plasma (SPECTR-R, INTERBALL, CLUSTER, WIND) demonstrate such an ESS property, which confirms the universality of this property, Budaev et al. (Reference Budaev, Savin and Zelenyi2011). Such observations lead to the hypothesis of the universality of the scaling in turbulence boundary layers which is currently widely discussed in the literature (see Budaev et al.
Reference Budaev, Savin and Zelenyi2011 and other related papers). With the exact result
$S_{3}({\it\tau})$
is seen to be linear almost over up to three orders of magnitude in time (figure 17). All data from edge plasma in fusion devices (tokamaks T-10, HYBTOK-II, JT-60U, heliotron LHD, linear NAGDIS-II (Budaev et al.
Reference Budaev, Ohno, Masuzaki, Morisaki, Komori and Takamura2008a
,Reference Budaev, Savin, Zelenyi, Ohno, Takamura and Amata
b
)) and space plasma (SPECTR-R, INTERBALL, CLUSTER, WIND) demonstrate such an ESS property, which confirms the universality of this property, Budaev et al. (Reference Budaev, Savin and Zelenyi2011). Such observations lead to the hypothesis of the universality of the scaling in turbulence boundary layers which is currently widely discussed in the literature (see Budaev et al.
Reference Budaev, Savin and Zelenyi2011 and other related papers). With the exact result
![]() ${\it\zeta}(3)=1$
and by using the ESS property, with experimental data one can obtain rather accurate values of
${\it\zeta}(3)=1$
and by using the ESS property, with experimental data one can obtain rather accurate values of
![]() ${\it\zeta}(q)$
considering
${\it\zeta}(q)$
considering
![]() ${\it\zeta}(q)/{\it\zeta}(3)$
by plotting
${\it\zeta}(q)/{\it\zeta}(3)$
by plotting
![]() $S(q)$
as a function of
$S(q)$
as a function of
![]() $S(3)$
.
$S(3)$
.

Figure 17. The ESS plot of the structure function
![]() $S_{q}({\it\tau})$
of different orders (
$S_{q}({\it\tau})$
of different orders (
![]() $q=2,3,4,5,6,7,8$
from bottom up) versus the third-order structure function: (a) the magnetic field
$q=2,3,4,5,6,7,8$
from bottom up) versus the third-order structure function: (a) the magnetic field
![]() $B_{x}$
in the TBL near MP, (b) plasma density in edge of T-10 tokamak, (c) plasma density in NAGDIS-II device, (d) SW ion flux, BMSW data SPECTR-R on 28.09.2011 (for
$B_{x}$
in the TBL near MP, (b) plasma density in edge of T-10 tokamak, (c) plasma density in NAGDIS-II device, (d) SW ion flux, BMSW data SPECTR-R on 28.09.2011 (for
![]() $q=2,3,4,5,6,7,8,9$
from bottom up). A linear behaviour is interpreted that the ESS holds.
$q=2,3,4,5,6,7,8,9$
from bottom up). A linear behaviour is interpreted that the ESS holds.
From this point, we are going to discuss some critical issues regarding the ESS property and determination of the intermittency exponents.
The property of ESS suggests that scaling properties in turbulence should be investigated as a function of the generalized scale
![]() ${\it\Omega}(l)$
, rather than a function of the resolution scale
${\it\Omega}(l)$
, rather than a function of the resolution scale
![]() $l$
. This is similar to critical phenomena in a finite size system in which the scaling properties are considered as a function of a correlation length, depending on the system size and diverging at the critical point. The ESS property can become fully compatible with a generalized scale transformation moment hierarchy in the log-Poisson She–Leveque–Dubrulle model (see appendix B) in terms of a generalized scale
$l$
. This is similar to critical phenomena in a finite size system in which the scaling properties are considered as a function of a correlation length, depending on the system size and diverging at the critical point. The ESS property can become fully compatible with a generalized scale transformation moment hierarchy in the log-Poisson She–Leveque–Dubrulle model (see appendix B) in terms of a generalized scale
![]() ${\it\Omega}(l)=\langle \langle {\it\varepsilon}_{l}\rangle ^{-1}{\it\delta}{\it\upsilon}_{l}^{3}\rangle$
, (see Dubrulle Reference Dubrulle1994) i.e. depending on the scale defined by the third-order moment. The She–Leveque–Dubrulle model postulates that the moment hierarchy originates from some hidden symmetry of the NSE, Dubrulle (Reference Dubrulle1994). The plasma turbulence is treated by governing equations which are more complicated than the NSE. At the same time, all these governing equations remain formally invariant (as with the NSE) under any affine contraction of the space–time
${\it\Omega}(l)=\langle \langle {\it\varepsilon}_{l}\rangle ^{-1}{\it\delta}{\it\upsilon}_{l}^{3}\rangle$
, (see Dubrulle Reference Dubrulle1994) i.e. depending on the scale defined by the third-order moment. The She–Leveque–Dubrulle model postulates that the moment hierarchy originates from some hidden symmetry of the NSE, Dubrulle (Reference Dubrulle1994). The plasma turbulence is treated by governing equations which are more complicated than the NSE. At the same time, all these governing equations remain formally invariant (as with the NSE) under any affine contraction of the space–time
![]() $x\rightarrow x/{\it\lambda}$
,
$x\rightarrow x/{\it\lambda}$
,
![]() $t\rightarrow t/{\it\lambda}^{1-h}$
, (of scale ratios
$t\rightarrow t/{\it\lambda}^{1-h}$
, (of scale ratios
![]() ${\it\lambda}$
), see discussion in Cartes et al. (Reference Cartes, Bustamante, Pouquet and Brachet2009). There are no limitations to suggest that hidden symmetry, similar to NSE, can regulate plasma dynamics: symmetry transforms for MHD equations and other equations used for a description of plasma dynamics are considered in Gridnev (Reference Gridnev1968), Nucci (Reference Nucci1984), Samokhin (Reference Samokhin1985), Gusyatnikova et al. (Reference Gusyatnikova, Samokhin, Titov, Vinogradov and Yamaguzhin1989), Bogoyavlenskij (Reference Bogoyavlenskij2002). Thus, observation of the ESS property for plasma data is an argument to examine the scalings proposed by the log-Poisson models in the same way as in hydrodynamics.
${\it\lambda}$
), see discussion in Cartes et al. (Reference Cartes, Bustamante, Pouquet and Brachet2009). There are no limitations to suggest that hidden symmetry, similar to NSE, can regulate plasma dynamics: symmetry transforms for MHD equations and other equations used for a description of plasma dynamics are considered in Gridnev (Reference Gridnev1968), Nucci (Reference Nucci1984), Samokhin (Reference Samokhin1985), Gusyatnikova et al. (Reference Gusyatnikova, Samokhin, Titov, Vinogradov and Yamaguzhin1989), Bogoyavlenskij (Reference Bogoyavlenskij2002). Thus, observation of the ESS property for plasma data is an argument to examine the scalings proposed by the log-Poisson models in the same way as in hydrodynamics.
Questions regarding similarity of the energy transfer cascade process in neutral flow and magnetofluids can arise on this way. In laboratory plasma, dissipation occurs on different scales, including large scales, which supposes an inverse cascade process. While in hydrodynamics, theoretical models assume a single direct cascade to small scales in terms of a scalar cascade approach. However in 3-D hydrodyamic flows, the existence of an inverse cascade is still an open question (see discussions in Paret & Tabeling Reference Paret and Tabeling1998; Boffetta et al. Reference Boffetta, Cenedese, Espa and Musacchio2005; Celani, Musacchio & Vincenzi Reference Celani, Musacchio and Vincenzi2010). Strictly speaking, in 3-D, the scalar approach is insufficient for a description of both the hydrodynamics and plasma dynamics, and turbulence should be studied using vector Lie cascades (see discussion in appendix A). However, the main features of cascades can be revealed using the scalar approach in terms of multifractals. The multifractal approach to the intermittency proposes self-similarity analysis independently of the issue of cascade direction (direct or inverse) – multifractal measures are a very general outcome of stochastic cascades.
It is worth noting that the absolute value of the velocity differences are often used to construct structure functions from experimental space data. Such structure functions of absolute values of velocity are not described by any theory. Whereas it is often the first step to make meaningful analysis of statistics from experimental data.
A fundamental open question connected to intermittency is the dependency of velocity statistics at various temporal scales on large scale forcing and boundary conditions: the so-called problem of universality (see Arneodo et al. Reference Arneodo, Benzi, Berg, Biferale, Bodenschatz, Busse, Calzavarini, Castaing, Cencini and Chevillard2008). Universality features are linked to the degree of anisotropy and non-homogeneities of the turbulent statistics. Different forms of anisotropy might have different effects on the small scales of turbulence. In hydrodynamics, the conjecture of local isotropy has received much attention, and has been tested in hydrodynamics flows with various kinds of anisotropy (see e.g. Biferale & Procaccia Reference Biferale and Procaccia2005). Understanding the way turbulence tends towards local isotropy from various states of anisotropy remains an important challenge in the study of turbulence. Different forms of anisotropy might have different effects on the small scales of plasma turbulence. In hydrodynamics, the conjecture of local isotropy has received much attention, and has been tested in flows with various kinds of anisotropy (see e.g. Biferale & Procaccia Reference Biferale and Procaccia2005). Finite Reynolds number effects and anisotropy may lead to a discrepancy of longitudinal and transverse components of the structure functions and scaling exponents (Biferale & Procaccia Reference Biferale and Procaccia2005). These authors have suggested an approach to treat the anisotropy problem in the following way: it is necessary to decompose the structure function of each order into the symmetry group determined by the large-scale flow and intermittency exponents calculated sector-by-sector. In a system where the large-scale isotropy is broken, for example in the plasma TBL, such an approach will help to improve intermittency investigation in plasma turbulence. This is an important consideration in the case of interpreting SW measurements in terms of anisotropic turbulence theories (see, e.g. Chen et al. Reference Chen, Wicks, Horbury and Schekochihin2010).
To summarise, ESS is a procedure that remarkably extends the range of scaling for structure functions and thus allows improved determination of intermittency exponents. In spite of several attempts to explain the success of ESS (see discussion, e.g. in Chakraborty, Frisch & Ray Reference Chakraborty, Frisch and Ray2010), the latter is still not fully understood. It was shown by Chakraborty et al. (Reference Chakraborty, Frisch and Ray2010), that by the process of ESS, the sub-leading terms to the leading scaling exponent are made smaller. This was shown for the Burgers equation and speculated for the NSE. ESS has been applied to Burgers turbulence at high Reynolds numbers and a gain of about three-quarters of a decade was numerically observed: there is a reduction of the subdominant contributions to scaling when going from the standard structure function representation to the ESS one (Chakraborty et al. Reference Chakraborty, Frisch and Ray2010).
4. Log-Poisson models of intermittent turbulence
4.1. Comparison with She–Leveque–Dubrulle model
The phenomenon of intermittency is explained in the framework of the log-Poisson models. The log-Poisson models were developed by the generalization of
![]() ${\it\beta}$
-model incorporating asymmetry and the hypothesis of scale invariance and cascade. The assumption of the existence of a random multiplicative process for the inertial range dynamics is important. Over a finite range of scales, a quantized cascade provides a log-Poisson process containing an infinite number of discrete values for the multipliers. It considerably contrasts to previous discrete cascade models which contain a finite number of multipliers: the
${\it\beta}$
-model incorporating asymmetry and the hypothesis of scale invariance and cascade. The assumption of the existence of a random multiplicative process for the inertial range dynamics is important. Over a finite range of scales, a quantized cascade provides a log-Poisson process containing an infinite number of discrete values for the multipliers. It considerably contrasts to previous discrete cascade models which contain a finite number of multipliers: the
![]() ${\it\alpha}$
-model and
${\it\alpha}$
-model and
![]() $p$
-model contain two multipliers, the random
$p$
-model contain two multipliers, the random
![]() ${\it\beta}$
-model contains three multipliers. Comparative study of the velocity and magnetic field in the interplanetary medium regarding scalings proposed by the
${\it\beta}$
-model contains three multipliers. Comparative study of the velocity and magnetic field in the interplanetary medium regarding scalings proposed by the
![]() ${\it\alpha}$
-model,
${\it\alpha}$
-model,
![]() $p$
-model, the random
$p$
-model, the random
![]() ${\it\beta}$
-model, IK model has been done in a wide range of scales (see Carbone et al.
Reference Carbone, Veltry and Bruno1996; Budaev et al.
Reference Budaev, Savin and Zelenyi2011). The log-Poisson intermittency model reproduces these experimental and numerical findings in hydrodynamic and MHD (see Carbone et al.
Reference Carbone, Veltry and Bruno1996; Müller & Biskamp Reference Müller and Biskamp2003; Budaev et al.
Reference Budaev, Savin and Zelenyi2011) turbulence very well.
${\it\beta}$
-model, IK model has been done in a wide range of scales (see Carbone et al.
Reference Carbone, Veltry and Bruno1996; Budaev et al.
Reference Budaev, Savin and Zelenyi2011). The log-Poisson intermittency model reproduces these experimental and numerical findings in hydrodynamic and MHD (see Carbone et al.
Reference Carbone, Veltry and Bruno1996; Müller & Biskamp Reference Müller and Biskamp2003; Budaev et al.
Reference Budaev, Savin and Zelenyi2011) turbulence very well.
The She–Leveque–Dubrulle model (Dubrulle Reference Dubrulle1994; She & Leveque Reference She and Leveque1994) is explained in appendix B. It assumes the existence of a limiting value
![]() ${\it\varepsilon}_{l}^{\infty }$
associated with the most dissipative structures. Advantages of the log-Poisson models are the consideration of intermittent turbulence properties such as the scale invariance, power law scaling for dissipation energy of the most intermittent dissipative structures,
${\it\varepsilon}_{l}^{\infty }$
associated with the most dissipative structures. Advantages of the log-Poisson models are the consideration of intermittent turbulence properties such as the scale invariance, power law scaling for dissipation energy of the most intermittent dissipative structures,
![]() ${\it\varepsilon}_{l}^{\infty }\sim l^{-{\it\Delta}},l\rightarrow 0$
where the parameter
${\it\varepsilon}_{l}^{\infty }\sim l^{-{\it\Delta}},l\rightarrow 0$
where the parameter
![]() ${\it\Delta}$
is associated with the geometry (dimension) of dissipative structures. To treat the plasma turbulence problem, we can suggest a geometry of dissipative structures from experimental observation of theoretical consideration. In this subsection, we review the comparison of experimental scalings with the prediction of the She–Leveque–Dubrulle model:
${\it\Delta}$
is associated with the geometry (dimension) of dissipative structures. To treat the plasma turbulence problem, we can suggest a geometry of dissipative structures from experimental observation of theoretical consideration. In this subsection, we review the comparison of experimental scalings with the prediction of the She–Leveque–Dubrulle model:
For 3-D isotropic hydrodynamic turbulence, She & Leveque (Reference She and Leveque1994) proposed that
![]() ${\it\Delta}={\it\beta}=2/3$
. The fitting of experimental data to scaling (4.1) is a way to classify the intermittency property.
${\it\Delta}={\it\beta}=2/3$
. The fitting of experimental data to scaling (4.1) is a way to classify the intermittency property.
She & Waymire (Reference She and Waymire1995) considered a stochastic multiplicative cascade in which complicated topological structures, namely, dissipative structures of different dimensions (in particular, those having fractal dimensions), can be formed simultaneously. In probability theory, such a process is described by the Khintchine–Levy approach (She & Waymire Reference She and Waymire1995). This approach is important for interpretation of the experimental data when experimental scalings deviate insignificantly from scaling (4.1) with fixed
![]() ${\it\Delta}$
and
${\it\Delta}$
and
![]() ${\it\beta}$
values. The deviation can arise from the complicated geometry of the dissipative structures, or from the fact that structures of different dimensions are present in the process simultaneously. This is why a real turbulent process can be characterized by the fitting values of
${\it\beta}$
values. The deviation can arise from the complicated geometry of the dissipative structures, or from the fact that structures of different dimensions are present in the process simultaneously. This is why a real turbulent process can be characterized by the fitting values of
![]() ${\it\Delta}$
and
${\it\Delta}$
and
![]() ${\it\beta}$
.
${\it\beta}$
.
The log-Poisson model reproduces experimental and numerical results in hydrodynamic (see Frish Reference Frish1995) and plasma turbulence rather well (see Budaev et al.
Reference Budaev, Savin and Zelenyi2011). In figure 18, the structure function scalings
![]() ${\it\zeta}(q)$
of space and fusion devices data are shown in the same plot with the scalings predicted by the K41 and the standard log-Poisson (She–Leveque, SL) models. The scalings are anomalously deviated from the K41 scaling. Many experimental spectra can be described by the log-Poisson model (4.1) with adjusted parameters
${\it\zeta}(q)$
of space and fusion devices data are shown in the same plot with the scalings predicted by the K41 and the standard log-Poisson (She–Leveque, SL) models. The scalings are anomalously deviated from the K41 scaling. Many experimental spectra can be described by the log-Poisson model (4.1) with adjusted parameters
![]() ${\it\Delta}$
and
${\it\Delta}$
and
![]() ${\it\beta}$
:
${\it\beta}$
:
![]() ${\it\Delta}=0.12{-}0.8$
,
${\it\Delta}=0.12{-}0.8$
,
![]() ${\it\beta}=0.25{-}0.7$
, see table 1. It is worth stressing that different observables (magnetic field, velocity, density, fluxes) have the closed multifractal measures which characterize intermittency (table 1).
${\it\beta}=0.25{-}0.7$
, see table 1. It is worth stressing that different observables (magnetic field, velocity, density, fluxes) have the closed multifractal measures which characterize intermittency (table 1).

Figure 18. (a) The scaling law of the high-order structure function
![]() ${\it\zeta}(q)/{\it\zeta}(3)$
for the Earth’s magnetosphere and edge plasma fluctuations in fusion devices. The dashed line shows the Kolmogorov K41 scaling
${\it\zeta}(q)/{\it\zeta}(3)$
for the Earth’s magnetosphere and edge plasma fluctuations in fusion devices. The dashed line shows the Kolmogorov K41 scaling
![]() $q/3$
, the solid line shows the log-Poisson model prediction for
$q/3$
, the solid line shows the log-Poisson model prediction for
![]() ${\it\beta}={\it\Delta}=2/3$
by the She–Leveque model (SL). (b) The deviation of the scaling laws of the structure function from Kolmogorov K41spectrum. The edge plasma in T-10 tokamak: (T-10 n far SOL) is the plasma density, (T-10
${\it\beta}={\it\Delta}=2/3$
by the She–Leveque model (SL). (b) The deviation of the scaling laws of the structure function from Kolmogorov K41spectrum. The edge plasma in T-10 tokamak: (T-10 n far SOL) is the plasma density, (T-10
![]() ${\it\Gamma}$
far SOL) is the particle flux; plasma density in NAGDIS-II in the attached mode (N-II attach) and detached mode (N-II detach); the ion flux in the TBL of the Earth’s magnetosphere (TBL ion flux), the magnetic field in the TBL of the Earth’s magnetosphere (TBL
${\it\Gamma}$
far SOL) is the particle flux; plasma density in NAGDIS-II in the attached mode (N-II attach) and detached mode (N-II detach); the ion flux in the TBL of the Earth’s magnetosphere (TBL ion flux), the magnetic field in the TBL of the Earth’s magnetosphere (TBL
![]() $B_{x}$
, 19.06.1998), the magnetic field in the MSH outside TBL of the Earth’s magnetosphere (MSH
$B_{x}$
, 19.06.1998), the magnetic field in the MSH outside TBL of the Earth’s magnetosphere (MSH
![]() $B_{x}$
) and in the SW from the Geotail data (SW,
$B_{x}$
) and in the SW from the Geotail data (SW,
![]() $B_{x}$
).
$B_{x}$
).
Table 1. Indicies
![]() ${\it\Delta}$
and
${\it\Delta}$
and
![]() ${\it\beta}$
.
${\it\beta}$
.

Values of
![]() ${\it\Delta}$
between
${\it\Delta}$
between
![]() ${\sim}1/3$
and
${\sim}1/3$
and
![]() $2/3$
are found (table 1); these cases can be interpreted as an evidence of dominant contribution of 1-D (filament-like) dissipative structures to the process. Such dissipative structures appear to have not a trivial geometrical topology but a fractal one. Only in the velocity shear layer in tokamaks (where the destruction of turbulent eddies is assumed) and in MSH far from TBL of the Earth’s magnetosphere, non-intermittent signals with
$2/3$
are found (table 1); these cases can be interpreted as an evidence of dominant contribution of 1-D (filament-like) dissipative structures to the process. Such dissipative structures appear to have not a trivial geometrical topology but a fractal one. Only in the velocity shear layer in tokamaks (where the destruction of turbulent eddies is assumed) and in MSH far from TBL of the Earth’s magnetosphere, non-intermittent signals with
![]() ${\it\beta}\approx 1$
were observed.
${\it\beta}\approx 1$
were observed.
To verify the hypotheses regarding power laws in the log-Poisson model, we can analyse the scalings for the relative moments
and examine the dependence
The index
![]() ${\it\delta}_{q}$
can be changed between
${\it\delta}_{q}$
can be changed between
![]() ${\it\delta}_{0}$
, as averaged flow scales
${\it\delta}_{0}$
, as averaged flow scales
![]() ${\it\Pi}_{0}(l)\sim l^{{\it\delta}0}$
, and
${\it\Pi}_{0}(l)\sim l^{{\it\delta}0}$
, and
![]() ${\it\delta}_{\infty }$
, consistent with limit scaling
${\it\delta}_{\infty }$
, consistent with limit scaling
![]() ${\it\Pi}_{\infty }(l)\sim l^{{\it\delta}\infty }$
. A dependence of
${\it\Pi}_{\infty }(l)\sim l^{{\it\delta}\infty }$
. A dependence of
![]() ${\it\delta}_{q}$
on
${\it\delta}_{q}$
on
![]() $q$
for different models:
$q$
for different models:
-
(I)
 ${\it\delta}_{q}\equiv 0$
– Kolmogorov K41.
${\it\delta}_{q}\equiv 0$
– Kolmogorov K41. -
(II)
 ${\it\delta}_{q}\equiv \text{const.}$
, isolated vorticities in the turbulence
${\it\delta}_{q}\equiv \text{const.}$
, isolated vorticities in the turbulence -
(III)
 ${\it\delta}_{0}=0$
,
${\it\delta}_{0}=0$
,
 ${\it\delta}_{\infty }=2/3$
– She–Leveque model.
${\it\delta}_{\infty }=2/3$
– She–Leveque model. -
(IV)
 ${\it\delta}_{0}=\text{const.}$
,
${\it\delta}_{0}=\text{const.}$
,
 ${\it\delta}_{\infty }$
is limited, She–Leveque–Dubrulle model
${\it\delta}_{\infty }$
is limited, She–Leveque–Dubrulle model
 ${\it\delta}_{q}={\it\delta}_{\infty }+{\it\zeta}_{3}{\rm\Delta}Q(q)$
, where
${\it\delta}_{q}={\it\delta}_{\infty }+{\it\zeta}_{3}{\rm\Delta}Q(q)$
, where
 $Q(q)$
-monotonic decay function
$Q(q)$
-monotonic decay function
 $Q(0)=1$
,
$Q(0)=1$
,
 $Q(\infty )=0$
, e.g.
$Q(\infty )=0$
, e.g.
 $Q(q)=\exp (-a_{c}q)$
.
$Q(q)=\exp (-a_{c}q)$
.
Figure 19 illustrates experimental observations of the case (IV). We point out that these results support hypothesis of moments hierarchy and generalized scale invariance of the plasma turbulence in terms of She–Leveque–Dubrulle model (see appendix B).

Figure 19. Index
![]() ${\it\delta}_{q}$
versus
${\it\delta}_{q}$
versus
![]() $q$
. Magnetic field
$q$
. Magnetic field
![]() $B_{x}$
in the Earth’s magnetosphere TBL, plasma density in SOL (T-10 SOL) at
$B_{x}$
in the Earth’s magnetosphere TBL, plasma density in SOL (T-10 SOL) at
![]() $r=31~\text{cm}$
and in the far SOL (T-10 far SOL) at
$r=31~\text{cm}$
and in the far SOL (T-10 far SOL) at
![]() $r=36~\text{cm}$
in the T-10 tokamak.
$r=36~\text{cm}$
in the T-10 tokamak.
4.2. Anisotropic turbulence cascade and dimension of dissipative structures
The scaling properties depend on a topology of singular dissipative structures (see Frish Reference Frish1995). The dimension of dissipative structures
![]() $\mathsf{D}$
(see figure 20
a) relates to the probability distribution of active turbulent zones in intermittent turbulence. Therefore it is important to know which dissipative structures are dominant (if structures of different topology co-exist) and determine the scaling properties.
$\mathsf{D}$
(see figure 20
a) relates to the probability distribution of active turbulent zones in intermittent turbulence. Therefore it is important to know which dissipative structures are dominant (if structures of different topology co-exist) and determine the scaling properties.

Figure 20. (a) Diagram of singular objects (dissipative structures in magnetic field
![]() $B$
) of different dimension
$B$
) of different dimension
![]() $D$
in a unit cube. The probability of having a given
$D$
in a unit cube. The probability of having a given
![]() ${\it\delta}{\it\upsilon}_{l}$
in a sphere of radius
${\it\delta}{\it\upsilon}_{l}$
in a sphere of radius
![]() $l$
by an object with dimension
$l$
by an object with dimension
![]() $D$
is
$D$
is
![]() $\mathsf{P}(l)\sim l^{3\text{-}D}$
at
$\mathsf{P}(l)\sim l^{3\text{-}D}$
at
![]() $l\rightarrow 0$
(see Frish Reference Frish1995). (b) Diagram of the nonlinear interaction of filamentary dissipative structures (
$l\rightarrow 0$
(see Frish Reference Frish1995). (b) Diagram of the nonlinear interaction of filamentary dissipative structures (
![]() $D=1$
) in the cross-field direction.
$D=1$
) in the cross-field direction.
In the She–Leveque model of 3-D isotropic hydrodynamics, dissipative structures are considered to be 1-D filaments. In the Biskamp–Mueller model (BM) of 3-D isotropic MHD turbulence, dissipative structures are assumed to be 2-D current sheets (Müller & Biskamp Reference Müller and Biskamp2003). A diagram of the process when nonlinear interaction across the magnetic field is of Kolmogorov’s type locality, i.e. only modes with close
![]() $k\bot$
interact nonlinearly, is presented in figure 20(b). This scheme illustrates the condition in the SOL (edge plasma) of tokamaks and other fusion devices: the magnetic field lines are open and turbulence is characterized by flute-like structures along the magnetic field (which could be a result of interchange instability). Inside the Earth’s magnetosphere, field-aligned perturbations are also observed. In boundary layers with a high ratio of thermal to magnetic pressure, the jets are extended along the direction of the mean flow velocity (see Savin et al.
Reference Savin, Skalsky, Zelenyi, Avanov, Borodkova, Klimov, Lutsenko, Panov, Romanov and Smirnov2005 and references therein). In the general case, as was discussed in the pioneering work by Zeldovich et al. (Reference Zeldovich, Molchanov, Ruzmaikin and Sokolov1987), the filamentary structures produce the dominant contribution to intermittent manifestation of magnetized plasma dynamics.
$k\bot$
interact nonlinearly, is presented in figure 20(b). This scheme illustrates the condition in the SOL (edge plasma) of tokamaks and other fusion devices: the magnetic field lines are open and turbulence is characterized by flute-like structures along the magnetic field (which could be a result of interchange instability). Inside the Earth’s magnetosphere, field-aligned perturbations are also observed. In boundary layers with a high ratio of thermal to magnetic pressure, the jets are extended along the direction of the mean flow velocity (see Savin et al.
Reference Savin, Skalsky, Zelenyi, Avanov, Borodkova, Klimov, Lutsenko, Panov, Romanov and Smirnov2005 and references therein). In the general case, as was discussed in the pioneering work by Zeldovich et al. (Reference Zeldovich, Molchanov, Ruzmaikin and Sokolov1987), the filamentary structures produce the dominant contribution to intermittent manifestation of magnetized plasma dynamics.
In the framework of the log-Poisson model, to consider a geometry of the most singular dissipative structures we have to treat a scaling of energy dissipation
![]() ${\it\varepsilon}_{l}^{\infty }\sim l^{-{\it\Delta}}$
and the scaling of velocity
${\it\varepsilon}_{l}^{\infty }\sim l^{-{\it\Delta}}$
and the scaling of velocity
![]() ${\it\upsilon}_{l}\sim l^{1/g}$
(Müller & Biskamp Reference Müller and Biskamp2003) with the parameter
${\it\upsilon}_{l}\sim l^{1/g}$
(Müller & Biskamp Reference Müller and Biskamp2003) with the parameter
![]() $g=3$
for K41,
$g=3$
for K41,
![]() $g=4$
for IK. In a random cascade model, the intermittency index
$g=4$
for IK. In a random cascade model, the intermittency index
![]() ${\it\beta}$
relates with
${\it\beta}$
relates with
![]() ${\it\Delta}$
and co-dimension
${\it\Delta}$
and co-dimension
![]() $C_{0}$
of the most singular dissipative structures:
$C_{0}$
of the most singular dissipative structures:
![]() ${\it\beta}=1-{\it\Delta}/C_{0}$
(see Politano & Pouquet Reference Politano and Pouquet1995; Boldyrev Reference Boldyrev2002)
${\it\beta}=1-{\it\Delta}/C_{0}$
(see Politano & Pouquet Reference Politano and Pouquet1995; Boldyrev Reference Boldyrev2002)
![]() $C_{0}=3-D$
, where
$C_{0}=3-D$
, where
![]() $D$
is the dimension of dissipative structures. In 3-D,
$D$
is the dimension of dissipative structures. In 3-D,
![]() $C_{0}=2$
for filaments (
$C_{0}=2$
for filaments (
![]() $D=1$
),
$D=1$
),
![]() $C_{0}=1$
for micro-sheets (
$C_{0}=1$
for micro-sheets (
![]() $D=2$
). The log-Poisson model scaling:
$D=2$
). The log-Poisson model scaling:
Usually
![]() ${\it\Delta}$
and
${\it\Delta}$
and
![]() $g$
are related assuming an equal scaling for the time scale
$g$
are related assuming an equal scaling for the time scale
![]() $t_{l}^{\infty }$
of the rate
$t_{l}^{\infty }$
of the rate
![]() ${\it\varepsilon}_{l}^{\infty }\sim E^{\infty }/t_{l}^{\infty }$
(
${\it\varepsilon}_{l}^{\infty }\sim E^{\infty }/t_{l}^{\infty }$
(
![]() $E^{\infty }$
is the amount of the energy dissipated in the most singular structures) and for the nonlinear transfer time
$E^{\infty }$
is the amount of the energy dissipated in the most singular structures) and for the nonlinear transfer time
![]() $t_{l}^{NL}$
of the energy cascade rate
$t_{l}^{NL}$
of the energy cascade rate
![]() ${\it\varepsilon}\sim {\it\delta}{\it\upsilon}_{l}^{2}/t_{l}^{NL}$
. From
${\it\varepsilon}\sim {\it\delta}{\it\upsilon}_{l}^{2}/t_{l}^{NL}$
. From
![]() ${\it\varepsilon}_{l}^{\infty }\sim l^{-{\it\Delta}}$
and
${\it\varepsilon}_{l}^{\infty }\sim l^{-{\it\Delta}}$
and
![]() ${\it\upsilon}_{l}\sim l^{1/g}$
, we obtain
${\it\upsilon}_{l}\sim l^{1/g}$
, we obtain
![]() ${\it\Delta}=2/g$
. The hydrodynamic SL formula results from
${\it\Delta}=2/g$
. The hydrodynamic SL formula results from
![]() $C_{0}=2$
,
$C_{0}=2$
,
![]() $g=3$
,
$g=3$
,
![]() ${\it\Delta}=2/3$
. The IK MHD model assumes
${\it\Delta}=2/3$
. The IK MHD model assumes
![]() $g=4$
,
$g=4$
,
![]() ${\it\Delta}=1/2$
, and
${\it\Delta}=1/2$
, and
![]() $C_{0}=1$
with dissipative structures interpreted as 2-D current sheets. In DNS of 3-D isotropic MHD turbulence (the BM model, BM Müller & Biskamp Reference Müller and Biskamp2003) scalings are reproduced well with the combination
$C_{0}=1$
with dissipative structures interpreted as 2-D current sheets. In DNS of 3-D isotropic MHD turbulence (the BM model, BM Müller & Biskamp Reference Müller and Biskamp2003) scalings are reproduced well with the combination
![]() $g=3$
,
$g=3$
,
![]() ${\it\Delta}=2/3$
, and
${\it\Delta}=2/3$
, and
![]() $C_{0}=1$
implying hydrodynamic scaling and sheet-like dissipative structures. To consider anisotropy statistics of the cascade strength, we may follow the phenomenological interpretation of Biskamp and Mueller by dropping the scaling equality of
$C_{0}=1$
implying hydrodynamic scaling and sheet-like dissipative structures. To consider anisotropy statistics of the cascade strength, we may follow the phenomenological interpretation of Biskamp and Mueller by dropping the scaling equality of
![]() $t_{l}^{NL}$
and
$t_{l}^{NL}$
and
![]() $t_{l}^{\infty \prime }$
. Instead,
$t_{l}^{\infty \prime }$
. Instead,
![]() $t_{l}^{\infty }$
is fixed to the K41 time scale,
$t_{l}^{\infty }$
is fixed to the K41 time scale,
![]() $t_{l}^{\infty }\sim l/{\it\delta}{\it\upsilon}_{l}\sim l^{1-1/g}$
,
$t_{l}^{\infty }\sim l/{\it\delta}{\it\upsilon}_{l}\sim l^{1-1/g}$
,
![]() ${\it\Delta}=1-1/g$
, which with
${\it\Delta}=1-1/g$
, which with
![]() $C_{0}=1$
leads to Müller & Biskamp (Reference Müller and Biskamp2003):
$C_{0}=1$
leads to Müller & Biskamp (Reference Müller and Biskamp2003):
As an alternative we can consider the same scaling
![]() $t_{l}^{\infty }\sim l/{\it\delta}{\it\upsilon}_{l}\sim l^{1-1/gf}$
with
$t_{l}^{\infty }\sim l/{\it\delta}{\it\upsilon}_{l}\sim l^{1-1/gf}$
with
![]() $C_{0}=2$
of 1-D filament-like structures (see figure 20
b). On this basis, the anomalous scaling that captures 1-D filament-like structures was proposed by Budaev (Reference Budaev2009):
$C_{0}=2$
of 1-D filament-like structures (see figure 20
b). On this basis, the anomalous scaling that captures 1-D filament-like structures was proposed by Budaev (Reference Budaev2009):
The quantity
![]() $g_{f}/3$
expresses the cascade strength relative to the isotropic K41 case (here we use the notation
$g_{f}/3$
expresses the cascade strength relative to the isotropic K41 case (here we use the notation
![]() $g_{f}$
to distinguish from the case
$g_{f}$
to distinguish from the case
![]() $g$
in (4.5)). The modified transfer time
$g$
in (4.5)). The modified transfer time
![]() $t_{l}^{NL}\sim (l/l_{0})^{{\it\theta}}~(l/{\it\delta}{\it\upsilon}_{l})$
can be considered detaching
$t_{l}^{NL}\sim (l/l_{0})^{{\it\theta}}~(l/{\it\delta}{\it\upsilon}_{l})$
can be considered detaching
![]() $t_{l}^{NL}$
and
$t_{l}^{NL}$
and
![]() $t_{l}^{\infty }$
to characterize the strength of the field-perpendicular and field-parallel polarized fluctuations. Here,
$t_{l}^{\infty }$
to characterize the strength of the field-perpendicular and field-parallel polarized fluctuations. Here,
![]() $l_{0}$
is an arbitrary reference length, and
$l_{0}$
is an arbitrary reference length, and
![]() ${\it\theta}$
is a dimensionless efficiency parameter. Assuming a constant energy cascade
${\it\theta}$
is a dimensionless efficiency parameter. Assuming a constant energy cascade
![]() ${\it\varepsilon}\sim {\it\delta}{\it\upsilon}_{l}^{2}/t_{l}^{NL}=\text{const.}$
,
${\it\varepsilon}\sim {\it\delta}{\it\upsilon}_{l}^{2}/t_{l}^{NL}=\text{const.}$
,
![]() $t_{l}^{NL}\sim l^{(1+{\it\theta})2/3}$
. In a standard phenomenology
$t_{l}^{NL}\sim l^{(1+{\it\theta})2/3}$
. In a standard phenomenology
![]() $t_{l}^{NL}\sim l^{2/g}$
. In a such approach, the cascade efficiency is controlled by the
$t_{l}^{NL}\sim l^{2/g}$
. In a such approach, the cascade efficiency is controlled by the
![]() $(l/l_{0})^{{\it\theta}}$
factor (Müller & Biskamp Reference Müller and Biskamp2003):
$(l/l_{0})^{{\it\theta}}$
factor (Müller & Biskamp Reference Müller and Biskamp2003):
-
(i)
 ${\it\theta}=0~(g,g_{f}=3)$
yields the isotropic K41 cascade;
${\it\theta}=0~(g,g_{f}=3)$
yields the isotropic K41 cascade; -
(ii)
 ${\it\theta}<0~(g,g_{f}>3)$
corresponds to a cascade enhancement;
${\it\theta}<0~(g,g_{f}>3)$
corresponds to a cascade enhancement; -
(iii)
 ${\it\theta}>0~(g,g_{f}<3)$
corresponds to a cascade depletion.
${\it\theta}>0~(g,g_{f}<3)$
corresponds to a cascade depletion.
Scaling laws (4.5) and (6.5) are helpful to classify experimental data and to prove the hypothesis of a topology and the dimension of dominant dissipative structures.
For the T-10 tokamak scaling (4.6) was tested in Budaev (Reference Budaev2009). In the main edge region of T-10 (
![]() $30~\text{cm}<r<34~\text{cm}$
), the scaling is described by the model with 1-D dissipative structures (4.6), figure 21(a). Only in the far edge (far SOL) region (
$30~\text{cm}<r<34~\text{cm}$
), the scaling is described by the model with 1-D dissipative structures (4.6), figure 21(a). Only in the far edge (far SOL) region (
![]() $r>34~\text{cm}$
), the scaling is close to the scaling (4.5) of the model which captured 2-D sheet-like dissipative structures. This result gives evidence of the dominant presence of 1-D singular dissipative structures in edge plasma of a fusion device. Observation of space plasma (see examples in figure 21
b) demonstrate scaling properties which captured 1-D filamentary and 2-D sheet-like dissipative structures. Table 2 lists values of
$r>34~\text{cm}$
), the scaling is close to the scaling (4.5) of the model which captured 2-D sheet-like dissipative structures. This result gives evidence of the dominant presence of 1-D singular dissipative structures in edge plasma of a fusion device. Observation of space plasma (see examples in figure 21
b) demonstrate scaling properties which captured 1-D filamentary and 2-D sheet-like dissipative structures. Table 2 lists values of
![]() $g$
and
$g$
and
![]() $g_{f}$
in space and laboratory plasmas. In most experiments, the parameter
$g_{f}$
in space and laboratory plasmas. In most experiments, the parameter
![]() $g_{f}$
is close to 3: filament-like dissipative structures (1-D topology) dominate intermittent turbulence. It appears that the intermittency observed in space and laboratory plasmas displays universal properties.
$g_{f}$
is close to 3: filament-like dissipative structures (1-D topology) dominate intermittent turbulence. It appears that the intermittency observed in space and laboratory plasmas displays universal properties.

Figure 21. (a) Scaling for the structure function (its deviation from the K41 prediction). Edge plasma of the T-10 tokamak. Shown are the plasma density at
![]() $r=34~\text{cm}$
in the SOL region (triangles) and the cross-field particle flux
$r=34~\text{cm}$
in the SOL region (triangles) and the cross-field particle flux
![]() ${\it\Gamma}$
at
${\it\Gamma}$
at
![]() $r=36~\text{cm}$
in the far SOL region (circles). The K41 model (dashed curves), the log-Poisson model with two-dimension 2-D (solid curves – fitting by (4.5) with
$r=36~\text{cm}$
in the far SOL region (circles). The K41 model (dashed curves), the log-Poisson model with two-dimension 2-D (solid curves – fitting by (4.5) with
![]() $g=2.85$
) and one-dimension 1-D (dotted curves – fitting by (4.6) with
$g=2.85$
) and one-dimension 1-D (dotted curves – fitting by (4.6) with
![]() $g_{f}=3.03$
) dissipative structures in three dimensions with anisotropy from magnetic field. (b) Scalings for the structure function. SPECTR-R, 20.03.12, ion flux, TBL, 12-21 UT, 3 Hz (circles), CLUSTER-4, 20.03.12, ion flux, SW/BS/MSH/MP (triangles). Kolmogorov K41 model (dashed line). The log-Poisson model with two-dimension 2-D (dashed-dotted curves – fitting by (4.5) with
$g_{f}=3.03$
) dissipative structures in three dimensions with anisotropy from magnetic field. (b) Scalings for the structure function. SPECTR-R, 20.03.12, ion flux, TBL, 12-21 UT, 3 Hz (circles), CLUSTER-4, 20.03.12, ion flux, SW/BS/MSH/MP (triangles). Kolmogorov K41 model (dashed line). The log-Poisson model with two-dimension 2-D (dashed-dotted curves – fitting by (4.5) with
![]() $g=2.90$
); and one-dimension 1-D (solid curves – fitting by (4.6) with
$g=2.90$
); and one-dimension 1-D (solid curves – fitting by (4.6) with
![]() $g_{f}=3.008$
) dissipative structures in 3-D with anisotropy from magnetic field.
$g_{f}=3.008$
) dissipative structures in 3-D with anisotropy from magnetic field.
Table 2. Indicies
![]() $g$
and
$g$
and
![]() $g_{f}$
.
$g_{f}$
.

The above approach makes it possible to utilize the language of the structure function’s scaling in order to characterize turbulent structures of different spatial scales. The results of the above analysis provide insight into the topology of the structures responsible for dissipation in plasma turbulence. The theoretical prediction of scaling laws depending on dissipative structure dimension and cascade are summarized in table 3. All cascade models of intermittent turbulence have adjustable parameters that are difficult to determine from first principles and physical arguments and that provide enough freedom to account for the experimental data (e.g. determined by the scaling
![]() ${\it\zeta}(q)$
of the structure functions). The scaling
${\it\zeta}(q)$
of the structure functions). The scaling
![]() ${\it\zeta}(q)$
is helpful to validate cascade models of developed turbulence with intermittency.
${\it\zeta}(q)$
is helpful to validate cascade models of developed turbulence with intermittency.
Table 3. Scaling laws predicted by different cascade models.

The results of the above analysis in the framework of the log-Poisson model can be interpreted by considering the topology of the structures responsible for a dissipation in the plasma TBL. They can be associated both with the large-scale coherent structures (which are vivid in experiments) and with small-scale structures (which are usually not seen) of intermittent turbulence. We note that structures of different topology can coexist in the framework of the log-Poisson model (She & Waymire Reference She and Waymire1995).
A theoretical analysis (She & Waymire Reference She and Waymire1995) of a stochastic multiplicative cascade (such as the log-Poisson cascade) shows that the process can involve generating dissipative structures of different (in particular, fractal) geometries (as was also discussed by Zeldovich et al. Reference Zeldovich, Molchanov, Ruzmaikin and Sokolov1987). As was discussed above, the properties of the experimental scalings for 1-D dissipative structures are adequately described by the log-Poisson model. The approach used here does not provide information on the particular spatial shape of quasi-1-D dissipative structures. From the properties of MHD flows, it is possible to assume that they have complex shape, stretched predominantly along the magnetic field. Additional experimental observations are needed to clarify this issue.
5. Comparison with hydrodynamic turbulence
In this section we present some recent experimental results of intermittency in the study of hydrodynamic flow for comparison with plasma turbulence. Developed turbulence was measured in wind tunnels, atmosphere, channels, liquids etc. (see Clauser Reference Clauser1956; Monin & Yaglom Reference Monin and Yaglom1971, Reference Monin and Yaglom1975; reviews McKeon & Sreenivasan Reference McKeon and Sreenivasan2007; Marusic et al.
Reference Marusic, McKeon, Monkewitz, Nagib, Smits and Sreenivasan2010). Turbulence intermittency was observed in turbulent flows with Reynolds number (estimated by Taylor’s microscale)
![]() $\mathit{Re}\sim 10^{2}{-}10^{4}$
. Most experimental data was obtained by using local probes (hot-wire anemometer). Modern methods of turbulence visualisation have confirmed the existence of intermittent coherent structures in the boundary layer of turbulent flows. The visualization of the developed turbulence registered long-lived filamentary structures of different lengths existing in the flow (see Camusi et al.
Reference Camusi, Felli, Pereira, Aloisio and Di Marko2008). A significant new result obtained in recent years is the experimental observation of very large-scale motion (VLSM) in a flow (see Marusic et al.
Reference Marusic, McKeon, Monkewitz, Nagib, Smits and Sreenivasan2010). These structures are coupled with small-scale fluctuations and contain a significant fraction of the overall energy of the flow, the energy of the VLSM is increased with the Reynolds number.
$\mathit{Re}\sim 10^{2}{-}10^{4}$
. Most experimental data was obtained by using local probes (hot-wire anemometer). Modern methods of turbulence visualisation have confirmed the existence of intermittent coherent structures in the boundary layer of turbulent flows. The visualization of the developed turbulence registered long-lived filamentary structures of different lengths existing in the flow (see Camusi et al.
Reference Camusi, Felli, Pereira, Aloisio and Di Marko2008). A significant new result obtained in recent years is the experimental observation of very large-scale motion (VLSM) in a flow (see Marusic et al.
Reference Marusic, McKeon, Monkewitz, Nagib, Smits and Sreenivasan2010). These structures are coupled with small-scale fluctuations and contain a significant fraction of the overall energy of the flow, the energy of the VLSM is increased with the Reynolds number.
Intermittency is a typical property of hydrodynamic TBLs (see, e.g. Cadot, Douady & Couder Reference Cadot, Douady and Couder1995; Camusi et al.
Reference Camusi, Felli, Pereira, Aloisio and Di Marko2008; Marusic et al.
Reference Marusic, McKeon, Monkewitz, Nagib, Smits and Sreenivasan2010). Fourier spectra of the velocity pulsations in TBLs are broadband and statistics are non-Gaussian. Below, we demonstrate the intermittency property observed in the low-turbulent aerodynamic T-36I wind tunnel at TsAGI (Russia) by Brutyan et al. (Reference Brutyan, Budaev, Wolkov, Zhitlukhin, Karpov, Klimov, Menshov, Podkovyrov, Urusov and Uspenskii2013). The test section of 2600 mm had a rectangular cross section of
![]() $500~\text{mm}\times 350~\text{mm}$
of the velocity of
$500~\text{mm}\times 350~\text{mm}$
of the velocity of
![]() $8{-}55~\text{m}~\text{s}^{-1}$
. Forced turbulization of the boundary layer was implemented by means of a stationary vortex generator installed in the front of the test section.
$8{-}55~\text{m}~\text{s}^{-1}$
. Forced turbulization of the boundary layer was implemented by means of a stationary vortex generator installed in the front of the test section.

Figure 22. (a) Velocity pulsations (in arbitrary units) and (b) PDF – in TBL over the surface at
![]() $y=2~\text{mm}$
, mean flow
$y=2~\text{mm}$
, mean flow
![]() $U=30~\text{m}~\text{s}^{-1}$
, T-36I wind tunnel. (c) The Fourier spectrum
$U=30~\text{m}~\text{s}^{-1}$
, T-36I wind tunnel. (c) The Fourier spectrum
![]() $S(f)$
of velocity pulsations in TBL over the surface at
$S(f)$
of velocity pulsations in TBL over the surface at
![]() $y=0.2~\text{mm}$
,
$y=0.2~\text{mm}$
,
![]() $x=1515~\text{mm}$
, mean flow
$x=1515~\text{mm}$
, mean flow
![]() $U=10~\text{m}~\text{s}^{-1}$
, T-36I wind tunnel. The fit by power law
$U=10~\text{m}~\text{s}^{-1}$
, T-36I wind tunnel. The fit by power law
![]() $f^{-1.97}$
is shown by a line.
$f^{-1.97}$
is shown by a line.
Typically, velocity pulsations in the TBL have intermittent structure with non-Gaussian statistics (figure 22
a,b) contrary to the near-Gaussian statistics in the main flow. Fourier spectra of the velocity pulsations in TBLs are broadband in the frequency range from 10 Hz to 10 kHz (figure 22
c). The Hurst exponent of the time-series measured in the TBL varies from 0.6 to 0.8. The TBL is characterized by a multifractal property: the PDF of the velocity increments
![]() ${\it\delta}_{l}U(t)$
at different time scales
${\it\delta}_{l}U(t)$
at different time scales
![]() $l$
demonstrate an evolution from ‘quasi-Gaussian’ at large scale from
$l$
demonstrate an evolution from ‘quasi-Gaussian’ at large scale from
![]() ${\sim}10^{-1}$
to
${\sim}10^{-1}$
to
![]() ${\sim}10^{-2}~\text{s}$
to fat tailed PDF’s at small scales. Multifractal spectra
${\sim}10^{-2}~\text{s}$
to fat tailed PDF’s at small scales. Multifractal spectra
![]() $D(h)$
are typically broadened and have a convex shape similar to the observations in space and laboratory plasma (figure 23).
$D(h)$
are typically broadened and have a convex shape similar to the observations in space and laboratory plasma (figure 23).

Figure 23. Multifractal spectra
![]() $D(h)$
versus the normalized Hölder exponent
$D(h)$
versus the normalized Hölder exponent
![]() $h^{\ast }=1+(h-h_{Dmax})$
(centred around 1 by subtracting
$h^{\ast }=1+(h-h_{Dmax})$
(centred around 1 by subtracting
![]() $h_{Dmax}$
), TBL ion flux from Spectr-R (SW Spectr), TBL ion flux Interball-I on 19.06.1998, cross-field flux in edge T-10 tokamak (T-10 flux SOL); aerodynamic flow velocity pulsation in TBL at different locations
$h_{Dmax}$
), TBL ion flux from Spectr-R (SW Spectr), TBL ion flux Interball-I on 19.06.1998, cross-field flux in edge T-10 tokamak (T-10 flux SOL); aerodynamic flow velocity pulsation in TBL at different locations
![]() $y=0.4~\text{mm}$
and
$y=0.4~\text{mm}$
and
![]() $y=1.5~\text{mm}$
over the surface,
$y=1.5~\text{mm}$
over the surface,
![]() $U=10~\text{m}~\text{s}^{-1}$
, T-36I wind tunnel.
$U=10~\text{m}~\text{s}^{-1}$
, T-36I wind tunnel.
The ESS property is shown in figure 24(a). Typically, the structure function scaling
![]() ${\it\zeta}(q)$
is a nonlinear function of
${\it\zeta}(q)$
is a nonlinear function of
![]() $q$
, figure 24(b) similar to the intermittent plasma data. The scalings deviate from the K41 scaling. The experimental spectra can be described by the log-Poisson model (4.1) with adjusted parameters
$q$
, figure 24(b) similar to the intermittent plasma data. The scalings deviate from the K41 scaling. The experimental spectra can be described by the log-Poisson model (4.1) with adjusted parameters
![]() ${\it\Delta}$
and
${\it\Delta}$
and
![]() ${\it\beta}$
in the range
${\it\beta}$
in the range
![]() ${\it\Delta}=0.2{-}0.4$
,
${\it\Delta}=0.2{-}0.4$
,
![]() ${\it\beta}=0.2{-}0.8$
. The results can be interpreted as an evidence of dominant contribution of 1-D filament-like dissipative structures to the turbulent process. It supports observations of long-lived filamentary structures, including VLSM, in hydrodynamic TBLs. The scalings in figure 24(b) illustrate similarity of hydrodynamic TBLs with plasma TBLs. Such observations open a way for the detailed investigation of generalized self-similarity, including attempts at turbulence control (e.g. as was demonstrated in first experiments with fractal boundary surface to test impact on the spectral and statistical properties in Brutyan et al. (Reference Brutyan, Budaev, Wolkov, Zhitlukhin, Karpov, Klimov, Menshov, Podkovyrov, Urusov and Uspenskii2013)). Thus the comparative study of intermittency in plasma and neutral fluid TBLs is helpful for the validation of developed turbulence models, including the log-Poisson model, to reveal universal features of the intermittency.
${\it\beta}=0.2{-}0.8$
. The results can be interpreted as an evidence of dominant contribution of 1-D filament-like dissipative structures to the turbulent process. It supports observations of long-lived filamentary structures, including VLSM, in hydrodynamic TBLs. The scalings in figure 24(b) illustrate similarity of hydrodynamic TBLs with plasma TBLs. Such observations open a way for the detailed investigation of generalized self-similarity, including attempts at turbulence control (e.g. as was demonstrated in first experiments with fractal boundary surface to test impact on the spectral and statistical properties in Brutyan et al. (Reference Brutyan, Budaev, Wolkov, Zhitlukhin, Karpov, Klimov, Menshov, Podkovyrov, Urusov and Uspenskii2013)). Thus the comparative study of intermittency in plasma and neutral fluid TBLs is helpful for the validation of developed turbulence models, including the log-Poisson model, to reveal universal features of the intermittency.

Figure 24. (a) ESS property of the intermittent turbulence in boundary layer: dependence of the structure functions of different orders
![]() $q$
on the third-order structure function, velocity pulsations at
$q$
on the third-order structure function, velocity pulsations at
![]() $y=20~\text{mm}$
,
$y=20~\text{mm}$
,
![]() $x=1515~\text{mm}$
,
$x=1515~\text{mm}$
,
![]() $U=10~\text{m}~\text{s}^{-1}$
, T-36I wind tunnel. (b) Scaling of structure functions – the deviation from the K41 model (dashed line). Log-Poisson model of She–Leveque (SL-solid line) and scaling Biscamp–Mueller (4.5) (BM log-Poisson) are shown; aerodynamic flow velocity pulsation at in TBL at different locations
$U=10~\text{m}~\text{s}^{-1}$
, T-36I wind tunnel. (b) Scaling of structure functions – the deviation from the K41 model (dashed line). Log-Poisson model of She–Leveque (SL-solid line) and scaling Biscamp–Mueller (4.5) (BM log-Poisson) are shown; aerodynamic flow velocity pulsation at in TBL at different locations
![]() $y=0.9~\text{mm}$
,
$y=0.9~\text{mm}$
,
![]() $y=4~\text{mm}$
,
$y=4~\text{mm}$
,
![]() $y=30~\text{mm}$
,
$y=30~\text{mm}$
,
![]() $U=10~\text{m}~\text{s}^{-1}$
, T-36I wind tunnel; TBL ion flux data Spectr-R (SW Spectr), TBL ion flux Interball 19.06.1998, cross-field flux in edge T-10 tokamak (T-10 flux SOL).
$U=10~\text{m}~\text{s}^{-1}$
, T-36I wind tunnel; TBL ion flux data Spectr-R (SW Spectr), TBL ion flux Interball 19.06.1998, cross-field flux in edge T-10 tokamak (T-10 flux SOL).
6. Scalings of intermittent plasma transport
The statistical description of transport processes in turbulent plasma is an alternative approach to the traditional characterization of transport based on the computation of effective transport diffusion coefficients assuming Einstein’s law of diffusion. Traditionally, a displacement of plasma particles with time
![]() ${\it\tau}$
is considered as
${\it\tau}$
is considered as
![]() $\langle {\it\delta}x^{2}\rangle \propto \mathit{D}{\it\tau}$
with a constant (or independent on time scale) diffusion coefficient
$\langle {\it\delta}x^{2}\rangle \propto \mathit{D}{\it\tau}$
with a constant (or independent on time scale) diffusion coefficient
![]() $\mathit{D}$
. In such models,
$\mathit{D}$
. In such models,
![]() $\mathit{D}$
is estimated from some assumptions supposing some dominant physical mechanism and eliminating other contributions. In such an approach, effects of the nonlinear coupling of modes with different scales (large and small) are excluded which could lead to a significant deviation of the model predictions from the real plasma properties. Because plasma transport is a multi-scale process, the statistical approach is most appropriative for a self-consistent description of turbulence and transport phenomena.
$\mathit{D}$
is estimated from some assumptions supposing some dominant physical mechanism and eliminating other contributions. In such an approach, effects of the nonlinear coupling of modes with different scales (large and small) are excluded which could lead to a significant deviation of the model predictions from the real plasma properties. Because plasma transport is a multi-scale process, the statistical approach is most appropriative for a self-consistent description of turbulence and transport phenomena.
To understand the transport analysis, we note that according to the cascade paradigm, the turbulent energy fluxes
![]() ${\it\varepsilon}$
are (on average) conserved from scale-to-scale during the cascade. In hydrodynamics, the cascade starts at a large outer scale, large structures break-up into smaller eddies due to instability or nonlinear interactions, the flux through the latter being multiplicatively modulated by the former. The variability at scale ratio
${\it\varepsilon}$
are (on average) conserved from scale-to-scale during the cascade. In hydrodynamics, the cascade starts at a large outer scale, large structures break-up into smaller eddies due to instability or nonlinear interactions, the flux through the latter being multiplicatively modulated by the former. The variability at scale ratio
![]() ${\it\lambda}$
is
${\it\lambda}$
is
![]() ${\it\varepsilon}_{{\it\lambda}}$
is the energy flux non-dimensionalized by the ensemble mean flux,
${\it\varepsilon}_{{\it\lambda}}$
is the energy flux non-dimensionalized by the ensemble mean flux,
![]() $L_{eff}$
is the effective outer scale of the cascade,
$L_{eff}$
is the effective outer scale of the cascade,
![]() $l$
is the scale of an eddy, the angular brackets indicate statistical averaging and
$l$
is the scale of an eddy, the angular brackets indicate statistical averaging and
![]() $K(q)$
is a convex function which characterizes the multiscaling (see Lovejoy, Schertzer & Stanway Reference Lovejoy, Schertzer and Stanway2001). This fundamental cascade equation describes the variability from the weak fluctuations (low
$K(q)$
is a convex function which characterizes the multiscaling (see Lovejoy, Schertzer & Stanway Reference Lovejoy, Schertzer and Stanway2001). This fundamental cascade equation describes the variability from the weak fluctuations (low
![]() $q$
) up to strong fluctuations (high
$q$
) up to strong fluctuations (high
![]() $q$
) at all scales. Considering
$q$
) at all scales. Considering
![]() ${\it\varepsilon}_{{\it\lambda}}$
as a stochastic 1-D multifractal density field (e.g. generated by a multiplicative cascade process; see appendix B) denoted
${\it\varepsilon}_{{\it\lambda}}$
as a stochastic 1-D multifractal density field (e.g. generated by a multiplicative cascade process; see appendix B) denoted
![]() ${\it\varphi}_{{\it\lambda}}$
where
${\it\varphi}_{{\it\lambda}}$
where
![]() ${\it\lambda}>1$
is the ratio of the largest scale of interest to the smallest scale of homogeneity displaying singularities
${\it\lambda}>1$
is the ratio of the largest scale of interest to the smallest scale of homogeneity displaying singularities
![]() $h$
:
$h$
:
The statistical moments of the multifractal field are described by the moment scaling function
![]() $\mathit{K}(q)$
:
$\mathit{K}(q)$
:
If we assume the dynamics as being controlled by scale invariant turbulent cascades of various (scale-by-scale) conserved fluxes
![]() ${\it\varphi}$
, then in a scaling regime, the fluctuations
${\it\varphi}$
, then in a scaling regime, the fluctuations
![]() ${\rm\Delta}f\,({\rm\Delta}x)$
in an observable
${\rm\Delta}f\,({\rm\Delta}x)$
in an observable
![]() $f$
(e.g. density or velocity of plasma fluctuations) over a distance
$f$
(e.g. density or velocity of plasma fluctuations) over a distance
![]() ${\rm\Delta}x$
are related to the turbulent fluxes by a relation of the form
${\rm\Delta}x$
are related to the turbulent fluxes by a relation of the form
![]() ${\rm\Delta}f\;({\rm\Delta}x)={\it\varphi}{\rm\Delta}x^{H}$
. This relation is a generalization of the classical laws of turbulence. For example, the Kolmogorov (Reference Kolmogorov1941a
,Reference Kolmogorov
b
) law for velocity fluctuations has
${\rm\Delta}f\;({\rm\Delta}x)={\it\varphi}{\rm\Delta}x^{H}$
. This relation is a generalization of the classical laws of turbulence. For example, the Kolmogorov (Reference Kolmogorov1941a
,Reference Kolmogorov
b
) law for velocity fluctuations has
![]() $H=1/3$
and
$H=1/3$
and
![]() ${\it\varphi}={\it\varepsilon}^{{\it\eta}}$
,
${\it\varphi}={\it\varepsilon}^{{\it\eta}}$
,
![]() ${\it\eta}=1/3$
(
${\it\eta}=1/3$
(
![]() ${\it\varepsilon}$
is the energy flux) (see Stolle, Lovejoy & Schertzer Reference Stolle, Lovejoy and Schertzer2009). Without knowing
${\it\varepsilon}$
is the energy flux) (see Stolle, Lovejoy & Schertzer Reference Stolle, Lovejoy and Schertzer2009). Without knowing
![]() ${\it\eta}$
or
${\it\eta}$
or
![]() $H$
– nor even the physical nature of the flux – we can use this to estimate the normalized (non-dimensional) flux at the smallest resolution of our data (see Stolle et al.
Reference Stolle, Lovejoy and Schertzer2009):
$H$
– nor even the physical nature of the flux – we can use this to estimate the normalized (non-dimensional) flux at the smallest resolution of our data (see Stolle et al.
Reference Stolle, Lovejoy and Schertzer2009):
Regarding energy flux,
![]() ${\it\varphi}^{\prime }={\it\varepsilon}^{{\it\eta}}/\langle {\it\varepsilon}^{{\it\eta}}\rangle$
is used to investigate diffusion process in multifractals. Averaging over stochastic multifractals (see Lovejoy, Schertzer & Silas Reference Lovejoy, Schertzer and Silas1998; Lovejoy et al.
Reference Lovejoy, Schertzer and Stanway2001) yields the coefficient of diffusion
${\it\varphi}^{\prime }={\it\varepsilon}^{{\it\eta}}/\langle {\it\varepsilon}^{{\it\eta}}\rangle$
is used to investigate diffusion process in multifractals. Averaging over stochastic multifractals (see Lovejoy, Schertzer & Silas Reference Lovejoy, Schertzer and Silas1998; Lovejoy et al.
Reference Lovejoy, Schertzer and Stanway2001) yields the coefficient of diffusion
![]() $\mathit{D}_{eff}$
$\mathit{D}_{eff}$
where
![]() $K_{{\it\eta}}({\it\eta}q)=qH-{\it\zeta}(q)$
, assuming
$K_{{\it\eta}}({\it\eta}q)=qH-{\it\zeta}(q)$
, assuming
![]() $H=1/3$
and
$H=1/3$
and
![]() ${\it\eta}=1/3$
(see details in Stolle et al.
Reference Stolle, Lovejoy and Schertzer2009), relates to the scaling of the high-order structure function
${\it\eta}=1/3$
(see details in Stolle et al.
Reference Stolle, Lovejoy and Schertzer2009), relates to the scaling of the high-order structure function
![]() ${\it\zeta}(q)$
. In multifractals, there is a one-to-one relationship between moments and field values (singularities), thus, there is a critical order of singularity controlling the diffusion process:
${\it\zeta}(q)$
. In multifractals, there is a one-to-one relationship between moments and field values (singularities), thus, there is a critical order of singularity controlling the diffusion process:
![]() $\mathit{K}(-1)$
in (6.5).
$\mathit{K}(-1)$
in (6.5).
The log-Poisson model could be used to estimate a transport scaling law based on the self-similarity index responsible for the percolation effect in turbulent plasma. In such an approach (see Budaev Reference Budaev2009; Budaev et al.
Reference Budaev, Savin and Zelenyi2011) the diffusion scaling law depends on the structure function scaling
![]() ${\it\zeta}(q)$
assuming a log-Poisson scaling. Hence, a displacement of particles with time
${\it\zeta}(q)$
assuming a log-Poisson scaling. Hence, a displacement of particles with time
![]() ${\it\tau}$
is scaled as
${\it\tau}$
is scaled as
with an exponent
![]() ${\it\alpha}\propto 1+K(-1)$
. This index was estimated from scaling
${\it\alpha}\propto 1+K(-1)$
. This index was estimated from scaling
![]() ${\it\zeta}(q)$
by using experimental measures (see tables 1 and 2) of scaling measured in space and laboratory devices (Budaev et al.
Reference Budaev, Savin and Zelenyi2011), see table 4. The normal diffusion law (as classic diffusion implies that
${\it\zeta}(q)$
by using experimental measures (see tables 1 and 2) of scaling measured in space and laboratory devices (Budaev et al.
Reference Budaev, Savin and Zelenyi2011), see table 4. The normal diffusion law (as classic diffusion implies that
![]() ${\it\alpha}=1$
) is observed in quiet SW, in MSH out of the Earth’s magnetosphere TBL and sheared flows in the vicinity of X-points with destroyed magnetic structure in fusion devices, Budaev et al. (Reference Budaev, Savin and Zelenyi2011). Superdiffusive transport with scaling exponent
${\it\alpha}=1$
) is observed in quiet SW, in MSH out of the Earth’s magnetosphere TBL and sheared flows in the vicinity of X-points with destroyed magnetic structure in fusion devices, Budaev et al. (Reference Budaev, Savin and Zelenyi2011). Superdiffusive transport with scaling exponent
![]() ${\it\alpha}$
close to 2 is discussed in Savin et al. (Reference Savin, Amata, Budaev, Zelenyi, Kronberg, Buechner, Safrankova, Nemecek, Blecki and Kozak2014) for the observations of SPS at deformed BS, in BS/MSH. The most of transport scaling exponent estimated for data from TBL
${\it\alpha}$
close to 2 is discussed in Savin et al. (Reference Savin, Amata, Budaev, Zelenyi, Kronberg, Buechner, Safrankova, Nemecek, Blecki and Kozak2014) for the observations of SPS at deformed BS, in BS/MSH. The most of transport scaling exponent estimated for data from TBL
![]() ${\it\alpha}\approx 1.2{-}1.8>1$
(Budaev et al.
Reference Budaev, Savin and Zelenyi2011), i.e. such scaling invokes superdiffusion. Similar observations were registered in hydrodynamics TBL: the scaling
${\it\alpha}\approx 1.2{-}1.8>1$
(Budaev et al.
Reference Budaev, Savin and Zelenyi2011), i.e. such scaling invokes superdiffusion. Similar observations were registered in hydrodynamics TBL: the scaling
![]() ${\it\alpha}\approx 1.4$
(see Brutyan et al.
Reference Brutyan, Budaev, Wolkov, Zhitlukhin, Karpov, Klimov, Menshov, Podkovyrov, Urusov and Uspenskii2013). These results support a view that the intermittent transport in TBLs display the universality predicted by the log-Poisson model.
${\it\alpha}\approx 1.4$
(see Brutyan et al.
Reference Brutyan, Budaev, Wolkov, Zhitlukhin, Karpov, Klimov, Menshov, Podkovyrov, Urusov and Uspenskii2013). These results support a view that the intermittent transport in TBLs display the universality predicted by the log-Poisson model.
Table 4. The scaling exponent
![]() ${\it\alpha}$
of transport in space and laboratory plasmas.
${\it\alpha}$
of transport in space and laboratory plasmas.

7. Conclusions
Fluctuations observed both in space and laboratory plasma are characterized by the generalized (extended) self-similarity in an extended scale range. The generalized self-similarity (scale invariance) is described in frame of the log-Poisson model which allows different functional dependences of the scaling on the geometry of the particular dissipative structures. 1-D (filamentary) and 2-D (sheet-like) dissipative structures emerging in the cascade process were studied. Many of the scalings experimentally obtained both in cosmic and fusion conditions have been found to be quite close to the model one for 1-D dissipative structures. The question of whether intermittent plasma flows are really dominated by the presence of 1-D dissipative structures requires additional theoretical and experimental efforts. Turbulent transport scaling can be evaluated using the universal log-Poisson model parameters. The average squared displacement of a given particle can be described as:
![]() $\langle {\it\delta}x^{2}\rangle \propto {\it\tau}^{{\it\alpha}}$
where
$\langle {\it\delta}x^{2}\rangle \propto {\it\tau}^{{\it\alpha}}$
where
![]() ${\it\alpha}$
is estimated from self-similarity scaling measured in space and laboratory plasma. In the TBLs
${\it\alpha}$
is estimated from self-similarity scaling measured in space and laboratory plasma. In the TBLs
![]() ${\it\alpha}\approx 1.2{-}1.8>1$
assuming the superdiffusion regime. It appears that intermittent turbulence in a magnetofluid is similar to the hydrodynamic analogue. This demonstrates the universal properties of intermittent turbulence for many natural phenomena.
${\it\alpha}\approx 1.2{-}1.8>1$
assuming the superdiffusion regime. It appears that intermittent turbulence in a magnetofluid is similar to the hydrodynamic analogue. This demonstrates the universal properties of intermittent turbulence for many natural phenomena.
Acknowledgements
Authors are grateful Professor G. N. Zastenker, BMSW Team and Dr M. Riazantseva for providing the SPECTR-R data and help in the data analysis; we also thank ACE, WIND and Cluster CIS teams for providing their plasma data via CSDS and SPDF, the Russian Academy of Sciences OFN-15 and P-22 programs, Professors N. Ohno, S. Takamura, M. Brutyan, I. Menshov, S. Masuzaki, Drs N. Asakura, S. Grashin for providing experimental data and fruitful discussions.
Appendix A. Statistical description of multifractal cascade process
This appendix offers an explanation of the multifractal formalism meant to analyse statistical self-similarity. In mathematics, a stochastic process
![]() $X(t)$
is called statistically self-similar for exponent
$X(t)$
is called statistically self-similar for exponent
![]() $H$
if for
$H$
if for
![]() $\forall {\it\lambda}>0,{\it\lambda}^{-H}X({\it\lambda}t)$
is the same process as
$\forall {\it\lambda}>0,{\it\lambda}^{-H}X({\it\lambda}t)$
is the same process as
![]() $X(t)$
(in statistics). Stochastic homogeneous signals are characterized by a single global Hurst exponent
$X(t)$
(in statistics). Stochastic homogeneous signals are characterized by a single global Hurst exponent
![]() $H$
and have the same scaling properties at all time intervals. Widely used examples of such processes are fractional Brownian motion and Lėvy walks. The Brownian motion is self-similar with an exponent
$H$
and have the same scaling properties at all time intervals. Widely used examples of such processes are fractional Brownian motion and Lėvy walks. The Brownian motion is self-similar with an exponent
![]() $H=1/2$
. The definition above describes only a monofractal process.
$H=1/2$
. The definition above describes only a monofractal process.
For the monofractal process being self-similar with an exponent
![]() $H$
, the probability density functions (PDF)
$H$
, the probability density functions (PDF)
![]() $P_{l}({\it\delta}X)$
of increments
$P_{l}({\it\delta}X)$
of increments
![]() ${\it\delta}_{l}X$
at scales
${\it\delta}_{l}X$
at scales
![]() $l$
and
$l$
and
![]() $L={\it\lambda}l$
are related by
$L={\it\lambda}l$
are related by
The
![]() $q$
th-order moments (structure functions)
$q$
th-order moments (structure functions)
![]() $S(q,l)=\langle |{\it\delta}_{l}X|^{q}\rangle$
at scales
$S(q,l)=\langle |{\it\delta}_{l}X|^{q}\rangle$
at scales
![]() $l$
and
$l$
and
![]() $L={\it\lambda}l$
are related by
$L={\it\lambda}l$
are related by
Here
![]() $\langle \cdots \rangle$
is the statistical averaging. This is a ‘monofractal’ process with exponent
$\langle \cdots \rangle$
is the statistical averaging. This is a ‘monofractal’ process with exponent
![]() ${\it\zeta}_{q}=qH$
.
${\it\zeta}_{q}=qH$
.
Another class of stochastic process includes multifractal signals that are described by many local Hurst exponents (or Hölder exponents) quantifying the local singular behaviour and local scaling in time series. According to this definition, the Hölder exponent
![]() $h(t_{0})$
of a function
$h(t_{0})$
of a function
![]() $f$
at the point
$f$
at the point
![]() $t_{0}$
is the greatest
$t_{0}$
is the greatest
![]() $h$
so that
$h$
so that
![]() $f$
is Lipschitz at
$f$
is Lipschitz at
![]() $t_{0}$
, i.e. there exist a constant
$t_{0}$
, i.e. there exist a constant
![]() $A$
and a polynomial
$A$
and a polynomial
![]() $Q_{n}(t)$
of order
$Q_{n}(t)$
of order
![]() $n$
so that for all
$n$
so that for all
![]() $t$
in the neighbourhood of
$t$
in the neighbourhood of
![]() $t_{0}$
we have,
$t_{0}$
we have,
This measures the degree of irregularity of
![]() $f$
at the point
$f$
at the point
![]() $t_{0}$
.
$t_{0}$
.
In order to account for multifractality, one has to generalize the classical definition of self-similarity. This was originally proposed in the field of developed turbulence (see Frish Reference Frish1995). The definition of the multifractal self-similarity as follows. A process is self-similar if the increment PDF’s at scales
![]() $l$
and
$l$
and
![]() $L={\it\lambda}l({\it\lambda}>1)$
are related by the relationship,
$L={\it\lambda}l({\it\lambda}>1)$
are related by the relationship,
where the self-similarity kernel
![]() $G_{l,L}(u)$
depends only on
$G_{l,L}(u)$
depends only on
![]() $l/L$
. The PDF
$l/L$
. The PDF
![]() $P_{l}({\it\delta}X)$
can be obtained through a ‘geometrical convolution’ between the kernel
$P_{l}({\it\delta}X)$
can be obtained through a ‘geometrical convolution’ between the kernel
![]() $G_{l,L}$
and the PDF
$G_{l,L}$
and the PDF
![]() $P_{L}$
. In case of monofractal self-similar process of exponent
$P_{L}$
. In case of monofractal self-similar process of exponent
![]() $H,G_{l,L}$
is the Dirac delta function
$H,G_{l,L}$
is the Dirac delta function
![]() $G_{l,L}(u)={\it\delta}(u-H\ln (l/L))$
. In the multifractal case, the moments (structure functions) at scales
$G_{l,L}(u)={\it\delta}(u-H\ln (l/L))$
. In the multifractal case, the moments (structure functions) at scales
![]() $l$
and
$l$
and
![]() $L={\it\lambda}l$
are related by
$L={\it\lambda}l$
are related by
with nonlinear spectrum
![]() ${\it\zeta}(q)$
.
${\it\zeta}(q)$
.
For fractional Brownian motion (which is a monofractal process and the only self-similar Gaussian process) the PDFs of increments
![]() ${\it\delta}_{l}X(t)$
at different time scales
${\it\delta}_{l}X(t)$
at different time scales
![]() $l$
are the Gaussian for all scales
$l$
are the Gaussian for all scales
![]() $l$
. For a
$l$
. For a
![]() ${\it\alpha}$
-stable Levy process (a monofractal process with one scaling exponent) distribution function is non-Gaussian (e.g. PDF with heavy tails).
${\it\alpha}$
-stable Levy process (a monofractal process with one scaling exponent) distribution function is non-Gaussian (e.g. PDF with heavy tails).
A multifractal model originated from the phenomenological assumptions that the successive cascade steps define the fraction of the flux transmitted to smaller scales and that a cascade from scale ratio
![]() ${\it\lambda}$
to scale ratio
${\it\lambda}$
to scale ratio
![]() ${\it\Lambda}={\it\lambda}{\it\lambda}^{\prime }$
is a rescaled version (by scale ratio
${\it\Lambda}={\it\lambda}{\it\lambda}^{\prime }$
is a rescaled version (by scale ratio
![]() ${\it\lambda}$
) of a cascade from ratio 1 to
${\it\lambda}$
) of a cascade from ratio 1 to
![]() ${\it\lambda}^{\prime }$
.
${\it\lambda}^{\prime }$
.
One possible interpretation of the multifractal formalism is the multiplicative cascade paradigm, that for any
![]() $l<L$
, the multifractal theory predicts:
$l<L$
, the multifractal theory predicts:
Then, according to the scaling properties of velocity, the generator
![]() $W(l,L)$
is a random quantity proportional to
$W(l,L)$
is a random quantity proportional to
![]() $(l/L)^{h}$
. It turns out that for
$(l/L)^{h}$
. It turns out that for
![]() $l_{1}<l_{2}<l_{3}$
we have
$l_{1}<l_{2}<l_{3}$
we have
The property of the generator
![]() $W$
defines a statistics of the process. The hypothesis on universal multifractal process (see Schertzer et al.
Reference Schertzer, Lovejoy, Hubert, Ern and Weiping2002) establishes renormalized nonlinear mixing over finite range of scales (i.e. in the TBL of a turbulent flow). It opens a way for the continuous scale cascade paradigm to overcome a problem of discrete scales in models.
$W$
defines a statistics of the process. The hypothesis on universal multifractal process (see Schertzer et al.
Reference Schertzer, Lovejoy, Hubert, Ern and Weiping2002) establishes renormalized nonlinear mixing over finite range of scales (i.e. in the TBL of a turbulent flow). It opens a way for the continuous scale cascade paradigm to overcome a problem of discrete scales in models.
In discrete cascades, a finite cascade step is assumed: the ratio of scales is
![]() $1/2\leqslant {\it\lambda}<1$
. Continuous cascade scales (so-called continuous cascades) are also used. For this, it is necessary to decrease the step value between consecutive steps of a discrete cascade. Such a cascade can be formally (mathematically) considered (see Schertzer et al.
Reference Schertzer, Lovejoy, Hubert, Ern and Weiping2002) for any
$1/2\leqslant {\it\lambda}<1$
. Continuous cascade scales (so-called continuous cascades) are also used. For this, it is necessary to decrease the step value between consecutive steps of a discrete cascade. Such a cascade can be formally (mathematically) considered (see Schertzer et al.
Reference Schertzer, Lovejoy, Hubert, Ern and Weiping2002) for any
![]() ${\it\lambda}<1$
and even
${\it\lambda}<1$
and even
![]() ${\it\lambda}<1/2$
, but statistical relations between different structures depend not on the metric of the ordinary space, but on a metric related with the parametrization. The distance between structures on a given scale is determined by the hierarchy level in the cascade. So, the distance between centres of adjacent cells is not homogeneous anymore.
${\it\lambda}<1/2$
, but statistical relations between different structures depend not on the metric of the ordinary space, but on a metric related with the parametrization. The distance between structures on a given scale is determined by the hierarchy level in the cascade. So, the distance between centres of adjacent cells is not homogeneous anymore.
Although stochastic multifractal cascade models of turbulence respect various symmetries of the dynamical equations, namely, the scaling and the energy flux conservation, there is nonetheless a large gap between the deterministic (i.e. Navier–Stokes or MHD) equations for the vector velocity field and phenomenological cascades for the scalar energy flux. In order to bridge the gap, an extension to vector cascades called ‘Lie cascades’ (see, e.g. Schertzer et al. Reference Schertzer, Lovejoy, Hubert, Ern and Weiping2002) has been considered. Strictly speaking, in 3-D, the scalar approach is already insufficient and turbulence should be studied using Lie cascades. However, in this framework, the extra symmetries which must be respected are not yet known. In Lie cascades, new symmetries emerge that have not been studied to date. However, the main features of cascades can be revealed using the scalar approach.
Involving statistical independence in the cascade and developing Kolmogorov’s theory, Parisi and Frisch in the frame of a multifractal formalism assumed (see Frish Reference Frish1995) that the velocity field has local scale-invariance with continuous spectrum exponents
![]() $h$
(Hölder exponents) each of which belongs to a given fractal set
$h$
(Hölder exponents) each of which belongs to a given fractal set
![]() ${\it\Omega}_{h}$
with dimension
${\it\Omega}_{h}$
with dimension
![]() $D(h)$
:
$D(h)$
:
![]() ${\it\delta}{\it\upsilon}_{l}(\boldsymbol{x},t)\sim (l/L)^{h}$
, for
${\it\delta}{\it\upsilon}_{l}(\boldsymbol{x},t)\sim (l/L)^{h}$
, for
![]() $\boldsymbol{x}\in {\it\Omega}_{h}$
, for
$\boldsymbol{x}\in {\it\Omega}_{h}$
, for
![]() $h$
ranges in
$h$
ranges in
![]() $h\in [h_{min},h_{max}]$
,
$h\in [h_{min},h_{max}]$
,
![]() $L$
-maximal scale in the process. In K41 model
$L$
-maximal scale in the process. In K41 model
![]() $h=\text{const.}=1/3$
. The probability of having a given
$h=\text{const.}=1/3$
. The probability of having a given
![]() ${\it\delta}{\it\upsilon}_{l}$
in a sphere of radius
${\it\delta}{\it\upsilon}_{l}$
in a sphere of radius
![]() $l$
(on the set with dimension
$l$
(on the set with dimension
![]() $D(h)$
) is
$D(h)$
) is
![]() $P_{h}(l)\sim (l/L)^{3-D(h)}$
. So, the structure function assumes the form:
$P_{h}(l)\sim (l/L)^{3-D(h)}$
. So, the structure function assumes the form:
where
![]() ${\it\mu}(h)$
is a smooth function independent of
${\it\mu}(h)$
is a smooth function independent of
![]() $l$
. If
$l$
. If
![]() $l/L\ll 1$
, using a saddle point estimate, one obtains:
$l/L\ll 1$
, using a saddle point estimate, one obtains:
![]() ${\it\zeta}(q)\cong h^{\ast }q+3-D(h^{\ast })$
, where
${\it\zeta}(q)\cong h^{\ast }q+3-D(h^{\ast })$
, where
![]() $h^{\ast }$
is a solution of the equation
$h^{\ast }$
is a solution of the equation
![]() $D^{\prime }(h^{\ast }(q))=q$
and
$D^{\prime }(h^{\ast }(q))=q$
and
![]() $D^{\prime \prime }(h^{\ast }(q))<0$
. The scaling
$D^{\prime \prime }(h^{\ast }(q))<0$
. The scaling
![]() ${\it\zeta}(q)$
depends on the shape of
${\it\zeta}(q)$
depends on the shape of
![]() $D(h)$
, which has a convex shape.
$D(h)$
, which has a convex shape.
![]() $D(h)$
is called the singularity spectrum or multifractal spectrum. From the analogy between the multifractal formalism and statistical thermodynamics, the variables
$D(h)$
is called the singularity spectrum or multifractal spectrum. From the analogy between the multifractal formalism and statistical thermodynamics, the variables
![]() $h$
and
$h$
and
![]() $D(h)$
play the same role as the energy and entropy in the thermodynamics, whereas instead of the inverse of temperature and free energy, we have
$D(h)$
play the same role as the energy and entropy in the thermodynamics, whereas instead of the inverse of temperature and free energy, we have
![]() $q$
and
$q$
and
![]() ${\it\zeta}(q)$
(Muzy, Bacry & Arneodo Reference Muzy, Bacry and Arneodo1991; Arneodo, Bacry & Muzy Reference Arneodo, Bacry and Muzy1995).
${\it\zeta}(q)$
(Muzy, Bacry & Arneodo Reference Muzy, Bacry and Arneodo1991; Arneodo, Bacry & Muzy Reference Arneodo, Bacry and Muzy1995).
Several methods can be used for estimation of multifractal spectrum (see, e.g. Parisi & Frisch Reference Parisi, Frisch, Ghil, Benzi and Parisi1985; Halsey et al.
Reference Halsey, Jensen, Kadanoff, Procaccia and Shraiman1986; Chhabra & Jensen Reference Chhabra and Jensen1989; Harte Reference Harte2001). To estimate the scaling
![]() ${\it\zeta}(q)$
and singularity spectrum
${\it\zeta}(q)$
and singularity spectrum
![]() $D(h)$
from experimental data, the wavelet analysis can be used.
$D(h)$
from experimental data, the wavelet analysis can be used.
The WT of the function
![]() $X(t)$
is defined as
$X(t)$
is defined as
![]() $T_{{\it\Psi}}(t,l)=(1/l)\int _{-\infty }^{+\infty }{\it\Psi}((t^{\prime }-t)/l)X(t^{\prime })\,\text{d}t^{\prime }$
, where
$T_{{\it\Psi}}(t,l)=(1/l)\int _{-\infty }^{+\infty }{\it\Psi}((t^{\prime }-t)/l)X(t^{\prime })\,\text{d}t^{\prime }$
, where
![]() ${\it\Psi}$
is the analysing wavelet,
${\it\Psi}$
is the analysing wavelet,
![]() $l\in R^{+}$
is a scale parameter and
$l\in R^{+}$
is a scale parameter and
![]() $t\in R$
is a space parameter. The WT
$t\in R$
is a space parameter. The WT
![]() $T_{{\it\Psi}}(t,l)$
(WT) is an analogue of the increments of the variable
$T_{{\it\Psi}}(t,l)$
(WT) is an analogue of the increments of the variable
![]() ${\it\delta}_{l}X(t)=X(t+l)-X(t)$
, but in practice, WT provides information about scaling properties in more detail than the increments. Usually, Morlet wavelets are used to analyse experimental data (see, e.g. Mallat Reference Mallat1999). This allows analysis of the process
${\it\delta}_{l}X(t)=X(t+l)-X(t)$
, but in practice, WT provides information about scaling properties in more detail than the increments. Usually, Morlet wavelets are used to analyse experimental data (see, e.g. Mallat Reference Mallat1999). This allows analysis of the process
![]() $X(t)$
both in physical space and in scale space. Wavelet analysis is available to study scale-invariance properties of the signal.
$X(t)$
both in physical space and in scale space. Wavelet analysis is available to study scale-invariance properties of the signal.
As was proven by Muzy et al. (Reference Muzy, Bacry and Arneodo1991) and Arneodo et al. (Reference Arneodo, Bacry and Muzy1995), Arneodo, Muzy & Roux (Reference Arneodo, Muzy and Roux1997) the WTMM (local maxima of
![]() $T_{{\it\Psi}}(t,l)$
at a given scale
$T_{{\it\Psi}}(t,l)$
at a given scale
![]() $l$
) detect all the singularities of a signal under investigation. The skeleton from the modulus maxima lines contains all information about the hierarchical distribution of the singularities in the signal. The WTMM method includes a construction of a partition function which scales, in the limit
$l$
) detect all the singularities of a signal under investigation. The skeleton from the modulus maxima lines contains all information about the hierarchical distribution of the singularities in the signal. The WTMM method includes a construction of a partition function which scales, in the limit
![]() $l\rightarrow 0^{+}$
, as:
$l\rightarrow 0^{+}$
, as:
where
![]() $\{t_{i}\}_{i}$
are the WTMM and
$\{t_{i}\}_{i}$
are the WTMM and
![]() $q\in R$
. Scaling exponent
$q\in R$
. Scaling exponent
![]() ${\it\zeta}(q)$
of the structure function of order
${\it\zeta}(q)$
of the structure function of order
![]() $q$
one can get the Hausdorf dimension
$q$
one can get the Hausdorf dimension
![]() $D(h)$
of the subset of
$D(h)$
of the subset of
![]() $R$
for which the increments behaves as
$R$
for which the increments behaves as
![]() ${\it\delta}_{l}X\sim l^{h}$
.
${\it\delta}_{l}X\sim l^{h}$
.
According to the theorem (Muzy et al.
Reference Muzy, Bacry and Arneodo1991; Arneodo et al.
Reference Arneodo, Bacry and Muzy1995, Reference Arneodo, Muzy and Roux1997),
![]() $D(h)$
, the singularity spectrum of the function
$D(h)$
, the singularity spectrum of the function
![]() $X$
, is obtained by Legendre transformation of the function
$X$
, is obtained by Legendre transformation of the function
![]() ${\it\zeta}_{q}$
defined above,
${\it\zeta}_{q}$
defined above,
![]() $D(h)=\min _{q}(qh-{\it\zeta}(q))$
.
$D(h)=\min _{q}(qh-{\it\zeta}(q))$
.
In practice, the scaling exponents are calculated numerically as (Muzy et al. Reference Muzy, Bacry and Arneodo1991; Arneodo et al. Reference Arneodo, Bacry and Muzy1995, Reference Arneodo, Muzy and Roux1997):
and
where
![]() $\tilde{T}_{{\it\Psi}}(q,t_{i}(l),l)=|T_{{\it\Psi}}(t_{i}(l),l)|^{q}/\sum _{t_{i_{i}}}|T_{{\it\Psi}}(t_{i}(l),l)|^{q}$
. The set of Hölder exponent and corresponding singularity spectrum
$\tilde{T}_{{\it\Psi}}(q,t_{i}(l),l)=|T_{{\it\Psi}}(t_{i}(l),l)|^{q}/\sum _{t_{i_{i}}}|T_{{\it\Psi}}(t_{i}(l),l)|^{q}$
. The set of Hölder exponent and corresponding singularity spectrum
![]() $D(h)$
are extracted from the log–log plot of
$D(h)$
are extracted from the log–log plot of
![]() $h(q)$
and
$h(q)$
and
![]() $D(h(q))$
. When increasing
$D(h(q))$
. When increasing
![]() $|q|$
, oscillations become larger in the logarithmic presentation of
$|q|$
, oscillations become larger in the logarithmic presentation of
![]() $Z(q,l)$
versus
$Z(q,l)$
versus
![]() $l$
, which very quickly deteriorate the power-low scaling behaviour observed for
$l$
, which very quickly deteriorate the power-low scaling behaviour observed for
![]() $q=0$
. To make easier and more reliable the regression linear fit estimate of
$q=0$
. To make easier and more reliable the regression linear fit estimate of
![]() ${\it\zeta}(q)$
, we can analyse
${\it\zeta}(q)$
, we can analyse
![]() $\log _{2}(Z(q,l)/Z(0,l))$
as a function of
$\log _{2}(Z(q,l)/Z(0,l))$
as a function of
![]() $\log _{2}(l)$
. The
$\log _{2}(l)$
. The
![]() ${\it\zeta}(q)$
spectrum evaluated from experimental data may provide a test for various cascade models of turbulence. To test the analysis code used for the multifractal analysis, the numerical simulation of fractional Brownian motion can be used, this has the linear dependence of
${\it\zeta}(q)$
spectrum evaluated from experimental data may provide a test for various cascade models of turbulence. To test the analysis code used for the multifractal analysis, the numerical simulation of fractional Brownian motion can be used, this has the linear dependence of
![]() ${\it\zeta}(q)$
on
${\it\zeta}(q)$
on
![]() $q$
.
$q$
.
Appendix B. She–Leveque–Dubrulle model
In this appendix, the log-Poisson model of intermittent turbulence proposed by She, Leveque and Dubrulle is explained. The log-Poisson models were developed by the generalization of
![]() ${\it\beta}$
-model incorporating asymmetry and hypothesis of scale invariance and cascade. The She–Leveque–Dubrulle model (Dubrulle Reference Dubrulle1994; She & Leveque Reference She and Leveque1994) assumes the existence of a limiting value
${\it\beta}$
-model incorporating asymmetry and hypothesis of scale invariance and cascade. The She–Leveque–Dubrulle model (Dubrulle Reference Dubrulle1994; She & Leveque Reference She and Leveque1994) assumes the existence of a limiting value
![]() ${\it\varepsilon}_{l}^{\infty }$
associated with the most dissipative structures. This model makes use of the dimensionless dissipation energy
${\it\varepsilon}_{l}^{\infty }$
associated with the most dissipative structures. This model makes use of the dimensionless dissipation energy
![]() ${\rm\pi}_{l}={\it\varepsilon}_{l}/{\it\varepsilon}_{l}^{\infty }$
and of the following three similarity hypotheses:
${\rm\pi}_{l}={\it\varepsilon}_{l}/{\it\varepsilon}_{l}^{\infty }$
and of the following three similarity hypotheses:
-
(I) The scaling for the structure function is the same as that in the K62 model, with the mutually dependent exponents,
 ${\it\zeta}(q)=q/3+{\it\phi}(q/3)$
, specifically,
${\it\zeta}(q)=q/3+{\it\phi}(q/3)$
, specifically,
 $\langle {\it\varepsilon}_{l}^{q}\rangle \sim l^{{\it\phi}(q)}$
, where
$\langle {\it\varepsilon}_{l}^{q}\rangle \sim l^{{\it\phi}(q)}$
, where
 ${\it\varepsilon}_{l}$
is the mean dissipation rate measured within the cells (say, spheres, or cubes) of size
${\it\varepsilon}_{l}$
is the mean dissipation rate measured within the cells (say, spheres, or cubes) of size
 $l$
. This scaling describes a local inhomogeneity (intermittency).
$l$
. This scaling describes a local inhomogeneity (intermittency). -
(II) The hierarchy of the moments of the mean dissipation rate is described by a power dependence,
(B 1)It is assumed that this property arises from the hidden symmetries of dynamic equations, such as the N–S equation in hydrodynamics and MHD equations in plasma physics. The exponent $$\begin{eqnarray}\frac{\langle {\rm\pi}_{l}^{q+1}\rangle }{\langle {\rm\pi}_{l}^{q}\rangle }=A_{q}\left(\frac{\langle {\rm\pi}_{l}^{q}\rangle }{\langle {\rm\pi}_{l}^{q-1}\rangle }\right)^{{\it\beta}}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\langle {\rm\pi}_{l}^{q+1}\rangle }{\langle {\rm\pi}_{l}^{q}\rangle }=A_{q}\left(\frac{\langle {\rm\pi}_{l}^{q}\rangle }{\langle {\rm\pi}_{l}^{q-1}\rangle }\right)^{{\it\beta}}.\end{eqnarray}$$
 ${\it\beta}$
characterizes the degree of intermittency (for non-intermittent homogeneous developed turbulence in, e.g. the K41 model, we have
${\it\beta}$
characterizes the degree of intermittency (for non-intermittent homogeneous developed turbulence in, e.g. the K41 model, we have
 ${\it\beta}=1$
).
${\it\beta}=1$
).
-
(III) The scaling for singular (
 $l\rightarrow 0$
) dissipative structures has the form
$l\rightarrow 0$
) dissipative structures has the form
 ${\it\varepsilon}_{l}\sim l^{-{\it\Delta}}$
, where the parameter
${\it\varepsilon}_{l}\sim l^{-{\it\Delta}}$
, where the parameter
 ${\it\Delta}$
is associated with the geometry of dissipative structures (She & Leveque Reference She and Leveque1994; Frish Reference Frish1995).
${\it\Delta}$
is associated with the geometry of dissipative structures (She & Leveque Reference She and Leveque1994; Frish Reference Frish1995).
These three hypotheses assume the existence of power laws associated with the self-similarity symmetries of a turbulent process. By analysing hypotheses (I)–(III), one can derive the scaling for the structure functions.
Dependence (B 1) yields
Let us write the hierarchy in expanded form,
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\langle {\rm\pi}_{l}^{2}\rangle =\langle {\rm\pi}_{l}\rangle ^{{\it\beta}+1}\\ \langle {\rm\pi}_{l}^{3}\rangle =\langle {\rm\pi}_{l}^{2}\rangle ^{{\it\beta}+1}\langle {\rm\pi}_{l}\rangle ^{-{\it\beta}}\\ \cdots \\ \langle {\rm\pi}_{l}^{q}\rangle =\langle {\rm\pi}_{l}\rangle ^{{\it\psi}},\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\langle {\rm\pi}_{l}^{2}\rangle =\langle {\rm\pi}_{l}\rangle ^{{\it\beta}+1}\\ \langle {\rm\pi}_{l}^{3}\rangle =\langle {\rm\pi}_{l}^{2}\rangle ^{{\it\beta}+1}\langle {\rm\pi}_{l}\rangle ^{-{\it\beta}}\\ \cdots \\ \langle {\rm\pi}_{l}^{q}\rangle =\langle {\rm\pi}_{l}\rangle ^{{\it\psi}},\end{array}\right\}\end{eqnarray}$$
where
In shortcut form, we have
In terms of the third-order moments, the
![]() $q$
th-order scaling for the velocity can then be written as
$q$
th-order scaling for the velocity can then be written as
The hierarchy of the moments can be explained by considering invariance under the generalized scale transformation, in which case the scaling should be considered with respect to the generalized scale determined by the third moment of the distribution function. This is the ESS property.

Figure 25. Scheme of a random anisotropic multiplicative cascade in the log-Poisson model.
Table 5. List of acronyms and abbreviations.

Let us briefly describe the hierarchy in the log-Poisson model. Consider a multiplicative cascade turbulent energy process in a system with hierarchical turbulent cells or with velocity fluctuations of different amplitudes on different scales. Let us divide the entire region into small cubic cells of side
![]() $l_{0}$
and introduce the energy dissipation rate
$l_{0}$
and introduce the energy dissipation rate
![]() ${\it\varepsilon}_{l}$
for each of the cells. In the steady state, the energy dissipation flux is the same as the energy influx into the system on the largest scales. In the K41 model, this energy dissipation flux is constant. Let us then divide each of the cells into smaller cubic cells of side
${\it\varepsilon}_{l}$
for each of the cells. In the steady state, the energy dissipation flux is the same as the energy influx into the system on the largest scales. In the K41 model, this energy dissipation flux is constant. Let us then divide each of the cells into smaller cubic cells of side
![]() ${\it\lambda}l_{0}$
, where
${\it\lambda}l_{0}$
, where
![]() $0<{\it\lambda}<1$
, and repeat this procedure with the same
$0<{\it\lambda}<1$
, and repeat this procedure with the same
![]() ${\it\lambda}$
for all smaller scales. As a result, we arrive to a hierarchy of cells such as that shown in figure 25. Let us consider two hierarchical levels: the levels
${\it\lambda}$
for all smaller scales. As a result, we arrive to a hierarchy of cells such as that shown in figure 25. Let us consider two hierarchical levels: the levels
![]() $l$
with the flux
$l$
with the flux
![]() ${\it\varepsilon}_{l}$
and the level
${\it\varepsilon}_{l}$
and the level
![]() $l^{\prime }={\it\lambda}l$
with the new cells. Assume that the dissipation energy flux through a fraction
$l^{\prime }={\it\lambda}l$
with the new cells. Assume that the dissipation energy flux through a fraction
![]() $y$
of these new cells is
$y$
of these new cells is
![]() $1-y$
and that the dissipation energy flux through the remaining fraction of the same cells is
$1-y$
and that the dissipation energy flux through the remaining fraction of the same cells is
![]() ${\it\varepsilon}_{1}^{\prime }={\it\beta}_{1}{\it\varepsilon}_{l}$
. Provided that the energy flux along the cascade is conserved, we have
${\it\varepsilon}_{1}^{\prime }={\it\beta}_{1}{\it\varepsilon}_{l}$
. Provided that the energy flux along the cascade is conserved, we have
![]() $y{\it\beta}_{1}+(1-y){\it\beta}_{2}=1$
. Assume then that the division into cells is random, i.e. that a fixed observation point can occur in any of the new, smaller scale cells with equal probability. A large number
$y{\it\beta}_{1}+(1-y){\it\beta}_{2}=1$
. Assume then that the division into cells is random, i.e. that a fixed observation point can occur in any of the new, smaller scale cells with equal probability. A large number
![]() $m$
of divisions ends with the spatial scale
$m$
of divisions ends with the spatial scale
![]() $l_{m}=l_{0}{\it\lambda}^{m}$
. The energy moment
$l_{m}=l_{0}{\it\lambda}^{m}$
. The energy moment
![]() $\langle {\it\varepsilon}_{l}^{q}\rangle \sim l^{{\it\phi}(q)}$
, averaged over the entire large initial region, obeys the scaling law
$\langle {\it\varepsilon}_{l}^{q}\rangle \sim l^{{\it\phi}(q)}$
, averaged over the entire large initial region, obeys the scaling law
here
![]() $W={\it\varepsilon}_{i+1}/{\it\varepsilon}_{i}$
is the cascade factor that describes the process and is defined by
$W={\it\varepsilon}_{i+1}/{\it\varepsilon}_{i}$
is the cascade factor that describes the process and is defined by
 $$\begin{eqnarray}W=\left\{\begin{array}{@{}ll@{}}0\quad & \text{with probability }1-y{\it\beta}_{1}-(1-y){\it\beta}_{2}\\ 1/{\it\beta}_{1}\quad & \text{with probability }y{\it\beta}_{1}\\ 1/{\it\beta}_{2}\quad & \text{with probability }(1-y){\it\beta}_{2}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}W=\left\{\begin{array}{@{}ll@{}}0\quad & \text{with probability }1-y{\it\beta}_{1}-(1-y){\it\beta}_{2}\\ 1/{\it\beta}_{1}\quad & \text{with probability }y{\it\beta}_{1}\\ 1/{\it\beta}_{2}\quad & \text{with probability }(1-y){\it\beta}_{2}.\end{array}\right.\end{eqnarray}$$
Accordingly, we can find the
![]() ${\it\beta}_{1}$
value with probability
${\it\beta}_{1}$
value with probability
![]() $y$
and the
$y$
and the
![]() ${\it\beta}_{2}$
value with probability
${\it\beta}_{2}$
value with probability
![]() $(1-y)$
. Assume that the fraction
$(1-y)$
. Assume that the fraction
![]() $y$
is small and that the parameter of the cascade is also small,
$y$
is small and that the parameter of the cascade is also small,
![]() ${\it\lambda}=1-C_{0}/y$
. For a small
${\it\lambda}=1-C_{0}/y$
. For a small
![]() $y$
value, we have
$y$
value, we have
![]() ${\it\beta}_{1}<1$
and
${\it\beta}_{1}<1$
and
![]() ${\it\beta}_{2}>1$
, in which case the structures with
${\it\beta}_{2}>1$
, in which case the structures with
![]() ${\it\beta}_{2}$
are the most intense, singular structures. Using definition (B 10), we obtain
${\it\beta}_{2}$
are the most intense, singular structures. Using definition (B 10), we obtain
The parameter
![]() $C_{0}$
is related to the fractal dimension of structures with the fraction of energy
$C_{0}$
is related to the fractal dimension of structures with the fraction of energy
![]() ${\it\beta}_{2}$
. The number of such cells is
${\it\beta}_{2}$
. The number of such cells is
![]() $N_{m}=N_{0}((1-y)/{\it\lambda}^{3})^{m}$
, the side of a cubic cell at the
$N_{m}=N_{0}((1-y)/{\it\lambda}^{3})^{m}$
, the side of a cubic cell at the
![]() $m$
th hierarchical level being
$m$
th hierarchical level being
![]() $l_{n}=l_{0}{\it\lambda}^{m}$
. The fractal dimension calculated for a small
$l_{n}=l_{0}{\it\lambda}^{m}$
. The fractal dimension calculated for a small
![]() $y$
value by the box-counting method is
$y$
value by the box-counting method is
That is, the parameter
![]() $C_{0}$
is the co-dimension of the structure that involves only cells characterized by the parameter
$C_{0}$
is the co-dimension of the structure that involves only cells characterized by the parameter
![]() ${\it\beta}_{2}$
: for 1-D, or filamentary, structures, we have
${\it\beta}_{2}$
: for 1-D, or filamentary, structures, we have
![]() $C_{0}=2$
and, for 2-D sheet-like structures, we have
$C_{0}=2$
and, for 2-D sheet-like structures, we have
![]() $C_{0}=1$
. We can then use the Kolmogorov formula for the dissipation rate,
$C_{0}=1$
. We can then use the Kolmogorov formula for the dissipation rate,
![]() ${\it\varepsilon}_{l}\approx {\it\delta}_{l}{\it\upsilon}^{3}/l$
, so the scaling for the structure velocity function is
${\it\varepsilon}_{l}\approx {\it\delta}_{l}{\it\upsilon}^{3}/l$
, so the scaling for the structure velocity function is
This scaling coincides with scaling (B 12). The parameter
![]() ${\it\beta}={\it\beta}_{1}$
, which characterizes the degree of intermittency, can be determined from numerical or laboratory experiments (for non-intermittent turbulence, we have
${\it\beta}={\it\beta}_{1}$
, which characterizes the degree of intermittency, can be determined from numerical or laboratory experiments (for non-intermittent turbulence, we have
![]() ${\it\beta}=1$
).
${\it\beta}=1$
).
Under the additional assumption that velocity fluctuations near the most dissipative structures are non-intermittent, we can reduce scaling (B 14) to She–Leveque scaling (B 9).
The logarithm of the dissipation energy
![]() ${\it\varepsilon}_{l}$
obeys the Poisson distribution,
${\it\varepsilon}_{l}$
obeys the Poisson distribution,
![]() $P(\mathit{y},{\it\mu})=({\it\mu}^{y}\text{e}^{-{\it\mu}})/{\it\Gamma}(\mathit{y}+1)$
, for
$P(\mathit{y},{\it\mu})=({\it\mu}^{y}\text{e}^{-{\it\mu}})/{\it\Gamma}(\mathit{y}+1)$
, for
![]() $y=\ln {\it\varepsilon}_{l}/\ln {\it\beta}$
; here
$y=\ln {\it\varepsilon}_{l}/\ln {\it\beta}$
; here
![]() ${\it\mu}>0$
is the parameter of the distribution,
${\it\mu}>0$
is the parameter of the distribution,
![]() ${\it\Gamma}(y)$
is the Gamma function.
${\it\Gamma}(y)$
is the Gamma function.