1. Introduction
One of the main branches of constructive mathematics is that of recursive or ‘Russian’ constructivism, where to justify the existence of mathematical objects, one must show how to compute them. A rather extreme interpretation of this philosophy is the axiom of Church’s thesis, which states that all functions from
![]() $\mathbb{N}$
to
$\mathbb{N}$
to
![]() $\mathbb{N}$
are computable. Despite (or perhaps because of) its highly non-classical nature, it has been well studied by logicians and turns out to be consistent with a wide variety of formal theories for constructive mathematics. This is usually proved using realizability models based on computable functions, starting with Kleene’s model of Heyting arithmetic (Kleene Reference Kleene1945), but with many later variants and generalisations. See, for example, Troelstra and van Dalen (Reference Troelstra and van Dalen1988, Chapter 4, Section 4) for a standard reference.
$\mathbb{N}$
are computable. Despite (or perhaps because of) its highly non-classical nature, it has been well studied by logicians and turns out to be consistent with a wide variety of formal theories for constructive mathematics. This is usually proved using realizability models based on computable functions, starting with Kleene’s model of Heyting arithmetic (Kleene Reference Kleene1945), but with many later variants and generalisations. See, for example, Troelstra and van Dalen (Reference Troelstra and van Dalen1988, Chapter 4, Section 4) for a standard reference.
When interpreting Church’s thesis in type theory, an additional complication is introduced. Logical statements are usually interpreted in type theory using the propositions-as-types interpretation. Applying this to Church’s thesis would give us the type below.
However, it is straightforward to use function extensionality to show that this type is empty. Footnote 1 It is therefore impossible in any case to show that the above “untruncated” version of Church’s thesis is consistent with univalence, since univalence implies function extensionality Univalent Foundations Program (2013, Theorem 4.9.4).
To have any hope of showing Church’s thesis is consistent with univalence, we need a different formulation. We will use the interpretation of logical statements advocated in Univalent Foundations Program (2013, Section 3.7), and commonly used in homotopy type theory and elsewhere. In this approach, one uses the higher inductive type of propositional truncation at disjunction and existential quantifiers, which ensures that the resulting type is always an hproposition (i.e. that any two of its elements are equal). This yields the following version of Church’s thesis, which is the one we will study here.
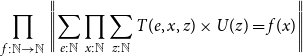 \begin{equation*} \prod_{f : \mathbb{N} \to \mathbb{N}}\left\|{\sum_{e : \mathbb{N}}\prod_{x : \mathbb{N}}\sum_{z : \mathbb{N}}T(e, x, z) \times U(z) = f(x)}\right\|\end{equation*}
\begin{equation*} \prod_{f : \mathbb{N} \to \mathbb{N}}\left\|{\sum_{e : \mathbb{N}}\prod_{x : \mathbb{N}}\sum_{z : \mathbb{N}}T(e, x, z) \times U(z) = f(x)}\right\|\end{equation*}
It is well known that Church’s thesis holds in the internal logic of Hyland’s effective topos (see for instance van Oosten Reference van Oosten2008, Section 3.1 for a standard reference). Similar arguments show that in fact it already holds in its simpler subcategory of assemblies, and even in cubical assemblies, when they are viewed as regular locally cartesian closed categories and thereby, following Awodey and Bauer (Reference Awodey and Bauer2004) or Maietti (Reference Maietti2005) as models of extensional type theory with propositional truncation. However, the interpretation of cubical type theory in cubical assemblies due to the second author (Uemura Reference Uemura2019) is very different to the interpretation of extensional type theory. We draw attention in particular to the fact that for extensional type theory hpropositions are implemented as maps where in the internal logic each fibre has at most one element. Footnote 2 On the other hand in the interpretation of cubical type theory, each fibre can have multiple elements as long as any two elements are joined by a path, telling us to always treat them as “propositionally equal.” For propositional truncation, we do not strictly identify elements by quotienting, but instead add new paths. Our first result is that Church’s thesis is in fact false in the interpretation of cubical type theory in cubical assemblies, even though it holds in the internal logic.
To show Church’s thesis is consistent with univalence, we will combine cubical assemblies with the work of Rijke, Shulman and Spitters on lex modalities and
![]() $\Sigma$
-closed reflective subuniverses in Rijke et al. (Reference Rijke, Shulman and Spitters2020). We will construct a lex modality where Church’s thesis is forced to hold, and then use properties of cubical assemblies to show that the modality is non-trivial. Our model can also be viewed as a kind of stack model akin to those used by Coquand, Ruch and Sattler for various independence and consistency results, including the independence of countable choice from homotopy type theory (Coquand et al. Reference Coquand, Ruch and Sattler2021), although our formulation will be quite different to theirs.
$\Sigma$
-closed reflective subuniverses in Rijke et al. (Reference Rijke, Shulman and Spitters2020). We will construct a lex modality where Church’s thesis is forced to hold, and then use properties of cubical assemblies to show that the modality is non-trivial. Our model can also be viewed as a kind of stack model akin to those used by Coquand, Ruch and Sattler for various independence and consistency results, including the independence of countable choice from homotopy type theory (Coquand et al. Reference Coquand, Ruch and Sattler2021), although our formulation will be quite different to theirs.
Mike Shulman has pointed out that the overall construction may be seen as analogous to an existing result on exact completions. Menni (Reference Menni2001) showed that under certain conditions, the ex/reg completion of a category is equivalent to a category of sheaves in the ex/lex completion, over a topology generated by maps that are regular epimorphisms in the original category. The effective topos is the ex/reg completion of assemblies, and so a category of sheaves in the ex/lex completion of assemblies. Analogously, we think of cubical assemblies as an “
![]() $\infty$
-exact completion” of assemblies. We view the lex modality as analogous to the topology in Menni’s construction. Since the lex modality is generated by only some, rather than all, regular epimorphisms we obtain only an approximation to the yet-to-be defined
$\infty$
-exact completion” of assemblies. We view the lex modality as analogous to the topology in Menni’s construction. Since the lex modality is generated by only some, rather than all, regular epimorphisms we obtain only an approximation to the yet-to-be defined
![]() $\infty$
-effective topos.
$\infty$
-effective topos.
As part of our proof, we will give a generalisation of the Coquand–Huber–MÖrtberg (Coquand et al. Reference Coquand, Huber and MÖrtberg2018) construction of higher inductive types to arbitrary Orton–Pitts models. This will be used to define the higher inductive types of propositional truncation and nullification, which play an essential role in our proof.
2. Models of Type Theories
In this article, we use models of different kinds of type theories: extensional dependent type theory and intensional dependent type theory (with the univalence axiom). All of them are based on the notion of a category with families (Dybjer Reference Dybjer1996).
Definition 1. Let
![]() $\mathcal{C}$
be a category. A cwf-structure over
$\mathcal{C}$
be a category. A cwf-structure over
![]() $\mathcal{C}$
is a pair (T, E) of presheaves
$\mathcal{C}$
is a pair (T, E) of presheaves
![]() $T : \mathcal{C}^{\mathrm{op}} \to \mathbf{Set}$
and
$T : \mathcal{C}^{\mathrm{op}} \to \mathbf{Set}$
and
![]() $E : \left(\int_{\mathcal{C}}T\right)^{\mathrm{op}} \to \mathbf{Set}$
such that, for any object
$E : \left(\int_{\mathcal{C}}T\right)^{\mathrm{op}} \to \mathbf{Set}$
such that, for any object
![]() $\Gamma \in \mathcal{C}$
and element
$\Gamma \in \mathcal{C}$
and element
![]() $X \in T(\Gamma)$
, the presheaf
$X \in T(\Gamma)$
, the presheaf
is representable. The representing object for this presheaf is denoted by
![]() $\chi(X) : \{X\} \to \Gamma$
or
$\chi(X) : \{X\} \to \Gamma$
or
![]() $\chi(X) : \Gamma.X \to \Gamma$
. A category with families, cwf in short, is a triple
$\chi(X) : \Gamma.X \to \Gamma$
. A category with families, cwf in short, is a triple
![]() $\mathcal{E} = (\mathbb{C}^{\mathcal{E}}, \mathbb{T}^{\mathcal{E}}, \mathbb{E}^{\mathcal{E}})$
such that
$\mathcal{E} = (\mathbb{C}^{\mathcal{E}}, \mathbb{T}^{\mathcal{E}}, \mathbb{E}^{\mathcal{E}})$
such that
![]() $\mathbb{C}^{\mathcal{E}}$
is a category with a terminal object and
$\mathbb{C}^{\mathcal{E}}$
is a category with a terminal object and
![]() $(\mathbb{T}^{\mathcal{E}}, \mathbb{E}^{\mathcal{E}})$
is a cwf-structure over
$(\mathbb{T}^{\mathcal{E}}, \mathbb{E}^{\mathcal{E}})$
is a cwf-structure over
![]() $\mathbb{C}^{\mathcal{E}}$
.
$\mathbb{C}^{\mathcal{E}}$
.
In general, a model
![]() $\mathcal{E}$
of a type theory consists of a category with families
$\mathcal{E}$
of a type theory consists of a category with families
![]() $(\mathbb{C}^{\mathcal{E}}, \mathbb{T}^{\mathcal{E}}, \mathbb{E}^{\mathcal{E}})$
and algebraic operations on the presheaves
$(\mathbb{C}^{\mathcal{E}}, \mathbb{T}^{\mathcal{E}}, \mathbb{E}^{\mathcal{E}})$
and algebraic operations on the presheaves
![]() $\mathbb{T}^{\mathcal{E}}$
and
$\mathbb{T}^{\mathcal{E}}$
and
![]() $\mathbb{E}^{\mathcal{E}}$
. An object
$\mathbb{E}^{\mathcal{E}}$
. An object
![]() $\Gamma$
of
$\Gamma$
of
![]() $\mathbb{C}^{\mathcal{E}}$
is called a context. An element X of
$\mathbb{C}^{\mathcal{E}}$
is called a context. An element X of
![]() $\mathbb{T}^{\mathcal{E}}(\Gamma)$
is called a type and written
$\mathbb{T}^{\mathcal{E}}(\Gamma)$
is called a type and written
![]() $\Gamma \vdash_{\mathcal{E}} X$
. An element a of
$\Gamma \vdash_{\mathcal{E}} X$
. An element a of
![]() $\mathbb{E}^{\mathcal{E}}(\Gamma, X)$
is called an element of type X and written
$\mathbb{E}^{\mathcal{E}}(\Gamma, X)$
is called an element of type X and written
![]() $\Gamma \vdash_{\mathcal{E}} a : X$
. The subscript of
$\Gamma \vdash_{\mathcal{E}} a : X$
. The subscript of
![]() $\vdash_{\mathcal{E}}$
is omitted when the model
$\vdash_{\mathcal{E}}$
is omitted when the model
![]() $\mathcal{E}$
is clear from the context. An algebraic operation on those presheaves is expressed by the schema
$\mathcal{E}$
is clear from the context. An algebraic operation on those presheaves is expressed by the schema
where
![]() $\Gamma \vdash \mathcal{J}_{j}$
and
$\Gamma \vdash \mathcal{J}_{j}$
and
![]() $\Gamma \vdash A(\mathcal{J}_{1}, \dots, \mathcal{J}_{n})$
are either of the form
$\Gamma \vdash A(\mathcal{J}_{1}, \dots, \mathcal{J}_{n})$
are either of the form
![]() $\Gamma.X_{1}.\dots.X_{m} \vdash Y$
or of the form
$\Gamma.X_{1}.\dots.X_{m} \vdash Y$
or of the form
![]() $\Gamma.X_{1}.\dots.X_{m} \vdash b : Y$
with
$\Gamma.X_{1}.\dots.X_{m} \vdash b : Y$
with
![]() $(\Gamma \vdash X_{1}), \dots, (\Gamma.X_{1}.\dots.X_{m-1} \vdash X_{m})$
. In this schema, we always assume that the operation
$(\Gamma \vdash X_{1}), \dots, (\Gamma.X_{1}.\dots.X_{m-1} \vdash X_{m})$
. In this schema, we always assume that the operation
![]() $A(\mathcal{J}_{1}, \dots, \mathcal{J}_{n})$
is stable under reindexing: if
$A(\mathcal{J}_{1}, \dots, \mathcal{J}_{n})$
is stable under reindexing: if
![]() $f : \Delta \to \Gamma$
is a morphism in
$f : \Delta \to \Gamma$
is a morphism in
![]() $\mathbb{C}^{\mathcal{E}}$
, then we have
$\mathbb{C}^{\mathcal{E}}$
, then we have
![]() $A(\mathcal{J}_{1}, \dots, \mathcal{J}_{n}) \cdot f = A(\mathcal{J}_{1} \cdot f, \dots,\mathcal{J}_{n} \cdot f)$
.
$A(\mathcal{J}_{1}, \dots, \mathcal{J}_{n}) \cdot f = A(\mathcal{J}_{1} \cdot f, \dots,\mathcal{J}_{n} \cdot f)$
.
Example 2. Let
![]() $\mathcal{E}$
be a cwf. We say
$\mathcal{E}$
be a cwf. We say
![]() $\mathcal{E}$
supports dependent product types if it has operations
$\mathcal{E}$
supports dependent product types if it has operations
such that the map
![]() $\mathbb{E}(\Gamma.X, Y) \ni b \mapsto \lambda(X, Y, b) \in \mathbb{E}(\Gamma, \Pi(X, Y))$
is bijective.
$\mathbb{E}(\Gamma.X, Y) \ni b \mapsto \lambda(X, Y, b) \in \mathbb{E}(\Gamma, \Pi(X, Y))$
is bijective.
We omit explicit definitions of other well-known type constructors such as dependent sum types, extensional and intensional identity types, inductive types, higher inductive types and universes.
For a model
![]() $\mathcal{E}$
of a type theory, we denote by
$\mathcal{E}$
of a type theory, we denote by
![]() $[\![{-}]\!]^{\mathcal{E}}$
the interpretation of the type theory in the model
$[\![{-}]\!]^{\mathcal{E}}$
the interpretation of the type theory in the model
![]() $\mathcal{E}$
.
$\mathcal{E}$
.
Definition 3. By a model of univalent type theory, we mean a cwf that supports dependent product types, dependent sum types, intensional identity types, unit type, finite coproducts, natural numbers, propositional truncation and a countable chain
of univalent universes.
2.1 Internal languages
Formally we will work with models of type theories, but we will construct types and terms of those models in a syntactic way using their internal languages. Let
![]() $\mathcal{E} = (\mathbb{C}^{\mathcal{E}}, \mathbb{T}^{\mathcal{E}}, \mathbb{E}^{\mathcal{E}},\dots)$
be a model of a type theory. For a context
$\mathcal{E} = (\mathbb{C}^{\mathcal{E}}, \mathbb{T}^{\mathcal{E}}, \mathbb{E}^{\mathcal{E}},\dots)$
be a model of a type theory. For a context
![]() $\Gamma \in \mathbb{C}^{\mathcal{E}}$
and a type
$\Gamma \in \mathbb{C}^{\mathcal{E}}$
and a type
![]() $\Gamma \vdash X$
, we introduce a variable x and write
$\Gamma \vdash X$
, we introduce a variable x and write
![]() $(\Gamma, x : X)$
for the context
$(\Gamma, x : X)$
for the context
![]() $\Gamma.X$
. For another type
$\Gamma.X$
. For another type
![]() $\Gamma \vdash Y$
, the weakening
$\Gamma \vdash Y$
, the weakening
![]() $\Gamma, x : X \vdash Y$
is interpreted as the reindexing
$\Gamma, x : X \vdash Y$
is interpreted as the reindexing
![]() $\Gamma.X \vdash Y \cdot \chi(X)$
. For an element
$\Gamma.X \vdash Y \cdot \chi(X)$
. For an element
![]() $\Gamma \vdash a : X$
and a type
$\Gamma \vdash a : X$
and a type
![]() $\Gamma, x : X \vdash Y(x)$
, the substitution
$\Gamma, x : X \vdash Y(x)$
, the substitution
![]() $\Gamma \vdash Y(a)$
is interpreted as the reindexing
$\Gamma \vdash Y(a)$
is interpreted as the reindexing
![]() $\Gamma \vdash Y \cdot \bar{a}$
, where
$\Gamma \vdash Y \cdot \bar{a}$
, where
![]() $\bar{a} : \Gamma \to \Gamma.X$
is the section of
$\bar{a} : \Gamma \to \Gamma.X$
is the section of
![]() $\Gamma.X \to \Gamma$
corresponding to the element
$\Gamma.X \to \Gamma$
corresponding to the element
![]() $\Gamma \vdash a : X$
. All type and term constructors of the type theory are soundly interpreted in
$\Gamma \vdash a : X$
. All type and term constructors of the type theory are soundly interpreted in
![]() $\mathcal{E}$
in a natural way. Note that types and terms built in the internal language are stable under reindexing.
$\mathcal{E}$
in a natural way. Note that types and terms built in the internal language are stable under reindexing.
2.2 W-types with reductions
We will later use W-types with reductions to construct higher inductive types. So that we can use them internally in type theory we give below a new, split formulation. This is based on the non-dependent special case of the version in Swan (Reference Swan2018).
Let
![]() $\mathcal{E} = (\mathbb{C}^{\mathcal{E}}, \mathbb{T}^{\mathcal{E}}, \mathbb{E}^{\mathcal{E}},\dots)$
be a model of a type theory with dependent product types, dependent sum types and extensional identity types. A polynomial with reductions over a context
$\mathcal{E} = (\mathbb{C}^{\mathcal{E}}, \mathbb{T}^{\mathcal{E}}, \mathbb{E}^{\mathcal{E}},\dots)$
be a model of a type theory with dependent product types, dependent sum types and extensional identity types. A polynomial with reductions over a context
![]() $\Gamma \in \mathbb{C}^{\mathcal{E}}$
consists of the following data:
$\Gamma \in \mathbb{C}^{\mathcal{E}}$
consists of the following data:
-
a type
 $\Gamma \vdash Y$
of constructors;
$\Gamma \vdash Y$
of constructors; -
a type
 $\Gamma, y : Y \vdash X(y)$
of arities;
$\Gamma, y : Y \vdash X(y)$
of arities; -
a type
 $\Gamma, y : Y \vdash R(y)$
together with an element
$\Gamma, y : Y \vdash R(y)$
together with an element
 $\Gamma, y : Y, r : R(y) \vdash k(y, r) : X(y)$
which we refer to as the reductions.
$\Gamma, y : Y, r : R(y) \vdash k(y, r) : X(y)$
which we refer to as the reductions.
An algebra for a polynomial with reductions (Y, X, R, k) over
![]() $\Gamma \in \mathbb{C}^{\mathcal{E}}$
is a type
$\Gamma \in \mathbb{C}^{\mathcal{E}}$
is a type
![]() $\Gamma \vdash W$
together with an element
$\Gamma \vdash W$
together with an element
![]() $\Gamma, y : Y, \alpha : X(y) \to W \vdash s(y, \alpha) : W$
such that
$\Gamma, y : Y, \alpha : X(y) \to W \vdash s(y, \alpha) : W$
such that
![]() $\Gamma, y : Y, \alpha : X(y) \to W, r : R(y) \vdash s(y, \alpha) =\alpha(k(y, r))$
. Algebras for (Y, X, R, k) form a category in the obvious way and we refer to the initial algebra (if it exists) as the W-type with reductions for the polynomial with reductions.
$\Gamma, y : Y, \alpha : X(y) \to W, r : R(y) \vdash s(y, \alpha) =\alpha(k(y, r))$
. Algebras for (Y, X, R, k) form a category in the obvious way and we refer to the initial algebra (if it exists) as the W-type with reductions for the polynomial with reductions.
3. Orton–Pitts Construction
Assumption 4. Let
![]() $\mathcal{E}$
be a model of dependent type theory that supports dependent product types, dependent sum types, extensional identity types, unit type, finite colimits, natural numbers, propositional truncation and a countable chain of universes. We further assume that every context
$\mathcal{E}$
be a model of dependent type theory that supports dependent product types, dependent sum types, extensional identity types, unit type, finite colimits, natural numbers, propositional truncation and a countable chain of universes. We further assume that every context
![]() $\Gamma \in \mathbb{C}^{\mathcal{E}}$
is isomorphic to
$\Gamma \in \mathbb{C}^{\mathcal{E}}$
is isomorphic to
![]() $1.X$
for some type X over the terminal object 1. Suppose the following:
$1.X$
for some type X over the terminal object 1. Suppose the following:
-
 $\mathcal{E}$
has a type
$\mathcal{E}$
has a type
 $1 \vdash \mathbb{I}$
equipped with two constants 0 and 1 and two binary operators
$1 \vdash \mathbb{I}$
equipped with two constants 0 and 1 and two binary operators
 $\sqcap$
and
$\sqcap$
and
 $\sqcup$
;
$\sqcup$
; -
 $\mathcal{E}$
has types
$\mathcal{E}$
has types
 $1 \vdash \mathbb{F}$
and
$1 \vdash \mathbb{F}$
and
 $\varphi : \mathbb{F} \vdash [\varphi]$
such that
$\varphi : \mathbb{F} \vdash [\varphi]$
such that
 $\varphi : \mathbb{F}, x : [\varphi], y : [\varphi] \vdash x = y$
. An element of
$\varphi : \mathbb{F}, x : [\varphi], y : [\varphi] \vdash x = y$
. An element of
 $\mathbb{F}$
is called a cofibrant proposition. We often omit
$\mathbb{F}$
is called a cofibrant proposition. We often omit
 $[-]$
and regard an element
$[-]$
and regard an element
 $\varphi : \mathbb{F}$
itself as a type;
$\varphi : \mathbb{F}$
itself as a type; -
 $\mathbb{I}$
and
$\mathbb{I}$
and
 $\mathbb{F}$
satisfy
$\mathbb{F}$
satisfy
 $\mathtt{ax_{1}}$
–
$\mathtt{ax_{1}}$
–
 $\mathtt{ax_{9}}$
given by Orton and Pitts (Reference Orton and Pitts2018);
$\mathtt{ax_{9}}$
given by Orton and Pitts (Reference Orton and Pitts2018); -
 $\mathbb{F}$
satisfies propositional extensionality:
$\mathbb{F}$
satisfies propositional extensionality:
 $\prod_{\varphi, \psi : \mathbb{F}}(\varphi \Leftrightarrow \psi) \Rightarrow (\varphi = \psi)$
;
$\prod_{\varphi, \psi : \mathbb{F}}(\varphi \Leftrightarrow \psi) \Rightarrow (\varphi = \psi)$
; -
the exponential functor
 $(-)^{\mathbb{I}} : \mathbb{C}^{\mathcal{E}} \to \mathbb{C}^{\mathcal{E}}$
has a right adjoint;
$(-)^{\mathbb{I}} : \mathbb{C}^{\mathcal{E}} \to \mathbb{C}^{\mathcal{E}}$
has a right adjoint; -
 $\mathcal{E}$
has W-types with reductions for those polynomials with reductions where R is of the form
$\mathcal{E}$
has W-types with reductions for those polynomials with reductions where R is of the form
 $[ \varphi ]$
for an element
$[ \varphi ]$
for an element
 $\Gamma, y : Y \vdash \varphi : \mathbb{F}$
, and they are stable under reindexing. We say
$\Gamma, y : Y \vdash \varphi : \mathbb{F}$
, and they are stable under reindexing. We say
 $\mathcal{E}$
has cofibrant W-types with reductions.
$\mathcal{E}$
has cofibrant W-types with reductions.
Note that the axioms in Orton and Pitts (Reference Orton and Pitts2018) are written in the internal language of an elementary topos, but they are easily translated into dependent type theory with
![]() $\mathbb{I}$
and
$\mathbb{I}$
and
![]() $\mathbb{F}$
as above. We require propositional extensionality which trivially holds when
$\mathbb{F}$
as above. We require propositional extensionality which trivially holds when
![]() $\mathbb{F}$
is a subobject of the subobject classifier of an elementary topos.
$\mathbb{F}$
is a subobject of the subobject classifier of an elementary topos.
Under these assumptions, following Orton and Pitts, we will build a model
![]() $\widetilde{\mathcal{E}}$
of univalent type theory as follows:
$\widetilde{\mathcal{E}}$
of univalent type theory as follows:
-
the base category
 $\mathbb{C}^{\widetilde{\mathcal{E}}}$
is that of
$\mathbb{C}^{\widetilde{\mathcal{E}}}$
is that of
 $\mathcal{E}$
;
$\mathcal{E}$
; -
the types
 $\Gamma \vdash_{\widetilde{\mathcal{E}}} X$
are the types
$\Gamma \vdash_{\widetilde{\mathcal{E}}} X$
are the types
 $\Gamma \vdash_{\mathcal{E}} X$
equipped with a ‘fibration structure’;
$\Gamma \vdash_{\mathcal{E}} X$
equipped with a ‘fibration structure’; -
the elements
 $\Gamma \vdash_{\widetilde{\mathcal{E}}} a : X$
are the elements
$\Gamma \vdash_{\widetilde{\mathcal{E}}} a : X$
are the elements
 $\Gamma \vdash_{\mathcal{E}} a : X$
of the underlying type X in
$\Gamma \vdash_{\mathcal{E}} a : X$
of the underlying type X in
 $\mathcal{E}$
;
$\mathcal{E}$
;
By the construction given in Orton and Pitts (Reference Orton and Pitts2018), this model
![]() $\widetilde{\mathcal{E}}$
supports dependent product types, dependent sum types, identity types, unit type, finite coproducts and natural numbers. For a countable chain of univalent universes, use the right adjoint to
$\widetilde{\mathcal{E}}$
supports dependent product types, dependent sum types, identity types, unit type, finite coproducts and natural numbers. For a countable chain of univalent universes, use the right adjoint to
![]() $(-)^{\mathbb{I}}$
as in Licata et al. (Reference Licata, Orton, Pitts and Spitters2018). It remains to show that
$(-)^{\mathbb{I}}$
as in Licata et al. (Reference Licata, Orton, Pitts and Spitters2018). It remains to show that
![]() $\widetilde{\mathcal{E}}$
supports propositional truncation, which will be proved in Section 3.1 using cofibrant W-types with reductions. We call a model of univalent type theory of the form
$\widetilde{\mathcal{E}}$
supports propositional truncation, which will be proved in Section 3.1 using cofibrant W-types with reductions. We call a model of univalent type theory of the form
![]() $\widetilde{\mathcal{E}}$
an Orton–Pitts model.
$\widetilde{\mathcal{E}}$
an Orton–Pitts model.
3.1 Higher inductive types in Orton–Pitts models
We are still working with a model
![]() $\mathcal{E}$
of type theory that satisfies Assumption 4. We will show how to construct higher inductive types in
$\mathcal{E}$
of type theory that satisfies Assumption 4. We will show how to construct higher inductive types in
![]() $\widetilde{\mathcal{E}}$
. Our techniques are fairly general, although we will focus on the higher inductive types (HITs) that we will need for the main theorem. The techniques developed by Coquand, Huber and MÖrtberg in Coquand et al. (Reference Coquand, Huber and MÖrtberg2018) are already very close to working in arbitrary Orton–Pitts models. The main exception is that the underlying objects for the HITs are given by certain initial algebras, which are constructed directly for cubical sets. This definition does not quite work for cubical assemblies for two reasons. Firstly we are using a different cube category, and secondly we are working internally in assemblies. Rather than proving the same results again for cubical assemblies, we will use a more general approach based on W-types with reductions that covers both cases. The first author already showed in Swan (Reference Swan2018), Section 4 that (non-split) W-types with locally decidable reductions can be constructed in any category of presheaf assemblies and we will see later how to ensure that we get in fact split W-types with reductions in presheaf assemblies.
$\widetilde{\mathcal{E}}$
. Our techniques are fairly general, although we will focus on the higher inductive types (HITs) that we will need for the main theorem. The techniques developed by Coquand, Huber and MÖrtberg in Coquand et al. (Reference Coquand, Huber and MÖrtberg2018) are already very close to working in arbitrary Orton–Pitts models. The main exception is that the underlying objects for the HITs are given by certain initial algebras, which are constructed directly for cubical sets. This definition does not quite work for cubical assemblies for two reasons. Firstly we are using a different cube category, and secondly we are working internally in assemblies. Rather than proving the same results again for cubical assemblies, we will use a more general approach based on W-types with reductions that covers both cases. The first author already showed in Swan (Reference Swan2018), Section 4 that (non-split) W-types with locally decidable reductions can be constructed in any category of presheaf assemblies and we will see later how to ensure that we get in fact split W-types with reductions in presheaf assemblies.
Finally, we will also make some minor adjustments related to the fact that we do not assume the interval object has reversals.
When we construct higher inductive types, we will use formulations based on
![]() $\mathsf{Path}$
types, following Coquand, Huber and MÖrtberg. Technically these formulations can only be stated in cubical type theory, and not in intensional type theory in general. However, it is straightforward to derive versions based on
$\mathsf{Path}$
types, following Coquand, Huber and MÖrtberg. Technically these formulations can only be stated in cubical type theory, and not in intensional type theory in general. However, it is straightforward to derive versions based on
![]() $\mathsf{Id}$
types using the equivalence of
$\mathsf{Id}$
types using the equivalence of
![]() $\mathsf{Path}$
and
$\mathsf{Path}$
and
![]() $\mathsf{Id}$
types, which are then valid in
$\mathsf{Id}$
types, which are then valid in
![]() $\widetilde{\mathcal{E}}$
. We note that although computation rules hold definitionally for both point and path constructors for the
$\widetilde{\mathcal{E}}$
. We note that although computation rules hold definitionally for both point and path constructors for the
![]() $\mathsf{Path}$
type versions, after translating to
$\mathsf{Path}$
type versions, after translating to
![]() $\mathsf{Id}$
types, the definitional equality only holds for point constructors. However, neither definitional equality will be needed for our end result.
$\mathsf{Id}$
types, the definitional equality only holds for point constructors. However, neither definitional equality will be needed for our end result.
We will review a key idea in the techniques developed by Coquand et al. (Reference Coquand, Huber and MÖrtberg2018) for constructing higher inductive types. We first recall the Orton–Pitts definition of Kan composition.
Definition 5. (Orton–Pitts) Suppose we are given a type
![]() $\Gamma \vdash_{\mathcal{E}} A$
. A Kan composition operator is an operation that takes as input
$\Gamma \vdash_{\mathcal{E}} A$
. A Kan composition operator is an operation that takes as input
![]() $\varepsilon \in \{0, 1\}$
,
$\varepsilon \in \{0, 1\}$
,
![]() $\gamma : \mathbb{I} \to \Gamma$
and
$\gamma : \mathbb{I} \to \Gamma$
and
![]() $u : \prod_{i : \mathbb{I}} \; ((i = \varepsilon) \vee \varphi) \to A(p(i))$
and returns an element
$u : \prod_{i : \mathbb{I}} \; ((i = \varepsilon) \vee \varphi) \to A(p(i))$
and returns an element
![]() $a : A(p(1 - \varepsilon)) $
together with a proof that for
$a : A(p(1 - \varepsilon)) $
together with a proof that for
![]() $p : \varphi$
,
$p : \varphi$
,
![]() $a = u(1 - \varepsilon, p)$
.
$a = u(1 - \varepsilon, p)$
.
We now recall the Coquand–Huber–MÖrtberg definitions of homogeneous Kan composition and transport. In order to apply their techniques to arbitrary Orton–Pitts models, we will make the following minor adjustment. They work in a setting where the interval type has an involution operation, allowing them to use a ‘one directional’ definition of Kan composition. That is, instead of the definition above, which takes a direction argument
![]() $\varepsilon \in \{0, 1\}$
, they only consider the simpler definition with
$\varepsilon \in \{0, 1\}$
, they only consider the simpler definition with
![]() $\varepsilon$
fixed as 0, where the other direction can be derived using the involution operator, if necessary. In the more general setting of an arbitrary Orton–Pitts model, we need to follow the Orton–Pitts definition of Kan composition, and similarly define homogenous composition and transport so that they take a direction as input.
$\varepsilon$
fixed as 0, where the other direction can be derived using the involution operator, if necessary. In the more general setting of an arbitrary Orton–Pitts model, we need to follow the Orton–Pitts definition of Kan composition, and similarly define homogenous composition and transport so that they take a direction as input.
Definition 6 (Coquand–Huber–MÖrtberg) Suppose we are given a type
![]() $\Gamma \vdash_{\mathcal{E}} A$
. A homogeneous Kan composition operator is an operation in context
$\Gamma \vdash_{\mathcal{E}} A$
. A homogeneous Kan composition operator is an operation in context
![]() $\Gamma$
that takes as input
$\Gamma$
that takes as input
![]() $\varepsilon \in \{0, 1\}$
and
$\varepsilon \in \{0, 1\}$
and
![]() $u : \prod_{i : \mathbb{I}} \; ((i = \varepsilon) \vee \varphi) \to A $
and returns
$u : \prod_{i : \mathbb{I}} \; ((i = \varepsilon) \vee \varphi) \to A $
and returns
![]() $a : A$
such that for
$a : A$
such that for
![]() $p : \varphi$
,
$p : \varphi$
,
![]() $a = u(1 - \varepsilon, p)$
.
$a = u(1 - \varepsilon, p)$
.
Definition 7 (Coquand–Huber–MÖrtberg) Given a type
![]() $\Gamma \vdash_{\mathcal{E}} A$
, a transport operator is an operation that takes as input
$\Gamma \vdash_{\mathcal{E}} A$
, a transport operator is an operation that takes as input
![]() $\varepsilon \in \{0, 1\}$
, a path
$\varepsilon \in \{0, 1\}$
, a path
![]() $\gamma : \mathbb{I} \to \Gamma$
such that
$\gamma : \mathbb{I} \to \Gamma$
such that
![]() $ \varphi \to \prod_{i, j : \mathbb{I}} \gamma(i) = \gamma(j)$
, and
$ \varphi \to \prod_{i, j : \mathbb{I}} \gamma(i) = \gamma(j)$
, and
![]() $u_0 : A(\gamma(\varepsilon))$
and returns
$u_0 : A(\gamma(\varepsilon))$
and returns
![]() $u_1 : A(\gamma(1 - \varepsilon))$
such that
$u_1 : A(\gamma(1 - \varepsilon))$
such that
![]() $ \varphi \to u_0 = u_1 $
.
$ \varphi \to u_0 = u_1 $
.
We can now see the key lemma used in the construction of higher inductive types.
Lemma 8 (Coquand–Huber–MÖrtberg) Given both a homogeneous Kan composition operator and a transport operator on a type
![]() $\Gamma \vdash_{\mathcal{E}} A$
we can construct a Kan composition operator on
$\Gamma \vdash_{\mathcal{E}} A$
we can construct a Kan composition operator on
![]() $\Gamma \vdash_{\mathcal{E}} A$
.
$\Gamma \vdash_{\mathcal{E}} A$
.
Proof. This appears as Coquand et al. (Reference Coquand, Huber and MÖrtberg2018, Lemma 2.5). We simply observe that given a transport operator for both directions
![]() $\varepsilon \in \{0, 1\}$
we can produce also a Kan composition operator for both directions, by applying the Coquand–Huber–MÖrtberg argument twice, once for each direction.
$\varepsilon \in \{0, 1\}$
we can produce also a Kan composition operator for both directions, by applying the Coquand–Huber–MÖrtberg argument twice, once for each direction.
We can also think of types with homogeneous Kan composition as ‘locally fibrant.’ We show below how to use W-types with reductions to construct local fibrant replacements, i.e. how to freely add homogeneous Kan composition to arbitrary types.
Definition 9. Given a type
![]() $\Gamma \vdash_{\mathcal{E}} A$
, we define the local fibrant replacement of A,
$\Gamma \vdash_{\mathcal{E}} A$
, we define the local fibrant replacement of A,
![]() $\mathsf{LFR}(A)$
to be the W-type with reductions defined as follows.
$\mathsf{LFR}(A)$
to be the W-type with reductions defined as follows.
-
When
 $a : A$
, we add an element
$a : A$
, we add an element
 $\mathsf{inc}(a)$
to
$\mathsf{inc}(a)$
to
 $\mathsf{LFR}(A)$
.
$\mathsf{LFR}(A)$
. -
When
 $\varphi : \mathbb{F}$
,
$\varphi : \mathbb{F}$
,
 $\varepsilon \in \{0, 1\}$
and
$\varepsilon \in \{0, 1\}$
and
 $u : \sum_{i : \mathbb{I}} ((i = \varepsilon) \vee \varphi) \;\to\; \mathsf{LFR}(A)$
, we add an element
$u : \sum_{i : \mathbb{I}} ((i = \varepsilon) \vee \varphi) \;\to\; \mathsf{LFR}(A)$
, we add an element
 $\mathsf{hcomp}(\varphi, \varepsilon, u)$
to
$\mathsf{hcomp}(\varphi, \varepsilon, u)$
to
 $\mathsf{LFR}(A)$
.
$\mathsf{LFR}(A)$
. -
If
 $p : \varphi$
and
$p : \varphi$
and
 $\varepsilon$
and u are as above then
$\varepsilon$
and u are as above then
 $\mathsf{hcomp}(\varphi, \varepsilon, u)$
reduces to
$\mathsf{hcomp}(\varphi, \varepsilon, u)$
reduces to
 $u(1 - \varepsilon, p)$
.
$u(1 - \varepsilon, p)$
.
Formally, we define the constructors Y to be the coproduct
![]() $A + (\mathbb{F} \times 2)$
. We take the arity
$A + (\mathbb{F} \times 2)$
. We take the arity
![]() $X(\mathsf{inl}(a))$
to be the empty type for
$X(\mathsf{inl}(a))$
to be the empty type for
![]() $a : A$
and
$a : A$
and
![]() $X(\mathsf{inr}(\varphi, \varepsilon))$
to be
$X(\mathsf{inr}(\varphi, \varepsilon))$
to be
![]() $\sum_{i : \mathbb{I}} \varphi \vee (i = \varepsilon)$
for
$\sum_{i : \mathbb{I}} \varphi \vee (i = \varepsilon)$
for
![]() $(\varphi, \varepsilon) : \mathbb{F} \times 2$
. We take the reductions
$(\varphi, \varepsilon) : \mathbb{F} \times 2$
. We take the reductions
![]() $R(\mathsf{inl}(a))$
to be
$R(\mathsf{inl}(a))$
to be
![]() $\bot$
for
$\bot$
for
![]() $a : A$
and
$a : A$
and
![]() $R(\mathsf{inr}(\varphi, \varepsilon))$
to be
$R(\mathsf{inr}(\varphi, \varepsilon))$
to be
![]() $\varphi$
together with the map
$\varphi$
together with the map
![]() $p : \varphi \vdash (1 - \varepsilon, p) : \sum_{i : \mathbb{I}} \varphi \vee (i = \varepsilon)$
.
$p : \varphi \vdash (1 - \varepsilon, p) : \sum_{i : \mathbb{I}} \varphi \vee (i = \varepsilon)$
.
Theorem. The model
![]() $\widetilde{\mathcal{E}}$
supports suspensions.
$\widetilde{\mathcal{E}}$
supports suspensions.
Proof. Suppose we are given a type
![]() $\Gamma \vdash_{\widetilde{\mathcal{E}}} X$
. We first construct the naÏve suspension,
$\Gamma \vdash_{\widetilde{\mathcal{E}}} X$
. We first construct the naÏve suspension,
![]() $\mathsf{Susp}_0(X)$
as the pushout below.
$\mathsf{Susp}_0(X)$
as the pushout below.
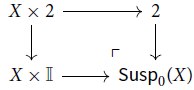
We next take the local fibrant replacement, to get
![]() $\mathsf{LFR}(\mathsf{Susp}_0(X))$
. This is then an initial
$\mathsf{LFR}(\mathsf{Susp}_0(X))$
. This is then an initial
![]() $\mathsf{Susp}(X)$
algebra, as defined by Coquand et al. (Reference Coquand, Huber and MÖrtberg2018), Section 2.2 and so we can then proceed with the same proof as they do there, observing that their argument produces by symmetry a transport operator in both directions.
$\mathsf{Susp}(X)$
algebra, as defined by Coquand et al. (Reference Coquand, Huber and MÖrtberg2018), Section 2.2 and so we can then proceed with the same proof as they do there, observing that their argument produces by symmetry a transport operator in both directions.
Theorem The model
![]() $\widetilde{\mathcal{E}}$
supports propositional truncation.
$\widetilde{\mathcal{E}}$
supports propositional truncation.
Proof. Suppose we are given a type
![]() $\Gamma \vdash_{\widetilde{\mathcal{E}}}A$
. We first define the underlying object of
$\Gamma \vdash_{\widetilde{\mathcal{E}}}A$
. We first define the underlying object of
![]() $\| A \|$
to be the W-type with reductions defined as follows.
$\| A \|$
to be the W-type with reductions defined as follows.
-
When
 $a : A$
, we add an element
$a : A$
, we add an element
 $\mathsf{inc}(a)$
to
$\mathsf{inc}(a)$
to
 $\| A \|$
.
$\| A \|$
. -
When
 $\varphi : \mathbb{F}$
,
$\varphi : \mathbb{F}$
,
 $\varepsilon \in \{0, 1\}$
and
$\varepsilon \in \{0, 1\}$
and
 $u : \sum_{i : \mathbb{I}} ((i = \varepsilon) \vee \varphi) \;\to\; \|A \| $
, we add an element
$u : \sum_{i : \mathbb{I}} ((i = \varepsilon) \vee \varphi) \;\to\; \|A \| $
, we add an element
 $\mathsf{hcomp}(\varphi, \varepsilon, u)$
to
$\mathsf{hcomp}(\varphi, \varepsilon, u)$
to
 $\| A \|$
.
$\| A \|$
. -
If
 $p : \varphi$
and
$p : \varphi$
and
 $\varepsilon$
and u are as above, then
$\varepsilon$
and u are as above, then
 $\mathsf{hcomp}(\varphi, \varepsilon, u)$
reduces to
$\mathsf{hcomp}(\varphi, \varepsilon, u)$
reduces to
 $u(1-\varepsilon, p)$
.
$u(1-\varepsilon, p)$
. -
If
 $x, y : \| A \|$
and
$x, y : \| A \|$
and
 $i : \mathbb{I}$
, then
$i : \mathbb{I}$
, then
 $\| A \|$
contains an element of the form
$\| A \|$
contains an element of the form
 $\mathsf{sq}(x, y, i)$
.
$\mathsf{sq}(x, y, i)$
. -
If x, y, i are as above and
 $i = 0$
, then
$i = 0$
, then
 $\mathsf{sq}(x, y, i)$
reduces to x.
$\mathsf{sq}(x, y, i)$
reduces to x. -
If x, y, i are as above and
 $i = 1$
, then
$i = 1$
, then
 $\mathsf{sq}(x, y, i)$
reduces to y.
$\mathsf{sq}(x, y, i)$
reduces to y.
Formally, we define this by taking the coproduct of two polynomials with reductions. The first is the one we used before for
![]() $\mathsf{LFR}$
. The second has constructors
$\mathsf{LFR}$
. The second has constructors
![]() $Y := \mathbb{I}$
, with the arity defined by
$Y := \mathbb{I}$
, with the arity defined by
![]() $X(i) := 2$
, and reductions
$X(i) := 2$
, and reductions
![]() $R(i) := (i = 0) \lor (i = 1)$
together with the map
$R(i) := (i = 0) \lor (i = 1)$
together with the map
![]() $p : (i = 0) \lor (i = 1) \vdash k(p) : 2$
defined by
$p : (i = 0) \lor (i = 1) \vdash k(p) : 2$
defined by
![]() $k(p) = 0$
if
$k(p) = 0$
if
![]() $p : i = 0$
and
$p : i = 0$
and
![]() $k(p) = 1$
if
$k(p) = 1$
if
![]() $p : i = 1$
.
$p : i = 1$
.
The remainder of the proof is the same as the syntactic description of propositional truncation by Coquand et al. (Reference Coquand, Huber and MÖrtberg2018), Section 3.3.4.
We now construct a new higher inductive type, which is a simplified version of the higher inductive type
![]() $\mathcal{J}_F$
defined by Rijke et al. (Reference Rijke, Shulman and Spitters2020, Section 2.2). Given families of types
$\mathcal{J}_F$
defined by Rijke et al. (Reference Rijke, Shulman and Spitters2020, Section 2.2). Given families of types
![]() $\Gamma \vdash_{\widetilde{\mathcal{E}}} A$
and
$\Gamma \vdash_{\widetilde{\mathcal{E}}} A$
and
![]() $\Gamma, a : A \vdash_{\widetilde{\mathcal{E}}} B(a)$
we will construct a higher inductive type
$\Gamma, a : A \vdash_{\widetilde{\mathcal{E}}} B(a)$
we will construct a higher inductive type
![]() $\mathcal{K}^\Gamma_B$
defined as follows.
$\mathcal{K}^\Gamma_B$
defined as follows.
-
When
 $a : A$
and
$a : A$
and
 $f : B(a) \to \mathcal{K}_B$
, we add an element
$f : B(a) \to \mathcal{K}_B$
, we add an element
 $\mathsf{ext}(a, f)$
to
$\mathsf{ext}(a, f)$
to
 $\mathcal{K}_B$
.
$\mathcal{K}_B$
. -
When
 $a : A$
,
$a : A$
,
 $f : B(a) \to \mathcal{K}_B$
and
$f : B(a) \to \mathcal{K}_B$
and
 $b : B(a)$
we add an element
$b : B(a)$
we add an element
 $\mathsf{isext}(a, f, b)$
to
$\mathsf{isext}(a, f, b)$
to
 $\mathsf{Path}(\mathsf{ext}(a, f), f(b))$
.
$\mathsf{Path}(\mathsf{ext}(a, f), f(b))$
.
We require that
![]() $\mathcal{K}_B$
satisfies the following elimination rule. Suppose we are given a family of types
$\mathcal{K}_B$
satisfies the following elimination rule. Suppose we are given a family of types
![]() $\Gamma, x : \mathcal{K}_B \vdash_{\widetilde{\mathcal{E}}} P(x)$
together with the terms below.
$\Gamma, x : \mathcal{K}_B \vdash_{\widetilde{\mathcal{E}}} P(x)$
together with the terms below.
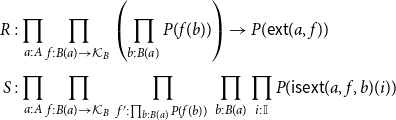 \begin{align*} R &: \prod_{a : A} \prod_{f : B(a) \to \mathcal{K}_B} \left(\prod_{b : B(a)} P(f(b))\right) \to P(\mathsf{ext}(a, f)) \\[4pt] S &: \prod_{a : A} \prod_{f : B(a) \to \mathcal{K}_B} \,\prod_{f' : \prod_{b : B(a)} P(f(b))} \,\prod_{b : B(a)} \prod_{i : \mathbb{I}} P(\mathsf{isext}(a, f, b)(i))\end{align*}
\begin{align*} R &: \prod_{a : A} \prod_{f : B(a) \to \mathcal{K}_B} \left(\prod_{b : B(a)} P(f(b))\right) \to P(\mathsf{ext}(a, f)) \\[4pt] S &: \prod_{a : A} \prod_{f : B(a) \to \mathcal{K}_B} \,\prod_{f' : \prod_{b : B(a)} P(f(b))} \,\prod_{b : B(a)} \prod_{i : \mathbb{I}} P(\mathsf{isext}(a, f, b)(i))\end{align*}
Suppose further that S satisfies the equalities
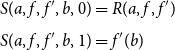 \begin{align*} S(a, f, f', b, 0) &= R(a, f, f') \\[4pt] S(a, f, f', b, 1) &= f'(b)\end{align*}
\begin{align*} S(a, f, f', b, 0) &= R(a, f, f') \\[4pt] S(a, f, f', b, 1) &= f'(b)\end{align*}
Then we have a choice of term
![]() $\Gamma, x : \mathcal{K}_B \vdash s(x) : P(x)$
satisfying the following computation rules for
$\Gamma, x : \mathcal{K}_B \vdash s(x) : P(x)$
satisfying the following computation rules for
![]() $a : A$
,
$a : A$
,
![]() $f : B(a) \to \mathcal{K}_B$
and
$f : B(a) \to \mathcal{K}_B$
and
![]() $b :B(a)$
.
$b :B(a)$
.
Moreover the choice of term is strictly preserved by reindexing.
We use the techniques developed by Coquand, Huber and MÖrtberg together with W-types with reductions for constructing the actual objects. In order to give
![]() $\mathcal{K}^\Gamma_B$
the structure of a fibration, we need to define a composition operator. We will do this by freely adding an
$\mathcal{K}^\Gamma_B$
the structure of a fibration, we need to define a composition operator. We will do this by freely adding an
![]() $\mathsf{hcomp}$
operator, and then combining it with a transport operator, which we will explicitly define.
$\mathsf{hcomp}$
operator, and then combining it with a transport operator, which we will explicitly define.
Definition 10. Let
![]() $\Gamma \vdash_{\mathcal{E}} X$
be a type. We define the naÏve cone,
$\Gamma \vdash_{\mathcal{E}} X$
be a type. We define the naÏve cone,
![]() $\mathsf{Cone}(X)$
to be the following pushout
Footnote 3
.
$\mathsf{Cone}(X)$
to be the following pushout
Footnote 3
.
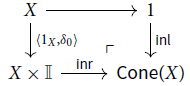
We can now define
![]() $\mathcal{K}^\Gamma_B$
to be the following W-type with reductions.
$\mathcal{K}^\Gamma_B$
to be the following W-type with reductions.
-
When
 $a : A$
,
$a : A$
,
 $c : \mathsf{Cone}(B(a))$
and
$c : \mathsf{Cone}(B(a))$
and
 $f : B(a) \to \mathcal{K}_B$
, we add an element
$f : B(a) \to \mathcal{K}_B$
, we add an element
 $\mathsf{pastecone}(a, c, f)$
to
$\mathsf{pastecone}(a, c, f)$
to
 $\mathcal{K}_B$
.
$\mathcal{K}_B$
. -
If a, c, f are as above and c is of the form
 $\mathsf{inr}(b, 1)$
for
$\mathsf{inr}(b, 1)$
for
 $b : B(a)$
, then
$b : B(a)$
, then
 $\mathsf{pastecone}(a, c, f)$
reduces to f(b).
$\mathsf{pastecone}(a, c, f)$
reduces to f(b). -
When
 $\varphi : \mathbb{F}$
,
$\varphi : \mathbb{F}$
,
 $\varepsilon : \{ 0, 1 \}$
and
$\varepsilon : \{ 0, 1 \}$
and
 $u : \sum_{i : \mathbb{I}} ((i = 0) \vee \varphi) \;\to\; \mathcal{K}_B$
, we add an element
$u : \sum_{i : \mathbb{I}} ((i = 0) \vee \varphi) \;\to\; \mathcal{K}_B$
, we add an element
 $\mathsf{hcomp}(\varphi, \varepsilon, u)$
to
$\mathsf{hcomp}(\varphi, \varepsilon, u)$
to
 $\mathcal{K}_B$
.
$\mathcal{K}_B$
. -
If
 $p : \varphi$
, and
$p : \varphi$
, and
 $\varepsilon$
and u are as above then
$\varepsilon$
and u are as above then
 $\mathsf{hcomp}(\varphi, \varepsilon, u)$
reduces to
$\mathsf{hcomp}(\varphi, \varepsilon, u)$
reduces to
 $u(1 - \varepsilon, p)$
.
$u(1 - \varepsilon, p)$
.
To check that this really is a W-type with reductions, we need to define the polynomial with reductions. We take it to be the coproduct of the following two polynomials with reductions.
We define the first component of the coproduct as follows. We take the constructors Y to be
![]() $\sum_{a : A} \mathsf{Cone}(B(a))$
and the arities X(a, c) to be B(a). We take the reductions
$\sum_{a : A} \mathsf{Cone}(B(a))$
and the arities X(a, c) to be B(a). We take the reductions
![]() $R(a, \mathsf{inl}(\ast))$
to be
$R(a, \mathsf{inl}(\ast))$
to be
![]() $\bot$
and
$\bot$
and
![]() $R(a, \mathsf{inr}(b, i))$
to be
$R(a, \mathsf{inr}(b, i))$
to be
![]() $(i = 1)$
together with the map
$(i = 1)$
together with the map
![]() $R(a, \mathsf{inr}(b, i)) \vdash b : B(a)$
. Note that
$R(a, \mathsf{inr}(b, i)) \vdash b : B(a)$
. Note that
![]() $R : \left(\sum_{a : A}\mathsf{Cone}(B(a))\right) \to \mathbb{F}$
is well-defined because we have
$R : \left(\sum_{a : A}\mathsf{Cone}(B(a))\right) \to \mathbb{F}$
is well-defined because we have
![]() $(0 = 1) = \bot$
by propositional extensionality.
$(0 = 1) = \bot$
by propositional extensionality.
The second component in the coproduct is the polynomial with reductions that we used for local fibrant replacement.
Lemma 11. We construct a transport operator for
![]() $\mathcal{K}^\Gamma_B$
.
$\mathcal{K}^\Gamma_B$
.
Proof. We give a proof for the direction
![]() $\varepsilon =0$
. The construction for the other direction is exactly the same by symmetry.
$\varepsilon =0$
. The construction for the other direction is exactly the same by symmetry.
Suppose we are given
![]() $\varphi : \mathbb{F}$
and a path
$\varphi : \mathbb{F}$
and a path
![]() $\gamma$
in
$\gamma$
in
![]() $\Gamma$
which is constant on
$\Gamma$
which is constant on
![]() $\varphi$
. We need to define a transport operator, which is a map
$\varphi$
. We need to define a transport operator, which is a map
![]() $t : \mathcal{K}_{B(\gamma(0))} \to \mathcal{K}_{B(\gamma(1))}$
such that t is the identity when
$t : \mathcal{K}_{B(\gamma(0))} \to \mathcal{K}_{B(\gamma(1))}$
such that t is the identity when
![]() $\varphi$
is true. Formally this map can be defined by giving an appropriate algebra structure on
$\varphi$
is true. Formally this map can be defined by giving an appropriate algebra structure on
![]() $\mathcal{K}_{B(\gamma(1))}$
and then using the initiality of
$\mathcal{K}_{B(\gamma(1))}$
and then using the initiality of
![]() $\mathcal{K}_{B(\gamma(0))}$
. However, for clarity we will present the proof as an argument by higher recursion on the definition of
$\mathcal{K}_{B(\gamma(0))}$
. However, for clarity we will present the proof as an argument by higher recursion on the definition of
![]() $\mathcal{K}_{B(\gamma(0))}$
.
$\mathcal{K}_{B(\gamma(0))}$
.
We need to show how to define
![]() $t(\mathsf{pastecone}(a, c, f))$
and
$t(\mathsf{pastecone}(a, c, f))$
and
![]() $t(\mathsf{hcomp}(\psi, \varepsilon, u))$
, and then check that the definition respects the reduction equations. For the latter, we define the transport operator so that it preserves the
$t(\mathsf{hcomp}(\psi, \varepsilon, u))$
, and then check that the definition respects the reduction equations. For the latter, we define the transport operator so that it preserves the
![]() $\mathsf{hcomp}$
structure, which determines it uniquely, following Coquand et al. (Reference Coquand, Huber and MÖrtberg2018). For the former, we recall that
$\mathsf{hcomp}$
structure, which determines it uniquely, following Coquand et al. (Reference Coquand, Huber and MÖrtberg2018). For the former, we recall that
![]() $\mathsf{Cone}(B(a))$
was defined as a pushout, and so we can split into a further two cases. Either c is of the form
$\mathsf{Cone}(B(a))$
was defined as a pushout, and so we can split into a further two cases. Either c is of the form
![]() $\mathsf{inl}(\ast)$
, or it is of the form
$\mathsf{inl}(\ast)$
, or it is of the form
![]() $\mathsf{inr}(b, i)$
where
$\mathsf{inr}(b, i)$
where
![]() $b : B(a)$
and
$b : B(a)$
and
![]() $i : \mathbb{I}$
. Now in addition to the reduction equation, we have to also satisfy
$i : \mathbb{I}$
. Now in addition to the reduction equation, we have to also satisfy
![]() $t(\mathsf{inl}(\ast)) = t(\mathsf{inr}(b, 0))$
in order to eliminate out of the pushout.
$t(\mathsf{inl}(\ast)) = t(\mathsf{inr}(b, 0))$
in order to eliminate out of the pushout.
Write
![]() $t_A$
for the transport
$t_A$
for the transport
![]() $A(\gamma(0)) \to A(\gamma(1))$
and
$A(\gamma(0)) \to A(\gamma(1))$
and
![]() $t_B$
for the transport
$t_B$
for the transport
![]() $\prod_{a : A(\Gamma(0))} B(a) \to B(t_A(a)) $
ensuring that
$\prod_{a : A(\Gamma(0))} B(a) \to B(t_A(a)) $
ensuring that
![]() $t_A(a) = a$
and
$t_A(a) = a$
and
![]() $t_B(b) = b$
when
$t_B(b) = b$
when
![]() $\varphi = \top$
, for all
$\varphi = \top$
, for all
![]() $a : A(\gamma(0))$
and
$a : A(\gamma(0))$
and
![]() $b : B(a)$
. Write
$b : B(a)$
. Write
![]() $t_B^{-1}$
for the homotopy inverse
$t_B^{-1}$
for the homotopy inverse
![]() $\prod_{a : A(\Gamma(0))} B(t_A(a)) \to B(a)$
, again ensuring that
$\prod_{a : A(\Gamma(0))} B(t_A(a)) \to B(a)$
, again ensuring that
![]() $t_B^{-1}(b) = b$
when
$t_B^{-1}(b) = b$
when
![]() $\varphi = \top$
. Since we are only guaranteed the existence of a homotopy inverse, not a strict inverse, we do not necessarily have
$\varphi = \top$
. Since we are only guaranteed the existence of a homotopy inverse, not a strict inverse, we do not necessarily have
![]() $t_B^{-1} \circ t_B = 1_{B(a)}$
. We can however construct paths
$t_B^{-1} \circ t_B = 1_{B(a)}$
. We can however construct paths
![]() $p : \prod_{a : A(\Gamma(0))} \prod_{b : B(a)} \mathbb{I} \to B(a)$
satisfying for all
$p : \prod_{a : A(\Gamma(0))} \prod_{b : B(a)} \mathbb{I} \to B(a)$
satisfying for all
![]() $a : A(\Gamma(0))$
and
$a : A(\Gamma(0))$
and
![]() $b : B(a)$
that
$b : B(a)$
that
![]() $p(a, b, 0) = t_B^{-1}(t_B(b)) $
and
$p(a, b, 0) = t_B^{-1}(t_B(b)) $
and
![]() $p(a, b, 1) = b$
. Furthermore, we may assume that for any a, b and i, if
$p(a, b, 1) = b$
. Furthermore, we may assume that for any a, b and i, if
![]() $\varphi = \top$
then
$\varphi = \top$
then
![]() $p(a, b, i) = b$
.
$p(a, b, i) = b$
.
We define
![]() $t(\mathsf{pastecone}(a, \mathsf{inl}(\ast), f))$
to be of the form
$t(\mathsf{pastecone}(a, \mathsf{inl}(\ast), f))$
to be of the form
![]() $\mathsf{pastecone}(t_A(a), \mathsf{inl}(\ast), f')$
, where we still need to define a function
$\mathsf{pastecone}(t_A(a), \mathsf{inl}(\ast), f')$
, where we still need to define a function
![]() $f' : B(t_A(a)) \to \mathcal{K}_{B(\gamma(1))}$
. Note that we may assume by recursion that for each
$f' : B(t_A(a)) \to \mathcal{K}_{B(\gamma(1))}$
. Note that we may assume by recursion that for each
![]() $b : B(a)$
, t(f(b)) has already been defined and belongs to
$b : B(a)$
, t(f(b)) has already been defined and belongs to
![]() $\mathcal{K}_{B(\gamma(1))}$
. Hence, we can simply define f’ to be
$\mathcal{K}_{B(\gamma(1))}$
. Hence, we can simply define f’ to be
![]() $t \circ f \circ t_B^{-1}$
.
$t \circ f \circ t_B^{-1}$
.
The obvious first attempt at defining
![]() $t(\mathsf{pastecone}(a, \mathsf{inr}(b, i), f))$
would be
$t(\mathsf{pastecone}(a, \mathsf{inr}(b, i), f))$
would be
![]() $\mathsf{pastecone}(t_A(a), \mathsf{inr}(t_B(b), i), t \circ f \circ t_B^{-1})$
. Note however that this does not satisfy the reduction equations. This is because when
$\mathsf{pastecone}(t_A(a), \mathsf{inr}(t_B(b), i), t \circ f \circ t_B^{-1})$
. Note however that this does not satisfy the reduction equations. This is because when
![]() $i = 1$
,
$i = 1$
,
![]() $\mathsf{pastecone}(a, \mathsf{inr}(b, i), f)$
reduces to f(b) and
$\mathsf{pastecone}(a, \mathsf{inr}(b, i), f)$
reduces to f(b) and
![]() $\mathsf{pastecone}(t_A(a), \mathsf{inr}(t_B(b), i), t \circ f \circ t_B^{-1})$
reduces to
$\mathsf{pastecone}(t_A(a), \mathsf{inr}(t_B(b), i), t \circ f \circ t_B^{-1})$
reduces to
![]() $t(f(t_B^{-1}(t_B(b))))$
which is not necessarily strictly equal to t(f(b)). We fix this using the
$t(f(t_B^{-1}(t_B(b))))$
which is not necessarily strictly equal to t(f(b)). We fix this using the
![]() $\mathsf{hcomp}$
constructor, following the construction of homotopy pushouts in Coquand et al. (Reference Coquand, Huber and MÖrtberg2018), Section 2.3. We define
$\mathsf{hcomp}$
constructor, following the construction of homotopy pushouts in Coquand et al. (Reference Coquand, Huber and MÖrtberg2018), Section 2.3. We define
![]() $\psi : \mathbb{F}$
to be
$\psi : \mathbb{F}$
to be
![]() $\varphi \vee (i = 0) \vee (i = 1)$
. We then define
$\varphi \vee (i = 0) \vee (i = 1)$
. We then define
![]() $u : \sum_{j : \mathbb{I}} (\psi \vee (j = 0)) \to \mathcal{K}_{B(\gamma(a))}$
as follows.
$u : \sum_{j : \mathbb{I}} (\psi \vee (j = 0)) \to \mathcal{K}_{B(\gamma(a))}$
as follows.
 \begin{equation*} u(j, \ast) :\equiv \begin{cases} \mathsf{pastecone}(t_A(a), \mathsf{inr}(t_B(b), i), t \circ f \circ t_B^{-1}) & j = 0 \\ \mathsf{pastecone}(a, \mathsf{inr}(b, i), t \circ f) & \varphi = \top \\ \mathsf{pastecone}(t_A(a), \mathsf{inl}(\ast), t \circ f \circ t_B^{-1}) & i = 0 \\ t(f(p(a, b, j))) & i = 1 \end{cases} \end{equation*}
\begin{equation*} u(j, \ast) :\equiv \begin{cases} \mathsf{pastecone}(t_A(a), \mathsf{inr}(t_B(b), i), t \circ f \circ t_B^{-1}) & j = 0 \\ \mathsf{pastecone}(a, \mathsf{inr}(b, i), t \circ f) & \varphi = \top \\ \mathsf{pastecone}(t_A(a), \mathsf{inl}(\ast), t \circ f \circ t_B^{-1}) & i = 0 \\ t(f(p(a, b, j))) & i = 1 \end{cases} \end{equation*}
We then define
![]() $t(\mathsf{pastecone}(a, \mathsf{inr}(b, i), f))$
to be
$t(\mathsf{pastecone}(a, \mathsf{inr}(b, i), f))$
to be
![]() $\mathsf{hcomp}(\psi, 0, u)$
. The reduction equation for
$\mathsf{hcomp}(\psi, 0, u)$
. The reduction equation for
![]() $\mathsf{hcomp}$
then ensures that we do satisfy the reduction equation for
$\mathsf{hcomp}$
then ensures that we do satisfy the reduction equation for
![]() $\mathsf{pastecone}$
and also retain the necessary equations for the pushout and furthermore ensures that the resulting map
$\mathsf{pastecone}$
and also retain the necessary equations for the pushout and furthermore ensures that the resulting map
![]() $t : \mathcal{K}_{B(\gamma(0))} \to \mathcal{K}_{B(\gamma(1))}$
is (one direction of) a transport operator.
$t : \mathcal{K}_{B(\gamma(0))} \to \mathcal{K}_{B(\gamma(1))}$
is (one direction of) a transport operator.
Theorem We construct a fibration structure for each
![]() $\mathcal{K}_B$
, which is strictly preserved by reindexing.
$\mathcal{K}_B$
, which is strictly preserved by reindexing.
Proof. By Lemmas 11 and 8.
Lemma 12. We construct terms
![]() $\mathsf{ext}$
and
$\mathsf{ext}$
and
![]() $\mathsf{isext}$
for
$\mathsf{isext}$
for
![]() $\mathcal{K}_B$
that satisfy the appropriate equations.
$\mathcal{K}_B$
that satisfy the appropriate equations.
Proof.
Lemma 13.
![]() $\mathcal{K}_B$
satisfies the necessary induction principle.
$\mathcal{K}_B$
satisfies the necessary induction principle.
Proof. Suppose we are given a family of types
![]() $\Gamma, x : \mathcal{K}_B \vdash_{\widetilde{\mathcal{E}}} P(x)$
together with the terms below.
$\Gamma, x : \mathcal{K}_B \vdash_{\widetilde{\mathcal{E}}} P(x)$
together with the terms below.
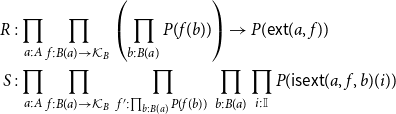 \begin{align*} R &: \prod_{a : A} \prod_{f : B(a) \to \mathcal{K}_B} \left(\prod_{b : B(a)} P(f(b))\right) \to P(\mathsf{ext}(a, f)) \\ S &: \prod_{a : A} \prod_{f : B(a) \to \mathcal{K}_B} \, \prod_{f' : \prod_{b : B(a)} P(f(b))} \, \prod_{b : B(a)} \prod_{i : \mathbb{I}} P(\mathsf{isext}(a, f, b)(i)) \end{align*}
\begin{align*} R &: \prod_{a : A} \prod_{f : B(a) \to \mathcal{K}_B} \left(\prod_{b : B(a)} P(f(b))\right) \to P(\mathsf{ext}(a, f)) \\ S &: \prod_{a : A} \prod_{f : B(a) \to \mathcal{K}_B} \, \prod_{f' : \prod_{b : B(a)} P(f(b))} \, \prod_{b : B(a)} \prod_{i : \mathbb{I}} P(\mathsf{isext}(a, f, b)(i)) \end{align*}
We need to define a term
![]() $\Gamma, x : \mathcal{K}_B \vdash s(x) : P(x)$
satisfying the appropriate equalities. We define s by higher recursion on the construction of
$\Gamma, x : \mathcal{K}_B \vdash s(x) : P(x)$
satisfying the appropriate equalities. We define s by higher recursion on the construction of
![]() $\mathcal{K}_B$
. We first deal with the case
$\mathcal{K}_B$
. We first deal with the case
![]() $s(\mathsf{pastecone}(a, c, f))$
. Recalling that
$s(\mathsf{pastecone}(a, c, f))$
. Recalling that
![]() $\mathsf{Cone}(B(a))$
is defined as a pushout, we can split into the two cases
$\mathsf{Cone}(B(a))$
is defined as a pushout, we can split into the two cases
![]() $c = \mathsf{inl}(\ast)$
and
$c = \mathsf{inl}(\ast)$
and
![]() $c = \mathsf{inr}(b, i)$
for some
$c = \mathsf{inr}(b, i)$
for some
![]() $b : B(a)$
and
$b : B(a)$
and
![]() $i : \mathbb{I}$
.
$i : \mathbb{I}$
.
We define
It is straightforward to check that this does preserve the reduction and pushout equations and so does give a well defined map. One can show it is a section again by higher recursion and the computation rules are satisfied by definition.
Finally, to define
![]() $s(\mathsf{hcomp}(\varphi, \varepsilon, u))$
, we use the fibration structure on
$s(\mathsf{hcomp}(\varphi, \varepsilon, u))$
, we use the fibration structure on
![]() $\Gamma, x : \mathcal{K}_B \vdash_{\mathcal{E}} P(x)$
.
$\Gamma, x : \mathcal{K}_B \vdash_{\mathcal{E}} P(x)$
.
3.2 Internal cubical models
Let
![]() $\mathcal{S}$
be a model of dependent type theory with dependent product types, dependent sum types, extensional identity types, unit type, finite colimits, W-types and a countable chain of universes. We also assume that every context of
$\mathcal{S}$
be a model of dependent type theory with dependent product types, dependent sum types, extensional identity types, unit type, finite colimits, W-types and a countable chain of universes. We also assume that every context of
![]() $\mathcal{S}$
is isomorphic to
$\mathcal{S}$
is isomorphic to
![]() $1.X$
for some type
$1.X$
for some type
![]() $1 \vdash_{\mathcal{S}} X$
. In particular, the category
$1 \vdash_{\mathcal{S}} X$
. In particular, the category
![]() $\mathbb{C}^{\mathcal{S}}$
is finitely complete so that internal categories in
$\mathbb{C}^{\mathcal{S}}$
is finitely complete so that internal categories in
![]() $\mathbb{C}^{\mathcal{S}}$
make sense. Let
$\mathbb{C}^{\mathcal{S}}$
make sense. Let
![]() $\Box$
denote the internal category in
$\Box$
denote the internal category in
![]() $\mathbb{C}^{\mathcal{S}}$
in which the objects are the natural numbers and the morphisms from n to m are the order-preserving functions
$\mathbb{C}^{\mathcal{S}}$
in which the objects are the natural numbers and the morphisms from n to m are the order-preserving functions
![]() $\mathbf{2}^{n} \to \mathbf{2}^{m}$
. Note that
$\mathbf{2}^{n} \to \mathbf{2}^{m}$
. Note that
![]() $\mathcal{S}$
has a natural number object since it has W-types. Spitters (Reference Spitters2016) has observed that
$\mathcal{S}$
has a natural number object since it has W-types. Spitters (Reference Spitters2016) has observed that
![]() $\Box$
is equivalent to the opposite of the category of free finitely generated distributive lattices. We will refer to internal presheaves over
$\Box$
is equivalent to the opposite of the category of free finitely generated distributive lattices. We will refer to internal presheaves over
![]() $\Box$
as internal cubical objects.
$\Box$
as internal cubical objects.
Theorem Under those assumptions, the category of internal cubical objects in
![]() $\mathcal{S}$
is part of a model of type theory that satisfies Assumption 4.
$\mathcal{S}$
is part of a model of type theory that satisfies Assumption 4.
Example 14. Let
![]() $\mathcal{A}$
be a partial combinatory algebra. It is well-known that the category
$\mathcal{A}$
be a partial combinatory algebra. It is well-known that the category
![]() $\mathbf{Asm}(\mathcal{A})$
of assemblies on
$\mathbf{Asm}(\mathcal{A})$
of assemblies on
![]() $\mathcal{A}$
is part of a model of type theory with dependent product types, dependent sum types, extensional identity types, unit type and finite colimits. It is also known that
$\mathcal{A}$
is part of a model of type theory with dependent product types, dependent sum types, extensional identity types, unit type and finite colimits. It is also known that
![]() $\mathbf{Asm}(\mathcal{A})$
has W-types (an explicit construction is found in van den Berg Reference van den Berg2006, Section 2.2). Assuming a countable chain of Grothendieck universes in the set theory,
$\mathbf{Asm}(\mathcal{A})$
has W-types (an explicit construction is found in van den Berg Reference van den Berg2006, Section 2.2). Assuming a countable chain of Grothendieck universes in the set theory,
![]() $\mathbf{Asm}(\mathcal{A})$
has a countable chain of universes, since for each Grothendieck universe one may implement a universe in assemblies as the uniform assembly on the set of small assemblies. Thus, the category
$\mathbf{Asm}(\mathcal{A})$
has a countable chain of universes, since for each Grothendieck universe one may implement a universe in assemblies as the uniform assembly on the set of small assemblies. Thus, the category
![]() $\mathbf{CAsm}(\mathcal{A})$
of internal cubical objects in
$\mathbf{CAsm}(\mathcal{A})$
of internal cubical objects in
![]() $\mathbf{Asm}(\mathcal{A})$
is part of a model of type theory that satisfies Assumption 4.
$\mathbf{Asm}(\mathcal{A})$
is part of a model of type theory that satisfies Assumption 4.
It is shown in Orton and Pitts (Reference Orton and Pitts2018) that, when
![]() $\mathcal{S} = \mathbf{Set}$
, the category of presheaves over
$\mathcal{S} = \mathbf{Set}$
, the category of presheaves over
![]() $\Box$
satisfies all the axioms of Orton and Pitts if we take
$\Box$
satisfies all the axioms of Orton and Pitts if we take
![]() $\mathbb{F}$
to be the presheaf of locally decidable propositions. The proof works for an arbitrary
$\mathbb{F}$
to be the presheaf of locally decidable propositions. The proof works for an arbitrary
![]() $\mathcal{S}$
and one can show that the category of internal cubical objects in
$\mathcal{S}$
and one can show that the category of internal cubical objects in
![]() $\mathcal{S}$
is part of a model of type theory satisfying Assumption 3 except the existence of cofibrant W-types with reductions (see also Uemura Reference Uemura2019). To construct cofibrant W-types with reductions, we recall the following from Swan (Reference Swan2018).
$\mathcal{S}$
is part of a model of type theory satisfying Assumption 3 except the existence of cofibrant W-types with reductions (see also Uemura Reference Uemura2019). To construct cofibrant W-types with reductions, we recall the following from Swan (Reference Swan2018).
Theorem Let
![]() $\mathcal{E}$
be a locally cartesian closed category with finite colimits and disjoint coproducts and W-types, and let
$\mathcal{E}$
be a locally cartesian closed category with finite colimits and disjoint coproducts and W-types, and let
![]() $\mathbf{C}$
be an internal category in
$\mathbf{C}$
be an internal category in
![]() $\mathcal{E}$
. Then the category
$\mathcal{E}$
. Then the category
![]() $\mathcal{P}(\mathbf{C})$
of internal presheaves over
$\mathcal{P}(\mathbf{C})$
of internal presheaves over
![]() $\mathbf{C}$
has all locally decidable W-types with reductions.
$\mathbf{C}$
has all locally decidable W-types with reductions.
We furthermore observe that one can show that this construction is stable under pullback up to isomorphism using a technique similar to the one used by Gambino and Hyland for ordinary W-types (Gambino and Hyland Reference Gambino and Hyland2004). The reason is that pointed polynomial endofunctors are stable under pullback because they are constructed from
![]() $\Sigma$
types,
$\Sigma$
types,
![]() $\Pi$
types and pushouts, all of which are preserved by pullback, and in locally cartesian closed categories, the initial algebras of such pointed endofunctors are also stable under pullback. However, to ensure that the construction is strictly preserved requires a little more work.
$\Pi$
types and pushouts, all of which are preserved by pullback, and in locally cartesian closed categories, the initial algebras of such pointed endofunctors are also stable under pullback. However, to ensure that the construction is strictly preserved requires a little more work.
We show how to use the non-split version above to construct split W-types with reductions. The essential idea is to carry out the construction given above “pointwise,” expanding out the method suggested by Coquand et al. (Reference Coquand, Huber and MÖrtberg2018, Section 2.2). Since we define cubical sets here as a category of presheaves in the usual, contravariant sense, we work with contravariant presheaves here, although the original proof in Swan (Reference Swan2018) is phrased in terms of covariant presheaves. We also make minor adjustments to fit with the ‘split’ version appearing in Section 2.2.
Suppose that we are given a context
![]() $\Gamma \in \mathcal{P}(\mathbf{C})$
together with a type
$\Gamma \in \mathcal{P}(\mathbf{C})$
together with a type
![]() $Y \in \mathcal{P}(\int_\mathbf{C} \Gamma)$
, a type
$Y \in \mathcal{P}(\int_\mathbf{C} \Gamma)$
, a type
![]() $X \in \mathcal{P}(\int_C \{Y\})$
, a locally decidable monomorphism
$X \in \mathcal{P}(\int_C \{Y\})$
, a locally decidable monomorphism
![]() $R \rightarrowtail Y$
and a map
$R \rightarrowtail Y$
and a map
![]() $k : \prod_{y : R} X(y)$
over
$k : \prod_{y : R} X(y)$
over
![]() $\int_\mathbf{C} \Gamma$
.
$\int_\mathbf{C} \Gamma$
.
We need to show how to define a strict version of the W-type with reductions W(Y, X, R). We will refer to the new strict version as W’(Y, X, R). This should be an element of
![]() $\mathcal{P}(\int_\mathbf{C} \Gamma)$
, so in particular we need to define a family of types
$\mathcal{P}(\int_\mathbf{C} \Gamma)$
, so in particular we need to define a family of types
![]() $W'(Y, X, R)(c, \gamma)$
indexed by objects c of
$W'(Y, X, R)(c, \gamma)$
indexed by objects c of
![]() $\mathbf{C}$
and elements
$\mathbf{C}$
and elements
![]() $\gamma : \Gamma(c)$
.
$\gamma : \Gamma(c)$
.
We fix such a c and
![]() $\gamma$
. We first note that we have a locally decidable polynomial with reductions
$\gamma$
. We first note that we have a locally decidable polynomial with reductions
![]() $Y_\gamma, X_\gamma, R_\gamma$
in the internal presheaf category
$Y_\gamma, X_\gamma, R_\gamma$
in the internal presheaf category
![]() $\mathcal{P}(\int_\mathbf{C} \mathbf{C}(-,c))$
given by reindexing along the map
$\mathcal{P}(\int_\mathbf{C} \mathbf{C}(-,c))$
given by reindexing along the map
![]() $\mathbf{C}(-,c) \to \Gamma$
given by Yoneda. We then carry out the ‘non-strict’ construction to get a presheaf
$\mathbf{C}(-,c) \to \Gamma$
given by Yoneda. We then carry out the ‘non-strict’ construction to get a presheaf
![]() $W(Y_\gamma, X_\gamma, R_\gamma)$
on
$W(Y_\gamma, X_\gamma, R_\gamma)$
on
![]() $\int_\mathbf{C} \mathbf{C}(-,c)$
and finally we define
$\int_\mathbf{C} \mathbf{C}(-,c)$
and finally we define
![]() $W'(Y, X, R)(c, \gamma)$
to be
$W'(Y, X, R)(c, \gamma)$
to be
![]() $W(Y_\gamma, X_\gamma, R_\gamma) (c, 1_c)$
.
$W(Y_\gamma, X_\gamma, R_\gamma) (c, 1_c)$
.
For completeness, we unfold the definitions to obtain the following explicit description of
![]() $W'(Y, X, R)(c, \gamma)$
. We first define the dependent W-type
$W'(Y, X, R)(c, \gamma)$
. We first define the dependent W-type
![]() $N_0$
of normal forms indexed by the objects (d, f) of
$N_0$
of normal forms indexed by the objects (d, f) of
![]() $\int_\mathbf{C} \mathbf{C}(-,c)$
.
$\int_\mathbf{C} \mathbf{C}(-,c)$
.
If (d, f) is an object of
![]() $\int_\mathbf{C} \mathbf{C}(-,c)$
, we add an element to
$\int_\mathbf{C} \mathbf{C}(-,c)$
, we add an element to
![]() $N_0(d, f)$
of the form
$N_0(d, f)$
of the form
![]() $\sup\!(y, \alpha)$
whenever y is an element of
$\sup\!(y, \alpha)$
whenever y is an element of
![]() $Y(d, \Gamma(f)(\gamma))$
that does not belong to the subobject
$Y(d, \Gamma(f)(\gamma))$
that does not belong to the subobject
![]() $R(d, \Gamma(f)(\gamma))$
and
$R(d, \Gamma(f)(\gamma))$
and
![]() $\alpha$
is an element of the following type.
$\alpha$
is an element of the following type.
The next step is to define maps
![]() $N_0(d, f) \to N_0(e, f \circ g)$
whenever
$N_0(d, f) \to N_0(e, f \circ g)$
whenever
![]() $g \colon e \to d$
and
$g \colon e \to d$
and
![]() $f \colon d \to c$
in
$f \colon d \to c$
in
![]() $\mathbf{C}$
. Say that we are given an element of
$\mathbf{C}$
. Say that we are given an element of
![]() $N_0(d, f)$
of the form
$N_0(d, f)$
of the form
![]() $\sup\!(y, \alpha)$
. We recall that
$\sup\!(y, \alpha)$
. We recall that
![]() $N_0(g)(\!\sup\!(y, \alpha))$
is defined by splitting into cases depending on whether or not y belongs to the subobject
$N_0(g)(\!\sup\!(y, \alpha))$
is defined by splitting into cases depending on whether or not y belongs to the subobject
![]() $R(d, \Gamma(f)(\gamma))$
. If it does, we define
$R(d, \Gamma(f)(\gamma))$
. If it does, we define
![]() $N_0(g)(\!\sup\!(y, \alpha))$
to be
$N_0(g)(\!\sup\!(y, \alpha))$
to be
![]() $\alpha(g,k(y))$
. Otherwise, we define
$\alpha(g,k(y))$
. Otherwise, we define
![]() $N_0(g)(\!\sup\!(y, \alpha))$
to be
$N_0(g)(\!\sup\!(y, \alpha))$
to be
![]() $\sup\!(Y(g)(y), \alpha')$
where
$\sup\!(Y(g)(y), \alpha')$
where
![]() $\alpha'(h, x)$
is defined to be
$\alpha'(h, x)$
is defined to be
![]() $\alpha(g \circ h, x)$
.
$\alpha(g \circ h, x)$
.
We then define N(d, f) for each
![]() $f : d \to c$
to be the subobject of
$f : d \to c$
to be the subobject of
![]() $N_0(d, f)$
consisting of hereditarily natural elements and verify that this does indeed define a presheaf on
$N_0(d, f)$
consisting of hereditarily natural elements and verify that this does indeed define a presheaf on
![]() $\int_\mathbf{C} \mathbf{C}(-,c)$
. But this is identical to Swan (Reference Swan2018), Section 4 so we omit the details.
$\int_\mathbf{C} \mathbf{C}(-,c)$
. But this is identical to Swan (Reference Swan2018), Section 4 so we omit the details.
If we then define
![]() $W'(Y, X, R)(c, \gamma)$
to be
$W'(Y, X, R)(c, \gamma)$
to be
![]() $N(c, 1_c)$
, then this is strictly stable under reindexing by definition.
$N(c, 1_c)$
, then this is strictly stable under reindexing by definition.
One can construct by recursion an isomorphism between N(d, f) and
![]() $W(Y, X, R)(d, \Gamma(f)(\gamma))$
for each
$W(Y, X, R)(d, \Gamma(f)(\gamma))$
for each
![]() $f : d \to c$
. In particular, this gives us an isomorphism between
$f : d \to c$
. In particular, this gives us an isomorphism between
![]() $N(c, 1_c)$
and
$N(c, 1_c)$
and
![]() $W(Y, X, R)(c, \gamma)$
, and so we have a canonical isomorphism between
$W(Y, X, R)(c, \gamma)$
, and so we have a canonical isomorphism between
![]() $W'(Y, X, R)(c, \gamma)$
and
$W'(Y, X, R)(c, \gamma)$
and
![]() $W(Y, X, R)(c, \gamma)$
. It follows that we can assign an initial algebra structure to
$W(Y, X, R)(c, \gamma)$
. It follows that we can assign an initial algebra structure to
![]() $W'(Y, X, R)(c, \gamma)$
by transferring the algebra structure on
$W'(Y, X, R)(c, \gamma)$
by transferring the algebra structure on
![]() $W(Y, X, R)(c, \gamma)$
via the isomorphism.
$W(Y, X, R)(c, \gamma)$
via the isomorphism.
3.3 Discrete types
We introduce a class of types in an Orton–Pitts model for future use. Let
![]() $\mathcal{E}$
be a model of type theory satisfying Assumption 4.
$\mathcal{E}$
be a model of type theory satisfying Assumption 4.
Definition 15. A type
![]() $1 \vdash X$
is said to be discrete if the map
$1 \vdash X$
is said to be discrete if the map
![]() $\lambda x.\lambda i.x : X \to X^{\mathbb{I}}$
is an isomorphism.
$\lambda x.\lambda i.x : X \to X^{\mathbb{I}}$
is an isomorphism.
The proofs of the following propositions are found in Uemura (Reference Uemura2019).
Proposition 16. Every discrete type
![]() $1 \vdash X$
carries a fibration structure.
$1 \vdash X$
carries a fibration structure.
Proposition 17. If a type
![]() $1 \vdash X$
has decidable equality, then it is discrete.
$1 \vdash X$
has decidable equality, then it is discrete.
Corollary 18. The natural number object in
![]() $\mathcal{E}$
is discrete.
$\mathcal{E}$
is discrete.
4. Church’s Thesis
We consider a dependent type theory with dependent product types, dependent sum types, identity types, unit type, disjoint finite coproducts, propositional truncation and natural numbers. In such a dependent type theory, one can define Kleene’s computation predicate T(e, x, z) and result extraction function U(z) as primitive recursive functions
![]() $T : \mathbb{N} \times \mathbb{N} \times \mathbb{N} \to \mathbf{2}$
and
$T : \mathbb{N} \times \mathbb{N} \times \mathbb{N} \to \mathbf{2}$
and
![]() $U : \mathbb{N} \to\mathbb{N}$
. The statement T(e, x, z) means that z codes a computation on Turing machine e with input x and U(z) is the output of the computation. Church’s Thesis is the following axiom.
$U : \mathbb{N} \to\mathbb{N}$
. The statement T(e, x, z) means that z codes a computation on Turing machine e with input x and U(z) is the output of the computation. Church’s Thesis is the following axiom.
Since the type
![]() $\sum_{z : \mathbb{N}}T(e, x, z) \times U(z) = f(x)$
is a proposition, Church’s Thesis is equivalent to the type
$\sum_{z : \mathbb{N}}T(e, x, z) \times U(z) = f(x)$
is a proposition, Church’s Thesis is equivalent to the type
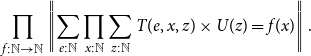 \begin{equation*} \prod_{f : \mathbb{N} \to \mathbb{N}}\left\|{\sum_{e : \mathbb{N}}\prod_{x : \mathbb{N}}\sum_{z : \mathbb{N}}T(e, x, z) \times U(z) = f(x)}\right\|.\end{equation*}
\begin{equation*} \prod_{f : \mathbb{N} \to \mathbb{N}}\left\|{\sum_{e : \mathbb{N}}\prod_{x : \mathbb{N}}\sum_{z : \mathbb{N}}T(e, x, z) \times U(z) = f(x)}\right\|.\end{equation*}
4.1 Failure of Church’s thesis in internal cubical models
Let
![]() $\mathcal{S}$
be a model of type theory as in Section 3.2. We have seen that the category
$\mathcal{S}$
be a model of type theory as in Section 3.2. We have seen that the category
![]() $\mathcal{P}(\Box)$
of internal cubical objects in
$\mathcal{P}(\Box)$
of internal cubical objects in
![]() $\mathcal{S}$
is part of a model of type theory satisfying Assumption 3. In this section, we show the following theorem.
$\mathcal{S}$
is part of a model of type theory satisfying Assumption 3. In this section, we show the following theorem.
Theorem The negation of Church’s Thesis holds in the model of univalent type theory
![]() $\widetilde{\mathcal{P}(\Box)}$
.
$\widetilde{\mathcal{P}(\Box)}$
.
To prove Theorem 4.1, we recall from Uemura (Reference Uemura2019) the notion of a codiscrete presheaf and some useful propositions. The constant presheaf functor
![]() $\Delta : \mathcal{S} \to \mathcal{P}(\Box)$
extends to a morphism of cwf’s and preserves (at least up to isomorphism) several type constructors. Here, we only need the following.
$\Delta : \mathcal{S} \to \mathcal{P}(\Box)$
extends to a morphism of cwf’s and preserves (at least up to isomorphism) several type constructors. Here, we only need the following.
Proposition 19 The morphism
![]() $\Delta : \mathcal{S} \to \mathcal{P}(\Box)$
of cwf’s preserves dependent product types, dependent sum types, extensional identity types and natural number objects.
$\Delta : \mathcal{S} \to \mathcal{P}(\Box)$
of cwf’s preserves dependent product types, dependent sum types, extensional identity types and natural number objects.
A constant presheaf
![]() $\Delta X$
is regarded as a type in
$\Delta X$
is regarded as a type in
![]() $\widetilde{\mathcal{P}(\Box)}$
by the following proposition and Proposition 16.
$\widetilde{\mathcal{P}(\Box)}$
by the following proposition and Proposition 16.
Proposition 20. Constant presheaves are discrete.
For types
![]() $1 \vdash_{\mathcal{S}} X$
and
$1 \vdash_{\mathcal{S}} X$
and
![]() $x : X \vdash_{\mathcal{S}} Y(x)$
, one can define a type
$x : X \vdash_{\mathcal{S}} Y(x)$
, one can define a type
![]() $x : \Delta X \vdash_{\mathcal{P}(\Box)} \nabla_{X}Y(x)$
called the codiscrete presheaf which has the following properties.
$x : \Delta X \vdash_{\mathcal{P}(\Box)} \nabla_{X}Y(x)$
called the codiscrete presheaf which has the following properties.
Proposition 21.
![]() $\nabla_{X}$
is the right adjoint to the evaluation functor
$\nabla_{X}$
is the right adjoint to the evaluation functor
![]() $(-)_{0}$
at
$(-)_{0}$
at
![]() $0 \in \Box$
: for any type
$0 \in \Box$
: for any type
![]() $x : \Delta X \vdash_{\mathcal{P}(\Box)} Z(x)$
, we have a natural bijection between the set of elements
$x : \Delta X \vdash_{\mathcal{P}(\Box)} Z(x)$
, we have a natural bijection between the set of elements
![]() $x : \Delta X, z : Z(x) \vdash_{\mathcal{P}(\Box)} b : \nabla_{X}Y(x)$
and the set of elements
$x : \Delta X, z : Z(x) \vdash_{\mathcal{P}(\Box)} b : \nabla_{X}Y(x)$
and the set of elements
![]() $x : X, z : Z_{0}(x) \vdash_{\mathcal{S}} b : Y(x)$
. Note that
$x : X, z : Z_{0}(x) \vdash_{\mathcal{S}} b : Y(x)$
. Note that
![]() $(\Delta X)_{0} = X$
and thus
$(\Delta X)_{0} = X$
and thus
![]() $Z_{0}$
is a type in
$Z_{0}$
is a type in
![]() $\mathcal{S}$
over X.
$\mathcal{S}$
over X.
Proposition 22. For a type
![]() $x : X \vdash_{\mathcal{S}}Y(x)$
, the type
$x : X \vdash_{\mathcal{S}}Y(x)$
, the type
![]() $x : \Delta X \vdash_{\mathcal{P}(\Box)} \nabla_{X}Y(x)$
has a composition structure and is a proposition in
$x : \Delta X \vdash_{\mathcal{P}(\Box)} \nabla_{X}Y(x)$
has a composition structure and is a proposition in
![]() $\widetilde{\mathcal{P}(\Box)}$
.
$\widetilde{\mathcal{P}(\Box)}$
.
Proof of Theorem 4.1. We define types
![]() $f : \mathbb{N} \to \mathbb{N} \vdash C'(f) :\equiv \sum_{e : \mathbb{N}}\prod_{x : \mathbb{N}}\sum_{z : \mathbb{N}}T(e, x, z) \times U(x) = f(x)$
and
$f : \mathbb{N} \to \mathbb{N} \vdash C'(f) :\equiv \sum_{e : \mathbb{N}}\prod_{x : \mathbb{N}}\sum_{z : \mathbb{N}}T(e, x, z) \times U(x) = f(x)$
and
![]() $f : \mathbb{N} \to \mathbb{N} \vdash C(f) :\equiv \left\|{C'(f)}\right\|$
. Let N denote the natural number object in
$f : \mathbb{N} \to \mathbb{N} \vdash C(f) :\equiv \left\|{C'(f)}\right\|$
. Let N denote the natural number object in
![]() $\mathcal{S}$
. Then Church’s Thesis is interpreted in
$\mathcal{S}$
. Then Church’s Thesis is interpreted in
![]() $\widetilde{\mathcal{P}(\Box)}$
as
$\widetilde{\mathcal{P}(\Box)}$
as
![]() $\prod_{f : \Delta(N \to N)}[\![{C}]\!]^{\widetilde{\mathcal{P}(\Box)}}(f)$
by Proposition 19. We will construct two functions in
$\prod_{f : \Delta(N \to N)}[\![{C}]\!]^{\widetilde{\mathcal{P}(\Box)}}(f)$
by Proposition 19. We will construct two functions in
![]() $\widetilde{\mathcal{P}(\Box)}$
:
$\widetilde{\mathcal{P}(\Box)}$
:
-
 $\prod_{f : \Delta(N \to N)}[\![{C}]\!]^{\widetilde{\mathcal{P}(\Box)}}(f) \to \nabla_{N \to N}[\![{C'}]\!]^{\mathcal{S}}(f)$
;
$\prod_{f : \Delta(N \to N)}[\![{C}]\!]^{\widetilde{\mathcal{P}(\Box)}}(f) \to \nabla_{N \to N}[\![{C'}]\!]^{\mathcal{S}}(f)$
; -
 $\left(\prod_{f : \Delta(N \to N)}\nabla_{N \to N}[\![{C'}]\!]^{\mathcal{S}}(f)\right) \to \mathbf{0}$
.
$\left(\prod_{f : \Delta(N \to N)}\nabla_{N \to N}[\![{C'}]\!]^{\mathcal{S}}(f)\right) \to \mathbf{0}$
.
Then we readily get a function
![]() $\left(\prod_{f : \Delta(N \to N)}[\![{C}]\!]^{\widetilde{\mathcal{P}(\Box)}}(f)\right) \to \mathbf{0}$
.
$\left(\prod_{f : \Delta(N \to N)}[\![{C}]\!]^{\widetilde{\mathcal{P}(\Box)}}(f)\right) \to \mathbf{0}$
.
For the former one, it suffices to give a function
![]() $[\![{C'}]\!]^{\widetilde{\mathcal{P}(\Box)}}(f) \to \nabla_{N \to N}[\![{C'}]\!]^{\mathcal{S}}(f)$
for all
$[\![{C'}]\!]^{\widetilde{\mathcal{P}(\Box)}}(f) \to \nabla_{N \to N}[\![{C'}]\!]^{\mathcal{S}}(f)$
for all
![]() $f : \Delta(N \to N)$
by the recursion principle of the propositional truncation because the codomain is a proposition by Proposition 22. By the adjunction
$f : \Delta(N \to N)$
by the recursion principle of the propositional truncation because the codomain is a proposition by Proposition 22. By the adjunction
![]() $(-)_{0} \dashv \nabla_{N \to N}$
, it suffices to give a function
$(-)_{0} \dashv \nabla_{N \to N}$
, it suffices to give a function
![]() $[\![{C'}]\!]^{\widetilde{\mathcal{P}(\Box)}}_{0} \to [\![{C'}]\!]^{\mathcal{S}}$
but we have an isomorphism
$[\![{C'}]\!]^{\widetilde{\mathcal{P}(\Box)}}_{0} \to [\![{C'}]\!]^{\mathcal{S}}$
but we have an isomorphism
![]() $[\![{C'}]\!]^{\widetilde{\mathcal{P}(\Box)}} \cong (\Delta[\![{C'}]\!]^{\mathcal{S}})_{0} = [\![{C'}]\!]^{\mathcal{S}}$
by Proposition 19.
$[\![{C'}]\!]^{\widetilde{\mathcal{P}(\Box)}} \cong (\Delta[\![{C'}]\!]^{\mathcal{S}})_{0} = [\![{C'}]\!]^{\mathcal{S}}$
by Proposition 19.
For the latter function, observe that
![]() $\prod_{f : \Delta(N \to N)}\nabla_{N \to N}[\![{C'}]\!]^{\mathcal{S}}(f) \cong \nabla_{1}\left(\prod_{f : N \to N}[\![{C'}]\!]^{\mathcal{S}}(f)\right)$
and that
$\prod_{f : \Delta(N \to N)}\nabla_{N \to N}[\![{C'}]\!]^{\mathcal{S}}(f) \cong \nabla_{1}\left(\prod_{f : N \to N}[\![{C'}]\!]^{\mathcal{S}}(f)\right)$
and that
![]() $\nabla_{1}\mathbf{0} \cong \mathbf{0}$
. Then we apply
$\nabla_{1}\mathbf{0} \cong \mathbf{0}$
. Then we apply
![]() $\nabla_{1}$
to the function
$\nabla_{1}$
to the function
![]() $\left(\prod_{f : N \to N}[\![{C'}]\!]^{\mathcal{S}}(f)\right) \to \mathbf{0}$
in
$\left(\prod_{f : N \to N}[\![{C'}]\!]^{\mathcal{S}}(f)\right) \to \mathbf{0}$
in
![]() $\mathcal{S}$
obtained from the inconsistency of Church’s Thesis with the axiom of choice and function extensionality.
$\mathcal{S}$
obtained from the inconsistency of Church’s Thesis with the axiom of choice and function extensionality.
5. Null Types
Let
![]() $\mathcal{E}$
be a model of univalent type theory. Based on Rijke, Shulman and Spitters’ null types (Rijke et al. Reference Rijke, Shulman and Spitters2020), we define a notion of null structure as follows.
$\mathcal{E}$
be a model of univalent type theory. Based on Rijke, Shulman and Spitters’ null types (Rijke et al. Reference Rijke, Shulman and Spitters2020), we define a notion of null structure as follows.
Let
![]() $a : A \vdash B(a)$
be a proposition in
$a : A \vdash B(a)$
be a proposition in
![]() $\mathcal{E}$
. For a type
$\mathcal{E}$
. For a type
![]() $\Gamma \vdash X$
in
$\Gamma \vdash X$
in
![]() $\mathcal{E}$
, we define a proposition
$\mathcal{E}$
, we define a proposition
![]() $\Gamma \vdash \mathsf{isNull}_{B}(X)$
as
$\Gamma \vdash \mathsf{isNull}_{B}(X)$
as
and call a term of
![]() $\mathsf{isNull}_{B}(X)$
a B-null structure on X. A B-null type is a type
$\mathsf{isNull}_{B}(X)$
a B-null structure on X. A B-null type is a type
![]() $\Gamma \vdash X$
equipped with a B-null structure n on X. That is, a B-null type has a witness that the canonical map
$\Gamma \vdash X$
equipped with a B-null structure n on X. That is, a B-null type has a witness that the canonical map
![]() $X \to X^{B(a)}$
is an equivalence for each a.
$X \to X^{B(a)}$
is an equivalence for each a.
Definition 23. We define a cwf
![]() $\mathcal{E}_{B}$
as follows:
$\mathcal{E}_{B}$
as follows:
-
the contexts are those of
 $\mathcal{E}$
;
$\mathcal{E}$
; -
the types are the B-null types in
 $\mathcal{E}$
;
$\mathcal{E}$
; -
the elements of
 $\Gamma \vdash_{\mathcal{E}_{B}} X$
are those of the underlying type X in
$\Gamma \vdash_{\mathcal{E}_{B}} X$
are those of the underlying type X in
 $\mathcal{E}$
.
$\mathcal{E}$
.
We have the obvious forgetful morphism
![]() $\mathcal{E}_{B} \to \mathcal{E}$
of cwf’s.
$\mathcal{E}_{B} \to \mathcal{E}$
of cwf’s.
For a proposition
![]() $a : A \vdash B(a)$
, a nullification operator assigns
$a : A \vdash B(a)$
, a nullification operator assigns
-
each type
 $\Gamma \vdash X$
a B-null type
$\Gamma \vdash X$
a B-null type
 $\Gamma \vdash \mathcal{L}_{B}X$
and an element
$\Gamma \vdash \mathcal{L}_{B}X$
and an element
 $\Gamma \vdash \eta_{X} : X \to \mathcal{L}_{B}X$
; and
$\Gamma \vdash \eta_{X} : X \to \mathcal{L}_{B}X$
; and -
each pair of type
 $\Gamma \vdash X$
and B-null type
$\Gamma \vdash X$
and B-null type
 $\Gamma \vdash Y$
an element
$\Gamma \vdash Y$
an element
 $\Gamma \vdash e : \mathsf{isEquiv}(\lambda(f : \mathcal{L}_{B}X \to Y).f \circ \eta_{X}$
.
$\Gamma \vdash e : \mathsf{isEquiv}(\lambda(f : \mathcal{L}_{B}X \to Y).f \circ \eta_{X}$
.
We also require that a nullification operator is preserved by reindexing.
We review some properties of null types. See Rijke et al. (Reference Rijke, Shulman and Spitters2020) for further details.
Proposition 24. Let
![]() $\Gamma \vdash X$
and
$\Gamma \vdash X$
and
![]() $\Gamma, x : X \vdash Y(x)$
be types in
$\Gamma, x : X \vdash Y(x)$
be types in
![]() $\mathcal{E}$
.
$\mathcal{E}$
.
-
There exists a term of type
 $\Gamma \vdash (\!\prod_{x : X}\mathsf{isNull}_{B}(Y(x))) \to \mathsf{isNull}_{B}(\!\prod_{x : X}Y(x))$
.
$\Gamma \vdash (\!\prod_{x : X}\mathsf{isNull}_{B}(Y(x))) \to \mathsf{isNull}_{B}(\!\prod_{x : X}Y(x))$
. -
There exists a term of type
 $\Gamma \vdash \mathsf{isNull}_{B}(X) \to (\!\prod_{x : X}\mathsf{isNull}_{B}(Y(x))) \to \mathsf{isNull}_{B}(\!\sum_{x : X}Y(x))$
.
$\Gamma \vdash \mathsf{isNull}_{B}(X) \to (\!\prod_{x : X}\mathsf{isNull}_{B}(Y(x))) \to \mathsf{isNull}_{B}(\!\sum_{x : X}Y(x))$
. -
There exists a term of type
 $\Gamma \vdash \mathsf{isNull}_{B}(X) \to \prod_{x_{0}, x_{1} : X}\mathsf{isNull}_{B}(\mathsf{Id}_{X}(x_{0}, x_{1}))$
.
$\Gamma \vdash \mathsf{isNull}_{B}(X) \to \prod_{x_{0}, x_{1} : X}\mathsf{isNull}_{B}(\mathsf{Id}_{X}(x_{0}, x_{1}))$
.
Consequently,
![]() $\mathcal{E}_{B}$
supports dependent product, dependent sum and intensional identity types preserved by the morphism
$\mathcal{E}_{B}$
supports dependent product, dependent sum and intensional identity types preserved by the morphism
![]() $\mathcal{E}_{B} \to \mathcal{E}$
.
$\mathcal{E}_{B} \to \mathcal{E}$
.
For a universe U, we define a subuniverse
![]() $U_{B}$
of U as
$U_{B}$
of U as
Proposition 25. The universe
![]() $U_{B}$
has a B-null structure.
$U_{B}$
has a B-null structure.
Proof. Our condition that each B(a) is a proposition corresponds to Rijke, Shulman and Spitters’ notion of topological modality. They prove in Rijke et al. (Reference Rijke, Shulman and Spitters2020, Corollary 3.11 and Theorem 3.12) that any such modality is lex and hence that the universe of modal types is itself modal.
Proposition 26. If a nullification operator
![]() $\mathcal{L}_{B}$
exists, then it preserves propositions.
$\mathcal{L}_{B}$
exists, then it preserves propositions.
Proof. This is true for any modality by Rijke et al. (Reference Rijke, Shulman and Spitters2020, Lemma 1.28).
Corollary 27. Suppose that
![]() $\mathcal{E}$
has a nullification operator
$\mathcal{E}$
has a nullification operator
![]() $\mathcal{L}_{B}$
. Then
$\mathcal{L}_{B}$
. Then
![]() $a : A \vdash \mathcal{L}_{B}B(a)$
is contractible.
$a : A \vdash \mathcal{L}_{B}B(a)$
is contractible.
Proof. Since
![]() $\mathcal{L}_{B}B(a)$
is a proposition, it suffices to find an element of
$\mathcal{L}_{B}B(a)$
is a proposition, it suffices to find an element of
![]() $\prod_{a : A}\mathcal{L}_{B}B(a)$
. Assume that
$\prod_{a : A}\mathcal{L}_{B}B(a)$
. Assume that
![]() $a : A$
is given. Since
$a : A$
is given. Since
![]() $\mathcal{L}_{B}B(a)$
is B-null, it is enough to give a function
$\mathcal{L}_{B}B(a)$
is B-null, it is enough to give a function
![]() $B(a) \to \mathcal{L}_{B}B(a)$
, so take the constructor
$B(a) \to \mathcal{L}_{B}B(a)$
, so take the constructor
![]() $\eta_{B(a)} : B(a) \to \mathcal{L}_{B}B(a)$
.
$\eta_{B(a)} : B(a) \to \mathcal{L}_{B}B(a)$
.
Corollary 28. Suppose that
![]() $\mathcal{E}$
has a nullification operator
$\mathcal{E}$
has a nullification operator
![]() $\mathcal{L}_{B}$
. Then
$\mathcal{L}_{B}$
. Then
![]() $X \mapsto \mathcal{L}_{B}\left\|{X}\right\|$
gives propositional truncation in the model
$X \mapsto \mathcal{L}_{B}\left\|{X}\right\|$
gives propositional truncation in the model
![]() $\mathcal{E}_{B}$
.
$\mathcal{E}_{B}$
.
Proof. By Proposition 26,
![]() $\mathcal{L}_{B}\left\|{X}\right\|$
is a proposition. For any B-null proposition Z, we have equivalences
$\mathcal{L}_{B}\left\|{X}\right\|$
is a proposition. For any B-null proposition Z, we have equivalences
5.1 Null types in Orton–Pitts models
Let
![]() $\widetilde{\mathcal{E}}$
be an Orton–Pitts model.
$\widetilde{\mathcal{E}}$
be an Orton–Pitts model.
Definition 29. A type
![]() $a : A \vdash B(a)$
in
$a : A \vdash B(a)$
in
![]() $\mathcal{E}$
or
$\mathcal{E}$
or
![]() $\widetilde{\mathcal{E}}$
is said to be well-supported if the propositional truncation
$\widetilde{\mathcal{E}}$
is said to be well-supported if the propositional truncation
![]() $a : A \vdash_{\mathcal{E}} \left\|{B(a)}\right\|$
taken in the model
$a : A \vdash_{\mathcal{E}} \left\|{B(a)}\right\|$
taken in the model
![]() $\mathcal{E}$
of extensional dependent type theory is inhabited.
$\mathcal{E}$
of extensional dependent type theory is inhabited.
Proposition 30. Let
![]() $1 \vdash_{\mathcal{E}} X$
be a type and
$1 \vdash_{\mathcal{E}} X$
be a type and
![]() $a : A \vdash_{\widetilde{\mathcal{E}}} B(a)$
a proposition. If X is discrete and B is well-supported, then X has a B-null structure.
$a : A \vdash_{\widetilde{\mathcal{E}}} B(a)$
a proposition. If X is discrete and B is well-supported, then X has a B-null structure.
Proof. We show that, for any
![]() $a : A$
, the function
$a : A$
, the function
![]() $k_{a} :\equiv \lambda x.\lambda b.x : X \to (B(a) \to X)$
is an isomorphism in the internal language of
$k_{a} :\equiv \lambda x.\lambda b.x : X \to (B(a) \to X)$
is an isomorphism in the internal language of
![]() $\mathcal{E}$
. Since B is well-supported,
$\mathcal{E}$
. Since B is well-supported,
![]() $k_{a}$
is injective. To prove surjectivity, we assume that
$k_{a}$
is injective. To prove surjectivity, we assume that
![]() $f : B(a) \to X$
is given. By the well-supportedness of B, there exists some element
$f : B(a) \to X$
is given. By the well-supportedness of B, there exists some element
![]() $b : B(a)$
. We show that
$b : B(a)$
. We show that
![]() $f = k_{a}(f(b))$
. Assume
$f = k_{a}(f(b))$
. Assume
![]() $b' : B(a)$
is given. Since B is a proposition in
$b' : B(a)$
is given. Since B is a proposition in
![]() $\widetilde{E}$
, we have a path
$\widetilde{E}$
, we have a path
![]() $p : \mathbb{I} \to B(a)$
such that
$p : \mathbb{I} \to B(a)$
such that
![]() $p0 = b'$
and
$p0 = b'$
and
![]() $p1 = b$
. By the discreteness of X the path
$p1 = b$
. By the discreteness of X the path
![]() $f \circ p : \mathbb{I} \to X$
is constant, which implies that
$f \circ p : \mathbb{I} \to X$
is constant, which implies that
![]() $f(b') = f(b)$
. Hence, we have
$f(b') = f(b)$
. Hence, we have
![]() $f = k_{a}(f(b))$
by function extensionality.
$f = k_{a}(f(b))$
by function extensionality.
We easily deduce the following corollaries.
Corollary 31. If B is well-supported, then
![]() $\mathbf{0}$
has a B-null structure.
$\mathbf{0}$
has a B-null structure.
Corollary 32. If B is well-supported, then
![]() $\mathbb{N}$
has a B-null structure.
$\mathbb{N}$
has a B-null structure.
Proposition 33. Let
![]() $a : A \vdash_{\widetilde{\mathcal{E}}} B(a)$
be a proposition and
$a : A \vdash_{\widetilde{\mathcal{E}}} B(a)$
be a proposition and
![]() $\Gamma \vdash_{\widetilde{\mathcal{E}}} X$
and
$\Gamma \vdash_{\widetilde{\mathcal{E}}} X$
and
![]() $\Gamma \vdash_{\widetilde{\mathcal{E}}} Y$
types. Then there exists a term of type
$\Gamma \vdash_{\widetilde{\mathcal{E}}} Y$
types. Then there exists a term of type
Proof. We proceed in the internal language of
![]() $\mathcal{E}$
. Suppose that X and Y has a B-null structure. Assume that
$\mathcal{E}$
. Suppose that X and Y has a B-null structure. Assume that
![]() $a : A$
is given. Since the function
$a : A$
is given. Since the function
![]() $(X + Y) \to (B(a) \to (X + Y))$
factors as
$(X + Y) \to (B(a) \to (X + Y))$
factors as
it suffices to show that the function
![]() $\Phi : ((B(a) \to X) + (B(a) \to Y)) \to (B(a) \to (X + Y))$
is an isomorphism. The injectivity of
$\Phi : ((B(a) \to X) + (B(a) \to Y)) \to (B(a) \to (X + Y))$
is an isomorphism. The injectivity of
![]() $\Phi$
follows from the well-supportedness of B. To prove the surjectivity, we assume that
$\Phi$
follows from the well-supportedness of B. To prove the surjectivity, we assume that
![]() $f : B(a) \to (X + Y)$
is given. We show that
$f : B(a) \to (X + Y)$
is given. We show that
![]() $(\forall_{b : B(a)}fb \in X) \lor (\forall_{b : B(a)}fb \in Y)$
. Since B is well-supported, there exists some element
$(\forall_{b : B(a)}fb \in X) \lor (\forall_{b : B(a)}fb \in Y)$
. Since B is well-supported, there exists some element
![]() $b_{0} : B(a)$
. We know that
$b_{0} : B(a)$
. We know that
![]() $fb_{0} \in X \lor fb_{0} \in Y$
. Suppose that
$fb_{0} \in X \lor fb_{0} \in Y$
. Suppose that
![]() $fb_{0} \in X$
. Assume
$fb_{0} \in X$
. Assume
![]() $b : B(a)$
is given. Since B is a proposition in
$b : B(a)$
is given. Since B is a proposition in
![]() $\widetilde{\mathcal{E}}$
, we have a path
$\widetilde{\mathcal{E}}$
, we have a path
![]() $p : \mathbb{I} \to B(a)$
such that
$p : \mathbb{I} \to B(a)$
such that
![]() $p0 = b_{0}$
and
$p0 = b_{0}$
and
![]() $p1 = b$
. Since the exponential functor
$p1 = b$
. Since the exponential functor
![]() $(-)^{\mathbb{I}}$
preserves colimits because it has a right adjoint, we have
$(-)^{\mathbb{I}}$
preserves colimits because it has a right adjoint, we have
![]() $(\forall_{i : \mathbb{I}}f(pi) \in X) \lor (\forall_{i : \mathbb{I}}f(pi) \in Y)$
. Now
$(\forall_{i : \mathbb{I}}f(pi) \in X) \lor (\forall_{i : \mathbb{I}}f(pi) \in Y)$
. Now
![]() $f(p0) \in X$
and thus we have
$f(p0) \in X$
and thus we have
![]() $\forall_{i : \mathbb{I}}f(pi) \in X$
. In particular,
$\forall_{i : \mathbb{I}}f(pi) \in X$
. In particular,
![]() $fb \in X$
. In a similar manner, we have
$fb \in X$
. In a similar manner, we have
![]() $\forall_{b : B(a)}fb \in Y$
assuming
$\forall_{b : B(a)}fb \in Y$
assuming
![]() $fb_{0} \in Y$
. Hence, we get
$fb_{0} \in Y$
. Hence, we get
![]() $(\forall_{b : B(a)}fb \in X) \lor (\forall_{b : B(a)}fb \in Y)$
.
$(\forall_{b : B(a)}fb \in X) \lor (\forall_{b : B(a)}fb \in Y)$
.
By Corollary 18, and Propositions 24, 30 and 33, for any type X defined in dependent type theory only using dependent product types, dependent sum types, identity types, unit type, disjoint finite coproducts and natural numbers, the underlying type of
![]() $[\![{X}]\!]^{\widetilde{\mathcal{E}}_{B}}$
is equal to
$[\![{X}]\!]^{\widetilde{\mathcal{E}}_{B}}$
is equal to
![]() $[\![{X}]\!]^{\widetilde{\mathcal{E}}}$
for any well-supported proposition B in
$[\![{X}]\!]^{\widetilde{\mathcal{E}}}$
for any well-supported proposition B in
![]() $\widetilde{\mathcal{E}}$
. In particular, in this case if
$\widetilde{\mathcal{E}}$
. In particular, in this case if
![]() $[\![{X}]\!]^{\widetilde{\mathcal{E}}}$
is inhabited, then so is
$[\![{X}]\!]^{\widetilde{\mathcal{E}}}$
is inhabited, then so is
![]() $[\![{X}]\!]^{\widetilde{\mathcal{E}}_{B}}$
.
$[\![{X}]\!]^{\widetilde{\mathcal{E}}_{B}}$
.
Example 34. Markov’s Principle is the following axiom.
It is equivalent to the type
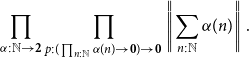 \begin{equation*} \prod_{\alpha : \mathbb{N} \to \mathbf{2}}\prod_{p : (\prod_{n : \mathbb{N}}\alpha(n) \to \mathbf{0}) \to \mathbf{0}}\left\|{\sum_{n : \mathbb{N}}\alpha(n)}\right\|. \end{equation*}
\begin{equation*} \prod_{\alpha : \mathbb{N} \to \mathbf{2}}\prod_{p : (\prod_{n : \mathbb{N}}\alpha(n) \to \mathbf{0}) \to \mathbf{0}}\left\|{\sum_{n : \mathbb{N}}\alpha(n)}\right\|. \end{equation*}
For a decidable predicate
![]() $\alpha : \mathbb{N} \to \mathbf{2}$
, the proposition
$\alpha : \mathbb{N} \to \mathbf{2}$
, the proposition
![]() $\left\|{\sum_{n : \mathbb{N}}\alpha(n)}\right\|$
is equivalent to the type
$\left\|{\sum_{n : \mathbb{N}}\alpha(n)}\right\|$
is equivalent to the type
![]() $\sum_{n : \mathbb{N}}\alpha(n) \times \prod_{k : \mathbb{N}}\alpha(k) \to n \leq k$
which is defined without propositional truncation. Hence, if the model
$\sum_{n : \mathbb{N}}\alpha(n) \times \prod_{k : \mathbb{N}}\alpha(k) \to n \leq k$
which is defined without propositional truncation. Hence, if the model
![]() $\mathcal{E}$
of extensional dependent type theory satisfies Markov’s Principle, then so does the model
$\mathcal{E}$
of extensional dependent type theory satisfies Markov’s Principle, then so does the model
![]() $\widetilde{\mathcal{E}}_{B}$
of univalent type theory for any well-supported proposition B in
$\widetilde{\mathcal{E}}_{B}$
of univalent type theory for any well-supported proposition B in
![]() $\widetilde{\mathcal{E}}$
.
$\widetilde{\mathcal{E}}$
.
We now show how to define nullification operators in Orton–Pitts models. Following Rijke et al. (Reference Rijke, Shulman and Spitters2020), Section 2.2, we will first define an operator
![]() $\mathcal{J}_B$
, although we will only consider the case of nullification, since that is all we need here.
$\mathcal{J}_B$
, although we will only consider the case of nullification, since that is all we need here.
Lemma 35. For types
![]() $a : A \vdash_{\widetilde{\mathcal{E}}} B(a)$
and
$a : A \vdash_{\widetilde{\mathcal{E}}} B(a)$
and
![]() $\Gamma \vdash_{\widetilde{\mathcal{E}}} X$
, we have the higher inductive
$\Gamma \vdash_{\widetilde{\mathcal{E}}} X$
, we have the higher inductive
![]() $\mathcal{J}_B(X)$
defined as follows.
$\mathcal{J}_B(X)$
defined as follows.
-
When
 $x : X$
, then
$x : X$
, then
 $\mathcal{J}_B(X)$
contains an element
$\mathcal{J}_B(X)$
contains an element
 $\alpha^B_X(x)$
.
$\alpha^B_X(x)$
. -
When
 $a : A$
and
$a : A$
and
 $f : B(a) \to \mathcal{K}_B$
, then
$f : B(a) \to \mathcal{K}_B$
, then
 $\mathcal{J}_B(X)$
contains an element
$\mathcal{J}_B(X)$
contains an element
 $\mathsf{ext}(a, f)$
.
$\mathsf{ext}(a, f)$
. -
When
 $a : A$
,
$a : A$
,
 $f : B(a) \to \mathcal{K}_B$
and
$f : B(a) \to \mathcal{K}_B$
and
 $b : B(a)$
then
$b : B(a)$
then
 $\mathsf{Id}(\mathsf{ext}(a, f), f(b))$
contains an element
$\mathsf{Id}(\mathsf{ext}(a, f), f(b))$
contains an element
 $\mathsf{isext}(a, f, b)$
.
$\mathsf{isext}(a, f, b)$
.
Proof.
![]() $\mathcal{J}_B(X)$
differs from
$\mathcal{J}_B(X)$
differs from
![]() $\mathcal{K}_B$
by having an extra point constructor
$\mathcal{K}_B$
by having an extra point constructor
![]() $\alpha^B_X : X \to \mathcal{J}_B(X)$
.
$\alpha^B_X : X \to \mathcal{J}_B(X)$
.
We define A’ to be the type
![]() $A + X$
and define the family of types
$A + X$
and define the family of types
![]() $a : A' \vdash B'(a)$
as follows.
$a : A' \vdash B'(a)$
as follows.
We can then take
![]() $\mathcal{J}_B(X)$
to be
$\mathcal{J}_B(X)$
to be
![]() $\mathcal{K}_{B'}$
, as defined in Section 3.1. We take
$\mathcal{K}_{B'}$
, as defined in Section 3.1. We take
![]() $\alpha^B_X(x)$
to be
$\alpha^B_X(x)$
to be
![]() $\mathsf{ext}(\mathsf{inr}(x), \bot_{\mathcal{K}_B})$
where
$\mathsf{ext}(\mathsf{inr}(x), \bot_{\mathcal{K}_B})$
where
![]() $\bot_{\mathcal{K}_B}$
is the unique map from 0 to
$\bot_{\mathcal{K}_B}$
is the unique map from 0 to
![]() $\mathcal{K}_B$
.
$\mathcal{K}_B$
.
Theorem.
![]() $\widetilde{\mathcal{E}}$
has a nullification operator
$\widetilde{\mathcal{E}}$
has a nullification operator
![]() $\mathcal{L}_{B}$
for every type
$\mathcal{L}_{B}$
for every type
![]() $a : A \vdash_{\widetilde{\mathcal{E}}} B(a)$
.
$a : A \vdash_{\widetilde{\mathcal{E}}} B(a)$
.
Proof. This follows from Rijke et al. (Reference Rijke, Shulman and Spitters2020, Theorem 2.18), observing that for the case of nullification the pushout appearing there is just a suspension, which we have already shown how to implement in Theorem 3.1, and we showed in Lemma 35 how to implement their
![]() $\mathcal{J}$
operator.
$\mathcal{J}$
operator.
6. Church’s Thesis in Null Types
Consider a dependent type theory with dependent product types, dependent sum types, identity types, unit type, disjoint finite coproducts, propositional truncation and natural numbers. Let
![]() $a : A\vdash B(a)$
be a type in this type theory where A and B are definable only using dependent product types, dependent sum types, identity type of
$a : A\vdash B(a)$
be a type in this type theory where A and B are definable only using dependent product types, dependent sum types, identity type of
![]() $\mathbf{2}$
, unit type, finite coproducts and natural numbers. We define
$\mathbf{2}$
, unit type, finite coproducts and natural numbers. We define
![]() $a : A \vdash C(a) := \left\|{B(a)}\right\|$
. For an Orton–Pitts model
$a : A \vdash C(a) := \left\|{B(a)}\right\|$
. For an Orton–Pitts model
![]() $\widetilde{\mathcal{E}}$
, the underlying types of the interpretations
$\widetilde{\mathcal{E}}$
, the underlying types of the interpretations
![]() $[\![{A}]\!]^{\widetilde{\mathcal{E}}}$
and
$[\![{A}]\!]^{\widetilde{\mathcal{E}}}$
and
![]() $[\![{B}]\!]^{\widetilde{\mathcal{E}}}$
are
$[\![{B}]\!]^{\widetilde{\mathcal{E}}}$
are
![]() $[\![{A}]\!]^{\mathcal{E}}$
and
$[\![{A}]\!]^{\mathcal{E}}$
and
![]() $[\![{B}]\!]^{\mathcal{E}}$
, respectively.
$[\![{B}]\!]^{\mathcal{E}}$
, respectively.
Theorem Let
![]() $\widetilde{\mathcal{E}}$
be an Orton–Pitts model. Suppose that
$\widetilde{\mathcal{E}}$
be an Orton–Pitts model. Suppose that
![]() $[\![{B}]\!]^{\widetilde{\mathcal{E}}}$
is well-supported. Then the proposition C holds in the model of univalent type theory
$[\![{B}]\!]^{\widetilde{\mathcal{E}}}$
is well-supported. Then the proposition C holds in the model of univalent type theory
![]() $\widetilde{\mathcal{E}}_{[\![{C}]\!]^{\widetilde{\mathcal{E}}}}$
.
$\widetilde{\mathcal{E}}_{[\![{C}]\!]^{\widetilde{\mathcal{E}}}}$
.
Proof. Let
![]() $D = [\![{C}]\!]^{\widetilde{\mathcal{E}}}$
. By assumption
$D = [\![{C}]\!]^{\widetilde{\mathcal{E}}}$
. By assumption
![]() $[\![{B}]\!]^{\widetilde{\mathcal{E}}}$
is well-supported and so is its truncation D. By Corollary 18 and Propositions 24, 30 and 33, the underlying types of
$[\![{B}]\!]^{\widetilde{\mathcal{E}}}$
is well-supported and so is its truncation D. By Corollary 18 and Propositions 24, 30 and 33, the underlying types of
![]() $[\![{A}]\!]^{\widetilde{\mathcal{E}}_D}$
and
$[\![{A}]\!]^{\widetilde{\mathcal{E}}_D}$
and
![]() $[\![{B}]\!]^{\widetilde{\mathcal{E}}_D}$
are equal to
$[\![{B}]\!]^{\widetilde{\mathcal{E}}_D}$
are equal to
![]() $[\![{A}]\!]^{\widetilde{\mathcal{E}}}$
and
$[\![{A}]\!]^{\widetilde{\mathcal{E}}}$
and
![]() $[\![{B}]\!]^{\widetilde{\mathcal{E}}}$
, respectively. Hence, we have
$[\![{B}]\!]^{\widetilde{\mathcal{E}}}$
, respectively. Hence, we have
![]() $[\![{C}]\!]^{\widetilde{\mathcal{E}}_{D}} = \mathcal{L}_{D}[\![{C}]\!]^{\widetilde{\mathcal{E}}}$
by Corollary 5, and this type is inhabited by Corollary 27.
$[\![{C}]\!]^{\widetilde{\mathcal{E}}_{D}} = \mathcal{L}_{D}[\![{C}]\!]^{\widetilde{\mathcal{E}}}$
by Corollary 5, and this type is inhabited by Corollary 27.
Corollary 36. Let
![]() $\mathcal{S}$
be a model of type theory as in Section 3.2. If the proposition C holds in
$\mathcal{S}$
be a model of type theory as in Section 3.2. If the proposition C holds in
![]() $\mathcal{S}$
, then C also holds in the model of univalent type theory
$\mathcal{S}$
, then C also holds in the model of univalent type theory
![]() $\widetilde{\mathcal{E}}_{[\![{C}]\!]^{\widetilde{\mathcal{E}}}}$
where
$\widetilde{\mathcal{E}}_{[\![{C}]\!]^{\widetilde{\mathcal{E}}}}$
where
![]() $\mathcal{E} = \mathcal{P}(\Box)$
.
$\mathcal{E} = \mathcal{P}(\Box)$
.
Proof. Since
![]() $C = \left\|{B}\right\|$
holds in
$C = \left\|{B}\right\|$
holds in
![]() $\mathcal{S}$
, the type
$\mathcal{S}$
, the type
![]() $[\![{B}]\!]^{\mathcal{S}}$
is well-supported. Then
$[\![{B}]\!]^{\mathcal{S}}$
is well-supported. Then
![]() $[\![{B}]\!]^{\widetilde{\mathcal{E}}} = [\![{B}]\!]^{\mathcal{E}}$
is also well-supported because the constant presheaf functor
$[\![{B}]\!]^{\widetilde{\mathcal{E}}} = [\![{B}]\!]^{\mathcal{E}}$
is also well-supported because the constant presheaf functor
![]() $\mathcal{S} \to \mathcal{E}$
preserves all structures of the type theory. Then use Theorem 6.
$\mathcal{S} \to \mathcal{E}$
preserves all structures of the type theory. Then use Theorem 6.
Example 37. Recall that Church’s Thesis is equivalent to the type
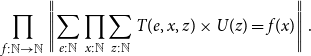 \begin{equation*} \prod_{f : \mathbb{N} \to \mathbb{N}}\left\|{\sum_{e : \mathbb{N}}\prod_{x : \mathbb{N}}\sum_{z : \mathbb{N}}T(e, x, z) \times U(z) = f(x)}\right\|. \end{equation*}
\begin{equation*} \prod_{f : \mathbb{N} \to \mathbb{N}}\left\|{\sum_{e : \mathbb{N}}\prod_{x : \mathbb{N}}\sum_{z : \mathbb{N}}T(e, x, z) \times U(z) = f(x)}\right\|. \end{equation*}
Also note that the equality of natural numbers is decidable, and thus there exists a function
![]() $=_{\mathbb{N}} : \mathbb{N} \to \mathbb{N} \to \mathbf{2}$
such that the type
$=_{\mathbb{N}} : \mathbb{N} \to \mathbb{N} \to \mathbf{2}$
such that the type
![]() $U(z) = f(x)$
is equivalent to
$U(z) = f(x)$
is equivalent to
![]() $(U(z) =_{\mathbb{N}} f(x)) = 1$
. Therefore, Church’s Thesis is equivalent to a type of the form
$(U(z) =_{\mathbb{N}} f(x)) = 1$
. Therefore, Church’s Thesis is equivalent to a type of the form
with a type
![]() $a : A \vdash B(a)$
definable only using dependent product types, dependent sum types, identity of
$a : A \vdash B(a)$
definable only using dependent product types, dependent sum types, identity of
![]() $\mathbf{2}$
, unit type, finite coproducts and natural numbers. Since Church’s Thesis holds in the category
$\mathbf{2}$
, unit type, finite coproducts and natural numbers. Since Church’s Thesis holds in the category
![]() $\mathbf{Asm}(\mathcal{K}_{1})$
of assemblies on Kleene’s first model
$\mathbf{Asm}(\mathcal{K}_{1})$
of assemblies on Kleene’s first model
![]() $\mathcal{K}_{1}$
, by Corollary 36 the model of univalent type theory
$\mathcal{K}_{1}$
, by Corollary 36 the model of univalent type theory
![]() $\widetilde{\mathcal{E}}_{[\![{C}]\!]^{\widetilde{\mathcal{E}}}}$
satisfies Church’s Thesis where
$\widetilde{\mathcal{E}}_{[\![{C}]\!]^{\widetilde{\mathcal{E}}}}$
satisfies Church’s Thesis where
![]() $\mathcal{E} = \mathbf{CAsm}(\mathcal{K}_{1})$
.
$\mathcal{E} = \mathbf{CAsm}(\mathcal{K}_{1})$
.
We can now prove our second main result, which informally says that univalent type theory is consistent with the main principles of Recursive Constructive Mathematics.
Theorem Martin–LÖf type theory remains consistent when all of the following extra structure and axioms are added.
-
(1). Propositional truncation.
-
(2). The axiom of univalence.
-
(3). Church’s Thesis.
-
(4). Markov’s Principle.
Proof. We prove consistency by constructing a model where all of the above holds and where there is no element of type
![]() $\bot$
. Consider the Orton–Pitts model
$\bot$
. Consider the Orton–Pitts model
![]() $\widetilde{\mathcal{E}}$
with
$\widetilde{\mathcal{E}}$
with
![]() $\mathcal{E} = \mathbf{CAsm}(\mathcal{K}_{1})$
. We have seen that
$\mathcal{E} = \mathbf{CAsm}(\mathcal{K}_{1})$
. We have seen that
![]() $\widetilde{\mathcal{E}}$
satisfies Church’s Thesis in Example 37. It remains to show that
$\widetilde{\mathcal{E}}$
satisfies Church’s Thesis in Example 37. It remains to show that
![]() $\widetilde{\mathcal{E}}$
satisfies Markov’s Principle and
$\widetilde{\mathcal{E}}$
satisfies Markov’s Principle and
![]() $\bot$
is empty in this model.
$\bot$
is empty in this model.
Using well supportness again, and Example 34 we see that to show Markov’s principle holds, it suffices to show it holds in cubical assemblies (as a model of extensional type theory). Again, we observe that the type corresponding to Markov’s principle is preserved by the constant presheaves functor, and so it suffices to show that Markov’s principle holds in assemblies, which is again a standard argument.
Using well supportness once more, and Corollary 31, we see that
![]() $\bot$
is the same in null types as in cubical assemblies. It follows that it has no global sections, i.e. there is no element of type
$\bot$
is the same in null types as in cubical assemblies. It follows that it has no global sections, i.e. there is no element of type
![]() $\bot$
in the model.
$\bot$
in the model.
We can use Theorem 6 for other principles.
Example 38. Brouwer’s Continuity Principle is the following axiom.
The standard ordering
![]() $<$
on
$<$
on
![]() $\mathbb{N}$
is decidable, and thus Brouwer’s Continuity Principle is an instance of Theorem 6.
$\mathbb{N}$
is decidable, and thus Brouwer’s Continuity Principle is an instance of Theorem 6.
We obtain a new proof of the following result due to Coquand et al. (Reference Coquand, Ruch and Sattler2021).
Theorem Martin–LÖf type theory remains consistent when all of the following extra structure and axioms are added.
-
(1). Propositional truncation.
-
(2). The axiom of univalence.
-
(3). Brouwer’s Continuity Principle.
Proof. This is the same as for Theorem 6. See e.g. van Oosten (Reference van Oosten2008), Proposition 3.1.6 for a proof that Brouwer’s principle holds in the the effective topos (the same proof applies for assemblies).
The original proof by Coquand, Ruch and Sattler used cubical sheaves. Mike Shulman has pointed out that it can also be proved using the main result of Shulman (Reference Shulman2019): there are well-known examples of Grothendieck toposes where Brouwer’s continuity principle holds, and using a Grothendieck
![]() $(\infty, 1)$
-topos whose corresponding 1-topos of hsets is such a topos, one obtains a model of univalent type theory where Brouwer’s continuity principle holds. Both the Coquand–Ruch–Sattler proof and Shulman’s proof can also be said to use modalities, although in a very different way to our proof.
$(\infty, 1)$
-topos whose corresponding 1-topos of hsets is such a topos, one obtains a model of univalent type theory where Brouwer’s continuity principle holds. Both the Coquand–Ruch–Sattler proof and Shulman’s proof can also be said to use modalities, although in a very different way to our proof.
7. Conclusion and Further Work
We have constructed a model of type theory that satisfies the main axiom of homotopy type theory (univalence) and the main axioms of recursive constructive mathematics (Church’s thesis and Markov’s principle). However, in both fields, there are additional axioms that are natural to consider, but which we have left for future work.
With regards to homotopy type theory, we expect that the remaining higher inductive types appearing in Univalent Foundations Program (2013) can be implemented following the technique suggested in Rijke et al. (Reference Rijke, Shulman and Spitters2020), Remark 3.24 together with the technique of Coquand et al. (Reference Coquand, Huber and MÖrtberg2018) for constructing the necessary higher inductive types in cubical assemblies.
The situation with the remaining axioms of recursive constructive mathematics is more difficult. The axiom of countable choice is often included, but it is unclear whether countable choice holds in our model, or how to adjust the model to ensure countable choice does hold. The other main axiom of recursive constructive mathematics is extended Church’s thesis, which states that certain partial functions from
![]() $\mathbb{N}$
to
$\mathbb{N}$
to
![]() $\mathbb{N}$
are computable. The main issue here is that it is unclear what is the most natural way to formulate partial functions in homotopy type theory. Much progress on this has been made by EscardÓ and Knapp (Reference EscardÓ and Knapp2017). However, as they show, a weak form of countable choice is needed for their definition to work as expected. We expect that for any reasonable formulation of extended Church’s thesis Theorem 6 can be used to construct a model where it holds.
$\mathbb{N}$
are computable. The main issue here is that it is unclear what is the most natural way to formulate partial functions in homotopy type theory. Much progress on this has been made by EscardÓ and Knapp (Reference EscardÓ and Knapp2017). However, as they show, a weak form of countable choice is needed for their definition to work as expected. We expect that for any reasonable formulation of extended Church’s thesis Theorem 6 can be used to construct a model where it holds.
Another open problem is to find a good definition of
![]() $(\infty, 1)$
-effective topos, which should be to the effective topos what
$(\infty, 1)$
-effective topos, which should be to the effective topos what
![]() $(\infty, 1)$
-toposes are to Grothendieck toposes. In particular, the effective topos should be recovered as the localisation of the hsets in the
$(\infty, 1)$
-toposes are to Grothendieck toposes. In particular, the effective topos should be recovered as the localisation of the hsets in the
![]() $(\infty, 1)$
-effective topos, and commonly seen theorems and definitions in the effective topos should be special cases of corresponding higher versions. One possible definition is cubical assemblies. We can now see another possibility in the form of reflective subuniverses of cubical assemblies. However, our definition is dependent on a particular choice of axioms that satisfy the necessary conditions to apply Theorem 6, so we leave open the problem of finding a ‘natural’ definition that satisfies axioms such as Church’s thesis without needing to ensure they hold in the definition. One possible approach is to try to find a version of our construction that applies to all well supported maps at once. Another possibility is to further develop an alternative, more direct approach by Van den Berg (2020).
$(\infty, 1)$
-effective topos, and commonly seen theorems and definitions in the effective topos should be special cases of corresponding higher versions. One possible definition is cubical assemblies. We can now see another possibility in the form of reflective subuniverses of cubical assemblies. However, our definition is dependent on a particular choice of axioms that satisfy the necessary conditions to apply Theorem 6, so we leave open the problem of finding a ‘natural’ definition that satisfies axioms such as Church’s thesis without needing to ensure they hold in the definition. One possible approach is to try to find a version of our construction that applies to all well supported maps at once. Another possibility is to further develop an alternative, more direct approach by Van den Berg (2020).
Acknowledgements
The first author is grateful for some helpful discussions on higher inductive types with Simon Huber, Anders MÖrtberg and Christian Sattler at the Hausdorff Research Institute for Mathematics during the trimester program Types, Sets and Constructions. We are grateful to Benno van den Berg, Thierry Coquand and Mike Shulman for helpful comments and corrections.
Financial support
The second author is supported by the research programme ‘The Computational Content of Homotopy Type Theory’ with project number 613.001.602, which is financed by the Netherlands Organisation for Scientific Research (NWO).



