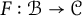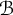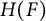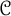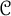1 Introduction
1.1 Background
The main objective of the present paper is to present a version of the Tannaka–Krein type reconstruction theorems. It is known that if
![]() ${\mathcal B}$
is a
${\mathcal B}$
is a
![]() $\mathbb {k}$
-linear abelian locally finite category and
$\mathbb {k}$
-linear abelian locally finite category and
![]() $F:{\mathcal B}\to \mathrm {vect\,}_{\mathbb {k}}$
is a fiber functor, that is, an exact faithful functor, then the coend
$F:{\mathcal B}\to \mathrm {vect\,}_{\mathbb {k}}$
is a fiber functor, that is, an exact faithful functor, then the coend
has structure of
![]() $\mathbb {k}$
-coalgebra, and the functor F factorizes as
$\mathbb {k}$
-coalgebra, and the functor F factorizes as

where
![]() $f:\mathrm {Comod}(C)\to \mathrm {vect\,}_{\mathbb {k}}$
is the forgetful functor, and
$f:\mathrm {Comod}(C)\to \mathrm {vect\,}_{\mathbb {k}}$
is the forgetful functor, and
![]() $\widehat {F}$
is a category equivalence. We refer the reader to [Reference Husemöller12, Reference Majid18, Reference Rivano22] and the references therein. If, moreover,
$\widehat {F}$
is a category equivalence. We refer the reader to [Reference Husemöller12, Reference Majid18, Reference Rivano22] and the references therein. If, moreover,
![]() ${\mathcal B}$
is a monoidal rigid category and F is a monoidal functor, then it is possible to endow the coalgebra C with structure of Hopf algebra. Succinctly, monoidality of
${\mathcal B}$
is a monoidal rigid category and F is a monoidal functor, then it is possible to endow the coalgebra C with structure of Hopf algebra. Succinctly, monoidality of
![]() ${\mathcal B}$
gives C a product, turning it into a bialgebra, and rigidity of
${\mathcal B}$
gives C a product, turning it into a bialgebra, and rigidity of
![]() ${\mathcal B}$
endows C with an antipode.
${\mathcal B}$
endows C with an antipode.
Some generalizations of this result appeared in the literature. We only mention some of them. In these more general versions, a fiber functor
![]() $F:{\mathcal B}\to {\mathcal C}$
is considered, where
$F:{\mathcal B}\to {\mathcal C}$
is considered, where
![]() ${\mathcal C}$
is an arbitrary monoidal category. In some versions, the object C is not a Hopf algebra in
${\mathcal C}$
is an arbitrary monoidal category. In some versions, the object C is not a Hopf algebra in
![]() ${\mathcal C}$
. For example, in [Reference Bruguières and Virelizier5], it is shown that if the functor F has a right adjoint
${\mathcal C}$
. For example, in [Reference Bruguières and Virelizier5], it is shown that if the functor F has a right adjoint
![]() $G:{\mathcal C}\to {\mathcal B}$
, then the associated monad to this adjunction
$G:{\mathcal C}\to {\mathcal B}$
, then the associated monad to this adjunction
![]() $T=F\circ G:{\mathcal C}\to {\mathcal C}$
is a bimonad, and there is a commutative diagram
$T=F\circ G:{\mathcal C}\to {\mathcal C}$
is a bimonad, and there is a commutative diagram

Here,
![]() $f: {\mathcal C}^T\to {\mathcal C}$
is the forgetful functor. Beck’s monadicity theorem implies that the functor
$f: {\mathcal C}^T\to {\mathcal C}$
is the forgetful functor. Beck’s monadicity theorem implies that the functor
![]() $\widehat {F}:{\mathcal B}\to {\mathcal C}^T$
is a monoidal equivalence. Rigidity of both monoidal categories
$\widehat {F}:{\mathcal B}\to {\mathcal C}^T$
is a monoidal equivalence. Rigidity of both monoidal categories
![]() ${\mathcal B}, {\mathcal C}$
implies that T has a Hopf monad structure. In [Reference Lyubashenko16, Reference Lyubashenko17], Lyubashenko reconstructed the object C as a coend
${\mathcal B}, {\mathcal C}$
implies that T has a Hopf monad structure. In [Reference Lyubashenko16, Reference Lyubashenko17], Lyubashenko reconstructed the object C as a coend
![]() $\int ^{B\in {\mathcal B}} F(B)\boxtimes F(B)^*$
, belonging to some completion of the Deligne tensor product
$\int ^{B\in {\mathcal B}} F(B)\boxtimes F(B)^*$
, belonging to some completion of the Deligne tensor product
![]() ${\mathcal C} \boxtimes {\mathcal C}$
, and it turns out to be a squared coalgebra. In the work of Majid [Reference Majid18, Reference Majid19], he started with a monoidal functor
${\mathcal C} \boxtimes {\mathcal C}$
, and it turns out to be a squared coalgebra. In the work of Majid [Reference Majid18, Reference Majid19], he started with a monoidal functor
![]() $F:{\mathcal B}\to {\mathcal C}$
, where
$F:{\mathcal B}\to {\mathcal C}$
, where
![]() ${\mathcal C}$
is a braided monoidal category, and he reconstructed a Hopf algebra
${\mathcal C}$
is a braided monoidal category, and he reconstructed a Hopf algebra
![]() $C=\int ^{B\in {\mathcal B}} F(B)^*{\otimes } F(B)$
, and set up a commutative diagram
$C=\int ^{B\in {\mathcal B}} F(B)^*{\otimes } F(B)$
, and set up a commutative diagram

With this generality, the functor
![]() $\widehat {F}$
no longer need to be an equivalence.
$\widehat {F}$
no longer need to be an equivalence.
1.2 Our approach
The point of view of this paper owes a lot to [Reference Schauenburg23]. However, we shall work only with finite categories. Let
![]() $\mathbb {k}$
be an arbitrary field, and let
$\mathbb {k}$
be an arbitrary field, and let
![]() ${\mathcal B}, {\mathcal C}$
be finite
${\mathcal B}, {\mathcal C}$
be finite
![]() $\mathbb {k}$
-linear abelian categories. Assume that both
$\mathbb {k}$
-linear abelian categories. Assume that both
![]() ${\mathcal C}, {\mathcal B}$
are rigid monoidal categories and
${\mathcal C}, {\mathcal B}$
are rigid monoidal categories and
![]() $F:{\mathcal B}\to {\mathcal C}$
is a monoidal functor. If F has a section
$F:{\mathcal B}\to {\mathcal C}$
is a monoidal functor. If F has a section
![]() $G:{\mathcal C}\to {\mathcal B}$
, that is,
$G:{\mathcal C}\to {\mathcal B}$
, that is,
![]() $F\circ G\simeq \mathrm { Id\,}_{\mathcal C}$
as monoidal functors, then it is possible to endow
$F\circ G\simeq \mathrm { Id\,}_{\mathcal C}$
as monoidal functors, then it is possible to endow
![]() ${\mathcal B}$
with an action of
${\mathcal B}$
with an action of
![]() ${\mathcal C}$
such that F is a monoidal
${\mathcal C}$
such that F is a monoidal
![]() ${\mathcal C}$
-module functor. This action behaves well together with the monoidal product of
${\mathcal C}$
-module functor. This action behaves well together with the monoidal product of
![]() ${\mathcal B}$
, in a sense that we call monoidal module category.
${\mathcal B}$
, in a sense that we call monoidal module category.
Under these conditions, we aim at constructing a Hopf algebra
![]() $H\in {\mathcal C}$
and obtaining a kind of Radford projection theorem in this categorical setting.
$H\in {\mathcal C}$
and obtaining a kind of Radford projection theorem in this categorical setting.
The reconstruction of such Hopf algebra is given in some steps, which we describe as follows. If
![]() ${\mathcal B}$
is a right
${\mathcal B}$
is a right
![]() ${\mathcal C}$
-module category and
${\mathcal C}$
-module category and
![]() $F:{\mathcal B}\to {\mathcal C}$
is an exact faithful module functor, then we construct a coalgebra
$F:{\mathcal B}\to {\mathcal C}$
is an exact faithful module functor, then we construct a coalgebra
![]() $C(F)\in {\mathcal C}$
as
$C(F)\in {\mathcal C}$
as
Here
![]() $\oint $
stands for the relative coend, a new tool, developed in [Reference Bortolussi and Mombelli4], in the context of module categories. This tool is one of the new features that we incorporate in these reconstruction theorems. The coproduct and counit of
$\oint $
stands for the relative coend, a new tool, developed in [Reference Bortolussi and Mombelli4], in the context of module categories. This tool is one of the new features that we incorporate in these reconstruction theorems. The coproduct and counit of
![]() $C(F)$
are defined using universal properties of the dinatural transformations associated with the relative coend. See Proposition 7.2. Moreover, we show that the functor F factorizes as
$C(F)$
are defined using universal properties of the dinatural transformations associated with the relative coend. See Proposition 7.2. Moreover, we show that the functor F factorizes as

Here,
![]() $f:{}^C{\mathcal C}\to {\mathcal C} $
is the forgetful functor and
$f:{}^C{\mathcal C}\to {\mathcal C} $
is the forgetful functor and
![]() $\widehat {F}: {\mathcal B}\to {}^C{\mathcal C}$
is an equivalence of
$\widehat {F}: {\mathcal B}\to {}^C{\mathcal C}$
is an equivalence of
![]() ${\mathcal C}$
-module categories. The existence of
${\mathcal C}$
-module categories. The existence of
![]() $\widehat {F}$
is stated in Proposition 7.4, and the proof that it is an equivalence of categories is given in Theorem 7.7.
$\widehat {F}$
is stated in Proposition 7.4, and the proof that it is an equivalence of categories is given in Theorem 7.7.
If, in addition,
![]() ${\mathcal C}$
is a braided rigid monoidal
${\mathcal C}$
is a braided rigid monoidal
![]() ${\mathcal C}$
-module category,
${\mathcal C}$
-module category,
![]() ${\mathcal B}$
is a rigid monoidal category, and F is a monoidal functor, then we endow the coalgebra
${\mathcal B}$
is a rigid monoidal category, and F is a monoidal functor, then we endow the coalgebra
![]() $C(F)$
with a product, turning it into a bialgebra in
$C(F)$
with a product, turning it into a bialgebra in
![]() ${\mathcal C}$
. Rigidity of
${\mathcal C}$
. Rigidity of
![]() ${\mathcal B}$
allows to define an antipode on
${\mathcal B}$
allows to define an antipode on
![]() $C(F)$
, making it into a braided Hopf algebra. These results are stated in Theorem 7.11 and Corollary 7.19.
$C(F)$
, making it into a braided Hopf algebra. These results are stated in Theorem 7.11 and Corollary 7.19.
The contents of the paper are the following. In Section 3, we give a brief account of some basic facts about tensor categories and module categories that will be used throughout the paper. In Section 4, we review the notion of relative (co)end of a functor in the setting of module categories over a tensor category
![]() ${\mathcal C}$
. This tool was developed by the second author in [Reference Bortolussi and Mombelli4] as generalization of the usual (co)end. Let
${\mathcal C}$
. This tool was developed by the second author in [Reference Bortolussi and Mombelli4] as generalization of the usual (co)end. Let
![]() ${\mathcal C}$
be a tensor category,
${\mathcal C}$
be a tensor category,
![]() ${\mathcal M}$
be a left
${\mathcal M}$
be a left
![]() ${\mathcal C}$
-module category, and
${\mathcal C}$
-module category, and
![]() ${\mathcal A}$
be some target category. If a functor
${\mathcal A}$
be some target category. If a functor
![]() $S:{\mathcal M}^{\mathrm {{op}}}\times {\mathcal M}\to {\mathcal A}$
has a prebalancing, that is, natural isomorphisms
$S:{\mathcal M}^{\mathrm {{op}}}\times {\mathcal M}\to {\mathcal A}$
has a prebalancing, that is, natural isomorphisms
then the relative coend
is an object in
![]() $ {\mathcal A}$
equipped with dinatural transformations
$ {\mathcal A}$
equipped with dinatural transformations
![]() $\pi _M:S(M,M)\xrightarrow {. .} \oint ^{M\in {\mathcal M}} (S,\beta )$
, such that it satisfies some extra condition (see, for example, (4.3)), and it is universal with this property. When
$\pi _M:S(M,M)\xrightarrow {. .} \oint ^{M\in {\mathcal M}} (S,\beta )$
, such that it satisfies some extra condition (see, for example, (4.3)), and it is universal with this property. When
![]() ${\mathcal C}=\mathrm {vect\,}_{\mathbb {k}}$
, the relative (co)end coincides with the usual (co)end.
${\mathcal C}=\mathrm {vect\,}_{\mathbb {k}}$
, the relative (co)end coincides with the usual (co)end.
Since relative (co)ends are objects defined by a universal property, they may not exist in general. Section 4.1 is devoted to prove that all relative coends, used in this work, actually exist. In this section, it is crucial that all categories, the tensor category
![]() ${\mathcal C}$
and the module category
${\mathcal C}$
and the module category
![]() ${\mathcal M}$
are finite. We also require that the action
${\mathcal M}$
are finite. We also require that the action
![]() $ {\mathcal C}\times {\mathcal M}\to {\mathcal M}$
is exact in each variable, allowing us to use [Reference Douglas, Schommer-Pries and Snyder9, Theorem 2.24], that says that there is an equivalence of module categories
$ {\mathcal C}\times {\mathcal M}\to {\mathcal M}$
is exact in each variable, allowing us to use [Reference Douglas, Schommer-Pries and Snyder9, Theorem 2.24], that says that there is an equivalence of module categories
![]() ${\mathcal M}\simeq {\mathcal C}_A$
, for some algebra
${\mathcal M}\simeq {\mathcal C}_A$
, for some algebra
![]() $A\in {\mathcal C}.$
$A\in {\mathcal C}.$
In Section 5, we review the definition of a Hopf algebra H in a braided tensor category
![]() ${\mathcal C}$
and its tensor category of comodules
${\mathcal C}$
and its tensor category of comodules
![]() ${^H}{\mathcal C}$
. We also review the definition of H-H-Yetter–Drinfeld modules in this setting, which produces a braided tensor category
${^H}{\mathcal C}$
. We also review the definition of H-H-Yetter–Drinfeld modules in this setting, which produces a braided tensor category
![]() ${^H_H}{\mathcal YD}({\mathcal C})$
. Then we introduce a notion of a
${^H_H}{\mathcal YD}({\mathcal C})$
. Then we introduce a notion of a
![]() ${\mathcal C}$
-module category
${\mathcal C}$
-module category
![]() ${\mathcal B}$
with a compatible tensor structure in the sense that there is a natural isomorphism
${\mathcal B}$
with a compatible tensor structure in the sense that there is a natural isomorphism
for all
![]() $X\in {\mathcal C},\,B\in {\mathcal B}$
, satisfying certain axioms. Note that there is a second reasonable notion of a monoidal module category, where the action
$X\in {\mathcal C},\,B\in {\mathcal B}$
, satisfying certain axioms. Note that there is a second reasonable notion of a monoidal module category, where the action
![]() $X\triangleright -$
is a monoidal functor, and this definition is not equivalent. Under the presence of a monoidal functor
$X\triangleright -$
is a monoidal functor, and this definition is not equivalent. Under the presence of a monoidal functor
![]() $F:{\mathcal B}\to {\mathcal C}$
, compatibility of the monoidal product in
$F:{\mathcal B}\to {\mathcal C}$
, compatibility of the monoidal product in
![]() ${\mathcal B}$
and the action of
${\mathcal B}$
and the action of
![]() ${\mathcal C}$
on
${\mathcal C}$
on
![]() ${\mathcal B}$
is equivalent to the existence of a section to F, that is a monoidal functor
${\mathcal B}$
is equivalent to the existence of a section to F, that is a monoidal functor
![]() $G:{\mathcal C}\to {\mathcal B}$
such that there is a monoidal natural isomorphism
$G:{\mathcal C}\to {\mathcal B}$
such that there is a monoidal natural isomorphism
![]() $F\circ G\simeq \mathrm {Id\,}.$
$F\circ G\simeq \mathrm {Id\,}.$
2 Preliminaries
Throughout this paper,
![]() $\mathbb {k}$
will denote an arbitrary field. We shall denote by
$\mathbb {k}$
will denote an arbitrary field. We shall denote by
![]() $\mathrm {vect\,}_{\mathbb {k}}$
the category of finite-dimensional
$\mathrm {vect\,}_{\mathbb {k}}$
the category of finite-dimensional
![]() $\mathbb {k}$
-vector spaces.
$\mathbb {k}$
-vector spaces.
A finite category [Reference Etingof and Ostrik10] is an abelian
![]() $\mathbb {k}$
-linear category such that it has only a finite number of isomorphism classes of simple objects, Hom spaces are finite-dimensional
$\mathbb {k}$
-linear category such that it has only a finite number of isomorphism classes of simple objects, Hom spaces are finite-dimensional
![]() $\mathbb {k}$
-vector spaces, all objects have finite length, and every simple object has a projective cover. All these conditions are equivalent to requiring that the category is equivalent to the category of finite-dimensional representations of a finite-dimensional
$\mathbb {k}$
-vector spaces, all objects have finite length, and every simple object has a projective cover. All these conditions are equivalent to requiring that the category is equivalent to the category of finite-dimensional representations of a finite-dimensional
![]() $\mathbb {k}$
-algebra.
$\mathbb {k}$
-algebra.
If
![]() ${\mathcal M}, {\mathcal N}$
are categories and
${\mathcal M}, {\mathcal N}$
are categories and
![]() $F:{\mathcal M}\to {\mathcal N}$
is a functor, we shall denote by
$F:{\mathcal M}\to {\mathcal N}$
is a functor, we shall denote by
![]() $F^{\mathrm {{ra}}}, F^{\mathrm {{la}}}:{\mathcal N}\to {\mathcal M}$
its right and left adjoints, respectively. We shall denote by
$F^{\mathrm {{ra}}}, F^{\mathrm {{la}}}:{\mathcal N}\to {\mathcal M}$
its right and left adjoints, respectively. We shall denote by
![]() ${\mathcal M}^{\mathrm {{op}}}$
the opposite category. If
${\mathcal M}^{\mathrm {{op}}}$
the opposite category. If
![]() $f:M\to N$
is a morphism in
$f:M\to N$
is a morphism in
![]() ${\mathcal M}$
, sometimes we shall denote by
${\mathcal M}$
, sometimes we shall denote by
![]() $f^{\mathrm {{op}}}:N\to M$
the same map but understood as a morphism in
$f^{\mathrm {{op}}}:N\to M$
the same map but understood as a morphism in
![]() ${\mathcal M}^{\mathrm {{op}}}$
.
${\mathcal M}^{\mathrm {{op}}}$
.
Any abelian
![]() $\mathbb {k}$
-linear category
$\mathbb {k}$
-linear category
![]() ${\mathcal M}$
has a canonical action of the category of finite-dimensional
${\mathcal M}$
has a canonical action of the category of finite-dimensional
![]() $\mathbb {k}$
-vector spaces
$\mathbb {k}$
-vector spaces
See, for example, [Reference Schauenburg23, Lemma 2.2.2]. Any additive
![]() $\mathbb {k}$
-linear functor
$\mathbb {k}$
-linear functor
![]() $F:{\mathcal M}\to {\mathcal N}$
between abelian
$F:{\mathcal M}\to {\mathcal N}$
between abelian
![]() $\mathbb {k}$
-linear categories respects the action of
$\mathbb {k}$
-linear categories respects the action of
![]() $\mathrm { vect\,}_{\mathbb {k}}$
, that is, there are natural isomorphisms
$\mathrm { vect\,}_{\mathbb {k}}$
, that is, there are natural isomorphisms
![]() $V\in \mathrm {vect\,}_{\mathbb {k}}$
,
$V\in \mathrm {vect\,}_{\mathbb {k}}$
,
![]() $M\in {\mathcal M}$
, satisfying certain axioms.
$M\in {\mathcal M}$
, satisfying certain axioms.
From now on, all categories will be assumed to be finite abelian
![]() $\mathbb {k}$
-linear categories, and all functors will be additive
$\mathbb {k}$
-linear categories, and all functors will be additive
![]() $\mathbb {k}$
-linear. Here,
$\mathbb {k}$
-linear. Here,
![]() $\mathbb {k}$
is an arbitrary field. All our proofs work in the presence of an associator, but for simplicity we assume in the presentation that the categories are strict.
$\mathbb {k}$
is an arbitrary field. All our proofs work in the presence of an associator, but for simplicity we assume in the presentation that the categories are strict.
3 Representations of tensor categories
3.1 Finite tensor categories
A finite tensor category
![]() ${\mathcal C}$
is a monoidal rigid category, with simple unit object
${\mathcal C}$
is a monoidal rigid category, with simple unit object
![]() $ \mathbf {1}\in {\mathcal C}$
. We refer to [Reference Etingof and Ostrik10] for more details on finite tensor categories. Without loss of generality, we shall assume that tensor categories in this work are strict.
$ \mathbf {1}\in {\mathcal C}$
. We refer to [Reference Etingof and Ostrik10] for more details on finite tensor categories. Without loss of generality, we shall assume that tensor categories in this work are strict.
If
![]() ${\mathcal C}, {\mathcal D}$
are monoidal categories, a monoidal functor is a functor
${\mathcal C}, {\mathcal D}$
are monoidal categories, a monoidal functor is a functor
![]() $F:{\mathcal C}\to {\mathcal D}$
equipped with natural isomorphisms
$F:{\mathcal C}\to {\mathcal D}$
equipped with natural isomorphisms
such that
If
![]() $(F,\xi ), (\widetilde {F}, \widetilde {\xi }):{\mathcal C}\to {\mathcal D}$
are two monoidal functors, a monoidal natural transformation between F and
$(F,\xi ), (\widetilde {F}, \widetilde {\xi }):{\mathcal C}\to {\mathcal D}$
are two monoidal functors, a monoidal natural transformation between F and
![]() $\widetilde {F}$
is a natural transformation
$\widetilde {F}$
is a natural transformation
![]() $\alpha :F\to \widetilde {F}$
such that
$\alpha :F\to \widetilde {F}$
such that
for any
![]() $A,B\in {\mathcal C}$
.
$A,B\in {\mathcal C}$
.
If
![]() ${\mathcal C}$
is a category, for any
${\mathcal C}$
is a category, for any
![]() $X\in {\mathcal C}$
, we shall denote by
$X\in {\mathcal C}$
, we shall denote by
the evaluation and coevaluation. By abuse of notation, we shall also denote by
the evaluation and coevaluation for the left duals. We will use the following basic result. If
![]() $f:X\to Y$
is an isomorphism in
$f:X\to Y$
is an isomorphism in
![]() ${\mathcal C}$
, then
${\mathcal C}$
, then
 $$ \begin{align}\begin{aligned} (\mathrm{id\,}_{ {}^*X}{\otimes} f )\mbox{coev}_X&= ({}^*f{\otimes} \mathrm{id\,}_Y )\mbox{coev}_Y, \\\mbox{ev}_Y (f{\otimes} \mathrm{id\,}_Y)&=\mbox{ev}_X (\mathrm{id\,}_X{\otimes} {}^*f). \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} (\mathrm{id\,}_{ {}^*X}{\otimes} f )\mbox{coev}_X&= ({}^*f{\otimes} \mathrm{id\,}_Y )\mbox{coev}_Y, \\\mbox{ev}_Y (f{\otimes} \mathrm{id\,}_Y)&=\mbox{ev}_X (\mathrm{id\,}_X{\otimes} {}^*f). \end{aligned}\end{align} $$
It is well known that for any pair of objects
![]() $X, Y\in {\mathcal C}$
, there are canonical natural isomorphisms
$X, Y\in {\mathcal C}$
, there are canonical natural isomorphisms
These isomorphisms allow us to compute coevaluation and evaluation maps of duals; more precisely, we shall need the following identity:
We are going to make use, very often, of the canonical natural isomorphisms
 $$ \begin{align}\begin{aligned} &\psi^Z_{X,Y}:\operatorname{Hom}_{\mathcal B}(X{\otimes} {}^*Y,Z)\to \operatorname{Hom}_{\mathcal B}(X,Z{\otimes} Y),\\&\psi^Z_{X,Y}(f)=(f{\otimes}\mathrm{id\,}_Y)(\mathrm{id\,}_X{\otimes} \mbox{coev}_Y). \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} &\psi^Z_{X,Y}:\operatorname{Hom}_{\mathcal B}(X{\otimes} {}^*Y,Z)\to \operatorname{Hom}_{\mathcal B}(X,Z{\otimes} Y),\\&\psi^Z_{X,Y}(f)=(f{\otimes}\mathrm{id\,}_Y)(\mathrm{id\,}_X{\otimes} \mbox{coev}_Y). \end{aligned}\end{align} $$
And, its inverse
 $$ \begin{align}\begin{aligned} \bar{\psi}^Z_{X,Y}:\operatorname{Hom}_{\mathcal B}(X,Z{\otimes} Y)\to \operatorname{Hom}_{\mathcal B}(X{\otimes} {}^*Y,Z) \\\bar{\psi}^Z_{X,Y}(g)=(\mathrm{id\,}_Z{\otimes}\mbox{ev}_Y)(g{\otimes}\mathrm{id\,}_{{}^*Y}). \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \bar{\psi}^Z_{X,Y}:\operatorname{Hom}_{\mathcal B}(X,Z{\otimes} Y)\to \operatorname{Hom}_{\mathcal B}(X{\otimes} {}^*Y,Z) \\\bar{\psi}^Z_{X,Y}(g)=(\mathrm{id\,}_Z{\otimes}\mbox{ev}_Y)(g{\otimes}\mathrm{id\,}_{{}^*Y}). \end{aligned}\end{align} $$
We shall also need the following basic fact.
Lemma 3.1 For any pair
![]() $V,W\in {\mathcal C}$
, the evaluation of
$V,W\in {\mathcal C}$
, the evaluation of
![]() $V{\otimes } W$
is given by
$V{\otimes } W$
is given by
3.2 Module categories over tensor categories
A left module category over
![]() ${\mathcal C}$
is a category
${\mathcal C}$
is a category
![]() ${\mathcal M}$
together with a
${\mathcal M}$
together with a
![]() $\mathbb {k}$
-bilinear bifunctor
$\mathbb {k}$
-bilinear bifunctor
![]() $\rhd : {\mathcal C} \times {\mathcal M} \to {\mathcal M}$
, exact in each variable, endowed with natural associativity and unit isomorphisms
$\rhd : {\mathcal C} \times {\mathcal M} \to {\mathcal M}$
, exact in each variable, endowed with natural associativity and unit isomorphisms
These isomorphisms are subject to the following conditions:

for any
![]() $X, Y, Z\in {\mathcal C}, M\in {\mathcal M}$
, as well as
$X, Y, Z\in {\mathcal C}, M\in {\mathcal M}$
, as well as
Sometimes we shall also say that
![]() ${\mathcal M}$
is a
${\mathcal M}$
is a
![]() ${\mathcal C}$
-module category or a representation of
${\mathcal C}$
-module category or a representation of
![]() ${\mathcal C}$
.
${\mathcal C}$
.
Let
![]() ${\mathcal M}$
and
${\mathcal M}$
and
![]() ${\mathcal M}'$
be a pair of
${\mathcal M}'$
be a pair of
![]() ${\mathcal C}$
-module categories. A module functor is a pair
${\mathcal C}$
-module categories. A module functor is a pair
![]() $(F,c)$
, where
$(F,c)$
, where
![]() $F:{\mathcal M}\to {\mathcal M}'$
is a functor equipped with natural isomorphisms
$F:{\mathcal M}\to {\mathcal M}'$
is a functor equipped with natural isomorphisms
for
![]() $X\in {\mathcal C}$
,
$X\in {\mathcal C}$
,
![]() $M\in {\mathcal M}$
, such that
$M\in {\mathcal M}$
, such that

for any
![]() $X, Y\in {\mathcal C}$
,
$X, Y\in {\mathcal C}$
,
![]() $M\in {\mathcal M}$
, as well as
$M\in {\mathcal M}$
, as well as
Module functors are composable, if
![]() ${\mathcal M}"$
is a
${\mathcal M}"$
is a
![]() ${\mathcal C}$
-module category and
${\mathcal C}$
-module category and
![]() $(G,d): {\mathcal M}' \to {\mathcal M}"$
is another module functor, then the composition
$(G,d): {\mathcal M}' \to {\mathcal M}"$
is another module functor, then the composition
is also a module functor.
A natural module transformation, between module functors
![]() $(F,c)$
and
$(F,c)$
and
![]() $(G,d)$
, is a natural transformation
$(G,d)$
, is a natural transformation
![]() $\theta : F \to G$
such that
$\theta : F \to G$
such that
for any
![]() $X\in {\mathcal C}$
,
$X\in {\mathcal C}$
,
![]() $M\in {\mathcal M}$
. The vector space of natural module transformations will be denoted by
$M\in {\mathcal M}$
. The vector space of natural module transformations will be denoted by
![]() $\mathrm {Nat\,}_{\!m}(F,G)$
. Two module functors
$\mathrm {Nat\,}_{\!m}(F,G)$
. Two module functors
![]() $F, G$
are equivalent if there exists a natural module isomorphism
$F, G$
are equivalent if there exists a natural module isomorphism
![]() $\theta :F \to G$
. We denote by
$\theta :F \to G$
. We denote by
![]() $\operatorname {Fun}_{{\mathcal C}}({\mathcal M}, {\mathcal M}')$
the category whose objects are module functors
$\operatorname {Fun}_{{\mathcal C}}({\mathcal M}, {\mathcal M}')$
the category whose objects are module functors
![]() $(F, c)$
from
$(F, c)$
from
![]() ${\mathcal M}$
to
${\mathcal M}$
to
![]() ${\mathcal M}'$
and arrows module natural transformations.
${\mathcal M}'$
and arrows module natural transformations.
Two
![]() ${\mathcal C}$
-modules
${\mathcal C}$
-modules
![]() ${\mathcal M}$
and
${\mathcal M}$
and
![]() ${\mathcal M}'$
are equivalent if there exist module functors
${\mathcal M}'$
are equivalent if there exist module functors
![]() $F:{\mathcal M}\to {\mathcal M}'$
,
$F:{\mathcal M}\to {\mathcal M}'$
,
![]() $G:{\mathcal M}'\to {\mathcal M}$
, and natural module isomorphisms
$G:{\mathcal M}'\to {\mathcal M}$
, and natural module isomorphisms
![]() $\mathrm {Id\,}_{{\mathcal M}'} \to F\circ G$
,
$\mathrm {Id\,}_{{\mathcal M}'} \to F\circ G$
,
![]() $\mathrm {Id\,}_{{\mathcal M}} \to G\circ F$
.
$\mathrm {Id\,}_{{\mathcal M}} \to G\circ F$
.
A module category will be called strict if isomorphisms m and l are identities. Any module category is equivalent to a strict one. We will often assume that the module category is strict without further mention.
A right module category over
![]() ${\mathcal C}$
is a category
${\mathcal C}$
is a category
![]() ${\mathcal M}$
equipped with an exact bifunctor
${\mathcal M}$
equipped with an exact bifunctor
![]() $\triangleleft : {\mathcal M}\times {\mathcal C}\to {\mathcal M}$
and natural isomorphisms
$\triangleleft : {\mathcal M}\times {\mathcal C}\to {\mathcal M}$
and natural isomorphisms
such that

as well as
If
![]() ${\mathcal M}, {\mathcal M}'$
are right
${\mathcal M}, {\mathcal M}'$
are right
![]() ${\mathcal C}$
-modules, a module functor from
${\mathcal C}$
-modules, a module functor from
![]() ${\mathcal M}$
to
${\mathcal M}$
to
![]() $ {\mathcal M}'$
is a pair
$ {\mathcal M}'$
is a pair
![]() $(T, d)$
where
$(T, d)$
where
![]() $T:{\mathcal M} \to {\mathcal M}'$
is a functor and
$T:{\mathcal M} \to {\mathcal M}'$
is a functor and
![]() $d_{M,X}:T(M\triangleleft X)\to T(M)\triangleleft X$
are natural isomorphisms such that for any
$d_{M,X}:T(M\triangleleft X)\to T(M)\triangleleft X$
are natural isomorphisms such that for any
![]() $X, Y\in {\mathcal C}$
,
$X, Y\in {\mathcal C}$
,
![]() $M\in {\mathcal M}$
:
$M\in {\mathcal M}$
:

as well as
3.3 The internal Hom
Let
![]() ${\mathcal C}$
be a tensor category and
${\mathcal C}$
be a tensor category and
![]() ${\mathcal M}$
be a left
${\mathcal M}$
be a left
![]() ${\mathcal C}$
-module category. For any pair of objects
${\mathcal C}$
-module category. For any pair of objects
![]() $M, N\in {\mathcal M}$
, the internal Hom is an object
$M, N\in {\mathcal M}$
, the internal Hom is an object
![]() $\underline {\operatorname {Hom}}(M,N)\in {\mathcal C}$
representing the left exact functor
$\underline {\operatorname {Hom}}(M,N)\in {\mathcal C}$
representing the left exact functor
This means that there are natural isomorphisms
The internal Hom for right
![]() ${\mathcal C}$
-module categories is defined similarly.
${\mathcal C}$
-module categories is defined similarly.
The next technical result will be needed later. Recall natural isomorphisms
![]() $\phi ^l$
defined in (3.5).
$\phi ^l$
defined in (3.5).
Lemma 3.2 Let
![]() ${\mathcal M}$
be a right
${\mathcal M}$
be a right
![]() ${\mathcal C}$
-module category with action given by
${\mathcal C}$
-module category with action given by
![]() $\triangleleft : {\mathcal M}\times {\mathcal C}\to {\mathcal M}$
. If
$\triangleleft : {\mathcal M}\times {\mathcal C}\to {\mathcal M}$
. If
![]() $(F,c):{\mathcal M}\to {\mathcal C}$
is a module functor, then, for any
$(F,c):{\mathcal M}\to {\mathcal C}$
is a module functor, then, for any
![]() $B\in {\mathcal M}$
,
$B\in {\mathcal M}$
,
![]() $X\in {\mathcal C}$
, the following diagrams commute.
$X\in {\mathcal C}$
, the following diagrams commute.


Proof The proof follows by simply checking that morphisms
satisfy rigidity axioms.
4 The (co)end for module categories
In this section, we recall the notion of relative (co)ends, a tool developed in [Reference Bortolussi and Mombelli4] in the context of representations of tensor categories, generalizing the well-known notion of (co)ends in category theory.
Let
![]() ${\mathcal C}$
be a tensor category and
${\mathcal C}$
be a tensor category and
![]() ${\mathcal M}$
be a left
${\mathcal M}$
be a left
![]() ${\mathcal C}$
-module category. Assume that
${\mathcal C}$
-module category. Assume that
![]() ${\mathcal A}$
is a category and
${\mathcal A}$
is a category and
![]() $S:{\mathcal M}^{\mathrm {{op}}}\times {\mathcal M}\to {\mathcal A}$
is a functor equipped with natural isomorphisms
$S:{\mathcal M}^{\mathrm {{op}}}\times {\mathcal M}\to {\mathcal A}$
is a functor equipped with natural isomorphisms
for any
![]() $X\in {\mathcal C}, M,N\in {\mathcal M}$
. We shall say that
$X\in {\mathcal C}, M,N\in {\mathcal M}$
. We shall say that
![]() $\beta $
is a prebalancing of the functor S. Sometimes we shall say that it is a
$\beta $
is a prebalancing of the functor S. Sometimes we shall say that it is a
![]() ${\mathcal C}$
-prebalancing to emphasize the dependence on
${\mathcal C}$
-prebalancing to emphasize the dependence on
![]() ${\mathcal C}$
.
${\mathcal C}$
.
Definition 4.1 The relative end of the pair
![]() $(S,\beta )$
is an object
$(S,\beta )$
is an object
![]() $E\in {\mathcal A}$
equipped with dinatural transformations
$E\in {\mathcal A}$
equipped with dinatural transformations
![]() $\pi _M: E\xrightarrow {. .} S(M,M)$
such that
$\pi _M: E\xrightarrow {. .} S(M,M)$
such that

for any
![]() $X\in {\mathcal C}, M\in {\mathcal M}$
, and is universal with this property. This means that, if
$X\in {\mathcal C}, M\in {\mathcal M}$
, and is universal with this property. This means that, if
![]() $\widetilde {E}\in {\mathcal A}$
is another object with dinatural transformations
$\widetilde {E}\in {\mathcal A}$
is another object with dinatural transformations
![]() $\xi _M:\widetilde {E}\xrightarrow {. .} S(M,M)$
, such that they fulfill (4.2), there exists a unique morphism
$\xi _M:\widetilde {E}\xrightarrow {. .} S(M,M)$
, such that they fulfill (4.2), there exists a unique morphism
![]() $h:\widetilde {E}\to E$
such that
$h:\widetilde {E}\to E$
such that
![]() $\xi _M= \pi _M\circ h $
.
$\xi _M= \pi _M\circ h $
.
The relative end depends on the choice of the prebalancing. We will denote the relative end as
![]() $\oint _{M\in {\mathcal M}} (S,\beta )$
, or sometimes simply as
$\oint _{M\in {\mathcal M}} (S,\beta )$
, or sometimes simply as
![]() $\oint _{M\in {\mathcal M}} S$
, when the prebalancing
$\oint _{M\in {\mathcal M}} S$
, when the prebalancing
![]() $\beta $
is understood from the context.
$\beta $
is understood from the context.
The relative coend of the pair
![]() $(S,\beta )$
is defined dually. This is an object
$(S,\beta )$
is defined dually. This is an object
![]() $C\in {\mathcal A}$
equipped with dinatural transformations
$C\in {\mathcal A}$
equipped with dinatural transformations
![]() $\pi _M:S(M,M)\xrightarrow {. .} C$
such that
$\pi _M:S(M,M)\xrightarrow {. .} C$
such that

for any
![]() $X\in {\mathcal C}, M\in {\mathcal M}$
, universal with this property. This means that, if
$X\in {\mathcal C}, M\in {\mathcal M}$
, universal with this property. This means that, if
![]() $\widetilde {C}\in {\mathcal A}$
is another object with dinatural transformations
$\widetilde {C}\in {\mathcal A}$
is another object with dinatural transformations
![]() $\lambda _M: S(M,M) \xrightarrow {. .} \widetilde {C}$
such that they satisfy (4.3), there exists a unique morphism
$\lambda _M: S(M,M) \xrightarrow {. .} \widetilde {C}$
such that they satisfy (4.3), there exists a unique morphism
![]() $g:C\to \widetilde {C}$
such that
$g:C\to \widetilde {C}$
such that
![]() $g \circ \pi _M=\lambda _M$
. The relative coend will be denoted
$g \circ \pi _M=\lambda _M$
. The relative coend will be denoted
![]() $\oint ^{M\in {\mathcal M}} (S,\beta )$
, or simply as
$\oint ^{M\in {\mathcal M}} (S,\beta )$
, or simply as
![]() $\oint ^{M\in {\mathcal M}} S$
.
$\oint ^{M\in {\mathcal M}} S$
.
A similar definition can be made for right
![]() ${\mathcal C}$
-module categories. Let
${\mathcal C}$
-module categories. Let
![]() ${\mathcal A}$
be a category, and let
${\mathcal A}$
be a category, and let
![]() ${\mathcal N}$
be a right
${\mathcal N}$
be a right
![]() ${\mathcal C}$
-module category endowed with a functor
${\mathcal C}$
-module category endowed with a functor
![]() $S:{\mathcal N}^{\mathrm {{op}}}\times {\mathcal N}\to {\mathcal A}$
with a prebalancing
$S:{\mathcal N}^{\mathrm {{op}}}\times {\mathcal N}\to {\mathcal A}$
with a prebalancing
for any
![]() $M,N\in {\mathcal N}$
,
$M,N\in {\mathcal N}$
,
![]() $X\in {\mathcal C}$
.
$X\in {\mathcal C}$
.
Definition 4.2 The relative end for S is an object
![]() $E\in {\mathcal A}$
equipped with dinatural transformations
$E\in {\mathcal A}$
equipped with dinatural transformations
![]() $\lambda _N:E\xrightarrow { .. } S(N,N)$
such that
$\lambda _N:E\xrightarrow { .. } S(N,N)$
such that

for any
![]() $N\in {\mathcal N}$
,
$N\in {\mathcal N}$
,
![]() $X\in {\mathcal C}$
. We shall also denote this relative end by
$X\in {\mathcal C}$
. We shall also denote this relative end by
![]() $\oint _{N\in {\mathcal N}} (S, \gamma )$
.
$\oint _{N\in {\mathcal N}} (S, \gamma )$
.
Similarly, the relative coend is an object
![]() $C\in {\mathcal B}$
with dinatural transformations
$C\in {\mathcal B}$
with dinatural transformations
![]() $\lambda _N: S(N,N)\xrightarrow { .. } C$
such that
$\lambda _N: S(N,N)\xrightarrow { .. } C$
such that

for any
![]() $N\in {\mathcal N}$
,
$N\in {\mathcal N}$
,
![]() $X\in {\mathcal C}$
. We shall also denote this relative coend by
$X\in {\mathcal C}$
. We shall also denote this relative coend by
![]() $\oint ^{N\in {\mathcal N}} (S, \gamma )$
.
$\oint ^{N\in {\mathcal N}} (S, \gamma )$
.
In the next proposition, we collect some results about the relative (co)end that will be useful. The reader is referred to [Reference Bortolussi and Mombelli4, Proposition 3.3] and [Reference Bortolussi and Mombelli4, Proposition 4.2].
Proposition 4.3 Assume that
![]() ${\mathcal M}, {\mathcal N}$
are left
${\mathcal M}, {\mathcal N}$
are left
![]() ${\mathcal C}$
-module categories and that
${\mathcal C}$
-module categories and that
![]() $S, \widetilde {S}:{\mathcal M}^{\mathrm {{op}}}\times {\mathcal M}\to {\mathcal A}$
are functors equipped with
$S, \widetilde {S}:{\mathcal M}^{\mathrm {{op}}}\times {\mathcal M}\to {\mathcal A}$
are functors equipped with
![]() ${\mathcal C}$
-prebalancings
${\mathcal C}$
-prebalancings
![]() $X\in {\mathcal C}, M,N\in {\mathcal M}$
. The following assertions holds:
$X\in {\mathcal C}, M,N\in {\mathcal M}$
. The following assertions holds:
-
(i) Assume that the module ends
 $\oint _{M\in {\mathcal M}} (S,\beta ), \oint _{M\in {\mathcal M}} (\widetilde {S},\widetilde {\beta })$
exist and have dinatural transformations
$\oint _{M\in {\mathcal M}} (S,\beta ), \oint _{M\in {\mathcal M}} (\widetilde {S},\widetilde {\beta })$
exist and have dinatural transformations
 $\pi , \widetilde {\pi }$
, respectively. If
$\pi , \widetilde {\pi }$
, respectively. If
 $\gamma :S\to \widetilde {S}$
is a natural transformation such that (4.6)then there exists a unique map
$\gamma :S\to \widetilde {S}$
is a natural transformation such that (4.6)then there exists a unique map $$ \begin{align} \widetilde{\beta}^X_{M,N} \gamma_{(M,X\triangleright N)}=\gamma_{(X^*\triangleright M,N)} \beta^X_{M,N}, \end{align} $$
$$ \begin{align} \widetilde{\beta}^X_{M,N} \gamma_{(M,X\triangleright N)}=\gamma_{(X^*\triangleright M,N)} \beta^X_{M,N}, \end{align} $$
 $\widehat {\gamma }: \oint _{M\in {\mathcal M}} (S,\beta )\to \oint _{M\in {\mathcal M}} (\widetilde {S},\widetilde {\beta })$
such that for any
$\widehat {\gamma }: \oint _{M\in {\mathcal M}} (S,\beta )\to \oint _{M\in {\mathcal M}} (\widetilde {S},\widetilde {\beta })$
such that for any $$ \begin{align*}\widetilde{\pi}_M \widehat{\gamma}= \gamma_{(M,M)} \pi_M\end{align*} $$
$$ \begin{align*}\widetilde{\pi}_M \widehat{\gamma}= \gamma_{(M,M)} \pi_M\end{align*} $$
 $M\in {\mathcal M}$
. If
$M\in {\mathcal M}$
. If
 $\gamma $
is a natural isomorphism, then
$\gamma $
is a natural isomorphism, then
 $\widehat {\gamma }$
is an isomorphism.
$\widehat {\gamma }$
is an isomorphism.
-
(ii) For any pair of
 ${\mathcal C}$
-module functors
${\mathcal C}$
-module functors
 $(F, c), (G, d):{\mathcal M}\to {\mathcal N},$
the functor has a canonical prebalancing given by
$(F, c), (G, d):{\mathcal M}\to {\mathcal N},$
the functor has a canonical prebalancing given by $$ \begin{align*}\operatorname{Hom}_{{\mathcal N}}(F(-), G(-)): {\mathcal M}^{\mathrm{{op}}}\times {\mathcal M}\to \mathrm{vect\,}_{\mathbb{k}}\end{align*} $$
(4.7)
$$ \begin{align*}\operatorname{Hom}_{{\mathcal N}}(F(-), G(-)): {\mathcal M}^{\mathrm{{op}}}\times {\mathcal M}\to \mathrm{vect\,}_{\mathbb{k}}\end{align*} $$
(4.7) $$ \begin{align} \beta^X_{M,N}: \operatorname{Hom}_{{\mathcal N}}(F(M), G(X\triangleright N))\to \operatorname{Hom}_{{\mathcal N}}(F(X^*\triangleright M), G(N)) \end{align} $$
for any
$$ \begin{align} \beta^X_{M,N}: \operatorname{Hom}_{{\mathcal N}}(F(M), G(X\triangleright N))\to \operatorname{Hom}_{{\mathcal N}}(F(X^*\triangleright M), G(N)) \end{align} $$
for any $$ \begin{align*}\beta^X_{M,N}(\alpha)= (ev_X\triangleright \mathrm{id\,}_{G(N)}) m^{-1}_{X^*,X,G(N)} (\mathrm{id\,}_{X^*}\triangleright d_{X,N}\alpha)c_{X^*,M},\end{align*} $$
$$ \begin{align*}\beta^X_{M,N}(\alpha)= (ev_X\triangleright \mathrm{id\,}_{G(N)}) m^{-1}_{X^*,X,G(N)} (\mathrm{id\,}_{X^*}\triangleright d_{X,N}\alpha)c_{X^*,M},\end{align*} $$
 $X\in {\mathcal C}, M, N\in {\mathcal M}$
. There is an isomorphism
$X\in {\mathcal C}, M, N\in {\mathcal M}$
. There is an isomorphism  $$ \begin{align*}\mathrm{Nat\,}_{\!m}(F,G)\simeq \oint_{M\in {\mathcal M}} (\operatorname{Hom}_{{\mathcal N}}(F(-), G(-)), \beta).\end{align*} $$
$$ \begin{align*}\mathrm{Nat\,}_{\!m}(F,G)\simeq \oint_{M\in {\mathcal M}} (\operatorname{Hom}_{{\mathcal N}}(F(-), G(-)), \beta).\end{align*} $$
The next result will be needed later. It follows from a combination of [Reference Bortolussi and Mombelli4, Proposition 3.3] (ii) and [Reference Bortolussi and Mombelli4, Lemma 3.6]. Let
![]() ${\mathcal M}$
be a left
${\mathcal M}$
be a left
![]() ${\mathcal C}$
-module category, then
${\mathcal C}$
-module category, then
![]() ${\mathcal N}={\mathcal M}^{\mathrm {{op}}}$
is a right
${\mathcal N}={\mathcal M}^{\mathrm {{op}}}$
is a right
![]() ${\mathcal C}$
-module category with right action given by
${\mathcal C}$
-module category with right action given by
Assume that
![]() ${\mathcal A}$
is a category equipped with a functor
${\mathcal A}$
is a category equipped with a functor
together with a prebalancing
The functor
has a natural prebalancing
The proof of the next statement is similar to the proof of [Reference Bortolussi and Mombelli4, Proposition 3.3(ii)].
Proposition 4.4 If the coend
![]() $\oint _{M\in {\mathcal N}} (S,\beta )$
exists, then for any object
$\oint _{M\in {\mathcal N}} (S,\beta )$
exists, then for any object
![]() $U\in {\mathcal A}$
, the end
$U\in {\mathcal A}$
, the end
![]() $\oint _{M\in {\mathcal M}} \operatorname {Hom}_{\mathcal A}( S( -, -), U)$
exists, and there is an isomorphism
$\oint _{M\in {\mathcal M}} \operatorname {Hom}_{\mathcal A}( S( -, -), U)$
exists, and there is an isomorphism
Moreover, if
![]() $\oint _{M\in {\mathcal M}} \operatorname {Hom}_{\mathcal A}(S( -, -),U)$
exists for any
$\oint _{M\in {\mathcal M}} \operatorname {Hom}_{\mathcal A}(S( -, -),U)$
exists for any
![]() $U\in {\mathcal A}$
, then the coend
$U\in {\mathcal A}$
, then the coend
![]() $\oint ^{M\in {\mathcal N}} (S,\beta )$
exists.
$\oint ^{M\in {\mathcal N}} (S,\beta )$
exists.
The proof of the next result is completely analogous to the proof in the case of usual coend.
Lemma 4.5 Let
![]() ${\mathcal M}$
be a right
${\mathcal M}$
be a right
![]() ${\mathcal C}$
-module category,
${\mathcal C}$
-module category,
![]() $S:{\mathcal M}^{\mathrm {{op}}}\times {\mathcal M}\to {\mathcal A}$
a functor equipped with a prebalancing
$S:{\mathcal M}^{\mathrm {{op}}}\times {\mathcal M}\to {\mathcal A}$
a functor equipped with a prebalancing
![]() $\gamma $
. If
$\gamma $
. If
![]() $F:{\mathcal A}\to {\mathcal A}'$
is a right exact functor, then there is an isomorphism
$F:{\mathcal A}\to {\mathcal A}'$
is a right exact functor, then there is an isomorphism
We shall also need the next result.
Lemma 4.6 Let
![]() ${\mathcal M}, {\mathcal N}$
be right
${\mathcal M}, {\mathcal N}$
be right
![]() ${\mathcal C}$
-module categories, and let
${\mathcal C}$
-module categories, and let
![]() $(J,c):{\mathcal M}\to {\mathcal N}$
be an equivalence of
$(J,c):{\mathcal M}\to {\mathcal N}$
be an equivalence of
![]() ${\mathcal C}$
-module categories. Assume that
${\mathcal C}$
-module categories. Assume that
![]() $S:{\mathcal N}^{\mathrm {{op}}}\times {\mathcal N}\to {\mathcal A}$
is a functor equipped with a prebalancing
$S:{\mathcal N}^{\mathrm {{op}}}\times {\mathcal N}\to {\mathcal A}$
is a functor equipped with a prebalancing
![]() $\beta $
. The functor
$\beta $
. The functor
![]() $S(J(-), J(-)):{\mathcal M}^{\mathrm {{op}}}\times {\mathcal M}\to {\mathcal A}$
has a prebalancing
$S(J(-), J(-)):{\mathcal M}^{\mathrm {{op}}}\times {\mathcal M}\to {\mathcal A}$
has a prebalancing
![]() $\gamma $
given by
$\gamma $
given by
for any
![]() $M,N\in {\mathcal M}$
. There is an isomorphism
$M,N\in {\mathcal M}$
. There is an isomorphism
Proof We only sketch the proof. Let
![]() $\lambda _N:S(N,N)\to \oint ^{N\in {\mathcal N}} (S,\beta )$
be the associated dinatural transformations. If we define
$\lambda _N:S(N,N)\to \oint ^{N\in {\mathcal N}} (S,\beta )$
be the associated dinatural transformations. If we define
![]() $\pi _M=\lambda _{J(M)}$
, for any
$\pi _M=\lambda _{J(M)}$
, for any
![]() $M\in {\mathcal M}$
, one can verify that these are dinatural transformations and they satisfy (4.5). Universality of
$M\in {\mathcal M}$
, one can verify that these are dinatural transformations and they satisfy (4.5). Universality of
![]() $\pi $
follows from the universality of
$\pi $
follows from the universality of
![]() $\lambda $
and the fact that J is an equivalence of categories.
$\lambda $
and the fact that J is an equivalence of categories.
4.1 Existence of (co)ends
In this section, we shall prove that certain (co)ends exists. All these (co)ends will be used in subsequent sections. We shall use ideas from [Reference Shimizu24, Reference Shimizu25].
Let
![]() ${\mathcal C}$
be a tensor category, and let
${\mathcal C}$
be a tensor category, and let
![]() ${\mathcal B}$
be a right
${\mathcal B}$
be a right
![]() ${\mathcal C}$
-module category. Since our definition of module category includes that the action is right exact in each variable, the hypothesis of [Reference Douglas, Schommer-Pries and Snyder9, Theorem 2.24] are fulfilled. This means that there exists an algebra
${\mathcal C}$
-module category. Since our definition of module category includes that the action is right exact in each variable, the hypothesis of [Reference Douglas, Schommer-Pries and Snyder9, Theorem 2.24] are fulfilled. This means that there exists an algebra
![]() $A\in {\mathcal C}$
such that
$A\in {\mathcal C}$
such that
as module categories. Consider
![]() ${\mathcal C}$
as a right
${\mathcal C}$
as a right
![]() ${\mathcal C}$
-module category with the regular action. We shall denote by
${\mathcal C}$
-module category with the regular action. We shall denote by
![]() $\mathrm {Rex\,}_{\mathcal C}({\mathcal B}, {\mathcal C})$
the category of right exact
$\mathrm {Rex\,}_{\mathcal C}({\mathcal B}, {\mathcal C})$
the category of right exact
![]() ${\mathcal C}$
-module functors. The functor
${\mathcal C}$
-module functors. The functor
is an equivalence of categories, since, under identification (4.8), the functor
![]() $\Phi $
is the composition of equivalences
$\Phi $
is the composition of equivalences
Here,
![]() $R: {\mathcal C}_{A} \to \mathrm {Rex\,}_{\mathcal C}({}_A{\mathcal C},{\mathcal C})$
is the functor given by
$R: {\mathcal C}_{A} \to \mathrm {Rex\,}_{\mathcal C}({}_A{\mathcal C},{\mathcal C})$
is the functor given by
![]() $R(V)(W)=V{\otimes }_{A} W.$
Let be
$R(V)(W)=V{\otimes }_{A} W.$
Let be
![]() $(F,c)\in \mathrm {Rex\,}_{\mathcal C}({\mathcal B}, {\mathcal C})$
. In particular, we have natural isomorphisms
$(F,c)\in \mathrm {Rex\,}_{\mathcal C}({\mathcal B}, {\mathcal C})$
. In particular, we have natural isomorphisms
for
![]() $B\in {\mathcal B}, X\in {\mathcal C}$
. Consider the functor
$B\in {\mathcal B}, X\in {\mathcal C}$
. Consider the functor
This functor possesses a
![]() ${\mathcal C}$
-prebalancing
${\mathcal C}$
-prebalancing
Proposition 4.7 Let
![]() ${\mathcal B}$
be a right
${\mathcal B}$
be a right
![]() ${\mathcal C}$
-module category. For any right exact
${\mathcal C}$
-module category. For any right exact
![]() ${\mathcal C}$
-module functor
${\mathcal C}$
-module functor
![]() $(F,c):{\mathcal B}\to {\mathcal C}$
, the coend
$(F,c):{\mathcal B}\to {\mathcal C}$
, the coend
exists. Moreover, the functor
![]() $(F,c)\mapsto \widetilde {C}(F,c)$
is a quasi-inverse of
$(F,c)\mapsto \widetilde {C}(F,c)$
is a quasi-inverse of
![]() $\Phi $
.
$\Phi $
.
Proof For any
![]() $D\in {\mathcal B}$
, we have
$D\in {\mathcal B}$
, we have
 $$ \begin{align*} \mathrm{Nat\,}_{\! m}(\Phi(D), F)& \simeq \oint_{B\in {\mathcal B}} \operatorname{Hom}_{\mathcal C}(\Phi(D)(B), F(B))\\ &\simeq \oint_{B\in {\mathcal B}} \operatorname{Hom}_{\mathcal C}(\underline{\operatorname{Hom}}_{{\mathcal B}}(B,D)^*, F(B))\\ &\simeq \oint_{B\in {\mathcal B}} \operatorname{Hom}_{\mathcal C}( {}^*F(B), \underline{\operatorname{Hom}}_{{\mathcal B}}(B,D))\\ &\simeq \oint_{B\in {\mathcal B}} \operatorname{Hom}_{\mathcal B}(B \triangleleft {}^*F(B), D)\\ &\simeq \operatorname{Hom}_{\mathcal B}( \oint^{B\in {\mathcal B}} B \triangleleft {}^*F(B), D)\\ &=\operatorname{Hom}_{{\mathcal B}^{\mathrm{{op}}}}(D, \oint^{B\in {\mathcal B}} B \triangleleft {}^*F(B)). \end{align*} $$
$$ \begin{align*} \mathrm{Nat\,}_{\! m}(\Phi(D), F)& \simeq \oint_{B\in {\mathcal B}} \operatorname{Hom}_{\mathcal C}(\Phi(D)(B), F(B))\\ &\simeq \oint_{B\in {\mathcal B}} \operatorname{Hom}_{\mathcal C}(\underline{\operatorname{Hom}}_{{\mathcal B}}(B,D)^*, F(B))\\ &\simeq \oint_{B\in {\mathcal B}} \operatorname{Hom}_{\mathcal C}( {}^*F(B), \underline{\operatorname{Hom}}_{{\mathcal B}}(B,D))\\ &\simeq \oint_{B\in {\mathcal B}} \operatorname{Hom}_{\mathcal B}(B \triangleleft {}^*F(B), D)\\ &\simeq \operatorname{Hom}_{\mathcal B}( \oint^{B\in {\mathcal B}} B \triangleleft {}^*F(B), D)\\ &=\operatorname{Hom}_{{\mathcal B}^{\mathrm{{op}}}}(D, \oint^{B\in {\mathcal B}} B \triangleleft {}^*F(B)). \end{align*} $$
The first isomorphism is Proposition 4.3(ii), and the fifth isomorphism is Proposition 4.4. Observe that, to prove the existence of the fourth isomorphism, one has to check that the natural isomorphisms
commute with the respective prebalancings and then use Proposition 4.3(i). This calculation is left to the reader. This proves both that the coend
![]() $\widetilde {C}(F,c)$
exists and that the quasi-inverse of
$\widetilde {C}(F,c)$
exists and that the quasi-inverse of
![]() $\Phi $
is given by
$\Phi $
is given by
For a pair of module functors
![]() $(F,c), (\widetilde F, \tilde c):{\mathcal B}\to {\mathcal C}$
, the functor
$(F,c), (\widetilde F, \tilde c):{\mathcal B}\to {\mathcal C}$
, the functor
has a canonical prebalancing, given by
 $$ \begin{align}\begin{aligned} \beta^X_{A,B}& : \widetilde{F}(B){\otimes} {}^*F(A \triangleleft X) \to \widetilde{F}(B \triangleleft {}^*X){\otimes} {}^*F(A), \\\beta^X_{A,B}& =(\tilde{c}^{-1}_{B, {}^*X}{\otimes} \mathrm{id\,})(\mathrm{id\,}_{\widetilde F(B)}{\otimes} (\phi^l_{F(A),X})^{-1} {}^*(c^{-1}_{A,X})). \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \beta^X_{A,B}& : \widetilde{F}(B){\otimes} {}^*F(A \triangleleft X) \to \widetilde{F}(B \triangleleft {}^*X){\otimes} {}^*F(A), \\\beta^X_{A,B}& =(\tilde{c}^{-1}_{B, {}^*X}{\otimes} \mathrm{id\,})(\mathrm{id\,}_{\widetilde F(B)}{\otimes} (\phi^l_{F(A),X})^{-1} {}^*(c^{-1}_{A,X})). \end{aligned}\end{align} $$
As a consequence of Lemma 4.5, one can apply
![]() $\widetilde F $
to the coend in Proposition 4.7. Thus, we get the next result.
$\widetilde F $
to the coend in Proposition 4.7. Thus, we get the next result.
Corollary 4.8 For any pair of right exact
![]() ${\mathcal C}$
-module functors
${\mathcal C}$
-module functors
![]() $F, \widetilde F:{\mathcal B}\to {\mathcal C}$
, the coend
$F, \widetilde F:{\mathcal B}\to {\mathcal C}$
, the coend
exists.
5 Hopf algebras in braided tensor categories
5.1 Hopf algebras in braided tensor categories
Let us briefly recall the notion of Hopf algebras in braided tensor categories, and how their corepresentation categories are again tensor categories. For more details, the reader is referred to [Reference Majid19, Reference Majid20, Reference Takeuchi26] and the references therein.
A braided tensor category is a pair
![]() $({\mathcal C},\sigma )$
where
$({\mathcal C},\sigma )$
where
![]() ${\mathcal C}$
is a tensor category and
${\mathcal C}$
is a tensor category and
![]() $\sigma _{V,W}:V{\otimes } W\to W{\otimes } V$
is a braiding, that is, a family of natural isomorphisms satisfying
$\sigma _{V,W}:V{\otimes } W\to W{\otimes } V$
is a braiding, that is, a family of natural isomorphisms satisfying
 $$ \begin{align} &\sigma_{V,U{\otimes} W}=(\mathrm{id\,}_U{\otimes} \sigma_{V,W})(\sigma_{V,U}{\otimes}\mathrm{id\,}_W), \nonumber\\ &\sigma_{V{\otimes} U, W}=(\sigma_{V,W}{\otimes}\mathrm{id\,}_U) (\mathrm{id\,}_V{\otimes} \sigma_{U,W}). \end{align} $$
$$ \begin{align} &\sigma_{V,U{\otimes} W}=(\mathrm{id\,}_U{\otimes} \sigma_{V,W})(\sigma_{V,U}{\otimes}\mathrm{id\,}_W), \nonumber\\ &\sigma_{V{\otimes} U, W}=(\sigma_{V,W}{\otimes}\mathrm{id\,}_U) (\mathrm{id\,}_V{\otimes} \sigma_{U,W}). \end{align} $$
Remark 5.1 Note that in the above axioms we are assuming that
![]() ${\mathcal C}$
is a strict tensor category.
${\mathcal C}$
is a strict tensor category.
The braiding fulfills the braid relation, whence the name. We illustrate this identity in terms of string diagrams, which we read bottom to top.

Definition 5.2 A bialgebra in
![]() ${\mathcal C}$
is a collection
${\mathcal C}$
is a collection
![]() $(H,m,u,\Delta ,\varepsilon )$
, where
$(H,m,u,\Delta ,\varepsilon )$
, where
![]() $(H,m,u)$
is an algebra,
$(H,m,u)$
is an algebra,
![]() $(H,\Delta ,\varepsilon )$
is a coalgebra, and
$(H,\Delta ,\varepsilon )$
is a coalgebra, and
![]() $\Delta , \varepsilon $
are algebra morphisms. That is,
$\Delta , \varepsilon $
are algebra morphisms. That is,
We illustrate the first identity:

If H is a bialgebra, then the space
![]() $\operatorname {Hom}_{\mathcal C}(H,H)$
has a convolution product with unit given by
$\operatorname {Hom}_{\mathcal C}(H,H)$
has a convolution product with unit given by
![]() $u\circ \varepsilon $
. If the identity
$u\circ \varepsilon $
. If the identity
![]() $\mathrm {id\,}_H$
has an inverse S under the convolution product, then H is a Hopf algebra, and S is called the antipode. The next theorem is well known (see, for example, [Reference Majid19]).
$\mathrm {id\,}_H$
has an inverse S under the convolution product, then H is a Hopf algebra, and S is called the antipode. The next theorem is well known (see, for example, [Reference Majid19]).
Theorem 5.3 If H is a Hopf algebra in a braided tensor category
![]() ${\mathcal C}$
, then the category of left H-comodules
${\mathcal C}$
, then the category of left H-comodules
![]() ${}^H{\mathcal C}$
is a tensor category. Moreover, if
${}^H{\mathcal C}$
is a tensor category. Moreover, if
![]() ${\mathcal C}$
is a finite tensor category, then
${\mathcal C}$
is a finite tensor category, then
![]() ${}^H{\mathcal C}$
is also a finite tensor category, and the forgetful functor
${}^H{\mathcal C}$
is also a finite tensor category, and the forgetful functor
![]() $f:{}^H{\mathcal C}\to {\mathcal C}$
is an exact faithful monoidal functor.
$f:{}^H{\mathcal C}\to {\mathcal C}$
is an exact faithful monoidal functor.
The tensor product of two left H-comodules is given as follows: if
![]() $(V,\rho _V)$
,
$(V,\rho _V)$
,
![]() $(W, \rho _W)$
are objects in
$(W, \rho _W)$
are objects in
![]() ${}^H{\mathcal C}$
, then the tensor product
${}^H{\mathcal C}$
, then the tensor product
![]() $V{\otimes } W$
in
$V{\otimes } W$
in
![]() ${\mathcal C}$
has a left H-comodule structure given by
${\mathcal C}$
has a left H-comodule structure given by

If
![]() $(V, \rho _V)\in {}^H{\mathcal C}$
, then
$(V, \rho _V)\in {}^H{\mathcal C}$
, then
![]() ${}^*V\in {}^H{\mathcal C}$
. The coaction is given by
${}^*V\in {}^H{\mathcal C}$
. The coaction is given by
The coaction of the right dual
![]() $V^*$
is defined similarly.
$V^*$
is defined similarly.
For any
![]() $V\in {\mathcal C}$
, we can endow V with a trivial H-comodule structure given by
$V\in {\mathcal C}$
, we can endow V with a trivial H-comodule structure given by
5.2 Yetter–Drinfeld modules
Let H be a finite-dimensional Hopf algebra in
![]() $\mathrm {vect\,}_{\mathbb {k}}$
. Then we shall denote by
$\mathrm {vect\,}_{\mathbb {k}}$
. Then we shall denote by
![]() ${}^H_H{\mathcal YD}$
the category of finite-dimensional Yetter–Drinfeld modules. An object
${}^H_H{\mathcal YD}$
the category of finite-dimensional Yetter–Drinfeld modules. An object
![]() $V\in {}^H_H{\mathcal YD}(\mathrm {vect\,}_{\mathbb {k}})$
is a left H-module
$V\in {}^H_H{\mathcal YD}(\mathrm {vect\,}_{\mathbb {k}})$
is a left H-module
![]() $\cdot :H{\otimes _{\mathbb {k}}} V\to V$
and a left H-comodule
$\cdot :H{\otimes _{\mathbb {k}}} V\to V$
and a left H-comodule
![]() $\lambda :V\to H{\otimes _{\mathbb {k}}} V$
such that
$\lambda :V\to H{\otimes _{\mathbb {k}}} V$
such that
for any
![]() $h\in H, v\in V$
. If
$h\in H, v\in V$
. If
![]() $V\in {}^H_H{\mathcal YD}(\mathrm {vect\,}_{\mathbb {k}})$
, the map
$V\in {}^H_H{\mathcal YD}(\mathrm {vect\,}_{\mathbb {k}})$
, the map
![]() $\sigma _X: V{\otimes _{\mathbb {k}}} X\to X{\otimes _{\mathbb {k}}} V$
, given by
$\sigma _X: V{\otimes _{\mathbb {k}}} X\to X{\otimes _{\mathbb {k}}} V$
, given by
![]() $\sigma _X(v{\otimes } x)=v_{\left ( -1 \right )}\cdot x{\otimes } v_{\left ( 0 \right )}$
, is a half-braiding for V.
$\sigma _X(v{\otimes } x)=v_{\left ( -1 \right )}\cdot x{\otimes } v_{\left ( 0 \right )}$
, is a half-braiding for V.
This notion had been generalized in [Reference Bespalov3] to Hopf algebras H inside a braided tensor category
![]() ${\mathcal C}$
:
${\mathcal C}$
:
Definition 5.4 Let H be a Hopf algebra in a braided tensor category
![]() ${\mathcal C}$
. Then an H-H-Yetter–Drinfeld module V is an object
${\mathcal C}$
. Then an H-H-Yetter–Drinfeld module V is an object
![]() $V\in {\mathcal C}$
, together with a structure of H-module
$V\in {\mathcal C}$
, together with a structure of H-module
![]() $m:H\otimes V\to V$
and structure of H-comodule in
$m:H\otimes V\to V$
and structure of H-comodule in
![]() $\rho :V\to H\otimes V$
in the tensor category
$\rho :V\to H\otimes V$
in the tensor category
![]() ${\mathcal C}$
, compatible in the following way:
${\mathcal C}$
, compatible in the following way:

The category
![]() ${^H_H}{\mathcal YD}({\mathcal C})$
consists of Yetter–Drinfeld modules and of H-linear and H-colinear morphisms. It becomes a tensor category with the usual tensor product of H-modules and H-comodules
${^H_H}{\mathcal YD}({\mathcal C})$
consists of Yetter–Drinfeld modules and of H-linear and H-colinear morphisms. It becomes a tensor category with the usual tensor product of H-modules and H-comodules
![]() $V\otimes W$
. An useful feature of this tensor category is that it admits, by construction, a braiding
$V\otimes W$
. An useful feature of this tensor category is that it admits, by construction, a braiding
which is given on objects
![]() $(V, m_V, \rho _V)$
and
$(V, m_V, \rho _V)$
and
![]() $(W, m_W, \rho _W)$
by
$(W, m_W, \rho _W)$
by
and is invertible if H has a bijective antipode
 $$ \begin{align*} (c_{(V, m_V, \rho_V), (W, m_W, \rho_W)} )^{-1} &:= c^{-1}_{V,W} \circ (m_W \otimes \mathrm{id\,}_V ) \circ (c^{-1}_{H,W} \otimes \mathrm{id\,}_V ) \\ &\circ (\mathrm{id\,}_W \otimes S^{-1} \otimes \mathrm{id\,}_V ) \circ (\mathrm{id\,}_W \otimes \rho_V ). \end{align*} $$
$$ \begin{align*} (c_{(V, m_V, \rho_V), (W, m_W, \rho_W)} )^{-1} &:= c^{-1}_{V,W} \circ (m_W \otimes \mathrm{id\,}_V ) \circ (c^{-1}_{H,W} \otimes \mathrm{id\,}_V ) \\ &\circ (\mathrm{id\,}_W \otimes S^{-1} \otimes \mathrm{id\,}_V ) \circ (\mathrm{id\,}_W \otimes \rho_V ). \end{align*} $$
If
![]() ${\mathcal C}$
is rigid, then the dual object in
${\mathcal C}$
is rigid, then the dual object in
![]() ${\mathcal C}$
with the standard dual action and coaction gives a dual object in
${\mathcal C}$
with the standard dual action and coaction gives a dual object in
![]() ${^H_H}{\mathcal YD}({\mathcal C})$
. The structure is summarized in the following statement proven in [Reference Bespalov3].
${^H_H}{\mathcal YD}({\mathcal C})$
. The structure is summarized in the following statement proven in [Reference Bespalov3].
Theorem 5.5 Let H be a Hopf algebra in
![]() ${\mathcal C}$
. The Yetter–Drinfeld modules over H in
${\mathcal C}$
. The Yetter–Drinfeld modules over H in
![]() ${\mathcal C}$
have a natural structure of a braided tensor category
${\mathcal C}$
have a natural structure of a braided tensor category
![]() ${^H_H}{\mathcal YD}({\mathcal C})$
. If
${^H_H}{\mathcal YD}({\mathcal C})$
. If
![]() ${\mathcal C}$
is rigid, then so is
${\mathcal C}$
is rigid, then so is
![]() ${^H_H}{\mathcal YD}({\mathcal C})$
.
${^H_H}{\mathcal YD}({\mathcal C})$
.
Recall that the Drinfeld center
![]() $\mathcal {Z}(\mathcal {B})$
is a braided tensor category associated with any tensor category
$\mathcal {Z}(\mathcal {B})$
is a braided tensor category associated with any tensor category
![]() $\mathcal {B}$
. The construction of Yetter–Drinfeld modules gives a realization of a special case of the construction of a relative Drinfeld center
$\mathcal {B}$
. The construction of Yetter–Drinfeld modules gives a realization of a special case of the construction of a relative Drinfeld center
![]() $\mathcal {Z}_{\mathcal C}(\mathcal {B})$
, a braided tensor category associated with any tensor category
$\mathcal {Z}_{\mathcal C}(\mathcal {B})$
, a braided tensor category associated with any tensor category
![]() $\mathcal {B}$
with a braided subcategory
$\mathcal {B}$
with a braided subcategory
![]() ${\mathcal C}\hookrightarrow \mathcal {Z}(\mathcal {B})$
. More precisely, we have
${\mathcal C}\hookrightarrow \mathcal {Z}(\mathcal {B})$
. More precisely, we have
6 Monoidal module categories
Assume that
![]() ${\mathcal C}$
,
${\mathcal C}$
,
![]() ${\mathcal B}$
tensor categories. We shall define what means that a tensor category
${\mathcal B}$
tensor categories. We shall define what means that a tensor category
![]() ${\mathcal C}$
acts on
${\mathcal C}$
acts on
![]() ${\mathcal B}$
.
${\mathcal B}$
.
Definition 6.1 We call
![]() ${\mathcal B}$
a monoidal left
${\mathcal B}$
a monoidal left
![]() ${\mathcal C}$
-module category if
${\mathcal C}$
-module category if
![]() ${\mathcal B}$
is a left
${\mathcal B}$
is a left
![]() ${\mathcal C}$
-module category, with action given by
${\mathcal C}$
-module category, with action given by
![]() $\triangleright :{\mathcal C}\times {\mathcal B}\to {\mathcal B}, $
such that
$\triangleright :{\mathcal C}\times {\mathcal B}\to {\mathcal B}, $
such that
![]() $ \mathbf {1}\triangleright \mathbf {1}\simeq \mathbf {1},$
and there are natural isomorphisms
$ \mathbf {1}\triangleright \mathbf {1}\simeq \mathbf {1},$
and there are natural isomorphisms
![]() $l_{X,B}: X \triangleright B\xrightarrow {\;\simeq \; } (X\triangleright \mathbf {1}){\otimes } B,$
for any
$l_{X,B}: X \triangleright B\xrightarrow {\;\simeq \; } (X\triangleright \mathbf {1}){\otimes } B,$
for any
![]() $X\in {\mathcal C}$
,
$X\in {\mathcal C}$
,
![]() $B\in {\mathcal B}$
, such that
$B\in {\mathcal B}$
, such that

for any
![]() $X, Y\in {\mathcal C}$
,
$X, Y\in {\mathcal C}$
,
![]() $B\in {\mathcal B}$
. Similarly, we shall say that
$B\in {\mathcal B}$
. Similarly, we shall say that
![]() ${\mathcal B}$
is a monoidal right
${\mathcal B}$
is a monoidal right
![]() ${\mathcal C}$
-module category, with action
${\mathcal C}$
-module category, with action
![]() $\triangleleft :{\mathcal B}\times {\mathcal C}\to {\mathcal B}, $
such that
$\triangleleft :{\mathcal B}\times {\mathcal C}\to {\mathcal B}, $
such that
and there are natural isomorphisms
![]() $l_{B,X}: B \triangleleft X\to B{\otimes } ( \mathbf {1} \triangleleft X),$
such that for any
$l_{B,X}: B \triangleleft X\to B{\otimes } ( \mathbf {1} \triangleleft X),$
such that for any
![]() $X, Y\in {\mathcal C}$
,
$X, Y\in {\mathcal C}$
,
![]() $B\in {\mathcal B}$
,
$B\in {\mathcal B}$
,

Example 6.2
-
(i) Any tensor category
 ${\mathcal C}$
is a monoidal
${\mathcal C}$
is a monoidal
 $\mathrm {vect\,}_{\mathbb {k}}$
-module category, with the canonical action
$\mathrm {vect\,}_{\mathbb {k}}$
-module category, with the canonical action  $$ \begin{align*} \bullet: \mathrm{vect\,}_{\mathbb{k}} \times {\mathcal C}\to {\mathcal C}. \end{align*} $$
$$ \begin{align*} \bullet: \mathrm{vect\,}_{\mathbb{k}} \times {\mathcal C}\to {\mathcal C}. \end{align*} $$
-
(ii) Let
 ${\mathcal C}$
be a tensor category. Any tensor subcategory
${\mathcal C}$
be a tensor category. Any tensor subcategory
 ${\mathcal D}$
acts on
${\mathcal D}$
acts on
 ${\mathcal C}$
by In particular, any tensor category acts on itself.
${\mathcal C}$
by In particular, any tensor category acts on itself. $$ \begin{align*}X \triangleright Y=X{\otimes} Y.\end{align*} $$
$$ \begin{align*}X \triangleright Y=X{\otimes} Y.\end{align*} $$
-
(iii) Let
 $({\mathcal C}, \sigma )$
be a braided tensor category and
$({\mathcal C}, \sigma )$
be a braided tensor category and
 ${\mathcal D}\subseteq {\mathcal C}$
be a tensor subcategory. Then
${\mathcal D}\subseteq {\mathcal C}$
be a tensor subcategory. Then
 ${\mathcal D}^{\mathrm {{rev}}}$
acts on
${\mathcal D}^{\mathrm {{rev}}}$
acts on
 ${\mathcal C}$
as In this case,
${\mathcal C}$
as In this case, $$ \begin{align*}X \triangleright Y=Y{\otimes} X.\end{align*} $$
$$ \begin{align*}X \triangleright Y=Y{\otimes} X.\end{align*} $$
 $l_{X,B}=\sigma _{B,X}$
.
$l_{X,B}=\sigma _{B,X}$
.
-
(iv) Let
 ${\mathcal C}$
be a tensor category and
${\mathcal C}$
be a tensor category and
 $C\in {\mathcal C}$
be a coalgebra. Then the category
$C\in {\mathcal C}$
be a coalgebra. Then the category
 ${}^C{\mathcal C}$
, of left C-comodules in
${}^C{\mathcal C}$
, of left C-comodules in
 ${\mathcal C}$
, is a right
${\mathcal C}$
, is a right
 ${\mathcal C}$
-module category. The action is given as follows. If
${\mathcal C}$
-module category. The action is given as follows. If
 $(W,\rho )\in {}^C{\mathcal C}$
, then
$(W,\rho )\in {}^C{\mathcal C}$
, then
 $W \triangleleft Y=W{\otimes } Y$
, where the coaction on
$W \triangleleft Y=W{\otimes } Y$
, where the coaction on
 $W{\otimes } Y$
is given by
$W{\otimes } Y$
is given by
 $\rho {\otimes } \mathrm {id\,}_Y.$
$\rho {\otimes } \mathrm {id\,}_Y.$
Definition 6.3 If
![]() ${\mathcal B}$
,
${\mathcal B}$
,
![]() ${\mathcal B}'$
are right monoidal
${\mathcal B}'$
are right monoidal
![]() ${\mathcal C}$
-module categories, a monoidal module functor is a collection
${\mathcal C}$
-module categories, a monoidal module functor is a collection
![]() $(F,c,\xi ):{\mathcal B}\to {\mathcal B}'$
where
$(F,c,\xi ):{\mathcal B}\to {\mathcal B}'$
where
![]() $(F,c)$
is a
$(F,c)$
is a
![]() ${\mathcal C}$
-module functor,
${\mathcal C}$
-module functor,
![]() $(F, \xi )$
is a monoidal functor, and equation
$(F, \xi )$
is a monoidal functor, and equation
is fulfilled for any
![]() $B\in {\mathcal B}$
,
$B\in {\mathcal B}$
,
![]() $V\in {\mathcal C}$
.
$V\in {\mathcal C}$
.
6.1 Sections of monoidal functors
Definition 6.4 Let
![]() ${\mathcal C}, {\mathcal B}$
be tensor categories. If
${\mathcal C}, {\mathcal B}$
be tensor categories. If
![]() $F:{\mathcal B}\to {\mathcal C}$
is a tensor functor, a section to F is a right exact tensor functor
$F:{\mathcal B}\to {\mathcal C}$
is a tensor functor, a section to F is a right exact tensor functor
![]() $G:{\mathcal C}\to {\mathcal B}$
such that
$G:{\mathcal C}\to {\mathcal B}$
such that
![]() $F\circ G\simeq \mathrm {Id\,}_{\mathcal C}$
as monoidal functors.
$F\circ G\simeq \mathrm {Id\,}_{\mathcal C}$
as monoidal functors.
Example 6.5
-
(1) Any (linear) tensor functor
 $F:{\mathcal B} \to \mathrm {vect\,}_{\mathbb {k}}$
has a canonical section given by
$F:{\mathcal B} \to \mathrm {vect\,}_{\mathbb {k}}$
has a canonical section given by  $$ \begin{align*}G:\mathrm{vect\,}_{\mathbb{k}} \to {\mathcal B},\end{align*} $$
$$ \begin{align*}G:\mathrm{vect\,}_{\mathbb{k}} \to {\mathcal B},\end{align*} $$
 $$ \begin{align*}G(V)= V \bullet \mathbf{1}.\end{align*} $$
$$ \begin{align*}G(V)= V \bullet \mathbf{1}.\end{align*} $$
Here, the action
 $\bullet :\mathrm {vect\,}_{\mathbb {k}}\times {\mathcal B}\to {\mathcal B}$
is the one presented in (2.1).
$\bullet :\mathrm {vect\,}_{\mathbb {k}}\times {\mathcal B}\to {\mathcal B}$
is the one presented in (2.1). -
(2) The previous example can be generalized to other kinds of fiber functors. If
 ${\mathcal C}$
is a tensor category that acts on another tensor category
${\mathcal C}$
is a tensor category that acts on another tensor category
 ${\mathcal B}$
, then any monoidal functor
${\mathcal B}$
, then any monoidal functor
 $F:{\mathcal B}\to {\mathcal C}$
that is also a
$F:{\mathcal B}\to {\mathcal C}$
that is also a
 ${\mathcal C}$
-module functor has a section given by
${\mathcal C}$
-module functor has a section given by
 $G:{\mathcal C}\to {\mathcal B}$
,
$G:{\mathcal C}\to {\mathcal B}$
,
 $G(V)=V\triangleright \mathbf {1}$
. See Proposition 6.6 below.
$G(V)=V\triangleright \mathbf {1}$
. See Proposition 6.6 below. -
(3) If
 $({\mathcal C},\sigma )$
is a braided tensor category and
$({\mathcal C},\sigma )$
is a braided tensor category and
 $H\in {\mathcal C}$
is a Hopf algebra with unit given by
$H\in {\mathcal C}$
is a Hopf algebra with unit given by
 $u: \mathbf {1}\to H$
, then the forgetful functor
$u: \mathbf {1}\to H$
, then the forgetful functor
 $f: {}^H{\mathcal C}\to {\mathcal C}$
has a section given by
$f: {}^H{\mathcal C}\to {\mathcal C}$
has a section given by
 $G:{\mathcal C}\to {}^H{\mathcal C}$
,
$G:{\mathcal C}\to {}^H{\mathcal C}$
,
 $G(V)=(V,\rho ^t_V)$
. Here,
$G(V)=(V,\rho ^t_V)$
. Here,
 $\rho ^t_V=u{\otimes } \mathrm {id\,}_V$
is the trivial comodule structure.
$\rho ^t_V=u{\otimes } \mathrm {id\,}_V$
is the trivial comodule structure. -
(4) Let H be a Hopf algebra and R be a Hopf algebra in the category of Yetter–Drinfeld modules
 ${}^H_H{\mathcal YD}$
. Consider the corresponding Hopf algebra obtained by bosonization
${}^H_H{\mathcal YD}$
. Consider the corresponding Hopf algebra obtained by bosonization
 $R\# H$
. Let us consider the functor The action of H on V is given by
$R\# H$
. Let us consider the functor The action of H on V is given by $$ \begin{align*}F:\operatorname{Rep}(R\# H)\to \operatorname{Rep}(H), \quad F(V)=V.\end{align*} $$
$$ \begin{align*}F:\operatorname{Rep}(R\# H)\to \operatorname{Rep}(H), \quad F(V)=V.\end{align*} $$
 $h\cdot v= (1\# h)\cdot v$
. The functor F has a section given by
$h\cdot v= (1\# h)\cdot v$
. The functor F has a section given by
 $G:\operatorname {Rep}(H)\to \operatorname {Rep}(R\# H)$
given by
$G:\operatorname {Rep}(H)\to \operatorname {Rep}(R\# H)$
given by
 $G(V)=V$
, where the action of
$G(V)=V$
, where the action of
 $R\# H$
on V is given by
$R\# H$
on V is given by  $$ \begin{align*}(r\# h)\cdot v=\varepsilon(r) h\cdot v.\end{align*} $$
$$ \begin{align*}(r\# h)\cdot v=\varepsilon(r) h\cdot v.\end{align*} $$
-
(5) Let
 $({\mathcal C},\sigma )$
be a braided tensor category. The forgetful functor from the center of
$({\mathcal C},\sigma )$
be a braided tensor category. The forgetful functor from the center of
 ${\mathcal C}$
,
${\mathcal C}$
,
 $f :Z({\mathcal C})\to {\mathcal C}$
, has a section given by the inclusion
$f :Z({\mathcal C})\to {\mathcal C}$
, has a section given by the inclusion
 ${\mathcal C} \hookrightarrow Z({\mathcal C})$
,
${\mathcal C} \hookrightarrow Z({\mathcal C})$
,
 $V\mapsto (V,\sigma )$
.
$V\mapsto (V,\sigma )$
.
Proposition 6.6 Let
![]() ${\mathcal B}, {\mathcal C}$
be tensor categories, and let
${\mathcal B}, {\mathcal C}$
be tensor categories, and let
![]() $(F,\xi ):{\mathcal B}\to {\mathcal C}$
be a monoidal functor. The following notions are equivalent:
$(F,\xi ):{\mathcal B}\to {\mathcal C}$
be a monoidal functor. The following notions are equivalent:
-
(i) The functor F has a section.
-
(ii)
 ${\mathcal B}$
is a right monoidal
${\mathcal B}$
is a right monoidal
 ${\mathcal C}$
-module category (in the sense of Definition 6.1) and F is a monoidal module functor.
${\mathcal C}$
-module category (in the sense of Definition 6.1) and F is a monoidal module functor.
Proof Let us only give a sketch of the proof. (i) implies (ii): assume that
![]() $(G, \zeta ):{\mathcal C}\to {\mathcal B}$
is a monoidal section to F. Let
$(G, \zeta ):{\mathcal C}\to {\mathcal B}$
is a monoidal section to F. Let
![]() $\alpha :F\circ G\to \mathrm {Id\,}$
be a natural monoidal isomorphism. Define the right action of
$\alpha :F\circ G\to \mathrm {Id\,}$
be a natural monoidal isomorphism. Define the right action of
![]() ${\mathcal C}$
on
${\mathcal C}$
on
![]() ${\mathcal B}$
as
${\mathcal B}$
as
for any
![]() $B\in {\mathcal B}$
,
$B\in {\mathcal B}$
,
![]() $V\in {\mathcal C}$
. The associativity of this action is given by
$V\in {\mathcal C}$
. The associativity of this action is given by
for any
![]() $B\in {\mathcal B}$
,
$B\in {\mathcal B}$
,
![]() $V, W\in {\mathcal C}$
. Turns out that
$V, W\in {\mathcal C}$
. Turns out that
![]() ${\mathcal B}$
is a monoidal module category with isomorphisms
${\mathcal B}$
is a monoidal module category with isomorphisms
With this action, F is a module functor. The module structure of the functor F is given by
Since
![]() $c_{ \mathbf {1},V}=\alpha _V$
, then it follows that equation (6.5) is fulfilled, that is,
$c_{ \mathbf {1},V}=\alpha _V$
, then it follows that equation (6.5) is fulfilled, that is,
![]() $(F,\xi , c)$
is a monoidal module functor.
$(F,\xi , c)$
is a monoidal module functor.
Let us prove now that (ii) implies (i): assume that
![]() $(F,\xi , c):{\mathcal B}\to {\mathcal C}$
is a monoidal
$(F,\xi , c):{\mathcal B}\to {\mathcal C}$
is a monoidal
![]() ${\mathcal C}$
-module functor. Define
${\mathcal C}$
-module functor. Define
![]() $G:{\mathcal C}\to {\mathcal B}$
,
$G:{\mathcal C}\to {\mathcal B}$
,
![]() $G(V)= \mathbf {1} \triangleleft V $
. Axiom (6.4) implies that isomorphisms
$G(V)= \mathbf {1} \triangleleft V $
. Axiom (6.4) implies that isomorphisms
endow G with the structure of monoidal functor. Define natural isomorphisms
![]() $\alpha _V:F(G(V))=F( \mathbf {1} \triangleleft V)\to V$
,
$\alpha _V:F(G(V))=F( \mathbf {1} \triangleleft V)\to V$
,
![]() $\alpha _V=c_{ \mathbf {1}, V}$
. Let us check that they are monoidal natural isomorphisms. For this, we need to verify that equation
$\alpha _V=c_{ \mathbf {1}, V}$
. Let us check that they are monoidal natural isomorphisms. For this, we need to verify that equation
is satisfied. Using that c satisfies diagram (3.18), it follows that the right-hand side of equation (6.6) is equal to
 $$ \begin{align*} &=(c_{ \mathbf{1}, V}{\otimes} \mathrm{id\,}_W) c_{ \mathbf{1} \triangleleft V, W} F(l^{-1}_{ \mathbf{1} \triangleleft V,W}) \xi_{ \mathbf{1} \triangleleft V, \mathbf{1} \triangleleft W}\\ &=(c_{ \mathbf{1}, V}{\otimes} \mathrm{id\,}_W) (\mathrm{id\,}_{F( \mathbf{1} \triangleleft V)}{\otimes} c_{ \mathbf{1}, W} ) \xi^{-1}_{ \mathbf{1} \triangleleft V, \mathbf{1} \triangleleft W} F(l_{ \mathbf{1} \triangleleft V,W}) F(l^{-1}_{ \mathbf{1} \triangleleft V,W}) \xi_{ \mathbf{1} \triangleleft V, \mathbf{1} \triangleleft W}\\ &=(c_{ \mathbf{1}, V}{\otimes} c_{ \mathbf{1}, W}). \end{align*} $$
$$ \begin{align*} &=(c_{ \mathbf{1}, V}{\otimes} \mathrm{id\,}_W) c_{ \mathbf{1} \triangleleft V, W} F(l^{-1}_{ \mathbf{1} \triangleleft V,W}) \xi_{ \mathbf{1} \triangleleft V, \mathbf{1} \triangleleft W}\\ &=(c_{ \mathbf{1}, V}{\otimes} \mathrm{id\,}_W) (\mathrm{id\,}_{F( \mathbf{1} \triangleleft V)}{\otimes} c_{ \mathbf{1}, W} ) \xi^{-1}_{ \mathbf{1} \triangleleft V, \mathbf{1} \triangleleft W} F(l_{ \mathbf{1} \triangleleft V,W}) F(l^{-1}_{ \mathbf{1} \triangleleft V,W}) \xi_{ \mathbf{1} \triangleleft V, \mathbf{1} \triangleleft W}\\ &=(c_{ \mathbf{1}, V}{\otimes} c_{ \mathbf{1}, W}). \end{align*} $$
The second equation follows from (6.5)
Remark 6.7 Constructions in Proposition 6.6 are reciprocal in the following sense. If
![]() ${\mathcal B}$
is a right monoidal
${\mathcal B}$
is a right monoidal
![]() ${\mathcal C}$
-module category and
${\mathcal C}$
-module category and
![]() $G:{\mathcal C}\to {\mathcal B}$
is the monoidal functor
$G:{\mathcal C}\to {\mathcal B}$
is the monoidal functor
![]() $G(V)= \mathbf {1}\triangleleft V$
, then one can endow
$G(V)= \mathbf {1}\triangleleft V$
, then one can endow
![]() ${\mathcal B}$
with a right
${\mathcal B}$
with a right
![]() ${\mathcal C}$
-module structure
${\mathcal C}$
-module structure
for any
![]() $B\in {\mathcal B}$
,
$B\in {\mathcal B}$
,
![]() $V\in {\mathcal C}$
. Turns out, that the identity functor
$V\in {\mathcal C}$
. Turns out, that the identity functor
![]() $\mathrm {Id\,}: ({\mathcal B}, \triangleleft )\to ({\mathcal B}, \blacktriangleleft )$
is an equivalence of module categories.
$\mathrm {Id\,}: ({\mathcal B}, \triangleleft )\to ({\mathcal B}, \blacktriangleleft )$
is an equivalence of module categories.
6.2 Some natural module transformations
It is known that natural transformations between additive functors are additive. For example, if
![]() $(F,\xi )$
is an additive monoidal functor, then natural isomorphisms
$(F,\xi )$
is an additive monoidal functor, then natural isomorphisms
are additive in each variable. In this section, we shall study what happens when F is a monoidal module functor. We aim at proving that
![]() $\xi $
is a module natural transformation in the second variable.
$\xi $
is a module natural transformation in the second variable.
Lemma 6.8 If
![]() ${\mathcal B}$
is a right monoidal
${\mathcal B}$
is a right monoidal
![]() ${\mathcal C}$
-module category, then for any
${\mathcal C}$
-module category, then for any
![]() $A\in {\mathcal B}$
, the functor
$A\in {\mathcal B}$
, the functor
![]() $L_A:{\mathcal B}\to {\mathcal B}$
,
$L_A:{\mathcal B}\to {\mathcal B}$
,
![]() $L_A(B)=A{\otimes } B$
is a
$L_A(B)=A{\otimes } B$
is a
![]() ${\mathcal C}$
-module functor.
${\mathcal C}$
-module functor.
Proof For any
![]() $B\in {\mathcal B}, V\in {\mathcal C}$
, the module structure of the functor
$B\in {\mathcal B}, V\in {\mathcal C}$
, the module structure of the functor
![]() $L_A$
is given by
$L_A$
is given by
Let us prove that
![]() $\eta $
satisfies (3.18). Using that isomorphisms l satisfy diagram (6.4), it follows that for any
$\eta $
satisfies (3.18). Using that isomorphisms l satisfy diagram (6.4), it follows that for any
![]() $C\in {\mathcal B}$
and any
$C\in {\mathcal B}$
and any
![]() $V, W\in {\mathcal C}$
, we have that
$V, W\in {\mathcal C}$
, we have that
On one hand, we have that
 $$ \begin{align*} \eta_{B,V{\otimes} W}& = l^{-1}_{A{\otimes} B, V{\otimes} W}(\mathrm{id\,}_A{\otimes} l_{B,V{\otimes} W})\\ &= l^{-1}_{(A{\otimes} B)\triangleleft V, W}(l^{-1}_{A{\otimes} B,V}{\otimes} \mathrm{id\,}_{ \mathbf{1} \triangleleft W})(\mathrm{id\,}_{A{\otimes} B}{\otimes} l_{ \mathbf{1} \triangleleft V,W}) (\mathrm{ id\,}_{A{\otimes} B}{\otimes} l^{-1}_{ \mathbf{1} \triangleleft V,W})\\ &\quad (\mathrm{id\,}_A{\otimes} l_{B,V}{\otimes} \mathrm{id\,}_{ \mathbf{1} \triangleleft W})(\mathrm{id\,}_A{\otimes} l_{B\triangleleft V,W})\\ & = l^{-1}_{(A{\otimes} B)\triangleleft V, W}(l^{-1}_{A{\otimes} B,V}{\otimes} \mathrm{id\,}_{ \mathbf{1} \triangleleft W}) (\mathrm{id\,}_A{\otimes} l_{B,V}{\otimes} \mathrm{id\,}_{ \mathbf{1} \triangleleft W})(\mathrm{id\,}_A{\otimes} l_{B\triangleleft V,W}). \end{align*} $$
$$ \begin{align*} \eta_{B,V{\otimes} W}& = l^{-1}_{A{\otimes} B, V{\otimes} W}(\mathrm{id\,}_A{\otimes} l_{B,V{\otimes} W})\\ &= l^{-1}_{(A{\otimes} B)\triangleleft V, W}(l^{-1}_{A{\otimes} B,V}{\otimes} \mathrm{id\,}_{ \mathbf{1} \triangleleft W})(\mathrm{id\,}_{A{\otimes} B}{\otimes} l_{ \mathbf{1} \triangleleft V,W}) (\mathrm{ id\,}_{A{\otimes} B}{\otimes} l^{-1}_{ \mathbf{1} \triangleleft V,W})\\ &\quad (\mathrm{id\,}_A{\otimes} l_{B,V}{\otimes} \mathrm{id\,}_{ \mathbf{1} \triangleleft W})(\mathrm{id\,}_A{\otimes} l_{B\triangleleft V,W})\\ & = l^{-1}_{(A{\otimes} B)\triangleleft V, W}(l^{-1}_{A{\otimes} B,V}{\otimes} \mathrm{id\,}_{ \mathbf{1} \triangleleft W}) (\mathrm{id\,}_A{\otimes} l_{B,V}{\otimes} \mathrm{id\,}_{ \mathbf{1} \triangleleft W})(\mathrm{id\,}_A{\otimes} l_{B\triangleleft V,W}). \end{align*} $$
The second equation follows from using (6.7). On the other hand,
is equal to
 $$ \begin{align*} &=(l^{-1}_{A{\otimes} B, V} \triangleleft\mathrm{id\,}_W)(\mathrm{id\,}_A{\otimes} l_{B,V}{\otimes} \mathrm{id\,}_{ \mathbf{1} \triangleleft W}) l^{-1}_{A{\otimes} (B \triangleleft V), W} (\mathrm{id\,}_A{\otimes} l_{B \triangleleft V, W})\\ &=(l^{-1}_{A{\otimes} B, V} \triangleleft\mathrm{id\,}_W) l^{-1}_{A{\otimes} B {\otimes} ( \mathbf{1}\triangleleft V), W} (\mathrm{id\,}_A{\otimes} l_{B,V}{\otimes} \mathrm{id\,}_{ \mathbf{1} \triangleleft W}) (\mathrm{id\,}_A{\otimes} l_{B \triangleleft V, W})\\ & =l^{-1}_{(A{\otimes} B)\triangleleft V, W}(l^{-1}_{A{\otimes} B,V}{\otimes} \mathrm{id\,}_{ \mathbf{1} \triangleleft W}) (\mathrm{id\,}_A{\otimes} l_{B,V}{\otimes} \mathrm{id\,}_{ \mathbf{1} \triangleleft W})(\mathrm{id\,}_A{\otimes} l_{B\triangleleft V,W}). \end{align*} $$
$$ \begin{align*} &=(l^{-1}_{A{\otimes} B, V} \triangleleft\mathrm{id\,}_W)(\mathrm{id\,}_A{\otimes} l_{B,V}{\otimes} \mathrm{id\,}_{ \mathbf{1} \triangleleft W}) l^{-1}_{A{\otimes} (B \triangleleft V), W} (\mathrm{id\,}_A{\otimes} l_{B \triangleleft V, W})\\ &=(l^{-1}_{A{\otimes} B, V} \triangleleft\mathrm{id\,}_W) l^{-1}_{A{\otimes} B {\otimes} ( \mathbf{1}\triangleleft V), W} (\mathrm{id\,}_A{\otimes} l_{B,V}{\otimes} \mathrm{id\,}_{ \mathbf{1} \triangleleft W}) (\mathrm{id\,}_A{\otimes} l_{B \triangleleft V, W})\\ & =l^{-1}_{(A{\otimes} B)\triangleleft V, W}(l^{-1}_{A{\otimes} B,V}{\otimes} \mathrm{id\,}_{ \mathbf{1} \triangleleft W}) (\mathrm{id\,}_A{\otimes} l_{B,V}{\otimes} \mathrm{id\,}_{ \mathbf{1} \triangleleft W})(\mathrm{id\,}_A{\otimes} l_{B\triangleleft V,W}). \end{align*} $$
The second and third equalities follow from the naturality of l.
Proposition 6.9 Assume that
![]() ${\mathcal B}$
is a monoidal right
${\mathcal B}$
is a monoidal right
![]() ${\mathcal C}$
-module category and that
${\mathcal C}$
-module category and that
![]() $(F, c, \xi ):{\mathcal B}\to {\mathcal C}$
a monoidal module functor. The following assertions hold.
$(F, c, \xi ):{\mathcal B}\to {\mathcal C}$
a monoidal module functor. The following assertions hold.
-
(i) The category
 ${\mathcal B}$
has structure of
${\mathcal B}$
has structure of
 ${\mathcal C}$
-bimodule category.
${\mathcal C}$
-bimodule category. -
(ii) There are
 ${\mathcal C}$
-module functors such that
${\mathcal C}$
-module functors such that $$ \begin{align*}H, \widetilde{H}:{\mathcal B}\boxtimes_{\mathcal C} {\mathcal B}\to {\mathcal C}\end{align*} $$
for any
$$ \begin{align*}H, \widetilde{H}:{\mathcal B}\boxtimes_{\mathcal C} {\mathcal B}\to {\mathcal C}\end{align*} $$
for any $$ \begin{align*}H(A\boxtimes B)=F(A{\otimes} B), \quad \widetilde{H}(A\boxtimes B)=F(A){\otimes} F(B),\end{align*} $$
$$ \begin{align*}H(A\boxtimes B)=F(A{\otimes} B), \quad \widetilde{H}(A\boxtimes B)=F(A){\otimes} F(B),\end{align*} $$
 $A, B\in {\mathcal B}$
.
$A, B\in {\mathcal B}$
.
-
(iii) The monoidal structure of the functor F defines a natural module isomorphism
 $\xi :\widetilde {H} \to H$
.
$\xi :\widetilde {H} \to H$
.
Proof (i). From Proposition 6.6, there is a section
![]() $G:{\mathcal C}\to {\mathcal B}$
of the functor F. Define the left action
$G:{\mathcal C}\to {\mathcal B}$
of the functor F. Define the left action
![]() $\triangleright :{\mathcal C}\times {\mathcal B}\to {\mathcal B}$
as
$\triangleright :{\mathcal C}\times {\mathcal B}\to {\mathcal B}$
as
![]() $V\triangleright B=G(V){\otimes } B$
. With this action,
$V\triangleright B=G(V){\otimes } B$
. With this action,
![]() ${\mathcal B}$
becomes a
${\mathcal B}$
becomes a
![]() ${\mathcal C}$
-bimodule category. Thus, we can consider the Deligne tensor product over
${\mathcal C}$
-bimodule category. Thus, we can consider the Deligne tensor product over
![]() ${\mathcal C}$
,
${\mathcal C}$
,
![]() ${\mathcal B}\boxtimes _{\mathcal C} {\mathcal B}$
. This category has an obvious right
${\mathcal B}\boxtimes _{\mathcal C} {\mathcal B}$
. This category has an obvious right
![]() ${\mathcal C}$
-module category structure.
${\mathcal C}$
-module category structure.
One can prove that functors
![]() ${\mathcal B}\times {\mathcal B}\to {\mathcal C}$
given by
${\mathcal B}\times {\mathcal B}\to {\mathcal C}$
given by
are
![]() ${\mathcal C}$
-balanced, thus defining functors H and
${\mathcal C}$
-balanced, thus defining functors H and
![]() $\widetilde {H}$
. The (right)
$\widetilde {H}$
. The (right)
![]() ${\mathcal C}$
-module structure of the functor
${\mathcal C}$
-module structure of the functor
![]() $\widetilde {H}$
is the one inherited from the functor F. The module structure of the functor H is more involved. One can prove that natural transformations
$\widetilde {H}$
is the one inherited from the functor F. The module structure of the functor H is more involved. One can prove that natural transformations
are
![]() ${\mathcal C}$
-balanced, thus defining natural transformations
${\mathcal C}$
-balanced, thus defining natural transformations
for any
![]() $X\in {\mathcal B}\boxtimes _{\mathcal C} {\mathcal B}$
,
$X\in {\mathcal B}\boxtimes _{\mathcal C} {\mathcal B}$
,
![]() $V\in {\mathcal C}$
. One can prove also that
$V\in {\mathcal C}$
. One can prove also that
![]() $(H,e)$
is a module functor. Note that e is the module structure resulting from the composition of module structures of F and the functor
$(H,e)$
is a module functor. Note that e is the module structure resulting from the composition of module structures of F and the functor
![]() $L_A$
, presented in Lemma 6.8. This proves (ii).
$L_A$
, presented in Lemma 6.8. This proves (ii).
(iii). To prove that
![]() $\xi $
is a natural module transformation in the second variable, we need to verify that the diagram
$\xi $
is a natural module transformation in the second variable, we need to verify that the diagram

is commutative for any
![]() $A, B\in {\mathcal B}$
,
$A, B\in {\mathcal B}$
,
![]() $V\in {\mathcal C}$
. Here,
$V\in {\mathcal C}$
. Here,
We have
 $$ \begin{align*} e_{A,B,V} &\xi_{A,B\triangleleft V}= c_{A{\otimes} B, V} F(l^{-1}_{A{\otimes} B, V}(\mathrm{id\,}_A{\otimes} l_{B,V}))\xi_{A,B\triangleleft V}\\ &=(\mathrm{id\,}{\otimes} c_{ \mathbf{1}, V}) \xi^{-1}_{A{\otimes} B, \mathbf{1}\triangleleft V} F(\mathrm{id\,}_A{\otimes} l_{B,V}) \xi_{A,B\triangleleft V}\\ &=(\mathrm{id\,}{\otimes} c_{ \mathbf{1}, V}) \xi^{-1}_{A{\otimes} B, \mathbf{1}\triangleleft V} \xi_{A,B{\otimes} ( \mathbf{1} \triangleleft V)}(\mathrm{id\,}_{F(A)}{\otimes} F(l_{B,V}))\\ &=(\mathrm{id\,}{\otimes} c_{ \mathbf{1}, V}) (\xi_{A,B}{\otimes} \mathrm{id\,}_{F( \mathbf{1} \triangleleft V)})(\mathrm{id\,}_{F(A)}{\otimes} \xi^{-1}_{B, \mathbf{1} \triangleleft V}) (\mathrm{ id\,}_{F(A)}{\otimes} F(l_{B,V}))\\ &=(\xi_{A,B}{\otimes} \mathrm{id\,}_{ V}) (\mathrm{id\,}_{F(A)}{\otimes} (\mathrm{id\,}_{F(B)}{\otimes} c_{ \mathbf{1}, V})\xi^{-1}_{B, \mathbf{1} \triangleleft V} F(l_{B,V})) \\ &=(\xi_{A,B}{\otimes} \mathrm{id\,}_{ V}) (\mathrm{id\,}_{F(A)}{\otimes} c_{B, V}). \end{align*} $$
$$ \begin{align*} e_{A,B,V} &\xi_{A,B\triangleleft V}= c_{A{\otimes} B, V} F(l^{-1}_{A{\otimes} B, V}(\mathrm{id\,}_A{\otimes} l_{B,V}))\xi_{A,B\triangleleft V}\\ &=(\mathrm{id\,}{\otimes} c_{ \mathbf{1}, V}) \xi^{-1}_{A{\otimes} B, \mathbf{1}\triangleleft V} F(\mathrm{id\,}_A{\otimes} l_{B,V}) \xi_{A,B\triangleleft V}\\ &=(\mathrm{id\,}{\otimes} c_{ \mathbf{1}, V}) \xi^{-1}_{A{\otimes} B, \mathbf{1}\triangleleft V} \xi_{A,B{\otimes} ( \mathbf{1} \triangleleft V)}(\mathrm{id\,}_{F(A)}{\otimes} F(l_{B,V}))\\ &=(\mathrm{id\,}{\otimes} c_{ \mathbf{1}, V}) (\xi_{A,B}{\otimes} \mathrm{id\,}_{F( \mathbf{1} \triangleleft V)})(\mathrm{id\,}_{F(A)}{\otimes} \xi^{-1}_{B, \mathbf{1} \triangleleft V}) (\mathrm{ id\,}_{F(A)}{\otimes} F(l_{B,V}))\\ &=(\xi_{A,B}{\otimes} \mathrm{id\,}_{ V}) (\mathrm{id\,}_{F(A)}{\otimes} (\mathrm{id\,}_{F(B)}{\otimes} c_{ \mathbf{1}, V})\xi^{-1}_{B, \mathbf{1} \triangleleft V} F(l_{B,V})) \\ &=(\xi_{A,B}{\otimes} \mathrm{id\,}_{ V}) (\mathrm{id\,}_{F(A)}{\otimes} c_{B, V}). \end{align*} $$
The second equality follows from (6.5), the third equality follows from the naturality of
![]() $\xi $
, and the fourth one follows from (3.1). The last equality follows from (6.5).
$\xi $
, and the fourth one follows from (3.1). The last equality follows from (6.5).
7 Fiber functors and reconstruction results
It is a classical result that, out of a fiber functor, which is a monoidal, exact, and faithful functor
![]() $F:{\mathcal B}\to \mathrm {vect\,}_{\mathbb {k}}$
, one can reconstruct a (usual) Hopf algebra H such that
$F:{\mathcal B}\to \mathrm {vect\,}_{\mathbb {k}}$
, one can reconstruct a (usual) Hopf algebra H such that
![]() ${\mathcal B}$
is monoidally equivalent to the category of left H-comodules. We shall generalize these reconstruction theorems for a fiber functor
${\mathcal B}$
is monoidally equivalent to the category of left H-comodules. We shall generalize these reconstruction theorems for a fiber functor
![]() $F:{\mathcal B}\to {\mathcal C}$
, where
$F:{\mathcal B}\to {\mathcal C}$
, where
![]() ${\mathcal C}$
is an arbitrary braided tensor category acting monoidally on
${\mathcal C}$
is an arbitrary braided tensor category acting monoidally on
![]() ${\mathcal B}$
. The reconstruction of the Hopf algebra from these data will be described in a similar way as the case
${\mathcal B}$
. The reconstruction of the Hopf algebra from these data will be described in a similar way as the case
![]() ${\mathcal C}=\mathrm {vect\,}_{\mathbb {k}}$
. See, for example, [Reference Majid19, Reference Schauenburg23]. The main new ingredient will be the use of the relative coend, introduced in [Reference Bortolussi and Mombelli4], and the splitting condition, that is, the existence of a section
${\mathcal C}=\mathrm {vect\,}_{\mathbb {k}}$
. See, for example, [Reference Majid19, Reference Schauenburg23]. The main new ingredient will be the use of the relative coend, introduced in [Reference Bortolussi and Mombelli4], and the splitting condition, that is, the existence of a section
![]() $G:{\mathcal C}\to {\mathcal B}$
of F. While dealing with the relative (co)end, the primary new challenge will be demonstrated that some dinatural transformations satisfy equation (4.5).
$G:{\mathcal C}\to {\mathcal B}$
of F. While dealing with the relative (co)end, the primary new challenge will be demonstrated that some dinatural transformations satisfy equation (4.5).
7.1 Coalgebras constructed from a coend
Let
![]() ${\mathcal C}$
be a tensor category, and let
${\mathcal C}$
be a tensor category, and let
![]() ${\mathcal B}$
be a right
${\mathcal B}$
be a right
![]() ${\mathcal C}$
-module category. For the rest of this section,
${\mathcal C}$
-module category. For the rest of this section,
![]() $(F,c):{\mathcal B}\to {\mathcal C}$
will denote a right exact module functor.
$(F,c):{\mathcal B}\to {\mathcal C}$
will denote a right exact module functor.
Consider the functor
This functor has a canonical prebalancing given by
 $$ \begin{align} &\beta^X_{A,B}: F(B){\otimes} {}^*F(A \triangleleft X) \to F(B \triangleleft {}^*X){\otimes} {}^*F(A), \nonumber\\ &\beta^X_{A,B}=(c^{-1}_{B, {}^*X}{\otimes} \mathrm{id\,}_{{}^*F(A)})(\mathrm{id\,}_{F(B)}{\otimes} (\phi^l_{F(A),X})^{-1} {}^*(c^{-1}_{A,X})). \end{align} $$
$$ \begin{align} &\beta^X_{A,B}: F(B){\otimes} {}^*F(A \triangleleft X) \to F(B \triangleleft {}^*X){\otimes} {}^*F(A), \nonumber\\ &\beta^X_{A,B}=(c^{-1}_{B, {}^*X}{\otimes} \mathrm{id\,}_{{}^*F(A)})(\mathrm{id\,}_{F(B)}{\otimes} (\phi^l_{F(A),X})^{-1} {}^*(c^{-1}_{A,X})). \end{align} $$
We define
Let
![]() $\pi _B:F(B){\otimes } {}^*F(B)\to C(F)$
be the associated dinatural transformations. Existence of this coend follows from Corollary 4.8. The following lemma is a generalization of [Reference Schauenburg23, Lemma 2.1.9]. Recall that for any
$\pi _B:F(B){\otimes } {}^*F(B)\to C(F)$
be the associated dinatural transformations. Existence of this coend follows from Corollary 4.8. The following lemma is a generalization of [Reference Schauenburg23, Lemma 2.1.9]. Recall that for any
![]() $M, N\in {\mathcal B}$
,
$M, N\in {\mathcal B}$
,
![]() $X\in {\mathcal C}$
, we have natural isomorphisms
$X\in {\mathcal C}$
, we have natural isomorphisms
described in (3.7).
Lemma 7.1 The functor
![]() $V\mapsto \mathrm {Nat\,}_{\! m}(F, V{\otimes } F)$
is represented by
$V\mapsto \mathrm {Nat\,}_{\! m}(F, V{\otimes } F)$
is represented by
![]() $C(F)$
. That is, for any
$C(F)$
. That is, for any
![]() $V\in {\mathcal C}$
, there are natural isomorphisms
$V\in {\mathcal C}$
, there are natural isomorphisms
 $$ \begin{align} &\omega: \operatorname{Hom}_{\mathcal C}(C(F),V)\to \mathrm{Nat\,}_{\! m}(F, V{\otimes} F), \nonumber\\ &\omega(g)_B= (g{\otimes} \mathrm{id\,}_{F(B)})\psi^{C(F)}_{F(B),F(B)}(\pi_B). \end{align} $$
$$ \begin{align} &\omega: \operatorname{Hom}_{\mathcal C}(C(F),V)\to \mathrm{Nat\,}_{\! m}(F, V{\otimes} F), \nonumber\\ &\omega(g)_B= (g{\otimes} \mathrm{id\,}_{F(B)})\psi^{C(F)}_{F(B),F(B)}(\pi_B). \end{align} $$
Proof Fix some object
![]() $V\in {\mathcal C}$
. The functor
$V\in {\mathcal C}$
. The functor
![]() $V{\otimes } F$
is a right module functor, then we can consider the prebalancing of the functor
$V{\otimes } F$
is a right module functor, then we can consider the prebalancing of the functor
given by
Note that here we are considering
![]() ${\mathcal B}^{\mathrm {{op}}}$
as a left
${\mathcal B}^{\mathrm {{op}}}$
as a left
![]() ${\mathcal C}$
-module category, with action
${\mathcal C}$
-module category, with action
![]() $X\triangleright B:=B\triangleleft {}^*X$
. Proposition 4.3(ii) tells us that there is an isomorphism
$X\triangleright B:=B\triangleleft {}^*X$
. Proposition 4.3(ii) tells us that there is an isomorphism
From the proof of Proposition 4.4, one can see that the dinatural transformations of the end
![]() $\oint _{B\in {\mathcal B}} \operatorname {Hom}_{\mathcal C}(F(B){\otimes } {}^*F(B),V)$
are given by
$\oint _{B\in {\mathcal B}} \operatorname {Hom}_{\mathcal C}(F(B){\otimes } {}^*F(B),V)$
are given by
Here, we are using identification
It follows by a straightforward computation that
for any
![]() $M, N\in {\mathcal B}$
and any
$M, N\in {\mathcal B}$
and any
![]() $f\in \operatorname {Hom}_{\mathcal B}(F(M \triangleleft {}^*X){\otimes } {}^*F(N ),V)$
. This implies, using Proposition 4.3(i) that, for any
$f\in \operatorname {Hom}_{\mathcal B}(F(M \triangleleft {}^*X){\otimes } {}^*F(N ),V)$
. This implies, using Proposition 4.3(i) that, for any
![]() $V\in {\mathcal C}$
, there exists an isomorphism
$V\in {\mathcal C}$
, there exists an isomorphism
such that
![]() $\mu _B\circ \widehat {\psi }^V= \psi ^V_{F(B),F(B)}\circ \widehat {\pi }_B.$
For any
$\mu _B\circ \widehat {\psi }^V= \psi ^V_{F(B),F(B)}\circ \widehat {\pi }_B.$
For any
![]() $V\in {\mathcal C}$
, we have that
$V\in {\mathcal C}$
, we have that
 $$ \begin{align*} \operatorname{Hom}_{\mathcal C}(C(F),V)&\simeq \oint_{B\in {\mathcal B}} \operatorname{Hom}_{\mathcal C}(F(B){\otimes} {}^*F(B),V)\\ &\simeq \oint_{B\in {\mathcal B}} \operatorname{Hom}_{\mathcal C}(F(B),V{\otimes} F(B))\\ &\simeq \mathrm{Nat\,}_{\! m}(F, V{\otimes} F). \end{align*} $$
$$ \begin{align*} \operatorname{Hom}_{\mathcal C}(C(F),V)&\simeq \oint_{B\in {\mathcal B}} \operatorname{Hom}_{\mathcal C}(F(B){\otimes} {}^*F(B),V)\\ &\simeq \oint_{B\in {\mathcal B}} \operatorname{Hom}_{\mathcal C}(F(B),V{\otimes} F(B))\\ &\simeq \mathrm{Nat\,}_{\! m}(F, V{\otimes} F). \end{align*} $$
The first isomorphism is Proposition 4.4. Tracing this chain of isomorphisms, one can see that the composition coincides with
![]() $\omega $
defined by equation (7.2).
$\omega $
defined by equation (7.2).
Proposition 7.2 Let
![]() ${\mathcal C}$
be a tensor category, and let
${\mathcal C}$
be a tensor category, and let
![]() ${\mathcal B}$
be a right
${\mathcal B}$
be a right
![]() ${\mathcal C}$
-module category. Let
${\mathcal C}$
-module category. Let
![]() $(F,c):{\mathcal B}\to {\mathcal C}$
be a right exact module functor. The object
$(F,c):{\mathcal B}\to {\mathcal C}$
be a right exact module functor. The object
![]() $C(F)\in {\mathcal C}$
has a coalgebra structure
$C(F)\in {\mathcal C}$
has a coalgebra structure
![]() $\Delta :C(F)\to C(F){\otimes } C(F)$
,
$\Delta :C(F)\to C(F){\otimes } C(F)$
,
![]() $\varepsilon :C(F)\to \mathbf {1}$
determined by diagrams
$\varepsilon :C(F)\to \mathbf {1}$
determined by diagrams


for any
![]() $B\in {\mathcal B}$
.
$B\in {\mathcal B}$
.
Proof It follows by a straightforward computation that the maps
are dinatural maps. It follows from diagram (3.20) that
![]() $ \mbox {ev}_{F(B)}$
satisfies (4.5). It follows from diagram (3.21) and the fact that
$ \mbox {ev}_{F(B)}$
satisfies (4.5). It follows from diagram (3.21) and the fact that
![]() $\pi $
satisfies (4.5) that
$\pi $
satisfies (4.5) that
![]() $(\pi _B{\otimes } \pi _B )(\mathrm {id\,}{\otimes } \mbox {coev}_{F(B)} {\otimes }\mathrm {id\,})$
also satisfies equation (4.5). Whence, the existence of
$(\pi _B{\otimes } \pi _B )(\mathrm {id\,}{\otimes } \mbox {coev}_{F(B)} {\otimes }\mathrm {id\,})$
also satisfies equation (4.5). Whence, the existence of
![]() $\Delta $
and
$\Delta $
and
![]() $\varepsilon $
follows from the universal property of the relative coend.
$\varepsilon $
follows from the universal property of the relative coend.
The proof that
![]() $(C(F),\Delta , \varepsilon )$
is a coalgebra is standard, and it follows from diagrams (7.3) and (7.4).
$(C(F),\Delta , \varepsilon )$
is a coalgebra is standard, and it follows from diagrams (7.3) and (7.4).
Let
![]() ${\mathcal C}$
be a tensor category, and let
${\mathcal C}$
be a tensor category, and let
![]() $C\in {\mathcal C}$
be a coalgebra. The category
$C\in {\mathcal C}$
be a coalgebra. The category
![]() ${}^C{\mathcal C}$
, of left C-comodules in
${}^C{\mathcal C}$
, of left C-comodules in
![]() ${\mathcal C}$
, is a right
${\mathcal C}$
, is a right
![]() ${\mathcal C}$
-module category. The action is given as follows. If
${\mathcal C}$
-module category. The action is given as follows. If
![]() $(W,\rho )\in {}^C{\mathcal C}$
, then
$(W,\rho )\in {}^C{\mathcal C}$
, then
![]() $W \triangleleft Y=W{\otimes } Y$
, where the coaction on
$W \triangleleft Y=W{\otimes } Y$
, where the coaction on
![]() $W{\otimes } Y$
is given by
$W{\otimes } Y$
is given by
![]() $\rho {\otimes } \mathrm {id\,}_Y.$
The forgetful functor
$\rho {\otimes } \mathrm {id\,}_Y.$
The forgetful functor
![]() $f:{}^C{\mathcal C}\to {\mathcal C}$
is a
$f:{}^C{\mathcal C}\to {\mathcal C}$
is a
![]() ${\mathcal C}$
-module functor. The next result says that the coalgebra reconstructed from the forgetful functor f coincides with C.
${\mathcal C}$
-module functor. The next result says that the coalgebra reconstructed from the forgetful functor f coincides with C.
In this case, the functor
![]() $S^f$
has a prebalancing given by
$S^f$
has a prebalancing given by
for any
![]() $A, B\in {}^C{\mathcal C}$
,
$A, B\in {}^C{\mathcal C}$
,
![]() $X\in {\mathcal C}$
.
$X\in {\mathcal C}$
.
Lemma 7.3 There exists an isomorphism of coalgebras
![]() $C(f)\simeq C$
in
$C(f)\simeq C$
in
![]() ${\mathcal C}$
.
${\mathcal C}$
.
Proof In this particular case, if
![]() $T\in {\mathcal C}$
is an object, and
$T\in {\mathcal C}$
is an object, and
![]() $\lambda _W:W{\otimes } {}^*W\to T$
is a dinatural transformation, equation (4.5) writes as
$\lambda _W:W{\otimes } {}^*W\to T$
is a dinatural transformation, equation (4.5) writes as
for any
![]() $W\in {}^C{\mathcal C}, V\in {\mathcal C}.$
$W\in {}^C{\mathcal C}, V\in {\mathcal C}.$
If
![]() $W\in {}^C{\mathcal C}$
has comodule structure given by
$W\in {}^C{\mathcal C}$
has comodule structure given by
![]() $\rho _W\to C{\otimes } W$
, then we define
$\rho _W\to C{\otimes } W$
, then we define
![]() $\pi _W:W{\otimes } {}^*W\to C,$
the morphisms given by
$\pi _W:W{\otimes } {}^*W\to C,$
the morphisms given by
![]() $\pi _W=\bar {\psi }^C_{W,W}(\rho )$
. Recall that natural isomorphisms
$\pi _W=\bar {\psi }^C_{W,W}(\rho )$
. Recall that natural isomorphisms
![]() $\bar {\psi }$
were defined in (3.8). Maps
$\bar {\psi }$
were defined in (3.8). Maps
![]() $\pi _W$
are dinatural transformations, and they satisfy equation (7.5).
$\pi _W$
are dinatural transformations, and they satisfy equation (7.5).
Let
![]() $A\in {\mathcal C}$
be another object, equipped with dinatural transformations
$A\in {\mathcal C}$
be another object, equipped with dinatural transformations
![]() $\lambda _W:W{\otimes } {}^*W\to A$
such that they satisfy equation (7.5). Define h as the composition
$\lambda _W:W{\otimes } {}^*W\to A$
such that they satisfy equation (7.5). Define h as the composition
Since
![]() $\lambda $
is dinatural, and it satisfies (7.5), one can see that
$\lambda $
is dinatural, and it satisfies (7.5), one can see that
![]() $h\circ \pi _W= \lambda _W$
. This proves that, indeed,
$h\circ \pi _W= \lambda _W$
. This proves that, indeed,
![]() $C(f)\simeq C$
.
$C(f)\simeq C$
.
Proposition 7.4 Let
![]() ${\mathcal B}$
be a right
${\mathcal B}$
be a right
![]() ${\mathcal C}$
-module category, and let
${\mathcal C}$
-module category, and let
![]() $(F,c):{\mathcal B}\to {\mathcal C}$
be a right exact module functor. Set
$(F,c):{\mathcal B}\to {\mathcal C}$
be a right exact module functor. Set
![]() $C=C(F)$
the coalgebra defined in Proposition 7.2.
$C=C(F)$
the coalgebra defined in Proposition 7.2.
-
1. The functor
 $(F,c):{\mathcal B}\to {\mathcal C}$
factorizes as (7.6)Here,
$(F,c):{\mathcal B}\to {\mathcal C}$
factorizes as (7.6)Here,
 $f:{}^C{\mathcal C} \to {\mathcal C}$
is the forgetful functor, and the functor
$f:{}^C{\mathcal C} \to {\mathcal C}$
is the forgetful functor, and the functor
 $\widehat {F}$
is a
$\widehat {F}$
is a
 ${\mathcal C}$
-module functor.
${\mathcal C}$
-module functor.
-
2. If F is exact (resp. faithful), then
 $\widehat {F}$
is exact (resp. faithful).
$\widehat {F}$
is exact (resp. faithful).
Proof 1. For any
![]() $A\in {\mathcal B}$
, define
$A\in {\mathcal B}$
, define
![]() $\widehat {F}(A)=(F(A),\rho _A),$
where
$\widehat {F}(A)=(F(A),\rho _A),$
where
Using diagrams (7.3) and (7.4), one can prove that
2. Clearly, if F is faithful, then
![]() $\widehat {F}$
is faithful. Assume that F is left exact. Let
$\widehat {F}$
is faithful. Assume that F is left exact. Let
![]() $f:A\to B$
be a morphism in
$f:A\to B$
be a morphism in
![]() ${\mathcal B}$
with kernel
${\mathcal B}$
with kernel
![]() $k=\ker f: K\to A$
. Since F is left exact, then
$k=\ker f: K\to A$
. Since F is left exact, then
![]() $F(k)=\ker F(f)$
. We only need to prove that the morphism
$F(k)=\ker F(f)$
. We only need to prove that the morphism
![]() $F(k):F(K)\to F(A)$
is a map of C-comodules. That is, we need to prove the equality
$F(k):F(K)\to F(A)$
is a map of C-comodules. That is, we need to prove the equality
Using the naturality of
![]() $\psi $
, it follows that
$\psi $
, it follows that
 $$ \begin{align*} \psi^C_{F(A),F(A)}(\pi_A) F(k)&= \psi^C_{F(K),F(A)}(\pi_A (F(k){\otimes} \mathrm{id\,}))\\ &=\psi^C_{F(K),F(A)}(\pi_K (\mathrm{id\,} {\otimes} {}^*F(k)))\\ &=(\mathrm{id\,} {\otimes} F(k)) \psi^C_{F(K),F(K)}(\pi_K ). \end{align*} $$
$$ \begin{align*} \psi^C_{F(A),F(A)}(\pi_A) F(k)&= \psi^C_{F(K),F(A)}(\pi_A (F(k){\otimes} \mathrm{id\,}))\\ &=\psi^C_{F(K),F(A)}(\pi_K (\mathrm{id\,} {\otimes} {}^*F(k)))\\ &=(\mathrm{id\,} {\otimes} F(k)) \psi^C_{F(K),F(K)}(\pi_K ). \end{align*} $$
The second equality follows from the dinaturality of
![]() $\pi $
, and the third equality follows again by the naturality of
$\pi $
, and the third equality follows again by the naturality of
![]() $\psi $
. The proof that if F is right exact then
$\psi $
. The proof that if F is right exact then
![]() $\widehat {F}$
is right exact follows similarly.
$\widehat {F}$
is right exact follows similarly.
7.2 Some auxiliary results
In this section, we shall present some technical results that will be used later. In particular, these results will be used in the proof of our main result Theorem 7.7.
Let
![]() ${\mathcal B}$
be a right
${\mathcal B}$
be a right
![]() ${\mathcal C}$
-module category, and
${\mathcal C}$
-module category, and
![]() $(F,c):{\mathcal B}\to {\mathcal C}$
be a module functor. To make calculations easier, we shall assume that the associativity of the
$(F,c):{\mathcal B}\to {\mathcal C}$
be a module functor. To make calculations easier, we shall assume that the associativity of the
![]() ${\mathcal C}$
-module category
${\mathcal C}$
-module category
![]() ${\mathcal B}$
is trivial. Recall the relative coend
${\mathcal B}$
is trivial. Recall the relative coend
presented in Proposition 4.7. Let us denote by
the associated dinatural transformations. Analogous to the definition of
![]() $\Delta $
, given in (7.3), we shall define a map
$\Delta $
, given in (7.3), we shall define a map
Lemma 7.5 There exists a unique morphism
![]() $\delta : \widetilde {C}(F,c)\to \widetilde {C}(F,c)\triangleleft C(F,c)$
such that
$\delta : \widetilde {C}(F,c)\to \widetilde {C}(F,c)\triangleleft C(F,c)$
such that

Proof Let us denote
![]() $ d_{B,V}$
the following natural isomorphism:
$ d_{B,V}$
the following natural isomorphism:
Recall from equation (4.9) that the prebalancing used in the coend
![]() $\widetilde {C}(F,c)$
is given by
$\widetilde {C}(F,c)$
is given by
Using that c satisfies (3.18), it is not difficult to prove that
for any
![]() $B\in {\mathcal B}$
,
$B\in {\mathcal B}$
,
![]() $V\in {\mathcal C}$
. The naturality of
$V\in {\mathcal C}$
. The naturality of
![]() $\phi ^l$
and c implies that
$\phi ^l$
and c implies that
for any
![]() $B\in {\mathcal B}$
,
$B\in {\mathcal B}$
,
![]() $V\in {\mathcal C}$
. Whence, using (3.6), it follows that
$V\in {\mathcal C}$
. Whence, using (3.6), it follows that
In this case, if
![]() $A\in {\mathcal B}$
, a dinatural transformation
$A\in {\mathcal B}$
, a dinatural transformation
![]() $\nu _B: B\triangleleft {}^*F(B)\to A$
satisfies equation (4.5) if and only if
$\nu _B: B\triangleleft {}^*F(B)\to A$
satisfies equation (4.5) if and only if
Using that dinatural transformations
![]() $\lambda $
and
$\lambda $
and
![]() $\pi $
both satisfy (4.5) and using (7.13), it follows that dinatural transformation
$\pi $
both satisfy (4.5) and using (7.13), it follows that dinatural transformation
also satisfies (7.14). Now, existence of the map
![]() $\delta : \widetilde {C}(F,c)\to \widetilde {C}(F,c)\triangleleft C(F,c)$
satisfying (7.10) follows from the universal property of the relative coend.
$\delta : \widetilde {C}(F,c)\to \widetilde {C}(F,c)\triangleleft C(F,c)$
satisfying (7.10) follows from the universal property of the relative coend.
For any
![]() $A, B\in {\mathcal B}$
and
$A, B\in {\mathcal B}$
and
![]() $V\in {\mathcal C}$
, define
$V\in {\mathcal C}$
, define
 $$ \begin{align} &\widetilde{\psi}^V_{B,A}:\operatorname{Hom}_{\mathcal B}(B\triangleleft {}^*V,A)\to \operatorname{Hom}_{\mathcal B}(B,A \triangleleft V), \nonumber\\ &\widetilde{\psi}^V_{B,A}(f)=(f\triangleleft \mathrm{id\,}_V)(\mathrm{id\,}_B \triangleleft \mbox{coev}_V). \end{align} $$
$$ \begin{align} &\widetilde{\psi}^V_{B,A}:\operatorname{Hom}_{\mathcal B}(B\triangleleft {}^*V,A)\to \operatorname{Hom}_{\mathcal B}(B,A \triangleleft V), \nonumber\\ &\widetilde{\psi}^V_{B,A}(f)=(f\triangleleft \mathrm{id\,}_V)(\mathrm{id\,}_B \triangleleft \mbox{coev}_V). \end{align} $$
Compare with natural isomorphisms given in (3.7). For any
![]() $B\in {\mathcal B}$
, define also
$B\in {\mathcal B}$
, define also
One could check that, using Lemma 4.5, whenever F is right exact,
![]() $F(\widetilde {C})=C$
. The dinatural transformations of
$F(\widetilde {C})=C$
. The dinatural transformations of
![]() $F(\widetilde {C})$
is given by
$F(\widetilde {C})$
is given by
![]() $F(\lambda _B)$
. In particular, this implies that
$F(\lambda _B)$
. In particular, this implies that
for any
![]() $B\in {\mathcal B}$
. Using definition of
$B\in {\mathcal B}$
. Using definition of
![]() $\Delta :C\to C{\otimes } C$
given by diagram (7.2), one can see that
$\Delta :C\to C{\otimes } C$
given by diagram (7.2), one can see that
If
![]() $h_1, h_2:C{\otimes } F(B)\to C{\otimes } C{\otimes } F(B)$
are defined as
$h_1, h_2:C{\otimes } F(B)\to C{\otimes } C{\otimes } F(B)$
are defined as
then it is a standard result that the kernel of the difference
![]() $h_1-h_2$
is
$h_1-h_2$
is
![]() $\rho _B$
. Using the above, we have the following.
$\rho _B$
. Using the above, we have the following.
Proposition 7.6 Assume that the module functor
![]() $(F,c):{\mathcal B}\to {\mathcal C}$
is faithful and exact. The map
$(F,c):{\mathcal B}\to {\mathcal C}$
is faithful and exact. The map
![]() $\widetilde {\rho }_B:B\to \widetilde {C} \triangleleft F(B)$
is the kernel of the difference of morphisms
$\widetilde {\rho }_B:B\to \widetilde {C} \triangleleft F(B)$
is the kernel of the difference of morphisms

where
![]() $\widetilde {h}_1= \mathrm {id\,}_{\widetilde {C} } \triangleleft \rho _B$
and
$\widetilde {h}_1= \mathrm {id\,}_{\widetilde {C} } \triangleleft \rho _B$
and
![]() $\widetilde {h}_2= \delta \triangleleft \mathrm {id\,}_{F(B)}.$
$\widetilde {h}_2= \delta \triangleleft \mathrm {id\,}_{F(B)}.$
Proof Note that we are using that F is right exact so that
![]() $F(\widetilde {C})=C$
. See Lemma 4.5. Using (7.17), (7.18), and the naturality of c, one can prove that
$F(\widetilde {C})=C$
. See Lemma 4.5. Using (7.17), (7.18), and the naturality of c, one can prove that
This implies that
![]() $F (\widetilde {\rho }_B)=\ker F(\widetilde {h}_1-\widetilde {h}_2)=F(\ker \widetilde {h}_1-\widetilde {h}_2)$
, since F is also left exact. The result follows, since F is faithful.
$F (\widetilde {\rho }_B)=\ker F(\widetilde {h}_1-\widetilde {h}_2)=F(\ker \widetilde {h}_1-\widetilde {h}_2)$
, since F is also left exact. The result follows, since F is faithful.
7.3 Reconstruction results
The following theorem is one of our main results and is a generalization of [Reference Schauenburg23, Theorem 2.2.8].
Theorem 7.7 Let
![]() ${\mathcal C}$
be a tensor category, and let
${\mathcal C}$
be a tensor category, and let
![]() ${\mathcal B}$
be a right
${\mathcal B}$
be a right
![]() ${\mathcal C}$
-module category. Let
${\mathcal C}$
-module category. Let
![]() $(F,c):{\mathcal B}\to {\mathcal C}$
be an exact and faithful module functor. Let
$(F,c):{\mathcal B}\to {\mathcal C}$
be an exact and faithful module functor. Let
![]() $C=\oint ^{B\in {\mathcal B}} F(B){\otimes } {}^*F(B)\in {\mathcal C}$
be the relative coend coalgebra introduced in Proposition 7.2 and consider its category of comodules
$C=\oint ^{B\in {\mathcal B}} F(B){\otimes } {}^*F(B)\in {\mathcal C}$
be the relative coend coalgebra introduced in Proposition 7.2 and consider its category of comodules
![]() ${}^C{\mathcal C}$
. Then the functor F factorizes into an equivalence of
${}^C{\mathcal C}$
. Then the functor F factorizes into an equivalence of
![]() ${\mathcal C}$
-module categories
${\mathcal C}$
-module categories
![]() $\widehat {F}: {\mathcal B}\stackrel {\sim }{\longrightarrow } {}^C{\mathcal C}$
and the forgetful functor
$\widehat {F}: {\mathcal B}\stackrel {\sim }{\longrightarrow } {}^C{\mathcal C}$
and the forgetful functor
![]() $f:{}^C{\mathcal C} \to {\mathcal C}$
:
$f:{}^C{\mathcal C} \to {\mathcal C}$
:

Proof Recall that we denote by
the dinatural transformations of the relative coend
![]() $C(F)$
. The definition of the functor
$C(F)$
. The definition of the functor
![]() $\widehat {F}:{\mathcal B}\to {}^C{\mathcal C}$
was given in Proposition 7.4. Since F is faithful,
$\widehat {F}:{\mathcal B}\to {}^C{\mathcal C}$
was given in Proposition 7.4. Since F is faithful,
![]() $\widehat {F}$
is also faithful. We need to prove that
$\widehat {F}$
is also faithful. We need to prove that
![]() $\widehat {F}$
is essentially surjective and full.
$\widehat {F}$
is essentially surjective and full.
Let us prove first that
![]() $\widehat {F}$
is essentially surjective. Take
$\widehat {F}$
is essentially surjective. Take
![]() $(M,\rho )\in {}^C{\mathcal C}$
. We endowed
$(M,\rho )\in {}^C{\mathcal C}$
. We endowed
![]() $C{\otimes } M$
structure of left C-comodule via
$C{\otimes } M$
structure of left C-comodule via
![]() $\Delta $
, then
$\Delta $
, then
![]() $\rho :M\to C{\otimes } M$
is actually a morphism in
$\rho :M\to C{\otimes } M$
is actually a morphism in
![]() ${}^C{\mathcal C}$
. We begin with the observation that
${}^C{\mathcal C}$
. We begin with the observation that
![]() $(M,\rho )$
is the kernel (in
$(M,\rho )$
is the kernel (in
![]() ${}^C{\mathcal C}$
) of the difference of morphisms
${}^C{\mathcal C}$
) of the difference of morphisms

Recall from Proposition 7.4 that for any
![]() $A\in {\mathcal B}$
, the object
$A\in {\mathcal B}$
, the object
![]() $F(A)$
has a left H-comodule structure given by
$F(A)$
has a left H-comodule structure given by
![]() $\rho _A=\psi ^C_{F(A),F(A)}(\pi _A).$
Hence, for any
$\rho _A=\psi ^C_{F(A),F(A)}(\pi _A).$
Hence, for any
![]() $V\in {\mathcal C}$
, the object
$V\in {\mathcal C}$
, the object
![]() $F(A){\otimes } V$
has a left comodule structure given by
$F(A){\otimes } V$
has a left comodule structure given by
![]() $\rho _A{\otimes }\mathrm {id\,}_V$
. The next claim will be crucial for the proof. To prove this claim, it is essential that the dinatural maps
$\rho _A{\otimes }\mathrm {id\,}_V$
. The next claim will be crucial for the proof. To prove this claim, it is essential that the dinatural maps
![]() $\pi $
satisfy equation (4.5).
$\pi $
satisfy equation (4.5).
Claim 7.1 For any
![]() $A\in {\mathcal B}$
,
$A\in {\mathcal B}$
,
![]() $V\in {\mathcal C},$
morphisms
$V\in {\mathcal C},$
morphisms
![]() $c_{A,V}:F(A\triangleleft V)\to F(A){\otimes } V$
are C-comodule maps.
$c_{A,V}:F(A\triangleleft V)\to F(A){\otimes } V$
are C-comodule maps.
Proof of Claim
We need to prove that
This equation is equivalent to
Since
![]() $\pi $
satisfies equation (4.5), it follows that
$\pi $
satisfies equation (4.5), it follows that
Using the description of the prebalancing
![]() $\beta $
given in (4.10), we obtain that
$\beta $
given in (4.10), we obtain that
 $$ \begin{align} \pi_{A\triangleleft V}& = \pi_A (\mathrm{id\,}_{F(A)}{\otimes} {}^*(c_{A\triangleleft V, V^*} F(\mathrm{id\,}_A \triangleleft \mbox{coev}_{V^*})) ) (\mathrm{id\,}{\otimes} \phi^l_{F(A\triangleleft V),V^*}) \nonumber\\ &\quad (c_{A,V}{\otimes} \mathrm{id\,}_{{}^*F(A\triangleleft V)}). \end{align} $$
$$ \begin{align} \pi_{A\triangleleft V}& = \pi_A (\mathrm{id\,}_{F(A)}{\otimes} {}^*(c_{A\triangleleft V, V^*} F(\mathrm{id\,}_A \triangleleft \mbox{coev}_{V^*})) ) (\mathrm{id\,}{\otimes} \phi^l_{F(A\triangleleft V),V^*}) \nonumber\\ &\quad (c_{A,V}{\otimes} \mathrm{id\,}_{{}^*F(A\triangleleft V)}). \end{align} $$
It follows from the naturality of c that
Using equation (3.18), it follows that
Whence
 $$ \begin{align} \pi_{A\triangleleft V}&=\pi_A (\mathrm{id\,}_{F(A)}{\otimes} {}^*(\mathrm{id\,}_{F(A)}{\otimes} \mbox{coev}_{V^*})) (\mathrm{id\,}_{F(A)}{\otimes} {}^*(c^{-1}_{A,V}{\otimes} \mathrm{id\,}_{V^*} ) ) \nonumber\\ &(\mathrm{id\,}_{F(A)}{\otimes} \phi^l_{F(A\triangleleft V),V^*})(c_{A,V}{\otimes} \mathrm{id\,}_{{}^*F(A\triangleleft V)})\\ &=\pi_A (\mathrm{id\,}_{F(A)}{\otimes} {}^*(\mathrm{id\,}_{F(A)}{\otimes} \mbox{coev}_{V^*})) (\mathrm{id\,}_{F(A)}{\otimes} \phi^l_{V^*,F(A){\otimes} V} )\nonumber\\ & ( c_{A,V}{\otimes} {}^*(c^{-1}_{A,V}) ).\nonumber \end{align} $$
$$ \begin{align} \pi_{A\triangleleft V}&=\pi_A (\mathrm{id\,}_{F(A)}{\otimes} {}^*(\mathrm{id\,}_{F(A)}{\otimes} \mbox{coev}_{V^*})) (\mathrm{id\,}_{F(A)}{\otimes} {}^*(c^{-1}_{A,V}{\otimes} \mathrm{id\,}_{V^*} ) ) \nonumber\\ &(\mathrm{id\,}_{F(A)}{\otimes} \phi^l_{F(A\triangleleft V),V^*})(c_{A,V}{\otimes} \mathrm{id\,}_{{}^*F(A\triangleleft V)})\\ &=\pi_A (\mathrm{id\,}_{F(A)}{\otimes} {}^*(\mathrm{id\,}_{F(A)}{\otimes} \mbox{coev}_{V^*})) (\mathrm{id\,}_{F(A)}{\otimes} \phi^l_{V^*,F(A){\otimes} V} )\nonumber\\ & ( c_{A,V}{\otimes} {}^*(c^{-1}_{A,V}) ).\nonumber \end{align} $$
The second equality follows from the naturality of
![]() $\phi ^l$
. It follows by a tedious, but straightforward, computation that
$\phi ^l$
. It follows by a tedious, but straightforward, computation that
 $$ \begin{align} \big({}^*(\mathrm{id\,}_{F(A)}{\otimes}\mbox{coev}_{V^*}){\otimes} \mathrm{id\,}_{F(A){\otimes} V} \big)&\big( \phi^l_{V^*,F(A){\otimes} V}{\otimes}\mathrm{ id\,}_{F(A){\otimes} V}\big) \nonumber\\ &\big(\mathrm{id\,}_{V}{\otimes}\mbox{coev}_{F(A){\otimes} V}\big)= \mbox{coev}_{F(A)}{\otimes}\mathrm{id\,}_{V}. \end{align} $$
$$ \begin{align} \big({}^*(\mathrm{id\,}_{F(A)}{\otimes}\mbox{coev}_{V^*}){\otimes} \mathrm{id\,}_{F(A){\otimes} V} \big)&\big( \phi^l_{V^*,F(A){\otimes} V}{\otimes}\mathrm{ id\,}_{F(A){\otimes} V}\big) \nonumber\\ &\big(\mathrm{id\,}_{V}{\otimes}\mbox{coev}_{F(A){\otimes} V}\big)= \mbox{coev}_{F(A)}{\otimes}\mathrm{id\,}_{V}. \end{align} $$
Let us prove now equation (7.20). The right-hand side of (7.20) is equal to
 $$ \begin{align*} &=(\pi_{A\triangleleft V} {\otimes}\mathrm{id\,}_{F(A){\otimes} V} ) (\mathrm{id\,}{\otimes} c_{A,V}) (\mathrm{id\,}_{F(A\triangleleft V)}{\otimes} \mbox{coev}_{F(A\triangleleft V)}) \\ &= \big(\pi_A {\otimes}\mathrm{id\,}_{F(A){\otimes} V} \big) \big(\mathrm{id\,}_{F(A)}{\otimes} {}^*(\mathrm{id\,}_{F(A)}{\otimes} \mbox{coev}_{V^*}){\otimes}\mathrm{id\,}_{F(A){\otimes} V}\big)\\ & \big(\mathrm{id\,}_{F(A)}{\otimes} \phi^l_{V^*,F(A){\otimes} V}{\otimes} \mathrm{id\,}_{F(A){\otimes} V} \big) \big( c_{A,V} {\otimes} {}^*(c^{-1}_{A,V}){\otimes} \mathrm{id\,}_{F(A){\otimes} V} \big)\\ & (\mathrm{id\,}{\otimes} c_{A,V}) (\mathrm{id\,}_{F(A\triangleleft V)} {\otimes}\mbox{coev}_{F(A\triangleleft V)}) \\ &=\big(\pi_A {\otimes}\mathrm{id\,}_{F(A){\otimes} V} \big) \big(\mathrm{id\,}_{F(A)}{\otimes} {}^*(\mathrm{id\,}_{F(A)}{\otimes} \mbox{coev}_{V^*}){\otimes}\mathrm{id\,}_{F(A){\otimes} V}\big)\\ & \big(\mathrm{id\,}_{F(A)}{\otimes} \phi^l_{V^*,F(A){\otimes} V}{\otimes} \mathrm{id\,}_{F(A){\otimes} V} \big) \big( c_{A,V}{\otimes} \mbox{coev}_{F(A){\otimes} V} \big)\\ &=(\pi_A{\otimes} \mathrm{id\,}_{F(A){\otimes} V}) (\mathrm{id\,}_{F(A)} {\otimes} \mbox{coev}_{F(A)}{\otimes} \mathrm{id\,}_V) c_{A,V}. \end{align*} $$
$$ \begin{align*} &=(\pi_{A\triangleleft V} {\otimes}\mathrm{id\,}_{F(A){\otimes} V} ) (\mathrm{id\,}{\otimes} c_{A,V}) (\mathrm{id\,}_{F(A\triangleleft V)}{\otimes} \mbox{coev}_{F(A\triangleleft V)}) \\ &= \big(\pi_A {\otimes}\mathrm{id\,}_{F(A){\otimes} V} \big) \big(\mathrm{id\,}_{F(A)}{\otimes} {}^*(\mathrm{id\,}_{F(A)}{\otimes} \mbox{coev}_{V^*}){\otimes}\mathrm{id\,}_{F(A){\otimes} V}\big)\\ & \big(\mathrm{id\,}_{F(A)}{\otimes} \phi^l_{V^*,F(A){\otimes} V}{\otimes} \mathrm{id\,}_{F(A){\otimes} V} \big) \big( c_{A,V} {\otimes} {}^*(c^{-1}_{A,V}){\otimes} \mathrm{id\,}_{F(A){\otimes} V} \big)\\ & (\mathrm{id\,}{\otimes} c_{A,V}) (\mathrm{id\,}_{F(A\triangleleft V)} {\otimes}\mbox{coev}_{F(A\triangleleft V)}) \\ &=\big(\pi_A {\otimes}\mathrm{id\,}_{F(A){\otimes} V} \big) \big(\mathrm{id\,}_{F(A)}{\otimes} {}^*(\mathrm{id\,}_{F(A)}{\otimes} \mbox{coev}_{V^*}){\otimes}\mathrm{id\,}_{F(A){\otimes} V}\big)\\ & \big(\mathrm{id\,}_{F(A)}{\otimes} \phi^l_{V^*,F(A){\otimes} V}{\otimes} \mathrm{id\,}_{F(A){\otimes} V} \big) \big( c_{A,V}{\otimes} \mbox{coev}_{F(A){\otimes} V} \big)\\ &=(\pi_A{\otimes} \mathrm{id\,}_{F(A){\otimes} V}) (\mathrm{id\,}_{F(A)} {\otimes} \mbox{coev}_{F(A)}{\otimes} \mathrm{id\,}_V) c_{A,V}. \end{align*} $$
The second equality follows from equation (7.22), the third equality follows from (3.3), and the last equality follows from (7.23). This finishes the proof of the claim.
It follows from Claim that natural isomorphisms c endow the functor
![]() $\widehat {F}$
with structure of module functor. Let
$\widehat {F}$
with structure of module functor. Let
be the object defined in Proposition 4.7, together with the map
presented in diagram (7.10). Since
![]() $F(\widetilde {C})=C$
, it also follows from Claim 7.1 that there are C-comodule isomorphisms
$F(\widetilde {C})=C$
, it also follows from Claim 7.1 that there are C-comodule isomorphisms
Hence,
![]() $(M,\rho )$
is the kernel of the difference of morphisms
$(M,\rho )$
is the kernel of the difference of morphisms

where
![]() $h_1= \delta \triangleleft \mathrm {id\,}_M, h_2=\mathrm {id\,}_{\widetilde {C}} \triangleleft \rho $
. Since F is left exact,
$h_1= \delta \triangleleft \mathrm {id\,}_M, h_2=\mathrm {id\,}_{\widetilde {C}} \triangleleft \rho $
. Since F is left exact,
![]() $(M,\rho )\simeq F( \ker (h_1-h_2))$
. This proves that
$(M,\rho )\simeq F( \ker (h_1-h_2))$
. This proves that
![]() $\widehat {F}$
is essentially surjective.
$\widehat {F}$
is essentially surjective.
Let us prove now that
![]() $\widehat {F}$
is full. Take
$\widehat {F}$
is full. Take
![]() $A, B\in {\mathcal B}$
and
$A, B\in {\mathcal B}$
and
![]() $f:F(A)\to F(B)$
a C-comodule morphism. We have a commutative diagram
$f:F(A)\to F(B)$
a C-comodule morphism. We have a commutative diagram

This implies that we have a commutative diagram

Where
![]() $h^A_1= \mathrm {id\,}_H{\otimes } \rho _A, h^A_2=\Delta {\otimes } \mathrm {id\,}_{F(A)}.$
Note that, by the universal property of the kernel, the map
$h^A_1= \mathrm {id\,}_H{\otimes } \rho _A, h^A_2=\Delta {\otimes } \mathrm {id\,}_{F(A)}.$
Note that, by the universal property of the kernel, the map
![]() $f:F(A)\to F(B)$
is the unique morphism fitting in this diagram. Define
$f:F(A)\to F(B)$
is the unique morphism fitting in this diagram. Define
See Proposition 4.7 for the definition of this coend. Using Proposition 7.6, for any
![]() $B\in {\mathcal B}$
, we have an exact sequence
$B\in {\mathcal B}$
, we have an exact sequence
where
![]() $\widetilde {h}_B=\mathrm {id\,}_{\widetilde {C} } \triangleleft \rho _B- \delta \triangleleft \mathrm {id\,}_{F(B)}.$
For the definition of
$\widetilde {h}_B=\mathrm {id\,}_{\widetilde {C} } \triangleleft \rho _B- \delta \triangleleft \mathrm {id\,}_{F(B)}.$
For the definition of
![]() $\delta $
and
$\delta $
and
![]() $ \widetilde {\rho }_B$
, see (7.9) and (7.10). Since f is a comodule morphism, by the universal property of the kernel, there exists a unique morphism
$ \widetilde {\rho }_B$
, see (7.9) and (7.10). Since f is a comodule morphism, by the universal property of the kernel, there exists a unique morphism
![]() $\eta $
that fits into the diagram
$\eta $
that fits into the diagram

Applying F to this diagram, we obtain diagram (7.25). By the uniqueness of f, we get that
![]() $F(\eta )=f$
, proving that
$F(\eta )=f$
, proving that
![]() $\widehat {F}$
is full.
$\widehat {F}$
is full.
7.4 Hopf algebras in
 ${\mathcal C}$
constructed from a coend
${\mathcal C}$
constructed from a coend
In the case
![]() ${\mathcal B}$
is a monoidal
${\mathcal B}$
is a monoidal
![]() ${\mathcal C}$
-module category and the functor
${\mathcal C}$
-module category and the functor
![]() $(F,c,\xi ):{\mathcal B}\to {\mathcal C}$
is a monoidal module functor, one can endow the coalgebra
$(F,c,\xi ):{\mathcal B}\to {\mathcal C}$
is a monoidal module functor, one can endow the coalgebra
![]() $C=C(F)$
with a Hopf algebra structure. In this section, we shall explain the construction of the product and antipode on
$C=C(F)$
with a Hopf algebra structure. In this section, we shall explain the construction of the product and antipode on
![]() $C(F).$
The new hypothesis needed to construct such Hopf algebra is that
$C(F).$
The new hypothesis needed to construct such Hopf algebra is that
![]() ${\mathcal C}$
possesses a braiding.
${\mathcal C}$
possesses a braiding.
To construct the product
![]() $m:C(F){\otimes } C(F)\to C(F)$
, we shall use ideas from [Reference Majid19]. In few words, we shall construct some natural module transformation
$m:C(F){\otimes } C(F)\to C(F)$
, we shall use ideas from [Reference Majid19]. In few words, we shall construct some natural module transformation
![]() $F{\otimes } F\to C(F){\otimes } F{\otimes } F$
and use Lemma 7.1 to find
$F{\otimes } F\to C(F){\otimes } F{\otimes } F$
and use Lemma 7.1 to find
![]() $m:C(F){\otimes } C(F)\to C(F)$
.
$m:C(F){\otimes } C(F)\to C(F)$
.
Lemma 7.8 Let
![]() ${\mathcal C}$
be a braided tensor category,
${\mathcal C}$
be a braided tensor category,
![]() ${\mathcal B}$
be a monoidal
${\mathcal B}$
be a monoidal
![]() ${\mathcal C}$
-module category, and a monoidal module functor
${\mathcal C}$
-module category, and a monoidal module functor
![]() $(F,c,\xi ):{\mathcal B}\to {\mathcal C}$
. Let us denote
$(F,c,\xi ):{\mathcal B}\to {\mathcal C}$
. Let us denote
![]() $ d_{B,V}$
the following natural isomorphism:
$ d_{B,V}$
the following natural isomorphism:
Then, for any
![]() $B\in {\mathcal B}$
,
$B\in {\mathcal B}$
,
![]() $V\in {\mathcal C}$
, we have
$V\in {\mathcal C}$
, we have
Proof It follows by a straightforward calculation using (3.18).
Recall, from Proposition 6.9, the functors
determined by
for any
![]() $A, B\in {\mathcal B}$
. Recall also that we are denoting by
$A, B\in {\mathcal B}$
. Recall also that we are denoting by
![]() $\pi _B:F(B){\otimes } {}^*F(B)\to C(F)$
the dinatural transformations and the associated left
$\pi _B:F(B){\otimes } {}^*F(B)\to C(F)$
the dinatural transformations and the associated left
![]() $C(F)$
-coaction
$C(F)$
-coaction
![]() $\rho _B=\psi ^C_{F(B),F(B)}(\pi _B).$
$\rho _B=\psi ^C_{F(B),F(B)}(\pi _B).$
Remark 7.9 In the case
![]() ${\mathcal C}=\mathrm {vect\,}_{\mathbb {k}}$
, the following proposition is trivial, since it only says that some natural transformation is additive. In the general case, where
${\mathcal C}=\mathrm {vect\,}_{\mathbb {k}}$
, the following proposition is trivial, since it only says that some natural transformation is additive. In the general case, where
![]() ${\mathcal C}$
is arbitrary, it is far from obvious, and it is a crucial step toward the reconstruction of the product in
${\mathcal C}$
is arbitrary, it is far from obvious, and it is a crucial step toward the reconstruction of the product in
![]() $C(F)$
. Its proof will highlight the importance of all required axioms.
$C(F)$
. Its proof will highlight the importance of all required axioms.
For later use,
![]() $\pi $
has to satisfy equation (4.5), using prebalancing (7.1). This means that
$\pi $
has to satisfy equation (4.5), using prebalancing (7.1). This means that
Proposition 7.10 Let
![]() ${\mathcal C}$
be a braided tensor category,
${\mathcal C}$
be a braided tensor category,
![]() ${\mathcal B}$
be a monoidal
${\mathcal B}$
be a monoidal
![]() ${\mathcal C}$
-module category, and
${\mathcal C}$
-module category, and
![]() $(F,c,\xi ):{\mathcal B}\to {\mathcal C}$
be a monoidal module functor. The natural transformation
$(F,c,\xi ):{\mathcal B}\to {\mathcal C}$
be a monoidal module functor. The natural transformation
![]() $\mu : \widetilde {H} \to C(F){\otimes } \widetilde {H}$
determined by the composition
$\mu : \widetilde {H} \to C(F){\otimes } \widetilde {H}$
determined by the composition
is a natural module transformation. That is,
![]() $\mu \in \mathrm {Nat\,}_{\! m}( \widetilde {H}, C(F){\otimes } \widetilde {H})$
.
$\mu \in \mathrm {Nat\,}_{\! m}( \widetilde {H}, C(F){\otimes } \widetilde {H})$
.
Proof It follows from Proposition 6.9 that
![]() $\xi $
is a natural module transformation. Once it has been established that the diagram
$\xi $
is a natural module transformation. Once it has been established that the diagram

is commutative, the proof will follow. Recall, from the proof of Proposition 6.9, that
We shall also keep the notation
Using the definition of
![]() $\rho _A$
, one can see that diagram (7.29) amounts to
$\rho _A$
, one can see that diagram (7.29) amounts to
 $$ \begin{align} \begin{split} &(\mathrm{id\,}_{C(F)}{\otimes} e_{A,B,V})(\pi_{A{\otimes} B \triangleleft V}{\otimes}\mathrm{id\,}_{F(A{\otimes} B \triangleleft V)})(\mathrm{id\,}_{F(A{\otimes} B \triangleleft V)}{\otimes}\mbox{coev}_{F(A{\otimes} B \triangleleft V)} )=\\ &=(\pi_{A{\otimes} B}{\otimes}\mathrm{id\,}_{_{F(A{\otimes} B)}{\otimes} V})(\mathrm{id\,}_{F(A{\otimes} B)} {\otimes} \mbox{coev}_{F(A{\otimes} B) }{\otimes}\mathrm{id\,}_V)e_{A,B,V}. \end{split} \end{align} $$
$$ \begin{align} \begin{split} &(\mathrm{id\,}_{C(F)}{\otimes} e_{A,B,V})(\pi_{A{\otimes} B \triangleleft V}{\otimes}\mathrm{id\,}_{F(A{\otimes} B \triangleleft V)})(\mathrm{id\,}_{F(A{\otimes} B \triangleleft V)}{\otimes}\mbox{coev}_{F(A{\otimes} B \triangleleft V)} )=\\ &=(\pi_{A{\otimes} B}{\otimes}\mathrm{id\,}_{_{F(A{\otimes} B)}{\otimes} V})(\mathrm{id\,}_{F(A{\otimes} B)} {\otimes} \mbox{coev}_{F(A{\otimes} B) }{\otimes}\mathrm{id\,}_V)e_{A,B,V}. \end{split} \end{align} $$
Using the dinaturality of
![]() $\pi $
, one can see that the left-hand side of (7.30) is equal to
$\pi $
, one can see that the left-hand side of (7.30) is equal to
 $$ \begin{align*}&=\big(\pi_{(A{\otimes} B )\triangleleft V} (F(\eta_{B,V}){\otimes} {}^*F(\eta^{-1}_{A,B,V})){\otimes} e_{A,B,V}\big)(\mathrm{id\,}_{F(A{\otimes} B \triangleleft V)}{\otimes}\mbox{coev}_{F(A{\otimes} B \triangleleft V)} )\\ &=\big(\pi_{(A{\otimes} B )\triangleleft V} {\otimes} c_{A{\otimes} B,V}\big) \big(F(\eta_{A,B,V}) {\otimes} \mbox{coev}_{F((A{\otimes} B) \triangleleft V)}\big)\\ &=\big(\pi_{(A{\otimes} B )\triangleleft V} {\otimes} \mathrm{id\,}\big) \big(F(\eta_{A,B,V}) {\otimes} \mathrm{id\,}{\otimes} c_{A{\otimes} B,V}\big) \big(\mathrm{id\,}{\otimes} \mbox{coev}_{F((A{\otimes} B) \triangleleft V)}\big)\\ &=\big(\pi_{(A{\otimes} B )\triangleleft V} {\otimes} \mathrm{id\,}\big) \big(F(\eta_{A,B,V}) {\otimes} \mathrm{id\,}{\otimes} c_{A{\otimes} B,V}\big) \big(\mathrm{id\,}{\otimes} d^{-1}_{A{\otimes} B,V}{\otimes} c^{-1}_{A{\otimes} B,V}\big)\\ &(\mathrm{id\,}_{F(A{\otimes} B\triangleleft V){\otimes} {}^*V{\otimes} \mbox{coev}_{A{\otimes} B}{\otimes} \mathrm{id\,}_V }) ( \mathrm{id\,}_{F(A{\otimes} B\triangleleft V)}{\otimes}\mbox{coev}_V)\\ &=\big(\pi_{(A{\otimes} B )\triangleleft V} {\otimes} \mathrm{id\,}\big) \big(F(\eta_{A,B,V}) {\otimes} d^{-1}_{A{\otimes} B,V}{\otimes} \mathrm{id\,}_{F(A{\otimes} B){\otimes} V}\big)\\ &(\mathrm{id\,}_{F(A{\otimes} B\triangleleft V){\otimes} {}^*V}{\otimes} \mbox{coev}_{A{\otimes} B}{\otimes} \mathrm{id\,}_V ) ( \mathrm{id\,}_{F(A{\otimes} B\triangleleft V)}{\otimes}\mbox{coev}_V)\\ &=(\pi_{A{\otimes} B}{\otimes}\mathrm{id\,}_{_{F(A{\otimes} B)}{\otimes} V})(\mathrm{id\,}_{F(A{\otimes} B)} {\otimes} \mbox{coev}_{F(A{\otimes} B) }{\otimes}\mathrm{id\,}_V)e_{A,B,V}. \end{align*} $$
$$ \begin{align*}&=\big(\pi_{(A{\otimes} B )\triangleleft V} (F(\eta_{B,V}){\otimes} {}^*F(\eta^{-1}_{A,B,V})){\otimes} e_{A,B,V}\big)(\mathrm{id\,}_{F(A{\otimes} B \triangleleft V)}{\otimes}\mbox{coev}_{F(A{\otimes} B \triangleleft V)} )\\ &=\big(\pi_{(A{\otimes} B )\triangleleft V} {\otimes} c_{A{\otimes} B,V}\big) \big(F(\eta_{A,B,V}) {\otimes} \mbox{coev}_{F((A{\otimes} B) \triangleleft V)}\big)\\ &=\big(\pi_{(A{\otimes} B )\triangleleft V} {\otimes} \mathrm{id\,}\big) \big(F(\eta_{A,B,V}) {\otimes} \mathrm{id\,}{\otimes} c_{A{\otimes} B,V}\big) \big(\mathrm{id\,}{\otimes} \mbox{coev}_{F((A{\otimes} B) \triangleleft V)}\big)\\ &=\big(\pi_{(A{\otimes} B )\triangleleft V} {\otimes} \mathrm{id\,}\big) \big(F(\eta_{A,B,V}) {\otimes} \mathrm{id\,}{\otimes} c_{A{\otimes} B,V}\big) \big(\mathrm{id\,}{\otimes} d^{-1}_{A{\otimes} B,V}{\otimes} c^{-1}_{A{\otimes} B,V}\big)\\ &(\mathrm{id\,}_{F(A{\otimes} B\triangleleft V){\otimes} {}^*V{\otimes} \mbox{coev}_{A{\otimes} B}{\otimes} \mathrm{id\,}_V }) ( \mathrm{id\,}_{F(A{\otimes} B\triangleleft V)}{\otimes}\mbox{coev}_V)\\ &=\big(\pi_{(A{\otimes} B )\triangleleft V} {\otimes} \mathrm{id\,}\big) \big(F(\eta_{A,B,V}) {\otimes} d^{-1}_{A{\otimes} B,V}{\otimes} \mathrm{id\,}_{F(A{\otimes} B){\otimes} V}\big)\\ &(\mathrm{id\,}_{F(A{\otimes} B\triangleleft V){\otimes} {}^*V}{\otimes} \mbox{coev}_{A{\otimes} B}{\otimes} \mathrm{id\,}_V ) ( \mathrm{id\,}_{F(A{\otimes} B\triangleleft V)}{\otimes}\mbox{coev}_V)\\ &=(\pi_{A{\otimes} B}{\otimes}\mathrm{id\,}_{_{F(A{\otimes} B)}{\otimes} V})(\mathrm{id\,}_{F(A{\otimes} B)} {\otimes} \mbox{coev}_{F(A{\otimes} B) }{\otimes}\mathrm{id\,}_V)e_{A,B,V}. \end{align*} $$
The second equality follows from the definition of
![]() $e_{A,B,V}$
and (3.3), and the fourth follows from (3.21). The last equation follows by using (7.28) and (7.27).
$e_{A,B,V}$
and (3.3), and the fourth follows from (3.21). The last equation follows by using (7.28) and (7.27).
Theorem 7.11 Assume that
![]() $({\mathcal C},\sigma )$
is a braided tensor category,
$({\mathcal C},\sigma )$
is a braided tensor category,
![]() ${\mathcal B}$
is a monoidal right
${\mathcal B}$
is a monoidal right
![]() ${\mathcal C}$
-module category, and
${\mathcal C}$
-module category, and
![]() $(F,c,\xi ):{\mathcal B}\to {\mathcal C}$
is an exact and faithful monoidal module functor with monoidal structure
$(F,c,\xi ):{\mathcal B}\to {\mathcal C}$
is an exact and faithful monoidal module functor with monoidal structure
The relative coend coalgebra
![]() $C(F)$
from Theorem 7.7 has an algebra structure, with unit
$C(F)$
from Theorem 7.7 has an algebra structure, with unit
![]() $u=\pi _{\mathbf {1}}$
and product
$u=\pi _{\mathbf {1}}$
and product
![]() $m:C(F){\otimes } C(F)\to C(F)$
determined by
$m:C(F){\otimes } C(F)\to C(F)$
determined by
 $$ \begin{align} \begin{split}&(m{\otimes} \mathrm{id\,})(\pi_A{\otimes} \pi_B{\otimes} \mathrm{id\,}_{F(A){\otimes} F(B)})(\mathrm{id\,}{\otimes} \sigma_{F(A), F(B){\otimes} {}^*F(B)}{\otimes} \mathrm{id\,}_{F(B)})\\ &(\mathrm{id\,}_{F(A)}{\otimes} \mbox{coev}_{F(A)}{\otimes} \mathrm{id\,}_{F(B)}{\otimes} \mbox{coev}_{F(B)})=(\mathrm{id\,}_{C(F)}{\otimes} \xi^{-1}_{A,B})\rho_{A{\otimes} B} \xi_{A,B}, \end{split} \end{align} $$
$$ \begin{align} \begin{split}&(m{\otimes} \mathrm{id\,})(\pi_A{\otimes} \pi_B{\otimes} \mathrm{id\,}_{F(A){\otimes} F(B)})(\mathrm{id\,}{\otimes} \sigma_{F(A), F(B){\otimes} {}^*F(B)}{\otimes} \mathrm{id\,}_{F(B)})\\ &(\mathrm{id\,}_{F(A)}{\otimes} \mbox{coev}_{F(A)}{\otimes} \mathrm{id\,}_{F(B)}{\otimes} \mbox{coev}_{F(B)})=(\mathrm{id\,}_{C(F)}{\otimes} \xi^{-1}_{A,B})\rho_{A{\otimes} B} \xi_{A,B}, \end{split} \end{align} $$
for any
![]() $A,B\in {\mathcal B}$
. The object
$A,B\in {\mathcal B}$
. The object
![]() $C(F)$
becomes a bialgebra in
$C(F)$
becomes a bialgebra in
![]() ${\mathcal C}$
. Moreover, the equivalence of
${\mathcal C}$
. Moreover, the equivalence of
![]() ${\mathcal C}$
-module categories
${\mathcal C}$
-module categories
![]() $\widehat {F}:{\mathcal B}\to {}^{C(F)}{\mathcal C}$
is an equivalence of tensor categories.
$\widehat {F}:{\mathcal B}\to {}^{C(F)}{\mathcal C}$
is an equivalence of tensor categories.
Proof Recall from Lemma 7.3 that, if
![]() $f:{}^{C{\otimes } C}{\mathcal C}\to {\mathcal C}$
is the forgetful functor, then
$f:{}^{C{\otimes } C}{\mathcal C}\to {\mathcal C}$
is the forgetful functor, then
![]() $C(f)= C{\otimes } C$
and the dinatural transformations of this coend are given by
$C(f)= C{\otimes } C$
and the dinatural transformations of this coend are given by
Since the functor
![]() $F:{\mathcal B}\to {\mathcal C}$
factorizes as
$F:{\mathcal B}\to {\mathcal C}$
factorizes as
![]() $F=f\circ \widehat {F}$
, then the functor
$F=f\circ \widehat {F}$
, then the functor
![]() $\widetilde {H}={\otimes }\circ (F\boxtimes F): {\mathcal B}\boxtimes _{\mathcal C}{\mathcal B}\to {\mathcal C}$
factorizes as
$\widetilde {H}={\otimes }\circ (F\boxtimes F): {\mathcal B}\boxtimes _{\mathcal C}{\mathcal B}\to {\mathcal C}$
factorizes as

Using Lemma 4.6, since
![]() $\widehat {F}$
is an equivalence of right
$\widehat {F}$
is an equivalence of right
![]() ${\mathcal C}$
-module categories, it follows that
${\mathcal C}$
-module categories, it follows that
Lemma 4.6 also explains how to compute dinatural transformations of this coend. If
![]() $\pi _X: \widetilde {H}(X){\otimes } {}^*\widetilde {H}(X)\to C(F){\otimes } C(F)$
,
$\pi _X: \widetilde {H}(X){\otimes } {}^*\widetilde {H}(X)\to C(F){\otimes } C(F)$
,
![]() $X\in {\mathcal B}\boxtimes _{\mathcal C}{\mathcal B}$
, are the dinatural transformations associated with this coend, then
$X\in {\mathcal B}\boxtimes _{\mathcal C}{\mathcal B}$
, are the dinatural transformations associated with this coend, then
 $$ \begin{align*}\pi_{A\boxtimes B}&=\lambda_{(F(A){\otimes} F(B),\rho)}=\big(\mathrm{id\,}_{C(F){\otimes} C(F)}{\otimes} \mbox{ev}_D\big)\big(\mathrm{id\,}_C{\otimes}\sigma_{F(A),C}{\otimes} \mathrm{ id\,}_{F(B){\otimes} {}^*D}\big)\\ & \big(\pi_A{\otimes} \mathrm{id\,}_{F(A)}{\otimes} \pi_B{\otimes}\mathrm{id\,}\big) (\mathrm{id\,}_{F(A)}{\otimes} \mbox{coev}_{F(A)}{\otimes} \mathrm{id\,}_{F(B)}{\otimes} \mbox{coev}_{F(B)}{\otimes} \mathrm{id\,}_{{}^*D}), \end{align*} $$
$$ \begin{align*}\pi_{A\boxtimes B}&=\lambda_{(F(A){\otimes} F(B),\rho)}=\big(\mathrm{id\,}_{C(F){\otimes} C(F)}{\otimes} \mbox{ev}_D\big)\big(\mathrm{id\,}_C{\otimes}\sigma_{F(A),C}{\otimes} \mathrm{ id\,}_{F(B){\otimes} {}^*D}\big)\\ & \big(\pi_A{\otimes} \mathrm{id\,}_{F(A)}{\otimes} \pi_B{\otimes}\mathrm{id\,}\big) (\mathrm{id\,}_{F(A)}{\otimes} \mbox{coev}_{F(A)}{\otimes} \mathrm{id\,}_{F(B)}{\otimes} \mbox{coev}_{F(B)}{\otimes} \mathrm{id\,}_{{}^*D}), \end{align*} $$
for any
![]() $A,B\in {\mathcal B}$
. Here,
$A,B\in {\mathcal B}$
. Here,
![]() $D=F(A){\otimes } F(B)$
. Here,
$D=F(A){\otimes } F(B)$
. Here,
![]() $\rho :F(A){\otimes } F(B)\to C(F){\otimes } F(A){\otimes } F(B) $
is the comodule structure of the tensor product according to formula (5.6). It follows from Lemma 7.1 that there is an isomorphism
$\rho :F(A){\otimes } F(B)\to C(F){\otimes } F(A){\otimes } F(B) $
is the comodule structure of the tensor product according to formula (5.6). It follows from Lemma 7.1 that there is an isomorphism
 $$ \begin{align*} \begin{split} \omega: \operatorname{Hom}_{\mathcal C}(C(F){\otimes} C(F),C(F))\to \mathrm{Nat\,}_{\! m}(\widetilde{H}, C(F){\otimes} \widetilde{H}),\\ \omega(g)_X= (g{\otimes} \mathrm{id\,}_{\widetilde{H}(X)})\psi^{C(F){\otimes} C(F)}_{\widetilde{H}(X),\widetilde{H}(X)}(\pi_X). \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} \omega: \operatorname{Hom}_{\mathcal C}(C(F){\otimes} C(F),C(F))\to \mathrm{Nat\,}_{\! m}(\widetilde{H}, C(F){\otimes} \widetilde{H}),\\ \omega(g)_X= (g{\otimes} \mathrm{id\,}_{\widetilde{H}(X)})\psi^{C(F){\otimes} C(F)}_{\widetilde{H}(X),\widetilde{H}(X)}(\pi_X). \end{split} \end{align*} $$
Since, by Proposition 7.10,
![]() $(\mathrm {id\,}_{C(F)}{\otimes } \xi ^{-1}_{A,B}) \rho _{A{\otimes } B} \xi _{A,B}$
is a natural module transformation, that is,
$(\mathrm {id\,}_{C(F)}{\otimes } \xi ^{-1}_{A,B}) \rho _{A{\otimes } B} \xi _{A,B}$
is a natural module transformation, that is,
then there exists a morphism
![]() $m:C(F){\otimes } C(F)\to C(F)$
such that
$m:C(F){\otimes } C(F)\to C(F)$
such that
Using the rigidity axioms, the naturality of
![]() $\sigma $
, and the formula for
$\sigma $
, and the formula for
![]() $\pi _{A\boxtimes B}$
, this equation implies (7.31). Using (7.31), it follows that
$\pi _{A\boxtimes B}$
, this equation implies (7.31). Using (7.31), it follows that
It follows also from (7.31) that
![]() $\xi $
is a comodule morphism, giving the functor
$\xi $
is a comodule morphism, giving the functor
![]() $\widehat {F}$
structure of monoidal functor.
$\widehat {F}$
structure of monoidal functor.
Definition 7.12 For any monoidal module functor
![]() $F:{\mathcal B}\to {\mathcal C}$
, we shall denote by
$F:{\mathcal B}\to {\mathcal C}$
, we shall denote by
the bialgebra with product given by Theorem (7.11) and coproduct (7.3).
Remark 7.13 In Theorem 7.11, some hypothesis on the functor
![]() $F:{\mathcal B}\to {\mathcal C}$
are superfluous. It follows from [Reference Deligne8, Corollaire 2.10] that if F is right exact, then it is exact and faithful.
$F:{\mathcal B}\to {\mathcal C}$
are superfluous. It follows from [Reference Deligne8, Corollaire 2.10] that if F is right exact, then it is exact and faithful.
Let
![]() $(H,\Delta , m)$
be a bialgebra in
$(H,\Delta , m)$
be a bialgebra in
![]() ${\mathcal C}$
. In the next results, we shall be devoted to prove that the bialgebra reconstructed in Theorem 7.11, from the forgetful functor
${\mathcal C}$
. In the next results, we shall be devoted to prove that the bialgebra reconstructed in Theorem 7.11, from the forgetful functor
![]() $f:{}^H{\mathcal C}\to {\mathcal C}$
, coincides with the original bialgebra H.
$f:{}^H{\mathcal C}\to {\mathcal C}$
, coincides with the original bialgebra H.
In Lemma 7.3, we already proved that the reconstructed coalgebra coincides with H. Moreover, if
![]() $(W, \rho _W)\in {}^H{\mathcal C}$
, then we have defined dinatural transformations
$(W, \rho _W)\in {}^H{\mathcal C}$
, then we have defined dinatural transformations
See (3.8) for the definition of isomorphisms
![]() $\bar {\psi } $
. In order to see that the reconstructed multiplication coincides with the product of H, we only need to prove that the original product m satisfies diagram (7.31). This will be done in the next proposition.
$\bar {\psi } $
. In order to see that the reconstructed multiplication coincides with the product of H, we only need to prove that the original product m satisfies diagram (7.31). This will be done in the next proposition.
Proposition 7.14 Let
![]() $(H,\Delta , m)$
be a bialgebra in
$(H,\Delta , m)$
be a bialgebra in
![]() ${\mathcal C}$
. Using dinatural transformations
${\mathcal C}$
. Using dinatural transformations
![]() $\pi _W:W{\otimes } {}^*W\to H,\ \pi _W=\bar {\psi }^H_{W,W}(\rho _W),$
we have that equation
$\pi _W:W{\otimes } {}^*W\to H,\ \pi _W=\bar {\psi }^H_{W,W}(\rho _W),$
we have that equation
 $$ \begin{align*} m (\pi_V{\otimes} \pi_W{\otimes} \mathrm{id\,}_{V{\otimes} W})&(\mathrm{id\,}_{V{\otimes} {}^*V}{\otimes} \sigma_{V, W{\otimes} {}^*W}{\otimes} \mathrm{id\,}_W)(\mathrm{id\,}{\otimes} \mbox{coev}_V{\otimes}\mathrm{id\,}{\otimes} \mbox{coev}_W)= \\ &=\rho_{V{\otimes} W} \end{align*} $$
$$ \begin{align*} m (\pi_V{\otimes} \pi_W{\otimes} \mathrm{id\,}_{V{\otimes} W})&(\mathrm{id\,}_{V{\otimes} {}^*V}{\otimes} \sigma_{V, W{\otimes} {}^*W}{\otimes} \mathrm{id\,}_W)(\mathrm{id\,}{\otimes} \mbox{coev}_V{\otimes}\mathrm{id\,}{\otimes} \mbox{coev}_W)= \\ &=\rho_{V{\otimes} W} \end{align*} $$
holds for any pair
![]() $(V, \rho _V), (W,\rho _W)\in {}^H{\mathcal C}$
.
$(V, \rho _V), (W,\rho _W)\in {}^H{\mathcal C}$
.
Proof It follows using the naturality of
![]() $\sigma $
and (5.6).
$\sigma $
and (5.6).
7.5 The antipode of
 $H(F)$
$H(F)$
In the next results, we shall construct an antipode
![]() $S:H(F)\to H(F)$
, making the bialgebra
$S:H(F)\to H(F)$
, making the bialgebra
![]() $ H(F)$
a Hopf algebra in
$ H(F)$
a Hopf algebra in
![]() ${\mathcal C}$
.
${\mathcal C}$
.
Lemma 7.15 Let
![]() $({\mathcal C},\sigma )$
be a braided tensor category, and let
$({\mathcal C},\sigma )$
be a braided tensor category, and let
![]() ${\mathcal B}$
be a monoidal right
${\mathcal B}$
be a monoidal right
![]() ${\mathcal C}$
-module category. Let
${\mathcal C}$
-module category. Let
![]() $(F,c):{\mathcal B}\to {\mathcal C}$
be an exact and faithful monoidal module functor. For any
$(F,c):{\mathcal B}\to {\mathcal C}$
be an exact and faithful monoidal module functor. For any
![]() $B\in {\mathcal B}$
,
$B\in {\mathcal B}$
,
![]() $V\in {\mathcal C}$
, there are natural isomorphisms
$V\in {\mathcal C}$
, there are natural isomorphisms
such that the diagram

is commutative.
Proof We shall freely use the fact that
![]() $F({}^*B)= {}^*F(B)$
, for any
$F({}^*B)= {}^*F(B)$
, for any
![]() $B\in {\mathcal B}$
. Since we are under the same hypothesis as Theorem 7.7, the functor
$B\in {\mathcal B}$
. Since we are under the same hypothesis as Theorem 7.7, the functor
![]() $F:{\mathcal B}\to {}^H{\mathcal C}$
is full. Since
$F:{\mathcal B}\to {}^H{\mathcal C}$
is full. Since
![]() $F({}^*B \triangleleft {}^*V)$
is a left H-comodule and the composition
$F({}^*B \triangleleft {}^*V)$
is a left H-comodule and the composition
is an isomorphism, we can endow
![]() ${}^*F(B \triangleleft V)$
with some H-comodule structure such that h is a H-comodule map. Fullness of F implies that there exist some
${}^*F(B \triangleleft V)$
with some H-comodule structure such that h is a H-comodule map. Fullness of F implies that there exist some
![]() $t_{B,V}$
such that
$t_{B,V}$
such that
![]() $F(t_{B,V})=h$
.
$F(t_{B,V})=h$
.
We shall use the same notation as in previous sections. We denote by
the dinatural transformations of the relative coend
![]() $H(F)$
. Also, recall from Proposition 7.4 that for any
$H(F)$
. Also, recall from Proposition 7.4 that for any
![]() $A\in {\mathcal B}$
, we have that
$A\in {\mathcal B}$
, we have that
![]() $(F(A),\rho _A)$
is a left
$(F(A),\rho _A)$
is a left
![]() $H(F)$
-comodule, with structure given by
$H(F)$
-comodule, with structure given by
Henceforth, for simplicity, we shall denote
![]() $H=H(F)$
.
$H=H(F)$
.
Lemma 7.16 Let
![]() $({\mathcal C},\sigma )$
be a braided tensor category, and let
$({\mathcal C},\sigma )$
be a braided tensor category, and let
![]() ${\mathcal B}$
be a monoidal right
${\mathcal B}$
be a monoidal right
![]() ${\mathcal C}$
-module category. For any
${\mathcal C}$
-module category. For any
![]() $B\in {\mathcal B}$
,
$B\in {\mathcal B}$
,
![]() $V\in {\mathcal C}$
, let us recall morphisms
$V\in {\mathcal C}$
, let us recall morphisms
![]() $ d_{B,V}$
, defined in Lemma 7.8, as
$ d_{B,V}$
, defined in Lemma 7.8, as
Then, for any
![]() $B\in {\mathcal B}$
,
$B\in {\mathcal B}$
,
![]() $V\in {\mathcal C}$
, we have
$V\in {\mathcal C}$
, we have
Proof Using Lemma 7.15, there are natural isomorphisms
![]() $t_{B,V}: {}^*(B \triangleleft V)\to {}^*B \triangleleft {}^*V$
such that
$t_{B,V}: {}^*(B \triangleleft V)\to {}^*B \triangleleft {}^*V$
such that
The naturality of
![]() $\phi ^l$
and c implies that
$\phi ^l$
and c implies that
for any
![]() $B\in {\mathcal B}$
,
$B\in {\mathcal B}$
,
![]() $V\in {\mathcal C}$
. Using the dinaturality of
$V\in {\mathcal C}$
. Using the dinaturality of
![]() $\pi $
, we obtain that
$\pi $
, we obtain that
for any
![]() $B\in {\mathcal B}$
,
$B\in {\mathcal B}$
,
![]() $V\in {\mathcal C}$
. Also, dinatural transformations
$V\in {\mathcal C}$
. Also, dinatural transformations
![]() $\pi $
satisfy (4.5); this implies that, for any
$\pi $
satisfy (4.5); this implies that, for any
![]() $B\in {\mathcal B}$
,
$B\in {\mathcal B}$
,
![]() $V\in {\mathcal C}$
, we have
$V\in {\mathcal C}$
, we have
 $$ \begin{align} \begin{split} \pi_{B \triangleleft {}^*V}& = \pi_B \big(\mathrm{id\,}_{F(B)}{\otimes} F({}^*(\mathrm{id\,}_B\triangleleft \mbox{coev}_V )) \big) \big(\mathrm{id\,}_{F(B)}{\otimes} d^{-1}_{B\triangleleft {}^*V,V} \big)\\ &\big( c_{B,{}^*V} {\otimes} \mathrm{id\,}_{{}^*F(B\triangleleft {}^*V)}\big). \end{split} \end{align} $$
$$ \begin{align} \begin{split} \pi_{B \triangleleft {}^*V}& = \pi_B \big(\mathrm{id\,}_{F(B)}{\otimes} F({}^*(\mathrm{id\,}_B\triangleleft \mbox{coev}_V )) \big) \big(\mathrm{id\,}_{F(B)}{\otimes} d^{-1}_{B\triangleleft {}^*V,V} \big)\\ &\big( c_{B,{}^*V} {\otimes} \mathrm{id\,}_{{}^*F(B\triangleleft {}^*V)}\big). \end{split} \end{align} $$
Next, when it is not absolutely necessary, as a space saving measure, we shall write the identities
![]() $\mathrm {id\,}$
, without using subscripts. Using the definition or
$\mathrm {id\,}$
, without using subscripts. Using the definition or
![]() $\rho $
, we obtain that
$\rho $
, we obtain that
is equal to
 $$ \begin{align*} &=(\sigma^{-1}_{ {}^*V, H}{\otimes} \mathrm{id\,}_{ {}^* F(B)})(\mathrm{id\,}_H{\otimes} d_{B,V}) (\pi_{{}^*(B\triangleleft V)}{\otimes} \mathrm{id\,})(\mathrm{id\,}{\otimes} \mbox{coev}_{{}^*F(B\triangleleft V)})d^{-1}_{B,V}\\ &=(\sigma^{-1}_{ {}^*V, H}{\otimes} \mathrm{id\,}_{ {}^* F(B)}) (\pi_{{}^*B\triangleleft {}^*V} {\otimes} d_{B,V}) (F(t_{B,V}){\otimes} {}^*F(t^{-1}_{B,V}){\otimes} \mathrm{id\,})\\ &(\mathrm{id\,}{\otimes} \mbox{coev}_{{}^*F(B\triangleleft V)})d^{-1}_{B,V}\\ &=(\sigma^{-1}_{ {}^*V, H}{\otimes} \mathrm{id\,}_{ {}^* F(B)}) (\pi_{{}^*B\triangleleft {}^*V} {\otimes} d_{B,V}) (F(t_{B,V}){\otimes} \mathrm{id\,}_{{}^*F({}^*B \triangleleft {}^*V)} {\otimes} F(t^{-1}_{B,V}))\\ &(\mathrm{id\,}{\otimes} \mbox{coev}_{F({}^*B\triangleleft {}^*V)})d^{-1}_{B,V}\\ &=(\sigma^{-1}_{ {}^*V, H}{\otimes} \mathrm{id\,}_{ {}^* F(B)})(\pi_{{}^*B}{\otimes} \mathrm{id\,}) (\mathrm{id\,}{\otimes} F({}^*(\mathrm{id\,}_{{}^*B}\triangleleft \mbox{coev}_V )){\otimes} \mathrm{ id\,})(\mathrm{id\,}{\otimes} d_{{}^*B \triangleleft {}^*V,V}{\otimes} \mathrm{id\,})\\ & (c_{{}^*B, {}^*V}{\otimes} \mathrm{id\,})\big(F(t_{B,V})d^{-1}_{B,V}{\otimes} \mathrm{id\,}_{{}^*F({}^*B \triangleleft {}^*V)} {\otimes} d_{B,V} F(t^{-1}_{B,V})\big) (\mathrm{id\,}{\otimes} d^{-1}_{{}^*B,{}^*V}{\otimes} c^{-1}_{{}^*B, {}^*V} )\\ &(\mathrm{id\,}{\otimes} \mbox{coev}_{{}^*F(B)}{\otimes} \mathrm{id\,}_{{}^*V})(\mathrm{id\,}_{{}^* F(B\triangleleft V)} {\otimes} \mbox{coev}_{{}^*V} )\\ &=(\sigma^{-1}_{ {}^*V, H}{\otimes} \mathrm{id\,}_{ {}^* F(B)})(\pi_{{}^*B}{\otimes} \mathrm{id\,}) (\mathrm{id\,}{\otimes} ({}^*(\mbox{coev}_V){\otimes} \mathrm{id\,}_{{}^*B}))d_{B,{}^*V{\otimes} V }{\otimes} \mathrm{id\,})\\ &(\mathrm{id\,}{\otimes} d_{{}^*B \triangleleft {}^*V,V}{\otimes} \mathrm{id\,}) \big(c_{{}^*B, {}^*V} F(t_{B,V})d^{-1}_{B,V}{\otimes} \mathrm{id\,}_{{}^*F({}^*B \triangleleft {}^*V)} {\otimes} d_{B,V} F(t^{-1}_{B,V})c^{-1}_{{}^*B, {}^*V}\big)\\ & (\mathrm{id\,}{\otimes} d^{-1}_{{}^*B,{}^*V}{\otimes} \mathrm{id\,} ) (\mathrm{id\,}{\otimes} \mbox{coev}_{{}^*F(B)}{\otimes} \mathrm{id\,}_{{}^*V})(\mathrm{id\,}_{{}^* F(B\triangleleft V)} {\otimes} \mbox{coev}_{{}^*V} )\\ &= (\mathrm{id\,}_{{}^*V} {\otimes} \pi_{{}^*B}{\otimes} \mathrm{id\,}) (\sigma^{-1}_{ {}^*V, F({}^*B){\otimes} {}^*F({}^*B) }{\otimes} \mathrm{id\,})(\mathrm{id\,} {\otimes} \mbox{ev}_{{}^*V}{\otimes} \mathrm{id\,}_{{}^*F({}^*B){\otimes} {}^*V{\otimes} {}^*F(B)})\\ &(\sigma_{{}^*V, {}^*F(B)}{\otimes} \mathrm{id\,}_{{}^{**}V{\otimes} {}^*F({}^*B)} {\otimes} \sigma_{{}^*V, {}^*F(B)}) (\mathrm{id\,}_{{}^*V{\otimes} {}^*F(B){\otimes} {}^{**}V}{\otimes} \mbox{coev}_{{}^*F(B)}{\otimes} \mathrm{id\,}_{{}^*V})\\ &(\mathrm{id\,}{\otimes} \mbox{coev}_{{}^*V})\\ &=(\mathrm{id\,}_{{}^*V}{\otimes} \rho_{{}^* B}). \end{align*} $$
$$ \begin{align*} &=(\sigma^{-1}_{ {}^*V, H}{\otimes} \mathrm{id\,}_{ {}^* F(B)})(\mathrm{id\,}_H{\otimes} d_{B,V}) (\pi_{{}^*(B\triangleleft V)}{\otimes} \mathrm{id\,})(\mathrm{id\,}{\otimes} \mbox{coev}_{{}^*F(B\triangleleft V)})d^{-1}_{B,V}\\ &=(\sigma^{-1}_{ {}^*V, H}{\otimes} \mathrm{id\,}_{ {}^* F(B)}) (\pi_{{}^*B\triangleleft {}^*V} {\otimes} d_{B,V}) (F(t_{B,V}){\otimes} {}^*F(t^{-1}_{B,V}){\otimes} \mathrm{id\,})\\ &(\mathrm{id\,}{\otimes} \mbox{coev}_{{}^*F(B\triangleleft V)})d^{-1}_{B,V}\\ &=(\sigma^{-1}_{ {}^*V, H}{\otimes} \mathrm{id\,}_{ {}^* F(B)}) (\pi_{{}^*B\triangleleft {}^*V} {\otimes} d_{B,V}) (F(t_{B,V}){\otimes} \mathrm{id\,}_{{}^*F({}^*B \triangleleft {}^*V)} {\otimes} F(t^{-1}_{B,V}))\\ &(\mathrm{id\,}{\otimes} \mbox{coev}_{F({}^*B\triangleleft {}^*V)})d^{-1}_{B,V}\\ &=(\sigma^{-1}_{ {}^*V, H}{\otimes} \mathrm{id\,}_{ {}^* F(B)})(\pi_{{}^*B}{\otimes} \mathrm{id\,}) (\mathrm{id\,}{\otimes} F({}^*(\mathrm{id\,}_{{}^*B}\triangleleft \mbox{coev}_V )){\otimes} \mathrm{ id\,})(\mathrm{id\,}{\otimes} d_{{}^*B \triangleleft {}^*V,V}{\otimes} \mathrm{id\,})\\ & (c_{{}^*B, {}^*V}{\otimes} \mathrm{id\,})\big(F(t_{B,V})d^{-1}_{B,V}{\otimes} \mathrm{id\,}_{{}^*F({}^*B \triangleleft {}^*V)} {\otimes} d_{B,V} F(t^{-1}_{B,V})\big) (\mathrm{id\,}{\otimes} d^{-1}_{{}^*B,{}^*V}{\otimes} c^{-1}_{{}^*B, {}^*V} )\\ &(\mathrm{id\,}{\otimes} \mbox{coev}_{{}^*F(B)}{\otimes} \mathrm{id\,}_{{}^*V})(\mathrm{id\,}_{{}^* F(B\triangleleft V)} {\otimes} \mbox{coev}_{{}^*V} )\\ &=(\sigma^{-1}_{ {}^*V, H}{\otimes} \mathrm{id\,}_{ {}^* F(B)})(\pi_{{}^*B}{\otimes} \mathrm{id\,}) (\mathrm{id\,}{\otimes} ({}^*(\mbox{coev}_V){\otimes} \mathrm{id\,}_{{}^*B}))d_{B,{}^*V{\otimes} V }{\otimes} \mathrm{id\,})\\ &(\mathrm{id\,}{\otimes} d_{{}^*B \triangleleft {}^*V,V}{\otimes} \mathrm{id\,}) \big(c_{{}^*B, {}^*V} F(t_{B,V})d^{-1}_{B,V}{\otimes} \mathrm{id\,}_{{}^*F({}^*B \triangleleft {}^*V)} {\otimes} d_{B,V} F(t^{-1}_{B,V})c^{-1}_{{}^*B, {}^*V}\big)\\ & (\mathrm{id\,}{\otimes} d^{-1}_{{}^*B,{}^*V}{\otimes} \mathrm{id\,} ) (\mathrm{id\,}{\otimes} \mbox{coev}_{{}^*F(B)}{\otimes} \mathrm{id\,}_{{}^*V})(\mathrm{id\,}_{{}^* F(B\triangleleft V)} {\otimes} \mbox{coev}_{{}^*V} )\\ &= (\mathrm{id\,}_{{}^*V} {\otimes} \pi_{{}^*B}{\otimes} \mathrm{id\,}) (\sigma^{-1}_{ {}^*V, F({}^*B){\otimes} {}^*F({}^*B) }{\otimes} \mathrm{id\,})(\mathrm{id\,} {\otimes} \mbox{ev}_{{}^*V}{\otimes} \mathrm{id\,}_{{}^*F({}^*B){\otimes} {}^*V{\otimes} {}^*F(B)})\\ &(\sigma_{{}^*V, {}^*F(B)}{\otimes} \mathrm{id\,}_{{}^{**}V{\otimes} {}^*F({}^*B)} {\otimes} \sigma_{{}^*V, {}^*F(B)}) (\mathrm{id\,}_{{}^*V{\otimes} {}^*F(B){\otimes} {}^{**}V}{\otimes} \mbox{coev}_{{}^*F(B)}{\otimes} \mathrm{id\,}_{{}^*V})\\ &(\mathrm{id\,}{\otimes} \mbox{coev}_{{}^*V})\\ &=(\mathrm{id\,}_{{}^*V}{\otimes} \rho_{{}^* B}). \end{align*} $$
The second equality follows from (7.37), the third equality follows from (3.3), the fourth one follows from (7.38), and the fifth equality follows from (7.36). The sixth equality follows by using (3.6) and (7.35), and the last equality follows by using the rigidity axioms and (5.1).
Recall that sometimes we are denoting
![]() $H=H(F)$
.
$H=H(F)$
.
Theorem 7.17 Let
![]() ${\mathcal C}$
be a tensor category, and let
${\mathcal C}$
be a tensor category, and let
![]() ${\mathcal B}$
be a monoidal right
${\mathcal B}$
be a monoidal right
![]() ${\mathcal C}$
-module category. Let
${\mathcal C}$
-module category. Let
![]() $(F,c):{\mathcal B}\to {\mathcal C}$
be an exact and faithful monoidal module functor. There exists a map
$(F,c):{\mathcal B}\to {\mathcal C}$
be an exact and faithful monoidal module functor. There exists a map
![]() $S:H(F)\to H(F)$
such that it corresponds, under isomorphism
$S:H(F)\to H(F)$
such that it corresponds, under isomorphism
presented in (7.2), to the natural module transformation
![]() $\alpha :F\to H(F){\otimes } F,$
$\alpha :F\to H(F){\otimes } F,$
 $$ \begin{align*} \alpha_B=(\mbox{ev}_{F(B)}&{\otimes} \mathrm{id\,}_{H(F){\otimes} F(B)})(\mathrm{id\,}_{F(B)}{\otimes} \sigma^{-1}_{{}^*F(B),H(F)}{\otimes} \mathrm{id\,}_{F(B)})\\ & (\mathrm{id\,}_{F(B)}{\otimes} \rho_{{}^*B}{\otimes} \mathrm{id\,}_{F(B)})(\mathrm{id\,}_{F(B)}{\otimes} \mbox{coev}_{F(B)}). \end{align*} $$
$$ \begin{align*} \alpha_B=(\mbox{ev}_{F(B)}&{\otimes} \mathrm{id\,}_{H(F){\otimes} F(B)})(\mathrm{id\,}_{F(B)}{\otimes} \sigma^{-1}_{{}^*F(B),H(F)}{\otimes} \mathrm{id\,}_{F(B)})\\ & (\mathrm{id\,}_{F(B)}{\otimes} \rho_{{}^*B}{\otimes} \mathrm{id\,}_{F(B)})(\mathrm{id\,}_{F(B)}{\otimes} \mbox{coev}_{F(B)}). \end{align*} $$
That is,
![]() $\omega (S)=\alpha $
.
$\omega (S)=\alpha $
.
Proof We only need to prove that, indeed,
![]() $\alpha $
is a module natural transformation, that is,
$\alpha $
is a module natural transformation, that is,
for any
![]() $B\in {\mathcal B}$
,
$B\in {\mathcal B}$
,
![]() $V\in {\mathcal C}$
. Equations (3.20) and (3.21) imply that
$V\in {\mathcal C}$
. Equations (3.20) and (3.21) imply that
 $$ \begin{align} \mbox{ev}_{F(B\triangleleft V )} = \mbox{ev}_{F(B)}\big(\mathrm{id\,}{\otimes} \mbox{ev}_V{\otimes} \mathrm{id\,} \big)\big(c_{B,V}{\otimes} d_{B,V}\big), \nonumber\\ \mbox{coev}_{F(B\triangleleft V )}= \big( d^{-1}_{B,V}{\otimes} c^{-1}_{B,V}\big)\big(\mathrm{id\,}{\otimes} \mbox{coev}_{F(B)}{\otimes}\mathrm{id\,}\big) \mbox{coev}_V. \end{align} $$
$$ \begin{align} \mbox{ev}_{F(B\triangleleft V )} = \mbox{ev}_{F(B)}\big(\mathrm{id\,}{\otimes} \mbox{ev}_V{\otimes} \mathrm{id\,} \big)\big(c_{B,V}{\otimes} d_{B,V}\big), \nonumber\\ \mbox{coev}_{F(B\triangleleft V )}= \big( d^{-1}_{B,V}{\otimes} c^{-1}_{B,V}\big)\big(\mathrm{id\,}{\otimes} \mbox{coev}_{F(B)}{\otimes}\mathrm{id\,}\big) \mbox{coev}_V. \end{align} $$
Using the definition of
![]() $\alpha $
, we obtain that
$\alpha $
, we obtain that
![]() $(\mathrm {id\,}_H{\otimes } c_{B,V}) \alpha _{B\triangleleft V} c^{-1}_{B,V}$
is equal to
$(\mathrm {id\,}_H{\otimes } c_{B,V}) \alpha _{B\triangleleft V} c^{-1}_{B,V}$
is equal to
 $$ \begin{align*} &= (\mbox{ev}_{F(B\triangleleft V)}{\otimes} \mathrm{id\,}_{H{\otimes} F(B){\otimes} V)})(\mathrm{id\,}_{F(B\triangleleft V)}{\otimes} \sigma^{-1}_{{}^*F(B\triangleleft V),H}{\otimes} c_{B,V} )\\ & (\mathrm{id\,}_{F(B\triangleleft V)}{\otimes} \rho_{{}^*(B\triangleleft V)}{\otimes} \mathrm{id\,}_{F(B\triangleleft V)})(\mathrm{id\,}_{F(B\triangleleft V)}{\otimes} \mbox{coev}_{F(B\triangleleft V)})c^{-1}_{B,V}\\ &=(\mbox{ev}_{F(B)}{\otimes} \mathrm{id\,}_{H{\otimes} F(B){\otimes} V)}) \big(\mathrm{id\,}{\otimes} \mbox{ev}_V{\otimes} \mathrm{id\,}_{{}^*F(B) {\otimes} H{\otimes} F(B){\otimes} V} \big)\\ & (\mathrm{id\,}_{F(B){\otimes} V}{\otimes} \sigma^{-1}_{{}^*V{\otimes} {}^*F(B),H}{\otimes} \mathrm{id\,}_{F(B){\otimes} V} ) \big(c_{B,V}{\otimes} \mathrm{id\,}_{H}{\otimes} d_{B,V} {\otimes} c_{B,V}\big)\\ &(\mathrm{id\,}_{F(B\triangleleft V)}{\otimes} \rho_{{}^*(B\triangleleft V)}{\otimes} \mathrm{id\,}_{F(B\triangleleft V)})\big( \mathrm{id\,}_{F(B\triangleleft V)}{\otimes} d^{-1}_{B,V}{\otimes} c^{-1}_{B,V}\big) \\ &\big(\mathrm{id\,}_{F(B\triangleleft V){\otimes} {}^*V}{\otimes} \mbox{coev}_{F(B)}{\otimes}\mathrm{id\,}_V\big) (\mathrm{id\,}_{F(B\triangleleft V)}{\otimes} \mbox{coev}_V) c^{-1}_{B,V}\\ &=(\mbox{ev}_{F(B)}{\otimes} \mathrm{id\,}_{H{\otimes} F(B){\otimes} V)}) \big(\mathrm{id\,}{\otimes} \mbox{ev}_V{\otimes} \mathrm{id\,}_{{}^*F(B) {\otimes} H{\otimes} F(B){\otimes} V} \big)\\ &(\mathrm{id\,}{\otimes} \sigma^{-1}_{{}^*F(B),H}{\otimes} \mathrm{id\,})(\mathrm{id\,}{\otimes} \sigma^{-1}_{{}^*V,H}{\otimes} \mathrm{id\,}) \big(\mathrm{id\,}{\otimes} (\mathrm{ id\,}_{H}{\otimes} d_{B,V} ) \rho_{{}^*(B\triangleleft V)} d^{-1}_{B,V} {\otimes} \mathrm{id\,} \big)\\ &\big(\mathrm{id\,}_{F(B\triangleleft V){\otimes} {}^*V}{\otimes} \mbox{coev}_{F(B)}{\otimes}\mathrm{id\,}_V\big) (\mathrm{id\,}_{F(B\triangleleft V)}{\otimes} \mbox{coev}_V)\\ &=\alpha_B{\otimes}\mathrm{id\,}_V. \end{align*} $$
$$ \begin{align*} &= (\mbox{ev}_{F(B\triangleleft V)}{\otimes} \mathrm{id\,}_{H{\otimes} F(B){\otimes} V)})(\mathrm{id\,}_{F(B\triangleleft V)}{\otimes} \sigma^{-1}_{{}^*F(B\triangleleft V),H}{\otimes} c_{B,V} )\\ & (\mathrm{id\,}_{F(B\triangleleft V)}{\otimes} \rho_{{}^*(B\triangleleft V)}{\otimes} \mathrm{id\,}_{F(B\triangleleft V)})(\mathrm{id\,}_{F(B\triangleleft V)}{\otimes} \mbox{coev}_{F(B\triangleleft V)})c^{-1}_{B,V}\\ &=(\mbox{ev}_{F(B)}{\otimes} \mathrm{id\,}_{H{\otimes} F(B){\otimes} V)}) \big(\mathrm{id\,}{\otimes} \mbox{ev}_V{\otimes} \mathrm{id\,}_{{}^*F(B) {\otimes} H{\otimes} F(B){\otimes} V} \big)\\ & (\mathrm{id\,}_{F(B){\otimes} V}{\otimes} \sigma^{-1}_{{}^*V{\otimes} {}^*F(B),H}{\otimes} \mathrm{id\,}_{F(B){\otimes} V} ) \big(c_{B,V}{\otimes} \mathrm{id\,}_{H}{\otimes} d_{B,V} {\otimes} c_{B,V}\big)\\ &(\mathrm{id\,}_{F(B\triangleleft V)}{\otimes} \rho_{{}^*(B\triangleleft V)}{\otimes} \mathrm{id\,}_{F(B\triangleleft V)})\big( \mathrm{id\,}_{F(B\triangleleft V)}{\otimes} d^{-1}_{B,V}{\otimes} c^{-1}_{B,V}\big) \\ &\big(\mathrm{id\,}_{F(B\triangleleft V){\otimes} {}^*V}{\otimes} \mbox{coev}_{F(B)}{\otimes}\mathrm{id\,}_V\big) (\mathrm{id\,}_{F(B\triangleleft V)}{\otimes} \mbox{coev}_V) c^{-1}_{B,V}\\ &=(\mbox{ev}_{F(B)}{\otimes} \mathrm{id\,}_{H{\otimes} F(B){\otimes} V)}) \big(\mathrm{id\,}{\otimes} \mbox{ev}_V{\otimes} \mathrm{id\,}_{{}^*F(B) {\otimes} H{\otimes} F(B){\otimes} V} \big)\\ &(\mathrm{id\,}{\otimes} \sigma^{-1}_{{}^*F(B),H}{\otimes} \mathrm{id\,})(\mathrm{id\,}{\otimes} \sigma^{-1}_{{}^*V,H}{\otimes} \mathrm{id\,}) \big(\mathrm{id\,}{\otimes} (\mathrm{ id\,}_{H}{\otimes} d_{B,V} ) \rho_{{}^*(B\triangleleft V)} d^{-1}_{B,V} {\otimes} \mathrm{id\,} \big)\\ &\big(\mathrm{id\,}_{F(B\triangleleft V){\otimes} {}^*V}{\otimes} \mbox{coev}_{F(B)}{\otimes}\mathrm{id\,}_V\big) (\mathrm{id\,}_{F(B\triangleleft V)}{\otimes} \mbox{coev}_V)\\ &=\alpha_B{\otimes}\mathrm{id\,}_V. \end{align*} $$
The second equality follows from (7.39) and the naturality of
![]() $\sigma $
, and the third equality follows by (5.1). The last equality follows from (7.34) and rigidity axioms.
$\sigma $
, and the third equality follows by (5.1). The last equality follows from (7.34) and rigidity axioms.
Remark 7.18 The above result is the most sensitive statement to prove in order to prove the existence of the antipode for
![]() $H(F)$
. In the case
$H(F)$
. In the case
![]() ${\mathcal C}=\mathrm {vect\,}_{\mathbb {k}}$
, the isomorphism
${\mathcal C}=\mathrm {vect\,}_{\mathbb {k}}$
, the isomorphism
lands in the space of all natural transformations. So, in that case, there is nothing to prove, and the existence of S is guaranteed by the fact that
![]() $\omega $
is an isomorphism.
$\omega $
is an isomorphism.
Corollary 7.19 The bialgebra
![]() $H(F)$
, from Definition 7.12, is actually a Hopf algebra. The antipode
$H(F)$
, from Definition 7.12, is actually a Hopf algebra. The antipode
![]() $S:H(F)\to H(F)$
is determined as the unique morphism such that
$S:H(F)\to H(F)$
is determined as the unique morphism such that

is commutative. Here,
Proof Taking the map
![]() $S:H(F)\to H(F)$
defined in Theorem 7.17, and using the definition of
$S:H(F)\to H(F)$
defined in Theorem 7.17, and using the definition of
![]() $\alpha $
, one can prove that S satisfies diagram (7.40).
$\alpha $
, one can prove that S satisfies diagram (7.40).
Axioms
follow from (7.40) by a lengthy, but straightforward, computation.
Remark 7.20 A version of the Hopf algebra
![]() $H(F)$
has been previously considered in the work of Lyubashenko [Reference Lyubashenko16, Reference Lyubashenko17] when F is some fiber functor and in [Reference Lyubashenko14, Reference Lyubashenko15] when F is the identity functor. See also the work of Schauenburg [Reference Schauenburg23], where
$H(F)$
has been previously considered in the work of Lyubashenko [Reference Lyubashenko16, Reference Lyubashenko17] when F is some fiber functor and in [Reference Lyubashenko14, Reference Lyubashenko15] when F is the identity functor. See also the work of Schauenburg [Reference Schauenburg23], where
![]() ${\mathcal C}$
is the category of finite-dimensional vector spaces. However, there are new ingredients in our definition. We require that
${\mathcal C}$
is the category of finite-dimensional vector spaces. However, there are new ingredients in our definition. We require that
![]() ${\mathcal B}$
is actually a monoidal
${\mathcal B}$
is actually a monoidal
![]() ${\mathcal C}$
-module category and the functor F is a monoidal module functor. The use of the relative coend is another new feature of our construction.
${\mathcal C}$
-module category and the functor F is a monoidal module functor. The use of the relative coend is another new feature of our construction.
Let
![]() $(H,\Delta , m, S)$
be a Hopf algebra in
$(H,\Delta , m, S)$
be a Hopf algebra in
![]() ${\mathcal C}$
. In the next proposition, we shall see that the reconstructed antipode given in Theorem 7.17, out of the forgetful functor
${\mathcal C}$
. In the next proposition, we shall see that the reconstructed antipode given in Theorem 7.17, out of the forgetful functor
![]() $f:{}^H{\mathcal C}\to {\mathcal C}$
, coincides with the original antipode
$f:{}^H{\mathcal C}\to {\mathcal C}$
, coincides with the original antipode
![]() $S:H\to H$
.
$S:H\to H$
.
Proposition 7.21 Let
![]() $(H,\Delta , m, S)$
be a Hopf algebra in
$(H,\Delta , m, S)$
be a Hopf algebra in
![]() ${\mathcal C}$
. Using the identification
${\mathcal C}$
. Using the identification
![]() $H=H(f)$
proven in Lemma 7.3, the reconstructed antipode obtained in Corollary 7.19 coincides with the antipode S of H.
$H=H(f)$
proven in Lemma 7.3, the reconstructed antipode obtained in Corollary 7.19 coincides with the antipode S of H.
Proof Let us denote by
![]() $\widehat {S}:H\to H$
the map reconstructed in Proposition 7.19. For any
$\widehat {S}:H\to H$
the map reconstructed in Proposition 7.19. For any
![]() $V\in {\mathcal C}$
, recall the isomorphism (7.2)
$V\in {\mathcal C}$
, recall the isomorphism (7.2)
 $$ \begin{align*} \begin{split} \omega: \operatorname{Hom}_{\mathcal C}(H(f),V)\to \mathrm{Nat\,}_{\! m}(f, V{\otimes} f),\\ \omega(g)_{(W,\rho_W)}= (g{\otimes} \mathrm{id\,}_{W})\psi^{H}_{W,W}(\pi_W) \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} \omega: \operatorname{Hom}_{\mathcal C}(H(f),V)\to \mathrm{Nat\,}_{\! m}(f, V{\otimes} f),\\ \omega(g)_{(W,\rho_W)}= (g{\otimes} \mathrm{id\,}_{W})\psi^{H}_{W,W}(\pi_W) \end{split} \end{align*} $$
for any
![]() $(W,\rho _W)\in {}^H{\mathcal C}$
. Corollary 7.17 implies that, if
$(W,\rho _W)\in {}^H{\mathcal C}$
. Corollary 7.17 implies that, if
![]() $\alpha :f\to H{\otimes } f$
is the module natural transformation defined as
$\alpha :f\to H{\otimes } f$
is the module natural transformation defined as
 $$ \begin{align*} \alpha_{(W,\rho_W)}=( \mbox{ev}_{W}&{\otimes} \mathrm{id\,}_{H{\otimes} W})(\mathrm{id\,}_{W}{\otimes} \sigma^{-1}_{{}^*W,H}{\otimes} \mathrm{id\,}_{ W})\\ & (\mathrm{id\,}_{W}{\otimes} \rho_{{}^*W} {\otimes}\mathrm{id\,}_{W})(\mathrm{id\,}_W{\otimes} \mbox{coev}_W), \end{align*} $$
$$ \begin{align*} \alpha_{(W,\rho_W)}=( \mbox{ev}_{W}&{\otimes} \mathrm{id\,}_{H{\otimes} W})(\mathrm{id\,}_{W}{\otimes} \sigma^{-1}_{{}^*W,H}{\otimes} \mathrm{id\,}_{ W})\\ & (\mathrm{id\,}_{W}{\otimes} \rho_{{}^*W} {\otimes}\mathrm{id\,}_{W})(\mathrm{id\,}_W{\otimes} \mbox{coev}_W), \end{align*} $$
for any
![]() $(W,\rho _W)\in {}^H{\mathcal C}$
, then
$(W,\rho _W)\in {}^H{\mathcal C}$
, then
Using formula (5.7) for
![]() $\rho _{{}^*W}$
, we get that
$\rho _{{}^*W}$
, we get that
for any
![]() $(W,\rho _W)\in {}^H{\mathcal C}$
. Whence
$(W,\rho _W)\in {}^H{\mathcal C}$
. Whence
![]() $S=\widehat {S}$
.
$S=\widehat {S}$
.
8 Examples and applications
8.1 Generic example
The next example was treated along the paper. At the end, we proved that the reconstructed Hopf algebra from the forgetful functor
![]() $F:{^H}{\mathcal C}\to {\mathcal C}$
coincides with
$F:{^H}{\mathcal C}\to {\mathcal C}$
coincides with
![]() $H.$
$H.$
Example 8.1 Let H be a Hopf algebra in a braided finite tensor category
![]() ${\mathcal C}$
and consider the tensor category
${\mathcal C}$
and consider the tensor category
![]() ${\mathcal B}={^H}{\mathcal C}$
. Then the forgetful functor admits an exact faithful monoidal functor
${\mathcal B}={^H}{\mathcal C}$
. Then the forgetful functor admits an exact faithful monoidal functor
![]() $F:{^H}{\mathcal C}\to {\mathcal C}$
and the counit
$F:{^H}{\mathcal C}\to {\mathcal C}$
and the counit
![]() $\varepsilon _H$
gives rise to a monoidal section
$\varepsilon _H$
gives rise to a monoidal section
![]() ${^H}{\mathcal C}\leftarrow {\mathcal C}$
that turns
${^H}{\mathcal C}\leftarrow {\mathcal C}$
that turns
![]() ${^H}{\mathcal C}$
into a
${^H}{\mathcal C}$
into a
![]() ${\mathcal C}$
-module category.
${\mathcal C}$
-module category.
Example 8.2 Let
![]() $H\subset L$
be Hopf algebras in
$H\subset L$
be Hopf algebras in
![]() $\mathrm {vect\,}_{\mathbb {k}}$
with
$\mathrm {vect\,}_{\mathbb {k}}$
with
![]() $\iota :H\to L$
the inclusion, and assume that there is a left-inverse Hopf algebra map
$\iota :H\to L$
the inclusion, and assume that there is a left-inverse Hopf algebra map
![]() $\pi :H\rightarrow L$
, called projection. Then we have the restriction functor
$\pi :H\rightarrow L$
, called projection. Then we have the restriction functor
![]() $\iota ^*\,:\operatorname {Rep}(H)\leftarrow \operatorname {Rep}(L)$
and in addition
$\iota ^*\,:\operatorname {Rep}(H)\leftarrow \operatorname {Rep}(L)$
and in addition
![]() ${\mathcal B}=\operatorname {Rep}(L)$
becomes a modules category over
${\mathcal B}=\operatorname {Rep}(L)$
becomes a modules category over
![]() ${\mathcal C}=Rep(H)$
via
${\mathcal C}=Rep(H)$
via
![]() $\pi ^*:\,\operatorname {Rep}(H)\leftarrow \operatorname {Rep}(L)$
. Assume that H is quasitriangular. Hence, our result shows that there exists a Hopf algebra
$\pi ^*:\,\operatorname {Rep}(H)\leftarrow \operatorname {Rep}(L)$
. Assume that H is quasitriangular. Hence, our result shows that there exists a Hopf algebra
![]() $C\in \operatorname {Rep}(H)$
such that there is an equivalence of monoidal modular categories
$C\in \operatorname {Rep}(H)$
such that there is an equivalence of monoidal modular categories
We now discuss how this is related to the classical Radford Projection Theorem [Reference Radford21]. This result states that the existence of a Hopf algebra projection
![]() $\pi $
implies that L is isomorphic to a Radford biproduct
$\pi $
implies that L is isomorphic to a Radford biproduct
where R is a Hopf algebra in
![]() ${^H_H}{\mathcal YD}(\mathrm {Vect\,}_{\mathbb {k}})$
. In our case, we have assumed that H is quasitriangular and
${^H_H}{\mathcal YD}(\mathrm {Vect\,}_{\mathbb {k}})$
. In our case, we have assumed that H is quasitriangular and
![]() $\iota ^*$
lifts to a braided functor to the center of
$\iota ^*$
lifts to a braided functor to the center of
![]() ${\mathcal B}$
. This gives rise to a choice of a functor
${\mathcal B}$
. This gives rise to a choice of a functor
![]() $\operatorname {Rep}(H)\to {^H_H}{\mathcal YD}(\mathrm {Vect\,}_{\mathbb {k}})$
and shows R to be in the image – more explicitly the R-matrix of H determines the H-coaction from the H-action. Then this R is precisely the dual of our Hopf algebra C.
$\operatorname {Rep}(H)\to {^H_H}{\mathcal YD}(\mathrm {Vect\,}_{\mathbb {k}})$
and shows R to be in the image – more explicitly the R-matrix of H determines the H-coaction from the H-action. Then this R is precisely the dual of our Hopf algebra C.
8.2 Generic consequences
Our results has certain general implications, for example:
Example 8.3 If
![]() $({\mathcal C}, \sigma )$
is a braided tensor category, then the forgetful functor
$({\mathcal C}, \sigma )$
is a braided tensor category, then the forgetful functor
![]() $f:Z({\mathcal C})\to {\mathcal C}$
has a section
$f:Z({\mathcal C})\to {\mathcal C}$
has a section
![]() $G:{\mathcal C}\to Z({\mathcal C})$
,
$G:{\mathcal C}\to Z({\mathcal C})$
,
![]() $G(V)=(V, \sigma _V)$
. Theorems 7.7 and 7.17 imply that there exists a Hopf algebra
$G(V)=(V, \sigma _V)$
. Theorems 7.7 and 7.17 imply that there exists a Hopf algebra
![]() $H\in {\mathcal C}$
such that
$H\in {\mathcal C}$
such that
![]() $Z({\mathcal C})\simeq {}^H{\mathcal C}$
. For
$Z({\mathcal C})\simeq {}^H{\mathcal C}$
. For
![]() ${\mathcal C}=\operatorname {Rep}(H)$
for a factorizable Hopf algebra H, this can be obtained from the defining equivalence
${\mathcal C}=\operatorname {Rep}(H)$
for a factorizable Hopf algebra H, this can be obtained from the defining equivalence
![]() $Z({\mathcal C})\simeq {}^H{\mathcal C}\boxtimes {}^H{\mathcal C}$
, but in the non-nondegenerate case or the case without fiber functor, we are not aware of such a result. In general, we recover thereby the recent result [Reference Liu and Zhu13].
$Z({\mathcal C})\simeq {}^H{\mathcal C}\boxtimes {}^H{\mathcal C}$
, but in the non-nondegenerate case or the case without fiber functor, we are not aware of such a result. In general, we recover thereby the recent result [Reference Liu and Zhu13].
8.3 Lifting and cocycles deformations
In the classification of (e.g., pointed) Hopf algebras H, the strategy in the Andruskiewisch–Schneider program [Reference Andruskiewitsch and Schneider1] is to consider the coradical
![]() $H_0$
(which is assumed to be a Hopf algebra, for example, a group ring) and classify the possible Nichols algebras R, and then obtain H as a lifting of
$H_0$
(which is assumed to be a Hopf algebra, for example, a group ring) and classify the possible Nichols algebras R, and then obtain H as a lifting of
![]() $\mathrm {gr}(H)=R\#H_0$
. It is an important question to determine whether this lifting is a
$\mathrm {gr}(H)=R\#H_0$
. It is an important question to determine whether this lifting is a
![]() $2$
-cocycle twist, and the observation is that this holds in almost all cases [Reference Angiono and Garcia Iglesias2].
$2$
-cocycle twist, and the observation is that this holds in almost all cases [Reference Angiono and Garcia Iglesias2].
We view this problem in our setting: since a main assumption is that
![]() $H_0\subset H$
, we have a tensor functor
$H_0\subset H$
, we have a tensor functor
![]() $\iota ^*:\,\mathrm {Comod}(H_0)\to \mathrm {Comod}(H)$
. The lifting is a
$\iota ^*:\,\mathrm {Comod}(H_0)\to \mathrm {Comod}(H)$
. The lifting is a
![]() $2$
-cocycle twist precisely iff there is a tensor functor
$2$
-cocycle twist precisely iff there is a tensor functor
![]() $\mathrm {Comod}(H_0)\leftarrow \mathrm {Comod}(H)$
, if the
$\mathrm {Comod}(H_0)\leftarrow \mathrm {Comod}(H)$
, if the
![]() $2$
-cocycle is trivial then it comes from a Hopf algebra projection
$2$
-cocycle is trivial then it comes from a Hopf algebra projection
![]() $\pi $
, and then our relative coend is
$\pi $
, and then our relative coend is
![]() $R^*$
.
$R^*$
.
While this view does not allow to decide the difficult question when a lifting is a
![]() $2$
-cocycle twist, it shows the natural categorical context of this question and it produces general statements, for example, if R as a coalgebra has a trivial lifting, then there is a monoidal section and hence the lifting is tensor functor and thus the lifting comes from a
$2$
-cocycle twist, it shows the natural categorical context of this question and it produces general statements, for example, if R as a coalgebra has a trivial lifting, then there is a monoidal section and hence the lifting is tensor functor and thus the lifting comes from a
![]() $2$
-cocycle twist.
$2$
-cocycle twist.
8.4 The logarithmic Kazhdan Lusztig conjecture
In conformal field theory, there is in good situations a modular tensor category of representations of a vertex algebra
![]() $\mathcal {V}$
, which reflects the analytic properties, for example, of solution spaces to certain differential equations (e.g., the braiding reflects the monodromy around the singularity
$\mathcal {V}$
, which reflects the analytic properties, for example, of solution spaces to certain differential equations (e.g., the braiding reflects the monodromy around the singularity
![]() $z=0$
). One is often confronted with the very difficult question to determine the representation category of representations of a vertex subalgebra
$z=0$
). One is often confronted with the very difficult question to determine the representation category of representations of a vertex subalgebra
![]() $\mathcal {W}\subset \mathcal {V}$
if the representation theory of
$\mathcal {W}\subset \mathcal {V}$
if the representation theory of
![]() $\mathcal {V}$
is known, for example, being a free-field realization. A brief introduction, references, and an account for the statements below can be found in [Reference Creutzig, Lentner and Rupert6, Reference Creutzig, Lentner and Rupert7].
$\mathcal {V}$
is known, for example, being a free-field realization. A brief introduction, references, and an account for the statements below can be found in [Reference Creutzig, Lentner and Rupert6, Reference Creutzig, Lentner and Rupert7].
Categorically, one can understand as
![]() $\operatorname {Rep}(\mathcal {W})$
being a modular tensor category and
$\operatorname {Rep}(\mathcal {W})$
being a modular tensor category and
![]() $A=\mathcal {V}$
being a commutative algebra in this category and
$A=\mathcal {V}$
being a commutative algebra in this category and
![]() ${\mathcal C}=\operatorname {Rep}(\mathcal {V})$
is the category of local A-modules
${\mathcal C}=\operatorname {Rep}(\mathcal {V})$
is the category of local A-modules
![]() $\operatorname {Rep}^\mathrm{loc}(A)$
. Then, by the results in [Reference Creutzig, Lentner and Rupert6, Section 3], we have under suitable conditions that
$\operatorname {Rep}^\mathrm{loc}(A)$
. Then, by the results in [Reference Creutzig, Lentner and Rupert6, Section 3], we have under suitable conditions that
![]() $\operatorname {Rep}(\mathcal {W})$
is a relative Drinfeld center of
$\operatorname {Rep}(\mathcal {W})$
is a relative Drinfeld center of
![]() $\operatorname {Rep}(A)$
with respect to the subcategory
$\operatorname {Rep}(A)$
with respect to the subcategory
![]() ${\mathcal C}=\operatorname {Rep}^\mathrm{loc}(A)$
. In the cases relevant to logarithmic (i.e., nonsemisimple) conformal field theory, it is often the case that all simple modules in
${\mathcal C}=\operatorname {Rep}^\mathrm{loc}(A)$
. In the cases relevant to logarithmic (i.e., nonsemisimple) conformal field theory, it is often the case that all simple modules in
![]() $\operatorname {Rep}(A)$
are already in
$\operatorname {Rep}(A)$
are already in
![]() $\operatorname {Rep}^\mathrm{loc}(A)$
. This gives rise via the socle filtration to a monoidal section functor (see [Reference Creutzig, Lentner and Rupert6, Section 4])
$\operatorname {Rep}^\mathrm{loc}(A)$
. This gives rise via the socle filtration to a monoidal section functor (see [Reference Creutzig, Lentner and Rupert6, Section 4])
Then the results in our paper produce a Hopf algebra
![]() $R^*$
such that
$R^*$
such that
and in this case the mentioned equivalence to the relative Drinfeld center means explicitly (see Section 5.2)
For example, the celebrated and notoriously difficult logarithmic Kazhdan Lusztig conjecture considers the lattice vertex algebra
![]() $\mathcal {V}_\Lambda $
of the root lattice of a semisimple complex finite-dimensional Lie algebra
$\mathcal {V}_\Lambda $
of the root lattice of a semisimple complex finite-dimensional Lie algebra
![]() $\mathfrak {g}$
rescaled by an integer p, whose category of representations is the category of vector spaces graded by an abelian group
$\mathfrak {g}$
rescaled by an integer p, whose category of representations is the category of vector spaces graded by an abelian group
Then it asserts that
![]() $\mathcal {V}_\Lambda $
contains as kernel of screening operators a certain vertex algebra
$\mathcal {V}_\Lambda $
contains as kernel of screening operators a certain vertex algebra
![]() $\mathcal {W}_p(\mathfrak {g})\subset \mathcal {V}_\Lambda $
, whose category of representation is conjectured to be equivalent to the category of representations of the small quantum group
$\mathcal {W}_p(\mathfrak {g})\subset \mathcal {V}_\Lambda $
, whose category of representation is conjectured to be equivalent to the category of representations of the small quantum group
![]() $u_q(\mathfrak {g})$
for
$u_q(\mathfrak {g})$
for
![]() $q=e^{\pi i / p}$
. In the first author’s paper [Reference Creutzig, Lentner and Rupert6], the approach is to view the small quantum group category as a category of Yetter–Drinfeld modules over the Nichols algebra
$q=e^{\pi i / p}$
. In the first author’s paper [Reference Creutzig, Lentner and Rupert6], the approach is to view the small quantum group category as a category of Yetter–Drinfeld modules over the Nichols algebra
![]() $\mathcal {N}$
$\mathcal {N}$
and develop the categorical tools above to reduce the equivalence in question to proving that
In the case
![]() $\mathfrak {sl}_2$
, the abelian category could be determined and this gives a systematic proof of the conjecture in this case (initially we have used more complicated proof methods for the case
$\mathfrak {sl}_2$
, the abelian category could be determined and this gives a systematic proof of the conjecture in this case (initially we have used more complicated proof methods for the case
![]() $\mathfrak {sl}_2,p=2$
in [Reference Creutzig, Lentner and Rupert6], while [Reference Gannon and Negron11] has used very different arguments for
$\mathfrak {sl}_2,p=2$
in [Reference Creutzig, Lentner and Rupert6], while [Reference Gannon and Negron11] has used very different arguments for
![]() $\mathfrak {sl}_2,p$
). A main motivation for writing the present paper is that now we have the clear statement that the category
$\mathfrak {sl}_2,p$
). A main motivation for writing the present paper is that now we have the clear statement that the category
![]() $\operatorname {Rep}(A)$
is for abstract reasons given as category of representations of a Hopf algebra
$\operatorname {Rep}(A)$
is for abstract reasons given as category of representations of a Hopf algebra
![]() $\mathcal {N}$
in
$\mathcal {N}$
in
![]() ${\mathcal C}$
, and it now remains to determine that
${\mathcal C}$
, and it now remains to determine that
![]() $\mathcal {N}$
is, indeed, the expected Nichols algebra, namely the Nichols algebra of screenings.
$\mathcal {N}$
is, indeed, the expected Nichols algebra, namely the Nichols algebra of screenings.
9 Questions
Question 9.1 The result should be applicable if
![]() ${\mathcal C}$
is merely locally finite tensor category and/or if
${\mathcal C}$
is merely locally finite tensor category and/or if
![]() $\mathcal {N}$
is infinite. The example we have in mind is maybe the quantum group
$\mathcal {N}$
is infinite. The example we have in mind is maybe the quantum group
![]() $U_q(\mathfrak {g})$
at generic q.
$U_q(\mathfrak {g})$
at generic q.
Question 9.2 For given classes of semisimple modular tensor categories
![]() $\mathcal {C}$
(for example, the category of representations of an affine Lie algebra at positive integer level), can we classify semisimple Hopf algebras over
$\mathcal {C}$
(for example, the category of representations of an affine Lie algebra at positive integer level), can we classify semisimple Hopf algebras over
![]() $\mathcal {C}$
?
$\mathcal {C}$
?
Question 9.3 Is there a general argument that the embedding of the coradical
![]() $H_0$
into a pointed Hopf algebra H admits a categorical section of comodule categories, if we assume in addition that the Yetter–Drinfeld module
$H_0$
into a pointed Hopf algebra H admits a categorical section of comodule categories, if we assume in addition that the Yetter–Drinfeld module
![]() $H_1/H_0$
is semisimple over
$H_1/H_0$
is semisimple over
![]() $H_0$
?
$H_0$
?
Acknowledgements
The work of both authors was partially done during the Workshop on Hopf algebras and Tensor categories held in May 2023, in Marburg, Germany. We thank the organizers, and in particular to Istvan Heckenberger. The attendance of M.M., to this workshop, was possible due to a grant of the Alexander von Humboldt Foundation, under a Research Group Linkage Programme. Part of the work of M.M. was done during a visit at Hamburg University. M.M. thanks Christoph Schweigert for the warm hospitality and for providing us with reference [Reference Husemöller12].