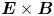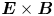1. Introduction
Current sheets are ubiquitous in space plasmas and are an important factor in how the Sun controls the near-Earth plasma environment (Chen Reference Chen1993; Yamada, Kulsrud & Ji Reference Yamada, Kulsrud and Ji2010; Petrukovich et al. Reference Petrukovich, Artemyev, Vasko, Nakamura and Zelenyi2015; Chen, Liu & Hu Reference Chen, Liu and Hu2021; Chitta, Priest & Cheng Reference Chitta, Priest and Cheng2021; Wilson et al. Reference Wilson, Brosius, Gopalswamy, Nieves-Chinchilla, Szabo, Hurley, Phan, Kasper, Lugaz and Richardson2021). For example, during geomagnetically active periods, the solar wind compresses the magnetosphere creating ion-scale current sheets (Takahashi & Hones Reference Takahashi and Hones1988; Schindler & Hesse Reference Schindler and Hesse2008, Reference Schindler and Hesse2010; Ganguli et al. Reference Ganguli, Crabtree, Fletcher and Amatucci2020) in the magnetotail that have substructures embedded in the current density (McComas et al. Reference McComas, Russell, Elphic and Bame1986; Schindler & Birn Reference Schindler and Birn1993; Sergeev et al. Reference Sergeev, Mitchel, Russell and Williams1993; Sanny et al. Reference Sanny, McPherron, Russell, Baker, Pulkkinen and Nishida1994; Hoshino et al. Reference Hoshino, Nishida, Mukai, Saito, Yamamoto and Kokubun1996; Sitnov, Guzdar & Swisdak Reference Sitnov, Guzdar and Swisdak2003; Asano et al. Reference Asano, Mukai, Hoshino, Saito, Hayakawa and Nagai2004; Runov et al. Reference Runov, Sergeev, Nakamura, Baumjohann, Vöros, Volwerk, Asano, Klecker, Rème and Balogh2004, Reference Runov, Sergeev, Nakamura, Baumjohann, Apatenkov, Asano, Takada, Volwerk, Vörös and Zhang2006; Petrukovich et al. Reference Petrukovich, Artemyev, Malova, Popov, Nakamura and Zelenyi2011; Norgren et al. Reference Norgren, Graham, Khotyaintsev, André, Vaivads, Hesse, Eriksson, Lindqvist, Lavraud and Burch2018; DuBois et al. Reference DuBois, Crabtree, Ganguli, Malaspina and Amatucci2022). These gyro-scale current sheets are dominated by ambipolar effects that lead to unique physics such as multi-scale substructures and sheared $\boldsymbol{E} \times \boldsymbol{B}$![]() flows that have recently been observed (DuBois et al. Reference DuBois, Crabtree, Ganguli, Malaspina and Amatucci2022). Other features that are not captured in the Harris equilibrium (Harris Reference Harris1962), such as unequal sheared flows in electrons and ions, intense electrostatic lower hybrid emissions in the centre of the current sheet where the density gradient is negligible, non-gyrotropic electron distribution functions, etc., are also observed in gyro-scale current sheets (DuBois et al. Reference DuBois, Crabtree, Ganguli, Malaspina and Amatucci2022). In this article, we attempt to explain the features observed in a gyro-scale current sheet prior to magnetic reconnection from in situ data using our kinetic current sheet model (Ganguli et al. Reference Ganguli, Crabtree, Fletcher and Amatucci2020; DuBois et al. Reference DuBois, Crabtree, Ganguli, Malaspina and Amatucci2022) in which the ambipolar electric field is self-consistently generated at the gyro-scale by compression. We find that the global compression is the ultimate common physical origin for these seemingly unrelated observational features. Central to the phenomena is the generation of the perpendicular ambipolar electric field, which acts as a surrogate for the global compression.
flows that have recently been observed (DuBois et al. Reference DuBois, Crabtree, Ganguli, Malaspina and Amatucci2022). Other features that are not captured in the Harris equilibrium (Harris Reference Harris1962), such as unequal sheared flows in electrons and ions, intense electrostatic lower hybrid emissions in the centre of the current sheet where the density gradient is negligible, non-gyrotropic electron distribution functions, etc., are also observed in gyro-scale current sheets (DuBois et al. Reference DuBois, Crabtree, Ganguli, Malaspina and Amatucci2022). In this article, we attempt to explain the features observed in a gyro-scale current sheet prior to magnetic reconnection from in situ data using our kinetic current sheet model (Ganguli et al. Reference Ganguli, Crabtree, Fletcher and Amatucci2020; DuBois et al. Reference DuBois, Crabtree, Ganguli, Malaspina and Amatucci2022) in which the ambipolar electric field is self-consistently generated at the gyro-scale by compression. We find that the global compression is the ultimate common physical origin for these seemingly unrelated observational features. Central to the phenomena is the generation of the perpendicular ambipolar electric field, which acts as a surrogate for the global compression.
1.1. Origin of the ambipolar electric field
As a current sheet is compressed to gyro-scale sizes, an effective charge imbalance arises in a non-uniform collisionless plasma due to the difference in the electron and ion gyro-radii (ρe,i), averaged over the plasma distribution. This generates a localized ambipolar electric field perpendicular to the magnetic field. The ambipolar electric field is a kinetic effect that can arise even for negligible electron pressure gradients, e.g. when density and temperature gradients are in opposite directions (Ganguli et al. Reference Ganguli, Crabtree, Fletcher and Amatucci2020). Interestingly, the electron pressure gradient in the centre of gyro-scale magnetotail current sheets is often found to be flat (Runov et al. Reference Runov, Sergeev, Nakamura, Baumjohann, Apatenkov, Asano, Takada, Volwerk, Vörös and Zhang2006), and yet this region is characterized by a localized electric field on the electron scale and consequently with sheared electron flow. This means that the electron flow is composed predominantly of $\boldsymbol{E} \times \boldsymbol{B}$![]() drift, with negligible diamagnetic drift. However, since the electric field is on a scale size smaller than the ion gyro-radius, the ions do not have a velocity equal to the $\boldsymbol{E} \times \boldsymbol{B}$
drift, with negligible diamagnetic drift. However, since the electric field is on a scale size smaller than the ion gyro-radius, the ions do not have a velocity equal to the $\boldsymbol{E} \times \boldsymbol{B}$![]() drift (Ganguli et al. Reference Ganguli, Crabtree, Fletcher and Amatucci2020), and the ambipolar electric field must be balanced partially by a divergence in the ion stress tensor. This electric field renormalizes the gyro frequencies, making them shear dependent, and affects the particle orbits which separates the ion and electron scale physics through gyro averaging of the gradients. This leads to a current in the cross-field (‘Hall’) direction (Ganguli et al. Reference Ganguli, Crabtree, Fletcher and Amatucci2020).
drift (Ganguli et al. Reference Ganguli, Crabtree, Fletcher and Amatucci2020), and the ambipolar electric field must be balanced partially by a divergence in the ion stress tensor. This electric field renormalizes the gyro frequencies, making them shear dependent, and affects the particle orbits which separates the ion and electron scale physics through gyro averaging of the gradients. This leads to a current in the cross-field (‘Hall’) direction (Ganguli et al. Reference Ganguli, Crabtree, Fletcher and Amatucci2020).
Historically, the Hall current forms in plasmas where a sufficiently large collision frequency renders the ions unmagnetized while leaving the electrons unaffected so that the electrons can $\boldsymbol{E} \times \boldsymbol{B}$![]() drift in the cross-field direction. This is a collisional effect, which can be large scale. In current sheet physics, ‘Hall current’ is often informally used to refer to any cross-field current, which is usually explained as a diamagnetic effect due to a pressure gradient, even in the collisionless magnetosphere. In a collisionless plasma, a cross-field current can also arise as a result of current sheet compression below an ion gyro-diameter, which can maintain a transverse electric field localized to electron scales in a nearly uniform quasi-neutral plasma (Ganguli, Lee & Palmadesso Reference Ganguli, Lee and Palmadesso1988a,Reference Ganguli, Lee and Palmadessob; Ganguli et al. Reference Ganguli, Crabtree, Fletcher and Amatucci2020). This introduces novel kinetic features in the current sheet, including unequal and sheared $\boldsymbol{E} \times \boldsymbol{B}$
drift in the cross-field direction. This is a collisional effect, which can be large scale. In current sheet physics, ‘Hall current’ is often informally used to refer to any cross-field current, which is usually explained as a diamagnetic effect due to a pressure gradient, even in the collisionless magnetosphere. In a collisionless plasma, a cross-field current can also arise as a result of current sheet compression below an ion gyro-diameter, which can maintain a transverse electric field localized to electron scales in a nearly uniform quasi-neutral plasma (Ganguli, Lee & Palmadesso Reference Ganguli, Lee and Palmadesso1988a,Reference Ganguli, Lee and Palmadessob; Ganguli et al. Reference Ganguli, Crabtree, Fletcher and Amatucci2020). This introduces novel kinetic features in the current sheet, including unequal and sheared $\boldsymbol{E} \times \boldsymbol{B}$![]() drifts because the gyro-averaged ion $\boldsymbol{E} \times \boldsymbol{B}$
drifts because the gyro-averaged ion $\boldsymbol{E} \times \boldsymbol{B}$![]() drift is less than that of the electrons. The unequal drift causes a localized cross-field current resulting in a structured current density, and under certain conditions, the $\boldsymbol{E} \times \boldsymbol{B}$
drift is less than that of the electrons. The unequal drift causes a localized cross-field current resulting in a structured current density, and under certain conditions, the $\boldsymbol{E} \times \boldsymbol{B}$![]() shear-driven electron-ion hybrid (EIH) instability can generate waves in the lower hybrid frequency range (Ganguli et al. Reference Ganguli, Lee and Palmadesso1988a, Reference Ganguli, Crabtree, Fletcher and Amatucci2020; Amatucci et al. Reference Amatucci, Ganguli, Walker, Gatling, Balkey and McCulloch2003; DuBois et al. Reference DuBois, Thomas, Amatucci and Ganguli2013).
shear-driven electron-ion hybrid (EIH) instability can generate waves in the lower hybrid frequency range (Ganguli et al. Reference Ganguli, Lee and Palmadesso1988a, Reference Ganguli, Crabtree, Fletcher and Amatucci2020; Amatucci et al. Reference Amatucci, Ganguli, Walker, Gatling, Balkey and McCulloch2003; DuBois et al. Reference DuBois, Thomas, Amatucci and Ganguli2013).
The EIH instability is driven by the curvature of the cross-field flow and not the density gradient (Ganguli et al. Reference Ganguli, Lee and Palmadesso1988a), which makes it ideal for anomalous effects at the field reversal region where the density (pressure) gradient is found to be negligible. Additionally, experiments (DuBois et al. Reference DuBois, Thomas, Amatucci and Ganguli2014) and simulations (Fletcher et al. Reference Fletcher, Crabtree, Ganguli, Malaspina, Tejero and Chu2019) show that the EIH instability can be the dominant source of emissions, even in the presence of a density gradient. The resulting turbulence affects the current sheet dynamics through anomalous resistivity, viscosity and cross-field diffusion. These inevitable gyro-scale current sheet phenomena have not been comprehensively studied but, based on recent studies (Ganguli et al. Reference Ganguli, Crabtree, Fletcher and Amatucci2020; DuBois et al. Reference DuBois, Crabtree, Ganguli, Malaspina and Amatucci2022), could be quite consequential.
1.2. Magnetic reconnection
Reconnection can occur as a current sheet with a reversed magnetic field configuration is compressed (Schindler & Birn Reference Schindler and Birn1993; Nakamura et al. Reference Nakamura, Baumjohann, Asano, Runov, Balogh, Owen, Fazakerley, Fujimoto, Klecker and Rème2006; Sitnov et al. Reference Sitnov, Swisdak, Guzdar and Runov2006; Schindler & Hesse Reference Schindler and Hesse2008; Artemyev & Zelenyi Reference Artemyev and Zelenyi2013; Borovsky & Valdivia Reference Borovsky and Valdivia2018; Artemyev et al. Reference Artemyev, Angelopoulos, Runov and Petrukovich2019). Simulations and theoretical treatments (Uzdensky, Loureiro & Schekochihin Reference Uzdensky, Loureiro and Schekochihin2010; Daughton et al. Reference Daughton, Roytershteyn, Karimabadi, Yin, Albright, Bergen and Bowers2011) envision that large-scale reorganization of the magnetotail could be a multi-scale process with forcing and feedback between reconnection at different sites. This indicates that the cumulative effect of reconnection at gyro-scale current sheets is important in a large-scale topological magnetic reorganization. Studies (Hwang et al. Reference Hwang, Goldstein, Moore, Walsh, Baishev, Moiseyev, Shevtsov and Yumoto2014; Xu et al. Reference Xu, Fu, Norgren, Hwang and Liu2018) have suggested a possible connection between gyro-scale current sheets and reconnection, but the physics is still unclear. NASA's Magnetospheric Multiscale (MMS) mission (Burch et al. Reference Burch, Moore, Torbert and Giles2016) can resolve micro-scale features, so for the first time, it is possible to investigate gyro-scale current sheets in detail and assess their contributions to the generalized Ohm's Law and their role in magnetic reconnection.
Understanding how the frozen-in condition is broken to enable reconnection is an important open problem in space plasmas. Mechanisms include pressure anisotropy (Cai & Lee Reference Cai and Lee1997; Le et al. Reference Le, Egedal, Daughton, Fox and Katz2009; Egedal, Le & Daughton Reference Egedal, Le and Daughton2013; Torbert et al. Reference Torbert, Burch, Giles, Gershman, Pollock, Dorelli, Avanov, Argall, Shuster and Strangeway2016a; Egedal et al. Reference Egedal, Ng, Le, Daughton, Wetherton, Dorelli, Gershman and Rager2019; Greess et al. Reference Greess, Egedal, Stanier, Daughton, Olson, Lê, Myers, Millet-Ayala, Clark and Wallace2021), electron inertia (Sonnerup Reference Sonnerup1988; Valentini et al. Reference Valentini, Trávníček, Califano, Hellinger and Mangeney2007; Torbert et al. Reference Torbert, Burch, Giles, Gershman, Pollock, Dorelli, Avanov, Argall, Shuster and Strangeway2016a; Korovinskiy et al. Reference Korovinskiy, Kiehas, Panov, Semenov, Erkaev, Divin and Kubyshkin2021) and anomalous resistivity due to wave–particle interactions (Vaivads et al. Reference Vaivads, André, Buchert, Wahlund, Fazakerley and Cornilleau-Wehrlin2004; Silin et al. Reference Silin, Büchner and Vaivads2005; Che Reference Che2017; Khotyaintsev et al. Reference Khotyaintsev, Graham, Norgren and Vaivads2019). It has been found (Torbert et al. Reference Torbert, Burch, Giles, Gershman, Pollock, Dorelli, Avanov, Argall, Shuster and Strangeway2016a) that pressure and inertial terms may not be sufficient to balance the generalized Ohm's Law alone, and 3-D simulations showed enhanced fluctuations that imply waves may also play an important role in balancing the generalized Ohm's Law.
Lower hybrid waves have long been observed in current sheets and are postulated to be a potential source for anomalous resistivity. Generally, the density gradient driven lower-hybrid drift instability is cited as the source for lower hybrid waves at the centre of current sheets (Huba, Gladd & Papadopoulos Reference Huba, Gladd and Papadopoulos1978; Gurnett et al. Reference Gurnett, Anderson, Tsurutani, Smith, Paschmann, Haerendel, Bame and Russell1979; Chen et al. Reference Chen, Wang, Le Contel, Rager, Hesse, Drake, Dorelli, Ng, Bessho and Graham2020; Yoo et al. Reference Yoo, Ji, Ambat, Wang, Ji, Lo, Li, Ren, Jara-Almonte and Chen2020). However, observations (Runov et al. Reference Runov, Sergeev, Nakamura, Baumjohann, Apatenkov, Asano, Takada, Volwerk, Vörös and Zhang2006) show that the density gradient is negligible near the centre, which would require inward transport of lower hybrid waves that were generated away from the centre (Daughton Reference Daughton2003). It is not clear if this transport can be sustained in a strongly sheared magnetic field geometry formed when a guide field is present. We find that $\boldsymbol{E} \times \boldsymbol{B}$![]() velocity shear due to the perpendicular ambipolar electric field can naturally arise in the centre of current sheets around the magnetic reversal and can drive lower hybrid waves (DuBois et al. Reference DuBois, Crabtree, Ganguli, Malaspina and Amatucci2022). These waves, which in the absence of velocity shear reduce to the modified two stream instability for a non-zero wave vector along the magnetic field (Mcbride et al. Reference Mcbride, Ott, Boris and Orens1972), are consistent with the local plasma conditions at the current sheet centre and require no extraordinary arguments to justify their existence. The importance of the perpendicular ambipolar electric field in compressed current sheets is further emphasized by particle-in-cell (PIC) simulations (Romero & Ganguli Reference Romero and Ganguli1993) and laboratory experiments (Matsubara & Tanikawa Reference Matsubara and Tanikawa2000) that show shear-driven lower hybrid waves can contribute to substantial anomalous resistivity, viscosity and cross-field diffusion.
velocity shear due to the perpendicular ambipolar electric field can naturally arise in the centre of current sheets around the magnetic reversal and can drive lower hybrid waves (DuBois et al. Reference DuBois, Crabtree, Ganguli, Malaspina and Amatucci2022). These waves, which in the absence of velocity shear reduce to the modified two stream instability for a non-zero wave vector along the magnetic field (Mcbride et al. Reference Mcbride, Ott, Boris and Orens1972), are consistent with the local plasma conditions at the current sheet centre and require no extraordinary arguments to justify their existence. The importance of the perpendicular ambipolar electric field in compressed current sheets is further emphasized by particle-in-cell (PIC) simulations (Romero & Ganguli Reference Romero and Ganguli1993) and laboratory experiments (Matsubara & Tanikawa Reference Matsubara and Tanikawa2000) that show shear-driven lower hybrid waves can contribute to substantial anomalous resistivity, viscosity and cross-field diffusion.
Agyrotropy in the electron distribution function has been observed in gyro-scale current sheets (Lapenta et al. Reference Lapenta, Berchem, Zhou, Walker, El-Alaoui, Goldstein, Paterson, Giles, Pollock and Russell2017; Chen et al. Reference Chen, Wang, Le Contel, Rager, Hesse, Drake, Dorelli, Ng, Bessho and Graham2020). It has been argued that non-gyrotropic distributions are caused by meandering gyro orbits (Lapenta et al. Reference Lapenta, Berchem, Zhou, Walker, El-Alaoui, Goldstein, Paterson, Giles, Pollock and Russell2017) or acceleration due to wave effects (Chen et al. Reference Chen, Wang, Le Contel, Rager, Hesse, Drake, Dorelli, Ng, Bessho and Graham2020). When a guide field is present, as in the case discussed here, meandering orbits are absent. It is also unclear how heating due to wave–particle interactions driven by a local instability can create agyrotropy. However, it has recently been shown that strong agyrotropy can be generated by a localized perpendicular electric field with scale lengths less than an ion gyro-radius (i.e. ambipolar electric field) (Ganguli et al. Reference Ganguli, Crabtree, Fletcher, Tejero, Malaspina and Cohen2018, Reference Ganguli, Crabtree, Fletcher and Amatucci2020; DuBois et al. Reference DuBois, Crabtree, Ganguli, Malaspina and Amatucci2022). The formation of non-gyrotropic electron distribution functions has also been suggested to be an indicator of reconnection in both PIC simulations and in situ observations (Mahajan & Hazeltine Reference Mahajan and Hazeltine2000; Scudder & Daughton Reference Scudder and Daughton2008).
This paper focuses on the importance of the perpendicular ambipolar electric field in a compressed, gyro-scale current sheet located in the Earth's magnetotail through MMS data analysis. Section 2 discusses the MMS data products and analysis techniques used in the study. Section 3 begins with a summary of previous results which characterize the current sheet, ambipolar electric field and $\boldsymbol{E} \times \boldsymbol{B}$![]() velocity shear-driven lower hybrid waves (§ 3.1). Section 3.2 discusses new calculations of the terms in the generalized Ohm's Law including the anomalous resistivity and viscosity due to wave turbulence with electrons and the off-diagonal pressure tensor terms. Section 4 concludes with a discussion of the impact on reconnection physics.
velocity shear-driven lower hybrid waves (§ 3.1). Section 3.2 discusses new calculations of the terms in the generalized Ohm's Law including the anomalous resistivity and viscosity due to wave turbulence with electrons and the off-diagonal pressure tensor terms. Section 4 concludes with a discussion of the impact on reconnection physics.
2. Data and methodology
The MMS mission comprises four identical spacecraft that fly in a pyramid-like formation to study kinetic-scale structures and dynamics in the electron diffusion region of thin and reconnecting current sheets. On July 3, 2017, the MMS spacecraft crossed a current sheet in the magnetotail at approximately 5:27:07 UTC. During this event, the MMS spacecraft were in the night side of Earth's plasma sheet on the dusk side of midnight, far from the magnetopause. We use high time resolution burst data from the fluxgate magnetometer (FGM) for magnetic field measurements (Russell et al. Reference Russell, Anderson, Baumjohann, Bromund, Dearborn, Fischer, Le, Leinweber, Leneman and Magnes2016), fast plasma investigation (FPI) for velocity, density, temperature, pressure tensor and distribution function measurements (Pollock et al. Reference Pollock, Moore, Jacques, Burch, Gliese, Saito, Omoto, Avanov, Barrie and Coffey2016), and from the FIELDS instrument (Torbert et al. Reference Torbert, Russell, Magnes, Ergun, Lindqvist, Le Contel, Vaith, Macri, Myers and Rau2016b) for electric field and electrostatic fluctuation measurements. The FGM burst measurements are at 128 Samples/s, the FIELDs burst measurements are at 8192 Samples/s, and the FPI burst measurements are at 6 Samples/s for ions and 33 Samples/s for electrons. All data are initially in the geocentric solar ecliptic (GSE) coordinate system.
Vector data are rotated from the GSE coordinate system into the local current sheet LMN coordinate system (figure 1) using the transformation matrix [L,M,N] = [[−0.67, −0.68, −0.30], [−0.70, 0.71, −0.04], [−0.24, −0.18, 0.95]], where $\hat{L}$![]() is the outflow direction, $\hat{M}$
is the outflow direction, $\hat{M}$![]() is the direction of the guide field and $\hat{N}$
is the direction of the guide field and $\hat{N}$![]() is the direction normal to the current sheet. The transformation matrix is calculated from the minimum variance analysis (Denton et al. Reference Denton, Sonnerup, Russell, Hasegawa, Phan, Strangeway, Giles, Ergun, Lindqvist and Torbert2018). Details of the calculated transformation matrix can be found in the supplemental material of DuBois et al. (Reference DuBois, Crabtree, Ganguli, Malaspina and Amatucci2022).
is the direction normal to the current sheet. The transformation matrix is calculated from the minimum variance analysis (Denton et al. Reference Denton, Sonnerup, Russell, Hasegawa, Phan, Strangeway, Giles, Ergun, Lindqvist and Torbert2018). Details of the calculated transformation matrix can be found in the supplemental material of DuBois et al. (Reference DuBois, Crabtree, Ganguli, Malaspina and Amatucci2022).

Figure 1. Local current sheet LMN coordinate system, where $\hat{L}$![]() is the outflow direction, $\hat{M}$
is the outflow direction, $\hat{M}$![]() is the direction of the guide field and $\hat{N}$
is the direction of the guide field and $\hat{N}$![]() is the direction normal to the current sheet.
is the direction normal to the current sheet.
For the analysis in § 3, current sheet parameters such as velocity (V cs) and width (L cs) are important for determining if the current sheet is gyro-scale and for calculations of gradients. The reversal magnetic field (BL) data from each spacecraft are shifted in time (dt) to minimize the difference between reversal times. The current sheet velocity is then estimated as ${V_{\textrm{cs}}} = \textrm{d}N/\textrm{d}t$![]() , where dN is the spacecraft distance from one another in $\hat{N}$
, where dN is the spacecraft distance from one another in $\hat{N}$![]() . Here, L cs is estimated using the variance of BL (Staniland et al. Reference Staniland, Dougherty, Masters and Bunce2020). When BL is steady, the variance is approximately 0, but when BL diverges during a current sheet crossing, the variance is large. The beginning and ending times of the variance increase are used to identify the boundaries of the current sheet. Here, V cs is used to convert the difference between the beginning/ending times to L cs, which is normalized to ρi to show how the current sheet scale size compares with the ion-scale size. To smooth the data and infer dc level profiles of plasma parameters (figure 2), a boxcar average lowpass filter (~3 Hz) is applied to the time series.
. Here, L cs is estimated using the variance of BL (Staniland et al. Reference Staniland, Dougherty, Masters and Bunce2020). When BL is steady, the variance is approximately 0, but when BL diverges during a current sheet crossing, the variance is large. The beginning and ending times of the variance increase are used to identify the boundaries of the current sheet. Here, V cs is used to convert the difference between the beginning/ending times to L cs, which is normalized to ρi to show how the current sheet scale size compares with the ion-scale size. To smooth the data and infer dc level profiles of plasma parameters (figure 2), a boxcar average lowpass filter (~3 Hz) is applied to the time series.

Figure 2. (a) EN (solid, blue) and ne (dash, orange), (b) the electron distribution function for t = 6 s (pink box), (c) t = 7.67 s (green box), (d) t = 9 s (yellow box), (e) Ve (dot-dash, grey) and ${V_{E \times B}}$![]() (solid, blue) in $\hat{L}$
(solid, blue) in $\hat{L}$![]() , and (f) ωs (solid, blue) and ${\omega ^\ast }$
, and (f) ωs (solid, blue) and ${\omega ^\ast }$![]() (dash, orange) frequencies (right vertical axis). The spectrogram of electrostatic fluctuation power spectral density as a function of time is shown in panels (a,e,f). The top axis shows distance normalized to ${\rho _i}$
(dash, orange) frequencies (right vertical axis). The spectrogram of electrostatic fluctuation power spectral density as a function of time is shown in panels (a,e,f). The top axis shows distance normalized to ${\rho _i}$![]() . The vertical dotted lines indicate the times for which the electron distribution functions in panels (b–d) were calculated.
. The vertical dotted lines indicate the times for which the electron distribution functions in panels (b–d) were calculated.
For the calculations of the terms in the generalized Ohm's Law (§ 3.2), the quantities are calculated from each MMS spacecraft individually. The average quantities (denoted by $\langle x\rangle$![]() ) are calculated from the boxcar average technique (above), and the fluctuation quantities (denoted by $\delta x$
) are calculated from the boxcar average technique (above), and the fluctuation quantities (denoted by $\delta x$![]() ) are calculated by applying a lowpass filter with a cutoff frequency of 20 Hz to the raw data to filter out any high frequency noise and then subtracting the boxcar average. This ensures that only lower hybrid frequencies (3 to 20 Hz) are considered for the calculations of the terms in the generalized Ohm's Law, although including higher frequencies did not significantly affect the results discussed in § 3.2. We then account for time shifts between spacecraft using the same BL shifting technique described above to get the dt between the reference spacecraft (MMS1) and the remaining spacecraft. The calculations from MMS2 and MMS3 spacecraft data are then shifted in time using the dt. Once the time shift is accounted for, the spacecraft data are averaged together.
) are calculated by applying a lowpass filter with a cutoff frequency of 20 Hz to the raw data to filter out any high frequency noise and then subtracting the boxcar average. This ensures that only lower hybrid frequencies (3 to 20 Hz) are considered for the calculations of the terms in the generalized Ohm's Law, although including higher frequencies did not significantly affect the results discussed in § 3.2. We then account for time shifts between spacecraft using the same BL shifting technique described above to get the dt between the reference spacecraft (MMS1) and the remaining spacecraft. The calculations from MMS2 and MMS3 spacecraft data are then shifted in time using the dt. Once the time shift is accounted for, the spacecraft data are averaged together.
3. Results and discussion
3.1. Previous velocity shear-driven lower hybrid wave results
The first evidence of velocity shear-driven lower hybrid waves in a compressed gyro-scale current sheet was previously reported by DuBois et al. (Reference DuBois, Crabtree, Ganguli, Malaspina and Amatucci2022). The four MMS spacecraft traversed a gyro-scale current sheet of width ${L_{\textrm{cs}}}\sim 0.6{\rho _i}$![]() and crossed the magnetic reversal at approximately 5:27:07.02 UTC. DuBois et al. (Reference DuBois, Crabtree, Ganguli, Malaspina and Amatucci2022, figure 1) shows a full summary of the plasma parameters in LMN coordinates for this event.
and crossed the magnetic reversal at approximately 5:27:07.02 UTC. DuBois et al. (Reference DuBois, Crabtree, Ganguli, Malaspina and Amatucci2022, figure 1) shows a full summary of the plasma parameters in LMN coordinates for this event.
At the BL reversal (t = 7.02 s), there is a guide field (${B_M}\sim 10\ \textrm{nT}$![]() ), and the magnetic field normal to the current sheet (BN) is flat and near-zero inside the current sheet. The electric field normal to the current sheet (EN) is the perpendicular ambipolar electric field (figure 2(a) – solid, blue) and has a scale length ${\rho _e} < {L_E} < {\rho _i}$
), and the magnetic field normal to the current sheet (BN) is flat and near-zero inside the current sheet. The electric field normal to the current sheet (EN) is the perpendicular ambipolar electric field (figure 2(a) – solid, blue) and has a scale length ${\rho _e} < {L_E} < {\rho _i}$![]() , calculated from the half-width at half-max of EN. A spectrogram of the EN burst data reveals lower hybrid fluctuations (figure 2, left vertical axis), which are intense around the peak of the ${V_{E \times B}}$
, calculated from the half-width at half-max of EN. A spectrogram of the EN burst data reveals lower hybrid fluctuations (figure 2, left vertical axis), which are intense around the peak of the ${V_{E \times B}}$![]() flow. The ion velocity (Vi) is significantly smaller than the electron velocity (Ve), which indicates that the ions experience negligible electric field due to gyro averaging (Ganguli et al. Reference Ganguli, Crabtree, Fletcher and Amatucci2020). The electron density (ne) is nearly constant during the fluctuations (figure 2(a) – dashed, orange), which are localized around the field reversal region.
flow. The ion velocity (Vi) is significantly smaller than the electron velocity (Ve), which indicates that the ions experience negligible electric field due to gyro averaging (Ganguli et al. Reference Ganguli, Crabtree, Fletcher and Amatucci2020). The electron density (ne) is nearly constant during the fluctuations (figure 2(a) – dashed, orange), which are localized around the field reversal region.
Non-gyrotropic distribution functions were observed in this event (Chen et al. Reference Chen, Wang, Le Contel, Rager, Hesse, Drake, Dorelli, Ng, Bessho and Graham2020). Figure 2(b–d) shows the electron distribution functions calculated for t = 6 s (figure 2(b), pink), t = 7.67 s (figure 2(c), green) and t = 9 s (figure 2(d), yellow). The vertical dotted lines in figure 2(a,e,f) note the times of distribution functions. Figure 2(c) shows that the agyrotropy is correlated to the sheared perpendicular ambipolar electric field, while in figure 2(b,d), the electron distribution function is observed to be significantly less agyrotropic where the shear of the ambipolar electric field is reduced. This indicates that the agyrotropy is proportional to the shear of the electric field. This observation is supported by a kinetic model (Ganguli et al. Reference Ganguli, Crabtree, Fletcher and Amatucci2020; DuBois et al. Reference DuBois, Crabtree, Ganguli, Malaspina and Amatucci2022), which establishes that the shear in the perpendicular ambipolar field is responsible for breaking the gyrotropy in the equilibrium distribution function, as opposed to the postulated wave heating (Chen et al. Reference Chen, Wang, Le Contel, Rager, Hesse, Drake, Dorelli, Ng, Bessho and Graham2020).
The perpendicular ambipolar electric field breaks gyrotropy of the electron distribution function through the asymmetry in temperature in the gyro plane that arises due to the gradient in EN included in the parameter $\eta (x) = 1 + (\textrm{d}{V_{E \times B}}/\textrm{d}x)/\varOmega$![]() , where the gradient of the $\boldsymbol{E} \times \boldsymbol{B}$
, where the gradient of the $\boldsymbol{E} \times \boldsymbol{B}$![]() velocity, $\textrm{d}{V_{E \times B}}/\textrm{d}x$
velocity, $\textrm{d}{V_{E \times B}}/\textrm{d}x$![]() , is the velocity shear, and $\varOmega$
, is the velocity shear, and $\varOmega$![]() is the cyclotron frequency (Ganguli et al. Reference Ganguli, Crabtree, Fletcher and Amatucci2020). Increasing compression intensifies shear making $\textrm{d}{V_{E \times B}}/\textrm{d}x \to - \varOmega$
is the cyclotron frequency (Ganguli et al. Reference Ganguli, Crabtree, Fletcher and Amatucci2020). Increasing compression intensifies shear making $\textrm{d}{V_{E \times B}}/\textrm{d}x \to - \varOmega$![]() . Consequently, as $\eta \to 0$
. Consequently, as $\eta \to 0$![]() , the renormalized gyro frequency $\textrm{(}\varOmega \to \sqrt \eta \varOmega )$
, the renormalized gyro frequency $\textrm{(}\varOmega \to \sqrt \eta \varOmega )$![]() becomes vanishingly small and the gyro-radius becomes large representing the larger temperature, but the particles still gyrate around the magnetic field, albeit in non-circular orbits. For $\eta < 0$
becomes vanishingly small and the gyro-radius becomes large representing the larger temperature, but the particles still gyrate around the magnetic field, albeit in non-circular orbits. For $\eta < 0$![]() , the orbits are no longer simple gyration (Ganguli et al. Reference Ganguli, Lee and Palmadesso1988b) and the particles are effectively unmagnetized and accelerated by the electric field to high energies. This explains the origin of agyrotropy in the equilibrium distribution of compressed plasma layers and is notable because Scudder & Mozer (Reference Scudder and Mozer2005) found from data analysis that non-gyrotropic distribution functions could be generated by a quasi-static electric field, but the source of such an electric field was unknown. Theoretical arguments by Mahajan & Hazeltine (Reference Mahajan and Hazeltine2000) and Scudder & Daughton (Reference Scudder and Daughton2008) suggest that the non-gyrotropic distribution function may be an indicator for imminent magnetic reconnection. Our data analysis confirms that non-gyrotropic distribution functions arise due to the localized perpendicular ambipolar electric field by their strong correlation. Physically, this is because the equilibrium electron $\boldsymbol{E} \times \boldsymbol{B}$
, the orbits are no longer simple gyration (Ganguli et al. Reference Ganguli, Lee and Palmadesso1988b) and the particles are effectively unmagnetized and accelerated by the electric field to high energies. This explains the origin of agyrotropy in the equilibrium distribution of compressed plasma layers and is notable because Scudder & Mozer (Reference Scudder and Mozer2005) found from data analysis that non-gyrotropic distribution functions could be generated by a quasi-static electric field, but the source of such an electric field was unknown. Theoretical arguments by Mahajan & Hazeltine (Reference Mahajan and Hazeltine2000) and Scudder & Daughton (Reference Scudder and Daughton2008) suggest that the non-gyrotropic distribution function may be an indicator for imminent magnetic reconnection. Our data analysis confirms that non-gyrotropic distribution functions arise due to the localized perpendicular ambipolar electric field by their strong correlation. Physically, this is because the equilibrium electron $\boldsymbol{E} \times \boldsymbol{B}$![]() velocity is strongly sheared (DuBois et al. Reference DuBois, Crabtree, Ganguli, Malaspina and Amatucci2022), which makes the equilibrium electron ${\eta _e} \to 0$
velocity is strongly sheared (DuBois et al. Reference DuBois, Crabtree, Ganguli, Malaspina and Amatucci2022), which makes the equilibrium electron ${\eta _e} \to 0$![]() and the ion ${\eta _i} < 0$
and the ion ${\eta _i} < 0$![]() . This configuration is unstable to EIH waves (discussed in § 1.1), which can heat the electrons and relax the velocity gradient resulting in a larger value of ${\eta _e}$
. This configuration is unstable to EIH waves (discussed in § 1.1), which can heat the electrons and relax the velocity gradient resulting in a larger value of ${\eta _e}$![]() in the saturated state. This demonstrates the critical role of the perpendicular ambipolar electric field, which may be considered as a surrogate for compression, and its importance to current sheet evolution. It can ultimately lead to reconnection (Scudder & Mozer Reference Scudder and Mozer2005) if the electric field is sufficiently strong.
in the saturated state. This demonstrates the critical role of the perpendicular ambipolar electric field, which may be considered as a surrogate for compression, and its importance to current sheet evolution. It can ultimately lead to reconnection (Scudder & Mozer Reference Scudder and Mozer2005) if the electric field is sufficiently strong.
A large $\boldsymbol{E} \times \boldsymbol{B}$![]() velocity shear (figure 2(e) – solid, blue) in $\hat{L}({V_{E \times B - L}})$
velocity shear (figure 2(e) – solid, blue) in $\hat{L}({V_{E \times B - L}})$![]() peaks with the wave activity. Here, ${V_{E \times B - L}}$
peaks with the wave activity. Here, ${V_{E \times B - L}}$![]() is nearly equal to the total electron flow (figure 2(e) – dashed, grey) in $\hat{L}$
is nearly equal to the total electron flow (figure 2(e) – dashed, grey) in $\hat{L}$![]() , ${V_{eL}}$
, ${V_{eL}}$![]() , which indicates that the electrons are $\boldsymbol{E} \times \boldsymbol{B}$
, which indicates that the electrons are $\boldsymbol{E} \times \boldsymbol{B}$![]() drifting. It has been previously shown that velocity shear becomes important when ${\omega _s}/{\omega _{LH}} > 1$
drifting. It has been previously shown that velocity shear becomes important when ${\omega _s}/{\omega _{LH}} > 1$![]() (Romero & Ganguli Reference Romero and Ganguli1993) and for this event, ${\omega _s}/{\omega _{LH}} \approx 8$
(Romero & Ganguli Reference Romero and Ganguli1993) and for this event, ${\omega _s}/{\omega _{LH}} \approx 8$![]() . Additionally, the diamagnetic drift velocity $[{\boldsymbol{V}_{\textrm{drift}}} = \boldsymbol{\nabla }{P_e} \times \boldsymbol{B}/({n_e}{B^2})]$
. Additionally, the diamagnetic drift velocity $[{\boldsymbol{V}_{\textrm{drift}}} = \boldsymbol{\nabla }{P_e} \times \boldsymbol{B}/({n_e}{B^2})]$![]() in $\hat{L}$
in $\hat{L}$![]() is small in the region of the wave localization because ${V_{eL}} \approx {V_{E \times B - L}}$
is small in the region of the wave localization because ${V_{eL}} \approx {V_{E \times B - L}}$![]() . The observed lower hybrid waves are characterized as shear-driven EIH waves because the diamagnetic drift frequency (${\omega ^\ast } ={-} {k_ \bot }{\boldsymbol{V}_{\textrm{drift}}}$
. The observed lower hybrid waves are characterized as shear-driven EIH waves because the diamagnetic drift frequency (${\omega ^\ast } ={-} {k_ \bot }{\boldsymbol{V}_{\textrm{drift}}}$![]() in figure 2(f) – dashed, orange, right vertical axis) is significantly smaller than the shear frequency (${\omega _s} \sim {\boldsymbol{V}_{E \times B}}/{L_E}$
in figure 2(f) – dashed, orange, right vertical axis) is significantly smaller than the shear frequency (${\omega _s} \sim {\boldsymbol{V}_{E \times B}}/{L_E}$![]() in figure 2(f) – solid, blue, right vertical axis). The wavenumber $({k_ \bot })$
in figure 2(f) – solid, blue, right vertical axis). The wavenumber $({k_ \bot })$![]() in the calculation of the diamagnetic drift frequency can be estimated using a time shift method (Norgren et al. Reference Norgren, Vaivads, Khotyaintsev and André2012). This rules out the density gradient as the driving mechanism (Romero & Ganguli Reference Romero and Ganguli1993; DuBois et al. Reference DuBois, Thomas, Amatucci and Ganguli2014, Reference DuBois, Crabtree, Ganguli, Malaspina and Amatucci2022; Ganguli et al. Reference Ganguli, Crabtree, Fletcher and Amatucci2020). The observed waves also have a long wavelength with ${k_ \bot }{\rho _e} \approx 0.18$
in the calculation of the diamagnetic drift frequency can be estimated using a time shift method (Norgren et al. Reference Norgren, Vaivads, Khotyaintsev and André2012). This rules out the density gradient as the driving mechanism (Romero & Ganguli Reference Romero and Ganguli1993; DuBois et al. Reference DuBois, Thomas, Amatucci and Ganguli2014, Reference DuBois, Crabtree, Ganguli, Malaspina and Amatucci2022; Ganguli et al. Reference Ganguli, Crabtree, Fletcher and Amatucci2020). The observed waves also have a long wavelength with ${k_ \bot }{\rho _e} \approx 0.18$![]() and ${k_ \bot }{L_E} \approx 1$
and ${k_ \bot }{L_E} \approx 1$![]() indicating they are shear-driven lower hybrid fluctuations.
indicating they are shear-driven lower hybrid fluctuations.
The current density, calculated from the moments data $[\boldsymbol{J} = e({n_i}{\boldsymbol{V}_i} - {n_e}{\boldsymbol{V}_e})]$![]() , shows the electron current density $({J_e})$
, shows the electron current density $({J_e})$![]() is dominant (figure 3(a) – solid, orange) because ${V_i} \ll {V_e}$
is dominant (figure 3(a) – solid, orange) because ${V_i} \ll {V_e}$![]() and it is comparable to the cross-field current, ${J_{\textrm{cf}}} = en(\boldsymbol{E} \times \boldsymbol{B})$
and it is comparable to the cross-field current, ${J_{\textrm{cf}}} = en(\boldsymbol{E} \times \boldsymbol{B})$![]() (figure 3 – dot, purple). The large peak in JeL (figure 3(a) – solid, orange) is localized to the region of EN and the shear-driven lower hybrid waves, and the scale size is less than ${\rho _i}$
(figure 3 – dot, purple). The large peak in JeL (figure 3(a) – solid, orange) is localized to the region of EN and the shear-driven lower hybrid waves, and the scale size is less than ${\rho _i}$![]() . This indicates the formation of a gyro-scale current sheet. This is notable because previous studies (Hwang et al. Reference Hwang, Goldstein, Moore, Walsh, Baishev, Moiseyev, Shevtsov and Yumoto2014; Xu et al. Reference Xu, Fu, Norgren, Hwang and Liu2018) have shown a connection between current sheets with substructures in J and the onset of magnetic reconnection.
. This indicates the formation of a gyro-scale current sheet. This is notable because previous studies (Hwang et al. Reference Hwang, Goldstein, Moore, Walsh, Baishev, Moiseyev, Shevtsov and Yumoto2014; Xu et al. Reference Xu, Fu, Norgren, Hwang and Liu2018) have shown a connection between current sheets with substructures in J and the onset of magnetic reconnection.

Figure 3. Current densities (a) JL, (b) JM and (c) JN. The electron (orange, solid) and ion (blue, dashed) current densities are calculated from moments data. The total current density (red, dash-dot) is the sum of the electron and ion components. The cross-field current (purple, dot) is shown for comparison.
These previous results demonstrated that a localized perpendicular ambipolar electric field develops in a gyro-scale current sheet with scale size ${L_{\textrm{CS}}} < {\rho _i}$![]() and results in a sheared $\boldsymbol{E} \times \boldsymbol{B}$
and results in a sheared $\boldsymbol{E} \times \boldsymbol{B}$![]() velocity that drives lower hybrid fluctuations. Not only does this indicate a new mechanism to generate intense electrostatic turbulence near the magnetic field reversal, but these shear-driven lower hybrid waves can be used as a diagnostic to indicate if the system is in a path to magnetic reconnection since they imply the existence of a sheared electron flow and a non-gyrotropic electron distribution function, both of which may be prerequisites for magnetic reconnection (Mahajan & Hazeltine Reference Mahajan and Hazeltine2000; Scudder & Mozer Reference Scudder and Mozer2005; Scudder & Daughton Reference Scudder and Daughton2008). The shear-driven lower hybrid waves are also ideally localized in the current sheet centre and can contribute to anomalous dissipation, indicating they may play a significant role in magnetic reconnection (Romero & Ganguli Reference Romero and Ganguli1993; Ganguli et al. Reference Ganguli, Keskinen, Romero, Heelis, Moore and Pollock1994; Walker et al. Reference Walker, Amatucci, Ganguli, Antoniades, Bowles and Koepke1997; Amatucci et al. Reference Amatucci, Walker, Ganguli, Duncan, Antoniades, Bowles, Gavrishchaka and Koepke1998; Matsubara & Tanikawa Reference Matsubara and Tanikawa2000; Kumar, Mattoo & Jha Reference Kumar, Mattoo and Jha2002).
velocity that drives lower hybrid fluctuations. Not only does this indicate a new mechanism to generate intense electrostatic turbulence near the magnetic field reversal, but these shear-driven lower hybrid waves can be used as a diagnostic to indicate if the system is in a path to magnetic reconnection since they imply the existence of a sheared electron flow and a non-gyrotropic electron distribution function, both of which may be prerequisites for magnetic reconnection (Mahajan & Hazeltine Reference Mahajan and Hazeltine2000; Scudder & Mozer Reference Scudder and Mozer2005; Scudder & Daughton Reference Scudder and Daughton2008). The shear-driven lower hybrid waves are also ideally localized in the current sheet centre and can contribute to anomalous dissipation, indicating they may play a significant role in magnetic reconnection (Romero & Ganguli Reference Romero and Ganguli1993; Ganguli et al. Reference Ganguli, Keskinen, Romero, Heelis, Moore and Pollock1994; Walker et al. Reference Walker, Amatucci, Ganguli, Antoniades, Bowles and Koepke1997; Amatucci et al. Reference Amatucci, Walker, Ganguli, Duncan, Antoniades, Bowles, Gavrishchaka and Koepke1998; Matsubara & Tanikawa Reference Matsubara and Tanikawa2000; Kumar, Mattoo & Jha Reference Kumar, Mattoo and Jha2002).
3.2. Impact on magnetic reconnection
One of the essential questions in reconnection physics is what effect breaks the frozen-in condition (where magnetic field lines move with the plasma)? One way for the frozen-in condition to be broken is through anomalous processes caused by the interaction of wave turbulence with electrons. Anomalous terms can be added to the generalized Ohm's Law,
where the first term on the right side of the equation $({\boldsymbol{\eta }_{\boldsymbol{R}}}\boldsymbol{\cdot }\boldsymbol{J})$![]() is the anomalous resistivity (drag) due to the interaction of wave turbulence and electrons, the second term $(\boldsymbol{T})$
is the anomalous resistivity (drag) due to the interaction of wave turbulence and electrons, the second term $(\boldsymbol{T})$![]() is the anomalous viscosity (momentum transport), the third term $(\boldsymbol{\nabla }\boldsymbol{\cdot }{\bar{\boldsymbol{P}}_e})$
is the anomalous viscosity (momentum transport), the third term $(\boldsymbol{\nabla }\boldsymbol{\cdot }{\bar{\boldsymbol{P}}_e})$![]() is the electron pressure tensor, and the last term $({\boldsymbol{V}_{\boldsymbol{e}}}\boldsymbol{\cdot }\boldsymbol{\nabla }{\boldsymbol{V}_{\boldsymbol{e}}})$
is the electron pressure tensor, and the last term $({\boldsymbol{V}_{\boldsymbol{e}}}\boldsymbol{\cdot }\boldsymbol{\nabla }{\boldsymbol{V}_{\boldsymbol{e}}})$![]() is the electron inertia. The anomalous terms can compete with other effects during the reconnection process. Due to measurement uncertainties, it is difficult to determine the dominance of any term unambiguously. For example, the magnitude of the anomalous terms depends on the wave amplitudes and is likely to change throughout the current sheet evolution due to the magnitude of compression. The time evolution of the pressure tensor term may also vary with current sheet evolution. Therefore, it is reasonable to account for all effects in determining the generalized Ohm's Law balance unless an unambiguous determination can be made for the dominance of a single process. In this section, we focus on estimating the anomalous, off-diagonal pressure tensor and electron inertia terms directly from MMS data in a gyro-scale current.
is the electron inertia. The anomalous terms can compete with other effects during the reconnection process. Due to measurement uncertainties, it is difficult to determine the dominance of any term unambiguously. For example, the magnitude of the anomalous terms depends on the wave amplitudes and is likely to change throughout the current sheet evolution due to the magnitude of compression. The time evolution of the pressure tensor term may also vary with current sheet evolution. Therefore, it is reasonable to account for all effects in determining the generalized Ohm's Law balance unless an unambiguous determination can be made for the dominance of a single process. In this section, we focus on estimating the anomalous, off-diagonal pressure tensor and electron inertia terms directly from MMS data in a gyro-scale current.
It was previously thought that density gradient driven lower hybrid drift waves could provide the anomalous resistivity necessary to trigger magnetic reconnection (Davidson & Gladd Reference Davidson and Gladd1975; Silin et al. Reference Silin, Büchner and Vaivads2005). However, magnetotail observations and theoretical calculations now suggest that lower hybrid drift waves are unlikely to be the source because the waves are localized far from the magnetic field reversal region (Huba & Ganguli Reference Huba and Ganguli1983) where magnetic reconnection is likely to be initiated, and the centre of current sheets are characterized by the lack of a density gradient (Runov et al. Reference Runov, Sergeev, Nakamura, Baumjohann, Apatenkov, Asano, Takada, Volwerk, Vörös and Zhang2006), which is necessary to drive lower hybrid drift waves. Drake, Gladd & Huba (Reference Drake, Gladd and Huba1981) argued that the lower hybrid drift instability may be supported at the centre due to a strongly varying magnetic field; but the model does not consider a guide field and the strong ambipolar electric field, which will also exist and intensify due to compression and substantially affect particle dynamics. One-dimensional PIC simulations by Birn, Schindler & Hesse (Reference Birn, Schindler and Hesse2004) that were initialized with a Harris equilibrium but were compressed by inflowing boundary conditions show the self-consistent formation of a transverse electric field, consistent with our kinetic model. In figure 2(e), we show that the net cross-field electron drift is close to the electron $\boldsymbol{E} \times \boldsymbol{B}$![]() drift, implying that the diamagnetic drift that is necessary to drive the lower hybrid drift instability is almost non-existent in the data. Two-dimensional simulations (Daughton Reference Daughton2003; Silin et al. Reference Silin, Büchner and Vaivads2005) showed that it may be possible for an electromagnetic lower hybrid drift wave to radiate inward to the centre if the current sheet is sufficiently thin. However, these simulations do not consider a realistic 3-D geometry in which the wave propagation characteristics may not convect the energy towards the centre. We find (DuBois et al. Reference DuBois, Crabtree, Ganguli, Malaspina and Amatucci2022) that the shear-driven EIH waves, which are ideally generated in the centre of the current sheet where magnetic reconnection is likely to be initiated, need no supplementary arguments to justify their presence in the centre of the current sheet. In addition, their predominant electrostatic nature ensures that they remain localized to the generation region to contribute robustly to anomalous dissipation.
drift, implying that the diamagnetic drift that is necessary to drive the lower hybrid drift instability is almost non-existent in the data. Two-dimensional simulations (Daughton Reference Daughton2003; Silin et al. Reference Silin, Büchner and Vaivads2005) showed that it may be possible for an electromagnetic lower hybrid drift wave to radiate inward to the centre if the current sheet is sufficiently thin. However, these simulations do not consider a realistic 3-D geometry in which the wave propagation characteristics may not convect the energy towards the centre. We find (DuBois et al. Reference DuBois, Crabtree, Ganguli, Malaspina and Amatucci2022) that the shear-driven EIH waves, which are ideally generated in the centre of the current sheet where magnetic reconnection is likely to be initiated, need no supplementary arguments to justify their presence in the centre of the current sheet. In addition, their predominant electrostatic nature ensures that they remain localized to the generation region to contribute robustly to anomalous dissipation.
Laboratory experiments (Matsubara & Tanikawa Reference Matsubara and Tanikawa2000; Kumar et al. Reference Kumar, Mattoo and Jha2002) have shown that the EIH instability can contribute to anomalous dissipation. The EIH anomalous resistivity estimated from PIC simulations by Romero & Ganguli (Reference Romero and Ganguli1993) showed that the sheared cross-field electron current is greatly reduced due to the growth of the EIH instability, indicating the presence of both anomalous resistivity and viscosity. It was also shown that the resistivity was proportional to the shear frequency, which is proportional to the global compression, thus implying that increasing compression may result in a larger anomalous resistivity and a faster reconnection rate. Additionally, theoretical arguments (Mahajan & Hazeltine Reference Mahajan and Hazeltine2000; Scudder & Daughton Reference Scudder and Daughton2008) suggest that non-gyrotropic distribution functions are an indicator of the possibility for magnetic reconnection to occur, and the source of non-gyrotropic distribution functions is the localized ambipolar electric field (§ 3.1).
The anomalous resistivity $({\boldsymbol{\eta }_R})$![]() due to the shear-driven EIH waves can be estimated directly from MMS data,
due to the shear-driven EIH waves can be estimated directly from MMS data,
where, ${\boldsymbol{\nu }_\alpha }$![]() is the anomalous collision frequency,
is the anomalous collision frequency,
The electron density fluctuation quantity $(\delta {n_e})$![]() is calculated by taking the raw FPI qmoments burst data and subtracting the quasi-static profile (indicated by $\langle {n_e}\rangle$
is calculated by taking the raw FPI qmoments burst data and subtracting the quasi-static profile (indicated by $\langle {n_e}\rangle$![]() ). The qmoments data products (Rager et al. Reference Rager, Dorelli, Gershman, Uritsky, Avanov, Torbert, Burch, Ergun, Egedal and Schiff2018) are computed at one quarter of the 30 ms resolution time of the FPI moments burst data and have sufficient resolution for $\delta {n_e}$
). The qmoments data products (Rager et al. Reference Rager, Dorelli, Gershman, Uritsky, Avanov, Torbert, Burch, Ergun, Egedal and Schiff2018) are computed at one quarter of the 30 ms resolution time of the FPI moments burst data and have sufficient resolution for $\delta {n_e}$![]() determination. The electric field fluctuation quantity $(\delta \boldsymbol{E})$
determination. The electric field fluctuation quantity $(\delta \boldsymbol{E})$![]() can be similarly calculated using the electric field burst data. The anomalous resistivity in $\hat{M}({\eta _{RM}})$
can be similarly calculated using the electric field burst data. The anomalous resistivity in $\hat{M}({\eta _{RM}})$![]() is the resistivity in the reconnection direction of the current sheet. Figure 4 shows ${\eta _{RM}}$
is the resistivity in the reconnection direction of the current sheet. Figure 4 shows ${\eta _{RM}}$![]() calculated from $\delta {E_M}$
calculated from $\delta {E_M}$![]() and $\delta {n_e}$
and $\delta {n_e}$![]() using the methodology described in § 2, overlaid on the spectrogram of shear-driven lower hybrid waves. The anomalous resistivity is relatively constant in the time prior to the fluctuations, and then begins to quickly increase during the time of the shear-driven EIH waves. The anomalous resistivity due to the interaction between shear-driven lower hybrid wave turbulence and electrons is estimated to have a peak value of ${\eta _{RM}} = 4 \pm 2.9\ \mathrm{k\Omega }\ \textrm{m}$
using the methodology described in § 2, overlaid on the spectrogram of shear-driven lower hybrid waves. The anomalous resistivity is relatively constant in the time prior to the fluctuations, and then begins to quickly increase during the time of the shear-driven EIH waves. The anomalous resistivity due to the interaction between shear-driven lower hybrid wave turbulence and electrons is estimated to have a peak value of ${\eta _{RM}} = 4 \pm 2.9\ \mathrm{k\Omega }\ \textrm{m}$![]() . This is similar to what Silin et al. (Reference Silin, Büchner and Vaivads2005) estimated using spacecraft potential to infer the electron density for lower hybrid fluctuations observed in Cluster data. The anomalous resistivity term in the generalized Ohm's Law can be calculated using ${\eta _{RM}}$
. This is similar to what Silin et al. (Reference Silin, Büchner and Vaivads2005) estimated using spacecraft potential to infer the electron density for lower hybrid fluctuations observed in Cluster data. The anomalous resistivity term in the generalized Ohm's Law can be calculated using ${\eta _{RM}}$![]() and the current density, JM (figure 3(b) – dash-dot, red). Figure 5(a) shows that the anomalous resistivity term (solid, white) is nearly 0 prior to the shear-driven lower hybrid waves and then, during the time of the waves, begins to decrease and has a minimum value of ${({\eta _R}J)_M} ={-} 0.18 \pm 0.12\ \textrm{mV}\ {\textrm{m}^{ - 1}}$
and the current density, JM (figure 3(b) – dash-dot, red). Figure 5(a) shows that the anomalous resistivity term (solid, white) is nearly 0 prior to the shear-driven lower hybrid waves and then, during the time of the waves, begins to decrease and has a minimum value of ${({\eta _R}J)_M} ={-} 0.18 \pm 0.12\ \textrm{mV}\ {\textrm{m}^{ - 1}}$![]() .
.

Figure 4. Anomalous resistivity in $\hat{M}$![]() (white) overlaid on spectrogram of lower hybrid fluctuations.
(white) overlaid on spectrogram of lower hybrid fluctuations.

Figure 5. (a) Anomalous resistivity term ${({\eta _R}J)_M}$![]() (solid, white) and anomalous viscosity term T (yellow, dashed) estimated from data. (b) Cross-field diffusion coefficient (solid, white). (c) Electron inertial term (solid, white). Plots are overlaid on the spectrogram of lower hybrid fluctuations (left vertical axis).
(solid, white) and anomalous viscosity term T (yellow, dashed) estimated from data. (b) Cross-field diffusion coefficient (solid, white). (c) Electron inertial term (solid, white). Plots are overlaid on the spectrogram of lower hybrid fluctuations (left vertical axis).
It has also been shown that the anomalous viscosity $(\boldsymbol{T})$![]() associated with lower hybrid waves can be calculated directly from MMS data (Graham et al. Reference Graham, Khotyaintsev, André, Vaivads, Divin, Drake, Norgren, Le Contel, Lindqvist and Rager2022). To estimate the anomalous viscosity in $\hat{M}$
associated with lower hybrid waves can be calculated directly from MMS data (Graham et al. Reference Graham, Khotyaintsev, André, Vaivads, Divin, Drake, Norgren, Le Contel, Lindqvist and Rager2022). To estimate the anomalous viscosity in $\hat{M}$![]() , we use
, we use

where $\delta V$![]() is the fluctuation quantity of the electron flow (subscript indicates direction in LMN), $\delta B$
is the fluctuation quantity of the electron flow (subscript indicates direction in LMN), $\delta B$![]() is the fluctuation quantity of the magnetic field and $\langle \delta V\delta B\rangle$
is the fluctuation quantity of the magnetic field and $\langle \delta V\delta B\rangle$![]() is calculated by multiplying the fluctuation quantities together, followed by calculating the boxcar average. Figure 5(a) shows the anomalous viscosity in $\hat{M}$
is calculated by multiplying the fluctuation quantities together, followed by calculating the boxcar average. Figure 5(a) shows the anomalous viscosity in $\hat{M}$![]() estimated directly from MMS data (dashed, yellow). The anomalous viscosity begins to increase during the time of the shear-driven lower hybrid waves, remains localized to the region of the waves and has a peak value of ${T_M} = 0.43 \pm 0.28\ \textrm{mV}\ {\textrm{m}^{ - 1}}$
estimated directly from MMS data (dashed, yellow). The anomalous viscosity begins to increase during the time of the shear-driven lower hybrid waves, remains localized to the region of the waves and has a peak value of ${T_M} = 0.43 \pm 0.28\ \textrm{mV}\ {\textrm{m}^{ - 1}}$![]() , and is in the opposite direction of the anomalous resistivity.
, and is in the opposite direction of the anomalous resistivity.
The cross-field diffusion coefficient $({D_ \bot })$![]() , which is related to anomalous viscosity, can be estimated directly from MMS data using
, which is related to anomalous viscosity, can be estimated directly from MMS data using
where the density gradient is taken in $\hat{N}$![]() or the direction of motion of the spacecraft across the current sheet. The cross-field diffusion coefficient is shown in figure 5(b), where there is a large increase as soon as shear-driven lower hybrid waves are observed and then quickly decreases back to near-zero as the shear-driven waves disappear. This sudden increase in the cross-field diffusion indicates anomalous electron drift and diffusion across the current sheet, which can modify the reconnection process. This was similarly observed in laboratory experiments (Matsubara & Tanikawa Reference Matsubara and Tanikawa2000).
or the direction of motion of the spacecraft across the current sheet. The cross-field diffusion coefficient is shown in figure 5(b), where there is a large increase as soon as shear-driven lower hybrid waves are observed and then quickly decreases back to near-zero as the shear-driven waves disappear. This sudden increase in the cross-field diffusion indicates anomalous electron drift and diffusion across the current sheet, which can modify the reconnection process. This was similarly observed in laboratory experiments (Matsubara & Tanikawa Reference Matsubara and Tanikawa2000).
The electron inertia term in $\hat{M}({I_{eM}})$![]() can also be calculated directly from the MMS data (figure 5c) using
can also be calculated directly from the MMS data (figure 5c) using
where, again, the gradient is taken in $\hat{N}$![]() because this is the direction of motion of the spacecraft across the current sheet, and VeN and VeM are boxcar averaged (quasi-static) electron velocities. The electron inertial term peaks at $- 0.7 \pm 0.15\ \textrm{mV}\ {\textrm{m}^{ - 1}}$
because this is the direction of motion of the spacecraft across the current sheet, and VeN and VeM are boxcar averaged (quasi-static) electron velocities. The electron inertial term peaks at $- 0.7 \pm 0.15\ \textrm{mV}\ {\textrm{m}^{ - 1}}$![]() during the time of the intense ambipolar electric field and is comparable to the other terms in the generalized Ohm's Law. As we have already shown, the majority of the electron flow consists of the $\boldsymbol{E} \times \boldsymbol{B}$
during the time of the intense ambipolar electric field and is comparable to the other terms in the generalized Ohm's Law. As we have already shown, the majority of the electron flow consists of the $\boldsymbol{E} \times \boldsymbol{B}$![]() velocity. Since the $\boldsymbol{E} \times \boldsymbol{B}$
velocity. Since the $\boldsymbol{E} \times \boldsymbol{B}$![]() velocity also has a component in $\hat{M}$
velocity also has a component in $\hat{M}$![]() , the quasi-static electron velocities are related to the quasi-static ambipolar electric field. This shows how the ambipolar effect can enhance the inertial term, which is typically considered to be less important and usually ignored in estimates of the generalized Ohm's Law balance.
, the quasi-static electron velocities are related to the quasi-static ambipolar electric field. This shows how the ambipolar effect can enhance the inertial term, which is typically considered to be less important and usually ignored in estimates of the generalized Ohm's Law balance.
A previous study (Egedal et al. Reference Egedal, Ng, Le, Daughton, Wetherton, Dorelli, Gershman and Rager2019) of MMS data has shown that the off-diagonal pressure tensor can be responsible for breaking the frozen-in condition, but significant lower hybrid fluctuations were not detected in the reconnecting current sheet. Another study (Torbert et al. Reference Torbert, Burch, Giles, Gershman, Pollock, Dorelli, Avanov, Argall, Shuster and Strangeway2016a) has shown that the pressure and inertial terms may not actually be sufficient to balance the generalized Ohm's Law. We calculate the off-diagonal pressure tensor terms in $\hat{M}$![]() from MMS moments data using
from MMS moments data using
The pressure tensor terms depend on gradients in $\hat{L}$![]() and $\hat{N}$
and $\hat{N}$![]() , assuming $\partial /\partial M\sim 0$
, assuming $\partial /\partial M\sim 0$![]() (Egedal et al. Reference Egedal, Ng, Le, Daughton, Wetherton, Dorelli, Gershman and Rager2019). Figures 6(a) and 6(b) show the pressure terms, PLM and PMN, respectively, for each spacecraft. The signals have been shifted in time using the method described in § 2. There are several methods that can be used to calculate the gradients of the two terms in (3.7). First, if the spacecraft are moving across the current sheet in the same direction of the gradient, then one can take the direct gradient of the pressure by converting time to distance using the current sheet velocity. If there is a steady increase or decrease in the signals with no variations between the spacecraft signals, and the spacecraft motion is in the same direction as the gradient, then the gradient can also be calculated using $(\max - \min )/({x_{\max }} - {x_{\min }})$
(Egedal et al. Reference Egedal, Ng, Le, Daughton, Wetherton, Dorelli, Gershman and Rager2019). Figures 6(a) and 6(b) show the pressure terms, PLM and PMN, respectively, for each spacecraft. The signals have been shifted in time using the method described in § 2. There are several methods that can be used to calculate the gradients of the two terms in (3.7). First, if the spacecraft are moving across the current sheet in the same direction of the gradient, then one can take the direct gradient of the pressure by converting time to distance using the current sheet velocity. If there is a steady increase or decrease in the signals with no variations between the spacecraft signals, and the spacecraft motion is in the same direction as the gradient, then the gradient can also be calculated using $(\max - \min )/({x_{\max }} - {x_{\min }})$![]() , where ${x_{\max }}$
, where ${x_{\max }}$![]() is the position of the spacecraft in the gradient direction when the signal is the maximum point and ${x_{\min }}$
is the position of the spacecraft in the gradient direction when the signal is the maximum point and ${x_{\min }}$![]() is the position of the spacecraft in the gradient direction when the signal is at the minimum point. A more straightforward method depends on if there are variations in the signals for each spacecraft and can be used regardless of whether the spacecraft direction and the gradient direction are the same.
is the position of the spacecraft in the gradient direction when the signal is at the minimum point. A more straightforward method depends on if there are variations in the signals for each spacecraft and can be used regardless of whether the spacecraft direction and the gradient direction are the same.

Figure 6. Off-diagonal pressure tensor terms (a) PLM and (b) PMN measured by MMS1 (solid, black), MMS2 (dashed, yellow) and MMS3 (dash-dot, green). (c) Resulting pressure tensor gradient estimated from PMN data (solid, white) overlaid on the spectrogram of shear-driven lower hybrid fluctuations.
For our case of interest, the spacecraft are moving across the current sheet in $\hat{N}$![]() , making the second term in (3.7) straightforward to calculate using the third method. Figure 6(b) illustrates that during the time of the shear-driven lower hybrid waves, the MMS1 (solid, black) and MMS2 (dashed, yellow) measure relatively the same signal, while MMS3 (dash dot, green) is noticeably different. Therefore, the gradient can be calculated using $({P_{MN1}} - {P_{MN3}})/({N_1} - {N_3})$
, making the second term in (3.7) straightforward to calculate using the third method. Figure 6(b) illustrates that during the time of the shear-driven lower hybrid waves, the MMS1 (solid, black) and MMS2 (dashed, yellow) measure relatively the same signal, while MMS3 (dash dot, green) is noticeably different. Therefore, the gradient can be calculated using $({P_{MN1}} - {P_{MN3}})/({N_1} - {N_3})$![]() . This calculation can likewise be completed using MMS2 and MMS3 data, and then the average can be taken. The first term in (3.7) requires taking the gradient with respect to $\hat{L}$
. This calculation can likewise be completed using MMS2 and MMS3 data, and then the average can be taken. The first term in (3.7) requires taking the gradient with respect to $\hat{L}$![]() , which means only the third method is applicable to this calculation since spacecraft motion across the current sheet is in $\hat{N}$
, which means only the third method is applicable to this calculation since spacecraft motion across the current sheet is in $\hat{N}$![]() . Looking at figure 6(a), the PLM data have no variations between spacecraft during the region of interest (between 7 and 8 seconds). Therefore, the gradient of the PLM term in (3.7) cannot be estimated directly from the data. The pressure tensor gradient is therefore estimated using only the PMN term (figure 6c). There is a peak of approximately $- 2.8 \pm 4.5\ \textrm{mV}\ {\textrm{m}^{ - 1}}$
. Looking at figure 6(a), the PLM data have no variations between spacecraft during the region of interest (between 7 and 8 seconds). Therefore, the gradient of the PLM term in (3.7) cannot be estimated directly from the data. The pressure tensor gradient is therefore estimated using only the PMN term (figure 6c). There is a peak of approximately $- 2.8 \pm 4.5\ \textrm{mV}\ {\textrm{m}^{ - 1}}$![]() in the pressure tensor gradient during the time of the shear-driven lower hybrid fluctuations.
in the pressure tensor gradient during the time of the shear-driven lower hybrid fluctuations.
Interestingly, the related off-diagonal terms in the pressure tensor can be generated due to compression in a 2-D magnetic field, as was shown in studies of dipolarization fronts by Ganguli et al. (Reference Ganguli, Crabtree, Fletcher, Tejero, Malaspina and Cohen2018, Reference Ganguli, Crabtree, Fletcher and Amatucci2020). In a 2-D magnetic field, compression creates the 2-D ambipolar potential, $\varPhi \textrm{(}x,z\textrm{)}$![]() , which generates ${E_\parallel } \propto \partial \varPhi /\partial z$
, which generates ${E_\parallel } \propto \partial \varPhi /\partial z$![]() along the magnetic field line. Pressure anisotropy must arise to balance the ${E_\parallel }$
along the magnetic field line. Pressure anisotropy must arise to balance the ${E_\parallel }$![]() in a collisionless plasma. This indicates that the off-diagonal pressure tensor terms may be related to the ambipolar electric field through compression.
in a collisionless plasma. This indicates that the off-diagonal pressure tensor terms may be related to the ambipolar electric field through compression.
4. Conclusions
In situ measurements show that a localized perpendicular ambipolar electric field develops in a gyro-scale current sheet as it is compressed to a scale size of L cs < 2ρi. This perpendicular ambipolar electric field results in a strong electron sheared $\boldsymbol{E} \times \boldsymbol{B}$![]() velocity, which drives electrostatic lower hybrid fluctuations. A non-gyrotropic electron distribution function is observed and is shown to be generated by the shear in the perpendicular ambipolar electric field. This is noteworthy because it has been previously suggested that the presence of non-gyrotropic electron distribution functions may be a precursor to magnetic reconnection occurring. The sheared flow and non-gyrotropic electron distribution function observed in the current sheet cannot be described using the Harris equilibrium.
velocity, which drives electrostatic lower hybrid fluctuations. A non-gyrotropic electron distribution function is observed and is shown to be generated by the shear in the perpendicular ambipolar electric field. This is noteworthy because it has been previously suggested that the presence of non-gyrotropic electron distribution functions may be a precursor to magnetic reconnection occurring. The sheared flow and non-gyrotropic electron distribution function observed in the current sheet cannot be described using the Harris equilibrium.
The terms in generalized Ohm's Law can be estimated directly from the data. During the time of shear-driven lower hybrid waves, the cross-field diffusion increases rapidly from approximately 0 to $(30 \pm 12) \times {10^9}\ {\textrm{m}^2}\ {\textrm{s}^{ - 1}}$![]() and decreases back to near-zero as the shear-driven lower hybrid waves disappear. The cross-field diffusion relates the particle flow and the fluctuations in $\hat{N}$
and decreases back to near-zero as the shear-driven lower hybrid waves disappear. The cross-field diffusion relates the particle flow and the fluctuations in $\hat{N}$![]() . So, this rapid increase and decrease around the time of the shear-driven lower hybrid waves indicates that the waves can modify the reconnection process through the diffusion of momentum across the current sheet. The data also show that the wave-induced effects (anomalous resistivity and viscosity), pressure anisotropy effects and electron inertia peak during the time of the shear-driven lower hybrid fluctuations, and we find that all terms are comparable at the moment of the measurement. Therefore, the roles of the anomalous resistivity, viscosity, pressure tensor and electron inertia terms should be equally treated in determining the balance in the generalized Ohm's Law and the breaking of the frozen-in condition. It is noted that the relative influence of the different terms in the generalized Ohm's Law will very likely change as time proceeds, and the current sheet becomes more compressed and closer to reconnection. In future work, a statistical study of gyro-scale current sheets of different thicknesses will be conducted to compare how the terms in generalized Ohm's Law evolve and if certain terms become more significant than others.
. So, this rapid increase and decrease around the time of the shear-driven lower hybrid waves indicates that the waves can modify the reconnection process through the diffusion of momentum across the current sheet. The data also show that the wave-induced effects (anomalous resistivity and viscosity), pressure anisotropy effects and electron inertia peak during the time of the shear-driven lower hybrid fluctuations, and we find that all terms are comparable at the moment of the measurement. Therefore, the roles of the anomalous resistivity, viscosity, pressure tensor and electron inertia terms should be equally treated in determining the balance in the generalized Ohm's Law and the breaking of the frozen-in condition. It is noted that the relative influence of the different terms in the generalized Ohm's Law will very likely change as time proceeds, and the current sheet becomes more compressed and closer to reconnection. In future work, a statistical study of gyro-scale current sheets of different thicknesses will be conducted to compare how the terms in generalized Ohm's Law evolve and if certain terms become more significant than others.
These results are significant because they stress the importance of the perpendicular ambipolar electric field, which is the surrogate of global compression, in the current sheet physics and its impact on the reconnection process. The perpendicular ambipolar electric field can act as a free energy source to drive electrostatic lower hybrid fluctuations, which can provide anomalous resistivity and viscosity. It has also been suggested that the off-diagonal pressure tensor terms may be related to the ambipolar electric field through compression. This, and the fact that all terms were found to be comparable, indicate that multiple processes may be necessary to trigger magnetic reconnection. Therefore, breaking the frozen-in condition depends on the kinetic-scale features and dynamics occurring within gyro-scale current sheets.
In a forthcoming article (Crabtree et al. Reference Crabtree, Ganguli, DuBois and Sen2024), we generalize our model to 2-D and formally show that the primary driver of physics in the current sheet is the global compression. The compression results in thinning of the current sheet, which generates the highly inhomogeneous transverse ambipolar electric field when sufficiently thin. This, in turn, leads to velocity shear-driven phenomena and also introduces anisotropy in the pressure tensor, both of which affect the balance of the generalized Ohm's Law. The intensity of these phenomena is proportional to the scale size of the current sheet and hence to the intensity of the compression.
Acknowledgements
All MMS data used in this manuscript are publicly available and can be found online at the MMS Science Data Center. This work was supported by the Naval Research Laboratory Base Program.
Editor Troy Carter thanks the referees for their advice in evaluating this article.
Declaration of interests
The authors report no conflict of interest.