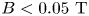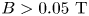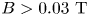1 Introduction
A spherical object or dust grain attains an equilibrium potential (or floating potential) when it is immersed in a plasma. At the floating potential, it draws a net zero current, i.e. the net flux of electrons and ions to the surface of the spherical object is zero. In low-temperature plasmas, where the electron temperature is much higher than the ion temperature (![]() $T_e \gg T_i$), the floating potential of the spherical particle mainly depends on the flux of energetic electrons to its surface and is always negative with respect to the plasma potential. In a dusty plasma, which is an admixture of the plasma species and submicron to micron-sized solid particles, the charge on the dust grains determines their collective dynamics such as dust acoustic waves (Barkan, Merlino & D'Angelo Reference Barkan, Merlino and D'Angelo1995; Bandyopadhyay et al. Reference Bandyopadhyay, Prasad, Sen and Kaw2008; Dharodi, Tiwari & Das Reference Dharodi, Tiwari and Das2014; Choudhary, Mukherjee & Bandyopadhyay Reference Choudhary, Mukherjee and Bandyopadhyay2016) and vortex motion (Law et al. Reference Law, Steel, Annaratone and Allen1998; Vaulina et al. Reference Vaulina, Samarian, Petrov, James and Melandso2004; Saitou & Ishihara Reference Saitou and Ishihara2013; Choudhary, Mukherjee & Bandyopadhyay Reference Choudhary, Mukherjee and Bandyopadhyay2017, Reference Choudhary, Mukherjee and Bandyopadhyay2018; Choudhary et al. Reference Choudhary, Bergert, Mitic and Thoma2020). In a dusty plasma, a dust particles are assumed to be spherical capacitors, which allows us to determine the surface potential and the net charge on it.
$T_e \gg T_i$), the floating potential of the spherical particle mainly depends on the flux of energetic electrons to its surface and is always negative with respect to the plasma potential. In a dusty plasma, which is an admixture of the plasma species and submicron to micron-sized solid particles, the charge on the dust grains determines their collective dynamics such as dust acoustic waves (Barkan, Merlino & D'Angelo Reference Barkan, Merlino and D'Angelo1995; Bandyopadhyay et al. Reference Bandyopadhyay, Prasad, Sen and Kaw2008; Dharodi, Tiwari & Das Reference Dharodi, Tiwari and Das2014; Choudhary, Mukherjee & Bandyopadhyay Reference Choudhary, Mukherjee and Bandyopadhyay2016) and vortex motion (Law et al. Reference Law, Steel, Annaratone and Allen1998; Vaulina et al. Reference Vaulina, Samarian, Petrov, James and Melandso2004; Saitou & Ishihara Reference Saitou and Ishihara2013; Choudhary, Mukherjee & Bandyopadhyay Reference Choudhary, Mukherjee and Bandyopadhyay2017, Reference Choudhary, Mukherjee and Bandyopadhyay2018; Choudhary et al. Reference Choudhary, Bergert, Mitic and Thoma2020). In a dusty plasma, a dust particles are assumed to be spherical capacitors, which allows us to determine the surface potential and the net charge on it.
In recent years, the research field of dusty or complex plasmas has been of interest due to its applications in space or solar plasmas (Goertz Reference Goertz1984, Reference Goertz1989; Mendis & Rosenberg Reference Mendis and Rosenberg1994), plasma processing technologies (Selwyn, Heidenreich & Haller Reference Selwyn, Heidenreich and Haller1991; Watanabe Reference Watanabe1997), fusion devices (Winter Reference Winter2000), colloidal solutions (Löwen et al. Reference Löwen, Royall, Ivlev and Morfill2011), etc. For studying the collective dynamics of the dust grain medium, the charge on the dust grains has to be known. In the last more than three decades, various experimental methods have been used to obtain the dust charge in an unmagnetized dusty plasma (Wu & Miller Reference Wu and Miller1990; Barkan, D'Angelo & Merlino Reference Barkan, D'Angelo and Merlino1994; Goree Reference Goree1994; Walch, Horanyi & Robertson Reference Walch, Horanyi and Robertson1994; Khrapak et al. Reference Khrapak, Ratynskaia, Zobnin, Usachev, Yaroshenko, Thoma, Kretschmer, Höfner, Morfill and Petrov2005). The experimentally measured dust charge values were compared with theoretically obtained values using the orbital motion limited (OML) approximation (Mott-Smith & Langmuir Reference Mott-Smith and Langmuir1926; Allen Reference Allen1992) and numerical simulations (Khrapak et al. Reference Khrapak, Ratynskaia, Zobnin, Usachev, Yaroshenko, Thoma, Kretschmer, Höfner, Morfill and Petrov2005). The OML theory describes the charging mechanism of submicron to micron-sized particles (![]() $r <\lambda _{De}$) in the plasma environment. Here,
$r <\lambda _{De}$) in the plasma environment. Here, ![]() $r$ is the radius of the particle and
$r$ is the radius of the particle and ![]() $\lambda _{De}$ is the electron Debye length. For large dust grains or spherical objects (
$\lambda _{De}$ is the electron Debye length. For large dust grains or spherical objects (![]() $r > \lambda _{De}$), the thin sheath theory (TS) or the modified OML theory (Willis et al. Reference Willis, Coppins, Bacharis and Allen2010) is suitable to understand the charging mechanism in an unmagnetized plasma.
$r > \lambda _{De}$), the thin sheath theory (TS) or the modified OML theory (Willis et al. Reference Willis, Coppins, Bacharis and Allen2010) is suitable to understand the charging mechanism in an unmagnetized plasma.
Nowadays, magnetized dusty plasma is a popular research topic among the dusty plasma community. It is well known that the dynamics of dusty plasmas depends on the characteristics of the background plasma that can be changed in the presence of an external magnetic field. Therefore, the ![]() $B$-field is considered as an external parameter to control the dynamics of the dust grain medium which may allow to us study fluid dynamics, solid state phenomena, turbulence, etc. at a microscopic level (Morfill & Ivlev Reference Morfill and Ivlev2009; Bonitz, Henning & Block Reference Bonitz, Henning and Block2010). Since the dust charge depends on the background plasma, the estimation of the accurate charge on dust grains (magnetic or non-magnetic) is a challenge depending on the magnetization of the plasma particles. In the last few years, theoretical as well as experimental works have been carried out to estimate the charge on dust grains in the magnetized plasma. Tsytovich, Sato & Morfill (Reference Tsytovich, Sato and Morfill2003) performed simulations to understand the charging mechanism of micron-sized dust particles in a magnetized plasma. It has been claimed that the
$B$-field is considered as an external parameter to control the dynamics of the dust grain medium which may allow to us study fluid dynamics, solid state phenomena, turbulence, etc. at a microscopic level (Morfill & Ivlev Reference Morfill and Ivlev2009; Bonitz, Henning & Block Reference Bonitz, Henning and Block2010). Since the dust charge depends on the background plasma, the estimation of the accurate charge on dust grains (magnetic or non-magnetic) is a challenge depending on the magnetization of the plasma particles. In the last few years, theoretical as well as experimental works have been carried out to estimate the charge on dust grains in the magnetized plasma. Tsytovich, Sato & Morfill (Reference Tsytovich, Sato and Morfill2003) performed simulations to understand the charging mechanism of micron-sized dust particles in a magnetized plasma. It has been claimed that the ![]() $B$-field influences the dust charging mechanism at a strong
$B$-field influences the dust charging mechanism at a strong ![]() $B$-field when the electron gyration radius is greater than the dust radius. Lange (Reference Lange2016) performed a simulation of a magnetized radio-frequency (rf) plasma and observed a smaller dust surface potential (or charge) at a lower magnetic field. The simulation of Patacchini, Hutchinson & Lapenta (Reference Patacchini, Hutchinson and Lapenta2007) demonstrated the decrease of the dust charge at all values of magnetic field in a collisonless plasma. A recent simulation (Kodanova et al. Reference Kodanova, Bastykova, Ramazanov, Nigmetova, Maiorov and Moldabekov2019) suggests that the dust charge starts to decrease after a critical value of
$B$-field when the electron gyration radius is greater than the dust radius. Lange (Reference Lange2016) performed a simulation of a magnetized radio-frequency (rf) plasma and observed a smaller dust surface potential (or charge) at a lower magnetic field. The simulation of Patacchini, Hutchinson & Lapenta (Reference Patacchini, Hutchinson and Lapenta2007) demonstrated the decrease of the dust charge at all values of magnetic field in a collisonless plasma. A recent simulation (Kodanova et al. Reference Kodanova, Bastykova, Ramazanov, Nigmetova, Maiorov and Moldabekov2019) suggests that the dust charge starts to decrease after a critical value of ![]() $B$-field in a magnetized plasma. Yukihiro et al. (Reference Yukihiro, Gakushi, Takatoshi and Osamu2009) reported a higher dust surface potential or large dust charge in a weakly magnetized plasma. Apart from analytical and numerical simulation studies, a few experiments have been performed to obtain the dust charge in a magnetized plasma. Kalita et al. (Reference Kalita, Kakati, Saikia, Bandyopadhyay and Kausik2015) have measured the dust charge in a weakly magnetized plasma (
$B$-field in a magnetized plasma. Yukihiro et al. (Reference Yukihiro, Gakushi, Takatoshi and Osamu2009) reported a higher dust surface potential or large dust charge in a weakly magnetized plasma. Apart from analytical and numerical simulation studies, a few experiments have been performed to obtain the dust charge in a magnetized plasma. Kalita et al. (Reference Kalita, Kakati, Saikia, Bandyopadhyay and Kausik2015) have measured the dust charge in a weakly magnetized plasma (![]() $B < 0.05\ \textrm {T}$) and found the role of the
$B < 0.05\ \textrm {T}$) and found the role of the ![]() $B$-field to be negligible on the dust charging mechanism. Tadsen, Greiner & Piel (Reference Tadsen, Greiner and Piel2018) have observed a reduction of the dust charge up to 50 % for nano-sized particles at a low magnetic field (
$B$-field to be negligible on the dust charging mechanism. Tadsen, Greiner & Piel (Reference Tadsen, Greiner and Piel2018) have observed a reduction of the dust charge up to 50 % for nano-sized particles at a low magnetic field (![]() $B < 0.01\ \textrm {T}$) in an rf discharge. In this work, the charge on nano-sized non-magnetic particles is determined by fitting the theoretical dispersion relation of dust-acoustic waves to the experimentally observed dispersion relation. An experimental work of Melzer et al. (Reference Melzer, Krüger, Schütt and Mulsow2019) shows a reduction in the dust charge at low magnetic field (
$B < 0.01\ \textrm {T}$) in an rf discharge. In this work, the charge on nano-sized non-magnetic particles is determined by fitting the theoretical dispersion relation of dust-acoustic waves to the experimentally observed dispersion relation. An experimental work of Melzer et al. (Reference Melzer, Krüger, Schütt and Mulsow2019) shows a reduction in the dust charge at low magnetic field (![]() $B < 0.02\ \textrm {T}$) and nearly constant value up to
$B < 0.02\ \textrm {T}$) and nearly constant value up to ![]() $B > 5\ \textrm {T}$. In their work, the charge on micron-sized dust grains is extracted by a normal mode analysis of the dust cluster in the magnetized rf plasma. A similar rf discharge configuration and normal mode analysis technique were used to get the charge on micron-sized paramagnetic particles at low
$B > 5\ \textrm {T}$. In their work, the charge on micron-sized dust grains is extracted by a normal mode analysis of the dust cluster in the magnetized rf plasma. A similar rf discharge configuration and normal mode analysis technique were used to get the charge on micron-sized paramagnetic particles at low ![]() $B$-field (
$B$-field (![]() $B < 0.01\ \textrm {T}$) and observed a nearly constant value of the dust charge (Puttscher & Melzer Reference Puttscher and Melzer2014). The inconsistencies in the numerically, as well as experimentally, observed values of the dust charge leave many open questions on the charging mechanism of spherical particles (magnetic and non-magnetic) in a magnetized plasma. Does the dust charge remain unchanged even though the magnetic field modifies the background plasma? How does it depend on the density of the plasma species and the background gas in the presence of a
$B < 0.01\ \textrm {T}$) and observed a nearly constant value of the dust charge (Puttscher & Melzer Reference Puttscher and Melzer2014). The inconsistencies in the numerically, as well as experimentally, observed values of the dust charge leave many open questions on the charging mechanism of spherical particles (magnetic and non-magnetic) in a magnetized plasma. Does the dust charge remain unchanged even though the magnetic field modifies the background plasma? How does it depend on the density of the plasma species and the background gas in the presence of a ![]() $B$-field? Do magnetic particles attain similar charges than non-magnetic particles? Does the surface potential of a dust grain show a size dependence in a magnetized plasma? Why does the experimentally estimated dust charge not vary according to the theoretical models?
$B$-field? Do magnetic particles attain similar charges than non-magnetic particles? Does the surface potential of a dust grain show a size dependence in a magnetized plasma? Why does the experimentally estimated dust charge not vary according to the theoretical models?
To answer some of these questions, a better understanding of the dust charging in an rf magnetized plasma is required. It is sometimes difficult to measure a small variation in the charge of micron-sized dust grains (![]() $r < \lambda _{De}$) while the background plasma parameters are changing in the presence of an external magnetic field. In laboratory experiments, it is easy to directly measure the surface potential of a large spherical conducting body (
$r < \lambda _{De}$) while the background plasma parameters are changing in the presence of an external magnetic field. In laboratory experiments, it is easy to directly measure the surface potential of a large spherical conducting body (![]() $r > \lambda _{De}$), which can be considered as a large dust grain in a magnetized plasma. The surface potential variation of a spherical probe (or large dust grain) in presence of an external magnetic field can provide information on a background plasma to minimize the errors in measuring the charge on micron-sized particles (
$r > \lambda _{De}$), which can be considered as a large dust grain in a magnetized plasma. The surface potential variation of a spherical probe (or large dust grain) in presence of an external magnetic field can provide information on a background plasma to minimize the errors in measuring the charge on micron-sized particles (![]() $r < \lambda _{De}$) in a magnetized dusty plasma. It is well known that the charge on an individual dust particle is higher (more negative) than that of a particle in the dust grain cluster. However, the variation of the dust charge of a single dust grain and dust cluster would be similar. Sometimes the surface potential of a large dust grain also helps us to understand the interactions among the micron-sized dust grains in a magnetized plasma. Keeping this in mind, experiments are planned to measure the surface potential of magnetic and non-magnetic spherical probes (or large dust particles) in a magnetized rf discharge.
$r < \lambda _{De}$) in a magnetized dusty plasma. It is well known that the charge on an individual dust particle is higher (more negative) than that of a particle in the dust grain cluster. However, the variation of the dust charge of a single dust grain and dust cluster would be similar. Sometimes the surface potential of a large dust grain also helps us to understand the interactions among the micron-sized dust grains in a magnetized plasma. Keeping this in mind, experiments are planned to measure the surface potential of magnetic and non-magnetic spherical probes (or large dust particles) in a magnetized rf discharge.
The investigations are carried out in a magnetized complex plasma device where an rf glow discharge is ignited between two electrodes, and a superconducting electromagnet is used to introduce the magnetic field. The surface potential of various sized magnetic (stainless steel (SS), SS-430, ![]() $\mu _r = 1800$) and non-magnetic (bronze,
$\mu _r = 1800$) and non-magnetic (bronze, ![]() $\mu _r \sim 1$) spherical probes (or large dust grains) has been measured in the unmagnetized and magnetized plasma at various discharge conditions. At a lower magnetic field, the magnitude of the surface potential of a spherical object increases to a maximum value and then starts to decrease with an increasing of the strength of the
$\mu _r \sim 1$) spherical probes (or large dust grains) has been measured in the unmagnetized and magnetized plasma at various discharge conditions. At a lower magnetic field, the magnitude of the surface potential of a spherical object increases to a maximum value and then starts to decrease with an increasing of the strength of the ![]() $B$-field. This trend is found to be independent of the size and type of material of the spherical object. However, the charging mechanism of magnetic and non-magnetic spherical objects depends on the magnetic field. The charge or surface potential of a non-magnetic spherical probe in the plasma is found to be smaller (less negative) than that of a magnetic sphere after a threshold value of a
$B$-field. This trend is found to be independent of the size and type of material of the spherical object. However, the charging mechanism of magnetic and non-magnetic spherical objects depends on the magnetic field. The charge or surface potential of a non-magnetic spherical probe in the plasma is found to be smaller (less negative) than that of a magnetic sphere after a threshold value of a ![]() $B$-field. Experimentally observed results are explained on the basis of the current collection to the surface of the object in the presence of a magnetic field.
$B$-field. Experimentally observed results are explained on the basis of the current collection to the surface of the object in the presence of a magnetic field.
The manuscript is organized as follows. Section 2 deals with the detailed description of the experimental set-up and the magnetized plasma production. The surface floating potential variation at various discharge conditions in unmagnetized and magnetized plasmas are discussed in § 3. Qualitative and quantitative explanations of the surface potential variation for magnetic and non-magnetic spheres are given in § 4. A brief summary of the work along with concluding remarks is provided in § 5.
2 Experimental set-up and diagnostics
The experimental set-up (magnetized dusty plasma device) consists of an aluminium vacuum chamber and a superconducting electromagnet, which is shown in figure 1(a). This device was previously used to study the dusty plasma in a strong magnetic field (Schwabe et al. Reference Schwabe, Konopka, Bandyopadhyay and Morfill2011). The schematic diagram of the experimental set-up is presented in figure 1(b). The superconducting electromagnet has a Helmholtz coil configuration to produce a uniform magnetic field at the centre of the vacuum chamber. The superconducting magnet consists of a helium compressor, a cooling head, eight sensors for temperature measurements, and a superconducting magnet power supply (0 to 80 A). At first, the plasma chamber is evacuated below ![]() $10^{-2}$ Pa using a pumping system consisting of a rotary and turbo molecular pump (known as a TMP). The experiments are performed in an argon plasma and the pressure of the argon gas inside the chamber is controlled by a mass flow controller (known as an MFC) and a gate valve controller. A 13.56 MHz rf generator with matching network is used to ignite the gas discharge between a stainless steel electrode (lower) and an indium tin oxide (ITO) coated glass electrode (upper) of 6.5 cm diameter. Both electrodes are separated by 3 cm. For the comparative study, stainless steel (SS-430,
$10^{-2}$ Pa using a pumping system consisting of a rotary and turbo molecular pump (known as a TMP). The experiments are performed in an argon plasma and the pressure of the argon gas inside the chamber is controlled by a mass flow controller (known as an MFC) and a gate valve controller. A 13.56 MHz rf generator with matching network is used to ignite the gas discharge between a stainless steel electrode (lower) and an indium tin oxide (ITO) coated glass electrode (upper) of 6.5 cm diameter. Both electrodes are separated by 3 cm. For the comparative study, stainless steel (SS-430, ![]() $\mu _r = 1800$, magnetic) spherical probes of radius 1.0 mm, 1.25 mm and 1.7 mm and a bronze (non-magnetic,
$\mu _r = 1800$, magnetic) spherical probes of radius 1.0 mm, 1.25 mm and 1.7 mm and a bronze (non-magnetic, ![]() $\mu _r \sim 1$) spherical probe of radius 1.5 mm are used. Opposite radial ports are used to insert the spherical probes and the emissive probe for measuring the floating and plasma potentials. The measurements are taken in the homogeneous plasma region where the magnetic field is uniform. The spherical probes are placed in the plasma using a ceramic tube of diameter 2 mm which protrudes into the plasma by a feed-through in the chamber wall and holds the spherical probes at its end. To avoid the floating potential perturbation due to the connecting aluminium tube (it holds ceramic tube), the length of the ceramic tube is taken longer so that it only remains in contact with the plasma, as is shown in figure 1(c). We have made a connection to the spherical probe in such a way as to keep the connection area as small as possible compared with the total surface area. For measuring the time-averaged floating potential (
$\mu _r \sim 1$) spherical probe of radius 1.5 mm are used. Opposite radial ports are used to insert the spherical probes and the emissive probe for measuring the floating and plasma potentials. The measurements are taken in the homogeneous plasma region where the magnetic field is uniform. The spherical probes are placed in the plasma using a ceramic tube of diameter 2 mm which protrudes into the plasma by a feed-through in the chamber wall and holds the spherical probes at its end. To avoid the floating potential perturbation due to the connecting aluminium tube (it holds ceramic tube), the length of the ceramic tube is taken longer so that it only remains in contact with the plasma, as is shown in figure 1(c). We have made a connection to the spherical probe in such a way as to keep the connection area as small as possible compared with the total surface area. For measuring the time-averaged floating potential (![]() $V_f$) of a spherical probe (or large dust grain), a high-impedance voltage divider (1200 : 1) is used. The spherical probe is connected to a high-value resistor (
$V_f$) of a spherical probe (or large dust grain), a high-impedance voltage divider (1200 : 1) is used. The spherical probe is connected to a high-value resistor (![]() $R_1 = 120\ \textrm {M}{\rm \Omega}$) to minimize the current flowing in the voltage divider circuit. First the voltage drop (
$R_1 = 120\ \textrm {M}{\rm \Omega}$) to minimize the current flowing in the voltage divider circuit. First the voltage drop (![]() $V_2$) with respect to ground due to this small current is measured across a low value resistor (
$V_2$) with respect to ground due to this small current is measured across a low value resistor (![]() $R_2 = 100\ \textrm {k}{\rm \Omega}$) and then the floating potential of the spherical probe (
$R_2 = 100\ \textrm {k}{\rm \Omega}$) and then the floating potential of the spherical probe (![]() $V_f$) is calculated by using the expression,
$V_f$) is calculated by using the expression, ![]() $V_f = (R_1 + R_2) V_2 /R_2$. In the present set of experiments, an emissive probe made of tungsten of radius 0.05 mm, placed perpendicular to the magnetic field lines, is used to measure the time-averaged plasma potential (
$V_f = (R_1 + R_2) V_2 /R_2$. In the present set of experiments, an emissive probe made of tungsten of radius 0.05 mm, placed perpendicular to the magnetic field lines, is used to measure the time-averaged plasma potential (![]() $V_p$). Floating potential method technique is used to measure
$V_p$). Floating potential method technique is used to measure ![]() $V_p$ in the absence and presence of the magnetic field (Fujita et al. Reference Fujita, Nowak, Hoegger and Schneider1980; Bradley, Thompson & Gonzalvo Reference Bradley, Thompson and Gonzalvo2001; Balan et al. Reference Balan, Schrittwieser, Ioniţă, Cabral, Figueiredo, Fernandes, Varandas, Adámek, Hron and Stöckel2003; Sheehan et al. Reference Sheehan, Raitses, Hershkowitz, Kaganovich and Fisch2011; Choudhary Reference Choudhary2017). It has been claimed in some studies that the floating potential method underestimates the plasma potential (Schrittwieser et al. Reference Schrittwieser, Ionita, Balan, Varandas, Figueiredo, Stoeckel, Adamek, Hron, Ryszawy and Tichy2005; Sheehan et al. Reference Sheehan, Raitses, Hershkowitz, Kaganovich and Fisch2011). In view of this, we have compared the plasma potential values obtained from the cold single Langmuir probe and the emissive probe. The floating potential method estimates the plasma potential lower by
$V_p$ in the absence and presence of the magnetic field (Fujita et al. Reference Fujita, Nowak, Hoegger and Schneider1980; Bradley, Thompson & Gonzalvo Reference Bradley, Thompson and Gonzalvo2001; Balan et al. Reference Balan, Schrittwieser, Ioniţă, Cabral, Figueiredo, Fernandes, Varandas, Adámek, Hron and Stöckel2003; Sheehan et al. Reference Sheehan, Raitses, Hershkowitz, Kaganovich and Fisch2011; Choudhary Reference Choudhary2017). It has been claimed in some studies that the floating potential method underestimates the plasma potential (Schrittwieser et al. Reference Schrittwieser, Ionita, Balan, Varandas, Figueiredo, Stoeckel, Adamek, Hron, Ryszawy and Tichy2005; Sheehan et al. Reference Sheehan, Raitses, Hershkowitz, Kaganovich and Fisch2011). In view of this, we have compared the plasma potential values obtained from the cold single Langmuir probe and the emissive probe. The floating potential method estimates the plasma potential lower by ![]() $<$2 V than estimated by a cold probe. This potential difference is within the error of
$<$2 V than estimated by a cold probe. This potential difference is within the error of ![]() $<$15 %. Thus, the floating potential method is useful to get an approximate value of plasma potential to obtain
$<$15 %. Thus, the floating potential method is useful to get an approximate value of plasma potential to obtain ![]() $V_s$.
$V_s$.

Figure 1. (a) Magnetized dusty plasma device. (b) Schematic diagram of the experiment set-up (1) superconducting electromagnet, (2) and (3) are superconductor coils, (4) power supply for magnet, (5) vacuum chamber, (6) upper electrode, (7) lower electrode, (8) 13.56 MHz rf generator with matching network, (9) emissive probe and (10) spherical probes. The direction of the magnetic field along the ![]() $Z$-direction is represented by a blue arrow. (c) Schematic diagram of the spherical probe (1) conducting (non-conducting) sphere, (2) connecting wire (insulation shielded), (3) ceramic tube of diameter 2 mm and (4) aluminium tube of diameter 6 mm.
$Z$-direction is represented by a blue arrow. (c) Schematic diagram of the spherical probe (1) conducting (non-conducting) sphere, (2) connecting wire (insulation shielded), (3) ceramic tube of diameter 2 mm and (4) aluminium tube of diameter 6 mm.
3 Measurements of surface potential of spherical objects
A spherical object or dust grain immersed in a plasma attains a negative potential to balance both the electron and ion currents to its surface. This equilibrium surface potential with respect to the plasma potential (![]() $V_p$) is termed as surface potential (
$V_p$) is termed as surface potential (![]() $V_s = V_p - V_f$) of the spherical object (Chen Reference Chen2003; Conde Reference Conde2011). It is stated in Willis et al. (Reference Willis, Coppins, Bacharis and Allen2010) that different analytical theories are valid for estimating the surface potential of an object in a Maxwellian plasma. The OML theory (Allen Reference Allen1992) is applicable for small objects (
$V_s = V_p - V_f$) of the spherical object (Chen Reference Chen2003; Conde Reference Conde2011). It is stated in Willis et al. (Reference Willis, Coppins, Bacharis and Allen2010) that different analytical theories are valid for estimating the surface potential of an object in a Maxwellian plasma. The OML theory (Allen Reference Allen1992) is applicable for small objects (![]() $\rho = r/\lambda _{De} \ll 1$) and the surface potential is derived by balancing the electron and ion fluxes to the surface of an object (Willis et al. Reference Willis, Coppins, Bacharis and Allen2010; Beadles, Wang & Horányi Reference Beadles, Wang and Horányi2017)
$\rho = r/\lambda _{De} \ll 1$) and the surface potential is derived by balancing the electron and ion fluxes to the surface of an object (Willis et al. Reference Willis, Coppins, Bacharis and Allen2010; Beadles, Wang & Horányi Reference Beadles, Wang and Horányi2017)
where ![]() $\varPhi = -V_s/T_e$,
$\varPhi = -V_s/T_e$, ![]() $T_e$ and
$T_e$ and ![]() $T_i$ are the electron and ion temperatures,
$T_i$ are the electron and ion temperatures, ![]() $m_e$ and
$m_e$ and ![]() $M_i$ are the electron and ion masses, respectively. For the large spherical object (
$M_i$ are the electron and ion masses, respectively. For the large spherical object (![]() $\rho \gg 1$), the TS is applicable to obtain
$\rho \gg 1$), the TS is applicable to obtain ![]() $V_s$. The surface potential for such spherical objects can be estimated by (Stangeby Reference Stangeby2000; Willis et al. Reference Willis, Coppins, Bacharis and Allen2010)
$V_s$. The surface potential for such spherical objects can be estimated by (Stangeby Reference Stangeby2000; Willis et al. Reference Willis, Coppins, Bacharis and Allen2010)
In the transition region between OML and TS theory, the orbital motion (known as OM) theory estimates the surface potential. Then ![]() $V_s$ is found to be a straight line fit on a log plot between the OML limit and TS limit (Willis et al. Reference Willis, Coppins, Bacharis and Allen2010; Beadles et al. Reference Beadles, Wang and Horányi2017). It is clear from (3.2) and (3.3) that the floating surface potential (
$V_s$ is found to be a straight line fit on a log plot between the OML limit and TS limit (Willis et al. Reference Willis, Coppins, Bacharis and Allen2010; Beadles et al. Reference Beadles, Wang and Horányi2017). It is clear from (3.2) and (3.3) that the floating surface potential (![]() $V_s$) of a large spherical object or small dust grain has an approximately linear relation with
$V_s$) of a large spherical object or small dust grain has an approximately linear relation with ![]() $T_e$,
$T_e$,
Here ![]() $\alpha$ is a constant varying from
$\alpha$ is a constant varying from ![]() $\sim$2.5 to 4 in the transition region between the OML and TS (
$\sim$2.5 to 4 in the transition region between the OML and TS (![]() $0.1 < \rho <10$) for an unmagnetized argon plasma (
$0.1 < \rho <10$) for an unmagnetized argon plasma (![]() $T_i \ll T_e$) (Willis et al. Reference Willis, Coppins, Bacharis and Allen2010; Beadles et al. Reference Beadles, Wang and Horányi2017). In a magnetized plasma,
$T_i \ll T_e$) (Willis et al. Reference Willis, Coppins, Bacharis and Allen2010; Beadles et al. Reference Beadles, Wang and Horányi2017). In a magnetized plasma, ![]() $V_s$ also depends on
$V_s$ also depends on ![]() $T_e$ but the value of
$T_e$ but the value of ![]() $\alpha$ may be lower or higher than that of an unmagnetized plasma. For finding the value of the floating surface potential,
$\alpha$ may be lower or higher than that of an unmagnetized plasma. For finding the value of the floating surface potential, ![]() $V_s = V_p - V_f$, of a spherical conducting probe in the plasma, it is necessary to measure the plasma potential (
$V_s = V_p - V_f$, of a spherical conducting probe in the plasma, it is necessary to measure the plasma potential (![]() $V_p$) as a reference potential. By knowing the surface potential (
$V_p$) as a reference potential. By knowing the surface potential (![]() $V_s$), the charge on the surface (
$V_s$), the charge on the surface (![]() $Q_s$) of a small dust grain (
$Q_s$) of a small dust grain (![]() $r <\lambda _{De}$) and large dust grain (
$r <\lambda _{De}$) and large dust grain (![]() $r >\lambda _{De}$) can be estimated using the different approximations (Delzanno & Tang Reference Delzanno and Tang2015).
$r >\lambda _{De}$) can be estimated using the different approximations (Delzanno & Tang Reference Delzanno and Tang2015).
3.1 Surface potential of spherical probes in unmagnetized plasma
The present work deals with spherical probes (large dust grains) of radius larger than the electron Debye length, i.e. ![]() $r > \lambda _{De}$. Stainless steel spheres of radius 1.0 mm, 1.25 mm and 1.7 mm are used to study the size dependence of the surface potential. A pair of spherical probes of different sizes (separated by 14 mm) is placed in the plasma volume, as shown in the schematic diagram (see figure 1b). It should be noted that both probes are placed in the horizontal (
$r > \lambda _{De}$. Stainless steel spheres of radius 1.0 mm, 1.25 mm and 1.7 mm are used to study the size dependence of the surface potential. A pair of spherical probes of different sizes (separated by 14 mm) is placed in the plasma volume, as shown in the schematic diagram (see figure 1b). It should be noted that both probes are placed in the horizontal (![]() $X$–
$X$–![]() $Y$) plane. The distance between the probes is decided after successive measurements of
$Y$) plane. The distance between the probes is decided after successive measurements of ![]() $V_f$ for both spherical probes at similar discharge conditions in the presence of a
$V_f$ for both spherical probes at similar discharge conditions in the presence of a ![]() $B$-field. These successive measurements are taken at the centre of the plasma volume whereas the simultaneous measurements on both sides of the centre are performed to keep both probes in the homogeneous plasma background. The difference between the successive and simultaneous measured values of
$B$-field. These successive measurements are taken at the centre of the plasma volume whereas the simultaneous measurements on both sides of the centre are performed to keep both probes in the homogeneous plasma background. The difference between the successive and simultaneous measured values of ![]() $V_f$ at the same discharge condition are found to be
$V_f$ at the same discharge condition are found to be ![]() $<$0.3 V, which is
$<$0.3 V, which is ![]() $<$2–3 % of the actual value. Therefore, we neglect the shadow/potential overlapping effect of an individual sphere on each other during the simultaneous measurements of
$<$2–3 % of the actual value. Therefore, we neglect the shadow/potential overlapping effect of an individual sphere on each other during the simultaneous measurements of ![]() $V_f$ for the comparative study. It is known that dust grains (
$V_f$ for the comparative study. It is known that dust grains (![]() $\mathrm {\mu }\textrm {m}$ to mm) respond only to a very low frequency external field (
$\mathrm {\mu }\textrm {m}$ to mm) respond only to a very low frequency external field (![]() $\sim$1 to 100Hz). They do not respond to a high frequency field of an rf discharge. In view of this, it is our aim to measure the time-averaged or DC potential of the spherical probes in the rf discharge.
$\sim$1 to 100Hz). They do not respond to a high frequency field of an rf discharge. In view of this, it is our aim to measure the time-averaged or DC potential of the spherical probes in the rf discharge.
Figures 2(a) and 2(b) show the time-averaged ![]() $V_p$,
$V_p$, ![]() $V_f$ and
$V_f$ and ![]() $V_s$ for different rf powers at constant pressure and for different pressures at constant power, respectively. We see a slight variation in the potentials at different discharge conditions in the absence of the magnetic field (
$V_s$ for different rf powers at constant pressure and for different pressures at constant power, respectively. We see a slight variation in the potentials at different discharge conditions in the absence of the magnetic field (![]() $B = 0\ \textrm {T}$). To see the effect of the object size on
$B = 0\ \textrm {T}$). To see the effect of the object size on ![]() $V_s$ at a given discharge condition (
$V_s$ at a given discharge condition (![]() $P = 12\ \textrm {W}$ and
$P = 12\ \textrm {W}$ and ![]() $p = 30 \ \textrm {Pa}$), the floating potential of the stainless steel spherical probes of different sizes are measured. The variation of
$p = 30 \ \textrm {Pa}$), the floating potential of the stainless steel spherical probes of different sizes are measured. The variation of ![]() $V_s$ for different sized spherical probes is depicted in figure 3. For finding the theoretical values of
$V_s$ for different sized spherical probes is depicted in figure 3. For finding the theoretical values of ![]() $V_s$ for the given discharge conditions, the plasma density (
$V_s$ for the given discharge conditions, the plasma density (![]() $n$) and electron temperature are measured using the double probe (Johnson & Malter Reference Johnson and Malter1950; Nobata Reference Nobata1963; Choudhary Reference Choudhary2017).
$n$) and electron temperature are measured using the double probe (Johnson & Malter Reference Johnson and Malter1950; Nobata Reference Nobata1963; Choudhary Reference Choudhary2017).

Figure 2. (a) Time-averaged floating potential (![]() $V_f$), plasma potential (
$V_f$), plasma potential (![]() $V_p$) and surface potential (
$V_p$) and surface potential (![]() $V_s$) of the spherical stainless steel probe (
$V_s$) of the spherical stainless steel probe (![]() $r = 1.7 \ \textrm {mm}$) for different input rf powers at fixed pressure,
$r = 1.7 \ \textrm {mm}$) for different input rf powers at fixed pressure, ![]() $p = 30\ \textrm {Pa}$ in an unmagnetized plasma. (b) The
$p = 30\ \textrm {Pa}$ in an unmagnetized plasma. (b) The ![]() $V_f$,
$V_f$, ![]() $V_p$ and
$V_p$ and ![]() $V_s$ of the same spherical probe for different argon pressures at fixed rf power
$V_s$ of the same spherical probe for different argon pressures at fixed rf power ![]() $P = 12\ \textrm {W}$ in an unmagnetized plasma. The plotted values of
$P = 12\ \textrm {W}$ in an unmagnetized plasma. The plotted values of ![]() $V_f$ and
$V_f$ and ![]() $V_p$ are averaged over few data sets at given discharge condition.
$V_p$ are averaged over few data sets at given discharge condition.

Figure 3. Experimental and theoretical surface potentials (![]() $V_s$) of different sized stainless steel spherical probes (
$V_s$) of different sized stainless steel spherical probes (![]() $r = 1$, 1.25 and 1.7 mm) at rf power,
$r = 1$, 1.25 and 1.7 mm) at rf power, ![]() $P = 12\ \textrm {W}$ and gas pressure,
$P = 12\ \textrm {W}$ and gas pressure, ![]() $p = 30\ \textrm {Pa}$ in an unmagnetized plasma. The error in measuring the plasma potential is
$p = 30\ \textrm {Pa}$ in an unmagnetized plasma. The error in measuring the plasma potential is ![]() ${<}\pm$5 % and floating potential is
${<}\pm$5 % and floating potential is ![]() ${<}\pm$2 %. Both errors are included over the average values.
${<}\pm$2 %. Both errors are included over the average values.
The double probe is made of two tungsten wires (or single probes) of radius 0.15 mm and length 8 mm. Both probes are separated by ![]() $\sim$7 mm. At
$\sim$7 mm. At ![]() $p = 30\ \textrm {Pa}$, the plasma is moderately collisional; therefore the collisionless OML theory (Mott-Smith & Langmuir Reference Mott-Smith and Langmuir1926; Chen Reference Chen2003) of the cylindrical probe underestimates the plasma density. To measure the approximate plasma density, the collisional model for the ion current to the cylindrical probe is used (Tichy et al. Reference Tichy, Kudrna, Behnke, Csambal and Klagge1997; Kudrna & Passoth Reference Kudrna and Passoth2007). The variation of
$p = 30\ \textrm {Pa}$, the plasma is moderately collisional; therefore the collisionless OML theory (Mott-Smith & Langmuir Reference Mott-Smith and Langmuir1926; Chen Reference Chen2003) of the cylindrical probe underestimates the plasma density. To measure the approximate plasma density, the collisional model for the ion current to the cylindrical probe is used (Tichy et al. Reference Tichy, Kudrna, Behnke, Csambal and Klagge1997; Kudrna & Passoth Reference Kudrna and Passoth2007). The variation of ![]() $T_e$ and
$T_e$ and ![]() $n$ with different rf powers is depicted in figure 4. At this discharge condition,
$n$ with different rf powers is depicted in figure 4. At this discharge condition, ![]() $\lambda _{De}$ is
$\lambda _{De}$ is ![]() $\sim$0.3 mm, which gives
$\sim$0.3 mm, which gives ![]() $2 <\rho < 6$. The theoretically estimated values corresponding to this
$2 <\rho < 6$. The theoretically estimated values corresponding to this ![]() $\rho$ (Willis et al. Reference Willis, Coppins, Bacharis and Allen2010) are plotted with experimental data (figure 3) and found to be in good agreement within the error of
$\rho$ (Willis et al. Reference Willis, Coppins, Bacharis and Allen2010) are plotted with experimental data (figure 3) and found to be in good agreement within the error of ![]() $\sim$10 %, which is expected due to the plasma collisionality. It confirms that the surface potential of a spherical object depends on its size in a low-temperature unmagnetized plasma (
$\sim$10 %, which is expected due to the plasma collisionality. It confirms that the surface potential of a spherical object depends on its size in a low-temperature unmagnetized plasma (![]() $T_e \gg T_i$).
$T_e \gg T_i$).

Figure 4. Plasma density (![]() $n$) and electron temperature (
$n$) and electron temperature (![]() $T_e$) at different rf powers. The measurements are carried out at fixed argon pressure,
$T_e$) at different rf powers. The measurements are carried out at fixed argon pressure, ![]() $p = 30\ \textrm {Pa}$ in unmagnetized plasma.
$p = 30\ \textrm {Pa}$ in unmagnetized plasma.
3.2 Surface potential of spherical probes in magnetized plasma
For producing the magnetized plasma, a ![]() $B$-field perpendicular to the plane of electrode (in the
$B$-field perpendicular to the plane of electrode (in the ![]() $Z$-direction) is applied. In figure 5 the surface potential of the SS probe of radius 1.25 mm and bronze probe of radius 1.5 mm at various strengths of the magnetic field are presented. It should be noted that the
$Z$-direction) is applied. In figure 5 the surface potential of the SS probe of radius 1.25 mm and bronze probe of radius 1.5 mm at various strengths of the magnetic field are presented. It should be noted that the ![]() $B$-field is uniform in the entire plasma region at
$B$-field is uniform in the entire plasma region at ![]() $B = 0.2\ \textrm {T}$. The plots in figure 5(a) show the variation of
$B = 0.2\ \textrm {T}$. The plots in figure 5(a) show the variation of ![]() $V_s$ for different input rf powers,
$V_s$ for different input rf powers, ![]() $P = 3.5$, 6.5 and 12 W at a fixed pressure,
$P = 3.5$, 6.5 and 12 W at a fixed pressure, ![]() $p = 30\ \textrm {Pa}$. It is clearly seen in this figure that
$p = 30\ \textrm {Pa}$. It is clearly seen in this figure that ![]() $V_s$ first increases (becomes more negative) at low
$V_s$ first increases (becomes more negative) at low ![]() $B$ (
$B$ (![]() $B < 0.05\ \textrm {T}$), attains a maximum value and after that it starts to decrease (becomes less negative) at higher magnetic field strength (
$B < 0.05\ \textrm {T}$), attains a maximum value and after that it starts to decrease (becomes less negative) at higher magnetic field strength (![]() $B > 0.05\ \textrm {T}$). The rate of change of
$B > 0.05\ \textrm {T}$). The rate of change of ![]() $V_s$ is observed to be different in the low
$V_s$ is observed to be different in the low ![]() $B$-field region (
$B$-field region (![]() $B < 0.05\ \textrm {T}$) and high
$B < 0.05\ \textrm {T}$) and high ![]() $B$-field region (
$B$-field region (![]() $B > 0.05\ \textrm {T}$) at a given input power. It is also noticed that
$B > 0.05\ \textrm {T}$) at a given input power. It is also noticed that ![]() $V_s$ attains its maximum value at low
$V_s$ attains its maximum value at low ![]() $B$-field at a lower input power (
$B$-field at a lower input power (![]() $P = 3.5\ \textrm {W}$) and at high
$P = 3.5\ \textrm {W}$) and at high ![]() $B$-field at a higher input power (
$B$-field at a higher input power (![]() $P = 12\ \textrm {W}$).
$P = 12\ \textrm {W}$).

Figure 5. (a) Time–averaged surface potential (![]() $V_s$) of the stainless steel spherical probe (
$V_s$) of the stainless steel spherical probe (![]() $r = 1.25\ \textrm {mm}$) for different rf powers at fixed pressure,
$r = 1.25\ \textrm {mm}$) for different rf powers at fixed pressure, ![]() $p = 30\ \textrm {Pa}$, in the plasma at different strengths of the magnetic field. The dotted line represents the shifting of the maxima of
$p = 30\ \textrm {Pa}$, in the plasma at different strengths of the magnetic field. The dotted line represents the shifting of the maxima of ![]() $V_s$ with increasing the input rf power. (b) Time-averaged
$V_s$ with increasing the input rf power. (b) Time-averaged ![]() $V_s$ of the stainless steel spherical probe (
$V_s$ of the stainless steel spherical probe (![]() $r = 1.25\ \textrm {mm}$) for different argon pressures at rf power,
$r = 1.25\ \textrm {mm}$) for different argon pressures at rf power, ![]() $P = 12\ \textrm {W}$ in magnetized plasma. (c) Time–averaged
$P = 12\ \textrm {W}$ in magnetized plasma. (c) Time–averaged ![]() $V_s$ of the bronze spherical probe (
$V_s$ of the bronze spherical probe (![]() $r = 1.5\ \textrm {mm}$) for different argon pressures at rf power,
$r = 1.5\ \textrm {mm}$) for different argon pressures at rf power, ![]() $P = 12\ \textrm {W}$ in the plasma at different strengths of magnetic field. Here, the plotted values of
$P = 12\ \textrm {W}$ in the plasma at different strengths of magnetic field. Here, the plotted values of ![]() $V_s$ are averaged over few data sets at given discharge condition.
$V_s$ are averaged over few data sets at given discharge condition.
The variation of ![]() $V_s$ at a given power (
$V_s$ at a given power (![]() $P = 12\ \textrm {W}$) and different pressures,
$P = 12\ \textrm {W}$) and different pressures, ![]() $p = 15$, 30 and 50 Pa with the magnetic field strength is presented in figure 5(b). The rate of change of
$p = 15$, 30 and 50 Pa with the magnetic field strength is presented in figure 5(b). The rate of change of ![]() $V_s$ is less at higher pressures for
$V_s$ is less at higher pressures for ![]() $B > 0.05\ \textrm {T}$. It confirms the
$B > 0.05\ \textrm {T}$. It confirms the ![]() $V_s$ dependence on the plasma collisionality. Moreover,
$V_s$ dependence on the plasma collisionality. Moreover, ![]() $V_s$ achieves its maximum value at lower
$V_s$ achieves its maximum value at lower ![]() $B$ if the gas pressure is reduced. A similar trend of
$B$ if the gas pressure is reduced. A similar trend of ![]() $V_s$ variation is observed for the different sized magnetic spherical probes in the presence of a
$V_s$ variation is observed for the different sized magnetic spherical probes in the presence of a ![]() $B$-field. The variation of
$B$-field. The variation of ![]() $V_s$ against
$V_s$ against ![]() $B$ for a non-magnetic sphere (bronze) is depicted in figure 5(c). The surface potential shows a similar trend to that of the magnetic sphere (figure 5b) in the presence of a
$B$ for a non-magnetic sphere (bronze) is depicted in figure 5(c). The surface potential shows a similar trend to that of the magnetic sphere (figure 5b) in the presence of a ![]() $B$-field. However, the rate of change of
$B$-field. However, the rate of change of ![]() $V_s$ for the non-magnetic and magnetic sphere are different at the same discharge conditions.
$V_s$ for the non-magnetic and magnetic sphere are different at the same discharge conditions.
3.3 Comparison of surface potentials
The ![]() $V_s$ data of the magnetic probes and the non-magnetic probe are compared to see the fundamental differences in the charging mechanism in a magnetized plasma. Comparison of
$V_s$ data of the magnetic probes and the non-magnetic probe are compared to see the fundamental differences in the charging mechanism in a magnetized plasma. Comparison of ![]() $V_s$ for the magnetic and non-magnetic spheres at different
$V_s$ for the magnetic and non-magnetic spheres at different ![]() $B$-field is depicted in figure 6. We take simultaneous measurements of the floating potential of a pair of spherical probes at a given discharge condition. At the same discharge condition, the floating potential is measured for different pairs of spherical probes with different sizes. It should be noted that the error in
$B$-field is depicted in figure 6. We take simultaneous measurements of the floating potential of a pair of spherical probes at a given discharge condition. At the same discharge condition, the floating potential is measured for different pairs of spherical probes with different sizes. It should be noted that the error in ![]() $V_f$ measurement is
$V_f$ measurement is ![]() ${<}\pm$2 % and the reference potential (
${<}\pm$2 % and the reference potential (![]() $V_p$) is common for all measurements at similar discharge conditions. This gives almost an accurate trend of the potential difference. In figure 6(a) the surface potential of the bronze probe has been subtracted from the magnetic ones. It is reconstructed from the
$V_p$) is common for all measurements at similar discharge conditions. This gives almost an accurate trend of the potential difference. In figure 6(a) the surface potential of the bronze probe has been subtracted from the magnetic ones. It is reconstructed from the ![]() $V_s$ data for different sized (
$V_s$ data for different sized (![]() $r = 1.0\ \textrm {mm}$, 1.25 mm and 1.7 mm) SS and bronze (
$r = 1.0\ \textrm {mm}$, 1.25 mm and 1.7 mm) SS and bronze (![]() $r = 1.5\ \textrm {mm}$) probes to compare the size dependence in the presence of the
$r = 1.5\ \textrm {mm}$) probes to compare the size dependence in the presence of the ![]() $B$-field. It is clear from figure 6(a) that the smaller sized magnetic sphere (e.g.
$B$-field. It is clear from figure 6(a) that the smaller sized magnetic sphere (e.g. ![]() $r = 1\ \textrm {mm}$) has a higher value of
$r = 1\ \textrm {mm}$) has a higher value of ![]() $V_s$ than the non-magnetic sphere (e.g.
$V_s$ than the non-magnetic sphere (e.g. ![]() $r = 1.5\ \textrm {mm}$) above
$r = 1.5\ \textrm {mm}$) above ![]() $B > 0.03\ \textrm {T}$. This difference in
$B > 0.03\ \textrm {T}$. This difference in ![]() $V_s$ increases with increasing
$V_s$ increases with increasing ![]() $B$-field. It means that equally sized magnetic and non-magnetic spherical objects or dust grains have different charges in a magnetized rf discharge. Figure 6(b) compares the surface potential of the different sized magnetic spheres to see the role of the
$B$-field. It means that equally sized magnetic and non-magnetic spherical objects or dust grains have different charges in a magnetized rf discharge. Figure 6(b) compares the surface potential of the different sized magnetic spheres to see the role of the ![]() $B$-field in the determination of
$B$-field in the determination of ![]() $V_s$. It is seen in figure 6(b) that the difference in
$V_s$. It is seen in figure 6(b) that the difference in ![]() $V_s$ for different sized magnetic probes decreases with increasing magnetic field and remains almost constant at higher
$V_s$ for different sized magnetic probes decreases with increasing magnetic field and remains almost constant at higher ![]() $B$-field (
$B$-field (![]() $B > 0.05\ \textrm {T}$). It shows that
$B > 0.05\ \textrm {T}$). It shows that ![]() $\alpha$ remains almost constant for all sized spherical probes at higher
$\alpha$ remains almost constant for all sized spherical probes at higher ![]() $B$-field,
$B$-field, ![]() $B > 0.05\ \textrm {T}$. In other words,
$B > 0.05\ \textrm {T}$. In other words, ![]() $V_s$ has a much weaker size dependence in a magnetized rf plasma.
$V_s$ has a much weaker size dependence in a magnetized rf plasma.

Figure 6. (a) The surface potential difference (![]() $V_d$) for non-magnetic (bronze) and magnetic (SS) spherical probes at pressure,
$V_d$) for non-magnetic (bronze) and magnetic (SS) spherical probes at pressure, ![]() $p = 30\ \textrm {Pa}$ and rf power,
$p = 30\ \textrm {Pa}$ and rf power, ![]() $p = 12\ \textrm {W}$ in the plasma at various strengths of the magnetic field. (b) The difference of
$p = 12\ \textrm {W}$ in the plasma at various strengths of the magnetic field. (b) The difference of ![]() $V_s$ for different sized magnetic (SS) spherical probes at pressure,
$V_s$ for different sized magnetic (SS) spherical probes at pressure, ![]() $p = 30\ \textrm {Pa}$ and rf power,
$p = 30\ \textrm {Pa}$ and rf power, ![]() $P = 12\ \textrm {W}$ in magnetized plasma.
$P = 12\ \textrm {W}$ in magnetized plasma.
4 Discussion
The surface potential of a spherical probe or dust grain is determined by the electron and ion currents to its surface. In a low-temperature plasma, where ![]() $T_i \ll T_e$, the surface potential is mainly determined by
$T_i \ll T_e$, the surface potential is mainly determined by ![]() $T_e$. Since
$T_e$. Since ![]() $v_{\textrm {the}}\gg v_{\textrm {thi}}$, the surface potential is always negative with respect to the plasma potential. Here,
$v_{\textrm {the}}\gg v_{\textrm {thi}}$, the surface potential is always negative with respect to the plasma potential. Here, ![]() $v_{\textrm {the}}$ and
$v_{\textrm {the}}$ and ![]() $v_{\textrm {thi}}$ are the electron and ion thermal velocities, respectively. In an unmagnetized rf discharge plasma (at
$v_{\textrm {thi}}$ are the electron and ion thermal velocities, respectively. In an unmagnetized rf discharge plasma (at ![]() $B = 0\ \textrm {T}$), the surface potential of a spherical object of the radius
$B = 0\ \textrm {T}$), the surface potential of a spherical object of the radius ![]() $r > \lambda _{De}$ is estimated using the theoretical value of
$r > \lambda _{De}$ is estimated using the theoretical value of ![]() $\alpha$ in the transition region between OML and TS regions (Willis et al. Reference Willis, Coppins, Bacharis and Allen2010, Reference Willis, Coppins, Bacharis and Allen2012). A slight variation in
$\alpha$ in the transition region between OML and TS regions (Willis et al. Reference Willis, Coppins, Bacharis and Allen2010, Reference Willis, Coppins, Bacharis and Allen2012). A slight variation in ![]() $T_e$ (see figure 4) with increasing the power and pressure demonstrates a negligible change in
$T_e$ (see figure 4) with increasing the power and pressure demonstrates a negligible change in ![]() $V_s$ in the unmagnetized plasma (see figure 2).
$V_s$ in the unmagnetized plasma (see figure 2).
With the application of a magnetic field, the gyroradius of electrons (![]() $r_{\textrm {ge}} = m_e v_{\textrm {the}}/e B$) and of ions (
$r_{\textrm {ge}} = m_e v_{\textrm {the}}/e B$) and of ions (![]() $r_{\textrm {gi}} = m_i v_{\textrm {thi}}/e B$) decreases with increasing
$r_{\textrm {gi}} = m_i v_{\textrm {thi}}/e B$) decreases with increasing ![]() $B$-field. Due to the mass differences, electrons are magnetized at lower magnetic field than ions, i.e.
$B$-field. Due to the mass differences, electrons are magnetized at lower magnetic field than ions, i.e. ![]() $r_{\textrm {ge}} \ll r_{\textrm {gi}}$. The electrons and ions are considered to be magnetized when the gyration frequency of the respective species (
$r_{\textrm {ge}} \ll r_{\textrm {gi}}$. The electrons and ions are considered to be magnetized when the gyration frequency of the respective species (![]() $\omega _{\textrm {ce}/\textrm {ci}}$) is higher than the collisional frequency (
$\omega _{\textrm {ce}/\textrm {ci}}$) is higher than the collisional frequency (![]() $\nu _{e-n/i-n}$), i.e.
$\nu _{e-n/i-n}$), i.e. ![]() $r_{\textrm {ge}/i}<\lambda _{e-n/i-n}$. Here
$r_{\textrm {ge}/i}<\lambda _{e-n/i-n}$. Here ![]() $\lambda _{e/i}$ is the collisional mean free path for the respective species. In our experiments (
$\lambda _{e/i}$ is the collisional mean free path for the respective species. In our experiments (![]() $p = 15$ to 50 Pa and
$p = 15$ to 50 Pa and ![]() $P = 3.5$ to 12 W),
$P = 3.5$ to 12 W), ![]() $n$ and
$n$ and ![]() $T_e$ are observed to varybetween
$T_e$ are observed to varybetween ![]() ${\sim }6\times 10^{14}\ \textrm {m}^{-3}$ and
${\sim }6\times 10^{14}\ \textrm {m}^{-3}$ and ![]() $3\times 10^{15}\ \textrm {m}^{-3}$ and 3–5 eV, respectively. The mean free path of electrons,
$3\times 10^{15}\ \textrm {m}^{-3}$ and 3–5 eV, respectively. The mean free path of electrons, ![]() $\lambda _{e-n} = 1/n_g \sigma _{e-n} \sim 14\text {--}3\ \textrm {mm}$ and ions,
$\lambda _{e-n} = 1/n_g \sigma _{e-n} \sim 14\text {--}3\ \textrm {mm}$ and ions, ![]() $\lambda _{i-n} = 1/n_g \sigma _{i-n} \sim 0.2\text {--}0.08\ \textrm {mm}$. Here
$\lambda _{i-n} = 1/n_g \sigma _{i-n} \sim 0.2\text {--}0.08\ \textrm {mm}$. Here ![]() $\sigma _{e-n} \sim 2\times 10^{-20}\ \textrm {m}^{2}$ and
$\sigma _{e-n} \sim 2\times 10^{-20}\ \textrm {m}^{2}$ and ![]() $\sigma _{i-n} \sim 1\times 10^{-18}\ \textrm {m}^{2}$ are the collision cross-sections of electrons and ions with argon atoms, respectively
$\sigma _{i-n} \sim 1\times 10^{-18}\ \textrm {m}^{2}$ are the collision cross-sections of electrons and ions with argon atoms, respectively
(Benyoucef et al. Reference Benyoucef, Yousfi, Belmadani and Settaouti2010), and ![]() $n_g$ is the neutral gas density. The electron gyroradius varies between
$n_g$ is the neutral gas density. The electron gyroradius varies between ![]() $r_{\textrm {ge}} \sim 0.5\text {--}0.7\ \textrm {mm}$ for
$r_{\textrm {ge}} \sim 0.5\text {--}0.7\ \textrm {mm}$ for ![]() $B = 0.01\ \textrm {T}$ at given discharge conditions. Therefore, the condition
$B = 0.01\ \textrm {T}$ at given discharge conditions. Therefore, the condition ![]() $r_{\textrm {ge}} < \lambda _{e-n}$ meets even below
$r_{\textrm {ge}} < \lambda _{e-n}$ meets even below ![]() $B = 0.01\ \textrm {T}$. With an increasing of the strength of the magnetic field (
$B = 0.01\ \textrm {T}$. With an increasing of the strength of the magnetic field (![]() $B > 0.01\ \textrm {T}$),
$B > 0.01\ \textrm {T}$), ![]() $r_{\textrm {ge}}$ continuously decreases and electrons are fully magnetized. Ions are assumed to be at room temperature, i.e.
$r_{\textrm {ge}}$ continuously decreases and electrons are fully magnetized. Ions are assumed to be at room temperature, i.e. ![]() $T_i \sim 0.03\ \textrm {eV}$. The ion gyroradius
$T_i \sim 0.03\ \textrm {eV}$. The ion gyroradius ![]() $r_{\textrm {gi}}$ at
$r_{\textrm {gi}}$ at ![]() $B = 0.2\ \textrm {T}$ is estimated as
$B = 0.2\ \textrm {T}$ is estimated as ![]() $\sim$0.5 mm, which indicates that ions get magnetized at high magnetic field,
$\sim$0.5 mm, which indicates that ions get magnetized at high magnetic field, ![]() $B > 0.2\ \textrm {T}$. It essentially means that in the range of the magnetic field (
$B > 0.2\ \textrm {T}$. It essentially means that in the range of the magnetic field (![]() $B< 0.2\ \textrm {T}$), only electrons are magnetized but ions are assumed to be unmagnetized. In a magnetized plasma, the currents
$B< 0.2\ \textrm {T}$), only electrons are magnetized but ions are assumed to be unmagnetized. In a magnetized plasma, the currents ![]() $I_e$ and
$I_e$ and ![]() $I_i$ to the surface of a spherical probe are altered when the condition,
$I_i$ to the surface of a spherical probe are altered when the condition, ![]() $r_{\textrm {ge}/i} < \lambda _{De}$, is satisfied. Here
$r_{\textrm {ge}/i} < \lambda _{De}$, is satisfied. Here ![]() $\lambda _{De}= \sqrt {\epsilon _0 k_B T_e/e^2 n_e}$ is the electron Debye length. In the present work,
$\lambda _{De}= \sqrt {\epsilon _0 k_B T_e/e^2 n_e}$ is the electron Debye length. In the present work, ![]() $\lambda _{De}$ varies between
$\lambda _{De}$ varies between ![]() $\sim$0.2 and 0.5 mm for the given range of plasma parameters. It shows that the electron current gets changed as a
$\sim$0.2 and 0.5 mm for the given range of plasma parameters. It shows that the electron current gets changed as a ![]() $B$-field is introduced. The ions do not fulfil this criteria at
$B$-field is introduced. The ions do not fulfil this criteria at ![]() $B< 0.2\ \textrm {T}$, therefore, the ion current to the surface of the spherical object is considered to be unaffected.
$B< 0.2\ \textrm {T}$, therefore, the ion current to the surface of the spherical object is considered to be unaffected.
In an unmagnetized plasma, a constant flux of energetic electrons is lost to the chamber wall. The magnetic field confines the electrons, which definitely reduces the electrons loss to the chamber wall. Therefore, it is expected that the density of the energetic electrons would be increased as the magnetic field is introduced. To see the effect of the ![]() $B$-field on the electron population, the EEDF is measured using a tungsten cylindrical probe of length
$B$-field on the electron population, the EEDF is measured using a tungsten cylindrical probe of length ![]() $l_p = 8\ \textrm {mm}$ and radius
$l_p = 8\ \textrm {mm}$ and radius ![]() $r_p = 0.15\ \textrm {mm}$. The probe is positioned perpendicular to the discharge axis or magnetic field lines. At discharge condition (
$r_p = 0.15\ \textrm {mm}$. The probe is positioned perpendicular to the discharge axis or magnetic field lines. At discharge condition (![]() $P = 12\ \textrm {W}$ and
$P = 12\ \textrm {W}$ and ![]() $p = 30\ \textrm {Pa}$),
$p = 30\ \textrm {Pa}$), ![]() $r_p <\lambda _{De}$, therefore, the conventional probe theory of a cylindrical probe is used to get the EEDF. It should be noted that the plasma anisotropy in the presence of the magnetic field depends on the parameter
$r_p <\lambda _{De}$, therefore, the conventional probe theory of a cylindrical probe is used to get the EEDF. It should be noted that the plasma anisotropy in the presence of the magnetic field depends on the parameter ![]() $B/p$ and this value should be higher than
$B/p$ and this value should be higher than ![]() $3\times 10^{-2}$ T/Pa (Behnke et al. Reference Behnke, Passoth, Csambal, Tichý, Kudrna, Trunec and Brablec1999). Since in our set of experiments, the ratio of
$3\times 10^{-2}$ T/Pa (Behnke et al. Reference Behnke, Passoth, Csambal, Tichý, Kudrna, Trunec and Brablec1999). Since in our set of experiments, the ratio of ![]() $B/p$ varies from
$B/p$ varies from ![]() ${\sim }1\times 10^{-4}$ to
${\sim }1\times 10^{-4}$ to ![]() $2\times 10^{-3}$ T/Pa, it does not exceed
$2\times 10^{-3}$ T/Pa, it does not exceed ![]() $3\times 10^{-2}$ T/Pa. Therefore, we do not expect any substantial anisotropy of the plasma or EEDF in our measurements. It should also be noted that the second derivative probe method gives a reliable EEDF in the range of the diffusion parameter (Demidov et al. Reference Demidov, Ratynskaia, Armstrong and Rypdal1999)
$3\times 10^{-2}$ T/Pa. Therefore, we do not expect any substantial anisotropy of the plasma or EEDF in our measurements. It should also be noted that the second derivative probe method gives a reliable EEDF in the range of the diffusion parameter (Demidov et al. Reference Demidov, Ratynskaia, Armstrong and Rypdal1999) ![]() $\varPsi = r_p ({\ln (\pi l_p/4 r_p)}/{\gamma r_{\textrm {ge}}})< 30$ (Popov et al. Reference Popov, Ivanova, Dimitrova, Kovačič, Gyergyek and Čerček2012). Here,
$\varPsi = r_p ({\ln (\pi l_p/4 r_p)}/{\gamma r_{\textrm {ge}}})< 30$ (Popov et al. Reference Popov, Ivanova, Dimitrova, Kovačič, Gyergyek and Čerček2012). Here, ![]() $\gamma$ is constant and we assumed
$\gamma$ is constant and we assumed ![]() $\gamma \sim 4/3$ for our pressure regime. In our case, the diffusion parameter has the value
$\gamma \sim 4/3$ for our pressure regime. In our case, the diffusion parameter has the value ![]() $\varPsi < 15$ for
$\varPsi < 15$ for ![]() $B < 0.1\ \textrm {T}$; therefore, this method is used to get the EEDF to show the increase in the energetic electron population as the
$B < 0.1\ \textrm {T}$; therefore, this method is used to get the EEDF to show the increase in the energetic electron population as the ![]() $B$-field is turned on. The EEDF is estimated from the second derivative of the probe I-V characteristics with respect to the probe voltage (Godyak Reference Godyak1990; Kudrna & Passoth Reference Kudrna and Passoth2007; Popov et al. Reference Popov, Ivanova, Dimitrova, Kovačič, Gyergyek and Čerček2012),
$B$-field is turned on. The EEDF is estimated from the second derivative of the probe I-V characteristics with respect to the probe voltage (Godyak Reference Godyak1990; Kudrna & Passoth Reference Kudrna and Passoth2007; Popov et al. Reference Popov, Ivanova, Dimitrova, Kovačič, Gyergyek and Čerček2012),
where ![]() $E = \textrm {eV} = e(V_p - V_b)$,
$E = \textrm {eV} = e(V_p - V_b)$, ![]() $I_e$ is the electron current to probe,
$I_e$ is the electron current to probe, ![]() $V_b$ is the probe bias,
$V_b$ is the probe bias, ![]() $V_p$ is the plasma potential and
$V_p$ is the plasma potential and ![]() $A_p$ is the area of probe. The EEDF with magnetic field at
$A_p$ is the area of probe. The EEDF with magnetic field at ![]() $p = 30\ \textrm {Pa}$ and
$p = 30\ \textrm {Pa}$ and ![]() $P = 12\ \textrm {W}$ is shown in figure 7(a). The population of the cold (or lower energy) electrons, which are reaching the probe, decreases with increasing
$P = 12\ \textrm {W}$ is shown in figure 7(a). The population of the cold (or lower energy) electrons, which are reaching the probe, decreases with increasing ![]() $B$-field whereas the population of the energetic electrons increases at low
$B$-field whereas the population of the energetic electrons increases at low ![]() $B < 0.05\ \textrm {T}$ (see inset image). It means that the energetic electrons can easily reach this probe surface at low
$B < 0.05\ \textrm {T}$ (see inset image). It means that the energetic electrons can easily reach this probe surface at low ![]() $B$-field.
$B$-field.

Figure 7. (a) Electron energy distribution function (EEDF) with external magnetic field at gas pressure, ![]() $p = 30\ \textrm {Pa}$ and rf power,
$p = 30\ \textrm {Pa}$ and rf power, ![]() $P = 12\ \textrm {W}$. The inset image represents the enhancement of the energetic electron population with the application of a magnetic field. (b) The plots of ln(EEPF) for given EEDF at various strengths of the magnetic field.
$P = 12\ \textrm {W}$. The inset image represents the enhancement of the energetic electron population with the application of a magnetic field. (b) The plots of ln(EEPF) for given EEDF at various strengths of the magnetic field.
It is obvious that the average electron energy will increase due to the increase of the density of energetic electrons. It means ![]() $T_e$ is expected to increase while the magnetic field is introduced. Since the variation in
$T_e$ is expected to increase while the magnetic field is introduced. Since the variation in ![]() $T_e$ affects the surface potential of a spherical object (see (3.3)), it is measured using a double or single probe at various strengths of the
$T_e$ affects the surface potential of a spherical object (see (3.3)), it is measured using a double or single probe at various strengths of the ![]() $B$-field. The inverse slope of
$B$-field. The inverse slope of ![]() $\ln (\textrm {EEPF})=$
$\ln (\textrm {EEPF})=$ ![]() $\ln ({F(E)}/{\sqrt {E}})$ with respect to
$\ln ({F(E)}/{\sqrt {E}})$ with respect to ![]() $E$ (see figure 7b) gives
$E$ (see figure 7b) gives ![]() $T_e$. It should be noted that the single probe used to obtain the EEDF is not compensated and overestimates
$T_e$. It should be noted that the single probe used to obtain the EEDF is not compensated and overestimates ![]() $T_e$, therefore, errors concerning
$T_e$, therefore, errors concerning ![]() $T_e$ are expected at low
$T_e$ are expected at low ![]() $B$-field. At higher
$B$-field. At higher ![]() $B$ (
$B$ (![]() $B > 0.09\ \textrm {T}$), the secondary plasma around the probe tip during the positive bias does not give true I–V characteristics, which is also a cause of error in the
$B > 0.09\ \textrm {T}$), the secondary plasma around the probe tip during the positive bias does not give true I–V characteristics, which is also a cause of error in the ![]() $T_e$ measurement even though it is rf compensated. In view of this, a double probe is used to obtain the approximate value of
$T_e$ measurement even though it is rf compensated. In view of this, a double probe is used to obtain the approximate value of ![]() $T_e$ up to
$T_e$ up to ![]() $B \sim 0.15\ \textrm {T}$. The double probe theory (Johnson & Malter Reference Johnson and Malter1950) estimates reliable plasma parameters (
$B \sim 0.15\ \textrm {T}$. The double probe theory (Johnson & Malter Reference Johnson and Malter1950) estimates reliable plasma parameters (![]() $n$ and
$n$ and ![]() $T_e$) in rf discharges if electrons obey the Maxwellian distribution, i.e. the EEDF should be Maxwellian in the presence of the
$T_e$) in rf discharges if electrons obey the Maxwellian distribution, i.e. the EEDF should be Maxwellian in the presence of the ![]() $B$-field. In figure 7(b),
$B$-field. In figure 7(b), ![]() $\ln (\textrm {EEPF})$ is plotted against the electron energy
$\ln (\textrm {EEPF})$ is plotted against the electron energy ![]() $E$ for different values of
$E$ for different values of ![]() $B$. The
$B$. The ![]() $\ln (\textrm {EEPF})$ against
$\ln (\textrm {EEPF})$ against ![]() $E$ shows the characteristics of a Maxwellian plasma (Godyak, Piejak & Alexandrovich Reference Godyak, Piejak and Alexandrovich1993) in the experiments. Figure 8 represents the variation of the electron temperature (
$E$ shows the characteristics of a Maxwellian plasma (Godyak, Piejak & Alexandrovich Reference Godyak, Piejak and Alexandrovich1993) in the experiments. Figure 8 represents the variation of the electron temperature (![]() $T_e$) with magnetic field at
$T_e$) with magnetic field at ![]() $p = 30\ \textrm {Pa}$ and
$p = 30\ \textrm {Pa}$ and ![]() $P = 6.5$ and
$P = 6.5$ and ![]() $12\ \textrm {W}$.
$12\ \textrm {W}$.

Figure 8. Electron temperature (![]() $T_e$) variation with magnetic field at pressure,
$T_e$) variation with magnetic field at pressure, ![]() $p = 30 \ \textrm {Pa}$ and rf powers,
$p = 30 \ \textrm {Pa}$ and rf powers, ![]() $P = 6.5$ and 12 W.
$P = 6.5$ and 12 W.
In the magnetized plasma, the net electron current ![]() $I_e$ to the spherical probe is a sum of the electron currents to different positions on the probe (Patacchini et al. Reference Patacchini, Hutchinson and Lapenta2007). In the present experiments, it is difficult to estimate the electron current as a function of position (with respect to the magnetic field direction) on the spherical probe surface (Patacchini et al. Reference Patacchini, Hutchinson and Lapenta2007). Therefore, a simple model which considers the net electron current (
$I_e$ to the spherical probe is a sum of the electron currents to different positions on the probe (Patacchini et al. Reference Patacchini, Hutchinson and Lapenta2007). In the present experiments, it is difficult to estimate the electron current as a function of position (with respect to the magnetic field direction) on the spherical probe surface (Patacchini et al. Reference Patacchini, Hutchinson and Lapenta2007). Therefore, a simple model which considers the net electron current (![]() $I_e$) in two possible directions along the
$I_e$) in two possible directions along the ![]() $B$-field (
$B$-field (![]() $I_{e\parallel }$) and transverse to the
$I_{e\parallel }$) and transverse to the ![]() $B$-field (
$B$-field (![]() $I_{e\perp }$) is used to explain the observed results qualitatively. Here
$I_{e\perp }$) is used to explain the observed results qualitatively. Here ![]() $I_{e\parallel }$ and
$I_{e\parallel }$ and ![]() $I_{e\perp }$ are assumed to be the electron current components at a given position on the spherical probe with respect to the magnetic field direction. The total electron current to the surface of a spherical probe is
$I_{e\perp }$ are assumed to be the electron current components at a given position on the spherical probe with respect to the magnetic field direction. The total electron current to the surface of a spherical probe is ![]() $I_e = I_{e\parallel } + I_{e\perp }$, which determines the floating surface potential of a probe in a magnetized plasma. It should be noted that the electron motion transverse to the
$I_e = I_{e\parallel } + I_{e\perp }$, which determines the floating surface potential of a probe in a magnetized plasma. It should be noted that the electron motion transverse to the ![]() $B$-field is much more hindered than that along the
$B$-field is much more hindered than that along the ![]() $B$-field in the moderately collisional plasma. In other words,
$B$-field in the moderately collisional plasma. In other words, ![]() $I_{e\perp }$ is reduced much more than
$I_{e\perp }$ is reduced much more than ![]() $I_{e\parallel }$ in a magnetized plasma (Sanmartin Reference Sanmartin1970; Bohm, Burhop & Messey Reference Bohm, Burhop, Messey, Guthrie and Wakerling1994), i.e.
$I_{e\parallel }$ in a magnetized plasma (Sanmartin Reference Sanmartin1970; Bohm, Burhop & Messey Reference Bohm, Burhop, Messey, Guthrie and Wakerling1994), i.e. ![]() $D_{e\perp } < D_{e\parallel }$, where
$D_{e\perp } < D_{e\parallel }$, where ![]() $D_{e\perp }$ and
$D_{e\perp }$ and ![]() $D_{e\parallel }$ are the transverse and longitudinal diffusion coefficients, respectively.
$D_{e\parallel }$ are the transverse and longitudinal diffusion coefficients, respectively.
There are two possible diffusion processes: the first one is the drain diffusion and the second one is the collisional diffusion. In drain diffusion, electrons may change their direction and cross the ![]() $B$-field during the motion in rf oscillating sheath field of a spherical object. In collisional diffusion, the gyrating electrons collide with background neutrals and diffuse across the
$B$-field during the motion in rf oscillating sheath field of a spherical object. In collisional diffusion, the gyrating electrons collide with background neutrals and diffuse across the ![]() $B$-field with a higher rate (Bohm et al. Reference Bohm, Burhop, Messey, Guthrie and Wakerling1994). The drain diffusion mainly dominates over the collision diffusion in a low pressure magnetized plasma. Since the present work is performed in a moderately collisional plasma, the collisional diffusion process is considered to be more effective. For moderately collisional low-temperature magnetized plasmas, the collisional transverse diffusion coefficient is
$B$-field with a higher rate (Bohm et al. Reference Bohm, Burhop, Messey, Guthrie and Wakerling1994). The drain diffusion mainly dominates over the collision diffusion in a low pressure magnetized plasma. Since the present work is performed in a moderately collisional plasma, the collisional diffusion process is considered to be more effective. For moderately collisional low-temperature magnetized plasmas, the collisional transverse diffusion coefficient is ![]() $D_{e\perp } = D_{e0}/(1 + \omega ^2_{\textrm {ce}} \tau ^2_e)$, where
$D_{e\perp } = D_{e0}/(1 + \omega ^2_{\textrm {ce}} \tau ^2_e)$, where ![]() $D_{e0} = \lambda _{e-n} v_{\textrm {the}}/3$ is the diffusion coefficient in the absence of a
$D_{e0} = \lambda _{e-n} v_{\textrm {the}}/3$ is the diffusion coefficient in the absence of a ![]() $B$-field,
$B$-field, ![]() $\omega _{\textrm {ce}} = e B/m_e$ is the electron cyclotron frequency and
$\omega _{\textrm {ce}} = e B/m_e$ is the electron cyclotron frequency and ![]() $\tau _e = \lambda _{e-n}/v_{\textrm {the}}$ is the electron–neutral collision time (Chen Reference Chen1984; Bohm et al. Reference Bohm, Burhop, Messey, Guthrie and Wakerling1994; Curreli & Chen Reference Curreli and Chen2014).
$\tau _e = \lambda _{e-n}/v_{\textrm {the}}$ is the electron–neutral collision time (Chen Reference Chen1984; Bohm et al. Reference Bohm, Burhop, Messey, Guthrie and Wakerling1994; Curreli & Chen Reference Curreli and Chen2014).
In a collisionless magnetized plasma, the electron motion is restricted by the magnetic field in the transverse direction. Therefore, the ![]() $D_{e\parallel }$ (or
$D_{e\parallel }$ (or ![]() $I_{e\parallel }$) play a dominant role in the determination of the surface potential (or charge) of the dust grain in the presence of magnetic field (Patacchini et al. Reference Patacchini, Hutchinson and Lapenta2007). The logarithmic plots of transverse diffusion coefficient,
$I_{e\parallel }$) play a dominant role in the determination of the surface potential (or charge) of the dust grain in the presence of magnetic field (Patacchini et al. Reference Patacchini, Hutchinson and Lapenta2007). The logarithmic plots of transverse diffusion coefficient, ![]() $\ln ({D_{e\perp })}$, are shown in figure 9 which show a reduction in
$\ln ({D_{e\perp })}$, are shown in figure 9 which show a reduction in ![]() $D_{e\perp }$ after a magnetic field strength of 0.01 T. The value of
$D_{e\perp }$ after a magnetic field strength of 0.01 T. The value of ![]() $D_{e\perp }$ increases with the pressure while the magnetic field strength (
$D_{e\perp }$ increases with the pressure while the magnetic field strength (![]() $B > 0.02\ \textrm {T}$) is kept constant, which is also illustrated in figure 9.
$B > 0.02\ \textrm {T}$) is kept constant, which is also illustrated in figure 9.

Figure 9. Logarithm plots of transverse diffusion coefficient (![]() $D_{e\perp }$) for different argon pressures at various strengths of magnetic field.
$D_{e\perp }$) for different argon pressures at various strengths of magnetic field.
In the low magnetic field regime (![]() $B < 0.05\ \textrm {T}$), the increase in
$B < 0.05\ \textrm {T}$), the increase in ![]() $T_e$ (see figure 8) enhances the surface potential (more negative) of a spherical probe according to (3.3). Now, the probe collects a higher net current (
$T_e$ (see figure 8) enhances the surface potential (more negative) of a spherical probe according to (3.3). Now, the probe collects a higher net current (![]() $I_e$) than
$I_e$) than ![]() $I_{e0}$. Here,
$I_{e0}$. Here, ![]() $I_{e0}$ represents an equilibrium electron current to the spherical probe in unmagnetized plasma. This can also be understood on the basis of energetic electron population. Experimentally, the dominating role of energetic electrons in the charging process of a spherical object or dust grain in the plasma have been confirmed (Arnas, Mikikian & Doveil Reference Arnas, Mikikian and Doveil1999). Since the Larmor radius of the energetic electrons (
$I_{e0}$ represents an equilibrium electron current to the spherical probe in unmagnetized plasma. This can also be understood on the basis of energetic electron population. Experimentally, the dominating role of energetic electrons in the charging process of a spherical object or dust grain in the plasma have been confirmed (Arnas, Mikikian & Doveil Reference Arnas, Mikikian and Doveil1999). Since the Larmor radius of the energetic electrons (![]() $T_e > 20\ \textrm {eV}$) lies between 1.5 mm and 0.4 mm for
$T_e > 20\ \textrm {eV}$) lies between 1.5 mm and 0.4 mm for ![]() $B < 0.05\ \textrm {T}$, energetic electrons are considered to be weakly magnetized. Since
$B < 0.05\ \textrm {T}$, energetic electrons are considered to be weakly magnetized. Since ![]() $D_{e\perp }$ decreases in this
$D_{e\perp }$ decreases in this ![]() $B$-field regime (
$B$-field regime (![]() $B < 0.05\ \textrm {T}$), the net electron current to spherical surface should be lowered. However, the opposite behaviour (large
$B < 0.05\ \textrm {T}$), the net electron current to spherical surface should be lowered. However, the opposite behaviour (large ![]() $I_e$ or
$I_e$ or ![]() $V_s$) is observed at low
$V_s$) is observed at low ![]() $B$-field because of the confinement of energetic electrons (or higher
$B$-field because of the confinement of energetic electrons (or higher ![]() $T_e$). The higher charges on the dust grains or more negative surface potential in a weakly magnetized plasma is also observed numerically by Yukihiro et al. (Reference Yukihiro, Gakushi, Takatoshi and Osamu2009). They claimed a larger absorption cross-section for electron capture on the dust surface in the presence of a magnetic field. In the present study, higher charges on a spherical probe are due to the increase of
$T_e$). The higher charges on the dust grains or more negative surface potential in a weakly magnetized plasma is also observed numerically by Yukihiro et al. (Reference Yukihiro, Gakushi, Takatoshi and Osamu2009). They claimed a larger absorption cross-section for electron capture on the dust surface in the presence of a magnetic field. In the present study, higher charges on a spherical probe are due to the increase of ![]() $T_e$ for the higher magnetic field (see figure 8).
$T_e$ for the higher magnetic field (see figure 8).
At higher ![]() $B$-field (
$B$-field (![]() $B > 0.05\ \textrm {T}$), a lower value of the mean free path (
$B > 0.05\ \textrm {T}$), a lower value of the mean free path (![]() $r_{\textrm {ge}} < \lambda _{e-n}$) increases the electron–neutral collision frequency, resulting in a reduction of
$r_{\textrm {ge}} < \lambda _{e-n}$) increases the electron–neutral collision frequency, resulting in a reduction of ![]() $T_e$. A slight reduction in
$T_e$. A slight reduction in ![]() $T_e$ at higher
$T_e$ at higher ![]() $B$ is seen in figure 8. At fixed gas pressure, transverse diffusion coefficient (
$B$ is seen in figure 8. At fixed gas pressure, transverse diffusion coefficient (![]() $D_{e\perp }$) decreases with the increasing magnetic field (see figure 9) which causes a reduction in
$D_{e\perp }$) decreases with the increasing magnetic field (see figure 9) which causes a reduction in ![]() $I_{e\perp }$. It is also observed in numerical simulations that
$I_{e\perp }$. It is also observed in numerical simulations that ![]() $I_{e\parallel }$ starts to decrease with an increase of the
$I_{e\parallel }$ starts to decrease with an increase of the ![]() $B$-field. However, this reduction in
$B$-field. However, this reduction in ![]() $I_{e\parallel }$ is small compared with the reduction in
$I_{e\parallel }$ is small compared with the reduction in ![]() $I_{e\perp }$ in the magnetic field regime (
$I_{e\perp }$ in the magnetic field regime (![]() $B < 0.15\ \textrm {T}$). Therefore, it is assumed that the reduction in
$B < 0.15\ \textrm {T}$). Therefore, it is assumed that the reduction in ![]() $I_{e\perp }$ to the spherical probe could be a possible cause of lower or less negative surface potential at high
$I_{e\perp }$ to the spherical probe could be a possible cause of lower or less negative surface potential at high ![]() $B$-field (
$B$-field (![]() $B > 0.05\ \textrm {T}$), which is shown in figure 5.
$B > 0.05\ \textrm {T}$), which is shown in figure 5.
Since ![]() $D_{e\perp }$ (or
$D_{e\perp }$ (or ![]() $I_{e\perp }$) varies with
$I_{e\perp }$) varies with ![]() $1/B^2$ at a given pressure,
$1/B^2$ at a given pressure, ![]() $V_s$ should have a
$V_s$ should have a ![]() $1/B^2$ dependence. In figure 10(a),
$1/B^2$ dependence. In figure 10(a), ![]() $V_s$ is plotted against
$V_s$ is plotted against ![]() $1/B^2$ for different spherical probes between
$1/B^2$ for different spherical probes between ![]() $B = 0.06\ \textrm {T}$ and 0.2 T. Figure 10(a) clearly indicates that
$B = 0.06\ \textrm {T}$ and 0.2 T. Figure 10(a) clearly indicates that ![]() $V_s$ decreases linearly with
$V_s$ decreases linearly with ![]() $1/B^2$ between
$1/B^2$ between ![]() $B \sim 0.06\ \textrm {T}$ and 0.15 T for an rf power of 12 W. However, the upper
$B \sim 0.06\ \textrm {T}$ and 0.15 T for an rf power of 12 W. However, the upper ![]() $B$-field value shifts to a slightly lower value (
$B$-field value shifts to a slightly lower value (![]() $B > 0.10\ \textrm {T}$) for the low power discharge (
$B > 0.10\ \textrm {T}$) for the low power discharge (![]() $P = 6.5$). Since plasma density is different in both cases (
$P = 6.5$). Since plasma density is different in both cases (![]() $P = 12\ \textrm {W}$ and 6.5 W) at
$P = 12\ \textrm {W}$ and 6.5 W) at ![]() $p = 30\ \textrm {Pa}$, different rates of reduction of
$p = 30\ \textrm {Pa}$, different rates of reduction of ![]() $V_s$ with
$V_s$ with ![]() $1/B^2$ are expected. The plots of
$1/B^2$ are expected. The plots of ![]() $V_s$ against
$V_s$ against ![]() $1/B^2$ for different pressures at given power (
$1/B^2$ for different pressures at given power (![]() $P = 12\ \textrm {W}$) are shown in figure 10(b). We also see a linear variation of
$P = 12\ \textrm {W}$) are shown in figure 10(b). We also see a linear variation of ![]() $V_s$ with
$V_s$ with ![]() $1/B^2$ below
$1/B^2$ below ![]() $B < 0.12\ \textrm {T}$ and a nonlinear reduction in
$B < 0.12\ \textrm {T}$ and a nonlinear reduction in ![]() $V_s$ above
$V_s$ above ![]() $B > 0.12\ \textrm {T}$ (above
$B > 0.12\ \textrm {T}$ (above ![]() $p \geq 30\ \textrm {Pa}$). For the low pressure case (
$p \geq 30\ \textrm {Pa}$). For the low pressure case (![]() $p = 15\ \textrm {Pa}$), the nonlinear behaviour of
$p = 15\ \textrm {Pa}$), the nonlinear behaviour of ![]() $V_s$ is observed at a magnetic field of
$V_s$ is observed at a magnetic field of ![]() $>$0.10 T. The different linear rates of
$>$0.10 T. The different linear rates of ![]() $V_s$ at different pressures (figure 10b) are expected because of different plasma backgrounds (plasma density and
$V_s$ at different pressures (figure 10b) are expected because of different plasma backgrounds (plasma density and ![]() $T_e$) at a fixed input rf power and different gas pressures. In a similar plasma background, we could expect a constant linear rate of
$T_e$) at a fixed input rf power and different gas pressures. In a similar plasma background, we could expect a constant linear rate of ![]() $V_s$ with
$V_s$ with ![]() $1/B^2$ at different pressures according to the theoretical estimation as shown in figure 9. It shows that the reduction in
$1/B^2$ at different pressures according to the theoretical estimation as shown in figure 9. It shows that the reduction in ![]() $I_e$ (or
$I_e$ (or ![]() $V_s$) is mainly due to the lower value of
$V_s$) is mainly due to the lower value of ![]() $I_{e\perp }$ in this magnetic field regime.
$I_{e\perp }$ in this magnetic field regime.

Figure 10. (a) Surface potential variation with ![]() $1/B^2$ for different spherical probes at pressure
$1/B^2$ for different spherical probes at pressure ![]() $p = 30\ \textrm {Pa}$ and rf powers,
$p = 30\ \textrm {Pa}$ and rf powers, ![]() $P = 6.5\ \textrm {W}$ and 12 W. The values of
$P = 6.5\ \textrm {W}$ and 12 W. The values of ![]() $1/B^2$ are correspond to
$1/B^2$ are correspond to ![]() $B = 0.06\ \textrm {T}$ to 0.2 T (b)
$B = 0.06\ \textrm {T}$ to 0.2 T (b) ![]() $V_s$ variation against
$V_s$ variation against ![]() $1/B^2$ for bronze probe (
$1/B^2$ for bronze probe (![]() $r = 1.7\ \textrm {mm}$) at rf power 12 W and different pressures. The values of
$r = 1.7\ \textrm {mm}$) at rf power 12 W and different pressures. The values of ![]() $1/B^2$ are correspond to
$1/B^2$ are correspond to ![]() $B = 0.04\ \textrm {T}$ to 0.2 T.
$B = 0.04\ \textrm {T}$ to 0.2 T.
At strong magnetic field strength, the contribution of ![]() $I_{e\perp }$ to
$I_{e\perp }$ to ![]() $I_e$ starts to reduce and a larger contribution comes from
$I_e$ starts to reduce and a larger contribution comes from ![]() $I_{e\parallel }$ (Sanmartin Reference Sanmartin1970). Hence the role of
$I_{e\parallel }$ (Sanmartin Reference Sanmartin1970). Hence the role of ![]() $D_{e\parallel }$ (or
$D_{e\parallel }$ (or ![]() $I_{e\parallel }$) becomes more important in the determination of the surface potential. In the present experiments,
$I_{e\parallel }$) becomes more important in the determination of the surface potential. In the present experiments, ![]() $V_s$ does not decrease linearly with
$V_s$ does not decrease linearly with ![]() $1/B^2$ above
$1/B^2$ above ![]() $B > 0.12\ \textrm {T}$ (figure 10) except for the low density plasmas (
$B > 0.12\ \textrm {T}$ (figure 10) except for the low density plasmas (![]() $p = 30\ \textrm {Pa}$,
$p = 30\ \textrm {Pa}$, ![]() $P = 6.5\ \textrm {W}$ and
$P = 6.5\ \textrm {W}$ and ![]() $p = 15\ \textrm {Pa}$,
$p = 15\ \textrm {Pa}$, ![]() $P = 12\ \textrm {W}$). In moderately collisional plasma, a reduction in
$P = 12\ \textrm {W}$). In moderately collisional plasma, a reduction in ![]() $I_{e\parallel }$ is expected while the magnetic field increases but it could be comparable or larger than that of
$I_{e\parallel }$ is expected while the magnetic field increases but it could be comparable or larger than that of ![]() $I_{e\perp }$ at strong
$I_{e\perp }$ at strong ![]() $B$-field (Sanmartin Reference Sanmartin1970). The nonlinear characteristics of
$B$-field (Sanmartin Reference Sanmartin1970). The nonlinear characteristics of ![]() $V_s$ against
$V_s$ against ![]() $1/B^2$ above
$1/B^2$ above ![]() $B > 0.12\ \textrm {T}$ (see figure 10) is expected due to a dominant role of
$B > 0.12\ \textrm {T}$ (see figure 10) is expected due to a dominant role of ![]() $I_{e\parallel }$ along with
$I_{e\parallel }$ along with ![]() $I_{e\perp }$ for determining the surface potential. In some other experiments and simulations a reduction in
$I_{e\perp }$ for determining the surface potential. In some other experiments and simulations a reduction in ![]() $V_s$ of a spherical object with increasing magnetic field has also been reported (Dote, Amemiya & Ichimiya Reference Dote, Amemiya and Ichimiya1964; Lange Reference Lange2016; Tadsen et al. Reference Tadsen, Greiner and Piel2018).
$V_s$ of a spherical object with increasing magnetic field has also been reported (Dote, Amemiya & Ichimiya Reference Dote, Amemiya and Ichimiya1964; Lange Reference Lange2016; Tadsen et al. Reference Tadsen, Greiner and Piel2018).
It is known that the current ![]() $I_{e\perp }$ to the spherical probe decreases with increasing
$I_{e\perp }$ to the spherical probe decreases with increasing ![]() $\omega _{\textrm {ce}} \tau _e$ or decreasing
$\omega _{\textrm {ce}} \tau _e$ or decreasing ![]() $D_{e\perp }$. At given finite
$D_{e\perp }$. At given finite ![]() $B$-field,
$B$-field, ![]() $D_{e\perp }$ increases with increasing electron–neutral collisions or gas pressure, which leads to an increase of
$D_{e\perp }$ increases with increasing electron–neutral collisions or gas pressure, which leads to an increase of ![]() $I_{e\perp }$. At finite
$I_{e\perp }$. At finite ![]() $B$-field (
$B$-field (![]() $B > 0.01\ \textrm {T}$),
$B > 0.01\ \textrm {T}$), ![]() $D_{e\perp }$ has a slightly larger value at higher pressure (
$D_{e\perp }$ has a slightly larger value at higher pressure (![]() $p = 50\ \textrm {Pa}$) than at lower pressure (
$p = 50\ \textrm {Pa}$) than at lower pressure (![]() $p = 15\ \textrm {Pa}$), as shown in figure 9. The difference in
$p = 15\ \textrm {Pa}$), as shown in figure 9. The difference in ![]() $D_{e\perp }$ for different pressures at finite
$D_{e\perp }$ for different pressures at finite ![]() $B$-field is one of the possible causes for the different values of
$B$-field is one of the possible causes for the different values of ![]() $V_s$ in the presence of a magnetic field (figure 5b). The spherical surface collects more electron current at higher pressure (
$V_s$ in the presence of a magnetic field (figure 5b). The spherical surface collects more electron current at higher pressure (![]() $\,p = 50\ \textrm {Pa}$) because of the large value of
$\,p = 50\ \textrm {Pa}$) because of the large value of ![]() $D_{e\perp }$. The lower value of
$D_{e\perp }$. The lower value of ![]() $D_{e\perp }$ causes a smaller electron current to the spherical probe. Therefore, the spherical probe has a higher value (more negative) of
$D_{e\perp }$ causes a smaller electron current to the spherical probe. Therefore, the spherical probe has a higher value (more negative) of ![]() $V_s$ at
$V_s$ at ![]() $p = 50\ \textrm {Pa}$ than at
$p = 50\ \textrm {Pa}$ than at ![]() $p = 15\ \textrm {Pa}$ (figure 5) in the magnetized plasma (
$p = 15\ \textrm {Pa}$ (figure 5) in the magnetized plasma (![]() $B > 0.05\ \textrm {T}$). These results confirm the dominating role of the collisional diffusion over the drain diffusion in a moderately collisional magnetized plasma.
$B > 0.05\ \textrm {T}$). These results confirm the dominating role of the collisional diffusion over the drain diffusion in a moderately collisional magnetized plasma.
It should be noted that in an unmagnetized plasma (![]() $B = 0\ \textrm {T}$), the dust charge or surface potential decreases with an increase of the pressure due to the higher ion–neutral collision frequency (Khrapak et al. Reference Khrapak, Ratynskaia, Zobnin, Usachev, Yaroshenko, Thoma, Kretschmer, Höfner, Morfill and Petrov2005). It is also known that collisions of plasma species with neutrals retard the motion along the magnetic field, hence reduction in
$B = 0\ \textrm {T}$), the dust charge or surface potential decreases with an increase of the pressure due to the higher ion–neutral collision frequency (Khrapak et al. Reference Khrapak, Ratynskaia, Zobnin, Usachev, Yaroshenko, Thoma, Kretschmer, Höfner, Morfill and Petrov2005). It is also known that collisions of plasma species with neutrals retard the motion along the magnetic field, hence reduction in ![]() $I_{e/i \parallel }$ is expected with increasing the gas pressure. Since ions are unmagnetized below the magnetic field of
$I_{e/i \parallel }$ is expected with increasing the gas pressure. Since ions are unmagnetized below the magnetic field of ![]() $<$0.2 T, the role of ions is negligible compared with the electrons in the determination of the surface potential in this given magnetic field regime (
$<$0.2 T, the role of ions is negligible compared with the electrons in the determination of the surface potential in this given magnetic field regime (![]() $B < 0.2\ \textrm {T}$). Due to the smaller gyroradius of electrons (higher gyrofrequency) above
$B < 0.2\ \textrm {T}$). Due to the smaller gyroradius of electrons (higher gyrofrequency) above ![]() $B > 0.05 \ \textrm {T}$, the electron–neutral collision frequency is found to be larger. It means that collisions lower the
$B > 0.05 \ \textrm {T}$, the electron–neutral collision frequency is found to be larger. It means that collisions lower the ![]() $I_{e\parallel }$ more effectively than
$I_{e\parallel }$ more effectively than ![]() $I_{i \parallel }$ in the magnetized discharge. Hence the role of ion current for determining the surface potential at different pressures (
$I_{i \parallel }$ in the magnetized discharge. Hence the role of ion current for determining the surface potential at different pressures (![]() $p = 15$ to 50 Pa) is assumed to be negligible above
$p = 15$ to 50 Pa) is assumed to be negligible above ![]() $B > 0.05\ \textrm {T}$. The higher negative value of
$B > 0.05\ \textrm {T}$. The higher negative value of ![]() $V_s$ at higher pressure also confirms a dominant role of
$V_s$ at higher pressure also confirms a dominant role of ![]() $I_{e\perp }$ in the reduction of the net electron current (
$I_{e\perp }$ in the reduction of the net electron current (![]() $I_e$) or the surface potential in the magnetized plasma.
$I_e$) or the surface potential in the magnetized plasma.
The difference in ![]() $V_s$ for magnetic (stainless steel) and non-magnetic (bronze) spherical objects (figure 6) is understood on the basis of field line distribution around a spherical body in a magnetized plasma. Since
$V_s$ for magnetic (stainless steel) and non-magnetic (bronze) spherical objects (figure 6) is understood on the basis of field line distribution around a spherical body in a magnetized plasma. Since ![]() $I_{e\perp }$ decreases faster than
$I_{e\perp }$ decreases faster than ![]() $I_{e\parallel }$ with the magnetic field,
$I_{e\parallel }$ with the magnetic field, ![]() $I_{e\perp }$ mainly responsible for the reduction in
$I_{e\perp }$ mainly responsible for the reduction in ![]() $I_e$ (or
$I_e$ (or ![]() $V_s$). The magnetic flux density on either side of the magnetic sphere is less than that inside of it in the presence of a magnetic field (see figure 3.7 of Fagan (Reference Fagan2013)), which enhances
$V_s$). The magnetic flux density on either side of the magnetic sphere is less than that inside of it in the presence of a magnetic field (see figure 3.7 of Fagan (Reference Fagan2013)), which enhances ![]() $I_{e\perp }$ to the object surface due to the large value of
$I_{e\perp }$ to the object surface due to the large value of ![]() $D_{e\perp }$ that varies with
$D_{e\perp }$ that varies with ![]() $1/B^2$. Thus, the electron current,
$1/B^2$. Thus, the electron current, ![]() $I_e$, to the magnetic sphere increases, making the surface of the spherical object more negative (higher
$I_e$, to the magnetic sphere increases, making the surface of the spherical object more negative (higher ![]() $V_s$) in the presence of
$V_s$) in the presence of ![]() $B$-field. In the case of the non-magnetic object (copper bronze), the magnetic flux density on either side of the sphere is slightly larger than that inside of it due to the diamagnetic characteristics of copper. The
$B$-field. In the case of the non-magnetic object (copper bronze), the magnetic flux density on either side of the sphere is slightly larger than that inside of it due to the diamagnetic characteristics of copper. The ![]() $B$-field line density on either side of the non-magnetic sphere is expected to be higher than that around the magnetic sphere, which reduces
$B$-field line density on either side of the non-magnetic sphere is expected to be higher than that around the magnetic sphere, which reduces ![]() $I_{e\perp }$ to the object surface. The lower value of the electron current (
$I_{e\perp }$ to the object surface. The lower value of the electron current (![]() $I_e$) to the non-magnetic sphere makes the surface less negative. Hence a magnetic sphere has a higher value (more negative) of
$I_e$) to the non-magnetic sphere makes the surface less negative. Hence a magnetic sphere has a higher value (more negative) of ![]() $V_s$ than that of a non-magnetic sphere (see figure 6a) above a finite value of
$V_s$ than that of a non-magnetic sphere (see figure 6a) above a finite value of ![]() $B$-field (
$B$-field (![]() $B > 0.03\ \textrm {T}$).
$B > 0.03\ \textrm {T}$).
The qualitative description presented here provides a better understanding of the observed surface potential variation for magnetic and non-magnetic spherical probes (or large dust grains) in a magnetized rf discharge. We have provided a possible charging mechanism of magnetic and non-magnetic particles based on the reduction of electron current to spherical surface. To the best of our knowledge, at present there is no analytical or simulation work for a moderately collisional magnetized plasma to support our claim. Therefore it may be possible that another charging mechanism of magnetic and non-magnetic spherical particles plays a role in a magnetized plasma.
5 Conclusion
The surface potential of magnetic (stainless steel) and non-magnetic (bronze) spherical objects in a magnetized rf discharge at various discharge conditions is measured. A 13.56 MHz rf generator is used to produce the plasma between a transparent ITO coated glass electrode and a metal electrode. A superconducting electromagnet with Helmholtz coils configuration is used to introduce an external magnetic field. The vacuum chamber is placed at the centre of the magnet to perform the experiments in a uniform magnetic field. The surface potential of different sized magnetic spherical probes (![]() $r = 1.0\ \textrm {mm}$, 1.25 mm and 1.7 mm) is measured and compared with a non-magnetic spherical probe (
$r = 1.0\ \textrm {mm}$, 1.25 mm and 1.7 mm) is measured and compared with a non-magnetic spherical probe (![]() $r = 1.5\ \textrm {mm}$) in the plasma at different strengths of the
$r = 1.5\ \textrm {mm}$) in the plasma at different strengths of the ![]() $B$-field. The main findings of the experimental studies are listed below.
$B$-field. The main findings of the experimental studies are listed below.
(i) The surface potential (
 $V_s$) of the spherical object (
$V_s$) of the spherical object ( $r >\lambda _{De}$) depends on its size in the unmagnetized plasma.
$r >\lambda _{De}$) depends on its size in the unmagnetized plasma.(ii) The surface potential of a spherical object either magnetic or non-magnetic increases at the low magnetic field (
 $B < 0.05\ \textrm {T}$), attains a maximum value and starts to decrease with further increasing the strength of the external magnetic field (
$B < 0.05\ \textrm {T}$), attains a maximum value and starts to decrease with further increasing the strength of the external magnetic field ( $B > 0.05\ \textrm {T}$). The rate of change of the surface potential in the magnetized plasma strongly depends on the gas pressure as well as the plasma parameters (
$B > 0.05\ \textrm {T}$). The rate of change of the surface potential in the magnetized plasma strongly depends on the gas pressure as well as the plasma parameters ( $n$ and
$n$ and  $T_e$).
$T_e$).(iii) The surface potential of magnetic spherical objects or large dust grains is found to be higher (more negative) than that of a non-magnetic sphere at the higher magnetic field (
 $B > 0.04\ \textrm {T}$).
$B > 0.04\ \textrm {T}$).(iv) The surface potential of the spherical objects loses its size dependence characteristics in the rf discharge with the application of an external magnetic field (
 $B > 0.05\ \textrm {T}$).
$B > 0.05\ \textrm {T}$).
The magnetic field reduces the loss of energetic electrons to the wall and confines them in the plasma volume. The average energy of bulk plasma electrons or ![]() $T_e$ increases due to the confinement of energetic electrons. An increase in energetic electron population or
$T_e$ increases due to the confinement of energetic electrons. An increase in energetic electron population or ![]() $T_e$ at lower
$T_e$ at lower ![]() $B$ (
$B$ (![]() $B < 0.05$) increases the electron current to the probe surface. Hence, the surface potential increases (more negative) with
$B < 0.05$) increases the electron current to the probe surface. Hence, the surface potential increases (more negative) with ![]() $B$ and attains its peak value between
$B$ and attains its peak value between ![]() $B = 0.01\ \textrm {T}$ and 0.05 T for different discharge conditions. With an increase of the
$B = 0.01\ \textrm {T}$ and 0.05 T for different discharge conditions. With an increase of the ![]() $B$-field (
$B$-field (![]() $B > 0.05\ \textrm {T}$), the electron motion transverse to the
$B > 0.05\ \textrm {T}$), the electron motion transverse to the ![]() $B$-field as well as along the
$B$-field as well as along the ![]() $B$-field is hindered, resulting in a lower electron current to the probe surface. The reduction of the net electron current makes the spherical object less negative. Since ions are assumed to be unmagnetized for the given range of the magnetic field, the role of the magnetic field on the ion current is considered to be negligible. Thus, the electron current determines the surface potential, given by the balance of the electron and ion currents. The value of
$B$-field is hindered, resulting in a lower electron current to the probe surface. The reduction of the net electron current makes the spherical object less negative. Since ions are assumed to be unmagnetized for the given range of the magnetic field, the role of the magnetic field on the ion current is considered to be negligible. Thus, the electron current determines the surface potential, given by the balance of the electron and ion currents. The value of ![]() $V_s$ depends on the magnetic field line density around a spherical object which affects the current to the surface of the object. Therefore, the surface potential is lower (or less negative) for a non-magnetic sphere than for a magnetic sphere in the magnetized plasma.
$V_s$ depends on the magnetic field line density around a spherical object which affects the current to the surface of the object. Therefore, the surface potential is lower (or less negative) for a non-magnetic sphere than for a magnetic sphere in the magnetized plasma.
This work highlights the role of the external magnetic field as well as the types of material of the spherical objects (large dust grains) on the surface potential in a low-temperature plasma. These findings will directly help to estimate the true charges on submicron to micron-sized dust grains (![]() $r < \lambda _{De}$) in magnetized dusty plasma experiments. It has been confirmed that electron temperature increases as the magnetic field is introduced, which definitely indicates the higher dust charges at lower magnetic field. However, many simulations and experimental works suggest either no change or less negative charge on the dust grain at low
$r < \lambda _{De}$) in magnetized dusty plasma experiments. It has been confirmed that electron temperature increases as the magnetic field is introduced, which definitely indicates the higher dust charges at lower magnetic field. However, many simulations and experimental works suggest either no change or less negative charge on the dust grain at low ![]() $B$-field. We expect the reduction in the charge of dust particles (
$B$-field. We expect the reduction in the charge of dust particles (![]() $r < \lambda _{De}$) to be similar as for a spherical probe (
$r < \lambda _{De}$) to be similar as for a spherical probe (![]() $r > \lambda _{De}$) in a strong magnetic field. Interestingly, the smaller magnetic or paramagnetic dust grains may acquire a more negative charge on their surface as compared with the non-magnetic dust grains in a magnetized dusty plasma. In the future, our focus will be on the direct or indirect measurement of the charge on dust grains (
$r > \lambda _{De}$) in a strong magnetic field. Interestingly, the smaller magnetic or paramagnetic dust grains may acquire a more negative charge on their surface as compared with the non-magnetic dust grains in a magnetized dusty plasma. In the future, our focus will be on the direct or indirect measurement of the charge on dust grains (![]() $r < \lambda _{De}$) in a magnetized dusty plasma to understand the dynamics of the dust grain medium. The reported experimental work may be a motive for researchers to develop an analytical or simulation model to understand the charging mechanism of magnetic and non-magnetic spherical particles in a strongly magnetized plasma.
$r < \lambda _{De}$) in a magnetized dusty plasma to understand the dynamics of the dust grain medium. The reported experimental work may be a motive for researchers to develop an analytical or simulation model to understand the charging mechanism of magnetic and non-magnetic spherical particles in a strongly magnetized plasma.
Acknowledgements
This work is supported by the Deutsche Forschungsgemeinschaft (DFG). The authors are grateful to F. Becker for his assistance in making spherical probes and supporting experiments. The authors are also thankful to M. Kretschmer for the experimental assistance.
Editor Edward Thomas thanks the referees for their advice in evaluating this article.