Introduction
One way of studying glacier variations with climate is to evaluate the energy balance at the glacier surface during the melt season. This involves measuring or estimating the different energy sources and sinks. Important sources of energy include solar and terrestrial radiation and turbulent heat exchange with the overlying atmosphere. Important sinks include heat conduction into the glacier and, most importantly for present purposes, the latent heat needed for melting. The study of glacier energy balance has made much progress since the 1930s (Ångstrom, 1933), but the use of simple climate data to calculate the energy balance, first identified by Sverdrup (1935), is still not entirely solved because of the theoretical and instrumental difficulties. Even now, the measurement of energy balance on a glacier is far from a routine exercise and is only done for selected ‘experiments’ on a few glaciers (Oerlemans and Vugts, 1993; Reference Konzelmann and BraithwaiteOhmura and others, 1994), although most people acknowledge that the energy balance is fundamental to understanding links between glaciers and climate.
Most energy-balance studies have demonstrated the predominance of radiation in the overall energy balance (Reference KeelerOhmura, 2001) where the net radiation absorbed by the glacier is the relatively small difference between large radiation sources (incoming shortwave and longwave radiation) and large radiation sinks (reflected shortwave and emitted longwave). However, if we are concerned about the effects of global warming on the cryosphere, the key factor is the temperature sensitivity of glacier melt that is important. This reflects the cumulative effect of temperature changes on the individual energy-balance components: glacier melting increases with temperature because various energy sources increase with temperature. Reference KeelerOhmura (2001) correctly points out that incoming longwave radiation is an important energy source and, because of its obvious link to temperature, says that this explains the relation between glacier melt and temperature. However, the temperature sensitivity of the longwave radiation, described by the Stefan–Boltzmann equation, is found to be fairly small compared with the temperature sensitivity of turbulent heat transfer (Reference Konzelmann and BraithwaiteKuhn, 1979; Reference Bøggild, Olesen, Ahlstrøm and JørgensenBraithwaite, 1981, Reference Braithwaite1995; Reference Braithwaite and OlesenBraithwaite and Olesen, 1990b), and the latter is mainly responsible for the increased melt with higher temperatures (Reference BraithwaiteBraithwaite and Olesen, 1990a).
It is obviously desirable to determine energy balance for longer periods on more glaciers. It would be difficult to measure turbulent fluxes routinely by direct measurements using eddy-correlation methods or to collect data at several instrument heights to estimate turbulent fluxes by the gradient method. The alternative is to estimate turbulent fluxes from simple climate data collected at one height (e.g. 1–2m above the glacier surface). Ideally this should be done with automatic recording instruments that need only occasional visits for servicing and downloading data. With the development of reliable data loggers over the last 20 years, the main focus is now on the instruments and methodology of estimating glacier energy balances with the simple data that can be collected by unsupervised instruments. Reference Braithwaite, Konzelmann, Marty and OlesenBraithwaite and others (1998b) suggested the term ‘reconnaissance energy-balance study’ for an approach where the larger energy-balance components (radiation and ablation) are measured and the smaller components (turbulent fluxes) are estimated from simple data for wind speed and temperature. This is in contrast to very comprehensive studies (e.g. involving tall instrument masts and instruments that need close supervision) which require major logistics (Reference AmbachAmbach, 1963; Oerlemans and Vugts, 1993; Reference Konzelmann and BraithwaiteOhmura and others, 1994). Ski-equipped aircraft and snow scooters can be used for heavy lifting to support studies in the accumulation areas of large glaciers, but studies in ablation areas may still involve manual handling of equipment with, at best, support from small helicopters that are agile enough to land on rough glacier surfaces.
For the present paper, I concentrate on the calculation of turbulent heat fluxes from simple climate data. I discuss archive data that were collected mainly by old-fashioned and labour-intensive methods (e.g. manual measurement of daily ablation) but I argue that the basic approach could be used by others with modern equipment. The results may indicate small revisions of already published energy-balance studies (Reference Braithwaite and OlesenBraithwaite and Olesen, 1990b; Reference Braithwaite and OlesenBraithwaite and others, 1998a) but this is not the main point of the paper. The main point is to illustrate a technique that could be used for future work.
Turbulent Heat-Transfer Coefficient
The measurement or calculation of turbulent transfer over glacier surfaces is difficult both from the point of view of theory and measurement. Reference Meesters, Bink, Vugts, Cannemeijer and HennekenMorris (1989) gives an extended review with references to earlier work, and an accessible and concise treatment of this complex subject is given by Paterson (1994). The key concept there is calculation of the turbulent heat flux H in Wm–2 using a transfer coefficient A:
where P is the atmospheric pressure, u and T are wind speed and temperature measured at screen height and Ts is the glacier surface temperature, which is 0˚C for a melting surface.
The use of ‘transfer coefficient’ by Paterson (1994, p. 65) is confusingly close to the ‘heat-transfer coefficient’ of Reference Konzelmann and BraithwaiteKuhn (1979). The essential difference is that the independent variable in the first case is wind speed multiplied by temperature while in the second case it is temperature alone. I prefer to call Kuhn’s concept the ‘temperature sensitivity of sensible-heat flux’ (e.g. in Wm–2 K–1) and to reserve ‘heat-transfer coefficient’ for Paterson’s dimensionless quantity.
The expression for H in Equation (1) is fairly general if A is unspecified. Some theoretical assumptions about the vertical profiles of temperature and wind speed over the glacier surface are needed to derive values of A (Reference GarrattGrainger and Lister, 1966; Reference Meesters, Bink, Vugts, Cannemeijer and HennekenMorris, 1989).
The simplest, and possibly most elegant, treatment of sensible-heat flux assumes that both wind speed and temperature increase as the natural logarithm of the height above the surface, i.e. the so-called logarithmic profile for a neutral boundary layer (Reference Duynkerke and van den BroekeGarratt, 1992, p. 45; Paterson, 1994, p. 60–66). Paterson (1994) derives a formula for A for this case where the transfer coefficient depends only upon the logarithm of z/z 0, where z is the instrument height (ideally 1–2m above the surface) and z 0 is the effective roughness of the glacier surface. Figure 1 shows the relation between transfer coefficient and effective surface roughness. The Reference Ambach and KirchlechnerAmbach and Kirchlechner (1988) value is based on a detailed energy-balance study in Greenland where Reference AmbachAmbach (1963) found different roughness values for wind speed, air temperature and humidity. Reference KuhnMeesters and others (1997) give values of 2.7, 1.6 and 2.8×10–3 for separate transfer coefficients for wind, temperature and moisture for a site in Greenland. The roughness value in Figure 1 is the effective roughness of Reference Meesters, Bink, Vugts, Cannemeijer and HennekenMorris (1989) that gives the same heat-transfer coefficient as calculated with separate roughness values for wind, temperature and humidity. Reference Braithwaite and OlesenBraithwaite and Olesen (1990b) followed Reference Ambach and KirchlechnerAmbach and Kirchlechner (1988) in assuming a transfer coefficient of 1.9×10–3 because the Reference Havens, Müller and WilmotHay and Fitzharris (1988) value (3.9×10–3) then seemed too high. However, several authors have assumed a surface roughness of 10–3m corresponding to an A value of 2.9×10–3 (Van de Wal and Russell, 1994; Reference Braithwaite, Konzelmann, Marty and OlesenBraithwaite and others, 1998b). Reference Braithwaite, Konzelmann, Marty and OlesenDenby and Smeets (2000) found heat-transfer coefficients of 3.6 and 3.5×10–3 for one site on an Icelandic glacier using two different methods (eddy-correlation and profile methods). Further downslope from that Icelandic site they found values of 2.1 and 1.9×10–3 for the same two methods. They also found an increase in heat-transfer coefficient through the season, which they explain by increasing surface roughness.
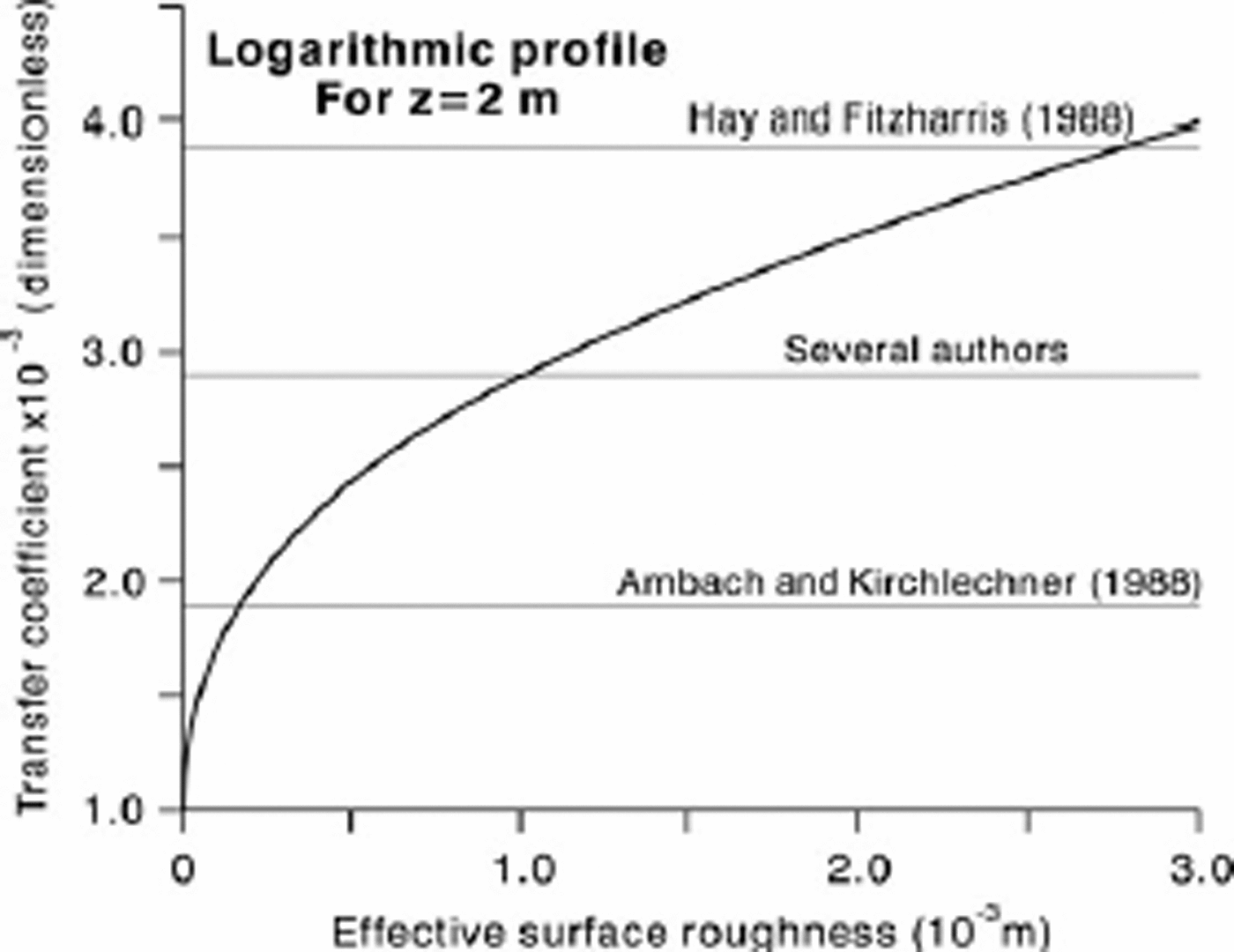
Fig. 1. Dimensionless exchange coefficient versus assumed surface roughness length assuming logarithmic (neutral) profile and 2m instrument height.
One objection to the assumptions underlying Figure 1 is that the boundary layer over a melting glacier surface is aerodynamically stable rather than neutral, so turbulence is inhibited to a greater or lesser degree by buoyancy forces. Using the more general log-linear wind profile, with the scale height of Monin and Obukhov (Reference Duynkerke and van den BroekeGarratt, 1992, p. 52–54), the heat-transfer coefficient is lowered as the temperature increases due to increasing stability. This is not a big effect for the relatively high wind speeds over the Greenland ice sheet, and the transfer coefficient is close to the value predicted for the neutral boundary layer but is much reduced with lower wind speeds of about 3 ms–1 or less (Reference Braithwaite, Konzelmann, Marty and OlesenBraithwaite and others, 1998b).
A more fundamental objection to the assumptions underlying Figure 1 is connected with katabatic flow on sloping ice and snow surfaces where the wind has a downslope component so the wind profile does not solely reflect turbulent conditions (Reference Meesters, Bink, Vugts, Cannemeijer and HennekenMorris, 1989; Reference Denby and SmeetsDuynkerke and Van den Broeke, 1994; Van den Broeke and others, 1994). This difficulty has been known for some time (Reference Hay and FitzharrisHolmgren, 1971; Reference MunroMunro and Davies, 1978), but as a result of a recent conference (Reference Munro and DaviesOerlemans and Van den Broeke, 2002) it is now hard to ignore. For the estimation of sensible-heat flux from simple climate data the key issue appears to be the height of the measurement instruments compared with the height of the constant flux layer underlying the katabatic flow layer (Reference Meesters, Bink, Vugts, Cannemeijer and HennekenMorris, 1989; Reference Müller and Roskin-SharlinMunro, 2004). This is beyond the scope of the present paper.
From this brief discussion, it seems that calculation of sensible-heat flux from simple climate data (e.g. temperature and wind speed ∽2m above the glacier surface) involves problems. Rolstad and Oerlemans (2005) neatly avoid difficulties with stability and katabatic flows as they calculate the sensible-heat flux as the residual in the energy-balance equation and then estimate the necessary heat-transfer coefficient A. They find values of 2.0±0.5, 2.5±1.1, 1.3±0.6 and 2.1±0.6×10–3 for a site on the Greenland ice sheet, for two seasons at one site in Iceland and at one site on a Swiss glacier. In their approach, radiative heat fluxes are measured directly or estimated from simple climate data measured with an automatic weather station, and the value of A is chosen to fit the energy-balance equation with the mean ablation measured at the site. No assumptions about turbulence (wind profile, surface roughness or aerodynamic stability) are needed for such an empirical approach, although errors in other terms (e.g. for radiation components) may accumulate. I attempt something similar to estimate new values of A from field data at six field sites, including daily measurements of ablation to avoid the problem of error accumulation.
Data
Data from six sites are analyzed in this paper (Table 1). The key point to the present study is that ablation was measured directly every day at all six sites so the energy-balance calculation can be checked on a daily basis. The reader should note that the studies cited below, spanning nearly 40 years, expressed energy-balance terms in a variety of units. For present purposes, all data have been converted into Wm–2 which now seems to be accepted as a standard unit.
Table 1. Locations of the sites used for this study. Detailed references to the data are given in the text
The usual formulation of the energy-balance equation is to calculate melt energy (the amount of melt in mass-balance terms multiplied by the latent heat of fusion) as the residual in the energy-balance equation. It is not possible to measure melt directly. What can be measured, although somewhat inaccurately, is the ablation, which is the net loss of material from the glacier surface by melting and vapour transfer together. Although the latter may involve a large latent energy flux, i.e. condensation or sublimation, it only causes a very small mass change. This is why studies of glacier energy balance usually treat ablation and melting as essentially identical in mass-balance terms and use measured ablation to evaluate melt energy. If one wanted to calculate ablation energy, it would be melt energy plus latent-heat flux. Reference Braithwaite, Konzelmann, Marty and OlesenBraithwaite and others (1998b) give an example from North Greenland where the largest daily value of latent-heat flux is –71Wm–2, which gives a mass loss of only 2 kgm–2 d–1 by sublimation, which is undetectable using ablation stakes (Reference Braithwaite and OlesenBraithwaite and others, 1998a). Estimation of melt energy from ablation data will break down in climates with very low melt and high sublimation (e.g. on very high mountains or in some parts of the Antarctic) but this does not apply to the present datasets.
Fritz Müller (1926–1980) was a pioneer of short-term measurements of ablation in parallel with measurements needed to calculate the energy balance of the melting glacier surface. Reference MorrisMüller and Keeler (1969) describe efforts to measure the ablation involving both the lowering of the glacier surface and the change in near-surface density due to growth and decay of ‘weathering crust’. Reference MorrisMüller and Keeler (1969) list components of the daily energy balance for summer periods in 1961 and 1962 (White Glacier, Axel Heiberg Island, Canada) and for 33 days in 1963 (Sverdrup Glacier, Devon Island, Canada). More detailed data for these studies can be found in Reference HolmgrenKeeler (1964), Reference Grainger and ListerHavens and others (1965) and Reference Müller and KeelerMüller and Roskin-Sharlin (1967). Data for a further energy-balance study for summer 1960 on White Glacier are given by Reference AndrewsAndrews (1964).
Müller’s emphasis on daily ablation measurements was continued in Greenland work, where Nordbogletscher, South Greenland, and Qamanârssûp sermia, West Greenland, were the sites of multi-summer studies where daily ablation was measured in parallel with collection of climate data. This allowed Reference BraithwaiteBraithwaite and Olesen (1990a, Reference Braithwaite and Olesenb) to develop a simple energy-balance model to calculate daily ablation over five to seven seasons. The long series of daily measurements were only possible because the stations were operated mainly for political reasons in connection with the planning of hydropower stations in Greenland. It will never again be possible to measure daily ablation manually for so many hundreds of days.
Kronprins Christians Land and Hans Tausen ice cap, North Greenland, were the sites of reconnaissance energy-balance studies in 1993 and 1994 (Reference KeelerKonzelmann and Braithwaite, 1995; Reference Braithwaite and OlesenBraithwaite and others, 1998a, Reference Braithwaite, Konzelmann, Marty and Olesenb). Daily data on ablation were collected in parallel with high-quality measurements of radiation balance and of simple climate data.
Aside from ablation data, collected manually at all sites by resident field teams, climate data for the two Canadian sites and for Nordbogletscher and Qamanârssûp sermia were collected with relatively primitive instruments which were read manually. Climate data for Kronprins Christians Land and Hans Tausen ice cap were recorded on digital data loggers but they were still supervised manually. Future workers will rely more on automatic instruments with only brief visits to the field site.
Empirical Estimates of Heat-Transfer Coefficient
The formulation of the sensible-heat flux in terms of the dimensionless heat-transfer coefficient prompts the hypothesis that melt energy should be highly correlated with the product of wind speed and temperature. For convenience, this product is pre-multiplied by (1:29 × 10-2)P, where P is average atmospheric pressure in Pascal at the location in question, to give a ‘wind–temperature variable’. The slope of the regression line between melt energy and this variable is, by hypothesis, an estimate of the heat-transfer coefficient A. This implies the assumption that none of the other terms in the energy balance are highly correlated with the wind–temperature variable, which seems reasonable. If any other term were well correlated with the wind–temperature variable the prime candidate would probably be the latent-heat flux.
Statistics for the six sites are summarized inTable 2 and in Figure 2. Correlations between melt energy and the wind–temperature variable are in all cases quite high (+0.69 to +0.93) compared with the correlation between net radiation and the wind–temperature variable (–0.10 to +0.21). In all six cases the intercept is positive and in five out of the six cases the intercept is significantly greater than zero (with 95% probability). This fits with the notion that there can be ablation even when turbulent heat transfer is zero (e.g. because air temperature is 0˚C). There is a range of slope values, but four out of the six are not significantly different from 2:9 × 10-3, which is the value A would have for a neutral boundary layer with surface roughness of 1mm and instrument height of 2 m (Fig. 1). The other two slope values (Sverdrup Glacier and Hans Tausen ice cap) are much bigger although they also have very wide confidence intervals (95% probability). It would be too hasty to conclude that these high A values simply reflect higher surface roughness in these two cases. There are relatively small ranges of temperature and wind speed in the measuring periods for these two sites, so the high slope values may be artefacts of short records.
Table 2. Intercept and slope in regression equations linking ablation to the wind–temperature variable with 95% confidence intervals
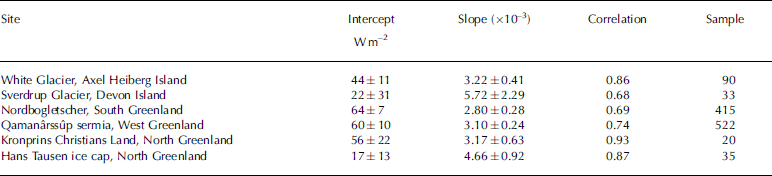
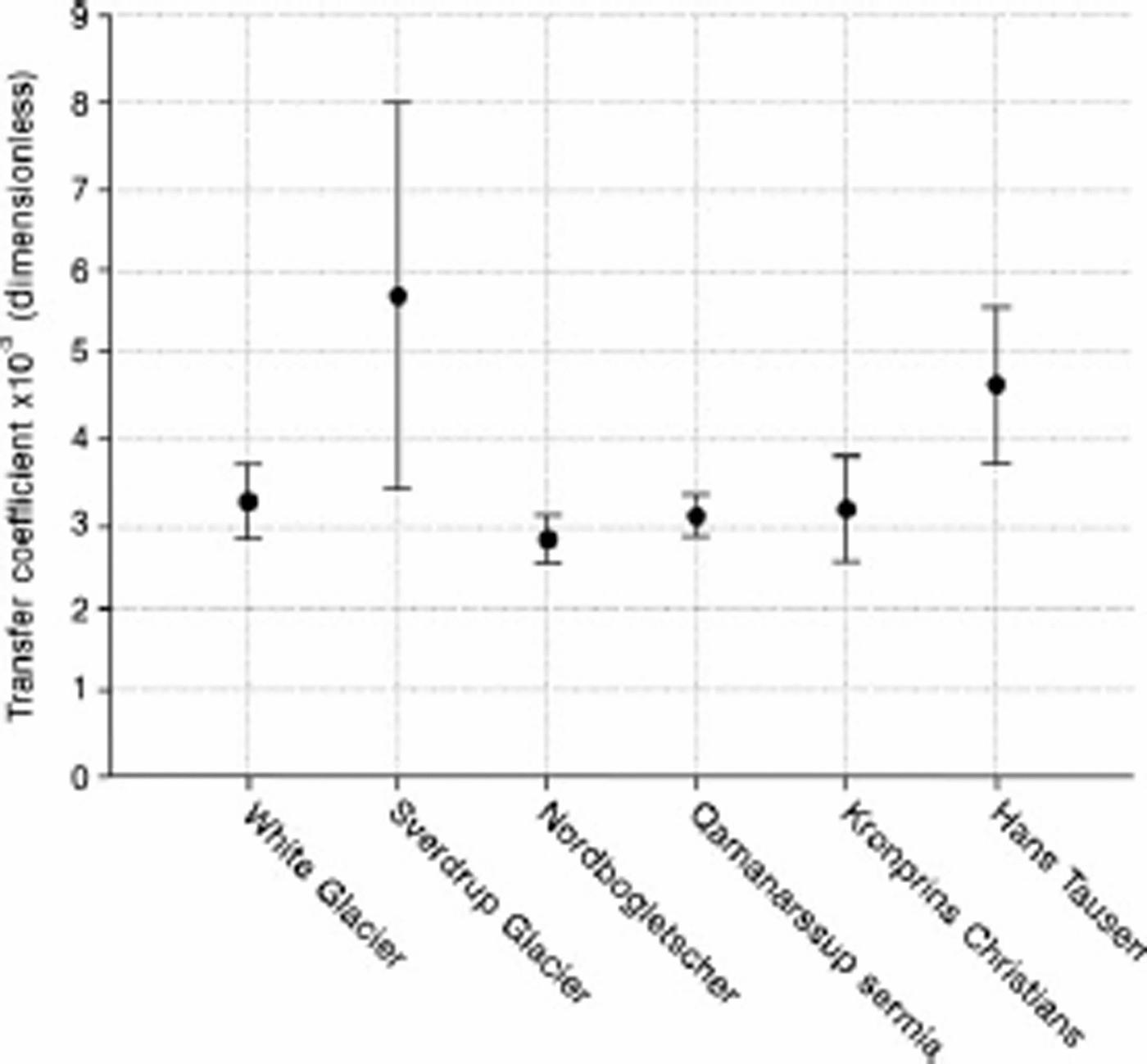
Fig. 2. Mean and 95% confidence interval for sensible-heat flux transfer coefficient at six sites.
The data for White and Sverdrup Glaciers are pooled in Figure 3, with a new regression equation for the combined sample. By inspection of the scatter plot we can see that the high slope for Sverdrup Glacier (Table 2) is because many points are clustered near the origin. The combined sample has a more even point distribution and a lower slope. Scatter plots for Nordbogletscher and Qamanârssûp sermia (Figs 4 and 5) are remarkably similar. Data from Kronprins Christians Land and Hans Tausen ice cap are pooled in Figure 6, and the result is again a more even point distribution and lower slope. The slopes of regression equations in Figures 3–6 suggest values of 3.3, 2.8, 3.1 and 4:1 × 10-3 for the heat-transfer coefficient. These values suggest higher values of sensible-heat flux than calculated originally (e.g. using 1.9×10–3 (Reference Braithwaite and OlesenBraithwaite and Olesen, 1990b) and 2.9×10–3 (Reference Braithwaite, Konzelmann, Marty and OlesenBraithwaite and others, 1998b)), but the purpose of this paper is not to revise energy balances calculated previously.

Fig. 3. Melt energy (calculated from measured ablation) versus wind–temperature variable at two sites in Arctic Canada. Sverdrup: Sverdrup Glacier, Devon Island; Lower ice: White Glacier, Axel Heiberg Island.
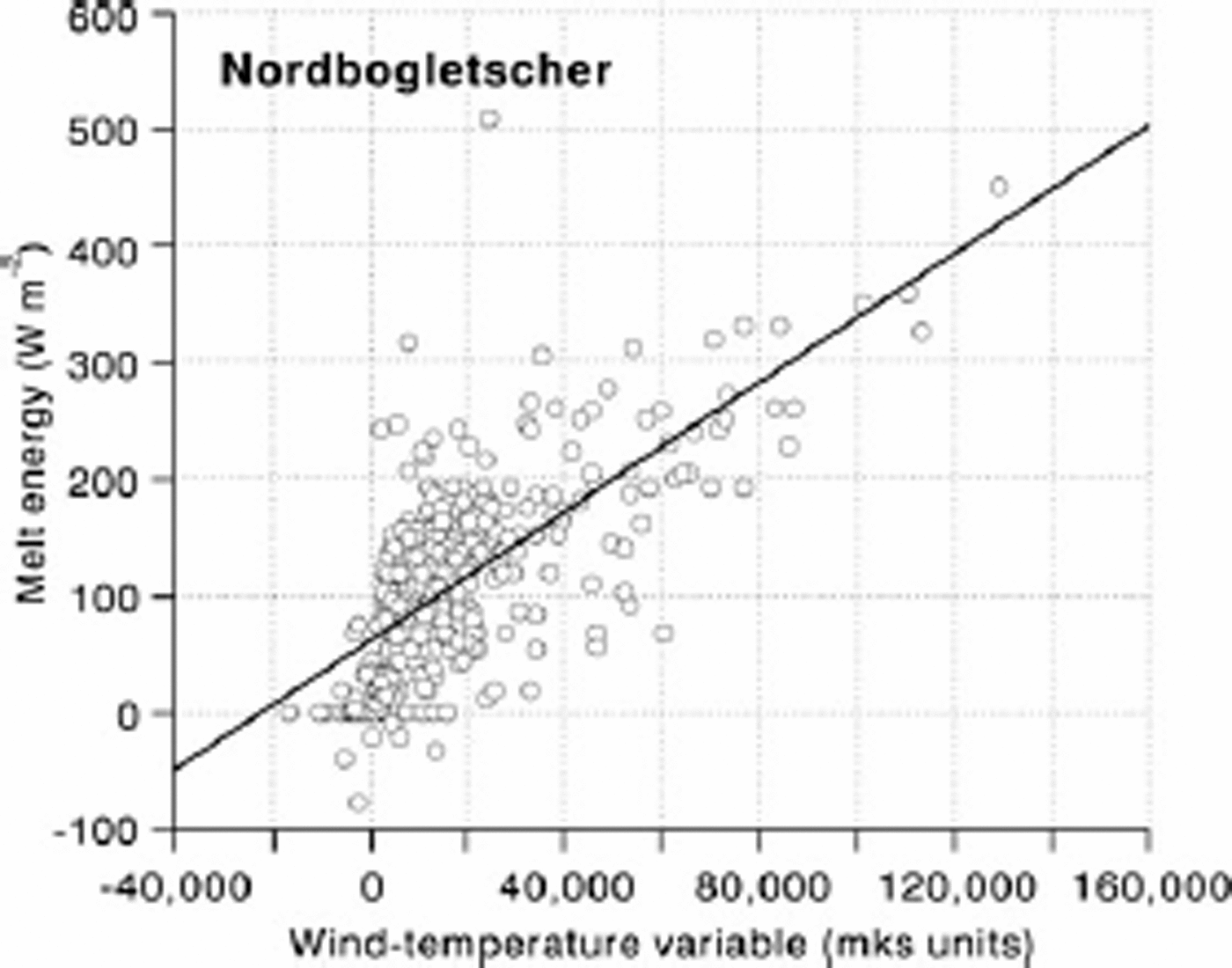
Fig. 4. Melt energy (calculated from measured ablation) versus wind–temperature variable at stake 53, Nordbogletscher, South Greenland.
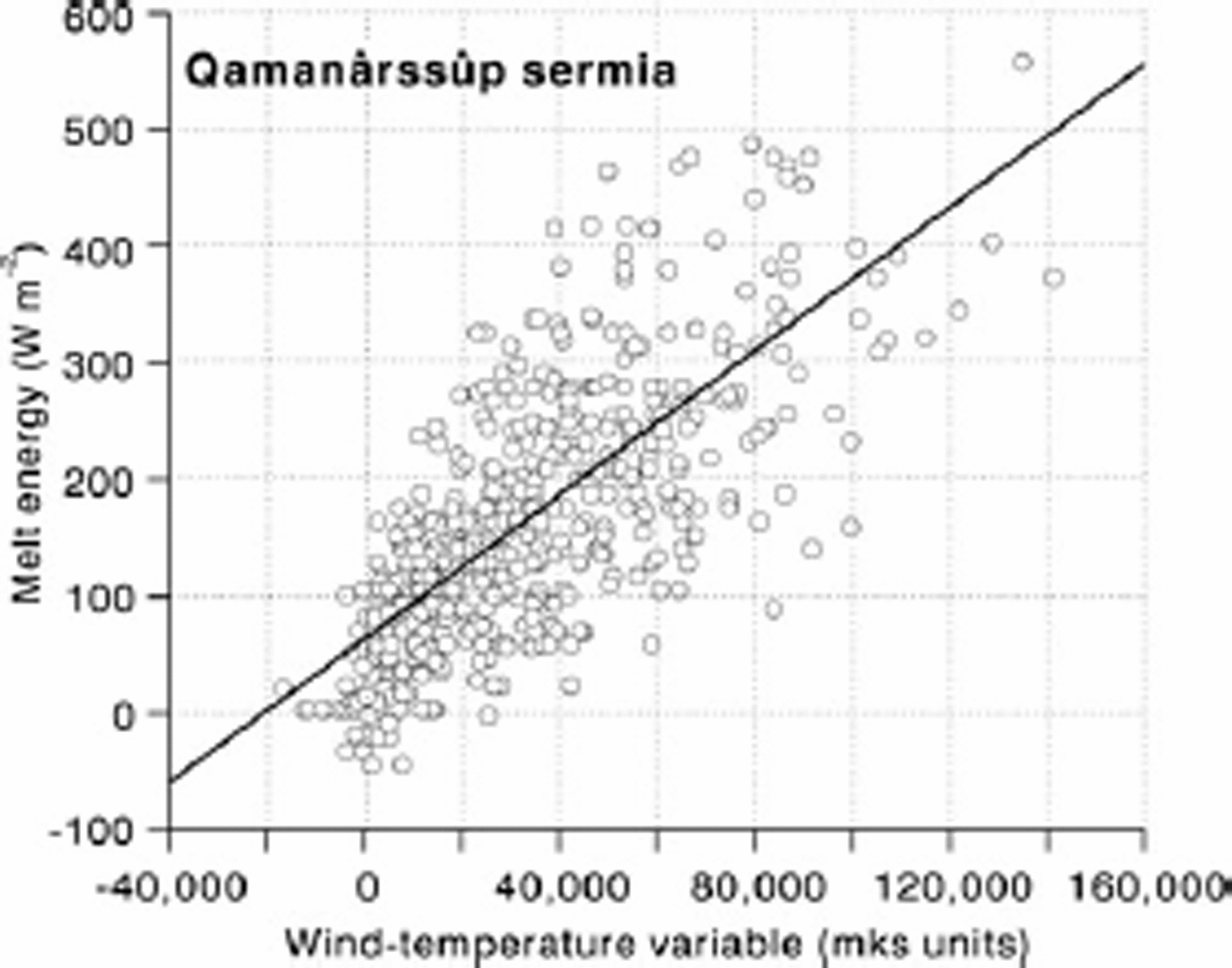
Fig. 5. Melt energy (calculated from measured ablation) versus wind–temperature variable at stake 751, Qamanârssûp sermia, West Greenland.
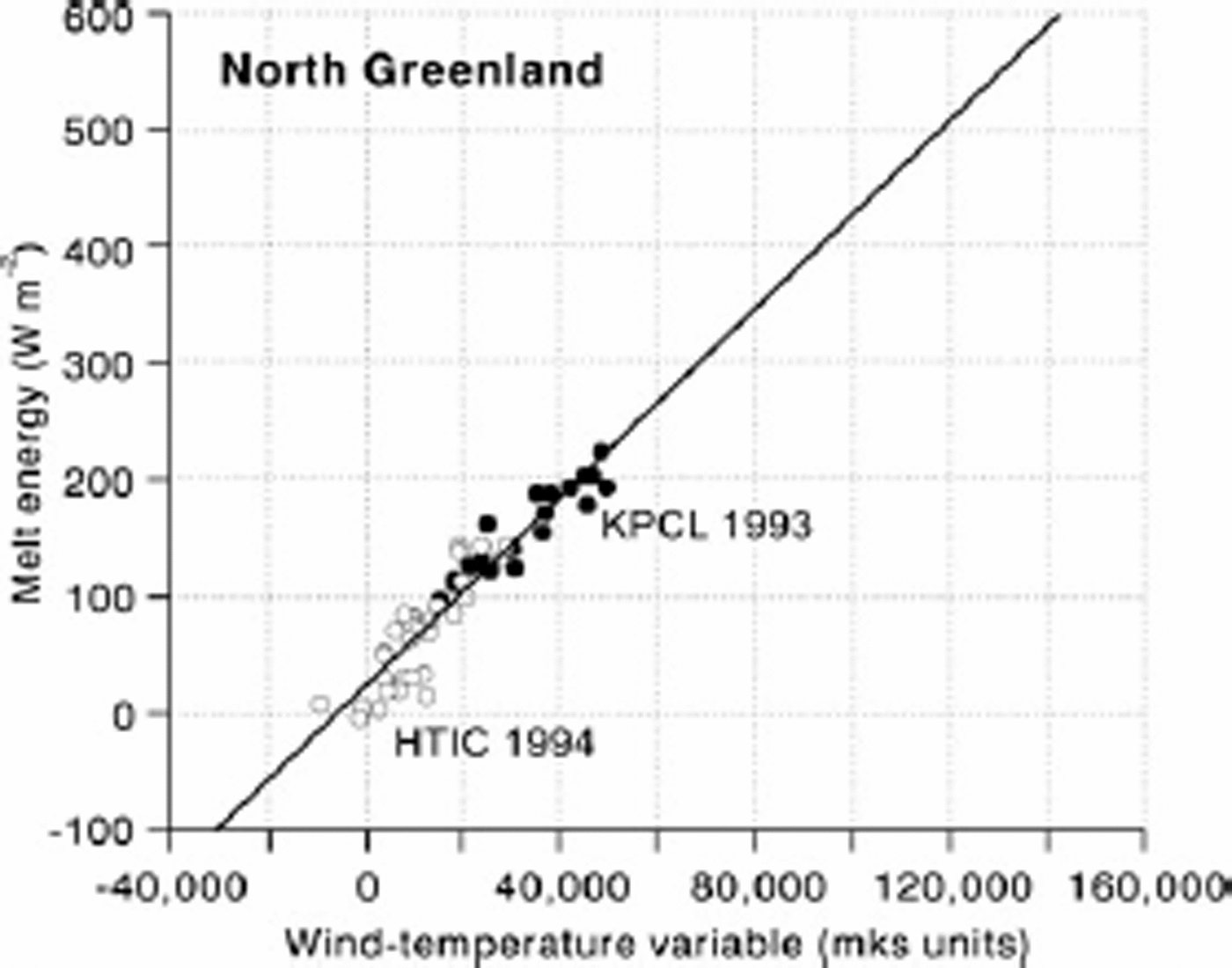
Fig. 6. Melt energy (calculated from measured ablation) versus wind–temperature variable at two sites in North Greenland. KPCL: Kronprins Christians Land; HTIC: Hans Tausen ice cap.
Part of the scatter in Figures 3–6 must be due to errors in the measured ablation. Reference MorrisMüller and Keeler (1969) discuss these for the datasets in Figure 3. There are some negative values for melt energy in Figures 4 and 5 which must be due to measurement errors for ablation. However, it would be invalid to simply suppress these particular values, because the whole dataset is permeated with such errors. Reference Braithwaite and OlesenBraithwaite and others (1998a) suggest a standard deviation of ±6kgm–2 d–1 for random errors in daily ablation measurements, i.e. equivalent to ±23Wm–2 in terms of melt energy, although some much larger errors can arise due to gross errors in reading stakes or recording the data.
The fact that two out of the six slopes in Table 2 seem anomalous, and these are associated with quite short records, suggests that one should look at short-term variations in slope. This is done by splitting the two large samples up into smaller samples for each month (Table 3). Month-to-month variations in slope are quite large (e.g. ranging from 1.0 to 4.2×10–3 at Qamanârssûp sermia). The variations in Table 3 suggest that the present method of determining heat-transfer coefficient should not be applied to very short records, as even with 20–30 days of record there are substantial variations. There is, perhaps surprisingly, no great difference between monthly averages although one might have expected systematic changes in surface roughness throughout the melt season (Reference Braithwaite, Konzelmann, Marty and OlesenDenby and Smeets, 2000). It is curious that the averages of monthly slopes at Nordbogletscher and Qamanârssûp sermia are much closer together than the slopes in Table 2. Presumably, this is due to the different definitions of sample space.
Table 3. Monthly values of slope in the regression line linking ablation energy to wind–temperature variable for two sites.
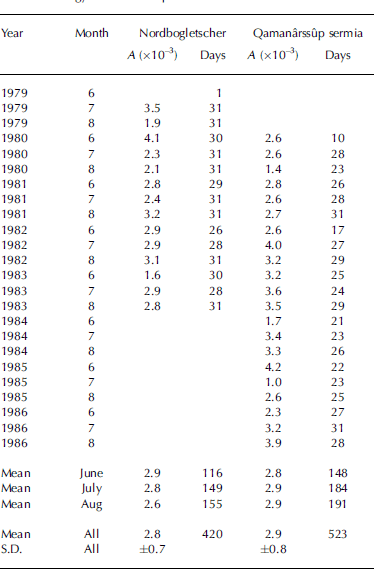
Future Work
The data analyzed in the present study are based on daily measurements of ablation stakes and simple meteorological data. Future workers will have to rely on occasional visits to unsupervised automatic instruments. Daily measurements of ice ablation could be made automatically with a sonic ranging sensor or pressure transducer (Reference BauerBøggild and others, 2004) connected to a modern data logger that will also record the necessary temperature and wind data. These climate data can be collected at hourly intervals which would permit the study of diurnal variations in temperature and wind speed that might be useful in assessing the characteristic effects of katabatic flow.
Collection of detailed data for radiative components would also make the method of Rolstad and Oerlemans (2005) possible so that two estimates could be obtained for heat-transfer coefficient. If this is done for a number of sites it will then be possible to study inter-site variations in heat-transfer coefficient (e.g. due to effects of sample size) and variations in aerodynamic situations at different sites and in different periods.
There is ample evidence to show that ablation varies greatly within a few metres of an ablation stake (e.g. by ±10 to ±15% of total ablation (Reference ÅngströmBauer, 1961; Reference Braithwaite and OlesenBraithwaite and others, 1998a)). Rolstad and Oerlemans (2005) call this ‘differential melt’. This uncertainty will be transmitted to any quantity calculated from the measured ablation (e.g. the heat-transfer coefficient in the present case). In future work, daily ablation will only be available from one point, but a stake farm of up to ten stakes could be established around this point if there is time to drill extra stakes. The record of daily measurements at the one point could then be adjusted to fit the mean ablation of the stake farm.
Conclusions
Melt energy is correlated with the wind–temperature variable, and the slope of the regression line is an estimate of the dimensionless heat-transfer coefficient for sensible-heat flux. In four out of the six cases studied, results are in fair agreement with values already reported in the literature, i.e. in the range 2.8–3.2×10–3. Rather high values in the other two cases, i.e. 4.7 and 5.7×10–3, may be artefacts of short records and/or the results of katabatic flow. The suggested method for calculating heat-transfer coefficient should only be used for at least 20–30 days of record.
Acknowledgements
This paper was written during a period of research leave from the University of Manchester and I thank my colleagues for covering my teaching and administration duties. I thank the scientific editor of this paper (J.O. Hagen) and three anonymous referees for their invaluable comments.











