List of Symbols
List of Symbols

1. Introduction
Fluctuations in the mass of the Earth’s ice sheets have profound implications for the Earth’s radiation balance, ocean circulation and sea level that, in the 21st century, may have considerable political and economic consequences (Reference SolomonSolomon and others, 2007). The potential of radar altimeters on Earth-orbiting satellites to reveal these fluctuations has already been demonstrated with the 10 year time series from the European Space Agency (ESA) European Remote-sensing Satellite (ERS). A new and improved radar altimeter, the Synthetic Aperture Radar Interferometric Radar Altimeter (SIRAL), is carried by the ESA CryoSat-2 satellite (Reference WinghamWingham and others, 2006). This paper is concerned with density measurements made in the dry snow zone of the Greenland ice sheet as part of the calibration and validation (cal/val) activities in support of CryoSat-2.
The general objective of the land-ice cal/val activities has been to estimate the variance in the uncertainty in the trend in spatially averaged land-ice mass that will be measured by SIRAL. Here we are particularly concerned with the elements of this uncertainty that arise because of fluctuations in accumulation and near-surface density. We do not consider other components arising from errors in estimation of postglacial rebound or instrument system errors. Although the density data reported in this paper are of considerable interest in considering retrieval errors associated with variations in the penetration of radar waves into the near-surface snow, this component of the uncertainty will be considered in detail elsewhere.
We consider a column of densifying firn whose surface lies at a height z = h
S in an inertial frame {x, z, t} and whose base, fixed in the inertial frame, lies at sufficient depth that the firn has reached the density of ice, ρ
i. The mass fluxes per unit area at the surface and base of the column are
![]() and
and
![]() , which we suppose are the only sources of mass gain or loss. If
, which we suppose are the only sources of mass gain or loss. If
![]() is the rate of change of height, and we associate with it a mass change,
is the rate of change of height, and we associate with it a mass change,
![]() , that we suppose equal to the change in mass of the column, we will generally commit an error which, written as an equivalent rate of change of height, is
, that we suppose equal to the change in mass of the column, we will generally commit an error which, written as an equivalent rate of change of height, is
In this paper our first purpose is to use field measurements from the Greenland ice sheet to determine how this average error varies with the observation interval. In applying Equation (1) to the situation in Greenland, we must acknowledge that the ice (1) undergoes horizontal motion and (2) is subject to a nonzero strain rate. With regard to (1), Equation (1) is unchanged if we subject the material column to a constant horizontal velocity, save that
![]() and
and
![]() are no longer those at a fixed location. In fact, because the time periods that concern us are short, we shall suppose that, at a given location,
are no longer those at a fixed location. In fact, because the time periods that concern us are short, we shall suppose that, at a given location,
![]() is constant in both time and space. With regard to (2), we shall suppose that the strain rate is sufficiently small that the mass loss through the walls of the column may be ignored in comparison with that from its base. This is reasonable if the depth at which the firn reaches the density of ice is small in comparison with the ice thickness.
is constant in both time and space. With regard to (2), we shall suppose that the strain rate is sufficiently small that the mass loss through the walls of the column may be ignored in comparison with that from its base. This is reasonable if the depth at which the firn reaches the density of ice is small in comparison with the ice thickness.
In the following, we use as the vertical coordinate the depth, s (positive downwards), of the firn beneath the surface. Its relation to the inertial elevation is
In the frame {s, t} the velocity of the firn relative to the surface, v, is related to the velocity, u, observed in the inertial frame via
At the surface the mass flux satisfies the kinematic boundary condition:
where v S is the velocity of the material at the surface and ρ S its density. Introducing a compaction velocity,
and substituting Equations (4) and (5) into Equation (1) yields

The compaction velocity is the difference between the velocity at a point at fixed depth in the column that has reached the density of ice, and the velocity at the surface. Equation (6) shows that the error is entirely associated with processes that occur at or near the surface; it does not depend on the ice flux at the base,
![]() .
.
Since we do not have continuous measurements of
![]() ,
,
![]() or ρ
S over the observation time interval, t ∊ {0, Δt}, it is necessary to integrate Equation (6). We move from the Eulerian approach of Equations (1–6) to a Lagrangian approach, in which the compaction velocity is defined as the difference between the ice velocity at the base of the column and the velocity of a material particle which lies at the surface at the start of the observation period and is then overlain by the accumulating snow. This allows us to use the measurements we have, namely Δl, the depth of snow accumulated over time Δt (i.e. the depth of the accumulation layer); Δm
S, the mass per unit area of the accumulation layer; Δh
S, the change in surface elevation; and (indirectly) Δc, the compaction in the underlying snow. The error, Δε, is defined by the integral of Equation (1) over time, namely
or ρ
S over the observation time interval, t ∊ {0, Δt}, it is necessary to integrate Equation (6). We move from the Eulerian approach of Equations (1–6) to a Lagrangian approach, in which the compaction velocity is defined as the difference between the ice velocity at the base of the column and the velocity of a material particle which lies at the surface at the start of the observation period and is then overlain by the accumulating snow. This allows us to use the measurements we have, namely Δl, the depth of snow accumulated over time Δt (i.e. the depth of the accumulation layer); Δm
S, the mass per unit area of the accumulation layer; Δh
S, the change in surface elevation; and (indirectly) Δc, the compaction in the underlying snow. The error, Δε, is defined by the integral of Equation (1) over time, namely
where Δm
F is the mass lost per unit area at the base of the column over the observation time interval. Defining the mean density of the accumulation layer as
![]() = Δm
s/Δl, we show in Appendix A that Equation (6) integrates to give
= Δm
s/Δl, we show in Appendix A that Equation (6) integrates to give
with an approximation error that is small compared to the measurement errors for our observation periods. If

no error, Δε, occurs. Unless the compacted firn has been subjected to abrupt changes, experience shows that the compaction does not greatly differ from that given by Equation (9), so the terms on the right-hand side of Equation (8) largely cancel. It is then natural to regard Δε as the error resulting from fluctuations from a time-invariant state described by m 0, ρ 0(s) and c 0 and satisfying Equation (9). For time interval Δt we write

with

We show in Appendix A that
![]() is the harmonic mean of ρ
0(s) over the accumulation layer. Substitution from Equation (10) in Equation (8) gives
is the harmonic mean of ρ
0(s) over the accumulation layer. Substitution from Equation (10) in Equation (8) gives

in which the first two terms on the right-hand side describe the result of surface fluctuations of either mass and density and the third the result of compaction fluctuations. This separation is useful, for, if it turns out that Δc
1 is small, then the error may be largely reduced by knowledge (from observations or models) of
![]() and Δm
S alone. Conversely, if Δc
1 is large, knowledge of the density structure of the firn is also needed.
and Δm
S alone. Conversely, if Δc
1 is large, knowledge of the density structure of the firn is also needed.
To the extent that the fluctuations do vary about a constant state, we expect the average error to reduce with time; if it does not, then the terms in Equation (12) will identify secular changes in the surface fluctuations or the densification. Our second purpose in this paper is therefore to investigate the relative magnitude of the terms in this equation. In doing so, though, we note that, to an extent, the magnitude of the terms in Equation (12) is dependent on the definition we use of the time-invariant state: the total error in Equation (1) or Equation (7) is not.
Our data show (section 5.2) that the ratio
![]() is of order 0.1 for subannual timescales, decreasing to order 0.01 on a 2 year timescale. Hence, for our observation periods, the mass and density fluctuations may be separated by expanding
is of order 0.1 for subannual timescales, decreasing to order 0.01 on a 2 year timescale. Hence, for our observation periods, the mass and density fluctuations may be separated by expanding

so that

Our final purpose in this paper is to investigate the effect of spatial averaging on the magnitude of the error in calculating the mass-balance trend from elevation measurements, with particular reference to the CryoSat radar altimeter data. For discrete sites, xj weighted by wj , the spatial mean of Δε/Δt is given by

where
![]() is the covariance of Δε/Δt. Thus the effect of short-term fluctuations on the accuracy of the trend measured by satellite altimeter depends on their spatial correlation. We report measurements which have allowed us to determine
is the covariance of Δε/Δt. Thus the effect of short-term fluctuations on the accuracy of the trend measured by satellite altimeter depends on their spatial correlation. We report measurements which have allowed us to determine
![]() and, for the first time, quantify the contributions to this covariance from accumulation, surface density and compaction.
and, for the first time, quantify the contributions to this covariance from accumulation, surface density and compaction.
2. The Cryosat Traverse
Measurements have been made along a 365 km section of the Expéditions Glaciologiques Internationales au Groenland (EGIG) line from site T05 to site T41, and then along a 184 km track north to Summit Station (Fig. 1). Repeated traverses, coordinated with airborne observations made using an airborne version of SIRAL, the Airborne Synthetic Aperture Radar Interferometric Radar Altimeter System (ASIRAS), were made in spring and autumn 2004 and spring and summer 2006. Table 1 shows the positions of the sites. Temperatures at 15 m depth, T 15, were measured in 1990 by Reference Fischer, Wagenbach, Laternser and HaeberliFischer and others (1995), who give a lapse rate for temperature with altitude over the western EGIG line (T05 to T41) of −0.0094 K m−1 (including the effect of changing latitude). For the region between T41 and Summit they give lapse rates of −0.0072 Km−1 and −0.71 K (degree latitude)−1. Using these lapse rates we have calculated approximate values of T 15 (shown in parentheses in Table 1) for intermediate sites. Reference BoxBox (2002) gives a mean annual air temperature of T m = −29.7°C at Summit for the period 1991–2000, higher than the value of T 15 = −31.6°C measured in 1990. Similarly Reference Steffen and BoxSteffen and Box (2001) find the mean annual air temperature measured in 1997 at Summit, T m = −29.5°C, is higher than the 10 m temperature T 10 = −31.1 °C for the same year. At Crawford Point, not far from T05, T m = −16.8°C and T 10 = −18.4°C for 1996. The traverse runs from a site (T05) which is clearly in the percolation zone, with summer meltwater refreezing within the snowpack in thick ice layers, through a transition zone to T21, which can be regarded as the start of the dry snow zone. From here to Summit Station, air temperatures above 0°C are rare and any meltwater refreezes in the surface layer.
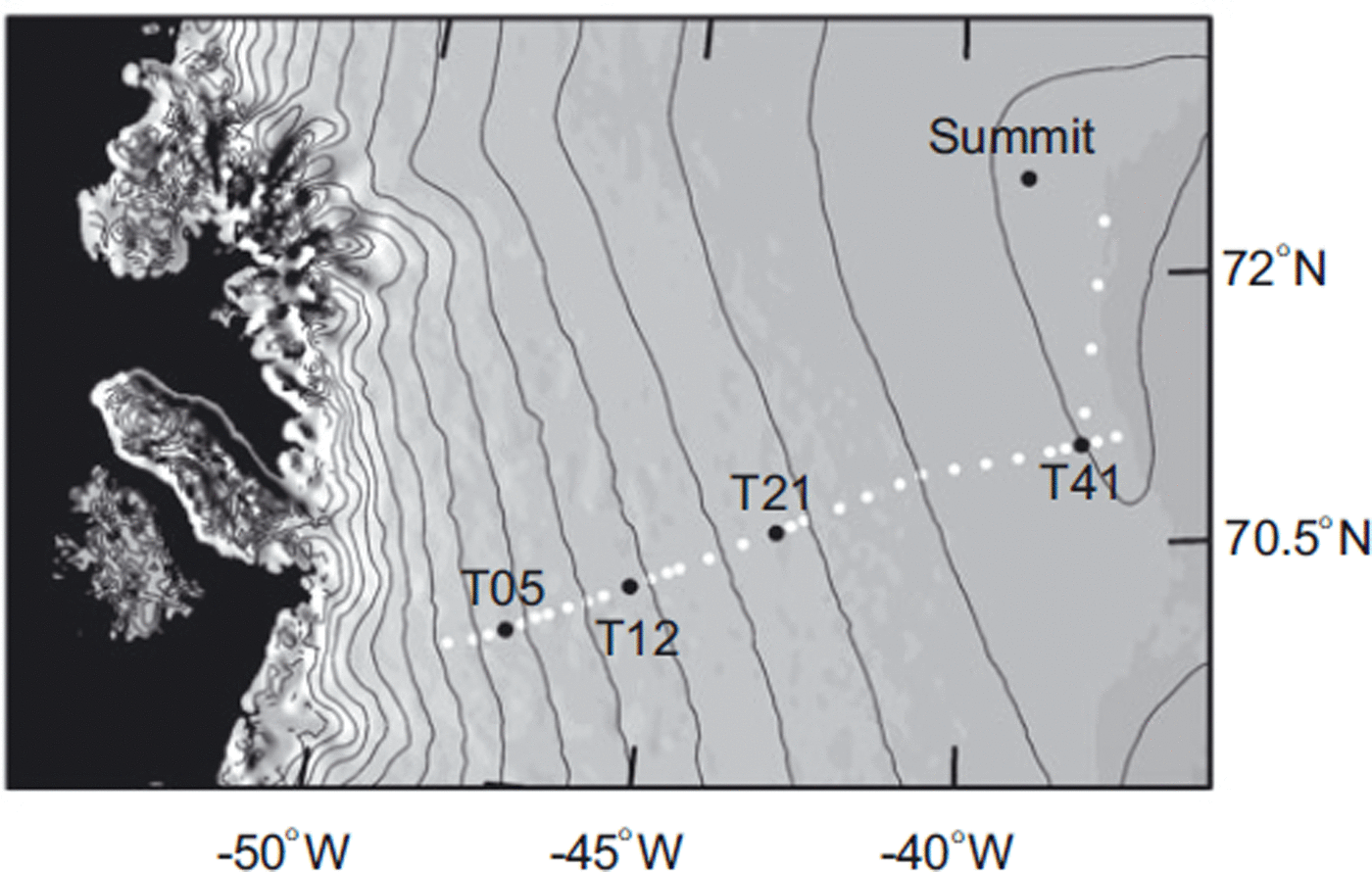
Fig. 1. The CryoSat traverse. Sites T05 to T41 lie along the EGIG line.
Table 1. Temperature at a depth of 15 m, T 15, and the mean and standard deviation of the annual accumulation series at the CryoSat traverse sites with x the distance along the traverse. Elevations are given in metres above the WGS84 ellipsoid. Values in parentheses are approximate values calculated using the lapse rates
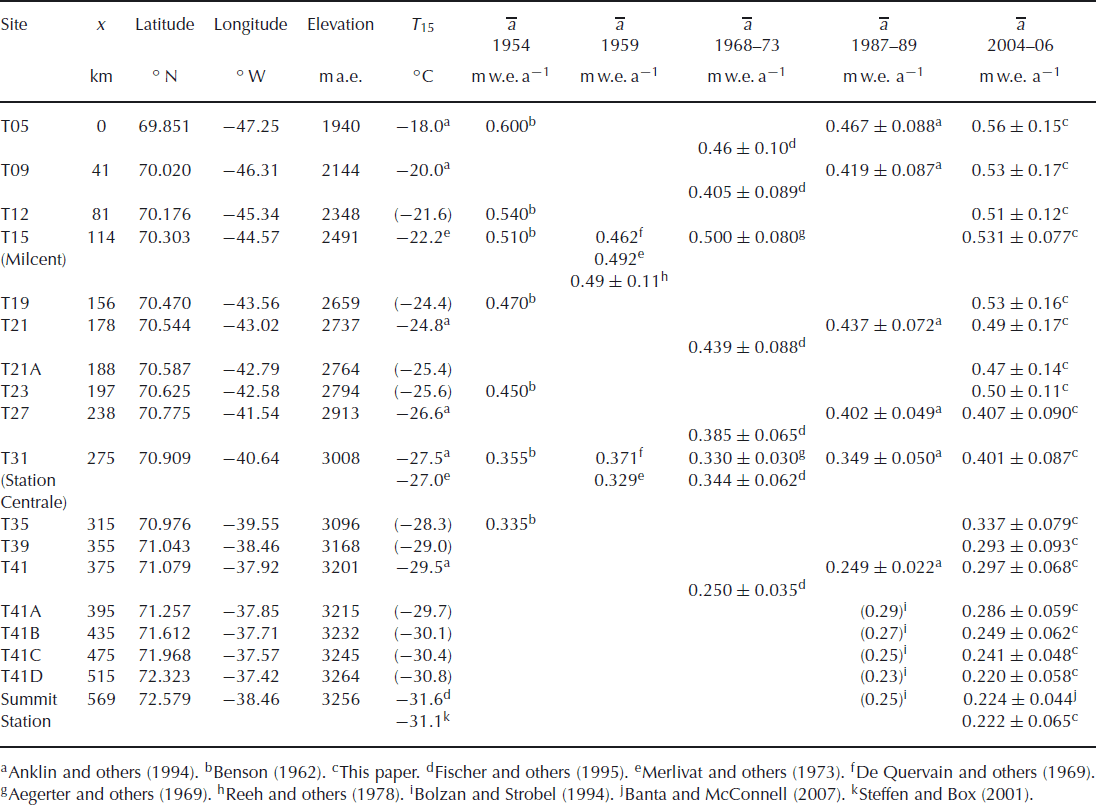
Mean annual accumulation was determined by Reference BensonBenson (1962) in 1955 and Reference De Quervain, Brandenberger, Reinwarth, Renaud, Roch and SchneiderDe Quervain and others (1969) in 1959 using stratigraphic methods and by Reference Aegerter, Oeschger, Renaud and SchumacherAegerter and others (1969) and Reference Merlivat, Ravoire, Vergnaud and LoriusMerlivat and others (1973) using tritium analysis of shallow cores collected during the EGIG II crossing in 1968. In 1973 Reference Reeh, Clausen, Dansgaard, Gundestrup, Hammer and JohnsenReeh and others (1978) collected a deep core at ‘Milcent’ (T15) covering 796 years. Values determined by analysis of shallow cores collected in 1990 using H2O2 (Reference Anklin, Stauffer, Geis and WagenbachAnklin and others, 1994) and δ18O (Reference Fischer, Wagenbach, Laternser and HaeberliFischer and others, 1995) gave no evidence of a significant temporal change in accumulation rates over the 40 years from 1955. Reference Bolzan and StrobelBolzan and Strobel (1994) produced a map of accumulation in the Summit region based on shallow cores collected in 1987, and we have used this to provide interpolated values for our sites T41A to Summit Station. Table 1 shows the historic data for the CryoSat traverse sites, with standard deviations where known. The traverse runs through a region of relatively high accumulation from T05 to T19; from there on accumulation decreases with elevation.
In spring 2004 the traverse began at T12 and ended at Summit Station, with an extended period spent at T21 making measurements over a 1 km2 grid to coincide with an ASIRAS overflight on 6 May. At Summit Station measurements were made using existing boreholes (‘Katie’, ‘Karl’ and ‘Geoff’) and augered holes (4 m from ‘Geoff’ and 1 m from ‘Katie’) all of which lie on a 50 m radius circle 200 m north of the station. In autumn 2004 the traverse began at Summit Station. Since the fragile summer surface hoar layer could not be preserved while a site was reoccupied, sites T41A, T39, T23 and T21A were left untouched for resurvey in spring 2006 (when the summer layer would be protected by a harder winter layer). The traverse ended at T21 where repeat measurements over the 1 km2 grid again coincided with an ASIRAS overflight on 14 September. In spring 2006 the traverse began in the transition zone at T12, where measurements were made over a 1 km2 grid to coincide with an ASIRAS overflight on 25 April, and ended at Summit Station. Delays at the start meant there was insufficient time to profile all sites on the traverse, so T21, T21A, T23 and T27 were omitted. Finally in summer 2006 the traverse began at Summit Station and ended at T05, with profiles collected at all sites. Profiles over a 1 km2 grid at T05 were collected by other members of the ESA CryoSat cal/val team in spring and autumn 2004 (Reference ParryParry and others, 2007).
3. Methods
Density profiles were measured using a neutron probe which forms part of the ice geophysical logging system (IGLS) developed by Reference Morris and CooperMorris and Cooper (2003). It contains an annular source of fast neutrons around a cylindrical detector of slow neutrons. The fast neutrons lose energy by scattering in the snow, and the count rate of slow neutrons arriving back at the detector is related to snow density. Theoretical calibration equations have been derived by Reference MorrisMorris (2008). A Kovacs auger, driven by a Porter and Cable 110 V electric drill, was used to make 5 cm access holes, using a 1.25 m aluminium guide tube to ensure the hole was not enlarged in the upper softer layers of the snow. At some sites it proved more difficult to remove chippings and produce a deep hole, but at most sites depths around 13 m were achieved. The data were recorded on a Panasonic CF-29 Toughbook computer, kept inside a work tent with the IGLS logger. It functioned at very low temperatures (around −30°C) without problems.
In autumn 2004 the shaft encoder system on the winch failed at site T35 because an associated plastic drive belt snapped. (This was replaced by a metal drive chain for the 2006 field seasons.) For sites T35, T31 and T27 the neutron probe was used in time-based mode with the winch operated manually. Data were obtained at 2 cm intervals over 64 s counting periods. This method was accurate but very slow, so at site T21, where a large number of repeat profiles were needed, an alternative automatic method was devised. The cable was run out to a known depth, the winch was set to run at the slowest speed and data collected at 1 s intervals in time-based mode. The times were converted to depth assuming constant winch speed. The densities were averaged over 1 cm, traversed in ∼10 s at the winch speeds used.
The access holes drilled in spring 2004 were protected by a large snow block so it was possible to reuse the holes in the autumn by digging down to the spring surface. At sites with higher accumulation (T21–T31), new shallow holes were drilled 1 m away, so the summer layer could be profiled. Below the spring surface the density profiles in the new holes matched those in the reused holes. Hence there is no indication that the presence of the hole affected compaction rates below this level, i.e. below ∼1 m depth. In 2006 an improved system was adopted. Holes drilled in the spring were capped with 1 m lengths of 5 cm diameter white plastic tubing, closed with tape at the upper end. The tubes were then removed, without disturbing the new snow, and the holes reprofiled in the summer. Figure 2 shows density profiles for spring 2004 and summer 2006 at site T41 as an example of the data obtained using the neutron probe. The profiles show the variation between denser winter snow and less dense snow formed during the summer from a mixture of surface hoar and precipitation. The noise in the data has been reduced by simple averaging, which is equivalent to extending the counting period and preferable to more complex signal-processing filters at this stage. Missing data near the surface have been interpolated with a constant density. The annual density peaks have been numbered, with peak 0 just below the spring 2004 surface. Our observations indicate that the density peaks lie in winter snow but are formed during the following summer, when warmer temperatures promote densification in the near-surface layer (e.g. Reference Zwally and LiZwally and Li, 2002). The pattern of peaks is consistent over the traverse, although at lower altitude melt-layer peaks are also found.
In Figure 2a the vertical axis, l, has been chosen so that the lowest density peak (N = 13, not shown) lies at the same level in each profile. For convenience we have set l = 0 at the spring 2004 surface so that for these data l = −s. In this l-representation the compression of the snow as a result of densification over time is clearly apparent. Each layer remains recognizable as it moves downwards and increases in density. In Figure 2b the vertical axis, q, is the water equivalent accumulation measured from the spring 2004 surface. In this q-representation it is apparent that the mass of snow between given peaks does not change with time.
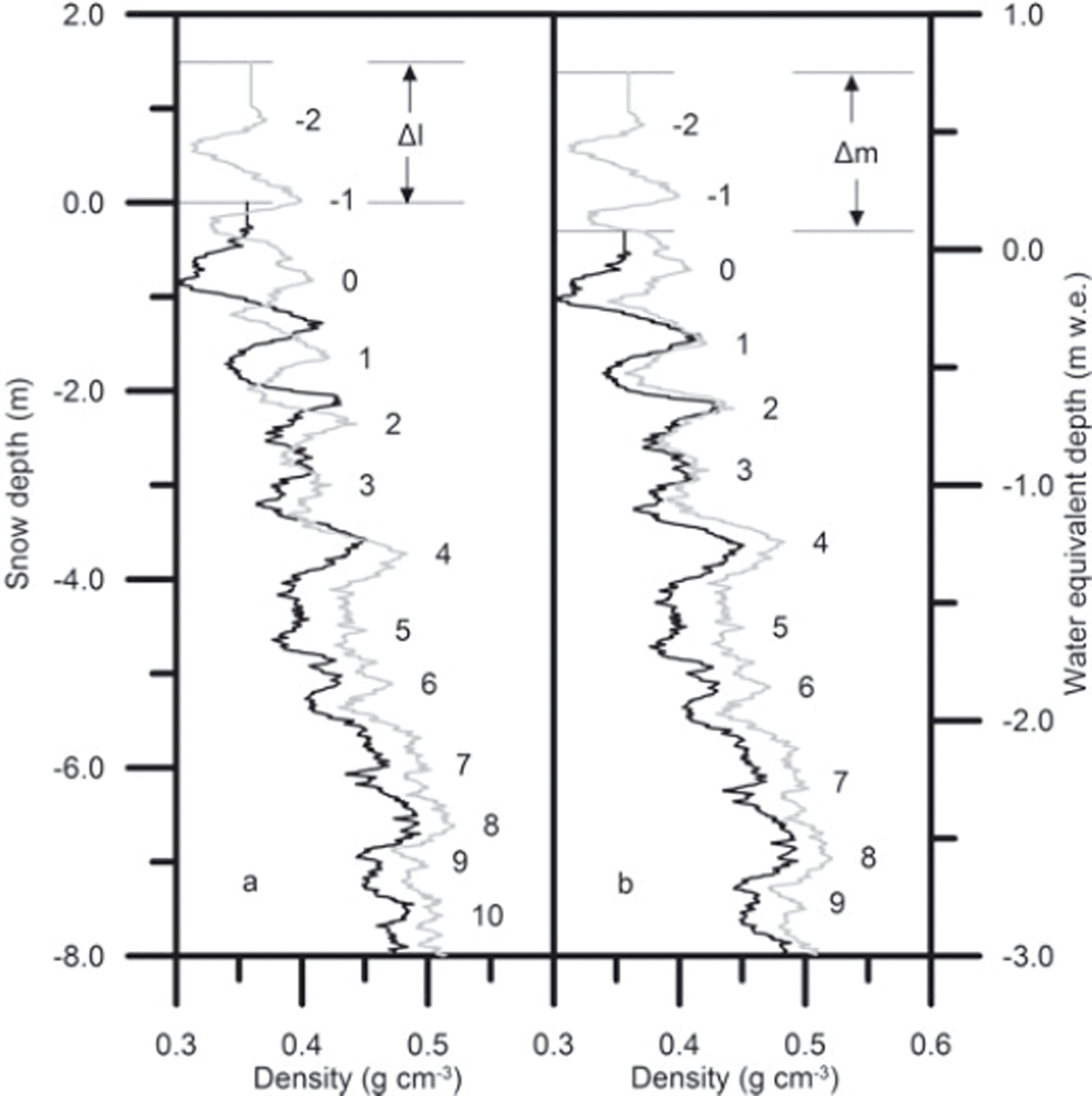
Fig. 2. Density profiles collected in spring 2004 (black) and summer 2006 (grey) at T41. (a) Density vs snow depth, with l = 0 at the spring 2004 surface and the profiles matched at peak 13 (not shown). (b) Density vs accumulated mass, with q = 0 at the start of the measured profile in spring 2004.
Dual-frequency GPS measurements of the position of a point on the snow surface were made at each site. The point was marked with a 4 m aluminium pole, and the relative height of the surface (with respect to the bottom of the pole) was also recorded. The pole was installed 1 m from the access hole to avoid disturbing the snow to be profiled.
The nature of the ice-sheet surface was recorded with digital photographs. About 10 km uphill from T31 the character of the surface and wind regime changed markedly. Below this altitude the katabatic wind was persistent, the upper snow layer was wind-packed and the surface marked by sastrugi. Above this altitude there was little wind and the surface was very smooth, with undisturbed surface hoar in the summer. Comparison with the summer night-time wind field calculated by Reference NiederbäumerNiederbäumer (1999), using a model of katabatic flow, suggests that the transition point occurs where the wind speed (calculated at ∼12 m above the snow surface) is ∼8 m s−1.
4. Analysis
4.1. Determination of ρ 0(s)
Our observations do not provide all the quantities that are needed to determine the error and its separate parts. In particular, we are limited because the measurements are taken only at particular intervals and because our density profiles do not generally extend deep enough that the density is that of ice. We need, therefore, to appeal to a model of the density to complete the problem. We choose to fit a model of the form suggested by Reference Herron and LangwayHerron and Langway (1980) to derive the time-invariant density profile, ρ 0(s), from our measured profiles (Appendix A) and use this as an estimate for ρ(s) where necessary.
4.2. Determination of Δm
S and

For the periods from 2004 to 2006 it is possible to determine Δm
S and
![]() directly from the density profiles for a known Δt. Values of
directly from the density profiles for a known Δt. Values of
![]() when Δt is an integral number of years can also be obtained, by averaging from the surface to the appropriate peak in the density profile (Fig. 2). For the two short periods, spring–autumn 2004 and spring–summer 2006, the surface layer was too thin for accurate density measurements to be made. However, we can identify the thickness of the accumulation layer, i.e.
when Δt is an integral number of years can also be obtained, by averaging from the surface to the appropriate peak in the density profile (Fig. 2). For the two short periods, spring–autumn 2004 and spring–summer 2006, the surface layer was too thin for accurate density measurements to be made. However, we can identify the thickness of the accumulation layer, i.e.
![]() .
.
4.3. Determination of Δm 0
The gradient of a plot of q against N gives the mean annual accumulation rate,
![]() . We use this to estimate the long-term component of mass input over time, Δt, i.e.
. We use this to estimate the long-term component of mass input over time, Δt, i.e.
![]() . The mass between peaks gives the annual accumulation series.
. The mass between peaks gives the annual accumulation series.
4.4. Determination of Δh S
The Eulerian elevation change, Δh S, for each site has been determined by repeated GPS measurements of the ellipsoidal height of the snow surface at each stake (to give the Lagrangian elevation change) followed by addition of the (negative) convective elevation change, Δx ∂h S/∂x, (see Table 5 in Appendix B). The distance travelled by the stake downstream over time Δt is known from the GPS measurements. The local slope, ∂h S/∂x, has been estimated from the local slope of the surface return given by ASIRAS data collected in 2004. Above T41 the convective elevation changes are negligible compared to the instrumental error in Δh S. Below T23 the correction for convective elevation change is significant, especially over the longer time periods.
The surface height change, Δh S, may also be determined from comparison of density profiles at each site. Δh S is related to Δl by

where uN is the velocity at peak N. Using Equation (3) and adapting Equation (5) for peak N leads to

where
![]() is the compaction below peak N. We write
is the compaction below peak N. We write

(by analogy with Equation (A12)), where
![]() is the harmonic mean density of the material at peak N over time Δt and Δc
1N
is the fluctuation in compaction below N. Then
is the harmonic mean density of the material at peak N over time Δt and Δc
1N
is the fluctuation in compaction below N. Then

where
![]() is estimated as the harmonic mean of the values of ρ
0 at the depth of peak N at t = 0 and t = Δt. Δm
F is unknown, but if the system is in equilibrium with the century-scale mean annual accumulation, it will be slightly higher than Δm
0 (see Fig. 3). For our density profiles the lowest peak is deep enough for fluctuations in
is estimated as the harmonic mean of the values of ρ
0 at the depth of peak N at t = 0 and t = Δt. Δm
F is unknown, but if the system is in equilibrium with the century-scale mean annual accumulation, it will be slightly higher than Δm
0 (see Fig. 3). For our density profiles the lowest peak is deep enough for fluctuations in
![]() to be negligible, so we set
to be negligible, so we set
![]() , where a
1 is a constant which we optimize to obtain the best match with the GPS data. The uncertainty in Δh
S is estimated from the standard error in
, where a
1 is a constant which we optimize to obtain the best match with the GPS data. The uncertainty in Δh
S is estimated from the standard error in
![]() , the instrumental error in Δl (±0.02 m) and an estimated 5% error in
, the instrumental error in Δl (±0.02 m) and an estimated 5% error in
![]() . Table 2 shows that the individual values of a
1 for each site are not significantly different from each other. There is no evidence of a trend in a
1 with distance along the traverse. We therefore choose to use the mean for all sites, a
1 = 0.027 m w.e. a−1, to adjust the density data.
. Table 2 shows that the individual values of a
1 for each site are not significantly different from each other. There is no evidence of a trend in a
1 with distance along the traverse. We therefore choose to use the mean for all sites, a
1 = 0.027 m w.e. a−1, to adjust the density data.

Fig. 3. The Greenland common accumulation record (Reference AndersenAndersen and others, 2006) (black) extended using a 13 year running mean of annual accumulation (grey) from the ‘Katie’ core collected near Summit Station (Reference Banta and McConnellBanta and McConnell, 2007).
Table 2. Mean estimates of individual mass-balance trends, a 1j , at the CryoSat traverse sites

A third method of determining elevation change uses the measurements of snow surface height with respect to the bottom of the aluminium marker poles. To obtain Δh S it is necessary to estimate the downward movement of the pole. As with a 1, the data do not justify using individual values for each pole, so we use the best mean value for all sites, a relatively small value of 0.025 m a−1 Δt. The mass-balance trend is again set to a 1 = 0.027 m w.e. a−1. The elevation changes calculated using these values are given in Tables 6 and 7 in Appendix B.
5. Results
5.1. Mean annual accumulation
The last column of Table 1 shows the mean and standard deviation of the annual accumulation series derived from the density profiles collected in 2004 and 2006 at each site along the CryoSat traverse. Reference Hawley, Morris and McConnellHawley and others (2008) have shown that the neutron-probe method and the traditional methods based on chemical and isotopic analysis produce statistically indistinguishable accumulation series for the ‘Katie’ core collected near Summit Station. The variability of the neutron-probe series is slightly higher, probably due to the variability of the timing (in the year) of the annual density peak. This effect is also apparent at other sites, where the 2004–06 CryoSat data generally have larger values of standard deviation than the 1987–89 chemistry-based data. These higher standard deviations are appropriate for the early stratigraphic data from 1954 and 1959, which also use density fluctuations to identify annual layers.
The mean accumulations shown in Table 1 apply to relatively short time-spans and need to be set in the context of longer records. Figure 3 shows the most recent part of the 1800 year common accumulation record derived for Greenland by Reference AndersenAndersen and others (2006) from five Greenland ice cores (‘Dye-3’, ‘Milcent’(T15), ‘Crête’, ‘GRIP’ and ‘NGRIP’). It shows an 11.9 year periodicity and agrees broadly with a smoothed normalized accumulation record from the ‘Katie’ core which we have used to extend the common record to the year 2000. It appears that the period from 1984 was one of lower accumulation. This is supported to some extent by the ‘Central Western’ record of Reference Banta and McConnellBanta and McConnell (2007) which shows a minimum around 1995.
5.2. Mean surface density
Figure 4a shows the (arithmetic) mean density of surface layers accumulated over ∼2 year periods. The best straight ine through the spring 2004–spring 2006 data is

The density decreases with distance, x, along the traverse. This is as expected, since Δt is long enough for post-depositional densification to have occurred in the accumulation layer. Densification rates depend on mean annual temperature and accumulation, which both decrease with distance along the traverse (Table 1). This decrease is also apparent in the time-invariant density at the surface, ρ 0(0), shown in Figure 4b. The best straight line through these values is
As would be expected, at a given site Equation (21) gives lower densities than Equation (20).
Figure 4c shows the minimum density recorded by the neutron probe at each site, as a function of distance along the traverse. These minimum densities occur in summer layers at or near the surface. The lower envelope of the data is given by the curve

This gives an upper estimate of the minimum value of
![]() which we can use with Equation (21) to estimate the surface density fluctuation,
which we can use with Equation (21) to estimate the surface density fluctuation,
![]() , over a summer period. These data indicate that the proportion of low-density snow input over the summer increases with x. Our observations of the snow surface (section 3) suggest an explanation for this trend. Although thin layers of hoar crystals were observed in the upper 1 m of snow at all sites, thick very low-density surface hoar was only observed above T31. Below this site, winds were stronger and more snow was input in dense, wind-packed layers.
, over a summer period. These data indicate that the proportion of low-density snow input over the summer increases with x. Our observations of the snow surface (section 3) suggest an explanation for this trend. Although thin layers of hoar crystals were observed in the upper 1 m of snow at all sites, thick very low-density surface hoar was only observed above T31. Below this site, winds were stronger and more snow was input in dense, wind-packed layers.

Fig. 4. (a) The mean density,
![]() , of snow accumulated over the periods spring 2004–spring 2006 (●), spring 2004–summer 2006 (○) and autumn 2004–summer 2006 (◊). The dashed line is the best fit to the spring 2004–spring 2006 data. (b) The time-invariant density at the snow surface, ρ
0(0), derived from profiles measured in spring 2004 (○), autumn 2004 (◊), spring 2006 (∆) and summer 2006 (●). The dashed line is the best fit to the summer 2006 data. (c) The minimum density observed in profiles measured in spring 2004 (○), spring 2006 (∆) and summer 2006 (●). The solid curve is an upper estimate of the minimum value of
, of snow accumulated over the periods spring 2004–spring 2006 (●), spring 2004–summer 2006 (○) and autumn 2004–summer 2006 (◊). The dashed line is the best fit to the spring 2004–spring 2006 data. (b) The time-invariant density at the snow surface, ρ
0(0), derived from profiles measured in spring 2004 (○), autumn 2004 (◊), spring 2006 (∆) and summer 2006 (●). The dashed line is the best fit to the summer 2006 data. (c) The minimum density observed in profiles measured in spring 2004 (○), spring 2006 (∆) and summer 2006 (●). The solid curve is an upper estimate of the minimum value of
![]() .
.
5.3. Local variability
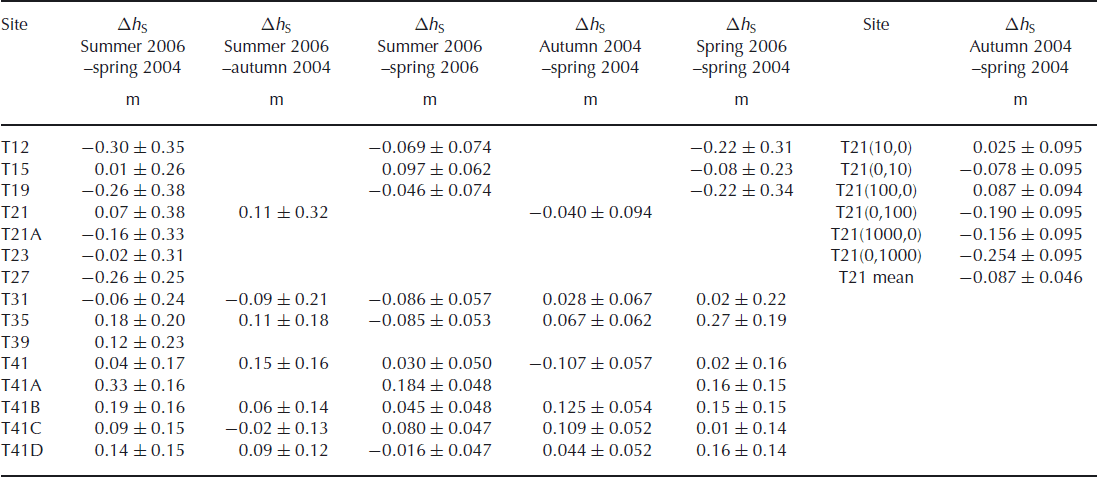
Figure 5a shows density profiles measured over the 1 km2 nested grid at T21 in spring 2004 over a period of 9 days. The profiles were remeasured in autumn 2004 over a 10 day period with high winds and drifting snow. The lowest peak of each autumn profile has been matched to the corresponding peak in the spring profile for the same gridpoint. The correction for compaction below peak N has been calculated separately for each gridpoint, and the resulting elevation changes are shown in Table 6 in Appendix B. For these profiles the mean elevation change from spring 2004 is −0.151 ± 0.042 m and the variance from this mean is 0.016 m2. Pole data taken at the same time (over 8 days in spring and 1 day in autumn 2004) over seven points of the same grid give a mean elevation change of −0.087 ± 0.046 m, with variance of 0.015 m2 (Table 7). The mean elevation change rate for the density profile data is −0.423 ± 0.116 m a−1 with sample variance 0.122 m2 a−2. The mean elevation change rate for the pole data is −0.258 ± 0.136 m a−1 with sample variance 0.129 m2 a−2. The differences between the mean elevation change and change rate for the two methods are not statistically significant (two-tailed t test, α = 0.05).
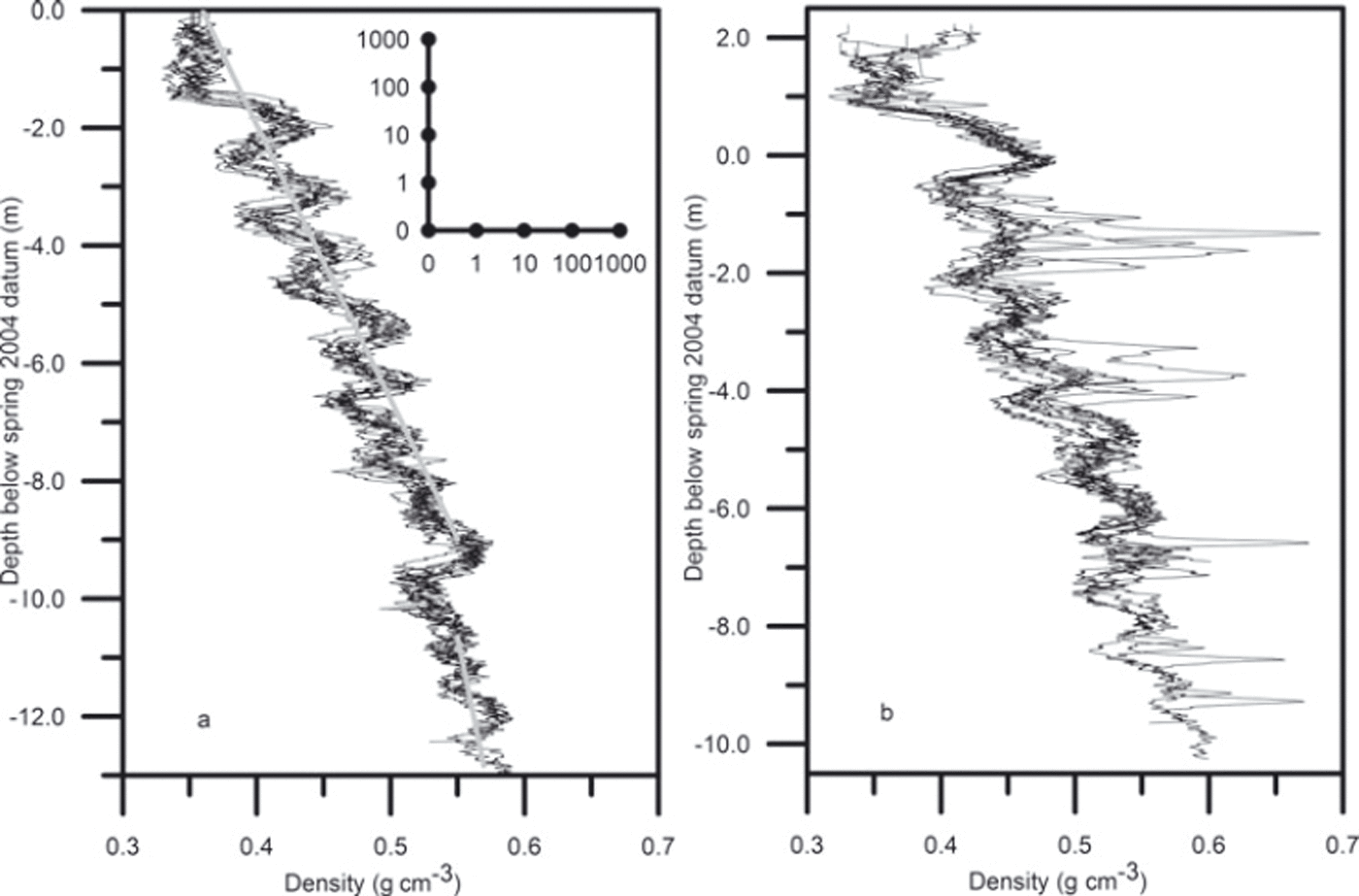
Fig. 5. Density profiles from (a) site T21 (spring 2004) and (b) site T12 (spring 2006) collected at points separated by approximately 1, 10, 100 and 1000 m on a 1 km2 nested grid, shown schematically in (a). The grey curves are fitted to the density profile at the central point of the T21 grid, above and below 0.55 g cm−3. At T12 high-density melt layers appear in some profiles in some years.
Figure 5b shows density profiles measured at points on the 1 km2 nested grid at T12 over a period of 7 days in spring 2006. Winds were moderate with some drifting snow. The lowest peak in each profile has been matched to the corresponding peak in the spring 2004 profile at T12 (7,−1). The same correction for compaction below this peak has been applied to all points on the grid, and the resulting elevation changes are shown in Table 6. For these profiles, the mean elevation change from spring 2004 is −0.156 ± 0.053 m and the variance from this mean is 0.025 m2. This variance is greater than at T21 partly because the presence of melt layers increases the variation in density and partly because only one profile from 2004 is available for matching. The mean elevation change rate for the period is −0.077 ± 0.026 m a−1 and the variance 6.03 × 10−3 m2 a−2.
5.4. Elevation change rate
Because the time, Δt, between repeated measurements varies along the traverse, we plot the spatial variability of the rate of change, Δh S/Δt, rather than that of Δh S. In Figure 6 the grey points show data from density profiles and pole measurements made within 1 m of the GPS measurements, which are shown in black. The error bars are larger for the data from the density profiles and pole data because both sets of data are derived using the mean annual accumulation and the density at peak N (section 4.4). At each site the scatter is within the range expected from the variance measured over the 1 km2 grids (section 5.3).
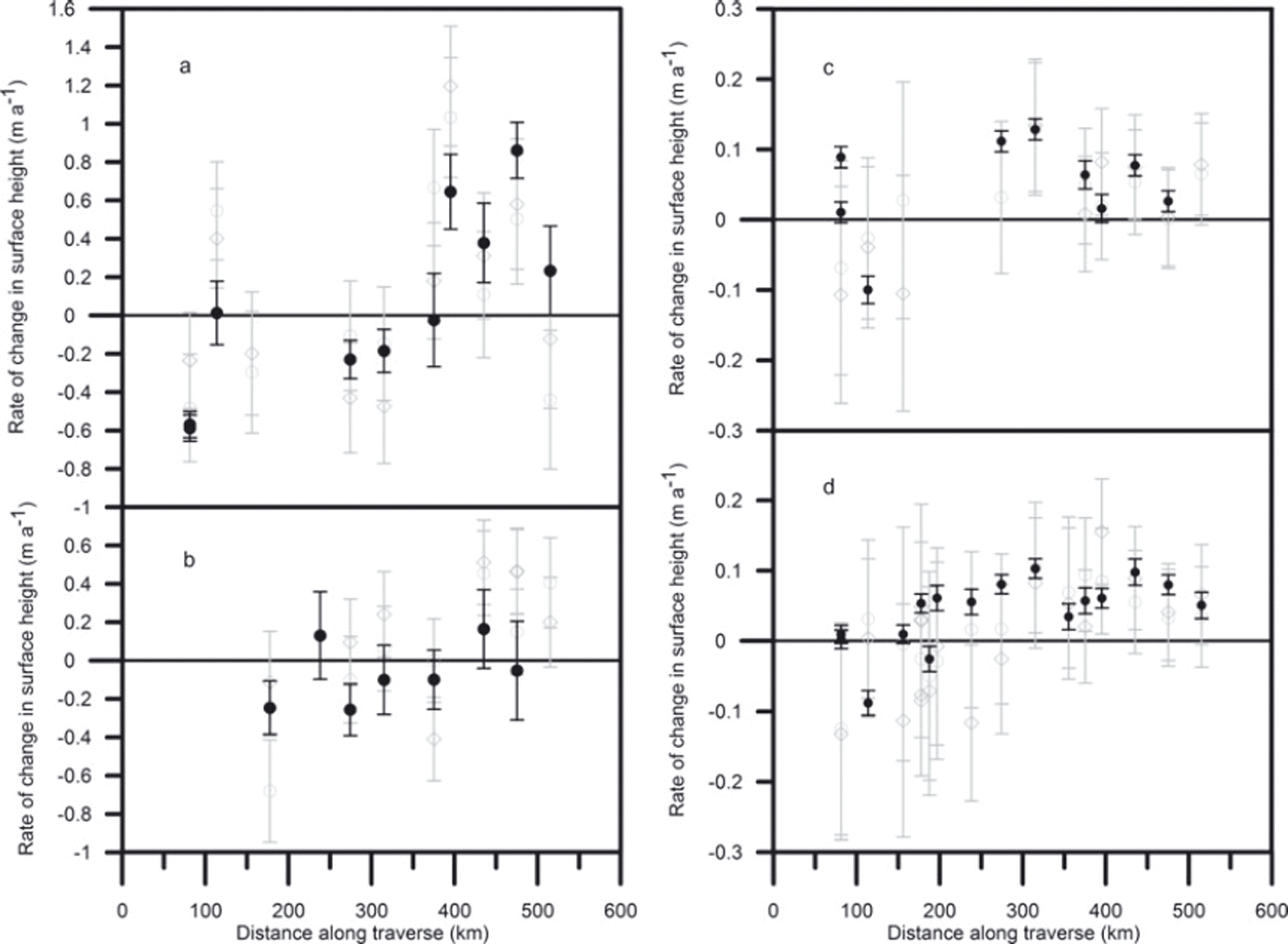
Fig. 6. The rate of change in surface elevation, Δh S/Δt, for (a) spring–summer 2006, (b) spring–autumn 2004, (c) spring 2004–spring 2006 and (d) spring 2004–summer 2006 determined from GPS (●), density profile (○) and pole (◊) measurements. The mean of nine density profile measurements over a 1 km2 grid was −0.423 m a−1, with standard deviation 0.35 m a−1, at T21 over the period spring–autumn 2004, and −0.077 m a−1, with standard deviation 0.078 m a−1, at T12 over the period spring 2004–spring 2006.
Figure 6a shows that sites towards the end of the traverse (T41A–T41D) gained in elevation over June and the first half of July 2006, whereas sites below T41 (except T15) lost elevation. Figure 6b shows that sites T41 and below (except T27) lost elevation over the period mid-May to mid-August 2004 and two sites above T41 gained elevation, although at rates lower than those seen in 2006. Figure 6c shows a small increase in elevation over the 2 year period from spring 2004 to spring 2006 at all sites except T15 and T19. These increases are consistent with satellite laser altimeter measurements of elevation change over the period 2003–07 in the region (Reference Pritchard, Arthern, Vaughan and EdwardsPritchard and others, 2009). Figure 6d shows a small increase in elevation for all sites above T21A for the period from spring 2004 to summer 2006. Sites T21A and T15 lost elevation. For the 241 km above T31 the elevation increased by an average rate of 0.068 m a−1; for the 193 km below T31 the elevation decreased, with an average elevation change rate of −0.017 m a−1.
For time periods greater than 1 year the fact that the time window changes by a few days between sites will not be significant; the effects of a storm captured at one site but not at another will not be important if all sites experience many storms. However, elevation change rates over a single summer, with Δt ranging from 47 days between visits to T41D in 2006 to 130 days between visits to T21 in 2004, will be influenced by individual storms and more scatter is to be expected. In summer 2006, for example, snowfall of ∼2 cm occurred at site T41C just before the surface elevation was measured. This produced a contribution to the elevation change rate of ∼0.13 m a−1, i.e. about one-quarter of the difference between the mean elevation change rates for T41C and T41D. Similarly snowfall and drifting snow preceded measurements at T12 in spring 2006 and may have increased the surface elevation, thus producing a decrease in elevation change rate over the summer. However, it would require an increase of ∼16 cm to explain all the difference between T12 and T15. Despite the scatter, there does seem to be evidence of increased elevation on the summit plateau and decreased elevation at the lower altitudes over the summer periods.
5.5. Contributions to the error
The contributions of short-term fluctuations to Δε/Δt over the longer periods, from 2004 to 2006, are shown in Figure 7a–c, with the total shown in Figure 7d. As in the case of the total elevation change, the error bars are estimated using the standard error in
![]() , the instrumental error in Δl (±0.2 m) and an estimated 5% error in density. There is no trend in the contribution to the error from mass fluctuations, which suggests that Δm
1 decreases with distance along the traverse at approximately the same rate as
, the instrumental error in Δl (±0.2 m) and an estimated 5% error in density. There is no trend in the contribution to the error from mass fluctuations, which suggests that Δm
1 decreases with distance along the traverse at approximately the same rate as
![]() . This is quite possible if
. This is quite possible if
![]() which decreases along the traverse (Table 1). Similarly, there is no clear trend in the contribution from compaction fluctuations. However, there is a relation between
which decreases along the traverse (Table 1). Similarly, there is no clear trend in the contribution from compaction fluctuations. However, there is a relation between
![]() , particularly apparent below T31. Table 3 shows that over the longer periods the contribution from compaction fluctuations offsets the contribution from
, particularly apparent below T31. Table 3 shows that over the longer periods the contribution from compaction fluctuations offsets the contribution from
![]() We would expect that an increase in accumulation would produce an instantaneous increase in pressure throughout the snow cover and hence compaction, with a lag time dependent on temperature, pressure and type of snow (e.g. Reference Arthern and WinghamArthern and Wingham, 1998; Reference Zwally and LiZwally and Li, 2002). The rapidity of the response is, however, significant; within 2 years much of the effect of accumulation variability is counteracted by densification in the underlying snow. The contribution from surface density fluctuations is relatively small and there is no evidence that it becomes more important with distance along the traverse. This leaves the term Δm
1/Δtρ
i as the dominant contribution to Δε/Δt, and thus suggests that a reasonable estimate of the error can be made from a knowledge of mass fluctuations alone. For 1996–2005 we have annual accumulation at all sites from T5 to T41D and can calculate the annual mass contribution to Δε/Δt. Figure 8 shows the mean contribution over the period. Comparison with Figure 7a shows the mean value along the traverse is not significantly different for the annual and ∼2 year periods (0.03 m a−1 rather than 0.01 m a−1), but averaging over 9 years reduces the noise in the annual data.
We would expect that an increase in accumulation would produce an instantaneous increase in pressure throughout the snow cover and hence compaction, with a lag time dependent on temperature, pressure and type of snow (e.g. Reference Arthern and WinghamArthern and Wingham, 1998; Reference Zwally and LiZwally and Li, 2002). The rapidity of the response is, however, significant; within 2 years much of the effect of accumulation variability is counteracted by densification in the underlying snow. The contribution from surface density fluctuations is relatively small and there is no evidence that it becomes more important with distance along the traverse. This leaves the term Δm
1/Δtρ
i as the dominant contribution to Δε/Δt, and thus suggests that a reasonable estimate of the error can be made from a knowledge of mass fluctuations alone. For 1996–2005 we have annual accumulation at all sites from T5 to T41D and can calculate the annual mass contribution to Δε/Δt. Figure 8 shows the mean contribution over the period. Comparison with Figure 7a shows the mean value along the traverse is not significantly different for the annual and ∼2 year periods (0.03 m a−1 rather than 0.01 m a−1), but averaging over 9 years reduces the noise in the annual data.
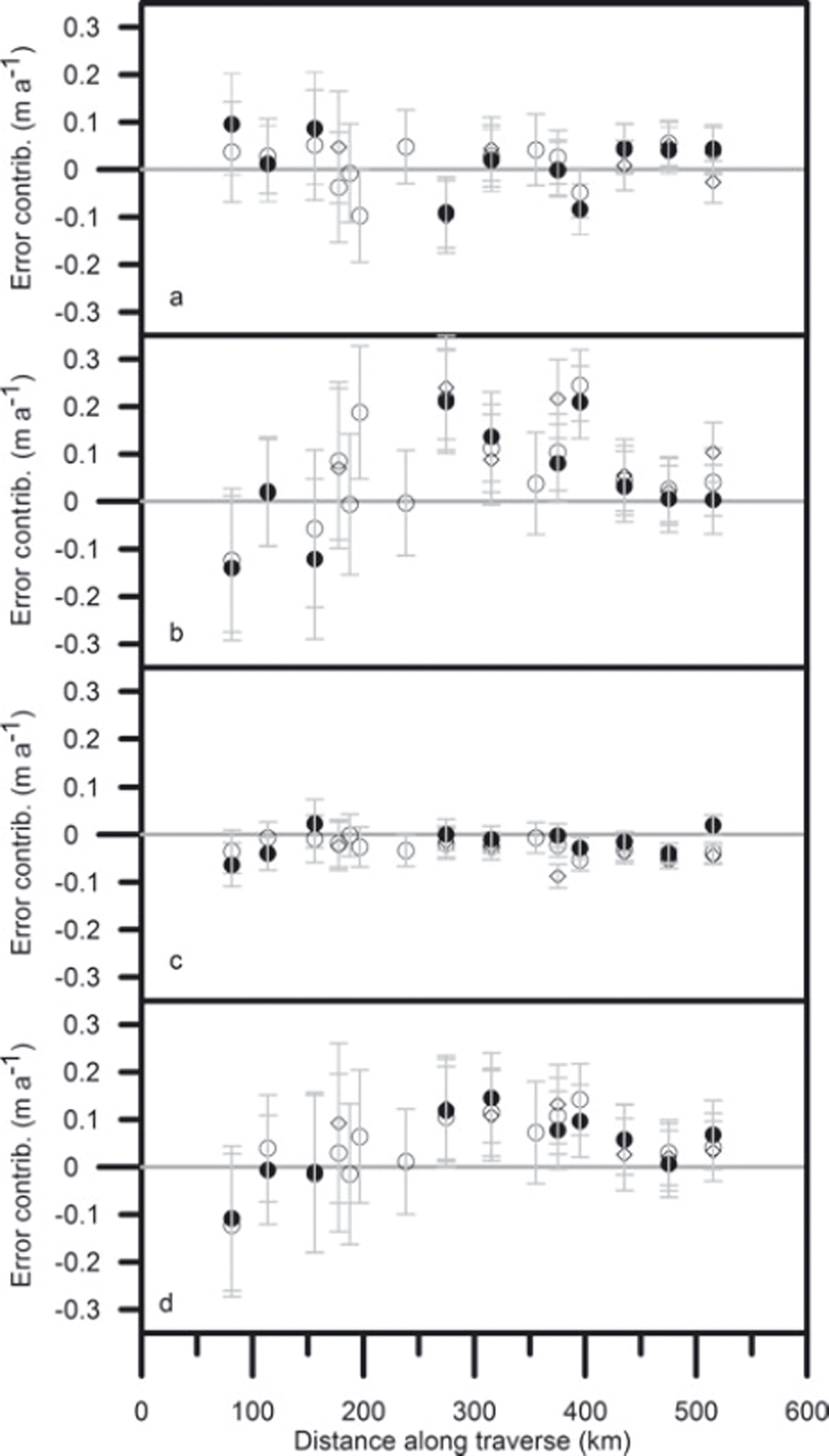
Fig. 7. The contribution of (a) mass, (b) compaction and (c) density fluctuations to the error in mass-balance trend, Δε/Δt (shown in (d)), over the periods spring 2004–summer 2006 (○), autumn 2004–summer 2006 (◊) and spring 2004–spring 2006 (●).
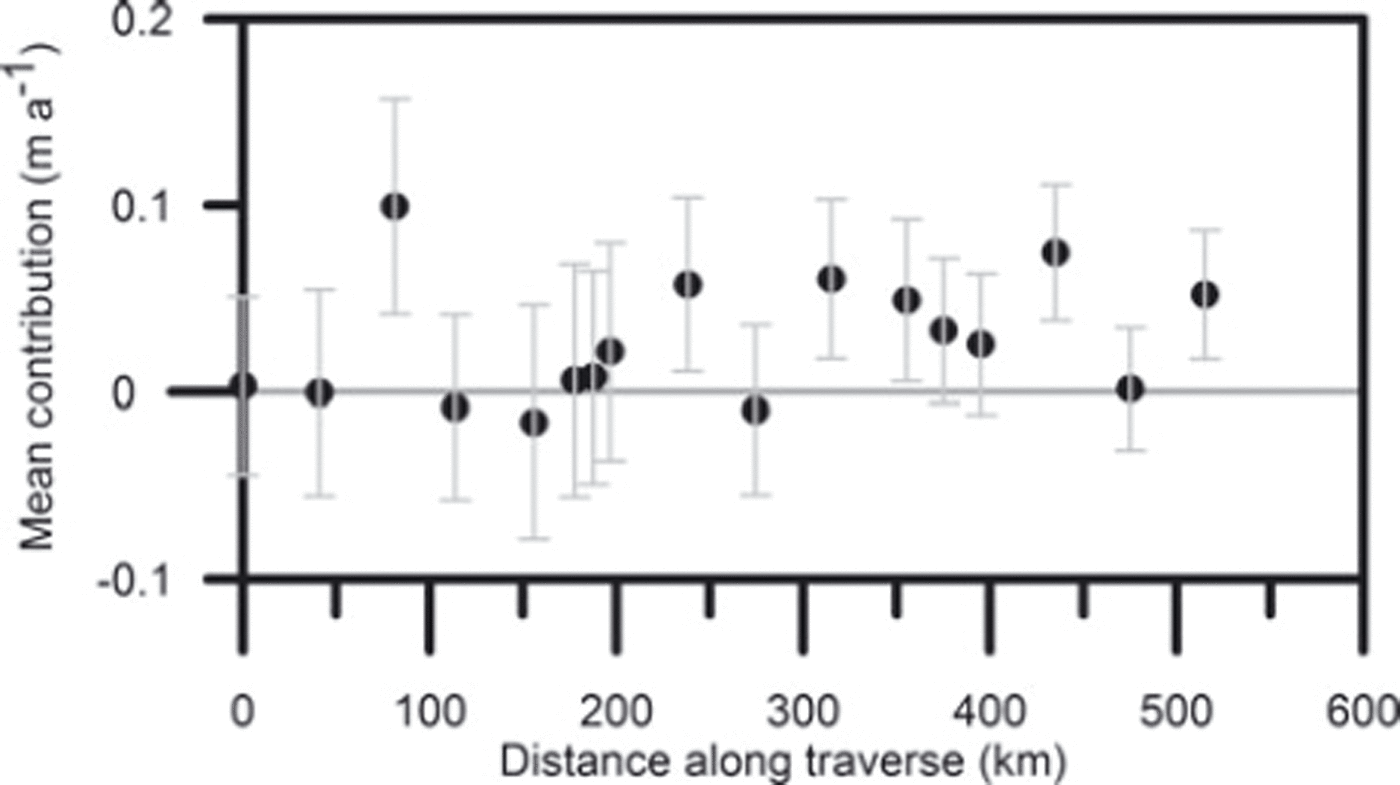
Fig. 8. The mean of the contributions to Δε/Δt from annual accumulation fluctuations over the period 1996–2005.
Table 3. Gradients of plots of Δc
1/Δt against
![]()
We now consider the short summer periods, for which we do not have direct measurements of surface density. Contributions to Δε/Δt from (1) mass and density and (2) compaction are shown in Figure 9a and b, respectively. We have used the GPS surface elevation rates to calculate the compaction contribution in 2004 as the neutron-probe values are derived from profiles separated by 1 m and are thus less reliable. For the 2004 summer period, there is an increase in the contribution from mass and density fluctuations with distance along the traverse, and a corresponding decrease in the contribution from compaction fluctuations.

Fig. 9. The contribution of (a) mass and density, (b) compaction and (c) mass fluctuations to the error in mass-balance trend, Δε/Δt (shown in (d)), over the periods spring 2004–autumn 2004 (◊) and spring 2006–summer 2006 (●).
Using the estimate for the minimum value of
![]() shown in Figure 4c to derive an estimate for
shown in Figure 4c to derive an estimate for
![]() for the short summer periods, we separate the contributions from mass and density. The estimated contribution from mass fluctuations is shown in Figure 9c. It increases with distance along the traverse, indicating the importance of summer low-density snow input at the higher elevations and also suggesting that, over the first 300 km of the traverse, summer accumulation rates are less than the mean annual rate. This is consistent with our observations of a transition point at ∼10 km from T31, i.e. ∼285 km along the traverse. For both summer periods the contribution from density fluctuations is ∼0.1 ± 0.05 m a−1 throughout the traverse.
for the short summer periods, we separate the contributions from mass and density. The estimated contribution from mass fluctuations is shown in Figure 9c. It increases with distance along the traverse, indicating the importance of summer low-density snow input at the higher elevations and also suggesting that, over the first 300 km of the traverse, summer accumulation rates are less than the mean annual rate. This is consistent with our observations of a transition point at ∼10 km from T31, i.e. ∼285 km along the traverse. For both summer periods the contribution from density fluctuations is ∼0.1 ± 0.05 m a−1 throughout the traverse.
For the 2004 summer period the contribution from compaction fluctuations offsets two-thirds of the contribution
![]() over the whole traverse (Table 3). However, over the short 2006 summer period the compaction and mass fluctuations are not correlated. This suggests the large elevation change rates seen in Figure 6a arise because there has not been time for densification below the surface layer to counteract changes in the surface mass input. However, it is also possible that surface height measurements made in summer 2006 at sites with very low-density surface snow have larger errors than the ±0.02 m used to calculate the error bars shown in Figure 9. The overall conclusion is that for the shorter periods it is necessary to take surface density into account when estimating the error, Δε/Δt.
over the whole traverse (Table 3). However, over the short 2006 summer period the compaction and mass fluctuations are not correlated. This suggests the large elevation change rates seen in Figure 6a arise because there has not been time for densification below the surface layer to counteract changes in the surface mass input. However, it is also possible that surface height measurements made in summer 2006 at sites with very low-density surface snow have larger errors than the ±0.02 m used to calculate the error bars shown in Figure 9. The overall conclusion is that for the shorter periods it is necessary to take surface density into account when estimating the error, Δε/Δt.
At T12, with mean annual temperature T m ≈ −21.66°C, high-density melt layers have been observed in some profiles (Fig. 5). Profiles from other sites do not show melt layers and there is no evidence of melt at T12 in the period spring 2004–summer 2006. Snow-pit data show that very thin ice layers can occur at all sites, but these are not resolved by the neutron-probe density measurements. If melt occurs, and the meltwater is refrozen below the surface layer, the effect would be to produce a more negative value of Δm 1 and, because the ice layer would increase the resistance to the overburden pressure, a more positive value of Δc 1.
5.6. Spatial covariances
Using 5 years of ERS measurements, Reference Wingham, Ridout, Scharroo, Arthern and ShumWingham and others (1998) have determined the spatial covariance, C h, of measured elevation change rates in Antarctica. They report a root-mean covariance of 0.049 m a−1 for points at zero separation, falling to ∼0.004 ma−1 for separations greater than ∼500 km. The element of this covariance which arises from errors associated with the satellite technique can be estimated; it falls from a zero value of 0.0413 to ∼0.004 m a−1 for separations greater than ∼400 km. The remaining covariance includes unresolved height changes due to changes in penetration of the altimeter signal and the effect of fluctuations in density and compaction. Taking fluctuations in accumulation as the dominant term, Reference Wingham, Ridout, Scharroo, Arthern and ShumWingham and others (1998) deduce a correlation scale of ∼200 km for fluctuations in accumulation from the 5 year mean over the region of ERS coverage in Antarctica.
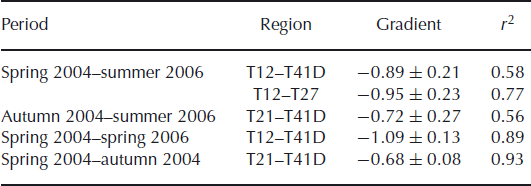
Figure 10 shows the covariance in the contribution made by annual accumulation fluctuations to the error, Δε/Δt, for the 9 years from 1996 to 2005, as a function of distance along the traverse. Since the data are not stationary, the covariances depend on absolute position rather than separation; for stationary data the contours would be straight lines with a gradient of +1. Values range from a variance of 0.056 m2 a−2 at T12 (80 km from the start of the traverse) and covariances of −0.016 m2 a−2 between sites at each end of the traverse. This anticorrelation may arise because post-depositional melting at the lower sites has transferred mass between annual layers and distorted the annual accumulation series or may reflect real climatic behaviour. Stacking data from neighbouring sites smooths the covariance matrix, but the overall picture remains the same: fluctuations in the contributions from mass decorrelate over distances of 100–200 km. Table 4 shows the root-mean covariance
![]() over 100 km elements of the traverse calculated using a simple interpolation scheme that allocates each section of the traverse a covariance equal to the mean of the values from sites at each end, weighted according to the length of the section. They range from 0.044 ± 0.004 m a−1 for the 100 km from T41 to T41C to 0.101 ± 0.006 m a−1 for the 106 km from T12 to T21A. Over the 434 km from T12 to T41D,
over 100 km elements of the traverse calculated using a simple interpolation scheme that allocates each section of the traverse a covariance equal to the mean of the values from sites at each end, weighted according to the length of the section. They range from 0.044 ± 0.004 m a−1 for the 100 km from T41 to T41C to 0.101 ± 0.006 m a−1 for the 106 km from T12 to T21A. Over the 434 km from T12 to T41D,
![]() . The CryoSat data span a much shorter period of ∼28 months, but it is still possible to investigate the spatial covariance of the error, Δε/Δt, and the individual contributions to it. Figure 11 shows the covariances of the error as a function of distance along the traverse for the only period for which we have data at all sites from T12 to T41D, spring 2004–summer 2006. This example is drawn from a population of time intervals for which the mean error is presumed zero, so we calculate
. The CryoSat data span a much shorter period of ∼28 months, but it is still possible to investigate the spatial covariance of the error, Δε/Δt, and the individual contributions to it. Figure 11 shows the covariances of the error as a function of distance along the traverse for the only period for which we have data at all sites from T12 to T41D, spring 2004–summer 2006. This example is drawn from a population of time intervals for which the mean error is presumed zero, so we calculate
![]() (and similarly for the covariances of the contributions). The highest values are found in the upper part of the traverse. For the spring 2004–summer 2006 period the root-mean covariances
(and similarly for the covariances of the contributions). The highest values are found in the upper part of the traverse. For the spring 2004–summer 2006 period the root-mean covariances
![]() and
and
![]() over 100 km elements of the traverse are shown in Table 4. The uncertainties in the root-mean covariances of the contributions have been calculated from the individual uncertainties, shown as error bars in Figures 7 and 9. The mean elevation change rate decreases with elevation (as shown in Fig. 6d) but the only area for which the mean error,
over 100 km elements of the traverse are shown in Table 4. The uncertainties in the root-mean covariances of the contributions have been calculated from the individual uncertainties, shown as error bars in Figures 7 and 9. The mean elevation change rate decreases with elevation (as shown in Fig. 6d) but the only area for which the mean error,
![]() , is less than
, is less than
![]() is T12–T21A. Table 4 shows that
is T12–T21A. Table 4 shows that
![]() does not vary significantly over the traverse. However,
does not vary significantly over the traverse. However,
![]() is significantly smaller for T12–T21A and
is significantly smaller for T12–T21A and
![]() is larger for T41–T41C. This is not unexpected, since local variability in the density profile, and hence in the resistance to an applied compactive force, decreases with elevation (Fig. 5). The square root of the sum of covariances from the three contributions to fluctuations in elevation change is greater than the root-mean covariance of the total. This is as expected, since we have already indicated that the fluctuations in mass input and compaction are not independent (section 5.5).
is larger for T41–T41C. This is not unexpected, since local variability in the density profile, and hence in the resistance to an applied compactive force, decreases with elevation (Fig. 5). The square root of the sum of covariances from the three contributions to fluctuations in elevation change is greater than the root-mean covariance of the total. This is as expected, since we have already indicated that the fluctuations in mass input and compaction are not independent (section 5.5).
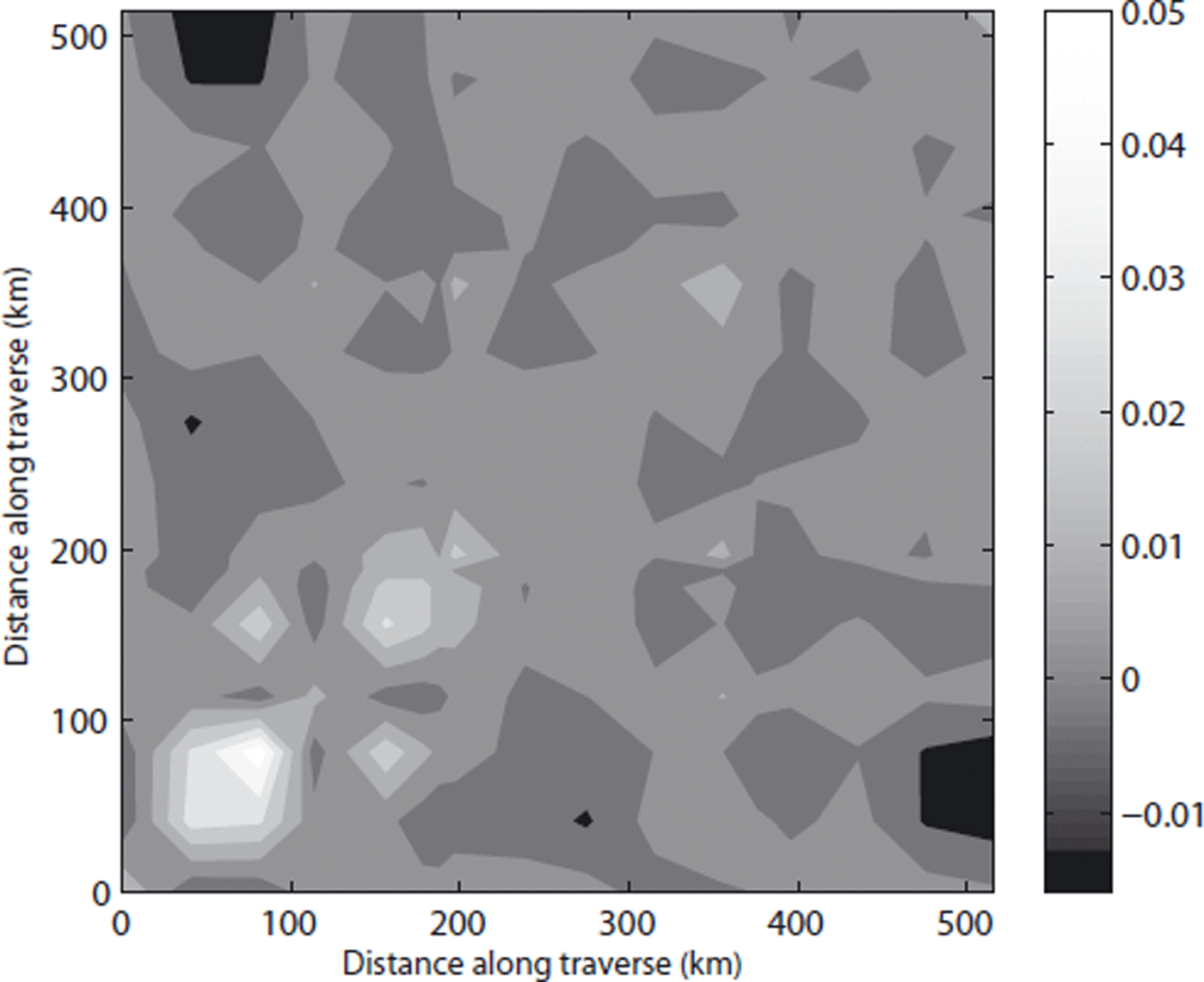
Fig. 10. The spatial covariance, C a, of the annual mass contribution to Δε/Δt for 1996–2005. The units are m2 a−2.
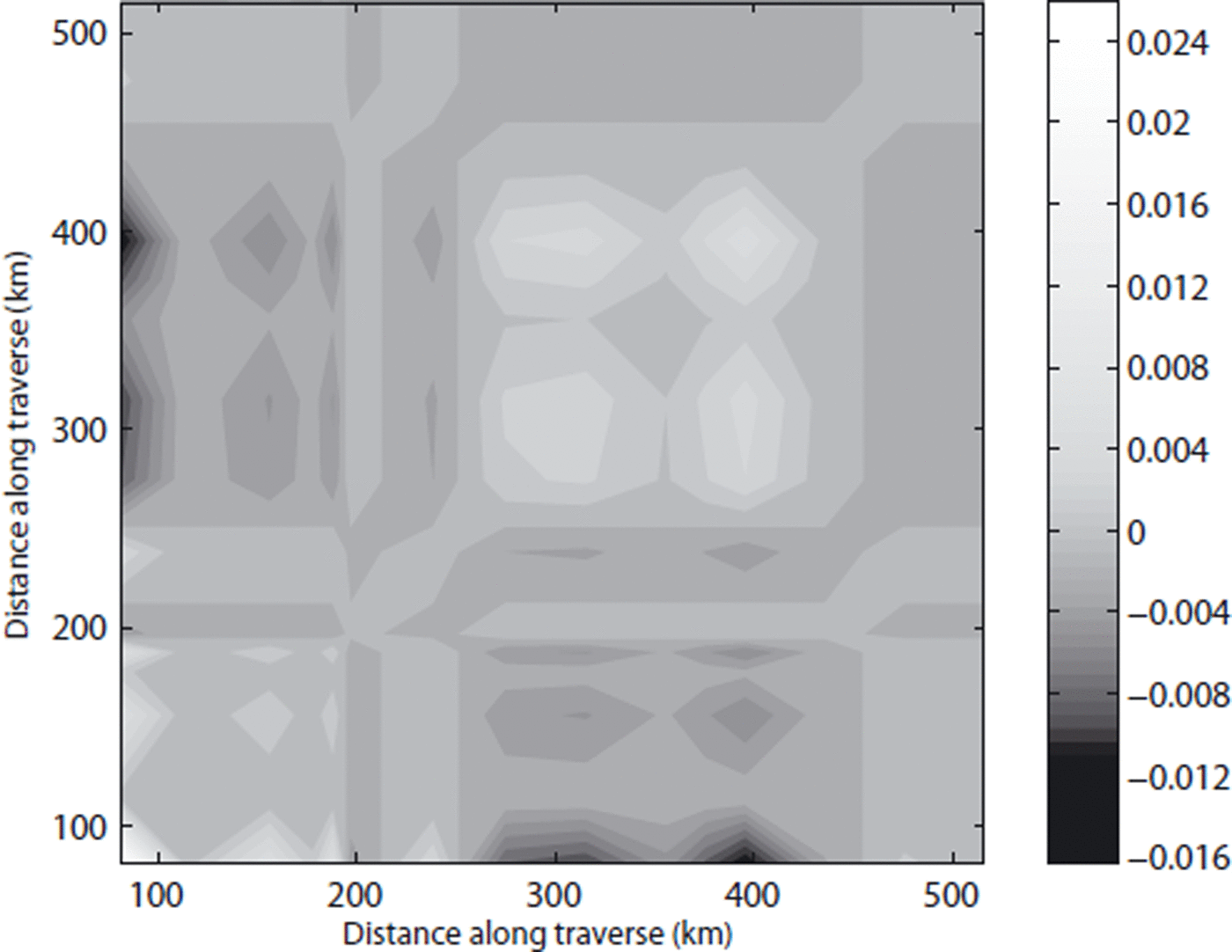
Fig. 11. The spatial covariance,
![]() , of the error, Δε/Δt, over the period spring 2004–summer 2006. The contours are at intervals of 0.005 m2 a−2.
, of the error, Δε/Δt, over the period spring 2004–summer 2006. The contours are at intervals of 0.005 m2 a−2.
Table 4. The mean elevation change rate, mean error and root-mean covariances for spring 2004–summer 2006 and for the annual accumulation series
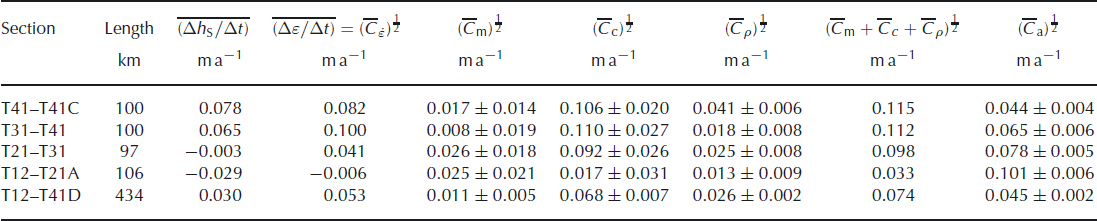
6. Conclusions
From snow density profiles made along the EGIG line and north to Summit Station we have derived recent mean annual accumulation rates,
![]() , which are consistent with those reported by other workers (Table 1). Our measurements suggest that the mass outflow may be slightly greater than
, which are consistent with those reported by other workers (Table 1). Our measurements suggest that the mass outflow may be slightly greater than
![]() , although the imbalance, a
1 = 0.027 ± 0.024 m w.e. a−1, is small; of the order of the standard error in
, although the imbalance, a
1 = 0.027 ± 0.024 m w.e. a−1, is small; of the order of the standard error in
![]() . In terms of elevation, the mass-balance trend is −a
1
ρ
w/ρ
i = −0.029 ± 0.026 m a−1; less than the mean error over the traverse for a 28 month period,
. In terms of elevation, the mass-balance trend is −a
1
ρ
w/ρ
i = −0.029 ± 0.026 m a−1; less than the mean error over the traverse for a 28 month period,
![]() . That is, during our observation period the increase in surface height from short-term fluctuations outweighed any decrease from the long-term mass-balance trend.
. That is, during our observation period the increase in surface height from short-term fluctuations outweighed any decrease from the long-term mass-balance trend.
The elevation change rates over the 2 years from spring 2004 to spring 2006 (Fig. 6c) are consistent with satellite laser altimeter measurements of elevation change over the period 2003–07 in the region (Reference Pritchard, Arthern, Vaughan and EdwardsPritchard and others, 2009). Over the period spring 2004–summer 2006, for which we have most data, the mean elevation change rate on the Summit plateau above 3000 m (T31) was 0.068 m a−1 . For the lower part of the traverse from 2350 to 3000 m (T12–T31), the mean elevation change rate was −0.017 m a−1 . However, in both cases the mean error,
![]() and 0.017 m a−1, respectively, is greater than the mean elevation change rate, so that the implied mass-balance change is not significantly different from zero. In the high summer of 2006, the elevation change rate increased to ∼0.6 m a−1 at the highest sites on the Summit plateau and decreased to ∼−0.6 m a−1 at the lowest site (Fig. 6a). This is consistent with ERS-1/2 satellite radar altimeter data which show a seasonal variation in surface elevation at Summit (Reference Zwally and LiZwally and Li, 2002), with elevation change rates of ∼0.7 m a−1 in the July–September period.
and 0.017 m a−1, respectively, is greater than the mean elevation change rate, so that the implied mass-balance change is not significantly different from zero. In the high summer of 2006, the elevation change rate increased to ∼0.6 m a−1 at the highest sites on the Summit plateau and decreased to ∼−0.6 m a−1 at the lowest site (Fig. 6a). This is consistent with ERS-1/2 satellite radar altimeter data which show a seasonal variation in surface elevation at Summit (Reference Zwally and LiZwally and Li, 2002), with elevation change rates of ∼0.7 m a−1 in the July–September period.
We find that the density of the surface snow layer decreases significantly with increasing elevation. Over the traverse the time-invariant surface density, ρ
0(0), decreases from 0.39 to 0.31 g cm−3 (Fig. 4b) and the mean density over the accumulation layer,
![]() , decreases from 0.40 to 0.33 g cm−3 for Δt = 22–28 months (Fig. 4a). Measurements of
, decreases from 0.40 to 0.33 g cm−3 for Δt = 22–28 months (Fig. 4a). Measurements of
![]() for Δt = 2–22 years show an increasing spatial divergence; after 10 years the value at T12 is 0.48 g cm−3 and at T41D 0.38 g cm−3. Hence using a fixed value of 0.40 g cm−3 (e.g. Reference ZwallyZwally and others, 2005) to convert decadal elevation change to mass change introduces a 10–20% error over the CryoSat traverse.
for Δt = 2–22 years show an increasing spatial divergence; after 10 years the value at T12 is 0.48 g cm−3 and at T41D 0.38 g cm−3. Hence using a fixed value of 0.40 g cm−3 (e.g. Reference ZwallyZwally and others, 2005) to convert decadal elevation change to mass change introduces a 10–20% error over the CryoSat traverse.
In order to reduce speckle error, satellite radar altimeter data have to be spatially averaged over a scale of ∼100 km. The consequences of doing this along the CryoSat traverse are summarized in Table 4. Over a 28 month period the error in calculating mass balance from the mean elevation change rate,
![]() , varied from −0.006 to 0.100 m a−1, with lowest values below T31. The specified system accuracy for the CryoSat mission over an area of (100 km)2 is ±0.033 m a−1 . If the traverse results can be applied over a 100 km wide strip, we expect the uncertainty arising from short-term fluctuations below T21A to be less than the system accuracy for observation periods longer than ∼3 years. Above T21A a longer observation period is needed to reduce uncertainty to the desired level. Summing the mean covariances of contributions arising from fluctuations in mass, compaction and density produces too high an estimate for the error because mass and compaction fluctuations are correlated. Our observations suggest that over periods of ∼2 years compaction offsets the effect of the change in surface elevation because of mass fluctuations with density
, varied from −0.006 to 0.100 m a−1, with lowest values below T31. The specified system accuracy for the CryoSat mission over an area of (100 km)2 is ±0.033 m a−1 . If the traverse results can be applied over a 100 km wide strip, we expect the uncertainty arising from short-term fluctuations below T21A to be less than the system accuracy for observation periods longer than ∼3 years. Above T21A a longer observation period is needed to reduce uncertainty to the desired level. Summing the mean covariances of contributions arising from fluctuations in mass, compaction and density produces too high an estimate for the error because mass and compaction fluctuations are correlated. Our observations suggest that over periods of ∼2 years compaction offsets the effect of the change in surface elevation because of mass fluctuations with density
![]() . This leaves Δm
1/Δtρ
i as the dominant contribution to the error, and a good estimate can be made without a knowledge of surface density. This is, however, not the case for the shorter summer periods.
. This leaves Δm
1/Δtρ
i as the dominant contribution to the error, and a good estimate can be made without a knowledge of surface density. This is, however, not the case for the shorter summer periods.
Acknowledgements
This project is a contribution to the calibration and validation of the ESA CryoSat satellite altimeter and is supported by ESA and by UK Natural Environment Research Council (NERC) Consortium grant NER/O/S/2003/00620. We thank the British Antarctic Survey for the loan of a Trimble geodetic GPS survey system in spring 2004 and the NERC Geophysical Equipment Facilty for the loan of a Leica system for the two traverses in 2006. Logistic support for the traverses was provided by Air Greenland and Veco Polar Resources. G. Somers, J. Pailthorpe, H. Chamberlain and M. Hignell gave invaluable assistance in the field and T. Benham provided Figure 1. Finally we thank M.T. Gudmundsson and two anonymous reviewers for extensive and helpful comments on an earlier version of the paper.
Appendix A
Integrating Equation (6) over time gives
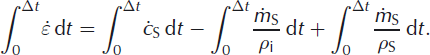
We need to express the last term in terms of the measured thickness, Δl, of the snow accumulated over time Δt, rather than ρ S(t), which we do not observe. Changing the variable from t to s
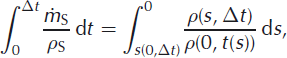
where s(0, Δt) is the distance moved in time Δt by a material particle lying at the surface at time t = 0. The distinction between the numerator and the denominator in Equation (A2) can be illuminated by supposing the interval Δt is short, in which case
where D/Dt denotes the material derivative. The final term in Equation (A4) accounts for the densification that occurs in the accumulated layer. Substituting from Equations (A3) and (A4) into Equation (A2) and retaining only the first-order terms provides

We estimate the magnitude of the second term in the parentheses by appealing to a densification model. For a given site, we derive the time-invariant density by fitting equations of the form suggested by Reference Herron and LangwayHerron and Langway (1980),

to the measured density profiles. k 0 and b are constants with different values for the ranges 0 ≤ ρ 0 ≤ 0.55 g cm−3 and 0.55 g cm−3 ≤ ρ 0 0.73 g cm−3.Other choices of model equation would of course be possible, but Equation (A6) is well established and, given that we do not need to predict the values of k 0 and b a priori, is sufficiently accurate for our purpose. Using ρ 0(0), which is independent of t, as an estimate for ρ(0, 0) we obtain

The magnitude of this correction term increases with Δl, so there is a limit on the length of the observation time period for which the approximation Equation (A7) may be used. For our spring 2004–summer 2006 data the correction term decreases from 0.06 to 0.03 as accumulation decreases along the traverse. The effect of neglecting this term on the contributions to Δε/Δt is small compared to the uncertainty arising from measurement errors (section 4.4; Fig. 7). Hence we write Equation (A5) as
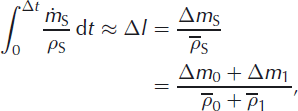
using the variables defined in Equation (10), with at maximum a 6% error for the largest Δt we consider in this paper.
We now consider how to express the other two terms of the right-hand side of Equation (A1). Integrating
![]() over time gives
over time gives

by definition of the time-invariant compaction. For the time-invariant density,
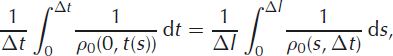
the harmonic mean over the accumulated layer, which we denote by
![]() . Using Equation (A6)
. Using Equation (A6)

So we may write

Finally,

Substitution from Equations (A5), (A12) and (A13) into Equation (A1) leads to Equation (12) in section 1.
Appendix B
Table 5. Eulerian elevation change, Δh S, calculated from GPS measurements at the CryoSat traverse sites corrected for convective elevation changes, Δx(∂h S/∂x). The formal one-sigma errors quoted are those arising from the processing system and do not account for GPS orbit or clock errors or for mis-modelling. Thus they should be regarded as minimum ‘instrumental’ errors in Δh S
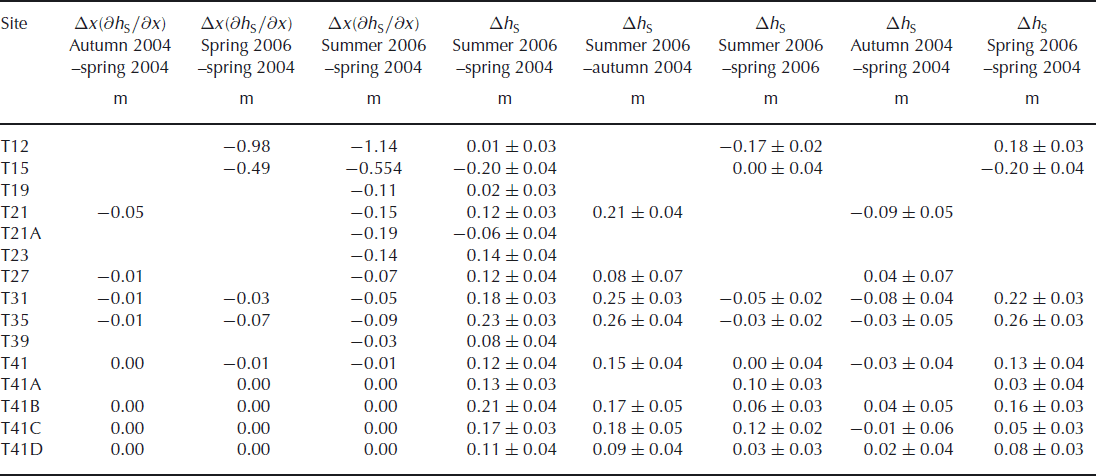
Table 6. Elevation change, Δh S, determined from density profiles at the CryoSat traverse sites
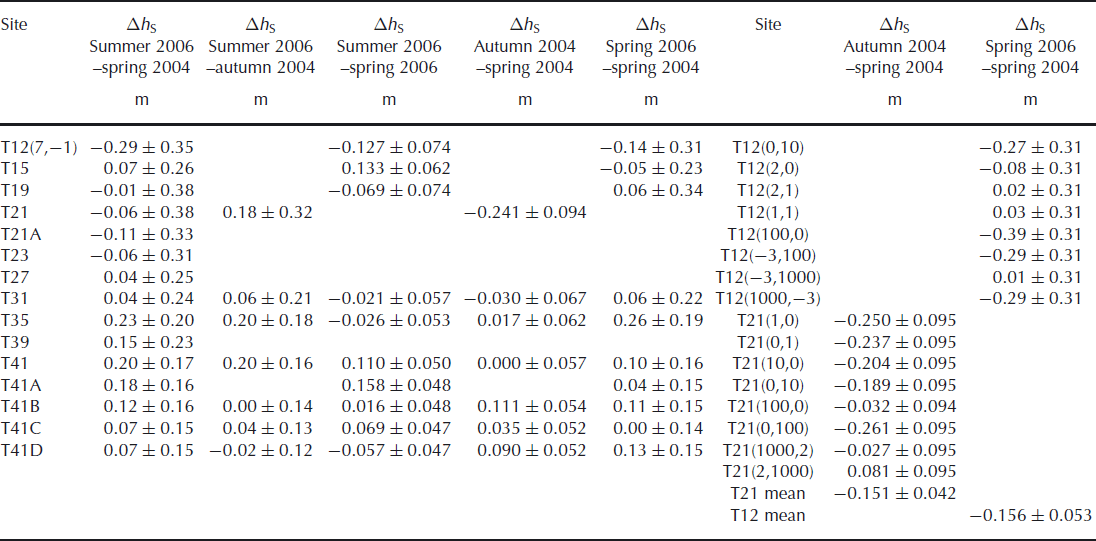
Table 7. Elevation change, Δh S, determined from pole measurements at the CryoSat traverse sites