Impact statement
In the context of increased probability of coastal erosion and flooding associated with climate change, there is a pressing need to predict future shorelines at both short- (daily) and medium-term (decadal) timescales. Such predictions are essential for the assessment of the climate resilience of the world’s coastlines and the delivery of effective, economic and data-informed coastal management. Coastal managers currently lack these predictions and there are many different modelling approaches to inform where increased coastal protection, adaption measures or future infrastructure developments should be focussed. Promising modelling advances have recently been made, particularly in the context of reduced complexity models. This paper reviews various numerical modelling approaches to predicting shoreline and coastal morphological change, comments on some of the most promising methods used to-date, provides some guidance on model selection, and highlights important future research directions and challenges to progress.
Introduction
Global climate change is expected to result in geographically widespread differences in; storm frequency and intensity (Dorland et al., Reference Dorland, Tol and Palutikof1999; Masselink et al., Reference Masselink, Russell, Rennie, Brooks and Spencer2020); wave climate variability (Scott et al., Reference Scott, Masselink, O’hare, Saulter, Poate, Russell, Davidson and Conley2016; Castelle et al., Reference Castelle, Dodet, Masselink and Scott2018; Morim et al., Reference Morim, Hemer, Cartwright, Strauss and Andutta2018; Chowdhury et al., Reference Chowdhury, Behera and Reeve2019; Morim et al., Reference Morim, Hemer, Wang, Cartwright, Trenham, Semedo, Young, Bricheno, Camus, Casas-Prat, Erikson, Mentaschi, Mori, Shimura, Timmermans, Aarnes, Breivik, Behrens, Dobrynin, Menendez, Staneva, Wehner, Wolf, Kamranzad, Webb, Stopa and Andutta2019; Meucci et al., Reference Meucci, Young, Hemer, Kirezci and Ranasinghe2020); rising sea levels (Nicholls et al., Reference Nicholls, Hanson, Lowe, Warrick, Lu and Long2014; Fox-Kemper et al., Reference Fox-Kemper, Hewitt, Xiao, Aðalgeirsdóttir, Drijfhout, Edwards, Golledge, Hemer, Kopp, Krinner, Mix, Notz, Nowicki, Nurhati, Ruiz, Sallée, Slangen, Yu, Masson-Delmotte, Zhai, Pirani, Connors, Péan, Berger, Caud, Chen, Goldfarb, Gomis, Huang, Leitzell, Lonnoy, Matthews, Maycock, Waterfield, Yelekçi, Yu and Zhou2021) and significant morphological changes and impacts to vulnerable coastlines (Enríquez et al., Reference Enríquez, Marcos, Álvarez-Ellacuría, Orfila and Gomis2017; Wiggins et al., Reference Wiggins, Scott, Masselink, Russell and Mccarroll2019; Vousdoukas et al., Reference Vousdoukas, Ranasinghe, Mentaschi, Plomaritis, Athanasiou, Luijendijk and Feyen2020). The common assumption that the morphology remains unchanged during sea level rise is inaccurate for projecting coastal evolution on decadal and climate change timescales (Anderson et al., Reference Anderson, Fletcher, Barbee, Romine, Lemmo and Delevaux2018a). Morphodynamic change can result in loss of land and infrastructure through erosion and can significantly change the likelihood of wave overtopping and flooding. Consequently, the development of methodological approaches for predicting morphodynamic change over daily-to-decadal timescales remains a topical and ongoing research focus for coastal scientists and engineers.
Whilst the focus of this paper is on shoreline modelling of sedimentary coastlines, it is important to recognise that this information can be derived from models of varying complexity, ranging from simple one-dimensional models that predict the shoreline evolution with time, to complex three-dimensional models of morphodynamic evolution. Coastal state indicators refer to a reduced set of parameters that enable a simplistic and quantitative description of the state and evolution of the coast (Davidson et al., Reference Davidson, Van Koningsveld, De Kruif, Rawson, Holman, Lamberti, Medina, Kroon and Aarninkhof2007). Although shorelines are certainly an important state indicator (Boak and Turner, Reference Boak and Turner2005; Davidson et al., Reference Davidson, Van Koningsveld, De Kruif, Rawson, Holman, Lamberti, Medina, Kroon and Aarninkhof2007), it should also be recognised that shoreline definition is highly variable and not a unique example. Indicators like beach volume (Burvingt et al., Reference Burvingt, Masselink, Scott, Davidson and Russell2018) or the momentary coastline position (Van Koningsveld et al., Reference Van Koningsveld, Davidson and Huntley2005), are amongst other useful state indicators relevant to coastal management (Davidson et al., Reference Davidson, Van Koningsveld, De Kruif, Rawson, Holman, Lamberti, Medina, Kroon and Aarninkhof2007). This paper aims to review a range of modelling approaches, whilst retaining an emphasis on shoreline modelling.
Figure 1 illustrates the variety and the spatial/temporal scales of processes that shape coastal morphology. Also shown is the partitioning of the days-to-decades timescale addressed in this contribution into short- (days-to-weeks), medium- (months-to-decades) and long-term (>decades) categories, used throughout the following sections and – for convenience – simply referred to as short, medium and long timescales, without further elaboration. Cross-shore and longshore gradients in sediment fluxes, wave set-up and changing water levels are some of the principal processes driving coastal change at short-to-medium timescales on wave-dominated coastlines (Davidson et al., Reference Davidson, Splinter and Turner2013), whereas, over longer timescales (multi-decadal/centurial), eustatic and isostatic sea level change may have a more significant influence on shoreline change. Eustatic sea level change refers to a global change in sea level, while isostatic (or ‘relative’) sea level change refers to localised changes in land height, relative to sea level (Rovere et al., Reference Rovere, Stocchi and Vacchi2016). Additionally, cross-shore processes often represent shorter time periods (days-to-months) relative to durations surrounding longshore processes (weeks-to-years) (Winter, Reference Winter2012), although often overlap within the same categorised timescales. Thus, Figure 1 not only illustrates the typical time and space scales of hydro- and morpho-dynamic processes, but it also suggests the relative importance and need for consideration of these processes in morpho-dynamic models, providing an initial guide for both model development and choice. The morphology and dominating driving processes of coastal change also vary significantly between sites, presenting a variety of different challenges and requiring differing emphasis on underlying equations. For example, some models are restricted by their underlying physics to either cross-shore or longshore transport-dominated coastlines.
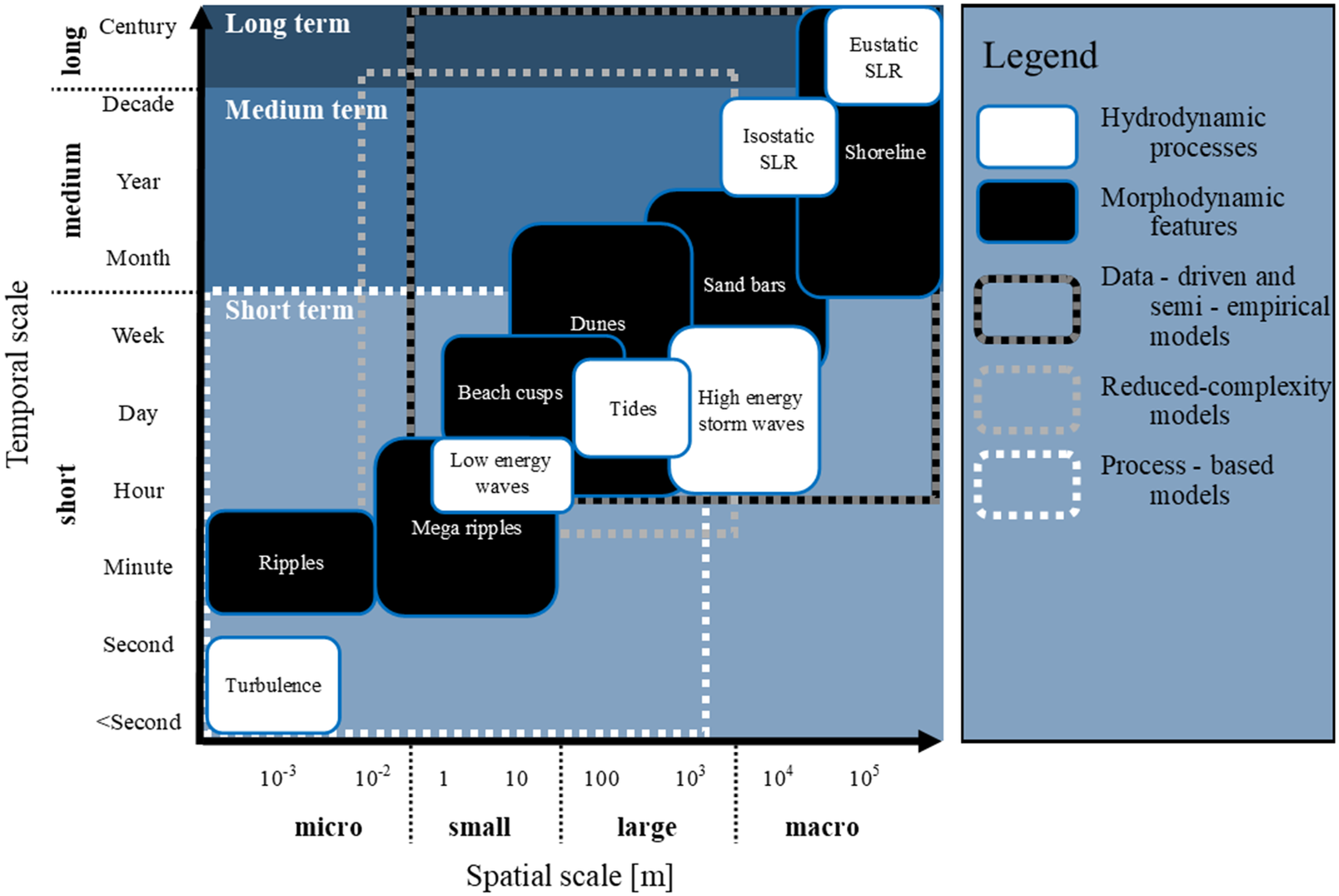
Figure 1. A schematic diagram representing approximate spatial and temporal modelling scales that are appropriate to hydrodynamic processes (white box) and morphodynamic features (black box). Typical temporal/spatial scales are represented for each model class (as described in Figure 2). Timescale classifications (short-to-long) are represented and referred to throughout the paper. SLR refers to sea level rise. Aspects of this figure have been modified from Fenster et al. (Reference Fenster, Dolan and Elder1993) and Winter (Reference Winter2012).
A suggested classification of approaches to modelling coastal evolution is presented in section ‘The modelling complexity spectrum’, with special reference to equilibrium models in section ‘Equilibrium concepts’, which have emerged as particularly useful means of generating stable, computationally-efficient, long-term models of coastal processes. These sections (‘The modelling complexity spectrum’ and ‘Equilibrium concepts’) present the framework for a more general overview of shoreline modelling on timescales of days-to-decades, presented in section ‘Modelling approaches’, followed by a discussion and concluding remarks on the future direction and challenges in shoreline modelling (section ‘Discussion and concluding remarks’).
The modelling complexity spectrum
Models of coastal morphodynamic evolution vary greatly in their complexity, computational demands, stability and prediction horizon. Each method has its own advantages/disadvantages, simplifications and assumptions. Therefore, classifying models can ensure that a model is appropriately selected based upon user requirements, the availability of calibration data and accepted best practices. Classification of coastal models (cf. De Vriend, Reference De Vriend1997; Wolinsky, Reference Wolinsky2009; Reeve et al., Reference Reeve, Karunarathna, Pan, Horrillo-Caraballo, Rózyński and Ranasinghe2016) is becoming increasingly challenging as models are developed and combined. Models are generally classified based upon spatial (metres/km), temporal scales (short-term/long-term) or dimensions (e.g. profile, depth-averaged coastal area, 3D models). As technology and process knowledge advances, new developments are based on coupling different models, each of which can resolve different temporal/spatial scales and/or processes.
Simple conceptual models of coastal evolution have been around for many decades (Dean, Reference Dean1977; Bruun, Reference Bruun1988; Hanson and Kraus, Reference Hanson and Kraus1989). In the 1990s, the advent of modern computers, better field measurements/coastal monitoring technology and improved coastal process understanding, led to a commonly adopted approach to predicting coastal change through the appropriate mathematical aggregation of small-scale processes into physics-based (process) models. Although this approach is fundamentally sound and incredibly powerful for predicting a range of hydrodynamic processes and shorter-term morphodynamic responses, it has been hindered in the area of medium-to-long term (years/decades) application by computational complexity (e.g. speed, stability and sensitivity to initial conditions), especially at regional spatial scales. The continual evolution of physics-based, process models and improved computational capabilities are now starting to mitigate some of these traditional limitations (Dastgheib et al., Reference Dastgheib, Roelvink and Wang2008; Van Der Wegen and Roelvink, Reference Van Der Wegen and Roelvink2008; O’Shea and Murphy, Reference O’shea and Murphy2020), and may potentially be the best solution in the future. However, process models were challenged in the late 1990s by the arrival of an increasing number of high-quality, long-term, morphodynamic datasets and a more heretic approach to modelling coastal processes in the form of data-driven modelling (Hsu et al., Reference Hsu, Ou and Wang1994; Southgate et al., Reference Southgate, Wijnberg, Larson, Capobianco and Jansen2003), which omitted much of the process knowledge and was far more empirical. Some debate emerged in the community of coastal scientists as to the most productive method of predicting medium-to-long term coastal evolution. The quality and duration of such datasets continue to develop today, with better long-term monitoring in place in some areas (Kroon et al., Reference Kroon, Larson, Möller, Yokoki, Rozynski, Cox and Larroude2008; Senechal et al., Reference Senechal, Gouriou, Castelle, Parisot, Capo, Bujan and Howa2009; Turner et al., Reference Turner, Harley, Short, Simmonds, Bracs, Phillips and Splinter2016; Ludka et al., Reference Ludka, Guza, O’reilly, Merrifield, Flick, Bak, Hesser, Bucciarelli, Olfe, Woodward, Boyd, Smith, Okihiro, Grenzeback, Parry and Boyd2019; Castelle et al., Reference Castelle, Bujan, Marieu and Ferreira2020) and improved technology, including coastal video monitoring systems (Holman et al., Reference Holman, Sallenger, Lippmann and Haines1993; Davidson et al., Reference Davidson, Van Koningsveld, De Kruif, Rawson, Holman, Lamberti, Medina, Kroon and Aarninkhof2007; Kroon et al., Reference Kroon, Davidson, Aarninkhof, Archetti, Armaroli, Gonzalez, Medri, Osorio, Aagaard, Holman and Spanhoff2007; Siegle et al., Reference Siegle, Huntley and Davidson2007; Smit et al., Reference Smit, Aarninkhof, Wijnberg, González, Kingston, Southgate, Ruessink, Holman, Siegle, Davidson and Medina2007) and satellite data (e.g. Luijendijk et al., Reference Luijendijk, Hagenaars, Ranasinghe, Baart, Donchyts and Aarninkhof2018; Vos et al., Reference Vos, Harley, Splinter, Simmons and Turner2019a,Reference Vos, Splinter, Harley, Simmons and Turnerb; Castelle et al., Reference Castelle, Masselink, Scott, Stokes, Konstantinou, Marieu and Bujan2021). However, the polarisation of modelling approaches has significantly blurred into a plethora of reduced-complexity models that attempt to combine the most impactful processes with the stability and computational efficiency of data-driven models.
Consistent with an anticipated broader evolution towards more reduced complexity models, it is therefore perhaps better to consider coastal morphodynamic models as a continuum. Figures 2 and 3 demonstrate such a complexity-spectrum and the appropriate application of the models. The ‘bottom-up’ approach to coastal modelling adopted by process models is positioned at the base of the diagram and represents the most complex and inclusive process models (Figure 2). The complexity spectrum progresses upwards through reduced-complexity and semi-empirical models to purely data-driven (top-down) models at the top. The advantages (green) and disadvantages (red) with progression up and down the complexity spectrum are indicated at each side of the diagram. Moving towards the top of the diagram, models become simpler, more stable and computationally efficient, with the potential for longer model runs. This progression (upwards) is accompanied by the negative effects (red) of reduced generality, an increased need for calibration data and reduced capacity to deal with system complexities (e.g. structures, complex geology and sources and sinks of sediment). Example models have been illustrated for each level of the complexity spectrum.
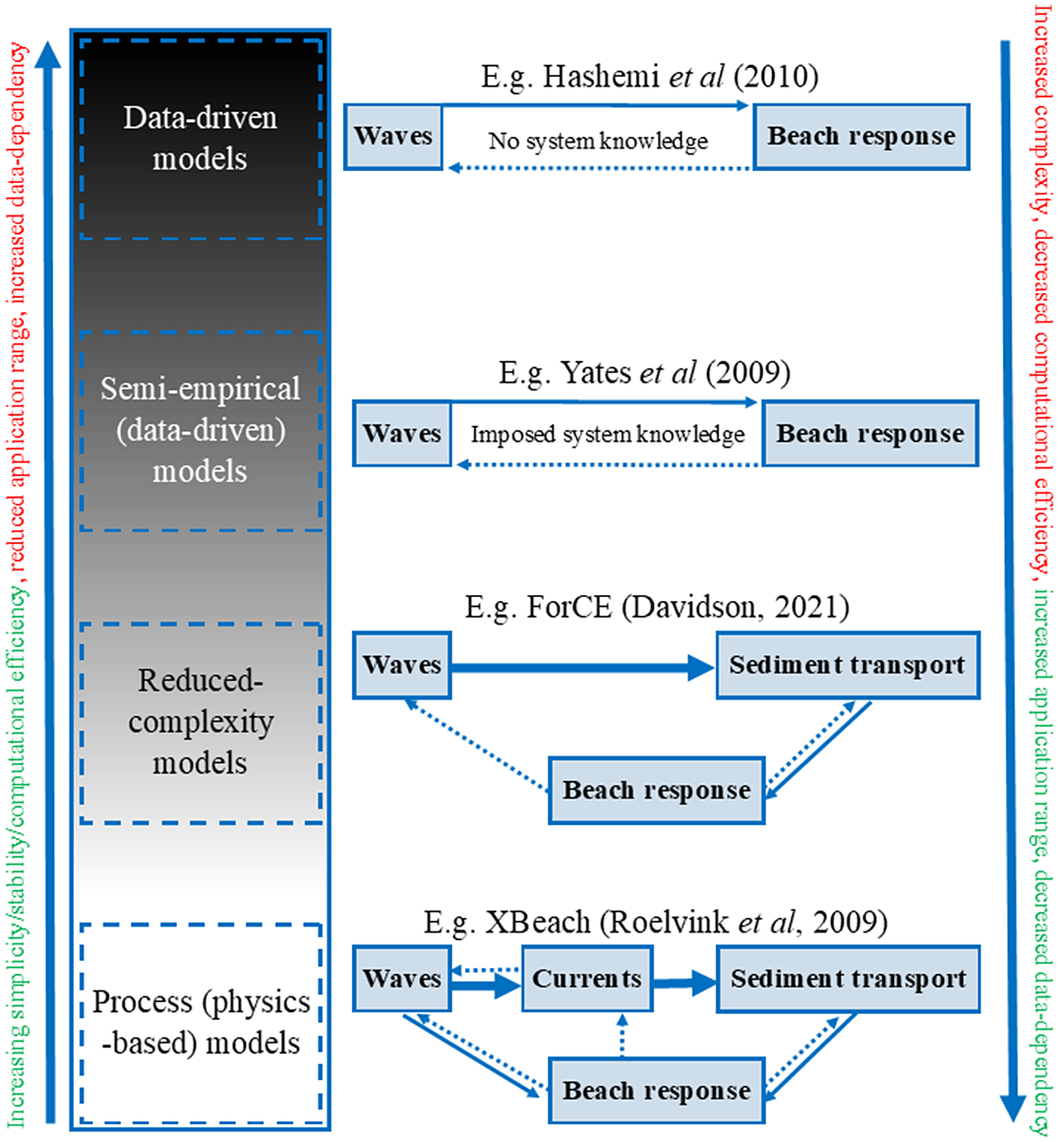
Figure 2. The morphodynamic modelling complexity spectrum (left), with corresponding simplified model examples on the right. Advantages/disadvantages are shown in green/red, respectively.
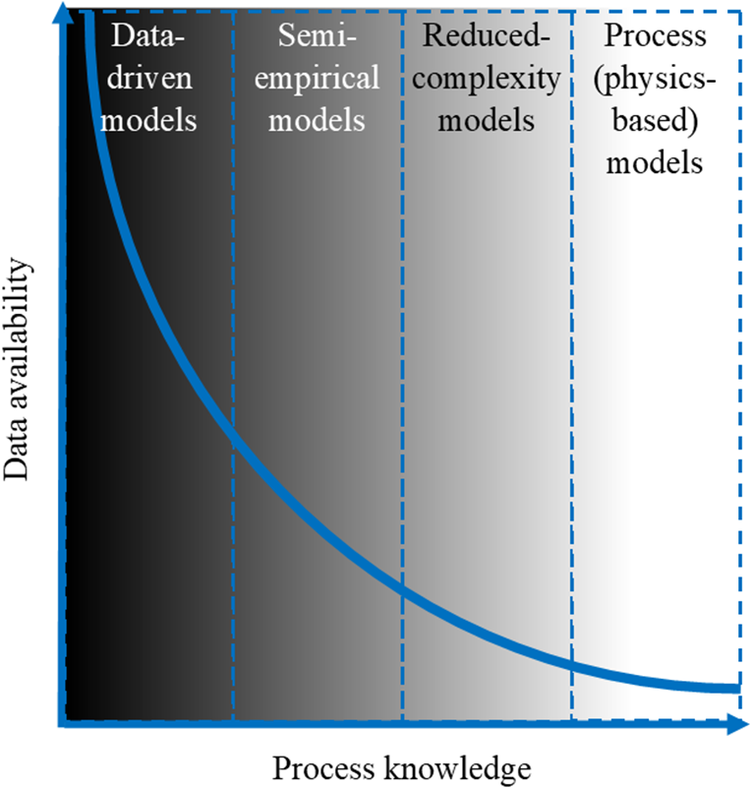
Figure 3. Schematic diagram demonstrating the relationship between typical model classifications (classified according to Figure 3), the availability of data and the current knowledge of processes.
Figure 3 illustrates how the appropriate model choice trajectory is functionally dependent (amongst other factors discussed previously) on both data availability and process knowledge. A high level of process understanding will facilitate process models with high fidelity, even in the absence of relevant calibration data. Conversely, in the absence of sufficient process understanding, but an abundance of relevant data, one may proceed with a data-driven modelling approach (Figure 2).
Equilibrium concepts
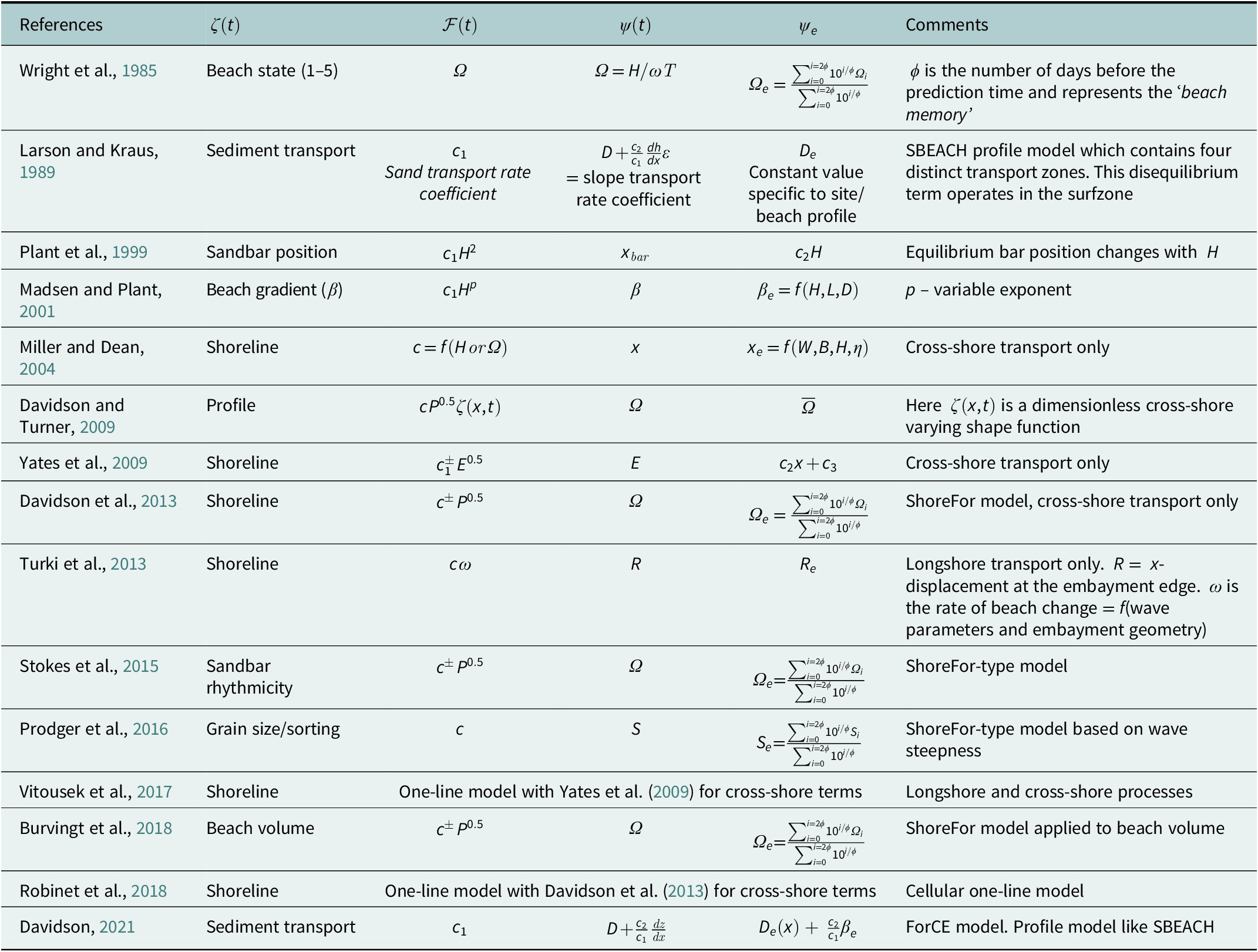
Although beaches respond to, and are spatially translated by, eustatic and isostatic changes in sea level, they are remarkably persistent in time, often remaining for many centuries in the same location. The longevity of beaches and adaption to sea level change (e.g. raised beaches) strongly suggests that beaches are systems in a state of dynamic equilibrium. Therefore, it is not surprising that models with strongly embedded equilibrium concepts (Table 1) have been particularly successful in predicting a plethora of coastal morphodynamic processes. In the short-to-medium term (days-to-years), beaches can be modelled as systems that are perturbed around an underlying static equilibrium state. However, over the longer (multi-decadal) timescales, changes in sea level and wave climate demand a model that displays perturbations around a dynamic underlying equilibrium condition.
Table 1. Summary table of a selection of prominent models with (embedded) equilibrium components for a range of coastal processes
Note:
![]() $ \zeta, $
modelled variable; x, shoreline position; z, bed level; H, E, P, D, Wave height, energy, power and dissipation; c, Model tuning coefficient(s) (NB. including subscripts if more than one and values vary for each table row);
$ \zeta, $
modelled variable; x, shoreline position; z, bed level; H, E, P, D, Wave height, energy, power and dissipation; c, Model tuning coefficient(s) (NB. including subscripts if more than one and values vary for each table row);
![]() $ \varOmega $
, dimensionless fall velocity; S, wave steepness; subscript e, represents equilibrium value. Other symbols are defined in the comments column.
$ \varOmega $
, dimensionless fall velocity; S, wave steepness; subscript e, represents equilibrium value. Other symbols are defined in the comments column.
Equilibrium models are based upon the theory that the modelled process will vary temporally around a static or dynamically varying equilibrium value. Equilibrium models can be represented using the following simple generalisation:
where
![]() $ \frac{d\zeta}{d t} $
represents temporal change in some aspect of the beach morphology (e.g. shoreline position or beach volume),
$ \frac{d\zeta}{d t} $
represents temporal change in some aspect of the beach morphology (e.g. shoreline position or beach volume),
![]() $ \mu $
is a (tuneable) response rate parameter,
$ \mu $
is a (tuneable) response rate parameter,
![]() $ \mathcal{F} $
is a forcing term (usually related to incident waves),
$ \mathcal{F} $
is a forcing term (usually related to incident waves),
![]() $ \psi $
is a dependent parameter (typically the shoreline location, dimensionless fall velocity or wave energy) and
$ \psi $
is a dependent parameter (typically the shoreline location, dimensionless fall velocity or wave energy) and
![]() $ {\psi}_e $
is the long-term (or weighted) average of antecedent values of
$ {\psi}_e $
is the long-term (or weighted) average of antecedent values of
![]() $ \psi $
. Note that in static equilibrium models,
$ \psi $
. Note that in static equilibrium models,
![]() $ {\psi}_e $
is constant in time, but in dynamic equilibrium systems it varies temporally. In simple equilibrium models
$ {\psi}_e $
is constant in time, but in dynamic equilibrium systems it varies temporally. In simple equilibrium models
![]() $ \chi \hskip0.3em =\hskip0.3em 1 $
, whilst in more complex models,
$ \chi \hskip0.3em =\hskip0.3em 1 $
, whilst in more complex models,
![]() $ \chi $
is a spatially varying shape function. Davidson and Turner (Reference Davidson and Turner2009), for example, used
$ \chi $
is a spatially varying shape function. Davidson and Turner (Reference Davidson and Turner2009), for example, used
![]() $ \chi $
to describe the cross-shore behaviour of morphological change in a profile model. The ‘additional terms’ in Equation (1) are stated in recognition that the model may have source or sink terms governed by other processes (e.g. sea level rise). A characteristic of equilibrium systems is that they tend asymptotically to the underlying equilibrium value with time under conditions of constant forcing (
$ \chi $
to describe the cross-shore behaviour of morphological change in a profile model. The ‘additional terms’ in Equation (1) are stated in recognition that the model may have source or sink terms governed by other processes (e.g. sea level rise). A characteristic of equilibrium systems is that they tend asymptotically to the underlying equilibrium value with time under conditions of constant forcing (
![]() $ \mathcal{F}\hskip0.3em =\hskip0.3em \mathrm{constant},\hskip0.3em {\psi}_e\hskip0.3em =\hskip0.3em \mathrm{constant}\Big). $
The sign of the bracketed quantity in Equation (1) can be referred to as the disequilibrium and controls the direction of change (positive or negative), whilst the response rate and forcing term dictate the magnitude of the change.
$ \mathcal{F}\hskip0.3em =\hskip0.3em \mathrm{constant},\hskip0.3em {\psi}_e\hskip0.3em =\hskip0.3em \mathrm{constant}\Big). $
The sign of the bracketed quantity in Equation (1) can be referred to as the disequilibrium and controls the direction of change (positive or negative), whilst the response rate and forcing term dictate the magnitude of the change.
Table 1 presents some illustrative, but not exhaustive, examples of published equilibrium models for a range of coastal phenomena, indicating the versatility and applicability of this class of model to nearshore systems. Equilibrium models are represented across a broad range of the complexity spectrum (Figure 2; excluding pure data-driven models) and are most prevalent in the semi-empirical and reduced-complexity models, discussed in the following section. That said, embedding equilibrium concepts within process models to improve skill, stability and long-term predictions, are an ongoing area of research. Possibly one of the earliest examples of a model in the form of Equation (1) is the Wright et al. (Reference Wright, Short and Green1985) beach state prediction model (Table 1), which introduced the important concept of ‘beach memory’ and meant that future predicted beach states were crucially affected by antecedent wave conditions.
Modelling approaches
Here, we use the complexity spectrum (Figure 2) as a framework for the discussion of a range of modelling approaches, starting with data-driven models and progressing to more complex physics-based process models. We detail a wide range of models beyond the traditional shoreline models, for example, profile models, whereby a shoreline value may be extracted.
Data-driven models
Data-driven models are essentially a ‘black box’ technology, mapping the forcing directly to morphodynamic response, with no imposed/intervening system knowledge. The key advantage of this approach is that gaps in system knowledge are no longer an obstacle to prediction and can be instead learned by an algorithm. Data-driven models involve making predictions of unseen/future coastal state based on empirical relationships between the model forcing and response timeseries, with no prior knowledge of the internal processes involved.
This class of model has grown in popularity alongside the emergence of long-term morphodynamic datasets. Manual methods of coastal monitoring, through in-situ survey for example, have previously taken considerable time and labour to generate, limiting the application of data-driven models to a small number of coastal locations. However, the volume of available coastal morphodynamic datasets has increased significantly in recent years, including data sources like coastal video systems and drone technology, and – most notably – satellite-derived shoreline data (e.g. Luijendijk et al., Reference Luijendijk, Hagenaars, Ranasinghe, Baart, Donchyts and Aarninkhof2018; Vos et al., Reference Vos, Harley, Splinter, Simmons and Turner2019a; Castelle et al., Reference Castelle, Masselink, Scott, Stokes, Konstantinou, Marieu and Bujan2021), making the use of fully data-driven models a more realistic opportunity and opening the door for the emergence of machine-learning techniques.
Goldstein et al. (Reference Goldstein, Coco and Plant2019) present a detailed review of such machine-learning techniques within the context of coastal applications. Goldstein et al. (Reference Goldstein, Coco and Plant2019) note that machine-learning models fundamentally differ from statistical/empirical models, as there are no assumptions or hypothesis about the structure of the relationship in the data, and instead there is an automated searching for rules and relationships. Additionally, in machine learning, no restrictive assumptions about the data are made, for example, no specific distribution is required for residuals. Therefore, statistical and machine-learning modelling techniques are discussed separately in the following sections.
Statistical models
Statistical models infer relationships between variables, to understand and extrapolate beyond the limits of the dataset. Morphodynamic datasets are often irregularly sampled in time, making decomposition of the signals using conventional spectral analysis difficult, leading early investigators to use Empirical Orthogonal Function (EOF) analysis to decompose the temporal evolution of different modes of morphology, whereby different modes can represent key beach processes (e.g. cross-shore/longshore transport), enabling analysis and prediction of coastal changes (e.g. Winant et al., Reference Winant, Inman and Nordstrom1975; Aranuvachapun and Johnson, Reference Aranuvachapun and Johnson1978; Wijnberg and Terwindt, Reference Wijnberg and Terwindt1995; Reeve et al., Reference Reeve, Li and Thurston2001). Winant et al. (Reference Winant, Inman and Nordstrom1975) were the first to apply this technique to coastal modelling, followed by an extension to 3-dimensions by Hsu et al. (Reference Hsu, Liaw, Wang and Ou1986) and Medina et al. (Reference Medina, Vidal, Losada and Roldan1992), using both cross-shore and longshore eigenfunctions to describe temporal morphological variations. Canonical Correlation Analysis (CCA) has been used in a similar fashion to study bar dynamics (Różyński, Reference Różyński2003) and to link beach profile evolution to wave forcing (Larson et al., Reference Larson, Capobianco and Hanson2000; Horrillo-Caraballo and Reeve, Reference Horrillo-Caraballo and Reeve2008; Horrillo-Caraballo and Reeve, Reference Horrillo-Caraballo and Reeve2010).
Bayesian networks (BN), a probabilistic graphical model that explicitly represents the conditional dependencies that link variables, have also been applied to shoreline prediction problems, with most developments occurring since the 1990s. Nodes within these networks represent variables, while arrows demonstrate the cause-effect relationships between associated nodal points. The simplicity of this approach means it is intuitive and provides a fast and computationally-efficient solution. Studies have demonstrated positive results, with BN shoreline models replicating up to 71% (Gutierrez et al., Reference Gutierrez, Plant and Thieler2011) and 88% (Beuzen et al., Reference Beuzen, Turner, Blenkinsopp, Atkinson, Flocard and Baldock2018) of shoreline variability. Beuzen et al. (Reference Beuzen, Turner, Blenkinsopp, Atkinson, Flocard and Baldock2018) developed a BN to model shoreline change during storm events at Narrabeen-Collaroy, Australia, tested against 10 years of data. Multiple BNs were investigated within the study, with the most successful model able to reproduce up to 88% of the variability in the training dataset. Plant and Stockdon (Reference Plant and Stockdon2012) developed a BN to predict barrier-island response to extreme conditions, predicting dune-crest elevation as a function of dune-base elevation, storm-induced mean water level and storm-induced extreme run-up. The computational efficiency of BNs conveniently facilitates Monte Carlo simulations of shoreline change (Wikle and Berliner, Reference Wikle and Berliner2007), which are now a popular technique within coastal literature.
Machine-learning models
Machine learning models are algorithms that enable the computer to ‘learn’ from a dataset, based on inferred relationships. Artificial Neural Networks (ANNs) are a prominent data-driven methodology which have been used to link wave information directly to shoreline (e.g. Alizadeh et al., Reference Alizadeh, Vafakhah, Azarmsa and Torabi2011) and profile response (e.g. Hashemi et al., Reference Hashemi, Ghadampour and Neill2010). ANNs consist of a series of node layers connecting an input layer (here, wave parameters) to an output layer (beach response), via one or more hidden layers. During training, the relations between the input and output datasets are ‘learnt’ and the relationships quantified within the hidden layers. The term ‘deep learning’ is often used to describe ANNs, whereby the greater the number of hidden layers, the ‘deeper’ the learning.
There are various types of ANN, which have been applied to a wide range of coastal problems. ANNs may be classified due to their structure, data-flow direction or density of neurons. A Feed Forward Neural Network (FFNN) (e.g. Hashemi et al., Reference Hashemi, Ghadampour and Neill2010; Goncalves et al., Reference Goncalves, Awange, Krueger, Heck and Coelho2012; Rajasree et al., Reference Rajasree, Deo and Sheela Nair2016; López et al., Reference López, Aragonés, Villacampa and Compañ2018) is the most simple form of ANN, with input data travelling in only one direction and weightings remaining consistent. Goncalves et al. (Reference Goncalves, Awange, Krueger, Heck and Coelho2012) utilised a multi-layer FFNN to model short-term shoreline change and directly compared results with linear regression and robust parameter estimation models (whereby a normal distribution is assumed, and the effects of outliers are isolated and ‘down-weighted’), while Rajasree et al. (Reference Rajasree, Deo and Sheela Nair2016) used a multi-layer FFNN to model long-term shoreline simulations, trained with past satellite images. Hashemi et al. (Reference Hashemi, Ghadampour and Neill2010) and López et al. (Reference López, Aragonés, Villacampa and Compañ2018) both utilised a 3-layer FFNN with backpropagation to model a cross-shore profile, demonstrating reasonable success.
A multi-layer perceptron ANN comprises a fully connected network. Weightings are learnt, modified and improved through iterative comparison between predicted outputs and the training dataset, and data propagation is bi-directional. Alizadeh et al. (Reference Alizadeh, Vafakhah, Azarmsa and Torabi2011) provided input wind and wave data into a multi-layer perceptron ANN to model shoreline position outputs and demonstrated good comparison with validation data. More recently, Simmons and Splinter (Reference Simmons and Splinter2022) demonstrated that a multi-layer perceptron ANN proved the most skilful under storm conditions when compared to process and reduced-complexity models.
Recurrent Neural Networks (RNNs) differ from the more basic ANNs due to the addition of a ‘memory’, which enables the incorporation of dependencies of data points upon previous data points. Zeinali et al. (Reference Zeinali, Dehgani and Talebbeydokhti2021) utilise a non-linear RNN to model short-term shoreline changes in Narrabeen, Australia, which performed well when compared to the training data. The study also explored a generalised regression, radial-based function and time delay ANN. These methods proved to be simpler than the RNN algorithms, but not as skilful.
Recent blind tests of data-driven models applied to Tairua Beach, New Zealand (Montaño et al., Reference Montaño, Coco, Antolínez, Beuzen, Bryan, Cagigal, Castelle, Davidson, Goldstein, Ibaceta, Idier, Ludka, Masoud-Ansari, Méndez, Murray, Plant, Ratliff, Robinet, Rueda, Sénéchal, Simmons, Splinter, Stephens, Townend, Vitousek and Vos2020) have showed that data-driven models performed comparably to semi-empirical models. However, a specific challenge to the data-driven class of model is the lack of generality when predictions are extrapolated to encompass new sites or forcing conditions that were outside the parameter space of their training datasets. To some extent, generality can be improved by the addition of noise to input variables to avoid over-tuning ANNs to specific data (Reed and Marks, Reference Reed and Marks1999), for example, but the lack of generality remains a major limitation of this modelling type.
Semi-empirical models
Semi-empirical models link wave parameters (e.g. wave height, period and direction) directly to coastal response via equations that implicitly impose some system knowledge, without the intermediate steps of computing the details of complex wave shoaling and dissipation, the generation of nearshore currents or even sediment transport. These models are generally quite simple models, which whilst demanding some calibration data, are less data-dependent than their data-driven model counterparts. Frequently, the simplicity of these models restricts their widespread application, with some prominent models only being applicable to coastlines dominated by either longshore and/or cross-shore transport processes, for example. Generally, the computation of shoreline change due to gradients in longshore transport involves the intermediate steps of computing sediment flux and applying the conservation of volume principles; such models are discussed in section ‘Reduced-complexity models’.
A range of semi-empirical models is presented in Table 1 for the prediction of the temporal evolution of a range of nearshore processes on cross-shore transport-dominated coastlines, including: shoreline position (Miller and Dean, Reference Miller and Dean2004; Yates et al., Reference Yates, Guza and O’reilly2009; Davidson et al., Reference Davidson, Splinter and Turner2013; Vitousek et al., Reference Vitousek, Barnard, Limber, Erikson and Cole2017), beach volume (Burvingt et al., Reference Burvingt, Masselink, Scott, Davidson and Russell2018), beach profile (Hsu et al., Reference Hsu, Ou and Wang1994; Tinker et al., Reference Tinker, O’hare, Masselink, Butt and Russell2009), beach gradient (Madsen and Plant, Reference Madsen and Plant2001), sediment sorting and grain size (Prodger et al., Reference Prodger, Russell, Davidson, Miles and Scott2016) and sand bar location/rhythmicity (Plant et al., Reference Plant, Holman, Freilich and Birkemeier1999). Equilibrium models (section ‘Equilibrium concepts’) feature heavily amongst the semi-empirical class. When incident wave energy exceeds the antecedent average values, beaches tend to erode, shorelines recede landward, beach profiles flatten, sediments coarsen and become better sorted, and bars migrate offshore and straighten. The reverse is true when wave energy is less than the antecedent average value.
The empirical model of Wright et al. (Reference Wright, Short and Green1985) developed the foundation for subsequent profile models (Hsu et al., Reference Hsu, Ou and Wang1994; Davidson and Turner, Reference Davidson and Turner2009), while Miller and Dean (Reference Miller and Dean2004) were amongst one of the first to develop a semi-empirical model to forecast shoreline change, setting the path for similar models (Yates et al., Reference Yates, Guza and O’reilly2009).
Shoreline rotation is a key process within some embayments that is perhaps lacking in previous equilibrium models. Turki et al. (Reference Turki, Medina, Coco and Gonzalez2013) and Jaramillo et al. (Reference Jaramillo, Gonzalez, Medina and Turki2021) both present an equilibrium model for shoreline rotation, utilising the foundations provided by Miller and Dean (Reference Miller and Dean2004) and further developed by Yates et al. (Reference Yates, Guza and O’reilly2009).
In a simultaneous, but independent, development to Yates et al. (Reference Yates, Guza and O’reilly2009), Davidson and Turner (Reference Davidson and Turner2009) proposed an equilibrium profile model with a forcing term proportional to the squared dimensionless fall velocity and a constant (static) equilibrium term, equal to the mean dimensionless fall velocity. The shoreline extracted from this profile evolution agreed well with observations and led to a further reduction into a shoreline model by Davidson et al. (Reference Davidson, Turner and Guza2011), demonstrating its use in the projection of coastal change in the absence of measured waves using a Monte Carlo simulation forced by synthetic waves. This method of long-term projection was later extended (Davidson et al., Reference Davidson, Turner, Splinter and Harley2017) where short-term predictions (≤7 days) forced by forecasted waves were complemented by projections using a statistical analysis of Monte Carlo simulations, forced by synthetic waves to produce a seamless assessment of beach evolution across multiple (short-to-long term) timescales (Davidson et al., Reference Davidson, Steele and Saulter2019; Steele et al., Reference Steele, Davidson, Saulter, Fournier and Upton2019).
While the shoreline model of Davidson et al. (Reference Davidson, Turner and Guza2011) demonstrated promising results at Gold Coast, Australia, it performed less well at other test sites, leading to the development of the ShoreFor model (Davidson et al., Reference Davidson, Splinter and Turner2013), which included a dynamic equilibrium term that was functionally dependent on a weighted average of the antecedent dimensionless fall velocity (Table 1). Splinter et al. (Reference Splinter, Turner, Davidson, Barnard, Castelle and Oltman-Shay2014) demonstrated that the resulting ShoreFor model skilfully predicted shoreline evolution at eight different global locations and that the model-free parameters related systematically to site-specific variables including wave and sediment parameters, promising more generic application of the model on cross-shore transport-dominated coasts without the need for extensive calibration.
Reduced-complexity models
Reduced-complexity models include key processes, focussing only on specific aspects that are crucial to the representation of that process (van Maanen et al., Reference Van Maanen, Nicholls, French, Barkwith, Bonaldo, Burningham, Brad Murray, Payo, Sutherland, Thornhill, Townend, Van Der Wegen and Walkden2016) at the target spatial and temporal scales (Figure 1). In a shoreline modelling context, this class of model covers a wide range of complexity space in Figure 2 (relative to data-driven models), and often involves increased dimensionality, more detailed treatment of wave shoaling and dissipation, explicit calculation of sediment transport and application of the principles of conservation of mass/volume. This type of model is generally better equipped to deal with more complex coastal environments, where simpler data-driven or semi-empirical models might struggle to replicate reality. Models are very diverse within this category, but some might include the effects of both significant longshore and cross-shore sediment transport components, natural headlands and coastal structures, for example.
Beach profile models
Beach profile models include a shoreline data point and usefully extend the morphodynamic prediction in a cross-shore direction, in some cases facilitating the explicit modelling of the shoaling and dissipation of incident waves and changing sea level. Practically, profile models are very useful as they lend themselves to the prediction of coastal overtopping and flooding. The most versatile of these models in terms of daily to decadal projections are simplified further by depth-averaging. The further reduction of complexity in some of the models discussed here comes from the direct link between wave dissipation to sediment transport without explicit consideration of the intermediate process of generating surf zone currents.
The SBEACH model (Larson and Kraus, Reference Larson and Kraus1989) explicitly modelled wave shoaling, dissipation and setup across the beach profile. The model was designed to forecast storm-induced beach change; however, the model formulation is both simple and sufficiently numerically efficient to facilitate projection to much longer time periods, providing the solutions remain skilful and stable. For the computation of sediment transport, the profile was divided into four morphodynamic zones. Sediment transport was computed in the surfzone and values at the surfzone boundaries were systematically attenuated at different rates through the other zones. Sediment transport in the surfzone was governed by an equilibrium equation (Table 1). This equilibrium term is a fixed, site-specific dissipation value (static equilibrium), with the profile evolution obtained by applying the principle of conservation of mass to the cross-shore distribution of sediment flux. The SBEACH model has been widely applied to a range of field and laboratory settings and demonstrates skilful predictions (Larson and Kraus, Reference Larson and Kraus1989; Rosati et al., Reference Rosati, Wise, Kraus and Larson1993; Sommerfeld, Reference Sommerfeld1996).
The FORecasting Coastal Evolution (ForCE) model (Davidson, Reference Davidson2021) fundamentally follows a similar method to that of SBEACH. Unlike SBEACH, ForCE has a single sediment transport equation (one zone, not four), which varies in magnitude in a cross-shore direction scaled by the spatial distribution in wave energy dissipation derived from a Battjes and Janssen (Reference Battjes and Janssen1978) wave model. The ForCE model is computationally simple and stable and allows for changing water levels due to tides, surge and longer-term sea-level rise (dynamic equilibrium).
Wolinsky and Murray (Reference Wolinsky and Murray2009) developed a shoreline evolution model which predicts the evolution over long timescales of decades to millennia. This applied conservation principles through application of the shoreline Exner Equation for the conservation of sediment mass (Paola and Voller, Reference Paola and Voller2005), and necessarily included not only the impacts of sea level rise, but also carefully accounted for the inland topography and substrate lithology. Results from the model suggested that shoreline retreat is highly dependent on the inland morphology and can potentially cause considerable deviation from simple Bruun (Reference Bruun1962) law projections of shoreline recession due to sea level rise.
There have been many other profile translation models which can resolve coastal changes at short- to long-term timescales. Of these, the shoreline translation model of Cowell et al. (Reference Cowell, Roy and Jones1995) affords a probabilistic estimate of profile change, allowing for open sediment budgets, storm variability, effects of mixed sediment sizes, and variable resistance in substrate material. Kinsela et al. (Reference Kinsela, Morris, Linklater and Hanslow2017) introduced a mechanism for including short-term variability and Beuzen et al. (Reference Beuzen, Turner, Blenkinsopp, Atkinson, Flocard and Baldock2018) used a shoreline translation mode to examine the impact of coastal structures. McCarroll et al. (Reference Mccarroll, Masselink, Valiente, Scott, Wiggins, Kirby and Davidson2021) presented a rules-based solution based on the measured beach profile, which allowed for a variety of inland morphologies, including coastal structures.
Whilst many of the profile models discussed here include the capacity to include longshore gradients in sediment transport, this process is not modelled directly in most of the examples discussed above.
One-line models
Here, the term ‘one-line model’ represents the temporal evolution of the shoreline (rather than the beach profile). An early review of the evolution of one-line models can be found in Hanson (Reference Hanson1989), which details the evolution of one-line models from their conception (Pelnard-Considère, Reference Pelnard-Considère1957) to a more generalised application, including a variety of coastal structures and nature complexities (Hanson and Kraus, Reference Hanson and Kraus1989). In an attempt to encapsulate cross-shore processes, subsequent early extension of one-line models to a multiple n-line format (e.g. Perlin and Dean, Reference Perlin and Dean1983) initially proved more difficult to validate and received much less practical engineering application (Hanson, Reference Hanson1989).
The initial restrictive ‘small wave angle’ assumption imposed in the early analytical one-line models was partially relaxed with the advent of numerical 1D modelling approaches. The ‘small wave angle’ assumption enables simplification of equations, based upon the foundation that the sine or tangent of the angle is approximately equal to the angle in question, providing the angle is ‘small’ (Larson et al., Reference Larson, Hanson and Kraus1987). Hanson and Kraus (Reference Hanson and Kraus1989) developed one of the best-known and widely used one-line models, GENESIS (GENEralized model for SImulating Shoreline change) (Krueger et al., Reference Krueger, Gravens and Kraus1988; Young et al., Reference Young, Pilkey, Bush and Thieler1995; Carley et al., Reference Carley, Turner, Couriel, Jackson and Mcgrath1999; Szmytkiewicz et al., Reference Szmytkiewicz, Biegowski, Kaczmarek, Okrój, Ostrowski, Pruszak, Różyńsky and Skaja2000; Wamsley et al., Reference Wamsley, Kraus and Hanson2003; Hanson and Kraus, Reference Hanson and Kraus2011). The model considers sediment transport forced by oblique wave approach and longshore gradients in wave height and is one of the most ubiquitous models for the prediction of shoreline evolution on longshore transport-dominated beaches over 1–100 months for coastlines 1–100 km long. The ease of application and versatility of the GENESIS model in a variety of coastal settings led to an abundance of similar one-line modelling approaches, for example, ONELINE (Kamphuis, Reference Kamphuis1993), LITPACK (Kristensen et al., Reference Kristensen, Dronen, Deigaard and Fredsoe2016), UNIBEST-CL+ (Deltares, 2011) and LONGMOOR (Tonnon et al., Reference Tonnon, Huisman, Stam and Van Rijn2018). Although the GENESIS model and other similar counterparts (Deltares, 2011; Kristensen et al., Reference Kristensen, Dronen, Deigaard and Fredsoe2016) have been broadly applied worldwide, they have also been criticised in the literature (e.g. Young et al., Reference Young, Pilkey, Bush and Thieler1995) for their simplifying assumptions and the reduced complexity philosophy.
Models combining cross-shore and longshore sediment transport processes
A clear limitation of the early one-line models is the omission of cross-shore transport processes, which can be the dominant driver for shoreline change at some coastal localities. Models combining cross-shore and longshore transport processes promise much greater versatility in terms of their generic application.
The earlier attempts to extend one-line models to include cross-shore transport processes adopted by the n-line approach have been surpassed by the inclusion of semi-empirical models (section ‘Semi-empirical models’), which are well suited to integration with one-line models. These models predict the impact of cross-shore sediment transport on shoreline evolution, whereby the cross-shore transport direction is dictated by a disequilibrium term (Hanson et al., Reference Hanson, Larson, Kraus and Capobianco1997; Hanson and Larson, Reference Hanson and Larson1998; Vitousek et al., Reference Vitousek, Barnard, Limber, Erikson and Cole2017; Robinet et al., Reference Robinet, Idier, Castelle and Marieu2018). Hanson et al. (Reference Hanson, Larson, Kraus and Capobianco1997) and Hanson and Larson (Reference Hanson and Larson1998) presented one of the first examples of this approach, whereby the magnitude of the cross-shore transport term was functionally dependent on the product of the Shield’s parameter, sediment fall velocity and the sediment grain size. The direction of transport, (onshore/offshore), was dictated by a comparison of the instantaneous fall velocity with a critical threshold value, not unlike the later equilibrium models, discussed in section ‘Equilibrium concepts’ (e.g. Davidson and Turner, Reference Davidson and Turner2009; Davidson et al., Reference Davidson, Turner and Guza2011, Reference Davidson, Splinter and Turner2013).
Coupling of models is becoming a more common approach to enable the inclusion of more processes, with Vitousek et al. (Reference Vitousek, Barnard, Limber, Erikson and Cole2017) presenting one of the first models to explicitly couple the one-line modelling format with an equilibrium shoreline model. CoSMoS-COAST is a hybrid one-line model which integrates the Yates et al. (Reference Yates, Guza and O’reilly2009) model for shoreline displacement due to cross-shore transport processes with a one-line model, and also includes terms that allow for a simple Brunn-law (Bruun, Reference Bruun1962) displacement of the shoreline due to sea level rise. The model was developed with the aim of predicting both medium- and long-term shoreline evolution, with a particular focus on responses to climate change. A key strength of CoSMoS-COAST was the use of an extended Kalman filter, enabling efficient calibration with limited data, assimilation of real-time data and the estimation of confidence intervals for model-free parameters and predictions.
Robinet et al. (Reference Robinet, Idier, Castelle and Marieu2018) developed a very similar model to Vitousek et al. (Reference Vitousek, Barnard, Limber, Erikson and Cole2017), integrating the Kamphuis (Reference Kamphuis1993) longshore transport model with the ShoreFor model (Davidson et al., Reference Davidson, Splinter and Turner2013) for the prediction of cross-shore terms. The resulting LX-Shore model included an accurate description of the nearshore wave field, derived from a spectral wave model and a cellular approach to shoreline modelling (as opposed to a one-line approach), which facilitated the modelling of complex morphologies (e.g. sand spits).
Consideration of dune evolution is a key consideration when predicting shoreline change at some coastal locations. Antolínez et al. (Reference Antolínez, Méndez, Anderson, Ruggiero and Kaminsky2019) developed a COupled CrOss-shOre, loNg-shorE and foreDune evolution model, COCOONED, that included the CERC longshore transport model in a one-line equation. Cross-shore transport was determined by the Miller and Dean (Reference Miller and Dean2004) equilibrium shoreline model. The model is applicable to similar time and space scales to CoSMoS-COAST, also including sediment source/sink and sea level terms, but additionally including the impacts of foredune erosion on shoreline change. A similar longshore/cross-shore transport one-line model was proposed by Palalane and Larson (Reference Palalane and Larson2020), which also parametrised dune growth by aeolian transport as well as erosion.
Process models
Process, physics-based or bottom-up modelling approaches occupy the base of the complexity spectrum (Figure 2). This class exhibits a broad range of diversity, including depth-averaged models (1D/2D), depth-resolving models (2D/3D), coastal profile and area models. Sherwood et al. (Reference Sherwood, Van Dongeren, Doyle, Hegermiller, Hsu, Kalra, Olabarrieta, Penko, Rafati, Roelvink, Van Der Lugt, Veeramony and Warner2022) provide a more thorough overview of the classification and application of process-based models. The application of detailed process-based models (e.g. Mike 21, Delft 3D, XBeach or Telemac) is an established modelling approach, including the detailed physics of wave propagation, dissipation, generation of nearshore currents, sediment transport and the resulting morphological change with multiple feedback loops (Warren and Bach, Reference Warren and Bach1992; Lesser et al., Reference Lesser, Roelvink, Van Kester and Stelling2004; Roelvink et al., Reference Roelvink, Reniers, Van Dongeren, Van Thiel De Vries, Mccall and Lescinski2009; Villaret et al., Reference Villaret, Hervouet, Kopmann, Merkel and Davies2013). This class of model has proved very successful in predicting a range of nearshore phenomena including storm/dune erosion and wave overtopping.
Process models are computationally expensive, meaning medium-to-long term projections are often challenging. The upscaling of processes represented in the bottom-up approach can range from centimetres to several kilometres. Therefore, errors resulting from imperfect physics and empirical representation of model components can cause an aggregation of errors, which lead to instabilities and inaccuracies in long model runs. In principle, the inclusion of more detailed physics in process models means that this class of model is the most widely applicable, least dependent on data for calibration and best able to deal with coastal complexities (e.g. coastal structures, complex natural coastlines and estuaries). However, whilst process models have proved to be the most effective way of predicting waves, currents and sediment transport in the short-to-medium term (days-to-years), their application to longer-term projections of morphological change still remain a significant challenge. The complexity and non-linearity of process models not only causes problems with long-term stability and computational complexity, but it also renders long-term projections extremely sensitive to very subtle changes in the initial conditions. Moreover, the Monte Carlo or ensemble models runs, which are required to establish the probability of given long-term projections, are reasonably straightforward for the less complex models, but remain significantly challenging for complex process models. For these reasons, the discussion of these models here is relatively brief. Combining process models with data-driven approaches may offer the potential to maintain the complexity of process models with reduced computational demand. This is a novel method, requiring significant future development, however, Itzkin et al. (Reference Itzkin, Moore, Ruggiero, Hovenga and Hacker2022) applied this approach to model dune and beach evolution with reasonable success over multi-year timescales.
Discussion and concluding remarks
This paper presents an overview of shoreline evolution models in terms of a modelling complexity spectrum (Figure 2). The appropriate choice of model complexity depends not only on the intended space-/time- scales to be modelled (Figure 1), and the target environment, it strongly pivots on the balance between current system knowledge and the availability of relevant data (Figure 3). At present, deficiencies in both system knowledge and the widespread availability of data, coupled with the diverse nature and complexity of coastal systems, has meant that the most promising approaches to modelling shoreline evolution on timescales of days-to-decades are reduced-complexity models, positioned in the centre of the complexity spectrum.
Providing only short-term predictions are required, the diverse and complex nature of coastal systems is best approached through process-based models at the base of the complexity spectrum. However, the complexity and hence computational cost of this class of model, coupled with a sensitivity to small variations in initial conditions, currently renders medium-to-long-term forecasts with these types of models very challenging, particularly at large space and timescales, and when Monte Carlo or ensemble simulations are required to generate probabilistic projections.
Conversely, data-driven models provide the required computational efficiency to generate multi-decadal projections of shoreline change with ease, but in the absence of extensive and widespread data, they lack the generality required to cope with system complexities like anthropogenic structures, hard rock geology, complex wave transformations, supra-tidal morphology (e.g. cliffs and dunes), mixed grain size beaches and potential additional sources/sinks of sediment (e.g. from estuaries or anthropogenic input). This means that these models have limited ability to extrapolate accurately beyond the parameter space of their training dataset. Therefore, the ability of these models to provide accurate morphological forecasts over the long-term with changing wave climates and sea level is questionable. For these reasons, reduced-complexity models occupy the promising middle ground between process models and data-driven models.
The simplicity of reduced-complexity models means that it is relatively easy to embed data-assimilation methods (e.g. Kalman filters) within their algorithms. This has the advantage of efficiently calibrating models, making effective use of noisy data and assigning confidence limits to model-free parameters and estimates, ultimately improving the accuracy of predictions (Long and Plant, Reference Long and Plant2012; Vitousek et al., Reference Vitousek, Barnard, Limber, Erikson and Cole2017; Ciritci and Turk, Reference Ciritci and Turk2020; Ibaceta et al., Reference Ibaceta, Splinter, Harley and Turner2020; Alvarez-Cuesta et al., Reference Alvarez-Cuesta, Toimil and Losada2021).
Proceeding with the notion that reduced-complexity models offer the most realistic (immediate) vehicle for the prediction of coastal morphodynamic change on daily-to-decadal timescales (short-to-medium term) and beyond, what then are the future challenges that need to be addressed within this class of model before they become suitable effective and applied coastal management tools? The answers to this question are dependent on the target prediction horizon of the required forecast and discussed below accordingly, from short to long timescales. Medium- and long-term timescales have been discussed in conjunction, due to the shared challenges they face, particularly with regards to uncertainties surrounding model forcing.
Short term timescales
Over the short-term (days-to-weeks), management objectives include the prediction of coastal evolution due to storms or storm sequences. The challenges within this timeframe include, optimising the complexity of the models so they can adequately cope with complex coastal environments and facilitate wide-spread regional application, whilst maintaining sufficient computational efficiency, skill and stability. Specifically, these complexities include coastal structures, mixed-beach sediments, sediment bypassing, dune-dynamics and limited sediment supply. Many of these challenges have already been partially solved in existing models, but bringing them together seamlessly in a single efficient model remains a significant challenge.
Short-term (weather) data used as forcing are intrinsic to the shoreline modelling problem, directly impacting the skill of the shoreline models that they drive. The application of ensemble approaches (e.g. Saetra and Bidlot, Reference Saetra and Bidlot2004; Alves et al., Reference Alves, Wittmann, Sestak, Schauer, Stripling, Bernier, Mclean, Chao, Chawla, Tolman, Nelson and Klotz2013; Bunney and Saulter, Reference Bunney and Saulter2015) is considered the best practice in mitigating the initial condition uncertainty on short-term timescales (Siddorn et al., Reference Siddorn, Good, Harris, Lewis, Maksymczuk, Martin and Saulter2016; Steele et al., Reference Steele, Neal, Bunney, Evans, Fournier, Gill, Mylne and Saulter2017). A pioneering example application is described in the context of shoreline evolution by Steele et al. (Reference Steele, Davidson, Saulter, Fournier and Upton2019).
Medium-to-long term timescales
Over the medium-term (months-to-decades), models are required to resolve morphological changes over seasonal, interannual and longer-term climate change timescales. Here, models must consider slower and more poorly understood sediment transport processes, which become increasingly significant over longer timescales, including the erosion of cliff-backed coastlines of various lithology (Walkden and Dickson, Reference Walkden and Dickson2008), natural and anthropogenic sediment source-sinks (e.g. river inputs and beach replenishment) and sediment transport between the surfzone on offshore regions beyond the depth of closure (Harley et al., Reference Harley, Masselink, Ruiz De Alegría-Arzaburu, Valiente and Scott2022).
With the inclusion of more processes (complexity) required to achieve more widespread geographical application of models, care must be taken to maintain sufficient stability and computational efficiency, also required to model medium-to-long term coastal change. Here several methodologies can be invoked. Firstly, it has been demonstrated that the inherently stable equilibrium models discussed in section ‘Equilibrium concepts’ are appropriate to a plethora of coastal processes and that embedding equilibrium processes in more complex models can significantly enhance stability. Secondly, complex processes can be accurately encapsulated by data learning methodologies, including Artificial Neural Networks (ANN). Thus, embedding ANNs within more complex models can also increase computational efficiency (Itzkin et al. (Reference Itzkin, Moore, Ruggiero, Hovenga and Hacker2022).
Medium-to-long term projections present even more challenges in terms of the provision of realistic (climate) forcing conditions for morphodynamic models. Wave forcing models required by morphological models must inherently account for much greater unknowns. These include the ‘internal variability’, ‘model uncertainty’ and ‘scenario uncertainty’ (Hawkins and Sutton, Reference Hawkins and Sutton2009). Internal variability is associated with the natural fluctuations and chaotic nature of the climate system. Model uncertainty arises from the differences in the way individual models have been designed to replicate real-world processes. Scenario uncertainty is associated with future global economic and emissions trajectories. To account for these uncertainties and represent the possible future pathways, sets of emissions scenarios have been generated, with Representative Concentration Pathways (RCPs; Moss et al., Reference Moss, Edmonds, Hibbard, Manning, Rose, Van Vuuren, Carter, Emori, Kainuma, Kram, Meehl, Mitchell, Nakicenovic, Riahi, Smith, Stouffer, Thomson, Weyant and Wilbanks2010, Van Vuuren et al., Reference Van Vuuren, Edmonds, Kainuma, Riahi, Thomson, Hibbard, Hurtt, Kram, Krey, Lamarque, Masui, Meinshausen, Nakicenovic, Smith and Rose2011) or Shared Socioeconomic Pathways (SSPs; Riahi et al., Reference Riahi, Van Vuuren, Kriegler, Edmonds, O’neill, Fujimori, Bauer, Calvin, Dellink, Fricko, Lutz, Popp, Cuaresma, Kc, Leimbach, Jiang, Kram, Rao, Emmerling, Ebi, Hasegawa, Havlik, Humpenöder, Da Silva, Smith, Stehfest, Bosetti, Eom, Gernaat, Masui, Rogelj, Strefler, Drouet, Krey, Luderer, Harmsen, Takahashi, Baumstark, Doelman, Kainuma, Klimont, Marangoni, Lotze-Campen, Obersteiner, Tabeau and Tavoni2017). Ensemble approaches, for example, Monte Carlo simulations, are commonly adopted to generate wave-forcing input parameters for coastal models (Davidson et al., Reference Davidson, Lewis and Turner2010; Antolínez et al., Reference Antolínez, Méndez, Camus, Vitousek, González, Ruggiero and Barnard2016; Davidson et al., Reference Davidson, Turner, Splinter and Harley2017; Antolínez et al., Reference Antolínez, Méndez, Anderson, Ruggiero and Kaminsky2019; D’Anna et al., Reference D’anna, Idier, Castelle, Rohmer, Cagigal and Mendez2022), providing a probabilistic description of wave conditions and enabling uncertainty to be easily quantified. Vitousek et al. (Reference Vitousek, Cagigal, Montaño, Rueda, Mendez, Coco and Barnard2021) provide a literature review and detailed description of the application of an ensemble approach using a Kalman filter, to simulate wave forcing for shoreline modelling. The use of ensemble forcing, where possible, is deemed necessary to account for intrinsic uncertainties (Vitousek et al., Reference Vitousek, Cagigal, Montaño, Rueda, Mendez, Coco and Barnard2021).
Although sea level forcing can somewhat be considered of secondary importance in the context of shoreline modelling on short timescales, the impact of sea level rise cannot be neglected on medium-to-long timescales. Data suggests that while seasonal and interannual variability in wave conditions will continue to dominate the morphological response up until 2050, sea level rise is likely to be the main driver of coastal change beyond that (Howard et al., Reference Howard, Palmer and Bricheno2019; D’Anna et al., Reference D’anna, Castelle, Idier, Rohmer, Le Cozannet, Thieblemont and Bricheno2021; Davidson, Reference Davidson2021; D’Anna et al., Reference D’anna, Idier, Castelle, Rohmer, Cagigal and Mendez2022). There is currently no single model that can compute all the different contributions to both global and regional sea-level change directly – with the latest estimates compiled by determining the individual contributions to sea level separately and then combining these for different emissions scenarios (Fox-Kemper et al., Reference Fox-Kemper, Hewitt, Xiao, Aðalgeirsdóttir, Drijfhout, Edwards, Golledge, Hemer, Kopp, Krinner, Mix, Notz, Nowicki, Nurhati, Ruiz, Sallée, Slangen, Yu, Masson-Delmotte, Zhai, Pirani, Connors, Péan, Berger, Caud, Chen, Goldfarb, Gomis, Huang, Leitzell, Lonnoy, Matthews, Maycock, Waterfield, Yelekçi, Yu and Zhou2021). To correctly inform local shoreline modelling, regional sea level projections are more appropriate than global means, (e.g. Chen et al., Reference Chen, Dangendorf, Narayan, O’driscoll, Tsimplis, Su, Mayer and Pohlmann2014; Hermans et al., Reference Hermans, Tinker, Palmer, Katsman, Vermeersen and Slangen2020; Tinker et al., Reference Tinker, Palmer, Copsey, Howard, Lowe and Hermans2020). Relative sea level uncertainty varies greatly with geographical location – particularly in tectonically active areas and those where ocean dynamics may be subject to large changes – providing a further reminder of the care needed in the selection, treatment and interpretation of any forcing data (e.g. Vannitsem et al., Reference Vannitsem, Bremnes, Demaeyer, Evans, Flowerdew, Hemri, Lerch, Roberts, Theis, Atencia, Ben Bouallègue, Bhend, Dabernig, De Cruz, Hieta, Mestre, Moret, Plenković, Schmeits, Taillardat, Van Den Bergh, Van Schaeybroeck, Whan and Ylhaisi2021).
While differences exist between general circulation models (large-scale, numerical, climate models) in the detail of how wind fields are going to change in the future, there is generally better consensus in long-term trends of large-scale atmospheric patterns. Therefore, an alternative approach, potentially particularly well suited to seamless forecasts spanning short- to long-term (weather-to-climate) timescales, considers these weather patterns and climate indices that can be related directly to shoreline variability. Studies are starting to exploit this link to explain erosion/accretion events (Barnard et al., Reference Barnard, Short, Harley, Splinter, Vitousek, Turner, Allan, Banno, Bryan, Doria, Hansen, Kato, Kuriyama, Randall-Goodwin, Ruggiero, Walker and Heathfield2015; Castelle et al., Reference Castelle, Dodet, Masselink and Scott2017) and estimate shoreline evolution (e.g. Robinet et al., Reference Robinet, Castelle, Idier, Le Cozannet, Déqué and Charles2016; Anderson et al., Reference Anderson, Ruggiero, Antolínez, Méndez and Allan2018b; Wiggins et al., Reference Wiggins, Scott, Masselink, Mccarroll and Russell2020; Montaño et al., Reference Montaño, Coco, Cagigal, Mendez, Rueda, Bryan and Harley2021; Scott et al., Reference Scott, Mccarroll, Masselink, Castelle, Dodet, Saulter, Scaife and Dunstone2021).
Extending reduced-complexity models to the long-term presents new challenges which are beyond the scope of detailed discussion here, but will likely include the use of rules-based modelling approaches (Castelle and Masselink, Reference Castelle and Masselink2023) and models with highly flexible grids and dynamic boundary conditions to cope with the high levels of coastal distortion (Roelvink et al., Reference Roelvink, Huisman, Elghandour, Ghonim and Reyns2020), as well as a comprehensive consideration of eustatic and isostatic sea level variations.
Final remarks
Inevitably, the future direction of daily-to-decadal modelling of shoreline evolution will continue to be dynamic within complexity space (Figure 2). Progression towards the process-based end of the complexity spectrum will be facilitated by increasing computational capabilities and improved process knowledge. Conversely, the rapidly increasing availability of coastal data (e.g. satellite data) and data assimilation techniques promises increasing opportunity to migrate towards the data-driven end of the complexity spectrum. Therefore, occupying the promising middle ground, reduced-complexity models are well-positioned to benefit from the anticipated advances/drivers in both directions, building on their established potential for providing immediate practical, community-accessible capability for the seamless prediction/projection of shoreline change across timescales, through which further effective and efficient progress can be made.
Open peer review
To view the open peer review materials for this article, please visit http://doi.org/10.1017/cft.2023.5.
Acknowledgements
E.H. would like to acknowledge the financial support from the School of Biological and Marine Sciences, University of Plymouth. The authors thank Teil Howard and Jonathan Tinker (Met Office) for their feedback on the final draft of the manuscript.
Competing interest
The authors declare none.







Comments
Dear Editor,
We were invited to author a commissioned review article for Cambridge Prisms: Coastal Futures, within the Coastal Engineering sub-topic, with the title “Shoreline modelling at timescales of days to decades”. This paper is a collaboration between the University of Plymouth and the Met Office, UK. Emily Hunt, a PhD student at the University of Plymouth, is acting as lead author, with co-authors Dr Mark Davidson, Dr Tim Scott, Dr Paul Russell (University of Plymouth) and Dr Edward Steele (Met Office) making up Emily Hunt’s PhD supervisory team. Dr Edward Steele is a Science Manager for the Met Office, and Dr Jessica Amies is an Industry Specialist at the Met Office, specializing in Oceanography. The expertise and knowledge of this team combines to make for a comprehensive review on the current state of knowledge of shoreline models.
Thank you for this opportunity and your consideration.