Time-dependent measurement of high-power laser light reflection by low-Z foam plasma

Abstract

Porous materials have many applications for laser–matter interaction experiments related to inertial confinement fusion. Obtaining new knowledge about the properties of the laser-produced plasma of porous media is a challenging task. In this work, we report, for the first time to the best of our knowledge, the time-dependent measurement of the reflected light of a terawatt laser pulse from the laser-produced plasma of low-Z foam material of overcritical density. The experiments have been performed with the ABC laser, with targets constituted by foam of overcritical density and by solid media of the same chemical composition. We implemented in the MULTI-FM code a model for the light reflection to reproduce and interpret the experimental results. Using the simulations together with the experimental results, we indicate a criterion for estimating the homogenization time of the laser-produced plasma, whose measurement is challenging with direct diagnostic techniques and still not achieved.

1. Introduction

Porous materials, or foams, have a non-trivial internal structure, constituted by randomly arranged solid parts, which can be filaments or membranes, separated by empty spaces^{[ 1 ]}. These materials have a wide range of application in the laser–plasma interaction experiments. They are used for the study of equations of state^{[ 2 , 3 ]} and shock waves^{[ 4 , 5 ]}, for increasing the efficiency of absorption of laser energy^{[ 6 , 7 ]} and of its conversion into X-rays^{[ 8 ]}, as bright neutron sources^{[ 9 ]}, and to enhance electron acceleration by short laser pulses^{[ 10 – 13 ]}. In the direct-drive approach towards inertial confinement fusion (ICF), foams of overcritical density have been suggested to be employed as absorbers for the fusion capsule being able to increase the ablation loading on the target surface^{[ 14 ]}. Foams of subcritical density showed the ability of smoothing spatial inhomogeneities of the laser profile^{[ 15 – 18 ]} and have been suggested as liners in the indirect drive approach in ICF to delay the closing of the entrance holes of the hohlraum and to improve the capsule drive^{[ 19 ]}.

The peculiarity of laser-produced plasma in a porous material is the non-equilibrium nature of its state associated with the homogenization process. For a large-pore foam with a pore size of about 10 μm, the plasma homogenization has a comparable duration of a nanosecond laser pulse of terawatt power. The laser interaction with the partially homogenized plasma has a number of important distinguishing features compared with the case of a solid target. First, radiation absorption occurs volumetrically at the homogenization depth not only in the case of a foam with an average density lower than the critical plasma density (subcritical foam), but also in one with a supercritical average density (overcritical foam)^{[ 20 ]}. This is the reason for the higher absorption efficiency of laser radiation in the plasma of a porous substance compared with the plasma of a solid target. Experimentally, the absorption efficiency of foams has been measured to be up to 90% for the first harmonic of a nanosecond Nd-laser radiation^{[ 6 , 7 , 21 , 22 ]}. The plasma homogenization process determines the features of energy transfer in the foam target. In the inhomogeneous foam plasma, the diffusion of plasma electrons and the directed hydrodynamic motion of the substance are largely suppressed owing to the density oscillations within the pores. As a result, the rate of energy transfer is significantly lower (by a factor of 1.5–2) than the speed of the shock wave in a solid substance with the same density^{[ 17 , 18 , 23 , 24 ]}.

Despite many experiments performed in the last few decades and the actual experimental interest about laser–foam interaction, numerically simulating the behavior of porous materials under intense laser pulse irradiation is still a challenging task. Modeling a foam as a homogeneous material of the same average density proved to be unsuccessful when compared with the experiments^{[ 18 , 25 – 28 ]}. The very different spatial scales present in the problem, with thicknesses of the solid parts ranging from tens of nanometers to micrometers, and the experimental size of the typical plasma being of the order of hundreds of micrometers or millimeters, are a serious limitation for studying the foam behavior from first principles. This makes the accurate numerical simulation of such foam plasmas a very challenging task. In fact, reproducing the internal structure of the foam material in a numerical simulation implies a high computational cost and requires the use of parallel codes and supercomputers, with quite long computational time. Recently, effective models have been developed and implemented in existing serial codes to allow reproducing the features of laser–foam interaction and energy transport in reasonable computational time^{[ 24 , 28 , 29 ]}. In particular, the MULTI-FM code^{[ 26 ]} is based on the use of limiters for the thermal conductivity and pressure gradient which depend on the homogenization degree of the plasma, and proved to be in very good agreement with the experimental data^{[ 24 , 26 ]}. The speed of the shock wave generated by the laser action on an overcritical foam was measured in the experiments in Ref. [24] and was reproduced with very good agreement by the simulations done with the MULTI-FM code. The results of Ref. [24] also indicate that a one-dimensional code as MULTI-FM can account for most of the relevant physical aspects of the problem in a planar configuration of irradiation with overcritical foams with large pores. As shown in the following, the one-dimensional model also gives results close to the experimental results for light reflection, because the reflection process occurs in a weakly homogenized plasma in the initial period of time less than 1 ns, when the two-dimensional energy transfer effects do not have a significant effect.

In all the available models and codes, the fraction of energy absorbed in the plasma, which can be deduced from the fraction of reflected laser light energy, is a semi-empirical parameter. The experimental and theoretical analysis of light reflection is very important for understanding the physics of laser interaction with foams as well as the properties of the laser-produced plasma in foam targets. The reflected light from foam plasmas has been measured, so far, both through a time-integrated diagnostic^{[ 17 , 21 , 30 , 31 ]} and through a time-resolved diagnostic, but in this case only devoted to the study of plasma instabilities in subcritical foam targets with a pore size of the order of a few micrometers, at most^{[ 32 – 35 ]}.

In this work, we report, for the first time to the best of our knowledge, the time-dependent measurement of the total laser light reflected during the irradiation of overcritical foam targets by a powerful nanosecond laser pulse, at intensities relevant for ICF. The average pore size of the samples is of 40 μm, resulting in a homogenization time of the order of the laser pulse duration, which allows for investigating the influence of the plasma homogenization degree on the interaction with the laser. Our measurements indicate that the internal structure of the foam has an evident effect on the reflected light compared with the case of a solid medium of the same chemical composition. We developed a new model for light reflection in the inhomogeneous foam plasma and we implemented it in the MULTI-FM code. By using the MULTI-FM code together with the experimental data, we indicate a possible strategy for estimating the homogenization time of the foam plasma, the direct measurement of which is experimentally challenging and still not achieved, despite the importance of this parameter for many applications of foams in laser–matter interaction experiments. The homogenization degree of the foam plasma determines all the peculiar features of the interaction of porous materials with laser pulses^{[ 24 , 26 , 28 , 29 ]} and the measurement of the duration of the homogenization phase is particularly relevant for large-pore foams. The simulations performed with the MULTI-FM code confirm the high time-integrated absorption efficiency of about 90% of thick layers of foam of overcritical density reported in the literature^{[ 21 ]}.

2. Experimental results

The experiments were carried out at the ABC laser facility, located in the ENEA Research Center in Frascati. The ABC laser is a Nd:glass–phosphate laser, able to deliver two counter-propagating synchronized beams with a maximum energy of 100 J each and a time duration of 3 ns full width at half maximum (FWHM). The experimental setup is shown in Figure 1. One of the two beams of the ABC laser with wavelength ${\lambda}_L=1054$ nm was focalized by an f/1 lens with an intensity I_L ≅ 10¹⁴ W/cm² and a spot diameter of 100 μm on the target placed at the center of the experimental chamber. To a very good approximation, the focal spot had a circular shape with a super-Gaussian intensity profile. The mean laser energy over all shots was 40.2 J, with a standard deviation of 3.4 J. The targets used in the experiments were constituted by planar foils of freestanding polystyrene foam with an average density ${\rho}_p=10$ mg/cm³ and an average pore size of ${\delta}_0\cong 40$ μm, corresponding to a wall thickness ${b}_0\cong 1$ μm. The targets were realized from capsules of a chemical mixture containing polystyrene, which were let fall in a vertical furnace. The heating caused the formation of the pores in the capsules, which were subsequently cooled down and cut. By varying the heating and cooling conditions, as well as the initial chemical mixture and capsule size, the pore size and the thickness of the solid parts could be controlled. The density of the targets was measured by weighting a defined volume of material, whereas the features of the internal structure were determined by an electron microscope. The thickness of the foam layer was varied during the experiment.

Figure 1 The experimental setup used in the campaign. The photodiode A is used to monitor the time dependency of the incident laser energy profile, whereas the photodiode B collects the laser light reflected by the plasma. A Faraday cup provides, by a time-of-flight analysis, information on the energetic content of the plasma. An optical streak camera, placed on the equatorial plane at 90° from the target normal, is used to monitor the evolution of both the plasma created on the front surface by the laser–target interaction and the plasma produced on the rear side of the target by the blow-off of the shock wave generated in the foam. An optical spectrometer is placed along the same line of sight for a spectrally resolved monitoring of the plasma self-emission.

The main beam was deflected by two mirrors before entering the interaction chamber. The light refracted by the first mirror was focused by a lens on the calibrated photodiode A, which allowed for a reliable on-line measurement of the energy delivered by the laser. The beam was circularly polarized by a λ/4 waveplate. A large fraction of the laser light was reflected by the plasma within the angle covered by the focusing lens, which in our case was $\alpha =28{}^{\circ}$ . We estimated this fraction to be about 80% of the total reflected light according to the results of Refs. [36, 37], in which the angular dependence of the reflectivity of solid and foam targets has been measured at the ABC and the KANAL-2 laser facilities, respectively, with laser parameters comparable to the present experiments. The circular polarization was conserved to great accuracy in the reflection process in the plasma. In fact, the p-component could be partly absorbed by the plasma through resonant absorption, which, however, in our experimental conditions represented no more than 5% of the total absorption^{[ 24 ]}. A second passage through the waveplate transformed the circular polarization into linear polarization, with the axis perpendicular to the original. Therefore, the reflected light was rejected by the polarizer and then focused on the photodiode B. The calibrated photodiode B allowed for a suitable characterization of the reflected light. A relative calibration procedure has been carried out for the photodiode B, to reliably compare the A and B signals and their integrals, for estimating the absorption and reflection efficiencies of the targets. To this end, we made a series of shots at low energy with a mirror placed after the λ/4 waveplate. We recorded the A and B signals and, assuming a perfect reflection from the mirror, we obtained the relative attenuation.

As a reference for the shots with the foam, we firstly irradiated a thick solid homogeneous slab of polystyrene of density ${\rho}_P=1.05$ g/cm³, collecting several shots. A typical result, shot 5207, is reported in Figure 2(a). As it can be seen from Figure 2(a), the profile of the signal B_r is nearly identical to that of signal A. This means that the plasma is generated at the very beginning of the irradiation and the reflection is stable during the whole laser duration, as expected from the irradiation of a solid target. The B signal shows that a fraction of the laser light, around 70%, is not reflected and is absorbed by the plasma. This series of shots also allowed us to determine the timing between the A and B signals, which proved to be very stable and reliable for all the shots.

Figure 2 Typical time-dependent and integrated results from the shots performed in the campaign for the reflected light. In the shot 5207 the target was solid polystyrene, whereas in all the others it was a polystyrene foam. The labels “A” and “B” in the legends, according to Figure 1, indicate the photodiode from which the signal was recorded. Each signal is normalized to the maximum of the corresponding A signal, with the exception of B_r. The origin of the time axes corresponds to the time at which the main pulse hits the target. (a) The results of the shot with solid polystyrene. The signal named B_r is the B signal normalized to one. (b) The comparison between the shot in (a) and one of the shots with foam polystyrene (shot 5251). The inset in (b) shows an enlarged view of the reflection from the chamber window. (c) Typical reflected light signals recorded in the campaign. The foam thickness is indicated in the legend, next to the shot number. (d) The values of the integral of the B signals for all the shots of the campaign, plotted versus the target thickness and normalized to the integral of the corresponding A signal. The horizontal dashed line indicates the value of the integral of the B signal for the shot on solid polystyrene, with its error indicated by the gray shading.

Many shots have been collected with various foam targets of different thicknesses. In Figure 2(b) we report a typical B signal obtained in the campaign with foam targets (shot 5251), along with the laser temporal profile and the solid polystyrene signal (shot 5207) of Figure 2(a). Figure 2(b) shows that a remarkable difference is observed between the reflection efficiency of the foam compared with the solid target.

Figure 2(c) shows the data from several shots with foam targets of different thicknesses, which can be retrieved from Figure 2(d). The curves in the figure indicate that the features of the reflection process do not have a significative dependence on the target thickness, because the time durations of the B signals are comparable for targets of various thicknesses. This indicates that the plasma density is large enough throughout the whole laser duration to reflect the light, even after that the shock formed inside the material reached the backside of the slab.

The data reported in Figure 2(d) are the integrals of the B curves normalized to the integral of the corresponding A signal for each shot, plotted versus the target thickness. The uncertainties on the calculation of the integrals have been evaluated considering the uncertainty on the amplitude and on the timing of the A and B signals for each shot. It is well known that, during the laser–matter interaction, high-intensity electromagnetic pulses (EMPs) are generated, which have been recently measured at the ABC facility as reported in Ref. [38]. These EMPs can couple with the diagnostic instrumentation, the cables, and the scopes. To avoid any contamination on the photodiode signals from EMPs, accurate shielding was ensured on them and on the cables. The scopes were not placed in the interaction chamber room, to protect them from the electromagnetic disturbances. As it can be seen from Figure 2, the signals show no evidence of EMP pollution in the whole time of interaction. We can therefore assume that the uncertainty on the measurement due to EMP is negligible.

Another source of uncertainty may come from the background noise on the scope. The acquired signals from the A and B photodiodes are much longer than the time of duration of the laser light or the reflected light from the targets. By analyzing the signals for $t>300$ ns and by comparison with acquisitions on null shots where the laser was fired at full energy but did not actually hit the target, it was possible to estimate the uncertainty for each of the discussed shots and for the laser temporal profile. The error for the normalized signals was $\delta {V}_{\mathrm{A}}=0.1$ for the normalized A signals and $\delta {V}_{\mathrm{B}}=0.005$ for the normalized B signals. For all the shots, the uncertainty on the B signal is sufficiently low to reliably distinguish between the observed oscillations.

The time uncertainty for the A and B signals was determined by the time resolution of the scope recording them. The A signals were acquired by a Tektronix TDS684B scope, and led to $\delta {t}_{\mathrm{A}}=200$ ps. The B signals were acquired by a Tektronix DPO7354C scope, for $\delta {t}_{\mathrm{B}}=100$ ps. The early peak at around –3 ns in Figure 2(b) is relative to a partial reflection from the chamber window. This does not affect the reflected light signal and constitutes a reference for checking the timing among signals from different shots. The acquisitions setup was stable throughout the whole campaign; therefore, all the considerations on the timing apply for all the shots presented in this work. As can be seen from Figure 2(b), the timing between the B signals for the shots 5207 and 5251 is sufficiently accurate for the purposes of the present work.

The thickness of each target was measured by using an optical microscope with a camera connected to a PC. The total error was determined as $\delta T=20$ μm and reported in Figure 2(d) for each shot.

The data in Figure 2(d) confirm that the reflection efficiency does not depend in an appreciable way on the thickness of the irradiated sample. Moreover, the fluctuations in the integral value are related to the variable morphology of the internal structure of the samples. The average reflected fraction of the incident laser light of the foam targets within the angle covered by the focusing lens results to be about 0.1. Considering that in our experiments we can estimate that the focusing lens collects approximately 80% of the reflected light, we obtain a total reflectivity of around 0.12, in agreement with the results of Refs. [21, 22]. This value is about three times lower than that of the solid target, for which, at the same way, the total reflectivity results to be approximately 0.32.

It is important to note that in the majority of the shots, the B signal has a first part with evident oscillations and a smoother trailing edge, where some oscillations are still present. Both features are not related to the laser temporal profile and do not appear in the shots with the homogeneous target, as seen in Figure 2(a). This fact can be interpreted as the manifestation of the effect of the internal structure of the foam as follows. The irradiation of the solid parts of the target evaporates the cold material transforming it into plasma. The random distribution of the solid parts inside the target volume causes an inhomogeneous spatial distribution of the plasma density, which produces pronounced oscillations in the B signals in the time range from 1 to 3 ns after the beginning of irradiation, until the inhomogeneities are reduced. The ablation of the target implies that the homogenizing region moves towards the rear side of the target and encounters regions of still non-homogenized plasma, which perturb the shape of the critical reflective region, leading to the trailing edge oscillations in the B signals from 3 ns onwards. This interpretation is supported by the model implemented in the MULTI-FM code, showing how the reflected light features are determined by the inhomogeneity of the laser-produced plasma and by the timescale of the homogenization process.

During the interaction with the laser, the plasma was monitored by a large number of diagnostics^{[ 39 , 40 ]}. An optical streak camera placed on the equatorial plane at 90° from the optical axis of the main beam recorded the images of the self-emitted light from the plasma. The camera is Hamamatsu C5680, operating in the spectral range 200–850 nm, with a time resolution of 2 ps. The magnification of the camera was set to include in the image both the front and the rear surfaces of the foam targets, to monitor the evolution of the plasma plume on the laser side and the breakthrough of the shock wave on the rear side. This allowed for the measurement of the speed of the shock wave inside the foam, resulting in an almost-constant value among the several shots on foam targets of 125 ± 40 μm/ns, in accordance with Refs. [24, 41]. Along the same line of sight, an Ocean Optics HR4000CG-UV-NIR spectrometer operating in the range 200–1100 nm allowed for a spectral analysis of the plasma emission; the associated typical measurements are given in Figure 3(a). For the detection of the charged particles escaping from the target, a Faraday cup was used for time-of-flight measurements, as indicated in Figure 1. The device was placed at an angle of 54° from the target normal, at a distance of 55 cm from it, and was connected to a Tektronix TDS684B oscilloscope. In Figure 3(b) a typical signal from the foam plasma is reported in the ion energy domain per unit of atomic mass. From this plot it is possible to see the contribution of thermal ions with energies up to 4 keV/A, with a peak at about 1 keV/A, where A is the atomic mass.

Figure 3 Typical signals obtained from the plasma diagnostics in the performed campaign: (a) typical spectra obtained with the spectrometer for the solid (shot 5207) and the foam (shot 5238) targets; (b) a typical signal obtained for the same latter shot on a foam target from a Faraday cup placed at 54° from the target normal; the oscillations for energies higher than 5 keV/a.m.u are due to EMP fields coupling to the detector. Here it is possible to see the thermal component of the plasma, with main peak at about 1 keV/a.m.u.

It is well known that some parametric instabilities, such as stimulated Raman scattering (SRS) and stimulated Brillouin scattering (SBS), can give a contribution to the light reflection^{[ 42 , 43 ]}. The onset of the parametric instabilities, including the two-plasmon decay (TPD), is known to occur when phase-matching conditions are fulfilled, and is enhanced when the characteristic length of the plasma density gradient is large^{[ 42 , 43 ]}. Experiments about the irradiation of foams of subcritical density with small pores^{[ 32 – 34 ]} reported a very low contribution to the scattered laser light in the focusing optics due to SRS, of about 1% or less of the incident energy. The SBS light scattered in the focusing optics was measured to be lower than 8% of the incident light^{[ 33 , 34 ]}. In the same experiment of Ref. [34], a signature of the TPD instability was also found. In these cases, all the foam plasmas can be considered to be homogeneous for the whole pulse duration, with a very long density scale length, conditions which are favorable for the onset of all the parametric instabilities^{[ 32 – 34 ]}.

In our experiments, the plasma characteristics are opposite. The foam plasma produced in our campaign has a homogenization time comparable to the duration of the laser pulse and is overcritical. At the beginning of the irradiation, the laser pulse interacts with the pore walls, evaporating them and creating a very inhomogeneous turbulent plasma^{[ 20 ]}. In this regime, which corresponds also to the maximum reflection of the laser light (see Figure 2(c)), the matching conditions required for the development of the parametric instabilities are mainly violated. As the homogenization process completes, the laser penetration depth decreases progressively, until the critical surface is formed in the homogeneous foam plasma^{[ 24 , 26 ]}. With the plasma being overcritical, we expect a shorter scale length of the plasma density gradient in the corona compared with Refs. [32–34], as indicated by the simulations with the MULTI-FM code^{[ 24 , 26 ]}, and therefore a smaller contribution of the parametric instabilities^{[ 42 , 43 ]} with respect to what was observed for the mentioned experiments on subcritical foams. The comparison of the data obtained from the spectrometer for the solid and the foam target shown in Figure 3(a) gives further information on this issue. The peak seen at $2{\lambda}_L/3$ in the shot 5207 with the solid target is a clear indication of the excitation of the TPD instability^{[ 43 ]}. This peak is absent from the shot with the foam target, as expected according to the previous discussion. Moreover, SBS is further reduced because, during the laser interaction with the foam and up to the plasma homogenization, the ions are predominantly heated by the plasma collisions inside the pores^{[ 20 , 44 ]}, and this is known to contribute to the SBS suppression^{[ 29 , 45 ]}. Based on the results of Refs. [32–35] and of the previous considerations, we expect a small contribution from the SRS and SBS instabilities to the reflected light. Therefore, in the following, we consider that the whole measured reflected light originates from the critical surface of the plasma. Indeed, dedicated experiments for the precise determination of the SRS and the SBS effects on the reflected light in our experimental conditions will be interesting and useful for the community and we plan to perform them in the near future.

3. Reflection model in the MULTI-FM code

An algorithm for modeling the reflection of laser light in porous media has been implemented in the MULTI-FM code^{[ 24 , 26 ]}. MULTI-FM is a one-dimensional code and is a modification of the MULTI code^{[ 46 ]} for the modeling of the properties of porous media under high-power laser irradiation, where an effective model of absorption of laser energy, thermal conductivity, and response to pressure gradients has been implemented^{[ 24 ]}. The homogenization degree of the plasma is controlled by the parameter $\mathrm{IsFoam}\left(x,t\right)$ , defined at each numerical cell for each simulation time step as

(1) $$\begin{align}\mathrm{IsFoam}\left(x,t\right)=1-\frac{H\left(x,t\right)}{H_c},\end{align}$$

where

(2) $$\begin{align}H\left(x,t\right)=2{\int}_{0}^{t}\frac{\hbox{d}t^{\prime }}{\tau_0\left(x,t^{\prime}\right)},\kern1.2em 0\le H\left(x,t\right)\le H\left(x,{t}_{{h}}\right),\end{align}$$

in which ${t}_{{h}}$ is the homogenization time and

(3) $$\begin{align}{\tau}_0\left(x,t^{\prime}\right)&\approx 2.4\cdot {10}^{-3}\frac{Z^4{\left({\delta}_0-{b}_0\right)}^2{\rho}_p}{A^{1/2}\;T{\left(x,t^\prime \right)}^{5/2}}\notag\\[4pt]&\approx 2.4\cdot {10}^{-3}\frac{Z^4{\delta}_0^2{\rho}_p}{A^{1/2}\;T{\left(x,t^\prime \right)}^{5/2}}\end{align}$$

is the time scale (in second) of the homogenization process^{[ 26 ]}, where $Z$ is the average degree of ionization, ${\delta}_0$ is the average pore size of the foam, ${b}_0$ is the average solid parts thickness, ${\rho}_p$ is the initial average density of the foam, $A$ is the average mass number, and $T\left(x,t^{\prime}\right)$ is the temperature of the foam plasma.

At the beginning of the simulation at the time ${t}_0=0$ , $H\left(x,{t}_0\right)=0.$ At $t={t}_{{h}}$ we have

(4) $$\begin{align}H\left(x,{t}_{{h}}\right)={H}_c=\left\{\displaystyle\begin{array}{c}1,\kern5.039997em {\rho}_p\ge {\rho}_{\mathrm{cr},}\\[7pt] {}1-{\left[\frac{{\left(1-{\rho}_p/{\rho}_{\mathrm{cr}}\right)}^{\alpha }}{{\left(1-{\rho}_p/{\rho}_{{s}}\right)}^{\alpha }}\right]}^2,\kern0.24em {\rho}_p\le {\rho}_{\mathrm{cr}},\end{array}\right.\end{align}$$

where ${\rho}_{{s}}$ is the density of the solid parts and $\alpha$ is the fractal parameter, connecting the structural characteristics of the foam to its average density through the relation

(5) $$\begin{align}\frac{\delta_0}{b_0}\approx {\left(\frac{\rho_{{s}}}{\rho_p}\right)}^{\alpha }.\end{align}$$

The parameter $\alpha$ depends on the shape of the solid elements and is approximately equal to $\alpha ={\left(\nu +1\right)}^{-1}$ , with $\nu =$ 0, 1, 2, corresponding to planar (membrane), cylindrical (filament), or spherical (cluster) solid elements, respectively. As found in Refs. [24, 47] for the mixed membrane–filament foam type such as that in the present experiment, $\alpha =0.8$ is the most adequate value.

In the beginning of the simulation, IsFoam is equal to one in each cell, because the plasma is completely inhomogeneous. As the homogenization progresses, the value of IsFoam decreases to zero, reaching this value at the complete homogenization of the plasma in the numerical cell. The IsFoam parameter controls the contributions of two absorption mechanisms, namely the foam-like absorption in the areas where the density is greater than the critical density, and inverse bremsstrahlung absorption in the areas where the density is less than the critical density, through the absorption coefficient defined as

(6) $$\begin{align}K\left(x,t\right)=\left\{\begin{array}{ll}\begin{array}{l}\left\{\vphantom{\left[{K}_{{f}}\left(x,t\right)\cdot\mathrm{IsFoam}\Big(x,t\Big)\right]^2}\left[{K}_{{f}}\left(x,t\right)\cdot\mathrm{IsFoam}\left(x,t\right)\right]^2\right.\\+\left.\left\{{K}_{{b}}\left(x,t\right)\cdot\left[1-\mathrm{IsFoam}\left(x,t\right)\right]\right\}\vphantom{\left[{K}_{{f}}\left(x,t\right)\cdot\mathrm{IsFoam}\Big(x,t\Big)\right]^2}\right\}^{1/2},\end{array}&\\& \kern-6pc\rho \left(x,t\right)<{\rho}_{\mathrm{cr}},\\[6pt]{}{K}_{{f}}\left(x,t\right)\cdot \mathrm{IsFoam}\left(x,t\right),&\\& \kern-6pc\rho \left(x,t\right)\ge {\rho}_{\mathrm{cr}},\end{array} \right.\end{align}$$

where foam-like absorption coefficient ${K}_{{f}}$ is^{[ 48 ]}

(7) $$\begin{align}{K}_{{f}}\left(x,t\right)&=\frac{\delta_0}{b_0{L}_{p0}}\left\{\frac{1}{\left(1-\frac{b_0}{\delta_0}\right){\left[1-H\left(x,t\right)\right]}^{1/2}}-1\right\},\notag\\&\kern10pc0\le t\le {t}_{{h}},\end{align}$$

and ${L}_{p0}$ is the initial transparency length,

(8) $$\begin{align}{L}_{p0}\approx \frac{\pi^2}{2}\frac{\rho_{{s}}}{\rho_p}{b}_0,\end{align}$$

whereas ${K}_{{b}}$ is the well-known inverse bremsstrahlung absorption coefficient^{[ 42 ]} and $\rho \left(x,t\right)$ is the plasma density. Moreover, the $\mathrm{IsFoam}$ parameter regulates the electron conductivity and the response to pressure gradients in the heat and momentum equations as

$$\begin{align*}q\left(x,t\right)=-\left[1-\mathrm{IsFoam}\left(x,t\right)\right]\left[\kappa \left(x,t\right)\frac{\partial {T}_{{e}}\left(x,t\right)}{\partial x}\right],\end{align*}$$

(9) $$\begin{align}\frac{\partial }{\partial t}v\left(x,t\right)=-\left[1-\mathrm{IsFoam}\left(x,t\right)\right]\frac{\partial }{\partial m}P\left(x,t\right),\end{align}$$

where $v\left(x,t\right)$ is the velocity of the plasma, $m$ is the Lagrangian mass coordinate, $P\left(x,t\right)$ is the pressure, $q\left(x,t\right)$ is the heat flux, $\kappa \left(x,t\right)$ is the Spitzer conductivity, and ${T}_{{e}}\left(x,t\right)$ is the electron temperature. The dependence (Equation (8)) of the geometric transparency length on the foam parameters is confirmed by the results of experiments in Ref. [21], where the laser radiation passing through the foam layers of different thickness has been measured. The homogenization time (Equation (3)) is confirmed by the experiments in Refs. [6, 7, 14, 18, 22, 24] where the speed of the absorbed laser energy transfer in a porous substance of supercritical and subcritical density was measured.

We implemented an algorithm for reproducing the reflection of light in the foam target by mimicking the internal structure of the sample, in the frames of the effective model already developed. The pores in the foam material are delimited by the randomly distributed membranes or filaments. Therefore, the fraction of the transverse section of the laser beam interacting with solid parts per unit length is given by the ratio between the area of the transverse section of the target occupied by the solid parts and the empty area. Moreover, this ratio changes as the solid parts thickness grows due to laser heating, as the plasma homogenization continues. When this process is completed, the critical surface is completely formed and the laser light is reflected by the amount characteristic of an overcritical homogeneous plasma.

The algorithm for light reflection implemented in the code considers the pores as separated by partially reflective solid walls of infinitesimal thickness, as shown in Figure 4. The first wall is placed at ${\delta}_0/2$ from the target front surface. As described in Ref. [46], in the MULTI code it is assumed that, in general, two laser beams propagate in the numerical grid with $N$ cells at each time instant, the incident beam with intensity ${I}_{+}$ and the reflected beam with intensity ${I}_{-}$ . The energy deposited in one cell is calculated by integrating the deposition term

$$\begin{align*}S={\partial}_x{I}_{+}-{\partial}_x{I}_{-}.\end{align*}$$

Figure 4 Scheme of the mechanism of reflection and transmission of light in the target, following the algorithm described in the text. Here δ₀ is the pore size parameter required by the algorithm.

The specific deposition, after spatial discretization, is given by the expression

$$\begin{align*}{\left(\frac{S}{\rho}\right)}_i=\frac{I_{+,i+1}-{I}_{+,i}-{I}_{-,i+1}+{I}_{-,i}}{{\Delta m}_i},\end{align*}$$

where ${\rho}_i$ is the density of the plasma in the $i$ th cell and ${\Delta m}_i$ is its thickness in Lagrangian coordinates. $S$ and $\rho$ are cell-centered quantities, ${I}_{+}$ and ${I}_{-}$ are defined at the cell interfaces, and ${I}_{+,N+1}$ is the known incident laser intensity given at the beginning of the simulation. For each time step, the calculation of the laser energy deposition starts from the $\left(N+1\right)$ th interface towards the 0th interface. At each numerical cell, the value of ${\mathrm{IsFoam}}_i$ is checked to determine the homogenization degree of the plasma, as well as the ratio ${\rho}_i/{\rho}_{\mathrm{cr}}$ between the density of the cell ${\rho}_i$ and the critical density ${\rho}_{\mathrm{cr}}$ . If ${\rho}_i/{\rho}_{\mathrm{cr}}<1$ the ray can propagate through the cell and its intensity decreases as

(10) $$\begin{align}{I}_{+,i}={I}_{+,i+1}\;\exp \left(-{K}_i\cdot {\Delta x}_i\right),\end{align}$$

where ${K}_i$ is the absorption coefficient of Equation (6) and ${\Delta x}_i$ is the thickness of the $i$ th numerical cell. When ${\rho}_i/{\rho}_{\mathrm{cr}}\ge 1$ , the plasma in the current cell is overcritical: if ${\mathrm{IsFoam}}_i>0$ the plasma is not completely homogeneous, the laser beam is assumed to be free to propagate through the cell and its intensity decreases as in Equation (10); if ${\mathrm{IsFoam}}_i=0$ , the plasma is completely homogeneous and must behave as an ordinary plasma. Therefore, in this last case the laser beam propagation is stopped, the ray is reflected, and a fraction of its energy is deposited in the numerical cell, according to the parameter $\varDelta$ which is defined at the beginning of the simulation, as in the original MULTI code^{[ 46 ]}. The optimal value for this parameter has been set by matching the simulated reflected light with the shots made on solid polystyrene, obtaining $\varDelta =0.72$ . In fact, the fraction of the light reflected at the critical surface of the solid target should reasonably be the same as the reflected at the solid parts of the foam.

As the numerical grid is traversed following the laser propagation, one of the interfaces between the numerical cells can be identified as a pore wall. The placement of the pore walls is determined before the start of the simulation. The intensity incident on the wall ${I}_{{w}}$ is split into the reflected ${I_{{w}}}^{\mathrm{R}}$ and transmitted ${I_{{w}}}^{\mathrm{T}}$ intensities as

(11) $$\begin{align}{I_{{w}}}^{\mathrm{R}}&=\left(\chi \cdot {\mathrm{IsFoam}}_{{w}+1/2}\right)\;{I}_{{w}},\notag\\[-2pt]{I_{{w}}}^{\mathrm{T}}&=\left(1-\chi \cdot {\mathrm{IsFoam}}_{{w}+1/2}\right)\;{I}_{{w}},\end{align}$$

where ${\mathrm{IsFoam}}_{{w}+1/2}$ is the value of the IsFoam parameter in the numerical cell just before the wall along the laser path and $\chi$ is the reflectivity of the wall and its value is related to the features of the internal structure of the foam. This parameter could be, approximately, determined as the ratio of the pore size and the transparency length, obtaining, according to Equations (5) and (8),

(12) $$\begin{align}\chi \approx \frac{2}{\pi^2}{\left(\frac{\rho_p}{\rho_{{s}}}\right)}^{\left(1-\alpha \right)}=\frac{2}{\pi^2}{\left(\frac{b_0}{\delta_0}\right)}^{\left(1-\alpha \right)/\alpha }.\end{align}$$

The reflectivity increases with the increasing fractal parameter $\alpha$ , that corresponds to passing to a membrane-like shape for the solid parts of the foam. The reflectivity also increases by increasing the foam average density, corresponding to lowering the pore size while keeping the solid parts thickness fixed, according to Equation (5). Under the considered conditions ( ${\rho}_p=10$ mg/cm³, ${\rho}_{{s}}=1$ g/cm³, ${\delta}_0=40$ μm, ${b}_0=1$ μm, $\alpha =0.8$ ), according to Equation (12) the reflectivity could be estimated as 0.08, which is in good agreement with the experimental results, as shown in the next subsection. According to Equation (3), for a given average density, the homogenization time decreases quite strongly with the decreasing pore size, as ${\tau}_0\propto {\delta_0}^2$ . In a foam with a pore size of about 40 μm, such as those considered here, the homogenization time is about 2 ns, whereas in a small-pore foam with a pore size of several micrometers (with a wall thickness of several hundreds of micrometers), the homogenization time is several tens of picoseconds. The reflectivity of such a small-pore foam reaches that of a homogeneous plasma with a density equal to the density of the foam in a very short time, of the order of several tens of picoseconds, significantly shorter than the laser pulse duration.

As can be seen from Equation (11),

$$\begin{align*}{I_{{w}}}^{\mathrm{R}}+{I_{{w}}}^{\mathrm{T}}={I}_{{w}},\end{align*}$$

so that conservation of energy is assured at each pore wall. As the IsFoam parameter represents the degree of homogenization of the plasma in the foam material, it is related to the expansion of the walls of the pores under the action of the laser: the more the walls expand in the pores, the more efficient the laser absorption, the less the laser is reflected/transmitted.

After the splitting process on the pore wall, the laser is propagated through the numerical grid both toward the front and back sides of the target, and is absorbed by the plasma as described previously. As the propagation reaches another pore wall, the intensity is split again into reflected and transmitted and the propagation is repeated, together with absorption. As the code is Lagrangian, the compression of the target under laser irradiation also affects the wall spacing, as, quite reasonably, should happen in reality. The algorithm also simulates the trapping of the laser light into the porous material, due to the reflection on several solid elements forming the internal structure. This process is particularly relevant for foams with large pores ( ${\delta}_0\sim 40$ μm) such as those used in our experiments, for which the homogenization time is long and of the order of the laser pulse duration. In fact, the reflection–transmission mechanism of the laser light proposed here is realized during the homogenization time, because after that moment the plasma is comparable to that from a solid medium, and the reflection of laser light is associated with the critical density surface.

4. Simulation results

We simulated the reflected light observed in the experiments using the MULTI-FM code. In the simulations, the target was a 10 mg/cm³ foam of polystyrene with ${\delta}_0=40$ μm and ${b}_0=1$ μm. The pore walls in the numerical mesh were placed at a distance ${\delta}_0$ from each other, with the first wall at 20 μm from the target front surface. As an example, we consider here the target to be 320 μm thick, as in the shot 5251 above, which led to 8 pore walls in the mesh. We performed a series of simulations with a random, reasonably small, displacement of the pore walls from their original locations and we verified that an uneven spacing of the pore walls in the numerical mesh does not affect the results in a relevant way. The transparency length of this target is longer than its thickness, indicating that a small fraction of the laser light is transmitted through the target at the beginning of irradiation. The laser pulse intensity was taken as $I={10}^{14}$ W/cm² with a ${\sin}^2t$ laser temporal profile, which are the best approximations for the ABC pulse intensity and temporal shape averaged on all the shots. The flux limiter has been taken as 0.06 and the equation of state for both the solid and the foam targets was obtained from the SESAME library^{[ 49 ]}. Changing the thickness of the target in the simulations did not change in a substantial way the profile of the reflected light, as shown by the experimental data.

Figure 5 shows the comparison between the simulated reflected light collected by the focusing optics for the 320 μm target and the experimental measurements, for both porous and solid targets. The profile of the light reflected by the solid target is smooth in the simulations as in the shot 5207, confirming the reliable behavior of the original MULTI code. The sudden drop of the reflected light by the solid target with the density equal to the foam target indicates the instant when the whole plasma becomes subcritical, after the shock traversed the sample. The comparison of the simulations for the foam targets with the experiments indicated the best value for the $\chi$ parameter of our model to be 0.1 that is in good agreement with the model of Equation (12) and experimental data. As can be seen, good agreement is found between the simulations and the experiments both for the rising and for the trailing edges of the signals for the porous targets. Moreover, also the temporal duration of the reflected light is comparable with the experiment, indicating that the main physics of the process is satisfactorily captured. This good agreement between one-dimensional simulations and experiments is a consequence of the fact that the maximum reflection occurs in a weakly homogenized plasma in the initial period of time shorter than 1 ns, when two-dimensional energy transfer effects do not have a significant effect.

Figure 5 The comparison between the B signals for shots 5245, 5251, and 5256 on foam targets, as well as for the shot 5207 on the solid target and the simulated ones. In the simulation, the foam target was 320 μm thick, its average density was ${\rho}_p=10$ mg/cm³, δ₀ = 40 μm, and $\chi$ = 0.1. The dashed red line is the simulated B signal for a homogeneous target with the same density as the foam targets.

The simulated signal decreases from about 1.4 ns to around 1.8 ns from the beginning of the irradiation, and then increases again until 2 ns. This behavior is linked with the homogenization process of the plasma. At the beginning of the irradiation, when the plasma is weakly homogenized, the foam-like absorption is dominant and the reflected light curve follows quite closely that for the solid target. As the homogenization develops and sufficiently extended regions of subcritical plasma appear in the pores, the contribution of the inverse bremsstrahlung absorption increases. At around 1.4 ns, the reflected light starts to decrease as the absorption efficiency increases due to both foam-like and inverse bremsstrahlung mechanisms. As the homogenization process continues and the pores become more and more filled with supercritical density plasma, both absorption mechanisms begin to function weakly. As a result, at around 1.8 ns, the reflection starts to grow again. At around 2 ns, the homogenization is reached at some point in the foam plasma and the reflection is now due to the presence of a region of homogeneous plasma of overcritical density. The small oscillations from this instant on are related to plasma regions not yet homogenized ahead of the critical surface, which implies continuous jumps between homogenized and non-homogenized plasmas. The presence of this strong drop in the simulated reflected light signals is related to the crossover implemented in the code between the two regimes of plasma behavior, that before homogenization, described by the foam model discussed previously, and that of a homogeneous plasma after homogenization. In reality, this transition is seen as a reduction of the oscillations in the amplitude of the signal. We leave the improvement of the crossover in the code to future work. Owing to its relation with the plasma homogenization, the time of beginning of the small oscillations may change appreciably with the changing pore size. This time is reduced by about 800 ps when the pores are scaled to 20 μm, indicating a significant change in the homogenization time and therefore an experimentally observable effect. The initially oscillating behavior of the simulated reflected light, which ends at the instant when plasma homogenization is attained, suggests that the time-dependent measurements of the reflected light, in conjunction with the simulations, could allow for an estimate of the homogenization time of the foam plasma. This oscillating behavior can be retrieved, with the only exception of shot 5221, also in all the shots in Figure 2(c), lasting until around 2–2.5 ns, when the signal becomes smoother. This observation indicates a potential strategy for the determination of the homogenization time by the careful analysis of the reflected laser light, identifying the time at which the initial large oscillations become smoother, with the help of numerical simulations. This strategy could lead to obtaining information about this fundamental characteristic of the plasma from a porous material, whose measurement is known to be very challenging with other techniques.

As is apparent from the results of Figure 6, the homogeneous target in the Orange simulation has a completely different behavior from the foam target in the Red and Black simulations under laser irradiation, and the structure of the shock wave is also very different. Even if the reflected energy is a small fraction of the total, including the reflection model in the simulation changes the plasma behavior in a noticeable way. The reflection and transmission of light at the pore walls, as well as the trapping of the laser light between adjacent walls, are the origins of the step-like structure of the temperature, pressure, and specific laser energy deposition profiles in the beginning of the simulation. In the density plot, the wall position is signaled by the spikes generated by the compression of the plasma due to the pressure differences. The presence of a shock wave from t = 2 ns in the Red and Black simulations is the signature of the homogenization of the plasma into the foam target, which implies that the reflection is due, from that instant on, to the presence of the critical surface, as indicated also by the peak in the laser energy deposition profile. At $t=2$ ns the homogenization is reached also in the Black simulation, but the shock wave is less evident because of the smaller gradient in the physical quantities before shock formation. The density jump at the shock in the Red simulation is larger than in the Black simulation and the pressure in the Red simulation is as high as in the Black simulation, but it is sustained for a longer time. The timing of plasma blowoff measured with the optical streak camera for the corresponding target thickness is in agreement with the simulated timing obtained from the Red simulation, which predicts a speed of 130 μm/ns^{[ 24 ]}.

Figure 6 The profiles of the density, temperature, pressure, and specific laser energy deposition for selected times indicated at the top of the picture. The red and the black lines correspond to simulations of foam targets with the laser light reflection turned on (“Red simulation” in the text) and off (“Black simulation” in the text), respectively. For both simulations, the blue-framed plots correspond to times before the homogenization time, whereas the green-framed plots correspond to times after the homogenization time. The target and laser parameters are the same as in Figure 5 for both simulations. The orange lines correspond to a simulation (“Orange simulation” in the text) with the same target thickness, target density, and laser intensity as Red and Black simulations but with a homogeneous target. All the plot values are referred to the coordinates of the target at the zero time of the simulation, for better representation.

The described effects of the reflection of light in foams might seem paradoxical at first glance. Indeed, the scattering effect in a solid target under normal inverse bremsstrahlung absorption in the evaporated part of the target would simply be equivalent to a decrease in the energy that goes to generate the ablation pressure on the target surface, weakening the shock wave, reducing the pressure behind the shock wave front, and reducing its speed. In the case of a porous substance, when the absorption is volumetric, the scattering effect has a specific manifestation, reducing the total amount of energy entering the target. However, in contrast to a solid target, this decrease, because of the volumetric absorption, applies to the entire target, including that part of it in which a shock wave is formed after the homogenization process is completed. This means that the scattering effect reduces the level of preheating of the substance ahead of a shock wave front, making it stronger, despite the overall decrease in the energy entering the target. This explanation is clearer if one looks at the temporal profiles of the reflected and transmitted light for the Red and Black simulations, shown in Figure 7.

Figure 7 The reflected (dashed lines) and transmitted (solid lines) for the Black (black lines) and the Red (red lines) simulations.

As the target thickness is 320 μm in both simulations, which is shorter than the initial transparency length of the target, at the beginning of both simulations some laser light is transmitted. At later times, when the density of the laser-produced plasma falls below the critical density, the laser light passes through again, as seen from around 3 ns in Figure 7. In the Black simulation the initially transmitted light is larger than in the Red simulation, because of the absence of laser light reflection, which indicates an overestimation of the foam transparency and therefore of the preheat of the material in the bulk of the target. The features of the absorbing properties of laser-produced plasma of porous target are manifested until the ablation of the target has terminated. In the calculation corresponding to Figure 7, this time is approximately 3.1 ns. At this stage, the integral fraction of the scattered light is about twice as high as the fraction of the transmitted light.

By using the MULTI-FM simulations, we can estimate the absorption efficiency for foam targets with the parameters similar to those used in the campaign. By simulating different thicknesses of the foam targets, as in the experiments, we can calculate the transmitted fraction of the laser energy and therefore the fraction of the energy absorbed in the plasma. Table 1 shows the simulated fractions of reflected and transmitted energy as well as the fraction of absorbed laser energy obtained from MULTI-FM simulations performed for different shots. For thin foams, due to the small number of solid pore walls present in the sample, the transmitted light is as high as half of the reflected light. As the thickness of the target is increased, its transmissivity decreases, because of the larger number of reflective areas in the target and the thicker plasma produced by the laser. However, the reflected light is approximately constant as the thickness is increased, as also found in the experiments. This indicates that the high absorption efficiency of the foam prevents the reflected laser light to come out of the laser-generated plasma, and the larger number of solid parts lowers the loss of energy through transmission. In the case of large thickness of the sample, larger than the transparency length, the reflected and transmitted fractions of the laser light are around 12% and 1%–2%, respectively.

Table 1 The absorption efficiency for some shots and target thicknesses obtained from MULTI-FM simulations until the time of complete ablation of the target.

Note that the numerical calculation of the fraction of transmitted light in low reflection conditions is important for assessing the overall energy balance. Indeed, by separating the processes of reflection of laser light at the critical density in the overcritical plasma and its scattering associated with parametric instabilities, the fraction of transmitted light can be written as 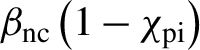${\beta}_{\mathrm{nc}}\left(1-{\chi}_{\mathrm{pi}}\right)$ , where ${\beta}_{\mathrm{nc}}$ is the fraction of transmitted light in numerical calculation using the MULTI-FM code without taking into account stimulated scattering, whereas ${\chi}_{\mathrm{pi}}$ is hypothetical fraction of scattered light due to induced plasma processes. Here ${\chi}_{\mathrm{pi}}$ is limited by the experimental values of the total fraction of reflected and scattered light to be ${\chi}_{\mathrm{pi}}<10\%\hbox{--} 12\%$ . Therefore, a possible correction to the transmitted light in the MULTI-FM simulations cannot exceed about 10%. The simulated transmittance of 1%–4% corrected by a factor about 0.9, according to the considerations just explained, together with the experimental value of the total reflected and scattered light of 10%–12%, leads to an absorption efficiency of about 85%–90%, in very good agreement with the literature^{[ 21 , 22 ]} and much higher than that for a solid target of the same chemical composition, which we measured to be around 70%.

5. Conclusions

In this work we have presented, for the first time, the time-resolved measurement of the reflected light of a terawatt Nd-laser pulse from a target made from a foam of overcritical density with large pores, obtained in experiments performed at the ABC facility. We have found that the internal structure of the foam manifests itself by inducing oscillations of the reflected light signals. We have developed an algorithm to numerically model the light reflection process in the foam, which depends on the degree of homogenization of the laser-produced plasma. We have implemented the algorithm in the MULTI-FM code and the results of the simulations of reflected light signal are in good agreement with the experimental results presented in this work. This agreement indirectly indicates a small contribution of stimulated scattering to the total signal of reflected light from the laser-produced foam plasma.

The comparison with the light reflected by a solid target with the same chemical composition shows that the foams reflect significantly less laser light than the solid. We found that the foam targets reflected about 12% of the incident laser light, whereas the light reflected by the solid targets with the same chemical composition as the foam was about 32% of the total. Moreover, the profile of the reflected light signal was very different and strongly related to the internal structure of the porous material. The low reflection of the laser radiation in conjunction with the conclusion of many studies on the hydrodynamic nature of absorbed laser energy transfer in low-Z foams^{[ 6 , 14 , 18 , 21 , 24 , 26 , 47 ]} is the basis for their effective use as materials for laser energy absorbers of ICF targets, which can provide a smooth supply of a laser-driven pressure for the compressed part of the target for several nanoseconds.

The recorded time-dependent signal of the reflected light, together with the simulation performed with the MULTI-FM code, indicates a strategy for the estimation of the homogenization time of the laser-produced plasma of the porous substance, by a careful time-dependent analysis of the reflected laser light in dedicated experiments, together with simulations with suitable modeling of the foam plasma behavior. Finally, the MULTI-FM code has been used to estimate the absorption efficiency of the foam, which resulted to be about 90%, in very good agreement with the results of Refs. [21, 22].

The results of this work can be extended by varying the parameters of the foam targets, in terms of pore size and average density. This kind of parametric scan will be fundamental to checking the correctness of the value of the reflectivity parameter $\chi$ and to further investigating the possibility of estimating the homogenization time of the laser-generated plasma from the accurate time-dependent reflection measurements, supported by the simulations done with the MULTI-FM code. The measurement of the transmitted light, in addition to the reflected light, in the parametric scan will allow a precise estimation of the absorption efficiency of the foam samples over a wide range of target characteristics, to better test the reliability of our model. We also plan to add the spectral resolution to the time-dependent reflected light, to determine the role of parametric instabilities over the range of pore sizes and densities.