1. Introduction and main results
1.1. The transcendental Bézout problem
The classical Bézout theorem states that the number of common zeros of n polynomials in n variables is generically bounded by the product of their degrees. The transcendental Bézout problem is concerned with the count of zeros of entire maps
![]() $\mathbb {C}^n \to \mathbb {C}^n$
. It is motivated by a number of influential mathematical ideas. The starting point is Serre’s famous G.A.G.A. [Reference Serre32], by now understood as a meta-mathematical principle stating that complex projective analytic geometry reduces to algebraic geometry. A prototypical result is a theorem of Chow [Reference Chow11], by which every closed complex submanifold of
$\mathbb {C}^n \to \mathbb {C}^n$
. It is motivated by a number of influential mathematical ideas. The starting point is Serre’s famous G.A.G.A. [Reference Serre32], by now understood as a meta-mathematical principle stating that complex projective analytic geometry reduces to algebraic geometry. A prototypical result is a theorem of Chow [Reference Chow11], by which every closed complex submanifold of
![]() $\mathbb {C} P^n$
is necessarily algebraic (i.e., is given as the set of solutions of a system of polynomial equations). However, as the following simple example shows, Chow’s theorem fails in the affine setting.
$\mathbb {C} P^n$
is necessarily algebraic (i.e., is given as the set of solutions of a system of polynomial equations). However, as the following simple example shows, Chow’s theorem fails in the affine setting.
Example 1.1. Consider an analytic function
![]() $f:\mathbb {C} \to \mathbb {C}$
given by
$f:\mathbb {C} \to \mathbb {C}$
given by
Zeros of f form an infinite discrete set
![]() $\{(2k+1)\pi i, \; k \in \mathbb {Z}\}$
. It is not biholomorphically equivalent to any algebraic (and hence finite) proper subset of
$\{(2k+1)\pi i, \; k \in \mathbb {Z}\}$
. It is not biholomorphically equivalent to any algebraic (and hence finite) proper subset of
![]() $\mathbb {C}$
.
$\mathbb {C}$
.
In order to revive at least some parts of G.A.G.A. in the affine framework, one needs a substitute of the notion of the degree of a polynomial for entire mappings
![]() $f:\mathbb {C}^n \to \mathbb {C}^n$
. As it is put in [Reference Gol’dberg, Levin and Ostrovskii18], “A transcendental entire function that can be expanded into an infinite power series can be viewed as a “polynomial of infinite degree”, and the fact that the degree is infinite brings no additional information to the statement that an entire function is not a polynomial.” To this end, one introduces the maximum modulus
$f:\mathbb {C}^n \to \mathbb {C}^n$
. As it is put in [Reference Gol’dberg, Levin and Ostrovskii18], “A transcendental entire function that can be expanded into an infinite power series can be viewed as a “polynomial of infinite degree”, and the fact that the degree is infinite brings no additional information to the statement that an entire function is not a polynomial.” To this end, one introduces the maximum modulus
where
![]() $B_r$
stands for the closed ball of radius r. This quantity has at least two degree-like features. First, assume thatFootnote
1
$B_r$
stands for the closed ball of radius r. This quantity has at least two degree-like features. First, assume thatFootnote
1
Then, remarkably, f is a polynomial of the total degree
![]() $\leq k$
. This is a minor generalization of Liouville’s classical theorem. Thus, one can distinguish polynomials in terms of the maximum modulus.
$\leq k$
. This is a minor generalization of Liouville’s classical theorem. Thus, one can distinguish polynomials in terms of the maximum modulus.
In what follows, let
![]() $\zeta (f,r)$
denote the number of zeros of a continuous map
$\zeta (f,r)$
denote the number of zeros of a continuous map
![]() $f: \mathbb {C}^n \to \mathbb {C}^n$
inside the ball
$f: \mathbb {C}^n \to \mathbb {C}^n$
inside the ball
![]() $B_r$
.
$B_r$
.
The second feature of the maximum modulus of an entire function
![]() $f: \mathbb {C} \to \mathbb {C}$
is given by the following statement which readily follows from Jensen’s formula: if
$f: \mathbb {C} \to \mathbb {C}$
is given by the following statement which readily follows from Jensen’s formula: if
![]() $f(0)\neq 0$
, then for every
$f(0)\neq 0$
, then for every
![]() $a>1$
,
$a>1$
,
where C is a positive constant depending on a and
![]() $f(0)$
. For instance, in Example 1.1, both
$f(0)$
. For instance, in Example 1.1, both
![]() $\zeta $
and
$\zeta $
and
![]() $\log \mu $
grow linearly in r.
$\log \mu $
grow linearly in r.
These two features might have given a hope that
![]() $\log \mu (f,r)$
is an appropriate substitute of the degree for an entire map
$\log \mu (f,r)$
is an appropriate substitute of the degree for an entire map
![]() $f: \mathbb {C}^n \to \mathbb {C}^n$
(this was known as the transcendental Bézout problem). However, this analogy was overturned by Cornalba and Shiffman [Reference Cornalba and Shiffman13] who famously constructed, for
$f: \mathbb {C}^n \to \mathbb {C}^n$
(this was known as the transcendental Bézout problem). However, this analogy was overturned by Cornalba and Shiffman [Reference Cornalba and Shiffman13] who famously constructed, for
![]() $n=2$
, an entire map f with
$n=2$
, an entire map f with
![]() $\log \mu (f,r) \leq C_{\epsilon } r^\epsilon $
for every
$\log \mu (f,r) \leq C_{\epsilon } r^\epsilon $
for every
![]() $\epsilon>0$
(and hence of growth order zero), with
$\epsilon>0$
(and hence of growth order zero), with
![]() $\zeta (f,r)$
growing arbitrarily fast. As Griffiths wrote in [Reference Griffiths19] “This is the first instance known to this author when the analogue of a general result in algebraic geometry fails to hold in analytic geometry.”
$\zeta (f,r)$
growing arbitrarily fast. As Griffiths wrote in [Reference Griffiths19] “This is the first instance known to this author when the analogue of a general result in algebraic geometry fails to hold in analytic geometry.”
1.2. Coarse zero count
One of the motivations for the present paper is to further explore the Cornalba–Shiffman example using the notion of coarse zero count introduced in [Reference Buhovsky, Payette, Polterovich, Polterovich, Shelukhin and Stojisavljević9], which is based on topological persistence. The idea, roughly speaking, is to discard the zeros corresponding to small oscillations of the map. It turns out that with such a count, we are able to get a Jensen-type estimate (1.1), albeit with a possibly non-sharp power of
![]() $\log \mu (f,r)$
in the right-hand side; see (1.2) below.
$\log \mu (f,r)$
in the right-hand side; see (1.2) below.
Given a continuous map
![]() $f: \mathbb {C}^n \to \mathbb {C}^n$
and positive numbers
$f: \mathbb {C}^n \to \mathbb {C}^n$
and positive numbers
![]() $\delta , r>0$
, we define the counting function
$\delta , r>0$
, we define the counting function
![]() $\zeta (f,r,\delta )$
of
$\zeta (f,r,\delta )$
of
![]() $\delta $
-coarse zeros of f inside a ball
$\delta $
-coarse zeros of f inside a ball
![]() $B_r$
as the number of connected components of the set
$B_r$
as the number of connected components of the set
![]() $f^{-1}(B_\delta )\cap B_r$
which contain zeros of f; see Figure 1.
$f^{-1}(B_\delta )\cap B_r$
which contain zeros of f; see Figure 1.
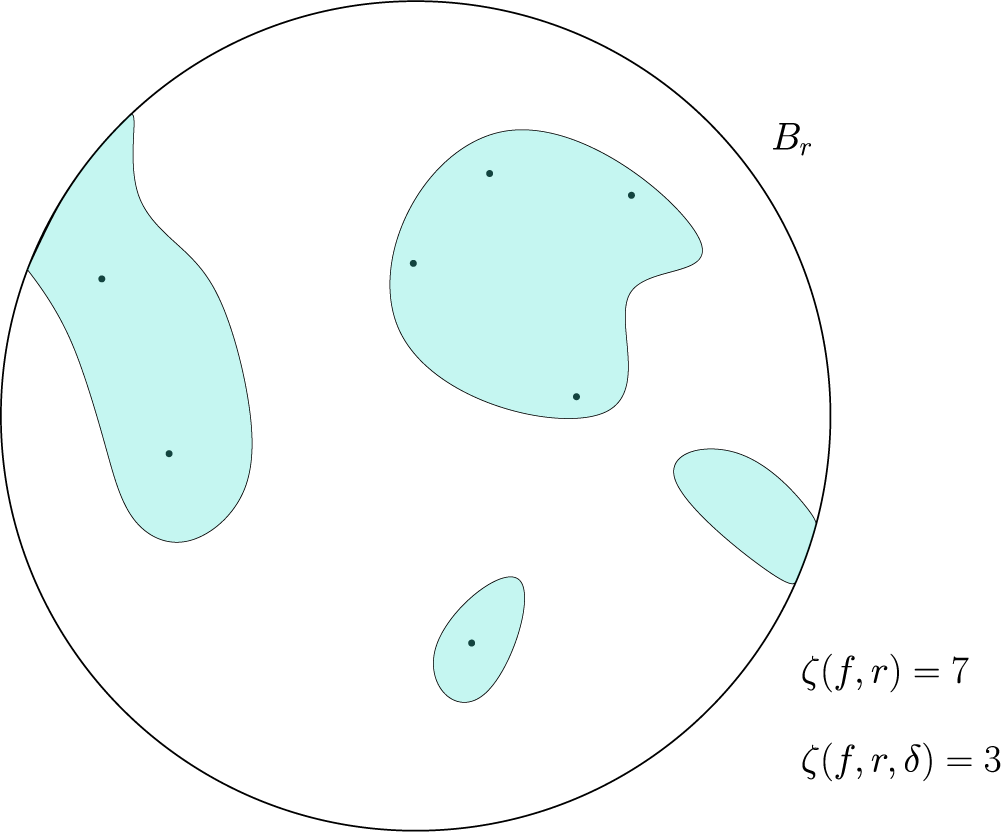
Figure 1 Dots represent zeros of f, whereas shaded regions depict the set
![]() $f^{-1}(B_\delta )$
.
$f^{-1}(B_\delta )$
.
Theorem 1.2. For any analytic map
![]() $f: \mathbb {C}^n \to \mathbb {C}^n$
and any
$f: \mathbb {C}^n \to \mathbb {C}^n$
and any
![]() $a>1$
,
$a>1$
,
![]() $r>0$
, and
$r>0$
, and
![]() $\delta \in (0, \frac {\mu (f, ar)}{2})$
, we have
$\delta \in (0, \frac {\mu (f, ar)}{2})$
, we have
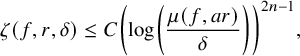 $$ \begin{align} \zeta(f,r,\delta) \leq C \left(\log\left(\frac{\mu(f, ar)}{\delta}\right)\right)^{2n-1}, \end{align} $$
$$ \begin{align} \zeta(f,r,\delta) \leq C \left(\log\left(\frac{\mu(f, ar)}{\delta}\right)\right)^{2n-1}, \end{align} $$
where the constant C depends only on a and n.
This theorem is proved in Section 2.1. Its generalization in the framework of topological persistence is presented in Section 6.
Note that by Liouville’s theorem, unless f is constant,
![]() $\mu (f, ar)$
is unbounded. Therefore, for any given
$\mu (f, ar)$
is unbounded. Therefore, for any given
![]() $\delta> 0,$
the condition
$\delta> 0,$
the condition
![]() $\delta \in (0,\mu (f,ar)/2)$
holds for all r large enough.
$\delta \in (0,\mu (f,ar)/2)$
holds for all r large enough.
Remark 1.3. Consider a higher-dimensional generalization of Example 1.1: take an analytic map
![]() $f:\mathbb {C}^n \to \mathbb {C}^n$
given by
$f:\mathbb {C}^n \to \mathbb {C}^n$
given by
It is easy to see that
![]() $\log \mu (f,r)$
grows linearly in r and
$\log \mu (f,r)$
grows linearly in r and
![]() $\zeta (f,r,\delta )$
grows as
$\zeta (f,r,\delta )$
grows as
![]() $r^n$
when
$r^n$
when
![]() $r \to \infty $
, for
$r \to \infty $
, for
![]() $\delta $
sufficiently small. It would be interesting to understand whether the power of the logarithm in (1.2) is sharp or it can be improved, possibly, to n.
$\delta $
sufficiently small. It would be interesting to understand whether the power of the logarithm in (1.2) is sharp or it can be improved, possibly, to n.
It follows from Theorem 1.2 that for the Cornalba-Shiffman example, the coarse count of zeros grows slower than any positive power of r; see Theorem 1.5 below for precise asymptotics.
Remark 1.4. Consider a function f of growth order
![]() $\leq \rho ;$
that is, for all
$\leq \rho ;$
that is, for all
![]() $\epsilon>0$
, there exist positive constants
$\epsilon>0$
, there exist positive constants
![]() $A_{\epsilon }, B$
, such that
$A_{\epsilon }, B$
, such that
everywhere. Then by (1.2),
![]() $\zeta (f,r,\delta )$
grows slower than
$\zeta (f,r,\delta )$
grows slower than
![]() $r^{(2n-1)\rho +\epsilon }$
for every
$r^{(2n-1)\rho +\epsilon }$
for every
![]() $\epsilon>0.$
At the same time, it was shown in [Reference Carlson10, equation (1.9)] that for any
$\epsilon>0.$
At the same time, it was shown in [Reference Carlson10, equation (1.9)] that for any
![]() $\alpha>0$
,
$\alpha>0$
,
![]() $\zeta (f+c, r)$
grows slower than
$\zeta (f+c, r)$
grows slower than
![]() $r^{(2n-1)\rho +1 +\alpha }$
for almost all
$r^{(2n-1)\rho +1 +\alpha }$
for almost all
![]() $c>0$
small enough. Although the growth rate in (1.2) is slightly sharper, it is interesting to note that the power
$c>0$
small enough. Although the growth rate in (1.2) is slightly sharper, it is interesting to note that the power
![]() $(2n-1)\rho $
appears in both bounds.
$(2n-1)\rho $
appears in both bounds.
1.3. Cornalba–Shiffman example: a coarse perspective
Let us remind the Cornalba–Shiffman construction. Let
![]() $g:\mathbb {C} \to \mathbb {C}$
be given by
$g:\mathbb {C} \to \mathbb {C}$
be given by
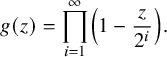 $$ \begin{align*} g(z)=\prod_{i=1}^\infty \left( 1- \frac{z}{2^i} \right).\end{align*} $$
$$ \begin{align*} g(z)=\prod_{i=1}^\infty \left( 1- \frac{z}{2^i} \right).\end{align*} $$
For
![]() $k\geq 1$
an integer, let
$k\geq 1$
an integer, let
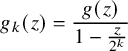 $$ \begin{align*}g_k(z)=\frac{g(z)}{1-\frac{z}{2^k}} \end{align*} $$
$$ \begin{align*}g_k(z)=\frac{g(z)}{1-\frac{z}{2^k}} \end{align*} $$
be the function defined by the same product with k-th term excluded. All the infinite products converge uniformly on compact subsets of
![]() $\mathbb {C}$
, and hence, g and
$\mathbb {C}$
, and hence, g and
![]() $g_k$
are holomorphic by Weierstrass’ theorem. For a positive integer c, we define a polynomial
$g_k$
are holomorphic by Weierstrass’ theorem. For a positive integer c, we define a polynomial
![]() $P_c:\mathbb {C} \rightarrow \mathbb {C}$
as
$P_c:\mathbb {C} \rightarrow \mathbb {C}$
as
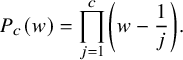 $$ \begin{align*}P_c(w)=\prod_{j=1}^c \left( w- \frac{1}{j} \right).\end{align*} $$
$$ \begin{align*}P_c(w)=\prod_{j=1}^c \left( w- \frac{1}{j} \right).\end{align*} $$
Given a strictly increasing sequence of positive integers
![]() $\mathfrak {c}=\{c_i \}$
,
$\mathfrak {c}=\{c_i \}$
,
![]() $c_1<c_2<\ldots $
define
$c_1<c_2<\ldots $
define
![]() $f:\mathbb {C}^2\to \mathbb {C}$
as
$f:\mathbb {C}^2\to \mathbb {C}$
as
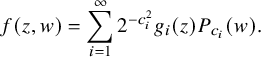 $$ \begin{align*}f(z,w)=\sum_{i=1}^\infty 2^{-c_i^2}g_i(z)P_{c_i}(w).\end{align*} $$
$$ \begin{align*}f(z,w)=\sum_{i=1}^\infty 2^{-c_i^2}g_i(z)P_{c_i}(w).\end{align*} $$
f converges uniformly on compact sets and is hence holomorphic by Weierstrass’ theorem in several variables. Finally, we define a map
![]() $F:\mathbb {C}^2 \rightarrow \mathbb {C}^2$
,
$F:\mathbb {C}^2 \rightarrow \mathbb {C}^2$
,
![]() $F(z,w)=(g(z),f(z,w)).$
As shown in [Reference Cornalba and Shiffman13], for all
$F(z,w)=(g(z),f(z,w)).$
As shown in [Reference Cornalba and Shiffman13], for all
![]() $\mathfrak {c}$
, F is of order zero. However, the zero set of F is given by
$\mathfrak {c}$
, F is of order zero. However, the zero set of F is given by
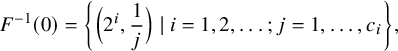 $$ \begin{align*}F^{-1}(0)=\left\lbrace \Big(2^i,\frac{1}{j} \Big) ~|~ i=1,2,\ldots; j=1,\ldots ,c_i \right\rbrace ,\end{align*} $$
$$ \begin{align*}F^{-1}(0)=\left\lbrace \Big(2^i,\frac{1}{j} \Big) ~|~ i=1,2,\ldots; j=1,\ldots ,c_i \right\rbrace ,\end{align*} $$
as depicted in Figure 2. The dots represent zeros of F, and the number of zeros
![]() $\zeta (F,r)=\zeta (F,r,0)$
equals the number of dots inside the circle.
$\zeta (F,r)=\zeta (F,r,0)$
equals the number of dots inside the circle.
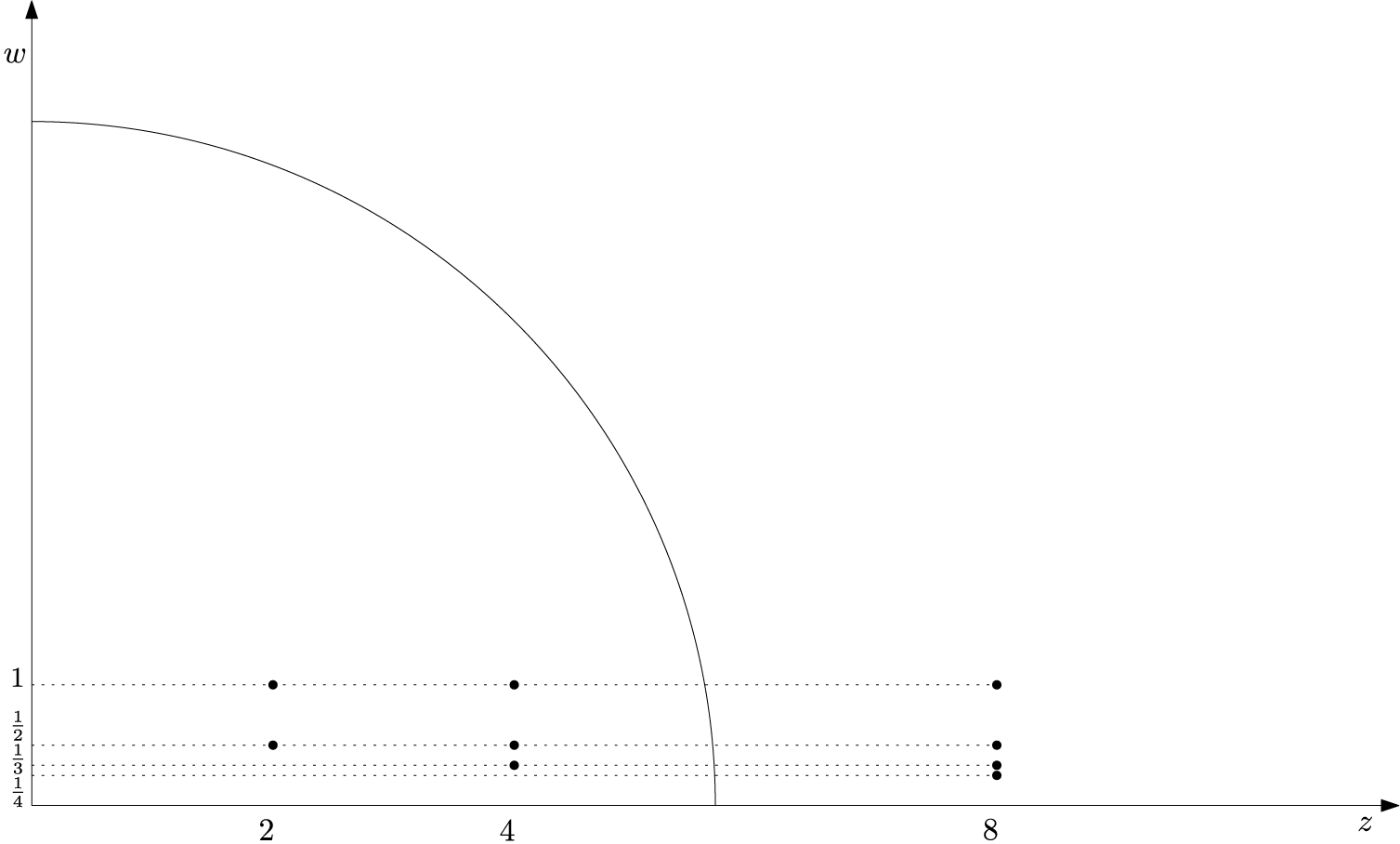
Figure 2 Classical count of zeros.
We now see that by taking
![]() $\mathfrak {c}$
, which increases sufficiently fast,
$\mathfrak {c}$
, which increases sufficiently fast,
![]() $\zeta (F,r)$
can grow arbitrarily fast, which disproves the two-dimensional transcendental Bézout problem. More precisely, in [Reference Cornalba and Shiffman13], Cornalba and Shiffman made a remark that
$\zeta (F,r)$
can grow arbitrarily fast, which disproves the two-dimensional transcendental Bézout problem. More precisely, in [Reference Cornalba and Shiffman13], Cornalba and Shiffman made a remark that
![]() $c_i=2^{2^i}$
would suffice. Indeed, it is not difficult to check that for
$c_i=2^{2^i}$
would suffice. Indeed, it is not difficult to check that for
![]() $\lambda>0$
, if
$\lambda>0$
, if
![]() $c_i=\lfloor 2^{\lambda i } \rfloor $
, then
$c_i=\lfloor 2^{\lambda i } \rfloor $
, then
![]() $\zeta (F,r)=\Theta (r^\lambda )$
(i.e., the order of growth of the number of zeros is
$\zeta (F,r)=\Theta (r^\lambda )$
(i.e., the order of growth of the number of zeros is
![]() $\lambda ),$
while for
$\lambda ),$
while for
![]() $c_i=2^{2^i}$
,
$c_i=2^{2^i}$
,
![]() $\log \zeta (F,r)= \Theta (r)$
and the order of growth of
$\log \zeta (F,r)= \Theta (r)$
and the order of growth of
![]() $\zeta (F,r)$
is infinite. Here and further on, we write
$\zeta (F,r)$
is infinite. Here and further on, we write
![]() $a(r)=\Theta (b(r))$
if
$a(r)=\Theta (b(r))$
if
![]() $a(r)=O(b(r))$
and
$a(r)=O(b(r))$
and
![]() $b(r)=O(a(r))$
as
$b(r)=O(a(r))$
as
![]() $r \to \infty $
; we will also write
$r \to \infty $
; we will also write
![]() $a(r) \sim b(r)$
if
$a(r) \sim b(r)$
if
![]() $\lim _{r\to \infty } a(r)/b(r)=1$
.
$\lim _{r\to \infty } a(r)/b(r)=1$
.
Let us re-examine the same class of examples from the coarse point of view. The following result is proved in Section 3.
Theorem 1.5. Let
![]() $\mathfrak {c}$
be an arbitrary increasing sequence of positive integers. When
$\mathfrak {c}$
be an arbitrary increasing sequence of positive integers. When
![]() $r\to +\infty $
it holds
$r\to +\infty $
it holds
and for a fixed
![]() $\delta>0$
$\delta>0$
Let us explain the geometric picture behind Theorem 1.5, while referring the reader to Section 3 for detailed proofs. For a fixed
![]() $\delta $
, we show that the set
$\delta $
, we show that the set
![]() $\{|F|\leq \delta \}$
, while possibly being complicated for small radius r, stabilizes for large radii and can be described rather accurately. More precisely, we show that there exists
$\{|F|\leq \delta \}$
, while possibly being complicated for small radius r, stabilizes for large radii and can be described rather accurately. More precisely, we show that there exists
![]() $k_0$
, which depends only on
$k_0$
, which depends only on
![]() $\delta $
, such that
$\delta $
, such that
![]() $\{|F|\leq \delta \}$
contains intervals
$\{|F|\leq \delta \}$
contains intervals
![]() $\{2^k \} \times [0,1]$
for all
$\{2^k \} \times [0,1]$
for all
![]() $k\geq k_0.$
Thus, for
$k\geq k_0.$
Thus, for
![]() $k\geq k_0$
, the zeros on each of the intervals
$k\geq k_0$
, the zeros on each of the intervals
![]() $\{2^k \} \times [0,1]$
are counted coarsely as one zero, and the coarse count increases at the rate
$\{2^k \} \times [0,1]$
are counted coarsely as one zero, and the coarse count increases at the rate
![]() $\log r.$
This implies
$\log r.$
This implies
![]() $\zeta (F,r,\delta )=O(\log r).$
Furthermore, for
$\zeta (F,r,\delta )=O(\log r).$
Furthermore, for
![]() $k\geq k_0$
,
$k\geq k_0$
,
![]() $\{ |F|\leq \delta \}$
will never intersect hyperplanes
$\{ |F|\leq \delta \}$
will never intersect hyperplanes
![]() $H_k= \{ (w,z) ~|~ Re(z)=2^k+2^{k-1} \}.$
In other words,
$H_k= \{ (w,z) ~|~ Re(z)=2^k+2^{k-1} \}.$
In other words,
![]() $\{|F|\leq \delta \}$
consists of parts contained between those hyperplanes and which contain intervals
$\{|F|\leq \delta \}$
consists of parts contained between those hyperplanes and which contain intervals
![]() $\{2^k \} \times [0,1],$
as shown on Figure 3 (shaded regions represent the set
$\{2^k \} \times [0,1],$
as shown on Figure 3 (shaded regions represent the set
![]() $\{ |F|\leq \delta \}$
). This implies that
$\{ |F|\leq \delta \}$
). This implies that
![]() $\zeta (F,r,\delta )= \Theta (\log r),$
which we can improve to
$\zeta (F,r,\delta )= \Theta (\log r),$
which we can improve to
![]() $\zeta (F,r,\delta ) \sim \log r$
as claimed by Theorem 1.5.
$\zeta (F,r,\delta ) \sim \log r$
as claimed by Theorem 1.5.
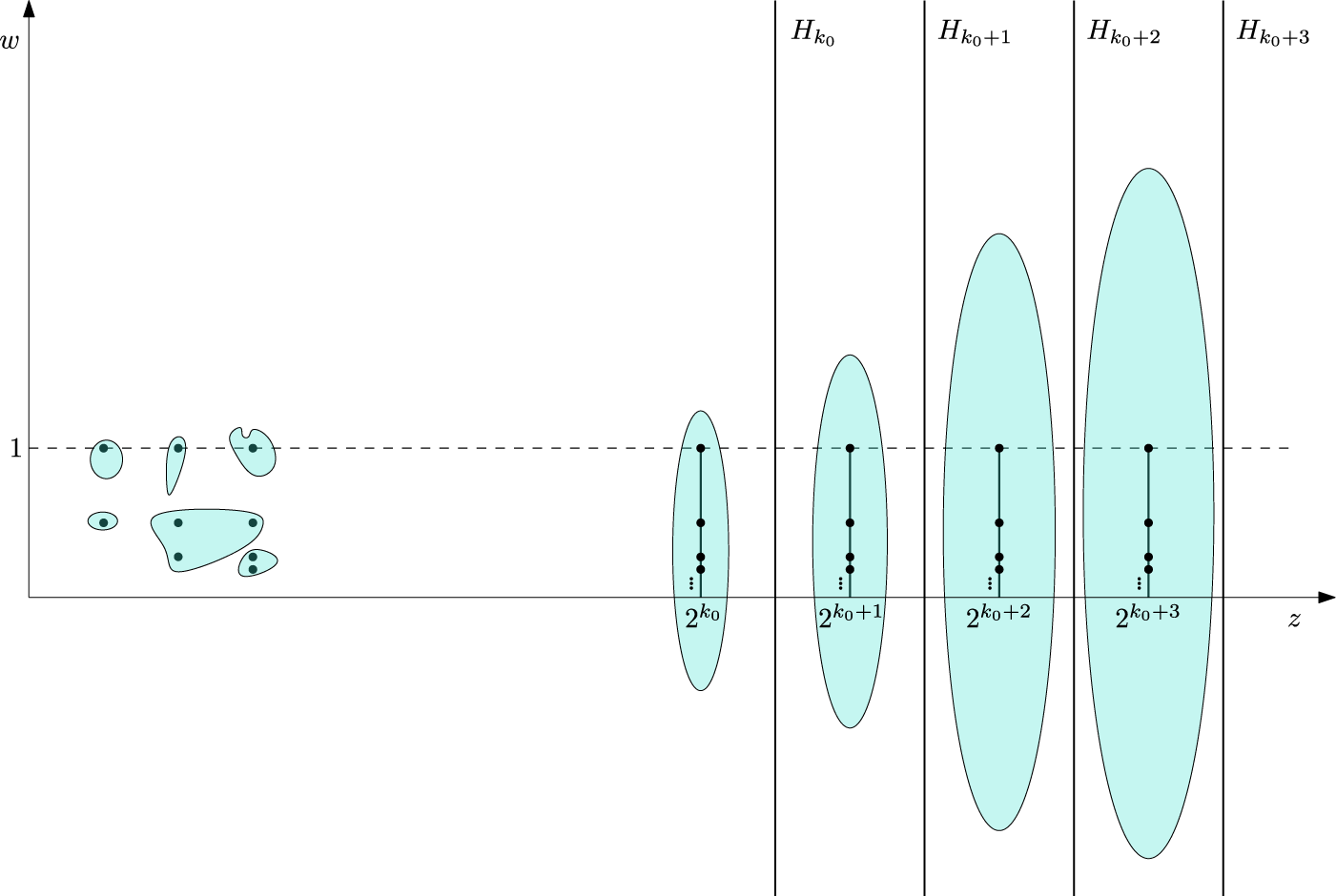
Figure 3 Coarse count of zeros.
Putting together Theorems 1.2 and 1.5, we come to the following conclusion. It follows from Theorem 1.2 for
![]() $n=2$
that
$n=2$
that
On the logarithmic scale, this inequality tells us that for fixed a and
![]() $\delta $
,
$\delta $
,
when
![]() $r\to +\infty .$
Theorem 1.5 implies that (1.3) is asymptotically sharp as
$r\to +\infty .$
Theorem 1.5 implies that (1.3) is asymptotically sharp as
In other words, Cornalba–Shiffman examples exhibit highly oscillatory behavior on small scales, which increases the count of zeros in an uncontrollable way and contradicts the transcendental Bézout problem. However, equality (1.4) shows that if we discard small oscillations, the same examples behave essentially as predicted by the coarse version of the transcendental Bézout problem.
1.4. Islands vs peninsulas
A connected component of
![]() $f^{-1}(B_\delta )\cap B_r$
is called an island if it is disjoint from
$f^{-1}(B_\delta )\cap B_r$
is called an island if it is disjoint from
![]() $S_r=\partial B_r$
, and a peninsula otherwise. We prove the following result in Section 2.3: this is a combination of Corollary 2.11 and Corollary 2.9.
$S_r=\partial B_r$
, and a peninsula otherwise. We prove the following result in Section 2.3: this is a combination of Corollary 2.11 and Corollary 2.9.
Theorem 1.6. Every island has nonempty interior which contains at least one zero of
![]() $f.$
$f.$
Let
![]() $\zeta ^0(f,r,\delta )$
denote the number of islands, and let
$\zeta ^0(f,r,\delta )$
denote the number of islands, and let
![]() $\tau (f,r,\delta )$
denote the total number of zeros of f with multiplicities contained in islands in
$\tau (f,r,\delta )$
denote the total number of zeros of f with multiplicities contained in islands in
![]() $B_r.$
Since an island can contain more than one zero, clearly,
$B_r.$
Since an island can contain more than one zero, clearly,
The following result is a consequence of Rouché’s theorem for analytic mappings; see Section 4.
Theorem 1.7. For all
![]() $a>1$
,
$a>1$
,
![]() $r>0$
and
$r>0$
and
![]() $\delta \in (0, \mu (f, ar)/2)$
,
$\delta \in (0, \mu (f, ar)/2)$
,
where
![]() $C_1$
depends only on a and n.
$C_1$
depends only on a and n.
Note that in view of Remark 1.3, estimate (1.5) is sharp.
Remark 1.8. Estimates analogous to (1.5) for the usual count of zeros have been proven under positive lower bounds on the Jacobian of f in [Reference Ji22, Reference Li23, Reference Li and Taylor24]. Upper bounds in Theorems 1.2 and 1.7 apply to all holomorphic mappings
![]() $f: \mathbb {C}^n \to \mathbb {C}^n.$
A detailed comparison of our results with those in [Reference Ji22, Reference Li23, Reference Li and Taylor24] is carried out in Section 5. In particular, we give a different proof of a result from [Reference Li and Taylor24] using Theorem 1.7.
$f: \mathbb {C}^n \to \mathbb {C}^n.$
A detailed comparison of our results with those in [Reference Ji22, Reference Li23, Reference Li and Taylor24] is carried out in Section 5. In particular, we give a different proof of a result from [Reference Li and Taylor24] using Theorem 1.7.
In general,
![]() $\zeta (f,r,\delta )$
and
$\zeta (f,r,\delta )$
and
![]() $\zeta ^0(f,r,\delta )$
can behave rather differently. Indeed, this is the case for the Cornalba-Shiffman example, as we discuss below.
$\zeta ^0(f,r,\delta )$
can behave rather differently. Indeed, this is the case for the Cornalba-Shiffman example, as we discuss below.
Let F be a Cornalba-Shiffman map defined previously. It is natural to ask what is the possible growth of the coarse count of islands
![]() $\zeta ^0(F,r,\delta ).$
We show that, as opposed to
$\zeta ^0(F,r,\delta ).$
We show that, as opposed to
![]() $\zeta (F,r,\delta )$
,
$\zeta (F,r,\delta )$
,
![]() $\zeta ^0(F,r,\delta )$
can grow arbitrarily slow, with an upper bound depending on
$\zeta ^0(F,r,\delta )$
can grow arbitrarily slow, with an upper bound depending on
![]() $\mathfrak {c}.$
More precisely, in Section 4, we prove the following theorem.
$\mathfrak {c}.$
More precisely, in Section 4, we prove the following theorem.
Theorem 1.9. Let
![]() $\lambda , \delta>0$
,
$\lambda , \delta>0$
,
![]() $l\geq 1$
an integer and write
$l\geq 1$
an integer and write
![]() $\exp _2(x)=2^x.$
If
$\exp _2(x)=2^x.$
If
 $c_i=\lfloor \underbrace {\exp _2 \ldots \exp _2}_{l \text { times}} (\lambda i ) \rfloor $
, then there exists a constant
$c_i=\lfloor \underbrace {\exp _2 \ldots \exp _2}_{l \text { times}} (\lambda i ) \rfloor $
, then there exists a constant
![]() $m_{l,\lambda ,\delta }$
such that for all
$m_{l,\lambda ,\delta }$
such that for all
 $r\geq \underbrace {\exp _2 \ldots \exp _2}_{l+1 \text { times}}(1)$
, it holds
$r\geq \underbrace {\exp _2 \ldots \exp _2}_{l+1 \text { times}}(1)$
, it holds
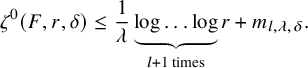 $$ \begin{align*} \zeta^0(F,r,\delta)\leq \frac{1}{\lambda}\underbrace{\log \ldots \log}_{l+1 \text{ times}} r + m_{l,\lambda,\delta}. \end{align*} $$
$$ \begin{align*} \zeta^0(F,r,\delta)\leq \frac{1}{\lambda}\underbrace{\log \ldots \log}_{l+1 \text{ times}} r + m_{l,\lambda,\delta}. \end{align*} $$
In particular, for
![]() $c_i=2^{2^i}$
as in [Reference Cornalba and Shiffman13], we have that
$c_i=2^{2^i}$
as in [Reference Cornalba and Shiffman13], we have that
![]() $\zeta ^0(F,r,\delta )=O(\log \log \log r).$
$\zeta ^0(F,r,\delta )=O(\log \log \log r).$
From the geometric perspective, the slow growth of
![]() $\zeta ^0(F,r,\delta )$
is due to elongation of
$\zeta ^0(F,r,\delta )$
is due to elongation of
![]() $\{|F|\leq \delta \}$
in the w-direction. Namely, as r increases, new groups of zeros of roughly the same modulus r appear, while the components of
$\{|F|\leq \delta \}$
in the w-direction. Namely, as r increases, new groups of zeros of roughly the same modulus r appear, while the components of
![]() $\{|F|\leq \delta \}$
which contain these zeros grow in the w-direction faster than r (the diameter of their w-projection grows faster than r). Hence, it takes larger r for a component of
$\{|F|\leq \delta \}$
which contain these zeros grow in the w-direction faster than r (the diameter of their w-projection grows faster than r). Hence, it takes larger r for a component of
![]() $\{|F|\leq \delta \}$
to be fully contained in
$\{|F|\leq \delta \}$
to be fully contained in
![]() $B_r$
(i.e., to contribute to
$B_r$
(i.e., to contribute to
![]() $\zeta ^0(F,r,\delta )).$
$\zeta ^0(F,r,\delta )).$
1.5. Discussion
Below, we discuss some extensions of our results as well as directions for further research.
1.5.1. Analytic mappings from
 $\mathbb {C}^n$
to
$\mathbb {C}^n$
to
 $\mathbb {C}^k$
$\mathbb {C}^k$
A bound analogous to Theorem 1.2 holds for entire mappings
![]() $f: \mathbb {C}^n \to \mathbb {C}^k.$
It appears as Theorem 2.6 in Section 2.2. To have geometric meaning in this case, the definition of
$f: \mathbb {C}^n \to \mathbb {C}^k.$
It appears as Theorem 2.6 in Section 2.2. To have geometric meaning in this case, the definition of
![]() $\zeta (f,r,\delta )$
should be generalized. To this end, we look at coarse homology groups of the zero set: for
$\zeta (f,r,\delta )$
should be generalized. To this end, we look at coarse homology groups of the zero set: for
![]() $0 \leq d \leq 2n-1,$
set
$0 \leq d \leq 2n-1,$
set
Considering generic algebraic maps
![]() $f,$
we expect only
$f,$
we expect only
![]() $0 \leq d \leq n-k$
to have geometric significance. Of particular interest is
$0 \leq d \leq n-k$
to have geometric significance. Of particular interest is
![]() $d = n-k,$
since this is the dimension where vanishing cycles appear. We prove the upper bound
$d = n-k,$
since this is the dimension where vanishing cycles appear. We prove the upper bound
under the same assumptions on the parameters
![]() $a,r,\delta $
as in Theorem 1.2.
$a,r,\delta $
as in Theorem 1.2.
1.5.2. Affine varieties
It would be interesting to generalize our main results to more general affine algebraic varieties
![]() $Y \subset \mathbb {C}^N$
. The starting case would be varieties which compactify to smooth projective varieties
$Y \subset \mathbb {C}^N$
. The starting case would be varieties which compactify to smooth projective varieties
![]() $X \subset \mathbb {C} P^N$
by a normal crossings divisor
$X \subset \mathbb {C} P^N$
by a normal crossings divisor
![]() $D = X \setminus Y.$
We expect that the methods of [Reference Cornalba and Griffiths12] combined with those of [Reference Buhovsky, Payette, Polterovich, Polterovich, Shelukhin and Stojisavljević9] – in particular, the subadditivity theorem for persistence barcodes – should be useful for this purpose. See also Section 6.
$D = X \setminus Y.$
We expect that the methods of [Reference Cornalba and Griffiths12] combined with those of [Reference Buhovsky, Payette, Polterovich, Polterovich, Shelukhin and Stojisavljević9] – in particular, the subadditivity theorem for persistence barcodes – should be useful for this purpose. See also Section 6.
1.5.3. Harmonic mappings
We expect that an analogue of Theorem 1.2 should hold in the context of harmonic maps. Namely, suppose that
![]() $h=(h_1,\ldots ,h_d): \mathbb {R}^d \to \mathbb {R}^d$
is a harmonic map in the sense that
$h=(h_1,\ldots ,h_d): \mathbb {R}^d \to \mathbb {R}^d$
is a harmonic map in the sense that
![]() $h_j:\mathbb {R}^d \to \mathbb {R}$
is harmonic for all j (this is equivalent to the map being harmonic in the variational sense [Reference Hélein and Wood21, Section 2.2, Examples 3, 4] where
$h_j:\mathbb {R}^d \to \mathbb {R}$
is harmonic for all j (this is equivalent to the map being harmonic in the variational sense [Reference Hélein and Wood21, Section 2.2, Examples 3, 4] where
![]() $\mathbb {R}^d$
is endowed with the standard Euclidean metric). In this case, we expect that the coarse counts
$\mathbb {R}^d$
is endowed with the standard Euclidean metric). In this case, we expect that the coarse counts
![]() $\zeta (h,r,\delta ), \zeta ^0(h,r,\delta )$
being defined analogously to the above, satisfy the upper bound
$\zeta (h,r,\delta ), \zeta ^0(h,r,\delta )$
being defined analogously to the above, satisfy the upper bound
for all
![]() $a>1$
,
$a>1$
,
![]() $r>0$
, and
$r>0$
, and
![]() $\delta \in (0, \mu (h,C_1 ar)/2),$
where
$\delta \in (0, \mu (h,C_1 ar)/2),$
where
![]() $C_1 \geq 1$
depends on d only, and
$C_1 \geq 1$
depends on d only, and
![]() $C_2$
depends only on a and
$C_2$
depends only on a and
![]() $d.$
(By Liouville’s theorem, the condition on
$d.$
(By Liouville’s theorem, the condition on
![]() $\delta $
holds for all r large enough, if our mapping is not constant.) This bound is sharp asymptotically in r for all fixed
$\delta $
holds for all r large enough, if our mapping is not constant.) This bound is sharp asymptotically in r for all fixed
![]() $\delta> 0,$
as can be seen from the example
$\delta> 0,$
as can be seen from the example
![]() $h = (h_1, \ldots , h_d)$
where
$h = (h_1, \ldots , h_d)$
where
![]() $h_i(x_1,\ldots ,x_d) = (e^{x_{i+1}} \sin (x_{i}))$
for
$h_i(x_1,\ldots ,x_d) = (e^{x_{i+1}} \sin (x_{i}))$
for
![]() $1 \leq i \leq d-1$
and
$1 \leq i \leq d-1$
and
![]() $h_d(x_1,\ldots ,x_d) = (e^{x_{1}} \sin (x_{d})).$
Note that
$h_d(x_1,\ldots ,x_d) = (e^{x_{1}} \sin (x_{d})).$
Note that
![]() $\log \mu (h,ar)$
is closely related to the notion of the doubling index of the harmonic function (see, for example, [Reference Logunov25, Equation (12)]).
$\log \mu (h,ar)$
is closely related to the notion of the doubling index of the harmonic function (see, for example, [Reference Logunov25, Equation (12)]).
An outline of the argument is as follows. First, replace Proposition 2.2 by an analogous estimate for real polynomials of degree k on a ball in
![]() $\mathbb {R}^d$
in terms of
$\mathbb {R}^d$
in terms of
![]() $k^d$
. Second, replace Proposition 2.1 by suitable Cauchy estimates, which hold for entire harmonic maps (see, for example, [Reference Axler, Bourdon and Ramey4, Theorem 2.4], [Reference Evans16, Chapter 2.2, Proof of Theorem 10]). The rest of the argument follows our proof of Theorem 1.2 directly. Note that the only property required from a harmonic mapping is that it satisfies Cauchy’s estimates; hence, inequality (1.6) should extend to a certain ‘quasi-analytic’ class of mappings.
$k^d$
. Second, replace Proposition 2.1 by suitable Cauchy estimates, which hold for entire harmonic maps (see, for example, [Reference Axler, Bourdon and Ramey4, Theorem 2.4], [Reference Evans16, Chapter 2.2, Proof of Theorem 10]). The rest of the argument follows our proof of Theorem 1.2 directly. Note that the only property required from a harmonic mapping is that it satisfies Cauchy’s estimates; hence, inequality (1.6) should extend to a certain ‘quasi-analytic’ class of mappings.
It would be interesting to realize this outline and to optimize the constant
![]() $C_1 \geq 1.$
$C_1 \geq 1.$
1.5.4. Near-holomorphic mappings
Let us also note that the proof of Theorem 1.2 yields the following stronger result about the coarse count of zeros of continuous functions that are close to holomorphic ones.
Denote by
![]() $d_{C^0}(f,g)$
the
$d_{C^0}(f,g)$
the
![]() $C^0$
-distance between continuous mappings
$C^0$
-distance between continuous mappings
![]() $f,g: \mathbb{C}^n \to \mathbb{C}^n$
.
$f,g: \mathbb{C}^n \to \mathbb{C}^n$
.
Corollary 1.10. Fix
![]() $b<1$
and
$b<1$
and
![]() $\delta>0$
, and let
$\delta>0$
, and let
![]() $h: \mathbb {C}^n \to \mathbb {C}^n$
be a continuous function such that there exists a holomorphic function
$h: \mathbb {C}^n \to \mathbb {C}^n$
be a continuous function such that there exists a holomorphic function
![]() $f: \mathbb {C}^n \to \mathbb {C}^n$
with
$f: \mathbb {C}^n \to \mathbb {C}^n$
with
![]() $d_{C^0}(h,f) < \frac {b}{2} \delta $
. Then
$d_{C^0}(h,f) < \frac {b}{2} \delta $
. Then
where C depends on
![]() $a,b,n$
only.
$a,b,n$
only.
1.5.5. A dynamical interlude
A dynamical counterpart of the transcendental Bézout problem is the count of periodic orbits of entire maps
![]() $f: \mathbb {C}^n \to \mathbb {C}^n$
. Here, by a k-periodic orbit, we mean a fixed point of the iteration
$f: \mathbb {C}^n \to \mathbb {C}^n$
. Here, by a k-periodic orbit, we mean a fixed point of the iteration
![]() $f^{\circ k}= f \circ \cdots \circ f$
(k times). There exists a vast literature on the orbit growth of algebraic maps f (see, for example, [Reference Artin and Mazur3]). For instance, it follows from the Bézout theorem that if the components of f are generic polynomials of degree
$f^{\circ k}= f \circ \cdots \circ f$
(k times). There exists a vast literature on the orbit growth of algebraic maps f (see, for example, [Reference Artin and Mazur3]). For instance, it follows from the Bézout theorem that if the components of f are generic polynomials of degree
![]() $\leq d$
, the number of k-periodic orbits does not exceed
$\leq d$
, the number of k-periodic orbits does not exceed
![]() $d^{kn}$
. Can one expect a bound on the number of k-periodic orbits in the ball of radius r in terms of the maximum modulus function
$d^{kn}$
. Can one expect a bound on the number of k-periodic orbits in the ball of radius r in terms of the maximum modulus function
![]() $\mu (f,r)$
? The naive answer is ‘no’ due to the Cornalba-Shiffman examples. Nevertheless, Theorem 1.2 above readily yields such a bound on the coarse count
$\mu (f,r)$
? The naive answer is ‘no’ due to the Cornalba-Shiffman examples. Nevertheless, Theorem 1.2 above readily yields such a bound on the coarse count
![]() $\zeta (f_k,r,\delta )$
, where
$\zeta (f_k,r,\delta )$
, where
One can check that the maximum modulus function behaves nicely under the composition and the sum:
Fix
![]() $a>1$
and
$a>1$
and
![]() $\delta>0$
, set
$\delta>0$
, set
![]() $\tilde \mu (r):= \mu (f, r)$
, and put
$\tilde \mu (r):= \mu (f, r)$
, and put
By Theorem 1.2, we have the desired estimate
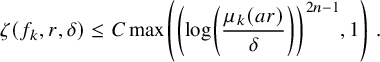 $$ \begin{align} \zeta (f_k,r,\delta) \leq C \max\left( \left( \log \left( \frac{\mu_k(a r)}{\delta}\right) \right)^{2n-1}, 1\right)\;. \end{align} $$
$$ \begin{align} \zeta (f_k,r,\delta) \leq C \max\left( \left( \log \left( \frac{\mu_k(a r)}{\delta}\right) \right)^{2n-1}, 1\right)\;. \end{align} $$
A few questions are in order.
Question 1.11. Can one find a transcendental entire map f for which estimate (1.7) is sharp?
A natural playground for testing this question are transcendental Hénon maps whose entropy as restricted to a family of concentric discs grows arbitrarily fast [Reference Arosio, Benini, Fornæss and Peters2].
Further, recall that a k-periodic orbit of an entire map
![]() $f: \mathbb {C}^n \to \mathbb {C}^n$
is called primitive if it is not m-periodic with
$f: \mathbb {C}^n \to \mathbb {C}^n$
is called primitive if it is not m-periodic with
![]() $m < k$
. Denote by
$m < k$
. Denote by
![]() $\nu _k(f,r)$
the number of primitive k-periodic orbits lying in the ball of radius r.
$\nu _k(f,r)$
the number of primitive k-periodic orbits lying in the ball of radius r.
Question 1.12. Does there exist a transcendental entire map f of order
![]() $0$
(i.e., the modulus
$0$
(i.e., the modulus
![]() $\mu (f,r)$
grows slower than
$\mu (f,r)$
grows slower than
![]() $e^{r^\epsilon }$
for every
$e^{r^\epsilon }$
for every
![]() $\epsilon>0$
) such that
$\epsilon>0$
) such that
![]() $\nu _k(f,r)$
grows arbitrarily fast in k and r?
$\nu _k(f,r)$
grows arbitrarily fast in k and r?
For instance, taking
![]() $f(z) = F(z)+z$
, where F is a Cornalba-Shiffman map, we see that
$f(z) = F(z)+z$
, where F is a Cornalba-Shiffman map, we see that
![]() $\nu _1(f,r)$
can grow arbitrarily fast. Can one generalize this construction to
$\nu _1(f,r)$
can grow arbitrarily fast. Can one generalize this construction to
![]() $k \geq 2$
?
$k \geq 2$
?
Finally, let us mention that the failure of the transcendental Bézout theorem appears as one of the substantial difficulties in the work [Reference Gutman, Qiao and Tsukamoto20] dealing with a dynamical problem of a completely different nature – namely, with embeddings of
![]() $\mathbb {Z}^k$
-actions into the shift action on the infinite dimensional cube (see (2) on p. 1450 in [Reference Gutman, Qiao and Tsukamoto20]). In particular, the authors analyze the structure of zeroes of so-called tiling-like band-limited maps (see p.1477 and Lemma 5.9). It would be interesting to perform our coarse count of zeroes (i.e., to calculate
$\mathbb {Z}^k$
-actions into the shift action on the infinite dimensional cube (see (2) on p. 1450 in [Reference Gutman, Qiao and Tsukamoto20]). In particular, the authors analyze the structure of zeroes of so-called tiling-like band-limited maps (see p.1477 and Lemma 5.9). It would be interesting to perform our coarse count of zeroes (i.e., to calculate
![]() $\zeta $
) for this class of examples.
$\zeta $
) for this class of examples.
Organization of the paper
In Section 2.1, we prove Theorem 1.2, providing our solution of the persistent transcendental Bézout problem. This result is extended in Section 2.2 to maps
![]() $\mathbb {C}^n \to \mathbb {C}^m$
and higher homology groups, and in Section 6, it is reformulated and generalized in the context of topological persistence. Section 2.3 contains a proof of Theorem 1.6 on the structure of islands.
$\mathbb {C}^n \to \mathbb {C}^m$
and higher homology groups, and in Section 6, it is reformulated and generalized in the context of topological persistence. Section 2.3 contains a proof of Theorem 1.6 on the structure of islands.
In Sections 3 and 4, we study the Cornalba-Shiffman example and prove Theorems 1.5, 1.7 and 1.9.
A comparison of our results with an earlier work of Li and Taylor [Reference Li and Taylor24] on the transcendental Bézout problem can be found in Section 5.
2. Proofs
2.1. Proof of Theorem 1.2
In order to prove Theorem 1.2, we will approximate an analytic map by a polynomial. To this end, we first recall a version of the classical Cauchy estimates for complex analytic mappings.
Proposition 2.1. Let
![]() $f: \mathbb {C}^n \to \mathbb {C}^m$
be a complex analytic mapping,
$f: \mathbb {C}^n \to \mathbb {C}^m$
be a complex analytic mapping,
![]() $a>1,$
and
$a>1,$
and
![]() $R_k = f-p_k$
be the Taylor remainder for the approximation of f by the Taylor polynomial mapping
$R_k = f-p_k$
be the Taylor remainder for the approximation of f by the Taylor polynomial mapping
![]() $p_k$
at
$p_k$
at
![]() $0$
of degree
$0$
of degree
![]() $<k.$
Then for all
$<k.$
Then for all
![]() $r>0, k \geq 0,$
$r>0, k \geq 0,$
for the constant
![]() $C_{a} = \frac {a}{a-1}$
depending only on
$C_{a} = \frac {a}{a-1}$
depending only on
![]() $a.$
$a.$
We give a proof for clarity.
Proof. Let
![]() $v \in S^{2n-1} \subset \mathbb {C}^n$
and
$v \in S^{2n-1} \subset \mathbb {C}^n$
and
![]() $u \in B_r(\mathbb {C}) \subset \mathbb {C}.$
Write a point z in
$u \in B_r(\mathbb {C}) \subset \mathbb {C}.$
Write a point z in
![]() $B_r = B_r(\mathbb {C}^n)$
as
$B_r = B_r(\mathbb {C}^n)$
as
![]() $z = u v.$
Then
$z = u v.$
Then
![]() $R_k(z) = f(uv)-p_k(uv).$
Now take
$R_k(z) = f(uv)-p_k(uv).$
Now take
![]() $v' \in S^{2m-1}$
, and set
$v' \in S^{2m-1}$
, and set
![]() $g(u) = \langle f(uv),v'\rangle , q_k(u) = \langle p_k(uv), v' \rangle .$
Then
$g(u) = \langle f(uv),v'\rangle , q_k(u) = \langle p_k(uv), v' \rangle .$
Then
![]() $q_k$
is the Taylor polynomial of g of degree
$q_k$
is the Taylor polynomial of g of degree
![]() $<k$
, and
$<k$
, and
![]() $r_k = g - q_k$
is the corresponding Taylor remainder. It is enough to bound
$r_k = g - q_k$
is the corresponding Taylor remainder. It is enough to bound
![]() $r_k(u)$
uniformly in
$r_k(u)$
uniformly in
![]() $v,v'$
for
$v,v'$
for
![]() $u \in B_r(\mathbb {C}).$
$u \in B_r(\mathbb {C}).$
Let
![]() $0<r<\rho .$
We use the following integral formula for the Cauchy remainder; see [Reference Ahlfors1, pages 125-126]: for
$0<r<\rho .$
We use the following integral formula for the Cauchy remainder; see [Reference Ahlfors1, pages 125-126]: for
![]() $u,w$
with
$u,w$
with
![]() $|u|=r$
,
$|u|=r$
,
![]() $|w|=\rho $
,
$|w|=\rho $
,
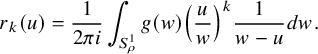 $$\begin{align*}r_k(u) = \frac{1}{2\pi i} \int_{S^1_{\rho}} g(w) \Big(\frac{u}{w}\Big)^k \frac{1}{w-u} dw. \end{align*}$$
$$\begin{align*}r_k(u) = \frac{1}{2\pi i} \int_{S^1_{\rho}} g(w) \Big(\frac{u}{w}\Big)^k \frac{1}{w-u} dw. \end{align*}$$
Therefore,
and picking
![]() $\rho = ar,$
we get
$\rho = ar,$
we get
So taking maxima over
![]() $u, v$
and
$u, v$
and
![]() $v',$
we obtain
$v',$
we obtain
Next, we highlight topological properties of polynomials needed for the proof of Theorem 1.2.
Proposition 2.2. Let
![]() $k \geq 1.$
Let
$k \geq 1.$
Let
![]() $p_1,\ldots , p_n: \mathbb {C}^n \to \mathbb {C}$
be complex polynomials of degree at most
$p_1,\ldots , p_n: \mathbb {C}^n \to \mathbb {C}$
be complex polynomials of degree at most
![]() $k.$
Set
$k.$
Set
![]() $p:\mathbb {C}^n \to \mathbb {C}^n$
,
$p:\mathbb {C}^n \to \mathbb {C}^n$
,
![]() $p = (p_1,\ldots ,p_n)$
for the induced polynomial mapping, and assume p is proper. Let B be a closed ball in
$p = (p_1,\ldots ,p_n)$
for the induced polynomial mapping, and assume p is proper. Let B be a closed ball in
![]() $\mathbb {C}^n$
, denote by
$\mathbb {C}^n$
, denote by
![]() $ h= |p|^2 $
and by
$ h= |p|^2 $
and by
![]() $\operatorname {Crit}(h|_{\partial B})$
the set of critical points of
$\operatorname {Crit}(h|_{\partial B})$
the set of critical points of
![]() $h|_{\partial B} .$
Then
$h|_{\partial B} .$
Then
![]() $p^{-1}(0)$
is a finite set of at most
$p^{-1}(0)$
is a finite set of at most
![]() $k^n$
points, whereas
$k^n$
points, whereas
![]() $\operatorname {Crit}(h|_{\partial B})$
has at most
$\operatorname {Crit}(h|_{\partial B})$
has at most
![]() $5k(10k)^{2n-2} $
connected components.
$5k(10k)^{2n-2} $
connected components.
Proof. First, we estimate the number of connected components of
![]() $\operatorname {Crit}(h|_{\partial B}).$
If
$\operatorname {Crit}(h|_{\partial B}).$
If
![]() $h|_{\partial B}$
is constant, the claim immediately follows. Otherwise, there exists a point
$h|_{\partial B}$
is constant, the claim immediately follows. Otherwise, there exists a point
![]() $N \in \partial B$
which is regular for
$N \in \partial B$
which is regular for
![]() $h|_{\partial B}.$
Consider complex linear coordinates
$h|_{\partial B}.$
Consider complex linear coordinates
![]() $(z_1,\ldots , z_n)$
,
$(z_1,\ldots , z_n)$
,
![]() $z_j = x_{2j-1}+i x_{2j},$
in which B is the unit ball, so
$z_j = x_{2j-1}+i x_{2j},$
in which B is the unit ball, so
![]() $\partial B$
is the unit sphere, and N is the base vector
$\partial B$
is the unit sphere, and N is the base vector
![]() $(0,\ldots ,0,i).$
Note that h is a real polynomial of degree at most
$(0,\ldots ,0,i).$
Note that h is a real polynomial of degree at most
![]() $2 k$
in
$2 k$
in
![]() $x_1,\ldots , x_{2n}.$
Following [Reference Nonez28], we consider inverse stereographic projection
$x_1,\ldots , x_{2n}.$
Following [Reference Nonez28], we consider inverse stereographic projection
![]() $\theta :\mathbb {R}^{2n-1} \to \partial B \setminus \{N\}$
,
$\theta :\mathbb {R}^{2n-1} \to \partial B \setminus \{N\}$
,
![]() $\theta (u_1,\ldots ,u_{2n-1}) = (x_1,\ldots ,x_{2n})$
,
$\theta (u_1,\ldots ,u_{2n-1}) = (x_1,\ldots ,x_{2n})$
,
![]() $x_j = \frac {2u_j}{|u|^2+1}$
for
$x_j = \frac {2u_j}{|u|^2+1}$
for
![]() $1 \leq j \leq 2n-1$
,
$1 \leq j \leq 2n-1$
,
![]() $x_{2n} = \frac {|u|^2-1}{|u|^2+1}.$
Then
$x_{2n} = \frac {|u|^2-1}{|u|^2+1}.$
Then
![]() $\theta ^*h = \frac {q}{(|u|^2+1)^{2k}}$
for a polynomial q in
$\theta ^*h = \frac {q}{(|u|^2+1)^{2k}}$
for a polynomial q in
![]() $u_1,\ldots ,u_{2n-1}$
of degree at most
$u_1,\ldots ,u_{2n-1}$
of degree at most
![]() $4k.$
The critical points of
$4k.$
The critical points of
![]() $\theta ^*h$
are in bijection with those of
$\theta ^*h$
are in bijection with those of
![]() $h|_{\partial B}$
and are given by
$h|_{\partial B}$
and are given by
![]() $2n-1$
polynomial equations
$2n-1$
polynomial equations
![]() $\partial _{u_j} q(u) (|u|^2+1) - 4k u_j q(u)= 0$
,
$\partial _{u_j} q(u) (|u|^2+1) - 4k u_j q(u)= 0$
,
![]() $1 \leq j \leq 2n-1,$
each one of degree at most
$1 \leq j \leq 2n-1,$
each one of degree at most
![]() $4k+1 \leq 5k.$
By an estimate of Milnor [Reference Milnor27, Theorem 2], we obtain that the total Betti number of
$4k+1 \leq 5k.$
By an estimate of Milnor [Reference Milnor27, Theorem 2], we obtain that the total Betti number of
![]() $\operatorname {Crit}(h|_{\partial B})$
is bounded by
$\operatorname {Crit}(h|_{\partial B})$
is bounded by
![]() $5k(10k)^{2n-2}.$
Since 0-th Betti number counts path components, we get that the total number of path components of
$5k(10k)^{2n-2}.$
Since 0-th Betti number counts path components, we get that the total number of path components of
![]() $\operatorname {Crit}(h|_{\partial B})$
is not greater than
$\operatorname {Crit}(h|_{\partial B})$
is not greater than
![]() $5k(10k)^{2n-2}.$
Finally, the number of connected components is less than or equal to the number of path components,Footnote
2
and the claim follows.
$5k(10k)^{2n-2}.$
Finally, the number of connected components is less than or equal to the number of path components,Footnote
2
and the claim follows.
For the second part of the proposition, it is enough to notice that since p is proper,
![]() $p^{-1}(0)$
is compact and thus consists of a finite set of points by [Reference Rudin31, Theorem 14.3.1]. The number of these points is bounded by
$p^{-1}(0)$
is compact and thus consists of a finite set of points by [Reference Rudin31, Theorem 14.3.1]. The number of these points is bounded by
![]() $k^n$
in view of Bézout’s theorem (see [Reference Fulton17, Example 8.4.6] for example).
$k^n$
in view of Bézout’s theorem (see [Reference Fulton17, Example 8.4.6] for example).
Remark 2.3. As can be seen from the proof, the exponent
![]() $2n-1$
in Proposition 2.2 is a boundary effect. We currently do not know if it can be improved.
$2n-1$
in Proposition 2.2 is a boundary effect. We currently do not know if it can be improved.
Last, we formulate a lemma which connects Proposition 2.2 to the coarse count of zeros of near-polynomial maps.
Lemma 2.4. Let
![]() $f: \mathbb {C}^n \to \mathbb {C}^n$
be a continuous map,
$f: \mathbb {C}^n \to \mathbb {C}^n$
be a continuous map,
![]() $p:\mathbb {C}^n \to \mathbb {C}^n$
a proper complex polynomial map,
$p:\mathbb {C}^n \to \mathbb {C}^n$
a proper complex polynomial map,
![]() $h=|p|^2,\ \mathrm{and}\ B\subset \mathbb {C}^n$
a closed ball. Assume that
$h=|p|^2,\ \mathrm{and}\ B\subset \mathbb {C}^n$
a closed ball. Assume that
![]() $|f(z)-p(z)|<\delta /2$
for all
$|f(z)-p(z)|<\delta /2$
for all
![]() $z\in B.$
Let
$z\in B.$
Let
![]() $\Omega $
be a connected component of
$\Omega $
be a connected component of
![]() $f^{-1}(B_\delta )\cap B$
which contains a zero of
$f^{-1}(B_\delta )\cap B$
which contains a zero of
![]() $f.$
Then
$f.$
Then
![]() $\Omega $
contains either a zero of p or a connected component of
$\Omega $
contains either a zero of p or a connected component of
![]() $\operatorname {Crit}(h|_{\partial B}).$
$\operatorname {Crit}(h|_{\partial B}).$
Proof. First, we prove that
![]() $\Omega $
contains a local minimum of
$\Omega $
contains a local minimum of
![]() $h.$
Let
$h.$
Let
![]() $z_0$
be a zero of f in
$z_0$
be a zero of f in
![]() $\Omega .$
Then
$\Omega .$
Then
![]() $ |p(z_0)| \leq |f(z_0)| + |p(z_0)-f(z_0)| < \delta /2 $
. It follows that
$ |p(z_0)| \leq |f(z_0)| + |p(z_0)-f(z_0)| < \delta /2 $
. It follows that
![]() $ \min _\Omega |p| < \delta /2 $
, and let
$ \min _\Omega |p| < \delta /2 $
, and let
![]() $ z_1 \in \Omega $
be a point where this minumum is achieved. Then
$ z_1 \in \Omega $
be a point where this minumum is achieved. Then
![]() $ |f(z_1)| \leq |p(z_1)|+|f(z_1)-p(z_1)| < \delta /2 + \delta /2 = \delta $
; hence,
$ |f(z_1)| \leq |p(z_1)|+|f(z_1)-p(z_1)| < \delta /2 + \delta /2 = \delta $
; hence,
![]() $ \Omega $
contains a neighborhood of
$ \Omega $
contains a neighborhood of
![]() $ z_1 $
in
$ z_1 $
in
![]() $ B_r $
, and therefore,
$ B_r $
, and therefore,
![]() $ z_1 $
is, in fact, a local minimum of the function
$ z_1 $
is, in fact, a local minimum of the function
![]() $ |p| $
, and hence also of the function h, on
$ |p| $
, and hence also of the function h, on
![]() $ B_r.$
$ B_r.$
Now, if
![]() $z_1\in \partial B$
, then
$z_1\in \partial B$
, then
![]() $z_1 \in \operatorname {Crit}(h|_{\partial B})$
, and let Z be a connected component of
$z_1 \in \operatorname {Crit}(h|_{\partial B})$
, and let Z be a connected component of
![]() $\operatorname {Crit}(h|_{\partial B})$
which contains
$\operatorname {Crit}(h|_{\partial B})$
which contains
![]() $z_1.$
Since h is constant on Z, we have that for every
$z_1.$
Since h is constant on Z, we have that for every
![]() $z\in Z$
, it holds
$z\in Z$
, it holds
![]() $|f(z)|\leq |p(z)|+|f(z)-p(z)|<\delta /2+\delta /2=\delta .$
Thus,
$|f(z)|\leq |p(z)|+|f(z)-p(z)|<\delta /2+\delta /2=\delta .$
Thus,
![]() $z\in f^{-1}(B_\delta )\cap B$
, and therefore,
$z\in f^{-1}(B_\delta )\cap B$
, and therefore,
![]() $Z\subset f^{-1}(B_\delta )\cap B.$
We claim that, in fact,
$Z\subset f^{-1}(B_\delta )\cap B.$
We claim that, in fact,
![]() $Z\subset \Omega .$
Indeed,
$Z\subset \Omega .$
Indeed,
![]() $Z\cap \Omega \neq \emptyset $
, and since both Z and
$Z\cap \Omega \neq \emptyset $
, and since both Z and
![]() $\Omega $
are connected, so is
$\Omega $
are connected, so is
![]() $Z\cup \Omega .$
However,
$Z\cup \Omega .$
However,
![]() $Z\cup \Omega \subset f^{-1}(B_\delta )\cap B$
, and since
$Z\cup \Omega \subset f^{-1}(B_\delta )\cap B$
, and since
![]() $\Omega $
is a connected component of
$\Omega $
is a connected component of
![]() $f^{-1}(B_\delta )\cap B$
,
$f^{-1}(B_\delta )\cap B$
,
![]() $Z\subset \Omega $
as claimed.
$Z\subset \Omega $
as claimed.
In case
![]() $z_1 \in B \setminus \partial B,$
we have that
$z_1 \in B \setminus \partial B,$
we have that
![]() $p(z_1)=0$
because p is an open mapping. Indeed, since p is proper, it is a finite mapping, and as it is equidimensional, it is therefore an open mapping [Reference D’Angelo14, Proposition 3, Section 2.1.3].
$p(z_1)=0$
because p is an open mapping. Indeed, since p is proper, it is a finite mapping, and as it is equidimensional, it is therefore an open mapping [Reference D’Angelo14, Proposition 3, Section 2.1.3].
Proof of Theorem 1.2.
By Proposition 2.1, we can approximate
![]() $ f $
by a Taylor polynomial mapping
$ f $
by a Taylor polynomial mapping
![]() $ p $
at
$ p $
at
![]() $ 0 $
of degree
$ 0 $
of degree
![]() $ <k $
such that
$ <k $
such that
![]() $ |f-p| \leq C_{a} a^{-k} \mu (f,ar) $
on
$ |f-p| \leq C_{a} a^{-k} \mu (f,ar) $
on
![]() $ B_r $
. Here, we choose
$ B_r $
. Here, we choose
![]() $ k $
to be the minimal positive integer such that
$ k $
to be the minimal positive integer such that
![]() $ C_a a^{-k} \mu (f,ar) < \delta /2 $
. We can slightly perturb
$ C_a a^{-k} \mu (f,ar) < \delta /2 $
. We can slightly perturb
![]() $ p $
to make it proper by adding a homogeneous polynomial of degree k, while
$ p $
to make it proper by adding a homogeneous polynomial of degree k, while
![]() $ |f-p|<\delta /2 $
continues to hold on
$ |f-p|<\delta /2 $
continues to hold on
![]() $ B_r.$
Indeed, p being proper is equivalent to
$ B_r.$
Indeed, p being proper is equivalent to
![]() $|p(z)|\to \infty $
as
$|p(z)|\to \infty $
as
![]() $|z|\to \infty $
, which can be achieved by such a perturbation. Lemma 2.4 implies that
$|z|\to \infty $
, which can be achieved by such a perturbation. Lemma 2.4 implies that
![]() $\zeta (f,r,\delta )$
is bounded from above by the total number of zeros of p and connected components of
$\zeta (f,r,\delta )$
is bounded from above by the total number of zeros of p and connected components of
![]() $\operatorname {Crit}(h|_{\partial B}).$
Now, Proposition 2.2 gives us that
$\operatorname {Crit}(h|_{\partial B}).$
Now, Proposition 2.2 gives us that
![]() $\zeta (f,r,\delta )\leq k^n+5k(10k)^{2n-2}$
, which proves the claim.
$\zeta (f,r,\delta )\leq k^n+5k(10k)^{2n-2}$
, which proves the claim.
Remark 2.5. Theorem 1.2 also holds for analytic maps
![]() $f:\mathbb {C}^n \to \mathbb {C}^m$
with
$f:\mathbb {C}^n \to \mathbb {C}^m$
with
![]() $m<n.$
Indeed, if
$m<n.$
Indeed, if
![]() $m<n$
, we can include
$m<n$
, we can include
![]() $\iota :\mathbb {C}^m\to \mathbb {C}^n$
and define
$\iota :\mathbb {C}^m\to \mathbb {C}^n$
and define
![]() $\tilde {f}=\iota \circ f.$
Now
$\tilde {f}=\iota \circ f.$
Now
![]() $\zeta (f,r,\delta )=\zeta (\tilde {f},r,\delta )$
,
$\zeta (f,r,\delta )=\zeta (\tilde {f},r,\delta )$
,
![]() $\mu (f,ar)=\mu (\tilde {f},ar)$
and (1.2) for f follows from the same inequality for
$\mu (f,ar)=\mu (\tilde {f},ar)$
and (1.2) for f follows from the same inequality for
![]() $\tilde {f}.$
$\tilde {f}.$
2.2. Higher-dimensional counts
A similar approach leads to a proof of the following more general statement, albeit with a slightly weaker exponent on the right-hand side. See also Section 6. Consider the invariants
![]() $\zeta _d(f,r,\delta )$
from Section 1.5.1.
$\zeta _d(f,r,\delta )$
from Section 1.5.1.
Theorem 2.6. For any analytic map
![]() $f: \mathbb {C}^n \to \mathbb {C}^m$
,
$f: \mathbb {C}^n \to \mathbb {C}^m$
,
![]() $m\leq n$
and any
$m\leq n$
and any
![]() $a>1$
,
$a>1$
,
![]() $r>0$
, an integer
$r>0$
, an integer
![]() $ 0 \leq d \leq 2n -1$
, and
$ 0 \leq d \leq 2n -1$
, and
![]() $\delta \in (0, \frac {\mu (f, ar)}{2})$
, we have
$\delta \in (0, \frac {\mu (f, ar)}{2})$
, we have
 $$ \begin{align} \zeta_d(f,r,\delta) \leq C \left(\log\left(\frac{\mu(f, ar)}{\delta}\right)\right)^{2n}, \end{align} $$
$$ \begin{align} \zeta_d(f,r,\delta) \leq C \left(\log\left(\frac{\mu(f, ar)}{\delta}\right)\right)^{2n}, \end{align} $$
where the constant C depends only on a and n.
Proof. First, we notice that it is enough to prove the theorem in the case
![]() $m=n$
by the same reasoning as in Remark 2.5.
$m=n$
by the same reasoning as in Remark 2.5.
By Proposition 2.1, we can approximate
![]() $ f $
by a Taylor polynomial mapping
$ f $
by a Taylor polynomial mapping
![]() $ p $
at
$ p $
at
![]() $ 0 $
of degree
$ 0 $
of degree
![]() $ <k $
such that
$ <k $
such that
![]() $ |f-p| \leq C_{a} a^{-k} \mu (f,ar) $
on
$ |f-p| \leq C_{a} a^{-k} \mu (f,ar) $
on
![]() $ B_r $
. Here, we choose
$ B_r $
. Here, we choose
![]() $ k $
to be the minimal positive integer such that
$ k $
to be the minimal positive integer such that
![]() $ C_a a^{-k} \mu (f,ar) < \delta /2 $
. Since
$ C_a a^{-k} \mu (f,ar) < \delta /2 $
. Since
![]() $ ||f|-|p|| \leq |f-p| < \delta /2 $
, there exist natural maps
$ ||f|-|p|| \leq |f-p| < \delta /2 $
, there exist natural maps
It follows that
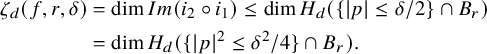 $$ \begin{align*} \zeta_d(f,r,\delta) &= \dim Im ( i_2 \circ i_1) \leq \dim H_d(\{|p|\leq \delta/2\} \cap B_r) \\ &= \dim H_d(\{ |p|^2 \leq \delta^2/4\} \cap B_r). \end{align*} $$
$$ \begin{align*} \zeta_d(f,r,\delta) &= \dim Im ( i_2 \circ i_1) \leq \dim H_d(\{|p|\leq \delta/2\} \cap B_r) \\ &= \dim H_d(\{ |p|^2 \leq \delta^2/4\} \cap B_r). \end{align*} $$
Identifying
![]() $\mathbb {C}^n=\mathbb {R}^{2n}$
, we have that
$\mathbb {C}^n=\mathbb {R}^{2n}$
, we have that
![]() $|p|^2$
is a real polynomial of degree
$|p|^2$
is a real polynomial of degree
![]() $<2k$
and
$<2k$
and
![]() $\{ |p|^2 \leq \delta ^2/4\}\cap B_r$
is defined by two polynomial inequalities
$\{ |p|^2 \leq \delta ^2/4\}\cap B_r$
is defined by two polynomial inequalities
By [Reference Milnor27, Theorem 3], we have that
![]() $\dim H_d(\{ |p|^2 \leq \delta ^2/4\} \cap B_r)$
is bounded by
$\dim H_d(\{ |p|^2 \leq \delta ^2/4\} \cap B_r)$
is bounded by
![]() $\frac {1}{2}(4k+2k)(3+2k)^{2n-1} $
, which finishes the proof.
$\frac {1}{2}(4k+2k)(3+2k)^{2n-1} $
, which finishes the proof.
Remark 2.7. In the proofs of Theorem 2.6 and Proposition 2.2, we used results of Milnor which relate to Betti numbers defined using Čech cohomology. These Betti numbers coincide with ones coming from singular homology, as explained in [Reference Milnor27], due to the fact that semialgebraic sets admit triangulations.
2.3. Zeros and islands
In this section, we prove Theorem 1.6, which is a combination of Corollary 2.11 and Corollary 2.9. It is a structure theorem for islands of analytic mappings. We start with the following general result which is possibly known, but we could not locate it in the literature.
Proposition 2.8. Let
![]() $g: U \to \mathbb {C}^m,$
for an open set
$g: U \to \mathbb {C}^m,$
for an open set
![]() $U \subset \mathbb {C}^n,$
for
$U \subset \mathbb {C}^n,$
for
![]() $n \geq m \geq 1,$
be a holomorphic mapping. Then every point
$n \geq m \geq 1,$
be a holomorphic mapping. Then every point
![]() $q\in U$
of non-degenerate minimum of
$q\in U$
of non-degenerate minimum of
![]() $h=|g|^2$
must be a zero of
$h=|g|^2$
must be a zero of
![]() $g.$
$g.$
Proof. Write
![]() $g = u + iv,$
where
$g = u + iv,$
where
![]() $u, v$
are the real and imaginary part of g, respectively, and i is the imaginary unit. Then
$u, v$
are the real and imaginary part of g, respectively, and i is the imaginary unit. Then
![]() $h = |u|^2 + |v|^2.$
Now
$h = |u|^2 + |v|^2.$
Now
![]() $d_q h = 2\langle u, d_q u \rangle + 2 \langle v, d_q v \rangle ,$
while
$d_q h = 2\langle u, d_q u \rangle + 2 \langle v, d_q v \rangle ,$
while
![]() $d_q g = d_q u + i d_q v.$
This shows that if q is a critical point of
$d_q g = d_q u + i d_q v.$
This shows that if q is a critical point of
![]() $h,$
then
$h,$
then
![]() $g(q) \in \mathbb {C}^m$
is orthogonal to the image of
$g(q) \in \mathbb {C}^m$
is orthogonal to the image of
![]() $d_q g.$
Therefore, as
$d_q g.$
Therefore, as
![]() $n \geq m,$
if
$n \geq m,$
if
![]() $g(q) \neq 0,$
then the kernel
$g(q) \neq 0,$
then the kernel
![]() $K = \ker d_q g$
is a nontrivial complex-linear subspace of
$K = \ker d_q g$
is a nontrivial complex-linear subspace of
![]() $\mathbb {C}^n.$
Now, as
$\mathbb {C}^n.$
Now, as
![]() $d_q g$
vanishes on
$d_q g$
vanishes on
![]() $K,$
writing the second order Taylor approximation
$K,$
writing the second order Taylor approximation
of g at
![]() $q,$
where
$q,$
where
![]() $d^2_q g$
is the complex Hessian (or quadratic differential) of g at
$d^2_q g$
is the complex Hessian (or quadratic differential) of g at
![]() $q,$
we obtain that
$q,$
we obtain that
is the second order Taylor approximation of h at
![]() $q,$
where the brackets denote the Hermitian inner product on
$q,$
where the brackets denote the Hermitian inner product on
![]() $\mathbb {C}^m.$
Hence, the Hessian
$\mathbb {C}^m.$
Hence, the Hessian
![]() $d^2_q h$
is given on
$d^2_q h$
is given on
![]() $a,b \in K$
by
$a,b \in K$
by
Since
![]() $d^2_q g$
is a
$d^2_q g$
is a
![]() $\mathbb {C}^m$
-valued complex bilinear form,
$\mathbb {C}^m$
-valued complex bilinear form,
![]() $\langle d^2_q g, g(q)\rangle $
is a
$\langle d^2_q g, g(q)\rangle $
is a
![]() $\mathbb {C}$
-valued complex bilinear form. Therefore, by a classical observation (see [Reference Milnor26, Assertion 1, p.39]), the quadratic form of
$\mathbb {C}$
-valued complex bilinear form. Therefore, by a classical observation (see [Reference Milnor26, Assertion 1, p.39]), the quadratic form of
![]() $d^2_q h|_K$
has zero signature as the real part of a complex quadratic form. Therefore, it cannot be positive-definite. This contradicts the hypothesis that q is an interior non-degenerate minimum. Hence,
$d^2_q h|_K$
has zero signature as the real part of a complex quadratic form. Therefore, it cannot be positive-definite. This contradicts the hypothesis that q is an interior non-degenerate minimum. Hence,
![]() $g(q) = 0.$
$g(q) = 0.$
Corollary 2.9. Let
![]() $g: B_r \to \mathbb {C}^m$
be a holomorphic mapping on a ball
$g: B_r \to \mathbb {C}^m$
be a holomorphic mapping on a ball
![]() $B_r$
in
$B_r$
in
![]() $\mathbb {C}^n$
,
$\mathbb {C}^n$
,
![]() $n \geq m.$
Consider an island of
$n \geq m.$
Consider an island of
![]() $\{ |g| \leq \delta \}$
with nonempty interior
$\{ |g| \leq \delta \}$
with nonempty interior
![]() $V.$
Then V contains a zero of
$V.$
Then V contains a zero of
![]() $g.$
$g.$
Proof. Denote by K the island of
![]() $\{ |g|\leq \delta \}$
with interior
$\{ |g|\leq \delta \}$
with interior
![]() $V.$
First, we claim that
$V.$
First, we claim that
![]() $|g|$
is not constant on
$|g|$
is not constant on
![]() $K.$
To this end, let
$K.$
To this end, let
![]() $q\in V$
, L a complex line passing through q parametrized by
$q\in V$
, L a complex line passing through q parametrized by
![]() $z\in \mathbb {C}$
and denote by
$z\in \mathbb {C}$
and denote by
![]() $u(z)=\sum _{j=1}^n |g_j(z)|^2$
the restriction of
$u(z)=\sum _{j=1}^n |g_j(z)|^2$
the restriction of
![]() $|g|^2$
to
$|g|^2$
to
![]() $L.$
If
$L.$
If
![]() $|g|$
was constant on K, u would be constant on a neighborhood of q in L and we would have that
$|g|$
was constant on K, u would be constant on a neighborhood of q in L and we would have that
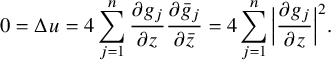 $$ \begin{align*}0=\Delta u = 4 \sum_{j=1}^n \frac{\partial g_j}{\partial z} \frac{\partial \bar{g}_j }{\partial \bar{z}}= 4 \sum_{j=1}^n \Big{|} \frac{\partial g_j}{\partial z} \Big{|}^2.\end{align*} $$
$$ \begin{align*}0=\Delta u = 4 \sum_{j=1}^n \frac{\partial g_j}{\partial z} \frac{\partial \bar{g}_j }{\partial \bar{z}}= 4 \sum_{j=1}^n \Big{|} \frac{\partial g_j}{\partial z} \Big{|}^2.\end{align*} $$
This implies that each
![]() $g_j$
is constant on a neighborhood of q and thus constant on the whole
$g_j$
is constant on a neighborhood of q and thus constant on the whole
![]() $L\cap B_r.$
Since L was taken arbitrarily, we conclude that g is constant, which is impossible since
$L\cap B_r.$
Since L was taken arbitrarily, we conclude that g is constant, which is impossible since
![]() $\{ |g| \leq \delta \}$
has an island by the assumption.
$\{ |g| \leq \delta \}$
has an island by the assumption.
Now, assume by contradiction that
![]() $0<\min _K |g|< \max _K |g|=\delta .$
Let
$0<\min _K |g|< \max _K |g|=\delta .$
Let
![]() $0<2\varepsilon < \min \{ \min _K |g| , \max _K |g| - \min _K |g| \}$
, and assume that
$0<2\varepsilon < \min \{ \min _K |g| , \max _K |g| - \min _K |g| \}$
, and assume that
![]() $g':K\to \mathbb {C}^m$
satisfies
$g':K\to \mathbb {C}^m$
satisfies
![]() $|g-g'|<\varepsilon $
on
$|g-g'|<\varepsilon $
on
![]() $K.$
Let
$K.$
Let
![]() $q,q' \in K$
for which
$q,q' \in K$
for which
![]() $|g(q)|=\min _K |g|$
,
$|g(q)|=\min _K |g|$
,
![]() $|g'(q')|=\min _K |g'|.$
Since
$|g'(q')|=\min _K |g'|.$
Since
we have that
![]() $q' \in V$
because
$q' \in V$
because
![]() $|g|$
equals
$|g|$
equals
![]() $\delta $
on
$\delta $
on
![]() $K\setminus V.$
Thus,
$K\setminus V.$
Thus,
![]() $|g'|$
has an interior local minimum
$|g'|$
has an interior local minimum
![]() $q'$
. By means of a transversality argument, we show the following proposition at the end of this subsection.
$q'$
. By means of a transversality argument, we show the following proposition at the end of this subsection.
Proposition 2.10. Assume K contains no zeros of
![]() $g.$
Then there exists an open set U,
$g.$
Then there exists an open set U,
![]() $K\subset U$
such that for every
$K\subset U$
such that for every
![]() $\varepsilon>0$
, there exists a holomorphic function
$\varepsilon>0$
, there exists a holomorphic function
![]() $g':U \to \mathbb {C}^m$
such that
$g':U \to \mathbb {C}^m$
such that
![]() $|g-g'|<\varepsilon $
on U and
$|g-g'|<\varepsilon $
on U and
![]() $|g'|^2$
is Morse.
$|g'|^2$
is Morse.
For
![]() $g'$
given by Proposition 2.10,
$g'$
given by Proposition 2.10,
![]() $q'$
must be a zero by Proposition 2.8. However, since
$q'$
must be a zero by Proposition 2.8. However, since
![]() $2\varepsilon < \min _K |g|$
, we have that
$2\varepsilon < \min _K |g|$
, we have that
![]() $0=|g'(q')|> |g(q')|-\varepsilon >\frac {1}{2} \min _K |g|>0$
, which is a contradiction.
$0=|g'(q')|> |g(q')|-\varepsilon >\frac {1}{2} \min _K |g|>0$
, which is a contradiction.
Corollary 2.11. Let
![]() $g: B_r \to \mathbb {C}^m$
be a holomorphic mapping on a ball
$g: B_r \to \mathbb {C}^m$
be a holomorphic mapping on a ball
![]() $B_r$
in
$B_r$
in
![]() $\mathbb {C}^n$
,
$\mathbb {C}^n$
,
![]() $n \geq m.$
Then every island of
$n \geq m.$
Then every island of
![]() $\{ |g| \leq \delta \}$
has nonempty interior.
$\{ |g| \leq \delta \}$
has nonempty interior.
Proof. Let K be an island with empty interior. Then
![]() $|g| = \delta $
on K, and we denote by
$|g| = \delta $
on K, and we denote by
![]() $K_i,i\geq 1$
a connected component of
$K_i,i\geq 1$
a connected component of
![]() $\{|g|\leq \delta + 1/i \} \cap B_r$
which contains
$\{|g|\leq \delta + 1/i \} \cap B_r$
which contains
![]() $K.$
$K.$
First, we claim that
![]() $\cap _{i\geq 1} K_i =K.$
Indeed,
$\cap _{i\geq 1} K_i =K.$
Indeed,
![]() $K \subset \cap _{i\geq 1} K_i$
by definition. However, since
$K \subset \cap _{i\geq 1} K_i$
by definition. However, since
![]() $\{ K_i \}$
is a nested sequence of connected compact sets,
$\{ K_i \}$
is a nested sequence of connected compact sets,
![]() $\cap _{i\geq 1} K_i$
is also compact and connected; see [Reference Engelking15, Corollary 6.1.19]. Since
$\cap _{i\geq 1} K_i$
is also compact and connected; see [Reference Engelking15, Corollary 6.1.19]. Since
![]() $|g|\leq \delta $
on
$|g|\leq \delta $
on
![]() $\cap _{i\geq 1} K_i$
, we have that
$\cap _{i\geq 1} K_i$
, we have that
![]() $\cap _{i\geq 1} K_i$
is a connected subset of
$\cap _{i\geq 1} K_i$
is a connected subset of
![]() $\{ |g| \leq \delta \}$
which contains K and thus has to be equal to K since K is a connected component.
$\{ |g| \leq \delta \}$
which contains K and thus has to be equal to K since K is a connected component.
Second, we claim that there exists
![]() $i_0$
such that for all
$i_0$
such that for all
![]() $i \geq i_0$
,
$i \geq i_0$
,
![]() $K_i$
are disjoint from
$K_i$
are disjoint from
![]() $\partial B_r.$
Indeed, if this was not the case, there would exist
$\partial B_r.$
Indeed, if this was not the case, there would exist
![]() $x_i \in K_i \cap \partial B_r$
, and by compactness of
$x_i \in K_i \cap \partial B_r$
, and by compactness of
![]() $\partial B_r$
we could assume
$\partial B_r$
we could assume
![]() $x_i \to x_\infty \in \partial B_r.$
This is not possible since
$x_i \to x_\infty \in \partial B_r.$
This is not possible since
![]() $x_\infty \in \cap _{i\geq 1} K_i = K$
, which is disjoint from
$x_\infty \in \cap _{i\geq 1} K_i = K$
, which is disjoint from
![]() $\partial B_r.$
$\partial B_r.$
Thus,
![]() $\{K_i \}, i\geq i_0$
is a sequence of islands in
$\{K_i \}, i\geq i_0$
is a sequence of islands in
![]() $B_r$
, each of which has a nonempty interior (since it contains an open neighborhood of K). By Corollary 2.9, there exists a sequence
$B_r$
, each of which has a nonempty interior (since it contains an open neighborhood of K). By Corollary 2.9, there exists a sequence
![]() $z_i\in K_i, i\geq i_0$
of zeros of g, and by compactness, we may assume that
$z_i\in K_i, i\geq i_0$
of zeros of g, and by compactness, we may assume that
![]() $z_i\to z_\infty \in K.$
This contradicts the fact that
$z_i\to z_\infty \in K.$
This contradicts the fact that
![]() $|g|=\delta $
of
$|g|=\delta $
of
![]() $K.$
$K.$
We note that the condition
![]() $n \geq m$
is essential for Proposition 2.8 and Corollaries 2.9, 2.11, as can be seen from the mapping
$n \geq m$
is essential for Proposition 2.8 and Corollaries 2.9, 2.11, as can be seen from the mapping
![]() $g:B_r \to \mathbb {C}^2$
,
$g:B_r \to \mathbb {C}^2$
,
![]() $B_r \subset \mathbb {C}$
,
$B_r \subset \mathbb {C}$
,
![]() $g(z) = (1,z).$
Similarly, so is non-degeneracy in Proposition 2.8, as shown by the example
$g(z) = (1,z).$
Similarly, so is non-degeneracy in Proposition 2.8, as shown by the example
![]() $g: B_r \to \mathbb {C}^2$
,
$g: B_r \to \mathbb {C}^2$
,
![]() $B_r \subset \mathbb {C}^2$
,
$B_r \subset \mathbb {C}^2$
,
![]() $g(z,w) = (z,1-z).$
$g(z,w) = (z,1-z).$
Proof of Proposition 2.10.
Denote by
![]() $g_z$
the complex differential of g with respect to
$g_z$
the complex differential of g with respect to
![]() $z=(z_1,\ldots , z_n)$
. Let U be such that the closure
$z=(z_1,\ldots , z_n)$
. Let U be such that the closure
![]() $\overline {U} \subset B_r$
and
$\overline {U} \subset B_r$
and
![]() $|g|>c > 0$
,
$|g|>c > 0$
,
![]() $|g_z| < C$
on U for some
$|g_z| < C$
on U for some
![]() $c,C.$
We argue as follows in the spirit of Thom’s parametric transversality theorem.
$c,C.$
We argue as follows in the spirit of Thom’s parametric transversality theorem.
The function
![]() $|g|^2= \bar {g}g$
is Morse on U whenever
$|g|^2= \bar {g}g$
is Morse on U whenever
![]() $\bar {g} g_z$
is transverse to
$\bar {g} g_z$
is transverse to
![]() $0$
as a mapping
$0$
as a mapping
![]() $U \to \mathbb {C}^n.$
Indeed, in this case by the proof of Proposition 2.8, at every critical point of
$U \to \mathbb {C}^n.$
Indeed, in this case by the proof of Proposition 2.8, at every critical point of
![]() $|g|^2,$
its Hessian will be the real part of a non-degenerate complex-valued symmetric bilinear form
$|g|^2,$
its Hessian will be the real part of a non-degenerate complex-valued symmetric bilinear form
![]() $2\bar {g} g_{zz},$
and as such, it will be non-degenerate.
$2\bar {g} g_{zz},$
and as such, it will be non-degenerate.
Denote by
![]() $A_i$
the standard basis in the space
$A_i$
the standard basis in the space
![]() ${\mathrm {Mat}}(m \times n,\mathbb {C})$
of
${\mathrm {Mat}}(m \times n,\mathbb {C})$
of
![]() $m \times n$
complex matrices. Choose
$m \times n$
complex matrices. Choose
![]() $\alpha>0$
small enough, and consider an
$\alpha>0$
small enough, and consider an
![]() $\alpha $
-net
$\alpha $
-net
![]() $b_j$
in a compact in
$b_j$
in a compact in
![]() $\mathbb {C}^m$
containing
$\mathbb {C}^m$
containing
![]() $A_i \left (U \right )$
for all i. Put
$A_i \left (U \right )$
for all i. Put
We look at the perturbation
The derivative of
![]() $\bar {G}G_z$
over
$\bar {G}G_z$
over
![]() $\epsilon _{ij}$
is
$\epsilon _{ij}$
is
Fix any point
![]() $z \in U$
, and choose j so that the second summand in (2.2) is smaller than
$z \in U$
, and choose j so that the second summand in (2.2) is smaller than
![]() $C\alpha $
. At the same time, at least one of the components of
$C\alpha $
. At the same time, at least one of the components of
![]() $\bar {g}(z)$
has absolute value
$\bar {g}(z)$
has absolute value
![]() $> c'$
, where
$> c'$
, where
![]() $c'$
depends only on c and n. Thus, the collection
$c'$
depends only on c and n. Thus, the collection
![]() $\{A_i \bar {g}\}$
contains elements
$\{A_i \bar {g}\}$
contains elements
![]() $c_1e_1, \dots , c_me_m$
, where
$c_1e_1, \dots , c_me_m$
, where
![]() $e_1, \dots , e_m$
is the standard basis of
$e_1, \dots , e_m$
is the standard basis of
![]() $\mathbb {C}^m$
, and
$\mathbb {C}^m$
, and
![]() $|c_i|> c'$
. As invertible matrices form an open set in
$|c_i|> c'$
. As invertible matrices form an open set in
![]() ${\mathrm {Mat}}(m \times m, \mathbb {C}),$
after the perturbation
${\mathrm {Mat}}(m \times m, \mathbb {C}),$
after the perturbation
![]() $\overline {(A_iz-b_j)}g_z$
of norm at most
$\overline {(A_iz-b_j)}g_z$
of norm at most
![]() $C\alpha $
, these vectors still span
$C\alpha $
, these vectors still span
![]() $\mathbb {C}^m$
, provided
$\mathbb {C}^m$
, provided
![]() $\alpha $
is small enough. It follows that
$\alpha $
is small enough. It follows that
![]() $\bar {G}G_z$
is transverse to
$\bar {G}G_z$
is transverse to
![]() $0$
. Thus, by Thom’s parametric transversality theorem, for almost all
$0$
. Thus, by Thom’s parametric transversality theorem, for almost all
![]() $\epsilon $
, we have that
$\epsilon $
, we have that
![]() $|G_\epsilon |^2$
is Morse. Choosing
$|G_\epsilon |^2$
is Morse. Choosing
![]() $g' = G_{\epsilon }$
for
$g' = G_{\epsilon }$
for
![]() $\epsilon $
sufficiently small then finishes the proof.
$\epsilon $
sufficiently small then finishes the proof.
3. Coarse analysis of the Cornalba-Shiffman example
The goal of this section is to prove Theorem 1.5. We will break down its proof into Propositions 3.1, 3.4 and 3.6. Since there are no zeros of F when
![]() $r< 2$
, we always assume
$r< 2$
, we always assume
![]() $r\geq 2.$
The following elementary estimate will be used repeatedly. For an integer
$r\geq 2.$
The following elementary estimate will be used repeatedly. For an integer
![]() $m\geq 1,$
$m\geq 1,$
 $$\begin{align*}2^{m(m+1)/2}< \prod_{i=0}^m (1+2^i) < 2^{(m+1)(m+2)/2}.\end{align*}$$
$$\begin{align*}2^{m(m+1)/2}< \prod_{i=0}^m (1+2^i) < 2^{(m+1)(m+2)/2}.\end{align*}$$
First, we estimate
![]() $\mu (F,r)$
as needed for the first part of Theorem 1.5.
$\mu (F,r)$
as needed for the first part of Theorem 1.5.
Proposition 3.1. For all
![]() $\mathfrak {c}$
and all
$\mathfrak {c}$
and all
![]() $r\geq 2$
, it holds
$r\geq 2$
, it holds
where
![]() $C=4+\log \left ( \prod _{i=1}^\infty (1+2^{-i}) \right ).$
$C=4+\log \left ( \prod _{i=1}^\infty (1+2^{-i}) \right ).$
Proof. Let
![]() $k\geq 1$
be an integer such that
$k\geq 1$
be an integer such that
![]() $2^k\leq r <2^{k+1}.$
In this case,
$2^k\leq r <2^{k+1}.$
In this case,
![]() $k \leq \log r < k+1.$
To prove the first inequality, it is enough to take
$k \leq \log r < k+1.$
To prove the first inequality, it is enough to take
![]() $(z,w)=(-r,0).$
Now
$(z,w)=(-r,0).$
Now
 $$ \begin{align*}|F(-r,0)|\geq |g(-r)|\geq |g(-2^k)|=\prod_{i=1}^\infty (1+2^{k-i}),\end{align*} $$
$$ \begin{align*}|F(-r,0)|\geq |g(-r)|\geq |g(-2^k)|=\prod_{i=1}^\infty (1+2^{k-i}),\end{align*} $$
and
 $$ \begin{align*}\prod_{i=1}^\infty (1+2^{k-i})>\prod_{i=1}^k (1+2^{k-i})=\prod_{j=0}^{k-1}(1+2^j)>2^{\frac{k(k-1)}{2}}> \left(\frac{r}{2} \right)^{\frac{k-1}{2}}.\end{align*} $$
$$ \begin{align*}\prod_{i=1}^\infty (1+2^{k-i})>\prod_{i=1}^k (1+2^{k-i})=\prod_{j=0}^{k-1}(1+2^j)>2^{\frac{k(k-1)}{2}}> \left(\frac{r}{2} \right)^{\frac{k-1}{2}}.\end{align*} $$
Since
![]() $\log r<k+1$
, we have that
$\log r<k+1$
, we have that
![]() $\frac {k-1}{2}>\frac {\log r -2}{2}$
, and hence,
$\frac {k-1}{2}>\frac {\log r -2}{2}$
, and hence,
![]() $|F(-r,0)|\geq \left (\frac {r}{2} \right )^{\frac {\log r}{2}-1}.$
Applying logarithm to both sides proves the first inequality.
$|F(-r,0)|\geq \left (\frac {r}{2} \right )^{\frac {\log r}{2}-1}.$
Applying logarithm to both sides proves the first inequality.
To prove the second inequality, we first notice that if
![]() $|z|\leq r$
, then
$|z|\leq r$
, then
 $$ \begin{align*}|g(z)|\leq \prod_{i=1}^\infty (1+2^{-i}|z|)<\prod_{i=1}^\infty (1+2^{k+1-i})=\prod_{j=0}^k (1+2^j) \cdot \prod_{i=1}^\infty (1+2^{-i}).\end{align*} $$
$$ \begin{align*}|g(z)|\leq \prod_{i=1}^\infty (1+2^{-i}|z|)<\prod_{i=1}^\infty (1+2^{k+1-i})=\prod_{j=0}^k (1+2^j) \cdot \prod_{i=1}^\infty (1+2^{-i}).\end{align*} $$
Denoting
![]() $C_1=\prod _{i=1}^\infty (1+2^{-i})$
and estimating
$C_1=\prod _{i=1}^\infty (1+2^{-i})$
and estimating
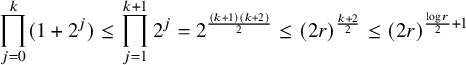 $$ \begin{align*}\prod_{j=0}^k (1+2^j) \leq \prod_{j=1}^{k+1} 2^j=2^{\frac{(k+1)(k+2)}{2}}\leq (2r)^{\frac{k+2}{2}}\leq (2r)^{\frac{\log r}{2}+1}\end{align*} $$
$$ \begin{align*}\prod_{j=0}^k (1+2^j) \leq \prod_{j=1}^{k+1} 2^j=2^{\frac{(k+1)(k+2)}{2}}\leq (2r)^{\frac{k+2}{2}}\leq (2r)^{\frac{\log r}{2}+1}\end{align*} $$
yields
Similarly,
for all
![]() $i\geq 1.$
Using this inequality, we further estimate that if
$i\geq 1.$
Using this inequality, we further estimate that if
![]() $|(z,w)|\leq r$
, then
$|(z,w)|\leq r$
, then
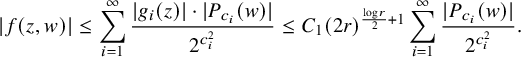 $$ \begin{align*}|f(z,w)|\leq \sum_{i=1}^\infty \frac{|g_i(z)| \cdot |P_{c_i}(w)|}{2^{c_i^2}}\leq C_1 (2r)^{\frac{\log r}{2}+1} \sum_{i=1}^\infty \frac{|P_{c_i}(w)|}{2^{c_i^2}}.\end{align*} $$
$$ \begin{align*}|f(z,w)|\leq \sum_{i=1}^\infty \frac{|g_i(z)| \cdot |P_{c_i}(w)|}{2^{c_i^2}}\leq C_1 (2r)^{\frac{\log r}{2}+1} \sum_{i=1}^\infty \frac{|P_{c_i}(w)|}{2^{c_i^2}}.\end{align*} $$
Morever,
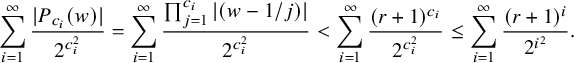 $$ \begin{align*}\sum_{i=1}^\infty \frac{|P_{c_i}(w)|}{2^{c_i^2}}=\sum_{i=1}^\infty \frac{\prod_{j=1}^{c_i}|(w-1/j)|}{2^{c_i^2}}<\sum_{i=1}^\infty \frac{(r+1)^{c_i}}{2^{c_i^2}}\leq \sum_{i=1}^\infty \frac{(r+1)^i}{2^{i^2}}.\end{align*} $$
$$ \begin{align*}\sum_{i=1}^\infty \frac{|P_{c_i}(w)|}{2^{c_i^2}}=\sum_{i=1}^\infty \frac{\prod_{j=1}^{c_i}|(w-1/j)|}{2^{c_i^2}}<\sum_{i=1}^\infty \frac{(r+1)^{c_i}}{2^{c_i^2}}\leq \sum_{i=1}^\infty \frac{(r+1)^i}{2^{i^2}}.\end{align*} $$
To bound the last term, we proceed as follows:
 $$ \begin{align*}\sum_{i=1}^\infty \frac{(r+1)^i}{2^{i^2}}&=\sum_{1\leq i \leq \log (r+1)} \left( \frac{r+1}{2^i} \right)^i + \sum_{ i> \log (r+1)} \left( \frac{r+1}{2^i} \right)^i <\\&< \sum_{1\leq i \leq \log (r+1)} (r+1)^i + \sum_{j=0}^\infty \frac{1}{2^j}< (r+2)^{\log (r+1)}+2<(2r)^{\log 2r}+2. \end{align*} $$
$$ \begin{align*}\sum_{i=1}^\infty \frac{(r+1)^i}{2^{i^2}}&=\sum_{1\leq i \leq \log (r+1)} \left( \frac{r+1}{2^i} \right)^i + \sum_{ i> \log (r+1)} \left( \frac{r+1}{2^i} \right)^i <\\&< \sum_{1\leq i \leq \log (r+1)} (r+1)^i + \sum_{j=0}^\infty \frac{1}{2^j}< (r+2)^{\log (r+1)}+2<(2r)^{\log 2r}+2. \end{align*} $$
Putting all the inequalities together, we obtain
Since
![]() $|F(z,w)|=\sqrt {|g(z)|^2+|f(z,w)|^2}$
, combining (3.1) and (3.2) proves the desired inequality.
$|F(z,w)|=\sqrt {|g(z)|^2+|f(z,w)|^2}$
, combining (3.1) and (3.2) proves the desired inequality.
We will now estimate
![]() $\zeta (F,r,\delta )$
from above. Before we carry out the relevant computations, let us explain the geometric intuition behind the estimate.
$\zeta (F,r,\delta )$
from above. Before we carry out the relevant computations, let us explain the geometric intuition behind the estimate.
Zeros of F belong to intervals
![]() $\{ 2^k \} \times [0,1]$
,
$\{ 2^k \} \times [0,1]$
,
![]() $k\geq 1.$
For a fixed
$k\geq 1.$
For a fixed
![]() $\delta $
, we wish to prove that there exists
$\delta $
, we wish to prove that there exists
![]() $k_0$
such that for all
$k_0$
such that for all
![]() $k\geq k_0$
, each of the intervals,
$k\geq k_0$
, each of the intervals,
![]() $\{ 2^k \} \times [0,1]$
is fully contained in
$\{ 2^k \} \times [0,1]$
is fully contained in
![]() $\{ |F|\leq \delta \}.$
This is the content of Corollary 3.3. Now, on each of these intervals all zeros belong to the same connected component of
$\{ |F|\leq \delta \}.$
This is the content of Corollary 3.3. Now, on each of these intervals all zeros belong to the same connected component of
![]() $\{|F|\leq \delta \}$
and are thus counted at most once in the coarse count
$\{|F|\leq \delta \}$
and are thus counted at most once in the coarse count
![]() $\zeta (F,r,\delta )$
; see Figure 4. In other words, each of the intervals
$\zeta (F,r,\delta )$
; see Figure 4. In other words, each of the intervals
![]() $\{ 2^k \} \times [0,1]$
,
$\{ 2^k \} \times [0,1]$
,
![]() $k\geq k_0$
contributes at most one to
$k\geq k_0$
contributes at most one to
![]() $\zeta (F,r,\delta )$
, and since they appear at rate
$\zeta (F,r,\delta )$
, and since they appear at rate
![]() $\log r$
, we have that
$\log r$
, we have that
The error term comes from zeros on intervals
![]() $\{2^k \}\times [0,1]$
for
$\{2^k \}\times [0,1]$
for
![]() $k<k_0$
where we cannot guarantee merging of zeros in
$k<k_0$
where we cannot guarantee merging of zeros in
![]() $\{ |F| \leq \delta \}$
(i.e., we observe no coarse effects). Moreover, since
$\{ |F| \leq \delta \}$
(i.e., we observe no coarse effects). Moreover, since
![]() $k_0$
depends only on
$k_0$
depends only on
![]() $\delta $
, the error terms only depends on
$\delta $
, the error terms only depends on
![]() $\mathfrak {c}$
and
$\mathfrak {c}$
and
![]() $\delta .$
These considerations are formally proven in Proposition 3.4.
$\delta .$
These considerations are formally proven in Proposition 3.4.
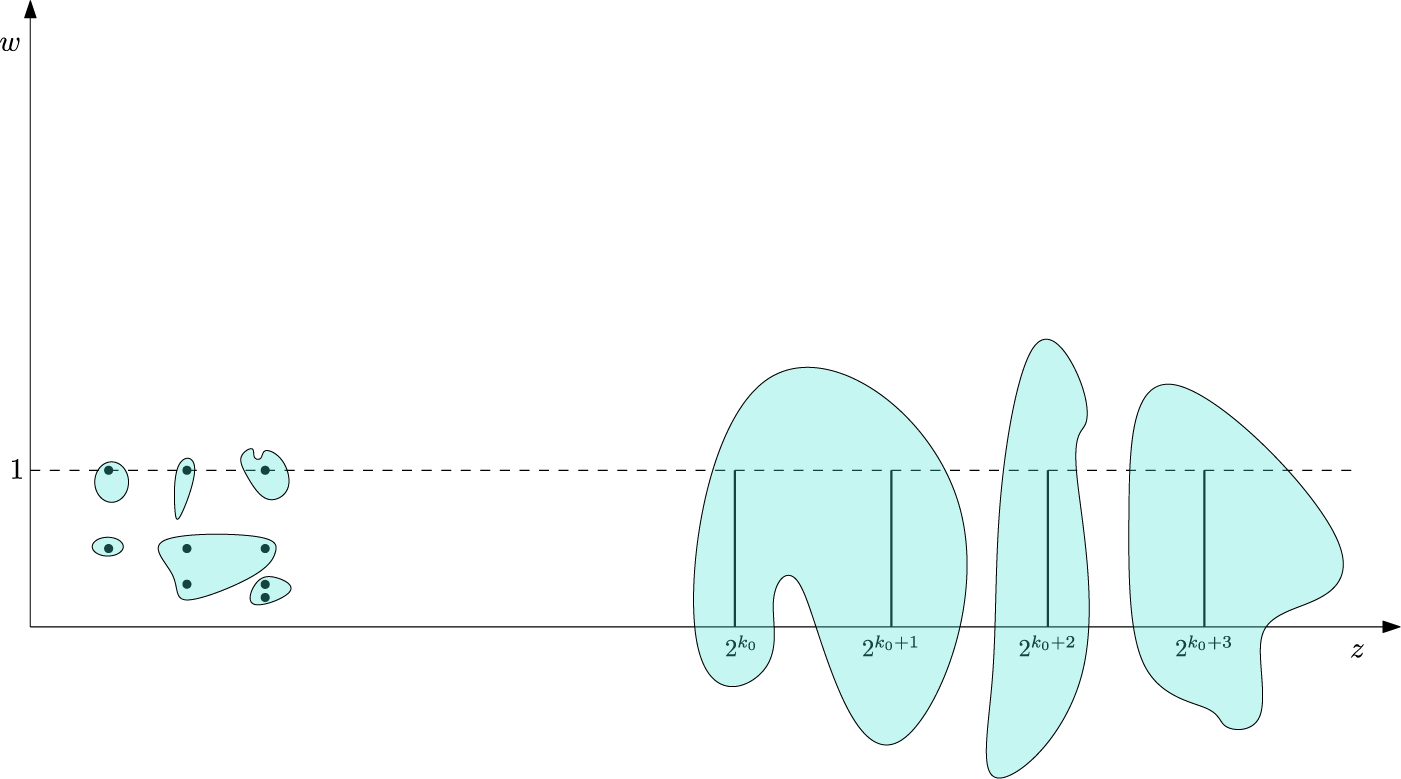
Figure 4 Merging of zeros starting from
![]() $2^{k_0}$
.
$2^{k_0}$
.
Lemma 3.2. For each
![]() $\delta \geq 2^{\frac {(i-1)i}{2}-c_i^2}$
, the whole interval
$\delta \geq 2^{\frac {(i-1)i}{2}-c_i^2}$
, the whole interval
![]() $\{2^i \} \times [0, 2^{c_i-\frac {(i-1)i}{2c_i}} \delta ^{\frac {1}{c_i}}]$
is contained in
$\{2^i \} \times [0, 2^{c_i-\frac {(i-1)i}{2c_i}} \delta ^{\frac {1}{c_i}}]$
is contained in
![]() $\{ |F|\leq \delta \}.$
$\{ |F|\leq \delta \}.$
Proof. First, we notice that
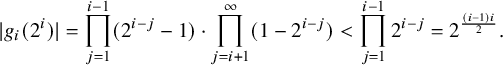 $$ \begin{align*}|g_i(2^i)| = \prod_{j=1}^{i-1}(2^{i-j}-1) \cdot \prod_{j=i+1}^\infty (1-2^{i-j}) < \prod_{j=1}^{i-1}2^{i-j} = 2^{\frac{(i-1)i}{2}}.\end{align*} $$
$$ \begin{align*}|g_i(2^i)| = \prod_{j=1}^{i-1}(2^{i-j}-1) \cdot \prod_{j=i+1}^\infty (1-2^{i-j}) < \prod_{j=1}^{i-1}2^{i-j} = 2^{\frac{(i-1)i}{2}}.\end{align*} $$
Second,
Now, if
![]() $w\in [0,1]$
,
$w\in [0,1]$
,
![]() $|P_{c_i}(w)|<1$
, and the claim follows by the assumption on
$|P_{c_i}(w)|<1$
, and the claim follows by the assumption on
![]() $\delta $
. If
$\delta $
. If
![]() $w\in (1, 2^{c_i-\frac {(i-1)i}{2c_i}} \delta ^{\frac {1}{c_i}}]$
,
$w\in (1, 2^{c_i-\frac {(i-1)i}{2c_i}} \delta ^{\frac {1}{c_i}}]$
,
![]() $|P_{c_i}(w)|<w^{c_i}$
, and thus,
$|P_{c_i}(w)|<w^{c_i}$
, and thus,
![]() $|F(2^i,w)|< 2^{\frac {(i-1)i}{2}-c_i^2} w^{c_i} \leq \delta $
, and the claim follows.
$|F(2^i,w)|< 2^{\frac {(i-1)i}{2}-c_i^2} w^{c_i} \leq \delta $
, and the claim follows.
Corollary 3.3. If
![]() $\delta \geq 2^{\frac {-i(i+1)}{2}}$
, then the whole interval
$\delta \geq 2^{\frac {-i(i+1)}{2}}$
, then the whole interval
![]() $\{2^i \} \times [0,1]$
is contained in
$\{2^i \} \times [0,1]$
is contained in
![]() $\{ |F|\leq \delta \}.$
$\{ |F|\leq \delta \}.$
Proof. Since
![]() $c_i^2\geq i^2$
,
$c_i^2\geq i^2$
,
![]() $\delta \geq 2^{\frac {-i(i+1)}{2}}$
implies that
$\delta \geq 2^{\frac {-i(i+1)}{2}}$
implies that
![]() $\delta \geq 2^{\frac {(i-1)i}{2}-c_i^2}$
, and thus,
$\delta \geq 2^{\frac {(i-1)i}{2}-c_i^2}$
, and thus,
by Lemma 3.2.
Proposition 3.4. The following estimates hold for
![]() $r>2:$
$r>2:$
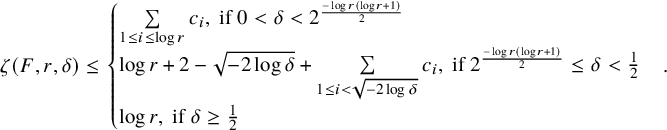 $$ \begin{align*}\zeta(F,r,\delta) \leq \begin{cases} \sum\limits_{1\leq i \leq \log r} c_i , \text{ if } 0<\delta<2^{\frac{-\log r(\log r +1)}{2}}\\ \log r+2- \sqrt{-2 \log \delta}+ \sum\limits_{1\leq i <\sqrt{-2 \log \delta} } c_i,\text{ if } 2^{\frac{-\log r(\log r +1)}{2}}\leq \delta < \frac{1}{2}\\ \log r ,\text{ if } \delta \geq \frac{1}{2}\\ \end{cases}.\end{align*} $$
$$ \begin{align*}\zeta(F,r,\delta) \leq \begin{cases} \sum\limits_{1\leq i \leq \log r} c_i , \text{ if } 0<\delta<2^{\frac{-\log r(\log r +1)}{2}}\\ \log r+2- \sqrt{-2 \log \delta}+ \sum\limits_{1\leq i <\sqrt{-2 \log \delta} } c_i,\text{ if } 2^{\frac{-\log r(\log r +1)}{2}}\leq \delta < \frac{1}{2}\\ \log r ,\text{ if } \delta \geq \frac{1}{2}\\ \end{cases}.\end{align*} $$
Proof. For a subset
![]() $S \subset \mathbb{C}^2,$
we write
$S \subset \mathbb{C}^2,$
we write
![]() $\dim H_0(S)$
for the number of its path components. First, we notice that for all
$\dim H_0(S)$
for the number of its path components. First, we notice that for all
![]() $r\geq 2$
,
$r\geq 2$
,
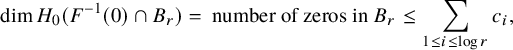 $$ \begin{align*}\dim H_0(F^{-1}(0) \cap B_r)= \text{ number of zeros in } B_r \leq \sum\limits_{1\leq i \leq \log r} c_i,\end{align*} $$
$$ \begin{align*}\dim H_0(F^{-1}(0) \cap B_r)= \text{ number of zeros in } B_r \leq \sum\limits_{1\leq i \leq \log r} c_i,\end{align*} $$
and hence,
![]() $\zeta (F,r,\delta ) \leq \sum \limits _{1\leq i \leq \log r} c_i$
, which proves the first case of the proposition.
$\zeta (F,r,\delta ) \leq \sum \limits _{1\leq i \leq \log r} c_i$
, which proves the first case of the proposition.
Now, we treat the third case (i.e.,
![]() $\delta \geq \frac {1}{2}).$
In this case, by Corollary 3.3, all intervals
$\delta \geq \frac {1}{2}).$
In this case, by Corollary 3.3, all intervals
![]() $\{2^i \} \times [0,1], i\geq 1$
are contained in
$\{2^i \} \times [0,1], i\geq 1$
are contained in
![]() $\{ |F|\leq \delta \}.$
Thus,
$\{ |F|\leq \delta \}.$
Thus,
![]() $\dim H_0(\{|F|\leq \delta \} \cap B_r)$
equals the number of intervals
$\dim H_0(\{|F|\leq \delta \} \cap B_r)$
equals the number of intervals
![]() $\{2^i \} \times [0,1], i\geq 1$
which intersect
$\{2^i \} \times [0,1], i\geq 1$
which intersect
![]() $B_r.$
This number is not greater than
$B_r.$
This number is not greater than
![]() $\log r$
, and thus,
$\log r$
, and thus,
![]() $ \zeta (F,r,\delta ) \leq \log r.$
$ \zeta (F,r,\delta ) \leq \log r.$
Finally, we treat the second case (i.e.,
![]() $2^{\frac {-\log r(\log r +1)}{2}}\leq \delta < \frac {1}{2}).$
Denote by
$2^{\frac {-\log r(\log r +1)}{2}}\leq \delta < \frac {1}{2}).$
Denote by
![]() $r_0>2$
the unique real number such that
$r_0>2$
the unique real number such that
![]() $\delta =2^{\frac {-\log r_0(\log r_0 +1)}{2}}.$
By the assumption,
$\delta =2^{\frac {-\log r_0(\log r_0 +1)}{2}}.$
By the assumption,
![]() $r_0\leq r.$
Let
$r_0\leq r.$
Let
![]() $k\geq 1$
be an integer such that
$k\geq 1$
be an integer such that
![]() $2^k<r_0 \leq 2^{k+1}.$
Now
$2^k<r_0 \leq 2^{k+1}.$
Now
![]() $2^{\frac {-(k+1)(k+2)}{2}}\leq \delta $
, and hence by Corollary 3.3,
$2^{\frac {-(k+1)(k+2)}{2}}\leq \delta $
, and hence by Corollary 3.3,
![]() $\{ |F|\leq \delta \}$
contains all interval
$\{ |F|\leq \delta \}$
contains all interval
![]() $\{2^i \}\times [0,1], i \geq k+1.$
Thus,
$\{2^i \}\times [0,1], i \geq k+1.$
Thus,
where
and
From (3.3), it follows that
Since
![]() $k<\log r_0 < \sqrt {-2 \log \delta }$
, we have that
$k<\log r_0 < \sqrt {-2 \log \delta }$
, we have that
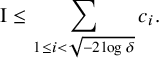 $$ \begin{align*}\textrm{I} \leq \sum_{1\leq i <\sqrt{-2 \log \delta} } c_i .\end{align*} $$
$$ \begin{align*}\textrm{I} \leq \sum_{1\leq i <\sqrt{-2 \log \delta} } c_i .\end{align*} $$
However,
![]() $r\geq r_0$
, and thus,
$r\geq r_0$
, and thus,
![]() $\log r \geq \log r_0>k$
as well as
$\log r \geq \log r_0>k$
as well as
Last, we use
![]() $\sqrt {-2\log \delta }<\log r_0+1 \leq k+2$
to obtain the desired inequality.
$\sqrt {-2\log \delta }<\log r_0+1 \leq k+2$
to obtain the desired inequality.
We will now provide a lower bound for
![]() $\zeta (F,r,\delta ).$
As before, we start by explaining the geometric intuition.
$\zeta (F,r,\delta ).$
As before, we start by explaining the geometric intuition.
As r increases, new zeros of F appear on intervals
![]() $\{2^k\} \times [0,1]$
(i.e., at a rate
$\{2^k\} \times [0,1]$
(i.e., at a rate
![]() $\log r).$
We wish to prove that zeros on different intervals will not be counted as one zero in the coarse count
$\log r).$
We wish to prove that zeros on different intervals will not be counted as one zero in the coarse count
![]() $\zeta (F,r,\delta ).$
Precisely, in Lemma 3.5, we prove that for a fixed
$\zeta (F,r,\delta ).$
Precisely, in Lemma 3.5, we prove that for a fixed
![]() $\delta $
, there exists
$\delta $
, there exists
![]() $k_0$
which depends only on
$k_0$
which depends only on
![]() $\delta $
, such that the set
$\delta $
, such that the set
![]() $\{ |F|\leq \delta \}$
does not intersect any of the hyperplanes
$\{ |F|\leq \delta \}$
does not intersect any of the hyperplanes
![]() $H_k=\{ Re(z)=2^k+2^{k-1} \}$
for
$H_k=\{ Re(z)=2^k+2^{k-1} \}$
for
![]() $k\geq k_0.$
Since
$k\geq k_0.$
Since
![]() $H_k$
separates intervals
$H_k$
separates intervals
![]() $\{2^k\} \times [0,1]$
and
$\{2^k\} \times [0,1]$
and
![]() $\{2^{k+1} \} \times [0,1]$
,
$\{2^{k+1} \} \times [0,1]$
,
![]() $\{|F|\leq \delta \}$
cannot contain zeros from different intervals for
$\{|F|\leq \delta \}$
cannot contain zeros from different intervals for
![]() $k\geq k_0$
; see Figure 5. Similarly to the case of the upper bound, this implies that
$k\geq k_0$
; see Figure 5. Similarly to the case of the upper bound, this implies that
where the error term comes from zeros on intervals
![]() $\{2^k \}\times [0,1]$
for
$\{2^k \}\times [0,1]$
for
![]() $k<k_0$
where we cannot guarantee separation of components of
$k<k_0$
where we cannot guarantee separation of components of
![]() $\{ |F| \leq \delta \}.$
These considerations are formally proven in Proposition 3.6.
$\{ |F| \leq \delta \}.$
These considerations are formally proven in Proposition 3.6.
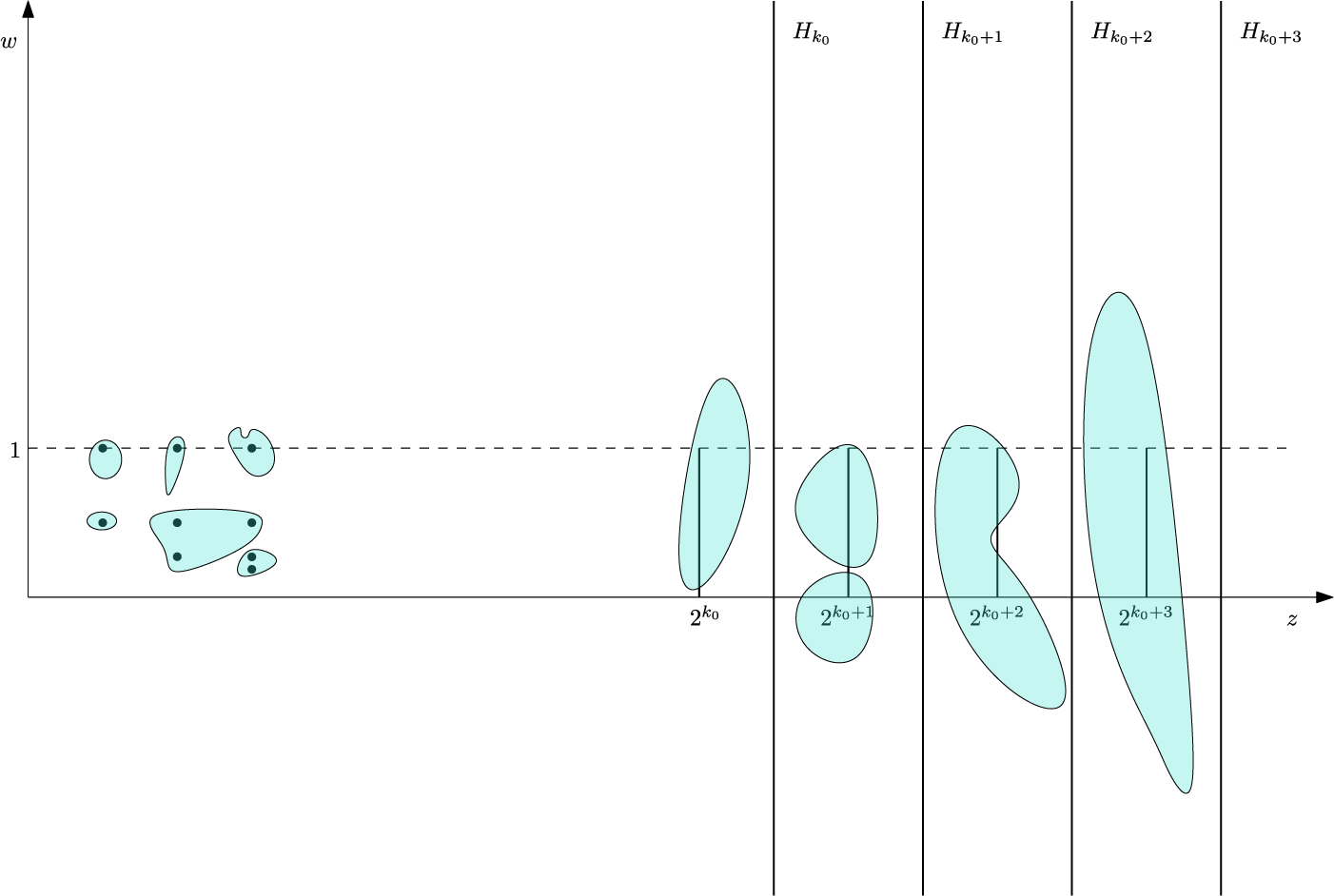
Figure 5 Separation of zeros starting from
![]() $2^{k_0}$
.
$2^{k_0}$
.
In the lemma and the proposition that follow, we denote by
![]() $C_0=\frac {1}{2}\prod _{i=1}^\infty \left (1-\frac {3}{2^{i+1}} \right ).$
$C_0=\frac {1}{2}\prod _{i=1}^\infty \left (1-\frac {3}{2^{i+1}} \right ).$
Lemma 3.5. Let
![]() $z\in \mathbb {C}$
be such that
$z\in \mathbb {C}$
be such that
![]() $Re(z)=2^k+2^{k-1}$
for some integer
$Re(z)=2^k+2^{k-1}$
for some integer
![]() $k\geq 1.$
Then for all
$k\geq 1.$
Then for all
![]() $w\in \mathbb {C}$
, it holds
$w\in \mathbb {C}$
, it holds
Proof. We estimate
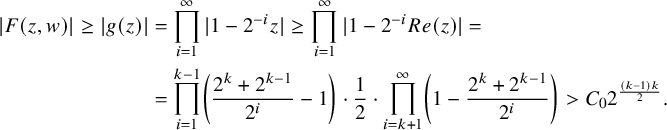 $$ \begin{align*}|F(z,w)|\geq |g(z)| &= \prod_{i=1}^\infty |1-2^{-i}z|\geq \prod_{i=1}^\infty |1-2^{-i} Re(z)|=\\&=\prod_{i=1}^{k-1} \left(\frac{2^k+2^{k-1}}{2^i}-1 \right)\cdot \frac{1}{2} \cdot \prod_{i=k+1}^\infty \left(1-\frac{2^k+2^{k-1}}{2^i} \right)>C_0 2^{\frac{(k-1)k}{2}}.\\[-40pt]\end{align*} $$
$$ \begin{align*}|F(z,w)|\geq |g(z)| &= \prod_{i=1}^\infty |1-2^{-i}z|\geq \prod_{i=1}^\infty |1-2^{-i} Re(z)|=\\&=\prod_{i=1}^{k-1} \left(\frac{2^k+2^{k-1}}{2^i}-1 \right)\cdot \frac{1}{2} \cdot \prod_{i=k+1}^\infty \left(1-\frac{2^k+2^{k-1}}{2^i} \right)>C_0 2^{\frac{(k-1)k}{2}}.\\[-40pt]\end{align*} $$
Proposition 3.6. For all
![]() $r\geq 2$
, it holds
$r\geq 2$
, it holds
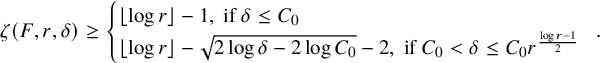 $$ \begin{align*}\zeta(F,r,\delta) \geq \begin{cases} \lfloor \log r \rfloor -1, \text{ if } \delta\leq C_0 \\ \lfloor \log r \rfloor -\sqrt{2\log \delta - 2 \log C_0} -2,\text{ if } C_0< \delta \leq C_0 r^{\frac{\log r -1}{2}}\end{cases}\!\!.\end{align*} $$
$$ \begin{align*}\zeta(F,r,\delta) \geq \begin{cases} \lfloor \log r \rfloor -1, \text{ if } \delta\leq C_0 \\ \lfloor \log r \rfloor -\sqrt{2\log \delta - 2 \log C_0} -2,\text{ if } C_0< \delta \leq C_0 r^{\frac{\log r -1}{2}}\end{cases}\!\!.\end{align*} $$
Proof. We first prove the case
![]() $\delta \leq C_0.$
By Lemma 3.5, we see that on each hyperplane
$\delta \leq C_0.$
By Lemma 3.5, we see that on each hyperplane
![]() $\{ Re(z)=2^i+2^{i-1} \}, i\geq 1$
, it holds
$\{ Re(z)=2^i+2^{i-1} \}, i\geq 1$
, it holds
![]() $|F(z,w)|>C_0\geq \delta .$
Hence,
$|F(z,w)|>C_0\geq \delta .$
Hence,
![]() $\{ |F|\leq \delta \}$
does not intersect any of these hyperplanes and in particular, zeros
$\{ |F|\leq \delta \}$
does not intersect any of these hyperplanes and in particular, zeros
![]() $(2^i,1),i\geq 1$
all belong to different connected components of
$(2^i,1),i\geq 1$
all belong to different connected components of
![]() $\{ |F|\leq \delta \}.$
In other words,
$\{ |F|\leq \delta \}.$
In other words,
which finishes the proof of the first case.
To prove the second case, we first denote by
![]() $r_0> 2$
the unique real number such that
$r_0> 2$
the unique real number such that
![]() $\delta = C_0 r_0^{\frac {\log r_0 -1}{2}}.$
By assumption,
$\delta = C_0 r_0^{\frac {\log r_0 -1}{2}}.$
By assumption,
![]() $r_0\leq r$
, and we denote by
$r_0\leq r$
, and we denote by
![]() $k\geq 1$
an integer such that
$k\geq 1$
an integer such that
![]() $2^k \leq r_0 < 2^{k+1}.$
Now
$2^k \leq r_0 < 2^{k+1}.$
Now
![]() $\delta < C_0 2^{\frac {k(k+1)}{2}}$
, and Lemma 3.5 implies that
$\delta < C_0 2^{\frac {k(k+1)}{2}}$
, and Lemma 3.5 implies that
![]() $\{ |F| \leq \delta \}$
does not intersect hyperplanes
$\{ |F| \leq \delta \}$
does not intersect hyperplanes
![]() $\{Re(z)=2^i+2^{i-1} \}, i\geq k+1.$
As in the first case, zeros
$\{Re(z)=2^i+2^{i-1} \}, i\geq k+1.$
As in the first case, zeros
![]() $(2^i,1),i\geq k+1$
belong to different connected components of
$(2^i,1),i\geq k+1$
belong to different connected components of
![]() $\{ |F|\leq \delta \}$
and thus
$\{ |F|\leq \delta \}$
and thus
Since
![]() $\log \delta =\log C_0 + \frac {1}{2}\log r_0 (\log r_0 -1)> \log C_0 + \frac {1}{2}(k-1)^2$
, we have that
$\log \delta =\log C_0 + \frac {1}{2}\log r_0 (\log r_0 -1)> \log C_0 + \frac {1}{2}(k-1)^2$
, we have that
![]() $k<\sqrt {2\log \delta - 2\log C_0}+1$
, and the claim follows.
$k<\sqrt {2\log \delta - 2\log C_0}+1$
, and the claim follows.
4. Counting islands
Let us start with the proof of Theorem 1.7, which, as was mentioned in the introduction, is a an easy corollary of Rouché’s theorem.
Proof of Theorem 1.7.
By Rouché’s theorem for analytic mappings from
![]() $\mathbb {C}^n$
to
$\mathbb {C}^n$
to
![]() $\mathbb {C}^n$
(see, for example, [Reference D’Angelo14, Section 2.1.3]), if
$\mathbb {C}^n$
(see, for example, [Reference D’Angelo14, Section 2.1.3]), if
![]() $g:\mathbb {C}^n \to \mathbb {C}^n$
is a polynomial mapping of degree at most k such that
$g:\mathbb {C}^n \to \mathbb {C}^n$
is a polynomial mapping of degree at most k such that
![]() $d_{C^0}(f|_{B_r},g|_{B_r}) < \delta /2,$
then
$d_{C^0}(f|_{B_r},g|_{B_r}) < \delta /2,$
then
By Bézout’s theorem, however,
By Proposition 2.1, it is enough to take k such that
![]() $C_a a^{-k} \mu (f,ar) < \delta /2.$
It is easy to see that the optimal such k satisfies
$C_a a^{-k} \mu (f,ar) < \delta /2.$
It is easy to see that the optimal such k satisfies
Combining the three displayed inequalities finishes the proof.
Before we give a formal proof of Theorem 1.9, let us briefly explain the geometric intuition as we did for the proof of Theorem 1.5. As we already explained, for a fixed
![]() $\delta $
, the sublevel set
$\delta $
, the sublevel set
![]() $\{ |F| \leq \delta \}$
stabilizes starting from
$\{ |F| \leq \delta \}$
stabilizes starting from
![]() $r=2^{k_0}$
into components which contain intervals
$r=2^{k_0}$
into components which contain intervals
![]() $\{2^k \} \times [0,1]$
,
$\{2^k \} \times [0,1]$
,
![]() $k\geq k_0$
, but which are separated by hyperplanes
$k\geq k_0$
, but which are separated by hyperplanes
![]() $H_k=\{ Re(z)=2^k+2^{k-1} \}. $
However, we will show that these components, in fact, contain intervals
$H_k=\{ Re(z)=2^k+2^{k-1} \}. $
However, we will show that these components, in fact, contain intervals
![]() $\{2^k \} \times [0,L(k)]$
, where
$\{2^k \} \times [0,L(k)]$
, where
![]() $L(k)$
can grow arbitrarily fast, the lower bound on growth depending on
$L(k)$
can grow arbitrarily fast, the lower bound on growth depending on
![]() $\mathfrak {c}.$
This follows from Lemma 3.2. In other words, components of
$\mathfrak {c}.$
This follows from Lemma 3.2. In other words, components of
![]() $\{|F|\leq \delta \}$
get elongated in w-direction, and thus, they partly remain outside of
$\{|F|\leq \delta \}$
get elongated in w-direction, and thus, they partly remain outside of
![]() $B_r$
for very large r, as shown on Figure 6. Due to this elongation, most of the components of
$B_r$
for very large r, as shown on Figure 6. Due to this elongation, most of the components of
![]() $\{|F|\leq \delta \}$
only contribute to
$\{|F|\leq \delta \}$
only contribute to
![]() $\zeta (F,r,\delta )$
and not to
$\zeta (F,r,\delta )$
and not to
![]() $\zeta ^0(F,r,\delta )$
, which leads to the upper bound given by Theorem 1.9.
$\zeta ^0(F,r,\delta )$
, which leads to the upper bound given by Theorem 1.9.
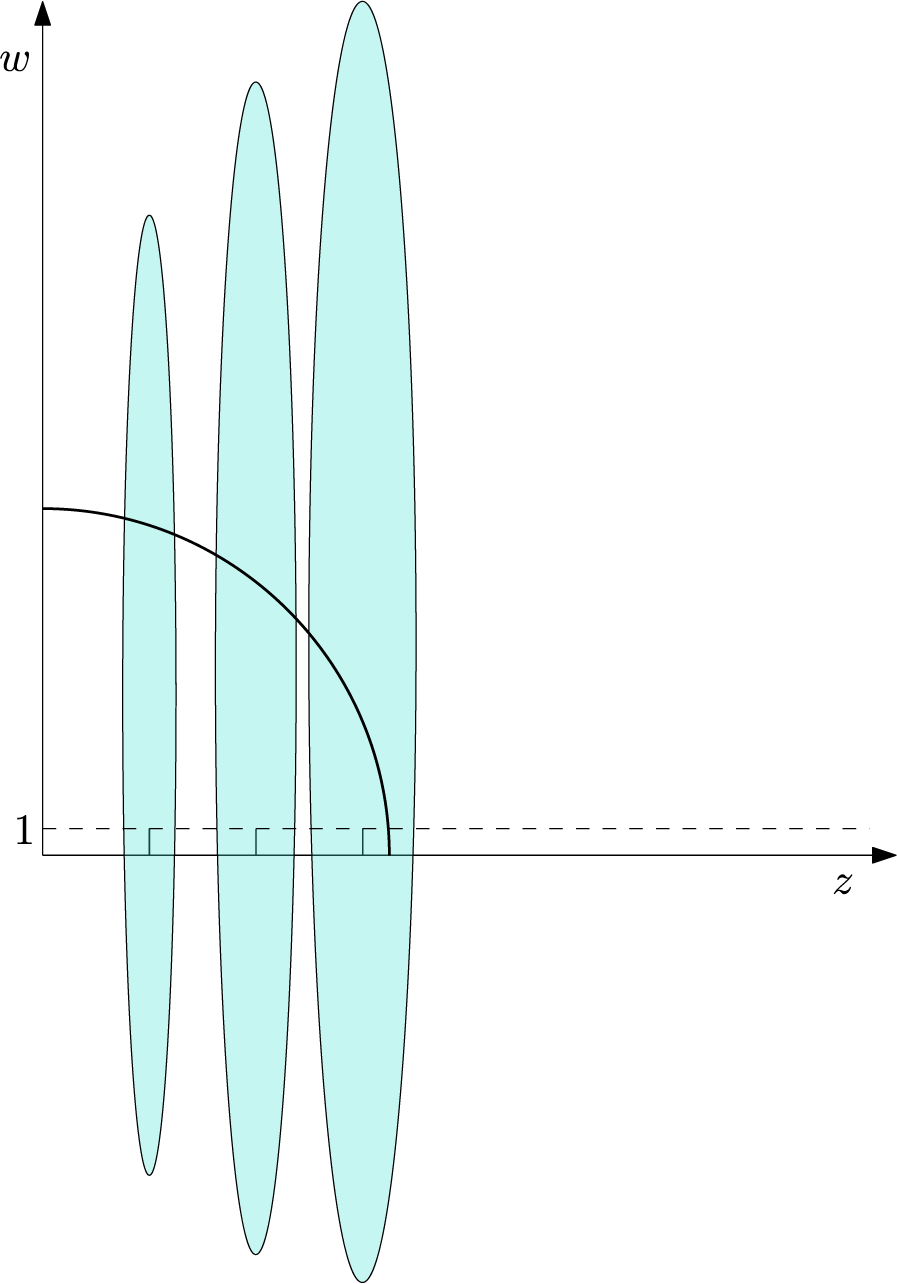
Figure 6 Components count for
![]() $\zeta (F,r,\delta )$
, but not for
$\zeta (F,r,\delta )$
, but not for
![]() $\zeta ^0(F,r,\delta )$
.
$\zeta ^0(F,r,\delta )$
.
Proof of Theorem 1.9.
Since
![]() $\zeta ^0(F,r,\delta )$
is decreasing in
$\zeta ^0(F,r,\delta )$
is decreasing in
![]() $\delta $
, it is enough to prove the statement for
$\delta $
, it is enough to prove the statement for
![]() $\delta \leq 1.$
Denote by
$\delta \leq 1.$
Denote by
![]() $b_i= 2^{c_i-\frac {(i-1)i}{2c_i}}\delta ^{\frac {1}{c_i}}.$
Let
$b_i= 2^{c_i-\frac {(i-1)i}{2c_i}}\delta ^{\frac {1}{c_i}}.$
Let
![]() $i_0(l,\lambda ,\delta )$
be the smallest index such that
$i_0(l,\lambda ,\delta )$
be the smallest index such that
-
1) For all
 $i\geq i_0$
,
$i\geq i_0$
,
 $\delta \geq \max (2^{-c_i},2^{\frac {(i-1)i}{2}-c_i^2})$
;
$\delta \geq \max (2^{-c_i},2^{\frac {(i-1)i}{2}-c_i^2})$
; -
2)
 $\log b_{i_0}\geq i_0$
;
$\log b_{i_0}\geq i_0$
; -
3) For all
 $i\geq i_0$
,
$i\geq i_0$
,
 $b_i$
is increasing.
$b_i$
is increasing.
Now,
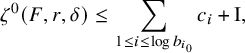 $$ \begin{align} \zeta^0(F,r,\delta) \leq \sum_{1\leq i \leq \log b_{i_0}} c_i + \textrm{I}, \end{align} $$
$$ \begin{align} \zeta^0(F,r,\delta) \leq \sum_{1\leq i \leq \log b_{i_0}} c_i + \textrm{I}, \end{align} $$
where
Since the first term of the right-hand side of this inequality depends only on
![]() $\delta $
and
$\delta $
and
![]() $\mathfrak {c}$
, we wish to estimate
$\mathfrak {c}$
, we wish to estimate
![]() $\textrm {I}$
. If
$\textrm {I}$
. If
![]() $r\leq b_{i_0}$
, then
$r\leq b_{i_0}$
, then
![]() $2^i>r$
and
$2^i>r$
and
![]() $\textrm {I}=0$
. Thus, we assume that
$\textrm {I}=0$
. Thus, we assume that
![]() $r>b_{i_0}.$
First, from 2), it follows that
$r>b_{i_0}.$
First, from 2), it follows that
Now, 3) implies that there exists a unique integer
![]() $k\geq i_0$
such that
$k\geq i_0$
such that
![]() $b_k\leq r <b_{k+1}.$
Due to 1), we may apply Lemma 3.2 to conclude that
$b_k\leq r <b_{k+1}.$
Due to 1), we may apply Lemma 3.2 to conclude that
![]() $\{ |F|\leq \delta \}$
contains intervals
$\{ |F|\leq \delta \}$
contains intervals
![]() $\{2^i \} \times [0,b_i]$
for all
$\{2^i \} \times [0,b_i]$
for all
![]() $i\geq i_0.$
This fact, combined with (4.2), implies
$i\geq i_0.$
This fact, combined with (4.2), implies
Going back to (4.1), we have that
 $$ \begin{align} \zeta^0(F,r,\delta) \leq \sum_{1\leq i \leq \log b_{i_0}} c_i -i_0 +k. \end{align} $$
$$ \begin{align} \zeta^0(F,r,\delta) \leq \sum_{1\leq i \leq \log b_{i_0}} c_i -i_0 +k. \end{align} $$
Finally, 1) gives us that
![]() $\delta ^{\frac {1}{c_k}}\geq \frac {1}{2}$
, and hence,
$\delta ^{\frac {1}{c_k}}\geq \frac {1}{2}$
, and hence,
![]() $2^{c_k-\frac {(k-1)k}{2c_k}-1}\leq b_k\leq r.$
Taking logarithms, we obtain that
$2^{c_k-\frac {(k-1)k}{2c_k}-1}\leq b_k\leq r.$
Taking logarithms, we obtain that
Since
![]() $\frac {(k-1)k}{2c_k}+1$
has an upper bound which only depends on
$\frac {(k-1)k}{2c_k}+1$
has an upper bound which only depends on
![]() $\lambda $
, taking logarithms l times gives us
$\lambda $
, taking logarithms l times gives us
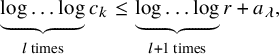 $$ \begin{align*}\underbrace{\log \ldots \log}_{l \text{ times}} c_k \leq \underbrace{\log \ldots \log}_{l+1 \text{ times}} r + a_{\lambda},\end{align*} $$
$$ \begin{align*}\underbrace{\log \ldots \log}_{l \text{ times}} c_k \leq \underbrace{\log \ldots \log}_{l+1 \text{ times}} r + a_{\lambda},\end{align*} $$
where
![]() $a_{\lambda }$
depends only on
$a_{\lambda }$
depends only on
![]() $\lambda .$
Substituting the desired value of
$\lambda .$
Substituting the desired value of
![]() $c_k$
in this inequality together with (4.3) finishes the proof.
$c_k$
in this inequality together with (4.3) finishes the proof.
5. Comparison with other results
The goal of this section is to compare the results of this paper to the results of [Reference Li and Taylor24]. More precisely, we will deduce Theorem 5.1 in [Reference Li and Taylor24] from Theorem 1.7, as well as show that Theorem 1.2 does not follow from Theorem 5.1 in [Reference Li and Taylor24]. We start by recalling this result.
For an entire map
![]() $f:\mathbb {C}^n\to \mathbb {C}^n$
, let
$f:\mathbb {C}^n\to \mathbb {C}^n$
, let
![]() $J_f$
denote the complex Jacobian matrix. Given a sequence of zeros
$J_f$
denote the complex Jacobian matrix. Given a sequence of zeros
![]() $\xi =\{ \xi _i\}\subset f^{-1}(0)$
, we define
$\xi =\{ \xi _i\}\subset f^{-1}(0)$
, we define
![]() $\zeta _\xi (f,r)$
to be the number of elements of
$\zeta _\xi (f,r)$
to be the number of elements of
![]() $\xi $
inside a ball
$\xi $
inside a ball
![]() $B_r.$
$B_r.$
Theorem 5.1 (Theorem 5.1 in [Reference Li and Taylor24]).
Let
![]() $f:\mathbb {C}^n\to \mathbb {C}^n$
be an entire map and
$f:\mathbb {C}^n\to \mathbb {C}^n$
be an entire map and
![]() $\xi =\{ \xi _i\}$
a sequence of zeros of
$\xi =\{ \xi _i\}$
a sequence of zeros of
![]() $f.$
If there exist real numbers
$f.$
If there exist real numbers
![]() $c>0$
and b such that
$c>0$
and b such that
then for any
![]() $a>1$
, it holds
$a>1$
, it holds
when
![]() $r\to \infty .$
$r\to \infty .$
First, we give a proof of Theorem 5.1 using Theorem 1.7. The strategy of the proof follows [Reference Ji22]. Namely, the main results of [Reference Ji22], Theorems 1.1 and 1.2, are proven using a lemma which was referred to as ‘Weak Bézout estimate’; see [Reference Ji22, Lemma 3.1]. This lemma establishes an inequality
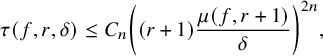 $$ \begin{align} \tau(f,r,\delta) \leq C_n \left( (r+1)\frac{\mu(f,r+1)}{\delta} \right)^{2n}, \end{align} $$
$$ \begin{align} \tau(f,r,\delta) \leq C_n \left( (r+1)\frac{\mu(f,r+1)}{\delta} \right)^{2n}, \end{align} $$
with
![]() $C_n$
which depends only on
$C_n$
which depends only on
![]() $n.$
The proof of (5.1) relies on a global version of the Chern-Levine-Nirenberg inequality; see [Reference Ji22, Theorem 2.1] and references therein. Substituting (5.1) with Theorem 1.7 and using the same general arguments as in [Reference Ji22] proves Theorem 5.1. To implement this strategy, we will need the following lemma.
$n.$
The proof of (5.1) relies on a global version of the Chern-Levine-Nirenberg inequality; see [Reference Ji22, Theorem 2.1] and references therein. Substituting (5.1) with Theorem 1.7 and using the same general arguments as in [Reference Ji22] proves Theorem 5.1. To implement this strategy, we will need the following lemma.
Lemma 5.2. Let
![]() $f:\mathbb {C}^n\to \mathbb {C}^n$
be an entire map and
$f:\mathbb {C}^n\to \mathbb {C}^n$
be an entire map and
![]() $\xi $
a zero of f such that
$\xi $
a zero of f such that
![]() $J_f(\xi )\neq 0.$
Then, for all
$J_f(\xi )\neq 0.$
Then, for all
![]() $z\in \mathbb {C}^n$
such that
$z\in \mathbb {C}^n$
such that
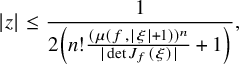 $$ \begin{align*}|z| \leq \frac{1}{2\left( n! \frac{(\mu(f,|\xi|+1))^n}{|\det J_f(\xi)|} +1 \right)},\end{align*} $$
$$ \begin{align*}|z| \leq \frac{1}{2\left( n! \frac{(\mu(f,|\xi|+1))^n}{|\det J_f(\xi)|} +1 \right)},\end{align*} $$
it holds
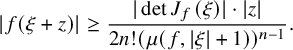 $$ \begin{align*}|f(\xi+z)|\geq \frac{ |\det J_f(\xi)| \cdot |z|}{2n! (\mu(f,|\xi|+1))^{n-1}}.\end{align*} $$
$$ \begin{align*}|f(\xi+z)|\geq \frac{ |\det J_f(\xi)| \cdot |z|}{2n! (\mu(f,|\xi|+1))^{n-1}}.\end{align*} $$
The proof of Lemma 5.2 can be extracted from the proof of Theorem 1.1 in [Reference Ji22]. We present it here for the sake of completeness. We will use the following auxiliary statement, which is a direct consequence of Schwarz lemma; see [Reference Ji22, Lemma 3.4] for details.
Lemma 5.3. Let
![]() $f:\mathbb {C}^n\to \mathbb {C}^n$
be an entire map such that
$f:\mathbb {C}^n\to \mathbb {C}^n$
be an entire map such that
![]() $f(0)=0, J_f(0)=0.$
Then for all z such that
$f(0)=0, J_f(0)=0.$
Then for all z such that
![]() $|z|\leq \frac {1}{2\mu (f,1)}$
, it holds
$|z|\leq \frac {1}{2\mu (f,1)}$
, it holds
![]() $|f(z)|\leq \frac {1}{2}|z|.$
$|f(z)|\leq \frac {1}{2}|z|.$
Proof of Lemma 5.2.
We start by proving the following auxiliary inequality:
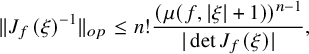 $$ \begin{align} \| J_f(\xi)^{-1} \|_{op} \leq n! \frac{(\mu(f,|\xi|+1))^{n-1}}{|\det J_f(\xi)|}, \end{align} $$
$$ \begin{align} \| J_f(\xi)^{-1} \|_{op} \leq n! \frac{(\mu(f,|\xi|+1))^{n-1}}{|\det J_f(\xi)|}, \end{align} $$
where
![]() $\| \cdot \|_{op}$
denotes the operator norm. Recall that
$\| \cdot \|_{op}$
denotes the operator norm. Recall that
and thus, we need to prove that
By Cauchy-Schwarz inequality,
and we are left to prove that
For each i and j,
![]() $\operatorname {adj}(J_f(\xi ))_{i,j}$
is a sum of
$\operatorname {adj}(J_f(\xi ))_{i,j}$
is a sum of
![]() $(n-1)!$
terms, each of which is a product of
$(n-1)!$
terms, each of which is a product of
![]() $n-1$
partial derivatives of
$n-1$
partial derivatives of
![]() $f.$
Thus,
$f.$
Thus,
Finally, Cauchy’s inequality yields that
![]() $\max _i |\partial _if(\xi )|\leq \mu (f,|\xi |+1)$
, which completes the proof of (5.2).
$\max _i |\partial _if(\xi )|\leq \mu (f,|\xi |+1)$
, which completes the proof of (5.2).
Now, let
![]() $g:\mathbb {C}^n \to \mathbb {C}^n$
be an entire map given by
$g:\mathbb {C}^n \to \mathbb {C}^n$
be an entire map given by
![]() $g(z)=(J_f(\xi ))^{-1}f(\xi +z).$
Since
$g(z)=(J_f(\xi ))^{-1}f(\xi +z).$
Since
![]() $g(0)=0$
and
$g(0)=0$
and
![]() $J_g(0)=\mathrm {id}_{\mathbb {C}^n}$
, we may apply Lemma 5.3 to the map
$J_g(0)=\mathrm {id}_{\mathbb {C}^n}$
, we may apply Lemma 5.3 to the map
![]() $g(z)-z$
, which gives us
$g(z)-z$
, which gives us
for all z, such that
![]() $|z|\leq \frac {1}{2\mu (g(z)-z, 1)}$
. Moreover,
$|z|\leq \frac {1}{2\mu (g(z)-z, 1)}$
. Moreover,
![]() $\mu (g(z)-z,1)\leq \mu (g,1)+1$
implies that (5.3) holds for all z with
$\mu (g(z)-z,1)\leq \mu (g,1)+1$
implies that (5.3) holds for all z with
![]() $|z| \leq \frac {1}{2(\mu (g,1)+1)}$
, and triangle inequality further implies that
$|z| \leq \frac {1}{2(\mu (g,1)+1)}$
, and triangle inequality further implies that
as long as
![]() $|z|\leq \frac {1}{2(\mu (g,1)+1)}.$
From the definition of g and (5.4), it follows that
$|z|\leq \frac {1}{2(\mu (g,1)+1)}.$
From the definition of g and (5.4), it follows that
for all z such that
![]() $|z|\leq \frac {1}{2(\mu (g,1)+1)}.$
Applying (5.2) to (5.5) yields
$|z|\leq \frac {1}{2(\mu (g,1)+1)}.$
Applying (5.2) to (5.5) yields
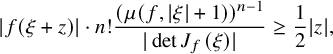 $$ \begin{align} |f(\xi+z)| \cdot n! \frac{(\mu(f,|\xi|+1))^{n-1}}{|\det J_f(\xi)|} \geq \frac{1}{2}|z|, \end{align} $$
$$ \begin{align} |f(\xi+z)| \cdot n! \frac{(\mu(f,|\xi|+1))^{n-1}}{|\det J_f(\xi)|} \geq \frac{1}{2}|z|, \end{align} $$
for all z such that
![]() $|z|\leq \frac {1}{2(\mu (g,1)+1)}.$
Using (5.2) again gives us
$|z|\leq \frac {1}{2(\mu (g,1)+1)}.$
Using (5.2) again gives us
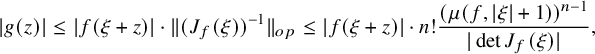 $$ \begin{align*}|g(z)|\leq |f(\xi+z)| \cdot \| (J_f(\xi))^{-1} \|_{op} \leq |f(\xi+z)| \cdot n! \frac{(\mu(f,|\xi|+1))^{n-1}}{|\det J_f(\xi)|},\end{align*} $$
$$ \begin{align*}|g(z)|\leq |f(\xi+z)| \cdot \| (J_f(\xi))^{-1} \|_{op} \leq |f(\xi+z)| \cdot n! \frac{(\mu(f,|\xi|+1))^{n-1}}{|\det J_f(\xi)|},\end{align*} $$
and thus,
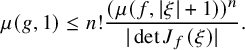 $$ \begin{align*}\mu(g,1)\leq n! \frac{(\mu(f,|\xi|+1))^n}{|\det J_f(\xi)|}.\end{align*} $$
$$ \begin{align*}\mu(g,1)\leq n! \frac{(\mu(f,|\xi|+1))^n}{|\det J_f(\xi)|}.\end{align*} $$
Combining the last inequality and (5.6) finishes the proof.
Proof of Theorem 5.1.
For simplicity, we assume that
![]() $b\geq 0$
and
$b\geq 0$
and
![]() $f(0)\neq 0.$
The general case readily reduces to this one.
$f(0)\neq 0.$
The general case readily reduces to this one.
Let
![]() $r\geq 0$
and
$r\geq 0$
and
![]() $\xi _i \in B_r.$
By the assumption
$\xi _i \in B_r.$
By the assumption
and since
![]() $\mu (f,|\xi _i|+1)\leq \mu (f,r+1)$
, Lemma 5.2 gives us that
$\mu (f,|\xi _i|+1)\leq \mu (f,r+1)$
, Lemma 5.2 gives us that
for all z such that
Since
![]() $\varepsilon <\frac {1}{2}<1$
, a connected component of
$\varepsilon <\frac {1}{2}<1$
, a connected component of
![]() $\{ |f|\leq \delta \}$
which contains
$\{ |f|\leq \delta \}$
which contains
![]() $\xi _i$
is itself fully contained in
$\xi _i$
is itself fully contained in
![]() $B_{r+1}.$
The same holds for each
$B_{r+1}.$
The same holds for each
![]() $\xi _j\in B_r$
, and thus,
$\xi _j\in B_r$
, and thus,
Finally, by (5.7),
![]() $\delta /2 \leq \mu (f,a(r+1))/2$
for all
$\delta /2 \leq \mu (f,a(r+1))/2$
for all
![]() $a>1$
, and we may apply Theorem 1.7, which yields
$a>1$
, and we may apply Theorem 1.7, which yields
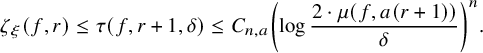 $$ \begin{align*}\zeta_{\xi}(f,r)\leq \tau(f,r+1,\delta) \leq C_{n,a} \left( \log \frac{2\cdot \mu(f,a(r+1))}{\delta} \right)^n.\end{align*} $$
$$ \begin{align*}\zeta_{\xi}(f,r)\leq \tau(f,r+1,\delta) \leq C_{n,a} \left( \log \frac{2\cdot \mu(f,a(r+1))}{\delta} \right)^n.\end{align*} $$
Substituting the expression for
![]() $\delta $
into this inequality and using
$\delta $
into this inequality and using
![]() $\mu (f,r+1)\leq \mu (f,a(r+1))$
gives us
$\mu (f,r+1)\leq \mu (f,a(r+1))$
gives us
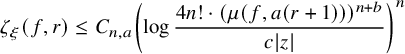 $$ \begin{align*}\zeta_{\xi}(f,r)\leq C_{n,a} \left( \log \frac{4n!\cdot (\mu(f,a(r+1)))^{n+b}}{c|z|} \right)^n\end{align*} $$
$$ \begin{align*}\zeta_{\xi}(f,r)\leq C_{n,a} \left( \log \frac{4n!\cdot (\mu(f,a(r+1)))^{n+b}}{c|z|} \right)^n\end{align*} $$
for all z such that
![]() $|z|\leq \varepsilon .$
Taking
$|z|\leq \varepsilon .$
Taking
![]() $|z|=\varepsilon $
yields
$|z|=\varepsilon $
yields
where
![]() $A,B,C$
depend on
$A,B,C$
depend on
![]() $n,a,b,c$
as indicated. This completes the proof.
$n,a,b,c$
as indicated. This completes the proof.
So far, we proved that Theorem 5.1 follows from Theorem 1.7. Now, we wish to show that Theorem 1.2 does not follow from Theorem 5.1. Namely, one may imagine the following scenario. Let
![]() $f:\mathbb {C}^n\to \mathbb {C}^n$
be an entire map. Although the classical count of zeros of f might not satisfy the transcendental Bézout bound, it may still happen that for a fixed
$f:\mathbb {C}^n\to \mathbb {C}^n$
be an entire map. Although the classical count of zeros of f might not satisfy the transcendental Bézout bound, it may still happen that for a fixed
![]() $\delta>0$
, we can choose a sequence of zeros
$\delta>0$
, we can choose a sequence of zeros
![]() $\{\xi _i\}$
from
$\{\xi _i\}$
from
![]() $f^{-1}(B_\delta )$
such that Theorem 5.1 applies to this sequence and
$f^{-1}(B_\delta )$
such that Theorem 5.1 applies to this sequence and
![]() $\zeta (f,r,\delta )=O(\zeta _\xi (f,r)).$
In this case, Theorem 5.1 would imply Theorem 1.2 (at least up to a constant which depends on
$\zeta (f,r,\delta )=O(\zeta _\xi (f,r)).$
In this case, Theorem 5.1 would imply Theorem 1.2 (at least up to a constant which depends on
![]() $\delta $
). However, our next result rules out this possibility.
$\delta $
). However, our next result rules out this possibility.
Proposition 5.4. Let
![]() $\mathfrak {c}=\{c_i \}$
be an increasing sequence of positive integers such that
$\mathfrak {c}=\{c_i \}$
be an increasing sequence of positive integers such that
![]() $\lim _{i\to +\infty } \frac {i}{c_i}=0$
and F the corresponding Cornalba-Shiffman map. For all real numbers
$\lim _{i\to +\infty } \frac {i}{c_i}=0$
and F the corresponding Cornalba-Shiffman map. For all real numbers
![]() $c>0$
and b, the inequality
$c>0$
and b, the inequality
holds for at most finitely many zeros
![]() $\xi \in F^{-1}(0).$
$\xi \in F^{-1}(0).$
Proof. Since the zeros of Cornalba-Shiffman maps are isolated and
![]() $\mu (F,r)\to + \infty $
as
$\mu (F,r)\to + \infty $
as
![]() $r\to +\infty $
, it is enough to prove the proposition for
$r\to +\infty $
, it is enough to prove the proposition for
![]() $b>0.$
Since
$b>0.$
Since
![]() $F(z,w)=(g(z),f(z,w))$
, we have that
$F(z,w)=(g(z),f(z,w))$
, we have that
All relevant infinite sums and products converge uniformly on compact sets, and thus, we may compute
 $$ \begin{align*}\partial_z g = \sum_{l=1}^\infty -2^{-l}g_l\end{align*} $$
$$ \begin{align*}\partial_z g = \sum_{l=1}^\infty -2^{-l}g_l\end{align*} $$
as well as
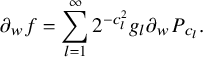 $$ \begin{align*}\partial_w f = \sum_{l=1}^\infty 2^{-c_l^2}g_l\partial_w P_{c_l}.\end{align*} $$
$$ \begin{align*}\partial_w f = \sum_{l=1}^\infty 2^{-c_l^2}g_l\partial_w P_{c_l}.\end{align*} $$
We wish to evaluate
![]() $J_F$
at zeros of
$J_F$
at zeros of
![]() $F.$
To this end, let us denote the zeros of F by
$F.$
To this end, let us denote the zeros of F by
![]() $\xi _{i,j}=(2^i,1/j)$
for
$\xi _{i,j}=(2^i,1/j)$
for
![]() $i\geq 1$
and
$i\geq 1$
and
![]() $1\leq j \leq c_i.$
We calculate
$1\leq j \leq c_i.$
We calculate
as well as
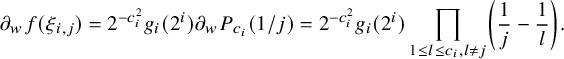 $$ \begin{align*}\partial_w f (\xi_{i,j}) = 2^{-c_i^2}g_i(2^i)\partial_w P_{c_i}(1/j)=2^{-c_i^2}g_i(2^i) \prod_{1\leq l\leq c_i, l\neq j} \left( \frac{1}{j}- \frac{1}{l} \right).\end{align*} $$
$$ \begin{align*}\partial_w f (\xi_{i,j}) = 2^{-c_i^2}g_i(2^i)\partial_w P_{c_i}(1/j)=2^{-c_i^2}g_i(2^i) \prod_{1\leq l\leq c_i, l\neq j} \left( \frac{1}{j}- \frac{1}{l} \right).\end{align*} $$
Since
![]() $\Big \vert \prod _{1\leq l\leq c_i, l\neq j} \left ( \frac {1}{j}- \frac {1}{l} \right )\Big \vert \leq 1,$
we get that for all i and j,
$\Big \vert \prod _{1\leq l\leq c_i, l\neq j} \left ( \frac {1}{j}- \frac {1}{l} \right )\Big \vert \leq 1,$
we get that for all i and j,
Moreover,
 $$ \begin{align*}g(2^i)= \prod_{l=1}^{i-1} (1-2^{i-l}) \cdot \prod_{l=i+1}^{\infty} (1-2^{i-l})= \prod_{l=1}^{i-1} (1-2^l) \cdot \prod_{l=1}^{\infty} (1-2^{-l}),\end{align*} $$
$$ \begin{align*}g(2^i)= \prod_{l=1}^{i-1} (1-2^{i-l}) \cdot \prod_{l=i+1}^{\infty} (1-2^{i-l})= \prod_{l=1}^{i-1} (1-2^l) \cdot \prod_{l=1}^{\infty} (1-2^{-l}),\end{align*} $$
and thus, we have that
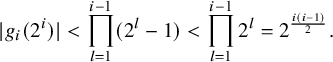 $$ \begin{align*}|g_i(2^i)|< \prod_{l=1}^{i-1} (2^l-1)<\prod_{l=1}^{i-1} 2^l=2^{\frac{i(i-1)}{2}}.\end{align*} $$
$$ \begin{align*}|g_i(2^i)|< \prod_{l=1}^{i-1} (2^l-1)<\prod_{l=1}^{i-1} 2^l=2^{\frac{i(i-1)}{2}}.\end{align*} $$
Combining this inequality with (5.8) yields
for all i and
![]() $j.$
By the assumption on
$j.$
By the assumption on
![]() $\mathfrak {c}$
, we have that for any
$\mathfrak {c}$
, we have that for any
![]() $b>0$
,
$b>0$
,
![]() $c_i^2\geq 5b(i+1)^2+i^2$
for all but finitely many
$c_i^2\geq 5b(i+1)^2+i^2$
for all but finitely many
![]() $i.$
Thus, for all but finitely many i, it holds
$i.$
Thus, for all but finitely many i, it holds
for all
![]() $j.$
Since
$j.$
Since
![]() $|\xi _{i,j}|=|(2^i,1/j)|<2^{i+1}$
, we have that
$|\xi _{i,j}|=|(2^i,1/j)|<2^{i+1}$
, we have that
Now, by Proposition 3.1,
where
![]() $C>0$
is an absolute constant. Putting (5.10), (5.11) and (5.12) together gives us
$C>0$
is an absolute constant. Putting (5.10), (5.11) and (5.12) together gives us
for all but finitely many indices
![]() $i,j.$
Since for every
$i,j.$
Since for every
![]() $a>0,2^{-2i+bC}<a$
for all but finitely many i, the proof follows.
$a>0,2^{-2i+bC}<a$
for all but finitely many i, the proof follows.
Remark 5.5. Different results in the spirit of Theorem 5.1 were obtained in [Reference Ji22] and [Reference Li23]. In one way or another, these results rely on lower bounds on
![]() $\det J_f$
at zeros of
$\det J_f$
at zeros of
![]() $f.$
Namely, in [Reference Ji22],
$f.$
Namely, in [Reference Ji22],
![]() $|\det J_f(\xi _i)|$
is assumed to be bounded from below by a constant, whereas in [Reference Li23], the upper bound for
$|\det J_f(\xi _i)|$
is assumed to be bounded from below by a constant, whereas in [Reference Li23], the upper bound for
![]() $\zeta _\xi (f,r)$
involves terms of the form
$\zeta _\xi (f,r)$
involves terms of the form
![]() $\log \frac {1}{\det J_f(\xi _i)}.$
From (5.9), it follows that by taking
$\log \frac {1}{\det J_f(\xi _i)}.$
From (5.9), it follows that by taking
![]() $\{c_i\}$
which increases sufficiently fast, we can make
$\{c_i\}$
which increases sufficiently fast, we can make
![]() $|\det J_F(\xi _{i,j})|$
of Cornalba-Shiffman maps decrease arbitrarily fast. Since, by Theorem 1.5,
$|\det J_F(\xi _{i,j})|$
of Cornalba-Shiffman maps decrease arbitrarily fast. Since, by Theorem 1.5,
![]() $\zeta (F,r,\delta )$
increases as
$\zeta (F,r,\delta )$
increases as
![]() $\log r$
independently of
$\log r$
independently of
![]() $\{c_i\}$
, we conclude that Theorem 1.2 cannot be deduced from the results of [Reference Ji22] and [Reference Li23] using the above-described strategy.
$\{c_i\}$
, we conclude that Theorem 1.2 cannot be deduced from the results of [Reference Ji22] and [Reference Li23] using the above-described strategy.
Remark 5.6. It is interesting to notice that Proposition 5.4 does not rule out a possibility that Theorem 1.7, or at least the same bound for
![]() $\zeta ^0$
, can be deduced from Theorem 5.1. Indeed, we have not proven any lower bound on the count of islands of Cornalba-Shiffman maps. As a matter of fact, it is not even clear if for each
$\zeta ^0$
, can be deduced from Theorem 5.1. Indeed, we have not proven any lower bound on the count of islands of Cornalba-Shiffman maps. As a matter of fact, it is not even clear if for each
![]() $\delta>0$
and each sequence
$\delta>0$
and each sequence
![]() $\{c_i\}$
,
$\{c_i\}$
,
![]() $\zeta ^0(F,r,\delta )\to +\infty $
as
$\zeta ^0(F,r,\delta )\to +\infty $
as
![]() $r\to +\infty .$
Namely, it may happen that starting from certain finite
$r\to +\infty .$
Namely, it may happen that starting from certain finite
![]() $r_0$
, all connected components of
$r_0$
, all connected components of
![]() $\{ |F|\leq \delta \}$
, which contain zeros of F, elongate all the way to infinity in the w-direction and thus never become islands, but rather remain peninsulas for all
$\{ |F|\leq \delta \}$
, which contain zeros of F, elongate all the way to infinity in the w-direction and thus never become islands, but rather remain peninsulas for all
![]() $r>r_0.$
$r>r_0.$
Question 5.7. Is it true that for each
![]() $\delta>0$
and all sequences
$\delta>0$
and all sequences
![]() $\mathfrak {c}$
,
$\mathfrak {c}$
,
![]() $\zeta ^0(F,r,\delta )\to +\infty $
as
$\zeta ^0(F,r,\delta )\to +\infty $
as
![]() $r \to +\infty $
? If so, what is the possible growth rate of
$r \to +\infty $
? If so, what is the possible growth rate of
![]() $\zeta ^0(F,r,\delta )$
depending on parameters
$\zeta ^0(F,r,\delta )$
depending on parameters
![]() $\delta $
and
$\delta $
and
![]() $\mathfrak {c}$
?
$\mathfrak {c}$
?
Remark 5.8. The main technical ingredient in [Reference Li and Taylor24] and [Reference Li23] is Theorem 3.6 from [Reference Li and Taylor24] (slightly modified in [Reference Li23]). Although the proof of this result has certain similarities with the proof of Theorem 1.7, it seems that the two approaches are fundamentally different. Namely, approximation of a holomorphic map by a polynomial is the key idea in the proof of Theorem 1.7, whereas it is not directly used in the proof of Theorem 3.6 in [Reference Li and Taylor24]. It would be interesting to explore how the methods of [Reference Li and Taylor24] and [Reference Li23] relate to the coarse counts of zeros. In the opposite direction, it would be interesting to deduce the results of [Reference Li23] using the same strategy as above, by proving a suitable analogue of Theorem 1.7.
6. Coarse counts and persistent homology
In this section, we discuss results generalizing Theorems 1.2 and 2.6, formulated in terms of persistent homology and barcodes.
6.1. Persistence modules and barcodes
Recall that for a Morse function
![]() $f:M \to \mathbb {R}$
on a compact manifold and a coefficient field
$f:M \to \mathbb {R}$
on a compact manifold and a coefficient field
![]() ${\mathbb {K}}$
, its barcode in degree
${\mathbb {K}}$
, its barcode in degree
![]() ${q} \in \mathbb {Z}$
is a finite multi-set
${q} \in \mathbb {Z}$
is a finite multi-set
![]() ${\mathcal {B}}_{q}(f;{\mathbb {K}})$
of intervals with multiplicities
${\mathcal {B}}_{q}(f;{\mathbb {K}})$
of intervals with multiplicities
![]() $(I_j,m_j),$
where
$(I_j,m_j),$
where
![]() $m_j \in \mathbb {N}$
and
$m_j \in \mathbb {N}$
and
![]() $I_j $
is finite, that is of the form
$I_j $
is finite, that is of the form
![]() $[a_j,b_j)$
or infinite, that is of the form
$[a_j,b_j)$
or infinite, that is of the form
![]() $[c_j,\infty ).$
The number of infinite bars is equal to the Betti number
$[c_j,\infty ).$
The number of infinite bars is equal to the Betti number
![]() $b_{q}(M;{\mathbb {K}}) = \dim H_{q}(M;{\mathbb {K}}).$
$b_{q}(M;{\mathbb {K}}) = \dim H_{q}(M;{\mathbb {K}}).$
This barcode is obtained algebraically from the persistence module
![]() $V_{q}(f;{\mathbb {K}})$
consisting of vector spaces
$V_{q}(f;{\mathbb {K}})$
consisting of vector spaces
![]() $V_{q}(f;{\mathbb {K}})^t = H_{q}(\{f \leq t\}; {\mathbb {K}})$
parametrized by
$V_{q}(f;{\mathbb {K}})^t = H_{q}(\{f \leq t\}; {\mathbb {K}})$
parametrized by
![]() $t\in \mathbb {R}$
and connecting maps
$t\in \mathbb {R}$
and connecting maps
![]() $\pi ^{s,t}: V_{q}(f;{\mathbb {K}})^s \to V_{q}(f;{\mathbb {K}})^t$
induced by the inclusions
$\pi ^{s,t}: V_{q}(f;{\mathbb {K}})^s \to V_{q}(f;{\mathbb {K}})^t$
induced by the inclusions
![]() $\{f \leq s \} \hookrightarrow \{f \leq t \}$
for
$\{f \leq s \} \hookrightarrow \{f \leq t \}$
for
![]() $s\leq t.$
These maps satisfy the structure relations of a persistence module:
$s\leq t.$
These maps satisfy the structure relations of a persistence module:
![]() $\pi ^{s,s} =\mathrm {id}_{V_{q}(f;{\mathbb {K}})^s}$
for all s and
$\pi ^{s,s} =\mathrm {id}_{V_{q}(f;{\mathbb {K}})^s}$
for all s and
![]() $\pi ^{s_2,s_3} \circ \pi ^{s_1,s_2} = \pi ^{s_1,s_3}$
for all
$\pi ^{s_2,s_3} \circ \pi ^{s_1,s_2} = \pi ^{s_1,s_3}$
for all
![]() $s_1 \leq s_2 \leq s_3.$
The total barcode of f is set to be
$s_1 \leq s_2 \leq s_3.$
The total barcode of f is set to be
where
![]() $\sqcup $
stands for the sum operation on multisets. This is the barcode of the persistence module
$\sqcup $
stands for the sum operation on multisets. This is the barcode of the persistence module
On a compact manifold M with boundary
![]() $\partial M$
and a Morse function
$\partial M$
and a Morse function
![]() $f: M \to \mathbb {R}$
in the sense of manifolds with boundary, we may define the persistence module and barcode of f as above.
$f: M \to \mathbb {R}$
in the sense of manifolds with boundary, we may define the persistence module and barcode of f as above.
One simple property of the barcode of this persistence module is that the number of bars in the barcode coincides with the number of their starting points. Another property is that the number of bars containing a given interval
![]() $[a,b]$
is
$[a,b]$
is
![]() $\dim {\mathrm {Im}}(\pi ^{a,b}).$
$\dim {\mathrm {Im}}(\pi ^{a,b}).$
Recall that the length of a finite bar
![]() $[a,b)$
is
$[a,b)$
is
![]() $b-a$
and the length of an infinite bar
$b-a$
and the length of an infinite bar
![]() $[c,\infty )$
is
$[c,\infty )$
is
![]() $+\infty .$
We require the following notion: for
$+\infty .$
We require the following notion: for
![]() $\delta \geq 0,$
let
$\delta \geq 0,$
let
![]() ${\mathcal {N}}_{\delta }(f;{\mathbb {K}})$
denote the number of bars of length
${\mathcal {N}}_{\delta }(f;{\mathbb {K}})$
denote the number of bars of length
![]() $>\delta $
in the barcode
$>\delta $
in the barcode
![]() ${\mathcal {B}}(f;{\mathbb {K}}).$
Similarly,
${\mathcal {B}}(f;{\mathbb {K}}).$
Similarly,
![]() ${\mathcal {N}}_{{q},\delta }(f;{\mathbb {K}})$
is the number of bars of length
${\mathcal {N}}_{{q},\delta }(f;{\mathbb {K}})$
is the number of bars of length
![]() $>\delta $
in the barcode
$>\delta $
in the barcode
![]() ${\mathcal {B}}_{q}(f;{\mathbb {K}})$
and
${\mathcal {B}}_{q}(f;{\mathbb {K}})$
and
![]() ${\mathcal {N}}_{\delta }(f;{\mathbb {K}}) = \sum _{q} {\mathcal {N}}_{{q},\delta }(f;{\mathbb {K}}).$
The definitions of
${\mathcal {N}}_{\delta }(f;{\mathbb {K}}) = \sum _{q} {\mathcal {N}}_{{q},\delta }(f;{\mathbb {K}}).$
The definitions of
![]() ${\mathcal {N}}_{{q},\delta }(f;{\mathbb {K}})$
and
${\mathcal {N}}_{{q},\delta }(f;{\mathbb {K}})$
and
![]() ${\mathcal {N}}_{\delta }(f;{\mathbb {K}})$
extend to any continuous function f on a compact manifold with boundary, as explained in detail in [Reference Buhovsky, Payette, Polterovich, Polterovich, Shelukhin and Stojisavljević9, Section 2.2].
${\mathcal {N}}_{\delta }(f;{\mathbb {K}})$
extend to any continuous function f on a compact manifold with boundary, as explained in detail in [Reference Buhovsky, Payette, Polterovich, Polterovich, Shelukhin and Stojisavljević9, Section 2.2].
We refer to [Reference Polterovich, Rosen, Samvelyan and Zhang30] for a systematic introduction to persistence modules with a view toward applications in topology and analysis. The only result which we require here is the following direct consequence of the algebraic isometry theorem [Reference Bauer and Lesnick5] (see [Reference Polterovich, Rosen, Samvelyan and Zhang30, Theorem 2.2.8, Equation (6.4)]).
Theorem 6.1. Let
![]() $f,g: M \to \mathbb {R}$
be two functions on a compact manifold M with boundary such that
$f,g: M \to \mathbb {R}$
be two functions on a compact manifold M with boundary such that
![]() $d_{C^0}(f,g) \leq c-\epsilon /2$
for
$d_{C^0}(f,g) \leq c-\epsilon /2$
for
![]() $c> \epsilon /2 > 0.$
Then for all
$c> \epsilon /2 > 0.$
Then for all
![]() ${q} \in \mathbb {Z}$
,
${q} \in \mathbb {Z}$
,
![]() ${\mathcal {N}}_{{q},2c}(f) \leq {\mathcal {N}}_{{q},\epsilon }(g).$
${\mathcal {N}}_{{q},2c}(f) \leq {\mathcal {N}}_{{q},\epsilon }(g).$
6.2. Bounds on barcodes of analytic functions
For a continuous map
![]() $f: \mathbb {C}^n \to \mathbb {C}^m,$
and
$f: \mathbb {C}^n \to \mathbb {C}^m,$
and
![]() $r>0,$
set
$r>0,$
set
Consider the invariants
![]() $\zeta _d(f,r,\delta )$
from Section 1.5.1. Note that
$\zeta _d(f,r,\delta )$
from Section 1.5.1. Note that
as shown in Lemma 6.4 and Remark 6.5 in [Reference Buhovsky, Payette, Polterovich, Polterovich, Shelukhin and Stojisavljević9]. Using the terminology and methods of persistence, we can prove the following result, which therefore generalizes Theorems 1.2 and 2.6.
Theorem 6.2. For any analytic map
![]() $f: \mathbb {C}^n \to \mathbb {C}^m$
,
$f: \mathbb {C}^n \to \mathbb {C}^m$
,
![]() $m\leq n$
and any
$m\leq n$
and any
![]() $a>1$
,
$a>1$
,
![]() $r>0$
, and
$r>0$
, and
![]() $\delta \in (0, \frac {\mu (f, ar)}{2})$
, we have
$\delta \in (0, \frac {\mu (f, ar)}{2})$
, we have
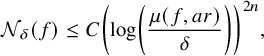 $$ \begin{align} {\mathcal{N}}_{\delta}(f) \leq C \left(\log\left(\frac{\mu(f, ar)}{\delta}\right)\right)^{2n}, \end{align} $$
$$ \begin{align} {\mathcal{N}}_{\delta}(f) \leq C \left(\log\left(\frac{\mu(f, ar)}{\delta}\right)\right)^{2n}, \end{align} $$
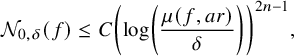 $$ \begin{align} {\mathcal{N}}_{0, \delta}(f) \leq C \left(\log\left(\frac{\mu(f, ar)}{\delta}\right)\right)^{2n-1}, \end{align} $$
$$ \begin{align} {\mathcal{N}}_{0, \delta}(f) \leq C \left(\log\left(\frac{\mu(f, ar)}{\delta}\right)\right)^{2n-1}, \end{align} $$
where the constant C depends only on a and n.
Since, given Theorem 6.1, this result reduces essentially to our proofs above and does not influence the main results of the paper, we only briefly sketch its proof.
Sketch of the proof.
First, we reduce as above to the case
![]() $m=n;$
see Remark 2.5. By Proposition 2.1, we can approximate
$m=n;$
see Remark 2.5. By Proposition 2.1, we can approximate
![]() $ f $
by a complex Taylor polynomial mapping
$ f $
by a complex Taylor polynomial mapping
![]() $ p $
at
$ p $
at
![]() $ 0 $
of degree
$ 0 $
of degree
![]() $ <k $
such that
$ <k $
such that
![]() $ |f-p| \leq C_{a} a^{-k} \mu (f,ar) $
on
$ |f-p| \leq C_{a} a^{-k} \mu (f,ar) $
on
![]() $ B_r $
. Here, we choose
$ B_r $
. Here, we choose
![]() $ k $
to be the minimal positive integer such that
$ k $
to be the minimal positive integer such that
![]() $ C_a a^{-k} \mu (f,ar) < \delta /2 $
. Furthermore, by a classical but lengthy transversality argument (which we omit), we may assume that
$ C_a a^{-k} \mu (f,ar) < \delta /2 $
. Furthermore, by a classical but lengthy transversality argument (which we omit), we may assume that
![]() $h=|p|^2$
has no critical points on
$h=|p|^2$
has no critical points on
![]() $\partial B_r$
and is Morse on
$\partial B_r$
and is Morse on
![]() $B_r$
and
$B_r$
and
![]() $h|_{\partial B_r}$
is Morse. Now, by Proposition 2.2, the number of critical points of h on
$h|_{\partial B_r}$
is Morse. Now, by Proposition 2.2, the number of critical points of h on
![]() $B_r$
is at most
$B_r$
is at most
![]() $C k^{2n},$
the number of critical points of h of index
$C k^{2n},$
the number of critical points of h of index
![]() $0$
is at most
$0$
is at most
![]() $C k^n,$
whereas the number of critical points of
$C k^n,$
whereas the number of critical points of
![]() $h|_{\partial B_r}$
is at most
$h|_{\partial B_r}$
is at most
![]() $C k^{2n-1}.$
The starting points of bars of degree
$C k^{2n-1}.$
The starting points of bars of degree
![]() $0$
correspond to critical points of h of index
$0$
correspond to critical points of h of index
![]() $0$
and to critical points of index
$0$
and to critical points of index
![]() $0$
of
$0$
of
![]() $h|_{\partial B_r}$
with gradient pointing inwards, whereas the endpoints of bars in general correspond to a subset of the critical points of h and of
$h|_{\partial B_r}$
with gradient pointing inwards, whereas the endpoints of bars in general correspond to a subset of the critical points of h and of
![]() $h|_{\partial B_r}.$
This follows from Morse theory for manifolds with boundary and was discussed in a more general framework in [Reference Buhovsky, Payette, Polterovich, Polterovich, Shelukhin and Stojisavljević9, Proposition 4.12]. Therefore,
$h|_{\partial B_r}.$
This follows from Morse theory for manifolds with boundary and was discussed in a more general framework in [Reference Buhovsky, Payette, Polterovich, Polterovich, Shelukhin and Stojisavljević9, Proposition 4.12]. Therefore,
![]() ${\mathcal {N}}_{\epsilon }(|p|) \leq C k^{2n}$
and
${\mathcal {N}}_{\epsilon }(|p|) \leq C k^{2n}$
and
![]() ${\mathcal {N}}_{0,\epsilon }(|p|) \leq C k^{2n-1}$
for any
${\mathcal {N}}_{0,\epsilon }(|p|) \leq C k^{2n-1}$
for any
![]() $\epsilon>0.$
Taking
$\epsilon>0.$
Taking
![]() $ ||f|-|p|| \leq |f-p| < c< \delta /2$
and
$ ||f|-|p|| \leq |f-p| < c< \delta /2$
and
![]() $0<\epsilon <c - \delta $
, Theorem 6.1 implies
$0<\epsilon <c - \delta $
, Theorem 6.1 implies
![]() ${\mathcal {N}}_{\delta }(|f|) \leq C k^{2n}$
and
${\mathcal {N}}_{\delta }(|f|) \leq C k^{2n}$
and
![]() ${\mathcal {N}}_{0,\delta }(|f|) \leq C k^{2n-1},$
which translates to the required bound by our choice of
${\mathcal {N}}_{0,\delta }(|f|) \leq C k^{2n-1},$
which translates to the required bound by our choice of
![]() $k.$
$k.$
Remark 6.3. An entire map
![]() $f:\mathbb {C}^n\to \mathbb {C}^n$
naturally gives rise to a persistence module
$f:\mathbb {C}^n\to \mathbb {C}^n$
naturally gives rise to a persistence module
![]() $H_*(\{ |f|\leq t \} \cap B_r )$
in two parameters r and
$H_*(\{ |f|\leq t \} \cap B_r )$
in two parameters r and
![]() $t.$
In this paper, we considered it as an r-parametrized family of persistence modules with one parameter t. It would be interesting to study this persistence module from the viewpoint of multiparameter persistence (see [Reference Botnan and Lesnick6] and references therein), for example, by using the recently introduced language of signed barcodes; see [Reference Botnan, Oppermann and Oudot7, Reference Botnan, Oppermann, Oudot and Scoccola8, Reference Oudot and Scoccola29].
$t.$
In this paper, we considered it as an r-parametrized family of persistence modules with one parameter t. It would be interesting to study this persistence module from the viewpoint of multiparameter persistence (see [Reference Botnan and Lesnick6] and references therein), for example, by using the recently introduced language of signed barcodes; see [Reference Botnan, Oppermann and Oudot7, Reference Botnan, Oppermann, Oudot and Scoccola8, Reference Oudot and Scoccola29].
Acknowledgements
We thank Misha Sodin and Steve Oudot for illuminating discussions, and the anonymous referee for numerous useful comments.
Competing interest
The authors have no competing interest to declare.
Funding statement
LB was partially supported by ERC Starting Grant 757585. IP was partially supported by NSERC and FRQNT. LP was partially supported by the Israel Science Foundation grant 1102/20. ES was partially supported by NSERC, Fondation Courtois, Alfred P. Sloan Foundation. VS was partially supported by the CRM-ISM postdoctoral fellowship and ERC Starting Grant 851701.














