Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-01-13T12:07:03.058Z Has data issue: false hasContentIssue false
  • English
  • Français

FINITE GROUPS WITH ABNORMAL MINIMAL NONNILPOTENT SUBGROUPS

Part of: Representation theory of groups

Published online by Cambridge University Press:  25 August 2022

ZHIGANG WANG Open the ORCID record for ZHIGANG WANG [Opens in a new window] ,
JINZHUAN CAI Open the ORCID record for JINZHUAN CAI [Opens in a new window] ,
INNA N. SAFONOVA Open the ORCID record for INNA N. SAFONOVA [Opens in a new window]  and
ALEXANDER N. SKIBA Open the ORCID record for ALEXANDER N. SKIBA [Opens in a new window]
ZHIGANG WANG
Affiliation:
School of Science, Hainan University, Haikou, Hainan 570228, PR China e-mail: wzhigang@hainanu.edu.cn
JINZHUAN CAI
Affiliation:
School of Science, Hainan University, Haikou, Hainan 570228, PR China e-mail: caijzh12@163.com
INNA N. SAFONOVA
Affiliation:
Department of Applied Mathematics and Computer Science, Belarusian State University, Minsk 220030, Belarus e-mail: safonova@bsu.by
ALEXANDER N. SKIBA*
Affiliation:
Department of Mathematics and Technologies of Programming, Francisk Skorina Gomel State University, Gomel 246019, Belarus
*
e-mail: alexander.skiba49@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

We describe finite soluble nonnilpotent groups in which every minimal nonnilpotent subgroup is abnormal. We also show that if G is a nonsoluble finite group in which every minimal nonnilpotent subgroup is abnormal, then G is quasisimple and $Z(G)$ is cyclic of order 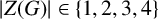$|Z(G)|\in \{1, 2, 3, 4\}$ .

Keywords

finite groupsoluble groupSchmidt groupabnormal subgroupquasisimple group

MSC classification

Primary: 20D10: Solvable groups, theory of formations, Schunck classes, Fitting classes, $pi$-length, ranks
Secondary: 20D15: Nilpotent groups, $p$-groups
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 107 , Issue 2 , April 2023 , pp. 261 - 270
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research was supported by the National Natural Science Foundation of China (Nos. 12171126 and 12101166) and Natural Science Foundation of Hainan Province (No. 621RC510). Research of the third author was supported by Ministry of Education of the Republic of Belarus (Grant 20211328).

References

Al-Sharo, K. A. and Skiba, A. N., ‘On finite groups with $\sigma$ -subnormal Schmidt subgroups’, Comm. Algebra 45 (2017), 4158–4165.CrossRefGoogle Scholar
Ballester-Bolinches, A., Esteban-Romero, R. and Robinson, D. J. S., ‘On finite minimal nonnilpotent groups’, Proc. Amer. Math. Soc. 133(12) (2005), 3455–3462.CrossRefGoogle Scholar
Ballester-Bolinches, A. and Ezquerro, L. M., Classes of Finite Groups (Springer, Dordrecht, 2006).Google Scholar
Conway, J. H., Curtis, R. T., Norton, S. P., Parker, R. A. and Wilson, R. A., Atlas of Finite Groups: Maximal Subgroups and Ordinary Characters for Simple Groups (Clarendon Press, Oxford, 1985).Google Scholar
Doerk, K. and Hawkes, T., Finite Soluble Groups (Walter de Gruyter, Berlin–New York, 1992).CrossRefGoogle Scholar
Gorenstein, D., Finite Groups (Harper and Row Publishers, New York–Evanston–London, 1968).Google Scholar
Gorenstein, D., Finite Simple Groups. An Introduction to their Classification (Plenum Press, New York–London, 1982).Google Scholar
Guo, W., Structure Theory for Canonical Classes of Finite Groups (Springer, Heidelberg–New York–Dordrecht–London, 2015).CrossRefGoogle Scholar
Hu, B. and Huang, J., ‘On finite groups with generalized $\sigma$ -subnormal Schmidt subgroups’, Comm. Algebra 46(7) (2018), 3127–3134.CrossRefGoogle Scholar
Huppert, B., Endliche Gruppen I (Springer-Verlag, Berlin–Heidelberg–New York, 1967).CrossRefGoogle Scholar
Liu, A.-M., Guo, W., Safonova, I. N. and Skiba, A. N., ‘A generalization of subnormality’, Mediterr. J. Math. 19 (2022), Article no. 98.CrossRefGoogle Scholar
Monakhov, V. S. and Knyagina, V. N., ‘On finite groups with some subnormal Schmidt subgroups’, Sib. Math. J. 45(6) (2004), 1316–1322.Google Scholar
Monakhov, V. S. and Knyagina, V. N., ‘Finite groups with Hall subnormally embedded Schmidt subgroups’, Comm. Algebra 48(1) (2020), 93–100.CrossRefGoogle Scholar
Shemetkov, L. A., Formations of Finite Groups (Nauka, Moscow, 1978).Google Scholar
Sun, F., Yi, X. and Kamornikov, S. F., ‘Finite groups with generalized subnormal Schmidt subgroups’, Sib. Math. J. 62(2) (2021), 450–456.CrossRefGoogle Scholar
Thompson, J. G., ‘Nonsolvable finite groups all of whose local subgroups are solvable’, Bull. Amer. Math. Soc. (N.S.) 74(3) (1968), 383–437.CrossRefGoogle Scholar
Vedernikov, V. A., ‘Finite groups with subnormal Schmidt subgroups’, Algebra Logika 46(6) (2007), 669–687.CrossRefGoogle Scholar
Weinstein, M. (ed.), Between Nilpotent and Solvable (Polygonal Publishing House, Passaic, NJ, 1982).Google Scholar
Yi, X. and Kamornikov, S. F., ‘Finite groups with $\sigma$ -subnormal Schmidt subgroups’, J. Algebra 560 (2020), 181–191.CrossRefGoogle Scholar