1. Introduction
Chirality, denoting the lack of superposition ability of structures on mirror images, is a characteristic of various assemblies, including carbon nanotubes, viruses and actin filaments, and is essential for their function. Since left- and right-handed amino acids lead to different protein structures, their homochirality is required for biological function such as gene encoding (Inaki, Liu & Matsuno Reference Inaki, Liu and Matsuno2016). Chiral proteins can sometimes lead to chiral mesoscale structures; some organisms with chiral body structures have chiral cells (Fan et al. Reference Fan, Zhang, Rahman, Stanton and Wan2019). Therefore, the chirality of proteins may be responsible for the chiral mesoscale structures found in cell media. Chiral mesoscale assemblies are formed in peptide amphiphiles with chiral amino acids (Gao et al. Reference Gao, Kewalramani, Valencia, Li, McCourt, Olvera de la Cruz and Bedzyk2019) and in many carbon-based systems, which have required great efforts to understand and characterize (Arnold et al. Reference Arnold, Green, Hulvat, Stupp and Hersam2006). However, the mechanism by which chirality manifests at the mesoscale is not well understood. Here, we propose ways of actuating and separating mesoscale chiral structures such as helices (Shimizu, Masuda & Minamikawa Reference Shimizu, Masuda and Minamikawa2005; McCourt et al. Reference McCourt, Kewalramani, Gao, Roth, Weigand, Olvera de la Cruz and Bedzyk2022), helicoidal scrolls (Nagarsekar et al. Reference Nagarsekar, Ashtikar, Steiniger, Thamm, Schacher and Fahr2016) and twisted ribbons (Oda et al. Reference Oda, Huc, Schmutz, Candau and MacKintosh1999).
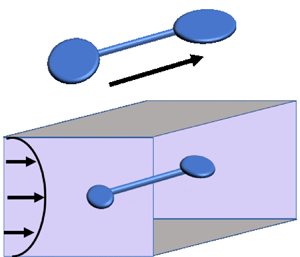
The question that arises is: under what conditions can these mesoscale chiral structures propel and separate? For instance, in Andreev, Son & Spivak (Reference Andreev, Son and Spivak2010), it was shown that in the absence of temperature gradients, chiral separation is possible only in non-stationary or nonlinear flows. However, in chemical and biological systems, various mesoscale structures move and function in an aqueous environment in the presence of thermal gradients induced by chemical reactions (Zhang et al. Reference Zhang, Duan, Lu, Zhao, Shklyaev, Liu, Huang and Sen2014). Temperature gradients may alter the liquid material parameters, and in particular viscosity, as this was demonstrated in laser-induced thermophoresis experiments (Schermer et al. Reference Schermer, Olson, Coleman and Bucholtz2011) and in associated theoretical work (Oppenheimer, Navardi & Stone Reference Oppenheimer, Navardi and Stone2016). In this paper, we show that the dependence of material parameters such as viscosity or density on temperature gives rise to propulsion and separation of a chiral suspension even in stationary linear flows (low Reynolds number flows). In particular, for a stationary Poiseuille flow, the segregation induced by chirality (characterized by the velocity ![]() ${v}^{{ch}}$) occurs in a direction normal to both the base flow and the temperature gradient; see figure 1.
${v}^{{ch}}$) occurs in a direction normal to both the base flow and the temperature gradient; see figure 1.

Figure 1. A chiral velocity ![]() ${v}^{{ch}}\hat {\boldsymbol {z}}$ – defined as the difference of the velocities of the left- and right-handed particles, averaged over their number density (number of particles per unit volume) – of
${v}^{{ch}}\hat {\boldsymbol {z}}$ – defined as the difference of the velocities of the left- and right-handed particles, averaged over their number density (number of particles per unit volume) – of ![]() $n$ chiral particles suspended in a classical liquid is induced by a vertical temperature gradient
$n$ chiral particles suspended in a classical liquid is induced by a vertical temperature gradient ![]() $\boldsymbol {\nabla } T= \partial _y T\hat {\boldsymbol {y}}$ and shear flow
$\boldsymbol {\nabla } T= \partial _y T\hat {\boldsymbol {y}}$ and shear flow ![]() $\boldsymbol {v} = u(y)\,\hat {\boldsymbol {x}}$ in a channel of width
$\boldsymbol {v} = u(y)\,\hat {\boldsymbol {x}}$ in a channel of width ![]() $d$. In a non-racemic suspension of chiral particles, the liquid is also perturbed by chirality and acquires a transverse velocity component
$d$. In a non-racemic suspension of chiral particles, the liquid is also perturbed by chirality and acquires a transverse velocity component ![]() $\delta v(y)\,\hat {\boldsymbol {z}}$ (not shown), perpendicular to the direction of the base flow
$\delta v(y)\,\hat {\boldsymbol {z}}$ (not shown), perpendicular to the direction of the base flow ![]() $u(y)\, \hat {\boldsymbol {x}}$.
$u(y)\, \hat {\boldsymbol {x}}$.
Our main result is an expression for the chiral velocity ![]() $\boldsymbol {v}^{{ch}}$ acquired by the suspended chiral particles. The chiral velocity is defined as the difference of the velocities of the left- and right-handed particles, averaged over their number density (number of particles per unit volume). To leading order in an expansion with respect to the temperature gradient, the chiral velocity is of the form
$\boldsymbol {v}^{{ch}}$ acquired by the suspended chiral particles. The chiral velocity is defined as the difference of the velocities of the left- and right-handed particles, averaged over their number density (number of particles per unit volume). To leading order in an expansion with respect to the temperature gradient, the chiral velocity is of the form
where ![]() $\Delta T$ is the temperature difference between the upper and lower channel walls,
$\Delta T$ is the temperature difference between the upper and lower channel walls, ![]() $R$ is the (micron scale) chiral particle radius,
$R$ is the (micron scale) chiral particle radius, ![]() $d$ is the (millimetre scale) channel width,
$d$ is the (millimetre scale) channel width, ![]() $U_0$ is a characteristic velocity scale of the base flow,
$U_0$ is a characteristic velocity scale of the base flow, ![]() $\gamma = \eta '/\eta$ is the logarithmic derivative of the viscosity, with a prime denoting differentiation with respect to temperature
$\gamma = \eta '/\eta$ is the logarithmic derivative of the viscosity, with a prime denoting differentiation with respect to temperature ![]() $T$,
$T$, ![]() $\chi$ is a geometric scalar coefficient characteristic of the particle shape, and the brackets
$\chi$ is a geometric scalar coefficient characteristic of the particle shape, and the brackets ![]() $\langle\ {\cdot}\ \rangle$ denote averaging over the channel width. Equation (1.1) is a consequence of the variation of liquid viscosity
$\langle\ {\cdot}\ \rangle$ denote averaging over the channel width. Equation (1.1) is a consequence of the variation of liquid viscosity ![]() $\eta$ with respect to temperature. Considerable effort has been expended in recent years in characterizing the response of active and biological liquids to viscosity gradients (Shoele & Eastham Reference Shoele and Eastham2018; Datt & Elfring Reference Datt and Elfring2019) (albeit based on the single-particle level; see the ensuing discussion).
$\eta$ with respect to temperature. Considerable effort has been expended in recent years in characterizing the response of active and biological liquids to viscosity gradients (Shoele & Eastham Reference Shoele and Eastham2018; Datt & Elfring Reference Datt and Elfring2019) (albeit based on the single-particle level; see the ensuing discussion).
The physical mechanism underlying the transverse chiral velocity (1.1) is the torque imparted on the base flow by the temperature gradient having the form ![]() $\boldsymbol {\nabla } T \times \nabla ^2 \boldsymbol {v} + (\boldsymbol {\nabla } T \boldsymbol {\cdot }\boldsymbol {\nabla })\, \textrm {curl}\,\boldsymbol {v}$, as will be discussed in detail in § 3, where
$\boldsymbol {\nabla } T \times \nabla ^2 \boldsymbol {v} + (\boldsymbol {\nabla } T \boldsymbol {\cdot }\boldsymbol {\nabla })\, \textrm {curl}\,\boldsymbol {v}$, as will be discussed in detail in § 3, where ![]() $\boldsymbol {v}$ is the velocity of the base flow, and
$\boldsymbol {v}$ is the velocity of the base flow, and ![]() $T$ is its temperature. With reference to figure 1, this torque is perpendicular to both pressure and temperature gradients, thus propelling the particles along its direction.
$T$ is its temperature. With reference to figure 1, this torque is perpendicular to both pressure and temperature gradients, thus propelling the particles along its direction.
Another aspect of the effect is that the motion of the chiral suspension in turn perturbs the base flow and endows it with a transverse velocity component ![]() $\delta v$. It is noteworthy that the chiral suspension also exerts a screw torque on the confining walls, in the direction of the base flow.
$\delta v$. It is noteworthy that the chiral suspension also exerts a screw torque on the confining walls, in the direction of the base flow.
It is important to realize that the hydrodynamic description developed in this paper implies averaging over the tumbling motion of the chiral particles and applies at time scales longer than the tumbling time (Andreev et al. Reference Andreev, Son and Spivak2010). It can be understood as a ‘continuum’ formulation for the motion of a chiral suspension, and thus differs from the majority of propulsion descriptions that are based on a resistance matrix at the level of a single suspended particle (Happel & Brenner Reference Happel and Brenner1965). The equivalence of the two approaches was discussed in the recent review article by Witten & Diamant (Reference Witten and Diamant2020).
The structure of this paper is as follows. In § 2, we describe the hydrodynamic equations of the base flow undisturbed by the chiral suspension. We have chosen an Arrhenius-type, temperature-dependent viscosity law that is valid over a large range of temperatures and is well-documented in the literature; see Fogel'son & Likhachev (Reference Fogel'son and Likhachev2001). In § 3, we introduce the chiral current, chiral velocity ![]() $v^{{ch}}$ and chiral stress following the symmetry arguments of Andreev et al. (Reference Andreev, Son and Spivak2010) (derived therein when the flow is isothermal). The chiral current is the difference of the left- and right-handed particle velocities weighted by the number of particles of each handedness. The chiral velocity
$v^{{ch}}$ and chiral stress following the symmetry arguments of Andreev et al. (Reference Andreev, Son and Spivak2010) (derived therein when the flow is isothermal). The chiral current is the difference of the left- and right-handed particle velocities weighted by the number of particles of each handedness. The chiral velocity ![]() $v^{{ch}}$ is equal to the chiral current divided by the number of particles per unit volume. Here, where non-isothermal flows are considered, one has to express the vorticity equation with respect to variations of material parameters with temperature. Our main result of the present paper appears in § 4, where we consider a suspension of chiral particles in a channel, whose base liquid is driven by crossed pressure and temperature gradients (see figure 1). Both the undisturbed by chirality flow and the chiral velocity
$v^{{ch}}$ is equal to the chiral current divided by the number of particles per unit volume. Here, where non-isothermal flows are considered, one has to express the vorticity equation with respect to variations of material parameters with temperature. Our main result of the present paper appears in § 4, where we consider a suspension of chiral particles in a channel, whose base liquid is driven by crossed pressure and temperature gradients (see figure 1). Both the undisturbed by chirality flow and the chiral velocity ![]() $v^{{ch}}$ can be expressed in closed form. Employing published material parameters, we estimate the magnitude of the chiral velocity and that of the liquid disturbed by chirality, henceforth denoted as
$v^{{ch}}$ can be expressed in closed form. Employing published material parameters, we estimate the magnitude of the chiral velocity and that of the liquid disturbed by chirality, henceforth denoted as ![]() $\delta v$. The main result obtained in this section is the linear dependence in
$\delta v$. The main result obtained in this section is the linear dependence in ![]() $\Delta T$ of the chiral velocity
$\Delta T$ of the chiral velocity ![]() $v^{{ch}}$ – defined as the difference of the velocities of the left- and right-handed particles, averaged over their number density (number of particles per unit volume) – obtained for small temperature gradients. Likewise, the velocity of the liquid disturbed by chirality also depends linearly on temperature gradients
$v^{{ch}}$ – defined as the difference of the velocities of the left- and right-handed particles, averaged over their number density (number of particles per unit volume) – obtained for small temperature gradients. Likewise, the velocity of the liquid disturbed by chirality also depends linearly on temperature gradients ![]() $\Delta T$. It is noteworthy that the chiral suspension exerts a screw torque on the confining walls, in the direction of the base flow. This was also observed earlier in the context of non-isothermal flows (Andreev et al. Reference Andreev, Son and Spivak2010), and here we calculate corrections due to the temperature variations. In § 5, we repeat the foregoing analysis for the practically important case of Couette flow. However, here the observables are quadratic with respect to
$\Delta T$. It is noteworthy that the chiral suspension exerts a screw torque on the confining walls, in the direction of the base flow. This was also observed earlier in the context of non-isothermal flows (Andreev et al. Reference Andreev, Son and Spivak2010), and here we calculate corrections due to the temperature variations. In § 5, we repeat the foregoing analysis for the practically important case of Couette flow. However, here the observables are quadratic with respect to ![]() $\Delta T$. As in the previously considered Poiseuille flow, all observables referred to in this section are perpendicular to the base flow plane, as depicted in figure 1.
$\Delta T$. As in the previously considered Poiseuille flow, all observables referred to in this section are perpendicular to the base flow plane, as depicted in figure 1.
In § 6, we analyse two additional thermal effects that may give rise to non-isothermal chiral particle propulsion. The first is to consider a non-isothermal liquid, driven for instance by a moving channel wall and endowed with viscous heating (see § 6.1), which increases the liquid temperature near the centre of the channel and thus diminishes its viscosity. The chiral velocity ![]() $\boldsymbol {v}^{{ch}}$ (see figure 1) depends then not on imposed temperature gradients but on the velocity scale introduced by the moving wall, and can be expressed in terms of the dimensionless Brinkman number. The second thermally related effect discussed in § 6.2 considers an alternative temperature-dependent mechanism whereby the chiral current is driven by gradients of temperature crossed with the gravitational force, in a Rayleigh–Bénard cell.
$\boldsymbol {v}^{{ch}}$ (see figure 1) depends then not on imposed temperature gradients but on the velocity scale introduced by the moving wall, and can be expressed in terms of the dimensionless Brinkman number. The second thermally related effect discussed in § 6.2 considers an alternative temperature-dependent mechanism whereby the chiral current is driven by gradients of temperature crossed with the gravitational force, in a Rayleigh–Bénard cell.
In the main body of this paper, we set the chirality parameter ![]() $\chi$ to be equal to 1. In Appendix A, we justify this choice by comparing our framework with the predictions of the single-particle theory of Makino & Doi (Reference Makino and Doi2004, Reference Makino and Doi2017). In addition, we show that the predictions of our theory (e.g. magnitude of chiral stress) are compatible to those found in systems of similar size in biology and technology (Kataoka & Troian Reference Kataoka and Troian1999; Ando & Yamamoto Reference Ando and Yamamoto2009).
$\chi$ to be equal to 1. In Appendix A, we justify this choice by comparing our framework with the predictions of the single-particle theory of Makino & Doi (Reference Makino and Doi2004, Reference Makino and Doi2017). In addition, we show that the predictions of our theory (e.g. magnitude of chiral stress) are compatible to those found in systems of similar size in biology and technology (Kataoka & Troian Reference Kataoka and Troian1999; Ando & Yamamoto Reference Ando and Yamamoto2009).
2. Hydrodynamic equations in the absence of chirality
Conservation of entropy in an incompressible flowing liquid (Landau & Lifshitz Reference Landau and Lifshitz1987) leads to heat advection and heat conduction as well as energy dissipation due to internal friction, termed viscous heating:
where summation is implied on repeated indices, ![]() $T$ is the liquid temperature,
$T$ is the liquid temperature, ![]() $c_p$ is the specific heat at constant pressure,
$c_p$ is the specific heat at constant pressure, ![]() $\rho$ is the density of the liquid,
$\rho$ is the density of the liquid, ![]() $k_{th}$ is the thermal conductivity of the liquid, and the liquid velocity
$k_{th}$ is the thermal conductivity of the liquid, and the liquid velocity ![]() $\boldsymbol {v}$ is determined from conservation of mass and linear momentum. Also,
$\boldsymbol {v}$ is determined from conservation of mass and linear momentum. Also, ![]() $\sigma _{ik}' = \eta ( {\partial u_i}/{\partial x_k} + {\partial u_k}/{\partial x_i} )$,
$\sigma _{ik}' = \eta ( {\partial u_i}/{\partial x_k} + {\partial u_k}/{\partial x_i} )$, ![]() $i,k = 1,2,3$, is the viscous stress tensor, and
$i,k = 1,2,3$, is the viscous stress tensor, and ![]() $\eta$ is the liquid viscosity. Rearranging the right-hand side of (2.1), one obtains
$\eta$ is the liquid viscosity. Rearranging the right-hand side of (2.1), one obtains
accompanied by fixed temperature boundary conditions on the vessel walls. Viscous heating can introduce hysteresis effects in Arrhenius-type viscosity laws (Davis et al. Reference Davis, Kriegsmann, Laurence and Rosenblat1983) and affect the motion of thin liquid films (Kirkinis & Andreev Reference Kirkinis and Andreev2019). In general, the viscous heating term is expected to be small and can be neglected. We will consider its effects on chiral particle propulsion in § 6.1.
Various temperature-dependent viscosity laws have been employed in the literature (see e.g. Potter & Graber Reference Potter and Graber1972; Davis et al. Reference Davis, Kriegsmann, Laurence and Rosenblat1983; Wall & Wilson Reference Wall and Wilson1996). Here, we will employ the well-documented Arrhenius-type temperature dependent viscosity law (Fogel'son & Likhachev Reference Fogel'son and Likhachev2001)
valid in the ![]() $243$–
$243$–![]() $373$ K temperature range, since it encompasses the linear and other exponential laws, appearing in the above references, as special cases. Here,
$373$ K temperature range, since it encompasses the linear and other exponential laws, appearing in the above references, as special cases. Here, ![]() $E$ is the activation energy,
$E$ is the activation energy, ![]() $R_g$ is the gas constant, and
$R_g$ is the gas constant, and ![]() $T_A$ is a temperature correction, unique to each viscous liquid; cf. Fogel'son & Likhachev (Reference Fogel'son and Likhachev2001) and table 1. If in a channel the lower wall
$T_A$ is a temperature correction, unique to each viscous liquid; cf. Fogel'son & Likhachev (Reference Fogel'son and Likhachev2001) and table 1. If in a channel the lower wall ![]() $y=0$ is kept at a temperature
$y=0$ is kept at a temperature ![]() $T_0$, then linearization of (2.3) leads to
$T_0$, then linearization of (2.3) leads to
where ![]() $\gamma = {E}/[{R_g(T_0 + T_A)^2}]$ is the logarithmic derivative of the viscosity (2.3), and
$\gamma = {E}/[{R_g(T_0 + T_A)^2}]$ is the logarithmic derivative of the viscosity (2.3), and ![]() $\eta (T_0) = \eta _0\exp \{{E}/{R_g(T_0+T_A)}\}$. We will employ parameter
$\eta (T_0) = \eta _0\exp \{{E}/{R_g(T_0+T_A)}\}$. We will employ parameter ![]() $\gamma$ in our investigations throughout this paper.
$\gamma$ in our investigations throughout this paper.
Table 1. Definitions and material parameter values (Fogel'son & Likhachev Reference Fogel'son and Likhachev2001).

The flowing liquid satisfies the Navier–Stokes equations and is considered incompressible:
where the Cauchy stress tensor ![]() $\sigma _{ik}$ is given by
$\sigma _{ik}$ is given by
and ![]() $p$ is the pressure.
$p$ is the pressure.
With a view towards understanding the structure of the vorticity equation leading to (3.8), we take the curl of both sides of (2.5a). Thus the left-hand side of (2.5a) just gives the vorticity equation for an inviscid liquid. The curl of the right-hand side of (2.5a) becomes
 \begin{align} \epsilon_{ijk}\,\partial_i\partial_l \sigma_{jl} &= 2\epsilon_{ijk}\left\{ \partial_i(\partial_l \eta) + (\partial_l \eta)\partial_i +(\partial_i\eta)\partial_l + \eta\,\partial_l\partial_i\right\} V_{jl} \nonumber\\ &= \left\{\epsilon_{ijk}\left[ \eta''\,\partial_iT\,\partial_lT + \eta'\,\partial_i\partial_lT \right]2V_{jl}+ \eta' \left[\partial_lT\,\partial_l\omega_k + \epsilon_{ijk}\,\partial_iT\,\partial_l^2 u_j\right] + \eta\,\partial_l^2 \omega_k \right\}, \end{align}
\begin{align} \epsilon_{ijk}\,\partial_i\partial_l \sigma_{jl} &= 2\epsilon_{ijk}\left\{ \partial_i(\partial_l \eta) + (\partial_l \eta)\partial_i +(\partial_i\eta)\partial_l + \eta\,\partial_l\partial_i\right\} V_{jl} \nonumber\\ &= \left\{\epsilon_{ijk}\left[ \eta''\,\partial_iT\,\partial_lT + \eta'\,\partial_i\partial_lT \right]2V_{jl}+ \eta' \left[\partial_lT\,\partial_l\omega_k + \epsilon_{ijk}\,\partial_iT\,\partial_l^2 u_j\right] + \eta\,\partial_l^2 \omega_k \right\}, \end{align}
where a prime denotes differentiation of the viscosity ![]() $\eta$ with respect to temperature
$\eta$ with respect to temperature ![]() $T$. It is clear that in the absence of nonlinear or non-stationary terms in the vorticity equation, the diffusion of vorticity is maintained in (2.7) by gradients of temperature. Also note that the linear terms in gradients of temperature in (2.7) match the terms of the chiral current introduced in (3.4).
$T$. It is clear that in the absence of nonlinear or non-stationary terms in the vorticity equation, the diffusion of vorticity is maintained in (2.7) by gradients of temperature. Also note that the linear terms in gradients of temperature in (2.7) match the terms of the chiral current introduced in (3.4).
To clarify the implications inherent in (2.7), we consider shear flow in a channel (see figure 1) whose walls are located at ![]() $y=0,d$, for which the liquid velocity, temperature and liquid vorticity become
$y=0,d$, for which the liquid velocity, temperature and liquid vorticity become
The boundary conditions for this flow are
where the upper channel wall is kept at a temperature ![]() $T_1>T_0$.
$T_1>T_0$.
For this flow, the vorticity equation becomes
by setting (2.7) equal to zero. The last term in (2.10) drops out for liquids satisfying ![]() $\partial _y^2 T =0$ (that is, liquids whose viscous heating displayed in (2.1) is unimportant). Retaining only leading-order terms in temperature gradients, we obtain the theoretical prediction (1.1) for the chiral current.
$\partial _y^2 T =0$ (that is, liquids whose viscous heating displayed in (2.1) is unimportant). Retaining only leading-order terms in temperature gradients, we obtain the theoretical prediction (1.1) for the chiral current.
3. Chiral current and chiral stress in non-isothermal flow
The effect that we discuss in this paper is critically dependent on the form of the chiral current, which is proportional to the chiral velocity as this was defined in the Introduction (see also (3.11) below). Thus in the ensuing paragraphs we justify the form of the chiral current on grounds of symmetry.
3.1. Conservation of particle number
Motion of chiral particles suspended in a classical liquid is associated with a chiral current ![]() $\boldsymbol {j}^\pm = n^\pm \boldsymbol {v}^\pm$, where
$\boldsymbol {j}^\pm = n^\pm \boldsymbol {v}^\pm$, where ![]() $n^\pm$ are the number densities (numbers of particles per unit volume) of right- and left-handed particles, respectively, and
$n^\pm$ are the number densities (numbers of particles per unit volume) of right- and left-handed particles, respectively, and ![]() $\boldsymbol {v}^{\pm }$ are their respective velocities. For simplicity, we consider an incompressible liquid where the right- and left-handed particles are mirror images of each other. We can thus define a chiral current
$\boldsymbol {v}^{\pm }$ are their respective velocities. For simplicity, we consider an incompressible liquid where the right- and left-handed particles are mirror images of each other. We can thus define a chiral current ![]() $\boldsymbol {j}^{{ch}}$ (cf. figure 1) of the form
$\boldsymbol {j}^{{ch}}$ (cf. figure 1) of the form
The chiral density ![]() $n^{{ch}} = n^+ - n^-$ satisfies the conservation law
$n^{{ch}} = n^+ - n^-$ satisfies the conservation law
where ![]() $\boldsymbol {j}(n) = -D\,\boldsymbol {\nabla } n - n \lambda _T\,\boldsymbol {\nabla } T - n \lambda _p\,\boldsymbol {\nabla } p$ is the particle current in the absence of chirality (Landau & Lifshitz Reference Landau and Lifshitz1987; Andreev et al. Reference Andreev, Son and Spivak2010), and
$\boldsymbol {j}(n) = -D\,\boldsymbol {\nabla } n - n \lambda _T\,\boldsymbol {\nabla } T - n \lambda _p\,\boldsymbol {\nabla } p$ is the particle current in the absence of chirality (Landau & Lifshitz Reference Landau and Lifshitz1987; Andreev et al. Reference Andreev, Son and Spivak2010), and ![]() $\boldsymbol {j}(n^{{ch}})$ is
$\boldsymbol {j}(n^{{ch}})$ is ![]() $\boldsymbol {j}(n)$ with
$\boldsymbol {j}(n)$ with ![]() $n$ replaced by
$n$ replaced by ![]() $n^{{ch}}$. The density
$n^{{ch}}$. The density ![]() $n=n^+ + n^-$ of chiral particles satisfies a similar conservation equation, which is affected by chirality in a non-racemic mixture
$n=n^+ + n^-$ of chiral particles satisfies a similar conservation equation, which is affected by chirality in a non-racemic mixture
so that (3.2) and (3.3) satisfy the Onsager principle of the symmetry of the kinetic coefficients (Landau & Lifshitz Reference Landau and Lifshitz1987).
3.2. Chiral current
In the presence of temperature gradients, a phenomenological expression for the chiral current ![]() $\boldsymbol {j}^{{ch}}$ (cf. (3.1)) based on symmetry considerations and which has a low power of derivatives of vorticity is
$\boldsymbol {j}^{{ch}}$ (cf. (3.1)) based on symmetry considerations and which has a low power of derivatives of vorticity is
where ![]() $n= n^+ + n^-$, and
$n= n^+ + n^-$, and ![]() $T, \boldsymbol {v}$ are the liquid's, undisturbed by chirality, temperature and velocity, respectively. The coefficients
$T, \boldsymbol {v}$ are the liquid's, undisturbed by chirality, temperature and velocity, respectively. The coefficients ![]() $\beta _1,\beta _2$ will be discussed below. As mentioned above, the magnitude of the chiral current is determined by the complicated tumbling motion of the particles caused by thermal fluctuations and the inhomogeneous flow. The phenomenological expression (3.4) is written to lowest order in the driving flow. At strong drives, thermal fluctuations are subdominant, and the magnitude of the chiral current is determined by averaging over corresponding Jeffery orbits in the non-uniform flow. This problem, but in a different context, was discussed in Kirkinis, Andreev & Spivak (Reference Kirkinis, Andreev and Spivak2012).
$\beta _1,\beta _2$ will be discussed below. As mentioned above, the magnitude of the chiral current is determined by the complicated tumbling motion of the particles caused by thermal fluctuations and the inhomogeneous flow. The phenomenological expression (3.4) is written to lowest order in the driving flow. At strong drives, thermal fluctuations are subdominant, and the magnitude of the chiral current is determined by averaging over corresponding Jeffery orbits in the non-uniform flow. This problem, but in a different context, was discussed in Kirkinis, Andreev & Spivak (Reference Kirkinis, Andreev and Spivak2012).
In Andreev et al. (Reference Andreev, Son and Spivak2010), the chiral current in an isothermal system was shown to be described by the expression
Insight into the physical origin of (3.4) may be obtained by applying (3.5) to a shear flow in the presence of temperature gradients. In particular, allowing temperature dependence of the liquid viscosity ![]() $\eta$ and implementing the resulting vorticity equation, (3.5) leads to
$\eta$ and implementing the resulting vorticity equation, (3.5) leads to
where a prime denotes differentiation with respect to temperature ![]() $T$, and we retained only leading-order terms in temperature gradients. Thus the coefficients
$T$, and we retained only leading-order terms in temperature gradients. Thus the coefficients ![]() $\beta _1$ and
$\beta _1$ and ![]() $\beta _2$ in (3.4) can be expressed in terms of the logarithmic derivative of viscosity with respect to temperature. We note that in the absence of temperature gradients, chiral separation is possible only in non-stationary or nonlinear flows (Andreev et al. Reference Andreev, Son and Spivak2010), as can be seen by inspection of the vorticity equation
$\beta _2$ in (3.4) can be expressed in terms of the logarithmic derivative of viscosity with respect to temperature. We note that in the absence of temperature gradients, chiral separation is possible only in non-stationary or nonlinear flows (Andreev et al. Reference Andreev, Son and Spivak2010), as can be seen by inspection of the vorticity equation
and (3.5). For example, such propulsion would be present in the nonlinear pressure-driven flow induced in a convergent or divergent channel (Landau & Lifshitz Reference Landau and Lifshitz1987, § 23). In the presence of temperature gradients, however, chiral separation is possible even in the creeping flow regime. This is important for biological systems, which operate at low Reynolds numbers. This can be seen by considering a liquid whose viscosity is a function of temperature. To leading order in ![]() $\Delta T$, the vorticity equation (3.7) is replaced by
$\Delta T$, the vorticity equation (3.7) is replaced by
 \begin{align} \eta\,\nabla^2
\textrm{curl}\,{\boldsymbol{v}} &\sim \eta'
\left[\boldsymbol{\nabla} T \times \nabla^2
{\boldsymbol{v}} + (\boldsymbol{\nabla} T
\boldsymbol{\cdot}\boldsymbol{\nabla})\,\textrm{curl}\,{\boldsymbol{v}}
\right]\nonumber\\ &\quad + \rho(\partial_t \textrm{curl} \,{\boldsymbol{v}}+
\textrm{curl} ({\boldsymbol{v}}
\boldsymbol{\cdot}\boldsymbol{\nabla}{\boldsymbol{v}}))
+O((\Delta T)^2),
\end{align}
\begin{align} \eta\,\nabla^2
\textrm{curl}\,{\boldsymbol{v}} &\sim \eta'
\left[\boldsymbol{\nabla} T \times \nabla^2
{\boldsymbol{v}} + (\boldsymbol{\nabla} T
\boldsymbol{\cdot}\boldsymbol{\nabla})\,\textrm{curl}\,{\boldsymbol{v}}
\right]\nonumber\\ &\quad + \rho(\partial_t \textrm{curl} \,{\boldsymbol{v}}+
\textrm{curl} ({\boldsymbol{v}}
\boldsymbol{\cdot}\boldsymbol{\nabla}{\boldsymbol{v}}))
+O((\Delta T)^2),
\end{align}
where a prime denotes differentiation with respect to temperature ![]() $T$. Comparison of the linear in
$T$. Comparison of the linear in ![]() $\boldsymbol {\nabla } T$ terms in (3.8) with (3.4) shows that the latter and (3.5) are equivalent when material parameters (here, the viscosity) vary with temperature. We note that an expression of magnetic origin for the diffusion of vorticity was also obtained in Kirkinis & Olvera de la Cruz (Reference Kirkinis and Olvera de la Cruz2023), leading to the actuation of a suspension of chiral particles in a magnetic liquid.
$\boldsymbol {\nabla } T$ terms in (3.8) with (3.4) shows that the latter and (3.5) are equivalent when material parameters (here, the viscosity) vary with temperature. We note that an expression of magnetic origin for the diffusion of vorticity was also obtained in Kirkinis & Olvera de la Cruz (Reference Kirkinis and Olvera de la Cruz2023), leading to the actuation of a suspension of chiral particles in a magnetic liquid.
When the spatial derivatives of ![]() $\boldsymbol {v}$ do not vanish, the linear in
$\boldsymbol {v}$ do not vanish, the linear in ![]() $\Delta T$ terms in (3.8) provide a scaling prediction for the magnitude of the chiral current (3.5), and equivalently for the chiral velocity
$\Delta T$ terms in (3.8) provide a scaling prediction for the magnitude of the chiral current (3.5), and equivalently for the chiral velocity ![]() ${v}^{{ch}}$ in the form (1.1). This is a main consequence of the symmetries leading to (3.4), and will be derived explicitly in § 4.
${v}^{{ch}}$ in the form (1.1). This is a main consequence of the symmetries leading to (3.4), and will be derived explicitly in § 4.
3.3. Chiral stress
A chiral suspension imparts stresses on the suspending liquid. To leading order in velocity gradients, these stresses, allowed by symmetry, read
where ![]() $V_{ij}$ is the rate-of-strain tensor. The first square bracket term of (3.9) introduced in Andreev et al. (Reference Andreev, Son and Spivak2010) was discussed in the recent review Witten & Diamant (Reference Witten and Diamant2020). The second square bracket term exists only when temperature gradients are present in the liquid.
$V_{ij}$ is the rate-of-strain tensor. The first square bracket term of (3.9) introduced in Andreev et al. (Reference Andreev, Son and Spivak2010) was discussed in the recent review Witten & Diamant (Reference Witten and Diamant2020). The second square bracket term exists only when temperature gradients are present in the liquid.
The coefficients ![]() $\beta$,
$\beta$, ![]() $\alpha$ and
$\alpha$ and ![]() $\alpha _1$ in (3.5) and (3.9) are determined in the low Reynolds number regime by studying the particle motion in the surrounding liquid (Happel & Brenner Reference Happel and Brenner1965). They may be estimated as
$\alpha _1$ in (3.5) and (3.9) are determined in the low Reynolds number regime by studying the particle motion in the surrounding liquid (Happel & Brenner Reference Happel and Brenner1965). They may be estimated as
where ![]() $R$ is the chiral particle radius, and
$R$ is the chiral particle radius, and ![]() $\chi$ is the degree of chirality in the shape of the particles. Equations (3.10a,b) provide the order of magnitude estimates of these coefficients. Their precise determination for a specific particle shape, however, requires solving hydrodynamic equations for a tumbling particle in the presence of temperature and velocity gradients, and is beyond the scope of our work. For simplicity, we consider an incompressible liquid where the right- and left-handed particles are mirror images of each other.
$\chi$ is the degree of chirality in the shape of the particles. Equations (3.10a,b) provide the order of magnitude estimates of these coefficients. Their precise determination for a specific particle shape, however, requires solving hydrodynamic equations for a tumbling particle in the presence of temperature and velocity gradients, and is beyond the scope of our work. For simplicity, we consider an incompressible liquid where the right- and left-handed particles are mirror images of each other.
3.4. Chiral velocity
The programme to be followed in this paper is as follows. First, we will determine the form of the base flow, undisturbed by chirality, and denoted by ![]() $\boldsymbol {v} = u(y)\,\hat {\boldsymbol {x}}$ with reference to figure 1. From this, we calculate the chiral velocity
$\boldsymbol {v} = u(y)\,\hat {\boldsymbol {x}}$ with reference to figure 1. From this, we calculate the chiral velocity ![]() $v^{{ch}}$ as
$v^{{ch}}$ as
which, through (3.5), gives rise to the main observable, that is, the chiral current ![]() $\boldsymbol {j}^{{ch}}$. We calculate explicitly the stresses imparted on the liquid and on the two channel walls by the chiral stress (3.9). The Cauchy stress tensor in (2.6) thus needs to be updated by the chiral contribution (3.9) to take into account the effects of the chiral suspension on the base liquid. Thus we calculate explicitly the chiral suspension-induced perturbation
$\boldsymbol {j}^{{ch}}$. We calculate explicitly the stresses imparted on the liquid and on the two channel walls by the chiral stress (3.9). The Cauchy stress tensor in (2.6) thus needs to be updated by the chiral contribution (3.9) to take into account the effects of the chiral suspension on the base liquid. Thus we calculate explicitly the chiral suspension-induced perturbation ![]() $\delta v$ of the liquid base flow.
$\delta v$ of the liquid base flow.
4. Chiral particle separation in crossed pressure and temperature gradients
4.1. Non-isothermal base Poiseuille flow (without chiral particles)
Consider pressure-driven flow in a channel with uneven heated walls (cf. figure 1). With ![]() $\boldsymbol {v} = u(y)\,\hat {\boldsymbol {x}}$,
$\boldsymbol {v} = u(y)\,\hat {\boldsymbol {x}}$, ![]() $\boldsymbol {\nabla } T= \partial _y T\hat {\boldsymbol {y}}$, the Navier–Stokes equations (2.5a,b) and energy balance (2.2) in the creeping flow approximation reduce to
$\boldsymbol {\nabla } T= \partial _y T\hat {\boldsymbol {y}}$, the Navier–Stokes equations (2.5a,b) and energy balance (2.2) in the creeping flow approximation reduce to
respectively, with boundary conditions
The energy equation temperature profile thus obtained is ![]() $T (y) = T_0 + ({y}/{d})\,\Delta T$. Let
$T (y) = T_0 + ({y}/{d})\,\Delta T$. Let
where ![]() $T_0$ and
$T_0$ and ![]() $T_1=T_0 +\Delta T$ are the lower and upper wall fixed temperatures, respectively,
$T_1=T_0 +\Delta T$ are the lower and upper wall fixed temperatures, respectively, ![]() $T_2 \equiv T= T_0 + ({y}/{d})\,\Delta T$, and
$T_2 \equiv T= T_0 + ({y}/{d})\,\Delta T$, and ![]() $E$,
$E$, ![]() $R_g$ and
$R_g$ and ![]() $T_A$ are the activation energy, gas constant and correction temperature as defined in table 1, respectively. The solution of the first equation of (4.1a,b) with boundary conditions (4.2a–c) becomes
$T_A$ are the activation energy, gas constant and correction temperature as defined in table 1, respectively. The solution of the first equation of (4.1a,b) with boundary conditions (4.2a–c) becomes
 \begin{equation} u = \frac{T_E^2d^2\, \partial_x p}{2\eta(T)\,(\Delta T)^2} \frac{\sum\limits_{\left\{i,j,k\right\}} {\rm e}^{X_{i}}\left\{{Ei}_1(X_i) \left[ \dfrac{{\rm e}^{X_{j}}}{X_k^2} - \dfrac{{\rm e}^{X_{k}}}{X_j^2} \right] + \dfrac{1}{X_jX_k} \left(\dfrac{1}{X_k} - \dfrac{1}{X_j} \right)\right\}} {\left[ {Ei}_1(X_0) - {Ei}_1(X_1) \right] {\rm e}^{X_{0} + X_{1}} + \dfrac{{\rm e}^{X_{0}}}{X_1} - \dfrac{{\rm e}^{X_{1}}}{X_0} }, \end{equation}
\begin{equation} u = \frac{T_E^2d^2\, \partial_x p}{2\eta(T)\,(\Delta T)^2} \frac{\sum\limits_{\left\{i,j,k\right\}} {\rm e}^{X_{i}}\left\{{Ei}_1(X_i) \left[ \dfrac{{\rm e}^{X_{j}}}{X_k^2} - \dfrac{{\rm e}^{X_{k}}}{X_j^2} \right] + \dfrac{1}{X_jX_k} \left(\dfrac{1}{X_k} - \dfrac{1}{X_j} \right)\right\}} {\left[ {Ei}_1(X_0) - {Ei}_1(X_1) \right] {\rm e}^{X_{0} + X_{1}} + \dfrac{{\rm e}^{X_{0}}}{X_1} - \dfrac{{\rm e}^{X_{1}}}{X_0} }, \end{equation}
where the ![]() $y$ dependence arises through
$y$ dependence arises through ![]() $X_2(T(y))$ (see (4.3a,b)), the symbol
$X_2(T(y))$ (see (4.3a,b)), the symbol ![]() $\{i,j,k\}$ means cyclic permutation of
$\{i,j,k\}$ means cyclic permutation of ![]() $i$,
$i$, ![]() $j$ and
$j$ and ![]() $k$, and
$k$, and
is the exponential integral.
4.2. Chiral velocity
Now consider the presence of chiral particles and define the chiral velocity (3.11), ![]() $\boldsymbol {v}^{{ch}} \equiv \boldsymbol {j}^{{ch}}/n$, relative to the liquid by employing (3.5). With respect to the geometry displayed in figure 1, it has the form
$\boldsymbol {v}^{{ch}} \equiv \boldsymbol {j}^{{ch}}/n$, relative to the liquid by employing (3.5). With respect to the geometry displayed in figure 1, it has the form ![]() $\boldsymbol {v}^{{ch}} = v^{{ch}}(y)\,\hat {\boldsymbol {z}}$, and its magnitude is
$\boldsymbol {v}^{{ch}} = v^{{ch}}(y)\,\hat {\boldsymbol {z}}$, and its magnitude is
 \begin{align} v^{{ch}} &=
\chi\,\frac{R^3}{d}\,\frac{X_2^4\,\Delta T\,
\partial_xp}{2\eta(T)\,T_E}\nonumber\\
&\quad \times \frac{\left[
{Ei}_1(X_1) - {Ei}_1(X_0) \right] {\rm e}^{X_{0} + X_{1}}
+\sum\limits_{i\neq j =0,1} \dfrac{( - 1)^i {\rm
e}^{X_{j}}}{X_i^2}
\left[\dfrac{1}{2}+\dfrac{1}{X_i}\left(\dfrac{1}{X_2}-\dfrac{1}{2}\right)
\right] } {\left[ {Ei}_1(X_0) - {Ei}_1(X_1)
\right] {\rm e}^{X_{0} + X_{1}} +
\dfrac{{\rm e}^{X_{0}}}{X_1} - \dfrac{{\rm
e}^{X_{1}}}{X_0}},
\end{align}
\begin{align} v^{{ch}} &=
\chi\,\frac{R^3}{d}\,\frac{X_2^4\,\Delta T\,
\partial_xp}{2\eta(T)\,T_E}\nonumber\\
&\quad \times \frac{\left[
{Ei}_1(X_1) - {Ei}_1(X_0) \right] {\rm e}^{X_{0} + X_{1}}
+\sum\limits_{i\neq j =0,1} \dfrac{( - 1)^i {\rm
e}^{X_{j}}}{X_i^2}
\left[\dfrac{1}{2}+\dfrac{1}{X_i}\left(\dfrac{1}{X_2}-\dfrac{1}{2}\right)
\right] } {\left[ {Ei}_1(X_0) - {Ei}_1(X_1)
\right] {\rm e}^{X_{0} + X_{1}} +
\dfrac{{\rm e}^{X_{0}}}{X_1} - \dfrac{{\rm
e}^{X_{1}}}{X_0}},
\end{align}
where the ![]() $y$-dependence again arises through
$y$-dependence again arises through ![]() $X_2(T(y))$ (see (4.3a,b)). In figure 2, we plot the closed-form expression (4.6) for the chiral velocity
$X_2(T(y))$ (see (4.3a,b)). In figure 2, we plot the closed-form expression (4.6) for the chiral velocity ![]() $\delta v$ in
$\delta v$ in ![]() ${\rm cm}\ {\rm s}^{-1}$ versus channel elevation
${\rm cm}\ {\rm s}^{-1}$ versus channel elevation ![]() $y$ in cm for two temperature variations
$y$ in cm for two temperature variations ![]() $\Delta T$ between the lower (at
$\Delta T$ between the lower (at ![]() $y=0$) and upper (at
$y=0$) and upper (at ![]() $y=0.1$ cm) channel walls. As can be seen in figure 2, velocity proliferation is favoured near the upper heated wall where viscosity is diminished. In addition, particle velocities are non-zero close to the solid walls located at
$y=0.1$ cm) channel walls. As can be seen in figure 2, velocity proliferation is favoured near the upper heated wall where viscosity is diminished. In addition, particle velocities are non-zero close to the solid walls located at ![]() $y=0,d$, even though no-slip boundary conditions are satisfied by the base liquid. This is the case because, according to (3.5), chiral particle velocities become prominent in the vicinity of large vorticity gradients, and these are present close to solid walls.
$y=0,d$, even though no-slip boundary conditions are satisfied by the base liquid. This is the case because, according to (3.5), chiral particle velocities become prominent in the vicinity of large vorticity gradients, and these are present close to solid walls.

Figure 2. Chiral particle velocity ![]() $v^{{ch}}$ in
$v^{{ch}}$ in ![]() ${\rm cm}\ {\rm s}^{-1}$ from (4.6), perpendicular to the
${\rm cm}\ {\rm s}^{-1}$ from (4.6), perpendicular to the ![]() $x$–
$x$–![]() $y$ plane formed by a base Poiseuille flow and the vertical temperature gradient directions (cf. figure 1). Here,
$y$ plane formed by a base Poiseuille flow and the vertical temperature gradient directions (cf. figure 1). Here, ![]() $y$ is the vertical channel coordinate in cm, and we employed the Arrhenius-type temperature dependent viscosity law (2.3) for a BM-4 oil (Fogel'son & Likhachev Reference Fogel'son and Likhachev2001). We have set
$y$ is the vertical channel coordinate in cm, and we employed the Arrhenius-type temperature dependent viscosity law (2.3) for a BM-4 oil (Fogel'son & Likhachev Reference Fogel'son and Likhachev2001). We have set ![]() $\chi =1$ (see the discussion in Appendix A).
$\chi =1$ (see the discussion in Appendix A).
Relation (4.6) is tidy but uninformative. To obtain an understanding of the effect, we average (4.6) over the channel width ![]() $d$, and expand with respect to
$d$, and expand with respect to ![]() $\Delta T$ to obtain
$\Delta T$ to obtain ![]() $\langle v^{{ch}} \rangle \sim 2\chi R^3 \gamma ({\Delta T}/{d})({\partial _x p}/{\eta })$, to leading order in
$\langle v^{{ch}} \rangle \sim 2\chi R^3 \gamma ({\Delta T}/{d})({\partial _x p}/{\eta })$, to leading order in ![]() $\Delta T$, where we defined the average of a function
$\Delta T$, where we defined the average of a function ![]() $f(y)$ with respect to the channel width to be
$f(y)$ with respect to the channel width to be ![]() $\langle\, f \rangle = ({1}/{d})\int _0^d f(y)\,{{\rm d}y}$,
$\langle\, f \rangle = ({1}/{d})\int _0^d f(y)\,{{\rm d}y}$, ![]() $R$ is chiral particle size,
$R$ is chiral particle size, ![]() $d$ is channel width, and
$d$ is channel width, and ![]() $\gamma$ is the logarithmic derivative of viscosity; see the discussion below (2.4). It is more illuminating, however, to replace the pressure gradient with a characteristic velocity
$\gamma$ is the logarithmic derivative of viscosity; see the discussion below (2.4). It is more illuminating, however, to replace the pressure gradient with a characteristic velocity ![]() $U_0$ of Poiseuille flow by averaging the (undisturbed by chirality) base Poiseuille profile
$U_0$ of Poiseuille flow by averaging the (undisturbed by chirality) base Poiseuille profile ![]() $u \sim {\partial _x p}/{2\eta (T_0)}\,(y^2 - yd)$ over the channel width
$u \sim {\partial _x p}/{2\eta (T_0)}\,(y^2 - yd)$ over the channel width ![]() $d$. This gives
$d$. This gives ![]() $U_0 = - ({\partial _x p}/{12\eta (T_0)})d^2$, and substituting into the expression for
$U_0 = - ({\partial _x p}/{12\eta (T_0)})d^2$, and substituting into the expression for ![]() $\langle v^{{ch}} \rangle$, we obtain the single-particle velocity
$\langle v^{{ch}} \rangle$, we obtain the single-particle velocity
Considering BM-4 oil (Fogel'son & Likhachev Reference Fogel'son and Likhachev2001), ![]() $\Delta T = {10}\ {\rm K}$ and the values displayed in table 1, (4.7) leads to the estimate
$\Delta T = {10}\ {\rm K}$ and the values displayed in table 1, (4.7) leads to the estimate
The Reynolds number is ![]() ${Re} \sim 3.4\times 10^{-3}$. Analogous results can be derived for silicon oils employed in the experiments of Ehrhard (Reference Ehrhard1993) and other liquids reported in the literature (Fogel'son & Likhachev Reference Fogel'son and Likhachev2001). Water can also be used, although it leads to Reynolds numbers higher than those reported here.
${Re} \sim 3.4\times 10^{-3}$. Analogous results can be derived for silicon oils employed in the experiments of Ehrhard (Reference Ehrhard1993) and other liquids reported in the literature (Fogel'son & Likhachev Reference Fogel'son and Likhachev2001). Water can also be used, although it leads to Reynolds numbers higher than those reported here.
4.3. Perturbation of liquid velocity by the chiral suspension
A chiral suspension imparts stresses on the suspending liquid. To leading order in gradients of vorticity, these stresses, allowed by symmetry, are given by (3.9)). Here, ![]() $n^{{ch}} = n^+ - n^-$ is the chiral density, and
$n^{{ch}} = n^+ - n^-$ is the chiral density, and ![]() $n^+$ and
$n^+$ and ![]() $n^-$ are the number densities of right- and left-handed particles, respectively. Thus the liquid velocity
$n^-$ are the number densities of right- and left-handed particles, respectively. Thus the liquid velocity ![]() $\boldsymbol {v}$ acquires a chirality-induced component
$\boldsymbol {v}$ acquires a chirality-induced component ![]() $\delta v$ perpendicular to the plane of the flow:
$\delta v$ perpendicular to the plane of the flow:
With the chiral correction (3.9), the Cauchy stress tensor reads
Conservation of linear momentum ![]() $\partial _j \sigma _{ij} = 0$ along the flow direction
$\partial _j \sigma _{ij} = 0$ along the flow direction ![]() $\hat {\boldsymbol {x}}: -\partial _xp +\partial _y (\eta \,\partial _yu)$
$\hat {\boldsymbol {x}}: -\partial _xp +\partial _y (\eta \,\partial _yu)$ ![]() $=0$ is now accompanied by its chirality-induced counterpart that is perpendicular to the base flow direction,
$=0$ is now accompanied by its chirality-induced counterpart that is perpendicular to the base flow direction,
and satisfies no-slip boundary conditions
The solution ![]() $\delta v$ of (4.11) with boundary conditions (4.12) is displayed in figure 3 in
$\delta v$ of (4.11) with boundary conditions (4.12) is displayed in figure 3 in ![]() ${\rm cm}\ {\rm s}^{-1}$ versus channel elevation
${\rm cm}\ {\rm s}^{-1}$ versus channel elevation ![]() $y$ in cm for two temperature variations
$y$ in cm for two temperature variations ![]() $\varDelta T$ between the lower (at
$\varDelta T$ between the lower (at ![]() $y=0$) and upper (at
$y=0$) and upper (at ![]() $y=0.1$ cm) channel walls, employing the Arrhenius-type temperature-dependent viscosity law (2.3). Its profile is skewed due to the reduction of viscosity close to the upper heated channel wall, which is also the location of high chiral velocity
$y=0.1$ cm) channel walls, employing the Arrhenius-type temperature-dependent viscosity law (2.3). Its profile is skewed due to the reduction of viscosity close to the upper heated channel wall, which is also the location of high chiral velocity ![]() $v^{{ch}}$.
$v^{{ch}}$.

Figure 3. Transverse chiral component of liquid velocity ![]() $\delta v$ in
$\delta v$ in ![]() ${\rm cm}\ {\rm s}^{-1}$, perpendicular to the
${\rm cm}\ {\rm s}^{-1}$, perpendicular to the ![]() $x$–
$x$–![]() $y$ plane formed by a Poiseuille flow and the temperature gradient directions (cf. figure 1) and obtained by solution of (4.11) with boundary conditions (4.12). Here,
$y$ plane formed by a Poiseuille flow and the temperature gradient directions (cf. figure 1) and obtained by solution of (4.11) with boundary conditions (4.12). Here, ![]() $y$ is the vertical channel coordinate in cm, and we employed the Arrhenius-type temperature dependent viscosity law (2.3) for a BM-4 oil (Fogel'son & Likhachev Reference Fogel'son and Likhachev2001), giving rise to the skewness of chiral velocity profiles. We have set
$y$ is the vertical channel coordinate in cm, and we employed the Arrhenius-type temperature dependent viscosity law (2.3) for a BM-4 oil (Fogel'son & Likhachev Reference Fogel'son and Likhachev2001), giving rise to the skewness of chiral velocity profiles. We have set ![]() $\chi =1$ (see the discussion in Appendix A).
$\chi =1$ (see the discussion in Appendix A).
To leading order in ![]() $\Delta T$, and averaging over the channel width
$\Delta T$, and averaging over the channel width ![]() $d$, we obtain
$d$, we obtain ![]() $\delta v \sim \chi R ({d\,\partial _x p}/{12\eta }) \gamma \,\Delta T$. Replacing the pressure gradient with its Poiseuille flow counterpart leads to
$\delta v \sim \chi R ({d\,\partial _x p}/{12\eta }) \gamma \,\Delta T$. Replacing the pressure gradient with its Poiseuille flow counterpart leads to
Employing the material parameters for BM-4 oil displayed in table 1, and setting ![]() $\Delta T = {10}\ {\rm K}$, we obtain the estimate
$\Delta T = {10}\ {\rm K}$, we obtain the estimate
which agrees well, in order of magnitude, with the exact solution displayed in figure 3. The momentum equation displayed in (4.11) was formulated by considering only the first term of the constitutive law (3.9), since the second term – for the material parameters employed in this paper – gives velocities that are one order of magnitude smaller than the ones derived here.
4.4. Screw torque in a non-racemic suspension
A non-racemic mixture will apply shear stresses on the channel walls that are perpendicular to the plane of the paper. These forces arise from the chiral momentum flux density (3.9) (Andreev et al. Reference Andreev, Son and Spivak2010). Employing the geometry of the channel Poiseuille flow displayed in figure 1, this stress is of the form
In figure 4, we display the chiral stress ![]() $\sigma _{zy}^{{{ch}}}$ as a function of channel width employing the exact form for the liquid velocity profile (4.4). Since the normal vectors to the two channel walls have opposite sign, the chiral suspension exerts on the walls two forces of opposite sign directed into and out of the page. Hence there is a screw torque exerted by the chiral flow on the confining walls, directed along the flow.
$\sigma _{zy}^{{{ch}}}$ as a function of channel width employing the exact form for the liquid velocity profile (4.4). Since the normal vectors to the two channel walls have opposite sign, the chiral suspension exerts on the walls two forces of opposite sign directed into and out of the page. Hence there is a screw torque exerted by the chiral flow on the confining walls, directed along the flow.

Figure 4. Distribution of the chiral stress ![]() $\sigma _{zy}^{{{ch}}}$ in (4.15) in
$\sigma _{zy}^{{{ch}}}$ in (4.15) in ![]() ${\rm dynes}\ \textrm {cm}^{-2}$ imparted by the chiral suspension on the liquid in a direction perpendicular to the
${\rm dynes}\ \textrm {cm}^{-2}$ imparted by the chiral suspension on the liquid in a direction perpendicular to the ![]() $x$–
$x$–![]() $y$ plane formed by the Poiseuille flow and the vertical temperature gradient (cf. figure 1), versus the vertical coordinate
$y$ plane formed by the Poiseuille flow and the vertical temperature gradient (cf. figure 1), versus the vertical coordinate ![]() $y$ of the channel in cm. We employed the Arrhenius-type temperature-dependent viscosity law (2.3) for a BM-4 oil (Fogel'son & Likhachev Reference Fogel'son and Likhachev2001). Since the normal vectors to the two channel walls have opposite sign, the chiral suspension exerts on the walls two forces of opposite sign directed into and out of the page. Hence there is a screw torque exerted by the chiral flow on the confining walls, directed along the base flow direction. We have set
$y$ of the channel in cm. We employed the Arrhenius-type temperature-dependent viscosity law (2.3) for a BM-4 oil (Fogel'son & Likhachev Reference Fogel'son and Likhachev2001). Since the normal vectors to the two channel walls have opposite sign, the chiral suspension exerts on the walls two forces of opposite sign directed into and out of the page. Hence there is a screw torque exerted by the chiral flow on the confining walls, directed along the base flow direction. We have set ![]() $\chi =1$ (see the discussion in Appendix A).
$\chi =1$ (see the discussion in Appendix A).
Calculating the average of the chiral stress ![]() $\langle \sigma _{zy}^{{{ch}}} \rangle$ over the channel width, and expanding with respect to
$\langle \sigma _{zy}^{{{ch}}} \rangle$ over the channel width, and expanding with respect to ![]() $\Delta T$, we obtain
$\Delta T$, we obtain
Expression (4.16) implies that a chiral stress exists even in the absence of temperature gradients. This was also noted in Andreev et al. (Reference Andreev, Son and Spivak2010). Replacing the pressure gradient by the base Poiseuille profile, as carried out in the foregoing sections and employing the material values appearing in table 1 for ![]() $\Delta T = 10\ {\rm K}$, (4.16) gives
$\Delta T = 10\ {\rm K}$, (4.16) gives
Doubling ![]() $\Delta T$, one needs to double only the number
$\Delta T$, one needs to double only the number ![]() $0.43$ in this last expression.
$0.43$ in this last expression.
5. Non-isothermal chiral separation and propulsion in Couette flow
The practically important case of Couette flow under a vertical temperature gradient in a channel whose upper wall slides with velocity ![]() $V$ also gives a commensurate chiral particle propulsion:
$V$ also gives a commensurate chiral particle propulsion: ![]() $\boldsymbol {v} = u(y)\,\hat {\boldsymbol {x}}$,
$\boldsymbol {v} = u(y)\,\hat {\boldsymbol {x}}$, ![]() $\boldsymbol {\nabla } T= \partial _y T\hat {\boldsymbol {y}}$. In this case, the Navier–Stokes and energy balance equations in the creeping flow approximation reduce to
$\boldsymbol {\nabla } T= \partial _y T\hat {\boldsymbol {y}}$. In this case, the Navier–Stokes and energy balance equations in the creeping flow approximation reduce to
with boundary conditions
The energy equation temperature profile thus obtained is ![]() $T (y) = T_0 + ({y}/{d})\,\Delta T$.
$T (y) = T_0 + ({y}/{d})\,\Delta T$.
The vorticity equation in the form (2.10) still holds, but because of the form of the Couette flow profile, contributions on the right-hand side of (2.10) will all be of second order in ![]() $\Delta T$. Employing the notation introduced in (4.3a,b), the chiral separation velocity takes the form
$\Delta T$. Employing the notation introduced in (4.3a,b), the chiral separation velocity takes the form
 \begin{equation} v^{{ch}} = \chi R^3\,\frac{V}{d^3}\,\frac{X_2^4 \left(\dfrac{1}{X_0} - \dfrac{1}{X_1}\right)^3\left(\dfrac{2}{X_2} - 1\right) {\rm e}^{X_0+X_1 - X_2}} {\left[ {Ei}_1(X_0) - {Ei}_1(X_1) \right] {\rm e}^{X_{0} + X_{1}} + \dfrac{{\rm e}^{X_{0}}}{X_1} - \dfrac{{\rm e}^{X_{1}}}{X_0}}. \end{equation}
\begin{equation} v^{{ch}} = \chi R^3\,\frac{V}{d^3}\,\frac{X_2^4 \left(\dfrac{1}{X_0} - \dfrac{1}{X_1}\right)^3\left(\dfrac{2}{X_2} - 1\right) {\rm e}^{X_0+X_1 - X_2}} {\left[ {Ei}_1(X_0) - {Ei}_1(X_1) \right] {\rm e}^{X_{0} + X_{1}} + \dfrac{{\rm e}^{X_{0}}}{X_1} - \dfrac{{\rm e}^{X_{1}}}{X_0}}. \end{equation}
In figure 5, we plot the closed-form expression (5.3) for the individual particle velocity ![]() $v^{{ch}}$ in cm s
$v^{{ch}}$ in cm s![]() $^{-1}$ versus channel elevation
$^{-1}$ versus channel elevation ![]() $y$ in cm for two temperature variations
$y$ in cm for two temperature variations ![]() $\Delta T$ between the lower (at
$\Delta T$ between the lower (at ![]() $y=0$) and upper (at
$y=0$) and upper (at ![]() $y=0.1$ cm) channel walls.
$y=0.1$ cm) channel walls.

Figure 5. Chiral particle velocity ![]() $v^{{ch}}$ in
$v^{{ch}}$ in ![]() ${\rm cm}\ {\rm s}^{-1}$ from (5.3), perpendicular to the
${\rm cm}\ {\rm s}^{-1}$ from (5.3), perpendicular to the ![]() $x$–
$x$–![]() $y$ plane formed by the Couette flow and temperature gradient directions (cf. figure 1). Here,
$y$ plane formed by the Couette flow and temperature gradient directions (cf. figure 1). Here, ![]() $y$ is the vertical channel coordinate in cm, and we employed the Arrhenius-type temperature-dependent viscosity law (2.3) for a BM-4 oil (Fogel'son & Likhachev Reference Fogel'son and Likhachev2001). The base flow is generated by the motion of the upper channel wall with velocity
$y$ is the vertical channel coordinate in cm, and we employed the Arrhenius-type temperature-dependent viscosity law (2.3) for a BM-4 oil (Fogel'son & Likhachev Reference Fogel'son and Likhachev2001). The base flow is generated by the motion of the upper channel wall with velocity ![]() $1\ {\rm cm}\ {\rm s}^{-1}$. We have set
$1\ {\rm cm}\ {\rm s}^{-1}$. We have set ![]() $\chi =1$ (see the discussion in Appendix A).
$\chi =1$ (see the discussion in Appendix A).
Averaging (5.3) over the channel width ![]() $d$, and expanding with respect to
$d$, and expanding with respect to ![]() $\Delta T$, we obtain the chiral separation velocities
$\Delta T$, we obtain the chiral separation velocities ![]() $\langle v^{{ch}} \rangle$, which are now quadratic with respect to the temperature gradient strength
$\langle v^{{ch}} \rangle$, which are now quadratic with respect to the temperature gradient strength ![]() $\Delta T$:
$\Delta T$:
 \begin{equation} \langle v^{{ch}} \rangle \sim 2\chi V \left(\frac{R}{d}\right)^3 \dfrac{T_A + T_0 - \dfrac{T_E}{2}}{(T_A + T_0)^4}\,T_E (\Delta T)^2 \end{equation}
\begin{equation} \langle v^{{ch}} \rangle \sim 2\chi V \left(\frac{R}{d}\right)^3 \dfrac{T_A + T_0 - \dfrac{T_E}{2}}{(T_A + T_0)^4}\,T_E (\Delta T)^2 \end{equation}
(see table 1 for the meaning of the various temperature scales). Considering the parameter values displayed in table 1, upper channel wall velocity ![]() $V=1\ {\rm cm}\ {\rm s}^{-1}$ and
$V=1\ {\rm cm}\ {\rm s}^{-1}$ and ![]() $\Delta T = 10$ K, we obtain
$\Delta T = 10$ K, we obtain
which agrees well with the corresponding curve of figure 5. The Reynolds number is ![]() ${Re} \sim 3.4\times 10^{-2}$. In a manner analogous to the pressure-driven flow of § 4, the suspension will give rise to a transverse chiral component of liquid velocity
${Re} \sim 3.4\times 10^{-2}$. In a manner analogous to the pressure-driven flow of § 4, the suspension will give rise to a transverse chiral component of liquid velocity ![]() $v^{ch}$ perpendicular to the plane of the flow, also calculated for an upper wall velocity
$v^{ch}$ perpendicular to the plane of the flow, also calculated for an upper wall velocity ![]() $1\ {\rm cm}\ {\rm s}^{-1}$ employing the nonlinear Arrhenius viscosity law (2.3) by solving for
$1\ {\rm cm}\ {\rm s}^{-1}$ employing the nonlinear Arrhenius viscosity law (2.3) by solving for ![]() $\delta v$ in (4.11) with boundary conditions (4.12) when the base flow is given by the Couette profile obtained from (5.1a,b) and (5.2a–d). The liquid transverse chiral velocity
$\delta v$ in (4.11) with boundary conditions (4.12) when the base flow is given by the Couette profile obtained from (5.1a,b) and (5.2a–d). The liquid transverse chiral velocity ![]() $\delta v$ obtained in this manner is displayed in figure 6.
$\delta v$ obtained in this manner is displayed in figure 6.

Figure 6. Transverse chiral component of liquid velocity ![]() $\delta v$ in
$\delta v$ in ![]() ${\rm cm}\ {\rm s}^{-1}$, perpendicular to the
${\rm cm}\ {\rm s}^{-1}$, perpendicular to the ![]() $x$–
$x$–![]() $y$ plane formed by the Couette flow and temperature gradient directions (cf. figure 1) by solving for
$y$ plane formed by the Couette flow and temperature gradient directions (cf. figure 1) by solving for ![]() $\delta v$ in (4.11) with boundary conditions (4.12), when the base flow is given by the Couette profile obtained from (5.1a,b) and (5.2a–d). Here,
$\delta v$ in (4.11) with boundary conditions (4.12), when the base flow is given by the Couette profile obtained from (5.1a,b) and (5.2a–d). Here, ![]() $y$ is the vertical channel coordinate in cm, and we employed the Arrhenius-type temperature-dependent viscosity law (2.3) for a BM-4 oil (Fogel'son & Likhachev Reference Fogel'son and Likhachev2001), giving rise to the skewness of the chiral velocity profiles. The base flow is generated by the motion of the upper channel wall with velocity
$y$ is the vertical channel coordinate in cm, and we employed the Arrhenius-type temperature-dependent viscosity law (2.3) for a BM-4 oil (Fogel'son & Likhachev Reference Fogel'son and Likhachev2001), giving rise to the skewness of the chiral velocity profiles. The base flow is generated by the motion of the upper channel wall with velocity ![]() $1\ {\rm cm}\ {\rm s}^{-1}$. We have set
$1\ {\rm cm}\ {\rm s}^{-1}$. We have set ![]() $\chi =1$ (see the discussion in Appendix A).
$\chi =1$ (see the discussion in Appendix A).
6. Related thermal effects
6.1. Viscous heating-induced chiral particle propulsion
We note the existence of two rather special related thermal effects for the propulsion of chiral particles. The first concerns the effects of viscous heating in the interior of a channel when the viscosity is temperature-dependent and thermal gradients are generated at the interior by viscous heating (Kirkinis & Andreev Reference Kirkinis and Andreev2019). Referring to the geometry displayed in figure 1, where ![]() $\boldsymbol {v} = u(y)\,\hat {\boldsymbol {x}}$,
$\boldsymbol {v} = u(y)\,\hat {\boldsymbol {x}}$, ![]() $\boldsymbol {\nabla }T= \partial _y T\hat {\boldsymbol {y}}$ (here, however, the two walls are kept at equal temperatures), one can follow the formulation of this problem developed by Davis et al. (Reference Davis, Kriegsmann, Laurence and Rosenblat1983):
$\boldsymbol {\nabla }T= \partial _y T\hat {\boldsymbol {y}}$ (here, however, the two walls are kept at equal temperatures), one can follow the formulation of this problem developed by Davis et al. (Reference Davis, Kriegsmann, Laurence and Rosenblat1983):
 \begin{equation} \frac{{\rm d}}{{\rm d}y}\left[\eta(T)\,\frac{{\rm d}u}{{\rm d}y}\right] = 0, \quad k_{th}\,\frac{{\rm d}^2T}{{{\rm d}y}^2} + \eta \left(\frac{{\rm d}u}{{\rm d}y}\right)^2 = 0 , \end{equation}
\begin{equation} \frac{{\rm d}}{{\rm d}y}\left[\eta(T)\,\frac{{\rm d}u}{{\rm d}y}\right] = 0, \quad k_{th}\,\frac{{\rm d}^2T}{{{\rm d}y}^2} + \eta \left(\frac{{\rm d}u}{{\rm d}y}\right)^2 = 0 , \end{equation}with boundary conditions
Employing the Arrhenius law, the problem can be solved only numerically. The interest here would be the effect of hysteresis present between the shear rate and shear stress, as this was studied in detail by Davis et al. (Reference Davis, Kriegsmann, Laurence and Rosenblat1983). When ![]() $|T-T_0|/T_0< 1$, a valid approximation to the Arrhenius law given as
$|T-T_0|/T_0< 1$, a valid approximation to the Arrhenius law given as ![]() $\eta (T) = \eta _0 \exp ({-\gamma (T-T_0)})$ and the solution of (6.1a,b) with boundary conditions (6.2a–c) can be obtained in closed form. The effect is quantified by the Brinkman number
$\eta (T) = \eta _0 \exp ({-\gamma (T-T_0)})$ and the solution of (6.1a,b) with boundary conditions (6.2a–c) can be obtained in closed form. The effect is quantified by the Brinkman number
where ![]() $\gamma$ is the logarithmic derivative of the viscosity defined in (2.4). Exact expressions for the particle velocity and temperature are then (Gavis & Laurence Reference Gavis and Laurence1968; Sukanek, Goldstein & Laurence Reference Sukanek, Goldstein and Laurence1973)
$\gamma$ is the logarithmic derivative of the viscosity defined in (2.4). Exact expressions for the particle velocity and temperature are then (Gavis & Laurence Reference Gavis and Laurence1968; Sukanek, Goldstein & Laurence Reference Sukanek, Goldstein and Laurence1973)
where
 \begin{equation} a = 1 + \tfrac{1}{8}\,Br,\quad b = \sinh^{ - 1}\left(\tfrac{1}{8}\,Br\right)^{1/2}\quad {\rm and}\quad c = \left( \frac{1+\dfrac{1}{8}\,Br}{\dfrac{1}{8}\,Br} \right)^{1/2}. \end{equation}
\begin{equation} a = 1 + \tfrac{1}{8}\,Br,\quad b = \sinh^{ - 1}\left(\tfrac{1}{8}\,Br\right)^{1/2}\quad {\rm and}\quad c = \left( \frac{1+\dfrac{1}{8}\,Br}{\dfrac{1}{8}\,Br} \right)^{1/2}. \end{equation}
It is thus easy to calculate the chiral velocity ![]() $v^{{ch}}$ in the form
$v^{{ch}}$ in the form
 \begin{equation} v^{{ch}} = - \chi V \left(\frac{R}{d}\right)^3\frac{32 b^{3} c \left( - 2+\cosh \left(\dfrac{\left( - 4 y +2 d \right) b}{d}\right)\right)}{\left(\cosh \left(\dfrac{\left( - 4 y +2 d \right) b}{d}\right)+1\right)^{2}}. \end{equation}
\begin{equation} v^{{ch}} = - \chi V \left(\frac{R}{d}\right)^3\frac{32 b^{3} c \left( - 2+\cosh \left(\dfrac{\left( - 4 y +2 d \right) b}{d}\right)\right)}{\left(\cosh \left(\dfrac{\left( - 4 y +2 d \right) b}{d}\right)+1\right)^{2}}. \end{equation}
Figure 7 displays three representative chiral velocity curves within the channel of width ![]() $0.1$ cm employing the exact expression (6.6). Viscous heating and diminishing of the liquid viscosity near the channel centre lead to increased particle velocities. For very high Brinkman numbers, the profiles display additional maxima at the interior.
$0.1$ cm employing the exact expression (6.6). Viscous heating and diminishing of the liquid viscosity near the channel centre lead to increased particle velocities. For very high Brinkman numbers, the profiles display additional maxima at the interior.

Figure 7. Chiral particle velocity ![]() $v^{{ch}}$ in
$v^{{ch}}$ in ![]() ${\rm cm}\ {\rm s}^{-1}$ from (6.6), perpendicular to the
${\rm cm}\ {\rm s}^{-1}$ from (6.6), perpendicular to the ![]() $x$–
$x$–![]() $y$ plane formed by the motion of the upper wall with velocity
$y$ plane formed by the motion of the upper wall with velocity ![]() $V=0.1 \ {\rm cm}\ {\rm s}^{-1}$. Most of the propulsion is generated at the interior, which is the location of increased temperature gradients due to viscous heating and thus of diminishing liquid viscosity. We have set
$V=0.1 \ {\rm cm}\ {\rm s}^{-1}$. Most of the propulsion is generated at the interior, which is the location of increased temperature gradients due to viscous heating and thus of diminishing liquid viscosity. We have set ![]() $\chi =1$ (see the discussion in Appendix A).
$\chi =1$ (see the discussion in Appendix A).
Averaging (6.6) over the width of the channel, and expanding for small ![]() $Br$, we obtain
$Br$, we obtain
For ![]() $Br=0.8$,
$Br=0.8$, ![]() $d=0.1$ cm and
$d=0.1$ cm and ![]() $V=0.1\ {\rm cm}\ {\rm s}^{-1}$, we find
$V=0.1\ {\rm cm}\ {\rm s}^{-1}$, we find
6.2. Rayleigh–Bénard convection-induced chiral particle propulsion
Another related thermally induced chiral particle propulsion effect can take place in a Rayleigh–Bénard cell (Chandrasekhar Reference Chandrasekhar1961), driven by variations of the liquid density with temperature (thus the viscosity is considered to be a constant in this subsection). Here, the coefficient of thermal expansion ![]() $\alpha _T$ is the logarithmic derivative of density with respect to temperature, in the same sense that
$\alpha _T$ is the logarithmic derivative of density with respect to temperature, in the same sense that ![]() $\gamma$ in (2.4) is the logarithmic derivative of viscosity. Diffusion of vorticity, perpendicular to the plane of the cell, is now expressed in the form
$\gamma$ in (2.4) is the logarithmic derivative of viscosity. Diffusion of vorticity, perpendicular to the plane of the cell, is now expressed in the form
where ![]() $\boldsymbol {g}$ is the gravitational acceleration,
$\boldsymbol {g}$ is the gravitational acceleration, ![]() $\rho = \rho _0 [1 - \alpha _T (T-T_0)]$,
$\rho = \rho _0 [1 - \alpha _T (T-T_0)]$, ![]() $\rho = \rho _0$ at
$\rho = \rho _0$ at ![]() $T=T_0$, and
$T=T_0$, and ![]() $\alpha _T \equiv -({1}/{\rho })({\partial \rho }/{\partial T})>0$ is the coefficient of thermal expansion (Landau & Lifshitz Reference Landau and Lifshitz1987, § 56).
$\alpha _T \equiv -({1}/{\rho })({\partial \rho }/{\partial T})>0$ is the coefficient of thermal expansion (Landau & Lifshitz Reference Landau and Lifshitz1987, § 56).
When both the temperature gradient and gravitational acceleration ![]() $\boldsymbol {g}$ lie on the plane of the cell, the chiral velocity arising from the underbraced term in (6.9) is
$\boldsymbol {g}$ lie on the plane of the cell, the chiral velocity arising from the underbraced term in (6.9) is
This effect is present when the Rayleigh number exceeds its critical value. It is separate from the one discussed in the present paper, and will be analysed in detail elsewhere.
7. Discussion
Following the constitutive relations introduced in Andreev et al. (Reference Andreev, Son and Spivak2010), but now with temperature-dependent material parameters, in this paper we developed a theory to calculate the thermally-induced chiral current ![]() $\boldsymbol {j}^{{ch}}$ in a suspension of
$\boldsymbol {j}^{{ch}}$ in a suspension of ![]() $n^+$ right-handed and
$n^+$ right-handed and ![]() $n^-$ left-handed chiral particles. The main result is the linear in
$n^-$ left-handed chiral particles. The main result is the linear in ![]() $\Delta T$ expression for the chiral velocity
$\Delta T$ expression for the chiral velocity ![]() $v^{{ch}}$ established in (4.7), and its commensurate chiral current (3.1) in crossed temperature and pressure gradients, as displayed in figure 1. The chiral suspension applies stresses on the base liquid; cf. (3.9). These stresses, allowed by symmetry, endow the base flow with a component that is transverse to the direction of both the flow and the temperature gradient. As remarked by Witten & Diamant (Reference Witten and Diamant2020, § 7.3) in reviewing Andreev et al. (Reference Andreev, Son and Spivak2010), this behaviour resembles the Hall effect.
$v^{{ch}}$ established in (4.7), and its commensurate chiral current (3.1) in crossed temperature and pressure gradients, as displayed in figure 1. The chiral suspension applies stresses on the base liquid; cf. (3.9). These stresses, allowed by symmetry, endow the base flow with a component that is transverse to the direction of both the flow and the temperature gradient. As remarked by Witten & Diamant (Reference Witten and Diamant2020, § 7.3) in reviewing Andreev et al. (Reference Andreev, Son and Spivak2010), this behaviour resembles the Hall effect.
The main concepts developed in this paper can be traced back to the theory of non-centrosymmetric media (Sturman & Fridkin Reference Sturman and Fridkin2021). More recently, these ideas were employed in the photo-induced separation of chiral isomers (Spivak & Andreev Reference Spivak and Andreev2009), the photo-galvanic effect (Deyo et al. Reference Deyo, Golub, Ivchenko and Spivak2009), the propulsion of chiral particles (Kirkinis et al. Reference Kirkinis, Andreev and Spivak2012) by taking advantage of their electric polarization and magnetic moment, and finally, passive propulsion and separation, taking advantage of the rotational degrees of freedom of the medium (Kirkinis & Olvera de la Cruz Reference Kirkinis and Olvera de la Cruz2023).
Acknowledgements
We are grateful for comments and suggestions of two anonymous referees that significantly improved the manuscript.
Funding
We thank the Department of Energy, Office of Basic Energy Sciences for support under contract DE-FG02-08ER46539 and the Center for Computation & Theory of Soft Materials at Robert R. McCormick School of Engineering and Applied Science, Northwestern University (M.O.C. and E.K.). The work of A.V.A. was supported, in part, by the US National Science Foundation through the MRSEC grant no. DMR-1719797, the Thouless Institute for Quantum Matter, and the College of Arts & Sciences at the University of Washington.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Particle shape dependence of the chirality parameter  $\chi$
$\chi$
In the Introduction (below (1.1)), we mentioned that ![]() $\chi$ is a geometric scalar coefficient characteristic of the particle shape and thus it should be described by an expression that vanishes for a non-chiral particle. For chiral particles of gradually varying chiral shape, it should change continuously. Below, we employ single-particle theory (Makino & Doi Reference Makino and Doi2004, Reference Makino and Doi2017) to obtain such a qualitative expression.
$\chi$ is a geometric scalar coefficient characteristic of the particle shape and thus it should be described by an expression that vanishes for a non-chiral particle. For chiral particles of gradually varying chiral shape, it should change continuously. Below, we employ single-particle theory (Makino & Doi Reference Makino and Doi2004, Reference Makino and Doi2017) to obtain such a qualitative expression.
The drift particle velocity in a linear shear flow has the form ![]() $\boldsymbol {V}^{sp}= \tilde {g} E$ (cf. Makino & Doi Reference Makino and Doi2004, Reference Makino and Doi2017), where the superscript ‘sp’ stands for ‘single particle’ (theory),
$\boldsymbol {V}^{sp}= \tilde {g} E$ (cf. Makino & Doi Reference Makino and Doi2004, Reference Makino and Doi2017), where the superscript ‘sp’ stands for ‘single particle’ (theory), ![]() $\tilde {g}$ is the third rank mobility tensor, and
$\tilde {g}$ is the third rank mobility tensor, and ![]() $E$ is the rate-of-strain tensor of the flow. For a paddle-like particle as displayed in figure 8, the form of the third rank tensor
$E$ is the rate-of-strain tensor of the flow. For a paddle-like particle as displayed in figure 8, the form of the third rank tensor ![]() $\tilde {g}$ was derived in closed form in the aforementioned references. Its coefficients
$\tilde {g}$ was derived in closed form in the aforementioned references. Its coefficients ![]() $g(a,h;\theta )$ in the particle frame of reference, which are homogeneous functions of degree 1 (in the variables
$g(a,h;\theta )$ in the particle frame of reference, which are homogeneous functions of degree 1 (in the variables ![]() $a$ and
$a$ and ![]() $h$), can be written succinctly in the form (Makino & Doi Reference Makino and Doi2017, (27))
$h$), can be written succinctly in the form (Makino & Doi Reference Makino and Doi2017, (27))
where ![]() $\theta$ is the angle formed between the two blades as depicted in figure 8(b). Thus the angle
$\theta$ is the angle formed between the two blades as depicted in figure 8(b). Thus the angle ![]() $\theta =0$ corresponds to a non-chiral particle, and there are angles where
$\theta =0$ corresponds to a non-chiral particle, and there are angles where ![]() $g$ reaches a maximum, which we employ here to characterize what is meant by the phrase ‘strong chirality’. Note that the drift velocity
$g$ reaches a maximum, which we employ here to characterize what is meant by the phrase ‘strong chirality’. Note that the drift velocity ![]() $\boldsymbol {V}^{sp}$ generates a back-flow in the liquid and a commensurate shear stress (Witten & Diamant Reference Witten and Diamant2020, § 7.3) proportional to
$\boldsymbol {V}^{sp}$ generates a back-flow in the liquid and a commensurate shear stress (Witten & Diamant Reference Witten and Diamant2020, § 7.3) proportional to

Figure 8. (a) Paddle-like chiral particle employed in the single-particle theory based on the resistance matrix formulation (Makino & Doi Reference Makino and Doi2004, Reference Makino and Doi2017). Centre-to-centre distance is ![]() $2h$, and the radius of each disk is
$2h$, and the radius of each disk is ![]() $a$. We take the characteristic size of the paddle-like chiral particle to be
$a$. We take the characteristic size of the paddle-like chiral particle to be ![]() $h\sim R$, according to the notation introduced in the present paper. (b) Definition of the angle
$h\sim R$, according to the notation introduced in the present paper. (b) Definition of the angle ![]() $\theta$ employed in the mobility tensor to characterize the degree of chirality of a single particle (Makino & Doi Reference Makino and Doi2017); see (A1).
$\theta$ employed in the mobility tensor to characterize the degree of chirality of a single particle (Makino & Doi Reference Makino and Doi2017); see (A1).
We show below that ![]() $\chi$ is proportional to
$\chi$ is proportional to ![]() $g$ in (A1). Consider a non-racemic chiral suspension characterized by the chiral stress (3.9). It is proportional to
$g$ in (A1). Consider a non-racemic chiral suspension characterized by the chiral stress (3.9). It is proportional to ![]() $n^{ch}\alpha \,\partial _y^2 u$. Considering the scaling forms
$n^{ch}\alpha \,\partial _y^2 u$. Considering the scaling forms ![]() $n^{ch}\sim R^{-3}$ and
$n^{ch}\sim R^{-3}$ and ![]() $\alpha \sim \chi R^4$, introduced in the main body of the paper, we obtain the chiral shear stress to be proportional to
$\alpha \sim \chi R^4$, introduced in the main body of the paper, we obtain the chiral shear stress to be proportional to ![]() $\chi R ({U_0}/{d^2})$. Comparison with (A2) leads to the conclusion that
$\chi R ({U_0}/{d^2})$. Comparison with (A2) leads to the conclusion that ![]() $\chi \propto \hat {g}(\theta )$, where
$\chi \propto \hat {g}(\theta )$, where ![]() $\hat {g}(\theta )$ is the dimensionless counterpart of coefficient (A1), whose length scale dimension has been factorized (this is possible because
$\hat {g}(\theta )$ is the dimensionless counterpart of coefficient (A1), whose length scale dimension has been factorized (this is possible because ![]() $g$ is a homogeneous function of
$g$ is a homogeneous function of ![]() $a$ and
$a$ and ![]() $h$ of degree 1). Thus
$h$ of degree 1). Thus ![]() $\chi$ vanishes for a non-chiral paddle-like particle of the type displayed in figure 8 (for
$\chi$ vanishes for a non-chiral paddle-like particle of the type displayed in figure 8 (for ![]() $\theta =0$), and it can acquire finite values for strongly chiral shapes.
$\theta =0$), and it can acquire finite values for strongly chiral shapes.
Single-particle theory, as described above, provides an estimate for the tensor ![]() $\hat {g}(\theta )$ to be of the order of
$\hat {g}(\theta )$ to be of the order of ![]() $0.03$ for strongly chiral particles. On the other hand, in this paper, which is based on the continuum theory, we have set
$0.03$ for strongly chiral particles. On the other hand, in this paper, which is based on the continuum theory, we have set ![]() $\chi =O(1)$ in evaluating the various observables. This is a rough estimate for strongly chiral particles that were shown in Kirkinis & Olvera de la Cruz (Reference Kirkinis and Olvera de la Cruz2023) to generate chiral forces of the same order of magnitude as those occurring in comparable-size systems employed in technology and biology; cf. Kataoka & Troian (Reference Kataoka and Troian1999) and Ando & Yamamoto (Reference Ando and Yamamoto2009).
$\chi =O(1)$ in evaluating the various observables. This is a rough estimate for strongly chiral particles that were shown in Kirkinis & Olvera de la Cruz (Reference Kirkinis and Olvera de la Cruz2023) to generate chiral forces of the same order of magnitude as those occurring in comparable-size systems employed in technology and biology; cf. Kataoka & Troian (Reference Kataoka and Troian1999) and Ando & Yamamoto (Reference Ando and Yamamoto2009).