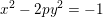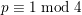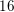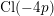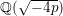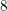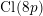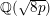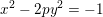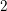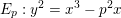1 Introduction
In [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13], Friedlander, Iwaniec, Mazur, and Rubin associated a quantity
![]() $\text{spin}(\mathfrak{a})\in \{0,\pm 1\}$
to each principal ideal
$\text{spin}(\mathfrak{a})\in \{0,\pm 1\}$
to each principal ideal
![]() $\mathfrak{a}$
in the ring of integers of a totally real number field
$\mathfrak{a}$
in the ring of integers of a totally real number field
![]() $K$
of degree
$K$
of degree
![]() $n\geqslant 3$
with a cyclic Galois group over
$n\geqslant 3$
with a cyclic Galois group over
![]() $\mathbb{Q}$
. Assuming a standard conjecture about short character sums, they proved that
$\mathbb{Q}$
. Assuming a standard conjecture about short character sums, they proved that
![]() $\text{spin}(\mathfrak{p})$
oscillates as
$\text{spin}(\mathfrak{p})$
oscillates as
![]() $\mathfrak{p}$
varies over principal prime ideals. The conjecture is unconditional in the low-degree case when
$\mathfrak{p}$
varies over principal prime ideals. The conjecture is unconditional in the low-degree case when
![]() $n=3$
, and precisely in this setting their result has arithmetic applications to the distribution of 2-Selmer groups of quadratic twists of certain elliptic curves.
$n=3$
, and precisely in this setting their result has arithmetic applications to the distribution of 2-Selmer groups of quadratic twists of certain elliptic curves.
In this paper, we will associate a similar ‘spin’ to ideals in the ring of integers
![]() ${\mathcal{O}}_{M}$
of the totally complex number field
${\mathcal{O}}_{M}$
of the totally complex number field
where
![]() $\unicode[STIX]{x1D701}_{8}$
is a primitive
$\unicode[STIX]{x1D701}_{8}$
is a primitive
![]() $8$
th root of unity and
$8$
th root of unity and
![]() $i=\unicode[STIX]{x1D701}_{8}^{2}$
. The essential part of our spin will come from symbols of the type
$i=\unicode[STIX]{x1D701}_{8}^{2}$
. The essential part of our spin will come from symbols of the type
where
![]() $(\frac{\cdot }{\cdot })$
is the quadratic residue symbol in
$(\frac{\cdot }{\cdot })$
is the quadratic residue symbol in
![]() $M$
and
$M$
and
![]() $r\in \text{Gal}(M/\mathbb{Q})$
is a fixed automorphism of order
$r\in \text{Gal}(M/\mathbb{Q})$
is a fixed automorphism of order
![]() $4$
. Following the basic strategy of [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13], we will also prove that the spin of prime ideals in
$4$
. Following the basic strategy of [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13], we will also prove that the spin of prime ideals in
![]() ${\mathcal{O}}_{M}$
oscillates. Unfortunately, the field
${\mathcal{O}}_{M}$
oscillates. Unfortunately, the field
![]() $M$
is of degree
$M$
is of degree
![]() $8$
over
$8$
over
![]() $\mathbb{Q}$
, and we are forced to assume the
$\mathbb{Q}$
, and we are forced to assume the
![]() $n=8$
case of [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13, Conjecture
$n=8$
case of [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13, Conjecture
![]() $C_{n}$
, p. 738]. Our result has applications to the arithmetic statistics of: (i) the
$C_{n}$
, p. 738]. Our result has applications to the arithmetic statistics of: (i) the
![]() $16$
-rank of the class group of
$16$
-rank of the class group of
![]() $\mathbb{Q}(\sqrt{-p})$
, (ii) the
$\mathbb{Q}(\sqrt{-p})$
, (ii) the
![]() $8$
-rank of the ordinary class group of the real quadratic field
$8$
-rank of the ordinary class group of the real quadratic field
![]() $\mathbb{Q}(\sqrt{2p})$
, (iii) the negative Pell equation
$\mathbb{Q}(\sqrt{2p})$
, (iii) the negative Pell equation
![]() $x^{2}-2py^{2}=-1$
, and (iv) the congruent number elliptic curve
$x^{2}-2py^{2}=-1$
, and (iv) the congruent number elliptic curve
![]() $y^{2}=x^{3}-p^{2}x$
.
$y^{2}=x^{3}-p^{2}x$
.
There are two main innovations that separate the present work from [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13]. First, we have the aforementioned arithmetic applications. Second, the Galois group of
![]() $M/\mathbb{Q}$
is dihedral of order
$M/\mathbb{Q}$
is dihedral of order
![]() $8$
, and hence is not cyclic, and this seemingly technical difference causes the original arguments in [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13] to break down. Fortunately, a lattice point counting argument offers a fix, which also substantially simplifies the proof in [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13].
$8$
, and hence is not cyclic, and this seemingly technical difference causes the original arguments in [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13] to break down. Fortunately, a lattice point counting argument offers a fix, which also substantially simplifies the proof in [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13].
Before stating our main results, we define the aforementioned spin
![]() $s_{\mathfrak{a}}$
of non-zero ideals
$s_{\mathfrak{a}}$
of non-zero ideals
![]() $\mathfrak{a}\subset {\mathcal{O}}_{M}$
. One can check that
$\mathfrak{a}\subset {\mathcal{O}}_{M}$
. One can check that
![]() $M/\mathbb{Q}$
is a totally complex dihedral extension of degree
$M/\mathbb{Q}$
is a totally complex dihedral extension of degree
![]() $8$
, that
$8$
, that
![]() ${\mathcal{O}}_{M}$
is a principal ideal domain, and that
${\mathcal{O}}_{M}$
is a principal ideal domain, and that
![]() $\unicode[STIX]{x1D701}_{8}$
generates the torsion subgroup of the unit group
$\unicode[STIX]{x1D701}_{8}$
generates the torsion subgroup of the unit group
![]() ${\mathcal{O}}_{M}^{\times }$
. We fix a subgroup
${\mathcal{O}}_{M}^{\times }$
. We fix a subgroup
![]() $V\leqslant {\mathcal{O}}_{M}^{\times }$
of rank
$V\leqslant {\mathcal{O}}_{M}^{\times }$
of rank
![]() $3$
such that
$3$
such that
![]() ${\mathcal{O}}_{M}^{\times }=\langle \unicode[STIX]{x1D701}_{8}\rangle \times V$
and fix a set of coset representatives
${\mathcal{O}}_{M}^{\times }=\langle \unicode[STIX]{x1D701}_{8}\rangle \times V$
and fix a set of coset representatives
![]() $\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{8}$
for
$\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{8}$
for
![]() $V^{2}$
in
$V^{2}$
in
![]() $V$
. We define a rational integer
$V$
. We define a rational integer
![]() $F$
as in (3.1); although
$F$
as in (3.1); although
![]() $F$
is an absolute constant, it is far too large to write out its decimal expansion. Suppose that
$F$
is an absolute constant, it is far too large to write out its decimal expansion. Suppose that
is a map such that
![]() $\unicode[STIX]{x1D713}(\unicode[STIX]{x1D6FC}\hspace{0.2em}{\rm mod}\hspace{0.2em}F)=\unicode[STIX]{x1D713}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{2}\hspace{0.2em}{\rm mod}\hspace{0.2em}F)$
for all
$\unicode[STIX]{x1D713}(\unicode[STIX]{x1D6FC}\hspace{0.2em}{\rm mod}\hspace{0.2em}F)=\unicode[STIX]{x1D713}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{2}\hspace{0.2em}{\rm mod}\hspace{0.2em}F)$
for all
![]() $\unicode[STIX]{x1D6FC}\in {\mathcal{O}}_{M}$
coprime to
$\unicode[STIX]{x1D6FC}\in {\mathcal{O}}_{M}$
coprime to
![]() $F$
and all
$F$
and all
![]() $\unicode[STIX]{x1D6FD}\in {\mathcal{O}}_{M}^{\times }$
. Fix once and for all an element of order
$\unicode[STIX]{x1D6FD}\in {\mathcal{O}}_{M}^{\times }$
. Fix once and for all an element of order
![]() $4$
in
$4$
in
![]() $\text{Gal}(M/\mathbb{Q})$
, denote it by
$\text{Gal}(M/\mathbb{Q})$
, denote it by
![]() $r$
, and define
$r$
, and define
![]() $[\cdot ]_{r}$
as in (1.1). Finally, let
$[\cdot ]_{r}$
as in (1.1). Finally, let
![]() $\mathfrak{a}$
be a non-zero ideal in
$\mathfrak{a}$
be a non-zero ideal in
![]() ${\mathcal{O}}_{M}$
. If
${\mathcal{O}}_{M}$
. If
![]() $(\mathfrak{a},F)\neq 1$
, define
$(\mathfrak{a},F)\neq 1$
, define
![]() $s_{\mathfrak{a}}=0$
. Otherwise, choose any generator
$s_{\mathfrak{a}}=0$
. Otherwise, choose any generator
![]() $\unicode[STIX]{x1D6FC}$
for
$\unicode[STIX]{x1D6FC}$
for
![]() $\mathfrak{a}$
and define
$\mathfrak{a}$
and define
The right-hand side above is independent of the choice of a generator
![]() $\unicode[STIX]{x1D6FC}$
for
$\unicode[STIX]{x1D6FC}$
for
![]() $\mathfrak{a}$
, as can be seen from (6.7) with
$\mathfrak{a}$
, as can be seen from (6.7) with
![]() $\unicode[STIX]{x1D70E}=r$
. Compare the definition of
$\unicode[STIX]{x1D70E}=r$
. Compare the definition of
![]() $s_{\mathfrak{a}}$
with the definition of
$s_{\mathfrak{a}}$
with the definition of
![]() $\text{spin}(\mathfrak{a})$
in [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13, (3.4), p. 706]. The most important difference is that
$\text{spin}(\mathfrak{a})$
in [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13, (3.4), p. 706]. The most important difference is that
![]() $r$
does not generate the Galois group
$r$
does not generate the Galois group
![]() $\text{Gal}(M/\mathbb{Q})$
, whereas in [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13], the automorphism
$\text{Gal}(M/\mathbb{Q})$
, whereas in [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13], the automorphism
![]() $\unicode[STIX]{x1D70E}$
does generate
$\unicode[STIX]{x1D70E}$
does generate
![]() $\text{Gal}(K/\mathbb{Q})$
. An application of the geometry of numbers bridges this gap while simplifying the proof of Friedlander et al. [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13, pp. 731–733]. Another difference is the extra averaging over generators of
$\text{Gal}(K/\mathbb{Q})$
. An application of the geometry of numbers bridges this gap while simplifying the proof of Friedlander et al. [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13, pp. 731–733]. Another difference is the extra averaging over generators of
![]() $\mathfrak{a}$
in the definition of
$\mathfrak{a}$
in the definition of
![]() $s_{\mathfrak{a}}$
above, necessary because, unlike in [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13], we cannot make simplifying assumptions about the field over which we work.
$s_{\mathfrak{a}}$
above, necessary because, unlike in [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13], we cannot make simplifying assumptions about the field over which we work.
We now state our main theorem and its consequences, all conditional on Conjecture 1, a standard conjecture about short character sums whose statement we postpone until § 3.3.
Theorem 1. Assume that Conjecture 1 holds with
![]() $\unicode[STIX]{x1D6FF}>0$
. Then there is a constant
$\unicode[STIX]{x1D6FF}>0$
. Then there is a constant
![]() $\unicode[STIX]{x1D6FF}^{\prime }>0$
depending only on
$\unicode[STIX]{x1D6FF}^{\prime }>0$
depending only on
![]() $\unicode[STIX]{x1D6FF}$
such that for all
$\unicode[STIX]{x1D6FF}$
such that for all
![]() $X>1$
, we have
$X>1$
, we have
where the sum is taken over prime ideals
![]() $\mathfrak{p}\subset {\mathcal{O}}_{M}$
of norm at most
$\mathfrak{p}\subset {\mathcal{O}}_{M}$
of norm at most
![]() $X$
and the implied constant depends only on
$X$
and the implied constant depends only on
![]() $\unicode[STIX]{x1D713}$
. Moreover, one can take
$\unicode[STIX]{x1D713}$
. Moreover, one can take
![]() $\unicode[STIX]{x1D6FF}^{\prime }=\unicode[STIX]{x1D6FF}/400$
.
$\unicode[STIX]{x1D6FF}^{\prime }=\unicode[STIX]{x1D6FF}/400$
.
Let
![]() $\text{Cl}(D)$
,
$\text{Cl}(D)$
,
![]() $\text{Cl}^{+}(D)$
,
$\text{Cl}^{+}(D)$
,
![]() $h(D)$
, and
$h(D)$
, and
![]() $h^{+}(D)$
denote the class group, the narrow class group, the class number, and the narrow class number, respectively, of the quadratic field of discriminant
$h^{+}(D)$
denote the class group, the narrow class group, the class number, and the narrow class number, respectively, of the quadratic field of discriminant
![]() $D$
. For a finite abelian group
$D$
. For a finite abelian group
![]() $G$
and an integer
$G$
and an integer
![]() $k\geqslant 1$
, we define the
$k\geqslant 1$
, we define the
![]() $2^{k}$
-rank of
$2^{k}$
-rank of
![]() $G$
to be
$G$
to be
![]() $\text{rk}_{2^{k}}G=\dim _{\mathbb{F}_{2}}(2^{k-1}G/2^{k}G)$
. A lot is known about the
$\text{rk}_{2^{k}}G=\dim _{\mathbb{F}_{2}}(2^{k-1}G/2^{k}G)$
. A lot is known about the
![]() $8$
-rank of
$8$
-rank of
![]() $\text{Cl}^{+}(dp)$
for
$\text{Cl}^{+}(dp)$
for
![]() $d$
fixed and
$d$
fixed and
![]() $p$
varying among the prime numbers (see [Reference StevenhagenSte89] and [Reference SmithSmi16]). We will prove some long-standing conjectures about the
$p$
varying among the prime numbers (see [Reference StevenhagenSte89] and [Reference SmithSmi16]). We will prove some long-standing conjectures about the
![]() $16$
-rank of
$16$
-rank of
![]() $\text{Cl}(-4p)$
and the
$\text{Cl}(-4p)$
and the
![]() $8$
-rank of
$8$
-rank of
![]() $\text{Cl}(8p)$
(see for instance [Reference Cohn and LagariasCL84] and in particular their density conjecture
$\text{Cl}(8p)$
(see for instance [Reference Cohn and LagariasCL84] and in particular their density conjecture
![]() $D_{j}(d)$
on p. 263).
$D_{j}(d)$
on p. 263).
Theorem 2. Assume that Conjecture 1 holds with
![]() $\unicode[STIX]{x1D6FF}>0$
and let
$\unicode[STIX]{x1D6FF}>0$
and let
![]() $\unicode[STIX]{x1D6FF}^{\prime }$
be as in Theorem 1. Let
$\unicode[STIX]{x1D6FF}^{\prime }$
be as in Theorem 1. Let
![]() $r\in \{0,8\}$
. For all
$r\in \{0,8\}$
. For all
![]() $X\geqslant 41$
, we have
$X\geqslant 41$
, we have
where the implied constant is absolute.
Theorem 3. Assume that Conjecture 1 holds with
![]() $\unicode[STIX]{x1D6FF}>0$
and let
$\unicode[STIX]{x1D6FF}>0$
and let
![]() $\unicode[STIX]{x1D6FF}^{\prime }$
be as in Theorem 1. Let
$\unicode[STIX]{x1D6FF}^{\prime }$
be as in Theorem 1. Let
![]() $r\in \{0,4\}$
. Then for all
$r\in \{0,4\}$
. Then for all
![]() $X\geqslant 113$
, we have
$X\geqslant 113$
, we have
where the implied constant is absolute.
Density results about the
![]() $2$
-parts of the narrow and ordinary class groups of
$2$
-parts of the narrow and ordinary class groups of
![]() $\mathbb{Q}(\sqrt{8p})$
have implications for the arithmetic statistics of the solvability of the negative Pell equation
$\mathbb{Q}(\sqrt{8p})$
have implications for the arithmetic statistics of the solvability of the negative Pell equation
with
![]() $x,y\in \mathbb{Z}$
. For each
$x,y\in \mathbb{Z}$
. For each
![]() $X\geqslant 3$
, let
$X\geqslant 3$
, let
Stevenhagen conjectured in [Reference StevenhagenSte93b] that
![]() $\lim _{X\rightarrow \infty }\unicode[STIX]{x1D6FF}^{-}(X)$
exists and is equal to
$\lim _{X\rightarrow \infty }\unicode[STIX]{x1D6FF}^{-}(X)$
exists and is equal to
![]() $1/3$
. We prove the following theorem.
$1/3$
. We prove the following theorem.
Theorem 4. Assume that Conjecture 1 holds. Let
![]() $\unicode[STIX]{x1D6FF}^{-}(X)$
be defined as above. Then
$\unicode[STIX]{x1D6FF}^{-}(X)$
be defined as above. Then
In particular,
![]() $|\unicode[STIX]{x1D6FF}^{-}(X)-1/3|\leqslant 1/48+o(X)$
as
$|\unicode[STIX]{x1D6FF}^{-}(X)-1/3|\leqslant 1/48+o(X)$
as
![]() $X\rightarrow \infty$
, so the bounds above are within
$X\rightarrow \infty$
, so the bounds above are within
![]() $2.08\%$
of Stevenhagen’s conjecture.
$2.08\%$
of Stevenhagen’s conjecture.
Finally, we state an application of Theorem 1 to the distribution of the Tate–Šafarevič groups
![]() $\unicode[STIX]{x0428}(E_{p})$
of the congruent number elliptic curves
$\unicode[STIX]{x0428}(E_{p})$
of the congruent number elliptic curves
Theorem 5. Assume that Conjecture 1 holds. Then
2 Discussion of results
2.1
 $16$
-rank of class groups
$16$
-rank of class groups
Aside from two recent results due to the authors [Reference MilovicMil17b, Reference Koymans and MilovicKM18], density results about the
![]() $16$
-rank of class groups in one-prime-parameter families
$16$
-rank of class groups in one-prime-parameter families
![]() $\{\mathbb{Q}(\sqrt{dp})\}_{p}$
(
$\{\mathbb{Q}(\sqrt{dp})\}_{p}$
(
![]() $d$
fixed and
$d$
fixed and
![]() $p$
varying) have remained elusive despite a large body of work on algebraic criteria for the
$p$
varying) have remained elusive despite a large body of work on algebraic criteria for the
![]() $16$
-rank in such families [Reference KaplanKap77, Reference OriatOri78, Reference Kaplan and WilliamsKW82, Reference Leonard and WilliamsLW82, Reference Kaplan and WilliamsKW84, Reference YamamotoYam84, Reference Kaplan, Williams and HardyKWH86, Reference StevenhagenSte93a, Reference Bruin and HemenwayBH13]. This gap between algebraic and analytic understanding of the
$16$
-rank in such families [Reference KaplanKap77, Reference OriatOri78, Reference Kaplan and WilliamsKW82, Reference Leonard and WilliamsLW82, Reference Kaplan and WilliamsKW84, Reference YamamotoYam84, Reference Kaplan, Williams and HardyKWH86, Reference StevenhagenSte93a, Reference Bruin and HemenwayBH13]. This gap between algebraic and analytic understanding of the
![]() $16$
-rank can be largely attributed to the absence of appropriate governing fields and the subsequent inability to apply the Čebotarev density theorem. More precisely, for a finite extension of number fields
$16$
-rank can be largely attributed to the absence of appropriate governing fields and the subsequent inability to apply the Čebotarev density theorem. More precisely, for a finite extension of number fields
![]() $E/F$
, let
$E/F$
, let
![]() $\text{Art}_{E/F}$
denote the corresponding Artin map. Cohn and Lagarias [Reference Cohn and LagariasCL83, Reference Cohn and LagariasCL84] conjectured that, for each integer
$\text{Art}_{E/F}$
denote the corresponding Artin map. Cohn and Lagarias [Reference Cohn and LagariasCL83, Reference Cohn and LagariasCL84] conjectured that, for each integer
![]() $k\geqslant 1$
and each integer
$k\geqslant 1$
and each integer
![]() $d\not \equiv 2\hspace{0.2em}{\rm mod}\hspace{0.2em}4$
, the map
$d\not \equiv 2\hspace{0.2em}{\rm mod}\hspace{0.2em}4$
, the map
is Frobenian, in the sense of Serre [Reference SerreSer12]. In other words, they conjectured that there exists a normal field extension
![]() $M_{d,k}/\mathbb{Q}$
for which there is a class function
$M_{d,k}/\mathbb{Q}$
for which there is a class function
satisfying
for all primes
![]() $p$
unramified in
$p$
unramified in
![]() $M_{d,k}/\mathbb{Q}$
; such a field
$M_{d,k}/\mathbb{Q}$
; such a field
![]() $M_{d,k}$
is called a governing field for
$M_{d,k}$
is called a governing field for
![]() $\{\text{rk}_{2^{k}}\text{Cl}^{+}(dp)\}_{p}$
. For
$\{\text{rk}_{2^{k}}\text{Cl}^{+}(dp)\}_{p}$
. For
![]() $k\leqslant 3$
, Stevenhagen [Reference StevenhagenSte89] proved these conjectures for all
$k\leqslant 3$
, Stevenhagen [Reference StevenhagenSte89] proved these conjectures for all
![]() $d\not \equiv 2\hspace{0.2em}{\rm mod}\hspace{0.2em}4$
. Perhaps the simplest case is
$d\not \equiv 2\hspace{0.2em}{\rm mod}\hspace{0.2em}4$
. Perhaps the simplest case is
![]() $d=-4$
, where one can take
$d=-4$
, where one can take
![]() $M_{-4,3}$
to be the field
$M_{-4,3}$
to be the field
![]() $M=\mathbb{Q}(\unicode[STIX]{x1D701}_{8},\sqrt{1+i})$
as above and where
$M=\mathbb{Q}(\unicode[STIX]{x1D701}_{8},\sqrt{1+i})$
as above and where
![]() $h(-4p)\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
if and only if
$h(-4p)\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
if and only if
![]() $p$
splits completely in
$p$
splits completely in
![]() $M$
. Hence, by the Čebotarev density theorem, the density of primes
$M$
. Hence, by the Čebotarev density theorem, the density of primes
![]() $p$
such that
$p$
such that
![]() $h(-4p)\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
is equal to
$h(-4p)\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
is equal to
![]() $1/[M:\mathbb{Q}]=1/8$
.
$1/[M:\mathbb{Q}]=1/8$
.
Cohn and Lagarias [Reference Cohn and LagariasCL84] ruled out some obvious candidates for
![]() $M_{-4,4}$
, i.e., the governing field for the
$M_{-4,4}$
, i.e., the governing field for the
![]() $16$
-rank of
$16$
-rank of
![]() $\text{Cl}(-4p)$
, and to this day no governing fields for the
$\text{Cl}(-4p)$
, and to this day no governing fields for the
![]() $16$
-rank in any family have been found. Nevertheless, we are able to show, in Theorem 2, that the density of primes
$16$
-rank in any family have been found. Nevertheless, we are able to show, in Theorem 2, that the density of primes
![]() $p$
such that
$p$
such that
![]() $h(-4p)\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}16$
exists and is equal to
$h(-4p)\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}16$
exists and is equal to
![]() $1/16$
. It is proved unconditionally in [Reference MilovicMil17a] that there are infinitely many primes
$1/16$
. It is proved unconditionally in [Reference MilovicMil17a] that there are infinitely many primes
![]() $p$
such that
$p$
such that
![]() $h(-4p)\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}16$
, but that result implies nothing about the density as in Theorem 1.
$h(-4p)\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}16$
, but that result implies nothing about the density as in Theorem 1.
The key innovation that allows us to go beyond the
![]() $8$
-rank is to use Vinogradov’s method [Reference VinogradovVin47, Reference VinogradovVin54] for studying the distribution of prime numbers instead of the heretofore used Čebotarev density theorem (as in [Reference SmithSmi16], for instance). Moreover, the current state-of-the-art bounds for the error term in the Čebotarev density theorem are essentially of size
$8$
-rank is to use Vinogradov’s method [Reference VinogradovVin47, Reference VinogradovVin54] for studying the distribution of prime numbers instead of the heretofore used Čebotarev density theorem (as in [Reference SmithSmi16], for instance). Moreover, the current state-of-the-art bounds for the error term in the Čebotarev density theorem are essentially of size
![]() $X\exp (-\sqrt{\log X})$
, far worse than the power-saving bound
$X\exp (-\sqrt{\log X})$
, far worse than the power-saving bound
![]() $X^{1-\unicode[STIX]{x1D6FF}^{\prime }}$
in Theorem 2. In fact, obtaining such a power-saving error term in the Čebotarev density theorem would be tantamount to proving a zero-free region for the associated Artin
$X^{1-\unicode[STIX]{x1D6FF}^{\prime }}$
in Theorem 2. In fact, obtaining such a power-saving error term in the Čebotarev density theorem would be tantamount to proving a zero-free region for the associated Artin
![]() $L$
-functions of the form
$L$
-functions of the form
![]() $\Re (s)>1-\unicode[STIX]{x1D6FF}^{\prime }$
, and this is well out of reach of current methods in analytic number theory. Nonetheless, the power-saving bound
$\Re (s)>1-\unicode[STIX]{x1D6FF}^{\prime }$
, and this is well out of reach of current methods in analytic number theory. Nonetheless, the power-saving bound
![]() $X^{1-\unicode[STIX]{x1D6FF}^{\prime }}$
does not prove the non-existence of a governing field – it merely suggests that one is unlikely to exist. We summarize this discussion with the following immediate corollary of Theorem 2.
$X^{1-\unicode[STIX]{x1D6FF}^{\prime }}$
does not prove the non-existence of a governing field – it merely suggests that one is unlikely to exist. We summarize this discussion with the following immediate corollary of Theorem 2.
Corollary 6. Assume Conjecture 1 with
![]() $\unicode[STIX]{x1D6FF}>0$
, and let
$\unicode[STIX]{x1D6FF}>0$
, and let
![]() $\unicode[STIX]{x1D6FF}^{\prime }$
be as in Theorem 1. At least one of the following two statements is true:
$\unicode[STIX]{x1D6FF}^{\prime }$
be as in Theorem 1. At least one of the following two statements is true:
– a governing field for
 $\text{rk}_{16}\text{Cl}(-4p)$
does
$\text{rk}_{16}\text{Cl}(-4p)$
does
 $\text{not}$
exist;
$\text{not}$
exist;– there exists a normal extension
 $L/\mathbb{Q}$
and two distinct unions of conjugacy classes in
$L/\mathbb{Q}$
and two distinct unions of conjugacy classes in
 $\text{Gal}(L/\mathbb{Q})$
, say
$\text{Gal}(L/\mathbb{Q})$
, say
 $S_{1}$
and
$S_{1}$
and
 $S_{2}$
, such that for all
$S_{2}$
, such that for all
 $X>0$
, we have where the implied constant is absolute. Here
$X>0$
, we have where the implied constant is absolute. Here $$\begin{eqnarray}\#\{p\leqslant X:(p,L/\mathbb{Q})\subset S_{1}\}-\#\{p\leqslant X:(p,L/\mathbb{Q})\subset S_{2}\}\ll X^{1-\unicode[STIX]{x1D6FF}^{\prime }},\end{eqnarray}$$
$$\begin{eqnarray}\#\{p\leqslant X:(p,L/\mathbb{Q})\subset S_{1}\}-\#\{p\leqslant X:(p,L/\mathbb{Q})\subset S_{2}\}\ll X^{1-\unicode[STIX]{x1D6FF}^{\prime }},\end{eqnarray}$$
 $(p,L/\mathbb{Q})$
denotes the Artin conjugacy class of
$(p,L/\mathbb{Q})$
denotes the Artin conjugacy class of
 $p$
in
$p$
in
 $\text{Gal}(L/\mathbb{Q})$
.
$\text{Gal}(L/\mathbb{Q})$
.
2.2 Real quadratic fields and the negative Pell equation
In the case
![]() $d<0$
, the narrow class group
$d<0$
, the narrow class group
![]() $\text{Cl}^{+}(dp)$
is the same as the ordinary class group
$\text{Cl}^{+}(dp)$
is the same as the ordinary class group
![]() $\text{Cl}(dp)$
. If
$\text{Cl}(dp)$
. If
![]() $d>0$
, however, then
$d>0$
, however, then
![]() $\text{Cl}^{+}(dp)$
and
$\text{Cl}^{+}(dp)$
and
![]() $\text{Cl}(dp)$
may be different; in fact,
$\text{Cl}(dp)$
may be different; in fact,
![]() $\text{Cl}^{+}(dp)=\text{Cl}(dp)$
if and only if the fundamental unit
$\text{Cl}^{+}(dp)=\text{Cl}(dp)$
if and only if the fundamental unit
![]() $\unicode[STIX]{x1D700}_{dp}$
of
$\unicode[STIX]{x1D700}_{dp}$
of
![]() $\mathbb{Q}(\sqrt{dp})$
has norm
$\mathbb{Q}(\sqrt{dp})$
has norm
![]() $-1$
. While Cohn and Lagarias stated their conjecture on the existence of governing fields only for narrow class groups, one can ask what happens for ordinary class groups. As mentioned before, Stevenhagen proved the conjecture of Cohn and Lagarias for the
$-1$
. While Cohn and Lagarias stated their conjecture on the existence of governing fields only for narrow class groups, one can ask what happens for ordinary class groups. As mentioned before, Stevenhagen proved the conjecture of Cohn and Lagarias for the
![]() $8$
-rank of narrow class groups of both imaginary and real quadratic fields. Theorem 3 is the first density result for the
$8$
-rank of narrow class groups of both imaginary and real quadratic fields. Theorem 3 is the first density result for the
![]() $8$
-rank of the ordinary class group in a family of real quadratic fields. Again the power-saving error term suggests that there is no governing field for
$8$
-rank of the ordinary class group in a family of real quadratic fields. Again the power-saving error term suggests that there is no governing field for
![]() $\text{rk}_{8}\text{Cl}(8p)$
in the family
$\text{rk}_{8}\text{Cl}(8p)$
in the family
![]() $\{\text{Cl}(8p)\}_{p\equiv 1\hspace{0.2em}{\rm mod}\hspace{0.2em}4}$
. To place Theorem 3 in context, we note that the
$\{\text{Cl}(8p)\}_{p\equiv 1\hspace{0.2em}{\rm mod}\hspace{0.2em}4}$
. To place Theorem 3 in context, we note that the
![]() $2$
-part of
$2$
-part of
![]() $\text{Cl}^{+}(8p)$
is cyclic, and, for
$\text{Cl}^{+}(8p)$
is cyclic, and, for
![]() $p\equiv 1\hspace{0.2em}{\rm mod}\hspace{0.2em}4$
, one has (for instance, see [Reference StevenhagenSte93a]):
$p\equiv 1\hspace{0.2em}{\rm mod}\hspace{0.2em}4$
, one has (for instance, see [Reference StevenhagenSte93a]):
–
 $h^{+}(8p)=h(8p)\equiv 2\hspace{0.2em}{\rm mod}\hspace{0.2em}4\Leftrightarrow p\text{ splits completely in }\mathbb{Q}(i)\text{ but not in }\mathbb{Q}(\unicode[STIX]{x1D701}_{8})$
;
$h^{+}(8p)=h(8p)\equiv 2\hspace{0.2em}{\rm mod}\hspace{0.2em}4\Leftrightarrow p\text{ splits completely in }\mathbb{Q}(i)\text{ but not in }\mathbb{Q}(\unicode[STIX]{x1D701}_{8})$
;–
 $h^{+}(8p)\equiv h(8p)+2\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}4\Leftrightarrow p\text{ splits completely in }\mathbb{Q}(\unicode[STIX]{x1D701}_{8})\text{ but not in }\mathbb{Q}(\unicode[STIX]{x1D701}_{8},\sqrt[4]{2})$
;
$h^{+}(8p)\equiv h(8p)+2\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}4\Leftrightarrow p\text{ splits completely in }\mathbb{Q}(\unicode[STIX]{x1D701}_{8})\text{ but not in }\mathbb{Q}(\unicode[STIX]{x1D701}_{8},\sqrt[4]{2})$
;–
 $h^{+}(8p)=h(8p)\equiv 4\hspace{0.2em}{\rm mod}\hspace{0.2em}8\Leftrightarrow p\text{ splits completely in }\mathbb{Q}(\unicode[STIX]{x1D701}_{8},\sqrt[4]{2})\text{ but not in }\mathbb{Q}(\unicode[STIX]{x1D701}_{16},\sqrt[4]{2})$
;
$h^{+}(8p)=h(8p)\equiv 4\hspace{0.2em}{\rm mod}\hspace{0.2em}8\Leftrightarrow p\text{ splits completely in }\mathbb{Q}(\unicode[STIX]{x1D701}_{8},\sqrt[4]{2})\text{ but not in }\mathbb{Q}(\unicode[STIX]{x1D701}_{16},\sqrt[4]{2})$
;–
 $h^{+}(8p)\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}8\Leftrightarrow p\text{ splits completely in }\mathbb{Q}(\unicode[STIX]{x1D701}_{16},\sqrt[4]{2})$
.
$h^{+}(8p)\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}8\Leftrightarrow p\text{ splits completely in }\mathbb{Q}(\unicode[STIX]{x1D701}_{16},\sqrt[4]{2})$
.
Hence, Theorem 3 in conjunction with the Čebotarev density theorem implies that
and
The 2-torsion subgroup
![]() $\text{Cl}^{+}(8p)[2]$
is generated by the classes of the ramified ideals
$\text{Cl}^{+}(8p)[2]$
is generated by the classes of the ramified ideals
![]() $\mathfrak{t}$
and
$\mathfrak{t}$
and
![]() $\mathfrak{p}$
lying above
$\mathfrak{p}$
lying above
![]() $2$
and
$2$
and
![]() $p$
, respectively. Since the
$p$
, respectively. Since the
![]() $2$
-part of
$2$
-part of
![]() $\text{Cl}^{+}(8p)$
is cyclic, we have
$\text{Cl}^{+}(8p)$
is cyclic, we have
![]() $\#\text{Cl}^{+}(8p)[2]=2$
, so exactly one of the three ideals
$\#\text{Cl}^{+}(8p)[2]=2$
, so exactly one of the three ideals
![]() $\mathfrak{t}$
,
$\mathfrak{t}$
,
![]() $\mathfrak{p}$
, and
$\mathfrak{p}$
, and
![]() $\mathfrak{t}\mathfrak{p}$
is in the trivial class in
$\mathfrak{t}\mathfrak{p}$
is in the trivial class in
![]() $\text{Cl}^{+}(8p)$
, while the remaining two are both in the non-trivial class in
$\text{Cl}^{+}(8p)$
, while the remaining two are both in the non-trivial class in
![]() $\text{Cl}^{+}(8p)[2]$
. Moreover, (1.4) has a solution over the integers if and only if
$\text{Cl}^{+}(8p)[2]$
. Moreover, (1.4) has a solution over the integers if and only if
![]() $\mathbb{Z}[\sqrt{2p}]$
has a unit of norm
$\mathbb{Z}[\sqrt{2p}]$
has a unit of norm
![]() $-1$
, which occurs if and only if the ideal
$-1$
, which occurs if and only if the ideal
![]() $\mathfrak{t}\mathfrak{p}=(\sqrt{2p})$
can be generated by a totally positive element in
$\mathfrak{t}\mathfrak{p}=(\sqrt{2p})$
can be generated by a totally positive element in
![]() $\mathbb{Z}[\sqrt{2p}]$
, i.e., if and only if
$\mathbb{Z}[\sqrt{2p}]$
, i.e., if and only if
![]() $\mathfrak{t}\mathfrak{p}$
is in the trivial class in
$\mathfrak{t}\mathfrak{p}$
is in the trivial class in
![]() $\text{Cl}^{+}(8p)$
. Stevenhagen conjectured in [Reference StevenhagenSte93b] that as
$\text{Cl}^{+}(8p)$
. Stevenhagen conjectured in [Reference StevenhagenSte93b] that as
![]() $p$
varies over all prime numbers, each of
$p$
varies over all prime numbers, each of
![]() $\mathfrak{t}$
,
$\mathfrak{t}$
,
![]() $\mathfrak{p}$
, and
$\mathfrak{p}$
, and
![]() $\mathfrak{t}\mathfrak{p}$
is in the trivial class in
$\mathfrak{t}\mathfrak{p}$
is in the trivial class in
![]() $\text{Cl}^{+}(8p)$
equally often, which is why we expect
$\text{Cl}^{+}(8p)$
equally often, which is why we expect
![]() $\lim _{X\rightarrow \infty }\unicode[STIX]{x1D6FF}^{-}(X)$
to exist and be equal to
$\lim _{X\rightarrow \infty }\unicode[STIX]{x1D6FF}^{-}(X)$
to exist and be equal to
![]() $1/3$
(
$1/3$
(
![]() $\unicode[STIX]{x1D6FF}^{-}(X)$
is defined following (1.4)).
$\unicode[STIX]{x1D6FF}^{-}(X)$
is defined following (1.4)).
Since
![]() $\mathbb{Z}[\sqrt{2p}]$
has a unit of norm
$\mathbb{Z}[\sqrt{2p}]$
has a unit of norm
![]() $-1$
if and only if the narrow class group
$-1$
if and only if the narrow class group
![]() $\text{Cl}^{+}(8p)$
coincides with the ordinary class group
$\text{Cl}^{+}(8p)$
coincides with the ordinary class group
![]() $\text{Cl}(8p)$
, we can obtain successively better upper and lower bounds for the proportion of primes
$\text{Cl}(8p)$
, we can obtain successively better upper and lower bounds for the proportion of primes
![]() $p$
for which (1.4) is solvable over
$p$
for which (1.4) is solvable over
![]() $\mathbb{Z}$
by comparing
$\mathbb{Z}$
by comparing
![]() $h^{+}(8p)$
and
$h^{+}(8p)$
and
![]() $h(8p)$
modulo successively higher powers of
$h(8p)$
modulo successively higher powers of
![]() $2$
. Note that (1.4) has no solutions (even over
$2$
. Note that (1.4) has no solutions (even over
![]() $\mathbb{Q}$
) whenever
$\mathbb{Q}$
) whenever
![]() $p\equiv 3\hspace{0.2em}{\rm mod}\hspace{0.2em}4$
, since in that case
$p\equiv 3\hspace{0.2em}{\rm mod}\hspace{0.2em}4$
, since in that case
![]() $-1$
is not a quadratic residue modulo
$-1$
is not a quadratic residue modulo
![]() $p$
. From this, the list of splitting criteria above, and the Čebotarev density theorem, one immediately deduces that
$p$
. From this, the list of splitting criteria above, and the Čebotarev density theorem, one immediately deduces that
Hence
![]() $|\unicode[STIX]{x1D6FF}^{-}(X)-1/3|\leqslant 1/24+o(X)$
as
$|\unicode[STIX]{x1D6FF}^{-}(X)-1/3|\leqslant 1/24+o(X)$
as
![]() $X\rightarrow \infty$
, i.e., at worst, the bounds above are within
$X\rightarrow \infty$
, i.e., at worst, the bounds above are within
![]() $4.17\%$
of Stevenhagen’s conjecture. Theorem 4 hence cuts the possible discrepancy from Stevenhagen’s conjecture in half. Although the problem of improving (2.1) may have been first explicitly stated in 1993 in [Reference StevenhagenSte93b, p. 127], in essence it has been open since the 1930s, when Rédei [Reference RédeiRed34], Reichardt [Reference ReichardtRei34], and Scholz [Reference ScholzSch35] supplied the algebraic criteria sufficient to deduce (2.1).
$4.17\%$
of Stevenhagen’s conjecture. Theorem 4 hence cuts the possible discrepancy from Stevenhagen’s conjecture in half. Although the problem of improving (2.1) may have been first explicitly stated in 1993 in [Reference StevenhagenSte93b, p. 127], in essence it has been open since the 1930s, when Rédei [Reference RédeiRed34], Reichardt [Reference ReichardtRei34], and Scholz [Reference ScholzSch35] supplied the algebraic criteria sufficient to deduce (2.1).
2.3 Other results on
 $2$
-parts of class groups of number fields
$2$
-parts of class groups of number fields
Finally, we would like to contrast our results concerning one-prime-parameter families with results on
![]() $2$
-parts of class groups in families parametrized by arbitrarily many primes. The first significant achievement for families with arbitrary discriminants was made by Fouvry and Klüners [Reference Fouvry and KlünersFK07], who translated Rédei’s theory on
$2$
-parts of class groups in families parametrized by arbitrarily many primes. The first significant achievement for families with arbitrary discriminants was made by Fouvry and Klüners [Reference Fouvry and KlünersFK07], who translated Rédei’s theory on
![]() $4$
-ranks of class groups to sums of characters conducive to analytic techniques and then successfully dealt with these sums, basing some of their work on the techniques developed by Heath-Brown in [Reference Heath-BrownHea93, Reference Heath-BrownHea94]. Fouvry and Klüners subsequently developed their methods in various settings [Reference Fouvry and KlünersFK10a, Reference Fouvry and KlünersFK10b, Reference Fouvry and KlünersFK10c, Reference Fouvry and KlünersFK11], most notably obtaining impressive upper and lower bounds for the solvability of the negative Pell equation
$4$
-ranks of class groups to sums of characters conducive to analytic techniques and then successfully dealt with these sums, basing some of their work on the techniques developed by Heath-Brown in [Reference Heath-BrownHea93, Reference Heath-BrownHea94]. Fouvry and Klüners subsequently developed their methods in various settings [Reference Fouvry and KlünersFK10a, Reference Fouvry and KlünersFK10b, Reference Fouvry and KlünersFK10c, Reference Fouvry and KlünersFK11], most notably obtaining impressive upper and lower bounds for the solvability of the negative Pell equation
![]() $x^{2}-dy^{2}=-1$
for general squarefree integers
$x^{2}-dy^{2}=-1$
for general squarefree integers
![]() $d>0$
. When specialized to the one-prime-parameter family
$d>0$
. When specialized to the one-prime-parameter family
![]() $d=2p$
with
$d=2p$
with
![]() $p$
prime, their results are as strong as the bounds in (2.1), so Theorem 4 can be viewed as the next natural step in the line of work initiated by Fouvry and Klüners.
$p$
prime, their results are as strong as the bounds in (2.1), so Theorem 4 can be viewed as the next natural step in the line of work initiated by Fouvry and Klüners.
A recent paper of Smith [Reference SmithSmi17] (see also [Reference SmithSmi16]) features ground-breaking distribution theorems about
![]() $2^{k}$
-ranks of class groups of imaginary quadratic fields for all
$2^{k}$
-ranks of class groups of imaginary quadratic fields for all
![]() $k\geqslant 3$
. The very deep methods that underlie these theorems require the number of prime parameters on average to go to infinity and hence are unlikely to yield results in the direction of Theorems 2, 3, or 4; from the standpoint of analytic number theory, Theorem 2 is a result about the distribution of prime numbers, while the main analytic techniques underlying the results of [Reference SmithSmi17] are consequences of a very careful study of the anatomy of the prime divisors of highly composite integers.
$k\geqslant 3$
. The very deep methods that underlie these theorems require the number of prime parameters on average to go to infinity and hence are unlikely to yield results in the direction of Theorems 2, 3, or 4; from the standpoint of analytic number theory, Theorem 2 is a result about the distribution of prime numbers, while the main analytic techniques underlying the results of [Reference SmithSmi17] are consequences of a very careful study of the anatomy of the prime divisors of highly composite integers.
3 Preliminaries
3.1 The governing field for the
 $8$
-rank of
$8$
-rank of
 $\text{Cl}(-4p)$
$\text{Cl}(-4p)$
As in § 1, let
![]() $M=\mathbb{Q}(\unicode[STIX]{x1D701}_{8},\sqrt{1+i})$
be the (minimal) governing field for the
$M=\mathbb{Q}(\unicode[STIX]{x1D701}_{8},\sqrt{1+i})$
be the (minimal) governing field for the
![]() $8$
-rank in the family
$8$
-rank in the family
![]() $\{\mathbb{Q}(\sqrt{-4p})\}_{p\equiv 1\hspace{0.2em}{\rm mod}\hspace{0.2em}4}$
. Using a computer algebra package such as Sage, one can readily check that:
$\{\mathbb{Q}(\sqrt{-4p})\}_{p\equiv 1\hspace{0.2em}{\rm mod}\hspace{0.2em}4}$
. Using a computer algebra package such as Sage, one can readily check that:
(P1) the ring of integers of every subfield of
 $M$
(including
$M$
(including
 $M$
itself) is a principal ideal domain;
$M$
itself) is a principal ideal domain;(P2) the discriminant
 $\unicode[STIX]{x1D6E5}_{M}$
of
$\unicode[STIX]{x1D6E5}_{M}$
of
 $M/\mathbb{Q}$
is equal to
$M/\mathbb{Q}$
is equal to
 $2^{22}$
, and
$2^{22}$
, and
 $2$
is totally ramified in
$2$
is totally ramified in
 $M/\mathbb{Q}$
; and
$M/\mathbb{Q}$
; and(P3) the torsion subgroup of the group of units in
 ${\mathcal{O}}_{M}$
is
${\mathcal{O}}_{M}$
is
 $\langle \unicode[STIX]{x1D701}_{8}\rangle$
.
$\langle \unicode[STIX]{x1D701}_{8}\rangle$
.
Recall that
![]() $\text{rk}_{8}\text{Cl}(-4p)=1$
if and only if
$\text{rk}_{8}\text{Cl}(-4p)=1$
if and only if
![]() $p$
splits completely in
$p$
splits completely in
![]() $M/\mathbb{Q}$
, that is, if and only if
$M/\mathbb{Q}$
, that is, if and only if
![]() $p$
is odd and every prime ideal
$p$
is odd and every prime ideal
![]() $\mathfrak{p}$
in
$\mathfrak{p}$
in
![]() ${\mathcal{O}}_{M}$
lying over
${\mathcal{O}}_{M}$
lying over
![]() $p$
is of degree
$p$
is of degree
![]() $1$
.
$1$
.
As noted in § 1,
![]() $M/\mathbb{Q}$
is a normal extension with Galois group isomorphic to the dihedral group
$M/\mathbb{Q}$
is a normal extension with Galois group isomorphic to the dihedral group
![]() $D_{8}$
of order
$D_{8}$
of order
![]() $8$
. We fix an automorphism
$8$
. We fix an automorphism
![]() $r\in \text{Gal}(M/\mathbb{Q})$
such that
$r\in \text{Gal}(M/\mathbb{Q})$
such that
![]() $r$
generates the order
$r$
generates the order
![]() $4$
subgroup
$4$
subgroup
![]() $\text{Gal}(M/\mathbb{Q}(\sqrt{-2}))$
, and we let
$\text{Gal}(M/\mathbb{Q}(\sqrt{-2}))$
, and we let
![]() $s\in \text{Gal}(M/\mathbb{Q})$
be the non-trivial automorphism fixing the subfield
$s\in \text{Gal}(M/\mathbb{Q})$
be the non-trivial automorphism fixing the subfield
![]() $K_{1}=\mathbb{Q}(i,\sqrt{1+i})$
. Then
$K_{1}=\mathbb{Q}(i,\sqrt{1+i})$
. Then
![]() $D_{8}\cong \text{Gal}(M/\mathbb{Q})\cong \langle r,s\rangle$
, with
$D_{8}\cong \text{Gal}(M/\mathbb{Q})\cong \langle r,s\rangle$
, with
![]() $r$
of order
$r$
of order
![]() $4$
,
$4$
,
![]() $s$
of order
$s$
of order
![]() $2$
, and
$2$
, and
![]() $sr=r^{3}s$
. Hereinafter, we refer to the following field diagram.
$sr=r^{3}s$
. Hereinafter, we refer to the following field diagram.

By the Čebotarëv density theorem, for each
![]() $\unicode[STIX]{x1D70C}\in ({\mathcal{O}}_{M}/(\unicode[STIX]{x1D6E5}_{M}))^{\times }$
, we can choose an inverse
$\unicode[STIX]{x1D70C}\in ({\mathcal{O}}_{M}/(\unicode[STIX]{x1D6E5}_{M}))^{\times }$
, we can choose an inverse
![]() $\unicode[STIX]{x1D70C}^{\prime }\in {\mathcal{O}}_{M}$
such that
$\unicode[STIX]{x1D70C}^{\prime }\in {\mathcal{O}}_{M}$
such that
![]() $\unicode[STIX]{x1D70C}^{\prime }{\mathcal{O}}_{M}$
is a prime of degree one. Fix a set of such
$\unicode[STIX]{x1D70C}^{\prime }{\mathcal{O}}_{M}$
is a prime of degree one. Fix a set of such
![]() $\unicode[STIX]{x1D70C}^{\prime }$
and call it
$\unicode[STIX]{x1D70C}^{\prime }$
and call it
![]() ${\mathcal{R}}$
. Define
${\mathcal{R}}$
. Define
![]() $F$
to be the rational integer
$F$
to be the rational integer
This is not really analogous to
![]() $F$
on [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13, p. 723], but we denote it by the same letter because it will play an analogous role later on in the estimation of certain congruence sums.
$F$
on [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13, p. 723], but we denote it by the same letter because it will play an analogous role later on in the estimation of certain congruence sums.
3.2 Quadratic reciprocity
Let
![]() $L$
be a number field and let
$L$
be a number field and let
![]() ${\mathcal{O}}_{L}$
be its ring of integers. We say that an ideal
${\mathcal{O}}_{L}$
be its ring of integers. We say that an ideal
![]() $\mathfrak{a}$
in
$\mathfrak{a}$
in
![]() ${\mathcal{O}}_{L}$
is odd if
${\mathcal{O}}_{L}$
is odd if
![]() $\text{N}(\mathfrak{a})$
is odd; similarly, an element
$\text{N}(\mathfrak{a})$
is odd; similarly, an element
![]() $\unicode[STIX]{x1D6FC}$
in
$\unicode[STIX]{x1D6FC}$
in
![]() ${\mathcal{O}}_{L}$
is called odd if the principal ideal generated by
${\mathcal{O}}_{L}$
is called odd if the principal ideal generated by
![]() $\unicode[STIX]{x1D6FC}$
is odd. If
$\unicode[STIX]{x1D6FC}$
is odd. If
![]() $\mathfrak{p}$
is an odd prime ideal in
$\mathfrak{p}$
is an odd prime ideal in
![]() ${\mathcal{O}}_{L}$
, and
${\mathcal{O}}_{L}$
, and
![]() $\unicode[STIX]{x1D6FC}$
is an element in
$\unicode[STIX]{x1D6FC}$
is an element in
![]() ${\mathcal{O}}_{L}$
, then one defines
${\mathcal{O}}_{L}$
, then one defines
 $$\begin{eqnarray}\biggl(\frac{\unicode[STIX]{x1D6FC}}{\mathfrak{p}}\biggr)_{L}=\left\{\begin{array}{@{}ll@{}}0\quad & \text{if }\unicode[STIX]{x1D6FC}\in \mathfrak{p},\\ 1\quad & \text{if }\unicode[STIX]{x1D6FC}\notin \mathfrak{p}\text{ and }\unicode[STIX]{x1D6FC}\text{ is a square modulo }\mathfrak{p},\\ -1\quad & \text{otherwise.}\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\biggl(\frac{\unicode[STIX]{x1D6FC}}{\mathfrak{p}}\biggr)_{L}=\left\{\begin{array}{@{}ll@{}}0\quad & \text{if }\unicode[STIX]{x1D6FC}\in \mathfrak{p},\\ 1\quad & \text{if }\unicode[STIX]{x1D6FC}\notin \mathfrak{p}\text{ and }\unicode[STIX]{x1D6FC}\text{ is a square modulo }\mathfrak{p},\\ -1\quad & \text{otherwise.}\end{array}\right.\end{eqnarray}$$
If
![]() $\mathfrak{b}$
is an odd ideal in
$\mathfrak{b}$
is an odd ideal in
![]() ${\mathcal{O}}_{L}$
, one defines
${\mathcal{O}}_{L}$
, one defines
If
![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in {\mathcal{O}}_{L}$
with
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in {\mathcal{O}}_{L}$
with
![]() $\unicode[STIX]{x1D6FD}$
odd, we define
$\unicode[STIX]{x1D6FD}$
odd, we define
A weak (but sufficient to us) version of the law of quadratic reciprocity for number fields can be stated as follows (see for instance [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13, Lemma 2.1, p. 703]).
Lemma 3.1. Suppose
![]() $L$
is a totally complex number field, and let
$L$
is a totally complex number field, and let
![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in {\mathcal{O}}_{L}$
be odd. Then
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in {\mathcal{O}}_{L}$
be odd. Then
where
![]() $\unicode[STIX]{x1D700}\in \{\pm 1\}$
depends only on the congruence classes of
$\unicode[STIX]{x1D700}\in \{\pm 1\}$
depends only on the congruence classes of
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
modulo
$\unicode[STIX]{x1D6FD}$
modulo
![]() $8{\mathcal{O}}_{L}$
.◻
$8{\mathcal{O}}_{L}$
.◻
When
![]() $\unicode[STIX]{x1D6FC}$
is not odd, the following supplement to the law of quadratic reciprocity will suffice for our purposes (see [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13, Proposition 2.2, p. 703]).
$\unicode[STIX]{x1D6FC}$
is not odd, the following supplement to the law of quadratic reciprocity will suffice for our purposes (see [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13, Proposition 2.2, p. 703]).
Lemma 3.2. Let
![]() $L$
be a totally complex number field, and let
$L$
be a totally complex number field, and let
![]() $\unicode[STIX]{x1D6FC}\in {\mathcal{O}}_{L}$
be non-zero. Then
$\unicode[STIX]{x1D6FC}\in {\mathcal{O}}_{L}$
be non-zero. Then
![]() $(\frac{\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6FD}})_{L}$
depends only on the congruence class of
$(\frac{\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6FD}})_{L}$
depends only on the congruence class of
![]() $\unicode[STIX]{x1D6FD}$
modulo
$\unicode[STIX]{x1D6FD}$
modulo
![]() $8\unicode[STIX]{x1D6FC}{\mathcal{O}}_{L}$
.◻
$8\unicode[STIX]{x1D6FC}{\mathcal{O}}_{L}$
.◻
3.3 Short character sums
Here we state the conjecture that we assume in the proof of Theorem 1. It stipulates power-savings in short character (modulo
![]() $q$
) sums of length
$q$
) sums of length
![]() $q^{1/8}$
and is essentially the same as the case
$q^{1/8}$
and is essentially the same as the case
![]() $n=8$
of Conjecture
$n=8$
of Conjecture
![]() $C_{n}$
in [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13, p. 738].
$C_{n}$
in [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13, p. 738].
Conjecture 1. There exist absolute constants
![]() $\unicode[STIX]{x1D6FF}>0$
and
$\unicode[STIX]{x1D6FF}>0$
and
![]() $C>0$
such that if
$C>0$
such that if
![]() $\unicode[STIX]{x1D712}$
is a non-principal real-valued Dirichlet character modulo a squarefree integer
$\unicode[STIX]{x1D712}$
is a non-principal real-valued Dirichlet character modulo a squarefree integer
![]() $q>2$
and
$q>2$
and
![]() $N<q^{1/8}$
, then
$N<q^{1/8}$
, then
for all integers
![]() $M$
.
$M$
.
We feel that Conjecture 1 is of a genuinely different nature than the arithmetic applications that follow. It is the oscillation of spins over the set of prime ideals that yields the various arithmetic applications. In the sieving methods we use, proving oscillation of spins over prime ideals requires us to first prove oscillation over the set of all ideals. There we encounter character sums in the number field
![]() $M$
that one wishes to relate to character sums in
$M$
that one wishes to relate to character sums in
![]() $\mathbb{Q}$
, where oscillation of character sums is better understood. In passing from
$\mathbb{Q}$
, where oscillation of character sums is better understood. In passing from
![]() $M$
to
$M$
to
![]() $\mathbb{Q}$
, one suffers from the fact that, in some fixed integral basis for
$\mathbb{Q}$
, one suffers from the fact that, in some fixed integral basis for
![]() ${\mathcal{O}}_{M}$
, a nicely chosen element of norm
${\mathcal{O}}_{M}$
, a nicely chosen element of norm
![]() $X$
generally has coordinates of size
$X$
generally has coordinates of size
![]() $X^{1/8}$
. Conductors of characters in question have size similar to the norm, while the length of character sums in question is essentially limited by the size of the coordinates. We also remark that thanks to the work of Burgess [Reference BurgessBur62, Reference BurgessBur63], Conjecture 1 is known to be true when
$X^{1/8}$
. Conductors of characters in question have size similar to the norm, while the length of character sums in question is essentially limited by the size of the coordinates. We also remark that thanks to the work of Burgess [Reference BurgessBur62, Reference BurgessBur63], Conjecture 1 is known to be true when
![]() $1/8$
is replaced with any real number
$1/8$
is replaced with any real number
![]() $\unicode[STIX]{x1D703}>1/4$
, in which case the exponent
$\unicode[STIX]{x1D703}>1/4$
, in which case the exponent
![]() $\unicode[STIX]{x1D6FF}$
and the constant
$\unicode[STIX]{x1D6FF}$
and the constant
![]() $C$
depend on
$C$
depend on
![]() $\unicode[STIX]{x1D703}$
.
$\unicode[STIX]{x1D703}$
.
Instead of directly appealing to Conjecture 1, we will instead need a corollary of Conjecture 1 for arithmetic progressions. For
![]() $q$
odd and squarefree, let
$q$
odd and squarefree, let
![]() $\unicode[STIX]{x1D712}_{q}$
be the real Dirichlet character
$\unicode[STIX]{x1D712}_{q}$
be the real Dirichlet character
![]() $(\frac{\cdot }{q})$
. Following [Reference Friedlander, Iwaniec, Mazur and RubinFIMR15, 7, pp. 924–925] we will prove the following corollary.
$(\frac{\cdot }{q})$
. Following [Reference Friedlander, Iwaniec, Mazur and RubinFIMR15, 7, pp. 924–925] we will prove the following corollary.
Corollary 7. Assume Conjecture 1. Then there exist absolute constants
![]() $\unicode[STIX]{x1D6FF}>0$
and
$\unicode[STIX]{x1D6FF}>0$
and
![]() $C>0$
such that for all odd squarefree integers
$C>0$
such that for all odd squarefree integers
![]() $q>1$
, all integers
$q>1$
, all integers
![]() $N<q^{1/8}$
, all integers
$N<q^{1/8}$
, all integers
![]() $M$
,
$M$
,
![]() $l$
, and
$l$
, and
![]() $k$
satisfying
$k$
satisfying
![]() $q\nmid k$
we have
$q\nmid k$
we have
 $$\begin{eqnarray}\biggl|\mathop{\sum }_{\substack{ M\leqslant n\leqslant M+N \\ n\equiv l\hspace{0.2em}{\rm mod}\hspace{0.2em}k}}\unicode[STIX]{x1D712}_{q}(n)\biggr|\leqslant Cq^{1/8-\unicode[STIX]{x1D6FF}}.\end{eqnarray}$$
$$\begin{eqnarray}\biggl|\mathop{\sum }_{\substack{ M\leqslant n\leqslant M+N \\ n\equiv l\hspace{0.2em}{\rm mod}\hspace{0.2em}k}}\unicode[STIX]{x1D712}_{q}(n)\biggr|\leqslant Cq^{1/8-\unicode[STIX]{x1D6FF}}.\end{eqnarray}$$
Proof. Write
![]() $n=km+l$
. Then we have
$n=km+l$
. Then we have
where
![]() $r$
satisfies
$r$
satisfies
![]() $kr\equiv l\hspace{0.2em}{\rm mod}\hspace{0.2em}q/(q,k)$
. It follows that
$kr\equiv l\hspace{0.2em}{\rm mod}\hspace{0.2em}q/(q,k)$
. It follows that
 $$\begin{eqnarray}\biggl|\mathop{\sum }_{\substack{ M\leqslant n\leqslant M+N \\ n\equiv l\hspace{0.2em}{\rm mod}\hspace{0.2em}k}}\unicode[STIX]{x1D712}_{q}(n)\biggr|\leqslant \biggl|\mathop{\sum }_{M^{\prime }\leqslant m\leqslant M^{\prime }+(N/k)}\unicode[STIX]{x1D712}_{q/(q,k)}(m)\biggr|,\end{eqnarray}$$
$$\begin{eqnarray}\biggl|\mathop{\sum }_{\substack{ M\leqslant n\leqslant M+N \\ n\equiv l\hspace{0.2em}{\rm mod}\hspace{0.2em}k}}\unicode[STIX]{x1D712}_{q}(n)\biggr|\leqslant \biggl|\mathop{\sum }_{M^{\prime }\leqslant m\leqslant M^{\prime }+(N/k)}\unicode[STIX]{x1D712}_{q/(q,k)}(m)\biggr|,\end{eqnarray}$$
where
![]() $M^{\prime }=(M-l)k^{-1}+r$
. By our assumption
$M^{\prime }=(M-l)k^{-1}+r$
. By our assumption
![]() $q\nmid k$
, we see that
$q\nmid k$
, we see that
![]() $q/(q,k)$
is an odd squarefree integer greater than one. Hence
$q/(q,k)$
is an odd squarefree integer greater than one. Hence
![]() $\unicode[STIX]{x1D712}_{q/(q,k)}$
is a non-principal real-valued Dirichlet character. Now apply Conjecture 1.◻
$\unicode[STIX]{x1D712}_{q/(q,k)}$
is a non-principal real-valued Dirichlet character. Now apply Conjecture 1.◻
3.4 Vinogradov’s method, after Friedlander, Iwaniec, Mazur, and Rubin
Vinogradov’s method [Reference VinogradovVin47, Reference VinogradovVin54] has been substantially simplified by Vaughan [Reference VaughanVau77], and Friedlander et al. [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13, §5, pp. 717–722] gave a nice generalization to number fields. Morally speaking, power-saving estimates in sums over primes follow from power-saving estimates in linear congruence sums (sums of type I) and general bilinear sums (sums of type II). Precisely, by [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13, Proposition 5.2, p. 722] with
![]() $\unicode[STIX]{x1D717}=\unicode[STIX]{x1D6FF}/4$
and
$\unicode[STIX]{x1D717}=\unicode[STIX]{x1D6FF}/4$
and
![]() $\unicode[STIX]{x1D703}=1/48$
, Theorem 1 is a direct consequence of the following two propositions.
$\unicode[STIX]{x1D703}=1/48$
, Theorem 1 is a direct consequence of the following two propositions.
Proposition 3.3. Assume Conjecture 1 holds with
![]() $\unicode[STIX]{x1D6FF}>0$
. Then for all
$\unicode[STIX]{x1D6FF}>0$
. Then for all
![]() $\unicode[STIX]{x1D716}>0$
, we have
$\unicode[STIX]{x1D716}>0$
, we have
uniformly for all non-zero ideals
![]() $\mathfrak{m}$
of
$\mathfrak{m}$
of
![]() ${\mathcal{O}}_{M}$
and all
${\mathcal{O}}_{M}$
and all
![]() $x\geqslant 2$
.
$x\geqslant 2$
.
Proposition 3.4. For each
![]() $\unicode[STIX]{x1D716}>0$
, there exists a constant
$\unicode[STIX]{x1D716}>0$
, there exists a constant
![]() $c_{\unicode[STIX]{x1D716}}>0$
such that
$c_{\unicode[STIX]{x1D716}}>0$
such that
uniformly for all
![]() $M,N\geqslant 2$
and all sequences of complex numbers
$M,N\geqslant 2$
and all sequences of complex numbers
![]() $\{v_{\mathfrak{a}}\}$
and
$\{v_{\mathfrak{a}}\}$
and
![]() $\{w_{\mathfrak{b}}\}$
satisfying
$\{w_{\mathfrak{b}}\}$
satisfying
![]() $|v_{\mathfrak{a}}|,|w_{\mathfrak{a}}|\leqslant c_{\unicode[STIX]{x1D716}}\text{N}(\mathfrak{a})^{\unicode[STIX]{x1D716}}$
.
$|v_{\mathfrak{a}}|,|w_{\mathfrak{a}}|\leqslant c_{\unicode[STIX]{x1D716}}\text{N}(\mathfrak{a})^{\unicode[STIX]{x1D716}}$
.
Note that Proposition 3.4 is unconditional – it is only for the sums of type I featuring in Proposition 3.3 that we have to assume Conjecture 1. The proof of Proposition 3.4 is rather standard at this point; similar results in slightly different settings can be found in [Reference Friedlander and IwaniecFI98, Reference Friedlander, Iwaniec, Mazur and RubinFIMR13, Reference MilovicMil17b, Reference MilovicMil18, Reference Koymans and MilovicKM18], among others. The substantially more difficult proof of Proposition 3.3 requires us to make a genuine improvement to the argument of Friedlander et al. [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13, §6].
3.5 A fundamental domain for the action of
 ${\mathcal{O}}_{M}^{\times }$
${\mathcal{O}}_{M}^{\times }$
In the definition of
![]() $s_{\mathfrak{a}}$
in (1.3), we chose a generator
$s_{\mathfrak{a}}$
in (1.3), we chose a generator
![]() $\unicode[STIX]{x1D6FC}$
for the ideal
$\unicode[STIX]{x1D6FC}$
for the ideal
![]() $\mathfrak{a}$
. As we will see in the proofs of Propositions 3.3 and 3.4, when summing over multiple ideals
$\mathfrak{a}$
. As we will see in the proofs of Propositions 3.3 and 3.4, when summing over multiple ideals
![]() $\mathfrak{a}$
, it will be useful to work with a compatible set of generators. Here we present a suitable set of such generators, given by a standard fundamental domain for the action of
$\mathfrak{a}$
, it will be useful to work with a compatible set of generators. Here we present a suitable set of such generators, given by a standard fundamental domain for the action of
![]() ${\mathcal{O}}_{M}^{\times }$
on
${\mathcal{O}}_{M}^{\times }$
on
![]() ${\mathcal{O}}_{M}$
.
${\mathcal{O}}_{M}$
.
Recall that
![]() ${\mathcal{O}}_{M}^{\times }=\langle \unicode[STIX]{x1D701}_{8}\rangle \times V$
, where
${\mathcal{O}}_{M}^{\times }=\langle \unicode[STIX]{x1D701}_{8}\rangle \times V$
, where
![]() $V$
is free of rank
$V$
is free of rank
![]() $3$
. The group
$3$
. The group
![]() $V$
acts on
$V$
acts on
![]() ${\mathcal{O}}_{M}$
by multiplication, i.e., there is an action
${\mathcal{O}}_{M}$
by multiplication, i.e., there is an action
given by
![]() $\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D707},\unicode[STIX]{x1D6FC})=\unicode[STIX]{x1D707}\unicode[STIX]{x1D6FC}$
. Up to units of finite order, the orbits of
$\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D707},\unicode[STIX]{x1D6FC})=\unicode[STIX]{x1D707}\unicode[STIX]{x1D6FC}$
. Up to units of finite order, the orbits of
![]() $\unicode[STIX]{x1D6F9}$
correspond to ideals in
$\unicode[STIX]{x1D6F9}$
correspond to ideals in
![]() ${\mathcal{O}}_{M}$
.
${\mathcal{O}}_{M}$
.
Fix an integral basis for
![]() ${\mathcal{O}}_{M}$
, say
${\mathcal{O}}_{M}$
, say
![]() $\unicode[STIX]{x1D702}=\{\unicode[STIX]{x1D702}_{1},\ldots ,\unicode[STIX]{x1D702}_{8}\}$
. If
$\unicode[STIX]{x1D702}=\{\unicode[STIX]{x1D702}_{1},\ldots ,\unicode[STIX]{x1D702}_{8}\}$
. If
![]() $\unicode[STIX]{x1D6FC}=a_{1}\unicode[STIX]{x1D702}_{1}+\cdots +a_{8}\unicode[STIX]{x1D702}_{8}\in {\mathcal{O}}_{M}$
with
$\unicode[STIX]{x1D6FC}=a_{1}\unicode[STIX]{x1D702}_{1}+\cdots +a_{8}\unicode[STIX]{x1D702}_{8}\in {\mathcal{O}}_{M}$
with
![]() $a_{i}\in \mathbb{Z}$
, we call
$a_{i}\in \mathbb{Z}$
, we call
![]() $a_{i}$
the coordinates of
$a_{i}$
the coordinates of
![]() $\unicode[STIX]{x1D6FC}$
in the basis
$\unicode[STIX]{x1D6FC}$
in the basis
![]() $\unicode[STIX]{x1D702}$
. The ideal in
$\unicode[STIX]{x1D702}$
. The ideal in
![]() ${\mathcal{O}}_{M}$
generated by
${\mathcal{O}}_{M}$
generated by
![]() $\unicode[STIX]{x1D6FC}$
is also generated by
$\unicode[STIX]{x1D6FC}$
is also generated by
![]() $\unicode[STIX]{x1D707}\unicode[STIX]{x1D6FC}$
for any unit
$\unicode[STIX]{x1D707}\unicode[STIX]{x1D6FC}$
for any unit
![]() $\unicode[STIX]{x1D707}\in V$
. As
$\unicode[STIX]{x1D707}\in V$
. As
![]() $V$
is infinite, one can choose
$V$
is infinite, one can choose
![]() $\unicode[STIX]{x1D707}$
so that the coordinates of
$\unicode[STIX]{x1D707}$
so that the coordinates of
![]() $\unicode[STIX]{x1D707}\unicode[STIX]{x1D6FC}$
in the integral basis
$\unicode[STIX]{x1D707}\unicode[STIX]{x1D6FC}$
in the integral basis
![]() $\unicode[STIX]{x1D702}$
are arbitrarily large. The following classical result ensures that one can choose
$\unicode[STIX]{x1D702}$
are arbitrarily large. The following classical result ensures that one can choose
![]() $\unicode[STIX]{x1D707}$
so that the coordinates of
$\unicode[STIX]{x1D707}$
so that the coordinates of
![]() $\unicode[STIX]{x1D707}\unicode[STIX]{x1D6FC}$
are reasonably small.
$\unicode[STIX]{x1D707}\unicode[STIX]{x1D6FC}$
are reasonably small.
Lemma 3.5. There exists a subset
![]() ${\mathcal{D}}$
of
${\mathcal{D}}$
of
![]() ${\mathcal{O}}_{M}$
such that:
${\mathcal{O}}_{M}$
such that:
(i)
 ${\mathcal{D}}$
is a fundamental domain for the action
${\mathcal{D}}$
is a fundamental domain for the action
 $\unicode[STIX]{x1D6F9}$
, i.e., for all
$\unicode[STIX]{x1D6F9}$
, i.e., for all
 $\unicode[STIX]{x1D6FC}\in {\mathcal{O}}_{M}$
, there exists a unique
$\unicode[STIX]{x1D6FC}\in {\mathcal{O}}_{M}$
, there exists a unique
 $\unicode[STIX]{x1D707}\in V$
such that
$\unicode[STIX]{x1D707}\in V$
such that
 $\unicode[STIX]{x1D707}\unicode[STIX]{x1D6FC}\in {\mathcal{D}}$
; and
$\unicode[STIX]{x1D707}\unicode[STIX]{x1D6FC}\in {\mathcal{D}}$
; and(ii) every non-zero ideal
 $\mathfrak{a}$
in
$\mathfrak{a}$
in
 ${\mathcal{O}}_{M}$
has exactly
${\mathcal{O}}_{M}$
has exactly
 $8$
generators in
$8$
generators in
 ${\mathcal{D}}$
; if
${\mathcal{D}}$
; if
 $\unicode[STIX]{x1D6FC}$
is one such generator, then all such generators are of the form
$\unicode[STIX]{x1D6FC}$
is one such generator, then all such generators are of the form
 $\unicode[STIX]{x1D701}_{8}^{j}\unicode[STIX]{x1D6FC}$
, where
$\unicode[STIX]{x1D701}_{8}^{j}\unicode[STIX]{x1D6FC}$
, where
 $j\in \{1,\ldots ,8\}$
; and
$j\in \{1,\ldots ,8\}$
; and(iii) there exists a constant
 $C=C(\unicode[STIX]{x1D702})>0$
such that for all
$C=C(\unicode[STIX]{x1D702})>0$
such that for all
 $\unicode[STIX]{x1D6FC}\in {\mathcal{D}}$
, the coordinates
$\unicode[STIX]{x1D6FC}\in {\mathcal{D}}$
, the coordinates
 $a_{i}$
of
$a_{i}$
of
 $\unicode[STIX]{x1D6FC}$
in the basis
$\unicode[STIX]{x1D6FC}$
in the basis
 $\unicode[STIX]{x1D702}$
satisfy
$\unicode[STIX]{x1D702}$
satisfy
 $|a_{i}|\leqslant C\cdot \text{N}(\unicode[STIX]{x1D6FC})^{1/8}$
.
$|a_{i}|\leqslant C\cdot \text{N}(\unicode[STIX]{x1D6FC})^{1/8}$
.
For a proof, see [Reference Koymans and MilovicKM18], based on [Reference LangLan86, Lemma 1, p. 131]. We are now ready to prove Propositions 3.3 and 3.4, thereby proving Theorem 1.
4 Proof of Theorem 1
As mentioned in § 3.4, thanks to [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13, Proposition 5.2, p. 722], Theorem 1 reduces to proving the appropriate estimates for sums of type I and sums of type II.
4.1 Sums of type I
In this section, we prove Proposition 3.3. Define
![]() $F$
as in (3.1). We recall that we fixed a rank
$F$
as in (3.1). We recall that we fixed a rank
![]() $3$
subgroup
$3$
subgroup
![]() $V$
of
$V$
of
![]() ${\mathcal{O}}_{M}$
and a set of representatives
${\mathcal{O}}_{M}$
and a set of representatives
![]() $\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{8}$
for
$\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{8}$
for
![]() $V/V^{2}$
. Let
$V/V^{2}$
. Let
![]() $\mathfrak{m}$
be an ideal of
$\mathfrak{m}$
be an ideal of
![]() ${\mathcal{O}}_{M}$
coprime with
${\mathcal{O}}_{M}$
coprime with
![]() $F$
. Recall the definition of
$F$
. Recall the definition of
![]() $s_{\mathfrak{a}}$
in (1.3). After using Lemma 3.5 to transform a sum over ideals in
$s_{\mathfrak{a}}$
in (1.3). After using Lemma 3.5 to transform a sum over ideals in
![]() ${\mathcal{O}}_{M}$
to a sum over elements in the fundamental domain
${\mathcal{O}}_{M}$
to a sum over elements in the fundamental domain
![]() ${\mathcal{D}}$
, our goal becomes to bound the following sum
${\mathcal{D}}$
, our goal becomes to bound the following sum
 $$\begin{eqnarray}A(x)=\frac{1}{64}\mathop{\sum }_{\substack{ \text{N}(\mathfrak{a})\leqslant x \\ (\mathfrak{a},F)=1,\mathfrak{m}\mid \mathfrak{a}}}\mathop{\sum }_{i=1}^{8}\mathop{\sum }_{j=1}^{8}[\unicode[STIX]{x1D707}_{i}\unicode[STIX]{x1D701}_{8}^{j}\unicode[STIX]{x1D6FC}]=\frac{1}{64}\mathop{\sum }_{i=1}^{8}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FC}\in {\mathcal{D}};\text{N}(\unicode[STIX]{x1D6FC})\leqslant x \\ (\unicode[STIX]{x1D6FC},F)=1,\mathfrak{m}\mid \unicode[STIX]{x1D6FC}}}[\unicode[STIX]{x1D707}_{i}\unicode[STIX]{x1D6FC}],\end{eqnarray}$$
$$\begin{eqnarray}A(x)=\frac{1}{64}\mathop{\sum }_{\substack{ \text{N}(\mathfrak{a})\leqslant x \\ (\mathfrak{a},F)=1,\mathfrak{m}\mid \mathfrak{a}}}\mathop{\sum }_{i=1}^{8}\mathop{\sum }_{j=1}^{8}[\unicode[STIX]{x1D707}_{i}\unicode[STIX]{x1D701}_{8}^{j}\unicode[STIX]{x1D6FC}]=\frac{1}{64}\mathop{\sum }_{i=1}^{8}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FC}\in {\mathcal{D}};\text{N}(\unicode[STIX]{x1D6FC})\leqslant x \\ (\unicode[STIX]{x1D6FC},F)=1,\mathfrak{m}\mid \unicode[STIX]{x1D6FC}}}[\unicode[STIX]{x1D707}_{i}\unicode[STIX]{x1D6FC}],\end{eqnarray}$$
where, for convenience of notation, we have set
![]() $[\unicode[STIX]{x1D6FD}]=\unicode[STIX]{x1D713}(\unicode[STIX]{x1D6FD}\hspace{0.2em}{\rm mod}\hspace{0.2em}F)[\unicode[STIX]{x1D6FD}]_{r}$
for
$[\unicode[STIX]{x1D6FD}]=\unicode[STIX]{x1D713}(\unicode[STIX]{x1D6FD}\hspace{0.2em}{\rm mod}\hspace{0.2em}F)[\unicode[STIX]{x1D6FD}]_{r}$
for
![]() $\unicode[STIX]{x1D6FD}\in {\mathcal{O}}_{M}$
. The rough strategy of our proof will be the same as the strategy in [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13, §6], although we will have to make the appropriate adjustments in numerous places. We can simplify several steps thanks to the special properties of the field
$\unicode[STIX]{x1D6FD}\in {\mathcal{O}}_{M}$
. The rough strategy of our proof will be the same as the strategy in [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13, §6], although we will have to make the appropriate adjustments in numerous places. We can simplify several steps thanks to the special properties of the field
![]() $M$
as described in § 3.1. At some point, however, the strategy of [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13, §6] will no longer suffice, and we will need a new ingredient.
$M$
as described in § 3.1. At some point, however, the strategy of [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13, §6] will no longer suffice, and we will need a new ingredient.
By making changes of variables
![]() $\unicode[STIX]{x1D6FC}\mapsto \unicode[STIX]{x1D707}_{i}^{-1}\unicode[STIX]{x1D6FC}$
, we rewrite the sum above as
$\unicode[STIX]{x1D6FC}\mapsto \unicode[STIX]{x1D707}_{i}^{-1}\unicode[STIX]{x1D6FC}$
, we rewrite the sum above as
 $$\begin{eqnarray}A(x)=\frac{1}{64}\mathop{\sum }_{i=1}^{8}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D707}_{i}{\mathcal{D}};\text{N}(\unicode[STIX]{x1D6FC})\leqslant x \\ (\unicode[STIX]{x1D6FC},F)=1,\mathfrak{m}\mid \unicode[STIX]{x1D6FC}}}[\unicode[STIX]{x1D6FC}]\end{eqnarray}$$
$$\begin{eqnarray}A(x)=\frac{1}{64}\mathop{\sum }_{i=1}^{8}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D707}_{i}{\mathcal{D}};\text{N}(\unicode[STIX]{x1D6FC})\leqslant x \\ (\unicode[STIX]{x1D6FC},F)=1,\mathfrak{m}\mid \unicode[STIX]{x1D6FC}}}[\unicode[STIX]{x1D6FC}]\end{eqnarray}$$
and after splitting the sum into congruence classes modulo
![]() $F$
, we get
$F$
, we get
 $$\begin{eqnarray}A(x)=\frac{1}{64}\mathop{\sum }_{i=1}^{8}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D70C}\hspace{0.2em}{\rm mod}\hspace{0.2em}F; \\ (\unicode[STIX]{x1D70C},F)=1}}\unicode[STIX]{x1D713}(\unicode[STIX]{x1D70C})A(x;\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}_{i}),\end{eqnarray}$$
$$\begin{eqnarray}A(x)=\frac{1}{64}\mathop{\sum }_{i=1}^{8}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D70C}\hspace{0.2em}{\rm mod}\hspace{0.2em}F; \\ (\unicode[STIX]{x1D70C},F)=1}}\unicode[STIX]{x1D713}(\unicode[STIX]{x1D70C})A(x;\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}_{i}),\end{eqnarray}$$
where
 $$\begin{eqnarray}A(x;\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}_{i})=\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D707}_{i}{\mathcal{D}};\text{N}(\unicode[STIX]{x1D6FC})\leqslant x \\ \unicode[STIX]{x1D6FC}\equiv \unicode[STIX]{x1D70C}\hspace{0.2em}{\rm mod}\hspace{0.2em}F \\ \unicode[STIX]{x1D6FC}\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}\mathfrak{m}}}[\unicode[STIX]{x1D6FC}]_{r}.\end{eqnarray}$$
$$\begin{eqnarray}A(x;\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}_{i})=\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D707}_{i}{\mathcal{D}};\text{N}(\unicode[STIX]{x1D6FC})\leqslant x \\ \unicode[STIX]{x1D6FC}\equiv \unicode[STIX]{x1D70C}\hspace{0.2em}{\rm mod}\hspace{0.2em}F \\ \unicode[STIX]{x1D6FC}\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}\mathfrak{m}}}[\unicode[STIX]{x1D6FC}]_{r}.\end{eqnarray}$$
Our goal is to estimate
![]() $A(x;\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}_{i})$
for each congruence class
$A(x;\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}_{i})$
for each congruence class
![]() $\unicode[STIX]{x1D70C}\hspace{0.2em}{\rm mod}\hspace{0.2em}F$
,
$\unicode[STIX]{x1D70C}\hspace{0.2em}{\rm mod}\hspace{0.2em}F$
,
![]() $(\unicode[STIX]{x1D70C},F)=1$
and unit
$(\unicode[STIX]{x1D70C},F)=1$
and unit
![]() $\unicode[STIX]{x1D707}_{i}$
. As a
$\unicode[STIX]{x1D707}_{i}$
. As a
![]() $\mathbb{Z}$
-module, the ring
$\mathbb{Z}$
-module, the ring
![]() ${\mathcal{O}}_{M}$
decomposes as
${\mathcal{O}}_{M}$
decomposes as
![]() ${\mathcal{O}}_{M}=\mathbb{Z}\oplus \mathbb{M}$
, where
${\mathcal{O}}_{M}=\mathbb{Z}\oplus \mathbb{M}$
, where
![]() $\mathbb{M}$
is a free
$\mathbb{M}$
is a free
![]() $\mathbb{Z}$
-module of rank
$\mathbb{Z}$
-module of rank
![]() $7$
, so that we can write
$7$
, so that we can write
for some
![]() $\unicode[STIX]{x1D714}_{2},\ldots ,\unicode[STIX]{x1D714}_{8}\in {\mathcal{O}}_{M}$
. This means that
$\unicode[STIX]{x1D714}_{2},\ldots ,\unicode[STIX]{x1D714}_{8}\in {\mathcal{O}}_{M}$
. This means that
![]() $\unicode[STIX]{x1D6FC}$
can be written uniquely as
$\unicode[STIX]{x1D6FC}$
can be written uniquely as
so the four summation conditions above are equivalent to
Part 3 of Lemma 3.5 implies that the conjugates of
![]() $\unicode[STIX]{x1D6FD}$
, say
$\unicode[STIX]{x1D6FD}$
, say
![]() $\unicode[STIX]{x1D6FD}^{(i)}$
for
$\unicode[STIX]{x1D6FD}^{(i)}$
for
![]() $1\leqslant i\leqslant 8$
, satisfy
$1\leqslant i\leqslant 8$
, satisfy
![]() $|\unicode[STIX]{x1D6FD}^{(i)}|\ll x^{1/8}$
for any embedding
$|\unicode[STIX]{x1D6FD}^{(i)}|\ll x^{1/8}$
for any embedding
![]() $M{\hookrightarrow}\mathbb{C}$
. Because our field
$M{\hookrightarrow}\mathbb{C}$
. Because our field
![]() $M$
and the integral basis
$M$
and the integral basis
![]() $\{1,\unicode[STIX]{x1D714}_{2},\ldots ,\unicode[STIX]{x1D714}_{8}\}$
is fixed, the implied constant is absolute.
$\{1,\unicode[STIX]{x1D714}_{2},\ldots ,\unicode[STIX]{x1D714}_{8}\}$
is fixed, the implied constant is absolute.
Perhaps the main step of [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13, §6] is a trick on p. 725, which we use to rewrite
![]() $[\unicode[STIX]{x1D6FC}]_{r}=(\frac{r(\unicode[STIX]{x1D6FC})}{\unicode[STIX]{x1D6FC}})$
as
$[\unicode[STIX]{x1D6FC}]_{r}=(\frac{r(\unicode[STIX]{x1D6FC})}{\unicode[STIX]{x1D6FC}})$
as
Morally speaking, this allows us to fix
![]() $\unicode[STIX]{x1D6FD}$
and vary
$\unicode[STIX]{x1D6FD}$
and vary
![]() $a$
, thereby creating a genuine character sum in which the variable of summation does not depend on the conductor of the character. If
$a$
, thereby creating a genuine character sum in which the variable of summation does not depend on the conductor of the character. If
![]() $\unicode[STIX]{x1D6FD}=r(\unicode[STIX]{x1D6FD})$
, then
$\unicode[STIX]{x1D6FD}=r(\unicode[STIX]{x1D6FD})$
, then
![]() $\unicode[STIX]{x1D6FD}$
does not contribute to the sum. So we can and will assume
$\unicode[STIX]{x1D6FD}$
does not contribute to the sum. So we can and will assume
![]() $\unicode[STIX]{x1D6FD}\neq r(\unicode[STIX]{x1D6FD})$
. By property (P1) in § 3.1, we can write
$\unicode[STIX]{x1D6FD}\neq r(\unicode[STIX]{x1D6FD})$
. By property (P1) in § 3.1, we can write
with
![]() $c_{0},c,\unicode[STIX]{x1D702}\in {\mathcal{O}}_{M}$
,
$c_{0},c,\unicode[STIX]{x1D702}\in {\mathcal{O}}_{M}$
,
![]() $c_{0}\mid F$
squarefree,
$c_{0}\mid F$
squarefree,
![]() $\unicode[STIX]{x1D702}\mid F^{\infty }$
, and
$\unicode[STIX]{x1D702}\mid F^{\infty }$
, and
![]() $(c,F)=1$
. Then
$(c,F)=1$
. Then
By Lemma 3.2, the factor
![]() $(\frac{c_{0}}{a+\unicode[STIX]{x1D6FD}})$
depends only on the congruence class of
$(\frac{c_{0}}{a+\unicode[STIX]{x1D6FD}})$
depends only on the congruence class of
![]() $a+\unicode[STIX]{x1D6FD}$
modulo
$a+\unicode[STIX]{x1D6FD}$
modulo
![]() $8c_{0}$
, and, as
$8c_{0}$
, and, as
![]() $c_{0}$
is squarefree and divides
$c_{0}$
is squarefree and divides
![]() $F$
, it depends only on
$F$
, it depends only on
![]() $\unicode[STIX]{x1D70C}$
.
$\unicode[STIX]{x1D70C}$
.
Next we claim that
where
![]() $\unicode[STIX]{x1D700}_{1}\in \{\pm 1\}$
depends only on
$\unicode[STIX]{x1D700}_{1}\in \{\pm 1\}$
depends only on
![]() $\unicode[STIX]{x1D70C}$
and
$\unicode[STIX]{x1D70C}$
and
![]() $\unicode[STIX]{x1D6FD}$
. Indeed,
$\unicode[STIX]{x1D6FD}$
. Indeed,
![]() $\unicode[STIX]{x1D70C}$
determines the congruence class of
$\unicode[STIX]{x1D70C}$
determines the congruence class of
![]() $a+\unicode[STIX]{x1D6FD}$
modulo
$a+\unicode[STIX]{x1D6FD}$
modulo
![]() $8$
and
$8$
and
![]() $c$
depends only on
$c$
depends only on
![]() $\unicode[STIX]{x1D6FD}$
, so an application of Lemma 3.1 proves the claim. Combining everything gives
$\unicode[STIX]{x1D6FD}$
, so an application of Lemma 3.1 proves the claim. Combining everything gives
where
![]() $\unicode[STIX]{x1D700}_{2}=\unicode[STIX]{x1D700}_{2}(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D6FD})\in \{\pm 1\}$
depends only on
$\unicode[STIX]{x1D700}_{2}=\unicode[STIX]{x1D700}_{2}(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D6FD})\in \{\pm 1\}$
depends only on
![]() $\unicode[STIX]{x1D70C}$
and
$\unicode[STIX]{x1D70C}$
and
![]() $\unicode[STIX]{x1D6FD}$
. Having rewritten
$\unicode[STIX]{x1D6FD}$
. Having rewritten
![]() $(\frac{r(\unicode[STIX]{x1D6FC})}{\unicode[STIX]{x1D6FC}})$
in a desirable form, we can now split
$(\frac{r(\unicode[STIX]{x1D6FC})}{\unicode[STIX]{x1D6FC}})$
in a desirable form, we can now split
![]() $A(x;\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}_{i})$
as follows
$A(x;\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}_{i})$
as follows
 $$\begin{eqnarray}\displaystyle A(x;\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}_{i}) & = & \displaystyle \mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D707}_{i}{\mathcal{D}};\text{N}(\unicode[STIX]{x1D6FC})\leqslant x \\ \unicode[STIX]{x1D6FC}\equiv \unicode[STIX]{x1D70C}\hspace{0.2em}{\rm mod}\hspace{0.2em}F \\ \unicode[STIX]{x1D6FC}\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}\mathfrak{m}}}\biggl(\frac{r(\unicode[STIX]{x1D6FC})}{\unicode[STIX]{x1D6FC}}\biggr)=\mathop{\sum }_{\substack{ a+\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D707}_{i}{\mathcal{D}};\text{N}(a+\unicode[STIX]{x1D6FD})\leqslant x \\ a+\unicode[STIX]{x1D6FD}\equiv \unicode[STIX]{x1D70C}\hspace{0.2em}{\rm mod}\hspace{0.2em}F \\ a+\unicode[STIX]{x1D6FD}\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}\mathfrak{m}}}\biggl(\frac{r(a+\unicode[STIX]{x1D6FD})}{a+\unicode[STIX]{x1D6FD}}\biggr)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FD}\in \mathbb{M}}\mathop{\sum }_{\substack{ a\in \mathbb{Z}; \\ a+\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D707}_{i}{\mathcal{D}},\text{N}(a+\unicode[STIX]{x1D6FD})\leqslant x \\ a+\unicode[STIX]{x1D6FD}\equiv \unicode[STIX]{x1D70C}\hspace{0.2em}{\rm mod}\hspace{0.2em}F \\ a+\unicode[STIX]{x1D6FD}\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}\mathfrak{m}}}\biggl(\frac{r(a+\unicode[STIX]{x1D6FD})}{a+\unicode[STIX]{x1D6FD}}\biggr)=\mathop{\sum }_{\unicode[STIX]{x1D6FD}\in \mathbb{M}}\mathop{\sum }_{\substack{ a\in \mathbb{Z}; \\ a+\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D707}_{i}{\mathcal{D}};\text{N}(a+\unicode[STIX]{x1D6FD})\leqslant x \\ a+\unicode[STIX]{x1D6FD}\equiv \unicode[STIX]{x1D70C}\hspace{0.2em}{\rm mod}\hspace{0.2em}F \\ a+\unicode[STIX]{x1D6FD}\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}\mathfrak{m}}}\unicode[STIX]{x1D700}_{2}(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D6FD})\biggl(\frac{a+\unicode[STIX]{x1D6FD}}{c}\biggr)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FD}\in \mathbb{M}}|T(x;\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}_{i})|,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle A(x;\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}_{i}) & = & \displaystyle \mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D707}_{i}{\mathcal{D}};\text{N}(\unicode[STIX]{x1D6FC})\leqslant x \\ \unicode[STIX]{x1D6FC}\equiv \unicode[STIX]{x1D70C}\hspace{0.2em}{\rm mod}\hspace{0.2em}F \\ \unicode[STIX]{x1D6FC}\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}\mathfrak{m}}}\biggl(\frac{r(\unicode[STIX]{x1D6FC})}{\unicode[STIX]{x1D6FC}}\biggr)=\mathop{\sum }_{\substack{ a+\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D707}_{i}{\mathcal{D}};\text{N}(a+\unicode[STIX]{x1D6FD})\leqslant x \\ a+\unicode[STIX]{x1D6FD}\equiv \unicode[STIX]{x1D70C}\hspace{0.2em}{\rm mod}\hspace{0.2em}F \\ a+\unicode[STIX]{x1D6FD}\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}\mathfrak{m}}}\biggl(\frac{r(a+\unicode[STIX]{x1D6FD})}{a+\unicode[STIX]{x1D6FD}}\biggr)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FD}\in \mathbb{M}}\mathop{\sum }_{\substack{ a\in \mathbb{Z}; \\ a+\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D707}_{i}{\mathcal{D}},\text{N}(a+\unicode[STIX]{x1D6FD})\leqslant x \\ a+\unicode[STIX]{x1D6FD}\equiv \unicode[STIX]{x1D70C}\hspace{0.2em}{\rm mod}\hspace{0.2em}F \\ a+\unicode[STIX]{x1D6FD}\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}\mathfrak{m}}}\biggl(\frac{r(a+\unicode[STIX]{x1D6FD})}{a+\unicode[STIX]{x1D6FD}}\biggr)=\mathop{\sum }_{\unicode[STIX]{x1D6FD}\in \mathbb{M}}\mathop{\sum }_{\substack{ a\in \mathbb{Z}; \\ a+\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D707}_{i}{\mathcal{D}};\text{N}(a+\unicode[STIX]{x1D6FD})\leqslant x \\ a+\unicode[STIX]{x1D6FD}\equiv \unicode[STIX]{x1D70C}\hspace{0.2em}{\rm mod}\hspace{0.2em}F \\ a+\unicode[STIX]{x1D6FD}\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}\mathfrak{m}}}\unicode[STIX]{x1D700}_{2}(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D6FD})\biggl(\frac{a+\unicode[STIX]{x1D6FD}}{c}\biggr)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FD}\in \mathbb{M}}|T(x;\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}_{i})|,\nonumber\end{eqnarray}$$
where
![]() $T(x;\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}_{i})$
is defined as
$T(x;\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}_{i})$
is defined as
 $$\begin{eqnarray}T(x;\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}_{i})=\mathop{\sum }_{\substack{ a\in \mathbb{Z}; \\ a+\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D707}_{i}{\mathcal{D}},\text{N}(a+\unicode[STIX]{x1D6FD})\leqslant x \\ a+\unicode[STIX]{x1D6FD}\equiv \unicode[STIX]{x1D70C}\hspace{0.2em}{\rm mod}\hspace{0.2em}F \\ a+\unicode[STIX]{x1D6FD}\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}\mathfrak{m}}}\biggl(\frac{a+\unicode[STIX]{x1D6FD}}{c}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}T(x;\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}_{i})=\mathop{\sum }_{\substack{ a\in \mathbb{Z}; \\ a+\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D707}_{i}{\mathcal{D}},\text{N}(a+\unicode[STIX]{x1D6FD})\leqslant x \\ a+\unicode[STIX]{x1D6FD}\equiv \unicode[STIX]{x1D70C}\hspace{0.2em}{\rm mod}\hspace{0.2em}F \\ a+\unicode[STIX]{x1D6FD}\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}\mathfrak{m}}}\biggl(\frac{a+\unicode[STIX]{x1D6FD}}{c}\biggr).\end{eqnarray}$$
From now on we treat
![]() $\unicode[STIX]{x1D6FD}$
as fixed and estimate
$\unicode[STIX]{x1D6FD}$
as fixed and estimate
![]() $T(x;\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}_{i})$
. Recall that
$T(x;\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}_{i})$
. Recall that
![]() $c$
is odd and hence no ramified prime can divide the ideal
$c$
is odd and hence no ramified prime can divide the ideal
![]() $(c)=c{\mathcal{O}}_{M}$
by property (P2) in § 3.1. This implies that
$(c)=c{\mathcal{O}}_{M}$
by property (P2) in § 3.1. This implies that
![]() $(c)$
can be factored as
$(c)$
can be factored as
where, similarly as in [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13, (6.21), p. 727],
![]() $\mathfrak{g}$
consists of all prime ideals dividing
$\mathfrak{g}$
consists of all prime ideals dividing
![]() $(c)$
that are of degree greater than one or unramified primes of degree one for which some conjugate is also a factor of
$(c)$
that are of degree greater than one or unramified primes of degree one for which some conjugate is also a factor of
![]() $(c)$
. By construction
$(c)$
. By construction
![]() $\mathfrak{q}$
consists of all the remaining primes dividing
$\mathfrak{q}$
consists of all the remaining primes dividing
![]() $c{\mathcal{O}}_{M}$
. Then
$c{\mathcal{O}}_{M}$
. Then
![]() $q:=N\mathfrak{q}$
is a squarefree integer and
$q:=N\mathfrak{q}$
is a squarefree integer and
![]() $g:=N\mathfrak{g}$
is a squarefull number coprime with
$g:=N\mathfrak{g}$
is a squarefull number coprime with
![]() $q$
. There exists a rational integer
$q$
. There exists a rational integer
![]() $b$
with
$b$
with
![]() $b\equiv \unicode[STIX]{x1D6FD}\hspace{0.2em}{\rm mod}\hspace{0.2em}\mathfrak{q}$
by an application of the Chinese remainder theorem. Again, as
$b\equiv \unicode[STIX]{x1D6FD}\hspace{0.2em}{\rm mod}\hspace{0.2em}\mathfrak{q}$
by an application of the Chinese remainder theorem. Again, as
![]() $c$
depends on
$c$
depends on
![]() $\unicode[STIX]{x1D6FD}$
and not on
$\unicode[STIX]{x1D6FD}$
and not on
![]() $a$
, so also
$a$
, so also
![]() $b$
is a rational integer that depends on
$b$
is a rational integer that depends on
![]() $\unicode[STIX]{x1D6FD}$
and not on
$\unicode[STIX]{x1D6FD}$
and not on
![]() $a$
. We get
$a$
. We get
Define
![]() $g_{0}$
as the radical of
$g_{0}$
as the radical of
![]() $g$
, i.e.,
$g$
, i.e.,
Note that the quadratic residue symbol
![]() $(\frac{\unicode[STIX]{x1D6FC}}{\mathfrak{g}})$
is periodic in
$(\frac{\unicode[STIX]{x1D6FC}}{\mathfrak{g}})$
is periodic in
![]() $\unicode[STIX]{x1D6FC}$
modulo
$\unicode[STIX]{x1D6FC}$
modulo
![]() $\mathfrak{g}^{\ast }=\prod _{\mathfrak{p}\mid \mathfrak{g}}\mathfrak{p}$
. Since
$\mathfrak{g}^{\ast }=\prod _{\mathfrak{p}\mid \mathfrak{g}}\mathfrak{p}$
. Since
![]() $\mathfrak{g}^{\ast }$
divides
$\mathfrak{g}^{\ast }$
divides
![]() $g_{0}$
, we conclude that the symbol
$g_{0}$
, we conclude that the symbol
![]() $(\frac{a+\unicode[STIX]{x1D6FD}}{\mathfrak{g}})$
is periodic of period
$(\frac{a+\unicode[STIX]{x1D6FD}}{\mathfrak{g}})$
is periodic of period
![]() $g_{0}$
as a function of
$g_{0}$
as a function of
![]() $a\in \mathbb{Z}$
. We split
$a\in \mathbb{Z}$
. We split
![]() $T(x;\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}_{i})$
into congruence classes modulo
$T(x;\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}_{i})$
into congruence classes modulo
![]() $g_{0}$
, giving
$g_{0}$
, giving
where
 $$\begin{eqnarray}T(x;\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}_{i},a_{0})=\mathop{\sum }_{\substack{ a\in \mathbb{Z}; \\ a+\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D707}_{i}{\mathcal{D}},\text{N}(a+\unicode[STIX]{x1D6FD})\leqslant x \\ a+\unicode[STIX]{x1D6FD}\equiv \unicode[STIX]{x1D70C}\hspace{0.2em}{\rm mod}\hspace{0.2em}F \\ a+\unicode[STIX]{x1D6FD}\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}\mathfrak{m} \\ a\equiv a_{0}\hspace{0.2em}{\rm mod}\hspace{0.2em}g_{0}}}\biggl(\frac{a+b}{\mathfrak{q}}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}T(x;\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}_{i},a_{0})=\mathop{\sum }_{\substack{ a\in \mathbb{Z}; \\ a+\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D707}_{i}{\mathcal{D}},\text{N}(a+\unicode[STIX]{x1D6FD})\leqslant x \\ a+\unicode[STIX]{x1D6FD}\equiv \unicode[STIX]{x1D70C}\hspace{0.2em}{\rm mod}\hspace{0.2em}F \\ a+\unicode[STIX]{x1D6FD}\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}\mathfrak{m} \\ a\equiv a_{0}\hspace{0.2em}{\rm mod}\hspace{0.2em}g_{0}}}\biggl(\frac{a+b}{\mathfrak{q}}\biggr).\end{eqnarray}$$
Note that
![]() $a+\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D707}_{i}{\mathcal{D}}$
implies that
$a+\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D707}_{i}{\mathcal{D}}$
implies that
![]() $a\ll x^{1/8}$
, where the implied constant depends only on one of the eight units
$a\ll x^{1/8}$
, where the implied constant depends only on one of the eight units
![]() $\unicode[STIX]{x1D707}_{i}$
. The condition
$\unicode[STIX]{x1D707}_{i}$
. The condition
![]() $\text{N}(a+\unicode[STIX]{x1D6FD})\leqslant x$
for fixed
$\text{N}(a+\unicode[STIX]{x1D6FD})\leqslant x$
for fixed
![]() $\unicode[STIX]{x1D6FD}$
and
$\unicode[STIX]{x1D6FD}$
and
![]() $x$
is a polynomial inequality of degree
$x$
is a polynomial inequality of degree
![]() $8$
in
$8$
in
![]() $a$
. So the summation variable
$a$
. So the summation variable
![]() $a\in \mathbb{Z}$
runs over a collection of at most
$a\in \mathbb{Z}$
runs over a collection of at most
![]() $8$
intervals whose endpoints depend on
$8$
intervals whose endpoints depend on
![]() $\unicode[STIX]{x1D6FD}$
and
$\unicode[STIX]{x1D6FD}$
and
![]() $x$
. But from
$x$
. But from
![]() $a\ll x^{1/8}$
we see that for the length
$a\ll x^{1/8}$
we see that for the length
![]() $L$
of each such interval we have
$L$
of each such interval we have
![]() $L\ll x^{1/8}$
.
$L\ll x^{1/8}$
.
Furthermore, the congruences
![]() $a+\unicode[STIX]{x1D6FD}\equiv \unicode[STIX]{x1D70C}\hspace{0.2em}{\rm mod}\hspace{0.2em}F$
,
$a+\unicode[STIX]{x1D6FD}\equiv \unicode[STIX]{x1D70C}\hspace{0.2em}{\rm mod}\hspace{0.2em}F$
,
![]() $a+\unicode[STIX]{x1D6FD}\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}\mathfrak{m}$
and
$a+\unicode[STIX]{x1D6FD}\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}\mathfrak{m}$
and
![]() $a\equiv a_{0}\hspace{0.2em}{\rm mod}\hspace{0.2em}g_{0}$
mean that
$a\equiv a_{0}\hspace{0.2em}{\rm mod}\hspace{0.2em}g_{0}$
mean that
![]() $a$
runs over a certain arithmetic progression of modulus
$a$
runs over a certain arithmetic progression of modulus
![]() $k$
, which divides
$k$
, which divides
![]() $g_{0}mF$
, where
$g_{0}mF$
, where
![]() $m:=\text{N}\mathfrak{m}$
. Hence, we see that the inner sum in (4.1) can be rewritten as at most
$m:=\text{N}\mathfrak{m}$
. Hence, we see that the inner sum in (4.1) can be rewritten as at most
![]() $8$
sums, each of which runs over an arithmetic progression of modulus
$8$
sums, each of which runs over an arithmetic progression of modulus
![]() $k$
in a single segment of length
$k$
in a single segment of length
![]() $\ll x^{1/8}$
.
$\ll x^{1/8}$
.
As
![]() $q=\text{N}(\mathfrak{q})$
is squarefree,
$q=\text{N}(\mathfrak{q})$
is squarefree,
![]() $(\frac{\cdot }{\mathfrak{q}})$
is the real primitive Dirichlet character of modulus
$(\frac{\cdot }{\mathfrak{q}})$
is the real primitive Dirichlet character of modulus
![]() $q$
, and hence we have at most
$q$
, and hence we have at most
![]() $8$
incomplete character sums of length
$8$
incomplete character sums of length
![]() $\ll x^{1/8}$
and modulus
$\ll x^{1/8}$
and modulus
![]() $q\ll x$
. When the modulus
$q\ll x$
. When the modulus
![]() $q$
of the Dirichlet character divides the modulus
$q$
of the Dirichlet character divides the modulus
![]() $k$
of the arithmetic progression, one can not expect to get cancellation. For now we assume that
$k$
of the arithmetic progression, one can not expect to get cancellation. For now we assume that
![]() $q\nmid k$
, and we will deal with the case
$q\nmid k$
, and we will deal with the case
![]() $q\mid k$
later on. Corollary 7 implies that
$q\mid k$
later on. Corollary 7 implies that
and hence that
Just as in [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13], the implied constant above does not depend on
![]() $\unicode[STIX]{x1D6FD}$
because Conjecture 1, and so also Corollary 7, encompasses all incomplete character sums of length
$\unicode[STIX]{x1D6FD}$
because Conjecture 1, and so also Corollary 7, encompasses all incomplete character sums of length
![]() $\ll x^{1/8}$
, regardless of the endpoints of the interval being summed over.
$\ll x^{1/8}$
, regardless of the endpoints of the interval being summed over.
We still need to deal with the case
![]() $q\mid k$
. Certainly, this implies
$q\mid k$
. Certainly, this implies
![]() $q\mid m$
. So (4.2) holds if
$q\mid m$
. So (4.2) holds if
![]() $q\nmid m$
. Hence, by the definition of
$q\nmid m$
. Hence, by the definition of
![]() $(c)$
and the factorization
$(c)$
and the factorization
![]() $(c)=\mathfrak{g}\mathfrak{q}$
, we have (4.2) unless
$(c)=\mathfrak{g}\mathfrak{q}$
, we have (4.2) unless
We write
![]() $A_{\Box }(x;\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}_{i})$
for the contribution to
$A_{\Box }(x;\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}_{i})$
for the contribution to
![]() $A(x;\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}_{i})$
with (4.3). We have
$A(x;\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}_{i})$
with (4.3). We have
Decompose
![]() ${\mathcal{O}}_{M}$
as
${\mathcal{O}}_{M}$
as
where
![]() $\mathbb{M}^{\prime }$
is a free
$\mathbb{M}^{\prime }$
is a free
![]() $\mathbb{Z}$
-module of rank
$\mathbb{Z}$
-module of rank
![]() $6$
. Then we get an injective map
$6$
. Then we get an injective map
![]() $\mathbb{M}^{\prime }\rightarrow {\mathcal{O}}_{M}$
given by
$\mathbb{M}^{\prime }\rightarrow {\mathcal{O}}_{M}$
given by
![]() $\unicode[STIX]{x1D6FC}\mapsto \unicode[STIX]{x1D6FC}-r(\unicode[STIX]{x1D6FC})$
. Since
$\unicode[STIX]{x1D6FC}\mapsto \unicode[STIX]{x1D6FC}-r(\unicode[STIX]{x1D6FC})$
. Since
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D707}_{i}{\mathcal{D}}$
and
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D707}_{i}{\mathcal{D}}$
and
![]() $\text{N}(\unicode[STIX]{x1D6FC})\leqslant x$
, we know that all the conjugates
$\text{N}(\unicode[STIX]{x1D6FC})\leqslant x$
, we know that all the conjugates
![]() $|\unicode[STIX]{x1D6FC}^{(k)}|$
are
$|\unicode[STIX]{x1D6FC}^{(k)}|$
are
![]() $\ll x^{1/8}$
. If we write
$\ll x^{1/8}$
. If we write
with
![]() $a,b\in \mathbb{Z}$
, and
$a,b\in \mathbb{Z}$
, and
![]() $m^{\prime }\in \mathbb{M}^{\prime }$
, then it follows that
$m^{\prime }\in \mathbb{M}^{\prime }$
, then it follows that
![]() $|a|,|b|\leqslant y$
and furthermore all the conjugates of
$|a|,|b|\leqslant y$
and furthermore all the conjugates of
![]() $\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FC}-r(\unicode[STIX]{x1D6FC})$
satisfy
$\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FC}-r(\unicode[STIX]{x1D6FC})$
satisfy
![]() $|\unicode[STIX]{x1D6FE}^{(k)}|\leqslant y$
for some
$|\unicode[STIX]{x1D6FE}^{(k)}|\leqslant y$
for some
![]() $y\asymp x^{1/8}$
. Therefore, we have
$y\asymp x^{1/8}$
. Therefore, we have
Since it is easier to count ideals than integers, we replace
![]() $\unicode[STIX]{x1D6FE}$
by the principal ideal it generates. We remark that an ideal
$\unicode[STIX]{x1D6FE}$
by the principal ideal it generates. We remark that an ideal
![]() $\mathfrak{b}$
with
$\mathfrak{b}$
with
![]() $\text{N}\mathfrak{b}\leqslant y^{8}$
has
$\text{N}\mathfrak{b}\leqslant y^{8}$
has
![]() $\ll (\log y)^{8}$
generators satisfying
$\ll (\log y)^{8}$
generators satisfying
![]() $|\unicode[STIX]{x1D6FE}^{(k)}|\leqslant y$
for all
$|\unicode[STIX]{x1D6FE}^{(k)}|\leqslant y$
for all
![]() $k$
. Hence
$k$
. Hence
Now we can use the multiplicative structure of the ideals in
![]() ${\mathcal{O}}_{M}$
, giving the bound
${\mathcal{O}}_{M}$
, giving the bound
 $$\begin{eqnarray}A_{\Box }(x;\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}_{i})\ll x^{1/4}(\log x)^{8}\mathop{\sum }_{\substack{ b\leqslant y^{8} \\ p\mid b\;\Longrightarrow \;p^{2}\mid mFb}}\unicode[STIX]{x1D70F}(b),\end{eqnarray}$$
$$\begin{eqnarray}A_{\Box }(x;\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}_{i})\ll x^{1/4}(\log x)^{8}\mathop{\sum }_{\substack{ b\leqslant y^{8} \\ p\mid b\;\Longrightarrow \;p^{2}\mid mFb}}\unicode[STIX]{x1D70F}(b),\end{eqnarray}$$
where
![]() $b$
runs over the positive rational integers and
$b$
runs over the positive rational integers and
![]() $\unicode[STIX]{x1D70F}(b)$
counts the number of ideals in
$\unicode[STIX]{x1D70F}(b)$
counts the number of ideals in
![]() $M$
with norm
$M$
with norm
![]() $b$
. Then we have
$b$
. Then we have
![]() $\unicode[STIX]{x1D70F}(b)\ll b^{\unicode[STIX]{x1D716}}$
. Note that we can assume
$\unicode[STIX]{x1D70F}(b)\ll b^{\unicode[STIX]{x1D716}}$
. Note that we can assume
![]() $m\leqslant x$
because otherwise
$m\leqslant x$
because otherwise
![]() $A(x)$
is the empty sum. Hence, recalling that
$A(x)$
is the empty sum. Hence, recalling that
![]() $y\asymp x^{1/8}$
, we conclude that
$y\asymp x^{1/8}$
, we conclude that
where the implied constant depends only on
![]() $\unicode[STIX]{x1D716}$
.
$\unicode[STIX]{x1D716}$
.
Define
![]() $A_{0}(x;\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}_{i})$
to be the contribution of
$A_{0}(x;\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}_{i})$
to be the contribution of
![]() $A(x;\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}_{i})$
of the terms
$A(x;\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}_{i})$
of the terms
![]() $\unicode[STIX]{x1D6FC}=a+\unicode[STIX]{x1D6FD}$
not satisfying (4.3). We have
$\unicode[STIX]{x1D6FC}=a+\unicode[STIX]{x1D6FD}$
not satisfying (4.3). We have
To estimate
![]() $A_{0}(x;\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}_{i})$
we can use (4.2) for every relevant
$A_{0}(x;\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}_{i})$
we can use (4.2) for every relevant
![]() $\unicode[STIX]{x1D6FD}$
. Unfortunately, the bound (4.2) is only good when
$\unicode[STIX]{x1D6FD}$
. Unfortunately, the bound (4.2) is only good when
![]() $g_{0}$
is small. So we make the further partition
$g_{0}$
is small. So we make the further partition
where the components run over
![]() $\unicode[STIX]{x1D6FC}=a+\unicode[STIX]{x1D6FD}$
with
$\unicode[STIX]{x1D6FC}=a+\unicode[STIX]{x1D6FD}$
with
![]() $\unicode[STIX]{x1D6FD}$
satisfying
$\unicode[STIX]{x1D6FD}$
satisfying
Here
![]() $Z$
is at our disposal and we choose it later. It is here that we must improve on the bounds of [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13]. In their proof they define three sums
$Z$
is at our disposal and we choose it later. It is here that we must improve on the bounds of [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13]. In their proof they define three sums
 $$\begin{eqnarray}\displaystyle \displaystyle g_{0}\leqslant Z\quad & \text{in the sum }A_{1}(x;\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}_{i}), & \displaystyle \nonumber\\ \displaystyle \displaystyle g_{0}>Z,g\leqslant Y\quad & \text{in the sum }A_{2}(x;\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}_{i}), & \displaystyle \nonumber\\ \displaystyle \displaystyle g_{0}>Z,g>Y\quad & \text{in the sum }A_{3}(x;\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}_{i}), & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle g_{0}\leqslant Z\quad & \text{in the sum }A_{1}(x;\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}_{i}), & \displaystyle \nonumber\\ \displaystyle \displaystyle g_{0}>Z,g\leqslant Y\quad & \text{in the sum }A_{2}(x;\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}_{i}), & \displaystyle \nonumber\\ \displaystyle \displaystyle g_{0}>Z,g>Y\quad & \text{in the sum }A_{3}(x;\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}_{i}), & \displaystyle \nonumber\end{eqnarray}$$
with
![]() $Z\leqslant Y$
at their disposal. Following the proof in [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13] would give
$Z\leqslant Y$
at their disposal. Following the proof in [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13] would give
and it is easily seen that there is no choice of
![]() $Z\leqslant Y$
that makes
$Z\leqslant Y$
that makes
![]() $A_{0}(x;\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}_{i})\ll x^{1-\unicode[STIX]{x1D703}_{1}}$
for some
$A_{0}(x;\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}_{i})\ll x^{1-\unicode[STIX]{x1D703}_{1}}$
for some
![]() $\unicode[STIX]{x1D703}_{1}>0$
. Our proof is conceptually simpler and provides sharper bounds.
$\unicode[STIX]{x1D703}_{1}>0$
. Our proof is conceptually simpler and provides sharper bounds.
We estimate
![]() $A_{1}(x;\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}_{i})$
as in [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13] by using (4.2) and summing over
$A_{1}(x;\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}_{i})$
as in [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13] by using (4.2) and summing over
![]() $\unicode[STIX]{x1D6FD}\in \mathbb{M}$
satisfying
$\unicode[STIX]{x1D6FD}\in \mathbb{M}$
satisfying
![]() $|\unicode[STIX]{x1D6FD}^{(1)}|,\ldots ,|\unicode[STIX]{x1D6FD}^{(8)}|\ll x^{1/8}$
to obtain
$|\unicode[STIX]{x1D6FD}^{(1)}|,\ldots ,|\unicode[STIX]{x1D6FD}^{(8)}|\ll x^{1/8}$
to obtain
Our next goal is to estimate
![]() $A_{2}(x;\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}_{i})$
. We keep the condition
$A_{2}(x;\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}_{i})$
. We keep the condition
![]() $\unicode[STIX]{x1D6FC}-r(\unicode[STIX]{x1D6FC})\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}\mathfrak{g}$
, giving
$\unicode[STIX]{x1D6FC}-r(\unicode[STIX]{x1D6FC})\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}\mathfrak{g}$
, giving
where
![]() $y\asymp x^{1/8}$
and
$y\asymp x^{1/8}$
and
Here
![]() $\mathbb{M}^{\prime \prime }$
is by definition the image of
$\mathbb{M}^{\prime \prime }$
is by definition the image of
![]() $\mathbb{M}^{\prime }$
under the map
$\mathbb{M}^{\prime }$
under the map
![]() $\unicode[STIX]{x1D6FD}\mapsto \unicode[STIX]{x1D6FD}-r(\unicode[STIX]{x1D6FD})$
. Let
$\unicode[STIX]{x1D6FD}\mapsto \unicode[STIX]{x1D6FD}-r(\unicode[STIX]{x1D6FD})$
. Let
![]() $\unicode[STIX]{x1D702}_{3},\ldots ,\unicode[STIX]{x1D702}_{8}$
be a
$\unicode[STIX]{x1D702}_{3},\ldots ,\unicode[STIX]{x1D702}_{8}$
be a
![]() $\mathbb{Z}$
-basis of
$\mathbb{Z}$
-basis of
![]() $\mathbb{M}^{\prime \prime }$
. We view
$\mathbb{M}^{\prime \prime }$
. We view
![]() $\mathbb{M}^{\prime \prime }\subseteq \mathbb{R}^{6}$
via
$\mathbb{M}^{\prime \prime }\subseteq \mathbb{R}^{6}$
via
![]() $a_{3}\unicode[STIX]{x1D702}_{3}+\cdots +a_{8}\unicode[STIX]{x1D702}_{8}\mapsto (a_{3},\ldots ,a_{8})$
. In this way, we identify
$a_{3}\unicode[STIX]{x1D702}_{3}+\cdots +a_{8}\unicode[STIX]{x1D702}_{8}\mapsto (a_{3},\ldots ,a_{8})$
. In this way, we identify
![]() $\mathbb{M}^{\prime \prime }$
with
$\mathbb{M}^{\prime \prime }$
with
![]() $\mathbb{Z}^{6}$
, so
$\mathbb{Z}^{6}$
, so
![]() $\mathbb{M}^{\prime \prime }$
becomes a lattice in
$\mathbb{M}^{\prime \prime }$
becomes a lattice in
![]() $\mathbb{R}^{6}$
. Furthermore, define
$\mathbb{R}^{6}$
. Furthermore, define
![]() $\unicode[STIX]{x1D6EC}_{\mathfrak{g}}$
as
$\unicode[STIX]{x1D6EC}_{\mathfrak{g}}$
as
Then it is easily seen that
![]() $\unicode[STIX]{x1D6EC}_{\mathfrak{g}}$
is a sublattice of
$\unicode[STIX]{x1D6EC}_{\mathfrak{g}}$
is a sublattice of
![]() $\mathbb{M}^{\prime \prime }$
.
$\mathbb{M}^{\prime \prime }$
.
We further define
where the constant
![]() $c_{1}>0$
is taken large enough such that
$c_{1}>0$
is taken large enough such that
Note that
![]() $S_{x}=x^{1/8}S_{1}$
, which implies that
$S_{x}=x^{1/8}S_{1}$
, which implies that
![]() $\text{Vol}(S_{x})=x^{3/4}\text{Vol}(S_{1})$
. Because
$\text{Vol}(S_{x})=x^{3/4}\text{Vol}(S_{1})$
. Because
![]() $S_{1}$
is a
$S_{1}$
is a
![]() $6$
-dimensional hypercube, it has
$6$
-dimensional hypercube, it has
![]() $12$
sides. Hence, there exist an absolute constant
$12$
sides. Hence, there exist an absolute constant
![]() $L$
and functions
$L$
and functions
![]() $\unicode[STIX]{x1D711}_{1},\ldots ,\unicode[STIX]{x1D711}_{12}:[0,1]^{5}\rightarrow \mathbb{R}^{6}$
satisfying a Lipschitz condition
$\unicode[STIX]{x1D711}_{1},\ldots ,\unicode[STIX]{x1D711}_{12}:[0,1]^{5}\rightarrow \mathbb{R}^{6}$
satisfying a Lipschitz condition
for
![]() $a,b\in [0,1]^{5}$
,
$a,b\in [0,1]^{5}$
,
![]() $i=1,\ldots ,12$
such that the boundary of
$i=1,\ldots ,12$
such that the boundary of
![]() $S_{1}$
, denoted by
$S_{1}$
, denoted by
![]() $\unicode[STIX]{x2202}S_{1}$
, is covered by the images of the
$\unicode[STIX]{x2202}S_{1}$
, is covered by the images of the
![]() $\unicode[STIX]{x1D711}_{i}$
. Then
$\unicode[STIX]{x1D711}_{i}$
. Then
![]() $x^{1/8}\unicode[STIX]{x1D711}_{1},\ldots ,x^{1/8}\unicode[STIX]{x1D711}_{12}$
are Lipschitz functions for
$x^{1/8}\unicode[STIX]{x1D711}_{1},\ldots ,x^{1/8}\unicode[STIX]{x1D711}_{12}$
are Lipschitz functions for
![]() $\unicode[STIX]{x2202}S_{x}=\unicode[STIX]{x2202}x^{1/8}S_{1}=x^{1/8}\unicode[STIX]{x2202}S_{1}$
. Hence, we can choose
$\unicode[STIX]{x2202}S_{x}=\unicode[STIX]{x2202}x^{1/8}S_{1}=x^{1/8}\unicode[STIX]{x2202}S_{1}$
. Hence, we can choose
![]() $x^{1/8}L$
as the Lipschitz constant for
$x^{1/8}L$
as the Lipschitz constant for
![]() $S_{x}$
.
$S_{x}$
.
We now apply [Reference WidmerWid10, Theorem 5.4], which gives
where
![]() $\unicode[STIX]{x1D706}_{\mathfrak{g},1},\ldots ,\unicode[STIX]{x1D706}_{\mathfrak{g},6}$
are the successive minima of
$\unicode[STIX]{x1D706}_{\mathfrak{g},1},\ldots ,\unicode[STIX]{x1D706}_{\mathfrak{g},6}$
are the successive minima of
![]() $\unicode[STIX]{x1D6EC}_{\mathfrak{g}}$
and
$\unicode[STIX]{x1D6EC}_{\mathfrak{g}}$
and
![]() $\ll _{L}$
means that the implied constant may depend on
$\ll _{L}$
means that the implied constant may depend on
![]() $L$
. Our next goal is to give a lower bound for
$L$
. Our next goal is to give a lower bound for
![]() $\unicode[STIX]{x1D706}_{\mathfrak{g},1}$
.
$\unicode[STIX]{x1D706}_{\mathfrak{g},1}$
.
So let
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6EC}_{\mathfrak{g}}$
be non-zero. Then
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6EC}_{\mathfrak{g}}$
be non-zero. Then
![]() $\mathfrak{g}\mid \unicode[STIX]{x1D6FE}$
and hence
$\mathfrak{g}\mid \unicode[STIX]{x1D6FE}$
and hence
![]() $g\mid \text{N}(\unicode[STIX]{x1D6FE})$
. Write
$g\mid \text{N}(\unicode[STIX]{x1D6FE})$
. Write
![]() $\unicode[STIX]{x1D6FE}=(a_{3},\ldots ,a_{8})$
. We fix some small
$\unicode[STIX]{x1D6FE}=(a_{3},\ldots ,a_{8})$
. We fix some small
![]() $\unicode[STIX]{x1D716}>0$
. If
$\unicode[STIX]{x1D716}>0$
. If
![]() $a_{3},\ldots ,a_{8}\leqslant c_{2}g^{1/8-\unicode[STIX]{x1D716}}$
for some sufficiently small absolute constant
$a_{3},\ldots ,a_{8}\leqslant c_{2}g^{1/8-\unicode[STIX]{x1D716}}$
for some sufficiently small absolute constant
![]() $c_{2}>0$
, we obtain
$c_{2}>0$
, we obtain
![]() $\text{N}(\unicode[STIX]{x1D6FE})<g$
. Since
$\text{N}(\unicode[STIX]{x1D6FE})<g$
. Since
![]() $g\mid \text{N}(\unicode[STIX]{x1D6FE})$
, we conclude that
$g\mid \text{N}(\unicode[STIX]{x1D6FE})$
, we conclude that
![]() $\text{N}(\unicode[STIX]{x1D6FE})=0$
, contradiction. Hence there is an
$\text{N}(\unicode[STIX]{x1D6FE})=0$
, contradiction. Hence there is an
![]() $i$
with
$i$
with
![]() $a_{i}>c_{2}g^{1/8-\unicode[STIX]{x1D716}}$
. This implies that the length of
$a_{i}>c_{2}g^{1/8-\unicode[STIX]{x1D716}}$
. This implies that the length of
![]() $\unicode[STIX]{x1D6FE}$
satisfies
$\unicode[STIX]{x1D6FE}$
satisfies
![]() $\Vert \unicode[STIX]{x1D6FE}\Vert \gg g^{1/8-\unicode[STIX]{x1D716}}$
and therefore
$\Vert \unicode[STIX]{x1D6FE}\Vert \gg g^{1/8-\unicode[STIX]{x1D716}}$
and therefore
By Minkowski’s second theorem and (4.7) we find that
Plugging (4.5) and (4.9) back into (4.4) gives
We rewrite the last sum as
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{\substack{ \mathfrak{g} \\ g_{0}>Z}}\frac{x}{g^{3/4-6\unicode[STIX]{x1D716}}} & = & \displaystyle x\mathop{\sum }_{\substack{ g\leqslant x \\ g\text{ squarefull} \\ g_{0}>Z}}\frac{\unicode[STIX]{x1D70F}(g)}{g^{3/4-6\unicode[STIX]{x1D716}}}\ll x^{1+\unicode[STIX]{x1D716}^{\prime }}\mathop{\sum }_{\substack{ g\leqslant x \\ g\text{ squarefull} \\ g_{0}>Z}}\frac{1}{g^{3/4-6\unicode[STIX]{x1D716}}}\nonumber\\ \displaystyle & = & \displaystyle x^{1+\unicode[STIX]{x1D716}^{\prime }}\mathop{\sum }_{\substack{ g\leqslant x \\ g\text{ squarefull} \\ g_{0}>Z}}g^{-1/4+6\unicode[STIX]{x1D716}}\frac{1}{g^{1/2}}\leqslant x^{1+\unicode[STIX]{x1D716}^{\prime }}Z^{-1/2+3\unicode[STIX]{x1D716}}\mathop{\sum }_{\substack{ g\leqslant x \\ g\text{ squarefull} \\ g_{0}>Z}}\frac{1}{g^{1/2}}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle x^{1+\unicode[STIX]{x1D716}^{\prime }}Z^{-1/2+3\unicode[STIX]{x1D716}}\mathop{\sum }_{\substack{ g\leqslant x \\ g\text{ squarefull}}}\frac{1}{g^{1/2}}\ll x^{1+\unicode[STIX]{x1D716}^{\prime }}Z^{-1/2+3\unicode[STIX]{x1D716}}\log x.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{\substack{ \mathfrak{g} \\ g_{0}>Z}}\frac{x}{g^{3/4-6\unicode[STIX]{x1D716}}} & = & \displaystyle x\mathop{\sum }_{\substack{ g\leqslant x \\ g\text{ squarefull} \\ g_{0}>Z}}\frac{\unicode[STIX]{x1D70F}(g)}{g^{3/4-6\unicode[STIX]{x1D716}}}\ll x^{1+\unicode[STIX]{x1D716}^{\prime }}\mathop{\sum }_{\substack{ g\leqslant x \\ g\text{ squarefull} \\ g_{0}>Z}}\frac{1}{g^{3/4-6\unicode[STIX]{x1D716}}}\nonumber\\ \displaystyle & = & \displaystyle x^{1+\unicode[STIX]{x1D716}^{\prime }}\mathop{\sum }_{\substack{ g\leqslant x \\ g\text{ squarefull} \\ g_{0}>Z}}g^{-1/4+6\unicode[STIX]{x1D716}}\frac{1}{g^{1/2}}\leqslant x^{1+\unicode[STIX]{x1D716}^{\prime }}Z^{-1/2+3\unicode[STIX]{x1D716}}\mathop{\sum }_{\substack{ g\leqslant x \\ g\text{ squarefull} \\ g_{0}>Z}}\frac{1}{g^{1/2}}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle x^{1+\unicode[STIX]{x1D716}^{\prime }}Z^{-1/2+3\unicode[STIX]{x1D716}}\mathop{\sum }_{\substack{ g\leqslant x \\ g\text{ squarefull}}}\frac{1}{g^{1/2}}\ll x^{1+\unicode[STIX]{x1D716}^{\prime }}Z^{-1/2+3\unicode[STIX]{x1D716}}\log x.\nonumber\end{eqnarray}$$
By picking
![]() $Z=X^{\unicode[STIX]{x1D6FF}/2}$
,
$Z=X^{\unicode[STIX]{x1D6FF}/2}$
,
![]() $\unicode[STIX]{x1D716}$
and
$\unicode[STIX]{x1D716}$
and
![]() $\unicode[STIX]{x1D716}^{\prime }$
sufficiently small, we get the desired result with
$\unicode[STIX]{x1D716}^{\prime }$
sufficiently small, we get the desired result with
![]() $\unicode[STIX]{x1D703}_{1}=\unicode[STIX]{x1D6FF}/4$
.
$\unicode[STIX]{x1D703}_{1}=\unicode[STIX]{x1D6FF}/4$
.
5 Sums of type II
Our goal in this section is to prove Proposition 3.4, thereby completing the proof of Theorem 1. A power-saving bound for the bilinear sum in Proposition 3.4 is possible because the symbol
is not multiplicative in
![]() $\unicode[STIX]{x1D6FC}$
but instead satisfies the following elegant identity, analogous to [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13, (3.8), p. 708]. Let
$\unicode[STIX]{x1D6FC}$
but instead satisfies the following elegant identity, analogous to [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13, (3.8), p. 708]. Let
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
be odd elements in
$\unicode[STIX]{x1D6FD}$
be odd elements in
![]() ${\mathcal{O}}_{M}$
. Then
${\mathcal{O}}_{M}$
. Then
where
and
![]() $\unicode[STIX]{x1D700}_{3}\in \{\pm 1\}$
depends only on the congruence classes of
$\unicode[STIX]{x1D700}_{3}\in \{\pm 1\}$
depends only on the congruence classes of
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
modulo
$\unicode[STIX]{x1D6FD}$
modulo
![]() $8$
(see Lemma 3.1). We remark here that the natural one-line proof of (5.1) should be contrasted with the rather involved proofs of [Reference Friedlander and IwaniecFI98, Lemma 20.1, p. 1021] and [Reference MilovicMil17b, Proposition 8, p. 31]. It would be very interesting to find a common source of these identities, if it exists.
$8$
(see Lemma 3.1). We remark here that the natural one-line proof of (5.1) should be contrasted with the rather involved proofs of [Reference Friedlander and IwaniecFI98, Lemma 20.1, p. 1021] and [Reference MilovicMil17b, Proposition 8, p. 31]. It would be very interesting to find a common source of these identities, if it exists.
With
![]() $\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{8}$
and
$\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{8}$
and
![]() $[\cdot ]=\unicode[STIX]{x1D713}(\cdot \hspace{0.2em}{\rm mod}\hspace{0.2em}F)[\cdot ]_{r}$
is as in the beginning of § 4.1, we see that the bilinear sum from Proposition 3.4 is equal to
$[\cdot ]=\unicode[STIX]{x1D713}(\cdot \hspace{0.2em}{\rm mod}\hspace{0.2em}F)[\cdot ]_{r}$
is as in the beginning of § 4.1, we see that the bilinear sum from Proposition 3.4 is equal to
where
Here
![]() ${\mathcal{D}}(X)=\{x\in {\mathcal{D}}:\text{N}(x)\leqslant X\}$
;
${\mathcal{D}}(X)=\{x\in {\mathcal{D}}:\text{N}(x)\leqslant X\}$
;
![]() $v_{\unicode[STIX]{x1D6FC}}$
(respectively
$v_{\unicode[STIX]{x1D6FC}}$
(respectively
![]() $w_{\unicode[STIX]{x1D6FD}}$
) depends only on the ideal generated by
$w_{\unicode[STIX]{x1D6FD}}$
) depends only on the ideal generated by
![]() $\unicode[STIX]{x1D6FC}$
(respectively
$\unicode[STIX]{x1D6FC}$
(respectively
![]() $\unicode[STIX]{x1D6FD}$
); and, the double sum over
$\unicode[STIX]{x1D6FD}$
); and, the double sum over
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
is assumed to be supported on
$\unicode[STIX]{x1D6FD}$
is assumed to be supported on
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
such that
$\unicode[STIX]{x1D6FD}$
such that
![]() $(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD},F)=1$
.
$(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD},F)=1$
.
The condition
![]() $(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD},F)=1$
is equivalent to the two conditions
$(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD},F)=1$
is equivalent to the two conditions
![]() $(\unicode[STIX]{x1D6FC},F)=1$
and
$(\unicode[STIX]{x1D6FC},F)=1$
and
![]() $(\unicode[STIX]{x1D6FD},F)=1$
. Hence we can decompose the sum (5.3) into
$(\unicode[STIX]{x1D6FD},F)=1$
. Hence we can decompose the sum (5.3) into
![]() $(\#({\mathcal{O}}_{M}/F{\mathcal{O}}_{M})^{\times })^{2}$
sums
$(\#({\mathcal{O}}_{M}/F{\mathcal{O}}_{M})^{\times })^{2}$
sums
![]() $B(M,N;\unicode[STIX]{x1D701},i,\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D70C}_{2})$
where we further restrict the support of
$B(M,N;\unicode[STIX]{x1D701},i,\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D70C}_{2})$
where we further restrict the support of
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
to fixed invertible congruence classes modulo
$\unicode[STIX]{x1D6FD}$
to fixed invertible congruence classes modulo
![]() $F$
, i.e.,
$F$
, i.e.,
Hence, with
![]() $\unicode[STIX]{x1D700}_{4}=\unicode[STIX]{x1D713}(\unicode[STIX]{x1D701}\unicode[STIX]{x1D707}_{i}\unicode[STIX]{x1D70C}_{1}\unicode[STIX]{x1D70C}_{2}\hspace{0.2em}{\rm mod}\hspace{0.2em}F)$
fixed for fixed
$\unicode[STIX]{x1D700}_{4}=\unicode[STIX]{x1D713}(\unicode[STIX]{x1D701}\unicode[STIX]{x1D707}_{i}\unicode[STIX]{x1D70C}_{1}\unicode[STIX]{x1D70C}_{2}\hspace{0.2em}{\rm mod}\hspace{0.2em}F)$
fixed for fixed
![]() $\unicode[STIX]{x1D701}$
,
$\unicode[STIX]{x1D701}$
,
![]() $\unicode[STIX]{x1D707}_{i}$
,
$\unicode[STIX]{x1D707}_{i}$
,
![]() $\unicode[STIX]{x1D70C}_{1}$
, and
$\unicode[STIX]{x1D70C}_{1}$
, and
![]() $\unicode[STIX]{x1D70C}_{2}$
, we have
$\unicode[STIX]{x1D70C}_{2}$
, we have
where we again note that the support of
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
is restricted to (5.4). To prove Proposition 3.4, it suffices to prove the desired estimate for each of the
$\unicode[STIX]{x1D6FD}$
is restricted to (5.4). To prove Proposition 3.4, it suffices to prove the desired estimate for each of the
sums
![]() $B(M,N;\unicode[STIX]{x1D701},i,\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D70C}_{2})$
. To this end, we now take advantage of the special non-multiplicativity of the spin symbol
$B(M,N;\unicode[STIX]{x1D701},i,\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D70C}_{2})$
. To this end, we now take advantage of the special non-multiplicativity of the spin symbol
![]() $[\cdot ]_{r}$
. By (5.1), we can unfold
$[\cdot ]_{r}$
. By (5.1), we can unfold
![]() $[\unicode[STIX]{x1D701}\unicode[STIX]{x1D707}_{i}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}]_{r}$
into the product
$[\unicode[STIX]{x1D701}\unicode[STIX]{x1D707}_{i}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}]_{r}$
into the product
The factor
![]() $\unicode[STIX]{x1D700}_{5}\in \{\pm 1\}$
depends only on the congruence classes
$\unicode[STIX]{x1D700}_{5}\in \{\pm 1\}$
depends only on the congruence classes
![]() $\unicode[STIX]{x1D701}\unicode[STIX]{x1D707}_{i}\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
and
$\unicode[STIX]{x1D701}\unicode[STIX]{x1D707}_{i}\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
and
![]() $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
, the factor
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
, the factor
![]() $[\unicode[STIX]{x1D701}\unicode[STIX]{x1D707}_{i}]_{r}$
does not depend on
$[\unicode[STIX]{x1D701}\unicode[STIX]{x1D707}_{i}]_{r}$
does not depend on
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
in any way, and the factor
$\unicode[STIX]{x1D6FD}$
in any way, and the factor
is determined by the congruence class
![]() $r(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD})r^{3}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD})\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
, by Lemma 3.2. As
$r(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD})r^{3}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD})\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
, by Lemma 3.2. As
![]() $8$
divides
$8$
divides
![]() $F$
, all of these congruence classes are determined by
$F$
, all of these congruence classes are determined by
![]() $\unicode[STIX]{x1D701}$
,
$\unicode[STIX]{x1D701}$
,
![]() $\unicode[STIX]{x1D707}_{i}$
,
$\unicode[STIX]{x1D707}_{i}$
,
![]() $\unicode[STIX]{x1D70C}_{1}$
and
$\unicode[STIX]{x1D70C}_{1}$
and
![]() $\unicode[STIX]{x1D70C}_{2}$
. Hence
$\unicode[STIX]{x1D70C}_{2}$
. Hence
where
![]() $\unicode[STIX]{x1D700}_{6}=\unicode[STIX]{x1D700}_{6}(\unicode[STIX]{x1D701},\unicode[STIX]{x1D707}_{i},\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D70C}_{2})$
depends only on
$\unicode[STIX]{x1D700}_{6}=\unicode[STIX]{x1D700}_{6}(\unicode[STIX]{x1D701},\unicode[STIX]{x1D707}_{i},\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D70C}_{2})$
depends only on
![]() $\unicode[STIX]{x1D701}$
,
$\unicode[STIX]{x1D701}$
,
![]() $\unicode[STIX]{x1D707}_{i}$
,
$\unicode[STIX]{x1D707}_{i}$
,
![]() $\unicode[STIX]{x1D70C}_{1}$
, and
$\unicode[STIX]{x1D70C}_{1}$
, and
![]() $\unicode[STIX]{x1D70C}_{2}$
but not on
$\unicode[STIX]{x1D70C}_{2}$
but not on
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
. Next, using (5.1) again, we get
$\unicode[STIX]{x1D6FD}$
. Next, using (5.1) again, we get
where
![]() $\unicode[STIX]{x1D700}_{7}$
depends only on
$\unicode[STIX]{x1D700}_{7}$
depends only on
![]() $\unicode[STIX]{x1D701}$
,
$\unicode[STIX]{x1D701}$
,
![]() $\unicode[STIX]{x1D707}_{i}$
,
$\unicode[STIX]{x1D707}_{i}$
,
![]() $\unicode[STIX]{x1D70C}_{1}$
, and
$\unicode[STIX]{x1D70C}_{1}$
, and
![]() $\unicode[STIX]{x1D70C}_{2}$
, and
$\unicode[STIX]{x1D70C}_{2}$
, and
The sum in (5.7) has exactly the same shape as [Reference Koymans and MilovicKM18, (3.2), p. 11]. Moreover, the function
![]() $\unicode[STIX]{x1D6FE}$
satisfies the properties (P1)–(P3) on [Reference Koymans and MilovicKM18, p. 11]; indeed, (P1) follows by Lemma 3.1, and (P2) is clear. For (P3), suppose that
$\unicode[STIX]{x1D6FE}$
satisfies the properties (P1)–(P3) on [Reference Koymans and MilovicKM18, p. 11]; indeed, (P1) follows by Lemma 3.1, and (P2) is clear. For (P3), suppose that
![]() $r(\unicode[STIX]{x1D6FC})r^{3}(\unicode[STIX]{x1D6FC}){\mathcal{O}}_{M}=\mathfrak{a}^{2}$
for some odd ideal
$r(\unicode[STIX]{x1D6FC})r^{3}(\unicode[STIX]{x1D6FC}){\mathcal{O}}_{M}=\mathfrak{a}^{2}$
for some odd ideal
![]() $\mathfrak{a}\subset {\mathcal{O}}_{M}$
. Then, as
$\mathfrak{a}\subset {\mathcal{O}}_{M}$
. Then, as
![]() $r(\unicode[STIX]{x1D6FC})r^{3}(\unicode[STIX]{x1D6FC})$
is fixed by
$r(\unicode[STIX]{x1D6FC})r^{3}(\unicode[STIX]{x1D6FC})$
is fixed by
![]() $r^{2}$
and is thus an odd element of
$r^{2}$
and is thus an odd element of
![]() $\mathbb{Q}(\unicode[STIX]{x1D701}_{8})$
, we have
$\mathbb{Q}(\unicode[STIX]{x1D701}_{8})$
, we have
for some odd ideal
![]() $\mathfrak{a}^{\prime }\subset \mathbb{Z}[\unicode[STIX]{x1D701}_{8}]$
. Taking norms to
$\mathfrak{a}^{\prime }\subset \mathbb{Z}[\unicode[STIX]{x1D701}_{8}]$
. Taking norms to
![]() $\mathbb{Q}$
, we get that
$\mathbb{Q}$
, we get that
Hence, if
![]() $\text{N}_{M/\mathbb{Q}}(\unicode[STIX]{x1D6FC})$
is not a square, we see that
$\text{N}_{M/\mathbb{Q}}(\unicode[STIX]{x1D6FC})$
is not a square, we see that
![]() $r(\unicode[STIX]{x1D6FC})r^{3}(\unicode[STIX]{x1D6FC})$
does not generate the square of an ideal in
$r(\unicode[STIX]{x1D6FC})r^{3}(\unicode[STIX]{x1D6FC})$
does not generate the square of an ideal in
![]() ${\mathcal{O}}_{M}$
, and so
${\mathcal{O}}_{M}$
, and so
which proves (P3). Proposition 3.4 now follows by [Reference Koymans and MilovicKM18, Proposition 3.6, p. 11].
6 Proof of Theorem 2
We will now deduce Theorem 2 from Theorem 1 by choosing the factor
![]() $\unicode[STIX]{x1D713}$
in the definition of
$\unicode[STIX]{x1D713}$
in the definition of
![]() $s_{\mathfrak{a}}$
appropriately. First note that Theorem 2 is equivalent to the statement that
$s_{\mathfrak{a}}$
appropriately. First note that Theorem 2 is equivalent to the statement that
where
 $$\begin{eqnarray}a_{p}=\left\{\begin{array}{@{}ll@{}}1\quad & \text{if }h(-4p)\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}16,\\ -1\quad & \text{if }h(-4p)\equiv 8\hspace{0.2em}{\rm mod}\hspace{0.2em}16,\\ 0\quad & \text{otherwise.}\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}a_{p}=\left\{\begin{array}{@{}ll@{}}1\quad & \text{if }h(-4p)\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}16,\\ -1\quad & \text{if }h(-4p)\equiv 8\hspace{0.2em}{\rm mod}\hspace{0.2em}16,\\ 0\quad & \text{otherwise.}\end{array}\right.\end{eqnarray}$$
We will use an algebraic criterion for the
![]() $16$
-rank due to Bruin and Hemenway [Reference Bruin and HemenwayBH13]. Let
$16$
-rank due to Bruin and Hemenway [Reference Bruin and HemenwayBH13]. Let
![]() $p$
be a prime number such that
$p$
be a prime number such that
![]() $h(-4p)\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
, i.e., such that
$h(-4p)\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
, i.e., such that
![]() $p$
splits completely in
$p$
splits completely in
![]() $M/\mathbb{Q}$
. As in § 3.1, set
$M/\mathbb{Q}$
. As in § 3.1, set
![]() $K_{1}=\mathbb{Q}(i,\sqrt{1+i})$
. Let
$K_{1}=\mathbb{Q}(i,\sqrt{1+i})$
. Let
![]() $\unicode[STIX]{x1D70C}$
be a prime in
$\unicode[STIX]{x1D70C}$
be a prime in
![]() ${\mathcal{O}}_{K_{1}}$
dividing
${\mathcal{O}}_{K_{1}}$
dividing
![]() $p$
, and let
$p$
, and let
![]() $\unicode[STIX]{x1D6FF}_{p}$
be an element of
$\unicode[STIX]{x1D6FF}_{p}$
be an element of
![]() ${\mathcal{O}}_{K_{1}}$
such that
${\mathcal{O}}_{K_{1}}$
such that
![]() $\text{N}_{K_{1}/\mathbb{Q}(i)}(\unicode[STIX]{x1D6FF}_{p})=p$
and such that
$\text{N}_{K_{1}/\mathbb{Q}(i)}(\unicode[STIX]{x1D6FF}_{p})=p$
and such that
![]() $\unicode[STIX]{x1D6FF}_{p}\notin \unicode[STIX]{x1D70C}{\mathcal{O}}_{K_{1}}$
. Bruin and Hemenway proved that
$\unicode[STIX]{x1D6FF}_{p}\notin \unicode[STIX]{x1D70C}{\mathcal{O}}_{K_{1}}$
. Bruin and Hemenway proved that
We will now interpret this symbol as a quadratic residue symbol in
![]() $M$
. Recall the definition of
$M$
. Recall the definition of
![]() $r$
and
$r$
and
![]() $s$
and the field diagram in § 3.1.
$s$
and the field diagram in § 3.1.
Let
![]() $\unicode[STIX]{x1D70B}$
be a prime in
$\unicode[STIX]{x1D70B}$
be a prime in
![]() ${\mathcal{O}}_{M}$
dividing
${\mathcal{O}}_{M}$
dividing
![]() $p$
such that
$p$
such that
We define elements
![]() $\unicode[STIX]{x1D70C}$
and
$\unicode[STIX]{x1D70C}$
and
![]() $\unicode[STIX]{x1D6FF}_{p}$
in
$\unicode[STIX]{x1D6FF}_{p}$
in
![]() ${\mathcal{O}}_{K_{1}}$
by setting
${\mathcal{O}}_{K_{1}}$
by setting
![]() $\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70B}\cdot s(\unicode[STIX]{x1D70B})$
and
$\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70B}\cdot s(\unicode[STIX]{x1D70B})$
and
Note that
![]() $\text{N}_{K_{1}/\mathbb{Q}(i)}(\unicode[STIX]{x1D6FF}_{p})=\unicode[STIX]{x1D6FF}_{p}\cdot r^{2}(\unicode[STIX]{x1D6FF}_{p})=p$
and
$\text{N}_{K_{1}/\mathbb{Q}(i)}(\unicode[STIX]{x1D6FF}_{p})=\unicode[STIX]{x1D6FF}_{p}\cdot r^{2}(\unicode[STIX]{x1D6FF}_{p})=p$
and
![]() $\unicode[STIX]{x1D6FF}_{p}\notin \unicode[STIX]{x1D70C}{\mathcal{O}}_{K_{1}}$
, so that
$\unicode[STIX]{x1D6FF}_{p}\notin \unicode[STIX]{x1D70C}{\mathcal{O}}_{K_{1}}$
, so that
![]() $\unicode[STIX]{x1D70C}$
and
$\unicode[STIX]{x1D70C}$
and
![]() $\unicode[STIX]{x1D6FF}_{p}$
satisfy the assumptions implicit in criterion (6.2). Next, note that since
$\unicode[STIX]{x1D6FF}_{p}$
satisfy the assumptions implicit in criterion (6.2). Next, note that since
![]() $p$
splits completely in
$p$
splits completely in
![]() $M/\mathbb{Q}$
, the inclusion
$M/\mathbb{Q}$
, the inclusion
![]() ${\mathcal{O}}_{K_{1}}{\hookrightarrow}{\mathcal{O}}_{M}$
induces an isomorphism of finite fields of order
${\mathcal{O}}_{K_{1}}{\hookrightarrow}{\mathcal{O}}_{M}$
induces an isomorphism of finite fields of order
![]() $p$
$p$
Hence
and so
The above quadratic residue symbol factors into five quadratic residue symbols, the first four of which are of the form
![]() $\big(\frac{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D70B})}{\unicode[STIX]{x1D70B}}\big)_{M}$
with
$\big(\frac{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D70B})}{\unicode[STIX]{x1D70B}}\big)_{M}$
with
![]() $\unicode[STIX]{x1D70E}$
in
$\unicode[STIX]{x1D70E}$
in
![]() $\{r,r^{2},sr,sr^{2}\}$
, and the last one of which is
$\{r,r^{2},sr,sr^{2}\}$
, and the last one of which is
![]() $\big(\frac{\sqrt{1+i}}{\unicode[STIX]{x1D70B}}\big)_{M}$
. For
$\big(\frac{\sqrt{1+i}}{\unicode[STIX]{x1D70B}}\big)_{M}$
. For
![]() $\unicode[STIX]{x1D70E}\in \text{Gal}(M/\mathbb{Q})$
, we set
$\unicode[STIX]{x1D70E}\in \text{Gal}(M/\mathbb{Q})$
, we set
We will now show that when
![]() $\unicode[STIX]{x1D70E}$
is an element of order
$\unicode[STIX]{x1D70E}$
is an element of order
![]() $2$
, the spin symbol
$2$
, the spin symbol
![]() $[\unicode[STIX]{x1D6FC}]_{\unicode[STIX]{x1D70E}}$
can be absorbed into the factor
$[\unicode[STIX]{x1D6FC}]_{\unicode[STIX]{x1D70E}}$
can be absorbed into the factor
![]() $\unicode[STIX]{x1D713}$
. One part of what follows is an adaptation of the treatment of such spins in [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13, §12, pp. 745–749].
$\unicode[STIX]{x1D713}$
. One part of what follows is an adaptation of the treatment of such spins in [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13, §12, pp. 745–749].
Proposition 6.1. Let
![]() $\unicode[STIX]{x1D6FC}\in {\mathcal{O}}_{M}$
be such that
$\unicode[STIX]{x1D6FC}\in {\mathcal{O}}_{M}$
be such that
![]() $(\unicode[STIX]{x1D6FC},F)=1$
, and let
$(\unicode[STIX]{x1D6FC},F)=1$
, and let
![]() $\unicode[STIX]{x1D70E}$
be an element of order
$\unicode[STIX]{x1D70E}$
be an element of order
![]() $2$
in
$2$
in
![]() $\text{Gal}(M/\mathbb{Q})$
such that
$\text{Gal}(M/\mathbb{Q})$
such that
![]() $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FC}))=1$
. Then
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FC}))=1$
. Then
![]() $[\unicode[STIX]{x1D6FC}]_{\unicode[STIX]{x1D70E}}$
depends only on
$[\unicode[STIX]{x1D6FC}]_{\unicode[STIX]{x1D70E}}$
depends only on
![]() $\unicode[STIX]{x1D70E}$
and on the congruence class of
$\unicode[STIX]{x1D70E}$
and on the congruence class of
![]() $\unicode[STIX]{x1D6FC}$
modulo
$\unicode[STIX]{x1D6FC}$
modulo
![]() $F$
.
$F$
.
The proof of our claim proceeds in two steps. The first step will be to reduce to the case
![]() $\unicode[STIX]{x1D6FC}\equiv 1\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
. The second step will be to use the ideas from Section 12 of [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13]. Recall the definitions of
$\unicode[STIX]{x1D6FC}\equiv 1\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
. The second step will be to use the ideas from Section 12 of [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13]. Recall the definitions of
![]() ${\mathcal{R}}$
and
${\mathcal{R}}$
and
![]() $F$
in § 3.1.
$F$
in § 3.1.
Proof. As
![]() $(\unicode[STIX]{x1D6FC},F)=1$
, we also have
$(\unicode[STIX]{x1D6FC},F)=1$
, we also have
![]() $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6E5}_{M})=1$
. Let
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6E5}_{M})=1$
. Let
![]() $\unicode[STIX]{x1D70C}^{\prime }\in {\mathcal{R}}$
be such that
$\unicode[STIX]{x1D70C}^{\prime }\in {\mathcal{R}}$
be such that
![]() $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70C}^{\prime }\equiv 1\hspace{0.2em}{\rm mod}\hspace{0.2em}\unicode[STIX]{x1D6E5}_{M}$
and in particular, by property (P2) from the beginning of § 3.1, such that
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70C}^{\prime }\equiv 1\hspace{0.2em}{\rm mod}\hspace{0.2em}\unicode[STIX]{x1D6E5}_{M}$
and in particular, by property (P2) from the beginning of § 3.1, such that
![]() $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70C}^{\prime }\equiv 1\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
. We emphasize two important facts. First, note that
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70C}^{\prime }\equiv 1\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
. We emphasize two important facts. First, note that
![]() $\unicode[STIX]{x1D70C}^{\prime }$
depends only on
$\unicode[STIX]{x1D70C}^{\prime }$
depends only on
![]() $\unicode[STIX]{x1D6FC}\hspace{0.2em}{\rm mod}\hspace{0.2em}\unicode[STIX]{x1D6E5}_{M}$
and hence only on
$\unicode[STIX]{x1D6FC}\hspace{0.2em}{\rm mod}\hspace{0.2em}\unicode[STIX]{x1D6E5}_{M}$
and hence only on
![]() $\unicode[STIX]{x1D6FC}\hspace{0.2em}{\rm mod}\hspace{0.2em}F$
. Second, as
$\unicode[STIX]{x1D6FC}\hspace{0.2em}{\rm mod}\hspace{0.2em}F$
. Second, as
![]() $\text{N}(\unicode[STIX]{x1D70C}^{\prime })$
divides
$\text{N}(\unicode[STIX]{x1D70C}^{\prime })$
divides
![]() $F$
and
$F$
and
![]() $(\unicode[STIX]{x1D70C}^{\prime })$
is a prime of degree
$(\unicode[STIX]{x1D70C}^{\prime })$
is a prime of degree
![]() $1$
, we have
$1$
, we have
Hence, each of the four factors on the right-hand side of
is non-zero. Using Lemma 3.1 and the assumption that
![]() $\unicode[STIX]{x1D70E}$
is an involution, we get
$\unicode[STIX]{x1D70E}$
is an involution, we get
where
![]() $\unicode[STIX]{x1D700}_{8}\in \{\pm 1\}$
depends only on
$\unicode[STIX]{x1D700}_{8}\in \{\pm 1\}$
depends only on
![]() $\unicode[STIX]{x1D70E}$
and the congruence classes of
$\unicode[STIX]{x1D70E}$
and the congruence classes of
![]() $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D70C}^{\prime })$
and
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D70C}^{\prime })$
and
![]() $\unicode[STIX]{x1D6FC}$
modulo
$\unicode[STIX]{x1D6FC}$
modulo
![]() $8$
, both of which depend only on
$8$
, both of which depend only on
![]() $\unicode[STIX]{x1D70E}$
and
$\unicode[STIX]{x1D70E}$
and
![]() $\unicode[STIX]{x1D6FC}\hspace{0.2em}{\rm mod}\hspace{0.2em}F$
. Furthermore,
$\unicode[STIX]{x1D6FC}\hspace{0.2em}{\rm mod}\hspace{0.2em}F$
. Furthermore,
![]() $(\frac{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D70C}^{\prime })}{\unicode[STIX]{x1D70C}^{\prime }})_{M}\in \{\pm 1\}$
also depends only on
$(\frac{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D70C}^{\prime })}{\unicode[STIX]{x1D70C}^{\prime }})_{M}\in \{\pm 1\}$
also depends only on
![]() $\unicode[STIX]{x1D70E}$
and
$\unicode[STIX]{x1D70E}$
and
![]() $\unicode[STIX]{x1D6FC}\hspace{0.2em}{\rm mod}\hspace{0.2em}F$
. This gives
$\unicode[STIX]{x1D6FC}\hspace{0.2em}{\rm mod}\hspace{0.2em}F$
. This gives
where
![]() $\unicode[STIX]{x1D700}_{9}\in \{\pm 1\}$
depends only on
$\unicode[STIX]{x1D700}_{9}\in \{\pm 1\}$
depends only on
![]() $\unicode[STIX]{x1D70E}$
and
$\unicode[STIX]{x1D70E}$
and
![]() $\unicode[STIX]{x1D6FC}\hspace{0.2em}{\rm mod}\hspace{0.2em}F$
. So from now on we may assume that
$\unicode[STIX]{x1D6FC}\hspace{0.2em}{\rm mod}\hspace{0.2em}F$
. So from now on we may assume that
![]() $\unicode[STIX]{x1D6FC}\equiv 1\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
.
$\unicode[STIX]{x1D6FC}\equiv 1\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
.
In the interest of not being repetitive, we now refer to the argument used to prove [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13, Proposition 12.1, p. 745]. Define
![]() $L$
to be the subfield of
$L$
to be the subfield of
![]() $M$
fixed by
$M$
fixed by
![]() $\langle \unicode[STIX]{x1D70E}\rangle$
. In our case, the discriminant ideal
$\langle \unicode[STIX]{x1D70E}\rangle$
. In our case, the discriminant ideal
![]() $\text{Disc}(M/L)$
is even, and in fact divides a power of
$\text{Disc}(M/L)$
is even, and in fact divides a power of
![]() $2{\mathcal{O}}_{L}$
. Although the proof of [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13, Proposition 12.1, p. 745] relies on
$2{\mathcal{O}}_{L}$
. Although the proof of [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13, Proposition 12.1, p. 745] relies on
![]() $\mathfrak{D}$
being odd in an essential way, we will overcome this by using the fact that
$\mathfrak{D}$
being odd in an essential way, we will overcome this by using the fact that
![]() ${\mathcal{O}}_{L}$
is a principal ideal domain.
${\mathcal{O}}_{L}$
is a principal ideal domain.
Similarly as in [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13, (12.4), p. 747], one can deduce that
where
![]() $\unicode[STIX]{x1D700}_{10}\in \{\pm 1\}$
depends only on
$\unicode[STIX]{x1D700}_{10}\in \{\pm 1\}$
depends only on
![]() $\unicode[STIX]{x1D70E}$
and
$\unicode[STIX]{x1D70E}$
and
![]() $\unicode[STIX]{x1D6FC}\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
, and where
$\unicode[STIX]{x1D6FC}\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
, and where
![]() $\unicode[STIX]{x1D6FE}$
and
$\unicode[STIX]{x1D6FE}$
and
![]() $\unicode[STIX]{x1D6FD}$
are defined via
$\unicode[STIX]{x1D6FD}$
are defined via
Defining the submodule
![]() ${\mathcal{M}}$
of
${\mathcal{M}}$
of
![]() ${\mathcal{O}}_{M}$
in the same way as on [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13, p. 747], i.e.,
${\mathcal{O}}_{M}$
in the same way as on [Reference Friedlander, Iwaniec, Mazur and RubinFIMR13, p. 747], i.e.,
![]() ${\mathcal{M}}={\mathcal{O}}_{L}+((1+\unicode[STIX]{x1D6FC})/2){\mathcal{O}}_{L}$
, we arrive at the identity
${\mathcal{M}}={\mathcal{O}}_{L}+((1+\unicode[STIX]{x1D6FC})/2){\mathcal{O}}_{L}$
, we arrive at the identity
where
![]() $\mathfrak{a}$
is an ideal in
$\mathfrak{a}$
is an ideal in
![]() ${\mathcal{O}}_{L}$
such that
${\mathcal{O}}_{L}$
such that
![]() ${\mathcal{O}}_{M}/{\mathcal{M}}\cong {\mathcal{O}}_{L}/\mathfrak{a}$
. Since
${\mathcal{O}}_{M}/{\mathcal{M}}\cong {\mathcal{O}}_{L}/\mathfrak{a}$
. Since
![]() ${\mathcal{O}}_{L}$
is a principal ideal domain (see (P1) in § 3.1), we obtain the equation
${\mathcal{O}}_{L}$
is a principal ideal domain (see (P1) in § 3.1), we obtain the equation
where now
![]() $D\in {\mathcal{O}}_{L}$
is some generator of the discriminant
$D\in {\mathcal{O}}_{L}$
is some generator of the discriminant
![]() $\text{Disc}(M/L)$
,
$\text{Disc}(M/L)$
,
![]() $a\in {\mathcal{O}}_{L}$
is some generator of the ideal
$a\in {\mathcal{O}}_{L}$
is some generator of the ideal
![]() $\mathfrak{a}$
, and
$\mathfrak{a}$
, and
![]() $u\in {\mathcal{O}}_{L}^{\times }$
. Then we have
$u\in {\mathcal{O}}_{L}^{\times }$
. Then we have
which, by Lemma 3.2, depends only on the congruence class
![]() $\unicode[STIX]{x1D6FD}\hspace{0.2em}{\rm mod}\hspace{0.2em}8D$
. One can check that
$\unicode[STIX]{x1D6FD}\hspace{0.2em}{\rm mod}\hspace{0.2em}8D$
. One can check that
![]() $16D$
divides
$16D$
divides
![]() $\unicode[STIX]{x1D6E5}_{M}$
for any involution
$\unicode[STIX]{x1D6E5}_{M}$
for any involution
![]() $\unicode[STIX]{x1D70E}\in \text{Gal}(M/\mathbb{Q})$
, and so
$\unicode[STIX]{x1D70E}\in \text{Gal}(M/\mathbb{Q})$
, and so
![]() $\unicode[STIX]{x1D6FD}\hspace{0.2em}{\rm mod}\hspace{0.2em}8D$
is completely determined by
$\unicode[STIX]{x1D6FD}\hspace{0.2em}{\rm mod}\hspace{0.2em}8D$
is completely determined by
![]() $\unicode[STIX]{x1D70E}$
and the congruence class
$\unicode[STIX]{x1D70E}$
and the congruence class
![]() $\unicode[STIX]{x1D6FC}\hspace{0.2em}{\rm mod}\hspace{0.2em}\unicode[STIX]{x1D6E5}_{M}$
. Hence, whenever
$\unicode[STIX]{x1D6FC}\hspace{0.2em}{\rm mod}\hspace{0.2em}\unicode[STIX]{x1D6E5}_{M}$
. Hence, whenever
![]() $\unicode[STIX]{x1D6FC}\equiv 1\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
, the symbol
$\unicode[STIX]{x1D6FC}\equiv 1\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
, the symbol
![]() $[w]_{\unicode[STIX]{x1D70E}}$
only depends on
$[w]_{\unicode[STIX]{x1D70E}}$
only depends on
![]() $\unicode[STIX]{x1D70E}$
and
$\unicode[STIX]{x1D70E}$
and
![]() $\unicode[STIX]{x1D6FC}\hspace{0.2em}{\rm mod}\hspace{0.2em}\unicode[STIX]{x1D6E5}_{M}$
. In conjunction with (6.5), this completes the proof of our proposition.◻
$\unicode[STIX]{x1D6FC}\hspace{0.2em}{\rm mod}\hspace{0.2em}\unicode[STIX]{x1D6E5}_{M}$
. In conjunction with (6.5), this completes the proof of our proposition.◻
If
![]() $\unicode[STIX]{x1D70C}$
is an invertible class modulo
$\unicode[STIX]{x1D70C}$
is an invertible class modulo
![]() $F$
and
$F$
and
![]() $\unicode[STIX]{x1D70E}\in \{r^{2},sr,sr^{2}\}$
, we define
$\unicode[STIX]{x1D70E}\in \{r^{2},sr,sr^{2}\}$
, we define
where
![]() $\unicode[STIX]{x1D6FC}$
is any element of
$\unicode[STIX]{x1D6FC}$
is any element of
![]() ${\mathcal{O}}_{M}$
such that
${\mathcal{O}}_{M}$
such that
![]() $\unicode[STIX]{x1D6FC}\equiv \unicode[STIX]{x1D70C}\hspace{0.2em}{\rm mod}\hspace{0.2em}F$
and such that
$\unicode[STIX]{x1D6FC}\equiv \unicode[STIX]{x1D70C}\hspace{0.2em}{\rm mod}\hspace{0.2em}F$
and such that
![]() $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FC}))=1$
; this is well-defined by Proposition 6.1. Moreover, define
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FC}))=1$
; this is well-defined by Proposition 6.1. Moreover, define
where
![]() $\unicode[STIX]{x1D6FC}$
is any element of
$\unicode[STIX]{x1D6FC}$
is any element of
![]() ${\mathcal{O}}_{M}$
such that
${\mathcal{O}}_{M}$
such that
![]() $\unicode[STIX]{x1D6FC}\equiv \unicode[STIX]{x1D70C}\hspace{0.2em}{\rm mod}\hspace{0.2em}F$
; this is well-defined by Lemma 3.2. We then define
$\unicode[STIX]{x1D6FC}\equiv \unicode[STIX]{x1D70C}\hspace{0.2em}{\rm mod}\hspace{0.2em}F$
; this is well-defined by Lemma 3.2. We then define
We now check that
![]() $\unicode[STIX]{x1D713}_{0}(\unicode[STIX]{x1D6FC}\hspace{0.6em}{\rm mod}\hspace{0.2em}F)=\unicode[STIX]{x1D713}_{0}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{2}\hspace{0.2em}{\rm mod}\hspace{0.2em}F)$
for all
$\unicode[STIX]{x1D713}_{0}(\unicode[STIX]{x1D6FC}\hspace{0.6em}{\rm mod}\hspace{0.2em}F)=\unicode[STIX]{x1D713}_{0}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{2}\hspace{0.2em}{\rm mod}\hspace{0.2em}F)$
for all
![]() $\unicode[STIX]{x1D6FC}\in {\mathcal{O}}_{M}$
coprime to
$\unicode[STIX]{x1D6FC}\in {\mathcal{O}}_{M}$
coprime to
![]() $F$
and all
$F$
and all
![]() $\unicode[STIX]{x1D6FD}\in {\mathcal{O}}_{M}^{\times }$
. Indeed, it is clear that
$\unicode[STIX]{x1D6FD}\in {\mathcal{O}}_{M}^{\times }$
. Indeed, it is clear that
![]() $\unicode[STIX]{x1D713}_{M}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{2}\hspace{0.2em}{\rm mod}\hspace{0.2em}F)=\unicode[STIX]{x1D713}_{M}(\unicode[STIX]{x1D6FC}\hspace{0.2em}{\rm mod}\hspace{0.2em}F)$
, and, for any
$\unicode[STIX]{x1D713}_{M}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{2}\hspace{0.2em}{\rm mod}\hspace{0.2em}F)=\unicode[STIX]{x1D713}_{M}(\unicode[STIX]{x1D6FC}\hspace{0.2em}{\rm mod}\hspace{0.2em}F)$
, and, for any
![]() $\unicode[STIX]{x1D70E}\in \text{Gal}(M/\mathbb{Q})$
, we have
$\unicode[STIX]{x1D70E}\in \text{Gal}(M/\mathbb{Q})$
, we have
From (6.4), we now deduce the following criterion for the
![]() $16$
-rank of
$16$
-rank of
![]() $\text{Cl}(-4p)$
, valid for all but finitely many primes
$\text{Cl}(-4p)$
, valid for all but finitely many primes
![]() $p$
.
$p$
.
Proposition 6.2. Let
![]() $p$
be a rational prime such that
$p$
be a rational prime such that
![]() $p$
splits completely in
$p$
splits completely in
![]() $M/\mathbb{Q}$
and such that
$M/\mathbb{Q}$
and such that
![]() $(p,F)=1$
. Let
$(p,F)=1$
. Let
![]() $\unicode[STIX]{x1D70B}$
be any prime in
$\unicode[STIX]{x1D70B}$
be any prime in
![]() ${\mathcal{O}}_{M}$
dividing
${\mathcal{O}}_{M}$
dividing
![]() $p$
. Then
$p$
. Then
Let
![]() $a_{p}$
be defined as (6.1). With
$a_{p}$
be defined as (6.1). With
![]() $\unicode[STIX]{x1D713}_{0}$
as in (6.6), we set
$\unicode[STIX]{x1D713}_{0}$
as in (6.6), we set
![]() $\unicode[STIX]{x1D713}=\unicode[STIX]{x1D713}_{0}$
and define
$\unicode[STIX]{x1D713}=\unicode[STIX]{x1D713}_{0}$
and define
![]() $s_{\mathfrak{a}}$
as in (1.3). If
$s_{\mathfrak{a}}$
as in (1.3). If
![]() $(p,F)=1$
,
$(p,F)=1$
,
![]() $p$
splits completely in
$p$
splits completely in
![]() $M/\mathbb{Q}$
, and
$M/\mathbb{Q}$
, and
![]() $\mathfrak{p}$
is any prime ideal in
$\mathfrak{p}$
is any prime ideal in
![]() ${\mathcal{O}}_{M}$
lying above
${\mathcal{O}}_{M}$
lying above
![]() $p$
, then Proposition 6.2 implies that
$p$
, then Proposition 6.2 implies that
Since there are only finitely many primes dividing
![]() $F$
, and since each unramified degree
$F$
, and since each unramified degree
![]() $1$
prime ideal
$1$
prime ideal
![]() $\mathfrak{p}$
in
$\mathfrak{p}$
in
![]() ${\mathcal{O}}_{M}$
has
${\mathcal{O}}_{M}$
has
![]() $8$
conjugates, we have
$8$
conjugates, we have
 $$\begin{eqnarray}\mathop{\sum }_{p\leqslant X}a_{p}=\mathop{\sum }_{\substack{ p\leqslant X \\ p\nmid F}}a_{p}+O(1)=\frac{1}{8}\mathop{\sum }_{\substack{ \text{N}(\mathfrak{p})=p\leqslant X \\ p\nmid F}}s_{\mathfrak{p}}+O(1)=\frac{1}{8}\mathop{\sum }_{\substack{ \text{N}(\mathfrak{p})=p\leqslant X}}s_{\mathfrak{p}}+O(1).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{p\leqslant X}a_{p}=\mathop{\sum }_{\substack{ p\leqslant X \\ p\nmid F}}a_{p}+O(1)=\frac{1}{8}\mathop{\sum }_{\substack{ \text{N}(\mathfrak{p})=p\leqslant X \\ p\nmid F}}s_{\mathfrak{p}}+O(1)=\frac{1}{8}\mathop{\sum }_{\substack{ \text{N}(\mathfrak{p})=p\leqslant X}}s_{\mathfrak{p}}+O(1).\end{eqnarray}$$
The number of prime ideals in
![]() ${\mathcal{O}}_{M}$
of degree at least
${\mathcal{O}}_{M}$
of degree at least
![]() $2$
and of norm
$2$
and of norm
![]() ${\leqslant}X$
is
${\leqslant}X$
is
so we have
Theorem 1 in conjunction with (6.8) now gives the desired estimate.
7 Proof of Theorem 3
To deduce Theorem 3 from Theorem 1, we will make a different choice for
![]() $\unicode[STIX]{x1D713}$
. Similarly as in the proof of Theorem 2, we define
$\unicode[STIX]{x1D713}$
. Similarly as in the proof of Theorem 2, we define
 $$\begin{eqnarray}b_{p}=\left\{\begin{array}{@{}ll@{}}1\quad & \text{if }h^{+}(8p)\equiv h(8p)\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}8,\\ -1\quad & \text{if }h^{+}(8p)+4\equiv h(8p)\equiv 4\hspace{0.2em}{\rm mod}\hspace{0.2em}8,\\ 0\quad & \text{otherwise},\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}b_{p}=\left\{\begin{array}{@{}ll@{}}1\quad & \text{if }h^{+}(8p)\equiv h(8p)\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}8,\\ -1\quad & \text{if }h^{+}(8p)+4\equiv h(8p)\equiv 4\hspace{0.2em}{\rm mod}\hspace{0.2em}8,\\ 0\quad & \text{otherwise},\end{array}\right.\end{eqnarray}$$
and note that Theorem 3 is equivalent to the estimate
Throughout, we fix a primitive
![]() $16$
th root of unity
$16$
th root of unity
![]() $\unicode[STIX]{x1D701}_{16}$
and we set
$\unicode[STIX]{x1D701}_{16}$
and we set
![]() $\unicode[STIX]{x1D701}_{8}=\unicode[STIX]{x1D701}_{16}^{2}$
,
$\unicode[STIX]{x1D701}_{8}=\unicode[STIX]{x1D701}_{16}^{2}$
,
![]() $i=\unicode[STIX]{x1D701}_{8}^{2}$
,
$i=\unicode[STIX]{x1D701}_{8}^{2}$
,
![]() $\sqrt{-2}=\unicode[STIX]{x1D701}_{8}+\unicode[STIX]{x1D701}_{8}^{3}$
, and
$\sqrt{-2}=\unicode[STIX]{x1D701}_{8}+\unicode[STIX]{x1D701}_{8}^{3}$
, and
![]() $\sqrt{2}=\unicode[STIX]{x1D701}_{8}+\unicode[STIX]{x1D701}_{8}^{-1}$
. As stated in the discussion prior to the statement of Theorem 3, for a prime number
$\sqrt{2}=\unicode[STIX]{x1D701}_{8}+\unicode[STIX]{x1D701}_{8}^{-1}$
. As stated in the discussion prior to the statement of Theorem 3, for a prime number
![]() $p\equiv 1\hspace{0.2em}{\rm mod}\hspace{0.2em}4$
, we have
$p\equiv 1\hspace{0.2em}{\rm mod}\hspace{0.2em}4$
, we have
![]() $h^{+}(8p)\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
if and only if
$h^{+}(8p)\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
if and only if
![]() $p$
splits completely in the number field
$p$
splits completely in the number field
Since
![]() $1+i=\unicode[STIX]{x1D701}_{8}\sqrt{2}$
, we have
$1+i=\unicode[STIX]{x1D701}_{8}\sqrt{2}$
, we have
![]() $M=\mathbb{Q}(\unicode[STIX]{x1D701}_{8},\sqrt{1+i})=\mathbb{Q}(\unicode[STIX]{x1D701}_{8},\unicode[STIX]{x1D701}_{16}\sqrt[4]{2})$
, and so
$M=\mathbb{Q}(\unicode[STIX]{x1D701}_{8},\sqrt{1+i})=\mathbb{Q}(\unicode[STIX]{x1D701}_{8},\unicode[STIX]{x1D701}_{16}\sqrt[4]{2})$
, and so
![]() $M\subset M^{\prime }$
is a quadratic extension, generated by
$M\subset M^{\prime }$
is a quadratic extension, generated by
![]() $\sqrt{\unicode[STIX]{x1D701}_{8}}$
. We now use a criterion of Kaplan and Williams [Reference Kaplan and WilliamsKW84, p. 26]. Suppose that
$\sqrt{\unicode[STIX]{x1D701}_{8}}$
. We now use a criterion of Kaplan and Williams [Reference Kaplan and WilliamsKW84, p. 26]. Suppose that
![]() $p\equiv 1\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
, i.e., that
$p\equiv 1\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
, i.e., that
![]() $h^{+}(8p)\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}4$
. Then we can write
$h^{+}(8p)\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}4$
. Then we can write
with
![]() $a,b,c,d\in \mathbb{Z}$
. After possibly interchanging
$a,b,c,d\in \mathbb{Z}$
. After possibly interchanging
![]() $a$
and
$a$
and
![]() $b$
, we can guarantee that
$b$
, we can guarantee that
![]() $a$
is odd. Replacing
$a$
is odd. Replacing
![]() $a$
by
$a$
by
![]() $-a$
and
$-a$
and
![]() $c$
by
$c$
by
![]() $-c$
is necessary, we can then ensure that
$-c$
is necessary, we can then ensure that
Assume now that
![]() $h^{+}(8p)\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
, i.e., that
$h^{+}(8p)\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
, i.e., that
![]() $p$
splits completely in
$p$
splits completely in
![]() $M^{\prime }/\mathbb{Q}$
; this forces the congruence conditions [Reference Kaplan and WilliamsKW84, p. 23]
$M^{\prime }/\mathbb{Q}$
; this forces the congruence conditions [Reference Kaplan and WilliamsKW84, p. 23]
With
![]() $b_{p}$
defined as in (7.1), and with
$b_{p}$
defined as in (7.1), and with
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
as on [Reference Kaplan and WilliamsKW84, p. 26], we have
$\unicode[STIX]{x1D6FD}$
as on [Reference Kaplan and WilliamsKW84, p. 26], we have
As
![]() $M\subset M^{\prime }$
, it must be that
$M\subset M^{\prime }$
, it must be that
![]() $h(-4p)\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
, so that with
$h(-4p)\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
, so that with
![]() $a_{p}$
as in the statement of Theorem 2, we get
$a_{p}$
as in the statement of Theorem 2, we get
In light of (6.8), it remains to express the factor
![]() $(-1)^{(a-1+b+2d)/8}$
in terms of a generator
$(-1)^{(a-1+b+2d)/8}$
in terms of a generator
![]() $\unicode[STIX]{x1D71B}$
for an ideal in
$\unicode[STIX]{x1D71B}$
for an ideal in
![]() ${\mathcal{O}}_{M}$
lying above
${\mathcal{O}}_{M}$
lying above
![]() $p$
. The main difficulty here lies in the sensitivity of the formula (7.4) to the conditions (7.3). Note that
$p$
. The main difficulty here lies in the sensitivity of the formula (7.4) to the conditions (7.3). Note that
and
The only units in
![]() $\mathbb{Z}[\sqrt{-2}]$
are
$\mathbb{Z}[\sqrt{-2}]$
are
![]() $\pm 1$
, so if
$\pm 1$
, so if
![]() $\text{N}_{M/\mathbb{Q}(\sqrt{-2})}(\unicode[STIX]{x1D71B})=c^{\prime }+d^{\prime }\sqrt{-2}$
, we must have either
$\text{N}_{M/\mathbb{Q}(\sqrt{-2})}(\unicode[STIX]{x1D71B})=c^{\prime }+d^{\prime }\sqrt{-2}$
, we must have either
![]() $(c^{\prime },d^{\prime })=(c,d)$
or
$(c^{\prime },d^{\prime })=(c,d)$
or
![]() $(c^{\prime },d^{\prime })=(-c,-d)$
. Note that
$(c^{\prime },d^{\prime })=(-c,-d)$
. Note that
![]() $d\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
if and only if
$d\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
if and only if
![]() $-d\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
, and also
$-d\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
, and also
![]() $d\equiv 4\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
if and only if
$d\equiv 4\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
if and only if
![]() $-d\equiv 4\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
. Hence, the factor
$-d\equiv 4\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
. Hence, the factor
![]() $(-1)^{d/4}$
in (7.4) is always equal to
$(-1)^{d/4}$
in (7.4) is always equal to
![]() $(-1)^{d^{\prime }/4}$
.
$(-1)^{d^{\prime }/4}$
.
The situation for
![]() $\mathbb{Z}[i]$
is slightly more complicated. Suppose
$\mathbb{Z}[i]$
is slightly more complicated. Suppose
![]() $\text{N}_{M/\mathbb{Q}(i)}(\unicode[STIX]{x1D71B})=a^{\prime }+b^{\prime }i$
. Define
$\text{N}_{M/\mathbb{Q}(i)}(\unicode[STIX]{x1D71B})=a^{\prime }+b^{\prime }i$
. Define
![]() $e(\unicode[STIX]{x1D71B})\in \{\pm 1\}$
by the equation
$e(\unicode[STIX]{x1D71B})\in \{\pm 1\}$
by the equation
Since
![]() $p={a^{\prime }}^{2}+{b^{\prime }}^{2}\equiv 1\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
, one of
$p={a^{\prime }}^{2}+{b^{\prime }}^{2}\equiv 1\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
, one of
![]() $a^{\prime }$
and
$a^{\prime }$
and
![]() $b^{\prime }$
must be congruent to
$b^{\prime }$
must be congruent to
![]() $0\hspace{0.2em}{\rm mod}\hspace{0.2em}4$
, and the other is then congruent to
$0\hspace{0.2em}{\rm mod}\hspace{0.2em}4$
, and the other is then congruent to
![]() $e(\unicode[STIX]{x1D71B})\hspace{0.2em}{\rm mod}\hspace{0.2em}4$
. If
$e(\unicode[STIX]{x1D71B})\hspace{0.2em}{\rm mod}\hspace{0.2em}4$
. If
![]() $e(\unicode[STIX]{x1D71B})=1$
, then either
$e(\unicode[STIX]{x1D71B})=1$
, then either
![]() $(a^{\prime },b^{\prime })$
or
$(a^{\prime },b^{\prime })$
or
![]() $(b^{\prime },a^{\prime })$
satisfies the same conditions as
$(b^{\prime },a^{\prime })$
satisfies the same conditions as
![]() $(a,b)$
in (7.2) and (7.3), and so
$(a,b)$
in (7.2) and (7.3), and so
![]() $(-1)^{(a-1+b)/8}=(-1)^{(a^{\prime }+b^{\prime }-1)/8}$
. If
$(-1)^{(a-1+b)/8}=(-1)^{(a^{\prime }+b^{\prime }-1)/8}$
. If
![]() $e(\unicode[STIX]{x1D71B})=-1$
, then either
$e(\unicode[STIX]{x1D71B})=-1$
, then either
![]() $(-a^{\prime },-b^{\prime })$
or
$(-a^{\prime },-b^{\prime })$
or
![]() $(-b^{\prime },-a^{\prime })$
satisfies the same conditions as
$(-b^{\prime },-a^{\prime })$
satisfies the same conditions as
![]() $(a,b)$
in (7.2) and (7.3), and so
$(a,b)$
in (7.2) and (7.3), and so
![]() $(-1)^{(a-1+b)/8}=(-1)^{(-a^{\prime }-b^{\prime }-1)/8}=(-1)^{(a^{\prime }+b^{\prime }+1)/8}$
. In any case,
$(-1)^{(a-1+b)/8}=(-1)^{(-a^{\prime }-b^{\prime }-1)/8}=(-1)^{(a^{\prime }+b^{\prime }+1)/8}$
. In any case,
![]() $(-1)^{(a-1+b)/8}=(-1)^{(a^{\prime }+b^{\prime }-e(\unicode[STIX]{x1D71B}))/8}$
, so that
$(-1)^{(a-1+b)/8}=(-1)^{(a^{\prime }+b^{\prime }-e(\unicode[STIX]{x1D71B}))/8}$
, so that
Note that the formula (7.5) holds regardless of the congruence classes of
![]() $a^{\prime }$
,
$a^{\prime }$
,
![]() $b^{\prime }$
, and
$b^{\prime }$
, and
![]() $d^{\prime }$
. In other words, we have managed to remove the dependence of the formula for
$d^{\prime }$
. In other words, we have managed to remove the dependence of the formula for
![]() $b_{p}$
on conditions of the shape (7.3).
$b_{p}$
on conditions of the shape (7.3).
Now let
![]() $\unicode[STIX]{x1D6FC}$
be any odd element in
$\unicode[STIX]{x1D6FC}$
be any odd element in
![]() ${\mathcal{O}}_{M}$
, not necessarily an element of norm
${\mathcal{O}}_{M}$
, not necessarily an element of norm
![]() $p$
. We define
$p$
. We define
![]() $a^{\prime \prime },b^{\prime \prime },c^{\prime \prime },d^{\prime \prime }\in \mathbb{Z}$
, and
$a^{\prime \prime },b^{\prime \prime },c^{\prime \prime },d^{\prime \prime }\in \mathbb{Z}$
, and
![]() $e(\unicode[STIX]{x1D6FC})\in \{\pm 1\}$
via equations
$e(\unicode[STIX]{x1D6FC})\in \{\pm 1\}$
via equations
Let
![]() $\unicode[STIX]{x1D70C}$
be an invertible congruence class modulo
$\unicode[STIX]{x1D70C}$
be an invertible congruence class modulo
![]() $F$
. Define
$F$
. Define
where
![]() $\unicode[STIX]{x1D6FC}$
is any element of
$\unicode[STIX]{x1D6FC}$
is any element of
![]() ${\mathcal{O}}_{M}$
such that
${\mathcal{O}}_{M}$
such that
![]() $\unicode[STIX]{x1D6FC}\equiv \unicode[STIX]{x1D70C}\hspace{0.2em}{\rm mod}\hspace{0.2em}F$
and
$\unicode[STIX]{x1D6FC}\equiv \unicode[STIX]{x1D70C}\hspace{0.2em}{\rm mod}\hspace{0.2em}F$
and
![]() $a^{\prime \prime }$
,
$a^{\prime \prime }$
,
![]() $b^{\prime \prime }$
,
$b^{\prime \prime }$
,
![]() $d^{\prime \prime }$
, and
$d^{\prime \prime }$
, and
![]() $e(\unicode[STIX]{x1D6FC})$
are defined via the equations (7.6); this is well-defined since
$e(\unicode[STIX]{x1D6FC})$
are defined via the equations (7.6); this is well-defined since
![]() $F$
is divisible by
$F$
is divisible by
![]() $16$
and
$16$
and
![]() $\exp (2\unicode[STIX]{x1D70B}i)=1$
. Finally, we define
$\exp (2\unicode[STIX]{x1D70B}i)=1$
. Finally, we define
where
![]() $\unicode[STIX]{x1D6FC}$
is any element of
$\unicode[STIX]{x1D6FC}$
is any element of
![]() ${\mathcal{O}}_{M}$
such that
${\mathcal{O}}_{M}$
such that
![]() $\unicode[STIX]{x1D6FC}\equiv \unicode[STIX]{x1D70C}\hspace{0.2em}{\rm mod}\hspace{0.2em}F$
; this is well-defined by Lemma 3.2.
$\unicode[STIX]{x1D6FC}\equiv \unicode[STIX]{x1D70C}\hspace{0.2em}{\rm mod}\hspace{0.2em}F$
; this is well-defined by Lemma 3.2.
Suppose
![]() $\unicode[STIX]{x1D6FC}\in {\mathcal{O}}_{M}$
is coprime to
$\unicode[STIX]{x1D6FC}\in {\mathcal{O}}_{M}$
is coprime to
![]() $F$
, and suppose
$F$
, and suppose
![]() $\unicode[STIX]{x1D6FD}\in {\mathcal{O}}_{M}^{\times }$
. Again, it is clear that
$\unicode[STIX]{x1D6FD}\in {\mathcal{O}}_{M}^{\times }$
. Again, it is clear that
Furthermore, because
![]() $\text{N}_{M/\mathbb{Q}(i)}(\unicode[STIX]{x1D6FD}^{2})=\text{N}_{M/\mathbb{Q}(i)}(\unicode[STIX]{x1D6FD})^{2}\in \{\pm 1\}$
and
$\text{N}_{M/\mathbb{Q}(i)}(\unicode[STIX]{x1D6FD}^{2})=\text{N}_{M/\mathbb{Q}(i)}(\unicode[STIX]{x1D6FD})^{2}\in \{\pm 1\}$
and
![]() $\text{N}_{M/\mathbb{Q}(\sqrt{-2})}(\unicode[STIX]{x1D6FD}^{2})=\text{N}_{M/\mathbb{Q}(\sqrt{-2})}(\unicode[STIX]{x1D6FD})^{2}=1$
, and because of the symmetry in (7.7) with respect to the transformation
$\text{N}_{M/\mathbb{Q}(\sqrt{-2})}(\unicode[STIX]{x1D6FD}^{2})=\text{N}_{M/\mathbb{Q}(\sqrt{-2})}(\unicode[STIX]{x1D6FD})^{2}=1$
, and because of the symmetry in (7.7) with respect to the transformation
![]() $(a^{\prime \prime }+b^{\prime \prime }-e(\unicode[STIX]{x1D6FC}))\mapsto -(a^{\prime \prime }+b^{\prime \prime }-e(\unicode[STIX]{x1D6FC}))$
, we also have
$(a^{\prime \prime }+b^{\prime \prime }-e(\unicode[STIX]{x1D6FC}))\mapsto -(a^{\prime \prime }+b^{\prime \prime }-e(\unicode[STIX]{x1D6FC}))$
, we also have
![]() $\unicode[STIX]{x1D713}_{t}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{2}\hspace{0.2em}{\rm mod}\hspace{0.2em}F)=\unicode[STIX]{x1D713}_{t}(\unicode[STIX]{x1D6FC}\hspace{0.2em}{\rm mod}\hspace{0.2em}F)$
.
$\unicode[STIX]{x1D713}_{t}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{2}\hspace{0.2em}{\rm mod}\hspace{0.2em}F)=\unicode[STIX]{x1D713}_{t}(\unicode[STIX]{x1D6FC}\hspace{0.2em}{\rm mod}\hspace{0.2em}F)$
.
Finally, with
![]() $\unicode[STIX]{x1D713}_{0}$
defined as in (6.6), we define two functions
$\unicode[STIX]{x1D713}_{0}$
defined as in (6.6), we define two functions
![]() $\unicode[STIX]{x1D713}_{1},\unicode[STIX]{x1D713}_{2}$
on
$\unicode[STIX]{x1D713}_{1},\unicode[STIX]{x1D713}_{2}$
on
![]() $({\mathcal{O}}_{M}/F{\mathcal{O}}_{M})^{\times }$
by setting
$({\mathcal{O}}_{M}/F{\mathcal{O}}_{M})^{\times }$
by setting
and
Now suppose
![]() $p$
splits completely in
$p$
splits completely in
![]() $M/\mathbb{Q}$
and let
$M/\mathbb{Q}$
and let
![]() $\unicode[STIX]{x1D71B}$
be any prime in
$\unicode[STIX]{x1D71B}$
be any prime in
![]() ${\mathcal{O}}_{M}$
of norm
${\mathcal{O}}_{M}$
of norm
![]() $p$
. Since
$p$
. Since
![]() $M^{\prime }=M(\sqrt{\unicode[STIX]{x1D701}_{8}})$
, we have
$M^{\prime }=M(\sqrt{\unicode[STIX]{x1D701}_{8}})$
, we have
so this can be detected by
![]() $\unicode[STIX]{x1D713}_{M^{\prime }}$
for
$\unicode[STIX]{x1D713}_{M^{\prime }}$
for
![]() $p$
coprime to
$p$
coprime to
![]() $F$
. With
$F$
. With
![]() $a^{\prime \prime }$
,
$a^{\prime \prime }$
,
![]() $b^{\prime \prime }$
, and
$b^{\prime \prime }$
, and
![]() $d^{\prime \prime }$
defined as in (7.6) with
$d^{\prime \prime }$
defined as in (7.6) with
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D71B}$
, we always have
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D71B}$
, we always have
![]() $a^{\prime \prime }+b^{\prime \prime }-e(\unicode[STIX]{x1D71B})\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
; as
$a^{\prime \prime }+b^{\prime \prime }-e(\unicode[STIX]{x1D71B})\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
; as
![]() $\exp (\unicode[STIX]{x1D70B}i)=\exp (-\unicode[STIX]{x1D70B}i)$
, we have
$\exp (\unicode[STIX]{x1D70B}i)=\exp (-\unicode[STIX]{x1D70B}i)$
, we have
Hence, from (7.5) and Proposition 6.2, supposing also that
![]() $(p,F)=1$
, we obtain
$(p,F)=1$
, we obtain
Now, with
![]() $\unicode[STIX]{x1D713}_{1}$
and
$\unicode[STIX]{x1D713}_{1}$
and
![]() $\unicode[STIX]{x1D713}_{2}$
as in (7.9) and (7.10), respectively, we set
$\unicode[STIX]{x1D713}_{2}$
as in (7.9) and (7.10), respectively, we set
![]() $\unicode[STIX]{x1D713}=\unicode[STIX]{x1D713}_{1}$
(respectively
$\unicode[STIX]{x1D713}=\unicode[STIX]{x1D713}_{1}$
(respectively
![]() $\unicode[STIX]{x1D713}=\unicode[STIX]{x1D713}_{2}$
) and define
$\unicode[STIX]{x1D713}=\unicode[STIX]{x1D713}_{2}$
) and define
![]() $s_{1,\mathfrak{a}}$
(respectively
$s_{1,\mathfrak{a}}$
(respectively
![]() $s_{2,\mathfrak{a}}$
) as in (1.3). If
$s_{2,\mathfrak{a}}$
) as in (1.3). If
![]() $(p,F)=1$
,
$(p,F)=1$
,
![]() $p$
splits completely in
$p$
splits completely in
![]() $M/\mathbb{Q}$
, and
$M/\mathbb{Q}$
, and
![]() $\mathfrak{p}$
is any prime ideal in
$\mathfrak{p}$
is any prime ideal in
![]() ${\mathcal{O}}_{M}$
lying above
${\mathcal{O}}_{M}$
lying above
![]() $p$
, then (7.11) implies that
$p$
, then (7.11) implies that
By the same argument as at the end of § 6, Theorem 1 applied to the sequences
![]() $\{s_{1,\mathfrak{a}}\}_{\mathfrak{a}}$
and
$\{s_{1,\mathfrak{a}}\}_{\mathfrak{a}}$
and
![]() $\{s_{2,\mathfrak{a}}\}_{\mathfrak{a}}$
proves Theorem 3.
$\{s_{2,\mathfrak{a}}\}_{\mathfrak{a}}$
proves Theorem 3.
8 Proof of Theorem 5
We start by recalling a criterion due to Bruin and Hemenway [Reference Bruin and HemenwayBH13, Theorem B, p. 66]. Suppose
![]() $p$
is a prime number that splits completely in
$p$
is a prime number that splits completely in
![]() $M/\mathbb{Q}$
and let
$M/\mathbb{Q}$
and let
![]() $\unicode[STIX]{x1D71B}$
be a prime in
$\unicode[STIX]{x1D71B}$
be a prime in
![]() ${\mathcal{O}}_{M}$
of absolute norm
${\mathcal{O}}_{M}$
of absolute norm
![]() $p$
. Then
$p$
. Then
(the right-hand side implies that
![]() $p\in W(3)\setminus W(2)$
, where
$p\in W(3)\setminus W(2)$
, where
![]() $W(e)$
is defined in [Reference Bruin and HemenwayBH13, p. 65]; see also [Reference Bruin and HemenwayBH13, Corollary 2.2, p. 67]). The above product differs from the product in (6.4) only by the factor
$W(e)$
is defined in [Reference Bruin and HemenwayBH13, p. 65]; see also [Reference Bruin and HemenwayBH13, Corollary 2.2, p. 67]). The above product differs from the product in (6.4) only by the factor
![]() $(\frac{\unicode[STIX]{x1D701}_{8}}{\unicode[STIX]{x1D71B}})_{M}$
. We thus define
$(\frac{\unicode[STIX]{x1D701}_{8}}{\unicode[STIX]{x1D71B}})_{M}$
. We thus define
![]() $\unicode[STIX]{x1D713}:({\mathcal{O}}_{M}/F{\mathcal{O}}_{M})^{\times }\rightarrow \mathbb{C}$
by
$\unicode[STIX]{x1D713}:({\mathcal{O}}_{M}/F{\mathcal{O}}_{M})^{\times }\rightarrow \mathbb{C}$
by
where
![]() $\unicode[STIX]{x1D713}_{0}$
is as in (6.6) and
$\unicode[STIX]{x1D713}_{0}$
is as in (6.6) and
![]() $\unicode[STIX]{x1D713}_{M^{\prime }}$
is as in (7.8). Theorem 1 applied to the sequence
$\unicode[STIX]{x1D713}_{M^{\prime }}$
is as in (7.8). Theorem 1 applied to the sequence
![]() $\{s_{\mathfrak{a}}\}_{\mathfrak{a}}$
, defined as in (1.3) with
$\{s_{\mathfrak{a}}\}_{\mathfrak{a}}$
, defined as in (1.3) with
![]() $\unicode[STIX]{x1D713}$
as above, now gives the desired result.
$\unicode[STIX]{x1D713}$
as above, now gives the desired result.
Acknowledgements
The authors would like to thank Jan-Hendrik Evertse, Étienne Fouvry, Zev Klagsbrun, Carlo Pagano, and Peter Stevenhagen for useful discussions related to this work. The first author is a doctoral student at Leiden University. The second author was also supported by an ALGANT Erasmus Mundus Scholarship and the National Science Foundation agreement No. DMS-1128155 for part of this research.