Dehn twist exact sequences through Lagrangian cobordism

Abstract

This paper introduces a new Lagrangian surgery construction that generalizes Lalonde–Sikorav and Polterovich’s well-known construction, and combines this with Biran and Cornea’s Lagrangian cobordism formalism. With these techniques, we build a framework which both recovers several known long exact sequences (Seidel’s exact sequence, including the fixed point version and Wehrheim and Woodward’s family version) in symplectic geometry in a uniform way, and yields a partial answer to a long-term open conjecture due to Huybrechts and Thomas; this also involved a new observation which relates projective twists with surgeries.

1 Introduction

1.1 Motivations and overview

Lagrangian cobordisms were first introduced by Arnold [Arn80a, Arn80b] and subsequently studied by Eliashberg [Eli84], Audin [Aud85], Chekanov [Che97], etc. More recently, Biran and Cornea, in their celebrated series of papers [BC13, BC14, BC17], considered Floer theories on them, and have achieved great success encapsulating information of the triangulated structures of the derived Fukaya category. A particularly attractive application is that they establish the long-expected relation between Lagrangian surgeries [LS91, Pol91] and the mapping cones in derived Fukaya categories.

A primary purpose of this paper is to revisit such surgery-cobordism relations with an emphasis on applications to Dehn twists. The underlying philosophy of our approach is to understand the functors between Fukaya categories via Lagrangian cobordisms. This functor-level point of view has been exploited in several other contexts by many authors [WMW, WW16, AS15] etc.

We explore this direction through the eyes of Lagrangian correspondences. Intuitively, one may regard Lagrangian correspondences as symplectic mirrors of kernels of Fourier–Mukai transforms. The observation is that almost all exact sequences involving Lagrangian Dehn twists can be interpreted as cone relations between these ‘kernels’. Explicitly, Lagrangian cobordism constructions geometrically realize all these cones on the correspondence level and provide a completely analogous picture on the symplectic side, versus various twist constructions on derived categories. This point of view greatly simplifies the proof of several known exact sequences and leads to new cone relations in Floer theory such as Lagrangian $\mathbb{C}\mathbb{P}^{n}$ -twists, partially verifying a conjecture due to Huybrechts and Thomas.

To this end, much work needs to be done on the general geometric framework. We designed a new approach to Lagrangian surgeries called the flow surgery, which is coordinate-free and easy to compare with other constructions such as Dehn twists. The construction also allows many variants open for future exploration.

Another geometric observation is that Dehn twists along various projective spaces are equivalent to Lagrangian surgeries with certain immersed spheres. Using the aforementioned idea from the complex side, we package this information in product symplectic manifolds.

Readers who are cautious about technical conditions throughout the paper will find a list by the end of this introduction.

1.2 Flow surgeries and flow handles

Recall that for two Lagrangians $L_{1}\pitchfork L_{2}=\{x\}$ , their Lagrangian surgery at $x$ is given by adding an explicit Lagrangian handle in the Darboux chart [LS91, Pol91]. Then a Lagrangian cobordism can be obtained by using ‘half’ of a Lagrangian handle of one dimension higher [BC13]. This line of thought has led to remarkable breakthroughs in both constructions of new examples of Lagrangian submanifolds [Pol91] and cobordism theory [BC13].

To implement this construction to Lagrangian ‘fiber sums’ (surgery along clean intersections), the patching of local models requires delicate consideration on the choice of connections on normal bundles. On top of that, in most of our applications, the main difficulty is to show that the resulting manifold is Hamiltonian isotopic to certain given Lagrangians, usually those obtained by Lagrangian Dehn twists.

Our basic idea to solve both problems at once is to use a reparametrized geodesic flow, mimicking the original construction of the symplectic Dehn twist by Seidel, to produce a new Lagrangian surgery operation called the flow surgery (see § 2.2). This flow surgery recovers the usual Lagrangian surgery when the auxiliary data is chosen appropriately, but has much better flexibility. For example, the resulting Lagrangian handle needs not be diffeomorphic to a punctured ball (or a bundle with punctured-ball fibers in the clean surgery case). Moreover, Biran and Cornea’s cobordism construction via surgeries is easily seen to fit into this framework.

The main examples we have are the following (see § 3 for relevant definitions).

Theorem 1.1. Consider the following embedded submanifolds in $M$ :

1. (1) $S^{n}{\hookrightarrow}M$ is a Lagrangian sphere embedding;

2. (2) $C{\hookrightarrow}M$ is a spherically coisotropic submanifold embedding;

3. (3) $S{\hookrightarrow}M$ is a Lagrangian embedding where $S$ is diffeomorphic to either $\mathbb{R}\mathbb{P}^{n}$ , $\mathbb{C}\mathbb{P}^{n}$ or $\mathbb{HP}^{n}$ ;

4. (4) $C_{P}{\hookrightarrow}M$ is a projectively coisotropic submanifold embedding.

Let $\unicode[STIX]{x1D70F}_{S^{n}}$ , $\unicode[STIX]{x1D70F}_{C}$ , $\unicode[STIX]{x1D70F}_{S}$ and $\unicode[STIX]{x1D70F}_{C_{P}}$ denote the corresponding Dehn twists. One has the following surgery equalities up to Hamiltonian isotopies in $M\times M^{-}$ (see § 2.2 for relevant notation).

1. (1) The graph of a Dehn twist along a sphere is the surgery of $S^{n}\times S^{n}$ with the diagonal, that is,

   (1.1) $$\begin{eqnarray}(S^{n}\times (S^{n})^{-})\text{\#}_{\unicode[STIX]{x1D6E5}_{S^{n}},E_{2}}\unicode[STIX]{x1D6E5}_{M}=\text{Graph}(\unicode[STIX]{x1D70F}_{S^{n}}^{-1}).\end{eqnarray}$$

2. (2) Let $\widetilde{C}{\hookrightarrow}M\times M^{-}$ be the Lagrangian submanifold associated to $C$ . Then the graph of family Dehn twist along $C$ is the surgery of an associated Lagrangian $\widetilde{C}$ and the diagonal, that is,

   (1.2) $$\begin{eqnarray}\widetilde{C}\text{\#}_{{\mathcal{D}},E_{2}}\unicode[STIX]{x1D6E5}_{M}=\text{Graph}(\unicode[STIX]{x1D70F}_{C}^{-1}).\end{eqnarray}$$

3. (3) The graph of projective twist along $S$ is the surgery of two copies of $S\times S^{-}$ along with the diagonal, that is,

   (1.3) $$\begin{eqnarray}(S\times S^{-})\text{\#}_{D^{\operatorname{op}},E_{2}}(S\times S^{-})\text{\#}_{\unicode[STIX]{x1D6E5}_{S},E_{2}}\unicode[STIX]{x1D6E5}_{M}=\text{Graph}(\unicode[STIX]{x1D70F}_{S}^{-1}).\end{eqnarray}$$

4. (4) Let $\widetilde{C}_{P}{\hookrightarrow}M\times M^{-}$ be the Lagrangian submanifold associated to $C_{P}$ . Then the graph of family Dehn twist along $C_{P}$ is the surgery of two copies of the associated Lagrangian $\widetilde{C}_{P}$ and the diagonal, that is,

   (1.4) $$\begin{eqnarray}\widetilde{C}_{P}\text{\#}_{{\mathcal{D}}^{\operatorname{op}},E_{2}}\widetilde{C}_{P}\text{\#}_{{\mathcal{D}},E_{2}}\unicode[STIX]{x1D6E5}_{M}=\text{Graph}(\unicode[STIX]{x1D70F}_{C_{P}}^{-1}).\end{eqnarray}$$

The surgery equalities immediately lead to the existence of corresponding Lagrangian cobordisms. Note that in case (1), a similar cobordism construction was established in [AS15] using Lefschetz fibrations independently.

To motivate our construction, we point out a direct point of view on projective twists via immersed Lagrangian submanifolds as follows: for each Lagrangian projective space $S$ , there is a naturally associated immersed Lagrangian sphere $S_{{\looparrowright}}$ . Then the Dehn twist of $L$ along $S$  is equivalent to performing a surgery with a copy of $S_{{\looparrowright}}$ for each intersection $L\cap S$ .

Example 1.2. The simplest instance of a projective twist can be demonstrated concretely in $M=T^{\ast }S^{1}$ , see Figure 1. Here we consider $S_{{\looparrowright}}\subset M$ to be an immersed circle with a unique transverse immersed point. Here $L$ is given by the cotangent fiber at a point, and we assume it passes through the unique immersed point of $S_{{\looparrowright}}$ . While the base is regarded as an $\mathbb{R}\mathbb{P}^{1}$ , the surgery Lagrangian $S_{{\looparrowright}}\text{\#}L$ is $\unicode[STIX]{x1D70F}_{\mathbb{R}\mathbb{P}^{1}}L$ . Here the surgery is performed through one of the branches of $S_{{\looparrowright}}$ at the immersed point.

This surgery can be recast into a Lagrangian cobordism in $T^{\ast }S^{1}\times \mathbb{C}$ . The cobordism can be constructed so that it naively satisfies Biran and Cornea’s definition, i.e., outside $T^{\ast }S^{1}\times K$ for some compact set $K$ , it is a union of products between rays and immersed Lagrangian submanifolds in $T^{\ast }S^{1}$ . However, it is evident that the self-intersection cannot be clean since they form a ray. In general, any surgery process involving resolution of an immersed point will suffer from the same shortcoming. Therefore, we will need a modification for the Floer theory to be well defined.

Figure 1. A surgery with an immersed $S^{1}$ .

For the general case, the above approach becomes rather technical. Our key novelty is to apply the surgery construction to Lagrangian submanifolds in product manifolds, such as the graph of projective twists, to package the same information in a way better suited for doing Floer theory, hence case (3). More precisely, one should imagine that the two copies of $S\times S^{-}$ in case (3) are obtained from breaking an immersed Lagrangian relevant to the Dehn twist, similar to the fact that $S_{{\looparrowright}}$ in Example 1.2 can be obtained as a Lagrangian surgery between two copies of zero section.

Remark 1.3. Formal proofs will only be given in the case of $S^{n}$ and $\mathbb{C}\mathbb{P}^{n}$ , since the $\mathbb{HP}^{n}$ and $\mathbb{R}\mathbb{P}^{n}$ cases will follow from the proof of $\mathbb{C}\mathbb{P}^{n}$ word by word. The common feature for these manifolds we used is the existence of a metric $g_{S}$ with the following property: for any point $x\in S$ , the injectivity radius at $x$ equals $\unicode[STIX]{x1D70B}$ , and $S\backslash B_{x}(\unicode[STIX]{x1D70B})$ is a smooth closed submanifold, where $B_{x}(\unicode[STIX]{x1D70B})$ is the open ball of radius $\unicode[STIX]{x1D70B}$ around $x$ in the round metric on $S$ .

We include a detailed discussion on gradings involved in Lagrangian surgeries (see § 4), which allows us to compute the connecting maps later on (Appendix A). But we emphasize that the grading is a vital part of the foundation of Lagrangian surgeries for an intrinsic reason. Consider the simple case when all the involved Lagrangians (including those considered in general surgery constructions) are $\mathbb{Z}$ -graded and embedded. According to the cone relation proved in [BC13], the algebra instructs that a surgery happen only at degree-zero cocycles. This principle was noticed first by Paul Seidel [Sei00].

Such a principle interprets several known phenomena in a uniform way. First of all there are two different surgeries at a single point (see [FOOO09, ch. 10]) and they should be viewed as two different cones $\text{Cone}(L_{0}\xrightarrow[{}]{c}L_{1})$ and $\text{Cone}(L_{1}[-n]\xrightarrow[{}]{c^{\vee }[-n]}L_{0})$ , which are a priori very different. When the resolved intersections involve generators with different degrees, in many cases this leads to obstructions in Floer theory, as exemplified in [FOOO09, ch. 10]. In better situations when resolved intersections have zero degree modulo $N$ , the surgery at least collapses $\mathbb{Z}$ -gradings to $\mathbb{Z}/N$ -gradings. This can also be checked directly on the Maslov classes of the surgered Lagrangians.

For our applications, we extend this principle to clean surgeries. The upshot is that, for two graded Lagrangians $L_{0},L_{1}$ with $L_{0}\cap L_{1}=D$ being a clean intersection with zero Maslov index, $L_{1}$ and $L_{0}[\text{dim}(D)+1]$ can be surgered to produce a graded Lagrangian. This matches well with predictions from homological algebra dictated by Lagrangian Floer theory with clean intersections [FOOO09, ch. 10]. It also extends the surgery exact sequence to the clean intersection case.

1.3 Cone relations in functor categories via Lagrangian cobordisms

From the surgery equalities in Theorem 1.1 and the corresponding cobordisms, we immediately recover Seidel’s exact sequence and Wehrheim and Woodward’s family Dehn twist sequence on the functor level, assuming all monotonicity conditions discussed in § 6, as follows.

Theorem 1.4 (See [Sei03, WW16, BC17], also Theorems 6.4 and 6.6).

Let $M$ be a monotone symplectic manifold. When $S^{n}\subset M$ is a monotone Lagrangian sphere, there is a cone in $\operatorname{End}(Tw\mathscr{F}uk(M))$ .

(1.5)

When $C\subset M$ is a spherically coisotropic submanifold with appropriate monotonicity assumptions (see Theorem 6.6), there is a cone in $\operatorname{End}(Tw\mathscr{F}uk(M))$ .

(1.6)

(Here, $C^{t}$ is the transpose of a Lagrangian correspondence, and $\circ$ denotes the composition. See § 5 for the precise definitions.)

Besides invoking Biran and Cornea’s general cobordism formalism and Theorem 1.1, we derived natural sufficient conditions for Lagrangian cobordisms to be monotone/exact in Lemma 6.3 and 6.2, which are particularly adapted to the surgery setting.

Through our methods, we can cover the case when $C\subset M$ is of codimension one, under the assumption that $\unicode[STIX]{x1D70B}_{1}(M)$ is torsion. For more general symplectic manifolds, our method reduces the problem of proving exact sequences to only checking the monotonicity conditions as in Theorem 6.6 for codimension one spherically coisotropic manifolds.

In another direction, since our construction holds for arbitrary symplectic manifolds, when combined with the general framework due to Fukaya et al. [FOOO09], it yields a proof for Seidel’s exact sequence in an arbitrary symplectic manifold.

Remark 1.5. There are interesting consequences of these cones of endofunctors of Fukaya categories. For example, one may prove that for the Milnor fibers of any $ADE$ -singularities, the auto-equivalences of the Fukaya category induced by compactly supported symplectomorphisms are split generated by those induced by compositions of Dehn twists along vanishing cycles, modulo aligning some technical ingredients (such as establishing the cobordism theory in the wrapped context, as pointed out to us by Sheel Ganatra). This is a generalization (though in a weaker categorical sense) of a result in dimension 4, which says that for surface $A_{n}$ -Milnor fibers, any symplectomorphism is Hamiltonian isotopic to certain compositions of Dehn twists along vanishing cycles [Eva11, Wu14]. This part will appear separately soon.

1.4 The Huybrechts–Thomas conjecture and projective twists

There is a natural extension of the Dehn twist along spheres to arbitrary rank-one symmetric spaces, which has been known for a long time. Seidel’s long exact sequence associated to a Dehn twist along a sphere should be viewed as the mirror of a spherical twist in derived categories [ST01]. Also, such a cone relation on the $A$ -side has become a foundational tool in the study of homological mirror symmetry, especially in the symplectic Picard–Lefschetz theory [Sei08a].

Since then, how to describe the effect of the Dehn twists along a rank-one symmetric space in Floer theory has remained a mystery.

Fortunately, one could at least formulate a conjectural algebraic expression from homological mirror symmetry in this case. On the $B$ -side, Huybrechts and Thomas [HT06] first defined $\mathbb{P}^{n}$ -objects in the derived category. Recall that an object ${\mathcal{E}}\in D^{b}(X)$ for a smooth projective variety is called a $\mathbb{P}^{n}$ -object if ${\mathcal{E}}\otimes \unicode[STIX]{x1D714}_{X}\cong {\mathcal{E}}$ and $\operatorname{Ext}^{\ast }({\mathcal{E}},{\mathcal{E}})$ is isomorphic as a graded ring to $H^{\ast }(\mathbb{P}^{n},\mathbb{C})$ . Then they constructed an auto-equivalence of $D^{b}(X)$ called the $\mathbb{P}^{n}$ -twist associated to ${\mathcal{E}}$ , which is the Fourier–Mukai transform with kernel

(1.7) $$\begin{eqnarray}\text{Cone}(\text{Cone}({\mathcal{E}}^{\vee }\boxtimes {\mathcal{E}}[-2]\xrightarrow[{}]{\bar{h}^{\vee }\times \operatorname{id}-\operatorname{id}\times \bar{h}}{\mathcal{E}}^{\vee }\boxtimes {\mathcal{E}})\xrightarrow[{}]{ev}{\mathcal{O}}_{\unicode[STIX]{x1D6E5}}).\end{eqnarray}$$

Here $\bar{h}\in \operatorname{hom}^{2}({\mathcal{E}},{\mathcal{E}})$ is a representative of the generator in cohomology. They then conjectured the $\mathbb{P}^{n}$ -twist is exactly the mirror auto-equivalence of the one induced by a Dehn twist along Lagrangian $\mathbb{C}\mathbb{P}^{n}$ on the derived Fukaya categories. Written explicitly in the derived Fukaya category, the conjecture reads as follows.

Conjecture 1.6 ([HT06], see also [Har11]).

Given a monotone Lagrangian $\mathbb{C}\mathbb{P}^{n}$ in $M^{4n}$ , denoted by $S$ , and a compact monotone Lagrangian $L$ , then in $D^{\unicode[STIX]{x1D70B}}\mathscr{F}uk(M)$

(1.8) $$\begin{eqnarray}\unicode[STIX]{x1D70F}_{\mathbb{C}\mathbb{P}^{n}}(L)\cong \text{Cone}(\text{Cone}(\text{hom}(S,L)\otimes S[-2]\xrightarrow[{}]{\unicode[STIX]{x1D707}^{2}(-,h)\times \operatorname{id}-\operatorname{id}\times \unicode[STIX]{x1D707}^{2}(h,-)}\text{hom}(S,L)\otimes S)\xrightarrow[{}]{ev}L).\end{eqnarray}$$

Here the right-hand side is an iterated mapping cone, $D^{\unicode[STIX]{x1D70B}}\mathscr{F}uk(M)$ denotes the Karoubi completion of the derived Fukaya category generated by compact Lagrangian branes, and $h\in \operatorname{hom}^{2}(S,S)$ is the Floer cochain in degree $2$ representing the dual of the hyperplane class in cohomology.

Richard Harris studied the conjecture in $A_{\infty }$ context: he formulated a projective twist as an $A_{\infty }$ -autoequivalence of an $A_{\infty }$ category [Har11]. His construction spelled out a conjectural algebraic expression about $\unicode[STIX]{x1D70F}_{S}L$ in the twisted complexes of a Fukaya category (up to quasi-isomorphisms, of course).

As an application of the surgery equalities in Theorem 1.1, we show the following cone relations.

Theorem 1.7 (See Theorem 6.7).

For any given monotone Lagrangian submanifolds $L_{0}$ , $L_{1}$ and $S$ in $M$ with minimal Maslov numbers at least two such that $S$ is diffeomorphic to $\mathbb{C}\mathbb{P}^{n}$ , there is a quasi-isomorphism of cochain complexes

(1.9) $$\begin{eqnarray}\displaystyle & & \displaystyle CF^{\ast }(L_{0},\unicode[STIX]{x1D70F}_{S}L_{1})\nonumber\\ \displaystyle & & \displaystyle \quad \cong \,\text{Cone}(CF^{\ast }(S,L_{1})\otimes CF^{\ast -2}(L_{0},S)\rightarrow CF^{\ast }(S,L_{1})\otimes CF^{\ast }(L_{0},S)\rightarrow CF^{\ast }(L_{0},L_{1})).\end{eqnarray}$$

Here, the right-hand side is an iterated mapping cone. That is, we used $\text{Cone}(A\rightarrow B\rightarrow C)$ as a shorthand for $\text{Cone}(\text{Cone}(A\rightarrow B)\rightarrow C)$ for chain complexes $A,B$ and $C$ . On the categorical level, Biran and Cornea’s cobordism framework and (1.3) imply a cone relation between product Lagrangians, and this translates, using the M’au–Wehrheim–Woodward functor [WMW], into a cone relation between endofunctors. This allows one to verify the ( $A_{\infty }$ ) Fukaya categorical version of the conjecture in the monotone case.

Theorem 1.8 (See Theorem 6.10).

Huybrechts–Thomas conjecture 1.6 is true modulo determination of connecting maps.

The proof of Theorem 1.8 follows from the construction of a cobordism representing an iterated cone on the functor level, see Theorem 1.1 and Lemma 4.18. With some extra work, our proof implies that, on the $A_{\infty }$ level, our geometric expression matches Harris’s construction up to quasi-isomorphisms. Our method applies well on $\mathbb{R}\mathbb{P}^{n}$ or $\mathbb{HP}^{n}$ , as well as their family versions (see Theorem 6.11). However, even if all the geodesics on a Lagrangian are closed, our method cannot apply when the geodesics do not have a common period. Examples of these manifolds include free quotient of spheres by finite groups of order greater than two, and their Dehn twists are studied in a forthcoming paper by the authors.

We should mention that the $A_{\infty }$ version should also hold for Fukaya categories of exact symplectic manifolds: however, at the time of writing, the construction of infinitesimal Fukaya categories is not fully carried out, and the wrapped version of Lagrangian cobordism theory in the present situation requires independent efforts (see [Gao17]).

Remark 1.9. While it is not difficult to find examples of Lagrangian $\mathbb{R}\mathbb{P}^{n}$ in problems in symplectic topology ([She15], [Wu14] etc.), the search of interesting examples of Lagrangian $\mathbb{C}\mathbb{P}^{n}$ is more intriguing. In [HT06] the authors suggested several sources of $\mathbb{P}^{n}$ -objects in derived categories. An interesting instance is given by sheaves pulled back from the zero section of a holomorphic Lagrangian fibration on a hyperkähler manifold. From the Strominger–Yau–Zaslow (SYZ) point of view, this should correspond to a Lagrangian $\mathbb{C}\mathbb{P}^{n}$ section on the SYZ mirror. While the role of $\mathbb{P}^{n}$ objects on either side of mirror symmetry remains widely open so far, it is interesting to know whether such objects split generate either side of mirror symmetry.

Another significant source of Lagrangian projective spaces is due to Manolescu [Man07]. In particular, he constructed a family of exact symplectic manifolds which admit certain symplectic fibrations. The monodromies of such fibrations are closely related to projective twists. Conjecturally, the Khovanov–Rozansky homology of a link can be recovered by $HF(L,L^{\prime })$ , where $L$ is certain Lagrangian submanifold on the fiber, and $L^{\prime }$ is the parallel transport of $L$ back to the same fiber over a path on the base. Therefore, it seems that the projective twist formula should imply interesting information on Khovanov–Rozansky homology, which will be explored in the future.

Remark 1.10. In a different direction, the $\mathbb{P}^{n}$ -cone relation should be interesting in understanding some basic problems in symplectic topology, such as mapping class groups of a symplectic manifold and the search of exotic Lagrangian submanifolds. For instance, while a Lagrangian $\mathbb{C}\mathbb{P}^{n}$ -twist is always smoothly isotopic to identity (see [Sei00, Proposition 4.6]), it is usually not Hamiltonian isotopic to identity. A simplest model result along this line is to generalize Seidel’s twisted Lagrangian sphere construction [Sei99]: in the plumbing of three $T^{\ast }\mathbb{C}\mathbb{P}^{n}$ , the iterated Dehn twists along $\mathbb{C}\mathbb{P}^{n}$ in the middle should generate an infinite subgroup of the symplectic mapping class group. It is not as clear how to obtain a free group in the mapping class group from two projective twists, though, as exhibited by Keating in the spherical case [Kea14].

Remark 1.11. With Theorem 1.1 the projective twist cone formula easily generalizes to $\mathbb{R}\mathbb{P}^{n}$ and $\mathbb{HP}^{n}$ . The only difference between the formulas is the grading shift of the first term, as specified in Theorem 6.10.

$\mathbb{R}\mathbb{P}^{n}$ also gains a special feature: in this case the associated sphere $S_{{\looparrowright}}$ is equivalent to $\mathbb{R}\mathbb{P}^{n}$ equipped with a non-trivial $\mathbb{Z}_{2}$ -local system in the Fukaya category (see [Dam12, AB14, She15]). Therefore, the iterated cone relation can be packaged directly into a long exact sequence without invoking the iterated cones.

Structure of the paper

The geometric construction on Lagrangian surgeries via flow handles is part of the technical heart of the paper, and will occupy the first three sections: § 2 describes the basic constructions, § 3 explains how flow surgeries could be compared to Dehn twists, and § 4 investigates the grading issues in Lagrangian surgeries in general. This proves Theorem 1.1, including the consideration of gradings. After briefly recalling the Wehrheim–Woodward quilted theory in § 5, we give proofs of all claimed long exact sequences in § 6. Appendix A is devoted to some computations of the connecting maps.

Conventions

• ∙ Throughout the paper, we assume any Lagrangian submanifold $L$ of a symplectic manifold $(M,\unicode[STIX]{x1D714})$ under consideration to be exact or monotone, which means the following.

  1. – (exactness) We have $\unicode[STIX]{x1D714}=d\unicode[STIX]{x1D6FC}$ for some $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6FA}^{1}(M)$ , and $\unicode[STIX]{x1D6FC}|_{L}=df$ for some smooth function $f$ on $L$ .

  2. – (monotonicity) For any $\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D70B}_{2}(M,L)$ , $\unicode[STIX]{x1D714}(\unicode[STIX]{x1D6FD})=\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FD})$ . Here $\unicode[STIX]{x1D706}>0$ and $\unicode[STIX]{x1D707}$ denotes the Maslov class, the minimal Maslov number satisfies $\unicode[STIX]{x1D707}_{\text{min}}\geqslant 2$ , and $M$ is compact without boundary.

  More precisely, results in §§2–4 do not involve Floer theory and are valid without these assumptions.

• ∙ All Lagrangian embeddings are assumed to be proper unless specified otherwise. In most situations, Lagrangian embeddings to $M$ are compact even in the exact setting, while Lagrangian embeddings to $M\times \mathbb{C}$ are usually non-compact.

• ∙ The Hamiltonian vector field $X_{h}$ of a Hamiltonian function $h$ is defined by $\unicode[STIX]{x1D704}_{X_{h}}\unicode[STIX]{x1D714}=\,\,\unicode[STIX]{x1D714}(X_{h},-)=-dh$ and the time- $t$ flow under $X_{h}$ is denoted as $\unicode[STIX]{x1D719}_{t}^{h}$ .

• ∙ We will also denote by $M^{-}=(M,-\unicode[STIX]{x1D714})$ the negation of the symplectic manifold $(M,\unicode[STIX]{x1D714})$ .

1.5 A note on coefficients

Throughout this paper we will use coefficient rings $\mathbb{Z}/2$ or $\unicode[STIX]{x1D6EC}_{\mathbb{Z}/2}$ . Using characteristic zero coefficients is possible up to checking orientations for the general framework on Lagrangian cobordisms for [BC13, BC14]. As far as the coefficients are concerned, however, the Huybrechts–Thomas conjecture might not hold in general for $\mathbb{C}$ -coefficients: for example, $\mathbb{C}\mathbb{P}^{2k}$ are not spin thus will be constrained to Fukaya categories defined over $\mathbb{Z}/2$ in many cases.

2 Dehn twist and Lagrangian surgeries

2.1 Dehn twist

Let $S$ be a connected closed manifold equipped with a Riemannian metric $g(\cdot ,\cdot )$ such that every geodesic is closed of length $2\unicode[STIX]{x1D70B}$ (i.e., the shortest period of every unit-speed geodesic is $2\unicode[STIX]{x1D70B}$ ). We identify $T^{\ast }S$ with $TS$ by $g$ and switch freely between the two. The following lemma is well known.

Lemma 2.1. The Hamiltonian $\unicode[STIX]{x1D70E}:T^{\ast }S\rightarrow \mathbb{R}$ defined by

$$\begin{eqnarray}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D709})=\Vert \unicode[STIX]{x1D709}\Vert\end{eqnarray}$$

for all $q\in S$ and $\unicode[STIX]{x1D709}\in T_{q}^{\ast }S$ has the property that its Hamiltonian vector field $X_{\unicode[STIX]{x1D70E}}$ generates the normalized geodesic flow on $T^{\ast }S\backslash \{0_{\text{section}}\}$ (this is the flow that parallel transports every tangent vector at unit-speed along the geodesic starting from it).

To define the Dehn twist, we need to introduce an auxiliary function. We first consider the case when $S$ is not diffeomorphic to a sphere. For $\unicode[STIX]{x1D716}>0$ small, we define a Dehn twist profile to be a smooth function $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D716}}^{\text{Dehn}}:\mathbb{R}^{+}\rightarrow \mathbb{R}$ such that (see Figure 2):

1. (1) $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D716}}^{\text{Dehn}}(r)=2\unicode[STIX]{x1D70B}-r$ for $r\ll \unicode[STIX]{x1D716}$ ;

2. (2) $0<\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D716}}^{\text{Dehn}}(r)<2\unicode[STIX]{x1D70B}$ for all $r<\unicode[STIX]{x1D716}$ ; and

3. (3) $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D716}}^{\text{Dehn}}(r)=0$ for $r\geqslant \unicode[STIX]{x1D716}$ .

Definition 2.2. If $S$ is not diffeomorphic to a sphere, the model Dehn twist $(\unicode[STIX]{x1D70F}_{S},\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D716}}^{\text{Dehn}})$ on $T^{\ast }S$ is given by

$$\begin{eqnarray}\unicode[STIX]{x1D70F}_{S}(\unicode[STIX]{x1D709})=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D716}}^{\text{Dehn}}(\Vert \unicode[STIX]{x1D709}\Vert )}^{\unicode[STIX]{x1D70E}}(\unicode[STIX]{x1D709})\end{eqnarray}$$

on $T^{\ast }S-\{0_{\text{section}}\}$ and identity on the zero section.

Figure 2. A Dehn twist profile $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D716}}^{\text{Dehn}}$ when $S\neq S^{n}$ .

We will simply write $\unicode[STIX]{x1D70F}_{S}$ instead of $(\unicode[STIX]{x1D70F}_{S},\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D716}}^{\text{Dehn}})$ .

When $S$ is diffeomorphic to a sphere, the spherical Dehn twist profile $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D716}}^{\text{Dehn},\text{sp}}$ is picked with (1), (2) above replaced by:

( $1^{\prime }$ )

$\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D716}}^{\text{Dehn},\text{sp}}(r)=\unicode[STIX]{x1D70B}-r$ for $r\ll \unicode[STIX]{x1D716}$ ; and

( $2^{\prime }$ )

$0<\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D716}}^{\text{Dehn},\text{sp}}(r)<\unicode[STIX]{x1D70B}$ for all $r<\unicode[STIX]{x1D716}$ .

In this case, the Dehn twist $(\unicode[STIX]{x1D70F}_{S},\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D716}}^{\text{Dehn},\text{sp}})$ is defined analogously but the antipodal map is used to extend smoothly along the zero section instead of the identity map.

Example 2.3. Let $T^{\ast }S^{1}=\mathbb{R}/2\unicode[STIX]{x1D70B}\mathbb{Z}\times \mathbb{R}$ with coordinates $(q,p)\in \mathbb{R}/2\unicode[STIX]{x1D70B}\mathbb{Z}\times \mathbb{R}$ be equipped with the standard symplectic form $\unicode[STIX]{x1D714}_{S^{1}}=dp\wedge dq$ . For a spherical profile $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D716}}^{\text{Dehn},\text{sp}}$ , $(\unicode[STIX]{x1D70F}_{S^{1}},\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D716}}^{\text{Dehn},\text{sp}})$ is defined by

$$\begin{eqnarray}\unicode[STIX]{x1D70F}_{S^{1}}(q,p)=\left\{\begin{array}{@{}ll@{}}\displaystyle \bigg(q+\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D716}}^{\text{Dehn},\text{sp}}(\Vert p\Vert )\frac{p}{\Vert p\Vert },p\bigg) & \text{for }p\neq 0,\\ (q+\unicode[STIX]{x1D70B},0) & \text{for }p=0.\end{array}\right.\end{eqnarray}$$

Consider the double cover $\unicode[STIX]{x1D704}_{\text{double}}:T^{\ast }S^{1}\rightarrow T^{\ast }\mathbb{RP}^{1}=\mathbb{R}/2\unicode[STIX]{x1D70B}\mathbb{Z}\times \mathbb{R}$ given by

(2.1) $$\begin{eqnarray}\unicode[STIX]{x1D704}_{\text{double}}(q,p)=(2q,{\textstyle \frac{1}{2}}p)=(\widetilde{q},\widetilde{p}).\end{eqnarray}$$

For $(\widetilde{q},\widetilde{p})=\unicode[STIX]{x1D704}_{\text{double}}(q,p)\in T^{\ast }\mathbb{RP}^{1}$ , we define

$$\begin{eqnarray}T(\widetilde{q},\widetilde{p})=\unicode[STIX]{x1D704}_{\text{double}}\circ \unicode[STIX]{x1D70F}_{S^{1}}(q,p)\end{eqnarray}$$

which is independent of the choice of the preimage $(q,p)$ of $(\widetilde{q},\widetilde{p})$ . It is an easy exercise to show that $T$ is Hamiltonian isotopic to $\unicode[STIX]{x1D70F}_{\mathbb{RP}^{1}}$ for the new Dehn twist profile under the change of coordinates (2.1). Also, if we identify $T^{\ast }\mathbb{RP}^{1}$ with $T^{\ast }S^{1}$ so that $\unicode[STIX]{x1D70F}_{S^{1}}$ is well defined on $T^{\ast }\mathbb{RP}^{1}$ , then $T$ is also Hamiltonian isotopic to $\unicode[STIX]{x1D70F}_{S^{1}}^{2}$ for an appropriate choice of spherical profile.

This example has the following well-known immediate generalizations.

Lemma 2.4. Let $\unicode[STIX]{x1D704}_{\text{double}}:T^{\ast }S^{n}\rightarrow T^{\ast }\mathbb{RP}^{n}$ be the symplectic double cover obtained from the double cover of the zero section. For $(\widetilde{q},\widetilde{p})=\unicode[STIX]{x1D704}_{\text{double}}(q,p)\in T^{\ast }\mathbb{RP}^{n}$ ,

$$\begin{eqnarray}T(\widetilde{q},\widetilde{p})=\unicode[STIX]{x1D704}_{\text{double}}\circ \unicode[STIX]{x1D70F}_{S^{n}}(q,p)\end{eqnarray}$$

is well defined and $T$ is Hamiltonian isotopic to $\unicode[STIX]{x1D70F}_{\mathbb{RP}^{n}}$ for an appropriate choice of auxiliary function defining $\unicode[STIX]{x1D70F}_{\mathbb{RP}^{n}}$ .

If $n>1$ , the choice of auxiliary function defining $\unicode[STIX]{x1D70F}_{\mathbb{RP}^{n}}$ is irrelevant up to Hamiltonian isotopy.

Proof. Since the Hamiltonian function is radial and invariant under the antipodal map on $S^{n}$ , the time- $t$ flow on $T^{\ast }\mathbb{R}\mathbb{P}^{n}$ lifts to a time- $t$ flow on $T^{\ast }S^{n}$ . More precisely, the function $\tilde{\unicode[STIX]{x1D70E}}:=\unicode[STIX]{x1D70E}\,\circ \,\unicode[STIX]{x1D704}_{\text{double}}:T^{\ast }S^{n}\rightarrow \mathbb{R}$ is given by $\tilde{\unicode[STIX]{x1D70E}}(\unicode[STIX]{x1D709})=\Vert \unicode[STIX]{x1D709}\Vert$ with respect to the pull-back bundle metric from $T^{\ast }\mathbb{RP}^{n}$ by $\unicode[STIX]{x1D704}_{\text{double}}$ so we have $\unicode[STIX]{x1D704}_{\text{double}}\circ \unicode[STIX]{x1D719}_{t}^{\tilde{\unicode[STIX]{x1D70E}}}=\unicode[STIX]{x1D719}_{t}^{\unicode[STIX]{x1D70E}}\circ \unicode[STIX]{x1D704}_{\text{double}}$ . In particular, we have

(2.2) $$\begin{eqnarray}\unicode[STIX]{x1D704}_{\text{double}}\circ \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D716}}^{\text{Dehn}}(\Vert \unicode[STIX]{x1D709}\Vert )}^{\tilde{\unicode[STIX]{x1D70E}}}(\unicode[STIX]{x1D709})=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D716}}^{\text{Dehn}}(\Vert \unicode[STIX]{x1D704}_{\text{double}}(\unicode[STIX]{x1D709})\Vert )}^{\unicode[STIX]{x1D70E}}\circ \unicode[STIX]{x1D704}_{\text{double}}(\unicode[STIX]{x1D709})\end{eqnarray}$$

for any Dehn twist profile $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D716}}^{\text{Dehn}}$ . Since the shortest period of geodesics of $S^{n}$ with respect to the pull-back Riemannian metric by $\unicode[STIX]{x1D704}_{\text{double}}$ is $4\unicode[STIX]{x1D70B}$ instead of $2\unicode[STIX]{x1D70B}$ , the left-hand side of (2.2) equals $\unicode[STIX]{x1D704}_{\text{double}}\circ \unicode[STIX]{x1D70F}_{S^{n}}(\unicode[STIX]{x1D709})$ when $\Vert \unicode[STIX]{x1D709}\Vert \neq 0$ . The right-hand side of (2.2) equals $\unicode[STIX]{x1D70F}_{\mathbb{RP}^{n}}\circ \unicode[STIX]{x1D704}_{\text{double}}(\unicode[STIX]{x1D709})$ when $\Vert \unicode[STIX]{x1D709}\Vert \neq 0$ , so the result follows.◻

Lemma 2.5 (See [Sei00] or [Har11]).

For $T^{\ast }S^{2}=T^{\ast }\mathbb{CP}^{1}$ , $\unicode[STIX]{x1D70F}_{S^{2}}^{2}$ is Hamiltonian isotopic to $\unicode[STIX]{x1D70F}_{\mathbb{CP}^{1}}$ .

As usual, one may globalize the model Dehn twist.

Definition 2.6. A Dehn twist along $S$ in $M$ is a compactly supported symplectomorphism defined by the model Dehn twist as above in a Weinstein neighborhood of $S$ and extended by identity outside.

For more details and the dependence of choices used to define $\unicode[STIX]{x1D70F}_{S}$ , see [Sei99] and [Sei03].

2.2 Lagrangian surgery through flow handles

2.2.1 Surgery at a point

We first recall the definition of a Lagrangian surgery at a transversal intersection point from [LS91], [Pol91] and [BC13].

Definition 2.7. Let $a(s),b(s)\in \mathbb{R}$ . A smooth curve $\unicode[STIX]{x1D6FE}(s)=a(s)\,+\,ib(s)\in \mathbb{C}$ is called $\unicode[STIX]{x1D706}$ -admissible if (see Figure 3):

• ∙ $(a(s),b(s))=(-s+\unicode[STIX]{x1D706},0)$ for $s\leqslant 0$ ;

• ∙ $a^{\prime }(s),b^{\prime }(s)<0$ for $s\in (0,\unicode[STIX]{x1D716})$ ; and

• ∙ $(a(s),b(s))=(0,-s)$ for $s\geqslant \unicode[STIX]{x1D716}$ (note that $b(\unicode[STIX]{x1D716})=-\unicode[STIX]{x1D716}$ ).

Figure 3. Picture of an admissible curve.

The part of a $\unicode[STIX]{x1D706}$ -admissible curve with $s\in [0,\unicode[STIX]{x1D716}]$ can be uniquely captured by $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}}(r):=a(b^{-1}(-r))\in [0,\unicode[STIX]{x1D706}]$ . The main property of an admissible curve can be translated into properties of $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}}$ as follows:

1. (1) $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}}(0)=\unicode[STIX]{x1D706}>0$ , and $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}}^{\prime }(r)<0$ for $r\in (0,\unicode[STIX]{x1D716})$ ;

2. (2) $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}}^{-1}(r)$ and $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}}(r)$ have vanishing derivatives of all orders at $r=\unicode[STIX]{x1D706}$ and $r=\unicode[STIX]{x1D716}$ , respectively.

Figure 4. Admissible and semi-admissible functions.

Such a function will also be called $\unicode[STIX]{x1D706}$ -admissible. We will frequently use the two equivalent descriptions of admissibility interchangeably.

We also define a class of semi-admissible functions, by relaxing (2) to:

$(2^{\prime })$ $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}}^{\prime }(0)=-\unicode[STIX]{x1D6FC}\in [-\infty ,0]$ . Here $\unicode[STIX]{x1D6FC}=\infty$ if $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}}$ is admissible.

See an example of admissible and semi-admissible function in Figure 4.

Note that in all definitions of (semi-)admissibility there is an extra variable $\unicode[STIX]{x1D716}$ . We will see that the dependence on $\unicode[STIX]{x1D716}$ is not significant in this paper: we fix $\unicode[STIX]{x1D716}$ for each pair of Lagrangian submanifolds $(L_{1},L_{2})$ once and for all. In any surgery constructions appearing later, the resulting surgery manifold yields a smooth family of Lagrangian isotopic submanifolds as $\unicode[STIX]{x1D716}$ varies. In the context of Dehn twists, this family becomes Hamiltonian isotopic. As a result, we will suppress the dependence of $\unicode[STIX]{x1D716}$ unless necessary.

Given a $\unicode[STIX]{x1D706}$ -admissible curve $\unicode[STIX]{x1D6FE}$ , define the handle

$$\begin{eqnarray}H_{\unicode[STIX]{x1D6FE}}=\Big\{(\unicode[STIX]{x1D6FE}(s)x_{1},\ldots ,\unicode[STIX]{x1D6FE}(s)x_{n})\mid s,x_{i}\in \mathbb{R},\sum \mathop{x}_{i}^{2}=1\Big\}\subset \mathbb{C}^{n}.\end{eqnarray}$$

Lemma 2.8. For a $\unicode[STIX]{x1D706}$ -admissible $\unicode[STIX]{x1D6FE}$ , $H_{\unicode[STIX]{x1D6FE}}$ is a Lagrangian submanifold of $(\mathbb{C}^{n},\sum dx_{i}\wedge dy_{i})$ .

Proof. Let $J$ be the standard complex structure on $\mathbb{C}^{n}$ and $g(\cdot ,\cdot ):=\unicode[STIX]{x1D714}(\cdot ,J\cdot )$ be the standard flat metric. Observe that $T_{\unicode[STIX]{x1D6FE}(s)x}H_{\unicode[STIX]{x1D6FE}}=\operatorname{Span}_{\mathbb{R}}\{\unicode[STIX]{x1D6FE}^{\prime }(s)x\}\,\oplus \,\unicode[STIX]{x1D6FE}(s)T_{x}S^{n-1}$ , for $x=(x_{1},\ldots ,x_{n})\in S^{n-1}\subset \mathbb{R}^{n}$ . A tangent vector in the second summand can be represented by $\unicode[STIX]{x1D6FE}(s)y=\unicode[STIX]{x1D6FE}(s)(y_{1},\ldots ,y_{n})$ , where $y\in \mathbb{R}^{n}$ and $g(x,y)=0$ . We have

$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D714}(\unicode[STIX]{x1D6FE}^{\prime }(s)x,\unicode[STIX]{x1D6FE}(s)y) & = & \displaystyle -g(\unicode[STIX]{x1D6FE}(s)^{\prime }x,J(\unicode[STIX]{x1D6FE}(s)y))\nonumber\\ \displaystyle & = & \displaystyle -g(a^{\prime }(s)x+b^{\prime }(s)J(x),-b(s)y+a(s)J(y))\nonumber\\ \displaystyle & = & \displaystyle a^{\prime }(s)b(s)g(x,y)-b^{\prime }(s)a(s)g(J(x),J(y))=0,\nonumber\end{eqnarray}$$

where $\unicode[STIX]{x1D6FE}(s)=(a(s),b(s))$ . The fact that $\unicode[STIX]{x1D714}|_{\unicode[STIX]{x1D6FE}(s)T_{x}S^{n-1}}=0$ is obvious, so the result follows.◻

As a consequence, we have the following corollary.

Corollary 2.9. Let $L_{1},L_{2}\subset (M,\unicode[STIX]{x1D714})$ be two Lagrangians transversely intersecting at $p$ . Let $\unicode[STIX]{x1D704}:U\rightarrow M$ be the Darboux chart around $p$ with a standard complex structure so that $\unicode[STIX]{x1D704}^{-1}(L_{1})\subset \mathbb{R}^{n}$ and $\unicode[STIX]{x1D704}^{-1}(L_{2})\subset i\mathbb{R}^{n}$ are disks centered at the origin. Then one can obtain a Lagrangian $L_{1}\text{\#}_{p,st}L_{2}$ by attaching a Lagrangian handle $\unicode[STIX]{x1D704}(H_{\unicode[STIX]{x1D6FE}})$ to $(L_{1}\cup L_{2})\backslash \unicode[STIX]{x1D704}(U)$ .

The Lagrangian $L_{1}\text{\#}_{p,st}L_{2}$ is called a Lagrangian surgery from $L_{1}$ to $L_{2}$ following [LS91, Pol91]. Note that, the Lagrangian $L_{2}\text{\#}_{p,st}L_{1}$ obtained by performing Lagrangian surgery from $L_{2}$ to $L_{1}$ is in general not even smoothly isotopic to $L_{1}\text{\#}_{p,st}L_{2}$ .

Now, we present an new approach to performing Lagrangian surgery which also motivates the definition of Lagrangian surgery along clean intersections.

Definition 2.10. Given the zero section $L\subset T^{\ast }L$ , a Riemannian metric $g$ on $L$ (hence inducing a bundle metric on $T^{\ast }L$ ), a point $x\in L$ , and a choice of $\unicode[STIX]{x1D70E}$ as in Lemma 2.1, we define the flow handle $H_{\unicode[STIX]{x1D708}}$ with respect to a $\unicode[STIX]{x1D706}$ -admissible function $\unicode[STIX]{x1D708}$ to be (see Figure 5)

$$\begin{eqnarray}H_{\unicode[STIX]{x1D708}}=\{\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D708}(\Vert p\Vert )}^{\unicode[STIX]{x1D70E}}(p)\in T^{\ast }L:p\in (T_{x}^{\ast }L)_{\unicode[STIX]{x1D716}}\backslash \{x\}\},\end{eqnarray}$$

where $(T_{x}^{\ast }L)_{\unicode[STIX]{x1D716}}$ denotes the cotangent vectors at $x\in L$ with length ${\leqslant}\unicode[STIX]{x1D716}$ .

The following elementary fact about geodesics will be repeatedly used.

Lemma 2.11. Let $L$ , $x$ and $H_{\unicode[STIX]{x1D708}}$ be as above. Let $\unicode[STIX]{x1D6FE}:[0,c]\rightarrow L$ be a unit-speed geodesic starting at $\unicode[STIX]{x1D6FE}(0)=x$ . Then there is an induced symplectic embedding $T^{\ast }[0,c]\rightarrow T^{\ast }L$ and

$$\begin{eqnarray}T^{\ast }[0,c]\cap H_{\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D6FC}}}=\bigg\{\bigg(\frac{\unicode[STIX]{x1D708}(\Vert p\Vert )p}{\Vert p\Vert },p\bigg)\in T^{\ast }[0,c]\,\biggr|\,p\in (0,\unicode[STIX]{x1D716}],\unicode[STIX]{x1D708}(p)\leqslant c\bigg\}.\end{eqnarray}$$

Proof. We have an embedding $\unicode[STIX]{x1D6FE}_{\ast }:T[0,c]\rightarrow TL$ . The tangent bundles can be dualized to an embedding $T^{\ast }[0,c]\rightarrow T^{\ast }L$ using the standard metric on $T[0,1]$ and $TL$ . To see that this embedding is symplectic when $\unicode[STIX]{x1D6FE}$ is a geodesic, we can pick a geodesic ball $U$ with a normal coordinate system $q=(q_{1},\ldots ,q_{n})$ centered at $x$ . We can assume $\unicode[STIX]{x1D6FE}(t)=(t,0,\ldots ,0)$ . Let $0\neq v\in T[0,c]$ and $\unicode[STIX]{x1D6FE}_{\ast }v\in TL$ . By definition, the dual of $\unicode[STIX]{x1D6FE}_{\ast }v\in TL$ , denoted by $(\unicode[STIX]{x1D6FE}_{\ast }v)^{\ast }:=\,\,g(-,\unicode[STIX]{x1D6FE}_{\ast }v)\in T^{\ast }L$ , vanishes when it is evaluated at vectors perpendicular to $\unicode[STIX]{x1D6FE}_{\ast }v$ . Since $U$ is a geodesic ball, vectors perpendicular to $\mathbb{R}\unicode[STIX]{x1D6FE}_{\ast }v=\mathbb{R}\unicode[STIX]{x2202}_{q_{1}}$ are spanned by vectors $\unicode[STIX]{x2202}_{q_{2}},\ldots ,\unicode[STIX]{x2202}_{q_{n}}$ . Therefore, $(\unicode[STIX]{x1D6FE}_{\ast }v)^{\ast }=|v|\,dq_{1}$ where $|v|$ is the norm of $v$ measured in standard metric in $[0,c]$ . As a result, the embedding $T^{\ast }[0,c]\rightarrow T^{\ast }L$ is given by $(q^{\prime },p^{\prime })\mapsto (q,p)=((q^{\prime },0,\ldots ,0),(p^{\prime },\ldots ,0))$ which is clearly symplectic. By definition, we have $T^{\ast }[0,c]\,\cap \,H_{\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D6FC}}}=\{(\unicode[STIX]{x1D708}(\Vert p\Vert )p/\Vert p\Vert ,p)\in T^{\ast }[0,c]\mid p\in (0,\unicode[STIX]{x1D716}],\unicode[STIX]{x1D708}(p)\leqslant c\}$ , so the result follows.◻

Figure 5. A flow handle.

Remark 2.12. The time-1 Hamiltonian flow of $\widetilde{\unicode[STIX]{x1D708}}(\Vert p\Vert )$ , where $\widetilde{\unicode[STIX]{x1D708}}^{\prime }(s)=\unicode[STIX]{x1D708}(s)$ , is $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D708}(\Vert p\Vert )}^{\unicode[STIX]{x1D70E}}$ . For this reason, the reader should keep in mind that $H_{\unicode[STIX]{x1D708}}$ is automatically Lagrangian for any choice of admissible $\unicode[STIX]{x1D708}$ . For our purposes, the discussion on $\unicode[STIX]{x1D708}$ will be more flexible so we suppress the role of the actual Hamiltonian function $\widetilde{\unicode[STIX]{x1D708}}$ unless otherwise specified.

Lemma 2.13. Let $S_{\unicode[STIX]{x1D706}}(T_{x}^{\ast }L)$ be the radius $\unicode[STIX]{x1D706}$ -sphere in the cotangent plane of $x$ . We use the exponential map on the cotangent bundle via the identification of $T^{\ast }L$ and $TL$ . If $\exp :S_{\unicode[STIX]{x1D706}}(T_{x}^{\ast }L)\rightarrow L$ is an embedding, and $\unicode[STIX]{x2202}H_{\unicode[STIX]{x1D708}}\,\cap \,L=\exp (S_{\unicode[STIX]{x1D706}}(T_{x}^{\ast }L))\subset L$ divides $L$ into two components, then $H_{\unicode[STIX]{x1D708}}$ glues with exactly one of the components, as well as $T_{x}^{\ast }L\setminus (T_{x}^{\ast }L)_{\unicode[STIX]{x1D716}}$ , to form a smooth Lagrangian submanifold coinciding with $T_{x}^{\ast }L$ outside a compact set for a $\unicode[STIX]{x1D706}$ -admissible $\unicode[STIX]{x1D708}$ .

Proof. The only thing left to prove is the smoothness of gluing on $\unicode[STIX]{x2202}H_{\unicode[STIX]{x1D708}}=\exp (S_{\unicode[STIX]{x1D706}}(T_{x}^{\ast }L))$ . Note that from the assumptions, $\unicode[STIX]{x1D706}$ is not a critical radius of the exponential map, hence the exponential map is a diffeomorphism near $S_{\unicode[STIX]{x1D706}}(T_{x}^{\ast }L)$ . The flow $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D708}(\Vert p\Vert )}^{\unicode[STIX]{x1D70E}}$ , followed by the projection to $L$ , is the same as $\exp (\unicode[STIX]{x1D708}(\Vert p\Vert )\cdot (p/\Vert p\Vert ))$ , which is a diffeomorphism. Therefore, near $\unicode[STIX]{x2202}H_{\unicode[STIX]{x1D708}}$ , the handle is a smooth Lagrangian section of $T^{\ast }L$ over the open shell $\exp (B_{\unicode[STIX]{x1D706}}(T_{x}^{\ast }L)\backslash \overline{B_{\unicode[STIX]{x1D706}-\unicode[STIX]{x1D6FF}}(T_{x}^{\ast }L)})$ , which is a smooth open submanifold of $L$ . Here, $B_{r}(T_{x}^{\ast }L)$ is the radius- $r$ ball of $T_{x}^{\ast }L$ centered at the origin. Moreover, the section has vanishing derivatives for all orders on the boundary component $S_{\unicode[STIX]{x1D706}}(T_{x}^{\ast }L)$ due to the assumption of admissibility on $\unicode[STIX]{x1D708}(r)$ near $r=0$ . The conclusion follows.◻

Example 2.14. One may match the Lagrangian handle $H_{\unicode[STIX]{x1D6FE}}$ and flow handle $H_{\unicode[STIX]{x1D708}}$ for an admissible $\unicode[STIX]{x1D6FE}$ and its corresponding admissible $\unicode[STIX]{x1D708}(r)=a(b^{-1}(-r))$ (see Definition 2.7 and the paragraph after it) via the identification between $T^{\ast }\mathbb{R}^{n}$ and $\mathbb{C}^{n}$ .

To see this, take an admissible curve $\unicode[STIX]{x1D6FE}(s)=(a(s),b(s))$ and its flow handle $H_{\unicode[STIX]{x1D6FE}}$ . We consider the flow handle

$$\begin{eqnarray}H_{\unicode[STIX]{x1D708}}=\bigg\{\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D708}(\Vert p\Vert )}^{\unicode[STIX]{x1D70E}}(0,p)=\bigg(0+\frac{p}{\Vert p\Vert }\cdot \unicode[STIX]{x1D708}(\Vert p\Vert ),p\bigg):p\in (T_{0}^{\ast }\mathbb{R}^{n})_{\unicode[STIX]{x1D716}}\bigg\}.\end{eqnarray}$$

We now identify $T^{\ast }\mathbb{R}^{n}$ with $\mathbb{C}^{n}$ by sending $(q,p)\mapsto q-ip$ , which matches the symplectic form $dp\wedge dq$ and $(1/-2i)\,dz\wedge d\bar{z}=dx\wedge dy$ . Then by definition

$$\begin{eqnarray}\displaystyle \bigg(\unicode[STIX]{x1D708}(\Vert p\Vert )\frac{p}{\Vert p\Vert },p\bigg) & \mapsto & \displaystyle \unicode[STIX]{x1D708}(\Vert p\Vert )\frac{p}{\Vert p\Vert }-ip\nonumber\\ \displaystyle & = & \displaystyle (\unicode[STIX]{x1D708}(\Vert p\Vert )-i\Vert p\Vert )\frac{p}{\Vert p\Vert }\nonumber\\ \displaystyle & = & \displaystyle (a(b^{-1}(-\Vert p\Vert ))+ib(b^{-1}(-\Vert p\Vert )))\frac{p}{\Vert p\Vert }\nonumber\\ \displaystyle & = & \displaystyle (a(s)+ib(s))x\nonumber\end{eqnarray}$$

by a change of variable $s=b^{-1}(-\Vert p\Vert )$ and $x=p/\Vert p\Vert$ . By this identification, we will simply use $H_{\unicode[STIX]{x1D708}}$ to denote both handles.

Corollary 2.15. Let $L_{1},L_{2}\subset (M,\unicode[STIX]{x1D714})$ be two Lagrangians transversely intersecting at $p$ . Under the assumption in Lemma 2.13, one can obtain a Lagrangian $L_{1}\text{\#}_{p}^{\unicode[STIX]{x1D708}}L_{2}$ by gluing: (1) $L_{2}\backslash U$ , for an $\unicode[STIX]{x1D716}$ -neighborhood $U$ of $p$ ; (2) the Lagrangian flow handle $H_{\unicode[STIX]{x1D708}}$ ; and (3) an open set in $L_{1}$ that glues with $H_{\unicode[STIX]{x1D708}}$ given by Lemma 2.13. For appropriately chosen $\unicode[STIX]{x1D708}$ , $L_{1}\text{\#}_{p}^{\unicode[STIX]{x1D708}}L_{2}$ coincides with $L_{1}\text{\#}_{p,st}L_{2}$ defined in Corollary 2.9.

Proof. Clearly $H_{\unicode[STIX]{x1D708}}$ glues smoothly with $L_{2}\backslash U$ and the open set in $L_{1}$ by Lemma 2.13, and the result is a smooth Lagrangian submanifold. Let $\unicode[STIX]{x1D708}(x)=a(b^{-1}(-x))$ be chosen as in Example 2.14 for an admissible curve. The flow handle is then identified with the standard Lagrangian handle defined by Lalonde and Sikorav, and Polterovich.◻

The following lemma addresses the independence of the surgery Lagrangians on the choice of profile functions.

Lemma 2.16. If $L_{1}$ is simply-connected, and the surgery profile and the injectivity radius of the exponential map at $x$ satisfies $\unicode[STIX]{x1D708}(0)<\operatorname{inj}_{g}(x)$ , then the Hamiltonian isotopy type of the surgery Lagrangian is independent of the choice of $\unicode[STIX]{x1D708}(r)$ .

Proof. For any two flow handles with different surgery profiles, there is a Lagrangian isotopy between them by a family of flow handles. We want to show that this Lagrangian isotopy can be extended to a symplectic isotopy using (a minor modification of) Banyaga’s isotopy extension theorem [MS98, Theorem 3.19].

Let $W$ be a Weinstein neighborhood of $L_{1}$ and ${\mathcal{N}}$ be a neighborhood of a flow handle in $W$ . Following the proof of [MS98, Theorem 3.19], it is sufficient to show that the relative cohomology $H^{2}(W,\unicode[STIX]{x2202}W\cup {\mathcal{N}};\mathbb{R})$ vanishes. But this cohomology is nothing but the second cohomology of the following space: take the Thom space of $T^{\ast }L_{1}$ (whose second cohomology vanishes when dim $L_{1}>2$ ), then collapse an additional cycle obtained from the connected sum of a fiber and the zero section. Therefore, the vanishing of $H^{2}(W,\unicode[STIX]{x2202}W\cup {\mathcal{N}};\mathbb{R})$ can be obtained by the long exact sequence of the relative cohomologies when $L_{1}$ is simply connected and dim $L_{1}>2$ . When $\operatorname{dim}L_{1}=2$ , the long exact sequence reads

$$\begin{eqnarray}\displaystyle H^{1}(L_{1};\mathbb{R})\cong H^{1}(D^{2}\text{\#}L_{1},S^{1};\mathbb{R}) & \rightarrow & \displaystyle H^{2}(W,\unicode[STIX]{x2202}W\cup D^{2}\text{\#}L_{1};\mathbb{R})\rightarrow H^{2}(W,\unicode[STIX]{x2202}W)\nonumber\\ \displaystyle & \rightarrow & \displaystyle H^{2}(D^{2}\text{\#}L_{1},S^{1};\mathbb{R}).\nonumber\end{eqnarray}$$

The last arrow is an isomorphism by restriction of the Thom form, hence the first arrow is again surjective. The rest of the argument will then go through. To argue the symplectic isotopy obtained by Banyaga’s argument is Hamiltonian, use the assumption of simply-connectedness again.◻

We give two examples of flow handles that are different from standard handles.

Example 2.17. Let $r(p)$ be the injectivity radius of $p$ . For different choices of $\unicode[STIX]{x1D708}(r)$ with $\unicode[STIX]{x1D708}(0)<r(p)$ , these handles will define a family of different Lagrangian surgeries which are all Lagrangian isotopic to each other.

The situation becomes more interesting when $\unicode[STIX]{x1D708}(0)>r(p)$ . Some simple instances are given by $S=\mathbb{R}\mathbb{P}^{n}$ , $\mathbb{C}\mathbb{P}^{n}$ or any finite cover of rank-one symmetric space. Take $\mathbb{C}\mathbb{P}^{n}$ and its standard Fubini–Study metric as an example, for any $p\in S$ , the flow surgery can be performed for $kr(p)<\unicode[STIX]{x1D708}(0)<(k+1)r(p)$ for any $k\in \mathbb{Z}$ . Later we will see that such surgeries are indeed iterated surgeries in the ordinary sense in Lemma 3.3 (although surgeries along clean intersections will be involved).

Example 2.18. A less standard example is essentially given by exotic spheres in [Sei14]. Given any $f\in \operatorname{Diff}^{+}(S^{n-1})$ , one may form an exotic sphere $S_{f}=B_{-}\bigcup _{f}B_{+}$ by gluing two copies $B_{\pm }$ of $B^{n}$ via $f$ . There is a Riemannian metric on $S_{f}$ so that all geodesics starting from the origins $0_{\pm }\in B_{\pm }$ are closed, passing through both $0_{\pm }$ , and of the same length [Sei14, Lemma 2.1]. Take $p=0_{-}\in B_{-}$ . When $\unicode[STIX]{x1D706}$ is below the injectivity radius, the corresponding flow handle surgery is the original one considered in [Pol91]. When $\unicode[STIX]{x1D708}(0)>r(p)$ , the generalized surgery defined above is identified with an iterated surgery along $p$ and $q=0_{+}\in B_{+}$ in a successive order, which is exactly the family constructed in [Sei14] by the geodesic flow.

The following lemma can be found in [Sei99], but we feel that it is instructive to sketch its proof from the point of view of flow handles to make our discussion complete.

Lemma 2.19 [Sei99].

Let $x\in S^{n}$ be a point and consider $L=\unicode[STIX]{x1D70F}_{S^{n}}(T_{x}^{\ast }S^{n})\subset T^{\ast }S^{n}$ . Then $S^{n}\text{\#}_{x}^{\unicode[STIX]{x1D708}}T_{x}^{\ast }S^{n}$ is Hamiltonian isotopic to $L$ through a compactly supported Hamiltonian, where $\unicode[STIX]{x1D708}$ is an admissible function such that $\unicode[STIX]{x1D708}(0)<r(x)$ , the injectivity radius of $x$ under the round metric.

Proof. Let $S^{n}$ be equipped with the round metric such that every embedded closed geodesic has length $2\unicode[STIX]{x1D70B}$ . This induces a metric on $T^{\ast }S^{n}$ which we will use throughout. Denote by $A:S^{n}\rightarrow S^{n}$ the antipodal map.

We consider two embeddings of open geodesic balls $B_{\unicode[STIX]{x1D70B}}(x){\hookrightarrow}S^{n}$ and $B_{\unicode[STIX]{x1D70B}}(A(x)){\hookrightarrow}S^{n}$ into the zero section, which are of radius $\unicode[STIX]{x1D70B}$ , and centered at $x$ and $A(x)$ , respectively. Also fix a normal coordinate system on each of these balls, which induces a trivialization (and a chart) on $T^{\ast }B_{\unicode[STIX]{x1D70B}}(x)$ and $T^{\ast }B_{\unicode[STIX]{x1D70B}}(A(x))$ .

The two embeddings give two symplectomorphisms $f_{x}:T^{\ast }B_{\unicode[STIX]{x1D70B}}(x)\rightarrow T^{\ast }S^{n}\backslash T_{A(x)}^{\ast }S^{n}$ and $f_{A(x)}:T^{\ast }B_{\unicode[STIX]{x1D70B}}(A(x))\rightarrow T^{\ast }S^{n}\backslash T_{x}^{\ast }S^{n}$ . Indeed, these symplectomorphisms come from the definition of the canonical symplectic form on a cotangent bundle, which patches the forms $dp\wedge dq$ for the two local charts on the zero section as above. Recall the notation of spherical Dehn twist profile from the paragraph following Lemma 2.1, and $\unicode[STIX]{x1D716}$ is an arbitrary small positive constant. Under these symplectomorphisms we have by Lemma 2.11

$$\begin{eqnarray}f_{x}^{-1}(L)=\bigg\{\bigg(\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D716}}^{\text{Dehn},\text{sp}}(\Vert p\Vert )\frac{p}{\Vert p\Vert },p\bigg)\in T^{\ast }B_{\unicode[STIX]{x1D70B}}(x):p\in \mathbb{R}^{n}\backslash \{0\}\bigg\}\end{eqnarray}$$

and

$$\begin{eqnarray}f_{A(x)}^{-1}(L)=\bigg\{\bigg(\unicode[STIX]{x1D70B}-\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D716}}^{\text{Dehn},\text{sp}}(\Vert p\Vert ))\frac{p}{\Vert p\Vert },p\bigg)\in T^{\ast }B_{\unicode[STIX]{x1D70B}}(A(x)):p\in B_{\unicode[STIX]{x1D716}}(0)\bigg\}.\end{eqnarray}$$

Here, we use the properties that $B_{\unicode[STIX]{x1D70B}}(x){\hookrightarrow}S^{n}$ are geodesic ball embeddings.

On the other hand, suppose $\unicode[STIX]{x1D708}=\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}}$ is such that $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}}(0)=\unicode[STIX]{x1D706}<\unicode[STIX]{x1D70B}=r(x)$ (see § 2.2.1). Then $f_{x}^{-1}(H_{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}}})$ is given by

$$\begin{eqnarray}\displaystyle f_{x}^{-1}(H_{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}}}) & = & \displaystyle \bigg\{\bigg(\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}}(\Vert p\Vert )\frac{p}{\Vert p\Vert },p\bigg)\in T^{\ast }B_{\unicode[STIX]{x1D70B}}(x):p\in \mathbb{R}^{n}\backslash \{0\}\bigg\}\nonumber\\ \displaystyle & & \displaystyle \cup \,\{(q,0)\in T^{\ast }B_{\unicode[STIX]{x1D70B}}(A(x)):q\in B_{\unicode[STIX]{x1D70B}}(0)\backslash B_{\unicode[STIX]{x1D706}}(0)\}.\nonumber\end{eqnarray}$$

Let $\unicode[STIX]{x1D6FF}>0$ be such that $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D716}}^{\text{Dehn},\text{sp}}(r)=\unicode[STIX]{x1D70B}-r$ for $r<\unicode[STIX]{x1D6FF}$ . We can pick $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}}$ such that $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}}(r)=\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D716}}^{\text{Dehn},\text{sp}}(r)$ for $r\geqslant \unicode[STIX]{x1D6FF}$ . The resulting $S^{n}\text{\#}_{x}^{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}}}T_{x}^{\ast }S^{n}$ hence coincides with $L$ outside $T^{\ast }B_{\unicode[STIX]{x1D6FF}}(A(x))$ . Inside $T^{\ast }B_{\unicode[STIX]{x1D6FF}}(A(x))$ , even though $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D716}}^{\text{Dehn},\text{sp}}$ is not an admissible function, both $S^{n}\text{\#}_{x}^{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}}}T_{x}^{\ast }S^{n}$ and $L$ are graphs of exact 1-forms (although the primitive function does not vanish near the boundary). Therefore, $S^{n}\text{\#}_{x}^{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}}}T_{x}^{\ast }S^{n}$ is Lagrangian isotopic to $L$ by varying the primitive function in $T^{\ast }B_{\unicode[STIX]{x1D6FF}}(A(x))$ but fixing them near the boundary, and hence Hamiltonian isotopic to $L$ by a compactly supported Hamiltonian due to the simply-connectedness of $T^{\ast }S^{n}$ and $L$ . (Extending an exact Lagrangian isotopy to a Hamiltonian isotopy is well known when the Lagrangian is compact, but when the exact Lagrangian has cylindrical ends, then it requires a relative version of Banyaga extension and the simply-connectedness assumption. See a completely parallel argument in Lemma 2.16.)◻

Remark 2.20. Consider the setting as in Corollary 2.15. For semi-admissible $\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D6FC}}$ that is not admissible, the gluing with $L_{1}$ cannot be smooth in general (for example, consider a semi-admissible profile where $\unicode[STIX]{x1D708}(0)<\unicode[STIX]{x1D70B}$ in the case when $L_{1}$ is a sphere with radius $1$ , then we will have a corner locus which is the circle that we glue along). Lemma 2.19 is an instance when a surgery using a semi-admissible profile $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D716}}^{\text{Dehn}}$ yields a smooth Lagrangian submanifold. Intuitively, the lemma regards $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D716}}^{\text{Dehn}}$ as a degenerate case of an admissible function. The point is that, when $\unicode[STIX]{x1D706}=r(p)$ , we only need to glue $\operatorname{Cl}(H_{\unicode[STIX]{x1D708}})$ with $L_{2}\backslash U$ (compare with Lemma 2.13, which exemplifies the more common case where $\operatorname{Cl}(H_{\unicode[STIX]{x1D708}})$ glues with an open subset of $L_{2}$ ), where $\operatorname{Cl}(\cdot )$ denotes the closure and $U$ is an $\unicode[STIX]{x1D716}$ -neighborhood of $p$ .

In the case when a semi-admissible function defines a smooth Lagrangian surgery manifold, we will continue to denote it as $L_{1}\text{\#}_{p}^{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D6FC}}}L_{2}$ . This applies to other surgeries along clean intersections and will be used several more times in a parametrized version in the paper.

2.2.2 Surgery along clean intersection

Let $L_{1}$ and $L_{2}$ be two Lagrangians in $(M,\unicode[STIX]{x1D714})$ which intersect cleanly at a submanifold $D$ . In other words, we have $T_{p}D=T_{p}L_{1}\cap T_{p}L_{2}$ for all $p\in D$ . The following well-known local proposition due to Pozniak allows us to extend the definition of flow handles to this case.

Proposition 2.21 [Poź99].

Let $L_{1},L_{2}\subset (M,\unicode[STIX]{x1D714})$ be two closed embedded Lagrangians with clean intersection at $L_{1}\cap L_{2}=D$ . Then there is a symplectic embedding $\unicode[STIX]{x1D711}$ from a neighborhood $U$ of $0_{\text{section}}\subset T^{\ast }L_{1}$ to $M$ such that $\unicode[STIX]{x1D711}(0_{\text{section}})=L_{1}$ and $\unicode[STIX]{x1D711}^{-1}(L_{2})\subset N_{D}^{\ast }$ , where $0_{\text{section}}$ is the zero section and $N_{D}^{\ast }$ is the conormal bundle of $D$ in $L_{1}$ .

Definition 2.22. Fix a metric $g$ on $L$ . We define the flow handle for $D\subset L$ with respect to an admissible function $\unicode[STIX]{x1D708}$ to be

$$\begin{eqnarray}H_{\unicode[STIX]{x1D708}}^{D}=\{\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D708}(\Vert \unicode[STIX]{x1D709}\Vert )}^{\unicode[STIX]{x1D70E}}(\unicode[STIX]{x1D709})\in T^{\ast }L:\unicode[STIX]{x1D709}\in (N_{D}^{\ast })_{\unicode[STIX]{x1D716}}\backslash D\},\end{eqnarray}$$

where $(N_{D}^{\ast })_{\unicode[STIX]{x1D716}}$ consists of covectors in the conormal bundle of $D$ in $L$ with length ${\leqslant}\unicode[STIX]{x1D716}$ .

Lemma 2.23. Let $S_{\unicode[STIX]{x1D706}}(N_{D}^{\ast })$ be the radius- $\unicode[STIX]{x1D706}$ sphere bundle in the conormal bundle of $D$ . If $\exp :S_{\unicode[STIX]{x1D706}}(N_{D}^{\ast })\rightarrow L$ is an embedding, and $\unicode[STIX]{x2202}H_{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}}}^{D}\cap L\subset L$ divides $L$ into two components, then $H_{\unicode[STIX]{x1D708}}^{D}$ glues with exactly one of the components to form a smooth Lagrangian submanifold coinciding with $N_{D}^{\ast }$ outside a compact set.

The proof is exactly the same as Lemma 2.13 and we omit it. Below, we call $r(D)>0$ the injectivity radius of $D$ , which is the supremum of $r>0$ such that the (dual) exponential map of $(N_{D}^{\ast })_{{\leqslant}r}$ is an embedding. It is positive since it is easy to check to be positive in a chart, and we only consider the case when $D$ is compact. As in the transversal intersection case, the surgery is always well defined when we choose $\unicode[STIX]{x1D708}(0)=\unicode[STIX]{x1D706}<r(D)$ . Using Proposition 2.21, we globalize the construction as follows.

Corollary 2.24. Let $L_{1},L_{2}\subset (M,\unicode[STIX]{x1D714})$ be two Lagrangians intersecting cleanly at $D$ . By choosing a metric on $L_{1}$ , a symplectic embedding $\unicode[STIX]{x1D704}:(T^{\ast }L_{1})_{\unicode[STIX]{x1D716}}\rightarrow M$ such that $\unicode[STIX]{x1D704}(0_{\text{section}})=L_{1}$ and $\unicode[STIX]{x1D704}^{-1}(L_{2})\subset N_{D}^{\ast }$ , one can obtain a Lagrangian $L_{1}\text{\#}_{D}^{\unicode[STIX]{x1D708}}L_{2}$ by attaching a Lagrangian flow handle $\unicode[STIX]{x1D704}(H_{\unicode[STIX]{x1D708}}^{D})$ to $(L_{1}\backslash U_{1})\cup (L_{2}\backslash U_{2})$ , with $U_{i}\subset L_{i}$ appropriate open neighborhoods of $D$ , and $\unicode[STIX]{x1D716}$ being sufficiently small.

As in Example 2.17, we denote $L_{1}\text{\#}_{D}^{\unicode[STIX]{x1D708}}L_{2}$ by $L_{1}\text{\#}_{D}L_{2}$ if $\unicode[STIX]{x1D706}<r(D)$ .

2.3 $E_{2}$ -flow surgery and its family version

We will introduce a generalization of flow handle which will be useful when performing surgeries on Lagrangian submanifolds in product symplectic manifolds later. Heuristically, our previous constructions have taken advantage of the fact that $\Vert p\Vert$ has a well-defined Hamiltonian flow on the whole cotangent bundle except for the zero section. More crucially, the resulting flow handle should have an embedded boundary in $L_{1}$ . Indeed, any Hamiltonian function with such properties will suffice for defining a meaningful Lagrangian handle.

A variant of the flow handle can therefore be defined as follows. Let $L=K_{1}^{n-m}\times K_{2}^{m}$ be a product manifold equipped with a product Riemannian metric. Then there is an orthogonal decomposition $T^{\ast }L=E_{1}\oplus E_{2}$ given by the two factors respectively. Let $D\subset L$ be of codimension $m$ and transverse to $\{p\}\times K_{2}$ for all $p\in K_{1}$ . Let $\unicode[STIX]{x1D70B}_{2}:T^{\ast }L\rightarrow E_{2}$ be the projection to $E_{2}$ . One may then use the function $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70B}}(\cdot )=\Vert \unicode[STIX]{x1D70B}_{2}(\cdot )\Vert _{g}:T^{\ast }L\rightarrow \mathbb{R}$ to define a new flow handle. Note that $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70B}}=\Vert \unicode[STIX]{x1D70B}_{2}(\cdot )\Vert _{g}$ is smooth on $T^{\ast }L\backslash E_{1}$ .

Figure 6. An $E_{2}$ -flow handle.

Definition 2.25. In the situation above, we define the $E_{2}$ -flow handle for $D$ (or flow handle along the $E_{2}$ -direction) with respect to an $\unicode[STIX]{x1D706}$ -admissible $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}}$ to be (see Figure 6)

$$\begin{eqnarray}H_{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}}}^{D,E_{2}}=\{\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}}(\Vert \unicode[STIX]{x1D70B}_{2}(\unicode[STIX]{x1D709})\Vert )}^{\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70B}}}(\unicode[STIX]{x1D709})\subset T^{\ast }L:\unicode[STIX]{x1D709}\in (N_{D}^{\ast })_{\unicode[STIX]{x1D716},E_{2}}\backslash D\},\end{eqnarray}$$

where $(N_{D}^{\ast })_{\unicode[STIX]{x1D716},E_{2}}$ consists of covectors $\unicode[STIX]{x1D709}$ in the conormal bundle of $D$ in $L$ such that $\Vert \unicode[STIX]{x1D70B}_{2}(\unicode[STIX]{x1D709})\Vert \leqslant \unicode[STIX]{x1D716}$ .

We note that for any point $\unicode[STIX]{x1D709}=(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2})\in E_{1}\oplus E_{2}$ , $\unicode[STIX]{x1D719}_{t}^{\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70B}}}(\unicode[STIX]{x1D709})=(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D719}_{t}^{\unicode[STIX]{x1D70E}}(\unicode[STIX]{x1D709}_{2}))$ so $E_{2}$ -flow is the normalized (co)geodesic flow on the second factor and is trivial on the first factor.

Let $S_{\unicode[STIX]{x1D706}}(E_{2}|_{D})$ be the radius- $\unicode[STIX]{x1D706}$ sphere bundle of $E_{2}$ over $D$ . We consider $\exp _{\unicode[STIX]{x1D706}}^{E_{2}}:S_{\unicode[STIX]{x1D706}}(E_{2}|_{D})\rightarrow L$ , which is the exponential map restricted on $S_{\unicode[STIX]{x1D706}}(E_{2}|_{D})$ along the leaves of the foliation given by second factor. We define the $E_{2}$ -injectivity radius $r^{E_{2}}(D)$ of $D$ as the supremum of $\unicode[STIX]{x1D706}$ such that $\exp _{s}^{E_{2}}$ is an embedding for all $s<\unicode[STIX]{x1D706}$ .

Lemma 2.26. Let $D\subset L=K_{1}\times K_{2}$ be of dimension $n-m$ and transversal to $\{p\}\times K_{2}$ for all $p\in K_{1}$ . If $\exp _{\unicode[STIX]{x1D706}}^{E_{2}}:S_{\unicode[STIX]{x1D706}}(E_{2}|_{D})\rightarrow L$ is an embedding and $\unicode[STIX]{x2202}H_{\unicode[STIX]{x1D708}}^{D,E_{2}}\subset L$ divides $L$ into two components, then $H_{\unicode[STIX]{x1D708}}^{D,E_{2}}$ glues with exactly one of the components of $L$ to form a smooth Lagrangian submanifold coinciding with $N_{D}^{\ast }$ outside a compact set.

Proof. The proof is again similar to that of Lemma 2.23.◻

Similarly to the cases we considered before, if $L_{1}=K_{1}\times K_{2}$ and $L_{2}$ are Lagrangians cleanly intersecting at $D$ as above, we can add an $E_{2}$ -flow handle to $L_{1}\cup L_{2}$ outside a tubular neighborhood of $D$ to get a new Lagrangian submanifold for $\unicode[STIX]{x1D706}<r^{E_{2}}(D)$ . We will denote the resulting Lagrangian submanifold by $L_{1}\text{\#}_{D,E_{2}}L_{2}$ , called the $E_{2}$ -flow surgery from $L_{1}$ to $L_{2}$ along  $D$ .

A family version of $E_{2}$ -flow surgery

We now consider the $E_{2}$ -flow surgery for a family over a symplectic base. Assume that we have a smooth manifold pair $(L=K_{1}\times K_{2},D)$ , a decomposition $T^{\ast }L=E_{1}\oplus E_{2}$ and a Lagrangian handle $H_{\unicode[STIX]{x1D708}}^{D,E_{2}}$ as above.

Let $(\mathscr{P},\unicode[STIX]{x1D714}_{\mathscr{P}})$ be a symplectic manifold equipped with a symplectic fiber bundle structure $\unicode[STIX]{x1D70B}:\mathscr{P}\rightarrow \mathscr{B}$ , such that it has a symplectic base $(\mathscr{B},\unicode[STIX]{x1D714}_{\mathscr{B}})$ and fibers symplectomorphic to $T^{\ast }L$ . Let $i:B{\hookrightarrow}\mathscr{B}$ be a Lagrangian submanifold such that the structure group $G$ of $i^{\ast }\mathscr{P}\rightarrow B$ is a subgroup of $\text{Isom}(L){\hookrightarrow}\text{Symp}(T^{\ast }L)$ . In particular, $G$ preserves $L$ and we make the following further assumptions on  $G$ .

1. (i) $G$ preserves $D$ , the subbundles $E_{1}$ and $E_{2}$ and $H_{\unicode[STIX]{x1D708}}^{D,E_{2}}$ .

2. (ii) For any loop $\unicode[STIX]{x1D6FE}:\mathbb{R}/\mathbb{Z}\rightarrow B$ , the symplectic monodromy around $\unicode[STIX]{x1D6FE}$ for the fiber bundle $\unicode[STIX]{x1D70B}:\mathscr{P}\rightarrow \mathscr{B}$ lies in $G$ .

3. (iii) Let $x\in \mathscr{P}$ , $b:=\unicode[STIX]{x1D70B}(x)\in B$ and $\mathscr{P}_{b}:=\unicode[STIX]{x1D70B}^{-1}(b)$ . Assume $\operatorname{Ker}_{x}$ is the symplectic orthogonal complement of the fiber $T_{x}\mathscr{P}_{b}\subset T_{x}\mathscr{P}$ at $x$ , then we ask $\unicode[STIX]{x1D714}_{\mathscr{P}}(v_{1},v_{2})=0$ for any $v_{1},v_{2}\in \operatorname{Ker}_{x}$ such that $\unicode[STIX]{x1D70B}_{\ast }v_{i}\in TB\subset T\mathscr{B}$ for both $i$ .

Since $L$ and $D$ are invariant under $G$ , we can use symplectic parallel transport to obtain a smooth manifold pair $(\mathscr{L},\mathscr{D})$ in $\mathscr{P}$ . More precisely, let $\mathscr{P}_{b}=T^{\ast }L$ be a reference fiber with based point $b\in B$ . We define $\mathscr{L}:=\bigcup _{\unicode[STIX]{x1D6FE}\in I_{B}}\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D6FE}}(L)$ , $\mathscr{D}:=\bigcup _{\unicode[STIX]{x1D6FE}\in I_{B}}\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D6FE}}(D)$ , where $I_{B}$ consists of all paths $\unicode[STIX]{x1D6FE}$ from $b$ to another point $b^{\prime }\in B$ and $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D6FE}}$ is the symplectic parallel transport along $\unicode[STIX]{x1D6FE}$ . As a result, $(\mathscr{L},\mathscr{D})$ has a compatible fiber bundle structure over the base $B$ , that is,

where the two bundle structures are compatible with the inclusions $\mathscr{D}{\hookrightarrow}\mathscr{L}{\hookrightarrow}i^{\ast }\mathscr{P}$ .

All previous symplectic constructions on $T^{\ast }L$ are $G$ -invariant, by assumption (i), hence can be glued over $B$ . For example, $N_{D}^{\ast }L$ glues into $N_{\mathscr{D}}^{\ast }\mathscr{L}:=\bigcup _{\unicode[STIX]{x1D6FE}\in I_{B}}\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D6FE}}(N_{D}^{\ast }L)$ . When $i^{\ast }\mathscr{P}$ is regarded as a vector bundle over $\mathscr{L}$ , it comes with a natural splitting $i^{\ast }\mathscr{P}=\mathscr{E}_{1}\,\oplus \,\mathscr{E}_{2}$ , where $\mathscr{E}_{i}:=\bigcup _{\unicode[STIX]{x1D6FE}\in I_{B}}(\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D6FE}})_{\ast }(E_{i})$ for $i=1,2$ . Moreover, the $E_{2}$ -handle $H_{\unicode[STIX]{x1D708}}^{D,E_{2}}$ on fibers can be glued together, which gives a smooth handle $\mathscr{H}_{\unicode[STIX]{x1D708}}:=\bigcup _{\unicode[STIX]{x1D6FE}\in I_{B}}\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D6FE}}(H_{\unicode[STIX]{x1D708}}^{D,E_{2}})\subset i^{\ast }\mathscr{P}$ . The fact that $\mathscr{H}_{\unicode[STIX]{x1D708}}{\hookrightarrow}\mathscr{P}\supset i^{\ast }\mathscr{P}$ is indeed a Lagrangian embedding follows from the assumptions (ii) and (iii) on $G$ .

Lemma 2.27. For two cleanly intersecting Lagrangians $\mathscr{L}_{0},\mathscr{L}_{1}\subset (M^{2n},\unicode[STIX]{x1D714})$ , if there is a neighborhood of $\mathscr{L}_{0}$ which can be identified with $(\mathscr{P},\unicode[STIX]{x1D714}_{\mathscr{P}})$ above (together with all the bundle structures and assumptions on $G$ ) such that $(\mathscr{L}_{0},\mathscr{L}_{1},\mathscr{L}_{0}\,\cap \,\mathscr{L}_{1})$ is identified with $(\mathscr{L},N_{\mathscr{D}}^{\ast }\mathscr{L},\mathscr{D})$ , then the family $E_{2}$ -surgery between $\mathscr{L}_{0}$ and $\mathscr{L}_{1}$ can be performed and gives a Lagrangian submanifold $\mathscr{L}_{0}\text{\#}_{\mathscr{D},E_{2}}^{\unicode[STIX]{x1D708}}\mathscr{L}_{1}$ of $(M,\unicode[STIX]{x1D714})$ .

Despite the fact that many assumptions are imposed on $(\mathscr{P},\unicode[STIX]{x1D714}_{\mathscr{P}})$ and $G$ , there are practical examples where Lemma 2.27 applies (see § 3.3).

Remark 2.28. It is easy to see that our construction works word by word as long as there is a decomposition of the vector bundle $T^{\ast }L=E_{1}\oplus E_{2}$ . However, one needs to impose technical conditions to make $exp_{\unicode[STIX]{x1D706}}^{E_{2}}:S_{\unicode[STIX]{x1D706}}\rightarrow L$ an embedding even for small $\unicode[STIX]{x1D706}$ . An easy condition is to assume that $E_{2}$ is integrable at least near $D$ , but it should also work in some cases when $E_{2}$ is completely non-integrable near $D$ but integrable outside a small neighborhood. Considerations along this line might result in delicate constructions of new Lagrangian submanifolds.

3 Isotopies: from surgeries to Dehn twists

This section contains the construction which relates Lagrangian surgeries to various kinds of Dehn twists. The general idea is the same as in Lemma 2.19, which may also be interpreted as deforming an admissible profile to a semi-admissible one. The deformation from an admissible profile to a semi-admissible profile will correspond to a Lagrangian isotopy between appropriate Lagrangians.

We first explain how this works in the $\mathbb{C}\mathbb{P}^{n}$ case, then give a proof of Theorem 1.1(1), (2), (3), (4) using family versions of this observation.

3.1 Fiber version

In this section, we are interested in $L$ being $\mathbb{RP}^{n}$ , $\mathbb{CP}^{m/2}$ or $\mathbb{HP}^{n}$ equipped with the Riemannian metric such that every geodesic is closed of length $2\unicode[STIX]{x1D70B}$ . All actual proofs will be given only in the case of $\mathbb{C}\mathbb{P}^{n}$ but are easily generalized. Let $x\in L$ be a point and $F_{x}=T_{x}^{\ast }L$ . We also let $D_{x}=\{y\in L\mid \text{dist}(x,y)=\unicode[STIX]{x1D70B}\}$ be the submanifold opposite to $x$ . In the case of $\mathbb{CP}^{m/2}$ , $D_{x}\simeq \mathbb{CP}^{m/2-1}$ .

Lemma 3.1. Let $x\in L$ be a point and $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}_{i}}$ , $i=1,2$ , be $\unicode[STIX]{x1D706}_{i}$ -admissible functions such that $(k-1)\unicode[STIX]{x1D70B}<\unicode[STIX]{x1D706}_{i}<k\unicode[STIX]{x1D70B}$ for some positive integer $k$ for both $i=1,2$ . Then $L\text{\#}_{x}^{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}_{i}}}F_{x}$ for $i=1,2$ are isotopic by a compactly supported Hamiltonian.

Moreover, if we choose a semi-admissible function $\unicode[STIX]{x1D708}_{k\unicode[STIX]{x1D70B}}^{\unicode[STIX]{x1D6FC}}:(0,\infty )\rightarrow [0,k\unicode[STIX]{x1D70B})$ that is monotonic decreasing and all orders of derivatives vanish at $r=\unicode[STIX]{x1D716}$ such that $\unicode[STIX]{x1D708}_{k\unicode[STIX]{x1D70B}}^{\unicode[STIX]{x1D6FC}}(r)=k\unicode[STIX]{x1D70B}-\unicode[STIX]{x1D6FC}r$ near $r=0$ $(\unicode[STIX]{x1D6FC}\geqslant 0)$ , then $L\text{\#}_{x}^{\unicode[STIX]{x1D708}_{k\unicode[STIX]{x1D70B}}^{\unicode[STIX]{x1D6FC}}}F_{x}$ (see Remark 2.20 for the definition of $L\text{\#}_{x}^{\unicode[STIX]{x1D708}_{k\unicode[STIX]{x1D70B}}^{\unicode[STIX]{x1D6FC}}}F_{x}$ when $\unicode[STIX]{x1D708}_{k\unicode[STIX]{x1D70B}}^{\unicode[STIX]{x1D6FC}}$ is semi-admissible) is a smooth Lagrangian that is isotopic to $L\text{\#}_{x}^{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}_{i}}}F_{x}$ by a compactly supported Hamiltonian.

Furthermore, these Hamiltonian isotopies can be chosen to be invariant under the action of the group of isometries of $L$ that fix $x$ .

Corollary 3.2. For $\unicode[STIX]{x1D70B}<\unicode[STIX]{x1D706}<2\unicode[STIX]{x1D70B}$ and $L$ being $\mathbb{RP}^{n}$ , $\mathbb{CP}^{m/2}$ or $\mathbb{HP}^{n}$ , $L\text{\#}_{x}^{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}}}F_{x}$ is Hamiltonian isotopic to $\unicode[STIX]{x1D70F}_{L}(F_{x})$ for an admissible $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}}$ .

Proof of Corollary 3.2.

Observe that when $\unicode[STIX]{x1D6FC}=1$ and $k=2$ , $\unicode[STIX]{x1D708}_{k\unicode[STIX]{x1D70B}}^{\unicode[STIX]{x1D6FC}}(r)$ is a Dehn twist profile (see Figure 7). The Corollary follows from Lemma 3.1.◻

Proof of Lemma 3.1.

For the first statement, we observe that the space of $\unicode[STIX]{x1D706}$ -admissible functions for $(k-1)\unicode[STIX]{x1D70B}<\unicode[STIX]{x1D706}<k\unicode[STIX]{x1D70B}$ is connected. A smooth isotopy $\{\unicode[STIX]{x1D708}_{t}\}$ from $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}_{1}}$ to $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}_{2}}$ in this space results in a smooth Lagrangian isotopy from $L\text{\#}_{x}^{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}_{1}}}F_{x}$ to $L\text{\#}_{x}^{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}_{2}}}F_{x}$ since $\unicode[STIX]{x2202}H_{\unicode[STIX]{x1D708}^{t}}$ does not pass any critical locus. This is a Hamiltonian isotopy because $H^{1}(L\text{\#}_{x}^{\unicode[STIX]{x1D708}_{t}}F_{x},\unicode[STIX]{x2202}^{\infty }(L\text{\#}_{x}^{\unicode[STIX]{x1D708}_{t}}F_{x});\mathbb{R})=0$ (cf. Example 2.17). Here, $\unicode[STIX]{x2202}^{\infty }(L\text{\#}_{x}^{\unicode[STIX]{x1D708}_{t}}F_{x})$ is the infinite end of $L\text{\#}_{x}^{\unicode[STIX]{x1D708}_{t}}F_{x}$ .

Figure 7. Isotopy from $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}_{1}}$ to $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70B}}$ to $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70B}}^{\unicode[STIX]{x1D6FC}}$ (Dehn twist profile).

For the second statement, we only consider the case that $k=1$ and $L=\mathbb{CP}^{m/2}$ , and the remaining cases are similar. In this case, denote $\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D6FC}}=\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70B}}^{\unicode[STIX]{x1D6FC}}$ . Then for a handle $H_{\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D6FC}}}$ at $x$ , $\operatorname{Cl}(H_{\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D6FC}}})\backslash H_{\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D6FC}}}=D_{x}=\mathbb{CP}^{m/2-1}$ . We pick a local chart $U\subset L$ with local coordinates $(q_{1},\ldots ,q_{m})$ adapted to $D_{x}$ in the sense that $U\cap D_{x}=\{q_{1}=q_{2}=0\}$ and $c(t)=(tq_{1},tq_{2},q_{3},\ldots ,q_{m})$ are unit-speed geodesics perpendicular to $D_{x}$ at $t=0$ , for any $(q_{1},\ldots ,q_{m})$ such that $|q_{1}|^{2}+|q_{2}|^{2}=1$ . It induces canonically a Darboux chart $T^{\ast }U$ in $T^{\ast }L$ . We write a point in $T^{\ast }U$ as $(q_{a},q_{b},p_{a},p_{b})$ , where $q_{a}=(q_{1},q_{2})$ , $q_{b}=(q_{3},\ldots ,q_{m})$ and similarly for $p_{a}$ and $p_{b}$ . Since $H_{\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D6FC}}}$ is defined by the geodesic flow, we have

(3.1) $$\begin{eqnarray}\displaystyle T^{\ast }U\cap H_{\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D6FC}}} & = & \displaystyle \{(q_{a},q_{b},p_{a},0)\mid q_{a}=-\unicode[STIX]{x1D6FC}p_{a}\neq 0\}\end{eqnarray}$$

(3.2) $$\begin{eqnarray}\displaystyle T^{\ast }U\cap D_{x} & = & \displaystyle \{(0,q_{b},0,0)\}\end{eqnarray}$$

when $U$ is sufficiently small. To see that it is true, we consider a unit-speed geodesic $\unicode[STIX]{x1D6FE}:[0,\unicode[STIX]{x1D70B}]\rightarrow L$ from $x$ to a point $x^{\prime }\in D_{x}$ . By Lemma 2.11, we have a symplectic embedding $T^{\ast }[0,\unicode[STIX]{x1D70B}]\rightarrow T^{\ast }L$ and

(3.3) $$\begin{eqnarray}\displaystyle T^{\ast }[0,\unicode[STIX]{x1D70B}]\cap H_{\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D6FC}}}=\bigg\{\bigg(\frac{\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D6FC}}(\Vert p\Vert )p}{\Vert p\Vert },p\bigg)\in T^{\ast }[0,\unicode[STIX]{x1D70B}]\,\biggr|\,p\in (0,\unicode[STIX]{x1D716}]\bigg\}. & & \displaystyle\end{eqnarray}$$

On the other hand, the symplectic embedding $T^{\ast }[0,\unicode[STIX]{x1D70B}]\cap T^{\ast }U\rightarrow T^{\ast }U$ is given by

(3.4) $$\begin{eqnarray}\displaystyle (q,p)\mapsto (q_{a},q_{b},p_{a},p_{b})=((\unicode[STIX]{x1D70B}-q)c_{1},c_{2},-pc_{1},0) & & \displaystyle\end{eqnarray}$$

for some $c_{1},c_{2}$ such that $|c_{1}|=1$ because $U$ is adapted to $D_{x}$ (by the same reasoning as in the proof of Lemma 2.11). When $p>0$ close to zero, $q=\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D6FC}}(\Vert p\Vert )p/\Vert p\Vert =\unicode[STIX]{x1D70B}-\unicode[STIX]{x1D6FC}p$ so we have $(\unicode[STIX]{x1D70B}-q)=\unicode[STIX]{x1D6FC}p$ and hence $(\unicode[STIX]{x1D70B}-q)c_{1}=\unicode[STIX]{x1D6FC}pc_{1}$ . Therefore, (3.3) and (3.4) imply (3.1) when we consider all possible unit-speed geodesics from $x$ to points on $D_{x}$ .

From the local description, it is clear that $H_{\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D6FC}}}$ and $D_{x}$ can be glued smoothly to become $\operatorname{Cl}(H_{\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D6FC}}})$ . The gluing from $H_{\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D6FC}}}$ to $F_{x}-B_{\unicode[STIX]{x1D716}}$ is the same as in the admissible case. It results in a smooth Lagrangian $L\text{\#}_{x}^{\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D6FC}}}F_{x}$ .

Finally, we want to show that $L\text{\#}_{x}^{\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D6FC}}}F_{x}$ is Hamiltonian isotopic to $L\text{\#}_{x}^{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}_{i}}}F_{x}$ . We can assume $\unicode[STIX]{x1D6FC}\neq 0$ , by a Hamiltonian perturbation if necessary. Locally near $D_{x}$ , we have

(3.5) $$\begin{eqnarray}\displaystyle & \displaystyle T^{\ast }U\cap (H_{\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D6FC}}}\cup D_{x})=\{(-\unicode[STIX]{x1D6FC}p_{a},q_{b},p_{a},0)\}=\bigg\{\bigg(q_{a},q_{b},-\frac{1}{\unicode[STIX]{x1D6FC}}q_{a},0\bigg)\bigg\} & \displaystyle\end{eqnarray}$$

(3.6) $$\begin{eqnarray}\displaystyle & \displaystyle T^{\ast }U\cap L=\{(q_{a},q_{b},0,0)\}. & \displaystyle\end{eqnarray}$$

Notice that, by the choice of $U$ , we have $\text{dist}^{2}(\cdot ,D_{x})=|q_{a}|^{2}:=|q_{1}|^{2}+|q_{2}|^{2}$ in $U$ . It implies that $H_{\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D6FC}}}\cup D_{x}$ is the graph of $d(-(1/2\unicode[STIX]{x1D6FC})\text{dist}^{2}(\cdot ,D_{x}))$ in $T^{\ast }U$ . Since the definition of the graph of $d(-(1/2\unicode[STIX]{x1D6FC})\text{dist}^{2}(\cdot ,D_{x}))$ is coordinate-free, by gluing charts that are adapted to $D_{x}$ , we know that there is a small $\unicode[STIX]{x1D6FF}>0$ such that $(H_{\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D6FC}}}\cup D_{x})\cap T^{\ast }B_{\unicode[STIX]{x1D6FF}}(D_{x})$ is the graph of $d(-(1/2\unicode[STIX]{x1D6FC})\text{dist}^{2}(\cdot ,D_{x}))$ over $B_{\unicode[STIX]{x1D6FF}}(D_{x})$ , where $B_{\unicode[STIX]{x1D6FF}}(D_{x})$ is the $\unicode[STIX]{x1D6FF}$ neighborhood of $D_{x}$ in $L$ . Take a smooth decreasing function $f(r):[0,\unicode[STIX]{x1D6FF}]\rightarrow \mathbb{R}$ so that $f=0$ near $r=0$ and $f(r)=-(1/2\unicode[STIX]{x1D6FC})r$ near $r=\unicode[STIX]{x1D6FF}$ . Denote $f_{t}(r)=tf(r)-(1-t)(1/2\unicode[STIX]{x1D6FC})r$ .

Then the graph of $d(f_{t}\circ \text{dist}^{2}(\cdot ,D_{x}))$ can be patched with $H_{\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D6FC}}}\backslash T^{\ast }B_{\unicode[STIX]{x1D6FF}}(D_{x})$ to give a Hamiltonian isotopy from $L\text{\#}_{x}^{\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D6FC}}}F_{x}$ to $L\text{\#}_{x}^{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}}}F_{x}$ for some admissible $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}}$ with $0<\unicode[STIX]{x1D706}<\unicode[STIX]{x1D70B}$ . We remark that the Hamiltonian isotopy is invariant under $\text{Isom}(L)_{x}$ , the isometry group of $L$ fixing  $x$ . This concludes the proof.

The following could be helpful to understand the construction. An alternative way to describe the isotopy $d(f_{t}\circ \text{dist}^{2}(\cdot ,D_{x}))$ is that we use a family of semi-admissible function $\{\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D6FC}_{t}}\}_{t\in [0,1)}$ ( $\unicode[STIX]{x1D6FC}_{t}>0$ ) such that $\unicode[STIX]{x1D6FC}_{0}=\unicode[STIX]{x1D6FC}$ and $\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D6FC}_{t}}$ approaches to $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}}$ when $t$ goes to $1$ . Then we will have $L\text{\#}_{x}^{\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D6FC}}}F_{x}=d(f_{t}\circ \text{dist}^{2}(\cdot ,D_{x}))$ near $D_{x}$ .◻

Later we will see that, when the surgery profile $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}}$ has $\unicode[STIX]{x1D706}$ exceeding the injectivity radius, there is no cobordism directly associated to such a surgery. To fit such a surgery into the cobordism framework, in general we need to decompose the surgery into several steps. The following lemma shows how this works in the case of $\mathbb{C}\mathbb{P}^{n}$ (which easily generalizes to $\mathbb{R}\mathbb{P}^{n}$ and $\mathbb{HP}^{n}$ ).

Lemma 3.3. Let $x\in \mathbb{CP}^{m/2}$ be a point and $F_{x}=T_{x}^{\ast }\mathbb{CP}^{m/2}$ . Let $D_{x}=\{y\in \mathbb{CP}^{m/2}\mid \text{dist}(x,y)=\unicode[STIX]{x1D70B}\}$ be the submanifold opposite to $x$ . Then there is an embedded Lagrangian $Q_{x}\subset T^{\ast }\mathbb{CP}^{m/2}$ such that:

1. (1) $Q_{x}=F_{x}$ away from a neighborhood of zero section;

2. (2) $Q_{x}$ is Hamiltonian isotopic to $\mathbb{CP}^{m/2}\text{\#}_{x,std}F_{x}$ ;

3. (3) $Q_{x}$ intersects cleanly with $\mathbb{CP}^{m/2}$ at $D_{x}$ ;

4. (4) $\mathbb{CP}^{m/2}\text{\#}_{D_{x}}Q_{x}$ is Hamiltonian isotopic to $\unicode[STIX]{x1D70F}_{\mathbb{CP}^{m/2}}(F_{x})$ .

As a result, as far as Hamiltonian isotopy class is concerned, we have $\mathbb{CP}^{m/2}\text{\#}_{D_{x}}(\mathbb{CP}^{m/2}\text{\#}_{x}F_{x})=\unicode[STIX]{x1D70F}_{\mathbb{CP}^{m/2}}(F_{x})$ .

Proof. Choose a semi-admissible profile $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70B}}^{0}$ such that $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70B}}^{0}=\unicode[STIX]{x1D70B}$ near $r=0$ and let $Q_{x}=\mathbb{C}\mathbb{P}^{m/2}\text{\#}_{x}^{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70B}}^{0}}F_{x}$ . Then (1), (3) follows from definition, and (2) is a consequence of Lemma 3.1 and Corollary 3.2.

To see (4), note that near $D_{x}$ , $Q_{x}$ coincides with the $\unicode[STIX]{x1D716}^{\prime }$ -disk conormal bundle at $D_{x}$ for some $\unicode[STIX]{x1D716}^{\prime }\ll \unicode[STIX]{x1D716}$ . Therefore, $\mathbb{C}\mathbb{P}^{m/2}\text{\#}_{D_{x}}^{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}}}Q_{x}$ coincides with $\mathbb{C}\mathbb{P}^{m/2}\text{\#}_{x}^{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}+\unicode[STIX]{x1D70B}}}F_{x}$ for any $0<\unicode[STIX]{x1D706}<\unicode[STIX]{x1D70B}$ and an appropriate choice of $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}+\unicode[STIX]{x1D70B}}$ (see Figure 8 for the demonstration). The latter is then Hamiltonian isotopic to $\mathbb{C}\mathbb{P}^{m/2}\text{\#}_{x}^{\unicode[STIX]{x1D708}_{2\unicode[STIX]{x1D70B}}^{0}}F_{x}=\unicode[STIX]{x1D70F}_{\mathbb{C}\mathbb{P}^{m/2}}(F_{x})$ by Corollary 3.2.◻

Figure 8. Left and middle: identification of $\mathbb{C}\mathbb{P}^{m/2}\text{\#}_{D_{x}}^{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}}}Q_{x}$ and $\mathbb{C}\mathbb{P}^{m/2}\text{\#}_{x}^{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}+\unicode[STIX]{x1D70B}}}F_{x}$ . Right: isotopy from an admissible function to a Dehn twist profile.

3.2 Product version

In this section we prove Theorem 1.1(1), (3). The proofs here are similar to that in the last section, and should be considered as family versions of it. In this subsection, we use $S$ to denote $S^{n}$ , $\mathbb{RP}^{n}$ , $\mathbb{CP}^{m/2}$ or $\mathbb{HP}^{n}$ equipped with the Riemannian metric such that every geodesic is closed of length $2\unicode[STIX]{x1D70B}$ .

For a symplectomorphism $\unicode[STIX]{x1D70F}:(M,\unicode[STIX]{x1D714})\rightarrow (M,\unicode[STIX]{x1D714})$ , we define the graph of $\unicode[STIX]{x1D70F}$ as

$$\begin{eqnarray}\displaystyle \text{Graph}(\unicode[STIX]{x1D70F}):=\{(p,\unicode[STIX]{x1D70F}(p))\in M\times M\mid p\in M\}. & & \displaystyle \nonumber\end{eqnarray}$$

In particular, $\text{Graph}(\unicode[STIX]{x1D70F})$ is a Lagrangian submanifold if we equip $M\times M$ with the symplectic form $\unicode[STIX]{x1D714}\oplus -\unicode[STIX]{x1D714}$ .

For the moment, let $S\subset (M,\unicode[STIX]{x1D714})$ be a Lagrangian sphere and $S^{-}:=S\subset M^{-}$ . One may consider the clean surgery of $L_{1}=S\times S^{-}$ and $L_{2}=\unicode[STIX]{x1D6E5}$ in $M\times M^{-}$ . In this case, they cleanly intersect along $D=\unicode[STIX]{x1D6E5}_{S}\subset S\times S^{-}$ . In Definition 2.25, take $E_{2}=S\times (T^{\ast }S)^{-}\subset T^{\ast }S\times (T^{\ast }S)^{-}$ , $E_{1}=T^{\ast }S\times S^{-}\subset T^{\ast }S\times (T^{\ast }S)^{-}$ and a $\unicode[STIX]{x1D70B}$ -admissible function $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70B}}$ .

Let $U\subset M$ be a Weinstein neighborhood of $S$ which can be identified with $T_{\unicode[STIX]{x1D716}}^{\ast }S$ , the open set of $T^{\ast }S$ consisting of covectors with length less than $\unicode[STIX]{x1D716}$ . It induces an identification between $U\times U$ , a Weinstein neighborhood of $L_{1}$ , and $T_{\unicode[STIX]{x1D716}}^{\ast }S\times T_{\unicode[STIX]{x1D716}}^{\ast }S$ . Now consider a point $(p,p)\in \unicode[STIX]{x1D6E5}_{U}:=\unicode[STIX]{x1D6E5}\cap (U\times U)$ , where $p$ can be considered as a point in $T_{\unicode[STIX]{x1D716}}^{\ast }S$ . The flow in Definition 2.25 defines a symplectomorphism fixing the first coordinate in $(T^{\ast }S\times (T^{\ast }S)^{-})\backslash E_{1}$ ; when restricted to $\unicode[STIX]{x1D6E5}_{U}$ , the $E_{2}$ -flow sends $(p,p)\mapsto (p,\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70B}}(\Vert p\Vert )}^{\unicode[STIX]{x1D70E}}(p))$ . Therefore, the image of $\unicode[STIX]{x1D6E5}_{U}\backslash \unicode[STIX]{x1D6E5}_{S}$ under the flow is an open subset of the graph of $\unicode[STIX]{x1D70F}_{S}^{-1}$ (the inverse owes to the negation of symplectic form on $M^{-}$ ), except that we have used an admissible profile for the handle which is not a Dehn twist profile. Lemma 3.4 below ensures that this could be compensated by a local Hamiltonian perturbation. Hence modulo Lemma 3.4, this shows that $(S\times S^{-})\text{\#}_{\unicode[STIX]{x1D6E5}_{S},E_{2}}^{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70B}}}\unicode[STIX]{x1D6E5}=\text{Graph}(\unicode[STIX]{x1D70F}_{S}^{-1})$ (see Figure 9). The whole construction applies when $S$ is $\mathbb{RP}^{n}$ , $\mathbb{CP}^{m/2}$ or $\mathbb{HP}^{n}$ , except that the admissible profile has $\unicode[STIX]{x1D708}(0)=2\unicode[STIX]{x1D70B}$ .

Figure 9. Obtaining the graph of a Dehn twist by $E_{2}$ -flow surgery.

Lemma 3.4. Let $S$ be $S^{n}$ , $\mathbb{RP}^{n}$ , $\mathbb{CP}^{m/2}$ or $\mathbb{HP}^{n}$ . Let $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}_{i}}$ be $\unicode[STIX]{x1D706}_{i}$ -admissible functions such that $(k-1)\unicode[STIX]{x1D70B}<\unicode[STIX]{x1D706}_{i}<k\unicode[STIX]{x1D70B}$ for some positive integer $k$ for both $i=1,2$ . Then the $E_{2}$ -flow surgered Lagrangian manifolds $(S\times S^{-})\text{\#}_{\unicode[STIX]{x1D6E5}_{S},E_{2}}^{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}_{i}}}\unicode[STIX]{x1D6E5}$ above with surgery profiles $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}_{i}}$ are Hamiltonian isotopic.

Moreover, if we choose a semi-admissible function $\unicode[STIX]{x1D708}_{k\unicode[STIX]{x1D70B}}^{\unicode[STIX]{x1D6FC}}$ such that $\unicode[STIX]{x1D708}_{k\unicode[STIX]{x1D70B}}^{\unicode[STIX]{x1D6FC}}(r)=k\unicode[STIX]{x1D70B}-\unicode[STIX]{x1D6FC}r$ near $r=0\;(\unicode[STIX]{x1D6FC}\geqslant 0)$ , then $(S\times S^{-})\text{\#}_{\unicode[STIX]{x1D6E5}_{S},E_{2}}^{\unicode[STIX]{x1D708}_{k\unicode[STIX]{x1D70B}}^{\unicode[STIX]{x1D6FC}}}\unicode[STIX]{x1D6E5}$ is a smooth Lagrangian that is Hamiltonian isotopic to $(S\times S^{-})\text{\#}_{\unicode[STIX]{x1D6E5}_{S},E_{2}}^{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}_{i}}}\unicode[STIX]{x1D6E5}$ .

Furthermore, these Hamiltonian isotopies can be chosen to be $\text{Isom}_{\unicode[STIX]{x1D6E5}}(S)$ invariant, where $\text{Isom}_{\unicode[STIX]{x1D6E5}}(S)$ is the diagonal isometry group in $\text{Isom}(S)\times \text{Isom}(S)$ acting on $T^{\ast }S\times (T^{\ast }S)^{-}$ .

We have the following corollary whose proof is similar to Corollary 3.2

Corollary 3.5 (Cf. Theorem 1.1(1)).

For $\unicode[STIX]{x1D70B}<\unicode[STIX]{x1D706}<2\unicode[STIX]{x1D70B}$ and $S$ being $\mathbb{RP}^{n}$ , $\mathbb{CP}^{m/2}$ or $\mathbb{HP}^{n}$ (respectively $0<\unicode[STIX]{x1D706}<\unicode[STIX]{x1D70B}$ and $S=S^{n}$ ), $\,(S\times S^{-})\text{\#}_{\unicode[STIX]{x1D6E5}_{S},E_{2}}^{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}}}\unicode[STIX]{x1D6E5}$ is Hamiltonian isotopic to $\text{Graph}(\unicode[STIX]{x1D70F}_{S}^{-1})$ .

Proof of Corollary 3.5.

When $\unicode[STIX]{x1D6FC}=1$ and $k=2$ (respectively $k=1$ ), $(S\times S^{-})\text{\#}_{\unicode[STIX]{x1D6E5}_{S},E_{2}}^{\unicode[STIX]{x1D708}_{k\unicode[STIX]{x1D70B}}^{\unicode[STIX]{x1D6FC}}}\unicode[STIX]{x1D6E5}$ coincides with $\text{Graph}(\unicode[STIX]{x1D70F}_{S}^{-1})$ . Therefore, the result follows from Lemma 3.4.◻

Proof of Lemma 3.4.

The proof of the first statement is exactly the same as Lemma 3.1. For the second statement, we again only consider the case that $k=1$ and $S=\mathbb{CP}^{m/2}$ and the remaining cases are similar.

Define $D^{\operatorname{op}}=\{(x,y)\in S\times S\mid \text{dist}(x,y)=\unicode[STIX]{x1D70B}\}$ . Projection to the first factor in $S\times S$ equips $D^{\operatorname{op}}$ with a $\mathbb{CP}^{m/2-1}$ -bundle structure over $S=\mathbb{CP}^{m/2}$ . Therefore, a tubular neighborhood of $D^{\operatorname{op}}$ in $S\times S^{-}$ is the total space $\widetilde{\mathscr{V}}$ of a fiber bundle $\unicode[STIX]{x1D70B}_{\widetilde{\mathscr{V}}}:\widetilde{\mathscr{V}}\rightarrow S$ , whose fibers $\mathscr{V}$ are total spaces of topological ${\mathcal{O}}(1)$ -bundles over $\mathbb{CP}^{m/2-1}$ . We pick an open subset $U^{B}\subset S$ and a local trivialization $U^{B}\times U^{F}\simeq \unicode[STIX]{x1D70B}_{\widetilde{\mathscr{V}}}^{-1}(U^{B})$ (so $U^{F}=\mathscr{V}$ ). Readers should note that the product structure of $U^{B}\times U^{F}$ is not compatible with the product structure of $L=S\times S^{-}$ , but $\{q\}\times U^{F}$ is an open set of $\{q\}\times S^{-}$ for any $q\in U^{B}$ . In other words, we should regard $U^{B}$ as a parameter space and points in $U^{B}$ are parameterizing some open subsets of $S^{-}$ .

Pick a chart $U^{B}\times U^{F^{\prime }}$ on $U^{B}\times U^{F}$ with local coordinates $(q^{B},q^{F})=(q_{1}^{B},\ldots ,q_{m}^{B},q_{1}^{F},\ldots ,q_{m}^{F})$ adapted to $D^{\operatorname{op}}$ in the sense that:

• ∙ $(U^{B}\times U^{F^{\prime }})\cap D^{\operatorname{op}}=\{q_{1}^{F}=q_{2}^{F}=0\}$ ;

• ∙ $c(t)=(q^{B},tq_{1}^{F},tq_{2}^{F},q_{3}^{F},\ldots ,q_{m}^{F})$ are unit-speed geodesics for all $(q^{B},q^{F})$ such that $|q_{1}^{F}|^{2}+|q_{2}^{F}|^{2}=1$ ; and

• ∙ $c(t)\in \{q^{B}\}\times S$ is perpendicular to $\{q^{B}\}\times D_{q^{B}}\subset \{q^{B}\}\times S$ at $t=0$ with respect to the metric on $\{q^{B}\}\times S=S$ , where $D_{q^{B}}$ is the submanifold opposite to $q^{B}\in S$ .

Note that $c(0)\in D^{\operatorname{op}}$ and the projection of $c(0)$ to the first factor is $q^{B}$ so $c(0)\in \{q^{B}\}\times D_{q^{B}}$ .

The inclusions $U^{B}\times U^{F^{\prime }}\subset U^{B}\times U^{F}\subset S\times S^{-}$ induces canonical inclusions $T^{\ast }(U^{B}\times U^{F^{\prime }})\subset T^{\ast }(U^{B}\times U^{F})\subset T^{\ast }(S\times S^{-})$ . We write a point in $T^{\ast }(U^{B}\times U^{F^{\prime }})$ as $(q^{B},p^{B},q_{a}^{F},q_{b}^{F},p_{a}^{F},p_{b}^{F})$ , where $q_{a}^{F}=(q_{1}^{F},q_{2}^{F})$ , $q_{b}^{F}=(q_{3}^{F},\ldots ,q_{m}^{F})$ and similarly for $p_{a}^{F}$ and $p_{b}^{F}$ . We consider points $(q^{B},p^{B})\in T^{\ast }U^{B}$ as points in $T^{\ast }S$ (because $U^{B}\subset S$ ).

For each point $(q^{B},p^{B})\in T^{\ast }S$ , there is a corresponding point $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70B}}(\Vert p^{B}\Vert )}^{\unicode[STIX]{x1D70E}}(q^{B},p^{B})\in T^{\ast }S^{-}$ such that $((q^{B},p^{B}),\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70B}}(\Vert p^{B}\Vert )}^{\unicode[STIX]{x1D70E}}(q^{B},p^{B}))\in H_{\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D6FC}}}\subset T^{\ast }S\times T^{\ast }S^{-}$ . There are also corresponding open sets $\{(q^{B},p^{B})\}\times T^{\ast }U^{F^{\prime }}\subset \{(q^{B},p^{B})\}\times T^{\ast }S^{-}$ and $\{q^{B}\}\times U^{F^{\prime }}\subset \{q^{B}\}\times S^{-}$ such that $\{q^{B}\}\times U^{F^{\prime }}$ is adapted to $\{q^{B}\}\times D_{q^{B}}$ in the sense that:

• ∙ $\{q^{B}\}\times U^{F^{\prime }}\cap \{q^{B}\}\times D_{q^{B}}=\{q^{B}\}\times \{q_{a}^{F}=0\}$ ; and

• ∙ $c(t)=(q^{B},tq_{1}^{F},tq_{2}^{F},q_{3}^{F},\ldots ,q_{m}^{F})$ are unit-speed geodesics and perpendicular to $D_{q^{B}}$ at $t=0$ , for any $q^{F}\in U^{F}$ such that $|q_{1}^{F}|^{2}+|q_{2}^{F}|^{2}=1$ .

Since $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70B}}(\Vert \cdot \Vert )}^{\unicode[STIX]{x1D70E}}(\cdot )$ is defined by the geodesic flow on $\{(q^{B},p^{B})\}\times T^{\ast }S^{-}=T^{\ast }S^{-}$ and $\{q^{B}\}\times U^{F^{\prime }}$ is adapted to $\{q^{B}\}\times D_{q^{B}}$ , we know that $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D6FC}}(\Vert p^{B}\Vert )}^{\unicode[STIX]{x1D70E}}(q^{B},p^{B})=(-\unicode[STIX]{x1D6FC}p_{a}^{F},q_{b}^{F},p_{a}^{F},0)$ when $p^{B}\neq 0$ small (as in the proof of Lemma 3.1). Now, we have a parametrized version of (3.5)

(3.7) $$\begin{eqnarray}\displaystyle & & \displaystyle T^{\ast }(U^{B}\times U^{F^{\prime }})\cap H_{\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D6FC}}}\nonumber\\ \displaystyle & & \displaystyle \quad =\{(q^{B},p^{B},-\unicode[STIX]{x1D6FC}p_{a}^{F},q_{b}^{F},p_{a}^{F},0)\mid p^{B}\neq 0,\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D6FC}}(\Vert p^{B}\Vert )}^{\unicode[STIX]{x1D70E}}(q^{B},p^{B})=(-\unicode[STIX]{x1D6FC}p_{a}^{F},q_{b}^{F},p_{a}^{F},0)\}\end{eqnarray}$$

when $U^{B}$ and $U^{F^{\prime }}$ are sufficiently small.

Here, both $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70B}}^{\unicode[STIX]{x1D6FC}}(\Vert p^{B}\Vert )}^{\unicode[STIX]{x1D70E}}(q^{B},p^{B})$ and $(-\unicode[STIX]{x1D6FC}p_{a}^{F},q_{b}^{F},p_{a}^{F},0)$ are considered as points in $T_{\unicode[STIX]{x1D716}}^{\ast }S$ although they belong to different factors of $T^{\ast }(S\times S^{-})$ . Therefore, in $T^{\ast }(U^{B}\times U^{F^{\prime }})\cap H_{\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D6FC}}}$ , fixing $q^{B}$ and letting $p^{B}$ go to $0$ linearly leads to fixing $q_{b}^{F}$ and letting $p_{a}^{F}$ go to zero linearly.

Since $H_{\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D6FC}}}$ is globally defined, the above discussion is true for any charts $U^{B}\times U^{F^{\prime }}$ on $U^{B}\times U^{F}$ adapted to $D^{\operatorname{op}}$ . From the discussion using local charts on $U^{B}\times U^{F}$ and the fact that $p_{a}^{F}$ goes to zero linearly as $p^{B}$ goes to $0$ linearly, we can see that $H_{\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D6FC}}}$ and $D^{\operatorname{op}}$ can be glued smoothly (linearity is not necessary for $H_{\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D6FC}}}$ and $D^{\operatorname{op}}$ to be glued smoothly but it is sufficient). The fact that $H_{\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D6FC}}}$ can be glued smoothly with $\unicode[STIX]{x1D6E5}$ is because all orders of derivatives of $\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D6FC}}$ vanish at $r=\unicode[STIX]{x1D716}$ . It results in a smooth Lagrangian, which we denote by $(S\times S^{-})\text{\#}_{\unicode[STIX]{x1D6E5}_{S},E_{2}}^{\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D6FC}}}\unicode[STIX]{x1D6E5}$ .

Finally, we show that $(S\times S^{-})\text{\#}_{\unicode[STIX]{x1D6E5}_{S},E_{2}}^{\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D6FC}}}\unicode[STIX]{x1D6E5}$ is Hamiltonian isotopic to $(S\times S^{-})\text{\#}_{\unicode[STIX]{x1D6E5}_{S},E_{2}}^{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}_{1}}}\unicode[STIX]{x1D6E5}$ . We can choose $\{\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D6FC}_{t}}\}_{t\in [0,1)}$ interpolating $\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D6FC}}$ and $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}_{1}}$ as in the proof of Lemma 3.1. This is a smooth Lagrangian isotopy which is invariant under the diagonal $\text{Isom}(S)$ action.◻

In parallel to Lemma 3.3, we have the following.

Lemma 3.6 (Theorem 1.1(3)).

Let $S$ be $\mathbb{RP}^{n}$ , $\mathbb{CP}^{m/2}$ or $\mathbb{HP}^{n}$ and

$$\begin{eqnarray}\displaystyle D^{\operatorname{op}}=\{(x,y)\in S\times S^{-}\mid \text{dist}(x,y)=\unicode[STIX]{x1D70B}\}. & & \displaystyle \nonumber\end{eqnarray}$$

Up to Hamiltonian isotopy in $T^{\ast }S\times (T^{\ast }S)^{-}$ , we have

$$\begin{eqnarray}\displaystyle (S\times S^{-})\text{\#}_{D^{\operatorname{op}},E_{2}}((S\times S^{-})\text{\#}_{\unicode[STIX]{x1D6E5}_{S},E_{2}}\unicode[STIX]{x1D6E5})=\text{Graph}(\unicode[STIX]{x1D70F}_{S}^{-1}). & & \displaystyle \nonumber\end{eqnarray}$$

Proof. The proof is similar to that of Lemma 3.3 and we again assume $S=\mathbb{CP}^{m/2}$ . We use the function $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70B}}^{0}$ in Lemma 3.3 to define ${\mathcal{S}}=(S\times S^{-})\text{\#}_{\unicode[STIX]{x1D6E5}_{S},E_{2}}^{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70B}}^{0}}\unicode[STIX]{x1D6E5}$ , which is Hamiltonian isotopic to $(S\times S^{-})\text{\#}_{\unicode[STIX]{x1D6E5}_{S},E_{2}}\unicode[STIX]{x1D6E5}$ by Lemma 3.4. Now, ${\mathcal{S}}$ intersects $S\times S^{-}$ cleanly along $D^{\operatorname{op}}$ . We can perform another $E_{2}$ -flow surgery from $S\times S^{-}$ to ${\mathcal{S}}$ . Then $S\times S^{-}\text{\#}_{D^{\operatorname{op}},E_{2}}{\mathcal{S}}$ is identical to $S\times S^{-}\text{\#}_{\unicode[STIX]{x1D6E5}_{S},E_{2}}^{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70B}+\unicode[STIX]{x1D706}}}\unicode[STIX]{x1D6E5}$ for some admissible function $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70B}+\unicode[STIX]{x1D706}}$ . By Lemmas 3.4 and 3.3, $S\times S^{-}\text{\#}_{\unicode[STIX]{x1D6E5}_{S},E_{2}}^{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70B}+\unicode[STIX]{x1D706}}}\unicode[STIX]{x1D6E5}$ is Hamiltonian isotopic to $S\times S^{-}\text{\#}_{\unicode[STIX]{x1D6E5}_{S},E_{2}}^{\unicode[STIX]{x1D708}_{2\unicode[STIX]{x1D70B}}^{0}}\unicode[STIX]{x1D6E5}=\text{Graph}(\unicode[STIX]{x1D70F}_{S}^{-1})$ so we obtain the result.◻

3.3 Family versions

One may also generalize the above example to the case of family Dehn twists [WW16] which we now recall. Let $G$ be $\operatorname{SO}(l+1)$ with Lie algebra $\mathfrak{g}$ . A connection one form on a principal $G$ bundle $\unicode[STIX]{x1D70B}:P\rightarrow B$ is a one form $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6FA}^{1}(P,\mathfrak{g})$ satisfying the following two conditions:

• ∙ $\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D709}_{P})=\unicode[STIX]{x1D709}$ for any $\unicode[STIX]{x1D709}\in \mathfrak{g}$ , where $\unicode[STIX]{x1D709}_{P}$ is the vector field generating the action of $\unicode[STIX]{x1D709}$ ;

• ∙ $g^{\ast }\unicode[STIX]{x1D6FC}=\operatorname{Ad}(g)^{-1}\unicode[STIX]{x1D6FC}$ for any $g\in G$ , where the adjoint action is on the values of $\unicode[STIX]{x1D6FC}$ .

We have a splitting

$$\begin{eqnarray}TP=\ker (\unicode[STIX]{x1D6FC})\oplus \ker (D\unicode[STIX]{x1D70B})\end{eqnarray}$$

which is invariant under the group action.

Suppose $B$ admits a symplectic structure $\unicode[STIX]{x1D714}_{B}$ . We equip $(T^{\ast }S^{l},\unicode[STIX]{x1D714}_{T^{\ast }S^{l}})$ with the Hamiltonian $G$ -action induced by the isometry of the zero section $G=\text{Isom}(S^{l})\subset \text{Symp}(T^{\ast }S^{l})$ , where $\unicode[STIX]{x1D714}_{T^{\ast }S^{l}}$ is the canonical symplectic structure on $T^{\ast }S^{l}$ . We denote the moment map by $\unicode[STIX]{x1D6F7}:T^{\ast }S^{l}\rightarrow \mathfrak{g}^{\vee }$ . The minimally coupling form on $P\times T^{\ast }S^{l}$ is defined by

(3.8) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D714}_{P\times T^{\ast }S^{l},\unicode[STIX]{x1D6FC}}:=\unicode[STIX]{x1D70B}_{P}^{\ast }\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D714}_{B}+\unicode[STIX]{x1D70B}_{S}^{\ast }\unicode[STIX]{x1D714}_{T^{\ast }S^{l}}+d\langle \unicode[STIX]{x1D70B}_{P}^{\ast }\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D70B}_{S}^{\ast }\unicode[STIX]{x1D6F7}\rangle \in \unicode[STIX]{x1D6FA}^{2}(P\times T^{\ast }S^{l}), & & \displaystyle\end{eqnarray}$$

where $\unicode[STIX]{x1D70B}_{P}:P\times T^{\ast }S^{l}\rightarrow P$ and $\unicode[STIX]{x1D70B}_{S}:P\times T^{\ast }S^{l}\rightarrow T^{\ast }S^{l}$ are projections to the first and second factors, respectively. The two form $\unicode[STIX]{x1D714}_{P\times T^{\ast }S^{l},\unicode[STIX]{x1D6FC}}$ has the property that $\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D709}_{P\times F}}\unicode[STIX]{x1D714}_{P\times F,\unicode[STIX]{x1D6FC}}=0$ and it descends to a symplectic form $\unicode[STIX]{x1D714}_{P(T^{\ast }S^{l})}$ on $P\times _{G}T_{\unicode[STIX]{x1D716}}^{\ast }S^{l}$ for some $\unicode[STIX]{x1D716}>0$ , where $\unicode[STIX]{x1D709}_{P\times F}$ is the vector field in $P\times F$ generating the diagonal action of $\unicode[STIX]{x1D709}$ and $T_{\unicode[STIX]{x1D716}}^{\ast }S^{l}$ consists of the cotangent vectors with norm less than $\unicode[STIX]{x1D716}$ . Moreover, $\unicode[STIX]{x1D70B}\circ \unicode[STIX]{x1D70B}_{P}:P\times T^{\ast }S^{l}\rightarrow B$ descends to a symplectic fiber bundle map $\unicode[STIX]{x1D70B}_{P(T^{\ast }S^{l})}:P\times _{G}T_{\unicode[STIX]{x1D716}}^{\ast }S^{l}\rightarrow B$ . An important feature of $\unicode[STIX]{x1D714}_{P(T^{\ast }S^{l})}$ is the following.

Lemma 3.7. We have $\unicode[STIX]{x1D714}_{P\times T^{\ast }S^{l},\unicode[STIX]{x1D6FC}}(v_{1},v_{2})=0$ for any $v_{1}\in \ker (\unicode[STIX]{x1D6FC})$ and $v_{2}\in T(T^{\ast }S^{l})$ . Therefore, the symplectic orthogonal complement of fibers of $\unicode[STIX]{x1D70B}_{P(T^{\ast }S^{l})}$ in $P\times _{G}T_{\unicode[STIX]{x1D716}}^{\ast }S^{l}$ is the image of $\ker (\unicode[STIX]{x1D6FC})$ under the quotient map $P\times T_{\unicode[STIX]{x1D716}}^{\ast }S^{l}\rightarrow P\times _{G}T_{\unicode[STIX]{x1D716}}^{\ast }S^{l}$ .

Proof. We have a decomposition $T(P\times T^{\ast }S^{l})=\ker (\unicode[STIX]{x1D6FC})\oplus \ker (D\unicode[STIX]{x1D70B})\oplus T(T^{\ast }S^{l})$ . Since $v_{1}\in \ker (\unicode[STIX]{x1D6FC})$ , we have $v_{1}\in \ker (\unicode[STIX]{x1D70B}_{S}^{\ast }\unicode[STIX]{x1D714}_{T^{\ast }S^{l}})$ and $v_{1}\in \ker (\unicode[STIX]{x1D70B}_{S}^{\ast }\,d\unicode[STIX]{x1D6F7})$ . Since $v_{2}\in T(T^{\ast }S^{l})$ , we have $v_{2}\in \ker (\unicode[STIX]{x1D70B}_{P}^{\ast }\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D714}_{B})$ and $v_{2}\in \ker (\unicode[STIX]{x1D70B}_{P}^{\ast }\,d\unicode[STIX]{x1D6FC})$ . The result follows from (3.8).◻

Corollary 3.8. For the symplectic fibration $\unicode[STIX]{x1D70B}_{P(T^{\ast }S^{l})}:P\times _{G}T_{\unicode[STIX]{x1D716}}^{\ast }S^{l}\rightarrow B$ , the monodromy of each loop in $B$ by symplectic parallel transport lies in $G$ .

Proof. By definition, those monodromies of parallel transports with respect to $\unicode[STIX]{x1D6FC}$ in $P$ lie in $G$ . Therefore, so is $P\times T_{\unicode[STIX]{x1D716}}^{\ast }S^{l}$ and hence $P\times _{G}T_{\unicode[STIX]{x1D716}}^{\ast }S^{l}$ . The result follows because symplectic orthogonal complement of fibers coincides with the image of $\ker (\unicode[STIX]{x1D6FC})$ , by Lemma 3.7.◻

Recall that a spherically fibered coisotropic manifold $i:C^{2n-l}{\hookrightarrow}M^{2n}$ is a coisotropic submanifold so that there is a fibration $\unicode[STIX]{x1D70C}:C\rightarrow B^{2n-2l}$ over a symplectic base, whose fibers are leaves of the characteristic foliation (also called null-leaves) and are diffeomorphic to $S^{l}$ . In other words, $\unicode[STIX]{x1D70C}^{\ast }\unicode[STIX]{x1D714}_{B}=i^{\ast }\unicode[STIX]{x1D714}_{M}$ . Moreover, we equip the fibers with round metrics such that all their geodesics are closed of length $2\unicode[STIX]{x1D70B}$ and ask that the structure group of $\unicode[STIX]{x1D70C}$ lie in $\operatorname{SO}(l+1)$ .

A neighborhood $U$ of $C$ can be symplectically identified with $P\times _{\operatorname{SO}(l+1)}T_{\unicode[STIX]{x1D716}}^{\ast }S^{l}$ , where $P$ is the principal $\operatorname{SO}(l+1)$ -bundle associated to $C$ . The family Dehn twist $\unicode[STIX]{x1D70F}_{C}$ can then be defined fiberwise as the fiberwise Hamiltonian function $\widetilde{\unicode[STIX]{x1D708}}_{\unicode[STIX]{x1D716}}^{\text{Dehn}}(\Vert p\Vert )$ (see Remark 2.12) is preserved by the structure group. With respect to the fiberwise metric $g^{v}$ , the function $h(\cdot )=\widetilde{\unicode[STIX]{x1D708}}(\Vert \cdot \Vert _{g^{v}})$ defines a flow along fibers whose time- $1$ map is the desired Dehn twist (with a continuation over $C$ defined by the fiberwise antipodal map on $C$ ).

Equivalently, we can choose a reference fiber $F=T^{\ast }S^{l}$ of the symplectic fibration $\unicode[STIX]{x1D70B}_{P(T^{\ast }S^{l})}$ and the family Dehn twist restricted to any fiber $F^{\prime }$ is defined to be $\unicode[STIX]{x1D70F}_{C}|_{F^{\prime }}:=\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D6FE}^{-1}}\circ \unicode[STIX]{x1D70F}_{S^{l}}\circ \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D6FE}}$ , where $\unicode[STIX]{x1D6FE}$ is a path from the base point of $F^{\prime }$ to the base point of $F$ , $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D6FE}}$ is symplectic parallel transport along $\unicode[STIX]{x1D6FE}$ and $\unicode[STIX]{x1D70F}_{S^{l}}$ is the Dehn twist on $F$ . By Corollary 3.8, $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D6FE}^{-1}}\,\circ \,\unicode[STIX]{x1D70F}_{S^{l}}\,\circ \,\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D6FE}}$ is independent of $\unicode[STIX]{x1D6FE}$ and gives a symplectomorphism of $F^{\prime }$ . The fiberwise symplectomorphisms patch together to a diffeomorphism $\unicode[STIX]{x1D70F}_{C}$ . To see that $\unicode[STIX]{x1D70F}_{C}$ is a symplectomorphism of $P\times _{\operatorname{SO}(l+1)}T_{\unicode[STIX]{x1D716}}^{\ast }S^{l}$ , it suffices to check that

(3.9) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D714}_{P(T^{\ast }S^{l})}((\unicode[STIX]{x1D70F}_{C})_{\ast }v_{1},(\unicode[STIX]{x1D70F}_{C})_{\ast }v_{2})=\unicode[STIX]{x1D714}_{P(T^{\ast }S^{l})}(v_{1},v_{2}) & & \displaystyle\end{eqnarray}$$

for any $v_{1},v_{2}\in \ker (\unicode[STIX]{x1D6FC})$ because $T(P\times _{\operatorname{SO}(l+1)}T_{\unicode[STIX]{x1D716}}^{\ast }S^{l})=\ker (\unicode[STIX]{x1D6FC})\oplus T(T_{\unicode[STIX]{x1D716}}^{\ast }S^{l})$ , $(\ker (\unicode[STIX]{x1D6FC}))^{\unicode[STIX]{x1D714}_{P(T^{\ast }S^{l})}}=T(T_{\unicode[STIX]{x1D716}}^{\ast }S^{l})$ by Lemma 3.7 and we already know that $\unicode[STIX]{x1D70F}_{C}$ is fiberwise symplectic. By construction, $(\unicode[STIX]{x1D70F}_{C})_{\ast }v_{i}\in \ker (\unicode[STIX]{x1D6FC})$ and $(\unicode[STIX]{x1D70B}_{P(T^{\ast }S^{l})}\circ \unicode[STIX]{x1D70F}_{C})_{\ast }v_{i}=(\unicode[STIX]{x1D70B}_{P(T^{\ast }S^{l})})_{\ast }v_{i}$ for $i=1,2$ so (3.9) follows from (3.8).

Now consider the natural Lagrangian embedding $\widetilde{C}:=C\times _{B}C{\hookrightarrow}M\times M$ , where $M$ is a symplectic manifold such that we have an inclusion $i:C^{2n-l}{\hookrightarrow}M^{2n}$ making $C$ a spherically fibered coisotropic manifold. Explicitly, the image of this map is

$$\begin{eqnarray}\widetilde{C}=\{(x,y)\in C\times C\subset M\times M:\unicode[STIX]{x1D70B}(x)=\unicode[STIX]{x1D70B}(y)\},\end{eqnarray}$$

where $\unicode[STIX]{x1D70B}:C\rightarrow B$ is the $S^{l}$ -bundle projection. Indeed, $\widetilde{C}=C^{t}\circ C$ is a composition Lagrangian in the sense of (5.2). Here we have abused the notation by identifying $C$ with its Lagrangian image in $B\times M$ defined by

$$\begin{eqnarray}\{(x,y)\in B\times C\subset B\times M:\unicode[STIX]{x1D70B}(y)=x\}.\end{eqnarray}$$

Note that $\widetilde{C}$ is a fiber bundle over $B$ with fiber $S^{l}\times S^{l}$ and structure group the diagonal $\operatorname{SO}(l+1)$ .

We continue to use $U$ to denote a neighborhood of $C$ in $M$ which can be identified with $P\times _{\operatorname{SO}(l+1)}T_{\unicode[STIX]{x1D716}}^{\ast }S^{l}$ . Consider a symplectic trivialization $U_{0}:=B_{0}\times T_{\unicode[STIX]{x1D716}}^{\ast }S^{l}$ of the symplectic fiber bundle $\unicode[STIX]{x1D70B}_{P(T^{\ast }S^{l})}:U=P\times _{\operatorname{SO}(l+1)}T_{\unicode[STIX]{x1D716}}^{\ast }S^{l}\rightarrow B$ for some contractible open set $B_{0}\subset B$ . Any point contained in $\unicode[STIX]{x1D6E5}\cap (U_{0}\times U_{0}^{-})\subset M\times M^{-}$ thus takes the form $((x,p),(x,p))$ , where $x\in B_{0}$ and $p\in T_{\unicode[STIX]{x1D716}}^{\ast }S^{l}$ . In this setting, the graph of $\unicode[STIX]{x1D70F}_{C}^{-1}$ in $U_{0}\times U_{0}^{-}$ consist of points

$$\begin{eqnarray}\text{Graph}(\unicode[STIX]{x1D70F}_{C}^{-1})=\{((x,p),(x,\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D708}^{\text{Dehn}}(\Vert p\Vert )}^{\unicode[STIX]{x1D70E}}(p)))\mid x\in B_{0},p\in T_{\unicode[STIX]{x1D716}}^{\ast }S^{l}\}.\end{eqnarray}$$

This is true for any contractible open subset $B_{0}\subset B$ and $\text{Graph}(\unicode[STIX]{x1D70F}_{C}^{-1})$ coincides with $\unicode[STIX]{x1D6E5}$ outside $U\times U^{-}$ .

As before, we want to realize $\text{Graph}(\unicode[STIX]{x1D70F}_{C}^{-1})$ as a surgery from $\widetilde{C}$ to $\unicode[STIX]{x1D6E5}$ . In this case, we want to perform a family $E_{2}$ -surgery.

In the notation of § 2.3, let $L=S^{l}\times (S^{l})^{-}$ , $D=\unicode[STIX]{x1D6E5}_{S^{l}}\subset L$ , $\mathscr{P}=U\times U^{-}$ , $\mathscr{B}=B\times B^{-}$ , $i:B\rightarrow \unicode[STIX]{x1D6E5}_{B}\subset \mathscr{B}$ be the diagonal embedding, $\mathscr{L}=\widetilde{C}$ , $N_{\mathscr{D}}^{\ast }\mathscr{L}=\unicode[STIX]{x1D6E5}_{U}$ , $\mathscr{D}=\unicode[STIX]{x1D6E5}_{U}\cap \widetilde{C}$ , and $G=\operatorname{SO}(l+1)=\text{Isom}_{\unicode[STIX]{x1D6E5}}(L)\subset \operatorname{SO}(l+1)\times \operatorname{SO}(l+1)$ is the diagonal isometry group. It is clear how to define the fiber bundle structures

compatible with the inclusions $\mathscr{D}{\hookrightarrow}\mathscr{L}{\hookrightarrow}i^{\ast }\mathscr{P}$ . As in the calculation for Lemma 3.7 and Corollary 3.8, we know that the symplectic orthogonal complement of the fibers of $\unicode[STIX]{x1D70B}:\mathscr{P}\rightarrow \mathscr{B}$ is given by the product horizontal distribution $\ker (\unicode[STIX]{x1D6FC})\oplus (\ker (\unicode[STIX]{x1D6FC}))^{-}$ and the symplectic monodromy for loops in $B$ lies in the diagonal isometry group $G$ . We leave it as an exercise for readers to check that $G$ satisfies all the other assumptions in § 2.3. As a result, we can define a global Lagrangian handle $\mathscr{H}_{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70B}}}\subset \mathscr{P}$ .

By the same token, we can define a projectively fibered coisotropic manifold which is a coisotropic manifold with null-leaves complex (or real, quaternionic) projective spaces. Family Dehn twists for these spaces are defined similarly.

Lemma 3.9. Let $C\subset (M,\unicode[STIX]{x1D714})$ be a spherically (respectively projectively) coisotropic submanifold with base $B$ . Let $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}_{i}}$ be $\unicode[STIX]{x1D706}_{i}$ -admissible functions such that $(k-1)\unicode[STIX]{x1D70B}<\unicode[STIX]{x1D706}_{i}<k\unicode[STIX]{x1D70B}$ for some positive integer $k$ for both $i=1,2$ . Then the family $E_{2}$ -flow surgered Lagrangian manifolds $\widetilde{C}\text{\#}_{\mathscr{D},E_{2}}^{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}_{i}}}\unicode[STIX]{x1D6E5}$ for $i=1,2$ are Hamiltonian isotopic.

Moreover, if we choose a semi-admissible function $\unicode[STIX]{x1D708}_{k\unicode[STIX]{x1D70B}}^{\unicode[STIX]{x1D6FC}}:(0,\infty )\rightarrow [0,k\unicode[STIX]{x1D70B})$ such that $\unicode[STIX]{x1D708}_{k\unicode[STIX]{x1D70B}}^{\unicode[STIX]{x1D6FC}}(r)=k\unicode[STIX]{x1D70B}-\unicode[STIX]{x1D6FC}r$ near $r=0\;(\unicode[STIX]{x1D6FC}\geqslant 0)$ , then $\widetilde{C}\text{\#}_{\mathscr{D},E_{2}}^{\unicode[STIX]{x1D708}_{k\unicode[STIX]{x1D70B}}^{\unicode[STIX]{x1D6FC}}}\unicode[STIX]{x1D6E5}$ is a smooth Lagrangian that is Hamiltonian isotopic to $\widetilde{C}\text{\#}_{\mathscr{D},E_{2}}^{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}_{i}}}\unicode[STIX]{x1D6E5}$ .

Corollary 3.10 (Theorem 1.1(2), (4)).

For spherically (respectively projectively) coisotropic submanifold $C$ , the family $E_{2}$ -flow clean surgery $\widetilde{C}\text{\#}_{\mathscr{D},E_{2}}\unicode[STIX]{x1D6E5}$ (respectively $\widetilde{C}\text{\#}_{\mathscr{D}^{\operatorname{op}},E_{2}}\widetilde{C}\text{\#}_{\mathscr{D},E_{2}}\unicode[STIX]{x1D6E5}$ ) is Hamiltonian isotopic to $\text{Graph}(\unicode[STIX]{x1D70F}_{C}^{-1})$ . Here $\mathscr{D}^{\operatorname{op}}$ is a $D^{\operatorname{op}}$ -bundle over the base $B$ and $D^{\operatorname{op}}$ is as in Lemma 3.6.

Proof of Lemma 3.9.

We give the proof for the spherical case and the other cases are similar. Since the construction in Lemma 3.4 is $\operatorname{SO}(l+1)$ invariant, we can apply Lemma 3.4 to $\widetilde{C}$ and $\unicode[STIX]{x1D6E5}_{U}$ inside $\mathscr{P}=U\times U^{-}$ fiberwise to obtain the desired Lagrangian isotopy from $\widetilde{C}\text{\#}_{\mathscr{D},E_{2}}^{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}_{1}}}\unicode[STIX]{x1D6E5}$ to $\widetilde{C}\text{\#}_{\mathscr{D},E_{2}}^{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}_{2}}}\unicode[STIX]{x1D6E5}$ and from $\widetilde{C}\text{\#}_{\mathscr{D},E_{2}}^{\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D6FC}}}\unicode[STIX]{x1D6E5}$ to $\widetilde{C}\text{\#}_{\mathscr{D},E_{2}}^{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}_{i}}}\unicode[STIX]{x1D6E5}$ .

What remains to show is that the Lagrangian isotopies are Hamiltonian isotopies. We prove the case where the Lagrangian isotopy is from $\widetilde{C}\text{\#}_{\mathscr{D},E_{2}}^{\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D6FC}}}\unicode[STIX]{x1D6E5}$ to $\widetilde{C}\text{\#}_{\mathscr{D},E_{2}}^{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}_{i}}}\unicode[STIX]{x1D6E5}$ . The other case is similar. Let $\unicode[STIX]{x1D704}_{K,t}:K\rightarrow T^{\ast }S^{l}\times (T^{\ast }S^{l})^{-1}$ be the Lagrangian isotopy from $(S\times S^{-})\text{\#}_{\unicode[STIX]{x1D6E5}_{S},E_{2}}^{\unicode[STIX]{x1D708}_{k\unicode[STIX]{x1D70B}}^{\unicode[STIX]{x1D6FC}}}\unicode[STIX]{x1D6E5}$ to $(S\times S^{-})\text{\#}_{\unicode[STIX]{x1D6E5}_{S},E_{2}}^{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}_{i}}}\unicode[STIX]{x1D6E5}$ in Lemma 3.4, which is $\operatorname{SO}(l+1)$ invariant. Let $b\in B$ be a reference based point. We define the Lagrangian isotopy $\unicode[STIX]{x1D704}_{\mathscr{K},t}:\mathscr{K}\rightarrow M\times M^{-}$ by

$$\begin{eqnarray}\unicode[STIX]{x1D704}_{\mathscr{K},t}(x)=\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D6FE}^{-1}}\circ \unicode[STIX]{x1D704}_{K,t}\circ \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D6FE}}(x),\end{eqnarray}$$

where $t\in [0,1]$ , $\unicode[STIX]{x1D6FE}:[0,1]\rightarrow B$ is a path from the based point of $x$ (i.e., projection of $x$ to $B$ ) to $b$ and $\mathscr{K}=\widetilde{C}\text{\#}_{\mathscr{D},E_{2}}^{\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D6FC}}}\unicode[STIX]{x1D6E5}$ . It is well defined because the monodromy of $\mathscr{K}\rightarrow B$ is inherited from $i^{\ast }\mathscr{P}\rightarrow B$ .

Since $\unicode[STIX]{x1D704}_{K,t}:L\rightarrow T^{\ast }S^{l}\times (T^{\ast }S^{l})^{-1}$ is a Hamiltonian isotopy, it is an exact isotopy (i.e $\unicode[STIX]{x1D703}_{0}:=\unicode[STIX]{x1D704}_{K,t}^{\ast }(\unicode[STIX]{x1D714}_{\text{can}}\oplus -\unicode[STIX]{x1D714}_{\text{can}})(\unicode[STIX]{x2202}\unicode[STIX]{x1D704}_{K,t}/\unicode[STIX]{x2202}t,\cdot )$ is exact). Since the fiberwise symplectic form and the isotopy are $\operatorname{SO}(l+1)$ -invariant, so is $\unicode[STIX]{x1D703}_{0}$ and its primitive. These primitives on fibers can be patched together to form a function $f:\mathscr{K}\rightarrow \mathbb{R}$ such that $\unicode[STIX]{x1D703}-df$ vanishes on fibers, where $\unicode[STIX]{x1D703}:=\unicode[STIX]{x1D704}_{\mathscr{K},t}^{\ast }(\unicode[STIX]{x1D714}_{M}\oplus -\unicode[STIX]{x1D714}_{M})(\unicode[STIX]{x2202}\unicode[STIX]{x1D704}_{\mathscr{K},t}/\unicode[STIX]{x2202}t,\cdot )$ . As a consequence of Lemma 3.7, the distribution of symplectic orthogonal complements of fibers of $\mathscr{P}\rightarrow \mathscr{B}$ coincides with $\ker (\unicode[STIX]{x1D6FC})\oplus (\ker (\unicode[STIX]{x1D6FC}))^{-}$ . Let $\operatorname{Ker}\subset T(\mathscr{K})$ be the horizontal distribution with respect to the fiber bundle $\mathscr{K}\rightarrow B$ that is mapped into (and actually also onto) the diagonal horizontal distribution $\ker (\unicode[STIX]{x1D6FC})_{\unicode[STIX]{x1D6E5}}\subset \ker (\unicode[STIX]{x1D6FC})\oplus (\ker (\unicode[STIX]{x1D6FC}))^{-}$ under the inclusion $\mathscr{K}\rightarrow \mathscr{P}$ . By definition, $\unicode[STIX]{x1D703}$ vanishes on $\operatorname{Ker}$ . Since $f$ is $\operatorname{SO}(l+1)$ -invariant, $df$ also vanishes on $\operatorname{Ker}$ and hence $\unicode[STIX]{x1D703}=df$ . This implies that $\unicode[STIX]{x1D704}_{\mathscr{K},t}$ is an exact, thus a Hamiltonian, isotopy.◻

Corollary 3.10 is now an immediate consequence of Lemma 3.9 by setting $k=1$ for spherical case and $k=2$ for the projective cases.

4 Gradings and energy

In this section we discuss the gradings in Lagrangian surgeries. We follow mostly the exposition in [AB14] to review the definition of gradings in § 4.1. The subsequent subsections provide computations for sufficient and necessary criteria to perform graded surgeries. Starting from § 5, all surgeries between graded Lagrangians will be graded surgeries. Our discussion stays in the $\mathbb{Z}$ -graded and exact case but the corresponding results for $\mathbb{Z}/N$ -gradings in the monotone setting can be obtained by modifying our argument using the setting in [Sei00] and the statements will be a modulo- $N$ reduction of what we have here.

4.1 Basic notions

We assume $2c_{1}(M)=0$ and fix once and for all a nowhere-vanishing section $\unicode[STIX]{x1D6FA}^{2}$ of $(\unicode[STIX]{x1D6EC}_{\mathbb{C}}^{\text{top}}(T^{\ast }M,J))^{\otimes 2}$ .

Let $\unicode[STIX]{x1D704}_{L}:L\rightarrow M$ be an exact Lagrangian immersion (i.e., $\unicode[STIX]{x1D704}_{L}^{\ast }\unicode[STIX]{x1D6FC}$ is exact). A grading on $(L,\unicode[STIX]{x1D704}_{L})$ (sometimes simply denoted by $\unicode[STIX]{x1D704}_{L}$ ) is defined as a continuous function $\unicode[STIX]{x1D703}_{L}:L\rightarrow \mathbb{R}$ such that $e^{2\unicode[STIX]{x1D70B}i\unicode[STIX]{x1D703}_{L}}=\text{Det}_{\unicode[STIX]{x1D6FA}}^{2}(\text{Im}(D\unicode[STIX]{x1D704}_{L}))$ , where $\text{Im}(D\unicode[STIX]{x1D704}_{L})$ is the image of $D\unicode[STIX]{x1D704}_{L}$ and $\text{Det}_{\unicode[STIX]{x1D6FA}}^{2}$ is defined as

$$\begin{eqnarray}\text{Det}_{\unicode[STIX]{x1D6FA}}^{2}(\unicode[STIX]{x1D6EC}_{p})=\text{Det}_{\unicode[STIX]{x1D6FA}}^{2}(X_{1},\ldots ,X_{n})=\frac{\unicode[STIX]{x1D6FA}^{2}(X_{1},\ldots ,X_{n})}{\Vert \unicode[STIX]{x1D6FA}^{2}(X_{1},\ldots ,X_{n})\Vert }\in S^{1}\end{eqnarray}$$

for any Lagrangian plane $\unicode[STIX]{x1D6EC}_{p}\subset T_{p}M$ at a point $p$ and any choice of a basis $\{X_{1},\ldots ,X_{n}\}$ for $\unicode[STIX]{x1D6EC}_{p}$ .

Given two transversal Lagrangian planes $\unicode[STIX]{x1D6EC}_{0},\unicode[STIX]{x1D6EC}_{1}$ (of dimension $n$ ) at the same point with a choice of $\unicode[STIX]{x1D703}_{0},\unicode[STIX]{x1D703}_{1}$ such that $e^{2\unicode[STIX]{x1D70B}i\unicode[STIX]{x1D703}_{j}}=\text{Det}_{\unicode[STIX]{x1D6FA}}^{2}(\unicode[STIX]{x1D6EC}_{j})$ for both $j$ , we can identify them as graded Lagrangian vector subspaces of $\mathbb{C}^{n}$ . The index of the pair $(\unicode[STIX]{x1D6EC}_{0},\unicode[STIX]{x1D703}_{0})$ and $(\unicode[STIX]{x1D6EC}_{1},\unicode[STIX]{x1D703}_{1})$ is defined as

(4.1) $$\begin{eqnarray}\text{Ind}((\unicode[STIX]{x1D6EC}_{0},\unicode[STIX]{x1D703}_{0}),(\unicode[STIX]{x1D6EC}_{1},\unicode[STIX]{x1D703}_{1}))=n+\unicode[STIX]{x1D703}_{1}-\unicode[STIX]{x1D703}_{0}-2\text{Angle}(\unicode[STIX]{x1D6EC}_{0},\unicode[STIX]{x1D6EC}_{1})\end{eqnarray}$$

where $\text{Angle}(\unicode[STIX]{x1D6EC}_{0},\unicode[STIX]{x1D6EC}_{1})=\sum _{j=1}^{n}\unicode[STIX]{x1D6FD}_{j}$ and $\unicode[STIX]{x1D6FD}_{j}\in (0,1/2)$ are such that there is a unitary basis $\{u_{1},\ldots ,u_{n}\}$ of $\unicode[STIX]{x1D6EC}_{0}$ satisfying $\unicode[STIX]{x1D6EC}_{1}=\operatorname{Span}_{\mathbb{R}}\{e^{2\unicode[STIX]{x1D70B}i\unicode[STIX]{x1D6FD}_{j}}u_{j}\}_{j=1}^{n}$ .

In general, when $\unicode[STIX]{x1D6EC}_{0}\cap \unicode[STIX]{x1D6EC}_{1}=\unicode[STIX]{x1D6EC}\neq \{0\}$ , the definition of index for the pair $(\unicode[STIX]{x1D6EC}_{0},\unicode[STIX]{x1D703}_{0})$ and $(\unicode[STIX]{x1D6EC}_{1},\unicode[STIX]{x1D703}_{1})$ is the same as above with the definition of $\text{Angle}(\unicode[STIX]{x1D6EC}_{0},\unicode[STIX]{x1D6EC}_{1})$ modified as follows. Pick a path of Lagrangian planes $\unicode[STIX]{x1D6EC}_{t}$ from $\unicode[STIX]{x1D6EC}_{0}$ to $\unicode[STIX]{x1D6EC}_{1}$ such that both the following hold.

• ∙ We have $\unicode[STIX]{x1D6EC}\subset \unicode[STIX]{x1D6EC}_{t}\subset \unicode[STIX]{x1D6EC}_{0}+\unicode[STIX]{x1D6EC}_{1}$ for all $t\in [0,1]$ .

• ∙ The image $\overline{\unicode[STIX]{x1D6EC}_{t}}$ of $\unicode[STIX]{x1D6EC}_{t}$ inside the symplectic vector space $(\unicode[STIX]{x1D6EC}_{0}+\unicode[STIX]{x1D6EC}_{1})/\unicode[STIX]{x1D6EC}$ is a positive definite path from $\overline{\unicode[STIX]{x1D6EC}_{0}}$ to $\overline{\unicode[STIX]{x1D6EC}_{1}}$ .

Let $\unicode[STIX]{x1D6FD}_{t}$ be a continuous path of real numbers such that $e^{2\unicode[STIX]{x1D70B}i\unicode[STIX]{x1D6FD}_{t}}=\text{Det}_{\unicode[STIX]{x1D6FA}}^{2}(\unicode[STIX]{x1D6EC}_{t})$ . Then, the Lagrangian angle is defined as

$$\begin{eqnarray}2\text{Angle}(\unicode[STIX]{x1D6EC}_{0},\unicode[STIX]{x1D6EC}_{1})=\unicode[STIX]{x1D6FD}_{1}-\unicode[STIX]{x1D6FD}_{0}.\end{eqnarray}$$

Equivalently, we can define $2\text{Angle}(\unicode[STIX]{x1D6EC}_{0},\unicode[STIX]{x1D6EC}_{1}):=2\text{Angle}(\overline{\unicode[STIX]{x1D6EC}_{0}},\overline{\unicode[STIX]{x1D6EC}_{1}})$ .

Definition 4.1. For two graded Lagrangian immersions $(\unicode[STIX]{x1D704}_{L_{1}}\!,\unicode[STIX]{x1D703}_{1})$ , $(\unicode[STIX]{x1D704}_{L_{2}}\!,\unicode[STIX]{x1D703}_{2})$ (not necessarily distinct), and points $p_{j}\in L_{j}$ for $j=1,2$ such that $\unicode[STIX]{x1D704}_{L_{1}}(p_{1})=\unicode[STIX]{x1D704}_{L_{2}}(p_{2})=p$ , the index for the ordered pair $(p_{1},p_{2})$ is

$$\begin{eqnarray}\text{Ind}_{(p_{1},p_{2})}(\unicode[STIX]{x1D704}_{L_{1}},\unicode[STIX]{x1D704}_{L_{2}})=\text{Ind}(((\unicode[STIX]{x1D704}_{L_{1}})_{\ast }T_{p_{1}}L_{1},\unicode[STIX]{x1D703}_{1}(p_{1})),((\unicode[STIX]{x1D704}_{L_{2}})_{\ast }T_{p_{2}}L_{2},\unicode[STIX]{x1D703}_{2}(p_{2}))).\end{eqnarray}$$

We also use the notation $\text{Ind}_{p}(L_{1},L_{2})$ to denote $\text{Ind}_{(p_{1},p_{2})}(\unicode[STIX]{x1D704}_{L_{1}},\unicode[STIX]{x1D704}_{L_{2}})$ if $\unicode[STIX]{x1D704}_{L_{1}}^{-1}(p)=\{p_{1}\}$ and $\unicode[STIX]{x1D704}_{L_{2}}^{-1}(p)=\{p_{2}\}$ . Note that if $L_{1}$ and $L_{2}$ are two Lagrangian embeddings such that $L_{1}$ intersects $L_{2}$ cleanly along a connected submanifold $D\subset M$ , then $\text{Ind}_{p}(L_{1},L_{2})=\text{Ind}_{q}(L_{1},L_{2})$ for all $p,q\in D$ . In this case, we denote the index as $\text{Ind}_{D}(L_{1},L_{2})$ .

Example 4.2. For a graded Lagrangian immersion $(\unicode[STIX]{x1D704}_{L},\unicode[STIX]{x1D703})$ and an integer $k$ , $\unicode[STIX]{x1D704}_{L}[k]$ is defined as $\unicode[STIX]{x1D704}_{L}[k]=(\unicode[STIX]{x1D704}_{L},\unicode[STIX]{x1D703}-k)$ . In particular, we have

$$\begin{eqnarray}\text{Ind}_{D}(\unicode[STIX]{x1D704}_{L_{1}}[k],\unicode[STIX]{x1D704}_{L_{2}}[k^{\prime }])=\text{Ind}_{D}(\unicode[STIX]{x1D704}_{L_{1}},\unicode[STIX]{x1D704}_{L_{2}})+k-k^{\prime }.\end{eqnarray}$$

Example 4.3. Let $M=\mathbb{C}^{n}$ be equipped with the standard symplectic form, complex structure and complex volume form. Let $L_{1}=\mathbb{R}^{n}=\{y_{1}=\cdots =y_{n}=0\}$ and $L_{2}=\{x_{1}=\cdots =x_{n-k}=y_{n-k+1}=\cdots =y_{n}=0\}$ be two Lagrangian planes for some $0\leqslant k\leqslant n$ . We have $\text{Det}_{\unicode[STIX]{x1D6FA}}^{2}(L_{1})=1$ and $\text{Det}_{\unicode[STIX]{x1D6FA}}^{2}(L_{2})=(-1)^{n-k}$ . Let $\unicode[STIX]{x1D703}_{L_{1}}=n-k-1$ and $\unicode[STIX]{x1D703}_{L_{2}}=(n-k)/2$ be the gradings of $L_{1}$ and $L_{2}$ . Then, we have $\text{Ind}_{0}(L_{1},L_{2})=(n)+(n-k)/2-(n-k-1)-2(n-k)(1/4)=k+1$ .

Definition 4.4. For a Lagrangian isotopy $\unicode[STIX]{x1D6F7}=(\unicode[STIX]{x1D6F7}_{t})_{t\in [0,1]}:L\times [0,1]\rightarrow (M,\unicode[STIX]{x1D714})$ , if $\unicode[STIX]{x1D6F7}_{0}$ is equipped with grading $\unicode[STIX]{x1D703}_{0}$ , then the induced grading on $\unicode[STIX]{x1D6F7}_{1}$ is defined as follows. There is a unique way to extend $\unicode[STIX]{x1D703}_{0}:L\times \{0\}\rightarrow \mathbb{R}$ continuously to $\unicode[STIX]{x1D703}:L\times [0,1]\rightarrow \mathbb{R}$ such that $e^{2\unicode[STIX]{x1D70B}i\unicode[STIX]{x1D703}(\cdot ,t)}=\text{Det}_{\unicode[STIX]{x1D6FA}}^{2}(\operatorname{Im}(D\unicode[STIX]{x1D6F7}_{t}(\cdot )))$ and the induced grading on $\unicode[STIX]{x1D6F7}_{1}$ is defined by $\unicode[STIX]{x1D703}(\cdot ,1)$ .

Example 4.5. Let $L=\mathbb{R}\subset (\mathbb{R}^{2},dx\wedge dy)$ and identify the latter with $\mathbb{C}$ equipped with the standard complex volume form. Consider $h:\mathbb{R}\rightarrow \mathbb{R}$ given by $h(q)=c(q^{2}/2)$ for some constant  $c$ . The graph of $dh$ , $\text{Graph}(dh)$ , is given by $\{(q,cq)\in T^{\ast }L\mid q\in L\}$ . By setting $q=x$ and $p=-y$ to identify $\mathbb{C}$ with $T^{\ast }L$ , $\text{Graph}(dh)$ is given by $\{(x,-cx)\in \mathbb{C}\}$ . Using our sign convention, $\text{Graph}(dh)$ is the time- $1$ Hamiltonian flow of $L$ generated by the Hamiltonian $-h\circ \unicode[STIX]{x1D70B}:T^{\ast }L\rightarrow \mathbb{R}$ , where $\unicode[STIX]{x1D70B}:T^{\ast }L\rightarrow L$ is the projection. If we give a grading to $L$ and induce from it a grading on $\text{Graph}(dh)$ by the Hamiltonian isotopy, then

$$\begin{eqnarray}\text{Ind}_{0}(L,\text{Graph}(dh))=\left\{\begin{array}{@{}ll@{}}1 & \text{if }c\leqslant 0,\\ 0 & \text{if }c>0.\end{array}\right.\end{eqnarray}$$

In short, the index equals the Morse index of $h$ at $q=0$ if $c\neq 0$ . We call the induced grading on $\text{Graph}(dh)$ by the Hamiltonian isotopy generated by $-h\circ \unicode[STIX]{x1D70B}$ the canonical induced grading on $\text{Graph}(dh)$ .

Example 4.6. Let $L=\mathbb{R}^{n}\subset (\mathbb{C}^{n},\sum _{i=1}^{n}dx_{i}\wedge dy_{i})$ . Consider $h:L\rightarrow \mathbb{R}$ given by $h(q)=c\sum _{j=1}^{k}(q_{j}^{2}/2)$ . If we let $q_{i}=x_{i}$ and $p_{i}=-y_{i}$ to identify $\mathbb{C}^{n}$ with $T^{\ast }L$ and equip $\text{Graph}(dh)$ with the canonical induced grading, then

$$\begin{eqnarray}\text{Ind}_{\mathbb{R}^{n-k}}(L,\text{Graph}(dh))=\left\{\begin{array}{@{}ll@{}}n & \text{if }c\leqslant 0,\\ n-k & \text{if }c>0,\end{array}\right.\end{eqnarray}$$

where $\mathbb{R}^{n-k}$ is the last $n-k$ $q_{i}$ coordinates.

Corollary 4.7. Let $h:L\rightarrow \mathbb{R}$ be a Morse–Bott function with Morse–Bott maximum at critical submanifold $D_{1}$ of dimension $k_{1}$ and minimum at $D_{2}$ of dimension $k_{2}$ . If the zero section $L\subset T^{\ast }L$ is graded and $\text{Graph}(dh)$ is equipped with the canonical induced grading, then $\text{Ind}_{D_{1}}(L,\text{Graph}(dh))=n$ and $\text{Ind}_{D_{2}}(L,\text{Graph}(dh))=n-k_{2}$ .

4.2 Local computation for surgery at a point

The grading of a Lagrangian surgery in the local model was considered by Seidel [Sei00], and we include an account for completeness. Let $H_{\unicode[STIX]{x1D6FE}}$ be a Lagrangian handle. We equip $\mathbb{C}^{n}$ with the standard complex volume form $\unicode[STIX]{x1D6FA}=dz_{1}\wedge \cdots \wedge dz_{n}$ .

Lemma 4.8 [Sei00].

Let $\mathbb{R}^{n}$ and $i\mathbb{R}^{n}$ be equipped with gradings $\unicode[STIX]{x1D703}_{r}$ and $\unicode[STIX]{x1D703}_{i}$ , respectively. Then, there is a grading $\unicode[STIX]{x1D703}_{H}$ on $H_{\unicode[STIX]{x1D6FE}}$ and a unique integer $m$ such that $\unicode[STIX]{x1D703}_{H}$ can be patched with $\unicode[STIX]{x1D703}_{r}+m$ and $\unicode[STIX]{x1D703}_{i}$ to give a grading on $\mathbb{R}^{n}\text{\#}_{0}i\mathbb{R}^{n}$ . If $\text{Ind}_{0}((\mathbb{R}^{n},\unicode[STIX]{x1D703}_{r}),(i\mathbb{R}^{n},\unicode[STIX]{x1D703}_{i}))=1$ , we have $m=0$ .

Proof. As shown in Example 2.14, $H_{\unicode[STIX]{x1D6FE}}=H_{\unicode[STIX]{x1D708}}$ for some flow handle $H_{\unicode[STIX]{x1D708}}$ . Since $H_{\unicode[STIX]{x1D708}}$ is obtained by Hamiltonian flow from $i\mathbb{R}^{n}\backslash \{0\}$ , $H_{\unicode[STIX]{x1D708}}$ is canonically graded by $\unicode[STIX]{x1D703}_{i}$ using the Hamiltonian isotopy. We call this grading $\unicode[STIX]{x1D703}_{H}$ and continuously extend it on $\operatorname{Cl}(H_{\unicode[STIX]{x1D708}})$ . Since $\mathbb{R}^{n}\cap \operatorname{Cl}(H_{\unicode[STIX]{x1D708}})$ has one grading induced from $\unicode[STIX]{x1D703}_{r}$ and one induced from $\unicode[STIX]{x1D703}_{H}$ , $\unicode[STIX]{x1D703}_{H}|_{\mathbb{R}^{n}\cap \operatorname{Cl}(H_{\unicode[STIX]{x1D708}})}-\unicode[STIX]{x1D703}_{r}|_{\mathbb{R}^{n}\cap \operatorname{Cl}(H_{\unicode[STIX]{x1D708}})}$ is a locally constant integer-valued function. If $\mathbb{R}^{n}\cap \operatorname{Cl}(H_{\unicode[STIX]{x1D708}})$ is connected, then there is a unique integer $m$ such that $\unicode[STIX]{x1D703}_{H}|_{\mathbb{R}^{n}\cap \operatorname{Cl}(H_{\unicode[STIX]{x1D708}})}=\unicode[STIX]{x1D703}_{r}|_{\mathbb{R}^{n}\cap \operatorname{Cl}(H_{\unicode[STIX]{x1D708}})}+m$ . If $\mathbb{R}^{n}\cap \operatorname{Cl}(H_{\unicode[STIX]{x1D708}})$ is not connected, then $n=1$ and one can check directly that the same conclusion holds. As a result, this $m$ is the unique integer such that $\unicode[STIX]{x1D703}_{H}$ can be patched with $\unicode[STIX]{x1D703}_{r}+m$ and $\unicode[STIX]{x1D703}_{i}$ to give a grading on $\mathbb{R}^{n}\text{\#}_{0}i\mathbb{R}^{n}$ . In what follows, we want to show that $m=0$ if $\text{Ind}_{0}((\mathbb{R}^{n},\unicode[STIX]{x1D703}_{r}),(i\mathbb{R}^{n},\unicode[STIX]{x1D703}_{i}))=1$ .

Pick a point $x=(x_{1},\ldots ,x_{n})\in S^{n-1}$ . Let $c(s)=\unicode[STIX]{x1D6FE}(s)x\in H_{\unicode[STIX]{x1D6FE}}$ , where $\unicode[STIX]{x1D6FE}$ is an admissible curve (see Definition 2.7), and denote the image curve by $\text{Im}(c)$ . The Lagrangian plane $\unicode[STIX]{x1D6EC}_{s}$ at $c(s)$ is spanned by $\{\unicode[STIX]{x1D6FE}^{\prime }(s)x\}\cup \{\unicode[STIX]{x1D6FE}(s)v_{j}\}_{j=2}^{n}$ , where $v_{j}\in T_{x}S^{n-1}$ forms an orthonormal basis. (See also the proof of Lemma 2.8.) Therefore, we have

$$\begin{eqnarray}\text{Det}_{\unicode[STIX]{x1D6FA}}^{2}(\unicode[STIX]{x1D6EC}_{s})=e^{i2(\arg (\unicode[STIX]{x1D6FE}^{\prime }(s))+(n-1)\arg (\unicode[STIX]{x1D6FE}(s)))}\end{eqnarray}$$

for all $s$ . There is a unique continuous function $\unicode[STIX]{x1D703}_{c}:\text{Im}(c)\rightarrow \mathbb{R}$ such that:

• ∙ $\unicode[STIX]{x1D703}_{c}(c(s))=n-1$ for $s<0$ ;

• ∙ $\unicode[STIX]{x1D703}_{c}(c(s))=n/2$ for $s>\unicode[STIX]{x1D716}$ ; and

• ∙ $e^{2\unicode[STIX]{x1D70B}i\unicode[STIX]{x1D703}_{c}(c(s))}=\text{Det}_{\unicode[STIX]{x1D6FA}}^{2}(\unicode[STIX]{x1D6EC}_{s})$ for all $s$ .

Therefore, we have $\unicode[STIX]{x1D703}_{c}-\unicode[STIX]{x1D703}_{H}|_{\text{Im}(c)}\in \mathbb{Z}$ and $\unicode[STIX]{x1D703}_{c}$ describes the change of Lagrangian planes from $\mathbb{R}^{n}$ to $i\mathbb{R}^{n}$ along the handle. By comparing with Example 4.3 (for $k=0$ ), we can see that if the graded Lagrangians $\mathbb{R}^{n}$ and $i\mathbb{R}^{n}$ inside $\mathbb{C}^{n}$ intersect at the origin with index  $1$ , then $m=0$ . In other words, $\unicode[STIX]{x1D703}_{c}$ determines a grading $(\unicode[STIX]{x1D703}_{c})_{H}$ on $H_{\unicode[STIX]{x1D708}}$ when we consider all possible $c=\unicode[STIX]{x1D6FE}x$ for $x\in S^{n-1}$ . The graded Lagrangians $(H_{\unicode[STIX]{x1D708}},(\unicode[STIX]{x1D703}_{c})_{H})$ , $(\mathbb{R}^{n},n-1)$ and $(i\mathbb{R}^{n},n/2)$ can be glued continuously. If the graded Lagrangians $\mathbb{R}^{n}$ and $i\mathbb{R}^{n}$ inside $\mathbb{C}^{n}$ intersect at the origin with index  $1$ , we can equip $\mathbb{R}^{n}$ and $i\mathbb{R}^{n}$ with gradings $n-1$ and $n/2$ by Example 4.3. This finishes the proof.◻

Corollary 4.9 [Sei00].

Let $\unicode[STIX]{x1D704}_{i}:L_{i}\rightarrow (M,\unicode[STIX]{x1D714})$ for $i=1,2$ be two graded Lagrangian immersions with gradings $\unicode[STIX]{x1D703}_{1}$ and $\unicode[STIX]{x1D703}_{2}$ , respectively, intersecting transversally at a point $p$ . If $\text{Ind}_{p}((L_{1},\unicode[STIX]{x1D703}_{1}),(L_{2},\unicode[STIX]{x1D703}_{2}))=1$ , then $\unicode[STIX]{x1D704}:L_{1}\text{\#}_{p}L_{2}\rightarrow (M,\unicode[STIX]{x1D714})$ can be equipped with a grading $\unicode[STIX]{x1D703}_{12}$ extending $\unicode[STIX]{x1D703}_{1}$ and $\unicode[STIX]{x1D703}_{2}$ . In this case, we call $L_{1}\text{\#}_{p}L_{2}$ together with its grading a graded surgery from $L_{1}$ to $L_{2}$ .

4.3 Local computation for surgery along clean intersection

This subsection discusses the grading for Lagrangian surgery along a clean intersection. We start with ordinary clean surgery (see § 2.2.2).

Lemma 4.10. Let $L_{1},N_{D}^{\ast }\subset T^{\ast }L_{1}$ be equipped with gradings $\unicode[STIX]{x1D703}_{r}$ and $\unicode[STIX]{x1D703}_{i}$ , respectively. For any $\unicode[STIX]{x1D706}$ -admissible function $\unicode[STIX]{x1D708}$ such that $\unicode[STIX]{x1D706}<r(D)$ , there is a grading $\unicode[STIX]{x1D703}_{H}$ on $H_{\unicode[STIX]{x1D708}}^{D}$ and a unique integer $m$ such that $\unicode[STIX]{x1D703}_{H}$ can be patched with $\unicode[STIX]{x1D703}_{i},\unicode[STIX]{x1D703}_{r}+m$ to become a grading on $L_{1}\text{\#}_{D}^{\unicode[STIX]{x1D708}}N_{D}^{\ast }$ .

Moreover, $m=0$ if and only if $\text{Ind}_{D}((L_{1},\unicode[STIX]{x1D703}_{r}),(N_{D}^{\ast },\unicode[STIX]{x1D703}_{i}))=\text{dim}(D)+1$ .

Immediately from Lemma 4.10, we have the following.

Corollary 4.11. Let $L_{1},L_{2}\subset (M,\unicode[STIX]{x1D714})$ be graded Lagrangians cleanly intersecting at $D$ . We can perform a graded surgery $L_{1}\text{\#}_{D}L_{2}$ from $L_{1}$ to $L_{2}$ along $D$ if and only if $\text{Ind}_{D}(L_{1},L_{2})=\text{dim}(D)+1$ .

Proof of Lemma 4.10.

The first statement of the lemma follows as in the first paragraph of the proof of Lemma 4.8. Therefore, we just need to prove that $m=0$ if and only if $\text{Ind}_{D}((L_{1},\unicode[STIX]{x1D703}_{r}),(N_{D}^{\ast },\unicode[STIX]{x1D703}_{i}))=\text{dim}(D)+1$ . Let $\text{dim}(D)=k$ .

Pick a Darboux chart such that in local coordinates $N_{D}^{\ast }$ is represented by points of the form $(q,p)=(q_{b},0,0,p_{f})$ . Here $(q,p)=(q_{b},q_{f},p_{b},p_{f})$ , $q_{b}=(q_{1},\ldots ,q_{k})$ , $q_{f}=(q_{k+1},\ldots ,q_{n})$ $p_{b}=(p_{1},\ldots ,p_{k})$ and $p_{f}=(p_{k+1},\ldots ,p_{n})$ . We also require $(q_{b},tq_{f})$ are unit-speed geodesics on $L_{1}$ as $t$ varies and perpendicular to $D$ at $t=0$ , for any $q$ such that $|q_{f}|^{2}=1$ . As a result, the handle $H_{\unicode[STIX]{x1D708}}^{D}$ in local coordinates is given by (here, we suppose that the surgery is supported in a sufficiently small region relative to the Darboux chart)

$$\begin{eqnarray}\bigg\{\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D708}(\Vert p_{f}\Vert )}^{\unicode[STIX]{x1D70E}}(q_{b},0,0,p_{f})=\bigg(q_{b},\unicode[STIX]{x1D708}(\Vert p_{f}\Vert )\frac{p_{f}}{\Vert p_{f}\Vert },0,p_{f}\bigg)\bigg\},\end{eqnarray}$$

where $q_{b}\in B^{k}\subset \mathbb{R}^{k},p_{f}\in B^{n-k}\subset \mathbb{R}^{n-k}$ and $B^{k},B^{n-k}$ are some small open balls centered at the origin.

We consider the standard complex volume form $\unicode[STIX]{x1D6FA}=dz_{1}\wedge \cdots \wedge dz_{n}$ in the chart. Let $e_{\unicode[STIX]{x1D70B}_{2}}\in S^{n-k-1}\subset \mathbb{R}^{n-k}$ be a vector in the unit sphere of last $n-k$ $p_{i}$ -coordinates. Let

$$\begin{eqnarray}c(r)=\bigg(0,\unicode[STIX]{x1D708}(\Vert re_{\unicode[STIX]{x1D70B}_{2}}\Vert )\frac{re_{\unicode[STIX]{x1D70B}_{2}}}{\Vert re_{\unicode[STIX]{x1D70B}_{2}}\Vert },0,re_{\unicode[STIX]{x1D70B}_{2}}\bigg)=(0,\unicode[STIX]{x1D708}(r)e_{\unicode[STIX]{x1D70B}_{2}},0,re_{\unicode[STIX]{x1D70B}_{2}})\end{eqnarray}$$

be a smooth curve on $H_{\unicode[STIX]{x1D708}}^{D}$ for $r\in (0,\unicode[STIX]{x1D716}]$ . We define $c(0)=\lim _{r\rightarrow 0^{+}}c(r)$ .

We want to understand how the Lagrangian planes change from $L_{1}$ to $N_{D}^{\ast }$ along the handle and it suffices to look at how the Lagrangian planes change along $c(r)$ . The Lagrangian plane $\unicode[STIX]{x1D6EC}_{r}$ at $c(r)$ is spanned by

$$\begin{eqnarray}\{(e_{j},0,0,0)\}_{j=1}^{k}\cup \{(0,\unicode[STIX]{x1D708}^{\prime }(r)e_{\unicode[STIX]{x1D70B}_{2}},0,e_{\unicode[STIX]{x1D70B}_{2}})\}\cup \bigg\{\bigg(0,\unicode[STIX]{x1D708}(r)\frac{e_{j}^{\bot }}{r},0,e_{j}^{\bot }\bigg)\bigg\}_{j=2}^{n-k},\end{eqnarray}$$

where $e_{j}\in \mathbb{R}^{k}$ are coordinate vectors and $e_{j}^{\bot }$ form an orthonormal basis for orthogonal complement of $e_{\unicode[STIX]{x1D70B}_{2}}$ in $\mathbb{R}^{n-k}$ .

Then we have

$$\begin{eqnarray}\text{Det}_{\unicode[STIX]{x1D6FA}}^{2}(\unicode[STIX]{x1D6EC}_{r})=e^{i2(\arg (\unicode[STIX]{x1D708}^{\prime }(r)-\sqrt{-1})+(n-k-1)\arg (\unicode[STIX]{x1D708}(r)/r-\sqrt{-1}))}\end{eqnarray}$$

for all $r$ . Here, the convention we use is still $z_{i}=q_{i}-\sqrt{-1}p_{i}$ . Observe that $\unicode[STIX]{x1D708}^{\prime }(\unicode[STIX]{x1D716})=0$ and $\unicode[STIX]{x1D708}(\unicode[STIX]{x1D716})/\unicode[STIX]{x1D716}=0$ . When $r$ goes to $0$ , $\unicode[STIX]{x1D708}^{\prime }(r)$ decreases monotonically to $-\infty$ . Similarly, $\unicode[STIX]{x1D708}(r)/r$ increases monotonically to infinity when $r$ goes to zero.

In particular, $\arg (\unicode[STIX]{x1D708}^{\prime }(r)-\sqrt{-1})$ increases from $\unicode[STIX]{x1D70B}$ to $3\unicode[STIX]{x1D70B}/2$ as $r$ increases and $\arg (\unicode[STIX]{x1D708}(r)/r-\sqrt{-1})$ ) decreases from $2\unicode[STIX]{x1D70B}$ to $3\unicode[STIX]{x1D70B}/2$ as $r$ increases. Therefore, there is a unique continuous function $\unicode[STIX]{x1D703}_{c}:\text{Im}(c)\rightarrow \mathbb{R}$ such that:

• ∙ $\unicode[STIX]{x1D703}_{c}(c(r))=n-k-1$ for $r=0$ ;

• ∙ $\unicode[STIX]{x1D703}_{c}(c(r))=(n-k)/2$ for $r=\unicode[STIX]{x1D716}$ ; and

• ∙ $e^{2\unicode[STIX]{x1D70B}i\unicode[STIX]{x1D703}_{c}(c(r))}=\text{Det}_{\unicode[STIX]{x1D6FA}}^{2}(\unicode[STIX]{x1D6EC}_{r})$ for all $r\in [0,\unicode[STIX]{x1D716}]$ .

By Example 4.3, we have $\text{Ind}_{\mathbb{R}^{k}}((\mathbb{R}^{n},n-k-1),(N^{\ast }(\mathbb{R}^{k}),(n-k)/2))=k+1$ . Hence, $m=0$ if and only if $\text{Ind}_{D}((L_{1},\unicode[STIX]{x1D703}_{r}),(N_{D}^{\ast },\unicode[STIX]{x1D703}_{i}))=k+1$ .◻

For the $E_{2}$ -flow surgery, we use the setting in § 2.3 and we have the following.

Lemma 4.12. Suppose $D\subset L=K_{1}\times K_{2}$ is a smooth submanifold of dimension $k$ which is transversal to $\{p\}\times K_{2}$ for all $p\in K_{1}$ . Let $L,N_{D}^{\ast }\subset T^{\ast }L$ be equipped with gradings $\unicode[STIX]{x1D703}_{r}$ and $\unicode[STIX]{x1D703}_{i}$ , respectively. For any $\unicode[STIX]{x1D706}$ -admissible function $\unicode[STIX]{x1D708}$ such that $\unicode[STIX]{x1D706}<r^{E_{2}}(D)$ , there is a grading $\unicode[STIX]{x1D703}_{H}$ on $H_{\unicode[STIX]{x1D708}}^{D,E_{2}}$ and a unique integer $m$ such that $\unicode[STIX]{x1D703}_{H}$ can be patched with $\unicode[STIX]{x1D703}_{r}+m$ and $\unicode[STIX]{x1D703}_{i}$ to become a grading on $L\text{\#}_{D,E_{2}}^{\unicode[STIX]{x1D708}}N_{D}^{\ast }$ .

Moreover, we have $m=0$ if and only if $\text{Ind}_{D}((L,\unicode[STIX]{x1D703}_{r}),(N_{D}^{\ast },\unicode[STIX]{x1D703}_{i}))=\text{dim}(D)+1$ .

Corollary 4.13. Let $L_{1}=K_{1}\times K_{2},L_{2}\subset (M,\unicode[STIX]{x1D714})$ be graded Lagrangians cleanly intersecting at $D$ . Suppose $D$ is transversal to $\{p\}\times K_{2}$ for all $p\in K_{1}$ . Then we can perform a graded $E_{2}$ -flow surgery $L_{1}\text{\#}_{D,E_{2}}L_{2}$ from $L_{1}$ to $L_{2}$ along $D$ if and only if $\text{Ind}_{D}(L_{1},L_{2})=\text{dim}(D)+1$ .

Proof of Lemma 4.12.

As explained before (cf. Lemmas 4.8 and 4.10), we just need to show that $m=0$ if and only if $\text{Ind}_{D}((L,\unicode[STIX]{x1D703}_{r}),(N_{D}^{\ast },\unicode[STIX]{x1D703}_{i}))=\text{dim}(D)+1$ . Again denote $k=\text{dim}(D)$ .

Pick a product chart $U=U_{1}\times U_{2}$ for $L=K_{1}\times K_{2}$ (i.e., $U_{i}\subset K_{i}$ for $i=1,2$ ). Points in $U$ are denoted by $q=(q_{b},q_{f})$ , where $q_{b}\in U_{1}$ and $q_{f}\in U_{2}$ . We also want that $(q_{b},tq_{f})$ is a unit-speed geodesic as $t$ varies and perpendicular to $D$ at $t=0$ , for any $q_{b},q_{f}$ such that $|q_{f}|=1$ . We can also assume the origin belongs to $D$ and denote a basis of the tangent space $T_{0}D$ of $D$ at the origin by $\{w^{1},\ldots ,w^{k}\}$ and $w^{j}=w_{b}^{j}+w_{f}^{j}$ , where $w_{b}^{j}$ and $w_{f}^{j}$ are the $q_{b}$ and $q_{f}$ components of $w^{j}$ , respectively. Since $D$ is transversal to the second factor, we can assume that $w_{b}^{j}$ are the unit coordinate vectors in the $q_{b}$ -plane for $1\leqslant j\leqslant k$ . Moreover, there is a $U_{2}$ -valued function $q_{f}^{D}(q_{b})$ of $q_{b}$ near the origin such that $(q_{b},q_{f}^{D}(q_{b}))\in D$ .

This chart gives a corresponding Darboux chart on $T^{\ast }L$ and we define $p_{b}^{D}$ as a function of $q_{b},p_{f}$ near the origin such that $(q_{b},q_{f}^{D}(q_{b}),p_{b}^{D}(q_{b},p_{f}),p_{f})\in N_{D}^{\ast }$ . Note that $p_{b}^{D}(\cdot ,\cdot )$ is linear on the second factor. Near the origin (close enough to the origin so that $q_{f}^{D}(q_{b})$ is well defined), the handle $H_{\unicode[STIX]{x1D708}}^{D,E_{2}}$ is given in local coordinates by

$$\begin{eqnarray}\bigg\{\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D708}(\Vert p_{b}\Vert )}^{\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70B}}}(q_{b},q_{f}^{D}(q_{b}),p_{b}^{D}(q_{b},p_{f}),p_{f})=\bigg(q_{b},q_{f}^{D}(q_{b})+\unicode[STIX]{x1D708}(\Vert p_{f}\Vert )\frac{p_{f}}{\Vert p_{f}\Vert },p_{b}^{D}(q_{b},p_{f}),p_{f}\bigg)\bigg\},\end{eqnarray}$$

where $q_{b}\in B^{k}\subset \mathbb{R}^{k},p_{f}\in B^{n-k}\subset \mathbb{R}^{n-k}$ and $B^{k},B^{n-k}$ are small open balls centered at the origin.

We consider the standard complex volume form $\unicode[STIX]{x1D6FA}=dz_{1}\wedge \cdots \wedge dz_{n}$ in the chart. Let $e_{\unicode[STIX]{x1D70B}_{2}}\in S^{n-k-1}\subset \mathbb{R}^{n-k}$ be a vector in the unit sphere in the $p_{f}$ coordinates. Let

$$\begin{eqnarray}\displaystyle c(r) & = & \displaystyle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D708}(\Vert re_{\unicode[STIX]{x1D70B}_{2}}\Vert )}^{\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70B}}}(0,0,p_{b}^{D}(0,re_{\unicode[STIX]{x1D70B}_{2}}),re_{\unicode[STIX]{x1D70B}_{2}})\nonumber\\ \displaystyle & = & \displaystyle \bigg(0,\unicode[STIX]{x1D708}(\Vert re_{\unicode[STIX]{x1D70B}_{2}}\Vert )\frac{re_{\unicode[STIX]{x1D70B}_{2}}}{\Vert re_{\unicode[STIX]{x1D70B}_{2}}\Vert },p_{b}^{D}(0,re_{\unicode[STIX]{x1D70B}_{2}}),re_{\unicode[STIX]{x1D70B}_{2}}\bigg)\nonumber\\ \displaystyle & = & \displaystyle (0,\unicode[STIX]{x1D708}(r)e_{\unicode[STIX]{x1D70B}_{2}},p_{b}^{D}(0,re_{\unicode[STIX]{x1D70B}_{2}}),re_{\unicode[STIX]{x1D70B}_{2}})\nonumber\end{eqnarray}$$

be a smooth curve in $H_{\unicode[STIX]{x1D708}}^{D,E_{2}}$ for $r\in (0,\unicode[STIX]{x1D716}]$ . We define $c(0)=\lim _{r\rightarrow 0^{+}}c(r)$ .

The Lagrangian plane $\unicode[STIX]{x1D6EC}_{r}$ of $H_{\unicode[STIX]{x1D708}}^{D,E_{2}}$ at $c(r)$ is spanned by

$$\begin{eqnarray}\{(w_{b}^{j},w_{f}^{j},\unicode[STIX]{x1D705}(r,w^{j}),0)\}_{j=1}^{k}\cup \{(0,\unicode[STIX]{x1D708}^{\prime }(r)e_{\unicode[STIX]{x1D70B}_{2}},p_{b}^{D}(0,e_{\unicode[STIX]{x1D70B}_{2}}),e_{\unicode[STIX]{x1D70B}_{2}})\}\cup \bigg\{\bigg(0,\frac{\unicode[STIX]{x1D708}(r)}{r}e_{j}^{\bot },p_{b}^{D}(0,e_{j}^{\bot }),e_{j}^{\bot }\bigg)\bigg\}_{j=2}^{n-k},\end{eqnarray}$$

where $\unicode[STIX]{x1D705}(r,w^{j})=\unicode[STIX]{x2202}_{q_{j}}p_{b}^{D}(0,re_{\unicode[STIX]{x1D70B}_{2}})=r(\unicode[STIX]{x2202}_{q_{j}}p_{b}^{D}(0,e_{\unicode[STIX]{x1D70B}_{2}}))$ is linear in $r$ and $e_{j}^{\bot }$ form an orthonormal basis for orthogonal complement of $e_{\unicode[STIX]{x1D70B}_{2}}$ in $\mathbb{R}^{n-k}$ . We note that $(0,\unicode[STIX]{x1D708}^{\prime }(r)e_{\unicode[STIX]{x1D70B}_{2}},p_{b}^{D}(0,e_{\unicode[STIX]{x1D70B}_{2}}),e_{\unicode[STIX]{x1D70B}_{2}})=c^{\prime }(r)$ and the computation uses the fact that $p_{b}^{D}(\cdot ,\cdot )$ is linear on the second factor.

Let $\unicode[STIX]{x1D705}_{j}(r,w^{j})$ be the coefficient of $w_{b}^{j}$ -component of $\unicode[STIX]{x1D705}(r,w^{j})$ (here, we identify the $q_{b}$ -plane and the $p_{b}$ -plane). Notice that

$$\begin{eqnarray}\text{Det}_{\unicode[STIX]{x1D6FA}}^{2}(\unicode[STIX]{x1D6EC}_{r})=e^{i2(\mathop{\sum }_{j=1}^{k}\arg (1-\unicode[STIX]{x1D705}_{j}(r,w^{j})\sqrt{-1})+\arg (\unicode[STIX]{x1D708}^{\prime }(r)-\sqrt{-1})+(n-k-1)\arg (\unicode[STIX]{x1D708}(r)/r-\sqrt{-1}))}\end{eqnarray}$$

for all $r$ (here, we use the fact that $w_{b}^{j}$ are unit coordinates vectors and we use the convention $z_{i}=q_{i}-\sqrt{-1}p_{i}$ ). Let $K(r)=\sum _{j=1}^{k}\arg (1-\unicode[STIX]{x1D705}_{j}(r,w^{j})\sqrt{-1})$ .

As in the proof of Lemma 4.10, $\arg (\unicode[STIX]{x1D708}^{\prime }(r)-\sqrt{-1})$ increases from $\unicode[STIX]{x1D70B}$ to $3\unicode[STIX]{x1D70B}/2$ as $r$ increases and $\arg (\unicode[STIX]{x1D708}(r)/r-\sqrt{-1})$ ) decreases from $2\unicode[STIX]{x1D70B}$ to $3\unicode[STIX]{x1D70B}/2$ as $r$ increases. Therefore, there is a unique continuous function $\unicode[STIX]{x1D703}_{c}:\text{Im}(c)\rightarrow \mathbb{R}$ such that:

• ∙ $\unicode[STIX]{x1D703}_{c}(c(r))=n-k-1+K(0)/\unicode[STIX]{x1D70B}=n-k-1$ for $r=0$ ;

• ∙ $\unicode[STIX]{x1D703}_{c}(c(r))=(n-k)/2+K(\unicode[STIX]{x1D716})/\unicode[STIX]{x1D70B}$ for $r=\unicode[STIX]{x1D716}$ ; and

• ∙ $e^{2\unicode[STIX]{x1D70B}i\unicode[STIX]{x1D703}_{c}(c(r))}=\text{Det}_{\unicode[STIX]{x1D6FA}}^{2}(\unicode[STIX]{x1D6EC}_{r})$ for all $r\in [0,\unicode[STIX]{x1D716}]$ .

On the other hand, we can lift a path of Lagrangian planes $\unicode[STIX]{x1D6EC}_{r}^{N}$ of $N_{D}^{\ast }$ over the path $c_{2}(r)=(0,0,p_{b}^{D}(0,re_{\unicode[STIX]{x1D70B}_{2}}),re_{\unicode[STIX]{x1D70B}_{2}})$ connecting the origin and $c(\unicode[STIX]{x1D716})$ . The Lagrangian plane $\unicode[STIX]{x1D6EC}_{r}^{N}$ is spanned by

$$\begin{eqnarray}\{(w_{b}^{j},w_{f}^{j},\unicode[STIX]{x1D705}(r,w^{j}),0)\}_{j=1}^{k}\cup \{(0,0,p_{b}^{D}(0,e_{\unicode[STIX]{x1D70B}_{2}}),e_{\unicode[STIX]{x1D70B}_{2}})\}\cup \{(0,0,p_{b}^{D}(0,e_{j}^{\bot }),e_{j}^{\bot })\}_{j=2}^{n-k}.\end{eqnarray}$$

Therefore, the grading of $N_{D}^{\ast }$ at the origin is the grading of $N_{D}^{\ast }$ at $c(\unicode[STIX]{x1D716})$ subtracted by $K(\unicode[STIX]{x1D716})/\unicode[STIX]{x1D70B}$ . If we extend $\unicode[STIX]{x1D703}_{c}$ continuously over $\text{Im}(c_{2})$ (note: $\text{Im}(c)\,\cap \,\text{Im}(c_{2})=\{c(\unicode[STIX]{x1D716})\}$ ), then $\unicode[STIX]{x1D703}_{c}(c_{2}(0))=(n-k)/2$ .

By an analogous calculation to Example 4.3, we have

$$\begin{eqnarray}\text{Ind}_{D}\bigg((L_{1},n-k-1),\bigg(N_{D}^{\ast },\frac{n-k}{2}\bigg)\bigg)=k+1\end{eqnarray}$$

and by comparing it with $\unicode[STIX]{x1D703}_{c}$ the result follows.◻

The following is a family version whose proof is similar.

Corollary 4.14. Let ${\mathcal{L}}_{0},{\mathcal{L}}_{1}\subset (M^{2n},\unicode[STIX]{x1D714})$ as in Lemma 2.27 and let the dimension of ${\mathcal{D}}$ be $k$ . Assume ${\mathcal{L}}_{0},{\mathcal{L}}_{1}$ are graded with grading $\unicode[STIX]{x1D703}_{r}$ and $\unicode[STIX]{x1D703}_{i}$ . Then $\text{Ind}_{{\mathcal{D}}}(({\mathcal{L}}_{1},\unicode[STIX]{x1D703}_{r}),(N^{\ast }{\mathcal{D}},\unicode[STIX]{x1D703}_{i}))=k+1$ if and only if ${\mathcal{L}}_{0}\text{\#}_{{\mathcal{D}},E_{2}}^{\unicode[STIX]{x1D708}}{\mathcal{L}}_{1}$ has a grading such that the grading restricted to ${\mathcal{L}}_{0},{\mathcal{L}}_{1}$ coincides with $\unicode[STIX]{x1D703}_{r}$ and  $\unicode[STIX]{x1D703}_{i}$ , respectively.

4.4 Diagonal in product

We recall from [WW10b, Remark 3.0.5] how to associate a canonical grading to the diagonal in $M\times M^{-}$ .

Let $(\mathbb{R}^{2n},\unicode[STIX]{x1D714}_{std})$ be the standard symplectic vector space and $\text{Lag}(\mathbb{R}^{2n})$ be the Lagrangian Grassmannian. An $N$ -fold Maslov cover $\text{Lag}^{N}(\mathbb{R}^{2n})$ is a $\mathbb{Z}_{N}$ covering $\text{Lag}^{N}(\mathbb{R}^{2n})\rightarrow \text{Lag}(\mathbb{R}^{2n})$ associated to the Maslov class in $\operatorname{Hom}(\unicode[STIX]{x1D70B}_{1}(\text{Lag}^{N}(\mathbb{R}^{2n})),\mathbb{Z})$ . More precisely, the modulo- $N$ reduction of the Maslov class defines a representation $\unicode[STIX]{x1D70B}_{1}(\text{Lag}^{N}(\mathbb{R}^{2n}))\rightarrow \mathbb{Z}_{N}$ and the $N$ -fold Maslov cover is given as $\text{Lag}^{N}(\mathbb{R}^{2n}):=\widetilde{\text{Lag}(\mathbb{R}^{2n})}\times _{\unicode[STIX]{x1D70B}_{1}(\text{Lag}^{N}(\mathbb{R}^{2n}))}\mathbb{Z}_{N}\rightarrow \text{Lag}(\mathbb{R}^{2n})$ , where $\widetilde{\text{Lag}(\mathbb{R}^{2n})}$ is the universal cover of $\text{Lag}(\mathbb{R}^{2n})$ .

More explicitly, for $\unicode[STIX]{x1D6EC}_{0}\in \text{Lag}(\mathbb{R}^{2n})$ , the $N$ -fold Maslov cover $\text{Lag}^{N}(\mathbb{R}^{2n},\unicode[STIX]{x1D6EC}_{0})$ of $\text{Lag}(\mathbb{R}^{2n})$ based at $\unicode[STIX]{x1D6EC}_{0}$ consists of homotopy classes of paths (relative to end points) $\widetilde{\unicode[STIX]{x1D6EC}}:[0,1]\rightarrow \text{Lag}(\mathbb{R}^{2n})$ such that $\widetilde{\unicode[STIX]{x1D6EC}}(0)=\unicode[STIX]{x1D6EC}_{0}$ , modulo loops whose Maslov index is a multiple of $N$ . If we identify $\mathbb{R}^{2n}$ with $\mathbb{C}^{n,-}$ (see the identification in Lemma 4.15), then we can equip $\mathbb{R}^{2n}$ with the standard complex volume form $\unicode[STIX]{x1D6FA}$ . A lift of a Lagrangian subspace $\unicode[STIX]{x1D6EC}\in \text{Lag}(\mathbb{R}^{2n})$ to $\widetilde{\text{Lag}(\mathbb{R}^{2n},\unicode[STIX]{x1D6EC}_{0})}$ determines a grading $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6EC}}:\unicode[STIX]{x1D6EC}\rightarrow \mathbb{R}$ (see § 4.1) which is a constant function. Conversely, a constant $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6EC}}$ on $\unicode[STIX]{x1D6EC}$ such that $e^{2\unicode[STIX]{x1D70B}i\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6EC}}}=\text{Det}_{\unicode[STIX]{x1D6FA}}^{2}(\unicode[STIX]{x1D6EC})$ determines a lift of $\unicode[STIX]{x1D6EC}$ to $\widetilde{\text{Lag}(\mathbb{R}^{2n},\unicode[STIX]{x1D6EC}_{0})}$ . Therefore, we also call of lift of $\unicode[STIX]{x1D6EC}$ to $\widetilde{\text{Lag}(\mathbb{R}^{2n},\unicode[STIX]{x1D6EC}_{0})}$ (respectively $\text{Lag}^{N}(\mathbb{R}^{2n},\unicode[STIX]{x1D6EC}_{0})$ ) a grading (respectively $\mathbb{Z}_{N}$ -grading) of $\unicode[STIX]{x1D6EC}$ .

Similarly, $(\mathbb{R}^{2n,-}\times \mathbb{R}^{2n},-\unicode[STIX]{x1D714}_{std}\,\oplus \,\unicode[STIX]{x1D714}_{std})$ is a symplectic vector space and $\unicode[STIX]{x1D6EC}_{0}^{-}\,\times \,\unicode[STIX]{x1D6EC}_{0}$ is a Lagrangian subspace so we can define the $N$ -fold Maslov cover $\text{Lag}^{N}(\mathbb{R}^{2n,-}\,\times \,\mathbb{R}^{2n},\unicode[STIX]{x1D6EC}_{0}^{-}\,\times \,\unicode[STIX]{x1D6EC}_{0})$ based at $\unicode[STIX]{x1D6EC}_{0}^{-}\times \unicode[STIX]{x1D6EC}_{0}$ . For any Lagrangian subspace $\unicode[STIX]{x1D6EC}\subset \mathbb{R}^{2n}$ and a path $\unicode[STIX]{x1D6FE}:[0,1]\rightarrow \text{Lag}(\mathbb{R}^{2n})$ from $\unicode[STIX]{x1D6FE}(0)=\unicode[STIX]{x1D6EC}$ to $\unicode[STIX]{x1D6FE}(1)=\unicode[STIX]{x1D6EC}_{0}$ , the induced path $(\unicode[STIX]{x1D6FE}^{-}\times \unicode[STIX]{x1D6FE})(t):=(\unicode[STIX]{x1D6FE}(t))^{-}\times \unicode[STIX]{x1D6FE}(t)$ from $\unicode[STIX]{x1D6EC}^{-}\times \unicode[STIX]{x1D6EC}$ to $\unicode[STIX]{x1D6EC}_{0}^{-}\times \unicode[STIX]{x1D6EC}_{0}$ gives an identification between $\text{Lag}^{N}(\mathbb{R}^{2n,-}\times \mathbb{R}^{2n},\unicode[STIX]{x1D6EC}_{0}^{-}\times \unicode[STIX]{x1D6EC}_{0})$ and $\text{Lag}^{N}(\mathbb{R}^{2n,-}\times \mathbb{R}^{2n},\unicode[STIX]{x1D6EC}^{-}\times \unicode[STIX]{x1D6EC})$ . If $\unicode[STIX]{x1D6FE}_{2}:[0,1]\rightarrow \text{Lag}(\mathbb{R}^{2n})$ is another path from $\unicode[STIX]{x1D6FE}_{2}(0)=\unicode[STIX]{x1D6EC}$ to $\unicode[STIX]{x1D6FE}_{2}(1)=\unicode[STIX]{x1D6EC}_{0}$ , then $(\unicode[STIX]{x1D6FE}^{-}\times \unicode[STIX]{x1D6FE})\ast ((\unicode[STIX]{x1D6FE}_{2}^{-1})^{-}\times \unicode[STIX]{x1D6FE}_{2}^{-1})$ , where $\unicode[STIX]{x1D6FE}_{2}^{-1}$ is the inverse path of $\unicode[STIX]{x1D6FE}_{2}$ and $\ast$ is the concatenation of path, has Maslov index $0$ so the identification between $\text{Lag}^{N}(\mathbb{R}^{2n,-}\,\times \,\mathbb{R}^{2n},\unicode[STIX]{x1D6EC}_{0}^{-}\,\times \,\unicode[STIX]{x1D6EC}_{0})$ and $\text{Lag}^{N}(\mathbb{R}^{2n,-}\,\times \,\mathbb{R}^{2n},\unicode[STIX]{x1D6EC}^{-}\,\times \,\unicode[STIX]{x1D6EC})$ is independent of the choice of $\unicode[STIX]{x1D6FE}$ . Therefore, $\unicode[STIX]{x1D6EC}^{-}\times \unicode[STIX]{x1D6EC}$ has a canonical lift to $\text{Lag}^{N}(\mathbb{R}^{2n,-}\times \mathbb{R}^{2n},\unicode[STIX]{x1D6EC}_{0}^{-}\times \unicode[STIX]{x1D6EC}_{0})$ , and hence a canonical ( $\mathbb{Z}_{N}$ )-grading.

To give a canonical grading to the diagonal $\unicode[STIX]{x1D6E5}\subset \mathbb{R}^{2n,-}\times \mathbb{R}^{2n}$ , it suffices to give once and for all an identification between $\text{Lag}^{N}(\mathbb{R}^{2n,-}\times \mathbb{R}^{2n},\unicode[STIX]{x1D6EC}^{-}\times \unicode[STIX]{x1D6EC})$ and $\text{Lag}^{N}(\mathbb{R}^{2n,-}\times \mathbb{R}^{2n},\unicode[STIX]{x1D6E5})$ . This is given by the concatenation of the two paths

$$\begin{eqnarray}(e^{Jt}\unicode[STIX]{x1D6EC}^{-}\times \unicode[STIX]{x1D6EC})_{t\in [0,\unicode[STIX]{x1D70B}/2]},\quad (\{(tx+Jy,x+tJy)\mid x,y\in \unicode[STIX]{x1D6EC}\})_{t\in [0,1]},\end{eqnarray}$$

where $J$ is an $\unicode[STIX]{x1D714}_{std}$ -compatible complex structure on $\mathbb{R}^{2n}$ . This canonical grading induces a canonical grading on $\unicode[STIX]{x1D6E5}_{M}\subset M^{-}\times M$ for any symplectic manifold $M$ .

In the following lemma, we consider the symplectic manifold $M=\mathbb{C}^{n,-}$ and compute the index between a product Lagrangian with the diagonal $\unicode[STIX]{x1D6E5}_{M}$ .

Lemma 4.15 (Cf. [WW10b, § 3]).

For any graded Lagrangian subspace $\unicode[STIX]{x1D6EC}\subset \mathbb{C}^{n,-}$ , we have

$$\begin{eqnarray}\text{Ind}_{\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6EC}}}(\unicode[STIX]{x1D6EC}^{-}\times \unicode[STIX]{x1D6EC},\unicode[STIX]{x1D6E5}_{\mathbb{ C}^{n,-}})=n,\end{eqnarray}$$

where $\unicode[STIX]{x1D6EC}^{-}\times \unicode[STIX]{x1D6EC}$ and $\unicode[STIX]{x1D6E5}_{\mathbb{C}^{n,-}}$ are equipped with their canonical gradings in $\mathbb{C}^{n}\times \mathbb{C}^{n,-}$ .

Proof. It suffices to consider $\unicode[STIX]{x1D6EC}=\mathbb{R}^{n}\subset \mathbb{C}^{n,-}$ and $J=-J_{std}=-\sqrt{-1}$ . Let $z_{i}=x_{i}+\sqrt{-1}y_{i}$ be the coordinates of $\mathbb{C}^{n}$ and $w_{i}=u_{i}+\sqrt{-1}v_{i}$ be the coordinates of $\mathbb{C}^{n,-}$ . We consider the standard complex volume form $\unicode[STIX]{x1D6FA}=dz_{1}\wedge \cdots \wedge dz_{n}\wedge d\bar{w_{1}}\wedge \cdots \wedge d\bar{w_{n}}$ on $\mathbb{C}^{n}\times \mathbb{C}^{n,-}$ and equip $\unicode[STIX]{x1D6EC}^{-}\times \unicode[STIX]{x1D6EC}$ with grading $0$ . We have $\text{Det}^{2}(e^{Jt}\unicode[STIX]{x1D6EC}^{-}\times \unicode[STIX]{x1D6EC})=e^{-i2nt}$ , which induces a grading of $-n/2$ on $e^{J(\unicode[STIX]{x1D70B}/2)}\unicode[STIX]{x1D6EC}^{-}\times \unicode[STIX]{x1D6EC}$ . We also have $\text{Det}^{2}(\{(tx+Jy,x+tJy)\mid x,y\in \unicode[STIX]{x1D6EC}\})=e^{-in\unicode[STIX]{x1D70B}}$ for all $t$ so the canonical grading on $\unicode[STIX]{x1D6E5}$ is $-n/2$ .

To calculate $\text{Angle}(\unicode[STIX]{x1D6EC}^{-}\times \unicode[STIX]{x1D6EC},\unicode[STIX]{x1D6E5})$ , we observe that $(\unicode[STIX]{x1D6EC}^{-}\times \unicode[STIX]{x1D6EC})\cap \unicode[STIX]{x1D6E5}=\text{Span}\{(\unicode[STIX]{x2202}_{x_{i}}+\unicode[STIX]{x2202}_{u_{i}})\}_{i=1}^{n}$ . We can use $\unicode[STIX]{x1D6EC}_{t}=(\unicode[STIX]{x1D6EC}^{-}\times \unicode[STIX]{x1D6EC})\cap \unicode[STIX]{x1D6E5}+\text{Span}\{(t(\unicode[STIX]{x2202}_{y_{i}}+\unicode[STIX]{x2202}_{v_{i}})+(1-t)(-\unicode[STIX]{x2202}_{x_{i}}+\unicode[STIX]{x2202}_{u_{i}}))\}$ from $\unicode[STIX]{x1D6EC}^{-}\times \unicode[STIX]{x1D6EC}$ to $\unicode[STIX]{x1D6E5}$ for the calculation of $\operatorname{Angle}(\unicode[STIX]{x1D6EC}^{-}\times \unicode[STIX]{x1D6EC},\unicode[STIX]{x1D6E5})$ . As a result, we have $2\text{Angle}(\unicode[STIX]{x1D6EC}^{-}\times \unicode[STIX]{x1D6EC},\unicode[STIX]{x1D6E5})=n/2$ and hence

$$\begin{eqnarray}\text{Ind}_{\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6EC}}}(\unicode[STIX]{x1D6EC}^{-}\times \unicode[STIX]{x1D6EC},\unicode[STIX]{x1D6E5}_{\mathbb{ C}^{n,-}})=2n+\bigg(\!-\frac{n}{2}\bigg)-0-\frac{n}{2}=n.\Box\end{eqnarray}$$

Corollary 4.16. Let $L$ be a Lagrangian in $M$ . With the canonical gradings of $L\times L\subset M\times M^{-}$ and $\unicode[STIX]{x1D6E5}\subset M\times M^{-}$ , one can perform graded clean surgery to obtain $(L\times L)[1]\text{\#}_{\unicode[STIX]{x1D6E5}_{L},E_{2}}\unicode[STIX]{x1D6E5}$ .

Proof. This is a direct consequence of Lemmas 4.12 and 4.15 because $\text{Ind}_{\unicode[STIX]{x1D6E5}_{L}}(L\times L[1],\unicode[STIX]{x1D6E5})=\text{Ind}_{\unicode[STIX]{x1D6E5}_{L}}(L\times L,\unicode[STIX]{x1D6E5})+1=\text{dim}(\unicode[STIX]{x1D6E5}_{L})+1$ (see Example 4.2).◻

Corollary 4.17 (Cf. Theorem 1.1(1)).

There is a graded clean surgery identity

$$\begin{eqnarray}(S^{n}\times S^{n})[1]\text{\#}_{\unicode[STIX]{x1D6E5}_{S^{n}},E_{2}}\unicode[STIX]{x1D6E5}=\text{Graph}(\unicode[STIX]{x1D70F}_{S^{n}}^{-1}).\end{eqnarray}$$

Proof. This is a direct consequence of Corollaries 3.5 and 4.16.◻

Lemma 4.18 (Cf. Theorem 1.1(3)).

There is a graded clean surgery identity

$$\begin{eqnarray}\mathbb{CP}^{m/2}\times \mathbb{CP}^{m/2}\text{\#}_{D^{\operatorname{op}},E_{2}}((\mathbb{CP}^{m/2}\times \mathbb{CP}^{m/2})[1]\text{\#}_{\unicode[STIX]{x1D6E5}_{\mathbb{CP}^{m/2}},E_{2}}\unicode[STIX]{x1D6E5})=\text{Graph}(\unicode[STIX]{x1D70F}_{\mathbb{CP}^{m/2}}^{-1}).\end{eqnarray}$$

Proof. By Corollary 4.16, we can obtain a graded Lagrangian

$$\begin{eqnarray}L=(\mathbb{CP}^{m/2}\times \mathbb{CP}^{m/2})[1]\text{\#}_{\unicode[STIX]{x1D6E5}_{\mathbb{CP}^{m/2}},E_{2}}\unicode[STIX]{x1D6E5}.\end{eqnarray}$$

As explained in the proof of Lemma 3.4 and Lemma 3.6, $L$ is Hamiltonian isotopic to a Lagrangian $Q$ cleanly intersecting with $\mathbb{CP}^{m/2}\times \mathbb{CP}^{m/2}$ along $D^{\operatorname{op}}$ such that $Q$ coincides with the graph of a Morse–Bott function with maximum at $D^{\operatorname{op}}$ near $D^{\operatorname{op}}$ . Therefore, we have $\text{Ind}_{D^{\operatorname{op}}}(\mathbb{CP}^{m/2}\times \mathbb{CP}^{m/2},Q)=2m-1$ . Here the first term $2m$ follows by Corollary 4.7 and the second term $-1$ comes from the grading shift of the first factor of $L$ . Since $D^{\operatorname{op}}$ is of dimension $2m-2$ , we get the result by applying Lemma 4.12.◻

The cases for $\mathbb{RP}^{n}$ and $\mathbb{HP}^{n}$ can be computed analogously.

Lemma 4.19 (Cf. Theorem 1.1(3)).

There are graded clean surgery identities

$$\begin{eqnarray}\mathbb{RP}^{n}\times \mathbb{RP}^{n}[1]\text{\#}_{D^{\operatorname{op}},E_{2}}((\mathbb{RP}^{n}\times \mathbb{RP}^{n})[1]\text{\#}_{\unicode[STIX]{x1D6E5}_{\mathbb{ RP}^{n}},E_{2}}\unicode[STIX]{x1D6E5})=\text{Graph}(\unicode[STIX]{x1D70F}_{\mathbb{RP}^{n}}^{-1})\end{eqnarray}$$

and

$$\begin{eqnarray}\mathbb{HP}^{n}\times \mathbb{HP}^{n}[-2]\text{\#}_{D^{\operatorname{op}},E_{2}}((\mathbb{HP}^{n}\times \mathbb{HP}^{n})[1]\text{\#}_{\unicode[STIX]{x1D6E5}_{\mathbb{ HP}^{n}},E_{2}}\unicode[STIX]{x1D6E5})=\text{Graph}(\unicode[STIX]{x1D70F}_{\mathbb{HP}^{n}}^{-1}),\end{eqnarray}$$

where $D^{\operatorname{op}}$ are defined similar to Lemma 4.18.

For the family Dehn twist, we have the following (see Corollary 3.10).

Lemma 4.20 (Cf. Theorem 1.1(2), (4)).

There are graded clean surgery identities

$$\begin{eqnarray}\displaystyle & \displaystyle \widetilde{C}_{S}[1]\text{\#}_{\mathscr{D},E_{2}}\unicode[STIX]{x1D6E5}=\text{Graph}(\unicode[STIX]{x1D70F}_{C_{S}}^{-1}), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \widetilde{C}_{R}[1]\text{\#}_{\mathscr{D}^{\operatorname{op}},E_{2}}\widetilde{C}_{R}[1]\text{\#}_{\mathscr{D},E_{2}}\unicode[STIX]{x1D6E5}=\text{Graph}(\unicode[STIX]{x1D70F}_{C_{R}}^{-1}), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \widetilde{C}_{C}\text{\#}_{\mathscr{D}^{\operatorname{op}},E_{2}}\widetilde{C}_{C}[1]\text{\#}_{\mathscr{D},E_{2}}\unicode[STIX]{x1D6E5}=\text{Graph}(\unicode[STIX]{x1D70F}_{C_{C}}^{-1}), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \widetilde{C}_{H}[-2]\text{\#}_{\mathscr{D}^{\operatorname{op}},E_{2}}\widetilde{C}_{H}[1]\text{\#}_{\mathscr{D},E_{2}}\unicode[STIX]{x1D6E5}=\text{Graph}(\unicode[STIX]{x1D70F}_{C_{H}}^{-1}), & \displaystyle \nonumber\end{eqnarray}$$

where $C_{S}$ (respectively $C_{R},C_{C},C_{H}$ ) is a spherically (respectively real projectively, complex projectively, quaternionic projectively) coisotropic submanifold.

5 Review of Lagrangian Floer theory, Lagrangian cobordisms and quilted Floer theory

We first fix conventions for Lagrangian Floer theory for the rest of the paper, which follows that of [Sei08a]. Note that this is different from the homology convention of [BC13].

Let $L_{0},L_{1}\subset (M,\unicode[STIX]{x1D714})$ be a pair of transversally intersecting graded compact Lagrangian submanifolds. For a generic one-parameter family of $\unicode[STIX]{x1D714}$ -compatible almost complex structure $\mathbf{J}=\{J_{t}\}_{t\in [0,1]}$ , let

(5.1) $$\begin{eqnarray}\displaystyle {\mathcal{M}}(p_{-},p_{+}) & = & \displaystyle \biggl\{u:\mathbb{R}\times [0,1]\rightarrow M:u_{s}(s,t)+J_{t}(u(s,t))u_{t}(s,t)=0,~u(s,0)\in L_{0}\nonumber\\ \displaystyle & & \displaystyle \text{and }u(s,1)\in L_{1}~\lim _{s\rightarrow +\infty }u(s,t)=p_{+},~\lim _{s\rightarrow -\infty }u(s,t)=p_{-}\biggr\}\bigg/\mathbb{R}.\end{eqnarray}$$

Then the Floer cochain complex $CF^{\ast }(L_{0},L_{1})$ is generated by $L_{0}\cap L_{1}$ as a graded vector space and equipped with a differential by counting rigid elements from ${\mathcal{M}}(p_{-},p_{+})$ , i.e.,

$$\begin{eqnarray}dp_{+}=\mathop{\sum }_{p_{-}\in L_{0}\cap L_{1}}\text{\#}{\mathcal{M}}^{0}(p_{-},p_{+})p_{-}.\end{eqnarray}$$

We refer to [Sei08a] for the definition of Fukaya category ${\mathcal{F}}uk(M)$ and the derived Fukaya category $D^{\unicode[STIX]{x1D70B}}{\mathcal{F}}uk(M)$ that involves higher operations defined using pseudo-holomorphic polygons.

Definition 5.1. Let $L_{i},L_{j}^{\prime }\subset (M,\unicode[STIX]{x1D714})$ , $1\leqslant i\leqslant k$ , $1\leqslant j\leqslant k^{\prime }$ be a collection of Lagrangian submanifolds. A Lagrangian cobordism $V$ from $(L_{1},\ldots ,L_{k})$ to $(L_{1}^{\prime },\ldots ,L_{k^{\prime }}^{\prime })$ is an embedded Lagrangian submanifold in $M\times \mathbb{C}$ so that the following condition holds (see Figure 10).

• ∙ There is a compact set $K\subset \mathbb{C}$ such that $V\backslash (M\times K)=(\bigsqcup _{i=1}^{k}L_{i}\times \unicode[STIX]{x1D6FE}_{i})\sqcup (\bigsqcup _{j=1}^{k^{\prime }}L_{j}^{\prime }\times \unicode[STIX]{x1D6FE}_{j}^{\prime })$ , where $\unicode[STIX]{x1D6FE}_{i}=(-\infty ,x_{i})\times \{a_{i}\}$ and $\unicode[STIX]{x1D6FE}_{j}^{\prime }=(x_{j}^{\prime },\infty )\times \{b_{j}^{\prime }\}$ for some $x_{i},a_{i},x_{j}^{\prime },b_{j}^{\prime }$ such that $a_{1}<\cdots <a_{k}$ and $b_{1}^{\prime }>\cdots >b_{k^{\prime }}^{\prime }$ .

Each $L_{i}\times \unicode[STIX]{x1D6FE}_{i}$ or $L_{j}^{\prime }\times \unicode[STIX]{x1D6FE}_{j}^{\prime }$ is called an end of the Lagrangian cobordism $V$ .

The counterclockwise order for the ends starting from $L_{1}^{\prime }$ is $L_{1}^{\prime },\ldots ,L_{k^{\prime }}^{\prime },L_{1},\ldots ,L_{k}$ . For the grading we always choose the quadratic complex volume form on $M\times \mathbb{C}$ to be the quadratic complex volume form on $M$ times the standard one on $\mathbb{C}$ . When $V$ is graded, the restriction induces a grading on each end. On an end, say $L_{i}\times \unicode[STIX]{x1D6FE}_{i}$ , we denote the induced grading as $\unicode[STIX]{x1D703}_{ii}$ . Since an end is a product Lagrangian, we can associate a grading $\unicode[STIX]{x1D703}_{i}$ to $L_{i}$ by requiring $\unicode[STIX]{x1D703}_{i}(p)=\unicode[STIX]{x1D703}_{ii}(p\times z)$ for all $p\in L_{i}$ and $z\in \unicode[STIX]{x1D6FE}_{i}$ . The same rule applies to $L_{j}^{\prime }\times \unicode[STIX]{x1D6FE}_{j}^{\prime }$ . We use this grading convention between a cobordism and its fiber Lagrangians over its ends throughout.

Figure 10. Projection of a Lagrangian cobordism.

The main result we will utilize from Biran and Cornea’s Lagrangian cobordism formalism reads as follows.

Theorem 5.2 [BC14].

If there exists a graded monotone (or exact) Lagrangian cobordism from monotone (or exact) Lagrangians $(L_{1}[k-1],L_{2}[k-2],\ldots ,L_{k})$ to $(L_{1}^{\prime }[k^{\prime }-1],L_{2}^{\prime }[k^{\prime }-2],\ldots ,L_{k^{\prime }}^{\prime })$ , then there is an isomorphism between iterated cones in ${\mathcal{D}}^{\unicode[STIX]{x1D70B}}{\mathcal{F}}uk(M)$ ,

$$\begin{eqnarray}\text{Cone}(L_{1}\rightarrow L_{2}\rightarrow \cdots \rightarrow L_{k})\cong \text{Cone}(L_{1}^{\prime }\rightarrow L_{2}^{\prime }\rightarrow \cdots \rightarrow L_{k^{\prime }}^{\prime }).\end{eqnarray}$$

Here $\text{Cone}(L_{1}\rightarrow L_{2}\rightarrow \cdots \rightarrow L_{k})=\text{Cone}(\cdots \text{Cone}(\text{Cone}(L_{1}\rightarrow L_{2})\rightarrow L_{3})\rightarrow \cdots \rightarrow L_{k})$ and the maps in the cones are given by counting appropriate pseudo-holomorphic polygons.

Note that $CF^{\ast }(K,\text{Cone}(L_{1}\rightarrow L_{2}\rightarrow \cdots \rightarrow L_{k}))=CF^{\ast }(K,L_{1}[k-1])\oplus \cdots \oplus CF^{\ast }(K,L_{k})$ as a graded vector space for any graded Lagrangian $K$ transversally intersecting each $L_{i}$ . It explains the seemingly weird grading shift of the Lagrangians $L_{i},L_{j}^{\prime }$ for the cobordism.

We dedicate the rest of this section to quilted Floer theory developed in [WW10b, WW10a, WW12, WMW].

Definition 5.3 [WW10b, Definition 2.1.3].

Given a sequence of symplectic manifolds $M_{0},\ldots ,M_{r+1}$ , a generalized Lagrangian correspondence $\text{}\underline{L}=(L_{01},\ldots ,L_{r(r+1)})$ is a sequence of Lagrangian submanifolds such that $L_{i(i+1)}\subset M_{i}^{-}\times M_{i+1}$ are compact Lagrangian submanifolds for all $i$ . A cyclic generalized Lagrangian correspondence is one such that $M_{0}=M_{r+1}$ .

For a Lagrangian correspondence $L_{01}\subset M_{0}^{-}\times M_{1}$ , $L_{01}^{t}\subset M_{1}^{-}\times M_{0}$ is defined to be $L_{01}^{t}=\{(x,y)\mid (y,x)\in L_{01}\}$ . Given two Lagrangian correspondences $L_{01}\subset M_{0}^{-}\times M_{1}$ and $L_{12}\subset M_{1}^{-}\times M_{2}$ , their geometric composition is defined as

(5.2) $$\begin{eqnarray}L_{01}\circ L_{12}=\{(x,z)\mid \exists y\text{ such that }(x,y)\in L_{01}\text{ and }(y,z)\in L_{12}\}.\end{eqnarray}$$

For the composition to work nicely, we require the following.

• ∙ $L_{01}\times L_{12}$ intersects $M_{0}^{-}\,\times \,\unicode[STIX]{x1D6E5}\,\times \,M_{2}$ transversally in $M_{0}^{-}\times M_{1}\times M_{1}^{-}\times M_{2}$ , where $\unicode[STIX]{x1D6E5}\subset M_{1}\times M_{1}^{-}$ is the diagonal.

• ∙ The projection $\unicode[STIX]{x1D70B}_{02}:L_{01}\times _{M_{1}}L_{12}\rightarrow L_{01}\circ L_{12}\subset M_{0}^{-}\times M_{2}$ is an embedding, where $L_{01}\times _{M_{1}}L_{12}$ is the fiber product between $\unicode[STIX]{x1D70B}_{01,1}:L_{01}\rightarrow M_{1}$ and $\unicode[STIX]{x1D70B}_{12,1}:L_{12}\rightarrow M_{1}$ , and $\unicode[STIX]{x1D70B}_{02}$ is the projection forgetting the $M_{1}$ factor.

In this case, the composition $L_{01}\circ L_{12}$ is called embedded. We refer to § 3.3 for a non-trivial example of Lagrangian correspondence and composition coming from coisotropic embeddings.

For a cyclic generalized Lagrangian correspondence $\text{}\underline{L}$ , the quilted Floer cohomology is defined to be

$$\begin{eqnarray}HF^{\ast }(\text{}\underline{L}):=HF^{\ast }(L_{01}\times L_{23}\cdots L_{(r-1)r},(L_{12}\times L_{34}\cdots L_{r(r+1)})^{T})\end{eqnarray}$$

in $M_{0}^{-}\times M_{1}\times \cdots \times M_{r-1}^{-}\times M_{r}$ when $r$ is odd, where $(-)^{T}:M_{1}^{-}\times M_{2}\times \cdots \times M_{r}^{-}\times M_{0}\rightarrow M_{0}^{-}\times M_{1}\times \cdots \times M_{r-1}^{-}\times M_{r}$ is given by transposition of the last factor to the first factor, combined with an overall sign change in the symplectic form. When $r$ is even, we have

$$\begin{eqnarray}HF^{\ast }(\text{}\underline{L}):=HF^{\ast }(L_{01}\times L_{23}\cdots L_{r(r+1)},(L_{12}\times L_{34}\cdots L_{(r-1)r}\times \unicode[STIX]{x1D6E5}_{M_{0}})^{T})\end{eqnarray}$$

in $M_{0}^{-}\times M_{1}\times \cdots \times M_{r}^{-}\times M_{r+1}$ , where $(-)^{T}$ is defined analogously.

It is worth pointing out that for the quilted Floer cohomology to be well defined, $\text{}\underline{L}$ needs to satisfy a monotonicity condition [WW10b, Definitnion 4.1.2(b)] stronger than having all $L_{i,(i+1)}$ to be monotone. For monotone Lagrangian submanifolds $L_{0}\subset \{\text{point}\}^{-}\times M_{0}$ and $L_{1}\subset M_{1}^{-}\times \{\text{point}\}$ , a sufficient condition for this stronger monotonicity to hold for $\text{}\underline{L}=(L_{0},L_{01},L_{1})$ is when $\unicode[STIX]{x1D70B}_{1}(L_{01})=1$ [WW10b, Lemma 4.1.3]. We refer readers to [WW10b] for further details on monotonicity, as well as orientation, grading and so forth for a generalized Lagrangian correspondence. The following theorems summarize the main properties that will concern us.

Theorem 5.4 [WW10b, Theorem 5.2.6].

For a cyclic generalized Lagrangian correspondence $\text{}\underline{L}$ such that:

• ∙ $M_{i}$ are all compact monotone with the same positive monotonicity constant, or are all exact;

• ∙ $L_{i(i+1)}$ are all compact, oriented and monotone (or all exact) with minimal Maslov number at least three;

• ∙ $M_{0}=M_{r+1}$ is a point;

• ∙ $L_{i(i+1)}=L_{i}\times L_{i+1}$ for Lagrangians $L_{i}\subset M_{i}$ and $L_{i+1}\subset M_{i+1}$ for some $1\leqslant i<r$ ,

there is a canonical isomorphism

$$\begin{eqnarray}HF^{\ast }(\text{}\underline{L})=HF^{\ast }(L_{01},L_{12},\ldots ,L_{(i-1)i},L_{i})\otimes HF^{\ast }(L_{i+1},L_{(i+1)(i+2)},\ldots ,L_{r(r+1)})\end{eqnarray}$$

with coefficients in a field.

Theorem 5.5 ([WW10b, Theorem 5.4.1] and [LL13, Theorems 1, 2]).

For a cyclic generalized Lagrangian correspondence $\text{}\underline{L}$ such that:

• ∙ $M_{i}$ are all compact monotone with the same positive monotonicity constant, or are all exact;

• ∙ $L_{i(i+1)}$ are all compact, oriented and monotone (or all exact) with minimal Maslov number at least three;

• ∙ $\text{}\underline{L}$ is monotone, relatively spin and graded in the sense of [WW10b, §4.3]; and

• ∙ $L_{(i-1)i}\circ L_{i(i+1)}$ is embedded in the sense above,

there is a canonical isomorphism

$$\begin{eqnarray}HF^{\ast }(\text{}\underline{L})=HF^{\ast }(L_{01},L_{12},\ldots ,L_{(i-1)i}\circ L_{i(i+1)},\ldots ,L_{r(r+1)})\end{eqnarray}$$

where the orientation and grading on the right are induced by those on $\text{}\underline{L}$ .

Remark 5.6. In [LL13], Theorem 5.5 was extended to greater generality than stated here, which should be useful for extending our results to negatively monotone cases.

For a graded symplectomorphism $\unicode[STIX]{x1D719}\in \text{Symp}(M)$ , the fixed point Floer cohomology can be defined as

$$\begin{eqnarray}HF^{\ast }(\unicode[STIX]{x1D719})=HF^{\ast }(\unicode[STIX]{x1D6E5},\text{Graph}(\unicode[STIX]{x1D719}))=HF^{\ast }(\text{Graph}(\unicode[STIX]{x1D719}^{-1}),\unicode[STIX]{x1D6E5}),\end{eqnarray}$$

where the Lagrangian Floer cohomologies take place in $M\times M^{-}$ (see [Sei00], [WW10b, Definition 3.0.6 and Remark 3.0.7] for the details of graded symplectomorphisms and the associated gradings on the graphs).

Remark 5.7. We follow the convention in [WW10b], where $HF^{\ast }(\unicode[STIX]{x1D719})=HF^{\ast }(\text{Graph}(\unicode[STIX]{x1D719}),\unicode[STIX]{x1D6E5})$ in $M^{-}\times M$ . Therefore, we have $HF^{\ast }(\unicode[STIX]{x1D719})=HF^{\ast }(\unicode[STIX]{x1D6E5},\text{Graph}(\unicode[STIX]{x1D719}))$ in $M\times M^{-}$ .

6 Proof of the long exact sequences

6.1 Exactness and monotonicity of surgery cobordisms

We construct Lagrangian cobordisms associated to the surgery identities in Theorem 1.1(1), (2), (3), (4) and deduce the long exact sequences in this section. Throughout the whole section, we assume all Lagrangians in $M$ to be $\mathbb{Z}$ or $\mathbb{Z}/N$ -graded.

Lemma 6.1. Let $L=L_{1}\text{\#}_{D}L_{2},L_{1}\text{\#}_{D,E_{2}}L_{2}$ or ${\mathcal{L}}_{1}\text{\#}_{{\mathcal{D}},E_{2}}{\mathcal{L}}_{2}$ as surgeries of graded Lagrangians. Then there is a graded Lagrangian cobordism $V$ from $L_{1}$ and $L_{2}$ (or ${\mathcal{L}}_{1}$ and ${\mathcal{L}}_{2}$ ) to $L$ .

Proof. We give the proof for $L=L_{1}\text{\#}_{D,E_{2}}L_{2}$ ; the proofs for $L_{1}\text{\#}_{D}L_{2}$ and ${\mathcal{L}}_{1}\text{\#}_{{\mathcal{D}},E_{2}}{\mathcal{L}}_{2}$ are similar. It suffices to consider $M=T^{\ast }L_{1}$ and $L_{2}=N_{D}^{\ast }$ is the conormal bundle of $D$ in $L_{1}$ . As usual, we assume that a product metric on $L_{1}=K_{1}\times K_{2}$ is chosen and $D\pitchfork (\{p\}\times K_{2})$ for all $p\in K_{1}$ so that the $E_{2}$ -flow clean surgery can be performed.

First note that $L_{1}\times \mathbb{R}$ intersects cleanly with $L_{2}\times i\mathbb{R}$ at $D\times \{0\}$ . Let the grading of $L_{i}$ be $\unicode[STIX]{x1D703}_{i}$ . We give a grading $\unicode[STIX]{x1D703}_{1r}$ to $L_{1}\times \mathbb{R}$ by requiring $\unicode[STIX]{x1D703}_{1r}(p,z)=\unicode[STIX]{x1D703}_{1}(p)$ for all $p\in L_{1}$ and $z\in \mathbb{R}$ . On the other hand, we equip $L_{2}\times i\mathbb{R}$ with grading $\unicode[STIX]{x1D703}_{2i}$ such that $\unicode[STIX]{x1D703}_{2i}(p,z)=\unicode[STIX]{x1D703}_{1}(p)-1/2$ for all $p\in L_{1}$ and $z\in \mathbb{R}$ . Then we have $\text{Ind}_{D\times \{0\}}(L_{1}\times \mathbb{R},L_{2}\times i\mathbb{R})=\text{Ind}_{D}(L_{1},L_{2})+\text{Ind}_{0}(\mathbb{R},i\mathbb{R})=\text{Ind}_{D}(L_{1},L_{2})$ . Moreover, we also have $\text{Ind}_{D}(L_{1},L_{2})=\text{dim}(D)+1$ by the assumption that graded $E_{2}$ -flow surgery from $L_{1}$ to $L_{2}$ can be performed and Lemma 4.12 .

Pick the standard metric on $\mathbb{R}$ . By Lemma 4.12, we can perform the graded Lagrangian surgery from $L_{1}\,\times \,\mathbb{R}$ to $L_{2}\,\times \,i\mathbb{R}$ resolving the clean intersection by a $(E_{2}\oplus \mathbb{R})$ -flow handle $H_{\unicode[STIX]{x1D708}}^{D,E_{2}\oplus \mathbb{R}}$ , where we canonically identify $T^{\ast }(L_{1}\times \mathbb{R})$ with an $E_{1}\oplus E_{2}\oplus \mathbb{R}$ bundle over $L_{1}\times \mathbb{R}$ . We note that $E_{2}\oplus \mathbb{R}$ -flow is well defined to give a smooth Lagrangian manifold because we stayed inside the injectivity radius (Lemma 2.26). Hence we have a graded embedded Lagrangian cobordism with four ends in $M\times \mathbb{C}$ .

Let $\unicode[STIX]{x1D70B}:M\times \mathbb{C}\rightarrow \mathbb{C}$ be the projection to the second factor and $\unicode[STIX]{x1D70B}_{H}=\unicode[STIX]{x1D70B}|_{H_{\unicode[STIX]{x1D708}}^{D,E_{2}\oplus \mathbb{R}}}$ . We define $S_{+}=\{(x,y)\in \mathbb{R}^{2}\mid y\geqslant x\}$ and $W=\unicode[STIX]{x1D70B}_{H}^{-1}(S_{+})$ . A direct check shows that $W$ is a smooth manifold with boundary $\unicode[STIX]{x1D70B}_{H}^{-1}(0)=L$ . Let $W_{0}=W\cap \unicode[STIX]{x1D70B}^{-1}([-3\unicode[STIX]{x1D716},0]\times [0,3\unicode[STIX]{x1D716}])$ . It has three boundary components, namely $L_{1}\times \{(-3\unicode[STIX]{x1D716},0)\}$ , $L_{2}\times (0,3\unicode[STIX]{x1D716})$ and $L\times \{(0,0)\}$ , while $L\times \{(0,0)\}$ is the only boundary component that is not cylindrical. One then applies a trick due to Biran and Cornea (see [BC13, §6]). This yields a Hamiltonian perturbation $\unicode[STIX]{x1D711}$ supported on $\unicode[STIX]{x1D70B}^{-1}([-\unicode[STIX]{x1D716},\unicode[STIX]{x1D716}]\times [-\unicode[STIX]{x1D716},\unicode[STIX]{x1D716}])$ , so that $\unicode[STIX]{x1D711}(W)$ has all three cylindrical ends. By extending $\unicode[STIX]{x1D711}(\unicode[STIX]{x1D70B}_{H}^{-1}(0))$ to infinity and bending the cylindrical end corresponding to $L_{2}$ to the left, we get the desired Lagrangian cobordism $V$ (see Figure 11).

Finally, by the identification of gradings from ends to fiber Lagrangians, we conclude that it is a cobordism from $L_{1}$ and $L_{2}$ to $L$ .◻

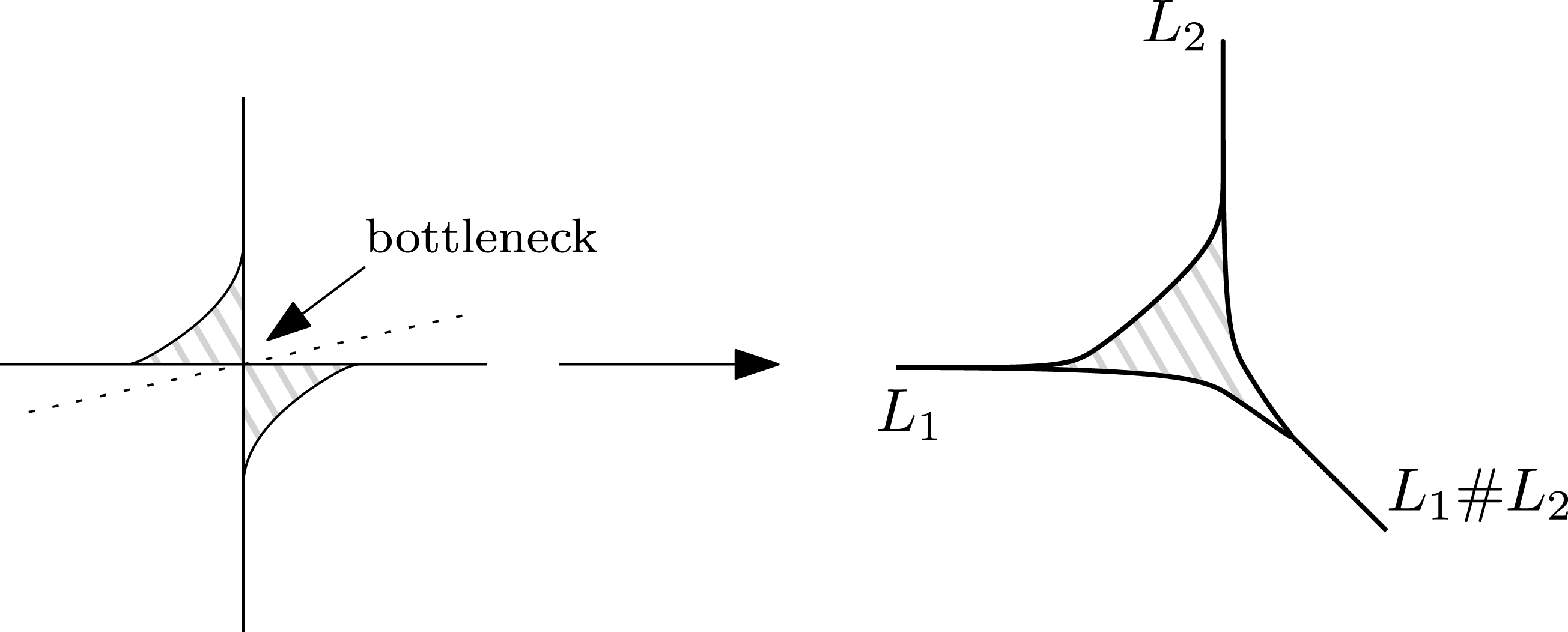
Figure 11. Construction of a surgery cobordism.

We call a cobordism obtained by Lemma 6.1 a surgery cobordism. When $D$ is a single point, it reduces to the usual Lagrangian surgery and Lemma 6.1 was discussed in [BC13, §6] in detail.

Lemma 6.2. Let $V$ be a surgery cobordism from $L_{1},L_{2}$ to $L$ and $D$ is connected. If $L_{1}$ and $L_{2}$ are exact Lagrangians, then $L$ is exact and $V$ is also exact.

Proof. We give the proof for $L=L_{1}\text{\#}_{D,E_{2}}L_{2}$ . Without loss of generality, we can assume $M=T^{\ast }L_{1}$ , $L_{2}=N_{D}^{\ast }$ is the conormal bundle. We first assume $\text{codim}_{L_{i}}(D)\geqslant 2$ .

Since the $E_{2}$ -flow handle $H_{\unicode[STIX]{x1D708}}^{D,E_{2}}$ is obtained by a Hamiltonian flow of $N_{D}^{\ast }\backslash D$ , it is immediate that $H_{\unicode[STIX]{x1D708}}^{D,E_{2}}$ is an exact Lagrangian. Let $f_{1},f_{2}$ and $f_{H}$ be primitives of $\unicode[STIX]{x1D6FC}$ restricted on $L_{1}$ , $L_{2}$ and $H_{\unicode[STIX]{x1D708}}^{D,E_{2}}$ , respectively. Since we assume that $D$ is of codimension two or higher, $(f_{i}-f_{H})|_{L_{i}\cap \overline{H_{\unicode[STIX]{x1D708}}^{D,E_{2}}}}$ are locally constant and hence constant for $i=1,2$ , where $\overline{H_{\unicode[STIX]{x1D708}}^{D,E_{2}}}$ denotes the closure of the handle. By possibly adding a constant to $f_{1}$ and $f_{2}$ , we can assume $f_{1}$ , $f_{2}$ and $f_{H}$ are chosen in such a way that they match together to give a primitive on $L$ .

Now we drop the codimension assumption and only assume $\text{codim}_{L_{i}}(D)\geqslant 1$ . We recall that in the proof of Lemma 6.1, the first step for constructing $V$ is to resolve $L_{1}\times \mathbb{R}$ and $L_{2}\times i\mathbb{R}$ along $D\times \{(0,0)\}$ , which has now $\text{codim}_{L_{i}\times \mathbb{R}}(D)\geqslant 2$ . This process preserves exactness by what we just proved. Then we cut the cobordism into a half, do Hamiltonian perturbation near $L\times \{(0,0)\}$ and extend the cylindrical end. All of these steps preserve the exactness of the Lagrangian and hence $V$ is exact. The restriction of $V$ to the fiber over $\{(0,0)\}$ is precisely $L$ , proving the exactness of the surgery.◻

Lemma 6.3. Let $V$ be a surgery cobordism from $L_{1},L_{2}$ to $L$ . If $L_{1}$ and $L_{2}$ are monotone Lagrangians such that either:

1. (1) $\unicode[STIX]{x1D70B}_{1}(L_{1},D)=1$ or $\unicode[STIX]{x1D70B}_{1}(L_{2},D)=1$ ; or

2. (2) the image of $\unicode[STIX]{x1D70B}_{1}(L_{i})$ in $\unicode[STIX]{x1D70B}_{1}(M)$ is torsion for either $i=1,2$ ,

then $L$ is monotone and $V$ is also monotone.

Proof. Again we give the proof for $L=L_{1}\text{\#}_{D,E_{2}}L_{2}$ and we first assume that $\text{codim}_{L_{i}}(D)\geqslant 2$ . For convenience we decompose $L=\mathring{L}_{1}\cup \mathring{L}_{2}$ . Here $\mathring{L}_{2}$ is the closure of the image of $L_{2}\backslash D$ under the $E_{2}$ -flow defining the surgery, and $\mathring{L}_{1}$ is the closure of the complement of $\mathring{L}_{2}$ .

In case (1) it suffices to prove the lemma when $\unicode[STIX]{x1D70B}_{1}(L_{2},D)=1$ , since the slight asymmetry of $L_{1}$ and $L_{2}$ will be irrelevant. First it is easy to see that $\unicode[STIX]{x1D70B}_{1}(U(D),U(D)\backslash D)=\unicode[STIX]{x1D70B}_{1}(N_{D}^{\ast },N_{D}^{\ast }\backslash D)=1$ by our assumption on $D$ , where $U(D)$ is a tubular neighborhood of $D$ in $L_{2}$ . Since the flow handle $H_{\unicode[STIX]{x1D708}}^{D,E_{2}}$ is obtained by applying an $E_{2}$ -flow to $N_{D}^{\ast }\backslash D$ , any path in $\mathring{L}_{2}$ with ends at $H_{\unicode[STIX]{x1D708}}^{D,E_{2}}$ can be homotoped to a path in $H_{\unicode[STIX]{x1D708}}^{D,E_{2}}$ , while $H_{\unicode[STIX]{x1D708}}^{D,E_{2}}$ in turn retracts to its boundary component that lies on $\mathring{L}_{1}$ .

The upshot is, we can find for any element in $\unicode[STIX]{x1D70B}_{2}(M,L)$ a representative $u:\mathbb{D}^{2}\rightarrow M$ with boundary completely lying in $\mathring{L}_{1}$ . Since $L_{1}$ is monotone, it finishes the proof for $L$ .

Case (2) is similar. Without loss of generality, assume the image of $\unicode[STIX]{x1D70B}_{1}(L_{2})\rightarrow \unicode[STIX]{x1D70B}_{1}(M)$ is torsion. Take again any disk $u:\mathbb{D}^{2}\rightarrow M$ with boundary on $L$ , and assume $\unicode[STIX]{x2202}u$ intersects $\unicode[STIX]{x2202}\mathring{L}_{2}$ transversally. For any segment $I\subset \unicode[STIX]{x2202}u$ contained in $\mathring{L}_{2}$ satisfying $\unicode[STIX]{x2202}I\subset \unicode[STIX]{x2202}\mathring{L}_{2}$ , one connects the two endpoints of $\unicode[STIX]{x2202}I$ by $I^{\prime }\subset \unicode[STIX]{x2202}\mathring{L}_{2}$ (the relevant boundary is connected due to the assumption of connectedness and codimension of $D$ ). By assumption, we can take a disk $v:\mathbb{D}^{2}\rightarrow M$ with $\unicode[STIX]{x2202}v=m[I\cup I^{\prime }]$ for some integer $m$ . Then one may decompose $mu$ so that $m[u]=[mu-v]+[v]$ , so that $\unicode[STIX]{x2202}v\subset \mathring{L}_{2}$ . By performing such a cutting iteratively, one may assume $\unicode[STIX]{x2202}(mu-v)\subset \mathring{L}_{1}$ . Since $\unicode[STIX]{x2202}v$ retracts to $L_{2}\cap \mathring{L}_{2}$ , the monotonicity follows from that of $L_{1}$ and $L_{2}$ with such a decomposition.

Now in either case the monotonicity of $V$ is argued in a similar way as Lemma 6.2 because all processes involved preserve monotonicity. The restriction to the fiber over the origin again removes the assumption of $\text{codim}_{L_{i}}D\geqslant 2$ as in Lemma 6.2.◻

6.2 Proof of long exact sequences

Theorem 6.4 [Sei03, WW16, BC17].

Let $(M,\unicode[STIX]{x1D714})$ be a monotone symplectic manifold and $S^{n}$ ( $n>1$ ) a graded embedded Lagrangian sphere. For any graded monotone Lagrangians $L_{1}$ and $L_{2}$ , there is a long exact sequence

$$\begin{eqnarray}\cdots \rightarrow HF^{\ast }(S^{n},L_{2})\otimes HF^{\ast }(L_{1},S^{n})\rightarrow HF^{\ast }(L_{1},L_{2})\rightarrow HF^{\ast }(L_{1},\unicode[STIX]{x1D70F}_{S^{n}}(L_{2}))\rightarrow \cdots \,.\end{eqnarray}$$

Proof. By Corollaries 3.5, 4.17 and Lemma 6.1, there is a Lagrangian cobordism $V$ from $S^{n}\times S^{n}[1]$ and the diagonal $\unicode[STIX]{x1D6E5}$ to $\text{Graph}(\unicode[STIX]{x1D70F}_{S^{n}}^{-1})$ in $M\times M^{-}$ , where $M^{-}=(M,-\unicode[STIX]{x1D714})$ . By Lemma 6.3, the monotonicity of $(M,\unicode[STIX]{x1D714})$ implies the same property for $S^{n}\times S^{n}[1]$ , $\unicode[STIX]{x1D6E5}\subset M\times M^{-}$ and the corresponding cobordism $V$ .

In either case, $\text{Graph}(\unicode[STIX]{x1D70F}_{S^{n}}^{-1})$ is a cone from $S^{n}\times S^{n}$ to $\unicode[STIX]{x1D6E5}$ in the derived Fukaya category of $M\times M^{-}$ by Theorem 5.2. In particular, we have a long exact sequence

$$\begin{eqnarray}\cdots \rightarrow HF^{\ast }(L_{1}\times L_{2},S^{n}\times S^{n})\rightarrow HF^{\ast }(L_{1}\times L_{2},\unicode[STIX]{x1D6E5})\rightarrow HF^{\ast }(L_{1}\times L_{2},\text{Graph}(\unicode[STIX]{x1D70F}_{S^{n}}^{-1}))\rightarrow \cdots \,.\end{eqnarray}$$

From the Kunneth formula, $HF^{\ast }(L_{1}\times L_{2},S^{n}\times S^{n})\cong HF^{\ast }(L_{1},S^{n})\times HF^{\ast }(S^{n},L_{2})$ (recall that there is a negation on the symplectic form of the second factor). The identity $HF^{\ast }(L_{1}\times L_{2},\unicode[STIX]{x1D6E5})\cong HF^{\ast }(L_{1},L_{2})$ is also well known: in view of Lagrangian correspondence,

$$\begin{eqnarray}HF^{\ast }(L_{1}\times L_{2},\unicode[STIX]{x1D6E5})=HF^{\ast }(L_{1},\unicode[STIX]{x1D6E5},L_{2})=HF^{\ast }(L_{1},\unicode[STIX]{x1D6E5}\circ L_{2})=HF^{\ast }(L_{1},L_{2})\end{eqnarray}$$

by Theorem 5.5.◻

Corollary 6.5 [Sei08b, WW16].

In the same situation as Theorem 6.4, $f\in \text{Symp}(M)$ , then

(6.1) $$\begin{eqnarray}\cdots \rightarrow HF^{\ast }(\unicode[STIX]{x1D70F}\circ f)\rightarrow HF^{\ast }(f)\rightarrow HF^{\ast }(f(S^{n}),S^{n})\rightarrow \cdots \,.\end{eqnarray}$$

Proof. The exact sequence follows from applying the cohomological functor $HF^{\ast }(-,\text{Graph}(f))$ to the cone given by the cobordism.◻

The above result is predicted by Seidel [Sei08b, Remark 2.11] in a slightly different form from here. This is solely due to the cohomological convention we took. In the following theorem, we assume all involved symplectic manifolds and Lagrangians have the same monotonicity constant with minimal Maslov number at least three.

Theorem 6.6 (Theorem 1.4, see also [WW16]).

Let $C$ be a spherically fibered coisotropic manifold over the base $(B,\unicode[STIX]{x1D714}_{B})$ in $(M,\unicode[STIX]{x1D714})$ . Given Lagrangians $L_{1}$ and $L_{2}$ and assume both the following monotonicity conditions.

1. (i) The generalized Lagrangian correspondence $(L_{1},C^{t},C,L_{2})$ is monotone in the sense of [WW10b].

2. (ii) The surgery cobordism corresponding to the surgery in Corollary 3.10 is monotone.

Then there is a long exact sequence

$$\begin{eqnarray}\cdots \rightarrow HF^{\ast }(L_{1}\times C,C^{t}\times L_{2})\rightarrow HF^{\ast }(L_{1},L_{2})\rightarrow HF^{\ast }(L_{1},\unicode[STIX]{x1D70F}_{C}(L_{2}))\rightarrow \cdots \,.\end{eqnarray}$$

In particular if the spherical fiber of $C$ has dimension ${>}1$ or $\unicode[STIX]{x1D70B}_{1}(M)$ is torsion, (ii) is automatic.

Proof. The proof is analogous to Theorem 6.4 with Corollaries 3.5 and 4.17 replaced by Corollary 3.10 and Lemma 4.20. Here we give a sketch. First, $(L_{1},C^{t},C,L_{2})$ being monotone implies $\widetilde{C}=C^{t}\circ C$ being monotone (see [WW10b, Remark 5.2.3]). The Lagrangian cobordism in Corollary 3.10 is monotone by Lemma 6.3. It is not hard to verify $\unicode[STIX]{x1D70B}_{1}(\widetilde{C},\widetilde{C}\cap \unicode[STIX]{x1D6E5})=1$ when $\text{codim}_{M}C\geqslant 2$ . Hence, Theorem 5.2 applies either in this case or when $\unicode[STIX]{x1D70B}_{1}(M)$ is torsion, and we obtain the long exact sequence

$$\begin{eqnarray}\cdots \rightarrow HF^{\ast }(L_{1}\times L_{2},\widetilde{C})\rightarrow HF^{\ast }(L_{1}\times L_{2},\unicode[STIX]{x1D6E5})\rightarrow HF^{\ast }(L_{1}\times L_{2},\text{Graph}(\unicode[STIX]{x1D70F}_{C}^{-1}))\rightarrow \cdots \,.\end{eqnarray}$$

With our assumption on the monotonicity of $(L_{1},C^{t},C,L_{2})$ , we apply Theorem 5.5 to obtain the desired result.◻

There is a similar result on the fixed point version of family Dehn twist, and we will not state it explicitly here.

The new proofs for Theorems 6.4 and 6.6 go through for projective Dehn twists, by using Lemma 4.19. The family versions and (family) fixed point versions for projective Dehn twists can be obtained similarly (cf. Lemma 4.20).

Theorem 6.7. Let $(M,\unicode[STIX]{x1D714})$ be a closed monotone symplectic manifold. Let $S$ be a graded Lagrangian submanifold diffeomorphic to a complex (or real, quaternionic) projective space. For graded monotone Lagrangians $L_{0}$ and $L_{1}$ , there is a quasi-isomorphism of cochain complexes

(6.2) $$\begin{eqnarray}\displaystyle & & \displaystyle CF^{\ast }(L_{0},\unicode[STIX]{x1D70F}_{S}L_{1})\nonumber\\ \displaystyle & & \displaystyle \quad \cong \,\text{Cone}(CF^{\ast }(S,L_{1})\otimes CF^{\ast -\dagger }(L_{0},S)\rightarrow CF^{\ast }(S,L_{1})\otimes CF^{\ast }(L_{0},S)\rightarrow CF^{\ast }(L_{0},L_{1})).\qquad\end{eqnarray}$$

for some maps in the mapping cones, where $\dagger =2,1,4$ , respectively, for complex, real and quaternionic projective space.

Similarly, let $C_{P}$ be a projectively coisotropic submanifold which satisfies the same monotonicity conditions as in Theorem 6.6,

(6.3) $$\begin{eqnarray}\displaystyle & & \displaystyle CF^{\ast }(L_{0},\unicode[STIX]{x1D70F}_{C_{P}}L_{1})\nonumber\\ \displaystyle & & \displaystyle \quad \cong \,\text{Cone}(CF^{\ast -\dagger }(L_{0}\times C_{P},C_{P}^{t}\times L_{1})\rightarrow CF^{\ast }(L_{0}\times C_{P},C_{P}^{t}\times L_{1})\rightarrow CF^{\ast }(L_{0},L_{1})).\end{eqnarray}$$

Proof. This is an immediate consequence of the cobordism of Theorem 1.1(3), (4), and [BC13, Theorem 2.2.1] by plugging in $N=L_{0}\times L_{1}$ as the testing Lagrangian.◻

Remark 6.8. From elementary homological algebra, (6.2) leads to the following long exact sequences (cf. Theorem 6.4),

$$\begin{eqnarray}\cdots \rightarrow HF^{\ast }(S,L_{1})\otimes HF^{\ast -\dagger }(L_{0},S)\rightarrow HF^{\ast }(S,L_{1})\otimes HF^{\ast }(L_{0},S)\rightarrow H^{\ast }(C)\cdots\end{eqnarray}$$

and

$$\begin{eqnarray}\cdots \rightarrow H^{\ast }(C)\rightarrow HF^{\ast }(L_{0},L_{1})\rightarrow HF^{\ast }(L_{0},\unicode[STIX]{x1D70F}_{S}(L_{1}))\rightarrow \cdots\end{eqnarray}$$

for some cochain complex $C$ . Geometrically, $C$ is the Floer complex between certain immersed Lagrangian submanifold and $L_{0}\times L_{1}$ in the ambient symplectic manifold $M\times M$ . The case is similar for projectively coisotropic submanifolds $C_{P}$ .

We have focused on the monotone case so far for concreteness of the exposition. For exact Lagrangian submanifolds, we have the following.

Theorem 6.9. Theorem 6.4 and the first half of Theorem 6.7 holds true for compact exact Lagrangian submanifolds, and Corollary 6.5 holds for exact symplectic manifolds.

The proof for the exact cases are almost completely identical to the monotone cases with Lemma 6.2 ensuring the exactness of the surgery cobordism involved, except for one instance, that the identity

$$\begin{eqnarray}HF^{\ast }(L_{1}\times L_{2},\unicode[STIX]{x1D6E5})\cong HF^{\ast }(L_{1},L_{2})\end{eqnarray}$$

does not fit into the general machinery of Lagrangian correspondences directly.

However, this statement is again well known to experts, and we give a rough argument here. The chain group has a natural bijection sending $L_{1}\times L_{2}\cap \unicode[STIX]{x1D6E5}\ni (x,x)\mapsto x\in L_{1}\cap L_{2}$ . For a $(J,J^{-})$ -holomorphic strip $u=(u^{1},u^{2}):\mathbb{R}\times [0,1]\rightarrow M\times M^{-}$ , where $J=(J_{t})_{t\in [0,1]}$ is a family of $\unicode[STIX]{x1D714}$ -compatible almost complex structures and $J^{-}=-J$ , one has an $J^{\prime }=(J^{\prime })_{t\in [0,1]}$ -holomorphic strip

(6.4) $$\begin{eqnarray}u^{\prime }(s,t)=\left\{\begin{array}{@{}ll@{}}u^{2}(2s,1-2t) & \text{when }0\leqslant t<1/2,\\ u^{1}(2s,2t-1) & \text{when }1/2\leqslant t\leqslant 1,\end{array}\right.\end{eqnarray}$$

where $J_{t}^{\prime }=J_{1-2t}$ for $t\in [0,1/2]$ and $J_{t}^{\prime }=J_{2t-1}$ for $t\in [1/2,1]$ . Conversely, given a $J^{\prime }$ -holomorphic strip $u^{\prime }$ , we can define $u=(u^{2},u^{1})$ , $u^{1}(s,t)=u^{\prime }(s/2,(1+t)/2)$ and $u^{2}(s,t)=u^{\prime }(s/2,(1-t)/2)$ . This gives a bijection between $\mathscr{M}((x,x),(y,y);J\oplus J^{-})$ , the moduli space of $J\oplus J^{-}$ -holomorphic strips connecting $(x,x)$ and $(y,y)$ , and $\mathscr{M}(x,y;J)$ , the $J$ -holomorphic strips connecting $x$ and $y$ , for $x,y\in L_{1}\cap L_{2}$ . This concludes our discussion on exact cases for the long exact sequences.

6.3 Cones in Fukaya categories

We may recapitulate results from § 6 on the functor level using results in [BC14, WMW]. We continue to use the monotone setting in this subsection.

The case of spherical twists and fibered Dehn twists are straightforward given the M’au–Wehrheim–Woodward $A_{\infty }$ -functor $\unicode[STIX]{x1D6F7}$ , which is

(6.5) $$\begin{eqnarray}\unicode[STIX]{x1D6F7}:\mathscr{F}uk(M\times M)\longrightarrow \text{fun}(\mathscr{F}uk^{\text{\#}}(M),\mathscr{F}uk^{\text{\#}}(M)),\end{eqnarray}$$

where $\mathscr{F}uk^{\text{\#}}(M)$ is the $A_{\infty }$ -category of generalized Lagrangians defined in [WMW]. When $G_{\unicode[STIX]{x1D719}}$ is a graph of a symplectomorphism $\unicode[STIX]{x1D719}$ , the functor $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D719}}:=\unicode[STIX]{x1D6F7}(G_{\unicode[STIX]{x1D719}})$ in $\text{fun}(\mathscr{F}uk(M),\mathscr{F}uk(M))$ is the functor induced by $\unicode[STIX]{x1D719}$ .

Given Corollaries 3.5, 4.17 and Lemma 6.1, we constructed a Lagrangian cobordism from $S^{n}\times S^{n}$ and $\unicode[STIX]{x1D6E5}$ to $\text{Graph}(\unicode[STIX]{x1D70F}_{S^{n}}^{-1})$ . The main result from [BC14] then gives a cone in $\mathscr{F}uk(M\times M)$

(6.6) $$\begin{eqnarray}S^{n}\times (S^{n})^{-}\rightarrow \unicode[STIX]{x1D6E5}\rightarrow \text{Graph}(\unicode[STIX]{x1D70F}_{S^{n}}^{-1})\xrightarrow[{}]{[1]}.\end{eqnarray}$$

Hence, under $\unicode[STIX]{x1D6F7}$ this turns into a cone of functors

(6.7) $$\begin{eqnarray}\text{hom}(S^{n},-)\otimes S^{n}\rightarrow \text{Id}_{Tw\mathscr{F}uk(M)}\rightarrow \unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D70F}_{S^{n}}}\xrightarrow[{}]{[1]}\end{eqnarray}$$

or, if $\unicode[STIX]{x1D719}\times \operatorname{id}$ is applied to the cobordism, the resulting cone reads

(6.8) $$\begin{eqnarray}\text{hom}(\unicode[STIX]{x1D719}(S^{n}),-)\otimes S^{n}\rightarrow \unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D719}}\rightarrow \unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D70F}_{S^{n}}\circ \unicode[STIX]{x1D719}}\xrightarrow[{}]{[1]}.\end{eqnarray}$$

Evaluating (6.7) at any object $L\subset \mathscr{F}uk(M)$ hence recovers Seidel’s cone relation [Sei08a]

(6.9) $$\begin{eqnarray}\rightarrow \text{hom}(S^{n},L)\otimes S^{n}\xrightarrow[{}]{ev}L\rightarrow \unicode[STIX]{x1D70F}_{S^{n}}L\xrightarrow[{}]{[1]}\end{eqnarray}$$

while further evaluating at another object gives the cohomological version: Theorem 6.4. Corollary 6.5 follows from (6.8) by considering the morphisms to the identity functor in simple cases. For the family Dehn twist Corollary 3.10, we may also interpret it as a cone of functors, but we need to go to the general Lagrangian correspondence framework; by the time of writing, it is not clear that the functor induced by $\widetilde{C}$ in $\text{fun}(\mathscr{F}uk^{\text{\#}}(M),\mathscr{F}uk^{\text{\#}}(M))$ can descend to a functor in $\text{fun}(\mathscr{F}uk(M),\mathscr{F}uk(M))$ even for spherically coisotropic manifolds.

For the case of projective twists, the same argument shows the following.

Theorem 6.10. Let $S\subset M$ be a monotone Lagrangian $\mathbb{C}\mathbb{P}^{n}$ (respectively $\mathbb{RP}^{n},\mathbb{HP}^{n}$ ). Then the auto-equivalence induced by Lagrangian $S$ -twist is equivalent to the following iterated cone in $\text{fun}(\mathscr{F}uk(M),\mathscr{F}uk(M))$

$$\begin{eqnarray}\text{Cone}(\text{hom}(S,-)\otimes S[-\dagger ]\rightarrow \text{hom}(S,-)\otimes S\rightarrow \text{id}_{\mathscr{F}uk(M)}),\end{eqnarray}$$

where $\dagger =2,1,4$ , respectively, for $\mathbb{C}\mathbb{P}^{n}$ , $\mathbb{RP}^{n}$ and $\mathbb{HP}^{n}$ . Evaluating an object $L$ on these functors recovers Theorem 1.8.

Proof. The construction from Lemma 3.6 gives a Lagrangian cobordism from $S\times S[-\dagger ]$ , $S\times S$ and $\unicode[STIX]{x1D6E5}$ to the graph of $\unicode[STIX]{x1D70F}_{S}^{-1}$ , and grading considerations from Lemmas 4.18, 4.19 endow the cobordism with a well-defined grading that matches those on the ends. The main theorem in [BC14] gives a quasi-isomorphism of iterated cones in $\mathscr{F}uk(M\times M^{-})$

$$\begin{eqnarray}\text{Cone}((S\times S)[-\dagger ]\rightarrow S\times S\rightarrow \unicode[STIX]{x1D6E5}_{M})\cong \text{Graph}(\unicode[STIX]{x1D70F}_{S}^{-1}).\end{eqnarray}$$

The desired assertion is simply the image of this equality under the M’au–Wehrheim–Woodward functor $\unicode[STIX]{x1D6F7}$ .◻

Similarly, by replacing Lemma 3.6 with Corollary 3.10, and Lemmas 4.18 and 4.19 with Lemma 4.20, we have the following.

Theorem 6.11. Given a projectively coisotropic manifold $C\subset M$ satisfying the monotonicity assumptions in Theorem 6.6, the auto-equivalence induced by the family projective twist is equivalent to the following iterated cone in the category $\text{fun}(\mathscr{F}uk^{\text{\#}}(M),\mathscr{F}uk^{\text{\#}}(M))$ ,

$$\begin{eqnarray}\text{Cone}(\widetilde{C}[-\dagger ]\rightarrow \widetilde{C}\rightarrow \text{id}_{\mathscr{F}uk^{\text{\#}}(M)}),\end{eqnarray}$$

where $\dagger =2,1,4$ , respectively, if the projective fiber is $\mathbb{C}\mathbb{P}^{l}$ , $\mathbb{RP}^{l}$ and $\mathbb{HP}^{l}$ .

We remark that the functor $\widetilde{C}$ should be regarded as the composite of the functors $C^{t}:\mathscr{F}uk^{\text{\#}}(M)\rightarrow \mathscr{F}uk^{\text{\#}}(B)$ and $C:\mathscr{F}uk^{\text{\#}}(B)\rightarrow \mathscr{F}uk^{\text{\#}}(M)$ .