1. Introduction
The existence of a characteristic altitudinal structure in the δ 18O and δD values in snow on a high mountain was first discovered in data obtained from surface snow-pit samples taken along a vertical transect on Mount Logan, Yukon Territory, Canada (Reference Holdsworth, Fogarasi and KrouseHoldsworth and others, 1991; referred to hereafter as HFK, 1991). The profile there was interpreted as consisting of the planetary boundary layer (PBL), an intermediate “mixed layer” (previously abbreviated ML and hereafter as MXL) and then part of the quasi-geostrophic (G) flow region above. Insufficient data at other high-altitude sites had precluded this complete structure from being recognized elsewhere, although a partial profile was found on Mount Bona–Churchill, Alaska, U.S.A. Data extending to almost 7 km altitude have now been obtained from Cerro Aconcagua in the southern Andes of South America. These new data support the interpretation given to the earlier data and indicate the general nature of the vertical variation of the stable isotopes of water in the lower half of the troposphere as seen in precipitation in regions of high relief.
In this paper, new data are presented and results discussed in terms of the regional and local air-mass dynamics typical of cyclonic conditions that produce precipitation at particular sites. The MXL occurs prominently in all the profiles. The layer contains snow derived from both the PBL and the G flow region. The use of these latter two terms for atmospheric domains in a cyclone is approximate but convenient. Both terms have wide use in meteorology and are borrowed from that literature. For a detailed analysis of the complete cyclonic system, they should be referred to, generally, as the lower air-mass region and the upper air-mass region. The terminology will be clarified when the structure of a cyclone is presented. For convenient reference to the earlier work we retain the terms (PBL and G) used there. For the Saint Elias Mountains (Yukon Territory and Alaska) sites and for Cerro Aconcagua, we interpret the MXL in terms of a cyclone model since regular cyclogenesis is observed in the Pacific Ocean west of these sites and synoptic charts show the prevalence of occluded frontal systems along the coastline. The systems are usually stalled, allowing major, prolonged precipitation to occur inland. For the Saint Elias Mountains (Fig. 1) an estimated >85% of all the air originates over the Pacific Ocean (Reference Bryson and HareBryson and Hare, 1974), and under precipitating conditions nearly all of the moisture originates from polar-front cyclones in the Gulf of Alaska.

Fig. 1. Map of Alaska, U.S.A., and Yukon Territory, Canada, showing mountains referred to in the text. V (▲), Mount Vancouver (4785 m); S (▲), Mount Steele (5073 m). Mount Bona (5029 m) is indistinguishable from adjacent Mount Churchill (4766 m). Mount Saint Elias (5489 m) is on the Alaska–Yukon border. These peaks, as well as others clustered around Mount Logan (5957 m), all lie in the Saint Elias Mountains. Other symbols are: WH (□), Whitehorse; SK (□), Sitka; YT (□), Yakutat; AK (□), Anchorage; FB (□), Fairbanks.
That cyclones and their associated fronts can deliver snow with markedly different δ values over short time intervals was known earlier for areas where frontal systems could be tracked instrumentally (Reference DansgaardDansgaard, 1961), but the mechanism of frontal precipitation was not applied to specific ice-core sites. Reference Hage, Gray and LintonHage and others (1975) reported large variations in δ 18O (∼10‰) within and between individual snowstorms, but they did not develop a meteorological model to explain the data. If, as is common practice, annual averages of δ are used for analytical purposes, then the details of the cyclonic processes become obscured if a sufficient vertical range of δ(z) data is unavailable. Here, the investigation is largely driven by new spatial data coupled with what is already known about the structure of cyclones that are stalled by topography. The recognition that two separate fractionation schemes exist, with δs separated by over 10‰, within a single cyclone, is key to interpreting the data of HFK (1991) and the new data presented here. These results have important implications for the proper interpretation of isotopic and chemical time series derived from ice cores retrieved from high-altitude sites. In this paper the sites where observations were made are described in section 2. The results are then presented and discussed (section 3) and their significance demonstrated in terms of the structure of a polar-front cyclone model (section 4). Section 5 contains a summary and the main conclusions.
2. Snow-Sampling Sites Used in this Study
The sites where data were obtained for this study are (1) grouped north of 60° N within the Saint Elias Mountains and (2) on Cerro Aconcagua at 32.6° S, 70° W. Sites exploited within Canada have already been documented (HFK, 1991).
The two new sites, one in Alaska and the other in Argentina, are now briefly described:
(1) Mount Bona–Mount Churchill massif, Alaska (Fig. 1)
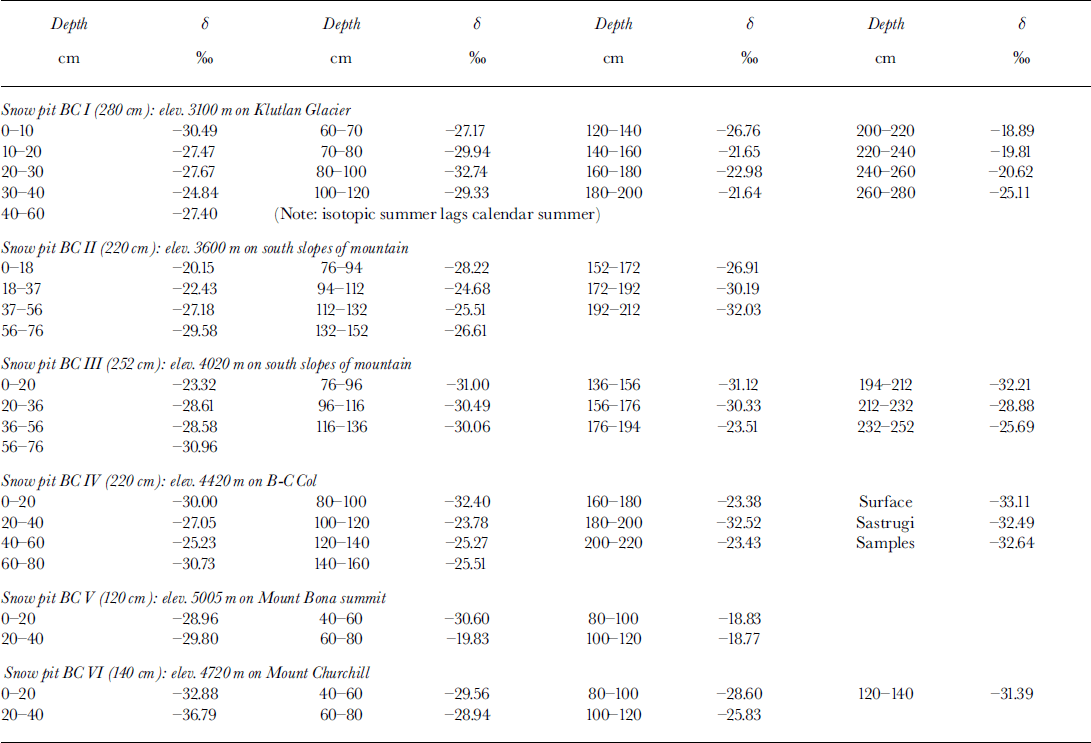
Mount Bona (61°23′ N, 141°45′ W; 5029 m; Fig. 2) is the highest peak on the massif which is connected to a glacier-filled tilted crater on the north side. The highest part of the discontinuous rim of this crater is Mount Churchill (4767 m a.s.l.), about 4 km to the north of the summit of Mount Bona. Between the two peaks is a saddle, Bona–Churchill Col (B-C Col), about 4400 m high. This is a potential deep (>100 m) ice-core site. Ice flows off the southeastern flanks of the massif to feed Klutlan Glacier. In summer 1991, samples were taken from six snow pits, the lowest being near the top of Klutlan Glacier at about 3000 m, and the highest being on the summit of Mount Bona >2000 m above the lowest site.
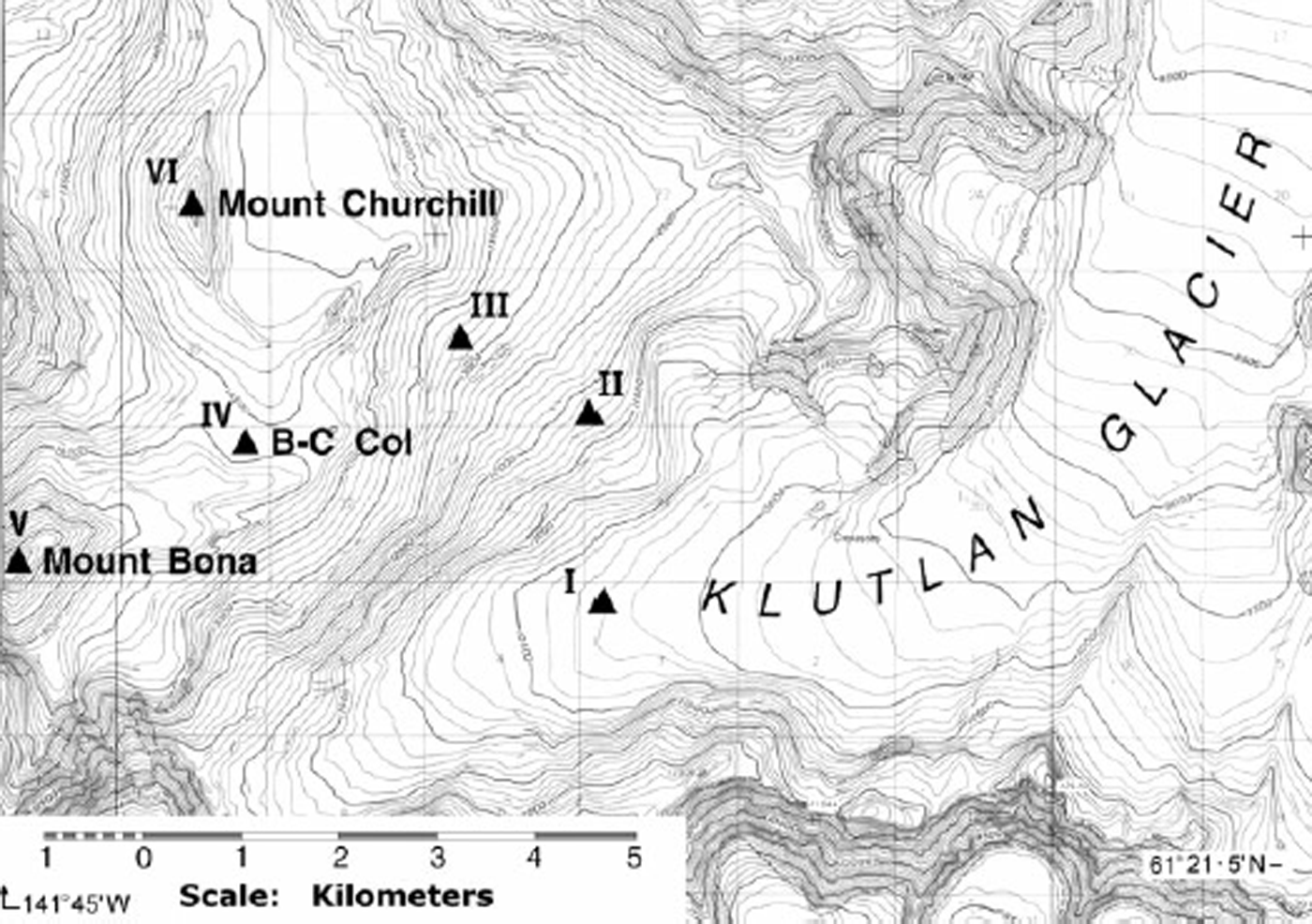
Fig 2. Map of Mount Bona and Mount Churchill and the upper part of Klutlan Glacier, Alaska. Snow-pit sampling sites (I–VI) are marked by the symbol ▲ Map is modified from U.S. Department of the Interior (U.S. Geological Survey) maps: McCarthy B2 and B3 Quadrangle at a scale of 1 : 63 360.
Snow pits, varying in depth from 280 cm (Klutlan Glacier) to 120 cm on the summit of Mount Bona, were dug back to the previous summer layer, as determined from visual pit stratigraphy, grain-size and hardness. The sampling interval was generally 20 cm, but in some cases it was 10 cm where stratigraphy became complex. Separate samples were taken for stable-isotope analyses and for major-anion analyses. The purpose of these latter samples was to help identify the seasonal layers in the profiles. This was usually accomplished by using nitrate concentrations.
(2) Cerro Aconcagua, Argentina (summit altitude: 6959 m) (Fig. 3)
In December 1996, an ascent was made via the northwest ridge route. Although this mountain does not offer a deep ice-core site, it does provide an opportunity to study the nature of the vertical structure of the atmosphere on the highest peak in the Americas using the stable-isotopic composition of the seasonal snow cover. Snow banks along this route were sampled wherever possible from 4430 to 6930 m a.s.l. Generally, these banks seemed to consist mainly of snow accumulated since the previous summer, but some were deep and dense enough to be pseudo-perennial. Because of logistics constraints, bulk sampling was done either down a vertical profile to bedrock (or moraine) or to hard ice, usually covering a distance of < 1 m. Each sample run was taken to be close to an annual bulk sample. Even if this is not the case and snow accumulation for 2 years was collected, the normal isotopic difference between successive years (a few per mil) is small compared with the differences among samples. Annuality is not a strict condition for the present purposes. A single snowfall arriving at all levels as part of a major cyclonic storm system would provide sufficient samples for this study, assuming that any post-depositional processes (e.g. ablation) were not grossly dissimilar throughout the transect.

Fig. 3. Map of part of Cerro Aconcagua, Argentina, showing the snow sites sampled in December 1996. All sites were in the northwest sector. The locations sampled by Reference Grabczak, Niewodniczanski and RózańkiGrabczak and others (1989) were in the northeast sector.
Snow was collected in heavy-duty zip-lock plastic bags. The snow was later melted down and the water poured into 50 mL plastic bottles and then frozen. Refreezing was repeated in Mendoza before the return to Calgary.
This sample set is relatively consistent in terms of the aspect of the sites, which generally faced north or northwest. Cyclonic activity in the southeast Pacific results in storms predominantly bringing snow to the site from the north and west, as may be seen on satellite imagery. Earlier snow sampling on Cerro Aconcagua was done by Reference Grabczak, Niewodniczanski and RózańkiGrabczak and others (1989), but they sampled at only two locations on the Glacier de los Polacos route at 5200 and 6910 m altitude (on the northeast side of the mountain). Because those samples came from a different sector of the mountain and in a different year, the data are not directly used to augment the current dataset but they are presented and discussed later in the interpretation section.
3. Results and Discussion
New data
Isotope data from the Alaskan sites (Mount Bona, Mount Churchill and Klutlan Glacier) are presented in Figure 4. Note that these data apply to snow that accumulated from the end of summer 1990 up to summer 1991. For comparison, data for Mount Logan are also presented, but, to avoid confusion, only the PBL and the G flow region sequences are shown (as dashed lines) because in the MXL on Mount Logan the multiyear data are quite scattered and would interfere with the newer dataset. In addition, the PBL sequences from the Greenland and Antarctic ice sheets, as well as some altitude-limited data for the Queen Elizabeth Islands, Canadian Arctic Archipelago, are shown (see HFK, 1991).

Fig. 4. Variation of δ 18O with altitude for Klutlan Glacier, Mount Bona and Mount Churchill sites. Dashed curves show data for Mount Logan (upper) in the geostrophic flow region and for Mount Logan (lower) in the planetary boundary layer (HFK, 1991). Gulf of Alaska sea-level data point (□) is derived from International Atomic Energy Agency (IAEA)/World Meteorological Organization (WMO) data (Reference Rozanski, Araguás-Araguás, Gonfiantini, Swart, Lohmann, McKenzie and SavinRozanski and others, 1993). Other curves in the planetary boundary layer are taken from HFK (1991). The Alaskan data are deduced to lie predominantly in the mixed layer.
It is apparent that the Alaskan data apply mainly to the MXL in that region. The top of the PBL sequence is drawn on the basis of an expected similarity to data from Mount Logan (see fig. 5 in HFK, 1991).While not conclusive on their own, overall, these data are seen to be quite compatible with the more detailed results from Mount Logan. Other incomplete δ(z) profiles are described in HFK (1991).

Fig. 5. Variation of δ 18O in snow with altitude on Cerro Aconcagua. Sampling sites are shown in Figure 3, and data given in Appendix 2. The sea-level intercepts are estimated from IAEA/WMO data (Reference Rozanski, Araguás-Araguás, Gonfiantini, Swart, Lohmann, McKenzie and SavinRozanski and others, 1993) and from other sources. Only the highest-altitude data points derived from the work of Reference Grabczak, Niewodniczanski and RózańkiGrabczak and others (1989) (G1985) have been plotted. The geographic position of their site (sampled in 1985) was on the other side of the mountain from the site sampled in 1996. The lower sequence (approximate PBL) is derived from moisture originating south of the polar front, and the upper sequence evidently derives from subtropical maritime moisture sources.
The isotope data shown in Figure 5 are from Cerro Aconcagua. These data are sparse, both spatially and temporally, but they are all that could be obtained in 1996. The preceding winter was reported to be dry, and so the residual snow banks were both scarce and thin. The data may be provisionally associated with the previously discussed atmospheric structure as shown by the connected solid lines. Curved lines connecting data points below about 5000 m are drawn (see section 4) assuming that the moisture for the snow comes from cyclones originating in the Pacific Ocean and stalling off the coast of Chile. The three plotted δ 18O values at coastal (Chilean) sea-level sites are derived from data found in Reference Gat and GonfiantiniGat and Gonfiantini (1981), Reference Jouzel, Russell, Suozzo, Koster, White and BroeckerJouzel and others (1987) and Reference Rozanski, Araguás-Araguás, Gonfiantini, Swart, Lohmann, McKenzie and SavinRozanski and others (1993), and take into account possible storm trajectories as seen on satellite imagery. Curves shown are constructed to be consistent with the theoretical dδ/dz values obtained from equations given in Reference Sonntag, Münnich, Jacob, Rozanski, Street-Perrott, Beran and RatcliffeSonntag and others (1983). Appendix 1 gives the derivation of the slope dδ/dz. The data bar (G1985) is derived from snow profiles sampled in 1985 and analyzed by Reference Grabczak, Niewodniczanski and RózańkiGrabczak and others (1989). The large difference between those data and the more modern data could be due to several factors. For instance, the high-altitude snowpack in 1996 could have sustained 18O enrichment by prolonged evaporation due to the reported very low winter snowfall. The raw data for Figures 4 and 5 are given in Appendix 2.
It will be noted that in HFK (1991) and in Figures 4 and 5 there are various types of slopes (dδ/dz) in the mixed layer. This can be understood by noting that both the separation of the two isotopic fractionation curves and the thickness of the mixed layer may vary with time. Assuming a uniform variation of δ from the lower edge of the upper air mass to the upper edge of the lower air mass, it becomes evident how a ramp, cliff (HFK, 1991) or overhang (Fig. 5) occurs in the mixed layer. Deviation from a straight line, as seen in the jagged profile in Figure 4, may result from layering within the mixed layer which is in general not completely mixed (the cliff profile is the nearest to this condition).
Wind scouring from higher elevations and deposition at lower sites
The question of how much the (annual) δ value of the snow can be shifted by wind scour at a high-altitude site in winter is examined with two examples, noting that the scoured-site δ becomes less negative and the recipient-site δ more negative. There are also secondary effects such as evaporative enrichment due to preferential loss of 16O at the scoured site.
-
(a) At Northwest Col (NW Col) on Mount Logan the mean annual δ 18O value varied ±1.25‰ from a mean of −31‰ over 3 years, based on snow pits dug there each year. If variable wind scour from peaks above is involved then this range is an upper limit for that process. But this does not give the total shift, only a relative one. However, because the NW Col δ value lies fairly concordantly on what is interpreted to be an upper fractionation curve (HFK, 1991) the total δ shift can still hardly be more than a few per mil. In section 5 a comprehensive list of factors is given showing other influences on δ.
-
(b) On the Agassiz Ice Cap, Ellesmere Island, Canadian Arctic Archipelago, Reference Fisher, Koerner, Paterson, Dansgaard, Gundestrup and ReehFisher and others (1983) interpreted an inversion of δ between two ice-core sites (one on the crest and one downslope) as being caused by winter wind scour. As section 5 shows, this may not be the only factor. However, assuming that it is the only factor, then in order to obtain a “normal” dδ/dz slope (Reference Sonntag, Münnich, Jacob, Rozanski, Street-Perrott, Beran and RatcliffeSonntag and others, 1983; HFK, 1991) between the two sites, the lowersite δ 18O has to be higher by +1.55‰ and the upper-site value lower by −1.55‰. This is therefore the maximum shift caused by wind scour.
If it is supposed that in Figure 4 the Mount Bona δ point has been shifted (to a more positive value) by losing winter snow and denying the existence of the upper curve, the point would have to be back-shifted about −15‰ in order to even approximately lie on an extension of the lower curve. The same argument would apply to Figure 5. This proposition is physically unreasonable. Therefore, winter wind scour is not considered to be a significant factor in modifying the δ(z) distributions shown here. This was also a stated conclusion in HFK (1991) using other arguments.
Averaging intervals for site values
A note is necessary about δ-data averaging intervals. To standardize the procedure as much as possible and thus to make data useful for other purposes, annual averaging has been attempted wherever suitable data were available. For Mount Logan the seasonal oscillation in δ is of order 10‰, and for the Mount Bona–Churchill region 8‰. At least 10 samples per year were taken in each snow pit. However, it is clear that some data (Aconcagua) may not be strictly annual. This does not prevent useful information from being extracted from the data, as long as the sampling protocol is consistent for that profile. In fact, if samples could be collected simultaneously at all levels up to and beyond an ice-core site during (or just after) a single, suitably located, cyclonic system storm, one snowfall would be sufficient to establish the profiles seen in HFK (1991) and in this paper.
Comparison of new data with earlier data
In Figure 6 our data are compared to those in Figure 2 of Reference Petit, White, Young, Jouzel and KorotkevichPetit and others (1991). In our figure the deuterium excess, as defined by d ≡ δD − 8δ 18O, is plotted against δD. On theoretical grounds, d is considered to vary with sea surface temperature, wind speed and humidity, and δD is used as a (rough) “temperature proxy” (Reference Petit, White, Young, Jouzel and KorotkevichPetit and others, 1991). This is done because in some cases mean annual site temperatures are not known. Because this is the case for the Aconcagua sites, and because of the short time-scale for the data, as well as the need to be consistent, we have followed the same procedure.

Fig. 6. Plot of d vs δD (‰) following Reference Petit, White, Young, Jouzel and KorotkevichPetit and others (1991). The enveloped areas represent fields of multi-year averaged data for surface snow from the Antarctic (Reference Petit, White, Young, Jouzel and KorotkevichPetit and others, 1991; Qin and others, 1994). Low d values are from low-altitude sites; data at the left end of the largest envelope are from the highest-altitude (coldest) sites. Selected high-altitude data are from sites detailed in Figures 2 and 3 and in HFK (1991). Data are annual or multi-annual except for Cerro Aconcagua (see Fig. 5 and Appendix 2) where they are only approximately annual. In general, the highest d values occur at the highest-altitude sites. The “Eclipse” site is 40 km north of Mount Logan (Reference Holdsworth, Krouse and PeakeHoldsworth and others, 1988), and the point is an annual value for 1990.The point marked Tibet is from a mountain glacier site and is a sub-annual value (Reference Aizen, Aizen, Melack and MartmaAizen and others, 1996).
From Figure 6, it is clear that the mountain datasets form a different distribution from the ice-sheet data. There are distinct data groupings for a specific mountain region (e.g. Saint Elias Mountains), and considerable data divergence occurs between regions: one for Mount Logan (Saint Elias Mountains region) for a specific year and the other for Cerro Aconcagua. The single point (open circle) for a low-altitude site (Hailougou glacier) in southeastern Tibet, northern Himalaya (Reference Aizen, Aizen, Melack and MartmaAizen and others, 1996), aligns closely with the higheraltitude Aconcagua data. The reason for this is not known, but clearly more data are needed.
The Alaskan and Yukon data support the previously noted result that d increases with altitude, or roughly with decreasing temperature, but in a non-linear way (see also Reference FisherFisher, 1991). However, the Saint Elias Mountains data display dd/dδD gradients steeper than the large ice sheets. In contrast, while the Cerro Aconcagua data define a similar slope to the other mountain data, it is of opposite sign. Thus, the data show that each mountain region should be studied as a separate isotopic–meteorologic “system” involving cyclone dynamics and moisture trajectory history from sea-level source to site.
The standard δD vs δ 18O plots can also be used to show the variation of d as a function of altitude. In Figure 7 the Cerro Aconcagua data have been partitioned into two groups, and the standard “meteoric-line” slope of 8 has been drawn through each of them (altitudes are indicated beside each point). Although the data are very sparse, the lower sites average d ≈ 10‰, while the upper sites average about 20‰, consistent with Figure 6. For the Saint Elias Mountains we have used selected data from Mount Logan (Fig. 7), as only these have a large enough altitude span to illustrate this effect. The Mount Logan lower-altitude line is coincident at its upper end with the lower-altitude Aconcagua line, so only the lower portion is shown by the dashed-dotted line. The Mount Logan upper line has a value of d = 16‰ (somewhat lower than for the upper Aconcagua line). These data are sufficient to show that the less numerous Aconcagua data are quite compatible with the most reliable Mount Logan data, despite the relative roughness of the sampling on Aconcagua (section 2).
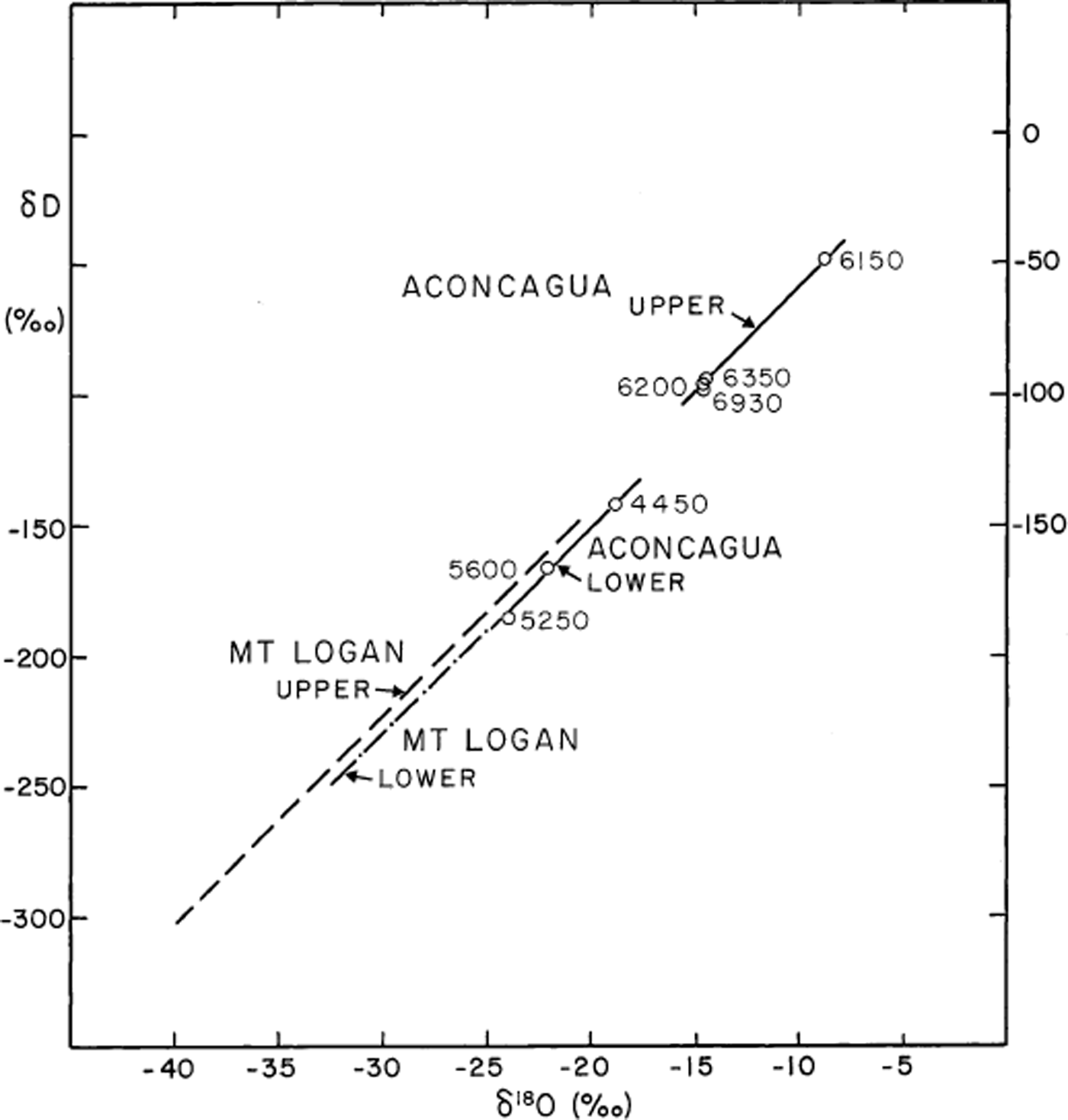
Fig. 7. Plot δD vs δ 18O for snow from Mount Logan (HFK, 1991) and Aconcagua. Data are partitioned according to altitude; for Cerro Aconcagua, altitude values are given in meters.
A standard practice, due to Reference DansgaardDansgaard (1964), is to establish an empirical (linear) relationship between mean annual δ values of precipitation and site temperature. This is referred to as the empirical linear method (ELM). We next illustrate the conventional use of ELM by comparing the mean annual δ 18O of snow with mean annual air temperature (T) at different sites and stations in the Yukon/Alaska region where recent temperature data are very well established. Using the ELM, the line joining sea-level stations to the high-altitude mountain sites may be compared with previously published (δ vs T) lines for the major ice sheets (Reference Rozanski, Araguás-Araguás, Gonfiantini, Swart, Lohmann, McKenzie and SavinRozanski and others 1993). Table 1 lists the datasets, and their sources, used to construct Figure 8. It is seen that there is a close concordance between the “Saint Elias line” (ML-BC-MW-A-Y) and the “Greenland line” (SWG).
Table 1. Isotope (δ 18O) and temperature (T) data for sites referred to in Figure 8
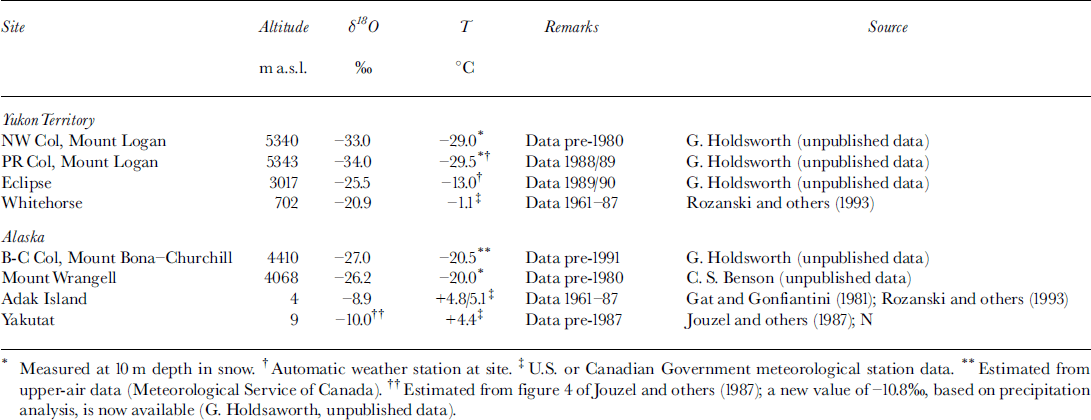

Fig. 8. Conventional plot of site mean δ 18O vs site mean air temperature (T). Asfar as possible (δ, T ) data are matched so that within close limits they cover approximately the same (usually annual) time period (Table 1). Solid circles (●): ML, Mount Logan (lower circle is Prospectors-Russell Col (PR Col; 5343 m); upper circle is NW Col (5340 m)); BC, Mount Bona-Churchill Col (4410 m); MW, Mount Wrangell, Alaska (4068 m). Solid diamonds (♦): A, Adak Island, Alaska (4 m); T, Takutat, Alaska (8.5 m). The line running through these points is a least-squares fit. Other points are: E, Eclipse (3017 m); WH, Whitehorse (702 m; see Fig. 1). These latter two points represent isotopically light precipitation, and most of the departure from the line joining A, T to ML is expected from their geographic coordinates. Other lines, taken from Reference Rozanski, Araguás-Araguás, Gonfiantini, Swart, Lohmann, McKenzie and SavinRozanski and others (1993), are as follows: SWG (fine solid line), south and West Greenland; AP, Antarctic Peninsula; EA, East Antarctica. Straight lines connecting points do not imply a relationship that may be usedfor interpreting ice core δ’s but follow the usual practice of applying the ELM (section 3).
In a geographic comparison with other data, the Mount Logan ice-core 20th-century long-term mean δ 18O (−33 per mil) and latitude (60.5° N) point falls far below the general clustering of data points shown in figure 10a of Reference Rozanski, Araguás-Araguás, Gonfiantini, Swart, Lohmann, McKenzie and SavinRozanski and others (1993). Those authors did not consider data from high-altitude (low-temperature) sites, which are clearly delineated from sites previously studied.
The δ vs T line for the Saint Elias Mountains shown in Figure 8 is broadly consistent with the relationship originally found by Reference DansgaardDansgaard (1964) for mid-to high-latitude sites. (These data apply, as do the earlier data, to the spatial domain and over a limited (20th century) time-span.)
4. Description of the Cyclone-Water-Isotope Model
A brief outline is now given of the cyclone mechanism for producing the observed δ(z) profiles shown in section 3. First, the structure of a polar-front cyclone is presented, and second, the isotopic fractionation schemes within it are described. This system is shown to be able to explain the stepped δ(z) profiles. The discussion of a cyclone is restricted here to the North Pacific, but a Southern Hemisphere cyclone will produce the same vertical isotope profile as a Northern Hemisphere one.
Description of the typical cyclone
Cyclones form in the northeast Pacific region in preferred centres of action (COAs) (Terada and Hanzawa, 1984). These COAs are generally associated with the polar-front zone (PFZ; Reference HoldsworthHoldsworth, 2001a). COAs show seasonal movement as well as significant decadal-scale east–west displacements (Reference Christoforou and HameedChristoforou and Hameed, 1997). Cyclones travel east or northeastward and usually stall and occlude along the Alaska coastline due to the topographic barrier (Reference PutninsPutnins, 1966) or migrate into southwest Alaska. Figure 9a shows a typical mature, occluded, cyclone in the Gulf of Alaska. Figure 9b shows the closest available surface synoptic map and the position of the occluded front. During the occlusion process, when the cold front overtakes the warm front, warm moist air from low latitudes and along the trajectory is shunted, as an upper layer, northeastward over the warm-front zone, while cold air from north of the polar front is pushed northward at low levels. The warm-front zone contains a mixture of air (moisture) from the upper layer and air (moisture) from the lower layer, with zone slopes typically close to 0.5° (Reference McBean and StewartMcBean and Stewart, 1991). The thickness of this mixed (or entrainment) zone increases from the surface (1000 mbar level) along the frontal zone. This is due to the continued wind-shear-induced entrainment of air as the frontal zone increases in altitude. For a typical cyclone that becomes occluded off the Alaska coastline, the warm-front zone may reach, in a distance of at least 300 km, an altitude of >3 km where it intersects the massif of Mount Logan (Fig. 10). Appendix 3 presents a physical basis for the geometry of the front shown in Figure 10.
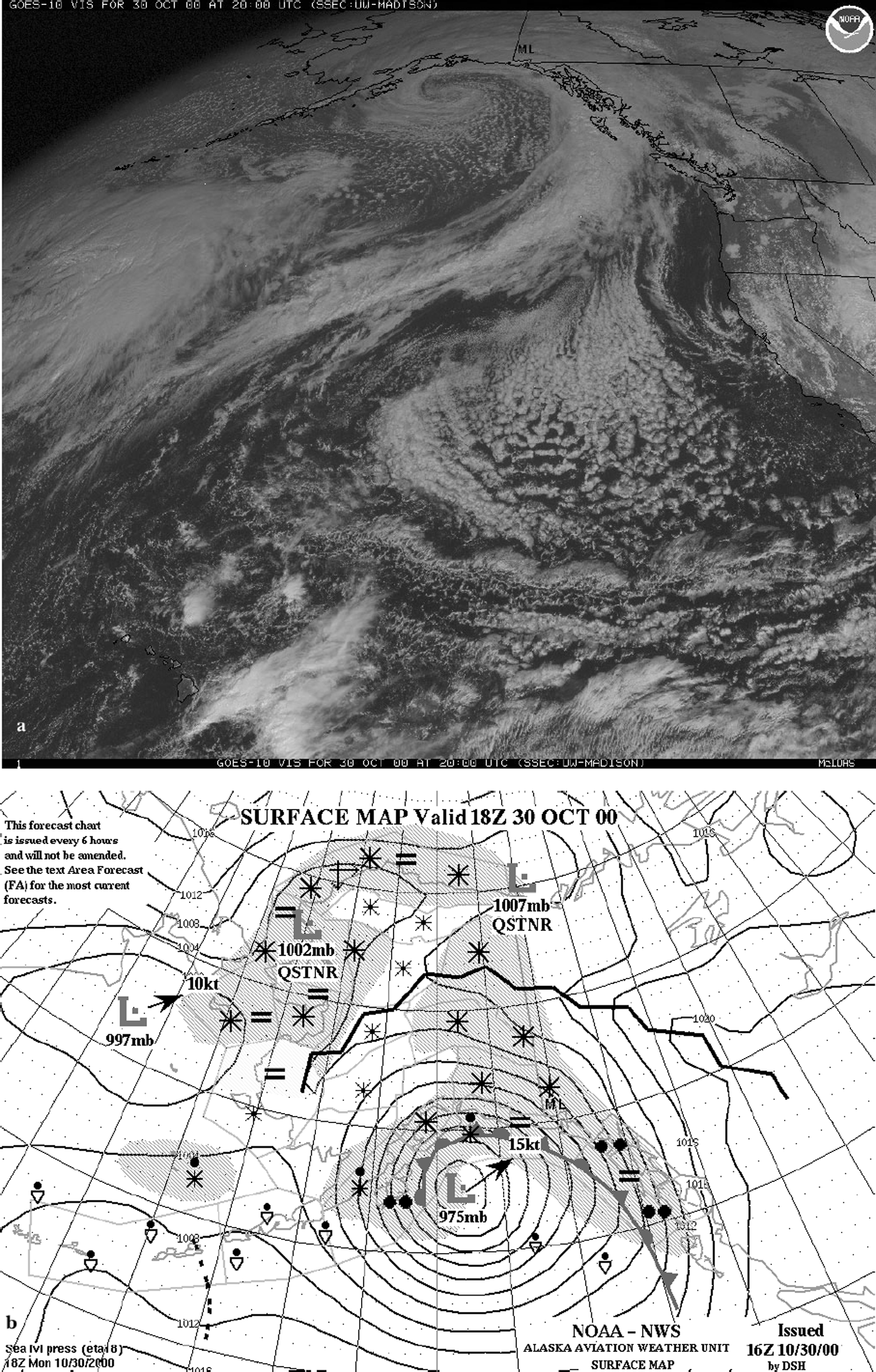
Fig. 9. (a) Geostationary-Orbiting Operational Environmental Satellite 10 (GOES 10) visible image of the Gulf of Alaska region for 30 October 2000 at 2000 GMT showing stalled cyclone delivering precipitation to the Saint Elias Mountains. (Image courtesy of U.S. National Oceanic and Atmospheric Administration and the University of Wisconsin, Madison.) See Figure 1 for the location of Mount Logan shown by black triangle. Moisture advected from low latitudes is raised over the warm-front zone (see Fig 10). (b) Synoptic surface map for the Gulf of Alaska region for 30 October 2000 at 1800 GMT. Map is courtesy of Alaska Aviation Weather Unit, Anchorage. For definition of symbols see: www.alaska.net/aawu/symbols.gif. The occluded frontal system (marked by alternating barbs and semicircles) is situated off the Alaska coastline with centre coordinates 55° N, 148° W. Precipitation is shown by shaded areas. Mount Logan (black triangle) is located just below the farthest right asterisk symbol (representing snowfall).

Fig. 10. Schematic diagram of a warm frontal zone extending into the Saint Elias Mountains. M, Malaspina Glacier; S, Seward Glacier. The position of the cyclone centre and an occluded frontal system in the Gulf of Alaska correspond to kilometre zero on the horizontal scale (similar to Fig. 9b). Mount Logan (NW COL marks the upper drill site) is intersected by three atmospheric layers as explained in the text. Air movement in the lower layer (shown by open arrows) is from the south, while air movement in the upper layer (shown by solid arrows) is from the southwest. Wind shear generates entrainment of one air mass into the other to produce the warm-frontal zone, of thickness Z mxl which is determined by differential wind shear and distance from the cyclone centre. This zone produces the mixed layer (MXL) defined by the stable isotopes. Appendix 3 gives meteorological information on warm fronts.
The air layer below the frontal zone at this location is 1–1.5 km thick and constitutes what is normally referred to as the planetary boundary layer (PBL). This air has its most recent origin from north of the PFZ and is thus derived from high latitudes. In contrast, air above the warm-front zone has its origins far south of the PFZ, as Figure 9a indicates. In winter, the farthest moisture is frequently drawn from close to Hawaii (22° N). Examination of synoptic charts (such as seen in Fig. 9b) reveals that occluded frontal systems usually become stationary along the coastline, and hence the structure of the atmosphere at Mount Logan during major precipitation events is approximately the same during each major storm. That conclusion is consistent with the observed isotope data, which are mean values over the annual snowpack. Isotope anomalies produced by variations of the “standard-model” occluded cyclone largely disappear during the annual averaging process. Processes such as the Pacific Decadal Oscillation and El Niño-Southern Oscillation (Reference Moore, Holdsworth and AlversonMoore and others, 2001) will modify cyclone intensity and tracking, but we are not yet able to provide any information explaining how this could affect the δ(z) profiles presented here. The few stationary fronts that are seen on charts north of Mount Logan are dry, and hence are no longer relevant to precipitation arriving on Mount Logan.
Isotopic fractionation scheme
The origin and structure of a typical Gulf of Alaska cyclone shows that moisture in the cyclone is drawn from two main regions. At low elevations in the western and eastern sectors of the developed cyclone, moisture originates from north of the polar front and has relatively short trajectories to Mount Logan. The sea-water source is usually colder than about 12°C. At high elevations (above the warm front) moisture originates along a track that often starts as far south as 22–30° N where sea water temperatures are usually >20°C. These moisture trajectories targeted for Mount Logan above 5 km can be very long (up to 3800 km).
Hence, there are two water-isotope fractionation sequences operating in moisture flows arriving simultaneously at different altitude bands in the interior of the Saint Elias Mountains. The lower scheme is defined very clearly by the isotope data usually below about 3.5 km altitude and has similar slopes to the major ice-sheet sequences (HFK, 1991). The upper sequence is not well represented by the data because the air mass containing it only intersects less than one vertical kilometre of the mountain. However, the model predicts its existence. In addition, many of these data are obtained from snow pits dug on separate sub-peaks of Mount Logan rather than being obtained from sites linked by snowfields on the same side of the mountain (as for the lower sequence). The data, covering five individual years, were obtained each year from the last (summer-to-summer) annual layer. Data for two of those years (1987, 2000) are incomplete but still fit very closely to the full profiles established earlier (HFK, 1991).
The middle layer (MXL) is inferred to be a zone comprised of a mixture of air/moisture from the lower and upper layers, and hence the isotopic content is derived from two sources. The slope (dδ/dz) in the middle layer is quite variable. As explained in section 3, this is largely due to the dynamics of the cyclone.
5. Summary and Conclusions
Vertical profiles of the stable isotopes of snow in high mountains reveal a structure that is basically a reflection of the structure of the atmosphere during precipitation events. Thus it is a primary structure as opposed to a secondary or post-depositional structure. In the case of the Saint Elias Mountains, this structure is linked to synoptic-scale polar-front cyclones. These cyclones contain moisture from two quite different air masses. It is evidently possible to have precipitation occurring simultaneously within those air masses during a cyclonic storm, but this is not a necessary condition. The important result is that layering occurs in the atmosphere as a result of cyclonic activity. These layers are sub-horizontal and evidently may persist after a precipitation event. Stationary fronts seen on synoptic charts are an example of this. Thus residual layering from exhausted cyclones could drift large distances and influence other types of precipitation events such as convection. Atmospheric layering is of profound importance to high-altitude ice-core sites. Thus the observation by Reference Newell, Thouret, Cho, Stoller, Marenco and SmitNewell and others (1999) that layering in the atmosphere is more widespread than was previously realized is very significant.
Our results have important implications for the use of the isotopic thermometer as used in ice-core paleoclimate reconstructions. The standard linear thermometer (section 3) or a quadratic version (Reference Johnsen, Dahl-Jensen, Dansgaard and GundestrupJohnsen and others, 1995; Reference GreveGreve, 1997) must be established and always used in the same part of the atmosphere or in the same generic air mass as the ice-core site; otherwise the calibration of the thermometer will be altered when temporal changes occur in the vertical distributions of the water isotopes. This problem with the paleo-thermometer is of particular importance when a site (which is near the mixed zone) experiences a change from one climatic state to another. Reference HoldsworthHoldsworth (2001b) discusses this with two applications of the model.
Reference FisherFisher (1992) presented an earlier review of the factors recognized to cause variations in δ at ice-core sites. This list is now updated, and the major factors now formally recognized to modulate δ are as follows:
-
(1) Changes in source and site air temperature (Reference DansgaardDansgaard, 1964) (all time-scales)
-
(2) Changes in air-mass circulation patterns (e.g. north–south shifts in centres of action), changing the source of moisture for precipitation and variations in the trajectories of water vapour arriving at the site (see, e.g., Reference Newell and ZhuNewell and Zhu, 1994) (shorter time-scales)
-
(3) Changes in the relative contributions of moisture, from multiple sources, to the ice-core site (Reference Charles, Rind, Jouzel, Koster and FairbanksCharles and others, 1994) (potentially all, but especially long, time-scales)
-
(4) Changes in the timing of seasonal precipitation (Reference Steig, Grootes and StuiverSteig and others, 1994; Reference Krinner, Genthon and JouzelKrinner and others, 1997; Reference SchlosserSchlosser, 1999) (all time-scales)
-
(5) Variations arising from changes in atmospheric (air-mass) structure at an ice-core site, which is in, or near the edge of, the mixed layer. This mechanism was implicit in the conclusions of HFK (1991), and its consequences are developed further in this paper. In particular, variations in thickness of the warm-front zone may have a major effect on δ at a given site. Only ice-core sites that are permanently in the PBL below semi-stationary frontal structures, or well above such frontal structures, will not be affected by this mechanism.
-
(6) Variations in the height at which precipitation starts forming in an idealized Rayleigh isotope distillation sequence (Reference PierrehumbertPierrehumbert, 1999)
-
(7) Post-(original) deposition changes may also occur and include: the effects of wind scour and redeposition of snow at another (lower) location (Reference Fisher, Koerner, Paterson, Dansgaard, Gundestrup and ReehFisher and others, 1983) changes in ice dynamics on divides, domes or saddle points (e.g. Reference Holdsworth, Krouse, Nosal, Spencer and MayewskiHoldsworth and others, 1989). This includes such effects as side-slope ice flow from higher elevations into the saddle and divide migrations as a result of (2) (Reference Waddington and MarriottWaddington and Marriott, 1986) (medium to long time-scales) as well as significant variations in snow surface elevation at the site with time (e.g. Reference Cuffey and ClowCuffey and Clow, 1997; Reference GreveGreve, 1997) (long time-scales for large ice sheets).
The relative influence of each of the above factors will clearly vary with location of the ice-core site, either on a specific mountain glacier or on an ice sheet or between the two types of glacier.
Acknowledgements
The first author acknowledges support from the National Water Research Institute (Environment Canada) in Saskatoon for the fieldwork done on Mount Logan that laid the foundation for the present study, and for partial publication costs. The fieldwork and sampling done on Mount Bona–Churchill were supported partly by the Isotope Science Laboratory, The University of Calgary (Natural Sciences and Engineering Research Council funding to H.R.K.) and partly by the U.S. Geological Survey, Denver, CO. Travel to Cerro Aconcagua was partially supported by a grant from the Inter American Institute to R. S. Bradley at the University of Massachusetts. The isotopic analyses were done at the Isotope Science Laboratory, The University of Calgary (taylor-s@phas.ucalgary.ca). Stratigraphic and chemical data (not included in Appendix 2) are available from the first author. D. A. Fisher constructively reviewed an earlier version of the paper, while helpful comments by J. B. Johnson and M. Sturm (scientific editors) and two reviewers greatly improved the manuscript.
Appendix 1
Derivation of Slope and Curvature of δ(Z) Graphs
The δ(z) data presented in HFK (1991) (and in Figs 4 and 5 of this paper) show increasing dδ/dz slope values with increasing altitude. This is qualitatively consistent with a model presented by Reference Sonntag, Münnich, Jacob, Rozanski, Street-Perrott, Beran and RatcliffeSonntag and others (1983). Following is a brief description of their model:
Moisture is advected from an ocean source of constant temperature following a Rayleigh batch condensation process. Thus the value of δ(z) is dependent on the temperature at elevation z where the moisture condenses and is precipitated. (Here, δ is taken as δ 18O). The isotope fractionation factor α e(T) relevant to 18O is obtained from Reference MajoubeMajoube (1971) (see Reference Sonntag, Münnich, Jacob, Rozanski, Street-Perrott, Beran and RatcliffeSonntag and others, 1983). The magnitude of the atmospheric lapse rate, ΔT/Δz, is held constant. A “characteristic” scale height z s is defined by z s = T 0/(ΔT/Δz), where T 0 is a “characteristic” temperature taken as ≈15°C. (This value was given by Reference Sonntag, Münnich, Jacob, Rozanski, Street-Perrott, Beran and RatcliffeSonntag and others (1983) for mid-latitudes but has not been modified for more northerly latitudes. The results are not very sensitive to a precise value of T 0 and hence z s.)
An equation was derived by Reference Sonntag, Münnich, Jacob, Rozanski, Street-Perrott, Beran and RatcliffeSonntag and others (1983) incorporating the above parameters (their equation 5). We have re-derived it to obtain the following expression:
This relationship is used only for obtaining approximate slopes and curvatures of the distillation curve.
Aconcagua: sites bulk-sampled (December 1996)
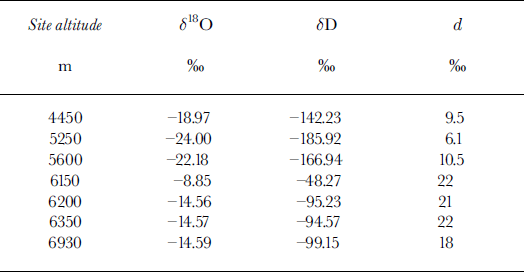
Appendix 2
Raw δ 18O Data for Bona–Churchill and Aconcagua Sites
Mount Bona-Churchill samples (May-June 1991)
Differentiating Equation (Al) with respect to z gives the slope:
Differentiating Equation (A2) with respect to z gives the curvature:

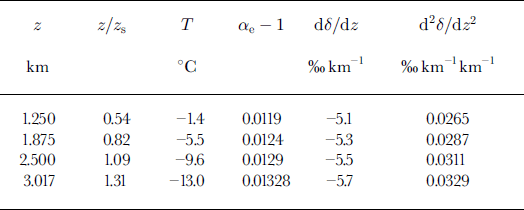
The lapse rate is here given a value of −6.5°C km−1 based on upper-air data for Yakutat, Alaska, and values of temperature at an automatic weather station (Eclipse site as listed in Table 1) in the interior Saint Elias Mountains. The “characteristic” scale height thus has a value z s ≈ 2.3 km. Sonntag and others derived a value of 2.5 km for their application, but the difference makes a negligible effect in Equations (A2) and (A3).
Table 2 gives values of dδ/dz (‰ km−1) and d2 δ/dz 2 (‰ km−1 km−1) for prescribed values of the variables appearing in Equations (A2) and (A3). Column 5 shows an increasing slope with height and an average dδ/dz of −5.4‰ km−1. The empirical curve slopes for the Saint Elias Mountains lower curve lie between −4 and −6‰ km−1, with a mean of about −5‰ km−1. Column 6 shows that the curvature is always positive (convex upwards) as the detailed field data show. Although the theoretical curvature is less than the observed, this general feature is used in constructing curves with sparse data, such as shown in Figure 5.
Table 2. Slope and curvature of δ(z) curves
Appendix 3
The Slope and Structure of Warm Fronts
In glaciated regions of high relief, the topography and thermal character of the air above the glaciers is not conducive to the passage of frontal systems. A study of cyclones in the Gulf of Alaska has shown that most cyclones stall off the Alaska coastline, occlude, and then either decay or move northwestward towards southeast Alaska. In the process, the Saint Elias Mountains are subjected to a quasi-static atmospheric structure during precipitation, so that a large mountain (e.g. Mount Logan) is subjected to repeated precipitation events, involving moisture of different origin, in two principal altitude bands, which, at that location, roughly correspond to the planetary boundary layer and the geostrophic flow region (above 5000 m), respectively. In order to show that Figure 10 is a realistic reconstruction of a frontal zone, we refer to a detailed synoptic-scale study in the Gulf of Alaska region by Reference McBean and StewartMcBean and Stewart (1991). Using the temperature data, it was shown that the upper-air moisture above the fronts must have been advected from much lower latitudes. In addition, potential temperatures (fig. 9 of Reference McBean and StewartMcBean and Stewart, 1991) for November 1980 indicate a warm-frontal slope of about 0.7°. The density of operational radiosonde data is not sufficient to define the structure of the front (thickness, curvature), but these features are discussed in theoretical treatments (Reference HessHess, 1959; Reference HoltonHolton, 1979). The simplest equation given for the slope of a front (z vertical and y perpendicular to the plan trace of the front) is (Reference HoltonHolton, 1979):

where f is the Coriolis parameter (s−1), g is the acceleration of gravity (ms−2), and T m is the mean temperature (K) of the air at the given altitude where a change in horizontal wind speed, du g (m s−1), across the front is associated with a temperature change of dT (K). The equation ignores any frontal curvature terms. Using actual data (quoted in Reference HessHess, 1959; Reference McBean and StewartMcBean and Stewart, 1991), slopes of between 1/50 (1.15°) and 1/400 (0.14°) are found to occur for different fronts. The slope shown in Figure 10 has been given a (high) value of 1.1° by way of example, because a front stalled by topography would probably develop a steeper slope (see, e.g., Reference Keyser and ShapiroKeyser and Shapiro, 1986) than one free to move over open ocean (Reference McBean and StewartMcBean and Stewart, 1991). One way to check this diagram would be to collect snow-pit samples on Mount Saint Elias for isotope analyses to determine δ(z) as was done on Mount Logan. (Note that Mount Saint Elias (Fig. 1) is not formally shown in Figure 10.)
The difference in the δ 18O value in precipitation on either side of a warm front has rarely been measured directly. Reference DansgaardDansgaard (1961) did this for a moving warm front (slope 0.72°) and found a Δδ 18O value of at least 16‰. The difference between the Mount Logan sequences as seen in the snow-pit samples (HFK, 1991) is of this order (>10‰). Therefore, empirical evidence and theory exists to enable us to interpret our isotopic profiles in terms of a warm-front system. However, this is the first time that a discrete width of the warm frontal zone has been indirectly determined in mountainous regions. It should be noted that the two main distillation sequences are not an example of the “Boyle effect” (Reference HoldsworthHoldsworth, 2001b).














