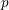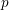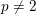1 Introduction
Which prime powers can occur as divisors of irreducible character degrees of finite groups? This question has a long history with many important results and famous open problems. In 1996 Geoffrey Robinson put forward a conjecture on the maximal power of a prime that may divide a character degree. To formulate it, we need to introduce the notion of the defect of a character. Let
![]() $G$
be a finite group and
$G$
be a finite group and
![]() $p$
be a prime. Then the
$p$
be a prime. Then the
![]() $p$
-defect of an irreducible character
$p$
-defect of an irreducible character
![]() $\unicode[STIX]{x1D712}\in \operatorname{Irr}(G)$
is the integer
$\unicode[STIX]{x1D712}\in \operatorname{Irr}(G)$
is the integer
![]() $\operatorname{def}(\unicode[STIX]{x1D712})$
such that
$\operatorname{def}(\unicode[STIX]{x1D712})$
such that
![]() $|G|_{p}=p^{\operatorname{def}(\unicode[STIX]{x1D712})}\unicode[STIX]{x1D712}(1)_{p}$
; here
$|G|_{p}=p^{\operatorname{def}(\unicode[STIX]{x1D712})}\unicode[STIX]{x1D712}(1)_{p}$
; here
![]() $n_{p}$
denotes the
$n_{p}$
denotes the
![]() $p$
-part of an integer
$p$
-part of an integer
![]() $n$
. The answer proposed by Robinson [Reference RobinsonRob96] is as follows.
$n$
. The answer proposed by Robinson [Reference RobinsonRob96] is as follows.
Conjecture (Robinson). Let
![]() $G$
be a finite group,
$G$
be a finite group,
![]() $p$
a prime and
$p$
a prime and
![]() $\unicode[STIX]{x1D712}\in \operatorname{Irr}(G)$
lying in a
$\unicode[STIX]{x1D712}\in \operatorname{Irr}(G)$
lying in a
![]() $p$
-block of
$p$
-block of
![]() $G$
with defect group
$G$
with defect group
![]() $D$
. Then
$D$
. Then
with equality if and only if
![]() $D$
is abelian.
$D$
is abelian.
The height of a character
![]() $\unicode[STIX]{x1D712}$
in a block with defect group
$\unicode[STIX]{x1D712}$
in a block with defect group
![]() $D$
is defined to be the integer
$D$
is defined to be the integer
![]() $\operatorname{ht}(\unicode[STIX]{x1D712})$
such that
$\operatorname{ht}(\unicode[STIX]{x1D712})$
such that
![]() $\unicode[STIX]{x1D712}(1)_{p}|D|=p^{\operatorname{ht}(\unicode[STIX]{x1D712})}|G|_{p}$
. So the conjecture claims that
$\unicode[STIX]{x1D712}(1)_{p}|D|=p^{\operatorname{ht}(\unicode[STIX]{x1D712})}|G|_{p}$
. So the conjecture claims that
with equality if and only if
![]() $D$
is abelian. For abelian defect groups
$D$
is abelian. For abelian defect groups
![]() $D$
, this is the assertion of the direction of Brauer’s famous height-zero conjecture, the proof of which has recently been completed by Kessar and Malle [Reference Kessar and MalleKM13]. Thus Robinson’s conjecture generalises this direction of Brauer’s height-zero conjecture. For
$D$
, this is the assertion of the direction of Brauer’s famous height-zero conjecture, the proof of which has recently been completed by Kessar and Malle [Reference Kessar and MalleKM13]. Thus Robinson’s conjecture generalises this direction of Brauer’s height-zero conjecture. For
![]() $G$
a
$G$
a
![]() $p$
-group it reduces to the classical assertion that
$p$
-group it reduces to the classical assertion that
![]() $\unicode[STIX]{x1D712}(1)$
always divides
$\unicode[STIX]{x1D712}(1)$
always divides
![]() $|G:Z(G)|$
.
$|G:Z(G)|$
.
In 1941, Brauer [Reference BrauerBra41] proved that
![]() $p^{\operatorname{ht}(\unicode[STIX]{x1D712})}\leqslant |D|/p^{2}$
for blocks with non-abelian defect group
$p^{\operatorname{ht}(\unicode[STIX]{x1D712})}\leqslant |D|/p^{2}$
for blocks with non-abelian defect group
![]() $D$
, and in 1968 he showed [Reference BrauerBra68] that
$D$
, and in 1968 he showed [Reference BrauerBra68] that
![]() $p^{\operatorname{ht}(\unicode[STIX]{x1D712})}\leqslant |D|/\text{exp}(Z(D))$
. In 1961, Fong [Reference FongFon61] proved Robinson’s conjecture for the class of
$p^{\operatorname{ht}(\unicode[STIX]{x1D712})}\leqslant |D|/\text{exp}(Z(D))$
. In 1961, Fong [Reference FongFon61] proved Robinson’s conjecture for the class of
![]() $p$
-solvable groups, long before its formulation, and in 1979, Watanabe [Reference WatanabeWat78/79] showed that in Fong’s result the inequality is always strict when
$p$
-solvable groups, long before its formulation, and in 1979, Watanabe [Reference WatanabeWat78/79] showed that in Fong’s result the inequality is always strict when
![]() $D$
is non-abelian.
$D$
is non-abelian.
Our main result is the following theorem.
Theorem 1. Robinson’s conjecture holds for all finite groups for all odd primes.
Our proof crucially relies on the reduction given by Murai [Reference MuraiMur98, Theorem 4.6] of Robinson’s conjecture to quasi-simple groups. We improve this reduction in Theorem 2.3 to show that in fact any minimal counterexample has to occur for a block of a quasi-simple group. We then appeal to the classification of finite simple groups and the deep results on the block theory of these groups, as well as to the proven direction of Brauer’s height-zero conjecture, to verify that their blocks do not provide minimal counterexamples. While we handle many quasi-simple groups for all primes, our restriction that
![]() $p\neq 2$
comes from the fact that not enough seems yet to be known on quasi-isolated blocks of exceptional groups of Lie type in bad characteristic. This case seems out of reach at present.
$p\neq 2$
comes from the fact that not enough seems yet to be known on quasi-isolated blocks of exceptional groups of Lie type in bad characteristic. This case seems out of reach at present.
According to Robinson [Reference RobinsonRob96, Theorem 5.1], his conjecture would follow from a strengthened form of Dade’s ordinary conjecture (see also Eaton [Reference EatonEat04]). In this sense our result can be seen as further evidence towards Dade’s (as yet unproven) conjecture.
Remark 1. It is always the case that the degree of an irreducible character divides the index of any (maximal) abelian normal subgroup. The corresponding sharpening of (RC) where
![]() $Z(D)$
is replaced by a maximal abelian normal subgroup of
$Z(D)$
is replaced by a maximal abelian normal subgroup of
![]() $D$
fails to hold, though. The smallest counterexample is
$D$
fails to hold, though. The smallest counterexample is
![]() $G=\operatorname{GL}_{2}(3)$
with
$G=\operatorname{GL}_{2}(3)$
with
![]() $p=2$
.
$p=2$
.
The paper is organised as follows. In § 2 we show that minimal counterexamples occur for quasi-simple groups. We then deal with the sporadic and the exceptional covering groups in § 3, and the alternating groups in § 4. The groups of Lie type for their defining prime are considered in § 5. The non-defining good primes are then dealt with in § 6, while the case of odd bad primes is considered in § 7. In that final section we also give the proof of Theorem 1.
2 General results
Throughout this paper, we fix a prime
![]() $p$
. Let
$p$
. Let
![]() $\unicode[STIX]{x1D708}$
be the exponential valuation associated to
$\unicode[STIX]{x1D708}$
be the exponential valuation associated to
![]() $p$
, normalised so that
$p$
, normalised so that
![]() $\unicode[STIX]{x1D708}(p)=1$
. For a finite group
$\unicode[STIX]{x1D708}(p)=1$
. For a finite group
![]() $G$
and a subgroup
$G$
and a subgroup
![]() $H$
of
$H$
of
![]() $G$
, we write
$G$
, we write
![]() $\unicode[STIX]{x1D708}(G)$
and
$\unicode[STIX]{x1D708}(G)$
and
![]() $\unicode[STIX]{x1D708}(G:H)$
for
$\unicode[STIX]{x1D708}(G:H)$
for
![]() $\unicode[STIX]{x1D708}(|G|)$
and
$\unicode[STIX]{x1D708}(|G|)$
and
![]() $\unicode[STIX]{x1D708}(|G:H|)$
, respectively.
$\unicode[STIX]{x1D708}(|G:H|)$
, respectively.
We start out by showing, based on the reduction of Murai [Reference MuraiMur98]. that a minimal counterexample to Robinson’s conjecture (RC) necessarily has to occur for a block of a quasi-simple group. Let
![]() $G$
be a finite group and
$G$
be a finite group and
![]() $B$
a
$B$
a
![]() $p$
-block of
$p$
-block of
![]() $G$
. We say that
$G$
. We say that
![]() $(G,B)$
is a minimal counterexample to (RC) if (RC) fails for
$(G,B)$
is a minimal counterexample to (RC) if (RC) fails for
![]() $B$
but does hold for all
$B$
but does hold for all
![]() $p$
-blocks
$p$
-blocks
![]() $B_{1}$
of groups
$B_{1}$
of groups
![]() $G_{1}$
with
$G_{1}$
with
![]() $|G_{1}/Z(G_{1})|<|G/Z(G)|$
. The following result [Reference Kessar and MalleKM13, Theorem 1.1] allows us to focus on
$|G_{1}/Z(G_{1})|<|G/Z(G)|$
. The following result [Reference Kessar and MalleKM13, Theorem 1.1] allows us to focus on
![]() $p$
-blocks of finite groups with non-abelian defect groups.
$p$
-blocks of finite groups with non-abelian defect groups.
Theorem 2.1 (Kessar and Malle).
If
![]() $B$
is a
$B$
is a
![]() $p$
-block of a finite group with abelian defect groups then all ordinary irreducible characters in
$p$
-block of a finite group with abelian defect groups then all ordinary irreducible characters in
![]() $B$
have height zero. In particular, they satisfy (RC).
$B$
have height zero. In particular, they satisfy (RC).
Murai showed that if (RC) fails, then there is already a block of a quasi-simple group for which the conjecture does not hold. In our proofs, we will show that blocks of quasi-simple groups are not minimal counterexamples to (RC). Thus we need to make the connection between Murai’s reduction and our results.
Lemma 2.2. Let
![]() $G$
be a finite group. Assume that (RC) holds for all quasi-simple groups
$G$
be a finite group. Assume that (RC) holds for all quasi-simple groups
![]() $L$
such that
$L$
such that
![]() $|L/Z(L)|\leqslant |G/Z(G)|$
. Then no
$|L/Z(L)|\leqslant |G/Z(G)|$
. Then no
![]() $p$
-block of
$p$
-block of
![]() $G$
is a minimal counterexample to (RC).
$G$
is a minimal counterexample to (RC).
Proof. Assume that some
![]() $p$
-block of
$p$
-block of
![]() $G$
is a minimal counterexample, so that
$G$
is a minimal counterexample, so that
![]() $G$
is non-abelian. Let
$G$
is non-abelian. Let
![]() $N$
be a subgroup of
$N$
be a subgroup of
![]() $G$
such that
$G$
such that
![]() $Z(G)\leqslant N$
and
$Z(G)\leqslant N$
and
![]() $N/Z(G)$
is a maximal normal subgroup of
$N/Z(G)$
is a maximal normal subgroup of
![]() $G/Z(G)$
.
$G/Z(G)$
.
We claim that the condition of [Reference MuraiMur98, Theorem 4.3] holds for
![]() $N$
, that is, that (RC) holds for every
$N$
, that is, that (RC) holds for every
![]() $p$
-block of every central extension of
$p$
-block of every central extension of
![]() $H/N$
for every subgroup
$H/N$
for every subgroup
![]() $H$
with
$H$
with
![]() $N\leqslant H\leqslant G$
. Let
$N\leqslant H\leqslant G$
. Let
![]() $L_{1}$
be a central extension of
$L_{1}$
be a central extension of
![]() $H/N$
. If
$H/N$
. If
![]() $H<G$
, then
$H<G$
, then
![]() $|L_{1}/Z(L_{1})|\leqslant |H/N|<|G/Z(G)|$
, hence the claim holds for
$|L_{1}/Z(L_{1})|\leqslant |H/N|<|G/Z(G)|$
, hence the claim holds for
![]() $L_{1}$
since
$L_{1}$
since
![]() $G$
was chosen minimal. Thus we have that
$G$
was chosen minimal. Thus we have that
![]() $H=G$
, and
$H=G$
, and
![]() $L_{1}$
is a central extension of the simple group
$L_{1}$
is a central extension of the simple group
![]() $G/N$
. If
$G/N$
. If
![]() $G/N$
is of prime order, then
$G/N$
is of prime order, then
![]() $L_{1}$
is abelian, and (RC) is trivially true. If
$L_{1}$
is abelian, and (RC) is trivially true. If
![]() $G/N$
is non-abelian simple, then
$G/N$
is non-abelian simple, then
![]() $L=[L_{1},L_{1}]$
is quasi-simple. Since
$L=[L_{1},L_{1}]$
is quasi-simple. Since
![]() $|L/Z(L)|=|G/N|\leqslant |G/Z(G)|$
, it follows by assumption that (RC) holds for every
$|L/Z(L)|=|G/N|\leqslant |G/Z(G)|$
, it follows by assumption that (RC) holds for every
![]() $p$
-block of
$p$
-block of
![]() $L$
. Then (RC) holds for every
$L$
. Then (RC) holds for every
![]() $p$
-block of
$p$
-block of
![]() $L_{1}$
by the proof of [Reference MuraiMur98, Theorem 4.4], and the claim follows.
$L_{1}$
by the proof of [Reference MuraiMur98, Theorem 4.4], and the claim follows.
Now the result follows from the same argument as for [Reference MuraiMur98, Theorem 4.6]. ◻
Theorem 2.3. Let
![]() $p$
be a prime. If no
$p$
be a prime. If no
![]() $p$
-block of a quasi-simple group is a minimal counterexample to (RC), then (RC) is true for every
$p$
-block of a quasi-simple group is a minimal counterexample to (RC), then (RC) is true for every
![]() $p$
-block of any finite group.
$p$
-block of any finite group.
Proof. If (RC) is true for all quasi-simple groups, then we are done by [Reference MuraiMur98, Theorem 4.6]. Otherwise, assume that
![]() $G$
is a quasi-simple group which is a counterexample to (RC) with
$G$
is a quasi-simple group which is a counterexample to (RC) with
![]() $|G/Z(G)|$
minimal among quasi-simple groups. By assumption there exists a finite group
$|G/Z(G)|$
minimal among quasi-simple groups. By assumption there exists a finite group
![]() $H$
such that (RC) does not hold for some
$H$
such that (RC) does not hold for some
![]() $p$
-block of
$p$
-block of
![]() $H$
and
$H$
and
![]() $|H/Z(H)|<|G/Z(G)|$
. By Lemma 2.2, there is a quasi-simple group
$|H/Z(H)|<|G/Z(G)|$
. By Lemma 2.2, there is a quasi-simple group
![]() $L$
such that
$L$
such that
![]() $|L/Z(L)|\leqslant |H/Z(H)|$
and (RC) does not hold for some
$|L/Z(L)|\leqslant |H/Z(H)|$
and (RC) does not hold for some
![]() $p$
-block of
$p$
-block of
![]() $L$
. However, we have
$L$
. However, we have
![]() $|L/Z(L)|<|G/Z(G)|$
, contradicting the choice of
$|L/Z(L)|<|G/Z(G)|$
, contradicting the choice of
![]() $G$
. This completes the proof.◻
$G$
. This completes the proof.◻
Corollary 2.4. If no block of a quasi-simple group with cyclic center is a minimal counterexample to (RC), then (RC) is true for all finite groups.
Proof. By Theorem 2.3 we may assume that a minimal counterexample to (RC) is a
![]() $p$
-block
$p$
-block
![]() $B$
of a quasi-simple group
$B$
of a quasi-simple group
![]() $G$
. Let
$G$
. Let
![]() $D$
be a defect group of
$D$
be a defect group of
![]() $B$
. Let
$B$
. Let
![]() $\unicode[STIX]{x1D712}\in \operatorname{Irr}(B)$
and
$\unicode[STIX]{x1D712}\in \operatorname{Irr}(B)$
and
![]() $K:=\ker (\unicode[STIX]{x1D712})\cap Z(G)$
. Then
$K:=\ker (\unicode[STIX]{x1D712})\cap Z(G)$
. Then
![]() $N:=\mathbf{O}_{p}(K)\leqslant D$
and
$N:=\mathbf{O}_{p}(K)\leqslant D$
and
![]() $\bar{D}=D/N$
is a defect group of the
$\bar{D}=D/N$
is a defect group of the
![]() $p$
-block
$p$
-block
![]() $\bar{B}$
of
$\bar{B}$
of
![]() $G/K$
dominated by
$G/K$
dominated by
![]() $B$
. Let
$B$
. Let
![]() $\bar{\unicode[STIX]{x1D712}}\in \operatorname{Irr}(\bar{B})$
such that
$\bar{\unicode[STIX]{x1D712}}\in \operatorname{Irr}(\bar{B})$
such that
![]() $\unicode[STIX]{x1D712}$
is the inflation of
$\unicode[STIX]{x1D712}$
is the inflation of
![]() $\bar{\unicode[STIX]{x1D712}}$
. Now clearly
$\bar{\unicode[STIX]{x1D712}}$
. Now clearly
![]() $\operatorname{def}(\unicode[STIX]{x1D712})=|N|\operatorname{def}(\bar{\unicode[STIX]{x1D712}})$
, while
$\operatorname{def}(\unicode[STIX]{x1D712})=|N|\operatorname{def}(\bar{\unicode[STIX]{x1D712}})$
, while
![]() $|Z(D)|\leqslant |N|\cdot |Z(\bar{D})|$
, so
$|Z(D)|\leqslant |N|\cdot |Z(\bar{D})|$
, so
![]() $\bar{B}$
is a counterexample as well. As
$\bar{B}$
is a counterexample as well. As
![]() $\unicode[STIX]{x1D712}$
is irreducible,
$\unicode[STIX]{x1D712}$
is irreducible,
![]() $Z(G/K)$
is cyclic by Schur’s lemma. The claim follows.◻
$Z(G/K)$
is cyclic by Schur’s lemma. The claim follows.◻
3 Sporadic groups
In this section we verify Robinson’s conjecture for
![]() $p$
-blocks of covering groups of the sporadic simple groups, as well as for those of exceptional covering groups of groups of Lie type. We start by recording some general observations.
$p$
-blocks of covering groups of the sporadic simple groups, as well as for those of exceptional covering groups of groups of Lie type. We start by recording some general observations.
Lemma 3.1. Let
![]() $B$
be a
$B$
be a
![]() $p$
-block with defect group
$p$
-block with defect group
![]() $D$
such that
$D$
such that
![]() $|Z(D)|=p$
. Then Robinson’s conjecture holds for
$|Z(D)|=p$
. Then Robinson’s conjecture holds for
![]() $B$
.
$B$
.
Proof. If
![]() $B$
contains characters of defect at most 1, then by a well-known result of Brauer (see [Reference BrauerBra41]) the block has defect 1, and the defect group
$B$
contains characters of defect at most 1, then by a well-known result of Brauer (see [Reference BrauerBra41]) the block has defect 1, and the defect group
![]() $D$
is cyclic, hence abelian.◻
$D$
is cyclic, hence abelian.◻
Corollary 3.2. Robinson’s conjecture holds for all
![]() $p$
-blocks with a non-abelian defect group of order
$p$
-blocks with a non-abelian defect group of order
![]() $p^{3}$
.
$p^{3}$
.
For convenience we will also use the following result [Reference SambaleSam14, Theorem 13.6].
Theorem 3.3 (Sambale).
Robinson’s conjecture holds for all
![]() $2$
-blocks with defect group of order
$2$
-blocks with defect group of order
![]() $16$
.
$16$
.
Lemma 3.4. Let
![]() $N$
be a normal subgroup of
$N$
be a normal subgroup of
![]() $G$
of
$G$
of
![]() $p^{\prime }$
-order. Write
$p^{\prime }$
-order. Write
![]() $\overline{G}=G/N$
. Let
$\overline{G}=G/N$
. Let
![]() $\overline{B}$
be a
$\overline{B}$
be a
![]() $p$
-block of
$p$
-block of
![]() $\overline{G}$
, and
$\overline{G}$
, and
![]() $B$
a
$B$
a
![]() $p$
-block of
$p$
-block of
![]() $G$
dominating
$G$
dominating
![]() $\overline{B}$
. If
$\overline{B}$
. If
![]() $B$
satisfies Robinson’s conjecture then so does
$B$
satisfies Robinson’s conjecture then so does
![]() $\overline{B}$
.
$\overline{B}$
.
Proof. This is a direct consequence of [Reference NavarroNav98, Theorem 9.9(c)]. In fact, the sets
![]() $\operatorname{Irr}(B)$
and
$\operatorname{Irr}(B)$
and
![]() $\operatorname{Irr}(\overline{B})$
are identified under inflation, and the defect groups of
$\operatorname{Irr}(\overline{B})$
are identified under inflation, and the defect groups of
![]() $B$
and
$B$
and
![]() $\overline{B}$
are isomorphic.◻
$\overline{B}$
are isomorphic.◻
Theorem 3.5. Let
![]() $G$
be quasi-simple such that
$G$
be quasi-simple such that
![]() $S=G/Z(G)$
is one of the
$S=G/Z(G)$
is one of the
![]() $26$
sporadic simple groups or
$26$
sporadic simple groups or
![]() $^{2}\!F_{4}(2)^{\prime }$
. Then for all
$^{2}\!F_{4}(2)^{\prime }$
. Then for all
![]() $p$
, Robinson’s conjecture holds for all
$p$
, Robinson’s conjecture holds for all
![]() $p$
-blocks of
$p$
-blocks of
![]() $G$
.
$G$
.
Proof. By Theorem 2.1, we need only consider
![]() $p$
-blocks of
$p$
-blocks of
![]() $G$
with non-abelian defect groups. It turns out that there are at most two kinds of such
$G$
with non-abelian defect groups. It turns out that there are at most two kinds of such
![]() $p$
-blocks in each case. The blocks of defect 3 are not counterexamples by Lemma 3.2, nor are those of defect 4 when
$p$
-blocks in each case. The blocks of defect 3 are not counterexamples by Lemma 3.2, nor are those of defect 4 when
![]() $p=2$
by Theorem 3.3. The remaining blocks are listed in Table 1, where
$p=2$
by Theorem 3.3. The remaining blocks are listed in Table 1, where
![]() $B$
is a
$B$
is a
![]() $p$
-block of
$p$
-block of
![]() $G$
with defect
$G$
with defect
![]() $d$
,
$d$
,
![]() $m$
is the maximal height of the irreducible characters in
$m$
is the maximal height of the irreducible characters in
![]() $B$
and
$B$
and
![]() $\unicode[STIX]{x1D708}_{Z}=\unicode[STIX]{x1D708}(P:Z(P))$
for some defect group
$\unicode[STIX]{x1D708}_{Z}=\unicode[STIX]{x1D708}(P:Z(P))$
for some defect group
![]() $P$
of
$P$
of
![]() $B$
. We denote by
$B$
. We denote by
![]() $B_{0}$
the principal
$B_{0}$
the principal
![]() $p$
-block of
$p$
-block of
![]() $G$
, and the notation
$G$
, and the notation
![]() $B_{0}^{(j)}$
means that there are
$B_{0}^{(j)}$
means that there are
![]() $j$
$j$
![]() $p$
-blocks of
$p$
-blocks of
![]() $G$
with the same invariants
$G$
with the same invariants
![]() $d,m$
and
$d,m$
and
![]() $\unicode[STIX]{x1D708}_{Z}$
as the
$\unicode[STIX]{x1D708}_{Z}$
as the
![]() $p$
-block
$p$
-block
![]() $B_{0}$
.
$B_{0}$
.
Table 1. Blocks of sporadic simple groups with non-abelian defect
![]() $d\geqslant 4+\unicode[STIX]{x1D6FF}_{2,p}$
.
$d\geqslant 4+\unicode[STIX]{x1D6FF}_{2,p}$
.

Here are some details of how to construct the table. The heights and defects of blocks of
![]() $G$
are obtained from the GAP character table library [GAP18]. The structure of defect groups of many non-principal
$G$
are obtained from the GAP character table library [GAP18]. The structure of defect groups of many non-principal
![]() $2$
-blocks of sporadic simple groups and their covering groups is given by Landrock [Reference LandrockLan78]. (See also the proof of [Reference Kessar and MalleKM13, Proposition 8.1].)
$2$
-blocks of sporadic simple groups and their covering groups is given by Landrock [Reference LandrockLan78]. (See also the proof of [Reference Kessar and MalleKM13, Proposition 8.1].)
In some cases, the center of a Sylow
![]() $p$
-subgroup of
$p$
-subgroup of
![]() $G$
is available using GAP [GAP18] or is shown in [Reference SyskinSys80]. For the remaining cases, we apply one of the following straightforward observations.
$G$
is available using GAP [GAP18] or is shown in [Reference SyskinSys80]. For the remaining cases, we apply one of the following straightforward observations.
(1) If
 $Q\leqslant P$
, then
$Q\leqslant P$
, then
 $\unicode[STIX]{x1D708}(P:Z(P))\geqslant \unicode[STIX]{x1D708}(Q:Z(Q))$
.
$\unicode[STIX]{x1D708}(P:Z(P))\geqslant \unicode[STIX]{x1D708}(Q:Z(Q))$
.(2) If
 $Q\unlhd P$
, then
$Q\unlhd P$
, then
 $\unicode[STIX]{x1D708}(P:Z(P))\geqslant \unicode[STIX]{x1D708}(P/Q:Z(P/Q))+\unicode[STIX]{x1D708}(Q:Z(Q))$
.
$\unicode[STIX]{x1D708}(P:Z(P))\geqslant \unicode[STIX]{x1D708}(P/Q:Z(P/Q))+\unicode[STIX]{x1D708}(Q:Z(Q))$
.
Also, we analyse the structure of the centraliser of some element in
![]() $G$
of order
$G$
of order
![]() $p$
given in [Reference SyskinSys80] and the references therein.
$p$
given in [Reference SyskinSys80] and the references therein.
If
![]() $G=J_{4}$
and
$G=J_{4}$
and
![]() $P$
is a Sylow
$P$
is a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $G$
, then
$G$
, then
![]() $|P|=2^{21}$
and according to [Reference SyskinSys80] the centraliser
$|P|=2^{21}$
and according to [Reference SyskinSys80] the centraliser
![]() $C_{G}(z)$
of a 2-central involution
$C_{G}(z)$
of a 2-central involution
![]() $z$
in
$z$
in
![]() $G$
has the structure
$G$
has the structure
![]() $EM$
, where
$EM$
, where
![]() $E$
is an extra-special group
$E$
is an extra-special group
![]() $2_{-}^{1+12}$
and the derived subgroup
$2_{-}^{1+12}$
and the derived subgroup
![]() $M^{\prime }$
has index
$M^{\prime }$
has index
![]() $2$
in
$2$
in
![]() $M$
and is isomorphic to the
$M$
and is isomorphic to the
![]() $6$
-fold cover of
$6$
-fold cover of
![]() $M_{22}$
. So
$M_{22}$
. So
![]() $\unicode[STIX]{x1D708}_{Z}\geqslant 12+6=18$
.
$\unicode[STIX]{x1D708}_{Z}\geqslant 12+6=18$
.
If
![]() $G=Co_{1}$
and
$G=Co_{1}$
and
![]() $P$
is a Sylow
$P$
is a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $G$
, then
$G$
, then
![]() $|P|=2^{21}$
and
$|P|=2^{21}$
and
![]() $G$
has a 2-central involution
$G$
has a 2-central involution
![]() $z$
such that
$z$
such that
![]() $\mathbf{O}_{2}(C)$
is an extra-special group
$\mathbf{O}_{2}(C)$
is an extra-special group
![]() $2_{-}^{1+8}$
and
$2_{-}^{1+8}$
and
![]() $C/\mathbf{O}_{2}(C)$
is isomorphic to
$C/\mathbf{O}_{2}(C)$
is isomorphic to
![]() $\operatorname{O}_{8}^{+}(2)$
, where
$\operatorname{O}_{8}^{+}(2)$
, where
![]() $C=C_{G}(z)$
. Since the Sylow
$C=C_{G}(z)$
. Since the Sylow
![]() $2$
-subgroups of
$2$
-subgroups of
![]() $\operatorname{O}_{8}^{+}(2)$
have center of order
$\operatorname{O}_{8}^{+}(2)$
have center of order
![]() $2$
, it follows that
$2$
, it follows that
![]() $\unicode[STIX]{x1D708}_{Z}\geqslant 8+11=19$
.
$\unicode[STIX]{x1D708}_{Z}\geqslant 8+11=19$
.
If
![]() $G=Fi_{24}^{\prime }$
then Sylow
$G=Fi_{24}^{\prime }$
then Sylow
![]() $2$
-subgroups of
$2$
-subgroups of
![]() $G$
have order
$G$
have order
![]() $2^{21}$
and
$2^{21}$
and
![]() $G$
has a central involution
$G$
has a central involution
![]() $z$
such that
$z$
such that
![]() $\mathbf{O}_{2}(C)$
is an extra-special group
$\mathbf{O}_{2}(C)$
is an extra-special group
![]() $2_{-}^{1+12}$
and
$2_{-}^{1+12}$
and
![]() $C/\mathbf{O}_{2}(C)$
has a subgroup isomorphic to
$C/\mathbf{O}_{2}(C)$
has a subgroup isomorphic to
![]() $3.\operatorname{U}_{4}(3).2$
, where
$3.\operatorname{U}_{4}(3).2$
, where
![]() $C=C_{G}(z)$
. Since a Sylow
$C=C_{G}(z)$
. Since a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $\operatorname{U}_{4}(3)$
has center of order
$\operatorname{U}_{4}(3)$
has center of order
![]() $2$
, it follows that
$2$
, it follows that
![]() $\unicode[STIX]{x1D708}_{Z}\geqslant 12+6=18$
.
$\unicode[STIX]{x1D708}_{Z}\geqslant 12+6=18$
.
The Sylow
![]() $3$
-subgroups of
$3$
-subgroups of
![]() $3.O^{\prime }N$
are extra-special groups of order
$3.O^{\prime }N$
are extra-special groups of order
![]() $3^{1+8}$
and exponent
$3^{1+8}$
and exponent
![]() $3$
.
$3$
.
Suppose
![]() $G=HN$
. If
$G=HN$
. If
![]() $P$
is a Sylow
$P$
is a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $G$
, then
$G$
, then
![]() $|P|=2^{14}$
and the centraliser of a 2-central involution of
$|P|=2^{14}$
and the centraliser of a 2-central involution of
![]() $G$
is the extension of
$G$
is the extension of
![]() $2_{-}^{1+8}$
by the wreath product of
$2_{-}^{1+8}$
by the wreath product of
![]() $\mathfrak{A}_{5}$
by
$\mathfrak{A}_{5}$
by
![]() $C_{2}$
. This implies that
$C_{2}$
. This implies that
![]() $\unicode[STIX]{x1D708}_{Z}\geqslant 9$
. If
$\unicode[STIX]{x1D708}_{Z}\geqslant 9$
. If
![]() $P$
is a Sylow
$P$
is a Sylow
![]() $3$
-subgroup of
$3$
-subgroup of
![]() $G$
, then
$G$
, then
![]() $|P|=3^{6}$
and the centraliser of a 3-central element of order
$|P|=3^{6}$
and the centraliser of a 3-central element of order
![]() $3$
in
$3$
in
![]() $G$
is a
$G$
is a
![]() $3$
-constrained extension of the extra-special group of order
$3$
-constrained extension of the extra-special group of order
![]() $3^{5}$
by
$3^{5}$
by
![]() $\operatorname{SL}_{2}(5)$
. Therefore, we have
$\operatorname{SL}_{2}(5)$
. Therefore, we have
![]() $\unicode[STIX]{x1D708}_{Z}\geqslant 5$
in this case. This also holds if
$\unicode[STIX]{x1D708}_{Z}\geqslant 5$
in this case. This also holds if
![]() $P$
is a Sylow
$P$
is a Sylow
![]() $5$
-subgroup of
$5$
-subgroup of
![]() $G$
.
$G$
.
If
![]() $G=Ly$
then
$G=Ly$
then
![]() $G$
has a Sylow
$G$
has a Sylow
![]() $2$
-subgroup isomorphic to that of
$2$
-subgroup isomorphic to that of
![]() $2.\mathfrak{A}_{11}$
, hence
$2.\mathfrak{A}_{11}$
, hence
![]() $\unicode[STIX]{x1D708}_{Z}=7$
for the principal
$\unicode[STIX]{x1D708}_{Z}=7$
for the principal
![]() $2$
-block of
$2$
-block of
![]() $G$
. Note that
$G$
. Note that
![]() $G$
has another
$G$
has another
![]() $2$
-block with non-abelian defect groups which are actually isomorphic to the Sylow
$2$
-block with non-abelian defect groups which are actually isomorphic to the Sylow
![]() $2$
-subgroups of
$2$
-subgroups of
![]() $2.\mathfrak{A}_{8}$
. So
$2.\mathfrak{A}_{8}$
. So
![]() $\unicode[STIX]{x1D708}_{Z}=6$
in this case. For
$\unicode[STIX]{x1D708}_{Z}=6$
in this case. For
![]() $p=3$
,
$p=3$
,
![]() $G$
has an element of order
$G$
has an element of order
![]() $3$
whose centraliser in
$3$
whose centraliser in
![]() $G$
is a faithful split extension of a special group of order
$G$
is a faithful split extension of a special group of order
![]() $3^{6}$
and exponent
$3^{6}$
and exponent
![]() $3$
by
$3$
by
![]() $\operatorname{SL}_{2}(5)$
, which implies
$\operatorname{SL}_{2}(5)$
, which implies
![]() $\unicode[STIX]{x1D708}_{Z}\geqslant 5$
for
$\unicode[STIX]{x1D708}_{Z}\geqslant 5$
for
![]() $B_{0}$
. Finally, if
$B_{0}$
. Finally, if
![]() $P$
is a Sylow
$P$
is a Sylow
![]() $5$
-subgroup of
$5$
-subgroup of
![]() $G$
, then we consider the centraliser of an element of order
$G$
, then we consider the centraliser of an element of order
![]() $3$
in
$3$
in
![]() $G$
which has a subgroup isomorphic to a faithful split extension of a special group of order
$G$
which has a subgroup isomorphic to a faithful split extension of a special group of order
![]() $5^{5}$
and exponent 5 by a cyclic group of order
$5^{5}$
and exponent 5 by a cyclic group of order
![]() $5$
. It then follows that
$5$
. It then follows that
![]() $\unicode[STIX]{x1D708}_{Z}=5$
for
$\unicode[STIX]{x1D708}_{Z}=5$
for
![]() $B_{0}$
.
$B_{0}$
.
Suppose
![]() $G=Th$
. A Sylow
$G=Th$
. A Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $G$
has order
$G$
has order
![]() $2^{15}$
and the centraliser of any involution of
$2^{15}$
and the centraliser of any involution of
![]() $G$
is a
$G$
is a
![]() $2$
-constrained extension of
$2$
-constrained extension of
![]() $2_{-}^{1+8}$
by
$2_{-}^{1+8}$
by
![]() $\mathfrak{A}_{9}$
, which implies
$\mathfrak{A}_{9}$
, which implies
![]() $\unicode[STIX]{x1D708}_{Z}\geqslant 13$
in this case. If
$\unicode[STIX]{x1D708}_{Z}\geqslant 13$
in this case. If
![]() $P$
is a Sylow
$P$
is a Sylow
![]() $3$
-subgroup of
$3$
-subgroup of
![]() $G$
, then by [Reference SyskinSys80], we have
$G$
, then by [Reference SyskinSys80], we have
![]() $|Z(P)|=3$
, and so
$|Z(P)|=3$
, and so
![]() $\unicode[STIX]{x1D708}_{Z}=9$
.
$\unicode[STIX]{x1D708}_{Z}=9$
.
Suppose
![]() $G=B$
, the Baby Monster. If
$G=B$
, the Baby Monster. If
![]() $P$
is a Sylow
$P$
is a Sylow
![]() $p$
-subgroup of
$p$
-subgroup of
![]() $G$
, then we investigate the maximal subgroups
$G$
, then we investigate the maximal subgroups
![]() $2.^{2}\!E_{6}(2).2$
,
$2.^{2}\!E_{6}(2).2$
,
![]() $Fi_{23}$
and
$Fi_{23}$
and
![]() $HN.2$
of
$HN.2$
of
![]() $G$
from [Reference Conway, Curtis, Norton, Parker and WilsonCCNPW84] or [Reference WilsonWil09, Table 5.7] to get the desired estimate of
$G$
from [Reference Conway, Curtis, Norton, Parker and WilsonCCNPW84] or [Reference WilsonWil09, Table 5.7] to get the desired estimate of
![]() $\unicode[STIX]{x1D708}_{Z}$
for the cases
$\unicode[STIX]{x1D708}_{Z}$
for the cases
![]() $p=2,3$
and
$p=2,3$
and
![]() $5$
, respectively.
$5$
, respectively.
Finally, suppose
![]() $G=M$
, the Monster. For
$G=M$
, the Monster. For
![]() $p=2$
we use the maximal subgroup
$p=2$
we use the maximal subgroup
![]() $2.B$
of
$2.B$
of
![]() $G$
to obtain
$G$
to obtain
![]() $\unicode[STIX]{x1D708}_{Z}\geqslant 35$
. For
$\unicode[STIX]{x1D708}_{Z}\geqslant 35$
. For
![]() $p=3$
we look at the maximal subgroup
$p=3$
we look at the maximal subgroup
![]() $3.Fi_{24}$
of
$3.Fi_{24}$
of
![]() $G$
to obtain
$G$
to obtain
![]() $\unicode[STIX]{x1D708}_{Z}\geqslant 15$
. According to [Reference Gorenstein, Lyons and SolomonGLS98, Table 5.3z], a Sylow
$\unicode[STIX]{x1D708}_{Z}\geqslant 15$
. According to [Reference Gorenstein, Lyons and SolomonGLS98, Table 5.3z], a Sylow
![]() $5$
-subgroup of
$5$
-subgroup of
![]() $G$
has an extra-special subgroup
$G$
has an extra-special subgroup
![]() $5^{1+6}$
of exponent
$5^{1+6}$
of exponent
![]() $5$
, hence
$5$
, hence
![]() $\unicode[STIX]{x1D708}_{Z}\geqslant 6$
, and a Sylow
$\unicode[STIX]{x1D708}_{Z}\geqslant 6$
, and a Sylow
![]() $7$
-subgroup of
$7$
-subgroup of
![]() $G$
has an extra-special subgroup
$G$
has an extra-special subgroup
![]() $7^{1+4}$
of exponent
$7^{1+4}$
of exponent
![]() $7$
, hence
$7$
, hence
![]() $\unicode[STIX]{x1D708}_{Z}\geqslant 4$
. Now the table is established, finishing the proof.◻
$\unicode[STIX]{x1D708}_{Z}\geqslant 4$
. Now the table is established, finishing the proof.◻
Theorem 3.6. Let
![]() $G$
be an exceptional covering group of a simple group of Lie type or of the alternating groups
$G$
be an exceptional covering group of a simple group of Lie type or of the alternating groups
![]() $\mathfrak{A}_{6}$
or
$\mathfrak{A}_{6}$
or
![]() $\mathfrak{A}_{7}$
. Then Robinson’s conjecture holds for all
$\mathfrak{A}_{7}$
. Then Robinson’s conjecture holds for all
![]() $p$
-blocks of
$p$
-blocks of
![]() $G$
for all primes
$G$
for all primes
![]() $p$
.
$p$
.
Proof. The Schur multipliers of the groups mentioned in the theorem can be found in [Reference Conway, Curtis, Norton, Parker and WilsonCCNPW84] and [Reference Malle and TestermanMT11, Table 24.3]. For convenience, we list them in Table 2. The character tables of all these groups can be found in GAP [GAP18], as well as the defects of
![]() $p$
-blocks and the heights of irreducible characters of
$p$
-blocks and the heights of irreducible characters of
![]() $G$
.
$G$
.
Table 2. Non-generic Schur multipliers.

Table 3. Blocks of exceptional covering groups with non-abelian defect
![]() $d\geqslant 4$
.
$d\geqslant 4$
.

As we only list exceptional coverings, we do not consider the simple groups themselves, nor
![]() $2.\operatorname{L}_{2}(4)=2.\mathfrak{A}_{5}$
,
$2.\operatorname{L}_{2}(4)=2.\mathfrak{A}_{5}$
,
![]() $2.\operatorname{L}_{2}(9)=2.\mathfrak{A}_{6}$
,
$2.\operatorname{L}_{2}(9)=2.\mathfrak{A}_{6}$
,
![]() $2.\operatorname{L}_{3}(2)=2.\operatorname{L}_{2}(7)$
,
$2.\operatorname{L}_{3}(2)=2.\operatorname{L}_{2}(7)$
,
![]() $3.\operatorname{L}_{3}(4)$
,
$3.\operatorname{L}_{3}(4)$
,
![]() $2.\operatorname{L}_{4}(2)=2.\mathfrak{A}_{8}$
,
$2.\operatorname{L}_{4}(2)=2.\mathfrak{A}_{8}$
,
![]() $2.\operatorname{U}_{4}(2)=2.\operatorname{S}_{4}(3)$
,
$2.\operatorname{U}_{4}(2)=2.\operatorname{S}_{4}(3)$
,
![]() $4.\operatorname{U}_{4}(3)$
,
$4.\operatorname{U}_{4}(3)$
,
![]() $3.\operatorname{U}_{6}(2)$
,
$3.\operatorname{U}_{6}(2)$
,
![]() $2.\operatorname{O}_{7}(3)$
or
$2.\operatorname{O}_{7}(3)$
or
![]() $3.^{2}\!E_{6}(2)$
. Also, by Corollary 2.4 we only need to look at coverings with cyclic center. Observe that when the universal covering group has non-cyclic center, then often all cyclic
$3.^{2}\!E_{6}(2)$
. Also, by Corollary 2.4 we only need to look at coverings with cyclic center. Observe that when the universal covering group has non-cyclic center, then often all cyclic
![]() $p$
-subgroups of the center of a given order are conjugate under the outer automorphism group [Reference Conway, Curtis, Norton, Parker and WilsonCCNPW84], and then just one such extension has to be considered in each case.
$p$
-subgroups of the center of a given order are conjugate under the outer automorphism group [Reference Conway, Curtis, Norton, Parker and WilsonCCNPW84], and then just one such extension has to be considered in each case.
By Theorem 2.1 and Lemma 3.2 we may focus on
![]() $p$
-blocks
$p$
-blocks
![]() $B$
of
$B$
of
![]() $G$
with non-abelian defect groups
$G$
with non-abelian defect groups
![]() $P$
of defect
$P$
of defect
![]() $d\geqslant 4$
. In particular, we have
$d\geqslant 4$
. In particular, we have
![]() $p=2$
or
$p=2$
or
![]() $3$
and by Theorem 3.3 we may assume
$3$
and by Theorem 3.3 we may assume
![]() $d\geqslant 5$
when
$d\geqslant 5$
when
![]() $p=2$
. We list them in Table 3, where
$p=2$
. We list them in Table 3, where
![]() $d,m,\unicode[STIX]{x1D708}_{Z},B_{0}$
and
$d,m,\unicode[STIX]{x1D708}_{Z},B_{0}$
and
![]() $B_{0}^{(j)}$
have the same meaning as in Table 1. (Notice that in some cases we need to study the centraliser of some
$B_{0}^{(j)}$
have the same meaning as in Table 1. (Notice that in some cases we need to study the centraliser of some
![]() $p$
-element of
$p$
-element of
![]() $G$
. Again, we do not try to get the exact number, so sometimes the numbers in Table 3 are just lower bounds on
$G$
. Again, we do not try to get the exact number, so sometimes the numbers in Table 3 are just lower bounds on
![]() $\unicode[STIX]{x1D708}_{Z}$
big enough for our purpose.)◻
$\unicode[STIX]{x1D708}_{Z}$
big enough for our purpose.)◻
4 Alternating groups
We next discuss alternating groups. For odd primes these have essentially been dealt with by Bessenrodt and Olsson [Reference Bessenrodt and OlssonBO97].
Theorem 4.1. Let
![]() $H$
be quasi-simple such that
$H$
be quasi-simple such that
![]() $H/Z(H)=\mathfrak{A}_{n}$
with
$H/Z(H)=\mathfrak{A}_{n}$
with
![]() $n\geqslant 5$
. Then for all primes
$n\geqslant 5$
. Then for all primes
![]() $p$
, Robinson’s conjecture holds for all
$p$
, Robinson’s conjecture holds for all
![]() $p$
-blocks of
$p$
-blocks of
![]() $H$
.
$H$
.
Proof. By Theorem 3.6 we may assume that
![]() $H=\mathfrak{A}_{n}$
or the
$H=\mathfrak{A}_{n}$
or the
![]() $2$
-fold cover
$2$
-fold cover
![]() $2.\mathfrak{A}_{n}$
of
$2.\mathfrak{A}_{n}$
of
![]() $\mathfrak{A}_{n}$
. Bessenrodt and Olsson showed that Robinson’s conjecture holds for all
$\mathfrak{A}_{n}$
. Bessenrodt and Olsson showed that Robinson’s conjecture holds for all
![]() $p$
-blocks of
$p$
-blocks of
![]() $2.\mathfrak{S}_{n}$
, for all primes
$2.\mathfrak{S}_{n}$
, for all primes
![]() $p$
(see [Reference Bessenrodt and OlssonBO97, Theorem 4.9]). Therefore, for
$p$
(see [Reference Bessenrodt and OlssonBO97, Theorem 4.9]). Therefore, for
![]() $p$
odd, the result follows by Lemma 3.4 and the Clifford theory with respect to
$p$
odd, the result follows by Lemma 3.4 and the Clifford theory with respect to
![]() $p$
-blocks.
$p$
-blocks.
So now let
![]() $p=2$
. Let
$p=2$
. Let
![]() $b$
be a
$b$
be a
![]() $2$
-block of
$2$
-block of
![]() $H$
. We first assume
$H$
. We first assume
![]() $H=\mathfrak{A}_{n}$
. Let
$H=\mathfrak{A}_{n}$
. Let
![]() $G$
be the symmetric group
$G$
be the symmetric group
![]() $\mathfrak{S}_{n}$
,
$\mathfrak{S}_{n}$
,
![]() $B$
a
$B$
a
![]() $2$
-block of
$2$
-block of
![]() $G$
covering
$G$
covering
![]() $b$
, and
$b$
, and
![]() $P$
a defect group of
$P$
a defect group of
![]() $B$
. By the proven Nakayama conjecture [Reference OlssonOls93, Theorem 11.1], the
$B$
. By the proven Nakayama conjecture [Reference OlssonOls93, Theorem 11.1], the
![]() $2$
-blocks of
$2$
-blocks of
![]() $G$
are parameterised by the
$G$
are parameterised by the
![]() $2$
-cores of partitions of
$2$
-cores of partitions of
![]() $n$
. If
$n$
. If
![]() $B$
corresponds to a
$B$
corresponds to a
![]() $2$
-core
$2$
-core
![]() $\unicode[STIX]{x1D705}$
, then by [Reference OlssonOls93, Proposition 11.3],
$\unicode[STIX]{x1D705}$
, then by [Reference OlssonOls93, Proposition 11.3],
![]() $P$
is isomorphic to a Sylow
$P$
is isomorphic to a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $\mathfrak{S}_{2w}$
, where
$\mathfrak{S}_{2w}$
, where
![]() $w:=(n-|\unicode[STIX]{x1D705}|)/2$
is the so-called weight of
$w:=(n-|\unicode[STIX]{x1D705}|)/2$
is the so-called weight of
![]() $B$
. Let
$B$
. Let
![]() $Q=P\cap \mathfrak{A}_{n}$
, a defect group of
$Q=P\cap \mathfrak{A}_{n}$
, a defect group of
![]() $b$
, isomorphic to a Sylow
$b$
, isomorphic to a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $\mathfrak{A}_{2w}$
.
$\mathfrak{A}_{2w}$
.
If
![]() $w\leqslant 2$
then
$w\leqslant 2$
then
![]() $Q$
is abelian, and if
$Q$
is abelian, and if
![]() $w=3$
then
$w=3$
then
![]() $Q$
is non-abelian of order
$Q$
is non-abelian of order
![]() $p^{3}$
. For these two cases, the result follows by Theorem 2.1 and by Corollary 3.2, respectively. So we may assume
$p^{3}$
. For these two cases, the result follows by Theorem 2.1 and by Corollary 3.2, respectively. So we may assume
![]() $w>3$
in the following. Write
$w>3$
in the following. Write
![]() $w=2^{a_{1}}+\cdots +2^{a_{t}}$
, where
$w=2^{a_{1}}+\cdots +2^{a_{t}}$
, where
![]() $a_{1}>\cdots >a_{t}\geqslant 0$
. Then, if we denote by
$a_{1}>\cdots >a_{t}\geqslant 0$
. Then, if we denote by
![]() $X_{i}=C_{2}\wr \cdots \wr C_{2}$
the iterated wreath product of
$X_{i}=C_{2}\wr \cdots \wr C_{2}$
the iterated wreath product of
![]() $a_{i}$
copies of the group
$a_{i}$
copies of the group
![]() $C_{2}$
of order
$C_{2}$
of order
![]() $2$
, then by [Reference OlssonOls93, Proposition 11.3],
$2$
, then by [Reference OlssonOls93, Proposition 11.3],
![]() $P$
is isomorphic to
$P$
is isomorphic to
![]() $X_{a_{1}+1}\times \cdots \times X_{a_{t}+1}$
. Hence
$X_{a_{1}+1}\times \cdots \times X_{a_{t}+1}$
. Hence
![]() $\unicode[STIX]{x1D708}(P:Z(P))=2w-2t$
. By [Reference OlssonOls93, Proposition 11.9], the heights of characters in
$\unicode[STIX]{x1D708}(P:Z(P))=2w-2t$
. By [Reference OlssonOls93, Proposition 11.9], the heights of characters in
![]() $B$
are bounded by
$B$
are bounded by
![]() $w-t$
. So the heights of characters in
$w-t$
. So the heights of characters in
![]() $b$
are also bounded by
$b$
are also bounded by
![]() $w-t$
, and thus the result follows.
$w-t$
, and thus the result follows.
Now we assume
![]() $H=2.\mathfrak{A}_{n}$
and let
$H=2.\mathfrak{A}_{n}$
and let
![]() $G$
be a
$G$
be a
![]() $2$
-fold cover
$2$
-fold cover
![]() $2.\mathfrak{S}_{n}$
of
$2.\mathfrak{S}_{n}$
of
![]() $\mathfrak{S}_{n}$
. By [Reference NavarroNav98, Theorem 9.10], there is a bijection between the set of
$\mathfrak{S}_{n}$
. By [Reference NavarroNav98, Theorem 9.10], there is a bijection between the set of
![]() $2$
-blocks of
$2$
-blocks of
![]() $G$
and those of
$G$
and those of
![]() $\mathfrak{S}_{n}$
. If
$\mathfrak{S}_{n}$
. If
![]() $B$
corresponds to a
$B$
corresponds to a
![]() $2$
-block of
$2$
-block of
![]() $\mathfrak{S}_{n}$
with weight
$\mathfrak{S}_{n}$
with weight
![]() $w$
, then a defect group
$w$
, then a defect group
![]() $P$
is a Sylow
$P$
is a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $2.\mathfrak{S}_{2w}$
, hence a defect group
$2.\mathfrak{S}_{2w}$
, hence a defect group
![]() $Q$
of
$Q$
of
![]() $b$
is a Sylow
$b$
is a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $2.\mathfrak{A}_{2w}$
. Note that we may assume that
$2.\mathfrak{A}_{2w}$
. Note that we may assume that
![]() $w\geqslant 2$
, and that the Sylow
$w\geqslant 2$
, and that the Sylow
![]() $2$
-subgroups of
$2$
-subgroups of
![]() $2.\mathfrak{A}_{4}$
and
$2.\mathfrak{A}_{4}$
and
![]() $2.\mathfrak{A}_{6}$
are the quaternion groups
$2.\mathfrak{A}_{6}$
are the quaternion groups
![]() $Q_{8},Q_{16}$
respectively. In addition, if
$Q_{8},Q_{16}$
respectively. In addition, if
![]() $w>3$
then by [Reference WagnerWag77, Lemma 3.2] we have
$w>3$
then by [Reference WagnerWag77, Lemma 3.2] we have
![]() $|Z(Q)|=2$
. Thus we always have
$|Z(Q)|=2$
. Thus we always have
![]() $|Z(Q)|=2$
for
$|Z(Q)|=2$
for
![]() $w\geqslant 2$
. Now the result follows by Lemma 3.1. ◻
$w\geqslant 2$
. Now the result follows by Lemma 3.1. ◻
5 Groups of Lie type in their defining characteristic
In this section let
![]() $\mathbf{G}$
be a simple algebraic group of simply connected type over an algebraically closed field of characteristic
$\mathbf{G}$
be a simple algebraic group of simply connected type over an algebraically closed field of characteristic
![]() $p$
and
$p$
and
![]() $F:\mathbf{G}\rightarrow \mathbf{G}$
a Steinberg endomorphism such that
$F:\mathbf{G}\rightarrow \mathbf{G}$
a Steinberg endomorphism such that
![]() $G=\mathbf{G}^{F}$
is quasi-simple.
$G=\mathbf{G}^{F}$
is quasi-simple.
Theorem 5.1. Let
![]() $B$
be a
$B$
be a
![]() $p$
-block of
$p$
-block of
![]() $G=\mathbf{G}^{F}$
, where
$G=\mathbf{G}^{F}$
, where
![]() $\mathbf{G}$
is as above. Then
$\mathbf{G}$
is as above. Then
![]() $B$
is not a minimal counterexample to Robinson’s conjecture.
$B$
is not a minimal counterexample to Robinson’s conjecture.
Proof. First note that we need not consider
![]() $\mathbf{G}$
of type
$\mathbf{G}$
of type
![]() $A_{1}$
since Sylow
$A_{1}$
since Sylow
![]() $p$
-subgroups of these groups are abelian. Let
$p$
-subgroups of these groups are abelian. Let
![]() $q$
be the absolute value of the eigenvalues of
$q$
be the absolute value of the eigenvalues of
![]() $F$
in its action on the character group of an
$F$
in its action on the character group of an
![]() $F$
-stable maximal torus of
$F$
-stable maximal torus of
![]() $\mathbf{G}$
. Let
$\mathbf{G}$
. Let
![]() $N$
be the number of positive roots of the root system of
$N$
be the number of positive roots of the root system of
![]() $\mathbf{G}$
. First assume that
$\mathbf{G}$
. First assume that
![]() $G$
is not a Suzuki or Ree group. By the results of Lusztig [Reference LusztigLus84], for any
$G$
is not a Suzuki or Ree group. By the results of Lusztig [Reference LusztigLus84], for any
![]() $\unicode[STIX]{x1D712}\in \operatorname{Irr}(G)$
there are integers
$\unicode[STIX]{x1D712}\in \operatorname{Irr}(G)$
there are integers
![]() $a_{\unicode[STIX]{x1D712}}\geqslant 0$
,
$a_{\unicode[STIX]{x1D712}}\geqslant 0$
,
![]() $n_{\unicode[STIX]{x1D712}}\geqslant 1$
and a product of cyclotomic polynomials
$n_{\unicode[STIX]{x1D712}}\geqslant 1$
and a product of cyclotomic polynomials
![]() $f\in \mathbb{Z}[X]$
(in particular,
$f\in \mathbb{Z}[X]$
(in particular,
![]() $f$
is not divisible by
$f$
is not divisible by
![]() $X$
) such that
$X$
) such that
Let
![]() $A_{\unicode[STIX]{x1D712}}:=a_{\unicode[STIX]{x1D712}}+\deg (f)$
be the degree of the degree polynomial of
$A_{\unicode[STIX]{x1D712}}:=a_{\unicode[STIX]{x1D712}}+\deg (f)$
be the degree of the degree polynomial of
![]() $\unicode[STIX]{x1D712}$
. Then the Alvis–Curtis–Kawanaka–Lusztig dual
$\unicode[STIX]{x1D712}$
. Then the Alvis–Curtis–Kawanaka–Lusztig dual
![]() $\unicode[STIX]{x1D713}:=\operatorname{D}_{\mathbf{G}}(\unicode[STIX]{x1D712})$
has the property that
$\unicode[STIX]{x1D713}:=\operatorname{D}_{\mathbf{G}}(\unicode[STIX]{x1D712})$
has the property that
(see, for example, [Reference LusztigLus84, (8.5.12)]). Now duality is an involution, so
![]() $\operatorname{D}_{\mathbf{G}}^{2}(\unicode[STIX]{x1D712})=\operatorname{D}_{\mathbf{G}}(\unicode[STIX]{x1D713})=\unicode[STIX]{x1D712}$
, that is,
$\operatorname{D}_{\mathbf{G}}^{2}(\unicode[STIX]{x1D712})=\operatorname{D}_{\mathbf{G}}(\unicode[STIX]{x1D713})=\unicode[STIX]{x1D712}$
, that is,
![]() $a_{\unicode[STIX]{x1D712}}=N-A_{\unicode[STIX]{x1D713}}$
. Hence the precise power of
$a_{\unicode[STIX]{x1D712}}=N-A_{\unicode[STIX]{x1D713}}$
. Hence the precise power of
![]() $p$
dividing
$p$
dividing
![]() $\unicode[STIX]{x1D712}(1)$
is
$\unicode[STIX]{x1D712}(1)$
is
![]() $q^{N-A_{\unicode[STIX]{x1D713}}}$
, with
$q^{N-A_{\unicode[STIX]{x1D713}}}$
, with
![]() $\unicode[STIX]{x1D713}=\operatorname{D}_{\mathbf{G}}(\unicode[STIX]{x1D712})$
.
$\unicode[STIX]{x1D713}=\operatorname{D}_{\mathbf{G}}(\unicode[STIX]{x1D712})$
.
We now claim that for all
![]() $\unicode[STIX]{x1D712}\in \operatorname{Irr}(G)$
we have
$\unicode[STIX]{x1D712}\in \operatorname{Irr}(G)$
we have
![]() $\unicode[STIX]{x1D712}(1)_{p}<q^{N-1}$
unless
$\unicode[STIX]{x1D712}(1)_{p}<q^{N-1}$
unless
![]() $\unicode[STIX]{x1D712}$
is the Steinberg character of
$\unicode[STIX]{x1D712}$
is the Steinberg character of
![]() $G$
(see, for example, [Reference CarterCar85, § 6]). By what we said before, it is sufficient for this to see that
$G$
(see, for example, [Reference CarterCar85, § 6]). By what we said before, it is sufficient for this to see that
![]() $A_{\unicode[STIX]{x1D713}}>1$
unless
$A_{\unicode[STIX]{x1D713}}>1$
unless
![]() $\unicode[STIX]{x1D712}=\operatorname{D}_{\mathbf{G}}(\unicode[STIX]{x1D713})$
is the Steinberg character, that is, unless
$\unicode[STIX]{x1D712}=\operatorname{D}_{\mathbf{G}}(\unicode[STIX]{x1D713})$
is the Steinberg character, that is, unless
![]() $\unicode[STIX]{x1D713}=1_{G}$
. Clearly,
$\unicode[STIX]{x1D713}=1_{G}$
. Clearly,
![]() $A_{\unicode[STIX]{x1D712}}=0$
means
$A_{\unicode[STIX]{x1D712}}=0$
means
![]() $\unicode[STIX]{x1D713}=1_{G}$
. The explicit formulas for
$\unicode[STIX]{x1D713}=1_{G}$
. The explicit formulas for
![]() $A_{\unicode[STIX]{x1D713}}$
given, for example, in [Reference CarterCar85, § 13] show that
$A_{\unicode[STIX]{x1D713}}$
given, for example, in [Reference CarterCar85, § 13] show that
![]() $A_{\unicode[STIX]{x1D713}}>1$
in all other cases.
$A_{\unicode[STIX]{x1D713}}>1$
in all other cases.
Now the Steinberg character is of
![]() $p$
-defect
$p$
-defect
![]() $0$
, so certainly does not provide a counterexample. All other blocks have full defect, that is, any
$0$
, so certainly does not provide a counterexample. All other blocks have full defect, that is, any
![]() $U\in \operatorname{Syl}_{p}(G)$
is a defect group (see [Reference Cabanes and EnguehardCE04, Theorem 6.18]). Note that
$U\in \operatorname{Syl}_{p}(G)$
is a defect group (see [Reference Cabanes and EnguehardCE04, Theorem 6.18]). Note that
![]() $|U|=q^{N}$
. Then
$|U|=q^{N}$
. Then
![]() $|Z(U)|=q$
unless
$|Z(U)|=q$
unless
![]() $G$
is of type
$G$
is of type
![]() $B_{n}(2^{f})$
(
$B_{n}(2^{f})$
(
![]() $n\geqslant 2$
),
$n\geqslant 2$
),
![]() $F_{4}(2^{f})$
or
$F_{4}(2^{f})$
or
![]() $G_{2}(3^{f})$
, while in the latter cases
$G_{2}(3^{f})$
, while in the latter cases
![]() $|Z(U)|=q^{2}$
; see [Reference Gorenstein, Lyons and SolomonGLS98, Theorem 3.3.1]. Hence we are done in the case when
$|Z(U)|=q^{2}$
; see [Reference Gorenstein, Lyons and SolomonGLS98, Theorem 3.3.1]. Hence we are done in the case when
![]() $|Z(U)|=q$
, as then
$|Z(U)|=q$
, as then
In the cases when
![]() $|Z(U)|=q^{2}$
it is again easy to check from the values of
$|Z(U)|=q^{2}$
it is again easy to check from the values of
![]() $A_{\unicode[STIX]{x1D713}}$
in [Reference CarterCar85, § 13] that here in fact
$A_{\unicode[STIX]{x1D713}}$
in [Reference CarterCar85, § 13] that here in fact
![]() $\unicode[STIX]{x1D712}(1)_{p}<q^{N-2}$
unless
$\unicode[STIX]{x1D712}(1)_{p}<q^{N-2}$
unless
![]() $\unicode[STIX]{x1D712}$
is the Steinberg character, which again allows us to conclude.
$\unicode[STIX]{x1D712}$
is the Steinberg character, which again allows us to conclude.
For the Suzuki and Ree groups, the above arguments do go through mutatis mutandis, replacing, for example, cyclotomic polynomials over
![]() $\mathbb{Z}$
by cyclotomic polynomials over
$\mathbb{Z}$
by cyclotomic polynomials over
![]() $\mathbb{Z}[\sqrt{p}]$
. Here we always have
$\mathbb{Z}[\sqrt{p}]$
. Here we always have
![]() $|Z(U)|=q^{2}$
(see [Reference ReeRee61b, (5.6)], [Reference ReeRee61a, Theorem 4.14]; note that in this case
$|Z(U)|=q^{2}$
(see [Reference ReeRee61b, (5.6)], [Reference ReeRee61a, Theorem 4.14]; note that in this case
![]() $q$
is not an integer), but again all
$q$
is not an integer), but again all
![]() $a_{\unicode[STIX]{x1D712}}$
for
$a_{\unicode[STIX]{x1D712}}$
for
![]() $\unicode[STIX]{x1D712}$
not the Steinberg character are at most
$\unicode[STIX]{x1D712}$
not the Steinberg character are at most
![]() $N-2$
.◻
$N-2$
.◻
For primes
![]() $p$
that are good for
$p$
that are good for
![]() $\mathbf{G}$
, this result also follows from [Reference GeckGec03, Theorem 1].
$\mathbf{G}$
, this result also follows from [Reference GeckGec03, Theorem 1].
6 Good primes
To conform with the usual notation in block theory of finite reductive groups, from now on we change our notation and consider
![]() $\ell$
-blocks, for a prime
$\ell$
-blocks, for a prime
![]() $\ell$
, and let
$\ell$
, and let
![]() $p$
denote the characteristic of the underlying field of a linear algebraic group. Let us start out with the following completely elementary observation, which can be thought of as an analogue of (RC) for conjugacy class lengths.
$p$
denote the characteristic of the underlying field of a linear algebraic group. Let us start out with the following completely elementary observation, which can be thought of as an analogue of (RC) for conjugacy class lengths.
Lemma 6.1. Let
![]() $D$
be a non-abelian
$D$
be a non-abelian
![]() $\ell$
-group. Then
$\ell$
-group. Then
![]() $|C_{D}(t)|>|Z(D)|$
for all
$|C_{D}(t)|>|Z(D)|$
for all
![]() $t\in D$
.
$t\in D$
.
Proof. If
![]() $t\in Z(D)$
the claim holds. Else
$t\in Z(D)$
the claim holds. Else
![]() $\langle Z(D),t\rangle$
centralises
$\langle Z(D),t\rangle$
centralises
![]() $t$
and has order larger than
$t$
and has order larger than
![]() $|Z(D)|$
.◻
$|Z(D)|$
.◻
Roughly speaking, Robinson’s conjecture for groups of Lie type in cross characteristic should be a consequence of this observation. In order to explain this, let us look at the principal
![]() $\ell$
-block
$\ell$
-block
![]() $B_{0}$
of a finite reductive group
$B_{0}$
of a finite reductive group
![]() $G$
in characteristic different from
$G$
in characteristic different from
![]() $\ell$
. Then
$\ell$
. Then
![]() $\operatorname{Irr}(B)\subseteq {\mathcal{E}}_{\ell }(G,1)=\bigsqcup _{t}{\mathcal{E}}(G,t)$
, where
$\operatorname{Irr}(B)\subseteq {\mathcal{E}}_{\ell }(G,1)=\bigsqcup _{t}{\mathcal{E}}(G,t)$
, where
![]() $t$
runs over the
$t$
runs over the
![]() $\ell$
-elements of the dual group
$\ell$
-elements of the dual group
![]() $G^{\ast }$
. Moreover, by the Jordan decomposition of characters, there are bijections
$G^{\ast }$
. Moreover, by the Jordan decomposition of characters, there are bijections
![]() $J_{t}:{\mathcal{E}}(G,t)\rightarrow {\mathcal{E}}(C_{G^{\ast }}(t),1)$
with
$J_{t}:{\mathcal{E}}(G,t)\rightarrow {\mathcal{E}}(C_{G^{\ast }}(t),1)$
with
![]() $\unicode[STIX]{x1D712}(1)=|G^{\ast }:C_{G^{\ast }}(t)|_{p^{\prime }}J_{t}(\unicode[STIX]{x1D712})(1)$
. In particular, this means that
$\unicode[STIX]{x1D712}(1)=|G^{\ast }:C_{G^{\ast }}(t)|_{p^{\prime }}J_{t}(\unicode[STIX]{x1D712})(1)$
. In particular, this means that
![]() $\unicode[STIX]{x1D712}$
and
$\unicode[STIX]{x1D712}$
and
![]() $J_{t}(\unicode[STIX]{x1D712})$
have the same defect in their ambient groups. Fix a Sylow
$J_{t}(\unicode[STIX]{x1D712})$
have the same defect in their ambient groups. Fix a Sylow
![]() $\ell$
-subgroup
$\ell$
-subgroup
![]() $D$
of
$D$
of
![]() $G^{\ast }$
; then any
$G^{\ast }$
; then any
![]() $\ell$
-element
$\ell$
-element
![]() $t\in G^{\ast }$
has a conjugate in
$t\in G^{\ast }$
has a conjugate in
![]() $D$
, and obviously
$D$
, and obviously
![]() $|G^{\ast }:C_{G^{\ast }}(t)|_{\ell }\leqslant |D:C_{D}(t)|\leqslant |D:Z(D)|$
by Lemma 6.1, with strict inequality when
$|G^{\ast }:C_{G^{\ast }}(t)|_{\ell }\leqslant |D:C_{D}(t)|\leqslant |D:Z(D)|$
by Lemma 6.1, with strict inequality when
![]() $D$
is non-abelian. Thus, for example, when all elements of
$D$
is non-abelian. Thus, for example, when all elements of
![]() $J_{t}(\operatorname{Irr}(B)\cap {\mathcal{E}}(G,t))$
have degree prime to
$J_{t}(\operatorname{Irr}(B)\cap {\mathcal{E}}(G,t))$
have degree prime to
![]() $\ell$
, the desired conclusion follows (assuming that
$\ell$
, the desired conclusion follows (assuming that
![]() $G$
and
$G$
and
![]() $G^{\ast }$
have isomorphic Sylow
$G^{\ast }$
have isomorphic Sylow
![]() $\ell$
-subgroups, or at least that their centers are of the same order).
$\ell$
-subgroups, or at least that their centers are of the same order).
6.1 Unipotent blocks
We now make this heuristic precise. For a prime
![]() $\ell$
not dividing
$\ell$
not dividing
![]() $q$
we denote by
$q$
we denote by
![]() $d_{\ell }(q)$
the order of
$d_{\ell }(q)$
the order of
![]() $q$
modulo
$q$
modulo
![]() $\ell$
when
$\ell$
when
![]() $\ell$
is odd, respectively the order of
$\ell$
is odd, respectively the order of
![]() $q$
modulo 4 when
$q$
modulo 4 when
![]() $\ell =2$
. We employ freely the notions from
$\ell =2$
. We employ freely the notions from
![]() $d$
-Harish-Chandra theory, such as
$d$
-Harish-Chandra theory, such as
![]() $d$
-split Levi subgroups,
$d$
-split Levi subgroups,
![]() $d$
-cuspidal pairs and
$d$
-cuspidal pairs and
![]() $d$
-Harish-Chandra series, as laid out in [Reference Broué, Malle and MichelBMM93], as well as the language of Lusztig series explained, for example, in [Reference Cabanes and EnguehardCE04, § 8]. The following estimate will prove useful.
$d$
-Harish-Chandra series, as laid out in [Reference Broué, Malle and MichelBMM93], as well as the language of Lusztig series explained, for example, in [Reference Cabanes and EnguehardCE04, § 8]. The following estimate will prove useful.
Proposition 6.2. Let
![]() $\mathbf{H}$
be connected reductive with Frobenius map
$\mathbf{H}$
be connected reductive with Frobenius map
![]() $F$
with respect to an
$F$
with respect to an
![]() $\mathbb{F}_{q}$
-rational structure. Let
$\mathbb{F}_{q}$
-rational structure. Let
![]() $\ell$
be a prime and
$\ell$
be a prime and
![]() $d=d_{\ell }(q)$
. Let
$d=d_{\ell }(q)$
. Let
![]() $\unicode[STIX]{x1D712}\in {\mathcal{E}}(\mathbf{H}^{F},1)$
be a unipotent character in the
$\unicode[STIX]{x1D712}\in {\mathcal{E}}(\mathbf{H}^{F},1)$
be a unipotent character in the
![]() $d$
-Harish-Chandra series of the
$d$
-Harish-Chandra series of the
![]() $d$
-cuspidal pair
$d$
-cuspidal pair
![]() $(\mathbf{L},\unicode[STIX]{x1D706})$
of
$(\mathbf{L},\unicode[STIX]{x1D706})$
of
![]() $\mathbf{H}$
. Then
$\mathbf{H}$
. Then
Proof. This follows directly from the character formula for unipotent characters in
![]() $d$
-Harish-Chandra series; see [Reference MalleMal07, Theorem 4.2].◻
$d$
-Harish-Chandra series; see [Reference MalleMal07, Theorem 4.2].◻
For a prime
![]() $\ell$
we consider the following property of a connected reductive group
$\ell$
we consider the following property of a connected reductive group
![]() $\mathbf{G}$
with Frobenius map
$\mathbf{G}$
with Frobenius map
![]() $F$
with respect to an
$F$
with respect to an
![]() $\mathbb{F}_{q}$
-rational structure; here,
$\mathbb{F}_{q}$
-rational structure; here,
![]() $d=d_{\ell }(q)$
.
$d=d_{\ell }(q)$
.
- (
 $\ddagger$
)
$\ddagger$
) For any
 $d$
-split Levi subgroup
$d$
-split Levi subgroup
 $\mathbf{L}\leqslant \mathbf{G}$
, an
$\mathbf{L}\leqslant \mathbf{G}$
, an
 $F$
-stable reductive subgroup
$F$
-stable reductive subgroup
 $\mathbf{H}\leqslant \mathbf{G}$
is the centraliser of an
$\mathbf{H}\leqslant \mathbf{G}$
is the centraliser of an
 $\ell$
-element in
$\ell$
-element in
 $C_{\mathbf{G}}^{\circ }([\mathbf{L},\mathbf{L}])^{F}$
if and only if its dual
$C_{\mathbf{G}}^{\circ }([\mathbf{L},\mathbf{L}])^{F}$
if and only if its dual
 $\mathbf{H}^{\ast }\leqslant \mathbf{G}^{\ast }$
is the centraliser of an
$\mathbf{H}^{\ast }\leqslant \mathbf{G}^{\ast }$
is the centraliser of an
 $\ell$
-element in
$\ell$
-element in
 $C_{\mathbf{G}^{\ast }}^{\circ }([\mathbf{L}^{\ast },\mathbf{L}^{\ast }])^{F}$
.
$C_{\mathbf{G}^{\ast }}^{\circ }([\mathbf{L}^{\ast },\mathbf{L}^{\ast }])^{F}$
.
Lemma 6.3. Let
![]() $\mathbf{G}$
be simple,
$\mathbf{G}$
be simple,
![]() $\ell$
a good prime for
$\ell$
a good prime for
![]() $\mathbf{G}$
not dividing
$\mathbf{G}$
not dividing
![]() $q$
. Then (
$q$
. Then (
![]() $\ddagger$
) holds for
$\ddagger$
) holds for
![]() $\mathbf{G}$
unless when
$\mathbf{G}$
unless when
![]() $\mathbf{G}$
is of type
$\mathbf{G}$
is of type
![]() $A_{n-1}$
and either
$A_{n-1}$
and either
![]() $F$
is untwisted and
$F$
is untwisted and
![]() $\ell |(n,q-1)$
, or
$\ell |(n,q-1)$
, or
![]() $F$
is twisted and
$F$
is twisted and
![]() $\ell |(n,q+1)$
.
$\ell |(n,q+1)$
.
Proof. There is an isogeny
![]() $\unicode[STIX]{x1D70B}:\mathbf{G}\rightarrow \mathbf{G}_{\operatorname{ad}}$
with
$\unicode[STIX]{x1D70B}:\mathbf{G}\rightarrow \mathbf{G}_{\operatorname{ad}}$
with
![]() $F$
-stable kernel, which on the level of finite groups restricts to a homomorphism
$F$
-stable kernel, which on the level of finite groups restricts to a homomorphism
![]() $\mathbf{G}^{F}\rightarrow \mathbf{G}_{\operatorname{ad}}^{F}$
. This induces a bijection between the sets of
$\mathbf{G}^{F}\rightarrow \mathbf{G}_{\operatorname{ad}}^{F}$
. This induces a bijection between the sets of
![]() $F$
-stable Levi subgroups of
$F$
-stable Levi subgroups of
![]() $\mathbf{G}$
and of
$\mathbf{G}$
and of
![]() $\mathbf{G}_{\operatorname{ad}}$
, preserving the property of being
$\mathbf{G}_{\operatorname{ad}}$
, preserving the property of being
![]() $d$
-split. By our assumptions on
$d$
-split. By our assumptions on
![]() $\ell$
, centralisers of
$\ell$
, centralisers of
![]() $\ell$
-elements in
$\ell$
-elements in
![]() $\mathbf{G}$
are Levi subgroups. Also, by our assumptions
$\mathbf{G}$
are Levi subgroups. Also, by our assumptions
![]() $Z(\mathbf{G})$
has order prime to
$Z(\mathbf{G})$
has order prime to
![]() $\ell$
, so the order of the kernel of
$\ell$
, so the order of the kernel of
![]() $\unicode[STIX]{x1D70B}$
and the index
$\unicode[STIX]{x1D70B}$
and the index
![]() $|\mathbf{G}_{\operatorname{ad}}^{F}:\unicode[STIX]{x1D70B}(\mathbf{G}^{F})|$
are prime to
$|\mathbf{G}_{\operatorname{ad}}^{F}:\unicode[STIX]{x1D70B}(\mathbf{G}^{F})|$
are prime to
![]() $\ell$
. Thus,
$\ell$
. Thus,
![]() $\unicode[STIX]{x1D70B}$
induces a bijection between centralisers of
$\unicode[STIX]{x1D70B}$
induces a bijection between centralisers of
![]() $\ell$
-elements in
$\ell$
-elements in
![]() $\mathbf{G}^{F}$
and
$\mathbf{G}^{F}$
and
![]() $\mathbf{G}_{\operatorname{ad}}^{F}$
as required for (
$\mathbf{G}_{\operatorname{ad}}^{F}$
as required for (
![]() $\ddagger$
).
$\ddagger$
).
If
![]() $\mathbf{G}$
is not of type
$\mathbf{G}$
is not of type
![]() $B_{n}$
or
$B_{n}$
or
![]() $C_{n}$
, then
$C_{n}$
, then
![]() $\mathbf{G}_{\operatorname{ad}}$
and
$\mathbf{G}_{\operatorname{ad}}$
and
![]() $(\mathbf{G}^{\ast })_{\operatorname{ad}}$
are isomorphic, and our claim follows. For
$(\mathbf{G}^{\ast })_{\operatorname{ad}}$
are isomorphic, and our claim follows. For
![]() $\mathbf{G}=\operatorname{Sp}_{2n}$
all
$\mathbf{G}=\operatorname{Sp}_{2n}$
all
![]() $d$
-split Levi subgroups have the form
$d$
-split Levi subgroups have the form
![]() $\mathbf{L}=\operatorname{Sp}_{2m}\prod _{i}\operatorname{GL}_{n_{i}}$
with
$\mathbf{L}=\operatorname{Sp}_{2m}\prod _{i}\operatorname{GL}_{n_{i}}$
with
![]() $e\sum n_{i}+m=n$
, where
$e\sum n_{i}+m=n$
, where
![]() $e=d/(d,2)$
(see [Reference Broué, Malle and MichelBMM93, p. 49]) and
$e=d/(d,2)$
(see [Reference Broué, Malle and MichelBMM93, p. 49]) and
![]() $C_{\mathbf{G}}^{\circ }([\mathbf{L},\mathbf{L}])=\operatorname{Sp}_{2(n-k)}$
for some
$C_{\mathbf{G}}^{\circ }([\mathbf{L},\mathbf{L}])=\operatorname{Sp}_{2(n-k)}$
for some
![]() $k\geqslant m$
. Thus the claim for
$k\geqslant m$
. Thus the claim for
![]() $\operatorname{Sp}_{2n}$
follows by induction, and hence also for its dual
$\operatorname{Sp}_{2n}$
follows by induction, and hence also for its dual
![]() $\operatorname{SO}_{2n+1}$
, and then by the preceding argument for all groups isogenous to these.◻
$\operatorname{SO}_{2n+1}$
, and then by the preceding argument for all groups isogenous to these.◻
Theorem 6.4. Let
![]() $\mathbf{G}$
be simple,
$\mathbf{G}$
be simple,
![]() $\ell >2$
a good prime for
$\ell >2$
a good prime for
![]() $\mathbf{G}$
different from the defining characteristic of
$\mathbf{G}$
different from the defining characteristic of
![]() $\mathbf{G}$
,
$\mathbf{G}$
,
![]() $\ell \neq 3$
if
$\ell \neq 3$
if
![]() $\mathbf{G}^{F}=^{3}\!D_{4}(q)$
,
$\mathbf{G}^{F}=^{3}\!D_{4}(q)$
,
![]() $\ell \not |(n,q-1)$
if
$\ell \not |(n,q-1)$
if
![]() $\mathbf{G}$
is of type
$\mathbf{G}$
is of type
![]() $A_{n-1}$
and
$A_{n-1}$
and
![]() $F$
is untwisted, and
$F$
is untwisted, and
![]() $\ell \not |(n,q+1)$
if
$\ell \not |(n,q+1)$
if
![]() $\mathbf{G}$
is of type
$\mathbf{G}$
is of type
![]() $A_{n-1}$
and
$A_{n-1}$
and
![]() $F$
is twisted. Then the unipotent
$F$
is twisted. Then the unipotent
![]() $\ell$
-blocks of
$\ell$
-blocks of
![]() $\mathbf{G}^{F}$
satisfy (RC).
$\mathbf{G}^{F}$
satisfy (RC).
Proof. Under our assumptions on
![]() $\ell$
, by [Reference Cabanes and EnguehardCE94, Theorem] the unipotent
$\ell$
, by [Reference Cabanes and EnguehardCE94, Theorem] the unipotent
![]() $\ell$
-blocks of
$\ell$
-blocks of
![]() $\mathbf{G}$
are in bijection with the
$\mathbf{G}$
are in bijection with the
![]() $\mathbf{G}^{F}$
-conjugacy classes of
$\mathbf{G}^{F}$
-conjugacy classes of
![]() $d$
-cuspidal unipotent pairs
$d$
-cuspidal unipotent pairs
![]() $(\mathbf{L},\unicode[STIX]{x1D706})$
of
$(\mathbf{L},\unicode[STIX]{x1D706})$
of
![]() $\mathbf{G}$
, where
$\mathbf{G}$
, where
![]() $d=d_{\ell }(q)$
. We write
$d=d_{\ell }(q)$
. We write
![]() $b(\mathbf{L},\unicode[STIX]{x1D706})$
for the corresponding unipotent
$b(\mathbf{L},\unicode[STIX]{x1D706})$
for the corresponding unipotent
![]() $\ell$
-block of
$\ell$
-block of
![]() $\mathbf{G}^{F}$
.
$\mathbf{G}^{F}$
.
Let
![]() $B=b(\mathbf{L},\unicode[STIX]{x1D706})$
be an
$B=b(\mathbf{L},\unicode[STIX]{x1D706})$
be an
![]() $\ell$
-block, and assume that
$\ell$
-block, and assume that
![]() $\unicode[STIX]{x1D712}\in \operatorname{Irr}(B)$
. Then by [Reference Cabanes and EnguehardCE94, Theorem (iii)] there is an
$\unicode[STIX]{x1D712}\in \operatorname{Irr}(B)$
. Then by [Reference Cabanes and EnguehardCE94, Theorem (iii)] there is an
![]() $\ell$
-element
$\ell$
-element
![]() $t\in \mathbf{G}^{\ast F}$
such that
$t\in \mathbf{G}^{\ast F}$
such that
![]() $\unicode[STIX]{x1D712}\in {\mathcal{E}}(\mathbf{G}^{F},t)$
, and
$\unicode[STIX]{x1D712}\in {\mathcal{E}}(\mathbf{G}^{F},t)$
, and
![]() $\unicode[STIX]{x1D712}$
is a constituent of
$\unicode[STIX]{x1D712}$
is a constituent of
![]() $R_{\mathbf{H}}^{\mathbf{G}}(\hat{t}\unicode[STIX]{x1D712}_{t})$
where
$R_{\mathbf{H}}^{\mathbf{G}}(\hat{t}\unicode[STIX]{x1D712}_{t})$
where
![]() $\mathbf{H}\leqslant \mathbf{G}$
is dual to
$\mathbf{H}\leqslant \mathbf{G}$
is dual to
![]() $\mathbf{H}^{\ast }:=C_{\mathbf{G}^{\ast }}(t)$
and
$\mathbf{H}^{\ast }:=C_{\mathbf{G}^{\ast }}(t)$
and
![]() $\unicode[STIX]{x1D712}_{t}\in {\mathcal{E}}(\mathbf{H}^{F},1)$
. Moreover,
$\unicode[STIX]{x1D712}_{t}\in {\mathcal{E}}(\mathbf{H}^{F},1)$
. Moreover,
![]() $\unicode[STIX]{x1D712}_{t}$
lies in the
$\unicode[STIX]{x1D712}_{t}$
lies in the
![]() $d$
-Harish-Chandra series of a
$d$
-Harish-Chandra series of a
![]() $d$
-cuspidal pair
$d$
-cuspidal pair
![]() $(\mathbf{L}_{t},\unicode[STIX]{x1D706}_{t})$
of
$(\mathbf{L}_{t},\unicode[STIX]{x1D706}_{t})$
of
![]() $\mathbf{H}$
such that
$\mathbf{H}$
such that
![]() $[\mathbf{L},\mathbf{L}]=[\mathbf{L}_{t},\mathbf{L}_{t}]$
.
$[\mathbf{L},\mathbf{L}]=[\mathbf{L}_{t},\mathbf{L}_{t}]$
.
By Lemma 6.3,
![]() $\mathbf{G}$
satisfies (
$\mathbf{G}$
satisfies (
![]() $\ddagger$
), so there is an
$\ddagger$
), so there is an
![]() $\ell$
-element
$\ell$
-element
![]() $t^{\prime }\in C_{\mathbf{G}}^{\circ }([\mathbf{L},\mathbf{L}])^{F}=C_{\mathbf{G}}^{\circ }([\mathbf{L}_{t},\mathbf{L}_{t}])^{F}$
with centraliser
$t^{\prime }\in C_{\mathbf{G}}^{\circ }([\mathbf{L},\mathbf{L}])^{F}=C_{\mathbf{G}}^{\circ }([\mathbf{L}_{t},\mathbf{L}_{t}])^{F}$
with centraliser
![]() $\mathbf{H}$
. According to [Reference Cabanes and EnguehardCE94, Theorem (ii)], any Sylow
$\mathbf{H}$
. According to [Reference Cabanes and EnguehardCE94, Theorem (ii)], any Sylow
![]() $\ell$
-subgroup
$\ell$
-subgroup
![]() $D$
of
$D$
of
![]() $C_{\mathbf{G}}^{\circ }([\mathbf{L},\mathbf{L}])^{F}$
is a defect group of
$C_{\mathbf{G}}^{\circ }([\mathbf{L},\mathbf{L}])^{F}$
is a defect group of
![]() $b(\mathbf{L},\unicode[STIX]{x1D706})$
. Since
$b(\mathbf{L},\unicode[STIX]{x1D706})$
. Since
![]() $Z^{\circ }(\mathbf{L}_{t})\leqslant C_{\mathbf{H}}^{\circ }([\mathbf{L}_{t},\mathbf{L}_{t}])\leqslant C_{\mathbf{G}}^{\circ }([\mathbf{L}_{t},\mathbf{L}_{t}])$
we may assume
$Z^{\circ }(\mathbf{L}_{t})\leqslant C_{\mathbf{H}}^{\circ }([\mathbf{L}_{t},\mathbf{L}_{t}])\leqslant C_{\mathbf{G}}^{\circ }([\mathbf{L}_{t},\mathbf{L}_{t}])$
we may assume
![]() $Z^{\circ }(\mathbf{L}_{t})_{\ell }^{F}\leqslant D$
. Then
$Z^{\circ }(\mathbf{L}_{t})_{\ell }^{F}\leqslant D$
. Then
using that
![]() $C_{\mathbf{H}}(Z^{\circ }(\mathbf{L}_{t})_{\ell }^{F})=\mathbf{L}_{t}$
since
$C_{\mathbf{H}}(Z^{\circ }(\mathbf{L}_{t})_{\ell }^{F})=\mathbf{L}_{t}$
since
![]() $\mathbf{L}_{t}$
is
$\mathbf{L}_{t}$
is
![]() $d$
-split in
$d$
-split in
![]() $\mathbf{H}$
(see [Reference Cabanes and EnguehardCE94, Proposition 3.3(ii)]). As
$\mathbf{H}$
(see [Reference Cabanes and EnguehardCE94, Proposition 3.3(ii)]). As
![]() $D$
is an
$D$
is an
![]() $\ell$
-group, this shows that
$\ell$
-group, this shows that
![]() $Z(D)\leqslant Z^{\circ }(\mathbf{L}_{t})_{\ell }^{F}$
. With Proposition 6.2 this yields
$Z(D)\leqslant Z^{\circ }(\mathbf{L}_{t})_{\ell }^{F}$
. With Proposition 6.2 this yields
Moreover, this inequality is strict unless
![]() $Z(D)=Z^{\circ }(\mathbf{L}_{t})_{\ell }^{F}$
. But in the latter case all elements of
$Z(D)=Z^{\circ }(\mathbf{L}_{t})_{\ell }^{F}$
. But in the latter case all elements of
![]() $D$
centralise
$D$
centralise
![]() $Z^{\circ }(\mathbf{L}_{t})_{\ell }^{F}$
, so lie in
$Z^{\circ }(\mathbf{L}_{t})_{\ell }^{F}$
, so lie in
![]() $C_{\mathbf{H}}(Z^{\circ }(\mathbf{L}_{t})_{\ell }^{F})=\mathbf{L}_{t}$
, whence
$C_{\mathbf{H}}(Z^{\circ }(\mathbf{L}_{t})_{\ell }^{F})=\mathbf{L}_{t}$
, whence
is abelian. ◻
6.2 Linear and unitary groups for odd primes
We now turn to groups of type
![]() $A_{n-1}$
. We may and will assume that
$A_{n-1}$
. We may and will assume that
![]() $\ell |n$
, as otherwise we are in the situation of Theorem 6.4. As customary, we let
$\ell |n$
, as otherwise we are in the situation of Theorem 6.4. As customary, we let
![]() $\operatorname{GL}_{n}(-q)$
denote
$\operatorname{GL}_{n}(-q)$
denote
![]() $\operatorname{GU}_{n}(q)$
, and similarly for
$\operatorname{GU}_{n}(q)$
, and similarly for
![]() $\operatorname{SL}_{n}(-q)$
.
$\operatorname{SL}_{n}(-q)$
.
We will need the following inequalities between coefficients of
![]() $\ell$
-adic expansions.
$\ell$
-adic expansions.
Lemma 6.5. Let
![]() $\ell >2$
be a prime and
$\ell >2$
be a prime and
![]() $a\geqslant 1$
an integer. Let
$a\geqslant 1$
an integer. Let
![]() $n$
be a positive integer with
$n$
be a positive integer with
![]() $\ell$
-adic expansion
$\ell$
-adic expansion
![]() $n=\sum _{i}a_{i}\ell ^{i}$
, where
$n=\sum _{i}a_{i}\ell ^{i}$
, where
![]() $a_{0}=0$
. Suppose
$a_{0}=0$
. Suppose
![]() $n=\sum _{j}n_{j}\ell ^{b_{j}}$
with
$n=\sum _{j}n_{j}\ell ^{b_{j}}$
with
![]() $n_{j}>0$
,
$n_{j}>0$
,
![]() $b_{j}\geqslant 0$
. Set
$b_{j}\geqslant 0$
. Set
![]() $s_{i}:=\sum _{j\mid b_{j}=i}n_{j}$
. Then
$s_{i}:=\sum _{j\mid b_{j}=i}n_{j}$
. Then
where
![]() $k=\min \{a,b_{j}\}$
, unless
$k=\min \{a,b_{j}\}$
, unless
![]() $a_{i}=s_{i}$
for all
$a_{i}=s_{i}$
for all
![]() $i$
and either
$i$
and either
![]() $n=\ell ^{k}$
, or
$n=\ell ^{k}$
, or
![]() $n=2\ell$
and
$n=2\ell$
and
![]() $k=1$
.
$k=1$
.
Proof. Note that
![]() $n=\sum _{j}n_{j}\ell ^{b_{j}}=\sum _{i}s_{i}\ell ^{i}$
. Clearly we can get from the
$n=\sum _{j}n_{j}\ell ^{b_{j}}=\sum _{i}s_{i}\ell ^{i}$
. Clearly we can get from the
![]() $\ell$
-adic expansion of
$\ell$
-adic expansion of
![]() $n$
to the representation
$n$
to the representation
![]() $n=\sum _{i}s_{i}\ell ^{i}$
by repeatedly replacing a summand
$n=\sum _{i}s_{i}\ell ^{i}$
by repeatedly replacing a summand
![]() $\ell ^{i}$
by
$\ell ^{i}$
by
![]() $\ell$
summands
$\ell$
summands
![]() $\ell ^{i-1}$
, and each such step does increase the coefficient sum by
$\ell ^{i-1}$
, and each such step does increase the coefficient sum by
![]() $\ell -1$
. Thus if
$\ell -1$
. Thus if
![]() $(a_{i})_{i}\neq (s_{i})_{i}$
then
$(a_{i})_{i}\neq (s_{i})_{i}$
then
![]() $\sum _{i}(s_{i}-a_{i})\geqslant \ell -1\geqslant 2$
and hence
$\sum _{i}(s_{i}-a_{i})\geqslant \ell -1\geqslant 2$
and hence
as claimed (since
![]() $k=0$
if all
$k=0$
if all
![]() $b_{j}=0$
).
$b_{j}=0$
).
So now assume that
![]() $a_{i}=s_{i}$
for all
$a_{i}=s_{i}$
for all
![]() $i$
, that is, the
$i$
, that is, the
![]() $n_{j}$
with
$n_{j}$
with
![]() $b_{j}=i$
sum to
$b_{j}=i$
sum to
![]() $a_{i}$
. As
$a_{i}$
. As
![]() $a_{0}=0$
this means that
$a_{0}=0$
this means that
![]() $b_{j}>0$
for all
$b_{j}>0$
for all
![]() $j$
. Then
$j$
. Then
unless there is exactly one non-zero
![]() $b_{j}=k$
, and
$b_{j}=k$
, and
![]() $n_{j}\leqslant 2$
, with
$n_{j}\leqslant 2$
, with
![]() $b_{j}=1$
when
$b_{j}=1$
when
![]() $n_{j}=2$
.◻
$n_{j}=2$
.◻
Lemma 6.6. Let
![]() $\ell >2$
,
$\ell >2$
,
![]() $\unicode[STIX]{x1D716}\in \{\pm 1\}$
,
$\unicode[STIX]{x1D716}\in \{\pm 1\}$
,
![]() $\tilde{G}=\operatorname{GL}_{n}(\unicode[STIX]{x1D716}q)$
and
$\tilde{G}=\operatorname{GL}_{n}(\unicode[STIX]{x1D716}q)$
and
![]() $G=\operatorname{SL}_{n}(\unicode[STIX]{x1D716}q)$
, with
$G=\operatorname{SL}_{n}(\unicode[STIX]{x1D716}q)$
, with
![]() $(q-\unicode[STIX]{x1D716})_{\ell }=\ell ^{a}$
. Let
$(q-\unicode[STIX]{x1D716})_{\ell }=\ell ^{a}$
. Let
![]() $\tilde{D}$
,
$\tilde{D}$
,
![]() $D=\tilde{D}\cap G$
be Sylow
$D=\tilde{D}\cap G$
be Sylow
![]() $\ell$
-subgroups of
$\ell$
-subgroups of
![]() $\tilde{G}$
,
$\tilde{G}$
,
![]() $G$
respectively.
$G$
respectively.
(a) Then
 $|Z(\tilde{D})|=\ell ^{a\sum a_{i}}$
and
$|Z(\tilde{D})|=\ell ^{a\sum a_{i}}$
and
 $|Z(D)|=|Z(\tilde{D})|/\ell ^{a-k}$
where
$|Z(D)|=|Z(\tilde{D})|/\ell ^{a-k}$
where
 $n=\sum a_{i}\ell ^{i}$
is the
$n=\sum a_{i}\ell ^{i}$
is the
 $\ell$
-adic expansion of
$\ell$
-adic expansion of
 $n$
and
$n$
and
 $k=\min \{a,i\mid a_{i}\neq 0\}$
.
$k=\min \{a,i\mid a_{i}\neq 0\}$
.(b) Let
 $1\neq Z\leqslant \mathbf{O}_{\ell }(Z(G))$
and assume that
$1\neq Z\leqslant \mathbf{O}_{\ell }(Z(G))$
and assume that
 $(n,\ell ^{a})\neq (3,3)$
. Then
$(n,\ell ^{a})\neq (3,3)$
. Then
 $|Z(D/Z)|\leqslant \ell |Z(D)/Z|$
with strict inequality if
$|Z(D/Z)|\leqslant \ell |Z(D)/Z|$
with strict inequality if
 $n\neq \ell ^{k}$
.
$n\neq \ell ^{k}$
.
Proof. We assume
![]() $\unicode[STIX]{x1D716}=1$
, the case
$\unicode[STIX]{x1D716}=1$
, the case
![]() $\unicode[STIX]{x1D716}=-1$
being entirely similar. A Sylow
$\unicode[STIX]{x1D716}=-1$
being entirely similar. A Sylow
![]() $\ell$
-subgroup
$\ell$
-subgroup
![]() $P$
of
$P$
of
![]() $\operatorname{GL}_{\ell ^{i}}(q)$
is an iterated wreath product
$\operatorname{GL}_{\ell ^{i}}(q)$
is an iterated wreath product
![]() $C_{\ell ^{a}}\wr C_{\ell }\wr \cdots \wr C_{\ell }$
(with
$C_{\ell ^{a}}\wr C_{\ell }\wr \cdots \wr C_{\ell }$
(with
![]() $i$
factors
$i$
factors
![]() $C_{\ell }$
). Let
$C_{\ell }$
). Let
![]() $B=C_{\ell ^{a}}^{\ell ^{i}}$
denote its base group. There is a complement
$B=C_{\ell ^{a}}^{\ell ^{i}}$
denote its base group. There is a complement
![]() $R$
to
$R$
to
![]() $B$
in
$B$
in
![]() $P$
consisting of permutation matrices, hence lying in
$P$
consisting of permutation matrices, hence lying in
![]() $\operatorname{SL}_{\ell ^{i}}(q)$
as
$\operatorname{SL}_{\ell ^{i}}(q)$
as
![]() $\ell$
is odd. Then
$\ell$
is odd. Then
![]() $Z(P)$
is contained inside
$Z(P)$
is contained inside
![]() $B$
, as
$B$
, as
![]() $R$
acts faithfully by permutations on the set of cyclic factors of
$R$
acts faithfully by permutations on the set of cyclic factors of
![]() $B$
. It is clear that
$B$
. It is clear that
![]() $Z(P)$
is just the central diagonal subgroup
$Z(P)$
is just the central diagonal subgroup
![]() $Z_{0}\cong C_{\ell ^{a}}$
of
$Z_{0}\cong C_{\ell ^{a}}$
of
![]() $B$
. Then
$B$
. Then
![]() $R$
still acts faithfully on the quotient
$R$
still acts faithfully on the quotient
![]() $B/Z_{0}$
. Direct computation shows that the elements of
$B/Z_{0}$
. Direct computation shows that the elements of
![]() $B$
whose image is central in
$B$
whose image is central in
![]() $P/Z_{0}$
are of the form
$P/Z_{0}$
are of the form
![]() $(a,a,\ldots ,az,az,\ldots ,az^{2},az^{2},\ldots )$
with blocks of length
$(a,a,\ldots ,az,az,\ldots ,az^{2},az^{2},\ldots )$
with blocks of length
![]() $\ell ^{i-1}$
and
$\ell ^{i-1}$
and
![]() $z$
of order dividing
$z$
of order dividing
![]() $\ell$
. Thus
$\ell$
. Thus
![]() $|Z(P/Z_{0})|=\ell$
.
$|Z(P/Z_{0})|=\ell$
.
Now for
![]() $n$
arbitrary,
$n$
arbitrary,
![]() $\tilde{D}$
is contained in a block diagonal subgroup
$\tilde{D}$
is contained in a block diagonal subgroup
![]() $\prod _{i}\operatorname{GL}_{\ell ^{i}}(q)^{a_{i}}$
of
$\prod _{i}\operatorname{GL}_{\ell ^{i}}(q)^{a_{i}}$
of
![]() $\tilde{G}$
. From the above description we see that
$\tilde{G}$
. From the above description we see that
![]() $Z(\tilde{D})$
is the product of the central
$Z(\tilde{D})$
is the product of the central
![]() $\ell$
-subgroups of the factors and that
$\ell$
-subgroups of the factors and that
![]() $Z(D)=Z(\tilde{D})\cap G$
. Then the determinant condition gives (a).
$Z(D)=Z(\tilde{D})\cap G$
. Then the determinant condition gives (a).
Part (b) also follows from the above observations when
![]() $n=\ell ^{i}$
. When the
$n=\ell ^{i}$
. When the
![]() $\ell$
-adic expansion of
$\ell$
-adic expansion of
![]() $n$
has at least two summands, again a direct computation shows that
$n$
has at least two summands, again a direct computation shows that
![]() $Z(P/Z)=Z(P)/Z=Z_{0}/Z$
for any
$Z(P/Z)=Z(P)/Z=Z_{0}/Z$
for any
![]() $Z\leqslant Z_{0}$
, as claimed.◻
$Z\leqslant Z_{0}$
, as claimed.◻
Lemma 6.7. Assume that
![]() $2<\ell |(n,q-\unicode[STIX]{x1D716})$
. Let
$2<\ell |(n,q-\unicode[STIX]{x1D716})$
. Let
![]() $\unicode[STIX]{x1D712}$
be a unipotent character of
$\unicode[STIX]{x1D712}$
be a unipotent character of
![]() $\operatorname{GL}_{m}(\unicode[STIX]{x1D716}q)$
. Then
$\operatorname{GL}_{m}(\unicode[STIX]{x1D716}q)$
. Then
![]() $\operatorname{def}(\unicode[STIX]{x1D712})\geqslant ma$
where
$\operatorname{def}(\unicode[STIX]{x1D712})\geqslant ma$
where
![]() $\ell ^{a}=(q-\unicode[STIX]{x1D716})_{\ell }$
.
$\ell ^{a}=(q-\unicode[STIX]{x1D716})_{\ell }$
.
Proof. The degree polynomial of
![]() $\unicode[STIX]{x1D712}$
is not divisible by
$\unicode[STIX]{x1D712}$
is not divisible by
![]() $x-\unicode[STIX]{x1D716}$
, while
$x-\unicode[STIX]{x1D716}$
, while
![]() $x-\unicode[STIX]{x1D716}$
divides the order polynomial of
$x-\unicode[STIX]{x1D716}$
divides the order polynomial of
![]() $\operatorname{GL}_{m}(\unicode[STIX]{x1D716}q)$
exactly
$\operatorname{GL}_{m}(\unicode[STIX]{x1D716}q)$
exactly
![]() $m$
times. Thus
$m$
times. Thus
![]() $\ell ^{\operatorname{def}(\unicode[STIX]{x1D712})}\geqslant (q-\unicode[STIX]{x1D716})_{\ell }^{m}=\ell ^{ma}$
.◻
$\ell ^{\operatorname{def}(\unicode[STIX]{x1D712})}\geqslant (q-\unicode[STIX]{x1D716})_{\ell }^{m}=\ell ^{ma}$
.◻
Theorem 6.8. Let
![]() $G=\operatorname{SL}_{n}(\unicode[STIX]{x1D716}q)$
, let
$G=\operatorname{SL}_{n}(\unicode[STIX]{x1D716}q)$
, let
![]() $\ell >2$
and assume that
$\ell >2$
and assume that
![]() $\ell |(n,q-\unicode[STIX]{x1D716})$
. Then for any
$\ell |(n,q-\unicode[STIX]{x1D716})$
. Then for any
![]() $Z\leqslant Z(G)$
the unipotent
$Z\leqslant Z(G)$
the unipotent
![]() $\ell$
-blocks of
$\ell$
-blocks of
![]() $G/Z$
do not provide counterexamples to (RC).
$G/Z$
do not provide counterexamples to (RC).
Proof. First assume that
![]() $\unicode[STIX]{x1D716}=1$
, so
$\unicode[STIX]{x1D716}=1$
, so
![]() $G=\operatorname{SL}_{n}(q)$
. As
$G=\operatorname{SL}_{n}(q)$
. As
![]() $\ell |(q-1)$
, the principal block
$\ell |(q-1)$
, the principal block
![]() $B$
is the unique unipotent
$B$
is the unique unipotent
![]() $\ell$
-block of
$\ell$
-block of
![]() $G$
[Reference Cabanes and EnguehardCE04, Theorem 22.9]. Let
$G$
[Reference Cabanes and EnguehardCE04, Theorem 22.9]. Let
![]() $\tilde{B}$
denote the principal
$\tilde{B}$
denote the principal
![]() $\ell$
-block of
$\ell$
-block of
![]() $\operatorname{GL}_{n}(q)$
. Then the characters in
$\operatorname{GL}_{n}(q)$
. Then the characters in
![]() $\operatorname{Irr}(B)$
are constituents of the restriction to
$\operatorname{Irr}(B)$
are constituents of the restriction to
![]() $G$
of the characters in
$G$
of the characters in
![]() $\operatorname{Irr}(\tilde{B})$
. Let
$\operatorname{Irr}(\tilde{B})$
. Let
![]() $\tilde{\unicode[STIX]{x1D712}}\in \operatorname{Irr}(\tilde{B})$
. Then there is an
$\tilde{\unicode[STIX]{x1D712}}\in \operatorname{Irr}(\tilde{B})$
. Then there is an
![]() $\ell$
-element
$\ell$
-element
![]() $t\in \operatorname{GL}_{n}(q)$
with
$t\in \operatorname{GL}_{n}(q)$
with
![]() $\tilde{\unicode[STIX]{x1D712}}\in {\mathcal{E}}(\tilde{G},t)$
. The centraliser
$\tilde{\unicode[STIX]{x1D712}}\in {\mathcal{E}}(\tilde{G},t)$
. The centraliser
![]() $\mathbf{H}:=C_{\operatorname{GL}_{n}}(t)$
of
$\mathbf{H}:=C_{\operatorname{GL}_{n}}(t)$
of
![]() $t$
has the rational form
$t$
has the rational form
![]() $\mathbf{H}^{F}=\prod _{j}\operatorname{GL}_{n_{j}}(q^{\ell ^{b_{j}}})$
for suitable integers
$\mathbf{H}^{F}=\prod _{j}\operatorname{GL}_{n_{j}}(q^{\ell ^{b_{j}}})$
for suitable integers
![]() $n_{j},b_{j}$
with
$n_{j},b_{j}$
with
![]() $\sum _{j}n_{j}\ell ^{b_{j}}=n$
. The unipotent characters of
$\sum _{j}n_{j}\ell ^{b_{j}}=n$
. The unipotent characters of
![]() $\mathbf{H}^{F}$
are just the outer tensor products of the unipotent characters of the various factors. Using that
$\mathbf{H}^{F}$
are just the outer tensor products of the unipotent characters of the various factors. Using that
![]() $\ell ^{a+b_{j}}$
is the precise power of
$\ell ^{a+b_{j}}$
is the precise power of
![]() $\ell$
dividing
$\ell$
dividing
![]() $q^{\ell ^{b_{j}}}-1$
, we thus get, with Lemma 6.7,
$q^{\ell ^{b_{j}}}-1$
, we thus get, with Lemma 6.7,
where
![]() $s_{i}$
is the sum over all
$s_{i}$
is the sum over all
![]() $n_{j}$
with
$n_{j}$
with
![]() $b_{j}=i$
. By Lemma 6.6 the center of a Sylow
$b_{j}=i$
. By Lemma 6.6 the center of a Sylow
![]() $\ell$
-subgroup
$\ell$
-subgroup
![]() $\tilde{D}$
of
$\tilde{D}$
of
![]() $\operatorname{GL}_{n}(q)$
has order
$\operatorname{GL}_{n}(q)$
has order
![]() $\ell ^{a\sum a_{i}}$
, where
$\ell ^{a\sum a_{i}}$
, where
![]() $n=\sum _{i}a_{i}\ell ^{i}$
is the
$n=\sum _{i}a_{i}\ell ^{i}$
is the
![]() $\ell$
-adic expansion of
$\ell$
-adic expansion of
![]() $n$
. Thus we are in the situation of Lemma 6.5. First assume that we are not in one of the exceptions mentioned there. Then
$n$
. Thus we are in the situation of Lemma 6.5. First assume that we are not in one of the exceptions mentioned there. Then
![]() $\ell ^{\operatorname{def}(\tilde{\unicode[STIX]{x1D712}})}>\ell ^{k+1}|Z(\tilde{D})|$
with
$\ell ^{\operatorname{def}(\tilde{\unicode[STIX]{x1D712}})}>\ell ^{k+1}|Z(\tilde{D})|$
with
![]() $k=\min \{a,b_{j}\}$
. Let
$k=\min \{a,b_{j}\}$
. Let
![]() $\unicode[STIX]{x1D712}$
be a constituent of
$\unicode[STIX]{x1D712}$
be a constituent of
![]() $\tilde{\unicode[STIX]{x1D712}}|_{G}$
and
$\tilde{\unicode[STIX]{x1D712}}|_{G}$
and
![]() $D=\tilde{D}\cap G$
a Sylow
$D=\tilde{D}\cap G$
a Sylow
![]() $\ell$
-subgroup of
$\ell$
-subgroup of
![]() $G$
. Then
$G$
. Then
![]() $\ell ^{\operatorname{def}(\unicode[STIX]{x1D712})}>\ell |Z(D)|$
by Lemma 6.6(a). Now let
$\ell ^{\operatorname{def}(\unicode[STIX]{x1D712})}>\ell |Z(D)|$
by Lemma 6.6(a). Now let
![]() $Z\leqslant Z(G)$
be a central
$Z\leqslant Z(G)$
be a central
![]() $\ell$
-subgroup in the kernel of
$\ell$
-subgroup in the kernel of
![]() $\unicode[STIX]{x1D712}$
. Then for a Sylow
$\unicode[STIX]{x1D712}$
. Then for a Sylow
![]() $\ell$
-subgroup
$\ell$
-subgroup
![]() $\bar{D}=D/Z$
of
$\bar{D}=D/Z$
of
![]() $G/Z$
we have
$G/Z$
we have
![]() $|Z(\bar{D})|\leqslant \ell |Z(D)|/|Z|$
when
$|Z(\bar{D})|\leqslant \ell |Z(D)|/|Z|$
when
![]() $n\neq \ell ^{k}$
by Lemma 6.6(b), whence
$n\neq \ell ^{k}$
by Lemma 6.6(b), whence
![]() $\ell ^{\operatorname{def}(\unicode[STIX]{x1D712})}>|Z(\bar{D})|$
for
$\ell ^{\operatorname{def}(\unicode[STIX]{x1D712})}>|Z(\bar{D})|$
for
![]() $G/Z$
as claimed.
$G/Z$
as claimed.
Now assume that
![]() $n=2\ell$
and
$n=2\ell$
and
![]() $k=1$
. Then we still get
$k=1$
. Then we still get
![]() $\ell ^{\operatorname{def}(\tilde{\unicode[STIX]{x1D712}})}>\ell ^{k}|Z(\tilde{D})|$
. Since in this case
$\ell ^{\operatorname{def}(\tilde{\unicode[STIX]{x1D712}})}>\ell ^{k}|Z(\tilde{D})|$
. Since in this case
![]() $|Z(\bar{D})|=|Z(D)|/|Z|$
we may conclude as before. Finally, assume that
$|Z(\bar{D})|=|Z(D)|/|Z|$
we may conclude as before. Finally, assume that
![]() $n=\ell ^{k}$
, with
$n=\ell ^{k}$
, with
![]() $k\leqslant a$
. Here
$k\leqslant a$
. Here
![]() $\mathbf{H}^{F}=\operatorname{GL}_{1}(q^{n})$
, and
$\mathbf{H}^{F}=\operatorname{GL}_{1}(q^{n})$
, and
![]() $\tilde{\unicode[STIX]{x1D712}}$
decomposes into
$\tilde{\unicode[STIX]{x1D712}}$
decomposes into
![]() $n=\ell ^{k}$
characters upon restriction to
$n=\ell ^{k}$
characters upon restriction to
![]() $G$
, so
$G$
, so
![]() $\operatorname{def}(\unicode[STIX]{x1D712})=2k$
. Furthermore,
$\operatorname{def}(\unicode[STIX]{x1D712})=2k$
. Furthermore,
![]() $|Z(\bar{D})|=|Z(D)|/\ell ^{k-1}$
. If
$|Z(\bar{D})|=|Z(D)|/\ell ^{k-1}$
. If
![]() $k>1$
this implies that
$k>1$
this implies that
![]() $\ell ^{\operatorname{def}(\bar{\unicode[STIX]{x1D712}})}\geqslant \ell ^{k}>|Z(\bar{D})|$
, for
$\ell ^{\operatorname{def}(\bar{\unicode[STIX]{x1D712}})}\geqslant \ell ^{k}>|Z(\bar{D})|$
, for
![]() $\bar{\unicode[STIX]{x1D712}}\in \operatorname{Irr}(G/Z)$
a character with inflation
$\bar{\unicode[STIX]{x1D712}}\in \operatorname{Irr}(G/Z)$
a character with inflation
![]() $\unicode[STIX]{x1D712}$
. When
$\unicode[STIX]{x1D712}$
. When
![]() $k=1$
,
$k=1$
,
![]() $\unicode[STIX]{x1D712}$
is faithful and so does not descend to any proper quotient of
$\unicode[STIX]{x1D712}$
is faithful and so does not descend to any proper quotient of
![]() $G$
. In the excluded case that
$G$
. In the excluded case that
![]() $n=\ell ^{a}=3$
and
$n=\ell ^{a}=3$
and
![]() $Z\neq 1$
the Sylow 3-subgroups of
$Z\neq 1$
the Sylow 3-subgroups of
![]() $G/Z$
are abelian.
$G/Z$
are abelian.
The proof for
![]() $\operatorname{SU}_{n}(q)$
is completely analogous, with
$\operatorname{SU}_{n}(q)$
is completely analogous, with
![]() $q-1$
replaced by
$q-1$
replaced by
![]() $q+1$
throughout.◻
$q+1$
throughout.◻
7 Exceptional groups
In this section we consider blocks of exceptional groups for non-defining primes. We first get the Suzuki and Ree groups out of the way.
Proposition 7.1. Let
![]() $G$
be quasi-simple such that
$G$
be quasi-simple such that
![]() $S:=G/Z(G)$
is one of the following groups:
$S:=G/Z(G)$
is one of the following groups:
![]() $^{2}\!B_{2}(q^{2})$
with
$^{2}\!B_{2}(q^{2})$
with
![]() $q^{2}=2^{2m+1}>2$
,
$q^{2}=2^{2m+1}>2$
,
![]() $^{2}G_{2}(q^{2})$
with
$^{2}G_{2}(q^{2})$
with
![]() $q^{2}=3^{2m+1}>3$
, or
$q^{2}=3^{2m+1}>3$
, or
![]() $^{2}\!F_{4}(q^{2})$
with
$^{2}\!F_{4}(q^{2})$
with
![]() $q^{2}=2^{2m+1}>2$
. Then Robinson’s conjecture holds for all
$q^{2}=2^{2m+1}>2$
. Then Robinson’s conjecture holds for all
![]() $p$
-blocks of
$p$
-blocks of
![]() $G$
.
$G$
.
Proof. If
![]() $p$
is the defining characteristic of
$p$
is the defining characteristic of
![]() $G$
, we conclude by Theorem 5.1.
$G$
, we conclude by Theorem 5.1.
If
![]() $S=^{2}\!B_{2}(q^{2})$
with
$S=^{2}\!B_{2}(q^{2})$
with
![]() $q^{2}=2^{2m+1}>2$
, then by Theorem 3.6 we may assume that
$q^{2}=2^{2m+1}>2$
, then by Theorem 3.6 we may assume that
![]() $Z(G)=1$
. Here, all Sylow subgroups for odd primes are cyclic. Similarly, if
$Z(G)=1$
. Here, all Sylow subgroups for odd primes are cyclic. Similarly, if
![]() $G=^{2}G_{2}(q^{2})$
with
$G=^{2}G_{2}(q^{2})$
with
![]() $q^{2}=3^{2m+1}>3$
, then
$q^{2}=3^{2m+1}>3$
, then
![]() $Z(G)=1$
and again all Sylow
$Z(G)=1$
and again all Sylow
![]() $p$
-subgroups for primes
$p$
-subgroups for primes
![]() $p\neq 3$
are abelian.
$p\neq 3$
are abelian.
Finally, suppose
![]() $G=^{2}\!F_{4}(q^{2})$
with
$G=^{2}\!F_{4}(q^{2})$
with
![]() $q^{2}=2^{2m+1}>2$
. For
$q^{2}=2^{2m+1}>2$
. For
![]() $p=3$
, the
$p=3$
, the
![]() $3$
-blocks of
$3$
-blocks of
![]() $G$
have been determined in [Reference MalleMal90]. In particular, we only need to consider the principal
$G$
have been determined in [Reference MalleMal90]. In particular, we only need to consider the principal
![]() $3$
-block
$3$
-block
![]() $B_{0}$
. By [Reference MalleMal91, Proposition 1.2(1)], we have
$B_{0}$
. By [Reference MalleMal91, Proposition 1.2(1)], we have
![]() $|Z(P)|=3$
for
$|Z(P)|=3$
for
![]() $P\in \operatorname{Syl}_{3}(P)$
, hence (RC) holds for
$P\in \operatorname{Syl}_{3}(P)$
, hence (RC) holds for
![]() $3$
-blocks of
$3$
-blocks of
![]() $G$
by Lemma 3.1. Thus (RC) holds for all
$G$
by Lemma 3.1. Thus (RC) holds for all
![]() $p$
-blocks of
$p$
-blocks of
![]() $G=^{2}\!F_{4}(q^{2})$
for all primes
$G=^{2}\!F_{4}(q^{2})$
for all primes
![]() $p$
. ◻
$p$
. ◻
7.1 Unipotent blocks
Let
![]() $\mathbf{G}$
be a simple algebraic group with a Frobenius endomorphism
$\mathbf{G}$
be a simple algebraic group with a Frobenius endomorphism
![]() $F:\mathbf{G}\rightarrow \mathbf{G}$
such that
$F:\mathbf{G}\rightarrow \mathbf{G}$
such that
![]() $G:=\mathbf{G}^{F}$
is a finite quasi-simple exceptional group of Lie type. We investigate
$G:=\mathbf{G}^{F}$
is a finite quasi-simple exceptional group of Lie type. We investigate
![]() $\ell$
-blocks of
$\ell$
-blocks of
![]() $\mathbf{G}^{F}$
for primes
$\mathbf{G}^{F}$
for primes
![]() $\ell >2$
different from the defining characteristic of
$\ell >2$
different from the defining characteristic of
![]() $\mathbf{G}$
, and we assume, moreover, that
$\mathbf{G}$
, and we assume, moreover, that
![]() $\ell$
is a bad prime for
$\ell$
is a bad prime for
![]() $\mathbf{G}$
, or
$\mathbf{G}$
, or
![]() $\ell =3$
for
$\ell =3$
for
![]() $G=^{3}\!D_{4}(q)$
.
$G=^{3}\!D_{4}(q)$
.
Table 4. Centers of Sylow
![]() $\ell$
-subgroups
$\ell$
-subgroups
![]() $P\in \operatorname{Syl}_{\ell }(G)$
. Here
$P\in \operatorname{Syl}_{\ell }(G)$
. Here
![]() $\unicode[STIX]{x1D716},\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D702}\in \{\pm 1\}$
with
$\unicode[STIX]{x1D716},\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D702}\in \{\pm 1\}$
with
![]() $q\equiv \unicode[STIX]{x1D716}\;(\text{mod}\;3)$
and
$q\equiv \unicode[STIX]{x1D716}\;(\text{mod}\;3)$
and
![]() $q\equiv \unicode[STIX]{x1D702}\;(\text{mod}\;5)$
.
$q\equiv \unicode[STIX]{x1D702}\;(\text{mod}\;5)$
.

We first discuss unipotent blocks. Again, we only need to consider those of non-abelian defect. For the principal block, one needs to determine
![]() $|Z(P)|$
for
$|Z(P)|$
for
![]() $P\in \operatorname{Syl}_{\ell }(G)$
. For all groups except for type
$P\in \operatorname{Syl}_{\ell }(G)$
. For all groups except for type
![]() $E_{6}$
and
$E_{6}$
and
![]() $\ell =3$
, and for type
$\ell =3$
, and for type
![]() $E_{7}$
and
$E_{7}$
and
![]() $\ell =2$
, Sylow
$\ell =2$
, Sylow
![]() $\ell$
-subgroups of
$\ell$
-subgroups of
![]() $G$
and
$G$
and
![]() $G^{\ast }$
are isomorphic as
$G^{\ast }$
are isomorphic as
![]() $G\cong G^{\ast }$
.
$G\cong G^{\ast }$
.
Proposition 7.2. Let
![]() $G$
be quasi-simple of exceptional Lie type. The structure of centralisers of
$G$
be quasi-simple of exceptional Lie type. The structure of centralisers of
![]() $\ell$
-central semisimple
$\ell$
-central semisimple
![]() $\ell$
-elements
$\ell$
-elements
![]() $t\in G$
, where
$t\in G$
, where
![]() $\ell >2$
is a bad prime for
$\ell >2$
is a bad prime for
![]() $G$
, and the size of
$G$
, and the size of
![]() $Z(P)$
for
$Z(P)$
for
![]() $P\in \operatorname{Syl}_{\ell }(G)$
are as given in Table 4.
$P\in \operatorname{Syl}_{\ell }(G)$
are as given in Table 4.
Proof. The centralisers of semisimple elements in
![]() $\mathbf{G}$
can be classified with the algorithm of Borel and de Siebenthal. It turns out that the only centralisers
$\mathbf{G}$
can be classified with the algorithm of Borel and de Siebenthal. It turns out that the only centralisers
![]() $C_{G}(t)$
of
$C_{G}(t)$
of
![]() $\ell$
-elements
$\ell$
-elements
![]() $t\notin Z(G)$
of
$t\notin Z(G)$
of
![]() $\ell ^{\prime }$
-index in
$\ell ^{\prime }$
-index in
![]() $G$
are as listed in Table 4. (In fact, these can also be found on the website of Frank Lübeck.)
$G$
are as listed in Table 4. (In fact, these can also be found on the website of Frank Lübeck.)
Now if
![]() $P\in \operatorname{Syl}_{\ell }(G)$
and
$P\in \operatorname{Syl}_{\ell }(G)$
and
![]() $t\in Z(P)$
then
$t\in Z(P)$
then
![]() $C_{G}(t)$
has
$C_{G}(t)$
has
![]() $\ell ^{\prime }$
-index in
$\ell ^{\prime }$
-index in
![]() $G$
. Thus
$G$
. Thus
![]() $t$
occurs in the table, and
$t$
occurs in the table, and
![]() $P\leqslant C_{G}(t)$
. Then
$P\leqslant C_{G}(t)$
. Then
![]() $|Z(P)|$
can be read off from the structure of
$|Z(P)|$
can be read off from the structure of
![]() $C_{G}(t)$
.◻
$C_{G}(t)$
.◻
Lemma 7.3. Let
![]() $G$
be quasi-simple of exceptional Lie type. If
$G$
be quasi-simple of exceptional Lie type. If
![]() $G$
has a non-principal unipotent
$G$
has a non-principal unipotent
![]() $\ell$
-block of non-abelian defect for a bad prime
$\ell$
-block of non-abelian defect for a bad prime
![]() $\ell >2$
, then
$\ell >2$
, then
![]() $\ell =3$
and the block and its defect groups are as given in Table 5.
$\ell =3$
and the block and its defect groups are as given in Table 5.
Table 5. Non-principal unipotent
![]() $3$
-blocks of non-abelian defect. Here
$3$
-blocks of non-abelian defect. Here
![]() $\unicode[STIX]{x1D716}\in \{\pm 1\}$
with
$\unicode[STIX]{x1D716}\in \{\pm 1\}$
with
![]() $q\equiv \unicode[STIX]{x1D716}\;(\text{mod}\;3)$
.
$q\equiv \unicode[STIX]{x1D716}\;(\text{mod}\;3)$
.

Proof. The non-principal unipotent
![]() $\ell$
-blocks of exceptional groups were determined by Enguehard [Reference EnguehardEng00]. In Table 5 we label these blocks by the smallest Harish-Chandra vertex
$\ell$
-blocks of exceptional groups were determined by Enguehard [Reference EnguehardEng00]. In Table 5 we label these blocks by the smallest Harish-Chandra vertex
![]() $(\mathbf{L},\unicode[STIX]{x1D706})$
above which (some of) their unipotent characters lie, in the notation of [Reference EnguehardEng00]. The defect groups are described in [Reference EnguehardEng00]. From this, the information on the center can readily be derived. For example, for
$(\mathbf{L},\unicode[STIX]{x1D706})$
above which (some of) their unipotent characters lie, in the notation of [Reference EnguehardEng00]. The defect groups are described in [Reference EnguehardEng00]. From this, the information on the center can readily be derived. For example, for
![]() $G=E_{8}(q)$
and
$G=E_{8}(q)$
and
![]() $\ell =3$
, [Reference EnguehardEng00, p. 364] states that a defect group
$\ell =3$
, [Reference EnguehardEng00, p. 364] states that a defect group
![]() $D$
is isomorphic to a Sylow 3-subgroup of
$D$
is isomorphic to a Sylow 3-subgroup of
![]() $F_{4}(q)$
, whence
$F_{4}(q)$
, whence
![]() $|Z(D)|=3$
by Table 4. ◻
$|Z(D)|=3$
by Table 4. ◻
Proposition 7.4. The unipotent
![]() $\ell$
-blocks of quasi-simple groups of exceptional Lie type for bad primes
$\ell$
-blocks of quasi-simple groups of exceptional Lie type for bad primes
![]() $\ell \neq 2$
do not provide counterexamples to Robinson’s conjecture.
$\ell \neq 2$
do not provide counterexamples to Robinson’s conjecture.
Proof. Let
![]() $G$
be quasi-simple of exceptional Lie type,
$G$
be quasi-simple of exceptional Lie type,
![]() $\ell >2$
be a bad prime for
$\ell >2$
be a bad prime for
![]() $G$
and
$G$
and
![]() $B$
a unipotent
$B$
a unipotent
![]() $\ell$
-block.
$\ell$
-block.
If
![]() $B$
is the principal
$B$
is the principal
![]() $\ell$
-block of
$\ell$
-block of
![]() $G$
, then by Lemma 3.1 we may assume that
$G$
, then by Lemma 3.1 we may assume that
![]() $Z(P)$
is of order at least
$Z(P)$
is of order at least
![]() $\ell ^{2}$
, where
$\ell ^{2}$
, where
![]() $P$
is a Sylow
$P$
is a Sylow
![]() $\ell$
-subgroup of
$\ell$
-subgroup of
![]() $G$
. Thus, by Table 4 we may assume that
$G$
. Thus, by Table 4 we may assume that
![]() $G$
is in fact simple, and of type
$G$
is in fact simple, and of type
![]() $E_{7}$
with
$E_{7}$
with
![]() $\ell =3$
.
$\ell =3$
.
Assume first that
![]() $q\equiv 1\;(\text{mod}\;3)$
. Here, according to Enguehard’s description in [Reference EnguehardEng00, Theorem B], a character
$q\equiv 1\;(\text{mod}\;3)$
. Here, according to Enguehard’s description in [Reference EnguehardEng00, Theorem B], a character
![]() $\unicode[STIX]{x1D712}\in {\mathcal{E}}(G,t)$
lies in the principal 3-block if
$\unicode[STIX]{x1D712}\in {\mathcal{E}}(G,t)$
lies in the principal 3-block if
![]() $t$
is a 3-element, and, moreover, the Jordan correspondent of
$t$
is a 3-element, and, moreover, the Jordan correspondent of
![]() $\unicode[STIX]{x1D712}$
in
$\unicode[STIX]{x1D712}$
in
![]() ${\mathcal{E}}(C_{G^{\ast }}(t),1)$
lies in a Harish-Chandra series with Harish-Chandra vertex either a torus or a Levi subgroup of type
${\mathcal{E}}(C_{G^{\ast }}(t),1)$
lies in a Harish-Chandra series with Harish-Chandra vertex either a torus or a Levi subgroup of type
![]() $E_{6}$
. First assume that
$E_{6}$
. First assume that
![]() $\unicode[STIX]{x1D712}$
has Harish-Chandra vertex
$\unicode[STIX]{x1D712}$
has Harish-Chandra vertex
![]() $E_{6}$
. Then
$E_{6}$
. Then
![]() $\mathbf{H}=C_{\mathbf{G}^{\ast }}(t)$
has a Levi subgroup of type
$\mathbf{H}=C_{\mathbf{G}^{\ast }}(t)$
has a Levi subgroup of type
![]() $E_{6}$
and thus is of type
$E_{6}$
and thus is of type
![]() $E_{6}$
or
$E_{6}$
or
![]() $E_{7}$
. Then the formula for Jordan decomposition shows that
$E_{7}$
. Then the formula for Jordan decomposition shows that
![]() $\unicode[STIX]{x1D6F7}_{1}\unicode[STIX]{x1D6F7}_{3}^{3}\unicode[STIX]{x1D6F7}_{9}$
divides
$\unicode[STIX]{x1D6F7}_{1}\unicode[STIX]{x1D6F7}_{3}^{3}\unicode[STIX]{x1D6F7}_{9}$
divides
![]() $|G|/\unicode[STIX]{x1D712}(1)$
and so
$|G|/\unicode[STIX]{x1D712}(1)$
and so
![]() $|G|_{3}/\unicode[STIX]{x1D712}(1)_{3}\geqslant 3^{4}(q-1)_{3}$
. If
$|G|_{3}/\unicode[STIX]{x1D712}(1)_{3}\geqslant 3^{4}(q-1)_{3}$
. If
![]() $\unicode[STIX]{x1D712}$
has trivial Harish-Chandra vertex then by the same argument we are done when
$\unicode[STIX]{x1D712}$
has trivial Harish-Chandra vertex then by the same argument we are done when
![]() $\mathbf{H}$
has
$\mathbf{H}$
has
![]() $\mathbb{F}_{q}$
-rank at least 2. Note that
$\mathbb{F}_{q}$
-rank at least 2. Note that
![]() $\mathbf{H}$
has
$\mathbf{H}$
has
![]() $\mathbb{F}_{q}$
-rank at least 1 as by Table 4 every 3-element centralises a split torus of rank 1. Now if
$\mathbb{F}_{q}$
-rank at least 1 as by Table 4 every 3-element centralises a split torus of rank 1. Now if
![]() $\mathbf{H}$
has
$\mathbf{H}$
has
![]() $\mathbb{F}_{q}$
-rank equal to 1, then all of its unipotent characters have degree prime to 3, and it is easy to see that
$\mathbb{F}_{q}$
-rank equal to 1, then all of its unipotent characters have degree prime to 3, and it is easy to see that
![]() $|G:\unicode[STIX]{x1D712}(1)|_{3}\geqslant 3(q-1)_{3}>|Z(P)|$
.
$|G:\unicode[STIX]{x1D712}(1)|_{3}\geqslant 3(q-1)_{3}>|Z(P)|$
.
Let us now consider the non-principal unipotent blocks listed in Table 5. Here only
![]() $G=E_{7}(q)$
with
$G=E_{7}(q)$
with
![]() $\ell =3$
is relevant, with
$\ell =3$
is relevant, with
![]() $B$
the block whose characters have Harish-Chandra vertex
$B$
the block whose characters have Harish-Chandra vertex
![]() $D_{4}$
. As before, by [Reference EnguehardEng00, Theorem B] the characters in
$D_{4}$
. As before, by [Reference EnguehardEng00, Theorem B] the characters in
![]() $B$
lie in
$B$
lie in
![]() ${\mathcal{E}}(G,t)$
for 3-elements
${\mathcal{E}}(G,t)$
for 3-elements
![]() $t$
whose centraliser
$t$
whose centraliser
![]() $\mathbf{H}=C_{\mathbf{G}^{\ast }}(t)$
either has a split Levi subgroup of type
$\mathbf{H}=C_{\mathbf{G}^{\ast }}(t)$
either has a split Levi subgroup of type
![]() $D_{4}$
, or
$D_{4}$
, or
![]() $\mathbf{H}^{F}=\unicode[STIX]{x1D6F7}_{1}\unicode[STIX]{x1D6F7}_{3}.^{3}\!D_{4}(q)$
(see [Reference EnguehardEng00, Proposition 17]). In either case
$\mathbf{H}^{F}=\unicode[STIX]{x1D6F7}_{1}\unicode[STIX]{x1D6F7}_{3}.^{3}\!D_{4}(q)$
(see [Reference EnguehardEng00, Proposition 17]). In either case
![]() $|G|/\unicode[STIX]{x1D712}(1)$
is divisible by
$|G|/\unicode[STIX]{x1D712}(1)$
is divisible by
![]() $3(q-1)_{3}$
, sufficient for our claim.
$3(q-1)_{3}$
, sufficient for our claim.
The same line of argument applies when
![]() $q\equiv -1\;(\text{mod}\;3)$
.◻
$q\equiv -1\;(\text{mod}\;3)$
.◻
7.2 Isolated 5-blocks in
 $E_{8}(q)$
$E_{8}(q)$
We now consider certain
![]() $5$
-blocks. Recall that an element
$5$
-blocks. Recall that an element
![]() $t\in \mathbf{G}^{\ast F}$
is called quasi-isolated if
$t\in \mathbf{G}^{\ast F}$
is called quasi-isolated if
![]() $C_{\mathbf{G}^{\ast }}(t)$
is not contained in any proper
$C_{\mathbf{G}^{\ast }}(t)$
is not contained in any proper
![]() $F$
-stable Levi subgroup of
$F$
-stable Levi subgroup of
![]() $\mathbf{G}^{\ast }$
. It is isolated if
$\mathbf{G}^{\ast }$
. It is isolated if
![]() $C_{\mathbf{G}^{\ast }}^{\circ }(t)$
is not contained in a proper
$C_{\mathbf{G}^{\ast }}^{\circ }(t)$
is not contained in a proper
![]() $F$
-stable Levi subgroup.
$F$
-stable Levi subgroup.
Proposition 7.5. Let
![]() $B$
be an isolated
$B$
be an isolated
![]() $5$
-block of
$5$
-block of
![]() $G=E_{8}(q)$
. Then
$G=E_{8}(q)$
. Then
![]() $B$
is not a minimal counterexample to (RC).
$B$
is not a minimal counterexample to (RC).
Table 6. Isolated 5-blocks in
![]() $E_{8}(q)$
,
$E_{8}(q)$
,
![]() $q\equiv 1\;(\text{mod}\;5)$
.
$q\equiv 1\;(\text{mod}\;5)$
.

Proof. Let
![]() $d=d_{5}(q)$
be the order of
$d=d_{5}(q)$
be the order of
![]() $q$
modulo 5. The isolated non-unipotent 5-blocks of
$q$
modulo 5. The isolated non-unipotent 5-blocks of
![]() $G$
were determined in [Reference Kessar and MalleKM13, Proposition 6.10]. The ones of non-abelian defect are listed in Table 6 for
$G$
were determined in [Reference Kessar and MalleKM13, Proposition 6.10]. The ones of non-abelian defect are listed in Table 6 for
![]() $d=1$
. For
$d=1$
. For
![]() $d=2$
one obtains their Ennola duals, while there are none when
$d=2$
one obtains their Ennola duals, while there are none when
![]() $d=4$
. Let
$d=4$
. Let
![]() $s\in G$
be an isolated
$s\in G$
be an isolated
![]() $5^{\prime }$
-element. One of the results in [Reference Kessar and MalleKM13] is that the intersections of the 5-blocks with
$5^{\prime }$
-element. One of the results in [Reference Kessar and MalleKM13] is that the intersections of the 5-blocks with
![]() ${\mathcal{E}}(G,s)$
are exactly the
${\mathcal{E}}(G,s)$
are exactly the
![]() $d$
-Harish-Chandra series. Unfortunately, the subdivision of the whole of
$d$
-Harish-Chandra series. Unfortunately, the subdivision of the whole of
![]() ${\mathcal{E}}_{5}(G,s)$
into 5-blocks was not determined in [Reference Kessar and MalleKM13]. We claim that the analogue of [Reference Cabanes and EnguehardCE94, Theorem (iii)] and [Reference EnguehardEng00, Theorem B] continues to hold. That is, for any
${\mathcal{E}}_{5}(G,s)$
into 5-blocks was not determined in [Reference Kessar and MalleKM13]. We claim that the analogue of [Reference Cabanes and EnguehardCE94, Theorem (iii)] and [Reference EnguehardEng00, Theorem B] continues to hold. That is, for any
![]() $5$
-element
$5$
-element
![]() $t\in C_{G}(s)$
the intersections of the 5-blocks in
$t\in C_{G}(s)$
the intersections of the 5-blocks in
![]() ${\mathcal{E}}_{5}(G,s)$
with the Lusztig series
${\mathcal{E}}_{5}(G,s)$
with the Lusztig series
![]() ${\mathcal{E}}(G,st)$
coincide with the
${\mathcal{E}}(G,st)$
coincide with the
![]() $d$
-Harish-Chandra series.
$d$
-Harish-Chandra series.
Let
![]() $\mathbf{H}=C_{\mathbf{G}^{\ast }}(s)$
as in Table 6. Then 5 is a good prime for
$\mathbf{H}=C_{\mathbf{G}^{\ast }}(s)$
as in Table 6. Then 5 is a good prime for
![]() $\mathbf{H}$
and does not divide
$\mathbf{H}$
and does not divide
![]() $|Z(\mathbf{H})^{F}|$
, so the centralisers of all
$|Z(\mathbf{H})^{F}|$
, so the centralisers of all
![]() $5$
-elements in
$5$
-elements in
![]() $\mathbf{H}^{F}$
are Levi subgroups of
$\mathbf{H}^{F}$
are Levi subgroups of
![]() $\mathbf{H}$
and hence of
$\mathbf{H}$
and hence of
![]() $\mathbf{G}^{\ast }$
, and in fact
$\mathbf{G}^{\ast }$
, and in fact
![]() $d$
-split Levi subgroups of
$d$
-split Levi subgroups of
![]() $\mathbf{H}$
. According to the argument given in [Reference EnguehardEng00, p. 368], to show our claim it suffices to verify the validity of the analogues of [Reference EnguehardEng00, Propositions 20 and 22] in our situation. For Proposition 20 this holds by part (a) of the argument given there. Indeed, by inspection the centraliser of any 5-element in
$\mathbf{H}$
. According to the argument given in [Reference EnguehardEng00, p. 368], to show our claim it suffices to verify the validity of the analogues of [Reference EnguehardEng00, Propositions 20 and 22] in our situation. For Proposition 20 this holds by part (a) of the argument given there. Indeed, by inspection the centraliser of any 5-element in
![]() $\mathbf{H}$
is either
$\mathbf{H}$
is either
![]() $d$
-split, or classical of rank at most 3 and with just one unipotent
$d$
-split, or classical of rank at most 3 and with just one unipotent
![]() $5$
-block. Proposition 22 continues to hold here by part (c) of its proof, as we had just seen above that the centralisers of 5-elements
$5$
-block. Proposition 22 continues to hold here by part (c) of its proof, as we had just seen above that the centralisers of 5-elements
![]() $t\in \mathbf{H}^{F}$
are Levi subgroups. This proves the claim.
$t\in \mathbf{H}^{F}$
are Levi subgroups. This proves the claim.
Thus, the 5-blocks listed in Table 6 only contain characters
![]() $\unicode[STIX]{x1D712}\in {\mathcal{E}}(G,st)$
that lie in the principal
$\unicode[STIX]{x1D712}\in {\mathcal{E}}(G,st)$
that lie in the principal
![]() $d$
-series, and their defect groups are Sylow 5-subgroups of
$d$
-series, and their defect groups are Sylow 5-subgroups of
![]() $\mathbf{H}^{F}$
. We can then argue exactly as in the proof of Theorem 6.4 to prove our assertion.◻
$\mathbf{H}^{F}$
. We can then argue exactly as in the proof of Theorem 6.4 to prove our assertion.◻
7.3 Quasi-isolated 3-blocks
Theorem 7.6. Let
![]() $B$
be a quasi-isolated
$B$
be a quasi-isolated
![]() $3$
-block of a quasi-simple exceptional group of Lie type. Then
$3$
-block of a quasi-simple exceptional group of Lie type. Then
![]() $B$
is not a minimal counterexample to (RC).
$B$
is not a minimal counterexample to (RC).
Proof. Let
![]() $G$
be a quasi-simple exceptional group of Lie type and
$G$
be a quasi-simple exceptional group of Lie type and
![]() $d=d_{3}(q)$
. The isolated non-unipotent 3-blocks of
$d=d_{3}(q)$
. The isolated non-unipotent 3-blocks of
![]() $G$
were determined in [Reference Kessar and MalleKM13]. For most of those blocks we can apply exactly the same argument as in the proof of Proposition 7.5. Let
$G$
were determined in [Reference Kessar and MalleKM13]. For most of those blocks we can apply exactly the same argument as in the proof of Proposition 7.5. Let
![]() $s\in \mathbf{G}^{\ast F}$
be a quasi-isolated
$s\in \mathbf{G}^{\ast F}$
be a quasi-isolated
![]() $3^{\prime }$
-element and
$3^{\prime }$
-element and
![]() $\mathbf{H}=C_{\mathbf{G}^{\ast }}(s)$
. If
$\mathbf{H}=C_{\mathbf{G}^{\ast }}(s)$
. If
![]() $\mathbf{H}$
has only classical factors, then 3 is a good prime for
$\mathbf{H}$
has only classical factors, then 3 is a good prime for
![]() $\mathbf{H}$
and we may conclude by noticing that the analogues of [Reference EnguehardEng00, Propositions 20 and 22] are satisfied. The only cases for which this approach fails are when
$\mathbf{H}$
and we may conclude by noticing that the analogues of [Reference EnguehardEng00, Propositions 20 and 22] are satisfied. The only cases for which this approach fails are when
![]() $\mathbf{H}$
has a factor of type
$\mathbf{H}$
has a factor of type
![]() $E_{6}$
(in
$E_{6}$
(in
![]() $G$
of type
$G$
of type
![]() $E_{7}$
), or of type
$E_{7}$
), or of type
![]() $E_{7}$
(in
$E_{7}$
(in
![]() $G$
of type
$G$
of type
![]() $E_{8}$
).
$E_{8}$
).
Table 7. Harish-Chandra series in some quasi-isolated 3-blocks,
![]() $q\equiv 1\;(\text{mod}\;3)$
.
$q\equiv 1\;(\text{mod}\;3)$
.

Let us consider these cases, listed from [Reference Kessar and MalleKM13, Tables 4 and 6] in Table 7 for
![]() $d=1$
(for
$d=1$
(for
![]() $d=2$
again we have the Ennola dual situations). Blocks 8 and 9 for
$d=2$
again we have the Ennola dual situations). Blocks 8 and 9 for
![]() $E_{7}(q)$
have defect groups with centers of the same size
$E_{7}(q)$
have defect groups with centers of the same size
![]() $(q-1)_{3}$
, so for our question we do not need to know the precise block distribution. Block 10 has defect groups with center of order 3, while defect groups for block 11 are abelian, so (RC) holds for these blocks independent of the block distribution.
$(q-1)_{3}$
, so for our question we do not need to know the precise block distribution. Block 10 has defect groups with center of order 3, while defect groups for block 11 are abelian, so (RC) holds for these blocks independent of the block distribution.
Finally assume that
![]() $G=E_{8}(q)$
and
$G=E_{8}(q)$
and
![]() $s\in \mathbf{G}^{\ast F}$
is an isolated involution with
$s\in \mathbf{G}^{\ast F}$
is an isolated involution with
![]() $\mathbf{H}=C_{\mathbf{G}^{\ast }}(s)$
of rational type
$\mathbf{H}=C_{\mathbf{G}^{\ast }}(s)$
of rational type
![]() $E_{7}(q)A_{1}(q)$
. Here block 5 has abelian defect groups, and the size of the centers of the defect groups of blocks 3 and 4 is not smaller than for block 5, so we need to be more careful. Now note with Proposition 6.2 that the only characters in
$E_{7}(q)A_{1}(q)$
. Here block 5 has abelian defect groups, and the size of the centers of the defect groups of blocks 3 and 4 is not smaller than for block 5, so we need to be more careful. Now note with Proposition 6.2 that the only characters in
![]() ${\mathcal{E}}_{3}(G,s)$
with potentially too small defect are those lying in the Harish-Chandra series of a cuspidal character of type
${\mathcal{E}}_{3}(G,s)$
with potentially too small defect are those lying in the Harish-Chandra series of a cuspidal character of type
![]() $E_{7}[\pm \unicode[STIX]{x1D709}]$
. Such characters occur in
$E_{7}[\pm \unicode[STIX]{x1D709}]$
. Such characters occur in
![]() ${\mathcal{E}}(G,st)$
only for 3-elements
${\mathcal{E}}(G,st)$
only for 3-elements
![]() $t\in \mathbf{H}^{F}$
with
$t\in \mathbf{H}^{F}$
with
![]() $C_{\mathbf{G}^{\ast }}(st)$
of rational type
$C_{\mathbf{G}^{\ast }}(st)$
of rational type
![]() $E_{7}(q).\unicode[STIX]{x1D6F7}_{1}$
. But this is a proper 1-split Levi subgroup of
$E_{7}(q).\unicode[STIX]{x1D6F7}_{1}$
. But this is a proper 1-split Levi subgroup of
![]() $\mathbf{H}$
, and thus [Reference EnguehardEng00, Proposition 20] continues to hold by (b) of its proof, and Proposition 22 by (c) of its proof. Hence all characters in
$\mathbf{H}$
, and thus [Reference EnguehardEng00, Proposition 20] continues to hold by (b) of its proof, and Proposition 22 by (c) of its proof. Hence all characters in
![]() ${\mathcal{E}}_{3}(G,s)$
lying in Harish-Chandra series above
${\mathcal{E}}_{3}(G,s)$
lying in Harish-Chandra series above
![]() $E_{7}[\pm \unicode[STIX]{x1D709}]$
fall into block 5, and we may conclude as in the previous cases.◻
$E_{7}[\pm \unicode[STIX]{x1D709}]$
fall into block 5, and we may conclude as in the previous cases.◻
We are now ready to prove our main result.
Proof of Theorem 1.
According to Theorem 2.3, we have to show that no
![]() $p$
-block of a quasi-simple group
$p$
-block of a quasi-simple group
![]() $G$
is a minimal counterexample to Robinson’s conjecture. We invoke the classification of finite simple groups. If
$G$
is a minimal counterexample to Robinson’s conjecture. We invoke the classification of finite simple groups. If
![]() $G$
is a covering group of a sporadic simple group or of
$G$
is a covering group of a sporadic simple group or of
![]() $^{2}\!F_{4}(2)^{\prime }$
, the claim holds by Theorem 3.5. For
$^{2}\!F_{4}(2)^{\prime }$
, the claim holds by Theorem 3.5. For
![]() $G$
a covering group of an alternating group
$G$
a covering group of an alternating group
![]() $\mathfrak{A}_{n}$
,
$\mathfrak{A}_{n}$
,
![]() $n\geqslant 5$
, we showed the assertion in Theorem 4.1. Thus,
$n\geqslant 5$
, we showed the assertion in Theorem 4.1. Thus,
![]() $G$
is such that
$G$
is such that
![]() $S=G/Z(G)$
is simple of Lie type. If
$S=G/Z(G)$
is simple of Lie type. If
![]() $G$
is an exceptional covering group, then we are done by Theorem 3.6.
$G$
is an exceptional covering group, then we are done by Theorem 3.6.
It remains to consider the case when
![]() $G$
is a non-exceptional covering of a simple group of Lie type
$G$
is a non-exceptional covering of a simple group of Lie type
![]() $S=G/Z(G)$
, and
$S=G/Z(G)$
, and
![]() $G\neq ^{2}\!F_{4}(2)^{\prime }$
. The Suzuki and Ree groups have been handled in Proposition 7.1. Thus, without loss we may assume that
$G\neq ^{2}\!F_{4}(2)^{\prime }$
. The Suzuki and Ree groups have been handled in Proposition 7.1. Thus, without loss we may assume that
![]() $G=\mathbf{G}^{F}$
for
$G=\mathbf{G}^{F}$
for
![]() $\mathbf{G}$
a simple algebraic group of simply connected type with a Frobenius endomorphism
$\mathbf{G}$
a simple algebraic group of simply connected type with a Frobenius endomorphism
![]() $F$
. If
$F$
. If
![]() $p$
is the defining characteristic of
$p$
is the defining characteristic of
![]() $G$
, then the claim is in Theorem 5.1. So now assume that
$G$
, then the claim is in Theorem 5.1. So now assume that
![]() $\ell$
is not the defining characteristic, and
$\ell$
is not the defining characteristic, and
![]() $B$
is an
$B$
is an
![]() $\ell$
-block of
$\ell$
-block of
![]() $G$
. By Corollary 2.4 we may assume that
$G$
. By Corollary 2.4 we may assume that
![]() $G$
has cyclic center. Then by the reduction theorem of Bonnafé, Dat and Rouquier [Reference Bonnafé, Dat and RouquierBDR17, Theorem 7.7] we may assume that
$G$
has cyclic center. Then by the reduction theorem of Bonnafé, Dat and Rouquier [Reference Bonnafé, Dat and RouquierBDR17, Theorem 7.7] we may assume that
![]() $B$
is in fact an isolated block of
$B$
is in fact an isolated block of
![]() $G$
, as otherwise it is Morita equivalent to an
$G$
, as otherwise it is Morita equivalent to an
![]() $\ell$
-block of a strictly smaller group with the same defect group and thus cannot be a minimal counterexample. Observe that the Bonnafé–Dat–Rouquier Morita equivalence is compatible with Lusztig series and thus with central characters. Hence it carries over to blocks of central quotients of
$\ell$
-block of a strictly smaller group with the same defect group and thus cannot be a minimal counterexample. Observe that the Bonnafé–Dat–Rouquier Morita equivalence is compatible with Lusztig series and thus with central characters. Hence it carries over to blocks of central quotients of
![]() $G$
.
$G$
.
By the result of Enguehard [Reference EnguehardEng13, Theorem 1.4], if
![]() $B$
is isolated but not unipotent, and
$B$
is isolated but not unipotent, and
![]() $\ell$
is good for
$\ell$
is good for
![]() $G$
, not equal to 3 when
$G$
, not equal to 3 when
![]() $G=^{3}\!D_{4}(q)$
, then there exists a height-preserving bijection between
$G=^{3}\!D_{4}(q)$
, then there exists a height-preserving bijection between
![]() $\operatorname{Irr}(B)$
and the characters in an
$\operatorname{Irr}(B)$
and the characters in an
![]() $\ell$
-block with isomorphic defect group of a strictly smaller group, if the Mackey formula does hold for
$\ell$
-block with isomorphic defect group of a strictly smaller group, if the Mackey formula does hold for
![]() $G$
. The only simple groups for which the Mackey formula is not known to hold are
$G$
. The only simple groups for which the Mackey formula is not known to hold are
![]() $^{2}\!E_{6}(2)$
,
$^{2}\!E_{6}(2)$
,
![]() $E_{7}(2)$
and
$E_{7}(2)$
and
![]() $E_{8}(2)$
, but for these, all Sylow
$E_{8}(2)$
, but for these, all Sylow
![]() $\ell$
-subgroups for good primes
$\ell$
-subgroups for good primes
![]() $\ell$
are abelian. We are hence left to consider unipotent blocks, as well as isolated blocks for primes
$\ell$
are abelian. We are hence left to consider unipotent blocks, as well as isolated blocks for primes
![]() $\ell >2$
which are bad for
$\ell >2$
which are bad for
![]() $G$
.
$G$
.
If
![]() $\ell$
is good for
$\ell$
is good for
![]() $\mathbf{G}$
, then the unipotent blocks are treated in Theorem 6.4 (respectively, in Theorem 6.8 for groups of type
$\mathbf{G}$
, then the unipotent blocks are treated in Theorem 6.4 (respectively, in Theorem 6.8 for groups of type
![]() $A$
). The only groups for which 5 is a bad prime are those of type
$A$
). The only groups for which 5 is a bad prime are those of type
![]() $E_{8}$
, and their isolated 5-blocks have been handled in Propositions 7.4 and 7.5. Finally, the isolated 3-blocks of exceptional groups do not provide minimal counterexamples to (RC) by Theorem 7.6.◻
$E_{8}$
, and their isolated 5-blocks have been handled in Propositions 7.4 and 7.5. Finally, the isolated 3-blocks of exceptional groups do not provide minimal counterexamples to (RC) by Theorem 7.6.◻
Acknowledgements
We thank the anonymous referees for some helpful remarks and for alerting us to the early history of Robinson’s conjecture.