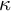1 Introduction
In this paper, we study certain aspects of the Galvin property of ultrafilters.
Definition 1.1. Let U be a uniform ultrafilter over
![]() $\kappa $
. We say that U has the Galvin property if for any sequence
$\kappa $
. We say that U has the Galvin property if for any sequence
![]() ${\langle } A_i{\rangle }_{ i<2^\kappa }$
, there is
${\langle } A_i{\rangle }_{ i<2^\kappa }$
, there is
![]() $I\in [ 2^\kappa ]^{\kappa }$
such that
$I\in [ 2^\kappa ]^{\kappa }$
such that
![]() $\bigcap _{i\in I}A_i\in U$
.
$\bigcap _{i\in I}A_i\in U$
.
More generally, if
![]() $\lambda \leq \kappa $
and U is a uniform ultrafilter over
$\lambda \leq \kappa $
and U is a uniform ultrafilter over
![]() $\kappa $
, we denote by
$\kappa $
, we denote by
![]() $\mathrm{Gal}(U,\lambda ,2^\kappa )$
the statement that for any
$\mathrm{Gal}(U,\lambda ,2^\kappa )$
the statement that for any
![]() ${\langle } A_i{\rangle }_{i<2^\kappa }$
, there is
${\langle } A_i{\rangle }_{i<2^\kappa }$
, there is
![]() $I\in [2^\kappa ]^\lambda $
such that
$I\in [2^\kappa ]^\lambda $
such that
![]() $\bigcap _{i\in I}A_i\in U$
. Galvin proved in 1973 every normal ultrafilter has the Galvin property. Gitik and Benhamou [Reference Benhamou and Gitik7] recently improved this result to show that any product of
$\bigcap _{i\in I}A_i\in U$
. Galvin proved in 1973 every normal ultrafilter has the Galvin property. Gitik and Benhamou [Reference Benhamou and Gitik7] recently improved this result to show that any product of
![]() $\kappa $
-complete p-points over
$\kappa $
-complete p-points over
![]() $\kappa $
has the Galvin property.Footnote
1
Benhamou [Reference Benhamou1] then proved what appears to be a slight improvement of this result.
$\kappa $
has the Galvin property.Footnote
1
Benhamou [Reference Benhamou1] then proved what appears to be a slight improvement of this result.
Theorem 1.2 Suppose that U is Rudin–Keisler equivalent to an n-fold sum of
![]() $\kappa $
-complete p-points (see Definition 2.4). Then U has the Galvin property.
$\kappa $
-complete p-points (see Definition 2.4). Then U has the Galvin property.
The main theorem of this paper shows that under natural combinatorial hypotheses which hold in all known canonical inner models, the converse of the above theorem is true.
Main Theorem 1.1 Assume the Ultrapower Axiom and that every irreducible ultrafilter is Dodd sound. If U is a
![]() $\kappa $
-complete ultrafilter on
$\kappa $
-complete ultrafilter on
![]() $\kappa $
with the Galvin property, then U is Rudin–Keisler equivalent to an iterated sum of
$\kappa $
with the Galvin property, then U is Rudin–Keisler equivalent to an iterated sum of
![]() $\kappa $
-complete p-points on
$\kappa $
-complete p-points on
![]() $\kappa $
.
$\kappa $
.
The hypotheses of this theorem will be discussed and explained further later in the Introduction.
The study of the Galvin property is motivated by its presence in various areas of set theory and infinite combinatorics [Reference Benhamou and Dobrinen2–Reference Benhamou and Gitik8, Reference Garti, Hayut, Horowitz and Menachem16]. One particularly noteworthy incarnation of the Galvin property is the maximal class in the Tukey order, which we shall now explain in more detail.
Definition 1.3. For two posets
![]() $(P,\leq _P),(Q,\leq _Q)$
Footnote
2
, we say that
$(P,\leq _P),(Q,\leq _Q)$
Footnote
2
, we say that
![]() $P\leq _T Q$
if there is a cofinal map
$P\leq _T Q$
if there is a cofinal map
![]() $f:Q\rightarrow P$
.Footnote
3
We say that
$f:Q\rightarrow P$
.Footnote
3
We say that
![]() $P,Q$
are Tukey equivalent and denote
$P,Q$
are Tukey equivalent and denote
![]() $P\equiv _TQ$
, if
$P\equiv _TQ$
, if
![]() $P\leq _T Q$
and
$P\leq _T Q$
and
![]() $Q\leq _TP$
.
$Q\leq _TP$
.
The Tukey order finds its origins in the Moore–Smith convergence notions of nets and is of particular interest when considering the poset
![]() $(U,\supseteq ),$
where U is an ultrafilter. The Tukey order restricted to ultrafilters over
$(U,\supseteq ),$
where U is an ultrafilter. The Tukey order restricted to ultrafilters over
![]() $\omega $
has been extensively studied by Isbell [Reference Isbell20], Milovich [Reference Milovich27, Reference Milovich28], Dobrinen and Todorcevic [Reference Dobrinen12, Reference Dobrinen13, Reference Dobrinen and Todorcevic15], Raghavan, Dobrinen, and Blass [Reference Blass, Dobrinen and Raghavan10, Reference Raghavan and Todorcevic32], and many others. Lately, this investigation has been stretched to ultrafilters over uncountable cardinals and in particular to measurable cardinals by Benhamou and Dobrinen [Reference Benhamou and Dobrinen2]. It turns out that the Tukey order on
$\omega $
has been extensively studied by Isbell [Reference Isbell20], Milovich [Reference Milovich27, Reference Milovich28], Dobrinen and Todorcevic [Reference Dobrinen12, Reference Dobrinen13, Reference Dobrinen and Todorcevic15], Raghavan, Dobrinen, and Blass [Reference Blass, Dobrinen and Raghavan10, Reference Raghavan and Todorcevic32], and many others. Lately, this investigation has been stretched to ultrafilters over uncountable cardinals and in particular to measurable cardinals by Benhamou and Dobrinen [Reference Benhamou and Dobrinen2]. It turns out that the Tukey order on
![]() $\sigma $
-complete ultrafilters over measurable cardinal behaves differently from the one on
$\sigma $
-complete ultrafilters over measurable cardinal behaves differently from the one on
![]() $\omega $
and requires a new theory to be developed. One of these differences revolves around the maximal class. For a given
$\omega $
and requires a new theory to be developed. One of these differences revolves around the maximal class. For a given
![]() $\lambda $
, a uniform ultrafilter U on
$\lambda $
, a uniform ultrafilter U on
![]() $\kappa $
is called Tukey-top with respect to
$\kappa $
is called Tukey-top with respect to
![]() $\lambda $
if its Tukey class is above every
$\lambda $
if its Tukey class is above every
![]() $\lambda $
-directed poset of size
$\lambda $
-directed poset of size
![]() $2^\kappa $
. It turns out that an ultrafilter U is Tukey-top with respect to
$2^\kappa $
. It turns out that an ultrafilter U is Tukey-top with respect to
![]() $\lambda $
if and only if
$\lambda $
if and only if
![]() $\neg \mathrm{Gal}(U,\lambda ,2^\kappa )$
. In particular, a uniform ultrafilter over
$\neg \mathrm{Gal}(U,\lambda ,2^\kappa )$
. In particular, a uniform ultrafilter over
![]() $\kappa $
is Tukey-top with respect to
$\kappa $
is Tukey-top with respect to
![]() $\kappa $
if and only if it is non-Galvin.
$\kappa $
if and only if it is non-Galvin.
Working in ZFC (with no additional set theoretic hypotheses), Isbell [Reference Isbell20] constructed ultrafilters on
![]() $\omega $
which are non-Galvin, this construction was accomplished independently by Juhász [Reference Juhász23]. The first construction of non-Galvin ultrafilters over measurable cardinals is due to Garti, Shelah, and Benhamou [Reference Benhamou, Garti and Sehlah6], using the existence of Kurepa trees to prevent a certain ultrafilter from having the Galvin property. This connection between Kurepa trees and the Galvin property is further explored in this paper, where we define (Definition 3.3) a diamond-like principle
$\omega $
which are non-Galvin, this construction was accomplished independently by Juhász [Reference Juhász23]. The first construction of non-Galvin ultrafilters over measurable cardinals is due to Garti, Shelah, and Benhamou [Reference Benhamou, Garti and Sehlah6], using the existence of Kurepa trees to prevent a certain ultrafilter from having the Galvin property. This connection between Kurepa trees and the Galvin property is further explored in this paper, where we define (Definition 3.3) a diamond-like principle
![]() $\Diamond ^*_{\mathrm{thin}}(W)$
, and a slight weakening (Definition 3.12) of it that ensures that an ultrafilter is non-Galvin (Lemma 3.5).
$\Diamond ^*_{\mathrm{thin}}(W)$
, and a slight weakening (Definition 3.12) of it that ensures that an ultrafilter is non-Galvin (Lemma 3.5).
In [Reference Benhamou and Dobrinen2], Isbell’s construction together with other features from [Reference Benhamou1] enabled the construction of a non-Galvin ultrafilter over a
![]() $\kappa $
-compact cardinal. Here, we improve this initial large cardinal, isolate the notion of a non-Galvin cardinal (Definition 5.1), and prove the following.
$\kappa $
-compact cardinal. Here, we improve this initial large cardinal, isolate the notion of a non-Galvin cardinal (Definition 5.1), and prove the following.
Main Theorem 1.2 Suppose that
![]() $\kappa $
is a non-Galvin cardinal, then
$\kappa $
is a non-Galvin cardinal, then
![]() $\kappa $
carries a
$\kappa $
carries a
![]() $\kappa $
-complete ultrafilter U such that
$\kappa $
-complete ultrafilter U such that
![]() $\neg \mathrm{Gal}(U,\kappa ,\kappa ^+)$
. In particular, if in addition
$\neg \mathrm{Gal}(U,\kappa ,\kappa ^+)$
. In particular, if in addition
![]() $2^\kappa =\kappa ^+$
, then U is a non-Galvin ultrafilter.
$2^\kappa =\kappa ^+$
, then U is a non-Galvin ultrafilter.
We also prove that
![]() $\kappa $
-compactness implies non-Galvinness (Theorem 5.7), that some degree of Dodd soundness implies it (Corollary 3.11), and that in the known canonical inner models, a
$\kappa $
-compactness implies non-Galvinness (Theorem 5.7), that some degree of Dodd soundness implies it (Corollary 3.11), and that in the known canonical inner models, a
![]() $\kappa $
-compact cardinal is a limit of non-Galvin cardinals (Proposition 6.9).
$\kappa $
-compact cardinal is a limit of non-Galvin cardinals (Proposition 6.9).
In [Reference Benhamou and Gitik9], Gitik and Benhamou noted that although the existence of a non-Galvin ultrafilter is equiconsistent with a measurable cardinal, the latter assumption (measurability) does not outright imply that there is a non-Galvin ultrafilter. More precisely, in Kunen’s model
![]() $L[U]$
, since every
$L[U]$
, since every
![]() $\sigma $
-complete ultrafilter is Rudin–Keisler equivalent to a power of the normal ultrafilter U, Theorem 1.2 can be invoked to deduce the Galvin property for every
$\sigma $
-complete ultrafilter is Rudin–Keisler equivalent to a power of the normal ultrafilter U, Theorem 1.2 can be invoked to deduce the Galvin property for every
![]() $\sigma $
-complete ultrafilter in
$\sigma $
-complete ultrafilter in
![]() $L[U]$
. Being the simplest example of a canonical inner model which can accommodate a measurable cardinal, the result in
$L[U]$
. Being the simplest example of a canonical inner model which can accommodate a measurable cardinal, the result in
![]() $L[U]$
suggests that the Galvin property, like many other combinatorial properties of ultrafilters, has a rigid form in the canonical inner models. Indeed, the result from
$L[U]$
suggests that the Galvin property, like many other combinatorial properties of ultrafilters, has a rigid form in the canonical inner models. Indeed, the result from
![]() $L[U]$
was later generalized [Reference Benhamou1] to the Mitchell–Steel models
$L[U]$
was later generalized [Reference Benhamou1] to the Mitchell–Steel models
![]() $L[E]$
up to a measurable limit of superstrong cardinalFootnote
4
(see Theorem 1.2). These results in the inner models suggest the following question [Reference Benhamou1, Question 5.1].
$L[E]$
up to a measurable limit of superstrong cardinalFootnote
4
(see Theorem 1.2). These results in the inner models suggest the following question [Reference Benhamou1, Question 5.1].
Question 1.4. Is there an inner model with a non-Galvin ultrafilter?
In this paper, we take a more ambitious approach and work under the Ultrapower Axiom (UA)Footnote 5 which is a combinatorial principle discovered by Goldberg [Reference Goldberg17]. The advantage of UA is that with one simple axiom, which holds in all known canonical inner models, many of the usual principles are captured; for example, the linearity of the Mitchell order and instances of GCH. More relevant for our purposes, the presence of UA imposes rigidity on the structure of ultrafilters.
Theorem 1.5 (UA)
Let W be a
![]() $\sigma $
-complete ultrafilter. Then W can be written as the n-fold sum of irreducible ultrafilters.Footnote
6
$\sigma $
-complete ultrafilter. Then W can be written as the n-fold sum of irreducible ultrafilters.Footnote
6
In [Reference Benhamou1], this kind of characterization, together with further fine structural properties of the Mitchell–Steel extender models
![]() $L[E]$
was already used to prove the following.
$L[E]$
was already used to prove the following.
Theorem 1.6 If
![]() $L[E]$
is an iterable Mitchell–Steel model containing no superstrong cardinals, then every
$L[E]$
is an iterable Mitchell–Steel model containing no superstrong cardinals, then every
![]() $\kappa $
-complete ultrafilter in
$\kappa $
-complete ultrafilter in
![]() $L[E]$
has the Galvin property.
$L[E]$
has the Galvin property.
The point here is that in
![]() $L[E]$
every
$L[E]$
every
![]() $\kappa $
-complete ultrafilter takes the form of Theorem 1.2 and therefore satisfies the Galvin property.
$\kappa $
-complete ultrafilter takes the form of Theorem 1.2 and therefore satisfies the Galvin property.
The existence of canonical inner models with superstrong cardinals is open, though provable from widely believed conjectures: the fine structure for inner models with superstrong cardinals has been developed assuming iterability hypotheses [Reference Steel35]. Therefore, the current knowledge about canonical inner models does not quite reach the level where a
![]() $\kappa $
-complete non-Galvin ultrafilter exists, although our results below show that the conditional canonical inner models built based on iterability hypotheses can contain non-Galvin ultrafilters.
$\kappa $
-complete non-Galvin ultrafilter exists, although our results below show that the conditional canonical inner models built based on iterability hypotheses can contain non-Galvin ultrafilters.
Here, we shall prove the following stronger (in several senses) result.
Main Theorem 1.3 (UA)
Assume that every irreducible ultrafilter is Dodd sound (see Definition 2.1(6)). Then a uniform
![]() $\sigma $
-complete ultrafilter over a regular cardinal has the Galvin property if and only if it is a D-limit of n-fold sums of
$\sigma $
-complete ultrafilter over a regular cardinal has the Galvin property if and only if it is a D-limit of n-fold sums of
![]() $\kappa $
-complete p-points over
$\kappa $
-complete p-points over
![]() $\kappa $
.
$\kappa $
.
We note that in the above theorem, the ultrafilter D might be just a
![]() $\sigma $
-complete ultrafilter over a cardinals
$\sigma $
-complete ultrafilter over a cardinals
![]() $\lambda <\kappa $
(see Theorem 2.10). By results of Schlutzenberg [Reference Schlutzenberg34], in the Mitchell–Steel extender models
$\lambda <\kappa $
(see Theorem 2.10). By results of Schlutzenberg [Reference Schlutzenberg34], in the Mitchell–Steel extender models
![]() $L[E]$
, every irreducible ultrafilter is Dodd sound, so the assumption in the theorem holds in
$L[E]$
, every irreducible ultrafilter is Dodd sound, so the assumption in the theorem holds in
![]() $L[E]$
. Hence, Theorem 1.3 implies that in the canonical inner models of the form of
$L[E]$
. Hence, Theorem 1.3 implies that in the canonical inner models of the form of
![]() $L[E]$
, even above a superstrong cardinal, the n-fold sum of p-points, in fact, characterizes the ultrafilters with the Galvin property. This characterization implies, for example, that
$L[E]$
, even above a superstrong cardinal, the n-fold sum of p-points, in fact, characterizes the ultrafilters with the Galvin property. This characterization implies, for example, that
![]() $\sigma $
-complete ultrafilters over successor cardinals always possess the Galvin property (Corollary 6.2).
$\sigma $
-complete ultrafilters over successor cardinals always possess the Galvin property (Corollary 6.2).
As a corollary, we obtain the characterization of the Tukey-top ultrafilters.
Corollary 1.7 (UA)
Assume that every irreducible ultrafilter is Dodd sound, then a
![]() $\sigma $
-complete ultrafilter over a regular cardinal is Tukey-top if and only if it is not a D-sum of n-fold sums of
$\sigma $
-complete ultrafilter over a regular cardinal is Tukey-top if and only if it is not a D-sum of n-fold sums of
![]() $\kappa $
-complete p-points over
$\kappa $
-complete p-points over
![]() $\kappa $
.
$\kappa $
.
This corollary may come as a bit of a surprise if one is familiar with the Tukey order on
![]() $\omega $
: Dobrinen and Raghavan proved independently that it is consistent that there are non-Tukey-top ultrafilters on
$\omega $
: Dobrinen and Raghavan proved independently that it is consistent that there are non-Tukey-top ultrafilters on
![]() $\omega $
that are not n-fold sums of p-points [Reference Blass, Dobrinen and Raghavan10], more specifically, a generic ultrafilter for
$\omega $
that are not n-fold sums of p-points [Reference Blass, Dobrinen and Raghavan10], more specifically, a generic ultrafilter for
![]() $P(\omega \times \omega )/\text {fin}\cdot \text {fin}$
is such an ultrafilter; this result was stretched by Dobrinen in [Reference Dobrinen13, Reference Dobrinen14].
$P(\omega \times \omega )/\text {fin}\cdot \text {fin}$
is such an ultrafilter; this result was stretched by Dobrinen in [Reference Dobrinen13, Reference Dobrinen14].
One might suspect that under these very restrictive assumptions, we again run into the situation where every
![]() $\kappa $
-complete ultrafilter has the Galvin property, but by Theorem 1.2, a non-Galvin cardinal suffices to guarantee the existence of a non-Galvin ultrafilter. Our next result suggests that in the canonical inner models, non-Galvin cardinals are exactly the large cardinal assumption needed to ensure the existence of non-Galvin ultrafilters.
$\kappa $
-complete ultrafilter has the Galvin property, but by Theorem 1.2, a non-Galvin cardinal suffices to guarantee the existence of a non-Galvin ultrafilter. Our next result suggests that in the canonical inner models, non-Galvin cardinals are exactly the large cardinal assumption needed to ensure the existence of non-Galvin ultrafilters.
Main Theorem 1.4 (UA)
Assume that every irreducible ultrafilter is Dodd sound. If there is a
![]() $\kappa $
-complete non-Galvin ultrafilter on an uncountable cardinal
$\kappa $
-complete non-Galvin ultrafilter on an uncountable cardinal
![]() $\kappa $
, then there is a non-Galvin cardinal.
$\kappa $
, then there is a non-Galvin cardinal.
One feature which seems to require more effort is to obtain a non-Galvin ultrafilter which extends the club filter (i.e., q-point). The ultrafilters that were constructed in [Reference Benhamou and Dobrinen2] from a
![]() $\kappa $
-compact cardinal extended the club filter and it is not clear at this point whether a non-Galvin cardinal implies the existence of such ultrafilters. Nonetheless, in the canonical inner models, the implication holds. In fact, the existence of a non-Galvin ultrafilter is equivalent to the existence of a non-Galvin q-point.
$\kappa $
-compact cardinal extended the club filter and it is not clear at this point whether a non-Galvin cardinal implies the existence of such ultrafilters. Nonetheless, in the canonical inner models, the implication holds. In fact, the existence of a non-Galvin ultrafilter is equivalent to the existence of a non-Galvin q-point.
Main Theorem 1.5 (UA)
Assume every irreducible ultrafilter is Dodd sound. Suppose
![]() $\kappa $
is an uncountable cardinal that carries a
$\kappa $
is an uncountable cardinal that carries a
![]() $\kappa $
-complete non-Galvin ultrafilter. Then the Ketonen least non-Galvin
$\kappa $
-complete non-Galvin ultrafilter. Then the Ketonen least non-Galvin
![]() $\kappa $
-complete ultrafilter on
$\kappa $
-complete ultrafilter on
![]() $\kappa $
extends the closed unbounded filter.
$\kappa $
extends the closed unbounded filter.
The organization of this paper is as follows:
-
• In Section 2, we collect some basic definitions and facts from the theory of ultrafilters.
-
• In Section 3, we establish the connection between non-Galvin ultrafilters and various diamond-like principles.
-
• In Section 4, we use partial soundness to conclude that some ultrafilter is non-Galvin and define the corresponding diamond
 $\diamondsuit ^-_{\mathrm{thin}}$
.
$\diamondsuit ^-_{\mathrm{thin}}$
. -
• In Section 5, we introduce the non-Galvin cardinals and prove Main Theorem 1.2.
-
• In Section 6, we work in the canonical inner models and prove Main Theorems 1.1, 1.3, 1.4, 1.5.
-
• In Section 7, we state some open questions and suggest further directions.
1.1 Notation
Our notation is mostly standard. Let
![]() $\kappa $
be a cardinal, and let X be any set. Then
$\kappa $
be a cardinal, and let X be any set. Then
![]() $[X]^\kappa =\{Y\in P(X)\mid |Y|=\kappa \}$
and
$[X]^\kappa =\{Y\in P(X)\mid |Y|=\kappa \}$
and
![]() $[X]^{<\kappa }=\{Y\in P(X)\mid |Y|<\kappa \}$
. When X is a set of ordinals, we identify elements of
$[X]^{<\kappa }=\{Y\in P(X)\mid |Y|<\kappa \}$
. When X is a set of ordinals, we identify elements of
![]() $[X]^{<\kappa }$
with their increasing enumerations. We write
$[X]^{<\kappa }$
with their increasing enumerations. We write
![]() ${}^{<\kappa }X$
for the set of all functions
${}^{<\kappa }X$
for the set of all functions
![]() $f\colon \gamma \rightarrow X$
, where
$f\colon \gamma \rightarrow X$
, where
![]() $\gamma <\kappa $
and
$\gamma <\kappa $
and
![]() ${}^\alpha X$
for the set of all functions
${}^\alpha X$
for the set of all functions
![]() $f\colon \alpha \rightarrow X$
. Let
$f\colon \alpha \rightarrow X$
. Let
![]() $\kappa $
be regular. For two subsets of
$\kappa $
be regular. For two subsets of
![]() $\kappa $
, we write
$\kappa $
, we write
![]() $X\subseteq ^* Y$
to denote that
$X\subseteq ^* Y$
to denote that
![]() $X\setminus Y$
is bounded in
$X\setminus Y$
is bounded in
![]() $\kappa $
. Similarly, for
$\kappa $
. Similarly, for
![]() $f,g\colon \kappa \rightarrow \kappa $
, we denote
$f,g\colon \kappa \rightarrow \kappa $
, we denote
![]() $f\leq ^* g$
if there is
$f\leq ^* g$
if there is
![]() $\alpha <\kappa $
such that for every
$\alpha <\kappa $
such that for every
![]() $\alpha \leq \beta <\kappa $
,
$\alpha \leq \beta <\kappa $
,
![]() $f(\beta )\leq g(\beta )$
. We say that
$f(\beta )\leq g(\beta )$
. We say that
![]() $C\subseteq \kappa $
is a closed unbounded (or club) subset of
$C\subseteq \kappa $
is a closed unbounded (or club) subset of
![]() $\kappa $
if it is a closed subset with respect to the order topology on
$\kappa $
if it is a closed subset with respect to the order topology on
![]() $\kappa $
and unbounded in the ordinals below
$\kappa $
and unbounded in the ordinals below
![]() $\kappa $
. The club filter over
$\kappa $
. The club filter over
![]() $\kappa $
is the filter:
$\kappa $
is the filter:
If
![]() $f\colon A\rightarrow B$
is a function, then
$f\colon A\rightarrow B$
is a function, then
![]() $f"(X)=\{f(x)\mid x\in X\}$
and
$f"(X)=\{f(x)\mid x\in X\}$
and
![]() $f^{-1}[Y]=\{a\in A\mid f(a)\in Y\}$
.
$f^{-1}[Y]=\{a\in A\mid f(a)\in Y\}$
.
2 Preliminaries
We only consider
![]() $\sigma $
-complete ultrafilters over regular cardinals in this paper. We will, however, consider ultrafilters on
$\sigma $
-complete ultrafilters over regular cardinals in this paper. We will, however, consider ultrafilters on
![]() $\kappa $
that fail to be uniform or
$\kappa $
that fail to be uniform or
![]() $\kappa $
-complete. For a
$\kappa $
-complete. For a
![]() $\sigma $
-complete ultrafilter U, we denote by
$\sigma $
-complete ultrafilter U, we denote by
![]() $M_U$
the transitive collapse of the ultrapower of the universe of sets by U and by
$M_U$
the transitive collapse of the ultrapower of the universe of sets by U and by
![]() $j_U\colon V\rightarrow M_U$
the usual ultrapower embedding. Given an elementary embedding
$j_U\colon V\rightarrow M_U$
the usual ultrapower embedding. Given an elementary embedding
![]() $j\colon V\rightarrow M$
and an object
$j\colon V\rightarrow M$
and an object
![]() $A\in M$
, we let
$A\in M$
, we let
![]() $\rho =\min \{\alpha \mid A\in V_{j(\alpha )}\}$
and define
$\rho =\min \{\alpha \mid A\in V_{j(\alpha )}\}$
and define
![]() $D(j,A):=\{X\subseteq V_\rho \mid A\in j(X)\}$
. When A is an ordinal, we will always replace
$D(j,A):=\{X\subseteq V_\rho \mid A\in j(X)\}$
. When A is an ordinal, we will always replace
![]() $V_{\rho }$
in the above definition by
$V_{\rho }$
in the above definition by
![]() $\rho $
. If M is any model of ZFC and f is a function or relation defined in the language of set theory, the relativization of f to this model is denoted by
$\rho $
. If M is any model of ZFC and f is a function or relation defined in the language of set theory, the relativization of f to this model is denoted by
![]() $(f)^M$
; for example, if
$(f)^M$
; for example, if
![]() $\kappa \in M$
, we might consider
$\kappa \in M$
, we might consider
![]() $(\kappa ^+)^M$
,
$(\kappa ^+)^M$
,
![]() $V_\kappa ^M$
, etc.
$V_\kappa ^M$
, etc.
The primary large cardinals we will be interested in are measurable cardinals. We say that a cardinal
![]() $\kappa $
is measurable if it carries a non-principal
$\kappa $
is measurable if it carries a non-principal
![]() $\kappa $
-complete ultrafilter. In the Introduction, we also mentioned the compact cardinals, which can be characterized using the filter extension property: we say
$\kappa $
-complete ultrafilter. In the Introduction, we also mentioned the compact cardinals, which can be characterized using the filter extension property: we say
![]() $\kappa $
has the
$\kappa $
has the
![]() $\lambda $
-filter extension property if every
$\lambda $
-filter extension property if every
![]() $\kappa $
-complete filter on
$\kappa $
-complete filter on
![]() $\lambda $
can be extended to a
$\lambda $
can be extended to a
![]() $\kappa $
-complete ultrafilter. A
$\kappa $
-complete ultrafilter. A
![]() $\kappa $
-compact cardinal is a cardinal
$\kappa $
-compact cardinal is a cardinal
![]() $\kappa $
which has that
$\kappa $
which has that
![]() $\kappa $
-filter extension property. For more background on large cardinals, we refer the reader to [Reference Kanamori25].
$\kappa $
-filter extension property. For more background on large cardinals, we refer the reader to [Reference Kanamori25].
Definition 2.1 (Special properties of ultrafilters)
Let U be an ultrafilter over a regular cardinal
![]() $\kappa $
. We say that:
$\kappa $
. We say that:
-
(1) A function f on
 $\kappa $
is said to be constant (mod U) if there is a set
$\kappa $
is said to be constant (mod U) if there is a set
 $A\in U$
such that
$A\in U$
such that
 $f\restriction A$
is constant. A function f is unbounded (mod U) if
$f\restriction A$
is constant. A function f is unbounded (mod U) if
 $\forall \alpha <\kappa $
,
$\forall \alpha <\kappa $
,
 $f^{-1}[\alpha ]\notin U$
. A function f is almost one-to-one (mod U) if there is a set
$f^{-1}[\alpha ]\notin U$
. A function f is almost one-to-one (mod U) if there is a set
 $A\in U$
such that
$A\in U$
such that
 $f\restriction A$
is almost one-to-one in the sense that for any x,
$f\restriction A$
is almost one-to-one in the sense that for any x,
 $\{\alpha \in A : f(\alpha ) = x\}$
is bounded below
$\{\alpha \in A : f(\alpha ) = x\}$
is bounded below
 $\kappa $
.
$\kappa $
. -
(2) U is a p-point if every function
 $f\colon \kappa \rightarrow \kappa $
which is unbounded
$f\colon \kappa \rightarrow \kappa $
which is unbounded
 $(\text {mod }U)$
is almost one-to-one
$(\text {mod }U)$
is almost one-to-one
 $(\text {mod }U)$
.Footnote
7
$(\text {mod }U)$
.Footnote
7
-
(3) U is
 $\mu $
-indecomposable if for any function
$\mu $
-indecomposable if for any function
 $f\colon \kappa \rightarrow \mu $
, there is
$f\colon \kappa \rightarrow \mu $
, there is
 $\mu '<\mu $
such that
$\mu '<\mu $
such that
 $f^{-1}[\mu ']\in U$
.
$f^{-1}[\mu ']\in U$
. -
(4) U is weakly normal if whenever
 $f\colon A\rightarrow \kappa $
is such that
$f\colon A\rightarrow \kappa $
is such that
 $A\in U$
and f is regressive, there is
$A\in U$
and f is regressive, there is
 $A'\subseteq A$
,
$A'\subseteq A$
,
 $A'\in U$
such that
$A'\in U$
such that
 $f"[A']$
is bounded.Footnote
8
$f"[A']$
is bounded.Footnote
8
-
(5) U is
 $\alpha $
-sound if the function
$\alpha $
-sound if the function
 $j^\alpha \colon P(\kappa )\rightarrow M_U$
defined by
$j^\alpha \colon P(\kappa )\rightarrow M_U$
defined by
 $j^\alpha (X)=j_U(X)\cap \alpha $
belongs to
$j^\alpha (X)=j_U(X)\cap \alpha $
belongs to
 $M_U$
.
$M_U$
. -
(6) U is Dodd sound if it is
 $[\text {id}]_U$
-sound.
$[\text {id}]_U$
-sound. -
(7) U is
 $\kappa $
-irreducible if every ultrafilter W on an ordinal
$\kappa $
-irreducible if every ultrafilter W on an ordinal
 $\lambda <\kappa $
that is Rudin–Frolík below U is principal (see Definition 2.15).
$\lambda <\kappa $
that is Rudin–Frolík below U is principal (see Definition 2.15).
Remark 2.2.
-
(1) The concept of Dodd soundness arose in inner model theory, where it serves as a strong form of the initial segment condition [Reference Schimmerling33]. Though on first glance, it may appear quite different, the Dodd soundness of a mouse is essentially equivalent to the Dodd soundness of its last extender as defined above. The formulation of Dodd soundness given here is due to Goldberg [Reference Goldberg17].
-
(2) Note that if U is
 $\alpha $
-sound, then
$\alpha $
-sound, then
 $\{j_U(A)\cap \alpha \mid A\subseteq \kappa \}\in M_U$
. This is in fact equivalent. Indeed, if
$\{j_U(A)\cap \alpha \mid A\subseteq \kappa \}\in M_U$
. This is in fact equivalent. Indeed, if
 $\{j_U(A)\cap \alpha \mid A\subseteq \kappa \}\in M_U$
, then it is the inverse of the transitive collapse of
$\{j_U(A)\cap \alpha \mid A\subseteq \kappa \}\in M_U$
, then it is the inverse of the transitive collapse of
 $\{j(S)\cap [\text {id}]_U\mid S\in P(\kappa )\}$
.
$\{j(S)\cap [\text {id}]_U\mid S\in P(\kappa )\}$
. -
(3) Note that if U is an ultrafilter over a regular cardinal
 $\kappa $
, and
$\kappa $
, and
 $\lambda <\kappa $
is such that
$\lambda <\kappa $
is such that
 $\lambda \in U$
, then automatically, U is a p-point as for any function
$\lambda \in U$
, then automatically, U is a p-point as for any function
 $f:\kappa \rightarrow \kappa $
,
$f:\kappa \rightarrow \kappa $
,
 $f\restriction \lambda $
is bounded and hence there are no unbounded functions mod U.
$f\restriction \lambda $
is bounded and hence there are no unbounded functions mod U. -
(4) If U is irreducible and uniform on
 $\lambda $
, then U is
$\lambda $
, then U is
 $\lambda $
-irreducible.
$\lambda $
-irreducible.
Proposition 2.3 Let
![]() $f\colon \kappa \rightarrow \kappa $
be any function, and let U be an ultrafilter over
$f\colon \kappa \rightarrow \kappa $
be any function, and let U be an ultrafilter over
![]() $\kappa $
.
$\kappa $
.
-
(1) f is unbounded mod U if and only if
 $\sup _{\alpha <\kappa }j_U(\alpha )\leq [f]_U$
.
$\sup _{\alpha <\kappa }j_U(\alpha )\leq [f]_U$
. -
(2) f is almost one-to-one mod U if and only if there is a (monotone) function
 $g\colon \kappa \rightarrow \kappa $
such that
$g\colon \kappa \rightarrow \kappa $
such that
 $j_U(g)([f]_U)=[g\circ f]_U\geq [\text {id}]_U$
.
$j_U(g)([f]_U)=[g\circ f]_U\geq [\text {id}]_U$
.
Proof
![]() $(1)$
is trivial. For
$(1)$
is trivial. For
![]() $(2)$
, suppose that f is almost one-to-one on
$(2)$
, suppose that f is almost one-to-one on
![]() $A\in U$
, and let for each
$A\in U$
, and let for each
![]() $\alpha <\kappa \ g(\alpha )=\sup f^{-1}[\alpha +1]\cap A$
. Then for each
$\alpha <\kappa \ g(\alpha )=\sup f^{-1}[\alpha +1]\cap A$
. Then for each
![]() $\xi \in A\ g(f(\xi ))=\sup f^{-1}[f(\xi )+1]\cap A\geq \xi $
, hence
$\xi \in A\ g(f(\xi ))=\sup f^{-1}[f(\xi )+1]\cap A\geq \xi $
, hence
![]() $[g\circ f]_U\geq [\text {id}]_U$
. For the other direction, let g be a monotone function such that
$[g\circ f]_U\geq [\text {id}]_U$
. For the other direction, let g be a monotone function such that
![]() $[g\circ f]_U\geq [\text {id}]_U$
. Then there is a set
$[g\circ f]_U\geq [\text {id}]_U$
. Then there is a set
![]() $A\in U$
such that for each
$A\in U$
such that for each
![]() $\alpha \in A$
,
$\alpha \in A$
,
![]() $g\circ f(\alpha )\geq \alpha $
. Hence, if
$g\circ f(\alpha )\geq \alpha $
. Hence, if
![]() $\beta \in f^{-1}[\alpha ]$
, then
$\beta \in f^{-1}[\alpha ]$
, then
![]() $g(\alpha )\geq g(f(\beta ))\geq \beta $
, hence
$g(\alpha )\geq g(f(\beta ))\geq \beta $
, hence
![]() $f^{-1}[\alpha ]\subseteq g(\alpha )+1$
.
$f^{-1}[\alpha ]\subseteq g(\alpha )+1$
.
Definition 2.4. Suppose U is an ultrafilter over X and for each
![]() $\alpha \in X$
,
$\alpha \in X$
,
![]() $U_\alpha $
is an ultrafilter over
$U_\alpha $
is an ultrafilter over
![]() $X_\alpha $
. Define the limit
$X_\alpha $
. Define the limit
and the sum
where
![]() $(Y)_\alpha =\{\beta \in X_\alpha \mid (\alpha ,\beta )\in Y\}$
is the
$(Y)_\alpha =\{\beta \in X_\alpha \mid (\alpha ,\beta )\in Y\}$
is the
![]() $\alpha {\text {th}}$
fiber of Y.
$\alpha {\text {th}}$
fiber of Y.
The key property of sums is that they yield ultrafilters that represent iterated ultrapowers.
Lemma 2.5 [Reference Goldberg17, Corollary 5.2.7]
If U is an ultrafilter on X and
![]() $\langle W_\alpha \rangle _{\alpha \in X}$
is a sequence of ultrafilters, then letting
$\langle W_\alpha \rangle _{\alpha \in X}$
is a sequence of ultrafilters, then letting
![]() $W^* = [\alpha \mapsto W_\alpha ]_U$
,
$W^* = [\alpha \mapsto W_\alpha ]_U$
,
![]() $M_{\sum _U {\langle } W_\alpha {\rangle }_{\alpha \in X}} = (M_{W^*})^{M_U}$
and
$M_{\sum _U {\langle } W_\alpha {\rangle }_{\alpha \in X}} = (M_{W^*})^{M_U}$
and
![]() $j_{\sum _U {\langle } W_\alpha {\rangle }_{\alpha \in x}} = (j_{W^*})^{M_U}\circ j_U$
. Moreover,
$j_{\sum _U {\langle } W_\alpha {\rangle }_{\alpha \in x}} = (j_{W^*})^{M_U}\circ j_U$
. Moreover,
![]() $U\text {-}\lim {\langle } W_\alpha {\rangle }_{\alpha \in X} = j_U^{-1}[W^*].$
$U\text {-}\lim {\langle } W_\alpha {\rangle }_{\alpha \in X} = j_U^{-1}[W^*].$
The sum construction is often used to obtain an ultrafilter representing an iterated ultrapower in this way, and in this context, the choice of the sequence
![]() $\langle W_\alpha \rangle _{\alpha \in X}$
representing
$\langle W_\alpha \rangle _{\alpha \in X}$
representing
![]() $W^*$
is usually irrelevant and distracting. For this reason, we introduce a notation that allows us to remain agnostic about this choice.
$W^*$
is usually irrelevant and distracting. For this reason, we introduce a notation that allows us to remain agnostic about this choice.
Definition 2.6. If U is an ultrafilter over X and
![]() $M_U$
satisfies that
$M_U$
satisfies that
![]() $W^*$
is an ultrafilter, then
$W^*$
is an ultrafilter, then
![]() $U^\frown W^*$
denotes
$U^\frown W^*$
denotes
![]() $\sum _U {\langle } W_\alpha {\rangle }_{\alpha \in X}$
, where
$\sum _U {\langle } W_\alpha {\rangle }_{\alpha \in X}$
, where
![]() $W_\alpha $
is a sequence of ultrafilters such that
$W_\alpha $
is a sequence of ultrafilters such that
![]() $W^* = [\alpha \mapsto W_\alpha ]_U$
.
$W^* = [\alpha \mapsto W_\alpha ]_U$
.
Technically, the definition of
![]() $U^\frown W^*$
depends on the choice of the underlying sets of
$U^\frown W^*$
depends on the choice of the underlying sets of
![]() $W_\alpha $
. This ambiguity causes no issues, however, since if
$W_\alpha $
. This ambiguity causes no issues, however, since if
![]() $W_\alpha '$
is another sequence such that
$W_\alpha '$
is another sequence such that
![]() $W^* = [\alpha \mapsto W_\alpha ']_U$
, then letting
$W^* = [\alpha \mapsto W_\alpha ']_U$
, then letting
![]() $Z = \sum _U {\langle } W_\alpha {\rangle }_{\alpha \in X}$
and
$Z = \sum _U {\langle } W_\alpha {\rangle }_{\alpha \in X}$
and
![]() $Z' = \sum _U {\langle } W^{\prime }_\alpha {\rangle }_{\alpha \in X}$
, there is a set
$Z' = \sum _U {\langle } W^{\prime }_\alpha {\rangle }_{\alpha \in X}$
, there is a set
![]() $S\in Z\cap Z'$
such that
$S\in Z\cap Z'$
such that
![]() $Z \cap P(S) = Z'\cap P(S)$
.
$Z \cap P(S) = Z'\cap P(S)$
.
Definition 2.7. We define recursively when U is an n-fold sum of p-points. W is a one-fold sum of p-points if W is a p-point. We say that W is an
![]() $(n+1)$
-fold sum of p-points if there are n-fold sums of p-points
$(n+1)$
-fold sum of p-points if there are n-fold sums of p-points
![]() $U_\alpha $
and a p-point ultrafilter U such that U is Rudin–Keisler equivalent to
$U_\alpha $
and a p-point ultrafilter U such that U is Rudin–Keisler equivalent to
![]() $\sum _{U}{\langle } U_\alpha {\rangle }_{\alpha <\kappa }$
.
$\sum _{U}{\langle } U_\alpha {\rangle }_{\alpha <\kappa }$
.
We shall now prove a slight improvement of the form of ultrafilters which have the Galvin property in Theorem 1.2, this will be turn out to be an exact characterization of the ultrafilters with the Galvin property under UA plus every irreducible is Dodd sound in Main Theorem 1.3. We need the definition of the modified diagonal intersection.
Definition 2.8. Suppose that W is a
![]() $\kappa $
-complete ultrafilter over
$\kappa $
-complete ultrafilter over
![]() $\kappa $
, and let
$\kappa $
, and let
![]() $\pi _W:\kappa \rightarrow \kappa $
be the function which represents
$\pi _W:\kappa \rightarrow \kappa $
be the function which represents
![]() $\kappa $
mod W. For a sequence
$\kappa $
mod W. For a sequence
![]() ${\langle } A_i{\rangle }_{i<\kappa }$
of subsets of
${\langle } A_i{\rangle }_{i<\kappa }$
of subsets of
![]() $\kappa $
, we define the modified diagonal intersection by
$\kappa $
, we define the modified diagonal intersection by
Fact 2.9. If W is a
![]() $\kappa $
-complete ultrafilter over
$\kappa $
-complete ultrafilter over
![]() $\kappa $
and
$\kappa $
and
![]() ${\langle } A_i{\rangle }_{i<\kappa }\subseteq W$
, then:
${\langle } A_i{\rangle }_{i<\kappa }\subseteq W$
, then:
-
(1)
 $\Delta ^W_{i<\kappa }A_i\in W$
.
$\Delta ^W_{i<\kappa }A_i\in W$
. -
(2) For every
 $i_0<\kappa $
,
$i_0<\kappa $
,
 $(\Delta ^W_{i<\kappa }A_i)\setminus (\pi ^{-1}[i_0+1])\subseteq A_{i_0}$
.
$(\Delta ^W_{i<\kappa }A_i)\setminus (\pi ^{-1}[i_0+1])\subseteq A_{i_0}$
.
Theorem 2.10 Suppose that
![]() $\lambda <\kappa $
, let D be any ultrafilter over
$\lambda <\kappa $
, let D be any ultrafilter over
![]() $\lambda $
, and let
$\lambda $
, and let
![]() ${\langle } W_\xi {\rangle }_{ \xi <\lambda }$
be a sequence of n-fold sums of
${\langle } W_\xi {\rangle }_{ \xi <\lambda }$
be a sequence of n-fold sums of
![]() $\kappa $
-complete p-point ultrafilters over
$\kappa $
-complete p-point ultrafilters over
![]() $\kappa $
. Then
$\kappa $
. Then
![]() $\sum _{D}{\langle } W_\xi {\rangle }_{\xi <\lambda }$
has the Galvin property.
$\sum _{D}{\langle } W_\xi {\rangle }_{\xi <\lambda }$
has the Galvin property.
Proof Denote by
![]() $Z:=\sum _{D}{\langle } W_\xi {\rangle }_{\xi <\lambda }$
, and let us assume for simplicity of notation that
$Z:=\sum _{D}{\langle } W_\xi {\rangle }_{\xi <\lambda }$
, and let us assume for simplicity of notation that
![]() $n=2$
. Hence,
$n=2$
. Hence,
![]() $Z=\sum _{D}{\langle }\sum _{U_\xi }{\langle } U_{\xi ,\eta }{\rangle }_{\eta <\kappa }{\rangle }_{\xi <\lambda }$
, where each
$Z=\sum _{D}{\langle }\sum _{U_\xi }{\langle } U_{\xi ,\eta }{\rangle }_{\eta <\kappa }{\rangle }_{\xi <\lambda }$
, where each
![]() $U_{\xi }$
and
$U_{\xi }$
and
![]() $U_{\xi ,\eta }$
is a
$U_{\xi ,\eta }$
is a
![]() $\kappa $
-complete p-point over
$\kappa $
-complete p-point over
![]() $\kappa $
. For
$\kappa $
. For
![]() $A\in Z$
, define
$A\in Z$
, define
 $$ \begin{align*}A^{(2)}_{i,j}&=\{k<\kappa\mid {\langle} i,j,k{\rangle}\in A\},\\A^{(1)}_i&=\{j<\kappa\mid A^{(2)}_{i,j}\in U_{i,j}\},\\A^{(0)}&=\{i<\lambda\mid A^{(1)}_i\in U_i\}.\end{align*} $$
$$ \begin{align*}A^{(2)}_{i,j}&=\{k<\kappa\mid {\langle} i,j,k{\rangle}\in A\},\\A^{(1)}_i&=\{j<\kappa\mid A^{(2)}_{i,j}\in U_{i,j}\},\\A^{(0)}&=\{i<\lambda\mid A^{(1)}_i\in U_i\}.\end{align*} $$
Note that
For any
![]() $W\in \{U_i\mid i<\lambda \}\cup \{U_{i,j}\mid i<\lambda ,\ j<\kappa \}$
, choose
$W\in \{U_i\mid i<\lambda \}\cup \{U_{i,j}\mid i<\lambda ,\ j<\kappa \}$
, choose
![]() $\pi _W:\kappa \rightarrow \kappa $
such that
$\pi _W:\kappa \rightarrow \kappa $
such that
![]() $[\pi _W]_W=\kappa $
and
$[\pi _W]_W=\kappa $
and
![]() $\pi _W$
is almost one-to-one. Such a function exists since W is a
$\pi _W$
is almost one-to-one. Such a function exists since W is a
![]() $\kappa $
-complete p-point. Define
$\kappa $
-complete p-point. Define
![]() $\rho _W:\kappa \rightarrow \kappa $
by
$\rho _W:\kappa \rightarrow \kappa $
by
Next, we define
Note that
![]() $\rho ^{(1)},\rho ^{(2)}:\kappa \rightarrow \kappa $
since
$\rho ^{(1)},\rho ^{(2)}:\kappa \rightarrow \kappa $
since
![]() $\kappa $
is regular. Now we are ready to prove the theorem. Let
$\kappa $
is regular. Now we are ready to prove the theorem. Let
![]() ${\langle } A_i{\rangle }_{i<2^\kappa }$
be a sequence of sets in Z. Since
${\langle } A_i{\rangle }_{i<2^\kappa }$
be a sequence of sets in Z. Since
![]() $\lambda <\kappa $
, we can assume without loss of generality that there is a set
$\lambda <\kappa $
, we can assume without loss of generality that there is a set
![]() $A^{(0)}_*\in D$
such that for every
$A^{(0)}_*\in D$
such that for every
![]() $i<2^\kappa $
,
$i<2^\kappa $
,
![]() $A_*^{(0)}=(A_i)^{(0)}$
. Let
$A_*^{(0)}=(A_i)^{(0)}$
. Let
![]() $\mathcal {N}$
be an elementary substructure of
$\mathcal {N}$
be an elementary substructure of
![]() $H(\theta )$
for some large enough
$H(\theta )$
for some large enough
![]() $\theta $
such that:
$\theta $
such that:
-
(1)
 $|\mathcal {N}|=\kappa $
.
$|\mathcal {N}|=\kappa $
. -
(2)
 ${}^{<\kappa }\mathcal {N}\subseteq \mathcal {N}$
.
${}^{<\kappa }\mathcal {N}\subseteq \mathcal {N}$
. -
(3)
 $\kappa \subseteq \mathcal {N}$
and
$\kappa \subseteq \mathcal {N}$
and
 $\kappa ^+\cap \mathcal {N}\in \kappa ^+$
.
$\kappa ^+\cap \mathcal {N}\in \kappa ^+$
. -
(4)
 ${\langle } A_i{\rangle }_{i<2^\kappa }\in \mathcal {N}$
.
${\langle } A_i{\rangle }_{i<2^\kappa }\in \mathcal {N}$
.
Let
![]() $\alpha ^*=\kappa ^+\cap \mathcal {N}$
.
$\alpha ^*=\kappa ^+\cap \mathcal {N}$
.
Claim 2.11 For every
![]() ${\langle }\alpha _1,\alpha _2{\rangle }\in [\kappa ]^2$
and
${\langle }\alpha _1,\alpha _2{\rangle }\in [\kappa ]^2$
and
![]() $\delta <\alpha ^*$
, there is
$\delta <\alpha ^*$
, there is
![]() $\delta <\beta <\alpha ^*$
such that:
$\delta <\beta <\alpha ^*$
such that:
-
(1)
 $\forall i\in (A_*)^{(0)}, (A_{\beta })^{(1)}_i\cap \alpha _1=(A_{\alpha ^*})^{(1)}_i\cap \alpha _1$
.
$\forall i\in (A_*)^{(0)}, (A_{\beta })^{(1)}_i\cap \alpha _1=(A_{\alpha ^*})^{(1)}_i\cap \alpha _1$
. -
(2)
 $\forall i\in (A_*)^{(0)}\forall j<\alpha _1, \ (A_{\beta })^{(2)}_{i,j}\cap \alpha _2=(A_{\alpha ^*})^{(2)}_{i,j}\cap \alpha _2$
.
$\forall i\in (A_*)^{(0)}\forall j<\alpha _1, \ (A_{\beta })^{(2)}_{i,j}\cap \alpha _2=(A_{\alpha ^*})^{(2)}_{i,j}\cap \alpha _2$
.
Proof Consider the statement
![]() $H(\theta )\models \phi (\alpha _1,\alpha _2,\delta )$
as witnessed by
$H(\theta )\models \phi (\alpha _1,\alpha _2,\delta )$
as witnessed by
![]() $\alpha ^*$
and since
$\alpha ^*$
and since
![]() $\alpha _1,\alpha _2,\delta \in \mathcal {N}$
, the elementarity of
$\alpha _1,\alpha _2,\delta \in \mathcal {N}$
, the elementarity of
![]() $\mathcal {N}$
implies that there is such
$\mathcal {N}$
implies that there is such
![]() $\beta \in \mathcal {N}$
and, in particular,
$\beta \in \mathcal {N}$
and, in particular,
![]() $\beta <\alpha ^*$
.
$\beta <\alpha ^*$
.
Define a sequence
![]() ${\langle } \mu _i\mid i<\kappa {\rangle }$
inductively, suppose that
${\langle } \mu _i\mid i<\kappa {\rangle }$
inductively, suppose that
![]() ${\langle } \mu _j\mid j<i{\rangle }$
was defined. Let
${\langle } \mu _j\mid j<i{\rangle }$
was defined. Let
![]() $\delta =\sup _{j<i}\mu _j+1\in \mathcal {N}$
and apply the claim to
$\delta =\sup _{j<i}\mu _j+1\in \mathcal {N}$
and apply the claim to
![]() $\delta $
and
$\delta $
and
to produce
![]() $\mu _i>\delta $
(and thus
$\mu _i>\delta $
(and thus
![]() $\mu _i\neq \mu _j$
for all
$\mu _i\neq \mu _j$
for all
![]() $j<i$
). We claim that
$j<i$
). We claim that
To see this, we define for every
![]() $\xi \in (A_*)^{(0)}$
,
$\xi \in (A_*)^{(0)}$
,
and for every
![]() $\xi \in (A_*)^{(0)}$
,
$\xi \in (A_*)^{(0)}$
,
![]() $\eta \in (A_*)^{(1)}_\xi $
, define
$\eta \in (A_*)^{(1)}_\xi $
, define
Let
 $$ \begin{align*}A_*=\bigcup_{\xi\in A_*^{(0)}}\bigcup_{\eta\in (A_*)^{(1)}_\xi}\{\xi\}\times\{\eta\}\times (A_*)^{(2)}_{\xi,\eta}.\end{align*} $$
$$ \begin{align*}A_*=\bigcup_{\xi\in A_*^{(0)}}\bigcup_{\eta\in (A_*)^{(1)}_\xi}\{\xi\}\times\{\eta\}\times (A_*)^{(2)}_{\xi,\eta}.\end{align*} $$
Claim 2.12 For every
![]() ${\langle }\alpha ,\beta ,\gamma {\rangle }\in A_*$
, and for every
${\langle }\alpha ,\beta ,\gamma {\rangle }\in A_*$
, and for every
![]() $i<\kappa $
,
$i<\kappa $
,
![]() $\alpha \in (A_{\mu _i})^{(0)}$
,
$\alpha \in (A_{\mu _i})^{(0)}$
,
![]() $\beta \in (A_{\mu _i})^{(1)}_{\alpha }$
and
$\beta \in (A_{\mu _i})^{(1)}_{\alpha }$
and
![]() $\gamma \in (A_{\mu _i})^{(2)}_{\alpha ,\beta }$
.
$\gamma \in (A_{\mu _i})^{(2)}_{\alpha ,\beta }$
.
Proof of claim
Let
![]() ${\langle } \alpha ,\beta ,\gamma {\rangle }\in A_*$
. By definition of
${\langle } \alpha ,\beta ,\gamma {\rangle }\in A_*$
. By definition of
![]() $A_*$
,
$A_*$
,
![]() $\alpha \in (A_*)^{(0)}$
,
$\alpha \in (A_*)^{(0)}$
,
![]() $\beta \in (A_*)^{(1)}_\alpha $
and
$\beta \in (A_*)^{(1)}_\alpha $
and
![]() $\gamma \in (A_*)^{(2)}_{\alpha ,\beta }$
. In particular,
$\gamma \in (A_*)^{(2)}_{\alpha ,\beta }$
. In particular,
For
![]() $i<\kappa $
, we note first that
$i<\kappa $
, we note first that
![]() $\alpha \in (A_{\mu _i})^{(0)}$
since we assume
$\alpha \in (A_{\mu _i})^{(0)}$
since we assume
![]() $(A_{\mu _i})^{(0)}=(A_*)^{(0)}$
. Now to see that
$(A_{\mu _i})^{(0)}=(A_*)^{(0)}$
. Now to see that
![]() $\beta \in (A_{\mu _i})^{(1)}_\alpha $
, split into cases. If
$\beta \in (A_{\mu _i})^{(1)}_\alpha $
, split into cases. If
![]() $i<\pi _{U_\alpha }(\beta )$
, then
$i<\pi _{U_\alpha }(\beta )$
, then
![]() $\beta \in (A_{\mu _i})^{(1)}_\alpha $
by the definition of the modified diagonal intersection. If
$\beta \in (A_{\mu _i})^{(1)}_\alpha $
by the definition of the modified diagonal intersection. If
![]() $i\geq \pi _{U_{\alpha }}(\beta )$
, then
$i\geq \pi _{U_{\alpha }}(\beta )$
, then
![]() $\beta <\rho _{U_\alpha }(i)$
. Also, by
$\beta <\rho _{U_\alpha }(i)$
. Also, by
![]() $(*)$
,
$(*)$
,
![]() $\alpha <\pi _{U_\alpha }(\beta )\leq i$
and therefore
$\alpha <\pi _{U_\alpha }(\beta )\leq i$
and therefore
![]() $\rho _{U_\alpha }(i)\leq \sup _{\alpha <i}\rho _{U_\alpha }(i)=\rho ^{(1)}(i)$
. By the choice of
$\rho _{U_\alpha }(i)\leq \sup _{\alpha <i}\rho _{U_\alpha }(i)=\rho ^{(1)}(i)$
. By the choice of
![]() $\mu _i$
, (1) of Claim 2.11
$\mu _i$
, (1) of Claim 2.11
Finally for
![]() $\gamma $
, if
$\gamma $
, if
![]() $i<\pi _{U_{\alpha ,\beta }}(\gamma )$
, then
$i<\pi _{U_{\alpha ,\beta }}(\gamma )$
, then
![]() $\gamma \in (A_{\mu _i})^{(2)}_{\alpha ,\beta }$
. If
$\gamma \in (A_{\mu _i})^{(2)}_{\alpha ,\beta }$
. If
![]() $i\geq \pi _{U_{\alpha ,\beta }}(\gamma )$
, then as in the previous paragraph,
$i\geq \pi _{U_{\alpha ,\beta }}(\gamma )$
, then as in the previous paragraph,
![]() $\beta <\pi _{U_{\alpha ,\beta }}(\gamma )\leq i$
and thus
$\beta <\pi _{U_{\alpha ,\beta }}(\gamma )\leq i$
and thus
We conclude that
![]() $\gamma \in (A_{\alpha ^*})^{(2)}_{\alpha ,\beta }\cap \rho ^{(2)}(i)$
. By the choice of
$\gamma \in (A_{\alpha ^*})^{(2)}_{\alpha ,\beta }\cap \rho ^{(2)}(i)$
. By the choice of
![]() $\mu _i$
and (2) of Claim 2.11,
$\mu _i$
and (2) of Claim 2.11,
![]() $\gamma \in (A_{\mu _i})^{(2)}_{\alpha ,\beta }\cap \rho ^{(2)}(i)$
.
$\gamma \in (A_{\mu _i})^{(2)}_{\alpha ,\beta }\cap \rho ^{(2)}(i)$
.
By the claim, that for every
![]() ${\langle }\alpha ,\beta ,\gamma {\rangle }\in A_*$
and every
${\langle }\alpha ,\beta ,\gamma {\rangle }\in A_*$
and every
![]() $i<\kappa $
,
$i<\kappa $
,
![]() ${\langle } \alpha ,\beta ,\gamma {\rangle }\in A_{\mu _i}$
, namely
${\langle } \alpha ,\beta ,\gamma {\rangle }\in A_{\mu _i}$
, namely
![]() $A_*\subseteq \bigcap _{i<\kappa }A_{\mu _i}$
. Finally, we note that
$A_*\subseteq \bigcap _{i<\kappa }A_{\mu _i}$
. Finally, we note that
![]() $A_*\in Z$
. Indeed,
$A_*\in Z$
. Indeed,
![]() $(A_*)^{(0)}\in D$
by the choice of
$(A_*)^{(0)}\in D$
by the choice of
![]() $(A_*)^{(0)}$
. Also, for every
$(A_*)^{(0)}$
. Also, for every
![]() $i<\kappa $
, and
$i<\kappa $
, and
![]() $\alpha \in (A_*)^{(0)}$
,
$\alpha \in (A_*)^{(0)}$
,
![]() $\alpha \in (A_{\mu _i})^{(0)}$
and so
$\alpha \in (A_{\mu _i})^{(0)}$
and so
![]() $(A_{\mu _i})^{(1)}_\alpha \in U_\alpha $
. We conclude
$(A_{\mu _i})^{(1)}_\alpha \in U_\alpha $
. We conclude
![]() $(A_*)^{(1)}_\alpha \in U_\alpha $
. Also, for
$(A_*)^{(1)}_\alpha \in U_\alpha $
. Also, for
![]() $\beta \in (A_*)^{(1)}_{\alpha }$
,
$\beta \in (A_*)^{(1)}_{\alpha }$
,
![]() $\beta \in (A_{\mu _i})^{(1)}_{\alpha }$
and therefore
$\beta \in (A_{\mu _i})^{(1)}_{\alpha }$
and therefore
![]() $(A_{\mu _i})^{(2)}_{\alpha ,\beta }\in U_{\alpha ,\beta }$
. It follows that
$(A_{\mu _i})^{(2)}_{\alpha ,\beta }\in U_{\alpha ,\beta }$
. It follows that
![]() $(A_*)^{(2)}_{\alpha ,\beta }\in U_{\alpha ,\beta }$
. Hence,
$(A_*)^{(2)}_{\alpha ,\beta }\in U_{\alpha ,\beta }$
. Hence,
![]() $A_*\in Z$
, and in particular,
$A_*\in Z$
, and in particular,
![]() $\bigcap _{i<\kappa }A_{\mu _i}\in Z$
.
$\bigcap _{i<\kappa }A_{\mu _i}\in Z$
.
Recall that the sequence of
![]() ${\langle } U_\alpha {\rangle }_{\alpha \in X}$
is called discrete if there is a sequence of pairwise disjoint sets
${\langle } U_\alpha {\rangle }_{\alpha \in X}$
is called discrete if there is a sequence of pairwise disjoint sets
![]() ${\langle } A_\alpha {\rangle }_{\alpha \in X}$
such that
${\langle } A_\alpha {\rangle }_{\alpha \in X}$
such that
![]() $A_\alpha \in U_\alpha $
. We say that
$A_\alpha \in U_\alpha $
. We say that
![]() ${\langle } U_\alpha {\rangle }_{\alpha \in X}$
is discrete mod U, if there is
${\langle } U_\alpha {\rangle }_{\alpha \in X}$
is discrete mod U, if there is
![]() $Y\in U$
,
$Y\in U$
,
![]() $Y\subseteq X$
such
$Y\subseteq X$
such
![]() ${\langle } U_\alpha {\rangle }_{\alpha \in Y}$
is discrete.
${\langle } U_\alpha {\rangle }_{\alpha \in Y}$
is discrete.
Fact 2.13.
![]() $\sum _U{\langle } U_\alpha {\rangle }_{\alpha <\kappa }\equiv _{RK} U\text {-}\lim {\langle } U_\alpha {\rangle }_{\alpha <\kappa }$
iff
$\sum _U{\langle } U_\alpha {\rangle }_{\alpha <\kappa }\equiv _{RK} U\text {-}\lim {\langle } U_\alpha {\rangle }_{\alpha <\kappa }$
iff
![]() ${\langle } U_\alpha {\rangle }_{ \alpha <\kappa }$
is discrete mod U.
${\langle } U_\alpha {\rangle }_{ \alpha <\kappa }$
is discrete mod U.
Proposition 2.14 If U is a p-point ultrafilter, then any sequence
![]() ${\langle } U_\alpha {\rangle }_{ \alpha <\kappa }$
of distinct
${\langle } U_\alpha {\rangle }_{ \alpha <\kappa }$
of distinct
![]() $\kappa $
-complete ultrafilters is discrete mod U.
$\kappa $
-complete ultrafilters is discrete mod U.
Proof See [Reference Kanamori24, Corollary 5.15].
Definition 2.15. (Orderings of ultrafilters)
Let
![]() $U,W$
be ultrafilters over ordinals
$U,W$
be ultrafilters over ordinals
![]() $\kappa ,\lambda $
(resp.) define:
$\kappa ,\lambda $
(resp.) define:
-
(1) The Rudin–Keisler order by
 $U\leq _{RK}W$
if there is a function
$U\leq _{RK}W$
if there is a function
 $\pi \colon \lambda \rightarrow \kappa $
such that
$\pi \colon \lambda \rightarrow \kappa $
such that
 $U=\{B\subseteq \kappa \mid \pi ^{-1}[B]\in W\}$
.
$U=\{B\subseteq \kappa \mid \pi ^{-1}[B]\in W\}$
. -
(2) The Rudin–Frolík order by
 $U\leq _{RF}W$
if there is a set
$U\leq _{RF}W$
if there is a set
 $I\in U$
and a discrete sequence
$I\in U$
and a discrete sequence
 ${\langle } W_i{\rangle }_{i\in I}$
of ultrafilters over
${\langle } W_i{\rangle }_{i\in I}$
of ultrafilters over
 $\kappa $
such that
$\kappa $
such that
 $W=U\text {-}\lim {\langle } W_i{\rangle }_{i\in I}$
.
$W=U\text {-}\lim {\langle } W_i{\rangle }_{i\in I}$
. -
(3) The Ketonen order by
 $U<_{\mathbb{k}}W$
if
$U<_{\mathbb{k}}W$
if
 $j_W"U$
is contained in a countably complete ultrafilter
$j_W"U$
is contained in a countably complete ultrafilter
 $U^*$
of
$U^*$
of
 $M_W$
such that
$M_W$
such that
 $[id]_W\in U^*$
.
$[id]_W\in U^*$
.
For more background on ultrafilters, their orderings, and the Ultrapower Axiom, we refer the reader to [Reference Kanamori24] and [Reference Goldberg17].
We also record here the definition and basic properties of the canonical functions.
Definition 2.16. For every
![]() $\eta <\kappa ^+$
, we fix a cofinal sequence
$\eta <\kappa ^+$
, we fix a cofinal sequence
![]() ${\langle } \eta _i{\rangle }_{i<\mathrm {cf}(\eta )}$
. Define recursively the canonical functions
${\langle } \eta _i{\rangle }_{i<\mathrm {cf}(\eta )}$
. Define recursively the canonical functions
![]() $f_\alpha \colon \kappa \rightarrow \kappa $
for
$f_\alpha \colon \kappa \rightarrow \kappa $
for
![]() $\alpha <\kappa ^+$
as follows:
$\alpha <\kappa ^+$
as follows:
![]() $f_0=0$
is the constant function with value
$f_0=0$
is the constant function with value
![]() $0$
. Given
$0$
. Given
![]() $f_\alpha $
, define
$f_\alpha $
, define
![]() $f_{\alpha +1}(x)=f_\alpha (x)+1$
. For limit
$f_{\alpha +1}(x)=f_\alpha (x)+1$
. For limit
![]() $\eta <\kappa ^+$
, we split into cases:
$\eta <\kappa ^+$
, we split into cases:
-
(1) If
 $\mathrm {cf}(\eta )<\kappa $
, define
$\mathrm {cf}(\eta )<\kappa $
, define
 $f_\eta (x)=\sup _{i<\mathrm {cf}(\eta )}f_{\eta _i}(x)$
.
$f_\eta (x)=\sup _{i<\mathrm {cf}(\eta )}f_{\eta _i}(x)$
. -
(2) If
 $\mathrm {cf}(\eta )=\kappa $
, define
$\mathrm {cf}(\eta )=\kappa $
, define
 $f_\eta (x)=\sup _{i<x}f_{\eta _i}(x)$
.
$f_\eta (x)=\sup _{i<x}f_{\eta _i}(x)$
.
It is not hard to see that the canonical functions are increasing modulo the bounded ideal, but the main reason we are interested in those functions is the following.
Proposition 2.17 Let
![]() $k\colon N\rightarrow M$
be an elementary embedding (not necessarily definable in N) with critical point
$k\colon N\rightarrow M$
be an elementary embedding (not necessarily definable in N) with critical point
![]() $\kappa $
. Then for every
$\kappa $
. Then for every
![]() $\alpha <(\kappa ^+)^N$
,
$\alpha <(\kappa ^+)^N$
,
![]() $k(f_\alpha )(\kappa )=\alpha $
.
$k(f_\alpha )(\kappa )=\alpha $
.
Proof By induction on
![]() $\alpha $
. Clearly, for
$\alpha $
. Clearly, for
![]() $\alpha =0$
,
$\alpha =0$
,
![]() $k(f_0)(\kappa )=0$
and if
$k(f_0)(\kappa )=0$
and if
![]() $k(f_\alpha )(\kappa )=\alpha $
, then by elementarity
$k(f_\alpha )(\kappa )=\alpha $
, then by elementarity
![]() $k(f_{\alpha +1})(\kappa )=\alpha +1$
. For limit
$k(f_{\alpha +1})(\kappa )=\alpha +1$
. For limit
![]() $\eta $
, if
$\eta $
, if
![]() $\mathrm {cf}(\eta )<\kappa $
, then the functions used in the definition of
$\mathrm {cf}(\eta )<\kappa $
, then the functions used in the definition of
![]() $f_\eta $
are
$f_\eta $
are
![]() ${\langle } f_{\eta _i}{\rangle }_{i<\mathrm {cf}(\eta )}$
are pointwise mapped by k; that is,
${\langle } f_{\eta _i}{\rangle }_{i<\mathrm {cf}(\eta )}$
are pointwise mapped by k; that is,
![]() $k({\langle } f_{\eta _i}\mid i<\mathrm {cf}(\eta ){\rangle })={\langle } k(f_{\eta _i})\mid i<\mathrm {cf}(\eta ){\rangle }$
. It follows by elementarity and the definition of
$k({\langle } f_{\eta _i}\mid i<\mathrm {cf}(\eta ){\rangle })={\langle } k(f_{\eta _i})\mid i<\mathrm {cf}(\eta ){\rangle }$
. It follows by elementarity and the definition of
![]() $f_\eta $
that
$f_\eta $
that
![]() $k(f_\eta )(\kappa )=\sup _{i<\mathrm {cf}(\eta )}k(f_{\eta _i})(\kappa )$
. Hence, by the induction hypothesis,
$k(f_\eta )(\kappa )=\sup _{i<\mathrm {cf}(\eta )}k(f_{\eta _i})(\kappa )$
. Hence, by the induction hypothesis,
![]() $k(f_\eta )(\kappa )=\sup _{i<\mathrm {cf}(\eta )}\eta _i=\eta $
. If
$k(f_\eta )(\kappa )=\sup _{i<\mathrm {cf}(\eta )}\eta _i=\eta $
. If
![]() $\mathrm {cf}(\eta )=\kappa $
, then the sequence
$\mathrm {cf}(\eta )=\kappa $
, then the sequence
![]() ${\langle } f_{\eta _i}\mid i<\kappa {\rangle }$
is stretched by k to
${\langle } f_{\eta _i}\mid i<\kappa {\rangle }$
is stretched by k to
![]() $k({\langle } f_{\eta _i}\mid i<\kappa {\rangle })={\langle } f^{\prime }_{\eta _i}\mid i<k(\kappa ){\rangle }$
but for every
$k({\langle } f_{\eta _i}\mid i<\kappa {\rangle })={\langle } f^{\prime }_{\eta _i}\mid i<k(\kappa ){\rangle }$
but for every
![]() $i<\kappa $
, as
$i<\kappa $
, as
![]() $k(i)=i$
, we have
$k(i)=i$
, we have
![]() $f^{\prime }_{\eta _i}=k(f_{\eta _i})$
. Again by the definition of
$f^{\prime }_{\eta _i}=k(f_{\eta _i})$
. Again by the definition of
![]() $f_\eta $
, elementarity, and the induction hypothesis, we conclude that
$f_\eta $
, elementarity, and the induction hypothesis, we conclude that
3 Diamond-like principle and the Galvin property
In [Reference Benhamou, Garti and Sehlah6], a relation between Kurepa trees and the Galvin property has been established to construct a
![]() $\kappa $
-complete non-Galvin ultrafilter. In this section, we exploit the deep connection between Kurepa trees and diamond principles which was first observed by Jensen [Reference Jensen and Kunen22], to find new combinatorial properties of ultrafilters which ensures the Galvin property.
$\kappa $
-complete non-Galvin ultrafilter. In this section, we exploit the deep connection between Kurepa trees and diamond principles which was first observed by Jensen [Reference Jensen and Kunen22], to find new combinatorial properties of ultrafilters which ensures the Galvin property.
Definition 3.1. Let S be a stationary set.
![]() $\diamondsuit ^*(S)$
is the assertion that there is a sequence
$\diamondsuit ^*(S)$
is the assertion that there is a sequence
![]() ${\langle }\mathcal {A}_\alpha {\rangle }_{\alpha \in S}$
such that
${\langle }\mathcal {A}_\alpha {\rangle }_{\alpha \in S}$
such that
![]() $\mathcal {A}_\alpha \subseteq P(\alpha )$
and:
$\mathcal {A}_\alpha \subseteq P(\alpha )$
and:
-
(1)
 $|\mathcal {A}_\alpha |\leq \alpha $
.
$|\mathcal {A}_\alpha |\leq \alpha $
. -
(2) For every
 $X\subseteq \kappa $
, there is a club C such that for each
$X\subseteq \kappa $
, there is a club C such that for each
 $\alpha \in C\cap S$
,
$\alpha \in C\cap S$
,
 $C\cap \alpha ,X\cap \alpha \in \mathcal {A}_\alpha $
.
$C\cap \alpha ,X\cap \alpha \in \mathcal {A}_\alpha $
.
Proposition 3.2 If
![]() $\diamondsuit ^*(S)$
holds, then any ultrafilter U over a regular cardinal
$\diamondsuit ^*(S)$
holds, then any ultrafilter U over a regular cardinal
![]() $\kappa $
satisfying
$\kappa $
satisfying
![]() $\text {Club}_\kappa \cup \{S\}\subseteq U$
and
$\text {Club}_\kappa \cup \{S\}\subseteq U$
and
![]() $\mathrm {cf}^{M_U}([\text {id}]_U)\leq \operatorname {\mathrm {crit}}(j_U)$
must be non-Galvin.
$\mathrm {cf}^{M_U}([\text {id}]_U)\leq \operatorname {\mathrm {crit}}(j_U)$
must be non-Galvin.
Proof Suppose otherwise, and let
![]() $C_X$
for every
$C_X$
for every
![]() $X\subseteq \kappa $
be the club guaranteed by item
$X\subseteq \kappa $
be the club guaranteed by item
![]() $(2)$
of
$(2)$
of
![]() $\diamondsuit ^*(S)$
. Then
$\diamondsuit ^*(S)$
. Then
![]() $C_X\in U$
. Also, for each
$C_X\in U$
. Also, for each
![]() $\alpha \in S$
, let
$\alpha \in S$
, let
![]() ${\langle } I^\alpha _i{\rangle }_{i<\mathrm { cf}(\alpha )}$
be a partition of
${\langle } I^\alpha _i{\rangle }_{i<\mathrm { cf}(\alpha )}$
be a partition of
![]() $\mathcal {A}_\alpha $
such that
$\mathcal {A}_\alpha $
such that
![]() $|I^\alpha _i|<\alpha $
. Now for each
$|I^\alpha _i|<\alpha $
. Now for each
![]() $X\subseteq \kappa $
, consider the function
$X\subseteq \kappa $
, consider the function
![]() $f_X:C_{X}\cap S\rightarrow \kappa $
defined by
$f_X:C_{X}\cap S\rightarrow \kappa $
defined by
![]() $f_X(\alpha )=i<\mathrm {cf}(\alpha )$
for the unique i such that
$f_X(\alpha )=i<\mathrm {cf}(\alpha )$
for the unique i such that
![]() $X\cap \alpha \in I^\alpha _i$
. Since
$X\cap \alpha \in I^\alpha _i$
. Since
![]() $cf^{M_U}([id]_U)\leq \operatorname {\mathrm {crit}}(j_U)$
, there is a function
$cf^{M_U}([id]_U)\leq \operatorname {\mathrm {crit}}(j_U)$
, there is a function
![]() $\pi :\kappa \rightarrow On$
such that
$\pi :\kappa \rightarrow On$
such that
![]() $i<\mathrm {cf}(\alpha )\leq \pi (\alpha )$
and
$i<\mathrm {cf}(\alpha )\leq \pi (\alpha )$
and
![]() $[\pi ]_U=\operatorname {\mathrm {crit}}(j_U)$
. It follows that there is
$[\pi ]_U=\operatorname {\mathrm {crit}}(j_U)$
. It follows that there is
![]() $A_X\subseteq C_{X}\cap S$
,
$A_X\subseteq C_{X}\cap S$
,
![]() $A_X\in U$
and
$A_X\in U$
and
![]() $\gamma _X<\kappa $
such that for every
$\gamma _X<\kappa $
such that for every
![]() $\alpha \in A_X$
,
$\alpha \in A_X$
,
![]() $f_X(\alpha )=\gamma _X$
. There are
$f_X(\alpha )=\gamma _X$
. There are
![]() $2^\kappa $
-many subsets with the same
$2^\kappa $
-many subsets with the same
![]() $\gamma _X=\gamma ^*$
. Now apply Galvin’s property to those
$\gamma _X=\gamma ^*$
. Now apply Galvin’s property to those
![]() $2^\kappa $
-many sets in order find
$2^\kappa $
-many sets in order find
![]() $\kappa $
-many distinct subsets of
$\kappa $
-many distinct subsets of
![]() $\kappa $
,
$\kappa $
,
![]() ${\langle } X_\xi {\rangle }_{\xi <\kappa }$
for which
${\langle } X_\xi {\rangle }_{\xi <\kappa }$
for which
![]() $A^*:=\bigcap _{\xi <\kappa }A_{X_\xi }\in U$
. Now for each
$A^*:=\bigcap _{\xi <\kappa }A_{X_\xi }\in U$
. Now for each
![]() $\alpha \in A^*\cap S$
,
$\alpha \in A^*\cap S$
,
![]() $|I^\alpha _{\gamma ^*}|<\alpha $
. Since
$|I^\alpha _{\gamma ^*}|<\alpha $
. Since
![]() $\kappa $
is regular, we may apply Födor’s lemma to find a stationary set
$\kappa $
is regular, we may apply Födor’s lemma to find a stationary set
![]() $S'\subseteq A^*\cap S$
and
$S'\subseteq A^*\cap S$
and
![]() $\theta <\kappa $
such that
$\theta <\kappa $
such that
![]() $|I^\alpha _{\gamma ^*}|=\theta $
for each
$|I^\alpha _{\gamma ^*}|=\theta $
for each
![]() $\alpha \in S'$
. Consider
$\alpha \in S'$
. Consider
![]() ${\langle } X_i{\rangle }_{i<\theta ^{+}}$
and for each
${\langle } X_i{\rangle }_{i<\theta ^{+}}$
and for each
![]() $i\neq j<\theta ^{+}$
, let
$i\neq j<\theta ^{+}$
, let
![]() $\beta _{i,j}<\kappa $
be high enough so that
$\beta _{i,j}<\kappa $
be high enough so that
![]() $X_i\cap \beta _{i,j}\neq X_j\cap \beta _{i,j}$
. Take any
$X_i\cap \beta _{i,j}\neq X_j\cap \beta _{i,j}$
. Take any
![]() $\alpha \in S'\setminus \sup _{i\neq j<\theta ^{+}}\beta _{i,j}$
. To reach a contradiction, note that on one hand, since
$\alpha \in S'\setminus \sup _{i\neq j<\theta ^{+}}\beta _{i,j}$
. To reach a contradiction, note that on one hand, since
![]() $\alpha \in S'$
,
$\alpha \in S'$
,
![]() $|I^{\alpha }_{\gamma ^*}|=\theta $
. On the other hand, for every
$|I^{\alpha }_{\gamma ^*}|=\theta $
. On the other hand, for every
![]() $i\neq j<\theta ^{+}$
,
$i\neq j<\theta ^{+}$
,
![]() $X_i\cap \alpha \in I^{\alpha }_{\gamma ^*}$
and the sets
$X_i\cap \alpha \in I^{\alpha }_{\gamma ^*}$
and the sets
![]() $X_i\cap \alpha $
are all distinct.
$X_i\cap \alpha $
are all distinct.
Let us introduce a similar guessing principle
![]() $\diamondsuit ^*_{\mathrm{thin}}(U)$
to the one above, which can be formulated in terms of the ultrapower and does not involve the club filter. Then we will prove that
$\diamondsuit ^*_{\mathrm{thin}}(U)$
to the one above, which can be formulated in terms of the ultrapower and does not involve the club filter. Then we will prove that
![]() $\diamondsuit ^*_{\mathrm{thin}}(U)$
implies that U is non-Galvin.
$\diamondsuit ^*_{\mathrm{thin}}(U)$
implies that U is non-Galvin.
Definition 3.3. An ultrafilter W on a regular cardinal
![]() $\kappa $
satisfies
$\kappa $
satisfies
![]() $\diamondsuit ^*_{\mathrm{thin}}(W)$
if there is a sequence of sets
$\diamondsuit ^*_{\mathrm{thin}}(W)$
if there is a sequence of sets
![]() $\langle \mathcal A_\alpha \rangle _{\alpha < \kappa }$
such that:
$\langle \mathcal A_\alpha \rangle _{\alpha < \kappa }$
such that:
-
(1) For all
 $A\subseteq \kappa $
, for W-almost all
$A\subseteq \kappa $
, for W-almost all
 $\alpha $
,
$\alpha $
,
 $A\cap \alpha \in \mathcal A_\alpha $
.
$A\cap \alpha \in \mathcal A_\alpha $
. -
(2)
 $\alpha \mapsto |A_\alpha |$
is not almost one-to-one mod W.
$\alpha \mapsto |A_\alpha |$
is not almost one-to-one mod W.
The sequence
![]() ${\langle }\mathcal {A}_\alpha {\rangle }_{\alpha <\kappa }$
is called a
${\langle }\mathcal {A}_\alpha {\rangle }_{\alpha <\kappa }$
is called a
![]() $\diamondsuit ^*_{\mathrm{thin}}(U)$
-sequence.
$\diamondsuit ^*_{\mathrm{thin}}(U)$
-sequence.
In the ultrapower, this is expressed as follows.
Lemma 3.4
![]() $\diamondsuit ^*_{\mathrm{thin}}(U)$
is equivalent to the existence of a set
$\diamondsuit ^*_{\mathrm{thin}}(U)$
is equivalent to the existence of a set
![]() $A\in M_U$
such that:
$A\in M_U$
such that:
-
(1)
 $\{j_U(S)\cap [id]_U\mid S\subseteq \kappa \}\subseteq A$
.
$\{j_U(S)\cap [id]_U\mid S\subseteq \kappa \}\subseteq A$
. -
(2) There is no function
 $f\colon \kappa \rightarrow \kappa $
such that
$f\colon \kappa \rightarrow \kappa $
such that
 $j_U(f)(|A|^M)\geq [id]_U$
.
$j_U(f)(|A|^M)\geq [id]_U$
.
Proof The witnessing
![]() $\diamondsuit ^*_{\mathrm{thin}}(U)$
-sequence is just the sequence
$\diamondsuit ^*_{\mathrm{thin}}(U)$
-sequence is just the sequence
![]() ${\langle } \mathcal {A}_\alpha {\rangle }_{\alpha <\kappa }$
representing A in
${\langle } \mathcal {A}_\alpha {\rangle }_{\alpha <\kappa }$
representing A in
![]() $M_U$
. Clearly, condition
$M_U$
. Clearly, condition
![]() $(1)$
is equivalent to the fact that for every
$(1)$
is equivalent to the fact that for every
![]() $S\subseteq \kappa $
,
$S\subseteq \kappa $
,
![]() $\{\alpha <\kappa \mid S\cap \alpha \in \mathcal {A}_\alpha \}\in U$
. By Proposition 2.3, condition
$\{\alpha <\kappa \mid S\cap \alpha \in \mathcal {A}_\alpha \}\in U$
. By Proposition 2.3, condition
![]() $(2)$
is equivalent to the function
$(2)$
is equivalent to the function
![]() $\alpha \mapsto |\mathcal {A}_\alpha |$
not being almost one-to-one mod U.
$\alpha \mapsto |\mathcal {A}_\alpha |$
not being almost one-to-one mod U.
Lemma 3.5 If
![]() $\diamondsuit ^*_{\mathrm{thin}}(W)$
, then W is non-Galvin.
$\diamondsuit ^*_{\mathrm{thin}}(W)$
, then W is non-Galvin.
Proof Assume toward contradiction that W has the Galvin property. Enumerate
![]() $\mathcal {A}_\alpha =\{A_{\alpha ,i}\mid i<|\mathcal {A}_\alpha |\}$
. For every set X, there is
$\mathcal {A}_\alpha =\{A_{\alpha ,i}\mid i<|\mathcal {A}_\alpha |\}$
. For every set X, there is
![]() $B_X\in W$
such that for every for every
$B_X\in W$
such that for every for every
![]() $\alpha \in B_X$
,
$\alpha \in B_X$
,
![]() $X\cap \alpha \in \mathcal {A}_\alpha $
. By our assumption, there are
$X\cap \alpha \in \mathcal {A}_\alpha $
. By our assumption, there are
![]() $\kappa $
-many distinct sets
$\kappa $
-many distinct sets
![]() $\{X_i\mid i<\kappa \}$
such that
$\{X_i\mid i<\kappa \}$
such that
![]() $B:=\bigcap _{i<\kappa }B_{X_i}\in W$
. Note that the key property of B is that for every
$B:=\bigcap _{i<\kappa }B_{X_i}\in W$
. Note that the key property of B is that for every
![]() $i<\kappa $
and for all
$i<\kappa $
and for all
![]() $\alpha \in B$
,
$\alpha \in B$
,
![]() $X_i\cap \alpha \in \mathcal {A}_\alpha $
. Since the function
$X_i\cap \alpha \in \mathcal {A}_\alpha $
. Since the function
![]() $\alpha \mapsto |\mathcal {A}_\alpha |$
is not almost one-to-one mod W, there is
$\alpha \mapsto |\mathcal {A}_\alpha |$
is not almost one-to-one mod W, there is
![]() $\theta <\kappa $
and an unbounded subset
$\theta <\kappa $
and an unbounded subset
![]() $B'\subseteq B$
such that for every
$B'\subseteq B$
such that for every
![]() $\alpha \in B'$
,
$\alpha \in B'$
,
![]() $|\mathcal {A}_\alpha |=\theta $
. Consider
$|\mathcal {A}_\alpha |=\theta $
. Consider
![]() $\{ X_i\mid i<\theta ^+\}$
. For every
$\{ X_i\mid i<\theta ^+\}$
. For every
![]() $i\neq j<\theta ^+$
, find
$i\neq j<\theta ^+$
, find
![]() $\alpha _{i,j}<\kappa $
such that
$\alpha _{i,j}<\kappa $
such that
![]() $X_i\cap \alpha _{i,j}\neq X_j\cap \alpha _{i,j}$
and take
$X_i\cap \alpha _{i,j}\neq X_j\cap \alpha _{i,j}$
and take
![]() $\alpha ^*=\sup _{i,j<\theta ^+}\alpha _{i,j}$
. By regularity of
$\alpha ^*=\sup _{i,j<\theta ^+}\alpha _{i,j}$
. By regularity of
![]() $\kappa $
,
$\kappa $
,
![]() $\alpha ^*<\kappa $
. Since
$\alpha ^*<\kappa $
. Since
![]() $B'$
is unbounded there exists some
$B'$
is unbounded there exists some
![]() $\beta ^*\in B'$
with
$\beta ^*\in B'$
with
![]() $\beta ^*>\alpha ^*$
. It follows that for every
$\beta ^*>\alpha ^*$
. It follows that for every
![]() $i<\theta ^+$
,
$i<\theta ^+$
,
![]() $X_i\cap \beta ^*\in \mathcal {A}_{\beta ^*}$
, and also for every
$X_i\cap \beta ^*\in \mathcal {A}_{\beta ^*}$
, and also for every
![]() $i\neq j$
, since
$i\neq j$
, since
![]() $\alpha _{i,j}<\beta ^*$
,
$\alpha _{i,j}<\beta ^*$
,
![]() $X_i\cap \beta ^*\neq X_j\cap \beta ^*$
. It follows that
$X_i\cap \beta ^*\neq X_j\cap \beta ^*$
. It follows that
![]() $i\mapsto X_i\cap \beta ^*$
is a one-to-one function from
$i\mapsto X_i\cap \beta ^*$
is a one-to-one function from
![]() $\theta ^+$
into
$\theta ^+$
into
![]() $\mathcal {A}_{\beta ^*}$
. This contradicts the fact that
$\mathcal {A}_{\beta ^*}$
. This contradicts the fact that
![]() $\beta ^*\in B'$
and thus
$\beta ^*\in B'$
and thus
![]() $|\mathcal {A}_{\beta ^*}|=\theta $
.
$|\mathcal {A}_{\beta ^*}|=\theta $
.
Corollary 3.6 Suppose that
![]() $\kappa $
is regular and U is an ultrafilter extending the club filter on
$\kappa $
is regular and U is an ultrafilter extending the club filter on
![]() $\kappa $
. Assume that there is a sequence of sets
$\kappa $
. Assume that there is a sequence of sets
![]() ${\langle } \mathcal {A}_\alpha {\rangle }_{ \alpha <\kappa }$
such that:
${\langle } \mathcal {A}_\alpha {\rangle }_{ \alpha <\kappa }$
such that:
-
(1) For every
 $\alpha <\kappa $
,
$\alpha <\kappa $
,
 $|\mathcal {A}_\alpha |<\alpha $
.
$|\mathcal {A}_\alpha |<\alpha $
. -
(2) For every
 $X\subseteq \kappa $
,
$X\subseteq \kappa $
,
 $\{\alpha <\kappa \mid X\cap \alpha \in \mathcal {A}_\alpha \}\in U$
.
$\{\alpha <\kappa \mid X\cap \alpha \in \mathcal {A}_\alpha \}\in U$
.
Then
![]() $\diamondsuit ^*_{\mathrm{thin}}(U)$
holds and, in particular, U is non-Galvin.
$\diamondsuit ^*_{\mathrm{thin}}(U)$
holds and, in particular, U is non-Galvin.
Proof It remains to show that
![]() $\alpha \mapsto |\mathcal {A}_\alpha |$
is not one-to-one on a set in U. If
$\alpha \mapsto |\mathcal {A}_\alpha |$
is not one-to-one on a set in U. If
![]() $A\in U$
, then A is stationary since
$A\in U$
, then A is stationary since
![]() $\text {Club}_\kappa \subseteq U$
. By Födor applied to the function
$\text {Club}_\kappa \subseteq U$
. By Födor applied to the function
![]() $\alpha \mapsto |\mathcal {A}_\alpha |$
restricted to A, there is an unbounded subset
$\alpha \mapsto |\mathcal {A}_\alpha |$
restricted to A, there is an unbounded subset
![]() $S'\subseteq A$
and
$S'\subseteq A$
and
![]() $\theta <\kappa $
such that for every
$\theta <\kappa $
such that for every
![]() $\alpha \in S'$
,
$\alpha \in S'$
,
![]() $|\mathcal {A}_\alpha |=\theta $
. In particular,
$|\mathcal {A}_\alpha |=\theta $
. In particular,
![]() $\alpha \mapsto |\mathcal {A}_\alpha |$
is not almost one-to-one on A.
$\alpha \mapsto |\mathcal {A}_\alpha |$
is not almost one-to-one on A.
The most important class of ultrafilters which satisfy
![]() $\diamondsuit ^*_{\mathrm{thin}}$
are the non p-point Dodd sound ultrafilters as will be proven in Lemma 3.8. To prove that lemma, we will need the following characterization due to Goldberg of Dodd sound ultrafilters [Reference Goldberg17, Theorem 4.3.26]:
$\diamondsuit ^*_{\mathrm{thin}}$
are the non p-point Dodd sound ultrafilters as will be proven in Lemma 3.8. To prove that lemma, we will need the following characterization due to Goldberg of Dodd sound ultrafilters [Reference Goldberg17, Theorem 4.3.26]:
Theorem 3.7 A uniform ultrafilter U on an ordinal
![]() $\delta $
is Dodd sound if and only if there is a sequence
$\delta $
is Dodd sound if and only if there is a sequence
![]() ${\langle } \mathcal {A}_\alpha {\rangle }_{\alpha <\delta }$
such that for any sequence
${\langle } \mathcal {A}_\alpha {\rangle }_{\alpha <\delta }$
such that for any sequence
![]() ${\langle } S_\alpha \subseteq \alpha {\rangle }_{\alpha < \delta }$
, the following are equivalent:
${\langle } S_\alpha \subseteq \alpha {\rangle }_{\alpha < \delta }$
, the following are equivalent:
-
(a) There is a set
 $S\subseteq \kappa $
such that for U-almost every
$S\subseteq \kappa $
such that for U-almost every
 $\alpha $
,
$\alpha $
,
 $S\cap \alpha =S_\alpha $
.
$S\cap \alpha =S_\alpha $
. -
(b) For U-almost every
 $\alpha $
,
$\alpha $
,
 $S_\alpha \in \mathcal {A}_\alpha $
.
$S_\alpha \in \mathcal {A}_\alpha $
.
Lemma 3.8 Let
![]() $\kappa $
be regular, and let U a non p-point Dodd sound ultrafilter, then
$\kappa $
be regular, and let U a non p-point Dodd sound ultrafilter, then
![]() $\diamondsuit ^*_{\mathrm{thin}}(U)$
.
$\diamondsuit ^*_{\mathrm{thin}}(U)$
.
Proof Assume that U is a non p-point Dodd sound ultrafilter. Let
![]() ${\langle }\mathcal {A}_\alpha {\rangle }_{\alpha <\kappa }$
be the sequence obtained by Theorem 3.7. Note that for every
${\langle }\mathcal {A}_\alpha {\rangle }_{\alpha <\kappa }$
be the sequence obtained by Theorem 3.7. Note that for every
![]() $S\subseteq \kappa $
, the sequence
$S\subseteq \kappa $
, the sequence
![]() ${\langle } S\cap \alpha {\rangle }_{\alpha <\kappa }$
satisfies condition
${\langle } S\cap \alpha {\rangle }_{\alpha <\kappa }$
satisfies condition
![]() $(a)$
of Theorem 3.7. By the theorem, we conclude that for U-almost every
$(a)$
of Theorem 3.7. By the theorem, we conclude that for U-almost every
![]() $\alpha $
,
$\alpha $
,
![]() $S\cap \alpha \in \mathcal {A}_\alpha $
. It follows that
$S\cap \alpha \in \mathcal {A}_\alpha $
. It follows that
![]() $j_U(S)\cap [id]_U\in [\alpha \mapsto \mathcal {A}_\alpha ]$
and
$j_U(S)\cap [id]_U\in [\alpha \mapsto \mathcal {A}_\alpha ]$
and
![]() $\{j_U(S)\cap [id]_U\mid S\subseteq \kappa \}\subseteq [\alpha \mapsto \mathcal {A}_\alpha ]_U$
. Similarly, from the implication
$\{j_U(S)\cap [id]_U\mid S\subseteq \kappa \}\subseteq [\alpha \mapsto \mathcal {A}_\alpha ]_U$
. Similarly, from the implication
![]() $(b)$
to
$(b)$
to
![]() $(a)$
we deduce that
$(a)$
we deduce that
![]() $[\alpha \mapsto \mathcal {A}_\alpha ]_U\subseteq \{j_U(S)\cap [\text {id}]_U\mid S\subseteq \kappa \}$
. By Dodd soundness, the function
$[\alpha \mapsto \mathcal {A}_\alpha ]_U\subseteq \{j_U(S)\cap [\text {id}]_U\mid S\subseteq \kappa \}$
. By Dodd soundness, the function
![]() $j^{[\text {id}]_U}\colon P(\kappa )\rightarrow \{j_U (S)\cap [\text {id}]_U\mid S\subseteq \kappa \}$
defined by
$j^{[\text {id}]_U}\colon P(\kappa )\rightarrow \{j_U (S)\cap [\text {id}]_U\mid S\subseteq \kappa \}$
defined by
![]() $j^{[\text {id}]_U}(S)=j(S)\cap [\text {id}]_U$
belongs to
$j^{[\text {id}]_U}(S)=j(S)\cap [\text {id}]_U$
belongs to
![]() $M_U$
. Thus
$M_U$
. Thus
![]() $M_U\models |[\alpha \mapsto \mathcal {A}_\alpha ]_U|=2^\kappa $
. Finally,
$M_U\models |[\alpha \mapsto \mathcal {A}_\alpha ]_U|=2^\kappa $
. Finally,
![]() $\alpha \mapsto |\mathcal {A}_\alpha |$
cannot be an almost one-to-one function mod U: otherwise, the class of any unbounded function
$\alpha \mapsto |\mathcal {A}_\alpha |$
cannot be an almost one-to-one function mod U: otherwise, the class of any unbounded function
![]() $\kappa \leq [\pi ]_U$
would also be an almost one-to-one mod U. To see this, suppose that
$\kappa \leq [\pi ]_U$
would also be an almost one-to-one mod U. To see this, suppose that
![]() $[\tau ]_U=\kappa $
, then
$[\tau ]_U=\kappa $
, then
![]() $[\alpha \mapsto 2^{\tau (\alpha )}]_U=2^\kappa $
and by our assumption, this is represented by an almost one-to-one function mod U
Footnote
9
. Let
$[\alpha \mapsto 2^{\tau (\alpha )}]_U=2^\kappa $
and by our assumption, this is represented by an almost one-to-one function mod U
Footnote
9
. Let
![]() $X\in U$
be the set witnessing that
$X\in U$
be the set witnessing that
![]() $\alpha \mapsto 2^{\tau (\alpha )}$
is almost one-to-one mod U. Also we let
$\alpha \mapsto 2^{\tau (\alpha )}$
is almost one-to-one mod U. Also we let
![]() $Y\in U$
be such that for every
$Y\in U$
be such that for every
![]() $\alpha \in Y$
,
$\alpha \in Y$
,
![]() $\tau (\alpha )\leq \pi (\alpha )$
. We claim that
$\tau (\alpha )\leq \pi (\alpha )$
. We claim that
![]() $\pi \restriction X\cap Y$
is almost one-to-one as for any
$\pi \restriction X\cap Y$
is almost one-to-one as for any
![]() $\gamma <\kappa $
,
$\gamma <\kappa $
,
 $$ \begin{align*}\{\alpha<\kappa\mid \pi(\alpha)&<\gamma\}\cap X\cap Y\subseteq\{\alpha<\kappa\mid \tau(\alpha)<\gamma\}\cap X\cap Y\subseteq\\&\subseteq\{\alpha<\kappa\mid 2^{\tau(\alpha)}\leq 2^\gamma\}\cap X\cap Y.\end{align*} $$
$$ \begin{align*}\{\alpha<\kappa\mid \pi(\alpha)&<\gamma\}\cap X\cap Y\subseteq\{\alpha<\kappa\mid \tau(\alpha)<\gamma\}\cap X\cap Y\subseteq\\&\subseteq\{\alpha<\kappa\mid 2^{\tau(\alpha)}\leq 2^\gamma\}\cap X\cap Y.\end{align*} $$
The right most set is bounded by the choice of X. We conclude that U is a p-point contradiction.
Note that an ultrafilter U satisfying
![]() $\diamondsuit ^*_{\mathrm{thin}}(U)$
need not be Dodd sound since by Lemma 3.4, we only cover the set
$\diamondsuit ^*_{\mathrm{thin}}(U)$
need not be Dodd sound since by Lemma 3.4, we only cover the set
![]() $\{j_U(S)\cap [id]_U\mid S\subseteq \kappa \}$
. However, at least for
$\{j_U(S)\cap [id]_U\mid S\subseteq \kappa \}$
. However, at least for
![]() $\kappa $
-complete Dodd sound ultrafilters, the second requirement of
$\kappa $
-complete Dodd sound ultrafilters, the second requirement of
![]() $\diamondsuit ^*_{\mathrm{thin}}(U)$
regarding the function
$\diamondsuit ^*_{\mathrm{thin}}(U)$
regarding the function
![]() $\alpha \mapsto |\mathcal {A}_\alpha |$
is equivalent to U not being a p-point.
$\alpha \mapsto |\mathcal {A}_\alpha |$
is equivalent to U not being a p-point.
Proposition 3.9 Let
![]() $\kappa $
be measurable and U be a
$\kappa $
be measurable and U be a
![]() $\kappa $
-complete Dodd sound ultrafilter over
$\kappa $
-complete Dodd sound ultrafilter over
![]() $\kappa $
, and let
$\kappa $
, and let
![]() $[\alpha \mapsto \mathcal {A}_\alpha ]_U=\{j_U(S)\cap [\text {id}]_U\mid S\subseteq \kappa \}$
. Then U is a non p-point ultrafilter if and only if the function
$[\alpha \mapsto \mathcal {A}_\alpha ]_U=\{j_U(S)\cap [\text {id}]_U\mid S\subseteq \kappa \}$
. Then U is a non p-point ultrafilter if and only if the function
![]() $\alpha \mapsto |\mathcal {A}_\alpha |$
is not almost one-to-one mod U.
$\alpha \mapsto |\mathcal {A}_\alpha |$
is not almost one-to-one mod U.
Proof One direction follows from the previous lemma. Let us prove the other, note that
![]() $\alpha \mapsto |\mathcal {A}_\alpha |$
cannot be bounded on a set in U, just otherwise, suppose that
$\alpha \mapsto |\mathcal {A}_\alpha |$
cannot be bounded on a set in U, just otherwise, suppose that
![]() $\theta <\kappa $
is such that
$\theta <\kappa $
is such that
![]() $B^*:=\{\alpha <\kappa \mid |\mathcal {A}_\alpha |\leq \theta \}\in U$
. Take any
$B^*:=\{\alpha <\kappa \mid |\mathcal {A}_\alpha |\leq \theta \}\in U$
. Take any
![]() $\theta ^+$
-many sets
$\theta ^+$
-many sets
![]() $\{ X_i\mid i<\theta ^+\}$
such that there is
$\{ X_i\mid i<\theta ^+\}$
such that there is
![]() $\gamma <\kappa $
such that for all
$\gamma <\kappa $
such that for all
![]() $i\neq j<\theta ^+$
,
$i\neq j<\theta ^+$
,
![]() $X_i\cap \gamma \neq X_j\cap \gamma $
. For each
$X_i\cap \gamma \neq X_j\cap \gamma $
. For each
![]() $i<\theta ^+$
, Denote by
$i<\theta ^+$
, Denote by
![]() $B_i:=\{\alpha <\kappa \mid X_i\cap \alpha \in \mathcal {A}_\alpha \}\in U$
. By
$B_i:=\{\alpha <\kappa \mid X_i\cap \alpha \in \mathcal {A}_\alpha \}\in U$
. By
![]() $\kappa $
-completeness and fineness, there is
$\kappa $
-completeness and fineness, there is
![]() $\gamma ^*\in B^*\cap (\bigcap _{i<\theta ^+}B_i)\setminus \gamma $
. It follows that
$\gamma ^*\in B^*\cap (\bigcap _{i<\theta ^+}B_i)\setminus \gamma $
. It follows that
![]() $|\mathcal {A}_{\gamma ^*}|=\theta $
but also for each
$|\mathcal {A}_{\gamma ^*}|=\theta $
but also for each
![]() $i<\theta ^+$
,
$i<\theta ^+$
,
![]() $X_i\cap \gamma ^*\in \mathcal {A}_{\gamma ^*}$
are all distinct sets. Contradiction. We conclude that
$X_i\cap \gamma ^*\in \mathcal {A}_{\gamma ^*}$
are all distinct sets. Contradiction. We conclude that
![]() $\alpha \mapsto |\mathcal {A}_\alpha |$
is an unbounded function mod U which is also not almost one-to-one according to
$\alpha \mapsto |\mathcal {A}_\alpha |$
is an unbounded function mod U which is also not almost one-to-one according to
![]() $(1)$
. Hence, U is not a p-point.
$(1)$
. Hence, U is not a p-point.
We cannot drop the
![]() $\kappa $
-completeness assumption here.
$\kappa $
-completeness assumption here.
Example 3.10. Suppose that W is a fine normal ultrafilter over
![]() $P_\kappa (\lambda )$
for
$P_\kappa (\lambda )$
for
![]() $\kappa <\lambda $
, where
$\kappa <\lambda $
, where
![]() $\lambda $
is a regular cardinal. By [Reference Goldberg17, Theorems 4.4.37 and 4.4.25], there is a Dodd sound non uniform ultrafilter U on
$\lambda $
is a regular cardinal. By [Reference Goldberg17, Theorems 4.4.37 and 4.4.25], there is a Dodd sound non uniform ultrafilter U on
![]() $\lambda $
(and therefore p-point) which is Rudin–Keisler equivalent to W. Note that there is no function which is unbounded (and therefore no function which is almost one-to-one) mod U. In particular,
$\lambda $
(and therefore p-point) which is Rudin–Keisler equivalent to W. Note that there is no function which is unbounded (and therefore no function which is almost one-to-one) mod U. In particular,
![]() $\alpha \mapsto |\mathcal {A}_\alpha |$
is not almost one-to-one mod U. Also, note that U satisfies
$\alpha \mapsto |\mathcal {A}_\alpha |$
is not almost one-to-one mod U. Also, note that U satisfies
![]() $\diamondsuit ^*_{\mathrm{thin}}(U)$
and therefore is an example of a non-Galvin ultrafilter over
$\diamondsuit ^*_{\mathrm{thin}}(U)$
and therefore is an example of a non-Galvin ultrafilter over
![]() $\lambda $
which is uniform and not
$\lambda $
which is uniform and not
![]() $\lambda $
-complete.
$\lambda $
-complete.
Corollary 3.11 If U is a non p-point, Dodd sound ultrafilter over a regular cardinal
![]() $\kappa $
, then U is non-Galvin.
$\kappa $
, then U is non-Galvin.
In attempt to pinpoint the exact guessing principle that catches non-Galvinness, we note that the usage of
![]() $\diamondsuit ^*_{\mathrm{thin}}(W)$
in the argument of Lemma 3.5 can be replaced with the following weakening.
$\diamondsuit ^*_{\mathrm{thin}}(W)$
in the argument of Lemma 3.5 can be replaced with the following weakening.
Definition 3.12. Let
![]() $\kappa \leq \lambda \leq 2^\kappa $
. An ultrafilter W on a regular cardinal
$\kappa \leq \lambda \leq 2^\kappa $
. An ultrafilter W on a regular cardinal
![]() $\kappa $
satisfies
$\kappa $
satisfies
![]() $\diamondsuit ^*_{\text {par}}(W,\lambda )$
if there is a sequence of sets
$\diamondsuit ^*_{\text {par}}(W,\lambda )$
if there is a sequence of sets
![]() $\langle X_\alpha \rangle _{\alpha <\lambda }$
,
$\langle X_\alpha \rangle _{\alpha <\lambda }$
,
![]() $A\in M_W$
such that:
$A\in M_W$
such that:
-
(1)
 $\{j_U(X_\alpha )\cap [id]_U\mid \alpha <\lambda \}\subseteq A$
.
$\{j_U(X_\alpha )\cap [id]_U\mid \alpha <\lambda \}\subseteq A$
. -
(2) For any function
 $f:\kappa \rightarrow \kappa $
,
$f:\kappa \rightarrow \kappa $
,
 $j_U(f)(|A|^{M_W})<[id]_W$
.
$j_U(f)(|A|^{M_W})<[id]_W$
.
Clearly,
![]() $\diamondsuit ^*_{\mathrm{thin}}(W)$
implies
$\diamondsuit ^*_{\mathrm{thin}}(W)$
implies
![]() $\diamondsuit ^*_{\text {par}}(W,2^\kappa )$
which in turn imply
$\diamondsuit ^*_{\text {par}}(W,2^\kappa )$
which in turn imply
![]() $\diamondsuit ^*_{\text {par}}(W,\lambda )$
for any
$\diamondsuit ^*_{\text {par}}(W,\lambda )$
for any
![]() $\lambda \in [\kappa ,2^\kappa ]$
.
$\lambda \in [\kappa ,2^\kappa ]$
.
Proposition 3.13
![]() $\diamondsuit ^*_{\mathrm{par}}(W,\lambda )$
implies that
$\diamondsuit ^*_{\mathrm{par}}(W,\lambda )$
implies that
![]() $\neg \mathrm{Gal}(W,\kappa ,\lambda ).$
$\neg \mathrm{Gal}(W,\kappa ,\lambda ).$
Proof The argument of Lemma 3.5 gives this stronger result.
The principle
![]() $\diamondsuit ^*_{\text {par}}(W,\lambda )$
is equivalent to the existence of a set
$\diamondsuit ^*_{\text {par}}(W,\lambda )$
is equivalent to the existence of a set
![]() $K\subseteq P(\kappa )$
of size
$K\subseteq P(\kappa )$
of size
![]() $\lambda $
and a sequence
$\lambda $
and a sequence
![]() ${\langle } A_\alpha {\rangle }_{\alpha <\kappa }$
such that:
${\langle } A_\alpha {\rangle }_{\alpha <\kappa }$
such that:
-
(1) For every
 $X\in K$
,
$X\in K$
,
 $\{\alpha <\kappa \mid X\cap \alpha \in A_\alpha \}\in W$
.
$\{\alpha <\kappa \mid X\cap \alpha \in A_\alpha \}\in W$
. -
(2) The function
 $\alpha \mapsto |A_\alpha |$
is not almost one-to-one mod W.
$\alpha \mapsto |A_\alpha |$
is not almost one-to-one mod W.
The referee pointed out to us the strong similarity of
![]() $\diamondsuit ^*_{\text {par}}$
to the notion of pseudo-Kurepa families due to Todorcevic [Reference Todorcevic36]. Indeed, many of the initial segments of the sets in K must be equal in order for the sets
$\diamondsuit ^*_{\text {par}}$
to the notion of pseudo-Kurepa families due to Todorcevic [Reference Todorcevic36]. Indeed, many of the initial segments of the sets in K must be equal in order for the sets
![]() $A_\alpha $
of asymptotically bounded cardinality to exist.
$A_\alpha $
of asymptotically bounded cardinality to exist.
Next, we would like to provide two closure properties of the class of ultrafilters satisfying
![]() $\diamondsuit ^*_{\mathrm{thin}}$
.
$\diamondsuit ^*_{\mathrm{thin}}$
.
Lemma 3.14 Suppose U is an ultrafilter on
![]() $\kappa $
and Z is the U-limit of a discrete sequence of ultrafilters
$\kappa $
and Z is the U-limit of a discrete sequence of ultrafilters
![]() $W_\xi $
on
$W_\xi $
on
![]() $\kappa $
such that
$\kappa $
such that
![]() $\diamondsuit ^*_{\mathrm{thin}}(W_\xi )$
. Then
$\diamondsuit ^*_{\mathrm{thin}}(W_\xi )$
. Then
![]() $\diamondsuit ^*_{\mathrm{thin}}(Z)$
.
$\diamondsuit ^*_{\mathrm{thin}}(Z)$
.
Proof Fix a partition of
![]() $\kappa $
into sets
$\kappa $
into sets
![]() $S_\xi \in W_\xi $
. For each
$S_\xi \in W_\xi $
. For each
![]() $\xi < \kappa $
, let
$\xi < \kappa $
, let
![]() $\langle \mathcal A^\xi _\alpha \rangle _{\alpha < \kappa }$
witness that
$\langle \mathcal A^\xi _\alpha \rangle _{\alpha < \kappa }$
witness that
![]() $\diamondsuit ^*_{\mathrm{thin}}(W_\xi )$
. Then let
$\diamondsuit ^*_{\mathrm{thin}}(W_\xi )$
. Then let
![]() $\mathcal A_\alpha = \mathcal A^\xi _\alpha $
, where
$\mathcal A_\alpha = \mathcal A^\xi _\alpha $
, where
![]() $\xi < \kappa $
is unique such that
$\xi < \kappa $
is unique such that
![]() $\alpha \in S_\xi $
. Fixing
$\alpha \in S_\xi $
. Fixing
![]() $A\subseteq \kappa $
, we would like to show that
$A\subseteq \kappa $
, we would like to show that
![]() $B:=\{\alpha <\kappa \mid A\cap \alpha \in \mathcal {A}_{\alpha }\}\in U\text {-}\lim {\langle } W_\xi {\rangle }_{\xi <\kappa }$
. For any
$B:=\{\alpha <\kappa \mid A\cap \alpha \in \mathcal {A}_{\alpha }\}\in U\text {-}\lim {\langle } W_\xi {\rangle }_{\xi <\kappa }$
. For any
![]() $\xi <\kappa $
, then
$\xi <\kappa $
, then
![]() $B_\xi :=\{\alpha \in S_\xi \mid A\cap \alpha \in \mathcal {A}^\xi _\alpha \}\in W_\xi $
. Since for each
$B_\xi :=\{\alpha \in S_\xi \mid A\cap \alpha \in \mathcal {A}^\xi _\alpha \}\in W_\xi $
. Since for each
![]() $\alpha \in S_\xi $
,
$\alpha \in S_\xi $
,
![]() $\mathcal {A}_\alpha =\mathcal {A}^\xi _\alpha $
, we conclude that
$\mathcal {A}_\alpha =\mathcal {A}^\xi _\alpha $
, we conclude that
![]() $B_\xi \subseteq B$
and therefore
$B_\xi \subseteq B$
and therefore
![]() $B\in W_\xi $
. It follows that
$B\in W_\xi $
. It follows that
![]() $B\in U\text {-}\lim {\langle } W_\xi {\rangle }_{\xi <\kappa }$
. It remains to show that
$B\in U\text {-}\lim {\langle } W_\xi {\rangle }_{\xi <\kappa }$
. It remains to show that
![]() $c(\alpha )=|\mathcal {A}_\alpha |$
is not almost one-to-one on any set
$c(\alpha )=|\mathcal {A}_\alpha |$
is not almost one-to-one on any set
![]() $B\in W$
. Suppose otherwise, and let
$B\in W$
. Suppose otherwise, and let
![]() $B\in W$
witness that c is almost one-to-one. Pick any
$B\in W$
witness that c is almost one-to-one. Pick any
![]() $\xi <\kappa $
such that
$\xi <\kappa $
such that
![]() $B\in W_\xi $
to reach a contradiction note that
$B\in W_\xi $
to reach a contradiction note that
![]() $B\cap S_\xi \in W_\xi $
, and the function c is almost one-to-one on this set. However, for every
$B\cap S_\xi \in W_\xi $
, and the function c is almost one-to-one on this set. However, for every
![]() $\alpha \in B\cap S_\xi $
,
$\alpha \in B\cap S_\xi $
,
![]() $\mathcal {A}^\xi _\alpha =\mathcal {A}_\alpha =c(\alpha )$
and so
$\mathcal {A}^\xi _\alpha =\mathcal {A}_\alpha =c(\alpha )$
and so
![]() $\alpha \mapsto |\mathcal {A}^\xi _\alpha |$
is almost one-to-one on
$\alpha \mapsto |\mathcal {A}^\xi _\alpha |$
is almost one-to-one on
![]() $B\cap S_\xi $
, contradicting
$B\cap S_\xi $
, contradicting
![]() $\diamondsuit ^*_{\mathrm{thin}}(W_\xi )$
.
$\diamondsuit ^*_{\mathrm{thin}}(W_\xi )$
.
Lemma 3.15 Suppose U is an n-fold sum of p-points on
![]() $\kappa $
and
$\kappa $
and
![]() $\langle W_\xi \rangle _{\xi < \kappa }$
is a sequence of (not necessarily discrete)
$\langle W_\xi \rangle _{\xi < \kappa }$
is a sequence of (not necessarily discrete)
![]() $\kappa $
-complete ultrafilters on
$\kappa $
-complete ultrafilters on
![]() $\kappa $
such that
$\kappa $
such that
![]() $\diamondsuit ^*_{\mathrm{thin}}(W_\xi )$
. Then letting
$\diamondsuit ^*_{\mathrm{thin}}(W_\xi )$
. Then letting
![]() $Z = U\text {-}\lim {\langle } W_\xi {\rangle }_{\xi < \kappa }$
, we have
$Z = U\text {-}\lim {\langle } W_\xi {\rangle }_{\xi < \kappa }$
, we have
![]() $\diamondsuit ^*_{\mathrm{thin}}(Z)$
.
$\diamondsuit ^*_{\mathrm{thin}}(Z)$
.
Proof We first consider the case that U is a p-point. Then replace U with
![]() $U_W = D(j_U, W)$
, where W is the point in
$U_W = D(j_U, W)$
, where W is the point in
![]() $M_U$
represented by
$M_U$
represented by
![]() $\xi \mapsto W_\xi $
. Note that
$\xi \mapsto W_\xi $
. Note that
![]() $U_W$
is Rudin–Keisler below an ultrafilter on
$U_W$
is Rudin–Keisler below an ultrafilter on
![]() $\kappa $
which implies that
$\kappa $
which implies that
![]() $U_W$
concentrates on a set of (
$U_W$
concentrates on a set of (
![]() $\kappa $
-complete) ultrafilters of size
$\kappa $
-complete) ultrafilters of size
![]() $\kappa $
. By enumerating those ultrafilters
$\kappa $
. By enumerating those ultrafilters
![]() $W^{\prime }_\xi $
for
$W^{\prime }_\xi $
for
![]() $\xi <\kappa $
, we can shift
$\xi <\kappa $
, we can shift
![]() $U_W$
to an ultrafilter
$U_W$
to an ultrafilter
![]() $U'$
on
$U'$
on
![]() $\kappa $
such that
$\kappa $
such that
![]() $[\text {id}]_{U_W}$
is identified with
$[\text {id}]_{U_W}$
is identified with
![]() $[\xi \mapsto W^{\prime }_\xi ]_{U'}$
. Also, note that
$[\xi \mapsto W^{\prime }_\xi ]_{U'}$
. Also, note that
![]() $U'-\text {lim} W^{\prime }_\xi =U-\text {lim} W_\xi $
since the factor map
$U'-\text {lim} W^{\prime }_\xi =U-\text {lim} W_\xi $
since the factor map
![]() $k\colon M_{U'}\rightarrow M_U$
sends
$k\colon M_{U'}\rightarrow M_U$
sends
![]() $k([\xi \mapsto W^{\prime }_\xi ]_{U'})=W$
and thus
$k([\xi \mapsto W^{\prime }_\xi ]_{U'})=W$
and thus
Since
![]() $U'\leq _{RK}U$
, and U is a p-point,
$U'\leq _{RK}U$
, and U is a p-point,
![]() $U'$
is also a p-point (see [Reference Kanamori24, Corollary 2.8]). The sequence
$U'$
is also a p-point (see [Reference Kanamori24, Corollary 2.8]). The sequence
![]() ${\langle } W^{\prime }_\xi {\rangle }_{ \xi <\kappa }$
represents the identity in
${\langle } W^{\prime }_\xi {\rangle }_{ \xi <\kappa }$
represents the identity in
![]() $U'$
, it is one-to-one mod
$U'$
, it is one-to-one mod
![]() $U'$
, since all the
$U'$
, since all the
![]() $W^{\prime }_\xi $
’s are
$W^{\prime }_\xi $
’s are
![]() $\kappa $
-complete, by Proposition 2.14 the sequence is discrete on a set in
$\kappa $
-complete, by Proposition 2.14 the sequence is discrete on a set in
![]() $U'$
.Footnote
10
This allows us to apply the previous lemma, obtaining thin diamond for
$U'$
.Footnote
10
This allows us to apply the previous lemma, obtaining thin diamond for
![]() $U'\text {-}\lim {\langle } W^{\prime }_\xi {\rangle }_{\xi <\kappa } = U\text {-}\lim {\langle } W_\xi {\rangle }_{\xi < \kappa }$
.
$U'\text {-}\lim {\langle } W^{\prime }_\xi {\rangle }_{\xi <\kappa } = U\text {-}\lim {\langle } W_\xi {\rangle }_{\xi < \kappa }$
.
Now suppose the lemma is true for n-fold sums of p-points, and we will prove it when U is an
![]() $(n+1)$
-fold sum. We can fix a p-point D such that U is the D-limit of a sequence of n-fold sum p-points
$(n+1)$
-fold sum. We can fix a p-point D such that U is the D-limit of a sequence of n-fold sum p-points
![]() $U_\xi $
on
$U_\xi $
on
![]() $\kappa $
. As in the previous paragraph, since D is a p-point, we may assume that the
$\kappa $
. As in the previous paragraph, since D is a p-point, we may assume that the
![]() $U_\xi $
’s are discrete. Let
$U_\xi $
’s are discrete. Let
![]() $U^* = [\xi \mapsto U_\xi ]_D$
, then by elementarity,
$U^* = [\xi \mapsto U_\xi ]_D$
, then by elementarity,
![]() $M_D\models \ U^*$
is an n-fold sum of p-points. Applying the induction hypothesis in
$M_D\models \ U^*$
is an n-fold sum of p-points. Applying the induction hypothesis in
![]() $M_D$
to
$M_D$
to
![]() $U^*$
and the ultrafilters
$U^*$
and the ultrafilters
![]() $j_D(\langle W_\xi \rangle _{\xi < \kappa })={\langle } Z^*_\xi {\rangle }_{ \xi <j_D(\kappa )}$
, we conclude that
$j_D(\langle W_\xi \rangle _{\xi < \kappa })={\langle } Z^*_\xi {\rangle }_{ \xi <j_D(\kappa )}$
, we conclude that
![]() $Z^*=U^*\text {-}\lim {\langle } Z^*_\xi {\rangle }_{\xi <j_D(\kappa )}$
satisfies
$Z^*=U^*\text {-}\lim {\langle } Z^*_\xi {\rangle }_{\xi <j_D(\kappa )}$
satisfies
![]() $\diamondsuit ^*_{\mathrm{thin}}(Z^*)$
. Let
$\diamondsuit ^*_{\mathrm{thin}}(Z^*)$
. Let
![]() $[\alpha \mapsto Z_\alpha ]_D=Z^*$
and assume without loss of generality that for every
$[\alpha \mapsto Z_\alpha ]_D=Z^*$
and assume without loss of generality that for every
![]() $\alpha <\kappa $
,
$\alpha <\kappa $
,
![]() $\diamondsuit ^*_{\mathrm{thin}}(Z_\alpha )$
holds. We claim that
$\diamondsuit ^*_{\mathrm{thin}}(Z_\alpha )$
holds. We claim that
from which it follows that
![]() $\diamondsuit ^*_{\mathrm{thin}}(Z)$
, by the argument of the previous paragraph. To see
$\diamondsuit ^*_{\mathrm{thin}}(Z)$
, by the argument of the previous paragraph. To see
![]() $(*)$
, since we assumed that the
$(*)$
, since we assumed that the
![]() $U_\alpha $
’s are discrete, by the theory of sums and limits of ultrapower
$U_\alpha $
’s are discrete, by the theory of sums and limits of ultrapower
hence
4 Partial Dodd soundness and skies
A finer analysis of the diamond-like principles of the previous section reveals that partial soundness suffices for an ultrafilter to be non-Galvin. To better understand this improvement, let us prove the following theorem in terms of general elementary embeddings.
Theorem 4.1 Suppose that
![]() $j\colon V\rightarrow M$
is an elementary embedding with
$j\colon V\rightarrow M$
is an elementary embedding with
![]() $\operatorname {\mathrm {crit}}(j)=\kappa $
such that
$\operatorname {\mathrm {crit}}(j)=\kappa $
such that
![]() $\lambda =\sup \{j(f)(\kappa )\mid f\colon \kappa \rightarrow \kappa \}$
and
$\lambda =\sup \{j(f)(\kappa )\mid f\colon \kappa \rightarrow \kappa \}$
and
![]() $\{j(A)\cap \lambda \mid A\subseteq \kappa \}\in M$
. Then there is
$\{j(A)\cap \lambda \mid A\subseteq \kappa \}\in M$
. Then there is
![]() $\xi $
such that
$\xi $
such that
![]() $D:=D(j,\xi )$
and
$D:=D(j,\xi )$
and
![]() $\neg \mathrm {Gal}({D,\kappa ,2^\kappa })$
.
$\neg \mathrm {Gal}({D,\kappa ,2^\kappa })$
.
Remark 4.2. Note that from the assumptions of the theorem it follows that
![]() $\lambda <j(\kappa )$
, indeed, if
$\lambda <j(\kappa )$
, indeed, if
![]() $\lambda =j(\kappa )$
, then since we are assuming
$\lambda =j(\kappa )$
, then since we are assuming
![]() $\{j(A)\cap \lambda \mid A\subseteq \kappa \}\in M$
, we have
$\{j(A)\cap \lambda \mid A\subseteq \kappa \}\in M$
, we have
![]() $j"P(\kappa )\in M$
and therefore
$j"P(\kappa )\in M$
and therefore
![]() $\{j(f)(\kappa )\mid f:\kappa \rightarrow \kappa \}\in M$
. It follows that
$\{j(f)(\kappa )\mid f:\kappa \rightarrow \kappa \}\in M$
. It follows that
![]() $M\models cf(j(\kappa ))=2^\kappa $
. But by elementarity,
$M\models cf(j(\kappa ))=2^\kappa $
. But by elementarity,
![]() $M\models j(\kappa )$
is regular. Contradiction.
$M\models j(\kappa )$
is regular. Contradiction.
Proof Denote
![]() $\mathcal {A}=\{j(A)\cap \lambda \mid A\subseteq \kappa \}\in M$
. Enumerate
$\mathcal {A}=\{j(A)\cap \lambda \mid A\subseteq \kappa \}\in M$
. Enumerate
![]() $V_\kappa $
in V,
$V_\kappa $
in V,
![]() $f\colon \kappa \rightarrow V_\kappa $
such that for every
$f\colon \kappa \rightarrow V_\kappa $
such that for every
![]() $x\in V_\kappa $
,
$x\in V_\kappa $
,
![]() $f^{-1}[x]$
is unbounded in
$f^{-1}[x]$
is unbounded in
![]() $\kappa $
. Since
$\kappa $
. Since
![]() $\mathcal {A}\in (V_{j(\kappa )})^M$
, there is
$\mathcal {A}\in (V_{j(\kappa )})^M$
, there is
![]() $j(\kappa )>\xi \geq \lambda $
such that
$j(\kappa )>\xi \geq \lambda $
such that
![]() $j(f)(\xi )=\mathcal {A}$
. By similar arguments, we can ensure that there are some functions
$j(f)(\xi )=\mathcal {A}$
. By similar arguments, we can ensure that there are some functions
![]() $g, h: \kappa \rightarrow \kappa $
such that for the same
$g, h: \kappa \rightarrow \kappa $
such that for the same
![]() $\xi $
we will also have
$\xi $
we will also have
![]() $\kappa =j(g)(\xi )$
and
$\kappa =j(g)(\xi )$
and
![]() $\lambda =j(h)(\xi )$
. Let
$\lambda =j(h)(\xi )$
. Let
![]() $D=D(j,\xi )$
,
$D=D(j,\xi )$
,
![]() $j_D\colon V\rightarrow M_D$
be the ultrapower, and let
$j_D\colon V\rightarrow M_D$
be the ultrapower, and let
![]() $k_D\colon M_D\rightarrow M$
be the factor map
$k_D\colon M_D\rightarrow M$
be the factor map
![]() $k_D([\phi ]_D)=j(\phi )(\xi )$
. Note that
$k_D([\phi ]_D)=j(\phi )(\xi )$
. Note that
and therefore
![]() $\kappa ,\lambda ,\mathcal {A}\in Im(k_D)$
. It follows that
$\kappa ,\lambda ,\mathcal {A}\in Im(k_D)$
. It follows that
![]() $\operatorname {\mathrm {crit}}(k_D)>\kappa $
and
$\operatorname {\mathrm {crit}}(k_D)>\kappa $
and
![]() $[g]_D=\kappa $
. Since
$[g]_D=\kappa $
. Since
the elementarity of
![]() $k_D$
implies that
$k_D$
implies that
![]() $[h]_D\leq [id]_D$
. Recall that for any function
$[h]_D\leq [id]_D$
. Recall that for any function
![]() $\phi \colon \kappa \rightarrow \kappa $
,
$\phi \colon \kappa \rightarrow \kappa $
,
![]() $j(\phi )(\kappa )<\lambda $
thus by elementarity of
$j(\phi )(\kappa )<\lambda $
thus by elementarity of
![]() $k_D$
,
$k_D$
,
By our initial assumption,
![]() $\lambda>j(\alpha \mapsto 2^\alpha )(\kappa )=2^\kappa $
and since
$\lambda>j(\alpha \mapsto 2^\alpha )(\kappa )=2^\kappa $
and since
![]() $M\models |\mathcal {A}|=2^\kappa $
,
$M\models |\mathcal {A}|=2^\kappa $
,
Denote by
![]() $B_\alpha =f(\alpha )$
, note that and fix a set
$B_\alpha =f(\alpha )$
, note that and fix a set
![]() $X^*\in D$
such that if
$X^*\in D$
such that if
![]() $\alpha \in X^*$
then
$\alpha \in X^*$
then
![]() $|B_\alpha |=2^{g(\alpha )}<h(\alpha )$
. Pick any
$|B_\alpha |=2^{g(\alpha )}<h(\alpha )$
. Pick any
![]() $2^\kappa $
distinct subsets of
$2^\kappa $
distinct subsets of
![]() $\kappa $
,
$\kappa $
,
![]() ${\langle } A_\alpha {\rangle }_{ \alpha <2^\kappa }$
, then
${\langle } A_\alpha {\rangle }_{ \alpha <2^\kappa }$
, then
![]() $j(A_\alpha )\cap \lambda \in \mathcal {A}$
and by elementarity
$j(A_\alpha )\cap \lambda \in \mathcal {A}$
and by elementarity
![]() $j_D(A_\alpha )\cap \lambda '\in B$
. It follows that
$j_D(A_\alpha )\cap \lambda '\in B$
. It follows that
We claim that
![]() ${\langle } X_\alpha {\rangle }_{ \alpha <2^\kappa }$
witness that
${\langle } X_\alpha {\rangle }_{ \alpha <2^\kappa }$
witness that
![]() $\neg \mathrm{Gal}(U,\kappa ,2^\kappa )$
. Otherwise, there is
$\neg \mathrm{Gal}(U,\kappa ,2^\kappa )$
. Otherwise, there is
![]() $I\in [2^\kappa ]^\kappa $
such that
$I\in [2^\kappa ]^\kappa $
such that
![]() $X_I:=\cap _{i\in I}X_i\in D$
. Let us argue that there must be
$X_I:=\cap _{i\in I}X_i\in D$
. Let us argue that there must be
![]() $\theta <\kappa $
such that
$\theta <\kappa $
such that
To see this, assume otherwise, then for each
![]() $\theta <\kappa $
, we can define
$\theta <\kappa $
, we can define
then
![]() $\rho \colon \kappa \rightarrow \kappa $
is well-defined. Since
$\rho \colon \kappa \rightarrow \kappa $
is well-defined. Since
![]() $2^{j_D(g)([id]_D)}=2^{[g]_D}=2^\kappa $
, we conclude that
$2^{j_D(g)([id]_D)}=2^{[g]_D}=2^\kappa $
, we conclude that
![]() $j_D(\rho )(\kappa )\geq j_D(h)([\text {id}]_D)=[h]_D$
, contradicting
$j_D(\rho )(\kappa )\geq j_D(h)([\text {id}]_D)=[h]_D$
, contradicting
![]() $(*)$
. We proceed as before, find
$(*)$
. We proceed as before, find
![]() $\beta \in X_I\cap X^*$
such that the restriction of
$\beta \in X_I\cap X^*$
such that the restriction of
![]() $\theta $
-many of the sets in I to
$\theta $
-many of the sets in I to
![]() $h(\beta )$
are distinct. This produces a contradiction.
$h(\beta )$
are distinct. This produces a contradiction.
Let us define the concept of a sky of an elementary embedding at
![]() $\delta $
, which was first considered in the case that
$\delta $
, which was first considered in the case that
![]() $\delta =\omega $
by Puritz [Reference Puritz30, Reference Puritz, Luxemburg and Robinson31] and generalized to measurable cardinals later by Kanamori [Reference Kanamori24]. This concept will enable us to simplify our future definitions.
$\delta =\omega $
by Puritz [Reference Puritz30, Reference Puritz, Luxemburg and Robinson31] and generalized to measurable cardinals later by Kanamori [Reference Kanamori24]. This concept will enable us to simplify our future definitions.
Definition 4.3. Let
![]() $j:V\rightarrow M$
be an elementary embedding where M is transitive, and let
$j:V\rightarrow M$
be an elementary embedding where M is transitive, and let
![]() $\kappa $
be any cardinal. We define a transitive relation on
$\kappa $
be any cardinal. We define a transitive relation on
![]() $[\sup (j"{\kappa }),j(\kappa ))$
:
$[\sup (j"{\kappa }),j(\kappa ))$
:
![]() $\alpha \preceq \beta $
if there is a function
$\alpha \preceq \beta $
if there is a function
![]() $f:\kappa \rightarrow \kappa $
such that
$f:\kappa \rightarrow \kappa $
such that
![]() $j(f)(\beta )\geq \alpha $
. We derive the equivalence relation
$j(f)(\beta )\geq \alpha $
. We derive the equivalence relation
![]() $\alpha \equiv \beta $
if
$\alpha \equiv \beta $
if
![]() $\alpha \preceq \beta $
and
$\alpha \preceq \beta $
and
![]() $\beta \preceq \alpha $
. A sky of j at
$\beta \preceq \alpha $
. A sky of j at
![]() $\kappa $
is a
$\kappa $
is a
![]() $\equiv $
-equivalence class. We denote by
$\equiv $
-equivalence class. We denote by
![]() $sky(\alpha )$
the sky of
$sky(\alpha )$
the sky of
![]() $\alpha $
at
$\alpha $
at
![]() $\kappa $
for the unique
$\kappa $
for the unique
![]() $\kappa $
such that
$\kappa $
such that
![]() $\alpha \in [\sup (j"{\kappa }),j(\kappa ))$
.
$\alpha \in [\sup (j"{\kappa }),j(\kappa ))$
.
Note that the only interesting situation is when
![]() $\kappa $
is not a continuity point of j. Since M is transitive,
$\kappa $
is not a continuity point of j. Since M is transitive,
![]() $\prec $
is a well-defined well-ordering of the skies. Moreover, since
$\prec $
is a well-defined well-ordering of the skies. Moreover, since
![]() $\alpha \leq \beta $
implies
$\alpha \leq \beta $
implies
![]() $\alpha \preceq \beta $
, then each sky is a half-open interval.
$\alpha \preceq \beta $
, then each sky is a half-open interval.
Suppose now that U is a
![]() $\sigma $
-complete ultrafilter over
$\sigma $
-complete ultrafilter over
![]() $\kappa $
. It is clear that for any
$\kappa $
. It is clear that for any
![]() $\alpha <j_U(\kappa )$
,
$\alpha <j_U(\kappa )$
,
![]() $\alpha \preceq [id]_U$
as
$\alpha \preceq [id]_U$
as
![]() $\alpha =[f]_U$
for some
$\alpha =[f]_U$
for some
![]() $f:\kappa \rightarrow \kappa $
and therefore
$f:\kappa \rightarrow \kappa $
and therefore
![]() $\alpha =j_U(f)([id]_U)$
. So
$\alpha =j_U(f)([id]_U)$
. So
![]() $sky([id]_U)$
is the maximal sky. This simple observation, together with Proposition 2.3, leads to an elegant characterization of p-points in terms of skies.
$sky([id]_U)$
is the maximal sky. This simple observation, together with Proposition 2.3, leads to an elegant characterization of p-points in terms of skies.
Corollary 4.4 Let U be a
![]() $\sigma $
-complete ultrafilter over
$\sigma $
-complete ultrafilter over
![]() $\kappa $
, then U is a p-point if and only if
$\kappa $
, then U is a p-point if and only if
![]() $j_U$
has a unique sky at
$j_U$
has a unique sky at
![]() $\kappa $
.
$\kappa $
.
We can now reformulate Theorem 4.1 in terms of skies.
Corollary 4.5 Suppose that U is a
![]() $\kappa $
-complete,
$\kappa $
-complete,
![]() $\lambda $
-sound ultrafilter over
$\lambda $
-sound ultrafilter over
![]() $\kappa $
such that
$\kappa $
such that
![]() $\lambda $
is the least element of the second sky at
$\lambda $
is the least element of the second sky at
![]() $\kappa $
. Then U is non-Galvin.
$\kappa $
. Then U is non-Galvin.
Proof By the definition of
![]() $\xi $
in the proof of Theorem 4.1, we can choose
$\xi $
in the proof of Theorem 4.1, we can choose
![]() $\xi =[\text {id}]_U$
and the theorem ensures that
$\xi =[\text {id}]_U$
and the theorem ensures that
![]() $U=D(j_U,[\text {id}]_U)$
is non-Galvin.
$U=D(j_U,[\text {id}]_U)$
is non-Galvin.
Note that a embedding j with critical point
![]() $\kappa $
has at least two skies at
$\kappa $
has at least two skies at
![]() $\kappa $
if and only if
$\kappa $
if and only if
![]() $\sup \{j(f)(\kappa )\mid f\colon \kappa \rightarrow \kappa \}<j(\kappa )$
.
$\sup \{j(f)(\kappa )\mid f\colon \kappa \rightarrow \kappa \}<j(\kappa )$
.
Corollary 4.6 Suppose that there is a superstrong embedding
![]() $j\colon V\rightarrow M$
with
$j\colon V\rightarrow M$
with
![]() $\operatorname {\mathrm {crit}}(j)=\kappa $
and at least two skies. Then
$\operatorname {\mathrm {crit}}(j)=\kappa $
and at least two skies. Then
![]() $\kappa $
carries a non-Galvin ultrafilter.
$\kappa $
carries a non-Galvin ultrafilter.
The reason that
![]() $\diamondsuit ^*_{\mathrm{thin}}$
(Definition 3.1) is not equivalent to Dodd soundness is that we are only trying to cover
$\diamondsuit ^*_{\mathrm{thin}}$
(Definition 3.1) is not equivalent to Dodd soundness is that we are only trying to cover
![]() $\{j_U(S)\cap [id]_U\mid S\subseteq \kappa \}$
with a set A in
$\{j_U(S)\cap [id]_U\mid S\subseteq \kappa \}$
with a set A in
![]() $M_U$
, while in Dodd soundness we need the actual set
$M_U$
, while in Dodd soundness we need the actual set
![]() $\{j_U(S)\cap [id]_U\mid S\subseteq \kappa \}$
to be in
$\{j_U(S)\cap [id]_U\mid S\subseteq \kappa \}$
to be in
![]() $M_U$
. Let us call this property covering soundness. The innovation here is to work with covering
$M_U$
. Let us call this property covering soundness. The innovation here is to work with covering
![]() $\lambda $
-soundness which is just the ability to cover
$\lambda $
-soundness which is just the ability to cover
![]() $\{j_U(S)\cap \lambda \mid S\subseteq \kappa \}$
.
$\{j_U(S)\cap \lambda \mid S\subseteq \kappa \}$
.
However, without any further assumptions, we can always take
![]() $P^{M_U}(\lambda )$
as our covering set, so covering
$P^{M_U}(\lambda )$
as our covering set, so covering
![]() $\lambda $
-soundness is always true. What makes
$\lambda $
-soundness is always true. What makes
![]() $\diamondsuit ^*_{\mathrm{thin}}$
nontrivial is the second requirement that there is no function
$\diamondsuit ^*_{\mathrm{thin}}$
nontrivial is the second requirement that there is no function
![]() $f:\kappa \rightarrow \kappa $
such that
$f:\kappa \rightarrow \kappa $
such that
![]() $j_U(f)(|A|^{M_U})\geq [id]_U$
. This rules out our previous example of
$j_U(f)(|A|^{M_U})\geq [id]_U$
. This rules out our previous example of
![]() $P^{M_U}(\lambda )$
or any other trivial example. Equipped with our new terminology of skies, we note that
$P^{M_U}(\lambda )$
or any other trivial example. Equipped with our new terminology of skies, we note that
![]() $(2)$
of Definition 3.1 is in fact equivalent to
$(2)$
of Definition 3.1 is in fact equivalent to
![]() $|A|^M$
not laying the top sky (namely
$|A|^M$
not laying the top sky (namely
![]() $sky(|A|^{M_U})\prec sky([id]_U)$
).
$sky(|A|^{M_U})\prec sky([id]_U)$
).
Assuming (full)
![]() $\lambda $
-soundness, the results of this section ensure that the “covering” set could be chosen to be precisely
$\lambda $
-soundness, the results of this section ensure that the “covering” set could be chosen to be precisely
![]() $\{j_U(S)\cap \lambda \mid S\subseteq \kappa \}$
. Moreover, with this choice, the
$\{j_U(S)\cap \lambda \mid S\subseteq \kappa \}$
. Moreover, with this choice, the
![]() $M_U$
-cardinality of the covering set is
$M_U$
-cardinality of the covering set is
![]() $2^\kappa $
. Then, under the assumption on
$2^\kappa $
. Then, under the assumption on
![]() $\lambda $
in Theorem 4.1, there is no function
$\lambda $
in Theorem 4.1, there is no function
![]() $f:\kappa \rightarrow \kappa $
such that
$f:\kappa \rightarrow \kappa $
such that
![]() $j_U(f)(2^\kappa )\geq \lambda $
.
$j_U(f)(2^\kappa )\geq \lambda $
.
Bearing the idea of skies in mind, we see the following common theme: if A is the covering set and
![]() $\lambda $
is the degree of covering soundness, then
$\lambda $
is the degree of covering soundness, then
![]() $sky(|A|^{M_U})\prec sky(\lambda )$
. Let us formulate a diamond-like principle which generalize both Theorem 4.1 and
$sky(|A|^{M_U})\prec sky(\lambda )$
. Let us formulate a diamond-like principle which generalize both Theorem 4.1 and
![]() $\diamondsuit ^*_{\mathrm{thin}}(U)$
. It corresponds to covering
$\diamondsuit ^*_{\mathrm{thin}}(U)$
. It corresponds to covering
![]() $\lambda $
-soundness, allowing
$\lambda $
-soundness, allowing
![]() $\lambda $
to lay in an arbitrary sky (except the least one). This diamond-like principle is essential to prove the characterization of
$\lambda $
to lay in an arbitrary sky (except the least one). This diamond-like principle is essential to prove the characterization of
![]() $\sigma $
-complete non-Galvin ultrafilters.
$\sigma $
-complete non-Galvin ultrafilters.
Definition 4.7. Let U be an ultrafilter over a regular cardinal
![]() $\kappa $
.
$\kappa $
.
![]() $\diamondsuit ^-_{\mathrm{thin}}(U)$
is the statement that there is
$\diamondsuit ^-_{\mathrm{thin}}(U)$
is the statement that there is
![]() $A\in M_U$
and
$A\in M_U$
and
![]() $\lambda <j_U(\kappa )$
such that:
$\lambda <j_U(\kappa )$
such that:
-
(1)
 $\{j_U(S)\cap \lambda \mid S\subseteq \kappa \}\subseteq A$
.
$\{j_U(S)\cap \lambda \mid S\subseteq \kappa \}\subseteq A$
. -
(2) There is no function
 $f\colon \kappa \rightarrow \kappa $
such that
$f\colon \kappa \rightarrow \kappa $
such that
 $j_U(f)(|A|^M)\geq \lambda $
Footnote
11
.
$j_U(f)(|A|^M)\geq \lambda $
Footnote
11
.
Clearly,
![]() $\diamondsuit ^*_{\mathrm{thin}}(U)$
implies
$\diamondsuit ^*_{\mathrm{thin}}(U)$
implies
![]() $\diamondsuit ^-_{\mathrm{thin}}(U)$
by taking
$\diamondsuit ^-_{\mathrm{thin}}(U)$
by taking
![]() $\lambda =[id]_U$
.
$\lambda =[id]_U$
.
Corollary 4.8 If U is an ultrafilter over a regular cardinal
![]() $\kappa $
which is
$\kappa $
which is
![]() $\lambda $
-sound where
$\lambda $
-sound where
![]() $\lambda $
is such that for every function
$\lambda $
is such that for every function
![]() $f:\kappa \rightarrow \kappa $
,
$f:\kappa \rightarrow \kappa $
,
![]() $j_U(f)(\kappa )<\lambda $
, then
$j_U(f)(\kappa )<\lambda $
, then
![]() $\diamondsuit ^-_{\mathrm{thin}}(U)$
.
$\diamondsuit ^-_{\mathrm{thin}}(U)$
.
Proof By
![]() $\lambda $
-soundness of U,
$\lambda $
-soundness of U,
![]() $A:=\{j_U(S)\cap \lambda \mid S\subseteq \kappa \}\in M_U$
and
$A:=\{j_U(S)\cap \lambda \mid S\subseteq \kappa \}\in M_U$
and
![]() $M_U\models |A|=2^\kappa $
. There cannot be a function
$M_U\models |A|=2^\kappa $
. There cannot be a function
![]() $g:\kappa \rightarrow \kappa $
such that
$g:\kappa \rightarrow \kappa $
such that
![]() $j_U(g)(2^\kappa )\geq \lambda $
, since otherwise, the function
$j_U(g)(2^\kappa )\geq \lambda $
, since otherwise, the function
![]() $g'(\alpha )=g(2^\alpha )$
would be a function from
$g'(\alpha )=g(2^\alpha )$
would be a function from
![]() $\kappa $
to
$\kappa $
to
![]() $\kappa $
such that
$\kappa $
such that
![]() $j_U(g')(\kappa )\geq \lambda $
, contradicting the assumptions of the corollary.
$j_U(g')(\kappa )\geq \lambda $
, contradicting the assumptions of the corollary.
Theorem 4.9
![]() $\diamondsuit ^-_{\mathrm{thin}}(U)$
implies that U is non-Galvin.
$\diamondsuit ^-_{\mathrm{thin}}(U)$
implies that U is non-Galvin.
Proof Fix any
![]() ${\langle } X_\alpha {\rangle }_{\alpha <2^\kappa }$
sequence of distinct subsets of
${\langle } X_\alpha {\rangle }_{\alpha <2^\kappa }$
sequence of distinct subsets of
![]() $\kappa $
.
$\kappa $
.
![]() $[\alpha \mapsto A_\alpha ]_U=A$
and
$[\alpha \mapsto A_\alpha ]_U=A$
and
![]() $[f]_U=\lambda =j_U(f)([id]_U)$
. By our assumption,
$[f]_U=\lambda =j_U(f)([id]_U)$
. By our assumption,
We claim that
![]() ${\langle } B_\alpha {\rangle }_{ \alpha <2^\kappa }$
witness that
${\langle } B_\alpha {\rangle }_{ \alpha <2^\kappa }$
witness that
![]() $\neg \mathrm{Gal}(U,\kappa ,2^\kappa )$
. Otherwise, there is
$\neg \mathrm{Gal}(U,\kappa ,2^\kappa )$
. Otherwise, there is
![]() $I\in [2^\kappa ]^\kappa $
such that
$I\in [2^\kappa ]^\kappa $
such that
![]() $B_I:=\cap _{i\in I}B_i\in U$
. Consider the map
$B_I:=\cap _{i\in I}B_i\in U$
. Consider the map
![]() $\xi \mapsto |A_\xi |$
, note that
$\xi \mapsto |A_\xi |$
, note that
![]() $|A_\xi |\leq \pi (\xi )$
where
$|A_\xi |\leq \pi (\xi )$
where
![]() $j_U(\pi )([\text {id}]_U)=|A|$
, and therefore there must be
$j_U(\pi )([\text {id}]_U)=|A|$
, and therefore there must be
![]() $\theta <\kappa $
such that
$\theta <\kappa $
such that
Just assume otherwise, then for each
![]() $\theta <\kappa $
, we can define
$\theta <\kappa $
, we can define
then
![]() $g\colon \kappa \rightarrow \kappa $
is well-defined. Since
$g\colon \kappa \rightarrow \kappa $
is well-defined. Since
![]() $j_U(\pi )([\text {id}]_D)=|A|$
we conclude that
$j_U(\pi )([\text {id}]_D)=|A|$
we conclude that
![]() $j_U(g)(|A|)\geq j_U(f)([\text {id}]_D)=\lambda $
, contradicting condition
$j_U(g)(|A|)\geq j_U(f)([\text {id}]_D)=\lambda $
, contradicting condition
![]() $(2)$
. Now the continuation is as before, we find
$(2)$
. Now the continuation is as before, we find
![]() $\beta \in B_I$
such that
$\beta \in B_I$
such that
![]() $f(\beta )$
is high enough so that the restriction of
$f(\beta )$
is high enough so that the restriction of
![]() $\theta ^{+}$
-many of the sets in I to
$\theta ^{+}$
-many of the sets in I to
![]() $f(\beta )$
are distinct. This produces a contradiction.
$f(\beta )$
are distinct. This produces a contradiction.
The advantage of using the class of ultrafilters satisfying
![]() $\diamondsuit ^-_{\mathrm{thin}}(U)$
over the class satisfying
$\diamondsuit ^-_{\mathrm{thin}}(U)$
over the class satisfying
![]() $\diamondsuit ^*_{\mathrm{thin}}$
, is that is it upward closed with respect to the Rudin–Keisler ordering.
$\diamondsuit ^*_{\mathrm{thin}}$
, is that is it upward closed with respect to the Rudin–Keisler ordering.
Lemma 4.10 Suppose that
![]() $\diamondsuit ^-_{\mathrm{thin}}(U)$
holds and
$\diamondsuit ^-_{\mathrm{thin}}(U)$
holds and
![]() $U\leq _{RK}W$
, then
$U\leq _{RK}W$
, then
![]() $\diamondsuit ^-_{\mathrm{thin}}(W)$
holds.
$\diamondsuit ^-_{\mathrm{thin}}(W)$
holds.
Proof Let
![]() $k:M_U\rightarrow M_W$
be an elementary embedding such that
$k:M_U\rightarrow M_W$
be an elementary embedding such that
![]() $j_W=k\circ j_U$
and
$j_W=k\circ j_U$
and
![]() $A,\lambda $
witnessing
$A,\lambda $
witnessing
![]() $\diamondsuit ^-_{\mathrm{thin}}(U)$
. For every
$\diamondsuit ^-_{\mathrm{thin}}(U)$
. For every
![]() $S\subseteq \kappa $
, we have
$S\subseteq \kappa $
, we have
Hence
![]() $\{j_W(S)\cap k(\lambda )\mid S\subseteq \kappa \}\subseteq k(A)\in M_W$
. By elementarity,
$\{j_W(S)\cap k(\lambda )\mid S\subseteq \kappa \}\subseteq k(A)\in M_W$
. By elementarity,
![]() $|k(A)|^{M_W}=k(|A|^{M_U})$
. Suppose toward contradiction that there is a function
$|k(A)|^{M_W}=k(|A|^{M_U})$
. Suppose toward contradiction that there is a function
![]() $g:\kappa \rightarrow \kappa $
such that
$g:\kappa \rightarrow \kappa $
such that
![]() $j_W(g)(k(|A|^{M_U}))\geq k(\lambda )$
, then
$j_W(g)(k(|A|^{M_U}))\geq k(\lambda )$
, then
![]() $k(j_U(g)(|A|))\geq k(\lambda )$
and by elementarity if k,
$k(j_U(g)(|A|))\geq k(\lambda )$
and by elementarity if k,
![]() $j_U(g)(|A|)\geq \lambda $
, contradiction.
$j_U(g)(|A|)\geq \lambda $
, contradiction.
Lemma 4.11 Suppose that Z is an ultrafilter on
![]() $\kappa $
which is the U-limit of a discrete sequence of ultrafilters
$\kappa $
which is the U-limit of a discrete sequence of ultrafilters
![]() $W_\xi $
on
$W_\xi $
on
![]() $\kappa $
and such that
$\kappa $
and such that
![]() $\diamondsuit ^-_{\mathrm{thin}}(W_\xi )$
. Then
$\diamondsuit ^-_{\mathrm{thin}}(W_\xi )$
. Then
![]() $\diamondsuit ^-_{\mathrm{thin}}(Z)$
.
$\diamondsuit ^-_{\mathrm{thin}}(Z)$
.
Proof Fix a partition of
![]() $\kappa $
into sets
$\kappa $
into sets
![]() $S_\xi \in W_\xi $
. For each
$S_\xi \in W_\xi $
. For each
![]() $\xi < \kappa $
, let
$\xi < \kappa $
, let
![]() $\langle \mathcal A^\xi _\alpha \rangle _{\alpha < \kappa }$
and
$\langle \mathcal A^\xi _\alpha \rangle _{\alpha < \kappa }$
and
![]() $f_\xi $
witness that
$f_\xi $
witness that
![]() $\diamondsuit ^-_{\mathrm{thin}}(W_\xi )$
. Then let
$\diamondsuit ^-_{\mathrm{thin}}(W_\xi )$
. Then let
![]() $\mathcal A_\alpha = \mathcal A^\xi _\alpha $
, where
$\mathcal A_\alpha = \mathcal A^\xi _\alpha $
, where
![]() $\xi < \kappa $
is unique such that
$\xi < \kappa $
is unique such that
![]() $\alpha \in S_\xi $
and
$\alpha \in S_\xi $
and
![]() $f(\alpha )=f_\xi (\alpha )$
. Let
$f(\alpha )=f_\xi (\alpha )$
. Let
![]() $A\subseteq \kappa $
, we would like to show that
$A\subseteq \kappa $
, we would like to show that
![]() $B:=\{\alpha <\kappa \mid A\cap f(\alpha )\in \mathcal {A}_{\alpha }\}\in U\text {-}\lim {\langle } W_\xi {\rangle }_{\xi <\kappa }$
. Take any
$B:=\{\alpha <\kappa \mid A\cap f(\alpha )\in \mathcal {A}_{\alpha }\}\in U\text {-}\lim {\langle } W_\xi {\rangle }_{\xi <\kappa }$
. Take any
![]() $\xi <\kappa $
, then
$\xi <\kappa $
, then
![]() $B_\xi :=\{\alpha \in S_\xi \mid A\cap f_\xi (\alpha )\in \mathcal {A}^\xi _\alpha \}\in W_\xi $
. Since for each
$B_\xi :=\{\alpha \in S_\xi \mid A\cap f_\xi (\alpha )\in \mathcal {A}^\xi _\alpha \}\in W_\xi $
. Since for each
![]() $\alpha \in S_\xi $
and
$\alpha \in S_\xi $
and
![]() $f(\alpha )=f_\xi (\alpha )$
,
$f(\alpha )=f_\xi (\alpha )$
,
![]() $\mathcal {A}_\alpha =\mathcal {A}^\xi _\alpha $
, we conclude that
$\mathcal {A}_\alpha =\mathcal {A}^\xi _\alpha $
, we conclude that
![]() $B_\xi \subseteq B$
and therefore
$B_\xi \subseteq B$
and therefore
![]() $B\in W_\xi $
. It follows that
$B\in W_\xi $
. It follows that
![]() $B\in U\text {-}\lim {\langle } W_\xi {\rangle }_{\xi <\kappa }$
. It remains to show that
$B\in U\text {-}\lim {\langle } W_\xi {\rangle }_{\xi <\kappa }$
. It remains to show that
![]() $c(\alpha )=|\mathcal {A}_\alpha |$
is in a lower sky than f. Suppose otherwise and let
$c(\alpha )=|\mathcal {A}_\alpha |$
is in a lower sky than f. Suppose otherwise and let
![]() $g:\kappa \rightarrow \kappa $
such that for some
$g:\kappa \rightarrow \kappa $
such that for some
![]() $B\in W$
,
$B\in W$
,
![]() $\alpha \in B\rightarrow g(c(\alpha ))\geq f(\alpha )$
. Pick any
$\alpha \in B\rightarrow g(c(\alpha ))\geq f(\alpha )$
. Pick any
![]() $\xi <\kappa $
such that
$\xi <\kappa $
such that
![]() $B\in W_\xi $
to reach a contradiction note that
$B\in W_\xi $
to reach a contradiction note that
![]() $B\cap S_\xi \in W_\xi $
, and for every
$B\cap S_\xi \in W_\xi $
, and for every
![]() $\alpha \in B\cap S_\xi $
,
$\alpha \in B\cap S_\xi $
,
![]() $g(|A^\xi |_\alpha )=g(c(\alpha ))\geq f(\alpha )=f_\xi (\alpha )$
. However, the sky
$g(|A^\xi |_\alpha )=g(c(\alpha ))\geq f(\alpha )=f_\xi (\alpha )$
. However, the sky
![]() $\alpha \mapsto |\mathcal {A}^\xi _\alpha |$
is below the sky of
$\alpha \mapsto |\mathcal {A}^\xi _\alpha |$
is below the sky of
![]() $f_\xi $
, contradicting the choice of
$f_\xi $
, contradicting the choice of
![]() $f_\xi $
.
$f_\xi $
.
For a non-discrete sequence, we have the following.
Lemma 4.12 Suppose that Z is an ultrafilter over
![]() $\kappa $
which is Rudin–Keisler equivalent to
$\kappa $
which is Rudin–Keisler equivalent to
![]() $\sum _U{\langle } W_\xi {\rangle }_{\xi <\lambda }$
, where U is any ultrafilter over
$\sum _U{\langle } W_\xi {\rangle }_{\xi <\lambda }$
, where U is any ultrafilter over
![]() $\lambda \leq \kappa $
and
$\lambda \leq \kappa $
and
![]() $W_\xi 's$
are ultrafilters over
$W_\xi 's$
are ultrafilters over
![]() $\kappa $
such that
$\kappa $
such that
![]() $\diamondsuit ^-_{\mathrm{thin}}(W_\xi )$
holds. Then
$\diamondsuit ^-_{\mathrm{thin}}(W_\xi )$
holds. Then
![]() $\diamondsuit ^-_{\mathrm{thin}}(Z)$
holds.
$\diamondsuit ^-_{\mathrm{thin}}(Z)$
holds.
Proof Let
![]() $W^*=[\xi \mapsto W_\xi ]_U$
. By our assumption,
$W^*=[\xi \mapsto W_\xi ]_U$
. By our assumption,
Let
![]() $j_{W^*}:M_{U}\rightarrow M_{W^*}$
be the ultrapower of
$j_{W^*}:M_{U}\rightarrow M_{W^*}$
be the ultrapower of
![]() $M_U$
by
$M_U$
by
![]() $W^*$
. It follows that there is
$W^*$
. It follows that there is
![]() $A\in M_{W^*}$
and
$A\in M_{W^*}$
and
![]() $\lambda <j_{W^*}(j_U(\kappa ))$
such that
$\lambda <j_{W^*}(j_U(\kappa ))$
such that
![]() $\{j_{W^*}(S)\cap \lambda \mid S\in P(j_U(\kappa ))^{M_U}\}\subseteq A$
and there is no function
$\{j_{W^*}(S)\cap \lambda \mid S\in P(j_U(\kappa ))^{M_U}\}\subseteq A$
and there is no function
![]() $f:j_U(\kappa )\rightarrow j_U(\kappa )\in M_U$
such that
$f:j_U(\kappa )\rightarrow j_U(\kappa )\in M_U$
such that
![]() $j_{W^*}(f)(|A|^{M_{W^*}})\geq \lambda $
. Note that
$j_{W^*}(f)(|A|^{M_{W^*}})\geq \lambda $
. Note that
![]() $M_{W^*}=M_{\sum _U{\langle } W_\xi {\rangle }_{\xi <\lambda }}$
and
$M_{W^*}=M_{\sum _U{\langle } W_\xi {\rangle }_{\xi <\lambda }}$
and
![]() $j_{\sum _U{\langle } W_\xi {\rangle }_{\xi <\lambda }}=j_{W^*}\circ j_U$
. We claim that A and
$j_{\sum _U{\langle } W_\xi {\rangle }_{\xi <\lambda }}=j_{W^*}\circ j_U$
. We claim that A and
![]() $\lambda $
witness that
$\lambda $
witness that
![]() $\diamondsuit ^-_{\mathrm{thin}}(\sum _U{\langle } W_\xi {\rangle }_{\xi <\lambda })$
. Indeed, for any
$\diamondsuit ^-_{\mathrm{thin}}(\sum _U{\langle } W_\xi {\rangle }_{\xi <\lambda })$
. Indeed, for any
![]() $X\subseteq \kappa $
,
$X\subseteq \kappa $
,
![]() $j_U(X)\in P(j_U(\kappa ))^{M_U}$
and therefore
$j_U(X)\in P(j_U(\kappa ))^{M_U}$
and therefore
![]() $j_{W^*}(j_U(X))\cap \lambda \in A$
. Similarly, for any function
$j_{W^*}(j_U(X))\cap \lambda \in A$
. Similarly, for any function
![]() $f:\kappa \rightarrow \kappa $
,
$f:\kappa \rightarrow \kappa $
,
![]() $j_U(f):j_U(\kappa )\rightarrow j_U(\kappa )\in M_U$
and therefore
$j_U(f):j_U(\kappa )\rightarrow j_U(\kappa )\in M_U$
and therefore
![]() $j_{W^*}(j_U(f))(|A|^{M_{W^*}})<\lambda $
.
$j_{W^*}(j_U(f))(|A|^{M_{W^*}})<\lambda $
.
5 Non-Galvin cardinals
As pointed out in the Introduction, a measurable cardinal does not imply the existence of a non-Galvin ultrafilter [Reference Benhamou and Gitik9]. In [Reference Benhamou1], the question regarding which large cardinal properties imply the existence of non-Galvin ultrafilters was raised and in [Reference Benhamou and Dobrinen2] a
![]() $\kappa $
-compact cardinal was proven to carry such an ultrafilter. We open this section with a new large cardinal property.
$\kappa $
-compact cardinal was proven to carry such an ultrafilter. We open this section with a new large cardinal property.
Definition 5.1.
![]() $\kappa $
is called non-Galvin cardinal if there are elementary embeddings
$\kappa $
is called non-Galvin cardinal if there are elementary embeddings
![]() $j\colon V\rightarrow M$
,
$j\colon V\rightarrow M$
,
![]() $i\colon V\rightarrow N$
,
$i\colon V\rightarrow N$
,
![]() $k\colon N\rightarrow M$
such that:
$k\colon N\rightarrow M$
such that:
-
(1)
 $k\circ i=j$
.
$k\circ i=j$
. -
(2)
 $\operatorname {\mathrm {crit}}(j)=\kappa $
,
$\operatorname {\mathrm {crit}}(j)=\kappa $
,
 $\operatorname {\mathrm {crit}}(k)=i(\kappa )$
.
$\operatorname {\mathrm {crit}}(k)=i(\kappa )$
. -
(3)
 ${}^{\kappa }N\subseteq N$
and
${}^{\kappa }N\subseteq N$
and
 ${}^{\kappa }M\subseteq M.$
${}^{\kappa }M\subseteq M.$
-
(4) There is
 $A\in M$
such that
$A\in M$
such that
 $i"\kappa ^+\subseteq A$
and
$i"\kappa ^+\subseteq A$
and
 $M\models |A|<i(\kappa )$
.
$M\models |A|<i(\kappa )$
.
Note that by condition
![]() $(4)$
,
$(4)$
,
![]() $\kappa \subseteq A$
and that A can be chosen so that
$\kappa \subseteq A$
and that A can be chosen so that
![]() $\min (A\setminus \kappa )=i(\kappa )$
.
$\min (A\setminus \kappa )=i(\kappa )$
.
The next proposition implies that we may assume that the embedding j in the definition of non-Galvin cardinals is an ultrapower embedding and the embedding i is an extender ultrapower derived from it.
Proposition 5.2 Suppose that
![]() $j\colon V\rightarrow M$
,
$j\colon V\rightarrow M$
,
![]() $i\colon V\rightarrow N$
,
$i\colon V\rightarrow N$
,
![]() $k\colon N\rightarrow M$
and
$k\colon N\rightarrow M$
and
![]() $A\in M$
are as in Definition 5.1. Then there is a
$A\in M$
are as in Definition 5.1. Then there is a
![]() $\kappa $
-complete ultrafilter U over
$\kappa $
-complete ultrafilter U over
![]() $V_\kappa $
and
$V_\kappa $
and
![]() $\rho <j_U(\kappa )$
which, together with the ultrapower by the
$\rho <j_U(\kappa )$
which, together with the ultrapower by the
![]() $(\kappa ,\rho )$
-extender E derived from
$(\kappa ,\rho )$
-extender E derived from
![]() $j_U$
and
$j_U$
and
![]() $[\text {id}]_U$
, witnesses that
$[\text {id}]_U$
, witnesses that
![]() $\kappa $
is non-Galvin. Namely, the following hold:
$\kappa $
is non-Galvin. Namely, the following hold:
-
(1)
 $k_{E}\circ j_{E}=j_U$
.
$k_{E}\circ j_{E}=j_U$
. -
(2)
 $\operatorname {\mathrm {crit}}(j_U)=\kappa $
,
$\operatorname {\mathrm {crit}}(j_U)=\kappa $
,
 $\operatorname {\mathrm {crit}}(k_{E})=\rho =j_{E}(\kappa )$
.
$\operatorname {\mathrm {crit}}(k_{E})=\rho =j_{E}(\kappa )$
. -
(3)
 ${}^\kappa M_{E}\subseteq M_{E}$
and
${}^\kappa M_{E}\subseteq M_{E}$
and
 ${}^\kappa M_U\subseteq M_U$
.
${}^\kappa M_U\subseteq M_U$
. -
(4)
 $j_{E}"\kappa ^+\subseteq [\text {id}]_U$
and
$j_{E}"\kappa ^+\subseteq [\text {id}]_U$
and
 $M_U\models |[\text {id}]_U|<j_{E}(\kappa )$
.
$M_U\models |[\text {id}]_U|<j_{E}(\kappa )$
.
Proof We may assume
![]() $\sup (A) = \sup i"\kappa ^+$
and
$\sup (A) = \sup i"\kappa ^+$
and
![]() $A\cap i(\kappa ) = \kappa $
. Let U be the ultrafilter derived from j using A. Let
$A\cap i(\kappa ) = \kappa $
. Let U be the ultrafilter derived from j using A. Let
![]() $\bar A = [\text {id}]_U$
, and let
$\bar A = [\text {id}]_U$
, and let
![]() $k_U : M_U\to M$
be the unique elementary embedding with
$k_U : M_U\to M$
be the unique elementary embedding with
![]() $k_U\circ j_U = j$
and
$k_U\circ j_U = j$
and
![]() $k_U(\bar A) = A$
. Note that
$k_U(\bar A) = A$
. Note that
![]() $\kappa $
and
$\kappa $
and
![]() $i(\kappa )$
are in the range of
$i(\kappa )$
are in the range of
![]() $k_U$
since these ordinals are definable in M using A as a parameter:
$k_U$
since these ordinals are definable in M using A as a parameter:
![]() $\kappa $
is the least ordinal not in A, and
$\kappa $
is the least ordinal not in A, and
![]() $i(\kappa ) = |\sup (A)|^M$
. Therefore
$i(\kappa ) = |\sup (A)|^M$
. Therefore
![]() $k_U(\kappa ) = \kappa $
. Let
$k_U(\kappa ) = \kappa $
. Let
![]() $\rho $
be such that
$\rho $
be such that
![]() $k_U(\rho ) = i(\kappa )$
.
$k_U(\rho ) = i(\kappa )$
.
Let E be the extender of length
![]() $\rho $
derived from
$\rho $
derived from
![]() $j_U$
. Let
$j_U$
. Let
![]() $k_E : M_E\to M_U$
denote the unique factor embedding with
$k_E : M_E\to M_U$
denote the unique factor embedding with
![]() $k_E \circ j_E = j_U$
and
$k_E \circ j_E = j_U$
and
![]() $k_E\restriction \rho = \text {id}.$
$k_E\restriction \rho = \text {id}.$

We will verify (1), (2), (3), and (4). Of course, (1) is true essentially by the definition of
![]() $k_E$
.
$k_E$
.
For (2), note that
![]() $\operatorname {\mathrm {crit}}(j_U) = \kappa $
since
$\operatorname {\mathrm {crit}}(j_U) = \kappa $
since
![]() $k_U\circ j_U = j$
and
$k_U\circ j_U = j$
and
![]() $k_U(\kappa ) = \kappa $
. The fact that
$k_U(\kappa ) = \kappa $
. The fact that
![]() $\operatorname {\mathrm {crit}}(k_E) \geq \rho $
follows from the definition of
$\operatorname {\mathrm {crit}}(k_E) \geq \rho $
follows from the definition of
![]() $k_E$
. To see
$k_E$
. To see
![]() $\operatorname {\mathrm {crit}}(k_E) = \rho $
and
$\operatorname {\mathrm {crit}}(k_E) = \rho $
and
![]() $k_E(\rho ) = j_U(\kappa )$
, we will show thatFootnote
12
$k_E(\rho ) = j_U(\kappa )$
, we will show thatFootnote
12
This will establish that
![]() $\operatorname {\mathrm {crit}}(k_E) =\rho $
and
$\operatorname {\mathrm {crit}}(k_E) =\rho $
and
![]() $k_E(\rho ) = j_U(\kappa )$
since
$k_E(\rho ) = j_U(\kappa )$
since
![]() $k_E$
is the inverse of the transitive collapse of
$k_E$
is the inverse of the transitive collapse of
![]() $\text {Hull}^{M_U}(j_U"V\cup \rho )$
. To prove this equality, it suffices to show the inclusion
$\text {Hull}^{M_U}(j_U"V\cup \rho )$
. To prove this equality, it suffices to show the inclusion
![]() $\text {Hull}^{M_U}(j_U"V\cup \rho )\cap j_U(\kappa )\subseteq \rho $
.
$\text {Hull}^{M_U}(j_U"V\cup \rho )\cap j_U(\kappa )\subseteq \rho $
.
Since
![]() $k\circ i=j$
and since
$k\circ i=j$
and since
![]() $\operatorname {\mathrm {crit}}(k)=i(\kappa )$
, we have
$\operatorname {\mathrm {crit}}(k)=i(\kappa )$
, we have
![]() $\text {Hull}^M(j"V\cup i(\kappa ))\subseteq k"N$
, and therefore
$\text {Hull}^M(j"V\cup i(\kappa ))\subseteq k"N$
, and therefore
![]() $\text {Hull}^M(j"V\cup i(\kappa ))\cap j(\kappa ) \subseteq k"N\cap j(\kappa ) = i(\kappa )$
. Since
$\text {Hull}^M(j"V\cup i(\kappa ))\cap j(\kappa ) \subseteq k"N\cap j(\kappa ) = i(\kappa )$
. Since
we have
In particular,
 $$ \begin{align*}\mathrm{Hull}^{M_U}(j_U"V\cup \rho)\cap j_U(\kappa) &\subseteq k_U^{-1}[\mathrm{Hull}^M(j"V\cup i(\kappa))\cap j(\kappa)] \\ &= k_U^{-1}(i(\kappa)) = \rho.\end{align*} $$
$$ \begin{align*}\mathrm{Hull}^{M_U}(j_U"V\cup \rho)\cap j_U(\kappa) &\subseteq k_U^{-1}[\mathrm{Hull}^M(j"V\cup i(\kappa))\cap j(\kappa)] \\ &= k_U^{-1}(i(\kappa)) = \rho.\end{align*} $$
Since
![]() $k_E(\rho ) = j_U(\kappa )> \rho $
and
$k_E(\rho ) = j_U(\kappa )> \rho $
and
![]() $k_E \circ j_E = j_U$
, it follows
$k_E \circ j_E = j_U$
, it follows
![]() $\rho = j_E(\kappa )$
. Note also that
$\rho = j_E(\kappa )$
. Note also that
![]() $\rho < j_U(\kappa )$
, and so the fact that
$\rho < j_U(\kappa )$
, and so the fact that
![]() $k_E(\rho ) = j_U(\kappa )$
implies
$k_E(\rho ) = j_U(\kappa )$
implies
![]() $k_E(\rho ) \neq \rho $
and hence
$k_E(\rho ) \neq \rho $
and hence
![]() $\operatorname {\mathrm {crit}}(k_E) = \rho $
.
$\operatorname {\mathrm {crit}}(k_E) = \rho $
.
For (3), the inner model
![]() $M_U$
is closed under
$M_U$
is closed under
![]() $\kappa $
-sequences since it is the ultrapower of V by a
$\kappa $
-sequences since it is the ultrapower of V by a
![]() $\kappa $
-complete ultrafilter. The inner model
$\kappa $
-complete ultrafilter. The inner model
![]() $M_E$
is closed under
$M_E$
is closed under
![]() $\kappa $
-sequences by Lemma 5.3, since
$\kappa $
-sequences by Lemma 5.3, since
![]() $\mathrm {cf}(\rho )> \kappa $
and
$\mathrm {cf}(\rho )> \kappa $
and
![]() ${}^\kappa \rho \subseteq M_E$
. To see that
${}^\kappa \rho \subseteq M_E$
. To see that
![]() $\mathrm {cf}(\rho )> \kappa $
, note that
$\mathrm {cf}(\rho )> \kappa $
, note that
![]() $\mathrm {cf}(i(\kappa ))> \kappa $
since N satisfies that
$\mathrm {cf}(i(\kappa ))> \kappa $
since N satisfies that
![]() $i(\kappa )$
is regular and N is closed under
$i(\kappa )$
is regular and N is closed under
![]() $\kappa $
-sequences. Therefore M satisfies that
$\kappa $
-sequences. Therefore M satisfies that
![]() $\mathrm {cf}(i(\kappa ))> \kappa $
. By the elementarity of
$\mathrm {cf}(i(\kappa ))> \kappa $
. By the elementarity of
![]() $k_U$
, and since
$k_U$
, and since
![]() $k_U(\rho ) = i(\kappa )$
,
$k_U(\rho ) = i(\kappa )$
,
![]() $M_U$
satisfies
$M_U$
satisfies
![]() $\mathrm {cf}(\rho )> \kappa $
. Here, we use that
$\mathrm {cf}(\rho )> \kappa $
. Here, we use that
![]() $k_U(\kappa ) = \kappa $
.
$k_U(\kappa ) = \kappa $
.
Finally, we verify (4). By elementarity of
![]() $k_U$
, since
$k_U$
, since
![]() $|A| < i(\kappa )$
, we have
$|A| < i(\kappa )$
, we have
![]() $|\bar A| < \rho $
. So we just have to show that
$|\bar A| < \rho $
. So we just have to show that
![]() $j_E"\kappa ^+\subseteq \bar A.$
Suppose
$j_E"\kappa ^+\subseteq \bar A.$
Suppose
![]() $\alpha \in j_E"\kappa ^+.$
We claim that
$\alpha \in j_E"\kappa ^+.$
We claim that
![]() $k_U(\alpha )\in \text {ran}(i)$
. Let
$k_U(\alpha )\in \text {ran}(i)$
. Let
![]() ${\preceq }$
be a well order of
${\preceq }$
be a well order of
![]() $\kappa $
of order type
$\kappa $
of order type
![]() $j_E^{-1}(\alpha )$
. Then
$j_E^{-1}(\alpha )$
. Then
![]() $j_E({\preceq })$
has order type
$j_E({\preceq })$
has order type
![]() $\alpha $
. Note that
$\alpha $
. Note that
Thus
![]() $k_U(\alpha )$
, which is the order type of
$k_U(\alpha )$
, which is the order type of
![]() $k_U(j_E({\preceq }))$
is equal to the order type of
$k_U(j_E({\preceq }))$
is equal to the order type of
![]() $i({\preceq })$
, which is in the range of i. It follows that
$i({\preceq })$
, which is in the range of i. It follows that
![]() $(k_U\circ j_E)"\kappa ^+\subseteq i"\kappa ^+\subseteq A$
. Since
$(k_U\circ j_E)"\kappa ^+\subseteq i"\kappa ^+\subseteq A$
. Since
![]() $k_U(\bar {A}) = A$
, we conclude that
$k_U(\bar {A}) = A$
, we conclude that
![]() $j_E"\kappa ^+\subseteq k_U^{-1}[A]\subseteq \bar A$
.
$j_E"\kappa ^+\subseteq k_U^{-1}[A]\subseteq \bar A$
.
The proof of the following lemma, which was cited in the previous proposition, appears in [Reference Hamkins18, Lemma 2.9].
Lemma 5.3 Suppose E is an extender of length
![]() $\rho $
with
$\rho $
with
![]() $\operatorname {\mathrm {crit}}(j_E) = \kappa $
. If
$\operatorname {\mathrm {crit}}(j_E) = \kappa $
. If
![]() ${}^\kappa \rho \subseteq M_E$
, then
${}^\kappa \rho \subseteq M_E$
, then
![]() ${}^\kappa M_E\subseteq M_E$
. In particular, if E is the extender of length
${}^\kappa M_E\subseteq M_E$
. In particular, if E is the extender of length
![]() $\rho $
derived from an elementary embedding
$\rho $
derived from an elementary embedding
![]() $j : V\to M$
where
$j : V\to M$
where
![]() ${}^\kappa M\subseteq M$
,
${}^\kappa M\subseteq M$
,
![]() $\mathrm {cf}(\rho )> \kappa $
, and
$\mathrm {cf}(\rho )> \kappa $
, and
![]() $M\vDash \rho ^\kappa = \rho $
, then
$M\vDash \rho ^\kappa = \rho $
, then
![]() ${}^\kappa M_E\subseteq M_E$
.
${}^\kappa M_E\subseteq M_E$
.
Let us turn to the proof of Main Theorem 1.2.
Theorem 5.4 Suppose that
![]() $\kappa $
is a non-Galvin cardinal. Then there exists a
$\kappa $
is a non-Galvin cardinal. Then there exists a
![]() $\kappa $
-complete ultrafilter U over
$\kappa $
-complete ultrafilter U over
![]() $\kappa $
such that
$\kappa $
such that
![]() $\neg \mathrm {Gal}({U,\kappa ,\kappa ^+})$
. In particular, if
$\neg \mathrm {Gal}({U,\kappa ,\kappa ^+})$
. In particular, if
![]() $2^\kappa =\kappa ^+$
then U is non-Galvin.
$2^\kappa =\kappa ^+$
then U is non-Galvin.
Proof We use the notation of 5.1. As before, we can fix an ordinal
![]() $\nu <j(\kappa )$
such that for some sequence
$\nu <j(\kappa )$
such that for some sequence
![]() $\vec {A} = \langle A_\alpha \rangle _{\alpha < \kappa }$
such that
$\vec {A} = \langle A_\alpha \rangle _{\alpha < \kappa }$
such that
![]() $A = j(\vec {A})_\nu $
and for some sequence
$A = j(\vec {A})_\nu $
and for some sequence
![]() $\vec {\kappa } = \langle \kappa _\alpha \rangle _{\alpha < \kappa }$
,
$\vec {\kappa } = \langle \kappa _\alpha \rangle _{\alpha < \kappa }$
,
![]() $i(\kappa ) = j(\vec {\kappa })_\nu .$
Let
$i(\kappa ) = j(\vec {\kappa })_\nu .$
Let
![]() $U=D(j,\nu )$
be the ultrafilter on
$U=D(j,\nu )$
be the ultrafilter on
![]() $\kappa $
derived from j using
$\kappa $
derived from j using
![]() $\nu $
. Since
$\nu $
. Since
![]() $\operatorname {\mathrm {crit}}(j)=\kappa $
, U is a
$\operatorname {\mathrm {crit}}(j)=\kappa $
, U is a
![]() $\kappa $
-complete ultrafilter over
$\kappa $
-complete ultrafilter over
![]() $\kappa $
. We will show
$\kappa $
. We will show
![]() $\neg \mathrm {Gal}({U,\kappa ,\kappa ^+})$
.
$\neg \mathrm {Gal}({U,\kappa ,\kappa ^+})$
.
Let
![]() $\langle f_\xi \rangle _{\xi < \kappa ^+}$
denote the sequence of canonical functions on
$\langle f_\xi \rangle _{\xi < \kappa ^+}$
denote the sequence of canonical functions on
![]() $\kappa $
(see Definition 2.16). For
$\kappa $
(see Definition 2.16). For
![]() $\xi < \kappa ^+$
, define
$\xi < \kappa ^+$
, define
Note that
![]() $B_\xi \in U$
since
$B_\xi \in U$
since
and
The point here is that in N,
![]() $\vec g = i(\vec f)$
is the sequence of canonical functions on
$\vec g = i(\vec f)$
is the sequence of canonical functions on
![]() $i(\kappa )$
, and since
$i(\kappa )$
, and since
![]() $\operatorname {\mathrm {crit}}(k) = i(\kappa )$
, by Proposition 2.17, for any
$\operatorname {\mathrm {crit}}(k) = i(\kappa )$
, by Proposition 2.17, for any
![]() $\eta < i(\kappa ^+)$
,
$\eta < i(\kappa ^+)$
,
![]() $k(g_\eta )(i(\kappa )) = \eta $
. The fact that
$k(g_\eta )(i(\kappa )) = \eta $
. The fact that
![]() $k(i(f_\xi ))(i(\kappa )) = i(\xi )$
follows from this observation when
$k(i(f_\xi ))(i(\kappa )) = i(\xi )$
follows from this observation when
![]() $\eta = i(\xi )$
(and thus
$\eta = i(\xi )$
(and thus
![]() $i(f_\xi ) = g_{i(\xi )}$
).
$i(f_\xi ) = g_{i(\xi )}$
).
Suppose
![]() $\sigma \subseteq \kappa ^+$
and
$\sigma \subseteq \kappa ^+$
and
![]() $\bigcap _{\xi \in \sigma } B_\xi \in U$
. We must show that
$\bigcap _{\xi \in \sigma } B_\xi \in U$
. We must show that
![]() $|\sigma | < \kappa $
. Since
$|\sigma | < \kappa $
. Since
![]() $|A|^M < i(\kappa )$
, it suffices to show that
$|A|^M < i(\kappa )$
, it suffices to show that
![]() $i(\sigma )\subseteq A$
: then
$i(\sigma )\subseteq A$
: then
![]() $\text {ot}(i(\sigma )) < \text {ot}(A) < i(\kappa )$
, and hence
$\text {ot}(i(\sigma )) < \text {ot}(A) < i(\kappa )$
, and hence
![]() $N\vDash \text {ot}(i(\sigma )) < i(\kappa )$
, which by elementarity implies
$N\vDash \text {ot}(i(\sigma )) < i(\kappa )$
, which by elementarity implies
![]() $\text {ot}(\sigma ) < \kappa $
.
$\text {ot}(\sigma ) < \kappa $
.
The proof that
![]() $i(\sigma )\subseteq A$
is similar to the calculation in the previous paragraph: Since
$i(\sigma )\subseteq A$
is similar to the calculation in the previous paragraph: Since
![]() $\bigcap _{\xi \in \sigma } B_\xi \in U$
, for all
$\bigcap _{\xi \in \sigma } B_\xi \in U$
, for all
![]() $\eta \in j(\sigma )$
,
$\eta \in j(\sigma )$
,
![]() $j(\vec f)_\eta (i(\kappa )) \in A$
. Fix
$j(\vec f)_\eta (i(\kappa )) \in A$
. Fix
![]() $\xi \in i(\sigma )$
, and we will prove that
$\xi \in i(\sigma )$
, and we will prove that
![]() $\xi \in A$
. We have
$\xi \in A$
. We have
![]() $k(\xi )\in j(\sigma )$
, so
$k(\xi )\in j(\sigma )$
, so
![]() $j(\vec f)_{k(\xi )}(i(\kappa ))\in A$
. But
$j(\vec f)_{k(\xi )}(i(\kappa ))\in A$
. But
![]() $j(\vec f)_{k(\xi )} = k(g_\xi )$
, hence
$j(\vec f)_{k(\xi )} = k(g_\xi )$
, hence
![]() $k(g_\xi )(i(\kappa )) = \xi $
. It follows that
$k(g_\xi )(i(\kappa )) = \xi $
. It follows that
![]() $\xi \in A$
.
$\xi \in A$
.
Remark 5.5. Note that in condition
![]() $(4)$
the Definition 5.1 of non-Galvin cardinal it is important to work with
$(4)$
the Definition 5.1 of non-Galvin cardinal it is important to work with
![]() $\kappa ^+$
instead of
$\kappa ^+$
instead of
![]() $2^\kappa $
for there are no canonical functions in general up to
$2^\kappa $
for there are no canonical functions in general up to
![]() $2^\kappa $
.
$2^\kappa $
.
Remark 5.6. As proven in [Reference Benhamou and Dobrinen2], if
![]() $\kappa $
is
$\kappa $
is
![]() $\kappa $
-compact then there are
$\kappa $
-compact then there are
![]() $2^{2^\kappa }$
-many
$2^{2^\kappa }$
-many
![]() $\kappa $
-complete non-Galvin ultrafilters that extend the closed unbounded filter on
$\kappa $
-complete non-Galvin ultrafilters that extend the closed unbounded filter on
![]() $\kappa $
. On the other hand, assuming the Ultrapower Axiom and that every irreducible ultrafilter is Dodd sound, the least non-Galvin cardinal carries a unique non-Galvin ultrafilter that extends the closed unbounded filter on
$\kappa $
. On the other hand, assuming the Ultrapower Axiom and that every irreducible ultrafilter is Dodd sound, the least non-Galvin cardinal carries a unique non-Galvin ultrafilter that extends the closed unbounded filter on
![]() $\kappa $
. Under these assumptions, if
$\kappa $
. Under these assumptions, if
![]() $\kappa $
carries distinct non-Galvin ultrafilters extending the closed unbounded filter, then the Ketonen least distinct such ultrafilters are precisely the least two extensions of the closed unbounded filter concentrating on singular cardinals (see the proof of Theorem 6.6). These ultrafilters are irreducible (and in fact are Mitchell points) by [Reference Goldberg17, Corollary 8.2.13 and Proposition 8.3.39]. Therefore
$\kappa $
carries distinct non-Galvin ultrafilters extending the closed unbounded filter, then the Ketonen least distinct such ultrafilters are precisely the least two extensions of the closed unbounded filter concentrating on singular cardinals (see the proof of Theorem 6.6). These ultrafilters are irreducible (and in fact are Mitchell points) by [Reference Goldberg17, Corollary 8.2.13 and Proposition 8.3.39]. Therefore
![]() $D_0 \lhd D_1$
, so
$D_0 \lhd D_1$
, so
![]() $\kappa $
carries a non-Galvin ultrafilter in
$\kappa $
carries a non-Galvin ultrafilter in
![]() $\text {Ult}(V,D_1)$
, and so
$\text {Ult}(V,D_1)$
, and so
![]() $\kappa $
is not the least non-Galvin cardinal.
$\kappa $
is not the least non-Galvin cardinal.
As a first upper bound for the non-Galvin cardinals we have the following.
Theorem 5.7 If
![]() $\kappa $
is
$\kappa $
is
![]() $\kappa $
-compact, then
$\kappa $
-compact, then
![]() $\kappa $
is a non-Galvin cardinal.
$\kappa $
is a non-Galvin cardinal.
Proof Let U be a normal ultrafilter on
![]() $\kappa $
. Since
$\kappa $
. Since
![]() $|P^{M_U}(P_\kappa (\kappa ^+))| = 2^\kappa $
, there is a transitive model M with
$|P^{M_U}(P_\kappa (\kappa ^+))| = 2^\kappa $
, there is a transitive model M with
By Hayut’s result [Reference Hayut19, Corollary 6], there is a transitive model N, an elementary embedding
![]() $j_0\colon M\rightarrow N$
, with
$j_0\colon M\rightarrow N$
, with
![]() $\operatorname {\mathrm {crit}}(j_0)=\kappa $
along with some
$\operatorname {\mathrm {crit}}(j_0)=\kappa $
along with some
![]() $s\in N$
,
$s\in N$
,
![]() $s\subseteq j_0(\kappa )^+$
such that
$s\subseteq j_0(\kappa )^+$
such that
![]() $j_0"\kappa ^+\subseteq s$
with
$j_0"\kappa ^+\subseteq s$
with
![]() $|s|^N<j_0(\kappa )$
. Define
$|s|^N<j_0(\kappa )$
. Define
![]() $\mathcal {W}$
the
$\mathcal {W}$
the
![]() $\kappa $
-complete ultrafilter on
$\kappa $
-complete ultrafilter on
![]() $P_\kappa (\kappa ^+)$
derived from
$P_\kappa (\kappa ^+)$
derived from
![]() $j_0$
and s. Note that
$j_0$
and s. Note that
![]() $\mathcal {W}$
is fine since
$\mathcal {W}$
is fine since
![]() $j_0"\kappa ^+\subseteq s$
and it measures all the subsets of
$j_0"\kappa ^+\subseteq s$
and it measures all the subsets of
![]() $P_\kappa (\kappa ^+)$
in
$P_\kappa (\kappa ^+)$
in
![]() $M_U$
. Let
$M_U$
. Let
![]() $j_{\mathcal {W}}\colon M_U\rightarrow M_{\mathcal {W}}$
be the ultrapower of
$j_{\mathcal {W}}\colon M_U\rightarrow M_{\mathcal {W}}$
be the ultrapower of
![]() $M_U$
by
$M_U$
by
![]() $\mathcal {W}$
defined in V, and
$\mathcal {W}$
defined in V, and
![]() $j\colon V\to M_{\mathcal {W}}$
be the embedding
$j\colon V\to M_{\mathcal {W}}$
be the embedding
![]() $j = j_{\mathcal {W}}\circ j_U$
. Let
$j = j_{\mathcal {W}}\circ j_U$
. Let
![]() $\lambda = j_{\mathcal {W}}(\kappa )<j(\kappa ),$
and let E be the extender of length
$\lambda = j_{\mathcal {W}}(\kappa )<j(\kappa ),$
and let E be the extender of length
![]() $\lambda $
derived from j.
$\lambda $
derived from j.
Claim 5.8
E is also the extender of length
![]() $\lambda $
derived from
$\lambda $
derived from
![]() $j_{\mathcal {W}}.$
$j_{\mathcal {W}}.$
Proof For any
![]() $X\subseteq \kappa $
, we have that
$X\subseteq \kappa $
, we have that
Thus for all
![]() $\alpha <\lambda $
,
$\alpha <\lambda $
,
![]() $\alpha \in j(X)$
iff
$\alpha \in j(X)$
iff
![]() $\alpha \in j_{\mathcal {W}}(X)$
.
$\alpha \in j_{\mathcal {W}}(X)$
.
Finally, let
![]() $i\colon V\to N_E$
be the ultrapower of V by E and
$i\colon V\to N_E$
be the ultrapower of V by E and
![]() $A = [\text {id}]_{\mathcal {W}}\in M_{\mathcal {W}}$
. We claim that
$A = [\text {id}]_{\mathcal {W}}\in M_{\mathcal {W}}$
. We claim that
![]() $i,j,A$
witness that
$i,j,A$
witness that
![]() $\kappa $
is a non-Galvin cardinal. Indeed,
$\kappa $
is a non-Galvin cardinal. Indeed,
![]() $i(\kappa )\geq \lambda $
. To see that
$i(\kappa )\geq \lambda $
. To see that
![]() $i(\kappa )\leq \lambda $
, we compute the ultrapower
$i(\kappa )\leq \lambda $
, we compute the ultrapower
![]() $i'$
of
$i'$
of
![]() $M_U$
by E, and since
$M_U$
by E, and since
![]() $M_U$
is closed under
$M_U$
is closed under
![]() $\kappa $
-sequences, it follows that
$\kappa $
-sequences, it follows that
![]() $i(\kappa )=i'(\kappa )$
. By the previous claim,
$i(\kappa )=i'(\kappa )$
. By the previous claim,
![]() $j_{\mathcal {W}}$
also factors through
$j_{\mathcal {W}}$
also factors through
![]() $i'$
and thus
$i'$
and thus
![]() $j_{\mathcal {W}}(\kappa )=k'(i'(\kappa ))\geq i'(\kappa )=i(\kappa )$
, as wanted.
$j_{\mathcal {W}}(\kappa )=k'(i'(\kappa ))\geq i'(\kappa )=i(\kappa )$
, as wanted.
By the usual argument about the derived extender, the factor map
![]() $k\colon N_E\rightarrow M_{\mathcal {W}}$
has critical point
$k\colon N_E\rightarrow M_{\mathcal {W}}$
has critical point
![]() $i(\kappa )$
(see, for example, [Reference Jech21, Lemma 20.29(ii)]). Also,
$i(\kappa )$
(see, for example, [Reference Jech21, Lemma 20.29(ii)]). Also,
![]() $M_{\mathcal {W}}\models |A|<j_{\mathcal {W}}(\kappa )=i(\kappa )$
and since
$M_{\mathcal {W}}\models |A|<j_{\mathcal {W}}(\kappa )=i(\kappa )$
and since
![]() $\mathcal {W}$
is fine,
$\mathcal {W}$
is fine,
![]() $j_{\mathcal {W}}"\kappa ^+\subseteq A$
.
$j_{\mathcal {W}}"\kappa ^+\subseteq A$
.
Claim 5.9 For every
![]() $\alpha <\kappa ^+$
,
$\alpha <\kappa ^+$
,
![]() $i(\alpha )=j_{\mathcal {W}}(\alpha )$
.
$i(\alpha )=j_{\mathcal {W}}(\alpha )$
.
Proof Note that
![]() $i(U)\in N_E$
is a normal measure on
$i(U)\in N_E$
is a normal measure on
![]() $i(\kappa )$
, let
$i(\kappa )$
, let
![]() $X\in i(U)$
be any set,
$X\in i(U)$
be any set,
![]() $k(X)\in j(U)=j_{\mathcal {W}}(j_U(U))$
. Note that
$k(X)\in j(U)=j_{\mathcal {W}}(j_U(U))$
. Note that
![]() $j_{\mathcal {W}}(j_U(U))$
is generated by
$j_{\mathcal {W}}(j_U(U))$
is generated by
![]() $j_{\mathcal {W}}" j_U(U)$
by Theorem 6 and Corollary 8 of [Reference Blass11, Section 3]. Therefore, there is a set
$j_{\mathcal {W}}" j_U(U)$
by Theorem 6 and Corollary 8 of [Reference Blass11, Section 3]. Therefore, there is a set
![]() $Y\in j_U(U)$
such that
$Y\in j_U(U)$
such that
![]() $j_{\mathcal {W}}(Y)\subseteq k(X)$
. Since U is normal, there is a set
$j_{\mathcal {W}}(Y)\subseteq k(X)$
. Since U is normal, there is a set
![]() $A\in U$
such that
$A\in U$
such that
![]() $j_U(A)\subseteq ^* Y$
and
$j_U(A)\subseteq ^* Y$
and
![]() $j(A)\subseteq ^* k(X)$
, which in turn implies that
$j(A)\subseteq ^* k(X)$
, which in turn implies that
![]() $i(A)\subseteq ^* X$
. Now we note that
$i(A)\subseteq ^* X$
. Now we note that
![]() $i(A)\in R$
, where R is the
$i(A)\in R$
, where R is the
![]() $N_E$
-ultrafilter (external) derived from k and
$N_E$
-ultrafilter (external) derived from k and
![]() $j_{\mathcal {W}}(\kappa )$
. We conclude that
$j_{\mathcal {W}}(\kappa )$
. We conclude that
![]() $i(U)\subseteq R$
and thus that
$i(U)\subseteq R$
and thus that
![]() $i(U)=R$
(as two
$i(U)=R$
(as two
![]() $N_E$
-ultrafilters). So k factors through
$N_E$
-ultrafilters). So k factors through
![]() $j_{i(U)}$
and
$j_{i(U)}$
and
![]() $k'\colon M_{i(U)}\rightarrow M_{\mathcal {W}}$
has critical point
$k'\colon M_{i(U)}\rightarrow M_{\mathcal {W}}$
has critical point
![]() $>j_{\mathcal {W}}(\kappa )$
(since
$>j_{\mathcal {W}}(\kappa )$
(since
![]() $k'(j_{\mathcal {W}}(\kappa ))=k'([\text {id}]_{i(U)})=k(id)(j_{\mathcal {W}}(\kappa ))=j_{\mathcal {W}}(\kappa )$
). To conclude the claim, let
$k'(j_{\mathcal {W}}(\kappa ))=k'([\text {id}]_{i(U)})=k(id)(j_{\mathcal {W}}(\kappa ))=j_{\mathcal {W}}(\kappa )$
). To conclude the claim, let
![]() $\alpha <\kappa ^+$
and
$\alpha <\kappa ^+$
and
![]() $f\colon \kappa \rightarrow \kappa $
be the canonical function such that
$f\colon \kappa \rightarrow \kappa $
be the canonical function such that
![]() $j_U(f)(\kappa )=\alpha $
, then
$j_U(f)(\kappa )=\alpha $
, then
By elementarity,
![]() $i(f)\colon i(\kappa )\rightarrow i(\kappa )$
is the canonical function for
$i(f)\colon i(\kappa )\rightarrow i(\kappa )$
is the canonical function for
![]() $i(\alpha )$
. Since
$i(\alpha )$
. Since
![]() $j_{i(U)}$
is the ultrapower by a normal ultrafilter over
$j_{i(U)}$
is the ultrapower by a normal ultrafilter over
![]() $j_{\mathcal {W}}(\kappa )$
, we conclude that
$j_{\mathcal {W}}(\kappa )$
, we conclude that
as desired.
![]() $\kappa $
is superstrong with an inaccessible target (which simply means that there is an elementary
$\kappa $
is superstrong with an inaccessible target (which simply means that there is an elementary
![]() $j : V\to M$
such that
$j : V\to M$
such that
![]() $\operatorname {\mathrm {crit}}(j) = \kappa $
,
$\operatorname {\mathrm {crit}}(j) = \kappa $
,
![]() $V_{j(\kappa )}\subseteq M$
, and
$V_{j(\kappa )}\subseteq M$
, and
![]() $j(\kappa )$
is inaccessible in V), then by the argument of 4.1,
$j(\kappa )$
is inaccessible in V), then by the argument of 4.1,
![]() $\kappa $
is a non-Galvin cardinal. Moreover, any subcompact cardinal is a limit of cardinals that are superstrong with an inaccessible target.
$\kappa $
is a non-Galvin cardinal. Moreover, any subcompact cardinal is a limit of cardinals that are superstrong with an inaccessible target.
Hayut proved [Reference Hayut19] that
![]() $\kappa ^+$
-
$\kappa ^+$
-
![]() $\Pi ^1_1$
-subcompactness implies
$\Pi ^1_1$
-subcompactness implies
![]() $\kappa $
-compactness and he conjectures that these notions are equiconsistent.Footnote
13
So morally speaking,
$\kappa $
-compactness and he conjectures that these notions are equiconsistent.Footnote
13
So morally speaking,
![]() $\kappa $
-compact cardinals should be strictly greater than non-Galvin ultrafilters in the large cardinal hierarchy. In the next section, we will see that at least under UA this is the case. Finally, we establish the connection between Dodd soundness and non-Galvin cardinals.
$\kappa $
-compact cardinals should be strictly greater than non-Galvin ultrafilters in the large cardinal hierarchy. In the next section, we will see that at least under UA this is the case. Finally, we establish the connection between Dodd soundness and non-Galvin cardinals.
Lemma 5.10 Suppose that U is a
![]() $\kappa $
-complete non p-point
$\kappa $
-complete non p-point
![]() $\lambda $
-sound ultrafilter, and let E be the
$\lambda $
-sound ultrafilter, and let E be the
![]() $(\kappa ,\lambda )$
-extender derived from
$(\kappa ,\lambda )$
-extender derived from
![]() $j_U$
and
$j_U$
and
![]() $\lambda =\sup \{j_U(f)(\kappa )\mid f\colon \kappa \rightarrow \kappa \}$
. Then
$\lambda =\sup \{j_U(f)(\kappa )\mid f\colon \kappa \rightarrow \kappa \}$
. Then
![]() $j_E"2^\kappa \in M_U$
and moreover
$j_E"2^\kappa \in M_U$
and moreover
![]() $j_U,j_E,k_E$
and
$j_U,j_E,k_E$
and
![]() $j_E"2^\kappa $
witness that
$j_E"2^\kappa $
witness that
![]() $\kappa $
is a non-Galvin cardinal.
$\kappa $
is a non-Galvin cardinal.
Proof Derive the extender E from
![]() $\lambda ,$
i.e.,
$\lambda ,$
i.e.,
![]() $E={\langle } E_a\mid a\in [\lambda ]^{<\omega }{\rangle }$
, where
$E={\langle } E_a\mid a\in [\lambda ]^{<\omega }{\rangle }$
, where
![]() $E_a$
is an ultrafilter over
$E_a$
is an ultrafilter over
![]() $[\kappa ]^{|a|}$
defined by
$[\kappa ]^{|a|}$
defined by
By
![]() $\lambda $
-soundness of U,
$\lambda $
-soundness of U,
![]() $E\in M_U$
and we let
$E\in M_U$
and we let
![]() $i=j_E\colon M\rightarrow M_E$
. Note that
$i=j_E\colon M\rightarrow M_E$
. Note that
![]() $j_E"P(\kappa )$
can be calculated in
$j_E"P(\kappa )$
can be calculated in
![]() $M_U$
and therefore
$M_U$
and therefore
![]() $j_E"P(\kappa )\in M_U$
. Also, note that
$j_E"P(\kappa )\in M_U$
. Also, note that
![]() $j_E(\kappa )\geq \lambda $
and since
$j_E(\kappa )\geq \lambda $
and since
![]() $E\in M_U$
, we must have that for every
$E\in M_U$
, we must have that for every
![]() $a\in [\lambda ]^{<\omega }$
,
$a\in [\lambda ]^{<\omega }$
,
![]() $j_{E_a}(\kappa )<\lambda $
hence
$j_{E_a}(\kappa )<\lambda $
hence
![]() $j_E(\kappa )\leq \lambda $
. We conclude that the critical point of the factor map
$j_E(\kappa )\leq \lambda $
. We conclude that the critical point of the factor map
![]() $k_E\colon M_E\rightarrow M_U$
is
$k_E\colon M_E\rightarrow M_U$
is
![]() $\lambda = j_E(\kappa )$
. Finally, observe that
$\lambda = j_E(\kappa )$
. Finally, observe that
![]() $j_E"2^\kappa \in M_U$
. To see this, simply note that
$j_E"2^\kappa \in M_U$
. To see this, simply note that
![]() $j_E\restriction On=(j_E)^{M_U}\restriction On$
Footnote
14
and therefore
$j_E\restriction On=(j_E)^{M_U}\restriction On$
Footnote
14
and therefore
![]() $j_E"2^\kappa =(j_E)^{M_U}{}"2^\kappa \in M_U$
.
$j_E"2^\kappa =(j_E)^{M_U}{}"2^\kappa \in M_U$
.
6 In the canonical inner models
In this section, we work within the framework of
![]() $UA$
and “every irreducible is Dodd sound.” By results of Goldberg [Reference Goldberg17] and Schlutzenberg [Reference Schlutzenberg34], these assumptions hold in the extender models
$UA$
and “every irreducible is Dodd sound.” By results of Goldberg [Reference Goldberg17] and Schlutzenberg [Reference Schlutzenberg34], these assumptions hold in the extender models
![]() $L[E]$
. Our first goal of this section is to prove Main Theorem 1.3 regarding the characterization of
$L[E]$
. Our first goal of this section is to prove Main Theorem 1.3 regarding the characterization of
![]() $\sigma $
-complete non-Galvin ultrafilters. To do that, we will need some preparatory results.
$\sigma $
-complete non-Galvin ultrafilters. To do that, we will need some preparatory results.
Theorem 6.1 (UA)
Suppose
![]() $\kappa $
is either successor or strongly inaccessible and U is a
$\kappa $
is either successor or strongly inaccessible and U is a
![]() $\kappa $
-irreducible non-
$\kappa $
-irreducible non-
![]() $\kappa $
-complete ultrafilter on
$\kappa $
-complete ultrafilter on
![]() $\kappa $
. Then
$\kappa $
. Then
![]() $\diamondsuit ^{-}_{\mathrm{thin}}(U)$
.
$\diamondsuit ^{-}_{\mathrm{thin}}(U)$
.
Proof By [Reference Goldberg17, Theorems 8.2.22 and 8.2.23],
![]() $M_U$
is closed under
$M_U$
is closed under
![]() ${<}\kappa $
-sequences and every
${<}\kappa $
-sequences and every
![]() $A\in [M_U]^\kappa $
is covered by some
$A\in [M_U]^\kappa $
is covered by some
![]() $B\in M_U$
such that
$B\in M_U$
such that
![]() $|B|^{M_U} = \kappa $
. By the assumptions of the theorem, U is not
$|B|^{M_U} = \kappa $
. By the assumptions of the theorem, U is not
![]() $\kappa $
-complete and therefore
$\kappa $
-complete and therefore
![]() $\operatorname {\mathrm {crit}}(j_U)<\kappa $
. Let
$\operatorname {\mathrm {crit}}(j_U)<\kappa $
. Let
![]() $E^\kappa _\omega =\{\nu <\kappa \mid \mathrm {cf}(\nu )=\omega \}$
, define the function
$E^\kappa _\omega =\{\nu <\kappa \mid \mathrm {cf}(\nu )=\omega \}$
, define the function
![]() $g:E^\kappa _\omega \rightarrow \kappa $
by
$g:E^\kappa _\omega \rightarrow \kappa $
by
![]() $g(\nu )=\rho $
for the minimal measurable cardinal
$g(\nu )=\rho $
for the minimal measurable cardinal
![]() $\rho $
such that
$\rho $
such that
![]() $j_U(\rho )>\nu $
. By [Reference Goldberg17, Lemma 4.2.36],
$j_U(\rho )>\nu $
. By [Reference Goldberg17, Lemma 4.2.36],
![]() $g(\nu )$
is well defined and
$g(\nu )$
is well defined and
![]() $g(\nu )\leq \nu $
. Since
$g(\nu )\leq \nu $
. Since
![]() $\mathrm {cf}(\nu )=\omega $
,
$\mathrm {cf}(\nu )=\omega $
,
![]() $g(\nu )<\nu $
. By Födor, there is an unbounded
$g(\nu )<\nu $
. By Födor, there is an unbounded
![]() $S\subseteq E^\kappa _{\omega }$
and
$S\subseteq E^\kappa _{\omega }$
and
![]() $\kappa ^*<\kappa $
such that for every
$\kappa ^*<\kappa $
such that for every
![]() $\nu \in S$
,
$\nu \in S$
,
![]() $g(\nu )=\kappa ^*$
. In particular,
$g(\nu )=\kappa ^*$
. In particular,
![]() $j_U(\kappa ^*)\geq \kappa $
. If
$j_U(\kappa ^*)\geq \kappa $
. If
![]() $j_U(\kappa ^*)>\kappa $
, let
$j_U(\kappa ^*)>\kappa $
, let
![]() $\gamma =\kappa ^*$
, otherwise
$\gamma =\kappa ^*$
, otherwise
![]() $\kappa $
is a limit of
$\kappa $
is a limit of
![]() $M_U$
-strongly inaccessible cardinals. Let
$M_U$
-strongly inaccessible cardinals. Let
![]() $\kappa ^*<\gamma <\kappa $
be the least strongly inaccessible cardinal. In any case,
$\kappa ^*<\gamma <\kappa $
be the least strongly inaccessible cardinal. In any case,
![]() $j_U(\gamma )>\kappa $
and since
$j_U(\gamma )>\kappa $
and since
![]() $M_U$
is closed under
$M_U$
is closed under
![]() $<\kappa $
-sequences,
$<\kappa $
-sequences,
![]() $\gamma $
is a strongly inaccessible cardinal in V. Therefore,
$\gamma $
is a strongly inaccessible cardinal in V. Therefore,
![]() $j_U"P_\kappa (\kappa )$
is covered by a set
$j_U"P_\kappa (\kappa )$
is covered by a set
![]() $B\in M_U$
of cardinality less than
$B\in M_U$
of cardinality less than
![]() $j_U(\gamma )$
. Let
$j_U(\gamma )$
. Let
![]() $A= \{\bigcup S: S\in [B]^\kappa \cap M_U\}$
. Then
$A= \{\bigcup S: S\in [B]^\kappa \cap M_U\}$
. Then
![]() $|A|^{M_U} < j_U(\gamma )$
, and for any
$|A|^{M_U} < j_U(\gamma )$
, and for any
![]() $S\subseteq \kappa $
,
$S\subseteq \kappa $
,
![]() $j_U(S)\cap \kappa _*\in A$
where
$j_U(S)\cap \kappa _*\in A$
where
![]() $\kappa _* =\sup j_U"\kappa \geq j_U(\gamma )$
. Note that
$\kappa _* =\sup j_U"\kappa \geq j_U(\gamma )$
. Note that
![]() $\kappa _*> j_U(f)(\alpha )$
for any
$\kappa _*> j_U(f)(\alpha )$
for any
![]() $f : \kappa \to \kappa $
and
$f : \kappa \to \kappa $
and
![]() $\alpha < \kappa _*$
and, in particular, there is no function
$\alpha < \kappa _*$
and, in particular, there is no function
![]() $f:\kappa \rightarrow \kappa $
such that
$f:\kappa \rightarrow \kappa $
such that
![]() $j_U(f)(|A|^{M_U})\geq \kappa _*$
. We conclude that A witnesses
$j_U(f)(|A|^{M_U})\geq \kappa _*$
. We conclude that A witnesses
![]() $\diamondsuit ^-_{\mathrm{thin}}(U)$
.
$\diamondsuit ^-_{\mathrm{thin}}(U)$
.
Corollary 6.2 (UA)
If U is a
![]() $\sigma $
-complete ultrafilter over
$\sigma $
-complete ultrafilter over
![]() $\kappa ^+$
then
$\kappa ^+$
then
![]() $\diamondsuit ^-_{\mathrm{thin}}(U)$
and, in particular, U is non-Galvin.
$\diamondsuit ^-_{\mathrm{thin}}(U)$
and, in particular, U is non-Galvin.
Proof By [Reference Goldberg17, Lemma 8.2.24],
![]() $U=\sum _{D}{\langle } W_\xi {\rangle }_{\xi <\lambda _D}$
, where D is an ultrafilter over
$U=\sum _{D}{\langle } W_\xi {\rangle }_{\xi <\lambda _D}$
, where D is an ultrafilter over
![]() $\lambda _D<\kappa ^+$
,
$\lambda _D<\kappa ^+$
,
![]() ${\langle } W_\xi {\rangle }_{\xi <\lambda _D}$
is discrete and
${\langle } W_\xi {\rangle }_{\xi <\lambda _D}$
is discrete and
![]() $M_D\models W=[\xi \mapsto W_\xi ]_D$
is
$M_D\models W=[\xi \mapsto W_\xi ]_D$
is
![]() $j_D(\kappa ^+)$
-irreducible which cannot be
$j_D(\kappa ^+)$
-irreducible which cannot be
![]() $j_D(\kappa ^+)$
-complete. By the previous theorem,
$j_D(\kappa ^+)$
-complete. By the previous theorem,
![]() $M_D\models \diamondsuit ^-_{\mathrm{thin}}(W)$
. Therefore, for D-almost all
$M_D\models \diamondsuit ^-_{\mathrm{thin}}(W)$
. Therefore, for D-almost all
![]() $\xi $
,
$\xi $
,
![]() $\diamondsuit ^-_{\mathrm{thin}}(W_\xi )$
which by Lemma 4.11, implies that
$\diamondsuit ^-_{\mathrm{thin}}(W_\xi )$
which by Lemma 4.11, implies that
![]() $\diamondsuit ^-_{\mathrm{thin}}(\sum _D{\langle } W_\xi {\rangle }_{\xi <\lambda _D})$
holds.
$\diamondsuit ^-_{\mathrm{thin}}(\sum _D{\langle } W_\xi {\rangle }_{\xi <\lambda _D})$
holds.
Theorem 6.3 (UA)
Assume that every irreducible is Dodd sound. If W is a
![]() $\kappa $
-complete ultrafilter over
$\kappa $
-complete ultrafilter over
![]() $\kappa $
, then the following are equivalent:
$\kappa $
, then the following are equivalent:
-
(1) W has the Galvin property.
-
(2)
 $\neg \diamondsuit ^-_{\mathrm{thin}}(W)$
.
$\neg \diamondsuit ^-_{\mathrm{thin}}(W)$
. -
(3) W is an n-fold sum of
 $\kappa $
-complete p-points over
$\kappa $
-complete p-points over
 $\kappa $
$\kappa $
Proof Let W be
![]() $\kappa $
-complete ultrafilter. If W is an n-fold sum of
$\kappa $
-complete ultrafilter. If W is an n-fold sum of
![]() $\kappa $
-complete p-points then by Theorem 2.10, W has the Galvin property which by Theorem 4.9 implies
$\kappa $
-complete p-points then by Theorem 2.10, W has the Galvin property which by Theorem 4.9 implies
![]() $\neg \diamondsuit ^-_{\mathrm{thin}}(W)$
. Let W be a
$\neg \diamondsuit ^-_{\mathrm{thin}}(W)$
. Let W be a
![]() $\kappa $
-complete ultrafilter over
$\kappa $
-complete ultrafilter over
![]() $\kappa $
which is not an n-fold sum of
$\kappa $
which is not an n-fold sum of
![]() $\kappa $
-complete p-points. Let
$\kappa $
-complete p-points. Let
![]() $U\leq _{RF}W$
be irreducible, which exists since W is nontrivial. If U is not a p-point then by the assumptions of the theorem, U is a non p-point ultrafilter Dodd sound over
$U\leq _{RF}W$
be irreducible, which exists since W is nontrivial. If U is not a p-point then by the assumptions of the theorem, U is a non p-point ultrafilter Dodd sound over
![]() $\kappa $
and therefore by Lemma 3.8,
$\kappa $
and therefore by Lemma 3.8,
![]() $\diamondsuit ^*_{\mathrm{thin}}(U)$
holds and thus also
$\diamondsuit ^*_{\mathrm{thin}}(U)$
holds and thus also
![]() $\diamondsuit ^-_{\mathrm{thin}}(U)$
. Since
$\diamondsuit ^-_{\mathrm{thin}}(U)$
. Since
![]() $U\leq _{RK} W$
, Lemma 4.10 applies, so we can conclude that
$U\leq _{RK} W$
, Lemma 4.10 applies, so we can conclude that
![]() $\diamondsuit ^-_{\mathrm{thin}}(W)$
. Hence, we may restrict ourselves to the case where there is a p-point RF-below W (and this p-point must be
$\diamondsuit ^-_{\mathrm{thin}}(W)$
. Hence, we may restrict ourselves to the case where there is a p-point RF-below W (and this p-point must be
![]() $\kappa $
-complete). By [Reference Goldberg17, Theorem 5.3.14], there is a
$\kappa $
-complete). By [Reference Goldberg17, Theorem 5.3.14], there is a
![]() $\leq _{RF}$
-maximal
$\leq _{RF}$
-maximal
![]() $U \leq _{\text {RF}} W$
that is an n-fold sum of
$U \leq _{\text {RF}} W$
that is an n-fold sum of
![]() $\kappa $
-complete p-points over
$\kappa $
-complete p-points over
![]() $\kappa $
. Let
$\kappa $
. Let
![]() $\langle W_\xi {\rangle }_{\xi < \kappa }$
be a discrete sequence with
$\langle W_\xi {\rangle }_{\xi < \kappa }$
be a discrete sequence with
![]() $W = U\text {-}\lim {\langle } W_\xi {\rangle }_{\xi < \kappa }$
. By the choice of U, the embedding
$W = U\text {-}\lim {\langle } W_\xi {\rangle }_{\xi < \kappa }$
. By the choice of U, the embedding
![]() $j_U:V\rightarrow M_U$
can be factored as a finite iterated ultrapower
$j_U:V\rightarrow M_U$
can be factored as a finite iterated ultrapower
where in
![]() $M_k$
,
$M_k$
,
![]() $j_{k,k+1}$
is the ultrapower embedding associated with a
$j_{k,k+1}$
is the ultrapower embedding associated with a
![]() $\kappa _{k}$
-complete p-point
$\kappa _{k}$
-complete p-point
![]() $U_k$
over
$U_k$
over
![]() $\kappa _{k}$
and
$\kappa _{k}$
and
![]() $\kappa _k=j_{0,k}(\kappa )$
. Also, denote by
$\kappa _k=j_{0,k}(\kappa )$
. Also, denote by
![]() $Z_k$
the ultrafilter associated with
$Z_k$
the ultrafilter associated with
![]() $j_{0,k}$
; i.e.,
$j_{0,k}$
; i.e.,
For this notation, see Definition 2.6. Since
![]() $W_\xi $
is nonprincipal, there is an irreducible ultrafilter
$W_\xi $
is nonprincipal, there is an irreducible ultrafilter
![]() $D_\xi \leq _{\text {RF}} W_\xi $
. Suppose that
$D_\xi \leq _{\text {RF}} W_\xi $
. Suppose that
![]() $D_\xi $
is
$D_\xi $
is
![]() $\rho _\xi $
-complete uniform ultrafilter over
$\rho _\xi $
-complete uniform ultrafilter over
![]() $\delta _\xi $
for some
$\delta _\xi $
for some
![]() $\rho _\xi \leq \delta _\xi \leq \kappa $
. Note that
$\rho _\xi \leq \delta _\xi \leq \kappa $
. Note that
![]() $\sum _U D_\xi \leq _{RF}W$
. Let m be the least such that
$\sum _U D_\xi \leq _{RF}W$
. Let m be the least such that
![]() $\kappa _{m-1}<\delta ^*:=[\xi \mapsto \delta _\xi ]_U\leq \kappa _{m}$
, where
$\kappa _{m-1}<\delta ^*:=[\xi \mapsto \delta _\xi ]_U\leq \kappa _{m}$
, where
![]() $\kappa _{-1}$
is defined to be
$\kappa _{-1}$
is defined to be
![]() $0$
. Let
$0$
. Let
![]() $D^*=[\xi \mapsto D_\xi ]_{U}$
is an
$D^*=[\xi \mapsto D_\xi ]_{U}$
is an
![]() $M_U$
-ultrafilter over
$M_U$
-ultrafilter over
![]() $\delta ^*$
. Note that
$\delta ^*$
. Note that
![]() $D^*\in M_{m}$
since
$D^*\in M_{m}$
since
![]() $M_n\subseteq M_m$
and since
$M_n\subseteq M_m$
and since
![]() $\operatorname {\mathrm {crit}}(j_{m,n})=\kappa _{m}$
it is an
$\operatorname {\mathrm {crit}}(j_{m,n})=\kappa _{m}$
it is an
![]() $M_m$
-ultrafilter. Moreover,
$M_m$
-ultrafilter. Moreover,
![]() $M_n^{\kappa _{m}}\cap M_{m}=M_n^{\kappa _{m}}\cap M_n$
and therefore
$M_n^{\kappa _{m}}\cap M_{m}=M_n^{\kappa _{m}}\cap M_n$
and therefore
![]() $(j_{D^*})^{M_{m}}\restriction M_n=(j_{D^*})^{M_n}$
. By elementarity of
$(j_{D^*})^{M_{m}}\restriction M_n=(j_{D^*})^{M_n}$
. By elementarity of
![]() $j_{D^*}^{M_m}$
,
$j_{D^*}^{M_m}$
,
![]() $j_{D^*}^{M_n}\circ j_{m,n}=j_{D^*}^{M_{m}}(j_{m,n})\circ j_{D^*}^{M_{m}}$
and we have that
$j_{D^*}^{M_n}\circ j_{m,n}=j_{D^*}^{M_{m}}(j_{m,n})\circ j_{D^*}^{M_{m}}$
and we have that
Claim 6.4 If
![]() $M_{m}\models D^*$
is not
$M_{m}\models D^*$
is not
![]() $\kappa _m$
-complete, then
$\kappa _m$
-complete, then
![]() $\diamondsuit ^-_{\mathrm{thin}}(W)$
holds.
$\diamondsuit ^-_{\mathrm{thin}}(W)$
holds.
Proof of claim
Since
![]() $D_\xi $
is irreducible, by our assumption, it is a non
$D_\xi $
is irreducible, by our assumption, it is a non
![]() $\kappa $
-complete Dodd sound ultrafilter. Note that in this case
$\kappa $
-complete Dodd sound ultrafilter. Note that in this case
![]() $m>0$
, since if
$m>0$
, since if
![]() $m=0$
, the
$m=0$
, the
![]() $D^*$
must be
$D^*$
must be
![]() $\kappa $
-complete. Let us split unto cases:
$\kappa $
-complete. Let us split unto cases:
-
Case 1: If
 $\delta ^*=\kappa _m$
, then
$\delta ^*=\kappa _m$
, then
 $D^*$
is a uniform ultrafilter on
$D^*$
is a uniform ultrafilter on
 $\kappa _m$
and it must be
$\kappa _m$
and it must be
 $\kappa _m$
-irreducible. By Theorem 6.1,
$\kappa _m$
-irreducible. By Theorem 6.1,
 $M_m\models \diamondsuit ^-_{\mathrm{thin}}(D^*)$
holds. By Lemma 3.15, we conclude that
$M_m\models \diamondsuit ^-_{\mathrm{thin}}(D^*)$
holds. By Lemma 3.15, we conclude that
 $\diamondsuit ^-_{\mathrm{thin}}(Z_m^\frown D^*)$
holds in V (see Definition 2.6 for this notation), and hence by Lemma 4.10
$\diamondsuit ^-_{\mathrm{thin}}(Z_m^\frown D^*)$
holds in V (see Definition 2.6 for this notation), and hence by Lemma 4.10
 $\diamondsuit ^-_{\mathrm{thin}}(W)$
follows as well.
$\diamondsuit ^-_{\mathrm{thin}}(W)$
follows as well. -
Case 2: Assume that
 $\delta ^*<\kappa _m$
.
$\delta ^*<\kappa _m$
.-
Case 2(b): Assume
 $\operatorname {\mathrm {crit}}(j_{D^*}^{M_m})>\kappa _{m-1}$
. Note that the two-step iteration ultrapower
$\operatorname {\mathrm {crit}}(j_{D^*}^{M_m})>\kappa _{m-1}$
. Note that the two-step iteration ultrapower
 $j_{D^*}^{M_{m}}\circ j_{U_{m-1}}$
is given by a
$j_{D^*}^{M_{m}}\circ j_{U_{m-1}}$
is given by a
 $\kappa _{m-1}$
-complete p-point on
$\kappa _{m-1}$
-complete p-point on
 $\kappa _{m-1}$
in
$\kappa _{m-1}$
in
 $M_m$
(see [Reference Benhamou1, Lemma 1.11]), which contradicts the maximality of U.
$M_m$
(see [Reference Benhamou1, Lemma 1.11]), which contradicts the maximality of U. -
Case 2(c): Assume
 $\operatorname {\mathrm {crit}}(j_{D^*}^{M_{m}})\leq \kappa _{m-1}<\delta ^*<\kappa _m$
. Since
$\operatorname {\mathrm {crit}}(j_{D^*}^{M_{m}})\leq \kappa _{m-1}<\delta ^*<\kappa _m$
. Since
 $D^*$
is an irreducible uniform ultrafilter over
$D^*$
is an irreducible uniform ultrafilter over
 $\lambda _{D^*}\geq \kappa _{m-1}^+$
,
$\lambda _{D^*}\geq \kappa _{m-1}^+$
,
 $D^*$
is
$D^*$
is
 $\kappa _{m-1}^+$
-irreducible and therefore by [Reference Goldberg17, Theorem 8.2.22],
$\kappa _{m-1}^+$
-irreducible and therefore by [Reference Goldberg17, Theorem 8.2.22],
 $M_{D^*}$
is closed under
$M_{D^*}$
is closed under
 $\kappa _{m-1}$
-sequences which in turn implies that
$\kappa _{m-1}$
-sequences which in turn implies that
 $P(\kappa _{m-1})\subseteq M_{D^*}$
. By Lemma [Reference Goldberg17, Lemma 4.2.36],
$P(\kappa _{m-1})\subseteq M_{D^*}$
. By Lemma [Reference Goldberg17, Lemma 4.2.36],
 $j^{M_m}_{D^*}(\kappa _{m-1})>\kappa _{m-1}$
. Let
$j^{M_m}_{D^*}(\kappa _{m-1})>\kappa _{m-1}$
. Let
 $\lambda =j^{M_m}_{D^*}(\kappa _{m-1})$
. We claim that
$\lambda =j^{M_m}_{D^*}(\kappa _{m-1})$
. We claim that
 ${U_{m-1}}^\frown D^*$
is
${U_{m-1}}^\frown D^*$
is
 $\lambda $
-sound and that for every function
$\lambda $
-sound and that for every function
 $f:\kappa _{m-1}\rightarrow \kappa _{m-1}$
,
$f:\kappa _{m-1}\rightarrow \kappa _{m-1}$
,
 $j_{{U_{m-1}}^\frown D^*}(f)(\kappa _{m-1})<\lambda $
which by Corollary 4.8 implies that
$j_{{U_{m-1}}^\frown D^*}(f)(\kappa _{m-1})<\lambda $
which by Corollary 4.8 implies that
 $\diamondsuit ^-_{\mathrm{thin}}({U_{m-1}}^\frown D^*)$
. Indeed, for any function
$\diamondsuit ^-_{\mathrm{thin}}({U_{m-1}}^\frown D^*)$
. Indeed, for any function
 $f:\kappa _{m-1}\rightarrow \kappa _{m-1}$
, since
$f:\kappa _{m-1}\rightarrow \kappa _{m-1}$
, since
 $j^{M_m}_{D^*}(\kappa _{m-1})>\kappa _{m-1}$
,
$j^{M_m}_{D^*}(\kappa _{m-1})>\kappa _{m-1}$
,
 $j^{M_m}_{D^*}(j_{U_{m-1}}(f))(\kappa _{m-1})=j_{D^*}^{M_m} (j_{U_{m-1}}(f)\restriction \kappa _{m-1})(\kappa _{m-1})=j_{D^*}^{M_m}(f)(\kappa _{m-1}),$
and
$j^{M_m}_{D^*}(j_{U_{m-1}}(f))(\kappa _{m-1})=j_{D^*}^{M_m} (j_{U_{m-1}}(f)\restriction \kappa _{m-1})(\kappa _{m-1})=j_{D^*}^{M_m}(f)(\kappa _{m-1}),$
and
 $j_{D^*}^{M_m}(f):j_{D^*}^{M_m}(\kappa _{m-1})\rightarrow j_{D^*}^{M_m}(\kappa _{m-1})$
. Hence
$j_{D^*}^{M_m}(f):j_{D^*}^{M_m}(\kappa _{m-1})\rightarrow j_{D^*}^{M_m}(\kappa _{m-1})$
. Hence
 $j_{D^*}^{M_m}(f)(\kappa _{m-1})<j_{D^*}^{M_m}(\kappa _{m-1})$
.
$j_{D^*}^{M_m}(f)(\kappa _{m-1})<j_{D^*}^{M_m}(\kappa _{m-1})$
.To see that
 ${U_{m-1}}^\frown D^*$
is
${U_{m-1}}^\frown D^*$
is
 $\lambda $
-sound, derive the
$\lambda $
-sound, derive the
 $(\kappa _{m-1},\lambda )$
-extender E from
$(\kappa _{m-1},\lambda )$
-extender E from
 $j_{D^*}^{M_m}$
inside
$j_{D^*}^{M_m}$
inside
 $M_m$
. Note that E is also the
$M_m$
. Note that E is also the
 $(\kappa _{m-1},\lambda )$
-extender derived from
$(\kappa _{m-1},\lambda )$
-extender derived from
 $j_{D^*}\circ j_{m-1,m}$
since for
$j_{D^*}\circ j_{m-1,m}$
since for
 $\alpha <j_{D^*}^{M_m}(\kappa _{m-1}),$
we have that
$\alpha <j_{D^*}^{M_m}(\kappa _{m-1}),$
we have that $\alpha \in j_{D^*}^{M_m}(j_{m-1,m}(X))\cap j_{D^*}^{M_m}(\kappa _{m-1})$
iff
$\alpha \in j_{D^*}^{M_m}(j_{m-1,m}(X))\cap j_{D^*}^{M_m}(\kappa _{m-1})$
iff
 $\alpha \in j_{D^*}^{M_m}(j_{m-1,m}(X)\cap \kappa _{m-1})$
iff
$\alpha \in j_{D^*}^{M_m}(j_{m-1,m}(X)\cap \kappa _{m-1})$
iff
 $ \alpha \in j^{M_m}_{D^*}(X)$
.
$ \alpha \in j^{M_m}_{D^*}(X)$
.Now,
 $D^*$
is a uniform ultrafilter over
$D^*$
is a uniform ultrafilter over
 $\delta ^*>\kappa _{m-1}$
, hence we have that
$\delta ^*>\kappa _{m-1}$
, hence we have that
 $j^{M_m}_{D^*}(\kappa )<[id]_{D^*}$
and since
$j^{M_m}_{D^*}(\kappa )<[id]_{D^*}$
and since
 $D^*$
is Dodd sound we have that
$D^*$
is Dodd sound we have that
 $E\in (M_{D^*})^{M_m}$
. In particular,
$E\in (M_{D^*})^{M_m}$
. In particular,
 $\{j_E(X)\mid X\subseteq \kappa _{m-1}\}\in (M_{D^*})^{M_{m}}$
, where
$\{j_E(X)\mid X\subseteq \kappa _{m-1}\}\in (M_{D^*})^{M_{m}}$
, where
 $j_E:M_{m-1}\rightarrow M_E$
. Let
$j_E:M_{m-1}\rightarrow M_E$
. Let
 $k_E:M_E\rightarrow (M_{D^*})^{M_{m}}$
be the factor map. It follows that
$k_E:M_E\rightarrow (M_{D^*})^{M_{m}}$
be the factor map. It follows that
 $\operatorname {\mathrm {crit}}(k_E)= j_{D^*}^{M_m}(\kappa _{m-1})$
. Finally, note that
$\operatorname {\mathrm {crit}}(k_E)= j_{D^*}^{M_m}(\kappa _{m-1})$
. Finally, note that
 $j_{{U_{m-1}}^\frown D^*}(X)\cap j^{M_m}_{D^*}(\kappa _{m-1})=j_E(X)$
, hence as desired. We conclude that
$j_{{U_{m-1}}^\frown D^*}(X)\cap j^{M_m}_{D^*}(\kappa _{m-1})=j_E(X)$
, hence as desired. We conclude that $$ \begin{align*}\{j_{{U_{m-1}}^\frown D^*}(X)\cap j^{M_m}_{D^*}(\kappa_{m-1})\mid X\subseteq \kappa_{m-1}\}\in (M_{D^*})^{M_m}\end{align*} $$
$$ \begin{align*}\{j_{{U_{m-1}}^\frown D^*}(X)\cap j^{M_m}_{D^*}(\kappa_{m-1})\mid X\subseteq \kappa_{m-1}\}\in (M_{D^*})^{M_m}\end{align*} $$
 $M_{m-1}\models \diamondsuit ^-_{\mathrm{thin}}({U_{m-1}}^\frown D^*)$
. By Lemma 4.12
$M_{m-1}\models \diamondsuit ^-_{\mathrm{thin}}({U_{m-1}}^\frown D^*)$
. By Lemma 4.12
 $\diamondsuit ^-_{\mathrm{thin}}({Z_{m-1}}^\frown {U_{m-1}}^\frown D^*$
) , and this ultrafilter is Rudin–Keisler below W.
$\diamondsuit ^-_{\mathrm{thin}}({Z_{m-1}}^\frown {U_{m-1}}^\frown D^*$
) , and this ultrafilter is Rudin–Keisler below W.
-
By the claim, we may assume that for
![]() $M_m\models D^*$
is
$M_m\models D^*$
is
![]() $\kappa _m$
-complete over
$\kappa _m$
-complete over
![]() $\kappa _m$
. It follows again that in
$\kappa _m$
. It follows again that in
![]() $M_m$
,
$M_m$
,
![]() $D^*$
cannot be a p-point, as this would contradict the maximality of U, recalling that
$D^*$
cannot be a p-point, as this would contradict the maximality of U, recalling that
![]() $\sum _U D_\xi \leq _{RF}W$
and that this ultrafilter
$\sum _U D_\xi \leq _{RF}W$
and that this ultrafilter
![]() $\sum _UD_\xi $
can be represented as an (
$\sum _UD_\xi $
can be represented as an (
![]() $n+1$
)-fold sum of
$n+1$
)-fold sum of
![]() $\kappa $
-complete p-points by (6.1). Since
$\kappa $
-complete p-points by (6.1). Since
![]() $D^*$
is irreducible in
$D^*$
is irreducible in
![]() $M_m$
,
$M_m$
,
![]() $M_m\models D^*$
is Dodd-sound and non p-point. By Lemma 3.8
$M_m\models D^*$
is Dodd-sound and non p-point. By Lemma 3.8
![]() $M_m\models \diamondsuit ^*_{\mathrm{thin}}(D^*)$
holds. In particular,
$M_m\models \diamondsuit ^*_{\mathrm{thin}}(D^*)$
holds. In particular,
![]() $\diamondsuit ^-_{\mathrm{thin}}(D^*)$
holds. In any case, Lemma 3.15 applies to conclude that
$\diamondsuit ^-_{\mathrm{thin}}(D^*)$
holds. In any case, Lemma 3.15 applies to conclude that
![]() $\diamondsuit ^-_{\mathrm{thin}}({Z_m}^\frown D^*)$
holds, and since this ultrafilter is
$\diamondsuit ^-_{\mathrm{thin}}({Z_m}^\frown D^*)$
holds, and since this ultrafilter is
![]() $RK$
-below W, Lemma 4.10 ensures that
$RK$
-below W, Lemma 4.10 ensures that
![]() $\diamondsuit ^-_{\mathrm{thin}}(W)$
holds.
$\diamondsuit ^-_{\mathrm{thin}}(W)$
holds.
Theorem 6.5 (UA)
Assume that every irreducible ultrafilter is Dodd sound. For every
![]() $\sigma $
-complete ultrafilter W over
$\sigma $
-complete ultrafilter W over
![]() $\kappa $
, the following are equivalent:
$\kappa $
, the following are equivalent:
-
(1) W has the Galvin property.
-
(2)
 $\neg \diamondsuit ^-_{\mathrm{thin}}(W)$
.
$\neg \diamondsuit ^-_{\mathrm{thin}}(W)$
. -
(3) W is the D-sum of n-fold sums of
 $\kappa $
-complete p-points over
$\kappa $
-complete p-points over
 $\kappa $
and D is a
$\kappa $
and D is a
 $\sigma $
-complete ultrafilter on
$\sigma $
-complete ultrafilter on
 $\lambda <\kappa $
.
$\lambda <\kappa $
.
Proof The proof that
![]() $(3)\Rightarrow (1)\Rightarrow (2)$
is in the previous theorem. It remains to prove that
$(3)\Rightarrow (1)\Rightarrow (2)$
is in the previous theorem. It remains to prove that
![]() $\neg \diamondsuit ^-_{\mathrm{thin}}(W)$
implies that W is a D-sum of n-fold sums of
$\neg \diamondsuit ^-_{\mathrm{thin}}(W)$
implies that W is a D-sum of n-fold sums of
![]() $\kappa $
-complete p-points over
$\kappa $
-complete p-points over
![]() $\kappa $
. Equivalently, let us prove the contrapositive, suppose that W is a
$\kappa $
. Equivalently, let us prove the contrapositive, suppose that W is a
![]() $\sigma $
-complete ultrafilter over
$\sigma $
-complete ultrafilter over
![]() $\kappa $
which is not an n-fold sum of p-points. Now, let us move to the general case, suppose that W is just
$\kappa $
which is not an n-fold sum of p-points. Now, let us move to the general case, suppose that W is just
![]() $\sigma $
-complete. By [Reference Goldberg17, Lemma 8.2.24], there is a countably complete ultrafilter
$\sigma $
-complete. By [Reference Goldberg17, Lemma 8.2.24], there is a countably complete ultrafilter
![]() $D\leq _{RF} W$
on
$D\leq _{RF} W$
on
![]() $\lambda <\kappa $
such that if
$\lambda <\kappa $
such that if
![]() $W=D\text {-}\lim {\langle } W_\xi {\rangle }_{\xi <\lambda }$
, then
$W=D\text {-}\lim {\langle } W_\xi {\rangle }_{\xi <\lambda }$
, then
![]() $M_D\models Z=[\xi \mapsto W_\xi ]_D$
is
$M_D\models Z=[\xi \mapsto W_\xi ]_D$
is
![]() $j_D(\kappa )$
-irreducible. If Z is not
$j_D(\kappa )$
-irreducible. If Z is not
![]() $j_D(\kappa )$
-complete, then by Theorem 6.1.
$j_D(\kappa )$
-complete, then by Theorem 6.1.
![]() $M_D\models \diamondsuit ^-_{\mathrm{thin}}(Z)$
and therefore
$M_D\models \diamondsuit ^-_{\mathrm{thin}}(Z)$
and therefore
![]() $W=D\text {-}\lim {\langle } W_\xi {\rangle }_{\xi <\lambda }$
will also satisfy
$W=D\text {-}\lim {\langle } W_\xi {\rangle }_{\xi <\lambda }$
will also satisfy
![]() $\diamondsuit ^-_{\mathrm{thin}}$
by Lemma 4.11. If Z is
$\diamondsuit ^-_{\mathrm{thin}}$
by Lemma 4.11. If Z is
![]() $j_D(\kappa )$
-complete, then Z is a
$j_D(\kappa )$
-complete, then Z is a
![]() $j_D(\kappa )$
-complete ultrafilter which is not a
$j_D(\kappa )$
-complete ultrafilter which is not a
![]() $D'$
-sum of n-fold sums of p-points and we fall into the first case where we assumed that W was
$D'$
-sum of n-fold sums of p-points and we fall into the first case where we assumed that W was
![]() $\kappa $
-complete (inside
$\kappa $
-complete (inside
![]() $M_D$
and replacing
$M_D$
and replacing
![]() $\kappa $
by
$\kappa $
by
![]() $j_D(\kappa )$
). We conclude that
$j_D(\kappa )$
). We conclude that
![]() $\diamondsuit ^-_{\mathrm{thin}}(Z)$
holds and again, it follows from that
$\diamondsuit ^-_{\mathrm{thin}}(Z)$
holds and again, it follows from that
![]() $\diamondsuit ^-_{\mathrm{thin}}(W)$
holds.
$\diamondsuit ^-_{\mathrm{thin}}(W)$
holds.
Next, we turn to the proof of Main Theorem 1.5.
Theorem 6.6 (UA)
Assume that every irreducible ultrafilter is Dodd sound. Suppose
![]() $\kappa $
is an uncountable cardinal that carries a
$\kappa $
is an uncountable cardinal that carries a
![]() $\kappa $
-complete non-Galvin ultrafilter. Then the Ketonen least non-Galvin
$\kappa $
-complete non-Galvin ultrafilter. Then the Ketonen least non-Galvin
![]() $\kappa $
-complete ultrafilter on
$\kappa $
-complete ultrafilter on
![]() $\kappa $
extends the closed unbounded filter.
$\kappa $
extends the closed unbounded filter.
Proof We claim that in this context, the Ketonen least non-Galvin ultrafilter U is equal to the Ketonen least ultrafilter W on a regular cardinal
![]() $\delta $
extending the closed unbounded filter and concentrating on singular cardinals. First, note that W is irreducible by [Reference Goldberg17, Corollary 8.2.12].
$\delta $
extending the closed unbounded filter and concentrating on singular cardinals. First, note that W is irreducible by [Reference Goldberg17, Corollary 8.2.12].
Claim 6.7
W is
![]() $\delta $
-complete
$\delta $
-complete
Proof of Claim 6.7
Suppose toward a contradiction that W is not
![]() $\delta $
-complete, and let
$\delta $
-complete, and let
![]() $\mu =crit(j_W)<\delta $
. Since W is Dodd sound,
$\mu =crit(j_W)<\delta $
. Since W is Dodd sound,
![]() $j_W$
is a
$j_W$
is a
![]() $2^{<\delta }$
-supercompact embedding (see [Reference Goldberg17, Lemma 4.3.4]), and so
$2^{<\delta }$
-supercompact embedding (see [Reference Goldberg17, Lemma 4.3.4]), and so
![]() $j_W$
witnesses that
$j_W$
witnesses that
![]() $\mu $
is
$\mu $
is
![]() $2^{<\delta }$
-supercompact. In particular,
$2^{<\delta }$
-supercompact. In particular,
![]() $\mu $
is
$\mu $
is
![]() $2^\mu $
-supercompact, and therefore every
$2^\mu $
-supercompact, and therefore every
![]() $\mu $
-complete filter on
$\mu $
-complete filter on
![]() $\mu $
extends to a
$\mu $
extends to a
![]() $\mu $
-complete ultrafilter. This yields a
$\mu $
-complete ultrafilter. This yields a
![]() $\mu $
-complete ultrafilter
$\mu $
-complete ultrafilter
![]() $W'$
on
$W'$
on
![]() $\mu $
extending the closed unbounded filter on
$\mu $
extending the closed unbounded filter on
![]() $\mu $
adjoined with the set of singular cardinals less than
$\mu $
adjoined with the set of singular cardinals less than
![]() $\mu $
. Since
$\mu $
. Since
![]() $\mu <\delta $
, it follows that
$\mu <\delta $
, it follows that
![]() $W'<_{\mathbb {k}}W$
(see [Reference Goldberg17, Lemma 3.3.15]) contradicting the minimality of W.
$W'<_{\mathbb {k}}W$
(see [Reference Goldberg17, Lemma 3.3.15]) contradicting the minimality of W.
End of proof of Theorem 6.6. Note that W is not a p-point since W extends the closed unbounded filter but is not normal; therefore by Corollary 3.11, W is non-Galvin, and hence U is below W in the Ketonen order.
Conversely, since U is the Ketonen least non-Galvin ultrafilter, by Theorem 1.2, U is irreducible and not a p-point. Without loss of generality, we can assume that U is Dodd sound. Moreover, U is a
![]() $\gamma $
-complete ultrafilter on
$\gamma $
-complete ultrafilter on
![]() $\gamma $
for some measurable cardinal
$\gamma $
for some measurable cardinal
![]() $\gamma $
.
$\gamma $
.
Let
![]() $\lambda = \sup \{j_U(f)(\gamma ) \mid f\colon \gamma \rightarrow \gamma \}$
. Since U is not a p-point,
$\lambda = \sup \{j_U(f)(\gamma ) \mid f\colon \gamma \rightarrow \gamma \}$
. Since U is not a p-point,
![]() $\lambda \leq [\text {id}]_U$
. Since U is Dodd sound,
$\lambda \leq [\text {id}]_U$
. Since U is Dodd sound,
![]() $\{j_U(A)\cap \lambda : A\subseteq \gamma \}\in M_U$
, which implies
$\{j_U(A)\cap \lambda : A\subseteq \gamma \}\in M_U$
, which implies
and hence
![]() $\{j_U(f)(\gamma ) \mid f\colon \gamma \rightarrow \gamma \}\in M_U$
, which implies that
$\{j_U(f)(\gamma ) \mid f\colon \gamma \rightarrow \gamma \}\in M_U$
, which implies that
![]() $M_U$
satisfies
$M_U$
satisfies
![]() $\mathrm {cf}(\lambda ) \leq 2^\gamma $
.
$\mathrm {cf}(\lambda ) \leq 2^\gamma $
.
Let D be the ultrafilter on
![]() $\gamma $
derived from
$\gamma $
derived from
![]() $j_U$
using
$j_U$
using
![]() $\lambda $
. Then D is below U in the Ketonen order. Since
$\lambda $
. Then D is below U in the Ketonen order. Since
![]() $\mathrm {cf}^{M_U}(\lambda ) \leq 2^\gamma $
, D concentrates on singular cardinals. Moreover, for any
$\mathrm {cf}^{M_U}(\lambda ) \leq 2^\gamma $
, D concentrates on singular cardinals. Moreover, for any
![]() $f\in \gamma ^\gamma $
,
$f\in \gamma ^\gamma $
,
![]() $\lambda $
is closed under
$\lambda $
is closed under
![]() $j_U(f)$
– that is,
$j_U(f)$
– that is,
![]() $j_U(f)[\lambda ]\subseteq \lambda $
– so D concentrates on the set of closure points of f. It follows that D extends the closed unbounded filter. Therefore, W is below D in the Ketonen order, so by the transitivity of the Ketonen order, W is below U in the Ketonen order. It follows that
$j_U(f)[\lambda ]\subseteq \lambda $
– so D concentrates on the set of closure points of f. It follows that D extends the closed unbounded filter. Therefore, W is below D in the Ketonen order, so by the transitivity of the Ketonen order, W is below U in the Ketonen order. It follows that
![]() $U = W$
as claimed. This implies that U extends the club filter, which proves the theorem.
$U = W$
as claimed. This implies that U extends the club filter, which proves the theorem.
Let us turn our attention to the non-Galvin cardinals. Main Theorem 1.4, which we now prove, shows that the existence of a non-Galvin cardinal is exactly the large cardinal assumption needed to conclude the existence of non-Galvin ultrafilters in an inner model.
Theorem 6.8 (UA)
Assume that every irreducible ultrafilter is Dodd sound. If there is a
![]() $\kappa $
-complete non-Galvin ultrafilter on an uncountable cardinal
$\kappa $
-complete non-Galvin ultrafilter on an uncountable cardinal
![]() $\kappa $
, then there is a non-Galvin cardinal.
$\kappa $
, then there is a non-Galvin cardinal.
Proof Let W be a non-Galvin ultrafilter on
![]() $\kappa $
. By Theorem 1.5, W is Rudin–Keisler equivalent to an n-fold sum of irreducible ultrafilters. By Theorem 1.2, it is impossible that all these ultrafilters are p-points (even on measure one sets) so
$\kappa $
. By Theorem 1.5, W is Rudin–Keisler equivalent to an n-fold sum of irreducible ultrafilters. By Theorem 1.2, it is impossible that all these ultrafilters are p-points (even on measure one sets) so
![]() $\kappa $
must carry an irreducible ultrafilter U which is not a p-point. By our assumption, every irreducible is Dodd sound. Since U is a
$\kappa $
must carry an irreducible ultrafilter U which is not a p-point. By our assumption, every irreducible is Dodd sound. Since U is a
![]() $\kappa $
-complete, non p-point, Dodd sound ultrafilter, Lemma 5.10 applies, and we conclude that
$\kappa $
-complete, non p-point, Dodd sound ultrafilter, Lemma 5.10 applies, and we conclude that
![]() $\kappa $
is a non-Galvin cardinal.
$\kappa $
is a non-Galvin cardinal.
Proposition 6.9 (UA)
If
![]() $\kappa $
is
$\kappa $
is
![]() $\kappa $
-compact and no cardinal
$\kappa $
-compact and no cardinal
![]() $\nu < \kappa $
is
$\nu < \kappa $
is
![]() $\kappa $
-supercompact, then
$\kappa $
-supercompact, then
![]() $\kappa $
a limit of non-Galvin cardinals.
$\kappa $
a limit of non-Galvin cardinals.
Proof Since
![]() $\kappa $
is
$\kappa $
is
![]() $\kappa $
-compact, a theorem of Kunen [Reference Kunen, Gandy and Yates26, Lemma 3] implies that for every
$\kappa $
-compact, a theorem of Kunen [Reference Kunen, Gandy and Yates26, Lemma 3] implies that for every
![]() $\xi < (2^{\kappa })^+$
, there is a countably complete ultrafilter U on
$\xi < (2^{\kappa })^+$
, there is a countably complete ultrafilter U on
![]() $\kappa $
such that
$\kappa $
such that
![]() $j_U(\xi )> \xi $
. Let
$j_U(\xi )> \xi $
. Let
![]() $U_\xi $
denote the Ketonen least such ultrafilter. By [Reference Goldberg17, Lemma 7.4.34] and [Reference Goldberg17, Proposition 8.3.39],
$U_\xi $
denote the Ketonen least such ultrafilter. By [Reference Goldberg17, Lemma 7.4.34] and [Reference Goldberg17, Proposition 8.3.39],
![]() $U_\xi $
is a Mitchell point: for any ultrafilter
$U_\xi $
is a Mitchell point: for any ultrafilter
![]() $W<_{\mathbb {k}} U$
, W lies below U in the Mitchell order.
$W<_{\mathbb {k}} U$
, W lies below U in the Mitchell order.
Since
![]() $\kappa $
is strongly inaccessible, there is an
$\kappa $
is strongly inaccessible, there is an
![]() $\omega $
-club
$\omega $
-club
![]() $C\subseteq (2^\kappa )^+$
such that for all
$C\subseteq (2^\kappa )^+$
such that for all
![]() $\xi \in C$
, for all countably complete ultrafilters D of rank less than
$\xi \in C$
, for all countably complete ultrafilters D of rank less than
![]() $\xi $
in the Ketonen order,
$\xi $
in the Ketonen order,
![]() $j_D(\xi ) = \xi $
. For
$j_D(\xi ) = \xi $
. For
![]() $\xi \in C$
,
$\xi \in C$
,
![]() $U_\xi $
is a uniform irreducible ultrafilter on
$U_\xi $
is a uniform irreducible ultrafilter on
![]() $\kappa $
, and so it follows from [Reference Goldberg17, Theorem 8.2.23] that
$\kappa $
, and so it follows from [Reference Goldberg17, Theorem 8.2.23] that
![]() $U_\xi $
witnesses
$U_\xi $
witnesses
![]() $\operatorname {\mathrm {crit}}(j_{U_\xi })$
is
$\operatorname {\mathrm {crit}}(j_{U_\xi })$
is
![]() ${<}\kappa $
-supercompact. Since
${<}\kappa $
-supercompact. Since
![]() $\kappa $
is measurable, it follows that
$\kappa $
is measurable, it follows that
![]() $\operatorname {\mathrm {crit}}(j_{U_\xi })$
is
$\operatorname {\mathrm {crit}}(j_{U_\xi })$
is
![]() $\kappa $
-supercompact, and so by the assumptions of the proposition,
$\kappa $
-supercompact, and so by the assumptions of the proposition,
![]() $\operatorname {\mathrm {crit}}(j_{U_\xi }) = \kappa $
. In other words,
$\operatorname {\mathrm {crit}}(j_{U_\xi }) = \kappa $
. In other words,
![]() $U_\xi $
is
$U_\xi $
is
![]() $\kappa $
-complete.
$\kappa $
-complete.
Now, let W witness that
![]() $\kappa $
is a non-Galvin cardinal. Fix
$\kappa $
is a non-Galvin cardinal. Fix
![]() $\xi \in C$
larger than the Ketonen rank of W. Then W is below
$\xi \in C$
larger than the Ketonen rank of W. Then W is below
![]() $U_\xi $
in the Mitchell order, and so
$U_\xi $
in the Mitchell order, and so
![]() $\kappa $
is non-Galvin in
$\kappa $
is non-Galvin in
![]() $M_{U_\xi }$
. It follows that
$M_{U_\xi }$
. It follows that
![]() $\kappa $
is a limit of non-Galvin cardinals.
$\kappa $
is a limit of non-Galvin cardinals.
In particular, the least cardinal
![]() $\kappa $
that is
$\kappa $
that is
![]() $\kappa $
-compact is larger than the least non-Galvin cardinal assuming UA.Footnote
15
$\kappa $
-compact is larger than the least non-Galvin cardinal assuming UA.Footnote
15
7 Open problems
Question 7.1. Is it consistent that there is a
![]() $\kappa $
-complete uniform ultrafilter U over
$\kappa $
-complete uniform ultrafilter U over
![]() $\kappa $
satisfying the Galvin property that is not an n-fold sum of
$\kappa $
satisfying the Galvin property that is not an n-fold sum of
![]() $\kappa $
-complete p-points over
$\kappa $
-complete p-points over
![]() $\kappa $
?
$\kappa $
?
Recently, Gitik gave a positive answer to this question, thus our characterization of ultrafilters with the Galvin property cannot be proved in ZFC. The following question seems more plausible for a positive answer in ZFC.
Question 7.2. Is every uniform
![]() $\kappa $
-complete ultrafilter U over
$\kappa $
-complete ultrafilter U over
![]() $\kappa ^+$
non-Galvin, i.e.,
$\kappa ^+$
non-Galvin, i.e.,
![]() $\neg \mathrm{Gal}(U,\kappa ^+,\kappa ^{++})$
holds?
$\neg \mathrm{Gal}(U,\kappa ^+,\kappa ^{++})$
holds?
Under UA, the answer is positive by Corollary 6.2.
Question 7.3. Does a non-Galvin cardinal entail the existence of a non-Galvin ultrafilter which extends the club filter?
By Main Theorem 1.2, a non-Galvin cardinal entails the existence of a non-Galvin ultrafilter. Assuming UA and that every irreducible is Dodd sound, Main Theorem 1.5 shows that a non-Galvin cardinal also entails the existence of
![]() $\kappa $
-complete non-Galvin ultrafilter which extends the club filter.
$\kappa $
-complete non-Galvin ultrafilter which extends the club filter.
Question 7.4. Does every fine normal ultrafilter over
![]() $P_\kappa (\kappa ^+)$
satisfy
$P_\kappa (\kappa ^+)$
satisfy
![]() $\mathrm{Gal}(U,\kappa ,2^{\kappa ^{+}})$
?
$\mathrm{Gal}(U,\kappa ,2^{\kappa ^{+}})$
?
The answer would be interesting even under
![]() $UA$
. This is the first step toward answering the more general problem.
$UA$
. This is the first step toward answering the more general problem.
Question 7.5. Characterize the Tukey-top ultrafilters on
![]() $\kappa $
with respect to
$\kappa $
with respect to
![]() $\lambda <\kappa $
assuming UA plus every irreducible is Dodd sound.
$\lambda <\kappa $
assuming UA plus every irreducible is Dodd sound.
Question 7.6. Is there a similar characterization under
![]() $UA$
for
$UA$
for
![]() $\sigma $
-complete ultrafilters with the Galvin property over singular cardinals?
$\sigma $
-complete ultrafilters with the Galvin property over singular cardinals?
We believe that such a characterization exists and that similar methods to those appearing in this paper should be useful.
In the absence of GCH, we have the following questions which are open.
Question 7.7. If we replace
![]() $i"\kappa ^+$
by
$i"\kappa ^+$
by
![]() $i"2^\kappa $
in the definition of non-Galvin cardinal, do we get a
$i"2^\kappa $
in the definition of non-Galvin cardinal, do we get a
![]() $\kappa $
-complete ultrafilter such that
$\kappa $
-complete ultrafilter such that
![]() $\neg \mathrm{Gal}(U,\kappa ,2^\kappa )$
?
$\neg \mathrm{Gal}(U,\kappa ,2^\kappa )$
?
More generally:
Question 7.8. Is it consistent that there is a
![]() $\kappa $
-complete ultrafilter U such that
$\kappa $
-complete ultrafilter U such that
![]() $\neg \mathrm{Gal}(U,\kappa ,\kappa ^+)$
but
$\neg \mathrm{Gal}(U,\kappa ,\kappa ^+)$
but
![]() $\mathrm{Gal}(U,\kappa ,2^\kappa )$
?
$\mathrm{Gal}(U,\kappa ,2^\kappa )$
?
The result of this paper resolves these two questions under UA plus every irreducible is Dodd sound.
The following two questions address the assumptions in the main theorems of this paper.
Question 7.9. Is it consistent that there is a cardinal
![]() $\kappa $
which is
$\kappa $
which is
![]() $\kappa ^+$
-supercompact and that every irreducible ultrafilter is Dodd sound?
$\kappa ^+$
-supercompact and that every irreducible ultrafilter is Dodd sound?
Question 7.10. Does UA imply that every irreducible ultrafilter is Rudin–Keisler equivalent to a Dodd sound ultrafilter?
Let us conclude this paper with a diamond-like principle which is a reasonable candidate to be equivalent to non-Galvin ultrafilters. Such a principle would be valuable as there is no known formulation of the Galvin property in terms of the ultrapower. This would be also interesting from the point of view of the Tukey order since this order involves functions which typically have domains of size
![]() $2^\kappa $
, and thus not available in the ultrapower.
$2^\kappa $
, and thus not available in the ultrapower.
Definition 7.11. We say that
![]() $\diamondsuit ^-_{\text {par}}(U)$
holds if and only if there is
$\diamondsuit ^-_{\text {par}}(U)$
holds if and only if there is
![]() $A\in M_U$
,
$A\in M_U$
,
![]() $\lambda $
and
$\lambda $
and
![]() ${\langle } X_i{\rangle }_{i<2^\kappa }\subseteq P(\kappa )$
such that:
${\langle } X_i{\rangle }_{i<2^\kappa }\subseteq P(\kappa )$
such that:
-
(1)
 $\{j_U(X_i)\cap \lambda \mid i<2^\kappa \}\subseteq A$
.
$\{j_U(X_i)\cap \lambda \mid i<2^\kappa \}\subseteq A$
. -
(2) There is no function
 $f:\kappa \rightarrow \kappa $
such that
$f:\kappa \rightarrow \kappa $
such that
 $j_U(f)(|A|^{M_U})\geq \lambda $
.
$j_U(f)(|A|^{M_U})\geq \lambda $
.
The argument of Theorem 4.9 can be adjusted to conclude that
![]() $\diamondsuit ^-_{\text {par}}(U)$
implies that U is non-Galvin.
$\diamondsuit ^-_{\text {par}}(U)$
implies that U is non-Galvin.
Question 7.12. Is
![]() $\diamondsuit ^-_{\mathrm{par}}(U)$
equivalent to U being non-Galvin?
$\diamondsuit ^-_{\mathrm{par}}(U)$
equivalent to U being non-Galvin?
The next question seeks an analogous result on
![]() $\omega $
to the one of this paper.
$\omega $
to the one of this paper.
Question 7.13. Is it consistent that every ultrafilter on
![]() $\omega $
which is not Tukey-top is an n-fold sum of p-points?
$\omega $
which is not Tukey-top is an n-fold sum of p-points?
Acknowledgments
We would like to thank the referee of this paper for their clever remarks and contribution to the presentation of the current version of this paper. We would also like to thank Natasha Dobrinen for providing valuable corrections regarding the theory of the Tukey order on ultrafilters over a countable set. Finally, we would like to thank Moti Gitik for insightful discussions and comments.