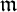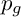1 Introduction and notations
Let
![]() $(A,\mathfrak m)$
be an excellent two-dimensional normal local ring, and let I be an
$(A,\mathfrak m)$
be an excellent two-dimensional normal local ring, and let I be an
![]() $\mathfrak m$
-primary ideal of A. The integral closure
$\mathfrak m$
-primary ideal of A. The integral closure
![]() $\bar {I}$
of I is the ideal consisting of all solutions z of some equation with coefficients
$\bar {I}$
of I is the ideal consisting of all solutions z of some equation with coefficients
![]() $c_i \in I^i $
:
$c_i \in I^i $
:
![]() $Z ^n +c_1 Z^{n-1} +c_2 Z^{n-2} + \dots + c_{n-1} Z + c_n=0$
. Then
$Z ^n +c_1 Z^{n-1} +c_2 Z^{n-2} + \dots + c_{n-1} Z + c_n=0$
. Then
![]() $ I \subseteq \bar {I} \subseteq \sqrt {I}$
. We say that I is integrally closed if
$ I \subseteq \bar {I} \subseteq \sqrt {I}$
. We say that I is integrally closed if
![]() $I = \bar {I}$
and I is normal if
$I = \bar {I}$
and I is normal if
![]() $I^n= {\overline {I^n}} $
for every positive integer n. By a classical result of Rees [Reference Rossi29], under our assumptions, the filtration
$I^n= {\overline {I^n}} $
for every positive integer n. By a classical result of Rees [Reference Rossi29], under our assumptions, the filtration
![]() $\{\overline {I^n}\}_{n \in \mathbb N}$
is a good I-filtration of A and it is called the normal filtration.
$\{\overline {I^n}\}_{n \in \mathbb N}$
is a good I-filtration of A and it is called the normal filtration.
We may define the Hilbert–Samuel function
![]() $\bar {H}_I(n):=\ell _A(A/\overline {I^{n+1}})$
for all integers
$\bar {H}_I(n):=\ell _A(A/\overline {I^{n+1}})$
for all integers
![]() $n \ge 0$
, and it becomes a polynomial for large n. (Here,
$n \ge 0$
, and it becomes a polynomial for large n. (Here,
![]() $\ell _A(M) $
is the length of the A-module M.) This polynomial is called the normal Hilbert polynomial
$\ell _A(M) $
is the length of the A-module M.) This polynomial is called the normal Hilbert polynomial
 $$ \begin{align*} \bar{P}_I(n) =\bar e_0(I) \binom{n+2}{2} -\bar e_1(I) \binom{n+1}{1} +\bar e_2(I), \end{align*} $$
$$ \begin{align*} \bar{P}_I(n) =\bar e_0(I) \binom{n+2}{2} -\bar e_1(I) \binom{n+1}{1} +\bar e_2(I), \end{align*} $$
and the coefficients
![]() $\overline {e}_i(I)$
,
$\overline {e}_i(I)$
,
![]() $i=0,1,2,$
are the normal Hilbert coefficients.
$i=0,1,2,$
are the normal Hilbert coefficients.
A rich literature is available on the normal Hilbert coefficients
![]() $\bar e_i(I)$
, and this study is considered an important part of the theory of blowing-up rings (see, e.g., [Reference Corso, Polini and Rossi2], [Reference Cutkosky3], [Reference Itoh10], [Reference Itoh11], [Reference Kato12], [Reference Némethi and Okuma17]–[Reference Okuma19], [Reference Tomari33]).
$\bar e_i(I)$
, and this study is considered an important part of the theory of blowing-up rings (see, e.g., [Reference Corso, Polini and Rossi2], [Reference Cutkosky3], [Reference Itoh10], [Reference Itoh11], [Reference Kato12], [Reference Némethi and Okuma17]–[Reference Okuma19], [Reference Tomari33]).
From the geometric side, any integrally closed
![]() $\mathfrak m$
-primary ideal I of
$\mathfrak m$
-primary ideal I of
![]() $A $
is represented on some resolution (see [Reference Masuti, Sarkar and Verma16]). Let
$A $
is represented on some resolution (see [Reference Masuti, Sarkar and Verma16]). Let
be a resolution of singularities with an anti-nef cycle
![]() $Z>0$
on X, so that
$Z>0$
on X, so that
![]() $I =I_Z= H^0(\mathcal {O}_X(-Z))$
and
$I =I_Z= H^0(\mathcal {O}_X(-Z))$
and
![]() $I\mathcal {O}_X=\mathcal {O}_X(-Z)$
. We say that
$I\mathcal {O}_X=\mathcal {O}_X(-Z)$
. We say that
![]() $I = I_Z$
is represented by
$I = I_Z$
is represented by
![]() $Z $
on X. The aim of this paper is to join the algebraic and the geometric information on A taking advantage of the theory of the Hilbert functions and of the theory of the resolution of singularities.
$Z $
on X. The aim of this paper is to join the algebraic and the geometric information on A taking advantage of the theory of the Hilbert functions and of the theory of the resolution of singularities.
For a coherent
![]() $\mathcal {O}_X$
-module
$\mathcal {O}_X$
-module
![]() $\mathcal {F}$
, we write
$\mathcal {F}$
, we write
![]() $h^i(\mathcal {F})=\ell _A(H^i(X, \mathcal {F}))$
. If
$h^i(\mathcal {F})=\ell _A(H^i(X, \mathcal {F}))$
. If
![]() $I=I_Z$
is an
$I=I_Z$
is an
![]() $\mathfrak m$
-primary integrally closed ideal of A represented by Z on X, one can define for every integer
$\mathfrak m$
-primary integrally closed ideal of A represented by Z on X, one can define for every integer
![]() $n \ge 0$
a decreasing chain of integers
$n \ge 0$
a decreasing chain of integers
![]() $q(nI):= q(\overline {I^n}) = h^1(\mathcal {O}_X(-nZ))$
where
$q(nI):= q(\overline {I^n}) = h^1(\mathcal {O}_X(-nZ))$
where
![]() $q(0I) := p_g(A)$
is the geometric genus of A. It is proved that
$q(0I) := p_g(A)$
is the geometric genus of A. It is proved that
![]() $q(nI) $
stabilizes for every I and
$q(nI) $
stabilizes for every I and
![]() $n\ge p_g(A)$
. We denote it by
$n\ge p_g(A)$
. We denote it by
![]() $q(\infty I)$
.
$q(\infty I)$
.
These integers are independent of the representation, and they are strictly related to the normal Hilbert polynomial. The keys of our approach can be considered Theorem 2.2 and Proposition 2.6, consequences of Kato’s Riemann–Roch formula (see [Reference Lipman14], [Reference Okuma, Watanabe and Yoshida24]). In particular, the following holds:
-
(1)
 $\overline {P}_I(n)=\ell _A(A/\overline {I^{n+1}})$
for all
$\overline {P}_I(n)=\ell _A(A/\overline {I^{n+1}})$
for all
 $n \ge p_g(A)-1$
.
$n \ge p_g(A)-1$
. -
(2)
 $\bar e_1(I)-e_0(I) + \ell _A(A/I) =p_g(A) - q(I)$
.
$\bar e_1(I)-e_0(I) + \ell _A(A/I) =p_g(A) - q(I)$
. -
(3)
 $\bar e_2(I)= p_g(A)-q(nI)=p_g(A)-q(\infty I)$
for all
$\bar e_2(I)= p_g(A)-q(nI)=p_g(A)-q(\infty I)$
for all
 $n \ge p_g(A)$
.
$n \ge p_g(A)$
.
Moreover, we have
 $$ \begin{align*} \bar e_0(I)= -Z^2,\qquad \bar e_1(I)= \dfrac{-Z^2+ZK_X}{2}. \end{align*} $$
$$ \begin{align*} \bar e_0(I)= -Z^2,\qquad \bar e_1(I)= \dfrac{-Z^2+ZK_X}{2}. \end{align*} $$
This makes the bridge between the theory of the normal Hilbert coefficients and the theory of the singularities. This is the line already traced by Lipman [Reference Masuti, Sarkar and Verma16], Cutkosky [Reference Franciosi and Tenni4], and more recently by Okuma, Watanabe, and Yoshida (see [Reference Okuma, Watanabe and Yoshida23]–[Reference Pinkham25]).
Let
![]() $(A,\mathfrak m)$
be a two-dimensional excellent normal local domain containing an algebraically closed field
$(A,\mathfrak m)$
be a two-dimensional excellent normal local domain containing an algebraically closed field
![]() $k= A/\mathfrak m$
. It is known that A is a rational singularity (see [Reference Artin1]) if and only if every integrally closed
$k= A/\mathfrak m$
. It is known that A is a rational singularity (see [Reference Artin1]) if and only if every integrally closed
![]() $\mathfrak m$
-primary ideal I of A is normal (see [Reference Franciosi and Tenni4], [Reference Masuti, Sarkar and Verma16]), equivalently
$\mathfrak m$
-primary ideal I of A is normal (see [Reference Franciosi and Tenni4], [Reference Masuti, Sarkar and Verma16]), equivalently
![]() $\bar e_2(I)=0$
, that is, I is a
$\bar e_2(I)=0$
, that is, I is a
![]() $p_g$
-ideal, as proved in [Reference Okuma, Watanabe and Yoshida23], [Reference Okuma, Watanabe and Yoshida24]. Inspired by a paper by Okuma [Reference Okuma, Watanabe and Yoshida22], we investigate the integrally closed
$p_g$
-ideal, as proved in [Reference Okuma, Watanabe and Yoshida23], [Reference Okuma, Watanabe and Yoshida24]. Inspired by a paper by Okuma [Reference Okuma, Watanabe and Yoshida22], we investigate the integrally closed
![]() $\mathfrak m$
-primary ideals of elliptic singularities (see [Reference Yau38]) and of strongly elliptic singularities (see [Reference Yau41]). All the preliminary results are contained in §2.
$\mathfrak m$
-primary ideals of elliptic singularities (see [Reference Yau38]) and of strongly elliptic singularities (see [Reference Yau41]). All the preliminary results are contained in §2.
In §3, we prove the main results of the paper. We define the elliptic and the strongly elliptic ideals aimed by the study of nonrational singularities. We recall that if Q is a minimal reduction of I, then we denote by
![]() $\bar {\mathrm {r}}(I):= \min \{ r \;|\; \overline {I^{n+1}} = Q \overline {I^n}\;, \text {for all} \; n \ge r\}$
, the normal reduction number of I and this integer exists and does not depend on the choice of Q. Okuma proved that if A is an elliptic singularity, then
$\bar {\mathrm {r}}(I):= \min \{ r \;|\; \overline {I^{n+1}} = Q \overline {I^n}\;, \text {for all} \; n \ge r\}$
, the normal reduction number of I and this integer exists and does not depend on the choice of Q. Okuma proved that if A is an elliptic singularity, then
![]() $\bar {\mathrm {r}}(I) = 2$
for any integrally closed
$\bar {\mathrm {r}}(I) = 2$
for any integrally closed
![]() $\mathfrak m$
-primary ideal of A (see [Reference Okuma, Watanabe and Yoshida22, Theorem 3.3]). According to Okuma’s result, we define elliptic ideals to be the integrally closed
$\mathfrak m$
-primary ideal of A (see [Reference Okuma, Watanabe and Yoshida22, Theorem 3.3]). According to Okuma’s result, we define elliptic ideals to be the integrally closed
![]() $\mathfrak m$
-primary ideals satisfying
$\mathfrak m$
-primary ideals satisfying
![]() $\bar {\mathrm {r}}(I)= 2$
. In Theorem 3.2, we prove that elliptic ideals satisfy
$\bar {\mathrm {r}}(I)= 2$
. In Theorem 3.2, we prove that elliptic ideals satisfy
![]() $\bar e_2(I)=\bar {e}_1(I) -e_0(I) + \ell _A( A/I)>0 $
attaining the minimal value according to the inequality proved by Sally [Reference Wagreich35] and Itoh [Reference Kato12]. In particular, if I is an elliptic ideal, then
$\bar e_2(I)=\bar {e}_1(I) -e_0(I) + \ell _A( A/I)>0 $
attaining the minimal value according to the inequality proved by Sally [Reference Wagreich35] and Itoh [Reference Kato12]. In particular, if I is an elliptic ideal, then
![]() $p_g(A)> q(I)=q(\infty I)$
. If A is not a rational singularity, then elliptic ideals always exist (see Proposition 3.3). In particular, we prove the following proposition.
$p_g(A)> q(I)=q(\infty I)$
. If A is not a rational singularity, then elliptic ideals always exist (see Proposition 3.3). In particular, we prove the following proposition.
Proposition 1.1 (See Proposition 3.3)
If A is not a rational singularity, then for any
![]() $\mathfrak m$
-primary integrally closed ideal I of A,
$\mathfrak m$
-primary integrally closed ideal I of A,
![]() $\overline {I^{n}}$
is either a
$\overline {I^{n}}$
is either a
![]() $p_g$
-ideal or an elliptic ideal for every
$p_g$
-ideal or an elliptic ideal for every
![]() $n \ge p_g(A)$
.
$n \ge p_g(A)$
.
Yau in [Reference Yau41], Laufer in [Reference Masuti, Ozeki and Rossi15], and Wagreich in [Reference Yau38] introduced interesting classes of elliptic singularities. An excellent two-dimensional normal local ring A is a strongly elliptic singularity if
![]() $ p_g(A)=1$
, that is,
$ p_g(A)=1$
, that is,
![]() $p_g$
is almost minimal.
$p_g$
is almost minimal.
Among the elliptic ideals, in Theorem 3.9, we define strongly elliptic ideals those for which
![]() $\bar e_2 =1 $
and equivalent conditions are given. The following result characterizes algebraically the strongly elliptic singularities.
$\bar e_2 =1 $
and equivalent conditions are given. The following result characterizes algebraically the strongly elliptic singularities.
Theorem 1.2 (See Theorem 3.14)
Let
![]() $(A,\mathfrak m)$
be a two-dimensional excellent normal local domain containing an algebraically closed field
$(A,\mathfrak m)$
be a two-dimensional excellent normal local domain containing an algebraically closed field
![]() $k= A/\mathfrak m$
, and assume that
$k= A/\mathfrak m$
, and assume that
![]() $p_g(A)>0$
. The following conditions are equivalent
$p_g(A)>0$
. The following conditions are equivalent
![]() $:$
$:$
-
(1) A is a strongly elliptic singularity.
-
(2) Every integrally closed ideal of A is either a
 $p_g$
-ideal or a strongly elliptic ideal.
$p_g$
-ideal or a strongly elliptic ideal.
Notice that
![]() $p_g$
-ideals are always normal, but elliptic ideals are not necessary normal (see Proposition 3.16 and Examples 3.15 and 3.25). Moreover, if A is strongly elliptic and I is not a
$p_g$
-ideals are always normal, but elliptic ideals are not necessary normal (see Proposition 3.16 and Examples 3.15 and 3.25). Moreover, if A is strongly elliptic and I is not a
![]() $p_g$
-ideal, then Proposition 3.16 and Theorem 3.23 give necessary and sufficient conditions for being I normal.
$p_g$
-ideal, then Proposition 3.16 and Theorem 3.23 give necessary and sufficient conditions for being I normal.
Theorem 1.3. Let
![]() $(A,\mathfrak m)$
be a two-dimensional excellent normal local domain containing an algebraically closed field
$(A,\mathfrak m)$
be a two-dimensional excellent normal local domain containing an algebraically closed field
![]() $k= A/\mathfrak m$
. Assume that A is a strongly elliptic singularity. If
$k= A/\mathfrak m$
. Assume that A is a strongly elliptic singularity. If
![]() $I = I_Z $
is an elliptic ideal
$I = I_Z $
is an elliptic ideal
![]() $($
equivalently, I is not a
$($
equivalently, I is not a
![]() $p_g$
-ideal
$p_g$
-ideal
![]() $)$
and D is the minimally elliptic cycle on X, then
$)$
and D is the minimally elliptic cycle on X, then
![]() $I^2$
is integrally closed
$I^2$
is integrally closed
![]() $($
equivalently, I is normal
$($
equivalently, I is normal
![]() $)$
if and only if
$)$
if and only if
![]() $- Z D \ge 3$
and if
$- Z D \ge 3$
and if
![]() $- ZD \le 2$
, then
$- ZD \le 2$
, then
![]() $I^2 = QI$
.
$I^2 = QI$
.
For any normal surface singularity which is not rational,
![]() $p_g$
-ideals and elliptic ideals exist plentifully. But this is no longer true for strongly elliptic ideals.
$p_g$
-ideals and elliptic ideals exist plentifully. But this is no longer true for strongly elliptic ideals.
In §4, we show that there exist excellent two-dimensional normal local rings having no strongly elliptic ideals (see Example 4.8). Finally, Corollary 4.7 gives necessary and sufficient conditions for the existence of strongly elliptic ideals in terms of the existence of certain cohomological cycles. When there exist, we present an effective geometric construction (see Example 4.9).
2 Preliminaries and normal reduction number
Let
![]() $(A,\mathfrak m)$
be an excellent two-dimensional normal local domain containing an algebraically closed field
$(A,\mathfrak m)$
be an excellent two-dimensional normal local domain containing an algebraically closed field
![]() $k= A/\mathfrak m$
, and let I be an integrally closed
$k= A/\mathfrak m$
, and let I be an integrally closed
![]() $\mathfrak m$
-primary ideal of A. With the already introduced notation, then there exists a resolution
$\mathfrak m$
-primary ideal of A. With the already introduced notation, then there exists a resolution
![]() $X \to \ \operatorname {\mathrm {Spec}} A$
and a cycle Z such that I is represented on X by Z. When we write
$X \to \ \operatorname {\mathrm {Spec}} A$
and a cycle Z such that I is represented on X by Z. When we write
![]() $I_Z$
, we always assume that
$I_Z$
, we always assume that
![]() $\mathcal {O}_X(-Z) $
is generated by global sections, namely
$\mathcal {O}_X(-Z) $
is generated by global sections, namely
![]() $I \mathcal {O}_X=\mathcal {O}_X(-Z)$
, and note that
$I \mathcal {O}_X=\mathcal {O}_X(-Z)$
, and note that
![]() $I_Z= H^0(X, \mathcal {O}_X(-Z))$
. Recall that the geometric genus
$I_Z= H^0(X, \mathcal {O}_X(-Z))$
. Recall that the geometric genus
![]() $p_g(A)= h^1(\mathcal {O}_X)$
is independent of the choice of the resolution.
$p_g(A)= h^1(\mathcal {O}_X)$
is independent of the choice of the resolution.
Okuma, Watanabe, and Yoshida introduced a natural extension of the integrally closed ideals in a two-dimensional rational singularity, that is, the
![]() $p_g$
-ideals. With the previous notation,
$p_g$
-ideals. With the previous notation,
and if the equality holds, then Z is called a
![]() $p_g$
-cycle and
$p_g$
-cycle and
![]() $I=I_Z$
is called a
$I=I_Z$
is called a
![]() $p_g$
-ideal. In [Reference Okuma, Watanabe and Yoshida23], [Reference Okuma, Watanabe and Yoshida24], the authors characterized the
$p_g$
-ideal. In [Reference Okuma, Watanabe and Yoshida23], [Reference Okuma, Watanabe and Yoshida24], the authors characterized the
![]() $p_g$
-ideals in terms of the normal Hilbert polynomial. They proved that A is a rational singularity if and only if every integrally closed
$p_g$
-ideals in terms of the normal Hilbert polynomial. They proved that A is a rational singularity if and only if every integrally closed
![]() $\mathfrak m$
-primary ideal is a
$\mathfrak m$
-primary ideal is a
![]() $p_g$
-ideal. Starting by
$p_g$
-ideal. Starting by
![]() $p_g(A)$
, we define the following chain of integers.
$p_g(A)$
, we define the following chain of integers.
Definition 2.1. We define
![]() $q(I):= h^1(\mathcal {O}_X(-Z))$
and more in general
$q(I):= h^1(\mathcal {O}_X(-Z))$
and more in general
![]() $q(nI):= q(\overline {I^n}) = h^1(\mathcal {O}_X(-nZ))$
for every integer
$q(nI):= q(\overline {I^n}) = h^1(\mathcal {O}_X(-nZ))$
for every integer
![]() $n \ge 1$
.
$n \ge 1$
.
We put
![]() $q(0 I)=h^1(\mathcal {O}_X)=p_g(A)$
. Notice that
$q(0 I)=h^1(\mathcal {O}_X)=p_g(A)$
. Notice that
![]() $q(nI)$
is in general very difficult to compute, but it is independent of the representation (see [Reference Okuma, Watanabe and Yoshida23, Lemma 3.4]). These invariants are strictly related to the normal Hilbert polynomial, and their interplay is very important in our approach.
$q(nI)$
is in general very difficult to compute, but it is independent of the representation (see [Reference Okuma, Watanabe and Yoshida23, Lemma 3.4]). These invariants are strictly related to the normal Hilbert polynomial, and their interplay is very important in our approach.
The following formula is called a Riemann–Roch formula. The result was proved in [Reference Lipman14] in the complex case, but it holds in any characteristic (see [Reference Watanabe and Yoshida40]).
Theorem 2.2 (Kato’s Riemann–Roch formula [Reference Watanabe and Yoshida40, Theorem 2.2])
Let
![]() $I=I_Z$
be an
$I=I_Z$
be an
![]() $\mathfrak m$
-primary integrally closed ideal represented by an anti-nef cycle Z on X. Then we have
$\mathfrak m$
-primary integrally closed ideal represented by an anti-nef cycle Z on X. Then we have
 $$ \begin{align*} \ell_A(A/I) + q(I) =-\dfrac{Z^2+K_XZ}{2} + p_g(A), \end{align*} $$
$$ \begin{align*} \ell_A(A/I) + q(I) =-\dfrac{Z^2+K_XZ}{2} + p_g(A), \end{align*} $$
where
![]() $K_X$
denotes the canonical divisor.
$K_X$
denotes the canonical divisor.
We recall here the properties of the sequence
![]() $\{q(nI)\}$
. Propositions 2.3 and 2.5 on
$\{q(nI)\}$
. Propositions 2.3 and 2.5 on
![]() $I = I_Z$
follow from the long exact sequence attached to the short exact sequence
$I = I_Z$
follow from the long exact sequence attached to the short exact sequence
(see [Reference Okuma, Watanabe and Yoshida24, Lemma 3.1]).
Proposition 2.3. With the previous notation, the following facts hold
![]() $:$
$:$
-
(1)
 $0 \le q(I) \le p_g(A)$
.
$0 \le q(I) \le p_g(A)$
. -
(2)
 $q(kI) \ge q((k+1)I)$
for every integer
$q(kI) \ge q((k+1)I)$
for every integer
 $k \ge 0$
and if
$k \ge 0$
and if
 $q(nI) = q((n+1)I)$
for some
$q(nI) = q((n+1)I)$
for some
 $n\ge 0$
, then
$n\ge 0$
, then
 $q(nI) = q(mI)$
for every
$q(nI) = q(mI)$
for every
 $m\ge n$
. Hence,
$m\ge n$
. Hence,
 $q(nI) = q((n+1)I)$
for every I and
$q(nI) = q((n+1)I)$
for every I and
 $n\ge p_g(A)$
. We denote it by
$n\ge p_g(A)$
. We denote it by
 $q(\infty I)$
.
$q(\infty I)$
.
We use the above sequence for computing the following important algebraic numerical invariants of the normal filtration
![]() $\{\overline {I^n}\}$
. Let
$\{\overline {I^n}\}$
. Let
![]() $\mathbb {Z}_{+}$
denote the set of positive integers.
$\mathbb {Z}_{+}$
denote the set of positive integers.
Definition 2.4 (cf. [Reference Rees26])
Let
![]() $I \subset A$
be
$I \subset A$
be
![]() $\mathfrak m$
-primary integrally closed ideal, and let Q be a minimal reduction of I. Define:
$\mathfrak m$
-primary integrally closed ideal, and let Q be a minimal reduction of I. Define:
 $$ \begin{align*} \operatorname{\mathrm{nr}}(I) &:= \min\{r \in \mathbb{Z}_{+} \,|\, \overline{I^{r+1}}=Q\overline{I^r}\}, \\ \bar{\mathrm{r}}(I) &:= \min\{ r \in \mathbb{Z}_{+} \;|\; \overline{I^{n+1}} = Q \overline{I^n} \; \mbox{for all } n \ge r\}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{nr}}(I) &:= \min\{r \in \mathbb{Z}_{+} \,|\, \overline{I^{r+1}}=Q\overline{I^r}\}, \\ \bar{\mathrm{r}}(I) &:= \min\{ r \in \mathbb{Z}_{+} \;|\; \overline{I^{n+1}} = Q \overline{I^n} \; \mbox{for all } n \ge r\}. \end{align*} $$
We call
![]() $\bar {\mathrm {r}}(I)$
the normal reduction number and
$\bar {\mathrm {r}}(I)$
the normal reduction number and
![]() $\operatorname {\mathrm {nr}}(I)$
the relative normal reduction number.
$\operatorname {\mathrm {nr}}(I)$
the relative normal reduction number.
The normal reduction number exists (see [Reference Okuma, Watanabe and Yoshida21], [Reference Rossi29]), and it has been studied by many authors in the context of the Hilbert function and of the Hilbert polynomial (see, e.g., [Reference Corso, Polini and Rossi2], [Reference Cutkosky3], [Reference Itoh10], [Reference Kato12], [Reference Okuma19]). The main difficulty of the normal filtration with respect to the I-adic filtration is that the Rees algebra of the normal filtration is not generated by the part of degree one because
![]() $I \overline {I^n} \neq \overline {I^{n+1}}$
. By the definition, we deduce that
$I \overline {I^n} \neq \overline {I^{n+1}}$
. By the definition, we deduce that
![]() $\operatorname {\mathrm {nr}}(I) \le \bar {\mathrm {r}}(I)$
and we see that, in general, they do not coincide. Note that the definitions of
$\operatorname {\mathrm {nr}}(I) \le \bar {\mathrm {r}}(I)$
and we see that, in general, they do not coincide. Note that the definitions of
![]() $\operatorname {\mathrm {nr}}(I)$
and of
$\operatorname {\mathrm {nr}}(I)$
and of
![]() $\bar {\mathrm {r}}(I)$
are independent on the choice of a minimal reduction Q of I (see, e.g., [Reference Itoh10, Theorem 4.5]). It is also a consequence of the following result in [Reference Rees26, §2].
$\bar {\mathrm {r}}(I)$
are independent on the choice of a minimal reduction Q of I (see, e.g., [Reference Itoh10, Theorem 4.5]). It is also a consequence of the following result in [Reference Rees26, §2].
Proposition 2.5. The following statements hold.
-
(1) For any integer
 $n \ge 1$
, we have
$n \ge 1$
, we have  $$ \begin{align*} 2 \cdot q(nI) + \ell_A(\overline{I^{n+1}}/Q\overline{I^n}) =q((n+1)I)+q((n-1)I). \end{align*} $$
$$ \begin{align*} 2 \cdot q(nI) + \ell_A(\overline{I^{n+1}}/Q\overline{I^n}) =q((n+1)I)+q((n-1)I). \end{align*} $$
-
(2) We have
 $$ \begin{align*} \operatorname{\mathrm{nr}}(I) &= \min\{n \in \mathbb{Z}_{+} \,| \, q((n-1)I)- q(nI) = q(nI) - q((n+1)I) \},\\[6pt] \bar{\mathrm{r}}(I) &= \min\{n \in \mathbb{Z}_{+} \,|\, q((n-1)I)=q(nI) \}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{nr}}(I) &= \min\{n \in \mathbb{Z}_{+} \,| \, q((n-1)I)- q(nI) = q(nI) - q((n+1)I) \},\\[6pt] \bar{\mathrm{r}}(I) &= \min\{n \in \mathbb{Z}_{+} \,|\, q((n-1)I)=q(nI) \}. \end{align*} $$
From the propositions above, we have that
![]() $\bar {\mathrm {r}}(I) \le p_g(A) +1$
. In [Reference Rees26, Theorem 2.9], the authors showed that
$\bar {\mathrm {r}}(I) \le p_g(A) +1$
. In [Reference Rees26, Theorem 2.9], the authors showed that
![]() $p_g(A) \ge \binom {\operatorname {\mathrm {nr}}(I)}{2}$
.
$p_g(A) \ge \binom {\operatorname {\mathrm {nr}}(I)}{2}$
.
Rossi [Reference Sally32, Corollary 1.5] proved the following upper bound on the reduction number
![]() $r(I)$
for every
$r(I)$
for every
![]() $\mathfrak m$
-primary ideal I (here,
$\mathfrak m$
-primary ideal I (here,
![]() $r(I)$
denotes the reduction number for the I-adic filtration) in a two-dimensional Cohen–Macaulay local ring A in terms of the Hilbert coefficients:
$r(I)$
denotes the reduction number for the I-adic filtration) in a two-dimensional Cohen–Macaulay local ring A in terms of the Hilbert coefficients:
The bound gives, as a consequence, several interesting results, in particular a positive answer to a long-standing conjecture stated by Sally in the case of local Cohen–Macaulay rings of almost minimal multiplicity (see [Reference Sally32], [Reference Valabrega and Valla34]). Later, the inequality was extended by Rossi and Valla (see [Reference Tomari33, Theorem 4.3] for special multiplicative I-filtrations). The result does not include the normal filtration. It is natural to ask if the same bound also holds for
![]() $\bar {\mathrm {r}}(I)$
. The answer is negative as we will show later, but we prove that the analogue upper bound holds true for
$\bar {\mathrm {r}}(I)$
. The answer is negative as we will show later, but we prove that the analogue upper bound holds true for
![]() $\operatorname {\mathrm {nr}}(I)$
. We need some preliminary results.
$\operatorname {\mathrm {nr}}(I)$
. We need some preliminary results.
From Riemann–Roch formula (Theorem 2.2), we get
 $$ \begin{align*} \ell_A(A/\overline{I^{n+1}})+q((n+1)I) =-\dfrac{(n+1)^2Z^2+(n+1)ZK_X}{2} + p_g(A). \end{align*} $$
$$ \begin{align*} \ell_A(A/\overline{I^{n+1}})+q((n+1)I) =-\dfrac{(n+1)^2Z^2+(n+1)ZK_X}{2} + p_g(A). \end{align*} $$
Using this, we can express
![]() $\bar {e}_0(I), \bar {e}_1(I), \bar {e}_2(I)$
as follows.
$\bar {e}_0(I), \bar {e}_1(I), \bar {e}_2(I)$
as follows.
Proposition 2.6 [Reference Okuma, Watanabe and Yoshida24, Theorem 3.2]
Assume that
![]() $I = I_Z$
is represented by a cycle
$I = I_Z$
is represented by a cycle
![]() $Z> 0$
on a resolution X of
$Z> 0$
on a resolution X of
![]() $\operatorname {\mathrm {Spec}}(A)$
. Let
$\operatorname {\mathrm {Spec}}(A)$
. Let
![]() $\bar {P}_I(n)$
be the normal Hilbert polynomial of I. Then
$\bar {P}_I(n)$
be the normal Hilbert polynomial of I. Then
![]() $:$
$:$
-
(1)
 $\overline {P}_I(n)=\ell _A(A/\overline {I^{n+1}})$
for all
$\overline {P}_I(n)=\ell _A(A/\overline {I^{n+1}})$
for all
 $n \ge p_g(A)-1$
.
$n \ge p_g(A)-1$
. -
(2)
 $\bar e_0(I)=e_0(I)$
.
$\bar e_0(I)=e_0(I)$
. -
(3)
 $\bar e_1(I)-e_0(I) + \ell _A(A/I) =p_g(A) - q(I)$
.
$\bar e_1(I)-e_0(I) + \ell _A(A/I) =p_g(A) - q(I)$
. -
(4)
 $\bar e_2(I)= p_g(A)-q(nI)=p_g(A)-q(\infty I)$
for all
$\bar e_2(I)= p_g(A)-q(nI)=p_g(A)-q(\infty I)$
for all
 $n \ge p_g(A)$
.
$n \ge p_g(A)$
.
Moreover, we have
 $$ \begin{align*} \bar e_0(I)= -Z^2,\qquad \bar e_1(I)= \dfrac{-Z^2+ZK_X}{2}. \end{align*} $$
$$ \begin{align*} \bar e_0(I)= -Z^2,\qquad \bar e_1(I)= \dfrac{-Z^2+ZK_X}{2}. \end{align*} $$
Theorem 2.7. Let
![]() $(A,\mathfrak m)$
be an excellent two-dimensional normal local domain containing an algebraically closed field
$(A,\mathfrak m)$
be an excellent two-dimensional normal local domain containing an algebraically closed field
![]() $k= A/\mathfrak m$
. Let
$k= A/\mathfrak m$
. Let
![]() $I \subset A$
be an
$I \subset A$
be an
![]() $\mathfrak m$
-primary integrally closed ideal. Then
$\mathfrak m$
-primary integrally closed ideal. Then
If we put
![]() $r=\operatorname {\mathrm {nr}}(I)$
, equality holds if and only if the following conditions hold true
$r=\operatorname {\mathrm {nr}}(I)$
, equality holds if and only if the following conditions hold true
![]() $:$
$:$
-
(1)
 $\ell _A(\overline {I^{n+1}}/Q\overline {I^n}) =1$
for
$\ell _A(\overline {I^{n+1}}/Q\overline {I^n}) =1$
for
 $n= 1,\ldots , r-1$
if
$n= 1,\ldots , r-1$
if
 $r>1,$
$r>1,$
-
(2)
 $q((r-1)I)=q(\infty I)$
.
$q((r-1)I)=q(\infty I)$
.
When this is the case,
![]() $\operatorname {\mathrm {nr}}(I)=\bar {\mathrm {r}}(I)$
,
$\operatorname {\mathrm {nr}}(I)=\bar {\mathrm {r}}(I)$
,
![]() $q(I)=p_g(A)-\bar {\mathrm {r}}(I)+1$
, and
$q(I)=p_g(A)-\bar {\mathrm {r}}(I)+1$
, and
![]() $\bar {e}_2(I)=p_g(A)- q(\infty I) = r(r-1)/2$
.
$\bar {e}_2(I)=p_g(A)- q(\infty I) = r(r-1)/2$
.
Proof. By virtue of Proposition 2.6, it is enough to show
If we put
![]() $\Delta q(n) : = q(nI) - q((n+1)I)$
for every integer
$\Delta q(n) : = q(nI) - q((n+1)I)$
for every integer
![]() $n \ge 0$
, then
$n \ge 0$
, then
![]() $\Delta q(n) $
is nonnegative and decreasing since
$\Delta q(n) $
is nonnegative and decreasing since
![]() $\ell _A(\overline {I^{n+1}}/Q\overline {I^n}) =\Delta q(n-1) -\Delta q(n)$
. We have
$\ell _A(\overline {I^{n+1}}/Q\overline {I^n}) =\Delta q(n-1) -\Delta q(n)$
. We have
Put
![]() $a=p_g(A)-q(I)$
. Then
$a=p_g(A)-q(I)$
. Then
![]() $\Delta q(0)=a\ge \operatorname {\mathrm {nr}}(I)-1$
and
$\Delta q(0)=a\ge \operatorname {\mathrm {nr}}(I)-1$
and
![]() $\operatorname {\mathrm {nr}}(I)=a+1$
if and only if
$\operatorname {\mathrm {nr}}(I)=a+1$
if and only if
Now, assume
![]() $\operatorname {\mathrm {nr}}(I)=a+1$
. Then
$\operatorname {\mathrm {nr}}(I)=a+1$
. Then
![]() $a=r-1$
and for every n with
$a=r-1$
and for every n with
![]() $1 \le n \le a=r-1$
, we have
$1 \le n \le a=r-1$
, we have
Moreover, for every
![]() $n \ge a+1$
, we have
$n \ge a+1$
, we have
and thus
![]() $\overline {I^{n+1}}=Q\overline {I^n}$
. Hence,
$\overline {I^{n+1}}=Q\overline {I^n}$
. Hence,
![]() $\bar {\mathrm {r}}(I)=a+1=\operatorname {\mathrm {nr}}(I)$
. Furthermore,
$\bar {\mathrm {r}}(I)=a+1=\operatorname {\mathrm {nr}}(I)$
. Furthermore,
 $$ \begin{align*} \bar{e}_2(I)=p_g(A)-q(\infty I)=q(0 I)-q((r-1)I) = \sum_{i=0}^{r-2} \Delta q(i)= \dfrac{r(r-1)}{2}. \end{align*} $$
$$ \begin{align*} \bar{e}_2(I)=p_g(A)-q(\infty I)=q(0 I)-q((r-1)I) = \sum_{i=0}^{r-2} \Delta q(i)= \dfrac{r(r-1)}{2}. \end{align*} $$
One can prove the converse similarly.
Note that, if the equality holds in the previous result, then the normal filtration
![]() $\{\overline {I^n}\} $
has almost minimal multiplicity following the definition given in [Reference Tomari33, 2.1]. In the following example, we show that Theorem 2.7 does not hold if we replace
$\{\overline {I^n}\} $
has almost minimal multiplicity following the definition given in [Reference Tomari33, 2.1]. In the following example, we show that Theorem 2.7 does not hold if we replace
![]() $\operatorname {\mathrm {nr}}(I)$
by
$\operatorname {\mathrm {nr}}(I)$
by
![]() $\bar {r}(I)$
. The example shows that for all
$\bar {r}(I)$
. The example shows that for all
![]() $g \ge 2$
, there exist an excellent two-dimensional normal local ring A and an integrally closed
$g \ge 2$
, there exist an excellent two-dimensional normal local ring A and an integrally closed
![]() $\mathfrak m$
-primary ideal I such that
$\mathfrak m$
-primary ideal I such that
![]() $\operatorname {\mathrm {nr}}(I) =1, \bar {r}(I)={{g+1}}, q(I) = g-1$
and
$\operatorname {\mathrm {nr}}(I) =1, \bar {r}(I)={{g+1}}, q(I) = g-1$
and
![]() $\ell _A(A/I) = g$
.
$\ell _A(A/I) = g$
.
The following ideal I satisfies
![]() $\bar {e}_1(I)=\bar {e}_0(I)-\ell _A(A/I)+1$
, but
$\bar {e}_1(I)=\bar {e}_0(I)-\ell _A(A/I)+1$
, but
![]() $\bar {\mathrm {r}}(I)\not \le 2$
.
$\bar {\mathrm {r}}(I)\not \le 2$
.
Example 2.8 [Reference Reid27, Example 3.10]
Let
![]() $g \ge 2$
be an integer, and let K be a field of
$g \ge 2$
be an integer, and let K be a field of
![]() $\operatorname {\mathrm {char}} K=0$
or
$\operatorname {\mathrm {char}} K=0$
or
![]() $\operatorname {\mathrm {char}} K=p$
, where p does not divide
$\operatorname {\mathrm {char}} K=p$
, where p does not divide
![]() $2g+2$
. Then
$2g+2$
. Then
![]() $R=K[X,Y,Z]/(X^2-Y^{2g+2}-Z^{2g+2})$
is a graded normal K-algebra with
$R=K[X,Y,Z]/(X^2-Y^{2g+2}-Z^{2g+2})$
is a graded normal K-algebra with
![]() $\deg X=g+1$
,
$\deg X=g+1$
,
![]() $\deg Y=\deg Z=1$
. Let
$\deg Y=\deg Z=1$
. Let
![]() $A=R^{(g)}$
be the gth Veronese subring of R:
$A=R^{(g)}$
be the gth Veronese subring of R:
where
![]() $x, y, z$
denote, respectively, the image of
$x, y, z$
denote, respectively, the image of
![]() $X, Y, Z$
in R. Then A is a graded normal domain with
$X, Y, Z$
in R. Then A is a graded normal domain with
![]() $A_k=R_{kg}$
for every integer
$A_k=R_{kg}$
for every integer
![]() $k \ge 0$
. Let
$k \ge 0$
. Let
![]() $I=(y^g,y^{g-1}z) +A_{\ge 2}$
and
$I=(y^g,y^{g-1}z) +A_{\ge 2}$
and
![]() $Q=(y^g-z^{2g}, y^{g-1}z)$
. Then the following statements hold:
$Q=(y^g-z^{2g}, y^{g-1}z)$
. Then the following statements hold:
-
(1)
 $p_g(A)=g$
.
$p_g(A)=g$
. -
(2)
 $\operatorname {\mathrm {nr}}(I)=1$
and
$\operatorname {\mathrm {nr}}(I)=1$
and
 $\bar {\mathrm {r}}(I)=g+1$
. Indeed,
$\bar {\mathrm {r}}(I)=g+1$
. Indeed,-
(a)
 $\overline {I}=I$
and
$\overline {I}=I$
and
 $\overline {I^{n}}=I^n=QI^{n-1}$
for every
$\overline {I^{n}}=I^n=QI^{n-1}$
for every
 $n=2,\ldots , g$
.
$n=2,\ldots , g$
. -
(b)
 $\ell _A(\overline {I^{g+1}}/Q\overline {I^g})=1$
(
$\ell _A(\overline {I^{g+1}}/Q\overline {I^g})=1$
(
 $\overline {I^{g+1}}= I^{g+1} +(xy^{g^2-1})$
).
$\overline {I^{g+1}}= I^{g+1} +(xy^{g^2-1})$
). -
(c)
 $\overline {I^{n+1}}=Q \overline {I^{n}}$
for every
$\overline {I^{n+1}}=Q \overline {I^{n}}$
for every
 $n \ge g+1$
.
$n \ge g+1$
.
-
-
(3)
 $\bar {e}_0(I)=4g-2$
,
$\bar {e}_0(I)=4g-2$
,
 $\bar {e}_1(I)=3g-1$
,
$\bar {e}_1(I)=3g-1$
,
 $\bar {e}_2(I)=g$
, and
$\bar {e}_2(I)=g$
, and
 $\ell _A(A/I)=g$
.
$\ell _A(A/I)=g$
. -
(4)
 $q(nI)=g-n$
for every
$q(nI)=g-n$
for every
 $n=0,1,\ldots ,g$
;
$n=0,1,\ldots ,g$
;
 $q(gI)=q(\infty I)=0$
.
$q(gI)=q(\infty I)=0$
.
The first statement follows from that
![]() $a(A)=0$
and
$a(A)=0$
and
![]() $g=g(\operatorname {\mathrm {Proj}} (A))$
. For the convenience of the readers, we give a sketch of the proof in the case of
$g=g(\operatorname {\mathrm {Proj}} (A))$
. For the convenience of the readers, we give a sketch of the proof in the case of
![]() $g=2$
(see [Reference Reid27, Proof of Example 3.10]). Let
$g=2$
(see [Reference Reid27, Proof of Example 3.10]). Let
![]() $A=K[y^2,yz,z^2,xy,xz]=R^{(2)}$
with
$A=K[y^2,yz,z^2,xy,xz]=R^{(2)}$
with
![]() $\deg x=3$
and
$\deg x=3$
and
![]() $\deg y= \deg z=1$
, and
$\deg y= \deg z=1$
, and
![]() $I=(y^2,yz, z^4, xy,xz) \supset Q=(y^2-z^4,yz)$
. Then one can easily see that
$I=(y^2,yz, z^4, xy,xz) \supset Q=(y^2-z^4,yz)$
. Then one can easily see that
![]() $e_0(I)=\ell _A(A/Q)=4g-2=6$
,
$e_0(I)=\ell _A(A/Q)=4g-2=6$
,
![]() $\ell _A(A/I)=p_g(A)=g=2$
, and
$\ell _A(A/I)=p_g(A)=g=2$
, and
![]() $I^2=QI$
,
$I^2=QI$
,
![]() $\overline {I}=I$
. In particular,
$\overline {I}=I$
. In particular,
![]() $\operatorname {\mathrm {nr}}(I)=1$
.
$\operatorname {\mathrm {nr}}(I)=1$
.
Claim 1.
![]() $f_0 \in K[y,z]_{2n} \cap \overline {I^n} \Longrightarrow f_0 \in I^n$
for each
$f_0 \in K[y,z]_{2n} \cap \overline {I^n} \Longrightarrow f_0 \in I^n$
for each
![]() $n \ge 1$
.
$n \ge 1$
.
The normality of
![]() $I_0=(y^2,yz,z^4)K[y,z] \subset K[y,z]$
implies the above claim.
$I_0=(y^2,yz,z^4)K[y,z] \subset K[y,z]$
implies the above claim.
Claim 2.
![]() $0 \ne f_1 \in K[y,z]_{2n-3}$
,
$0 \ne f_1 \in K[y,z]_{2n-3}$
,
![]() $xf_1 \in \overline {I^n} \Longrightarrow n \ge 3$
.
$xf_1 \in \overline {I^n} \Longrightarrow n \ge 3$
.
By assumption and Claim 1, we have
![]() $(y^6+z^6)f_1^2=(xf_1)^2 \in \overline {I^{2n}} \cap K[y,z]_{2 \cdot 2n} \subset I^{2n}$
. The degree (in y and z) of any monomial in
$(y^6+z^6)f_1^2=(xf_1)^2 \in \overline {I^{2n}} \cap K[y,z]_{2 \cdot 2n} \subset I^{2n}$
. The degree (in y and z) of any monomial in
![]() $I^{2n}=(y^2, yz, z^4, xy, xz)$
is at least
$I^{2n}=(y^2, yz, z^4, xy, xz)$
is at least
![]() $4n=\deg (y^6+z^6) f_1^2$
. Hence,
$4n=\deg (y^6+z^6) f_1^2$
. Hence,
![]() $(y^6+z^6)f_1^2 \in (y^2, yz)^{2n}$
, and the highest power of z appearing in
$(y^6+z^6)f_1^2 \in (y^2, yz)^{2n}$
, and the highest power of z appearing in
![]() $(y^6+z^6) f_1^2$
is at most
$(y^6+z^6) f_1^2$
is at most
![]() $2n$
. Therefore,
$2n$
. Therefore,
![]() $n \ge 3$
.
$n \ge 3$
.
Claim 3. If
![]() $n \le 2$
, then
$n \le 2$
, then
![]() $\overline {I^n} \cap A_n \subset I^n \cap A_n$
.
$\overline {I^n} \cap A_n \subset I^n \cap A_n$
.
Any
![]() $f \in \overline {I^n} \cap A_n$
can be written as
$f \in \overline {I^n} \cap A_n$
can be written as
![]() $f=f_0+xf_1$
for some
$f=f_0+xf_1$
for some
![]() $f_0 \in K[y,z]_{2n}$
and
$f_0 \in K[y,z]_{2n}$
and
![]() $f_1 \in K[y,z]_{2n-3})$
. Let
$f_1 \in K[y,z]_{2n-3})$
. Let
![]() $\sigma \in \operatorname {\mathrm {Aut}}_{K[y,z]^{(2)}}(A)$
such that
$\sigma \in \operatorname {\mathrm {Aut}}_{K[y,z]^{(2)}}(A)$
such that
![]() $\sigma (x)=-x$
. Then, since
$\sigma (x)=-x$
. Then, since
![]() $\sigma (I)=I$
, we obtain
$\sigma (I)=I$
, we obtain
![]() $\sigma (f)=f_0 - xf_1 \in \overline {I^n}$
. Hence,
$\sigma (f)=f_0 - xf_1 \in \overline {I^n}$
. Hence,
By Claims 1 and 2, we have
![]() $f_0 \in I^n$
and
$f_0 \in I^n$
and
![]() $f_1=0$
. Therefore,
$f_1=0$
. Therefore,
![]() $f=f_0 \in I^n \cap A_n$
, as required.
$f=f_0 \in I^n \cap A_n$
, as required.
Claim 4.
![]() $xy^3 \in \overline {I^3} \setminus Q\overline {I^2}$
.
$xy^3 \in \overline {I^3} \setminus Q\overline {I^2}$
.
Since
![]() $(xy^3)^2=(y^6)^2+(y^3z^3)^2 \in (I^3)^2$
, we get
$(xy^3)^2=(y^6)^2+(y^3z^3)^2 \in (I^3)^2$
, we get
![]() $xy^3 \in \overline {I^3}$
. Assume
$xy^3 \in \overline {I^3}$
. Assume
![]() $xy^3 \in Q\overline {I^2}=(a,b)\overline {I^2}$
, where
$xy^3 \in Q\overline {I^2}=(a,b)\overline {I^2}$
, where
![]() $a=y^2-z^4$
and
$a=y^2-z^4$
and
![]() $b=yz$
. Then
$b=yz$
. Then
![]() $axy+bxz^3=xy^3=au+bv$
for some
$axy+bxz^3=xy^3=au+bv$
for some
![]() $u,v \in \overline {I^2}$
. Since
$u,v \in \overline {I^2}$
. Since
![]() $a,b$
form a regular sequence, we can take an element
$a,b$
form a regular sequence, we can take an element
![]() $h \in A_1$
, so that
$h \in A_1$
, so that
![]() $u-xy=bh$
and
$u-xy=bh$
and
![]() $xz^3-v =ah$
. So we may assume
$xz^3-v =ah$
. So we may assume
![]() $u,v \in A_2$
, and thus
$u,v \in A_2$
, and thus
![]() $u,v \in \overline {I^2} \cap A_2 \subset I^2$
. However, this yields
$u,v \in \overline {I^2} \cap A_2 \subset I^2$
. However, this yields
![]() $xy^3=au+bv \in QI^2=I^3$
, which is a contradiction.
$xy^3=au+bv \in QI^2=I^3$
, which is a contradiction.
Claim 5.
![]() $q(I)=1$
,
$q(I)=1$
,
![]() $q(2I)=q(\infty I)=0$
,
$q(2I)=q(\infty I)=0$
,
![]() $\ell _A(\overline {I^3}/Q\overline {I^2})=1$
, and
$\ell _A(\overline {I^3}/Q\overline {I^2})=1$
, and
![]() $\overline {I^{n+1}}=Q\overline {I^n}$
for each
$\overline {I^{n+1}}=Q\overline {I^n}$
for each
![]() $n \ge 3$
.
$n \ge 3$
.
By Proposition 2.3, we have
![]() $2=p_g(A)=q(0\cdot I)\ge q(I) \ge q(2\cdot I) \ge 0$
. If
$2=p_g(A)=q(0\cdot I)\ge q(I) \ge q(2\cdot I) \ge 0$
. If
![]() $q(I)=q(2\cdot I)$
, then
$q(I)=q(2\cdot I)$
, then
![]() $q(2 \cdot I)=q(3 \cdot I)$
. This implies
$q(2 \cdot I)=q(3 \cdot I)$
. This implies
![]() $\ell _A(\overline {I^3}/Q\overline {I^2})=0$
from Proposition 2.5. This contradicts Claim 4. Hence,
$\ell _A(\overline {I^3}/Q\overline {I^2})=0$
from Proposition 2.5. This contradicts Claim 4. Hence,
![]() $q(I)=1$
and
$q(I)=1$
and
![]() $q(2\cdot I)=0$
. The other assertions follow from Proposition 2.5. In particular,
$q(2\cdot I)=0$
. The other assertions follow from Proposition 2.5. In particular,
![]() $\bar {\mathrm {r}}(I)=3$
.
$\bar {\mathrm {r}}(I)=3$
.
Claim 6.
![]() $\bar{e_1}(I)=3g-2=5$
and
$\bar{e_1}(I)=3g-2=5$
and
![]() $\bar{e_2}(I)=g=2$
.
$\bar{e_2}(I)=g=2$
.
By Proposition 2.6, we have
 $$ \begin{align*} \bar e_1(I)&= e_0(I)-\ell_A(A/I)+p_g(A)-q(I)=6-2+2-1=5, \\ \bar e_2(I) &= p_g(A)-q(\infty I)=~2-0=2. \end{align*} $$
$$ \begin{align*} \bar e_1(I)&= e_0(I)-\ell_A(A/I)+p_g(A)-q(I)=6-2+2-1=5, \\ \bar e_2(I) &= p_g(A)-q(\infty I)=~2-0=2. \end{align*} $$
3 Elliptic and strongly elliptic ideals
We define the Rees algebra
![]() $\bar {\mathcal R}(I)$
and the associated graded ring
$\bar {\mathcal R}(I)$
and the associated graded ring
![]() $\bar {G}(I)$
associated with the normal filtration as follows:
$\bar {G}(I)$
associated with the normal filtration as follows:
 $$ \begin{align*} \bar{\mathcal R}(I) &:= \bigoplus_{n\ge 0}\overline{I^n} t^n \subset A[t]. \\ \bar{G}(I) &:= \bigoplus_{n\ge 0}\overline{I^n}/ \overline{I^{n+1}} \cong \bar{\mathcal R}(I)/\bar{\mathcal R}(I)(1). \end{align*} $$
$$ \begin{align*} \bar{\mathcal R}(I) &:= \bigoplus_{n\ge 0}\overline{I^n} t^n \subset A[t]. \\ \bar{G}(I) &:= \bigoplus_{n\ge 0}\overline{I^n}/ \overline{I^{n+1}} \cong \bar{\mathcal R}(I)/\bar{\mathcal R}(I)(1). \end{align*} $$
![]() $\bar {\mathcal R}(I)$
(resp.
$\bar {\mathcal R}(I)$
(resp.
![]() $\bar {G}(I)$
) is called the normal Rees algebra (resp. the normal associated graded ring) of I. We recall that the a-invariant of a graded d-dimensional ring R with maximal homogeneous graded ideal
$\bar {G}(I)$
) is called the normal Rees algebra (resp. the normal associated graded ring) of I. We recall that the a-invariant of a graded d-dimensional ring R with maximal homogeneous graded ideal
![]() $\mathfrak {M}$
was introduced by Goto and Watanabe [Reference Huneke9] and defined as
$\mathfrak {M}$
was introduced by Goto and Watanabe [Reference Huneke9] and defined as
![]() $a(R):= \max \{n | [H^d_{\mathfrak M}(R)]_n \neq 0\}$
, where
$a(R):= \max \{n | [H^d_{\mathfrak M}(R)]_n \neq 0\}$
, where
![]() $[H^d_{\mathfrak M}(R) ]_n$
denotes the homogeneous component of degree n of the graded R-module
$[H^d_{\mathfrak M}(R) ]_n$
denotes the homogeneous component of degree n of the graded R-module
![]() $H^d_{\mathfrak M}(R)$
.
$H^d_{\mathfrak M}(R)$
.
It is known that A is a rational singularity if and only if
![]() $\overline r(A)=1$
(see [Reference Reid27, Proposition 1.1]). In [Reference Okuma, Watanabe and Yoshida23], [Reference Okuma, Watanabe and Yoshida24], the authors introduced the notion of
$\overline r(A)=1$
(see [Reference Reid27, Proposition 1.1]). In [Reference Okuma, Watanabe and Yoshida23], [Reference Okuma, Watanabe and Yoshida24], the authors introduced the notion of
![]() $p_g$
-ideals, characterizing rational singularities.
$p_g$
-ideals, characterizing rational singularities.
Theorem 3.1 (cf. [Reference Goto and Shimoda7], [Reference Itoh10], [Reference Okuma, Watanabe and Yoshida23], [Reference Okuma, Watanabe and Yoshida24])
Let
![]() $(A,\mathfrak m)$
be a two-dimensional excellent normal nonregular local domain containing an algebraically closed field
$(A,\mathfrak m)$
be a two-dimensional excellent normal nonregular local domain containing an algebraically closed field
![]() $k= A/\mathfrak m. $
Let
$k= A/\mathfrak m. $
Let
![]() $I=I_Z$
be an
$I=I_Z$
be an
![]() $\mathfrak m$
-primary integrally closed ideal of A. Put
$\mathfrak m$
-primary integrally closed ideal of A. Put
![]() $\bar {G}=\bar {G}(I)$
and
$\bar {G}=\bar {G}(I)$
and
![]() $\bar {\mathcal R}=\bar {\mathcal R}(I)$
. Then the following conditions are equivalent
$\bar {\mathcal R}=\bar {\mathcal R}(I)$
. Then the following conditions are equivalent
![]() $:$
$:$
-
(1)
 $\bar {\mathrm {r}}(I)= 1$
.
$\bar {\mathrm {r}}(I)= 1$
. -
(2)
 $q(I)=p_g(A)$
.
$q(I)=p_g(A)$
. -
(3)
 $I^2=QI$
and
$I^2=QI$
and
 $\overline {I^n}=I^n$
for every
$\overline {I^n}=I^n$
for every
 $n \ge 1$
.
$n \ge 1$
. -
(4)
 $\bar e_1(I) = e_0(I)-\ell _A(A/I)$
.
$\bar e_1(I) = e_0(I)-\ell _A(A/I)$
. -
(5)
 $\bar e_2(I)=0$
.
$\bar e_2(I)=0$
. -
(6)
 $\bar {G}$
is Cohen–Macaulay with
$\bar {G}$
is Cohen–Macaulay with
 $a(\bar {G})< 0$
.
$a(\bar {G})< 0$
. -
(7)
 $\bar {\mathcal R}$
is Cohen–Macaulay.
$\bar {\mathcal R}$
is Cohen–Macaulay.
When this is the case, I is said to be a
![]() $p_g$
-ideal.
$p_g$
-ideal.
Proof. Since
![]() $QI^{n-1} \subset I^n \subset \overline {I^n}$
for every
$QI^{n-1} \subset I^n \subset \overline {I^n}$
for every
![]() $n \ge 2$
, (1)
$n \ge 2$
, (1)
![]() $\Leftrightarrow (3)$
is trivial. (1)
$\Leftrightarrow (3)$
is trivial. (1)
![]() $\Leftrightarrow $
(5) (resp. (6)
$\Leftrightarrow $
(5) (resp. (6)
![]() $\Leftrightarrow $
(7)) follows from [Reference Goto and Shimoda7, Part II, Proposition 8.1] (resp. [Reference Goto and Shimoda7, Part II, Corollary 1.2]). Moreover, the equivalence of (4), (5), and (7) follows from [Reference Goto and Shimoda7, Part II, Theorem 8.2]. (2)
$\Leftrightarrow $
(7)) follows from [Reference Goto and Shimoda7, Part II, Proposition 8.1] (resp. [Reference Goto and Shimoda7, Part II, Corollary 1.2]). Moreover, the equivalence of (4), (5), and (7) follows from [Reference Goto and Shimoda7, Part II, Theorem 8.2]. (2)
![]() $\Leftrightarrow $
(4) follows from Proposition 2.5.
$\Leftrightarrow $
(4) follows from Proposition 2.5.
It is known that A is a rational singularity if and only if any integrally closed
![]() $\mathfrak m$
-primary ideal is a
$\mathfrak m$
-primary ideal is a
![]() $p_g$
-ideal (see [Reference Okuma, Watanabe and Yoshida23], [Reference Okuma, Watanabe and Yoshida24]). We define
$p_g$
-ideal (see [Reference Okuma, Watanabe and Yoshida23], [Reference Okuma, Watanabe and Yoshida24]). We define
Then A is a rational singularity if and only if
![]() $\overline r(A)=1$
(see [Reference Reid27, Proposition 1.1]).
$\overline r(A)=1$
(see [Reference Reid27, Proposition 1.1]).
Okuma proved in [Reference Okuma, Watanabe and Yoshida22, Theorem 3.3] that if A is an elliptic singularity, then
![]() $\overline r(A)=2$
. For the definition of elliptic singularity, we refer to [Reference Yau38, p. 428] or [Reference Okuma, Watanabe and Yoshida22, Definition 2.1]. We investigate the integrally closed
$\overline r(A)=2$
. For the definition of elliptic singularity, we refer to [Reference Yau38, p. 428] or [Reference Okuma, Watanabe and Yoshida22, Definition 2.1]. We investigate the integrally closed
![]() $\mathfrak m$
-primary ideals such that
$\mathfrak m$
-primary ideals such that
![]() $\bar {\mathrm {r}}(I) =2$
with the aim to characterize elliptic singularities. Next result extends and completes a result by Itoh [Reference Kato12, Proposition 10], by using a different approach.
$\bar {\mathrm {r}}(I) =2$
with the aim to characterize elliptic singularities. Next result extends and completes a result by Itoh [Reference Kato12, Proposition 10], by using a different approach.
Theorem 3.2. Let
![]() $(A,\mathfrak m)$
be a two-dimensional excellent normal local domain containing an algebraically closed field
$(A,\mathfrak m)$
be a two-dimensional excellent normal local domain containing an algebraically closed field
![]() $k= A/\mathfrak m$
, and let
$k= A/\mathfrak m$
, and let
![]() $I \subset A$
be an
$I \subset A$
be an
![]() $\mathfrak m$
-primary integrally closed ideal. Put
$\mathfrak m$
-primary integrally closed ideal. Put
![]() $\bar {G}=\bar {G}(I)$
and
$\bar {G}=\bar {G}(I)$
and
![]() $\bar {\mathcal R}=\bar {\mathcal R}(I)$
. Then the following conditions are equivalent
$\bar {\mathcal R}=\bar {\mathcal R}(I)$
. Then the following conditions are equivalent
![]() $:$
$:$
-
(1)
 $\bar {\mathrm {r}}(I)=2$
.
$\bar {\mathrm {r}}(I)=2$
. -
(2)
 $p_g(A)> q(I)=q(\infty I)$
.
$p_g(A)> q(I)=q(\infty I)$
. -
(3)
 $\bar {e}_1(I) = e_0(I) -\ell _A( A/I) + \bar {e}_2(I)$
and
$\bar {e}_1(I) = e_0(I) -\ell _A( A/I) + \bar {e}_2(I)$
and
 $\bar {e}_2(I)>0$
.
$\bar {e}_2(I)>0$
. -
(4)
 $\ell _A(A/\overline {I^{n+1}}) = \bar {P}_I(n)$
for all
$\ell _A(A/\overline {I^{n+1}}) = \bar {P}_I(n)$
for all
 $n\ge 0$
and
$n\ge 0$
and
 $\bar {e}_2(I)>0$
.
$\bar {e}_2(I)>0$
. -
(5)
 $\bar {G}$
is Cohen–Macaulay with
$\bar {G}$
is Cohen–Macaulay with
 $a(\bar {G})=0$
.
$a(\bar {G})=0$
.
When this is the case, I is said to be an elliptic ideal and
![]() $\ell _A ([H^2_{\mathfrak M}(\bar {G})_0) = \ell _A(\overline {I^2}/QI) = \bar {e}_2(I)$
.
$\ell _A ([H^2_{\mathfrak M}(\bar {G})_0) = \ell _A(\overline {I^2}/QI) = \bar {e}_2(I)$
.
Proof.
![]() $(1) \Longleftrightarrow (2):$
It follows from Proposition 2.5(2).
$(1) \Longleftrightarrow (2):$
It follows from Proposition 2.5(2).
![]() $(2) \Longleftrightarrow (3):$
By Proposition 2.6, we have
$(2) \Longleftrightarrow (3):$
By Proposition 2.6, we have
 $$ \begin{align*} \bar{e}_1(I) &= e_0(I) -\ell_A( A/I) + \bar{e}_2(I) - \big\{q(I)-q(\infty I)\big\}. \\ \bar{e}_2(I) &= p_g(A) - q(\infty I) \ge 0. \end{align*} $$
$$ \begin{align*} \bar{e}_1(I) &= e_0(I) -\ell_A( A/I) + \bar{e}_2(I) - \big\{q(I)-q(\infty I)\big\}. \\ \bar{e}_2(I) &= p_g(A) - q(\infty I) \ge 0. \end{align*} $$
The assertion follows from here.
![]() $(2) \Longleftrightarrow (4):$
Assume
$(2) \Longleftrightarrow (4):$
Assume
![]() $I= I_Z = H^0(X,\mathcal {O}_X(-Z))$
for some resolution
$I= I_Z = H^0(X,\mathcal {O}_X(-Z))$
for some resolution
![]() $X \to \operatorname {\mathrm {Spec}} A$
. By Kato’s Riemann–Roch formula, for every integer
$X \to \operatorname {\mathrm {Spec}} A$
. By Kato’s Riemann–Roch formula, for every integer
![]() $n \ge 0$
, we have
$n \ge 0$
, we have
 $$ \begin{align*} \ell_A(A/\overline{I^{n+1}})+h^1(\mathcal{O}_X(-(n+1)Z)) =-\dfrac{(n+1)^2Z^2+(n+1) K_XZ}{2} +p_g(A). \end{align*} $$
$$ \begin{align*} \ell_A(A/\overline{I^{n+1}})+h^1(\mathcal{O}_X(-(n+1)Z)) =-\dfrac{(n+1)^2Z^2+(n+1) K_XZ}{2} +p_g(A). \end{align*} $$
Hence,
 $$ \begin{align*} \ell_A(A/\overline{I^{n+1}}) &= \bar{e}_0(I){n+2 \choose 2} - \bar{e}_1(I) {n+1 \choose 1} + \big\{p_g(A)-q((n+1)I) \big\} \\ &= \bar{P}_I(n)- \big\{q((n+1)I)-q(\infty I) \big\}. \end{align*} $$
$$ \begin{align*} \ell_A(A/\overline{I^{n+1}}) &= \bar{e}_0(I){n+2 \choose 2} - \bar{e}_1(I) {n+1 \choose 1} + \big\{p_g(A)-q((n+1)I) \big\} \\ &= \bar{P}_I(n)- \big\{q((n+1)I)-q(\infty I) \big\}. \end{align*} $$
Assume (4). By replacing
![]() $0$
to n in the above equation, we get
$0$
to n in the above equation, we get
![]() $q(I)=q(\infty I)$
, hence (2). Conversely, if
$q(I)=q(\infty I)$
, hence (2). Conversely, if
![]() $q(I)=q(\infty I)$
, then since
$q(I)=q(\infty I)$
, then since
![]() $q((n+1)I)=q(\infty I)$
for all
$q((n+1)I)=q(\infty I)$
for all
![]() $n \ge 1$
, the above equation implies (4).
$n \ge 1$
, the above equation implies (4).
![]() $(1) \Longrightarrow (5):$
Put
$(1) \Longrightarrow (5):$
Put
![]() $Q=(a,b)$
. Since
$Q=(a,b)$
. Since
![]() $\overline {I^{n+1}} \colon a=\overline {I^n}$
,
$\overline {I^{n+1}} \colon a=\overline {I^n}$
,
![]() $a^{*}$
, the image of a in
$a^{*}$
, the image of a in
![]() $\bar {G}$
is a nonzero divisor of
$\bar {G}$
is a nonzero divisor of
![]() $\bar {G}$
.
$\bar {G}$
.
By assumption, we have
![]() $\overline {I^{n+1} } \cap Q = Q {\overline {I^{n}}} \cap Q =Q {\overline {I^{n}}}$
for every
$\overline {I^{n+1} } \cap Q = Q {\overline {I^{n}}} \cap Q =Q {\overline {I^{n}}}$
for every
![]() $n \ge 2$
. On the other hand, we have
$n \ge 2$
. On the other hand, we have
![]() $\overline {I^2} \cap Q = QI$
by [Reference Itoh10, Theorem in p. 371] or [Reference Itoh11, Theorem]. Then it is well known that
$\overline {I^2} \cap Q = QI$
by [Reference Itoh10, Theorem in p. 371] or [Reference Itoh11, Theorem]. Then it is well known that
![]() $a^{*}$
,
$a^{*}$
,
![]() $b^{*}$
form a regular sequence in
$b^{*}$
form a regular sequence in
![]() $\bar {G}$
, and thus
$\bar {G}$
, and thus
![]() $\bar {G}$
is Cohen–Macaulay (see also [Reference Watanabe and Yoshida37]) and
$\bar {G}$
is Cohen–Macaulay (see also [Reference Watanabe and Yoshida37]) and
![]() $2=\bar {\mathrm {r}}(I)=a(\bar {G})+\dim A=a(\bar {G})+2$
. Thus,
$2=\bar {\mathrm {r}}(I)=a(\bar {G})+\dim A=a(\bar {G})+2$
. Thus,
![]() $a(\bar {G})=0$
, as required.
$a(\bar {G})=0$
, as required.
![]() $(5) \Longrightarrow (1):$
Since
$(5) \Longrightarrow (1):$
Since
![]() $\bar {G}$
is Cohen–Macaulay, we have
$\bar {G}$
is Cohen–Macaulay, we have
![]() $\bar {\mathrm {r}}(I)=a(\bar {G})+\dim A=0+2=2$
.
$\bar {\mathrm {r}}(I)=a(\bar {G})+\dim A=0+2=2$
.
We notice that if A is not a rational singularity, then elliptic ideals always exist.
Proposition 3.3. Let
![]() $(A,\mathfrak m)$
be a two-dimensional excellent normal local domain containing an algebraically closed field
$(A,\mathfrak m)$
be a two-dimensional excellent normal local domain containing an algebraically closed field
![]() $k= A/\mathfrak m$
, and let
$k= A/\mathfrak m$
, and let
![]() $I \subset A$
be an
$I \subset A$
be an
![]() $\mathfrak m$
-primary integrally closed ideal which is not a
$\mathfrak m$
-primary integrally closed ideal which is not a
![]() $p_g$
-ideal. Then there exists a positive integer n such that
$p_g$
-ideal. Then there exists a positive integer n such that
![]() $\overline {I^n} $
is an elliptic ideal. In particular, if A is not a rational singularity, then for any
$\overline {I^n} $
is an elliptic ideal. In particular, if A is not a rational singularity, then for any
![]() $\mathfrak m$
-primary integrally closed ideal I of A, then
$\mathfrak m$
-primary integrally closed ideal I of A, then
![]() $\overline {I^{n}}$
is either a
$\overline {I^{n}}$
is either a
![]() $p_g$
-ideal or an elliptic ideal for every
$p_g$
-ideal or an elliptic ideal for every
![]() $n \ge p_g(A)$
.
$n \ge p_g(A)$
.
Proof. Let n be a positive integer such that
![]() $\ell _A(A/\overline {I^{n}})=\bar {P}_I(n-1)$
. Since the integral closure of
$\ell _A(A/\overline {I^{n}})=\bar {P}_I(n-1)$
. Since the integral closure of
![]() $(\overline {I^n})^{p}$
coincides with
$(\overline {I^n})^{p}$
coincides with
![]() $\overline {I^{n p}}$
for p large, we have
$\overline {I^{n p}}$
for p large, we have
 $$ \begin{align*} \bar{e}_0(I^{n})= n^2 \bar{e}_0(I); \ \ \bar{e}_1(I^{n}) = n \bar{e}_1(I) + {n \choose 2} \bar{e}_0(I); \ \ \bar{e}_2(I^n)= \bar{e}_2(I). \end{align*} $$
$$ \begin{align*} \bar{e}_0(I^{n})= n^2 \bar{e}_0(I); \ \ \bar{e}_1(I^{n}) = n \bar{e}_1(I) + {n \choose 2} \bar{e}_0(I); \ \ \bar{e}_2(I^n)= \bar{e}_2(I). \end{align*} $$
After substituting the
![]() $\bar {e}_i(I^n)$
’s with the corresponding expressions in terms of the
$\bar {e}_i(I^n)$
’s with the corresponding expressions in terms of the
![]() $\bar {e}_i(I)$
’s we conclude that
$\bar {e}_i(I)$
’s we conclude that
 $$ \begin{align*} \bar{e}_2(I^n) - \bar{e}_1(I^n) + \bar{e}_0(I^n)-\ell_A(A/\overline{I^n}) &= \bar{e}_0(I) {n+1 \choose 2} - \bar{e}_1(I) n + \bar{e}_2(I) -\ell_A(A/\overline{I^n}) \\ &= \bar{P}_I(n-1) -\ell_A(A/\overline{I^n}) =0. \end{align*} $$
$$ \begin{align*} \bar{e}_2(I^n) - \bar{e}_1(I^n) + \bar{e}_0(I^n)-\ell_A(A/\overline{I^n}) &= \bar{e}_0(I) {n+1 \choose 2} - \bar{e}_1(I) n + \bar{e}_2(I) -\ell_A(A/\overline{I^n}) \\ &= \bar{P}_I(n-1) -\ell_A(A/\overline{I^n}) =0. \end{align*} $$
Since I is not a
![]() $p_g$
-ideal, then
$p_g$
-ideal, then
![]() $\bar {e}_2(I^n)= \bar {e}_2(I)>0. $
Hence, by Theorem 3.2, then
$\bar {e}_2(I^n)= \bar {e}_2(I)>0. $
Hence, by Theorem 3.2, then
![]() $\overline {I^n}$
is an elliptic ideal.
$\overline {I^n}$
is an elliptic ideal.
We denote by
![]() $\mathfrak {M} = \mathfrak m + \bar {\mathcal R}_{+} $
the homogeneous maximal ideal of
$\mathfrak {M} = \mathfrak m + \bar {\mathcal R}_{+} $
the homogeneous maximal ideal of
![]() $\bar {\mathcal R}$
. As usual, we say that
$\bar {\mathcal R}$
. As usual, we say that
![]() $\bar {\mathcal R}$
is
$\bar {\mathcal R}$
is
![]() $($
FLC
$($
FLC
![]() $)$
if
$)$
if
![]() $\ell _A(H^i_{\mathfrak {M}} (\bar {\mathcal R}))< \infty $
for every
$\ell _A(H^i_{\mathfrak {M}} (\bar {\mathcal R}))< \infty $
for every
![]() $i \le \dim A=2$
.
$i \le \dim A=2$
.
Proposition 3.4. Assume I is an elliptic ideal, then
![]() $\bar {\mathcal R}$
is
$\bar {\mathcal R}$
is
![]() $($
FLC
$($
FLC
![]() $)$
but not Cohen–Macaulay with
$)$
but not Cohen–Macaulay with
Proof. Note that
![]() $\bar {\mathcal R}_{\mathfrak M}$
is a universally catenary domain which is a homomorphic image of a Cohen–Macaulay local ring. Hence, it is an (FLC) because
$\bar {\mathcal R}_{\mathfrak M}$
is a universally catenary domain which is a homomorphic image of a Cohen–Macaulay local ring. Hence, it is an (FLC) because
![]() $\bar {\mathcal R}$
satisfies Serre condition
$\bar {\mathcal R}$
satisfies Serre condition
![]() $(S_2)$
. Thus,
$(S_2)$
. Thus,
![]() $H_{\mathfrak M}^0(\bar {\mathcal R})= H_{\mathfrak M}^1(\bar {\mathcal R})=0$
and
$H_{\mathfrak M}^0(\bar {\mathcal R})= H_{\mathfrak M}^1(\bar {\mathcal R})=0$
and
![]() $H_{\mathfrak M}^2(\bar {\mathcal R})$
has finite length.
$H_{\mathfrak M}^2(\bar {\mathcal R})$
has finite length.
Put
![]() $\mathcal {N}=\bar {\mathcal R}_{+}$
. Then we obtain two exact sequences of graded
$\mathcal {N}=\bar {\mathcal R}_{+}$
. Then we obtain two exact sequences of graded
![]() $\bar {\mathcal R}$
-modules.
$\bar {\mathcal R}$
-modules.
where
![]() ${}_h A$
can be regarded as
${}_h A$
can be regarded as
![]() $\bar {\mathcal R}/\mathcal {N}$
which is concentrated in degree
$\bar {\mathcal R}/\mathcal {N}$
which is concentrated in degree
![]() $0$
. One can easily see that
$0$
. One can easily see that
![]() $H_{\mathfrak M}^0(\mathcal {N})=H_{\mathfrak M}^1(\mathcal {N})=0$
, and we get
$H_{\mathfrak M}^0(\mathcal {N})=H_{\mathfrak M}^1(\mathcal {N})=0$
, and we get
For any integer
![]() $n \le -1$
, the first exact sequence (3.1) yields
$n \le -1$
, the first exact sequence (3.1) yields
In addition, the second exact sequence (3.2) yields
Then
![]() $[H_{\mathfrak M}^2(\bar {\mathcal R})]_{-1} \subset [H_{\mathfrak M}^2(\bar {\mathcal R})]_{-2} \subset \cdots \subset [H_{\mathfrak M}^2(\bar {\mathcal R})]_{n}=0$
for
$[H_{\mathfrak M}^2(\bar {\mathcal R})]_{-1} \subset [H_{\mathfrak M}^2(\bar {\mathcal R})]_{-2} \subset \cdots \subset [H_{\mathfrak M}^2(\bar {\mathcal R})]_{n}=0$
for
![]() $n \ll 0$
, and thus
$n \ll 0$
, and thus
![]() $[H_{\mathfrak M}^2(\bar {\mathcal R})]_{n}=0$
for all
$[H_{\mathfrak M}^2(\bar {\mathcal R})]_{n}=0$
for all
![]() $n \le -1$
.
$n \le -1$
.
For any integer
![]() $n \ge 1$
, the first exact sequence (3.1) yields
$n \ge 1$
, the first exact sequence (3.1) yields
Moreover, as
![]() $a(\bar {G})=0$
, we have
$a(\bar {G})=0$
, we have
Hence, we get
![]() $[H_{\mathcal {M}}^2(\bar {\mathcal R})]_n=0$
for all
$[H_{\mathcal {M}}^2(\bar {\mathcal R})]_n=0$
for all
![]() $n \ge 1$
.
$n \ge 1$
.
Since
![]() $a(\bar {\mathcal R})=-1$
, we have
$a(\bar {\mathcal R})=-1$
, we have
![]() $[H_{\mathfrak M}^3(\mathcal {N})]_1 \cong [H_{\mathfrak M}^3(\bar {\mathcal R})]_1=0$
. Hence, we get
$[H_{\mathfrak M}^3(\mathcal {N})]_1 \cong [H_{\mathfrak M}^3(\bar {\mathcal R})]_1=0$
. Hence, we get
as required.
Corollary 3.5. Let
![]() $(A,\mathfrak m)$
be a two-dimensional excellent normal local domain, and let
$(A,\mathfrak m)$
be a two-dimensional excellent normal local domain, and let
![]() $I \subset A$
be an
$I \subset A$
be an
![]() $\mathfrak m$
-primary integrally closed ideal.
$\mathfrak m$
-primary integrally closed ideal.
Then I is an elliptic ideal if and only if
![]() $0 \ne H^2_{\mathfrak M}(\bar {\mathcal R}) = [H^2_{\mathfrak M}(\bar {\mathcal R})]_0 \hookrightarrow H_{\mathfrak m}^2(A)$
, where the last map is induced from the natural surjection
$0 \ne H^2_{\mathfrak M}(\bar {\mathcal R}) = [H^2_{\mathfrak M}(\bar {\mathcal R})]_0 \hookrightarrow H_{\mathfrak m}^2(A)$
, where the last map is induced from the natural surjection
![]() $\bar {\mathcal R} \to {}_h A = \bar {\mathcal R}/\bar {\mathcal R}_{+}$
.
$\bar {\mathcal R} \to {}_h A = \bar {\mathcal R}/\bar {\mathcal R}_{+}$
.
Proof. Assume I is an elliptic ideal, then from the proof of Proposition 3.4 and Theorem 3.2, we conclude our assertions. Conversely, by our assumption, we can conclude that
![]() $\bar {G}(I)$
is Cohen–Macaulay with
$\bar {G}(I)$
is Cohen–Macaulay with
![]() $a(\bar {G}(I))=0$
by a similar argument as in the proof of Proposition 3.4. Hence, I is an elliptic ideal by Theorem 3.2.
$a(\bar {G}(I))=0$
by a similar argument as in the proof of Proposition 3.4. Hence, I is an elliptic ideal by Theorem 3.2.
For a cycle
![]() $C>0$
on X, we denote by
$C>0$
on X, we denote by
![]() $\chi (C)$
the Euler characteristic of
$\chi (C)$
the Euler characteristic of
![]() $\mathcal O_C$
.
$\mathcal O_C$
.
Definition 3.6. Let
![]() $Z_f$
denote the fundamental cycle, namely, the nonzero minimal anti-nef cycle on X. The ring A is called elliptic if
$Z_f$
denote the fundamental cycle, namely, the nonzero minimal anti-nef cycle on X. The ring A is called elliptic if
![]() $\chi (Z_f)=0$
.
$\chi (Z_f)=0$
.
The following result follows from Theorem 3.2 and [Reference Okuma, Watanabe and Yoshida22, Theorem 3.3].
Corollary 3.7. If A is an elliptic singularity, then for every integrally closed ideal
![]() $I \subset A$
, the following facts hold
$I \subset A$
, the following facts hold
![]() $:$
$:$
-
(1)
 $\bar {G}(I)$
is Cohen–Macaulay with
$\bar {G}(I)$
is Cohen–Macaulay with
 $a(\bar {G}(I))\le 0$
.
$a(\bar {G}(I))\le 0$
. -
(2) I is elliptic or a
 $p_g$
-ideal.
$p_g$
-ideal.
Since there always exists an ideal I with
![]() $q(I)=0$
, we have
$q(I)=0$
, we have
![]() $\bar r(A)=2$
.
$\bar r(A)=2$
.
The result above gives some evidence about a positive answer to the following question:
Question 3.8. Assume
![]() $\bar r(A) =2$
, is it true that A is an elliptic singularity?
$\bar r(A) =2$
, is it true that A is an elliptic singularity?
We can give a positive answer to Question 3.8 if
![]() $ \bar {e}_2(I) \le 1$
for all integrally closed
$ \bar {e}_2(I) \le 1$
for all integrally closed
![]() $\mathfrak m$
-primary ideals. In the following result, we describe the integrally closed
$\mathfrak m$
-primary ideals. In the following result, we describe the integrally closed
![]() $\mathfrak m$
-primary ideals satisfying this minimal condition.
$\mathfrak m$
-primary ideals satisfying this minimal condition.
Theorem 3.9. Let
![]() $(A,\mathfrak m)$
be a two-dimensional excellent normal local domain over an algebraically closed field. Let
$(A,\mathfrak m)$
be a two-dimensional excellent normal local domain over an algebraically closed field. Let
![]() $I \subset A$
be an
$I \subset A$
be an
![]() $\mathfrak m$
-primary integrally closed ideal, and let Q be a minimal reduction of I. Put
$\mathfrak m$
-primary integrally closed ideal, and let Q be a minimal reduction of I. Put
![]() $\bar {G}=\bar {G}(I)$
and
$\bar {G}=\bar {G}(I)$
and
![]() $\bar {\mathcal R}=\bar {\mathcal R}(I)$
. Then the following conditions are equivalent
$\bar {\mathcal R}=\bar {\mathcal R}(I)$
. Then the following conditions are equivalent
![]() $:$
$:$
-
(1)
 $\bar {r}(I)=2$
and
$\bar {r}(I)=2$
and
 $\ell _A(\overline {I^2}/Q I) =1$
.
$\ell _A(\overline {I^2}/Q I) =1$
. -
(2)
 $q(I)=q(\infty I)=p_g(A)-1$
.
$q(I)=q(\infty I)=p_g(A)-1$
. -
(3)
 $\bar {e}_2(I) =1$
.
$\bar {e}_2(I) =1$
. -
(4)
 $\bar {e}_1(I) = e_0(I) -\ell _A( A/I) + 1$
and
$\bar {e}_1(I) = e_0(I) -\ell _A( A/I) + 1$
and
 $\operatorname {\mathrm {nr}}(I)=\bar {\mathrm {r}}(I)$
.
$\operatorname {\mathrm {nr}}(I)=\bar {\mathrm {r}}(I)$
. -
(5)
 $\bar {G}$
is Cohen–Macaulay with
$\bar {G}$
is Cohen–Macaulay with
 $a(\bar {G})=0$
and
$a(\bar {G})=0$
and
 $\ell _A([H^2_{\mathfrak M}(\bar {G})]_0)=1$
.
$\ell _A([H^2_{\mathfrak M}(\bar {G})]_0)=1$
.
When this is the case, I is said to be a strongly elliptic ideal and
![]() $\bar {\mathcal R}$
is a Buchsbaum ring with
$\bar {\mathcal R}$
is a Buchsbaum ring with
![]() $\ell _A(H^2_{\mathfrak M}(\bar {\mathcal R})) = 1$
.
$\ell _A(H^2_{\mathfrak M}(\bar {\mathcal R})) = 1$
.
Proof.
![]() $(1) \Longrightarrow (2):$
By Theorem 3.2, we have
$(1) \Longrightarrow (2):$
By Theorem 3.2, we have
![]() $p_g(A)> q(I)=q(\infty I)$
. In particular,
$p_g(A)> q(I)=q(\infty I)$
. In particular,
![]() $q(2 I)=q(I)$
. By Proposition 2.5(1),
$q(2 I)=q(I)$
. By Proposition 2.5(1),
![]() $p_g(A)-q(I)=\ell _A(\overline {I^2}/QI)=1$
. Conversely,
$p_g(A)-q(I)=\ell _A(\overline {I^2}/QI)=1$
. Conversely,
![]() $(2) \Longrightarrow (1) $
again by Proposition 2.5.
$(2) \Longrightarrow (1) $
again by Proposition 2.5.
![]() $(2) \Longrightarrow (3):$
By Proposition 2.6(4), we have
$(2) \Longrightarrow (3):$
By Proposition 2.6(4), we have
![]() $(3) \Longrightarrow (2):$
Since
$(3) \Longrightarrow (2):$
Since
![]() $p_g(A)-q(\infty I)=\bar {e}_2(I)=1$
, by assumption, we have
$p_g(A)-q(\infty I)=\bar {e}_2(I)=1$
, by assumption, we have
![]() $p_g(A)-1 = q(\infty I) \le q(I) \le p_g(A)$
. If
$p_g(A)-1 = q(\infty I) \le q(I) \le p_g(A)$
. If
![]() $q(I)=p_g(A)$
, then I is a
$q(I)=p_g(A)$
, then I is a
![]() $p_g$
-ideal, and thus
$p_g$
-ideal, and thus
![]() $\bar {e}_2(I)=0$
. This is a contradiction. Hence,
$\bar {e}_2(I)=0$
. This is a contradiction. Hence,
![]() $q(\infty I) = q(I)=p_g(A)-1$
, as required.
$q(\infty I) = q(I)=p_g(A)-1$
, as required.
![]() $(1),(3) \Longrightarrow (4):$
It follows from Theorem 3.2
$(1),(3) \Longrightarrow (4):$
It follows from Theorem 3.2
![]() $(1)\Longrightarrow (3)$
and the fact that
$(1)\Longrightarrow (3)$
and the fact that
![]() $1< \operatorname {\mathrm {nr}}(I) \le \bar {\mathrm {r}}(I)=2. $
$1< \operatorname {\mathrm {nr}}(I) \le \bar {\mathrm {r}}(I)=2. $
![]() $(4) \Longrightarrow (1):$
By Proposition 2.5(1), we have
$(4) \Longrightarrow (1):$
By Proposition 2.5(1), we have
 $$ \begin{align*} \ell_A(\overline{I^2}/QI)&= (p_g(A)-q(I))-(q(I)-q(2I)), \\ \ell_A(\overline{I^3}/Q\overline{I^2})&= (q(I)-q(2I))-(q(2I)-q(3I)), \\ \vdots \qquad ~ &= ~ \qquad \vdots \end{align*} $$
$$ \begin{align*} \ell_A(\overline{I^2}/QI)&= (p_g(A)-q(I))-(q(I)-q(2I)), \\ \ell_A(\overline{I^3}/Q\overline{I^2})&= (q(I)-q(2I))-(q(2I)-q(3I)), \\ \vdots \qquad ~ &= ~ \qquad \vdots \end{align*} $$
By a similar argument as in [Reference Itoh10] and Proposition 2.6, we get
 $$ \begin{align*} \bar{e}_2(I) &= \sum_{n=1}^{\infty} n \cdot \ell_A(\overline{I^{n+1}}/Q\overline{I^n}), \\ \bar{e}_1(I)-\bar{e}_0(I)+\ell_A(A/I) &= \sum_{n=1}^{\infty} \ell_A(\overline{I^{n+1}}/Q\overline{I^n}). \end{align*} $$
$$ \begin{align*} \bar{e}_2(I) &= \sum_{n=1}^{\infty} n \cdot \ell_A(\overline{I^{n+1}}/Q\overline{I^n}), \\ \bar{e}_1(I)-\bar{e}_0(I)+\ell_A(A/I) &= \sum_{n=1}^{\infty} \ell_A(\overline{I^{n+1}}/Q\overline{I^n}). \end{align*} $$
Thus, our assumption implies
![]() $\ell _A(\overline {I^{n+1}}/Q\overline {I^n})=1$
for some unique integer
$\ell _A(\overline {I^{n+1}}/Q\overline {I^n})=1$
for some unique integer
![]() $n \ge 1$
. On the other hand, since
$n \ge 1$
. On the other hand, since
![]() $\operatorname {\mathrm {nr}}(I)=\bar {\mathrm {r}}(I)$
, we must have
$\operatorname {\mathrm {nr}}(I)=\bar {\mathrm {r}}(I)$
, we must have
![]() $n=1$
.
$n=1$
.
![]() $(1) \Longrightarrow (5):$
Suppose (1). Then Theorem 3.2
$(1) \Longrightarrow (5):$
Suppose (1). Then Theorem 3.2
![]() $(1)\Longrightarrow (5)$
implies that
$(1)\Longrightarrow (5)$
implies that
![]() $\bar {G}$
is Cohen–Macaulay with
$\bar {G}$
is Cohen–Macaulay with
![]() $a(\bar {G})=0$
.
$a(\bar {G})=0$
.
We remark that
![]() $\sqrt {\mathfrak M} = \sqrt {\bar G_+} $
in
$\sqrt {\mathfrak M} = \sqrt {\bar G_+} $
in
![]() $\bar G; $
hence, by [Reference Okuma19, Proposition 3.1], we have
$\bar G; $
hence, by [Reference Okuma19, Proposition 3.1], we have
![]() $[H_{\mathfrak M}^2(\bar G)]_0 \cong \overline {I^2}/QI \cong A/\mathfrak m$
has length
$[H_{\mathfrak M}^2(\bar G)]_0 \cong \overline {I^2}/QI \cong A/\mathfrak m$
has length
![]() $1$
. In particular, by Proposition 3.4,
$1$
. In particular, by Proposition 3.4,
![]() $H_{\mathfrak M}^2(\bar {\mathcal R})$
becomes an
$H_{\mathfrak M}^2(\bar {\mathcal R})$
becomes an
![]() $A/\mathfrak m$
-vector space, and thus
$A/\mathfrak m$
-vector space, and thus
![]() $\bar {\mathcal R}$
is Buchsbaum.
$\bar {\mathcal R}$
is Buchsbaum.
![]() $(5) \Longrightarrow (1):$
By Theorem 3.2
$(5) \Longrightarrow (1):$
By Theorem 3.2
![]() $(5) \Longrightarrow (1)$
, we have
$(5) \Longrightarrow (1)$
, we have
![]() $\bar {\mathrm {r}}(I)=2$
. In addition,
$\bar {\mathrm {r}}(I)=2$
. In addition,
![]() $\ell _A(\overline {I^2}/QI)=\ell _A([H_{\mathfrak M}^2(\bar {G})]_0)=1$
.
$\ell _A(\overline {I^2}/QI)=\ell _A([H_{\mathfrak M}^2(\bar {G})]_0)=1$
.
It is clear that if I is a strongly elliptic ideal, then I is an elliptic ideal. In some cases, they are equivalent. Notice that the converse is not true in general. For instance, let
![]() $A=k[[x^2,y^2,z^2,xy,xz,yz]]/(x^4+y^4+z^4)$
. Then A is a two-dimensional normal local domain with the maximal ideal
$A=k[[x^2,y^2,z^2,xy,xz,yz]]/(x^4+y^4+z^4)$
. Then A is a two-dimensional normal local domain with the maximal ideal
![]() $\mathfrak m=(x^2,y^2,z^2,xy,xz,yz)$
. Then
$\mathfrak m=(x^2,y^2,z^2,xy,xz,yz)$
. Then
![]() $\mathfrak m$
is a normal ideal, and
$\mathfrak m$
is a normal ideal, and
![]() $Q=(x^2,y^2)$
is a minimal reduction of
$Q=(x^2,y^2)$
is a minimal reduction of
![]() $\mathfrak m$
with
$\mathfrak m$
with
![]() $\mathfrak m^3=Q\mathfrak m^2$
. Moreover,
$\mathfrak m^3=Q\mathfrak m^2$
. Moreover,
![]() $\bar {\mathrm {r}}(\mathfrak m)=r(\mathfrak m)=2$
and
$\bar {\mathrm {r}}(\mathfrak m)=r(\mathfrak m)=2$
and
![]() $\ell _A(\mathfrak m^2/Q\mathfrak m)=3$
imply that
$\ell _A(\mathfrak m^2/Q\mathfrak m)=3$
imply that
![]() $\mathfrak m$
is an elliptic ideal but not a strongly elliptic ideal.
$\mathfrak m$
is an elliptic ideal but not a strongly elliptic ideal.
Notice that (1) is equivalent to (3) follows also from [Reference Itoh13].
Proposition 3.10. Let
![]() $(A,\mathfrak m)$
be a two-dimensional Gorenstein excellent normal local domain. Then
$(A,\mathfrak m)$
be a two-dimensional Gorenstein excellent normal local domain. Then
![]() $\mathfrak m$
is an elliptic ideal if and only if
$\mathfrak m$
is an elliptic ideal if and only if
![]() $\mathfrak m$
is a strongly elliptic ideal.
$\mathfrak m$
is a strongly elliptic ideal.
Proof. Assume
![]() $\mathfrak m$
is an elliptic ideal and Q be its minimal reduction. Since
$\mathfrak m$
is an elliptic ideal and Q be its minimal reduction. Since
![]() $\bar {r}(\mathfrak m)=2$
,
$\bar {r}(\mathfrak m)=2$
,
![]() $\mathfrak m \overline {\mathfrak m^2} \subset Q$
, and we have
$\mathfrak m \overline {\mathfrak m^2} \subset Q$
, and we have
![]() $\overline {\mathfrak m^2}/Q\mathfrak m \cong (\overline {\mathfrak m^2}+Q)/Q \hookrightarrow A/Q$
, whose image is contained in
$\overline {\mathfrak m^2}/Q\mathfrak m \cong (\overline {\mathfrak m^2}+Q)/Q \hookrightarrow A/Q$
, whose image is contained in
![]() $(Q:\mathfrak m)/Q$
. Since the latter has length
$(Q:\mathfrak m)/Q$
. Since the latter has length
![]() $1$
,
$1$
,
![]() $\ell _A (\overline {\mathfrak m^2}/Q\mathfrak m) =1$
and
$\ell _A (\overline {\mathfrak m^2}/Q\mathfrak m) =1$
and
![]() $\mathfrak m$
is strongly elliptic.
$\mathfrak m$
is strongly elliptic.
Example 3.11. Let
![]() $A=\mathbb {C}[[x,y,z]]/(x^a+y^b+z^c)$
be a Brieskorn hypersurface, where
$A=\mathbb {C}[[x,y,z]]/(x^a+y^b+z^c)$
be a Brieskorn hypersurface, where
![]() $2 \le a \le b \le c$
. Then:
$2 \le a \le b \le c$
. Then:
-
(1)
 $\mathfrak m$
is a
$\mathfrak m$
is a
 $p_g$
-ideal if and only if
$p_g$
-ideal if and only if
 $(a,b)=(2,2),(2,3)$
.
$(a,b)=(2,2),(2,3)$
. -
(2)
 $\mathfrak m$
is an elliptic ideal (equivalently strongly elliptic) if and only if
$\mathfrak m$
is an elliptic ideal (equivalently strongly elliptic) if and only if  $$ \begin{align*} (a,b)=(2,4),(2,5),(3,3),(3,4). \end{align*} $$
$$ \begin{align*} (a,b)=(2,4),(2,5),(3,3),(3,4). \end{align*} $$
In particular, if
![]() $p \ge 1$
and
$p \ge 1$
and
![]() $(a,b,c)=(2,4,4p+1)$
, then
$(a,b,c)=(2,4,4p+1)$
, then
![]() $p_g(A)=p$
and
$p_g(A)=p$
and
![]() $\mathfrak m$
is a (strongly) elliptic ideal. It follows from [Reference Rees26, Theorem 3.1 and Proposition 3.8].
$\mathfrak m$
is a (strongly) elliptic ideal. It follows from [Reference Rees26, Theorem 3.1 and Proposition 3.8].
Example 3.12. Proposition 3.10 does not hold if
![]() $I \neq \mathfrak m$
. Let A be any two-dimensional excellent normal local domain with
$I \neq \mathfrak m$
. Let A be any two-dimensional excellent normal local domain with
![]() $p_g(A)> 1$
. Then there exist always integrally closed ideals I with
$p_g(A)> 1$
. Then there exist always integrally closed ideals I with
![]() $q(I)=0$
. Since
$q(I)=0$
. Since
![]() $q(I)=q(2I)=0$
,
$q(I)=q(2I)=0$
,
![]() $\bar {r}(I) =2$
, and
$\bar {r}(I) =2$
, and
![]() $\bar {e}_2(I) = p_g(A)$
. Thus, 3.10 does not hold for such I.
$\bar {e}_2(I) = p_g(A)$
. Thus, 3.10 does not hold for such I.
We recall that an excellent normal local domain for which every integrally closed
![]() $\mathfrak m$
-primary ideal is a
$\mathfrak m$
-primary ideal is a
![]() $p_g$
-ideal is a rational singularity (
$p_g$
-ideal is a rational singularity (
![]() $p_g(A)=0$
). This result suggests to study the next step.
$p_g(A)=0$
). This result suggests to study the next step.
Definition 3.13 (e.g., [Reference Yau41])
An excellent normal local domain A is a strongly elliptic singularity if
![]() $p_g(A)=1$
.
$p_g(A)=1$
.
Note that any strong elliptic singularity is an elliptic singularity. The following result characterizes algebraically the strongly elliptic singularities.
Theorem 3.14. Let
![]() $(A,\mathfrak m)$
be a two-dimensional excellent normal local domain containing an algebraically closed field
$(A,\mathfrak m)$
be a two-dimensional excellent normal local domain containing an algebraically closed field
![]() $k= A/\mathfrak m$
and assume that
$k= A/\mathfrak m$
and assume that
![]() $p_g(A)>0$
. The following facts are equivalent
$p_g(A)>0$
. The following facts are equivalent
![]() $:$
$:$
-
(1) A is a strongly elliptic singularity.
-
(2) Every integrally closed ideal of A is either a
 $p_g$
-ideal or a strongly elliptic ideal.
$p_g$
-ideal or a strongly elliptic ideal.
Proof. It depends by the fact that always there exists an integrally closed ideal I of A such that
![]() $q(I)=0$
. Thus,
$q(I)=0$
. Thus,
![]() $p_g(A)= \bar {e}_2(I)$
.
$p_g(A)= \bar {e}_2(I)$
.
If A is a rational singularity, then every integrally closed
![]() $\mathfrak m$
-primary ideal is normal. This is not true if A is an elliptic singularity, even if we assume A is a strongly elliptic singularity.
$\mathfrak m$
-primary ideal is normal. This is not true if A is an elliptic singularity, even if we assume A is a strongly elliptic singularity.
Example 3.15.
-
(1) Let
 $A = k[ X,Y,Z]/ (X^3 + Y^3 + Z^3), $
then A is Gorenstein,
$A = k[ X,Y,Z]/ (X^3 + Y^3 + Z^3), $
then A is Gorenstein,
 $p_g(A) = 1$
, and the maximal ideal
$p_g(A) = 1$
, and the maximal ideal
 $\mathfrak m$
is normal. If we consider
$\mathfrak m$
is normal. If we consider
 $I = (x,y, z^2), $
then
$I = (x,y, z^2), $
then
 $I^2$
is not normal.
$I^2$
is not normal. -
(2) Cutkosky showed that if
 $A= \mathbb {Q}[[ X,Y,Z]]/ (X^3 +3 Y^3 +9 Z^3)$
(
$A= \mathbb {Q}[[ X,Y,Z]]/ (X^3 +3 Y^3 +9 Z^3)$
(
 $\mathbb {Q}$
rational numbers), then for every integrally closed ideal
$\mathbb {Q}$
rational numbers), then for every integrally closed ideal
 $I \subset A$
,
$I \subset A$
,
 $I^2 $
is also integrally closed and hence normal. This is because the elliptic curve does not have any
$I^2 $
is also integrally closed and hence normal. This is because the elliptic curve does not have any
 $\mathbb {Q}$
-rational point.
$\mathbb {Q}$
-rational point. -
(3) Let
 $A=k[x,y,z]/(x^2+y^4+z^4)$
,
$A=k[x,y,z]/(x^2+y^4+z^4)$
,
 $I=\mathfrak m=(x,y,z)$
, and
$I=\mathfrak m=(x,y,z)$
, and
 $Q=(y,z)$
. Then
$Q=(y,z)$
. Then
 $p_g(A)=1$
and
$p_g(A)=1$
and
 $ \overline {\mathfrak m^n}= x(y,z)^{n-2}+\mathfrak m^n$
for every
$ \overline {\mathfrak m^n}= x(y,z)^{n-2}+\mathfrak m^n$
for every
 $n \ge 2$
.
$n \ge 2$
.
Proposition 3.16. Let
![]() $(A,\mathfrak m)$
be a two-dimensional excellent normal local domain containing an algebraically closed field
$(A,\mathfrak m)$
be a two-dimensional excellent normal local domain containing an algebraically closed field
![]() $k= A/\mathfrak m. $
Assume that I is a strongly elliptic ideal. Then the following conditions are equivalent
$k= A/\mathfrak m. $
Assume that I is a strongly elliptic ideal. Then the following conditions are equivalent
![]() $:$
$:$
-
(1)
 $\overline {I^2}=I^2$
.
$\overline {I^2}=I^2$
. -
(2)
 $\overline {I^n}=I^n$
for some
$\overline {I^n}=I^n$
for some
 $n \ge 2$
.
$n \ge 2$
. -
(3)
 $\overline {I^n}=I^n$
for every
$\overline {I^n}=I^n$
for every
 $n \ge 2$
.
$n \ge 2$
.
Proof. By Theorem 3.9(1), we have
![]() $\ell _A(\overline {I^2}/QI)=1$
and
$\ell _A(\overline {I^2}/QI)=1$
and
![]() $\overline {I^n} = Q \overline {I^{n-1}}$
for
$\overline {I^n} = Q \overline {I^{n-1}}$
for
![]() $n\ge 3$
. Hence, if
$n\ge 3$
. Hence, if
![]() $I^2 = \overline {I^2}$
, then
$I^2 = \overline {I^2}$
, then
![]() $I^n = \overline {I^n}$
for all
$I^n = \overline {I^n}$
for all
![]() $n\ge 2$
.
$n\ge 2$
.
Conversely, assume that
![]() $I^2 \ne \overline {I^2}$
. Since
$I^2 \ne \overline {I^2}$
. Since
![]() $\ell _A(\overline {I^2}/QI)=1$
, we should have
$\ell _A(\overline {I^2}/QI)=1$
, we should have
![]() $I^2 = QI$
. This implies that
$I^2 = QI$
. This implies that
![]() $G(I) := \oplus _{n\ge 0} I^n/ I^{n+1}$
is Cohen–Macaulay with
$G(I) := \oplus _{n\ge 0} I^n/ I^{n+1}$
is Cohen–Macaulay with
![]() $a(G(I)) = -1$
(see [Reference Goto and Watanabe8], [Reference Watanabe and Yoshida37, Proposition 2.6]) and hence
$a(G(I)) = -1$
(see [Reference Goto and Watanabe8], [Reference Watanabe and Yoshida37, Proposition 2.6]) and hence
 $$ \begin{align*} \ell_A( A/ I^{n+1}) = e_0(I) \genfrac{(}{)}{0pt}{0}{n+2}{2} - e_1(I)\genfrac{(}{)}{0pt}{0}{n+1}{1} \end{align*} $$
$$ \begin{align*} \ell_A( A/ I^{n+1}) = e_0(I) \genfrac{(}{)}{0pt}{0}{n+2}{2} - e_1(I)\genfrac{(}{)}{0pt}{0}{n+1}{1} \end{align*} $$
with
![]() $e_0(I) = \bar e_0(I)$
and
$e_0(I) = \bar e_0(I)$
and
![]() $e_1(I) = e_0(I) - \ell _A(A/I)$
.
$e_1(I) = e_0(I) - \ell _A(A/I)$
.
On the other hand, by Theorem 3.2 and Corollary 3.9, we have
 $$ \begin{align*} \ell_A(A/\overline{I^{n+1}})&= \bar{P}_I(n)=\overline{e}_0(I){n+2 \choose 2} - \overline{e}_1(I){n+1 \choose 1} + \overline{e}_2(I) \\ &= e_0(I){n+2 \choose 2} - (e_0(I)-\ell_A(A/I)+1){n+1 \choose 1} +1 \\ &= \ell_A(A/I^{n+1})-n. \end{align*} $$
$$ \begin{align*} \ell_A(A/\overline{I^{n+1}})&= \bar{P}_I(n)=\overline{e}_0(I){n+2 \choose 2} - \overline{e}_1(I){n+1 \choose 1} + \overline{e}_2(I) \\ &= e_0(I){n+2 \choose 2} - (e_0(I)-\ell_A(A/I)+1){n+1 \choose 1} +1 \\ &= \ell_A(A/I^{n+1})-n. \end{align*} $$
This implies that
![]() $I^n \ne \overline {I^n}$
for all
$I^n \ne \overline {I^n}$
for all
![]() $n\ge 2$
.
$n\ge 2$
.
We can characterize the normal ideals in a strongly elliptic singularity. Before showing the results, let us recall some definitions and basic facts on cycles and a vanishing theorem for elliptic singularities. In the following, A is an elliptic singularity, and X is a resolution of
![]() $\operatorname {\mathrm {Spec}}(A)$
.
$\operatorname {\mathrm {Spec}}(A)$
.
For a cycle
![]() $C>0$
on X, we denote by
$C>0$
on X, we denote by
![]() $\chi (C)$
the Euler characteristic
$\chi (C)$
the Euler characteristic
![]() $\chi (\mathcal O_C)=h^0(\mathcal O_C)-h^1(\mathcal O_C)$
. Then
$\chi (\mathcal O_C)=h^0(\mathcal O_C)-h^1(\mathcal O_C)$
. Then
![]() $p_a(C):=1-\chi (C)$
is called the arithmetic genus of C. By the Riemann–Roch theorem, we have
$p_a(C):=1-\chi (C)$
is called the arithmetic genus of C. By the Riemann–Roch theorem, we have
![]() $\chi (C)=-(K_X+C)C/2$
, where
$\chi (C)=-(K_X+C)C/2$
, where
![]() $K_X$
is the canonical divisor on X. From this, if
$K_X$
is the canonical divisor on X. From this, if
![]() $C_1, C_2>0$
are cycles, we have
$C_1, C_2>0$
are cycles, we have
![]() $\chi (C_1+C_2)=\chi (C_1)+\chi (C_2)-C_1C_2$
. From the exact sequence
$\chi (C_1+C_2)=\chi (C_1)+\chi (C_2)-C_1C_2$
. From the exact sequence
we have
![]() $\chi (\mathcal O_{C_2}(-C_1))=-C_1C_2+\chi (C_2)$
.
$\chi (\mathcal O_{C_2}(-C_1))=-C_1C_2+\chi (C_2)$
.
If A is elliptic, then there exists a unique cycle
![]() $E_{min}$
, called the minimally elliptic cycle, such that
$E_{min}$
, called the minimally elliptic cycle, such that
![]() $\chi (E_{min})=0$
and
$\chi (E_{min})=0$
and
![]() $\chi (C)>0$
for all cycles
$\chi (C)>0$
for all cycles
![]() $0<C<E_{min}$
(see [Reference Masuti, Ozeki and Rossi15]). Moreover, we have the following (see [Reference Masuti, Ozeki and Rossi15, Propositions 3.1 and 3.2 and Corollary 4.2], [Reference Watanabe36, (6.4) and (6.5)], [Reference Yau38, p. 428]).
$0<C<E_{min}$
(see [Reference Masuti, Ozeki and Rossi15]). Moreover, we have the following (see [Reference Masuti, Ozeki and Rossi15, Propositions 3.1 and 3.2 and Corollary 4.2], [Reference Watanabe36, (6.4) and (6.5)], [Reference Yau38, p. 428]).
Proposition 3.17. Assume that A is elliptic. Then
![]() $\chi (C)\ge 0$
for any cycle
$\chi (C)\ge 0$
for any cycle
![]() $C>0$
on X and
$C>0$
on X and
![]() $C\ge E_{min}$
if
$C\ge E_{min}$
if
![]() $\chi (C)=0$
.
$\chi (C)=0$
.
Let us recall that the fundamental cycle
![]() $Z_f$
can be computed via a sequence of cycles:
$Z_f$
can be computed via a sequence of cycles:
where
![]() $E_{j_1}$
is an arbitrary component of E and
$E_{j_1}$
is an arbitrary component of E and
![]() $C_{i-1}E_{j_i}>0$
for
$C_{i-1}E_{j_i}>0$
for
![]() $2\le i \le m$
. Such a sequence
$2\le i \le m$
. Such a sequence
![]() $\{C_i\}$
is called a computation sequence for
$\{C_i\}$
is called a computation sequence for
![]() $Z_f$
. It is known that
$Z_f$
. It is known that
![]() $h^0(\mathcal O_{C_i})=1$
for
$h^0(\mathcal O_{C_i})=1$
for
![]() $1 \le i\le m$
(see [Reference Masuti, Ozeki and Rossi15, p. 1,260]).
$1 \le i\le m$
(see [Reference Masuti, Ozeki and Rossi15, p. 1,260]).
The following vanishing theorems are essential in our argument.
Theorem 3.18 (Röhr [Reference Sally31, 1.7])
Let L be a divisor on X such that
![]() $LC>-2\chi (C)$
for every cycle
$LC>-2\chi (C)$
for every cycle
![]() $C>0$
which occurs in a computation sequence for
$C>0$
which occurs in a computation sequence for
![]() $Z_f$
. Then
$Z_f$
. Then
![]() $H^1(\mathcal O_X(L))=0$
. If A is rational, then the converse holds, too.
$H^1(\mathcal O_X(L))=0$
. If A is rational, then the converse holds, too.
From Theorem 3.18 and Proposition 3.17, we have the following.
Corollary 3.19. Assume that A is an elliptic singularity. Let L be a nef divisor on X such that
![]() $L E_{min}>0$
. Then
$L E_{min}>0$
. Then
![]() $H^1(\mathcal O_X(L))=0$
.
$H^1(\mathcal O_X(L))=0$
.
Proposition 3.20. Assume that A is an elliptic singularity and D the minimally elliptic cycle on X. Let F be a nef divisor on X. If
![]() $FD>0$
, then
$FD>0$
, then
![]() $H^1(\mathcal O_X(F-D))=0$
, and from the exact sequence
$H^1(\mathcal O_X(F-D))=0$
, and from the exact sequence
![]() $0 \to \mathcal O_X(F-D) \to \mathcal O_X(F) \to \mathcal O_D(F) \to 0$
, the restriction map
$0 \to \mathcal O_X(F-D) \to \mathcal O_X(F) \to \mathcal O_D(F) \to 0$
, the restriction map
![]() $H^0(\mathcal O_X(F))\to H^0(\mathcal O_D(F))$
is surjective.
$H^0(\mathcal O_X(F))\to H^0(\mathcal O_D(F))$
is surjective.
Proof. If
![]() $F-D$
is nef, since
$F-D$
is nef, since
![]() $(F-D)D>0$
, we have
$(F-D)D>0$
, we have
![]() $H^1(\mathcal O_X(F-D))=0$
by Corollary 3.19. Assume that
$H^1(\mathcal O_X(F-D))=0$
by Corollary 3.19. Assume that
![]() $F-D$
is not nef. As in [Reference Goto and Nishida6, 1.4], we have a sequence
$F-D$
is not nef. As in [Reference Goto and Nishida6, 1.4], we have a sequence
![]() $\{D_i\}$
of cycles such that
$\{D_i\}$
of cycles such that
Since
![]() $F-Z_f$
is nef,
$F-Z_f$
is nef,
![]() $(F-D_{i-1}) E_{j_i}<0$
implies
$(F-D_{i-1}) E_{j_i}<0$
implies
![]() $D_{i-1}E_{j_i}>0$
, and
$D_{i-1}E_{j_i}>0$
, and
![]() $D\le Z_f$
, we see that
$D\le Z_f$
, we see that
![]() $D_s\le Z_f$
and
$D_s\le Z_f$
and
![]() $D_s$
occurs in a computation sequence for
$D_s$
occurs in a computation sequence for
![]() $Z_f$
. Then the equalities
$Z_f$
. Then the equalities
![]() $\chi (D)=\chi (D_s)=0$
and
$\chi (D)=\chi (D_s)=0$
and
![]() $\chi (D_i) = \chi (D_{i-1}) +\chi ( E_{j_i})-D_{i-1} E_{j_i}$
imply that
$\chi (D_i) = \chi (D_{i-1}) +\chi ( E_{j_i})-D_{i-1} E_{j_i}$
imply that
![]() $F E_{j_i}=0$
,
$F E_{j_i}=0$
,
![]() $D_{i-1} E_{j_i}=1$
, and
$D_{i-1} E_{j_i}=1$
, and
![]() $h^j(\mathcal O_{E_{j_i}}(F-D_{i-1}))=0$
for
$h^j(\mathcal O_{E_{j_i}}(F-D_{i-1}))=0$
for
![]() $j=0,1$
and
$j=0,1$
and
![]() $1\le i \le s$
. Since
$1\le i \le s$
. Since
we have
![]() $(F-D_s)D>0$
. Therefore, from the exact sequence
$(F-D_s)D>0$
. Therefore, from the exact sequence
we obtain
![]() $H^1(\mathcal O_X(F-D))=H^1(\mathcal O_X(F-D_s))=0$
.
$H^1(\mathcal O_X(F-D))=H^1(\mathcal O_X(F-D_s))=0$
.
Theorem 3.21 [Reference Giraud5, 2.7]
Let C be a Cohen–Macaulay projective scheme of pure dimension
![]() $1$
, and let
$1$
, and let
![]() $\mathcal F$
be a rank
$\mathcal F$
be a rank
![]() $1$
torsion-free sheaf on C. Assume that
$1$
torsion-free sheaf on C. Assume that
![]() $\deg \mathcal F|_{W}:= \chi (\mathcal F|_{W})-\chi (W)> -2\chi (W)$
for every subcurve
$\deg \mathcal F|_{W}:= \chi (\mathcal F|_{W})-\chi (W)> -2\chi (W)$
for every subcurve
![]() $W\subset C$
. Then
$W\subset C$
. Then
![]() $H^1(\mathcal F)=0$
.
$H^1(\mathcal F)=0$
.
To show the normality of an ideal I, the following is essential.
Proposition 3.22. Let
![]() $\mathcal L_1$
and
$\mathcal L_1$
and
![]() $\mathcal L_2$
be nef invertible sheaves on the minimally elliptic cycle D such that
$\mathcal L_2$
be nef invertible sheaves on the minimally elliptic cycle D such that
![]() $d_i:=\deg \mathcal L_i \ge 3$
for
$d_i:=\deg \mathcal L_i \ge 3$
for
![]() $i=1,2$
. Then the multiplication map
$i=1,2$
. Then the multiplication map
is surjective.
Proof. First, note that
![]() $\chi (W)>0$
for any cycle
$\chi (W)>0$
for any cycle
![]() $0<W\lneqq D$
by the definition of the minimally elliptic cycle. For any subscheme
$0<W\lneqq D$
by the definition of the minimally elliptic cycle. For any subscheme
![]() $\Lambda \subset D$
, we denote by
$\Lambda \subset D$
, we denote by
![]() $I_{\Lambda }\subset \mathcal O_D$
the ideal sheaf of
$I_{\Lambda }\subset \mathcal O_D$
the ideal sheaf of
![]() $\Lambda $
. For any cycle
$\Lambda $
. For any cycle
![]() $W\le D$
and any
$W\le D$
and any
![]() $p\in \operatorname {\mathrm {Supp}} (W)$
, we have
$p\in \operatorname {\mathrm {Supp}} (W)$
, we have
![]() $\deg (I_p\mathcal L_i)|_W=\deg \mathcal L_i|_W-1$
. Therefore, it follows from Theorem 3.21 that
$\deg (I_p\mathcal L_i)|_W=\deg \mathcal L_i|_W-1$
. Therefore, it follows from Theorem 3.21 that
![]() $H^1(I_p\mathcal L_i)=0$
for any point
$H^1(I_p\mathcal L_i)=0$
for any point
![]() $p \in \operatorname {\mathrm {Supp}}(D)$
. Hence,
$p \in \operatorname {\mathrm {Supp}}(D)$
. Hence,
![]() $\mathcal L_i$
is generated by global sections. Let
$\mathcal L_i$
is generated by global sections. Let
![]() $s\in H^0(\mathcal L_1)$
be a general section and consider the exact sequence
$s\in H^0(\mathcal L_1)$
be a general section and consider the exact sequence
where B is the zero-dimensional subscheme of D of degree
![]() $d_1=\deg \mathcal L_1$
defined by s. Note that since
$d_1=\deg \mathcal L_1$
defined by s. Note that since
![]() $\mathcal L_1$
is generated by global sections, each point of
$\mathcal L_1$
is generated by global sections, each point of
![]() $\operatorname {\mathrm {Supp}} (B)$
is a nonsingular point of
$\operatorname {\mathrm {Supp}} (B)$
is a nonsingular point of
![]() $\operatorname {\mathrm {Supp}} (D)$
and there exists
$\operatorname {\mathrm {Supp}} (D)$
and there exists
![]() $s_1\in H^0(\mathcal L_1)$
such that
$s_1\in H^0(\mathcal L_1)$
such that
![]() $\mathcal L_1|_B\cong s_1\mathcal O_B\cong \mathcal O_B$
. Let
$\mathcal L_1|_B\cong s_1\mathcal O_B\cong \mathcal O_B$
. Let
![]() $p\in \operatorname {\mathrm {Supp}}(B)$
be any point. The following fact makes our proof easier.
$p\in \operatorname {\mathrm {Supp}}(B)$
be any point. The following fact makes our proof easier.
Claim 7. Let
![]() $\mathfrak n \subset \mathcal O:=\mathcal O_{X,p}$
be the maximal ideal. Then we can take generators
$\mathfrak n \subset \mathcal O:=\mathcal O_{X,p}$
be the maximal ideal. Then we can take generators
![]() $x,y$
of
$x,y$
of
![]() $\mathfrak n$
, so that
$\mathfrak n$
, so that
![]() $\mathcal O_{D,p}=\mathcal O/(x^{n_p})$
with
$\mathcal O_{D,p}=\mathcal O/(x^{n_p})$
with
![]() $n_p\ge 1$
and
$n_p\ge 1$
and
![]() $\mathcal O_{B,p}\cong \mathcal O/(x^{n_p},y)$
. Hence, at p, the subschemes of B correspond to monomials
$\mathcal O_{B,p}\cong \mathcal O/(x^{n_p},y)$
. Hence, at p, the subschemes of B correspond to monomials
![]() $x^{\ell }$
with
$x^{\ell }$
with
![]() $\ell \le n_p$
.
$\ell \le n_p$
.
Proof of Claim 7
Since E is nonsingular at p, we have the generators
![]() $x,y\in \mathfrak n$
such that
$x,y\in \mathfrak n$
such that
![]() $\mathcal O_{D,p}=\mathcal O/(x^{n_p})$
. Assume that
$\mathcal O_{D,p}=\mathcal O/(x^{n_p})$
. Assume that
![]() $\mathcal O_{B,p}=\mathcal O/(x^{n_p}, f)$
, where
$\mathcal O_{B,p}=\mathcal O/(x^{n_p}, f)$
, where
![]() $f\in \mathfrak n$
. If
$f\in \mathfrak n$
. If
![]() $\ell _{\mathcal O}(\mathcal O/(x,f))=1$
, we can put
$\ell _{\mathcal O}(\mathcal O/(x,f))=1$
, we can put
![]() $y=f$
. Assume that
$y=f$
. Assume that
![]() $\ell _{\mathcal O}(\mathcal O/(x,f))\ge 2$
. Let
$\ell _{\mathcal O}(\mathcal O/(x,f))\ge 2$
. Let
![]() $0<W\le D$
be any cycle, and let
$0<W\le D$
be any cycle, and let
![]() $\mathcal O_{W,p}=\mathcal O/(x^{m_p})$
. Assume that
$\mathcal O_{W,p}=\mathcal O/(x^{m_p})$
. Assume that
![]() $p\in \operatorname {\mathrm {Supp}} (W)$
. Then the cokernel of
$p\in \operatorname {\mathrm {Supp}} (W)$
. Then the cokernel of
![]() $(I_p^2\mathcal L_1)|_W\to \mathcal L_1|_W$
is isomorphic to
$(I_p^2\mathcal L_1)|_W\to \mathcal L_1|_W$
is isomorphic to
![]() $\mathcal O/\mathfrak n^2+(x^{m_p})$
. If
$\mathcal O/\mathfrak n^2+(x^{m_p})$
. If
![]() $m_p=1$
, then
$m_p=1$
, then
![]() $\deg (I_p^2\mathcal L_1)|_W=\deg \mathcal L_1|_W-2$
. If
$\deg (I_p^2\mathcal L_1)|_W=\deg \mathcal L_1|_W-2$
. If
![]() $m_p\ge 2$
, then
$m_p\ge 2$
, then
![]() $\deg (I_p^2\mathcal L_1)|_W =\deg \mathcal L_1|_W-3\ge \ell _{\mathcal O}(\mathcal O/(x^{m_p},f))-3\ge 1$
. Thus, we have
$\deg (I_p^2\mathcal L_1)|_W =\deg \mathcal L_1|_W-3\ge \ell _{\mathcal O}(\mathcal O/(x^{m_p},f))-3\ge 1$
. Thus, we have
![]() $H^1(I_p^2\mathcal L_1)=0$
by Theorem 3.21, and the map
$H^1(I_p^2\mathcal L_1)=0$
by Theorem 3.21, and the map
![]() $H^0(I_p\mathcal L_1) \to I_p\mathcal L_1/I_p^2\mathcal L_1$
is surjective; however, this shows that we can take
$H^0(I_p\mathcal L_1) \to I_p\mathcal L_1/I_p^2\mathcal L_1$
is surjective; however, this shows that we can take
![]() $f=y$
.
$f=y$
.
Tensoring
![]() $\mathcal L_2$
with the sequence (3.3), we obtain the exact sequence
$\mathcal L_2$
with the sequence (3.3), we obtain the exact sequence
since
![]() $H^1(\mathcal L_2)=0$
. As seen above, we have general sections
$H^1(\mathcal L_2)=0$
. As seen above, we have general sections
![]() $s_1\in H^0(\mathcal L_1)$
and
$s_1\in H^0(\mathcal L_1)$
and
![]() $s_2\in H^0(\mathcal L_2)$
such that
$s_2\in H^0(\mathcal L_2)$
such that
![]() $s_1s_2\mapsto 1\in H^0(\mathcal O_B)$
. Thus, the sections of
$s_1s_2\mapsto 1\in H^0(\mathcal O_B)$
. Thus, the sections of
![]() $H^0(\mathcal L_1 \otimes \mathcal L_2)$
which map to
$H^0(\mathcal L_1 \otimes \mathcal L_2)$
which map to
![]() $1\in H^0(\mathcal O_B)$
are in the image of
$1\in H^0(\mathcal O_B)$
are in the image of
![]() $\gamma $
. It is now sufficient to show that for any subscheme
$\gamma $
. It is now sufficient to show that for any subscheme
![]() $B'\subset B$
of
$B'\subset B$
of
![]() $\deg B'<d_1$
, the image of
$\deg B'<d_1$
, the image of
![]() $\gamma $
contains a section
$\gamma $
contains a section
![]() $t \in H^0(\mathcal I_{B'}\mathcal L_1\otimes \mathcal L_2)$
such that
$t \in H^0(\mathcal I_{B'}\mathcal L_1\otimes \mathcal L_2)$
such that
![]() $\mathcal L_1\otimes \mathcal L_2/t\mathcal O_D \cong \mathcal O_{B'}\oplus \mathcal O_{\overline {B}}$
, where
$\mathcal L_1\otimes \mathcal L_2/t\mathcal O_D \cong \mathcal O_{B'}\oplus \mathcal O_{\overline {B}}$
, where
![]() $\operatorname {\mathrm {Supp}} (\overline {B}) \cap \operatorname {\mathrm {Supp}} (B)=\emptyset $
. To prove this, we write
$\operatorname {\mathrm {Supp}} (\overline {B}) \cap \operatorname {\mathrm {Supp}} (B)=\emptyset $
. To prove this, we write
![]() $\mathcal I_{B'}=\mathcal I_{B_1}\mathcal I_{B_2}$
(
$\mathcal I_{B'}=\mathcal I_{B_1}\mathcal I_{B_2}$
(
![]() $B_1, B_2\subset B'$
), so that
$B_1, B_2\subset B'$
), so that
![]() $\deg \mathcal I_{B_i}\mathcal L_i=d_i-\deg B_i\ge 2$
for
$\deg \mathcal I_{B_i}\mathcal L_i=d_i-\deg B_i\ge 2$
for
![]() $i=1,2$
(note that
$i=1,2$
(note that
![]() $\deg B_1 + \deg B_2 <d_1$
). Let
$\deg B_1 + \deg B_2 <d_1$
). Let
![]() $0<W\le D$
be any cycle, and let
$0<W\le D$
be any cycle, and let
![]() $p\in \operatorname {\mathrm {Supp}}(B)$
. We use the notation of the proof of Claim 7. Suppose that
$p\in \operatorname {\mathrm {Supp}}(B)$
. We use the notation of the proof of Claim 7. Suppose that
![]() $\mathcal O_{B_1,p}=\mathcal O/(x^{\ell _p},y)$
. Then
$\mathcal O_{B_1,p}=\mathcal O/(x^{\ell _p},y)$
. Then
![]() $\deg \mathcal L_1|_W=\sum _W m_p$
, where
$\deg \mathcal L_1|_W=\sum _W m_p$
, where
![]() $\sum _W$
means the sum over
$\sum _W$
means the sum over
![]() $p\in \operatorname {\mathrm {Supp}}(B) \cap \operatorname {\mathrm {Supp}}(W)$
, and the cokernel of
$p\in \operatorname {\mathrm {Supp}}(B) \cap \operatorname {\mathrm {Supp}}(W)$
, and the cokernel of
![]() $(I_{B_1}\mathcal L_1)|_W\to \mathcal L_1|_W$
is isomorphic to
$(I_{B_1}\mathcal L_1)|_W\to \mathcal L_1|_W$
is isomorphic to
![]() $\mathcal O/(x^{m_p}, x^{\ell _p},y)$
. Therefore,
$\mathcal O/(x^{m_p}, x^{\ell _p},y)$
. Therefore,
Since
![]() $\deg \mathcal I_{B_1}\mathcal L_1=d_1-\deg B_1\ge 2$
, by Theorem 3.21, we have
$\deg \mathcal I_{B_1}\mathcal L_1=d_1-\deg B_1\ge 2$
, by Theorem 3.21, we have
![]() $H^1(I_q\mathcal I_{B_1}\mathcal L_1)=0$
for any point
$H^1(I_q\mathcal I_{B_1}\mathcal L_1)=0$
for any point
![]() $q\in \operatorname {\mathrm {Supp}}(B)$
. Hence,
$q\in \operatorname {\mathrm {Supp}}(B)$
. Hence,
![]() $H^0(\mathcal I_{B_1}\mathcal L_1)$
has no base points. Clearly, the same results for
$H^0(\mathcal I_{B_1}\mathcal L_1)$
has no base points. Clearly, the same results for
![]() $\mathcal I_{B_2}\mathcal L_2$
hold. Therefore, for each
$\mathcal I_{B_2}\mathcal L_2$
hold. Therefore, for each
![]() $i=1,2$
, we have a section
$i=1,2$
, we have a section
![]() $t_i\in H^0(\mathcal I_{B_i}\mathcal L_i)$
such that
$t_i\in H^0(\mathcal I_{B_i}\mathcal L_i)$
such that
![]() $\mathcal L_i/t_i\mathcal O_D \cong \mathcal O_{B_i}\oplus \mathcal O_{\overline {B_i}}$
, where
$\mathcal L_i/t_i\mathcal O_D \cong \mathcal O_{B_i}\oplus \mathcal O_{\overline {B_i}}$
, where
![]() $\operatorname {\mathrm {Supp}} (\overline {B_i}) \cap \operatorname {\mathrm {Supp}} (B)=\emptyset $
. Then
$\operatorname {\mathrm {Supp}} (\overline {B_i}) \cap \operatorname {\mathrm {Supp}} (B)=\emptyset $
. Then
![]() $t:=t_1t_2$
satisfies the required property.
$t:=t_1t_2$
satisfies the required property.
Theorem 3.23. Let
![]() $(A,\mathfrak m)$
be a two-dimensional excellent normal local domain containing an algebraically closed field
$(A,\mathfrak m)$
be a two-dimensional excellent normal local domain containing an algebraically closed field
![]() $k= A/\mathfrak m$
. Assume that A is a strongly elliptic singularity. If
$k= A/\mathfrak m$
. Assume that A is a strongly elliptic singularity. If
![]() $I = I_Z $
is an elliptic ideal
$I = I_Z $
is an elliptic ideal
![]() $($
equivalently, I is not a
$($
equivalently, I is not a
![]() $p_g$
-ideal
$p_g$
-ideal
![]() $)$
and D is the minimally elliptic cycle on X, then
$)$
and D is the minimally elliptic cycle on X, then
![]() $I^2$
is integrally closed
$I^2$
is integrally closed
![]() $($
equivalently, I is normal
$($
equivalently, I is normal
![]() $)$
if and only if
$)$
if and only if
![]() $- Z D \ge 3$
and if
$- Z D \ge 3$
and if
![]() $- ZD \le 2$
, then
$- ZD \le 2$
, then
![]() $I^2 = QI$
.
$I^2 = QI$
.
Proof. Assume that
![]() $-ZD\le 2$
. Since
$-ZD\le 2$
. Since
![]() $H^1(\mathcal O_X(-Z))=0$
, by the Riemann–Roch theorem, we have
$H^1(\mathcal O_X(-Z))=0$
, by the Riemann–Roch theorem, we have
![]() $h^0(\mathcal O_D(-nZ))=-nZD$
for
$h^0(\mathcal O_D(-nZ))=-nZD$
for
![]() $n\ge 1$
. Hence,
$n\ge 1$
. Hence,
cannot be surjective. By Proposition 3.20, the map
cannot be surjective, too. Therefore,
![]() $I^2\ne I_{2Z}$
, and hence
$I^2\ne I_{2Z}$
, and hence
![]() $I^2 = QI$
.
$I^2 = QI$
.
Assume that
![]() $-ZD\ge 3$
. By Propositions 3.20 and 3.22, we have the following commutative diagram:
$-ZD\ge 3$
. By Propositions 3.20 and 3.22, we have the following commutative diagram:

where at least the maps other than
![]() $\alpha $
are surjective. By Proposition 3.20 and its proof, we have
$\alpha $
are surjective. By Proposition 3.20 and its proof, we have
![]() $I_{2Z}=I^2+H^0(\mathcal O_X(-2Z-D))$
,
$I_{2Z}=I^2+H^0(\mathcal O_X(-2Z-D))$
,
![]() $H^0(\mathcal O_X(-2Z-D))=H^0(\mathcal O_X(-2Z-D_s))$
, and
$H^0(\mathcal O_X(-2Z-D))=H^0(\mathcal O_X(-2Z-D_s))$
, and
![]() $-(Z+D_s)D\ge -ZD\ge 3$
. We have as above a surjective map
$-(Z+D_s)D\ge -ZD\ge 3$
. We have as above a surjective map
and
![]() $H^0(\mathcal O_X(-2Z-D_s)) \subset I H^0(\mathcal O_X(-Z-D_s))+H^0(\mathcal O_X(-2Z-D_s-D))$
. From these arguments, for
$H^0(\mathcal O_X(-2Z-D_s)) \subset I H^0(\mathcal O_X(-Z-D_s))+H^0(\mathcal O_X(-2Z-D_s-D))$
. From these arguments, for
![]() $m>0$
, we have
$m>0$
, we have
![]() $I_{2Z}\subset I^2+H^0(\mathcal O_X(-2Z-mD))$
. We denote by
$I_{2Z}\subset I^2+H^0(\mathcal O_X(-2Z-mD))$
. We denote by
![]() $H(m)$
the minimal anti-nef cycle on X such that
$H(m)$
the minimal anti-nef cycle on X such that
![]() $H(m)\ge 2Z+mD$
. Then
$H(m)\ge 2Z+mD$
. Then
![]() $H^0(\mathcal O_X(-2Z-mD))=H^0(\mathcal O_X(-H(m)))$
, and for an arbitrary
$H^0(\mathcal O_X(-2Z-mD))=H^0(\mathcal O_X(-H(m)))$
, and for an arbitrary
![]() $n\in \mathbb Z_{+}$
, there exists
$n\in \mathbb Z_{+}$
, there exists
![]() $m(n)\in \mathbb Z_{+}$
such that
$m(n)\in \mathbb Z_{+}$
such that
![]() $H(m(n))\ge nE$
. Therefore,
$H(m(n))\ge nE$
. Therefore,
![]() $H^0(\mathcal O_X(-2Z-mD))\subset I^2$
for sufficiently large m, and we obtain
$H^0(\mathcal O_X(-2Z-mD))\subset I^2$
for sufficiently large m, and we obtain
![]() $I_{2Z}=I^2$
.
$I_{2Z}=I^2$
.
Remark 3.24. Assume that A is elliptic. It follows from Proposition 4.5 and Corollary 3.19 that
![]() $q(I)=0$
if and only if
$q(I)=0$
if and only if
![]() $ZD\ne 0$
. By an argument similar to the proof of Theorem 3.23, we can prove that if
$ZD\ne 0$
. By an argument similar to the proof of Theorem 3.23, we can prove that if
![]() $ZD\ne 0$
, then
$ZD\ne 0$
, then
![]() $I=I_Z$
is normal if and only if
$I=I_Z$
is normal if and only if
![]() $-ZD\ge 3$
.
$-ZD\ge 3$
.
For elliptic ideals in an elliptic singularity (not strongly elliptic), Remark 3.24 cannot be applied because the condition
![]() $ZD \ne 0$
does not hold in general. Next example shows that the condition
$ZD \ne 0$
does not hold in general. Next example shows that the condition
![]() $0 < -ZD <3$
is not necessary for
$0 < -ZD <3$
is not necessary for
![]() $I_Z$
being not normal.
$I_Z$
being not normal.
Example 3.25. Suppose that
![]() $p\ge 1$
be an integer. Let
$p\ge 1$
be an integer. Let
![]() $ A=k[x,y,z]/(x^2+y^3+z^{6(p+1)})$
, and assume that X is the minimal resolution. Then E is a chain of
$ A=k[x,y,z]/(x^2+y^3+z^{6(p+1)})$
, and assume that X is the minimal resolution. Then E is a chain of
![]() $p+1$
nonsingular curves
$p+1$
nonsingular curves
![]() $E_0, E_1, \dots , E_p$
, where
$E_0, E_1, \dots , E_p$
, where
![]() $g(E_0)=1$
,
$g(E_0)=1$
,
![]() $E_0^2=-1$
,
$E_0^2=-1$
,
![]() $g(E_i)=0$
,
$g(E_i)=0$
,
![]() $E_i^2=-2$
,
$E_i^2=-2$
,
![]() $E_{i-1}E_i=1$
, for
$E_{i-1}E_i=1$
, for
![]() $1\le i \le p$
, and
$1\le i \le p$
, and
![]() $E_iE_j =0$
if
$E_iE_j =0$
if
![]() $|i-j| \ge 2$
. It is easy to see that A is elliptic and
$|i-j| \ge 2$
. It is easy to see that A is elliptic and
![]() $E_0$
is the minimally elliptic cycle. Furthermore,
$E_0$
is the minimally elliptic cycle. Furthermore,
![]() $\mathfrak m$
is a
$\mathfrak m$
is a
![]() $p_g$
-ideal and
$p_g$
-ideal and
![]() $p_g(A)=p+1$
by [Reference Rees26, 3.1 and 3.10]. Since A is not strongly elliptic, there is a non-
$p_g(A)=p+1$
by [Reference Rees26, 3.1 and 3.10]. Since A is not strongly elliptic, there is a non-
![]() $p_g$
-ideal
$p_g$
-ideal
![]() $I_Z$
such that
$I_Z$
such that
![]() $-ZE_0=0$
(see Theorem 3.14 and Proposition 4.5). Let
$-ZE_0=0$
(see Theorem 3.14 and Proposition 4.5). Let
![]() $W=\sum _{i=0}^p(p+1-i)E_i$
. Then
$W=\sum _{i=0}^p(p+1-i)E_i$
. Then
![]() $-W\sim K_X$
and the exceptional part of the divisors
$-W\sim K_X$
and the exceptional part of the divisors
![]() $\operatorname {\mathrm {div}}_X(x)$
,
$\operatorname {\mathrm {div}}_X(x)$
,
![]() $\operatorname {\mathrm {div}}_X(y)$
, and
$\operatorname {\mathrm {div}}_X(y)$
, and
![]() $\operatorname {\mathrm {div}}_X(z)$
are
$\operatorname {\mathrm {div}}_X(z)$
are
![]() $3W$
,
$3W$
,
![]() $2W$
, and E, respectively. For
$2W$
, and E, respectively. For
![]() $1\le n \le p+1$
, let
$1\le n \le p+1$
, let
![]() $D_n=\gcd (nE, W):=\sum _{i=0}^p\min (n,p+1-i)E_i$
. (Our cycle
$D_n=\gcd (nE, W):=\sum _{i=0}^p\min (n,p+1-i)E_i$
. (Our cycle
![]() $D_n$
coincides with
$D_n$
coincides with
![]() $C_{n-1}$
in [Reference Okuma, Watanabe and Yoshida22, 2.6].) Then
$C_{n-1}$
in [Reference Okuma, Watanabe and Yoshida22, 2.6].) Then
![]() $\mathcal O_X(-2D_n)$
is generated (cf. [Reference Okuma, Watanabe and Yoshida22, 3.6(4)]) and
$\mathcal O_X(-2D_n)$
is generated (cf. [Reference Okuma, Watanabe and Yoshida22, 3.6(4)]) and
![]() $D_n^2=-n$
. Let
$D_n^2=-n$
. Let
![]() $I_n=I_{2D_n}$
. Since the cohomological cycle of
$I_n=I_{2D_n}$
. Since the cohomological cycle of
![]() $(D_n)^{\bot }$
is
$(D_n)^{\bot }$
is
![]() $W-D_n$
, we have
$W-D_n$
, we have
![]() $q(I_n)=p_g(A)-n$
by Proposition 4.5; note that
$q(I_n)=p_g(A)-n$
by Proposition 4.5; note that
![]() $-(W-D_n)\sim K_X$
on a neighborhood of
$-(W-D_n)\sim K_X$
on a neighborhood of
![]() $\operatorname {\mathrm {Supp}}(W-D_n)=E_0\cup \cdots \cup E_{p-n}$
. Then
$\operatorname {\mathrm {Supp}}(W-D_n)=E_0\cup \cdots \cup E_{p-n}$
. Then
![]() $I_n=(x,y,z^{2n})$
. We have
$I_n=(x,y,z^{2n})$
. We have
![]() $D_nE_0=0$
for
$D_nE_0=0$
for
![]() $1\le n\le p$
and
$1\le n\le p$
and
![]() $D_{p+1}E_0=E_0^2=-1$
. Therefore, it follows from Remark 3.24 that
$D_{p+1}E_0=E_0^2=-1$
. Therefore, it follows from Remark 3.24 that
![]() $\overline {I_{p+1}^2}\ne I_{p+1}^2$
, since
$\overline {I_{p+1}^2}\ne I_{p+1}^2$
, since
![]() $-2D_{p+1}E_0=2$
. However, the condition
$-2D_{p+1}E_0=2$
. However, the condition
![]() $0<-ZE_0\le 2$
is not necessary for
$0<-ZE_0\le 2$
is not necessary for
![]() $I_Z$
being not normal. In fact, we have
$I_Z$
being not normal. In fact, we have
![]() $\overline {I_{n}^2}\ne I_{n}^2$
for all
$\overline {I_{n}^2}\ne I_{n}^2$
for all
![]() $1\le n \le p+1$
because
$1\le n \le p+1$
because
![]() $xz^n\not \in I_n^2$
and
$xz^n\not \in I_n^2$
and
![]() $(xz^n)^2\in I_n^4$
.
$(xz^n)^2\in I_n^4$
.
4 The existence of strongly elliptic ideals
Motivated by the fact that in every two-dimensional excellent normal local domain which is not a rational singularity elliptic ideals always exist, it is natural to ask if it is also true for strongly elliptic ideals. We need some more preliminaries for proving that the answer is negative, in particular there are two-dimensional excellent normal local domains with no integrally closed
![]() $\mathfrak m$
-primary ideals I with
$\mathfrak m$
-primary ideals I with
![]() $\bar e_2(I)=1$
. Assume
$\bar e_2(I)=1$
. Assume
![]() $(A,\mathfrak m)$
is a two-dimensional excellent normal local domain over an algebraically closed field.
$(A,\mathfrak m)$
is a two-dimensional excellent normal local domain over an algebraically closed field.
Let
![]() $\pi \colon X \to \operatorname {\mathrm {Spec}} A $
be a resolution of singularity with exceptional set
$\pi \colon X \to \operatorname {\mathrm {Spec}} A $
be a resolution of singularity with exceptional set
![]() $E=\bigcup E_i$
.
$E=\bigcup E_i$
.
Definition 4.1. Let
![]() $D\ge 0$
be a cycle on X, and let
$D\ge 0$
be a cycle on X, and let
 $$ \begin{align*} h(D)=\max \left\{h^1(\mathcal O_{B}) \,\bigg| \,B \in \sum \mathbb Z E_i, \; B\ge 0, \; \operatorname{\mathrm{Supp}} (B)\subset \operatorname{\mathrm{Supp}} (D)\right\}. \end{align*} $$
$$ \begin{align*} h(D)=\max \left\{h^1(\mathcal O_{B}) \,\bigg| \,B \in \sum \mathbb Z E_i, \; B\ge 0, \; \operatorname{\mathrm{Supp}} (B)\subset \operatorname{\mathrm{Supp}} (D)\right\}. \end{align*} $$
We put
![]() $h^1(\mathcal O_{B})=0$
if
$h^1(\mathcal O_{B})=0$
if
![]() $B=0$
. There exists a unique minimal cycle
$B=0$
. There exists a unique minimal cycle
![]() $C\ge 0$
such that
$C\ge 0$
such that
![]() $h^1(\mathcal O_C)=h(D)$
(cf. [Reference Rossi and Valla30, 4.8]). We call C the cohomological cycle of D. The cohomological cycle of E is denoted by
$h^1(\mathcal O_C)=h(D)$
(cf. [Reference Rossi and Valla30, 4.8]). We call C the cohomological cycle of D. The cohomological cycle of E is denoted by
![]() $C_X$
.
$C_X$
.
Note that
![]() $p_g(A)=h(E)$
, and that if A is Gorenstein and
$p_g(A)=h(E)$
, and that if A is Gorenstein and
![]() $\pi $
is the minimal resolution, then the canonical cycle
$\pi $
is the minimal resolution, then the canonical cycle
![]() $Z_{K_X}=C_X$
(see [Reference Rossi and Valla30, 4.20]). Clearly, the minimally elliptic cycle is the cohomological cycle of itself.
$Z_{K_X}=C_X$
(see [Reference Rossi and Valla30, 4.20]). Clearly, the minimally elliptic cycle is the cohomological cycle of itself.
Remark 4.2. (1) If
![]() $C_1$
and
$C_1$
and
![]() $C_2$
are cohomological cycles of some cycles on X such that
$C_2$
are cohomological cycles of some cycles on X such that
![]() $C_1 \le C_2$
and
$C_1 \le C_2$
and
![]() $h^1(\mathcal O_{C_1})<h^1(C_2)$
, then
$h^1(\mathcal O_{C_1})<h^1(C_2)$
, then
![]() $\operatorname {\mathrm {Supp}}(C_1) \ne \operatorname {\mathrm {Supp}}(C_2)$
.
$\operatorname {\mathrm {Supp}}(C_1) \ne \operatorname {\mathrm {Supp}}(C_2)$
.
(2) In general, for
![]() $q<p_g(A)$
, cohomological cycle C with
$q<p_g(A)$
, cohomological cycle C with
![]() $h^1(\mathcal O_C)=q$
is not unique. For example, there exists a singularity whose minimal good resolution has two minimally elliptic cycles (e.g., [Reference Okuma, Watanabe and Yoshida20]).
$h^1(\mathcal O_C)=q$
is not unique. For example, there exists a singularity whose minimal good resolution has two minimally elliptic cycles (e.g., [Reference Okuma, Watanabe and Yoshida20]).
The following result is a generalization of [Reference Pinkham25, 2.6].
Proposition 4.3. Assume that
![]() $p_g(A)>0$
, and let
$p_g(A)>0$
, and let
![]() $D\ge 0$
be a reduced cycle on X. Then the cohomological cycle C of D is the minimal cycle such that
$D\ge 0$
be a reduced cycle on X. Then the cohomological cycle C of D is the minimal cycle such that
![]() $H^0(X\setminus D, \mathcal O_X(K_X))=H^0(X,\mathcal O_X(K_X+C))$
. Therefore, if
$H^0(X\setminus D, \mathcal O_X(K_X))=H^0(X,\mathcal O_X(K_X+C))$
. Therefore, if
![]() $g\:X'\to X$
is the blowing-up at a point in
$g\:X'\to X$
is the blowing-up at a point in
![]() $\operatorname {\mathrm {Supp}} C$
and
$\operatorname {\mathrm {Supp}} C$
and
![]() $E'$
the exceptional set for g, then the cohomological cycle
$E'$
the exceptional set for g, then the cohomological cycle
![]() $C'$
of
$C'$
of
![]() $g^*D$
satisfies that
$g^*D$
satisfies that
![]() $g_*^{-1}C \le C' \le g^*C-E'$
and
$g_*^{-1}C \le C' \le g^*C-E'$
and
![]() $h^1(\mathcal O_{C'})=h^1(\mathcal O_C);$
we have
$h^1(\mathcal O_{C'})=h^1(\mathcal O_C);$
we have
![]() $C'=g^*C-E'$
if
$C'=g^*C-E'$
if
![]() $\mathcal O_X(K_X+C)$
is generated at the center of the blowing-up.
$\mathcal O_X(K_X+C)$
is generated at the center of the blowing-up.
Proof. Let
![]() $F>0$
be an arbitrary cycle with
$F>0$
be an arbitrary cycle with
![]() $\operatorname {\mathrm {Supp}}(F)\subset D$
. By the duality, we have
$\operatorname {\mathrm {Supp}}(F)\subset D$
. By the duality, we have
![]() $h^1(\mathcal O_F)=h^0( \mathcal {O}_F(K_X+F))$
. From the exact sequence
$h^1(\mathcal O_F)=h^0( \mathcal {O}_F(K_X+F))$
. From the exact sequence
and the Grauert–Riemenschneider vanishing theorem, we have
On the other hand, we have the inclusion
where the equality holds if F is sufficiently large; if the equality holds, we obtain
![]() $h^1(\mathcal O_F)=h(D)$
, because the upper bound
$h^1(\mathcal O_F)=h(D)$
, because the upper bound
![]() $\ell _A(H^0(X\setminus D, \mathcal O_X(K_X))/H^0(X,\mathcal O_X(K_X)))$
for
$\ell _A(H^0(X\setminus D, \mathcal O_X(K_X))/H^0(X,\mathcal O_X(K_X)))$
for
![]() $h^1(\mathcal O_F)$
depends only on
$h^1(\mathcal O_F)$
depends only on
![]() $\operatorname {\mathrm {Supp}}(D)$
. Clearly, the minimum of such cycles F exists as the maximal poles of rational forms in
$\operatorname {\mathrm {Supp}}(D)$
. Clearly, the minimum of such cycles F exists as the maximal poles of rational forms in
![]() $H^0(X\setminus D, \mathcal O_X(K_X))$
. Let
$H^0(X\setminus D, \mathcal O_X(K_X))$
. Let
![]() $D'=g^{-1}(D)$
. Since
$D'=g^{-1}(D)$
. Since
![]() $K_{X'}+g^*C-E'=g^*(K_X+C)$
, we have
$K_{X'}+g^*C-E'=g^*(K_X+C)$
, we have
Hence,
![]() $C' \le g^*C-E'$
. The inequality
$C' \le g^*C-E'$
. The inequality
![]() $g_*^{-1}C \le C'$
is clear. From (4.1), we have
$g_*^{-1}C \le C'$
is clear. From (4.1), we have
![]() $h^1(\mathcal O_{C'})=h^1(\mathcal O_C)$
. If
$h^1(\mathcal O_{C'})=h^1(\mathcal O_C)$
. If
![]() $\mathcal O_X(K_X+C)$
is generated at the center of the blowing-up, then
$\mathcal O_X(K_X+C)$
is generated at the center of the blowing-up, then
![]() $\mathcal O_{X'}(K_{X'}+g^*C-E')$
has no fixed components, and the minimality of the cycle
$\mathcal O_{X'}(K_{X'}+g^*C-E')$
has no fixed components, and the minimality of the cycle
![]() $g^*C-E'$
follows.
$g^*C-E'$
follows.
Definition 4.4. We define a reduced cycle
![]() $Z^{\bot }$
to be the sum of the components
$Z^{\bot }$
to be the sum of the components
![]() $E_i\subset E$
such that
$E_i\subset E$
such that
![]() $ZE_i=0$
.
$ZE_i=0$
.
From [Reference Okuma, Watanabe and Yoshida24, 3.4], we have the following.
Proposition 4.5. Let
![]() $I=I_Z$
be represented by a cycle Z on X and denote by C the cohomological cycle of
$I=I_Z$
be represented by a cycle Z on X and denote by C the cohomological cycle of
![]() $Z^{\bot }$
. Assume
$Z^{\bot }$
. Assume
![]() $\bar {r}(I)=2$
, then
$\bar {r}(I)=2$
, then
![]() $\mathcal O_C(-Z)\cong \mathcal O_C$
and
$\mathcal O_C(-Z)\cong \mathcal O_C$
and
![]() $h^1(\mathcal O_C)=q(I)$
.
$h^1(\mathcal O_C)=q(I)$
.
The converse of the result above is described as follows.
Proposition 4.6. If C is the cohomological cycle of a cycle on X with
![]() $h^1(\mathcal O_C)=q>0$
, then there exist a resolution
$h^1(\mathcal O_C)=q>0$
, then there exist a resolution
![]() $Y\to \operatorname {\mathrm {Spec}} A$
and a cycle
$Y\to \operatorname {\mathrm {Spec}} A$
and a cycle
![]() $Z>0$
on Y such that
$Z>0$
on Y such that
![]() $\mathcal O_Y(-Z)$
is generated and
$\mathcal O_Y(-Z)$
is generated and
![]() $q(I_Z)=q(\infty I_Z)=q$
.
$q(I_Z)=q(\infty I_Z)=q$
.
Proof. There exists a cycle W on X such that
![]() $WE_i<0$
for all
$WE_i<0$
for all
![]() $E_i$
and
$E_i$
and
![]() $\mathcal O_X(-W)$
is generated (cf. the proof of [Reference Okuma, Watanabe and Yoshida23, 4.5]). Let
$\mathcal O_X(-W)$
is generated (cf. the proof of [Reference Okuma, Watanabe and Yoshida23, 4.5]). Let
![]() $h\in I_W$
be a general element. First, we show that there exist a resolution
$h\in I_W$
be a general element. First, we show that there exist a resolution
![]() $Y\to \operatorname {\mathrm {Spec}} A$
and a cohomological cycle D on Y with
$Y\to \operatorname {\mathrm {Spec}} A$
and a cohomological cycle D on Y with
![]() $h^1(\mathcal {O}_D)=q$
such that if
$h^1(\mathcal {O}_D)=q$
such that if
![]() $Z_h$
is the exceptional part of
$Z_h$
is the exceptional part of
![]() $\operatorname {\mathrm {div}}_Y(h)$
, then
$\operatorname {\mathrm {div}}_Y(h)$
, then
![]() $Z_h^{\bot }=D_{red}$
. We obtain the resolution Y from X by taking blowing-ups appropriately as follows. Let
$Z_h^{\bot }=D_{red}$
. We obtain the resolution Y from X by taking blowing-ups appropriately as follows. Let
![]() $H\subset X$
be an irreducible component of the proper transform of
$H\subset X$
be an irreducible component of the proper transform of
![]() $\operatorname {\mathrm {div}}_{\operatorname {\mathrm {Spec}} A}(h)$
intersecting C at a point p, and let
$\operatorname {\mathrm {div}}_{\operatorname {\mathrm {Spec}} A}(h)$
intersecting C at a point p, and let
![]() $g\:X'\to X$
be the blowing-up at p. Let
$g\:X'\to X$
be the blowing-up at p. Let
![]() $C'$
be the cohomological cycle of
$C'$
be the cohomological cycle of
![]() $g^*C$
. Then
$g^*C$
. Then
![]() $h^1(\mathcal O_{C'})=q$
by Proposition 4.3. If the intersection number
$h^1(\mathcal O_{C'})=q$
by Proposition 4.3. If the intersection number
![]() $C'(g_*^{-1}H)$
is positive, then we take again the blowing-up at the intersection point. By the property of the intersection number of curves and Proposition 4.3, taking blowing-ups in this manner, we obtain a resolution
$C'(g_*^{-1}H)$
is positive, then we take again the blowing-up at the intersection point. By the property of the intersection number of curves and Proposition 4.3, taking blowing-ups in this manner, we obtain a resolution
![]() $Y\to \operatorname {\mathrm {Spec}} A$
and a cohomological cycle D which satisfy the conditions described above; in fact, for an exceptional prime divisor F on Y, we have that
$Y\to \operatorname {\mathrm {Spec}} A$
and a cohomological cycle D which satisfy the conditions described above; in fact, for an exceptional prime divisor F on Y, we have that
![]() $F\le Z_h^{\bot }$
if and only if F does not intersect the proper transform of
$F\le Z_h^{\bot }$
if and only if F does not intersect the proper transform of
![]() $\operatorname {\mathrm {div}}_{\operatorname {\mathrm {Spec}} A}(h)$
. Thus, it follows from [Reference Okuma, Watanabe and Yoshida22, 3.6] (cf. [Reference Okuma, Watanabe and Yoshida24, 3.4]) that
$\operatorname {\mathrm {div}}_{\operatorname {\mathrm {Spec}} A}(h)$
. Thus, it follows from [Reference Okuma, Watanabe and Yoshida22, 3.6] (cf. [Reference Okuma, Watanabe and Yoshida24, 3.4]) that
![]() $\mathcal O_Y(-nZ_h)$
is generated and
$\mathcal O_Y(-nZ_h)$
is generated and
![]() $h^1(\mathcal O_Y(-nZ_h))=q$
for
$h^1(\mathcal O_Y(-nZ_h))=q$
for
![]() $n\ge p_g(A)$
. Then the cycle
$n\ge p_g(A)$
. Then the cycle
![]() $Z:=p_g(A)Z_h$
satisfies the assertion.
$Z:=p_g(A)Z_h$
satisfies the assertion.
Corollary 4.7. There exists a strongly elliptic ideal in A if and only if there exists a cohomological cycle C of a cycle on a resolution
![]() $Y\to \operatorname {\mathrm {Spec}} A$
such that
$Y\to \operatorname {\mathrm {Spec}} A$
such that
![]() $h^1(\mathcal O_C)=p_g(A)-1$
.
$h^1(\mathcal O_C)=p_g(A)-1$
.
Example 4.8. Let C be a nonsingular curve of genus
![]() $g\ge 2$
and D an divisor on C with
$g\ge 2$
and D an divisor on C with
![]() $\deg D>0$
. Let
$\deg D>0$
. Let
![]() $A= \bigoplus _{n\ge 0} H^0( C, \mathcal O_C( nD))$
, and assume that
$A= \bigoplus _{n\ge 0} H^0( C, \mathcal O_C( nD))$
, and assume that
![]() $a(A)=0$
. Then
$a(A)=0$
. Then
![]() $p_g(A)=g$
and A has no strongly elliptic ideals because any cycle F on any resolution has
$p_g(A)=g$
and A has no strongly elliptic ideals because any cycle F on any resolution has
![]() $h^1(\mathcal O_F)=0$
or g. More precisely, if
$h^1(\mathcal O_F)=0$
or g. More precisely, if
![]() $Z E_0 = 0$
, where
$Z E_0 = 0$
, where
![]() $E_0\subset E$
denotes the curve of genus g, then
$E_0\subset E$
denotes the curve of genus g, then
![]() $I_Z$
is a
$I_Z$
is a
![]() $p_g$
-ideal; otherwise,
$p_g$
-ideal; otherwise,
![]() $q(\infty I_Z)=0$
.
$q(\infty I_Z)=0$
.
Next example shows that there are local normal Gorenstein domains that always have strongly elliptic ideals.
Example 4.9. Let C be a nonsingular curve of genus
![]() $g\ge 2$
, and put
$g\ge 2$
, and put
 $$ \begin{align*} A=\bigoplus_{n\ge 0}H^0(\mathcal O_C(nK_C)). \end{align*} $$
$$ \begin{align*} A=\bigoplus_{n\ge 0}H^0(\mathcal O_C(nK_C)). \end{align*} $$
Then A is a normal Gorenstein ring by [Reference Watanabe39]. Suppose that
![]() $f: X\to \operatorname {\mathrm {Spec}} A$
is the minimal resolution. We have
$f: X\to \operatorname {\mathrm {Spec}} A$
is the minimal resolution. We have
 $$ \begin{align*} p_g(A)=\sum_{n\ge 0}h^1(\mathcal O_C(nK_C))=g+1 \end{align*} $$
$$ \begin{align*} p_g(A)=\sum_{n\ge 0}h^1(\mathcal O_C(nK_C))=g+1 \end{align*} $$
by Pinkham’s formula [Reference Röhr28],
![]() $E\cong C$
,
$E\cong C$
,
![]() $\mathcal O_E(-E)\cong \mathcal O_E(K_E)$
, and
$\mathcal O_E(-E)\cong \mathcal O_E(K_E)$
, and
![]() $K_X=-2E$
(cf. [Reference Okuma, Watanabe and Yoshida23, 4.6]). Let
$K_X=-2E$
(cf. [Reference Okuma, Watanabe and Yoshida23, 4.6]). Let
![]() $Y\to X$
be the blowing-up at a point
$Y\to X$
be the blowing-up at a point
![]() $p\in E$
, and let
$p\in E$
, and let
![]() $E_1$
be the fiber of p and
$E_1$
be the fiber of p and
![]() $E_0$
the proper transform of E. By Proposition 4.3, we have
$E_0$
the proper transform of E. By Proposition 4.3, we have
![]() $C_Y=2E_0+E_1$
. It follows from (b) of the theorem in [Reference Rossi and Valla30, 4.8] that
$C_Y=2E_0+E_1$
. It follows from (b) of the theorem in [Reference Rossi and Valla30, 4.8] that
![]() $h^1(\mathcal O_{E_0})\le h^1(\mathcal O_{nE_0})<p_g(A)$
for every
$h^1(\mathcal O_{E_0})\le h^1(\mathcal O_{nE_0})<p_g(A)$
for every
![]() $n\ge 1$
. Hence, the cohomological cycle of
$n\ge 1$
. Hence, the cohomological cycle of
![]() $E_0$
is
$E_0$
is
![]() $E_0$
and
$E_0$
and
![]() $h^1(\mathcal O_{E_0})=g=p_g(A)-1$
. Therefore, A has a strongly elliptic ideal by Corollary 4.7.
$h^1(\mathcal O_{E_0})=g=p_g(A)-1$
. Therefore, A has a strongly elliptic ideal by Corollary 4.7.
Next, we construct a strongly elliptic ideal. Take a general linear form
![]() $L\in A_1\subset A$
, and suppose that
$L\in A_1\subset A$
, and suppose that
![]() $\sup (\operatorname {\mathrm {div}}_X(L)-E)\cap E$
consists of
$\sup (\operatorname {\mathrm {div}}_X(L)-E)\cap E$
consists of
![]() $\deg K_C$
points
$\deg K_C$
points
![]() $p_1, \dots , p_{2g-2} \in E$
. Let
$p_1, \dots , p_{2g-2} \in E$
. Let
![]() $\phi : X'\to X$
be the blowing-up at
$\phi : X'\to X$
be the blowing-up at
![]() $\{p_1, \dots , p_{2g-2}\}$
, and let
$\{p_1, \dots , p_{2g-2}\}$
, and let
![]() $F_0$
be the proper transform of E and
$F_0$
be the proper transform of E and
![]() $F_i=\pi ^{-1}(p_i)$
. Let
$F_i=\pi ^{-1}(p_i)$
. Let
![]() $Z=F_0+2(F_1+\cdots +F_{2g-2})$
. Then
$Z=F_0+2(F_1+\cdots +F_{2g-2})$
. Then
![]() $\mathcal O_{X'}(-Z)$
is generated,
$\mathcal O_{X'}(-Z)$
is generated,
![]() $ZC_{X'}\ne 0$
, and
$ZC_{X'}\ne 0$
, and
![]() $ZF_0=0$
. Thus,
$ZF_0=0$
. Thus,
![]() $q(I_Z)=g=p_g(A)-1$
(cf. [Reference Okuma, Watanabe and Yoshida24, 3.4]). Moreover, we have that
$q(I_Z)=g=p_g(A)-1$
(cf. [Reference Okuma, Watanabe and Yoshida24, 3.4]). Moreover, we have that
![]() $\ell _A(A/I_Z)=g$
by Theorem 2.2 and
$\ell _A(A/I_Z)=g$
by Theorem 2.2 and
![]() $I_Z=\overline {\mathfrak m^2}+(L)$
. Note that if C is not hyperelliptic, then
$I_Z=\overline {\mathfrak m^2}+(L)$
. Note that if C is not hyperelliptic, then
![]() $\mathfrak m^2$
is normal, because A is a standard graded ring.
$\mathfrak m^2$
is normal, because A is a standard graded ring.
Acknowledgments
We would like to thank Dr. János Nagy and Professor András Némethi for their remark on Proposition 4.3. We would also like to thank the referee for useful suggestions that improved the presentation of the paper. Kei-ichi Watanabe would like to thank the Department of Mathematics of the University of Genoa for the hospitality during his stay in Genoa, where this joint work started.