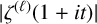 $|\zeta ^{(\ell )}(1+{i}t)|$
$|\zeta ^{(\ell )}(1+{i}t)|$Published online by Cambridge University Press: 05 January 2023
We investigate the large values of the derivatives of the Riemann zeta function 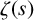 $\zeta (s)$ on the 1-line. We give a larger lower bound for
$\zeta (s)$ on the 1-line. We give a larger lower bound for 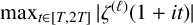 $\max _{t\in [T,2T]}|\zeta ^{(\ell )}(1+{i} t)|$, which improves the previous result established by Yang [‘Extreme values of derivatives of the Riemann zeta function’, Mathematika 68 (2022), 486–510].
$\max _{t\in [T,2T]}|\zeta ^{(\ell )}(1+{i} t)|$, which improves the previous result established by Yang [‘Extreme values of derivatives of the Riemann zeta function’, Mathematika 68 (2022), 486–510].
The first author is supported by the China Scholarship Council (CSC) for his study in France. The second author is supported by Natural Science Foundation of Tianjin City (Grant No. 19JCQNJC14200).