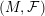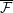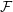1 Introduction
Given a Riemannian manifold
![]() $M$
, a singular Riemannian foliation
$M$
, a singular Riemannian foliation
![]() ${\mathcal{F}}$
on
${\mathcal{F}}$
on
![]() $M$
is, roughly speaking, a partition of
$M$
is, roughly speaking, a partition of
![]() $M$
into smooth connected and locally equidistant submanifolds of possibly varying dimension (the leaves of
$M$
into smooth connected and locally equidistant submanifolds of possibly varying dimension (the leaves of
![]() ${\mathcal{F}}$
), which is spanned by a family of smooth vector fields. The precise definition, given in § 2, was suggested by Molino, by combining the concepts of transnormal system of Bolton [Reference BoltonBol73] and of singular foliation by Sussmann [Reference SussmannSus73].
${\mathcal{F}}$
), which is spanned by a family of smooth vector fields. The precise definition, given in § 2, was suggested by Molino, by combining the concepts of transnormal system of Bolton [Reference BoltonBol73] and of singular foliation by Sussmann [Reference SussmannSus73].
A typical example of a singular Riemannian foliation is the decomposition of a Riemannian manifold
![]() $M$
into the orbits of an isometric group action
$M$
into the orbits of an isometric group action
![]() $G$
on
$G$
on
![]() $M$
. Such a foliation is called homogeneous. Another example of a foliation is given by the partition of a Euclidean vector bundle
$M$
. Such a foliation is called homogeneous. Another example of a foliation is given by the partition of a Euclidean vector bundle
![]() $E\rightarrow L$
, endowed with a metric connection, into the holonomy tubes around the zero section (cf. Example 2.7). Such a foliation, which we call a holonomy foliation, will be a sort-of prototype in the structural results that will appear later on. Holonomy foliations are in general not homogeneous (the zero section
$E\rightarrow L$
, endowed with a metric connection, into the holonomy tubes around the zero section (cf. Example 2.7). Such a foliation, which we call a holonomy foliation, will be a sort-of prototype in the structural results that will appear later on. Holonomy foliations are in general not homogeneous (the zero section
![]() $L$
is always a leaf but in general not a homogeneous manifold); however, they are locally homogeneous, in the sense that the infinitesimal foliation at every point of
$L$
is always a leaf but in general not a homogeneous manifold); however, they are locally homogeneous, in the sense that the infinitesimal foliation at every point of
![]() $E$
is homogeneous (cf. §§ 2.3 and 2.4). This construction is related to other important types of foliations, like polar foliations [Reference ToebenToe06] or Wilking’s dual foliation to the Sharafutdinov projection [Reference WilkingWil07]; see Remark 2.8.
$E$
is homogeneous (cf. §§ 2.3 and 2.4). This construction is related to other important types of foliations, like polar foliations [Reference ToebenToe06] or Wilking’s dual foliation to the Sharafutdinov projection [Reference WilkingWil07]; see Remark 2.8.
In general, the leaves of a singular Riemannian foliation might not be closed, even in the simple cases defined above. In the homogeneous case, consider for example the foliation on the flat torus
![]() $T^{2}$
by parallel lines, of irrational slope. These are non-closed orbits of an isometric
$T^{2}$
by parallel lines, of irrational slope. These are non-closed orbits of an isometric
![]() $\mathbb{R}$
-action on
$\mathbb{R}$
-action on
![]() $T^{2}$
.
$T^{2}$
.
Given a (regular) Riemannian foliation
![]() $(M,{\mathcal{F}})$
with non-closed leaves, Molino proved that replacing the leaves of
$(M,{\mathcal{F}})$
with non-closed leaves, Molino proved that replacing the leaves of
![]() ${\mathcal{F}}$
with their closure yields a new singular Riemannian foliation
${\mathcal{F}}$
with their closure yields a new singular Riemannian foliation
![]() $\overline{{\mathcal{F}}}$
(cf. [Reference MolinoMol88, ch. 5]). Moreover, he conjectured that the same result should hold true if one starts with a singular Riemannian foliation and this has become known, in recent decades, as Molino’s conjecture.
$\overline{{\mathcal{F}}}$
(cf. [Reference MolinoMol88, ch. 5]). Moreover, he conjectured that the same result should hold true if one starts with a singular Riemannian foliation and this has become known, in recent decades, as Molino’s conjecture.
Molino proved that the closure
![]() $\overline{{\mathcal{F}}}$
of a singular Riemannian foliation
$\overline{{\mathcal{F}}}$
of a singular Riemannian foliation
![]() $(M,{\mathcal{F}})$
is a transnormal system [Reference MolinoMol88], thus leaving to prove that it is a singular foliation as well. Moreover, in [Reference Molino and MizutaniMol94] he suggested a strategy to prove the conjecture for the case of orbit-like foliations, i.e. foliations which, roughly speaking, are locally diffeomorphic to the orbits of some proper isometric group action around each point (cf. § 2.4). A formal alternative proof in this case can be found in [Reference Alexandrino and RadeschiAR17]. Molino’s conjecture was also proved for polar foliations and then infinitesimally polar foliations in [Reference AlexandrinoAle06] and [Reference Alexandrino and LytchakAL11], respectively.
$(M,{\mathcal{F}})$
is a transnormal system [Reference MolinoMol88], thus leaving to prove that it is a singular foliation as well. Moreover, in [Reference Molino and MizutaniMol94] he suggested a strategy to prove the conjecture for the case of orbit-like foliations, i.e. foliations which, roughly speaking, are locally diffeomorphic to the orbits of some proper isometric group action around each point (cf. § 2.4). A formal alternative proof in this case can be found in [Reference Alexandrino and RadeschiAR17]. Molino’s conjecture was also proved for polar foliations and then infinitesimally polar foliations in [Reference AlexandrinoAle06] and [Reference Alexandrino and LytchakAL11], respectively.
These partial results do not cover every possible foliation. Since the 1980s there are examples of non-orbit-like foliations and, in recent years, there was shown the existence of a remarkably large class of ‘infinitesimal’ foliations that are neither homogeneous nor polar, the so-called Clifford foliations [Reference RadeschiRad14] (these infinitesimal foliations have been shown, however, to have an algebraic nature; cf. [Reference Lytchak and RadeschiLR16]). Therefore, it is important to give a complete answer to the conjecture, to fully understand the semi-local dynamic of singular Riemannian foliations.
The goal of this paper is to prove the full Molino’s conjecture.
Theorem (Molino’s conjecture). Let
![]() $(M,{\mathcal{F}})$
be a singular Riemannian foliation on a complete manifold
$(M,{\mathcal{F}})$
be a singular Riemannian foliation on a complete manifold
![]() $M$
and let
$M$
and let
![]() $\overline{{\mathcal{F}}}=\{\overline{L}\mid L\in {\mathcal{F}}\}$
be the partition of
$\overline{{\mathcal{F}}}=\{\overline{L}\mid L\in {\mathcal{F}}\}$
be the partition of
![]() $M$
into the closures of the leaves of
$M$
into the closures of the leaves of
![]() ${\mathcal{F}}$
. Then
${\mathcal{F}}$
. Then
![]() $(M,\overline{{\mathcal{F}}})$
is a singular Riemannian foliation.
$(M,\overline{{\mathcal{F}}})$
is a singular Riemannian foliation.
This result is in fact a direct consequence of the following.
Main theorem. Let
![]() $(M,{\mathcal{F}})$
be a singular Riemannian foliation, let
$(M,{\mathcal{F}})$
be a singular Riemannian foliation, let
![]() $L$
be a (possibly not closed) leaf, and let
$L$
be a (possibly not closed) leaf, and let
![]() $U$
be an
$U$
be an
![]() $\unicode[STIX]{x1D716}$
-neighbourhood around the closure of
$\unicode[STIX]{x1D716}$
-neighbourhood around the closure of
![]() $L$
. Then for
$L$
. Then for
![]() $\unicode[STIX]{x1D716}$
small enough, there are a metric
$\unicode[STIX]{x1D716}$
small enough, there are a metric
![]() $\text{g}^{\ell }$
on
$\text{g}^{\ell }$
on
![]() $U$
and a singular foliation
$U$
and a singular foliation
![]() $\widehat{{\mathcal{F}}}^{\ell }$
such that:
$\widehat{{\mathcal{F}}}^{\ell }$
such that:
-
(1)
 $(U,\text{g}^{\ell },\widehat{{\mathcal{F}}}^{\ell })$
is an orbit-like singular Riemannian foliation;
$(U,\text{g}^{\ell },\widehat{{\mathcal{F}}}^{\ell })$
is an orbit-like singular Riemannian foliation; -
(2) the foliation
 $\widehat{{\mathcal{F}}}^{\ell }$
coincides with
$\widehat{{\mathcal{F}}}^{\ell }$
coincides with
 ${\mathcal{F}}$
on
${\mathcal{F}}$
on
 $\overline{L}$
;
$\overline{L}$
; -
(3) the closure of
 $\widehat{{\mathcal{F}}}^{\ell }$
is contained in the closure of
$\widehat{{\mathcal{F}}}^{\ell }$
is contained in the closure of
 ${\mathcal{F}}$
.
${\mathcal{F}}$
.
In short, the foliation
![]() $\widehat{{\mathcal{F}}}^{\ell }$
is obtained by first constructing the linearized foliation
$\widehat{{\mathcal{F}}}^{\ell }$
is obtained by first constructing the linearized foliation
![]() ${\mathcal{F}}^{\ell }$
of
${\mathcal{F}}^{\ell }$
of
![]() ${\mathcal{F}}$
in
${\mathcal{F}}$
in
![]() $U$
, which is a subfoliation of
$U$
, which is a subfoliation of
![]() ${\mathcal{F}}$
spanned by the first-order approximations, around
${\mathcal{F}}$
spanned by the first-order approximations, around
![]() $L$
, of the vector fields tangent to
$L$
, of the vector fields tangent to
![]() ${\mathcal{F}}$
(see § 2.5 for a precise definition). The foliation
${\mathcal{F}}$
(see § 2.5 for a precise definition). The foliation
![]() $\widehat{{\mathcal{F}}}^{\ell }$
is then obtained from
$\widehat{{\mathcal{F}}}^{\ell }$
is then obtained from
![]() ${\mathcal{F}}^{\ell }$
by taking the ‘local closure’ of the leaves of
${\mathcal{F}}^{\ell }$
by taking the ‘local closure’ of the leaves of
![]() ${\mathcal{F}}^{\ell }$
. The foliations
${\mathcal{F}}^{\ell }$
. The foliations
![]() ${\mathcal{F}},{\mathcal{F}}^{\ell },\widehat{{\mathcal{F}}}^{\ell }$
, together with their closures, are then related by the following inclusions:
${\mathcal{F}},{\mathcal{F}}^{\ell },\widehat{{\mathcal{F}}}^{\ell }$
, together with their closures, are then related by the following inclusions:

Example 1.1. Consider a Euclidean vector bundle
![]() $E$
over a complete Riemannian manifold
$E$
over a complete Riemannian manifold
![]() $L$
, with a metric connection
$L$
, with a metric connection
![]() $\unicode[STIX]{x1D6FB}^{E}$
and a connection metric
$\unicode[STIX]{x1D6FB}^{E}$
and a connection metric
![]() $g^{E}$
(cf. Example 2.7). Let
$g^{E}$
(cf. Example 2.7). Let
![]() $H_{p}$
denote the holonomy group of
$H_{p}$
denote the holonomy group of
![]() $(E,\unicode[STIX]{x1D6FB}^{E})$
at
$(E,\unicode[STIX]{x1D6FB}^{E})$
at
![]() $p$
, acting by isometries on the Euclidean fiber
$p$
, acting by isometries on the Euclidean fiber
![]() $E_{p}$
, and let
$E_{p}$
, and let
![]() $(E_{p},{\mathcal{F}}_{p}^{0})$
be a singular Riemannian foliation preserved by the
$(E_{p},{\mathcal{F}}_{p}^{0})$
be a singular Riemannian foliation preserved by the
![]() $H_{p}$
-action. Finally, let
$H_{p}$
-action. Finally, let
![]() $K_{p}$
be the maximal connected group of isometries of
$K_{p}$
be the maximal connected group of isometries of
![]() $E_{p}$
that fixes each leaf of
$E_{p}$
that fixes each leaf of
![]() ${\mathcal{F}}_{p}^{0}$
as a set.
${\mathcal{F}}_{p}^{0}$
as a set.
Letting
![]() ${\mathcal{F}}$
be the partition of
${\mathcal{F}}$
be the partition of
![]() $E$
into the holonomy translates of the leaves of
$E$
into the holonomy translates of the leaves of
![]() ${\mathcal{F}}_{p}^{0}$
(i.e. for every leaf
${\mathcal{F}}_{p}^{0}$
(i.e. for every leaf
![]() ${\mathcal{L}}\in {\mathcal{F}}_{p}^{0}$
,
${\mathcal{L}}\in {\mathcal{F}}_{p}^{0}$
,
![]() $L_{{\mathcal{L}}}$
denotes the set of points in
$L_{{\mathcal{L}}}$
denotes the set of points in
![]() $E$
that can be reached via
$E$
that can be reached via
![]() $\unicode[STIX]{x1D6FB}^{E}$
-parallel translation from a point in
$\unicode[STIX]{x1D6FB}^{E}$
-parallel translation from a point in
![]() ${\mathcal{L}}$
), then
${\mathcal{L}}$
), then
![]() ${\mathcal{F}}$
is a singular Riemannian foliation. In this case, the linearized foliation
${\mathcal{F}}$
is a singular Riemannian foliation. In this case, the linearized foliation
![]() ${\mathcal{F}}^{\ell }$
is the foliation by the holonomy translates of the
${\mathcal{F}}^{\ell }$
is the foliation by the holonomy translates of the
![]() $K_{p}$
-orbits in
$K_{p}$
-orbits in
![]() $E_{p}$
, and the local closure of
$E_{p}$
, and the local closure of
![]() $\widehat{{\mathcal{F}}}^{\ell }$
is the foliation by the holonomy translates of the
$\widehat{{\mathcal{F}}}^{\ell }$
is the foliation by the holonomy translates of the
![]() $\overline{K}_{p}$
-orbits in
$\overline{K}_{p}$
-orbits in
![]() $E_{p}$
, where
$E_{p}$
, where
![]() $\overline{K}_{p}$
denotes the closure of
$\overline{K}_{p}$
denotes the closure of
![]() $K_{p}$
in
$K_{p}$
in
![]() $\mathsf{O}(E_{p})$
.
$\mathsf{O}(E_{p})$
.
This can be restated in the language of groupoids: defining
![]() $H$
as the holonomy groupoid of the connection
$H$
as the holonomy groupoid of the connection
![]() $\unicode[STIX]{x1D6FB}^{E}$
, then
$\unicode[STIX]{x1D6FB}^{E}$
, then
![]() ${\mathcal{F}}=\{H({\mathcal{L}})\mid {\mathcal{L}}\in {\mathcal{F}}_{p}^{0}\}$
,
${\mathcal{F}}=\{H({\mathcal{L}})\mid {\mathcal{L}}\in {\mathcal{F}}_{p}^{0}\}$
,
![]() ${\mathcal{F}}^{\ell }$
is given by the orbits of
${\mathcal{F}}^{\ell }$
is given by the orbits of
![]() $HK_{p}$
, and its local closure
$HK_{p}$
, and its local closure
![]() $\hat{{\mathcal{F}}}^{\ell }$
is given by the orbits of
$\hat{{\mathcal{F}}}^{\ell }$
is given by the orbits of
![]() $H\overline{K}_{p}$
.
$H\overline{K}_{p}$
.
This paper is organized as follows: after a section of preliminaries (§ 2) we show how Molino’s conjecture follows from the main theorem (§ 3). In § 4 we fix the setup in which we work for the rest of the paper. In § 5 we define three distributions of the tangent bundle
![]() $TU$
. We first use these to obtain information on the local structure of
$TU$
. We first use these to obtain information on the local structure of
![]() ${\mathcal{F}}^{\ell }$
and define the local closure
${\mathcal{F}}^{\ell }$
and define the local closure
![]() $\widehat{{\mathcal{F}}}^{\ell }$
(§ 6) and then to define the metric
$\widehat{{\mathcal{F}}}^{\ell }$
(§ 6) and then to define the metric
![]() $\text{g}^{\ell }$
used in the main theorem (§ 7). In this final section we also prove the main theorem.
$\text{g}^{\ell }$
used in the main theorem (§ 7). In this final section we also prove the main theorem.
2 Preliminaries
Given a Riemannian manifold
![]() $(M,\text{g})$
, a partition
$(M,\text{g})$
, a partition
![]() ${\mathcal{F}}$
of
${\mathcal{F}}$
of
![]() $M$
into complete connected submanifolds (the leaves of
$M$
into complete connected submanifolds (the leaves of
![]() ${\mathcal{F}}$
) is called a transnormal system if geodesics starting perpendicular to a leaf stay perpendicular to all leaves, and a singular foliation if every vector tangent to a leaf can be locally extended to a vector field everywhere tangent to the leaves.
${\mathcal{F}}$
) is called a transnormal system if geodesics starting perpendicular to a leaf stay perpendicular to all leaves, and a singular foliation if every vector tangent to a leaf can be locally extended to a vector field everywhere tangent to the leaves.
A singular Riemannian foliation will be denoted by the triple
![]() $(M,\text{g},{\mathcal{F}})$
. However, if the Riemannian metric of
$(M,\text{g},{\mathcal{F}})$
. However, if the Riemannian metric of
![]() $M$
is understood, we will drop it and simply write
$M$
is understood, we will drop it and simply write
![]() $(M,{\mathcal{F}})$
.
$(M,{\mathcal{F}})$
.
The following notation will be used throughout the rest of the paper. Given a point
![]() $p\in M$
, the leaf of
$p\in M$
, the leaf of
![]() ${\mathcal{F}}$
through
${\mathcal{F}}$
through
![]() $p$
will be denoted by
$p$
will be denoted by
![]() $L_{p}$
. A small relatively compact open subset
$L_{p}$
. A small relatively compact open subset
![]() $P\subset L$
is called a plaque. The tangent and normal spaces to
$P\subset L$
is called a plaque. The tangent and normal spaces to
![]() $L_{p}$
at
$L_{p}$
at
![]() $p$
are denoted by
$p$
are denoted by
![]() $T_{p}L_{p}$
and
$T_{p}L_{p}$
and
![]() $\unicode[STIX]{x1D708}_{p}L_{p}$
, respectively. Given some
$\unicode[STIX]{x1D708}_{p}L_{p}$
, respectively. Given some
![]() $\unicode[STIX]{x1D716}>0$
,
$\unicode[STIX]{x1D716}>0$
,
![]() $\unicode[STIX]{x1D708}_{p}^{\unicode[STIX]{x1D716}}L_{p}$
denotes the set of vectors
$\unicode[STIX]{x1D708}_{p}^{\unicode[STIX]{x1D716}}L_{p}$
denotes the set of vectors
![]() $x\in \unicode[STIX]{x1D708}_{p}L_{p}$
with norm
$x\in \unicode[STIX]{x1D708}_{p}L_{p}$
with norm
![]() ${<}\unicode[STIX]{x1D716}$
. If
${<}\unicode[STIX]{x1D716}$
. If
![]() $\unicode[STIX]{x1D716}$
is small enough that the normal exponential map
$\unicode[STIX]{x1D716}$
is small enough that the normal exponential map
![]() $\exp :\unicode[STIX]{x1D708}_{p}^{\unicode[STIX]{x1D716}}L_{p}\rightarrow M$
is a diffeomorphism onto the image, such image is called a slice of
$\exp :\unicode[STIX]{x1D708}_{p}^{\unicode[STIX]{x1D716}}L_{p}\rightarrow M$
is a diffeomorphism onto the image, such image is called a slice of
![]() $L_{p}$
at
$L_{p}$
at
![]() $p$
and it is denoted by
$p$
and it is denoted by
![]() $S_{p}$
. The slice foliation
$S_{p}$
. The slice foliation
![]() ${\mathcal{F}}|_{S_{p}}$
denotes the partition of
${\mathcal{F}}|_{S_{p}}$
denotes the partition of
![]() $S_{p}$
into the connected components of the intersections
$S_{p}$
into the connected components of the intersections
![]() $L\cap S_{p}$
, where
$L\cap S_{p}$
, where
![]() $L\in {\mathcal{F}}$
.
$L\in {\mathcal{F}}$
.
2.1 Vector fields of a singular Riemannian foliation
We review here the main notations about vector fields of a singular Riemannian foliation.
A vector field
![]() $V$
is called vertical if it is tangent to the leaves at each point. The set of smooth vertical vector fields is a Lie algebra, which is denoted by
$V$
is called vertical if it is tangent to the leaves at each point. The set of smooth vertical vector fields is a Lie algebra, which is denoted by
![]() $\mathfrak{X}(M,{\mathcal{F}})$
.
$\mathfrak{X}(M,{\mathcal{F}})$
.
A vector field
![]() $X$
is called foliated if its flow takes leaves to leaves or, equivalently, if
$X$
is called foliated if its flow takes leaves to leaves or, equivalently, if
![]() $[X,V]\in \mathfrak{X}(M,{\mathcal{F}})$
for every
$[X,V]\in \mathfrak{X}(M,{\mathcal{F}})$
for every
![]() $V\in \mathfrak{X}(M,{\mathcal{F}})$
. Any vertical vector field is foliated, but there are other foliated vector fields. A vector field is called basic if it is both foliated and everywhere normal to the leaves.
$V\in \mathfrak{X}(M,{\mathcal{F}})$
. Any vertical vector field is foliated, but there are other foliated vector fields. A vector field is called basic if it is both foliated and everywhere normal to the leaves.
2.2 Homothetic transformation lemma
One of the most fundamental results in the theory of singular Riemannian foliations is the homothetic transformation lemma. A deeper discussion of this lemma, with proof and applications, can be found in Molino [Reference MolinoMol88, ch. 6], in particular Lemma 6.1 and Proposition 6.7.
Let
![]() $(M,{\mathcal{F}})$
be a singular foliation, let
$(M,{\mathcal{F}})$
be a singular foliation, let
![]() $L$
be a leaf of
$L$
be a leaf of
![]() ${\mathcal{F}}$
, and let
${\mathcal{F}}$
, and let
![]() $P\subset L$
be a plaque. Let
$P\subset L$
be a plaque. Let
![]() $\unicode[STIX]{x1D716}>0$
be such that the normal exponential map
$\unicode[STIX]{x1D716}>0$
be such that the normal exponential map
![]() $\exp :\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D716}}P\rightarrow M$
is a diffeomorphism onto its image
$\exp :\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D716}}P\rightarrow M$
is a diffeomorphism onto its image
![]() $B_{\unicode[STIX]{x1D716}}(P)$
. For any two radii
$B_{\unicode[STIX]{x1D716}}(P)$
. For any two radii
![]() $r_{1},r_{2}=\unicode[STIX]{x1D706}r_{1}$
in
$r_{1},r_{2}=\unicode[STIX]{x1D706}r_{1}$
in
![]() $(0,\unicode[STIX]{x1D716})$
, it makes sense to define the homothetic transformation
$(0,\unicode[STIX]{x1D716})$
, it makes sense to define the homothetic transformation
The leaves of
![]() ${\mathcal{F}}$
intersect
${\mathcal{F}}$
intersect
![]() $B_{r_{i}}(P)$
,
$B_{r_{i}}(P)$
,
![]() $i=1,2$
, in plaques that foliate
$i=1,2$
, in plaques that foliate
![]() $B_{r_{i}}(P)$
. We call
$B_{r_{i}}(P)$
. We call
![]() ${\mathcal{F}}|_{B_{r_{i}}(P)}$
the foliation of
${\mathcal{F}}|_{B_{r_{i}}(P)}$
the foliation of
![]() $B_{r_{i}}(P)$
into the path components of such intersections. One then has the following result.
$B_{r_{i}}(P)$
into the path components of such intersections. One then has the following result.
Theorem 2.1 (Homothetic transformation lemma).
The homothetic transformation
![]() $h_{\unicode[STIX]{x1D706}}$
takes the leaves of
$h_{\unicode[STIX]{x1D706}}$
takes the leaves of
![]() $(B_{r_{1}},{\mathcal{F}}|_{B_{r_{1}}(P)})$
onto the leaves of
$(B_{r_{1}},{\mathcal{F}}|_{B_{r_{1}}(P)})$
onto the leaves of
![]() $(B_{r_{2}},{\mathcal{F}}|_{B_{r_{2}}(P)})$
.
$(B_{r_{2}},{\mathcal{F}}|_{B_{r_{2}}(P)})$
.
This result still holds, more generally, if we replace the plaque
![]() $P$
by an open subset
$P$
by an open subset
![]() $B$
of some submanifold
$B$
of some submanifold
![]() $N\subset M$
which is a union of leaves of the same dimension. In this case, we consider some
$N\subset M$
which is a union of leaves of the same dimension. In this case, we consider some
![]() $\unicode[STIX]{x1D716}>0$
such that
$\unicode[STIX]{x1D716}>0$
such that
![]() $\exp :\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D716}}B\rightarrow M$
is a diffeomorphism onto the image
$\exp :\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D716}}B\rightarrow M$
is a diffeomorphism onto the image
![]() $B_{\unicode[STIX]{x1D716}}(B)$
, and define the homothetic transformation around
$B_{\unicode[STIX]{x1D716}}(B)$
, and define the homothetic transformation around
![]() $B$
,
$B$
,
![]() $h_{\unicode[STIX]{x1D706}}:B_{r}(B)\rightarrow B_{\unicode[STIX]{x1D706}r}(B)$
, as before. In this case, an analogous version of the homothetic transformation lemma applies.
$h_{\unicode[STIX]{x1D706}}:B_{r}(B)\rightarrow B_{\unicode[STIX]{x1D706}r}(B)$
, as before. In this case, an analogous version of the homothetic transformation lemma applies.
2.3 Infinitesimal foliation
Let
![]() $(M,{\mathcal{F}})$
be a singular Riemannian foliation,
$(M,{\mathcal{F}})$
be a singular Riemannian foliation,
![]() $p\in M$
a point, and
$p\in M$
a point, and
![]() $S_{p}$
a slice at
$S_{p}$
a slice at
![]() $p$
.
$p$
.
Definition 2.2 (Infinitesimal foliation at
 $p$
).
$p$
).
The infinitesimal foliation of
![]() ${\mathcal{F}}$
at
${\mathcal{F}}$
at
![]() $p$
, denoted by
$p$
, denoted by
![]() $(\unicode[STIX]{x1D708}_{p}L_{p},{\mathcal{F}}_{p})$
, is defined as the partition of
$(\unicode[STIX]{x1D708}_{p}L_{p},{\mathcal{F}}_{p})$
, is defined as the partition of
![]() $\unicode[STIX]{x1D708}_{p}L_{p}$
whose leaf at
$\unicode[STIX]{x1D708}_{p}L_{p}$
whose leaf at
![]() $v\in \unicode[STIX]{x1D708}_{p}L_{p}$
is given by
$v\in \unicode[STIX]{x1D708}_{p}L_{p}$
is given by
where
![]() $L_{\text{exp}_{p}tv}$
denotes the leaf of
$L_{\text{exp}_{p}tv}$
denotes the leaf of
![]() $(S_{p},{\mathcal{F}}|_{S_{p}})$
through
$(S_{p},{\mathcal{F}}|_{S_{p}})$
through
![]() $\exp _{p}tv$
.
$\exp _{p}tv$
.
The leaf
![]() $L_{v}$
is well defined because, by the homothetic transformation lemma, if
$L_{v}$
is well defined because, by the homothetic transformation lemma, if
![]() $\exp _{p}t_{0}w$
belongs to the same leaf of
$\exp _{p}t_{0}w$
belongs to the same leaf of
![]() $\exp _{p}t_{0}v$
for some small
$\exp _{p}t_{0}v$
for some small
![]() $t_{0}$
, then
$t_{0}$
, then
![]() $\exp _{p}tw$
belongs to the same leaf of
$\exp _{p}tw$
belongs to the same leaf of
![]() $\exp _{p}tv$
for every
$\exp _{p}tv$
for every
![]() $t\in (0,t_{0})$
. In the following proposition we collect the important facts about infinitesimal foliations that we will need.
$t\in (0,t_{0})$
. In the following proposition we collect the important facts about infinitesimal foliations that we will need.
Theorem 2.3. Given a singular Riemannian foliation
![]() $(M,{\mathcal{F}})$
and a point
$(M,{\mathcal{F}})$
and a point
![]() $p\in M$
with infinitesimal foliation
$p\in M$
with infinitesimal foliation
![]() $(\unicode[STIX]{x1D708}_{p}L_{p},{\mathcal{F}}_{p})$
, then:
$(\unicode[STIX]{x1D708}_{p}L_{p},{\mathcal{F}}_{p})$
, then:
-
(1) the foliation
 $(\unicode[STIX]{x1D708}_{p}L_{p},{\mathcal{F}}_{p})$
is a singular Riemannian foliation with respect to the flat metric
$(\unicode[STIX]{x1D708}_{p}L_{p},{\mathcal{F}}_{p})$
is a singular Riemannian foliation with respect to the flat metric
 $\text{g}_{p}$
at
$\text{g}_{p}$
at
 $p$
;
$p$
; -
(2) the normal exponential map
 $\exp _{p}:\unicode[STIX]{x1D708}_{p}^{\unicode[STIX]{x1D716}}L_{p}\rightarrow M$
sends the leaves of
$\exp _{p}:\unicode[STIX]{x1D708}_{p}^{\unicode[STIX]{x1D716}}L_{p}\rightarrow M$
sends the leaves of
 ${\mathcal{F}}_{p}$
to the leaves of
${\mathcal{F}}_{p}$
to the leaves of
 $(S_{p},{\mathcal{F}}|_{S_{p}})$
;
$(S_{p},{\mathcal{F}}|_{S_{p}})$
; -
(3)
 $(\unicode[STIX]{x1D708}_{p}L_{p},{\mathcal{F}}_{p})$
is invariant under rescalings
$(\unicode[STIX]{x1D708}_{p}L_{p},{\mathcal{F}}_{p})$
is invariant under rescalings
 $r_{\unicode[STIX]{x1D706}}:\unicode[STIX]{x1D708}_{p}L_{p}\rightarrow \unicode[STIX]{x1D708}_{p}L_{p}$
,
$r_{\unicode[STIX]{x1D706}}:\unicode[STIX]{x1D708}_{p}L_{p}\rightarrow \unicode[STIX]{x1D708}_{p}L_{p}$
,
 $r_{\unicode[STIX]{x1D706}}(v)=\unicode[STIX]{x1D706}v$
.
$r_{\unicode[STIX]{x1D706}}(v)=\unicode[STIX]{x1D706}v$
.
Proof. (1) [Reference MolinoMol88, Proposition 6.5].
(2) Follows from the definitions of infinitesimal foliation and of slice foliation.
(3) Via the exponential map
![]() $\exp :\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D716}}L_{p}\rightarrow S_{p}$
, this corresponds to the homothetic transformation lemma on
$\exp :\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D716}}L_{p}\rightarrow S_{p}$
, this corresponds to the homothetic transformation lemma on
![]() $S_{p}$
.◻
$S_{p}$
.◻
The following fact will become very useful.
Proposition 2.4. Given singular Riemannian foliations
![]() $(M,{\mathcal{F}})$
,
$(M,{\mathcal{F}})$
,
![]() $(M^{\prime },{\mathcal{F}}^{\prime })$
and a foliated diffeomorphism
$(M^{\prime },{\mathcal{F}}^{\prime })$
and a foliated diffeomorphism
![]() $\unicode[STIX]{x1D719}:U\rightarrow U^{\prime }$
, between open sets
$\unicode[STIX]{x1D719}:U\rightarrow U^{\prime }$
, between open sets
![]() $U,U^{\prime }$
of
$U,U^{\prime }$
of
![]() $M,M^{\prime }$
respectively, sending a point
$M,M^{\prime }$
respectively, sending a point
![]() $p\in U$
to
$p\in U$
to
![]() $p^{\prime }\in U^{\prime }$
, the differential of
$p^{\prime }\in U^{\prime }$
, the differential of
![]() $\unicode[STIX]{x1D719}$
induces a linear, foliated isomorphism
$\unicode[STIX]{x1D719}$
induces a linear, foliated isomorphism
![]() $\unicode[STIX]{x1D719}_{\ast }:(\unicode[STIX]{x1D708}_{p}L_{p},{\mathcal{F}}_{p})\rightarrow (\unicode[STIX]{x1D708}_{p^{\prime }}L_{p^{\prime }},{\mathcal{F}}_{p^{\prime }}^{\prime })$
.
$\unicode[STIX]{x1D719}_{\ast }:(\unicode[STIX]{x1D708}_{p}L_{p},{\mathcal{F}}_{p})\rightarrow (\unicode[STIX]{x1D708}_{p^{\prime }}L_{p^{\prime }},{\mathcal{F}}_{p^{\prime }}^{\prime })$
.
Proof. By substituting
![]() $(M^{\prime },\text{g}^{\prime },{\mathcal{F}}^{\prime })$
with
$(M^{\prime },\text{g}^{\prime },{\mathcal{F}}^{\prime })$
with
![]() $(M,\unicode[STIX]{x1D719}^{\ast }g^{\prime },{\mathcal{F}})$
, the problem can be reduced to the case where
$(M,\unicode[STIX]{x1D719}^{\ast }g^{\prime },{\mathcal{F}})$
, the problem can be reduced to the case where
![]() $M=M^{\prime }$
,
$M=M^{\prime }$
,
![]() $\unicode[STIX]{x1D719}=\text{id}$
,
$\unicode[STIX]{x1D719}=\text{id}$
,
![]() $p=p^{\prime }$
, and
$p=p^{\prime }$
, and
![]() ${\mathcal{F}}={\mathcal{F}}^{\prime }$
is a singular Riemannian foliation with respect to two metrics,
${\mathcal{F}}={\mathcal{F}}^{\prime }$
is a singular Riemannian foliation with respect to two metrics,
![]() $\text{g}$
and
$\text{g}$
and
![]() $\tilde{\text{g}}$
. In the following, we will denote with a ‘tilde’ (
$\tilde{\text{g}}$
. In the following, we will denote with a ‘tilde’ (
![]() $\;\tilde{}\;$
) every geometric object related to the metric
$\;\tilde{}\;$
) every geometric object related to the metric
![]() $\tilde{\text{g}}$
, and without the tilde any geometric object related to
$\tilde{\text{g}}$
, and without the tilde any geometric object related to
![]() $\text{g}$
.
$\text{g}$
.
Let
![]() $S_{p}$
(respectively
$S_{p}$
(respectively
![]() $\widetilde{S}_{p}$
) denote a slice at
$\widetilde{S}_{p}$
) denote a slice at
![]() $p$
with respect to
$p$
with respect to
![]() $\text{g}$
(respectively
$\text{g}$
(respectively
![]() $\tilde{\text{g}}$
). Consider the set
$\tilde{\text{g}}$
). Consider the set
![]() $\{X_{1},\ldots ,X_{k}\}\subset \mathfrak{X}(M,{\mathcal{F}})$
,
$\{X_{1},\ldots ,X_{k}\}\subset \mathfrak{X}(M,{\mathcal{F}})$
,
![]() $k=\dim L_{p}$
, of vector fields such that
$k=\dim L_{p}$
, of vector fields such that
![]() $\{X_{1}(p),\ldots ,X_{k}(p)\}$
is a basis of
$\{X_{1}(p),\ldots ,X_{k}(p)\}$
is a basis of
![]() $T_{p}L_{p}$
. Denote by
$T_{p}L_{p}$
. Denote by
![]() $\unicode[STIX]{x1D6F7}_{i}^{t}$
the flow of
$\unicode[STIX]{x1D6F7}_{i}^{t}$
the flow of
![]() $X_{i}$
and define
$X_{i}$
and define
![]() $\unicode[STIX]{x1D6F7}_{(t_{1},\ldots ,t_{k})}=\unicode[STIX]{x1D6F7}_{k}^{t_{k}}\circ \cdots \circ \unicode[STIX]{x1D6F7}_{1}^{t_{1}}$
.
$\unicode[STIX]{x1D6F7}_{(t_{1},\ldots ,t_{k})}=\unicode[STIX]{x1D6F7}_{k}^{t_{k}}\circ \cdots \circ \unicode[STIX]{x1D6F7}_{1}^{t_{1}}$
.
Around
![]() $p$
, both
$p$
, both
![]() $S_{p}$
and
$S_{p}$
and
![]() $\widetilde{S}_{p}$
are transverse to
$\widetilde{S}_{p}$
are transverse to
![]() $\text{span}(X_{1},\ldots ,X_{k})$
and, up to possibly replacing
$\text{span}(X_{1},\ldots ,X_{k})$
and, up to possibly replacing
![]() $S_{p}$
and
$S_{p}$
and
![]() $\widetilde{S}_{p}$
with smaller open subsets, we can assume that for every
$\widetilde{S}_{p}$
with smaller open subsets, we can assume that for every
![]() $q\in S_{p}$
there exists a unique
$q\in S_{p}$
there exists a unique
![]() $\tilde{q}\in \widetilde{S}_{p}$
of the form
$\tilde{q}\in \widetilde{S}_{p}$
of the form
![]() $\tilde{q}=\unicode[STIX]{x1D6F7}_{(t_{1},\ldots ,t_{k})}(q)$
. This gives rise to a map
$\tilde{q}=\unicode[STIX]{x1D6F7}_{(t_{1},\ldots ,t_{k})}(q)$
. This gives rise to a map
![]() $H:S_{p}\rightarrow \widetilde{S}_{p}$
,
$H:S_{p}\rightarrow \widetilde{S}_{p}$
,
![]() $H(q)=\tilde{q}$
which is differentiable and, since
$H(q)=\tilde{q}$
which is differentiable and, since
![]() $q$
and
$q$
and
![]() $\tilde{q}$
belong to the same leaf of
$\tilde{q}$
belong to the same leaf of
![]() ${\mathcal{F}}$
, sends the leaves of
${\mathcal{F}}$
, sends the leaves of
![]() ${\mathcal{F}}|_{S_{p}}$
to the leaves of
${\mathcal{F}}|_{S_{p}}$
to the leaves of
![]() ${\mathcal{F}}|_{\widetilde{S}_{p}}$
. In other words, there is a foliated diffeomorphism
${\mathcal{F}}|_{\widetilde{S}_{p}}$
. In other words, there is a foliated diffeomorphism
![]() $H:(S_{p},{\mathcal{F}}|_{S_{p}})\rightarrow (\widetilde{S}_{p},{\mathcal{F}}|_{\widetilde{S}_{p}})$
.
$H:(S_{p},{\mathcal{F}}|_{S_{p}})\rightarrow (\widetilde{S}_{p},{\mathcal{F}}|_{\widetilde{S}_{p}})$
.
Consider the composition
![]() $\unicode[STIX]{x1D713}$
of foliated diffeomorphisms
$\unicode[STIX]{x1D713}$
of foliated diffeomorphisms
For any
![]() $\unicode[STIX]{x1D706}\in (0,1)$
, one can define a new foliated diffeomorphism
$\unicode[STIX]{x1D706}\in (0,1)$
, one can define a new foliated diffeomorphism
As
![]() $\unicode[STIX]{x1D706}\rightarrow 0$
, the maps
$\unicode[STIX]{x1D706}\rightarrow 0$
, the maps
![]() $\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}$
converge to the differential
$\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}$
converge to the differential
![]() $d_{0}\unicode[STIX]{x1D713}$
of
$d_{0}\unicode[STIX]{x1D713}$
of
![]() $\unicode[STIX]{x1D713}$
at
$\unicode[STIX]{x1D713}$
at
![]() $0$
. This is an invertible linear map (in particular a diffeomorphism) and, as a limit of foliated maps, it is itself foliated. Therefore, the map
$0$
. This is an invertible linear map (in particular a diffeomorphism) and, as a limit of foliated maps, it is itself foliated. Therefore, the map
satisfies the statement of the proposition. ◻
Remark 2.5. Given a singular Riemannian foliation
![]() $(M,{\mathcal{F}})$
and a submanifold
$(M,{\mathcal{F}})$
and a submanifold
![]() $N\subset M$
which is a union of leaves of the same dimension, the infinitesimal foliation at a point
$N\subset M$
which is a union of leaves of the same dimension, the infinitesimal foliation at a point
![]() $p\in M$
splits as a product
$p\in M$
splits as a product
![]() $(\unicode[STIX]{x1D708}_{p}(L_{p},N)\times \unicode[STIX]{x1D708}_{p}N,\{\text{pts.}\}\times {\mathcal{F}}_{p}|_{\unicode[STIX]{x1D708}_{p}N})$
, where
$(\unicode[STIX]{x1D708}_{p}(L_{p},N)\times \unicode[STIX]{x1D708}_{p}N,\{\text{pts.}\}\times {\mathcal{F}}_{p}|_{\unicode[STIX]{x1D708}_{p}N})$
, where
![]() $\unicode[STIX]{x1D708}_{p}(L_{p},N)=\unicode[STIX]{x1D708}_{p}L_{p}\cap T_{p}N$
. In this case, the foliation
$\unicode[STIX]{x1D708}_{p}(L_{p},N)=\unicode[STIX]{x1D708}_{p}L_{p}\cap T_{p}N$
. In this case, the foliation
![]() $(\unicode[STIX]{x1D708}_{p}N,{\mathcal{F}}_{p}|_{\unicode[STIX]{x1D708}_{p}N})$
is the ‘essential part’ of the infinitesimal foliation
$(\unicode[STIX]{x1D708}_{p}N,{\mathcal{F}}_{p}|_{\unicode[STIX]{x1D708}_{p}N})$
is the ‘essential part’ of the infinitesimal foliation
![]() $(\unicode[STIX]{x1D708}_{p}L_{p},{\mathcal{F}}_{p})$
. By abuse of notation, we will call the foliation
$(\unicode[STIX]{x1D708}_{p}L_{p},{\mathcal{F}}_{p})$
. By abuse of notation, we will call the foliation
![]() $(\unicode[STIX]{x1D708}_{p}N,{\mathcal{F}}_{p}|_{\unicode[STIX]{x1D708}_{p}N})$
the infinitesimal foliation at
$(\unicode[STIX]{x1D708}_{p}N,{\mathcal{F}}_{p}|_{\unicode[STIX]{x1D708}_{p}N})$
the infinitesimal foliation at
![]() $p$
as well and denote it by
$p$
as well and denote it by
![]() ${\mathcal{F}}_{p}$
.
${\mathcal{F}}_{p}$
.
Given a singular Riemannian foliation
![]() $(M,{\mathcal{F}})$
and a point
$(M,{\mathcal{F}})$
and a point
![]() $p\in M$
, the infinitesimal foliation
$p\in M$
, the infinitesimal foliation
![]() $(\unicode[STIX]{x1D708}_{p}L_{p},{\mathcal{F}}_{p})$
at
$(\unicode[STIX]{x1D708}_{p}L_{p},{\mathcal{F}}_{p})$
at
![]() $p$
contains the origin as a leaf of
$p$
contains the origin as a leaf of
![]() ${\mathcal{F}}_{p}$
. Based on this fact, we make the following definition.
${\mathcal{F}}_{p}$
. Based on this fact, we make the following definition.
Definition 2.6 (Infinitesimal foliation).
An infinitesimal foliation is a singular Riemannian foliation
![]() $(V,{\mathcal{F}})$
on a Euclidean vector space, with the origin
$(V,{\mathcal{F}})$
on a Euclidean vector space, with the origin
![]() $\{0\}$
being a zero-dimensional leaf.
$\{0\}$
being a zero-dimensional leaf.
2.4 Homogeneous and orbit-like foliations
A singular Riemannian foliation
![]() $(M,{\mathcal{F}})$
is called homogeneous (sometimes Riemannian homogeneous) if there exists a connected Lie group
$(M,{\mathcal{F}})$
is called homogeneous (sometimes Riemannian homogeneous) if there exists a connected Lie group
![]() $G$
acting by isometries on
$G$
acting by isometries on
![]() $M$
, whose orbits are precisely the leaves of
$M$
, whose orbits are precisely the leaves of
![]() ${\mathcal{F}}$
. Furthermore, a singular Riemannian foliation
${\mathcal{F}}$
. Furthermore, a singular Riemannian foliation
![]() $(M,{\mathcal{F}})$
is called orbit-like if at every point
$(M,{\mathcal{F}})$
is called orbit-like if at every point
![]() $p\in M$
, the infinitesimal foliation
$p\in M$
, the infinitesimal foliation
![]() $(\unicode[STIX]{x1D708}_{p}L_{p},{\mathcal{F}}_{p})$
is closed and homogeneous.
$(\unicode[STIX]{x1D708}_{p}L_{p},{\mathcal{F}}_{p})$
is closed and homogeneous.
Example 2.7 (Holonomy foliations).
An example of an orbit-like foliation, which will be useful to keep in mind later on, can be constructed as follows. Consider a Riemannian manifold
![]() $L$
and a Euclidean vector bundle
$L$
and a Euclidean vector bundle
![]() $E$
over
$E$
over
![]() $L$
, that is, a vector bundle over
$L$
, that is, a vector bundle over
![]() $L$
with an inner product
$L$
with an inner product
![]() $\langle \,,\,\rangle _{p}$
on each fiber
$\langle \,,\,\rangle _{p}$
on each fiber
![]() $E_{p}$
,
$E_{p}$
,
![]() $p\in L$
. Let
$p\in L$
. Let
![]() $\unicode[STIX]{x1D6FB}^{E}$
be a metric connection on
$\unicode[STIX]{x1D6FB}^{E}$
be a metric connection on
![]() $E$
, i.e. a connection on
$E$
, i.e. a connection on
![]() $E$
such that, for every vector field
$E$
such that, for every vector field
![]() $X$
on
$X$
on
![]() $L$
and sections
$L$
and sections
![]() $\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}$
of
$\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}$
of
![]() $E$
, one has
$E$
, one has
Given
![]() $(E,\unicode[STIX]{x1D6FB}^{E})$
, there is an induced Riemannian metric
$(E,\unicode[STIX]{x1D6FB}^{E})$
, there is an induced Riemannian metric
![]() $\text{g}^{E}$
on
$\text{g}^{E}$
on
![]() $E$
, called the connection metric. Moreover,
$E$
, called the connection metric. Moreover,
![]() $\unicode[STIX]{x1D6FB}^{E}$
induces a parallel transport on
$\unicode[STIX]{x1D6FB}^{E}$
induces a parallel transport on
![]() $E$
: given
$E$
: given
![]() $\unicode[STIX]{x1D709}_{0}\in E_{p}$
and a curve
$\unicode[STIX]{x1D709}_{0}\in E_{p}$
and a curve
![]() $\unicode[STIX]{x1D6FE}:[0,1]\rightarrow L$
with
$\unicode[STIX]{x1D6FE}:[0,1]\rightarrow L$
with
![]() $\unicode[STIX]{x1D6FE}(0)=p$
, there exists a unique lift
$\unicode[STIX]{x1D6FE}(0)=p$
, there exists a unique lift
![]() $\unicode[STIX]{x1D709}:[0,1]\rightarrow E$
of
$\unicode[STIX]{x1D709}:[0,1]\rightarrow E$
of
![]() $\unicode[STIX]{x1D6FE}$
, with
$\unicode[STIX]{x1D6FE}$
, with
![]() $\unicode[STIX]{x1D709}(0)=\unicode[STIX]{x1D709}_{0}$
such that
$\unicode[STIX]{x1D709}(0)=\unicode[STIX]{x1D709}_{0}$
such that
![]() $\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D6FE}^{\prime }(t)}^{E}\unicode[STIX]{x1D709}(t)=0$
for every
$\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D6FE}^{\prime }(t)}^{E}\unicode[STIX]{x1D709}(t)=0$
for every
![]() $t\in [0,1]$
. On
$t\in [0,1]$
. On
![]() $E$
one can now define a foliation
$E$
one can now define a foliation
![]() ${\mathcal{F}}^{E}$
, by declaring two vectors
${\mathcal{F}}^{E}$
, by declaring two vectors
![]() $\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2}\in E$
in the same leaf if they can be connected to one another via a composition of parallel transports. The leaves of
$\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2}\in E$
in the same leaf if they can be connected to one another via a composition of parallel transports. The leaves of
![]() ${\mathcal{F}}^{E}$
are usually referred to as the holonomy tubes around the zero section
${\mathcal{F}}^{E}$
are usually referred to as the holonomy tubes around the zero section
![]() $L\subset E$
and they define a singular Riemannian foliation on
$L\subset E$
and they define a singular Riemannian foliation on
![]() $(E,\text{g}^{E})$
. Moreover, the infinitesimal foliation at any point of
$(E,\text{g}^{E})$
. Moreover, the infinitesimal foliation at any point of
![]() $E$
is homogeneous: in fact, for any point
$E$
is homogeneous: in fact, for any point
![]() $p$
along the zero section
$p$
along the zero section
![]() $L$
, one can first construct the holonomy group
$L$
, one can first construct the holonomy group
![]() $H_{p}$
of the connection
$H_{p}$
of the connection
![]() $\unicode[STIX]{x1D6FB}^{E}$
, which acts by isometries on the fiber
$\unicode[STIX]{x1D6FB}^{E}$
, which acts by isometries on the fiber
![]() $E_{p}$
in such a way that the orbits of the identity component
$E_{p}$
in such a way that the orbits of the identity component
![]() $H_{p}^{0}$
are precisely the leaves of the infinitesimal foliation of
$H_{p}^{0}$
are precisely the leaves of the infinitesimal foliation of
![]() ${\mathcal{F}}^{E}$
at
${\mathcal{F}}^{E}$
at
![]() $p$
. Similarly, the infinitesimal foliation at a point
$p$
. Similarly, the infinitesimal foliation at a point
![]() $\unicode[STIX]{x1D709}\in E_{p}$
is given by the orbits in
$\unicode[STIX]{x1D709}\in E_{p}$
is given by the orbits in
![]() $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D709}}L_{\unicode[STIX]{x1D709}}$
of the identity component of the stabilizer
$\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D709}}L_{\unicode[STIX]{x1D709}}$
of the identity component of the stabilizer
![]() $H_{\unicode[STIX]{x1D709}}\subset H_{p}$
of
$H_{\unicode[STIX]{x1D709}}\subset H_{p}$
of
![]() $\unicode[STIX]{x1D709}$
. The foliation
$\unicode[STIX]{x1D709}$
. The foliation
![]() ${\mathcal{F}}^{E}$
coincides with its own linearization with respect to the zero section (see definition in § 2.5). Moreover, if the leaves of
${\mathcal{F}}^{E}$
coincides with its own linearization with respect to the zero section (see definition in § 2.5). Moreover, if the leaves of
![]() ${\mathcal{F}}^{E}$
are closed, then
${\mathcal{F}}^{E}$
are closed, then
![]() $(E,\text{g}^{E},{\mathcal{F}}^{E})$
is an orbit-like foliation.
$(E,\text{g}^{E},{\mathcal{F}}^{E})$
is an orbit-like foliation.
Remark 2.8. When
![]() $L\subset M$
is a submanifold of somewhat special geometry, the holonomy foliation on the normal bundle
$L\subset M$
is a submanifold of somewhat special geometry, the holonomy foliation on the normal bundle
![]() $E$
of
$E$
of
![]() $L$
, endowed with the Levi-Civita connection, induces via the normal exponential map a foliation on the whole of
$L$
, endowed with the Levi-Civita connection, induces via the normal exponential map a foliation on the whole of
![]() $M$
. For example, if
$M$
. For example, if
![]() $L$
has parallel focal structure, then the induced foliation on
$L$
has parallel focal structure, then the induced foliation on
![]() $M$
is a polar foliation [Reference ToebenToe06]. If
$M$
is a polar foliation [Reference ToebenToe06]. If
![]() $M$
is a complete, non-compact manifold with sectional curvature
$M$
is a complete, non-compact manifold with sectional curvature
![]() ${\geqslant}0$
and
${\geqslant}0$
and
![]() $L$
is a soul of
$L$
is a soul of
![]() $M$
[Reference Cheeger and GromollCG72], then the induced foliation on
$M$
[Reference Cheeger and GromollCG72], then the induced foliation on
![]() $M$
is Wilking’s dual foliation to the Sharafutdinov projection [Reference WilkingWil07].
$M$
is Wilking’s dual foliation to the Sharafutdinov projection [Reference WilkingWil07].
Although in principle the property of being orbit-like might depend on the metric, the following proposition shows in fact that being orbit-like is invariant under foliated diffeomorphisms.
Proposition 2.9. The following hold.
-
(1) Given a foliated linear isomorphism
 $\unicode[STIX]{x1D711}:(V,{\mathcal{F}})\rightarrow (V^{\prime },{\mathcal{F}}^{\prime })$
between infinitesimal foliations,
$\unicode[STIX]{x1D711}:(V,{\mathcal{F}})\rightarrow (V^{\prime },{\mathcal{F}}^{\prime })$
between infinitesimal foliations,
 $(V,{\mathcal{F}})$
is homogeneous if and only if
$(V,{\mathcal{F}})$
is homogeneous if and only if
 $(V^{\prime },{\mathcal{F}}^{\prime })$
is homogeneous.
$(V^{\prime },{\mathcal{F}}^{\prime })$
is homogeneous. -
(2) Given a foliated diffeomorphism
 $\unicode[STIX]{x1D719}:(M,{\mathcal{F}})\rightarrow (M^{\prime },{\mathcal{F}}^{\prime })$
between singular Riemannian foliations,
$\unicode[STIX]{x1D719}:(M,{\mathcal{F}})\rightarrow (M^{\prime },{\mathcal{F}}^{\prime })$
between singular Riemannian foliations,
 $(M,{\mathcal{F}})$
is orbit-like if and only if
$(M,{\mathcal{F}})$
is orbit-like if and only if
 $(M^{\prime },{\mathcal{F}}^{\prime })$
is orbit-like.
$(M^{\prime },{\mathcal{F}}^{\prime })$
is orbit-like.
Proof. (1) By the symmetric roles of
![]() $V$
and
$V$
and
![]() $V^{\prime }$
, it is enough to show that if
$V^{\prime }$
, it is enough to show that if
![]() $(V,{\mathcal{F}})$
is homogeneous, so is
$(V,{\mathcal{F}})$
is homogeneous, so is
![]() $(V^{\prime },{\mathcal{F}}^{\prime })$
. Suppose that
$(V^{\prime },{\mathcal{F}}^{\prime })$
. Suppose that
![]() $(V,{\mathcal{F}})$
is homogeneous and therefore the foliation
$(V,{\mathcal{F}})$
is homogeneous and therefore the foliation
![]() ${\mathcal{F}}$
is spanned by Killing fields. Recall that a vector field
${\mathcal{F}}$
is spanned by Killing fields. Recall that a vector field
![]() $X$
on a Euclidean space
$X$
on a Euclidean space
![]() $(V,\text{g})$
is Killing if and only if it is of the form
$(V,\text{g})$
is Killing if and only if it is of the form
![]() $X(v)=Av$
, where
$X(v)=Av$
, where
![]() $A$
is a skew-symmetric endomorphism of
$A$
is a skew-symmetric endomorphism of
![]() $V$
, in the sense that
$V$
, in the sense that
![]() $\text{g}(Av,v)=0$
for every
$\text{g}(Av,v)=0$
for every
![]() $v\in V$
. Letting
$v\in V$
. Letting
![]() $\{X_{1},\ldots ,X_{k}\}$
denote a set of Killing fields on
$\{X_{1},\ldots ,X_{k}\}$
denote a set of Killing fields on
![]() $V$
spanning the foliation
$V$
spanning the foliation
![]() ${\mathcal{F}}$
, the set
${\mathcal{F}}$
, the set
![]() $\{Y_{1},\ldots ,Y_{k}\}$
with
$\{Y_{1},\ldots ,Y_{k}\}$
with
![]() $Y_{i}(v^{\prime })=\unicode[STIX]{x1D711}_{\ast }(X_{i}(\unicode[STIX]{x1D711}^{-1}(v^{\prime })))$
spans the foliation
$Y_{i}(v^{\prime })=\unicode[STIX]{x1D711}_{\ast }(X_{i}(\unicode[STIX]{x1D711}^{-1}(v^{\prime })))$
spans the foliation
![]() ${\mathcal{F}}^{\prime }$
as well. Since
${\mathcal{F}}^{\prime }$
as well. Since
![]() $\unicode[STIX]{x1D711}$
is a linear map and the vector fields
$\unicode[STIX]{x1D711}$
is a linear map and the vector fields
![]() $X_{i}$
are linear, it follows that
$X_{i}$
are linear, it follows that
![]() $Y_{i}$
can be written as
$Y_{i}$
can be written as
![]() $Y_{i}(v^{\prime })=B_{i}v^{\prime }$
for some endomorphism
$Y_{i}(v^{\prime })=B_{i}v^{\prime }$
for some endomorphism
![]() $B_{i}:V^{\prime }\rightarrow V^{\prime }$
,
$B_{i}:V^{\prime }\rightarrow V^{\prime }$
,
![]() $i=1,\ldots ,k$
. Since
$i=1,\ldots ,k$
. Since
![]() $(V^{\prime },\text{g}^{\prime },{\mathcal{F}}^{\prime })$
is a singular Riemannian foliation, the leaf
$(V^{\prime },\text{g}^{\prime },{\mathcal{F}}^{\prime })$
is a singular Riemannian foliation, the leaf
![]() $L_{v^{\prime }}$
through
$L_{v^{\prime }}$
through
![]() $v^{\prime }$
lies in a distance sphere from the origin and in particular
$v^{\prime }$
lies in a distance sphere from the origin and in particular
![]() $\text{g}^{\prime }(T_{v^{\prime }}L_{v^{\prime }},v^{\prime })=0$
. Since
$\text{g}^{\prime }(T_{v^{\prime }}L_{v^{\prime }},v^{\prime })=0$
. Since
![]() $Y_{i}(v^{\prime })$
is tangent to
$Y_{i}(v^{\prime })$
is tangent to
![]() $L_{v^{\prime }}$
, it follows that
$L_{v^{\prime }}$
, it follows that
In other words,
![]() $B_{i}$
is skew symmetric and thus
$B_{i}$
is skew symmetric and thus
![]() $Y_{i}$
is a Killing field as well. Therefore, the foliation
$Y_{i}$
is a Killing field as well. Therefore, the foliation
![]() $(V^{\prime },{\mathcal{F}}^{\prime })$
is spanned by Killing vector fields and hence it is homogeneous as well.
$(V^{\prime },{\mathcal{F}}^{\prime })$
is spanned by Killing vector fields and hence it is homogeneous as well.
(2) Up to exchanging the roles of
![]() $M$
and
$M$
and
![]() $M^{\prime }$
, it is enough to show that if
$M^{\prime }$
, it is enough to show that if
![]() $(M,{\mathcal{F}})$
is orbit-like, so is
$(M,{\mathcal{F}})$
is orbit-like, so is
![]() $(M^{\prime },{\mathcal{F}}^{\prime })$
. Fixing a point
$(M^{\prime },{\mathcal{F}}^{\prime })$
. Fixing a point
![]() $p\in M$
, Proposition 2.4 states that the foliated diffeomorphism
$p\in M$
, Proposition 2.4 states that the foliated diffeomorphism
![]() $\unicode[STIX]{x1D719}$
induces a foliated linear isomorphism
$\unicode[STIX]{x1D719}$
induces a foliated linear isomorphism
![]() $\unicode[STIX]{x1D719}_{\ast }:(\unicode[STIX]{x1D708}_{p}L_{p},{\mathcal{F}}_{p})\longrightarrow (\unicode[STIX]{x1D708}_{p^{\prime }}L_{p^{\prime }},{\mathcal{F}}_{p^{\prime }})$
, where
$\unicode[STIX]{x1D719}_{\ast }:(\unicode[STIX]{x1D708}_{p}L_{p},{\mathcal{F}}_{p})\longrightarrow (\unicode[STIX]{x1D708}_{p^{\prime }}L_{p^{\prime }},{\mathcal{F}}_{p^{\prime }})$
, where
![]() $p^{\prime }=\unicode[STIX]{x1D719}(p)$
. Since
$p^{\prime }=\unicode[STIX]{x1D719}(p)$
. Since
![]() $(M,{\mathcal{F}})$
is orbit-like, it follows that
$(M,{\mathcal{F}})$
is orbit-like, it follows that
![]() $(\unicode[STIX]{x1D708}_{p}L_{p},{\mathcal{F}}_{p})$
is closed and homogeneous. From the first point above it follows that
$(\unicode[STIX]{x1D708}_{p}L_{p},{\mathcal{F}}_{p})$
is closed and homogeneous. From the first point above it follows that
![]() $(\unicode[STIX]{x1D708}_{p^{\prime }}L_{p^{\prime }},{\mathcal{F}}_{p^{\prime }})$
is homogeneous as well and by the continuity of
$(\unicode[STIX]{x1D708}_{p^{\prime }}L_{p^{\prime }},{\mathcal{F}}_{p^{\prime }})$
is homogeneous as well and by the continuity of
![]() $\unicode[STIX]{x1D719}_{\ast }$
one has that
$\unicode[STIX]{x1D719}_{\ast }$
one has that
![]() $(\unicode[STIX]{x1D708}_{p^{\prime }}L_{p^{\prime }},{\mathcal{F}}_{p^{\prime }})$
is closed. Since
$(\unicode[STIX]{x1D708}_{p^{\prime }}L_{p^{\prime }},{\mathcal{F}}_{p^{\prime }})$
is closed. Since
![]() $p^{\prime }$
was chosen arbitrarily, it follows that
$p^{\prime }$
was chosen arbitrarily, it follows that
![]() $(M^{\prime },{\mathcal{F}}^{\prime })$
is orbit-like.◻
$(M^{\prime },{\mathcal{F}}^{\prime })$
is orbit-like.◻
2.5 Linearization and linearized foliation
Let
![]() $(M,{\mathcal{F}})$
be a singular Riemannian foliation,
$(M,{\mathcal{F}})$
be a singular Riemannian foliation,
![]() $B\subset M$
a submanifold saturated by leaves, and
$B\subset M$
a submanifold saturated by leaves, and
![]() $U\subset M$
an
$U\subset M$
an
![]() $\unicode[STIX]{x1D716}$
-tubular neighbourhood of
$\unicode[STIX]{x1D716}$
-tubular neighbourhood of
![]() $B$
with metric projection
$B$
with metric projection
![]() $\mathsf{p}:U\rightarrow B$
. Given a vector field
$\mathsf{p}:U\rightarrow B$
. Given a vector field
![]() $V$
in
$V$
in
![]() $U$
tangent to the leaves of
$U$
tangent to the leaves of
![]() ${\mathcal{F}}$
, it is possible to produce a new vector field
${\mathcal{F}}$
, it is possible to produce a new vector field
![]() $V^{\ell }$
, called the linearization of
$V^{\ell }$
, called the linearization of
![]() $V$
with respect to
$V$
with respect to
![]() $B$
, as follows:
$B$
, as follows:
where
![]() $h_{\unicode[STIX]{x1D706}}:U\rightarrow U$
denotes the homothetic transformation around
$h_{\unicode[STIX]{x1D706}}:U\rightarrow U$
denotes the homothetic transformation around
![]() $B$
. From [Reference Mendes and RadeschiMR15, Proposition 5], the linearization
$B$
. From [Reference Mendes and RadeschiMR15, Proposition 5], the linearization
![]() $V^{\ell }$
is a smooth vector field invariant under the homothetic transformation
$V^{\ell }$
is a smooth vector field invariant under the homothetic transformation
![]() $h_{\unicode[STIX]{x1D706}}$
and it coincides with
$h_{\unicode[STIX]{x1D706}}$
and it coincides with
![]() $V$
along
$V$
along
![]() $B$
. On
$B$
. On
![]() $U$
, consider the module
$U$
, consider the module
![]() $\mathfrak{X}(U,{\mathcal{F}})^{\ell }$
given by the linearization, with respect to
$\mathfrak{X}(U,{\mathcal{F}})^{\ell }$
given by the linearization, with respect to
![]() $B$
, of the vector fields in
$B$
, of the vector fields in
![]() $\mathfrak{X}(U,{\mathcal{F}})$
:
$\mathfrak{X}(U,{\mathcal{F}})$
:
Let
![]() $\mathsf{D}$
be the pseudogroup of local diffeomorphisms of
$\mathsf{D}$
be the pseudogroup of local diffeomorphisms of
![]() $U$
, generated by the flows of linearized vector fields, and let
$U$
, generated by the flows of linearized vector fields, and let
![]() $(U,{\mathcal{F}}^{\ell })$
be the partition of
$(U,{\mathcal{F}}^{\ell })$
be the partition of
![]() $U$
into the orbits of diffeomorphisms in
$U$
into the orbits of diffeomorphisms in
![]() $\mathsf{D}$
. By Sussmann [Reference SussmannSus73, Theorem 4.1], such orbits are (possibly non-complete) smooth submanifolds of
$\mathsf{D}$
. By Sussmann [Reference SussmannSus73, Theorem 4.1], such orbits are (possibly non-complete) smooth submanifolds of
![]() $M$
. Moreover, as noted by Molino [Reference MolinoMol88, Lemma 6.3], this foliation is spanned, at each point, by the vector fields in
$M$
. Moreover, as noted by Molino [Reference MolinoMol88, Lemma 6.3], this foliation is spanned, at each point, by the vector fields in
![]() $\mathfrak{X}^{\ell }(U,{\mathcal{F}})$
.
$\mathfrak{X}^{\ell }(U,{\mathcal{F}})$
.
We call
![]() $(U,{\mathcal{F}}^{\ell })$
the linearized foliation of
$(U,{\mathcal{F}}^{\ell })$
the linearized foliation of
![]() ${\mathcal{F}}$
with respect to
${\mathcal{F}}$
with respect to
![]() $B$
. We will show, later, that the leaves of the linearized foliation are actually complete and have a particularly nice local structure (cf. § 6).
$B$
. We will show, later, that the leaves of the linearized foliation are actually complete and have a particularly nice local structure (cf. § 6).
Given a point
![]() $p\in B$
, define
$p\in B$
, define
![]() $U_{p}=\mathsf{p}^{-1}(p)\subset U$
and let
$U_{p}=\mathsf{p}^{-1}(p)\subset U$
and let
![]() ${\mathcal{F}}_{p}$
(respectively
${\mathcal{F}}_{p}$
(respectively
![]() $({\mathcal{F}}^{\ell })_{p}$
) denote the partition of
$({\mathcal{F}}^{\ell })_{p}$
) denote the partition of
![]() $U_{p}$
into the connected components of
$U_{p}$
into the connected components of
![]() $L\cap U_{p}$
, as
$L\cap U_{p}$
, as
![]() $L$
ranges through the leaves of
$L$
ranges through the leaves of
![]() ${\mathcal{F}}$
(respectively
${\mathcal{F}}$
(respectively
![]() ${\mathcal{F}}^{\ell }$
). If
${\mathcal{F}}^{\ell }$
). If
![]() $U_{p}$
is given the flat metric
$U_{p}$
is given the flat metric
![]() $\text{g}_{p}$
of
$\text{g}_{p}$
of
![]() $\unicode[STIX]{x1D708}_{p}B$
via the exponential map
$\unicode[STIX]{x1D708}_{p}B$
via the exponential map
![]() $\exp _{p}:\unicode[STIX]{x1D708}_{p}^{\unicode[STIX]{x1D716}}B\rightarrow U_{p}$
, then
$\exp _{p}:\unicode[STIX]{x1D708}_{p}^{\unicode[STIX]{x1D716}}B\rightarrow U_{p}$
, then
![]() ${\mathcal{F}}_{p}$
corresponds to the infinitesimal foliation at
${\mathcal{F}}_{p}$
corresponds to the infinitesimal foliation at
![]() $p$
(cf. Remark 2.5), which justifies the notation of
$p$
(cf. Remark 2.5), which justifies the notation of
![]() ${\mathcal{F}}_{p}$
for this foliation. Furthermore, as noted in [Reference MolinoMol88, § 6.4],
${\mathcal{F}}_{p}$
for this foliation. Furthermore, as noted in [Reference MolinoMol88, § 6.4],
![]() $({\mathcal{F}}^{\ell })_{p}$
is given by the linearization of
$({\mathcal{F}}^{\ell })_{p}$
is given by the linearization of
![]() $(U_{p},\text{g}_{p},{\mathcal{F}}_{p})$
with respect to the origin. In other words,
$(U_{p},\text{g}_{p},{\mathcal{F}}_{p})$
with respect to the origin. In other words,
![]() $({\mathcal{F}}^{\ell })_{p}=({\mathcal{F}}_{p})^{\ell }$
and it makes sense to denote this foliation simply by
$({\mathcal{F}}^{\ell })_{p}=({\mathcal{F}}_{p})^{\ell }$
and it makes sense to denote this foliation simply by
![]() ${\mathcal{F}}_{p}^{\ell }$
. Moreover, letting
${\mathcal{F}}_{p}^{\ell }$
. Moreover, letting
![]() $\mathsf{O}({\mathcal{F}}_{p})$
denote the Lie group of (linear) isometries of
$\mathsf{O}({\mathcal{F}}_{p})$
denote the Lie group of (linear) isometries of
![]() $(U_{p},\text{g}_{p})$
sending every leaf to itself, one has the following result.
$(U_{p},\text{g}_{p})$
sending every leaf to itself, one has the following result.
Proposition 2.10. The foliation
![]() $(U_{p},{\mathcal{F}}_{p}^{\ell })$
is homogeneous, given by the orbits of the identity component
$(U_{p},{\mathcal{F}}_{p}^{\ell })$
is homogeneous, given by the orbits of the identity component
![]() $H_{p}$
of
$H_{p}$
of
![]() $\mathsf{O}({\mathcal{F}}_{p})$
.
$\mathsf{O}({\mathcal{F}}_{p})$
.
Proof. We identify here
![]() $U_{p}$
with a neighbourhood of the origin in
$U_{p}$
with a neighbourhood of the origin in
![]() $\unicode[STIX]{x1D708}_{p}B$
via the exponential map and we think of
$\unicode[STIX]{x1D708}_{p}B$
via the exponential map and we think of
![]() ${\mathcal{F}}_{p}^{\ell }$
as the linearization of
${\mathcal{F}}_{p}^{\ell }$
as the linearization of
![]() ${\mathcal{F}}_{p}$
.
${\mathcal{F}}_{p}$
.
Given a vector field
![]() $V\in \mathfrak{X}(U_{p},{\mathcal{F}}_{p})$
, its linearization
$V\in \mathfrak{X}(U_{p},{\mathcal{F}}_{p})$
, its linearization
![]() $V^{\ell }$
is linear, in the sense that
$V^{\ell }$
is linear, in the sense that
![]() $V_{p}^{\ell }=A\cdot p$
for some
$V_{p}^{\ell }=A\cdot p$
for some
![]() $A\in \text{End}(U_{p})$
. Since
$A\in \text{End}(U_{p})$
. Since
![]() ${\mathcal{F}}_{p}$
is a singular Riemannian foliation, the leaves are tangent to the distance spheres around the origin and therefore perpendicular to the radial directions from the origin:
${\mathcal{F}}_{p}$
is a singular Riemannian foliation, the leaves are tangent to the distance spheres around the origin and therefore perpendicular to the radial directions from the origin:
![]() $\langle V_{p}^{\ell },p\rangle =0$
. In other words,
$\langle V_{p}^{\ell },p\rangle =0$
. In other words,
![]() $V_{p}^{\ell }=A\cdot p$
with
$V_{p}^{\ell }=A\cdot p$
with
![]() $A$
skew symmetric, which implies that the flow of
$A$
skew symmetric, which implies that the flow of
![]() $V^{\ell }$
is an isometry of
$V^{\ell }$
is an isometry of
![]() $U_{p}$
. Moreover, since
$U_{p}$
. Moreover, since
![]() $V^{\ell }$
is everywhere tangent to the leaves of
$V^{\ell }$
is everywhere tangent to the leaves of
![]() ${\mathcal{F}}_{p}^{\ell }$
, the flow of
${\mathcal{F}}_{p}^{\ell }$
, the flow of
![]() $V^{\ell }$
is a one-parameter group in
$V^{\ell }$
is a one-parameter group in
![]() $H_{p}$
, moving every leaf of
$H_{p}$
, moving every leaf of
![]() $({\mathcal{F}}_{p})^{\ell }$
to itself. In particular, the orbits of
$({\mathcal{F}}_{p})^{\ell }$
to itself. In particular, the orbits of
![]() $H_{p}$
are contained in the leaves of
$H_{p}$
are contained in the leaves of
![]() $({\mathcal{F}}_{p})^{\ell }$
.
$({\mathcal{F}}_{p})^{\ell }$
.
However, by definition of
![]() $H_{p}$
, the tangent space of an
$H_{p}$
, the tangent space of an
![]() $H_{p}$
-orbit through a point
$H_{p}$
-orbit through a point
![]() $q\in U_{p}$
is given by
$q\in U_{p}$
is given by
and such vector fields coincide precisely with the vector fields in
![]() $\mathfrak{X}(U_{p},{\mathcal{F}}_{p})^{\ell }$
. Therefore,
$\mathfrak{X}(U_{p},{\mathcal{F}}_{p})^{\ell }$
. Therefore,
![]() $H_{p}\cdot q$
is the integral manifold of
$H_{p}\cdot q$
is the integral manifold of
![]() $\mathfrak{X}(U_{p},{\mathcal{F}}_{p})^{\ell }$
through
$\mathfrak{X}(U_{p},{\mathcal{F}}_{p})^{\ell }$
through
![]() $q$
.◻
$q$
.◻
3 Molino’s conjecture, assuming the main theorem
Before proving the main theorem, we show how Molino’s conjecture follows from it as a corollary.
Proof of Molino’s conjecture.
Let
![]() $(M,{\mathcal{F}})$
be a singular Riemannian foliation and let
$(M,{\mathcal{F}})$
be a singular Riemannian foliation and let
![]() $\overline{{\mathcal{F}}}$
denote the closure of
$\overline{{\mathcal{F}}}$
denote the closure of
![]() ${\mathcal{F}}$
. Molino himself proved that
${\mathcal{F}}$
. Molino himself proved that
![]() $\overline{{\mathcal{F}}}$
is a partition into complete smooth closed submanifolds and that
$\overline{{\mathcal{F}}}$
is a partition into complete smooth closed submanifolds and that
![]() $\overline{{\mathcal{F}}}$
is a transnormal system. Therefore, in order to prove the conjecture, it is enough to show that for any leaf
$\overline{{\mathcal{F}}}$
is a transnormal system. Therefore, in order to prove the conjecture, it is enough to show that for any leaf
![]() $L\in {\mathcal{F}}$
with closure
$L\in {\mathcal{F}}$
with closure
![]() $\overline{L}$
and any vector
$\overline{L}$
and any vector
![]() $v\in \unicode[STIX]{x1D708}(L,\overline{L}):=\unicode[STIX]{x1D708}L\cap T\overline{L}$
, there exists a smooth extension of
$v\in \unicode[STIX]{x1D708}(L,\overline{L}):=\unicode[STIX]{x1D708}L\cap T\overline{L}$
, there exists a smooth extension of
![]() $v$
to a vector field
$v$
to a vector field
![]() $V$
everywhere tangent to the leaves of
$V$
everywhere tangent to the leaves of
![]() $\overline{{\mathcal{F}}}$
.
$\overline{{\mathcal{F}}}$
.
Let
![]() $U$
be a tubular neighbourhood of
$U$
be a tubular neighbourhood of
![]() $\overline{L}$
and let
$\overline{L}$
and let
![]() $(U,\widehat{{\mathcal{F}}}^{\ell })$
be the foliation satisfying the main theorem. Since
$(U,\widehat{{\mathcal{F}}}^{\ell })$
be the foliation satisfying the main theorem. Since
![]() $\widehat{{\mathcal{F}}}^{\ell }$
coincides with
$\widehat{{\mathcal{F}}}^{\ell }$
coincides with
![]() ${\mathcal{F}}$
along
${\mathcal{F}}$
along
![]() $\overline{L}$
, it follows that
$\overline{L}$
, it follows that
![]() $L$
is a leaf of
$L$
is a leaf of
![]() $\widehat{{\mathcal{F}}}^{\ell }$
as well. Since
$\widehat{{\mathcal{F}}}^{\ell }$
as well. Since
![]() $\widehat{{\mathcal{F}}}^{\ell }$
is an orbit-like foliation, by [Reference Alexandrino and RadeschiAR17, Theorem 1.6], given
$\widehat{{\mathcal{F}}}^{\ell }$
is an orbit-like foliation, by [Reference Alexandrino and RadeschiAR17, Theorem 1.6], given
![]() $v\in \unicode[STIX]{x1D708}(L,\overline{L})$
there is a vector field
$v\in \unicode[STIX]{x1D708}(L,\overline{L})$
there is a vector field
![]() $V$
extending
$V$
extending
![]() $v$
which is tangent to the closure of
$v$
which is tangent to the closure of
![]() $\widehat{{\mathcal{F}}}^{\ell }$
. Since this closure is contained in
$\widehat{{\mathcal{F}}}^{\ell }$
. Since this closure is contained in
![]() $\overline{{\mathcal{F}}}$
, it follows that
$\overline{{\mathcal{F}}}$
, it follows that
![]() $V$
is also tangent to
$V$
is also tangent to
![]() $\overline{{\mathcal{F}}}$
and this ends the proof of the conjecture.◻
$\overline{{\mathcal{F}}}$
and this ends the proof of the conjecture.◻
4 The setup
Fix a leaf
![]() $L$
and a distance tube
$L$
and a distance tube
![]() $U=B_{\unicode[STIX]{x1D716}}(L)$
around
$U=B_{\unicode[STIX]{x1D716}}(L)$
around
![]() $\overline{L}$
. Using the normal exponential map
$\overline{L}$
. Using the normal exponential map
![]() $\exp :\unicode[STIX]{x1D708}\overline{L}\rightarrow M$
,
$\exp :\unicode[STIX]{x1D708}\overline{L}\rightarrow M$
,
![]() $U$
can be identified with the
$U$
can be identified with the
![]() $\unicode[STIX]{x1D716}$
-tube
$\unicode[STIX]{x1D716}$
-tube
![]() $\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D716}}\overline{L}$
around the zero section. By the homothetic transformation lemma, the pull-back foliation
$\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D716}}\overline{L}$
around the zero section. By the homothetic transformation lemma, the pull-back foliation
![]() $\exp ^{-1}{\mathcal{F}}$
on
$\exp ^{-1}{\mathcal{F}}$
on
![]() $\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D716}}\overline{L}$
is invariant under the rescalings
$\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D716}}\overline{L}$
is invariant under the rescalings
![]() $r_{\unicode[STIX]{x1D706}}:\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D716}}\overline{L}\rightarrow \unicode[STIX]{x1D708}^{\unicode[STIX]{x1D716}}\overline{L}$
,
$r_{\unicode[STIX]{x1D706}}:\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D716}}\overline{L}\rightarrow \unicode[STIX]{x1D708}^{\unicode[STIX]{x1D716}}\overline{L}$
,
![]() $r_{\unicode[STIX]{x1D706}}(p,v)=(p,\unicode[STIX]{x1D706}v)$
for any
$r_{\unicode[STIX]{x1D706}}(p,v)=(p,\unicode[STIX]{x1D706}v)$
for any
![]() $\unicode[STIX]{x1D706}\in (0,1)$
.
$\unicode[STIX]{x1D706}\in (0,1)$
.
For this reason, in the following sections we will be considering the (slightly more general) setup:
-
∙
 $U$
is the
$U$
is the
 $\unicode[STIX]{x1D716}$
-tube around the zero section of some Euclidean vector bundle
$\unicode[STIX]{x1D716}$
-tube around the zero section of some Euclidean vector bundle
 $E\rightarrow B$
(in our case
$E\rightarrow B$
(in our case
 $B=\overline{L}$
), with projection
$B=\overline{L}$
), with projection
 $\mathsf{p}:U\rightarrow B$
;
$\mathsf{p}:U\rightarrow B$
; -
∙
 $\text{g}$
is a Riemannian metric on
$\text{g}$
is a Riemannian metric on
 $U$
with the same radial function as the Euclidean metric on each fiber of
$U$
with the same radial function as the Euclidean metric on each fiber of
 $E$
;
$E$
; -
∙
 $(U,\text{g},{\mathcal{F}})$
is a singular Riemannian foliation on
$(U,\text{g},{\mathcal{F}})$
is a singular Riemannian foliation on
 $U$
, invariant under rescalings
$U$
, invariant under rescalings
 $r_{\unicode[STIX]{x1D706}}$
. In particular, the zero section
$r_{\unicode[STIX]{x1D706}}$
. In particular, the zero section
 $B$
is saturated by leaves and the projection
$B$
is saturated by leaves and the projection
 $\mathsf{p}$
sends leaves onto leaves;
$\mathsf{p}$
sends leaves onto leaves; -
∙ the restriction
 ${\mathcal{F}}_{B}={\mathcal{F}}|_{B}$
is a regular Riemannian foliation;
${\mathcal{F}}_{B}={\mathcal{F}}|_{B}$
is a regular Riemannian foliation; -
∙ for every leaf
 $L\subseteq B$
and any point
$L\subseteq B$
and any point
 $p\in L$
, the normal exponential map
$p\in L$
, the normal exponential map
 $\unicode[STIX]{x1D708}_{p}^{\unicode[STIX]{x1D716}}L\rightarrow U$
is an embedding.
$\unicode[STIX]{x1D708}_{p}^{\unicode[STIX]{x1D716}}L\rightarrow U$
is an embedding.
5 Three distributions
Let
![]() $(U,\text{g},{\mathcal{F}})$
,
$(U,\text{g},{\mathcal{F}})$
,
![]() $\mathsf{p}:U\rightarrow B$
be as in § 4. In order to prove the main theorem, it is first needed to produce a nicer metric on
$\mathsf{p}:U\rightarrow B$
be as in § 4. In order to prove the main theorem, it is first needed to produce a nicer metric on
![]() $U$
and for this we first need to split the tangent space of
$U$
and for this we first need to split the tangent space of
![]() $U$
into three components. The first,
$U$
into three components. The first,
![]() ${\mathcal{K}}=\ker \mathsf{p}_{\ast }$
, is the distribution tangent to the fibers of
${\mathcal{K}}=\ker \mathsf{p}_{\ast }$
, is the distribution tangent to the fibers of
![]() $\mathsf{p}$
. For the remaining two notice that, since the foliation
$\mathsf{p}$
. For the remaining two notice that, since the foliation
![]() $(B,{\mathcal{F}}_{B})$
is regular, the tangent bundle
$(B,{\mathcal{F}}_{B})$
is regular, the tangent bundle
![]() $TB$
splits into a tangent and a normal part to the foliation:
$TB$
splits into a tangent and a normal part to the foliation:
![]() $TB=T{\mathcal{F}}|_{B}\oplus \unicode[STIX]{x1D708}{\mathcal{F}}|_{B}$
. The last two distributions will be constructed as (appropriately chosen) extensions
$TB=T{\mathcal{F}}|_{B}\oplus \unicode[STIX]{x1D708}{\mathcal{F}}|_{B}$
. The last two distributions will be constructed as (appropriately chosen) extensions
![]() ${\mathcal{T}}$
and
${\mathcal{T}}$
and
![]() ${\mathcal{N}}$
of
${\mathcal{N}}$
of
![]() $T{\mathcal{F}}|_{B}$
and
$T{\mathcal{F}}|_{B}$
and
![]() $\unicode[STIX]{x1D708}{\mathcal{F}}|_{B}$
, respectively, to the whole of
$\unicode[STIX]{x1D708}{\mathcal{F}}|_{B}$
, respectively, to the whole of
![]() $U$
; see Figure 1.
$U$
; see Figure 1.

Figure 1. The distributions at
![]() $q$
.
$q$
.
5.1 The distribution
 ${\mathcal{T}}$
${\mathcal{T}}$
From [Reference AlexandrinoAle10], there exists a distribution
![]() $\widehat{{\mathcal{T}}}$
of rank
$\widehat{{\mathcal{T}}}$
of rank
![]() $\dim {\mathcal{F}}|_{B}$
, which extends
$\dim {\mathcal{F}}|_{B}$
, which extends
![]() $T{\mathcal{F}}|_{B}$
and is everywhere tangent to the leaves of
$T{\mathcal{F}}|_{B}$
and is everywhere tangent to the leaves of
![]() ${\mathcal{F}}$
.
${\mathcal{F}}$
.
The distribution
![]() ${\mathcal{T}}$
is simply defined as the linearization of
${\mathcal{T}}$
is simply defined as the linearization of
![]() $\widehat{{\mathcal{T}}}$
with respect to
$\widehat{{\mathcal{T}}}$
with respect to
![]() $B$
, as follows: consider a family of vector fields
$B$
, as follows: consider a family of vector fields
![]() $\{V_{\unicode[STIX]{x1D6FC}}\}_{\unicode[STIX]{x1D6FC}}$
spanning
$\{V_{\unicode[STIX]{x1D6FC}}\}_{\unicode[STIX]{x1D6FC}}$
spanning
![]() $\widehat{{\mathcal{T}}}$
. Since
$\widehat{{\mathcal{T}}}$
. Since
![]() $\widehat{{\mathcal{T}}}|_{B}$
is tangent to
$\widehat{{\mathcal{T}}}|_{B}$
is tangent to
![]() $B$
, the vector fields
$B$
, the vector fields
![]() $V_{\unicode[STIX]{x1D6FC}}$
lie tangent to
$V_{\unicode[STIX]{x1D6FC}}$
lie tangent to
![]() $B$
as well and therefore it makes sense to consider their linearization
$B$
as well and therefore it makes sense to consider their linearization
![]() $V_{\unicode[STIX]{x1D6FC}}^{\ell }$
with respect to
$V_{\unicode[STIX]{x1D6FC}}^{\ell }$
with respect to
![]() $B$
. By the properties of the linearization, these linearized vector fields still span a smooth distribution of the same rank as
$B$
. By the properties of the linearization, these linearized vector fields still span a smooth distribution of the same rank as
![]() $\widehat{{\mathcal{T}}}$
, which we call
$\widehat{{\mathcal{T}}}$
, which we call
![]() ${\mathcal{T}}$
.
${\mathcal{T}}$
.
5.2 The distribution
 ${\mathcal{N}}$
${\mathcal{N}}$
At each point
![]() $q\in U$
with
$q\in U$
with
![]() $\mathsf{p}(q)=p$
, the slice
$\mathsf{p}(q)=p$
, the slice
![]() $S_{p}=\exp _{p}(\unicode[STIX]{x1D708}_{p}^{\unicode[STIX]{x1D716}}L_{p})$
contains
$S_{p}=\exp _{p}(\unicode[STIX]{x1D708}_{p}^{\unicode[STIX]{x1D716}}L_{p})$
contains
![]() $q$
as well as the whole
$q$
as well as the whole
![]() $\mathsf{p}$
-fiber
$\mathsf{p}$
-fiber
![]() $U_{p}$
through
$U_{p}$
through
![]() $p$
. In particular,
$p$
. In particular,
![]() ${\mathcal{K}}_{q}$
lies tangent to
${\mathcal{K}}_{q}$
lies tangent to
![]() $S_{p}$
. Moreover,
$S_{p}$
. Moreover,
![]() $S_{p}$
comes equipped with a flat metric
$S_{p}$
comes equipped with a flat metric
![]() $\text{g}_{p}$
, inherited from the metric on
$\text{g}_{p}$
, inherited from the metric on
![]() $\unicode[STIX]{x1D708}_{p}L$
via the diffeomorphism
$\unicode[STIX]{x1D708}_{p}L$
via the diffeomorphism
![]() $\exp _{p}:\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D716}}L_{p}\rightarrow S_{p}$
.
$\exp _{p}:\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D716}}L_{p}\rightarrow S_{p}$
.
Define
![]() $\widehat{{\mathcal{N}}}_{q}$
as the subspace of
$\widehat{{\mathcal{N}}}_{q}$
as the subspace of
![]() $T_{q}S_{p}$
which is
$T_{q}S_{p}$
which is
![]() $\text{g}_{p}$
-orthogonal to
$\text{g}_{p}$
-orthogonal to
![]() ${\mathcal{K}}_{q}$
. Finally, define
${\mathcal{K}}_{q}$
. Finally, define
![]() ${\mathcal{N}}$
as the linearization of
${\mathcal{N}}$
as the linearization of
![]() $\widehat{{\mathcal{N}}}$
, as defined in the previous section.
$\widehat{{\mathcal{N}}}$
, as defined in the previous section.
The distributions
![]() $\widehat{{\mathcal{N}}}$
and
$\widehat{{\mathcal{N}}}$
and
![]() ${\mathcal{N}}$
satisfy the following property.
${\mathcal{N}}$
satisfy the following property.
Proposition 5.1. For every smooth
![]() ${\mathcal{F}}_{B}$
-basic vector field
${\mathcal{F}}_{B}$
-basic vector field
![]() $X_{0}$
along a plaque
$X_{0}$
along a plaque
![]() $P$
in
$P$
in
![]() $B$
, there exists a smooth extension
$B$
, there exists a smooth extension
![]() $X$
to an open subset of
$X$
to an open subset of
![]() $U$
such that:
$U$
such that:
-
(i)
 $X$
is foliated and tangent to
$X$
is foliated and tangent to
 $\widehat{{\mathcal{N}}}$
;
$\widehat{{\mathcal{N}}}$
; -
(ii) the linearization
 $X^{\ell }$
of
$X^{\ell }$
of
 $X$
with respect to
$X$
with respect to
 $B$
is tangent to
$B$
is tangent to
 ${\mathcal{N}}$
and it is foliated with respect to both
${\mathcal{N}}$
and it is foliated with respect to both
 ${\mathcal{F}}$
and
${\mathcal{F}}$
and
 ${\mathcal{F}}^{\ell }$
.
${\mathcal{F}}^{\ell }$
.
Proof. (1) Fix a leaf
![]() $L$
in
$L$
in
![]() $B$
, a plaque
$B$
, a plaque
![]() $P\subset L$
, and a parametrization
$P\subset L$
, and a parametrization
where
![]() $k=\dim {\mathcal{F}}_{B}$
. We first show that there exists a small neighbourhood of
$k=\dim {\mathcal{F}}_{B}$
. We first show that there exists a small neighbourhood of
![]() $P$
in
$P$
in
![]() $U$
, on which any
$U$
, on which any
![]() ${\mathcal{F}}_{B}$
-basic vector field
${\mathcal{F}}_{B}$
-basic vector field
![]() $X_{0}$
along
$X_{0}$
along
![]() $P$
can be extended to a foliated vector field
$P$
can be extended to a foliated vector field
![]() $X^{\prime }$
, whose restriction to
$X^{\prime }$
, whose restriction to
![]() $\mathsf{p}^{-1}(P)$
is tangent to
$\mathsf{p}^{-1}(P)$
is tangent to
![]() $\widehat{{\mathcal{N}}}$
.
$\widehat{{\mathcal{N}}}$
.
Let
![]() $\unicode[STIX]{x2202}_{y_{1}},\ldots ,\unicode[STIX]{x2202}_{y_{k}}$
be coordinate vector fields on
$\unicode[STIX]{x2202}_{y_{1}},\ldots ,\unicode[STIX]{x2202}_{y_{k}}$
be coordinate vector fields on
![]() $P$
and let
$P$
and let
![]() $Y_{1},\ldots ,Y_{k}$
denote vector fields, linearized with respect to
$Y_{1},\ldots ,Y_{k}$
denote vector fields, linearized with respect to
![]() $L$
, that extend
$L$
, that extend
![]() $\unicode[STIX]{x2202}_{y_{1}},\ldots ,\unicode[STIX]{x2202}_{y_{k}}$
to a neighbourhood of
$\unicode[STIX]{x2202}_{y_{1}},\ldots ,\unicode[STIX]{x2202}_{y_{k}}$
to a neighbourhood of
![]() $P$
in
$P$
in
![]() $U$
. There is a foliated diffeomorphism
$U$
. There is a foliated diffeomorphism
where
![]() $\unicode[STIX]{x1D6F7}_{i}^{y_{i}}$
is the flow of
$\unicode[STIX]{x1D6F7}_{i}^{y_{i}}$
is the flow of
![]() $Y_{i}$
, after time
$Y_{i}$
, after time
![]() $y_{i}$
.
$y_{i}$
.
Furthermore, the foliation
![]() $(P\times S_{p},P\times {\mathcal{F}}_{S_{p}})$
locally splits as
$(P\times S_{p},P\times {\mathcal{F}}_{S_{p}})$
locally splits as
where
![]() $\unicode[STIX]{x1D708}(L,B)=\unicode[STIX]{x1D708}L\cap TB$
. Moreover, if
$\unicode[STIX]{x1D708}(L,B)=\unicode[STIX]{x1D708}L\cap TB$
. Moreover, if
![]() $S_{p}$
is endowed with the Euclidean metric
$S_{p}$
is endowed with the Euclidean metric
![]() $\text{g}_{p}$
on
$\text{g}_{p}$
on
![]() $\unicode[STIX]{x1D708}_{p}L$
, the splitting
$\unicode[STIX]{x1D708}_{p}L$
, the splitting
![]() $S_{p}=\unicode[STIX]{x1D708}_{p}(L,B)\times \unicode[STIX]{x1D708}_{p}B$
is in fact Riemannian.
$S_{p}=\unicode[STIX]{x1D708}_{p}(L,B)\times \unicode[STIX]{x1D708}_{p}B$
is in fact Riemannian.
The map
![]() $F$
satisfies the following.
$F$
satisfies the following.
-
∙ The set
 $P\times \{0\}\times \unicode[STIX]{x1D708}_{p}^{\unicode[STIX]{x1D716}}B$
is sent to
$P\times \{0\}\times \unicode[STIX]{x1D708}_{p}^{\unicode[STIX]{x1D716}}B$
is sent to
 $\mathsf{p}^{-1}(P)=\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D716}}B|_{P}$
.
$\mathsf{p}^{-1}(P)=\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D716}}B|_{P}$
. -
∙ The set
 $P\times \unicode[STIX]{x1D708}_{p}^{\unicode[STIX]{x1D716}}(L,B)\times \{0\}$
is sent to a neighbourhood of
$P\times \unicode[STIX]{x1D708}_{p}^{\unicode[STIX]{x1D716}}(L,B)\times \{0\}$
is sent to a neighbourhood of
 $P$
in
$P$
in
 $B$
.
$B$
. -
∙ Since
 $F$
is defined via linearized vector fields, each fiber
$F$
is defined via linearized vector fields, each fiber
 $\{p^{\prime }\}\times S_{p}\subset P\times S_{p}$
is sent, via
$\{p^{\prime }\}\times S_{p}\subset P\times S_{p}$
is sent, via
 $F$
, to the slice
$F$
, to the slice
 $S_{p^{\prime }}$
, isometrically with respect to the flat metrics on
$S_{p^{\prime }}$
, isometrically with respect to the flat metrics on
 $S_{p}$
and
$S_{p}$
and
 $S_{p^{\prime }}$
(cf. [Reference Mendes and RadeschiMR15]).
$S_{p^{\prime }}$
(cf. [Reference Mendes and RadeschiMR15]).
From the last point, it follows that the distribution of
![]() $P\times \unicode[STIX]{x1D708}_{p}(L,B)\times \unicode[STIX]{x1D708}_{p}B$
tangent to the second factor is sent, along
$P\times \unicode[STIX]{x1D708}_{p}(L,B)\times \unicode[STIX]{x1D708}_{p}B$
tangent to the second factor is sent, along
![]() $\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D716}}B|_{P}$
, precisely to the distribution
$\unicode[STIX]{x1D708}^{\unicode[STIX]{x1D716}}B|_{P}$
, precisely to the distribution
![]() $\widehat{{\mathcal{N}}}$
.
$\widehat{{\mathcal{N}}}$
.
Any
![]() ${\mathcal{F}}_{B}$
-basic vector field
${\mathcal{F}}_{B}$
-basic vector field
![]() $X_{0}$
along
$X_{0}$
along
![]() $P$
corresponds, via
$P$
corresponds, via
![]() $F$
, to a vector field along
$F$
, to a vector field along
![]() $P\times \{0\}\times \{0\}$
of the form
$P\times \{0\}\times \{0\}$
of the form
![]() $(0,x_{0},0)$
, where
$(0,x_{0},0)$
, where
![]() $x_{0}\in \unicode[STIX]{x1D708}_{p}(L,B)$
is a fixed vector. One can clearly extend such a vector field to the foliated vector field
$x_{0}\in \unicode[STIX]{x1D708}_{p}(L,B)$
is a fixed vector. One can clearly extend such a vector field to the foliated vector field
![]() $X^{\prime }=F_{\ast }(0,x_{0},0)$
. Since
$X^{\prime }=F_{\ast }(0,x_{0},0)$
. Since
![]() $F$
is a foliated map, the vector field
$F$
is a foliated map, the vector field
![]() $X^{\prime }$
is a foliated vector field, whose restriction to
$X^{\prime }$
is a foliated vector field, whose restriction to
![]() $B$
is tangent to
$B$
is tangent to
![]() $B$
by the second point above. Moreover, by the discussion above the restriction of
$B$
by the second point above. Moreover, by the discussion above the restriction of
![]() $X^{\prime }$
to
$X^{\prime }$
to
![]() $\mathsf{p}^{-1}(P)$
is tangent to
$\mathsf{p}^{-1}(P)$
is tangent to
![]() $\widehat{{\mathcal{N}}}$
.
$\widehat{{\mathcal{N}}}$
.
This proves the first claim, made at the beginning of the proof. In particular, since the plaque
![]() $P$
was chosen arbitrarily, this shows that the distribution
$P$
was chosen arbitrarily, this shows that the distribution
![]() $\widehat{{\mathcal{N}}}$
is foliated: that is, given a vector
$\widehat{{\mathcal{N}}}$
is foliated: that is, given a vector
![]() $y$
tangent to
$y$
tangent to
![]() $\widehat{{\mathcal{N}}}$
at a point
$\widehat{{\mathcal{N}}}$
at a point
![]() $q$
, there exists a foliated extension
$q$
, there exists a foliated extension
![]() $Y$
along a plaque containing
$Y$
along a plaque containing
![]() $q$
which is everywhere tangent to
$q$
which is everywhere tangent to
![]() $\widehat{{\mathcal{N}}}$
. It is easy to see that
$\widehat{{\mathcal{N}}}$
. It is easy to see that
![]() ${\mathcal{K}}$
and
${\mathcal{K}}$
and
![]() ${\mathcal{T}}$
are foliated as well. In particular, given the foliated vector field
${\mathcal{T}}$
are foliated as well. In particular, given the foliated vector field
![]() $X^{\prime }$
, the (unique) decomposition
$X^{\prime }$
, the (unique) decomposition
produces three vector fields
![]() $X_{{\mathcal{K}}}^{\prime },X_{{\mathcal{T}}}^{\prime },\,X_{\widehat{{\mathcal{N}}}}^{\prime }$
which are foliated. In particular, the vector field
$X_{{\mathcal{K}}}^{\prime },X_{{\mathcal{T}}}^{\prime },\,X_{\widehat{{\mathcal{N}}}}^{\prime }$
which are foliated. In particular, the vector field
![]() $X=(X^{\prime })_{\widehat{{\mathcal{N}}}}$
is foliated, everywhere tangent to
$X=(X^{\prime })_{\widehat{{\mathcal{N}}}}$
is foliated, everywhere tangent to
![]() $\widehat{{\mathcal{N}}}$
, and it extends
$\widehat{{\mathcal{N}}}$
, and it extends
![]() $X_{0}=(X_{0})_{\widehat{{\mathcal{N}}}}$
to an open set of
$X_{0}=(X_{0})_{\widehat{{\mathcal{N}}}}$
to an open set of
![]() $U$
, as we needed to show.
$U$
, as we needed to show.
(2) Since
![]() $X$
is tangent to
$X$
is tangent to
![]() $\widehat{{\mathcal{N}}}$
, its linearization
$\widehat{{\mathcal{N}}}$
, its linearization
![]() $X^{\ell }$
is tangent to the linearization of
$X^{\ell }$
is tangent to the linearization of
![]() $\widehat{{\mathcal{N}}}$
, which is
$\widehat{{\mathcal{N}}}$
, which is
![]() ${\mathcal{N}}$
. Moreover, since
${\mathcal{N}}$
. Moreover, since
![]() $X$
is foliated and
$X$
is foliated and
![]() $r_{\unicode[STIX]{x1D706}}:U\rightarrow U$
is a foliated map,
$r_{\unicode[STIX]{x1D706}}:U\rightarrow U$
is a foliated map,
![]() $X^{\ell }=\lim _{\unicode[STIX]{x1D706}\rightarrow 0}(r_{\unicode[STIX]{x1D706}}^{-1})_{\ast }X\circ r_{\unicode[STIX]{x1D706}}$
is foliated as well. Finally, since
$X^{\ell }=\lim _{\unicode[STIX]{x1D706}\rightarrow 0}(r_{\unicode[STIX]{x1D706}}^{-1})_{\ast }X\circ r_{\unicode[STIX]{x1D706}}$
is foliated as well. Finally, since
![]() $X$
is foliated, for every vector field
$X$
is foliated, for every vector field
![]() $V$
tangent to
$V$
tangent to
![]() ${\mathcal{F}}$
one has that
${\mathcal{F}}$
one has that
![]() $[X,V]$
is also tangent to
$[X,V]$
is also tangent to
![]() ${\mathcal{F}}$
. Since
${\mathcal{F}}$
. Since
![]() $r_{\unicode[STIX]{x1D706}}$
is a diffeomorphism, one computes
$r_{\unicode[STIX]{x1D706}}$
is a diffeomorphism, one computes
 $$\begin{eqnarray}\displaystyle [X^{\ell },V^{\ell }] & = & \displaystyle \lim _{\unicode[STIX]{x1D706}\rightarrow 0}[(r_{\unicode[STIX]{x1D706}}^{-1})_{\ast }X\circ r_{\unicode[STIX]{x1D706}},(r_{\unicode[STIX]{x1D706}}^{-1})_{\ast }V\circ r_{\unicode[STIX]{x1D706}}]\nonumber\\ \displaystyle & = & \displaystyle \lim _{\unicode[STIX]{x1D706}\rightarrow 0}(r_{\unicode[STIX]{x1D706}}^{-1})_{\ast }[X,V]\circ r_{\unicode[STIX]{x1D706}}\nonumber\\ \displaystyle & = & \displaystyle [X,V]^{\ell }.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle [X^{\ell },V^{\ell }] & = & \displaystyle \lim _{\unicode[STIX]{x1D706}\rightarrow 0}[(r_{\unicode[STIX]{x1D706}}^{-1})_{\ast }X\circ r_{\unicode[STIX]{x1D706}},(r_{\unicode[STIX]{x1D706}}^{-1})_{\ast }V\circ r_{\unicode[STIX]{x1D706}}]\nonumber\\ \displaystyle & = & \displaystyle \lim _{\unicode[STIX]{x1D706}\rightarrow 0}(r_{\unicode[STIX]{x1D706}}^{-1})_{\ast }[X,V]\circ r_{\unicode[STIX]{x1D706}}\nonumber\\ \displaystyle & = & \displaystyle [X,V]^{\ell }.\nonumber\end{eqnarray}$$
Since the linearization
![]() $V^{\ell }$
are precisely the vector fields generating
$V^{\ell }$
are precisely the vector fields generating
![]() ${\mathcal{F}}^{\ell }$
, it follows from the equation above that
${\mathcal{F}}^{\ell }$
, it follows from the equation above that
![]() $[X^{\ell },V^{\ell }]$
is tangent to
$[X^{\ell },V^{\ell }]$
is tangent to
![]() ${\mathcal{F}}^{\ell }$
whenever
${\mathcal{F}}^{\ell }$
whenever
![]() $V^{\ell }$
is and therefore
$V^{\ell }$
is and therefore
![]() $X^{\ell }$
is foliated with respect to
$X^{\ell }$
is foliated with respect to
![]() ${\mathcal{F}}^{\ell }$
.◻
${\mathcal{F}}^{\ell }$
.◻
6 Structure of
 ${\mathcal{F}}^{\ell }$
and the local closure
${\mathcal{F}}^{\ell }$
and the local closure
 $\widehat{{\mathcal{F}}}^{\ell }$
$\widehat{{\mathcal{F}}}^{\ell }$
Using the extensions
![]() $X^{\ell }$
defined in Proposition 5.1, one can prove the following.
$X^{\ell }$
defined in Proposition 5.1, one can prove the following.
Proposition 6.1. Around any point
![]() $p\in B$
there is a neighbourhood
$p\in B$
there is a neighbourhood
![]() $W$
of
$W$
of
![]() $p$
in
$p$
in
![]() $B$
such that
$B$
such that
![]() $(\mathsf{p}^{-1}(W),{\mathcal{F}}^{\ell }|_{\mathsf{p}^{-1}(W)})$
is foliated diffeomorphic to a product
$(\mathsf{p}^{-1}(W),{\mathcal{F}}^{\ell }|_{\mathsf{p}^{-1}(W)})$
is foliated diffeomorphic to a product
where
![]() $k=\dim {\mathcal{F}}|_{B}$
and
$k=\dim {\mathcal{F}}|_{B}$
and
![]() $m=\dim B$
.
$m=\dim B$
.
Proof. Let
![]() $W$
be a coordinate neighbourhood of
$W$
be a coordinate neighbourhood of
![]() $B$
around
$B$
around
![]() $p$
, with a foliated diffeomorphism
$p$
, with a foliated diffeomorphism
![]() $\unicode[STIX]{x1D711}:(W,{\mathcal{F}}|_{W})\rightarrow (\mathbb{D}^{k}\times \mathbb{D}^{m-k},\mathbb{D}^{k}\times \{\text{pts}.\})$
. Let
$\unicode[STIX]{x1D711}:(W,{\mathcal{F}}|_{W})\rightarrow (\mathbb{D}^{k}\times \mathbb{D}^{m-k},\mathbb{D}^{k}\times \{\text{pts}.\})$
. Let
![]() $\unicode[STIX]{x2202}/\unicode[STIX]{x2202}y_{1},\ldots ,\unicode[STIX]{x2202}/\unicode[STIX]{x2202}y_{k}$
denote a basis of vector fields in
$\unicode[STIX]{x2202}/\unicode[STIX]{x2202}y_{1},\ldots ,\unicode[STIX]{x2202}/\unicode[STIX]{x2202}y_{k}$
denote a basis of vector fields in
![]() $W$
tangent to the leaves of
$W$
tangent to the leaves of
![]() ${\mathcal{F}}|_{W}$
and let
${\mathcal{F}}|_{W}$
and let
![]() $V_{1},\ldots ,V_{k}$
denote vector fields on
$V_{1},\ldots ,V_{k}$
denote vector fields on
![]() $\mathsf{p}^{-1}(W)$
, linearized with respect to
$\mathsf{p}^{-1}(W)$
, linearized with respect to
![]() $B$
, extending
$B$
, extending
![]() $\unicode[STIX]{x2202}/\unicode[STIX]{x2202}y_{i}$
,
$\unicode[STIX]{x2202}/\unicode[STIX]{x2202}y_{i}$
,
![]() $i=1,\ldots ,k$
, and spanning the foliation
$i=1,\ldots ,k$
, and spanning the foliation
![]() ${\mathcal{T}}$
. Similarly, let
${\mathcal{T}}$
. Similarly, let
![]() $\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x_{1},\ldots ,\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x_{m-k}$
denote a basis of basic vector fields in
$\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x_{1},\ldots ,\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x_{m-k}$
denote a basis of basic vector fields in
![]() $W$
normal to the leaves and let
$W$
normal to the leaves and let
![]() $X_{1}^{\ell },\ldots ,X_{m-k}^{\ell }$
denote linearized vector fields in
$X_{1}^{\ell },\ldots ,X_{m-k}^{\ell }$
denote linearized vector fields in
![]() $\unicode[STIX]{x1D70B}^{-1}(W)$
defined as in Proposition 5.1, extending the vectors
$\unicode[STIX]{x1D70B}^{-1}(W)$
defined as in Proposition 5.1, extending the vectors
![]() $\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x_{i}$
,
$\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x_{i}$
,
![]() $i=1,\ldots ,m-k$
. Finally, define
$i=1,\ldots ,m-k$
. Finally, define
![]() $\unicode[STIX]{x1D6F7}_{i}^{t}$
and
$\unicode[STIX]{x1D6F7}_{i}^{t}$
and
![]() $\unicode[STIX]{x1D6F9}_{i}^{t}$
as the flows of
$\unicode[STIX]{x1D6F9}_{i}^{t}$
as the flows of
![]() $V_{i}$
and
$V_{i}$
and
![]() $X_{i}^{\ell }$
, respectively, after time
$X_{i}^{\ell }$
, respectively, after time
![]() $t$
, and let
$t$
, and let
Since the
![]() $V_{i}$
and
$V_{i}$
and
![]() $X_{i}^{\ell }$
are linearized, they take fibers of
$X_{i}^{\ell }$
are linearized, they take fibers of
![]() $\mathbb{D}^{k}\times \mathbb{D}^{m-k}\times U_{p}\rightarrow \mathbb{D}^{k}\times \mathbb{D}^{m-k}$
to fibers of
$\mathbb{D}^{k}\times \mathbb{D}^{m-k}\times U_{p}\rightarrow \mathbb{D}^{k}\times \mathbb{D}^{m-k}$
to fibers of
![]() $\mathsf{p}:\mathsf{p}^{-1}(W)\rightarrow W$
. Since the flows
$\mathsf{p}:\mathsf{p}^{-1}(W)\rightarrow W$
. Since the flows
![]() $\unicode[STIX]{x1D6F9}_{i}$
send the leaves of
$\unicode[STIX]{x1D6F9}_{i}$
send the leaves of
![]() ${\mathcal{F}}^{\ell }$
to leaves and the flows
${\mathcal{F}}^{\ell }$
to leaves and the flows
![]() $\unicode[STIX]{x1D6F7}_{i}$
take the leaves of
$\unicode[STIX]{x1D6F7}_{i}$
take the leaves of
![]() ${\mathcal{F}}^{\ell }$
to themselves, the leaves of
${\mathcal{F}}^{\ell }$
to themselves, the leaves of
![]() $\mathbb{D}^{k}\times (\mathbb{D}^{m-k},\{\text{pts.}\})\times (U_{p},{\mathcal{F}}_{p}^{\ell })$
are sent into the leaves of
$\mathbb{D}^{k}\times (\mathbb{D}^{m-k},\{\text{pts.}\})\times (U_{p},{\mathcal{F}}_{p}^{\ell })$
are sent into the leaves of
![]() ${\mathcal{F}}^{\ell }$
. Since the differential
${\mathcal{F}}^{\ell }$
. Since the differential
![]() $dG$
is invertible at
$dG$
is invertible at
![]() $(0,0,p)\in \mathbb{D}^{k}\times \mathbb{D}^{m-k}\times U_{p}$
, it is a diffeomorphism around
$(0,0,p)\in \mathbb{D}^{k}\times \mathbb{D}^{m-k}\times U_{p}$
, it is a diffeomorphism around
![]() $G(0,0,p)=p$
and, by dimensional reasons, the leaves of
$G(0,0,p)=p$
and, by dimensional reasons, the leaves of
![]() $(\mathbb{D}^{k}\times \mathbb{D}^{m-k}\times U_{p},\mathbb{D}^{k}\times \{\text{pts.}\}\times {\mathcal{F}}_{p}^{\ell })$
are mapped diffeomorphically onto the leaves of
$(\mathbb{D}^{k}\times \mathbb{D}^{m-k}\times U_{p},\mathbb{D}^{k}\times \{\text{pts.}\}\times {\mathcal{F}}_{p}^{\ell })$
are mapped diffeomorphically onto the leaves of
![]() $(\mathsf{p}^{-1}(W),{\mathcal{F}}^{\ell }|_{\mathsf{p}^{-1}(W)})$
.◻
$(\mathsf{p}^{-1}(W),{\mathcal{F}}^{\ell }|_{\mathsf{p}^{-1}(W)})$
.◻
The local closure of
 ${\mathcal{F}}^{\ell }$
${\mathcal{F}}^{\ell }$
Even though
![]() $(U_{p},{\mathcal{F}}_{p}^{\ell })$
is homogeneous for every
$(U_{p},{\mathcal{F}}_{p}^{\ell })$
is homogeneous for every
![]() $p\in B$
, it might be the case that its leaves are not closed, which happens when the group
$p\in B$
, it might be the case that its leaves are not closed, which happens when the group
![]() $H_{p}\subseteq \mathsf{O}(U_{p})$
defined in Proposition 2.10 is not closed. To obviate this problem we define a new foliation
$H_{p}\subseteq \mathsf{O}(U_{p})$
defined in Proposition 2.10 is not closed. To obviate this problem we define a new foliation
![]() $\widehat{{\mathcal{F}}}^{\ell }$
, called the local closure of
$\widehat{{\mathcal{F}}}^{\ell }$
, called the local closure of
![]() ${\mathcal{F}}^{\ell }$
, such that
${\mathcal{F}}^{\ell }$
, such that
![]() ${\mathcal{F}}^{\ell }\subset \widehat{{\mathcal{F}}}^{\ell }\subset \overline{{\mathcal{F}}^{\ell }}$
and whose restriction
${\mathcal{F}}^{\ell }\subset \widehat{{\mathcal{F}}}^{\ell }\subset \overline{{\mathcal{F}}^{\ell }}$
and whose restriction
![]() $\widehat{{\mathcal{F}}}_{p}^{\ell }$
to each
$\widehat{{\mathcal{F}}}_{p}^{\ell }$
to each
![]() $\mathsf{p}$
-fiber
$\mathsf{p}$
-fiber
![]() $U_{p}$
is homogeneous and closed.
$U_{p}$
is homogeneous and closed.
Recall that
![]() ${\mathcal{F}}^{\ell }$
is defined by the orbits of the pseudogroup
${\mathcal{F}}^{\ell }$
is defined by the orbits of the pseudogroup
![]() $\mathsf{D}$
of local diffeomorphisms, generated by the flows of linearized vector fields. For each
$\mathsf{D}$
of local diffeomorphisms, generated by the flows of linearized vector fields. For each
![]() $q\in U_{p}$
, consider the closure
$q\in U_{p}$
, consider the closure
![]() $\overline{H}_{p}$
of
$\overline{H}_{p}$
of
![]() $H_{p}$
in
$H_{p}$
in
![]() $\mathsf{O}(U_{p})$
and define the
$\mathsf{O}(U_{p})$
and define the
![]() $\widehat{{\mathcal{F}}}^{\ell }$
-leaf
$\widehat{{\mathcal{F}}}^{\ell }$
-leaf
![]() $\widehat{L}_{q}$
through
$\widehat{L}_{q}$
through
![]() $q$
to be the
$q$
to be the
![]() $\mathsf{D}$
-orbit of
$\mathsf{D}$
-orbit of
![]() $\overline{H}_{p}\cdot q$
:
$\overline{H}_{p}\cdot q$
:
Let
![]() ${\sim}$
denote the relation
${\sim}$
denote the relation
![]() $q\sim q^{\prime }$
if and only if
$q\sim q^{\prime }$
if and only if
![]() $q^{\prime }=\unicode[STIX]{x1D6F7}(h\cdot q)$
for some
$q^{\prime }=\unicode[STIX]{x1D6F7}(h\cdot q)$
for some
![]() $\unicode[STIX]{x1D6F7}\in \mathsf{D}$
and
$\unicode[STIX]{x1D6F7}\in \mathsf{D}$
and
![]() $h\in \overline{H}_{p}$
. In this way, the leaf of
$h\in \overline{H}_{p}$
. In this way, the leaf of
![]() $\widehat{{\mathcal{F}}}^{\ell }$
through
$\widehat{{\mathcal{F}}}^{\ell }$
through
![]() $q$
can be rewritten as
$q$
can be rewritten as
![]() $\{q^{\prime }\in U\mid q^{\prime }\sim q\}$
. As for the other foliations, for every
$\{q^{\prime }\in U\mid q^{\prime }\sim q\}$
. As for the other foliations, for every
![]() $p\in B$
we define
$p\in B$
we define
![]() $(U_{p},\widehat{{\mathcal{F}}}_{p}^{\ell })$
to be the partition of
$(U_{p},\widehat{{\mathcal{F}}}_{p}^{\ell })$
to be the partition of
![]() $U_{p}$
into the connected components of the intersections of
$U_{p}$
into the connected components of the intersections of
![]() $U_{p}$
with the leaves in
$U_{p}$
with the leaves in
![]() $\widehat{{\mathcal{F}}}^{\ell }$
.
$\widehat{{\mathcal{F}}}^{\ell }$
.
Proposition 6.2. The following hold:
-
(1)
 $\widehat{{\mathcal{F}}}^{\ell }$
is a well-defined partition of
$\widehat{{\mathcal{F}}}^{\ell }$
is a well-defined partition of
 $U$
;
$U$
; -
(2) for every
 $p\in B$
, the leaves of
$p\in B$
, the leaves of
 $\widehat{{\mathcal{F}}}_{p}^{\ell }$
are the orbits of
$\widehat{{\mathcal{F}}}_{p}^{\ell }$
are the orbits of
 $\overline{H}_{p}$
on
$\overline{H}_{p}$
on
 $U_{p}$
.
$U_{p}$
.
Proof. (1) One must prove that the relation
![]() ${\sim}$
defined above is an equivalence relation. For this, notice that, since any
${\sim}$
defined above is an equivalence relation. For this, notice that, since any
![]() $\unicode[STIX]{x1D6F7}\in \mathsf{D}$
defines a foliated isometry between
$\unicode[STIX]{x1D6F7}\in \mathsf{D}$
defines a foliated isometry between
![]() $(U_{p},{\mathcal{F}}_{p}^{\ell })$
and
$(U_{p},{\mathcal{F}}_{p}^{\ell })$
and
![]() $(U_{\unicode[STIX]{x1D6F7}(p)},{\mathcal{F}}_{\unicode[STIX]{x1D6F7}(p)}^{\ell })$
for any
$(U_{\unicode[STIX]{x1D6F7}(p)},{\mathcal{F}}_{\unicode[STIX]{x1D6F7}(p)}^{\ell })$
for any
![]() $p\in B$
, in particular it defines a foliated isometry between the respective closures
$p\in B$
, in particular it defines a foliated isometry between the respective closures
![]() $(U_{p},\overline{H}_{p})$
and
$(U_{p},\overline{H}_{p})$
and
![]() $(U_{\unicode[STIX]{x1D6F7}(p)},\overline{H}_{\unicode[STIX]{x1D6F7}(p)})$
. In particular, for any
$(U_{\unicode[STIX]{x1D6F7}(p)},\overline{H}_{\unicode[STIX]{x1D6F7}(p)})$
. In particular, for any
![]() $h\in \overline{H}_{p}$
and
$h\in \overline{H}_{p}$
and
![]() $\unicode[STIX]{x1D6F7}\in \mathsf{D}$
, one has
$\unicode[STIX]{x1D6F7}\in \mathsf{D}$
, one has
![]() $h^{\prime }=\unicode[STIX]{x1D6F7}\circ h\circ \unicode[STIX]{x1D6F7}^{-1}\in \overline{H}_{\unicode[STIX]{x1D6F7}(p)}$
.
$h^{\prime }=\unicode[STIX]{x1D6F7}\circ h\circ \unicode[STIX]{x1D6F7}^{-1}\in \overline{H}_{\unicode[STIX]{x1D6F7}(p)}$
.
– Reflexivity of
![]() ${\sim}$
: if
${\sim}$
: if
![]() $q^{\prime }\sim q$
, then
$q^{\prime }\sim q$
, then
![]() $q^{\prime }=\unicode[STIX]{x1D6F7}(h(q))$
for some
$q^{\prime }=\unicode[STIX]{x1D6F7}(h(q))$
for some
![]() $h\in \overline{H}_{p}$
and
$h\in \overline{H}_{p}$
and
![]() $\unicode[STIX]{x1D6F7}\in \mathsf{D}$
. Then
$\unicode[STIX]{x1D6F7}\in \mathsf{D}$
. Then
![]() $q^{\prime }=h^{\prime }(\unicode[STIX]{x1D6F7}(q))$
, where
$q^{\prime }=h^{\prime }(\unicode[STIX]{x1D6F7}(q))$
, where
![]() $h^{\prime }=\unicode[STIX]{x1D6F7}\circ h\circ \unicode[STIX]{x1D6F7}^{-1}\in \overline{H}_{\unicode[STIX]{x1D6F7}(p)}$
and therefore
$h^{\prime }=\unicode[STIX]{x1D6F7}\circ h\circ \unicode[STIX]{x1D6F7}^{-1}\in \overline{H}_{\unicode[STIX]{x1D6F7}(p)}$
and therefore
![]() $q=\unicode[STIX]{x1D6F7}^{-1}((h^{\prime })^{-1}q^{\prime })$
, which means that
$q=\unicode[STIX]{x1D6F7}^{-1}((h^{\prime })^{-1}q^{\prime })$
, which means that
![]() $q\sim q^{\prime }$
.
$q\sim q^{\prime }$
.
– Transitivity of
![]() ${\sim}$
: if
${\sim}$
: if
![]() $q^{\prime }\sim q$
and
$q^{\prime }\sim q$
and
![]() $q^{\prime \prime }\sim q^{\prime }$
, then
$q^{\prime \prime }\sim q^{\prime }$
, then
![]() $q^{\prime }=\unicode[STIX]{x1D6F7}(h(q))$
and
$q^{\prime }=\unicode[STIX]{x1D6F7}(h(q))$
and
![]() $q^{\prime \prime }=\unicode[STIX]{x1D6F9}(g(q^{\prime }))$
for some
$q^{\prime \prime }=\unicode[STIX]{x1D6F9}(g(q^{\prime }))$
for some
![]() $h\in \overline{H}_{p}$
,
$h\in \overline{H}_{p}$
,
![]() $g\in \overline{H}_{\unicode[STIX]{x1D6F7}(p)}$
, and
$g\in \overline{H}_{\unicode[STIX]{x1D6F7}(p)}$
, and
![]() $\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D6F9}\in \mathsf{D}$
. Then
$\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D6F9}\in \mathsf{D}$
. Then
![]() $q^{\prime \prime }=(\unicode[STIX]{x1D6F9}\circ \unicode[STIX]{x1D6F7})((g^{\prime }\circ h)(q))$
, where
$q^{\prime \prime }=(\unicode[STIX]{x1D6F9}\circ \unicode[STIX]{x1D6F7})((g^{\prime }\circ h)(q))$
, where
![]() $g^{\prime }=\unicode[STIX]{x1D6F7}^{-1}\circ g\circ \unicode[STIX]{x1D6F7}\in \overline{H}_{p}$
, and therefore
$g^{\prime }=\unicode[STIX]{x1D6F7}^{-1}\circ g\circ \unicode[STIX]{x1D6F7}\in \overline{H}_{p}$
, and therefore
![]() $q^{\prime \prime }\sim q$
.
$q^{\prime \prime }\sim q$
.
(2) Let
![]() $L^{\prime }$
denote a leaf of
$L^{\prime }$
denote a leaf of
![]() $\widehat{{\mathcal{F}}}^{\ell }$
. From (1), the intersection of
$\widehat{{\mathcal{F}}}^{\ell }$
. From (1), the intersection of
![]() $L^{\prime }$
with
$L^{\prime }$
with
![]() $U_{p}$
is a union of orbits of
$U_{p}$
is a union of orbits of
![]() $\overline{H}_{p}$
. On the other hand, we claim that the intersection
$\overline{H}_{p}$
. On the other hand, we claim that the intersection
![]() $L^{\prime }\cap U_{p}$
consists of countably many orbits of
$L^{\prime }\cap U_{p}$
consists of countably many orbits of
![]() $\overline{H}_{p}$
, so that each connected component of such intersection must consist of a single
$\overline{H}_{p}$
, so that each connected component of such intersection must consist of a single
![]() $\overline{H}_{p}$
-orbit. From the definition of
$\overline{H}_{p}$
-orbit. From the definition of
![]() $\widehat{{\mathcal{F}}}^{\ell }$
, it is enough to prove that the subgroup
$\widehat{{\mathcal{F}}}^{\ell }$
, it is enough to prove that the subgroup
![]() $\mathsf{D}_{p}\subset \mathsf{D}$
of diffeomorphisms fixing
$\mathsf{D}_{p}\subset \mathsf{D}$
of diffeomorphisms fixing
![]() $p$
moves every
$p$
moves every
![]() $\overline{H}_{p}$
-orbit in
$\overline{H}_{p}$
-orbit in
![]() $L^{\prime }\cap U_{p}$
to at most countably many orbits. For this, consider a piecewise-smooth loop
$L^{\prime }\cap U_{p}$
to at most countably many orbits. For this, consider a piecewise-smooth loop
![]() $\unicode[STIX]{x1D6FE}:[0,1]\rightarrow L_{p}$
with
$\unicode[STIX]{x1D6FE}:[0,1]\rightarrow L_{p}$
with
![]() $\unicode[STIX]{x1D6FE}(0)=\unicode[STIX]{x1D6FE}(1)=p$
. Using linearized vector fields with
$\unicode[STIX]{x1D6FE}(0)=\unicode[STIX]{x1D6FE}(1)=p$
. Using linearized vector fields with
![]() $\unicode[STIX]{x1D6FE}$
as integral curve, one can construct a continuous path
$\unicode[STIX]{x1D6FE}$
as integral curve, one can construct a continuous path
![]() $\unicode[STIX]{x1D6F7}_{t}:[0,1]\rightarrow \mathsf{D}$
of diffeomorphisms such that
$\unicode[STIX]{x1D6F7}_{t}:[0,1]\rightarrow \mathsf{D}$
of diffeomorphisms such that
![]() $\unicode[STIX]{x1D6F7}_{0}=\text{id}_{U}$
and
$\unicode[STIX]{x1D6F7}_{0}=\text{id}_{U}$
and
![]() $\unicode[STIX]{x1D6F7}_{t}(p)=\unicode[STIX]{x1D6FE}(t)$
, as described in [Reference Mendes and RadeschiMR15, Corollary 7]. Fixing some
$\unicode[STIX]{x1D6F7}_{t}(p)=\unicode[STIX]{x1D6FE}(t)$
, as described in [Reference Mendes and RadeschiMR15, Corollary 7]. Fixing some
![]() $\overline{H}_{p}$
-orbit
$\overline{H}_{p}$
-orbit
![]() ${\mathcal{O}}$
in
${\mathcal{O}}$
in
![]() $L^{\prime }\cap U_{p}$
, its image
$L^{\prime }\cap U_{p}$
, its image
![]() $\unicode[STIX]{x1D6F7}_{1}({\mathcal{O}})$
is again some
$\unicode[STIX]{x1D6F7}_{1}({\mathcal{O}})$
is again some
![]() $\overline{H}_{p}$
-orbit, which depends only on the class
$\overline{H}_{p}$
-orbit, which depends only on the class
![]() $[\unicode[STIX]{x1D6FE}]\in \unicode[STIX]{x1D70B}_{1}(L_{p},p)$
and not on the actual path
$[\unicode[STIX]{x1D6FE}]\in \unicode[STIX]{x1D70B}_{1}(L_{p},p)$
and not on the actual path
![]() $\unicode[STIX]{x1D6FE}$
, nor on the specific choice of
$\unicode[STIX]{x1D6FE}$
, nor on the specific choice of
![]() $\unicode[STIX]{x1D6F7}_{t}$
. This gives a map
$\unicode[STIX]{x1D6F7}_{t}$
. This gives a map
This map admits a section, namely: for every orbit
![]() ${\mathcal{O}}^{\prime }$
in
${\mathcal{O}}^{\prime }$
in
![]() $L^{\prime }\cap U_{p}$
, take a path
$L^{\prime }\cap U_{p}$
, take a path
![]() $\unicode[STIX]{x1D6FE}$
in
$\unicode[STIX]{x1D6FE}$
in
![]() $L^{\prime }$
from a point in a (fixed) orbit
$L^{\prime }$
from a point in a (fixed) orbit
![]() ${\mathcal{O}}$
to a point in
${\mathcal{O}}$
to a point in
![]() ${\mathcal{O}}^{\prime }$
. Under the projection
${\mathcal{O}}^{\prime }$
. Under the projection
![]() $\mathsf{p}:U\rightarrow B$
, the composition
$\mathsf{p}:U\rightarrow B$
, the composition
![]() $\mathsf{p}\circ \unicode[STIX]{x1D6FE}$
is a loop in
$\mathsf{p}\circ \unicode[STIX]{x1D6FE}$
is a loop in
![]() $L_{p}$
. The section of
$L_{p}$
. The section of
![]() $\unicode[STIX]{x2202}$
sends
$\unicode[STIX]{x2202}$
sends
![]() ${\mathcal{O}}^{\prime }$
to
${\mathcal{O}}^{\prime }$
to
![]() $[\mathsf{p}\circ \unicode[STIX]{x1D6FE}]\in \unicode[STIX]{x1D70B}_{1}(L_{p},p)$
. In particular, the map
$[\mathsf{p}\circ \unicode[STIX]{x1D6FE}]\in \unicode[STIX]{x1D70B}_{1}(L_{p},p)$
. In particular, the map
![]() $\unicode[STIX]{x2202}$
is surjective and therefore the set of
$\unicode[STIX]{x2202}$
is surjective and therefore the set of
![]() $\overline{H}_{p}$
-orbits in
$\overline{H}_{p}$
-orbits in
![]() $L^{\prime }\cap U_{p}$
has at most the cardinality of
$L^{\prime }\cap U_{p}$
has at most the cardinality of
![]() $\unicode[STIX]{x1D70B}_{1}(L_{p},p)$
, which is at most countable since
$\unicode[STIX]{x1D70B}_{1}(L_{p},p)$
, which is at most countable since
![]() $L_{p}$
is a manifold.◻
$L_{p}$
is a manifold.◻
As a corollary of Propositions 6.2 and 6.1, one gets the following result.
Corollary 6.3. Let
![]() $(U,{\mathcal{F}})$
be a singular Riemannian foliation as in § 4, let
$(U,{\mathcal{F}})$
be a singular Riemannian foliation as in § 4, let
![]() ${\mathcal{F}}^{\ell }$
be its linearized foliation, and
${\mathcal{F}}^{\ell }$
be its linearized foliation, and
![]() $\widehat{{\mathcal{F}}}^{\ell }$
the local closure. Then
$\widehat{{\mathcal{F}}}^{\ell }$
the local closure. Then
![]() $\widehat{{\mathcal{F}}}^{\ell }$
is a singular foliation with complete leaves. Moreover, around each point
$\widehat{{\mathcal{F}}}^{\ell }$
is a singular foliation with complete leaves. Moreover, around each point
![]() $p\in B$
there is a neighbourhood
$p\in B$
there is a neighbourhood
![]() $W$
of
$W$
of
![]() $p$
in
$p$
in
![]() $B$
such that
$B$
such that
![]() $(\mathsf{p}^{-1}(W),\widehat{{\mathcal{F}}}^{\ell }|_{\mathsf{p}^{-1}(W)})$
is foliated diffeomorphic to a product
$(\mathsf{p}^{-1}(W),\widehat{{\mathcal{F}}}^{\ell }|_{\mathsf{p}^{-1}(W)})$
is foliated diffeomorphic to a product
which can be given the structure of a singular Riemannian foliation.
Once it is shown that
![]() $\widehat{{\mathcal{F}}}^{\ell }$
is also a transnormal system with respect to some metric, then by the corollary above it is globally a singular Riemannian foliation.
$\widehat{{\mathcal{F}}}^{\ell }$
is also a transnormal system with respect to some metric, then by the corollary above it is globally a singular Riemannian foliation.
7 A new metric
Let
![]() ${\mathcal{T}},{\mathcal{N}},\,{\mathcal{K}}$
be the distributions as in the previous section. Clearly, one has
${\mathcal{T}},{\mathcal{N}},\,{\mathcal{K}}$
be the distributions as in the previous section. Clearly, one has
![]() $TU={\mathcal{T}}\oplus {\mathcal{N}}\oplus {\mathcal{K}}$
.
$TU={\mathcal{T}}\oplus {\mathcal{N}}\oplus {\mathcal{K}}$
.
Now define the new metric
![]() $\text{g}^{\ell }$
on
$\text{g}^{\ell }$
on
![]() $U$
, as the metric defined by the following properties:
$U$
, as the metric defined by the following properties:
-
∙
 ${\mathcal{T}}\oplus {\mathcal{N}}$
and
${\mathcal{T}}\oplus {\mathcal{N}}$
and
 ${\mathcal{K}}$
are orthogonal with respect to
${\mathcal{K}}$
are orthogonal with respect to
 $\text{g}^{\ell }$
;
$\text{g}^{\ell }$
; -
∙
 $\text{g}^{\ell }|_{{\mathcal{T}}\oplus {\mathcal{N}}}=\mathsf{p}^{\ast }\text{g}_{B}$
, where
$\text{g}^{\ell }|_{{\mathcal{T}}\oplus {\mathcal{N}}}=\mathsf{p}^{\ast }\text{g}_{B}$
, where
 $\text{g}_{B}$
denotes the restriction of the original metric on
$\text{g}_{B}$
denotes the restriction of the original metric on
 $B$
. In particular,
$B$
. In particular,
 ${\mathcal{T}}$
and
${\mathcal{T}}$
and
 ${\mathcal{N}}$
are also orthogonal to one another;
${\mathcal{N}}$
are also orthogonal to one another; -
∙ for any
 $q\in U_{p}$
, recall that
$q\in U_{p}$
, recall that
 ${\mathcal{K}}_{q}=T_{q}U_{p}$
and define
${\mathcal{K}}_{q}=T_{q}U_{p}$
and define
 $\text{g}^{\ell }|_{{\mathcal{K}}_{q}}=\text{g}_{p}$
as the flat metric on
$\text{g}^{\ell }|_{{\mathcal{K}}_{q}}=\text{g}_{p}$
as the flat metric on
 $U_{p}$
induced from
$U_{p}$
induced from
 $\exp _{p}:\unicode[STIX]{x1D708}_{p}B\rightarrow U_{p}$
.
$\exp _{p}:\unicode[STIX]{x1D708}_{p}B\rightarrow U_{p}$
.
These conditions characterize the metric
![]() $\text{g}^{\ell }$
uniquely. The most useful property of this metric is the following.
$\text{g}^{\ell }$
uniquely. The most useful property of this metric is the following.
Proposition 7.1. The triples
![]() $(U,\text{g}^{\ell },{\mathcal{F}}^{\ell })$
and
$(U,\text{g}^{\ell },{\mathcal{F}}^{\ell })$
and
![]() $(U,\text{g}^{\ell },\widehat{{\mathcal{F}}}^{\ell })$
are singular Riemannian foliations.
$(U,\text{g}^{\ell },\widehat{{\mathcal{F}}}^{\ell })$
are singular Riemannian foliations.
Proof. The arguments for
![]() ${\mathcal{F}}^{\ell }$
and
${\mathcal{F}}^{\ell }$
and
![]() $\widehat{{\mathcal{F}}}^{\ell }$
are identical; therefore, we will only check the proposition for
$\widehat{{\mathcal{F}}}^{\ell }$
are identical; therefore, we will only check the proposition for
![]() $(U,\text{g}^{\ell },\widehat{{\mathcal{F}}}^{\ell })$
(which is the only case we need for the main theorem anyway).
$(U,\text{g}^{\ell },\widehat{{\mathcal{F}}}^{\ell })$
(which is the only case we need for the main theorem anyway).
Moreover, the statement is local in nature; therefore, it is enough to prove the statement on certain open sets covering the whole of
![]() $U$
. For any point
$U$
. For any point
![]() $p\in B$
, let
$p\in B$
, let
![]() $W$
denote a neighbourhood of
$W$
denote a neighbourhood of
![]() $p$
in
$p$
in
![]() $B$
and
$B$
and
![]() $\mathsf{p}^{-1}(W)$
a neighbourhood of
$\mathsf{p}^{-1}(W)$
a neighbourhood of
![]() $p$
in
$p$
in
![]() $U$
. We need to check that
$U$
. We need to check that
![]() $(\mathsf{p}^{-1}(W),\text{g}^{\ell },\widehat{{\mathcal{F}}}^{\ell })$
is a singular Riemannian foliation. To prove this, we apply [Reference AlexandrinoAle10, Proposition 2.14], which states that it is enough to check two conditions:
$(\mathsf{p}^{-1}(W),\text{g}^{\ell },\widehat{{\mathcal{F}}}^{\ell })$
is a singular Riemannian foliation. To prove this, we apply [Reference AlexandrinoAle10, Proposition 2.14], which states that it is enough to check two conditions:
-
(1)
 $(\mathsf{p}^{-1}(W),g^{\prime },\widehat{{\mathcal{F}}}^{\ell })$
is a singular Riemannian foliation with respect to some Riemannian metric
$(\mathsf{p}^{-1}(W),g^{\prime },\widehat{{\mathcal{F}}}^{\ell })$
is a singular Riemannian foliation with respect to some Riemannian metric
 $g^{\prime }$
;
$g^{\prime }$
; -
(2) for every stratum
 $\unicode[STIX]{x1D6F4}\subset \mathsf{p}^{-1}(W)$
(i.e. union of leaves of the same dimension), the restriction of
$\unicode[STIX]{x1D6F4}\subset \mathsf{p}^{-1}(W)$
(i.e. union of leaves of the same dimension), the restriction of
 $\widehat{{\mathcal{F}}}^{\ell }$
to
$\widehat{{\mathcal{F}}}^{\ell }$
to
 $\unicode[STIX]{x1D6F4}$
is a (regular) Riemannian foliation.
$\unicode[STIX]{x1D6F4}$
is a (regular) Riemannian foliation.
The first condition is satisfied by Corollary 6.3. The second condition is equivalent to checking that, for every leaf
![]() $\widehat{L}_{q}$
of
$\widehat{L}_{q}$
of
![]() $\widehat{{\mathcal{F}}}^{\ell }|_{\mathsf{p}^{-1}(W)}$
and every basic vector field
$\widehat{{\mathcal{F}}}^{\ell }|_{\mathsf{p}^{-1}(W)}$
and every basic vector field
![]() $X$
along
$X$
along
![]() $\widehat{L}_{q}$
tangent to the stratum through
$\widehat{L}_{q}$
tangent to the stratum through
![]() $\widehat{L}_{q}$
, the norm
$\widehat{L}_{q}$
, the norm
![]() $\Vert X\Vert _{\text{g}^{\ell }}$
is constant along
$\Vert X\Vert _{\text{g}^{\ell }}$
is constant along
![]() $\widehat{L}_{q}$
.
$\widehat{L}_{q}$
.
By definition of the metric
![]() $\text{g}^{\ell }$
, the space
$\text{g}^{\ell }$
, the space
![]() $\unicode[STIX]{x1D708}\widehat{L}_{q}$
is given by
$\unicode[STIX]{x1D708}\widehat{L}_{q}$
is given by
![]() ${\mathcal{N}}|_{\widehat{L}_{q}}\oplus (\unicode[STIX]{x1D708}\widehat{L}_{q}\cap {\mathcal{K}})$
. From Proposition 5.1, along
${\mathcal{N}}|_{\widehat{L}_{q}}\oplus (\unicode[STIX]{x1D708}\widehat{L}_{q}\cap {\mathcal{K}})$
. From Proposition 5.1, along
![]() $\widehat{L}_{q}$
the space
$\widehat{L}_{q}$
the space
![]() ${\mathcal{N}}$
is spanned by linearized vector fields
${\mathcal{N}}$
is spanned by linearized vector fields
![]() $X_{i}^{\ell }$
, which are then
$X_{i}^{\ell }$
, which are then
![]() $\text{g}^{\ell }$
-basic (i.e. foliated and
$\text{g}^{\ell }$
-basic (i.e. foliated and
![]() $\text{g}^{\ell }$
-orthogonal to the leaves). In particular, any basic vector field
$\text{g}^{\ell }$
-orthogonal to the leaves). In particular, any basic vector field
![]() $\overline{X}$
along
$\overline{X}$
along
![]() $\widehat{L}_{q}$
splits as a sum
$\widehat{L}_{q}$
splits as a sum
![]() $\overline{X}=\overline{X}_{1}+\overline{X}_{2}$
, where
$\overline{X}=\overline{X}_{1}+\overline{X}_{2}$
, where
![]() $\overline{X}_{1}$
is tangent to
$\overline{X}_{1}$
is tangent to
![]() ${\mathcal{N}}$
,
${\mathcal{N}}$
,
![]() $\overline{X}_{2}$
is tangent to
$\overline{X}_{2}$
is tangent to
![]() ${\mathcal{N}}^{\prime }:=\unicode[STIX]{x1D708}\widehat{L}_{q}\cap {\mathcal{K}}$
, and
${\mathcal{N}}^{\prime }:=\unicode[STIX]{x1D708}\widehat{L}_{q}\cap {\mathcal{K}}$
, and
![]() $\text{g}^{\ell }(\overline{X}_{1},\overline{X}_{2})=0$
. Therefore, it is enough to check independently that for every basic vector field
$\text{g}^{\ell }(\overline{X}_{1},\overline{X}_{2})=0$
. Therefore, it is enough to check independently that for every basic vector field
![]() $\overline{X}$
along
$\overline{X}$
along
![]() $\widehat{L}_{q}$
, tangent to either
$\widehat{L}_{q}$
, tangent to either
![]() ${\mathcal{N}}$
or
${\mathcal{N}}$
or
![]() ${\mathcal{N}}^{\prime }$
, the norm of
${\mathcal{N}}^{\prime }$
, the norm of
![]() $\overline{X}$
is constant along
$\overline{X}$
is constant along
![]() $\widehat{L}_{q}$
.
$\widehat{L}_{q}$
.
If
![]() $\overline{X}$
is tangent to
$\overline{X}$
is tangent to
![]() ${\mathcal{N}}$
, then by the construction in Proposition 5.1 it projects to some basic vector field
${\mathcal{N}}$
, then by the construction in Proposition 5.1 it projects to some basic vector field
![]() $X$
along
$X$
along
![]() $\widehat{L}_{p}\subset B$
. Since
$\widehat{L}_{p}\subset B$
. Since
![]() $(B,\text{g}_{B},{\mathcal{F}}|_{B})$
is a Riemannian foliation, the norm
$(B,\text{g}_{B},{\mathcal{F}}|_{B})$
is a Riemannian foliation, the norm
![]() $\Vert X\Vert _{\text{g}_{B}}$
is constant along
$\Vert X\Vert _{\text{g}_{B}}$
is constant along
![]() $\widehat{L}_{p}$
. By the construction of the metric
$\widehat{L}_{p}$
. By the construction of the metric
![]() $\text{g}^{\ell }$
, one has
$\text{g}^{\ell }$
, one has
![]() $\Vert \overline{X}\Vert _{\text{g}^{\ell }}=\Vert X\Vert _{\text{g}_{B}}$
and, therefore, the norm of
$\Vert \overline{X}\Vert _{\text{g}^{\ell }}=\Vert X\Vert _{\text{g}_{B}}$
and, therefore, the norm of
![]() $\overline{X}$
is constant along
$\overline{X}$
is constant along
![]() $\widehat{L}_{q}$
.
$\widehat{L}_{q}$
.
If
![]() $\overline{X}$
is tangent to
$\overline{X}$
is tangent to
![]() ${\mathcal{N}}^{\prime }$
, then it is tangent to any fiber
${\mathcal{N}}^{\prime }$
, then it is tangent to any fiber
![]() $U_{p^{\prime }}$
,
$U_{p^{\prime }}$
,
![]() $p^{\prime }\in \widehat{L}_{p}$
. The restriction
$p^{\prime }\in \widehat{L}_{p}$
. The restriction
![]() $\overline{X}|_{U_{p^{\prime }}}$
is a basic vector field of
$\overline{X}|_{U_{p^{\prime }}}$
is a basic vector field of
![]() $(U_{p^{\prime }},\widehat{{\mathcal{F}}}_{p^{\prime }}^{\ell })$
along
$(U_{p^{\prime }},\widehat{{\mathcal{F}}}_{p^{\prime }}^{\ell })$
along
![]() $\widehat{L}_{q}\cap U_{p^{\prime }}$
and therefore the norm
$\widehat{L}_{q}\cap U_{p^{\prime }}$
and therefore the norm
![]() $\Vert \overline{X}|_{U_{p^{\prime }}}\Vert _{\text{g}_{p^{\prime }}}$
is locally constant along
$\Vert \overline{X}|_{U_{p^{\prime }}}\Vert _{\text{g}_{p^{\prime }}}$
is locally constant along
![]() $\widehat{L}_{q}\cap U_{p^{\prime }}$
. By the construction of
$\widehat{L}_{q}\cap U_{p^{\prime }}$
. By the construction of
![]() $\text{g}^{\ell }$
, it follows that
$\text{g}^{\ell }$
, it follows that
![]() $\Vert \overline{X}|_{U_{p^{\prime }}}\Vert _{\text{g}^{\ell }}$
is also locally constant along each
$\Vert \overline{X}|_{U_{p^{\prime }}}\Vert _{\text{g}^{\ell }}$
is also locally constant along each
![]() $\widehat{L}_{q}\cap U_{p^{\prime }}$
. However, given two points
$\widehat{L}_{q}\cap U_{p^{\prime }}$
. However, given two points
![]() $p^{\prime },p^{\prime \prime }\in \widehat{L}_{p}$
and a vertical, foliated vector field
$p^{\prime },p^{\prime \prime }\in \widehat{L}_{p}$
and a vertical, foliated vector field
![]() $V^{\ell }$
whose flow
$V^{\ell }$
whose flow
![]() $\unicode[STIX]{x1D6F7}$
moves
$\unicode[STIX]{x1D6F7}$
moves
![]() $p^{\prime }$
to
$p^{\prime }$
to
![]() $p^{\prime \prime }$
, one also has that
$p^{\prime \prime }$
, one also has that
![]() $\unicode[STIX]{x1D6F7}$
moves
$\unicode[STIX]{x1D6F7}$
moves
![]() $U_{p^{\prime }}$
isometrically to
$U_{p^{\prime }}$
isometrically to
![]() $U_{p^{\prime \prime }}$
and
$U_{p^{\prime \prime }}$
and
![]() $\overline{X}|_{U_{p^{\prime }}}$
to
$\overline{X}|_{U_{p^{\prime }}}$
to
![]() $\overline{X}|_{U_{p^{\prime \prime }}}$
. In particular,
$\overline{X}|_{U_{p^{\prime \prime }}}$
. In particular,
![]() $\Vert \overline{X}|_{U_{p^{\prime }}}\Vert _{\text{g}^{\ell }}=\Vert \overline{X}|_{U_{p^{\prime }}}\Vert _{\text{g}_{p^{\prime }}}$
does not really depend on the point
$\Vert \overline{X}|_{U_{p^{\prime }}}\Vert _{\text{g}^{\ell }}=\Vert \overline{X}|_{U_{p^{\prime }}}\Vert _{\text{g}_{p^{\prime }}}$
does not really depend on the point
![]() $p^{\prime }\in \widehat{L}_{p}$
and it is actually constant along the whole leaf
$p^{\prime }\in \widehat{L}_{p}$
and it is actually constant along the whole leaf
![]() $\widehat{L}_{q}$
.◻
$\widehat{L}_{q}$
.◻
With this in place, one can finally prove the main theorem.
Proof of the main theorem.
Let
![]() $U$
be an
$U$
be an
![]() $\unicode[STIX]{x1D716}$
-tubular neighbourhood around the closure
$\unicode[STIX]{x1D716}$
-tubular neighbourhood around the closure
![]() $\overline{L}$
of a leaf
$\overline{L}$
of a leaf
![]() $L\in {\mathcal{F}}$
. Letting
$L\in {\mathcal{F}}$
. Letting
![]() $B=\overline{L}$
, we are under the assumptions of § 4. In particular, it is possible to define the linearized foliation
$B=\overline{L}$
, we are under the assumptions of § 4. In particular, it is possible to define the linearized foliation
![]() ${\mathcal{F}}^{\ell }$
on
${\mathcal{F}}^{\ell }$
on
![]() $U$
, its local closure
$U$
, its local closure
![]() $\widehat{{\mathcal{F}}}^{\ell }$
, and the metric
$\widehat{{\mathcal{F}}}^{\ell }$
, and the metric
![]() $\text{g}^{\ell }$
as in Proposition 7.1. It is clear by construction that
$\text{g}^{\ell }$
as in Proposition 7.1. It is clear by construction that
![]() $\widehat{{\mathcal{F}}}^{\ell }|_{\overline{L}}={\mathcal{F}}|_{L}$
and that the closure of
$\widehat{{\mathcal{F}}}^{\ell }|_{\overline{L}}={\mathcal{F}}|_{L}$
and that the closure of
![]() $\widehat{{\mathcal{F}}}^{\ell }$
is contained in the closure of
$\widehat{{\mathcal{F}}}^{\ell }$
is contained in the closure of
![]() ${\mathcal{F}}$
. Moreover, by Corollary 6.3, the foliation
${\mathcal{F}}$
. Moreover, by Corollary 6.3, the foliation
![]() $(U,\text{g}^{\ell },\widehat{{\mathcal{F}}}^{\ell })$
is, locally around each point, foliated diffeomorphic to the orbit-like foliation
$(U,\text{g}^{\ell },\widehat{{\mathcal{F}}}^{\ell })$
is, locally around each point, foliated diffeomorphic to the orbit-like foliation
![]() $(\mathbb{D}^{k}\times \mathbb{D}^{m-k}\times U_{p},\mathbb{D}^{k}\times \{\text{pts.}\}\times \widehat{{\mathcal{F}}}_{p}^{\ell })$
. By Proposition 2.9, the foliation
$(\mathbb{D}^{k}\times \mathbb{D}^{m-k}\times U_{p},\mathbb{D}^{k}\times \{\text{pts.}\}\times \widehat{{\mathcal{F}}}_{p}^{\ell })$
. By Proposition 2.9, the foliation
![]() $(U,\text{g}^{\ell },\widehat{{\mathcal{F}}}^{\ell })$
is orbit-like as well and this concludes the proof.◻
$(U,\text{g}^{\ell },\widehat{{\mathcal{F}}}^{\ell })$
is orbit-like as well and this concludes the proof.◻
Acknowledgements
The authors thank Professor Lytchak and Professor Thorbergsson for consistent support.