1 Introduction
The linear regression model with multiplicative interaction terms of the form
is a workhorse model in the social sciences for examining whether the relationship between an outcome
![]() $Y$
and a key independent variable
$Y$
and a key independent variable
![]() $D$
varies with levels of a moderator
$D$
varies with levels of a moderator
![]() $X$
, which is often meant to capture differences in context. For example, we might expect that the effect of
$X$
, which is often meant to capture differences in context. For example, we might expect that the effect of
![]() $D$
on
$D$
on
![]() $Y$
grows with higher levels of
$Y$
grows with higher levels of
![]() $X$
. Such conditional hypotheses are ubiquitous in the social sciences and linear regression models with multiplicative interaction terms are the most widely used framework for testing them in applied work.Footnote
1
$X$
. Such conditional hypotheses are ubiquitous in the social sciences and linear regression models with multiplicative interaction terms are the most widely used framework for testing them in applied work.Footnote
1
A large body of literature advises scholars how to test such conditional hypotheses using multiplicative interaction models. For example, Brambor, Clark, and Golder (Reference Brambor, Clark and Golder2006) provide a simple checklist of dos and don’ts.Footnote
2
They recommend that scholars should (1) include in the model all constitutive terms (
![]() $D$
and
$D$
and
![]() $X$
) alongside the interaction term (
$X$
) alongside the interaction term (
![]() $D\cdot X$
), (2) not interpret the coefficients on the constitutive terms (
$D\cdot X$
), (2) not interpret the coefficients on the constitutive terms (
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D702}$
) as unconditional marginal effects, and (3) compute substantively meaningful marginal effects and confidence intervals, ideally with a plot that shows how the conditional marginal effect of
$\unicode[STIX]{x1D702}$
) as unconditional marginal effects, and (3) compute substantively meaningful marginal effects and confidence intervals, ideally with a plot that shows how the conditional marginal effect of
![]() $D$
on
$D$
on
![]() $Y$
changes across levels of the moderator
$Y$
changes across levels of the moderator
![]() $X$
.
$X$
.
The recommendations given in Brambor, Clark, and Golder (Reference Brambor, Clark and Golder2006) have been highly cited and are nowadays often considered the best practice in political science.Footnote 3 As our survey of five top political science journals from 2006 to 2015 suggests, most articles with interaction terms now follow these guidelines and routinely report interaction effects with the marginal-effect plots recommended in Brambor, Clark, and Golder (Reference Brambor, Clark and Golder2006). In addition, scholars today rarely leave out constitutive terms or misinterpret the coefficients on the constitutive terms as unconditional marginal effects. Clearly, empirical practice improved with the publication of Brambor, Clark, and Golder (Reference Brambor, Clark and Golder2006) and related advice.
Despite these advances, we contend that the current best practice guidelines for using multiplicative interaction models do not address key issues, especially in the common scenario where at least one of the interacted variables is continuous. In particular, we emphasize two important problems that are currently often overlooked and not detected by scholars using the existing guidelines.
First, while multiplicative interaction models allow the effect of the key independent variable
![]() $D$
to vary across levels of the moderator
$D$
to vary across levels of the moderator
![]() $X$
, they maintain the important assumption that the interaction effect is linear and follows the functional form given by
$X$
, they maintain the important assumption that the interaction effect is linear and follows the functional form given by
![]() $\unicode[STIX]{x2202}Y/\unicode[STIX]{x2202}D=\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}X$
. This linear interaction effect (LIE) assumption states that the effect of
$\unicode[STIX]{x2202}Y/\unicode[STIX]{x2202}D=\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}X$
. This linear interaction effect (LIE) assumption states that the effect of
![]() $D$
on
$D$
on
![]() $Y$
can only linearly change with
$Y$
can only linearly change with
![]() $X$
at a constant rate given by
$X$
at a constant rate given by
![]() $\unicode[STIX]{x1D6FD}$
. In other words, the LIE assumption implies that the heterogeneity in effects is such that as
$\unicode[STIX]{x1D6FD}$
. In other words, the LIE assumption implies that the heterogeneity in effects is such that as
![]() $X$
increases by one unit, the effect of
$X$
increases by one unit, the effect of
![]() $D$
on
$D$
on
![]() $Y$
changes by
$Y$
changes by
![]() $\unicode[STIX]{x1D6FD}$
and this change in the effect is constant across the whole range of
$\unicode[STIX]{x1D6FD}$
and this change in the effect is constant across the whole range of
![]() $X$
. Perhaps not surprisingly, this LIE assumption often fails in empirical settings because many interaction effects are not linear and some may not even be monotonic. In fact, replicating 46 interaction effects that appeared in 22 articles published in the top five political science journals between 2006 and 2015, we find that the effect of
$X$
. Perhaps not surprisingly, this LIE assumption often fails in empirical settings because many interaction effects are not linear and some may not even be monotonic. In fact, replicating 46 interaction effects that appeared in 22 articles published in the top five political science journals between 2006 and 2015, we find that the effect of
![]() $D$
on
$D$
on
![]() $Y$
changes linearly in only about 48% of cases. In roughly 70% of cases, we cannot even reject the null that the effect of the key independent variable of interest is equal at typical low and typical high levels of the moderator once we relax the LIE assumption that underlies the claim of an interaction effect in the original studies. This suggests that a large share of published work across all empirical political science subfields using multiplicative interaction models draws conclusions that rest on a modeling artifact that goes undetected even when applying the current best practice guidelines. It is worth noting that researchers can use a regression model as a linear approximation for the unknown true model. However, the linear marginal-effect plots in the studies that we review, as well as the accompanying discussions therein, show that many authors take the LIE assumption quite literally and treat the linear interaction model as the true model. That is, both in text and in their marginal-effect plots, researchers move beyond on-average conclusions and instead claim to have estimated the marginal effect of the treatment at specific values of the moderator, interpretations which rely heavily on the linear functional form being correct.Footnote
4
$Y$
changes linearly in only about 48% of cases. In roughly 70% of cases, we cannot even reject the null that the effect of the key independent variable of interest is equal at typical low and typical high levels of the moderator once we relax the LIE assumption that underlies the claim of an interaction effect in the original studies. This suggests that a large share of published work across all empirical political science subfields using multiplicative interaction models draws conclusions that rest on a modeling artifact that goes undetected even when applying the current best practice guidelines. It is worth noting that researchers can use a regression model as a linear approximation for the unknown true model. However, the linear marginal-effect plots in the studies that we review, as well as the accompanying discussions therein, show that many authors take the LIE assumption quite literally and treat the linear interaction model as the true model. That is, both in text and in their marginal-effect plots, researchers move beyond on-average conclusions and instead claim to have estimated the marginal effect of the treatment at specific values of the moderator, interpretations which rely heavily on the linear functional form being correct.Footnote
4
Second, another problem that is often overlooked is the issue of lack of common support. Scholars using multiplicative interaction models routinely report the effect of
![]() $D$
on
$D$
on
![]() $Y$
across a wide range of
$Y$
across a wide range of
![]() $X$
values by plugging the
$X$
values by plugging the
![]() $X$
values into the conditional marginal-effect formula
$X$
values into the conditional marginal-effect formula
![]() $\unicode[STIX]{x2202}Y/\unicode[STIX]{x2202}D=\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}X$
. However, often little attention is paid as to whether there is sufficient common support in the data when computing the conditional marginal effects. Ideally, to compute the marginal effect of
$\unicode[STIX]{x2202}Y/\unicode[STIX]{x2202}D=\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}X$
. However, often little attention is paid as to whether there is sufficient common support in the data when computing the conditional marginal effects. Ideally, to compute the marginal effect of
![]() $D$
at a given value of the moderator,
$D$
at a given value of the moderator,
![]() $x_{o}$
, there needs to be (1) a sufficient number of observations whose
$x_{o}$
, there needs to be (1) a sufficient number of observations whose
![]() $X$
values are close to
$X$
values are close to
![]() $x_{o}$
and (2) variation in the treatment,
$x_{o}$
and (2) variation in the treatment,
![]() $D$
, at
$D$
, at
![]() $x_{o}$
. If either of these two conditions fails, the conditional marginal-effect estimates are based on extrapolation or interpolation of the functional form to an area where there is no or only sparse data and therefore the effect estimates are fragile and model dependent (King and Zeng Reference King and Zeng2006). In our replications we find that this type of extrapolation is common in empirical practice. Typically articles report conditional marginal-effect estimates for the entire range of the moderator which often includes large intervals where there are no or very few observations. Similarly, some articles report conditional marginal-effect estimates for values of the moderator where there is no variation in the key independent variable of interest. Overall, our replications suggest that scholars are not sufficiently aware of the lack of common support problem and draw conclusions based on highly model dependent estimates. And according to our replications, these problems are common to all empirical subfields in political science.
$x_{o}$
. If either of these two conditions fails, the conditional marginal-effect estimates are based on extrapolation or interpolation of the functional form to an area where there is no or only sparse data and therefore the effect estimates are fragile and model dependent (King and Zeng Reference King and Zeng2006). In our replications we find that this type of extrapolation is common in empirical practice. Typically articles report conditional marginal-effect estimates for the entire range of the moderator which often includes large intervals where there are no or very few observations. Similarly, some articles report conditional marginal-effect estimates for values of the moderator where there is no variation in the key independent variable of interest. Overall, our replications suggest that scholars are not sufficiently aware of the lack of common support problem and draw conclusions based on highly model dependent estimates. And according to our replications, these problems are common to all empirical subfields in political science.
Our goal is not to point fingers. Indeed, in the vast majority of studies we replicate below researchers were employing the accepted best practices at the time of publication. Our goal is to improve empirical practice. To this end we develop a set of simple diagnostic tests that help researchers to detect these currently overlooked and important problems. In addition, we offer simple semiparametric modeling strategies that allow researchers to remain in their familiar regression framework and estimate conditional marginal effects while relaxing the LIE assumption and avoiding model dependency that stems from excessive extrapolation.
Our diagnostics and estimation strategies are easy to implement using standard software packages. We propose a revised checklist that augments the existing guidelines for best practice. We also make available the code and data that implements our methods and replicates our figures in R and STATA.Footnote 5
While the focus of our study is on interaction models, we emphasize that the issues of model misspecification and lack of common support are not unique to these models and also apply to regression models without interaction terms. However, these issues may more often go overlooked in interaction models because marginal-effect estimates involve three key variables—the treatment, moderator, and response—requiring different diagnostic approaches to assess both functional form and common support.
In fact, as we show below, the LIE assumption implies that the conditional effect of
![]() $D$
is the difference between two linear functions in
$D$
is the difference between two linear functions in
![]() $X$
and therefore the assumption is unlikely to hold unless both of these functions are indeed linear. Similarly, there is often insufficient common support in
$X$
and therefore the assumption is unlikely to hold unless both of these functions are indeed linear. Similarly, there is often insufficient common support in
![]() $X$
across different values of
$X$
across different values of
![]() $D$
if the distribution of
$D$
if the distribution of
![]() $D$
and/or
$D$
and/or
![]() $X$
is highly skewed, or if one of the variables does not vary in some regions of the joint support of
$X$
is highly skewed, or if one of the variables does not vary in some regions of the joint support of
![]() $D$
and
$D$
and
![]() $X$
.
$X$
.
The rest of the article proceeds as follows. In the next section we discuss the problems with the multiplicative interaction model. In the third section we introduce our diagnostic tools and estimation strategies. In the fourth section we apply them to the replication data. The last section provides our revised guidelines for best practice and concludes.
2 Multiplicative Interaction Models
Consider the classical linear multiplicative interaction model that is often assumed in empirical work and is given by the following regression equation:
In this model
![]() $Y$
is the outcome variable,
$Y$
is the outcome variable,
![]() $D$
is the key independent variable of interest or “treatment,”
$D$
is the key independent variable of interest or “treatment,”
![]() $X$
is the moderator—a variable that affects the direction and/or strength of the treatment effect,Footnote
6
$X$
is the moderator—a variable that affects the direction and/or strength of the treatment effect,Footnote
6
![]() $D\cdot X$
is the interaction term between
$D\cdot X$
is the interaction term between
![]() $D$
and
$D$
and
![]() $X$
,
$X$
,
![]() $Z$
is a vector of control variables, and
$Z$
is a vector of control variables, and
![]() $\unicode[STIX]{x1D707}$
and
$\unicode[STIX]{x1D707}$
and
![]() $\unicode[STIX]{x1D716}$
represent the constant and error terms, respectively.Footnote
7
$\unicode[STIX]{x1D716}$
represent the constant and error terms, respectively.Footnote
7
We focus on the cases where the treatment variable
![]() $D$
is either binary or continuous and the moderator
$D$
is either binary or continuous and the moderator
![]() $X$
is continuous. When
$X$
is continuous. When
![]() $D$
and
$D$
and
![]() $X$
are both binary or discrete with few unique values one should employ a fully saturated model that dummies out the treatment and the moderator and includes all interaction terms to obtain the treatment effect at each level of
$X$
are both binary or discrete with few unique values one should employ a fully saturated model that dummies out the treatment and the moderator and includes all interaction terms to obtain the treatment effect at each level of
![]() $X$
. Moreover, in the following discussion we focus on the interaction effect components of the model (
$X$
. Moreover, in the following discussion we focus on the interaction effect components of the model (
![]() $D$
,
$D$
,
![]() $X$
, and
$X$
, and
![]() $D\cdot X$
). When covariates
$D\cdot X$
). When covariates
![]() $Z$
are included in the model, we maintain the typical assumption that the model is correctly specified with respect to these covariates.
$Z$
are included in the model, we maintain the typical assumption that the model is correctly specified with respect to these covariates.
The coefficients of Model (1) are consistently estimated under the usual linear regression assumptions which imply that the functional form is correctly specified and that
![]() $\mathbb{E}[\unicode[STIX]{x1D716}\mid D,X,Z]=0$
. In the multiplicative interaction model this implies the LIE assumption which says that the marginal effect of the treatment
$\mathbb{E}[\unicode[STIX]{x1D716}\mid D,X,Z]=0$
. In the multiplicative interaction model this implies the LIE assumption which says that the marginal effect of the treatment
![]() $D$
on the outcome
$D$
on the outcome
![]() $Y$
is
$Y$
is
which is a linear function of the moderator
![]() $X$
. This LIE assumption implies that the effect of
$X$
. This LIE assumption implies that the effect of
![]() $D$
on
$D$
on
![]() $Y$
can only linearly change with
$Y$
can only linearly change with
![]() $X$
, so if
$X$
, so if
![]() $X$
increases by one unit, the effect of
$X$
increases by one unit, the effect of
![]() $D$
on
$D$
on
![]() $Y$
changes by
$Y$
changes by
![]() $\unicode[STIX]{x1D6FD}$
and this change in the effect is constant across the whole range of
$\unicode[STIX]{x1D6FD}$
and this change in the effect is constant across the whole range of
![]() $X$
. This is a strong assumption, because we often have little theoretical or empirical reason to believe that the heterogeneity in the effect of
$X$
. This is a strong assumption, because we often have little theoretical or empirical reason to believe that the heterogeneity in the effect of
![]() $D$
on
$D$
on
![]() $Y$
takes such a linear form. Instead, it might well be that the effect of
$Y$
takes such a linear form. Instead, it might well be that the effect of
![]() $D$
on
$D$
on
![]() $Y$
is nonlinear or nonmonotonic. For example, the effect might be small for low values of
$Y$
is nonlinear or nonmonotonic. For example, the effect might be small for low values of
![]() $X$
, large at medium values of
$X$
, large at medium values of
![]() $X$
, and then small again for high values of
$X$
, and then small again for high values of
![]() $X$
.
$X$
.
The LIE assumption in Equation (2) means that the relative effect of treatment
![]() $D=d_{1}$
vs.
$D=d_{1}$
vs.
![]() $D=d_{2}$
can be expressed by the difference between two linear functions in
$D=d_{2}$
can be expressed by the difference between two linear functions in
![]() $X$
:
$X$
:
 $$\begin{eqnarray}\displaystyle \mathit{Eff}(d_{1},d_{2}) & = & \displaystyle Y(D=d_{1}\mid X,Z)-Y(D=d_{2}\mid X,Z)\nonumber\\ \displaystyle & = & \displaystyle (\unicode[STIX]{x1D707}+\unicode[STIX]{x1D6FC}d_{1}+\unicode[STIX]{x1D702}X+\unicode[STIX]{x1D6FD}d_{1}X)-(\unicode[STIX]{x1D707}+\unicode[STIX]{x1D6FC}d_{2}+\unicode[STIX]{x1D702}X+\unicode[STIX]{x1D6FD}d_{2}X)\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FC}(d_{1}-d_{2})+\unicode[STIX]{x1D6FD}(d_{1}-d_{2})X.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathit{Eff}(d_{1},d_{2}) & = & \displaystyle Y(D=d_{1}\mid X,Z)-Y(D=d_{2}\mid X,Z)\nonumber\\ \displaystyle & = & \displaystyle (\unicode[STIX]{x1D707}+\unicode[STIX]{x1D6FC}d_{1}+\unicode[STIX]{x1D702}X+\unicode[STIX]{x1D6FD}d_{1}X)-(\unicode[STIX]{x1D707}+\unicode[STIX]{x1D6FC}d_{2}+\unicode[STIX]{x1D702}X+\unicode[STIX]{x1D6FD}d_{2}X)\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FC}(d_{1}-d_{2})+\unicode[STIX]{x1D6FD}(d_{1}-d_{2})X.\end{eqnarray}$$
This decomposition makes clear that under the LIE assumption, the effect of
![]() $D$
on
$D$
on
![]() $Y$
is the difference between two linear functions,
$Y$
is the difference between two linear functions,
![]() $\unicode[STIX]{x1D707}+\unicode[STIX]{x1D6FC}d_{1}+(\unicode[STIX]{x1D702}+\unicode[STIX]{x1D6FD}d_{1})X$
and
$\unicode[STIX]{x1D707}+\unicode[STIX]{x1D6FC}d_{1}+(\unicode[STIX]{x1D702}+\unicode[STIX]{x1D6FD}d_{1})X$
and
![]() $\unicode[STIX]{x1D707}+\unicode[STIX]{x1D6FC}d_{2}+(\unicode[STIX]{x1D702}+\unicode[STIX]{x1D6FD}d_{2})X$
, and therefore the LIE assumption will be most likely to hold if both functions are linear for all modeled contrasts of
$\unicode[STIX]{x1D707}+\unicode[STIX]{x1D6FC}d_{2}+(\unicode[STIX]{x1D702}+\unicode[STIX]{x1D6FD}d_{2})X$
, and therefore the LIE assumption will be most likely to hold if both functions are linear for all modeled contrasts of
![]() $d_{1}$
vs.
$d_{1}$
vs.
![]() $d_{2}$
.Footnote
8
$d_{2}$
.Footnote
8
![]() $^{,}$
Footnote
9
$^{,}$
Footnote
9
This illustrates how attempts to estimate interaction effects with multiplicative interaction models are susceptible to misspecification bias because the LIE assumption will fail if one or both functions are misspecified due to nonlinearities, nonmonotonicities, or a skewed distribution of
![]() $X$
and/or
$X$
and/or
![]() $D$
, resulting in bad influence points, etc. As our empirical survey shows below, in practice this LIE assumption often fails because at least one of the two functions is not linear.Footnote
10
$D$
, resulting in bad influence points, etc. As our empirical survey shows below, in practice this LIE assumption often fails because at least one of the two functions is not linear.Footnote
10
The decomposition in Equation (3) also highlights the issue of common support. Since the conditional effect of
![]() $D$
on
$D$
on
![]() $Y$
is the difference between two linear functions, it is important that the two functions share common support over
$Y$
is the difference between two linear functions, it is important that the two functions share common support over
![]() $X$
. In other words, at any given value of the moderator
$X$
. In other words, at any given value of the moderator
![]() $X=x_{0}$
, there should be (1) a sufficient number of data points in the neighborhood of
$X=x_{0}$
, there should be (1) a sufficient number of data points in the neighborhood of
![]() $X=x_{0}$
and (2) those data points should exhibit variation in the treatment,
$X=x_{0}$
and (2) those data points should exhibit variation in the treatment,
![]() $D$
. If, for example, in the neighborhood of
$D$
. If, for example, in the neighborhood of
![]() $X=x_{0}$
all data points are treated units (
$X=x_{0}$
all data points are treated units (
![]() $D=1$
), we have a lack of common support and, since there are no control units (
$D=1$
), we have a lack of common support and, since there are no control units (
![]() $D=0$
) in the same region at all, the estimated conditional effect will be driven by interpolation or extrapolation and thus model dependent.Footnote
11
$D=0$
) in the same region at all, the estimated conditional effect will be driven by interpolation or extrapolation and thus model dependent.Footnote
11
Multiplicative interaction models are susceptible to the lack of common support problem because if the goal is to estimate the conditional effect of
![]() $D$
across the range of
$D$
across the range of
![]() $X$
then this requires common support across the entire joint distribution of
$X$
then this requires common support across the entire joint distribution of
![]() $D$
and
$D$
and
![]() $X$
. Otherwise, estimation of the conditional marginal effect will rely on interpolation or extrapolation of at least one of the functions to an area where there is no or only very few observations. It is well known that such interpolation or extrapolation purely based on an assumed functional form results in fragile and model dependent estimates. Slight changes in the assumed functional form or data can lead to very different answers (King and Zeng Reference King and Zeng2006). In our empirical survey below we show that such interpolation or extrapolation is common in applied work using multiplicative interaction models.
$X$
. Otherwise, estimation of the conditional marginal effect will rely on interpolation or extrapolation of at least one of the functions to an area where there is no or only very few observations. It is well known that such interpolation or extrapolation purely based on an assumed functional form results in fragile and model dependent estimates. Slight changes in the assumed functional form or data can lead to very different answers (King and Zeng Reference King and Zeng2006). In our empirical survey below we show that such interpolation or extrapolation is common in applied work using multiplicative interaction models.
In sum, there are two problems with multiplicative interaction models. The LIE assumption states that the interaction effect is linear, but if this assumption fails, the conditional marginal-effect estimates are inconsistent and biased. In addition, the common support condition suggests that we need sufficient data on
![]() $X$
and
$X$
and
![]() $D$
because otherwise the estimates will be model dependent. Both problems are currently overlooked because they are not detected by scholars following the current best practice guidelines. In the next section we develop simple diagnostic tools and estimation strategies that allow scholars to diagnose these problems and estimate conditional marginal effects while relaxing the LIE assumption.
$D$
because otherwise the estimates will be model dependent. Both problems are currently overlooked because they are not detected by scholars following the current best practice guidelines. In the next section we develop simple diagnostic tools and estimation strategies that allow scholars to diagnose these problems and estimate conditional marginal effects while relaxing the LIE assumption.
3 Diagnostics
Before introducing the diagnostic tools, we present simulated data samples to highlight three scenarios: (1) linear marginal effect with a dichotomous treatment, (2) linear marginal effect with a continuous treatment, and (3) nonlinear marginal effect with a dichotomous treatment.
The data generating process (DGP) for both samples that contain a linear marginal effect is as follows:
![]() $Y_{i}$
is the outcome for unit
$Y_{i}$
is the outcome for unit
![]() $i$
, the moderator is
$i$
, the moderator is
![]() $X_{i}\stackrel{\text{i.i.d.}}{{\sim}}{\mathcal{N}}(3,1)$
, and the error term is
$X_{i}\stackrel{\text{i.i.d.}}{{\sim}}{\mathcal{N}}(3,1)$
, and the error term is
![]() $\unicode[STIX]{x1D716}_{i}\stackrel{\text{i.i.d.}}{{\sim}}{\mathcal{N}}(0,4)$
. Both samples share the same sets of
$\unicode[STIX]{x1D716}_{i}\stackrel{\text{i.i.d.}}{{\sim}}{\mathcal{N}}(0,4)$
. Both samples share the same sets of
![]() $X_{i}$
and
$X_{i}$
and
![]() $\unicode[STIX]{x1D716}_{i}$
, but in the first sample, the treatment indicator is
$\unicode[STIX]{x1D716}_{i}$
, but in the first sample, the treatment indicator is
![]() $D_{i}\stackrel{\text{i.i.d.}}{{\sim}}Bernoulli(0.5)$
, while in the second one it is
$D_{i}\stackrel{\text{i.i.d.}}{{\sim}}Bernoulli(0.5)$
, while in the second one it is
![]() $D_{i}\stackrel{\text{i.i.d.}}{{\sim}}{\mathcal{N}}(3,1)$
. The marginal effect of
$D_{i}\stackrel{\text{i.i.d.}}{{\sim}}{\mathcal{N}}(3,1)$
. The marginal effect of
![]() $D$
on
$D$
on
![]() $Y$
therefore is
$Y$
therefore is
![]() $ME_{D}=-9+3X$
.
$ME_{D}=-9+3X$
.
The DGP for the sample with a nonlinear marginal effect is:
![]() $Y_{i}$
is the outcome, the moderator is
$Y_{i}$
is the outcome, the moderator is
![]() $X_{i}\stackrel{\text{i.i.d.}}{{\sim}}{\mathcal{U}}(-3,3)$
, the treatment indicator is
$X_{i}\stackrel{\text{i.i.d.}}{{\sim}}{\mathcal{U}}(-3,3)$
, the treatment indicator is
![]() $D_{i}\stackrel{\text{i.i.d.}}{{\sim}}\mathit{Bernoulli}(0.5)$
, and the error term is
$D_{i}\stackrel{\text{i.i.d.}}{{\sim}}\mathit{Bernoulli}(0.5)$
, and the error term is
![]() $\unicode[STIX]{x1D701}_{i}\stackrel{\text{i.i.d.}}{{\sim}}{\mathcal{N}}(0,4)$
. The marginal effect of
$\unicode[STIX]{x1D701}_{i}\stackrel{\text{i.i.d.}}{{\sim}}{\mathcal{N}}(0,4)$
. The marginal effect of
![]() $D$
on
$D$
on
![]() $Y$
therefore is
$Y$
therefore is
![]() $ME_{D}=-5+2X^{2}$
. For simplicity, we do not include any control variables. Note that all three samples have 200 observations.
$ME_{D}=-5+2X^{2}$
. For simplicity, we do not include any control variables. Note that all three samples have 200 observations.
We now present a simple visual diagnostic to help researchers to detect potential problems with the LIE assumption and the lack of common support. The diagnostic that we recommend is a scatterplot of raw data. This diagnostic is simple to implement and powerful in the sense that it readily reveals the main problems associated with the LIE assumption and lack of common support.
If the treatment
![]() $D$
is binary, we recommend plotting the outcome
$D$
is binary, we recommend plotting the outcome
![]() $Y$
against the moderator
$Y$
against the moderator
![]() $X$
separately for the sample of treatment group observations (
$X$
separately for the sample of treatment group observations (
![]() $D=1$
) and the sample of control group observations (
$D=1$
) and the sample of control group observations (
![]() $D=0$
). In each sample we recommend superimposing a linear regression line as well as LOESS fits in each group (Cleveland and Devlin Reference Cleveland and Devlin1988).Footnote
12
The upper panel of Figure 1 presents examples of such a plot for the simulated data with the binary treatment in cases where the marginal effect is (a) linear and (b) nonlinear.
$D=0$
). In each sample we recommend superimposing a linear regression line as well as LOESS fits in each group (Cleveland and Devlin Reference Cleveland and Devlin1988).Footnote
12
The upper panel of Figure 1 presents examples of such a plot for the simulated data with the binary treatment in cases where the marginal effect is (a) linear and (b) nonlinear.

Figure 1. Linear Interaction Diagnostic (LID) plots: simulated samples. Note: The above plots show the relationships among the treatment
![]() $D$
, the outcome
$D$
, the outcome
![]() $Y$
, and the moderator
$Y$
, and the moderator
![]() $X$
using the raw data: (a) when
$X$
using the raw data: (a) when
![]() $D$
is binary and the true marginal effect is linear; (b) when
$D$
is binary and the true marginal effect is linear; (b) when
![]() $D$
is binary and the true marginal effect is nonlinear (quadratic); and (c) when
$D$
is binary and the true marginal effect is nonlinear (quadratic); and (c) when
![]() $D$
is continuous and the true marginal effect is linear.
$D$
is continuous and the true marginal effect is linear.
The first important issue to check is whether the relationship between
![]() $Y$
and
$Y$
and
![]() $X$
is reasonably linear in both groups. For this we can simply check if the linear regression lines (blue) and the LOESS fits (red) diverge considerably across the range of
$X$
is reasonably linear in both groups. For this we can simply check if the linear regression lines (blue) and the LOESS fits (red) diverge considerably across the range of
![]() $X$
values. In Figure 1(a), where the true DGP contains a linear marginal effect, the two lines are very close to each other in both groups indicating that both conditional expectation functions are well approximated with a linear fit as required by the LIE assumption. However, as Figure 1(b) shows, LOESS (i.e. locally weighted regression) and ordinary least squares (OLS) will diverge considerably when the true marginal effect is nonlinear, thus alerting the researcher to a possible misspecification error.
$X$
values. In Figure 1(a), where the true DGP contains a linear marginal effect, the two lines are very close to each other in both groups indicating that both conditional expectation functions are well approximated with a linear fit as required by the LIE assumption. However, as Figure 1(b) shows, LOESS (i.e. locally weighted regression) and ordinary least squares (OLS) will diverge considerably when the true marginal effect is nonlinear, thus alerting the researcher to a possible misspecification error.
We call these plots the Linear Interaction Diagnostic (LID) plots. In addition to shedding light on the validity of the LIE assumption, they provide other important insights as well. In Figure 1(a), the slope of
![]() $Y$
on
$Y$
on
![]() $X$
in the treatment group is apparently larger (less negative) than that of the control group (
$X$
in the treatment group is apparently larger (less negative) than that of the control group (
![]() $\hat{\unicode[STIX]{x1D702}}+\hat{\unicode[STIX]{x1D6FD}}>\hat{\unicode[STIX]{x1D702}}$
), suggesting a possible positive interaction effect of
$\hat{\unicode[STIX]{x1D702}}+\hat{\unicode[STIX]{x1D6FD}}>\hat{\unicode[STIX]{x1D702}}$
), suggesting a possible positive interaction effect of
![]() $D$
and
$D$
and
![]() $X$
on
$X$
on
![]() $Y$
. The LOESS fit in Figure 1(b) also gives evidence that the relationship between
$Y$
. The LOESS fit in Figure 1(b) also gives evidence that the relationship between
![]() $X$
and
$X$
and
![]() $Y$
differs between the two groups, (in fact, the functions are near mirror opposites), a result that is masked by the OLS fit.
$Y$
differs between the two groups, (in fact, the functions are near mirror opposites), a result that is masked by the OLS fit.
A final important issue to look out for is whether there is sufficient common support in the data. For this we can simply compare the distribution of
![]() $X$
in both groups and examine the range of
$X$
in both groups and examine the range of
![]() $X$
values for which there are a sufficient number of data points for the estimation of marginal effects. The box plots near the center of the figures display quantiles of the moderator at each level of the treatment. The dot in the center denotes the median, the end points of the thick bars denote the 25th and 75th percentiles, and the end points of the thin bars denote the 5th and 95th percentiles. In Figure 1(a), we see that both groups share a common support of
$X$
values for which there are a sufficient number of data points for the estimation of marginal effects. The box plots near the center of the figures display quantiles of the moderator at each level of the treatment. The dot in the center denotes the median, the end points of the thick bars denote the 25th and 75th percentiles, and the end points of the thin bars denote the 5th and 95th percentiles. In Figure 1(a), we see that both groups share a common support of
![]() $X$
for the range between about 1.5 to 4.5—whereas support exists across the entire range of
$X$
for the range between about 1.5 to 4.5—whereas support exists across the entire range of
![]() $X$
in Figure 1(b)—as we would expect given the simulation parameters.Footnote
13
$X$
in Figure 1(b)—as we would expect given the simulation parameters.Footnote
13
If the treatment and moderator are continuous, then visualizing the conditional relationship of
![]() $Y$
and
$Y$
and
![]() $D$
across levels of
$D$
across levels of
![]() $X$
is more complicated, but in our experience a simple binning approach is sufficient to detect most problems in typical political science data. Accordingly, we recommend that researchers split the sample into three roughly equal sized groups based on the moderator: low
$X$
is more complicated, but in our experience a simple binning approach is sufficient to detect most problems in typical political science data. Accordingly, we recommend that researchers split the sample into three roughly equal sized groups based on the moderator: low
![]() $X$
(first tercile), medium
$X$
(first tercile), medium
![]() $X$
(second tercile), and high
$X$
(second tercile), and high
![]() $X$
(third tercile). For each of the three groups we then plot
$X$
(third tercile). For each of the three groups we then plot
![]() $Y$
against
$Y$
against
![]() $D$
while again overlaying both the linear and LOESS fits.
$D$
while again overlaying both the linear and LOESS fits.
Panel (c) of Figure 1 presents an LID plot for the simulated data with the continuous treatment and linear marginal effect. The plot reveals that the conditional expectation function of
![]() $Y$
given
$Y$
given
![]() $D$
is well approximated by a linear model in all three samples of observations with low, medium, or high values on the moderator
$D$
is well approximated by a linear model in all three samples of observations with low, medium, or high values on the moderator
![]() $X$
.
$X$
.
There is also clear evidence of an interaction as the slope of the line which captures the relationship between
![]() $D$
on
$D$
on
![]() $Y$
is negative at low levels of
$Y$
is negative at low levels of
![]() $X$
, flat at medium levels of
$X$
, flat at medium levels of
![]() $X$
, and positive at high levels of
$X$
, and positive at high levels of
![]() $X$
. In this case of a continuous treatment and continuous moderator it is also useful to generate the LID plot in both directions to examine the conditional relationships of
$X$
. In this case of a continuous treatment and continuous moderator it is also useful to generate the LID plot in both directions to examine the conditional relationships of
![]() $D\mid X$
and
$D\mid X$
and
![]() $X\mid D$
as the standard linear interaction model assumes linearity in both directions. Moreover, it can be useful to visualize interactions using a three-dimensional surface plot generated by a generalized additive model (GAM, Hastie and Tibshirani Reference Hastie and Tibshirani1986).Footnote
14
$X\mid D$
as the standard linear interaction model assumes linearity in both directions. Moreover, it can be useful to visualize interactions using a three-dimensional surface plot generated by a generalized additive model (GAM, Hastie and Tibshirani Reference Hastie and Tibshirani1986).Footnote
14
4 Estimation Strategies
In this section we develop two simple estimation strategies to estimate the conditional marginal effect of
![]() $D$
on
$D$
on
![]() $Y$
across values of the moderator
$Y$
across values of the moderator
![]() $X$
. These approaches have the advantage that they remain in the regression framework familiar to applied researchers and at the same time relax the LIE assumption and flexibly allow for heterogeneity in how the conditional marginal effect changes across values of
$X$
. These approaches have the advantage that they remain in the regression framework familiar to applied researchers and at the same time relax the LIE assumption and flexibly allow for heterogeneity in how the conditional marginal effect changes across values of
![]() $X$
. When the marginal effect is indeed linear in
$X$
. When the marginal effect is indeed linear in
![]() $X$
, these strategies are less efficient than the linear interaction model, however, they offer protection against excessive model dependency and the lack of common support—a classic case of the bias-variance trade-off.
$X$
, these strategies are less efficient than the linear interaction model, however, they offer protection against excessive model dependency and the lack of common support—a classic case of the bias-variance trade-off.
4.1 Binning estimator
The first estimation approach is a binning estimator. Simply put, we break a continuous moderator into several bins represented by dummy variables and interact these dummy variables with the treatment indicator, with some adjustment to improve interpretability.Footnote
15
There are three steps to implement the estimator. First, we discretize the moderator variable
![]() $X$
into three bins (respectively corresponding to the three terciles) as before and create a dummy variable for each bin. More formally, we define three dummy variables that indicate the interval
$X$
into three bins (respectively corresponding to the three terciles) as before and create a dummy variable for each bin. More formally, we define three dummy variables that indicate the interval
![]() $X$
falls into:
$X$
falls into:
 $$\begin{eqnarray}G_{1}=\left\{\begin{array}{@{}ll@{}}1\quad & X<\unicode[STIX]{x1D6FF}_{1/3}\\ 0\quad & \text{otherwise}\\ \quad \end{array}\right.,\quad G_{2}=\left\{\begin{array}{@{}ll@{}}1\quad & X\in [\unicode[STIX]{x1D6FF}_{1/3},\unicode[STIX]{x1D6FF}_{2/3})\\ 0\quad & \text{otherwise}\end{array}\right.,\quad G_{3}=\left\{\begin{array}{@{}ll@{}}1\quad & X\geqslant \unicode[STIX]{x1D6FF}_{2/3}\\ 0\quad & \text{otherwise}\end{array}\right.,\end{eqnarray}$$
$$\begin{eqnarray}G_{1}=\left\{\begin{array}{@{}ll@{}}1\quad & X<\unicode[STIX]{x1D6FF}_{1/3}\\ 0\quad & \text{otherwise}\\ \quad \end{array}\right.,\quad G_{2}=\left\{\begin{array}{@{}ll@{}}1\quad & X\in [\unicode[STIX]{x1D6FF}_{1/3},\unicode[STIX]{x1D6FF}_{2/3})\\ 0\quad & \text{otherwise}\end{array}\right.,\quad G_{3}=\left\{\begin{array}{@{}ll@{}}1\quad & X\geqslant \unicode[STIX]{x1D6FF}_{2/3}\\ 0\quad & \text{otherwise}\end{array}\right.,\end{eqnarray}$$
in which
![]() $\unicode[STIX]{x1D6FF}_{1/3}$
and
$\unicode[STIX]{x1D6FF}_{1/3}$
and
![]() $\unicode[STIX]{x1D6FF}_{2/3}$
are respectively the first and second terciles of
$\unicode[STIX]{x1D6FF}_{2/3}$
are respectively the first and second terciles of
![]() $X$
. We can choose other numbers in the support of
$X$
. We can choose other numbers in the support of
![]() $X$
to create the bins but the advantage of using terciles is that we obtain estimates of the effect at typical low, medium, and high values of
$X$
to create the bins but the advantage of using terciles is that we obtain estimates of the effect at typical low, medium, and high values of
![]() $X$
. While three bins tend to work well in practice for typical political science data that we encountered, the researcher can create more than three bins in order to get a finer resolution of the effect heterogeneity. Increasing the number of bins requires a sufficiently large number of observations.
$X$
. While three bins tend to work well in practice for typical political science data that we encountered, the researcher can create more than three bins in order to get a finer resolution of the effect heterogeneity. Increasing the number of bins requires a sufficiently large number of observations.
Second, we pick an evaluation point within each bin,
![]() $x_{1}$
,
$x_{1}$
,
![]() $x_{2}$
, and
$x_{2}$
, and
![]() $x_{3}$
, where we want to estimate the conditional marginal effect of
$x_{3}$
, where we want to estimate the conditional marginal effect of
![]() $D$
on
$D$
on
![]() $Y$
. Typically, we choose
$Y$
. Typically, we choose
![]() $x_{1}$
,
$x_{1}$
,
![]() $x_{2}$
, and
$x_{2}$
, and
![]() $x_{3}$
to be the median of
$x_{3}$
to be the median of
![]() $X$
in each bin, but researchers are free to choose other numbers within the bins (for example, the means).
$X$
in each bin, but researchers are free to choose other numbers within the bins (for example, the means).
Third, we estimate a model that includes interactions between the bin dummies
![]() $G$
and the treatment indicator
$G$
and the treatment indicator
![]() $D$
, the bin dummies and the moderator
$D$
, the bin dummies and the moderator
![]() $X$
minus the evaluation points we pick (
$X$
minus the evaluation points we pick (
![]() $x_{1}$
,
$x_{1}$
,
![]() $x_{2}$
, and
$x_{2}$
, and
![]() $x_{3}$
), as well as the triple interactions. The last two terms are to capture the changing effect of
$x_{3}$
), as well as the triple interactions. The last two terms are to capture the changing effect of
![]() $D$
on
$D$
on
![]() $Y$
within each bin defined by
$Y$
within each bin defined by
![]() $G$
. Formally, we estimate the following model:
$G$
. Formally, we estimate the following model:
in which
![]() $\unicode[STIX]{x1D707}_{j}$
,
$\unicode[STIX]{x1D707}_{j}$
,
![]() $\unicode[STIX]{x1D6FC}_{j}$
,
$\unicode[STIX]{x1D6FC}_{j}$
,
![]() $\unicode[STIX]{x1D702}_{j}$
, and
$\unicode[STIX]{x1D702}_{j}$
, and
![]() $\unicode[STIX]{x1D6FD}_{j}$
(
$\unicode[STIX]{x1D6FD}_{j}$
(
![]() $j=1,2,3$
) are unknown coefficients.
$j=1,2,3$
) are unknown coefficients.
The binning estimator has several key advantages over the standard multiplicative interaction model given in Model (1). First, the binning estimator is much more flexible as it jointly fits the interaction components of the standard model to each bin separately, thereby relaxing the LIE assumption.Footnote
16
Since
![]() $(X-x_{j})$
equals zero at each evaluation point
$(X-x_{j})$
equals zero at each evaluation point
![]() $x_{j}$
, the conditional marginal effect of
$x_{j}$
, the conditional marginal effect of
![]() $D$
on
$D$
on
![]() $Y$
at the chosen evaluation points within each bin,
$Y$
at the chosen evaluation points within each bin,
![]() $x_{1}$
,
$x_{1}$
,
![]() $x_{2}$
, and
$x_{2}$
, and
![]() $x_{3}$
, is simply given by
$x_{3}$
, is simply given by
![]() $\unicode[STIX]{x1D6FC}_{1}$
,
$\unicode[STIX]{x1D6FC}_{1}$
,
![]() $\unicode[STIX]{x1D6FC}_{2}$
, and
$\unicode[STIX]{x1D6FC}_{2}$
, and
![]() $\unicode[STIX]{x1D6FC}_{3}$
, respectively. Here, the conditional marginal effects can vary freely across the three bins and therefore can take on any nonlinear or nonmonotonic pattern that might describe the heterogeneity in the effect of
$\unicode[STIX]{x1D6FC}_{3}$
, respectively. Here, the conditional marginal effects can vary freely across the three bins and therefore can take on any nonlinear or nonmonotonic pattern that might describe the heterogeneity in the effect of
![]() $D$
on
$D$
on
![]() $Y$
across low, medium, or high levels of
$Y$
across low, medium, or high levels of
![]() $X$
.Footnote
17
$X$
.Footnote
17
Second, since the bins are constructed based on the support of
![]() $X$
, the binning ensures that the conditional marginal effects are estimated at typical values of the moderator and do not rely on excessive extrapolation or interpolation.Footnote
18
$X$
, the binning ensures that the conditional marginal effects are estimated at typical values of the moderator and do not rely on excessive extrapolation or interpolation.Footnote
18
Third, the binning estimator is easy to implement using any regression software and the standard errors for the conditional marginal effects are directly estimated by the regression so there is no need to compute linear combinations of coefficients to compute the conditional marginal effects.
Fourth, the binning estimator provides a generalization that nests the standard multiplicative interaction model as a special case. It can therefore serve as a formal test on the validity of global LIE assumption imposed by the standard model. In particular, if the standard multiplicative interaction Model (1) is the true model, we have the following relationships:
 $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}_{j}-\unicode[STIX]{x1D702}_{j}x_{j}\quad j=1,2,3; & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}_{j}\quad j=1,2,3; & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{j}-\unicode[STIX]{x1D6FD}_{j}x_{j}\quad j=1,2,3; & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FD}_{j}\quad j=1,2,3. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}_{j}-\unicode[STIX]{x1D702}_{j}x_{j}\quad j=1,2,3; & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}_{j}\quad j=1,2,3; & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{j}-\unicode[STIX]{x1D6FD}_{j}x_{j}\quad j=1,2,3; & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FD}_{j}\quad j=1,2,3. & \displaystyle \nonumber\end{eqnarray}$$
The marginal effect of
![]() $D$
at
$D$
at
![]() $X=x_{j}$
(
$X=x_{j}$
(
![]() $j=1,2,3$
), therefore, is:
$j=1,2,3$
), therefore, is:
In the Appendix we formally show that when Model (1) is correct we have
in which
![]() $\hat{\unicode[STIX]{x1D6FC}}$
and
$\hat{\unicode[STIX]{x1D6FC}}$
and
![]() $\hat{\unicode[STIX]{x1D6FD}}$
are estimated from Model (1) and
$\hat{\unicode[STIX]{x1D6FD}}$
are estimated from Model (1) and
![]() $\hat{\unicode[STIX]{x1D6FC}}_{j}~(j=1,2,3)$
are estimated using Model (4). As mentioned above, we face a bias-variance trade-off. In the special case when the standard multiplicative interaction model is correct and therefore the global LIE assumption holds, then—as the sample size grows—the marginal-effect estimates from the binning estimator converge in probability on the unbiased marginal-effect estimates from the standard multiplicative interaction model given by
$\hat{\unicode[STIX]{x1D6FC}}_{j}~(j=1,2,3)$
are estimated using Model (4). As mentioned above, we face a bias-variance trade-off. In the special case when the standard multiplicative interaction model is correct and therefore the global LIE assumption holds, then—as the sample size grows—the marginal-effect estimates from the binning estimator converge in probability on the unbiased marginal-effect estimates from the standard multiplicative interaction model given by
![]() $ME(X)=\hat{\unicode[STIX]{x1D6FC}}+\hat{\unicode[STIX]{x1D6FD}}X$
. In this case, the standard estimator will be the most efficient estimator for the marginal effect at any given point in the range of the moderator and the estimates will be more precise than those from the binning estimator at the evaluation points simply because the linear model utilizes more information based on the modeling assumptions. However, when the linear interaction assumption does not hold, the standard estimator will be biased and inconsistent and researchers interested in minimizing bias are better off using the more flexible binning estimator that requires more degrees of freedom. Although the binning estimator may also have bias under this circumstance (the bias will disappear as the model becomes more and more flexible), disagreement between the binning estimates and estimates from the linear interaction model gives an indication the LIE assumption is invalid.
$ME(X)=\hat{\unicode[STIX]{x1D6FC}}+\hat{\unicode[STIX]{x1D6FD}}X$
. In this case, the standard estimator will be the most efficient estimator for the marginal effect at any given point in the range of the moderator and the estimates will be more precise than those from the binning estimator at the evaluation points simply because the linear model utilizes more information based on the modeling assumptions. However, when the linear interaction assumption does not hold, the standard estimator will be biased and inconsistent and researchers interested in minimizing bias are better off using the more flexible binning estimator that requires more degrees of freedom. Although the binning estimator may also have bias under this circumstance (the bias will disappear as the model becomes more and more flexible), disagreement between the binning estimates and estimates from the linear interaction model gives an indication the LIE assumption is invalid.
To illustrate the performance from the binning estimator we apply it to our simulated datasets that cover the cases of a binary treatment with linear and nonlinear marginal effects. The results are shown in Figure 2. To clarify the correspondence between the binning estimator and the standard multiplicative interaction model we superimpose the three estimates of the conditional marginal effects of
![]() $D$
on
$D$
on
![]() $Y$
,
$Y$
,
![]() $\hat{\unicode[STIX]{x1D6FC}}_{1}$
,
$\hat{\unicode[STIX]{x1D6FC}}_{1}$
,
![]() $\hat{\unicode[STIX]{x1D6FC}}_{2}$
and
$\hat{\unicode[STIX]{x1D6FC}}_{2}$
and
![]() $\hat{\unicode[STIX]{x1D6FC}}_{3}$
, and their 95% confidence intervals from the binning estimator in their appropriate places (i.e., at
$\hat{\unicode[STIX]{x1D6FC}}_{3}$
, and their 95% confidence intervals from the binning estimator in their appropriate places (i.e., at
![]() $X=x_{j}$
in bin
$X=x_{j}$
in bin
![]() $j$
) on the marginal-effect plot generated from the standard multiplicative interaction model as recommended by Brambor, Clark, and Golder (Reference Brambor, Clark and Golder2006).
$j$
) on the marginal-effect plot generated from the standard multiplicative interaction model as recommended by Brambor, Clark, and Golder (Reference Brambor, Clark and Golder2006).
In the case of a binary treatment, we also recommend to display at the bottom of the figure a stacked histogram that shows the distribution of the moderator
![]() $X$
. In this histogram the total height of the stacked bars refers to the distribution of the moderator in the pooled sample and the red and white shaded bars refer to the distribution of the moderator in the treatment and control groups, respectively. Adding such a histogram makes it easy to judge the degree to which there is common support in the data. In the case of a continuous treatment, we recommend a histogram at the bottom that simply shows the distribution of
$X$
. In this histogram the total height of the stacked bars refers to the distribution of the moderator in the pooled sample and the red and white shaded bars refer to the distribution of the moderator in the treatment and control groups, respectively. Adding such a histogram makes it easy to judge the degree to which there is common support in the data. In the case of a continuous treatment, we recommend a histogram at the bottom that simply shows the distribution of
![]() $X$
in the entire sample.Footnote
19
$X$
in the entire sample.Footnote
19
Figure 2(a) was generated using the DGP where the standard multiplicative interaction model is the correct model and therefore the LIE assumption holds. Hence, as Figure 2(a) shows, the conditional effect estimates from the binning estimator and the standard multiplicative interaction model are similar in both datasets. Even with a small sample size (i.e.,
![]() $N=200$
), the three estimates from the binning estimator, labeled L, M, and H, sit almost right on the estimated linear marginal-effect line from the true standard multiplicative interaction model. Note that the estimates from the binning estimator are only slightly less precise than those from the true multiplicative interaction model, which demonstrates that there is at best a modest cost in terms of decreased efficiency from using this more flexible estimator. We also see from the histogram that the three estimates from the binning estimator are computed at typical low, medium, and high values of
$N=200$
), the three estimates from the binning estimator, labeled L, M, and H, sit almost right on the estimated linear marginal-effect line from the true standard multiplicative interaction model. Note that the estimates from the binning estimator are only slightly less precise than those from the true multiplicative interaction model, which demonstrates that there is at best a modest cost in terms of decreased efficiency from using this more flexible estimator. We also see from the histogram that the three estimates from the binning estimator are computed at typical low, medium, and high values of
![]() $X$
with sufficient common support which is what we expect given the binning based on terciles.
$X$
with sufficient common support which is what we expect given the binning based on terciles.
Contrast these results with those in Figure 2(b), which were generated using our simulated data in which the true marginal effect of
![]() $D$
is nonlinear. In this case, the standard linear model indicates a slightly negative, but overall very weak, interaction effect, whereas the binning estimates reveal that the effect of
$D$
is nonlinear. In this case, the standard linear model indicates a slightly negative, but overall very weak, interaction effect, whereas the binning estimates reveal that the effect of
![]() $D$
is actually strongly conditioned by
$D$
is actually strongly conditioned by
![]() $X$
:
$X$
:
![]() $D$
exerts a positive effect in the low range of
$D$
exerts a positive effect in the low range of
![]() $X$
, a negative effect in the midrange of
$X$
, a negative effect in the midrange of
![]() $X$
, and a positive effect again in the high range of
$X$
, and a positive effect again in the high range of
![]() $X$
. In the event of such a nonlinear effect, the standard linear model delivers the wrong conclusion. When the estimates from the binning estimator are far off the line or when they are non-monotonic, we have evidence that the LIE assumption does not hold.
$X$
. In the event of such a nonlinear effect, the standard linear model delivers the wrong conclusion. When the estimates from the binning estimator are far off the line or when they are non-monotonic, we have evidence that the LIE assumption does not hold.
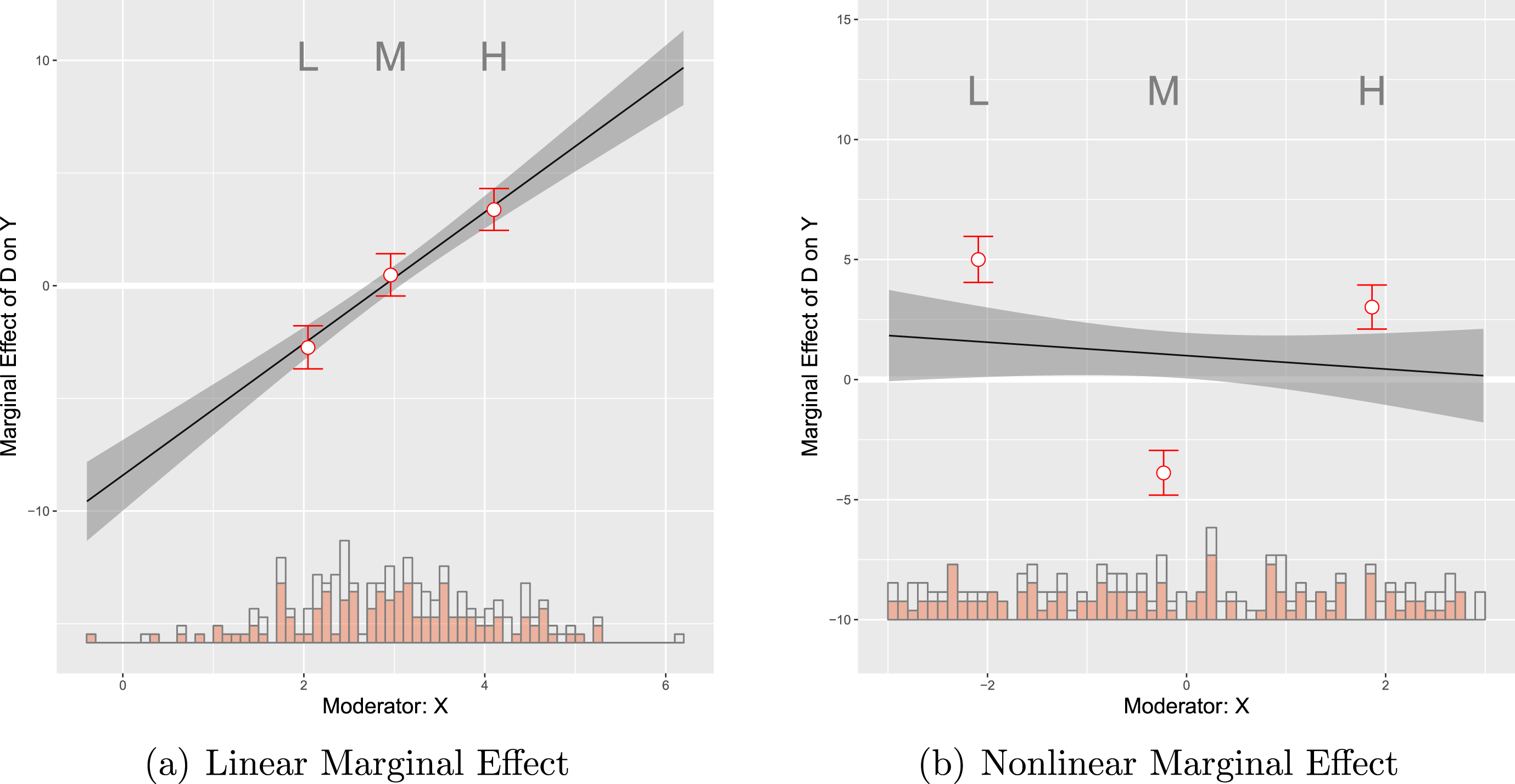
Figure 2. Conditional marginal effects from binning estimator: simulated samples. Note: The above plots show the estimated marginal effects using both the conventional linear interaction model and the binning estimator: (a) when the true marginal effect is linear; (b) when the true marginal effect is nonlinear (quadratic). In both cases, the treatment variable
![]() $D$
is dichotomous.
$D$
is dichotomous.
4.2 Kernel estimator
The second estimation strategy is a kernel smoothing estimator of the marginal effect, which is an application of semiparametric smooth varying-coefficient models (Li and Racine Reference Li and Racine2010). This approach provides a generalization that allows researchers to flexibly estimate the functional form of the marginal effect of
![]() $D$
on
$D$
on
![]() $Y$
across the values of
$Y$
across the values of
![]() $X$
by estimating a series of local effects with a kernel reweighting scheme. While the kernel estimator requires more computation and its output is less easily summarized than that of the binning estimator, it is also fully automated (e.g., researchers do not need to select a number of bins) and characterizes the marginal effect across the full range of the moderator, rather than at just a few evaluation points.
$X$
by estimating a series of local effects with a kernel reweighting scheme. While the kernel estimator requires more computation and its output is less easily summarized than that of the binning estimator, it is also fully automated (e.g., researchers do not need to select a number of bins) and characterizes the marginal effect across the full range of the moderator, rather than at just a few evaluation points.
Formally, the kernel smoothing method is based on the following semiparametric model:
in which
![]() $f(\cdot )$
,
$f(\cdot )$
,
![]() $g(\cdot )$
, and
$g(\cdot )$
, and
![]() $\unicode[STIX]{x1D6FE}(\cdot )$
are smooth functions of
$\unicode[STIX]{x1D6FE}(\cdot )$
are smooth functions of
![]() $X$
, and
$X$
, and
![]() $g(\cdot )$
captures the marginal effect of
$g(\cdot )$
captures the marginal effect of
![]() $D$
on
$D$
on
![]() $Y$
. It is easy to see that this kernel regression nests the standard interaction model given in Model (1) as a special case when
$Y$
. It is easy to see that this kernel regression nests the standard interaction model given in Model (1) as a special case when
![]() $f(X)=\unicode[STIX]{x1D707}+\unicode[STIX]{x1D702}X$
,
$f(X)=\unicode[STIX]{x1D707}+\unicode[STIX]{x1D702}X$
,
![]() $g(X)=\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}X$
and
$g(X)=\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}X$
and
![]() $\unicode[STIX]{x1D6FE}(X)=\unicode[STIX]{x1D6FE}$
. However, in the kernel regression the conditional effect of
$\unicode[STIX]{x1D6FE}(X)=\unicode[STIX]{x1D6FE}$
. However, in the kernel regression the conditional effect of
![]() $D$
on
$D$
on
![]() $Y$
need not to be linear as required by the LIE assumption, but can vary freely across the range of
$Y$
need not to be linear as required by the LIE assumption, but can vary freely across the range of
![]() $X$
. In addition, if covariates
$X$
. In addition, if covariates
![]() $Z$
are included in the model, the coefficients of those covariates are also allowed to vary freely across the range of
$Z$
are included in the model, the coefficients of those covariates are also allowed to vary freely across the range of
![]() $X$
resulting in a very flexible estimator that also helps to guard against misspecification bias with respect to the covariates.
$X$
resulting in a very flexible estimator that also helps to guard against misspecification bias with respect to the covariates.
We use a kernel based method to estimate Model (5). Specially, for each given
![]() $x_{0}$
in the support of
$x_{0}$
in the support of
![]() $X$
,
$X$
,
![]() $\hat{f}(x_{0})$
,
$\hat{f}(x_{0})$
,
![]() ${\hat{g}}(x_{0})$
, and
${\hat{g}}(x_{0})$
, and
![]() $\hat{\unicode[STIX]{x1D6FE}}(x_{0})$
are estimated by minimizing the following weighted least-squares objective function:
$\hat{\unicode[STIX]{x1D6FE}}(x_{0})$
are estimated by minimizing the following weighted least-squares objective function:
 $$\begin{eqnarray}\displaystyle & \displaystyle \left(\hat{\unicode[STIX]{x1D707}}(x_{0}),\hat{\unicode[STIX]{x1D6FC}}(x_{0}),\hat{\unicode[STIX]{x1D702}}(x_{0}),\hat{\unicode[STIX]{x1D6FD}}(x_{0}),\hat{\unicode[STIX]{x1D6FE}}(x_{0})\right)=\underset{\tilde{\unicode[STIX]{x1D707}},\tilde{\unicode[STIX]{x1D6FC}},\tilde{\unicode[STIX]{x1D702}},\tilde{\unicode[STIX]{x1D6FD}},\tilde{\unicode[STIX]{x1D6FE}}}{\text{argmin}}~L(\tilde{\unicode[STIX]{x1D707}},\tilde{\unicode[STIX]{x1D6FC}},\tilde{\unicode[STIX]{x1D702}},\tilde{\unicode[STIX]{x1D6FD}},\tilde{\unicode[STIX]{x1D6FE}}) & \displaystyle \nonumber\\ \displaystyle & \displaystyle L=\mathop{\sum }_{i}^{N}\left\{\left[Y_{i}-\tilde{\unicode[STIX]{x1D707}}-\tilde{\unicode[STIX]{x1D6FC}}D_{i}-\tilde{\unicode[STIX]{x1D702}}(X_{i}-x_{0})-\tilde{\unicode[STIX]{x1D6FD}}D_{i}(X_{i}-x_{0})-\tilde{\unicode[STIX]{x1D6FE}}Z_{i}\right]^{2}K\left(\frac{X_{i}-x_{0}}{h}\right)\right\}, & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \left(\hat{\unicode[STIX]{x1D707}}(x_{0}),\hat{\unicode[STIX]{x1D6FC}}(x_{0}),\hat{\unicode[STIX]{x1D702}}(x_{0}),\hat{\unicode[STIX]{x1D6FD}}(x_{0}),\hat{\unicode[STIX]{x1D6FE}}(x_{0})\right)=\underset{\tilde{\unicode[STIX]{x1D707}},\tilde{\unicode[STIX]{x1D6FC}},\tilde{\unicode[STIX]{x1D702}},\tilde{\unicode[STIX]{x1D6FD}},\tilde{\unicode[STIX]{x1D6FE}}}{\text{argmin}}~L(\tilde{\unicode[STIX]{x1D707}},\tilde{\unicode[STIX]{x1D6FC}},\tilde{\unicode[STIX]{x1D702}},\tilde{\unicode[STIX]{x1D6FD}},\tilde{\unicode[STIX]{x1D6FE}}) & \displaystyle \nonumber\\ \displaystyle & \displaystyle L=\mathop{\sum }_{i}^{N}\left\{\left[Y_{i}-\tilde{\unicode[STIX]{x1D707}}-\tilde{\unicode[STIX]{x1D6FC}}D_{i}-\tilde{\unicode[STIX]{x1D702}}(X_{i}-x_{0})-\tilde{\unicode[STIX]{x1D6FD}}D_{i}(X_{i}-x_{0})-\tilde{\unicode[STIX]{x1D6FE}}Z_{i}\right]^{2}K\left(\frac{X_{i}-x_{0}}{h}\right)\right\}, & \displaystyle \nonumber\end{eqnarray}$$
in which
![]() $K(\cdot )$
is a Gaussian kernel,
$K(\cdot )$
is a Gaussian kernel,
![]() $h$
is a bandwidth parameter that we automatically select via least-squares cross-validation,
$h$
is a bandwidth parameter that we automatically select via least-squares cross-validation,
![]() $\hat{f}(x_{0})=\hat{\unicode[STIX]{x1D707}}(x_{0})$
, and
$\hat{f}(x_{0})=\hat{\unicode[STIX]{x1D707}}(x_{0})$
, and
![]() ${\hat{g}}(x_{0})=\hat{\unicode[STIX]{x1D6FC}}(x_{0})$
. The two terms
${\hat{g}}(x_{0})=\hat{\unicode[STIX]{x1D6FC}}(x_{0})$
. The two terms
![]() $\unicode[STIX]{x1D702}(X-x_{0})$
and
$\unicode[STIX]{x1D702}(X-x_{0})$
and
![]() $\unicode[STIX]{x1D6FD}D(X-x_{0})$
are included to capture the influence of the first partial derivative of
$\unicode[STIX]{x1D6FD}D(X-x_{0})$
are included to capture the influence of the first partial derivative of
![]() $Y$
with respect to
$Y$
with respect to
![]() $X$
at each evaluation point of
$X$
at each evaluation point of
![]() $X$
, a common practice that reduces bias of the kernel estimator on the boundary of the support of
$X$
, a common practice that reduces bias of the kernel estimator on the boundary of the support of
![]() $X$
(e.g., Fan, Heckman, and Wand Reference Fan, Heckman and Wand1995). As a result, we obtain three smooth functions
$X$
(e.g., Fan, Heckman, and Wand Reference Fan, Heckman and Wand1995). As a result, we obtain three smooth functions
![]() $\hat{f}(\cdot )$
,
$\hat{f}(\cdot )$
,
![]() ${\hat{g}}(\cdot )$
, and
${\hat{g}}(\cdot )$
, and
![]() $\hat{\unicode[STIX]{x1D6FE}}(\cdot )$
, in which
$\hat{\unicode[STIX]{x1D6FE}}(\cdot )$
, in which
![]() ${\hat{g}}(\cdot )$
represents the estimated marginal effect of
${\hat{g}}(\cdot )$
represents the estimated marginal effect of
![]() $D$
on
$D$
on
![]() $Y$
with respect to
$Y$
with respect to
![]() $X$
.Footnote
20
We implement this estimation procedure in both R and STATA and compute standard errors and confidence intervals using a bootstrap.
$X$
.Footnote
20
We implement this estimation procedure in both R and STATA and compute standard errors and confidence intervals using a bootstrap.

Figure 3. Kernel smoothed estimates: simulated samples. Note: The above plots show the estimated marginal effects using the kernel estimator: (a) when the true marginal effect is linear; (b) when the true marginal effect is nonlinear (quadratic). In both cases, the treatment variable
![]() $D$
is dichotomous. The dotted line denotes the “true” marginal effect, while the solid line denotes the marginal-effect estimates.
$D$
is dichotomous. The dotted line denotes the “true” marginal effect, while the solid line denotes the marginal-effect estimates.
Figure 3 shows the results of our kernel estimator applied to the two simulated samples in which the true DGP contains either a linear or nonlinear marginal effect (the bandwidths are selected using a standard 5-fold cross-validation procedure). As in Figure 2, the x-axis is the moderator
![]() $X$
and the y-axis is the estimated effect of
$X$
and the y-axis is the estimated effect of
![]() $D$
on
$D$
on
![]() $Y$
. The confidence intervals are generated using 1,000 iterations of a nonparametric bootstrap where we resample the data with replacement. We again add our recommended (stacked) histograms at the bottom to judge the common support based on the distribution of the moderator.
$Y$
. The confidence intervals are generated using 1,000 iterations of a nonparametric bootstrap where we resample the data with replacement. We again add our recommended (stacked) histograms at the bottom to judge the common support based on the distribution of the moderator.
Figure 3 shows that the kernel estimator is able to accurately uncover both linear and nonlinear marginal effects. Figure 3(a) shows a strong linear interaction where the conditional marginal effect of
![]() $D$
on
$D$
on
![]() $Y$
grows constantly and monotonically with
$Y$
grows constantly and monotonically with
![]() $X$
. The marginal-effect estimates from the kernel estimator are close to those from the true multiplicative interaction model (red dashed line).Footnote
21
In addition, the kernel estimates in Figure 3(b) are a close approximation of the true quadratic marginal effect (red dashed line). In short, by utilizing a more flexible estimator, we are able to closely approximate the marginal effect whether the LIE assumption holds or not.
$X$
. The marginal-effect estimates from the kernel estimator are close to those from the true multiplicative interaction model (red dashed line).Footnote
21
In addition, the kernel estimates in Figure 3(b) are a close approximation of the true quadratic marginal effect (red dashed line). In short, by utilizing a more flexible estimator, we are able to closely approximate the marginal effect whether the LIE assumption holds or not.
Also note that toward the boundaries in Figure 3(a), where there is limited common support on
![]() $X$
, the conditional marginal-effect estimates are increasingly imprecisely estimated as expected given that even in this simulated data there is less data to estimate the marginal effects at these points. The fact that the confidence intervals grow wider at those points is desirable because it makes clear the increasing lack of common support.
$X$
, the conditional marginal-effect estimates are increasingly imprecisely estimated as expected given that even in this simulated data there is less data to estimate the marginal effects at these points. The fact that the confidence intervals grow wider at those points is desirable because it makes clear the increasing lack of common support.
5 Data
We now apply our diagnostic and estimation strategies to published papers that used classical linear interaction models and claimed an interaction effect. To broadly assess the practical validity of the assumptions of the multiplicative interaction model, we canvassed studies published in five top political science journals, The American Political Science Review (APSR), The American Journal of Political Science (AJPS), The Journal of Politics (JOP), International Organization (IO) and Comparative Political Studies (CPS). Sampling occurred in two stages. First, for all five journals, we used Google Scholar to identify every study which cited Brambor, Clark, and Golder (Reference Brambor, Clark and Golder2006), roughly 170 articles. Within these studies, we subset to cases which: used plain OLS or linear fixed-effect models; had a substantive claim tied to an interaction effect; and interacted at least one continuous variable. We excluded methods and review articles, as well as triple interactions because those models impose even more demanding assumptions.
Second, we conducted additional searches to identify all studies published in the APSR and AJPS which included the terms “regression” and “interaction” published since Brambor, Clark, and Golder (Reference Brambor, Clark and Golder2006), roughly 550 articles. We then subset to articles which did not cite Brambor, Clark, and Golder (Reference Brambor, Clark and Golder2006). In order to identify studies within this second sample which featured interaction models prominently, we selected articles which included a marginal-effect plot of the sort recommended by Brambor, Clark, and Golder (Reference Brambor, Clark and Golder2006) and then applied the same sampling filters as above. In the end, these two sampling strategies produced roughly 40 studies that met our sampling criteria.
After identifying these studies, we then sought out replication materials by emailing the authors and searching through the dataverses of the journals. (Again, we thank all authors who generously provided their replication data.) We excluded an additional 18 studies due to a lack of replication materials or an inability to replicate published findings, leaving a total of 22 studies from which we replicated 46 interaction effects. For studies that included multiple interaction effects, we focused on the most important ones which we identified as either: (1) those for which the authors generated a marginal-effect plot of the sort Brambor, Clark, and Golder (Reference Brambor, Clark and Golder2006) recommends, or, (2) if no such plots were included, those which were most relied upon for substantive claims. We excluded interaction effects where the marginal effect was statistically insignificant across the entire range of the moderator and/or where the authors did not claim to detect an interaction effect.Footnote 22
While we cannot guarantee that we did not miss a relevant article, we are confident that our literature review has identified a large portion of recent high-profile political science studies employing this modeling strategy and claiming an interaction effect.Footnote 23 The articles cover a broad range of topics and are drawn from all empirical subfields of political science. Roughly 37% of the interaction effects are from the APSR, 20% are from the AJPS, 22% are from CPS, 15% are from IO, and 7% are from JOP, respectively.
There are at least three reasons why the conclusions from our sample might provide a lower bound for the estimated share of published studies where the assumptions of the standard multiplicative interaction model do not hold. The first one is that we only focus on top journals. Second, for three journals we focus exclusively on the studies that cite Brambor, Clark, and Golder (Reference Brambor, Clark and Golder2006) and therefore presumably took special care to employ and interpret these models correctly. Third, we restrict our sample to the subset of potentially more reliable studies where the authors made replication data available and where we were able to successfully replicate the results.
It is important to emphasize that our replications and the conclusions that we draw from them are limited to reanalyzing the main models that underlie the interaction effect plots and tables presented in the original studies. Given the methodological focus of our article, we do not consider any additional evidence that the authors might have presented in their original studies to corroborate their substantive claims. Readers should keep this caveat in mind and consult the original studies and replication data to judge the credibility of the original claims in light of our replication results. Moreover, we emphasize that our results should not be interpreted as accusing any scholars of malpractice or incompetence. We remind readers that the authors of the studies that we replicate below were employing the accepted best practices at the time of publication, but following these existing guidelines for interaction models did not alert them to the problems that we describe below.
6 Results
Case 1: Linear Marginal Effects
We begin our discussion with a replication of Huddy, Mason, and Aarøe (Reference Huddy, Mason and Aarøe2015), an example of a study in which the assumptions of the multiplicative interaction model appear to hold well. This study uses a survey experiment and a multiplicative interaction model to test the hypothesis that a threat of electoral loss has a larger effect on anger if respondents are stronger partisan identifiers. The outcome is anger, the treatment is the threat of electoral loss (binary yes/no), and the moderator is the partisan identity of the respondent (continuous scale, 0 to 1). The key finding is that “Strongly identified partisans feel angrier than weaker partisans when threatened with electoral loss” (Huddy, Mason, and Aarøe Reference Huddy, Mason and Aarøe2015, p. 1).

Figure 4. Linear interaction effect: replication of Huddy, Mason, and Aarøe (Reference Huddy, Mason and Aarøe2015). Note: The above plots examine the marginal-effect plot in Huddy, Mason, and Aarøe (Reference Huddy, Mason and Aarøe2015): (a) linear interaction diagnostic plot; (b) marginal-effect estimates from the replicated model (black line) and the binning estimator (red dots); (c) marginal-effect estimates from the kernel estimator.
The upper panel in Figure 4 displays our diagnostic scatterplot applied to this data. We see that the relationship between anger and partisan identity is well approximated by a linear fit in both groups with and without threat, as the linear and LOESS lines are close to each other. This provides good support for the validity of the LIE assumption in this example. There seems to be a linear interaction, with the effect of threat on anger increasing with higher levels of partisan identity. In addition, the box plots suggest that there is sufficient common support for the range of partisan identity between about 0.3 to 1.
The middle panel in Figure 4 displays the conditional marginal-effect estimates of our binning estimator superimposed on the estimates from the multiplicative interaction model used by the authors. As expected given the scatterplot, the conditional marginal-effect estimates of the binning estimator for the threat effect at low, medium, and high levels of partisan identity line up very closely with the LIEs from the original model. The threat effect is almost twice as large at high compared to low levels of partisan identity and the difference between these two effects is statistically significant (
![]() $p<0.0001$
). The threat effect at medium levels falls about right in between the low and high estimates. In addition, the stacked histogram at the bottom again corroborates that there is sufficient common support with both treated and control observations across a wide range of values of the moderator. The lower right panel in Figure 4 presents the conditional marginal-effect estimates from the kernel estimator. The optimal bandwidth selected by cross-validation is relatively large. The result from the kernel estimation shows that the LIE assumption is supported by the data. The magnitude of the threat effect increases at an approximately constant rate with higher partisan identity.
$p<0.0001$
). The threat effect at medium levels falls about right in between the low and high estimates. In addition, the stacked histogram at the bottom again corroborates that there is sufficient common support with both treated and control observations across a wide range of values of the moderator. The lower right panel in Figure 4 presents the conditional marginal-effect estimates from the kernel estimator. The optimal bandwidth selected by cross-validation is relatively large. The result from the kernel estimation shows that the LIE assumption is supported by the data. The magnitude of the threat effect increases at an approximately constant rate with higher partisan identity.
Case 2: Lack of Common Support
The next example illustrates how the linear interaction model can mask a lack of common support in the data, which can occur when the treatment does not vary across a wide range of values of the moderator. Chapman (Reference Chapman2009) examines the effect of authorizations granted by the U.N. Security Council on public opinion of U.S. foreign policy, positing that this effect is conditional on public perceptions of member states’ interests. The outcome is the number of “rallies” (short term boosts in public opinion), the treatment is the granting of a U.N. authorization (binary yes/no) and the moderator is the preference distance between the U.S. and the Security Council (continuous scale,
![]() $-1$
to 0). In Figure 2 in the study, the author plots the marginal effect of U.N. authorization, and states, “[c]learly, the effect of authorization on rallies decreases as similarity increases” (p. 756).
$-1$
to 0). In Figure 2 in the study, the author plots the marginal effect of U.N. authorization, and states, “[c]learly, the effect of authorization on rallies decreases as similarity increases” (p. 756).
Figure 5. Lack of common support: Chapman (Reference Chapman2009). Note: The above plots examine the marginal-effect plot in Chapman (Reference Chapman2009): (a) linear interaction diagnostic plot; (b) marginal-effect estimates from the replicated model (black line) and the binning estimator (red dots); (c) marginal-effect estimates from the kernel estimator.
The upper panel in Figure 5 shows our diagnostic scatterplot for this model and the lower left panel in Figure 5 reproduces the original plot displayed in the study (Figure 2) but overlays the estimates from our binning estimator for low, medium, and high values of the moderator. Again, in the latter plot the stacked histogram at the bottom shows the distribution of the moderator in the treatment and control group with and without U.N. authorization, respectively.
As the plots show, there is a lack of common support. There are very few observations with a U.N. authorization and those observations are all clustered in a narrow range of moderator values of around
![]() $-0.5$
. In fact, as can be seen in the histogram at the bottom of the plot in the lower panel, or in the box plots in the upper panel of Figure 5, all the observations with a U.N. authorization fall into the lowest tercile of the moderator and the estimated marginal effect in this lowest bin is close to zero. In the medium and high bin, the effect of the U.N. authorizations cannot be estimated using the binning estimator because there is zero variation on the treatment variable for values of the moderator above about
$-0.5$
. In fact, as can be seen in the histogram at the bottom of the plot in the lower panel, or in the box plots in the upper panel of Figure 5, all the observations with a U.N. authorization fall into the lowest tercile of the moderator and the estimated marginal effect in this lowest bin is close to zero. In the medium and high bin, the effect of the U.N. authorizations cannot be estimated using the binning estimator because there is zero variation on the treatment variable for values of the moderator above about
![]() $-0.45$
.
$-0.45$
.
The common practice of fitting the standard multiplicative interaction model and computing the conditional marginal effects from this model will not alert the researcher to this problem. Here the effect estimates from the standard multiplicative interaction model for values of the moderator above
![]() $-0.45$
or below
$-0.45$
or below
![]() $-0.55$
are based purely on extrapolation that relies on the specified functional form, and are therefore model dependent and fragile.Footnote
24
This model and data cannot reliably answer the research question without assumptions as to how the effect of U.N. authorizations varies across the preference distance between the U.S. and the Security Council because the very few cases with and without authorizations are all concentrated in the narrow range of the moderator around
$-0.55$
are based purely on extrapolation that relies on the specified functional form, and are therefore model dependent and fragile.Footnote
24
This model and data cannot reliably answer the research question without assumptions as to how the effect of U.N. authorizations varies across the preference distance between the U.S. and the Security Council because the very few cases with and without authorizations are all concentrated in the narrow range of the moderator around
![]() $-0.5$
, while for other moderator values there is no variation in the treatment. This becomes yet again clear in the marginal-effect estimates from the kernel estimator (with a relatively large bandwidth chosen via cross-validation) displayed in the lower right panel of Figure 5. Once we move outside the narrow range where there is variation on the treatment, the confidence intervals from the marginal-effect estimates blow up, indicating that the effect cannot be estimated given the lack of common support. This shows the desired behavior of the kernel estimator in alerting researchers to the problem of lack of common support.
$-0.5$
, while for other moderator values there is no variation in the treatment. This becomes yet again clear in the marginal-effect estimates from the kernel estimator (with a relatively large bandwidth chosen via cross-validation) displayed in the lower right panel of Figure 5. Once we move outside the narrow range where there is variation on the treatment, the confidence intervals from the marginal-effect estimates blow up, indicating that the effect cannot be estimated given the lack of common support. This shows the desired behavior of the kernel estimator in alerting researchers to the problem of lack of common support.
Case 3: Severe Interpolation
The next published example illustrates how sparsity of data in various regions of a skewed moderator (as opposed to no variation at all in the treatment) can lead to misspecification. Malesky, Schuler, and Tran (Reference Malesky, Schuler and Tran2012) use a field experiment to examine whether legislative transparency interventions that have been found to have positive effects on legislator performance in democratic contexts produce the same benefits when exported to countries with authoritarian regimes. To this end the researchers randomly selected a subgroup of Vietnamese legislators for a transparency intervention which consisted of an online newspaper publishing a profile about legislators that featured transcripts and scorecards to document that legislator’s performance in terms of asking questions, critical questions in particular, in parliament. While the transparency intervention had no effect on average, the authors argue that the response of delegates to this transparency intervention is conditional on the level of Internet penetration in their province. To test this they regress the outcome, measured as the change in the number of questions asked by the legislator, on the treatment, a binary dummy for whether legislators were exposed to the transparency intervention or not, the moderator, measured as the number of Internet subscribers per 100 citizens in the province, and the interaction between the two (Table 5 in the original study).

Figure 6. Severe interpolation: Malesky, Schuler, and Tran (Reference Malesky, Schuler and Tran2012). Note: The above plots examine the marginal-effect plot in Malesky, Schuler, and Tran (Reference Malesky, Schuler and Tran2012): (a) the authors’ original plot; (b) marginal-effect estimates from the replicated model (black line) and the binning estimator (red dots); (c) marginal-effect estimates from the binning estimator after dropping four influential observations; (d) marginal-effect estimates from the kernel estimator.
Figure 6(a) reprints the marginal-effect plots presented by the authors in Figure 1 of their article which is based on plotting the conditional marginal effects from the standard multiplicative interaction model that they fit to the data. They write: “[t]he graphs show clearly that at low levels of Internet penetration, treatment has no impact on delegate behavior, but at high levels of Internet penetration, the treatment effect is large and significant” (p. 17). Based on this negative effect at higher levels of Internet penetration the authors conclude that, “delegates subjected to high treatment intensity demonstrate robust evidence of curtailed participation
![]() $[\ldots ]$
. These results make us cautious about the export of transparency without electoral sanctioning” (Malesky, Schuler, and Tran Reference Malesky, Schuler and Tran2012, p. 1).
$[\ldots ]$
. These results make us cautious about the export of transparency without electoral sanctioning” (Malesky, Schuler, and Tran Reference Malesky, Schuler and Tran2012, p. 1).
Figure 6(b) displays the marginal-effect estimates from our replication of the original model and the binning estimator. Our replication plots show two critical concerns. First, the effect of the transparency intervention appears nonmonotonic and nonlinear in the moderator. In fact, the point estimates from the binning estimator grow smaller between typical low and typical medium levels of Internet penetration, but then larger between typical medium and typical high levels of Internet penetration. None of the three estimates are significant, suggesting that the transparency intervention had no significant effect at either typical low, medium, or high levels of Internet penetration as measured by the median values in the low, medium, and high terciles.Footnote 25 This suggests that the LIE assumption employed in the original model does not hold and when relaxed by the binning estimator there is no compelling evidence of a negative interaction effect.
Second, as illustrated by the stacked histogram and the placement of the binned estimates (which lie at the median of Internet penetration in each bin), there are very few observations which exhibit levels of Internet penetration higher than about 2.5, which is the point above which the effect of the transparency intervention starts to become significant according to the original model.Footnote 26 In fact, for the range between 2.5 and 9, where the original model suggests a negative effect, there are very few observations and the results are based on interpolation of the likely incorrect linear functional form to an area far outside the bulk of the data (see Anderson (Reference Anderson2013) for a similar critique).Footnote 27 The linear downward trend that underlies the claim of a negative interaction is driven by the outliers with extremely high levels of Internet penetration that occur in two metropolitan areas. This interpolation suggests that the estimates are model dependent and fragile. To diagnose the robustness of the estimates we investigated how many leverage points need to be dropped before the findings change considerably when using the original model. The result of this robustness check is shown in Figure 6(c), where we see that once only four extreme leverage points—which make up less than 0.9% of all observations—are removed from the data the effect estimates from the original interaction model flatten, indicating no effect of the intervention at any level of Internet penetration.Footnote 28
Figure 6(d) shows the marginal-effect estimates from our kernel estimator. In Figure 6(d), we use a block bootstrap procedure to obtain the uncertainty estimates. The confidence intervals are much wider than those in Figures 6(b) and (c), which are based on cluster-robust standard errors. This is because when the number of clusters is relatively small (in this case, 64 in total, but much fewer in the right tail), cluster-robust standard errors can severely underestimate uncertainty (Cameron and Miller Reference Cameron and Miller2015).
Case 4: Nonlinearity
Our next example underscores how fitting linear interaction models can mask nonlinearities in interaction effects and therefore result in misspecification bias. Clark and Golder (Reference Clark and Golder2006) argue that the temporal proximity of presidential elections affects the number of parties that compete in an election, but that this effect is conditional on the number of presidential candidates. After estimating a linear interaction model, the authors plot the marginal effect in Figure 2 in their paper, which we replicated in the left plot of Figure 7, again superimposing the estimates from our binning estimator where we use four bins to discretize the moderator. The authors interpret their LIE estimates by writing that, “[i]t should be clear that temporally proximate presidential elections have a strong reductive effect on the number of parties when there are few presidential candidates. As predicted, this reductive effect declines as the number of candidates increases. Once the number of presidential candidates becomes sufficiently large, presidential elections stop having a significant effect on the number of parties,” (Clark and Golder Reference Clark and Golder2006, p. 702).Footnote 29
But as the estimates from the binning estimator in Figure 7 show, the story is more complicated. In fact, the moderator is skewed and for 59% of the observations takes on the lowest value of zero. Moreover, as in the Chapman (Reference Chapman2009) example above, there is no variation at all on the treatment variable in this first bin where the moderator takes on the value of zero, such that the treatment effect at this point is not identified given the absence of common support. This contradicts the original claim of a negative effect when there is a low effective number of candidates. And rather than evidencing a positive interaction, as the study claims, the effect is insignificant in the second bin, but then rapidly drops to be negative and significant at the third bin, only to increase again back to near zero in the last bin.Footnote 30 The LIE assumption does not hold and accordingly the linear interaction model is misspecified and exhibits a lack of common support for the majority of the data.
This is confirmed by the effect estimates from the kernel estimator which are shown in the right plot in Figure 7.Footnote 31 Consistent with the binning estimates, the marginal effect appears nonlinear and the confidence intervals blow up as the moderator approaches zero given that there is no variation in the treatment variable at this point. Contrary to the authors’ claims, the number of candidates in an election does not appear to moderate the effect of proximate elections in a consistent manner and the effect is not identified for a majority of the data due to the lack of common support.
Figure 7. Nonlinearity: Clark and Golder (Reference Clark and Golder2006). Note: The above plots examine the marginal-effect plot in Clark and Golder (Reference Clark and Golder2006): (a) marginal-effect estimates from the replicated model (black line) and the binning estimator (red dots); (b) marginal-effect estimates from the kernel estimator.
Summary of Replications
The previous cases highlight stark examples of some of the issues that can go undiagnosed if the standard linear interaction model is estimated and key assumptions go unchecked. But how common are such problems? How much should we trust published estimates from multiplicative interaction models in political science? To investigate this question we replicated 46 interaction effects from our sample of published work in the top five political science journals. To summarize these cases, we constructed a simple additive scoring system whereby cases were allocated single points for exhibiting (1) no statistically different treatment effects at typical low and typical high levels of the moderator, (2) severe extrapolation, and (3) nonlinear interaction effects.
We determined the first criterion by testing whether the marginal-effect estimate from the binning estimator at the median value in the low tercile of the moderator was statistically different from the effect estimate at the median of the high tercile of the moderator (
![]() $p<0.05$
, two-tailed). This criterion provides a formal test of the extent to which the data contains evidence of a significant interaction effect once we relax the stringent LIE assumption that underlies the claim of a significant interaction in the original study.
$p<0.05$
, two-tailed). This criterion provides a formal test of the extent to which the data contains evidence of a significant interaction effect once we relax the stringent LIE assumption that underlies the claim of a significant interaction in the original study.
We determined the second criterion of severe extrapolation by examining whether the L-Kurtosis of the moderator exceeds a threshold that indicates severe extrapolation. The L-Kurtosis is a robust and efficient measure of the degree to which the shape of the distribution is characterized by outliersFootnote 32 and therefore captures to what extent the estimates reported in the marginal-effect plots are based on extrapolation to moderator values where there is little or no data.Footnote 33
Finally, to determine whether the interaction effect is indeed linear as claimed in the original study, we reparameterize Model (4) as
such that the new model nests Model (1). We then test the null that the eight additional parameters are jointly equal to zero (i.e.,
![]() $\unicode[STIX]{x1D707}_{2^{\prime }}=\unicode[STIX]{x1D6FC}_{2^{\prime }}=\unicode[STIX]{x1D702}_{2^{\prime }}=\unicode[STIX]{x1D6FD}_{2^{\prime }}=\unicode[STIX]{x1D707}_{3^{\prime }}=\unicode[STIX]{x1D6FC}_{3^{\prime }}=\unicode[STIX]{x1D702}_{3^{\prime }}=\unicode[STIX]{x1D6FD}_{3^{\prime }}=0$
) using a standard Wald test. This criterion provides a formal test of whether the linear interaction model used in the original study can be rejected in favor of the more flexible binning estimator model that relaxes the LIE assumption. If we rejected the null, we obtained a piece of evidence against the linear interaction model. Hence, we allocated one point to the case for a nonlinear interaction effect. However, it is worth noting that failing the reject the null does not necessarily mean that the LIE assumption holds, especially when the sample size is small and the test is underpowered. We therefore regard this coding decision as lenient. Taken together, failing these three tests indicates that marginal-effect estimates based on a linear interaction model are likely to produce misleading results. In addition to our numerical summary we also display more complete analyses of each case in the Online Appendix B so that readers may examine them in more detail and come to their own conclusions.
$\unicode[STIX]{x1D707}_{2^{\prime }}=\unicode[STIX]{x1D6FC}_{2^{\prime }}=\unicode[STIX]{x1D702}_{2^{\prime }}=\unicode[STIX]{x1D6FD}_{2^{\prime }}=\unicode[STIX]{x1D707}_{3^{\prime }}=\unicode[STIX]{x1D6FC}_{3^{\prime }}=\unicode[STIX]{x1D702}_{3^{\prime }}=\unicode[STIX]{x1D6FD}_{3^{\prime }}=0$
) using a standard Wald test. This criterion provides a formal test of whether the linear interaction model used in the original study can be rejected in favor of the more flexible binning estimator model that relaxes the LIE assumption. If we rejected the null, we obtained a piece of evidence against the linear interaction model. Hence, we allocated one point to the case for a nonlinear interaction effect. However, it is worth noting that failing the reject the null does not necessarily mean that the LIE assumption holds, especially when the sample size is small and the test is underpowered. We therefore regard this coding decision as lenient. Taken together, failing these three tests indicates that marginal-effect estimates based on a linear interaction model are likely to produce misleading results. In addition to our numerical summary we also display more complete analyses of each case in the Online Appendix B so that readers may examine them in more detail and come to their own conclusions.
Table 1 provides a numerical summary of the results and Figure 8 displays the marginal effects from the binning estimator superimposed on the original marginal-effect estimates from the replicated multiplicative interaction models used in the original studies. In all, only 4 of the 41 cases where the data were sufficient to conduct all three testsFootnote 34 (9.8%) received a perfect score of zero indicating that the reported marginal effects meet all three criteria of differential treatment effects across the low and high levels of the moderator, no severe extrapolation, and linearity. We interpret this as a rather low fraction for a sample that consists only of top journal publications. Twelve cases (29.3%) received a score of 1, while 18 cases (43.9%) received a score of 2. Seven cases (17.1%) received a score of three, failing to pass a single one of the three tests.Footnote 35 We also find that there is considerable heterogeneity in the scores for interactions that are reported in the same article suggesting that checks for the linear interaction assumption and common support are not consistently applied.Footnote 36
Table 1. Replication Results by Journal.

The table displays the mean for each criterion for each journal, as well as the mean additive score for each journal. The unit of analysis is the interaction, not the article. Note that only 44 cases and 42 cases are used for the low vs. high and linearity tests, respectively, due to data limitations that prevented these tests.
Once we break out the results by journal, we find that the issues raised by our review are not unique to any one subfield or journal in political science. The JOP and CPS received the lowest (best) overall mean scores, 1.3 on our 0-to-3 scale, while APSR and AJPS tied for second with scores of 1.8. The highest (worst) score was 2.3 for IO. The mean scores here are computed using a small number of cases, and so their precision could rightly be questioned. Still, given that our sample is restricted to work published only in top political science journals, these results indicate that many findings in the discipline involving interaction effects in recent years may be modeling artifacts, and highlight a need for improved practices when employing multiplicative interaction models.
Figure 8. The assumptions of the linear interaction model rarely hold in published political science work. Note: The blue dashed vertical lines indicate the range of the moderators displayed in the original manuscripts.
7 Conclusion
Multiplicative interaction models are widely used in the social sciences to test conditional hypotheses. While empirical practice has improved following the publication of Brambor, Clark, and Golder (Reference Brambor, Clark and Golder2006) and related advice, this study demonstrates that there remain problems that are overlooked by scholars using the existing best practice guidelines. In particular, the multiplicative interaction model implies the key assumption that the interaction effects are linear, but our replications of published work in five top political science journals suggest that this assumption often does not hold in practice. In addition, as our replications also show, scholars often compute marginal effects in areas where there is no or only very limited common support, which results in fragile and model dependent estimates.
To improve empirical practice we develop a simple diagnostic that allows researchers to detect problems with the LIE assumption and/or lack of common support. In addition, we propose more flexible estimation strategies based on a simple binning estimator and a kernel estimator that allow researchers to estimate marginal effects without imposing the stringent linear interaction assumption while safeguarding against extrapolation to areas without (or with limited) common support. When applying these methods to our replications, we find that the key findings often change substantially. Given that our sample of replications only includes top journal articles, our findings here most likely understate the true extent of the problem in published work in political science. Overall, our replications suggest that a large portion of published findings employing multiplicative interaction models with at least one continuous variable are fragile and model dependent, and suggest a need to improve the current best practice guidelines.Footnote 37
We recommend that researchers engaged in modeling interaction effects and testing conditional hypotheses should conduct the following diagnostics:
(1) Checking the raw data. Generate the LID plot to check whether the conditional relationships between the outcome, treatment, and moderator are well approximated by a linear fit and check whether there is sufficient common support to compute the treatment effect across the values of the moderator. If additional covariates are involved in the model, the same diagnostic plots can be constructed after residualizing with respect to those covariates. If both the treatment and the moderator are continuous, a GAM plot can be used to further assist with these checks (see Appendix for details on GAM plots). Given the symmetry of interaction models, we also recommend that the diagnostic plots are constructed two ways to examine the marginal effects of
 $D\mid X$
and of
$D\mid X$
and of
 $X\mid D$
, as linearity is implied for both in the standard model. If the distribution of the variables is highly skewed and/or asymmetric we recommend that researchers use appropriate power and/or root transformations to reduce skewness, increase symmetry, and aid with linearizing the relationships between the variables (Mosteller and Tukey Reference Mosteller and Tukey1977).
$X\mid D$
, as linearity is implied for both in the standard model. If the distribution of the variables is highly skewed and/or asymmetric we recommend that researchers use appropriate power and/or root transformations to reduce skewness, increase symmetry, and aid with linearizing the relationships between the variables (Mosteller and Tukey Reference Mosteller and Tukey1977).(2) Applying the binning estimator. Compute the conditional marginal effects using the binning estimator. In our experience, three equal sized bins (one for each tercile) with the evaluation points set to the bin medians provide a reasonable default to get a good sense of the effect heterogeneity. More bins should be used if more detail is required and more data is available. The number of bins could be prespecified in a preanalysis plan to reduce subjectivity. Researchers should avoid computing marginal effects in areas where the data is too sparse either because there are no observations for those values of the moderator or there is no variation in the treatment. To aid with this we recommend to add a (stacked) histogram at the bottom of the marginal-effect plot to show the distribution of the moderator and detect problems with lack of common support.
(3) Applying the kernel estimator. In addition, generating the marginal-effect estimates using the kernel estimator is recommended to further evaluate the effect heterogeneity and relax the linearity assumption on the covariates. Researchers may also use other machine learning methods to gauge how treatment effects vary across different subgroups or levels of a moderator,Footnote 38 but we believe that the kernel method strikes a good balance between model complexity and interpretability, as well as accessibility to applied researchers.
(4) Be cautious when applying the linear interaction model. The standard linear interaction model and marginal-effect plots should only be used if the estimates from the binning and/or kernel estimator suggest that the interaction is really linear, and marginal effects should only be computed for areas with sufficient common support. If a standard linear interaction model is used in this case, the researchers should follow the existing guidelines as described in Brambor, Clark, and Golder (Reference Brambor, Clark and Golder2006) and related advice.
Following these revised guidelines would have solved the problems we discussed in the set of published studies that we replicated. Accordingly, we hope that applying these guidelines will lead to a further improvement in empirical practice.Footnote 39 That said, it is important to emphasize that following these revised guidelines does not guarantee that the model will be correctly specified. When other covariates are included in the model, it is important for researchers to apply all the usual regression diagnostics with respect to these covariatesFootnote 40 in addition to the checks we proposed here. Moreover, it is important to recognize that the checks cannot help with other common problems such as endogeneity or omitted variables that often affect inferences from regression models and can often only be solved through better research designs.
Supplementary material
For supplementary material accompanying this paper, please visithttps://doi.org/10.1017/pan.2018.46.
Appendix A
A.1 Proof
Model (1) and Model (4) in the main text are restated as follows:
It is to be proved that, if Model (1) is correct:
in which
![]() $\hat{\unicode[STIX]{x1D6FC}}$
and
$\hat{\unicode[STIX]{x1D6FC}}$
and
![]() $\hat{\unicode[STIX]{x1D6FD}}$
are estimated from Model (1) and
$\hat{\unicode[STIX]{x1D6FD}}$
are estimated from Model (1) and
![]() $\hat{\unicode[STIX]{x1D6FC}}_{j}$
are estimated from Model (4).
$\hat{\unicode[STIX]{x1D6FC}}_{j}$
are estimated from Model (4).
Proof. First, rewrite Model (4) as follows:
and define
![]() $\text{}\underline{\unicode[STIX]{x1D6FC}}_{j}=\unicode[STIX]{x1D6FC}_{j}-\unicode[STIX]{x1D6FD}_{j}x_{j}$
. When Model (1) is correct, if we regress
$\text{}\underline{\unicode[STIX]{x1D6FC}}_{j}=\unicode[STIX]{x1D6FC}_{j}-\unicode[STIX]{x1D6FD}_{j}x_{j}$
. When Model (1) is correct, if we regress
![]() $Y$
on
$Y$
on
![]() $G_{j}$
,
$G_{j}$
,
![]() $XG_{j}$
,
$XG_{j}$
,
![]() $DG_{j}$
,
$DG_{j}$
,
![]() $XDG_{j}$
(
$XDG_{j}$
(
![]() $j=1,2,3$
), and
$j=1,2,3$
), and
![]() $Z$
, we have:
$Z$
, we have:
Since
![]() $\hat{\text{}\underline{\unicode[STIX]{x1D6FC}}}_{j}=\hat{\unicode[STIX]{x1D6FC}}_{j}-\hat{\unicode[STIX]{x1D6FD}}_{j}x_{j}$
, we have
$\hat{\text{}\underline{\unicode[STIX]{x1D6FC}}}_{j}=\hat{\unicode[STIX]{x1D6FC}}_{j}-\hat{\unicode[STIX]{x1D6FD}}_{j}x_{j}$
, we have
![]() $\hat{\unicode[STIX]{x1D6FC}}_{j}\overset{p}{\rightarrow }\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD}x_{j}$
. Because
$\hat{\unicode[STIX]{x1D6FC}}_{j}\overset{p}{\rightarrow }\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD}x_{j}$
. Because
when Model (1) is correct, we have:
◻
A.2 Additional information on replication files
Table A1. Replication Results.
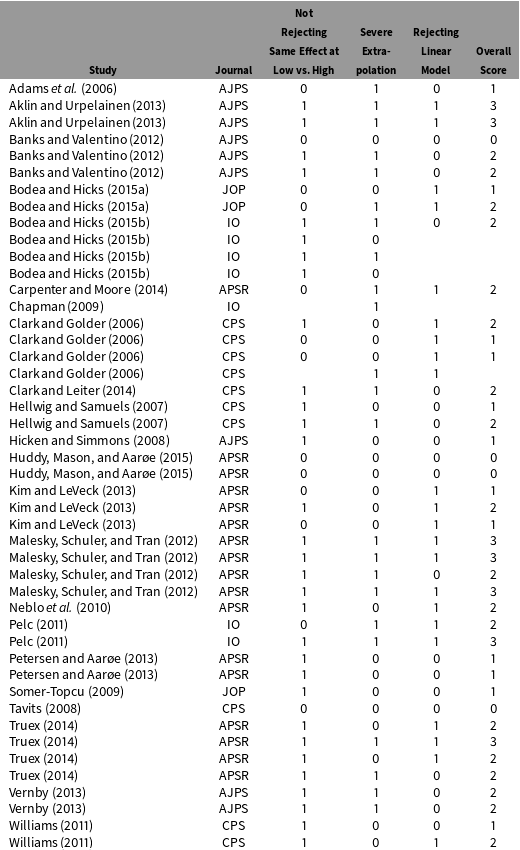
A.3 GAM Plot
In cases where both
![]() $D$
and
$D$
and
![]() $X$
are continuous, an alternative to the scatterplot is to use a generalized additive model (GAM) to plot the surface that describes how the average
$X$
are continuous, an alternative to the scatterplot is to use a generalized additive model (GAM) to plot the surface that describes how the average
![]() $Y$
changes across
$Y$
changes across
![]() $D$
and
$D$
and
![]() $X$
. While the statistical theory underlying GAMs is a bit more involved (Hastie and Tibshirani Reference Hastie and Tibshirani1986), the plots of the GAM surface can be easily constructed using canned routines in R. Figure A1 shows such a GAM plot for the simulated data from the second sample looking at the surface from four distinctive directions. Lighter color on the surface represents a higher value of
$X$
. While the statistical theory underlying GAMs is a bit more involved (Hastie and Tibshirani Reference Hastie and Tibshirani1986), the plots of the GAM surface can be easily constructed using canned routines in R. Figure A1 shows such a GAM plot for the simulated data from the second sample looking at the surface from four distinctive directions. Lighter color on the surface represents a higher value of
![]() $Y$
.
$Y$
.
Figure A1 has several features. First, it is obvious that holding
![]() $X$
constant,
$X$
constant,
![]() $Y$
is increasing in
$Y$
is increasing in
![]() $D$
and holding
$D$
and holding
![]() $D$
constant,
$D$
constant,
![]() $Y$
is increasing in
$Y$
is increasing in
![]() $X$
. Second, the slope of
$X$
. Second, the slope of
![]() $Y$
on
$Y$
on
![]() $D$
is larger with higher
$D$
is larger with higher
![]() $X$
than with lower
$X$
than with lower
![]() $X$
. Third, the surface of
$X$
. Third, the surface of
![]() $Y$
over
$Y$
over
![]() $D$
and
$D$
and
![]() $X$
is fairly smooth, with a gentle curvature in the middle but devoid of drastic humps, wrinkles, or holes. In the Online Appendix, we will see that the GAM plots of examples that likely violate the linearity assumption look quite different from those in Figure A1.
$X$
is fairly smooth, with a gentle curvature in the middle but devoid of drastic humps, wrinkles, or holes. In the Online Appendix, we will see that the GAM plots of examples that likely violate the linearity assumption look quite different from those in Figure A1.
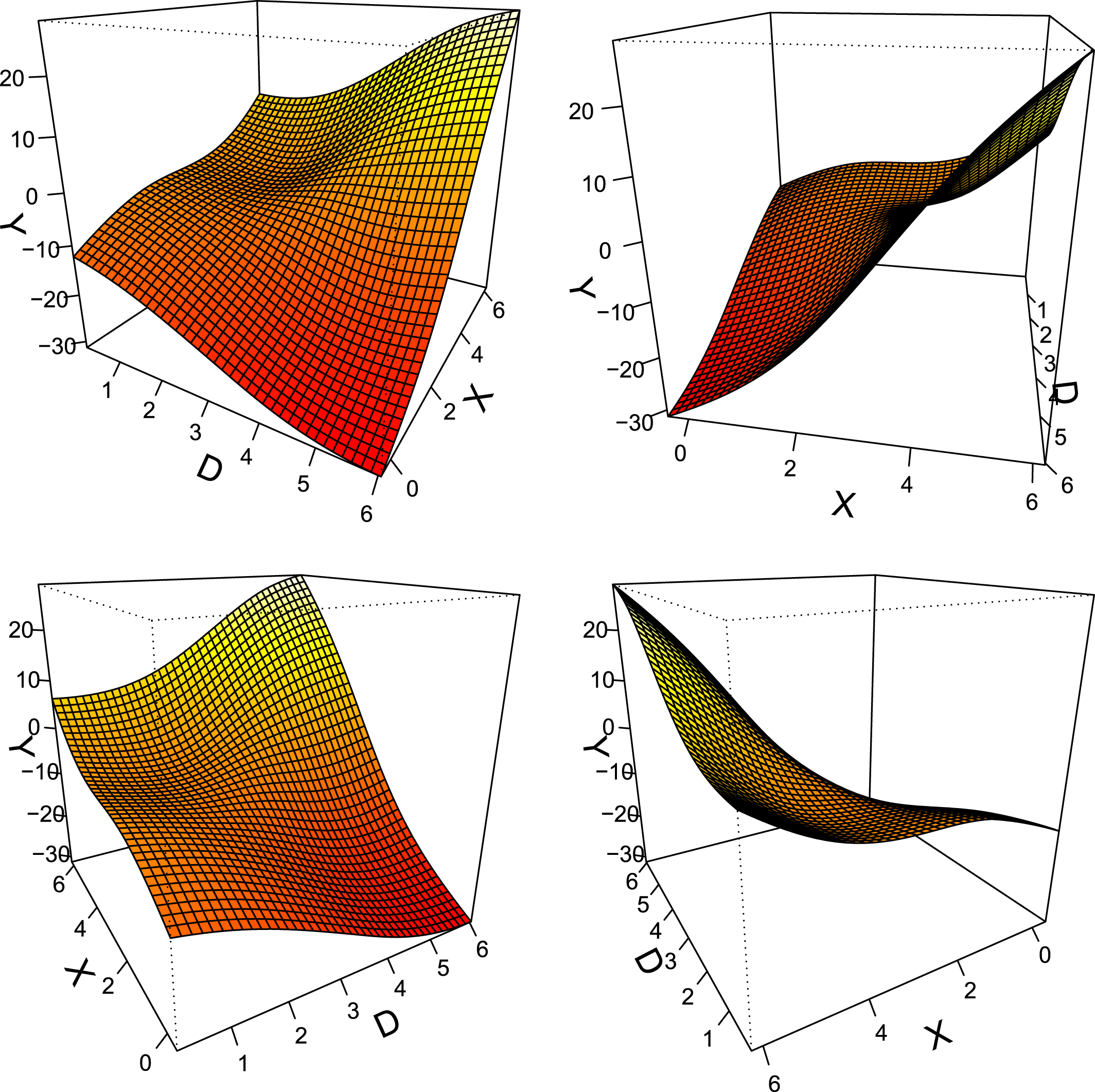
Figure A1. GAM plot: simulated sample with continuous treatment.













