No CrossRef data available.
Published online by Cambridge University Press: 15 September 2022
We prove that for any infinite sets of nonnegative integers
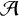 $\mathcal {A}$
and
$\mathcal {A}$
and
 $\mathcal {B}$
, there exist transcendental analytic functions
$\mathcal {B}$
, there exist transcendental analytic functions
 $f\in \mathbb {Z}\{z\}$
whose coefficients vanish for any indexes
$f\in \mathbb {Z}\{z\}$
whose coefficients vanish for any indexes
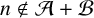 $n\not \in \mathcal {A}+\mathcal {B}$
and for which
$n\not \in \mathcal {A}+\mathcal {B}$
and for which
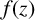 $f(z)$
is algebraic whenever z is algebraic and
$f(z)$
is algebraic whenever z is algebraic and
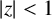 $|z|<1$
. As a consequence, we provide an affirmative answer for an asymptotic version of Mahler’s problem A.
$|z|<1$
. As a consequence, we provide an affirmative answer for an asymptotic version of Mahler’s problem A.
The authors are supported by National Council for Scientific and Technological Development, CNPq.