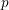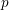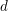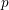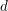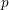1 Introduction
Let
![]() $F$
be a totally real field of degree
$F$
be a totally real field of degree
![]() $d=[F:\mathbb{Q}]>1$
. In this paper, we consider mod
$d=[F:\mathbb{Q}]>1$
. In this paper, we consider mod
![]() $p$
Hilbert modular forms associated to
$p$
Hilbert modular forms associated to
![]() $F$
. Recall that the weight of a (geometric) Hilbert modular form associated to
$F$
. Recall that the weight of a (geometric) Hilbert modular form associated to
![]() $F$
is a
$F$
is a
![]() $d$
-tuple of integers. Unlike the case of Hilbert modular forms in characteristic zero, or indeed mod
$d$
-tuple of integers. Unlike the case of Hilbert modular forms in characteristic zero, or indeed mod
![]() $p$
classical modular forms (i.e. the excluded case
$p$
classical modular forms (i.e. the excluded case
![]() $d=1$
), there are non-zero Hilbert modular forms in characteristic
$d=1$
), there are non-zero Hilbert modular forms in characteristic
![]() $p$
for which some components of the weight are negative. Indeed the partial Hasse invariants considered by Andreatta and Goren in [Reference Andreatta and GorenAG05] are examples of such forms, and they raise the question [Reference Andreatta and GorenAG05, Question 15.8] of whether all such forms are obtained from forms of non-negative weight by multiplication by partial Hasse invariants. We answer the question here in the affirmative, assuming
$p$
for which some components of the weight are negative. Indeed the partial Hasse invariants considered by Andreatta and Goren in [Reference Andreatta and GorenAG05] are examples of such forms, and they raise the question [Reference Andreatta and GorenAG05, Question 15.8] of whether all such forms are obtained from forms of non-negative weight by multiplication by partial Hasse invariants. We answer the question here in the affirmative, assuming
![]() $p$
is unramified in
$p$
is unramified in
![]() $F$
. In fact, we prove a stronger result along these lines (Corollary 1.2 below), which also immediately implies a vanishing result (Corollary 1.3) recently proven independently by Goldring and Koskivirta using methods different from ours (see [Reference Goldring and KoskivirtaGK17] and their forthcoming work with Stroh on related questions).
$F$
. In fact, we prove a stronger result along these lines (Corollary 1.2 below), which also immediately implies a vanishing result (Corollary 1.3) recently proven independently by Goldring and Koskivirta using methods different from ours (see [Reference Goldring and KoskivirtaGK17] and their forthcoming work with Stroh on related questions).
We now explain this in more detail and give the precise statements of our results. Let
![]() ${\mathcal{O}}_{F}$
denote the ring of integers of
${\mathcal{O}}_{F}$
denote the ring of integers of
![]() $F$
, and fix non-zero ideals
$F$
, and fix non-zero ideals
![]() $\mathfrak{n}$
and
$\mathfrak{n}$
and
![]() $\mathfrak{I}$
of
$\mathfrak{I}$
of
![]() ${\mathcal{O}}_{F}$
. We let
${\mathcal{O}}_{F}$
. We let
![]() $p$
be a prime which is relatively prime to
$p$
be a prime which is relatively prime to
![]() $\mathfrak{n}$
and the discriminant
$\mathfrak{n}$
and the discriminant
![]() $D_{F/\mathbb{Q}}$
. Assuming that
$D_{F/\mathbb{Q}}$
. Assuming that
![]() $\mathfrak{n}$
is sufficiently small (e.g. contained in
$\mathfrak{n}$
is sufficiently small (e.g. contained in
![]() $N{\mathcal{O}}_{F}$
for some integer
$N{\mathcal{O}}_{F}$
for some integer
![]() $N>3$
), then there is a scheme
$N>3$
), then there is a scheme
![]() $X=X^{\mathfrak{I}}(\mathfrak{n})$
, smooth of dimension
$X=X^{\mathfrak{I}}(\mathfrak{n})$
, smooth of dimension
![]() $d$
over
$d$
over
![]() $\mathbb{Z}_{p}$
, which parametrizes
$\mathbb{Z}_{p}$
, which parametrizes
![]() $d$
-dimensional abelian varieties with
$d$
-dimensional abelian varieties with
![]() ${\mathcal{O}}_{F}$
-action, together with suitable polarization data (depending on
${\mathcal{O}}_{F}$
-action, together with suitable polarization data (depending on
![]() $\mathfrak{I}$
) and level structure (depending on
$\mathfrak{I}$
) and level structure (depending on
![]() $\mathfrak{n}$
); see § 2. The scheme
$\mathfrak{n}$
); see § 2. The scheme
![]() $X$
is a model for a disjoint union of Hilbert modular varieties over
$X$
is a model for a disjoint union of Hilbert modular varieties over
![]() $\mathbb{C}$
with complex points
$\mathbb{C}$
with complex points
![]() $\unicode[STIX]{x1D6E4}_{i}\backslash \mathfrak{H}^{d}$
, where
$\unicode[STIX]{x1D6E4}_{i}\backslash \mathfrak{H}^{d}$
, where
![]() $\{\unicode[STIX]{x1D6E4}_{i}=\unicode[STIX]{x1D6E4}_{1}^{\mathfrak{I}}(\mathfrak{n})_{i}\}$
is a certain collection of congruence subgroup of
$\{\unicode[STIX]{x1D6E4}_{i}=\unicode[STIX]{x1D6E4}_{1}^{\mathfrak{I}}(\mathfrak{n})_{i}\}$
is a certain collection of congruence subgroup of
![]() $\operatorname{SL}_{2}(F)$
acting on
$\operatorname{SL}_{2}(F)$
acting on
![]() $d$
copies of the complex upper-half plane
$d$
copies of the complex upper-half plane
![]() $\mathfrak{H}$
via the
$\mathfrak{H}$
via the
![]() $d$
embeddings
$d$
embeddings
![]() $F\rightarrow \mathbb{R}$
. In this paper, we are only concerned with a geometric special fibre
$F\rightarrow \mathbb{R}$
. In this paper, we are only concerned with a geometric special fibre
![]() $\overline{X}:=X_{\overline{\mathbb{F}}_{p}}$
.
$\overline{X}:=X_{\overline{\mathbb{F}}_{p}}$
.
Let
![]() $\mathbb{B}$
denote the set of embeddings
$\mathbb{B}$
denote the set of embeddings
![]() $F\rightarrow \overline{\mathbb{Q}}_{p}$
; since
$F\rightarrow \overline{\mathbb{Q}}_{p}$
; since
![]() $p$
is unramified in
$p$
is unramified in
![]() $F$
, we may identify
$F$
, we may identify
![]() $\mathbb{B}$
with the set of ring homomorphisms
$\mathbb{B}$
with the set of ring homomorphisms
![]() ${\mathcal{O}}_{F}\rightarrow \overline{\mathbb{F}}_{p}$
. For
${\mathcal{O}}_{F}\rightarrow \overline{\mathbb{F}}_{p}$
. For
![]() $\unicode[STIX]{x1D6FD}\in \mathbb{B}$
, we let
$\unicode[STIX]{x1D6FD}\in \mathbb{B}$
, we let
![]() $\mathbf{e}_{\unicode[STIX]{x1D6FD}}$
denote the basis element of
$\mathbf{e}_{\unicode[STIX]{x1D6FD}}$
denote the basis element of
![]() $\mathbb{Z}^{\mathbb{B}}$
associated to
$\mathbb{Z}^{\mathbb{B}}$
associated to
![]() $\unicode[STIX]{x1D6FD}$
.
$\unicode[STIX]{x1D6FD}$
.
Let
![]() $\unicode[STIX]{x1D714}=s_{\ast }\unicode[STIX]{x1D6FA}_{\overline{{\mathcal{A}}}/\overline{X}}^{1}$
denote the sheaf of invariant differentials of the universal abelian variety
$\unicode[STIX]{x1D714}=s_{\ast }\unicode[STIX]{x1D6FA}_{\overline{{\mathcal{A}}}/\overline{X}}^{1}$
denote the sheaf of invariant differentials of the universal abelian variety
![]() $\unicode[STIX]{x1D70B}:\overline{{\mathcal{A}}}\rightarrow \overline{X}$
. Then
$\unicode[STIX]{x1D70B}:\overline{{\mathcal{A}}}\rightarrow \overline{X}$
. Then
![]() $\unicode[STIX]{x1D714}$
is, locally on
$\unicode[STIX]{x1D714}$
is, locally on
![]() $\overline{X}$
, free of rank one over
$\overline{X}$
, free of rank one over
![]() ${\mathcal{O}}_{\overline{X}}\otimes {\mathcal{O}}_{F}\cong \bigoplus _{\unicode[STIX]{x1D6FD}\in \mathbb{B}}{\mathcal{O}}_{\overline{X}}$
. Therefore,
${\mathcal{O}}_{\overline{X}}\otimes {\mathcal{O}}_{F}\cong \bigoplus _{\unicode[STIX]{x1D6FD}\in \mathbb{B}}{\mathcal{O}}_{\overline{X}}$
. Therefore,
![]() $\unicode[STIX]{x1D714}$
decomposes as a direct sum over
$\unicode[STIX]{x1D714}$
decomposes as a direct sum over
![]() $\unicode[STIX]{x1D6FD}\in \mathbb{B}$
of line bundles
$\unicode[STIX]{x1D6FD}\in \mathbb{B}$
of line bundles
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FD}}$
. For any
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FD}}$
. For any
![]() $\mathbf{k}=\sum k_{\unicode[STIX]{x1D6FD}}\mathbf{e}_{\unicode[STIX]{x1D6FD}}\in \mathbb{Z}^{\mathbb{B}}$
, we let
$\mathbf{k}=\sum k_{\unicode[STIX]{x1D6FD}}\mathbf{e}_{\unicode[STIX]{x1D6FD}}\in \mathbb{Z}^{\mathbb{B}}$
, we let
![]() $\unicode[STIX]{x1D714}^{\mathbf{k}}=\bigotimes _{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FD}}^{k_{\unicode[STIX]{x1D6FD}}}$
, and we define the space of
$\unicode[STIX]{x1D714}^{\mathbf{k}}=\bigotimes _{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FD}}^{k_{\unicode[STIX]{x1D6FD}}}$
, and we define the space of
![]() $\mathfrak{I}$
-polarized geometric Hilbert modular forms of level
$\mathfrak{I}$
-polarized geometric Hilbert modular forms of level
![]() $\mathfrak{n}$
, and weight
$\mathfrak{n}$
, and weight
![]() $\mathbf{k}$
over
$\mathbf{k}$
over
![]() $\overline{\mathbb{F}}_{p}$
to be the set of global sections:
$\overline{\mathbb{F}}_{p}$
to be the set of global sections:
Note that we may decompose
![]() $\mathbb{B}=\coprod \mathbb{B}_{\mathfrak{p}}$
, where the union is over the set of primes
$\mathbb{B}=\coprod \mathbb{B}_{\mathfrak{p}}$
, where the union is over the set of primes
![]() $\mathfrak{p}$
of
$\mathfrak{p}$
of
![]() ${\mathcal{O}}_{F}$
dividing
${\mathcal{O}}_{F}$
dividing
![]() $p$
, and
$p$
, and
![]() $\mathbb{B}_{\mathfrak{p}}=\{\unicode[STIX]{x1D6FD}:{\mathcal{O}}_{F}\rightarrow \overline{\mathbb{F}}_{p}\mid \ker (\unicode[STIX]{x1D6FD})=\mathfrak{p}\}$
. Let
$\mathbb{B}_{\mathfrak{p}}=\{\unicode[STIX]{x1D6FD}:{\mathcal{O}}_{F}\rightarrow \overline{\mathbb{F}}_{p}\mid \ker (\unicode[STIX]{x1D6FD})=\mathfrak{p}\}$
. Let
![]() $\unicode[STIX]{x1D70E}$
denote the Frobenius automorphism
$\unicode[STIX]{x1D70E}$
denote the Frobenius automorphism
![]() $x\mapsto x^{p}$
of
$x\mapsto x^{p}$
of
![]() $\overline{\mathbb{F}}_{p}$
; note that composition with
$\overline{\mathbb{F}}_{p}$
; note that composition with
![]() $\unicode[STIX]{x1D70E}$
defines a cyclic permutation of each
$\unicode[STIX]{x1D70E}$
defines a cyclic permutation of each
![]() $\mathbb{B}_{\mathfrak{p}}$
, of order
$\mathbb{B}_{\mathfrak{p}}$
, of order
![]() $|\mathbb{B}_{\mathfrak{p}}|=[F_{\mathfrak{p}}:\mathbb{Q}_{p}]$
. The partial Hasse invariant
$|\mathbb{B}_{\mathfrak{p}}|=[F_{\mathfrak{p}}:\mathbb{Q}_{p}]$
. The partial Hasse invariant
![]() $H_{\unicode[STIX]{x1D6FD}}^{\mathfrak{I}}$
, defined in [Reference Andreatta and GorenAG05, Definition 7.12], is an element of
$H_{\unicode[STIX]{x1D6FD}}^{\mathfrak{I}}$
, defined in [Reference Andreatta and GorenAG05, Definition 7.12], is an element of
![]() $M_{\mathbf{h}_{\unicode[STIX]{x1D6FD}}}^{\mathfrak{I}}(\mathfrak{n},\overline{\mathbb{F}}_{p})$
, i.e. a mod
$M_{\mathbf{h}_{\unicode[STIX]{x1D6FD}}}^{\mathfrak{I}}(\mathfrak{n},\overline{\mathbb{F}}_{p})$
, i.e. a mod
![]() $p$
Hilbert modular form of weight
$p$
Hilbert modular form of weight
![]() $\mathbf{h}_{\unicode[STIX]{x1D6FD}}$
, where
$\mathbf{h}_{\unicode[STIX]{x1D6FD}}$
, where
![]() $\mathbf{h}_{\unicode[STIX]{x1D6FD}}=p\mathbf{e}_{\unicode[STIX]{x1D70E}^{-1}\circ \unicode[STIX]{x1D6FD}}-\mathbf{e}_{\unicode[STIX]{x1D6FD}}$
. Note that
$\mathbf{h}_{\unicode[STIX]{x1D6FD}}=p\mathbf{e}_{\unicode[STIX]{x1D70E}^{-1}\circ \unicode[STIX]{x1D6FD}}-\mathbf{e}_{\unicode[STIX]{x1D6FD}}$
. Note that
![]() $\unicode[STIX]{x1D70E}^{-1}\circ \unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FD}$
if and only if
$\unicode[STIX]{x1D70E}^{-1}\circ \unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FD}$
if and only if
![]() $\unicode[STIX]{x1D6FD}\in \mathbb{B}_{\mathfrak{p}}$
for a prime
$\unicode[STIX]{x1D6FD}\in \mathbb{B}_{\mathfrak{p}}$
for a prime
![]() $\mathfrak{p}$
of degree one, in which case
$\mathfrak{p}$
of degree one, in which case
![]() $\mathbf{h}_{\unicode[STIX]{x1D6FD}}=(p-1)\mathbf{e}_{\unicode[STIX]{x1D6FD}}$
; otherwise the coefficient in
$\mathbf{h}_{\unicode[STIX]{x1D6FD}}=(p-1)\mathbf{e}_{\unicode[STIX]{x1D6FD}}$
; otherwise the coefficient in
![]() $\mathbf{h}_{\unicode[STIX]{x1D6FD}}$
of
$\mathbf{h}_{\unicode[STIX]{x1D6FD}}$
of
![]() $\mathbf{e}_{\unicode[STIX]{x1D6FD}}$
(respectively
$\mathbf{e}_{\unicode[STIX]{x1D6FD}}$
(respectively
![]() $\mathbf{e}_{\unicode[STIX]{x1D70E}^{-1}\circ \unicode[STIX]{x1D6FD}}$
) is
$\mathbf{e}_{\unicode[STIX]{x1D70E}^{-1}\circ \unicode[STIX]{x1D6FD}}$
) is
![]() $-1$
(respectively
$-1$
(respectively
![]() $p$
). For any
$p$
). For any
![]() $\mathbf{k}\in \mathbb{Z}^{\mathbb{B}}$
, multiplication by
$\mathbf{k}\in \mathbb{Z}^{\mathbb{B}}$
, multiplication by
![]() $H_{\unicode[STIX]{x1D6FD}}^{\mathfrak{I}}$
defines an injection
$H_{\unicode[STIX]{x1D6FD}}^{\mathfrak{I}}$
defines an injection
![]() $M_{\mathbf{k}-\mathbf{h}_{\unicode[STIX]{x1D6FD}}}^{\mathfrak{I}}(\mathfrak{n},\overline{\mathbb{F}}_{p}){\hookrightarrow}M_{\mathbf{k}}^{\mathfrak{I}}(\mathfrak{n},\overline{\mathbb{F}}_{p})$
. The key result is as follows.
$M_{\mathbf{k}-\mathbf{h}_{\unicode[STIX]{x1D6FD}}}^{\mathfrak{I}}(\mathfrak{n},\overline{\mathbb{F}}_{p}){\hookrightarrow}M_{\mathbf{k}}^{\mathfrak{I}}(\mathfrak{n},\overline{\mathbb{F}}_{p})$
. The key result is as follows.
Theorem 1.1. Suppose that
![]() $\mathbf{k}=\sum k_{\unicode[STIX]{x1D6FD}}\mathbf{e}_{\unicode[STIX]{x1D6FD}}\in \mathbb{Z}^{\mathbb{B}}$
, and that
$\mathbf{k}=\sum k_{\unicode[STIX]{x1D6FD}}\mathbf{e}_{\unicode[STIX]{x1D6FD}}\in \mathbb{Z}^{\mathbb{B}}$
, and that
![]() $\unicode[STIX]{x1D6FD}\in \mathbb{B}$
is such that
$\unicode[STIX]{x1D6FD}\in \mathbb{B}$
is such that
![]() $pk_{\unicode[STIX]{x1D6FD}}<k_{\unicode[STIX]{x1D70E}^{-1}\circ \unicode[STIX]{x1D6FD}}$
. Then multiplication by the partial Hasse invariant
$pk_{\unicode[STIX]{x1D6FD}}<k_{\unicode[STIX]{x1D70E}^{-1}\circ \unicode[STIX]{x1D6FD}}$
. Then multiplication by the partial Hasse invariant
![]() $H_{\unicode[STIX]{x1D6FD}}^{\mathfrak{I}}$
induces an isomorphism:
$H_{\unicode[STIX]{x1D6FD}}^{\mathfrak{I}}$
induces an isomorphism:
The proof of the theorem is based on properties of the Goren–Oort stratification established by Goren and Oort [Reference Goren and OortGO00] and Tian and Xiao [Reference Tian and XiaoTX16].
We will apply Theorem 1.1 to deduce a property of the weight filtration on Hilbert modular forms. To define the weight filtration, Andreatta and Goren prove [Reference Andreatta and GorenAG05, Theorem 8.19] that if
![]() $f$
is a non-zero element of
$f$
is a non-zero element of
![]() $M_{\mathbf{k}}^{\mathfrak{I}}(\mathfrak{n},\overline{\mathbb{F}}_{p})$
, then there is a unique maximal element of the set
$M_{\mathbf{k}}^{\mathfrak{I}}(\mathfrak{n},\overline{\mathbb{F}}_{p})$
, then there is a unique maximal element of the set
(under the usual partial ordering). The weight filtration
![]() $\unicode[STIX]{x1D6F7}(f)$
is then defined to be
$\unicode[STIX]{x1D6F7}(f)$
is then defined to be
![]() $\mathbf{k}-\sum n_{\unicode[STIX]{x1D6FD}}\mathbf{h}_{\unicode[STIX]{x1D6FD}}$
(i.e. the weight of
$\mathbf{k}-\sum n_{\unicode[STIX]{x1D6FD}}\mathbf{h}_{\unicode[STIX]{x1D6FD}}$
(i.e. the weight of
![]() $g$
), where
$g$
), where
![]() $\sum n_{\unicode[STIX]{x1D6FD}}\mathbf{e}_{\unicode[STIX]{x1D6FD}}$
is this maximal element.
$\sum n_{\unicode[STIX]{x1D6FD}}\mathbf{e}_{\unicode[STIX]{x1D6FD}}$
is this maximal element.
We now state the consequences of Theorem 1.1 in terms of two cones in
![]() $\mathbb{Q}^{\mathbb{B}}$
. We first define the minimal, standard and Hasse cones as follows
$\mathbb{Q}^{\mathbb{B}}$
. We first define the minimal, standard and Hasse cones as follows
 $$\begin{eqnarray}\displaystyle C^{\text{min}} & = & \displaystyle \biggl\{\mathop{\sum }_{\unicode[STIX]{x1D6FD}}x_{\unicode[STIX]{x1D6FD}}\mathbf{e}_{\unicode[STIX]{x1D6FD}}\in \mathbb{Q}^{\mathbb{B}}\,\biggr|\,px_{\unicode[STIX]{x1D6FD}}\geqslant x_{\unicode[STIX]{x1D70E}^{-1}\circ \unicode[STIX]{x1D6FD}}~\text{for all}~\unicode[STIX]{x1D6FD}\in \mathbb{B}\biggr\},\nonumber\\ \displaystyle C^{\text{st}} & = & \displaystyle \biggl\{\mathop{\sum }_{\unicode[STIX]{x1D6FD}}x_{\unicode[STIX]{x1D6FD}}\mathbf{e}_{\unicode[STIX]{x1D6FD}}\in \mathbb{Q}^{\mathbb{B}}\,\biggr|\,x_{\unicode[STIX]{x1D6FD}}\geqslant 0~\text{for all}~\unicode[STIX]{x1D6FD}\in \mathbb{B}\biggr\},\nonumber\\ \displaystyle C^{\text{Hasse}} & = & \displaystyle \biggl\{\mathop{\sum }_{\unicode[STIX]{x1D6FD}}y_{\unicode[STIX]{x1D6FD}}\mathbf{h}_{\unicode[STIX]{x1D6FD}}\in \mathbb{Q}^{\mathbb{B}}\,\biggr|\,y_{\unicode[STIX]{x1D6FD}}\geqslant 0~\text{for all}~\unicode[STIX]{x1D6FD}\in \mathbb{B}\biggr\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle C^{\text{min}} & = & \displaystyle \biggl\{\mathop{\sum }_{\unicode[STIX]{x1D6FD}}x_{\unicode[STIX]{x1D6FD}}\mathbf{e}_{\unicode[STIX]{x1D6FD}}\in \mathbb{Q}^{\mathbb{B}}\,\biggr|\,px_{\unicode[STIX]{x1D6FD}}\geqslant x_{\unicode[STIX]{x1D70E}^{-1}\circ \unicode[STIX]{x1D6FD}}~\text{for all}~\unicode[STIX]{x1D6FD}\in \mathbb{B}\biggr\},\nonumber\\ \displaystyle C^{\text{st}} & = & \displaystyle \biggl\{\mathop{\sum }_{\unicode[STIX]{x1D6FD}}x_{\unicode[STIX]{x1D6FD}}\mathbf{e}_{\unicode[STIX]{x1D6FD}}\in \mathbb{Q}^{\mathbb{B}}\,\biggr|\,x_{\unicode[STIX]{x1D6FD}}\geqslant 0~\text{for all}~\unicode[STIX]{x1D6FD}\in \mathbb{B}\biggr\},\nonumber\\ \displaystyle C^{\text{Hasse}} & = & \displaystyle \biggl\{\mathop{\sum }_{\unicode[STIX]{x1D6FD}}y_{\unicode[STIX]{x1D6FD}}\mathbf{h}_{\unicode[STIX]{x1D6FD}}\in \mathbb{Q}^{\mathbb{B}}\,\biggr|\,y_{\unicode[STIX]{x1D6FD}}\geqslant 0~\text{for all}~\unicode[STIX]{x1D6FD}\in \mathbb{B}\biggr\}.\nonumber\end{eqnarray}$$
Note that we have the containments
![]() $C^{\text{min}}\subset C^{\text{st}}\subset C^{\text{Hasse}}$
, each of which is an equality if and only if
$C^{\text{min}}\subset C^{\text{st}}\subset C^{\text{Hasse}}$
, each of which is an equality if and only if
![]() $p$
splits completely in
$p$
splits completely in
![]() $F$
.
$F$
.
Corollary 1.2. If
![]() $f$
is a non-zero form in
$f$
is a non-zero form in
![]() $M_{\mathbf{k}}^{\mathfrak{I}}(\mathfrak{n},\overline{\mathbb{F}}_{p})$
for some
$M_{\mathbf{k}}^{\mathfrak{I}}(\mathfrak{n},\overline{\mathbb{F}}_{p})$
for some
![]() $\mathbf{k}\in \mathbb{Z}^{\mathbb{B}}$
, then
$\mathbf{k}\in \mathbb{Z}^{\mathbb{B}}$
, then
![]() $\unicode[STIX]{x1D6F7}(f)\in C^{\text{min}}$
.
$\unicode[STIX]{x1D6F7}(f)\in C^{\text{min}}$
.
The motivation for the result arises from the first author’s work with Shu Sasaki, in the course of which we observed that an analogous property seems to hold for labelled weights of crystalline lifts of two-dimensional mod
![]() $p$
local Galois representations. As discussed above, this answers the question raised by Andreatta and Goren in [Reference Andreatta and GorenAG05, Question 15.8]; it also immediately implies the following result which has recently been independently proven by Goldring and Koskivirta [Reference Goldring and KoskivirtaGK17, Corollary 3.2.4].
$p$
local Galois representations. As discussed above, this answers the question raised by Andreatta and Goren in [Reference Andreatta and GorenAG05, Question 15.8]; it also immediately implies the following result which has recently been independently proven by Goldring and Koskivirta [Reference Goldring and KoskivirtaGK17, Corollary 3.2.4].
Corollary 1.3. If
![]() $M_{\mathbf{k}}^{\mathfrak{I}}(\mathfrak{n},\overline{\mathbb{F}}_{p})\neq 0$
, then
$M_{\mathbf{k}}^{\mathfrak{I}}(\mathfrak{n},\overline{\mathbb{F}}_{p})\neq 0$
, then
![]() $\mathbf{k}\in C^{\text{Hasse}}$
.
$\mathbf{k}\in C^{\text{Hasse}}$
.
2 Hilbert modular varieties
Let
![]() $F$
be a totally real field of degree
$F$
be a totally real field of degree
![]() $d>1$
, and
$d>1$
, and
![]() ${\mathcal{O}}_{F}$
its ring of integers. Let
${\mathcal{O}}_{F}$
its ring of integers. Let
![]() $p$
be a prime number which is unramified in
$p$
be a prime number which is unramified in
![]() $F$
, and
$F$
, and
![]() $\mathfrak{n}$
an ideal of
$\mathfrak{n}$
an ideal of
![]() ${\mathcal{O}}_{F}$
relatively prime to
${\mathcal{O}}_{F}$
relatively prime to
![]() $p$
. We also assume that
$p$
. We also assume that
![]() $\mathfrak{n}$
is contained in
$\mathfrak{n}$
is contained in
![]() $N{\mathcal{O}}_{F}$
for some
$N{\mathcal{O}}_{F}$
for some
![]() $N>3$
. For a prime ideal
$N>3$
. For a prime ideal
![]() $\mathfrak{p}$
of
$\mathfrak{p}$
of
![]() ${\mathcal{O}}_{F}$
dividing
${\mathcal{O}}_{F}$
dividing
![]() $p$
, let
$p$
, let
![]() $\unicode[STIX]{x1D705}_{\mathfrak{p}}={\mathcal{O}}_{F}/\mathfrak{p}$
, a finite field of order
$\unicode[STIX]{x1D705}_{\mathfrak{p}}={\mathcal{O}}_{F}/\mathfrak{p}$
, a finite field of order
![]() $p^{f_{\mathfrak{p}}}$
. Let
$p^{f_{\mathfrak{p}}}$
. Let
![]() $\unicode[STIX]{x1D705}$
be a finite field containing an isomorphic copy of each
$\unicode[STIX]{x1D705}$
be a finite field containing an isomorphic copy of each
![]() $\unicode[STIX]{x1D705}_{\mathfrak{p}}$
. We denote by
$\unicode[STIX]{x1D705}_{\mathfrak{p}}$
. We denote by
![]() $\mathbb{Q}_{\unicode[STIX]{x1D705}}$
the fraction field of
$\mathbb{Q}_{\unicode[STIX]{x1D705}}$
the fraction field of
![]() $W(\unicode[STIX]{x1D705})$
, and fix, once and for all, embeddings
$W(\unicode[STIX]{x1D705})$
, and fix, once and for all, embeddings
![]() $\mathbb{Q}_{\unicode[STIX]{x1D705}}{\hookrightarrow}\mathbb{Q}_{p}^{\text{ur}}\subset \overline{\mathbb{Q}}_{p}$
(inducing
$\mathbb{Q}_{\unicode[STIX]{x1D705}}{\hookrightarrow}\mathbb{Q}_{p}^{\text{ur}}\subset \overline{\mathbb{Q}}_{p}$
(inducing
![]() $\unicode[STIX]{x1D705}{\hookrightarrow}\overline{\mathbb{F}}_{p}$
), as well as embeddings
$\unicode[STIX]{x1D705}{\hookrightarrow}\overline{\mathbb{F}}_{p}$
), as well as embeddings
![]() $\overline{\mathbb{Q}}{\hookrightarrow}\overline{\mathbb{Q}}_{p}$
and
$\overline{\mathbb{Q}}{\hookrightarrow}\overline{\mathbb{Q}}_{p}$
and
![]() $\overline{\mathbb{Q}}{\hookrightarrow}\mathbb{C}$
.
$\overline{\mathbb{Q}}{\hookrightarrow}\mathbb{C}$
.
Let
![]() $\mathbb{B}=\text{Emb}(F,\mathbb{Q}_{\unicode[STIX]{x1D705}})$
. We write
$\mathbb{B}=\text{Emb}(F,\mathbb{Q}_{\unicode[STIX]{x1D705}})$
. We write
![]() $\mathbb{B}=\coprod _{\mathfrak{p}|p}\mathbb{B}_{\mathfrak{p}}$
, where
$\mathbb{B}=\coprod _{\mathfrak{p}|p}\mathbb{B}_{\mathfrak{p}}$
, where
for a prime ideal
![]() $\mathfrak{p}$
dividing
$\mathfrak{p}$
dividing
![]() $p$
. Since
$p$
. Since
![]() $p$
is unramified in
$p$
is unramified in
![]() $F$
,
$F$
,
![]() $\mathbb{B}$
is canonically identified with
$\mathbb{B}$
is canonically identified with
![]() $\operatorname{Hom}({\mathcal{O}}_{F},\unicode[STIX]{x1D705})$
. Using the fixed embeddings of
$\operatorname{Hom}({\mathcal{O}}_{F},\unicode[STIX]{x1D705})$
. Using the fixed embeddings of
![]() $\overline{\mathbb{Q}}$
into
$\overline{\mathbb{Q}}$
into
![]() $\overline{\mathbb{Q}}_{p}$
and
$\overline{\mathbb{Q}}_{p}$
and
![]() $\mathbb{C}$
, we can also identify
$\mathbb{C}$
, we can also identify
![]() $\mathbb{B}$
with the set of infinite places of
$\mathbb{B}$
with the set of infinite places of
![]() $F$
, and can think of
$F$
, and can think of
![]() $\mathbb{B}_{\mathfrak{p}}$
as the set of infinite places inducing the prime ideal
$\mathbb{B}_{\mathfrak{p}}$
as the set of infinite places inducing the prime ideal
![]() $\mathfrak{p}$
.
$\mathfrak{p}$
.
Let
![]() $\unicode[STIX]{x1D70E}$
denote the Frobenius automorphism of
$\unicode[STIX]{x1D70E}$
denote the Frobenius automorphism of
![]() $\mathbb{Q}_{\unicode[STIX]{x1D705}}$
, lifting
$\mathbb{Q}_{\unicode[STIX]{x1D705}}$
, lifting
![]() $x\mapsto x^{p}$
modulo
$x\mapsto x^{p}$
modulo
![]() $p$
. It acts on
$p$
. It acts on
![]() $\mathbb{B}$
by
$\mathbb{B}$
by
![]() $\unicode[STIX]{x1D6FD}\mapsto \unicode[STIX]{x1D70E}\circ \unicode[STIX]{x1D6FD}$
. It acts transitively on each
$\unicode[STIX]{x1D6FD}\mapsto \unicode[STIX]{x1D70E}\circ \unicode[STIX]{x1D6FD}$
. It acts transitively on each
![]() $\mathbb{B}_{\mathfrak{p}}$
. The decomposition
$\mathbb{B}_{\mathfrak{p}}$
. The decomposition
where
![]() $W(\unicode[STIX]{x1D705})_{\unicode[STIX]{x1D6FD}}$
is
$W(\unicode[STIX]{x1D705})_{\unicode[STIX]{x1D6FD}}$
is
![]() $W(\unicode[STIX]{x1D705})$
with the
$W(\unicode[STIX]{x1D705})$
with the
![]() ${\mathcal{O}}_{F}$
-action given via the embedding
${\mathcal{O}}_{F}$
-action given via the embedding
![]() $\unicode[STIX]{x1D6FD}$
, induces a decomposition
$\unicode[STIX]{x1D6FD}$
, induces a decomposition
for any
![]() ${\mathcal{O}}_{F}\otimes _{\mathbb{Z}}W(\unicode[STIX]{x1D705})$
-module
${\mathcal{O}}_{F}\otimes _{\mathbb{Z}}W(\unicode[STIX]{x1D705})$
-module
![]() $\unicode[STIX]{x1D6EC}$
.
$\unicode[STIX]{x1D6EC}$
.
Let
![]() $A$
be an abelian scheme over a scheme
$A$
be an abelian scheme over a scheme
![]() $S$
, with real multiplication defined by
$S$
, with real multiplication defined by
![]() $\unicode[STIX]{x1D704}:{\mathcal{O}}_{F}\rightarrow \operatorname{End}_{S}(A)$
. Then the dual abelian scheme
$\unicode[STIX]{x1D704}:{\mathcal{O}}_{F}\rightarrow \operatorname{End}_{S}(A)$
. Then the dual abelian scheme
![]() $A^{\vee }$
has an induced canonical real multiplication. We define
$A^{\vee }$
has an induced canonical real multiplication. We define
![]() ${\mathcal{P}}_{A}=\operatorname{Hom}_{{\mathcal{O}}_{F}}(A,A^{\vee })^{\text{sym}}$
, which we view as an étale sheaf on
${\mathcal{P}}_{A}=\operatorname{Hom}_{{\mathcal{O}}_{F}}(A,A^{\vee })^{\text{sym}}$
, which we view as an étale sheaf on
![]() $S$
of projective
$S$
of projective
![]() ${\mathcal{O}}_{F}$
-modules of rank one with a notion of positivity in which the positive elements correspond to
${\mathcal{O}}_{F}$
-modules of rank one with a notion of positivity in which the positive elements correspond to
![]() ${\mathcal{O}}_{F}$
-equivariant polarizations.
${\mathcal{O}}_{F}$
-equivariant polarizations.
Fix a representative
![]() $[(\mathfrak{I},\mathfrak{I}^{+})]\in \operatorname{Cl}^{+}(F)$
. Consider the functor
$[(\mathfrak{I},\mathfrak{I}^{+})]\in \operatorname{Cl}^{+}(F)$
. Consider the functor
that associates to a
![]() $\mathbb{Z}_{p}$
-scheme
$\mathbb{Z}_{p}$
-scheme
![]() $S$
, the set of all isomorphism classes of
$S$
, the set of all isomorphism classes of
![]() $\text{}\underline{A}/S=(A/S,\unicode[STIX]{x1D704},\unicode[STIX]{x1D706},\unicode[STIX]{x1D6FC})$
such that:
$\text{}\underline{A}/S=(A/S,\unicode[STIX]{x1D704},\unicode[STIX]{x1D706},\unicode[STIX]{x1D6FC})$
such that:
-
–
 $A$
is an abelian scheme of relative dimension
$A$
is an abelian scheme of relative dimension
 $d$
over
$d$
over
 $S$
;
$S$
; -
–
 $\unicode[STIX]{x1D704}:{\mathcal{O}}_{F}{\hookrightarrow}\text{End}_{S}(A)$
is a ring homomorphism endowing
$\unicode[STIX]{x1D704}:{\mathcal{O}}_{F}{\hookrightarrow}\text{End}_{S}(A)$
is a ring homomorphism endowing
 $A$
with real multiplication by
$A$
with real multiplication by
 ${\mathcal{O}}_{F}$
;
${\mathcal{O}}_{F}$
; -
– the map
 $\unicode[STIX]{x1D706}$
is an
$\unicode[STIX]{x1D706}$
is an
 ${\mathcal{O}}_{F}$
-linear isomorphism
${\mathcal{O}}_{F}$
-linear isomorphism
 $\unicode[STIX]{x1D706}:({\mathcal{P}}_{A},{\mathcal{P}}_{A}^{+})\rightarrow (\mathfrak{I},\mathfrak{I}^{+})$
of sheaves on the étale site of
$\unicode[STIX]{x1D706}:({\mathcal{P}}_{A},{\mathcal{P}}_{A}^{+})\rightarrow (\mathfrak{I},\mathfrak{I}^{+})$
of sheaves on the étale site of
 $S$
such that
$S$
such that
 $A\otimes _{{\mathcal{O}}_{F}}\mathfrak{I}\cong A^{\vee }$
;
$A\otimes _{{\mathcal{O}}_{F}}\mathfrak{I}\cong A^{\vee }$
; -
– the map
 $\unicode[STIX]{x1D6FC}:({\mathcal{O}}_{F}/\mathfrak{n})^{2}\rightarrow A[\mathfrak{n}]$
is an
$\unicode[STIX]{x1D6FC}:({\mathcal{O}}_{F}/\mathfrak{n})^{2}\rightarrow A[\mathfrak{n}]$
is an
 ${\mathcal{O}}_{F}$
-linear isomorphism of group schemes.
${\mathcal{O}}_{F}$
-linear isomorphism of group schemes.
Since
![]() $p$
is unramified in
$p$
is unramified in
![]() $F$
, the existence of
$F$
, the existence of
![]() $\unicode[STIX]{x1D706}$
is equivalent to
$\unicode[STIX]{x1D706}$
is equivalent to
![]() $\operatorname{Lie}(A)$
being a locally free
$\operatorname{Lie}(A)$
being a locally free
![]() $({\mathcal{O}}_{F}\otimes {\mathcal{O}}_{S})$
-module of rank one.
$({\mathcal{O}}_{F}\otimes {\mathcal{O}}_{S})$
-module of rank one.
There is a scheme
![]() $X^{\mathfrak{I}}(\mathfrak{n})=X$
of relative dimension
$X^{\mathfrak{I}}(\mathfrak{n})=X$
of relative dimension
![]() $d$
over
$d$
over
![]() $\operatorname{Spec}(\mathbb{Z}_{p})$
which represents the above functor. It is called the Hilbert modular scheme of polarization
$\operatorname{Spec}(\mathbb{Z}_{p})$
which represents the above functor. It is called the Hilbert modular scheme of polarization
![]() $\mathfrak{I}$
and level
$\mathfrak{I}$
and level
![]() $\unicode[STIX]{x1D6E4}(\mathfrak{n})$
, and is smooth over
$\unicode[STIX]{x1D6E4}(\mathfrak{n})$
, and is smooth over
![]() $\operatorname{Spec}(\mathbb{Z}_{p})$
.
$\operatorname{Spec}(\mathbb{Z}_{p})$
.
We let
![]() $X_{\unicode[STIX]{x1D705}}:=X\otimes _{\mathbb{Z}_{p}}\unicode[STIX]{x1D705}$
. It represents the above functor restricted to schemes over
$X_{\unicode[STIX]{x1D705}}:=X\otimes _{\mathbb{Z}_{p}}\unicode[STIX]{x1D705}$
. It represents the above functor restricted to schemes over
![]() $\unicode[STIX]{x1D705}$
. We denote the base extension of
$\unicode[STIX]{x1D705}$
. We denote the base extension of
![]() $X_{\unicode[STIX]{x1D705}}$
under our fixed embedding
$X_{\unicode[STIX]{x1D705}}$
under our fixed embedding
![]() $\unicode[STIX]{x1D705}\subset \overline{\mathbb{F}}_{p}$
by
$\unicode[STIX]{x1D705}\subset \overline{\mathbb{F}}_{p}$
by
![]() $\overline{X}$
.
$\overline{X}$
.
Let
![]() ${\mathcal{A}}/X$
(similarly,
${\mathcal{A}}/X$
(similarly,
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D705}}/X_{\unicode[STIX]{x1D705}}$
,
${\mathcal{A}}_{\unicode[STIX]{x1D705}}/X_{\unicode[STIX]{x1D705}}$
,
![]() $\overline{{\mathcal{A}}}/\overline{X}$
) denote the universal abelian scheme, and denote by
$\overline{{\mathcal{A}}}/\overline{X}$
) denote the universal abelian scheme, and denote by
![]() $\unicode[STIX]{x1D70B}$
the structural morphism in all cases. Let
$\unicode[STIX]{x1D70B}$
the structural morphism in all cases. Let
![]() $\unicode[STIX]{x1D714}_{{\mathcal{A}}/X}=\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D6FA}_{{\mathcal{A}}/X}^{1}$
denote the sheaf of invariant differentials. Similarly define
$\unicode[STIX]{x1D714}_{{\mathcal{A}}/X}=\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D6FA}_{{\mathcal{A}}/X}^{1}$
denote the sheaf of invariant differentials. Similarly define
![]() $\unicode[STIX]{x1D714}_{{\mathcal{A}}_{\unicode[STIX]{x1D705}}/X_{\unicode[STIX]{x1D705}}}$
and
$\unicode[STIX]{x1D714}_{{\mathcal{A}}_{\unicode[STIX]{x1D705}}/X_{\unicode[STIX]{x1D705}}}$
and
![]() $\unicode[STIX]{x1D714}_{\overline{{\mathcal{A}}}/\overline{X}}$
. When there is no possibility of confusion, we will simply use
$\unicode[STIX]{x1D714}_{\overline{{\mathcal{A}}}/\overline{X}}$
. When there is no possibility of confusion, we will simply use
![]() $\unicode[STIX]{x1D714}$
to denote any of these sheaves.
$\unicode[STIX]{x1D714}$
to denote any of these sheaves.
Since
![]() $p$
is unramified in
$p$
is unramified in
![]() $F$
, we know that
$F$
, we know that
![]() $\unicode[STIX]{x1D714}_{\overline{{\mathcal{A}}}/\overline{X}}$
is locally free of rank one over
$\unicode[STIX]{x1D714}_{\overline{{\mathcal{A}}}/\overline{X}}$
is locally free of rank one over
![]() ${\mathcal{O}}_{\overline{X}}\otimes _{\mathbb{Z}}{\mathcal{O}}_{F}\cong \bigoplus _{\unicode[STIX]{x1D6FD}\in \mathbb{B}}{\mathcal{O}}_{\overline{X}}$
. Therefore, we have
${\mathcal{O}}_{\overline{X}}\otimes _{\mathbb{Z}}{\mathcal{O}}_{F}\cong \bigoplus _{\unicode[STIX]{x1D6FD}\in \mathbb{B}}{\mathcal{O}}_{\overline{X}}$
. Therefore, we have
where, for each
![]() $\unicode[STIX]{x1D6FD}\in \mathbb{B}$
, the sheaf
$\unicode[STIX]{x1D6FD}\in \mathbb{B}$
, the sheaf
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FD}}$
is locally free of rank one over
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FD}}$
is locally free of rank one over
![]() ${\mathcal{O}}_{\overline{X}}$
.
${\mathcal{O}}_{\overline{X}}$
.
For
![]() $\unicode[STIX]{x1D6FD}\in \mathbb{B}$
, we let
$\unicode[STIX]{x1D6FD}\in \mathbb{B}$
, we let
![]() $\mathbf{e}_{\unicode[STIX]{x1D6FD}}$
denote the basis element of
$\mathbf{e}_{\unicode[STIX]{x1D6FD}}$
denote the basis element of
![]() $\mathbb{Z}^{\mathbb{B}}$
associated to
$\mathbb{Z}^{\mathbb{B}}$
associated to
![]() $\unicode[STIX]{x1D6FD}$
. For any
$\unicode[STIX]{x1D6FD}$
. For any
![]() $\mathbf{k}=\sum k_{\unicode[STIX]{x1D6FD}}\mathbf{e}_{\unicode[STIX]{x1D6FD}}\in \mathbb{Z}^{\mathbb{B}}$
, we define
$\mathbf{k}=\sum k_{\unicode[STIX]{x1D6FD}}\mathbf{e}_{\unicode[STIX]{x1D6FD}}\in \mathbb{Z}^{\mathbb{B}}$
, we define
3 Hilbert modular forms in characteristic
 $p$
$p$
Let notation be as in § 2. Let
![]() $R$
by any
$R$
by any
![]() $\unicode[STIX]{x1D705}$
-algebra. We define the space of
$\unicode[STIX]{x1D705}$
-algebra. We define the space of
![]() $\mathfrak{I}$
-polarized geometric Hilbert modular forms over
$\mathfrak{I}$
-polarized geometric Hilbert modular forms over
![]() $R$
of weight
$R$
of weight
![]() $\mathbf{k}=\sum k_{\unicode[STIX]{x1D6FD}}\mathbf{e}_{\unicode[STIX]{x1D6FD}}\in \mathbb{Z}^{\mathbb{B}}$
and level
$\mathbf{k}=\sum k_{\unicode[STIX]{x1D6FD}}\mathbf{e}_{\unicode[STIX]{x1D6FD}}\in \mathbb{Z}^{\mathbb{B}}$
and level
![]() $\unicode[STIX]{x1D6E4}(\mathfrak{n})$
to be
$\unicode[STIX]{x1D6E4}(\mathfrak{n})$
to be
Important examples of such modular forms are the partial Hasse invariants defined first in [Reference GorenGor01], and studied further in [Reference Andreatta and GorenAG05]. Let
![]() $\operatorname{Ver}:{\mathcal{A}}_{\unicode[STIX]{x1D705}}^{(p)}\rightarrow {\mathcal{A}}_{\unicode[STIX]{x1D705}}$
be the Verschiebung morphism of the universal abelian variety over
$\operatorname{Ver}:{\mathcal{A}}_{\unicode[STIX]{x1D705}}^{(p)}\rightarrow {\mathcal{A}}_{\unicode[STIX]{x1D705}}$
be the Verschiebung morphism of the universal abelian variety over
![]() $X_{\unicode[STIX]{x1D705}}$
. The induced morphism
$X_{\unicode[STIX]{x1D705}}$
. The induced morphism
![]() $\operatorname{Ver}^{\ast }:\unicode[STIX]{x1D714}_{{\mathcal{A}}_{\unicode[STIX]{x1D705}}/X_{\unicode[STIX]{x1D705}}}\rightarrow \unicode[STIX]{x1D714}_{{\mathcal{A}}_{\unicode[STIX]{x1D705}}^{(p)}/X_{\unicode[STIX]{x1D705}}}$
can be written as
$\operatorname{Ver}^{\ast }:\unicode[STIX]{x1D714}_{{\mathcal{A}}_{\unicode[STIX]{x1D705}}/X_{\unicode[STIX]{x1D705}}}\rightarrow \unicode[STIX]{x1D714}_{{\mathcal{A}}_{\unicode[STIX]{x1D705}}^{(p)}/X_{\unicode[STIX]{x1D705}}}$
can be written as
![]() $\operatorname{Ver}=\bigoplus _{\unicode[STIX]{x1D6FD}\in \mathbb{B}}\operatorname{Ver}_{\unicode[STIX]{x1D6FD}}^{\ast }$
, where
$\operatorname{Ver}=\bigoplus _{\unicode[STIX]{x1D6FD}\in \mathbb{B}}\operatorname{Ver}_{\unicode[STIX]{x1D6FD}}^{\ast }$
, where
gives a section of
![]() $\operatorname{Hom}(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FD}},\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70E}^{-1}\circ \unicode[STIX]{x1D6FD}}^{p})\cong \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FD}}^{-1}\otimes \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70E}^{-1}\circ \unicode[STIX]{x1D6FD}}^{p}$
, which we denote by
$\operatorname{Hom}(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FD}},\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70E}^{-1}\circ \unicode[STIX]{x1D6FD}}^{p})\cong \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FD}}^{-1}\otimes \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70E}^{-1}\circ \unicode[STIX]{x1D6FD}}^{p}$
, which we denote by
![]() $H_{\unicode[STIX]{x1D6FD}}^{\mathfrak{I}}$
. Thus,
$H_{\unicode[STIX]{x1D6FD}}^{\mathfrak{I}}$
. Thus,
![]() $H_{\unicode[STIX]{x1D6FD}}^{\mathfrak{I}}$
is a
$H_{\unicode[STIX]{x1D6FD}}^{\mathfrak{I}}$
is a
![]() $\mathfrak{I}$
-polarized geometric Hilbert modular forms over
$\mathfrak{I}$
-polarized geometric Hilbert modular forms over
![]() $\unicode[STIX]{x1D705}$
of weight
$\unicode[STIX]{x1D705}$
of weight
and level
![]() $\unicode[STIX]{x1D6E4}(\mathfrak{n})$
.
$\unicode[STIX]{x1D6E4}(\mathfrak{n})$
.
While we have not discussed
![]() $q$
-expansions in this article, we would like to point out that each
$q$
-expansions in this article, we would like to point out that each
![]() $H_{\unicode[STIX]{x1D6FD}}^{\mathfrak{I}}$
has
$H_{\unicode[STIX]{x1D6FD}}^{\mathfrak{I}}$
has
![]() $q$
-expansions equal to 1 at an unramified cusp on each connected component, which motivates the following question: given a mod
$q$
-expansions equal to 1 at an unramified cusp on each connected component, which motivates the following question: given a mod
![]() $p$
modular form
$p$
modular form
![]() $f$
, what is the maximum power of each
$f$
, what is the maximum power of each
![]() $H_{\unicode[STIX]{x1D6FD}}^{\mathfrak{I}}$
by which
$H_{\unicode[STIX]{x1D6FD}}^{\mathfrak{I}}$
by which
![]() $f$
is divisible? In [Reference Andreatta and GorenAG05, 8.19], it is proven that if
$f$
is divisible? In [Reference Andreatta and GorenAG05, 8.19], it is proven that if
![]() $f$
is a non-zero element of
$f$
is a non-zero element of
![]() $M_{\mathbf{k}}^{\mathfrak{I}}(\mathfrak{n},\overline{\mathbb{F}}_{p})$
, then there is a unique maximal element of the set
$M_{\mathbf{k}}^{\mathfrak{I}}(\mathfrak{n},\overline{\mathbb{F}}_{p})$
, then there is a unique maximal element of the set
(under the usual partial ordering). The weight filtration
![]() $\unicode[STIX]{x1D6F7}(f)$
is then defined to be
$\unicode[STIX]{x1D6F7}(f)$
is then defined to be
![]() $\mathbf{k}-\sum n_{\unicode[STIX]{x1D6FD}}\mathbf{h}_{\unicode[STIX]{x1D6FD}}$
(i.e. the weight of
$\mathbf{k}-\sum n_{\unicode[STIX]{x1D6FD}}\mathbf{h}_{\unicode[STIX]{x1D6FD}}$
(i.e. the weight of
![]() $g$
), where
$g$
), where
![]() $\sum n_{\unicode[STIX]{x1D6FD}}\mathbf{e}_{\unicode[STIX]{x1D6FD}}$
is this maximal element.
$\sum n_{\unicode[STIX]{x1D6FD}}\mathbf{e}_{\unicode[STIX]{x1D6FD}}$
is this maximal element.
4 The Goren–Oort Stratification
In this section, we recall the definition of the Goren–Oort stratification on
![]() $X_{\unicode[STIX]{x1D705}}$
and some of its properties proven in [Reference Goren and OortGO00]. We will then recall some key results proven by Tian and Xiao [Reference Tian and XiaoTX16] regarding the global structure of these strata, which we will use in the proof of our main theorem.
$X_{\unicode[STIX]{x1D705}}$
and some of its properties proven in [Reference Goren and OortGO00]. We will then recall some key results proven by Tian and Xiao [Reference Tian and XiaoTX16] regarding the global structure of these strata, which we will use in the proof of our main theorem.
Let
![]() $x=(A,\unicode[STIX]{x1D704},\unicode[STIX]{x1D706},\unicode[STIX]{x1D6FC})$
be a closed point of
$x=(A,\unicode[STIX]{x1D704},\unicode[STIX]{x1D706},\unicode[STIX]{x1D6FC})$
be a closed point of
![]() $X_{\unicode[STIX]{x1D705}}$
. The type of
$X_{\unicode[STIX]{x1D705}}$
. The type of
![]() $x$
is defined by
$x$
is defined by
where
![]() $\mathbb{D}$
denotes the contravariant Dieudonné module.
$\mathbb{D}$
denotes the contravariant Dieudonné module.
Let
![]() $T\subseteq \mathbb{B}$
. There is a locally closed subset
$T\subseteq \mathbb{B}$
. There is a locally closed subset
![]() $W_{T}$
of
$W_{T}$
of
![]() $X_{\unicode[STIX]{x1D705}}$
with the property that a closed point
$X_{\unicode[STIX]{x1D705}}$
with the property that a closed point
![]() $x$
of
$x$
of
![]() $X_{\unicode[STIX]{x1D705}}$
belongs to
$X_{\unicode[STIX]{x1D705}}$
belongs to
![]() $W_{T}$
if and only if
$W_{T}$
if and only if
![]() $\unicode[STIX]{x1D70F}(x)=T$
. We define
$\unicode[STIX]{x1D70F}(x)=T$
. We define
![]() $Z_{T}$
to be the Zariski closure of
$Z_{T}$
to be the Zariski closure of
![]() $W_{T}$
.
$W_{T}$
.
The following properties of this stratification are proven in [Reference Goren and OortGO00]:
-
– the collection
 $\{W_{T}:T\subseteq \mathbb{B}\}$
is a stratification of
$\{W_{T}:T\subseteq \mathbb{B}\}$
is a stratification of
 $X_{\unicode[STIX]{x1D705}}$
; we have
$X_{\unicode[STIX]{x1D705}}$
; we have
 $Z_{T}=\bigcup _{T^{\prime }\supseteq T}W_{T^{\prime }}$
;
$Z_{T}=\bigcup _{T^{\prime }\supseteq T}W_{T^{\prime }}$
; -
– each
 $W_{T}$
is non-empty, and equi-dimensional of dimension
$W_{T}$
is non-empty, and equi-dimensional of dimension
 $d-|T|$
;
$d-|T|$
; -
– each
 $Z_{T}$
is non-singular;
$Z_{T}$
is non-singular; -
– for any
 $T\subset \mathbb{B}$
, we have
$T\subset \mathbb{B}$
, we have
 $Z_{T}=\bigcap _{\unicode[STIX]{x1D6FD}\in T}Z(H_{\unicode[STIX]{x1D6FD}}^{\mathfrak{I}})$
scheme theoretically, where
$Z_{T}=\bigcap _{\unicode[STIX]{x1D6FD}\in T}Z(H_{\unicode[STIX]{x1D6FD}}^{\mathfrak{I}})$
scheme theoretically, where
 $Z(.)$
denotes the vanishing locus;
$Z(.)$
denotes the vanishing locus; -
–
 $W_{\mathbb{B}}=Z_{\mathbb{B}}$
is the non-empty finite set of all points
$W_{\mathbb{B}}=Z_{\mathbb{B}}$
is the non-empty finite set of all points
 $x=(A,\unicode[STIX]{x1D704},\unicode[STIX]{x1D706},\unicode[STIX]{x1D6FC})$
where
$x=(A,\unicode[STIX]{x1D704},\unicode[STIX]{x1D706},\unicode[STIX]{x1D6FC})$
where
 $A$
is a superspecial abelian variety.
$A$
is a superspecial abelian variety.
Lemma 4.1. Let
![]() $T\subset \mathbb{B}$
. Every connected component of
$T\subset \mathbb{B}$
. Every connected component of
![]() $Z_{T}$
intersects
$Z_{T}$
intersects
![]() $Z_{\mathbb{B}}$
non-trivially.
$Z_{\mathbb{B}}$
non-trivially.
Proof. This is [Reference Goren and OortGO00, Corollary 2.3.12]. ◻
We now recall some results proven in [Reference Tian and XiaoTX16] about the global structure of the strata
![]() $Z_{T}$
.
$Z_{T}$
.
Theorem 4.2 (Tian–Xiao).
Let
![]() $\mathfrak{p}|p$
be a prime ideal of
$\mathfrak{p}|p$
be a prime ideal of
![]() ${\mathcal{O}}_{F}$
such that
${\mathcal{O}}_{F}$
such that
![]() $f_{\mathfrak{p}}>1$
. Let
$f_{\mathfrak{p}}>1$
. Let
![]() $\unicode[STIX]{x1D6FD}_{0}\in \mathbb{B}_{\mathfrak{p}}$
. The Goren–Oort stratum
$\unicode[STIX]{x1D6FD}_{0}\in \mathbb{B}_{\mathfrak{p}}$
. The Goren–Oort stratum
![]() $Z_{\{\unicode[STIX]{x1D6FD}_{0}\}}$
is isomorphic to a
$Z_{\{\unicode[STIX]{x1D6FD}_{0}\}}$
is isomorphic to a
![]() $\mathbb{P}^{1}$
-bundle over the quaternionic Shimura variety
$\mathbb{P}^{1}$
-bundle over the quaternionic Shimura variety
![]() $X_{K}^{B}$
associated to
$X_{K}^{B}$
associated to
![]() $B^{\times }$
, where
$B^{\times }$
, where
![]() $B$
is the quaternion algebra over
$B$
is the quaternion algebra over
![]() $F$
that is ramified exactly at
$F$
that is ramified exactly at
![]() $\{\unicode[STIX]{x1D70E}^{-1}\circ \unicode[STIX]{x1D6FD}_{0},\unicode[STIX]{x1D6FD}_{0}\}$
, and
$\{\unicode[STIX]{x1D70E}^{-1}\circ \unicode[STIX]{x1D6FD}_{0},\unicode[STIX]{x1D6FD}_{0}\}$
, and
![]() $K$
is a level structure maximal at
$K$
is a level structure maximal at
![]() $p$
.
$p$
.
A much more general version of this result, which is based on an idea of Helm [Reference HelmHel10], is proven in [Reference Tian and XiaoTX16, Theorem 5.2], where such a recipe is given for
![]() $Z_{T}$
for an arbitrary subset
$Z_{T}$
for an arbitrary subset
![]() $T$
of
$T$
of
![]() $\mathbb{B}$
.
$\mathbb{B}$
.
Lemma 4.3. Let
![]() $\mathfrak{p}|p$
be a prime ideal of
$\mathfrak{p}|p$
be a prime ideal of
![]() ${\mathcal{O}}_{F}$
, and
${\mathcal{O}}_{F}$
, and
![]() $\unicode[STIX]{x1D6FD}_{0}\in \mathbb{B}_{\mathfrak{p}}$
. Let
$\unicode[STIX]{x1D6FD}_{0}\in \mathbb{B}_{\mathfrak{p}}$
. Let
![]() $T\subset \mathbb{B}$
be such that
$T\subset \mathbb{B}$
be such that
![]() $\unicode[STIX]{x1D6FD}_{0}\in T$
. We have the following isomorphism of line bundles on
$\unicode[STIX]{x1D6FD}_{0}\in T$
. We have the following isomorphism of line bundles on
![]() $Z_{T}$
:
$Z_{T}$
:
In particular, if
![]() $\mathbb{B}_{\mathfrak{p}}\subset T$
, then for all
$\mathbb{B}_{\mathfrak{p}}\subset T$
, then for all
![]() $\unicode[STIX]{x1D6FD}\in \mathbb{B}_{\mathfrak{p}}$
we have
$\unicode[STIX]{x1D6FD}\in \mathbb{B}_{\mathfrak{p}}$
we have
![]() $(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FD}}|_{Z_{T}})^{p^{f_{\mathfrak{p}}}}\cong {\mathcal{O}}_{Z_{T}}$
.
$(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FD}}|_{Z_{T}})^{p^{f_{\mathfrak{p}}}}\cong {\mathcal{O}}_{Z_{T}}$
.
Proof. Clearly, it is enough to prove this for
![]() $T=\{\unicode[STIX]{x1D6FD}_{0}\}$
. Recall that
$T=\{\unicode[STIX]{x1D6FD}_{0}\}$
. Recall that
![]() ${\mathcal{A}}$
denotes the universal abelian scheme over
${\mathcal{A}}$
denotes the universal abelian scheme over
![]() $\overline{X}$
. There is a short exact sequence
$\overline{X}$
. There is a short exact sequence
Isolating the
![]() $\unicode[STIX]{x1D6FD}_{0}$
-component and applying the isomorphism
$\unicode[STIX]{x1D6FD}_{0}$
-component and applying the isomorphism
![]() $\unicode[STIX]{x1D714}_{{\mathcal{A}}/\overline{X}}\cong \unicode[STIX]{x1D714}_{{\mathcal{A}}^{\vee }/\overline{X}}$
(induced by a choice of prime-to-
$\unicode[STIX]{x1D714}_{{\mathcal{A}}/\overline{X}}\cong \unicode[STIX]{x1D714}_{{\mathcal{A}}^{\vee }/\overline{X}}$
(induced by a choice of prime-to-
![]() $p$
polarization on the universal abelian variety), we deduce that
$p$
polarization on the universal abelian variety), we deduce that
![]() $\wedge ^{2}H_{\text{dR}}^{1}({\mathcal{A}}/\overline{X})_{\unicode[STIX]{x1D6FD}_{0}}$
is the trivial line bundle on
$\wedge ^{2}H_{\text{dR}}^{1}({\mathcal{A}}/\overline{X})_{\unicode[STIX]{x1D6FD}_{0}}$
is the trivial line bundle on
![]() $\overline{X}$
.
$\overline{X}$
.
Now, we consider the Verschiebung morphism
which has image equal to
![]() $(\unicode[STIX]{x1D714}^{(p)})_{\unicode[STIX]{x1D6FD}_{0}}=\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70E}^{-1}\circ \unicode[STIX]{x1D6FD}_{0}}^{p}$
. By definition, the vanishing of
$(\unicode[STIX]{x1D714}^{(p)})_{\unicode[STIX]{x1D6FD}_{0}}=\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70E}^{-1}\circ \unicode[STIX]{x1D6FD}_{0}}^{p}$
. By definition, the vanishing of
![]() $H_{\unicode[STIX]{x1D6FD}_{0}}^{\mathfrak{I}}$
is equivalent to
$H_{\unicode[STIX]{x1D6FD}_{0}}^{\mathfrak{I}}$
is equivalent to
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FD}_{0}}$
equalling the kernel of
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FD}_{0}}$
equalling the kernel of
![]() $\operatorname{Ver}_{\unicode[STIX]{x1D6FD}_{0}}$
. In particular, on
$\operatorname{Ver}_{\unicode[STIX]{x1D6FD}_{0}}$
. In particular, on
![]() $Z_{\{\unicode[STIX]{x1D6FD}_{0}\}}$
, we have a short exact sequence of sheaves
$Z_{\{\unicode[STIX]{x1D6FD}_{0}\}}$
, we have a short exact sequence of sheaves
This implies that on
![]() $Z_{\{\unicode[STIX]{x1D6FD}_{0}\}}$
we have
$Z_{\{\unicode[STIX]{x1D6FD}_{0}\}}$
we have
![]() ${\mathcal{O}}_{Z_{\unicode[STIX]{x1D6FD}_{0}}}\cong \wedge ^{2}H_{\text{dR}}^{1}({\mathcal{A}}/\overline{X})_{\unicode[STIX]{x1D6FD}_{0}}\cong \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FD}_{0}}\otimes \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70E}^{-1}\circ \unicode[STIX]{x1D6FD}_{0}}^{p}$
, as claimed.
${\mathcal{O}}_{Z_{\unicode[STIX]{x1D6FD}_{0}}}\cong \wedge ^{2}H_{\text{dR}}^{1}({\mathcal{A}}/\overline{X})_{\unicode[STIX]{x1D6FD}_{0}}\cong \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FD}_{0}}\otimes \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70E}^{-1}\circ \unicode[STIX]{x1D6FD}_{0}}^{p}$
, as claimed.
The last claim follows by applying the above result for all
![]() $\unicode[STIX]{x1D6FD}\in \mathbb{B}_{\mathfrak{p}}$
.◻
$\unicode[STIX]{x1D6FD}\in \mathbb{B}_{\mathfrak{p}}$
.◻
Lemma 4.4. Let
![]() $\unicode[STIX]{x1D6FD}_{0}\in \mathbb{B}_{\mathfrak{p}}$
be such that
$\unicode[STIX]{x1D6FD}_{0}\in \mathbb{B}_{\mathfrak{p}}$
be such that
![]() $f_{\mathfrak{p}}>1$
. By Theorem 4.2, the Goren–Oort stratum
$f_{\mathfrak{p}}>1$
. By Theorem 4.2, the Goren–Oort stratum
![]() $Z_{\{\unicode[STIX]{x1D6FD}_{0}\}}\subset \overline{X}$
is isomorphic to a
$Z_{\{\unicode[STIX]{x1D6FD}_{0}\}}\subset \overline{X}$
is isomorphic to a
![]() $\mathbb{P}^{1}$
-bundle over a quaternionic Shimura variety
$\mathbb{P}^{1}$
-bundle over a quaternionic Shimura variety
![]() $X_{K}^{B}$
. Let
$X_{K}^{B}$
. Let
![]() $x$
be a geometric point of
$x$
be a geometric point of
![]() $X_{K}^{B}$
, and denote by
$X_{K}^{B}$
, and denote by
![]() $\mathbb{P}_{x}^{1}$
the corresponding fibre of the
$\mathbb{P}_{x}^{1}$
the corresponding fibre of the
![]() $\mathbb{P}^{1}$
-bundle. Then, for
$\mathbb{P}^{1}$
-bundle. Then, for
![]() $\unicode[STIX]{x1D6FD}\in \mathbb{B}$
, we have the following equalities:
$\unicode[STIX]{x1D6FD}\in \mathbb{B}$
, we have the following equalities:
 $$\begin{eqnarray}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FD}}|_{\mathbb{P}_{x}^{1}}\cong \left\{\begin{array}{@{}ll@{}}{\mathcal{O}}_{\mathbb{P}_{x}^{1}}(p)\quad & \text{if}~\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FD}_{0},\\ {\mathcal{O}}_{\mathbb{P}_{x}^{1}}(-1)\quad & \text{if}~\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D70E}^{-1}\circ \unicode[STIX]{x1D6FD}_{0},\\ {\mathcal{O}}_{\mathbb{P}_{x}^{1}}\quad & \text{otherwise}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FD}}|_{\mathbb{P}_{x}^{1}}\cong \left\{\begin{array}{@{}ll@{}}{\mathcal{O}}_{\mathbb{P}_{x}^{1}}(p)\quad & \text{if}~\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FD}_{0},\\ {\mathcal{O}}_{\mathbb{P}_{x}^{1}}(-1)\quad & \text{if}~\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D70E}^{-1}\circ \unicode[STIX]{x1D6FD}_{0},\\ {\mathcal{O}}_{\mathbb{P}_{x}^{1}}\quad & \text{otherwise}.\end{array}\right.\end{eqnarray}$$
Proof. This is contained in [Reference Tian and XiaoTX16], but we sketch the proof for the convenience of the reader. The construction of the isomorphism between
![]() $Z_{\{\unicode[STIX]{x1D6FD}_{0}\}}$
and the
$Z_{\{\unicode[STIX]{x1D6FD}_{0}\}}$
and the
![]() $\mathbb{P}^{1}$
-bundle over
$\mathbb{P}^{1}$
-bundle over
![]() $X_{K}^{B}$
is given in [Reference Tian and XiaoTX16, §§5.11–5.24]. It is first shown that the connected components of Hilbert modular varieties and quaternionic Shimura varieties are naturally isomorphic with connected components of certain unitary Shimura varieties (respecting the Goren–Oort stratifications). Hence, it is enough to prove the above statement over appropriate unitary Shimura varieties. For the rest of this proof, we use notation directly from [Reference Tian and XiaoTX16]. To be more precise, it is enough to prove the statement with
$X_{K}^{B}$
is given in [Reference Tian and XiaoTX16, §§5.11–5.24]. It is first shown that the connected components of Hilbert modular varieties and quaternionic Shimura varieties are naturally isomorphic with connected components of certain unitary Shimura varieties (respecting the Goren–Oort stratifications). Hence, it is enough to prove the above statement over appropriate unitary Shimura varieties. For the rest of this proof, we use notation directly from [Reference Tian and XiaoTX16]. To be more precise, it is enough to prove the statement with
![]() $Z_{\{\unicode[STIX]{x1D6FD}_{0}\}}\subset \overline{X}$
replaced with
$Z_{\{\unicode[STIX]{x1D6FD}_{0}\}}\subset \overline{X}$
replaced with
![]() $\text{Sh}_{K^{\prime }}(G_{\emptyset }^{\prime })_{k_{0},\{\tilde{\unicode[STIX]{x1D6FD}}_{0}\}}\subset \text{Sh}_{K^{\prime }}(G_{\emptyset }^{\prime })_{k_{0}}$
,
$\text{Sh}_{K^{\prime }}(G_{\emptyset }^{\prime })_{k_{0},\{\tilde{\unicode[STIX]{x1D6FD}}_{0}\}}\subset \text{Sh}_{K^{\prime }}(G_{\emptyset }^{\prime })_{k_{0}}$
,
![]() $X_{K}^{B}$
replaced with
$X_{K}^{B}$
replaced with
![]() $\text{Sh}_{K^{\prime }}(G_{\{\unicode[STIX]{x1D70E}^{-1}\circ \tilde{\unicode[STIX]{x1D6FD}}_{0},\tilde{\unicode[STIX]{x1D6FD}}_{0}\}}^{\prime })_{k_{0}}$
, and
$\text{Sh}_{K^{\prime }}(G_{\{\unicode[STIX]{x1D70E}^{-1}\circ \tilde{\unicode[STIX]{x1D6FD}}_{0},\tilde{\unicode[STIX]{x1D6FD}}_{0}\}}^{\prime })_{k_{0}}$
, and
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FD}}$
replaced by
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FD}}$
replaced by
![]() $\unicode[STIX]{x1D714}_{\mathbf{A}^{\vee }/S,\tilde{\unicode[STIX]{x1D6FD}}}^{\circ }$
. The fibre of the
$\unicode[STIX]{x1D714}_{\mathbf{A}^{\vee }/S,\tilde{\unicode[STIX]{x1D6FD}}}^{\circ }$
. The fibre of the
![]() $\mathbb{P}^{1}$
-bundle over
$\mathbb{P}^{1}$
-bundle over
![]() $\text{Sh}_{K^{\prime }}(G_{\{\unicode[STIX]{x1D70E}^{-1}\circ \tilde{\unicode[STIX]{x1D6FD}}_{0},\tilde{\unicode[STIX]{x1D6FD}}_{0}\}}^{\prime })_{k_{0}}$
at a point
$\text{Sh}_{K^{\prime }}(G_{\{\unicode[STIX]{x1D70E}^{-1}\circ \tilde{\unicode[STIX]{x1D6FD}}_{0},\tilde{\unicode[STIX]{x1D6FD}}_{0}\}}^{\prime })_{k_{0}}$
at a point
![]() $\text{}\underline{B}/S$
on
$\text{}\underline{B}/S$
on
![]() $\text{Sh}_{K^{\prime }}(G_{\{\unicode[STIX]{x1D70E}^{-1}\circ \tilde{\unicode[STIX]{x1D6FD}}_{0},\tilde{\unicode[STIX]{x1D6FD}}_{0}\}}^{\prime })_{k_{0}}$
(where
$\text{Sh}_{K^{\prime }}(G_{\{\unicode[STIX]{x1D70E}^{-1}\circ \tilde{\unicode[STIX]{x1D6FD}}_{0},\tilde{\unicode[STIX]{x1D6FD}}_{0}\}}^{\prime })_{k_{0}}$
(where
![]() $\text{}\underline{B}$
denotes an abelian scheme
$\text{}\underline{B}$
denotes an abelian scheme
![]() $B/S$
with PEL structure) is the projectivization of
$B/S$
with PEL structure) is the projectivization of
![]() $H_{1}^{\text{dR}}(B/S)_{\unicode[STIX]{x1D70E}^{-1}\circ \tilde{\unicode[STIX]{x1D6FD}}_{0}}^{\circ }$
. In [Reference Tian and XiaoTX16, § 5.15], for any point
$H_{1}^{\text{dR}}(B/S)_{\unicode[STIX]{x1D70E}^{-1}\circ \tilde{\unicode[STIX]{x1D6FD}}_{0}}^{\circ }$
. In [Reference Tian and XiaoTX16, § 5.15], for any point
![]() $\text{}\underline{A}/S$
on
$\text{}\underline{A}/S$
on
![]() $\text{Sh}_{K^{\prime }}(G_{\emptyset }^{\prime })_{k_{0},\{\tilde{\unicode[STIX]{x1D6FD}}_{0}\}}$
, abelian schemes
$\text{Sh}_{K^{\prime }}(G_{\emptyset }^{\prime })_{k_{0},\{\tilde{\unicode[STIX]{x1D6FD}}_{0}\}}$
, abelian schemes
![]() $\text{}\underline{C}$
and
$\text{}\underline{C}$
and
![]() $\text{}\underline{B}$
along with isogenies
$\text{}\underline{B}$
along with isogenies
![]() $\unicode[STIX]{x1D719}_{A}:A\rightarrow C$
, and
$\unicode[STIX]{x1D719}_{A}:A\rightarrow C$
, and
![]() $\unicode[STIX]{x1D719}_{B}:B\rightarrow C$
are constructed such that
$\unicode[STIX]{x1D719}_{B}:B\rightarrow C$
are constructed such that
![]() $\text{}\underline{B}/S$
is a point on
$\text{}\underline{B}/S$
is a point on
![]() $\text{Sh}_{K^{\prime }}(G_{\{\unicode[STIX]{x1D70E}^{-1}\circ \tilde{\unicode[STIX]{x1D6FD}}_{0},\tilde{\unicode[STIX]{x1D6FD}}_{0}\}}^{\prime })_{k_{0}}$
. This data satisfies several properties including that
$\text{Sh}_{K^{\prime }}(G_{\{\unicode[STIX]{x1D70E}^{-1}\circ \tilde{\unicode[STIX]{x1D6FD}}_{0},\tilde{\unicode[STIX]{x1D6FD}}_{0}\}}^{\prime })_{k_{0}}$
. This data satisfies several properties including that
![]() $\unicode[STIX]{x1D719}_{A,\ast ,\unicode[STIX]{x1D70E}^{-1}\circ \tilde{\unicode[STIX]{x1D6FD}}_{0}}$
and
$\unicode[STIX]{x1D719}_{A,\ast ,\unicode[STIX]{x1D70E}^{-1}\circ \tilde{\unicode[STIX]{x1D6FD}}_{0}}$
and
![]() $\unicode[STIX]{x1D719}_{B,\ast ,\unicode[STIX]{x1D70E}^{-1}\circ \tilde{\unicode[STIX]{x1D6FD}}_{0}}$
are isomorphisms. The isomorphism between
$\unicode[STIX]{x1D719}_{B,\ast ,\unicode[STIX]{x1D70E}^{-1}\circ \tilde{\unicode[STIX]{x1D6FD}}_{0}}$
are isomorphisms. The isomorphism between
![]() $\text{Sh}_{K^{\prime }}(G_{\emptyset }^{\prime })_{k_{0},\{\tilde{\unicode[STIX]{x1D6FD}}_{0}\}}$
and the
$\text{Sh}_{K^{\prime }}(G_{\emptyset }^{\prime })_{k_{0},\{\tilde{\unicode[STIX]{x1D6FD}}_{0}\}}$
and the
![]() $\mathbb{P}^{1}$
-bundle over
$\mathbb{P}^{1}$
-bundle over
![]() $\text{Sh}_{K^{\prime }}(G_{\{\unicode[STIX]{x1D70E}^{-1}\circ \tilde{\unicode[STIX]{x1D6FD}}_{0},\tilde{\unicode[STIX]{x1D6FD}}_{0}\}}^{\prime })_{k_{0}}$
sends
$\text{Sh}_{K^{\prime }}(G_{\{\unicode[STIX]{x1D70E}^{-1}\circ \tilde{\unicode[STIX]{x1D6FD}}_{0},\tilde{\unicode[STIX]{x1D6FD}}_{0}\}}^{\prime })_{k_{0}}$
sends
![]() $\text{}\underline{A}/S$
to
$\text{}\underline{A}/S$
to
![]() $(\text{}\underline{B},J)$
, where
$(\text{}\underline{B},J)$
, where
![]() $J$
is the line in
$J$
is the line in
![]() $H_{1}^{\text{dR}}(B/S)_{\unicode[STIX]{x1D70E}^{-1}\circ \tilde{\unicode[STIX]{x1D6FD}}_{0}}^{\circ }$
given by
$H_{1}^{\text{dR}}(B/S)_{\unicode[STIX]{x1D70E}^{-1}\circ \tilde{\unicode[STIX]{x1D6FD}}_{0}}^{\circ }$
given by
![]() $J=\unicode[STIX]{x1D719}_{B,\ast ,\unicode[STIX]{x1D70E}^{-1}\circ \tilde{\unicode[STIX]{x1D6FD}}_{0}}^{-1}\unicode[STIX]{x1D719}_{A,\ast ,\unicode[STIX]{x1D70E}^{-1}\circ \tilde{\unicode[STIX]{x1D6FD}}_{0}}(\unicode[STIX]{x1D714}_{A^{\vee }/S,\unicode[STIX]{x1D70E}^{-1}\circ \tilde{\unicode[STIX]{x1D6FD}_{0}}}^{\circ })$
. This immediately implies that the restriction of
$J=\unicode[STIX]{x1D719}_{B,\ast ,\unicode[STIX]{x1D70E}^{-1}\circ \tilde{\unicode[STIX]{x1D6FD}}_{0}}^{-1}\unicode[STIX]{x1D719}_{A,\ast ,\unicode[STIX]{x1D70E}^{-1}\circ \tilde{\unicode[STIX]{x1D6FD}}_{0}}(\unicode[STIX]{x1D714}_{A^{\vee }/S,\unicode[STIX]{x1D70E}^{-1}\circ \tilde{\unicode[STIX]{x1D6FD}_{0}}}^{\circ })$
. This immediately implies that the restriction of
![]() $\unicode[STIX]{x1D714}_{A^{\vee }/S,\unicode[STIX]{x1D70E}^{-1}\circ \tilde{\unicode[STIX]{x1D6FD}_{0}}}^{\circ }$
to each fibre of the
$\unicode[STIX]{x1D714}_{A^{\vee }/S,\unicode[STIX]{x1D70E}^{-1}\circ \tilde{\unicode[STIX]{x1D6FD}_{0}}}^{\circ }$
to each fibre of the
![]() $\mathbb{P}^{1}$
-bundle is isomorphic to
$\mathbb{P}^{1}$
-bundle is isomorphic to
![]() ${\mathcal{O}}(-1)$
on
${\mathcal{O}}(-1)$
on
![]() $\mathbb{P}^{1}$
. Applying Lemma 4.3, it follows that the restriction of
$\mathbb{P}^{1}$
. Applying Lemma 4.3, it follows that the restriction of
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FD}_{0}}$
to each fibre of the corresponding
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FD}_{0}}$
to each fibre of the corresponding
![]() $\mathbb{P}^{1}$
-bundle is isomorphic to
$\mathbb{P}^{1}$
-bundle is isomorphic to
![]() ${\mathcal{O}}(p)$
.
${\mathcal{O}}(p)$
.
To prove the statement for
![]() $\unicode[STIX]{x1D6FD}\not \in \{\unicode[STIX]{x1D70E}^{-1}\circ \unicode[STIX]{x1D6FD}_{0},\unicode[STIX]{x1D6FD}_{0}\}$
, it is enough to note that, by construction (see [Reference Tian and XiaoTX16, proof of Lemma 5.18]),
$\unicode[STIX]{x1D6FD}\not \in \{\unicode[STIX]{x1D70E}^{-1}\circ \unicode[STIX]{x1D6FD}_{0},\unicode[STIX]{x1D6FD}_{0}\}$
, it is enough to note that, by construction (see [Reference Tian and XiaoTX16, proof of Lemma 5.18]),
![]() $H_{1}^{\text{dR}}(B/S)_{\tilde{\unicode[STIX]{x1D6FD}}}^{\circ }$
is canonically isomorphic to
$H_{1}^{\text{dR}}(B/S)_{\tilde{\unicode[STIX]{x1D6FD}}}^{\circ }$
is canonically isomorphic to
![]() $H_{1}^{\text{dR}}(A/S)_{\tilde{\unicode[STIX]{x1D6FD}}}^{\circ }$
since
$H_{1}^{\text{dR}}(A/S)_{\tilde{\unicode[STIX]{x1D6FD}}}^{\circ }$
since
![]() $\tilde{\unicode[STIX]{x1D6FD}}\not \in \tilde{\unicode[STIX]{x1D6E5}}(\{\unicode[STIX]{x1D6FD}_{0}\})^{+}\cup \tilde{\unicode[STIX]{x1D6E5}}(\{\unicode[STIX]{x1D6FD}_{0}\})^{-}=\{\tilde{\unicode[STIX]{x1D6FD}_{0}},\tilde{\unicode[STIX]{x1D6FD}_{0}}^{c}\}$
. This shows that
$\tilde{\unicode[STIX]{x1D6FD}}\not \in \tilde{\unicode[STIX]{x1D6E5}}(\{\unicode[STIX]{x1D6FD}_{0}\})^{+}\cup \tilde{\unicode[STIX]{x1D6E5}}(\{\unicode[STIX]{x1D6FD}_{0}\})^{-}=\{\tilde{\unicode[STIX]{x1D6FD}_{0}},\tilde{\unicode[STIX]{x1D6FD}_{0}}^{c}\}$
. This shows that
![]() $\unicode[STIX]{x1D714}_{A^{\vee }/S,\tilde{\unicode[STIX]{x1D6FD}}}^{\circ }$
depends canonically on
$\unicode[STIX]{x1D714}_{A^{\vee }/S,\tilde{\unicode[STIX]{x1D6FD}}}^{\circ }$
depends canonically on
![]() $\text{}\underline{B}$
, that is, the isomorphic image of
$\text{}\underline{B}$
, that is, the isomorphic image of
![]() $\unicode[STIX]{x1D714}_{\mathbf{A}^{\vee }/S,\tilde{\unicode[STIX]{x1D6FD}}}^{\circ }$
on the
$\unicode[STIX]{x1D714}_{\mathbf{A}^{\vee }/S,\tilde{\unicode[STIX]{x1D6FD}}}^{\circ }$
on the
![]() $\mathbb{P}^{1}$
-bundle is a pullback from the base, and hence has trivial fibres.◻
$\mathbb{P}^{1}$
-bundle is a pullback from the base, and hence has trivial fibres.◻
5 The main theorem
In this section, we prove our main theorem and discuss some of its consequences.
Theorem 5.1. Suppose that
![]() $\mathbf{k}=\sum k_{\unicode[STIX]{x1D6FD}}\mathbf{e}_{\unicode[STIX]{x1D6FD}}\in \mathbb{Z}^{\mathbb{B}}$
, and that
$\mathbf{k}=\sum k_{\unicode[STIX]{x1D6FD}}\mathbf{e}_{\unicode[STIX]{x1D6FD}}\in \mathbb{Z}^{\mathbb{B}}$
, and that
![]() $\unicode[STIX]{x1D6FD}_{0}\in \mathbb{B}$
is such that
$\unicode[STIX]{x1D6FD}_{0}\in \mathbb{B}$
is such that
![]() $pk_{\unicode[STIX]{x1D6FD}_{0}}<k_{\unicode[STIX]{x1D70E}^{-1}\circ \unicode[STIX]{x1D6FD}_{0}}$
for some
$pk_{\unicode[STIX]{x1D6FD}_{0}}<k_{\unicode[STIX]{x1D70E}^{-1}\circ \unicode[STIX]{x1D6FD}_{0}}$
for some
![]() $\unicode[STIX]{x1D6FD}_{0}\in \mathbb{B}$
. Then, multiplication by the partial Hasse invariant
$\unicode[STIX]{x1D6FD}_{0}\in \mathbb{B}$
. Then, multiplication by the partial Hasse invariant
![]() $H_{\unicode[STIX]{x1D6FD}_{0}}^{\mathfrak{I}}$
induces an isomorphism:
$H_{\unicode[STIX]{x1D6FD}_{0}}^{\mathfrak{I}}$
induces an isomorphism:
If
![]() $f_{\mathfrak{p}}=1$
, then a stronger result holds: we have
$f_{\mathfrak{p}}=1$
, then a stronger result holds: we have
![]() $M_{\mathbf{k}}^{\mathfrak{I}}(\mathfrak{n},\overline{\mathbb{F}}_{p})=0$
for all
$M_{\mathbf{k}}^{\mathfrak{I}}(\mathfrak{n},\overline{\mathbb{F}}_{p})=0$
for all
![]() $\mathbf{k}$
for which
$\mathbf{k}$
for which
![]() $k_{\unicode[STIX]{x1D6FD}_{0}}<0$
.
$k_{\unicode[STIX]{x1D6FD}_{0}}<0$
.
Proof. Let
![]() $\mathfrak{p}$
be a prime ideal of
$\mathfrak{p}$
be a prime ideal of
![]() ${\mathcal{O}}_{F}$
such that
${\mathcal{O}}_{F}$
such that
![]() $\unicode[STIX]{x1D6FD}_{0}\in \mathbb{B}_{\mathfrak{p}}$
. We distinguish two cases.
$\unicode[STIX]{x1D6FD}_{0}\in \mathbb{B}_{\mathfrak{p}}$
. We distinguish two cases.
Case 1:
![]() $f_{\mathfrak{p}}>1$
. Consider the short exact sequence
$f_{\mathfrak{p}}>1$
. Consider the short exact sequence
of sheaves on
![]() $\overline{X}$
, where the first map is multiplication by
$\overline{X}$
, where the first map is multiplication by
![]() $H_{\unicode[STIX]{x1D6FD}_{0}}^{\mathfrak{I}}$
. To prove the result, it is enough to show that
$H_{\unicode[STIX]{x1D6FD}_{0}}^{\mathfrak{I}}$
. To prove the result, it is enough to show that
![]() $H^{0}(\overline{X},{\mathcal{F}})$
vanishes. Clearly,
$H^{0}(\overline{X},{\mathcal{F}})$
vanishes. Clearly,
![]() ${\mathcal{F}}$
is supported on the vanishing locus of
${\mathcal{F}}$
is supported on the vanishing locus of
![]() $H_{\unicode[STIX]{x1D6FD}_{0}}^{\mathfrak{I}}$
, i.e.
$H_{\unicode[STIX]{x1D6FD}_{0}}^{\mathfrak{I}}$
, i.e.
![]() $Z_{\{\unicode[STIX]{x1D6FD}_{0}\}}$
, and we have
$Z_{\{\unicode[STIX]{x1D6FD}_{0}\}}$
, and we have
![]() $H^{0}(\overline{X},{\mathcal{F}})=H^{0}(Z_{\{\unicode[STIX]{x1D6FD}_{0}\}},\unicode[STIX]{x1D714}^{\mathbf{k}})$
. We show that the latter vanishes.
$H^{0}(\overline{X},{\mathcal{F}})=H^{0}(Z_{\{\unicode[STIX]{x1D6FD}_{0}\}},\unicode[STIX]{x1D714}^{\mathbf{k}})$
. We show that the latter vanishes.
By Theorem 4.2, the closed Goren–Oort stratum
![]() $Z_{\{\unicode[STIX]{x1D6FD}_{0}\}}$
is isomorphic to a
$Z_{\{\unicode[STIX]{x1D6FD}_{0}\}}$
is isomorphic to a
![]() $\mathbb{P}^{1}$
-bundle over a quaternionic Shimura variety
$\mathbb{P}^{1}$
-bundle over a quaternionic Shimura variety
![]() $X_{K}^{B}$
. Let
$X_{K}^{B}$
. Let
![]() $s\in H^{0}(Z_{\{\unicode[STIX]{x1D6FD}_{0}\}},\unicode[STIX]{x1D714}^{\mathbf{k}})$
. Let
$s\in H^{0}(Z_{\{\unicode[STIX]{x1D6FD}_{0}\}},\unicode[STIX]{x1D714}^{\mathbf{k}})$
. Let
![]() $x$
be a geometric point of
$x$
be a geometric point of
![]() $X_{K}^{B}$
, and denote by
$X_{K}^{B}$
, and denote by
![]() $\mathbb{P}_{x}^{1}$
the corresponding fibre of the
$\mathbb{P}_{x}^{1}$
the corresponding fibre of the
![]() $\mathbb{P}^{1}$
-bundle. By Lemma 4.4, we have
$\mathbb{P}^{1}$
-bundle. By Lemma 4.4, we have
By assumption
![]() $pk_{\unicode[STIX]{x1D6FD}_{0}}-k_{\unicode[STIX]{x1D70E}^{-1}\circ \unicode[STIX]{x1D6FD}_{0}}<0$
, so it follows that
$pk_{\unicode[STIX]{x1D6FD}_{0}}-k_{\unicode[STIX]{x1D70E}^{-1}\circ \unicode[STIX]{x1D6FD}_{0}}<0$
, so it follows that
![]() $H^{0}(\mathbb{P}_{x}^{1},\unicode[STIX]{x1D714}^{\mathbf{k}}|_{\mathbb{P}_{x}^{1}})=0$
. This shows that
$H^{0}(\mathbb{P}_{x}^{1},\unicode[STIX]{x1D714}^{\mathbf{k}}|_{\mathbb{P}_{x}^{1}})=0$
. This shows that
![]() $s|_{\mathbb{P}_{x}^{1}}=0$
for all geometric points
$s|_{\mathbb{P}_{x}^{1}}=0$
for all geometric points
![]() $x$
of
$x$
of
![]() $X_{K}^{B}$
. Hence,
$X_{K}^{B}$
. Hence,
![]() $s=0$
as claimed.
$s=0$
as claimed.
Case 2:
![]() $f_{\mathfrak{p}}=1$
. Here the assumption becomes
$f_{\mathfrak{p}}=1$
. Here the assumption becomes
![]() $k_{\unicode[STIX]{x1D6FD}_{0}}<0$
. We prove the stronger assertion that
$k_{\unicode[STIX]{x1D6FD}_{0}}<0$
. We prove the stronger assertion that
if
![]() $k_{\unicode[STIX]{x1D6FD}_{0}}<0$
. This will imply
$k_{\unicode[STIX]{x1D6FD}_{0}}<0$
. This will imply
![]() $M_{\mathbf{k}-\mathbf{h}_{\unicode[STIX]{x1D6FD}_{0}}}^{\mathfrak{I}}(\mathfrak{n},\overline{\mathbb{F}}_{p})=M_{\mathbf{k}}^{\mathfrak{I}}(\mathfrak{n},\overline{\mathbb{F}}_{p})=0$
.
$M_{\mathbf{k}-\mathbf{h}_{\unicode[STIX]{x1D6FD}_{0}}}^{\mathfrak{I}}(\mathfrak{n},\overline{\mathbb{F}}_{p})=M_{\mathbf{k}}^{\mathfrak{I}}(\mathfrak{n},\overline{\mathbb{F}}_{p})=0$
.
Write
![]() $\mathbb{B}=\{\unicode[STIX]{x1D6FD}_{0},\unicode[STIX]{x1D6FD}_{1},\ldots ,\unicode[STIX]{x1D6FD}_{d-1}\}$
, and, for
$\mathbb{B}=\{\unicode[STIX]{x1D6FD}_{0},\unicode[STIX]{x1D6FD}_{1},\ldots ,\unicode[STIX]{x1D6FD}_{d-1}\}$
, and, for
![]() $0\leqslant i\leqslant d-1$
, let
$0\leqslant i\leqslant d-1$
, let
![]() $T_{i}:=\mathbb{B}-\{\unicode[STIX]{x1D6FD}_{0},\ldots ,\unicode[STIX]{x1D6FD}_{i}\}$
. We prove by induction on
$T_{i}:=\mathbb{B}-\{\unicode[STIX]{x1D6FD}_{0},\ldots ,\unicode[STIX]{x1D6FD}_{i}\}$
. We prove by induction on
![]() $i$
that
$i$
that
for all
![]() $0\leqslant i\leqslant d-1$
.
$0\leqslant i\leqslant d-1$
.
We first prove the result for
![]() $i=0$
. By properties of the Goren–Oort stratification recalled in § 4, the closed stratum
$i=0$
. By properties of the Goren–Oort stratification recalled in § 4, the closed stratum
![]() $Z_{T_{0}}$
is equi-dimensional of dimension 1. Let
$Z_{T_{0}}$
is equi-dimensional of dimension 1. Let
![]() $W$
be an arbitrary connected component of
$W$
be an arbitrary connected component of
![]() $Z_{T_{0}}$
. By Lemma 4.1,
$Z_{T_{0}}$
. By Lemma 4.1,
![]() $W$
has a superspecial point on it. In particular,
$W$
has a superspecial point on it. In particular,
![]() $H_{\unicode[STIX]{x1D6FD}_{0}}^{\mathfrak{I}}$
has a non-empty vanishing locus on
$H_{\unicode[STIX]{x1D6FD}_{0}}^{\mathfrak{I}}$
has a non-empty vanishing locus on
![]() $W$
. This implies that
$W$
. This implies that
![]() $\deg (\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FD}_{0}}|_{W})>0$
on every connected component
$\deg (\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FD}_{0}}|_{W})>0$
on every connected component
![]() $W$
of
$W$
of
![]() $Z_{T_{0}}$
. By the second statement in Lemma 4.3, we find that for all
$Z_{T_{0}}$
. By the second statement in Lemma 4.3, we find that for all
![]() $1\leqslant i\leqslant d-1$
, the line bundle
$1\leqslant i\leqslant d-1$
, the line bundle
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FD}_{i}}$
restricts to a torsion line bundle on
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FD}_{i}}$
restricts to a torsion line bundle on
![]() $Z_{T_{0}}$
. Hence, on every connected component
$Z_{T_{0}}$
. Hence, on every connected component
![]() $W$
of
$W$
of
![]() $Z_{T_{0}}$
we have
$Z_{T_{0}}$
we have
Since every such connected component is projective, this proves that
![]() $H^{0}(Z_{T_{0}},\unicode[STIX]{x1D714}^{\mathbf{k}})=0$
.
$H^{0}(Z_{T_{0}},\unicode[STIX]{x1D714}^{\mathbf{k}})=0$
.
Now we prove the induction step. Assume that
![]() $1\leqslant i\leqslant d-1$
, and that the result holds for
$1\leqslant i\leqslant d-1$
, and that the result holds for
![]() $i-1$
. We prove that it holds also for
$i-1$
. We prove that it holds also for
![]() $i$
. Consider the short exact sequence
$i$
. Consider the short exact sequence
of sheaves on
![]() $Z_{T_{i}}$
, where the first map is multiplication by
$Z_{T_{i}}$
, where the first map is multiplication by
![]() $H_{\unicode[STIX]{x1D6FD}_{i}}^{\mathfrak{I}}|_{Z_{T_{i}}}$
. The sheaf
$H_{\unicode[STIX]{x1D6FD}_{i}}^{\mathfrak{I}}|_{Z_{T_{i}}}$
. The sheaf
![]() ${\mathcal{F}}$
is supported on the vanishing locus of
${\mathcal{F}}$
is supported on the vanishing locus of
![]() $H_{\unicode[STIX]{x1D6FD}_{i}}^{\mathfrak{I}}$
on
$H_{\unicode[STIX]{x1D6FD}_{i}}^{\mathfrak{I}}$
on
![]() $Z_{T_{i}}$
, which is
$Z_{T_{i}}$
, which is
![]() $Z_{T_{i-1}}$
, and we have
$Z_{T_{i-1}}$
, and we have
![]() $H^{0}(Z_{T_{i}},{\mathcal{F}})=H^{0}(Z_{T_{i-1}},\unicode[STIX]{x1D714}^{\mathbf{k}})=0$
, by the induction assumption. This shows that multiplication by
$H^{0}(Z_{T_{i}},{\mathcal{F}})=H^{0}(Z_{T_{i-1}},\unicode[STIX]{x1D714}^{\mathbf{k}})=0$
, by the induction assumption. This shows that multiplication by
![]() $H_{\unicode[STIX]{x1D6FD}_{i}}^{\mathfrak{I}}|_{Z_{T_{i}}}$
induces an isomorphism
$H_{\unicode[STIX]{x1D6FD}_{i}}^{\mathfrak{I}}|_{Z_{T_{i}}}$
induces an isomorphism
Since the
![]() $\unicode[STIX]{x1D6FD}_{0}$
-component of
$\unicode[STIX]{x1D6FD}_{0}$
-component of
![]() $\mathbf{k}-\mathbf{h}_{\unicode[STIX]{x1D6FD}_{i}}$
is negative, we can repeat the argument any number of times and deduce that for all
$\mathbf{k}-\mathbf{h}_{\unicode[STIX]{x1D6FD}_{i}}$
is negative, we can repeat the argument any number of times and deduce that for all
![]() $N>0$
, multiplication by
$N>0$
, multiplication by
![]() $(H_{\unicode[STIX]{x1D6FD}_{i}}^{\mathfrak{I}})^{N}|_{Z_{T_{i}}}$
induces an isomorphism
$(H_{\unicode[STIX]{x1D6FD}_{i}}^{\mathfrak{I}})^{N}|_{Z_{T_{i}}}$
induces an isomorphism
By Lemma 4.1,
![]() $H_{\unicode[STIX]{x1D6FD}_{i}}^{\mathfrak{I}}$
has a non-empty vanishing locus on any connected component of
$H_{\unicode[STIX]{x1D6FD}_{i}}^{\mathfrak{I}}$
has a non-empty vanishing locus on any connected component of
![]() $Z_{T_{i}}$
. This, along with the fact that every connected component of
$Z_{T_{i}}$
. This, along with the fact that every connected component of
![]() $Z_{T_{i}}$
is irreducible, implies that any non-zero section of
$Z_{T_{i}}$
is irreducible, implies that any non-zero section of
![]() $\unicode[STIX]{x1D714}^{\mathbf{k}}$
on
$\unicode[STIX]{x1D714}^{\mathbf{k}}$
on
![]() $Z_{T_{i}}$
is divisible by at most a finite power of
$Z_{T_{i}}$
is divisible by at most a finite power of
![]() $H_{\unicode[STIX]{x1D6FD}_{i}}^{\mathfrak{I}}|_{Z_{T_{i}}}$
. We therefore conclude that
$H_{\unicode[STIX]{x1D6FD}_{i}}^{\mathfrak{I}}|_{Z_{T_{i}}}$
. We therefore conclude that
![]() $H^{0}(Z_{T_{i}},\unicode[STIX]{x1D714}^{\mathbf{k}})=0$
. This completes the proof by induction. In particular, for
$H^{0}(Z_{T_{i}},\unicode[STIX]{x1D714}^{\mathbf{k}})=0$
. This completes the proof by induction. In particular, for
![]() $i=d-1$
, we obtain
$i=d-1$
, we obtain
This ends the proof of our main theorem. ◻
We note the following geometric interpretation of Theorem 5.1: if
![]() $\mathbf{k}\!=\!\sum k_{\unicode[STIX]{x1D6FD}}\mathbf{e}_{\unicode[STIX]{x1D6FD}}\in \mathbb{Z}^{\mathbb{B}}$
is such that
$\mathbf{k}\!=\!\sum k_{\unicode[STIX]{x1D6FD}}\mathbf{e}_{\unicode[STIX]{x1D6FD}}\in \mathbb{Z}^{\mathbb{B}}$
is such that
![]() $pk_{\unicode[STIX]{x1D6FD}_{0}}<k_{\unicode[STIX]{x1D70E}^{-1}\circ \unicode[STIX]{x1D6FD}_{0}}$
, then every Hilbert modular form of weight
$pk_{\unicode[STIX]{x1D6FD}_{0}}<k_{\unicode[STIX]{x1D70E}^{-1}\circ \unicode[STIX]{x1D6FD}_{0}}$
, then every Hilbert modular form of weight
![]() $\mathbf{k}$
vanishes on
$\mathbf{k}$
vanishes on
![]() $Z_{\{\unicode[STIX]{x1D6FD}_{0}\}}$
.
$Z_{\{\unicode[STIX]{x1D6FD}_{0}\}}$
.
We now prove some interesting consequences of Theorem 5.1. First, we define three cones in
![]() $\mathbb{Q}^{\mathbb{B}}$
.
$\mathbb{Q}^{\mathbb{B}}$
.
Definition 5.2. We define the minimal, standard and Hasse cones as follows:
 $$\begin{eqnarray}\displaystyle C^{\text{min}} & = & \displaystyle \biggl\{\mathop{\sum }_{\unicode[STIX]{x1D6FD}}x_{\unicode[STIX]{x1D6FD}}\mathbf{e}_{\unicode[STIX]{x1D6FD}}\in \mathbb{Q}^{\mathbb{B}}\,\biggr|\,px_{\unicode[STIX]{x1D6FD}}\geqslant x_{\unicode[STIX]{x1D70E}^{-1}\circ \unicode[STIX]{x1D6FD}}~\text{for all}~\unicode[STIX]{x1D6FD}\in \mathbb{B}\biggr\},\nonumber\\ \displaystyle C^{\text{st}} & = & \displaystyle \biggl\{\mathop{\sum }_{\unicode[STIX]{x1D6FD}}x_{\unicode[STIX]{x1D6FD}}\mathbf{e}_{\unicode[STIX]{x1D6FD}}\in \mathbb{Q}^{\mathbb{B}}\,\biggr|\,x_{\unicode[STIX]{x1D6FD}}\geqslant 0~\text{for all}~\unicode[STIX]{x1D6FD}\in \mathbb{B}\biggr\},\nonumber\\ \displaystyle C^{\text{Hasse}} & = & \displaystyle \biggl\{\mathop{\sum }_{\unicode[STIX]{x1D6FD}}y_{\unicode[STIX]{x1D6FD}}\mathbf{h}_{\unicode[STIX]{x1D6FD}}\in \mathbb{Q}^{\mathbb{B}}\,\biggr|\,y_{\unicode[STIX]{x1D6FD}}\geqslant 0~\text{for all}~\unicode[STIX]{x1D6FD}\in \mathbb{B}\biggr\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle C^{\text{min}} & = & \displaystyle \biggl\{\mathop{\sum }_{\unicode[STIX]{x1D6FD}}x_{\unicode[STIX]{x1D6FD}}\mathbf{e}_{\unicode[STIX]{x1D6FD}}\in \mathbb{Q}^{\mathbb{B}}\,\biggr|\,px_{\unicode[STIX]{x1D6FD}}\geqslant x_{\unicode[STIX]{x1D70E}^{-1}\circ \unicode[STIX]{x1D6FD}}~\text{for all}~\unicode[STIX]{x1D6FD}\in \mathbb{B}\biggr\},\nonumber\\ \displaystyle C^{\text{st}} & = & \displaystyle \biggl\{\mathop{\sum }_{\unicode[STIX]{x1D6FD}}x_{\unicode[STIX]{x1D6FD}}\mathbf{e}_{\unicode[STIX]{x1D6FD}}\in \mathbb{Q}^{\mathbb{B}}\,\biggr|\,x_{\unicode[STIX]{x1D6FD}}\geqslant 0~\text{for all}~\unicode[STIX]{x1D6FD}\in \mathbb{B}\biggr\},\nonumber\\ \displaystyle C^{\text{Hasse}} & = & \displaystyle \biggl\{\mathop{\sum }_{\unicode[STIX]{x1D6FD}}y_{\unicode[STIX]{x1D6FD}}\mathbf{h}_{\unicode[STIX]{x1D6FD}}\in \mathbb{Q}^{\mathbb{B}}\,\biggr|\,y_{\unicode[STIX]{x1D6FD}}\geqslant 0~\text{for all}~\unicode[STIX]{x1D6FD}\in \mathbb{B}\biggr\}.\nonumber\end{eqnarray}$$
It is easily seen that we always have containments
each of which is an equality if and only if
![]() $p$
splits completely in
$p$
splits completely in
![]() $F$
.
$F$
.
In [Reference Andreatta and GorenAG05, Question 15.8], Andreatta and Goren ask the following question. Over the complex numbers, a non-zero Hilbert modular form has weight in
![]() $C^{\text{st}}$
. In characteristic
$C^{\text{st}}$
. In characteristic
![]() $p$
this is no longer true as the example of the partial Hasse invariant shows. Note though that the filtration of a partial Hasse invariant is the trivial character (weight
$p$
this is no longer true as the example of the partial Hasse invariant shows. Note though that the filtration of a partial Hasse invariant is the trivial character (weight
![]() $(0,\ldots ,0)$
) that lies in
$(0,\ldots ,0)$
) that lies in
![]() $C^{\text{st}}$
. We therefore ask: is there an example of a modular form whose filtration is not in
$C^{\text{st}}$
. We therefore ask: is there an example of a modular form whose filtration is not in
![]() $C^{\text{st}}$
? is not in
$C^{\text{st}}$
? is not in
![]() $C^{\text{Hasse}}$
?
$C^{\text{Hasse}}$
?
As a corollary to our main theorem, we can answer that there are no such examples, and in fact the following stronger statement is true.
Corollary 5.3. If
![]() $f$
is a non-zero form in
$f$
is a non-zero form in
![]() $M_{\mathbf{k}}^{\mathfrak{I}}(\mathfrak{n},\overline{\mathbb{F}}_{p})$
for some
$M_{\mathbf{k}}^{\mathfrak{I}}(\mathfrak{n},\overline{\mathbb{F}}_{p})$
for some
![]() $\mathbf{k}\in \mathbb{Z}^{\mathbb{B}}$
, then
$\mathbf{k}\in \mathbb{Z}^{\mathbb{B}}$
, then
![]() $\unicode[STIX]{x1D6F7}(f)\in C^{\text{min}}$
.
$\unicode[STIX]{x1D6F7}(f)\in C^{\text{min}}$
.
Proof. This follows immediately from our main theorem. Let
![]() $\unicode[STIX]{x1D6F7}(f)=\sum _{\unicode[STIX]{x1D6FD}}w_{\unicode[STIX]{x1D6FD}}\mathbf{e}_{\unicode[STIX]{x1D6FD}}$
be the filtration of
$\unicode[STIX]{x1D6F7}(f)=\sum _{\unicode[STIX]{x1D6FD}}w_{\unicode[STIX]{x1D6FD}}\mathbf{e}_{\unicode[STIX]{x1D6FD}}$
be the filtration of
![]() $f$
. Then there are integers
$f$
. Then there are integers
![]() $n_{\unicode[STIX]{x1D6FD}}\geqslant 0$
, and
$n_{\unicode[STIX]{x1D6FD}}\geqslant 0$
, and
![]() $g\in M_{\unicode[STIX]{x1D6F7}(f)}^{\mathfrak{I}}(\mathfrak{n},\overline{\mathbb{F}}_{p})$
, where
$g\in M_{\unicode[STIX]{x1D6F7}(f)}^{\mathfrak{I}}(\mathfrak{n},\overline{\mathbb{F}}_{p})$
, where
and such that
![]() $g$
is not divisible by any partial Hasse invariant
$g$
is not divisible by any partial Hasse invariant
![]() $H_{\unicode[STIX]{x1D6FD}}^{\mathfrak{I}}$
. Hence, by Theorem 5.1, we must have
$H_{\unicode[STIX]{x1D6FD}}^{\mathfrak{I}}$
. Hence, by Theorem 5.1, we must have
![]() $pw_{\unicode[STIX]{x1D6FD}}\geqslant w_{\unicode[STIX]{x1D70E}^{-1}\circ \unicode[STIX]{x1D6FD}}$
for all
$pw_{\unicode[STIX]{x1D6FD}}\geqslant w_{\unicode[STIX]{x1D70E}^{-1}\circ \unicode[STIX]{x1D6FD}}$
for all
![]() $\unicode[STIX]{x1D6FD}\in \mathbb{B}$
, namely,
$\unicode[STIX]{x1D6FD}\in \mathbb{B}$
, namely,
![]() $\unicode[STIX]{x1D6F7}(f)=\sum _{\unicode[STIX]{x1D6FD}}w_{\unicode[STIX]{x1D6FD}}\mathbf{e}_{\unicode[STIX]{x1D6FD}}\in C^{\min }$
.◻
$\unicode[STIX]{x1D6F7}(f)=\sum _{\unicode[STIX]{x1D6FD}}w_{\unicode[STIX]{x1D6FD}}\mathbf{e}_{\unicode[STIX]{x1D6FD}}\in C^{\min }$
.◻
It follows that the phenomenon of negative weights for mod
![]() $p$
Hilbert modular forms is controlled by the weights of partial Hasse invariants. More precisely we deduce the following result, recently independently proven by Goldring and Koskivirta [Reference Goldring and KoskivirtaGK17, Corollary 3.2.4].
$p$
Hilbert modular forms is controlled by the weights of partial Hasse invariants. More precisely we deduce the following result, recently independently proven by Goldring and Koskivirta [Reference Goldring and KoskivirtaGK17, Corollary 3.2.4].
Corollary 5.4. If
![]() $M_{\mathbf{k}}^{\mathfrak{I}}(\mathfrak{n},\overline{\mathbb{F}}_{p})\neq 0$
, then
$M_{\mathbf{k}}^{\mathfrak{I}}(\mathfrak{n},\overline{\mathbb{F}}_{p})\neq 0$
, then
![]() $\mathbf{k}\in C^{\text{Hasse}}$
.
$\mathbf{k}\in C^{\text{Hasse}}$
.
Proof. Assume
![]() $f$
is a non-zero form in
$f$
is a non-zero form in
![]() $M_{\mathbf{k}}^{\mathfrak{I}}(\mathfrak{n},\overline{\mathbb{F}}_{p})$
. By Corollary 5.3, we know that
$M_{\mathbf{k}}^{\mathfrak{I}}(\mathfrak{n},\overline{\mathbb{F}}_{p})$
. By Corollary 5.3, we know that
By definition of filtration, there are non-negative integers
![]() $n_{\unicode[STIX]{x1D6FD}}$
such that
$n_{\unicode[STIX]{x1D6FD}}$
such that
![]() $\mathbf{k}=\unicode[STIX]{x1D6F7}(f)+\sum n_{\unicode[STIX]{x1D6FD}}\mathbf{h}_{\unicode[STIX]{x1D6FD}}$
, which clearly belongs to
$\mathbf{k}=\unicode[STIX]{x1D6F7}(f)+\sum n_{\unicode[STIX]{x1D6FD}}\mathbf{h}_{\unicode[STIX]{x1D6FD}}$
, which clearly belongs to
![]() $C^{\text{Hasse}}$
.◻
$C^{\text{Hasse}}$
.◻
Acknowledgements
We are grateful to Shu Sasaki for conversations on research setting the stage for this paper, to Wushi Goldring for informing us of his work with Koskivirta and Stroh, and to the referee for helpful remarks.