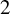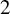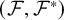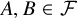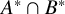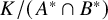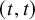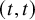1 Introduction
In a seminal paper of 1988 [Reference Frohardt6], Frohardt solved a big part of a famous question of Kantor which asks whether a finite group admitting a Kantor family is a p-group. Such groups are very important since they produce generalized quadrangles (GQs), the central Tits buildings of rank
![]() $2$
. In fact, groups with Kantor families yield the most important tool to construct GQs, and a large literature exists on these objects – see, for instance, [Reference Payne and Thas12, Reference Thas, Thas and Van Maldeghem14, Reference Thas16, Reference Buekenhout3, Reference Tits and Weiss22]. GQs constructed from Kantor families – by a procedure which is explained in Section 2.4 – carry an interesting automorphism group which locally fixes some point linewise, and are called “elation generalized quadrangles” (EGQs). The theory of EGQs was initially devised through the 1970s and 1980s (see [Reference Payne and Thas12, chapters 8–10] and [Reference Thas16]) in order to set up a framework to study automorphisms, and especially Moufang conditions, of GQs from a local point of view, much like translation planes were studied in the theory of projective planes. Together with a deep combinatorial theory, this enabled an almost entirely synthetic-geometric proof of the celebrated results of Fong and Seitz [Reference Fong and Seitz4, Reference Fong and Seitz5] on split BN-pairs of rank
$2$
. In fact, groups with Kantor families yield the most important tool to construct GQs, and a large literature exists on these objects – see, for instance, [Reference Payne and Thas12, Reference Thas, Thas and Van Maldeghem14, Reference Thas16, Reference Buekenhout3, Reference Tits and Weiss22]. GQs constructed from Kantor families – by a procedure which is explained in Section 2.4 – carry an interesting automorphism group which locally fixes some point linewise, and are called “elation generalized quadrangles” (EGQs). The theory of EGQs was initially devised through the 1970s and 1980s (see [Reference Payne and Thas12, chapters 8–10] and [Reference Thas16]) in order to set up a framework to study automorphisms, and especially Moufang conditions, of GQs from a local point of view, much like translation planes were studied in the theory of projective planes. Together with a deep combinatorial theory, this enabled an almost entirely synthetic-geometric proof of the celebrated results of Fong and Seitz [Reference Fong and Seitz4, Reference Fong and Seitz5] on split BN-pairs of rank
![]() $2$
, in the case of type
$2$
, in the case of type
![]() $\texttt {B}_2$
BN-pairs – see [Reference Payne and Thas12, chapters 8 and 9], [Reference Thas, Thas and Van Maldeghem14, chapters 10 and 11] and also the related recent note [Reference Thas18].
$\texttt {B}_2$
BN-pairs – see [Reference Payne and Thas12, chapters 8 and 9], [Reference Thas, Thas and Van Maldeghem14, chapters 10 and 11] and also the related recent note [Reference Thas18].
In [Reference Frohardt6], Frohardt also studied groups K with Kantor families
![]() $(\mathcal {F},\mathcal {F}^*)$
which have distinct members
$(\mathcal {F},\mathcal {F}^*)$
which have distinct members
![]() $A, B \in \mathcal {F}$
such that
$A, B \in \mathcal {F}$
such that
![]() $A^* \cap B^* \leq Z(K)$
(where
$A^* \cap B^* \leq Z(K)$
(where
![]() $Z(K)$
denotes the center of K) and
$Z(K)$
denotes the center of K) and
![]() $K/(A^* \cap B^*)$
is abelian. Such Kantor families are fundamental since almost all examples of Kantor families have this natural property – see, for example, the monograph [Reference Thas16] or Payne’s famous paper [Reference Payne10]. We also refer to Section 2.5 for more background information on this matter. Only a very few classes of finite groups are known which have Kantor families; the most used ones are elementary abelian groups, and Heisenberg groups defined over finite fields in odd characteristic, of dimension
$K/(A^* \cap B^*)$
is abelian. Such Kantor families are fundamental since almost all examples of Kantor families have this natural property – see, for example, the monograph [Reference Thas16] or Payne’s famous paper [Reference Payne10]. We also refer to Section 2.5 for more background information on this matter. Only a very few classes of finite groups are known which have Kantor families; the most used ones are elementary abelian groups, and Heisenberg groups defined over finite fields in odd characteristic, of dimension
![]() $3$
or
$3$
or
![]() $5$
(see, e.g., the monograph [Reference Thas16]). They all satisfy Frohardt’s condition.
$5$
(see, e.g., the monograph [Reference Thas16]). They all satisfy Frohardt’s condition.
Theorem 1.1 (D. Frohardt [Reference Frohardt6], 1988)
Let K be a finite group with a Kantor family
![]() $(\mathcal {F},\mathcal {F}^*)$
having distinct members
$(\mathcal {F},\mathcal {F}^*)$
having distinct members
![]() $A, B \in \mathcal {F}$
such that
$A, B \in \mathcal {F}$
such that
![]() $A^* \cap B^* \leq Z(K)$
and
$A^* \cap B^* \leq Z(K)$
and
![]() $K/(A^* \cap B^*)$
is abelian. Then one of the folowing three cases occurs:
$K/(A^* \cap B^*)$
is abelian. Then one of the folowing three cases occurs:
-
(1)
 $Z(K)$
and the elements of
$Z(K)$
and the elements of
 $\mathcal {F}$
are elementary abelian.
$\mathcal {F}$
are elementary abelian. -
(2)
 $Z(K)$
is an elementary abelian
$Z(K)$
is an elementary abelian
 $2$
-group and the elements of
$2$
-group and the elements of
 $\mathcal {F}$
have exponent
$\mathcal {F}$
have exponent
 $4$
.
$4$
. -
(3)
 $Z(K)$
has exponent
$Z(K)$
has exponent
 $4$
, and the elements of
$4$
, and the elements of
 $\mathcal {F}$
are elementary abelian
$\mathcal {F}$
are elementary abelian
 $2$
-groups.
$2$
-groups.
In loc. cit., Frohardt asked whether cases (2) and (3) actually occur.
In 2006, Rostermundt [Reference Rostermundt13] and, independently Thas [Reference Thas15], constructed an infinite class of examples (related to Hermitian varieties in projective dimension
![]() $3$
), which fitted in class (2), so class (3) became the final challenge. Frohardt’s problem resisted many years of tries (see, for instance, the work of Hachenberger [Reference Hachenberger7]), and the problem also occurs in the large literature of translation nets. Besides, the existence of elements in class (3) presented one of the main obstacles in classifying so-called “skew translation generalized quadrangles” (STGQs) – see [Reference Thas19, Reference Thas20] and also [Reference Thas21, Reference Bamberg, Glasby and Swartz1]. We also refer to Section 2.5 for some milestones in that classification theory.
$3$
), which fitted in class (2), so class (3) became the final challenge. Frohardt’s problem resisted many years of tries (see, for instance, the work of Hachenberger [Reference Hachenberger7]), and the problem also occurs in the large literature of translation nets. Besides, the existence of elements in class (3) presented one of the main obstacles in classifying so-called “skew translation generalized quadrangles” (STGQs) – see [Reference Thas19, Reference Thas20] and also [Reference Thas21, Reference Bamberg, Glasby and Swartz1]. We also refer to Section 2.5 for some milestones in that classification theory.
Payne’s first paper on STQGs [Reference Payne9] from 1975 marked the birth of the theory of STGQs. Pretty soon it became clear though that the “parity” of lines and points played a crucial role: In its long history, no examples were found of STGQs of even order
![]() $(t,t)$
for which the elation group was not abelian, while when t is odd it is easy to prove that the elation group cannot be abelian at all. Since one expects that such STGQs would have to meet the requirements of Frohardt’s theorem and since for STGQs of order
$(t,t)$
for which the elation group was not abelian, while when t is odd it is easy to prove that the elation group cannot be abelian at all. Since one expects that such STGQs would have to meet the requirements of Frohardt’s theorem and since for STGQs of order
![]() $(t,t)$
the elements of
$(t,t)$
the elements of
![]() $\mathcal {F}$
are always elementary abelian (see [Reference Thas20] for those details), such examples would conjecturally live in class (3) of Theorem 1.1. And indeed they do, if they would exist. The best result until 2020 was the same result when
$\mathcal {F}$
are always elementary abelian (see [Reference Thas20] for those details), such examples would conjecturally live in class (3) of Theorem 1.1. And indeed they do, if they would exist. The best result until 2020 was the same result when
![]() $(t,t) = (8,8)$
[Reference Bamberg, Glasby and Swartz1], with a very long and computer-aided technical proof. In the meanwhile, Ott has published a long paper [Reference Ott8] in which he showed that finite skew translation quadrangles of order
$(t,t) = (8,8)$
[Reference Bamberg, Glasby and Swartz1], with a very long and computer-aided technical proof. In the meanwhile, Ott has published a long paper [Reference Ott8] in which he showed that finite skew translation quadrangles of order
![]() $(t,t)$
with t not a square are translation GQs; that is, the associated elation group is an elementary abelian
$(t,t)$
with t not a square are translation GQs; that is, the associated elation group is an elementary abelian
![]() $2$
-group, and hence the quadrangle has a projective representation in some projective space. This essentially means that there is no “proper” theory of STGQs in this case.
$2$
-group, and hence the quadrangle has a projective representation in some projective space. This essentially means that there is no “proper” theory of STGQs in this case.
The present paper contains an alternative approach to the one of Ott, although we use one lemma of his paper. Our proof, which is geometric in nature, is very short in comparison with Ott’s proof, and we first completely classify STGQs of order
![]() $(t,t)$
which have a cyclic group of symmetries with center the elation point. We then use the lemma of Ott to reduce the general problem to the case of “cyclic STGQs.” In this paper, we also finally resolve Frohardt’s question by showing that class (3) of Theorem 1.1 is empty, and this will be done in Sections 4 and 5. The proof consists of a blend of synthetic geometrical and group theoretical techniques, which allows us to sufficiently understand the behavior of involutions to end the whole thing.
$(t,t)$
which have a cyclic group of symmetries with center the elation point. We then use the lemma of Ott to reduce the general problem to the case of “cyclic STGQs.” In this paper, we also finally resolve Frohardt’s question by showing that class (3) of Theorem 1.1 is empty, and this will be done in Sections 4 and 5. The proof consists of a blend of synthetic geometrical and group theoretical techniques, which allows us to sufficiently understand the behavior of involutions to end the whole thing.
Remark 1.2. On the combinatorial level, there is also an other interesting aspect to this result. If every line incident with some point in a finite GQ of even order
![]() $(t,t)$
is regular (see Section 2.2 for a formal definition of this very important notion), then it can be shown that the point itself is also regular ([Reference Payne and Thas12, section 1.5.2]). Ott’s result provides a group-theoretical converse if t is not a square: If a finite EGQ of even order
$(t,t)$
is regular (see Section 2.2 for a formal definition of this very important notion), then it can be shown that the point itself is also regular ([Reference Payne and Thas12, section 1.5.2]). Ott’s result provides a group-theoretical converse if t is not a square: If a finite EGQ of even order
![]() $(t,t)$
with t not a square, has a regular elation point (this is another way of defining STGQs in this specific case), then it is a translation quadrangle, so all the lines incident with x are regular.
$(t,t)$
with t not a square, has a regular elation point (this is another way of defining STGQs in this specific case), then it is a translation quadrangle, so all the lines incident with x are regular.
Organization
In Sections 2 and 3, we introduce the basic notions that we will need. In Section 4, we make a number of synthetic observations; we essentially show that in case (3) of Frohardt’s theorem, it is sufficient to work with Kantor families of type
![]() $(t,t)$
. This is done in the geometrical language of GQs. Then, in Section 5, we show that Frohardt’s class (3) is empty. And finally, in the last section, we classify cyclic STGQs (of finite order
$(t,t)$
. This is done in the geometrical language of GQs. Then, in Section 5, we show that Frohardt’s class (3) is empty. And finally, in the last section, we classify cyclic STGQs (of finite order
![]() $(t,t)$
). As a consequence, STGQs of even order
$(t,t)$
). As a consequence, STGQs of even order
![]() $(t,t)$
with t not a square are always translation quadrangles.
$(t,t)$
with t not a square are always translation quadrangles.
2 Synopsis of definitions
Let
![]() $\Gamma $
be a thick generalized quadrangle (GQ). It is a rank
$\Gamma $
be a thick generalized quadrangle (GQ). It is a rank
![]() $2$
geometry
$2$
geometry
![]() $\Gamma = (\mathcal {P},\mathcal {L},\mathbf {I})$
(where we call the elements of
$\Gamma = (\mathcal {P},\mathcal {L},\mathbf {I})$
(where we call the elements of
![]() $\mathcal {P}$
“points” and those of
$\mathcal {P}$
“points” and those of
![]() $\mathcal {L}$
“lines”) such that the following axioms are satisfied:
$\mathcal {L}$
“lines”) such that the following axioms are satisfied:
-
(a) there are no ordinary digons and triangles contained in
 $\Gamma $
;
$\Gamma $
; -
(b) each two elements of
 $\mathcal {P} \cup \mathcal {L}$
are contained in an ordinary quadrangle;
$\mathcal {P} \cup \mathcal {L}$
are contained in an ordinary quadrangle; -
(c) there exists an ordinary pentagon.
It can be shown that there are constants s and t such that each point is incident with
![]() $t + 1$
lines and each line is incident with
$t + 1$
lines and each line is incident with
![]() $s + 1$
points. We say that
$s + 1$
points. We say that
![]() $(s,t)$
is the order of
$(s,t)$
is the order of
![]() $\Gamma $
. Note that an ordinary quadrangle is just a (necessarily thin) GQ of order
$\Gamma $
. Note that an ordinary quadrangle is just a (necessarily thin) GQ of order
![]() $(1,1)$
– we call such a subgeometry also “apartment” (of
$(1,1)$
– we call such a subgeometry also “apartment” (of
![]() $\Gamma $
).
$\Gamma $
).
2.1 Subquadrangles
A subquadrangle (subGQ)
![]() $\Gamma ' = (\mathcal {P}',\mathcal {L}',\mathbf {I}')$
of a GQ
$\Gamma ' = (\mathcal {P}',\mathcal {L}',\mathbf {I}')$
of a GQ
![]() $\Gamma = (\mathcal {P},\mathcal {L},\mathbf {I})$
, is a GQ for which
$\Gamma = (\mathcal {P},\mathcal {L},\mathbf {I})$
, is a GQ for which
![]() $\mathcal {P}' \subseteq \mathcal {P}$
,
$\mathcal {P}' \subseteq \mathcal {P}$
,
![]() $\mathcal {L}' \subseteq \mathcal {L}$
, and
$\mathcal {L}' \subseteq \mathcal {L}$
, and
![]() $\mathbf {I}'$
is the incidence relation which is induced by
$\mathbf {I}'$
is the incidence relation which is induced by
![]() $\mathbf {I}$
on
$\mathbf {I}$
on
![]() $(\mathcal {P}' \times \mathcal {L}') \cup (\mathcal {L}' \times \mathcal {P}')$
.
$(\mathcal {P}' \times \mathcal {L}') \cup (\mathcal {L}' \times \mathcal {P}')$
.
2.2 Regularity
Let
![]() $\Gamma $
be a thick GQ of order
$\Gamma $
be a thick GQ of order
![]() $(s,t)$
. If X and Y are (not necessarily different) points, or lines,
$(s,t)$
. If X and Y are (not necessarily different) points, or lines,
![]() $X \sim Y$
denotes the fact that there is a line incident with both, or a point incident with both. Then
$X \sim Y$
denotes the fact that there is a line incident with both, or a point incident with both. Then
![]() $X^{\perp } := \{ Y \ \vert \ Y \sim X \}$
, and if S is a point set, or a line set,
$X^{\perp } := \{ Y \ \vert \ Y \sim X \}$
, and if S is a point set, or a line set,
![]() $S^{\perp } := \cap _{s \in S}s^{\perp }$
and
$S^{\perp } := \cap _{s \in S}s^{\perp }$
and
![]() $S^{\perp \perp } := {(S^{\perp })}^{\perp }$
.
$S^{\perp \perp } := {(S^{\perp })}^{\perp }$
.
A particularly important example is the case where
![]() $S = \{X,Y\}$
is a set of distinct noncollinear points (or nonconcurrent lines, but this is merely the dual situation, which we leave to the reader); then each line incident with X is incident with precisely one point of
$S = \{X,Y\}$
is a set of distinct noncollinear points (or nonconcurrent lines, but this is merely the dual situation, which we leave to the reader); then each line incident with X is incident with precisely one point of
![]() $\{ X,Y\}^{\perp }$
(so if
$\{ X,Y\}^{\perp }$
(so if
![]() $\Gamma $
is finite,
$\Gamma $
is finite,
![]() $\vert \{ X,Y\}^{\perp } \vert = t + 1$
). The set
$\vert \{ X,Y\}^{\perp } \vert = t + 1$
). The set
![]() $\{ X,Y\}^{\perp \perp }$
consists of all points which are collinear with every point of
$\{ X,Y\}^{\perp \perp }$
consists of all points which are collinear with every point of
![]() $\{X,Y\}^{\perp }$
, so
$\{X,Y\}^{\perp }$
, so
Let Z be any point of
![]() $\{X,Y\}^{\perp }$
; if each line incident with Z is incident with exactly one point of
$\{X,Y\}^{\perp }$
; if each line incident with Z is incident with exactly one point of
![]() $\{X,Y\}^{\perp \perp }$
, then this property is independent of the choice of Z, and we say that
$\{X,Y\}^{\perp \perp }$
, then this property is independent of the choice of Z, and we say that
![]() $\{ X,Y\}$
is regular. In the finite case, we could equivalently have asked that
$\{ X,Y\}$
is regular. In the finite case, we could equivalently have asked that
![]() $\vert \{ X,Y\}^{\perp \perp } \vert = t + 1$
.
$\vert \{ X,Y\}^{\perp \perp } \vert = t + 1$
.
We call a point/line X regular if
![]() $\{ X,Y \}$
is regular for all
$\{ X,Y \}$
is regular for all
![]() $Y \not \sim X$
.
$Y \not \sim X$
.
2.3 Symmetry
Isomorphisms and automorphisms of GQs are defined in the usual manner. See chapter 1 of [Reference Payne and Thas12]. The automorphism group of a GQ
![]() $\Gamma $
will be denoted by
$\Gamma $
will be denoted by
![]() $\mathrm {Aut}(\Gamma )$
.
$\mathrm {Aut}(\Gamma )$
.
Let X be a point or a line in a thick GQ
![]() $\Gamma $
. A symmetry with center X (in the case of a point) or axis X (in the case of a line) is an element of
$\Gamma $
. A symmetry with center X (in the case of a point) or axis X (in the case of a line) is an element of
![]() $\mathrm {Aut}(\Gamma )$
that fixes each element of
$\mathrm {Aut}(\Gamma )$
that fixes each element of
![]() $X^{\perp }$
. We say that X is a center of symmetry (point case) or an axis of symmetry (line case) if there exist Y and Z in
$X^{\perp }$
. We say that X is a center of symmetry (point case) or an axis of symmetry (line case) if there exist Y and Z in
![]() $X^{\perp }$
such that
$X^{\perp }$
such that
![]() $Y \not \sim Z$
, for which the group of all symmetries
$Y \not \sim Z$
, for which the group of all symmetries
![]() $\mathcal {S}(X)$
with center/axis X acts transitively on
$\mathcal {S}(X)$
with center/axis X acts transitively on
![]() $\{ Y,Z\}^{\perp } \setminus \{X\}$
. This definition does not depend on the choice of
$\{ Y,Z\}^{\perp } \setminus \{X\}$
. This definition does not depend on the choice of
![]() $(Y,Z)$
, and one easily shows that “transitive” implies “sharply transitive.” In the finite case, we could also have asked that
$(Y,Z)$
, and one easily shows that “transitive” implies “sharply transitive.” In the finite case, we could also have asked that
if the order of
![]() $\Gamma $
be
$\Gamma $
be
![]() $(s,t)$
.
$(s,t)$
.
Note that a center/axis of symmetry is necessarily regular.
We end this section with a very useful result of Benson.
Theorem 2.1 (C. T. Benson [Reference Benson2])
Let
![]() $\Gamma $
be a thick finite GQ of order
$\Gamma $
be a thick finite GQ of order
![]() $(s,t)$
, and let
$(s,t)$
, and let
![]() $\gamma $
be an automorphism of
$\gamma $
be an automorphism of
![]() $\Gamma $
. If N is the number of fixed points of
$\Gamma $
. If N is the number of fixed points of
![]() $\gamma $
, and M is the number of points x for which
$\gamma $
, and M is the number of points x for which
![]() $x^\gamma \ne x \sim x^\gamma $
, then
$x^\gamma \ne x \sim x^\gamma $
, then
2.4 Kantor families
In this section, we will recall the notion of Kantor family. Groups with Kantor families produce GQs, and vice versa, a certain type of GQ gives rise to Kantor families. We will only define finite Kantor families, as that is the case we will need in due course.
So suppose K is a finite group of order
![]() $u^2v$
for positive integers u and v, both at least
$u^2v$
for positive integers u and v, both at least
![]() $2$
. A Kantor family (of type
$2$
. A Kantor family (of type
![]() $(u,v)$
) in K is a pair
$(u,v)$
) in K is a pair
![]() $(\mathcal {F},\mathcal {F}^*)$
of sets of subgroups of K for which the properties below are satisfied:
$(\mathcal {F},\mathcal {F}^*)$
of sets of subgroups of K for which the properties below are satisfied:
-
(a)
 $\vert \mathcal {F} \vert = \vert \mathcal {F}^* \vert = v + 1$
, and there is a bijection
$\vert \mathcal {F} \vert = \vert \mathcal {F}^* \vert = v + 1$
, and there is a bijection
 $*: \mathcal {F} \mapsto \mathcal {F}^*$
which maps each
$*: \mathcal {F} \mapsto \mathcal {F}^*$
which maps each
 $A \in \mathcal {F}$
to
$A \in \mathcal {F}$
to
 $A^* \in \mathcal {F}^*$
such that
$A^* \in \mathcal {F}^*$
such that
 $A \leq A^*$
;
$A \leq A^*$
; -
(b) for each
 $A \in \mathcal {F}$
,
$A \in \mathcal {F}$
,
 $\vert A \vert = u$
and
$\vert A \vert = u$
and
 $\vert A^* \vert = uv$
;
$\vert A^* \vert = uv$
; -
(c) if
 $A, B, C$
are different elements in
$A, B, C$
are different elements in
 $\mathcal {F}$
, then
$\mathcal {F}$
, then
 $AB \cap C = \{ \mathrm {id} \}$
;
$AB \cap C = \{ \mathrm {id} \}$
; -
(d) if A and B are different elements in
 $\mathcal {F}$
, then
$\mathcal {F}$
, then
 $A \cap B^* = \{ \mathrm {id} \}$
.
$A \cap B^* = \{ \mathrm {id} \}$
.
From the data
![]() $\big (K,(\mathcal {F},\mathcal {F}^*)\big )$
, one constructs a thick GQ
$\big (K,(\mathcal {F},\mathcal {F}^*)\big )$
, one constructs a thick GQ
![]() $\Gamma = \Gamma \big (K,(\mathcal {F},\mathcal {F}^*)\big )$
of order
$\Gamma = \Gamma \big (K,(\mathcal {F},\mathcal {F}^*)\big )$
of order
![]() $(u,v)$
as follows. Its points are a symbol
$(u,v)$
as follows. Its points are a symbol
![]() $(\infty )$
, left cosets of type
$(\infty )$
, left cosets of type
![]() $gA^*$
(
$gA^*$
(
![]() $A \in \mathcal {F}$
and
$A \in \mathcal {F}$
and
![]() $g \in K$
) and the elements of K. Its lines are symbols
$g \in K$
) and the elements of K. Its lines are symbols
![]() $[ A ]$
(
$[ A ]$
(
![]() $A \in \mathcal {F}$
) and left cosets of type
$A \in \mathcal {F}$
) and left cosets of type
![]() $gA$
(
$gA$
(
![]() $A \in \mathcal {F}$
and
$A \in \mathcal {F}$
and
![]() $g \in K$
). The point
$g \in K$
). The point
![]() $(\infty )$
is incident with all lines of the first type and no other lines. A line
$(\infty )$
is incident with all lines of the first type and no other lines. A line
![]() $[A]$
is also incident with all points
$[A]$
is also incident with all points
![]() $gA^*$
. All other incidences are (reversed) containment. Elements of the group K act naturally as automorphisms of
$gA^*$
. All other incidences are (reversed) containment. Elements of the group K act naturally as automorphisms of
![]() $\Gamma $
, by left multiplication on the cosets, while fixing the symbolic point and symbolic lines. Then K fixes all the lines incident with
$\Gamma $
, by left multiplication on the cosets, while fixing the symbolic point and symbolic lines. Then K fixes all the lines incident with
![]() $(\infty )$
and acts sharply transitively on the points of
$(\infty )$
and acts sharply transitively on the points of
![]() $\Gamma $
which are not collinear with
$\Gamma $
which are not collinear with
![]() $(\infty )$
.
$(\infty )$
.
Conversely, let
![]() $\Omega $
be a thick GQ of order
$\Omega $
be a thick GQ of order
![]() $(u,v)$
, with an automorphism group L which fixes some point x linewise while acting sharply transitively on the points not collinear with x. We call such GQs elation generalized quadrangles (EGQs) with elation point x and elation group L. Then
$(u,v)$
, with an automorphism group L which fixes some point x linewise while acting sharply transitively on the points not collinear with x. We call such GQs elation generalized quadrangles (EGQs) with elation point x and elation group L. Then
![]() $\vert L \vert = u^2v$
. Now, take one arbitrary point y not collinear with x (due to the transitivity of L on these points, this choice is not important). For each line
$\vert L \vert = u^2v$
. Now, take one arbitrary point y not collinear with x (due to the transitivity of L on these points, this choice is not important). For each line
![]() $U \mathbf {I} y$
, let
$U \mathbf {I} y$
, let
![]() $\widetilde {u}$
be the point which is incident with U and collinear with x; let
$\widetilde {u}$
be the point which is incident with U and collinear with x; let
![]() $L_U^* := L_{\widetilde {u}}$
. Then with
$L_U^* := L_{\widetilde {u}}$
. Then with
![]() $\mathcal {F} := \{ L_U\ \vert \ U \mathbf {I} y \}$
and
$\mathcal {F} := \{ L_U\ \vert \ U \mathbf {I} y \}$
and
![]() $\mathcal {F}^* := \{ L_U^*\ \vert \ U \mathbf {I} y \}$
,
$\mathcal {F}^* := \{ L_U^*\ \vert \ U \mathbf {I} y \}$
,
![]() $(\mathcal {F},\mathcal {F}^*)$
is a Kantor family of type
$(\mathcal {F},\mathcal {F}^*)$
is a Kantor family of type
![]() $(u,v)$
in L. Also, we have a natural isomorphism
$(u,v)$
in L. Also, we have a natural isomorphism
which maps L to itself and
![]() $(\infty )$
to x.
$(\infty )$
to x.
2.5 Skew translation quadrangles
If
![]() $(\Gamma ,K)$
is an EGQ with elation point x and x is a center of symmetry such that the corresponding symmetry group
$(\Gamma ,K)$
is an EGQ with elation point x and x is a center of symmetry such that the corresponding symmetry group
![]() $\mathcal {S}$
is a subgroup of K, then we call
$\mathcal {S}$
is a subgroup of K, then we call
![]() $(\Gamma ,K)$
a skew translation generalized quadrangle (STGQ). In terms of Kantor families (using the notation of the previous subsection), a Kantor family
$(\Gamma ,K)$
a skew translation generalized quadrangle (STGQ). In terms of Kantor families (using the notation of the previous subsection), a Kantor family
![]() $(\mathcal {F},{\mathcal {F}}^*)$
gives rise to an STGQ if and only if there is a normal subgroup C of K such that for each
$(\mathcal {F},{\mathcal {F}}^*)$
gives rise to an STGQ if and only if there is a normal subgroup C of K such that for each
![]() $A \in \mathcal {F}$
, we have
$A \in \mathcal {F}$
, we have
![]() $A^* = AC$
(see [Reference Payne9] or [Reference Payne and Thas12, chapter 10]); C then corresponds to the group of symmetries with center the elation point. Note that for different
$A^* = AC$
(see [Reference Payne9] or [Reference Payne and Thas12, chapter 10]); C then corresponds to the group of symmetries with center the elation point. Note that for different
![]() $A, B$
in
$A, B$
in
![]() $\mathcal {F}$
, we have
$\mathcal {F}$
, we have
![]() $A^* \cap B^* = C$
. This type of GQ is very general: Each known finite GQ which is not isomorphic to the Hermitian quadrangle
$A^* \cap B^* = C$
. This type of GQ is very general: Each known finite GQ which is not isomorphic to the Hermitian quadrangle
![]() $\mathcal {H}(4,q^2)$
for some finite field
$\mathcal {H}(4,q^2)$
for some finite field
![]() $\mathbb {F}_q$
, is – modulo point-line duality – either an STGQ, or the Payne-derived quadrangle of an STGQ. More details on this statement can be found in [Reference Thas20]; for a more or less recent but rather detailed census on the known GQs, we also refer to [Reference Payne11].
$\mathbb {F}_q$
, is – modulo point-line duality – either an STGQ, or the Payne-derived quadrangle of an STGQ. More details on this statement can be found in [Reference Thas20]; for a more or less recent but rather detailed census on the known GQs, we also refer to [Reference Payne11].
We recall some basic (“decisive”) classification results in the large theory of STGQs. Much more can be found in [Reference Thas20]. The first result was first obtained by the author in [Reference Thas20] (see [Reference Thas19] for chronological details in its conception). It was also obtained in [Reference Bamberg, Glasby and Swartz1] with virtually the same proof.
Theorem 2.2. An STGQ of odd order
![]() $(t,t)$
is isomorphic to the symplectic quadrangle
$(t,t)$
is isomorphic to the symplectic quadrangle
![]() $\mathcal {W}(t)$
.
$\mathcal {W}(t)$
.
The symplectic quadrangle
![]() $\mathcal {W}(t)$
arises as the
$\mathcal {W}(t)$
arises as the
![]() $\mathbb {F}_t$
-rational points in a projective space
$\mathbb {F}_t$
-rational points in a projective space
![]() $\mathbb {P}^3(\mathbb {F}_t)$
, together with the absolute lines with respect to a symplectic polarity of
$\mathbb {P}^3(\mathbb {F}_t)$
, together with the absolute lines with respect to a symplectic polarity of
![]() $\mathbb {P}^3(\mathbb {F}_t)$
(see [Reference Payne and Thas12, chapter 3]); it is one of the natural geometric modules of the group
$\mathbb {P}^3(\mathbb {F}_t)$
(see [Reference Payne and Thas12, chapter 3]); it is one of the natural geometric modules of the group
![]() $\mathbf {PSp}_4(t)$
.
$\mathbf {PSp}_4(t)$
.
The most investigated type of STGQ is arguably the class of “flock quadrangles.” All the known flock quadrangles arise through Kantor families in one and the same type of elation group: finite Heisenberg groups of dimension
![]() $5$
(over a finite field). The next result proves the converse and is taken from [Reference Thas17].
$5$
(over a finite field). The next result proves the converse and is taken from [Reference Thas17].
Theorem 2.3. If
![]() $(\Gamma ,K)$
is an EGQ of order
$(\Gamma ,K)$
is an EGQ of order
![]() $(s,t)$
and K is isomorphic to a Heisenberg group of dimension
$(s,t)$
and K is isomorphic to a Heisenberg group of dimension
![]() $5$
over
$5$
over
![]() $\mathbb {F}_t$
, then
$\mathbb {F}_t$
, then
![]() $\Gamma $
is a flock quadrangle.
$\Gamma $
is a flock quadrangle.
The following result is one of the only known results on STGQs of even order
![]() $(t,t)$
; its proof takes up more than half of the paper [Reference Bamberg, Glasby and Swartz1] and is computer-aided.
$(t,t)$
; its proof takes up more than half of the paper [Reference Bamberg, Glasby and Swartz1] and is computer-aided.
Theorem 2.4. An STGQ of order
![]() $(8,8)$
is a translation generalized quadrangle.
$(8,8)$
is a translation generalized quadrangle.
Finally, we have Ott’s beautiful result:
Theorem 2.5 (Ott [Reference Ott8])
An STGQ
![]() $(\Gamma ,K)$
of even order
$(\Gamma ,K)$
of even order
![]() $(t,t)$
is a TGQ if t is not a square. In that case, K is an elementary abelian
$(t,t)$
is a TGQ if t is not a square. In that case, K is an elementary abelian
![]() $2$
-group.
$2$
-group.
3 Notation and setting for Sections 4 and 5
Let K be a finite group with a Kantor family
![]() $(\mathcal {F},\mathcal {F}^*)$
of type
$(\mathcal {F},\mathcal {F}^*)$
of type
![]() $(s,t)$
. The associated GQ with parameters
$(s,t)$
. The associated GQ with parameters
![]() $(s,t)$
is denoted
$(s,t)$
is denoted
![]() $\Gamma ^x$
, or
$\Gamma ^x$
, or
![]() $\Gamma $
, where the elation point is x. The Kantor family is defined relative to the point
$\Gamma $
, where the elation point is x. The Kantor family is defined relative to the point
![]() $z \not \sim x$
(unless we mention it otherwise). In Section 4 and Section 5, we assume the main assumptions of Frohardt’s Theorem 1.1 — this means that for certain distinct elements
$z \not \sim x$
(unless we mention it otherwise). In Section 4 and Section 5, we assume the main assumptions of Frohardt’s Theorem 1.1 — this means that for certain distinct elements
![]() $A, B \in \mathcal {F}$
, we suppose that
$A, B \in \mathcal {F}$
, we suppose that
![]() $K/(A^* \cap B^*)$
is abelian and that
$K/(A^* \cap B^*)$
is abelian and that
![]() $A^* \cap B^* \leq Z(K)$
, the center of K. Put
$A^* \cap B^* \leq Z(K)$
, the center of K. Put
![]() $A^* \cap B^* =: \mathcal {S}$
. We want to work solely in Theorem 1.1(3) in Sections 4 and 5 so that we furthermore assume the following properties:
$A^* \cap B^* =: \mathcal {S}$
. We want to work solely in Theorem 1.1(3) in Sections 4 and 5 so that we furthermore assume the following properties:
The elements of
![]() $\mathcal {F}$
are elementary abelian, and
$\mathcal {F}$
are elementary abelian, and
![]() $Z(K) =: Z$
has exponent
$Z(K) =: Z$
has exponent
![]() $4$
.
$4$
.
In particular, this means that
![]() $\Gamma $
is not a TGQ (and hence K is not abelian). On the other hand, we do know that s and t are powers of
$\Gamma $
is not a TGQ (and hence K is not abelian). On the other hand, we do know that s and t are powers of
![]() $2$
as a direct consequence of Theorem 1.1.
$2$
as a direct consequence of Theorem 1.1.
4 Preliminary properties and reduction to central STGQs of even order t
In this section, we observe some initial properties which narrow down the possibilities for elements in Theorem 1.1(3). In the final part of the proof of the main theorem, we will not need all these properties, but it is interesting to see how far one can go “synthetically.”
Below, we say that a group
![]() $G \leq K$
satisfies (*) if for any element
$G \leq K$
satisfies (*) if for any element
![]() $\alpha $
of G, we have that if
$\alpha $
of G, we have that if
![]() $\alpha $
fixes some point
$\alpha $
fixes some point
![]() $y \sim x \ne y$
,
$y \sim x \ne y$
,
![]() $\alpha $
also fixes
$\alpha $
also fixes
![]() $xy$
pointwise. We say that
$xy$
pointwise. We say that
![]() $G \leq K$
satisfies (*) at
$G \leq K$
satisfies (*) at
![]() $U \mathbf {I} x$
if this property is locally fulfilled at U.
$U \mathbf {I} x$
if this property is locally fulfilled at U.
First, note that for any line
![]() $W \mathbf {I} x$
, K acts transitively on
$W \mathbf {I} x$
, K acts transitively on
![]() $W \setminus \{x\}$
. As
$W \setminus \{x\}$
. As
![]() $\mathcal {S} \leq Z(K)$
, it hence follows that
$\mathcal {S} \leq Z(K)$
, it hence follows that
![]() $\mathcal {S}$
fixes
$\mathcal {S}$
fixes
![]() $[A]$
and
$[A]$
and
![]() $[B]$
pointwise (so
$[B]$
pointwise (so
![]() $\mathcal {S}$
is in the kernel of the action of K on the point set of
$\mathcal {S}$
is in the kernel of the action of K on the point set of
![]() $[A]$
, and
$[A]$
, and
![]() $[B]$
). As
$[B]$
). As
![]() $K/\mathcal {S}$
is abelian and transitive on both
$K/\mathcal {S}$
is abelian and transitive on both
![]() $[A] \setminus \{x\}$
and
$[A] \setminus \{x\}$
and
![]() $[B] \setminus \{x\}$
, we have that K has (*) at
$[B] \setminus \{x\}$
, we have that K has (*) at
![]() $[A]$
and
$[A]$
and
![]() $[B]$
.
$[B]$
.
Let
![]() $\eta \in Z^\times $
; if
$\eta \in Z^\times $
; if
![]() $\eta $
would fix an affine line (which is by definition a line not incident with x),
$\eta $
would fix an affine line (which is by definition a line not incident with x),
![]() $\eta $
is in some conjugate of an element of
$\eta $
is in some conjugate of an element of
![]() $\mathcal {F}$
, implying that
$\mathcal {F}$
, implying that
![]() $\eta ^2 = 1$
. Assume that
$\eta ^2 = 1$
. Assume that
![]() $\eta $
does not fix an affine line. Now, suppose there is an affine line U such that
$\eta $
does not fix an affine line. Now, suppose there is an affine line U such that
![]() $U^\eta $
does not intersect U. Take any element
$U^\eta $
does not intersect U. Take any element
![]() $V \in \{U,U^\eta \}^{\perp }$
which is not incident with x; choose the element
$V \in \{U,U^\eta \}^{\perp }$
which is not incident with x; choose the element
![]() $\beta $
in
$\beta $
in
![]() $K_V$
which sends
$K_V$
which sends
![]() $U^\eta $
to U; then
$U^\eta $
to U; then
![]() $\eta \beta $
fixes U and
$\eta \beta $
fixes U and
![]() $[\eta ,\beta ] = \mathrm {id}$
, so
$[\eta ,\beta ] = \mathrm {id}$
, so
![]() $\mathrm {id} = (\eta \beta )^2 = \eta ^2\beta ^2 = \eta ^2$
. So we may suppose that
$\mathrm {id} = (\eta \beta )^2 = \eta ^2\beta ^2 = \eta ^2$
. So we may suppose that
![]() $\eta $
fixes each point of
$\eta $
fixes each point of
![]() $x^{\perp }$
, that is,
$x^{\perp }$
, that is,
![]() $\eta $
is a symmetry with center x. In its turn, this implies that
$\eta $
is a symmetry with center x. In its turn, this implies that
![]() $\eta \in \mathcal {S}$
.
$\eta \in \mathcal {S}$
.
4.1 Reduction of parameters
In this subsection, we will show that
![]() $s = t$
, that is, the number of points incident with a line equals the number of lines incident with a point.
$s = t$
, that is, the number of points incident with a line equals the number of lines incident with a point.
Now, suppose that
![]() $\eta $
is a (nontrivial) symmetry with center x, and suppose that
$\eta $
is a (nontrivial) symmetry with center x, and suppose that
![]() $U \sim [A]$
is an affine line. Let
$U \sim [A]$
is an affine line. Let
![]() $\alpha \in A^*$
be an element which sends
$\alpha \in A^*$
be an element which sends
![]() $U^\eta $
to U such that
$U^\eta $
to U such that
![]() $\eta \alpha \ne \mathrm {id}$
(and note that such
$\eta \alpha \ne \mathrm {id}$
(and note that such
![]() $\alpha $
exist, of course). Then
$\alpha $
exist, of course). Then
![]() $\eta \alpha $
fixes U. As
$\eta \alpha $
fixes U. As
![]() $[\eta ,\alpha ] = \mathrm {id}$
,
$[\eta ,\alpha ] = \mathrm {id}$
,
![]() $\eta $
is an involution if and only if
$\eta $
is an involution if and only if
![]() $\alpha $
is an involution. As
$\alpha $
is an involution. As
![]() $(\mathcal {F},\mathcal {F}^*)$
is a Kantor family, we can write
$(\mathcal {F},\mathcal {F}^*)$
is a Kantor family, we can write
![]() $A^* = A\mathcal {S}$
(with
$A^* = A\mathcal {S}$
(with
![]() $A \cap \mathcal {S} = \{\mathrm {id}\}$
). We can write
$A \cap \mathcal {S} = \{\mathrm {id}\}$
). We can write
![]() $\alpha = \eta ^{-1}a$
, with
$\alpha = \eta ^{-1}a$
, with
![]() $a \in K_U$
so that the fixed points structure of
$a \in K_U$
so that the fixed points structure of
![]() $\alpha $
is that of a – precisely the points incident with
$\alpha $
is that of a – precisely the points incident with
![]() $[A]$
. Suppose
$[A]$
. Suppose
![]() $\alpha $
does not fix affine lines. Applying Theorem 2.1, we conclude
$\alpha $
does not fix affine lines. Applying Theorem 2.1, we conclude
which gives a contradiction unless
![]() $s = t$
since s and t are powers of
$s = t$
since s and t are powers of
![]() $2$
. In the other cases,
$2$
. In the other cases,
![]() $\alpha $
must fix affine lines, so that it is an involution, and hence
$\alpha $
must fix affine lines, so that it is an involution, and hence
![]() $\eta $
also is. So if
$\eta $
also is. So if
![]() $s \ne t$
, each element of Z is an involution, showing that case (3) of Frohardt’s theorem cannot occur under these assumptions. It follows that
$s \ne t$
, each element of Z is an involution, showing that case (3) of Frohardt’s theorem cannot occur under these assumptions. It follows that
![]() ${s = t}$
.
${s = t}$
.
4.2 The centralizers
 $C_B(\alpha )$
$C_B(\alpha )$
Now, consider the case where
![]() $s = t$
and t is even. Note that
$s = t$
and t is even. Note that
![]() $\mathcal {S}$
only consists of symmetries and involutions. Suppose
$\mathcal {S}$
only consists of symmetries and involutions. Suppose
![]() $\beta \in \mathcal {S}^\times $
is not an involution (it is then a symmetry); compose
$\beta \in \mathcal {S}^\times $
is not an involution (it is then a symmetry); compose
![]() $\beta $
with a hypothetical involution
$\beta $
with a hypothetical involution
![]() $\iota $
in Z which is not a symmetry. Then
$\iota $
in Z which is not a symmetry. Then
![]() $\beta \iota \in Z$
is not a symmetry, so it is an involution, and
$\beta \iota \in Z$
is not a symmetry, so it is an involution, and
![]() $\mathrm {id} = (\beta \iota )^2 = \beta ^2\iota ^2 = \beta ^2$
, a contradiction. So all involutions in
$\mathrm {id} = (\beta \iota )^2 = \beta ^2\iota ^2 = \beta ^2$
, a contradiction. So all involutions in
![]() $\mathcal {S}$
are symmetries, and whence all elements of
$\mathcal {S}$
are symmetries, and whence all elements of
![]() $\underline{\mathcal{S}}$
are symmetries. It follows easily that x is a regular point.
$\underline{\mathcal{S}}$
are symmetries. It follows easily that x is a regular point.
If K is abelian, the theory of translation GQs gives us that K is elementary abelian (see [Reference Thas, Thas and Van Maldeghem14, chapter 3]), so we may assume that K is not abelian. By Proposition 3.1 of Hachenberger [Reference Hachenberger7], it follows that
![]() $Z(K) = \mathcal {S}$
.
$Z(K) = \mathcal {S}$
.
Let
![]() $C \ne D$
be in
$C \ne D$
be in
![]() $\mathcal {F}$
; then
$\mathcal {F}$
; then
![]() $[K,K] = [C,D]$
(as
$[K,K] = [C,D]$
(as
![]() $K = CD\mathcal {S}$
)
$K = CD\mathcal {S}$
)
![]() $= \langle (cd)^2 \vert c \in C, d \in D \rangle $
. As this group is a subgroup of
$= \langle (cd)^2 \vert c \in C, d \in D \rangle $
. As this group is a subgroup of
![]() $\mathcal {S}$
, it follows that
$\mathcal {S}$
, it follows that
![]() $[K,K]$
is elementary abelian. As
$[K,K]$
is elementary abelian. As
![]() $\Phi (K) = K^2[K,K]$
(where
$\Phi (K) = K^2[K,K]$
(where
![]() $\Phi (K)$
denotes the Frattini subgroup of K), it easily follows that
$\Phi (K)$
denotes the Frattini subgroup of K), it easily follows that
![]() $\Phi (K)$
is the elementary abelian subgroup of
$\Phi (K)$
is the elementary abelian subgroup of
![]() $\mathcal {S}$
of all squares. Then on the other hand, if
$\mathcal {S}$
of all squares. Then on the other hand, if
![]() $s = \gamma ^2 \in \mathcal {S}$
is a square, there is an
$s = \gamma ^2 \in \mathcal {S}$
is a square, there is an
![]() $e \in E \in \mathcal {F}$
and
$e \in E \in \mathcal {F}$
and
![]() $c \in \mathcal {S}$
such that
$c \in \mathcal {S}$
such that
![]() $\gamma = ec$
(as
$\gamma = ec$
(as
![]() $K = \cup _{A \in \mathcal {F}}A^*$
), and
$K = \cup _{A \in \mathcal {F}}A^*$
), and
![]() $s = ecec = c^2$
. So
$s = ecec = c^2$
. So
![]() $\Phi (K) = \mathcal {S}^2$
. Also, for
$\Phi (K) = \mathcal {S}^2$
. Also, for
![]() $A \in \mathcal {F} \setminus \{ E\}$
, there is a unique
$A \in \mathcal {F} \setminus \{ E\}$
, there is a unique
![]() $B \in \mathcal {F}$
such that
$B \in \mathcal {F}$
such that
![]() $\gamma \in AE$
— write
$\gamma \in AE$
— write
![]() $\gamma ab$
with
$\gamma ab$
with
![]() $a \in A$
and
$a \in A$
and
![]() $b \in B$
. Then
$b \in B$
. Then
![]() $(ab)^2 = \gamma ^2 = s$
so that
$(ab)^2 = \gamma ^2 = s$
so that
![]() $s \in [K,K]$
. We have obtained that
$s \in [K,K]$
. We have obtained that
![]() $[K,K] = \mathcal {S}^2 = \Phi (K)$
.
$[K,K] = \mathcal {S}^2 = \Phi (K)$
.
Let
![]() $A \ne B$
be arbitrary in
$A \ne B$
be arbitrary in
![]() $\mathcal {F}$
. Now, let
$\mathcal {F}$
. Now, let
![]() $\alpha \in A^\times $
be arbitrary, and let
$\alpha \in A^\times $
be arbitrary, and let
![]() $\beta \in B^\times $
be such that
$\beta \in B^\times $
be such that
![]() $[\alpha ,\beta ] = \mathrm {id}$
. Put
$[\alpha ,\beta ] = \mathrm {id}$
. Put
![]() $\mathcal {F} \setminus \{A,B\} = \{C_1,\ldots ,C_{t - 1}\}$
. Then for each
$\mathcal {F} \setminus \{A,B\} = \{C_1,\ldots ,C_{t - 1}\}$
. Then for each
![]() $i \in \{1,\ldots ,t - 1\}$
there is precisely one triple
$i \in \{1,\ldots ,t - 1\}$
there is precisely one triple
![]() $(c_i,\beta _i,s_i) \in C_i \times B \times \mathcal {S}$
such that
$(c_i,\beta _i,s_i) \in C_i \times B \times \mathcal {S}$
such that
![]() $\alpha \beta = c_i\beta _is_i$
. Note that the maps
$\alpha \beta = c_i\beta _is_i$
. Note that the maps
![]() $\mu : \{ 1,\ldots ,t - 1\} \longrightarrow \mathcal {S}^\times : j \longrightarrow s_j$
and
$\mu : \{ 1,\ldots ,t - 1\} \longrightarrow \mathcal {S}^\times : j \longrightarrow s_j$
and
![]() $\mu ': \{ 1,\ldots ,t - 1\} \longrightarrow B \setminus \{\beta \}: j \longrightarrow \beta _j$
are surjective. Suppose that
$\mu ': \{ 1,\ldots ,t - 1\} \longrightarrow B \setminus \{\beta \}: j \longrightarrow \beta _j$
are surjective. Suppose that
![]() $s_e^2 = \mathrm {id}$
; then as
$s_e^2 = \mathrm {id}$
; then as
![]() $(\alpha \beta )^2 = \mathrm {id}$
,
$(\alpha \beta )^2 = \mathrm {id}$
,
![]() $[c_e,\beta _e] = \mathrm {id}$
, and so
$[c_e,\beta _e] = \mathrm {id}$
, and so
![]() $[\beta _e,c_e\beta _e s_e] = \mathrm {id} = [\beta _e,\alpha \beta ]$
, implying that
$[\beta _e,c_e\beta _e s_e] = \mathrm {id} = [\beta _e,\alpha \beta ]$
, implying that
![]() $[\alpha ,\beta _e] = \mathrm {id}$
. The converse is also true. So
$[\alpha ,\beta _e] = \mathrm {id}$
. The converse is also true. So
On the other hand, we have
![]() $t = \vert \alpha ^B \vert \times \vert C_B(\alpha ) \vert $
, so for any such
$t = \vert \alpha ^B \vert \times \vert C_B(\alpha ) \vert $
, so for any such
![]() $\alpha $
, the size of
$\alpha $
, the size of
![]() $\alpha ^K$
(which is the same as
$\alpha ^K$
(which is the same as
![]() $\alpha ^B$
) is a constant (
$\alpha ^B$
) is a constant (
![]() $\frac {t}{\ell }$
) independent of the choice of
$\frac {t}{\ell }$
) independent of the choice of
![]() $\alpha $
. As
$\alpha $
. As
![]() $\alpha ^K = \alpha ^B$
, it also follows that
$\alpha ^K = \alpha ^B$
, it also follows that
![]() $\alpha $
fixes precisely
$\alpha $
fixes precisely
![]() $\vert C_B(\alpha ) \vert = \ell $
points of
$\vert C_B(\alpha ) \vert = \ell $
points of
![]() $[A] \setminus \{x\}$
linewise.
$[A] \setminus \{x\}$
linewise.
Note at this point that if we prove that
![]() $\mathcal {S}$
is an elementary abelian
$\mathcal {S}$
is an elementary abelian
![]() $2$
-group, then each
$2$
-group, then each
![]() $A^*$
is also elementary abelian, and as K is covered by the
$A^*$
is also elementary abelian, and as K is covered by the
![]() $A^*$
s, it follows that K itself is elementary abelian, contradiction with the assumption that K has exponent
$A^*$
s, it follows that K itself is elementary abelian, contradiction with the assumption that K has exponent
![]() $4$
.
$4$
.
In the rest of this paper, we will denote the subgroup of
![]() $\mathcal {S}$
that consists of all its involutions by
$\mathcal {S}$
that consists of all its involutions by
![]() $\mathcal {I}$
.
$\mathcal {I}$
.
4.3 Extra info on
 $\mathcal {I}$
, and
$\mathcal {I}$
, and
 $\ell $
$\ell $
Keeping the same notation as before, we recall that
![]() $[K,K] = [C,D] = \{ (cd)^2 \vert c \in C, d \in D\}$
. Each
$[K,K] = [C,D] = \{ (cd)^2 \vert c \in C, d \in D\}$
. Each
![]() $(cd)^2 = cdcd = [c,d]$
is an element in
$(cd)^2 = cdcd = [c,d]$
is an element in
![]() $\mathcal {S}$
which obviously is an involution if it is nontrivial, so
$\mathcal {S}$
which obviously is an involution if it is nontrivial, so
![]() $[K,K] \leq \mathcal {I}$
. Also, note that the surjective morphism
$[K,K] \leq \mathcal {I}$
. Also, note that the surjective morphism
has kernel
![]() $\mathcal {I}$
, so that
$\mathcal {I}$
, so that
![]() $\mathcal {S}^2 \cong \mathcal {S}/\mathcal {I}$
. It follows that
$\mathcal {S}^2 \cong \mathcal {S}/\mathcal {I}$
. It follows that
![]() $\vert [ K, K ] \vert = \vert \mathcal {S}^2 \vert = t/\ell $
. We conclude that
$\vert [ K, K ] \vert = \vert \mathcal {S}^2 \vert = t/\ell $
. We conclude that
so that
![]() $\ell \geq \sqrt {t}$
.
$\ell \geq \sqrt {t}$
.
5 Solution of Frohardt’s problem
Recall that we suppose that
![]() $\Gamma $
is not a TGQ. For this part of the paper, we will invoke a result of Ott [Reference Ott8]. On page 413 of his paper (Proposition 4.2), Ott considers a maximal subgroup M of
$\Gamma $
is not a TGQ. For this part of the paper, we will invoke a result of Ott [Reference Ott8]. On page 413 of his paper (Proposition 4.2), Ott considers a maximal subgroup M of
![]() $\Phi (K)$
(in his paper, the notation G is used for our K and
$\Phi (K)$
(in his paper, the notation G is used for our K and
![]() $U_0$
is used for
$U_0$
is used for
![]() $\mathcal {S}$
). Then [Reference Ott8, Corollary 4.5, p. 414] says that
$\mathcal {S}$
). Then [Reference Ott8, Corollary 4.5, p. 414] says that
![]() $\vert M \vert = t/4$
. In this section, we only will use that observation of his paper. We do want to obtain a full solution of Frohardt’s problem, so we cannot rely on the main result of [Reference Ott8]: There, the case that t is a square is excluded, and we want to handle that too. Besides, after [Reference Ott8, Corollary 4.5, p. 414], the proof of the main result still takes about 20 pages, and we can rely on Equation (8) instead to obtain a very short approach to Frohardt’s problem.
$\vert M \vert = t/4$
. In this section, we only will use that observation of his paper. We do want to obtain a full solution of Frohardt’s problem, so we cannot rely on the main result of [Reference Ott8]: There, the case that t is a square is excluded, and we want to handle that too. Besides, after [Reference Ott8, Corollary 4.5, p. 414], the proof of the main result still takes about 20 pages, and we can rely on Equation (8) instead to obtain a very short approach to Frohardt’s problem.
So let
![]() $\vert M \vert = t/4$
; then as a maximal subgroup of the
$\vert M \vert = t/4$
; then as a maximal subgroup of the
![]() $2$
-group
$2$
-group
![]() $\Phi (K)$
, it has index 2 so that
$\Phi (K)$
, it has index 2 so that
![]() $\vert \Phi (K) \vert = t/2$
. But as
$\vert \Phi (K) \vert = t/2$
. But as
![]() $\Phi (K) = [K, K]$
, Equation (8) tells us that
$\Phi (K) = [K, K]$
, Equation (8) tells us that
![]() $\vert \Phi (K) \vert = t/\ell $
so that
$\vert \Phi (K) \vert = t/\ell $
so that
![]() $\ell = 2$
. As
$\ell = 2$
. As
![]() $\sqrt {t} \leq \ell $
by the previous section, it follows that
$\sqrt {t} \leq \ell $
by the previous section, it follows that
![]() $t \leq 4$
. For the cases
$t \leq 4$
. For the cases
![]() $t = 2$
and
$t = 2$
and
![]() $t = 4$
, it is well known that only the classical quadrangles
$t = 4$
, it is well known that only the classical quadrangles
![]() $\mathcal {W}(2)$
and
$\mathcal {W}(2)$
and
![]() $\mathcal {W}(4)$
occur (see [Reference Payne and Thas12, chapter 6]), which means that
$\mathcal {W}(4)$
occur (see [Reference Payne and Thas12, chapter 6]), which means that
![]() $\Gamma $
is a TGQ.
$\Gamma $
is a TGQ.
This shows that the class (3) in Frohardt’s Theorem 1.1 is empty, as all hypothetical members are TGQs, implying that K is elementary abelian.
6 STGQs of even order t, t not a square and cyclic STGQs
In this section, we will classify finite cyclic STGQs of order
![]() $(t,t)$
. As a corollary, we will give a short geometric proof of Ott’s main result [Reference Ott8]. In the latter case, we will furthermore assume that t is even and not a square (but we will be clear about the assumptions in each part of the section).
$(t,t)$
. As a corollary, we will give a short geometric proof of Ott’s main result [Reference Ott8]. In the latter case, we will furthermore assume that t is even and not a square (but we will be clear about the assumptions in each part of the section).
We will also rely on one extra (nontrivial) result of Ott’s paper [Reference Ott8], namely the fact that
![]() $\Phi (K) = \Phi (\mathcal {S})$
if
$\Phi (K) = \Phi (\mathcal {S})$
if
![]() $\Gamma $
is not a TGQ (under the assumptions of [Reference Ott8, Theorem 4.11]). It is our goal to give a very short alternative geometric approach to what follows after Theorem 4.11 in Ott’s paper (which is a long argument of 12 pages). Since we invoke that theorem, we also need to assume that t is not a square. Instead of “directly” obtaining the result, we choose a more interesting approach: We will completely classify cyclic STGQs of order
$\Gamma $
is not a TGQ (under the assumptions of [Reference Ott8, Theorem 4.11]). It is our goal to give a very short alternative geometric approach to what follows after Theorem 4.11 in Ott’s paper (which is a long argument of 12 pages). Since we invoke that theorem, we also need to assume that t is not a square. Instead of “directly” obtaining the result, we choose a more interesting approach: We will completely classify cyclic STGQs of order
![]() $(t, t)$
, cf. Theorem 6.2 (without any restrictions on t).
$(t, t)$
, cf. Theorem 6.2 (without any restrictions on t).
The following lemma reduces Ott’s theorem to a problem on cyclic STGQs.
Lemma 6.1. Let
![]() $(\Gamma ^x,K)$
be an STGQ of order
$(\Gamma ^x,K)$
be an STGQ of order
![]() $(t,t)$
with t even, and t not a square. Let
$(t,t)$
with t even, and t not a square. Let
![]() $\mathcal {S}$
be the group of symmetries with center x. Then we have that
$\mathcal {S}$
be the group of symmetries with center x. Then we have that
![]() $\mathcal {S}$
is cyclic.
$\mathcal {S}$
is cyclic.
Proof. As the group M of the previous section has size
![]() $t/4$
and is a maximal subgroup of
$t/4$
and is a maximal subgroup of
![]() $\Phi (K)$
(cf. Ott’s paper), we have that
$\Phi (K)$
(cf. Ott’s paper), we have that
![]() $\vert \Phi (K) \vert = t/2$
, and so
$\vert \Phi (K) \vert = t/2$
, and so
![]() $\vert \Phi (\mathcal {S}) \vert = t/2$
. As
$\vert \Phi (\mathcal {S}) \vert = t/2$
. As
![]() $[ \mathcal {S} : \Phi (\mathcal {S})] = 2$
, we have that
$[ \mathcal {S} : \Phi (\mathcal {S})] = 2$
, we have that
![]() $\mathcal {S}$
is generated by one element (a finite p-group P is cyclic if and only if the Frattini quotient
$\mathcal {S}$
is generated by one element (a finite p-group P is cyclic if and only if the Frattini quotient
![]() $P/\Phi (P)$
is cyclic).
$P/\Phi (P)$
is cyclic).
Angles in general STGQs
Let
![]() $(\widetilde {\Gamma }, \widetilde {K})$
be a general (not necessarily finite) STGQ with elation point x and associated group of symmetries (with center x)
$(\widetilde {\Gamma }, \widetilde {K})$
be a general (not necessarily finite) STGQ with elation point x and associated group of symmetries (with center x)
![]() $\mathcal {S}$
. Let
$\mathcal {S}$
. Let
![]() $(\widetilde {\mathcal {F}},\widetilde {\mathcal {F}}^*)$
be the associated Kantor family, and let
$(\widetilde {\mathcal {F}},\widetilde {\mathcal {F}}^*)$
be the associated Kantor family, and let
![]() $A \in \widetilde {\mathcal {F}}$
be arbitrary. Let A fix the line
$A \in \widetilde {\mathcal {F}}$
be arbitrary. Let A fix the line
![]() $U \sim [U] \mathbf {I} x$
, where U is not incident with x. Suppose that A fixes each point incident with
$U \sim [U] \mathbf {I} x$
, where U is not incident with x. Suppose that A fixes each point incident with
![]() $[U]$
. Define the angle spectrum of each element
$[U]$
. Define the angle spectrum of each element
![]() $a \in A^\times $
as follows. Let
$a \in A^\times $
as follows. Let
![]() $V \sim [U]$
, with V not incident with x; then the angle of a at V is the unique element s of
$V \sim [U]$
, with V not incident with x; then the angle of a at V is the unique element s of
![]() $\mathcal {S}$
for which
$\mathcal {S}$
for which
![]() $V^a = V^s$
. Then the angle spectrum of a is the set of all angles of a at V, where V varies over the lines in
$V^a = V^s$
. Then the angle spectrum of a is the set of all angles of a at V, where V varies over the lines in
![]() $[U]^\perp $
which are not incident with x.
$[U]^\perp $
which are not incident with x.
We now prove the following theorem (in whose statement we do not require extra assumptions for t).
Theorem 6.2 (Cyclic STGQs)
Suppose
![]() $(\Gamma ,K)$
is an STGQ of order t, and suppose that
$(\Gamma ,K)$
is an STGQ of order t, and suppose that
![]() $\mathcal {S}$
is cyclic. Then
$\mathcal {S}$
is cyclic. Then
![]() $t = p$
is a prime and
$t = p$
is a prime and
![]() $\Gamma \cong \mathcal {W}(p)$
.
$\Gamma \cong \mathcal {W}(p)$
.
Proof. For t odd, we already know that
![]() $\Gamma \cong \mathcal {W}(t)$
and as
$\Gamma \cong \mathcal {W}(t)$
and as
![]() $\mathcal {S}$
is elementary abelian in this case, it follows that t is prime (in which case
$\mathcal {S}$
is elementary abelian in this case, it follows that t is prime (in which case
![]() $\mathcal {S} \cong C_t$
).
$\mathcal {S} \cong C_t$
).
So now suppose that
![]() $s = t$
is even, with
$s = t$
is even, with
![]() $t = 2^h$
, and put
$t = 2^h$
, and put
![]() $\mathcal {S} = \langle \alpha \rangle $
. We suppose that
$\mathcal {S} = \langle \alpha \rangle $
. We suppose that
![]() $t \geq 4$
. Let
$t \geq 4$
. Let
![]() $y \not \sim x$
be some fixed point of
$y \not \sim x$
be some fixed point of
![]() $\Gamma $
, and if
$\Gamma $
, and if
![]() $U \mathbf {I} y$
, let
$U \mathbf {I} y$
, let
![]() $x_U := [U] \cap U$
, where
$x_U := [U] \cap U$
, where
![]() $[U]$
is the projection of U on x. Define the elements of the Kantor family of
$[U]$
is the projection of U on x. Define the elements of the Kantor family of
![]() $(\Gamma ,K)$
as
$(\Gamma ,K)$
as
![]() $\mathcal {F} = \{ K_U\ \vert \ U \mathbf {I} y \}$
and
$\mathcal {F} = \{ K_U\ \vert \ U \mathbf {I} y \}$
and
![]() $\mathcal {F}^* = \{ K_{x_U}\ \vert \ U \mathbf {I} y \}$
. Let
$\mathcal {F}^* = \{ K_{x_U}\ \vert \ U \mathbf {I} y \}$
. Let
![]() $A \in \mathcal {F}$
be arbitrary, with
$A \in \mathcal {F}$
be arbitrary, with
![]() $A = K_U$
and
$A = K_U$
and
![]() $U \mathbf {I} y$
, and let A act on
$U \mathbf {I} y$
, and let A act on
![]() $\mathcal {S}$
by conjugation. Define
$\mathcal {S}$
by conjugation. Define
![]() $N(A)$
to be the kernel of this action, and note that each element of
$N(A)$
to be the kernel of this action, and note that each element of
![]() $N(A)$
commutes with
$N(A)$
commutes with
![]() $\mathcal {S}$
and hence fixes
$\mathcal {S}$
and hence fixes
![]() $x_U$
linewise. Then
$x_U$
linewise. Then
![]() $A/N(A)$
is a subgroup of the automorphism group of
$A/N(A)$
is a subgroup of the automorphism group of
![]() $\mathcal {S}$
, which is well known to be isomorphic to
$\mathcal {S}$
, which is well known to be isomorphic to
![]() $C_2 \times C_{2^{h - 2}}$
. But as
$C_2 \times C_{2^{h - 2}}$
. But as
![]() $A/N(A)$
is elementary abelian, this implies that
$A/N(A)$
is elementary abelian, this implies that
where the latter is the
![]() $2$
-torsion subgroup of
$2$
-torsion subgroup of
![]() $C_2 \times C_{2^{h - 2}}$
. It follows that
$C_2 \times C_{2^{h - 2}}$
. It follows that
![]() $\vert N(A) \vert \in \{ t/4, t/2, t \}$
.
$\vert N(A) \vert \in \{ t/4, t/2, t \}$
.
Let
![]() $U, x_U, [U], A = K_U$
be as before, with U not incident with x arbitrary; then
$U, x_U, [U], A = K_U$
be as before, with U not incident with x arbitrary; then
![]() $N(A) \leq A$
has size
$N(A) \leq A$
has size
![]() $t, t/2$
or
$t, t/2$
or
![]() $t/4$
. Now, let
$t/4$
. Now, let
![]() $y \ne x_U$
be any other point on
$y \ne x_U$
be any other point on
![]() $[U]$
different from x.
$[U]$
different from x.
Any element of
 $N(A)^\times $
fixes
$N(A)^\times $
fixes
 $t/2 + 1$
points on
$t/2 + 1$
points on
 $[U]$
linewise, and all angles are given by
$[U]$
linewise, and all angles are given by
 $\mathrm {id}$
or
$\mathrm {id}$
or
 $\alpha ^{t/2}$
$\alpha ^{t/2}$
Let
![]() $a \in N(A)^\times $
. As a fixes the point
$a \in N(A)^\times $
. As a fixes the point
![]() $x_U$
linewise, it commutes with every element in
$x_U$
linewise, it commutes with every element in
![]() $\mathcal {S}$
. Suppose
$\mathcal {S}$
. Suppose
![]() $\beta $
is an angle of a; then
$\beta $
is an angle of a; then
![]() $\beta a$
fixes a line (not incident with x), so it is an involution. It follows that
$\beta a$
fixes a line (not incident with x), so it is an involution. It follows that
![]() $(\beta a)^2 = \beta ^2 = \mathrm {id}$
. So
$(\beta a)^2 = \beta ^2 = \mathrm {id}$
. So
![]() $\beta $
is the unique involution in
$\beta $
is the unique involution in
![]() $\mathcal {S}$
,
$\mathcal {S}$
,
![]() $\alpha ^{t/2}$
. Now, suppose a fixes
$\alpha ^{t/2}$
. Now, suppose a fixes
![]() $\lambda $
points on
$\lambda $
points on
![]() $[U] \setminus \{x\}$
linewise, so that
$[U] \setminus \{x\}$
linewise, so that
![]() $t - \lambda $
points remain in
$t - \lambda $
points remain in
![]() $[U] \setminus \{x\}$
which are all incident with precisely one fixed line (which is
$[U] \setminus \{x\}$
which are all incident with precisely one fixed line (which is
![]() $[U]$
). If we would have that
$[U]$
). If we would have that
![]() $\lambda < t/2$
, then
$\lambda < t/2$
, then
![]() $t/2 < t - \lambda < t$
. Considering the element
$t/2 < t - \lambda < t$
. Considering the element
![]() $a\alpha ^{t/2}$
, we see that it fixes
$a\alpha ^{t/2}$
, we see that it fixes
![]() $t - \lambda $
points in
$t - \lambda $
points in
![]() $[U] \setminus \{ x\}$
linewise. As we will observe in the next paragraph, this is a contradiction as
$[U] \setminus \{ x\}$
linewise. As we will observe in the next paragraph, this is a contradiction as
![]() $t - \lambda $
has to be a power of
$t - \lambda $
has to be a power of
![]() $2$
.
$2$
.
The map
 $\zeta $
$\zeta $
Now, let
![]() $a \in N(A)^\times $
be arbitrary; then a fixes
$a \in N(A)^\times $
be arbitrary; then a fixes
![]() $t/2$
points on
$t/2$
points on
![]() $[U]$
(besides x) linewise. Call this point set
$[U]$
(besides x) linewise. Call this point set
![]() $\mathcal {B}(a)$
. Let
$\mathcal {B}(a)$
. Let
![]() $B \ne A$
in
$B \ne A$
in
![]() $\mathcal {F}$
; then it is easy to see that
$\mathcal {F}$
; then it is easy to see that
![]() $\vert C_B(a) \vert = t/2$
, and the set
$\vert C_B(a) \vert = t/2$
, and the set
![]() $\mathcal {B}(a)$
can be identified with a unique subgroup of B (which acts sharply transitively on
$\mathcal {B}(a)$
can be identified with a unique subgroup of B (which acts sharply transitively on
![]() $\mathcal {B}(a)$
). As B is an elementary abelian
$\mathcal {B}(a)$
). As B is an elementary abelian
![]() $2$
-group (of order
$2$
-group (of order
![]() $t = 2^h$
), we can associate an
$t = 2^h$
), we can associate an
![]() $(h - 1)$
-dimensional projective space over
$(h - 1)$
-dimensional projective space over
![]() $\mathbb {F}_2$
with B, which we denote by
$\mathbb {F}_2$
with B, which we denote by
![]() $\Pi (B)$
; we then have that
$\Pi (B)$
; we then have that
![]() $\mathcal {B}(a)$
defines a hyperplane
$\mathcal {B}(a)$
defines a hyperplane
![]() $\Pi (a)$
in
$\Pi (a)$
in
![]() $\Pi (B)$
. Consider the map
$\Pi (B)$
. Consider the map
and note that
![]() $\zeta (\mathrm {id}) = \Pi (B)$
.
$\zeta (\mathrm {id}) = \Pi (B)$
.
For now, we suppose that
![]() $\underline{\zeta}$
is an injection (if it is not, we will later easily show that a contradiction arises).
$\underline{\zeta}$
is an injection (if it is not, we will later easily show that a contradiction arises).
Note that the dual spaces of
![]() $\zeta (N(A)^\times )$
are contained in (in fact, form) a subspace of
$\zeta (N(A)^\times )$
are contained in (in fact, form) a subspace of
![]() $\Pi (B)^* \simeq \Pi (B)$
(where
$\Pi (B)^* \simeq \Pi (B)$
(where
![]() $\Pi (B)^*$
is the dual space of
$\Pi (B)^*$
is the dual space of
![]() $\Pi (B)$
). If a and b are in
$\Pi (B)$
). If a and b are in
![]() $N(A)^\times $
, then
$N(A)^\times $
, then
![]() $ab = c$
is such that
$ab = c$
is such that
![]() $\zeta (c)$
is the third hyperplane on
$\zeta (c)$
is the third hyperplane on
![]() $\zeta (a) \cap \zeta (b)$
; in the dual space
$\zeta (a) \cap \zeta (b)$
; in the dual space
![]() $\Pi (B)^*$
,
$\Pi (B)^*$
,
![]() $\zeta (c)^*$
is the third point of the line
$\zeta (c)^*$
is the third point of the line
![]() $\zeta (a)^*\zeta (b)^*$
. It follows that
$\zeta (a)^*\zeta (b)^*$
. It follows that
![]() ${\zeta (N(A)^\times )}^* \simeq \zeta (N(A)^\times )$
is a subspace of
${\zeta (N(A)^\times )}^* \simeq \zeta (N(A)^\times )$
is a subspace of
![]() $\Pi (B)^* \simeq \Pi (B)$
.
$\Pi (B)^* \simeq \Pi (B)$
.
Subgroups of
 $N(A)$
which fix at least one arbitrary point
$N(A)$
which fix at least one arbitrary point
 $x' \ne x_U, x$
linewise have at least size
$x' \ne x_U, x$
linewise have at least size
 $t/8$
$t/8$
Let A be arbitrary in
![]() $\mathcal {F}$
as before, and keep using the same notation. Let
$\mathcal {F}$
as before, and keep using the same notation. Let
![]() $x' \ne x_U$
be arbitrary in
$x' \ne x_U$
be arbitrary in
![]() $[U] \setminus \{ x\}$
. Then the subgroup of A of elements which fix both
$[U] \setminus \{ x\}$
. Then the subgroup of A of elements which fix both
![]() $x_U$
and
$x_U$
and
![]() $x'$
linewise has at least size
$x'$
linewise has at least size
![]() $t/8$
. This follows from properties of the map
$t/8$
. This follows from properties of the map
![]() $\zeta $
as we will see below. Since the dual spaces of the elements in
$\zeta $
as we will see below. Since the dual spaces of the elements in
![]() $\zeta (N(A)^\times )$
form a subspace of
$\zeta (N(A)^\times )$
form a subspace of
![]() $\Pi (B)^* \simeq \Pi (B)$
, it follows that precisely one extra point
$\Pi (B)^* \simeq \Pi (B)$
, it follows that precisely one extra point
![]() $\widetilde {x}$
in
$\widetilde {x}$
in
![]() $[U] \setminus \{x_U,x\}$
is fixed linewise by
$[U] \setminus \{x_U,x\}$
is fixed linewise by
![]() $N(A)$
if
$N(A)$
if
![]() $\vert N(A) \vert = t/2$
(
$\vert N(A) \vert = t/2$
(
![]() ${\zeta (N(A)^\times )}^*$
then is a hyperplane), or precisely three extra points
${\zeta (N(A)^\times )}^*$
then is a hyperplane), or precisely three extra points
![]() $\widetilde {x}_1, \widetilde {x}_2, \widetilde {x}_3$
when
$\widetilde {x}_1, \widetilde {x}_2, \widetilde {x}_3$
when
![]() $\vert N(A) \vert = t/4$
(
$\vert N(A) \vert = t/4$
(
![]() ${\zeta (N(A)^\times )}^*$
then is a subspace of codimension
${\zeta (N(A)^\times )}^*$
then is a subspace of codimension
![]() $2$
). Suppose that
$2$
). Suppose that
![]() $x'$
is not one of the extra points. We distinguish three cases. Below, we put
$x'$
is not one of the extra points. We distinguish three cases. Below, we put
![]() $t = 2^h$
so that
$t = 2^h$
so that
![]() $\Pi (B)$
is a projective
$\Pi (B)$
is a projective
![]() $\mathbb {F}_2$
-space of dimension
$\mathbb {F}_2$
-space of dimension
![]() $h - 1$
.
$h - 1$
.
-
(0)
 $\underline{\vert N(A) \vert = t}$
. Since all angles are in
$\underline{\vert N(A) \vert = t}$
. Since all angles are in
 $\{ \mathrm {id}, \alpha ^{t/2}\}$
, the number of elements in
$\{ \mathrm {id}, \alpha ^{t/2}\}$
, the number of elements in
 $N(A)^\times $
which fix
$N(A)^\times $
which fix
 $x_U$
and
$x_U$
and
 $x'$
linewise is at least
$x'$
linewise is at least
 $t/2$
. (Let
$t/2$
. (Let
 $V \mathbf {I} x'$
,
$V \mathbf {I} x'$
,
 $V \ne [U]$
; then
$V \ne [U]$
; then
 $\vert N(A)_V \vert \leq 2$
.)
$\vert N(A)_V \vert \leq 2$
.) -
(1)
 $\underline{\vert N(A) \vert = t/2}$
. In this case, all elements of
$\underline{\vert N(A) \vert = t/2}$
. In this case, all elements of
 $\zeta (N(A)^\times )$
contain one fixed point r in
$\zeta (N(A)^\times )$
contain one fixed point r in
 $\Pi (B)$
(and all hyperplanes in
$\Pi (B)$
(and all hyperplanes in
 $\Pi (B)$
containing that point are contained in
$\Pi (B)$
containing that point are contained in
 $\zeta (N(A)^\times )$
). The number of elements in
$\zeta (N(A)^\times )$
). The number of elements in
 $N(A)^\times $
which fix
$N(A)^\times $
which fix
 $x_U$
and
$x_U$
and
 $x'$
linewise is the number of sets
$x'$
linewise is the number of sets
 $\mathcal {B}(a)$
(
$\mathcal {B}(a)$
(
 $a \in N(A)^\times $
) which contain besides r a second point
$a \in N(A)^\times $
) which contain besides r a second point
 $r'$
, and this equals the number of hyperplanes in
$r'$
, and this equals the number of hyperplanes in
 $\Pi (B)$
which contain two different points, hence a line:
$\Pi (B)$
which contain two different points, hence a line:
 $2^{h - 2} - 1 = t/4 - 1$
.
$2^{h - 2} - 1 = t/4 - 1$
. -
(2)
 $\underline{\vert N(A) \vert = t/4}$
. In this case, all elements of
$\underline{\vert N(A) \vert = t/4}$
. In this case, all elements of
 $\zeta (N(A)^\times )$
contain one fixed line R in
$\zeta (N(A)^\times )$
contain one fixed line R in
 $\Pi (B)$
(and all hyperplanes in
$\Pi (B)$
(and all hyperplanes in
 $\Pi (B)$
containing that line are contained in
$\Pi (B)$
containing that line are contained in
 $\zeta (N(A)^\times )$
). The number of elements in
$\zeta (N(A)^\times )$
). The number of elements in
 $N(A)^\times $
which fix
$N(A)^\times $
which fix
 $x_U$
and
$x_U$
and
 $x'$
linewise is the number of sets
$x'$
linewise is the number of sets
 $\mathcal {B}(a)$
(
$\mathcal {B}(a)$
(
 $a \in N(A)^\times $
) which contain both
$a \in N(A)^\times $
) which contain both
 $x_U$
and
$x_U$
and
 $x'$
, and this equals the number of hyperplanes in
$x'$
, and this equals the number of hyperplanes in
 $\Pi (B)$
which contain a given point and an extra line R, hence a plane:
$\Pi (B)$
which contain a given point and an extra line R, hence a plane:
 $2^{h - 3} - 1 = t/8 - 1$
.
$2^{h - 3} - 1 = t/8 - 1$
.
Alternative proof using angles
We have seen that all elements in
![]() $N(A)$
only allow angles contained in
$N(A)$
only allow angles contained in
![]() $\{ \mathrm {id}, \alpha ^{t/2} \}$
. Take any line Y on
$\{ \mathrm {id}, \alpha ^{t/2} \}$
. Take any line Y on
![]() $x'$
different from
$x'$
different from
![]() $[U]$
. Then
$[U]$
. Then
![]() $\vert N(A)_Y \vert \geq \vert N(A) \vert /2$
since at most one nontrivial angle can occur. And since
$\vert N(A)_Y \vert \geq \vert N(A) \vert /2$
since at most one nontrivial angle can occur. And since
![]() $[N(A),\mathcal {S}] = \{ \mathrm {id} \}$
, it also follows that
$[N(A),\mathcal {S}] = \{ \mathrm {id} \}$
, it also follows that
![]() $N(A)_Y$
fixes all lines on
$N(A)_Y$
fixes all lines on
![]() $x'$
. This gives us the same cases (0), (1), (2) as above.
$x'$
. This gives us the same cases (0), (1), (2) as above.
In the rest of the proof, we suppose that
![]() $t \geq 16$
(if
$t \geq 16$
(if
![]() $t = 8$
, we refer to [Reference Bamberg, Glasby and Swartz1]).
$t = 8$
, we refer to [Reference Bamberg, Glasby and Swartz1]).
Each element in A, where
 $A \in \mathcal {F}$
is arbitrary, has an angle spectrum which is a subset of
$A \in \mathcal {F}$
is arbitrary, has an angle spectrum which is a subset of
 $\{ \mathrm {id}, \alpha ^{t/2} \}$
; as a consequence, we have that
$\{ \mathrm {id}, \alpha ^{t/2} \}$
; as a consequence, we have that
 $[k, a] \in \{ \mathrm {id}, \alpha ^{t/2} \}$
for all
$[k, a] \in \{ \mathrm {id}, \alpha ^{t/2} \}$
for all
 $k \in K$
,
$k \in K$
,
 $a \in A$
,
$a \in A$
,
 $A \in \mathcal {F}$
$A \in \mathcal {F}$
First, suppose that
![]() $a \in N(A)^\times $
. Then we already know that only the angles
$a \in N(A)^\times $
. Then we already know that only the angles
![]() $\mathrm {id}$
and
$\mathrm {id}$
and
![]() $\alpha ^{t/2}$
can occur. Now, let
$\alpha ^{t/2}$
can occur. Now, let
![]() $k \in K^\times $
be arbitrary, and consider
$k \in K^\times $
be arbitrary, and consider
![]() $V^k$
. If a fixes
$V^k$
. If a fixes
![]() $V^k$
, we have that
$V^k$
, we have that
![]() $[k,a] = \mathrm {id}$
since it is a symmetry with center x which fixes
$[k,a] = \mathrm {id}$
since it is a symmetry with center x which fixes
![]() $V^k$
; if a does not fix
$V^k$
; if a does not fix
![]() $V^k$
, we have that
$V^k$
, we have that
![]() $[k,a] = \alpha ^{t/2}$
since it is a symmetry with center x which sends
$[k,a] = \alpha ^{t/2}$
since it is a symmetry with center x which sends
![]() $V^k$
to
$V^k$
to
![]() ${(V^{k})}^{\alpha ^{t/2}}$
. So if
${(V^{k})}^{\alpha ^{t/2}}$
. So if
![]() $N(A) = A$
, the statement is already proved.
$N(A) = A$
, the statement is already proved.
Suppose that
![]() $a \in A^\times \setminus N(A)^\times $
; then a induces (by conjugation) a nontrivial involutory automorphism of
$a \in A^\times \setminus N(A)^\times $
; then a induces (by conjugation) a nontrivial involutory automorphism of
![]() $\mathcal {S}$
. Let
$\mathcal {S}$
. Let
![]() $\gamma \ne \mathrm {id}$
be an angle of a. Then
$\gamma \ne \mathrm {id}$
be an angle of a. Then
![]() $\gamma a$
fixes a line not incident with x, so that it is an involution. Then
$\gamma a$
fixes a line not incident with x, so that it is an involution. Then
![]() $\gamma a \gamma a = \mathrm {id}$
, so that
$\gamma a \gamma a = \mathrm {id}$
, so that
![]() $\gamma ^a = \gamma ^{-1}$
. If a and
$\gamma ^a = \gamma ^{-1}$
. If a and
![]() $\gamma $
commute, it follows that
$\gamma $
commute, it follows that
![]() $\gamma $
is an involution, so
$\gamma $
is an involution, so
![]() $\gamma = \alpha ^{t/2}$
. Now, suppose a and
$\gamma = \alpha ^{t/2}$
. Now, suppose a and
![]() $\gamma $
do not commute. Consider the line
$\gamma $
do not commute. Consider the line
![]() $U \mathbf {I} x_U$
,
$U \mathbf {I} x_U$
,
![]() $U \ne [U]$
, which is supposed to be fixed by a. We identify the action of a on
$U \ne [U]$
, which is supposed to be fixed by a. We identify the action of a on
![]() $\mathcal {S}$
with the action of a on the lines incident with
$\mathcal {S}$
with the action of a on the lines incident with
![]() $x_U$
and different from
$x_U$
and different from
![]() $[U]$
(which we can do since
$[U]$
(which we can do since
![]() $\mathcal {S}$
acts sharply transitively on these lines: If
$\mathcal {S}$
acts sharply transitively on these lines: If
![]() $W \mathbf {I} x_U$
and
$W \mathbf {I} x_U$
and
![]() $W \ne [U]$
with
$W \ne [U]$
with
![]() $W = V^\alpha $
, then we identify W with
$W = V^\alpha $
, then we identify W with
![]() $\alpha \in \mathcal {S}$
). It is easy to calculate that the only nontrivial involutions in
$\alpha \in \mathcal {S}$
). It is easy to calculate that the only nontrivial involutions in
![]() $\mathrm {Aut}(\mathcal {S})$
are given by the following images of
$\mathrm {Aut}(\mathcal {S})$
are given by the following images of
![]() $\alpha $
:
$\alpha $
:
![]() $\nu _1:\ \alpha :\ \mapsto \ \alpha ^{t - 1}$
;
$\nu _1:\ \alpha :\ \mapsto \ \alpha ^{t - 1}$
;
![]() $\nu _2:\ \alpha :\ \mapsto \ \alpha ^{t/2 + 1}$
;
$\nu _2:\ \alpha :\ \mapsto \ \alpha ^{t/2 + 1}$
;
![]() $\nu _3:\ \alpha :\ \mapsto \ \alpha ^{(t - 1)(t/2 + 1)} = \alpha ^{t/2 - 1}$
.
$\nu _3:\ \alpha :\ \mapsto \ \alpha ^{(t - 1)(t/2 + 1)} = \alpha ^{t/2 - 1}$
.
In the first case,
![]() $\nu _1$
fixes precisely two elements (
$\nu _1$
fixes precisely two elements (
![]() $\mathrm {id}$
and
$\mathrm {id}$
and
![]() $\alpha ^{t/2}$
) of
$\alpha ^{t/2}$
) of
![]() $\mathcal {S}$
; in the second case
$\mathcal {S}$
; in the second case
![]() $t/2$
elements (all
$t/2$
elements (all
![]() $\alpha ^n$
with n even), and in the last case again two elements (
$\alpha ^n$
with n even), and in the last case again two elements (
![]() $\mathrm {id}$
and
$\mathrm {id}$
and
![]() $\alpha ^{t/2}$
). If a is of the first type or the third, at most two lines different from
$\alpha ^{t/2}$
). If a is of the first type or the third, at most two lines different from
![]() $[U]$
are fixed per point in
$[U]$
are fixed per point in
![]() $[U] \setminus \{x\}$
(in fact, one can easily show that it is precisely two per such point, but we do not need this equality). If a is of the second type, it fixes precisely
$[U] \setminus \{x\}$
(in fact, one can easily show that it is precisely two per such point, but we do not need this equality). If a is of the second type, it fixes precisely
![]() $t/2$
lines incident with
$t/2$
lines incident with
![]() $x_U$
and different from
$x_U$
and different from
![]() $[U]$
(and many more on other points as well, as we will later see).
$[U]$
(and many more on other points as well, as we will later see).
Now, suppose
![]() $a \in A^{\times }$
is of type 1 or type 3. Suppose a fixes the line U (not incident with x), and let
$a \in A^{\times }$
is of type 1 or type 3. Suppose a fixes the line U (not incident with x), and let
![]() $u^a = v$
with
$u^a = v$
with
![]() $u \mathbf {I} U$
, u not collinear with x. We suppose without loss of generality that u “defines the Kantor family” – that is, if
$u \mathbf {I} U$
, u not collinear with x. We suppose without loss of generality that u “defines the Kantor family” – that is, if
![]() $W \mathbf {I} u$
, then
$W \mathbf {I} u$
, then
![]() $K_W$
is an element of
$K_W$
is an element of
![]() $\mathcal {F}$
(and in particular,
$\mathcal {F}$
(and in particular,
![]() $K_U = A$
). For any such
$K_U = A$
). For any such
![]() $W \ne U$
, if
$W \ne U$
, if
![]() $B = K_W$
in
$B = K_W$
in
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $[W]$
is the line incident with x which meets W, define
$[W]$
is the line incident with x which meets W, define
![]() $U(B) = W$
as the line incident with u which meets
$U(B) = W$
as the line incident with u which meets
![]() $[W]$
, and let
$[W]$
, and let
![]() $V(B)$
be the line incident with v which meets
$V(B)$
be the line incident with v which meets
![]() $[W]$
. Let
$[W]$
. Let
![]() $u_B := U(B) \cap [W]$
and
$u_B := U(B) \cap [W]$
and
![]() $v_B := V(B) \cap [W]$
. Then as we have seen in a previous step, we have that
$v_B := V(B) \cap [W]$
. Then as we have seen in a previous step, we have that
![]() $B_{[u_B,v_B]}$
, the subgroup of B which fixes
$B_{[u_B,v_B]}$
, the subgroup of B which fixes
![]() $u_B$
and
$u_B$
and
![]() $v_B$
linewise, has size at least
$v_B$
linewise, has size at least
![]() $t/8$
. Note that
$t/8$
. Note that
![]() $U^{B_{[u_B,v_B]}}$
consists of lines in
$U^{B_{[u_B,v_B]}}$
consists of lines in
![]() $\{ [U], U(B), V(B) \}^{\perp }$
. As a consequence, since a maps u to v and fixes all points incident with
$\{ [U], U(B), V(B) \}^{\perp }$
. As a consequence, since a maps u to v and fixes all points incident with
![]() $[U]$
, it follows that a fixes all lines in
$[U]$
, it follows that a fixes all lines in
![]() $U^{B_{[u_B,v_B]}}$
. Letting B vary in
$U^{B_{[u_B,v_B]}}$
. Letting B vary in
![]() $\mathcal {F} \setminus \{A\}$
, we see that a has at least
$\mathcal {F} \setminus \{A\}$
, we see that a has at least
![]() $t(t/8 - 1) + 1$
fixed lines which are not collinear with x. Supposing that
$t(t/8 - 1) + 1$
fixed lines which are not collinear with x. Supposing that
![]() $t \geq 32$
(the case
$t \geq 32$
(the case
![]() $t = 16$
will be handled separately below), we see that type 1 and 3 are indeed not possible (since such elements would fix at most
$t = 16$
will be handled separately below), we see that type 1 and 3 are indeed not possible (since such elements would fix at most
![]() $2t$
such lines).
$2t$
such lines).
Finally, suppose that a is of type 2. Suppose
![]() $\gamma \ne \mathrm {id}$
is an angle of a; then we have seen that
$\gamma \ne \mathrm {id}$
is an angle of a; then we have seen that
![]() $\gamma ^a = \gamma ^{-1}$
. If we inspect the specific form of a and suppose that
$\gamma ^a = \gamma ^{-1}$
. If we inspect the specific form of a and suppose that
![]() $\gamma = \alpha ^n$
, we get that
$\gamma = \alpha ^n$
, we get that
so that
![]() $\alpha ^{n(t/2 + 2)} = \mathrm {id}$
. This is only possible if
$\alpha ^{n(t/2 + 2)} = \mathrm {id}$
. This is only possible if
![]() $n = t$
(
$n = t$
(
![]() $\gamma = \mathrm {id}$
) or
$\gamma = \mathrm {id}$
) or
![]() $n = t/2$
(
$n = t/2$
(
![]() $\gamma = \alpha ^{t/2}$
). Now, let
$\gamma = \alpha ^{t/2}$
). Now, let
![]() $k \in K^\times $
be arbitrary, and consider
$k \in K^\times $
be arbitrary, and consider
![]() $V^k$
. Similarly as in the case
$V^k$
. Similarly as in the case
![]() $a \in N(A)^\times $
, we have that either
$a \in N(A)^\times $
, we have that either
![]() $[k,a] = \mathrm {id}$
or
$[k,a] = \mathrm {id}$
or
![]() $[k,a] = \alpha ^{t/2}$
.
$[k,a] = \alpha ^{t/2}$
.
The claim is proved.
The case
 $t = 16$
$t = 16$
We use the notation of the preceding part of the proof. Suppose again that
![]() $a \in A^{\times }$
is of type 1 or type 3. Suppose that
$a \in A^{\times }$
is of type 1 or type 3. Suppose that
![]() $\vert N(B) \vert = t/4$
; then B contains elements of every type. Suppose
$\vert N(B) \vert = t/4$
; then B contains elements of every type. Suppose
![]() $\beta \in B$
is an element of type 2. We have seen moments ago that for such an element, only angles in
$\beta \in B$
is an element of type 2. We have seen moments ago that for such an element, only angles in
![]() $\{ \mathrm {id}, \alpha ^{t/2} \}$
can arise. Whence the same is true for all elements in
$\{ \mathrm {id}, \alpha ^{t/2} \}$
can arise. Whence the same is true for all elements in
![]() $\langle N(B), \beta \rangle $
(which is a group of size
$\langle N(B), \beta \rangle $
(which is a group of size
![]() $2\vert N(B) \vert $
). It follows that
$2\vert N(B) \vert $
). It follows that
![]() $\vert B_{U(B), V(B)} \vert \geq \vert \langle N(B), \beta \rangle \vert /2 = \vert N(B) \vert $
. Note that
$\vert B_{U(B), V(B)} \vert \geq \vert \langle N(B), \beta \rangle \vert /2 = \vert N(B) \vert $
. Note that
![]() $U^{B_{U(B),V(B)}}$
consists of lines in
$U^{B_{U(B),V(B)}}$
consists of lines in
![]() $\{ [U], U(B), V(B) \}^{\perp }$
. Hence in the counting argument above, we can actually replace
$\{ [U], U(B), V(B) \}^{\perp }$
. Hence in the counting argument above, we can actually replace
![]() $t/8$
by
$t/8$
by
![]() $t/4$
(such as in the cases
$t/4$
(such as in the cases
![]() $\vert N(B) \vert = t/2$
and
$\vert N(B) \vert = t/2$
and
![]() $\vert N(B) \vert = t$
), and we obtain that a has at least
$\vert N(B) \vert = t$
), and we obtain that a has at least
![]() $t(t/4 - 1) + 1$
fixed lines which are not collinear with x. When
$t(t/4 - 1) + 1$
fixed lines which are not collinear with x. When
![]() $t = 16$
, this amount is strictly larger than
$t = 16$
, this amount is strictly larger than
![]() $2t$
, so we have a contradiction. When a is of type 2, the argument is the same as above. So if
$2t$
, so we have a contradiction. When a is of type 2, the argument is the same as above. So if
![]() $k \in K$
, we have that either
$k \in K$
, we have that either
![]() $[k,a] = \mathrm {id}$
or
$[k,a] = \mathrm {id}$
or
![]() $[k,a] = \alpha ^{t/2}$
for any
$[k,a] = \alpha ^{t/2}$
for any
![]() $a \in A$
.
$a \in A$
.
We have that
 $[K, K] \leq C_2$
(up to isomorphism)
$[K, K] \leq C_2$
(up to isomorphism)
This is easy now: Consider any commutator
![]() $[u, v]$
with
$[u, v]$
with
![]() $u, v \in K$
; then u and v are products of elements contained in the members of
$u, v \in K$
; then u and v are products of elements contained in the members of
![]() $\mathcal {F}$
. It follows that such a commutator is a product of (conjugates of) elements
$\mathcal {F}$
. It follows that such a commutator is a product of (conjugates of) elements
![]() $[e, f]$
, with
$[e, f]$
, with
![]() $e, f$
elements of members in
$e, f$
elements of members in
![]() $\mathcal {F}$
. Whence
$\mathcal {F}$
. Whence
![]() $[u, v]$
is a product of copies of
$[u, v]$
is a product of copies of
![]() $\alpha ^{t/2}$
. The claim follows.
$\alpha ^{t/2}$
. The claim follows.
We have that
 $\Gamma \cong W(p)$
with
$\Gamma \cong W(p)$
with
 $s = p$
a prime
$s = p$
a prime
Let
![]() $\alpha \in \mathcal {S}$
. Then we can write
$\alpha \in \mathcal {S}$
. Then we can write
![]() $\alpha $
as
$\alpha $
as
![]() $a_1a_2 \cdots a_k$
with each
$a_1a_2 \cdots a_k$
with each
![]() $a_k$
contained in some element of
$a_k$
contained in some element of
![]() $\mathcal {F}$
; it follows that
$\mathcal {F}$
; it follows that
with
![]() $\ell $
a product of commutators, implying that the order of each such
$\ell $
a product of commutators, implying that the order of each such
![]() $\alpha $
is at most
$\alpha $
is at most
![]() $4$
. This means that
$4$
. This means that
![]() $s = \vert \mathcal {S} \vert \leq 4$
as
$s = \vert \mathcal {S} \vert \leq 4$
as
![]() $\mathcal {S}$
is cyclic. By [Reference Bamberg, Glasby and Swartz1], we conclude that
$\mathcal {S}$
is cyclic. By [Reference Bamberg, Glasby and Swartz1], we conclude that
![]() $\Gamma \cong \mathcal {W}(s)$
with
$\Gamma \cong \mathcal {W}(s)$
with
![]() $s \in \{ 2, 4\}$
. Only in the case
$s \in \{ 2, 4\}$
. Only in the case
![]() $\Gamma \cong \mathcal {W}(2)$
, we have that
$\Gamma \cong \mathcal {W}(2)$
, we have that
![]() $\mathcal {S}$
is cyclic.
$\mathcal {S}$
is cyclic.
Now, suppose that
![]() $\zeta $
is not an injection. Let
$\zeta $
is not an injection. Let
![]() $a, \widetilde {a}$
be different nontrivial elements of
$a, \widetilde {a}$
be different nontrivial elements of
![]() $N(A)$
for which
$N(A)$
for which
![]() $\zeta (a) = \zeta (\widetilde {a})$
. Then as they have the same spectrum, it follows that
$\zeta (a) = \zeta (\widetilde {a})$
. Then as they have the same spectrum, it follows that
![]() $a\widetilde {a}$
is a symmetry with axis
$a\widetilde {a}$
is a symmetry with axis
![]() $[U]$
. Let S be the “kernel” of
$[U]$
. Let S be the “kernel” of
![]() $\zeta $
: this is the subgroup of symmetries of
$\zeta $
: this is the subgroup of symmetries of
![]() $N(A)$
with axis
$N(A)$
with axis
![]() $[U]$
. Now,
$[U]$
. Now,
![]() $\Big (N(A)/S \Big )^\times $
induces a subspace of
$\Big (N(A)/S \Big )^\times $
induces a subspace of
![]() $\Pi (B)^*$
(instead of
$\Pi (B)^*$
(instead of
![]() $N(A)^\times $
). Putting
$N(A)^\times $
). Putting
![]() $\vert N(A) \vert = 2^{h - m}$
,
$\vert N(A) \vert = 2^{h - m}$
,
![]() $m \in \{ 0, 1, 2 \}$
and
$m \in \{ 0, 1, 2 \}$
and
![]() $\vert S \vert = 2^k$
, and using the same notation as before, we obtain that
$\vert S \vert = 2^k$
, and using the same notation as before, we obtain that
![]() $2^{h - m - k - 1} - 1$
elements of
$2^{h - m - k - 1} - 1$
elements of
![]() $\Big (N(A)/S \Big )^\times $
fix
$\Big (N(A)/S \Big )^\times $
fix
![]() $x_U$
and
$x_U$
and
![]() $x'$
linewise (note that elements of
$x'$
linewise (note that elements of
![]() $N(A)/S$
act naturally on the lines in
$N(A)/S$
act naturally on the lines in
![]() $[U]^\perp $
). As each element of S also fixes
$[U]^\perp $
). As each element of S also fixes
![]() $x_U$
and
$x_U$
and
![]() $x'$
linewise, we obtain that
$x'$
linewise, we obtain that
![]() $(2^{h - m - k - 1} - 1)2^k + 2^k - 1 = 2^{h - m - 1} - 1$
nontrivial elements of
$(2^{h - m - k - 1} - 1)2^k + 2^k - 1 = 2^{h - m - 1} - 1$
nontrivial elements of
![]() $N(A)$
fix
$N(A)$
fix
![]() $x_U$
and
$x_U$
and
![]() $x'$
linewise, which is the exact same result as in the injective case. Note that the short alternative approach using angles also works here! Now, the rest of the proof is the same. It follows that
$x'$
linewise, which is the exact same result as in the injective case. Note that the short alternative approach using angles also works here! Now, the rest of the proof is the same. It follows that
![]() $\Gamma \cong \mathcal {W}(2)$
.
$\Gamma \cong \mathcal {W}(2)$
.
The proof is complete.
Theorem 6.2 immediately leads to a very short proof of Ott’s result:
Corollary 6.3 (Ott’s result)
Let
![]() $(\Gamma ,K)$
be an STGQ of even order t. If t is not a square, then
$(\Gamma ,K)$
be an STGQ of even order t. If t is not a square, then
![]() $\Gamma $
is a TGQ and K is elementary abelian.
$\Gamma $
is a TGQ and K is elementary abelian.
Acknowledgments
The author wants to express his gratitude to an anonymous referee for some very helpful remarks.
Competing interest
The authors have no competing interest to declare.