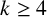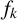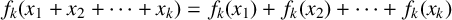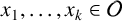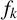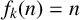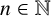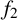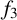MULTIPLICATIVE FUNCTIONS k-ADDITIVE ON GENERALISED OCTAGONAL NUMBERS

Abstract

Let $k\geq 4$ be an integer. We prove that the set $\mathcal {O}$ of all nonzero generalised octagonal numbers is a k-additive uniqueness set for the set of multiplicative functions. That is, if a multiplicative function $f_k$ satisfies the condition

$$ \begin{align*} f_k(x_1+x_2+\cdots+x_k)=f_k(x_1)+f_k(x_2)+\cdots+f_k(x_k) \end{align*} $$

for arbitrary $x_1,\ldots ,x_k\in \mathcal {O}$, then $f_k$ is the identity function $f_k(n)=n$ for all $n\in \mathbb {N}$. We also show that $f_2$ and $f_3$ are not determined uniquely.

1. Introduction

An arithmetic function $f:\mathbb {N}\to \mathbb {C}$ is called multiplicative if $f(1)=1$ and $f(mn)=f(m)f(n)$ whenever $\text {gcd}(m,n)=1$ . Let $\mathcal {M}$ denote the set of complex-valued multiplicative functions.

A set $E\subseteq \mathbb {N}$ is called an additive uniqueness set of a set of arithmetic functions $\mathcal {F}$ if $f\in \mathcal {F}$ is uniquely determined under the condition

(1.1) $$ \begin{align} f(m+n)=f(m)+f(n) \quad \text{for all } m,n\in E. \end{align} $$

For example, $\mathbb {N}$ and $\{1\}\cup 2\mathbb {N}$ are trivially additive uniqueness sets of $\mathcal {M}$ . This concept was first introduced by Spiro [12] in 1992. She proved that the set of primes is an additive uniqueness set of $\mathcal {M}_0=\{f\in \mathcal {M} \mid f(p_0)\neq 0 \ \text {for some prime}\ p_0\}$ . Spiro’s work has been extended in many directions.

Let $k\geq 2$ be a fixed integer. If there is only one function $f\in \mathcal {F}$ satisfying $f(x_1+x_2+\cdots +x_k)=f(x_1)+f(x_2)+\cdots +f(x_k)$ for arbitrary $x_i\in E$ , $i\in \{1,2,\ldots ,k\}$ , then E is called a k-additive uniqueness set of $\mathcal {F}$ .

In 2010, Fang [4] proved that the set of primes is a 3-additive uniqueness set of $\mathcal {M}_0$ . In 2013, Dubickas and Šarka [3] generalised Fang’s result to sums of an arbitrary number of primes. In 1999, Chung and Phong [2] showed that the set of positive triangular numbers $T_n=\tfrac 12n(n+1)$ , $n\in \mathbb {N}$ , and the set of positive tetrahedral numbers $ \textit {Te}_n=\tfrac 16n(n+1)(n+2)$ , $n\in \mathbb {N}$ , are new additive uniqueness sets for $\mathcal {M}$ and Park [10] extended their work to sums of k triangular numbers for $k\geq 3$ . Park [9] proved that the set of nonzero squares is a k-additive uniqueness set of $\mathcal {M}$ for every $k\geq 3$ , although it is not a 2-additive uniqueness set (see [1]). Recently, in [11], he showed that the set of positive cubes is a k-additive uniqueness set, like the set of positive squares, for multiplicative functions when $k\ge 3$ .

In 2018, Kim et al. [6] proved that the set of nonzero generalised pentagonal numbers $\mathcal {P}=\{\tfrac 12n(3n-1) \mid n\in \mathbb {Z}, n \ne 0\}$ , is an additive uniqueness set for $\mathcal {M}$ and the first author [5] extended their result to sums of k nonzero pentagonal numbers for $k\geq 3$ . Later, Kim et al. [7] showed that the set of positive pentagonal numbers and the set of positive hexagonal numbers $\mathcal {H}=\{n(2n-1)\,|\, n\in \mathbb {N}\}$ are new additive uniqueness sets for $\mathcal {M}$ . They also conjectured that among the sets of s-gonal numbers, only the sets of triangular, pentagonal and hexagonal numbers are additive uniqueness sets for $\mathcal {M}$ .

Let $\mathcal {O}=\{\mathcal {O}_m=m(3m-2) \mid m\in \mathbb {Z},m\neq 0\}$ be the set of nonzero generalised octagonal numbers. That is,

$$ \begin{align*} \mathcal{O}=\{1,5,8,16,21,33,40,56,65,85,\ldots\}. \end{align*} $$

The main result of this paper is the following theorem.

Theorem 1.1. Fix $k\ge 4$ . The set $\mathcal {O}$ of nonzero generalised octagonal numbers is a k-additive uniqueness set of $\mathcal {M}$ ; that is, if a multiplicative function $f_k$ satisfies

$$ \begin{align*} f_k(x_1+x_2+\cdots+x_k)=f_k(x_1)+f_k(x_2)+\cdots+f_k(x_k) \end{align*} $$

for arbitrary $x_1,\ldots ,x_k\in \mathcal {O}$ , then $f_k$ is the identity function.

In Sections 2 and 3, we will also show that $\mathcal {O}$ is neither an additive nor a $3$ -additive uniqueness set of $\mathcal {M}$ .

2. Non $2$ -additive uniqueness

Theorem 2.1. If a multiplicative function $f_2$ satisfies

$$ \begin{align*} f_2(a+b) = f_2(a)+f_2(b) \quad\text{ for }a,b \in \mathcal{O}, \end{align*} $$

then $f_2(2) = 2$ and $f_2(4)$ can be an arbitrary number. For other n, there are two possibilities for $f_2$ : either $f_2(n) = n$ or

$$ \begin{align*} f_2(n) = \begin{cases} 1 & \text{when}\ n\ \text{is odd},\\ 0 & \text{when}\ 8\mid n. \end{cases} \end{align*} $$

Proof. Trivially, $f_2(2) = 2$ .

Since $8$ and $16$ are generalised octagonal numbers and

$$ \begin{align*} f_2(3) \cdot f_2(8) = f_2(8) + f_2(16) = f_2(8) + f_2(8) + f_2(8), \end{align*} $$

if $f_2(8) \ne 0$ , then $f_2(3) = 3$ . Then, $f_2(5) = 5$ from

$$ \begin{align*} f_2(2)\cdot f_2(3) = f_2(1) + f_2(5) = 1+f_2(5). \end{align*} $$

Note that

$$ \begin{align*} f_2(13) &= f_2(5) + f_2(8) = 5 + f_2(8), \\ f_2(3) \cdot f_2(7) &= f_2(5) + f_2(16) = 5 + 2f_2(8), \\ f_2(2) \cdot f_2(11) &= f_2(1) + f_2(3) \cdot f_2(7) = 6 + 2f_2(8). \end{align*} $$

Thus, $f_2(8) = 8$ by solving

$$ \begin{align*} f_2(2) \cdot f_2(3) \cdot f_2(11) = f_2(1) + f_2(5) \cdot f_2(13) \Longleftrightarrow 3(6+2f_2(8)) = 1 + 5(5+f_2(8)). \end{align*} $$

Now assume that $f_2(8) = 0$ . Then,

$$ \begin{align*} f_2(13) = f_2(5 + 8) = f_2(5)\quad\text{and}\quad f_2(3) \cdot f_2(7) = f_2(5+16) = f_2(5). \end{align*} $$

Since

$$ \begin{align*} f_2(2) \cdot f_2(11) = f_2(1) + f_2(3) \cdot f_2(7) = 1 + f_2(5), \end{align*} $$

we obtain an equation $f_2(3)(1+f_2(5)) = 1 + f_2(5)^2$ from

$$ \begin{align*} f_2(2) \cdot f_2(3) \cdot f_2(11) = f_2(1) + f_2(5) \cdot f_2(13). \end{align*} $$

However, since $f_2(2) \cdot f_2(3) = 1+f_2(5)$ , we can conclude that

$$ \begin{align*} f_2(3) = f_2(5) = 1. \end{align*} $$

Note that if a generalised octagonal number is even, then it is divisible by $8$ . Also, the sum of two odd generalised octagonal numbers is singly even. So we cannot determine $f_2(4)$ . It can be an arbitrary value.

Now, we have two cases for the values of $f_2(n)$ for $n \le 8$ except $n=4$ :

$$ \begin{align*} &f_2(1) = 1, f_2(2) = 2, f_2(3) = 3, f_2(5) = 5, f_2(6) = 6, f_2(7) = 7, f_2(8) = 8;\\ &f_2(1) = 1, f_2(2) = 2, f_2(3) = 1, f_2(5) = 1, f_2(6) = 2, f_2(7) = 1, f_2(8) = 0. \end{align*} $$

Consider the first case. That is, let us show that $f_2(n)=n$ for all n except for  $4$ . We use induction on n. Suppose that $f_2(n)=n$ for $4\neq n<N$ . If N is not a prime power, then $N=ab$ with $\text {gcd}(a,b)=1$ and $f_2(N) = f_2(a) \cdot f_2(b) = ab =N$ by the multiplicativity of $f_2$ and the induction hypothesis. Thus, we may assume that $N=p^k$ is a prime power.

If $N = 2^r$ with $r \ge 4$ , then $f_2(N) = N$ from the equations

$$ \begin{align*} f_2(\mathcal{O}_{2^{r-2}} + \mathcal{O}_{2^{r-2}}) &= f_2( 2^{r-1}(3\cdot2^{r-3} - 1) + 2^{r-1}(3\cdot2^{r-3} - 1) ) \\ &= f_2(2^r) \cdot f_2(3\cdot2^{r-3} - 1) \\ &= f_2(2^r)\,(3\cdot2^{r-3} - 1) \end{align*} $$

and

$$ \begin{align*}f_2(\mathcal{O}_{2^{r-2}}) + f_2(\mathcal{O}_{2^{r-2}}) = 2 f_2( 2^{r-1} ) \cdot f_2(3\cdot2^{r-3} - 1) = 2^r (3\cdot2^{r-3} - 1),\end{align*} $$

since $3\cdot 2^{r-3}-1 < 2^r$ .

Now, suppose $N = 3^{2r+1}$ with $r \ge 1$ . In this case,

$$ \begin{align*} \mathcal{O}_{3^r} + \mathcal{O}_{-3^r} = 3^r(3\cdot3^r-2) + 3^r(3\cdot3^r+2) = 2 \cdot 3^{2r+1} \end{align*} $$

gives $f_2(3^{2r+1}) \kern1.3pt{=}\kern1.3pt 3^{2r+1}$ . Next, let us consider $N \kern1.3pt{=}\kern1.3pt 3^{2r}$ with $r \kern1.3pt{\ge}\kern1.3pt 2$ . Since ${3^2 \kern1.3pt{\equiv}\kern1.3pt -1 \pmod {5}}$ , we have $3^{2r} = 5m\pm 1$ with m even. Note that

$$ \begin{align*} \mathcal{O}_{-2m} + \mathcal{O}_{m+1} &= 4m(3m+1) + (m+1)(3m+1) = (3m+1)(5m+1), \\ \mathcal{O}_{-m+1} + \mathcal{O}_{2m} &= (m-1)(3m-1) + 4m(3m-1) = (3m-1)(5m-1). \end{align*} $$

Since $\gcd (m,3m+1) = \gcd (m+1,3m+1) = \gcd (3m+1,5m+1) = 1$ , and both of $4m$ and $3m+1$ are less than $5m+1$ , we can conclude that $f_2(5m+1) = 5m+1$ . Also, $f_2(5m-1) = 5m-1$ by the same method. Thus, $f_2(3^{2r}) = 3^{2r}$ .

The final case is $N = p^r$ with $p \ne 2,3$ . Note that $p^r = 6m\pm 1$ with $m \ge 2$ and

(*) $$ \begin{align} \begin{aligned} \mathcal{O}_{-4m} + \mathcal{O}_{-2m} = 8m(6m+1) + 4m(3m+1) = 12m(5m+1), \\ \mathcal{O}_{2m} + \mathcal{O}_{4m} = 8m(6m-1) + 4m(3m-1) = 12m(5m-1). \end{aligned} \end{align} $$

If $\gcd (8,m) = \gcd (4,3m\pm 1) = \gcd (4,5m\pm 1) = \gcd (3,5m\pm 1)$ , then (*) yields $f_2(6m\pm 1) = 6m\pm 1$ . However, otherwise, we must split each factor carefully. This part is complicated, so we break it into several cases. The proofs for $6m+1$ and $6m-1$ are similar, so we only treat $6m+1$ .

Case (i). $8m$ is a power of $2$ . In this case, letting $m = 2^r$ , $8m = 2^{r+3}$ is greater than $6m+1$ . So, we cannot apply the induction hypothesis to $f_2(8m)$ . However, note that

$$ \begin{align*} \mathcal{O}_{2^{r+1}} + \mathcal{O}_{2^{r+1}} = 2^{r+2}(3\cdot2^r-1) + 2^{r+2}(3\cdot2^r-1) = 2^{r+3}(3\cdot2^r-1) \end{align*} $$

and

$$ \begin{align*} 2^{r+2} = 4m < 6m+1 \quad\text{and}\quad 3\cdot2^r-1 = 3m-1 < 6m+1. \end{align*} $$

Thus, $f_2$ fixes $2^{r+3} = 8m$ .

Case (ii). $4(3m+1)$ is a power of $2$ . If we let $3m+1 = 2^r$ , then $4(3m+1) = 2^{r+2}$ and

$$ \begin{align*} \mathcal{O}_{2^r} + \mathcal{O}_{2^r} = 2^{r+1}(3\cdot2^{r-1}-1) + 2^{r+1}(3\cdot2^{r-1}-1) = 2^{r+2}(3\cdot2^{r-1}-1). \end{align*} $$

However, in this equation, $2^{r+1} = 2(3m+1)$ is not less than $6m+1$ . So, we apply this method again to verify $f_2(2^{r+1}) = 2^{r+1}$ .

Case (iii). The divisor $4(5m+1)$ of $12m(5m+1)$ is a power of $2$ . We can show that $f_2(4(5m+1)) = 4(5m+1)$ by applying the previous method twice.

Case (iv). The divisor $3(5m+1)$ of $12m(5m+1)$ is a power of $3$ . Since $\operatorname {ord}_5{3} = 4$ , we have $3(5m+1) = 3^{4r+1}$ . Thus,

$$ \begin{align*} \mathcal{O}_{3^{2r}} + \mathcal{O}_{-3^{2r}} = 3^{2r}(3\cdot3^{2r}-2) + 3^{2r}(3\cdot3^{2r}+2) = 2 \cdot 3^{4r+1}. \end{align*} $$

We can conclude that $f_2$ fixes $3(5m+1)$ .

Case (v). $4(5m+1) = 2^{a+2}\cdot 3$ with $a \ge 1$ . Since $\tfrac 134(5m+1)> 6m+1$ , we should check this case. Note that $5m+1$ is divisible by $2\cdot 3$ when $m = 6n+1$ with $n \ge 1$ . Then,

$$ \begin{align*} 5(6n+1)+1 = 2^a\cdot3 \Longleftrightarrow 5n+1 = 2^{a-1}. \end{align*} $$

If we take both sides modulo $5$ , we deduce that $a-1 = 4k$ . That is, $5n = 16^k-1$ with $k \ge 1$ . Calculating $6m+1$ :

$$ \begin{align*} 6m+1 &= 6(6n+1)+1 = 6^2 \times \frac{16^k-1}{5} + 7 \\ &= \frac{(6\cdot4^k)^2-1}{5} = \frac{1}{5}(6\cdot4^k+1)(6\cdot4^k-1). \end{align*} $$

Thus, $6m+1$ cannot be a power of a prime.

Case (vi). $3(5m+1) = 2\cdot 3^{b+1}$ with $b \ge 1$ . Note that $\tfrac 123(5m+1)> 6m+1$ . However, $m = 6n+1$ with $n \ge 1$ . Then,

$$ \begin{align*} 5(6n+1)+1 = 2\cdot3^b \Longleftrightarrow 5n+1 = 3^{b-1} \end{align*} $$

and thus $5n = 3^{4k} - 1$ with $k \ge 1$ . Thus,

$$ \begin{align*} 6m+1 = \tfrac{1}{5}(6\cdot9^k+1)(6\cdot9^k-1) \end{align*} $$

and this cannot be a power of p.

From (*) and Cases (i)–(vi), we can conclude that $f_2(6m+1) = 6m+1$ . Similarly, $f_2$ also fixes $6m-1$ . Hence, $f_2(n) = n$ except for $n=4$ .

By the same process, we can deduce the alternative with $f_2(2^r) = 0$ for $r \ge 3$ and $f_2(n) = 1$ if n is odd.

3. Non $3$ -additive uniqueness

Theorem 3.1. If a multiplicative function $f_3$ satisfies

$$ \begin{align*} f_3(a+b+c)=f_3(a)+f_3(b)+f_3(c) \end{align*} $$

for $a,b,c\in \mathcal {O}$ , then $f_3(n)=n$ for $n\neq 4$ , and $f_3(4)$ can be an arbitrary number.

Proof of Theorem 3.1.

Trivially, $f_3(3) = 3$ . Note that

$$ \begin{align*} f_3(7) &= f_3(5+1+1) = f_3(5) + 2,\\ f_3(11) &= f_3(5+5+1) = 2f_3(5)+1,\\ f_3(5)\cdot f_3(7) &= f_3(3)\cdot f_3(11) + f_3(1)+f_3(1). \end{align*} $$

If we set $a = f_3(5)$ , then $a(a+2) = 3(2a+1)+2$ . We obtain two solutions $a = -1$ and $a = 5$ .

If $f_3(5) = -1$ , then $f_3(8) = 2$ from

$$ \begin{align*} f_3(3) \cdot f_3(7) = 3 \cdot 1 = f_3(8+8+5) = 2f_3(8) -1. \end{align*} $$

However, this leads to a contradiction:

$$ \begin{align*} f_3(2) \cdot (-1) = f_3(2) \cdot f_3(5) &= f_3(8+1+1) = f_3(8) + 2 = 4, \\ f_3(2) = f_3(2) \cdot f_3(7) &= f_3(8+5+1) = f_3(8) = 2. \end{align*} $$

Thus, we can conclude that $f_3(5)=5$ . Then $f_3(n)=n$ for $n\le 8$ except $n=4$ . We can also find $f(9) = 9$ and $f(16) = 16$ from

$$ \begin{align*} f(2)\cdot f(9) = f(8+5+5) = 18, \quad f(2)\cdot f(9) = f(16+1+1) = f(16) + 2. \end{align*} $$

Let us show that $f_3(n)=n$ for all n except $n=4$ . We use induction on n. Suppose that $f_3(n)=n$ for $4\neq n<N$ . If N is not a prime power, then $N=ab$ with $\text {gcd}(a,b)=1$ and $f_3(N)=N$ by the multiplicativity of $f_3$ and the induction hypothesis. Thus, we may assume that N is a prime power.

If $N=3^r$ , then from the equalities

$$ \begin{align*} f_3(3\mathcal{O}_{3^{r-1}})&=3f_3(\mathcal{O}_{3^{r-1}})=3f_3(3^{r-1}(3^r-2))=3f_3(3^{r-1}) \cdot f_3(3^r-2)\\ &=f_3(3^r(3^r-2))=f_3(3^r) \cdot f_3(3^r-2), \end{align*} $$

we conclude that $f_3(3^r)=3^r$ since $f_3(3^r-2)=3^r-2$ by the induction hypothesis.

Now suppose that $N=2^{2s+1}$ with $s\ge 2$ . In this case,

$$ \begin{align*} \mathcal{O}_{2^s}+\mathcal{O}_{2^s}+\mathcal{O}_{-2^{s+1}}=2^{s+1}(3\cdot2^{s-1}-1)+2^{s+1}(3\cdot2^{s-1}-1)+2^{s+2}(3\cdot2^s+1)=9\cdot2^{2s+1} \end{align*} $$

yields $f_3(2^{2s+1})=2^{2s+1}$ since $3\cdot 2^{s-1}-1<2^{2s+1}$ , $3\cdot 2^s+1<2^{2s+1}$ . Next, assume that s is even and $N=2^{s+2}$ with $s\ge 4$ . In this case, from

$$ \begin{align*} \mathcal{O}_{2^{s-1}}+\mathcal{O}_{-2^{s-1}}+\mathcal{O}_{2^{s+1}} &=2^s(3\cdot2^{s-2}-1)+2^s(3\cdot2^{s-2}+1)+2^{s+2}(3\cdot2^s-1)\\ &=2^{s+2}(27\cdot2^{s-3}-1), \end{align*} $$

we have $f_3(2^{s+2})=2^{s+2}$ since $3\cdot 2^{s-2}\pm 1<2^{s+2}$ , $3\cdot 2^s-1<2^{s+2}$ and $27\cdot 2^{s-3}-1<2^{s+2}$ .

Now consider $N = p^r$ with $p \ne 2,3$ . Assume $N = p^r = 6m-1$ with $m \ge 1$ and $f_3(n) = n$ for all $n < N$ .

Note that

$$ \begin{align*} \mathcal{O}_m + \mathcal{O}_m + \mathcal{O}_{4m} &= m(3m-2) + m(3m-2) + 8m(6m-1) = 6m(9m-2), \\ \mathcal{O}_{2m} + \mathcal{O}_{2m} + \mathcal{O}_{4m} &= 4m(3m-1) + 4m(3m-1) + 8m(6m-1) = 8m(9m-2). \end{align*} $$

To calculate $f_3(6m-1)$ , we consider two cases.

Case (i). m is odd. In this case, $\gcd (m,3m-2) = \gcd (2,m) = \gcd (m,9m-2) = 1$ and every factor of the above two equations is less than $6m-1$ except $9m-2$ or a power of $2$ or $3$ . So, letting $x = f_3(6m-1)$ and $y = f_3(9m-2)$ , we can write

$$ \begin{align*} m(3m-2) + m(3m-2) + 8m\,x = 6m\,y, \\ 4m(3m-1) + 4m(3m-1) + 8m\,x = 8m\,y, \end{align*} $$

and these equations yield $x = f_3(6m-1) = 6m-1$ and $y = f_3(9m-2) = 9m-2$ .

Case (ii). m is even. Let $m = 2n$ . Then, we should check $f_3(12n-1)$ . Note that

$$ \begin{align*} \mathcal{O}_m + \mathcal{O}_m + \mathcal{O}_{4m} = 4n(3n-1) + 4n(3n-1) + 16n(12n-1) = 12n(9n-1) \end{align*} $$

and $\gcd (n,3n-1) \kern1.4pt{=}\kern1.4pt \gcd (2,12n-1) \kern1.4pt{=}\kern1.4pt \gcd (n,12n-1) \kern1.4pt{=}\kern1.4pt \gcd (n,9n-1) \kern1.4pt{=}\kern1.4pt 1$ , and every factor is less than $12n-1$ or a power of $2$ or $3$ . However, we have an exceptional case to check: $16n$ is a power of $2$ greater than $12n-1$ . In this case, we can use the equalities for $f_3(2^r)$ . So, $f_3$ fixes every factor. Thus, if we rearrange the equality

$$ \begin{align*} 4n(3n-1) + 4n(3n-1) + 16n\,f_3(12n-1) = 12n(9n-1), \end{align*} $$

we obtain $f_3(6m-1) = f_3(12n-1) = 12n-1$ .

For the case $N = p^r = 6m+1$ , we can use $\mathcal {O}_{-m} = m(3m+2)$ .

4. $4$ -additive uniqueness

Theorem 4.1. If a multiplicative function $f_4$ satisfies

$$ \begin{align*} f_4(a+b+c+d)=f_4(a)+f_4(b)+f_4(c)+f_4(d) \end{align*} $$

for $a,b,c,d\in \mathcal {O}$ , then $f_4$ is the identity function.

We will need the following lemma.

Lemma 4.2 (Kim et al. [8, Theorem 4.7]).

For any integer $k\ge 4$ , any positive integer n is a sum of k nonzero generalised octagonal numbers, except for $n=1,2,\ldots ,k-1$ and $k+b$ , where $b\in B=\{1,2,3,5,6,9,10,13,17\}$ .

Proof of Theorem 4.1.

By Lemma 4.2, every positive integer can be represented as a sum of four nonzero generalised octagonal numbers except for $1,2,3,5,6,7,9,10,13$ , $14,17,21$ . Note that it is sufficient to determine $f_4(n)$ for $n=2,3,5,7,9,13,17$ .

Trivially, $f_4(1)=1$ and $f_4(4)=4$ . Note that $f_4(12)=4f_4(3)=f_4(5+5+1+1)=2f_4(5)+2$ . Thus, $f_4(3)=\tfrac 12(f_4(5)+1)$ . Moreover,

$$ \begin{align*} f_4(8) &=f_4(5+1+1+1)=f_4(5)+3,\\ f_4(11) &=f_4(8+1+1+1)=f_4(5)+6. \end{align*} $$

Now observe that

$$ \begin{align*} f_4(40)&=f_4(8) \cdot f_4(5)=(f_4(5)+3) \cdot f_4(5)\\ &=f_4(33+5+1+1)=f_4(3) \cdot f_4(11)+f_4(5)+2=f_4(3)(f_4(5)+6)+f_4(5)+2. \end{align*} $$

After simplification,

$$ \begin{align*} f_4(5)^2+2f_4(5)=f_4(3)(f_4(5)+6)+2. \end{align*} $$

For convenience, let $f_4(5)=a$ . Then $2a^2+4a=(a+1)(a+6)+4$ and we obtain two solutions $f_4(5)=-2$ and $f_4(5)=5$ . The first solution yields $f_4(3)=-\tfrac 12$ and

$$ \begin{align*} f_4(16) &=3f_4(5)+1=-5,\\ f_4(21) &=f_4(3)(f_4(5)+3)-3=-\tfrac{7}{2}. \end{align*} $$

However, this leads to a contradiction:

$$ \begin{align*} f_4(48)& =f_4(21+21+5+1)=2f_4(21)+f_4(5)+1=-8\\ & =f_4(16) \cdot f_4(3)=\tfrac{5}{2}. \end{align*} $$

Thus, we can conclude that $f_4(3)=3$ , $f_4(5)=5$ and $f_4(7)=7$ . Since

$$ \begin{align*} f_4(30) &=f_4(2)\cdot f_4(3)\cdot f_4(5)=f_4(1+5+8+16),\\ f_4(18) &=f_4(2)\cdot f_4(9)=f_4(8+8+1+1),\\ f_4(26) &=f_4(13)\cdot f_4(2)=f_4(16+8+1+1),\\ f_4(34) &=f_4(17)\cdot f_4(2)=f_4(16+16+1+1), \end{align*} $$

we find $f_4(2)=2$ , $f_4(9)=9$ , $f_4(13)=13$ and $f_4(17)=17$ .

Since other numbers can be expressed as sums of four positive generalised octagonal numbers, we can conclude that $f_4$ is the identity function by induction.

5. $5$ -additive uniqueness

Theorem 5.1. If a multiplicative function $f_5$ satisfies

$$ \begin{align*} f_5(a+b+c+d+e)=f_5(a)+f_5(b)+f_5(c)+f_5(d)+f_5(e) \end{align*} $$

for $a,b,c,d,e\in \mathcal {O}$ , then $f_5$ is the identity function.

Proof of Theorem 5.1.

By Lemma 4.2, the exceptional set is

$$ \begin{align*}\{1,2,3,4\}\cup\{6,7,8,10,11,14,15,18,22\}.\end{align*} $$

Note that $f_5(5)=5$ and $f_5(9)=f_5(5+1+1+1+1)=f_5(5)+4=9$ . So it is sufficient to determine $f_5(n)$ for $n=2,3,4,7,8,11$ . Note that

$$ \begin{align*} f_5(16)=f_5(8+5+1+1+1)=f_5(8)+8. \end{align*} $$

Then

$$ \begin{align*} f_5(72)=9f_5(8)=f_5(16+16+16+16+8)=4f_5(16)+f_5(8)=5f_5(8)+32. \end{align*} $$

Therefore, $f_5(8)=8$ and from $f_5(24)=f_5(3) \cdot f_5(8)=f_5(8+5+5+5+1)= 16+f_5(8)$ , we get $f_5(3)=3$ . Similarly, from

$$ \begin{align*} f_5(30)&=5f_5(2) \cdot f_5(3)=f_5(8+8+8+5+1)=3f_5(8)+6,\\ f_5(36)&=9f_5(4)=f_5(5+5+5+5+16)=20+f_5(16),\\ f_5(21)&=f_5(3)\cdot f_5(7)=f_5(5+5+5+5+1)=21,\\ f_5(33)&=f_5(3)\cdot f_5(11)=f_5(8+8+8+8+1)=4f_5(8)+1, \end{align*} $$

we deduce that $f_5(2)=2$ , $f_5(4)=4$ , $f_5(7)=7$ and $f_5(11)=11$ , respectively.

Since other numbers can be represented as sums of five positive generalised octagonal numbers, we can conclude that $f_5$ is the identity function by induction.

6. Proof for k-additivity with $k\ge 6$

Let $k\geq 6$ and $f_k$ be k-additive on positive generalised octagonal numbers. That is, $f_k(x_1+x_2+\dotsb +x_k)=f_k(x_1)+f_k(x_2)+\dotsb +f_k(x_k)$ for arbitrary $x_1,\ldots ,x_k\in \mathcal {O}$ . Trivially, $f_k(1)=1$ and $f_k(k)=k$ .

Note that

$$ \begin{align*} (k-3)+18&=(k-3)\cdot1+5+5+8\\ &=(k-3)\cdot1+1+1+16,\\ (k-3)+37&=(k-3)\cdot1+8+8+21\\ &=(k-3)\cdot1+5+16+16,\\ (k-3)+42&=(k-3)\cdot1+5+16+21\\ &=(k-3)\cdot1+40+1+1,\\ (k-5)+64&=(k-5)\cdot1+8+8+16+16+16\\ &=(k-5)\cdot1+1+1+1+21+40. \end{align*} $$

Let $x=f_k(5)$ , $y=f_k(8)$ , $z=f_k(16)$ and $w=f_k(21)$ . The above equalities give rise to the system of equations

$$ \begin{align*} \begin{cases} 2x+y=2+z,\\ 2y+w=x+2z,\\ x+z+w=2+xy,\\ 2y+3z=3+xy+w. \end{cases} \end{align*} $$

The solutions are

$$ \begin{gather*} f_k(5)=f_k(8)=f_k(16)=f_k(21)=1,\\ f_k(5)=5, f_k(8)=8, f_k(16)=16, f_k(21)=21. \end{gather*} $$

Consider the first solution set $f_k(5)=f_k(8)=f_k(16)=f_k(21)=1$ . Arrange the positive generalised octagonal numbers into an increasing sequence and let $O_n$ denote the nth term. Then $f_k(O_1)=f_k(O_2)=f_k(O_3)=f_k(O_4)=f_k(O_5)=1$ . As seen in Section 5, every $O_n$ with $n\geq 6$ can be written as a sum of five positive generalised octagonal numbers. From the equality

(6.1) $$ \begin{align} (k-6)+1+1+1+16+21+O_f =(k-6)+40+O_a+O_b+O_c+O_d+O_e \end{align} $$

with $a,b,c,d,e<f$ , we infer that $f_k(O_n)=1$ for all $n\geq 6$ inductively. However, for sufficiently large n, $O_n$ can be represented as a sum of k positive generalised octagonal numbers. So $f_k(O_n)=k$ , which is a contradiction.

Hence, we conclude that $f_k(5)=5$ , $f_k(8)=8$ , $f_k(16)=16$ and $f_k(21)=21$ . Moreover, (6.1) yields $f_k(O_n)=O_n$ for every $n\geq 1$ .

If N is a sum of k positive generalised octagonal numbers, then $f_k(N)=N$ . Otherwise, choose an integer $M>k+17$ such that $\text {gcd}(M,N)=1$ . Then M and $MN$ can be represented as sums of k positive generalised octagonal numbers by Lemma 4.2. By the multiplicativity of $f_k$ , $Mf_k(N)=f_k(M) \cdot f_k(N)=f_k(MN)=MN$ . Therefore, $f_k(N)=N$ and this completes the proof.