Introduction
Repetitive structures abound in nature, providing a modular substrate for evolution. At the genomic level, repeated sequences are an economical way to achieve reprogrammability of a protein or system. For example, transcriptional activator-like effectors (TALEs) from the rice pathogen Xanthomonas bind specific sequences of DNA using repeated blocks of 33–34 amino acids that contain two variable residues that confer individual base pair specificity (Boch et al., Reference Boch, Scholze, Schornack, Landgraf, Hahn, Kay, Lahaye, Nickstadt and Bonas2009; Moscou and Bogdanove, Reference Moscou and Bogdanove2009). By varying these two residues and combining the repeat blocks, TALEs can target a wide range of DNA sequences. Repetitive structures also underlie adaptive response systems, such as antibodies, CRISPR-Cas systems (Hille et al., Reference Hille, Richter, Wong, Bratovič, Ressel and Charpentier2018), and polyketide synthases (Khosla et al., Reference Khosla, Gokhale, Jacobsen and Cane1999), which are capable of creating a large diversity of compounds from different combinations of repeated basic subunits that appear in different combinations in the synthesis enzymes.
As is clear even from these few examples, repetition can take different forms. Consider the case of nucleic acid targeting systems (Gaj et al., Reference Gaj, Gersbach and Barbas2013), including meganucleases, TALEs, zinc fingers and CRISPR-Cas (Fig. 1 a). All of these systems share the basic feature that mutagenesis of key regions results in altered substrate specificity; however, these systems differ in their levels of modularity in determining their nucleic acid binding specificity. In contrast to meganucleases, which have multiple scattered residues that determine the binding specificity, zinc finger repeats can bind to 3–4 base pairs allowing multiple repeats to be chained together to bind longer nucleic acids in a sequence specific manner. TALEs and CRISPRs also use repeats, but additionally have a one-to-one mapping between the repeat units (protein repeat subunit and guide RNA sequence respectively) and the individual bases of the target DNA, providing more extensive modularity (Fig. 1 a). For TALEs and CRISPRs, the regions in each repeat that confer binding specificity are also the most variable: for TALEs, it is the variable di-residue in each protein repeat unit, and for CRISPRs, it is the spacer RNA adjacent to each direct repeat.
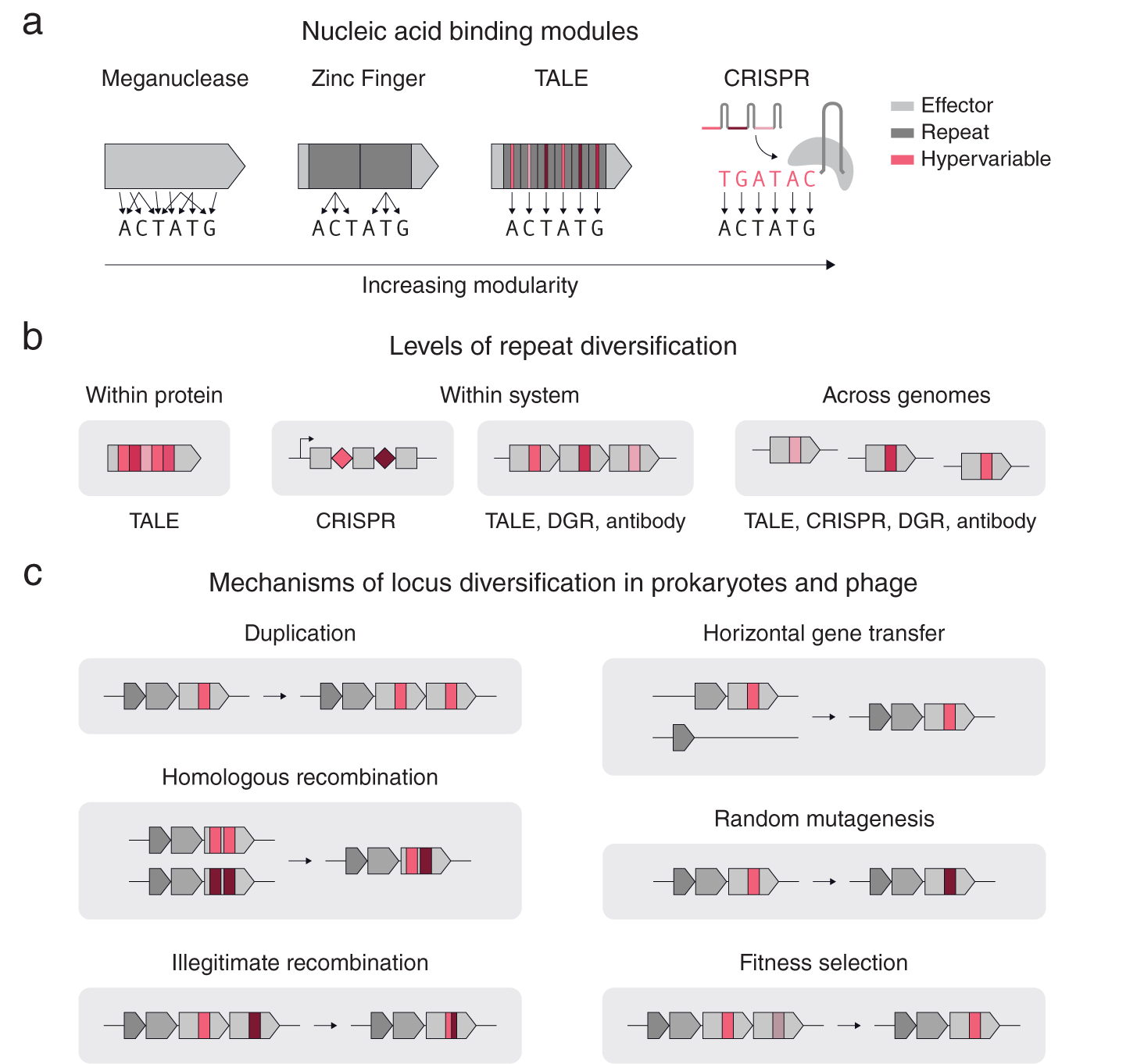
Fig. 1. Repeat structures in proteins and systems. (a) A comparison of different nucleic acid binding modules according to their modularity. Zinc Fingers, TALEs, and CRISPRs use repeats (dark grey), while TALEs and CRISPRs have hypervariable regions within their repeats that precisely determine the DNA binding specificity (red). (b) A schematic of different types of repeats and their diversification. (c) Basic mechanisms of diversification in prokaryotic genomes.
Repetition can also span across genomes (Fig. 1 b). Another example of cross-system repetition is diversity-generating retroelements (DGRs). DGRs consist of a target protein with a repeated downstream template region that is mutagenized in a targeted manner by an associated retrotransposon. In eukaryotic antibody systems, an array of highly related pseudogenes recombine in different combinations in individual cells to form different kinds of antibodies or T-cell receptors capable of binding to different substrates. Modular systems often contain diversification at multiple levels. For example, CRISPR-Cas systems have diversification within each system (multiple CRISPR repeats with different spacers) and across genomes (different CRISPR arrays near identical cas genes).
Multiple mechanisms exist for diversifying repeats at these three levels (Fig. 1 c). For genes with repeat units, illegitimate recombination and homologous recombination allow rapid diversification of the gene by shuffling the order of the repeats. Gene duplication, allows individual proteins to be repeated into arrays within a locus for subsequent diversification by random mutagenesis and DNA recombination. Horizontal gene transfer, homologous recombination and fitness selection additionally allow for rapid repeat diversification to occur across related genomes. Specialized mechanisms also exist for specific systems, such as Cas1–Cas2 spacer acquisition for CRISPR, or reverse transcriptase – Avd mediated homing mutagenesis for diversity generating retroelements (Roux et al., Reference Roux, Paul, Bagby, Allen, Attwood, Cavicchioli, Chistoserdova, Hallam, Hernandez, Hess, Liu, O’Malley, Peng, Rich, Saleska and Eloe-Fadrosh2020).
From within proteins to across genomes, these examples highlight how repeat elements serve as modular templates for complex adaptive response systems, facilitating the rapid modification of key components that interact with substrates while allowing the rest of the system to stay constant. This modularity reduces the evolutionary time required to adapt to new substrate requirements in quickly changing environments. We thus hypothesize that a key signature for adaptive response systems is the presence of diversifying repeats. At a genomic level, this would entail multiple (possibly neighbouring) copies of a CDS or non-coding region that have at least one region of hyper variation between the copies.
The exponentially increasing number of sequenced and annotated genomes (Koonin and Wolf, Reference Koonin and Wolf2008; Land et al., Reference Land, Hauser, Jun, Nookaew, Leuze, Ahn, Karpinets, Lund, Kora, Wassenaar, Poudel and Ussery2015) is enabling a new wave of bioinformatic mining through computational searches for genomic signatures or hallmarks, as opposed to just searching for sequence homology. These searches have already led to the discovery of a number of new molecular systems (Doron et al., Reference Doron, Melamed, Ofir, Leavitt, Lopatina, Keren, Amitai and Sorek2018; Yan et al., Reference Yan, Hunnewell, Alfonse, Carte, Keston-Smith, Sothiselvam, Garrity, Chong, Makarova, Koonin, Cheng and Scott2019; Makarova et al., Reference Makarova, Wolf, Iranzo, Shmakov, Alkhnbashi, Brouns, Charpentier, Cheng, Haft, Horvath, Moineau, Mojica, Scott, Shah, Siksnys, Terns, Venclovas, White, Yakunin, Yan, Zhang, Garrett, Backofen, Oost, Barrangou and Koonin2020; Roux et al., Reference Roux, Paul, Bagby, Allen, Attwood, Cavicchioli, Chistoserdova, Hallam, Hernandez, Hess, Liu, O’Malley, Peng, Rich, Saleska and Eloe-Fadrosh2020; Gao et al., Reference Gao, Altae-Tran, Böhning, Makarova, Segel, Schmid-Burgk, Koob, Wolf, Koonin and Zhang2020). Here we report a set of computational approaches to identify systems that contain evidence of repeat diversification, which may represent novel, potentially adaptive prokaryotic, eukaryotic, and viral systems. Our search reveals thousands of potentially diversified clusters of systems, five of which we studied in greater detail. Together, our results demonstrate the feasibility of using repetition as a hallmark signature to seed computational searches to identify candidate novel adaptive systems and highlight the many ways molecular repetition is used throughout nature.
Results
Establishing a computational pipeline to identify repeat signatures
We searched for diversified repeats in two contexts (Fig. 2 a,b): within protein repeats and repeated proteins within a system. Variation occurring on the protein or within system levels occurs at a faster evolutionary time scale than variation across organisms. We therefore reasoned that diversified repeats within these two contexts may be indicative of systems capable of responding to new selection pressures with minimal modification. Systems displaying either of these forms of diversified repeats can be mined from sequenced genomes by combining repeat motif detection algorithms with alignment scoring metrics that prioritize systems with localized hypervariation over those with random variation, which can be attributable to evolutionary drift. Localized hypervariation flanked by conserved regions can create a modular system, where small changes are embedded in the context of constant structure and function.
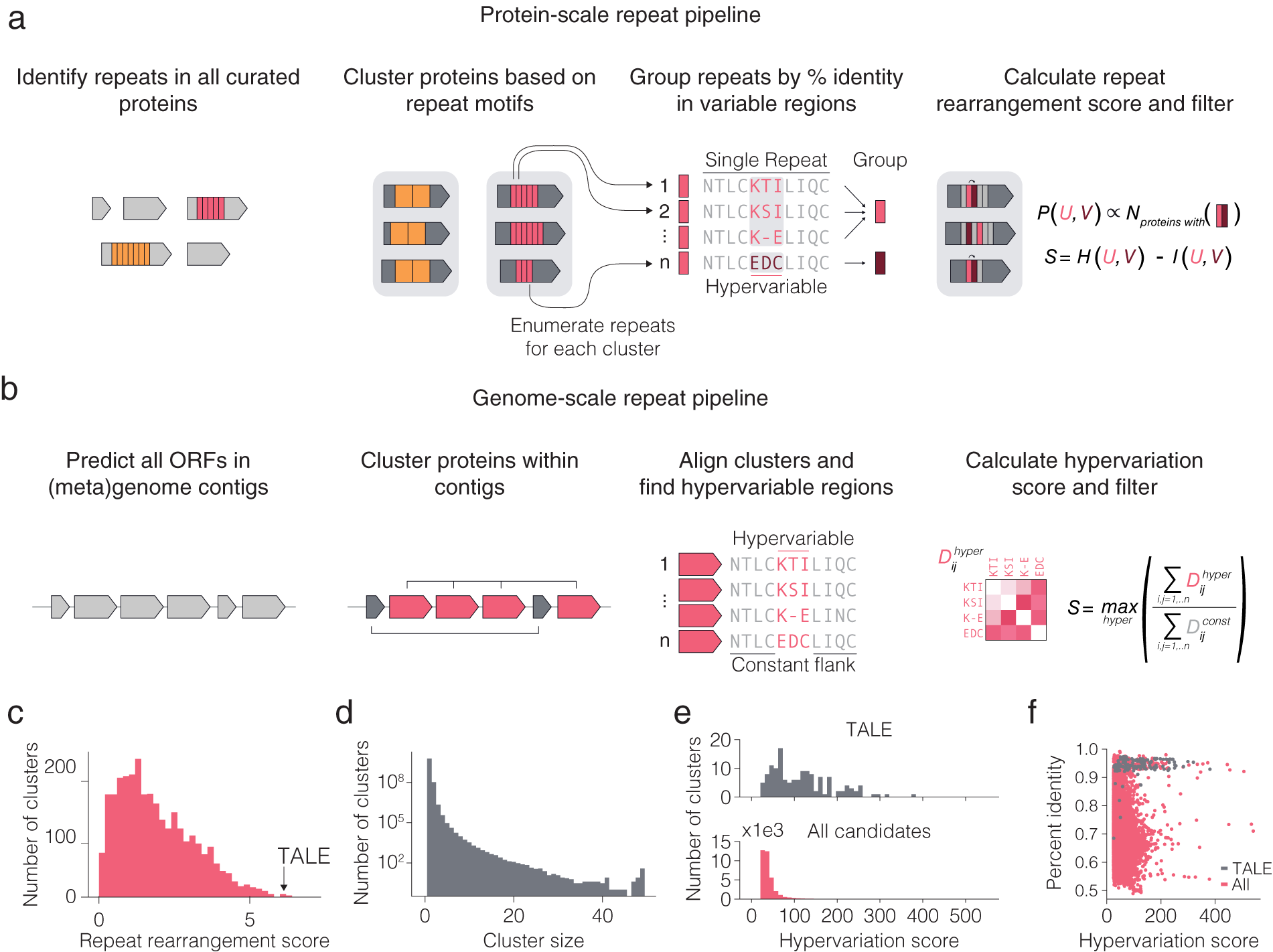
Fig. 2. Computational pipeline design for repeat protein analysis. (a) Schematic of protein-scale repeat pipeline. In the right most panel, N is the number of proteins containing a specific neighbouring repeat pair, while P (U,V) is the estimated joint distribution of neighbouring repeat pairs (u,v) obtained by counting the number of proteins with each specific pair of repeats and normalizing by the sum of all counts. The repeat rearrangement score, S, is the variation of information metric obtained by subtracting the mutual information, I (U,V), from the joint entropy, H (U,V). (b) Schematic of genome-scale repeat pipeline. The hypervariation score consists of computing an adjusted, non-redundant distance matrix between the hypervariable regions, and similarly for the constant regions. The hypervariation score, S, is the maximum ratio of the sum of the adjusted distance matrices over all hypervariable regions in the alignment. (c) Histogram of non-zero repeat rearrangement scores for hits from the protein-scale repeat pipeline, with an indicator for the score of the highest scoring TALE cluster. (d) Distribution of cluster sizes from the genome-scale repeat pipeline. ( e ) Distribution of the hypervariation score of all hits, with an indicator for score of the highest scoring TALE cluster. (f) Scatter plot of all within cluster percent identities and corresponding hypervariation score.
To computationally mine for these types of systems, we first developed a pipeline for identifying systems with diversified repeats at the protein level (Fig. 2 a). We searched all proteins in UniRef100 for repeat motifs, filtered for repeats with hypervariable positions, and then clustered the proteins with repeats into families on the basis of their repeat features. For each family of repeat proteins, the repeats found in the family were grouped into major repeat archetypes (e.g. TALE repeat) and subtypes (e.g. TALE repeats containing hypervariable residues HD vs. NI vs. NN) and used a repeat rearrangement scoring metric to identify protein families that display extensive rearrangement of the protein (Fig. 2 c,d). We identified 4,017 candidate hypervariable repeat protein clusters (Fig. 2 e). The representative TALE cluster scored among the highest of all candidates, suggesting that repeat protein families with both localized hypervariation and extensive rearrangement of repeats across different variants are exceptionally rare in nature. We identified three candidate systems for further analysis – a tomato transcription factor, a slime mold leucine-rich repeat (LRR) protein with only two hypervariable amino acids, and a bacterial cell-surface LRR protein.
We subsequently developed a pipeline for identifying systems with repeated, non-identical copies of the same protein (which we refer to as variants) in the locus (Fig. 2 b). Because genes with related functions tend to spatially cluster in prokaryotic genomes (Aravind, Reference Aravind2000), we restricted this search to prokaryotic genomes and metagenomes to find diversified systems for which inference of function would more likely be possible. For each genomic contig, we clustered all the proteins on that contig and retained clusters with six or more variants. Next, for each cluster, we aligned the proteins and used a hypervariation scoring metric to identify clusters with at least one region in the protein with high sequence variation flanked by two regions of high sequence conservation (Fig. 2 f). All candidate systems from the analysis were further clustered into 3,040 candidate families of systems. In addition to being diversified repeat proteins, TALEs can also be found in multiple copies with regions of hyper variation (insertion and deletions of entire repeats in the middle of the protein) in the same genomic contig. Representative TALE clusters scored similarly to many other clusters, suggesting that many other systems share the within-system diversification feature that natural TALE loci possess. In the following sections, we describe a number of interesting systems that came out of our initial analysis.
A locus containing tandem repeats of LRR proteins
Using both pipelines, we identified a genomic region in 17 isolates of Flavobacterium psychrophilum, a fish pathogen that causes bacterial cold water disease in rainbow trout (Duchaud et al., Reference Duchaud, Boussaha, Loux, Bernardet, Michel, Kerouault, Mondot, Nicolas, Bossy, Caron, Bessières, Gibrat, Claverol, Dumetz, Hénaff and Benmansour2007; Castillo et al., Reference Castillo, Christiansen, Dalsgaard, Madsen, Espejo and Middelboe2016). These regions contained up to 19 tandem repeats of a putative cell surface protein (Fig. 3 a). Each protein contains 2–14 internal LRRs (Fig. 3 b–d), a class of ~22-residue repeat motifs that contain several hypervariable positions. LRRs, which are also present in variable lymphocyte receptors (VLRs) in lampreys and hagfish (Herrin et al., Reference Herrin, Alder, Roux, Sina, Ehrhardt, Boydston, Turnbough and Cooper2008; Boehm et al., Reference Boehm, McCurley, Sutoh, Schorpp, Kasahara and Cooper2012), have been shown to mediate tight binding to diverse molecular targets (Kobe, Reference Kobe2001; Ng and Xavier, Reference Ng and Xavier2011). The F. psychrophilum LRR proteins also contain a conserved N-terminal secretion peptide and C-terminal type 9 secretion signal, which may provide an anchor to the cell surface via a conjugated lipoprotein (Lasica et al., Reference Lasica, Ksiazek, Madej and Potempa2017). Structural modelling suggests these proteins adopt a fold similar to known LRR proteins, with the repeat units arranged in a solenoidal configuration and the hypervariable residues concentrated on one side, forming a putative binding interface (Fig. 3 e). Although the exact function of these proteins is unknown, they have been suggested to play a role in bacterial adhesion (Duchaud et al., Reference Duchaud, Boussaha, Loux, Bernardet, Michel, Kerouault, Mondot, Nicolas, Bossy, Caron, Bessières, Gibrat, Claverol, Dumetz, Hénaff and Benmansour2007) and perhaps are also utilized by bacteriophage as receptors (Castillo et al., Reference Castillo, Christiansen, Dalsgaard, Madsen and Middelboe2015).
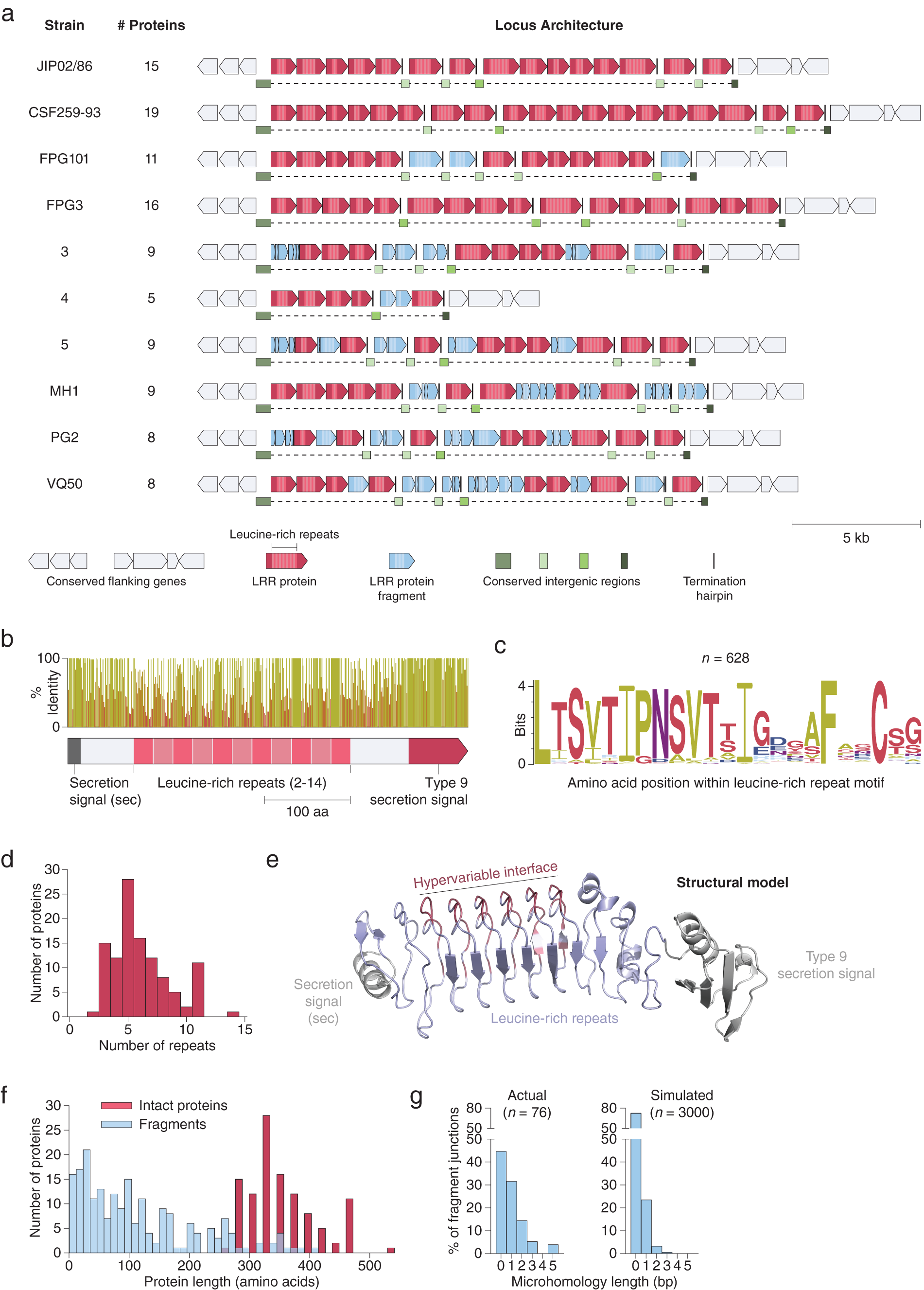
Fig. 3. Extensive signatures of modularity and recombination in a leucine-rich repeat (LRR) protein locus from Flavobacterium psychrophilum. (a) Graphical annotation of the LRR protein loci from ten strains of F. psychrophilum. (b) Domain architecture and sequence identity of a prototypical LRR protein (JIP02/86 #8). (c) Amino acid sequence logo of individual repeat units (n = 628) within intact LRR proteins. (d) Histogram of the number of repeat units within intact LRR proteins. (e) Structural model (trRosetta) of a prototypical LRR protein, highlighting the hypervariable positions (red) within the repeat units. The model was constructed from the first LRR protein in strain JIP02/86 (WP_011962357.1). (f) Size distribution of intact LRR proteins (red; n = 111) and protein fragments (blue; n = 206). (g) DNA microhomologies at high-confidence fragment-fragment junctions (left). Simulated microhomologies (right) based on random fragmentation of three intact loci (JIP02/86, CSF259-93, and FPG3).
Although independent instances of these LRR loci have been previously reported (Duchaud et al., Reference Duchaud, Boussaha, Loux, Bernardet, Michel, Kerouault, Mondot, Nicolas, Bossy, Caron, Bessières, Gibrat, Claverol, Dumetz, Hénaff and Benmansour2007; Castillo et al., Reference Castillo, Christiansen, Dalsgaard, Madsen and Middelboe2015), our examination of all the sequenced F. psychrophilum strains in Genbank reveals that each strain has significant differences in the number and lengths of LRR proteins as well as in the sequences of their repeat motifs, despite conservation of flanking genes (Fig. 3 a and Supplementary Fig. S1). Analysis of these loci at the nucleotide resolution revealed signatures of extensive recombination: The large stretches of DNA between LRR proteins, previously unannotated, in fact consist of broken fragments of LRR genes stuck together (Fig. 3 a, f). Indeed, every nucleotide is either part of an intact LRR gene, an LRR gene fragment, or one of two conserved types of putative intergenic regions (Fig. 3 a).
Given that these loci are marked by a complete absence of mobilome genes (e.g. transposons), we sought to further characterize the recombination within the LRR loci by mapping the boundaries of each gene fragment at single-nucleotide resolution (Supplementary Fig. S2a). Fragment-fragment junctions occur mostly within coding regions (Supplementary Fig. S2b) and are enriched in 1–5 base pair overlapping microhomologies relative to random fragmentation (Fig. 3 g). The pattern of fragmentation with junction microhomologies is consistent with illegitimate recombination, such as from strand slippage during replication or targeted DNA double-strand breaks (Darmon and Leach, Reference Darmon and Leach2014). Moreover, recombination within the LRR loci may occur on short timescales, as previous work reported that F. psychrophilum clones obtained after several days of phage challenge acquired differences in the DNA sequences of their LRR loci relative to the parental strain (Castillo et al., Reference Castillo, Christiansen, Dalsgaard, Madsen and Middelboe2015) (Supplementary Fig. S1).
Leucine-rich repeat (LRR) proteins from Dictyostelium purpureum
We also identified over 90 LRR proteins (O’Day et al., Reference O’Day, Suhre, Myre, Chatterjee-Chakraborty and Chavez2006) encoded in the genome of Dictyostelium purpureum, a species of social amoeba named for its distinctively purple spores. These proteins vary in the number of repeat motifs they contain (Fig. 4 a). The LRR motifs in D. purpureum were distinct from those in F. psychrophilum and contained two consecutive hypervariable residues within the motif, which bears resemblance to the variable di-residue found in TALEs (Fig. 4 b). The amino acid composition of the first hypervariable position is dominated by tyrosine (22%), aspartic acid (19%), histidine (13%), and asparagine (11%), while the amino acid composition of the second hypervariable position is dominated by aspartic acid (22%), tyrosine (15%), cysteine (10%), and asparagine (9%). Some pairs of hypervariable residues are more likely to be present than others, such as YD, YY, DD, YC and ND (Fig. 4 d). Structural modelling indicated an extended horseshoe-like structure (Fig. 4 c) with the hypervariable residues (sticks) forming an interface along a side of the horseshoe. The low frequency of the hydrophobic amino acids tryptophan, valine, leucine, isoleucine, methionine, phenylalanine, and alanine suggest the hypervariable interface is likely solvent exposed. Given their similarity to TALEs, these LRR proteins may bind specifically to nucleic acids, possibly in a manner similar to pumilio proteins (Adamala et al., Reference Adamala, Martin-Alarcon and Boyden2016), or other LRR proteins that bind to nucleic acids (Li et al., Reference Li, Deng, Petrucelli, Zhu, Mo, Zhang, Tam, Ariel, Zhao, Zhang, Ke, Li, Dokholyan, Duncan and Ting2019). Regardless of the substrate, however, the presence of numerous variable di-residue pairs suggest that these proteins could bind in a way that is possibly modular and reprogrammable.

Fig. 4. Leucine-rich repeat (LRR) proteins from Dictyostelium purpureum. (a) Repeat architectures of four representative D. purpureum LRR proteins. (b) Sequence logo of the LRR motifs. ( c ) Structural model of a representative LRR protein, with hypervariable residues shown as sticks. (d) Distribution of all pairs of hypervariable residues within a single LRR unit.
Tomato transcription factors
Using the within protein repeat pipeline, we identified a single nuclear transcription factor Y subunit gamma (NF-YC) gene, Solyc02g091030, in Solanum lycopersicum that contains an array of 12 tandem amino acid repeats of an unknown fold (Fig. 5 a). Unlike other systems described in this paper, the diversity in this protein is found at the transcriptome level and arises through splicing. At least 50 isoforms have been identified for this protein, the majority of which only contain differences in the repeat array itself. Each repeat is encoded by a separate exon, and all isoform differences occur as deletions at the 5′ of each exon. Each deletion is a multiple of three nucleotides, resulting in various isoforms differing by in-frame deletions. Deletions typically occur on a single repeat or on multiple adjacent repeats. Secondary structure prediction of the repeat unit shows that the 5′ deletions in each repeat occur in the only region of high confidence secondary structure (Fig. 5 b), suggesting that the deletions regulate the overall secondary and possibly tertiary structure of the repeat array. NF-Y genes are typically involved in maturation and adaptive stress response (Zhao et al., Reference Zhao, Wu, Kong, Lin, Zhang and Li2017). The NF-YC subunit is thought to dimerize with the NF-YB subunit in the cytoplasm before being imported into the nucleus where the dimer trimerizes with NF-YA, altering the ability of NF-YA to bind to promoters (Zhao et al., Reference Zhao, Wu, Kong, Lin, Zhang and Li2017). Expression of Solyc02g091030 does not vary greatly across different tissue types (Li et al., Reference Li, Li, Ju, Cao, Fu, Zhu, Zhu and Luo2016), suggesting it may have some role other than tissue-specific maturation. Other relatives of S. lycopersicum also possess variants of this transcription factor, such as Solanum pennellii, suggesting that the mechanism for this splicing based diversification may have evolved over the time scale of speciation.

Fig. 5. (a) Splicing isoforms for the Solanum lycopersicum transcription factor LOC101240705 (Solyc02g091030). A majority of isoforms differ only in the displayed region containing a tandem array of amino acid repeats. (b) Top: sequence logo of the 12 amino acid repeats without deletions. Bottom: PSIPRED secondary structure prediction of a representative repeat.
Secreted proteins containing a serine protease domain split over a hypervariable insert
We also identified tandem repeats of up to 14 proteins, each containing a serine protease domain, present in strains within Streptosporangiaceae, a Gram-positive family of bacteria within the Actinobacteria phylum that is widely distributed in soil (Fig. 6 a and Supplementary Fig. S3). The protease domain is relatively conserved (Fig. 6 b) but is likely to be catalytically inactive, as the active site serine is often substituted with aspartate, leucine, or other residues (Fig. 6 c). Of note, each protease domain contains an insertion in the middle that is highly variable across homologs, with a broad size range from less than 10 to over 200 amino acids (Fig. 6 b,d,e). Structural modelling indicates that these proteins retain the core serine protease fold and accommodate the insertion as a separate domain joined by flexible linkers (Fig. 6 f). These proteins also contain a predicted N-terminal secretion peptide (Fig. 6 b), suggesting extracellular localization.

Fig. 6. An array of serine proteases containing a hypervariable insert within the protease domain. (a) Graphical annotation of the protease locus from eight representative Streptosporangiceae strains. The hypervariable insert is shown in red. (b) Domain architecture and sequence identity of a prototypical protease (M. glauca #14). (c) Sequence logo of the catalytic serine and neighbouring residues from n = 223 proteases. (d) Histogram of hypervariable insert lengths. (e) Amino acid sequences of the inserts within the proteases from a representative locus (Herbidospora cretacea NBRC 15474). (f) Structural models (trRosetta) of representative proteases, constructed (left to right) from WP_061297158.1, WP_061297163.1, and WP_068929153.1.
The function of these proteins and the biochemical role of the hypervariable insert is not known. However, their predicted secretion into the extracellular environment suggests that they may play a role in interspecies bacterial conflict. For instance, we speculate that the hypervariable insert might act as a toxin that is supported by a serine protease scaffold and released upon secretion. Consistent with this hypothesis, over half of the analysed loci also encode a protease inhibitor that is predicted to be intracellular (Fig. 6 a), perhaps to mitigate toxicity to the host cell.
Alternating protein pairs from Photorhabdus implicated in self–non-self–recognition
We identified tandem repeats of a pair of proteins within strains of Photorhabdus (Fig. 7 a), a genus of symbiotic, bioluminescent, Gram-negative bacilli. Each pair consists of a long (L) protein (~530 amino acids) and a short (S) protein (~300 amino acids). L proteins are predicted to be intracellular, while S proteins contain a predicted secretion signal peptide at their N termini; however, neither protein has a known function or annotated domains. Eight repeats of the L–S pair (16 proteins total) are present in a single locus in P. thracensis DSM15199, and five repeats are present in P. khanii HGB 1456. Notably, the L protein consists of a 17–19 amino acid hypervariable region at the C terminus, whereas the other regions of the protein are nearly identical (Fig. 7 b–c). The S proteins are also variable, but the variable positions are distributed throughout its sequence. Using a yeast two-hybrid assay, we detected specific pairwise binding interactions between two sets of adjacent L and S proteins (Fig. 7 d,e). In our assay, the non-variable regions of each L protein were kept identical, and only the hypervariable insert was changed, indicating that the hypervariable residues in L determine binding specificity.
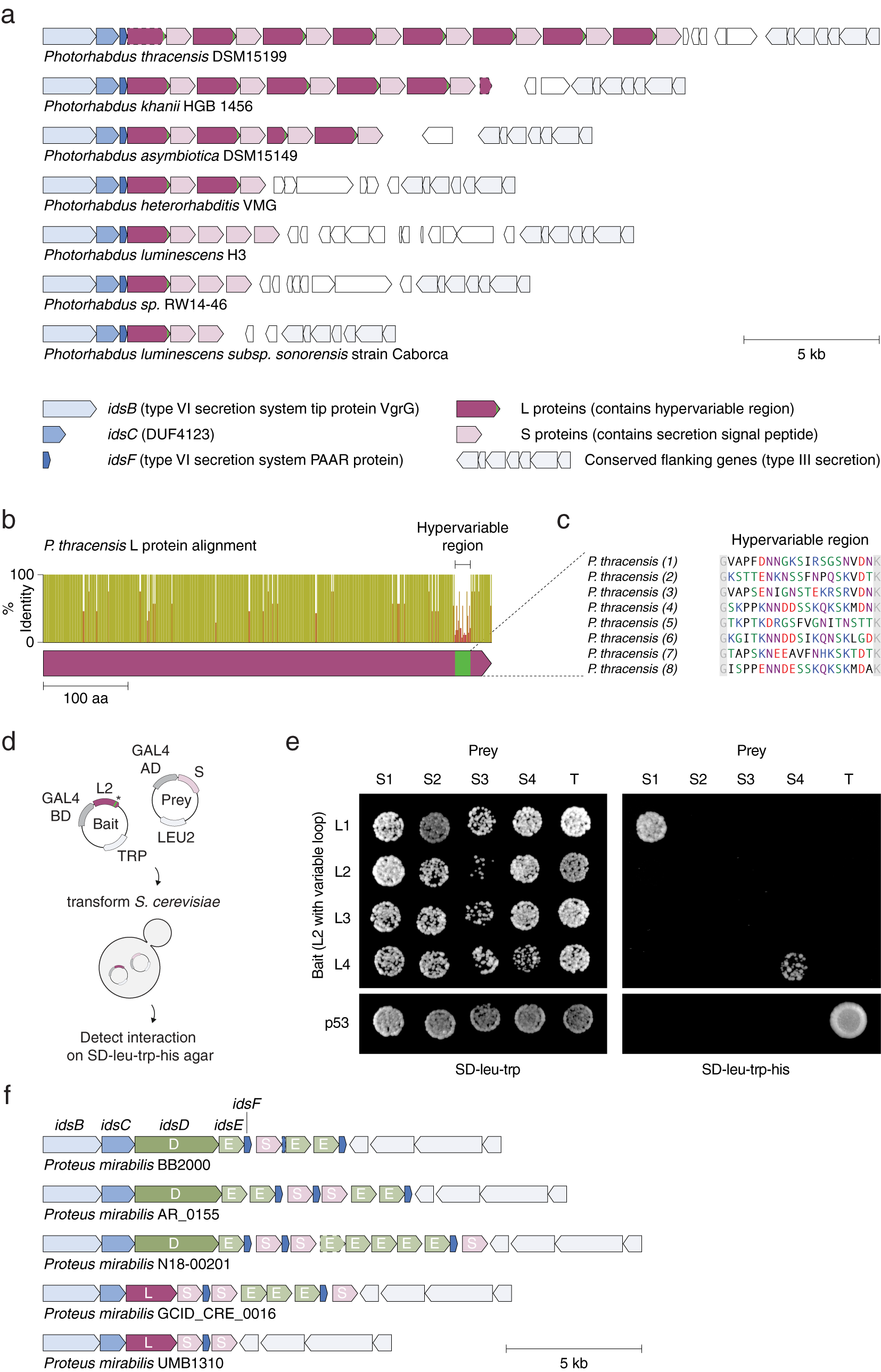
Fig. 7. An array of alternating protein pairs from Photorhabdus containing localized variation. (a) Graphical annotation of seven representative loci from Photorhabdus species. (b) Domain architecture and sequence identity of a prototypical L protein (P. thracensis #2). (c) Amino acid sequences of the hypervariable inserts within the fifteen L proteins shown in (a). (d–e) Yeast two-hybrid assay for P. thracensis L–S protein interactions (HIS3 reporter). The L protein #2 from P. thracensis (WP_046976484.1) was used as the fixed scaffold for all L proteins in the assay. (f) Comparison with the ids gene cluster from Proteus mirabilis, which confers self-identity and social recognition (Gibbs et al., Reference Gibbs, Urbanowski and Greenberg2008). The genes idsB, idsC and idsF are shared between the Photorhabdus and P. mirabilis loci.
The L–S locus resembles the ids gene cluster in Proteus mirabilis, which confers self-identity and social recognition between different P. mirabilis strains by mediating the formation of boundaries between swarming colonies (Gibbs et al., Reference Gibbs, Urbanowski and Greenberg2008). The ids locus consists of five genes (idsBCDEF) that are essential for social recognition (Fig. 7 f), three which (idsB, idsC, and idsF) are also present in the L–S locus. However, in the L–S locus, the ORFs encoding idsD and idsE that are usually present within the idsBCDEF operon are replaced by L and S, which have no sequence homology to idsD or idsE (Fig. 7 b). Like L and S, idsD and idsE also interact in a pairwise manner, and idsD contains a variable region at its C terminus that is responsible for conferring interaction specificity with idsE. Moreover, some ids loci also encode multiple copies of idsE, similar to the multiple S genes present in some of the Photorhabdus strains. Finally, in P. mirabilis, homologs of S are sometimes present within the ids locus, downstream of the idsBCDEF operon; likewise, homologs of idsE are sometimes present downstream of the L–S locus (Fig. 7 f).
The similarities between the L–S and ids loci suggest that the Photorhabdus L and S proteins may confer self- versus non-self–recognition between different Photorhabdus species. The pairwise binding specificity between adjacent L and S homologs, as well as the presence of multiple S genes in a locus with only one L gene (e.g. for Photorhabdus luminescens H3), is also consistent with a signature of interspecies conflict or recognition (Zhang et al., Reference Zhang, Souza, Anantharaman, Iyer and Aravind2012; Ross et al., Reference Ross, Verster, Radey, Schmidtke, Pope, Hoffman, Hajjar, Peterson, Borenstein and Mougous2019). However, since neither L nor S are predicted to be membrane proteins, in contrast to idsDE, the mechanism of recognition by L–S is likely distinct from that of idsDE.
Discussion
The approach presented here demonstrates the feasibility of identifying novel proteins and systems computationally using genomic hallmarks. We applied this method to systematically analyse all available proteins for protein repeat elements that contain strong localized variation within a fixed scaffold, as well as all available prokaryotic genomes and metagenomes for systems that contain multiple copies of the same protein with strong localized variation. This search revealed a number of interesting candidates that we examined in more depth.
Of the systems we selected for deeper analysis, some, such as the serine protease and the tomato NF-YC transcription factor, may involve unusual mechanisms of diversification. Additionally, three systems are implicated in interspecies conflict, a common theme in repeat-containing proteins and systems, such as TALEs, LRR-containing proteins, and CRISPR-Cas systems. Our findings here further highlight the role of diversified repeats in adaptive responses. The candidate systems from this study are found in widely divergent organisms, ranging from bacteria to plants and amoebae, underscoring the generality of the evolutionary strategy of using modular repeats. Furthermore, these findings highlight the importance of biodiversity in the discovery of new molecular systems.
By aggregating all available genomic sequencing data from multiple data sources, such as NCBI genomes, JGI, and NCBI WGS into a single database with a common format, we are able to implement comprehensive, domain-of-life wide discovery pipelines that far exceed the capacity of homology-based searches. By querying the database for non-homology-based features, such as spatially clustered proteins with hypervariation, or repeat proteins with rearrangement, we discovered systems with previously undescribed mechanisms and functions. We anticipate that the continued exponential growth of publicly-available genome sequences from all domains of life, along with expanded computational pipelines, will further empower the kinds of approaches described here and enable the discovery of additional protein families of interest.
Materials and Methods
Identifying hypervariable repeat proteins
All unique proteins (representatives of 100% sequence identity clusters) were downloaded from UniRef100. Proteins were first approximately searched for repeats using a fast kmer repeat detection approach. Specifically, for each protein, all kmers of length 12 were generated. Any kmer with less than four amino acids were discarded as low complexity. Each kmer’s amino acid sequence was then compressed using the following groupings: (A,G) , (I,L,V,M), (P), (F,W,Y), (D,E), (R,H,K), (S,T), (C), (N,Q). Proteins with less than three identical compressed kmers were discarded. Repeat proteins were filtered for evidence of hypervariation by analysing their dotplots. Specifically, protein dotplot matrices were generated by compressing their amino acids using the following groupings: (A), (G), (I,L,V), (M), (P), (F,W,Y), (D,E), (R,K), (H), (S,T), (C), (N,Q) and then computing the dotplot of the resulting compressed sequences. Proteins with hypervariable repeats contain dotplots with off-diagonal block identity matrices that contain a short internal segment of zeroes (signifying hypervariable positions). Repeats with hypervariable insertions and deletions can also be identified using a similar strategy in the dot plot, but as an identity matrix followed by zero band matrix and then a shifted identity matrix. To implement the off-diagonal pattern matching on the dotplot matrix representation, a 2D convolution was performed using five filters in total sized to 15 × 15 matrices (Supplementary Fig. S1). The hypervariable mismatch filters required a convolution value of 11 or higher to be considered hypervariable, while the indel filters required a convolution value of 12 or higher to be considered hypervariable. Using the hypervariable positions determined by the convolution filters as the reference for the repeat start and end points, the positional amino acid distribution of each repeat family was calculated and used as features for multi-dimensional clustering with hDBscan (McInnes et al., Reference McInnes, Healy and Astels2017), resulting in 4,017 clusters.
All proteins were then annotated for precise repeat boundaries using RADAR to capture repeats with accurate boundaries and allowing for mismatches (Heger and Holm, Reference Heger and Holm2000). For each cluster, the repeat rearrangement score for a given family was computed as follows. Because predictions for repeat start and end sites as determined by RADAR differ across different proteins in the same repeat cluster when repeat arrays are present, all repeats within the cluster were dephased using a linear optimization approach to produce consistent start and end positions for each repeat of the same archetype in the cluster. Specifically, a consensus start site was chosen so as to maximize the number of mismatches upstream from the start site of the first repeat in the proteins. All repeats in the family were clustered into major archetypes, and with each archetype, subtypes were formed on the basis of their hypervariable resides. Each repeat in every protein of the family was assigned a label based on the repeat subtype they belong to. An estimate for the repeat joint probability matrix, P, was generated as follows. Initialize P as a zero m × m matrix, where m is the number of repeat subtypes. For each protein, if repeat subtype i is followed by repeat subtype j in that protein, set Pij = Pij + 1, and we normalize P by the sum of P. The repeat rearrangement score is then the variation information of P, or the joint entropy of i, j minus the mutual information of i, j. Intuitively, the higher the score, the more similar P is to a uniform distribution, indicating that repeat units are used extensively in different combinations.
Identifying hypervariable, repeated proteins
All genomes from NCBI and assembled meta-genomes from JGI, NCBI WGS, and MG-RAST. We predicted all ORFs on all curated contigs larger than 5 kb. An ORF was considered a putative protein if it used any stop codon and satisfied one of the following conditions: (1) began with an ATG start codon and was at least 55 amino acids long, (2) began with a GTG or TTG start codon and was at least 200 amino acids long, or (3) began with a CTG codon and was at least 300 amino acids long. Within each contig, all putative proteins were clustered at a minimum identity of 45% and a minimum coverage of 30% using MMeqs2 Linclust (Steinegger and Söding, Reference Steinegger and Söding2017, Reference Steinegger and Söding2018), and all clusters with both six or more putative proteins and a median protein length of 100 amino acids or larger were retained for further analysis. Proteins from each cluster were then aligned using MAFFT with the default parameters (Katoh et al., Reference Katoh, Misawa, Kuma and Miyata2002).
Each cluster was then assigned a hypervariation score based on its alignment as follows. To emphasize hypervariation across amino acids with different biochemical properties, amino acids in the alignment were compressed into a 10 token alphabet based on biochemical properties using the following groupings: (A,S,T), (I,V,L,M), (W,F,Y), (D,E), (K,R), (N,Q), (H), (C), (P), (G). The distribution of each of the 10 tokens plus gaps at each position of the alignment was then computed. Positions with a Log2 Shannon entropy > = 0.92 or a gap percentage > = 15% were considered variable positions. The value 0.92 was chosen because we sought out positions that had at least as much entropy as a hypothetical ‘minimally hypervariable’ distribution consisting of two tokens each at 10% with one token at 80%. Stretches of variable positions in the alignment were grouped into hypervariable regions allowing for presence of occasional non-variable positions. Positions with a Log2 Shannon entropy of < 0.93 or gap percentage of < 15% were considered constant regions. Similarly, stretches of constant regions were grouped into constant regions allowing for the presence of occasional non-constant positions. Variable regions of < 6 positions and constant regions of < 7 positions were discarded. To pre-filter out alignments without localized variation, we assigned a score of 0 to alignments that either had 60% or more of its positions considered variable or had 30% or less of its total positional entropy contained in the identified hypervariable regions. For each constant region, the hamming distance between each sequence limited to the region’s boundaries was computed as a distance matrix. This distance matrix was then clustered using DBscan (Hahsler et al., Reference Hahsler, Piekenbrock and Doran2019) at 20% identity to estimate the count of unique, non-redundant sequences in the region. The discordance metric for the region was computed as the average value of the distance matrix times the non-redundant count. The discordance metric for the hypervariable regions were computed in an identical manner with an additional scaling obtained by multiplying by the length of the region and dividing by the number of hypervariable positions in the region. This rescaling helps prevent large gaps from artificially deflating the discordance of a hypervariable region. The divergence score of each hypervariable region was defined as the ratio of the discordance of the hypervariable region to the average discordance of the two closest flanking constant regions. The overall hypervariable score for the cluster was defined as the maximum of all divergence scores of hypervariable regions in the alignment that had at least one constant region upstream and at least one constant region downstream of the hypervariable region. All clusters with hypervariation scores of < 25 were discarded, leaving 42,129 systems. Because translated ORFs appearing in CRISPRs often appear hypervariable when clustered, we filtered out systems with 90% of its ORFs within 200 bp of a CRISPR containing 10 or more repeats. Removing translated CRISPRs resulted in 35,701 candidate systems.
All protein systems were ranked on the basis of their hypervariation score, and their loci were retrieved for further analysis. Representative proteins from each system were clustered at 30% identity and 30% coverage to group systems together into 3,040 families. By investigating the patterns of hypervariation, as well as putative functions of these families, we identified systems for further analysis.
Sequence analysis of candidate systems
Homologs of candidate genes were identified using BLAST or PSIBLAST searches followed by manual curation of genomic loci. Percent identity was calculated as the pairwise identity between non-gap residues at each position in the multiple sequence alignment. Sequence logos were generated using WebLogo3 without adjustment for composition. Structural models were generated using trRosetta (Yang et al., Reference Yang, Anishchenko, Park, Peng, Ovchinnikov and Baker2020). All models had an estimated TM-score of greater than 0.5.
Yeast two-hybrid assay
The L2 protein scaffold was cloned into pBGKT7 and the 19 amino acid hypervariable regions from L1–L4 were inserted. S proteins were cloned into pGADT7 (Takara). Y2HGold S. cerevisiae (Takara) were co-transformed with combinations of bait/prey plasmids and colonies selected on SD-leu-trp agar. Overnight liquid cultures were grown in SD-leu-trp, normalized by optical density, diluted, plated on SD-leu-trp and SD-leu-trp-his and grown for 2–3 days at 30°C. Yeast two-hybrid controls were performed using the SV40 large T antigen (T) and pGBKT7-53 (p53) plasmids (Takara).
Open Peer Review
To view the open peer review materials for this article, please visit http://doi.org/10.1017/qrd.2020.14.
Supplementary Materials
To view supplementary material for this article, please visit http://doi.org/10.1017/qrd.2020.14.
Acknowledgements
We thank Eugene Koonin and Kira Makarova for helpful discussions and the entire Zhang lab for support and advice.
Funding
F.Z. is supported by NIH grants (1R01-HG009761, 1R01-MH110049, and 1DP1-HL141201); the Howard Hughes Medical Institute; the Open Philanthropy Project, the Harold G. and Leila Mathers and Edward Mallinckrodt, Jr. Foundations; the Poitras Center for Neuropsychiatric Disorders Research at MIT; the Hock E. Tan and K. Lisa Yang Center for Autism Research at MIT; and by the Phillips family and J. and P. Poitras.
Conflict of interest
F.Z. is a scientific advisor and cofounder of Editas Medicine, Beam Therapeutics, Pairwise Plants, Arbor Biotechnologies, and Sherlock Biosciences.
Authorship contributions
F.Z. conceived of the project. H.A. and L.G. performed computational analyses. J.S. performed yeast two-hybrid assays. F.Z. supervised research. H.A., L.G., R.K.M., and F.Z. wrote the manuscript with input from all authors.
Data availability statement
All data are available in the manuscript or in the supplementary materials.










Comments
Comments to Author: This paper describes the use of bioinformatics for identification of repeat containing proteins in nature. The authors developed a computational algorithm for identification of repetitive nucleotide sequence elements in proteins and nucleic acids. Such repetitive sequences are known in CRISPR and other systems, and they generally confer important functions. However, in many cases these functions are unknown or not even studied. The study presented here is interesting as it enables identification of repetitive sequences not earlier identified and it further discuss the possible function of four of these sequences. The paper is very well written and even though there is no experimental validation of any of the findings, the paper stands as a very strong novel contribution to the field. I have no specific comments to the paper, which can be accepted as is.