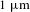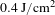Femtosecond laser-induced damage threshold in snow micro-structured targets

Abstract

Enhanced acceleration of protons to high energy by relatively modest high power ultra-short laser pulses, interacting with snow micro-structured targets was recently proposed. A notably increased proton energy was attributed to a combination of several mechanisms such as localized enhancement of the laser field intensity near the tip of $1~\unicode[STIX]{x03BC}\text{m}$ size whisker and increase in the hot electron concentration near the tip. Moreover, the use of mass-limited target prevents undesirable spread of absorbed laser energy out of the interaction zone. With increasing laser intensity a Coulomb explosion of the positively charged whisker will occur. All these mechanisms are functions of the local density profile and strongly depend on the laser pre-pulse structure. To clarify the effect of the pre-pulse on the state of the snow micro-structured target at the time of interaction with the main pulse, we measured the optical damage threshold (ODT) of the snow targets. ODT of $0.4~\text{J}/\text{cm}^{2}$ was measured by irradiating snow micro-structured targets with 50 fs duration pulses of Ti:Sapphire laser.

1 Introduction

Over the last two decades a variety of proton acceleration schemes were proposed and demonstrated (see Refs. [1, 2] for review), such as Target Normal Sheath Acceleration (TNSA)^[3–5], Radiation Pressure Acceleration (RPA)^{[6, 7]}, Break Out Afterburner (BOA)^{[8, 9]} and collisionless shock acceleration^{[10, 11]}. Some of these schemes considered mass-limited targets^[12] and nanostructure targets^[13–18] aimed to increase the efficiency of the laser–target interaction. A recent review on ‘targetry’ for application of laser–proton acceleration to cancer radiotherapy is reported in reference^[19]. Furthermore, these schemes require laser pulses exceeding 1 PW level on the target in order to accelerate protons to energies of about 150 MeV and are optimized for interaction of the main pulse with cold solid matter. In high power systems that include a regenerative amplifier, the energy leakage during amplification in regenerative amplifier (pre-pulse), is strongly focused on the target and can reach laser intensities of $10^{12}~\text{W}/\text{cm}^{2}$ . At these intensities, the laser pulse is strongly interacting with the target. Most of the schemes are sensitive to the presence of a pre-pulse that can produce a pre-plasma in front of the target. At high laser intensities required for proton acceleration, elimination of pre-plasma requires a ratio between the main pulse to the pre-pulse intensity (contrast ratio) higher than $10^{9}$ , which is a huge experimental challenge. Recently, we demonstrated a new approach to laser-based proton acceleration by using a moderate power laser system and micro-structured snow targets^[20–23]. Snow coated sapphire targets were found to absorb 95% of the incident laser light compared to flat bare sapphire targets^[20]. An enhancement by a factor of ten of the proton energy using snow targets was measured at moderate intensities^{[22, 23]}. Moreover, in this approach, it was shown that pre-formed plasma might be beneficial to the acceleration process^[23]. Numerical 2D particle-in-cell (PIC) code simulations^[23], with initial plasma conditions created by pre-pulse on the snow target surface at the time of the interaction with the main pulse, reproduced the obtained proton energy and explained the crucial role of the dynamic plasma produced by pre-pulse illumination of the snow target.

One of the parameters determining the state of the target after the interaction with the pre-pulse is the optical damage threshold (ODT). This feature is identified in the experiments reported here by the irreversible change of the surface as visible by a high magnification imaging system. The ODT is a consequence of multiphoton followed by impact ionization of the snow^[24–27]. The free electrons generated by ionization escape the target and due to charge separation, they pull the ions out of the target. The ODT may determine the plasma density gradient at the interaction of the main pulse with the target, and therefore is important for the protons acceleration mechanism.

In this paper, we report experiments aimed to measure the ODT and energy deposition in snow targets irradiated by a short pulse intense laser.

Investigating pre-pulse influence on micro-structure targets rises several challenges of probing the interaction in time and space at the relevant resolution i.e., few nanoseconds delay from the interaction, tens of femtosecond gate resolution and a few microns for spatial resolution. Therefore, an imaging system and gating technique with this characteristics were developed and used.

2 Experimental setup

The experiments were performed at the Hebrew University High Intensity Laser Facility with a Ti: Sapphire laser based on chirped pulse amplification (CPA) that can deliver a peak power of 1 TW in 50 fs with 10 Hz repetition rate. The laser minimal spot size diameter is $5~\unicode[STIX]{x03BC}\text{m}$ , leading to a maximum intensity of the main pulse of $5\times 10^{18}~\text{W}/\text{cm}^{2}$ , and it operates at a central wavelength of 800 nm. A pre-pulse of time duration same as the main pulse dictated by the leakage in the regenerative preamplifier precedes the main pulse by 10 ns. The main pulse to pre-pulse contrast ratio is 4000. In the experiments reported here, the laser fluence was varied in the range of 0.1–3 J/ $\text{cm}^{2}$ . This laser interacts with the snow target. The snow structured targets were grown in the interaction vacuum chamber, on a liquid nitrogen cooled sapphire substrate on which water vapor is deposited. The snow structure is determined by various parameters such as pressure, flow velocity, and temperature. The conditions of the snow growth followed the conditions in Refs. [28, 29], in order to achieve the morphology seen by the scanning electron microscope (SEM) in Refs. [28, 29]. The snow was deposited at a temperature down to $-170\,^{\circ }\text{C}$ and in the pressure range of 0.1–10 Torr. More details on the snow targets growth procedure are presented in Refs. [28, 29]. Typical snow target as imaged by an SEM is shown in Figure 1. The snow surface is highly structured with basically three roughness scales: (1) Pillars with a diameter of about $100~\unicode[STIX]{x03BC}\text{m}$ , (2) Spikes with a diameter of about $10~\unicode[STIX]{x03BC}\text{m}$ , and (3) Whiskers with a diameter of about $1~\unicode[STIX]{x03BC}\text{m}$ on the spikes^{[28, 29]}. For laser spot size of several microns, the laser may interact with one or few whiskers. The pre-pulse irradiating the target 10 ns before the main pulse may vaporize and ionize part of the whiskers, creating an expanding nonuniform plasma cloud, with a variety of density gradients and densities between sub-critical to solid density.

Figure 1. A typical SEM image of the target.

In order to determine the snow ODT, the laser energy on the target was decreased using filters, so that the main pulse intensity and fluence can mimic the pre-pulse interaction with the snow target. To capture the state of the snow target surface at the time of interaction of the main pulse with the target, the target was strobe illuminated by short pulse white-light source and imaged at three times: (1) Before the interaction of the laser with the snow target. (2) 7 ns after the interaction (around the delay between the pre-pulse and the main pulse, therefore simulating the conditions just before the arrival of the main pulse). (3) At longer times, minutes after the interaction. The measurements were conducted for different values of the laser fluence on the target, in the range of 0.1–3  $\text{J}/\text{cm}^{2}$ .

Figure 2. Experimental setup: Imaging system with one objective (Obj1) inside the vacuum chamber, and a second objective (Obj2) outside of the chamber, imaging the target on a CCD camera with magnification 16. The main laser pulse is split at beam splitter BS1 into two beams: A first beam that propagates to M3 and focuses with an off-axis parabolic mirror to interact with the target. A second delayed beam, that acts as a strobe and merges on the optical line of the imaging system at BS2. This delayed beam consists of white light with wavelength broaden by supercontinuum and delayed by 7 ns from the main beam.

The experimental setup is shown in Figure 2. To image the snow target before the interaction with the laser, the target was imaged with a telescope system to a CCD camera placed outside of the vacuum chamber. The telescope was built out of two objectives (labeled Obj1, Obj2 in Figure 2) that corrected aberrations with focal lengths ratio producing a magnification of 16. The first objective was placed in the vacuum chamber in a distance equal to a focal length from the target, transferring the image collimated to the second objective placed outside the chamber to image the target on the CCD camera. The resolution of the imaging system was $10~\unicode[STIX]{x03BC}\text{m}$ at a field of view of $400\times 300~\unicode[STIX]{x03BC}\text{m}$ .

Figure 3(a) shows a typical image of the target, illuminated by LED lamp, and imaged by the telescope. To obtain images at specific time suppressing smearing due to target expansion we have used a gating measurement, based on the short pulse duration probe beam. For this purpose, we have split the laser beam into two beams at the entrance of the vacuum chamber. The first beam was acting as the main laser beam interacting with the target, and the second beam was delayed by 7 ns and acted as a flash probe (strobe). Possible expansion of the target during the time duration of the probe beam was negligible. The fluence of the probe beam was $0.015~\text{J}/\text{cm}^{2}$ , its spot size was around $200~\unicode[STIX]{x03BC}\text{m}$ and its intensity was $3.1\times 10^{11}~\text{W}/\text{cm}^{2}$ . As is shown below, these values are below the threshold for damage. Figure 3(b) shows a typical image of the target, lighted by the strobe and imaged by the telescope. The main beam operated at 800 nm wavelength, while the delayed beam focused on the quartz plate produced femtosecond supercontinuum light and acted as a probe source. The supercontinuum generated in quartz crystals extends from ${\sim}350~\text{nm}$ and covers the entire visible range.

Chromatic filters placed in front of the CCD camera enabled separation between the main beam and the delay line. This measurement technique gives a controllable delayed probing with fast gating at the scale of the laser pulse (50–70 fs). Three images were recorded. The first image of the snow target, long before the interaction, was obtained by blocking the main beam and using the strobe alone. The second image, 7 ns after the interaction, of the order of the time duration between the pre-pulse and the main pulse of the laser system, was obtained using both beams of the laser, and the third image, long after the interaction, again by blocking the main beam and using the probe beam only; see Figure 4. We have controlled the main beam energy level by changing neutral density filters on its line, producing images for different laser fluences on the target to investigate the pre-pulse influence on the snow target. We have changed the fluence on the target in the range of 0.1– $3~\text{J}/\text{cm}^{2}$ .

Figure 3. Typical images of the snow micro-structure (a) illuminated by LED, (b) illuminated by gating strobe and (c) illuminated by the strobe with image processing to normalize light intensity.

3 Results

Two processing procedures had been applied on the images. First was image processing (enhancement, brightness, sharpness, etc.), as can be seen in Figure 3(c). The second method consisted of plotting the intensity as a function of distance along lines on the image. The intensity along a transection of the strobe images, where the damage was noticeable, was evaluated by averaging over a strip of few pixels (Figure 4). For each fluence, the intensity on the same transection stripe was chosen for the different times described above.

Figure 4. Transections of the strobe images for different fluences and at different times relatively to the laser–snow interaction. (a) Laser fluence of $1~\text{J}/\text{cm}^{2}$ , (b) fluence of $0.45~\text{J}/\text{cm}^{2}$ and (c) fluence of $0.35~\text{J}/\text{cm}^{2}$ . (1) At few minutes before the interaction, (2) 7 ns after the interaction and (3) long after the interaction (few minutes).

Processing and comparing the strobe images for different times, one can identify morphology changes of the snow pillar interface due to damage induced by the laser interaction. Damage is identified in the experiments presented here as an irreversible change in the target surface. We have seen that at fluence on target higher than $1~\text{J}/\text{cm}^{2}$ , a definite damage has been occurred to the target, as can be seen in Figures 4(a) and 5(a). At laser fluence on target less than $0.35~\text{J}/\text{cm}^{2}$ , we could not see any damage to the snow, with our imaging system and processing procedure [Figures 4(c) and 5(c)]. At fluence of the laser on the target of $0.45~\text{J}/\text{cm}^{2}$ we can hardly see any damage 7 ns after the interaction [Figures 4(b.2) and 5(b.2)], though long after the interaction due to thermal conductivity it is obvious that ablation occurred [Figures 4(b.3) and 5(b.3)]. From these results, we concluded that the laser fluence ODT is around $0.4~\text{J}/\text{cm}^{2}$ .

Figure 5. Strobe images of the snow micro-structures at different laser fluences and at different times according to laser–snow interaction. Laser at (a) 1, (b) 0.45 and (c) $0.35~\text{J}/\text{cm}^{2}$ . (1) Strobe image before the interaction, (2) an image 7 ns after the interaction and (3) long after the interaction (few minutes).

4 Discussion

The optical damage, caused by ablation in the case considered here, follows from the generation of free carriers and escape of the electrons from the solid. The electron–ion energy exchange time, as well as the conduction time, are much larger than the laser pulse duration^[26]. The electric field of charge separation pulls ions out of the target, creating a nonequilibrium mechanism of ablation. Following Gamaly et al. ^[26], the damage threshold fluence of snow can be estimated by

(1) $$\begin{eqnarray}F=\frac{3}{4}\left(e_{b}+I\right)\frac{l_{s}}{A}n_{e},\end{eqnarray}$$

where $e_{b}$ is the binding energy of the ions, $I$ is the ionization energy, $l_{s}=c/(\unicode[STIX]{x1D714}\unicode[STIX]{x1D705})$ is the absorption length (or the skin depth), $n_{e}$ is the free electrons density and $A$ is the absorption coefficient of the laser in snow, $c$ is the velocity of light, $\unicode[STIX]{x1D714}$ is the laser frequency and $\unicode[STIX]{x1D705}$ is the imaginary part of the index of refraction.

The electron density was calculated by a theoretical model describing the interaction of the laser with the snow target, which considers the snow target a micro-plasma^{[20, 27]}. In the model, the snow target is ionized by multiphoton and impact ionization, heated by inverse bremsstrahlung and cooled by hydrodynamic expansion and energy transfer to ions. At laser intensity $8\times 10^{12}~\text{W}/\text{cm}^{2}$ , corresponding to damage fluence measured here, it was found that the snow is fully single ionized, therefore the electron density is equal to the ion density. Following Refs. [26, 27], for the conditions considered here, the ratio of the skin depth and the absorption function is $l_{s}/A=\unicode[STIX]{x1D706}/(4\unicode[STIX]{x1D70B})$ . An average ionization potential of 13.9 eV per electron and the latent heat for vapor–solid transition in water of $2.8\times 10^{6}~\text{J}/\text{kg}$ for the binding energy were assumed. Therefore the damage threshold calculated from Eq. (1) is $F=0.98~\text{J}/\text{cm}^{2}$ , by a factor of two larger than the experimental value.

The higher estimated value of the ODT compared to the measured value might be related to the micro-structured size of the snow target. In recent years, it was shown that the interaction of intense short pulse lasers with mass-limited and structured targets is enhanced relatively to conventional slab targets. Such enhancement was reported for X-ray emission from carbon nanotubes placed on an Si substrate^{[30, 31]}, high harmonic generation from gold nano-spikes^[32], and in our recent experiments of proton acceleration from snow micro-structured targets^{[22, 23]}. ODT of protein nanolayer containing carbon nanotubes was measured recently and found to be lower than that of its sapphire substrate^[32]. In a previous work^{[20, 21]}, we demonstrated substantial absorption enhancement in snow wires relatively to a sapphire substrate. This high absorption of about 95%^[20] might lead to lower ODT than the estimated value. In addition, a similar level of agreement of the above, simplified model, with the experimental data was reported^[33].

5 Conclusion

ODT knowledge of the target material is a key factor for understanding the plasma parameters produced in the pre-pulse and furthermore understanding the laser–matter interaction. Therefore, with delicate pre-pulse settings, we expect to control more efficiently the laser–snow interaction experiments and to estimate the plasma density gradient, which is an important parameter for optimization of proton acceleration. A damage threshold of $0.4~\text{J}/\text{cm}^{2}$ was demonstrated to micro-structure snow target by a 50 fs laser pulse, much lower than the ODT of the sapphire substrate^[34–36]. Thus the laser system that will be used for the future experiments with the micro-structured targets must suppress unwanted pre-pulse to below this level.