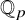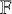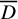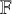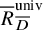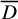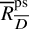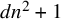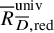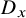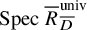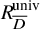1 Introduction
Let p be a prime number, and let K be a finite extension of
![]() ${\mathbb {Q}}_p$
of degree
${\mathbb {Q}}_p$
of degree
![]() $d=[K:{\mathbb {Q}}_p]$
with absolute Galois group
$d=[K:{\mathbb {Q}}_p]$
with absolute Galois group
![]() $G_K={\mathrm {Gal}}({{K}^{\mathrm {alg}}}/K)$
. In [Reference ChenevierChe11], Chenevier establishes the following results on the rigid variety
$G_K={\mathrm {Gal}}({{K}^{\mathrm {alg}}}/K)$
. In [Reference ChenevierChe11], Chenevier establishes the following results on the rigid variety
![]() ${\cal X}_n$
of continuous pseudocharacters of
${\cal X}_n$
of continuous pseudocharacters of
![]() $G_K$
of dimension n with coefficients in
$G_K$
of dimension n with coefficients in
![]() ${{{\mathbb {Q}}}^{\mathrm {alg}}_p}$
.
${{{\mathbb {Q}}}^{\mathrm {alg}}_p}$
.
Theorem (Chenevier).
-
(a) The open locus of regular points of
 ${\cal X}_n$
contains
${\cal X}_n$
contains
 ${\cal X}_n^{\operatorname {irr}}$
.
${\cal X}_n^{\operatorname {irr}}$
. -
(b) The open subvariety
 ${\cal X}_n^{\operatorname {irr}}\subset {\cal X}_n$
of irreducible pseudocharacters is Zariski dense in
${\cal X}_n^{\operatorname {irr}}\subset {\cal X}_n$
of irreducible pseudocharacters is Zariski dense in
 ${\cal X}_n$
.
${\cal X}_n$
. -
(c) The variety
 ${\cal X}_n$
is equidimensional of dimension
${\cal X}_n$
is equidimensional of dimension
 $dn^2+1$
.
$dn^2+1$
.
Moreover, [Reference ChenevierChe11] gives a precise description of the singular locus of the varieties
![]() ${\cal X}_n$
in terms of representation-theoretic data. Note that from any continuous pseudocharacter x of dimension n of
${\cal X}_n$
in terms of representation-theoretic data. Note that from any continuous pseudocharacter x of dimension n of
![]() $G_K$
with coefficients in
$G_K$
with coefficients in
![]() ${{{\mathbb {Q}}}^{\mathrm {alg}}_p}$
, one can reconstruct a semisimple n-dimensional continuous representation
${{{\mathbb {Q}}}^{\mathrm {alg}}_p}$
, one can reconstruct a semisimple n-dimensional continuous representation
![]() $\rho _x\colon G_K\to {\mathrm {GL}}_n({{{\mathbb {Q}}}^{\mathrm {alg}}_p})$
that is unique up to conjugation; one calls x irreducible if
$\rho _x\colon G_K\to {\mathrm {GL}}_n({{{\mathbb {Q}}}^{\mathrm {alg}}_p})$
that is unique up to conjugation; one calls x irreducible if
![]() $\rho _x$
is irreducible.
$\rho _x$
is irreducible.
The above results can be reinterpreted as results on the generic fibers of universal rings for pseudodeformations of a fixed residual pseudocharacter of
![]() $G_K$
as introduced by Chenevier in [Reference ChenevierChe14]. Note that we use the term pseudocharacter for what Chenevier in [Reference ChenevierChe14] calls determinant law and what is called pseudorepresentation in [Reference Wang EricksonWE13]; the term Taylor-pseudocharacter we use for what in [Reference TaylorTay91] was called a pseudocharacter. Pseudocharacters of dimension n of a group
$G_K$
as introduced by Chenevier in [Reference ChenevierChe14]. Note that we use the term pseudocharacter for what Chenevier in [Reference ChenevierChe14] calls determinant law and what is called pseudorepresentation in [Reference Wang EricksonWE13]; the term Taylor-pseudocharacter we use for what in [Reference TaylorTay91] was called a pseudocharacter. Pseudocharacters of dimension n of a group
![]() $\Gamma $
are certain polynomial laws in the sense of [Reference RobyRob63] that model the formal properties of the characteristic polynomial of n-dimensional representations of
$\Gamma $
are certain polynomial laws in the sense of [Reference RobyRob63] that model the formal properties of the characteristic polynomial of n-dimensional representations of
![]() $\Gamma $
. The simpler notion of Taylor-pseudocharacter refers to maps that model the formal properties of the trace of n-dimensional representations of
$\Gamma $
. The simpler notion of Taylor-pseudocharacter refers to maps that model the formal properties of the trace of n-dimensional representations of
![]() $\Gamma $
. The two notions agree for coefficient fields of characteristic zero or of characteristic
$\Gamma $
. The two notions agree for coefficient fields of characteristic zero or of characteristic
![]() $p>2n$
; see [Reference ChenevierChe14, Proposition 1.29]. Taylor-pseudocharacters have some defects in characteristic
$p>2n$
; see [Reference ChenevierChe14, Proposition 1.29]. Taylor-pseudocharacters have some defects in characteristic
![]() $p\le n$
. Pseudocharacters behave well independently of the characteristic (and n). Also, a pseudocharacter
$p\le n$
. Pseudocharacters behave well independently of the characteristic (and n). Also, a pseudocharacter
![]() ${D}$
of
${D}$
of
![]() $G_K$
of dimension n with coefficients in an algebraically closed field
$G_K$
of dimension n with coefficients in an algebraically closed field
![]() $\kappa $
is the pseudocharcter attached to a semisimple representation
$\kappa $
is the pseudocharcter attached to a semisimple representation
![]() $\rho _{D}\colon G_K\to {\mathrm {GL}}_n(\kappa )$
that is unique up to conjugation.
$\rho _{D}\colon G_K\to {\mathrm {GL}}_n(\kappa )$
that is unique up to conjugation.
Let now
![]() ${{\mathbb {F}}\,\!{}}$
be a finite field of characteristic p with ring of Witt vectors
${{\mathbb {F}}\,\!{}}$
be a finite field of characteristic p with ring of Witt vectors
![]() ${{W({{\mathbb {F}}\,\!{}})}}$
, and let
${{W({{\mathbb {F}}\,\!{}})}}$
, and let
![]() ${{\widehat {\mathcal {A}}r}_{{W({{\mathbb {F}}\,\!{}})}}}$
be the category of Noetherian
${{\widehat {\mathcal {A}}r}_{{W({{\mathbb {F}}\,\!{}})}}}$
be the category of Noetherian
![]() ${{W({{\mathbb {F}}\,\!{}})}}$
-algebras with residue field
${{W({{\mathbb {F}}\,\!{}})}}$
-algebras with residue field
![]() ${{\mathbb {F}}\,\!{}}$
. Let
${{\mathbb {F}}\,\!{}}$
. Let
![]() ${\overline {{D}}}$
be a continuous pseudocharacter of
${\overline {{D}}}$
be a continuous pseudocharacter of
![]() $G_K$
of dimension n with values in
$G_K$
of dimension n with values in
![]() ${{\mathbb {F}}\,\!{}}$
. If
${{\mathbb {F}}\,\!{}}$
. If
![]() ${{\mathbb {F}}\,\!{}}$
is sufficiently large,
${{\mathbb {F}}\,\!{}}$
is sufficiently large,
![]() ${\overline {{D}}}$
can be thought of as the pseudocharacter attached to a representation
${\overline {{D}}}$
can be thought of as the pseudocharacter attached to a representation
![]() ${\overline {\rho }}\colon G_K\to {\mathrm {GL}}_n({{\mathbb {F}}\,\!{}})$
, that is, morally as the characteristic polynomial law attached to
${\overline {\rho }}\colon G_K\to {\mathrm {GL}}_n({{\mathbb {F}}\,\!{}})$
, that is, morally as the characteristic polynomial law attached to
![]() ${\bar \rho }$
. It is shown in [Reference ChenevierChe14] that any residual
${\bar \rho }$
. It is shown in [Reference ChenevierChe14] that any residual
![]() ${\overline {{D}}}$
admits a universal pseudodeformation ring
${\overline {{D}}}$
admits a universal pseudodeformation ring
![]() ${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\overline {D}}}}}$
that represents the functor
${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\overline {D}}}}}$
that represents the functor
![]() ${{\widehat {\mathcal {A}}r}_{{W({{\mathbb {F}}\,\!{}})}}}\to {Sets}$
, that to any object R of
${{\widehat {\mathcal {A}}r}_{{W({{\mathbb {F}}\,\!{}})}}}\to {Sets}$
, that to any object R of
![]() ${{\widehat {\mathcal {A}}r}_{{W({{\mathbb {F}}\,\!{}})}}}$
assigns the set of pseudocharacter
${{\widehat {\mathcal {A}}r}_{{W({{\mathbb {F}}\,\!{}})}}}$
assigns the set of pseudocharacter
![]() ${D}_R$
of
${D}_R$
of
![]() $G_K$
with values in R and with residual pseudocharacter
$G_K$
with values in R and with residual pseudocharacter
![]() ${\overline {{D}}}$
. The above theorem now asserts that the absolutely irreducible locus of
${\overline {{D}}}$
. The above theorem now asserts that the absolutely irreducible locus of
![]() ${\mathrm {Spec}}\ {R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\overline {D}}}}}[1/p]$
is dense open in
${\mathrm {Spec}}\ {R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\overline {D}}}}}[1/p]$
is dense open in
![]() ${\mathrm {Spec}}\ {R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\overline {D}}}}}[1/p]$
and contained in the regular locus of
${\mathrm {Spec}}\ {R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\overline {D}}}}}[1/p]$
and contained in the regular locus of
![]() ${\mathrm {Spec}}\ {R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\overline {D}}}}}[1/p]$
, and that
${\mathrm {Spec}}\ {R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\overline {D}}}}}[1/p]$
, and that
![]() ${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\overline {D}}}}}[1/p]$
is equidimensional of dimension
${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\overline {D}}}}}[1/p]$
is equidimensional of dimension
![]() $dn^2+1$
; here x in
$dn^2+1$
; here x in
![]() ${X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}} :={\mathrm {Spec}}\ {R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\overline {D}}}}}$
with corresponding residue field
${X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}} :={\mathrm {Spec}}\ {R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\overline {D}}}}}$
with corresponding residue field
![]() ${\kappa ({x})} $
and pseudocharacter
${\kappa ({x})} $
and pseudocharacter
![]() ${D}_x$
is called irreducible if the semisimple representation
${D}_x$
is called irreducible if the semisimple representation
![]() $\rho _x:=\rho _{{D}_x\otimes _{{\kappa ({x})} }{{{{\kappa ({x})} }}^{\mathrm {alg}}}}\colon G_K\to {\mathrm {GL}}_n({{{\kappa ({x})} }}^{\mathrm {alg}})$
is irreducible.
$\rho _x:=\rho _{{D}_x\otimes _{{\kappa ({x})} }{{{{\kappa ({x})} }}^{\mathrm {alg}}}}\colon G_K\to {\mathrm {GL}}_n({{{\kappa ({x})} }}^{\mathrm {alg}})$
is irreducible.
The present work concerns the special fiber of
![]() ${\mathrm {Spec}}\ {R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\overline {D}}}}}$
, that is, the mod p reduction
${\mathrm {Spec}}\ {R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\overline {D}}}}}$
, that is, the mod p reduction
![]() ${\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}} = {R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\overline {D}}}}}/(p)$
of the ring
${\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}} = {R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\overline {D}}}}}/(p)$
of the ring
![]() ${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\overline {D}}}}}$
and the corresponding special fiber scheme
${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\overline {D}}}}}$
and the corresponding special fiber scheme
![]() ${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}} :={\mathrm {Spec}}\ {\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
. Our main results are natural analogs of the assertions in the above theorem of Chenevier. Before giving them, we point to some differences to the results of Chenevier and introduce some notions to deal with them.
${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}} :={\mathrm {Spec}}\ {\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
. Our main results are natural analogs of the assertions in the above theorem of Chenevier. Before giving them, we point to some differences to the results of Chenevier and introduce some notions to deal with them.
Let
![]() $\zeta _p\in {{K}^{\mathrm {alg}}}$
denote a primitive p-th root of unity. A first simple observation is that, already for
$\zeta _p\in {{K}^{\mathrm {alg}}}$
denote a primitive p-th root of unity. A first simple observation is that, already for
![]() $n=1$
, the space
$n=1$
, the space
![]() ${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
has empty regular locus, whenever
${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
has empty regular locus, whenever
![]() $\zeta _p$
lies in K. To address this problem, we study the natural determinant map
$\zeta _p$
lies in K. To address this problem, we study the natural determinant map
![]() ${\mathrm {det}}_{{\overline {{D}}}}\colon {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}\to {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\mathrm {det}}{{\overline {{D}}}}}}},{D}{\mapsto }{\mathrm {det}}{{D}}$
, where
${\mathrm {det}}_{{\overline {{D}}}}\colon {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}\to {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\mathrm {det}}{{\overline {{D}}}}}}},{D}{\mapsto }{\mathrm {det}}{{D}}$
, where
![]() ${\mathrm {det}}{D}$
is the constant coefficient of the pseudocharacter
${\mathrm {det}}{D}$
is the constant coefficient of the pseudocharacter
![]() ${D}$
; that is, if
${D}$
; that is, if
![]() ${D}$
is attached to an n-dimensional representation
${D}$
is attached to an n-dimensional representation
![]() $\rho $
, then
$\rho $
, then
![]() ${\mathrm {det}}{{D}}$
is attached to the one-dimensional representation
${\mathrm {det}}{{D}}$
is attached to the one-dimensional representation
![]() ${\mathrm {det}}\rho $
. Eventually, we show that
${\mathrm {det}}\rho $
. Eventually, we show that
![]() ${\mathrm {det}}{_{\overline {{D}}}}$
is formally smooth when restricted to a dense open subset of
${\mathrm {det}}{_{\overline {{D}}}}$
is formally smooth when restricted to a dense open subset of
![]() $ {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
. This subset is (slightly) smaller than the open of locus
$ {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
. This subset is (slightly) smaller than the open of locus
![]() $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}},{\operatorname {red}}}}})^{{\operatorname {irr}}}$
of irreducible points of
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}},{\operatorname {red}}}}})^{{\operatorname {irr}}}$
of irreducible points of
![]() $ {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
. There is a closed subset of the irreducible locus (of relatively small dimension) spanned by points that we call special such that when we restrict
$ {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
. There is a closed subset of the irreducible locus (of relatively small dimension) spanned by points that we call special such that when we restrict
![]() ${\mathrm {det}}_{{\overline {{D}}}}$
to the dense open subscheme of nonspecial irreducible points of
${\mathrm {det}}_{{\overline {{D}}}}$
to the dense open subscheme of nonspecial irreducible points of
![]() ${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
it is formally smooth. Because
${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
it is formally smooth. Because
![]() $ {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\mathrm {det}}{{\overline {{D}}}}}}}$
and its induced reduced subscheme
$ {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\mathrm {det}}{{\overline {{D}}}}}}}$
and its induced reduced subscheme
![]() $ {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\mathrm {det}}{{\overline {{D}}}},{\operatorname {red}}}}}$
are explicit and well understood, base change to reduced structures gives us access to
$ {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\mathrm {det}}{{\overline {{D}}}},{\operatorname {red}}}}}$
are explicit and well understood, base change to reduced structures gives us access to
![]() $ {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}},{{\operatorname {red}}}}}$
for which we deduce Chenevier’s dimension formula.
$ {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}},{{\operatorname {red}}}}}$
for which we deduce Chenevier’s dimension formula.
There are several equivalent ways to describe the locus of special points of
![]() $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}},{\operatorname {red}}}}})^{\operatorname {irr}}$
; see Subsection 5.1 and some basic results on Clifford theory explained in Section 2; each has its benefits. Let
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}},{\operatorname {red}}}}})^{\operatorname {irr}}$
; see Subsection 5.1 and some basic results on Clifford theory explained in Section 2; each has its benefits. Let
![]() ${\operatorname {ad}_{{\rho _x}}}$
denote the adjoint representation of
${\operatorname {ad}_{{\rho _x}}}$
denote the adjoint representation of
![]() $\rho _x$
, and let
$\rho _x$
, and let
![]() ${\operatorname {ad}_{{\rho _x}}^0}$
be its subrepresentation on trace zero matrices. Let x be a dimension
${\operatorname {ad}_{{\rho _x}}^0}$
be its subrepresentation on trace zero matrices. Let x be a dimension
![]() $1$
point of
$1$
point of
![]() $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}},{\operatorname {red}}}}})^{{\operatorname {irr}}}$
. The deformation theory as introduced by Mazur in [Reference MazurMaz89] yields that the map
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}},{\operatorname {red}}}}})^{{\operatorname {irr}}}$
. The deformation theory as introduced by Mazur in [Reference MazurMaz89] yields that the map
![]() ${\mathrm {det}}_{{\overline {{D}}}}$
is formally smooth at x if
${\mathrm {det}}_{{\overline {{D}}}}$
is formally smooth at x if
![]() ${H^2}({G_K},{\operatorname {ad}_{{\rho _x}}^0})$
vanishes. We call such an x special, if
${H^2}({G_K},{\operatorname {ad}_{{\rho _x}}^0})$
vanishes. We call such an x special, if
![]() ${H^2}({G_K},{\operatorname {ad}_{{\rho _x}}^0}){\neq }0$
. An important observation is that special points are induced from representations of smaller dimension of the group
${H^2}({G_K},{\operatorname {ad}_{{\rho _x}}^0}){\neq }0$
. An important observation is that special points are induced from representations of smaller dimension of the group
![]() $G_{K'}$
for
$G_{K'}$
for
![]() $K'$
a suitable extension of K. This link and induction give a strong dimension bound for the special locus
$K'$
a suitable extension of K. This link and induction give a strong dimension bound for the special locus
![]() $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\mathrm {spcl}}$
in
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\mathrm {spcl}}$
in
![]() $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}},{\operatorname {red}}}}})^{{\operatorname {irr}}}$
, that is, the Zariski closure of the special points of dimension
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}},{\operatorname {red}}}}})^{{\operatorname {irr}}}$
, that is, the Zariski closure of the special points of dimension
![]() $1$
therein. More precisely, one has: If
$1$
therein. More precisely, one has: If
![]() $\zeta _p\notin K$
, then x is special if and only if
$\zeta _p\notin K$
, then x is special if and only if
![]() $\rho _x$
is induced from a representation of
$\rho _x$
is induced from a representation of
![]() $G_{K(\zeta _p)}$
; if
$G_{K(\zeta _p)}$
; if
![]() $\zeta _p\in K$
, then x is special if and only if there exists a degree p Galois extension
$\zeta _p\in K$
, then x is special if and only if there exists a degree p Galois extension
![]() $K'$
of K such that
$K'$
of K such that
![]() $\rho _x$
is induced from a representation of
$\rho _x$
is induced from a representation of
![]() $G_{K'}$
. To state our main results, we also abbreviate
$G_{K'}$
. To state our main results, we also abbreviate
![]() $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{{\mathrm {n}\textrm {-}\mathrm {spcl}}}:=({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\operatorname {irr}}{\smallsetminus } ({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\mathrm {spcl}}$
and
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{{\mathrm {n}\textrm {-}\mathrm {spcl}}}:=({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\operatorname {irr}}{\smallsetminus } ({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\mathrm {spcl}}$
and
![]() $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\operatorname {red}}:={\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}{\smallsetminus } ({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\operatorname {irr}}$
.
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\operatorname {red}}:={\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}{\smallsetminus } ({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\operatorname {irr}}$
.
Theorem 1 (Theorem 5.5.1, equidimensionality).
The following assertions hold:
-
(a)
 $(\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{\overline {D}})^{\mathrm {n}\textrm {-}\mathrm {spcl}}\subset \overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{\overline {D}}$
is open and Zariski dense.
$(\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{\overline {D}})^{\mathrm {n}\textrm {-}\mathrm {spcl}}\subset \overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{\overline {D}}$
is open and Zariski dense. -
(b) If
 $\zeta _p\notin K$
, then
$\zeta _p\notin K$
, then
 $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{{{\mathrm {n}\textrm {-}\mathrm {spcl}}}}$
is regular.
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{{{\mathrm {n}\textrm {-}\mathrm {spcl}}}}$
is regular. -
(c) If
 $\zeta _p\in K$
, then
$\zeta _p\in K$
, then
 $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})_{\operatorname {red}}^{{{\mathrm {n}\textrm {-}\mathrm {spcl}}}}$
is regular, and
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})_{\operatorname {red}}^{{{\mathrm {n}\textrm {-}\mathrm {spcl}}}}$
is regular, and
 $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{{\operatorname {reg}}}$
is empty.
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{{\operatorname {reg}}}$
is empty. -
(d)
 ${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
is equidimensional of dimension
${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
is equidimensional of dimension
 $[K:{\mathbb {Q}}_p] n^2+1$
.
$[K:{\mathbb {Q}}_p] n^2+1$
.
Theorem 2 (Theorem 5.5.5, singular locus).
If
![]() $\zeta _p\notin K$
, then the following hold:
$\zeta _p\notin K$
, then the following hold:
-
(a) The closure of
 $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\mathrm {spcl}}$
in
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\mathrm {spcl}}$
in
 ${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
lies in
${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
lies in
 $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\operatorname {sing}}$
.
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\operatorname {sing}}$
. -
(b) If
 $n>2$
or
$n>2$
or
 $[K:{\mathbb {Q}}_p]>1$
, then
$[K:{\mathbb {Q}}_p]>1$
, then
 $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{{\operatorname {red}}}\subset ({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\operatorname {sing}}$
.
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{{\operatorname {red}}}\subset ({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\operatorname {sing}}$
. -
(c) If
 $n=2$
,
$n=2$
,
 $K={\mathbb {Q}}_p$
, and
$K={\mathbb {Q}}_p$
, and
 $x\in ({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{{\operatorname {red}}}$
is a direct sum
$x\in ({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{{\operatorname {red}}}$
is a direct sum
 ${D}_1\oplus {D}_2$
of one-dimensional characters
${D}_1\oplus {D}_2$
of one-dimensional characters
 ${D}_i$
, then
${D}_i$
, then
 $x\in ({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\operatorname {sing}}$
if and only if
$x\in ({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\operatorname {sing}}$
if and only if
 ${D}_2={D}_1(m)$
for
${D}_2={D}_1(m)$
for
 $m\in \{\pm 1\}$
.
$m\in \{\pm 1\}$
.
Theorem 3 (Theorem 5.5.7, Serre regularity).
The ring
![]() ${\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}},{\operatorname {red}}}}}$
satisfies Serre’s condition
${\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}},{\operatorname {red}}}}}$
satisfies Serre’s condition
![]() $(R_2)$
Footnote
1
, unless
$(R_2)$
Footnote
1
, unless
![]() $n=2$
,
$n=2$
,
![]() $K={\mathbb {Q}}_2$
and
$K={\mathbb {Q}}_2$
and
![]() ${\overline {{D}}}$
is trivial.
${\overline {{D}}}$
is trivial.
We in fact determine the exact dimension of
![]() $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\operatorname {red}}$
and
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\operatorname {red}}$
and
![]() $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\mathrm {spcl}}$
in Lemma 5.5.2 and Corollary 5.5.3. From this, depending on n and
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\mathrm {spcl}}$
in Lemma 5.5.2 and Corollary 5.5.3. From this, depending on n and
![]() $[K:{\mathbb {Q}}_p]$
, one can in general establish Serre’s condition
$[K:{\mathbb {Q}}_p]$
, one can in general establish Serre’s condition
![]() $(R_m)$
for some
$(R_m)$
for some
![]() $m=m_{K,n}>2$
.
$m=m_{K,n}>2$
.
It is a foundational and natural question to study the equidimensionality of
![]() ${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
and to better understand some geometric properties of
${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
and to better understand some geometric properties of
![]() ${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
, extending [Reference ChenevierChe11] to the special fiber. However, our true motivation was the expectation, that the equidimensionality proved here should help proving expected ring theoretic properties of the universal lifting ring
${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
, extending [Reference ChenevierChe11] to the special fiber. However, our true motivation was the expectation, that the equidimensionality proved here should help proving expected ring theoretic properties of the universal lifting ring
![]() $R_{\overline {\rho }}^{\square }$
attached to any continuous homomorphism
$R_{\overline {\rho }}^{\square }$
attached to any continuous homomorphism
![]() ${\bar \rho }\colon G_K\to {\mathrm {GL}}_n({{\mathbb {F}}\,\!{}})$
by Kisin in [Reference KisinKis09] as an important technical device to understand deformation rings as introduced in [Reference MazurMaz89] by Mazur. There should be a bootstrap argument to deduce from the dimension for
${\bar \rho }\colon G_K\to {\mathrm {GL}}_n({{\mathbb {F}}\,\!{}})$
by Kisin in [Reference KisinKis09] as an important technical device to understand deformation rings as introduced in [Reference MazurMaz89] by Mazur. There should be a bootstrap argument to deduce from the dimension for
![]() ${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
found here, that
${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
found here, that
![]() $R^\square _{{\overline {\rho }}}$
is flat over
$R^\square _{{\overline {\rho }}}$
is flat over
![]() ${{W({{\mathbb {F}}\,\!{}})}}$
of expected relative dimension
${{W({{\mathbb {F}}\,\!{}})}}$
of expected relative dimension
![]() $(d+1)n^2$
. This in turn would give the local complete intersection property of
$(d+1)n^2$
. This in turn would give the local complete intersection property of
![]() $R^\square _{{\overline {\rho }}}$
, the normality of the special fiber ring
$R^\square _{{\overline {\rho }}}$
, the normality of the special fiber ring
![]() $R^\square _{{\overline {\rho }}}/(p)$
, and it should allow one to deduce a bijection between the irreducible components of
$R^\square _{{\overline {\rho }}}/(p)$
, and it should allow one to deduce a bijection between the irreducible components of
![]() $R^\square _{{\overline {\rho }}}$
and of
$R^\square _{{\overline {\rho }}}$
and of
![]() $R^\square _{{\mathrm {det}}{\overline {\rho }}}$
, as expected from computations by us in the case
$R^\square _{{\mathrm {det}}{\overline {\rho }}}$
, as expected from computations by us in the case
![]() $n=2$
in [Reference Böckle and JuschkaBJ15], and then in further cases in [Reference Colmez, Dospinescu and PaškūnasCDP15], [Reference BabnikBab19] and [Reference IyengarIye20]. This in turn might prove, in light of recent results of [Reference Emerton and GeeEG19], the Zariski density of crystalline points, and thereby to complete work of many others, notably [Reference NakamuraNak14, § 4] by Nakamura, extending previous important work of Chenevier, in the case where
$n=2$
in [Reference Böckle and JuschkaBJ15], and then in further cases in [Reference Colmez, Dospinescu and PaškūnasCDP15], [Reference BabnikBab19] and [Reference IyengarIye20]. This in turn might prove, in light of recent results of [Reference Emerton and GeeEG19], the Zariski density of crystalline points, and thereby to complete work of many others, notably [Reference NakamuraNak14, § 4] by Nakamura, extending previous important work of Chenevier, in the case where
![]() ${\overline {\rho }}$
is absolutely irreducible, and of [Reference IyengarIye20] when
${\overline {\rho }}$
is absolutely irreducible, and of [Reference IyengarIye20] when
![]() ${\overline {\rho }}$
is trivial, under some technical hypotheses on K, p and n. This program has now been completed in work of the first author with A. Iyengar and V. Paškūnas in [Reference Böckle, Iyengar and PaškūnasBIP21] and [Reference Böckle, Iyengar and PaškūnasBIP22].
${\overline {\rho }}$
is trivial, under some technical hypotheses on K, p and n. This program has now been completed in work of the first author with A. Iyengar and V. Paškūnas in [Reference Böckle, Iyengar and PaškūnasBIP21] and [Reference Böckle, Iyengar and PaškūnasBIP22].
Let us give some further ideas of the proofs and indicate some of the auxiliary results and techniques developed in this article. Our overall strategy is similar to [Reference ChenevierChe11]. But we face new phenomena that have to be dealt with.
Above, we already mentioned special points x of
![]() $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}},{\operatorname {red}}}}})^{\operatorname {irr}}$
. They can exist when the cyclotomic character has finite order, that is, on the special but not the generic fiber. At such x, the representations
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}},{\operatorname {red}}}}})^{\operatorname {irr}}$
. They can exist when the cyclotomic character has finite order, that is, on the special but not the generic fiber. At such x, the representations
![]() $\rho _x$
is induced from a representation of
$\rho _x$
is induced from a representation of
![]() $G_{K'}$
for a proper cyclic extension
$G_{K'}$
for a proper cyclic extension
![]() $K'$
of K of degree dividing n. So it is important for us to define an induction for pseudocharacters. This we work out in Subsection 4.6; our present approach incorporates significant improvements due to the referee. Using induction of pseudorepresentation, we show that the locus of special representations can be covered by finitely many
$K'$
of K of degree dividing n. So it is important for us to define an induction for pseudocharacters. This we work out in Subsection 4.6; our present approach incorporates significant improvements due to the referee. Using induction of pseudorepresentation, we show that the locus of special representations can be covered by finitely many
![]() ${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}'}}}$
, where the
${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}'}}}$
, where the
![]() ${\overline {{D}}}'$
are continuous pseudocharacters of
${\overline {{D}}}'$
are continuous pseudocharacters of
![]() $G_{K'}$
for the
$G_{K'}$
for the
![]() $K'$
just mentioned, and in particular they are of dimension
$K'$
just mentioned, and in particular they are of dimension
![]() $n/[K':K]<n$
. Now, in an inductive procedure, the space
$n/[K':K]<n$
. Now, in an inductive procedure, the space
![]() ${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}'}}}$
is known to have dimension
${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}'}}}$
is known to have dimension
![]() $(d[K':K]) (n/[K':K])^2+1=dn^2/[K':K]+1$
, and this is much smaller than the lower dimension bound
$(d[K':K]) (n/[K':K])^2+1=dn^2/[K':K]+1$
, and this is much smaller than the lower dimension bound
![]() $dn^2+1$
that we establish for (all components of)
$dn^2+1$
that we establish for (all components of)
![]() ${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
. In particular, the special locus is nowhere dense in
${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
. In particular, the special locus is nowhere dense in
![]() ${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}},{\operatorname {red}}}}}$
. Another operation on pseudocharacters that we introduce in Subsection 4.5 is twisting by one-dimensional representations. We use it to prove the closedness of the special locus in the case
${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}},{\operatorname {red}}}}}$
. Another operation on pseudocharacters that we introduce in Subsection 4.5 is twisting by one-dimensional representations. We use it to prove the closedness of the special locus in the case
![]() $\zeta _p\notin K$
.
$\zeta _p\notin K$
.
A further important ingredient in our inductive argument to establish Theorem 1 is the proof that every neighborhood of some x in the reducible locus
![]() $( {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\operatorname {red}}$
contains a point of
$( {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\operatorname {red}}$
contains a point of
![]() $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\operatorname {irr}}$
. Here, we follow the argument used by Chenevier [Reference ChenevierChe11, Theorem 2.1], using, however, étale topology in place of rigid geometry. The key point in our setting is that étale locally
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\operatorname {irr}}$
. Here, we follow the argument used by Chenevier [Reference ChenevierChe11, Theorem 2.1], using, however, étale topology in place of rigid geometry. The key point in our setting is that étale locally
![]() $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\operatorname {red}}{\hookrightarrow } {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
is a closed immersion. Hence, if a neighborhood
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\operatorname {red}}{\hookrightarrow } {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
is a closed immersion. Hence, if a neighborhood
![]() $U\ \textrm{of\ some}\ x \in ({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\operatorname {red}}$
does not intersect
$U\ \textrm{of\ some}\ x \in ({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\operatorname {red}}$
does not intersect
![]() $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\operatorname {irr}}$
, the local behavior at x in
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\operatorname {irr}}$
, the local behavior at x in
![]() ${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
is similar to that of
${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
is similar to that of
![]() ${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_1}}}\times {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_2}}}$
for pseudocharacters such that
${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_1}}}\times {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_2}}}$
for pseudocharacters such that
![]() ${\overline {{D}}}={{\overline {{D}}}_1}\oplus {{\overline {{D}}}_2}$
, after completion at x. This will ultimately yield a contradiction by comparing dimensions (of tangent spaces); see Theorem 5.2.1 and its proof. Following a suggestion of the referee, in Subsection 5.3 we give a second independent proof of Theorem 5.2.1.
${\overline {{D}}}={{\overline {{D}}}_1}\oplus {{\overline {{D}}}_2}$
, after completion at x. This will ultimately yield a contradiction by comparing dimensions (of tangent spaces); see Theorem 5.2.1 and its proof. Following a suggestion of the referee, in Subsection 5.3 we give a second independent proof of Theorem 5.2.1.
On the technical side, we shall often work with dimension
![]() $1$
points
$1$
points
![]() $x\in {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
. The set of these is Zariski dense in
$x\in {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
. The set of these is Zariski dense in
![]() ${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
, so they allow us to see all irreducible components. At the same time, their residue fields
${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
, so they allow us to see all irreducible components. At the same time, their residue fields
![]() ${\kappa ({x})} $
are Laurent series fields over a finite field, and so finite-dimensional
${\kappa ({x})} $
are Laurent series fields over a finite field, and so finite-dimensional
![]() ${\kappa ({x})} $
-algebras carry a unique topology compatible with that of
${\kappa ({x})} $
-algebras carry a unique topology compatible with that of
![]() ${\kappa ({x})} $
. We make use of this in considering deformation functors at such points. This is especially useful if
${\kappa ({x})} $
. We make use of this in considering deformation functors at such points. This is especially useful if
![]() ${D}_x$
is irreducible or at least multiplicity free. This technique of studying deformation rings at dimension 1 points was introduced by Kisin over p-adic fields. We need to reprove some basic results, for instance in Subsection 3.3 and Subsection 4.8, building on [Reference ChenevierChe14], [Reference Wang-EricksonWE18] for pseudodeformations and on [Reference NekovářNek06] for Tate local duality over general coefficient rings such as
${D}_x$
is irreducible or at least multiplicity free. This technique of studying deformation rings at dimension 1 points was introduced by Kisin over p-adic fields. We need to reprove some basic results, for instance in Subsection 3.3 and Subsection 4.8, building on [Reference ChenevierChe14], [Reference Wang-EricksonWE18] for pseudodeformations and on [Reference NekovářNek06] for Tate local duality over general coefficient rings such as
![]() ${\kappa ({x})} $
or its ring of integers.
${\kappa ({x})} $
or its ring of integers.
Outline
We now give an outline of this work. Section 2 presents parts of Clifford theory to be used in Subsection 5.1 when defining and characterizing special points. Section 3 reviews the theory of deformations of Galois representation in the sense of Mazur with a strong emphasis on result related to deformation rings at dimension
![]() $1$
points where the residue field is a local equicharacteristic field. Section 4 is a detailed review of pseudocharacters following largely [Reference ChenevierChe14] with some noteworthy additions that are crucial for the main results of this work: We consider the locus of reducibility in the context of pseudocharacters, we introduce twisting and induction of pseudocharacters, and we give a special treatment to some elementary facts on equicharacteristic dimension
$1$
points where the residue field is a local equicharacteristic field. Section 4 is a detailed review of pseudocharacters following largely [Reference ChenevierChe14] with some noteworthy additions that are crucial for the main results of this work: We consider the locus of reducibility in the context of pseudocharacters, we introduce twisting and induction of pseudocharacters, and we give a special treatment to some elementary facts on equicharacteristic dimension
![]() $1$
points on pseudodeformation rings.
$1$
points on pseudodeformation rings.
The final Section 5 contains the proof of the main results of this work, Theorems 1 to 3 on the special fiber of universal pseudodeformation rings. We follow Chenevier’s proof for the generic fiber [Reference ChenevierChe11] and explain how to overcome all complications that arise in the special fiber. Much of these complications are packed into our definition of special points in Subsection 5.1; see Definition 5.1.2. nonspecial (irreducible) points will take the role of irreducible points in Chenevier’s work; they describe that part of the irreducible locus of the special fiber of the pseudodeformation space over which the determinant map is relatively formally smooth.
Subsection 5.1 also contains some technical result on the comparison of universal pseudodeformation and universal deformation rings over local fields where the residual pseudocharacter is a sum of two irreducible ones; see Lemma 5.1.6. In Subsection 5.2, we describe the induction procedure that proves the main result: Given a suitable induction hypothesis, we shows that the reducible locus is nowhere dense. In Subsection 5.4, we show that the nonspecial points are open and Zariski dense in the irreducible locus under some inductive hypotheses. By combining the previous subsections, it is then in Subsection 5.5 straightforward to prove Theorems 1 to 3.
Let us also note that in an appendix, we provide some results on commutative rings, on algebras over a field and on absolutely irreducible mod p representations of the absolute Galois group of a p-adic field. These results are mostly standard and they serve as a convenient reference. In addition, in Subsection A.4 we prove a variant of an important result of Vaccarino that we use in the construction of induction for pseudocharacters in Subsection 4.6.
Some notation and conventions
-
• Throughout, we fix a prime number p and a finite field
 ${{\mathbb {F}}\,\!{}}$
of characteristic p.
${{\mathbb {F}}\,\!{}}$
of characteristic p. -
• For any field E, we denote by
 ${{E}^{\mathrm {alg}}}$
an algebraic closure of E and by
${{E}^{\mathrm {alg}}}$
an algebraic closure of E and by
 $G_E={\mathrm {Gal}}({{E/E}^{\mathrm {alg}}})$
its absolute Galois group.
$G_E={\mathrm {Gal}}({{E/E}^{\mathrm {alg}}})$
its absolute Galois group. -
• We write
 ${\mathbb {Q}}_p$
for the p-adic completion of
${\mathbb {Q}}_p$
for the p-adic completion of
 ${\mathbb {Q}}$
and fix an algebraic closure
${\mathbb {Q}}$
and fix an algebraic closure
 ${{{\mathbb {Q}}}^{\mathrm {alg}}_p}$
of
${{{\mathbb {Q}}}^{\mathrm {alg}}_p}$
of
 ${\mathbb {Q}}_p$
. All algebraic extension fields of
${\mathbb {Q}}_p$
. All algebraic extension fields of
 ${\mathbb {Q}}_p$
will be considered as subfields of
${\mathbb {Q}}_p$
will be considered as subfields of
 ${{{\mathbb {Q}}}^{\mathrm {alg}}_p}$
.
${{{\mathbb {Q}}}^{\mathrm {alg}}_p}$
. -
• We fix a finite extension field K of
 ${\mathbb {Q}}_p$
of degree
${\mathbb {Q}}_p$
of degree
 $d=[K:{\mathbb {Q}}_p]$
inside
$d=[K:{\mathbb {Q}}_p]$
inside
 ${{{\mathbb {Q}}}^{\mathrm {alg}}_p}$
.
${{{\mathbb {Q}}}^{\mathrm {alg}}_p}$
. -
• Throughout,
 $\kappa $
will denote a finite field of characteristic p or a local field of residue characteristic p. It will take the role of a coefficient field for deformations and pseudodeformations. If such a coefficient field is meant to be finite, we usually write
$\kappa $
will denote a finite field of characteristic p or a local field of residue characteristic p. It will take the role of a coefficient field for deformations and pseudodeformations. If such a coefficient field is meant to be finite, we usually write
 ${{\mathbb {F}}\,\!{}}$
.
${{\mathbb {F}}\,\!{}}$
. -
• For a point x on a scheme X, we write
 ${\cal O}_{X,x}$
for the local ring at x and
${\cal O}_{X,x}$
for the local ring at x and
 ${\kappa ({x})} $
for its residue field; the latter is the second way in which the letter
${\kappa ({x})} $
for its residue field; the latter is the second way in which the letter
 $\kappa $
occurs; note that
$\kappa $
occurs; note that
 ${\kappa ({x})} $
can be any field.
${\kappa ({x})} $
can be any field. -
• For a complete Noetherian local ring R with finite residue field
 ${{\mathbb {F}}\,\!{}}$
, we call
${{\mathbb {F}}\,\!{}}$
, we call
 $x\in {\mathrm {Spec}}\ R$
with corresponding prime ideal
$x\in {\mathrm {Spec}}\ R$
with corresponding prime ideal
 ${\mathfrak {p}}_x\subset R$
a point of dimension
${\mathfrak {p}}_x\subset R$
a point of dimension
 $1$
if
$1$
if
 $R/{\mathfrak {p}}_x$
has Krull dimension
$R/{\mathfrak {p}}_x$
has Krull dimension
 $1$
. The residue field
$1$
. The residue field
 ${\kappa ({x})} $
will then either be a finite extension of
${\kappa ({x})} $
will then either be a finite extension of
 ${\mathbb {Q}}_p$
or of
${\mathbb {Q}}_p$
or of
 ${{\mathbb {F}}\,\!{}}((x))$
.
${{\mathbb {F}}\,\!{}}((x))$
. -
• By a ring, we mean a unital commutative ring. Algebras over a ring A do not need to be commutative. To make clear that an A-algebra is commutative, we will always speak of it as a commutative A-algebra.
-
• The categories
 ${\mathcal {A}r}_{\Lambda }$
and
${\mathcal {A}r}_{\Lambda }$
and
 ${\widehat {\mathcal {A}}r}_{\Lambda }$
of certain (pro-)Artinian local
${\widehat {\mathcal {A}}r}_{\Lambda }$
of certain (pro-)Artinian local
 $\Lambda $
-algebras, that have the same residue field as
$\Lambda $
-algebras, that have the same residue field as
 $\Lambda $
, are introduced at the beginning of Subsection 3.1.
$\Lambda $
, are introduced at the beginning of Subsection 3.1. -
• The category
 ${\mathcal {A}dm}_{\Lambda }$
of admissible
${\mathcal {A}dm}_{\Lambda }$
of admissible
 $\Lambda $
-algebras is introduced at the beginning of Subsection 4.4.
$\Lambda $
-algebras is introduced at the beginning of Subsection 4.4.
2 Clifford theory
Clifford theory provides a crucial input in determining conditions that characterize the special points that we will introduce in Definition 5.1.2, building on Lemma 5.1.1. In this section, we give the representation theoretic background. We also include some results for coefficient fields that are not algebraically closed. The results in Subsection 2.2, and most importantly Corollary 2.2.2, are probably well known. Those in Subsection 2.3, and in particular Lemma 2.3.1, seem of more exotic nature to us. We give proofs whenever we could not locate the results in the literature.
Throughout this section, G denotes a (possibly infinite) group and H a subgroup of finite index. If G is a topological group, we assume H to be open in G. We define
![]() $N:=\bigcap _{g\in G/H}H^g$
. It is of finite index and normal in G and the largest subgroup of H with this property. If H is normal, then
$N:=\bigcap _{g\in G/H}H^g$
. It is of finite index and normal in G and the largest subgroup of H with this property. If H is normal, then
![]() $N=H$
; if G is a topological group, then N is open in G. All representations will act on a free module of finite rank over some ring or field.
$N=H$
; if G is a topological group, then N is open in G. All representations will act on a free module of finite rank over some ring or field.
2.1 Generalities
Definition 2.1.1. For a representation
![]() $\rho \colon N\to {\mathrm {GL}}_m(A)$
over a ring A and
$\rho \colon N\to {\mathrm {GL}}_m(A)$
over a ring A and
![]() $g\in G$
, we define the conjugate of
$g\in G$
, we define the conjugate of
![]() $\rho $
by g as the representation
$\rho $
by g as the representation
Remark 2.1.2. Conjugation in the sense of Definition 2.1.1 defines an action of G on the set
![]() $\{[\rho ^g]{\>:\>} g\in G\}$
of isomorphism classes
$\{[\rho ^g]{\>:\>} g\in G\}$
of isomorphism classes
![]() $[\rho ^g]$
of representations
$[\rho ^g]$
of representations
![]() $\rho ^g$
of N. Since N acts trivially, the action factors via
$\rho ^g$
of N. Since N acts trivially, the action factors via
![]() $G/N$
and so, up to isomorphism, there are only finitely many conjugates of
$G/N$
and so, up to isomorphism, there are only finitely many conjugates of
![]() $\rho $
.
$\rho $
.
For the remainder of this subsection, let E denote a field of characteristic
![]() $p\ge 0$
. Unless said otherwise, any representation will be of finite dimension over E.
$p\ge 0$
. Unless said otherwise, any representation will be of finite dimension over E.
The following lemma will be used repeatedly.
Lemma 2.1.3 (Mackey’s tensor product theorem for induced representations; [Reference Curtis and ReinerCR62, Corollary 44.4]).
Let
![]() $\rho $
and
$\rho $
and
![]() $\rho '$
be representations of G and of H, respectively. Then
$\rho '$
be representations of G and of H, respectively. Then
We will also need:
Lemma 2.1.4. Let
![]() $\rho $
be a semisimple representation of H, and let
$\rho $
be a semisimple representation of H, and let
![]() $\nu ={\mathrm {Res}}_N^H\rho $
. Assume for parts (f) to (h) that H is normal in G, and so in turn
$\nu ={\mathrm {Res}}_N^H\rho $
. Assume for parts (f) to (h) that H is normal in G, and so in turn
![]() $N=H$
and
$N=H$
and
![]() $\nu =\rho $
. Then the following hold:
$\nu =\rho $
. Then the following hold:
-
(a) For any separable field extension
 $F\supset E$
the representation
$F\supset E$
the representation
 $\rho \otimes _EF$
is semisimple.
$\rho \otimes _EF$
is semisimple. -
(b) One has
 ${\mathrm {Res}}_N^G {\mathrm {Ind}}_H^G \rho \cong \bigoplus _{g\in G/H}({\mathrm {Res}}_N^H \rho )^g$
.
${\mathrm {Res}}_N^G {\mathrm {Ind}}_H^G \rho \cong \bigoplus _{g\in G/H}({\mathrm {Res}}_N^H \rho )^g$
. -
(c) If
 $\tau $
is an irreducible representation of G, then
$\tau $
is an irreducible representation of G, then
 ${\mathrm {Res}}_N^G\tau $
is semisimple, and all irreducible summands of
${\mathrm {Res}}_N^G\tau $
is semisimple, and all irreducible summands of
 ${\mathrm {Res}}_N^G\tau $
are conjugate to one another in the sense of Definition 2.1.1.
${\mathrm {Res}}_N^G\tau $
are conjugate to one another in the sense of Definition 2.1.1. -
(d) If
 $[G:N]$
is not a multiple of p, then
$[G:N]$
is not a multiple of p, then
 $ {\mathrm {Ind}}_H^G \rho $
is semisimple.
$ {\mathrm {Ind}}_H^G \rho $
is semisimple. -
(e) If
 $\nu $
is irreducible and if
$\nu $
is irreducible and if
 $G/N$
acts freely on
$G/N$
acts freely on
 $\{[\nu ^g]\!:\! g\in G\}$
, then
$\{[\nu ^g]\!:\! g\in G\}$
, then
 ${\mathrm {Ind}}_H^G \rho $
is irreducible.
${\mathrm {Ind}}_H^G \rho $
is irreducible. -
(f) The representation
 ${\mathrm {Ind}}_H^G\rho $
is absolutely irreducible if and only if
${\mathrm {Ind}}_H^G\rho $
is absolutely irreducible if and only if
 $\rho $
is absolutely irreducible and
$\rho $
is absolutely irreducible and
 $G/H$
acts freely on
$G/H$
acts freely on
 $\{[\rho ^g]{\>:\>} g\in G\}$
.
$\{[\rho ^g]{\>:\>} g\in G\}$
. -
(g) Let
 $\rho '$
be a second representation of H. Then
$\rho '$
be a second representation of H. Then
 $ {\mathrm {Ind}}_H^G \rho \cong {\mathrm {Ind}}_H^G \rho '$
if and only if (1)
$ {\mathrm {Ind}}_H^G \rho \cong {\mathrm {Ind}}_H^G \rho '$
if and only if (1) $$ \begin{align} \bigoplus_{g\in G/H} \rho^g \cong \bigoplus_{g\in G/H} (\rho')^g. \end{align} $$
$$ \begin{align} \bigoplus_{g\in G/H} \rho^g \cong \bigoplus_{g\in G/H} (\rho')^g. \end{align} $$
-
(h) If
 $\rho $
is irreducible in (g), then the isomorphism in (1) is equivalent to
$\rho $
is irreducible in (g), then the isomorphism in (1) is equivalent to
 $\rho '\cong \rho ^g$
for some
$\rho '\cong \rho ^g$
for some
 $g\in G$
.
$g\in G$
.
Proof. We denote by V the E-vector space underlying
![]() $\rho $
. Part (a) is [Reference Curtis and ReinerCR62, Corollary 69.8] with the ring A from there being the image of
$\rho $
. Part (a) is [Reference Curtis and ReinerCR62, Corollary 69.8] with the ring A from there being the image of
![]() $E[H]$
in
$E[H]$
in
![]() ${\mathrm {End}}_E(V)$
. Part (b) holds by [Reference Serre and ScottSer77, Proposition 22]. Part (c) follows from [Reference Curtis and ReinerCR62, Theorem 49.2]. For (d), note that
${\mathrm {End}}_E(V)$
. Part (b) holds by [Reference Serre and ScottSer77, Proposition 22]. Part (c) follows from [Reference Curtis and ReinerCR62, Theorem 49.2]. For (d), note that
![]() $\rho $
is a subrepresentation of
$\rho $
is a subrepresentation of
![]() ${\mathrm {Ind}}_N^H{\mathrm {Res}}_N^H\rho $
, and hence
${\mathrm {Ind}}_N^H{\mathrm {Res}}_N^H\rho $
, and hence
![]() ${\mathrm {Ind}}_H^G\rho $
is a subrepresentation of
${\mathrm {Ind}}_H^G\rho $
is a subrepresentation of
![]() ${\mathrm {Ind}}_N^G{\mathrm {Res}}_N^H\rho $
. By (c) applied to the irreducible summands of
${\mathrm {Ind}}_N^G{\mathrm {Res}}_N^H\rho $
. By (c) applied to the irreducible summands of
![]() $\rho $
, we see that
$\rho $
, we see that
![]() ${\mathrm {Res}}_N^H\rho $
is semisimple. Now, the result can be found in [Reference WebbWeb16, Chapter 5, Exercise 8].
${\mathrm {Res}}_N^H\rho $
is semisimple. Now, the result can be found in [Reference WebbWeb16, Chapter 5, Exercise 8].
To prove Part (e), let
![]() $V'\subset {\mathrm {Ind}}_H^G \rho $
be an irreducible G-subrepresentation. Then by (b) the representation
$V'\subset {\mathrm {Ind}}_H^G \rho $
be an irreducible G-subrepresentation. Then by (b) the representation
![]() ${\mathrm {Res}}_N^G V'$
contains
${\mathrm {Res}}_N^G V'$
contains
![]() $\nu ^g$
for some
$\nu ^g$
for some
![]() $g\in G$
. As
$g\in G$
. As
![]() $V'$
is a G-representation, we deduce
$V'$
is a G-representation, we deduce
![]() $ \nu ^g\subset {\mathrm {Res}}_N^G V'$
for all
$ \nu ^g\subset {\mathrm {Res}}_N^G V'$
for all
![]() $g\in G$
. By hypothesis, the
$g\in G$
. By hypothesis, the
![]() $\nu ^g$
,
$\nu ^g$
,
![]() $g\in G/N$
, are pairwise nonisomorphic, and hence
$g\in G/N$
, are pairwise nonisomorphic, and hence
![]() $\bigoplus _{g\in G/N} \nu ^g\subset {\mathrm {Res}}_H^G V'$
. By (b) the left-hand side is isomorphic to
$\bigoplus _{g\in G/N} \nu ^g\subset {\mathrm {Res}}_H^G V'$
. By (b) the left-hand side is isomorphic to
![]() $ {\mathrm {Res}}_N^G {\mathrm {Ind}}_H^G\rho $
so that for dimension reasons we must have
$ {\mathrm {Res}}_N^G {\mathrm {Ind}}_H^G\rho $
so that for dimension reasons we must have
![]() $V'={\mathrm {Ind}}_H^G\rho $
.
$V'={\mathrm {Ind}}_H^G\rho $
.
We next prove Part (f). Because the solution space of a linear system of equations has the same dimension over its field of definition and over any extension, one has
This allows one by base change
![]() $E\to {{E}^{\mathrm {alg}}}$
to reduce one direction of (f) to (e). For the converse, assume that
$E\to {{E}^{\mathrm {alg}}}$
to reduce one direction of (f) to (e). For the converse, assume that
![]() ${\mathrm {Ind}}_H^G\rho $
is absolutely irreducible. Because
${\mathrm {Ind}}_H^G\rho $
is absolutely irreducible. Because
![]() ${\mathrm {Ind}}_H^G$
is an exact functor,
${\mathrm {Ind}}_H^G$
is an exact functor,
![]() $\rho $
must be absolutely irreducible and hence also
$\rho $
must be absolutely irreducible and hence also
![]() $\rho ^g$
for all
$\rho ^g$
for all
![]() $g\in G$
. Because
$g\in G$
. Because
![]() ${\mathrm {Ind}}_H^G\rho $
is absolutely irreducible, Frobenius reciprocity yields
${\mathrm {Ind}}_H^G\rho $
is absolutely irreducible, Frobenius reciprocity yields
Hence,
![]() $\rho $
is isomorphic to
$\rho $
is isomorphic to
![]() $\rho ^g$
if and only if
$\rho ^g$
if and only if
![]() $g\in H$
, and this completes the proof of (f).
$g\in H$
, and this completes the proof of (f).
We now prove Part (g). Note that by (b) the only if direction is clear. For the other direction, note first that by [Reference Curtis and ReinerCR81, Lemma 10.12] we have
![]() ${\mathrm {Ind}}_H^G \rho \cong {\mathrm {Ind}}_H^G \rho ^g $
for all
${\mathrm {Ind}}_H^G \rho \cong {\mathrm {Ind}}_H^G \rho ^g $
for all
![]() $g\in G$
. Since induction and direct sum commute, we also have
$g\in G$
. Since induction and direct sum commute, we also have
 $$ \begin{align*}{\mathrm{Ind}}_H^G\big( \bigoplus_{g\in G/H} \rho^g \big)= \bigoplus_{g\in G/H} \big({\mathrm{Ind}}_H^G\rho^g \big) = \big({\mathrm{Ind}}_H^G\rho \big)^{\oplus [G:H]}.\end{align*} $$
$$ \begin{align*}{\mathrm{Ind}}_H^G\big( \bigoplus_{g\in G/H} \rho^g \big)= \bigoplus_{g\in G/H} \big({\mathrm{Ind}}_H^G\rho^g \big) = \big({\mathrm{Ind}}_H^G\rho \big)^{\oplus [G:H]}.\end{align*} $$
The same formula applies to
![]() $\rho '$
, and so our hypothesis gives
$\rho '$
, and so our hypothesis gives
![]() $({\mathrm {Ind}}_H^G\rho )^{\oplus [G:H]}\cong ({\mathrm {Ind}}_H^G\rho ')^{\oplus [G:H]}$
. The Krull–Schmidt theorem (see [Reference Curtis and ReinerCR62, Theorem 14.5]) now yields
$({\mathrm {Ind}}_H^G\rho )^{\oplus [G:H]}\cong ({\mathrm {Ind}}_H^G\rho ')^{\oplus [G:H]}$
. The Krull–Schmidt theorem (see [Reference Curtis and ReinerCR62, Theorem 14.5]) now yields
![]() ${\mathrm {Ind}}_H^G\rho \cong {\mathrm {Ind}}_H^G\rho '$
. Part (h) follows from the uniqueness of composition factors and the irreducibility of the
${\mathrm {Ind}}_H^G\rho \cong {\mathrm {Ind}}_H^G\rho '$
. Part (h) follows from the uniqueness of composition factors and the irreducibility of the
![]() $\rho ^g$
.
$\rho ^g$
.
2.2 Some results when p does not divide
 $[G:H]$
$[G:H]$
Suppose now that
![]() $\chi \colon G\to E^\times $
is a character of finite order
$\chi \colon G\to E^\times $
is a character of finite order
![]() ${m}$
so that E contains a primitive
${m}$
so that E contains a primitive
![]() ${m}$
-th root of unity
${m}$
-th root of unity
![]() $\zeta $
and
$\zeta $
and
![]() ${m}\cdot 1\in E^\times $
. We also set
${m}\cdot 1\in E^\times $
. We also set
![]() $H:={\operatorname {ker}{\chi }} $
so that H is normal in G and note that
$H:={\operatorname {ker}{\chi }} $
so that H is normal in G and note that
![]() . The following is a standard result of Clifford theory, for example, [Reference Curtis and ReinerCR62, Theorem 49.2, Corollary 50.6].
. The following is a standard result of Clifford theory, for example, [Reference Curtis and ReinerCR62, Theorem 49.2, Corollary 50.6].
Theorem 2.2.1. Let
![]() $\rho \colon G \to {\mathrm {GL}}_n(E)$
be an absolutely irreducible representation such that
$\rho \colon G \to {\mathrm {GL}}_n(E)$
be an absolutely irreducible representation such that
![]() $\rho \cong \rho \otimes \chi $
. Then the following hold:
$\rho \cong \rho \otimes \chi $
. Then the following hold:
-
(a) The order
 ${m}$
of
${m}$
of
 $\chi $
divides the degree n of
$\chi $
divides the degree n of
 $\rho $
.
$\rho $
. -
(b) There exists a Kummer extension
 $E'=E(\sqrt [{m}]{\lambda })$
of E for some
$E'=E(\sqrt [{m}]{\lambda })$
of E for some
 $\lambda \in E^\times $
and an absolutely irreducible representation
$\lambda \in E^\times $
and an absolutely irreducible representation
 $\rho ' \colon H \to {\mathrm {GL}}_{n/{m}}(E')$
such that
$\rho ' \colon H \to {\mathrm {GL}}_{n/{m}}(E')$
such that  $$ \begin{align*}\rho\otimes_EE' \cong{\mathrm{Ind}}_H^G \rho'.\end{align*} $$
$$ \begin{align*}\rho\otimes_EE' \cong{\mathrm{Ind}}_H^G \rho'.\end{align*} $$
-
(c) The representations
 $(\rho ')^g$
,
$(\rho ')^g$
,
 $g\in G/H$
, are pairwise nonisomorphic and absolutely irreducible, and one has
$g\in G/H$
, are pairwise nonisomorphic and absolutely irreducible, and one has
 ${\mathrm {Res}}^G_H\rho \otimes _EE'\cong \bigoplus _{g\in G/H}(\rho ')^g$
.
${\mathrm {Res}}^G_H\rho \otimes _EE'\cong \bigoplus _{g\in G/H}(\rho ')^g$
. -
(d) If E is local field, G is a topological group and
 $\rho $
is continuous, then so is
$\rho $
is continuous, then so is
 $\rho '$
.
$\rho '$
. -
(e) If in addition to (d), G is compact, then
 $\rho $
can be defined over the ring of integers
$\rho $
can be defined over the ring of integers
 ${\cal O}_E$
of E and
${\cal O}_E$
of E and
 $\rho '$
can be defined over
$\rho '$
can be defined over
 ${\cal O}_{E'}$
.
${\cal O}_{E'}$
.
Proof. Lacking a precise reference, we give a proof. Let A be an invertible
![]() $n\times n$
-matrix over E such that
$n\times n$
-matrix over E such that
From equation (2), one deduces
![]() $ A^{m} \rho (g) A^{-{m}} = \chi ^{m}(g) \rho (g)= \rho (g)$
for all
$ A^{m} \rho (g) A^{-{m}} = \chi ^{m}(g) \rho (g)= \rho (g)$
for all
![]() $g\in G$
. Since
$g\in G$
. Since
![]() $\rho $
is absolutely irreducible, [Reference Curtis and ReinerCR62, (29.13)] implies that
$\rho $
is absolutely irreducible, [Reference Curtis and ReinerCR62, (29.13)] implies that
![]() for some
for some
![]() $\lambda \in E$
. Define
$\lambda \in E$
. Define
![]() $E':=E(\sqrt [{m}]{\lambda })$
. Let
$E':=E(\sqrt [{m}]{\lambda })$
. Let
![]() $A'=\sqrt [{m}]{\lambda }^{-1}A$
in
$A'=\sqrt [{m}]{\lambda }^{-1}A$
in
![]() ${\mathrm {GL}}_n(E')$
so that equation (2) also holds for
${\mathrm {GL}}_n(E')$
so that equation (2) also holds for
![]() $A'$
and also
$A'$
and also
![]() . Since
. Since
![]() ${m} \cdot 1$
is invertible in E, it follows, using the Jordan form, that
${m} \cdot 1$
is invertible in E, it follows, using the Jordan form, that
![]() $A'$
is semisimple. Moreover,
$A'$
is semisimple. Moreover,
![]() $A'$
is diagonalizable over
$A'$
is diagonalizable over
![]() $E'$
since E contains a primitive
$E'$
since E contains a primitive
![]() ${m}$
-th root of unity.
${m}$
-th root of unity.
After a change of basis over
![]() $E'$
, we may write A as a block diagonal matrix with diagonal blocks
$E'$
, we may write A as a block diagonal matrix with diagonal blocks
![]() $A_1,\ldots ,A_{{m}}$
such that for
$A_1,\ldots ,A_{{m}}$
such that for
![]() $i=1,\ldots ,{m}$
each
$i=1,\ldots ,{m}$
each
![]() $A_i$
is a scalar matrix
$A_i$
is a scalar matrix
![]() with
with
![]() $ n_i\ge 0$
and
$ n_i\ge 0$
and
![]() $\sum _{i=1,\ldots ,{m}} n_i=n$
. For all
$\sum _{i=1,\ldots ,{m}} n_i=n$
. For all
![]() $g\in G$
and
$g\in G$
and
![]() $i,j=1,\ldots ,{m}$
, we decompose
$i,j=1,\ldots ,{m}$
, we decompose
![]() $\rho (g)$
correspondingly into blocks
$\rho (g)$
correspondingly into blocks
![]() $\rho _{i,j}(g)$
so that equation (2) turns into
$\rho _{i,j}(g)$
so that equation (2) turns into
Choose
![]() $g\in G$
such that
$g\in G$
such that
![]() $\chi (g)=\zeta $
. Then
$\chi (g)=\zeta $
. Then
![]() $\rho _{i,j}(g)$
is zero unless
$\rho _{i,j}(g)$
is zero unless
![]() $i-j\equiv 1\pmod {m}$
. Since
$i-j\equiv 1\pmod {m}$
. Since
![]() $\rho (g)$
is invertible, all
$\rho (g)$
is invertible, all
![]() $\rho _{i+1,i}(g)$
and
$\rho _{i+1,i}(g)$
and
![]() $\rho _{{m},1}(g)$
must be invertible and hence square matrices and of nonzero size. We deduce that all
$\rho _{{m},1}(g)$
must be invertible and hence square matrices and of nonzero size. We deduce that all
![]() $n_i$
are equal, hence nonzero, and hence equal to
$n_i$
are equal, hence nonzero, and hence equal to
![]() $n/{m}$
. In particular,
$n/{m}$
. In particular,
![]() ${m}$
divides n, proving (a).
${m}$
divides n, proving (a).
Next, for
![]() $h\in H$
and for all
$h\in H$
and for all
![]() $i,j=1,\ldots ,{m}$
, equation (3) becomes
$i,j=1,\ldots ,{m}$
, equation (3) becomes
![]() $\zeta ^{i-j}\rho _{i,j}(h)= \rho _{i,j}(h)$
so that
$\zeta ^{i-j}\rho _{i,j}(h)= \rho _{i,j}(h)$
so that
![]() $\rho (h)=\bigoplus _{i=1}^{m}\rho _{i,i}(h)$
is a block diagonal matrix and each
$\rho (h)=\bigoplus _{i=1}^{m}\rho _{i,i}(h)$
is a block diagonal matrix and each
![]() $\rho _{i,i}\colon H\to {\mathrm {GL}}_{n/{m}}(k)$
,
$\rho _{i,i}\colon H\to {\mathrm {GL}}_{n/{m}}(k)$
,
![]() $h\mapsto \rho _{i,i}(h),$
is a representation of dimension
$h\mapsto \rho _{i,i}(h),$
is a representation of dimension
![]() ${n}/{{m}}$
. In particular, the restriction satisfies
${n}/{{m}}$
. In particular, the restriction satisfies
 $$ \begin{align*}{\mathrm{Res}}^G_H\rho\otimes_EE'=\bigoplus_{i=1}^{m} \rho_{i,i}. \end{align*} $$
$$ \begin{align*}{\mathrm{Res}}^G_H\rho\otimes_EE'=\bigoplus_{i=1}^{m} \rho_{i,i}. \end{align*} $$
We choose
![]() $\rho '=\rho _{1,1}$
and consider
$\rho '=\rho _{1,1}$
and consider
![]() ${\mathrm {Ind}}_H^G \rho '$
. By [Reference Curtis and ReinerCR62, (10.8) Frobenius Reciprocity Theorem], we have
${\mathrm {Ind}}_H^G \rho '$
. By [Reference Curtis and ReinerCR62, (10.8) Frobenius Reciprocity Theorem], we have
Let
![]() $f\colon {\mathrm {Ind}}_H^G\rho '\to \rho \otimes _EE'$
be a nonzero G-homomorphism. Since
$f\colon {\mathrm {Ind}}_H^G\rho '\to \rho \otimes _EE'$
be a nonzero G-homomorphism. Since
![]() $\rho $
is irreducible, it must be surjective, and because
$\rho $
is irreducible, it must be surjective, and because
![]() $\dim \rho =n=m\cdot n/m=\dim {\mathrm {Ind}}_H^G\rho '$
, its kernel must be zero so that f is an isomorphism. Next, note that
$\dim \rho =n=m\cdot n/m=\dim {\mathrm {Ind}}_H^G\rho '$
, its kernel must be zero so that f is an isomorphism. Next, note that
![]() ${\mathrm {Ind}}_H^G$
is an exact functor; see [Reference Curtis and ReinerCR81, § 10, Exercise 20]. Hence,
${\mathrm {Ind}}_H^G$
is an exact functor; see [Reference Curtis and ReinerCR81, § 10, Exercise 20]. Hence,
![]() $\rho '$
is absolutely irreducible because
$\rho '$
is absolutely irreducible because
![]() $\rho $
is so. This completes the proof of (b).
$\rho $
is so. This completes the proof of (b).
Part (c) follows from Lemma 2.1.4
(b) and (f). Part (d) easily follows from the continuity of
![]() ${\mathrm {Res}}_H^G\rho \otimes _EE'\cong \bigoplus _{g\in G/H}(\rho ')^g$
, using that all linear topologies on a finite-dimensional vector space over
${\mathrm {Res}}_H^G\rho \otimes _EE'\cong \bigoplus _{g\in G/H}(\rho ')^g$
, using that all linear topologies on a finite-dimensional vector space over
![]() $E'$
that are compatible with the topology on
$E'$
that are compatible with the topology on
![]() $E'$
are equivalent.
$E'$
are equivalent.
Concerning (e), we only prove the first assertion; the proof of the second then follows from (d). For this, let V be the E-vector space underlying
![]() $\rho $
, and let T be an
$\rho $
, and let T be an
![]() ${\cal O}_E$
-lattice in V. The stabilizer of T is an open subgroup of
${\cal O}_E$
-lattice in V. The stabilizer of T is an open subgroup of
![]() ${\mathrm {GL}}_n(E)$
and hence, by the continuity of
${\mathrm {GL}}_n(E)$
and hence, by the continuity of
![]() $\rho $
, the latice T is fixed by an open subgroup
$\rho $
, the latice T is fixed by an open subgroup
![]() $G'$
of G. Therefore,
$G'$
of G. Therefore,
![]() $G/G'$
is finite. Thus,
$G/G'$
is finite. Thus,
![]() $T':=\bigcap _{g\in G/G'} gT$
is an
$T':=\bigcap _{g\in G/G'} gT$
is an
![]() ${\cal O}_E$
-lattice in V, and this lattice is clearly G-stable. Choosing an
${\cal O}_E$
-lattice in V, and this lattice is clearly G-stable. Choosing an
![]() ${\cal O}_E$
-basis of
${\cal O}_E$
-basis of
![]() $T'$
, that is then also an E-basis of V, assertion (e) for
$T'$
, that is then also an E-basis of V, assertion (e) for
![]() $\rho $
is clear.
$\rho $
is clear.
Corollary 2.2.2. Suppose that
![]() $\rho \colon G\to {\mathrm {GL}}_n(E)$
is a representation that is absolutely semisimple; this holds for instance if E is perfect. Then
$\rho \colon G\to {\mathrm {GL}}_n(E)$
is a representation that is absolutely semisimple; this holds for instance if E is perfect. Then
![]() $ \rho \cong \rho \otimes \chi $
holds if and only if there is a separable extension
$ \rho \cong \rho \otimes \chi $
holds if and only if there is a separable extension
![]() $E'$
of E of degree less than
$E'$
of E of degree less than
![]() ${m}^n\cdot (n^2)!$
and a representation
${m}^n\cdot (n^2)!$
and a representation
![]() $\rho ' \colon H \to {\mathrm {GL}}_{n/m}(E')$
such that
$\rho ' \colon H \to {\mathrm {GL}}_{n/m}(E')$
such that
![]() $\rho \otimes _EE'\cong {\mathrm {Ind}}_H^G \rho '$
. Furthermore, any such
$\rho \otimes _EE'\cong {\mathrm {Ind}}_H^G \rho '$
. Furthermore, any such
![]() $\rho '$
is absolutely semisimple, and one has
$\rho '$
is absolutely semisimple, and one has
![]() ${\mathrm {Res}}_H^G \rho \otimes _EE'= \bigoplus _{g\in G/H} (\rho ')^g$
.
${\mathrm {Res}}_H^G \rho \otimes _EE'= \bigoplus _{g\in G/H} (\rho ')^g$
.
Proof. If
![]() $\rho \otimes _EE'\cong {\mathrm {Ind}}_H^G\rho '$
, then Lemma 2.1.3 implies
$\rho \otimes _EE'\cong {\mathrm {Ind}}_H^G\rho '$
, then Lemma 2.1.3 implies
and this implies
![]() $\rho \otimes \chi \cong \rho $
by [Reference Curtis and ReinerCR62, 29.7].
$\rho \otimes \chi \cong \rho $
by [Reference Curtis and ReinerCR62, 29.7].
Conversely, suppose that
![]() $\rho \cong \rho \otimes \chi $
. After replacing E by a separable extension of degree at most
$\rho \cong \rho \otimes \chi $
. After replacing E by a separable extension of degree at most
![]() $(n^2)!$
(see Lemma A.2.7 and Remark A.2.8) we may assume that
$(n^2)!$
(see Lemma A.2.7 and Remark A.2.8) we may assume that
![]() $\rho $
is an absolutely completely reducible G-representation over
$\rho $
is an absolutely completely reducible G-representation over
![]() $E'$
, that is,
$E'$
, that is,
![]() $\rho =\oplus _{j\in J}\rho ^{\prime }_j$
for absolutely irreducible representations
$\rho =\oplus _{j\in J}\rho ^{\prime }_j$
for absolutely irreducible representations
![]() $\rho ^{\prime }_j$
for
$\rho ^{\prime }_j$
for
![]() $j\in J$
. We regroup this decomposition according to orbits under iterated twisting by
$j\in J$
. We regroup this decomposition according to orbits under iterated twisting by
![]() $\chi $
. This gives rise to a decomposition
$\chi $
. This gives rise to a decomposition
 $$ \begin{align} \rho\cong \bigoplus_{i\in I} \big( \bigoplus_{j=0}^{{m}_i-1} \rho_i\otimes \chi^j\big)^{\oplus r_i}, \end{align} $$
$$ \begin{align} \rho\cong \bigoplus_{i\in I} \big( \bigoplus_{j=0}^{{m}_i-1} \rho_i\otimes \chi^j\big)^{\oplus r_i}, \end{align} $$
for integers
![]() $r_i>0$
, absolutely irreducible representations
$r_i>0$
, absolutely irreducible representations
![]() $\rho _i\colon G\to {\mathrm {GL}}_{n_i}(E')$
, and divisors
$\rho _i\colon G\to {\mathrm {GL}}_{n_i}(E')$
, and divisors
![]() ${m}_i$
of
${m}_i$
of
![]() ${m}$
, for
${m}$
, for
![]() $i\in I$
so that
$i\in I$
so that
![]() $\rho _i\otimes \chi ^{{m}_i}\cong \rho _i$
, and no
$\rho _i\otimes \chi ^{{m}_i}\cong \rho _i$
, and no
![]() $\rho _i$
is isomorphic to
$\rho _i$
is isomorphic to
![]() $\rho _{i'}\otimes \chi ^j$
for some
$\rho _{i'}\otimes \chi ^j$
for some
![]() $j\in \{0,\ldots ,{m}_{i'}-1\}$
and
$j\in \{0,\ldots ,{m}_{i'}-1\}$
and
![]() $i'\in I$
. We have
$i'\in I$
. We have
![]() $G\supset H_i:={\operatorname {ker}{ \chi }}^{{m}_i}\supset H$
,
$G\supset H_i:={\operatorname {ker}{ \chi }}^{{m}_i}\supset H$
,
![]() $[H_i:H]={m}_i$
, and
$[H_i:H]={m}_i$
, and
![]() ${\mathrm {Res}}^G_{H_i}\chi $
is a character of order
${\mathrm {Res}}^G_{H_i}\chi $
is a character of order
![]() ${m}_i$
.
${m}_i$
.
By Theorem 2.2.1, we find Kummer extensions
![]() $E^{\prime }_i$
of
$E^{\prime }_i$
of
![]() $E'$
of degree dividing
$E'$
of degree dividing
![]() $m_i$
and representations
$m_i$
and representations
![]() $\rho _i^{\prime \prime }\colon H_i\to {\mathrm {GL}}_{n_i/{m}_i}(E^{\prime }_i)$
such that
$\rho _i^{\prime \prime }\colon H_i\to {\mathrm {GL}}_{n_i/{m}_i}(E^{\prime }_i)$
such that
![]() ${\mathrm {Ind}}_{H_i}^G\rho _i^{\prime \prime }\cong \rho _i\otimes _{E'}E^{\prime }_i$
. Let
${\mathrm {Ind}}_{H_i}^G\rho _i^{\prime \prime }\cong \rho _i\otimes _{E'}E^{\prime }_i$
. Let
be the trivial representation of H on
![]() $E'$
. Then
$E'$
. Then

where the second and fourth isomorphism follows from Lemma 2.1.3. Let
![]() $E"$
be the composite of the
$E"$
be the composite of the
![]() $E^{\prime }_i$
, and set
$E^{\prime }_i$
, and set
![]() $\rho ':=\bigoplus _{i\in I} ( {\mathrm {Res}}_H^{H_i} \rho _i^{\prime \prime }\otimes _{E^{\prime }_i}E")^{\oplus r_i}$
so that clearly
$\rho ':=\bigoplus _{i\in I} ( {\mathrm {Res}}_H^{H_i} \rho _i^{\prime \prime }\otimes _{E^{\prime }_i}E")^{\oplus r_i}$
so that clearly
![]() $[E":E']<m^n$
. The first assertion of the corollary is now evident from the above and from (4). The remaining assertions follow from Lemma 2.1.4
(b) and (d).
$[E":E']<m^n$
. The first assertion of the corollary is now evident from the above and from (4). The remaining assertions follow from Lemma 2.1.4
(b) and (d).
2.3 Some results when p divides
 $[G:H]$
$[G:H]$
Suppose for the remainder of this subsection that
![]() $p={\mathrm {Char}}\ E>0$
. Let
$p={\mathrm {Char}}\ E>0$
. Let
![]() $V=E^n$
, and let
$V=E^n$
, and let
![]() $\rho \colon G\to {\mathrm {Aut}}_E(V)$
be a representation such that the canonical map
$\rho \colon G\to {\mathrm {Aut}}_E(V)$
be a representation such that the canonical map
![]() $E\to {\mathrm {End}}_G(V)$
is an isomorphism.
$E\to {\mathrm {End}}_G(V)$
is an isomorphism.
Lemma 2.3.1. Suppose that
![]() $\rho $
is absolutely irreducible. Let
$\rho $
is absolutely irreducible. Let
![]() $H\subset G$
be a normal subgroup of index p, and set
$H\subset G$
be a normal subgroup of index p, and set
![]() $V_H:={\mathrm {Res}}_H^G \rho \otimes _E{{{E}^{\mathrm {alg}}}}$
. Then the following hold:
$V_H:={\mathrm {Res}}_H^G \rho \otimes _E{{{E}^{\mathrm {alg}}}}$
. Then the following hold:
-
(a) If
 $V_H$
is reducible, then
$V_H$
is reducible, then
 $V\otimes _E{{{E}^{\mathrm {alg}}}}\cong {\mathrm {Ind}}_H^G W$
for any irreducible submodule
$V\otimes _E{{{E}^{\mathrm {alg}}}}\cong {\mathrm {Ind}}_H^G W$
for any irreducible submodule
 $W\subset V_H$
.
$W\subset V_H$
. -
(b) If
 $V_H$
is irreducible, then we have:
$V_H$
is irreducible, then we have:-
(1) Any
 $E[G]$
-module W with
$E[G]$
-module W with
 ${\mathrm {Res}}_H^G W\cong {\mathrm {Res}}_H^GV$
is isomorphic to V.
${\mathrm {Res}}_H^G W\cong {\mathrm {Res}}_H^GV$
is isomorphic to V. -
(2)
 ${\mathrm {Ind}}_H^G V_H$
is indecomposable, its socle is isomorphic to
${\mathrm {Ind}}_H^G V_H$
is indecomposable, its socle is isomorphic to
 $V\otimes _E{{{E}^{\mathrm {alg}}}}$
,
$V\otimes _E{{{E}^{\mathrm {alg}}}}$
, -
(3)
 $V\otimes _E{{{E}^{\mathrm {alg}}}}$
is not induced from any H-module,
$V\otimes _E{{{E}^{\mathrm {alg}}}}$
is not induced from any H-module, -
(4) All irreducible subquotients of
 ${\mathrm {Ind}}_H^G V_H$
are isomorphic to
${\mathrm {Ind}}_H^G V_H$
are isomorphic to
 $V\otimes _E{{{E}^{\mathrm {alg}}}}$
.
$V\otimes _E{{{E}^{\mathrm {alg}}}}$
.
-
Proof. By Lemma 2.1.4
(c), we have
![]() $V_H=\oplus _{g\in G/H^*} W^g$
for some irreducible H-module W over
$V_H=\oplus _{g\in G/H^*} W^g$
for some irreducible H-module W over
![]() ${{{E}^{\mathrm {alg}}}}$
and some subgroup
${{{E}^{\mathrm {alg}}}}$
and some subgroup
![]() $H^*\subset G$
with
$H^*\subset G$
with
![]() $H\subset H^*$
. Since
$H\subset H^*$
. Since
![]() $G/H\cong {\mathbb {Z}}/p{\mathbb {Z}}$
, in Part (a) of the present lemma, we must have
$G/H\cong {\mathbb {Z}}/p{\mathbb {Z}}$
, in Part (a) of the present lemma, we must have
![]() $H^*=H$
, and then the assertion follows from Lemma 2.1.4
(e).
$H^*=H$
, and then the assertion follows from Lemma 2.1.4
(e).
We now prove (b). Let W be as in (1). By choosing the same underlying E vector space, we assume that
![]() ${\mathrm {Res}}_H^GW={\mathrm {Res}}_H^GV$
. Let
${\mathrm {Res}}_H^GW={\mathrm {Res}}_H^GV$
. Let
![]() $g\in G$
be a generator of
$g\in G$
be a generator of
![]() $G/H$
, and let
$G/H$
, and let
![]() $A,B\in {\mathrm {Aut}}_{E}({\mathrm {Res}}_H^G V)$
be the automorphisms given by the action of g on W and V, respectively. Because
$A,B\in {\mathrm {Aut}}_{E}({\mathrm {Res}}_H^G V)$
be the automorphisms given by the action of g on W and V, respectively. Because
![]() ${\mathrm {Res}}_H^GV$
is absolutely irreducible, there exists a nonzero scalar
${\mathrm {Res}}_H^GV$
is absolutely irreducible, there exists a nonzero scalar
![]() $\lambda \in E$
such that
$\lambda \in E$
such that
![]() $B=\lambda A$
. As
$B=\lambda A$
. As
![]() $g^p\in H$
, we find
$g^p\in H$
, we find
![]() $A^p=B^p=\lambda ^p A^p$
. Because
$A^p=B^p=\lambda ^p A^p$
. Because
![]() ${\mathrm {Char}}\ E=p>0$
, we must have
${\mathrm {Char}}\ E=p>0$
, we must have
![]() $\lambda =1$
, and so (1) is proved.
$\lambda =1$
, and so (1) is proved.
For (2), write
![]() ${\mathrm {Ind}}_H^G V_H=\bigoplus _{i\in I}W_i$
with indecomposable G-modules
${\mathrm {Ind}}_H^G V_H=\bigoplus _{i\in I}W_i$
with indecomposable G-modules
![]() $W_i$
. Let
$W_i$
. Let
![]() $W_i^{\prime }$
be an irreducible quotient of
$W_i^{\prime }$
be an irreducible quotient of
![]() $W_i$
as a G-submodule. From Lemma 2.1.4
(b) and (c) and the irreducibility of
$W_i$
as a G-submodule. From Lemma 2.1.4
(b) and (c) and the irreducibility of
![]() $V_H$
, we deduce
$V_H$
, we deduce
![]() ${\mathrm {Res}}_H^G W_i^{\prime }\cong V_H$
for all i, and by (1), we find
${\mathrm {Res}}_H^G W_i^{\prime }\cong V_H$
for all i, and by (1), we find
![]() $W_i^{\prime }\cong V\otimes _E{{{E}^{\mathrm {alg}}}}$
. The following inequality implies
$W_i^{\prime }\cong V\otimes _E{{{E}^{\mathrm {alg}}}}$
. The following inequality implies
![]() $\#I=1$
and the uniqueness of
$\#I=1$
and the uniqueness of
![]() $W_1'$
and thus gives (2):
$W_1'$
and thus gives (2):
 $$ \begin{align*} \#I &\le \dim_{{{E}^{\mathrm{alg}}}}{\mathrm{Hom}}_G( \bigoplus_i W_i,V\otimes_E{{{E}^{\mathrm{alg}}}}) \ = \ \dim_{{{E}^{\mathrm{alg}}}}{\mathrm{Hom}}_G( {\mathrm{Ind}}_H^GV_H,V\otimes_E{{{E}^{\mathrm{alg}}}}) \\ &= \dim_{{{E}^{\mathrm{alg}}}}{\mathrm{Hom}}_H( V_H,V_H) \ = \ 1. \end{align*} $$
$$ \begin{align*} \#I &\le \dim_{{{E}^{\mathrm{alg}}}}{\mathrm{Hom}}_G( \bigoplus_i W_i,V\otimes_E{{{E}^{\mathrm{alg}}}}) \ = \ \dim_{{{E}^{\mathrm{alg}}}}{\mathrm{Hom}}_G( {\mathrm{Ind}}_H^GV_H,V\otimes_E{{{E}^{\mathrm{alg}}}}) \\ &= \dim_{{{E}^{\mathrm{alg}}}}{\mathrm{Hom}}_H( V_H,V_H) \ = \ 1. \end{align*} $$
To see (3), observe that if
![]() $V\otimes _E{{{E}^{\mathrm {alg}}}}$
was induced, then by Lemma 2.1.4
(b) then
$V\otimes _E{{{E}^{\mathrm {alg}}}}$
was induced, then by Lemma 2.1.4
(b) then
![]() $V_H$
had to be reducible. For (4), note that we have
$V_H$
had to be reducible. For (4), note that we have
![]() ${\mathrm {Ind}}_H^G V_H\cong (V\otimes _E{{{E}^{\mathrm {alg}}}})\otimes _E{\mathrm {Ind}}_H^G E$
. Now, clearly the semisimplification of
${\mathrm {Ind}}_H^G V_H\cong (V\otimes _E{{{E}^{\mathrm {alg}}}})\otimes _E{\mathrm {Ind}}_H^G E$
. Now, clearly the semisimplification of
![]() ${\mathrm {Ind}}_H^G E$
is the trivial module
${\mathrm {Ind}}_H^G E$
is the trivial module
![]() $E^p$
, and this shows (4).
$E^p$
, and this shows (4).
For the remainder of this subsection, we shall also assume that E is a topological field, that
![]() $\rho $
is continuous and that G is topologically finitely generated, and we let
$\rho $
is continuous and that G is topologically finitely generated, and we let
![]() $\Phi (G)=G^p\overline {[G,G]}$
so that
$\Phi (G)=G^p\overline {[G,G]}$
so that
![]() $G/\Phi (G)$
is the maximal p-elementary abelian Hausdorff quotient of G, and we set
$G/\Phi (G)$
is the maximal p-elementary abelian Hausdorff quotient of G, and we set
![]() $m:=\dim _{{{\mathbb {F}}\,\!{}}_p}G/\Phi (G)$
. We note that the hypothesis on G holds for
$m:=\dim _{{{\mathbb {F}}\,\!{}}_p}G/\Phi (G)$
. We note that the hypothesis on G holds for
![]() $G=G_K$
with K a p-adic field by [Reference JannsenJan83, Satz 3.6].
$G=G_K$
with K a p-adic field by [Reference JannsenJan83, Satz 3.6].
In the sequel, we shall write
![]() ${\overline {{\mathrm {End}}}}(V)$
for the cokernel of the natural inclusion
${\overline {{\mathrm {End}}}}(V)$
for the cokernel of the natural inclusion
![]() $E{\hookrightarrow } {\mathrm {End}}_E(V)$
. We shall relate the nonvanishing of the module of G-invariants
$E{\hookrightarrow } {\mathrm {End}}_E(V)$
. We shall relate the nonvanishing of the module of G-invariants
![]() ${\overline{\mathrm{End}}}_G(V)$
of this cokernel to V being induced from a subgroup of G of p-power index. We assume that p divides n, since otherwise the trace splits the inclusion
${\overline{\mathrm{End}}}_G(V)$
of this cokernel to V being induced from a subgroup of G of p-power index. We assume that p divides n, since otherwise the trace splits the inclusion
![]() $E\to {\mathrm {End}}_E(V) \ G$
-equivariantly so that
$E\to {\mathrm {End}}_E(V) \ G$
-equivariantly so that
![]() ${\overline {{\mathrm {End}}}}_G(V)=0$
by our hypothesis
${\overline {{\mathrm {End}}}}_G(V)=0$
by our hypothesis
![]() $E= {\mathrm {End}}_G(V)$
.
$E= {\mathrm {End}}_G(V)$
.
Let
![]() ${\mathrm {End}}^{\prime }_{G}(V)$
be the subset of
${\mathrm {End}}^{\prime }_{G}(V)$
be the subset of
![]() $A\in {\mathrm {End}}_{E}(V)$
such that there exists a map
$A\in {\mathrm {End}}_{E}(V)$
such that there exists a map
![]() $\lambda _A\colon G\to E,g\mapsto \lambda _A(g)$
with
$\lambda _A\colon G\to E,g\mapsto \lambda _A(g)$
with
Again, because
![]() $E={\mathrm {End}}_G(V)$
, one has the short exact sequence
$E={\mathrm {End}}_G(V)$
, one has the short exact sequence
We write
![]() $\overline {A}\in {\overline {\mathrm {End}}}_G(V)$
for the class of
$\overline {A}\in {\overline {\mathrm {End}}}_G(V)$
for the class of
![]() $A\in {\mathrm {End}}^{\prime }_G(V)$
under this map. Recall that
$A\in {\mathrm {End}}^{\prime }_G(V)$
under this map. Recall that
![]() $f\in E[T]$
is p-linear if
$f\in E[T]$
is p-linear if
![]() $f=\sum _i a_i T^{p^i}$
and that the set
$f=\sum _i a_i T^{p^i}$
and that the set
![]() $E[T]^{\mathrm {p}\textrm {-}\mathrm {lin}}$
of p-linear polynomials in
$E[T]^{\mathrm {p}\textrm {-}\mathrm {lin}}$
of p-linear polynomials in
![]() $E[T]$
is a ring under addition and composition. The following lemma provides some basic properties of
$E[T]$
is a ring under addition and composition. The following lemma provides some basic properties of
![]() ${\mathrm {End}}_G'(V)$
.
${\mathrm {End}}_G'(V)$
.
Lemma 2.3.2. Let A be in
![]() ${\mathrm {End}}^{\prime }_G(V)$
. For
${\mathrm {End}}^{\prime }_G(V)$
. For
![]() $\lambda \in {{{E}^{\mathrm {alg}}}}$
, let
$\lambda \in {{{E}^{\mathrm {alg}}}}$
, let
![]() $V_\lambda $
and
$V_\lambda $
and
![]() $V^{\prime }_\lambda $
denote the eigenspace and generalized eigenspace of A for
$V^{\prime }_\lambda $
denote the eigenspace and generalized eigenspace of A for
![]() $\lambda $
. Suppose from Part (i) on that
$\lambda $
. Suppose from Part (i) on that
![]() $\rho $
is absolutely irreducible.
$\rho $
is absolutely irreducible.
-
(a) Each
 $\lambda _A$
is a continuous homomorphism
$\lambda _A$
is a continuous homomorphism
 $G\to (E,+)$
.
$G\to (E,+)$
. -
(b) The groups
 $H_{A}:={\mathop {\mathrm{Ker}}\nolimits }\, \lambda _{A}$
and
$H_{A}:={\mathop {\mathrm{Ker}}\nolimits }\, \lambda _{A}$
and
 $H_\rho :=\bigcap \{H_{A}\mid A\in {\mathrm {End}}^{\prime }_G(V)\}$
contain
$H_\rho :=\bigcap \{H_{A}\mid A\in {\mathrm {End}}^{\prime }_G(V)\}$
contain
 $\Phi (G)$
.
$\Phi (G)$
. -
(c)
 $\Lambda _{A}:=\lambda _{A}(G)\subset (E,+)$
is a finite-dimensional
$\Lambda _{A}:=\lambda _{A}(G)\subset (E,+)$
is a finite-dimensional
 ${{\mathbb {F}}\,\!{}}_p$
vector space.
${{\mathbb {F}}\,\!{}}_p$
vector space. -
(d) The multiset of eigenvalues of A with multiplicities is a torsor under
 $\Lambda _A:=\lambda _{A}(G)$
.
$\Lambda _A:=\lambda _{A}(G)$
. -
(e) The map
 $\lambda _{\scriptscriptstyle \bullet }\colon A\mapsto \lambda _A$
factors via an injective homomorphism
$\lambda _{\scriptscriptstyle \bullet }\colon A\mapsto \lambda _A$
factors via an injective homomorphism  $$ \begin{align*}{\overline{\mathrm{End}}}_G(V) \to {\mathrm{Hom}}_{\operatorname{cont}}(G,(E,+)),\overline{A}\mapsto \lambda_{\overline{A}}.\end{align*} $$
$$ \begin{align*}{\overline{\mathrm{End}}}_G(V) \to {\mathrm{Hom}}_{\operatorname{cont}}(G,(E,+)),\overline{A}\mapsto \lambda_{\overline{A}}.\end{align*} $$
-
(f)
 ${\mathrm {End}}^{\prime }_G(V)$
is a module for
${\mathrm {End}}^{\prime }_G(V)$
is a module for
 $E[T]^{\mathrm {p}\textrm {-}\mathrm {lin}}$
under
$E[T]^{\mathrm {p}\textrm {-}\mathrm {lin}}$
under
 $(f,A)\mapsto f(A)$
and one has
$(f,A)\mapsto f(A)$
and one has
 $\lambda _{f(A)}=f\circ \lambda _A$
.
$\lambda _{f(A)}=f\circ \lambda _A$
. -
(g) If
 ${\overline {\mathrm {End}}}_G(V)\neq 0$
, then there exist
${\overline {\mathrm {End}}}_G(V)\neq 0$
, then there exist
 $A\in {\mathrm {End}}^{\prime }_G(V)$
such that
$A\in {\mathrm {End}}^{\prime }_G(V)$
such that
 $\Lambda _A\cong ({{\mathbb {F}}\,\!{}}_p,+)$
and
$\Lambda _A\cong ({{\mathbb {F}}\,\!{}}_p,+)$
and
 $[G:H_A]=p$
.
$[G:H_A]=p$
. -
(h) The restriction
 $\rho |_{H_A}$
commutes with A; it preserves
$\rho |_{H_A}$
commutes with A; it preserves
 $V_\lambda $
and
$V_\lambda $
and
 $V^{\prime }_\lambda $
for all
$V^{\prime }_\lambda $
for all
 $\lambda \in {{{E}^{\mathrm {alg}}}}$
.
$\lambda \in {{{E}^{\mathrm {alg}}}}$
. -
(i) A is semisimple over
 ${{{E}^{\mathrm {alg}}}}$
.
${{{E}^{\mathrm {alg}}}}$
. -
(j) One has
 $\rho \otimes _E{{E}^{\mathrm {alg}}}\cong {\mathrm {Ind}}_{H_A}^{G_K} V_\lambda $
for any eigenvalue
$\rho \otimes _E{{E}^{\mathrm {alg}}}\cong {\mathrm {Ind}}_{H_A}^{G_K} V_\lambda $
for any eigenvalue
 $\lambda \in {{{E}^{\mathrm {alg}}}}$
of A.
$\lambda \in {{{E}^{\mathrm {alg}}}}$
of A. -
(k) Over
 ${{{E}^{\mathrm {alg}}}}$
the set
${{{E}^{\mathrm {alg}}}}$
the set
 ${\mathrm {End}}^{\prime }_{G_K}(V)$
is simultaneously diagonalizable.
${\mathrm {End}}^{\prime }_{G_K}(V)$
is simultaneously diagonalizable. -
(l) Suppose
 $\dim _{{{\mathbb {F}}\,\!{}}_p} E\ge m$
, then there exists
$\dim _{{{\mathbb {F}}\,\!{}}_p} E\ge m$
, then there exists
 $A\in {\mathrm {End}}_G'(V)$
with
$A\in {\mathrm {End}}_G'(V)$
with
 $H_\rho =H_A$
.
$H_\rho =H_A$
.
Proof. (a) The continuity of
![]() $\lambda _A$
follows from that of
$\lambda _A$
follows from that of
![]() $\rho $
. It is a homomorphism because of
$\rho $
. It is a homomorphism because of
To see (b) note that the image of
![]() $\lambda _A$
is p-elementary abelian because
$\lambda _A$
is p-elementary abelian because
![]() $p\cdot 1=0$
in E. By (a)
$p\cdot 1=0$
in E. By (a)
![]() $H_A={\mathop {\mathrm{Ker}}\nolimits }\, \lambda _A\supseteq \Phi (G)$
, and hence
$H_A={\mathop {\mathrm{Ker}}\nolimits }\, \lambda _A\supseteq \Phi (G)$
, and hence
![]() $H_\rho \supseteq \Phi (G)$
. Part (c) is clear from (a) and (b) since by assumption, G is topologically finitely generated and hence so is
$H_\rho \supseteq \Phi (G)$
. Part (c) is clear from (a) and (b) since by assumption, G is topologically finitely generated and hence so is
![]() $G/\Phi (G)$
. For Part (d), denote by
$G/\Phi (G)$
. For Part (d), denote by
![]() $\chi _A(T)\in E[T]$
the characteristic polynomial of A. Then equation (5) implies
$\chi _A(T)\in E[T]$
the characteristic polynomial of A. Then equation (5) implies
![]() $\chi _A(T)=\chi _A(T+\lambda _A(g))$
for all
$\chi _A(T)=\chi _A(T+\lambda _A(g))$
for all
![]() $g\in G_K$
, and this proves (d).
$g\in G_K$
, and this proves (d).
For (e), one easily verifies that
![]() $\lambda _\bullet $
is the boundary map of cohomology
$\lambda _\bullet $
is the boundary map of cohomology
![]() $H^0(G,{\overline {\mathrm {End}}}_E(V))\to H^1(G,E)$
induced from the sequence (6); Part (a) shows that the target module is
$H^0(G,{\overline {\mathrm {End}}}_E(V))\to H^1(G,E)$
induced from the sequence (6); Part (a) shows that the target module is
![]() $ {\mathrm {Hom}}_{\operatorname {cont}}(G,(E,+))$
; the cocyle condition is easily verified. Moreover,
$ {\mathrm {Hom}}_{\operatorname {cont}}(G,(E,+))$
; the cocyle condition is easily verified. Moreover,
![]() $\lambda _A$
is trivial if and only if
$\lambda _A$
is trivial if and only if
![]() $A\in {\mathrm {End}}_G(V)$
. Hence,
$A\in {\mathrm {End}}_G(V)$
. Hence,
![]() $\overline {A}\to \lambda _{\overline {A}}$
is defined and injective. The homomorphism property is straightforward.
$\overline {A}\to \lambda _{\overline {A}}$
is defined and injective. The homomorphism property is straightforward.
(f) Raising equation (5) to the power p and using
![]() ${\mathrm {Char}}(E)=p$
we find
${\mathrm {Char}}(E)=p$
we find
Since
![]() ${\mathrm {End}}_G'(V)$
is clearly an E-vector space and
${\mathrm {End}}_G'(V)$
is clearly an E-vector space and
![]() $\lambda _\bullet $
is E-linear, Part (f) follows. To see (g), let A be in
$\lambda _\bullet $
is E-linear, Part (f) follows. To see (g), let A be in
![]() ${\mathrm {End}}_G'(V){\smallsetminus } E$
so that
${\mathrm {End}}_G'(V){\smallsetminus } E$
so that
![]() $\Lambda _A\subset (E,+)$
is nontrivial and finite. Let
$\Lambda _A\subset (E,+)$
is nontrivial and finite. Let
![]() $\Lambda \subset \Lambda _A$
be a sub
$\Lambda \subset \Lambda _A$
be a sub
![]() ${{\mathbb {F}}\,\!{}}_p$
-vector space of codimension
${{\mathbb {F}}\,\!{}}_p$
-vector space of codimension
![]() $1$
, and let f be the p-linear polynomial
$1$
, and let f be the p-linear polynomial
![]() $\prod _{\lambda \in \Lambda }(T-\lambda )$
. Then
$\prod _{\lambda \in \Lambda }(T-\lambda )$
. Then
![]() $\Lambda _{f(A)}$
has order p by (f), and
$\Lambda _{f(A)}$
has order p by (f), and
![]() $H_A$
has index p by its definition in (b).
$H_A$
has index p by its definition in (b).
In (h), the asserted commutativity is clear from equation (5); the assertion on the
![]() $V_\lambda $
and
$V_\lambda $
and
![]() $V^{\prime }_\lambda $
is then immediate. For (i), choose an eigenvalue
$V^{\prime }_\lambda $
is then immediate. For (i), choose an eigenvalue
![]() $\lambda \in {{{E}^{\mathrm {alg}}}}$
for which
$\lambda \in {{{E}^{\mathrm {alg}}}}$
for which
![]() $\dim V_\lambda $
is minimal. By (c), we have
$\dim V_\lambda $
is minimal. By (c), we have
![]() $\dim V_\lambda \cdot \#\Lambda _A\le n$
with equality if and only if A is semisimple. Because A and
$\dim V_\lambda \cdot \#\Lambda _A\le n$
with equality if and only if A is semisimple. Because A and
![]() $\rho |_{H_A}\otimes _E{{{E}^{\mathrm {alg}}}}$
commute, the action of
$\rho |_{H_A}\otimes _E{{{E}^{\mathrm {alg}}}}$
commute, the action of
![]() $H_A$
preserves
$H_A$
preserves
![]() $V_\lambda $
. Let
$V_\lambda $
. Let
![]() $V_{{{E}^{\mathrm {alg}}}}:=V\otimes _E{{{E}^{\mathrm {alg}}}}$
. Frobenius reciprocity gives a nonzero homomorphism in
$V_{{{E}^{\mathrm {alg}}}}:=V\otimes _E{{{E}^{\mathrm {alg}}}}$
. Frobenius reciprocity gives a nonzero homomorphism in
Since
![]() $V_{{{E}^{\mathrm {alg}}}}$
is an irreducible
$V_{{{E}^{\mathrm {alg}}}}$
is an irreducible
![]() $G_K$
-representation, it follows that
$G_K$
-representation, it follows that
Hence, we must have equality and so A is semisimple. For (j), all but the last assertion follow from the proof for (i).
(k) Using equation (5), we compute for
![]() $A,B\in {\mathrm {End}}^{\prime }_{G_K}(V)$
and all
$A,B\in {\mathrm {End}}^{\prime }_{G_K}(V)$
and all
![]() $g\in G_K$
that
$g\in G_K$
that
Since
![]() $E={\mathrm {End}}_G(V)$
, we conclude that
$E={\mathrm {End}}_G(V)$
, we conclude that
![]() $AB-BA$
is a scalar matrix. We also know that A (and B) is semisimple. To conclude, we may work over
$AB-BA$
is a scalar matrix. We also know that A (and B) is semisimple. To conclude, we may work over
![]() ${{{E}^{\mathrm {alg}}}}$
so that we may assume that A has diagonal form. But then it is elementary to see that
${{{E}^{\mathrm {alg}}}}$
so that we may assume that A has diagonal form. But then it is elementary to see that
![]() $AB-BA$
has entries
$AB-BA$
has entries
![]() $0$
along the diagonal and hence this scalar matrix must be zero. It follows that any
$0$
along the diagonal and hence this scalar matrix must be zero. It follows that any
![]() $A,B\in {\mathrm {End}}^{\prime }_G(V)$
commute, and we conclude using (j).
$A,B\in {\mathrm {End}}^{\prime }_G(V)$
commute, and we conclude using (j).
(l) We need to show that for all
![]() $A,B\in {\mathrm {End}}_G'(V)$
there exist
$A,B\in {\mathrm {End}}_G'(V)$
there exist
![]() $\mu ,\nu \in E{\smallsetminus }\{0\}$
such that
$\mu ,\nu \in E{\smallsetminus }\{0\}$
such that
![]() $H_{\mu A+\nu B}= H_A\cap H_B$
. Let W be the
$H_{\mu A+\nu B}= H_A\cap H_B$
. Let W be the
![]() ${{\mathbb {F}}\,\!{}}_p$
-vector space
${{\mathbb {F}}\,\!{}}_p$
-vector space
![]() $G/(H_A\cap H_B)$
, and regard
$G/(H_A\cap H_B)$
, and regard
![]() $\lambda _A$
and
$\lambda _A$
and
![]() $\lambda _B$
as
$\lambda _B$
as
![]() ${{\mathbb {F}}\,\!{}}_p$
-linear maps
${{\mathbb {F}}\,\!{}}_p$
-linear maps
![]() $W\to E$
. Note that
$W\to E$
. Note that
![]() $d:=\dim _{{{\mathbb {F}}\,\!{}}_p}W\le m$
. Let
$d:=\dim _{{{\mathbb {F}}\,\!{}}_p}W\le m$
. Let
![]() $\underline {B}:=(b_1,\ldots ,b_d) $
be an
$\underline {B}:=(b_1,\ldots ,b_d) $
be an
![]() ${{\mathbb {F}}\,\!{}}_p$
basis of W. Suppose also without loss of generality that
${{\mathbb {F}}\,\!{}}_p$
basis of W. Suppose also without loss of generality that
![]() $\dim _{{{\mathbb {F}}\,\!{}}_p}G_K/H_A,\dim _{{{\mathbb {F}}\,\!{}}_p}G_K/H_B< d$
since otherwise we are done.
$\dim _{{{\mathbb {F}}\,\!{}}_p}G_K/H_A,\dim _{{{\mathbb {F}}\,\!{}}_p}G_K/H_B< d$
since otherwise we are done.
For
![]() $\nu \in {{{E}^{\mathrm {alg}}}}$
set
$\nu \in {{{E}^{\mathrm {alg}}}}$
set
![]() $C_\nu :=\lambda _A+\nu \lambda _B$
. Since the common kernel of
$C_\nu :=\lambda _A+\nu \lambda _B$
. Since the common kernel of
![]() $\lambda _A$
and
$\lambda _A$
and
![]() $\lambda _B$
is
$\lambda _B$
is
![]() $0\subset W$
, there exists
$0\subset W$
, there exists
![]() $\nu \in {{{E}^{\mathrm {alg}}}}$
such that
$\nu \in {{{E}^{\mathrm {alg}}}}$
such that
![]() $C_\nu $
is injective, that is, such that the vectors
$C_\nu $
is injective, that is, such that the vectors
![]() $(C_\nu b_i)_{i=1,\ldots ,d}$
are
$(C_\nu b_i)_{i=1,\ldots ,d}$
are
![]() ${{\mathbb {F}}\,\!{}}_p$
-linearly independent in E. This means that the Moore determinant of these vectors is nonzero. In other words, the determinant of the
${{\mathbb {F}}\,\!{}}_p$
-linearly independent in E. This means that the Moore determinant of these vectors is nonzero. In other words, the determinant of the
![]() $d\times d$
-square matrix with
$d\times d$
-square matrix with
![]() $(i,j)$
-entry given by
$(i,j)$
-entry given by
![]() $(\lambda _A(b_i)+\nu \lambda _B(b_i))^{p^{j-1}}$
is nonzero. As a function of
$(\lambda _A(b_i)+\nu \lambda _B(b_i))^{p^{j-1}}$
is nonzero. As a function of
![]() $\nu $
, this is a polynomial of degree at most
$\nu $
, this is a polynomial of degree at most
![]() $(p^d-1)/(p-1)$
. It is not identically zero because of its value at
$(p^d-1)/(p-1)$
. It is not identically zero because of its value at
![]() $\nu $
, and hence it can have at most
$\nu $
, and hence it can have at most
![]() $p^d-1<p^m-1$
zeros. It follows that for some
$p^d-1<p^m-1$
zeros. It follows that for some
![]() $\nu '\in E$
it is nonzero because
$\nu '\in E$
it is nonzero because
![]() $\#E\ge p^m$
, and this completes the proof of (l).
$\#E\ge p^m$
, and this completes the proof of (l).
We will later also need the following particular result:
Corollary 2.3.3. Suppose
![]() $\rho $
is a nontrivial extension of an absolutely irreducible representation
$\rho $
is a nontrivial extension of an absolutely irreducible representation
![]() $\rho _2$
by an absolutely irreducible representation
$\rho _2$
by an absolutely irreducible representation
![]() $\rho _1$
. Suppose further that
$\rho _1$
. Suppose further that
![]() $\rho _1$
and
$\rho _1$
and
![]() $\rho _2$
are not isomorphic and that the
$\rho _2$
are not isomorphic and that the
![]() $\rho _i$
are not induced from any normal index p subgroup of G. Then
$\rho _i$
are not induced from any normal index p subgroup of G. Then
![]() ${\overline {\mathrm {End}}}_G(V)=0$
.
${\overline {\mathrm {End}}}_G(V)=0$
.
Proof. Assume on the contrary that we can find
![]() $A\in {\mathrm {End}}_G'(V){\smallsetminus } E$
. We may assume that
$A\in {\mathrm {End}}_G'(V){\smallsetminus } E$
. We may assume that
![]() $\Lambda _A$
has order p by Lemma 2.3.2(g), and we also may assume
$\Lambda _A$
has order p by Lemma 2.3.2(g), and we also may assume
![]() $E={{{E}^{\mathrm {alg}}}}$
since this leaves
$E={{{E}^{\mathrm {alg}}}}$
since this leaves
![]() $\dim _E{\overline {\mathrm {End}}}_G(V)$
unchanged. Then
$\dim _E{\overline {\mathrm {End}}}_G(V)$
unchanged. Then
![]() $H_A$
has index p in G and we have p distinct subspaces
$H_A$
has index p in G and we have p distinct subspaces
![]() $V_\lambda $
of
$V_\lambda $
of
![]() $V_{{{E}^{\mathrm {alg}}}}$
that are stabilized by
$V_{{{E}^{\mathrm {alg}}}}$
that are stabilized by
![]() $H_A$
. By hypotheses and Lemma 2.3.1, the restrictions
$H_A$
. By hypotheses and Lemma 2.3.1, the restrictions
![]() $\rho _i|_{H_A}$
are absolutely irreducible. This already implies
$\rho _i|_{H_A}$
are absolutely irreducible. This already implies
![]() $p=2$
. We also find that the extension of
$p=2$
. We also find that the extension of
![]() $\rho _2$
by
$\rho _2$
by
![]() $\rho _1$
becomes trivial when restricted to
$\rho _1$
becomes trivial when restricted to
![]() $H_A$
, and that these restrictions must agree with the two distinct
$H_A$
, and that these restrictions must agree with the two distinct
![]() $V_\lambda $
. It follows by Frobenius reciprocity that we have a nonzero map
$V_\lambda $
. It follows by Frobenius reciprocity that we have a nonzero map
![]() ${\mathrm {Ind}}_{H_A}^G(\rho _2|_{H_A})\to \rho $
for
${\mathrm {Ind}}_{H_A}^G(\rho _2|_{H_A})\to \rho $
for
![]() $i=1,2$
. By Lemma 2.3.1(b)(4) all simple subquotients of
$i=1,2$
. By Lemma 2.3.1(b)(4) all simple subquotients of
![]() ${\mathrm {Ind}}_{H_A}^G(\rho _2|_{H_A})$
are isomorphic to
${\mathrm {Ind}}_{H_A}^G(\rho _2|_{H_A})$
are isomorphic to
![]() $\rho _2$
. But this is absurd, since
$\rho _2$
. But this is absurd, since
![]() $\rho $
is nonsplit and
$\rho $
is nonsplit and
![]() $\rho _2$
is not a submodule of
$\rho _2$
is not a submodule of
![]() $\rho $
. We reach a contradiction even for
$\rho $
. We reach a contradiction even for
![]() $p=2$
.
$p=2$
.
3 Deformations of Galois representation
This section recalls and augments the classical deformation theory [Reference MazurMaz89] of Mazur. Throughout we fix a profinite group G which often is
![]() $G_K$
for K a p-adic field.
$G_K$
for K a p-adic field.
In Subsection 3.1, we fix the basic categories relevant for all deformations functors that we shall study. We also recall some results on formal smoothness. Subsection 3.2 recalls Mazur’s deformation theory and some extensions for residual representations
![]() $G\to {\mathrm {GL}}_n(\kappa )$
where
$G\to {\mathrm {GL}}_n(\kappa )$
where
![]() $\kappa $
is a finite or a local field. Subsection 3.3 studies dimension
$\kappa $
is a finite or a local field. Subsection 3.3 studies dimension
![]() $1$
points on universal deformation rings. Except for some results on equicharacteristic dimension
$1$
points on universal deformation rings. Except for some results on equicharacteristic dimension
![]() $1$
points, all results are well documented in the literature. Subsection 3.4 gives a criterion for the determinant functor to be smooth. For this, we recall Tate local duality for coefficient modules over local fields.
$1$
points, all results are well documented in the literature. Subsection 3.4 gives a criterion for the determinant functor to be smooth. For this, we recall Tate local duality for coefficient modules over local fields.
3.1 Basic categories and functors and formal smoothness
The field
![]() $\kappa $
and the ring
$\kappa $
and the ring
![]() $\Lambda $
: From now on,
$\Lambda $
: From now on,
![]() $\kappa $
is either (a) a finite field of characteristic p that carries the discrete topology, or (b) a local field with its natural topology and with residue characteristic p. In the latter case,
$\kappa $
is either (a) a finite field of characteristic p that carries the discrete topology, or (b) a local field with its natural topology and with residue characteristic p. In the latter case,
![]() $\kappa $
is a finite extension of
$\kappa $
is a finite extension of
![]() ${\mathbb {Q}}_p$
or a finite extension of the formal Laurent series field
${\mathbb {Q}}_p$
or a finite extension of the formal Laurent series field
![]() ${{\mathbb {F}}\,\!{}}_p((t))$
. Depending on case (a) or (b), we define a topological ring
${{\mathbb {F}}\,\!{}}_p((t))$
. Depending on case (a) or (b), we define a topological ring
![]() $\Lambda $
. In case (b), we set
$\Lambda $
. In case (b), we set
![]() $\Lambda =\kappa $
. In case (a),
$\Lambda =\kappa $
. In case (a),
![]() $\Lambda $
is a Noetherian complete local ring with residue field
$\Lambda $
is a Noetherian complete local ring with residue field
![]() $\kappa $
and equipped with the topology defined by its maximal ideal
$\kappa $
and equipped with the topology defined by its maximal ideal
![]() ${\mathfrak {m}}_{\Lambda }$
.
${\mathfrak {m}}_{\Lambda }$
.
The categories
![]() ${\mathcal {A}r}_{\Lambda }$
and
${\mathcal {A}r}_{\Lambda }$
and
![]() ${\widehat {\mathcal {A}}r}_{\Lambda }$
: By
${\widehat {\mathcal {A}}r}_{\Lambda }$
: By
![]() ${\mathcal {A}r}_{\Lambda }$
, we denote the category of Artinian local
${\mathcal {A}r}_{\Lambda }$
, we denote the category of Artinian local
![]() $\Lambda $
-algebras A with residue field isomorphic to
$\Lambda $
-algebras A with residue field isomorphic to
![]() $\kappa $
and with local
$\kappa $
and with local
![]() $\Lambda $
-algebra homomorphisms as morphisms. For any local ring A, we denote by
$\Lambda $
-algebra homomorphisms as morphisms. For any local ring A, we denote by
![]() ${\mathfrak {m}}_A$
its maximal ideal. We regard any object A of
${\mathfrak {m}}_A$
its maximal ideal. We regard any object A of
![]() ${\mathcal {A}r}_{\Lambda }$
as a topological ring. In case (a), we give A the discrete topology. In case (b), the ring A is a
${\mathcal {A}r}_{\Lambda }$
as a topological ring. In case (a), we give A the discrete topology. In case (b), the ring A is a
![]() $\kappa $
-algebra of finite
$\kappa $
-algebra of finite
![]() $\kappa $
-dimension and we give A the unique topology that arises from any structure on A as a normed
$\kappa $
-dimension and we give A the unique topology that arises from any structure on A as a normed
![]() $\kappa $
-vector space. This topology on A is relevant whenever we talk about continuous maps to A or to any
$\kappa $
-vector space. This topology on A is relevant whenever we talk about continuous maps to A or to any
![]() ${\mathrm {GL}}_n(A)$
. We further define
${\mathrm {GL}}_n(A)$
. We further define
![]() ${\widehat {\mathcal {A}}r}_{\Lambda }$
as the category of complete Noetherian local
${\widehat {\mathcal {A}}r}_{\Lambda }$
as the category of complete Noetherian local
![]() $\Lambda $
-algebras with residue field
$\Lambda $
-algebras with residue field
![]() $\kappa $
and with local homomorphisms as morphisms. Any object of
$\kappa $
and with local homomorphisms as morphisms. Any object of
![]() ${\widehat {\mathcal {A}}r}_{\Lambda }$
is a limit of objects of
${\widehat {\mathcal {A}}r}_{\Lambda }$
is a limit of objects of
![]() ${\mathcal {A}r}_{\Lambda }$
. We equip an object A of
${\mathcal {A}r}_{\Lambda }$
. We equip an object A of
![]() ${\widehat {\mathcal {A}}r}_{\Lambda }$
with the weakest topology such that all maps
${\widehat {\mathcal {A}}r}_{\Lambda }$
with the weakest topology such that all maps
![]() $A\to A/{\mathfrak {m}}_A^m$
,
$A\to A/{\mathfrak {m}}_A^m$
,
![]() $m\ge 1$
, are continuous. In case (a), this simply means that A carries the
$m\ge 1$
, are continuous. In case (a), this simply means that A carries the
![]() ${\mathfrak {m}}_A$
-adic topology.
${\mathfrak {m}}_A$
-adic topology.
In
![]() ${\mathcal {A}r}_{\Lambda }$
, the coproduct of two objects
${\mathcal {A}r}_{\Lambda }$
, the coproduct of two objects
![]() $A,A'$
is their tensor product
$A,A'$
is their tensor product
![]() $A\otimes _{\Lambda } A'$
. For
$A\otimes _{\Lambda } A'$
. For
![]() $A,A'\in {\widehat {\mathcal {A}}r}_{\Lambda }$
, the coproduct is the completed tensor product
$A,A'\in {\widehat {\mathcal {A}}r}_{\Lambda }$
, the coproduct is the completed tensor product
![]() . Note that by [Reference GrothendieckGro64, Lemma
. Note that by [Reference GrothendieckGro64, Lemma
![]() ${0}_{\mathrm{IV}}$
.(19.7.1.2)] the ring
${0}_{\mathrm{IV}}$
.(19.7.1.2)] the ring
![]() $A\widehat {\otimes }_{\Lambda } A'$
lies again in
$A\widehat {\otimes }_{\Lambda } A'$
lies again in
![]() ${\widehat {\mathcal {A}}r}_{\Lambda }$
. From the discussion around the Cohen structure theorem in [Reference StacksSta18, §0323], one also deduces:
${\widehat {\mathcal {A}}r}_{\Lambda }$
. From the discussion around the Cohen structure theorem in [Reference StacksSta18, §0323], one also deduces:
Proposition 3.1.1. Let
![]() $A\in {\widehat {\mathcal {A}}r}_{\Lambda }$
and
$A\in {\widehat {\mathcal {A}}r}_{\Lambda }$
and
![]() $h:=\dim _\kappa {\mathfrak {m}}_A/({\mathfrak {m}}_{\Lambda },{\mathfrak {m}}_A^2)$
. Then there exists a surjective continuous homomorphism in
$h:=\dim _\kappa {\mathfrak {m}}_A/({\mathfrak {m}}_{\Lambda },{\mathfrak {m}}_A^2)$
. Then there exists a surjective continuous homomorphism in
![]() ${\widehat {\mathcal {A}}r}_{\Lambda }$
from the power series ring
${\widehat {\mathcal {A}}r}_{\Lambda }$
from the power series ring
![]() $\Lambda [[x_1,\ldots ,x_h]]$
onto A. Moreover, h is minimal with this property.
$\Lambda [[x_1,\ldots ,x_h]]$
onto A. Moreover, h is minimal with this property.
Further properties of
![]() ${\mathcal {A}r}_{\Lambda }$
and
${\mathcal {A}r}_{\Lambda }$
and
![]() ${\widehat {\mathcal {A}}r}_{\Lambda }$
can be found in [Reference StacksSta18, §06GB] and [Reference StacksSta18, §06GV].
${\widehat {\mathcal {A}}r}_{\Lambda }$
can be found in [Reference StacksSta18, §06GB] and [Reference StacksSta18, §06GV].
Functors on
![]() ${\mathcal {A}r}_{\Lambda }$
and
${\mathcal {A}r}_{\Lambda }$
and
![]() ${\widehat {\mathcal {A}}r}_{\Lambda }$
: We follow [Reference SchlessingerSch68]; see also [Reference StacksSta18, Chapter 06G7]. By
${\widehat {\mathcal {A}}r}_{\Lambda }$
: We follow [Reference SchlessingerSch68]; see also [Reference StacksSta18, Chapter 06G7]. By
![]() $\kappa [\varepsilon ]:=\kappa [ X]/(X^2)\in {\mathcal {A}r}_{\Lambda }$
, we denote the ring of dual numbers over
$\kappa [\varepsilon ]:=\kappa [ X]/(X^2)\in {\mathcal {A}r}_{\Lambda }$
, we denote the ring of dual numbers over
![]() $\kappa $
. Recall from [Reference SchlessingerSch68] that a small extension in
$\kappa $
. Recall from [Reference SchlessingerSch68] that a small extension in
![]() ${\mathcal {A}r}_{\Lambda }$
is a surjection
${\mathcal {A}r}_{\Lambda }$
is a surjection
![]() $f\colon B\to A$
in
$f\colon B\to A$
in
![]() ${\mathcal {A}r}_{\Lambda }$
whose kernel
${\mathcal {A}r}_{\Lambda }$
whose kernel
![]() ${\operatorname {ker}{f}}$
is isomorphic to
${\operatorname {ker}{f}}$
is isomorphic to
![]() $\kappa $
as a B-module, and in particular
$\kappa $
as a B-module, and in particular
![]() ${\operatorname {ker}{f}}$
is annihilated by
${\operatorname {ker}{f}}$
is annihilated by
![]() ${\mathfrak {m}}_B$
and thus
${\mathfrak {m}}_B$
and thus
![]() $({\operatorname {ker}{f}})^2=0$
.
$({\operatorname {ker}{f}})^2=0$
.
In the following, we consider covariant functors F from
![]() ${\mathcal {A}r}_{\Lambda }$
or
${\mathcal {A}r}_{\Lambda }$
or
![]() ${\widehat {\mathcal {A}}r}_{\Lambda }$
to
${\widehat {\mathcal {A}}r}_{\Lambda }$
to
![]() ${Sets}$
such that
${Sets}$
such that
![]() $F(\kappa )$
is a singleton.
$F(\kappa )$
is a singleton.
Definition 3.1.2. A covariant functor
![]() $F\colon {\widehat {\mathcal {A}}r}_{\Lambda }\to {Sets}$
is called continuous if the canonical map
$F\colon {\widehat {\mathcal {A}}r}_{\Lambda }\to {Sets}$
is called continuous if the canonical map
![]() is bijective for all
is bijective for all
![]() $A\in {\widehat {\mathcal {A}}r}_{\Lambda }$
.
$A\in {\widehat {\mathcal {A}}r}_{\Lambda }$
.
It is straightforward to see that there is a bijection between continuous functors
![]() ${\widehat {\mathcal {A}}r}_{\Lambda }\to {Sets}$
and functors
${\widehat {\mathcal {A}}r}_{\Lambda }\to {Sets}$
and functors
![]() ${\mathcal {A}r}_{\Lambda }\to {Sets}$
given by restriction. From now on, all functors on
${\mathcal {A}r}_{\Lambda }\to {Sets}$
given by restriction. From now on, all functors on
![]() ${\widehat {\mathcal {A}}r}_{\Lambda }$
will be continuous and we use the same symbol to denote them and their restriction to
${\widehat {\mathcal {A}}r}_{\Lambda }$
will be continuous and we use the same symbol to denote them and their restriction to
![]() ${\mathcal {A}r}_{\Lambda }$
. For any
${\mathcal {A}r}_{\Lambda }$
. For any
![]() $B\in {\widehat {\mathcal {A}}r}_{\Lambda }$
, we denote by
$B\in {\widehat {\mathcal {A}}r}_{\Lambda }$
, we denote by
![]() $h_B\colon {\widehat {\mathcal {A}}r}_{\Lambda }\to {Sets}$
the functor which is given by
$h_B\colon {\widehat {\mathcal {A}}r}_{\Lambda }\to {Sets}$
the functor which is given by
![]() $h_B(A):= {\mathrm {Hom}}_{{\widehat {\mathcal {A}}r}_{\Lambda }}(B,A)$
. A functor
$h_B(A):= {\mathrm {Hom}}_{{\widehat {\mathcal {A}}r}_{\Lambda }}(B,A)$
. A functor
![]() $F\colon {\widehat {\mathcal {A}}r}_{\Lambda }\to {Sets}$
is representable if it is isomorphic to
$F\colon {\widehat {\mathcal {A}}r}_{\Lambda }\to {Sets}$
is representable if it is isomorphic to
![]() $h_B$
for some
$h_B$
for some
![]() $B\in {\widehat {\mathcal {A}}r}_{\Lambda }$
.
$B\in {\widehat {\mathcal {A}}r}_{\Lambda }$
.
Definition 3.1.3 [Reference SchlessingerSch68, Definitions 2.2 – 2.7].
Let
![]() $F,F'\colon {\widehat {\mathcal {A}}r}_{\Lambda }\to {Sets}$
be functors.
$F,F'\colon {\widehat {\mathcal {A}}r}_{\Lambda }\to {Sets}$
be functors.
-
(a) The tangent space of F is
 $t_F:=F(\kappa [\varepsilon ])$
.
$t_F:=F(\kappa [\varepsilon ])$
. -
(b) A natural transformation
 $F'\to F$
is called smooth if for all small extensions
$F'\to F$
is called smooth if for all small extensions
 $B\to A$
in
$B\to A$
in
 ${\mathcal {A}r}_{\Lambda }$
, the map
${\mathcal {A}r}_{\Lambda }$
, the map
 $F'(B)\to F'(A)\times _{F(A)}F(B) $
is surjective; cf. [Reference SchlessingerSch68, Definition 2.2].
$F'(B)\to F'(A)\times _{F(A)}F(B) $
is surjective; cf. [Reference SchlessingerSch68, Definition 2.2]. -
(c) A pair
 $(A,\xi )$
consisting of an object A in
$(A,\xi )$
consisting of an object A in
 ${\widehat {\mathcal {A}}r}_{\Lambda }$
and a smooth natural transformation
${\widehat {\mathcal {A}}r}_{\Lambda }$
and a smooth natural transformation
 $\xi \colon h_A\to F$
is called a hull of F if the induced map
$\xi \colon h_A\to F$
is called a hull of F if the induced map
 $t_{h_A}\to t_F$
on tangent spaces is bijective; note that by Yoneda
$t_{h_A}\to t_F$
on tangent spaces is bijective; note that by Yoneda
 $\xi $
corresponds to some element of
$\xi $
corresponds to some element of
 $F(A)$
.
$F(A)$
.
Hulls are unique up to isomorphism but in general not up to unique isomorphism. If F is representable by some
![]() $A\in {\widehat {\mathcal {A}}r}_{\Lambda }$
, it clearly has a hull. Moreover, one has
$A\in {\widehat {\mathcal {A}}r}_{\Lambda }$
, it clearly has a hull. Moreover, one has
![]() $t_F\cong {\mathrm {Hom}}_\kappa ({\mathfrak {m}}_A/({\mathfrak {m}}_A^2,{\mathfrak {m}}_{\Lambda }),\kappa )$
.
$t_F\cong {\mathrm {Hom}}_\kappa ({\mathfrak {m}}_A/({\mathfrak {m}}_A^2,{\mathfrak {m}}_{\Lambda }),\kappa )$
.
Definition 3.1.4 (Formal smoothness).
We recall two notions of formal smoothness
-
(a) A homomorphism
 $R_1 \to R_2$
of topological rings with
$R_1 \to R_2$
of topological rings with
 $R_1$
and
$R_1$
and
 $R_2$
linearly topologized is called formally smooth if for every commutative solid diagram
$R_2$
linearly topologized is called formally smooth if for every commutative solid diagram 
of homomorphisms of topological rings with B a discrete ring and
 $B\to A$
surjective with square zero kernel, a dotted arrow exists which makes the diagram commute, cf. [Reference StacksSta18, Definition 07EB]
$B\to A$
surjective with square zero kernel, a dotted arrow exists which makes the diagram commute, cf. [Reference StacksSta18, Definition 07EB] -
(b) A morphism
 ${\varphi }\colon Y\to X$
of locally Noetherian schemes is called formally smooth at
${\varphi }\colon Y\to X$
of locally Noetherian schemes is called formally smooth at
 $y\in Y$
, if the induced morphism
$y\in Y$
, if the induced morphism
 $\widehat {{\cal O}}_{X,{\varphi }(x)}\to \widehat {{\cal O}}_{Y,y}$
of topological rings is formally smooth.
$\widehat {{\cal O}}_{X,{\varphi }(x)}\to \widehat {{\cal O}}_{Y,y}$
of topological rings is formally smooth.
Formal smoothness is related to smoothness of natural transformations between representable functors:
Proposition 3.1.5 [Reference SchlessingerSch68, Proposition 2.5(i)].
Let
![]() $R_1\to R_2$
be a morphism in
$R_1\to R_2$
be a morphism in
![]() ${\widehat {\mathcal {A}}r}_{\Lambda }$
, and set
${\widehat {\mathcal {A}}r}_{\Lambda }$
, and set
![]() $h=\dim R_2-\dim R_1$
. Then the following assertions are equivalent:
$h=\dim R_2-\dim R_1$
. Then the following assertions are equivalent:
-
(i)
 $R_1\to R_2$
is formally smooth.
$R_1\to R_2$
is formally smooth. -
(ii) The induced map of functors
 $h_{R_2}\to h_{R_1}$
is smooth.
$h_{R_2}\to h_{R_1}$
is smooth. -
(iii) There is an isomorphism
 $R_1[[x_1,\ldots ,x_h]]\to R_2$
of
$R_1[[x_1,\ldots ,x_h]]\to R_2$
of
 $R_1$
-algebras.
$R_1$
-algebras.
If any of (i)–(iii) holds, then h is called the relative dimension of
![]() $R_2$
over
$R_2$
over
![]() $R_1$
.
$R_1$
.
Note that (ii)
![]() $\Rightarrow $
(iii) is from [Reference SchlessingerSch68] and that (iii)
$\Rightarrow $
(iii) is from [Reference SchlessingerSch68] and that (iii)
![]() $\Rightarrow $
(i)
$\Rightarrow $
(i)
![]() $\Rightarrow $
(ii) are straightforward. A consequence of (ii)
$\Rightarrow $
(ii) are straightforward. A consequence of (ii)
![]() $\Rightarrow $
(i) of Proposition 3.1.5 is that a morphism in
$\Rightarrow $
(i) of Proposition 3.1.5 is that a morphism in
![]() ${\widehat {\mathcal {A}}r}_{\Lambda }$
is formally smooth if the lifting property in Definition 3.1.4(a) holds for all small extensions in
${\widehat {\mathcal {A}}r}_{\Lambda }$
is formally smooth if the lifting property in Definition 3.1.4(a) holds for all small extensions in
![]() ${\mathcal {A}r}_{\Lambda }$
.
${\mathcal {A}r}_{\Lambda }$
.
3.2 Mazur’s deformation theory and extensions
Our presentation of deformation functors follows Mazur [Reference MazurMaz89] and Kisin [Reference KisinKis09]. Consider a continuous representation
We write
![]() ${\operatorname {ad}_{{{\bar \rho }}}}$
for
${\operatorname {ad}_{{{\bar \rho }}}}$
for
![]() ${\mathrm {Mat}}_{n\times n}(\kappa )$
together with the action of G induced by
${\mathrm {Mat}}_{n\times n}(\kappa )$
together with the action of G induced by
![]() ${\bar \rho }$
composed with the conjugation action of
${\bar \rho }$
composed with the conjugation action of
![]() ${\mathrm {GL}}_n(\kappa )$
on
${\mathrm {GL}}_n(\kappa )$
on
![]() ${\mathrm {Mat}}_{n\times n}(\kappa )$
. By
${\mathrm {Mat}}_{n\times n}(\kappa )$
. By
![]() ${\operatorname {ad}_{{{\bar \rho }}}^0}$
, we denote the subrepresentation on trace zero matrices and by
${\operatorname {ad}_{{{\bar \rho }}}^0}$
, we denote the subrepresentation on trace zero matrices and by
![]() ${\operatorname {\overline {ad}}_{{{\bar \rho }}}}$
the quotient modulo the center
${\operatorname {\overline {ad}}_{{{\bar \rho }}}}$
the quotient modulo the center
![]() $\kappa $
. In the following, for a representation
$\kappa $
. In the following, for a representation
![]() $\rho $
into
$\rho $
into
![]() ${\mathrm {GL}}_n(A_1)$
and a ring homomorphism
${\mathrm {GL}}_n(A_1)$
and a ring homomorphism
![]() $A_1\to A_2$
we write
$A_1\to A_2$
we write
![]() $\rho \otimes _{A_1}A_2$
for the composition of
$\rho \otimes _{A_1}A_2$
for the composition of
![]() $\rho $
with
$\rho $
with
![]() ${\mathrm {GL}}_n(A_1)\to {\mathrm {GL}}_n(A_2)$
, cf. [Reference KisinKis03, p. 433].
${\mathrm {GL}}_n(A_1)\to {\mathrm {GL}}_n(A_2)$
, cf. [Reference KisinKis03, p. 433].
Definition 3.2.1. [Reference GouvêaGou01, Definitions 2.1 and 2.2].
Let A be in
![]() ${\mathcal {A}r}_{\Lambda }$
with residue map
${\mathcal {A}r}_{\Lambda }$
with residue map
![]() $A\to \kappa $
.
$A\to \kappa $
.
-
(a) A lifting of
 ${\overline {\rho }}$
to A is a continuous homomorphism
${\overline {\rho }}$
to A is a continuous homomorphism
 $\rho \colon G\to {\mathrm {GL}}_n(A)$
with
$\rho \colon G\to {\mathrm {GL}}_n(A)$
with
 $\rho \otimes _A \kappa ={\overline {\rho }}$
.
$\rho \otimes _A \kappa ={\overline {\rho }}$
. -
(b) The symbol
 $\Gamma _n(A)$
denotes the kernel of the canonical homomorphism
$\Gamma _n(A)$
denotes the kernel of the canonical homomorphism
 ${\mathrm {GL}}_n(A)\to {\mathrm {GL}}_n(\kappa )$
.
${\mathrm {GL}}_n(A)\to {\mathrm {GL}}_n(\kappa )$
. -
(c) A deformation of
 ${\overline {\rho }}$
to A is a
${\overline {\rho }}$
to A is a
 $\Gamma _n(A)$
-conjugacy class of a liftings of
$\Gamma _n(A)$
-conjugacy class of a liftings of
 $\bar \rho $
to A.
$\bar \rho $
to A. -
(d) The deformation functor
 ${\mathcal {D}}_{\bar \rho }$
, or
${\mathcal {D}}_{\bar \rho }$
, or
 ${\mathcal {D}}_{\Lambda ,{\bar \rho }}$
if we wish to indicate
${\mathcal {D}}_{\Lambda ,{\bar \rho }}$
if we wish to indicate
 $\Lambda $
, of
$\Lambda $
, of
 ${\overline {\rho }}$
is defined as
${\overline {\rho }}$
is defined as  $$ \begin{align*}{\mathcal{D}}_{{\overline{\rho}}}\colon {\mathcal{A}r}_{\Lambda}\,{\longrightarrow}\, {Sets}, \quad A\longmapsto \{\rho\colon G\,{\longrightarrow}\, {\mathrm{GL}}_n(A) {\>:\>}\rho\text{ is a deformation of } {\overline{\rho}}\}, \end{align*} $$
$$ \begin{align*}{\mathcal{D}}_{{\overline{\rho}}}\colon {\mathcal{A}r}_{\Lambda}\,{\longrightarrow}\, {Sets}, \quad A\longmapsto \{\rho\colon G\,{\longrightarrow}\, {\mathrm{GL}}_n(A) {\>:\>}\rho\text{ is a deformation of } {\overline{\rho}}\}, \end{align*} $$
In the following, for a profinite group H and a continuous H-module M we denote by
![]() $H^i(H,M)$
the i-th continuous group cohomology of H with coefficients in M. If M is discrete, details can be found in [Reference Neukirch, Schmidt and WingbergNSW00, Chapter 1]. For other coefficients we refer to the introduction of Subsection 3.4.
$H^i(H,M)$
the i-th continuous group cohomology of H with coefficients in M. If M is discrete, details can be found in [Reference Neukirch, Schmidt and WingbergNSW00, Chapter 1]. For other coefficients we refer to the introduction of Subsection 3.4.
The next definition is important in relation to the finiteness of
![]() ${\mathcal {D}}_{\bar \rho }({{\mathbb {F}}\,\!{}}[\varepsilon ])$
.
${\mathcal {D}}_{\bar \rho }({{\mathbb {F}}\,\!{}}[\varepsilon ])$
.
Definition 3.2.2. The following finiteness conditions go back to [Reference MazurMaz89, § 1.1].
-
(a) A profinite group G has property
 $\Phi _p$
if
$\Phi _p$
if
 $H^1(H,{{\mathbb {F}}\,\!{}}_p)$
is finite for all open subgroups H of G.
$H^1(H,{{\mathbb {F}}\,\!{}}_p)$
is finite for all open subgroups H of G. -
(b) The representation
 ${\overline {\rho }}$
satisfies condition
${\overline {\rho }}$
satisfies condition
 $\Phi _{{\overline {\rho }}}$
if
$\Phi _{{\overline {\rho }}}$
if
 $\dim _\kappa H^1(G,{\operatorname {ad}_{{{\overline {\rho }}}}})$
is finite.
$\dim _\kappa H^1(G,{\operatorname {ad}_{{{\overline {\rho }}}}})$
is finite.
Proposition 3.2.3. The following assertions hold:
-
(a) The profinite group
 $G_K$
satisfies Mazur’s condition
$G_K$
satisfies Mazur’s condition
 $\Phi _p$
.
$\Phi _p$
. -
(b) If a profinite group G satisfies
 $\Phi _p$
, then
$\Phi _p$
, then
 $\Phi _{\overline {\rho }}$
holds for any residual representation
$\Phi _{\overline {\rho }}$
holds for any residual representation
 ${\overline {\rho }}$
of G.
${\overline {\rho }}$
of G.
Proof. Part (a) is immediate from class field theory. If
![]() $\kappa $
is finite, then Part (b) is well-known; to deduce it one applies the inflation restriction sequence to
$\kappa $
is finite, then Part (b) is well-known; to deduce it one applies the inflation restriction sequence to
![]() $G\supset H:={\mathop {\mathrm{Ker}}\nolimits }\, {\operatorname {ad}_{{{\overline {\rho }}}}}$
. If
$G\supset H:={\mathop {\mathrm{Ker}}\nolimits }\, {\operatorname {ad}_{{{\overline {\rho }}}}}$
. If
![]() $\kappa $
is a local field, the assertion is proved later in Corollary 3.3.6. We invite the reader to check that there is no circular reasoning involved.
$\kappa $
is a local field, the assertion is proved later in Corollary 3.3.6. We invite the reader to check that there is no circular reasoning involved.
The versal hull of
![]() ${\mathcal {D}}_{\bar \rho }$
: Let
${\mathcal {D}}_{\bar \rho }$
: Let
![]() ${\bar \rho }$
be as in (7). The following result for finite
${\bar \rho }$
be as in (7). The following result for finite
![]() $\kappa $
is due to Mazur, with an extension due to Ramakrishna. For
$\kappa $
is due to Mazur, with an extension due to Ramakrishna. For
![]() $\kappa $
a p-adic field, a proof is given in [Reference KisinKis03, Lemma 9.3] by Kisin. The proof for local fields of positive characteristic is analogous.
$\kappa $
a p-adic field, a proof is given in [Reference KisinKis03, Lemma 9.3] by Kisin. The proof for local fields of positive characteristic is analogous.
Theorem 3.2.4 [Reference MazurMaz89, 1.1–1.6], [Reference GouvêaGou01, Theorem 3.3, p. 53, Theorem 4.2].
Assuming condition
![]() $\Phi _{\overline {\rho }}$
, the following hold:
$\Phi _{\overline {\rho }}$
, the following hold:
-
(a) One has
 $t_{{\mathcal {D}}_{\bar \rho }}\cong H^1(G,{\operatorname {ad}_{{{\bar \rho }}}})$
, and
$t_{{\mathcal {D}}_{\bar \rho }}\cong H^1(G,{\operatorname {ad}_{{{\bar \rho }}}})$
, and
 $h:=\dim _\kappa H^1(G,{\operatorname {ad}_{{{\bar \rho }}}})$
is finite.
$h:=\dim _\kappa H^1(G,{\operatorname {ad}_{{{\bar \rho }}}})$
is finite. -
(b) The functor
 ${\mathcal {D}}_{\overline {\rho }}$
has a hull; we write
${\mathcal {D}}_{\overline {\rho }}$
has a hull; we write
 $\rho ^{\operatorname {ver}}_{\overline {\rho }}\colon G{\longrightarrow } {\mathrm {GL}}_n( {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ,{\overline {\rho }}}}})$
for a representative of its versal deformation and
$\rho ^{\operatorname {ver}}_{\overline {\rho }}\colon G{\longrightarrow } {\mathrm {GL}}_n( {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ,{\overline {\rho }}}}})$
for a representative of its versal deformation and
 $ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ,{\overline {\rho }}}}}\in {\widehat {\mathcal {A}}r}_{\Lambda }$
for a versal deformation ring of
$ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ,{\overline {\rho }}}}}\in {\widehat {\mathcal {A}}r}_{\Lambda }$
for a versal deformation ring of
 ${\bar \rho }$
.
${\bar \rho }$
. -
(c) If
 $\kappa ={\mathrm {End}}_\kappa {{\overline {\rho }}}$
, then
$\kappa ={\mathrm {End}}_\kappa {{\overline {\rho }}}$
, then
 ${\mathcal {D}}_{\overline {\rho }}$
is representable; we write
${\mathcal {D}}_{\overline {\rho }}$
is representable; we write
 $\rho ^{\operatorname {univ}}_{\overline {\rho }}\colon G{\longrightarrow } \operatorname {GL}_n({R^{\operatorname {univ}}_{\Lambda ,{\overline {\rho }}}})$
for a representative of its universal deformation and
$\rho ^{\operatorname {univ}}_{\overline {\rho }}\colon G{\longrightarrow } \operatorname {GL}_n({R^{\operatorname {univ}}_{\Lambda ,{\overline {\rho }}}})$
for a representative of its universal deformation and
 ${R^{\operatorname {univ}}_{\Lambda ,{\overline {\rho }}}}\in {\widehat {\mathcal {A}}r}_{\Lambda } $
for the universal deformation ring of
${R^{\operatorname {univ}}_{\Lambda ,{\overline {\rho }}}}\in {\widehat {\mathcal {A}}r}_{\Lambda } $
for the universal deformation ring of
 ${\bar \rho }$
.
${\bar \rho }$
. -
(d) There is a surjection
 ${\varphi }\colon \Lambda [[x_1,\ldots ,x_h]]\to {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ,{\overline {\rho }}}}}$
in
${\varphi }\colon \Lambda [[x_1,\ldots ,x_h]]\to {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ,{\overline {\rho }}}}}$
in
 ${\widehat {\mathcal {A}}r}_{\Lambda }$
such that
${\widehat {\mathcal {A}}r}_{\Lambda }$
such that
 ${\mathop {\mathrm{Ker}}\nolimits }\, {\varphi }$
is generated by at most
${\mathop {\mathrm{Ker}}\nolimits }\, {\varphi }$
is generated by at most
 $\dim _\kappa H^2(G,{\operatorname {ad}_{{{\bar \rho }}}})$
elements.
$\dim _\kappa H^2(G,{\operatorname {ad}_{{{\bar \rho }}}})$
elements. -
(e) If
 $H^2(G,{\operatorname {ad}_{{{\bar \rho }}}})=0$
, then the natural map
$H^2(G,{\operatorname {ad}_{{{\bar \rho }}}})=0$
, then the natural map
 $\Lambda \to {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ,{\overline {\rho }}}}}$
is formally smooth of relative dimension h, or equivalently, the natural transformation
$\Lambda \to {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ,{\overline {\rho }}}}}$
is formally smooth of relative dimension h, or equivalently, the natural transformation
 ${\mathcal {D}}_{\bar \rho }\to h_{\Lambda }, [\rho \colon G\to {\mathrm {GL}}_n(A)]\mapsto A$
is smooth.
${\mathcal {D}}_{\bar \rho }\to h_{\Lambda }, [\rho \colon G\to {\mathrm {GL}}_n(A)]\mapsto A$
is smooth.
Remark 3.2.5. The existence of
![]() $ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ,{\overline {\rho }}}}}$
(and of
$ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ,{\overline {\rho }}}}}$
(and of
![]() $\rho ^{\operatorname {ver}}_{\overline {\rho }}$
) as a profinite topological ring does not require condition
$\rho ^{\operatorname {ver}}_{\overline {\rho }}$
) as a profinite topological ring does not require condition
![]() $\Phi _{\overline {\rho }}$
. The latter is needed for the rings to be Noetherian, that is, to lie in
$\Phi _{\overline {\rho }}$
. The latter is needed for the rings to be Noetherian, that is, to lie in
![]() ${\widehat {\mathcal {A}}r}_{\Lambda }$
.
${\widehat {\mathcal {A}}r}_{\Lambda }$
.
We shall later need to understand the change of
![]() $ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ,{\overline {\rho }}}}}$
under maps
$ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ,{\overline {\rho }}}}}$
under maps
![]() $\Lambda \to \Lambda '$
:
$\Lambda \to \Lambda '$
:
Lemma 3.2.6 (Cf. [Reference WilesWil95, p. 457]).
Let
![]() $\Lambda \to \Lambda '$
be a finite injective homomorphism of complete Noetherian local rings with finite residue fields
$\Lambda \to \Lambda '$
be a finite injective homomorphism of complete Noetherian local rings with finite residue fields
![]() $\kappa $
and
$\kappa $
and
![]() $\kappa '$
, respectively. Let
$\kappa '$
, respectively. Let
![]() ${\overline {\rho }}':={\overline {\rho }}\otimes _\kappa \kappa '$
. Let
${\overline {\rho }}':={\overline {\rho }}\otimes _\kappa \kappa '$
. Let
![]() $R_{\Lambda }$
be a hull for
$R_{\Lambda }$
be a hull for
![]() ${\mathcal {D}}_{\Lambda ,{\overline {\rho }}}$
and
${\mathcal {D}}_{\Lambda ,{\overline {\rho }}}$
and
![]() $R_{\Lambda '}$
for
$R_{\Lambda '}$
for
![]() ${\mathcal {D}}_{\Lambda ',\rho '}$
. Then
${\mathcal {D}}_{\Lambda ',\rho '}$
. Then
![]() $R_{\Lambda '}\cong R_{\Lambda }\otimes _{\Lambda }\Lambda '$
.
$R_{\Lambda '}\cong R_{\Lambda }\otimes _{\Lambda }\Lambda '$
.
3.3 Deformation rings at dimension
 ${\mathrm 1}$
points
${\mathrm 1}$
points
Suppose
![]() $\kappa $
is finite. Then for R in
$\kappa $
is finite. Then for R in
![]() ${\widehat {\mathcal {A}}r}_{\Lambda }$
and we call
${\widehat {\mathcal {A}}r}_{\Lambda }$
and we call
![]() $x\in {\mathrm {Spec}}\ R$
with corresponding prime ideal
$x\in {\mathrm {Spec}}\ R$
with corresponding prime ideal
![]() ${\mathfrak {p}}_x\subset R$
a point of dimension
${\mathfrak {p}}_x\subset R$
a point of dimension
![]() $1$
if
$1$
if
![]() $R/{\mathfrak {p}}_x$
has Krull dimension
$R/{\mathfrak {p}}_x$
has Krull dimension
![]() $1$
. For such x the field
$1$
. For such x the field
![]() ${\kappa ({x})} $
is either a finite extension of
${\kappa ({x})} $
is either a finite extension of
![]() ${\mathbb {Q}}_p$
or of
${\mathbb {Q}}_p$
or of
![]() ${{\mathbb {F}}\,\!{}}_p((t))$
. It has been first exploited by Kisin, for example, [Reference KisinKis03], that points x of dimension
${{\mathbb {F}}\,\!{}}_p((t))$
. It has been first exploited by Kisin, for example, [Reference KisinKis03], that points x of dimension
![]() $1$
with
$1$
with
![]() ${\kappa ({x})} \supset {\mathbb {Q}}_p$
on universal deformation rings can be much easier to understand than the closed point
${\kappa ({x})} \supset {\mathbb {Q}}_p$
on universal deformation rings can be much easier to understand than the closed point
![]() ${\mathrm {Spec}}{{\mathbb {F}}\,\!{}}$
. We recall this method and work it out further for dimension
${\mathrm {Spec}}{{\mathbb {F}}\,\!{}}$
. We recall this method and work it out further for dimension
![]() $1$
points x with
$1$
points x with
![]() ${\kappa ({x})} \supset {{\mathbb {F}}\,\!{}}_p((t))$
. The latter points will be an essential tool in our work.
${\kappa ({x})} \supset {{\mathbb {F}}\,\!{}}_p((t))$
. The latter points will be an essential tool in our work.
Let
![]() $\kappa $
be a finite field of characteristic p with the discrete topology. Let
$\kappa $
be a finite field of characteristic p with the discrete topology. Let
![]() $\Lambda $
be the ring of integers of a finite totally ramified extension L of
$\Lambda $
be the ring of integers of a finite totally ramified extension L of
![]() $W(\kappa )[1/p]$
. Let
$W(\kappa )[1/p]$
. Let
![]() ${\bar \rho }\colon G\to {\mathrm {GL}}_n(\kappa )$
be a continuous representation that satisfies
${\bar \rho }\colon G\to {\mathrm {GL}}_n(\kappa )$
be a continuous representation that satisfies
![]() $\Phi _{\overline {\rho }}$
with versal deformation
$\Phi _{\overline {\rho }}$
with versal deformation
Consider a continuous homomorphism
![]() $f\colon {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ,{\overline {\rho }}}}}\to E$
of
$f\colon {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ,{\overline {\rho }}}}}\to E$
of
![]() $\Lambda $
-algebras for a local field E. Denote by
$\Lambda $
-algebras for a local field E. Denote by
![]() $\mathfrak {p}$
the prime ideal
$\mathfrak {p}$
the prime ideal
![]() ${\mathop {\mathrm{Ker}}\nolimits }\, f$
. Then via f the field E is a finite extension of the fraction field
${\mathop {\mathrm{Ker}}\nolimits }\, f$
. Then via f the field E is a finite extension of the fraction field
![]() $E_f$
of
$E_f$
of
![]() $ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ,{\overline {\rho }}}}}/\mathfrak {p}$
, and
$ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ,{\overline {\rho }}}}}/\mathfrak {p}$
, and
![]() $\rho ^{\operatorname {ver}}_{\overline {\rho }}$
induces a representation
$\rho ^{\operatorname {ver}}_{\overline {\rho }}$
induces a representation
![]() $\rho _E\colon G\to {\mathrm {GL}}_n(E)$
. We may and will assume that
$\rho _E\colon G\to {\mathrm {GL}}_n(E)$
. We may and will assume that
![]() $E=E_f$
and that
$E=E_f$
and that
![]() $\rho _E(G)\subset {\mathrm {GL}}_n({\cal O})$
for
$\rho _E(G)\subset {\mathrm {GL}}_n({\cal O})$
for
![]() ${\cal O}$
the ring of integers of E – the latter by using strict equivalence.
${\cal O}$
the ring of integers of E – the latter by using strict equivalence.
Suppose first that E is of characteristic
![]() $0$
, in which case we follow [Reference KisinKis03, § 9]. Then f factors via a map
$0$
, in which case we follow [Reference KisinKis03, § 9]. Then f factors via a map
![]() $f[1/p]\colon {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ,{\overline {\rho }}}}}[1/p]\to E$
which is an L-algebra homomorphism, and E is a finite extension field of L. We denote by
$f[1/p]\colon {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ,{\overline {\rho }}}}}[1/p]\to E$
which is an L-algebra homomorphism, and E is a finite extension field of L. We denote by
![]() $\widehat {R}$
the completion of
$\widehat {R}$
the completion of
![]() $ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ,{\overline {\rho }}}}}[1/p]$
at the kernel of
$ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ,{\overline {\rho }}}}}[1/p]$
at the kernel of
![]() $f[1/p]$
. Then E is the residue field of
$f[1/p]$
. Then E is the residue field of
![]() $\widehat {R}$
. From the finiteness of
$\widehat {R}$
. From the finiteness of
![]() $L\to E$
, one easily deduces that in fact
$L\to E$
, one easily deduces that in fact
![]() $\widehat {R}$
is naturally a E-algebra. Moreover, we have a continuous homomorphism
$\widehat {R}$
is naturally a E-algebra. Moreover, we have a continuous homomorphism
![]() $\widehat {\rho }\colon G\to {\mathrm {GL}}_n(\widehat {R})$
induced from
$\widehat {\rho }\colon G\to {\mathrm {GL}}_n(\widehat {R})$
induced from
![]() $\rho ^{\operatorname {ver}}_{\overline {\rho }}$
. Clearly,
$\rho ^{\operatorname {ver}}_{\overline {\rho }}$
. Clearly,
![]() $\widehat {\rho }$
is a deformation of
$\widehat {\rho }$
is a deformation of
![]() $\rho _E$
. Using Remark 3.2.5, this provides one with a homomorphism
$\rho _E$
. Using Remark 3.2.5, this provides one with a homomorphism
Suppose now that E is of characteristic p. Then E is isomorphic to a Laurent series field
![]() $\kappa '(\!( x)\!)$
for a finite extension
$\kappa '(\!( x)\!)$
for a finite extension
![]() $\kappa '$
of the finite field
$\kappa '$
of the finite field
![]() $\kappa $
and with ring of integers
$\kappa $
and with ring of integers
![]() ${\cal O}\cong \kappa '[[x]]$
. Denote by
${\cal O}\cong \kappa '[[x]]$
. Denote by
![]() $\rho _{\cal O}$
the map
$\rho _{\cal O}$
the map
![]() $\rho _E$
with the range restricted to
$\rho _E$
with the range restricted to
![]() ${\mathrm {GL}}_n({\cal O})$
. It is a deformation of
${\mathrm {GL}}_n({\cal O})$
. It is a deformation of
![]() ${\bar \rho }':={\bar \rho }\otimes _\kappa \kappa '$
. Let
${\bar \rho }':={\bar \rho }\otimes _\kappa \kappa '$
. Let
![]() $\Lambda '=\Lambda \otimes _{W(\kappa )}W(\kappa ')$
, and consider the map
$\Lambda '=\Lambda \otimes _{W(\kappa )}W(\kappa ')$
, and consider the map
In the present case, we define
![]() $\widehat {R}$
as the completion of
$\widehat {R}$
as the completion of
![]() $ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ',{\overline {\rho }}'}}}\otimes _{\Lambda '} E$
at
$ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ',{\overline {\rho }}'}}}\otimes _{\Lambda '} E$
at
![]() ${\operatorname {ker}{f}}_E$
. By definition,
${\operatorname {ker}{f}}_E$
. By definition,
![]() $\widehat {R}$
is a E-algebra with residue field E. Moreover,
$\widehat {R}$
is a E-algebra with residue field E. Moreover,
![]() $\rho ^{\operatorname {ver}}_{\overline {\rho }}\otimes _{ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ,{\overline {\rho }}}}}} \widehat {R}$
defines a continuous representation
$\rho ^{\operatorname {ver}}_{\overline {\rho }}\otimes _{ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ,{\overline {\rho }}}}}} \widehat {R}$
defines a continuous representation
which is a deformation of
![]() $\rho _E$
. Again, this yields a homomorphism
$\rho _E$
. Again, this yields a homomorphism
Theorem 3.3.1. The map
![]() ${\varphi }$
is formally smooth. If
${\varphi }$
is formally smooth. If
![]() $ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ,{\overline {\rho }}}}}$
is universal, it is formally étale, and hence an isomorphism, by Proposition 3.1.5.
$ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ,{\overline {\rho }}}}}$
is universal, it is formally étale, and hence an isomorphism, by Proposition 3.1.5.
Remark 3.3.2. Before we give the proof, let us explain a difference depending on the characteristic of E, that will be resolved in Lemma 3.3.5. Suppose that
![]() ${R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ,{\overline {\rho }}}}}$
is a universal ring. Let
${R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ,{\overline {\rho }}}}}$
is a universal ring. Let
![]() ${X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {\rho }}}}} ={\mathrm {Spec}}\ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ,{\overline {\rho }}}}}$
, and let
${X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {\rho }}}}} ={\mathrm {Spec}}\ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ,{\overline {\rho }}}}}$
, and let
![]() $x\in {X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {\rho }}}}}$
be a point of dimension one so that
$x\in {X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {\rho }}}}}$
be a point of dimension one so that
![]() $E={\kappa ({x})} $
is a local field.
$E={\kappa ({x})} $
is a local field.
If E has characteristic zero, that is, if x lies on the generic fiber of
![]() $ {X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {\rho }}}}}$
, then
$ {X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {\rho }}}}}$
, then
![]() $\widehat {R}$
is the completion of the local ring
$\widehat {R}$
is the completion of the local ring
![]() ${\cal O}_{{X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {\rho }}}}},x}$
. Now, by Theorem 3.3.1 this completion is isomorphic to the universal ring
${\cal O}_{{X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {\rho }}}}},x}$
. Now, by Theorem 3.3.1 this completion is isomorphic to the universal ring
![]() $ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{E,\rho _E}}}$
, and so from the latter one can transfer many ring-theoretic properties to
$ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{E,\rho _E}}}$
, and so from the latter one can transfer many ring-theoretic properties to
![]() ${\cal O}_{{X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {\rho }}}}},x}$
.
${\cal O}_{{X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {\rho }}}}},x}$
.
If on the other hand E has characteristic p, that is, x lies on the special fiber
![]() ${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {\rho }}}}}$
, then
${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {\rho }}}}}$
, then
![]() $\widehat {R}$
is not isomorphic to the completion
$\widehat {R}$
is not isomorphic to the completion
![]() $\widehat {{\cal O}}_{{\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {\rho }}}}},x}$
of the local ring
$\widehat {{\cal O}}_{{\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {\rho }}}}},x}$
of the local ring
![]() ${\cal O}_{{\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {\rho }}}}},x}$
. It follows, however, from Lemma 3.3.5 below that we have an isomorphism
${\cal O}_{{\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {\rho }}}}},x}$
. It follows, however, from Lemma 3.3.5 below that we have an isomorphism
![]() $\widehat {R}\cong \widehat {{\cal O}}_{{\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {\rho }}}}},x}[[T]]$
. Via this route, Theorem 3.3.1 allows one again to deduce ring-theoretic properties of
$\widehat {R}\cong \widehat {{\cal O}}_{{\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {\rho }}}}},x}[[T]]$
. Via this route, Theorem 3.3.1 allows one again to deduce ring-theoretic properties of
![]() ${\cal O}_{{X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {\rho }}}}} ,x}$
from
${\cal O}_{{X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {\rho }}}}} ,x}$
from
![]() ${R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{E,\rho _E}}}$
.
${R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{E,\rho _E}}}$
.
Proof of Theorem 3.3.1.
If
![]() ${\mathrm {Char}}\ E=0$
, then this is [Reference KisinKis03, Proposition 9.5]. We give the proof if
${\mathrm {Char}}\ E=0$
, then this is [Reference KisinKis03, Proposition 9.5]. We give the proof if
![]() $p={\mathrm {Char}}\ E>0$
. It closely follows that of [Reference KisinKis03, Proposition 9.5]. We consider a commutative diagram
$p={\mathrm {Char}}\ E>0$
. It closely follows that of [Reference KisinKis03, Proposition 9.5]. We consider a commutative diagram

with
![]() $A\in {\mathcal {A}r}_E$
and
$A\in {\mathcal {A}r}_E$
and
![]() $I\subset A$
is a square zero ideal, with the solid arrows given, and we seek to construct a dashed arrow g so that the two triangular subdiagrams commute. If
$I\subset A$
is a square zero ideal, with the solid arrows given, and we seek to construct a dashed arrow g so that the two triangular subdiagrams commute. If
![]() ${{ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{E,\rho _E}}}}} $
is universal, we also have to show that the dashed arrow is unique. Note that A and I are finite-dimensional E-vector spaces. Also, the bottom arrow induces a pair of homomorphism
${{ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{E,\rho _E}}}}} $
is universal, we also have to show that the dashed arrow is unique. Note that A and I are finite-dimensional E-vector spaces. Also, the bottom arrow induces a pair of homomorphism
![]() $ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ',{\overline {\rho }}'}}}\to A/I$
and
$ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ',{\overline {\rho }}'}}}\to A/I$
and
![]() $E\to A/I$
, where the second one is simply the E-algebra structure map.
$E\to A/I$
, where the second one is simply the E-algebra structure map.
By possibly conjugating
![]() $\hat \rho $
by some matrix in
$\hat \rho $
by some matrix in
![]() $\Gamma _n(\widehat {R})$
, we can assume that
$\Gamma _n(\widehat {R})$
, we can assume that
![]() $\rho ^{\operatorname {ver}}_{\rho _E}\otimes _{{ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{E,\rho _E}}}}}\widehat {R}=\hat \rho $
. Following the proof in [Reference KisinKis03, Proposition 9.5], one shows that there exists an
$\rho ^{\operatorname {ver}}_{\rho _E}\otimes _{{ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{E,\rho _E}}}}}\widehat {R}=\hat \rho $
. Following the proof in [Reference KisinKis03, Proposition 9.5], one shows that there exists an
![]() ${\cal O}$
-subalgebra
${\cal O}$
-subalgebra
![]() $A^\circ $
of A such that
$A^\circ $
of A such that
-
(a)
 $A^\circ $
is free over
$A^\circ $
is free over
 ${\cal O}$
of rank equal to
${\cal O}$
of rank equal to
 $\dim _E A$
and
$\dim _E A$
and
 $A^\circ \otimes _{\cal O} E=A$
,
$A^\circ \otimes _{\cal O} E=A$
, -
(b) the image of
 $A^\circ $
under
$A^\circ $
under
 $A\to E$
is
$A\to E$
is
 ${\cal O}$
, and so
${\cal O}$
, and so
 $A^\circ \in {\widehat {\mathcal {A}}r}_{\kappa '}$
$A^\circ \in {\widehat {\mathcal {A}}r}_{\kappa '}$
-
(c) the image of
 $\rho ^{\operatorname {ver}}_{\rho _E}\otimes _{ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{E,\rho _E}}}}A$
lies in
$\rho ^{\operatorname {ver}}_{\rho _E}\otimes _{ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{E,\rho _E}}}}A$
lies in
 ${\mathrm {GL}}_n(A^\circ )$
,
${\mathrm {GL}}_n(A^\circ )$
, -
(d) the homomorphism
 $ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ',{\overline {\rho }}'}}}\to A/I$
factors via
$ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ',{\overline {\rho }}'}}}\to A/I$
factors via
 $A^\circ /I^\circ $
where
$A^\circ /I^\circ $
where
 $I^\circ =I\cap A^\circ $
.
$I^\circ =I\cap A^\circ $
.
Write
![]() $\rho _{A^\circ }$
for
$\rho _{A^\circ }$
for
![]() $\rho ^{\operatorname {ver}}_{\rho _E}\otimes _{ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{E,\rho _E}}}}A$
considered with its image in
$\rho ^{\operatorname {ver}}_{\rho _E}\otimes _{ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{E,\rho _E}}}}A$
considered with its image in
![]() ${\mathrm {GL}}_n(A^\circ )$
. Then
${\mathrm {GL}}_n(A^\circ )$
. Then
![]() $\rho _{A^\circ }$
reduces to
$\rho _{A^\circ }$
reduces to
![]() $\rho ^{\operatorname {ver}}_{{\overline {\rho }}'}\otimes _{ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ',{\overline {\rho }}'}}}}A^\circ /I^\circ $
modulo
$\rho ^{\operatorname {ver}}_{{\overline {\rho }}'}\otimes _{ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ',{\overline {\rho }}'}}}}A^\circ /I^\circ $
modulo
![]() $I^\circ $
, and thus by the versality of
$I^\circ $
, and thus by the versality of
![]() $ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ',{\overline {\rho }}'}}}$
there is a homomorphism
$ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ',{\overline {\rho }}'}}}$
there is a homomorphism
![]() $g^\circ \colon {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ',{\overline {\rho }}'}}}\to A^\circ $
such that
$g^\circ \colon {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ',{\overline {\rho }}'}}}\to A^\circ $
such that
![]() $\rho ^{\operatorname {ver}}_{{\overline {\rho }}'}\otimes _{ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ',{\overline {\rho }}'}}}}A^\circ $
is strictly equivalent to
$\rho ^{\operatorname {ver}}_{{\overline {\rho }}'}\otimes _{ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ',{\overline {\rho }}'}}}}A^\circ $
is strictly equivalent to
![]() $\rho _{A^\circ }$
. Let
$\rho _{A^\circ }$
. Let
![]() $g\colon \widehat {R}\to A$
be the homomorphism obtained from
$g\colon \widehat {R}\to A$
be the homomorphism obtained from
![]() $g^\circ \otimes {\mathrm {id}}$
under completion. It is now not difficult to see that both triangles in diagram (8) commute with this choice of g.
$g^\circ \otimes {\mathrm {id}}$
under completion. It is now not difficult to see that both triangles in diagram (8) commute with this choice of g.
It remains to show the uniqueness of g if
![]() ${ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ',{\overline {\rho }}'}}}}$
is universal. The argument in [Reference KisinKis03, Proposition 9.5] shows that there is in fact a directed system
${ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ',{\overline {\rho }}'}}}}$
is universal. The argument in [Reference KisinKis03, Proposition 9.5] shows that there is in fact a directed system
![]() $A_n^\circ $
,
$A_n^\circ $
,
![]() $n\in {\mathbb {N}_{\geq 1}}$
, satisfying (a) – (d) such that
$n\in {\mathbb {N}_{\geq 1}}$
, satisfying (a) – (d) such that
![]() $\bigcup _n A_n^\circ =A$
. Now if one has
$\bigcup _n A_n^\circ =A$
. Now if one has
![]() $g_1,g_2$
completing the diagram (8) to two commutative diagrams, there have to be homomorphisms
$g_1,g_2$
completing the diagram (8) to two commutative diagrams, there have to be homomorphisms
![]() $g_1^\circ ,g_2^\circ \colon {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ',{\overline {\rho }}'}}}\to A_n^\circ $
for n sufficiently large that give rise to
$g_1^\circ ,g_2^\circ \colon {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ',{\overline {\rho }}'}}}\to A_n^\circ $
for n sufficiently large that give rise to
![]() $g_1$
and
$g_1$
and
![]() $g_2$
, respectively. The corresponding deformations
$g_2$
, respectively. The corresponding deformations
![]() $G\to {\mathrm {GL}}_n(A_n^\circ )$
of
$G\to {\mathrm {GL}}_n(A_n^\circ )$
of
![]() $\bar \rho '$
do agree over A and hence they will agree for n sufficiently large, that is, they represent the same strict equivalence class. Because
$\bar \rho '$
do agree over A and hence they will agree for n sufficiently large, that is, they represent the same strict equivalence class. Because
![]() $ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ',{\overline {\rho }}'}}}$
is universal, they define the same ring maps
$ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ',{\overline {\rho }}'}}}$
is universal, they define the same ring maps
![]() $g_1^\circ =g_2^\circ $
and hence
$g_1^\circ =g_2^\circ $
and hence
![]() $g_1=g_2$
.
$g_1=g_2$
.
Applying Theorem 3.3.1 in the simplest nontrivial case will deduce the following corollary that will be used in the proof of Lemma 3.3.5.
Corollary 3.3.4. Let
![]() $\kappa $
be finite, let
$\kappa $
be finite, let
![]() $\kappa '$
be a finite extension of
$\kappa '$
be a finite extension of
![]() $\kappa $
and let
$\kappa $
and let
![]() $L=\kappa '((s))$
be the Laurent series field over
$L=\kappa '((s))$
be the Laurent series field over
![]() $\kappa '$
with uniformizer s. Let
$\kappa '$
with uniformizer s. Let
![]() ${\mathfrak {q}}$
be the kernel of the multiplication map
${\mathfrak {q}}$
be the kernel of the multiplication map
![]() $L\otimes _\kappa L\to L$
. Then
$L\otimes _\kappa L\to L$
. Then
![]() $X\mapsto s\otimes 1-1\otimes s$
induces a continuous L-algebra isomorphism
$X\mapsto s\otimes 1-1\otimes s$
induces a continuous L-algebra isomorphism
Proof. We first show that
![]() $\psi $
is an isomorphism in the case
$\psi $
is an isomorphism in the case
![]() $\kappa '=\kappa $
. Let
$\kappa '=\kappa $
. Let
![]() $G=\widehat {{\mathbb {Z}}}$
be the free profinite group on one topological generator
$G=\widehat {{\mathbb {Z}}}$
be the free profinite group on one topological generator
![]() $\gamma $
, and let
$\gamma $
, and let
![]() $\bar \rho \colon G\to {\mathrm {GL}}_1(\kappa )$
be the trivial representation given by
$\bar \rho \colon G\to {\mathrm {GL}}_1(\kappa )$
be the trivial representation given by
![]() $\gamma \mapsto 1$
. Because
$\gamma \mapsto 1$
. Because
![]() $H^1(G,\kappa )\cong \kappa $
and
$H^1(G,\kappa )\cong \kappa $
and
![]() $H^2(G,\kappa )=0$
, we have
$H^2(G,\kappa )=0$
, we have
![]() ${R^{\operatorname {univ}}_{\Lambda ,{\overline {\rho }}}}=\Lambda [[T]]$
for the resulting universal ring with universal deformation
${R^{\operatorname {univ}}_{\Lambda ,{\overline {\rho }}}}=\Lambda [[T]]$
for the resulting universal ring with universal deformation
![]() $\rho ^u\colon G\to {\mathrm {GL}}_1(\Lambda [[T]])$
given by
$\rho ^u\colon G\to {\mathrm {GL}}_1(\Lambda [[T]])$
given by
![]() $\gamma \mapsto 1+T$
.
$\gamma \mapsto 1+T$
.
Let
![]() $f\colon {R^{\operatorname {univ}}_{\Lambda ,{\overline {\rho }}}}=\Lambda [[T]]\rightarrow L$
be the specialization that is given by reduction mod p composed with the injection
$f\colon {R^{\operatorname {univ}}_{\Lambda ,{\overline {\rho }}}}=\Lambda [[T]]\rightarrow L$
be the specialization that is given by reduction mod p composed with the injection
![]() $\iota \colon \kappa [[T]]{\hookrightarrow } L=\kappa ((s)),T\mapsto s$
. The corresponding representation at L is
$\iota \colon \kappa [[T]]{\hookrightarrow } L=\kappa ((s)),T\mapsto s$
. The corresponding representation at L is
![]() $\rho _L\colon \Gamma \to {\mathrm {GL}}_1(L),\gamma \mapsto 1+s$
, and for its universal ring we find
$\rho _L\colon \Gamma \to {\mathrm {GL}}_1(L),\gamma \mapsto 1+s$
, and for its universal ring we find
![]() ${R^{\operatorname {univ}}_{L,\rho _L}}=L[[X]]$
with universal representation
${R^{\operatorname {univ}}_{L,\rho _L}}=L[[X]]$
with universal representation
Let
![]() $\widehat {R}$
be the completion of
$\widehat {R}$
be the completion of
![]() ${R^{\operatorname {univ}}_{\Lambda ,{\overline {\rho }}}}\otimes _{\Lambda } L=\kappa [[T]]\otimes _\kappa L$
at the kernel
${R^{\operatorname {univ}}_{\Lambda ,{\overline {\rho }}}}\otimes _{\Lambda } L=\kappa [[T]]\otimes _\kappa L$
at the kernel
![]() ${\mathfrak {q}}$
of the homomorphism
${\mathfrak {q}}$
of the homomorphism
![]() $f_L\colon \kappa [[T]]\otimes _\kappa L\to L$
that maps
$f_L\colon \kappa [[T]]\otimes _\kappa L\to L$
that maps
![]() $g(T)\otimes h\in \kappa [[T]]\otimes _\kappa L$
to
$g(T)\otimes h\in \kappa [[T]]\otimes _\kappa L$
to
![]() $g(s)h\in L$
. Under
$g(s)h\in L$
. Under
![]() $f_L$
, the nonzero elements of
$f_L$
, the nonzero elements of
![]() $\kappa [[T]]\otimes 1$
map to
$\kappa [[T]]\otimes 1$
map to
![]() $L^\times $
, and therefore
$L^\times $
, and therefore
![]() $\kappa [[T]]\otimes _\kappa L\to \widehat {R}$
extends to
$\kappa [[T]]\otimes _\kappa L\to \widehat {R}$
extends to
![]() $\kappa ((T))\otimes _\kappa L\to \widehat {R}$
, and completion gives an isomorphism
$\kappa ((T))\otimes _\kappa L\to \widehat {R}$
, and completion gives an isomorphism
![]() $\kappa ((T))\widehat {\otimes }_\kappa L\stackrel \simeq {\longrightarrow } \widehat {R}$
. We now invoke Theorem 3.3.1. It asserts that the L-algebra map
$\kappa ((T))\widehat {\otimes }_\kappa L\stackrel \simeq {\longrightarrow } \widehat {R}$
. We now invoke Theorem 3.3.1. It asserts that the L-algebra map
that, by its very definition, sends
![]() $\rho _L^u(\gamma )=1+s+X$
to
$\rho _L^u(\gamma )=1+s+X$
to
![]() $(\rho ^u\otimes _{\Lambda } L)(\gamma )=1+T\otimes 1$
, is an isomorphism. Because s on the left is mapped to
$(\rho ^u\otimes _{\Lambda } L)(\gamma )=1+T\otimes 1$
, is an isomorphism. Because s on the left is mapped to
![]() $1\otimes s$
on the right, we find that
$1\otimes s$
on the right, we find that
![]() $X\mapsto T\otimes 1-1\otimes s$
. This proves the assertion on
$X\mapsto T\otimes 1-1\otimes s$
. This proves the assertion on
![]() $\psi $
for
$\psi $
for
![]() $\kappa '=\kappa $
.
$\kappa '=\kappa $
.
To complete the proof, it remains to explain the reduction of a general finite extension
![]() $\kappa '\supset \kappa $
to the case
$\kappa '\supset \kappa $
to the case
![]() $\kappa '=\kappa $
just treated. For this observe that
$\kappa '=\kappa $
just treated. For this observe that
![]() $L\cong \kappa ' (\!( s )\!)\cong \kappa (\!( s )\!)\otimes _\kappa \kappa '$
so that
$L\cong \kappa ' (\!( s )\!)\cong \kappa (\!( s )\!)\otimes _\kappa \kappa '$
so that
![]() $L\otimes _\kappa L\to L$
can be written as the map
$L\otimes _\kappa L\to L$
can be written as the map
Since
![]() $\kappa '\supset \kappa $
is a finite Galois extension, the ring
$\kappa '\supset \kappa $
is a finite Galois extension, the ring
![]() $A:=\kappa '\otimes _\kappa \kappa '$
is isomorphic to the product of fields
$A:=\kappa '\otimes _\kappa \kappa '$
is isomorphic to the product of fields
![]() $(\kappa ')^{[\kappa ':\kappa ]}$
, and A contains a primitive idempotent corresponding to each factor. Under the multiplication map
$(\kappa ')^{[\kappa ':\kappa ]}$
, and A contains a primitive idempotent corresponding to each factor. Under the multiplication map
![]() $A\otimes A\to \kappa ',\lambda \otimes \mu \mapsto \lambda \mu $
, all but one of these map to zero. Hence, all but one of these primitive idempotents lie in
$A\otimes A\to \kappa ',\lambda \otimes \mu \mapsto \lambda \mu $
, all but one of these map to zero. Hence, all but one of these primitive idempotents lie in
![]() $\mathfrak {q}$
, and so they vanish under completion at
$\mathfrak {q}$
, and so they vanish under completion at
![]() $\mathfrak {q}$
. One deduces
$\mathfrak {q}$
. One deduces
![]() $L\widehat {\otimes }_\kappa L\cong L\widehat {\otimes }_{\kappa '} L$
, and this completes the reduction to
$L\widehat {\otimes }_\kappa L\cong L\widehat {\otimes }_{\kappa '} L$
, and this completes the reduction to
![]() $\kappa '=\kappa $
.
$\kappa '=\kappa $
.
The following result is needed in our applications of Theorem 3.3.1. Our focus is on the equicharacteristic case.
Lemma 3.3.5. Let R be in
![]() ${\widehat {\mathcal {A}}r}_\kappa $
so that
${\widehat {\mathcal {A}}r}_\kappa $
so that
![]() ${\mathrm {Char}}\ R=p$
, let
${\mathrm {Char}}\ R=p$
, let
![]() $\mathfrak {p}\in {\mathrm {Spec}}\ R$
be a point of dimension
$\mathfrak {p}\in {\mathrm {Spec}}\ R$
be a point of dimension
![]() $1$
so that
$1$
so that
![]() $\dim R/{\mathfrak {p}}=1$
. Let
$\dim R/{\mathfrak {p}}=1$
. Let
![]() ${\kappa ({\mathfrak {p}})} ={\mathrm {Quot}}(R/\mathfrak {p})$
, and consider the homomorphism
${\kappa ({\mathfrak {p}})} ={\mathrm {Quot}}(R/\mathfrak {p})$
, and consider the homomorphism
Set
![]() $\mathfrak {q}:={\operatorname {ker}{{\varphi }}} $
, and denote by
$\mathfrak {q}:={\operatorname {ker}{{\varphi }}} $
, and denote by
![]() $\widehat {R}$
the completion of
$\widehat {R}$
the completion of
![]() $R\otimes _\kappa {\kappa ({\mathfrak {p}})}$
at the maximal ideal
$R\otimes _\kappa {\kappa ({\mathfrak {p}})}$
at the maximal ideal
![]() $\mathfrak {q}$
and by
$\mathfrak {q}$
and by
![]() $\widehat {R}_{\mathfrak {p}}$
the completion of
$\widehat {R}_{\mathfrak {p}}$
the completion of
![]() $R_{\mathfrak {p}}$
at
$R_{\mathfrak {p}}$
at
![]() $R_{\mathfrak {p}}\mathfrak {p}$
. Then the following hold:
$R_{\mathfrak {p}}\mathfrak {p}$
. Then the following hold:
-
(a) One has an isomorphism
 $\widehat {R}_{\mathfrak {p}}[\![ T ]\!] \cong \widehat {R}$
.
$\widehat {R}_{\mathfrak {p}}[\![ T ]\!] \cong \widehat {R}$
. -
(b) If
 $\widehat {R}$
is formally smooth over
$\widehat {R}$
is formally smooth over
 ${\kappa ({\mathfrak {p}})}$
of dimension d, then
${\kappa ({\mathfrak {p}})}$
of dimension d, then
 $R_{\mathfrak {p}}$
is regular of dimension
$R_{\mathfrak {p}}$
is regular of dimension
 $d-1$
.
$d-1$
.
For a variant of Lemma 3.3.5 in the nonequicharacteristic case, see [Reference Böckle, Iyengar and PaškūnasBIP21, Lemma 3.36].
Proof. Consider
![]() $R\to R_{\mathfrak {p}} \to \widehat {R}_{\mathfrak {p}}$
. Tensoring with
$R\to R_{\mathfrak {p}} \to \widehat {R}_{\mathfrak {p}}$
. Tensoring with
![]() ${\kappa ({\mathfrak {p}})}$
over
${\kappa ({\mathfrak {p}})}$
over
![]() $\kappa $
, it yields a diagram
$\kappa $
, it yields a diagram

where
![]() $\iota $
denotes completion and where the dashed arrows
$\iota $
denotes completion and where the dashed arrows
![]() $\iota '$
and
$\iota '$
and
![]() $\iota "$
will now be constructed. For the existence of
$\iota "$
will now be constructed. For the existence of
![]() $\iota '$
, we use the universal property of localization. Thus, we need to show that
$\iota '$
, we use the universal property of localization. Thus, we need to show that
![]() $R{\smallsetminus }\mathfrak {p}\otimes 1$
is mapped under
$R{\smallsetminus }\mathfrak {p}\otimes 1$
is mapped under
![]() $\iota $
to the units in
$\iota $
to the units in
![]() $\widehat {R}$
. The ring
$\widehat {R}$
. The ring
![]() $\widehat {R}$
is local with residue map induced from
$\widehat {R}$
is local with residue map induced from
![]() ${\varphi }$
, and therefore we need to show that
${\varphi }$
, and therefore we need to show that
![]() ${\varphi }\circ \iota (R{\smallsetminus }\mathfrak {p}\otimes 1)$
lies in
${\varphi }\circ \iota (R{\smallsetminus }\mathfrak {p}\otimes 1)$
lies in
![]() ${\kappa ({\mathfrak {p}})}^\times $
, but this is clear from the definitions and the inclusion
${\kappa ({\mathfrak {p}})}^\times $
, but this is clear from the definitions and the inclusion
![]() $R/\mathfrak {p}{\hookrightarrow } {\kappa ({\mathfrak {p}})}$
. Regarding
$R/\mathfrak {p}{\hookrightarrow } {\kappa ({\mathfrak {p}})}$
. Regarding
![]() $\iota "$
, we first note that
$\iota "$
, we first note that
![]() $\mathfrak {p}\otimes _\kappa {\kappa ({\mathfrak {p}})}$
maps to
$\mathfrak {p}\otimes _\kappa {\kappa ({\mathfrak {p}})}$
maps to
![]() $\mathfrak {q}$
under
$\mathfrak {q}$
under
![]() $\iota $
and hence
$\iota $
and hence
![]() $\mathfrak {p}^n\otimes _\kappa {\kappa ({\mathfrak {p}})}$
to
$\mathfrak {p}^n\otimes _\kappa {\kappa ({\mathfrak {p}})}$
to
![]() $\mathfrak {q}^n$
. Hence, the existence of
$\mathfrak {q}^n$
. Hence, the existence of
![]() $\iota '$
gives a compatible system of homomorphisms
$\iota '$
gives a compatible system of homomorphisms
![]() $R_{\mathfrak {p}}/R_{\mathfrak {p}} \mathfrak {p}^n \to (R\otimes _\kappa {\kappa ({\mathfrak {p}})})/\mathfrak {q}^n$
, and this provides the construction of
$R_{\mathfrak {p}}/R_{\mathfrak {p}} \mathfrak {p}^n \to (R\otimes _\kappa {\kappa ({\mathfrak {p}})})/\mathfrak {q}^n$
, and this provides the construction of
![]() $ \iota "$
.
$ \iota "$
.
Let
![]() $\pi $
denote the reduction map
$\pi $
denote the reduction map
![]() $\pi \colon \widehat {R}\to {\kappa ({\mathfrak {p}})}$
, set
$\pi \colon \widehat {R}\to {\kappa ({\mathfrak {p}})}$
, set
![]() ${\varphi }'=\pi \circ \iota '$
and
${\varphi }'=\pi \circ \iota '$
and
![]() ${\varphi }"=\pi \circ \iota "$
and define
${\varphi }"=\pi \circ \iota "$
and define
![]() $\mathfrak {q}'={\operatorname {ker}{{\varphi }}} '$
and
$\mathfrak {q}'={\operatorname {ker}{{\varphi }}} '$
and
![]() $\mathfrak {q}"={\operatorname {ker}{{\varphi }}} "$
. Then the arguments just given provide a commutative diagram with canonical isomorphisms in the bottom row
$\mathfrak {q}"={\operatorname {ker}{{\varphi }}} "$
. Then the arguments just given provide a commutative diagram with canonical isomorphisms in the bottom row

where by slight abuse of notation we denote the middle and right vertical maps again
![]() $\iota '$
and
$\iota '$
and
![]() $\iota "$
. Note that by the Cohen structure theorem in equal characteristic the ring
$\iota "$
. Note that by the Cohen structure theorem in equal characteristic the ring
![]() $\widehat {R}_{\mathfrak {p}}$
contains
$\widehat {R}_{\mathfrak {p}}$
contains
![]() ${\kappa ({\mathfrak {p}})}$
as a subfield. Focusing on the right-most arrow and using that
${\kappa ({\mathfrak {p}})}$
as a subfield. Focusing on the right-most arrow and using that
![]() $R_{\mathfrak {p}}$
is regular if and only if
$R_{\mathfrak {p}}$
is regular if and only if
![]() $\widehat {R}_{\mathfrak {p}}$
is so, it will suffice to prove the following assertion.
$\widehat {R}_{\mathfrak {p}}$
is so, it will suffice to prove the following assertion.
Let
![]() $\mathcal {R}$
be a complete Noetherian local
$\mathcal {R}$
be a complete Noetherian local
![]() ${\kappa ({\mathfrak {p}})}$
-algebra with residue field
${\kappa ({\mathfrak {p}})}$
-algebra with residue field
![]() ${\kappa ({\mathfrak {p}})}$
and residue homomorphism
${\kappa ({\mathfrak {p}})}$
and residue homomorphism
![]() $\pi \colon \mathcal {R}\to {\kappa ({\mathfrak {p}})}$
, let
$\pi \colon \mathcal {R}\to {\kappa ({\mathfrak {p}})}$
, let
![]() $\psi \colon \mathcal {R}\otimes _\kappa {\kappa ({\mathfrak {p}})}\to {\kappa ({\mathfrak {p}})}$
be the homomorphism
$\psi \colon \mathcal {R}\otimes _\kappa {\kappa ({\mathfrak {p}})}\to {\kappa ({\mathfrak {p}})}$
be the homomorphism
![]() $r\otimes x\mapsto \pi (r)\cdot x$
, let
$r\otimes x\mapsto \pi (r)\cdot x$
, let
![]() $\mathfrak {Q}={\operatorname {ker}{ \psi }}$
and let
$\mathfrak {Q}={\operatorname {ker}{ \psi }}$
and let
![]() $\widehat {\mathcal {R}}$
be the completion of
$\widehat {\mathcal {R}}$
be the completion of
![]() $\mathcal {R}\otimes _\kappa {\kappa ({\mathfrak {p}})}$
at
$\mathcal {R}\otimes _\kappa {\kappa ({\mathfrak {p}})}$
at
![]() $\mathfrak {Q}$
. Then we assert that
$\mathfrak {Q}$
. Then we assert that
![]() $\widehat {\mathcal {R}}\cong \mathcal {R} [\![ t ]\!]$
.
$\widehat {\mathcal {R}}\cong \mathcal {R} [\![ t ]\!]$
.
To prove the assertion, note first that if
![]() $\mathcal {S}_1$
and
$\mathcal {S}_1$
and
![]() $\mathcal {S}_2$
are
$\mathcal {S}_2$
are
![]() ${\kappa ({\mathfrak {p}})}$
-algebras with maximal ideals
${\kappa ({\mathfrak {p}})}$
-algebras with maximal ideals
![]() $\mathfrak {P}_1$
and
$\mathfrak {P}_1$
and
![]() $\mathfrak {P}_2$
such that
$\mathfrak {P}_2$
such that
![]() ${\kappa ({\mathfrak {p}})}$
is in both cases the residue field, then the completion of
${\kappa ({\mathfrak {p}})}$
is in both cases the residue field, then the completion of
![]() $\mathcal {S}:=\mathcal {S}_1\otimes _{{\kappa ({\mathfrak {p}})}}\mathcal {S}_2$
at the maximal ideal
$\mathcal {S}:=\mathcal {S}_1\otimes _{{\kappa ({\mathfrak {p}})}}\mathcal {S}_2$
at the maximal ideal
![]() $\mathfrak {m}:=\mathfrak {P}_1\otimes _{{\kappa ({\mathfrak {p}})}}\mathcal {S}_2+\mathcal {S}_1\otimes _{{\kappa ({\mathfrak {p}})}}\mathfrak {P}_2$
is isomorphic to
$\mathfrak {m}:=\mathfrak {P}_1\otimes _{{\kappa ({\mathfrak {p}})}}\mathcal {S}_2+\mathcal {S}_1\otimes _{{\kappa ({\mathfrak {p}})}}\mathfrak {P}_2$
is isomorphic to
If furthermore
![]() $\mathcal {S}_1$
is complete with respect to
$\mathcal {S}_1$
is complete with respect to
![]() $\mathfrak {P}_1$
and if
$\mathfrak {P}_1$
and if
, then the completion of
![]() $\mathcal {S}$
at
$\mathcal {S}$
at
![]() $\mathfrak {m}$
is
$\mathfrak {m}$
is
![]() $\mathcal {S}_1 [\![ T ]\!]$
. We apply this to
$\mathcal {S}_1 [\![ T ]\!]$
. We apply this to
![]() $\mathcal {S}_1=\mathcal {R}$
,
$\mathcal {S}_1=\mathcal {R}$
,
![]() $\mathcal {S}_2= {\kappa ({\mathfrak {p}})}\otimes _\kappa {\kappa ({\mathfrak {p}})}$
,
$\mathcal {S}_2= {\kappa ({\mathfrak {p}})}\otimes _\kappa {\kappa ({\mathfrak {p}})}$
,
![]() $\mathfrak {P}_2={\operatorname {ker}{( {\kappa ({\mathfrak {p}})}\otimes _\kappa {\kappa ({\mathfrak {p}})}\to {\kappa ({\mathfrak {p}})},x\otimes y\mapsto xy)}}$
. Then by Corollary 3.3.4, we have
$\mathfrak {P}_2={\operatorname {ker}{( {\kappa ({\mathfrak {p}})}\otimes _\kappa {\kappa ({\mathfrak {p}})}\to {\kappa ({\mathfrak {p}})},x\otimes y\mapsto xy)}}$
. Then by Corollary 3.3.4, we have
, and we deduce
![]() $\widehat {\mathcal {R}}\cong \mathcal {R}[\![ T ]\!]$
.
$\widehat {\mathcal {R}}\cong \mathcal {R}[\![ T ]\!]$
.
Let us record the following consequence of Theorem 3.3.1 and Lemma 3.3.5.
Corollary 3.3.6. Suppose E is a local field and
![]() $\rho \colon G\to {\mathrm {GL}}_n(E)$
is a continuous homomorphism. Let
$\rho \colon G\to {\mathrm {GL}}_n(E)$
is a continuous homomorphism. Let
![]() $\kappa $
be the (finite) residue field of E, and let
$\kappa $
be the (finite) residue field of E, and let
![]() $\bar \rho $
be the semisimple reduction of
$\bar \rho $
be the semisimple reduction of
![]() $\rho $
to
$\rho $
to
![]() $\kappa $
. Then
$\kappa $
. Then
Proof. The corollary will follow from the simple fact that the rank of a coherent sheaf cannot decrease under specialization: Let
![]() ${\cal O}$
be the valuation ring of E. By possibly passing to a finite extension of E, we may assume that
${\cal O}$
be the valuation ring of E. By possibly passing to a finite extension of E, we may assume that
![]() $E^n$
contains a
$E^n$
contains a
![]() $\rho (G)$
-stable
$\rho (G)$
-stable
![]() ${\cal O}$
-lattice whose reduction is
${\cal O}$
-lattice whose reduction is
![]() $\bar \rho $
. Let
$\bar \rho $
. Let
![]() $R:= {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{{\cal O},{\overline {\rho }}}}}$
. We may assume that R is Noetherian, that is, that
$R:= {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{{\cal O},{\overline {\rho }}}}}$
. We may assume that R is Noetherian, that is, that
![]() $\dim _\kappa H^1(G,{\operatorname {ad}_{{{\bar \rho }}}})$
is finite since else there is nothing to show. Let also
$\dim _\kappa H^1(G,{\operatorname {ad}_{{{\bar \rho }}}})$
is finite since else there is nothing to show. Let also
![]() $ \widehat {R}$
and
$ \widehat {R}$
and
![]() $R':= {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{E,\rho }}}$
be as in Theorem 3.3.1, and denote by f a map
$R':= {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{E,\rho }}}$
be as in Theorem 3.3.1, and denote by f a map
![]() $f\colon R\to {\cal O}$
given by the versality of R.
$f\colon R\to {\cal O}$
given by the versality of R.
Denote by
![]() $\widehat {\Omega }_{R/{\cal O}}=\lim _n \Omega _{(R/{\mathfrak {m}}_R^n)/{\cal O}}$
the module of continuous Kähler differentials. Since R is a quotient of a power series ring over
$\widehat {\Omega }_{R/{\cal O}}=\lim _n \Omega _{(R/{\mathfrak {m}}_R^n)/{\cal O}}$
the module of continuous Kähler differentials. Since R is a quotient of a power series ring over
![]() ${\cal O}$
in finitely many variables, as an R-module
${\cal O}$
in finitely many variables, as an R-module
![]() $\widehat {\Omega }_{R/{\cal O}}$
is finitely generated. By Nakayama’s lemma, we have
$\widehat {\Omega }_{R/{\cal O}}$
is finitely generated. By Nakayama’s lemma, we have
Let
![]() ${\mathfrak {p}}=({\mathop {\mathrm{Ker}}\nolimits }\, f)$
, let
${\mathfrak {p}}=({\mathop {\mathrm{Ker}}\nolimits }\, f)$
, let
![]() ${\mathfrak {m}}_E={\mathop {\mathrm{Ker}}\nolimits }(R_{\mathfrak {p}}\to E)$
, with the map induced from f, and let
${\mathfrak {m}}_E={\mathop {\mathrm{Ker}}\nolimits }(R_{\mathfrak {p}}\to E)$
, with the map induced from f, and let
![]() $\widehat {{\mathfrak {m}}}_E$
be the maximal ideal of
$\widehat {{\mathfrak {m}}}_E$
be the maximal ideal of
![]() $\widehat {R}$
. Then by [Reference Böckle, Khare and ManningBKM21, Lemma 7.3], we have
$\widehat {R}$
. Then by [Reference Böckle, Khare and ManningBKM21, Lemma 7.3], we have
![]() $ \widehat {\Omega }_{R/{\cal O}}\otimes _RE\cong {\mathfrak {p}}/{\mathfrak {p}}^2\otimes _R E\cong {\mathfrak {m}}_E/{\mathfrak {m}}_E^2 $
, and furthermore from Lemma 3.3.5 and Theorem 3.3.1, again combined with [Reference Böckle, Khare and ManningBKM21, Lemma 7.3], we obtain
$ \widehat {\Omega }_{R/{\cal O}}\otimes _RE\cong {\mathfrak {p}}/{\mathfrak {p}}^2\otimes _R E\cong {\mathfrak {m}}_E/{\mathfrak {m}}_E^2 $
, and furthermore from Lemma 3.3.5 and Theorem 3.3.1, again combined with [Reference Böckle, Khare and ManningBKM21, Lemma 7.3], we obtain
![]() ${\mathfrak {m}}_E/{\mathfrak {m}}_E^2 \oplus E\cong \widehat {{\mathfrak {m}}}_E/\widehat {{\mathfrak {m}}}_E^2 \cong \widehat {\Omega }_{\widehat {R}/E}\otimes _{\widehat {R}}E\to \widehat {\Omega }_{R'/E}\otimes _{R'}E$
, where the last map is surjective. Hence,
${\mathfrak {m}}_E/{\mathfrak {m}}_E^2 \oplus E\cong \widehat {{\mathfrak {m}}}_E/\widehat {{\mathfrak {m}}}_E^2 \cong \widehat {\Omega }_{\widehat {R}/E}\otimes _{\widehat {R}}E\to \widehat {\Omega }_{R'/E}\otimes _{R'}E$
, where the last map is surjective. Hence,
By [Reference MazurMaz97, § 17, § 21], the dual of
![]() $\widehat {\Omega }_{R/{\cal O}}\otimes _R\kappa $
is the mod
$\widehat {\Omega }_{R/{\cal O}}\otimes _R\kappa $
is the mod
![]() ${\mathfrak {m}}_{\cal O}$
-tangent space of R at
${\mathfrak {m}}_{\cal O}$
-tangent space of R at
![]() ${\mathfrak {m}}_R$
and the dual of
${\mathfrak {m}}_R$
and the dual of
![]() $\widehat {\Omega }_{R'/E}\otimes _{R'}E$
is the tangent space of
$\widehat {\Omega }_{R'/E}\otimes _{R'}E$
is the tangent space of
![]() $R'$
at
$R'$
at
![]() ${\mathfrak {m}}_{R'}$
, and the latter can be identified with
${\mathfrak {m}}_{R'}$
, and the latter can be identified with
![]() $H^1(G,{\operatorname {ad}_{{{\bar \rho }}}})$
and
$H^1(G,{\operatorname {ad}_{{{\bar \rho }}}})$
and
![]() $H^1(G,{\operatorname {ad}_{{\rho }}} )$
, respectively. This proves the corollary.
$H^1(G,{\operatorname {ad}_{{\rho }}} )$
, respectively. This proves the corollary.
3.4 Relative formal smoothness of the determinant functor
A generalized Tate local duality: We recall a generalization of Tate local duality from [Reference NekovářNek06]. Let first G be a profinite group and M a discrete G-module. Then one defines the continuous cohomology
![]() $H^i(G,M)$
as
$H^i(G,M)$
as
, where
![]() ${\mathfrak {U}}$
is the set of all normal open subgroups of G; they form a basis of open neighborhoods near the identity of G. This applies for instance if M is a
${\mathfrak {U}}$
is the set of all normal open subgroups of G; they form a basis of open neighborhoods near the identity of G. This applies for instance if M is a
![]() $\kappa $
-vector space with a continuous G-action and if
$\kappa $
-vector space with a continuous G-action and if
![]() $\kappa $
is finite. Suppose, however, that
$\kappa $
is finite. Suppose, however, that
![]() $\kappa $
is a local field and that M is a finite-dimensional
$\kappa $
is a local field and that M is a finite-dimensional
![]() $\kappa $
-vector space that carries the natural topology induced from
$\kappa $
-vector space that carries the natural topology induced from
![]() $\kappa $
and a continuous
$\kappa $
and a continuous
![]() $\kappa $
-linear G-action. Let
$\kappa $
-linear G-action. Let
![]() ${\cal O}$
be the valuation ring of
${\cal O}$
be the valuation ring of
![]() $\kappa $
with maximal ideal
$\kappa $
with maximal ideal
![]() $\mathfrak {m}_{\cal O}$
and finite residue field
$\mathfrak {m}_{\cal O}$
and finite residue field
![]() ${{\mathbb {F}}\,\!{}}$
. Because G is compact a standard argument shows that M contains a G-stable
${{\mathbb {F}}\,\!{}}$
. Because G is compact a standard argument shows that M contains a G-stable
![]() ${\cal O}$
-lattice L. Suppose that G satisfies the finiteness condition (F) that for all open subgroups
${\cal O}$
-lattice L. Suppose that G satisfies the finiteness condition (F) that for all open subgroups
![]() $U\subset G$
and all
$U\subset G$
and all
![]() $i\ge 0$
one has
$i\ge 0$
one has
![]() $\dim _{{{\mathbb {F}}\,\!{}}} H^i(U,{{\mathbb {F}}\,\!{}})<\infty $
. In this case, one defines continuous cohomology via
$\dim _{{{\mathbb {F}}\,\!{}}} H^i(U,{{\mathbb {F}}\,\!{}})<\infty $
. In this case, one defines continuous cohomology via
and one shows that this definition is independent of any choices; it follows from [Reference NekovářNek06, 4.2.2] that this definition agrees with the one used in [Reference NekovářNek06]. Note that one also has
![]() $H^i(G,M)=Z^i(G,M)/B^i(G,M)$
, where
$H^i(G,M)=Z^i(G,M)/B^i(G,M)$
, where
![]() $Z^i(G,M)$
and
$Z^i(G,M)$
and
![]() $B^i(G,M)$
denotes the continuous i-cocycles and i-coboundaries, respectively, and one has
$B^i(G,M)$
denotes the continuous i-cocycles and i-coboundaries, respectively, and one has
![]() $H^0(G,M)=M^G$
. For
$H^0(G,M)=M^G$
. For
![]() $i=1$
,
$i=1$
,
![]() $Z^1(G,M)$
is the group of continuous maps
$Z^1(G,M)$
is the group of continuous maps
![]() $c\colon G\to M$
with
$c\colon G\to M$
with
![]() $c(gh)=gc(h)+c(g)$
for all
$c(gh)=gc(h)+c(g)$
for all
![]() $g,h\in G$
. Note, also, that all
$g,h\in G$
. Note, also, that all
![]() $1$
-coboundaries are continuous by the continuity of the action of G on M; the latter no longer holds for n-coboundaries with
$1$
-coboundaries are continuous by the continuity of the action of G on M; the latter no longer holds for n-coboundaries with
![]() $n\ge 2$
.
$n\ge 2$
.
The next result is a generalization of Tate local duality from finite field to local field coefficients. In the form needed, it is due to Nekovář. Let V be a finite-dimensional
![]() $\kappa $
-vector space with the topology induced from
$\kappa $
-vector space with the topology induced from
![]() $\kappa $
, and suppose that V carries a continuous
$\kappa $
, and suppose that V carries a continuous
![]() $\kappa $
-linear action by
$\kappa $
-linear action by
![]() $G_K$
. Write
$G_K$
. Write
![]() $V^\vee $
for the dual
$V^\vee $
for the dual
![]() ${\mathrm {Hom}}_\kappa (V,\kappa )$
of V and
${\mathrm {Hom}}_\kappa (V,\kappa )$
of V and
![]() $V(1)$
for the twist of V by the cyclotomic character. Set
$V(1)$
for the twist of V by the cyclotomic character. Set
![]() $h^j(K,V):=\dim _\kappa H^j(G_K,V)$
.
$h^j(K,V):=\dim _\kappa H^j(G_K,V)$
.
Theorem 3.4.1 (Tate and Nekovář).
The following assertions hold:
-
(a) One has
 $h^j(K,V)<\infty $
for
$h^j(K,V)<\infty $
for
 $j\in {\mathbb {Z}}$
and
$j\in {\mathbb {Z}}$
and
 $h^j(K,V)=0$
for
$h^j(K,V)=0$
for
 $j\notin \{0,1,2\}$
;
$j\notin \{0,1,2\}$
; -
(b) For
 $j\in \{0,1,2\}$
one has natural isomorphisms
$j\in \{0,1,2\}$
one has natural isomorphisms  $$ \begin{align*}H^{2-j}(G_K,V^\vee(1))\,\stackrel\simeq{\longrightarrow}\, H^j(G_K,V)^\vee;\end{align*} $$
$$ \begin{align*}H^{2-j}(G_K,V^\vee(1))\,\stackrel\simeq{\longrightarrow}\, H^j(G_K,V)^\vee;\end{align*} $$
-
(c) One has the Euler characteristic formula
 $$ \begin{align*}\sum_{j\ge0}(-1)^jh^j(K,V)= -[K:{\mathbb{Q}}_p]\cdot\dim_E V. \end{align*} $$
$$ \begin{align*}\sum_{j\ge0}(-1)^jh^j(K,V)= -[K:{\mathbb{Q}}_p]\cdot\dim_E V. \end{align*} $$
Proof. If
![]() $\kappa $
is finite, the above statement is just the usual Tate local duality. If
$\kappa $
is finite, the above statement is just the usual Tate local duality. If
![]() $\kappa $
is local, let
$\kappa $
is local, let
![]() ${\cal O}$
be its valuation ring. Because
${\cal O}$
be its valuation ring. Because
![]() $G_K$
is compact, one can find an
$G_K$
is compact, one can find an
![]() ${\cal O}$
-lattice T in V that is stable under
${\cal O}$
-lattice T in V that is stable under
![]() $G_K$
. Let
$G_K$
. Let
![]() $j\ge 0$
. Then [Reference NekovářNek06, Theorem 5.2.6] asserts that each
$j\ge 0$
. Then [Reference NekovářNek06, Theorem 5.2.6] asserts that each
![]() $H^j(G_K,T')$
,
$H^j(G_K,T')$
,
![]() $T'\in \{T,T^\vee (1)\}$
, is a finitely generated
$T'\in \{T,T^\vee (1)\}$
, is a finitely generated
![]() ${\cal O}$
-module and moreover it gives a spectral sequence
${\cal O}$
-module and moreover it gives a spectral sequence
Because
![]() ${\cal O}$
is regular and of dimension
${\cal O}$
is regular and of dimension
![]() $1$
, the groups
$1$
, the groups
![]() ${\mathrm {Ext}}^1_{\cal O}(\cdot ,{\cal O})$
are finitely generated
${\mathrm {Ext}}^1_{\cal O}(\cdot ,{\cal O})$
are finitely generated
![]() ${\cal O}$
-torsion modules and
${\cal O}$
-torsion modules and
![]() ${\mathrm {Ext}}^i_{\cal O}(\cdot ,{\cal O})=0$
for
${\mathrm {Ext}}^i_{\cal O}(\cdot ,{\cal O})=0$
for
![]() $i\ge 2$
. After tensoring the spectral sequence (9) with
$i\ge 2$
. After tensoring the spectral sequence (9) with
![]() $\kappa $
over
$\kappa $
over
![]() ${\cal O}$
, Parts (b) and (a) are clear. Part (c) follows from [Reference NekovářNek06, Theorem 4.6.9 and 5.2.11] applied to T, again after tensoring with
${\cal O}$
, Parts (b) and (a) are clear. Part (c) follows from [Reference NekovářNek06, Theorem 4.6.9 and 5.2.11] applied to T, again after tensoring with
![]() $\kappa $
over
$\kappa $
over
![]() ${\cal O}$
.
${\cal O}$
.
The determinant map: The determinant of representations induces a natural transformation
that maps the class of
![]() $\rho \colon G\to {\mathrm {GL}}_n(A)$
to the class of
$\rho \colon G\to {\mathrm {GL}}_n(A)$
to the class of
![]() ${\mathrm {det}}\circ \rho $
. The induced map on adjoint representations is the trace map in the short exact sequence
${\mathrm {det}}\circ \rho $
. The induced map on adjoint representations is the trace map in the short exact sequence
Using that
![]() ${\operatorname {ad}_{{{\bar \rho }}}}$
is self-dual it is easy to see that the sequence dual to the sequence (11) is
${\operatorname {ad}_{{{\bar \rho }}}}$
is self-dual it is easy to see that the sequence dual to the sequence (11) is
We have the following explicit result on
![]() ${\mathrm {det}}$
for
${\mathrm {det}}$
for
![]() $G=G_K$
and K a p-adic field with
$G=G_K$
and K a p-adic field with
![]() $d=[K:{\mathbb {Q}}_p]$
.
$d=[K:{\mathbb {Q}}_p]$
.
Lemma 3.4.2. Suppose that
![]() $H^0(G_K,{\operatorname {\overline {ad}}_{{{\bar \rho }}}} (1))=0$
. Then
$H^0(G_K,{\operatorname {\overline {ad}}_{{{\bar \rho }}}} (1))=0$
. Then
![]() ${\mathrm {det}}\colon {\mathcal {D}}_{{\bar \rho }}\to {\mathcal {D}}_{{\mathrm {det}}{\bar \rho }}$
is smooth of relative dimension
${\mathrm {det}}\colon {\mathcal {D}}_{{\bar \rho }}\to {\mathcal {D}}_{{\mathrm {det}}{\bar \rho }}$
is smooth of relative dimension
![]() $d(n^2-1)$
. This holds in particular, if
$d(n^2-1)$
. This holds in particular, if
![]() ,
,
![]() $\kappa \cong {\mathrm {End}}_{\kappa [G_K]}({\bar \rho })$
and
$\kappa \cong {\mathrm {End}}_{\kappa [G_K]}({\bar \rho })$
and
![]() $\zeta _p\in K$
.
$\zeta _p\in K$
.
Proof. Let
![]() $A\to B$
be a small extension in
$A\to B$
be a small extension in
![]() ${\mathcal {A}r}_{\Lambda }$
. Let I be its kernel so that
${\mathcal {A}r}_{\Lambda }$
. Let I be its kernel so that
![]() $I^2\subset {\mathfrak {m}}_A I=0$
. For the relative smoothness, we need to show the surjectivity of
$I^2\subset {\mathfrak {m}}_A I=0$
. For the relative smoothness, we need to show the surjectivity of
So suppose we are given deformations
![]() $\rho _B\in {\mathcal {D}}_{{\bar \rho }}(B)$
and
$\rho _B\in {\mathcal {D}}_{{\bar \rho }}(B)$
and
![]() $\tau _A\in {\mathcal {D}}_{{\mathrm {det}}{\bar \rho }}(A)$
with
$\tau _A\in {\mathcal {D}}_{{\mathrm {det}}{\bar \rho }}(A)$
with
![]() ${\mathrm {det}}\rho _B=\tau _A\otimes _A B\in {\mathcal {D}}_{{\mathrm {det}}{\bar \rho }}(B)$
. We need to find a deformation
${\mathrm {det}}\rho _B=\tau _A\otimes _A B\in {\mathcal {D}}_{{\mathrm {det}}{\bar \rho }}(B)$
. We need to find a deformation
![]() $\rho _A\in {\mathcal {D}}_{{\bar \rho }}(A)$
such that
$\rho _A\in {\mathcal {D}}_{{\bar \rho }}(A)$
such that
![]() $\rho _A\otimes _A B=\rho _B$
and
$\rho _A\otimes _A B=\rho _B$
and
![]() ${\mathrm {det}}\rho _A=\tau _A$
.
${\mathrm {det}}\rho _A=\tau _A$
.
Recall from [Reference MazurMaz89, p. 398] that there is a canonical obstruction class
![]() $\mathcal {O}(\rho _B)\in H^2(G_K,{\operatorname {ad}_{{\rho }}} )\otimes _\kappa I$
, which vanishes if and only if there exists a deformation of
$\mathcal {O}(\rho _B)\in H^2(G_K,{\operatorname {ad}_{{\rho }}} )\otimes _\kappa I$
, which vanishes if and only if there exists a deformation of
![]() ${\bar \rho }$
to A that lifts
${\bar \rho }$
to A that lifts
![]() $\rho _B$
. Because of the existence of the deformation
$\rho _B$
. Because of the existence of the deformation
![]() $\tau _A$
that maps to
$\tau _A$
that maps to
![]() ${\mathrm {det}}\rho _B$
, the obstruction class
${\mathrm {det}}\rho _B$
, the obstruction class
![]() $\mathcal {O}({\mathrm {det}}\rho _B)\in H^2(G_K,{\operatorname {ad}_{{{\mathrm {det}}{\bar \rho }}}} )\otimes _\kappa I$
vanishes. By Theorem 3.4.1, the long exact sequence of Galois cohomology arising from the sequence (11) gives the left exact sequence
$\mathcal {O}({\mathrm {det}}\rho _B)\in H^2(G_K,{\operatorname {ad}_{{{\mathrm {det}}{\bar \rho }}}} )\otimes _\kappa I$
vanishes. By Theorem 3.4.1, the long exact sequence of Galois cohomology arising from the sequence (11) gives the left exact sequence
By Theorem 3.4.1 the sequence is dual to the right exact sequence
that arises from the sequence (12). By our hypothesis, the map
![]() $H^0({\mathrm {diag}}(1))$
is an isomorphism, and so by duality the same holds for
$H^0({\mathrm {diag}}(1))$
is an isomorphism, and so by duality the same holds for
![]() $H^2({\mathrm {tr}})$
. By a short explicit computation, one sees that
$H^2({\mathrm {tr}})$
. By a short explicit computation, one sees that
![]() $\mathcal {O}(\rho _B)$
maps to
$\mathcal {O}(\rho _B)$
maps to
![]() $\mathcal {O}({\mathrm {det}}\rho _B)=0$
under
$\mathcal {O}({\mathrm {det}}\rho _B)=0$
under
![]() $H^2({\mathrm {tr}})\otimes _{\kappa }{\mathrm {id}}_I$
, and this implies the vanishing of
$H^2({\mathrm {tr}})\otimes _{\kappa }{\mathrm {id}}_I$
, and this implies the vanishing of
![]() $\mathcal {O}(\rho _B)$
.
$\mathcal {O}(\rho _B)$
.
We have now proved that there exists
![]() $\rho _A'\in {\mathcal {D}}_{\bar \rho }(A)$
mapping to
$\rho _A'\in {\mathcal {D}}_{\bar \rho }(A)$
mapping to
![]() $\rho _B\in {\mathcal {D}}_{\bar \rho }(B)$
. However, this lift need not satisfy
$\rho _B\in {\mathcal {D}}_{\bar \rho }(B)$
. However, this lift need not satisfy
![]() ${\mathrm {det}}\rho ^{\prime }_{A}=\tau _A$
. At this point, we note that our hypothesis in fact implies that
${\mathrm {det}}\rho ^{\prime }_{A}=\tau _A$
. At this point, we note that our hypothesis in fact implies that
![]() $H^2(G_K,{\operatorname {ad}_{{{\bar \rho }}}^0})=0$
so that
$H^2(G_K,{\operatorname {ad}_{{{\bar \rho }}}^0})=0$
so that
is surjective. Now,
![]() ${\mathrm {det}}\rho ^{\prime }_{A}$
and
${\mathrm {det}}\rho ^{\prime }_{A}$
and
![]() $\tau _A$
are deformations of
$\tau _A$
are deformations of
![]() $\tau _{B}$
and the space of all such deformations is a principal homogeneous space under
$\tau _{B}$
and the space of all such deformations is a principal homogeneous space under
![]() $H^1(G_K,\kappa )$
, that is, the tangent space of the deformation problem, by [Reference SchlessingerSch68, Remark 2.15], and likewise the deformations of
$H^1(G_K,\kappa )$
, that is, the tangent space of the deformation problem, by [Reference SchlessingerSch68, Remark 2.15], and likewise the deformations of
![]() $\rho _B$
form a principal homogeneous space under
$\rho _B$
form a principal homogeneous space under
![]() $H^1(G_K,{\operatorname {ad}_{{{\bar \rho }}}})$
. Since the map (13) is surjective we can thus alter
$H^1(G_K,{\operatorname {ad}_{{{\bar \rho }}}})$
. Since the map (13) is surjective we can thus alter
![]() $\rho ^{\prime }_A$
by a class in
$\rho ^{\prime }_A$
by a class in
![]() $H^1(G_K,{\operatorname {ad}_{{{\bar \rho }}}})$
into some other deformation
$H^1(G_K,{\operatorname {ad}_{{{\bar \rho }}}})$
into some other deformation
![]() $\rho _A$
of
$\rho _A$
of
![]() $\rho _B$
that also satisfies
$\rho _B$
that also satisfies
![]() ${\mathrm {det}}\rho _A=\tau _A$
. This completes the proof of the formal smoothness. Note also that if
${\mathrm {det}}\rho _A=\tau _A$
. This completes the proof of the formal smoothness. Note also that if
![]() , then the above two sequences are exact on both sides and hence
, then the above two sequences are exact on both sides and hence
![]() $H^0(G_K,\overline {{\operatorname {ad}_{{{\bar \rho }}}}}(1))=0$
.
$H^0(G_K,\overline {{\operatorname {ad}_{{{\bar \rho }}}}}(1))=0$
.
By Proposition 3.1.5, it follows that the natural map
![]() ${R^{\operatorname {univ}}_{{\mathrm {det}} {\bar {\rho }}}} \rightarrow {R^{\operatorname {univ}}_{{\bar {\rho }}}}$
is formally smooth of relative dimension
${R^{\operatorname {univ}}_{{\mathrm {det}} {\bar {\rho }}}} \rightarrow {R^{\operatorname {univ}}_{{\bar {\rho }}}}$
is formally smooth of relative dimension
![]() $h=h^1(K,{\operatorname {ad}_{{{\bar \rho }}}})-h^1(K,{\operatorname {ad}_{{{\mathrm {det}}{\bar \rho }}}} )$
. It remains to identify h with the number in the lemma. Since the map (13) is surjective, by the long exact sequence for
$h=h^1(K,{\operatorname {ad}_{{{\bar \rho }}}})-h^1(K,{\operatorname {ad}_{{{\mathrm {det}}{\bar \rho }}}} )$
. It remains to identify h with the number in the lemma. Since the map (13) is surjective, by the long exact sequence for
![]() $H^*(G_K,\cdot )$
applied to the sequence (11), we deduce
$H^*(G_K,\cdot )$
applied to the sequence (11), we deduce
Since
![]() $h^2(K,{\operatorname {ad}_{{{\bar \rho }}}^0})=0$
by hypothesis and the duality statement of Theorem 3.4.1, the Euler characteristic formula of Theorem 3.4.1 implies
$h^2(K,{\operatorname {ad}_{{{\bar \rho }}}^0})=0$
by hypothesis and the duality statement of Theorem 3.4.1, the Euler characteristic formula of Theorem 3.4.1 implies
![]() $h=d(n^2-1)$
.
$h=d(n^2-1)$
.
The last assertion is straightforward. If
![]() , then the sequence (11) splits; the second assumption now yields
, then the sequence (11) splits; the second assumption now yields
![]() $ H^0(G_K,{\operatorname {ad}_{{{\bar \rho }}}^0})=0$
. If now
$ H^0(G_K,{\operatorname {ad}_{{{\bar \rho }}}^0})=0$
. If now
![]() $\kappa $
has characteristic zero, then
$\kappa $
has characteristic zero, then
![]() $0=H^0(G_K,\kappa (1))\cong H^0(G_K,{\operatorname {ad}_{{{\bar \rho }}}}(1))$
and we are done. If on the other hand
$0=H^0(G_K,\kappa (1))\cong H^0(G_K,{\operatorname {ad}_{{{\bar \rho }}}}(1))$
and we are done. If on the other hand
![]() $\kappa $
has characteristic p and
$\kappa $
has characteristic p and
![]() $\zeta _p\in K$
, then
$\zeta _p\in K$
, then
![]() ${\operatorname {ad}_{{{\bar \rho }}}^0}={\operatorname {ad}_{{{\bar \rho }}}^0}(1)$
and we are done, as well.
${\operatorname {ad}_{{{\bar \rho }}}^0}={\operatorname {ad}_{{{\bar \rho }}}^0}(1)$
and we are done, as well.
Let
![]() ${\bar \rho }_1\colon G_K\to {\mathrm {GL}}_1(\kappa )$
be a continuous character, and denote by
${\bar \rho }_1\colon G_K\to {\mathrm {GL}}_1(\kappa )$
be a continuous character, and denote by
![]() ${\bar \rho }_0\colon G_K\to {\mathrm {GL}}_1(\kappa )$
the trivial character. If
${\bar \rho }_0\colon G_K\to {\mathrm {GL}}_1(\kappa )$
the trivial character. If
![]() $\kappa $
is finite, denote by
$\kappa $
is finite, denote by
![]() $\rho _1\colon G_K\to {\mathrm {GL}}_1(\Lambda )$
the Teichmüller lift of
$\rho _1\colon G_K\to {\mathrm {GL}}_1(\Lambda )$
the Teichmüller lift of
![]() ${\bar \rho }_1$
, if
${\bar \rho }_1$
, if
![]() $\kappa $
is a local field, set
$\kappa $
is a local field, set
![]() $\rho _1:={\bar \rho }_1$
. There is a natural isomorphism
$\rho _1:={\bar \rho }_1$
. There is a natural isomorphism
![]() ${\mathcal {D}}_{{\bar \rho }_0}\to {\mathcal {D}}_{{\bar \rho }_1}$
mapping a deformation
${\mathcal {D}}_{{\bar \rho }_0}\to {\mathcal {D}}_{{\bar \rho }_1}$
mapping a deformation
![]() $\rho \colon G_K\to {\mathrm {GL}}_1(A)$
to
$\rho \colon G_K\to {\mathrm {GL}}_1(A)$
to
![]() $\rho \otimes \rho _1$
. As already observed in [Reference MazurMaz89, § 1.4],
$\rho \otimes \rho _1$
. As already observed in [Reference MazurMaz89, § 1.4],
![]() ${\mathcal {D}}_{{\bar \rho }_0}$
is representable by the completed group ring
${\mathcal {D}}_{{\bar \rho }_0}$
is representable by the completed group ring
![]() $\Lambda [[G_K^{{\operatorname {ab}},p}]]$
, where
$\Lambda [[G_K^{{\operatorname {ab}},p}]]$
, where
![]() $G_K^{{\operatorname {ab}},p}$
is the completion of the abelianization
$G_K^{{\operatorname {ab}},p}$
is the completion of the abelianization
![]() $G_K^{\operatorname {ab}}$
of
$G_K^{\operatorname {ab}}$
of
![]() $G_K$
along normal open subgroups of p-power index; the universal homomorphism
$G_K$
along normal open subgroups of p-power index; the universal homomorphism
factors via
![]() $G_K^{{\operatorname {ab}},p}$
and sends
$G_K^{{\operatorname {ab}},p}$
and sends
![]() $g\in G_K^{{\operatorname {ab}},p}$
to itself as a unit element in
$g\in G_K^{{\operatorname {ab}},p}$
to itself as a unit element in
![]() $\Lambda [[G_K^{{\operatorname {ab}},p}]]$
. The reciprocity homomorphisms of local class field theory, yields an isomorphism
$\Lambda [[G_K^{{\operatorname {ab}},p}]]$
. The reciprocity homomorphisms of local class field theory, yields an isomorphism
where
![]() $K^{\times ,p}$
is the pro-p completion of the multiplicative group
$K^{\times ,p}$
is the pro-p completion of the multiplicative group
![]() $K^\times $
. The torsion subgroup of
$K^\times $
. The torsion subgroup of
![]() $K^{\times ,p}$
is naturally identified with the group
$K^{\times ,p}$
is naturally identified with the group
![]() $\mu _{p^\infty }(K)$
of p-power roots of unity in K. Combining this with
$\mu _{p^\infty }(K)$
of p-power roots of unity in K. Combining this with
![]() ${\mathrm {det}}$
from diagram (10), we have the following chain of natural ring homomorphisms in
${\mathrm {det}}$
from diagram (10), we have the following chain of natural ring homomorphisms in
![]() ${\widehat {\mathcal {A}}r}_{\Lambda }$
${\widehat {\mathcal {A}}r}_{\Lambda }$
Corollary 3.4.3 (Cf. [Reference NakamuraNak14, § 4]).
Let
![]() $\kappa $
be finite or a local field of characteristic p, and suppose
$\kappa $
be finite or a local field of characteristic p, and suppose
![]() $\Lambda =\kappa $
. Suppose that
$\Lambda =\kappa $
. Suppose that
![]() $H^0(G_K,{\operatorname {\overline {ad}}_{{{\bar \rho }}}} (1))=0$
. Then the following hold:
$H^0(G_K,{\operatorname {\overline {ad}}_{{{\bar \rho }}}} (1))=0$
. Then the following hold:
-
(a) Both morphisms in diagram (14) are formally smooth.
-
(b) Both morphism in the following induced diagram are formally smooth:
 $$ \begin{align*}\Lambda=\Lambda[\mu_{p^\infty}(K)]_{\operatorname{red}} \,{\longrightarrow}\, \Lambda[[ K^{\times,p} ]]_{\operatorname{red}} \,\stackrel\simeq{\longrightarrow}\, ( {R{{\phantom{\overline{m}}}}^{\operatorname{ver}}_{{\Lambda,{\mathrm{det}}{\overline{\rho}}}}})_{\operatorname{red}}\,{\longrightarrow}\, ( {R{{\phantom{\overline{m}}}}^{\operatorname{ver}}_{{\Lambda,{\overline{\rho}}}}})_{\operatorname{red}}.\end{align*} $$
$$ \begin{align*}\Lambda=\Lambda[\mu_{p^\infty}(K)]_{\operatorname{red}} \,{\longrightarrow}\, \Lambda[[ K^{\times,p} ]]_{\operatorname{red}} \,\stackrel\simeq{\longrightarrow}\, ( {R{{\phantom{\overline{m}}}}^{\operatorname{ver}}_{{\Lambda,{\mathrm{det}}{\overline{\rho}}}}})_{\operatorname{red}}\,{\longrightarrow}\, ( {R{{\phantom{\overline{m}}}}^{\operatorname{ver}}_{{\Lambda,{\overline{\rho}}}}})_{\operatorname{red}}.\end{align*} $$
The relative dimensions in both cases are
![]() $d+1$
and
$d+1$
and
![]() $d(n^2-1)$
, respectively.
$d(n^2-1)$
, respectively.
Proof. Let
![]() $q:={\operatorname {ord}{{\mu _{p^\infty }(K)}}}$
. By Lemma 3.4.2, the natural map
$q:={\operatorname {ord}{{\mu _{p^\infty }(K)}}}$
. By Lemma 3.4.2, the natural map
![]() ${R^{\operatorname {univ}}_{{\mathrm {det}} \rho }}{\longrightarrow } {R^{\operatorname {univ}}_{\rho }}$
is formally smooth of relative dimension
${R^{\operatorname {univ}}_{{\mathrm {det}} \rho }}{\longrightarrow } {R^{\operatorname {univ}}_{\rho }}$
is formally smooth of relative dimension
![]() $h=d(n^2-1)$
. From the theory of local fields, one has
$h=d(n^2-1)$
. From the theory of local fields, one has
![]() $K^{\times ,p}\cong {\mathbb {Z}}_p^{[K:{\mathbb {Q}}_p]+1}\times \mu _{p^\infty }(K)$
, where
$K^{\times ,p}\cong {\mathbb {Z}}_p^{[K:{\mathbb {Q}}_p]+1}\times \mu _{p^\infty }(K)$
, where
![]() $ \mu _{p^\infty }(K)$
is a finite cyclic group of p-power order q. By our hypothesis on the characteristic of
$ \mu _{p^\infty }(K)$
is a finite cyclic group of p-power order q. By our hypothesis on the characteristic of
![]() $\kappa $
, the right-hand morphism in diagram (14) can be identified with
$\kappa $
, the right-hand morphism in diagram (14) can be identified with
and parts (a) and (b) for it are now obvious. To see the second part of (b), note that the kernel of the reduction map
![]() $\kappa [x]/(x^q)\to \kappa $
is nilpotent. Hence, the kernel of the induced map
$\kappa [x]/(x^q)\to \kappa $
is nilpotent. Hence, the kernel of the induced map
![]() ${\varphi }\colon {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ,{\overline {\rho }}}}}\to {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ,{\overline {\rho }}}}}\otimes _{\kappa [x]/(x^q)}\kappa $
is nilpotent as well, and the map
${\varphi }\colon {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ,{\overline {\rho }}}}}\to {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ,{\overline {\rho }}}}}\otimes _{\kappa [x]/(x^q)}\kappa $
is nilpotent as well, and the map
![]() $ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ,{\overline {\rho }}}}}\to ( {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ,{\overline {\rho }}}}})_{\operatorname {red}}$
factors via
$ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ,{\overline {\rho }}}}}\to ( {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ,{\overline {\rho }}}}})_{\operatorname {red}}$
factors via
![]() ${\varphi }$
. At the same time, formal smoothness is preserved under base change. Hence,
${\varphi }$
. At the same time, formal smoothness is preserved under base change. Hence,
![]() $\kappa \to {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ,{\overline {\rho }}}}}\otimes _{\kappa [x]/(x^q)}\kappa $
is formally smooth, and therefore
$\kappa \to {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ,{\overline {\rho }}}}}\otimes _{\kappa [x]/(x^q)}\kappa $
is formally smooth, and therefore
![]() $ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ,{\overline {\rho }}}}}\otimes _{\kappa [x]/(x^q)}\kappa $
is regular and in particular a domain. We deduce that
$ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ,{\overline {\rho }}}}}\otimes _{\kappa [x]/(x^q)}\kappa $
is regular and in particular a domain. We deduce that
![]() $ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ,{\overline {\rho }}}}}\otimes _{\kappa [x]/(x^q)}\kappa \to ( {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ,{\overline {\rho }}}}})_{\operatorname {red}}$
is an isomorphism, and this completes (b).
$ {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ,{\overline {\rho }}}}}\otimes _{\kappa [x]/(x^q)}\kappa \to ( {R{{\phantom {\overline {m}}}}^{\operatorname {ver}}_{{\Lambda ,{\overline {\rho }}}}})_{\operatorname {red}}$
is an isomorphism, and this completes (b).
We end this subsection with a computation of
![]() $H^0(G_K,{\operatorname {ad}_{{{\overline {\rho }}}}}\otimes \chi )$
and a variant of Lemma 3.4.2 for certain reducible deformations.
$H^0(G_K,{\operatorname {ad}_{{{\overline {\rho }}}}}\otimes \chi )$
and a variant of Lemma 3.4.2 for certain reducible deformations.
Lemma 3.4.4. Let E be a finite or local field with its natural topology. Denote by
![]() $\rho _{i}\colon G_K\to {\mathrm {GL}}_{n_i}(E)$
continuous Galois representations for
$\rho _{i}\colon G_K\to {\mathrm {GL}}_{n_i}(E)$
continuous Galois representations for
![]() $i=1,2$
, and let
$i=1,2$
, and let
 $\rho =\left (\begin {array}{cc} \rho _{1}&c\\ 0&\rho _{2} \end {array}\right )$
be an extension of
$\rho =\left (\begin {array}{cc} \rho _{1}&c\\ 0&\rho _{2} \end {array}\right )$
be an extension of
![]() $\rho _1$
by
$\rho _1$
by
![]() $\rho _2$
. Let
$\rho _2$
. Let
![]() $\chi \colon G_K\to E^\times $
be a continuous character and write
$\chi \colon G_K\to E^\times $
be a continuous character and write
![]() $1$
for the trivial character. Suppose that
$1$
for the trivial character. Suppose that
-
(a)
 ${\mathrm {Hom}}_{G_K}(\rho _1,\rho _2\otimes \chi )=0$
and
${\mathrm {Hom}}_{G_K}(\rho _1,\rho _2\otimes \chi )=0$
and
 ${\mathrm {Hom}}_{G_K}(\rho _2,\rho _1\otimes \chi )=0$
.
${\mathrm {Hom}}_{G_K}(\rho _2,\rho _1\otimes \chi )=0$
. -
(b) For
 $i=1,2$
, we have
$i=1,2$
, we have
 ${\mathrm {End}}_{G_K}(\rho _i)\cong E$
if
${\mathrm {End}}_{G_K}(\rho _i)\cong E$
if
 $\chi =1$
and
$\chi =1$
and
 ${\mathrm {Hom}}_{G_K}(\rho _i,\rho _i\otimes \chi )=0$
if
${\mathrm {Hom}}_{G_K}(\rho _i,\rho _i\otimes \chi )=0$
if
 $\chi \neq 1$
.
$\chi \neq 1$
. -
(c) If
 $\chi =1$
, then the class
$\chi =1$
, then the class
 $c\in {\mathrm {Ext}}^1_{G_K}(\rho _2,\rho _1)$
is nontrivial,
$c\in {\mathrm {Ext}}^1_{G_K}(\rho _2,\rho _1)$
is nontrivial,
Then
![]() ${\mathrm {End}}_{G_K}(\rho )\cong E$
if
${\mathrm {End}}_{G_K}(\rho )\cong E$
if
![]() $\chi =1$
and
$\chi =1$
and
![]() ${\mathrm {Hom}}_{G_K}(\rho ,\rho \otimes \chi )=0$
if
${\mathrm {Hom}}_{G_K}(\rho ,\rho \otimes \chi )=0$
if
![]() $\chi \neq 1$
.
$\chi \neq 1$
.
Proof. To determine
![]() ${\mathrm {Hom}}_{G_K}(\rho ,\rho \otimes \chi )$
, we consider
${\mathrm {Hom}}_{G_K}(\rho ,\rho \otimes \chi )$
, we consider
![]() $A_{ij}\in {\mathrm {Mat}}_{n_i\times n_j}(E)$
for
$A_{ij}\in {\mathrm {Mat}}_{n_i\times n_j}(E)$
for
![]() $1\leq i,j\leq 2$
such that
$1\leq i,j\leq 2$
such that
 $$ \begin{align*} 0 &\stackrel{!}= \left(\begin{array}{cc} A_{11}&A_{12}\\ A_{21}&A_{22} \end{array}\right) \left(\begin{array}{cc} \rho_{1} & c\\ 0 & \rho_{2} \end{array}\right) - \left(\begin{array}{cc} \rho_{1}\otimes\chi & c\otimes\chi\\ 0 &\rho_{2}\otimes\chi \end{array}\right) \left(\begin{array}{cc} A_{11} &A_{12}\\ A_{21} &A_{22} \end{array}\right)\\ &= \left(\begin{array}{cc} A_{11}\rho_{1} &A_{11}c+A_{12}\rho_{2}\\ A_{21}\rho_{1} &A_{21}c+A_{22}\rho_{2} \end{array}\right) - \left(\begin{array}{cc} \rho_{1}\otimes\chi\cdot A_{11}+c\otimes \chi\cdot A_{21} &\rho_{1}\otimes\chi\cdot A_{12}+c\otimes\chi\cdot A_{22}\\ \rho_{2}\otimes\chi\cdot A_{21} &\rho_{2}\otimes\chi\cdot A_{22} \end{array}\right). \end{align*} $$
$$ \begin{align*} 0 &\stackrel{!}= \left(\begin{array}{cc} A_{11}&A_{12}\\ A_{21}&A_{22} \end{array}\right) \left(\begin{array}{cc} \rho_{1} & c\\ 0 & \rho_{2} \end{array}\right) - \left(\begin{array}{cc} \rho_{1}\otimes\chi & c\otimes\chi\\ 0 &\rho_{2}\otimes\chi \end{array}\right) \left(\begin{array}{cc} A_{11} &A_{12}\\ A_{21} &A_{22} \end{array}\right)\\ &= \left(\begin{array}{cc} A_{11}\rho_{1} &A_{11}c+A_{12}\rho_{2}\\ A_{21}\rho_{1} &A_{21}c+A_{22}\rho_{2} \end{array}\right) - \left(\begin{array}{cc} \rho_{1}\otimes\chi\cdot A_{11}+c\otimes \chi\cdot A_{21} &\rho_{1}\otimes\chi\cdot A_{12}+c\otimes\chi\cdot A_{22}\\ \rho_{2}\otimes\chi\cdot A_{21} &\rho_{2}\otimes\chi\cdot A_{22} \end{array}\right). \end{align*} $$
From hypothesis (a) and considering the (2,1)-entry, we deduce
![]() $A_{21}=0$
. From hypothesis (b) and considering the (1,1)- and (2,2)-entries, we deduce, depending on
$A_{21}=0$
. From hypothesis (b) and considering the (1,1)- and (2,2)-entries, we deduce, depending on
![]() $\chi $
the following: If
$\chi $
the following: If
![]() $\chi =1$
, then
$\chi =1$
, then
![]() $A_{ii}$
are scalar for
$A_{ii}$
are scalar for
![]() $i=1,2$
, say equal to
$i=1,2$
, say equal to
![]() for some
for some
![]() $\lambda _i\in E$
, respectively; if
$\lambda _i\in E$
, respectively; if
![]() $\chi \neq 1$
, then both
$\chi \neq 1$
, then both
![]() $A_{ii}=0$
. Considering the
$A_{ii}=0$
. Considering the
![]() $(1,2)$
-entry, we obtain the relation
$(1,2)$
-entry, we obtain the relation
If
![]() $\chi \neq 1$
, the left-hand side is zero, and from (a) we deduce
$\chi \neq 1$
, the left-hand side is zero, and from (a) we deduce
![]() $A_{12}=0$
so that the proof in this case is complete. If
$A_{12}=0$
so that the proof in this case is complete. If
![]() $\chi =1$
, then we have
$\chi =1$
, then we have
![]() $(\lambda _1-\lambda _2)c=\rho _{1}A_{12}-A_{12}\rho _{2}$
. Now,
$(\lambda _1-\lambda _2)c=\rho _{1}A_{12}-A_{12}\rho _{2}$
. Now,
![]() $g\mapsto \rho _{1}(g)A_{12}-A_{12}\rho _{2}(g)$
is a
$g\mapsto \rho _{1}(g)A_{12}-A_{12}\rho _{2}(g)$
is a
![]() $1$
-coboundary with values in
$1$
-coboundary with values in
![]() ${\mathrm {Hom}}_{G_K}(\rho _2,\rho _1)$
, and so if
${\mathrm {Hom}}_{G_K}(\rho _2,\rho _1)$
, and so if
![]() $\lambda _1\neq \lambda _2$
the last condition implies that c is the trivial class in
$\lambda _1\neq \lambda _2$
the last condition implies that c is the trivial class in
![]() ${\mathrm {Ext}}^1_{G_K}(\rho _2,\rho _1)$
which is excluded by hypothesis (c). This shows
${\mathrm {Ext}}^1_{G_K}(\rho _2,\rho _1)$
which is excluded by hypothesis (c). This shows
![]() $\lambda _1=\lambda _2$
, and
$\lambda _1=\lambda _2$
, and
![]() $A_{12}\in {\mathrm {Hom}}_{G_K}(\rho _2,\rho _1)$
, and hence
$A_{12}\in {\mathrm {Hom}}_{G_K}(\rho _2,\rho _1)$
, and hence
![]() $A_{12}=0$
, again by (a). This completes the proof.
$A_{12}=0$
, again by (a). This completes the proof.
For Proposition 5.3.3, we also need a variant of Corollary 3.4.3 for certain reducible
![]() ${\overline {\rho }}$
. So for the remainder of this subsection let
${\overline {\rho }}$
. So for the remainder of this subsection let
![]() ${\overline {\rho }}_i\colon G_K\to {\mathrm {GL}}_{n_i}(\kappa )$
,
${\overline {\rho }}_i\colon G_K\to {\mathrm {GL}}_{n_i}(\kappa )$
,
![]() $i=1,2$
, be absolutely irreducible, and assume that
$i=1,2$
, be absolutely irreducible, and assume that
![]() ${\overline {\rho }}_1$
is not isomorphic to
${\overline {\rho }}_1$
is not isomorphic to
![]() ${\overline {\rho }}_2(j)$
for
${\overline {\rho }}_2(j)$
for
![]() $j\in \{0,\pm 1\}$
. Let further
$j\in \{0,\pm 1\}$
. Let further
![]() ${\bar \rho }$
be a nonsplit extension of dimension
${\bar \rho }$
be a nonsplit extension of dimension
![]() $n=n_1+n_2$
that fits into a short exact sequence
$n=n_1+n_2$
that fits into a short exact sequence
![]() $0\to {\bar \rho }_1\to {\bar \rho }\to {\bar \rho }_2\to 0$
. Define the subfunctor
$0\to {\bar \rho }_1\to {\bar \rho }\to {\bar \rho }_2\to 0$
. Define the subfunctor
![]() ${\mathcal {D}}_{{\bar \rho }_1\subset {\bar \rho }}\subset {\mathcal {D}}_{\bar \rho }$
by mapping A in
${\mathcal {D}}_{{\bar \rho }_1\subset {\bar \rho }}\subset {\mathcal {D}}_{\bar \rho }$
by mapping A in
![]() ${\mathcal {A}r}_{\Lambda }$
to the set of
${\mathcal {A}r}_{\Lambda }$
to the set of
![]() $\Gamma _n(A)$
-conjugacy classes of liftings
$\Gamma _n(A)$
-conjugacy classes of liftings
![]() $\rho _A$
of
$\rho _A$
of
![]() $\bar \rho $
to A such that
$\bar \rho $
to A such that
![]() $\rho _A$
stabilizes an A-direct summand
$\rho _A$
stabilizes an A-direct summand
![]() $P_A$
of
$P_A$
of
![]() $A^n$
of rank
$A^n$
of rank
![]() $n_1$
so that the induced representation of
$n_1$
so that the induced representation of
![]() $\rho _A$
on
$\rho _A$
on
![]() $P_A$
is a deformation of
$P_A$
is a deformation of
![]() ${\bar \rho }_1$
; because of the shape of
${\bar \rho }_1$
; because of the shape of
![]() ${\overline {\rho }}$
the deformations described by
${\overline {\rho }}$
the deformations described by
![]() ${\mathcal {D}}_{{\bar \rho }_1\subset {\bar \rho }}$
are precisely the ‘reducible’ deformations of
${\mathcal {D}}_{{\bar \rho }_1\subset {\bar \rho }}$
are precisely the ‘reducible’ deformations of
![]() ${\bar \rho }$
. In fact:
${\bar \rho }$
. In fact:
Lemma 3.4.5.
![]() ${\mathcal {D}}_{{\bar \rho }_1\!\subset {\bar \rho }}\!\subset \!{\mathcal {D}}_{\bar \rho }$
is a relatively representable subfunctor in the sense of [Reference MazurMaz97,§ 19].
${\mathcal {D}}_{{\bar \rho }_1\!\subset {\bar \rho }}\!\subset \!{\mathcal {D}}_{\bar \rho }$
is a relatively representable subfunctor in the sense of [Reference MazurMaz97,§ 19].
Proof. In lack of a reference, we give a proof. Given a diagram
![]() $A\to B\leftarrow C$
in
$A\to B\leftarrow C$
in
![]() ${\mathcal {A}r}_{\Lambda }$
, one has to show that the induced diagram
${\mathcal {A}r}_{\Lambda }$
, one has to show that the induced diagram

is a pullback in the category of sets. To see this, suppose
![]() $(\rho _A,\rho _C)$
is an element in the top right and
$(\rho _A,\rho _C)$
is an element in the top right and
![]() $\rho _{A\times _BC}$
in the bottom left, both mapping to the same element in the bottom right. Then
$\rho _{A\times _BC}$
in the bottom left, both mapping to the same element in the bottom right. Then
![]() $(\rho _A,\rho _C)$
gives rise to a pair of subrepresentations
$(\rho _A,\rho _C)$
gives rise to a pair of subrepresentations
![]() $(\rho ^1_A,\rho ^1_C)$
that are deformations of
$(\rho ^1_A,\rho ^1_C)$
that are deformations of
![]() ${\bar \rho }_1$
and a pair of quotient representations
${\bar \rho }_1$
and a pair of quotient representations
![]() $(\rho ^2_A,\rho ^2_C)$
that are deformations of
$(\rho ^2_A,\rho ^2_C)$
that are deformations of
![]() ${\bar \rho }_2$
and each pair maps to the same element on B, say
${\bar \rho }_2$
and each pair maps to the same element on B, say
![]() $\rho ^1_B$
and
$\rho ^1_B$
and
![]() $\rho ^2_B$
, respectively. By our hypotheses on the
$\rho ^2_B$
, respectively. By our hypotheses on the
![]() ${\bar \rho }_i$
the respective deformation functors
${\bar \rho }_i$
the respective deformation functors
![]() ${\mathcal {D}}_{{\bar \rho }_i}$
are representable so that each pair patches to a deformations
${\mathcal {D}}_{{\bar \rho }_i}$
are representable so that each pair patches to a deformations
![]() $\rho ^1_{A\times _BC}$
of
$\rho ^1_{A\times _BC}$
of
![]() ${\bar \rho }_1$
and
${\bar \rho }_1$
and
![]() $\rho ^2_{A\times _BC}$
of
$\rho ^2_{A\times _BC}$
of
![]() ${\bar \rho }_2$
on
${\bar \rho }_2$
on
![]() $A\times _BC$
, respectively. It now follows from [Reference UrbanUrb99, Theorem] that
$A\times _BC$
, respectively. It now follows from [Reference UrbanUrb99, Theorem] that
![]() $\rho _{A\times _BC}$
lies in
$\rho _{A\times _BC}$
lies in
![]() ${\mathcal {D}}_{{\bar \rho }_1\subset {\bar \rho }}(A\times _BC)$
with
${\mathcal {D}}_{{\bar \rho }_1\subset {\bar \rho }}(A\times _BC)$
with
![]() $\rho ^1_{A\times _BC}$
as a sub and
$\rho ^1_{A\times _BC}$
as a sub and
![]() $\rho ^2_{A\times _BC}$
as a quotient representation.
$\rho ^2_{A\times _BC}$
as a quotient representation.
Now, by Lemma 3.4.4 we have
![]() ${\mathrm {End}}_{G_K}({\bar \rho })\cong \kappa $
so that
${\mathrm {End}}_{G_K}({\bar \rho })\cong \kappa $
so that
![]() ${\mathcal {D}}_{\bar \rho }$
is representable. By Lemma 3.4.5, it follows that
${\mathcal {D}}_{\bar \rho }$
is representable. By Lemma 3.4.5, it follows that
![]() ${\mathcal {D}}_{{\bar \rho }_1\subset {\bar \rho }}$
is a closed subfunctor that is representable by a quotient of
${\mathcal {D}}_{{\bar \rho }_1\subset {\bar \rho }}$
is a closed subfunctor that is representable by a quotient of
![]() $R^{\operatorname {univ}}_{\bar \rho }$
in
$R^{\operatorname {univ}}_{\bar \rho }$
in
![]() ${\widehat {\mathcal {A}}r}_{\Lambda }$
. Let
${\widehat {\mathcal {A}}r}_{\Lambda }$
. Let
![]() $\rho ^{\operatorname {univ}}_{{\bar \rho }_1\subset {\bar \rho }}\colon G_K\to {\mathrm {GL}}_n(R^{\operatorname {univ}}_{{\bar \rho }_1\subset {\bar \rho }} )$
be a universal representation for
$\rho ^{\operatorname {univ}}_{{\bar \rho }_1\subset {\bar \rho }}\colon G_K\to {\mathrm {GL}}_n(R^{\operatorname {univ}}_{{\bar \rho }_1\subset {\bar \rho }} )$
be a universal representation for
![]() ${\mathcal {D}}_{{\bar \rho }_1\subset {\bar \rho }}$
. By the shape of
${\mathcal {D}}_{{\bar \rho }_1\subset {\bar \rho }}$
. By the shape of
![]() ${\overline {\rho }}$
and the reducibility of
${\overline {\rho }}$
and the reducibility of
![]() $\rho ^{\operatorname {univ}}_{{\bar \rho }_1\subset {\bar \rho }}$
, we can choose a suitable basis for
$\rho ^{\operatorname {univ}}_{{\bar \rho }_1\subset {\bar \rho }}$
, we can choose a suitable basis for
![]() $\rho ^{\operatorname {univ}}_{{\bar \rho }_1\subset {\bar \rho }}$
so that
$\rho ^{\operatorname {univ}}_{{\bar \rho }_1\subset {\bar \rho }}$
so that
 $$ \begin{align*}\rho^{\operatorname{univ}}_{{\bar\rho}_1\subset{\bar\rho}}= \left(\begin{array}{cc} \rho^{\operatorname{univ},1}_{{\bar\rho}_1\subset{\bar\rho}} & *\\ 0 & \rho^{\operatorname{univ},2}_{{\bar\rho}_1\subset{\bar\rho}} \end{array}\right) \end{align*} $$
$$ \begin{align*}\rho^{\operatorname{univ}}_{{\bar\rho}_1\subset{\bar\rho}}= \left(\begin{array}{cc} \rho^{\operatorname{univ},1}_{{\bar\rho}_1\subset{\bar\rho}} & *\\ 0 & \rho^{\operatorname{univ},2}_{{\bar\rho}_1\subset{\bar\rho}} \end{array}\right) \end{align*} $$
for representations
![]() $\rho ^{\operatorname {univ},i}_{{\bar \rho }_1\subset {\bar \rho }}\colon G_K\to {\mathrm {GL}}_{n_i}(R^{\operatorname {univ}}_{{\bar \rho }_1\subset {\bar \rho }} )$
, and
$\rho ^{\operatorname {univ},i}_{{\bar \rho }_1\subset {\bar \rho }}\colon G_K\to {\mathrm {GL}}_{n_i}(R^{\operatorname {univ}}_{{\bar \rho }_1\subset {\bar \rho }} )$
, and
![]() $*$
a suitable nontrivial extension class. Here, the
$*$
a suitable nontrivial extension class. Here, the
![]() $\rho ^{\operatorname {univ},i}_{{\bar \rho }_1\subset {\bar \rho }}$
are unique up to conjugation.
$\rho ^{\operatorname {univ},i}_{{\bar \rho }_1\subset {\bar \rho }}$
are unique up to conjugation.
We now adapt the setting developed before Lemma 3.4.2 to the present situation. Namely, one has a natural functor
which for
![]() $A\in {\widehat {\mathcal {A}}r}_{\Lambda }$
attaches to
$A\in {\widehat {\mathcal {A}}r}_{\Lambda }$
attaches to
![]() $\rho _A\in {\mathcal {D}}_{{\bar \rho }_1\subset {\bar \rho }}(A)$
with
$\rho _A\in {\mathcal {D}}_{{\bar \rho }_1\subset {\bar \rho }}(A)$
with
![]() $\rho _A$
-stable direct summand
$\rho _A$
-stable direct summand
![]() $P_A(\cong A^{n_1})$
of
$P_A(\cong A^{n_1})$
of
![]() $A^n$
the pair
$A^n$
the pair
![]() $({\mathrm {det}} (\rho _{A|P_A}),{\mathrm {det}}(\rho _A\ {\mathop{\mathrm{mod}\ }\nolimits } P_A))$
of deformations of
$({\mathrm {det}} (\rho _{A|P_A}),{\mathrm {det}}(\rho _A\ {\mathop{\mathrm{mod}\ }\nolimits } P_A))$
of deformations of
![]() $({\mathrm {det}}{\overline {\rho }}_1,{\mathrm {det}}{\overline {\rho }}_2)$
. Let
$({\mathrm {det}}{\overline {\rho }}_1,{\mathrm {det}}{\overline {\rho }}_2)$
. Let
![]() ${\operatorname {ad}_{{{\bar \rho }_1\subset {\bar \rho }}}} \subset {\operatorname {ad}_{{{\bar \rho }}}}$
be the block upper triangular subspace of matrices that preserve
${\operatorname {ad}_{{{\bar \rho }_1\subset {\bar \rho }}}} \subset {\operatorname {ad}_{{{\bar \rho }}}}$
be the block upper triangular subspace of matrices that preserve
![]() $\bar \rho _1$
. Mapping matrices to the diagonal blocks gives a surjection
$\bar \rho _1$
. Mapping matrices to the diagonal blocks gives a surjection
![]() $\pi \colon {\operatorname {ad}_{{{\bar \rho }_1\subset {\bar \rho }}}} \subset {\operatorname {ad}_{{{\bar \rho }}}}\to {\operatorname {ad}_{{{\bar \rho }_1}}} \oplus {\operatorname {ad}_{{{\bar \rho }_2}}} $
, and we denote by
$\pi \colon {\operatorname {ad}_{{{\bar \rho }_1\subset {\bar \rho }}}} \subset {\operatorname {ad}_{{{\bar \rho }}}}\to {\operatorname {ad}_{{{\bar \rho }_1}}} \oplus {\operatorname {ad}_{{{\bar \rho }_2}}} $
, and we denote by
![]() ${\operatorname {ad}_{{{\bar \rho }_1\subset {\bar \rho }}} ^{00}}\subset {\operatorname {ad}_{{{\bar \rho }_1\subset {\bar \rho }}}} $
the inverse image of
${\operatorname {ad}_{{{\bar \rho }_1\subset {\bar \rho }}} ^{00}}\subset {\operatorname {ad}_{{{\bar \rho }_1\subset {\bar \rho }}}} $
the inverse image of
![]() ${\operatorname {ad}_{{{\bar \rho }_1}} ^0}\oplus {\operatorname {ad}_{{{\bar \rho }_2}} ^0}$
under
${\operatorname {ad}_{{{\bar \rho }_1}} ^0}\oplus {\operatorname {ad}_{{{\bar \rho }_2}} ^0}$
under
![]() $\pi $
, and by
$\pi $
, and by
![]() $\mathrm{rad}_{{\bar \rho }_1\subset {\bar \rho }}$
the kernel of
$\mathrm{rad}_{{\bar \rho }_1\subset {\bar \rho }}$
the kernel of
![]() $\pi $
.
$\pi $
.
Now, as in the proof of Lemma 3.4.2, obstructions to the smoothness of
![]() ${\mathrm {det}}^2$
lie in the group
${\mathrm {det}}^2$
lie in the group
![]() $H^2(G_K,{\operatorname {ad}_{{{\bar \rho }_1\subset {\bar \rho }}} ^{00}})$
. Using the short exact sequence
$H^2(G_K,{\operatorname {ad}_{{{\bar \rho }_1\subset {\bar \rho }}} ^{00}})$
. Using the short exact sequence
![]() $0\to \mathrm{rad}_{{\bar \rho }_1\subset {\bar \rho }}\to {\operatorname {ad}_{{{\bar \rho }_1\subset {\bar \rho }}} ^{00}}\to {\operatorname {ad}_{{{\bar \rho }_1}} ^0}\times {\operatorname {ad}_{{{\bar \rho }_2}} ^0}\to 0$
, and the vanishing of
$0\to \mathrm{rad}_{{\bar \rho }_1\subset {\bar \rho }}\to {\operatorname {ad}_{{{\bar \rho }_1\subset {\bar \rho }}} ^{00}}\to {\operatorname {ad}_{{{\bar \rho }_1}} ^0}\times {\operatorname {ad}_{{{\bar \rho }_2}} ^0}\to 0$
, and the vanishing of
![]() $H^2(G_K,\mathrm{rad}_{{\bar \rho }_1\subset {\bar \rho }})^*\cong H^0(G_K,{\mathrm {Hom}}({\bar \rho }_1,{\bar \rho }_2)(1))\cong {\mathrm {Hom}}_{G_K}({\bar \rho }_1,{\bar \rho }_2(1))$
, that relies on local Tate-duality from Theorem 3.4.1 and
$H^2(G_K,\mathrm{rad}_{{\bar \rho }_1\subset {\bar \rho }})^*\cong H^0(G_K,{\mathrm {Hom}}({\bar \rho }_1,{\bar \rho }_2)(1))\cong {\mathrm {Hom}}_{G_K}({\bar \rho }_1,{\bar \rho }_2(1))$
, that relies on local Tate-duality from Theorem 3.4.1 and
![]() ${\overline {\rho }}_1\not \cong {\bar \rho }_2(1)$
, one finds
${\overline {\rho }}_1\not \cong {\bar \rho }_2(1)$
, one finds
Again, from Tate local duality one deduces that
![]() ${\mathrm {det}}^2$
is formally smooth if
${\mathrm {det}}^2$
is formally smooth if
![]() $H^0(G_K,{\operatorname {\overline {ad}}_{{{\bar \rho }_i}}} (1))=0$
for
$H^0(G_K,{\operatorname {\overline {ad}}_{{{\bar \rho }_i}}} (1))=0$
for
![]() $i=1,2$
. Assuming this, the map of rings
$i=1,2$
. Assuming this, the map of rings
![]() $R^{\operatorname {univ}}_{{\mathrm {det}}{\bar \rho }_1}\hat \otimes _{\Lambda } R^{\operatorname {univ}}_{{\mathrm {det}}{\bar \rho }_2}\to R^{\operatorname {univ}}_{{\bar \rho }_1\subset {\bar \rho }} $
is formally smooth and the relative dimension is given by
$R^{\operatorname {univ}}_{{\mathrm {det}}{\bar \rho }_1}\hat \otimes _{\Lambda } R^{\operatorname {univ}}_{{\mathrm {det}}{\bar \rho }_2}\to R^{\operatorname {univ}}_{{\bar \rho }_1\subset {\bar \rho }} $
is formally smooth and the relative dimension is given by
To compute h, observe first that
![]() $H^1(G_K,{\operatorname {ad}_{{{\bar \rho }_1\subset {\bar \rho }}}} )\to H^1(G_K,{\operatorname {ad}_{{{\bar \rho }}}})$
is injective because
$H^1(G_K,{\operatorname {ad}_{{{\bar \rho }_1\subset {\bar \rho }}}} )\to H^1(G_K,{\operatorname {ad}_{{{\bar \rho }}}})$
is injective because
![]() ${\operatorname {ad}_{{{\bar \rho }}}}\!/\! {\operatorname {ad}_{{{\bar \rho }_1\subset {\bar \rho }}}} \cong {\mathrm {Hom}}_\kappa ({\bar \rho }_1,{\bar \rho }_2)$
and
${\operatorname {ad}_{{{\bar \rho }}}}\!/\! {\operatorname {ad}_{{{\bar \rho }_1\subset {\bar \rho }}}} \cong {\mathrm {Hom}}_\kappa ({\bar \rho }_1,{\bar \rho }_2)$
and
![]() ${\mathrm {Hom}}_{G_K}({\bar \rho }_1,{\bar \rho }_2)=0$
. The quantity
${\mathrm {Hom}}_{G_K}({\bar \rho }_1,{\bar \rho }_2)=0$
. The quantity
![]() $\dim H^1(G_K,\kappa )$
was computed in the proof of Corollary 3.4.3 to be
$\dim H^1(G_K,\kappa )$
was computed in the proof of Corollary 3.4.3 to be
![]() $1+d+\delta _p$
, where
$1+d+\delta _p$
, where
![]() $\delta _p=0$
if
$\delta _p=0$
if
![]() $\zeta _p\notin K$
and
$\zeta _p\notin K$
and
![]() $\delta _p=1$
if
$\delta _p=1$
if
![]() $\zeta _p\in K$
. Finally,
$\zeta _p\in K$
. Finally,
![]() $\dim H^1(G_K,{\operatorname {ad}_{{{\bar \rho }_1\subset {\bar \rho }}}} )$
is computed by the Euler–Poincaré formula of local Tate duality: Lemma 3.4.4 yields
$\dim H^1(G_K,{\operatorname {ad}_{{{\bar \rho }_1\subset {\bar \rho }}}} )$
is computed by the Euler–Poincaré formula of local Tate duality: Lemma 3.4.4 yields
![]() $ H^0(G_K,{\operatorname {ad}_{{{\bar \rho }_1\subset {\bar \rho }}}} )=H^0(G_K,{\operatorname {ad}_{{{\bar \rho }}}})\cong \kappa $
, and in the same way in which we deduced the isomorphism (15), we obtain
$ H^0(G_K,{\operatorname {ad}_{{{\bar \rho }_1\subset {\bar \rho }}}} )=H^0(G_K,{\operatorname {ad}_{{{\bar \rho }}}})\cong \kappa $
, and in the same way in which we deduced the isomorphism (15), we obtain
![]() $H^2(G_K,{\operatorname {ad}_{{{\bar \rho }_1\subset {\bar \rho }}}} )\cong H^2(G_K,{\operatorname {ad}_{{{\bar \rho }_1}}} \oplus {\operatorname {ad}_{{{\bar \rho }_2}}})$
, and by local Tate duality the latter has dimension
$H^2(G_K,{\operatorname {ad}_{{{\bar \rho }_1\subset {\bar \rho }}}} )\cong H^2(G_K,{\operatorname {ad}_{{{\bar \rho }_1}}} \oplus {\operatorname {ad}_{{{\bar \rho }_2}}})$
, and by local Tate duality the latter has dimension
![]() $2\delta _p$
. In total, we find
$2\delta _p$
. In total, we find
One also easily adapts the proof of Corollary 3.4.3. The following result summarizes the conclusions needed later. For the last assertion, one does not consider the map
![]() ${\mathrm {det}}^2$
but uses a variant of Theorem 3.2.4(e).
${\mathrm {det}}^2$
but uses a variant of Theorem 3.2.4(e).
Proposition 3.4.6 Let
![]() $\kappa $
be finite or a local field of characteristic p, let
$\kappa $
be finite or a local field of characteristic p, let
![]() $\Lambda ={\kappa }$
and suppose that
$\Lambda ={\kappa }$
and suppose that
![]() ${\bar \rho }$
is a nonsplit extension of
${\bar \rho }$
is a nonsplit extension of
![]() ${\bar \rho }_2$
by
${\bar \rho }_2$
by
![]() ${\bar \rho }_1$
and that
${\bar \rho }_1$
and that
![]() ${\bar \rho }_1$
is not isomorphic to
${\bar \rho }_1$
is not isomorphic to
![]() ${\bar \rho }_2(j)$
for
${\bar \rho }_2(j)$
for
![]() $j\in \{0,\pm 1\}$
.
$j\in \{0,\pm 1\}$
.
If
![]() $H^0(G_K,{\operatorname {\overline {ad}}_{{{\bar \rho }_i}}} (1))=0$
for
$H^0(G_K,{\operatorname {\overline {ad}}_{{{\bar \rho }_i}}} (1))=0$
for
![]() $i=1,2$
, then:
$i=1,2$
, then:
-
(a)
 $ {\mathrm {det}}^2\colon {\mathcal {D}}_{{\bar \rho }_1\subset {\bar \rho }}\to {\mathcal {D}}_{{\mathrm {det}}{\bar \rho }_1}\times {\mathcal {D}}_{{\mathrm {det}}{\bar \rho }_2}$
is formally smooth of relative dimension
$ {\mathrm {det}}^2\colon {\mathcal {D}}_{{\bar \rho }_1\subset {\bar \rho }}\to {\mathcal {D}}_{{\mathrm {det}}{\bar \rho }_1}\times {\mathcal {D}}_{{\mathrm {det}}{\bar \rho }_2}$
is formally smooth of relative dimension
 $d(n^2-n_1n_2-2)-1$
.
$d(n^2-n_1n_2-2)-1$
. -
(b) The ring
 $(R^{\operatorname {univ}}_{{\bar \rho }_1\subset {\bar \rho }})_{{\operatorname {red}}}$
is formally smooth over
$(R^{\operatorname {univ}}_{{\bar \rho }_1\subset {\bar \rho }})_{{\operatorname {red}}}$
is formally smooth over
 $\kappa $
of dimension
$\kappa $
of dimension
 $d(n^2-n_1n_2)+1$
.
$d(n^2-n_1n_2)+1$
.
If on the other hand
![]() $H^0(G_K,{\operatorname {ad}_{{{\bar \rho }_i}}} (1))=0$
for
$H^0(G_K,{\operatorname {ad}_{{{\bar \rho }_i}}} (1))=0$
for
![]() $i=1,2$
, then
$i=1,2$
, then
![]() $R^{\operatorname {univ}}_{{\bar \rho }_1\subset {\bar \rho }}$
is formally smooth over
$R^{\operatorname {univ}}_{{\bar \rho }_1\subset {\bar \rho }}$
is formally smooth over
![]() $\kappa $
of dimension
$\kappa $
of dimension
![]() $d(n^2-n_1n_2)+1$
.
$d(n^2-n_1n_2)+1$
.
4 Pseudocharacters and their deformations
In this section, we recall main definitions and results on polynomial laws and pseudocharacters. We assume that the reader is familiar with [Reference ChenevierChe11; Reference ChenevierChe14; Reference Wang-EricksonWE18]. Nevertheless, we will give many reminders. Each subsection gives a short survey over its contents. In Proposition 4.3.9, we prove an analog of the locus of reducibility of [Reference Bellaïche and ChenevierBC09, Proposition 1.5.1] in the context of pseudocharacters. In Subsections 4.5 and 4.6, we introduce twisting and induction as operations on pseudocharacters. In Proposition 4.7.4, we sketch the existence of a universal ring for continuous pseudodeformation where the residue field is a local field and in Proposition 4.7.6 we consider such rings under change of coefficients. These are adaptions of well-known results. Subsection 4.8 presents in detail several results on dimension
![]() $1$
points in universal pseudodeformation spaces.
$1$
points in universal pseudodeformation spaces.
Throughout this section, A will be a commutative unital ring with
![]() $0\neq 1$
. If A is local, we write
$0\neq 1$
. If A is local, we write
![]() ${\mathfrak {m}}_A$
for its maximal ideal and
${\mathfrak {m}}_A$
for its maximal ideal and
![]() ${\kappa ({A})}$
for its residue field. We write
${\kappa ({A})}$
for its residue field. We write
![]() ${\mathcal {A}lg}_A$
for the category of A-algebras and
${\mathcal {A}lg}_A$
for the category of A-algebras and
![]() ${\mathcal {CA}lg}_A$
for the full subcategory of commutative A-algebras. By
${\mathcal {CA}lg}_A$
for the full subcategory of commutative A-algebras. By
![]() $R,S$
, we always denote objects of
$R,S$
, we always denote objects of
![]() ${\mathcal {A}lg}_A$
and by B an object of
${\mathcal {A}lg}_A$
and by B an object of
![]() ${\mathcal {CA}lg}_A$
. For an A-algebra R, we denote by
${\mathcal {CA}lg}_A$
. For an A-algebra R, we denote by
![]() $R^o$
the A-algebra with the multiplication of R reversed. By G, we denote a group and by
$R^o$
the A-algebra with the multiplication of R reversed. By G, we denote a group and by
![]() $B[G]$
the group algebra over B for any
$B[G]$
the group algebra over B for any
![]() $B\in {\mathcal {CA}lg}_A$
. The letters
$B\in {\mathcal {CA}lg}_A$
. The letters
![]() $m,n$
(also with indices) will denote nonnegative integers. If
$m,n$
(also with indices) will denote nonnegative integers. If
![]() $\rho \colon G\to {\mathrm {GL}}_n(B)$
is a representation, then by
$\rho \colon G\to {\mathrm {GL}}_n(B)$
is a representation, then by
![]() $\rho ^{\mathrm {lin}}\colon B[G]\to {\mathrm {Mat}}_{n\times n}(B)$
we denote its linearization given by
$\rho ^{\mathrm {lin}}\colon B[G]\to {\mathrm {Mat}}_{n\times n}(B)$
we denote its linearization given by
![]() $\sum _ib_ig_i\mapsto \sum _ib_i\rho (g_i)$
.
$\sum _ib_ig_i\mapsto \sum _ib_i\rho (g_i)$
.
4.1 Pseudocharacters
In this subsection, we introduce pseudocharacters, Azumaya algebras and Cayley–Hamilton A-algebras. Of particular importance is Proposition 4.1.10, which says that a pseudocharacter is determined by its characteristic polynomial coefficients.
For an A-module M, we define the functor
![]() $\underline {M}\colon {\mathcal {CA}lg}_A\to {Sets},\ B\mapsto M \otimes _A B$
.
$\underline {M}\colon {\mathcal {CA}lg}_A\to {Sets},\ B\mapsto M \otimes _A B$
.
Definition 4.1.4 [Reference ChenevierChe14, § 1.1].
Let M and N be A-modules.
-
(a) An A-polynomial law
 $P\colon {M} \to {N}$
is a natural transformation
$P\colon {M} \to {N}$
is a natural transformation
 $\underline {M} \to \underline {N}$
. that is, P is a family of maps
$\underline {M} \to \underline {N}$
. that is, P is a family of maps
 $P_B\colon M \otimes _A B\to N \otimes _A B$
for all
$P_B\colon M \otimes _A B\to N \otimes _A B$
for all
 $B\in {\mathrm {Ob}}({\mathcal {CA}lg}_A)$
that induce commutative diagrams for every morphism in
$B\in {\mathrm {Ob}}({\mathcal {CA}lg}_A)$
that induce commutative diagrams for every morphism in
 ${\mathcal {CA}lg}_A$
.
${\mathcal {CA}lg}_A$
. -
(b) An A-polynomial law
 $P\colon {M} \to {N}$
is called homogeneous of degree n if
$P\colon {M} \to {N}$
is called homogeneous of degree n if  $$ \begin{align*}P_B(bx)=b^nP_B(x)\quad\text{ for all }B\in{\mathrm{Ob}}({\mathcal{CA}lg}_A),\ b\in B\text{ and }x\in M\otimes_A B.\end{align*} $$
$$ \begin{align*}P_B(bx)=b^nP_B(x)\quad\text{ for all }B\in{\mathrm{Ob}}({\mathcal{CA}lg}_A),\ b\in B\text{ and }x\in M\otimes_A B.\end{align*} $$
We let
 ${\cal P}^n_A(M,N)$
denote the set of all such.
${\cal P}^n_A(M,N)$
denote the set of all such.
Let
![]() $S,S'$
be objects in
$S,S'$
be objects in
![]() ${\mathcal {A}lg}_A$
so that in particular they are A-modules.
${\mathcal {A}lg}_A$
so that in particular they are A-modules.
-
(c) An A-polynomial law
 $P\colon S \to S'$
is called multiplicative if
$P\colon S \to S'$
is called multiplicative if  $$ \begin{align*}P_B(1)=1\quad\text{and}\quad P_B(xy)=P_B(x)P_B(y)\quad\text{for all }B\in{\mathrm{Ob}}({\mathcal{CA}lg}_A)\text{ and }x,y\in S\otimes_A B. \end{align*} $$
$$ \begin{align*}P_B(1)=1\quad\text{and}\quad P_B(xy)=P_B(x)P_B(y)\quad\text{for all }B\in{\mathrm{Ob}}({\mathcal{CA}lg}_A)\text{ and }x,y\in S\otimes_A B. \end{align*} $$
-
(d) We write
 ${\cal M}^n_A(S,S')$
for the set of multiplicative A-polynomial laws
${\cal M}^n_A(S,S')$
for the set of multiplicative A-polynomial laws
 $P\colon S\to S'$
that are homogeneous of degree n.
$P\colon S\to S'$
that are homogeneous of degree n. -
(d) A pseudocharacter on
 ${S}$
of dimension n is an A-polynomial law
${S}$
of dimension n is an A-polynomial law
 ${D}: {S} \to A$
that is multiplicative and homogeneous of degree n. We let
${D}: {S} \to A$
that is multiplicative and homogeneous of degree n. We let
 ${\mathcal {P}s\mathcal {R}}^n_{S}(A)$
be the set of all such.
${\mathcal {P}s\mathcal {R}}^n_{S}(A)$
be the set of all such. -
(e) If
 $S=A[G]$
in (d), we call
$S=A[G]$
in (d), we call
 ${D}$
an A-valued pseudocharacter on G of dimension n, and we write
${D}$
an A-valued pseudocharacter on G of dimension n, and we write
 ${\mathcal {P}s\mathcal {R}}^n_G(A)$
for
${\mathcal {P}s\mathcal {R}}^n_G(A)$
for
 ${\mathcal {P}s\mathcal {R}}^n_{A[G]}(A)$
; occasionally we write
${\mathcal {P}s\mathcal {R}}^n_{A[G]}(A)$
; occasionally we write
 ${D}\colon G\to A$
for
${D}\colon G\to A$
for
 ${D}\colon A[G]\to A $
, and then we explicitly refer to
${D}\colon A[G]\to A $
, and then we explicitly refer to
 ${D}$
as a pseudocharacter on G.
${D}$
as a pseudocharacter on G.
Remark 4.1.2 [Reference ChenevierChe14, after Example 1.2].
A homogeneous polynomial law P of degree n is uniquely determined by
![]() $P_{A[T_1,\ldots ,T_m]}\colon M[T_1,\ldots ,T_m]\to N[T_1,\ldots ,T_m]$
for all
$P_{A[T_1,\ldots ,T_m]}\colon M[T_1,\ldots ,T_m]\to N[T_1,\ldots ,T_m]$
for all
![]() $m\ge 0$
.
$m\ge 0$
.
Facts 4.1.3. The following facts are easy to verify.
-
(a) The only multiplicative polynomial law of degree zero is the constant map with value
 $1$
.
$1$
. -
(b) Multiplicative polynomial laws that are homogeneous of degree
 $1$
are A-algebra homomorphisms and vice versa.
$1$
are A-algebra homomorphisms and vice versa. -
(c) The composition of polynomial laws is a polynomial law; if both are homogeneous, the composition is homogeneous and its degree is the product of the individual degrees.
-
(d) The composition of multiplicative polynomial laws is multiplicative.
-
(e) If
 ${D}\colon S\to A$
is an A-valued pseudocharacter, then for any
${D}\colon S\to A$
is an A-valued pseudocharacter, then for any
 $B\in {\mathcal {CA}lg}_A$
, the base change
$B\in {\mathcal {CA}lg}_A$
, the base change
 ${D}\otimes _AB\colon S\otimes _AB\to B$
is a B-valued pseudocharacter.
${D}\otimes _AB\colon S\otimes _AB\to B$
is a B-valued pseudocharacter.
Definition 4.1.4 (pseudocharacter of a representation).
Let
![]() $\rho \colon G\to {\mathrm {GL}}_n(A)$
be a representation. The pseudocharacter
$\rho \colon G\to {\mathrm {GL}}_n(A)$
be a representation. The pseudocharacter
![]() ${D}_\rho $
attached to
${D}_\rho $
attached to
![]() $\rho $
is the polynomial law that to any
$\rho $
is the polynomial law that to any
![]() $B\in {\mathcal {CA}lg}_A$
attaches the composition of the determinant
$B\in {\mathcal {CA}lg}_A$
attaches the composition of the determinant
![]() ${\mathrm {det}}\colon {\mathrm {Mat}}_{n\times n}(B)\to B$
with the morphism
${\mathrm {det}}\colon {\mathrm {Mat}}_{n\times n}(B)\to B$
with the morphism
![]() $(\rho \otimes _AB)^{\mathrm {lin}}$
.
$(\rho \otimes _AB)^{\mathrm {lin}}$
.
Let
![]() ${D}$
be a pseudocharacter on G over A. Because
${D}$
be a pseudocharacter on G over A. Because
![]() ${D} $
is multiplicative, we have
${D} $
is multiplicative, we have
![]() ${D}(gh)={D}(g){D}(h)$
for
${D}(gh)={D}(g){D}(h)$
for
![]() $g,h\in G$
and
$g,h\in G$
and
![]() ${D}(1)=1$
. Thus, the map
${D}(1)=1$
. Thus, the map
![]() ${\varphi }\colon G\to A^\times , g\mapsto D_A(g)$
is a group homomorphism, and Definition 4.1.4 associates the pseudocharacter
${\varphi }\colon G\to A^\times , g\mapsto D_A(g)$
is a group homomorphism, and Definition 4.1.4 associates the pseudocharacter
![]() ${D}_{\varphi }$
to
${D}_{\varphi }$
to
![]() ${\varphi }$
.
${\varphi }$
.
Definition 4.1.5 (Determinant of a pseudocharacter).
We call
![]() ${\mathrm {det}} ({D}):= {D}_{\varphi }$
the determinant of
${\mathrm {det}} ({D}):= {D}_{\varphi }$
the determinant of
![]() ${D}$
.
${D}$
.
Reminder 4.1.6. From [Reference MilneMil80, § IV.1 – IV.2], we recall the notion of Azumaya algebra and some of its properties. Let first A be a local ring with residue field
![]() $\kappa $
. An algebra
$\kappa $
. An algebra
![]() $C\in {\mathcal {A}lg}_A$
is called an Azumaya A-algebra if C is free of finite rank as an A-module and if in
$C\in {\mathcal {A}lg}_A$
is called an Azumaya A-algebra if C is free of finite rank as an A-module and if in
![]() ${\mathcal {A}lg}_A$
the map
${\mathcal {A}lg}_A$
the map
is an isomorphism; equivalently, there exists a finite étale morphism
![]() $A\to B$
such that
$A\to B$
such that
![]() $C\otimes _AB\cong {\mathrm {Mat}}_{m\times m}(B)$
for some m. One calls m the degree of C; it satisfies
$C\otimes _AB\cong {\mathrm {Mat}}_{m\times m}(B)$
for some m. One calls m the degree of C; it satisfies
![]() ${\mathrm {rank}}_AC=m^2$
. Moreover, C carries a reduced norm map
${\mathrm {rank}}_AC=m^2$
. Moreover, C carries a reduced norm map
![]() ${\mathrm {det}}_C\colon C\to A$
characterized by the property that
${\mathrm {det}}_C\colon C\to A$
characterized by the property that
![]() ${\mathrm {det}}_C\otimes _AB$
is the determinant on
${\mathrm {det}}_C\otimes _AB$
is the determinant on
![]() ${\mathrm {Mat}}_{m\times m}(B)$
. Its extension to
${\mathrm {Mat}}_{m\times m}(B)$
. Its extension to
![]() $C[t]$
defines a reduced characteristic polynomial
$C[t]$
defines a reduced characteristic polynomial
![]() $\chi _c:={\mathrm {det}}_{C[t]}(t-c)\in A[t]$
, monic of degree m, for any
$\chi _c:={\mathrm {det}}_{C[t]}(t-c)\in A[t]$
, monic of degree m, for any
![]() $c\in C$
. Lastly,
$c\in C$
. Lastly,
![]() $C\otimes \kappa $
is a central simple algebra over
$C\otimes \kappa $
is a central simple algebra over
![]() $\kappa $
.
$\kappa $
.
Let now X be a scheme. An
![]() $\mathcal {O}_X$
-algebra
$\mathcal {O}_X$
-algebra
![]() ${\cal C}$
is called an Azumaya algebra over X if
${\cal C}$
is called an Azumaya algebra over X if
![]() ${\cal C}$
is coherent as an
${\cal C}$
is coherent as an
![]() $\mathcal {O}_X$
-module and if for all
$\mathcal {O}_X$
-module and if for all
![]() $x\in X$
, the stalk
$x\in X$
, the stalk
![]() ${\cal C}_x$
is an Azumaya algebra over
${\cal C}_x$
is an Azumaya algebra over
![]() $\mathcal {O}_{X,x}$
; equivalently, there exists a Zariski cover
$\mathcal {O}_{X,x}$
; equivalently, there exists a Zariski cover
![]() $\{U_i\}$
of X and for each i a finite étale surjective cover
$\{U_i\}$
of X and for each i a finite étale surjective cover
![]() $U_i^{\prime }\to U_i$
and an isomorphism
$U_i^{\prime }\to U_i$
and an isomorphism
![]() ${\cal C}\otimes _{\mathcal {O}_X}\mathcal {O}_{U^{\prime }_i}\stackrel \simeq \to {\mathrm {Mat}}_{m_i\times m_i}(\mathcal {O}_{U_i^{\prime }})$
for suitable
${\cal C}\otimes _{\mathcal {O}_X}\mathcal {O}_{U^{\prime }_i}\stackrel \simeq \to {\mathrm {Mat}}_{m_i\times m_i}(\mathcal {O}_{U_i^{\prime }})$
for suitable
![]() $m_i \in {\mathbb {N}_{\geq 1}}$
. In particular, the degree function
$m_i \in {\mathbb {N}_{\geq 1}}$
. In particular, the degree function
![]() $\underline {m}\colon X\to {\mathbb {N}_{\geq 1}}$
such that
$\underline {m}\colon X\to {\mathbb {N}_{\geq 1}}$
such that
![]() ${\mathrm {rank}}_{{\cal O}_X}{\cal C}=\underline m^2$
is locally constant. Also, the reduced norm exists as a map
${\mathrm {rank}}_{{\cal O}_X}{\cal C}=\underline m^2$
is locally constant. Also, the reduced norm exists as a map
![]() ${\mathrm {det}}_{\cal C}\colon {\cal C}\to {\cal O}_X$
. For
${\mathrm {det}}_{\cal C}\colon {\cal C}\to {\cal O}_X$
. For
![]() $X={\mathrm {Spec}}\ A$
affine, one calls
$X={\mathrm {Spec}}\ A$
affine, one calls
![]() $C={\cal C}(X)$
an Azumaya A-algebra.
$C={\cal C}(X)$
an Azumaya A-algebra.
Example 4.1.7. Let C be an Azumaya A-algebra of degree n with reduced norm
![]() ${\mathrm {det}}_C\colon \!C\to A$
.
${\mathrm {det}}_C\colon \!C\to A$
.
-
(a) The family of reduced norms
 $({\mathrm {det}}_C\otimes _AB\colon C\otimes _AB\to B)_{B\in {\mathcal {CA}lg}_A}$
defines a pseudocharacter, also called
$({\mathrm {det}}_C\otimes _AB\colon C\otimes _AB\to B)_{B\in {\mathcal {CA}lg}_A}$
defines a pseudocharacter, also called
 ${\mathrm {det}}_C$
, of dimension n; see [Reference ChenevierChe14, § 1.5].
${\mathrm {det}}_C$
, of dimension n; see [Reference ChenevierChe14, § 1.5]. -
(b) If
 ${D}\colon C\to A$
is any pseudocharacter of dimension
${D}\colon C\to A$
is any pseudocharacter of dimension
 $n'$
, then by [Reference ChenevierChe14, Lemma 2.15], we have
$n'$
, then by [Reference ChenevierChe14, Lemma 2.15], we have
 $n|n'$
and
$n|n'$
and
 ${D}={\mathrm {det}}_C^{n'/n}$
.
${D}={\mathrm {det}}_C^{n'/n}$
.
An important notion for pseudocharacters is that of characteristic polynomial.
Lemma 4.1.8 [Reference ChenevierChe14, § 1.10].
Let
![]() ${D}\in {\mathcal {P}s\mathcal {R}}^n_{S}(A)$
. Define
${D}\in {\mathcal {P}s\mathcal {R}}^n_{S}(A)$
. Define
![]() $\chi _{{D},B}(\cdot ,t)\colon {S}\otimes _A B{\longrightarrow } B[ t]$
by the formula
$\chi _{{D},B}(\cdot ,t)\colon {S}\otimes _A B{\longrightarrow } B[ t]$
by the formula
![]() $s\mapsto {D}_{B[ t]}(t-{s})$
for all
$s\mapsto {D}_{B[ t]}(t-{s})$
for all
![]() $B\in {\mathrm {Ob}}({\mathcal {CA}lg}_A)$
and
$B\in {\mathrm {Ob}}({\mathcal {CA}lg}_A)$
and
![]() $s\in {S}\otimes _AB$
. Then the following hold:
$s\in {S}\otimes _AB$
. Then the following hold:
-
(a)
 $\chi _{D}(\cdot ,t)\colon {S}\to A[t]$
is a multiplicative homogeneous polynomial law of degree n.
$\chi _{D}(\cdot ,t)\colon {S}\to A[t]$
is a multiplicative homogeneous polynomial law of degree n. -
(b) There exist unique A-polynomial laws
 $\Lambda _{{D},i}\colon {S} \to A$
of degree i,
$\Lambda _{{D},i}\colon {S} \to A$
of degree i,
 $i=0,\ldots ,n$
such that
$i=0,\ldots ,n$
such that  $$ \begin{align*}\chi_{D}(\cdot,t)=\sum_{i=0}^n (-1)^i \Lambda_{{D},i}(\cdot) t^{n-i} .\end{align*} $$
$$ \begin{align*}\chi_{D}(\cdot,t)=\sum_{i=0}^n (-1)^i \Lambda_{{D},i}(\cdot) t^{n-i} .\end{align*} $$
-
(c)
 $\Lambda _{{D},0}=1$
and
$\Lambda _{{D},0}=1$
and
 $\Lambda _{{D},n}={D}$
.
$\Lambda _{{D},n}={D}$
. -
(d) The maps
 ${s} \mapsto \sum _{i=0}^n (-1)^i \Lambda _{{D},i}({s}) {s}^{n-i}$
for all
${s} \mapsto \sum _{i=0}^n (-1)^i \Lambda _{{D},i}({s}) {s}^{n-i}$
for all
 $B\in {\mathrm {Ob}}({\mathcal {CA}lg}_A)$
and
$B\in {\mathrm {Ob}}({\mathcal {CA}lg}_A)$
and
 $s\in {S}\otimes _AB$
define a multiplicative A-polynomial law
$s\in {S}\otimes _AB$
define a multiplicative A-polynomial law
 $\chi _{D}\colon {S}\to {S}$
that is homogeneous of degree n.
$\chi _{D}\colon {S}\to {S}$
that is homogeneous of degree n.
Definition 4.1.9. [Reference ChenevierChe14, § 1.10] Let
![]() ${S}$
,
${S}$
,
![]() ${D}$
,
${D}$
,
![]() $\chi _{D}(\cdot ,t)$
and
$\chi _{D}(\cdot ,t)$
and
![]() $\Lambda _{{D},i}$
be as in Lemma 4.1.8.
$\Lambda _{{D},i}$
be as in Lemma 4.1.8.
-
(a) The polynomial law
 $\chi _{D}(\cdot ,t)$
is called the characteristic polynomial of
$\chi _{D}(\cdot ,t)$
is called the characteristic polynomial of
 ${D}$
.
${D}$
. -
(b) The polynomial law
 $\Lambda _{{D},i}$
is called the
$\Lambda _{{D},i}$
is called the
 $i^{\operatorname {th}}$
characteristic polynomial coefficient of
$i^{\operatorname {th}}$
characteristic polynomial coefficient of
 ${D}$
.
${D}$
. -
(c) The A-linear map
 ${{\mathrm {\tau }}_{D}:=\Lambda _{{D},1}}$
is called the trace associated with
${{\mathrm {\tau }}_{D}:=\Lambda _{{D},1}}$
is called the trace associated with
 ${D}$
.
${D}$
.
An important tool to extract properties of multiplicative homogeneous polynomial laws is Amitsur’s formula; see [Reference ChenevierChe14, Formula (1.5)]. It expresses values of such laws in terms of characteristic polynomial coefficients. Using this, one deduces the following result:
Proposition 4.1.10 [Reference ChenevierChe14, Corollary 1.14], [Reference Wang EricksonWE13, 1.1.9.15].
Let
![]() ${D}\in {\mathcal {P}s\mathcal {R}}_{G}^n(A)$
.
${D}\in {\mathcal {P}s\mathcal {R}}_{G}^n(A)$
.
-
(a) The characteristic polynomial coefficients
 $(\Lambda _{{D},i}\colon G\to A)_{i=1,\ldots ,n}$
characterize
$(\Lambda _{{D},i}\colon G\to A)_{i=1,\ldots ,n}$
characterize
 ${D}$
.
${D}$
. -
(b) Let
 $C \subset A$
be the subring generated by
$C \subset A$
be the subring generated by
 $\{\Lambda _{{D},i}(g){\>:\>} g\in G, i=1,\ldots ,n\}$
. Then
$\{\Lambda _{{D},i}(g){\>:\>} g\in G, i=1,\ldots ,n\}$
. Then
 ${D}$
factors through a unique C-valued pseudocharacter
${D}$
factors through a unique C-valued pseudocharacter
 ${D}_C$
on G of dimension n.
${D}_C$
on G of dimension n.
A natural operation on pseudocharacters is the formation of direct sums.Footnote 2
Definition 4.1.11 [Reference Wang EricksonWE13, § 1.1.11].
Let
![]() $S, S_1, S_2$
be
$S, S_1, S_2$
be
![]() ${\mathcal {A}lg}_A$
and B in
${\mathcal {A}lg}_A$
and B in
![]() ${\mathcal {CA}lg}_A$
.
${\mathcal {CA}lg}_A$
.
-
(a) The direct sum of multiplicative homogeneous A-polynomial laws
 $P_i\colon {S}_i\to B$
of degree
$P_i\colon {S}_i\to B$
of degree
 $n_i$
,
$n_i$
,
 $i=1,2$
, is the multiplicative homogeneous A-polynomial law of degree
$i=1,2$
, is the multiplicative homogeneous A-polynomial law of degree
 $n_1+n_2$
given by
$n_1+n_2$
given by  $$ \begin{align*}P_1{\oplus} P_2\colon S_1 \times S_2 \to B,\quad (x_1,x_2) \mapsto P_1(x_1)P_2(x_2). \end{align*} $$
$$ \begin{align*}P_1{\oplus} P_2\colon S_1 \times S_2 \to B,\quad (x_1,x_2) \mapsto P_1(x_1)P_2(x_2). \end{align*} $$
-
(b) The direct sum of pseudorepresentations
 ${D}_i\colon {S}\to A$
of dimension
${D}_i\colon {S}\to A$
of dimension
 $n_i$
,
$n_i$
,
 $i=1,2$
, is the pseudocharacter of dimension
$i=1,2$
, is the pseudocharacter of dimension
 $n_1+n_2$
given by
$n_1+n_2$
given by
 ${D}_1{\oplus } {D}_2\colon S \to A, x\mapsto {D}_1(x){D}_2(x)$
.
${D}_1{\oplus } {D}_2\colon S \to A, x\mapsto {D}_1(x){D}_2(x)$
.
Remark 4.1.12. Note that
![]() ${\mathrm {det}}^{n'/n}$
from Example 4.1.7 could now also be written as
${\mathrm {det}}^{n'/n}$
from Example 4.1.7 could now also be written as
![]() $ {\mathrm {det}}^{\oplus (n'/n)}$
.
$ {\mathrm {det}}^{\oplus (n'/n)}$
.
Lemma 4.1.13 [Reference Wang EricksonWE13, Lemma 1.1.11.7].
For
![]() $i=1,2$
, let
$i=1,2$
, let
![]() $\rho _i\colon G \to {\mathrm {GL}}_{n_i}(A)$
be a representation, and set
$\rho _i\colon G \to {\mathrm {GL}}_{n_i}(A)$
be a representation, and set
![]() $\rho :=\rho _1\oplus \rho _2$
. Then
$\rho :=\rho _1\oplus \rho _2$
. Then
![]() $ {D}_{\rho }={D}_{\rho _1}{\oplus }{D}_{\rho _2}$
for the associated pseudocharacters from Definition 4.1.4.
$ {D}_{\rho }={D}_{\rho _1}{\oplus }{D}_{\rho _2}$
for the associated pseudocharacters from Definition 4.1.4.
Lemma 4.1.14 [Reference ChenevierChe14, Lemma 2.2].
Let
![]() $S_1, S_2$
be in
$S_1, S_2$
be in
![]() ${\mathcal {A}lg}_A$
. Let
${\mathcal {A}lg}_A$
. Let
![]() $B\neq 0$
be in
$B\neq 0$
be in
![]() ${\mathcal {CA}lg}_A$
such that
${\mathcal {CA}lg}_A$
such that
![]() ${\mathrm {Spec}}\ B$
is connected. Let
${\mathrm {Spec}}\ B$
is connected. Let
![]() $P\colon S_1\times S_2 \longrightarrow B$
be a multiplicative A-polynomial law that is homogeneous of degree n. Then there exist for
$P\colon S_1\times S_2 \longrightarrow B$
be a multiplicative A-polynomial law that is homogeneous of degree n. Then there exist for
![]() $i=1,2$
unique
$i=1,2$
unique
![]() $n_i\ge 0$
with
$n_i\ge 0$
with
![]() $n_1+n_2=n$
and multiplicative homogeneous A-polynomial laws
$n_1+n_2=n$
and multiplicative homogeneous A-polynomial laws
![]() $P_i \colon S_i \to B$
of degree
$P_i \colon S_i \to B$
of degree
![]() $n_i$
such that
$n_i$
such that
![]() $P=P_1{\oplus } P_2$
.
$P=P_1{\oplus } P_2$
.
To any
![]() ${D}\in {\mathcal {P}s\mathcal {R}}^n_{S}(A)$
, one can naturally assign its kernel
${D}\in {\mathcal {P}s\mathcal {R}}^n_{S}(A)$
, one can naturally assign its kernel
![]() ${\mathop {\mathrm{Ker}}\nolimits }({D})$
.
${\mathop {\mathrm{Ker}}\nolimits }({D})$
.
Definition 4.1.15 [Reference ChenevierChe14, 1.17].
Let
![]() $P\colon \!M\to N$
be a polynomial law for A-modules M, N.
$P\colon \!M\to N$
be a polynomial law for A-modules M, N.
-
(a) The kernel
 ${\operatorname {ker}{(P)}} $
of P is the A-submodule of M defined as
${\operatorname {ker}{(P)}} $
of P is the A-submodule of M defined as  $$ \begin{align*}\{ x\in M{\>:\>} P( x\otimes b +m)=P(m) \quad\text{for all } B \in {{\mathrm{Ob}}}({\mathcal{CA}lg}_A),\ b \in B\text{ and }m \in M\otimes_A B \} \end{align*} $$
$$ \begin{align*}\{ x\in M{\>:\>} P( x\otimes b +m)=P(m) \quad\text{for all } B \in {{\mathrm{Ob}}}({\mathcal{CA}lg}_A),\ b \in B\text{ and }m \in M\otimes_A B \} \end{align*} $$
-
(b) If
 ${\operatorname {ker}{(P)}} =0$
, then P is called faithful.
${\operatorname {ker}{(P)}} =0$
, then P is called faithful.
Proposition 4.1.16 [Reference ChenevierChe14, 1.19–1.21].
For
![]() ${D}\in {\mathcal {P}s\mathcal {R}}^n_{S}(A)$
, the following hold.
${D}\in {\mathcal {P}s\mathcal {R}}^n_{S}(A)$
, the following hold.
-
(a)
 ${\operatorname {ker}{{D}}}$
is a two-sided ideal of
${\operatorname {ker}{{D}}}$
is a two-sided ideal of
 ${S}$
; there exists a unique
${S}$
; there exists a unique
 $\widetilde {{D}}\in {\mathcal {P}s\mathcal {R}}^n_{{S}/{\operatorname {ker}{{D}}} }(A)$
such that
$\widetilde {{D}}\in {\mathcal {P}s\mathcal {R}}^n_{{S}/{\operatorname {ker}{{D}}} }(A)$
such that
 ${D}=\widetilde {{D}}\circ \pi $
for
${D}=\widetilde {{D}}\circ \pi $
for
 $\pi $
the projection
$\pi $
the projection
 ${S}\to {S}/{\operatorname {ker}{{D}}} $
, and
${S}\to {S}/{\operatorname {ker}{{D}}} $
, and
 ${\operatorname {ker}{{D}}} $
is maximal with this property.
${\operatorname {ker}{{D}}} $
is maximal with this property. -
(b) If C is an Azumaya A-algebra, then its reduced norm
 ${\mathrm {det}}_C$
is faithful.
${\mathrm {det}}_C$
is faithful.
Over fields, the following is a fundamental result on faithful pseudocharacters.
Theorem 4.1.17 [Reference ChenevierChe14, Theorem 2.16].
Let k be a field such that k is perfect, or k has characteristic
![]() $p>0$
and
$p>0$
and
![]() $[k:k^p] <\infty $
. Let
$[k:k^p] <\infty $
. Let
![]() ${D}\colon {S}\to k$
be a pseudocharacter of dimension n. Then
${D}\colon {S}\to k$
be a pseudocharacter of dimension n. Then
![]() $S/{\operatorname {ker}{{D}}}$
is of finite k-dimension and semisimple as a ring.
$S/{\operatorname {ker}{{D}}}$
is of finite k-dimension and semisimple as a ring.
Choose a k-algebra isomorphism
![]() ${S}/{\operatorname {ker}{{D}}}\stackrel \simeq {\longrightarrow } \prod _{i=1}^s {S}_i$
, where each
${S}/{\operatorname {ker}{{D}}}\stackrel \simeq {\longrightarrow } \prod _{i=1}^s {S}_i$
, where each
![]() $S_i$
is a simple k-algebra. Let
$S_i$
is a simple k-algebra. Let
![]() $n_i$
be the degree of
$n_i$
be the degree of
![]() $S_i$
over its center
$S_i$
over its center
![]() $k_i$
, let
$k_i$
, let
![]() $f_i:=[k_i\cap {{k}^{\mathrm {sep}}}:k]$
, and let
$f_i:=[k_i\cap {{k}^{\mathrm {sep}}}:k]$
, and let
![]() $q_i$
be the smallest p-power such that
$q_i$
be the smallest p-power such that
![]() $k_i^{q_i}\subset {{k}^{\mathrm {sep}}}$
; note that all
$k_i^{q_i}\subset {{k}^{\mathrm {sep}}}$
; note that all
![]() $q_i=1$
if k is perfect. Then under the above isomorphism one has
$q_i=1$
if k is perfect. Then under the above isomorphism one has
 $$ \begin{align*}{D}=\bigoplus_{i=1}^s {\mathrm{det}}_{{S}_i}^{\oplus m_i}\end{align*} $$
$$ \begin{align*}{D}=\bigoplus_{i=1}^s {\mathrm{det}}_{{S}_i}^{\oplus m_i}\end{align*} $$
for some uniquely determined integers
![]() $m_i\ge 1$
, and one has
$m_i\ge 1$
, and one has
![]() $n= \sum _i m_i n_i q_i f_i$
.
$n= \sum _i m_i n_i q_i f_i$
.
Over algebraically closed field, the following consequence of Theorem 4.1.17 is important.
Theorem 4.1.18 [Reference ChenevierChe14, Theorem 2.12].
Suppose that k is an algebraically closed field and
![]() ${S}$
is a k-algebra. If
${S}$
is a k-algebra. If
![]() ${D}\colon {S} \to k$
is an n-dimensional pseudocharacter, then there is a semisimple representation
${D}\colon {S} \to k$
is an n-dimensional pseudocharacter, then there is a semisimple representation
![]() $\rho _{D}\colon {S} \to {\mathrm {Mat}}_{n\times n}(k)$
unique up to isomorphism with associated pseudocharacter
$\rho _{D}\colon {S} \to {\mathrm {Mat}}_{n\times n}(k)$
unique up to isomorphism with associated pseudocharacter
![]() ${D}$
, and one has
${D}$
, and one has
![]() ${\operatorname {ker}{\rho _{D}^{\mathrm {lin}} }} ={\operatorname {ker}{{D}}} $
.
${\operatorname {ker}{\rho _{D}^{\mathrm {lin}} }} ={\operatorname {ker}{{D}}} $
.
Definition 4.1.19. Let k be a field, and let
![]() ${D}\in {\mathcal {P}s\mathcal {R}}_G^n(k)$
.
${D}\in {\mathcal {P}s\mathcal {R}}_G^n(k)$
.
-
(a) We call
 $\rho _{{D}\otimes _k{{{k}}^{\mathrm {alg}}} }$
from Theorem 4.1.18 the semisimple representation associated to
$\rho _{{D}\otimes _k{{{k}}^{\mathrm {alg}}} }$
from Theorem 4.1.18 the semisimple representation associated to
 ${D}\otimes _k{{{k}}^{\mathrm {alg}}} $
.
${D}\otimes _k{{{k}}^{\mathrm {alg}}} $
. -
(b) We call
 ${D}$
${D}$
-
(1) irreducible if
 $\rho _{{D}\otimes _k{{{k}}^{\mathrm {alg}}} }$
is irreducible and reducible otherwise;
$\rho _{{D}\otimes _k{{{k}}^{\mathrm {alg}}} }$
is irreducible and reducible otherwise; -
(2) multiplicity free if
 $\rho _{{D}\otimes _k{{{k}}^{\mathrm {alg}}} }$
is a direct sum of pairwise nonisomorphic irreducible
$\rho _{{D}\otimes _k{{{k}}^{\mathrm {alg}}} }$
is a direct sum of pairwise nonisomorphic irreducible
 ${{{k}}^{\mathrm {alg}}} $
-linear representations of
${{{k}}^{\mathrm {alg}}} $
-linear representations of
 ${S}\otimes _k{{{k}}^{\mathrm {alg}}} $
;
${S}\otimes _k{{{k}}^{\mathrm {alg}}} $
; -
(3) split if
 ${D}={D}_\rho $
for some representation
${D}={D}_\rho $
for some representation
 $\rho \colon {S} \to {\mathrm {Mat}}_{n\times n}(k)$
;
$\rho \colon {S} \to {\mathrm {Mat}}_{n\times n}(k)$
;
-
Note that if k is finite, then every irreducible representation is split.
We record the following consequence that will be used in the proof of Lemma 12.
Corollary 4.1.20. Let
![]() ${\overline {{D}}}\colon {{\mathbb {F}}\,\!{}}[G]\to {{\mathbb {F}}\,\!{}}$
be an n-dimensional pseudocharacter. Let
${\overline {{D}}}\colon {{\mathbb {F}}\,\!{}}[G]\to {{\mathbb {F}}\,\!{}}$
be an n-dimensional pseudocharacter. Let
![]() ${{\mathbb {F}}\,\!{}}'$
be the extension of
${{\mathbb {F}}\,\!{}}'$
be the extension of
![]() ${{\mathbb {F}}\,\!{}}$
of degree
${{\mathbb {F}}\,\!{}}$
of degree
![]() $n!$
. Then
$n!$
. Then
![]() ${\overline {{D}}}\otimes _{{\mathbb {F}}\,\!{}}{{\mathbb {F}}\,\!{}}'$
is a direct sum of irreducible representations.
${\overline {{D}}}\otimes _{{\mathbb {F}}\,\!{}}{{\mathbb {F}}\,\!{}}'$
is a direct sum of irreducible representations.
Proof. Over finite fields the Brauer group is zero. Thus, by Theorem 4.1.14 we have an isomorphism
![]() ${{\mathbb {F}}\,\!{}}[G]/{\operatorname {ker}{{D}}}\stackrel \simeq {\longrightarrow } \prod _{i=1}^s {\mathrm {Mat}}_{d_i\times d_i}({{\mathbb {F}}\,\!{}}_i)$
for integers
${{\mathbb {F}}\,\!{}}[G]/{\operatorname {ker}{{D}}}\stackrel \simeq {\longrightarrow } \prod _{i=1}^s {\mathrm {Mat}}_{d_i\times d_i}({{\mathbb {F}}\,\!{}}_i)$
for integers
![]() $d_i\ge 1$
and finite field
$d_i\ge 1$
and finite field
![]() ${{\mathbb {F}}\,\!{}}_i$
over
${{\mathbb {F}}\,\!{}}_i$
over
![]() ${{\mathbb {F}}\,\!{}}$
such that
${{\mathbb {F}}\,\!{}}$
such that
![]() $n= \sum _i d_i f_im_i$
for
$n= \sum _i d_i f_im_i$
for
![]() $f_i=[{{\mathbb {F}}\,\!{}}_i:{{\mathbb {F}}\,\!{}}]$
. In particular, all
$f_i=[{{\mathbb {F}}\,\!{}}_i:{{\mathbb {F}}\,\!{}}]$
. In particular, all
![]() $f_i$
divide
$f_i$
divide
![]() $n!$
and hence
$n!$
and hence
![]() ${{\mathbb {F}}\,\!{}}'\supset {{\mathbb {F}}\,\!{}}_i$
for all i. Over perfect fields semisimple rings are absolutely semisimple (see Definition A.2.1 and Remark A.2.2) and thus
${{\mathbb {F}}\,\!{}}'\supset {{\mathbb {F}}\,\!{}}_i$
for all i. Over perfect fields semisimple rings are absolutely semisimple (see Definition A.2.1 and Remark A.2.2) and thus
![]() ${{\mathbb {F}}\,\!{}}'[G]/{\operatorname {ker}{({D}\otimes _{{\mathbb {F}}\,\!{}}{{\mathbb {F}}\,\!{}}')}} \stackrel \simeq {\longrightarrow } \prod _{i=1}^s \prod _{j=1}^{f_i} {\mathrm {Mat}}_{d_i\times d_i}({{\mathbb {F}}\,\!{}}')$
. We conclude using Lemma 4.1.14, Example 4.1.7
(b) and Remark 4.1.12.
${{\mathbb {F}}\,\!{}}'[G]/{\operatorname {ker}{({D}\otimes _{{\mathbb {F}}\,\!{}}{{\mathbb {F}}\,\!{}}')}} \stackrel \simeq {\longrightarrow } \prod _{i=1}^s \prod _{j=1}^{f_i} {\mathrm {Mat}}_{d_i\times d_i}({{\mathbb {F}}\,\!{}}')$
. We conclude using Lemma 4.1.14, Example 4.1.7
(b) and Remark 4.1.12.
Next, we recall the concept of the Cayley–Hamilton property for pseudocharacters.
Definition 4.1.21 [Reference ChenevierChe14, 1.17].
Let
![]() ${S}$
be an A-algebra, and let
${S}$
be an A-algebra, and let
![]() ${D}$
be in
${D}$
be in
![]() ${\mathcal {P}s\mathcal {R}}^n_{S}(A)$
.
${\mathcal {P}s\mathcal {R}}^n_{S}(A)$
.
-
(a) The Cayley–Hamilton ideal
 ${\mathrm {CH}}({D})$
of
${\mathrm {CH}}({D})$
of
 ${D}$
is the two-sided ideal of
${D}$
is the two-sided ideal of
 ${S}$
generated by the coefficients of the polynomialsFootnote
3
where m ranges over all positive integers and s over all elements of
${S}$
generated by the coefficients of the polynomialsFootnote
3
where m ranges over all positive integers and s over all elements of $$ \begin{align*}\chi_{{D},A[t_1,\ldots,t_m]}(s)\in {S}[t_1,\ldots,t_m],\end{align*} $$
$$ \begin{align*}\chi_{{D},A[t_1,\ldots,t_m]}(s)\in {S}[t_1,\ldots,t_m],\end{align*} $$
 ${S}[t_1,\ldots ,t_m]$
.Footnote
4
${S}[t_1,\ldots ,t_m]$
.Footnote
4
-
(b) One calls
 ${D}$
Cayley–Hamilton if
${D}$
Cayley–Hamilton if
 ${\mathrm {CH}}({D})=0$
, or, equivalently, if
${\mathrm {CH}}({D})=0$
, or, equivalently, if
 $\chi _{D}$
is identically zero.
$\chi _{D}$
is identically zero.
Proposition 4.1.22 [Reference ChenevierChe14,1.20f.], [Reference Wang EricksonWE13,1.1.8.6].
For
![]() ${D}\in {\mathcal {P}s\mathcal {R}}^n_{S}(A)$
, the following hold.
${D}\in {\mathcal {P}s\mathcal {R}}^n_{S}(A)$
, the following hold.
-
(a)
 ${\operatorname {ker}{(D)}} \supset {\mathrm {CH}}(D)$
, and hence
${\operatorname {ker}{(D)}} \supset {\mathrm {CH}}(D)$
, and hence
 ${D}$
factors via some
${D}$
factors via some
 $\widetilde {{D}}\in {\mathcal {P}s\mathcal {R}}^n_{{S}/{\mathrm {CH}}({D})}(A)$
.
$\widetilde {{D}}\in {\mathcal {P}s\mathcal {R}}^n_{{S}/{\mathrm {CH}}({D})}(A)$
. -
(b) If
 ${D}$
is Cayley–Hamilton and
${D}$
is Cayley–Hamilton and
 ${S}'\subset {S}$
is any A-subalgebra, then
${S}'\subset {S}$
is any A-subalgebra, then
 ${D}|_{{S}^{\prime }}$
is Cayley–Hamilton.
${D}|_{{S}^{\prime }}$
is Cayley–Hamilton. -
(c) For any morphism
 ${S}\to {S}'$
in
${S}\to {S}'$
in
 ${\mathcal {A}lg}_A$
, one has
${\mathcal {A}lg}_A$
, one has
 ${S}'/{\mathrm {CH}}({D}\otimes _{{S}}{S}')\cong ({S}/{\mathrm {CH}}({D}))\otimes _{{S}}{S}'$
.
${S}'/{\mathrm {CH}}({D}\otimes _{{S}}{S}')\cong ({S}/{\mathrm {CH}}({D}))\otimes _{{S}}{S}'$
.
Definition 4.1.23 [Reference ChenevierChe14, 1.17].
Let
![]() ${S}$
be an A-algebra, and let
${S}$
be an A-algebra, and let
![]() ${D}$
be in
${D}$
be in
![]() ${\mathcal {P}s\mathcal {R}}^n_{S}(A)$
.
${\mathcal {P}s\mathcal {R}}^n_{S}(A)$
.
-
(a) One calls
 ${S}_{D}^{\mathrm {CH}}:={S}/{\mathrm {CH}}({D})$
the Cayley–Hamilton quotient of
${S}_{D}^{\mathrm {CH}}:={S}/{\mathrm {CH}}({D})$
the Cayley–Hamilton quotient of
 ${S}$
with respect to
${S}$
with respect to
 ${D}$
.
${D}$
. -
(b) One calls the induced A-algebra homomorphism
 $\rho ^{\mathrm {CH}}_{D}\colon {S}\to {S}/{\mathrm {CH}}({D}) \ {D}$
the Cayley–Hamilton representation attached to
$\rho ^{\mathrm {CH}}_{D}\colon {S}\to {S}/{\mathrm {CH}}({D}) \ {D}$
the Cayley–Hamilton representation attached to
 ${D}$
.
${D}$
.
Any pseudocharacter
![]() ${D}\in {\mathcal {P}s\mathcal {R}}_{S}^n(A)$
possesses a factorization
${D}\in {\mathcal {P}s\mathcal {R}}_{S}^n(A)$
possesses a factorization
with
![]() $\widetilde {D}$
from Proposition 4.1.22
(a). In the special case
$\widetilde {D}$
from Proposition 4.1.22
(a). In the special case
![]() ${S}=A[G]$
, the factorization is a composition of a group homomorphism
${S}=A[G]$
, the factorization is a composition of a group homomorphism
![]() $G\to ({S}_{D}^{\mathrm {CH}})^\times $
with
$G\to ({S}_{D}^{\mathrm {CH}})^\times $
with
![]() $\widetilde {{D}}$
, that is,
$\widetilde {{D}}$
, that is,
![]() ${D}=\widetilde {{D}}\circ \rho ^{\mathrm {CH}}_{D}\colon A[G]\to A$
. Because of the following result and the good behavior of
${D}=\widetilde {{D}}\circ \rho ^{\mathrm {CH}}_{D}\colon A[G]\to A$
. Because of the following result and the good behavior of
![]() ${\mathrm {CH}}(\cdot )$
under base change, one might think of
${\mathrm {CH}}(\cdot )$
under base change, one might think of
![]() $\rho ^{\mathrm {CH}}_{D}$
as a natural substitute of a representation
$\rho ^{\mathrm {CH}}_{D}$
as a natural substitute of a representation
![]() $\rho $
with
$\rho $
with
![]() ${D}={D}_\rho $
when such a representation does not exist. First, we need one more piece of notation.
${D}={D}_\rho $
when such a representation does not exist. First, we need one more piece of notation.
Definition 4.1.24. Let
![]() $B\in {\mathcal {CA}lg}_A$
,
$B\in {\mathcal {CA}lg}_A$
,
![]() ${D}\in {\mathcal {P}s\mathcal {R}}_G^n(B)$
and
${D}\in {\mathcal {P}s\mathcal {R}}_G^n(B)$
and
![]() $X:={\mathrm {Spec}}\ B$
. Let
$X:={\mathrm {Spec}}\ B$
. Let
![]() $x\in X$
with residue homomorphism
$x\in X$
with residue homomorphism
![]() $\pi _x\colon B\to {\kappa ({x})} $
, and let
$\pi _x\colon B\to {\kappa ({x})} $
, and let
![]() $\overline x$
be a geometric point of X above x so that
$\overline x$
be a geometric point of X above x so that
![]() ${\kappa ({x})} {\hookrightarrow }{\kappa ({\overline x})}$
.
${\kappa ({x})} {\hookrightarrow }{\kappa ({\overline x})}$
.
-
(a) We call
 ${D}_x:=\pi _x\circ {D}$
the pseudocharacter of
${D}_x:=\pi _x\circ {D}$
the pseudocharacter of
 ${D}$
at x and set
${D}$
at x and set
 ${D}_{\bar x}:={D}_x\otimes _{{\kappa ({x})} } {\kappa ({\overline x})}$
.
${D}_{\bar x}:={D}_x\otimes _{{\kappa ({x})} } {\kappa ({\overline x})}$
. -
(b) We call
 $\rho _{\overline x}:=\rho _{{D}_{\overline x}} \colon G\to {\mathrm {GL}}_n({\kappa ({\overline x})})$
the (semisimple) representation at
$\rho _{\overline x}:=\rho _{{D}_{\overline x}} \colon G\to {\mathrm {GL}}_n({\kappa ({\overline x})})$
the (semisimple) representation at
 $\bar x$
.Footnote
5
$\bar x$
.Footnote
5
-
(c) We say that x has a property if
 ${D}_{\overline x}$
(or
${D}_{\overline x}$
(or
 $\rho _{\overline x}$
) satisfies this property.
$\rho _{\overline x}$
) satisfies this property.
If B is a universal ring for some space of pseudocharacters and
![]() $x\in {\mathrm {Spec}}\ B$
, then by writing
$x\in {\mathrm {Spec}}\ B$
, then by writing
![]() ${D}_x$
it will be implicitly understood that
${D}_x$
it will be implicitly understood that
![]() ${D}$
refers to the corresponding universal pseudocharacter.
${D}$
refers to the corresponding universal pseudocharacter.
The following is a significant generalization of Theorem 4.1.17 to families.
Proposition 4.1.25 (Cf. [Reference ChenevierChe14, Corollary 2.23]).
Let
![]() ${D}\in {\mathcal {P}s\mathcal {R}}_G^n(A)$
be such that
${D}\in {\mathcal {P}s\mathcal {R}}_G^n(A)$
be such that
![]() ${D}_x$
is irreducible for all
${D}_x$
is irreducible for all
![]() $x\in {\mathrm {Spec}}\ A$
. Then
$x\in {\mathrm {Spec}}\ A$
. Then
![]() $C:=A[G]_{D}^{\mathrm {CH}}$
is an A-Azumaya algebra of degree n, and
$C:=A[G]_{D}^{\mathrm {CH}}$
is an A-Azumaya algebra of degree n, and
![]() ${D}={\mathrm {det}}_C\circ \rho _{D}^{\mathrm {CH}}$
for
${D}={\mathrm {det}}_C\circ \rho _{D}^{\mathrm {CH}}$
for
![]() $\rho _{D}^{\mathrm {CH}}\colon A[G]\to C$
the Cayley–Hamilton representation restricted to G.
$\rho _{D}^{\mathrm {CH}}\colon A[G]\to C$
the Cayley–Hamilton representation restricted to G.
Remark 4.1.26. We shall use the notation
![]() $\rho _{D}$
for
$\rho _{D}$
for
![]() ${D}\in {\mathcal {P}s\mathcal {R}}_G^n(A)$
in two situations: Either A is an algebraically closed field and then it is the semisimple representation
${D}\in {\mathcal {P}s\mathcal {R}}_G^n(A)$
in two situations: Either A is an algebraically closed field and then it is the semisimple representation
![]() $\rho _{D}$
from Theorem 4.1.18. Or A is arbitrary and
$\rho _{D}$
from Theorem 4.1.18. Or A is arbitrary and
![]() $D_x$
is irreducible for all
$D_x$
is irreducible for all
![]() $x\in {\mathrm {Spec}}\ A$
, and then it is an abbreviation for
$x\in {\mathrm {Spec}}\ A$
, and then it is an abbreviation for
![]() $\rho _{D}^{\mathrm {CH}}$
. Because of Proposition 4.1.25, this assignment is well-defined.
$\rho _{D}^{\mathrm {CH}}$
. Because of Proposition 4.1.25, this assignment is well-defined.
4.2 Universal rings of pseudocharacters
Here, we recall the existence of a universal pseudodeformation ring and that irreducible points form an open subscheme. Moreover, we introduce morphisms related to the addition of pseudocharacters.
Proposition 4.2.1 [Reference ChenevierChe14, Proposition 1.6, Example 1.7].
The functor
![]() ${\mathcal {P}s\mathcal {R}}^n_{S}({\:\cdot \:})\colon {\mathcal {CA}lg}_A\to {Sets}$
is representable for any
${\mathcal {P}s\mathcal {R}}^n_{S}({\:\cdot \:})\colon {\mathcal {CA}lg}_A\to {Sets}$
is representable for any
![]() ${S}$
in
${S}$
in
![]() ${\mathcal {A}lg}_A$
by some ring
${\mathcal {A}lg}_A$
by some ring
![]() ${R^{\operatorname {univ}}_{S,n}}\in {\mathcal {CA}lg}_A$
. Moreover, for any
${R^{\operatorname {univ}}_{S,n}}\in {\mathcal {CA}lg}_A$
. Moreover, for any
![]() $B\in {\mathcal {CA}lg}_A$
, the natural map
$B\in {\mathcal {CA}lg}_A$
, the natural map
![]() $B\otimes _A {R^{\operatorname {univ}}_{S,n}}\rightarrow {R^{\operatorname {univ}}_{B\otimes _A{S},n}}$
is an isomorphism.
$B\otimes _A {R^{\operatorname {univ}}_{S,n}}\rightarrow {R^{\operatorname {univ}}_{B\otimes _A{S},n}}$
is an isomorphism.
The above means that there is a natural isomorphism
![]() $\operatorname {Hom}_{{\mathcal {CA}lg}}({R^{\operatorname {univ}}_{S,n}},{\:\cdot \:})\rightarrow {\mathcal {P}s\mathcal {R}}^n_{S}({\:\cdot \:})$
. Let the pseudocharacter corresponding to
$\operatorname {Hom}_{{\mathcal {CA}lg}}({R^{\operatorname {univ}}_{S,n}},{\:\cdot \:})\rightarrow {\mathcal {P}s\mathcal {R}}^n_{S}({\:\cdot \:})$
. Let the pseudocharacter corresponding to
![]() $\operatorname {id}_{{R^{\operatorname {univ}}_{S,n}}}$
be
$\operatorname {id}_{{R^{\operatorname {univ}}_{S,n}}}$
be
Definition 4.2.2. The commutative A-algebra
![]() ${R^{\operatorname {univ}}_{S,n}}$
and the A-scheme
${R^{\operatorname {univ}}_{S,n}}$
and the A-scheme
![]() ${X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{S},n}}} :=\operatorname {Spec}{R^{\operatorname {univ}}_{S,n}}$
are called the n-dimensional universal pseudocharacter ring and space, respectively, and
${X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{S},n}}} :=\operatorname {Spec}{R^{\operatorname {univ}}_{S,n}}$
are called the n-dimensional universal pseudocharacter ring and space, respectively, and
![]() ${D}^{\operatorname {univ}}_{{S},n}$
is called the n-dimensional universal pseudocharacter.
${D}^{\operatorname {univ}}_{{S},n}$
is called the n-dimensional universal pseudocharacter.
For
![]() ${S}={\mathbb {Z}}[ G]$
, we abbreviate
${S}={\mathbb {Z}}[ G]$
, we abbreviate
![]() ${R^{\operatorname {univ}}_{G,n}}:={R^{\operatorname {univ}}_{S,n}}$
,
${R^{\operatorname {univ}}_{G,n}}:={R^{\operatorname {univ}}_{S,n}}$
,
![]() ${D}^{\operatorname {univ}}_{G,n}:={D}^{\operatorname {univ}}_{{S},n}$
and
${D}^{\operatorname {univ}}_{G,n}:={D}^{\operatorname {univ}}_{{S},n}$
and
![]() ${X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{G,n}}} :={X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{S},n}}}$
.
${X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{G,n}}} :={X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{S},n}}}$
.
Remark 4.2.3.
-
(a) In [Reference ChenevierChe14], the ring
 ${R^{\operatorname {univ}}_{S,n}}$
is denoted by
${R^{\operatorname {univ}}_{S,n}}$
is denoted by
 $\Gamma _A^n({S})^{\operatorname {ab}}$
; in our notation A is implicit in the structural map of
$\Gamma _A^n({S})^{\operatorname {ab}}$
; in our notation A is implicit in the structural map of
 ${S}$
as an A-algebra.
${S}$
as an A-algebra. -
(b) For A-schemes X there is an obvious notion of
 $\mathcal {O}(X)$
-valued pseudocharacter
$\mathcal {O}(X)$
-valued pseudocharacter
 ${S}\to \mathcal {O}(X)$
of dimension n. The space
${S}\to \mathcal {O}(X)$
of dimension n. The space
 ${X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{S},n}}}$
represents the resulting functor of pseudocharacters on the category of A-schemes.
${X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{S},n}}}$
represents the resulting functor of pseudocharacters on the category of A-schemes.
Example 4.2.4. Recall the determinant
![]() ${\mathrm {det}}({D})\in {\mathcal {P}s\mathcal {R}}^1_{G}(A)$
of any
${\mathrm {det}}({D})\in {\mathcal {P}s\mathcal {R}}^1_{G}(A)$
of any
![]() ${D}\in {\mathcal {P}s\mathcal {R}}^n_{G}(A)$
from Definition 4.1.5. If we apply this to
${D}\in {\mathcal {P}s\mathcal {R}}^n_{G}(A)$
from Definition 4.1.5. If we apply this to
![]() ${D}^{\operatorname {univ}}_{A[G],n}$
, we obtain
${D}^{\operatorname {univ}}_{A[G],n}$
, we obtain
The last assertion in Proposition 4.2.1 and the universality of
![]() ${R^{\operatorname {univ}}_{A[G],1}}$
now yields a homomorphism in
${R^{\operatorname {univ}}_{A[G],1}}$
now yields a homomorphism in
![]() ${\mathcal {CA}lg}_A$
${\mathcal {CA}lg}_A$
and an induced morphism of schemes
![]() ${\mathrm {det}}\colon {X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{A[ G],n}}} \to {X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{A[ G],1}}}$
, both of which we denote by
${\mathrm {det}}\colon {X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{A[ G],n}}} \to {X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{A[ G],1}}}$
, both of which we denote by
![]() ${\mathrm {det}}$
.
${\mathrm {det}}$
.
Lemma 4.2.5 [Reference RobyRob63, Théorème III.4].
The following assertions hold:
-
(a) The canonical map
 ${R^{\operatorname {univ}}_{{S}_1\times {S}_2,n}} \rightarrow \bigoplus _{i=0}^n{R^{\operatorname {univ}}_{{S}_1,i}}\otimes {R^{\operatorname {univ}}_{{S}_2,n-i}}$
, induced from the universal property of these rings, is an isomorphism in
${R^{\operatorname {univ}}_{{S}_1\times {S}_2,n}} \rightarrow \bigoplus _{i=0}^n{R^{\operatorname {univ}}_{{S}_1,i}}\otimes {R^{\operatorname {univ}}_{{S}_2,n-i}}$
, induced from the universal property of these rings, is an isomorphism in
 ${\mathcal {CA}lg}_A$
.
${\mathcal {CA}lg}_A$
. -
(b) Let
 $B\neq 0$
be in
$B\neq 0$
be in
 ${\mathcal {CA}lg}_A$
such that
${\mathcal {CA}lg}_A$
such that
 ${\mathrm {Spec}}\ B$
is connected. Then any A-algebra homomorphism
${\mathrm {Spec}}\ B$
is connected. Then any A-algebra homomorphism
 ${R^{\operatorname {univ}}_{{S}_1\times {S}_2,n}} \rightarrow B$
corresponding to P factors via some summand
${R^{\operatorname {univ}}_{{S}_1\times {S}_2,n}} \rightarrow B$
corresponding to P factors via some summand
 ${R^{\operatorname {univ}}_{{S}_1,i}}\otimes {R^{\operatorname {univ}}_{{S}_2,n-i}}$
in Part (a).
${R^{\operatorname {univ}}_{{S}_1,i}}\otimes {R^{\operatorname {univ}}_{{S}_2,n-i}}$
in Part (a).
Corollary 4.2.6 [Reference Wang EricksonWE13, Lemma 1.1.11.7].
Suppose
![]() $n_1+n_2=n$
for
$n_1+n_2=n$
for
![]() $n_i\ge 0$
. Then the map
$n_i\ge 0$
. Then the map
is a morphism of affine A-schemes that corresponds to the ring homomorphism
where
![]() $\Delta $
is induced from the diagonal map
$\Delta $
is induced from the diagonal map
![]() $S\to S\times S$
and the universality of the rings.
$S\to S\times S$
and the universality of the rings.
4.3 Generalized matrix algebras
Generalized matrix algebras are important in the study of Cayley–Hamilton pseudocharacters over Henselian local rings and were introduced for that purpose in [Reference Bellaïche and ChenevierBC09, § 1.3] in the context of Taylor-pseudocharacters. This subsection recalls some basic result. In Proposition 4.3.9, we shall generalize [Reference Bellaïche and ChenevierBC09, Proposition 1.5.1], in Proposition 4.3.9 on the ideal of total reducibility to pseudocharacters.
Definition 4.3.1 (Cf. [Reference Bellaïche and ChenevierBC09, Definition 1.3.1]).
A generalized matrix algebra (or simply GMA) over A (of type
![]() $(n_1,\ldots ,n_r)$
) is an A-algebra
$(n_1,\ldots ,n_r)$
) is an A-algebra
![]() ${S}$
together with
${S}$
together with
-
(i) a set of orthogonal idempotents
 $e_1,\ldots ,e_r\in {S}$
with
$e_1,\ldots ,e_r\in {S}$
with
 $\sum _{i=1}^re_i=1_{S}$
, and
$\sum _{i=1}^re_i=1_{S}$
, and -
(ii) a set of A-algebra isomorphisms
 $\psi _i:e_i{S} e_i\stackrel {\sim }{\to }{\mathrm {Mat}}_{n_i\times n_i}(A)$
for
$\psi _i:e_i{S} e_i\stackrel {\sim }{\to }{\mathrm {Mat}}_{n_i\times n_i}(A)$
for
 $i=1,\ldots ,r$
$i=1,\ldots ,r$
such that the associated trace map
![]() ${\mathrm {\tau }}:{S}\to A, x\mapsto \sum _{i=1}{\mathrm {tr}}(\psi _i(e_ixe_i))$
is central, that is, it satisfies
${\mathrm {\tau }}:{S}\to A, x\mapsto \sum _{i=1}{\mathrm {tr}}(\psi _i(e_ixe_i))$
is central, that is, it satisfies
![]() ${\mathrm {\tau }}(xy)={\mathrm {\tau }}(yx)$
for all
${\mathrm {\tau }}(xy)={\mathrm {\tau }}(yx)$
for all
![]() $x,y\in {S}$
. The tuple
$x,y\in {S}$
. The tuple
![]() $\mathcal {E}:=\{e_i,\psi _i\}_{i=1,\ldots ,r}$
is called the data of idempotents of
$\mathcal {E}:=\{e_i,\psi _i\}_{i=1,\ldots ,r}$
is called the data of idempotents of
![]() ${S}$
. If we wish to emphasize the entire structure of a GMA, we write
${S}$
. If we wish to emphasize the entire structure of a GMA, we write
![]() $({S},{\cal E})$
instead of S. The dimension of
$({S},{\cal E})$
instead of S. The dimension of
![]() ${S}$
will be
${S}$
will be
![]() $\sum _in_i$
.
$\sum _in_i$
.
Notation 4.3.2. Let
![]() ${S}$
be an GMA over A of type
${S}$
be an GMA over A of type
![]() $(n_1,\ldots ,n_r)$
. For
$(n_1,\ldots ,n_r)$
. For
![]() $1\leq i\leq r$
and
$1\leq i\leq r$
and
![]() $1\leq k,l\leq n_i$
, we denote by
$1\leq k,l\leq n_i$
, we denote by
![]() $E_i^{k,l}$
the unique element in
$E_i^{k,l}$
the unique element in
![]() $e_i{S} e_i$
that maps under
$e_i{S} e_i$
that maps under
![]() $\psi _i$
to the matrix in
$\psi _i$
to the matrix in
![]() ${\mathrm {Mat}}_{n_i\times n_i}(A)$
that has 1 in the
${\mathrm {Mat}}_{n_i\times n_i}(A)$
that has 1 in the
![]() $(k,l)$
-entry and
$(k,l)$
-entry and
![]() $0$
everywhere else. For later use, we also introduce elements
$0$
everywhere else. For later use, we also introduce elements
![]() $E^j:=E^{i',i'}_{i+1}$
for
$E^j:=E^{i',i'}_{i+1}$
for
![]() $j=1,\ldots ,n$
, where
$j=1,\ldots ,n$
, where
![]() $i,i'\ge 1$
are unique such that
$i,i'\ge 1$
are unique such that
![]() $j=n_1+\ldots +n_i+i'$
with
$j=n_1+\ldots +n_i+i'$
with
![]() $1\le i'\le n_{i+1}$
. We write
$1\le i'\le n_{i+1}$
. We write
![]() ${\cal A}^j$
for
${\cal A}^j$
for
![]() $E^j {S} E^j$
and
$E^j {S} E^j$
and
![]() ${\varphi }^j$
for the isomorphism
${\varphi }^j$
for the isomorphism
![]() ${\cal A}^j\to A$
induced from
${\cal A}^j\to A$
induced from
![]() ${\mathrm {\tau }}$
.
${\mathrm {\tau }}$
.
The following result explains why GMA are generalizations of matrix algebras.
Lemma 4.3.3 (Structure of a GMA [Reference Bellaïche and ChenevierBC09, p. 21ff.]).
The following assertions hold:
-
(a) Let
 $({S},\mathcal {E})$
be a GMA over A of type
$({S},\mathcal {E})$
be a GMA over A of type
 $(n_1,\ldots ,n_r)$
, and define the following data:
$(n_1,\ldots ,n_r)$
, and define the following data:-
(1) A-modules
 ${\mathcal {A}}_{i,j}:=E_{i}^{1,1}SE_{j}^{1,1}$
for
${\mathcal {A}}_{i,j}:=E_{i}^{1,1}SE_{j}^{1,1}$
for
 $1\leq i,j\leq r$
,
$1\leq i,j\leq r$
, -
(2) isomorphisms
 ${\mathcal {A}}_{i,i}\cong A$
under
${\mathcal {A}}_{i,i}\cong A$
under
 ${\mathrm {\tau }}$
for
${\mathrm {\tau }}$
for
 $i=1,\ldots ,r$
,
$i=1,\ldots ,r$
, -
(3) A-linear maps
 ${\varphi }_{i,j,k}:{\mathcal {A}}_{i,j}\otimes _A{\mathcal {A}}_{j,k}\to {\mathcal {A}}_{i,k}$
induced from the product in
${\varphi }_{i,j,k}:{\mathcal {A}}_{i,j}\otimes _A{\mathcal {A}}_{j,k}\to {\mathcal {A}}_{i,k}$
induced from the product in
 ${S}$
.
${S}$
.
Then they satisfy the following conditions:
-
(UNIT) For
 $1\leq i,j\leq r$
, we have
$1\leq i,j\leq r$
, we have
 ${\mathcal {A}}_{i,i}=A$
and both
${\mathcal {A}}_{i,i}=A$
and both
 ${\varphi }_{i,i,j}$
and
${\varphi }_{i,i,j}$
and
 ${\varphi }_{i,j,j}$
agree with the A-module structure on
${\varphi }_{i,j,j}$
agree with the A-module structure on
 $A_{i,j}.$
$A_{i,j}.$
-
(ASSO) For
 $1\leq i,j,k,l\leq r$
and
$1\leq i,j,k,l\leq r$
and
 $x\otimes y\otimes z\in {\mathcal {A}}_{i,j}\otimes _A{\mathcal {A}}_{j,k}\otimes _A{\mathcal {A}}_{k,l}$
, we have
$x\otimes y\otimes z\in {\mathcal {A}}_{i,j}\otimes _A{\mathcal {A}}_{j,k}\otimes _A{\mathcal {A}}_{k,l}$
, we have  $$ \begin{align*}{\varphi}_{i,k,l}\big({\varphi}_{i,j,k}(x\otimes y)\otimes z\big)={\varphi}_{i,j,l}\big(x\otimes{\varphi}_{j,k,l}(y\otimes z)\big)\quad\text{in }{\mathcal{A}}_{i,l}.\end{align*} $$
$$ \begin{align*}{\varphi}_{i,k,l}\big({\varphi}_{i,j,k}(x\otimes y)\otimes z\big)={\varphi}_{i,j,l}\big(x\otimes{\varphi}_{j,k,l}(y\otimes z)\big)\quad\text{in }{\mathcal{A}}_{i,l}.\end{align*} $$
-
(COMM) For
 $1\leq i,j\leq r$
,
$1\leq i,j\leq r$
,
 $x\in {\mathcal {A}}_{i,j}$
and
$x\in {\mathcal {A}}_{i,j}$
and
 $y\in {\mathcal {A}}_{j,i}$
, we have
$y\in {\mathcal {A}}_{j,i}$
, we have
 ${\varphi }_{i,j,i}(x\otimes y)={\varphi }_{j,i,j}(y\otimes x)$
.
${\varphi }_{i,j,i}(x\otimes y)={\varphi }_{j,i,j}(y\otimes x)$
.
(17)and the latter is isomorphic to $$ \begin{align} \left( \begin{array}{ccc} {\mathrm{Mat}}_{n_1\times n_1}({\mathcal{A}}_{1,1})&\cdots&{\mathrm{Mat}}_{n_1\times n_r}({\mathcal{A}}_{1,r})\\ \vdots& \ddots&\vdots\\ {\mathrm{Mat}}_{n_r\times n_1}({\mathcal{A}}_{r,1})&\cdots&{\mathrm{Mat}}_{n_r\times n_r}({\mathcal{A}}_{r,r}) \end{array} \right) \end{align} $$
$$ \begin{align} \left( \begin{array}{ccc} {\mathrm{Mat}}_{n_1\times n_1}({\mathcal{A}}_{1,1})&\cdots&{\mathrm{Mat}}_{n_1\times n_r}({\mathcal{A}}_{1,r})\\ \vdots& \ddots&\vdots\\ {\mathrm{Mat}}_{n_r\times n_1}({\mathcal{A}}_{r,1})&\cdots&{\mathrm{Mat}}_{n_r\times n_r}({\mathcal{A}}_{r,r}) \end{array} \right) \end{align} $$
 ${S}$
.
${S}$
.
-
-
(b) Conversely, suppose we are given a family
 $({\mathcal {A}}_{i,j})_{1\leq i,j\leq r}$
of A-modules together with A-linear maps
$({\mathcal {A}}_{i,j})_{1\leq i,j\leq r}$
of A-modules together with A-linear maps
 ${\varphi }_{i,j,k}:{\mathcal {A}}_{i,j}\otimes _A{\mathcal {A}}_{j,k}\to {\mathcal {A}}_{i,k}$
for
${\varphi }_{i,j,k}:{\mathcal {A}}_{i,j}\otimes _A{\mathcal {A}}_{j,k}\to {\mathcal {A}}_{i,k}$
for
 $1\leq i,j,k\leq r$
satisfying the above conditions (UNIT), (ASSO) and (COMM). Then there is a unique structure of a GMA of type
$1\leq i,j,k\leq r$
satisfying the above conditions (UNIT), (ASSO) and (COMM). Then there is a unique structure of a GMA of type
 $(n_1,\ldots ,n_r)$
on the A-module
$(n_1,\ldots ,n_r)$
on the A-module
 ${S}:=\oplus _{i,j=1}^r {\mathrm {Mat}}_{n_i\times n_j}({\mathcal {A}}_{i,j})$
.
${S}:=\oplus _{i,j=1}^r {\mathrm {Mat}}_{n_i\times n_j}({\mathcal {A}}_{i,j})$
.
Next, we provide some technical lemmas:
Lemma 4.3.4. Let
![]() ${S}$
be a GMA over A of type
${S}$
be a GMA over A of type
![]() $(n_1,\ldots ,n_r)$
over A, and
$(n_1,\ldots ,n_r)$
over A, and
![]() $B\in {\mathrm {Ob}}({\mathcal {CA}lg}_A)$
. Then
$B\in {\mathrm {Ob}}({\mathcal {CA}lg}_A)$
. Then
![]() ${S}\otimes _A B$
is a GMA over B of type
${S}\otimes _A B$
is a GMA over B of type
![]() $(n_1,\ldots ,n_r)$
.
$(n_1,\ldots ,n_r)$
.
The proof of Lemma 4.3.4 is straightforward and left as an exercise.
Proposition 4.3.5 [Reference Wang-EricksonWE18, Proposition 2.23].
Given a GMA
![]() $({S},{\cal E})$
over A of dimension n, there exists a natural n-dimensional Cayley–Hamilton pseudocharacter
$({S},{\cal E})$
over A of dimension n, there exists a natural n-dimensional Cayley–Hamilton pseudocharacter
![]() ${\mathrm {det}}_{({S},{\cal E})}\colon {S}\to A$
, called the determinant of the GMA
${\mathrm {det}}_{({S},{\cal E})}\colon {S}\to A$
, called the determinant of the GMA
![]() $({S},{\cal E})$
, and given, for any B in
$({S},{\cal E})$
, and given, for any B in
![]() ${\mathcal {CA}lg}_A$
, by the formula
${\mathcal {CA}lg}_A$
, by the formula
 $$ \begin{align} {\mathrm{det}}_{({S}.{\cal E})}(x) = \sum_{\sigma\in{\mathfrak{S}}_n} {\mathrm{sgn}}(\sigma) \prod_{\mathrm{cycles\,}\gamma\mathrm{\,of\,}\sigma} {\varphi}^{l_0}\Big( \prod_{l\in \gamma} E^l x E^{\sigma(l)}\Big) \end{align} $$
$$ \begin{align} {\mathrm{det}}_{({S}.{\cal E})}(x) = \sum_{\sigma\in{\mathfrak{S}}_n} {\mathrm{sgn}}(\sigma) \prod_{\mathrm{cycles\,}\gamma\mathrm{\,of\,}\sigma} {\varphi}^{l_0}\Big( \prod_{l\in \gamma} E^l x E^{\sigma(l)}\Big) \end{align} $$
for any
![]() $x\in R\otimes _AB$
. Here, the product is first over the cycles
$x\in R\otimes _AB$
. Here, the product is first over the cycles
![]() $\gamma $
in the cycle decomposition of
$\gamma $
in the cycle decomposition of
![]() $\sigma $
and then over the elements l of the cycle
$\sigma $
and then over the elements l of the cycle
![]() $\gamma $
taken in the order that they appear in the cycle, where
$\gamma $
taken in the order that they appear in the cycle, where
![]() $l_0$
is a choice of initial element of
$l_0$
is a choice of initial element of
![]() $\gamma $
, and
$\gamma $
, and
![]() ${\varphi }^{l_0}$
is from Notation 4.3.2. We also have
${\varphi }^{l_0}$
is from Notation 4.3.2. We also have
![]() ${\mathrm {\tau }}=\Lambda ^1_{{D}_{\cal E}}$
.
${\mathrm {\tau }}=\Lambda ^1_{{D}_{\cal E}}$
.
The next results are auxiliary for Proposition 4.3.9 on the locus of reducibility of a GMA.
Lemma 4.3.6 [Reference ChenevierChe14, Lemma 1.12(i)].
One has
![]() ${D}(1+ss')={D}(1+s's)$
for all
${D}(1+ss')={D}(1+s's)$
for all
![]() $s, s' \in {S}$
.
$s, s' \in {S}$
.
Lemma 4.3.7. Let
![]() $({S},\mathcal {E})$
be a GMA, and let
$({S},\mathcal {E})$
be a GMA, and let
![]() $D\colon {S}\to A$
a pseudocharacter. Then for any
$D\colon {S}\to A$
a pseudocharacter. Then for any
![]() $x\in {\mathrm {Mat}}_{n_i\times n_j}({\mathcal {A}}_{i,j})$
for some
$x\in {\mathrm {Mat}}_{n_i\times n_j}({\mathcal {A}}_{i,j})$
for some
![]() $1\le i,j\le r$
with
$1\le i,j\le r$
with
![]() $i\neq j$
, we have
$i\neq j$
, we have
![]() $D(1+e_ixe_j)=1$
.
$D(1+e_ixe_j)=1$
.
Proof. By Lemma 4.3.6 we have
![]() $D(1+e_ixe_j)=D(1+e_je_ix)=D(1)=1$
.
$D(1+e_ixe_j)=D(1+e_je_ix)=D(1)=1$
.
Lemma 4.3.8 [Reference ChenevierChe14, Lemma 2.4].
Let
![]() ${S}$
be an A-algebra,
${S}$
be an A-algebra,
![]() $e \in {S}$
be an idempotent, and
$e \in {S}$
be an idempotent, and
![]() ${D}\colon {S} \to A$
be a pseudocharacter of dimension n. Suppose that
${D}\colon {S} \to A$
be a pseudocharacter of dimension n. Suppose that
![]() ${\mathrm {Spec}}(A)$
is connected.
${\mathrm {Spec}}(A)$
is connected.
-
(a) The polynomial law
 ${D}_e\colon e{S} e \to A$
,
${D}_e\colon e{S} e \to A$
,
 ${s} \mapsto {D}({s}+1-e)$
, is a pseudocharacter; its dimension
${s} \mapsto {D}({s}+1-e)$
, is a pseudocharacter; its dimension
 $r(e)$
satisfies
$r(e)$
satisfies
 $r(e)\leq n$
and one has
$r(e)\leq n$
and one has
 $r(1-e)+r(e)=n$
.
$r(1-e)+r(e)=n$
. -
(b) The restriction of
 ${D}$
to the A-subalgebra
${D}$
to the A-subalgebra
 $e{S} e\oplus (1-e){S}(1-e)$
is the sum
$e{S} e\oplus (1-e){S}(1-e)$
is the sum
 ${D}_e {\oplus }{D}_{1-e}$
. It is a pseudocharacter of dimension n.
${D}_e {\oplus }{D}_{1-e}$
. It is a pseudocharacter of dimension n. -
(c) If
 ${D}$
is faithful or Cayley–Hamilton, then
${D}$
is faithful or Cayley–Hamilton, then
 ${D}_e$
is faithful or Cayley–Hamilton, respectively.
${D}_e$
is faithful or Cayley–Hamilton, respectively. -
(d) Suppose that
 ${D}$
is Cayley–Hamilton. Then
${D}$
is Cayley–Hamilton. Then
 $e=1$
if and only if
$e=1$
if and only if
 ${D}(e)=1$
, and
${D}(e)=1$
, and
 $e=0$
if and only if
$e=0$
if and only if
 $r(e)=0$
. If
$r(e)=0$
. If
 $e_1, \dots , e_s$
is a family of nonzero orthogonal idempotents of
$e_1, \dots , e_s$
is a family of nonzero orthogonal idempotents of
 ${S}$
, then
${S}$
, then
 $s\leq n$
and
$s\leq n$
and
 $\sum _{i=1}^s r(e_i)\leq n$
. Further,
$\sum _{i=1}^s r(e_i)\leq n$
. Further,
 $\sum _{i=1}^s r(e_i)= n$
if and only if
$\sum _{i=1}^s r(e_i)= n$
if and only if
 $\sum _{i=1}^s e_i=1$
.
$\sum _{i=1}^s e_i=1$
.
The next result is the adaption of [Reference Bellaïche and ChenevierBC09, Proposition 1.5.1] to pseudocharacters.
Proposition 4.3.9. Let
![]() $({S},{\cal E})$
be a GMA over A, and let
$({S},{\cal E})$
be a GMA over A, and let
![]() ${\cal A}_{i,j}$
and
${\cal A}_{i,j}$
and
![]() ${\varphi }_{i,j,k}$
be as in Lemma 4.3.3. Define
${\varphi }_{i,j,k}$
be as in Lemma 4.3.3. Define
![]() $I= \sum _{i\neq j}{\mathcal {A}}_{i,j}{\mathcal {A}}_{j,i}$
as the ideal of total reducibility in A.
$I= \sum _{i\neq j}{\mathcal {A}}_{i,j}{\mathcal {A}}_{j,i}$
as the ideal of total reducibility in A.
-
(a)
-
(1) If
 $I=0$
, then the map
$I=0$
, then the map
 $\pi \colon {S}\to \sum _i e_i{S} e_i\subset {S}, x\mapsto \sum _i e_ixe_i$
is a ring homomorphism.
$\pi \colon {S}\to \sum _i e_i{S} e_i\subset {S}, x\mapsto \sum _i e_ixe_i$
is a ring homomorphism. -
(2) Denoting by
 $D_i$
the map
$D_i$
the map
 $e_i{S} e_i\stackrel {\psi _i}{\to } {\mathrm {Mat}}_{n_i\times n_i}(A)\stackrel {{\mathrm {det}}}{\to } A$
for
$e_i{S} e_i\stackrel {\psi _i}{\to } {\mathrm {Mat}}_{n_i\times n_i}(A)\stackrel {{\mathrm {det}}}{\to } A$
for
 $i=1,\ldots ,r$
, one has
$i=1,\ldots ,r$
, one has  $$ \begin{align*}{\mathrm{det}}_{({S},\mathcal{E})}= {\oplus}_{i=1}^r {D}_i\circ \pi \ {\mathop{\mathrm{mod}\ }\nolimits} I. \end{align*} $$
$$ \begin{align*}{\mathrm{det}}_{({S},\mathcal{E})}= {\oplus}_{i=1}^r {D}_i\circ \pi \ {\mathop{\mathrm{mod}\ }\nolimits} I. \end{align*} $$
-
-
(b) Suppose that there exist
 $m_i$
-dimensional pseudocharacters
$m_i$
-dimensional pseudocharacters
 ${D}^{\prime }_i\colon {S} \to A$
with
${D}^{\prime }_i\colon {S} \to A$
with
 $m_i>0$
for
$m_i>0$
for
 $i\in \{1,\ldots ,r\}$
such that one has
$i\in \{1,\ldots ,r\}$
such that one has
 ${\mathrm {det}}_{({S},\mathcal {E})}= {\oplus }_{i=1}^r {D}^{\prime }_i$
. Then
${\mathrm {det}}_{({S},\mathcal {E})}= {\oplus }_{i=1}^r {D}^{\prime }_i$
. Then
 $I=0$
and for a unique permutation
$I=0$
and for a unique permutation
 $\sigma \in {\mathfrak {S}_{{r}}}$
we have
$\sigma \in {\mathfrak {S}_{{r}}}$
we have
 $D_{\sigma (i)}'=D_i\circ \pi $
with
$D_{\sigma (i)}'=D_i\circ \pi $
with
 $D_i$
and
$D_i$
and
 $\pi $
from (i).
$\pi $
from (i).
Proof. Part (1) of (a) is a straightforward matrix calculation using
![]() ${\mathcal {A}}_{i,j}{\mathcal {A}}_{j,i}=0$
for all
${\mathcal {A}}_{i,j}{\mathcal {A}}_{j,i}=0$
for all
![]() $i\neq j$
from
$i\neq j$
from
![]() $\{1,\ldots ,r\}$
. To see Part (2) of (a), observe that equation (18) for
$\{1,\ldots ,r\}$
. To see Part (2) of (a), observe that equation (18) for
![]() $r=1$
is simply the Leibniz formula for matrix determinants. Hence, by our definitions we have the explicit formula
$r=1$
is simply the Leibniz formula for matrix determinants. Hence, by our definitions we have the explicit formula
 $$ \begin{align*}{D}_i \ {\mathop{\mathrm{mod}\ }\nolimits} I\colon e_i{S} e_i\,{\longrightarrow}\, A/I, \quad x\longmapsto \sum_{\sigma_i\in{\mathfrak{S}_{{n_i}}}} {\mathrm{sgn}}(\sigma_i) \prod_{\mathrm{cycles\,}\gamma_i\mathrm{\,of\,}\sigma_i} {\varphi}^{l}\Big( \prod_{l\in \gamma_i} E^l x E^{\sigma(l)}\Big)\ {\mathop{\mathrm{mod}\ }\nolimits} I,\end{align*} $$
$$ \begin{align*}{D}_i \ {\mathop{\mathrm{mod}\ }\nolimits} I\colon e_i{S} e_i\,{\longrightarrow}\, A/I, \quad x\longmapsto \sum_{\sigma_i\in{\mathfrak{S}_{{n_i}}}} {\mathrm{sgn}}(\sigma_i) \prod_{\mathrm{cycles\,}\gamma_i\mathrm{\,of\,}\sigma_i} {\varphi}^{l}\Big( \prod_{l\in \gamma_i} E^l x E^{\sigma(l)}\Big)\ {\mathop{\mathrm{mod}\ }\nolimits} I,\end{align*} $$
and using distributivity for
![]() $x\in {S}$
$x\in {S}$
 $$ \begin{align*} \prod_{i=1}^r ({D}_i\circ\pi)(x)\ {\mathop{\mathrm{mod}\ }\nolimits} I&= \prod_{i=1}^r\sum_{\sigma_i\in{\mathfrak{S}_{{n_i}}}} {\mathrm{sgn}}(\sigma_i) \prod_{\mathrm{cycles\,}\gamma_i\mathrm{\,of\,}\sigma_i} {\varphi}^{l}\Big( \prod_{l\in \gamma_i} E^l x E^{\sigma(l)}\Big)\ {\mathop{\mathrm{mod}\ }\nolimits} I\\ &=\sum_{\sigma_1\in{\mathfrak{S}_{{n_1}}}}\ldots\sum_{\sigma_r\in{\mathfrak{S}_{{n_r}}}} \prod_{i=1}^r {\mathrm{sgn}}(\sigma_i) \prod_{\mathrm{cycles\,}\gamma_i\mathrm{\,of\,}\sigma_i} {\varphi}^{l}\Big( \prod_{l\in \gamma_i} E^l x E^{\sigma(l)}\Big)\ {\mathop{\mathrm{mod}\ }\nolimits} I. \end{align*} $$
$$ \begin{align*} \prod_{i=1}^r ({D}_i\circ\pi)(x)\ {\mathop{\mathrm{mod}\ }\nolimits} I&= \prod_{i=1}^r\sum_{\sigma_i\in{\mathfrak{S}_{{n_i}}}} {\mathrm{sgn}}(\sigma_i) \prod_{\mathrm{cycles\,}\gamma_i\mathrm{\,of\,}\sigma_i} {\varphi}^{l}\Big( \prod_{l\in \gamma_i} E^l x E^{\sigma(l)}\Big)\ {\mathop{\mathrm{mod}\ }\nolimits} I\\ &=\sum_{\sigma_1\in{\mathfrak{S}_{{n_1}}}}\ldots\sum_{\sigma_r\in{\mathfrak{S}_{{n_r}}}} \prod_{i=1}^r {\mathrm{sgn}}(\sigma_i) \prod_{\mathrm{cycles\,}\gamma_i\mathrm{\,of\,}\sigma_i} {\varphi}^{l}\Big( \prod_{l\in \gamma_i} E^l x E^{\sigma(l)}\Big)\ {\mathop{\mathrm{mod}\ }\nolimits} I. \end{align*} $$
We have to compare the latter expression to
 $$ \begin{align*} {\mathrm{det}}_{({S}.{\cal E})}(x) \ {\mathop{\mathrm{mod}\ }\nolimits} I= \sum_{\sigma\in{\mathfrak{S}}_n} {\mathrm{sgn}}(\sigma) \prod_{\mathrm{cycles\,}\gamma\mathrm{\,of\,}\sigma} {\varphi}^{l_0}\Big( \prod_{l\in \gamma} E^l x E^{\sigma(l)}\Big)\ {\mathop{\mathrm{mod}\ }\nolimits} I. \end{align*} $$
$$ \begin{align*} {\mathrm{det}}_{({S}.{\cal E})}(x) \ {\mathop{\mathrm{mod}\ }\nolimits} I= \sum_{\sigma\in{\mathfrak{S}}_n} {\mathrm{sgn}}(\sigma) \prod_{\mathrm{cycles\,}\gamma\mathrm{\,of\,}\sigma} {\varphi}^{l_0}\Big( \prod_{l\in \gamma} E^l x E^{\sigma(l)}\Big)\ {\mathop{\mathrm{mod}\ }\nolimits} I. \end{align*} $$
Now, in the last expression, the term
![]() $ {\varphi }^{l_0}\Big ( \prod _{l\in \gamma } E^l x E^{\sigma (l)}\Big )\ {\mathop{\mathrm{mod}\ }\nolimits } I$
vanishes unless
$ {\varphi }^{l_0}\Big ( \prod _{l\in \gamma } E^l x E^{\sigma (l)}\Big )\ {\mathop{\mathrm{mod}\ }\nolimits } I$
vanishes unless
![]() $\gamma $
is contained in a single factor under the inclusion
$\gamma $
is contained in a single factor under the inclusion
![]() $ {\mathfrak {S}_{{n_1}}} \times \ldots \times {\mathfrak {S}_{{n_r}}} {\hookrightarrow } {\mathfrak {S}_{{n}}}$
, by the definition of I and using Lemma 4.3.3. This shows that
$ {\mathfrak {S}_{{n_1}}} \times \ldots \times {\mathfrak {S}_{{n_r}}} {\hookrightarrow } {\mathfrak {S}_{{n}}}$
, by the definition of I and using Lemma 4.3.3. This shows that
 $$ \begin{align*} {\mathrm{det}}_{({S}.{\cal E})}(x) \ {\mathop{\mathrm{mod}\ }\nolimits} I= \sum_{\sigma=(\sigma_1,\ldots,\sigma_r)\in{\mathfrak{S}_{{n_1}}} \times\ldots\times{\mathfrak{S}_{{n_r}}} } \prod_{i=1}^r{\mathrm{sgn}}(\sigma_i) \prod_{\mathrm{cycles\,}\gamma\mathrm{\,of\,}\sigma_i} {\varphi}^{l_0}\Big( \prod_{l\in \gamma} E^l x E^{\sigma(l)}\Big)\ {\mathop{\mathrm{mod}\ }\nolimits} I, \end{align*} $$
$$ \begin{align*} {\mathrm{det}}_{({S}.{\cal E})}(x) \ {\mathop{\mathrm{mod}\ }\nolimits} I= \sum_{\sigma=(\sigma_1,\ldots,\sigma_r)\in{\mathfrak{S}_{{n_1}}} \times\ldots\times{\mathfrak{S}_{{n_r}}} } \prod_{i=1}^r{\mathrm{sgn}}(\sigma_i) \prod_{\mathrm{cycles\,}\gamma\mathrm{\,of\,}\sigma_i} {\varphi}^{l_0}\Big( \prod_{l\in \gamma} E^l x E^{\sigma(l)}\Big)\ {\mathop{\mathrm{mod}\ }\nolimits} I, \end{align*} $$
and it completes the proof of (a).
We now prove (b). We begin by proving the following Claim: There is a unique permutation
![]() $\sigma \in {\mathfrak {S}_{{r}}}$
such that
$\sigma \in {\mathfrak {S}_{{r}}}$
such that
![]() ${D}_i=({D}^{\prime }_{\sigma (i)})_{e_i}$
and
${D}_i=({D}^{\prime }_{\sigma (i)})_{e_i}$
and
![]() $({D}^{\prime }_{i'})_{e_i}=1$
for
$({D}^{\prime }_{i'})_{e_i}=1$
for
![]() $i'\neq \sigma (i)$
. For this, we restrict
$i'\neq \sigma (i)$
. For this, we restrict
![]() ${\oplus }_{i'=1}^r {D}^{\prime }_{i'}$
to
${\oplus }_{i'=1}^r {D}^{\prime }_{i'}$
to
![]() $e_iSe_i$
so that
$e_iSe_i$
so that
By Lemma 4.3.8 the
![]() $ ({D}_{i'}^{\prime })_{e_i}$
are pseudocharacters of dimension
$ ({D}_{i'}^{\prime })_{e_i}$
are pseudocharacters of dimension
![]() $m_{i',i}:=\dim ({D}_{i'}^{\prime })_{e_i}\le m_{i'}$
. Now, under addition in the sense of Corollary 4.2.6 dimensions are added, and it follows that
$m_{i',i}:=\dim ({D}_{i'}^{\prime })_{e_i}\le m_{i'}$
. Now, under addition in the sense of Corollary 4.2.6 dimensions are added, and it follows that
But because
![]() $e_iSe_i={\mathrm {Mat}}_{n_i\times n_i}(A)$
, it follows from Example 4.1.7
(b) that each
$e_iSe_i={\mathrm {Mat}}_{n_i\times n_i}(A)$
, it follows from Example 4.1.7
(b) that each
![]() $m_{i',i}$
is divisible by
$m_{i',i}$
is divisible by
![]() $n_i$
. Hence, there is a unique map
$n_i$
. Hence, there is a unique map
![]() $\sigma \colon \{1,\ldots ,r\}\to \{1,\ldots ,r\}$
such that
$\sigma \colon \{1,\ldots ,r\}\to \{1,\ldots ,r\}$
such that
![]() $m_{\sigma (i),i}=n_i$
and
$m_{\sigma (i),i}=n_i$
and
![]() $m_{i',i}=0$
for
$m_{i',i}=0$
for
![]() $i'\neq \sigma (i)$
, and moreover
$i'\neq \sigma (i)$
, and moreover
![]() ${D}_i=({D}^{\prime }_{\sigma (i)})_{e_i}$
. It remains to show that
${D}_i=({D}^{\prime }_{\sigma (i)})_{e_i}$
. It remains to show that
![]() $\sigma $
is bijective. It will suffice to show that
$\sigma $
is bijective. It will suffice to show that
![]() $\sigma $
is surjective.
$\sigma $
is surjective.
For this, let
![]() $S^{\prime }_{i'}:=\oplus _{i\in \sigma ^{-1}(i')}e_iSe_i$
so that
$S^{\prime }_{i'}:=\oplus _{i\in \sigma ^{-1}(i')}e_iSe_i$
so that
![]() $S=\oplus _{i'}S^{\prime }_{i'}$
. The restriction of
$S=\oplus _{i'}S^{\prime }_{i'}$
. The restriction of
![]() $D^{\prime }_{i"}$
to
$D^{\prime }_{i"}$
to
![]() $S^{\prime }_{i'}$
is zero if
$S^{\prime }_{i'}$
is zero if
![]() $i"\neq i'$
, and the restriction of
$i"\neq i'$
, and the restriction of
![]() $D^{\prime }_{i'}$
to
$D^{\prime }_{i'}$
to
![]() $S^{\prime }_{i'}$
is a pseudocharacter with
$S^{\prime }_{i'}$
is a pseudocharacter with
 $$ \begin{align*} m_{i'}\stackrel{4.3.8}\ge \dim D^{\prime}_{i'} |_{S^{\prime}_{i'}}=\dim {\oplus}_{i"=1}^r{D}^{\prime}_{i"} |_{S^{\prime}_{i'}}=\dim {\mathrm{det}}_{({S},\mathcal{E})} |_{S^{\prime}_{i'}}=\sum_{i\in \sigma^{-1}(i')}n_i.\end{align*} $$
$$ \begin{align*} m_{i'}\stackrel{4.3.8}\ge \dim D^{\prime}_{i'} |_{S^{\prime}_{i'}}=\dim {\oplus}_{i"=1}^r{D}^{\prime}_{i"} |_{S^{\prime}_{i'}}=\dim {\mathrm{det}}_{({S},\mathcal{E})} |_{S^{\prime}_{i'}}=\sum_{i\in \sigma^{-1}(i')}n_i.\end{align*} $$
Summing over all
![]() $i'$
in the image of
$i'$
in the image of
![]() $\sigma $
implies
$\sigma $
implies
![]() $\sum _{i'\in \sigma (\{1,\ldots ,r\})}m_{i'}\ge n$
. However, all
$\sum _{i'\in \sigma (\{1,\ldots ,r\})}m_{i'}\ge n$
. However, all
![]() $m_{i'}$
are strictly positive and
$m_{i'}$
are strictly positive and
![]() $\sum _{i'=1}^r m_{i'}=n$
, and this implies that
$\sum _{i'=1}^r m_{i'}=n$
, and this implies that
![]() $\sigma $
is surjective, and hence the claim is proved.
$\sigma $
is surjective, and hence the claim is proved.
For simplicity of notation, we assume from here on, without loss of generality, that
![]() $\sigma ={\mathrm {id}}$
. We now show that
$\sigma ={\mathrm {id}}$
. We now show that
![]() $I=0$
. For this, it suffices to show that
$I=0$
. For this, it suffices to show that
![]() ${\mathcal {A}}_{i,j}{\mathcal {A}}_{j,i}=0$
for all
${\mathcal {A}}_{i,j}{\mathcal {A}}_{j,i}=0$
for all
![]() $i\neq j$
. By restricting to the subalgebra
$i\neq j$
. By restricting to the subalgebra
![]() ${S}'=e_i{S} e_i+e_j{S} e_j+e_i{S} e_j+e_j{S} e_i$
with
${S}'=e_i{S} e_i+e_j{S} e_j+e_i{S} e_j+e_j{S} e_i$
with
![]() $\mathcal {E}'=(e_i,\psi _i,e_j,\psi _j,)$
, that is, by considering
$\mathcal {E}'=(e_i,\psi _i,e_j,\psi _j,)$
, that is, by considering
![]() $D_{e_i+e_j}$
, and using
$D_{e_i+e_j}$
, and using
![]() ${\mathrm {det}}_{({S},\mathcal {E})}|_{S'}={\mathrm {det}}_{({S}',\mathcal {E}')}$
, we may assume
${\mathrm {det}}_{({S},\mathcal {E})}|_{S'}={\mathrm {det}}_{({S}',\mathcal {E}')}$
, we may assume
![]() $r=2$
for the proof of
$r=2$
for the proof of
![]() $I=0$
.
$I=0$
.
Let b be in
![]() ${\mathcal {A}}_{1,2}$
and c in
${\mathcal {A}}_{1,2}$
and c in
![]() ${\mathcal {A}}_{2,1}$
, and write x for
${\mathcal {A}}_{2,1}$
, and write x for
![]() $e_1E_1^{1,1}bE_2^{1,1}e_2$
and y for
$e_1E_1^{1,1}bE_2^{1,1}e_2$
and y for
![]() $e_2E_2^{1,1}ce:1^{1,1}e_1$
with
$e_2E_2^{1,1}ce:1^{1,1}e_1$
with
![]() $E^{k,l}_i$
from Notation 4.3.2. Using the description of GMAs from Lemma 4.3.3, one easily verifies that
$E^{k,l}_i$
from Notation 4.3.2. Using the description of GMAs from Lemma 4.3.3, one easily verifies that
Note moreover that by Lemma 4.3.6 we have
![]() $D(1+xy)=D(1+yx)$
for every pseudocharacter
$D(1+xy)=D(1+yx)$
for every pseudocharacter
![]() $D\colon {S}\to A$
. If we apply this to
$D\colon {S}\to A$
. If we apply this to
![]() $D_i^{\prime }$
and our earlier observations on
$D_i^{\prime }$
and our earlier observations on
![]() $(D^{\prime }_i)_{e_{i'}}$
, we find that
$(D^{\prime }_i)_{e_{i'}}$
, we find that
and similarly
![]() $D_2^{\prime }(1+xy)=1$
, and hence from hypothesis (2) that
$D_2^{\prime }(1+xy)=1$
, and hence from hypothesis (2) that
![]() ${\mathrm {det}}_{({S},\mathcal {E})}(1+E_1^{1,1}bc)=1$
. From the formula for
${\mathrm {det}}_{({S},\mathcal {E})}(1+E_1^{1,1}bc)=1$
. From the formula for
![]() ${\mathrm {det}}_{({S},\mathcal {E})}$
on
${\mathrm {det}}_{({S},\mathcal {E})}$
on
![]() $e_1{S} e_1+e_2{S} e_2 \cong {\mathrm {Mat}}_{n_1\times n_1}(A)\times {\mathrm {Mat}}_{n_2\times n_2}(A)$
, we deduce that
$e_1{S} e_1+e_2{S} e_2 \cong {\mathrm {Mat}}_{n_1\times n_1}(A)\times {\mathrm {Mat}}_{n_2\times n_2}(A)$
, we deduce that
and hence that
![]() $bc=0$
, as was to be shown.
$bc=0$
, as was to be shown.
For the second assertion, observe that by Lemma 4.3.7 we have
![]() $D_i^{\prime }(1+e_ixe_j)=1$
for any
$D_i^{\prime }(1+e_ixe_j)=1$
for any
![]() $i\neq j$
and
$i\neq j$
and
![]() $x\in {\mathrm {Mat}}_{n_i\times n_j}({\mathcal {A}}_{i,j})$
. It follows that
$x\in {\mathrm {Mat}}_{n_i\times n_j}({\mathcal {A}}_{i,j})$
. It follows that
![]() $D_i^{\prime }(1+u)=1$
for any u in the kernel of
$D_i^{\prime }(1+u)=1$
for any u in the kernel of
![]() $\pi $
. And now the second assertion follows from knowing the restriction of
$\pi $
. And now the second assertion follows from knowing the restriction of
![]() $D_i^{\prime }$
to
$D_i^{\prime }$
to
![]() $\sum _i e_i{S} e_i$
given in the first claim of the proof of (b).
$\sum _i e_i{S} e_i$
given in the first claim of the proof of (b).
The following result of Chenevier gives an application of GMAs to pseudocharacters.
Theorem 4.3.10 [Reference ChenevierChe14, Theorem 2.22], [Reference Wang EricksonWE13, Theorem 2.27].
Assume that A is a Henselian local ring with maximal ideal
![]() $m_A$
and residue field
$m_A$
and residue field
![]() ${\kappa ({A})}$
. Let
${\kappa ({A})}$
. Let
![]() ${S}$
be an A-algebra and suppose that
${S}$
be an A-algebra and suppose that
![]() ${D}\in {\mathcal {P}s\mathcal {R}}_{{S}}^n(A)$
is Cayley–Hamilton. Denote by
${D}\in {\mathcal {P}s\mathcal {R}}_{{S}}^n(A)$
is Cayley–Hamilton. Denote by
![]() ${\overline {{D}}}={D} \otimes _A {\kappa ({A})} \colon {S}/m_A{S}\longrightarrow {\kappa ({A})}$
the residual pseudocharacter of
${\overline {{D}}}={D} \otimes _A {\kappa ({A})} \colon {S}/m_A{S}\longrightarrow {\kappa ({A})}$
the residual pseudocharacter of
![]() ${D}$
. Suppose that
${D}$
. Suppose that
![]() ${\overline {{D}}}$
is split (see Definition 4.1.19). Then the following hold:
${\overline {{D}}}$
is split (see Definition 4.1.19). Then the following hold:
-
(a) If
 ${\overline {{D}}}$
is irreducible, then
${\overline {{D}}}$
is irreducible, then
 ${D} = {\mathrm {det}} \circ \rho $
for some A-algebra isomorphism
${D} = {\mathrm {det}} \circ \rho $
for some A-algebra isomorphism
 $\rho \colon {S} \stackrel {\sim }{\to } {\mathrm {Mat}}_{n\times n}(A)$
.
$\rho \colon {S} \stackrel {\sim }{\to } {\mathrm {Mat}}_{n\times n}(A)$
. -
(b) If
 ${\overline {{D}}}$
is multiplicity free, then
${\overline {{D}}}$
is multiplicity free, then
 ${S}$
is a generalized matrix algebra
${S}$
is a generalized matrix algebra
 $(S,{\cal E})$
and
$(S,{\cal E})$
and
 ${D}={\mathrm {det}}_{({S},{\cal E})}$
. If
${D}={\mathrm {det}}_{({S},{\cal E})}$
. If
 ${\overline {{D}}}=\bigoplus _{i=1}^l{\overline {{D}}}_i$
for irreducible
${\overline {{D}}}=\bigoplus _{i=1}^l{\overline {{D}}}_i$
for irreducible
 ${\overline {{D}}}_i$
, then the type of S is
${\overline {{D}}}_i$
, then the type of S is
 $(n_1,\ldots ,n_l)$
for
$(n_1,\ldots ,n_l)$
for
 $n_i$
the degree of
$n_i$
the degree of
 ${\overline {{D}}}_i$
.
${\overline {{D}}}_i$
.
4.4 Continuous pseudocharacters
In our application, mainly continuous pseudocharacters (of a profinite group G) will play a role. In this subsection, we will recall this concept and some of its properties. We denote throughout this subsection by G a profinite group. Let us refer to [Reference GrothendieckGro60, Chapter 0 § 7, Chapter 1 § 10] for a more thorough introduction to topological rings and formal schemes.
We introduce in Definition 4.4.2 a category of admissible
![]() $\kappa $
-algebras that is perhaps not standard. In Lemma 4.4.7, we prove a finiteness statement for continuous pseudocharacters on
$\kappa $
-algebras that is perhaps not standard. In Lemma 4.4.7, we prove a finiteness statement for continuous pseudocharacters on
![]() $G_K$
with
$G_K$
with
![]() $K \ p$
-adic and values in a finite field of characteristic p.
$K \ p$
-adic and values in a finite field of characteristic p.
Definition 4.4.1 (Cf. [Reference ChenevierChe14, § 2.30]).
Let A be a commutative topological ring. Then
![]() ${D}\in {\mathcal {P}s\mathcal {R}}^n_G(A)$
is called continuous if and only if the characteristic polynomial functions (restricted to G)
${D}\in {\mathcal {P}s\mathcal {R}}^n_G(A)$
is called continuous if and only if the characteristic polynomial functions (restricted to G)
![]() $\Lambda _{D,i}\colon G\to A$
are continuous for
$\Lambda _{D,i}\colon G\to A$
are continuous for
![]() $i=1,\ldots ,n$
.
$i=1,\ldots ,n$
.
We shall study continuity only for two types of commutative rings A that we now describe. Consider a directed set J with minimal element
![]() $0$
and an inverse system
$0$
and an inverse system
![]() $A_\lambda $
,
$A_\lambda $
,
![]() $\lambda \in J$
, of topological commutative rings with continuous transition maps and such that
$\lambda \in J$
, of topological commutative rings with continuous transition maps and such that
![]() $A_\lambda \to A_0$
is surjective with nilpotent kernel for any
$A_\lambda \to A_0$
is surjective with nilpotent kernel for any
![]() $\lambda \in J$
. Then the inverse limit
$\lambda \in J$
. Then the inverse limit
is a topological ring with respect to the weakest topology for which the projections to all
![]() $A_\lambda $
are continuous.
$A_\lambda $
are continuous.
Definition 4.4.2. Let
![]() $\kappa $
be a local or a finite field with its natural topology.
$\kappa $
be a local or a finite field with its natural topology.
-
(a) We say that a commutative topological ring A is
 $\kappa $
-admissible if there is an inverse system
$\kappa $
-admissible if there is an inverse system
 $(A_\lambda )_{\lambda \in J}$
as above expression (19) and an isomorphism of topological rings
$(A_\lambda )_{\lambda \in J}$
as above expression (19) and an isomorphism of topological rings
 $A\cong \lim _{\lambda \in J}A_\lambda $
such that each
$A\cong \lim _{\lambda \in J}A_\lambda $
such that each
 $A_\lambda $
is a finite-dimensional topological
$A_\lambda $
is a finite-dimensional topological
 $\kappa $
-algebra with the natural topology of a finite-dimensional
$\kappa $
-algebra with the natural topology of a finite-dimensional
 $\kappa $
-vector space.
$\kappa $
-vector space. -
(b) We denote by
 ${\mathcal {A}dm}_\kappa $
the category whose objects are
${\mathcal {A}dm}_\kappa $
the category whose objects are
 $\kappa $
-admissible commutative topological rings and whose morphisms are continuous
$\kappa $
-admissible commutative topological rings and whose morphisms are continuous
 $\kappa $
-algebra homomorphisms.
$\kappa $
-algebra homomorphisms.
Note that
![]() ${\widehat {\mathcal {A}}r}_\kappa $
is a full subcategory of
${\widehat {\mathcal {A}}r}_\kappa $
is a full subcategory of
![]() ${\mathcal {A}dm}_\kappa $
, but objects in
${\mathcal {A}dm}_\kappa $
, but objects in
![]() ${\mathcal {A}dm}_\kappa $
are in general only semilocal and with residue field of finite
${\mathcal {A}dm}_\kappa $
are in general only semilocal and with residue field of finite
![]() $\kappa $
-dimension.
$\kappa $
-dimension.
Definition 4.4.3 [Reference ChenevierChe14, § 3.9].
Let
![]() $W({{\mathbb {F}}\,\!{}})$
be the topological ring of Witt vectors over
$W({{\mathbb {F}}\,\!{}})$
be the topological ring of Witt vectors over
![]() ${{\mathbb {F}}\,\!{}}$
.
${{\mathbb {F}}\,\!{}}$
.
-
(a) A commutative topological ring A is admissible if there is an inverse system
 $(A_\lambda )_{\lambda \in J}$
as above expression (19) and an isomorphism of topological rings
$(A_\lambda )_{\lambda \in J}$
as above expression (19) and an isomorphism of topological rings
 $A\cong \lim _{\lambda \in J}A_\lambda $
such that each
$A\cong \lim _{\lambda \in J}A_\lambda $
such that each
 $A_\lambda $
carries the discrete topology.
$A_\lambda $
carries the discrete topology. -
(b) We denote by
 ${\mathcal {A}dm}_{{{W({{\mathbb {F}}\,\!{}})}}}$
the category whose objects are admissible commutative topological rings A together with a continuous homomorphism
${\mathcal {A}dm}_{{{W({{\mathbb {F}}\,\!{}})}}}$
the category whose objects are admissible commutative topological rings A together with a continuous homomorphism
 ${{W({{\mathbb {F}}\,\!{}})}} \to A$
and whose morphisms are continuous
${{W({{\mathbb {F}}\,\!{}})}} \to A$
and whose morphisms are continuous
 ${{W({{\mathbb {F}}\,\!{}})}}$
-algebra homomorphisms.
${{W({{\mathbb {F}}\,\!{}})}}$
-algebra homomorphisms.
Remark 4.4.4. Suppose A is admissible or
![]() $\kappa $
-admissible, and suppose that
$\kappa $
-admissible, and suppose that
![]() $A=\lim _{\lambda \in J}A_\lambda $
for an inverse system
$A=\lim _{\lambda \in J}A_\lambda $
for an inverse system
![]() $(A_\lambda )_{\lambda \in J}$
as in the above definitions. Then one can form the completed group ring as the inverse limit
$(A_\lambda )_{\lambda \in J}$
as in the above definitions. Then one can form the completed group ring as the inverse limit
where H ranges over all open normal subgroups of G; it contains
![]() $A[G]$
and is in fact the completion of
$A[G]$
and is in fact the completion of
![]() $A[G]$
with respect to the topology of
$A[G]$
with respect to the topology of
![]() $A[G]$
inherited from
$A[G]$
inherited from
![]() $A[[G]]$
.
$A[[G]]$
.
Using Amitsur’s formula, one can verify that the above definition of continuity is equivalent to the condition that for every commutative topological A-algebra B, with
![]() $B\in {\mathcal {A}dm}$
or
$B\in {\mathcal {A}dm}$
or
![]() ${\mathcal {A}dm}_\kappa $
, respectively, the map
${\mathcal {A}dm}_\kappa $
, respectively, the map
![]() $D_B\colon B[G] \to B$
is continuous; see [Reference Wang EricksonWE13, Definition 3.1.0.10]. This allows one also to extend
$D_B\colon B[G] \to B$
is continuous; see [Reference Wang EricksonWE13, Definition 3.1.0.10]. This allows one also to extend
![]() ${D}_B$
to a (continuous) pseudocharacter
${D}_B$
to a (continuous) pseudocharacter
![]() $B[[G]]\to B$
.
$B[[G]]\to B$
.
The following is the basic result on continuity if A is discrete.
Lemma 4.4.5 [Reference ChenevierChe14, Lemma 2.33].
Let A be a discrete, and let
![]() ${D}\colon A[G]\to A$
be a pseudocharacter. Then
${D}\colon A[G]\to A$
be a pseudocharacter. Then
![]() ${D}$
is continuous if and only if
${D}$
is continuous if and only if
![]() ${\operatorname {ker}{({D})}}$
is contained in the kernel of the canonical map
${\operatorname {ker}{({D})}}$
is contained in the kernel of the canonical map
![]() $A[G]\to A[G/H]$
for some normal open subgroup
$A[G]\to A[G/H]$
for some normal open subgroup
![]() $H\subset G$
. In this case, the natural representation
$H\subset G$
. In this case, the natural representation
![]() $G \longrightarrow ({B}[G]/{\operatorname {ker}{({D})}})^\times $
factors through
$G \longrightarrow ({B}[G]/{\operatorname {ker}{({D})}})^\times $
factors through
![]() $G/H$
.
$G/H$
.
We record the following consequence:
Corollary 4.4.6 [Reference ChenevierChe14, Example 2.34].
Let k be a discrete field, and let
![]() ${D}\in {\mathcal {P}s\mathcal {R}}^n_G({{{k}}^{\mathrm {alg}}} )$
be continuous. Then the representation
${D}\in {\mathcal {P}s\mathcal {R}}^n_G({{{k}}^{\mathrm {alg}}} )$
be continuous. Then the representation
![]() $\rho _{{D}} \colon G_K\to {\mathrm {GL}}_n({{{k}}^{\mathrm {alg}}} )$
associated by Theorem 4.1.18 is continuous, its image is finite and it is defined over a finite extension of k.
$\rho _{{D}} \colon G_K\to {\mathrm {GL}}_n({{{k}}^{\mathrm {alg}}} )$
associated by Theorem 4.1.18 is continuous, its image is finite and it is defined over a finite extension of k.
Proof. We provide a proof, expanding on [Reference ChenevierChe14, Example 2.34]: Because
![]() ${D}$
is continuous, we know by Lemma 4.4.5 that
${D}$
is continuous, we know by Lemma 4.4.5 that
![]() ${\operatorname {ker}{{D}}} $
contains the kernel of
${\operatorname {ker}{{D}}} $
contains the kernel of
![]() $k[G]\to k[G/H]$
for some open subgroup H of G. By Theorem 4.1.18, the kernels of
$k[G]\to k[G/H]$
for some open subgroup H of G. By Theorem 4.1.18, the kernels of
![]() $\rho _{D}^{\mathrm {lin}}$
and of
$\rho _{D}^{\mathrm {lin}}$
and of
![]() ${D}$
are the same, and hence
${D}$
are the same, and hence
![]() $\rho _{D}$
is continuous since it is trivial on the open subgroup H. Since
$\rho _{D}$
is continuous since it is trivial on the open subgroup H. Since
![]() $G/H$
is finite, this also shows that
$G/H$
is finite, this also shows that
![]() $\rho _{D}(G)\subset {\mathrm {GL}}_n({{{k}}^{\mathrm {alg}}} )$
is finite. It follows that the entries of the matrices in the image of
$\rho _{D}(G)\subset {\mathrm {GL}}_n({{{k}}^{\mathrm {alg}}} )$
is finite. It follows that the entries of the matrices in the image of
![]() $\rho _{D}$
lie in a finite extension of k, and this proves the last assertion.
$\rho _{D}$
lie in a finite extension of k, and this proves the last assertion.
When combined with earlier results, we deduce the following finiteness statement:
Proposition 4.4.7. Let
![]() ${{\mathbb {F}}\,\!{}}$
be a finite field of characteristic p, and let
${{\mathbb {F}}\,\!{}}$
be a finite field of characteristic p, and let
![]() $n\ge 1$
be an integer. Then there exist only finitely many continuous pseudocharacters
$n\ge 1$
be an integer. Then there exist only finitely many continuous pseudocharacters
![]() ${\overline {{D}}}\colon G_K\to {{\mathbb {F}}\,\!{}}$
on
${\overline {{D}}}\colon G_K\to {{\mathbb {F}}\,\!{}}$
on
![]() $G_K$
of dimension n.
$G_K$
of dimension n.
Denote by
![]() ${{\mathbb {F}}\,\!{}}'\supset {{\mathbb {F}}\,\!{}}$
the unique field extension of degree
${{\mathbb {F}}\,\!{}}'\supset {{\mathbb {F}}\,\!{}}$
the unique field extension of degree
![]() $n!$
. Then for any
$n!$
. Then for any
![]() ${\overline {{D}}}$
as above
${\overline {{D}}}$
as above
![]() ${\overline {{D}}}\otimes _{{\mathbb {F}}\,\!{}}{{\mathbb {F}}\,\!{}}'$
is a direct sum of split irreducible pseudocharacters
${\overline {{D}}}\otimes _{{\mathbb {F}}\,\!{}}{{\mathbb {F}}\,\!{}}'$
is a direct sum of split irreducible pseudocharacters
![]() ${\overline {{D}}}_i\colon G_K\to {{\mathbb {F}}\,\!{}}'$
on
${\overline {{D}}}_i\colon G_K\to {{\mathbb {F}}\,\!{}}'$
on
![]() $G_K$
.
$G_K$
.
Proof. The second part is immediate from Corollary 4.1.20. Hence, it suffices to prove the first part for split irreducible
![]() ${\overline {{D}}}$
. It moreover suffices to assume that
${\overline {{D}}}$
. It moreover suffices to assume that
![]() ${{\mathbb {F}}\,\!{}}$
contains the unique extension of the residue field of K of degree
${{\mathbb {F}}\,\!{}}$
contains the unique extension of the residue field of K of degree
![]() $n!$
. The result follows from Lemma A.3.1.
$n!$
. The result follows from Lemma A.3.1.
The next result shows the existence of a minimal ring of definition for any continuous pseudocharacter, and it gives an important result on their structure.
Lemma 4.4.8 [Reference ChenevierChe14, Lemma 3.10].
Let A be in
![]() ${\mathcal {A}dm}_{{{W({{\mathbb {F}}\,\!{}})}}}$
, let
${\mathcal {A}dm}_{{{W({{\mathbb {F}}\,\!{}})}}}$
, let
![]() ${D}\colon A[G]\to A$
be a continuous pseudocharacter and let
${D}\colon A[G]\to A$
be a continuous pseudocharacter and let
![]() $C \subset A$
be the closure of the
$C \subset A$
be the closure of the
![]() $W({{\mathbb {F}}\,\!{}})$
-algebra generated by the characteristic polynomial coefficients
$W({{\mathbb {F}}\,\!{}})$
-algebra generated by the characteristic polynomial coefficients
![]() $\Lambda _{{D},i}(g)$
for
$\Lambda _{{D},i}(g)$
for
![]() $g \in G$
and
$g \in G$
and
![]() $i\ge 1$
.
$i\ge 1$
.
-
(a) The ring C is an admissible profinite subring of A. In particular,
 $C=\varprojlim _{i}C_i$
is a finite product of local
$C=\varprojlim _{i}C_i$
is a finite product of local
 $W({{\mathbb {F}}\,\!{}})$
-algebras with finite residue fields.
$W({{\mathbb {F}}\,\!{}})$
-algebras with finite residue fields. -
(b) If further
 $\iota \colon A \longrightarrow A'$
is a continuous
$\iota \colon A \longrightarrow A'$
is a continuous
 $W({{\mathbb {F}}\,\!{}})$
-algebra homomorphism,
$W({{\mathbb {F}}\,\!{}})$
-algebra homomorphism,
 ${D}'\colon A'[G]\to A'$
is the induced pseudocharacter and
${D}'\colon A'[G]\to A'$
is the induced pseudocharacter and
 $C' \subset A'$
is the closure
$C' \subset A'$
is the closure
 $C' \subset A'$
of the
$C' \subset A'$
of the
 $W({{\mathbb {F}}\,\!{}})$
-algebra generated by the characteristic polynomial coefficients
$W({{\mathbb {F}}\,\!{}})$
-algebra generated by the characteristic polynomial coefficients
 $\Lambda _{{D}',i}(g)$
for
$\Lambda _{{D}',i}(g)$
for
 $g \in G$
and
$g \in G$
and
 $i\ge 1$
, then
$i\ge 1$
, then
 $\iota $
induces a surjection
$\iota $
induces a surjection
 $C \to C'$
in
$C \to C'$
in
 ${\mathcal {A}dm}_{{W({{\mathbb {F}}\,\!{}})}}$
.
${\mathcal {A}dm}_{{W({{\mathbb {F}}\,\!{}})}}$
.
We use the Lemma 4.4.8 to make the following useful definitions.
Definition 4.4.9 [Reference ChenevierChe14, Definition 3.11].
For a finite field
![]() ${{\mathbb {F}}\,\!{}}$
, one defines
${{\mathbb {F}}\,\!{}}$
, one defines
Definition 4.4.10 [Reference ChenevierChe14, Definition 3.12].
Let A be in
![]() ${\mathcal {A}dm}_{{W({{\mathbb {F}}\,\!{}})}}$
, let
${\mathcal {A}dm}_{{W({{\mathbb {F}}\,\!{}})}}$
, let
![]() ${D}\in {\mathcal {P}s\mathcal {R}}^n_G(A)$
be continuous, let
${D}\in {\mathcal {P}s\mathcal {R}}^n_G(A)$
be continuous, let
![]() $C \subset A$
be the ring from Lemma 4.4.8 and let
$C \subset A$
be the ring from Lemma 4.4.8 and let
![]() ${D}_C\colon C[G]\to C$
be the pseudocharacter from Proposition 4.1.10.
${D}_C\colon C[G]\to C$
be the pseudocharacter from Proposition 4.1.10.
-
(a) We call C the ring of definition of
 ${D}$
over
${D}$
over
 ${{W({{\mathbb {F}}\,\!{}})}}$
.
${{W({{\mathbb {F}}\,\!{}})}}$
. -
(b) If C is local so that
 ${\kappa ({C})} $
is finite, one calls
${\kappa ({C})} $
is finite, one calls
 ${D}$
residually constant.
${D}$
residually constant. -
(c) One calls
 ${D}$
residually equal to
${D}$
residually equal to
 $D_z$
for some
$D_z$
for some
 $z\in |G(n)|$
, if C is local and
$z\in |G(n)|$
, if C is local and
 ${D}_z\cong {D}_C\otimes _C{\kappa ({C})} $
.
${D}_z\cong {D}_C\otimes _C{\kappa ({C})} $
.
4.5 Twisting of pseudocharacters
In this subsection, we introduce a twisting operation for pseudocharacters that is the analog of the twist of a representation by a character, and we state some of its basic properties. Our approach require us to recall a number of results on the universal pseudocharacter that go back to Roby. Our main construction is only carried out for pseudocharacter of a topological group G. Our exposition of background material follows [Reference Wang EricksonWE13, Section 1.1].
Definition 4.4.11. Let M be an A-module. The divided power algebra of M relative to A is the commutative A-algebra
![]() $\Gamma _A(M)$
that is the quotient algebra of the polynomial algebra generated by the symbols
$\Gamma _A(M)$
that is the quotient algebra of the polynomial algebra generated by the symbols
![]() $m^{[i]}$
,
$m^{[i]}$
,
![]() $m\in M$
,
$m\in M$
,
![]() $i\in {\mathbb {N}}$
, subject to the relations
$i\in {\mathbb {N}}$
, subject to the relations
-
(i)
 $m^{[0]}=1$
for all
$m^{[0]}=1$
for all
 $m\in M$
,
$m\in M$
, -
(ii)
 $(am)^{[i]}=a^i m^{[i]}$
for
$(am)^{[i]}=a^i m^{[i]}$
for
 $a\in A$
,
$a\in A$
,
 $m\in M$
,
$m\in M$
,
 $i\in {\mathbb {N}}$
,
$i\in {\mathbb {N}}$
, -
(iii)
 $m^{[i]}m^{[j]}=\binom {i+j}i m^{[i+j]}$
for
$m^{[i]}m^{[j]}=\binom {i+j}i m^{[i+j]}$
for
 $m\in M$
,
$m\in M$
,
 $i,j\in {\mathbb {N}}$
and
$i,j\in {\mathbb {N}}$
and -
(iv)
 $(m+n)^{[i]}=\sum _{j=0}^i m^{[j]}n^{[i-j]}$
for
$(m+n)^{[i]}=\sum _{j=0}^i m^{[j]}n^{[i-j]}$
for
 $m,n\in M$
and
$m,n\in M$
and
 $i\in {\mathbb {N}}$
,
$i\in {\mathbb {N}}$
,
The ring
![]() $\Gamma _A(M)$
is a graded A-algebra
$\Gamma _A(M)$
is a graded A-algebra
![]() $\Gamma _A(M)=\bigoplus _{i\ge 0}\Gamma _A^i(M)$
with its i-th graded piece
$\Gamma _A(M)=\bigoplus _{i\ge 0}\Gamma _A^i(M)$
with its i-th graded piece
![]() $\Gamma ^i_A(M)$
being the A-module generated by the element
$\Gamma ^i_A(M)$
being the A-module generated by the element
![]() $m^{[i]}$
,
$m^{[i]}$
,
![]() $m\in M$
. The construction
$m\in M$
. The construction
![]() $M\mapsto \Gamma _A(M)$
defines a functor from A-modules to graded A-algebras. If
$M\mapsto \Gamma _A(M)$
defines a functor from A-modules to graded A-algebras. If
![]() ${\varphi }\colon M\to N$
is an A-module homomorphism, the induced map
${\varphi }\colon M\to N$
is an A-module homomorphism, the induced map
![]() $\Gamma _A({\varphi })\colon \Gamma _A(M)\to \Gamma _A(N)$
is characterized by
$\Gamma _A({\varphi })\colon \Gamma _A(M)\to \Gamma _A(N)$
is characterized by
![]() $m^{[i]}\mapsto ({\varphi }(m))^{[i]}$
,
$m^{[i]}\mapsto ({\varphi }(m))^{[i]}$
,
![]() $m\in M$
,
$m\in M$
,
![]() $i\in {\mathbb {N}}$
. One has compatibility with base change, that is, natural isomorphisms
$i\in {\mathbb {N}}$
. One has compatibility with base change, that is, natural isomorphisms
![]() $\Gamma _A^d(M)\otimes _AB\cong \Gamma ^d_B(M\otimes _AB)$
.
$\Gamma _A^d(M)\otimes _AB\cong \Gamma ^d_B(M\otimes _AB)$
.
Definition 4.5.2. The universal degree d homogenous polynomial law
![]() $L^d_M\in {\cal P}^d_A(M,\Gamma _A^d(M))$
is defined by the maps
$L^d_M\in {\cal P}^d_A(M,\Gamma _A^d(M))$
is defined by the maps
The universality of
![]() $L^d$
is expressed by the following result:
$L^d$
is expressed by the following result:
Theorem 4.5.3 [Reference RobyRob63, Théorème IV.1].
Let M, N be two A-modules, and let d be in
![]() ${\mathbb {N}}$
. There is a canonical isomorphism
${\mathbb {N}}$
. There is a canonical isomorphism
To describe the map in the converse direction, let
![]() $P\in {\cal P}^d_A(M,N)$
. Define the index set
$P\in {\cal P}^d_A(M,N)$
. Define the index set
![]() $I_d:=\{ \alpha =(\alpha _1,\ldots ,\alpha _d)\in {\mathbb {N}}^d\mid \sum \alpha _i=d \}$
. Given
$I_d:=\{ \alpha =(\alpha _1,\ldots ,\alpha _d)\in {\mathbb {N}}^d\mid \sum \alpha _i=d \}$
. Given
![]() $\alpha =(\alpha _1,\ldots ,\alpha _d)\in I_d$
set
$\alpha =(\alpha _1,\ldots ,\alpha _d)\in I_d$
set
![]() $T^\alpha =\prod _{j=1}^d T_j^{\alpha _j}$
for indeterminates
$T^\alpha =\prod _{j=1}^d T_j^{\alpha _j}$
for indeterminates
![]() $(T_1,\ldots ,T_d)$
, and set
$(T_1,\ldots ,T_d)$
, and set
![]() $m^{[\alpha ]}= \prod _{j=1}^d m_i^{[\alpha _i]}\in \Gamma _A^d(M)$
for
$m^{[\alpha ]}= \prod _{j=1}^d m_i^{[\alpha _i]}\in \Gamma _A^d(M)$
for
![]() $m=(m_1,\ldots ,m_d)\in M^d$
. Define now for all
$m=(m_1,\ldots ,m_d)\in M^d$
. Define now for all
![]() $\alpha \in I_d$
simultaneously maps
$\alpha \in I_d$
simultaneously maps
![]() $P^{[\alpha ]} \colon M^d\to N$
by
$P^{[\alpha ]} \colon M^d\to N$
by
for
![]() $m=(m_1,\ldots ,m_d)\in M^d$
. In the proof of Theorem 4.5.3 by Roby, it is shown that given any
$m=(m_1,\ldots ,m_d)\in M^d$
. In the proof of Theorem 4.5.3 by Roby, it is shown that given any
![]() $P\in {\cal P}^d_A(M,N)$
, there exists an A-module homomorphism
$P\in {\cal P}^d_A(M,N)$
, there exists an A-module homomorphism
![]() $f \colon \Gamma ^d_A(M)\to N$
such that
$f \colon \Gamma ^d_A(M)\to N$
such that
and that
![]() $f\circ L^d_M=P$
.
$f\circ L^d_M=P$
.
If M is a free A-module, the A-module
![]() $\Gamma _A^d(M)$
has the following explicit description.
$\Gamma _A^d(M)$
has the following explicit description.
Theorem 4.5.4 [Reference RobyRob63, Théorème IV.2].
Suppose that M is a free A-module with basis
![]() $(e_i)_{i\in I}$
. Then for
$(e_i)_{i\in I}$
. Then for
![]() $d\in {\mathbb {N}}$
, the A-module
$d\in {\mathbb {N}}$
, the A-module
![]() $\Gamma ^d_A(M)$
is free with basis
$\Gamma ^d_A(M)$
is free with basis
 $$ \begin{align*}\Big\{ e_{i_1}^{[k_1]}\cdot\ldots\cdot e_{i_j}^{[k_h]}\mid h\in{\mathbb{N}}, (i_1,\ldots,i_h)\in I^h, (k_1,\ldots,k_h)\in{\mathbb{N}_{\geq 1}}, \sum_{j=1}^h k_h=d\Big\}.\end{align*} $$
$$ \begin{align*}\Big\{ e_{i_1}^{[k_1]}\cdot\ldots\cdot e_{i_j}^{[k_h]}\mid h\in{\mathbb{N}}, (i_1,\ldots,i_h)\in I^h, (k_1,\ldots,k_h)\in{\mathbb{N}_{\geq 1}}, \sum_{j=1}^h k_h=d\Big\}.\end{align*} $$
If M is an A-algebra R, then [Reference RobyRob80] defines an A-algebra structure on each
![]() $\Gamma ^d_A(R)$
, different from that on
$\Gamma ^d_A(R)$
, different from that on
![]() $\Gamma _A(R)$
, by defining a multiplication
$\Gamma _A(R)$
, by defining a multiplication
![]() $\Gamma _A^d(R)\otimes _A\Gamma _A^d(R)\to \Gamma _A^d(R)$
, that we now recall. The multiplication map is defined as the composition of two maps. The first map exists for any A-module M, the second is built from the ring structure of R. Let first M be an arbitrary A-module. Then the map
$\Gamma _A^d(R)\otimes _A\Gamma _A^d(R)\to \Gamma _A^d(R)$
, that we now recall. The multiplication map is defined as the composition of two maps. The first map exists for any A-module M, the second is built from the ring structure of R. Let first M be an arbitrary A-module. Then the map
![]() $\beta _M\colon M\oplus M\to M\otimes _AM, (m,m')\mapsto m\otimes m'$
is a homogeneous polynomial law of degree
$\beta _M\colon M\oplus M\to M\otimes _AM, (m,m')\mapsto m\otimes m'$
is a homogeneous polynomial law of degree
![]() $2$
, and thus
$2$
, and thus
![]() $L^d_{M\otimes M}\circ \beta _M$
lies in
$L^d_{M\otimes M}\circ \beta _M$
lies in
![]() ${\cal P}^{2d}_A(M\oplus M,M\otimes M)$
. By Theorem 4.5.3, we have
${\cal P}^{2d}_A(M\oplus M,M\otimes M)$
. By Theorem 4.5.3, we have
![]() $L^d_{M\otimes M}\circ \beta _M=\eta _M\circ L^{2d}_{M\oplus M}$
for a unique A-linear map
$L^d_{M\otimes M}\circ \beta _M=\eta _M\circ L^{2d}_{M\oplus M}$
for a unique A-linear map
[Reference RobyRob63, Théorème III.4] gives an isomorphism
![]() $\bigoplus _{i=0}^e \Gamma _A^i(M)\otimes \Gamma _A^{e-i}(M)\to \Gamma _A^e(M)$
for any
$\bigoplus _{i=0}^e \Gamma _A^i(M)\otimes \Gamma _A^{e-i}(M)\to \Gamma _A^e(M)$
for any
![]() $e\in {\mathbb {N}}$
. It is further shown in [Reference RobyRob80, p. 869] that the maps
$e\in {\mathbb {N}}$
. It is further shown in [Reference RobyRob80, p. 869] that the maps
![]() $\Gamma _A^i(M)\otimes \Gamma _A^{2d-i}(M)\to \Gamma ^d_A(M\otimes M)$
induced from
$\Gamma _A^i(M)\otimes \Gamma _A^{2d-i}(M)\to \Gamma ^d_A(M\otimes M)$
induced from
![]() $\eta _M$
are zero for
$\eta _M$
are zero for
![]() $i\neq d$
, and that the induced map
$i\neq d$
, and that the induced map
![]() $\widetilde {\eta }_M\colon \Gamma _A^d(M)\otimes \Gamma _A^{d}(M)\to \Gamma ^d_A(M\otimes M)$
is given by the explicit formula
$\widetilde {\eta }_M\colon \Gamma _A^d(M)\otimes \Gamma _A^{d}(M)\to \Gamma ^d_A(M\otimes M)$
is given by the explicit formula
 $$ \begin{align} \widetilde{\eta}_M\big( m^{[\alpha]}\otimes n^{[\beta]}\big)= \sum_{\gamma\in {\mathrm{Mat}}_{d\times d}^{\alpha,\beta}({\mathbb{N}})} \prod_{(i,j)\in\{1,\ldots,d\}^2} (m_i\otimes n_j)^{[\gamma_{ij}]}, \end{align} $$
$$ \begin{align} \widetilde{\eta}_M\big( m^{[\alpha]}\otimes n^{[\beta]}\big)= \sum_{\gamma\in {\mathrm{Mat}}_{d\times d}^{\alpha,\beta}({\mathbb{N}})} \prod_{(i,j)\in\{1,\ldots,d\}^2} (m_i\otimes n_j)^{[\gamma_{ij}]}, \end{align} $$
for
![]() $m,n\in M^d$
,
$m,n\in M^d$
,
![]() $\alpha ,\beta \in I_d$
, and where
$\alpha ,\beta \in I_d$
, and where
![]() ${\mathrm {Mat}}_{d\times d}^{\alpha ,\beta }({\mathbb {N}})$
denotes the set of all matrices
${\mathrm {Mat}}_{d\times d}^{\alpha ,\beta }({\mathbb {N}})$
denotes the set of all matrices
![]() $\gamma =(\gamma _{ij})$
in
$\gamma =(\gamma _{ij})$
in
![]() ${\mathrm {Mat}}_{d\times d}({\mathbb {N}})$
whose rows sum to
${\mathrm {Mat}}_{d\times d}({\mathbb {N}})$
whose rows sum to
![]() $\beta $
and whose columns sum to
$\beta $
and whose columns sum to
![]() $\alpha $
. Let now
$\alpha $
. Let now
![]() $M=R$
be an A-algebra. Then the multiplication map
$M=R$
be an A-algebra. Then the multiplication map
![]() $\mu _R\colon R\otimes _AR\to R$
is A-linear, and thus it induces a graded map
$\mu _R\colon R\otimes _AR\to R$
is A-linear, and thus it induces a graded map
![]() $\Gamma _A(\mu _R)$
whose d-th graded piece is a homomorphism
$\Gamma _A(\mu _R)$
whose d-th graded piece is a homomorphism
![]() $\Gamma _A^d(\mu _R)\colon \Gamma _A^d(R\otimes R)\to \Gamma _A^d(R)$
. Roby defines
$\Gamma _A^d(\mu _R)\colon \Gamma _A^d(R\otimes R)\to \Gamma _A^d(R)$
. Roby defines
It is shown in [Reference RobyRob80, p. 870] that if R is unital, associative or commutative, respectively, then the same property holds for
![]() $\Gamma _A^d(R)$
with the multiplication
$\Gamma _A^d(R)$
with the multiplication
![]() $\mu _R^d$
, for any
$\mu _R^d$
, for any
![]() $d\in {\mathbb {N}}$
. It turns out that
$d\in {\mathbb {N}}$
. It turns out that
![]() $L^d_R$
is multiplicative with respect to this multiplication on
$L^d_R$
is multiplicative with respect to this multiplication on
![]() $\Gamma _A^d(R)$
. The key result is the following description of multiplicative polynomial laws:
$\Gamma _A^d(R)$
. The key result is the following description of multiplicative polynomial laws:
Theorem 4.5.5 [Reference RobyRob80, Théorème].
For A-algebras S,
![]() $S'$
, the following map is a bijection
$S'$
, the following map is a bijection
Suppose now that
![]() $R=A[G]$
for a group G. Note that the elements of G form an A-basis of
$R=A[G]$
for a group G. Note that the elements of G form an A-basis of
![]() $A[G]$
, and hence an A-basis of
$A[G]$
, and hence an A-basis of
![]() $\Gamma _A^n(A[G])$
is described in Theorem 4.5.4. Let
$\Gamma _A^n(A[G])$
is described in Theorem 4.5.4. Let
![]() ${D}\colon A[G]\to A$
be a pseudocharacter of dimension d. From Theorems 4.5.3 and 4.5.5 and using equation (20), we deduce:
${D}\colon A[G]\to A$
be a pseudocharacter of dimension d. From Theorems 4.5.3 and 4.5.5 and using equation (20), we deduce:
Proposition 4.5.6. There exists a unique homomorphism
![]() $f_{D}\colon \Gamma _A^d(A[G])\to A$
such that
$f_{D}\colon \Gamma _A^d(A[G])\to A$
such that
It is multiplicative for the product on
![]() $\Gamma _A^d(A[G])$
given by
$\Gamma _A^d(A[G])$
given by
![]() $\mu _{A[G]}^d$
.
$\mu _{A[G]}^d$
.
Let now
![]() $\chi \colon G\to A^\times $
be a group homomorphism. Define for
$\chi \colon G\to A^\times $
be a group homomorphism. Define for
![]() $\alpha =(\alpha _1,\ldots ,\alpha _d)$
and
$\alpha =(\alpha _1,\ldots ,\alpha _d)$
and
![]() $g=(g_1,\ldots ,g_d)\in G^d$
the notation
$g=(g_1,\ldots ,g_d)\in G^d$
the notation
![]() $\chi (g^{[\alpha ]})$
to by
$\chi (g^{[\alpha ]})$
to by
![]() $\chi (g^{[\alpha ]}):=\prod _{i=1}^d \chi (g_i)^{\alpha _i}$
. Because
$\chi (g^{[\alpha ]}):=\prod _{i=1}^d \chi (g_i)^{\alpha _i}$
. Because
![]() $\{g^{[\alpha ]}\mid \alpha \in I_d,g \in G^d \}$
is a basis of
$\{g^{[\alpha ]}\mid \alpha \in I_d,g \in G^d \}$
is a basis of
![]() $\Gamma _A^d(A[G])$
we have a unique A-linear map
$\Gamma _A^d(A[G])$
we have a unique A-linear map
![]() $f_{{D},\chi }\colon \Gamma _A^d(A[G])\to A$
such that
$f_{{D},\chi }\colon \Gamma _A^d(A[G])\to A$
such that
Proposition 4.5.7. Suppose that
![]() ${D}\in {\mathcal {P}s\mathcal {R}}_G^n(A)$
and that
${D}\in {\mathcal {P}s\mathcal {R}}_G^n(A)$
and that
![]() $\chi \colon G\to A^\times $
is a group homomorphism. Then the following hold:
$\chi \colon G\to A^\times $
is a group homomorphism. Then the following hold:
-
(a) The map
 $f_{{D},\chi }$
defined above is multiplicative.
$f_{{D},\chi }$
defined above is multiplicative.
Define the d-dimensional pseudocharacter
![]() ${D}\otimes \chi $
to be
${D}\otimes \chi $
to be
![]() $f_{{D},\chi }\circ L^d_{A[G]}$
.
$f_{{D},\chi }\circ L^d_{A[G]}$
.
-
(b) The characteristic polynomial coefficients of
 ${D}\otimes \chi $
satisfy the identities
${D}\otimes \chi $
satisfy the identities  $$ \begin{align*} \Lambda_{D\otimes \chi,i}(g)=\Lambda_{{D},i}(g)\cdot \chi(g)^i\quad \mbox{ for all } i \mbox{ and all } g\in G. \end{align*} $$
$$ \begin{align*} \Lambda_{D\otimes \chi,i}(g)=\Lambda_{{D},i}(g)\cdot \chi(g)^i\quad \mbox{ for all } i \mbox{ and all } g\in G. \end{align*} $$
-
(c) If
 ${D}$
and
${D}$
and
 $\chi $
are continuous, then so is
$\chi $
are continuous, then so is
 ${D}\otimes \chi $
.
${D}\otimes \chi $
. -
(d) If
 ${D}={D}_\rho $
for a representation
${D}={D}_\rho $
for a representation
 $\rho $
of G, then
$\rho $
of G, then
 ${D}\otimes \chi ={D}_{\rho \otimes \chi }$
.
${D}\otimes \chi ={D}_{\rho \otimes \chi }$
.
Proof. To see Part (a), we need to show that
![]() $f_{{D},\chi }(g\cdot h)=f_{{D},\chi }(g) f_{{D},\chi }(h)$
for
$f_{{D},\chi }(g\cdot h)=f_{{D},\chi }(g) f_{{D},\chi }(h)$
for
![]() $g=(g_1,\ldots ,g_d), h=(h_1,\ldots ,h_d) \in G^d$
and for
$g=(g_1,\ldots ,g_d), h=(h_1,\ldots ,h_d) \in G^d$
and for
![]() $\cdot $
the multiplication given by
$\cdot $
the multiplication given by
![]() $\mu ^d_{A[G]}$
. Using equation (21), we compute
$\mu ^d_{A[G]}$
. Using equation (21), we compute
 $$ \begin{align*} g^{[\alpha]}\cdot h^{[\beta]}&= \mu^d_{A[G]}\Big(\widetilde{\eta}_M\big( g^{[\alpha]}\otimes h^{[\beta]}\big)\Big) \ = \ \mu^d_{A[G]} \Big( \sum_{\gamma\in {\mathrm{Mat}}_{d\times d}^{\alpha,\beta}({\mathbb{N}})} \prod_{(i,j)\in\{1,\ldots,d\}^2} (g_i\otimes h_j)^{[\gamma_{ij}]}\Big)\\ &= \sum_{\gamma\in {\mathrm{Mat}}_{d\times d}^{\alpha,\beta}({\mathbb{N}})} \prod_{(i,j)\in\{1,\ldots,d\}^2} (g_i h_j)^{[\gamma_{ij}]}.\\ \end{align*} $$
$$ \begin{align*} g^{[\alpha]}\cdot h^{[\beta]}&= \mu^d_{A[G]}\Big(\widetilde{\eta}_M\big( g^{[\alpha]}\otimes h^{[\beta]}\big)\Big) \ = \ \mu^d_{A[G]} \Big( \sum_{\gamma\in {\mathrm{Mat}}_{d\times d}^{\alpha,\beta}({\mathbb{N}})} \prod_{(i,j)\in\{1,\ldots,d\}^2} (g_i\otimes h_j)^{[\gamma_{ij}]}\Big)\\ &= \sum_{\gamma\in {\mathrm{Mat}}_{d\times d}^{\alpha,\beta}({\mathbb{N}})} \prod_{(i,j)\in\{1,\ldots,d\}^2} (g_i h_j)^{[\gamma_{ij}]}.\\ \end{align*} $$
Observe that
![]() $\sum _{i,j}\gamma _{ij}=d$
for
$\sum _{i,j}\gamma _{ij}=d$
for
![]() $\gamma \in {\mathrm {Mat}}_{d\times d}^{\alpha ,\beta }({\mathbb {N}})$
and that index pairs
$\gamma \in {\mathrm {Mat}}_{d\times d}^{\alpha ,\beta }({\mathbb {N}})$
and that index pairs
![]() $(i,j)$
with
$(i,j)$
with
![]() $\gamma _{ij}=0$
can be ignored. We write
$\gamma _{ij}=0$
can be ignored. We write
![]() ${\underline \gamma }$
for the flattening of
${\underline \gamma }$
for the flattening of
![]() $\gamma $
truncated to length d, that is, we first regard
$\gamma $
truncated to length d, that is, we first regard
![]() $\gamma $
as a
$\gamma $
as a
![]() $d^2$
-tuple in one index and then omit the highest
$d^2$
-tuple in one index and then omit the highest
![]() $d^2-d$
indices, where
$d^2-d$
indices, where
![]() $\gamma _{ij}=0$
. Using in
$\gamma _{ij}=0$
. Using in
![]() $(*)$
the definition of
$(*)$
the definition of
![]() ${\mathrm {Mat}}_{d\times d}^{\alpha ,\beta }({\mathbb {N}})$
, we find
${\mathrm {Mat}}_{d\times d}^{\alpha ,\beta }({\mathbb {N}})$
, we find
 $$ \begin{align*} f_{{D},\chi}(g^{[\alpha]}\cdot h^{[\beta]})&= \sum_{\gamma\in {\mathrm{Mat}}_{d\times d}^{\alpha,\beta}({\mathbb{N}})} f_{{D},\chi}\Big(\prod_{(i,j)\in\{1,\ldots,d\}^2} (g_i h_j)^{[\gamma_{ij}]}\Big)\\ &= \sum_{\gamma\in {\mathrm{Mat}}_{d\times d}^{\alpha,\beta}({\mathbb{N}})} D^{[{\underline\gamma}]} ((g_ih_j)_{(i,j)\in {\underline\gamma}}) \Big(\prod_{(i,j)\in\{1,\ldots,d\}^2}\chi(g_ih_j)^{\gamma_{ij}}\Big)\\ &\stackrel{(*)}= \sum_{\gamma\in {\mathrm{Mat}}_{d\times d}^{\alpha,\beta}({\mathbb{N}})} D^{[{\underline\gamma}]} ((g_ih_j)_{(i,j)\in {\underline\gamma}}) \chi(g^{[\alpha]})\chi(h^{[\beta]})\\ &=\chi(g^{[\alpha]})\chi(h^{[\beta]}) f_{{D}}(g^{[\alpha]}\cdot h^{[\beta]}) \\ &\stackrel{f_{{D}}\mathrm{\, multipl.}}= \chi(g^{[\alpha]})\chi(h^{[\beta]}) f_{{D}}(g^{[\alpha]}) f_{{D}}(h^{[\beta]}) \ = \ f_{{D},\chi}(g^{[\alpha]})f_{{D},\chi}(h^{[\beta]}). \end{align*} $$
$$ \begin{align*} f_{{D},\chi}(g^{[\alpha]}\cdot h^{[\beta]})&= \sum_{\gamma\in {\mathrm{Mat}}_{d\times d}^{\alpha,\beta}({\mathbb{N}})} f_{{D},\chi}\Big(\prod_{(i,j)\in\{1,\ldots,d\}^2} (g_i h_j)^{[\gamma_{ij}]}\Big)\\ &= \sum_{\gamma\in {\mathrm{Mat}}_{d\times d}^{\alpha,\beta}({\mathbb{N}})} D^{[{\underline\gamma}]} ((g_ih_j)_{(i,j)\in {\underline\gamma}}) \Big(\prod_{(i,j)\in\{1,\ldots,d\}^2}\chi(g_ih_j)^{\gamma_{ij}}\Big)\\ &\stackrel{(*)}= \sum_{\gamma\in {\mathrm{Mat}}_{d\times d}^{\alpha,\beta}({\mathbb{N}})} D^{[{\underline\gamma}]} ((g_ih_j)_{(i,j)\in {\underline\gamma}}) \chi(g^{[\alpha]})\chi(h^{[\beta]})\\ &=\chi(g^{[\alpha]})\chi(h^{[\beta]}) f_{{D}}(g^{[\alpha]}\cdot h^{[\beta]}) \\ &\stackrel{f_{{D}}\mathrm{\, multipl.}}= \chi(g^{[\alpha]})\chi(h^{[\beta]}) f_{{D}}(g^{[\alpha]}) f_{{D}}(h^{[\beta]}) \ = \ f_{{D},\chi}(g^{[\alpha]})f_{{D},\chi}(h^{[\beta]}). \end{align*} $$
Concerning (b), note that
 $$ \begin{align*}{D}_{A[T']}(1-Tg')={D}_{A[T_1,\ldots,T_d]}\Big(\sum_{i=1}^dT_ig_i\Big)|_{g=(e,\ldots,e,g'),T=(1,0,\ldots,0,T')}\end{align*} $$
$$ \begin{align*}{D}_{A[T']}(1-Tg')={D}_{A[T_1,\ldots,T_d]}\Big(\sum_{i=1}^dT_ig_i\Big)|_{g=(e,\ldots,e,g'),T=(1,0,\ldots,0,T')}\end{align*} $$
so that
 $$ \begin{align*} \Lambda_{{D}\otimes \chi,i}(g')&=(-1)^i ({D}\otimes\chi)^{[d-i,0,\ldots,0,i]}(e,\ldots,e,g')\\ &=(-1)^i {D}^{[d-i,0,\ldots,0,i]}(e,\ldots,e,g') \chi((e,\ldots,e,g')^{[d-i,0,\ldots,0,i]})\\ &=(-1)^i {D}^{[d-i,0,\ldots,0,i]}(e,\ldots,e,g') \chi(g)^i \ = \ \Lambda_{{D},i}(g') \chi(g)^i. \end{align*} $$
$$ \begin{align*} \Lambda_{{D}\otimes \chi,i}(g')&=(-1)^i ({D}\otimes\chi)^{[d-i,0,\ldots,0,i]}(e,\ldots,e,g')\\ &=(-1)^i {D}^{[d-i,0,\ldots,0,i]}(e,\ldots,e,g') \chi((e,\ldots,e,g')^{[d-i,0,\ldots,0,i]})\\ &=(-1)^i {D}^{[d-i,0,\ldots,0,i]}(e,\ldots,e,g') \chi(g)^i \ = \ \Lambda_{{D},i}(g') \chi(g)^i. \end{align*} $$
Part (c) follows from (b) and Definition 4.4.1, Part (d) follows from (b) and the theorem of Brauer–Nesbitt.
Definition 4.5.8 (Twist of pseudocharacters).
We call the multiplicative polynomial law
![]() ${D}\otimes \chi \in {\mathcal {P}s\mathcal {R}}_G^n(A)$
from Proposition 4.5.7 the twist of
${D}\otimes \chi \in {\mathcal {P}s\mathcal {R}}_G^n(A)$
from Proposition 4.5.7 the twist of
![]() ${D}$
by
${D}$
by
![]() $\chi $
.
$\chi $
.
Remark 4.5.9. It should be interesting to define the tensor product of two pseudocharacters of any dimensions
![]() $n,n'$
.
$n,n'$
.
Lemma 4.5.10. Let
![]() ${D},{D}'$
be in
${D},{D}'$
be in
![]() ${\mathcal {P}s\mathcal {R}}_G^n(A)$
, and let
${\mathcal {P}s\mathcal {R}}_G^n(A)$
, and let
![]() $\chi \colon G\to A^\times $
be a group homomorphism. Then
$\chi \colon G\to A^\times $
be a group homomorphism. Then
![]() ${D}'={D}\otimes \chi $
if and only if
${D}'={D}\otimes \chi $
if and only if
![]() $\Lambda _{{D}',i}(g)=\Lambda _{{D},i}(g)\cdot \chi (g)^i$
for all i and all
$\Lambda _{{D}',i}(g)=\Lambda _{{D},i}(g)\cdot \chi (g)^i$
for all i and all
![]() $g\in G$
.
$g\in G$
.
Proof. Proposition 4.5.7 (b) shows that the condition given is necessary. That it is also sufficient follows from Proposition 4.1.10 (a), which says that a pseudocharacter is determined by its characteristic polynomial coefficients.
Corollary 4.5.11. Let
![]() ${D}$
be in
${D}$
be in
![]() ${\mathcal {P}s\mathcal {R}}_G^n(A)$
, and let
${\mathcal {P}s\mathcal {R}}_G^n(A)$
, and let
![]() $\chi \colon G\to A^\times $
be a character of finite order. Suppose that
$\chi \colon G\to A^\times $
be a character of finite order. Suppose that
![]() $\chi (g)-1$
lies in
$\chi (g)-1$
lies in
![]() $A^\times $
whenever
$A^\times $
whenever
![]() $g\in G{\smallsetminus } {\operatorname {ker}{\chi }} $
. Then the following hold:
$g\in G{\smallsetminus } {\operatorname {ker}{\chi }} $
. Then the following hold:
-
(a)
 ${D}={D}\otimes \chi $
if and only if
${D}={D}\otimes \chi $
if and only if  $$ \begin{align*}\forall g\in G, \forall i=0,\ldots, n: \Lambda_{{D},i}(g) = 0 \mbox{ or } {\operatorname{ord}{{\chi(g)}}} \mbox{ divides } i. \end{align*} $$
$$ \begin{align*}\forall g\in G, \forall i=0,\ldots, n: \Lambda_{{D},i}(g) = 0 \mbox{ or } {\operatorname{ord}{{\chi(g)}}} \mbox{ divides } i. \end{align*} $$
-
(b) Let I be the ideal of A generated by the set
Then the locus of
 ${\mathrm {Spec}}\ A$
on which
${\mathrm {Spec}}\ A$
on which
 $D=D\otimes \chi $
is the closed subscheme
$D=D\otimes \chi $
is the closed subscheme
 ${\mathrm {Spec}}\ A/I$
.
${\mathrm {Spec}}\ A/I$
.
Proof. To see Part (a), note that by Lemma 4.5.10 we have
![]() ${D}={D}\otimes \chi $
if and only if
${D}={D}\otimes \chi $
if and only if
Since
![]() $1-\chi ^i(g)$
is a unit in
$1-\chi ^i(g)$
is a unit in
![]() $A^\times $
whenever
$A^\times $
whenever
![]() ${\operatorname {ord}{{\chi (g)}}} \nmid i$
and is zero otherwise, the latter is clearly equivalent to the condition given in the corollary.
${\operatorname {ord}{{\chi (g)}}} \nmid i$
and is zero otherwise, the latter is clearly equivalent to the condition given in the corollary.
By Part (a), we have for any ideal J of A
and this implies Part (b).
4.6 Induction for pseudocharacters
In this subsection, we introduce the operation of inducing a pseudocharacter from a finite index subgroup. The main result is Theorem 4.6.7. Following a suggestion of the referee, we describe a construction that works in all cases.Footnote 6 The idea is a pullback to a universal situation. For this, we use Theorem A.4.4 which is a variant of an important result of Vaccarino. The uniqueness of the construction, that is, its characterizing property, is guaranteed by explicit formulas for the characteristic polynomial of the induction. The present subsection begins by recalling the construction of induction of a representation and then analyzes it to give in Lemma 4.6.6 a formula for the resulting characteristic polynomial. This is then used in the main result, Theorem 4.6.7.
We fix a group G and a subgroup
![]() $H\subset G$
of finite index
$H\subset G$
of finite index
![]() ${m}$
. As in Section 2, we set
${m}$
. As in Section 2, we set
![]() $N:=\bigcap _{g\in G/H}H^g$
. It is of finite index and normal in G, and the largest such subgroup contained in H. If G is a profinite group, we require H to be open, and then
$N:=\bigcap _{g\in G/H}H^g$
. It is of finite index and normal in G, and the largest such subgroup contained in H. If G is a profinite group, we require H to be open, and then
![]() $N\subset G$
is open, as well.
$N\subset G$
is open, as well.
Lemma 4.6.1. Let C be an Azumaya A-algebra. Consider a representation
![]() $\rho \colon H\to C^\times $
. There exists a representation
$\rho \colon H\to C^\times $
. There exists a representation
![]() $\rho ^*\colon G\to {\mathrm {GL}}_{m}(C)^\times $
such that for any étale extension
$\rho ^*\colon G\to {\mathrm {GL}}_{m}(C)^\times $
such that for any étale extension
![]() $A\to A'$
that splits C, there is an isomorphism
$A\to A'$
that splits C, there is an isomorphism
![]() $\rho ^*\otimes _AA'\cong {\mathrm {Ind}}_H^G (\rho \otimes _AA')$
of G-representations over A.
$\rho ^*\otimes _AA'\cong {\mathrm {Ind}}_H^G (\rho \otimes _AA')$
of G-representations over A.
The linearization
![]() $(\rho ^*)^{\mathrm {lin}}\colon A[G]\to {\mathrm {Mat}}_{m\times m}(C)$
of
$(\rho ^*)^{\mathrm {lin}}\colon A[G]\to {\mathrm {Mat}}_{m\times m}(C)$
of
![]() $\rho ^*$
takes values in the Azumaya algebra
$\rho ^*$
takes values in the Azumaya algebra
![]() ${\mathrm {Mat}}_{m\times m}(C)$
, and by Example 4.1.7 the associated pseudocharacter
${\mathrm {Mat}}_{m\times m}(C)$
, and by Example 4.1.7 the associated pseudocharacter
![]() ${D}_{\rho ^*}$
takes values in A.
${D}_{\rho ^*}$
takes values in A.
Proof. To prove the lemma, we adapt the description of the induced matrix representation from [Reference Curtis and ReinerCR81, pp. 227-230] to the setting of Azumaya algebras. Let
![]() $g_1,\ldots ,g_m$
be a set of representatives of left cosets of
$g_1,\ldots ,g_m$
be a set of representatives of left cosets of
![]() $G/H$
so that
$G/H$
so that
![]() $G=\bigsqcup _{i=1}^m g_i H$
. We extend
$G=\bigsqcup _{i=1}^m g_i H$
. We extend
![]() $\rho $
from H to G by defining
$\rho $
from H to G by defining
 $$ \begin{align*}\widetilde{\rho}\colon G \,{\longrightarrow}\, C,\quad g\longmapsto\left\{ \begin{array}{rl} \rho(g)&\text{if }g\in H,\\ 0&\text{if }g\in G{\smallsetminus} H. \end{array} \right. \end{align*} $$
$$ \begin{align*}\widetilde{\rho}\colon G \,{\longrightarrow}\, C,\quad g\longmapsto\left\{ \begin{array}{rl} \rho(g)&\text{if }g\in H,\\ 0&\text{if }g\in G{\smallsetminus} H. \end{array} \right. \end{align*} $$
Consider the map
 $$ \begin{align*}\rho^*\colon G\,{\longrightarrow}\, {\mathrm{Mat}}_{m\times m}(C),\quad g\longmapsto\left( \begin{array}{ccc} \widetilde{\rho}(g_1^{-1} g g_1)&\cdots&\widetilde{\rho}(g_1^{-1} g g_m)\\ \vdots&\ddots&\vdots\\ \widetilde{\rho}(g_m^{-1} g g_1)&\cdots&\widetilde{\rho}(g_m^{-1} g g_m) \end{array}\right). \end{align*} $$
$$ \begin{align*}\rho^*\colon G\,{\longrightarrow}\, {\mathrm{Mat}}_{m\times m}(C),\quad g\longmapsto\left( \begin{array}{ccc} \widetilde{\rho}(g_1^{-1} g g_1)&\cdots&\widetilde{\rho}(g_1^{-1} g g_m)\\ \vdots&\ddots&\vdots\\ \widetilde{\rho}(g_m^{-1} g g_1)&\cdots&\widetilde{\rho}(g_m^{-1} g g_m) \end{array}\right). \end{align*} $$
Define for
![]() $g\in G$
and
$g\in G$
and
![]() $j\in \{1,\ldots ,m\}$
the element
$j\in \{1,\ldots ,m\}$
the element
![]() $i_j\in \{1,\ldots ,m\}$
by the condition
$i_j\in \{1,\ldots ,m\}$
by the condition
![]() $ gg_{j}H= g_{i_j} H$
so that the map
$ gg_{j}H= g_{i_j} H$
so that the map
![]() $j\mapsto i_j$
is a permutation of
$j\mapsto i_j$
is a permutation of
![]() $\{1,\ldots ,m\}$
. This shows that
$\{1,\ldots ,m\}$
. This shows that
![]() $\rho ^*(g)$
is a monomial matrix over the skew field C which in each column j has a unique nonzero entry
$\rho ^*(g)$
is a monomial matrix over the skew field C which in each column j has a unique nonzero entry
![]() $\rho (g_{i_j}^{-1} g g_j)\in C^\times $
in row
$\rho (g_{i_j}^{-1} g g_j)\in C^\times $
in row
![]() $i_j$
. In particular, this also shows that
$i_j$
. In particular, this also shows that
![]() $\rho ^*(g)$
lies in
$\rho ^*(g)$
lies in
![]() ${\mathrm {GL}}_m(C)$
.
${\mathrm {GL}}_m(C)$
.
We claim that
![]() $\rho ^*$
has the properties asserted in the lemma. Let
$\rho ^*$
has the properties asserted in the lemma. Let
![]() $A\to A'$
be finite étale so that
$A\to A'$
be finite étale so that
![]() $C \otimes _A A'= {\mathrm {Mat}}_{r\times r}(A')$
for a suitable
$C \otimes _A A'= {\mathrm {Mat}}_{r\times r}(A')$
for a suitable
![]() $r\in {\mathbb {N}_{\geq 1}}$
. Then by our construction, that follows [Reference Curtis and ReinerCR81],
$r\in {\mathbb {N}_{\geq 1}}$
. Then by our construction, that follows [Reference Curtis and ReinerCR81],
![]() $\rho ^* \otimes _AA'$
is the matrix representation of the induced representation of
$\rho ^* \otimes _AA'$
is the matrix representation of the induced representation of
This implies the multiplicativity of the map
![]() $\rho ^*$
, that is, that it is a homomorphism. Moreover, it shows that
$\rho ^*$
, that is, that it is a homomorphism. Moreover, it shows that
![]() $\rho ^*\otimes _A A'$
is the usual induced representation of
$\rho ^*\otimes _A A'$
is the usual induced representation of
![]() $\rho \otimes _A A'$
.
$\rho \otimes _A A'$
.
Remark 4.6.2. It can be shown that
![]() $\rho \mapsto \rho ^*$
in Lemma 4.6.1 is uniquely characterized as the right adjoint of the restriction homomorphism from G-representations to H-representations on Azumaya algebras. In particular, up to isomorphism
$\rho \mapsto \rho ^*$
in Lemma 4.6.1 is uniquely characterized as the right adjoint of the restriction homomorphism from G-representations to H-representations on Azumaya algebras. In particular, up to isomorphism
![]() $\rho ^*$
is independent of the chosen representatives
$\rho ^*$
is independent of the chosen representatives
![]() $g_1,\ldots ,g_m$
of
$g_1,\ldots ,g_m$
of
![]() $G/H$
.
$G/H$
.
Definition 4.6.3. We call
![]() $\rho ^*$
from Lemma 4.6.1 the representation induced from
$\rho ^*$
from Lemma 4.6.1 the representation induced from
![]() $\rho $
under
$\rho $
under
![]() $H\subset G$
and denote it by
$H\subset G$
and denote it by
![]() ${\mathrm {Ind}}_H^G\rho $
.
${\mathrm {Ind}}_H^G\rho $
.
The reason for introducing induction with Azumaya algebra coefficients is to be able to formulate Theorem 4.6.7 (e); see Remark 4.6.9.
Example 4.6.4. Since we have just seen an explicit form of
![]() $\rho ^*$
, for later use we consider the following example: Let
$\rho ^*$
, for later use we consider the following example: Let
![]() $H\subset G$
be a normal subgroup of index p. Fix
$H\subset G$
be a normal subgroup of index p. Fix
![]() $g_0\in G{\smallsetminus } H$
, and set
$g_0\in G{\smallsetminus } H$
, and set
![]() $g_i:=g_0^i$
for
$g_i:=g_0^i$
for
![]() $i=1,\ldots ,p$
so that
$i=1,\ldots ,p$
so that
![]() $G=\bigsqcup _{i=1}^p g_i H$
and the map
$G=\bigsqcup _{i=1}^p g_i H$
and the map
is a group isomorphism. Let C be an Azumaya E-algebra for a field E of characteristic p, and let
![]() $\rho \colon H\to C^\times $
be a representation. Define the induced representation
$\rho \colon H\to C^\times $
be a representation. Define the induced representation
![]() $\rho ^*\colon G\to {\mathrm {Mat}}_{p\times p}(C)^\times $
as in the above proof. Let
$\rho ^*\colon G\to {\mathrm {Mat}}_{p\times p}(C)^\times $
as in the above proof. Let
![]() $A\in {\mathrm {Mat}}_{p\times p}(C)$
be the diagonal matrix with diagonal
$A\in {\mathrm {Mat}}_{p\times p}(C)$
be the diagonal matrix with diagonal
![]() $(i\cdot 1_C)_{i=0,\ldots ,p-1}$
. Then we claim that one has for all
$(i\cdot 1_C)_{i=0,\ldots ,p-1}$
. Then we claim that one has for all
![]() $g\in G$
the relation
$g\in G$
the relation
The reader is advised to compare this with Lemma 2.3.2. The claim asserts that
![]() $\lambda $
defines a nontrivial class in
$\lambda $
defines a nontrivial class in
![]() $H^0(G,C/E)$
with G acting on
$H^0(G,C/E)$
with G acting on
![]() $C/E$
via the adjoint representation of
$C/E$
via the adjoint representation of
![]() $\rho $
.
$\rho $
.
To prove the claim, let
![]() $g\in G$
. We shall verify
$g\in G$
. We shall verify
![]() $ \rho ^*(g)A-A\rho ^*(g)=\lambda (g) \rho ^*(g)$
. Observe that
$ \rho ^*(g)A-A\rho ^*(g)=\lambda (g) \rho ^*(g)$
. Observe that
![]() $\widetilde {\rho }(g_i^{-1}gg_j)=\widetilde {\rho }(g_0^{-i}gg_0^j)=0$
unless
$\widetilde {\rho }(g_i^{-1}gg_j)=\widetilde {\rho }(g_0^{-i}gg_0^j)=0$
unless
![]() $gH=g_0^{i-j}H$
, that is, unless
$gH=g_0^{i-j}H$
, that is, unless
![]() $\lambda (g)=i-j$
. In the following, we write a lower subscript
$\lambda (g)=i-j$
. In the following, we write a lower subscript
![]() ${}_{i,j}$
to indicate the
${}_{i,j}$
to indicate the
![]() $(i,j)$
-entry of a matrix in
$(i,j)$
-entry of a matrix in
![]() ${\mathrm {Mat}}_{p\times p}(C)$
. Then
${\mathrm {Mat}}_{p\times p}(C)$
. Then
 $$ \begin{align*} (\rho^*(g)A-A\rho^*(g))_{i,j}&= \rho^*(g)_{i,j}\cdot j - i\cdot \rho^*(g)_{i,j} \ = \ (j-i)\cdot \widetilde{\rho}(g_0^{-i}gg_0^j)\\ &\stackrel{\textrm{observ.}}= -\lambda(g)\cdot \rho^*(g)_{i,j}, \end{align*} $$
$$ \begin{align*} (\rho^*(g)A-A\rho^*(g))_{i,j}&= \rho^*(g)_{i,j}\cdot j - i\cdot \rho^*(g)_{i,j} \ = \ (j-i)\cdot \widetilde{\rho}(g_0^{-i}gg_0^j)\\ &\stackrel{\textrm{observ.}}= -\lambda(g)\cdot \rho^*(g)_{i,j}, \end{align*} $$
and this completes the proof of our assertion, and ends our example.
Presumably formulas for the characteristic polynomial of
![]() ${\mathrm {Ind}}_H^G\rho $
are well known. But we could not locate suitable references. So we develop this from scratch. We need to fix some notation: Let C be an Azumaya A-algebra of degree n. Recall from Reminder 4.1.6 that elements
${\mathrm {Ind}}_H^G\rho $
are well known. But we could not locate suitable references. So we develop this from scratch. We need to fix some notation: Let C be an Azumaya A-algebra of degree n. Recall from Reminder 4.1.6 that elements
![]() $c\in C$
have a reduced characteristic polynomial
$c\in C$
have a reduced characteristic polynomial
![]() $\chi _c$
; we define its coefficients
$\chi _c$
; we define its coefficients
![]() $\Lambda _{c,i}$
by
$\Lambda _{c,i}$
by
![]() $\chi _c(t)=\sum _{i=0}^n (-1)^i \Lambda _{c,i}(c) t^{n-i}$
. We write
$\chi _c(t)=\sum _{i=0}^n (-1)^i \Lambda _{c,i}(c) t^{n-i}$
. We write
![]() $\chi ^m_c$
for the reduced characteristic polynomial (of degree
$\chi ^m_c$
for the reduced characteristic polynomial (of degree
![]() $nm$
) of an element
$nm$
) of an element
![]() $c\in {\mathrm {Mat}}_{m\times m}(C)$
.
$c\in {\mathrm {Mat}}_{m\times m}(C)$
.
Lemma 4.6.5. Let
![]() $c=(c_{i,j})$
be in
$c=(c_{i,j})$
be in
![]() ${\mathrm {Mat}}_{m\times m}(C)$
. Suppose that there is a permutation
${\mathrm {Mat}}_{m\times m}(C)$
. Suppose that there is a permutation
![]() $\sigma \in {\mathfrak {S}_{{m}}}$
such that
$\sigma \in {\mathfrak {S}_{{m}}}$
such that
![]() $c_{i,j}=0$
for
$c_{i,j}=0$
for
![]() $i\neq \sigma (j)$
and such that
$i\neq \sigma (j)$
and such that
![]() $c_{\sigma (j),j}$
lies in
$c_{\sigma (j),j}$
lies in
![]() $C^\times $
for all j. Then
$C^\times $
for all j. Then
![]() $\chi ^m_c$
has the following description:
$\chi ^m_c$
has the following description:
Write
![]() $\sigma $
in its cycle decomposition
$\sigma $
in its cycle decomposition
![]() $\sigma =\sigma _1\cdot \ldots \cdot \sigma _v$
, where the
$\sigma =\sigma _1\cdot \ldots \cdot \sigma _v$
, where the
![]() $\sigma _l$
are disjoint cycles of length
$\sigma _l$
are disjoint cycles of length
![]() $m_l$
such that
$m_l$
such that
![]() $\sum _{l=1}^v m_l=m$
, and let
$\sum _{l=1}^v m_l=m$
, and let
![]() $j_l$
be in the support of
$j_l$
be in the support of
![]() $\sigma _l$
such that
$\sigma _l$
such that
![]() $\sigma _l=(j_l , \sigma (j_l), \ldots ,\sigma ^{m_l-1}(j_l))$
. Then
$\sigma _l=(j_l , \sigma (j_l), \ldots ,\sigma ^{m_l-1}(j_l))$
. Then
 $$ \begin{align*}\chi^m_c(t)= \prod_{l=1}^v \ \chi_{c(l)}(t^{m_l}) \qquad\text{with }c(l):=c_{j_l,\sigma^{m_l-1}(j_l)} c_{\sigma^{m_l-1}(j_l),\sigma^{m_l-2}(j_l)}\cdot\ldots\cdot c_{\sigma(j_l),j_l}. \end{align*} $$
$$ \begin{align*}\chi^m_c(t)= \prod_{l=1}^v \ \chi_{c(l)}(t^{m_l}) \qquad\text{with }c(l):=c_{j_l,\sigma^{m_l-1}(j_l)} c_{\sigma^{m_l-1}(j_l),\sigma^{m_l-2}(j_l)}\cdot\ldots\cdot c_{\sigma(j_l),j_l}. \end{align*} $$
Proof. Let
![]() $s_l=m_1+\ldots +m_{l-1}$
for
$s_l=m_1+\ldots +m_{l-1}$
for
![]() $l=1,\ldots ,v$
, with
$l=1,\ldots ,v$
, with
![]() $s_1=m_0=0$
, and let
$s_1=m_0=0$
, and let
![]() $\tau \in {\mathfrak {S}_{{m}}}$
be the permutation whose inverse is given by
$\tau \in {\mathfrak {S}_{{m}}}$
be the permutation whose inverse is given by
 $$ \begin{align*}\left(\begin{array}{cccc} s_1+1 & s_1+2 &\cdots & s_1+m_1\\ j_1 & \sigma(j_1) &\ldots &\sigma^{m_1-1}(j_i) \end{array}\right) \cdot\ldots\cdot \left(\begin{array}{cccc} s_v+1 & s_v+2 &\cdots & s_v+m_v\\ j_v &\sigma(j_v) &\ldots &\sigma^{m_v-1}(j_v) \end{array}\right), \end{align*} $$
$$ \begin{align*}\left(\begin{array}{cccc} s_1+1 & s_1+2 &\cdots & s_1+m_1\\ j_1 & \sigma(j_1) &\ldots &\sigma^{m_1-1}(j_i) \end{array}\right) \cdot\ldots\cdot \left(\begin{array}{cccc} s_v+1 & s_v+2 &\cdots & s_v+m_v\\ j_v &\sigma(j_v) &\ldots &\sigma^{m_v-1}(j_v) \end{array}\right), \end{align*} $$
and let
![]() $p=p_\tau $
in
$p=p_\tau $
in
![]() ${\mathrm {Mat}}_{m\times m}(C)$
be the permutation matrix attached to
${\mathrm {Mat}}_{m\times m}(C)$
be the permutation matrix attached to
![]() $\tau $
, that is, with
$\tau $
, that is, with
![]() $p_{i,j}=0$
for
$p_{i,j}=0$
for
![]() $i\neq \tau (j)$
and
$i\neq \tau (j)$
and
![]() $p_{\tau (j),j}=1_C$
for all j. Then one verifies that
$p_{\tau (j),j}=1_C$
for all j. Then one verifies that
![]() $p_\tau c p_\tau ^{-1}$
is a block diagonal matrix in
$p_\tau c p_\tau ^{-1}$
is a block diagonal matrix in
![]() ${\mathrm {Mat}}_{m\times m}(C)$
with v blocks on the diagonal, the
${\mathrm {Mat}}_{m\times m}(C)$
with v blocks on the diagonal, the
![]() $l^{\operatorname {th}}$
block lies in
$l^{\operatorname {th}}$
block lies in
![]() ${\mathrm {Mat}}_{m_l\times m_l}(C)$
and is of the form
${\mathrm {Mat}}_{m_l\times m_l}(C)$
and is of the form

By conjugating
![]() $B_l$
with the block diagonal matrix with entry at spot
$B_l$
with the block diagonal matrix with entry at spot
![]() $(i,i)$
the block given by
$(i,i)$
the block given by
![]() $ c_{\sigma ^{i-1}(j_l),\sigma ^{i-2}(j_l)}\cdot c_{\sigma ^{i-2}(j_l),\sigma ^{i-1}(j_l)}\cdot \ldots \cdot c_{\sigma (j_l),j_l} $
so that at
$ c_{\sigma ^{i-1}(j_l),\sigma ^{i-2}(j_l)}\cdot c_{\sigma ^{i-2}(j_l),\sigma ^{i-1}(j_l)}\cdot \ldots \cdot c_{\sigma (j_l),j_l} $
so that at
![]() $(1,1)$
the entry is
$(1,1)$
the entry is
![]() $1$
, the matrix
$1$
, the matrix
![]() $B_l$
is transferred to the block companion matrix
$B_l$
is transferred to the block companion matrix

It suffices by a genericity argument to assume that A is an algebraically closed field so that C is split over A. Then the claim that
![]() $B_l$
has characteristic polynomial
$B_l$
has characteristic polynomial
![]() $\chi _{c(l)}(t^{m_l})$
is a simple linear algebra calculation. In the case when
$\chi _{c(l)}(t^{m_l})$
is a simple linear algebra calculation. In the case when
![]() $c(l)$
is a diagonal matrix, after an obvious change of basis
$c(l)$
is a diagonal matrix, after an obvious change of basis
![]() $B^{\prime }_l$
becomes the direct sum of standard companion matrices each with the same type of last row as
$B^{\prime }_l$
becomes the direct sum of standard companion matrices each with the same type of last row as
![]() $B_l'$
and hence with characteristic polynomial
$B_l'$
and hence with characteristic polynomial
![]() $t^{m_l}-c(l)_{i,i}$
so that one finds
$t^{m_l}-c(l)_{i,i}$
so that one finds
![]() $\chi _{B_l}(t)=\chi _{c(l)}(t^{m_l})$
. In the general case, one uses that semisimple matrices are dense open in the set of all matrices, or a devissage argument once
$\chi _{B_l}(t)=\chi _{c(l)}(t^{m_l})$
. In the general case, one uses that semisimple matrices are dense open in the set of all matrices, or a devissage argument once
![]() $c(l)$
is in Jordan form.
$c(l)$
is in Jordan form.
A more heuristic argument for
![]() $\chi _{B_l}(t)=\chi _{c(l)}(t^{m_l})$
runs as follows. The matrix
$\chi _{B_l}(t)=\chi _{c(l)}(t^{m_l})$
runs as follows. The matrix
![]() $B_l^{m_l}$
is block scalar with diagonal scalar factor
$B_l^{m_l}$
is block scalar with diagonal scalar factor
![]() $c(l)\in C^\times $
. So by the Cayley–Hamilton theorem
$c(l)\in C^\times $
. So by the Cayley–Hamilton theorem
![]() $B_l^{m_l}$
is annihilated by
$B_l^{m_l}$
is annihilated by
![]() $\chi _{c(l)}(t)$
, and hence
$\chi _{c(l)}(t)$
, and hence
![]() $B_l$
is annihilated by
$B_l$
is annihilated by
![]() $\chi _{c(l)}(t^{m_l})$
, and for a generic
$\chi _{c(l)}(t^{m_l})$
, and for a generic
![]() $c(l)$
one would expect
$c(l)$
one would expect
![]() $\chi _{c(l)}(t^{m_l})$
to be the minimal polynomial of
$\chi _{c(l)}(t^{m_l})$
to be the minimal polynomial of
![]() $B_l$
.
$B_l$
.
Lemma 4.6.6. Let the hypotheses be as in Lemma 4.6.1 with
![]() $N\subset H\subset G$
, and let
$N\subset H\subset G$
, and let
![]() $g\in G$
. Let
$g\in G$
. Let
![]() $\gamma _{g,l}\in G$
,
$\gamma _{g,l}\in G$
,
![]() $l=1,\ldots ,v_g$
, form a set of representatives for the double coset space
$l=1,\ldots ,v_g$
, form a set of representatives for the double coset space
![]() $\langle g\rangle \backslash G/H$
so that
$\langle g\rangle \backslash G/H$
so that
![]() $G=\bigsqcup _{i=1,\ldots ,v_g} \langle g\rangle \gamma _{g,l} H$
, and let
$G=\bigsqcup _{i=1,\ldots ,v_g} \langle g\rangle \gamma _{g,l} H$
, and let
![]() $m_l=[\langle g\rangle \gamma _{g,l} H:H]$
so that
$m_l=[\langle g\rangle \gamma _{g,l} H:H]$
so that
![]() $m_l>0$
is minimal such that
$m_l>0$
is minimal such that
![]() $g^{m_l}\gamma _{g,l}H=\gamma _{g,l}H$
. Then one has
$g^{m_l}\gamma _{g,l}H=\gamma _{g,l}H$
. Then one has
 $$ \begin{align*}\chi_{{\mathrm{Ind}}_H^G\rho(g)}(t)= \prod_{l=1,\ldots,v_g} \chi_{\rho(\gamma_{g,l}^{-1} \cdot g^{m_l}\cdot \gamma_{g,l})}(t^{m_l}). \end{align*} $$
$$ \begin{align*}\chi_{{\mathrm{Ind}}_H^G\rho(g)}(t)= \prod_{l=1,\ldots,v_g} \chi_{\rho(\gamma_{g,l}^{-1} \cdot g^{m_l}\cdot \gamma_{g,l})}(t^{m_l}). \end{align*} $$
Moreover, on any left coset
![]() $g'N$
,
$g'N$
,
![]() $g'\in G$
, the map
$g'\in G$
, the map
![]() $g\to v_g$
is constant, and the double cosets space
$g\to v_g$
is constant, and the double cosets space
![]() $\langle g\rangle \backslash G/ H$
is independent of g, and hence so are the
$\langle g\rangle \backslash G/ H$
is independent of g, and hence so are the
![]() $m_l$
, and also one can choose uniform representatives
$m_l$
, and also one can choose uniform representatives
![]() $\gamma _{g,l}$
for
$\gamma _{g,l}$
for
![]() $\langle g\rangle \backslash G/ H$
, independently of
$\langle g\rangle \backslash G/ H$
, independently of
![]() $g\in g'N$
.
$g\in g'N$
.
If H is normal in G, the double coset space
![]() $\langle g\rangle \backslash G/H$
is in bijection with the right coset space
$\langle g\rangle \backslash G/H$
is in bijection with the right coset space
![]() $\langle g\rangle H \backslash G$
, and so
$\langle g\rangle H \backslash G$
, and so
![]() $v_g=[G:\langle g\rangle H ]$
and
$v_g=[G:\langle g\rangle H ]$
and
![]() $m_l=m':={\operatorname {ord}}_{G/H}(gH)$
is independent of l.
$m_l=m':={\operatorname {ord}}_{G/H}(gH)$
is independent of l.
Proof. We first recall the construction of
![]() ${\mathrm {Ind}}_H^G\rho $
from the proof of Lemma 4.6.1. As a convenient set of coset representatives for
${\mathrm {Ind}}_H^G\rho $
from the proof of Lemma 4.6.1. As a convenient set of coset representatives for
![]() $G/H$
, we take
$G/H$
, we take
![]() $\bigsqcup _{l=1,\ldots ,v_g}\{g^j\gamma _{g,l}:j=0,\ldots ,m_l-1\}$
. With this choice,
$\bigsqcup _{l=1,\ldots ,v_g}\{g^j\gamma _{g,l}:j=0,\ldots ,m_l-1\}$
. With this choice,
![]() $\rho ^*(g)$
is already in block diagonal form with
$\rho ^*(g)$
is already in block diagonal form with
![]() $v_g$
blocks and the size of the l-th block is
$v_g$
blocks and the size of the l-th block is
![]() $m_l$
. Moreover, by explicit computation, one finds that the l-th block has nonzero entries only at index pairs
$m_l$
. Moreover, by explicit computation, one finds that the l-th block has nonzero entries only at index pairs
![]() $(j,j-1)$
,
$(j,j-1)$
,
![]() $j=2,\ldots ,m_l$
, where the entry is
$j=2,\ldots ,m_l$
, where the entry is
![]() $1\in C$
, and at
$1\in C$
, and at
![]() $(1,m_l)$
, where the entry is
$(1,m_l)$
, where the entry is
![]() $\rho (\gamma _{g,l}^{-1}g^{m_l}\gamma _{g,l})$
. The asserted formula is now an immediate consequence of the formula in Lemma 4.6.5.
$\rho (\gamma _{g,l}^{-1}g^{m_l}\gamma _{g,l})$
. The asserted formula is now an immediate consequence of the formula in Lemma 4.6.5.
Concerning the constancy statement for all g in a fixed coset
![]() $g'N$
, observe that all assertions follow from the following observation: Let
$g'N$
, observe that all assertions follow from the following observation: Let
![]() $\tilde g=gn$
for some
$\tilde g=gn$
for some
![]() $n\in N$
, and let
$n\in N$
, and let
![]() $\langle g\rangle \gamma H$
be a double coset for some
$\langle g\rangle \gamma H$
be a double coset for some
![]() $\gamma \in G$
. Then by normality of N in G and using
$\gamma \in G$
. Then by normality of N in G and using
![]() $N\subset H$
, we have
$N\subset H$
, we have
and thus we have equality of double cosets
![]() $\langle g'\rangle \gamma H= \langle g\rangle \gamma H$
. The remaining assertions when H is normal in G we leave as exercises to the reader.
$\langle g'\rangle \gamma H= \langle g\rangle \gamma H$
. The remaining assertions when H is normal in G we leave as exercises to the reader.
Let now
be a pseudocharacter of dimension n with values in a commutative ring B. If G is a profinite group, we assume that
![]() ${D}_H$
is continuous. The following result establishes the existence of the induction of
${D}_H$
is continuous. The following result establishes the existence of the induction of
![]() ${D}_H$
.
${D}_H$
.
Theorem 4.6.7. There exists a unique pseudocharacter
![]() ${D}_G\colon B[G]\to B$
whose characteristic polynomial for each
${D}_G\colon B[G]\to B$
whose characteristic polynomial for each
![]() $g\in G$
is given as follows. Let
$g\in G$
is given as follows. Let
![]() $\gamma _{g,l}$
,
$\gamma _{g,l}$
,
![]() $l=1,\ldots ,v_g$
, be elements of G that form a set of representatives for the double coset space
$l=1,\ldots ,v_g$
, be elements of G that form a set of representatives for the double coset space
![]() $\langle g\rangle \backslash G/H$
, and define
$\langle g\rangle \backslash G/H$
, and define
![]() $m_l=[\langle g\rangle \gamma _{g,l} H:H]$
. Then
$m_l=[\langle g\rangle \gamma _{g,l} H:H]$
. Then
 $$ \begin{align} \chi_{{D}_G,B}(g,t)= \prod_{l=1,\ldots,v_g} \chi_{{D}_H,B}(\gamma_{g,l}^{-1} \cdot g^{m_l}\cdot \gamma_{g,l},t^{m_l}). \end{align} $$
$$ \begin{align} \chi_{{D}_G,B}(g,t)= \prod_{l=1,\ldots,v_g} \chi_{{D}_H,B}(\gamma_{g,l}^{-1} \cdot g^{m_l}\cdot \gamma_{g,l},t^{m_l}). \end{align} $$
The pseudocharacter
![]() ${D}_G$
has the following properties.
${D}_G$
has the following properties.
-
(a) One has
 $$ \begin{align*}{\mathrm{Res}}^G_N {D}_G\cong \bigoplus_{g\in G/H} \big({\mathrm{Res}}_N^H{D}_H\big)^g. \end{align*} $$
$$ \begin{align*}{\mathrm{Res}}^G_N {D}_G\cong \bigoplus_{g\in G/H} \big({\mathrm{Res}}_N^H{D}_H\big)^g. \end{align*} $$
-
(b) For any left coset
 $g'N$
,
$g'N$
,
 $g'\in G$
, in formula (22) the value of
$g'\in G$
, in formula (22) the value of
 $v_g$
and the elements
$v_g$
and the elements
 $\gamma _{g,l}$
can be taken independent of
$\gamma _{g,l}$
can be taken independent of
 $g\in g'N$
. Hence, if G is profinite and
$g\in g'N$
. Hence, if G is profinite and
 ${D}_H$
is continuous, then so is
${D}_H$
is continuous, then so is
 ${D}_G$
.
${D}_G$
. -
(c) The formation of
 ${D}_G$
commutes with base change, that is, the following holds. Let
${D}_G$
commutes with base change, that is, the following holds. Let
 $B\to B'$
be any homomorphism. Set
$B\to B'$
be any homomorphism. Set
 ${D}^{\prime }_H:={D}_H\otimes _BB'$
and
${D}^{\prime }_H:={D}_H\otimes _BB'$
and
 ${D}^{\prime }_G:={D}_G\otimes _BB'$
. Then equation (22) holds with
${D}^{\prime }_G:={D}_G\otimes _BB'$
. Then equation (22) holds with
 ${D}_H$
and
${D}_H$
and
 ${D}_G$
replaced by
${D}_G$
replaced by
 ${D}^{\prime }_H$
and
${D}^{\prime }_H$
and
 ${D}^{\prime }_G$
, respectively.
${D}^{\prime }_G$
, respectively. -
(d) For any geometric point
 $\overline x\to {\mathrm {Spec}}\ B$
the representations
$\overline x\to {\mathrm {Spec}}\ B$
the representations
 $\rho _{{D}_{G,\overline x}}$
is isomorphic to the semisimplification of
$\rho _{{D}_{G,\overline x}}$
is isomorphic to the semisimplification of
 ${\mathrm {Ind}}_H^G\rho _{{D}_{H,\overline x}}$
.
${\mathrm {Ind}}_H^G\rho _{{D}_{H,\overline x}}$
. -
(e) Suppose
 $U={\mathrm {Spec}}\ B'\subset {\mathrm {Spec}}\ B$
is affine open such that
$U={\mathrm {Spec}}\ B'\subset {\mathrm {Spec}}\ B$
is affine open such that
 ${D}_{H,x}$
is irreducible for all
${D}_{H,x}$
is irreducible for all
 $x\in U$
and set
$x\in U$
and set
 ${D}^{\prime }_H={D}_H\otimes _BB'$
and
${D}^{\prime }_H={D}_H\otimes _BB'$
and
 $C:=B'[G]/{\mathrm {CH}}(D^{\prime }_H)$
so that by Proposition 4.1.25, C is an Azumaya B-algebra and
$C:=B'[G]/{\mathrm {CH}}(D^{\prime }_H)$
so that by Proposition 4.1.25, C is an Azumaya B-algebra and
 $\psi =\rho _{D}^{\mathrm {CH}}:G\to C^\times $
is a representation such that
$\psi =\rho _{D}^{\mathrm {CH}}:G\to C^\times $
is a representation such that
 ${\mathrm {det}}_C\circ \psi ={D}^{\prime }_H$
. Then for
${\mathrm {det}}_C\circ \psi ={D}^{\prime }_H$
. Then for
 ${\mathrm {Ind}}_H^G\psi \colon G\to {\mathrm {GL}}_{m}(C)^\times $
from Definition 4.6.3, we have
${\mathrm {Ind}}_H^G\psi \colon G\to {\mathrm {GL}}_{m}(C)^\times $
from Definition 4.6.3, we have  $$ \begin{align*}{D}_G\otimes_BB'={D}_{{\mathrm{Ind}}_H^G\psi}.\end{align*} $$
$$ \begin{align*}{D}_G\otimes_BB'={D}_{{\mathrm{Ind}}_H^G\psi}.\end{align*} $$
-
(f) One has
 ${D}_G={D}_G \otimes \chi $
for any character
${D}_G={D}_G \otimes \chi $
for any character
 $\chi \colon G\to B^\times $
whose kernel contains H.
$\chi \colon G\to B^\times $
whose kernel contains H. -
(g) Suppose H is normal in G. Then
 $\chi _{{D}_G,B}(g,t)$
is a polynomial in
$\chi _{{D}_G,B}(g,t)$
is a polynomial in
 $t^{{\operatorname {ord}}_{G/H}(gH)}$
; and in particular its coefficients satisfy
$t^{{\operatorname {ord}}_{G/H}(gH)}$
; and in particular its coefficients satisfy
 $\Lambda _{{D}_G,i}(g)=0$
whenever
$\Lambda _{{D}_G,i}(g)=0$
whenever
 ${\operatorname {ord}}_{G/H}(gH) \nmid i$
.
${\operatorname {ord}}_{G/H}(gH) \nmid i$
.
Proof. Let us first consider the situation irrespective of any topology, that is, G is an abstract group and
![]() ${D}_H:B[H]\to B$
is a pseudocharacter on H of a finite index subgroup. Let
${D}_H:B[H]\to B$
is a pseudocharacter on H of a finite index subgroup. Let
![]() $\pi \colon {\mathrm {FG}}({X})\to G$
be a surjective group homomorphism from the free group on a suitable set of symbols
$\pi \colon {\mathrm {FG}}({X})\to G$
be a surjective group homomorphism from the free group on a suitable set of symbols
![]() ${X}$
. By the Nielsen–Schreier Theorem, any subgroup of
${X}$
. By the Nielsen–Schreier Theorem, any subgroup of
![]() ${\mathrm {FG}}({X})$
is free again, and so let
${\mathrm {FG}}({X})$
is free again, and so let
![]() ${X}_H\subset {\mathrm {FG}}({X})$
be a subset of free generators of
${X}_H\subset {\mathrm {FG}}({X})$
be a subset of free generators of
![]() $\pi ^{-1}(H)$
, and write
$\pi ^{-1}(H)$
, and write
![]() $\pi _H\colon {\mathrm {FG}}({X}_H)\to H$
for the restriction of
$\pi _H\colon {\mathrm {FG}}({X}_H)\to H$
for the restriction of
![]() $\pi $
to
$\pi $
to
![]() $\pi ^{-1}(H)$
.
$\pi ^{-1}(H)$
.
Recall from Theorem A.4.4 the following description of the universal pseudocharacter of the group ring
![]() ${\mathbb {Z}}\{{X}_H^{\pm }\}={\mathbb {Z}}[{\mathrm {FG}}({X}_H)]$
. Let
${\mathbb {Z}}\{{X}_H^{\pm }\}={\mathbb {Z}}[{\mathrm {FG}}({X}_H)]$
. Let
![]() $F_{{X}_H^{\pm }}(n)={\mathbb {Z}}[\xi _{{x},i,j}: {x}\in {X}_H, 1\le i,j\le n][\frac 1{{\mathrm {det}}(\xi _{x})}:{x}\in {X}_H]$
be the commutative
$F_{{X}_H^{\pm }}(n)={\mathbb {Z}}[\xi _{{x},i,j}: {x}\in {X}_H, 1\le i,j\le n][\frac 1{{\mathrm {det}}(\xi _{x})}:{x}\in {X}_H]$
be the commutative
![]() ${\mathbb {Z}}$
-algebra of the coefficients of the generic invertible
${\mathbb {Z}}$
-algebra of the coefficients of the generic invertible
![]() $n\times n$
-matrices
$n\times n$
-matrices
![]() $\xi _{x}=(\xi _{{x},i,j})_{i,j=1,\ldots ,n}\in {\mathrm {Mat}}_{n\times n}(F_{{X}^{\pm }_H}(n))$
of all
$\xi _{x}=(\xi _{{x},i,j})_{i,j=1,\ldots ,n}\in {\mathrm {Mat}}_{n\times n}(F_{{X}^{\pm }_H}(n))$
of all
![]() ${x}\in {X}_H$
. Define the representation
${x}\in {X}_H$
. Define the representation
and let
![]() $E_{{X}_H^{\pm }}(n)$
be the subring of
$E_{{X}_H^{\pm }}(n)$
be the subring of
![]() $F_{{X}_H^{\pm }}(n)$
generated by
$F_{{X}_H^{\pm }}(n)$
generated by
![]() ${\mathrm {det}}\circ \rho _{{X}_H^{\pm }}\big ( {\mathbb {Z}}\{{X}_H^{\pm }\}\big )$
. Then by Theorem A.4.4
${\mathrm {det}}\circ \rho _{{X}_H^{\pm }}\big ( {\mathbb {Z}}\{{X}_H^{\pm }\}\big )$
. Then by Theorem A.4.4
is the universal n-dimensional pseudocharacter of
![]() ${\mathbb {Z}}\{{X}_H^{\pm }\} $
(up to isomorphism).
${\mathbb {Z}}\{{X}_H^{\pm }\} $
(up to isomorphism).
Let
![]() $\alpha \colon E_{{X}_H^{\pm }}(n)\to B$
be the unique ring homomorphism (by universality of
$\alpha \colon E_{{X}_H^{\pm }}(n)\to B$
be the unique ring homomorphism (by universality of
![]() $ {D}_{{X}^{\pm }_H}$
) such that
$ {D}_{{X}^{\pm }_H}$
) such that
![]() $\alpha \circ {D}_{{X}^{\pm }_H} ={D}_H\circ \pi _H\colon {\mathbb {Z}}\{{X}_H^{\pm }\} \to B$
. Define
$\alpha \circ {D}_{{X}^{\pm }_H} ={D}_H\circ \pi _H\colon {\mathbb {Z}}\{{X}_H^{\pm }\} \to B$
. Define
with
![]() ${\mathrm {Ind}}_{{\mathrm {FG}}({X}_H)}^{{\mathrm {FG}}({X})}$
as in Lemma 4.6.1. Now, Lemma 4.6.6 shows that all characteristic polynomials of elements in
${\mathrm {Ind}}_{{\mathrm {FG}}({X}_H)}^{{\mathrm {FG}}({X})}$
as in Lemma 4.6.1. Now, Lemma 4.6.6 shows that all characteristic polynomials of elements in
![]() ${\mathrm {FG}}({X})$
lie in
${\mathrm {FG}}({X})$
lie in
![]() $E_{{X}_H^{\pm }}(n)$
, and it follows from [Reference ChenevierChe14, Corollary 1.14] (a consequence of Amitsur’s formula) that
$E_{{X}_H^{\pm }}(n)$
, and it follows from [Reference ChenevierChe14, Corollary 1.14] (a consequence of Amitsur’s formula) that
![]() ${\mathrm {Ind}}_{{\mathrm {FG}}({X}_H)}^{{\mathrm {FG}}({X})} {D}_{{X}^{\pm }_H}$
has ring of definition contained in
${\mathrm {Ind}}_{{\mathrm {FG}}({X}_H)}^{{\mathrm {FG}}({X})} {D}_{{X}^{\pm }_H}$
has ring of definition contained in
![]() $E_{{X}_H^{\pm }}(n)$
, and we regard it as a pseudocharacter
$E_{{X}_H^{\pm }}(n)$
, and we regard it as a pseudocharacter
We now claim that the composition
has kernel containing
![]() $K={\mathop {\mathrm{Ker}}\nolimits }(\pi \colon {\mathrm {FG}}({X})\to G)$
. For this, note first that by Lemma 2.1.4
(b) we have
$K={\mathop {\mathrm{Ker}}\nolimits }(\pi \colon {\mathrm {FG}}({X})\to G)$
. For this, note first that by Lemma 2.1.4
(b) we have
 $$ \begin{align*}{\mathrm{Res}}_{\pi^{-1}(N)}^{{\mathrm{FG}}({X})} {\mathrm{Ind}}_{{\mathrm{FG}}({X}_H)}^{{\mathrm{FG}}({X})} \rho_{{X}_H^{\pm}}=\bigoplus_{g\in G/H} \big({\mathrm{Res}}_{\pi^{-1}(N)}^{{\mathrm{FG}}({X}_H)} \rho_{{X}_H^{\pm}}\big)^{\tilde g}, \end{align*} $$
$$ \begin{align*}{\mathrm{Res}}_{\pi^{-1}(N)}^{{\mathrm{FG}}({X})} {\mathrm{Ind}}_{{\mathrm{FG}}({X}_H)}^{{\mathrm{FG}}({X})} \rho_{{X}_H^{\pm}}=\bigoplus_{g\in G/H} \big({\mathrm{Res}}_{\pi^{-1}(N)}^{{\mathrm{FG}}({X}_H)} \rho_{{X}_H^{\pm}}\big)^{\tilde g}, \end{align*} $$
for
![]() $\tilde g\in {\mathrm {FG}}({X}_H)$
a preimage of g under
$\tilde g\in {\mathrm {FG}}({X}_H)$
a preimage of g under
![]() $\pi $
. If we compose the equation with
$\pi $
. If we compose the equation with
![]() ${\mathrm {det}}$
and
${\mathrm {det}}$
and
![]() $\alpha $
, this gives
$\alpha $
, this gives
 $$ \begin{align} {\mathrm{Res}}_{\pi^{-1}(N)}^{{\mathrm{FG}}({X})} \Big(\alpha\circ {\mathrm{Ind}}_{{\mathrm{FG}}({X}_H)}^{{\mathrm{FG}}({X})} {D}_{{X}_H^{\pm}}\Big)=\bigoplus_{g\in G/H} \big({\mathrm{Res}}_{N}^{H} {D}_H\big)^g\circ\pi_H. \end{align} $$
$$ \begin{align} {\mathrm{Res}}_{\pi^{-1}(N)}^{{\mathrm{FG}}({X})} \Big(\alpha\circ {\mathrm{Ind}}_{{\mathrm{FG}}({X}_H)}^{{\mathrm{FG}}({X})} {D}_{{X}_H^{\pm}}\Big)=\bigoplus_{g\in G/H} \big({\mathrm{Res}}_{N}^{H} {D}_H\big)^g\circ\pi_H. \end{align} $$
The kernel of the right-hand side clearly contains K, and this proves the claim. As a consequence
![]() $ \alpha \circ {\mathrm {Ind}}_{{\mathrm {FG}}({X}_H)}^{{\mathrm {FG}}({X})} {D}_{{X}_H^{\pm }}$
factors via
$ \alpha \circ {\mathrm {Ind}}_{{\mathrm {FG}}({X}_H)}^{{\mathrm {FG}}({X})} {D}_{{X}_H^{\pm }}$
factors via
![]() $\pi \colon {\mathrm {FG}}({X})\to G$
, and using Proposition 4.1.16 we define
$\pi \colon {\mathrm {FG}}({X})\to G$
, and using Proposition 4.1.16 we define
as the unique pseudocharacter such that
![]() ${D}_G\circ \pi = \alpha \circ {\mathrm {Ind}}_{{\mathrm {FG}}({X}_H)}^{{\mathrm {FG}}({X})} {D}_{{X}_H^{\pm }}$
. Note that by its very construction and by Lemma 4.6.6,
${D}_G\circ \pi = \alpha \circ {\mathrm {Ind}}_{{\mathrm {FG}}({X}_H)}^{{\mathrm {FG}}({X})} {D}_{{X}_H^{\pm }}$
. Note that by its very construction and by Lemma 4.6.6,
![]() $ {\mathrm {Ind}}_{{\mathrm {FG}}({X}_H)}^{{\mathrm {FG}}({X})} {D}_{{X}_H^{\pm }}$
satisfies formula (22) and the formula is preserved under composition with
$ {\mathrm {Ind}}_{{\mathrm {FG}}({X}_H)}^{{\mathrm {FG}}({X})} {D}_{{X}_H^{\pm }}$
satisfies formula (22) and the formula is preserved under composition with
![]() $\alpha $
, and under passage via
$\alpha $
, and under passage via
![]() $\pi $
from
$\pi $
from
![]() ${\mathrm {FG}}({X})$
to G. This implies formula (22) for
${\mathrm {FG}}({X})$
to G. This implies formula (22) for
![]() ${D}_G$
. Since by Proposition 4.1.10, the characteristic polynomial
${D}_G$
. Since by Proposition 4.1.10, the characteristic polynomial
![]() $\chi _{{D}_G}(\cdot ,t)$
completely characterizes
$\chi _{{D}_G}(\cdot ,t)$
completely characterizes
![]() ${D}_G$
, the required uniqueness of
${D}_G$
, the required uniqueness of
![]() ${D}_G$
is also shown.
${D}_G$
is also shown.
We now prove Parts (a) to (f). Part (a) follows from equation (23) and our definition of
![]() ${D}_G$
. The first part of (b) follows from the construction of
${D}_G$
. The first part of (b) follows from the construction of
![]() ${D}_G$
and Lemma 4.6.6. To prove the continuity assertion in (b), we need to show that the characteristic polynomial coefficients of
${D}_G$
and Lemma 4.6.6. To prove the continuity assertion in (b), we need to show that the characteristic polynomial coefficients of
![]() ${D}_G$
are continuous. But this follows from the first part of (b), equation (22) and the continuity hypothesis on
${D}_G$
are continuous. But this follows from the first part of (b), equation (22) and the continuity hypothesis on
![]() ${D}_H$
.
${D}_H$
.
Part (c) is immediate from our construction which is based via pullback to the induction
![]() $ {\mathrm {Ind}}_{{\mathrm {FG}}({X}_H)}^{{\mathrm {FG}}({X})} {D}_{{X}_H^{\pm }}$
in a free group setting. To see (d), note first that by Part (c) formula (22) is preserved under base change to
$ {\mathrm {Ind}}_{{\mathrm {FG}}({X}_H)}^{{\mathrm {FG}}({X})} {D}_{{X}_H^{\pm }}$
in a free group setting. To see (d), note first that by Part (c) formula (22) is preserved under base change to
![]() ${\kappa ({\overline x})}$
, that is, the formula holds if we replace simultaneously
${\kappa ({\overline x})}$
, that is, the formula holds if we replace simultaneously
![]() ${D}_G$
by
${D}_G$
by
![]() ${D}_{G,\overline x}$
and
${D}_{G,\overline x}$
and
![]() ${D}_H$
by
${D}_H$
by
![]() ${D}_{H,\overline x}$
. By its definition,
${D}_{H,\overline x}$
. By its definition,
![]() $\rho _{{D}_{H,\overline x}}$
has characteristic polynomial
$\rho _{{D}_{H,\overline x}}$
has characteristic polynomial
![]() $\chi _{{D}_{H,\overline x}}$
, and by Lemma 4.6.6, the right-hand side of equation (22) over
$\chi _{{D}_{H,\overline x}}$
, and by Lemma 4.6.6, the right-hand side of equation (22) over
![]() ${\kappa ({\overline x})}$
is equal to
${\kappa ({\overline x})}$
is equal to
![]() $\chi _{{\mathrm {Ind}}_H^G\rho _{\overline x}}$
. This proves (d). For Part (e), note that over
$\chi _{{\mathrm {Ind}}_H^G\rho _{\overline x}}$
. This proves (d). For Part (e), note that over
![]() $B'$
we have equality of characteristic polynomials
$B'$
we have equality of characteristic polynomials
![]() $\chi _{\psi }=\chi _{{D}^{\prime }_H}$
from Proposition 4.1.25. Using Lemma 4.6.6 for
$\chi _{\psi }=\chi _{{D}^{\prime }_H}$
from Proposition 4.1.25. Using Lemma 4.6.6 for
![]() ${\mathrm {Ind}}_H^G\psi $
and formula (22) and Part (c) for
${\mathrm {Ind}}_H^G\psi $
and formula (22) and Part (c) for
![]() ${D}^{\prime }_H$
, we deduce
${D}^{\prime }_H$
, we deduce
![]() $\chi _{{D}_G\otimes _BB',B'}=\chi _{{\mathrm {Ind}}_H^G\psi } $
and hence Part (e).
$\chi _{{D}_G\otimes _BB',B'}=\chi _{{\mathrm {Ind}}_H^G\psi } $
and hence Part (e).
The proof of (f) will follow after pullback to
![]() ${\mathrm {FG}}({X})$
. To carry this out, let d be the order of
${\mathrm {FG}}({X})$
. To carry this out, let d be the order of
![]() $\chi $
and
$\chi $
and
![]() ${\mathbb {Z}}[\chi ]$
the extension of
${\mathbb {Z}}[\chi ]$
the extension of
![]() ${\mathbb {Z}}$
obtained by adjoining a primitive d-th root of unity. In an analogous way, we define
${\mathbb {Z}}$
obtained by adjoining a primitive d-th root of unity. In an analogous way, we define
![]() $F_{{X}^{\pm }}(n)[\chi ]$
and
$F_{{X}^{\pm }}(n)[\chi ]$
and
![]() $E_{{X}^{\pm }}(n)[\chi ]$
and we extend
$E_{{X}^{\pm }}(n)[\chi ]$
and we extend
![]() $\alpha \colon E_{{X}^{\pm }}(n)\to B$
to a homomorphism
$\alpha \colon E_{{X}^{\pm }}(n)\to B$
to a homomorphism
![]() $\alpha \colon E_{{X}^{\pm }}(n)[\chi ]\to B$
. Let now
$\alpha \colon E_{{X}^{\pm }}(n)[\chi ]\to B$
. Let now
![]() $\chi _E\colon G\to E_{{X}^{\pm }}(n)$
be the unique character such that
$\chi _E\colon G\to E_{{X}^{\pm }}(n)$
be the unique character such that
![]() $\alpha \circ \chi _E=\chi $
. By surjectivity of
$\alpha \circ \chi _E=\chi $
. By surjectivity of
![]() $\pi $
(and by applying
$\pi $
(and by applying
![]() $\alpha $
), it will suffice to show that
$\alpha $
), it will suffice to show that
But by construction of
![]() ${D}_{{X}^{\pm }_H}$
and Proposition 4.5.7
(d) this reduces to the same formula with
${D}_{{X}^{\pm }_H}$
and Proposition 4.5.7
(d) this reduces to the same formula with
![]() $\rho _{{X}^{\pm }_H}$
, and this formula holds by Mackey’s tensor product theorem formulated in Lemma 2.1.3.
$\rho _{{X}^{\pm }_H}$
, and this formula holds by Mackey’s tensor product theorem formulated in Lemma 2.1.3.
Finally, Part (g) follows from the last part of Lemma 4.6.6: The normality of H in G implies that
![]() $m_l={\operatorname {ord}}_{G/H}(gH)$
for all
$m_l={\operatorname {ord}}_{G/H}(gH)$
for all
![]() $l=1,\ldots ,v_g$
, and so the formula for
$l=1,\ldots ,v_g$
, and so the formula for
![]() $\chi _{{\mathrm {Ind}}_H^G\rho (g)}(t)$
in that lemma is a polynomial in
$\chi _{{\mathrm {Ind}}_H^G\rho (g)}(t)$
in that lemma is a polynomial in
![]() $t^{{\operatorname {ord}}_{G/H}(gH)}$
.
$t^{{\operatorname {ord}}_{G/H}(gH)}$
.
Definition 4.6.8. We call the pseudocharacter
![]() $D_G$
from Theorem 4.6.7 the induced pseudocharacter of
$D_G$
from Theorem 4.6.7 the induced pseudocharacter of
![]() ${D}_H$
under
${D}_H$
under
![]() $H\subset G$
and write
$H\subset G$
and write
![]() ${\mathrm {Ind}}_H^G{D}_H$
for it.
${\mathrm {Ind}}_H^G{D}_H$
for it.
Remark 4.6.9. Our construction of
![]() ${\mathrm {Ind}}_H^G{D}_H$
does not need the generality of Azumaya algebra coefficients in Definition 4.6.3. However, over the absolutely irreducible locus of
${\mathrm {Ind}}_H^G{D}_H$
does not need the generality of Azumaya algebra coefficients in Definition 4.6.3. However, over the absolutely irreducible locus of
![]() ${D}_H$
, one has an elementary construction of induction indicated in Theorem 4.6.7
(e). In fact, if B is for instance reduced and Noetherian and if the set U in Theorem 4.6.7
(e) is dense in
${D}_H$
, one has an elementary construction of induction indicated in Theorem 4.6.7
(e). In fact, if B is for instance reduced and Noetherian and if the set U in Theorem 4.6.7
(e) is dense in
![]() ${\mathrm {Spec}}\ B$
, one can uniquely reconstruct
${\mathrm {Spec}}\ B$
, one can uniquely reconstruct
![]() ${\mathrm {Ind}}_H^G{D}_H$
from this elementary construction. This approach had been pursued in an earlier version of this work.
${\mathrm {Ind}}_H^G{D}_H$
from this elementary construction. This approach had been pursued in an earlier version of this work.
Remark 4.6.10. In our approach to Theorem 4.6.7, we strongly rely on the explicit but somewhat technical formulas from Lemma 4.6.6. We use them to uniquely characterize the induction, once existence is shown. We also use these formulas in the existence part to show that
![]() ${\mathrm {Ind}}_{{\mathrm {FG}}({X}_H)}^{{\mathrm {FG}}({X})} {D}_{{X}^{\pm }_H}$
takes values in
${\mathrm {Ind}}_{{\mathrm {FG}}({X}_H)}^{{\mathrm {FG}}({X})} {D}_{{X}^{\pm }_H}$
takes values in
![]() $E_{{X}_H^{\pm }}(n)$
; initially the corresponding representation is only known to be defined over
$E_{{X}_H^{\pm }}(n)$
; initially the corresponding representation is only known to be defined over
![]() $F_{{X}_H^{\pm }}(n)$
. V. Paškūnas suggested in personal communication that perhaps one could avoid using Lemma 4.6.6, at least for the unique characterization of
$F_{{X}_H^{\pm }}(n)$
. V. Paškūnas suggested in personal communication that perhaps one could avoid using Lemma 4.6.6, at least for the unique characterization of
![]() ${\mathrm {Ind}}_H^G{D}_H$
. His remarks led to the following discussion, which sketches an alternative proof of Theorem 4.6.7:
${\mathrm {Ind}}_H^G{D}_H$
. His remarks led to the following discussion, which sketches an alternative proof of Theorem 4.6.7:
Suppose first that the target B of
![]() ${D}_H\colon H\to B$
is a domain, and let
${D}_H\colon H\to B$
is a domain, and let
![]() $\eta $
be the generic point of
$\eta $
be the generic point of
![]() ${\mathrm {Spec}}\ B$
. Then
${\mathrm {Spec}}\ B$
. Then
![]() ${\mathrm {Ind}}_H^G {D}_H$
is uniquely characterized by Theorem 4.6.7
(d) for the geometric point
${\mathrm {Ind}}_H^G {D}_H$
is uniquely characterized by Theorem 4.6.7
(d) for the geometric point
![]() $\overline x\colon {\mathrm {Spec}}\ {{\kappa ({\eta })}^{\mathrm {alg}}} \to {\mathrm {Spec}}\ B$
because it states that
$\overline x\colon {\mathrm {Spec}}\ {{\kappa ({\eta })}^{\mathrm {alg}}} \to {\mathrm {Spec}}\ B$
because it states that
![]() $({\mathrm {Ind}}_H^G {D}_H)_{\overline x}$
arises from
$({\mathrm {Ind}}_H^G {D}_H)_{\overline x}$
arises from
![]() ${\mathrm {Ind}}_H^G\rho _{{D}_{H,\overline x}}$
.
${\mathrm {Ind}}_H^G\rho _{{D}_{H,\overline x}}$
.
To handle the case of general B in a similar way, one can regard induction as a functorial type construction in the sense that for any group epimorphism
![]() ${\varphi }\colon G'\to G$
, any surjection of rings
${\varphi }\colon G'\to G$
, any surjection of rings
![]() $\alpha \colon B'\to B$
and any pseudocharacter
$\alpha \colon B'\to B$
and any pseudocharacter
![]() ${D}^{\prime }_{H'}\colon H'\to B'$
with
${D}^{\prime }_{H'}\colon H'\to B'$
with
![]() $H':={\varphi }^{-1}(H)$
such that
$H':={\varphi }^{-1}(H)$
such that
![]() $\alpha \circ {D}^{\prime }_H={D}_H\circ {\varphi }$
, one requires that
$\alpha \circ {D}^{\prime }_H={D}_H\circ {\varphi }$
, one requires that
![]() $ \alpha \circ ({\mathrm {Ind}}_{H'}^{G'}{D}^{\prime }_H)=({\mathrm {Ind}}_H^G{D}_H)\circ {\varphi }$
; this compatibility can be shown for our construction. Assuming this compatibility, the uniqueness of
$ \alpha \circ ({\mathrm {Ind}}_{H'}^{G'}{D}^{\prime }_H)=({\mathrm {Ind}}_H^G{D}_H)\circ {\varphi }$
; this compatibility can be shown for our construction. Assuming this compatibility, the uniqueness of
![]() ${\mathrm {Ind}}_H^G {D}_H$
follows from that of
${\mathrm {Ind}}_H^G {D}_H$
follows from that of
![]() ${\mathrm {Ind}}_{H'}^{G'}{D}^{\prime }_{H'}$
for a suitable
${\mathrm {Ind}}_{H'}^{G'}{D}^{\prime }_{H'}$
for a suitable
![]() ${D}^{\prime }_{H'}$
. And now one can apply the observation of the previous paragraph to the universal situation from the proof of Theorem 4.6.7, where
${D}^{\prime }_{H'}$
. And now one can apply the observation of the previous paragraph to the universal situation from the proof of Theorem 4.6.7, where
![]() ${D}^{\prime }_{H'}={D}_{{X}^{\pm }_H}$
and where
${D}^{\prime }_{H'}={D}_{{X}^{\pm }_H}$
and where
![]() $B'=E_{{X}_H^{\pm }}(n)$
is a domain. This shows that uniqueness follows from the stated functoriality and Theorem 4.6.7
(d).
$B'=E_{{X}_H^{\pm }}(n)$
is a domain. This shows that uniqueness follows from the stated functoriality and Theorem 4.6.7
(d).
Lastly, we indicate how to deduce that
![]() $E_{{X}_H^{\pm }}(n)$
is the ring of definition of
$E_{{X}_H^{\pm }}(n)$
is the ring of definition of
![]() ${\mathrm {Ind}}_{{\mathrm {FG}}({X}_H)}^{{\mathrm {FG}}({X})} {D}_{{X}^{\pm }_H}$
without the use of Lemma 4.6.6. For this, it suffices to assume that
${\mathrm {Ind}}_{{\mathrm {FG}}({X}_H)}^{{\mathrm {FG}}({X})} {D}_{{X}^{\pm }_H}$
without the use of Lemma 4.6.6. For this, it suffices to assume that
![]() ${X}$
is finite: To see this, let
${X}$
is finite: To see this, let
![]() $Y\subset {X}$
be finite such that
$Y\subset {X}$
be finite such that
![]() $Y\cup {X}_H$
generates
$Y\cup {X}_H$
generates
![]() ${\mathrm {FG}}({X})$
. Then one verifies that it suffices to consider the restriction of
${\mathrm {FG}}({X})$
. Then one verifies that it suffices to consider the restriction of
![]() ${D}_{{X}^{\pm }_H}$
to
${D}_{{X}^{\pm }_H}$
to
![]() ${\mathrm {FG}}(Y')$
for all finite subsets
${\mathrm {FG}}(Y')$
for all finite subsets
![]() $Y'\subset Y\cup {X}_H$
that contain Y. Assume now that
$Y'\subset Y\cup {X}_H$
that contain Y. Assume now that
![]() ${X}$
is finite and, by possibly adding generators, that
${X}$
is finite and, by possibly adding generators, that
![]() ${X}_H$
contains at least
${X}_H$
contains at least
![]() $n+4$
elements. We also assume that
$n+4$
elements. We also assume that
![]() ${D}_H$
is of degree
${D}_H$
is of degree
![]() $n>1$
, and we set
$n>1$
, and we set
![]() $m=\# X_H$
so that
$m=\# X_H$
so that
![]() $m\ge n+4$
.
$m\ge n+4$
.
Consider the morphism
![]() $\pi \colon {\mathrm {Spec}}\ F_{{X}_H^{\pm }}(n)\to {\mathrm {Spec}}\ E_{{X}_H^{\pm }}(n)$
. The ring
$\pi \colon {\mathrm {Spec}}\ F_{{X}_H^{\pm }}(n)\to {\mathrm {Spec}}\ E_{{X}_H^{\pm }}(n)$
. The ring
![]() $E_{{X}_H^{\pm }}(n) $
is a normal domain because it is the ring of invariants under the connected reductive group
$E_{{X}_H^{\pm }}(n) $
is a normal domain because it is the ring of invariants under the connected reductive group
![]() ${\mathrm {GL}}_n$
of the normal domain
${\mathrm {GL}}_n$
of the normal domain
![]() $F_{{X}_H^{\pm }}(n)$
. Let
$F_{{X}_H^{\pm }}(n)$
. Let
![]() $U\subset {\mathrm {Spec}}\ F_{{X}_H^{\pm }}(n)$
be the open subscheme over which the generic matrix representation
$U\subset {\mathrm {Spec}}\ F_{{X}_H^{\pm }}(n)$
be the open subscheme over which the generic matrix representation
![]() $ \rho _{{X}_H^{\pm }}\colon {\mathbb {Z}}\{{X}_H^{\pm }\}\to {\mathrm {Mat}}_{n\times n}(F_{{X}_H^{\pm }}(n)) ,{x}\mapsto \xi _{{x}}$
is irreducible, cf. [Reference ChenevierChe14, Example 2.20]. It is known that U is dense in
$ \rho _{{X}_H^{\pm }}\colon {\mathbb {Z}}\{{X}_H^{\pm }\}\to {\mathrm {Mat}}_{n\times n}(F_{{X}_H^{\pm }}(n)) ,{x}\mapsto \xi _{{x}}$
is irreducible, cf. [Reference ChenevierChe14, Example 2.20]. It is known that U is dense in
![]() ${\mathrm {Spec}}\ F_{{X}_H^{\pm }}(n)$
, and we will give a much stronger result in the next paragraph. It is also known that the induced map
${\mathrm {Spec}}\ F_{{X}_H^{\pm }}(n)$
, and we will give a much stronger result in the next paragraph. It is also known that the induced map
![]() $U\to V:=\pi (U)$
is a
$U\to V:=\pi (U)$
is a
![]() ${\mathrm {PGL}}_n$
-torsor, and V is open nonempty and hence also dense in the integral scheme
${\mathrm {PGL}}_n$
-torsor, and V is open nonempty and hence also dense in the integral scheme
![]() ${\mathrm {Spec}}\ E_{{X}_H^{\pm }}(n)$
, see [Reference NakamotoNak00, § 3 and Corollary 6.5]. It follows that
${\mathrm {Spec}}\ E_{{X}_H^{\pm }}(n)$
, see [Reference NakamotoNak00, § 3 and Corollary 6.5]. It follows that
![]() $\dim E_{{X}_H^{\pm }}(n)=\dim V=1+mn^2-(n^2-1)=(m-1)n^2+2$
because clearly
$\dim E_{{X}_H^{\pm }}(n)=\dim V=1+mn^2-(n^2-1)=(m-1)n^2+2$
because clearly
![]() $\dim F_{{X}_H^{\pm }}(n)=1+mn^2$
.
$\dim F_{{X}_H^{\pm }}(n)=1+mn^2$
.
We claim that V contains all points of codimension at most
![]() $1$
of
$1$
of
![]() ${\mathrm {Spec}}\ E_{{X}_H^{\pm }}(n)$
. For this, we shall show that the reducible locus
${\mathrm {Spec}}\ E_{{X}_H^{\pm }}(n)$
. For this, we shall show that the reducible locus
![]() $Z:={\mathrm {Spec}}\ F_{{X}_H^{\pm }}(n){\smallsetminus } U$
has dimension at most
$Z:={\mathrm {Spec}}\ F_{{X}_H^{\pm }}(n){\smallsetminus } U$
has dimension at most
![]() $(m-1)n^2$
from which it follows that
$(m-1)n^2$
from which it follows that
![]() $\pi (Z)={\mathrm {Spec}}\ E_{{X}_H^{\pm }}(n){\smallsetminus } V$
has codimension at least
$\pi (Z)={\mathrm {Spec}}\ E_{{X}_H^{\pm }}(n){\smallsetminus } V$
has codimension at least
![]() $2$
. Because Z is of finite type over
$2$
. Because Z is of finite type over
![]() ${\mathbb {Z}}$
, it suffices to analyze the dimensions after base change from
${\mathbb {Z}}$
, it suffices to analyze the dimensions after base change from
![]() ${\mathbb {Z}}$
to an algebraically closed field k. Then
${\mathbb {Z}}$
to an algebraically closed field k. Then
![]() $ \rho _{{X}_H^{\pm }}$
is reducible at a closed point if and only if there is a proper parabolic subgroup P of
$ \rho _{{X}_H^{\pm }}$
is reducible at a closed point if and only if there is a proper parabolic subgroup P of
![]() ${\mathrm {GL}}_n$
that contains the set of matrices
${\mathrm {GL}}_n$
that contains the set of matrices
![]() $ \rho _{{X}_H^{\pm }}({X}_H)$
, that is the set can by simultaneously conjugated by
$ \rho _{{X}_H^{\pm }}({X}_H)$
, that is the set can by simultaneously conjugated by
![]() ${\mathrm {GL}}_n$
to a standard parabolic P of
${\mathrm {GL}}_n$
to a standard parabolic P of
![]() ${\mathrm {GL}}_n$
. The stabilizer of this conjugation action is P itself and the dimension of P is at most
${\mathrm {GL}}_n$
. The stabilizer of this conjugation action is P itself and the dimension of P is at most
![]() $n^2-n+1$
, and there are only finitely many such standard P once a maximal torus and a Borel are chosen for
$n^2-n+1$
, and there are only finitely many such standard P once a maximal torus and a Borel are chosen for
![]() ${\mathrm {GL}}_n$
. It follows that the dimension over k of the set of reducible points is at most
${\mathrm {GL}}_n$
. It follows that the dimension over k of the set of reducible points is at most
![]() $m\dim P+(n^2-\dim P)=(m-1)\dim P +n^2=(m-1)n^2 - ((m-1)(n-1)-n^2 )$
and the claim on
$m\dim P+(n^2-\dim P)=(m-1)\dim P +n^2=(m-1)n^2 - ((m-1)(n-1)-n^2 )$
and the claim on
![]() $\dim Z$
follows from our hypothesis
$\dim Z$
follows from our hypothesis
![]() $m\ge n+4$
.
$m\ge n+4$
.
We now give an argument independent of Lemma 4.6.6 that show that
![]() ${\mathrm {Ind}}_{{\mathrm {FG}}({X}_H)}^{{\mathrm {FG}}({X})} {D}_{{X}^{\pm }_H}$
takes values in
${\mathrm {Ind}}_{{\mathrm {FG}}({X}_H)}^{{\mathrm {FG}}({X})} {D}_{{X}^{\pm }_H}$
takes values in
![]() $E_{{X}_H^{\pm }}(n)$
: Let
$E_{{X}_H^{\pm }}(n)$
: Let
![]() ${\mathrm {Spec}}\ B\subset V$
be any affine open subset. Then by Proposition 4.1.25 the pseudocharacter
${\mathrm {Spec}}\ B\subset V$
be any affine open subset. Then by Proposition 4.1.25 the pseudocharacter
![]() $ {D}_{{X}^{\pm }_H} \colon {\mathrm {FG}}({X}_H)\to E_{{X}_H^{\pm }}(n)\to B$
factors as a representation
$ {D}_{{X}^{\pm }_H} \colon {\mathrm {FG}}({X}_H)\to E_{{X}_H^{\pm }}(n)\to B$
factors as a representation
![]() $\rho _B\colon {\mathrm {FG}}({X}_H)\to C^\times $
for C an Azumaya B-algebra of degree n followed by the pseudocharacter associated to C in Example 4.1.7. By change of coefficients to an algebraic closure
$\rho _B\colon {\mathrm {FG}}({X}_H)\to C^\times $
for C an Azumaya B-algebra of degree n followed by the pseudocharacter associated to C in Example 4.1.7. By change of coefficients to an algebraic closure
![]() ${\mathbb {K}}$
of the generic point of
${\mathbb {K}}$
of the generic point of
![]() $ F_{{X}_H^{\pm }}$
, it follows that
$ F_{{X}_H^{\pm }}$
, it follows that
![]() $ {\mathrm {Ind}}_{{\mathrm {FG}}({X}_H)}^{{\mathrm {FG}}({X})} \rho _{{X}_H^{\pm }}$
and
$ {\mathrm {Ind}}_{{\mathrm {FG}}({X}_H)}^{{\mathrm {FG}}({X})} \rho _{{X}_H^{\pm }}$
and
![]() ${\mathrm {Ind}}_{{\mathrm {FG}}({X}_H)}^{{\mathrm {FG}}({X})} \rho _B$
, from Definition 4.6.3, are isomorphic over
${\mathrm {Ind}}_{{\mathrm {FG}}({X}_H)}^{{\mathrm {FG}}({X})} \rho _B$
, from Definition 4.6.3, are isomorphic over
![]() ${\mathbb {K}}$
. Hence,
${\mathbb {K}}$
. Hence,
![]() ${\mathrm {det}}\circ {\mathrm {Ind}}_{{\mathrm {FG}}({X}_H)}^{{\mathrm {FG}}({X})} \rho _{{X}_H^{\pm }}$
takes values in B. But because V contains all points of codimension at most
${\mathrm {det}}\circ {\mathrm {Ind}}_{{\mathrm {FG}}({X}_H)}^{{\mathrm {FG}}({X})} \rho _{{X}_H^{\pm }}$
takes values in B. But because V contains all points of codimension at most
![]() $1$
of the integral normal scheme
$1$
of the integral normal scheme
![]() ${\mathrm {Spec}}\ E_{{X}_H^{\pm }}(n)$
it follows that the intersection of all such rings B (inside
${\mathrm {Spec}}\ E_{{X}_H^{\pm }}(n)$
it follows that the intersection of all such rings B (inside
![]() ${\mathrm {Frac}} (E_{{X}_H^{\pm }}(n))$
) is equal to
${\mathrm {Frac}} (E_{{X}_H^{\pm }}(n))$
) is equal to
![]() $E_{{X}_H^{\pm }}(n)$
, and we are done.
$E_{{X}_H^{\pm }}(n)$
, and we are done.
For later use, we formulate the following simple finiteness result related to induction.
Lemma 4.6.11. Let k be a field, let
![]() $\chi \colon G\to k^\times $
be a character of finite order
$\chi \colon G\to k^\times $
be a character of finite order
![]() ${m}$
with kernel
${m}$
with kernel
![]() $H:={\operatorname {ker}{\chi }} $
and let
$H:={\operatorname {ker}{\chi }} $
and let
![]() ${D}$
be in
${D}$
be in
![]() ${\mathcal {P}s\mathcal {R}}_{G}^n({{{k}}^{\mathrm {alg}}} )$
. Define
${\mathcal {P}s\mathcal {R}}_{G}^n({{{k}}^{\mathrm {alg}}} )$
. Define
Then the following hold:
-
(a)
 ${\cal S}_{D}$
is finite.
${\cal S}_{D}$
is finite. -
(b)
 ${\cal S}_{D}$
is nonempty if and only if
${\cal S}_{D}$
is nonempty if and only if
 ${D}={D}\otimes \chi $
.
${D}={D}\otimes \chi $
.
If moreover G is profinite,
![]() ${{{k}}^{\mathrm {alg}}} $
carries the discrete topology and
${{{k}}^{\mathrm {alg}}} $
carries the discrete topology and
![]() ${D}$
is continuous, then there is a finite extension of k in
${D}$
is continuous, then there is a finite extension of k in
![]() $ {{{k}}^{\mathrm {alg}}} $
over which all
$ {{{k}}^{\mathrm {alg}}} $
over which all
![]() ${D}'\in {\cal S}_{D}$
are defined and split.
${D}'\in {\cal S}_{D}$
are defined and split.
Proof. By Theorem 4.1.18 and Corollary 4.4.6, the map
![]() $\rho \to {D}_\rho $
from semisimple representations of G over
$\rho \to {D}_\rho $
from semisimple representations of G over
![]() ${{{k}}^{\mathrm {alg}}} $
to pseudocharacters of G over
${{{k}}^{\mathrm {alg}}} $
to pseudocharacters of G over
![]() ${{{k}}^{\mathrm {alg}}} $
is a bijection, and the same holds over H. We also have
${{{k}}^{\mathrm {alg}}} $
is a bijection, and the same holds over H. We also have
![]() ${D}_\rho \otimes \chi ={D}_{\rho \otimes \chi }$
by Proposition 4.5.7
(d). Thus, (a) and (b) are really assertions on semisimple representations. Now, if
${D}_\rho \otimes \chi ={D}_{\rho \otimes \chi }$
by Proposition 4.5.7
(d). Thus, (a) and (b) are really assertions on semisimple representations. Now, if
![]() $\rho $
is a representation and if
$\rho $
is a representation and if
![]() $\rho ={\mathrm {Ind}}_H^G\rho '$
for some representation
$\rho ={\mathrm {Ind}}_H^G\rho '$
for some representation
![]() $\rho '$
, then
$\rho '$
, then
![]() $\rho '$
is a direct summand of the semisimple representation
$\rho '$
is a direct summand of the semisimple representation
![]() $\rho |_H$
by Lemma 2.1.4. Since up to isomorphism there are only finitely many such summands and since these are unique up to permutation, Part (a) follows. Part (b) is now immediate from Corollary 2.2.2. The last assertion is a consequence of Corollary 4.4.6 since
$\rho |_H$
by Lemma 2.1.4. Since up to isomorphism there are only finitely many such summands and since these are unique up to permutation, Part (a) follows. Part (b) is now immediate from Corollary 2.2.2. The last assertion is a consequence of Corollary 4.4.6 since
![]() ${\cal S}_{D}$
is finite.
${\cal S}_{D}$
is finite.
4.7 Pseudodeformations and their universal rings
This subsection recalls in Proposition 4.7.4 the main object of our interest, the universal pseudodeformation ring of a residual pseudocharacter
![]() ${\overline {{D}}}$
. Here, continuity plays a major role. We state basic results relevant to the present work. In addition to the usual treatment, we also give some special attention to functors
${\overline {{D}}}$
. Here, continuity plays a major role. We state basic results relevant to the present work. In addition to the usual treatment, we also give some special attention to functors
![]() ${\widehat {\mathcal {A}}r}_\kappa \to {Sets}$
where
${\widehat {\mathcal {A}}r}_\kappa \to {Sets}$
where
![]() $\kappa $
is a local field. The subsection also contains some results on deformations over formal schemes and on the locus of irreducibility.
$\kappa $
is a local field. The subsection also contains some results on deformations over formal schemes and on the locus of irreducibility.
We let
![]() ${{\mathbb {F}}\,\!{}}$
be either a finite or a local field; in the former case,
${{\mathbb {F}}\,\!{}}$
be either a finite or a local field; in the former case,
![]() $\Lambda $
is a complete Noetherian local commutative
$\Lambda $
is a complete Noetherian local commutative
![]() ${{W({{\mathbb {F}}\,\!{}})}}$
-algebra with residue field
${{W({{\mathbb {F}}\,\!{}})}}$
-algebra with residue field
![]() ${{\mathbb {F}}\,\!{}}$
. In the latter case,
${{\mathbb {F}}\,\!{}}$
. In the latter case,
![]() $\Lambda ={{\mathbb {F}}\,\!{}}$
. Recall the categories
$\Lambda ={{\mathbb {F}}\,\!{}}$
. Recall the categories
![]() ${\mathcal {A}r}_{\Lambda }$
and
${\mathcal {A}r}_{\Lambda }$
and
![]() ${\widehat {\mathcal {A}}r}_{\Lambda }$
from Subsection 3.1 and the topological conditions we impose on there objects and morphisms. By A, we denote a ring in
${\widehat {\mathcal {A}}r}_{\Lambda }$
from Subsection 3.1 and the topological conditions we impose on there objects and morphisms. By A, we denote a ring in
![]() ${\widehat {\mathcal {A}}r}_{{\mathbb {F}}\,\!{}}$
; its maximal ideal is
${\widehat {\mathcal {A}}r}_{{\mathbb {F}}\,\!{}}$
; its maximal ideal is
![]() ${\mathfrak {m}}_A$
and it comes with a natural reduction map
${\mathfrak {m}}_A$
and it comes with a natural reduction map
![]() $\pi _A\colon A\to A/{\mathfrak {m}}_A={{\mathbb {F}}\,\!{}}$
. We let G be a profinite group and we denote by
$\pi _A\colon A\to A/{\mathfrak {m}}_A={{\mathbb {F}}\,\!{}}$
. We let G be a profinite group and we denote by
![]() ${\overline {{D}}}\colon {{\mathbb {F}}\,\!{}}[G]\to {{\mathbb {F}}\,\!{}}$
a continuous pseudocharacter of dimension n.
${\overline {{D}}}\colon {{\mathbb {F}}\,\!{}}[G]\to {{\mathbb {F}}\,\!{}}$
a continuous pseudocharacter of dimension n.
Definition 4.7.1 [Reference Wang EricksonWE13, § 3.1.4.3].
-
(a) A pseudodeformation of
 ${\overline {{D}}}$
to A is a continuous pseudocharacter
${\overline {{D}}}$
to A is a continuous pseudocharacter
 ${D}\colon A[G]\to A$
such that
${D}\colon A[G]\to A$
such that
 ${D}\otimes _A{{\mathbb {F}}\,\!{}}=\pi _A\circ {D}\colon {{\mathbb {F}}\,\!{}}[G]\to {{\mathbb {F}}\,\!{}}$
is equal to
${D}\otimes _A{{\mathbb {F}}\,\!{}}=\pi _A\circ {D}\colon {{\mathbb {F}}\,\!{}}[G]\to {{\mathbb {F}}\,\!{}}$
is equal to
 ${\overline {{D}}}$
.
${\overline {{D}}}$
. -
(b) The functor
is called the pseudodeformation functor of the residual pseudocharacter $$ \begin{align*}{\mathcal{P}sD}_{{\overline{{D}}}}\colon{\widehat{\mathcal{A}}r}_{\Lambda}\to{Sets},\quad A\longmapsto \{{D}\colon G\,{\longrightarrow}\, A\text{ is a pseudodeformation of } {\overline{{D}}}\}, \end{align*} $$
$$ \begin{align*}{\mathcal{P}sD}_{{\overline{{D}}}}\colon{\widehat{\mathcal{A}}r}_{\Lambda}\to{Sets},\quad A\longmapsto \{{D}\colon G\,{\longrightarrow}\, A\text{ is a pseudodeformation of } {\overline{{D}}}\}, \end{align*} $$
 ${\overline {{D}}}$
.
${\overline {{D}}}$
.
Note that unlike in parts of [Reference Wang EricksonWE13] for us all pseudodeformations will be continuous.
Definition 4.7.2. Let
![]() $\pi \colon B\to {{\mathbb {F}}\,\!{}}$
be a morphism in
$\pi \colon B\to {{\mathbb {F}}\,\!{}}$
be a morphism in
![]() ${\mathcal {CA}lg}_{\Lambda }$
, and let
${\mathcal {CA}lg}_{\Lambda }$
, and let
![]() ${D}\colon B[G] \to B$
be a pseudocharacter such that
${D}\colon B[G] \to B$
be a pseudocharacter such that
![]() ${D}\otimes _B{{\mathbb {F}}\,\!{}}={\overline {{D}}}$
.
${D}\otimes _B{{\mathbb {F}}\,\!{}}={\overline {{D}}}$
.
An ideal I of B is called
![]() ${D}$
-open if the following conditions hold:
${D}$
-open if the following conditions hold:
-
(a) The map
 $\pi $
factors via
$\pi $
factors via
 $B/I$
and
$B/I$
and
 $B/I$
is a local Artin ring.
$B/I$
is a local Artin ring. -
(b)
 ${D}_I:={D}\otimes _BB/I$
is continuous if we equip
${D}_I:={D}\otimes _BB/I$
is continuous if we equip
 $B/I$
with the topology of an object in
$B/I$
with the topology of an object in
 ${\mathcal {A}r}_{\Lambda }$
.
${\mathcal {A}r}_{\Lambda }$
.
Lemma 4.7.3. With the notation from Definition 4.7.2, the
![]() ${D}$
-open ideals form a basis of a topology on B.
${D}$
-open ideals form a basis of a topology on B.
Proof. (Cf. [Reference Wang EricksonWE13, Theorem 3.1.4.6]) One has to show that if
![]() $I,I'$
are
$I,I'$
are
![]() ${D}$
-open ideals, then so is
${D}$
-open ideals, then so is
![]() $I\cap I'$
. Consider the injective homomorphism
$I\cap I'$
. Consider the injective homomorphism
For both
![]() $\Lambda $
that we consider, it is straightforward to see that
$\Lambda $
that we consider, it is straightforward to see that
![]() $\iota $
is a topological isomorphism onto its image. Now, a pseudocharacter is continuous if and only if this holds for its characteristic polynomial functions; cf. Definition 4.4.1. Since both I and
$\iota $
is a topological isomorphism onto its image. Now, a pseudocharacter is continuous if and only if this holds for its characteristic polynomial functions; cf. Definition 4.4.1. Since both I and
![]() $I'$
are
$I'$
are
![]() ${D}$
-open, it is now immediate that
${D}$
-open, it is now immediate that
![]() $I\cap I'$
is
$I\cap I'$
is
![]() ${D}$
-open.
${D}$
-open.
The following result is proved in [Reference ChenevierChe14, Proposition 3.3] for
![]() $\Lambda ={W({{\mathbb {F}}\,\!{}})}$
and in [Reference Wang EricksonWE13, Theorem 3.1.4.6] for
$\Lambda ={W({{\mathbb {F}}\,\!{}})}$
and in [Reference Wang EricksonWE13, Theorem 3.1.4.6] for
![]() $\Lambda \in {\widehat {\mathcal {A}}r}_{{W({{\mathbb {F}}\,\!{}})}}$
.
$\Lambda \in {\widehat {\mathcal {A}}r}_{{W({{\mathbb {F}}\,\!{}})}}$
.
Proposition 4.7.4. The pseudodeformation functor
![]() ${\mathcal {P}sD}_{\overline {{D}}}$
is prorepresentable by a topological
${\mathcal {P}sD}_{\overline {{D}}}$
is prorepresentable by a topological
![]() $\Lambda $
-algebra
$\Lambda $
-algebra
![]() ${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}}}}$
that is a filtered inverse limit of objects in
${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}}}}$
that is a filtered inverse limit of objects in
![]() ${\mathcal {A}r}_{\Lambda }$
, together with a universal pseudodeformation
${\mathcal {A}r}_{\Lambda }$
, together with a universal pseudodeformation
Proof. We recall a sketch of the proof from [Reference Wang EricksonWE13, Theorem 3.1.4.6] to indicate that it also applies to the case when
![]() $\Lambda =\kappa $
is a local field. Consider the universal ring
$\Lambda =\kappa $
is a local field. Consider the universal ring
![]() ${R^{\operatorname {univ}}_{\Lambda [G],n}}$
from Definition 4.2.2 with its universal pseudocharacter
${R^{\operatorname {univ}}_{\Lambda [G],n}}$
from Definition 4.2.2 with its universal pseudocharacter
![]() ${D}^{\operatorname {univ}}_{\Lambda [G]}\colon G {\longrightarrow } {R^{\operatorname {univ}}_{\Lambda [G],n}}$
on G. By definition,
${D}^{\operatorname {univ}}_{\Lambda [G]}\colon G {\longrightarrow } {R^{\operatorname {univ}}_{\Lambda [G],n}}$
on G. By definition,
![]() ${R^{\operatorname {univ}}_{\Lambda [G],n}}$
is a
${R^{\operatorname {univ}}_{\Lambda [G],n}}$
is a
![]() $\Lambda $
-algebra. The map
$\Lambda $
-algebra. The map
![]() ${\overline {{D}}}$
induces a
${\overline {{D}}}$
induces a
![]() $\Lambda $
-algebra homomorphism
$\Lambda $
-algebra homomorphism
![]() $\pi \colon {R^{\operatorname {univ}}_{\Lambda [G],n}}\rightarrow {{\mathbb {F}}\,\!{}}$
. By Lemma 4.7.3, the
$\pi \colon {R^{\operatorname {univ}}_{\Lambda [G],n}}\rightarrow {{\mathbb {F}}\,\!{}}$
. By Lemma 4.7.3, the
![]() ${D}$
-open ideals of
${D}$
-open ideals of
![]() ${R^{\operatorname {univ}}_{\Lambda [G],n}}$
form the basis of a topology on
${R^{\operatorname {univ}}_{\Lambda [G],n}}$
form the basis of a topology on
![]() ${R^{\operatorname {univ}}_{\Lambda [G],n}}$
, and one defines
${R^{\operatorname {univ}}_{\Lambda [G],n}}$
, and one defines
![]() ${R^{\operatorname {univ}}_{\Lambda ,{\overline {{D}}}}}$
as the completion of
${R^{\operatorname {univ}}_{\Lambda ,{\overline {{D}}}}}$
as the completion of
![]() ${R^{\operatorname {univ}}_{\Lambda [G],n}}$
with respect to this topology. It is then straightforward to establish the asserted properties for
${R^{\operatorname {univ}}_{\Lambda [G],n}}$
with respect to this topology. It is then straightforward to establish the asserted properties for
![]() ${R^{\operatorname {univ}}_{\Lambda ,{\overline {{D}}}}}$
together with the pseudocharacter
${R^{\operatorname {univ}}_{\Lambda ,{\overline {{D}}}}}$
together with the pseudocharacter
![]() ${D}^{\operatorname {univ}}_{\Lambda ,{\overline {{D}}}}:={D}^{\operatorname {univ}}_{\Lambda [G]}\otimes _{{R^{\operatorname {univ}}_{\Lambda [G,]}}{n}} {R^{\operatorname {univ}}_{\Lambda ,{\overline {{D}}}}}$
by verifying it for the restriction of
${D}^{\operatorname {univ}}_{\Lambda ,{\overline {{D}}}}:={D}^{\operatorname {univ}}_{\Lambda [G]}\otimes _{{R^{\operatorname {univ}}_{\Lambda [G,]}}{n}} {R^{\operatorname {univ}}_{\Lambda ,{\overline {{D}}}}}$
by verifying it for the restriction of
![]() ${\mathcal {P}sD}_{\overline {{D}}}$
to
${\mathcal {P}sD}_{\overline {{D}}}$
to
![]() ${\mathcal {A}r}_{\Lambda }$
.
${\mathcal {A}r}_{\Lambda }$
.
Definition 4.7.5. The ring
![]() ${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}}}} $
from Proposition 4.7.4 is called the universal (
${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}}}} $
from Proposition 4.7.4 is called the universal (
![]() $\Lambda $
-)pseudodeformation ring of
$\Lambda $
-)pseudodeformation ring of
![]() ${\overline {{D}}}$
, the pseudocharacter
${\overline {{D}}}$
, the pseudocharacter
![]() ${D}^{\operatorname {univ}}_{\Lambda ,{\overline {{D}}}}\colon {R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}}}} [G]\to {R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}}}} $
the universal (
${D}^{\operatorname {univ}}_{\Lambda ,{\overline {{D}}}}\colon {R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}}}} [G]\to {R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}}}} $
the universal (
![]() $\Lambda $
-)-pseudodeformation of
$\Lambda $
-)-pseudodeformation of
![]() ${\overline {{D}}}$
and the space
${\overline {{D}}}$
and the space
![]() ${X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}}}} :={\mathrm {Spec}}{R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}}}} $
the universal (
${X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}}}} :={\mathrm {Spec}}{R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}}}} $
the universal (
![]() $\Lambda $
-)pseudodeformation space of
$\Lambda $
-)pseudodeformation space of
![]() ${\overline {{D}}}$
; we write
${\overline {{D}}}$
; we write
![]() ${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{G,\Lambda ,{\overline {{D}}}}}}$
if there is a need to indicate G; we often drop the index
${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{G,\Lambda ,{\overline {{D}}}}}}$
if there is a need to indicate G; we often drop the index
![]() $\Lambda $
if it is clear from context.
$\Lambda $
if it is clear from context.
The ring
![]() ${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}}}} $
behaves well under change of the coefficient ring
${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}}}} $
behaves well under change of the coefficient ring
![]() $\Lambda $
.
$\Lambda $
.
Proposition 4.7.6 (Cf. [Reference WilesWil95, p. 457]).
Let
![]() $\bar f\colon {\kappa }\to {\kappa }'$
be a homomorphism between either two finite or two local fields, and let
$\bar f\colon {\kappa }\to {\kappa }'$
be a homomorphism between either two finite or two local fields, and let
![]() $f\colon \Lambda \to \Lambda '$
be a local homomorphisms of complete local Noetherian commutative rings that reduces on residue fields to
$f\colon \Lambda \to \Lambda '$
be a local homomorphisms of complete local Noetherian commutative rings that reduces on residue fields to
![]() $\bar f$
. Define
$\bar f$
. Define
![]() ${\overline {{D}}}':={\overline {{D}}}\otimes _{{\kappa }}{\kappa }'\colon {\kappa }'[G]\to {\kappa }'$
. Then one has a natural isomorphism
${\overline {{D}}}':={\overline {{D}}}\otimes _{{\kappa }}{\kappa }'\colon {\kappa }'[G]\to {\kappa }'$
. Then one has a natural isomorphism
Proof. The proof is as in [Reference WilesWil95, p. 457] for deformation rings: If
![]() $\bar f$
is the identity, one can proceed as follows. Any
$\bar f$
is the identity, one can proceed as follows. Any
![]() $A\in {\widehat {\mathcal {A}}r}_{\Lambda '}$
can be regarded as a ring in
$A\in {\widehat {\mathcal {A}}r}_{\Lambda '}$
can be regarded as a ring in
![]() ${\widehat {\mathcal {A}}r}_{\Lambda }$
via the action induced from f; the residue fields of A,
${\widehat {\mathcal {A}}r}_{\Lambda }$
via the action induced from f; the residue fields of A,
![]() $\Lambda $
and
$\Lambda $
and
![]() $\Lambda '$
are the same. Then the assertion follows rapidly by using the isomorphism
$\Lambda '$
are the same. Then the assertion follows rapidly by using the isomorphism
![]() ${\mathrm {Hom}}_{{\widehat {\mathcal {A}}r}_{\Lambda }}(A,B)\cong {\mathrm {Hom}}_{\Lambda '}(A\otimes _{\Lambda }\Lambda ',B)$
for
${\mathrm {Hom}}_{{\widehat {\mathcal {A}}r}_{\Lambda }}(A,B)\cong {\mathrm {Hom}}_{\Lambda '}(A\otimes _{\Lambda }\Lambda ',B)$
for
![]() $A\in {\widehat {\mathcal {A}}r}_{\Lambda }$
and
$A\in {\widehat {\mathcal {A}}r}_{\Lambda }$
and
![]() $B\in {\widehat {\mathcal {A}}r}_{\Lambda '}$
together with the universal properties of
$B\in {\widehat {\mathcal {A}}r}_{\Lambda '}$
together with the universal properties of
![]() ${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ',{\overline {{D}}}'}}}$
and
${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ',{\overline {{D}}}'}}}$
and
![]() ${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}}}} $
.
${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}}}} $
.
In the general case, define for any
![]() $B'\in {\widehat {\mathcal {A}}r}_{\Lambda '}$
the ring
$B'\in {\widehat {\mathcal {A}}r}_{\Lambda '}$
the ring
![]() $B"$
as the subring of
$B"$
as the subring of
![]() $B'$
of elements whose reduction to
$B'$
of elements whose reduction to
![]() ${\kappa }'$
lies in the subfield
${\kappa }'$
lies in the subfield
![]() ${\kappa }$
so that
${\kappa }$
so that
![]() $B"\in {\widehat {\mathcal {A}}r}_{\Lambda "}$
. The argument just given applies to
$B"\in {\widehat {\mathcal {A}}r}_{\Lambda "}$
. The argument just given applies to
![]() $\Lambda \to \Lambda "$
. For
$\Lambda \to \Lambda "$
. For
![]() $\Lambda "\to \Lambda '$
note first that any
$\Lambda "\to \Lambda '$
note first that any
![]() ${D}'\in {\mathcal {P}sD}_{\Lambda ',{\overline {{D}}}'}(B')$
takes values in
${D}'\in {\mathcal {P}sD}_{\Lambda ',{\overline {{D}}}'}(B')$
takes values in
![]() $B"$
because
$B"$
because
![]() ${\overline {{D}}}\!\phantom {|}'$
takes values in
${\overline {{D}}}\!\phantom {|}'$
takes values in
![]() ${\kappa }$
so that
${\kappa }$
so that
![]() ${D}'$
defines a
${D}'$
defines a
![]() ${D}"\in {\mathcal {P}sD}_{\Lambda ",{\overline {{D}}}}(B")$
. Conversely, if such a
${D}"\in {\mathcal {P}sD}_{\Lambda ",{\overline {{D}}}}(B")$
. Conversely, if such a
![]() ${D}"$
is given, we may form
${D}"$
is given, we may form
![]() ${D}"\otimes _{\Lambda "}\Lambda '$
and compose it with the natural
${D}"\otimes _{\Lambda "}\Lambda '$
and compose it with the natural
![]() $\Lambda '$
-homomorphism
$\Lambda '$
-homomorphism
![]() $B"\otimes _{\Lambda "}\Lambda '\to B'$
to get back to
$B"\otimes _{\Lambda "}\Lambda '\to B'$
to get back to
![]() ${D}'$
. This yields the following chain of isomorphisms
${D}'$
. This yields the following chain of isomorphisms
 $$ \begin{align*} {\mathrm{Hom}}_{\Lambda'}({R{{\phantom{\overline{m}}}}^{\operatorname{univ}}_{{\Lambda',{\overline{{D}}}'}}} ,B')&\cong{\mathcal{P}sD}_{\Lambda',{\overline{{D}}}'}(B') \ \cong \ {\mathcal{P}sD}_{\Lambda",{\overline{{D}}}}(B")\\ &\cong {\mathrm{Hom}}_{\Lambda"}({R{{\phantom{\overline{m}}}}^{\operatorname{univ}}_{{\Lambda",{\overline{{D}}}}}} ,B") \ \cong {\mathrm{Hom}}_{\Lambda"}({R{{\phantom{\overline{m}}}}^{\operatorname{univ}}_{{\Lambda",{\overline{{D}}}}}} ,B') \\ &\cong {\mathrm{Hom}}_{\Lambda'}({R{{\phantom{\overline{m}}}}^{\operatorname{univ}}_{{\Lambda",{\overline{{D}}}}}} \otimes_{\Lambda"}\Lambda',B') \end{align*} $$
$$ \begin{align*} {\mathrm{Hom}}_{\Lambda'}({R{{\phantom{\overline{m}}}}^{\operatorname{univ}}_{{\Lambda',{\overline{{D}}}'}}} ,B')&\cong{\mathcal{P}sD}_{\Lambda',{\overline{{D}}}'}(B') \ \cong \ {\mathcal{P}sD}_{\Lambda",{\overline{{D}}}}(B")\\ &\cong {\mathrm{Hom}}_{\Lambda"}({R{{\phantom{\overline{m}}}}^{\operatorname{univ}}_{{\Lambda",{\overline{{D}}}}}} ,B") \ \cong {\mathrm{Hom}}_{\Lambda"}({R{{\phantom{\overline{m}}}}^{\operatorname{univ}}_{{\Lambda",{\overline{{D}}}}}} ,B') \\ &\cong {\mathrm{Hom}}_{\Lambda'}({R{{\phantom{\overline{m}}}}^{\operatorname{univ}}_{{\Lambda",{\overline{{D}}}}}} \otimes_{\Lambda"}\Lambda',B') \end{align*} $$
We deduce
![]() ${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ',{\overline {{D}}}'}}} \cong {R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ",{\overline {{D}}}}}} \otimes _{\Lambda "}\Lambda '$
because any
${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ',{\overline {{D}}}'}}} \cong {R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ",{\overline {{D}}}}}} \otimes _{\Lambda "}\Lambda '$
because any
![]() $B'\in {\widehat {\mathcal {A}}r}_{\Lambda '}$
can occur as test objects.
$B'\in {\widehat {\mathcal {A}}r}_{\Lambda '}$
can occur as test objects.
The previous proposition justifies the following definition.
Definition 4.7.7. If
![]() ${{\mathbb {F}}\,\!{}}$
is finite, we call
${{\mathbb {F}}\,\!{}}$
is finite, we call
![]() ${\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}} :={R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{{\mathbb {F}}\,\!{}},{\overline {{D}}}}}} $
the universal mod p pseudodeformation ring of
${\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}} :={R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{{\mathbb {F}}\,\!{}},{\overline {{D}}}}}} $
the universal mod p pseudodeformation ring of
![]() ${\overline {{D}}}$
and we call
${\overline {{D}}}$
and we call
![]() ${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}:={X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{{\mathbb {F}}\,\!{}},{\overline {{D}}}}}}$
the special fiber of the universal pseudodeformation space of
${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}:={X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{{\mathbb {F}}\,\!{}},{\overline {{D}}}}}}$
the special fiber of the universal pseudodeformation space of
![]() ${\overline {{D}}}$
.
${\overline {{D}}}$
.
We shall also need to consider Cayley–Hamilton quotients. Recall from Remark 4.4.4 that
![]() ${D}^{\operatorname {univ}}_{\Lambda ,{\overline {{D}}}}$
induces a continuous pseudorepresentation (for which we shall use the same name)
${D}^{\operatorname {univ}}_{\Lambda ,{\overline {{D}}}}$
induces a continuous pseudorepresentation (for which we shall use the same name)
Let the following be the diagram induced from diagram (16)

Definition 4.7.8. For ‘object’ the algebra
![]() ${S^{{\operatorname {CH-univ}}}_{\Lambda ,{\overline {{D}}}}}$
, the CH-representation
${S^{{\operatorname {CH-univ}}}_{\Lambda ,{\overline {{D}}}}}$
, the CH-representation
![]() $\rho ^{\mathrm {CH}}_{\Lambda ,{\overline {{D}}}}$
, or the pseudocharacter
$\rho ^{\mathrm {CH}}_{\Lambda ,{\overline {{D}}}}$
, or the pseudocharacter
![]() ${D}^{\operatorname {CH-univ}}_{\Lambda ,{\overline {{D}}}}$
, respectively, we use the term universal Cayley–Hamilton object attached to
${D}^{\operatorname {CH-univ}}_{\Lambda ,{\overline {{D}}}}$
, respectively, we use the term universal Cayley–Hamilton object attached to
![]() ${\overline {{D}}}$
.
${\overline {{D}}}$
.
Remark 4.7.9. As explained in [Reference ChenevierChe14, Proposition 1.23], the factorization in diagram (24) has indeed a universal property.
Definition 4.7.10 (Cf. [Reference Wang EricksonWE13, 3.1.5]).
Suppose
![]() ${{\mathbb {F}}\,\!{}}$
is finite. Then we define condition
${{\mathbb {F}}\,\!{}}$
is finite. Then we define condition
![]() $\Phi _{\overline {{D}}}$
to be condition
$\Phi _{\overline {{D}}}$
to be condition
![]() $\Phi _{\rho _{{\overline {{D}}}\otimes _{{\mathbb {F}}\,\!{}}{{{{{\mathbb {F}}\,\!{}}}}^{\mathrm {alg}}} }}$
from Definition 3.2.2.
$\Phi _{\rho _{{\overline {{D}}}\otimes _{{\mathbb {F}}\,\!{}}{{{{{\mathbb {F}}\,\!{}}}}^{\mathrm {alg}}} }}$
from Definition 3.2.2.
We recall a criterion for
![]() ${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}}}} $
and
${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}}}} $
and
![]() ${S^{{\operatorname {CH-univ}}}_{\Lambda ,{\overline {{D}}}}}$
to be Noetherian.
${S^{{\operatorname {CH-univ}}}_{\Lambda ,{\overline {{D}}}}}$
to be Noetherian.
Proposition 4.7.11 [Reference Wang-EricksonWE18, Propositions 3.2 and 3.6].
The following hold if
![]() ${{\mathbb {F}}\,\!{}}$
is finite and
${{\mathbb {F}}\,\!{}}$
is finite and
![]() $\Phi _{\overline {{D}}}$
holds:
$\Phi _{\overline {{D}}}$
holds:
-
(a) The topological
 $\Lambda $
-algebra
$\Lambda $
-algebra
 ${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,\overline D}}}$
lies in
${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,\overline D}}}$
lies in
 ${\widehat {\mathcal {A}}r}_{\Lambda }$
.
${\widehat {\mathcal {A}}r}_{\Lambda }$
. -
(b) The CH-representation
 $\rho ^{\mathrm {CH}}_{\Lambda ,{\overline {{D}}}}$
is a continuous homomorphism.
$\rho ^{\mathrm {CH}}_{\Lambda ,{\overline {{D}}}}$
is a continuous homomorphism. -
(c) The ring
 ${S^{{\operatorname {CH-univ}}}_{\Lambda ,{\overline {{D}}}}}$
is module-finite as an
${S^{{\operatorname {CH-univ}}}_{\Lambda ,{\overline {{D}}}}}$
is module-finite as an
 ${R^{\operatorname {univ}}_{\Lambda ,{\overline {{D}}}}}$
-algebra, and therefore Noetherian.
${R^{\operatorname {univ}}_{\Lambda ,{\overline {{D}}}}}$
-algebra, and therefore Noetherian. -
(d) On
 ${S^{{\operatorname {CH-univ}}}_{\Lambda ,{\overline {{D}}}}}$
the profinite topology, the
${S^{{\operatorname {CH-univ}}}_{\Lambda ,{\overline {{D}}}}}$
the profinite topology, the
 $\mathfrak {m}_{\overline {{D}}}$
-adic topology, and the quotient topology from the surjection
$\mathfrak {m}_{\overline {{D}}}$
-adic topology, and the quotient topology from the surjection
 $\rho ^{\mathrm {CH}}_{\Lambda ,{\overline {{D}}}}$
are equivalent.
$\rho ^{\mathrm {CH}}_{\Lambda ,{\overline {{D}}}}$
are equivalent.
Remark 4.7.12. Suppose
![]() $G=G_K$
for K a p-adic field. Then by Propositions 3.2.3 and 4.7.11, the ring
$G=G_K$
for K a p-adic field. Then by Propositions 3.2.3 and 4.7.11, the ring
![]() ${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,\overline D}}}$
is Noetherian.
${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,\overline D}}}$
is Noetherian.
Corollary 4.7.13. Suppose
![]() ${{\mathbb {F}}\,\!{}}$
is finite and
${{\mathbb {F}}\,\!{}}$
is finite and
![]() $\Phi _{\overline {{D}}}$
holds. Let A be a quotient of
$\Phi _{\overline {{D}}}$
holds. Let A be a quotient of
![]() $R:={R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{W({{\mathbb {F}}\,\!{}}),{\overline {{D}}}}}}$
. Then A is the ring of definition of
$R:={R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{W({{\mathbb {F}}\,\!{}}),{\overline {{D}}}}}}$
. Then A is the ring of definition of
![]() $D_A={{D}^{\operatorname {univ}}_{{\overline {{D}}}}}\otimes _RA$
over
$D_A={{D}^{\operatorname {univ}}_{{\overline {{D}}}}}\otimes _RA$
over
![]() ${{W({{\mathbb {F}}\,\!{}})}}$
in the sense of Definition 4.4.10.
${{W({{\mathbb {F}}\,\!{}})}}$
in the sense of Definition 4.4.10.
Proof. Let
![]() $C\subset A$
be the ring of definition of
$C\subset A$
be the ring of definition of
![]() $D_A$
over
$D_A$
over
![]() ${{W({{\mathbb {F}}\,\!{}})}}$
, and let
${{W({{\mathbb {F}}\,\!{}})}}$
, and let
![]() $D_C$
be the pseudocharacter over C such that
$D_C$
be the pseudocharacter over C such that
![]() ${D}_C\otimes _CA={D}_A$
. By the universality of R we have a unique
${D}_C\otimes _CA={D}_A$
. By the universality of R we have a unique
![]() ${{W({{\mathbb {F}}\,\!{}})}}$
-algebra homomorphism
${{W({{\mathbb {F}}\,\!{}})}}$
-algebra homomorphism
![]() $R\to C$
such that
$R\to C$
such that
![]() $D_C={{D}^{\operatorname {univ}}_{{\overline {{D}}}}}\otimes _RC$
. We deduce that the composition
$D_C={{D}^{\operatorname {univ}}_{{\overline {{D}}}}}\otimes _RC$
. We deduce that the composition
![]() $R\to C{\hookrightarrow } A$
is equal to the initially given quotient map. Hence,
$R\to C{\hookrightarrow } A$
is equal to the initially given quotient map. Hence,
![]() $C{\hookrightarrow } A$
must be the identity.
$C{\hookrightarrow } A$
must be the identity.
We shall also need the following result which in parts can be traced back to the proof of Proposition 4.7.11 in [Reference Wang EricksonWE13].
Proposition 4.7.14. If
![]() ${{\mathbb {F}}\,\!{}}$
is finite and condition
${{\mathbb {F}}\,\!{}}$
is finite and condition
![]() $\Phi _{\overline {{D}}}$
is satisfied, then the following hold:
$\Phi _{\overline {{D}}}$
is satisfied, then the following hold:
-
(a) For any
 ${\varphi }\colon {R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,\overline D}}} \to A$
in
${\varphi }\colon {R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,\overline D}}} \to A$
in
 ${\widehat {\mathcal {A}}r}_{\Lambda }$
giving rise to the pseudocharacter
${\widehat {\mathcal {A}}r}_{\Lambda }$
giving rise to the pseudocharacter
 ${D}_A$
, the induced maps are isomorphisms.
${D}_A$
, the induced maps are isomorphisms. $$ \begin{align*}(\Lambda [[G]] \otimes _{\Lambda} A)^{\mathrm {CH}}_{{D}_A}\rightarrow ({R{{\phantom{\overline{m}}}}^{\operatorname{univ}}_{{\Lambda ,\overline{D}}}} [[G]]\otimes _{{R{{\phantom{\overline{m}}}}^{\operatorname{univ}}_{{\Lambda ,\overline{D}}}} }A)^{\mathrm {CH}}_{{D}_A}\rightarrow (A[[G]])^{\mathrm {CH}}_{{D}_A} \rightarrow {S^{{\operatorname{CH-univ}}}_{\Lambda ,\overline{D}}}\otimes _{{R{{\phantom{\overline{m}}}}^{\operatorname{univ}}_{{\Lambda ,\overline{D}}}}} A\end{align*} $$
$$ \begin{align*}(\Lambda [[G]] \otimes _{\Lambda} A)^{\mathrm {CH}}_{{D}_A}\rightarrow ({R{{\phantom{\overline{m}}}}^{\operatorname{univ}}_{{\Lambda ,\overline{D}}}} [[G]]\otimes _{{R{{\phantom{\overline{m}}}}^{\operatorname{univ}}_{{\Lambda ,\overline{D}}}} }A)^{\mathrm {CH}}_{{D}_A}\rightarrow (A[[G]])^{\mathrm {CH}}_{{D}_A} \rightarrow {S^{{\operatorname{CH-univ}}}_{\Lambda ,\overline{D}}}\otimes _{{R{{\phantom{\overline{m}}}}^{\operatorname{univ}}_{{\Lambda ,\overline{D}}}}} A\end{align*} $$
-
(b) The
 ${{\mathbb {F}}\,\!{}}$
-algebra
${{\mathbb {F}}\,\!{}}$
-algebra
 $({{\mathbb {F}}\,\!{}}[[G]])^{\mathrm {CH}}_{{\overline {{D}}}}$
is finite-dimensional as an
$({{\mathbb {F}}\,\!{}}[[G]])^{\mathrm {CH}}_{{\overline {{D}}}}$
is finite-dimensional as an
 ${{\mathbb {F}}\,\!{}}$
-vector space.
${{\mathbb {F}}\,\!{}}$
-vector space.
Proof. For (a) consider the maps in
They are injective with dense image. By the definition of the Cayley–Hamilton ideal, this still holds after passing to Cayley–Hamilton quotients. By [Reference Wang EricksonWE13, Corollary 1.2.2.9 and Proposition 3.2.2.1] the A-algebra
![]() $(A[[G]])^{\mathrm {CH}}_{{D}_A}$
is a finitely generated A-module and hence Noetherian. It follows that its subrings
$(A[[G]])^{\mathrm {CH}}_{{D}_A}$
is a finitely generated A-module and hence Noetherian. It follows that its subrings
![]() $(\Lambda [[G]] \otimes _{\Lambda } A)^{\mathrm {CH}}_{{D}_A}\subset ({R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,\overline D}}}[[G]]\otimes _{{R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,\overline D}}} }A)^{\mathrm {CH}}_{{D}_A}$
are also finite A-modules. By completeness of A and their density in
$(\Lambda [[G]] \otimes _{\Lambda } A)^{\mathrm {CH}}_{{D}_A}\subset ({R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,\overline D}}}[[G]]\otimes _{{R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,\overline D}}} }A)^{\mathrm {CH}}_{{D}_A}$
are also finite A-modules. By completeness of A and their density in
![]() $(A[[G]])^{\mathrm {CH}}_{{D}_A}$
, the inclusions must be equalities. By Proposition 4.1.22
(c), we also know that the formation of the Cayley–Hamilton quotient commutes with base change. Hence,
$(A[[G]])^{\mathrm {CH}}_{{D}_A}$
, the inclusions must be equalities. By Proposition 4.1.22
(c), we also know that the formation of the Cayley–Hamilton quotient commutes with base change. Hence,
![]() $({R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,\overline {D}}}} [[G]]\otimes _{{R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,\overline {D}}}}}A)^{\mathrm {CH}}_{{D}_A} \rightarrow {S^{{\operatorname {CH-univ}}}_{\Lambda ,\overline {D}}}\otimes _{{R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,\overline {D}}}}} A $
is an isomorphism, and this completes the proof of (a). Part (b) follows from [Reference Wang EricksonWE13, Theorem 1.3.3.2]; it is also a consequence of Part (a) and Proposition 4.7.11.
$({R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,\overline {D}}}} [[G]]\otimes _{{R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,\overline {D}}}}}A)^{\mathrm {CH}}_{{D}_A} \rightarrow {S^{{\operatorname {CH-univ}}}_{\Lambda ,\overline {D}}}\otimes _{{R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,\overline {D}}}}} A $
is an isomorphism, and this completes the proof of (a). Part (b) follows from [Reference Wang EricksonWE13, Theorem 1.3.3.2]; it is also a consequence of Part (a) and Proposition 4.7.11.
The next result concerns the reducible locus for multiplicity free
![]() ${\overline {{D}}}$
.
${\overline {{D}}}$
.
Corollary 4.7.15. Suppose
![]() ${\overline {{D}}}$
is split and multiplicity free over
${\overline {{D}}}$
is split and multiplicity free over
![]() ${{\mathbb {F}}\,\!{}}$
and equal to
${{\mathbb {F}}\,\!{}}$
and equal to
![]() ${{\overline {{D}}}_1}\oplus {{\overline {{D}}}_2}$
. Then the morphism
${{\overline {{D}}}_1}\oplus {{\overline {{D}}}_2}$
. Then the morphism
![]() $\iota _{{\overline {{D}}}_1,{\overline {{D}}}_2}\colon {X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_1}}} \widehat {\times } {X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_1}}} \to {X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}},({D}_1,{D}_2)\mapsto {{D}_1}\oplus {D}_2$
is a closed immersion.
$\iota _{{\overline {{D}}}_1,{\overline {{D}}}_2}\colon {X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_1}}} \widehat {\times } {X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_1}}} \to {X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}},({D}_1,{D}_2)\mapsto {{D}_1}\oplus {D}_2$
is a closed immersion.
Proof. We need to show that the ring homomorphism
corresponding to
![]() $\iota _{{\overline {{D}}}_1,{\overline {{D}}}_2}$
is surjective. Since both sides are complete Noetherian local rings with isomorphic residue field, it suffices to show the surjectivity for the induced map of the duals of their tangent spaces; that is, the injectivity of
$\iota _{{\overline {{D}}}_1,{\overline {{D}}}_2}$
is surjective. Since both sides are complete Noetherian local rings with isomorphic residue field, it suffices to show the surjectivity for the induced map of the duals of their tangent spaces; that is, the injectivity of
Consider
![]() $n_i$
-dimensional pseudodeformations
$n_i$
-dimensional pseudodeformations
![]() ${D}_i,{D}^{\prime }_i\in {\mathcal {P}sD}_{{\overline {{D}}}_i}({{\mathbb {F}}\,\!{}}[\varepsilon ])$
for
${D}_i,{D}^{\prime }_i\in {\mathcal {P}sD}_{{\overline {{D}}}_i}({{\mathbb {F}}\,\!{}}[\varepsilon ])$
for
![]() $i=1,2$
such that
$i=1,2$
such that
![]() ${D}:={D}_1\oplus {D}_2={D}^{\prime }_1\oplus {D}^{\prime }_2$
. We need to show
${D}:={D}_1\oplus {D}_2={D}^{\prime }_1\oplus {D}^{\prime }_2$
. We need to show
![]() ${D}_i={D}^{\prime }_i$
for
${D}_i={D}^{\prime }_i$
for
![]() $i=1,2$
.
$i=1,2$
.
Let
![]() $A={{\mathbb {F}}\,\!{}}[\varepsilon ]$
and let
$A={{\mathbb {F}}\,\!{}}[\varepsilon ]$
and let
![]() ${S}$
be the Cayley–Hamilton algebra
${S}$
be the Cayley–Hamilton algebra
![]() $A[G]/{\mathrm {CH}}({D})$
. Observe that
$A[G]/{\mathrm {CH}}({D})$
. Observe that
![]() ${\mathrm {CH}}({D})$
is contained in both,
${\mathrm {CH}}({D})$
is contained in both,
![]() ${\mathrm {CH}}({D}_i)$
and
${\mathrm {CH}}({D}_i)$
and
![]() ${\mathrm {CH}}({D}^{\prime }_i)$
: We explain this for
${\mathrm {CH}}({D}^{\prime }_i)$
: We explain this for
![]() ${D}_i$
. Recall
${D}_i$
. Recall
![]() $s\mapsto \chi _{{D},B}(\cdot )=\chi _{{D},B}(t,s)|_{t=s}$
from Lemma 4.1.8
(b). The equality
$s\mapsto \chi _{{D},B}(\cdot )=\chi _{{D},B}(t,s)|_{t=s}$
from Lemma 4.1.8
(b). The equality
![]() ${D}={D}_1\oplus {D}_2$
implies
${D}={D}_1\oplus {D}_2$
implies
for
![]() $n\in {\mathbb {N}}$
,
$n\in {\mathbb {N}}$
,
![]() $s_1,\ldots ,s_n\in {S}$
. The ideal
$s_1,\ldots ,s_n\in {S}$
. The ideal
![]() ${\mathrm {CH}}({D}_i)$
is generated by the coefficients of all polynomials
${\mathrm {CH}}({D}_i)$
is generated by the coefficients of all polynomials
![]() $\chi _{{D}_i,A[t_1,\ldots ,t_n]}(\sum _i s_it_i)$
. It follows from the displayed formula, that
$\chi _{{D}_i,A[t_1,\ldots ,t_n]}(\sum _i s_it_i)$
. It follows from the displayed formula, that
![]() ${\mathrm {CH}}({D})$
is zero modulo
${\mathrm {CH}}({D})$
is zero modulo
![]() ${\mathrm {CH}}({D}_i)$
, and this gives
${\mathrm {CH}}({D}_i)$
, and this gives
![]() ${\mathrm {CH}}({D}_i)\supset {\mathrm {CH}}({D})$
. As a consequence, we find that
${\mathrm {CH}}({D}_i)\supset {\mathrm {CH}}({D})$
. As a consequence, we find that
![]() ${D}_i$
and
${D}_i$
and
![]() ${D}^{\prime }_i$
factor via
${D}^{\prime }_i$
factor via
![]() ${S}$
.
${S}$
.
By Theorem 4.3.10
(b), the Cayley–Hamilton algebra is a GMA over A with
![]() ${D}={\mathrm {det}}_{({S},{\cal E})}$
for a datum of idempotents
${D}={\mathrm {det}}_{({S},{\cal E})}$
for a datum of idempotents
![]() ${\cal E}=\{e_j,\psi _j\}_{j=1,\ldots ,r}$
. The proof in [Reference ChenevierChe14, Theorem 2.22] shows that the idempotents
${\cal E}=\{e_j,\psi _j\}_{j=1,\ldots ,r}$
. The proof in [Reference ChenevierChe14, Theorem 2.22] shows that the idempotents
![]() $e_j$
correspond bijectively to the irreducible summands of
$e_j$
correspond bijectively to the irreducible summands of
![]() ${\overline {{D}}}$
, and so we write
${\overline {{D}}}$
, and so we write
![]() ${\overline {{D}}}=\oplus _{j} {\overline {{D}}}_{e_j}$
in the notation of Lemma 4.3.8. Write
${\overline {{D}}}=\oplus _{j} {\overline {{D}}}_{e_j}$
in the notation of Lemma 4.3.8. Write
![]() $J=\{1,\ldots ,r\}$
as a disjoint union
$J=\{1,\ldots ,r\}$
as a disjoint union
![]() $J=J_1\cup J_2$
such that
$J=J_1\cup J_2$
such that
![]() ${\overline {{D}}}_i=\oplus _{j\in J_i} {\overline {{D}}}_{e_j}$
, using that
${\overline {{D}}}_i=\oplus _{j\in J_i} {\overline {{D}}}_{e_j}$
, using that
![]() ${\overline {{D}}}$
is mulitplicity free.
${\overline {{D}}}$
is mulitplicity free.
Because
![]() ${S}$
is a GMA, the algebra
${S}$
is a GMA, the algebra
![]() $e_jSe_j$
is isomorphic to
$e_jSe_j$
is isomorphic to
![]() ${\mathrm {Mat}}_{n_j\times n_j}(A)$
for some
${\mathrm {Mat}}_{n_j\times n_j}(A)$
for some
![]() $n_j\in {\mathbb {N}}$
, and where
$n_j\in {\mathbb {N}}$
, and where
![]() $\sum _j n_j=n$
. It follows from Example 4.1.7 in particular that
$\sum _j n_j=n$
. It follows from Example 4.1.7 in particular that
![]() $({D}_i)_{e_j}$
is
$({D}_i)_{e_j}$
is
![]() $n_jf_{i,j}$
-dimensional for some
$n_jf_{i,j}$
-dimensional for some
![]() $f_{i,j}\in {\mathbb {N}}_0$
. Using
$f_{i,j}\in {\mathbb {N}}_0$
. Using
![]() $({D}_i)_{e_j}\ {\mathop{\mathrm{mod}\ }\nolimits }{(\varepsilon )}=({\overline {{D}}}_i)_{e_j}$
, we find
$({D}_i)_{e_j}\ {\mathop{\mathrm{mod}\ }\nolimits }{(\varepsilon )}=({\overline {{D}}}_i)_{e_j}$
, we find
![]() $f_{i,j}=1$
for
$f_{i,j}=1$
for
![]() $j\in J_i$
and
$j\in J_i$
and
![]() $f_{i,j}=0$
for
$f_{i,j}=0$
for
![]() $j\in J_{3-i}$
.
$j\in J_{3-i}$
.
Let
![]() $E_i=\sum _{j\in J_i}e_j$
. Then by Lemma 4.3.8, we have
$E_i=\sum _{j\in J_i}e_j$
. Then by Lemma 4.3.8, we have
![]() $\dim (({D}_i)_{E_i})=\dim ({D}_i)$
and
$\dim (({D}_i)_{E_i})=\dim ({D}_i)$
and
![]() $\dim (({D}_i)_{E_{3-i}})=0$
, and thus
$\dim (({D}_i)_{E_{3-i}})=0$
, and thus
![]() ${D}_i=({D}_i)_{E_i}=({D}_i)_{E_i}\oplus ({D}_{3-i})_{E_i}={D}_{E_i}$
. But the idempotent
${D}_i=({D}_i)_{E_i}=({D}_i)_{E_i}\oplus ({D}_{3-i})_{E_i}={D}_{E_i}$
. But the idempotent
![]() $E_i$
only depends on
$E_i$
only depends on
![]() ${\overline {{D}}}_i$
, and so arguing in the same way for the
${\overline {{D}}}_i$
, and so arguing in the same way for the
![]() ${D}^{\prime }_i$
, we find
${D}^{\prime }_i$
, we find
![]() ${D}^{\prime }_i={D}_{E_i}={D}^{\prime }_i$
, which concludes the proof.
${D}^{\prime }_i={D}_{E_i}={D}^{\prime }_i$
, which concludes the proof.
The locus of irreducible points shall be of special importance.
Definition 4.7.16. The irreducible locus of
![]() ${X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
is defined as
${X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
is defined as
and its reducible locus
![]() $({X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}} )^{\operatorname {red}}$
as the topological space
$({X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}} )^{\operatorname {red}}$
as the topological space
![]() ${X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}} {\smallsetminus } ({X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\operatorname {irr}}$
. We overline the notation for the corresponding subsets of
${X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}} {\smallsetminus } ({X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\operatorname {irr}}$
. We overline the notation for the corresponding subsets of
![]() ${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
.
${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
.
The argument in [Reference ChenevierChe14, Example 2.20] also proves.
Proposition 4.7.17. The subsets
![]() $({X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}} )^{\operatorname {irr}}\subset {X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
and
$({X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}} )^{\operatorname {irr}}\subset {X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
and
![]() $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\operatorname {irr}}\subset {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
are Zariski open.
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\operatorname {irr}}\subset {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
are Zariski open.
By Proposition 4.7.11
(c), we can associate to
![]() ${S^{{\operatorname {CH-univ}}}_{\Lambda ,{\overline {{D}}}}}$
a sheaf of coherent
${S^{{\operatorname {CH-univ}}}_{\Lambda ,{\overline {{D}}}}}$
a sheaf of coherent
![]() ${\cal O}_{{X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}}}}}$
-algebras
${\cal O}_{{X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}}}}}$
-algebras
![]() ${\mathcal {S}^{{\operatorname {CH-univ}}}_{\Lambda ,{\overline {{D}}}}}$
under the finiteness condition
${\mathcal {S}^{{\operatorname {CH-univ}}}_{\Lambda ,{\overline {{D}}}}}$
under the finiteness condition
![]() $\Phi _{\overline {{D}}}$
. The next result is not stated verbatim in [Reference ChenevierChe14]; however, its proof is that of [Reference ChenevierChe14, Corollary 2.23], with a continuity requirement added.
$\Phi _{\overline {{D}}}$
. The next result is not stated verbatim in [Reference ChenevierChe14]; however, its proof is that of [Reference ChenevierChe14, Corollary 2.23], with a continuity requirement added.
Proposition 4.7.18. Over
![]() $({X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}}}} )^{\operatorname {irr}}$
, the sheaf
$({X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}}}} )^{\operatorname {irr}}$
, the sheaf
![]() ${\mathcal {S}^{{\operatorname {CH-univ}}}_{\Lambda ,{\overline {{D}}}}}$
is an Azumaya
${\mathcal {S}^{{\operatorname {CH-univ}}}_{\Lambda ,{\overline {{D}}}}}$
is an Azumaya
![]() $\mathcal {O}_{{X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}}}}}$
-algebra of rank
$\mathcal {O}_{{X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}}}}}$
-algebra of rank
![]() $n^2$
equipped with its reduced norm.
$n^2$
equipped with its reduced norm.
Over affine open subsets of
![]() $({X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}}}})^{\operatorname {irr}}$
, Proposition 4.7.18 is a variant of Proposition 4.1.25 under some continuity constraints.
$({X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}}}})^{\operatorname {irr}}$
, Proposition 4.7.18 is a variant of Proposition 4.1.25 under some continuity constraints.
4.8 Pseudodeformations over local fields
In this subsection, we develop some results analogous to Subsection 3.3 for continuous pseudodeformations of a fixed one
![]() ${D}\colon {\kappa }[G]\to {\kappa }$
, where
${D}\colon {\kappa }[G]\to {\kappa }$
, where
![]() ${\kappa }$
is a local field. Also, continuity is an important theme; for instance, to deduce under weak hypotheses from the continuity of a pseudocharacter that of its associated representation.
${\kappa }$
is a local field. Also, continuity is an important theme; for instance, to deduce under weak hypotheses from the continuity of a pseudocharacter that of its associated representation.
Lemma 4.8.1. Let
![]() ${\kappa }$
be a local field with valuation ring
${\kappa }$
be a local field with valuation ring
![]() $\mathcal {O}_{\kappa }$
, and let
$\mathcal {O}_{\kappa }$
, and let
![]() ${D}\colon {\kappa }[G]\to {\kappa }$
be a continuous n-dimensional pseudocharacter. Then the following hold:
${D}\colon {\kappa }[G]\to {\kappa }$
be a continuous n-dimensional pseudocharacter. Then the following hold:
-
(a) There exists
 ${D}_{{\cal O}}\in {\mathcal {P}s\mathcal {R}}^n_{G}({\cal O}_{\kappa })$
such that
${D}_{{\cal O}}\in {\mathcal {P}s\mathcal {R}}^n_{G}({\cal O}_{\kappa })$
such that
 ${D}_{\cal O}\otimes _{{\cal O}_{\kappa }}{\kappa }={D}$
.
${D}_{\cal O}\otimes _{{\cal O}_{\kappa }}{\kappa }={D}$
.
Let
![]() $C\subset {\cal O}_{\kappa }$
be the admissible profinite subring of
$C\subset {\cal O}_{\kappa }$
be the admissible profinite subring of
![]() ${\cal O}_{\kappa }$
from Lemma 4.4.8, and let
${\cal O}_{\kappa }$
from Lemma 4.4.8, and let
![]() ${D}_C\in {\mathcal {P}s\mathcal {R}}^n_G(C)$
be such that
${D}_C\in {\mathcal {P}s\mathcal {R}}^n_G(C)$
be such that
![]() ${D}_C\otimes _C{\cal O}_{\kappa }={D}_{\cal O}$
. Then furthermore:
${D}_C\otimes _C{\cal O}_{\kappa }={D}_{\cal O}$
. Then furthermore:
-
(b) C is local, its residue field
 ${\kappa ({C})} $
is finite, either C is a finite field, or
${\kappa ({C})} $
is finite, either C is a finite field, or
 ${\kappa }$
is a finite extension of the fraction field of C,
${\kappa }$
is a finite extension of the fraction field of C,
 ${\overline {{D}}}:={D}_C\otimes _C{\kappa ({C})}$
is equal to
${\overline {{D}}}:={D}_C\otimes _C{\kappa ({C})}$
is equal to
 ${D}_z$
for some
${D}_z$
for some
 $z\in |G(n)|$
and
$z\in |G(n)|$
and
 ${D}_{\cal O}$
is residually equal to
${D}_{\cal O}$
is residually equal to
 ${D}_z$
in the sense of Definition 4.4.10.
${D}_z$
in the sense of Definition 4.4.10.
Proof. Let
![]() $\rho _{{D}\otimes _\kappa {{{\kappa }}^{\mathrm {alg}}} }$
be the representation from Theorem 4.1.18. For (a) observe first that the characteristic polynomial coefficients
$\rho _{{D}\otimes _\kappa {{{\kappa }}^{\mathrm {alg}}} }$
be the representation from Theorem 4.1.18. For (a) observe first that the characteristic polynomial coefficients
![]() $\Lambda _{{D},i}$
of
$\Lambda _{{D},i}$
of
![]() $\chi _{D}(g,{\:\cdot \:})$
are continuous for
$\chi _{D}(g,{\:\cdot \:})$
are continuous for
![]() $1\leq i\leq n$
, and hence the sets
$1\leq i\leq n$
, and hence the sets
![]() $\Lambda _{{D},i}(G)$
are compact in
$\Lambda _{{D},i}(G)$
are compact in
![]() ${\kappa }$
. Assume that for some
${\kappa }$
. Assume that for some
![]() $g\in G$
,
$g\in G$
,
![]() $\Lambda _{{D},i}(g)$
does not lie in
$\Lambda _{{D},i}(g)$
does not lie in
![]() $\mathcal {O}_{\kappa }$
. Then at least one eigenvalue of
$\mathcal {O}_{\kappa }$
. Then at least one eigenvalue of
![]() $\rho _{{D}\otimes _\kappa {{{\kappa }}^{\mathrm {alg}}} }(g)$
has valuation different from
$\rho _{{D}\otimes _\kappa {{{\kappa }}^{\mathrm {alg}}} }(g)$
has valuation different from
![]() $0$
, and, since we can pass to
$0$
, and, since we can pass to
![]() $g^{-1}$
, we may assume that this valuation is negative. Let
$g^{-1}$
, we may assume that this valuation is negative. Let
![]() $\lambda _1,\ldots ,\lambda _n\in {{{{\kappa }}}^{\mathrm {alg}}} $
denote the eigenvalues of
$\lambda _1,\ldots ,\lambda _n\in {{{{\kappa }}}^{\mathrm {alg}}} $
denote the eigenvalues of
![]() $\rho _{{D}\otimes _\kappa {{{\kappa }}^{\mathrm {alg}}} }(g)$
and index them so that
$\rho _{{D}\otimes _\kappa {{{\kappa }}^{\mathrm {alg}}} }(g)$
and index them so that
![]() $\lambda _1,\ldots ,\lambda _j$
are precisely those with negative valuation. Then for
$\lambda _1,\ldots ,\lambda _j$
are precisely those with negative valuation. Then for
![]() $n>0$
, the valuation of
$n>0$
, the valuation of
![]() $\Lambda _{{D},j}(g^n)$
is the valuation of
$\Lambda _{{D},j}(g^n)$
is the valuation of
![]() $(\lambda _1\cdot \ldots \cdot \lambda _j)^n$
. The latter valuations are unbounded. This contradicts the compactness of
$(\lambda _1\cdot \ldots \cdot \lambda _j)^n$
. The latter valuations are unbounded. This contradicts the compactness of
![]() $\Lambda _{{D},j}(G)$
and thus proves (a).
$\Lambda _{{D},j}(G)$
and thus proves (a).
We now prove (b). By Lemma 4.4.8, the ring C is a finite product
![]() $\prod _i C_i$
of local admissible profinite
$\prod _i C_i$
of local admissible profinite
![]() ${{W({{\mathbb {F}}\,\!{}})}}$
-algebras
${{W({{\mathbb {F}}\,\!{}})}}$
-algebras
![]() $C_i$
and the residue field of each
$C_i$
and the residue field of each
![]() $C_i$
is finite. Let
$C_i$
is finite. Let
![]() ${\mathfrak {m}}$
be the maximal ideal of
${\mathfrak {m}}$
be the maximal ideal of
![]() ${\cal O}_\kappa $
. Then
${\cal O}_\kappa $
. Then
![]() $C\cap {\mathfrak {m}}$
is topologically nilpotent and
$C\cap {\mathfrak {m}}$
is topologically nilpotent and
![]() $C/(C\cap {\mathfrak {m}})$
is a finite field that surjects onto the product of the residue fields of the
$C/(C\cap {\mathfrak {m}})$
is a finite field that surjects onto the product of the residue fields of the
![]() $C_i$
. It follows that C is local with finite residue field
$C_i$
. It follows that C is local with finite residue field
![]() $\kappa (C)$
.
$\kappa (C)$
.
It remains to show the assertion on the fraction field of C, since the last part of (b) follows from Lemma 4.4.8. For this, we may assume that C is infinite. Let
![]() $\kappa '$
be the fraction field of C. Because C is infinite and
$\kappa '$
be the fraction field of C. Because C is infinite and
![]() $\kappa (C)$
is finite, we find
$\kappa (C)$
is finite, we find
![]() $f\in C{\smallsetminus }\kappa (C)$
so that f has strictly positive valuation. Then
$f\in C{\smallsetminus }\kappa (C)$
so that f has strictly positive valuation. Then
![]() $\kappa '\supseteq \kappa (C)((f))$
is a nontrivially valued locally compact subfield of the locally compact field
$\kappa '\supseteq \kappa (C)((f))$
is a nontrivially valued locally compact subfield of the locally compact field
![]() $\kappa $
. It now follows from [Reference WeilWei67, I.§2. Corollary 2 of Theorem 3, p. 6] that
$\kappa $
. It now follows from [Reference WeilWei67, I.§2. Corollary 2 of Theorem 3, p. 6] that
![]() $[\kappa :\kappa ']$
is finite.
$[\kappa :\kappa ']$
is finite.
The following result is a generalization of Corollary 4.4.6.
Corollary 4.8.2. Let
![]() ${\kappa }$
be a local field, let A be in
${\kappa }$
be a local field, let A be in
![]() ${\mathcal {A}r}_{\kappa }$
and let
${\mathcal {A}r}_{\kappa }$
and let
![]() ${D}\in {\mathcal {P}s\mathcal {R}}^n_G(A)$
be continuous. Define
${D}\in {\mathcal {P}s\mathcal {R}}^n_G(A)$
be continuous. Define
![]() ${\overline {{D}}}$
as in Lemma 4.8.1, and assume that condition
${\overline {{D}}}$
as in Lemma 4.8.1, and assume that condition
![]() $\Phi _{\overline {{D}}}$
holds. Then the following hold:
$\Phi _{\overline {{D}}}$
holds. Then the following hold:
-
(a) If
 $A={\kappa }$
, then
$A={\kappa }$
, then
 $\rho _{{D}\otimes _{\kappa } {{{{\kappa }}}^{\mathrm {alg}}} }$
is continuous.
$\rho _{{D}\otimes _{\kappa } {{{{\kappa }}}^{\mathrm {alg}}} }$
is continuous. -
(b) If
 ${D}$
is split and irreducible, then
${D}$
is split and irreducible, then
 $\rho _{D}=\rho _{D}^{\mathrm {CH}}$
from Proposition 4.1.25 is a continuous representation to
$\rho _{D}=\rho _{D}^{\mathrm {CH}}$
from Proposition 4.1.25 is a continuous representation to
 ${\mathrm {Mat}}_{n\times n}(A)$
.
${\mathrm {Mat}}_{n\times n}(A)$
.
Proof. We first prove (a), and so here we assume
![]() $A={\kappa }$
. Set
$A={\kappa }$
. Set
![]() $\Lambda :={\cal O}_{\kappa }$
, and consider the diagram
$\Lambda :={\cal O}_{\kappa }$
, and consider the diagram

where
![]() ${\varphi }\colon {R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}}}} \to {\cal O}_{\kappa } $
is the map induced from the universal property of
${\varphi }\colon {R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}}}} \to {\cal O}_{\kappa } $
is the map induced from the universal property of
![]() ${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}}}} $
, and where
${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}}}} $
, and where
![]() $\iota \colon {\cal O}_{\kappa }\to {{{{\kappa }}}^{\mathrm {alg}}} $
is the natural inclusion. The first map is continuous by Proposition 4.7.11
(b), the second by Proposition 4.7.11
(d), which says that
$\iota \colon {\cal O}_{\kappa }\to {{{{\kappa }}}^{\mathrm {alg}}} $
is the natural inclusion. The first map is continuous by Proposition 4.7.11
(b), the second by Proposition 4.7.11
(d), which says that
![]() ${S^{{\operatorname {CH-univ}}}_{\Lambda ,{\overline {{D}}}}}$
carries the
${S^{{\operatorname {CH-univ}}}_{\Lambda ,{\overline {{D}}}}}$
carries the
![]() ${\mathfrak {m}}_{\overline {{D}}}$
-adic topology, By Proposition 4.7.11
(d), the ring
${\mathfrak {m}}_{\overline {{D}}}$
-adic topology, By Proposition 4.7.11
(d), the ring
![]() ${S^{{\operatorname {CH-univ}}}_{\Lambda ,{\overline {{D}}}}}\otimes _{{R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}}}} }{\cal O}_{\kappa }$
is finitely generated as an
${S^{{\operatorname {CH-univ}}}_{\Lambda ,{\overline {{D}}}}}\otimes _{{R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}}}} }{\cal O}_{\kappa }$
is finitely generated as an
![]() ${\cal O}_{{\kappa }}$
-module, and hence the
${\cal O}_{{\kappa }}$
-module, and hence the
![]() ${\mathfrak {m}}_{\overline {{D}}}$
-topology also coincides with the topology inherited from
${\mathfrak {m}}_{\overline {{D}}}$
-topology also coincides with the topology inherited from
![]() ${S^{{\operatorname {CH-univ}}}_{\Lambda ,{\overline {{D}}}}}\otimes _{{R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}}}} }{\kappa } \in {\mathcal {A}r}_{\kappa }$
; it follows that also the last map is continuous and that
${S^{{\operatorname {CH-univ}}}_{\Lambda ,{\overline {{D}}}}}\otimes _{{R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}}}} }{\kappa } \in {\mathcal {A}r}_{\kappa }$
; it follows that also the last map is continuous and that
![]() ${S^{{\operatorname {CH-univ}}}_{\Lambda ,{\overline {{D}}}}}\otimes _{{R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}}}} }{{{{\kappa }}}^{\mathrm {alg}}} $
has finite
${S^{{\operatorname {CH-univ}}}_{\Lambda ,{\overline {{D}}}}}\otimes _{{R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}}}} }{{{{\kappa }}}^{\mathrm {alg}}} $
has finite
![]() ${{{{\kappa }}}^{\mathrm {alg}}} $
-dimension. But then also the map
${{{{\kappa }}}^{\mathrm {alg}}} $
-dimension. But then also the map
is continuous. Hence, in the factorization of
![]() ${D}\colon {\kappa }[G]\to {{{{\kappa }}}^{\mathrm {alg}}} $
via
${D}\colon {\kappa }[G]\to {{{{\kappa }}}^{\mathrm {alg}}} $
via
![]() ${{{{\kappa }}}^{\mathrm {alg}}} [[G]]/{\operatorname {ker}{({D})}}$
given in Proposition 4.1.16, the first map is continuous. From Theorem 4.1.17, we know that
${{{{\kappa }}}^{\mathrm {alg}}} [[G]]/{\operatorname {ker}{({D})}}$
given in Proposition 4.1.16, the first map is continuous. From Theorem 4.1.17, we know that
![]() ${{{{\kappa }}}^{\mathrm {alg}}} [[G]]/{\operatorname {ker}{({D})}}$
is semisimple and finite-dimensional over
${{{{\kappa }}}^{\mathrm {alg}}} [[G]]/{\operatorname {ker}{({D})}}$
is semisimple and finite-dimensional over
![]() ${{{\kappa }}^{\mathrm {alg}}} $
and that its determinants are given by determinants of the simple matrix algebra factors of
${{{\kappa }}^{\mathrm {alg}}} $
and that its determinants are given by determinants of the simple matrix algebra factors of
![]() ${{{{\kappa }}}^{\mathrm {alg}}} [[G]]/{\operatorname {ker}{({D})}}$
. Hence, the second map in the factorization given in Proposition 4.1.16 is continuous and thus so is the composition
${{{{\kappa }}}^{\mathrm {alg}}} [[G]]/{\operatorname {ker}{({D})}}$
. Hence, the second map in the factorization given in Proposition 4.1.16 is continuous and thus so is the composition
![]() $\rho $
.
$\rho $
.
The proof of (b) is analogous. One has to replace
![]() ${\kappa }$
by A in most places and substitute Theorem 4.1.17 by Theorem 4.3.10.
${\kappa }$
by A in most places and substitute Theorem 4.1.17 by Theorem 4.3.10.
Remark 4.8.3. In an abstract setting,
![]() $\Phi _{\overline {{D}}}$
in Corollary 4.8.2 seems hard to check. In our concrete applications, we know
$\Phi _{\overline {{D}}}$
in Corollary 4.8.2 seems hard to check. In our concrete applications, we know
![]() ${\overline {{D}}}$
because of Proposition 3.2.3, so then the formulation is useful. A more natural condition to require would be
${\overline {{D}}}$
because of Proposition 3.2.3, so then the formulation is useful. A more natural condition to require would be
![]() $\Phi _{D}$
; we do suspect that this condition also suffices. Also, we wonder if the conclusion of Corollary 4.8.2 might hold without assuming
$\Phi _{D}$
; we do suspect that this condition also suffices. Also, we wonder if the conclusion of Corollary 4.8.2 might hold without assuming
![]() $\Phi _{\overline {{D}}}$
, and without invoking Lemma 4.8.1 just because
$\Phi _{\overline {{D}}}$
, and without invoking Lemma 4.8.1 just because
![]() $A\in {\mathcal {A}r}_{\kappa }$
.
$A\in {\mathcal {A}r}_{\kappa }$
.
Corollary 4.8.4. Let
![]() ${\kappa }$
be a local field, and let
${\kappa }$
be a local field, and let
![]() ${D}\in {\mathcal {P}s\mathcal {R}}^n_G({\kappa })$
be continuous. Define
${D}\in {\mathcal {P}s\mathcal {R}}^n_G({\kappa })$
be continuous. Define
![]() ${\overline {{D}}}$
as in Lemma 4.8.1, and assume that condition
${\overline {{D}}}$
as in Lemma 4.8.1, and assume that condition
![]() $\Phi _{\overline {{D}}}$
holds. Then there exists a finite extension
$\Phi _{\overline {{D}}}$
holds. Then there exists a finite extension
![]() ${\kappa }'$
of
${\kappa }'$
of
![]() ${\kappa }$
and split irreducible continuous
${\kappa }$
and split irreducible continuous
![]() ${D}_i\in {\mathcal {P}s\mathcal {R}}^{n_i}_G({\kappa }')$
,
${D}_i\in {\mathcal {P}s\mathcal {R}}^{n_i}_G({\kappa }')$
,
![]() $i=1,\ldots ,r$
such that
$i=1,\ldots ,r$
such that
Moreover,
![]() ${D}\in {\mathcal {P}s\mathcal {R}}^n_G({\cal O}_{{\kappa }})$
and
${D}\in {\mathcal {P}s\mathcal {R}}^n_G({\cal O}_{{\kappa }})$
and
![]() ${D}_i\in {\mathcal {P}s\mathcal {R}}^n_G({\cal O}_{{\kappa }'})$
for
${D}_i\in {\mathcal {P}s\mathcal {R}}^n_G({\cal O}_{{\kappa }'})$
for
![]() $i=1,\ldots ,r$
.
$i=1,\ldots ,r$
.
Proof. By Theorem 4.1.17, the
![]() ${\kappa }$
-algebra
${\kappa }$
-algebra
![]() ${S}:={\kappa }[[G]]/{\operatorname {ker}{({D}\otimes _{{\cal O}_\kappa }\kappa )}}$
has finite
${S}:={\kappa }[[G]]/{\operatorname {ker}{({D}\otimes _{{\cal O}_\kappa }\kappa )}}$
has finite
![]() ${\kappa }$
-dimension. Hence, Lemma A.2.3 allows us to find a finite extension
${\kappa }$
-dimension. Hence, Lemma A.2.3 allows us to find a finite extension
![]() ${\kappa }'$
of
${\kappa }'$
of
![]() ${\kappa }$
such that
${\kappa }$
such that
![]() ${S}\otimes _{\kappa }{\kappa }'/{\mathrm {Rad}}({S}\otimes _{\kappa }{\kappa }')$
is a product of matrix rings over
${S}\otimes _{\kappa }{\kappa }'/{\mathrm {Rad}}({S}\otimes _{\kappa }{\kappa }')$
is a product of matrix rings over
![]() ${\kappa }'$
. It follows that
${\kappa }'$
. It follows that
![]() ${\kappa }'[[G]]/{\operatorname {ker}{({D}\otimes _{{\cal O}_{\kappa }}{\kappa }')}}$
is a product of matrix algebras over
${\kappa }'[[G]]/{\operatorname {ker}{({D}\otimes _{{\cal O}_{\kappa }}{\kappa }')}}$
is a product of matrix algebras over
![]() ${\kappa }'$
. Hence, we have
${\kappa }'$
. Hence, we have
![]() ${D}\otimes _{{\kappa }}{\kappa }'=\oplus _{i=1}^r{D}_i$
for split irreducible
${D}\otimes _{{\kappa }}{\kappa }'=\oplus _{i=1}^r{D}_i$
for split irreducible
![]() ${D}_i\in {\mathcal {P}s\mathcal {R}}^{n_i}_G({\kappa }')$
. We find that
${D}_i\in {\mathcal {P}s\mathcal {R}}^{n_i}_G({\kappa }')$
. We find that
![]() $(\oplus _{i=1}^r\rho _{{D}_i})\otimes _{{\kappa }'}{{{{\kappa }}}^{\mathrm {alg}}} \cong \rho _{{D}\otimes _{{\cal O}_{\kappa }}{{{{\kappa }}}^{\mathrm {alg}}} }$
. Since the latter is continuous by Corollary 4.8.2, so are the
$(\oplus _{i=1}^r\rho _{{D}_i})\otimes _{{\kappa }'}{{{{\kappa }}}^{\mathrm {alg}}} \cong \rho _{{D}\otimes _{{\cal O}_{\kappa }}{{{{\kappa }}}^{\mathrm {alg}}} }$
. Since the latter is continuous by Corollary 4.8.2, so are the
![]() $\rho _{{D}_i}$
. Finally, Lemma 4.8.1 shows that the
$\rho _{{D}_i}$
. Finally, Lemma 4.8.1 shows that the
![]() ${D}_i$
can be defined over
${D}_i$
can be defined over
![]() ${\cal O}_{{\kappa }'}$
and
${\cal O}_{{\kappa }'}$
and
![]() ${D}$
over
${D}$
over
![]() ${\cal O}_{{\kappa }}$
.
${\cal O}_{{\kappa }}$
.
To prove a more general result than Corollary 4.8.4, we need some preparations.
Lemma 4.8.5. Let
![]() ${{\mathbb {F}}\,\!{}}$
be a finite field, let
${{\mathbb {F}}\,\!{}}$
be a finite field, let
![]() $A\in {\widehat {\mathcal {A}}r}_{{\mathbb {F}}\,\!{}}$
be a domain and let
$A\in {\widehat {\mathcal {A}}r}_{{\mathbb {F}}\,\!{}}$
be a domain and let
![]() ${\mathfrak {p}}\in {\mathrm {Spec}}\ A$
be a prime of dimension
${\mathfrak {p}}\in {\mathrm {Spec}}\ A$
be a prime of dimension
![]() $1$
, and consider the completion
$1$
, and consider the completion
![]() $\widehat {A}_{\mathfrak {p}}$
as a topological ring in
$\widehat {A}_{\mathfrak {p}}$
as a topological ring in
![]() ${\widehat {\mathcal {A}}r}_{{\kappa ({{\mathfrak {p}}})}}$
. Then the canonical map
${\widehat {\mathcal {A}}r}_{{\kappa ({{\mathfrak {p}}})}}$
. Then the canonical map
![]() $\iota \colon A\to \widehat {A}_{{\mathfrak {p}}}$
is continuous and injective, and
$\iota \colon A\to \widehat {A}_{{\mathfrak {p}}}$
is continuous and injective, and
![]() $A\to \iota (A)$
is a homeomorphism if
$A\to \iota (A)$
is a homeomorphism if
![]() $\iota (A)$
is equipped with the subspace topology.
$\iota (A)$
is equipped with the subspace topology.
Proof. The injectivity of
![]() $\iota $
is clear, since
$\iota $
is clear, since
![]() $A\to A_{\mathfrak {p}}$
is injective, as A is a domain, and completion is injective since
$A\to A_{\mathfrak {p}}$
is injective, as A is a domain, and completion is injective since
![]() $A_{\mathfrak {p}}$
is Noetherian.
$A_{\mathfrak {p}}$
is Noetherian.
Recall that A carries the
![]() ${\mathfrak {m}}_A$
-adic topology and that the topology on
${\mathfrak {m}}_A$
-adic topology and that the topology on
![]() $\widehat {A}_{\mathfrak {p}}$
is the weakest topology such that the canonical maps
$\widehat {A}_{\mathfrak {p}}$
is the weakest topology such that the canonical maps
![]() $\widehat {A}_{\mathfrak {p}}\to R_n:=A_{\mathfrak {p}}/{\mathfrak {p}}^n A_{\mathfrak {p}}\cong \widehat {A}_{\mathfrak {p}}/{\mathfrak {p}}^n \widehat {A}_{\mathfrak {p}}$
are continuous for all n, with
$\widehat {A}_{\mathfrak {p}}\to R_n:=A_{\mathfrak {p}}/{\mathfrak {p}}^n A_{\mathfrak {p}}\cong \widehat {A}_{\mathfrak {p}}/{\mathfrak {p}}^n \widehat {A}_{\mathfrak {p}}$
are continuous for all n, with
![]() $R_n$
carrying the unique topology as a finite-dimensional vector space with a continuous action of the local field
$R_n$
carrying the unique topology as a finite-dimensional vector space with a continuous action of the local field
![]() $\kappa ({\mathfrak {p}})$
. Let
$\kappa ({\mathfrak {p}})$
. Let
![]() $\iota _n\colon A\to \widehat {A}_{\mathfrak {p}}\to R_n$
be the canonical map. Because A and
$\iota _n\colon A\to \widehat {A}_{\mathfrak {p}}\to R_n$
be the canonical map. Because A and
![]() $\widehat {A}_{\mathfrak {p}}$
are topological modules, it remains to prove continuity near
$\widehat {A}_{\mathfrak {p}}$
are topological modules, it remains to prove continuity near
![]() $0$
, that is, we have to show the following two assertions: (i) For
$0$
, that is, we have to show the following two assertions: (i) For
![]() $n\in {\mathbb {N}}$
and
$n\in {\mathbb {N}}$
and
![]() $U\subset R_n$
an open neighborhood of
$U\subset R_n$
an open neighborhood of
![]() $0$
, there exists
$0$
, there exists
![]() $m\in {\mathbb {N}}$
such that
$m\in {\mathbb {N}}$
such that
![]() $\iota _n({\mathfrak {m}}_A^m)\subset U$
. (ii) For
$\iota _n({\mathfrak {m}}_A^m)\subset U$
. (ii) For
![]() $m\in {\mathbb {N}}$
, there exists
$m\in {\mathbb {N}}$
, there exists
![]() $n\in {\mathbb {N}}$
and
$n\in {\mathbb {N}}$
and
![]() $U\subset R_n$
open such that
$U\subset R_n$
open such that
![]() ${\mathfrak {m}}_A^m\supset \iota _n^{-1}(U)$
.
${\mathfrak {m}}_A^m\supset \iota _n^{-1}(U)$
.
Before we tackle (i) and (ii), we show the following assertion (iii): There exists
![]() $\omega \in {\mathfrak {m}}_A$
with nonzero image in
$\omega \in {\mathfrak {m}}_A$
with nonzero image in
![]() $A/{\mathfrak {p}}$
such that for each
$A/{\mathfrak {p}}$
such that for each
![]() $n\ge 1$
there exists a coefficient field
$n\ge 1$
there exists a coefficient field
![]() $K_n$
for
$K_n$
for
![]() $R_n$
such that
$R_n$
such that
![]() $K_n\supset {{\mathbb {F}}\,\!{}}[[\iota _n(\omega )]]$
– we also gather further properties of
$K_n\supset {{\mathbb {F}}\,\!{}}[[\iota _n(\omega )]]$
– we also gather further properties of
![]() ${{\mathbb {F}}\,\!{}}[[\iota _n(\omega )]]$
; recall that being a coefficient field means that
${{\mathbb {F}}\,\!{}}[[\iota _n(\omega )]]$
; recall that being a coefficient field means that
![]() $K_n\subset R_n$
is a subfield that under the reduction map
$K_n\subset R_n$
is a subfield that under the reduction map
![]() $R_n\to {\kappa ({{\mathfrak {p}}})}$
maps onto
$R_n\to {\kappa ({{\mathfrak {p}}})}$
maps onto
![]() ${\kappa ({{\mathfrak {p}}})}$
.
${\kappa ({{\mathfrak {p}}})}$
.
For the proof of (iii), let
![]() ${\cal O}$
be the ring of integers of the local field
${\cal O}$
be the ring of integers of the local field
![]() $K_1={\kappa ({{\mathfrak {p}}})}$
. The ring
$K_1={\kappa ({{\mathfrak {p}}})}$
. The ring
![]() ${\cal O}$
is also the integral closure of
${\cal O}$
is also the integral closure of
![]() $A/{\mathfrak {p}}{=\iota _1(A)}$
in
$A/{\mathfrak {p}}{=\iota _1(A)}$
in
![]() ${\kappa ({{\mathfrak {p}}})}$
. By [Reference WeilWei67, I.§4. Proposition 6, p. 22], for any
${\kappa ({{\mathfrak {p}}})}$
. By [Reference WeilWei67, I.§4. Proposition 6, p. 22], for any
![]() $\omega \in {\mathfrak {m}}{_A}$
with
$\omega \in {\mathfrak {m}}{_A}$
with
![]() $\iota _1(a)\neq 0$
the ring
$\iota _1(a)\neq 0$
the ring
![]() ${\cal O}$
is finite over
${\cal O}$
is finite over
![]() ${{\mathbb {F}}\,\!{}}{_p[[\iota _1(\omega )]]}$
, and hence a finite free
${{\mathbb {F}}\,\!{}}{_p[[\iota _1(\omega )]]}$
, and hence a finite free
![]() ${{\mathbb {F}}\,\!{}}{_p[[\iota _1(\omega )]]}$
-module. Because
${{\mathbb {F}}\,\!{}}{_p[[\iota _1(\omega )]]}$
-module. Because
![]() $A/{\mathfrak {p}}$
and
$A/{\mathfrak {p}}$
and
![]() ${\cal O}$
have the same quotient field, the field
${\cal O}$
have the same quotient field, the field
![]() $A/{\mathfrak {p}}$
is also a full
$A/{\mathfrak {p}}$
is also a full
![]() ${{\mathbb {F}}\,\!{}}{_p[[\iota _1(\omega )]]}$
-sublattice of
${{\mathbb {F}}\,\!{}}{_p[[\iota _1(\omega )]]}$
-sublattice of
![]() ${\kappa ({{\mathfrak {p}}})}$
and it follows that there exists
${\kappa ({{\mathfrak {p}}})}$
and it follows that there exists
![]() $j>0$
such that
$j>0$
such that
![]() $A/{\mathfrak {p}}{\supset \iota _1(\omega )^j{\cal O}}$
. Thus, for a uniformizer
$A/{\mathfrak {p}}{\supset \iota _1(\omega )^j{\cal O}}$
. Thus, for a uniformizer
![]() $t\in {\cal O}$
, all sufficiently large powers of t lie in
$t\in {\cal O}$
, all sufficiently large powers of t lie in
![]() $A/{\mathfrak {p}}$
. We now choose (a new!)
$A/{\mathfrak {p}}$
. We now choose (a new!)
![]() $\omega \in A$
such that
$\omega \in A$
such that
![]() $\iota _1(\omega )=t^e$
for some
$\iota _1(\omega )=t^e$
for some
![]() $e>0$
coprime to p. One easily verifies that
$e>0$
coprime to p. One easily verifies that
![]() $\iota _1(\omega )$
is a p-basis of
$\iota _1(\omega )$
is a p-basis of
![]() ${\kappa ({{\mathfrak {p}}})}$
. It follows from [Reference HochsterHoc14, Theorem 12], that
${\kappa ({{\mathfrak {p}}})}$
. It follows from [Reference HochsterHoc14, Theorem 12], that
![]() $K_n:=\bigcap R_n^{p^n}[\iota _n(\omega )]$
is a coefficient field for
$K_n:=\bigcap R_n^{p^n}[\iota _n(\omega )]$
is a coefficient field for
![]() $R_n$
. Because
$R_n$
. Because
![]() $K_n$
is complete, it contains
$K_n$
is complete, it contains
![]() ${{\mathbb {F}}\,\!{}}{[[\iota _n(\omega )]]}$
. Let
${{\mathbb {F}}\,\!{}}{[[\iota _n(\omega )]]}$
. Let
![]() ${\cal O}{_n}$
be the ring of integers of
${\cal O}{_n}$
be the ring of integers of
![]() $K_n$
. Then
$K_n$
. Then
![]() ${\cal O}{_n}$
is finite free over
${\cal O}{_n}$
is finite free over
![]() ${{\mathbb {F}}\,\!{}}{[[\iota _n(\omega )]]}$
. Also,
${{\mathbb {F}}\,\!{}}{[[\iota _n(\omega )]]}$
. Also,
![]() $A/{\mathfrak {p}}{\subset K_1}$
is finite free over
$A/{\mathfrak {p}}{\subset K_1}$
is finite free over
![]() ${{\mathbb {F}}\,\!{}}{[[\iota _1(\omega )]]}$
, and
${{\mathbb {F}}\,\!{}}{[[\iota _1(\omega )]]}$
, and
![]() $A/{\mathfrak {p}}{[1/\iota _1(\omega )]=}{\kappa ({{\mathfrak {p}}})}$
.
$A/{\mathfrak {p}}{[1/\iota _1(\omega )]=}{\kappa ({{\mathfrak {p}}})}$
.
We now prove (i). Let
![]() ${\mathfrak {p}}^{(n)}=\iota _n^{-1}(0)\supset {\mathfrak {p}}{^n}$
. Then
${\mathfrak {p}}^{(n)}=\iota _n^{-1}(0)\supset {\mathfrak {p}}{^n}$
. Then
![]() $A/{\mathfrak {p}}{^n\to A/}{\mathfrak {p}}^{(n)}A$
is surjective, and the induced map
$A/{\mathfrak {p}}{^n\to A/}{\mathfrak {p}}^{(n)}A$
is surjective, and the induced map
![]() $A/{\mathfrak {p}}^{(n)}A\to R_n$
is injective. Because the
$A/{\mathfrak {p}}^{(n)}A\to R_n$
is injective. Because the
![]() $A/{\mathfrak {p}}$
-modules
$A/{\mathfrak {p}}$
-modules
![]() ${\mathfrak {p}}{^i/}{\mathfrak {p}}{^{i+1}}$
are finitely generated over
${\mathfrak {p}}{^i/}{\mathfrak {p}}{^{i+1}}$
are finitely generated over
![]() $A/{\mathfrak {p}}$
and thus over
$A/{\mathfrak {p}}$
and thus over
![]() ${{\mathbb {F}}\,\!{}}{[[\iota _1(\omega )]]}$
, as a module over
${{\mathbb {F}}\,\!{}}{[[\iota _1(\omega )]]}$
, as a module over
![]() ${{\mathbb {F}}\,\!{}}{[[\iota _n(\omega )]]}$
the ring
${{\mathbb {F}}\,\!{}}{[[\iota _n(\omega )]]}$
the ring
![]() $A/{\mathfrak {p}}^{(n)}A$
is finite free. Moreover, it is an
$A/{\mathfrak {p}}^{(n)}A$
is finite free. Moreover, it is an
![]() ${{\mathbb {F}}\,\!{}}{[[\iota _n(\omega )]]}$
-lattice in the
${{\mathbb {F}}\,\!{}}{[[\iota _n(\omega )]]}$
-lattice in the
![]() ${{\mathbb {F}}\,\!{}}((\iota _n(\omega )))$
-vector space
${{\mathbb {F}}\,\!{}}((\iota _n(\omega )))$
-vector space
![]() $(A/{\mathfrak {p}}^{(n)}A)[1/\iota _n(\omega )]\subset R_n$
. By induction on n one also sees that
$(A/{\mathfrak {p}}^{(n)}A)[1/\iota _n(\omega )]\subset R_n$
. By induction on n one also sees that
![]() $(A/{\mathfrak {p}}^{(n)}A)[1/\iota _n(\omega )]= R_n$
: This is clearly true for
$(A/{\mathfrak {p}}^{(n)}A)[1/\iota _n(\omega )]= R_n$
: This is clearly true for
![]() $n=1$
by the previous paragraph. In the induction step, we know that under reduction
$n=1$
by the previous paragraph. In the induction step, we know that under reduction
![]() $(A/{\mathfrak {p}}^{(n)}A)[1/\iota _n(\omega )]$
maps onto
$(A/{\mathfrak {p}}^{(n)}A)[1/\iota _n(\omega )]$
maps onto
![]() $R_{n-1}$
. Moreover,
$R_{n-1}$
. Moreover,
![]() ${\mathfrak {p}}^{n-1}/{\mathfrak {p}}{^n[1/\iota _n(\omega )]}$
is a
${\mathfrak {p}}^{n-1}/{\mathfrak {p}}{^n[1/\iota _n(\omega )]}$
is a
![]() ${\kappa ({{\mathfrak {p}}})} =A/{\mathfrak {p}}{[1/\iota _1(\omega )]}$
-vector space, and it follows that
${\kappa ({{\mathfrak {p}}})} =A/{\mathfrak {p}}{[1/\iota _1(\omega )]}$
-vector space, and it follows that
![]() $(A/{\mathfrak {p}}^{(n)}A)[1/\iota _n(\omega )]$
is a
$(A/{\mathfrak {p}}^{(n)}A)[1/\iota _n(\omega )]$
is a
![]() ${\kappa ({{\mathfrak {p}}})}$
-vector space and thus equal to
${\kappa ({{\mathfrak {p}}})}$
-vector space and thus equal to
![]() $R_n$
. Now, the topology of
$R_n$
. Now, the topology of
![]() $R_n$
as a
$R_n$
as a
![]() $K_n$
or as a
$K_n$
or as a
![]() ${{\mathbb {F}}\,\!{}}{((\iota _1(\omega )))}$
-vector space is the same, and it follows that
${{\mathbb {F}}\,\!{}}{((\iota _1(\omega )))}$
-vector space is the same, and it follows that
![]() $\iota _n(A)$
is a compact open neighborhood of
$\iota _n(A)$
is a compact open neighborhood of
![]() $0$
in
$0$
in
![]() $R_n$
, and hence there exists
$R_n$
, and hence there exists
![]() $j>0$
such that
$j>0$
such that
![]() $\iota _n((\omega )^jA)\subset U$
, and also
$\iota _n((\omega )^jA)\subset U$
, and also
![]() $\iota _n(A)/\iota _n(\omega ^jA)$
is finite. It follows that
$\iota _n(A)/\iota _n(\omega ^jA)$
is finite. It follows that
![]() $A/({\mathfrak {p}}^{(n)}+\omega ^jA)$
is a local Artin ring, and so there exists
$A/({\mathfrak {p}}^{(n)}+\omega ^jA)$
is a local Artin ring, and so there exists
![]() $m>0$
such that
$m>0$
such that
![]() ${\mathfrak {m}}{_A^m}\subset {\mathfrak {p}}^{(n)}+\omega ^jA$
, and also
${\mathfrak {m}}{_A^m}\subset {\mathfrak {p}}^{(n)}+\omega ^jA$
, and also
![]() $\iota ({\mathfrak {m}_{A}^{n}})\subset U$
. This proves (i).
$\iota ({\mathfrak {m}_{A}^{n}})\subset U$
. This proves (i).
For (ii), we show first that there exists
![]() $n\in {\mathbb {N}}$
such that
$n\in {\mathbb {N}}$
such that
![]() ${\mathfrak {m}}_A^m\supset {\mathfrak {p}}^{(n)}$
: To see this, note that the ring maps
${\mathfrak {m}}_A^m\supset {\mathfrak {p}}^{(n)}$
: To see this, note that the ring maps
![]() $A\to A_{\mathfrak {p}}\to \widehat {A}_{\mathfrak {p}}$
are injective and the
$A\to A_{\mathfrak {p}}\to \widehat {A}_{\mathfrak {p}}$
are injective and the
![]() ${\mathfrak {p}}$
-adic topology on
${\mathfrak {p}}$
-adic topology on
![]() $\widehat {A}_{\mathfrak {p}}$
is separated, that is, we have
$\widehat {A}_{\mathfrak {p}}$
is separated, that is, we have
![]() $\bigcap _n{\mathfrak {p}}^{(n)}=0$
. The existence of n now follows from Chevalley’s lemma, [Reference ChevalleyChe43, Lemma 7], which asserts that the topology on A generated by the ideals
$\bigcap _n{\mathfrak {p}}^{(n)}=0$
. The existence of n now follows from Chevalley’s lemma, [Reference ChevalleyChe43, Lemma 7], which asserts that the topology on A generated by the ideals
![]() $({\mathfrak {p}}^{(n)})_{n\ge 0}$
is finer then the
$({\mathfrak {p}}^{(n)})_{n\ge 0}$
is finer then the
![]() ${\mathfrak {m}}_A$
-adic topology.
${\mathfrak {m}}_A$
-adic topology.
Now, by the choice of
![]() $\omega $
we have
$\omega $
we have
![]() $\omega A\subset {\mathfrak {m}}_A$
. Therefore,
$\omega A\subset {\mathfrak {m}}_A$
. Therefore,
![]() $\omega ^mA+{\mathfrak {p}}^{(n)}\subset {\mathfrak {m}}_A^m$
. It follows that
$\omega ^mA+{\mathfrak {p}}^{(n)}\subset {\mathfrak {m}}_A^m$
. It follows that
![]() $U=\iota _n(\omega ^mA)$
is an open neighborhood of
$U=\iota _n(\omega ^mA)$
is an open neighborhood of
![]() $0$
such that
$0$
such that
![]() $\iota _n^{-1}(\iota _n(A)\cap U)\subset {\mathfrak {m}}_A^m$
.
$\iota _n^{-1}(\iota _n(A)\cap U)\subset {\mathfrak {m}}_A^m$
.
Proposition 4.8.6. Suppose
![]() $\Phi _{\overline {{D}}}$
holds. Let
$\Phi _{\overline {{D}}}$
holds. Let
![]() ${\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}\to A$
be a morphism in
${\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}\to A$
be a morphism in
![]() ${\widehat {\mathcal {A}}r}_{{\mathbb {F}}\,\!{}}$
, and let
${\widehat {\mathcal {A}}r}_{{\mathbb {F}}\,\!{}}$
, and let
![]() ${D}_A$
be the corresponding pseudodeformation. Suppose A is a domain with fraction field
${D}_A$
be the corresponding pseudodeformation. Suppose A is a domain with fraction field
![]() ${\mathbb {K}}$
and that
${\mathbb {K}}$
and that
![]() ${D}_{\mathbb {K}}:={D}_A\otimes _A{\mathbb {K}}$
is multiplicity free. Then there exist
${D}_{\mathbb {K}}:={D}_A\otimes _A{\mathbb {K}}$
is multiplicity free. Then there exist
-
(i) a finite extension
 ${\mathbb {K}}'$
of
${\mathbb {K}}'$
of
 ${\mathbb {K}}$
with integral closure
${\mathbb {K}}$
with integral closure
 $A'$
of A in
$A'$
of A in
 ${\mathbb {K}}'$
, and
${\mathbb {K}}'$
, and -
(ii) continuous irreducible pseudocharacters
 ${D}^{\prime }_i\colon A'[G]\to A'$
,
${D}^{\prime }_i\colon A'[G]\to A'$
,
such that
![]() ${D}_A\otimes _AA'=\oplus _i{D}^{\prime }_i$
. The ring
${D}_A\otimes _AA'=\oplus _i{D}^{\prime }_i$
. The ring
![]() $A'$
lies in
$A'$
lies in
![]() $ {\widehat {\mathcal {A}}r}_{{{\mathbb {F}}\,\!{}}'}$
for some finite field
$ {\widehat {\mathcal {A}}r}_{{{\mathbb {F}}\,\!{}}'}$
for some finite field
![]() ${{\mathbb {F}}\,\!{}}'\supset {{\mathbb {F}}\,\!{}}$
. If
${{\mathbb {F}}\,\!{}}'\supset {{\mathbb {F}}\,\!{}}$
. If
![]() ${\overline {{D}}}$
is split, the ring of definition
${\overline {{D}}}$
is split, the ring of definition
![]() $A_i\subset A'$
of each
$A_i\subset A'$
of each
![]() ${D}_i^{\prime }$
lies in
${D}_i^{\prime }$
lies in
![]() ${\mathcal {A}dm}_{{\mathbb {F}}\,\!{}}$
and one has
${\mathcal {A}dm}_{{\mathbb {F}}\,\!{}}$
and one has
![]() ${\overline {{D}}}=\oplus _i({D}_i^{\prime }\otimes _{A_i}{\kappa ({A_i})})$
over
${\overline {{D}}}=\oplus _i({D}_i^{\prime }\otimes _{A_i}{\kappa ({A_i})})$
over
![]() ${{\mathbb {F}}\,\!{}}$
.
${{\mathbb {F}}\,\!{}}$
.
Proof. Define the rings
Then by Proposition 4.7.11, the A-algebra
![]() $S_A$
is finitely generated as an A-module, and the induced homomorphism
$S_A$
is finitely generated as an A-module, and the induced homomorphism
![]() $G\to S_A^\times $
is continuous if
$G\to S_A^\times $
is continuous if
![]() $S_A$
is equipped with the
$S_A$
is equipped with the
![]() ${\mathfrak {m}}_A$
-adic topology as an A-module. In particular, the
${\mathfrak {m}}_A$
-adic topology as an A-module. In particular, the
![]() ${\mathbb {K}}$
-algebra
${\mathbb {K}}$
-algebra
![]() $S_{\mathbb {K}}$
is of finite
$S_{\mathbb {K}}$
is of finite
![]() ${\mathbb {K}}$
-dimension.
${\mathbb {K}}$
-dimension.
Now, Lemma A.2.3 gives a finite extension
![]() ${\mathbb {K}}'$
of
${\mathbb {K}}'$
of
![]() ${\mathbb {K}}$
so that
${\mathbb {K}}$
so that
![]() $S':=S_{\mathbb {K}}\otimes _{\mathbb {K}}{\mathbb {K}}'/{\mathrm {Rad}}(S_{\mathbb {K}}\otimes _{\mathbb {K}}{\mathbb {K}}')$
is a product of matrix algebras
$S':=S_{\mathbb {K}}\otimes _{\mathbb {K}}{\mathbb {K}}'/{\mathrm {Rad}}(S_{\mathbb {K}}\otimes _{\mathbb {K}}{\mathbb {K}}')$
is a product of matrix algebras
![]() $S'=\prod _i{\mathrm {Mat}}_{n_i\times n_i}({\mathbb {K}}')$
. Since
$S'=\prod _i{\mathrm {Mat}}_{n_i\times n_i}({\mathbb {K}}')$
. Since
![]() ${D}_{{\mathbb {K}}'}:={D}_{\mathbb {K}}\otimes _{\mathbb {K}}{\mathbb {K}}'$
factors via
${D}_{{\mathbb {K}}'}:={D}_{\mathbb {K}}\otimes _{\mathbb {K}}{\mathbb {K}}'$
factors via
![]() $S'$
and is multiplicity free, it is the composition of
$S'$
and is multiplicity free, it is the composition of
![]() $G\to S_A^\times \to (S')^\times $
with
$G\to S_A^\times \to (S')^\times $
with
![]() $\prod _i {\mathrm {det}}_{n_i}$
where
$\prod _i {\mathrm {det}}_{n_i}$
where
![]() ${\mathrm {det}}_{n_i}$
is the determinant of
${\mathrm {det}}_{n_i}$
is the determinant of
![]() ${\mathrm {Mat}}_{n_i\times n_i}({\mathbb {K}}')$
. Write
${\mathrm {Mat}}_{n_i\times n_i}({\mathbb {K}}')$
. Write
![]() ${D}_{{\mathbb {K}}'}=\bigoplus _i {D}_i$
with
${D}_{{\mathbb {K}}'}=\bigoplus _i {D}_i$
with
![]() ${D}_i$
corresponding to
${D}_i$
corresponding to
![]() ${\mathrm {det}}_{n_i}$
on the i-th factor of
${\mathrm {det}}_{n_i}$
on the i-th factor of
![]() $S'$
.
$S'$
.
Let
![]() $A'$
be the integral closure of A in
$A'$
be the integral closure of A in
![]() ${\mathbb {K}}'$
. Because A is Nagata by Lemma A.1.1(a), the ring
${\mathbb {K}}'$
. Because A is Nagata by Lemma A.1.1(a), the ring
![]() $A'$
is finite over A and hence lies in
$A'$
is finite over A and hence lies in
![]() ${\mathcal {A}dm}_{{\mathbb {F}}\,\!{}}$
. Because A is complete Noetherian, so is
${\mathcal {A}dm}_{{\mathbb {F}}\,\!{}}$
. Because A is complete Noetherian, so is
![]() $A'$
, and because
$A'$
, and because
![]() $A'$
must be semilocal, it is a product of local rings. But
$A'$
must be semilocal, it is a product of local rings. But
![]() $A'$
is also a subring of the field
$A'$
is also a subring of the field
![]() ${\mathbb {K}}'$
, and thus
${\mathbb {K}}'$
, and thus
![]() $A'$
lies in
$A'$
lies in
![]() ${\widehat {\mathcal {A}}r}_{{{\mathbb {F}}\,\!{}}'}$
for some finite field extension
${\widehat {\mathcal {A}}r}_{{{\mathbb {F}}\,\!{}}'}$
for some finite field extension
![]() ${{\mathbb {F}}\,\!{}}'\supset {{\mathbb {F}}\,\!{}}$
. Let
${{\mathbb {F}}\,\!{}}'\supset {{\mathbb {F}}\,\!{}}$
. Let
![]() $S_{A'}:=S_A\otimes _AA'$
, and write
$S_{A'}:=S_A\otimes _AA'$
, and write
![]() $(S_A)'$
for the image of
$(S_A)'$
for the image of
![]() $S_{A'}$
in
$S_{A'}$
in
![]() $S'$
.
$S'$
.
Because
![]() ${D}_{{\mathbb {K}}'}=\bigoplus _i {D}_i$
, the attached characteristic polynomials satisfy
${D}_{{\mathbb {K}}'}=\bigoplus _i {D}_i$
, the attached characteristic polynomials satisfy
By hypothesis, the coefficients of
![]() ${D}_{{\mathbb {K}}'}$
lie in
${D}_{{\mathbb {K}}'}$
lie in
![]() $A\subset A'\subset {\mathbb {K}}'$
. Now, because
$A\subset A'\subset {\mathbb {K}}'$
. Now, because
![]() $A'$
is integrally closed, by [Reference MatsumuraMat89, Theorem 9.2] the coefficients of the
$A'$
is integrally closed, by [Reference MatsumuraMat89, Theorem 9.2] the coefficients of the
![]() $\chi _{{D}^{\prime }_i}(\cdot ,t) $
lie in
$\chi _{{D}^{\prime }_i}(\cdot ,t) $
lie in
![]() $A'$
. Hence, by Amitsur’s formula in the form Proposition 4.1.10, the
$A'$
. Hence, by Amitsur’s formula in the form Proposition 4.1.10, the
![]() ${D}_i^{\prime }$
take values in
${D}_i^{\prime }$
take values in
![]() $A'$
.
$A'$
.
Now, note that the proposition is trivial if A has Krull dimension
![]() $0$
, and so we assume it to be strictly positive from now on so that
$0$
, and so we assume it to be strictly positive from now on so that
![]() ${\mathrm {Spec}}\ A'{\smallsetminus }\{{\mathfrak {m}}_{A'}\}$
is a nonempty Jacobson scheme and thus the points of dimension
${\mathrm {Spec}}\ A'{\smallsetminus }\{{\mathfrak {m}}_{A'}\}$
is a nonempty Jacobson scheme and thus the points of dimension
![]() $1$
of
$1$
of
![]() ${\mathrm {Spec}}\ A'$
are very dense in it; see Definition A.1.10 and Proposition A.1.11. Moreover, the locus of irreducibility of each
${\mathrm {Spec}}\ A'$
are very dense in it; see Definition A.1.10 and Proposition A.1.11. Moreover, the locus of irreducibility of each
![]() $D_i$
is open in
$D_i$
is open in
![]() ${\mathrm {Spec}}\ A'$
by Proposition 4.7.17 and contains the generic point of
${\mathrm {Spec}}\ A'$
by Proposition 4.7.17 and contains the generic point of
![]() ${\mathrm {Spec}}\ A'$
by construction. Also, by Lemma A.1.1 the complete Noetherian local ring
${\mathrm {Spec}}\ A'$
by construction. Also, by Lemma A.1.1 the complete Noetherian local ring
![]() $A'$
is a Nagata ring and so the regular locus is open in
$A'$
is a Nagata ring and so the regular locus is open in
![]() ${\mathrm {Spec}}\ A'$
; it is nonempty because
${\mathrm {Spec}}\ A'$
; it is nonempty because
![]() $ A'$
is a domain. Hence, there exists a point
$ A'$
is a domain. Hence, there exists a point
![]() ${\mathfrak {p}}\in {\mathrm {Spec}}\ A'$
of dimension
${\mathfrak {p}}\in {\mathrm {Spec}}\ A'$
of dimension
![]() $1$
at which all
$1$
at which all
![]() $D_i$
are simultaneously irreducible and such that
$D_i$
are simultaneously irreducible and such that
![]() $A^{\prime }_{\mathfrak {p}}$
is regular local. The former condition on
$A^{\prime }_{\mathfrak {p}}$
is regular local. The former condition on
![]() ${\mathfrak {p}}$
implies by Proposition 4.7.18 that each
${\mathfrak {p}}$
implies by Proposition 4.7.18 that each
![]() ${D}_i$
when considered as a pseudocharacter
${D}_i$
when considered as a pseudocharacter
![]() $A^{\prime }_{\mathfrak {p}}[G]\to A^{\prime }_{\mathfrak {p}}$
is equal to the reduced norm composed with a representation
$A^{\prime }_{\mathfrak {p}}[G]\to A^{\prime }_{\mathfrak {p}}$
is equal to the reduced norm composed with a representation
![]() $G\to (C_i)^\times $
for
$G\to (C_i)^\times $
for
![]() $C_i$
an
$C_i$
an
![]() $A^{\prime }_{\mathfrak {p}}$
-Azumaya algebra. The latter condition implies that one has an inclusion of Brauer groups
$A^{\prime }_{\mathfrak {p}}$
-Azumaya algebra. The latter condition implies that one has an inclusion of Brauer groups
![]() ${\mathrm {Br}}(A^{\prime }_{\mathfrak {p}}){\hookrightarrow } {\mathrm {Br}}({\mathbb {K}}'$
) by [Reference Auslander and GoldmanAG60, Theorem 7.2], and hence that all
${\mathrm {Br}}(A^{\prime }_{\mathfrak {p}}){\hookrightarrow } {\mathrm {Br}}({\mathbb {K}}'$
) by [Reference Auslander and GoldmanAG60, Theorem 7.2], and hence that all
![]() $C_i$
have trivial Brauer class by the choice of
$C_i$
have trivial Brauer class by the choice of
![]() ${\mathbb {K}}'$
, that is
${\mathbb {K}}'$
, that is
![]() $C_i\cong {\mathrm {Mat}}_{n_i\times n_i}(A_{\mathfrak {p}})$
for suitable
$C_i\cong {\mathrm {Mat}}_{n_i\times n_i}(A_{\mathfrak {p}})$
for suitable
![]() $n_i>0$
. It follows that over
$n_i>0$
. It follows that over
![]() $A^{\prime }_{\mathfrak {p}}$
we have that
$A^{\prime }_{\mathfrak {p}}$
we have that
![]() ${D}'$
is the determinant of a direct sum of representations
${D}'$
is the determinant of a direct sum of representations
By our hypothesis,
![]() $G\to S_A^\times $
is continuous as is the induced pseudocharacter
$G\to S_A^\times $
is continuous as is the induced pseudocharacter
![]() ${D}\colon S_A\to A$
. Let
${D}\colon S_A\to A$
. Let
![]() $S_{\mathfrak {p}}$
be
$S_{\mathfrak {p}}$
be
![]() $S_A\otimes _A\widehat {A'}_{\mathfrak {p}}/{\mathrm {CH}}({D}')$
. Then by Lemma 4.8.5 also
$S_A\otimes _A\widehat {A'}_{\mathfrak {p}}/{\mathrm {CH}}({D}')$
. Then by Lemma 4.8.5 also
![]() $G\to S_{\mathfrak {p}}^\times $
is continuous, as is the induced pseudocharacter
$G\to S_{\mathfrak {p}}^\times $
is continuous, as is the induced pseudocharacter
![]() $S_{\mathfrak {p}}\to A'$
. From the above and Proposition 4.3.9, it follows that
$S_{\mathfrak {p}}\to A'$
. From the above and Proposition 4.3.9, it follows that
![]() $S_{\mathfrak {p}}$
is a GMA with trivial ideal of total reducibility. Now, the continuity of
$S_{\mathfrak {p}}$
is a GMA with trivial ideal of total reducibility. Now, the continuity of
![]() $G\to S_{\mathfrak {p}}^\times $
implies that of
$G\to S_{\mathfrak {p}}^\times $
implies that of
![]() ${D}_i\colon G\to {\mathrm {Mat}}_{n_i\times n_i}(\widehat {A'}_{\mathfrak {p}})^\times \stackrel {{\mathrm {det}}}\to \widehat {A'}_{\mathfrak {p}}$
obtained by applying the i-the projection and the determinant, and again from Lemma 4.8.5 we deduce that
${D}_i\colon G\to {\mathrm {Mat}}_{n_i\times n_i}(\widehat {A'}_{\mathfrak {p}})^\times \stackrel {{\mathrm {det}}}\to \widehat {A'}_{\mathfrak {p}}$
obtained by applying the i-the projection and the determinant, and again from Lemma 4.8.5 we deduce that
![]() ${D}_i\colon A'[G]\to A'$
is continuous.
${D}_i\colon A'[G]\to A'$
is continuous.
It remains to prove the last assertion, assuming that
![]() ${\overline {{D}}}$
is split: Let
${\overline {{D}}}$
is split: Let
![]() $A_i\subset A'$
be the ring of definition of
$A_i\subset A'$
be the ring of definition of
![]() ${D}_i^{\prime }$
, denote by
${D}_i^{\prime }$
, denote by
![]() ${D}_{i}\colon A_i[G]\to A_i$
the corresponding pseudocharacter and let
${D}_{i}\colon A_i[G]\to A_i$
the corresponding pseudocharacter and let
![]() ${\overline {{D}}}_i:={D}_i\otimes _{A_i}{\kappa ({A_i})}$
. Note that the
${\overline {{D}}}_i:={D}_i\otimes _{A_i}{\kappa ({A_i})}$
. Note that the
![]() ${\kappa ({A_i})}$
are the rings of definition of
${\kappa ({A_i})}$
are the rings of definition of
![]() ${\overline {{D}}}_i$
. Let
${\overline {{D}}}_i$
. Let
![]() ${{\mathbb {F}}\,\!{}}"$
be the smallest extension of
${{\mathbb {F}}\,\!{}}"$
be the smallest extension of
![]() ${{\mathbb {F}}\,\!{}}'$
that contains all
${{\mathbb {F}}\,\!{}}'$
that contains all
![]() ${\kappa ({A_i})}$
. Then
${\kappa ({A_i})}$
. Then
![]() ${\overline {{D}}}\otimes _{{\mathbb {F}}\,\!{}}{{\mathbb {F}}\,\!{}}"\cong \bigoplus _i {\overline {{D}}}_i\otimes _{{\kappa ({A_i})}}{{\mathbb {F}}\,\!{}}"$
. However,
${\overline {{D}}}\otimes _{{\mathbb {F}}\,\!{}}{{\mathbb {F}}\,\!{}}"\cong \bigoplus _i {\overline {{D}}}_i\otimes _{{\kappa ({A_i})}}{{\mathbb {F}}\,\!{}}"$
. However,
![]() ${\overline {{D}}}$
is split over
${\overline {{D}}}$
is split over
![]() ${{\mathbb {F}}\,\!{}}$
and so all
${{\mathbb {F}}\,\!{}}$
and so all
![]() ${\overline {{D}}}_i$
are defined over
${\overline {{D}}}_i$
are defined over
![]() ${{\mathbb {F}}\,\!{}}$
, and this shows
${{\mathbb {F}}\,\!{}}$
, and this shows
![]() ${\kappa ({A_i})}={{\mathbb {F}}\,\!{}}$
for all i by Lemma 4.4.8. We deduce
${\kappa ({A_i})}={{\mathbb {F}}\,\!{}}$
for all i by Lemma 4.4.8. We deduce
![]() $A_i\in {\mathcal {A}dm}_{{\mathbb {F}}\,\!{}}$
.
$A_i\in {\mathcal {A}dm}_{{\mathbb {F}}\,\!{}}$
.
Corollary 4.8.7. Let
![]() ${\kappa }$
be a finite or a local field, and let
${\kappa }$
be a finite or a local field, and let
![]() $\rho \colon G\to {\mathrm {GL}}_n(\kappa )$
be a continuous absolutely irreducible homomorphism with associated pseudocharacter
$\rho \colon G\to {\mathrm {GL}}_n(\kappa )$
be a continuous absolutely irreducible homomorphism with associated pseudocharacter
![]() ${D}$
. Suppose that
${D}$
. Suppose that
![]() $\Phi _{\overline {{D}}}$
holds for
$\Phi _{\overline {{D}}}$
holds for
![]() ${\overline {{D}}}$
attached to
${\overline {{D}}}$
attached to
![]() ${D}$
as in Lemma 4.8.1. Then the natural map
${D}$
as in Lemma 4.8.1. Then the natural map
![]() ${R^{\operatorname {univ}}_{\Lambda ,\rho }}\rightarrow {R^{\operatorname {univ}}_{\Lambda ,{D}}}$
induced from
${R^{\operatorname {univ}}_{\Lambda ,\rho }}\rightarrow {R^{\operatorname {univ}}_{\Lambda ,{D}}}$
induced from
![]() $\rho _A\mapsto {D}_{\rho _A}$
for
$\rho _A\mapsto {D}_{\rho _A}$
for
![]() $A\in {\mathcal {A}r}_\kappa $
is an isomorphism.
$A\in {\mathcal {A}r}_\kappa $
is an isomorphism.
Proof. If
![]() ${\kappa }$
is finite, the assertion is [Reference ChenevierChe14, Example 3.4]. For local
${\kappa }$
is finite, the assertion is [Reference ChenevierChe14, Example 3.4]. For local
![]() ${\kappa }$
, we need to show that the natural transformation of functors
${\kappa }$
, we need to show that the natural transformation of functors
![]() ${\mathcal {A}r}_{\kappa }\to {Sets}$
defined by
${\mathcal {A}r}_{\kappa }\to {Sets}$
defined by

is an isomorphism. Well definedness is clear. Injectivity follows from Theorem 4.3.10
(a) since
![]() $\rho _{D}$
is absolutely irreducible. To prove surjectivity, consider a pseudodeformation
$\rho _{D}$
is absolutely irreducible. To prove surjectivity, consider a pseudodeformation
![]() ${D}_A\colon A[G]\to A$
of
${D}_A\colon A[G]\to A$
of
![]() ${D}$
and note that by Theorem 4.3.10
(a) there exists a deformation
${D}$
and note that by Theorem 4.3.10
(a) there exists a deformation
![]() $\rho _A$
of
$\rho _A$
of
![]() $\rho _{D}$
to A with
$\rho _{D}$
to A with
![]() ${D}_A={D}_{\rho _A}$
. The continuity of
${D}_A={D}_{\rho _A}$
. The continuity of
![]() $\rho _A$
follows from Corollary 4.8.2
(b).
$\rho _A$
follows from Corollary 4.8.2
(b).
We now give an analog of Theorem 3.3.1 for pseudocharacters.
Corollary 4.8.8. Let
![]() ${{\mathbb {F}}\,\!{}}$
be a finite field and let
${{\mathbb {F}}\,\!{}}$
be a finite field and let
![]() ${\overline {{D}}}\in {\mathcal {P}s\mathcal {R}}_G^n({{\mathbb {F}}\,\!{}})$
be continuous. For
${\overline {{D}}}\in {\mathcal {P}s\mathcal {R}}_G^n({{\mathbb {F}}\,\!{}})$
be continuous. For
![]() $x\in {X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}}}}$
such that
$x\in {X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}}}}$
such that
![]() ${\kappa ({x})} $
is a local field and with residue map
${\kappa ({x})} $
is a local field and with residue map
![]() $\pi _x\colon {R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}}}} \to {\kappa ({x})} $
and associated pseudocharacter
$\pi _x\colon {R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}}}} \to {\kappa ({x})} $
and associated pseudocharacter
![]() ${D}_x\colon {\kappa ({x})} [G]\to {\kappa ({x})} $
, define the morphism
${D}_x\colon {\kappa ({x})} [G]\to {\kappa ({x})} $
, define the morphism
![]() $f_x=\pi _x\otimes {\mathrm {id}}\colon {R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}}}} \otimes _{\Lambda } {\kappa ({x})} \to {\kappa ({x})} $
, and the completion
$f_x=\pi _x\otimes {\mathrm {id}}\colon {R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}}}} \otimes _{\Lambda } {\kappa ({x})} \to {\kappa ({x})} $
, and the completion
![]() $\widehat {R}$
of
$\widehat {R}$
of
![]() ${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}}}} \otimes _{\Lambda } {\kappa ({x})} $
at
${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}}}} \otimes _{\Lambda } {\kappa ({x})} $
at
![]() ${\mathfrak {p}}={\mathop {\mathrm{Ker}}\nolimits }(f_x)$
. Denote by
${\mathfrak {p}}={\mathop {\mathrm{Ker}}\nolimits }(f_x)$
. Denote by
-
(i)
 $\widehat {{D}} \colon G\to {R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{{\overline {{D}}}}}}} \to \widehat {R}$
the completion at
$\widehat {{D}} \colon G\to {R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{{\overline {{D}}}}}}} \to \widehat {R}$
the completion at
 ${\mathfrak {p}}$
of the pseudocharacter
${\mathfrak {p}}$
of the pseudocharacter
 ${D}^{\operatorname {univ}}_{{\overline {{D}}}}\otimes _{\Lambda }{\kappa ({x})} $
, and by
${D}^{\operatorname {univ}}_{{\overline {{D}}}}\otimes _{\Lambda }{\kappa ({x})} $
, and by -
(ii)
 ${D}^{\operatorname {univ}}_{{D}_x}\colon G\to {R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\kappa ({x})} ,{{D}_x}}}}$
the universal pseudodeformation from Proposition 4.7.4 attached to
${D}^{\operatorname {univ}}_{{D}_x}\colon G\to {R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\kappa ({x})} ,{{D}_x}}}}$
the universal pseudodeformation from Proposition 4.7.4 attached to
 ${{D}_x}$
.
${{D}_x}$
.
Then the map
![]() ${\varphi }\colon {R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{D}_x}}} \to \widehat {R}$
induced from the universal property of
${\varphi }\colon {R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{D}_x}}} \to \widehat {R}$
induced from the universal property of
![]() $ {R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{D}_x}}}$
is an isomorphism.
$ {R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{D}_x}}}$
is an isomorphism.
Proof. We adapt the proof of Theorem 3.3.1. Thus, we need to show that
![]() ${\varphi }$
is formally étale. We abbreviate
${\varphi }$
is formally étale. We abbreviate
![]() ${\kappa }={\kappa ({x})} $
and let
${\kappa }={\kappa ({x})} $
and let
![]() ${\cal O}$
be the ring of integers of
${\cal O}$
be the ring of integers of
![]() $\kappa $
. Consider the commutative diagram
$\kappa $
. Consider the commutative diagram

where
![]() $A\in {{\widehat {\mathcal {A}}r}_{{\kappa }}}$
, the ideal
$A\in {{\widehat {\mathcal {A}}r}_{{\kappa }}}$
, the ideal
![]() $I\subset A$
satisfies
$I\subset A$
satisfies
![]() ${I^2}=0$
, and
${I^2}=0$
, and
![]() ${{D}}\colon A[G]\to A$
is continuous pseudodeformation of
${{D}}\colon A[G]\to A$
is continuous pseudodeformation of
![]() ${{D}_x}$
. The maps
${{D}_x}$
. The maps
![]() $\hat {\alpha }_{A/I}$
and
$\hat {\alpha }_{A/I}$
and
![]() $\alpha _A$
are homomorphisms in
$\alpha _A$
are homomorphisms in
![]() $\widehat {{\mathcal {A}r}_\kappa }$
. We will construct the dashed arrow
$\widehat {{\mathcal {A}r}_\kappa }$
. We will construct the dashed arrow
![]() $\hat {\alpha _A}$
so that the extended diagram commutes and show its uniqueness. Our first claim is that there is an
$\hat {\alpha _A}$
so that the extended diagram commutes and show its uniqueness. Our first claim is that there is an
![]() ${\cal O}$
-algebra
${\cal O}$
-algebra
![]() ${A_0}\subset A$
that as an
${A_0}\subset A$
that as an
![]() ${\cal O}$
-module is an
${\cal O}$
-module is an
![]() ${\cal O}$
-lattice in A and such that
${\cal O}$
-lattice in A and such that
![]() ${{D}}$
is valued in
${{D}}$
is valued in
![]() $A_0$
.
$A_0$
.
The proof is an induction over j for the composition
![]() ${D}_j={D}\pmod {{\mathfrak {m}}_A^j}$
of
${D}_j={D}\pmod {{\mathfrak {m}}_A^j}$
of
![]() ${D}$
with the quotient map
${D}$
with the quotient map
![]() $A\to A_j=A/{\mathfrak {m}}_A^j$
. For
$A\to A_j=A/{\mathfrak {m}}_A^j$
. For
![]() $j=1$
, the claim holds because
$j=1$
, the claim holds because
![]() ${D}_x={D}_1$
is valued in
${D}_x={D}_1$
is valued in
![]() ${\cal O}\subset {\kappa }$
. Suppose in the induction step that we have defined
${\cal O}\subset {\kappa }$
. Suppose in the induction step that we have defined
![]() $A_{j,0}\subset A_j$
as in the claim and we wish to construct
$A_{j,0}\subset A_j$
as in the claim and we wish to construct
![]() $A_{j+1,0}\subset A_{j+1}$
. Because the characteristic polynomial coefficients
$A_{j+1,0}\subset A_{j+1}$
. Because the characteristic polynomial coefficients
![]() $\Lambda _{i,{D}_{j+1}} $
,
$\Lambda _{i,{D}_{j+1}} $
,
![]() $i=1,\ldots ,n$
, are continuous and G is profinite and hence compact, the joint image of the
$i=1,\ldots ,n$
, are continuous and G is profinite and hence compact, the joint image of the
![]() $\Lambda _{i,{D}_{j+1}} (G)$
is bounded in
$\Lambda _{i,{D}_{j+1}} (G)$
is bounded in
![]() $A_{j+1}$
and hence there exists an
$A_{j+1}$
and hence there exists an
![]() ${\cal O}$
-sublattice
${\cal O}$
-sublattice
![]() $L\subset A_{j+1}$
that contains this joint image as well as
$L\subset A_{j+1}$
that contains this joint image as well as
![]() ${\cal O}\cdot 1$
, and such that
${\cal O}\cdot 1$
, and such that
![]() $L\pmod {{\mathfrak {m}}_A^j}=A_{j,0}$
. Now, using that
$L\pmod {{\mathfrak {m}}_A^j}=A_{j,0}$
. Now, using that
![]() $A_{j,0}$
is a ring and that
$A_{j,0}$
is a ring and that
![]() ${\mathfrak {m}}_A^j$
is annihilated by
${\mathfrak {m}}_A^j$
is annihilated by
![]() ${\mathfrak {m}}_A$
, it follows, for instance by considering a suitable
${\mathfrak {m}}_A$
, it follows, for instance by considering a suitable
![]() ${\cal O}$
-basis of L and the quotient
${\cal O}$
-basis of L and the quotient
![]() $L+{\mathfrak {m}}_A^j/L$
inside
$L+{\mathfrak {m}}_A^j/L$
inside
![]() ${\mathfrak {m}}_A^j/({\mathfrak {m}}_A^{j+1}+L\cap {\mathfrak {m}}_A^j)$
, that
${\mathfrak {m}}_A^j/({\mathfrak {m}}_A^{j+1}+L\cap {\mathfrak {m}}_A^j)$
, that
![]() $L\cdot L$
is an
$L\cdot L$
is an
![]() ${\cal O}$
-algebra that can be taken as
${\cal O}$
-algebra that can be taken as
![]() $A_{j+1,0}$
.
$A_{j+1,0}$
.
Let
![]() $C_x$
be the ring of definition of
$C_x$
be the ring of definition of
![]() ${D}_x$
. It is a quotient of
${D}_x$
. It is a quotient of
![]() ${R^{\operatorname {univ}}_{\Lambda ,{\overline {{D}}}}}$
and a subring of
${R^{\operatorname {univ}}_{\Lambda ,{\overline {{D}}}}}$
and a subring of
![]() ${\cal O}\subset {\kappa }$
. We let B be the subalgebra of
${\cal O}\subset {\kappa }$
. We let B be the subalgebra of
![]() $A_0$
that is the inverse image of
$A_0$
that is the inverse image of
![]() $C_x$
under the reduction map
$C_x$
under the reduction map
![]() $A_{0}\to {\cal O}$
modulo
$A_{0}\to {\cal O}$
modulo
![]() ${\mathfrak {m}}_A$
. Then
${\mathfrak {m}}_A$
. Then
![]() $B\in {\widehat {\mathcal {A}}r}_{\Lambda }$
and B is a coefficient ring for
$B\in {\widehat {\mathcal {A}}r}_{\Lambda }$
and B is a coefficient ring for
![]() ${D}$
. Denote by
${D}$
. Denote by
![]() ${D}_B\colon B[G]\to B$
the pseudocharacter such that
${D}_B\colon B[G]\to B$
the pseudocharacter such that
![]() $D_B\otimes _BA={D}$
. If
$D_B\otimes _BA={D}$
. If
![]() ${\kappa }$
has positive characteristic, it follows from Lemma 4.8.5 that
${\kappa }$
has positive characteristic, it follows from Lemma 4.8.5 that
![]() ${D}_B$
is continuous with B carrying the
${D}_B$
is continuous with B carrying the
![]() ${\mathfrak {m}}_B$
-adic topology. The same holds if
${\mathfrak {m}}_B$
-adic topology. The same holds if
![]() ${\kappa }$
is a p-dic field: Then B is a finite free
${\kappa }$
is a p-dic field: Then B is a finite free
![]() ${\mathbb {Z}}_p$
-module, and so the p-adic topology on B agrees with the
${\mathbb {Z}}_p$
-module, and so the p-adic topology on B agrees with the
![]() ${\mathfrak {m}}_B$
-adic topology on B. Therefore, the continuity of
${\mathfrak {m}}_B$
-adic topology on B. Therefore, the continuity of
![]() ${D}$
with respect to the topology on A as a continuous
${D}$
with respect to the topology on A as a continuous
![]() ${\kappa }$
-module implies the continuity of
${\kappa }$
-module implies the continuity of
![]() ${D}_B$
for the
${D}_B$
for the
![]() ${\mathfrak {m}}_B$
-adic topology on B.
${\mathfrak {m}}_B$
-adic topology on B.
Now, the universal property of
![]() ${R^{\operatorname {univ}}_{\Lambda ,{\overline {{D}}}}}$
yields a unique homomorphism
${R^{\operatorname {univ}}_{\Lambda ,{\overline {{D}}}}}$
yields a unique homomorphism
![]() $\beta _B\colon {R^{\operatorname {univ}}_{\Lambda ,{\overline {{D}}}}}\rightarrow B$
such that
$\beta _B\colon {R^{\operatorname {univ}}_{\Lambda ,{\overline {{D}}}}}\rightarrow B$
such that
![]() ${D}=\beta _B\circ {D}_B$
. Then
${D}=\beta _B\circ {D}_B$
. Then
![]() $\beta _B\otimes _{\Lambda }{\mathrm {id}}_{\kappa }$
is a homomorphism
$\beta _B\otimes _{\Lambda }{\mathrm {id}}_{\kappa }$
is a homomorphism
![]() ${R^{\operatorname {univ}}_{\Lambda ,{\overline {{D}}}}}\otimes _{\Lambda } {\kappa }\rightarrow A$
. Its composition with
${R^{\operatorname {univ}}_{\Lambda ,{\overline {{D}}}}}\otimes _{\Lambda } {\kappa }\rightarrow A$
. Its composition with
![]() $A\to {\kappa }$
has kernel
$A\to {\kappa }$
has kernel
![]() ${\mathfrak {p}}$
, and thus it induces a map
${\mathfrak {p}}$
, and thus it induces a map
![]() $({R^{\operatorname {univ}}_{\Lambda ,{\overline {{D}}}}}\otimes _{\Lambda } {\kappa })_{\mathfrak {p}}\rightarrow A$
. If m denotes the length of A, then
$({R^{\operatorname {univ}}_{\Lambda ,{\overline {{D}}}}}\otimes _{\Lambda } {\kappa })_{\mathfrak {p}}\rightarrow A$
. If m denotes the length of A, then
![]() ${\mathfrak {p}}^m$
maps to zero under that map so that it factors via
${\mathfrak {p}}^m$
maps to zero under that map so that it factors via
![]() $\widehat {R}\to A$
. This is the wanted map
$\widehat {R}\to A$
. This is the wanted map
![]() $\hat \alpha _A$
: The top triangle in the diagram commutes by construction, the bottom triangle because
$\hat \alpha _A$
: The top triangle in the diagram commutes by construction, the bottom triangle because
![]() $\beta _A \pmod I$
and the map
$\beta _A \pmod I$
and the map
![]() ${R^{\operatorname {univ}}_{\Lambda ,{\overline {{D}}}}}\rightarrow B/(I\cap B)\subset A/I$
must agree since they both give rise to
${R^{\operatorname {univ}}_{\Lambda ,{\overline {{D}}}}}\rightarrow B/(I\cap B)\subset A/I$
must agree since they both give rise to
![]() ${D}\pmod I$
.
${D}\pmod I$
.
Let us show the uniqueness of
![]() $\hat \alpha _A$
, and so let
$\hat \alpha _A$
, and so let
![]() $\alpha ^{\prime }_A$
be a second map
$\alpha ^{\prime }_A$
be a second map
![]() $\widehat {R}\to A$
that makes as a dashed arrow the diagram commute. Observe that by construction we have the equality of pseudocharacters
$\widehat {R}\to A$
that makes as a dashed arrow the diagram commute. Observe that by construction we have the equality of pseudocharacters
![]() ${\varphi }\circ {D}^{\operatorname {univ}}_{{D}_x}=\widehat {(\cdot )}\circ ({D}^{\operatorname {univ}}_{\overline {{D}}}\otimes _{\Lambda }\kappa )$
. Now composing the equality with either
${\varphi }\circ {D}^{\operatorname {univ}}_{{D}_x}=\widehat {(\cdot )}\circ ({D}^{\operatorname {univ}}_{\overline {{D}}}\otimes _{\Lambda }\kappa )$
. Now composing the equality with either
![]() $\hat \alpha _A$
or
$\hat \alpha _A$
or
![]() $\alpha ^{\prime }_A$
gives the same pseudocharacter. We claim that
$\alpha ^{\prime }_A$
gives the same pseudocharacter. We claim that
![]() $\hat \alpha _A\circ \widehat {(\cdot )}=\alpha ^{\prime }_A\circ \widehat {(\cdot )}$
as maps
$\hat \alpha _A\circ \widehat {(\cdot )}=\alpha ^{\prime }_A\circ \widehat {(\cdot )}$
as maps
![]() ${R^{\operatorname {univ}}_{\Lambda ,{\overline {{D}}}}}\otimes _{\Lambda } {\kappa }\rightarrow A$
. If the claim is shown, then uniqueness follows, because the induced diagonal map is reconstructed by localization and completion – the ideal
${R^{\operatorname {univ}}_{\Lambda ,{\overline {{D}}}}}\otimes _{\Lambda } {\kappa }\rightarrow A$
. If the claim is shown, then uniqueness follows, because the induced diagonal map is reconstructed by localization and completion – the ideal
![]() ${\mathfrak {p}}^m$
is mapped to zero in A.
${\mathfrak {p}}^m$
is mapped to zero in A.
To prove the latter claim, by the universal property of the tensor product of rings, it suffices to understand the ring maps on both factors of
![]() ${R^{\operatorname {univ}}_{\Lambda ,{\overline {{D}}}}}\otimes _{\Lambda } {\kappa }\rightarrow A$
separately. On the second factor, both maps are the scalar multiplication isomorphism
${R^{\operatorname {univ}}_{\Lambda ,{\overline {{D}}}}}\otimes _{\Lambda } {\kappa }\rightarrow A$
separately. On the second factor, both maps are the scalar multiplication isomorphism
![]() $\kappa \to \kappa \cdot 1,\alpha \mapsto \alpha \cdot 1$
, by the definition of
$\kappa \to \kappa \cdot 1,\alpha \mapsto \alpha \cdot 1$
, by the definition of
![]() $\widehat {(\cdot )}$
and the condition that the diagonal map be in
$\widehat {(\cdot )}$
and the condition that the diagonal map be in
![]() ${\widehat {\mathcal {A}}r}_\kappa $
. The restriction of either map
${\widehat {\mathcal {A}}r}_\kappa $
. The restriction of either map
![]() $\hat \alpha _A\circ \widehat {(\cdot )}$
or
$\hat \alpha _A\circ \widehat {(\cdot )}$
or
![]() $\alpha ^{\prime }_A\circ \widehat {(\cdot )}$
to the first factor
$\alpha ^{\prime }_A\circ \widehat {(\cdot )}$
to the first factor
![]() ${R^{\operatorname {univ}}_{\Lambda ,{\overline {{D}}}}}$
gives when composed with
${R^{\operatorname {univ}}_{\Lambda ,{\overline {{D}}}}}$
gives when composed with
![]() ${D}^{\operatorname {univ}}_{\overline {{D}}}\otimes _{\Lambda }\kappa $
the pseudocharacter
${D}^{\operatorname {univ}}_{\overline {{D}}}\otimes _{\Lambda }\kappa $
the pseudocharacter
![]() ${D}$
. Both restrictions to
${D}$
. Both restrictions to
![]() ${R^{\operatorname {univ}}_{\Lambda ,{\overline {{D}}}}}$
are subject to the universal property of this ring, and hence these restrictions agree, and the claim is shown.
${R^{\operatorname {univ}}_{\Lambda ,{\overline {{D}}}}}$
are subject to the universal property of this ring, and hence these restrictions agree, and the claim is shown.
Remark 4.8.9. We think that [Reference ChenevierChe14, Corollary 2.23(ii)] has to be formulated in a way similar to Corollary 4.8.8; only if
![]() ${\kappa ({x})} $
is a p-adic field, one can simply complete
${\kappa ({x})} $
is a p-adic field, one can simply complete
![]() $({R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {D}}}}} )_{{\mathfrak {p}}_x}$
to obtain a universal pseudodeformation ring for
$({R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {D}}}}} )_{{\mathfrak {p}}_x}$
to obtain a universal pseudodeformation ring for
![]() ${D}_x$
. In Corollary 4.8.8 we have only verified this for dimension
${D}_x$
. In Corollary 4.8.8 we have only verified this for dimension
![]() $1$
points.
$1$
points.
Corollary 4.8.10. Let
![]() ${\kappa }$
be a local field and let
${\kappa }$
be a local field and let
![]() ${D}\in {\mathcal {P}s\mathcal {R}}^n_G({\kappa })$
be continuous. Suppose that condition
${D}\in {\mathcal {P}s\mathcal {R}}^n_G({\kappa })$
be continuous. Suppose that condition
![]() $\Phi _{\overline {{D}}}$
, for
$\Phi _{\overline {{D}}}$
, for
![]() ${\overline {{D}}}$
from Lemma 4.8.1, is satisfied. Then the following hold:
${\overline {{D}}}$
from Lemma 4.8.1, is satisfied. Then the following hold:
-
(a) The ring
 ${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\kappa ,{D}}}}$
is Noetherian.
${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\kappa ,{D}}}}$
is Noetherian. -
(b) Suppose that
 ${D}$
is irreducible and that
${D}$
is irreducible and that
 $H^2(G,{\operatorname {ad}_{{\rho }}} )=0$
for
$H^2(G,{\operatorname {ad}_{{\rho }}} )=0$
for
 $\rho :=\rho _{{D}\otimes _{\kappa }{{{{\kappa }}}^{\mathrm {alg}}} }$
. Then
$\rho :=\rho _{{D}\otimes _{\kappa }{{{{\kappa }}}^{\mathrm {alg}}} }$
. Then
 ${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\kappa },{D}}}}$
is formally smooth over
${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\kappa },{D}}}}$
is formally smooth over
 ${\kappa }$
of relative dimension
${\kappa }$
of relative dimension
 $\dim _{{{{{\kappa }}}^{\mathrm {alg}}} } H^1(G,{\operatorname {ad}_{{\rho }}} )$
.
$\dim _{{{{{\kappa }}}^{\mathrm {alg}}} } H^1(G,{\operatorname {ad}_{{\rho }}} )$
.
Proof. Let C be the ring of definition of
![]() ${D}$
, let
${D}$
, let
![]() ${D}_C\colon C[G]\to C$
the continuous pseudocharacter from Lemma 4.8.1 such that
${D}_C\colon C[G]\to C$
the continuous pseudocharacter from Lemma 4.8.1 such that
![]() ${D}_C\otimes _C {\kappa }={D}$
and let
${D}_C\otimes _C {\kappa }={D}$
and let
![]() ${\overline {{D}}}':={D}_C\otimes _C\kappa (C)$
; note that
${\overline {{D}}}':={D}_C\otimes _C\kappa (C)$
; note that
![]() $\kappa (C)$
is finite; note also that continuity is clear because C carries the subspace topology of
$\kappa (C)$
is finite; note also that continuity is clear because C carries the subspace topology of
![]() $\kappa $
and we only require the continuity of the characteristic polynomial coefficients as functions
$\kappa $
and we only require the continuity of the characteristic polynomial coefficients as functions
![]() $G\to C$
. By Proposition 4.7.4 and our hypotheses, the ring
$G\to C$
. By Proposition 4.7.4 and our hypotheses, the ring
![]() ${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{W(\kappa (C)),{\overline {{D}}}'}}}$
is Noetherian. Part (a) follows by choosing
${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{W(\kappa (C)),{\overline {{D}}}'}}}$
is Noetherian. Part (a) follows by choosing
![]() $x\in {X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{W(\kappa (C)),{\overline {{D}}}'}}}$
as the point corresponding to
$x\in {X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{W(\kappa (C)),{\overline {{D}}}'}}}$
as the point corresponding to
![]() ${D}$
, and by applying Corollary 4.8.8 with this x; note that
${D}$
, and by applying Corollary 4.8.8 with this x; note that
![]() $\widehat {R}$
(in Corollary 4.8.8) is Noetherian as the completion of a Noetherian local ring.
$\widehat {R}$
(in Corollary 4.8.8) is Noetherian as the completion of a Noetherian local ring.
To see Part (b), let
![]() ${\kappa }'\supset {\kappa }$
be a finite extension over which
${\kappa }'\supset {\kappa }$
be a finite extension over which
![]() ${D}$
is split. Let
${D}$
is split. Let
![]() $\rho :=\rho _{{D}\otimes _{\kappa }{\kappa }'}\colon G\to {\mathrm {GL}}_n({\kappa }')$
be the continuous and absolutely irreducible representation with
$\rho :=\rho _{{D}\otimes _{\kappa }{\kappa }'}\colon G\to {\mathrm {GL}}_n({\kappa }')$
be the continuous and absolutely irreducible representation with
![]() ${D}_{\rho '}.={D}\otimes _{\kappa }{\kappa }'$
. Our hypotheses gives
${D}_{\rho '}.={D}\otimes _{\kappa }{\kappa }'$
. Our hypotheses gives
![]() $H^2(G,{\operatorname {ad}_{{\rho '}}} )=0$
and it will suffice to show that
$H^2(G,{\operatorname {ad}_{{\rho '}}} )=0$
and it will suffice to show that
![]() ${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\kappa }',{D}}}}$
is formally smooth over
${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\kappa }',{D}}}}$
is formally smooth over
![]() ${\kappa }'$
of dimension
${\kappa }'$
of dimension
![]() $\dim _{{\kappa }'} H^1(G,{\operatorname {ad}_{{\rho '}}} )$
. This follows from Corollary 4.8.7 and Theorem 3.2.4
(e).
$\dim _{{\kappa }'} H^1(G,{\operatorname {ad}_{{\rho '}}} )$
. This follows from Corollary 4.8.7 and Theorem 3.2.4
(e).
For later use, we also need variants of Corollary 4.8.7 and Corollary 4.8.8 for deformations of pairs of representations and pseudocharacters. Let
![]() ${\overline {{D}}}_1,{\overline {{D}}}_2\colon {{\mathbb {F}}\,\!{}}[G]\to {{\mathbb {F}}\,\!{}}$
be continuous pseudocharacters of dimensions
${\overline {{D}}}_1,{\overline {{D}}}_2\colon {{\mathbb {F}}\,\!{}}[G]\to {{\mathbb {F}}\,\!{}}$
be continuous pseudocharacters of dimensions
![]() $n_1$
and
$n_1$
and
![]() $n_2$
such that
$n_2$
such that
![]() $\Phi _{{\overline {{D}}}_i}$
holds for
$\Phi _{{\overline {{D}}}_i}$
holds for
![]() $i=1,2$
. Consider the functor
$i=1,2$
. Consider the functor
It is straightforward to see that
![]() ${\mathcal {P}sD}_{({\overline {{D}}}_1,{\overline {{D}}}_2)}$
is represented by
${\mathcal {P}sD}_{({\overline {{D}}}_1,{\overline {{D}}}_2)}$
is represented by
![]() ${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{(\Lambda ,{\overline {{D}}}_1,{\overline {{D}}}_2)}}} :={R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}_1}}} \widehat {\otimes } {R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}_2}}}$
and that the ring
${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{(\Lambda ,{\overline {{D}}}_1,{\overline {{D}}}_2)}}} :={R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}_1}}} \widehat {\otimes } {R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,{\overline {{D}}}_2}}}$
and that the ring
![]() ${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{(\Lambda ,{\overline {{D}}}_1,{\overline {{D}}}_2)}}}$
is Noetherian, using Propositions 4.7.4 and 4.7.11.
${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{(\Lambda ,{\overline {{D}}}_1,{\overline {{D}}}_2)}}}$
is Noetherian, using Propositions 4.7.4 and 4.7.11.
Let
![]() $x\in {X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{({\overline {{D}}}_1,{\overline {{D}}}_2)}}} :={\mathrm {Spec}}\ {R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{({\overline {{D}}}_1,{\overline {{D}}}_2)}}} $
be a point of dimension
$x\in {X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{({\overline {{D}}}_1,{\overline {{D}}}_2)}}} :={\mathrm {Spec}}\ {R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{({\overline {{D}}}_1,{\overline {{D}}}_2)}}} $
be a point of dimension
![]() $1$
such that
$1$
such that
![]() ${D}_{i,x}$
is irreducible for
${D}_{i,x}$
is irreducible for
![]() $i=1,2$
for the corresponding pair
$i=1,2$
for the corresponding pair
![]() $({D}_{1,x},{D}_{2,x})$
. As above, one can define a deformation functor for this pair an
$({D}_{1,x},{D}_{2,x})$
. As above, one can define a deformation functor for this pair an
![]() ${\mathcal {A}r}_{{\kappa ({x})} }$
. It is representable by
${\mathcal {A}r}_{{\kappa ({x})} }$
. It is representable by
![]() ${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\kappa ({x})} ,({D}_{1,x},{D}_{2,x})}}} :={R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\kappa ({x})} ,{D}_{1,x}}}} \widehat {\otimes }_{{\kappa ({x})} } {R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\kappa ({x})} ,{D}_{2,x}}}}$
, which is again complete local Noetherian. Let
${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\kappa ({x})} ,({D}_{1,x},{D}_{2,x})}}} :={R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\kappa ({x})} ,{D}_{1,x}}}} \widehat {\otimes }_{{\kappa ({x})} } {R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{{\kappa ({x})} ,{D}_{2,x}}}}$
, which is again complete local Noetherian. Let
![]() $\pi \colon R_x:={R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,({\overline {{D}}}_1,{\overline {{D}}}_2)}}} \otimes _{\Lambda } {\kappa ({x})} \to {\kappa ({x})} $
be the homomorphism induced from x, and let
$\pi \colon R_x:={R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{\Lambda ,({\overline {{D}}}_1,{\overline {{D}}}_2)}}} \otimes _{\Lambda } {\kappa ({x})} \to {\kappa ({x})} $
be the homomorphism induced from x, and let
be the natural homomorphism constructed as in Corollary 4.8.8, where
![]() $\widehat {R}_x$
denotes the completion of
$\widehat {R}_x$
denotes the completion of
![]() $R_x$
at
$R_x$
at
![]() ${\mathfrak {p}}_x:={\mathop {\mathrm{Ker}}\nolimits }\,\pi $
.
${\mathfrak {p}}_x:={\mathop {\mathrm{Ker}}\nolimits }\,\pi $
.
Let finally L be a finite extension of
![]() ${\kappa ({x})} $
over which there exist absolutely irreducible representations
${\kappa ({x})} $
over which there exist absolutely irreducible representations
![]() $\rho _i\colon G\to {\mathrm {GL}}_{n_i}(L)$
such that
$\rho _i\colon G\to {\mathrm {GL}}_{n_i}(L)$
such that
![]() ${D}_{\rho _i}={D}_{i,x}\otimes _{{\kappa ({x})} }L$
for
${D}_{\rho _i}={D}_{i,x}\otimes _{{\kappa ({x})} }L$
for
![]() $i=1,2$
. Define the functor
$i=1,2$
. Define the functor
Since the
![]() $\rho _i$
are absolutely irreducible, it is represented by
$\rho _i$
are absolutely irreducible, it is represented by
![]() ${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{L,(\rho _1,\rho _2)}}} :={R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{L,\rho _1}}} \widehat {\otimes }_L {R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{L,\rho _2}}}$
, and the latter ring is Noetherian local by Proposition 3.2.3 and Theorem 3.2.4 since we assume
${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{L,(\rho _1,\rho _2)}}} :={R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{L,\rho _1}}} \widehat {\otimes }_L {R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{L,\rho _2}}}$
, and the latter ring is Noetherian local by Proposition 3.2.3 and Theorem 3.2.4 since we assume
![]() $\Phi _{{\overline {{D}}}_i}$
,
$\Phi _{{\overline {{D}}}_i}$
,
![]() $i=1,2$
. As in Corollary 4.8.7 one has a natural homomorphism
$i=1,2$
. As in Corollary 4.8.7 one has a natural homomorphism
Proposition 4.8.11. The following hold:
-
(a) The maps
 $\psi $
and
$\psi $
and
 ${\varphi }$
are isomorphisms.
${\varphi }$
are isomorphisms. -
(b) Suppose
 $G=G_K$
and
$G=G_K$
and
 $H^0(G,{\operatorname {\overline {ad}}_{{\rho _i}}} )=0$
for
$H^0(G,{\operatorname {\overline {ad}}_{{\rho _i}}} )=0$
for
 $i=1,2$
. Then
$i=1,2$
. Then
 ${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{L,(\rho _1,\rho _2),{\operatorname {red}}}}} $
is formally smooth over L of dimension
${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{L,(\rho _1,\rho _2),{\operatorname {red}}}}} $
is formally smooth over L of dimension
 $d(n_1^2+n_2^2)+2$
and hence x is a smooth point on
$d(n_1^2+n_2^2)+2$
and hence x is a smooth point on
 ${X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{({\overline {{D}}}_1,{\overline {{D}}}_2),{\operatorname {red}}}}} $
with tangent space dimension
${X{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{({\overline {{D}}}_1,{\overline {{D}}}_2),{\operatorname {red}}}}} $
with tangent space dimension
 $d(n_1^2+n_2^2)+1$
.
$d(n_1^2+n_2^2)+1$
.
Proof. The two assertions in (a) are proved exactly as Corollary 4.8.7 and Corollary 4.8.8, and we omit the details. The first assertion in (b) follows from our description of
![]() ${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{L,(\rho _1,\rho _2),{\operatorname {red}}}}} $
as a completed tensor product and from Corollary 3.4.3. The second assertion now is a consequence of (a), of Proposition 4.7.6 and of Lemma 3.3.5.
${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{L,(\rho _1,\rho _2),{\operatorname {red}}}}} $
as a completed tensor product and from Corollary 3.4.3. The second assertion now is a consequence of (a), of Proposition 4.7.6 and of Lemma 3.3.5.
5 Equidimensionality and density of the regular locus
This section proves the main result of this work, the equidimensionality of the special fiber of universal pseudodeformation rings of expected dimension. The proof follows the steps of Chenevier’s proof of the equidimensionality of the generic fiber of the universal pseudocharacter space from [Reference ChenevierChe11]. The main contribution is to overcome the complications that arise in the special fiber.
There are certain points in the special fiber that have no counterpart in the generic fiber. We call them special points and describe them in Subsection 5.1; see Definition 5.1.2. nonspecial (irreducible) points will take the role of irreducible points in Chenevier’s work. Subsection 5.1 also contains some technical result, Lemma 5.1.6, on the comparison of universal pseudodeformation and universal deformation rings over local fields where the residual pseudocharacter is a sum of two irreducible ones.
In Subsection 5.2, we prove the inductive Theorem 5.2.1 to obtain our main result. If the nonspecial irreducible points are Zariski open dense in universal pseudodeformation spaces for
![]() ${\overline {{D}}}$
of dimension less than n, then irreducible points are Zariski dense for
${\overline {{D}}}$
of dimension less than n, then irreducible points are Zariski dense for
![]() ${\overline {{D}}}$
of dimension n. Subsection 5.3 gives an alternative proof of Theorem 5.2.1 following a suggestion of the referee. The main point of Subsection 5.4 is to show in Theorem 5.4.1 that the nonspecial irreducible points are dense open in the irreducible points. This uses induction of pseudocharacters from Subsection 4.6 as a main tool, and the proof in dimension n relies on results for dimension
${\overline {{D}}}$
of dimension n. Subsection 5.3 gives an alternative proof of Theorem 5.2.1 following a suggestion of the referee. The main point of Subsection 5.4 is to show in Theorem 5.4.1 that the nonspecial irreducible points are dense open in the irreducible points. This uses induction of pseudocharacters from Subsection 4.6 as a main tool, and the proof in dimension n relies on results for dimension
![]() $n'<n$
.
$n'<n$
.
Then in Subsection 5.5, we complete the proof of our main theorem Theorem 5.5.1 in a straightforward manner. In Theorem 5.5.5, we determine the singular locus of
![]() ${\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
when
${\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
when
![]() $\zeta _p\notin K$
. This allows us in Theorem 5.5.7 to establish Serre’s condition
$\zeta _p\notin K$
. This allows us in Theorem 5.5.7 to establish Serre’s condition
![]() $(R_2)$
for
$(R_2)$
for
![]() ${\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
except for one single
${\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
except for one single
![]() ${\overline {{D}}}$
.
${\overline {{D}}}$
.
In this section, we use the notation
![]() $K\supset {\mathbb {Q}}_p$
, d,
$K\supset {\mathbb {Q}}_p$
, d,
![]() $G_K$
,
$G_K$
,
![]() $\zeta _p$
,
$\zeta _p$
,
![]() ${\overline {{D}}}\colon G_K\to {{\mathbb {F}}\,\!{}}$
(continuous) with
${\overline {{D}}}\colon G_K\to {{\mathbb {F}}\,\!{}}$
(continuous) with
![]() ${{\mathbb {F}}\,\!{}}$
finite, as before. Often, we write n for
${{\mathbb {F}}\,\!{}}$
finite, as before. Often, we write n for
![]() $\dim {\overline {{D}}}$
. To emphasize K in universal objects, we sometimes write
$\dim {\overline {{D}}}$
. To emphasize K in universal objects, we sometimes write
![]() ${\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}}$
for
${\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}}$
for
![]() ${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{G_K,{{\mathbb {F}}\,\!{}},{\overline {{D}}}}}} $
and
${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{{G_K,{{\mathbb {F}}\,\!{}},{\overline {{D}}}}}} $
and
![]() ${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}}$
for
${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}}$
for
![]() ${\mathrm {Spec}}\ {\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}}$
. All results of this section only concern the special fiber of pseudodeformation spaces.
${\mathrm {Spec}}\ {\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}}$
. All results of this section only concern the special fiber of pseudodeformation spaces.
5.1 Special points
Let
![]() $\chi _{\mathrm cyc}\colon G_K\to {\mathbb {Z}}_p^\times $
denote the p-adic cyclotomic character. Let A be in
$\chi _{\mathrm cyc}\colon G_K\to {\mathbb {Z}}_p^\times $
denote the p-adic cyclotomic character. Let A be in
![]() ${\widehat {\mathcal {A}}r}_{{W({{\mathbb {F}}\,\!{}})}}$
(or a localization of such a ring), let
${\widehat {\mathcal {A}}r}_{{W({{\mathbb {F}}\,\!{}})}}$
(or a localization of such a ring), let
![]() $\rho \colon G_K\to {\mathrm {GL}}_n(A)$
be a continuous representation and
$\rho \colon G_K\to {\mathrm {GL}}_n(A)$
be a continuous representation and
![]() ${D}\colon G_K\to A$
be a continuous pseudocharacter. For
${D}\colon G_K\to A$
be a continuous pseudocharacter. For
![]() $i\in {\mathbb {Z}}$
, we shall denote by
$i\in {\mathbb {Z}}$
, we shall denote by
![]() $\rho (i)$
and
$\rho (i)$
and
![]() ${D}(i)$
the twist by
${D}(i)$
the twist by
![]() $\chi _{\mathrm cyc}^i$
of
$\chi _{\mathrm cyc}^i$
of
![]() $\rho $
and
$\rho $
and
![]() ${D}$
, respectively. An elementary but crucial observation in [Reference ChenevierChe11] was that
${D}$
, respectively. An elementary but crucial observation in [Reference ChenevierChe11] was that
![]() $H^2(G_K,{\operatorname {ad}_{{\rho }}} )=0$
whenever a
$H^2(G_K,{\operatorname {ad}_{{\rho }}} )=0$
whenever a
![]() $\rho \colon G_K\to {\mathrm {GL}}_n(E)$
is a continuous absolutely irreducible representation into a p-adic field E; this follows from local Tate duality in the form given in Theorem 3.4.1, which gives
$\rho \colon G_K\to {\mathrm {GL}}_n(E)$
is a continuous absolutely irreducible representation into a p-adic field E; this follows from local Tate duality in the form given in Theorem 3.4.1, which gives
together with the fact that
![]() $\chi _{\mathrm cyc}$
has infinite order. For representations into local (or finite) fields of characteristic p the order of
$\chi _{\mathrm cyc}$
has infinite order. For representations into local (or finite) fields of characteristic p the order of
![]() $\chi _{\mathrm cyc}\pmod p$
is finite, and so the situation has to be further analyzed.
$\chi _{\mathrm cyc}\pmod p$
is finite, and so the situation has to be further analyzed.
Lemma 5.1.1. Let E be a finite or local field of characteristic p, and let
![]() $\rho \colon G_K\to {\mathrm {GL}}_n(E)$
be a continuous absolutely irreducible representation. Then the following hold:
$\rho \colon G_K\to {\mathrm {GL}}_n(E)$
be a continuous absolutely irreducible representation. Then the following hold:
Suppose that
![]() $\zeta _p\notin K$
(Case I). Then the following assertions are equivalent:
$\zeta _p\notin K$
(Case I). Then the following assertions are equivalent:
-
(i)
 $H^2(G_K,{\operatorname {ad}_{{\rho }}} )$
is nonzero.
$H^2(G_K,{\operatorname {ad}_{{\rho }}} )$
is nonzero. -
(ii) The
 $G_K$
-representations
$G_K$
-representations
 $\rho $
and
$\rho $
and
 $\rho (1)$
are isomorphic.
$\rho (1)$
are isomorphic. -
(iii) There exists a finite separable extension
 $E'$
of E such that
$E'$
of E such that
 $\rho \otimes _EE'$
is induced from a continuous representation
$\rho \otimes _EE'$
is induced from a continuous representation
 $\tau $
of
$\tau $
of
 $G_{K'}$
over
$G_{K'}$
over
 $E'$
for
$E'$
for
 $K'=K(\zeta _p)$
.
$K'=K(\zeta _p)$
.
Suppose that
![]() $\zeta _p\in K$
(Case II). Then the map
$\zeta _p\in K$
(Case II). Then the map
![]() $H^2({\mathrm {Tr}})\colon H^2(G_K,{\operatorname {ad}_{{\rho }}} )\to H^2(G_K,E)\cong E$
is surjective, and the following assertions are equivalent:
$H^2({\mathrm {Tr}})\colon H^2(G_K,{\operatorname {ad}_{{\rho }}} )\to H^2(G_K,E)\cong E$
is surjective, and the following assertions are equivalent:
-
(i’)
 $H^2(G_K,{\operatorname {ad}_{{\rho }} ^0})$
is nonzero.
$H^2(G_K,{\operatorname {ad}_{{\rho }} ^0})$
is nonzero. -
(ii’)
 $H^0(G_K,{\operatorname {\overline {ad}}_{{\rho }}} )$
is nonzero.
$H^0(G_K,{\operatorname {\overline {ad}}_{{\rho }}} )$
is nonzero. -
(iii’) There exists a finite extension
 $E'$
of E and a Galois extension
$E'$
of E and a Galois extension
 $K'$
of K of degree p such that
$K'$
of K of degree p such that
 $\rho \otimes _EE'$
is induced from a continuous representation
$\rho \otimes _EE'$
is induced from a continuous representation
 $\tau $
over
$\tau $
over
 $E'$
of
$E'$
of
 $G_{K'}$
.
$G_{K'}$
. -
(iv’) The restriction
 $\rho \otimes _E{{E}^{\mathrm {alg}}}|_{G_{K'}}$
is reducible for some Galois extension
$\rho \otimes _E{{E}^{\mathrm {alg}}}|_{G_{K'}}$
is reducible for some Galois extension
 $K'$
of K of degree p.
$K'$
of K of degree p.
In both cases, if
![]() $\tau $
exists, then it is absolutely irreducible, and in particular
$\tau $
exists, then it is absolutely irreducible, and in particular
![]() ${\mathrm {End}}_{G_{K'}}(\tau )=E$
.
${\mathrm {End}}_{G_{K'}}(\tau )=E$
.
Proof. The equivalence of (i) and (ii) follows from the isomorphism (28) and the absolute irreducibility of
![]() $\rho $
. The duality in Theorem 3.4.1 also yields the equivalence of (i’) and (ii’), in a similar way. In all cases, the continuity and absolute irreducibility of
$\rho $
. The duality in Theorem 3.4.1 also yields the equivalence of (i’) and (ii’), in a similar way. In all cases, the continuity and absolute irreducibility of
![]() $\tau $
, if it exists, is implied by Lemma 2.1.4
(b) and (f).
$\tau $
, if it exists, is implied by Lemma 2.1.4
(b) and (f).
The equivalence of (ii) and (iii) now follows from Theorem 2.2.1. The equivalence of (iii’) and (iv’) is a consequence of Lemma 2.3.1. The implication (ii’)
![]() $\Rightarrow $
(iii’) follows from Lemma 2.3.2(g) and (j), and the implication (iii’)
$\Rightarrow $
(iii’) follows from Lemma 2.3.2(g) and (j), and the implication (iii’)
![]() $\Rightarrow $
(ii’) is shown in Example 4.6.4.
$\Rightarrow $
(ii’) is shown in Example 4.6.4.
Definition 5.1.2. We call
![]() $x\in ({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}})^{\operatorname {irr}}$
special if one of the following two conditions holds
$x\in ({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}})^{\operatorname {irr}}$
special if one of the following two conditions holds
-
(i)
 $\zeta _p\notin K$
and
$\zeta _p\notin K$
and
 ${D}_x={D}_x(1)$
,
${D}_x={D}_x(1)$
, -
(ii)
 $\zeta _p\in K$
and
$\zeta _p\in K$
and
 ${D}_x |_{G_{K'}}$
is reducible for some degree p Galois extension
${D}_x |_{G_{K'}}$
is reducible for some degree p Galois extension
 $K'$
of K;
$K'$
of K;
otherwise x is called nonspecial. We write
![]() $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}})^{\mathrm {spcl}}$
for
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}})^{\mathrm {spcl}}$
for
![]() $\{x\in ({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}})^{\operatorname {irr}}\mid \mbox { is special}\}$
and
$\{x\in ({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}})^{\operatorname {irr}}\mid \mbox { is special}\}$
and
![]() $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}})^{{\mathrm {n}\textrm {-}\mathrm {spcl}}}$
for
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}})^{{\mathrm {n}\textrm {-}\mathrm {spcl}}}$
for
![]() $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}})^{\operatorname {irr}}{\smallsetminus } ({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}})^{\mathrm {spcl}}$
.
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}})^{\operatorname {irr}}{\smallsetminus } ({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}})^{\mathrm {spcl}}$
.
Lemma 5.1.3. The set
![]() $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}})^{\mathrm {spcl}}$
is closed in
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}})^{\mathrm {spcl}}$
is closed in
![]() $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}})^{\operatorname {irr}}$
.
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}})^{\operatorname {irr}}$
.
Proof. If
![]() $\zeta _p\notin K$
, then the condition
$\zeta _p\notin K$
, then the condition
![]() ${D}={D}(1)$
is a closed condition in
${D}={D}(1)$
is a closed condition in
![]() ${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}}$
by Corollary 4.5.11, and this concludes the argument.
${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}}$
by Corollary 4.5.11, and this concludes the argument.
If
![]() $\zeta _p\in K$
, then note first that the set of Galois extensions
$\zeta _p\in K$
, then note first that the set of Galois extensions
![]() $K'$
of K of degree p is finite. Since by class field theory
$K'$
of K of degree p is finite. Since by class field theory
![]() $(G_{K^{\operatorname {ab}}})/(G_K^{\operatorname {ab}})^{\times p}$
is finite if K is a p-adic field. By [Reference ChenevierChe14, 2.20], the reducibility of a pseudocharacter over a field can be detected by the vanishing of certain determinants whose entries are traces of the pseudocharacter, evaluated at certain elements of the group in question. If
$(G_{K^{\operatorname {ab}}})/(G_K^{\operatorname {ab}})^{\times p}$
is finite if K is a p-adic field. By [Reference ChenevierChe14, 2.20], the reducibility of a pseudocharacter over a field can be detected by the vanishing of certain determinants whose entries are traces of the pseudocharacter, evaluated at certain elements of the group in question. If
![]() $n=\dim {D}$
, then
$n=\dim {D}$
, then
![]() $x\in ({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}})^{\mathrm {spcl}}$
if and only if for some degree p Galois extensions
$x\in ({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}})^{\mathrm {spcl}}$
if and only if for some degree p Galois extensions
![]() $K'$
over K and all
$K'$
over K and all
![]() $n^2$
tuples
$n^2$
tuples
![]() $(g_i)\in G_{K'}^{n^2}$
one has
$(g_i)\in G_{K'}^{n^2}$
one has
Hence,
![]() $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}})^{\mathrm {spcl}}$
is Zariski closed in
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}})^{\mathrm {spcl}}$
is Zariski closed in
![]() $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}})^{\operatorname {irr}}$
as a finite union (over
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}})^{\operatorname {irr}}$
as a finite union (over
![]() $K'$
) of closed subsets.
$K'$
) of closed subsets.
For
![]() $X\subset {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
locally closed, we set
$X\subset {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
locally closed, we set
![]() $\dot X:=X{\smallsetminus }\{{\mathfrak {m}}_{{\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}}\}$
. The following holds:
$\dot X:=X{\smallsetminus }\{{\mathfrak {m}}_{{\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}}\}$
. The following holds:
Facts 5.1.4.
-
(a)
 $ {\mathfrak {m}}_{{\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}}$
is the unique closed point of
$ {\mathfrak {m}}_{{\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}}$
is the unique closed point of
 $ {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
.
$ {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
. -
(b) For
 $i\ge 1$
, the dimension i points of
$i\ge 1$
, the dimension i points of
 $ {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
are the dimension
$ {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
are the dimension
 $i-1$
points of
$i-1$
points of
 ${\dot {\overline {X}}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{\overline {D}}}$
.
${\dot {\overline {X}}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{\overline {D}}}$
. -
(c) If
 $\dot X$
is nonempty, then the dimension
$\dot X$
is nonempty, then the dimension
 $0$
points of
$0$
points of
 $\dot X$
are very dense in
$\dot X$
are very dense in
 $\dot X$
; see Lemma A.1.8.
$\dot X$
; see Lemma A.1.8.
We call
![]() $x\in {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
regular, if
$x\in {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
regular, if
![]() ${\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
is regular at x, and singular otherwise.
${\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
is regular at x, and singular otherwise.
Notation 5.1.5. Let X be a locally closed subset of
![]() ${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
.
${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
.
-
(a) We use the superscripts
 ${\operatorname {irr}}$
,
${\operatorname {irr}}$
,
 ${\operatorname {red}}$
,
${\operatorname {red}}$
,
 ${\operatorname {reg}}$
,
${\operatorname {reg}}$
,
 ${\operatorname {sing}}$
on X to denote the subset of irreducible, reducible, regular and singular points, respectively; cf. Definition 4.7.16.
${\operatorname {sing}}$
on X to denote the subset of irreducible, reducible, regular and singular points, respectively; cf. Definition 4.7.16. -
(b) We write
 $X_{\operatorname {red}}$
(subscript!) for X with its induced reduced subscheme structure.
$X_{\operatorname {red}}$
(subscript!) for X with its induced reduced subscheme structure. -
(c) For attributes
 $a,b,c$
of X, if they apply, we write
$a,b,c$
of X, if they apply, we write
 $X^{a,b}$
for
$X^{a,b}$
for
 $X^a\cap X^b$
,
$X^a\cap X^b$
,
 $X^a_b$
for
$X^a_b$
for
 $X^a\cap X_b$
,
$X^a\cap X_b$
,
 $X_{a,b}$
for
$X_{a,b}$
for
 $X_a\cap X_b$
, and so on.
$X_a\cap X_b$
, and so on.
The remaining results in this section concern dimension
![]() $1$
points on
$1$
points on
![]() ${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
.
${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
.
Lemma 5.1.6. Let x be a closed point of
![]() $U:=({\dot {\overline {X}}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{\overline {D}}}})^{\operatorname {irr}}$
, let
$U:=({\dot {\overline {X}}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{\overline {D}}}})^{\operatorname {irr}}$
, let
![]() $D^{\prime }_x$
be the pseudocharacter
$D^{\prime }_x$
be the pseudocharacter
![]() ${\kappa ({x})} [G]\to {\kappa ({x})} ,g\mapsto 1\otimes _{{{W({{\mathbb {F}}\,\!{}})}}}D_x(g)$
and let
${\kappa ({x})} [G]\to {\kappa ({x})} ,g\mapsto 1\otimes _{{{W({{\mathbb {F}}\,\!{}})}}}D_x(g)$
and let
![]() $\widehat {R}$
be the universal pseudodeformation ring for
$\widehat {R}$
be the universal pseudodeformation ring for
![]() ${D}_x'$
from Corollary 4.8.8. Then the following hold:
${D}_x'$
from Corollary 4.8.8. Then the following hold:
-
(a) Suppose that
 $\zeta _p\notin K$
and that x is nonspecial. Then
$\zeta _p\notin K$
and that x is nonspecial. Then
 $\widehat {R}$
is regular of dimension
$\widehat {R}$
is regular of dimension
 $dn^2+1$
. If in addition
$dn^2+1$
. If in addition
 $U^{{\mathrm {n}\textrm {-}\mathrm {spcl}}}$
is nonempty, it is regular and equidimensional of dimension
$U^{{\mathrm {n}\textrm {-}\mathrm {spcl}}}$
is nonempty, it is regular and equidimensional of dimension
 $dn^2$
.
$dn^2$
. -
(b) Suppose that
 $\zeta _p\notin K$
and that x is special. Then
$\zeta _p\notin K$
and that x is special. Then
 $\widehat {R}$
is a complete intersection ring with
$\widehat {R}$
is a complete intersection ring with
 $\dim \widehat {R}\in \{dn^2+1,dn^2+2\}$
. Moreover, U is of dimension at most
$\dim \widehat {R}\in \{dn^2+1,dn^2+2\}$
. Moreover, U is of dimension at most
 $dn^2+1$
.
$dn^2+1$
. -
(c) Suppose that
 $\zeta _p\in K$
and that x is nonspecial. Then
$\zeta _p\in K$
and that x is nonspecial. Then
 $\widehat {R}_{\operatorname {red}}$
is regular of dimension
$\widehat {R}_{\operatorname {red}}$
is regular of dimension
 $dn^2+1$
. If in addition
$dn^2+1$
. If in addition
 $U^{{\mathrm {n}\textrm {-}\mathrm {spcl}}}_{\operatorname {red}}$
is nonempty, it is regular and equidimensional of dimension
$U^{{\mathrm {n}\textrm {-}\mathrm {spcl}}}_{\operatorname {red}}$
is nonempty, it is regular and equidimensional of dimension
 $dn^2$
.
$dn^2$
.
Proof. Consider the Galois representation
![]() $\rho _x\colon G_K\to {\mathrm {GL}}_n(L)$
with
$\rho _x\colon G_K\to {\mathrm {GL}}_n(L)$
with
![]() ${D}_{\rho _x}={D}^{\prime }_x$
from Theorem 4.3.10 that is defined over a finite extension L of
${D}_{\rho _x}={D}^{\prime }_x$
from Theorem 4.3.10 that is defined over a finite extension L of
![]() ${\kappa ({x})} $
. For (a) note that we have
${\kappa ({x})} $
. For (a) note that we have
![]() $H^2(G_K,{\operatorname {ad}_{{\rho _x}}})=0$
by Lemma 5.1.1, Case I and the definition of special. The Euler characteristic formula of Theorem 3.4.1 now yields
$H^2(G_K,{\operatorname {ad}_{{\rho _x}}})=0$
by Lemma 5.1.1, Case I and the definition of special. The Euler characteristic formula of Theorem 3.4.1 now yields
It follows from Lemma 3.3.5 and Remark 3.3.2 that x is a regular point of
![]() ${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
of dimension
${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
of dimension
![]() $dn^2+1-1=dn^2$
. Since x lies on U, it is also a regular point of U. To see that U is regular, let
$dn^2+1-1=dn^2$
. Since x lies on U, it is also a regular point of U. To see that U is regular, let
![]() $Y\subset U$
be the closed subscheme of singular points. We know that points of dimension at most
$Y\subset U$
be the closed subscheme of singular points. We know that points of dimension at most
![]() $1$
will be dense in the constructible set Y. Since the unique closed point of
$1$
will be dense in the constructible set Y. Since the unique closed point of
![]() $ {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
is not in U, points of dimension
$ {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
is not in U, points of dimension
![]() $1$
are dense in
$1$
are dense in
![]() $Y\subset U$
. However, as we just saw, such points are regular and cannot lie in Y. Therefore, Y must be empty. And again by the density of dimension
$Y\subset U$
. However, as we just saw, such points are regular and cannot lie in Y. Therefore, Y must be empty. And again by the density of dimension
![]() $1$
points in U, it follows that U is regular and equidimensional of dimension
$1$
points in U, it follows that U is regular and equidimensional of dimension
![]() $dn^2$
, proving (a).
$dn^2$
, proving (a).
For (b), we observe
![]() $H^2(G_K,{\operatorname {ad}_{{\rho _x}}})^\vee =H^0(G_K,{\operatorname {ad}_{{\rho _x}}}(1))={\mathrm {Hom}}_{G_K}(\rho _x,\rho _x(1))\cong L$
using Theorem 3.4.1, and in the last step that
$H^2(G_K,{\operatorname {ad}_{{\rho _x}}})^\vee =H^0(G_K,{\operatorname {ad}_{{\rho _x}}}(1))={\mathrm {Hom}}_{G_K}(\rho _x,\rho _x(1))\cong L$
using Theorem 3.4.1, and in the last step that
![]() $\rho _x\cong \rho _x(1)$
and that
$\rho _x\cong \rho _x(1)$
and that
![]() $\rho _x$
is absolutely irreducible. This time, the Euler characteristic formula provides a presentation
$\rho _x$
is absolutely irreducible. This time, the Euler characteristic formula provides a presentation
where the ideal I is generated by at most one element over
![]() ${\kappa ({x})} [\![ X_1,\ldots ,X_{dn^2+2} ]\!]$
. This proves the claims on
${\kappa ({x})} [\![ X_1,\ldots ,X_{dn^2+2} ]\!]$
. This proves the claims on
![]() $\widehat {R}_{\mathfrak {p}}$
. The remaining assertion follows from the density of dimension
$\widehat {R}_{\mathfrak {p}}$
. The remaining assertion follows from the density of dimension
![]() $1$
points in U and Lemma 3.3.5.
$1$
points in U and Lemma 3.3.5.
For (c), it follows from the nonspecialness of
![]() ${D}_x$
and from Corollary 3.4.3 that
${D}_x$
and from Corollary 3.4.3 that
![]() $({\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{\rho _x}}})_{\operatorname {red}}$
is regular local of dimension
$({\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{\rho _x}}})_{\operatorname {red}}$
is regular local of dimension
![]() $dn^2+1$
. From Proposition 4.7.6 and Corollary 4.8.7 we deduce
$dn^2+1$
. From Proposition 4.7.6 and Corollary 4.8.7 we deduce
![]() ${\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{D}_x}}}\otimes _{{\kappa ({x})} }L\cong {\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{\rho _x}}}$
, and the assertion on
${\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{D}_x}}}\otimes _{{\kappa ({x})} }L\cong {\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{\rho _x}}}$
, and the assertion on
![]() $\widehat {R}^{\mathfrak {p}}_{\operatorname {red}}$
follows. The remaining assertion follows from the density of dimension
$\widehat {R}^{\mathfrak {p}}_{\operatorname {red}}$
follows. The remaining assertion follows from the density of dimension
![]() $1$
points in U and Lemma 3.3.5.
$1$
points in U and Lemma 3.3.5.
We also need a similar result in certain reducible cases. It is adapted from [Reference ChenevierChe11, Lemma 2.2].
Lemma 5.1.7. For
![]() $i=1,2$
, let
$i=1,2$
, let
![]() ${\overline {{D}}}_i\colon G_K\to {{\mathbb {F}}\,\!{}}$
be pseudocharacters over a finite field
${\overline {{D}}}_i\colon G_K\to {{\mathbb {F}}\,\!{}}$
be pseudocharacters over a finite field
![]() ${{\mathbb {F}}\,\!{}}$
, let
${{\mathbb {F}}\,\!{}}$
, let
![]() $x_i\in {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_i}}}$
be irreducible nonspecial dimension
$x_i\in {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_i}}}$
be irreducible nonspecial dimension
![]() $1$
points and let L be a finite extension of both
$1$
points and let L be a finite extension of both
![]() ${\kappa ({x_i})}$
over which there exist absolutely irreducible representations
${\kappa ({x_i})}$
over which there exist absolutely irreducible representations
![]() $\rho _i\colon G_K\to {\mathrm {GL}}_{n_i}(L)$
with
$\rho _i\colon G_K\to {\mathrm {GL}}_{n_i}(L)$
with
![]() ${D}_{\rho _i}={D}_{x_i}\otimes _{{\kappa ({x})} }L$
. Let
${D}_{\rho _i}={D}_{x_i}\otimes _{{\kappa ({x})} }L$
. Let
![]() $\rho \colon G_K\to {\mathrm {GL}}_n(L)$
be a nontrivial extension of
$\rho \colon G_K\to {\mathrm {GL}}_n(L)$
be a nontrivial extension of
![]() $\rho _2$
by
$\rho _2$
by
![]() $\rho _1$
. Assume that
$\rho _1$
. Assume that
![]() ${D}_{x_1}\neq {D}_{x_2}(m)$
for any
${D}_{x_1}\neq {D}_{x_2}(m)$
for any
![]() $m\in \{1,\ldots ,p-1\}$
. Then the following hold:
$m\in \{1,\ldots ,p-1\}$
. Then the following hold:
-
(a) The representation
 $\rho $
exists; it satisfies
$\rho $
exists; it satisfies
 $L={\mathrm {End}}_{G_K}(\rho )$
; one has
$L={\mathrm {End}}_{G_K}(\rho )$
; one has
 ${D}_\rho ={D}_{\rho _1}\oplus {D}_{\rho _2}$
as pseudocharacters into L; the functor
${D}_\rho ={D}_{\rho _1}\oplus {D}_{\rho _2}$
as pseudocharacters into L; the functor
 ${\mathcal {D}}_{\rho }\colon {\mathcal {A}r}_L\to {Sets}$
is pro-representable.
${\mathcal {D}}_{\rho }\colon {\mathcal {A}r}_L\to {Sets}$
is pro-representable.
We write
![]() ${R^{\operatorname {univ}}_{\rho }}$
for the representing universal ring of
${R^{\operatorname {univ}}_{\rho }}$
for the representing universal ring of
![]() ${\mathcal {D}}_\rho $
and
${\mathcal {D}}_\rho $
and
![]() ${\rho ^{\operatorname {univ}}_\rho} \colon G_K\rightarrow \operatorname {GL}_n({R^{\operatorname {univ}}_{\rho }})$
for a universal deformation and
${\rho ^{\operatorname {univ}}_\rho} \colon G_K\rightarrow \operatorname {GL}_n({R^{\operatorname {univ}}_{\rho }})$
for a universal deformation and
![]() ${X^{\mathrm {univ}}_\rho} $
for
${X^{\mathrm {univ}}_\rho} $
for
![]() $\operatorname {Spec}{R^{\operatorname {univ}}_{\rho }}$
. Denote by
$\operatorname {Spec}{R^{\operatorname {univ}}_{\rho }}$
. Denote by
![]() $\widehat {R}$
the universal pseudodeformation ring for
$\widehat {R}$
the universal pseudodeformation ring for
![]() ${D}_\rho $
to
${D}_\rho $
to
![]() ${\mathcal {A}r}_L$
, by
${\mathcal {A}r}_L$
, by
![]() $\varphi \colon {X^{\mathrm {univ}}_\rho} \to \widehat {X} := {\mathrm {Spec}}\widehat {R}$
the map of L-schemes induced by sending
$\varphi \colon {X^{\mathrm {univ}}_\rho} \to \widehat {X} := {\mathrm {Spec}}\widehat {R}$
the map of L-schemes induced by sending
![]() ${\rho ^{\operatorname {univ}}_\rho} $
to its associated pseudocharacter
${\rho ^{\operatorname {univ}}_\rho} $
to its associated pseudocharacter
![]() ${D}_{{\rho ^{\operatorname {univ}}_\rho}}$
, and by
${D}_{{\rho ^{\operatorname {univ}}_\rho}}$
, and by
![]() $\operatorname {d}\varphi \colon {\mathbf {t}_{{X^{\mathrm {univ}}_\rho} ,\rho }}\rightarrow {\mathbf {t}_{\widehat {X},x}}$
the induced L-linear map on tangent spaces.
$\operatorname {d}\varphi \colon {\mathbf {t}_{{X^{\mathrm {univ}}_\rho} ,\rho }}\rightarrow {\mathbf {t}_{\widehat {X},x}}$
the induced L-linear map on tangent spaces.
-
(b) Suppose that
 $\rho ^{\prime }\in {\operatorname {ker}{\operatorname {d}\varphi }}\subset {\mathbf {t}_{{X^{\mathrm {univ}}_\rho} ,\rho }}\cong {\mathcal {D}}_{\rho }(L[\varepsilon ])$
, that is, that
$\rho ^{\prime }\in {\operatorname {ker}{\operatorname {d}\varphi }}\subset {\mathbf {t}_{{X^{\mathrm {univ}}_\rho} ,\rho }}\cong {\mathcal {D}}_{\rho }(L[\varepsilon ])$
, that is, that
 ${D}_{\rho '}={D}_\rho $
. Then with respect to a suitable basis
${D}_{\rho '}={D}_\rho $
. Then with respect to a suitable basis
 $\rho '$
is upper triangular and is the trivial deformations on the diagonal blocks.
$\rho '$
is upper triangular and is the trivial deformations on the diagonal blocks. -
(c) If
 $\zeta _p\notin K$
, then
$\zeta _p\notin K$
, then
 ${R^{\operatorname {univ}}_{\rho }}$
is formally smooth over L of dimension
${R^{\operatorname {univ}}_{\rho }}$
is formally smooth over L of dimension
 $\dim _L {\mathbf {t}_{{X^{\mathrm {univ}}_\rho} ,\rho }}=dn^2+1$
,
$\dim _L {\mathbf {t}_{{X^{\mathrm {univ}}_\rho} ,\rho }}=dn^2+1$
,  $$ \begin{align*}{\dim_L} {\operatorname{ker}{{\mathrm{d}}\varphi}} =d{n_1}{n_2}-1\quad\text{and}\quad {\dim_L}{\operatorname{im}{{\mathrm{d}}\varphi}} =d{n^2}-d{n_1}{n_2}+2.\end{align*} $$
$$ \begin{align*}{\dim_L} {\operatorname{ker}{{\mathrm{d}}\varphi}} =d{n_1}{n_2}-1\quad\text{and}\quad {\dim_L}{\operatorname{im}{{\mathrm{d}}\varphi}} =d{n^2}-d{n_1}{n_2}+2.\end{align*} $$
-
(d) If
 $\zeta _p\in K$
, then
$\zeta _p\in K$
, then
 ${R^{\operatorname {univ}}_{\rho ,{\operatorname {red}}}}$
is formally smooth over L of relative dimension
${R^{\operatorname {univ}}_{\rho ,{\operatorname {red}}}}$
is formally smooth over L of relative dimension
 $h-1$
for
$h-1$
for
 $h:=\dim _L {\mathbf {t}_{{X^{\mathrm {univ}}_\rho} ,\rho }}=dn^2+2$
. Denoting by
$h:=\dim _L {\mathbf {t}_{{X^{\mathrm {univ}}_\rho} ,\rho }}=dn^2+2$
. Denoting by
 $\varphi _{\operatorname {red}}\colon ({X^{\mathrm {univ}}_\rho} )_{\operatorname {red}}\to (\widehat {X})_{\operatorname {red}}$
the morphism on reduced L-schemes associated to
$\varphi _{\operatorname {red}}\colon ({X^{\mathrm {univ}}_\rho} )_{\operatorname {red}}\to (\widehat {X})_{\operatorname {red}}$
the morphism on reduced L-schemes associated to
 ${\varphi }$
and by
${\varphi }$
and by
 $\operatorname {d}\varphi _{\operatorname {red}}\colon {\mathbf {t}_{({X^{\mathrm {univ}}_\rho} )_{\operatorname {red}},\rho }}\rightarrow {\mathbf {t}_{(\widehat {X})_{\operatorname {red}},x}}$
the induced map on tangent spaces, there furthermore exists
$\operatorname {d}\varphi _{\operatorname {red}}\colon {\mathbf {t}_{({X^{\mathrm {univ}}_\rho} )_{\operatorname {red}},\rho }}\rightarrow {\mathbf {t}_{(\widehat {X})_{\operatorname {red}},x}}$
the induced map on tangent spaces, there furthermore exists
 $\delta \in \{0,1\}$
such that
$\delta \in \{0,1\}$
such that  $$ \begin{align*}{\dim_L} {\operatorname{ker}{{\mathrm{d}}\varphi}}_{\operatorname{red}}= d{n_1}{n_2}-1-\delta\quad\text{and}\quad {\dim_L}{\operatorname{im}{{\mathrm{d}}\varphi}}_{\operatorname{red}}=d{n^2}-d{n_1}{n_2}+2+\delta. \end{align*} $$
$$ \begin{align*}{\dim_L} {\operatorname{ker}{{\mathrm{d}}\varphi}}_{\operatorname{red}}= d{n_1}{n_2}-1-\delta\quad\text{and}\quad {\dim_L}{\operatorname{im}{{\mathrm{d}}\varphi}}_{\operatorname{red}}=d{n^2}-d{n_1}{n_2}+2+\delta. \end{align*} $$
Proof. We begin with (a). The Euler characteristic formula in Theorem 3.4.1 now gives
 $$ \begin{align*} \dim_L{\mathrm{Ext}}^1_{G_K}(\rho_{x_2},\rho_{x_1})&=\dim_L H^1(G_K,\rho_{x_1}\otimes\rho_{x_2}^\vee)\\ &=dn_1n_2+ \dim_L H^0(G_K,\rho_{x_1}\otimes\rho_{x_2}^\vee)+\dim_L H^2(G_K,\rho_{x_1}\otimes\rho_{x_2}^\vee), \end{align*} $$
$$ \begin{align*} \dim_L{\mathrm{Ext}}^1_{G_K}(\rho_{x_2},\rho_{x_1})&=\dim_L H^1(G_K,\rho_{x_1}\otimes\rho_{x_2}^\vee)\\ &=dn_1n_2+ \dim_L H^0(G_K,\rho_{x_1}\otimes\rho_{x_2}^\vee)+\dim_L H^2(G_K,\rho_{x_1}\otimes\rho_{x_2}^\vee), \end{align*} $$
which is strictly positive. Thus, there exists an nonzero element
![]() $c\in {\mathrm {Ext}}^1_{G_K}(\rho _{x_2},\rho _{x_1})$
. Setting
$c\in {\mathrm {Ext}}^1_{G_K}(\rho _{x_2},\rho _{x_1})$
. Setting
 $\rho =\left (\begin {array}{cc} \rho _{x_1}&c\\ 0&\rho _{x_2} \end {array}\right )$
and applying Lemma 3.4.4 and Theorem 3.2.4 completes the proof of (a). We observe for later, that in fact our assumptions imply that
$\rho =\left (\begin {array}{cc} \rho _{x_1}&c\\ 0&\rho _{x_2} \end {array}\right )$
and applying Lemma 3.4.4 and Theorem 3.2.4 completes the proof of (a). We observe for later, that in fact our assumptions imply that
and
![]() $H^0(G_K,\rho _{x_1}\otimes \rho _{x_2}^\vee )= {\mathrm {Hom}}_{G_K}(\rho _{x_2},\rho _{x_1})=0$
, so that
$H^0(G_K,\rho _{x_1}\otimes \rho _{x_2}^\vee )= {\mathrm {Hom}}_{G_K}(\rho _{x_2},\rho _{x_1})=0$
, so that
![]() $\dim _L{\mathrm {Ext}}^1_{G_K}(\rho _{x_2},\rho _{x_1})=d{n_1}{n_2}$
.
$\dim _L{\mathrm {Ext}}^1_{G_K}(\rho _{x_2},\rho _{x_1})=d{n_1}{n_2}$
.
For the proof of (b), we use the canonical identifications (see [Reference MazurMaz97, Proposition, p. 271])
to identify
![]() ${\operatorname {ker}{{\mathrm {d}}\varphi }}$
with the L-subspace of
${\operatorname {ker}{{\mathrm {d}}\varphi }}$
with the L-subspace of
![]() ${\mathcal {D}}_{\rho }(L[ \varepsilon ])$
, which consists of the deformations of
${\mathcal {D}}_{\rho }(L[ \varepsilon ])$
, which consists of the deformations of
![]() $\rho $
to
$\rho $
to
![]() $L[\varepsilon ]$
that map under
$L[\varepsilon ]$
that map under
![]() ${\mathrm {d}}\varphi $
to the trivial pseudodeformation to
${\mathrm {d}}\varphi $
to the trivial pseudodeformation to
![]() $L[\varepsilon ]$
of the residual pseudocharacter
$L[\varepsilon ]$
of the residual pseudocharacter
![]() ${D}_\rho $
associated with
${D}_\rho $
associated with
![]() $\rho $
. Let
$\rho $
. Let
![]() $\rho '$
be a deformation of
$\rho '$
be a deformation of
![]() $\rho $
whose associated pseudocharacter satisfies
$\rho $
whose associated pseudocharacter satisfies
![]() ${D}_{\rho '}={D}_\rho $
. The linearization of
${D}_{\rho '}={D}_\rho $
. The linearization of
![]() $\rho '$
gives a continuous homomorphism
$\rho '$
gives a continuous homomorphism
 $$ \begin{align*}L[\varepsilon][G_K]\,{\longrightarrow}\, \left(\begin{array}{cc} {\mathrm{Mat}}_{n_1\times n_1}(L[\varepsilon])&{\mathrm{Mat}}_{n_1\times n_2}({\mathcal{A}}_{12})\\ {\mathrm{Mat}}_{n_2\times n_1}({\mathcal{A}}_{21})&{\mathrm{Mat}}_{n_2\times n_2}(L[\varepsilon]) \end{array}\right)\rlap{,} \end{align*} $$
$$ \begin{align*}L[\varepsilon][G_K]\,{\longrightarrow}\, \left(\begin{array}{cc} {\mathrm{Mat}}_{n_1\times n_1}(L[\varepsilon])&{\mathrm{Mat}}_{n_1\times n_2}({\mathcal{A}}_{12})\\ {\mathrm{Mat}}_{n_2\times n_1}({\mathcal{A}}_{21})&{\mathrm{Mat}}_{n_2\times n_2}(L[\varepsilon]) \end{array}\right)\rlap{,} \end{align*} $$
which when composed with the determinant gives
![]() ${D}_{\rho '}$
so that by Theorem 4.3.10(b)
${D}_{\rho '}$
so that by Theorem 4.3.10(b)
![]() $\rho '$
factors via a GMA. By hypothesis, we must have
$\rho '$
factors via a GMA. By hypothesis, we must have
![]() ${\mathcal {A}}_{12}=L[\varepsilon ]$
and
${\mathcal {A}}_{12}=L[\varepsilon ]$
and
![]() ${\mathcal {A}}_{21}\subset \varepsilon L$
. Also by hypothesis, the residual pseudocharacter
${\mathcal {A}}_{21}\subset \varepsilon L$
. Also by hypothesis, the residual pseudocharacter
![]() ${D}_\rho $
is multiplicity free and split so that by Proposition 4.3.9
(b) the ideal of total reducibility
${D}_\rho $
is multiplicity free and split so that by Proposition 4.3.9
(b) the ideal of total reducibility
![]() ${\mathcal {A}}_{12}{\mathcal {A}}_{21}$
vanishes, and hence
${\mathcal {A}}_{12}{\mathcal {A}}_{21}$
vanishes, and hence
![]() ${\mathcal {A}}_{21}=0$
, and
${\mathcal {A}}_{21}=0$
, and
![]() $\rho '$
is upper triangular. Let
$\rho '$
is upper triangular. Let
![]() ${D}_1$
and
${D}_1$
and
![]() ${D}_2$
be the pseudocharacters described by the upper left and lower right diagonal blocks of
${D}_2$
be the pseudocharacters described by the upper left and lower right diagonal blocks of
![]() $\rho '$
. then again by Proposition 4.3.9
(b) (and by the nonsplitness of
$\rho '$
. then again by Proposition 4.3.9
(b) (and by the nonsplitness of
![]() $\rho $
) we have
$\rho $
) we have
![]() ${D}_i={D}_{\rho _i}$
,
${D}_i={D}_{\rho _i}$
,
![]() $i=1,2$
, and hence by Theorem 4.3.10
(a),
$i=1,2$
, and hence by Theorem 4.3.10
(a),
![]() $\rho '$
is the trivial deformations on the diagonal blocks.
$\rho '$
is the trivial deformations on the diagonal blocks.
For (c) and (d), we first compute
![]() ${\mathbf {t}_{{X^{\mathrm {univ}}_{\rho }},\rho }}=\dim _L H^1(G_K,{\operatorname {ad}_{{\rho }}} ) $
. It follows from Lemma 3.4.4 that
${\mathbf {t}_{{X^{\mathrm {univ}}_{\rho }},\rho }}=\dim _L H^1(G_K,{\operatorname {ad}_{{\rho }}} ) $
. It follows from Lemma 3.4.4 that
![]() $H^0(G_K,{\operatorname {ad}_{{\rho }}} )\cong L$
, and now formula Theorem 3.4.1
(c) yields
$H^0(G_K,{\operatorname {ad}_{{\rho }}} )\cong L$
, and now formula Theorem 3.4.1
(c) yields
By Theorem 3.4.1
(b), we have
![]() $\dim _L H^2(G_K,{\operatorname {ad}_{{\rho }}} )=\dim _L{\mathrm {Hom}}_{G_K}(\rho ,\rho (1))$
. The claimed expressions for
$\dim _L H^2(G_K,{\operatorname {ad}_{{\rho }}} )=\dim _L{\mathrm {Hom}}_{G_K}(\rho ,\rho (1))$
. The claimed expressions for
![]() $\dim _L{\mathbf {t}_{{X^{\mathrm {univ}}_{\rho }},\rho }}$
now follow from Lemma 3.4.4 with
$\dim _L{\mathbf {t}_{{X^{\mathrm {univ}}_{\rho }},\rho }}$
now follow from Lemma 3.4.4 with
![]() $\chi ={{\mathbb {F}}\,\!{}}(1)$
and our hypotheses. The claim on
$\chi ={{\mathbb {F}}\,\!{}}(1)$
and our hypotheses. The claim on
![]() ${R^{\operatorname {univ}}_{\rho }}$
in (c) now follows from Theorem 3.2.4. The claim on
${R^{\operatorname {univ}}_{\rho }}$
in (c) now follows from Theorem 3.2.4. The claim on
![]() ${R^{\operatorname {univ}}_{\rho }}$
in (d) follows from Corollary 3.4.3 provided that we show that
${R^{\operatorname {univ}}_{\rho }}$
in (d) follows from Corollary 3.4.3 provided that we show that
![]() $H^0(G_K,{\operatorname {\overline {ad}}_{{\rho }}} )=0$
. But under our hypotheses this follows from Corollary 2.3.3.
$H^0(G_K,{\operatorname {\overline {ad}}_{{\rho }}} )=0$
. But under our hypotheses this follows from Corollary 2.3.3.
For the assertions on
![]() ${\mathrm {d}}\varphi $
and
${\mathrm {d}}\varphi $
and
![]() ${\mathrm {d}}\varphi _{\operatorname {red}}$
in (c) and (d), we first give a formula for
${\mathrm {d}}\varphi _{\operatorname {red}}$
in (c) and (d), we first give a formula for
![]() $\dim _L{\operatorname {ker}{{\mathrm {d}}\varphi }} $
in either case. We consider lifts
$\dim _L{\operatorname {ker}{{\mathrm {d}}\varphi }} $
in either case. We consider lifts
![]() $\rho _1,\rho _2$
of
$\rho _1,\rho _2$
of
![]() $\rho $
to
$\rho $
to
![]() $L[\varepsilon ]$
whose associated deformation classes satisfy
$L[\varepsilon ]$
whose associated deformation classes satisfy
![]() $[\rho _1]=[\rho _2]\in {\operatorname {ker}{\operatorname {d}\varphi }} \subset {\mathbf {t}_{{X^{\mathrm {univ}}_{\rho }}}}\cong {\mathcal {D}}_{\rho }(L[ \varepsilon ])$
. By assertion, (b) we have
$[\rho _1]=[\rho _2]\in {\operatorname {ker}{\operatorname {d}\varphi }} \subset {\mathbf {t}_{{X^{\mathrm {univ}}_{\rho }}}}\cong {\mathcal {D}}_{\rho }(L[ \varepsilon ])$
. By assertion, (b) we have
 $\rho _i=\rho +\varepsilon \left (\begin {array}{cc} 0&c_i\\ 0&0 \end {array}\right )$
for some cocycle
$\rho _i=\rho +\varepsilon \left (\begin {array}{cc} 0&c_i\\ 0&0 \end {array}\right )$
for some cocycle
![]() $c_i\in Z^1(G_K,\rho _{x_1}\otimes \rho _{x_2}^\vee )$
. In order to obtain
$c_i\in Z^1(G_K,\rho _{x_1}\otimes \rho _{x_2}^\vee )$
. In order to obtain
![]() $\dim _L{\operatorname {ker}{{\mathrm {d}}\varphi }} $
, we determine when
$\dim _L{\operatorname {ker}{{\mathrm {d}}\varphi }} $
, we determine when
![]() $\rho _1$
is equivalent to
$\rho _1$
is equivalent to
![]() $\rho _2$
. In this case, there exists a matrix
$\rho _2$
. In this case, there exists a matrix
![]() $U \in {\mathrm {Mat}}_{n\times n}(L)$
such that
$U \in {\mathrm {Mat}}_{n\times n}(L)$
such that
 $$ \begin{align*} \rho+\varepsilon\left(\begin{array}{cc} 0&c_2\\ 0&0 \end{array}\right) &=\rho_2\\ &=(1+\varepsilon U)\rho_1(1-\varepsilon U)\\ &=(1+\varepsilon U)(\rho+ \varepsilon\left(\begin{array}{cc} 0&c_1\\ 0&0 \end{array}\right)) (1-\varepsilon U)\\ &=\rho+\varepsilon(U\rho-\rho U + \left(\begin{array}{cc} 0&c_1\\ 0&0 \end{array}\right)). \end{align*} $$
$$ \begin{align*} \rho+\varepsilon\left(\begin{array}{cc} 0&c_2\\ 0&0 \end{array}\right) &=\rho_2\\ &=(1+\varepsilon U)\rho_1(1-\varepsilon U)\\ &=(1+\varepsilon U)(\rho+ \varepsilon\left(\begin{array}{cc} 0&c_1\\ 0&0 \end{array}\right)) (1-\varepsilon U)\\ &=\rho+\varepsilon(U\rho-\rho U + \left(\begin{array}{cc} 0&c_1\\ 0&0 \end{array}\right)). \end{align*} $$
If we write
 $U =\left (\begin {array}{cc} U_{11}&U_{12}\\ U_{21}&U_{22} \end {array}\right )$
with matrices
$U =\left (\begin {array}{cc} U_{11}&U_{12}\\ U_{21}&U_{22} \end {array}\right )$
with matrices
![]() $U_{ij}\in {\mathrm {Mat}}_{n_i\times n_j}(L)$
for
$U_{ij}\in {\mathrm {Mat}}_{n_i\times n_j}(L)$
for
![]() $1\leq i,j\leq 2$
, then the above equality is equivalent to
$1\leq i,j\leq 2$
, then the above equality is equivalent to
 $$ \begin{align*} \left(\begin{array}{cc} 0&c_2-c_1\\ 0&0 \end{array}\right) =\left(\begin{array}{cc} U_{11}\rho_{x_1}&U_{11} c+U_{12}\rho_{x_2}\\ U_{21}\rho_{x_1}&U_{21} c+U_{22}\rho_{x_2} \end{array}\right) -\left(\begin{array}{cc} \rho_{x_1}U_{11}+cU_{21}&\rho_{x_1}U_{12}+cU_{22}\\ \rho_{x_2}U_{21}& \rho_{x_2}U_{22} \end{array}\right). \end{align*} $$
$$ \begin{align*} \left(\begin{array}{cc} 0&c_2-c_1\\ 0&0 \end{array}\right) =\left(\begin{array}{cc} U_{11}\rho_{x_1}&U_{11} c+U_{12}\rho_{x_2}\\ U_{21}\rho_{x_1}&U_{21} c+U_{22}\rho_{x_2} \end{array}\right) -\left(\begin{array}{cc} \rho_{x_1}U_{11}+cU_{21}&\rho_{x_1}U_{12}+cU_{22}\\ \rho_{x_2}U_{21}& \rho_{x_2}U_{22} \end{array}\right). \end{align*} $$
Because
![]() $\dim _L H^0(G_K,\rho _{x_i}\otimes \rho _{x_j}^\vee )=0$
and
$\dim _L H^0(G_K,\rho _{x_i}\otimes \rho _{x_j}^\vee )=0$
and
![]() $\dim _L H^0(G_K,\rho _{x_i}\otimes \rho _{x_i}^\vee )=1$
for
$\dim _L H^0(G_K,\rho _{x_i}\otimes \rho _{x_i}^\vee )=1$
for
![]() $1\leq i,j\leq 2$
and
$1\leq i,j\leq 2$
and
![]() $i\neq j$
, we deduce that
$i\neq j$
, we deduce that
![]() $U_{21}=0$
and that
$U_{21}=0$
and that
![]() $U_{11}$
and
$U_{11}$
and
![]() $U_{22}$
are scalar matrices. Finally, the map
$U_{22}$
are scalar matrices. Finally, the map
is a coboundary. Therefore,
![]() $c_2=(U_{11} +U_{22})c+c_1\in H^1(G_K,\rho _{x_1}\otimes \rho _{x_2}^\vee )$
and
$c_2=(U_{11} +U_{22})c+c_1\in H^1(G_K,\rho _{x_1}\otimes \rho _{x_2}^\vee )$
and
by the computation for (a). Using
![]() $\dim V=\dim {\operatorname {ker}{ \psi }}+\dim {\operatorname {im}{{\psi }}}$
for a vector space V and a linear map
$\dim V=\dim {\operatorname {ker}{ \psi }}+\dim {\operatorname {im}{{\psi }}}$
for a vector space V and a linear map
![]() $\psi $
with domain V, and the already computed dimension of
$\psi $
with domain V, and the already computed dimension of
![]() ${\mathbf {t}_{{X^{\mathrm {univ}}_{\rho }},\rho }}$
, the proof of (c) is complete.
${\mathbf {t}_{{X^{\mathrm {univ}}_{\rho }},\rho }}$
, the proof of (c) is complete.
For (d), consider the following diagram with left exact rows and where the middle and right vertical arrows are injective (by definition of
![]() ${\mathbf {t}_{}}$
):
${\mathbf {t}_{}}$
):

By a simple diagram, chase one deduces
![]() ${\operatorname {ker}{\varphi }}_{\operatorname {red}}={\operatorname {ker}{\varphi }} \cap {\mathbf {t}_{({X^{\mathrm {univ}}_{\rho }})_{\operatorname {red}},\rho }}\subset {\mathbf {t}_{{X^{\mathrm {univ}}_{\rho }},\rho }}$
. Next, consider the diagram
${\operatorname {ker}{\varphi }}_{\operatorname {red}}={\operatorname {ker}{\varphi }} \cap {\mathbf {t}_{({X^{\mathrm {univ}}_{\rho }})_{\operatorname {red}},\rho }}\subset {\mathbf {t}_{{X^{\mathrm {univ}}_{\rho }},\rho }}$
. Next, consider the diagram

with exact rows and where the left and middle vertical arrows are injective. Because of
![]() ${\operatorname {ker}{\varphi }}_{\operatorname {red}}={\operatorname {ker}{\varphi }}\cap {\mathbf {t}_{({X^{\mathrm {univ}}_{\rho }})_{\operatorname {red}},\rho }}$
the map
${\operatorname {ker}{\varphi }}_{\operatorname {red}}={\operatorname {ker}{\varphi }}\cap {\mathbf {t}_{({X^{\mathrm {univ}}_{\rho }})_{\operatorname {red}},\rho }}$
the map
![]() $\gamma $
is injective, and we deduce from the 9-Lemma that
$\gamma $
is injective, and we deduce from the 9-Lemma that
![]() $\dim {\operatorname {coker}{{\alpha }}} +\dim {\operatorname {coker}{{\gamma }}} =\dim {\operatorname {coker}{{\beta }}}$
. From the tangent space computations for (d) made so far, we deduce
$\dim {\operatorname {coker}{{\alpha }}} +\dim {\operatorname {coker}{{\gamma }}} =\dim {\operatorname {coker}{{\beta }}}$
. From the tangent space computations for (d) made so far, we deduce
![]() $\dim {\operatorname {coker}{{\beta }}} =1$
. Letting
$\dim {\operatorname {coker}{{\beta }}} =1$
. Letting
![]() $\delta :=\dim {\operatorname {coker}{{\alpha }}}$
, we must have
$\delta :=\dim {\operatorname {coker}{{\alpha }}}$
, we must have
![]() $0\le \delta \le 1$
and
$0\le \delta \le 1$
and
![]() $\dim {\operatorname {coker}{{\gamma }}} =1-\delta $
. Arguing as for (c) and using
$\dim {\operatorname {coker}{{\gamma }}} =1-\delta $
. Arguing as for (c) and using
![]() $\dim _L{\mathbf {t}_{{X^{\mathrm {univ}}_{\rho} ,{\operatorname {red}}},\rho }}=dn^2+1$
, the proof of (d) is complete, as well.
$\dim _L{\mathbf {t}_{{X^{\mathrm {univ}}_{\rho} ,{\operatorname {red}}},\rho }}=dn^2+1$
, the proof of (d) is complete, as well.
5.2 Zariski density of the irreducible locus
The aim of this subsection is to formulate an inductive procedure to prove Zariski density of the irreducible locus the special fibers of universal pseudodeformation spaces, and to establish some key steps. Our procedure is an adaption of an analogous result of Chenevier for the generic fiber; see [Reference ChenevierChe11, Théorème 2.1]. We shall prove the following main result.
Theorem 5.2.1. Let
![]() $n\ge 2$
be an integer. Suppose that for all pseudocharacters
$n\ge 2$
be an integer. Suppose that for all pseudocharacters
![]() ${\overline {{D}}}'\colon G_K\to {{\mathbb {F}}\,\!{}}$
on
${\overline {{D}}}'\colon G_K\to {{\mathbb {F}}\,\!{}}$
on
![]() $G_K$
of dimension
$G_K$
of dimension
![]() $n'<n$
the following hold:
$n'<n$
the following hold:
-
(a)
 ${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}'}}}$
is equidimensional of dimension
${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}'}}}$
is equidimensional of dimension
 $[K:{\mathbb {Q}}_p](n')^2+1$
,
$[K:{\mathbb {Q}}_p](n')^2+1$
, -
(b)
 $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}'}}})^{{{\mathrm {n}\textrm {-}\mathrm {spcl}}}}$
is Zariski dense in
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}'}}})^{{{\mathrm {n}\textrm {-}\mathrm {spcl}}}}$
is Zariski dense in
 ${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}'}}}$
.
${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}'}}}$
.
Then for all n-dimensional pseudocharacters
![]() ${\overline {{D}}} \colon G_K\to {{\mathbb {F}}\,\!{}}$
on
${\overline {{D}}} \colon G_K\to {{\mathbb {F}}\,\!{}}$
on
![]() $G_K$
the subspace
$G_K$
the subspace
![]() $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\operatorname {irr}}\subset {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
is Zariski dense.
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\operatorname {irr}}\subset {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
is Zariski dense.
Let us begin with some preparations. Let
![]() $n_1,n_2\ge 1$
be integers such that
$n_1,n_2\ge 1$
be integers such that
![]() $n=n_1+n_2$
. Let
$n=n_1+n_2$
. Let
![]() ${\overline {{D}}}_i\colon G_K\to {{\mathbb {F}}\,\!{}}$
be residual pseudocharacters on
${\overline {{D}}}_i\colon G_K\to {{\mathbb {F}}\,\!{}}$
be residual pseudocharacters on
![]() $G_K$
of dimension
$G_K$
of dimension
![]() $n_i$
. Addition
$n_i$
. Addition
![]() $({D}_1,{D}_2)\mapsto {D}_1{\oplus }{D}_2$
of pseudocharacters yields a morphism
$({D}_1,{D}_2)\mapsto {D}_1{\oplus }{D}_2$
of pseudocharacters yields a morphism
for
![]() ${\overline {{D}}}:={\overline {{D}}}_1\oplus {\overline {{D}}}_2$
. If
${\overline {{D}}}:={\overline {{D}}}_1\oplus {\overline {{D}}}_2$
. If
![]() ${{\overline {{D}}}_1}\neq {{\overline {{D}}}_2}$
, we define
${{\overline {{D}}}_1}\neq {{\overline {{D}}}_2}$
, we define
![]() ${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_1,{\overline {{D}}}_2}}} := {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_1}}} \hat {\times }_{{{\mathbb {F}}\,\!{}}} {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_2}}}$
and write
${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_1,{\overline {{D}}}_2}}} := {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_1}}} \hat {\times }_{{{\mathbb {F}}\,\!{}}} {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_2}}}$
and write
![]() $\iota _{{\overline {{D}}}_1,{\overline {{D}}}_2}$
for the above morphism. In the other case we let
$\iota _{{\overline {{D}}}_1,{\overline {{D}}}_2}$
for the above morphism. In the other case we let
![]() ${\mathbb {Z}}/2$
act on
${\mathbb {Z}}/2$
act on
![]() ${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_1}}} \hat {\times }_{{{\mathbb {F}}\,\!{}}} {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_1}}}$
by exchanging the factors; it preserves the diagonal, which we denote by
${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_1}}} \hat {\times }_{{{\mathbb {F}}\,\!{}}} {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_1}}}$
by exchanging the factors; it preserves the diagonal, which we denote by
![]() $\Delta _{{\overline {{D}}}_1}^{\operatorname {univ}}$
, and one has an induced morphism
$\Delta _{{\overline {{D}}}_1}^{\operatorname {univ}}$
, and one has an induced morphism
Note that away from the
![]() $\Delta ^{\operatorname {univ}}_{{\overline {{D}}}_1}$
, the morphism
$\Delta ^{\operatorname {univ}}_{{\overline {{D}}}_1}$
, the morphism
![]() ${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_1}}} \hat {\times }_{{{\mathbb {F}}\,\!{}}} {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_1}}} \to {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_1,{\overline {{D}}}_1} }}$
is an étale Galois cover with monodromy group
${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_1}}} \hat {\times }_{{{\mathbb {F}}\,\!{}}} {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_1}}} \to {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_1,{\overline {{D}}}_1} }}$
is an étale Galois cover with monodromy group
![]() ${\mathbb {Z}}/2$
.
${\mathbb {Z}}/2$
.
Lemma 5.2.2 [Reference ChenevierChe11, Lemme 1.1.].
For
![]() $i=1,2$
, let
$i=1,2$
, let
![]() $x_i\in {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_i}}}$
be irreducible points of dimension
$x_i\in {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_i}}}$
be irreducible points of dimension
![]() $1$
, and let L be a finite common extension of the residue fields
$1$
, and let L be a finite common extension of the residue fields
![]() ${\kappa ({x_i})}$
. If
${\kappa ({x_i})}$
. If
![]() ${\overline {{D}}}_1={\overline {{D}}}_2$
, assume also that
${\overline {{D}}}_1={\overline {{D}}}_2$
, assume also that
![]() $x_1\neq x_2$
. Let
$x_1\neq x_2$
. Let
![]() $x\in {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
be the point of dimension
$x\in {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
be the point of dimension
![]() $1$
with
$1$
with
![]() ${D}_{x_2}\otimes _{{\kappa ({x_1})}}L$
. Let
${D}_{x_2}\otimes _{{\kappa ({x_1})}}L$
. Let
![]() $\overline x\colon {\mathrm {Spec}}{\kappa ({x})} \to {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
be a geometric point over x.
$\overline x\colon {\mathrm {Spec}}{\kappa ({x})} \to {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
be a geometric point over x.
Then there is an étale neighborhood
![]() $({U},\overline u,{\varphi }_U\colon U\to {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})$
of
$({U},\overline u,{\varphi }_U\colon U\to {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})$
of
![]() $\overline {x}$
such that the base change
$\overline {x}$
such that the base change
of
![]() $\iota _{{\overline {{D}}}_1,{\overline {{D}}}_2}$
along
$\iota _{{\overline {{D}}}_1,{\overline {{D}}}_2}$
along
![]() ${\varphi }_U$
is a closed immersion with image
${\varphi }_U$
is a closed immersion with image
![]() $U^{\operatorname {red}}=\{u\in U\mid u\textrm { is reducible}\}$
. Moreover, if
$U^{\operatorname {red}}=\{u\in U\mid u\textrm { is reducible}\}$
. Moreover, if
![]() ${\overline {{D}}}_1={\overline {{D}}}_2$
, then we may choose U such that
${\overline {{D}}}_1={\overline {{D}}}_2$
, then we may choose U such that
![]() ${\varphi }_U(U)$
is disjoint from
${\varphi }_U(U)$
is disjoint from
![]() $\iota _{{\overline {{D}}}_1,{\overline {{D}}}_1}(\Delta _{{\overline {{D}}}_1}^{\operatorname {univ}})$
.
$\iota _{{\overline {{D}}}_1,{\overline {{D}}}_1}(\Delta _{{\overline {{D}}}_1}^{\operatorname {univ}})$
.
Proof. As recalled above Definition 4.7.8, the universal pseudodeformation
![]() ${{D}^{\operatorname {univ}}_{{\overline {{D}}}}}$
factors via the universal Cayley–Hamilton pseudodeformation and CH-representation
${{D}^{\operatorname {univ}}_{{\overline {{D}}}}}$
factors via the universal Cayley–Hamilton pseudodeformation and CH-representation
Consider the strictly local ring
![]() $\mathcal {O}_{\overline x}^{\operatorname {sh}}:= {\mathrm {colim}}_{({V}, \overline {{v}})} {\cal O}(V)$
for
$\mathcal {O}_{\overline x}^{\operatorname {sh}}:= {\mathrm {colim}}_{({V}, \overline {{v}})} {\cal O}(V)$
for
![]() $ {\cal O}(V):= \mathcal {O}_{{\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}}({V})$
, where
$ {\cal O}(V):= \mathcal {O}_{{\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}}({V})$
, where
![]() $({V},\overline {{v}})$
runs over all connected étale neighborhoods of
$({V},\overline {{v}})$
runs over all connected étale neighborhoods of
![]() $\overline {x}$
in
$\overline {x}$
in
![]() ${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
[Reference StacksSta18, Lemma 04HX]. Since by Proposition 4.1.22 the formation of the Cayley–Hamilton quotient
${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
[Reference StacksSta18, Lemma 04HX]. Since by Proposition 4.1.22 the formation of the Cayley–Hamilton quotient
![]() ${\overline {{S}}^{{\operatorname {CH-univ}}}_{{\overline {{D}}}}}$
commutes with arbitrary base change, for any étale neighborhood
${\overline {{S}}^{{\operatorname {CH-univ}}}_{{\overline {{D}}}}}$
commutes with arbitrary base change, for any étale neighborhood
![]() $({V}, \overline {{v}})$
of
$({V}, \overline {{v}})$
of
![]() $\overline {x}$
there is an isomorphism
$\overline {x}$
there is an isomorphism
From Theorem 4.3.10, it follows that
![]() $\overline {{S}}_{\overline x}:= {\mathrm {colim}}_{({V}, \overline {{v}})} \overline {{S}}_V$
is a GMA of type
$\overline {{S}}_{\overline x}:= {\mathrm {colim}}_{({V}, \overline {{v}})} \overline {{S}}_V$
is a GMA of type
![]() $(n_1,n_2)$
. In particular, there exists idempotents
$(n_1,n_2)$
. In particular, there exists idempotents
![]() $e_1,e_2\in \overline {{S}}_{\overline x}$
with
$e_1,e_2\in \overline {{S}}_{\overline x}$
with
![]() $e_1+e_2=1$
and for
$e_1+e_2=1$
and for
![]() $i=1,2$
an isomorphism
$i=1,2$
an isomorphism
![]() $\psi _{\overline x,i}\colon e_i\overline {{S}}_{\overline x}e_i\to {\mathrm {Mat}}_{n_i\times n_i}(\mathcal {O}_{\overline x}^{\operatorname {sh}})$
. Denote by
$\psi _{\overline x,i}\colon e_i\overline {{S}}_{\overline x}e_i\to {\mathrm {Mat}}_{n_i\times n_i}(\mathcal {O}_{\overline x}^{\operatorname {sh}})$
. Denote by
![]() ${\cal E}_{\overline x}:=(e_i,\psi _{\overline x,i})_{i=1,2}$
, then also the induced pseudocharacter to
${\cal E}_{\overline x}:=(e_i,\psi _{\overline x,i})_{i=1,2}$
, then also the induced pseudocharacter to
![]() ${\cal O}^{\operatorname {sh}}_{\overline x}$
factors via the natural Cayley–Hamilton pseudocharacter
${\cal O}^{\operatorname {sh}}_{\overline x}$
factors via the natural Cayley–Hamilton pseudocharacter
![]() ${D}_{\overline {{S}}_{\overline x},{\cal E}_{\overline x}}$
from Proposition 4.3.5.
${D}_{\overline {{S}}_{\overline x},{\cal E}_{\overline x}}$
from Proposition 4.3.5.
By Proposition 4.7.11, the ring
![]() ${\overline {{S}}^{{\operatorname {CH-univ}}}_{{\overline {{D}}}}}$
is module-finite as an
${\overline {{S}}^{{\operatorname {CH-univ}}}_{{\overline {{D}}}}}$
is module-finite as an
![]() ${\overline {R}^{\operatorname {univ}}_{{\overline {{D}}}}}$
-algebra and Noetherian. Note also that we constructed
${\overline {R}^{\operatorname {univ}}_{{\overline {{D}}}}}$
-algebra and Noetherian. Note also that we constructed
![]() $\overline {{S}}_{\overline s}$
and
$\overline {{S}}_{\overline s}$
and
![]() ${\cal O}_{\overline x}^{\operatorname {sh}}$
as direct limits over étale neighborhoods. Using spreading out principles from [Reference GrothendieckGro66, § 8.5], we can thus find a connected affine étale neighborhood
${\cal O}_{\overline x}^{\operatorname {sh}}$
as direct limits over étale neighborhoods. Using spreading out principles from [Reference GrothendieckGro66, § 8.5], we can thus find a connected affine étale neighborhood
![]() $(\overline u,U,{\varphi }\colon U\to {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})$
of
$(\overline u,U,{\varphi }\colon U\to {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})$
of
![]() $\overline x$
such that the
$\overline x$
such that the
![]() $e_i$
can be defined
$e_i$
can be defined
![]() $e_1+e_2=1$
, and such that one has isomorphism
$e_1+e_2=1$
, and such that one has isomorphism
whose base change under
![]() ${\cal O}(U)\to {\cal O}_{\overline x}^{\operatorname {sh}}$
is
${\cal O}(U)\to {\cal O}_{\overline x}^{\operatorname {sh}}$
is
![]() $\psi _{\overline x,i}$
. Hence,
$\psi _{\overline x,i}$
. Hence,
![]() $\overline {{S}}_U$
together with
$\overline {{S}}_U$
together with
![]() ${\cal E}_U:=(e_i,\psi _{U,i})_{i=1,2}$
is a GMA. By choosing U sufficiently ‘small’, we may also assume that the pseudocharacter
${\cal E}_U:=(e_i,\psi _{U,i})_{i=1,2}$
is a GMA. By choosing U sufficiently ‘small’, we may also assume that the pseudocharacter
![]() ${D}_U\colon {\cal O}(U)[G]\to {\cal O}(U)$
induced from
${D}_U\colon {\cal O}(U)[G]\to {\cal O}(U)$
induced from
![]() ${{D}^{\operatorname {univ}}_{{\overline {{D}}}}}$
factors via the induced CH-representation
${{D}^{\operatorname {univ}}_{{\overline {{D}}}}}$
factors via the induced CH-representation
![]() $G\to (\overline {{S}}_U)^\times $
composed with the natural Cayley–Hamilton pseudocharacter
$G\to (\overline {{S}}_U)^\times $
composed with the natural Cayley–Hamilton pseudocharacter
![]() ${D}_{\overline {{S}}_U, {\cal E}_U}$
.
${D}_{\overline {{S}}_U, {\cal E}_U}$
.
Let us write
 $$ \begin{align*}\overline{{S}}_{U}\cong \left(\begin{array}{cc} {\mathrm{Mat}}_{n_1\times n_1}(\mathcal{O}({U}))& {\mathrm{Mat}}_{n_1\times n_2}({\mathcal{A}}_{12})\\ {\mathrm{Mat}}_{n_2\times n_1}({\mathcal{A}}_{21})&{\mathrm{Mat}}_{n_2\times n_2}(\mathcal{O}({U})) \end{array}\right). \end{align*} $$
$$ \begin{align*}\overline{{S}}_{U}\cong \left(\begin{array}{cc} {\mathrm{Mat}}_{n_1\times n_1}(\mathcal{O}({U}))& {\mathrm{Mat}}_{n_1\times n_2}({\mathcal{A}}_{12})\\ {\mathrm{Mat}}_{n_2\times n_1}({\mathcal{A}}_{21})&{\mathrm{Mat}}_{n_2\times n_2}(\mathcal{O}({U})) \end{array}\right). \end{align*} $$
with finitely generated
![]() ${\cal O}(U)$
-modules
${\cal O}(U)$
-modules
![]() ${\mathcal {A}}_{12}$
and
${\mathcal {A}}_{12}$
and
![]() ${\mathcal {A}}_{21}$
together with the structure of a GMA described in Lemma 4.3.3. Let
${\mathcal {A}}_{21}$
together with the structure of a GMA described in Lemma 4.3.3. Let
![]() $I={\mathcal {A}}_{12}{\mathcal {A}}_{21}+{\mathcal {A}}_{21}{\mathcal {A}}_{12}={\mathcal {A}}_{12}{\mathcal {A}}_{21}$
be the ideal of total reducibility. From Proposition 4.3.9
(b), we deduce that there exist unique pseudocharacters
$I={\mathcal {A}}_{12}{\mathcal {A}}_{21}+{\mathcal {A}}_{21}{\mathcal {A}}_{12}={\mathcal {A}}_{12}{\mathcal {A}}_{21}$
be the ideal of total reducibility. From Proposition 4.3.9
(b), we deduce that there exist unique pseudocharacters
![]() ${D}_i\colon e_i\overline {{S}}_{U} e_i\to \mathcal {O}({U})/I$
for
${D}_i\colon e_i\overline {{S}}_{U} e_i\to \mathcal {O}({U})/I$
for
![]() $i=1,2$
such that
$i=1,2$
such that
Denote by
![]() $Z:={\mathrm {Spec}}(\mathcal {O}({U})/I)$
the locus of total reducibility, by
$Z:={\mathrm {Spec}}(\mathcal {O}({U})/I)$
the locus of total reducibility, by
![]() $f\colon Z\to U$
the induced closed immersion and by
$f\colon Z\to U$
the induced closed immersion and by
![]() $g\colon Z\to {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_1,{\overline {{D}}}_2}}}$
the morphism corresponding to the
$g\colon Z\to {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_1,{\overline {{D}}}_2}}}$
the morphism corresponding to the
![]() $\mathcal {O}(Z)$
-valued pseudocharacters
$\mathcal {O}(Z)$
-valued pseudocharacters
![]() $({D}_1,{D}_2)$
. Then the morphism
$({D}_1,{D}_2)$
. Then the morphism
![]() ${\varphi }_U\circ f$
corresponds to the
${\varphi }_U\circ f$
corresponds to the
![]() $\mathcal {O}(U)/I$
-valued pseudocharacter
$\mathcal {O}(U)/I$
-valued pseudocharacter
![]() $D_U\ {\mathop{\mathrm{mod}\ }\nolimits } I$
and there is a commutative diagram
$D_U\ {\mathop{\mathrm{mod}\ }\nolimits } I$
and there is a commutative diagram

since
![]() ${\varphi }_{U}\circ f$
and
${\varphi }_{U}\circ f$
and
![]() $\iota _{{\overline {{D}}}_1,{\overline {{D}}}_2}\circ g$
both correspond to
$\iota _{{\overline {{D}}}_1,{\overline {{D}}}_2}\circ g$
both correspond to
![]() ${D}_U\ {\mathop{\mathrm{mod}\ }\nolimits } I={D}_1{\oplus }{D}_2$
. We need to show that this diagram is Cartesian; then
${D}_U\ {\mathop{\mathrm{mod}\ }\nolimits } I={D}_1{\oplus }{D}_2$
. We need to show that this diagram is Cartesian; then
![]() $\iota _U=f$
is a closed immersion, by construction, that is, by [Reference StacksSta18, Definition 01JP] given any connected affine scheme W together with morphisms
$\iota _U=f$
is a closed immersion, by construction, that is, by [Reference StacksSta18, Definition 01JP] given any connected affine scheme W together with morphisms
![]() $f'\colon W\to {U}$
and
$f'\colon W\to {U}$
and
![]() $g'\colon W\to {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_1,{\overline {{D}}}_2}}}$
such that in the following diagram the solid square commutes
$g'\colon W\to {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_1,{\overline {{D}}}_2}}}$
such that in the following diagram the solid square commutes

we need to check that there exists a unique dashed arrow h making the diagram commute.
The morphism
![]() ${\varphi }_{U}\circ f'=\iota _{{\overline {{D}}}_1,{\overline {{D}}}_2}\circ g'$
defines an
${\varphi }_{U}\circ f'=\iota _{{\overline {{D}}}_1,{\overline {{D}}}_2}\circ g'$
defines an
![]() $\mathcal {O}(W)$
-valued pseudocharacter
$\mathcal {O}(W)$
-valued pseudocharacter
![]() ${D}^{\prime }_W$
, and the morphism
${D}^{\prime }_W$
, and the morphism
![]() $g'$
a pair
$g'$
a pair
![]() $({D}^{\prime }_1,{D}^{\prime }_2)$
of
$({D}^{\prime }_1,{D}^{\prime }_2)$
of
![]() $\mathcal {O}(W)$
-valued pseudocharacters of dimension
$\mathcal {O}(W)$
-valued pseudocharacters of dimension
![]() $n_j$
for
$n_j$
for
![]() $j=1,2$
. By Lemma 4.3.4, the base change
$j=1,2$
. By Lemma 4.3.4, the base change
![]() $\overline {{S}}_W$
of
$\overline {{S}}_W$
of
![]() $\overline {{S}}_U$
along
$\overline {{S}}_U$
along
![]() $f'$
is a generalized matrix algebra over
$f'$
is a generalized matrix algebra over
![]() ${\cal O}(W)$
of type
${\cal O}(W)$
of type
![]() $(n_1,n_2)$
. The definition of
$(n_1,n_2)$
. The definition of
![]() $\iota _{{\overline {{D}}}_1,{\overline {{D}}}_2}$
implies that
$\iota _{{\overline {{D}}}_1,{\overline {{D}}}_2}$
implies that
![]() ${D}^{\prime }_W={D}^{\prime }_1{{\oplus }} {D}^{\prime }_2$
, and from Proposition 4.3.9
(b) we conclude that the ideal
${D}^{\prime }_W={D}^{\prime }_1{{\oplus }} {D}^{\prime }_2$
, and from Proposition 4.3.9
(b) we conclude that the ideal
of total reducibility of
![]() $\overline {{S}}_W$
vanishes. Hence, there exists a unique morphism
$\overline {{S}}_W$
vanishes. Hence, there exists a unique morphism
![]() $h\colon W\to Z$
such that
$h\colon W\to Z$
such that
![]() $(f')^*$
factors as
$(f')^*$
factors as
![]() $\mathcal {O}({U})\stackrel {f^*}{\to } \mathcal {O}(Z) \stackrel {h^*}\to \mathcal {O}(W)$
. Note the
$\mathcal {O}({U})\stackrel {f^*}{\to } \mathcal {O}(Z) \stackrel {h^*}\to \mathcal {O}(W)$
. Note the
![]() $g^*\circ h^*$
determines a pair
$g^*\circ h^*$
determines a pair
![]() $({D}^{\prime \prime }_1,{D}^{\prime \prime }_2)$
of pseudocharacters
$({D}^{\prime \prime }_1,{D}^{\prime \prime }_2)$
of pseudocharacters
![]() $G\to {\cal O}(W)$
on G. From Proposition 4.3.9
(b), we deduce
$G\to {\cal O}(W)$
on G. From Proposition 4.3.9
(b), we deduce
![]() $\{{D}_1',{D}_2'\}=\{{D}_1^{\prime \prime },{D}_2^{\prime \prime }\}$
. The universal property of
$\{{D}_1',{D}_2'\}=\{{D}_1^{\prime \prime },{D}_2^{\prime \prime }\}$
. The universal property of
![]() ${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_1}}}\hat {\times }{\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_2}}}$
, and our definition of
${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_1}}}\hat {\times }{\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_2}}}$
, and our definition of
![]() $(\iota _{{\overline {{D}}}_1,{\overline {{D}}}_2},{\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_1,{\overline {{D}}}_2}}})$
implies that
$(\iota _{{\overline {{D}}}_1,{\overline {{D}}}_2},{\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_1,{\overline {{D}}}_2}}})$
implies that
![]() $(h')^*=g^*\circ h^*$
.
$(h')^*=g^*\circ h^*$
.
Next, we prove
![]() $Z=U^{\operatorname {red}}$
under the closed immersion f. By the definition of
$Z=U^{\operatorname {red}}$
under the closed immersion f. By the definition of
![]() $\iota _{{\overline {{D}}}_1,{\overline {{D}}}_2}$
the inclusion
$\iota _{{\overline {{D}}}_1,{\overline {{D}}}_2}$
the inclusion
![]() $\subseteq $
is obvious. Let therefore y be any point of
$\subseteq $
is obvious. Let therefore y be any point of
![]() $U^{\operatorname {red}}$
. To see that y lies on
$U^{\operatorname {red}}$
. To see that y lies on
![]() $f(Z)$
, let
$f(Z)$
, let
![]() ${D}_y$
be the reducible pseudocharacter corresponding
${D}_y$
be the reducible pseudocharacter corresponding
![]() ${\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}\to \mathcal {O}({U})\to {\kappa ({y})}$
. By Lemma 4.3.4, the base change
${\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}\to \mathcal {O}({U})\to {\kappa ({y})}$
. By Lemma 4.3.4, the base change
![]() ${S}_y:=\overline {{S}}_{U}\otimes _{\mathcal {O}({U})}{{{{\kappa ({y})}}}^{\mathrm {alg}}} $
of
${S}_y:=\overline {{S}}_{U}\otimes _{\mathcal {O}({U})}{{{{\kappa ({y})}}}^{\mathrm {alg}}} $
of
![]() $\overline {{S}}_{U}$
is also a generalized matrix algebra of type
$\overline {{S}}_{U}$
is also a generalized matrix algebra of type
![]() $(n_1,n_2)$
. Since
$(n_1,n_2)$
. Since
![]() ${D}_y$
is reducible, there exists pseudocharacters
${D}_y$
is reducible, there exists pseudocharacters
![]() ${D}_1,{D}_2\colon G_K\to {{{{\kappa ({y})}}}^{\mathrm {alg}}} $
on
${D}_1,{D}_2\colon G_K\to {{{{\kappa ({y})}}}^{\mathrm {alg}}} $
on
![]() $G_K$
such that
$G_K$
such that
![]() ${D}_y={D}_1{\oplus }{D}_2$
. By again applying Proposition 4.3.9, we find that the ideal of total reducibility of the generalized matrix algebra
${D}_y={D}_1{\oplus }{D}_2$
. By again applying Proposition 4.3.9, we find that the ideal of total reducibility of the generalized matrix algebra
![]() ${S}_y$
vanishes. Hence,
${S}_y$
vanishes. Hence,
![]() ${\cal O}(U)\to {\kappa ({y})}$
factors via
${\cal O}(U)\to {\kappa ({y})}$
factors via
![]() ${\cal O}(Z)$
as was to be shown.
${\cal O}(Z)$
as was to be shown.
For the final assertion, suppose from now on that
![]() ${{\overline {{D}}}_1}={{\overline {{D}}}_2}$
so that
${{\overline {{D}}}_1}={{\overline {{D}}}_2}$
so that
![]() $m:=n_1=n_2$
. Consider the maps
$m:=n_1=n_2$
. Consider the maps
for
![]() $i=1,2$
and
$i=1,2$
and
![]() $j=1,\ldots ,m$
, where
$j=1,\ldots ,m$
, where
![]() ${\bigwedge ^j}$
denotes the exterior power map on endomorphisms. For every
${\bigwedge ^j}$
denotes the exterior power map on endomorphisms. For every
![]() $g\in G$
, the vanishing locus of
$g\in G$
, the vanishing locus of
![]() ${\Lambda ^j_1}(g)-{\Lambda ^j_2}(g)\in {\cal O}(U)$
is a closed subscheme
${\Lambda ^j_1}(g)-{\Lambda ^j_2}(g)\in {\cal O}(U)$
is a closed subscheme
![]() ${Y_g}$
of U, and hence the intersection
${Y_g}$
of U, and hence the intersection
![]() $Y:=\bigcap _{g\in G} {Y_g}$
is closed in U. Since
$Y:=\bigcap _{g\in G} {Y_g}$
is closed in U. Since
![]() ${x_1}\neq {x_2}$
, we have
${x_1}\neq {x_2}$
, we have
![]() $(x_1,x_2)\notin {\varphi }(Y)$
, and thus
$(x_1,x_2)\notin {\varphi }(Y)$
, and thus
![]() $U'=U{\smallsetminus } Y$
is an étale neighborhood of
$U'=U{\smallsetminus } Y$
is an étale neighborhood of
![]() $\overline x$
as required for the last assertion.
$\overline x$
as required for the last assertion.
Proof (First proof of Theorem 5.2.1).
We suppose to the contrary that there exists a nonempty open affine
![]() ${V}\subset {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
such that
${V}\subset {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
such that
![]() $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{{\operatorname {irr}}}\cap {V}=\emptyset $
. Since
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{{\operatorname {irr}}}\cap {V}=\emptyset $
. Since
![]() ${V}\neq {\mathrm {Spec}}{{\mathbb {F}}\,\!{}}$
and the points of dimension
${V}\neq {\mathrm {Spec}}{{\mathbb {F}}\,\!{}}$
and the points of dimension
![]() $1$
are very dense in
$1$
are very dense in
![]() ${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
by Lemma A.1.8, there exists a point
${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
by Lemma A.1.8, there exists a point
![]() $x\in {V}$
of dimension
$x\in {V}$
of dimension
![]() $1$
that defines a reducible pseudodeformation
$1$
that defines a reducible pseudodeformation
of
![]() ${\overline {{D}}}$
. By Corollary 4.8.4, there exist a finite extension
${\overline {{D}}}$
. By Corollary 4.8.4, there exist a finite extension
![]() $L'/{\kappa ({x})} $
with finite residue field
$L'/{\kappa ({x})} $
with finite residue field
![]() ${{\mathbb {F}}\,\!{}}'\supset {{\mathbb {F}}\,\!{}}$
, residual pseudocharacter
${{\mathbb {F}}\,\!{}}'\supset {{\mathbb {F}}\,\!{}}$
, residual pseudocharacter
![]() ${\overline {{D}}}_i\colon G_K\to {{\mathbb {F}}\,\!{}}'$
on
${\overline {{D}}}_i\colon G_K\to {{\mathbb {F}}\,\!{}}'$
on
![]() $G_K$
of dimension
$G_K$
of dimension
![]() $n_i$
for some
$n_i$
for some
![]() $n_i\in {\mathbb {N}_0}$
with
$n_i\in {\mathbb {N}_0}$
with
![]() $n_1+n_2=n$
, and pseudocharacters
$n_1+n_2=n$
, and pseudocharacters
![]() ${D}_1,{D}_2\colon G_K\to \mathcal {O}_{L'}$
of
${D}_1,{D}_2\colon G_K\to \mathcal {O}_{L'}$
of
![]() $G_K$
corresponding to points
$G_K$
corresponding to points
![]() $(x_1,x_2)\in {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_1}}}\widehat {\times }{\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_2}}}$
such that
$(x_1,x_2)\in {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_1}}}\widehat {\times }{\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_2}}}$
such that
![]() ${D}_x\otimes _{{\kappa ({x})} }L'=({D}_1\oplus {D}_2)\otimes _{\mathcal {O}_{L'}}L'$
. By Lemma 5.2.6, we may and will assume
${D}_x\otimes _{{\kappa ({x})} }L'=({D}_1\oplus {D}_2)\otimes _{\mathcal {O}_{L'}}L'$
. By Lemma 5.2.6, we may and will assume
![]() ${{\mathbb {F}}\,\!{}}={{\mathbb {F}}\,\!{}}'$
.
${{\mathbb {F}}\,\!{}}={{\mathbb {F}}\,\!{}}'$
.
The inverse image of V under
![]() ${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_1}}}\widehat {\times }{\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_2}}}\to {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}},({D}_1,{D}_2)\mapsto {{D}_1}+{{D}_2}$
is an open neighborhood of
${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_1}}}\widehat {\times }{\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_2}}}\to {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}},({D}_1,{D}_2)\mapsto {{D}_1}+{{D}_2}$
is an open neighborhood of
![]() $(x_1,x_2)$
. By hypothesis (b) of Theorem 5.2.1, we may within this neighborhood replace the initially chosen pair by
$(x_1,x_2)$
. By hypothesis (b) of Theorem 5.2.1, we may within this neighborhood replace the initially chosen pair by
![]() $(x_1,x_2)$
such that both are irreducible and nonspecial, and by Lemma A.1.7 we may further assume that
$(x_1,x_2)$
such that both are irreducible and nonspecial, and by Lemma A.1.7 we may further assume that
![]() ${{D}_1}$
is not isomorphic to any of the finitely many
${{D}_1}$
is not isomorphic to any of the finitely many
![]() ${{D}_2}(m)$
,
${{D}_2}(m)$
,
![]() $m\in \{1,\ldots ,p-1\}$
, since
$m\in \{1,\ldots ,p-1\}$
, since
![]() $\dim {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_i}}}\ge 2$
. Let
$\dim {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_i}}}\ge 2$
. Let
![]() $U_i:=({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_i}}})^{{{\mathrm {n}\textrm {-}\mathrm {spcl}}}}$
. Then we observe that by Lemma 5.1.6 the schemes
$U_i:=({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_i}}})^{{{\mathrm {n}\textrm {-}\mathrm {spcl}}}}$
. Then we observe that by Lemma 5.1.6 the schemes
![]() $(U_i)_{\operatorname {red}}$
are regular, and if
$(U_i)_{\operatorname {red}}$
are regular, and if
![]() $\zeta _p \notin K$
, then
$\zeta _p \notin K$
, then
![]() ${U_i}=(U_i)_{\operatorname {red}}$
.
${U_i}=(U_i)_{\operatorname {red}}$
.
Let
![]() $\overline x$
be a geometric point above x. By Lemma 5.2.2, there exists an étale neighborhood
$\overline x$
be a geometric point above x. By Lemma 5.2.2, there exists an étale neighborhood
![]() $({U},\bar u,\varphi _{U}\colon {U}\to {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})$
of
$({U},\bar u,\varphi _{U}\colon {U}\to {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})$
of
![]() $\overline {x}$
such that the pullback of
$\overline {x}$
such that the pullback of
![]() $\iota _{{\overline {{D}}}_1,{\overline {{D}}}_2}$
along
$\iota _{{\overline {{D}}}_1,{\overline {{D}}}_2}$
along
![]() ${\varphi }_U$
${\varphi }_U$
is a closed immersion with image
![]() $U^{\operatorname {red}}$
. We may replace U by
$U^{\operatorname {red}}$
. We may replace U by
![]() ${\varphi }_U^{-1}(V)$
, which is nonempty since
${\varphi }_U^{-1}(V)$
, which is nonempty since
![]() $x\in V$
, and is étale over V, and we may shrink W accordingly. By further replacing U by an open subset (and accordingly W), we can assume that U is connected and affine. Since
$x\in V$
, and is étale over V, and we may shrink W accordingly. By further replacing U by an open subset (and accordingly W), we can assume that U is connected and affine. Since
![]() $W\to U$
is a closed immersion, the scheme W is affine. But we also have that
$W\to U$
is a closed immersion, the scheme W is affine. But we also have that
![]() $W\to U$
is surjective as a map of topological spaces since all points of V are reducible. Hence, the nil-reduction of
$W\to U$
is surjective as a map of topological spaces since all points of V are reducible. Hence, the nil-reduction of
![]() $W\to U$
is an isomorphism of schemes
$W\to U$
is an isomorphism of schemes
![]() $W_{\operatorname {red}}\to U_{\operatorname {red}}$
, and as a map of topological spaces
$W_{\operatorname {red}}\to U_{\operatorname {red}}$
, and as a map of topological spaces
![]() $W\to U$
is a homeomorphism. Since the base change of étale morphisms is étale, so is the map
$W\to U$
is a homeomorphism. Since the base change of étale morphisms is étale, so is the map
![]() $W\to {{\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_1,{\overline {{D}}}_2}}}}$
that is the base change of
$W\to {{\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_1,{\overline {{D}}}_2}}}}$
that is the base change of
![]() ${\varphi }_U$
under
${\varphi }_U$
under
![]() $\iota _{{\overline {{D}}}_1,{\overline {{D}}}_2}$
. Let
$\iota _{{\overline {{D}}}_1,{\overline {{D}}}_2}$
. Let
![]() $\widetilde {U}_i$
be the preimage of
$\widetilde {U}_i$
be the preimage of
![]() $U_i$
under the i-th projection
$U_i$
under the i-th projection
![]() ${{\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_1,{\overline {{D}}}_2}}}}\to {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_i}}}$
. We shrink W (and hence U) to a connected affine open so that the image of W in
${{\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_1,{\overline {{D}}}_2}}}}\to {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_i}}}$
. We shrink W (and hence U) to a connected affine open so that the image of W in
![]() ${{\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_1,{\overline {{D}}}_2}}}}$
lies in
${{\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_1,{\overline {{D}}}_2}}}}$
lies in
![]() $\widetilde {U}_1\cap \widetilde {U}_2$
.Footnote
7
We display the situation in the following diagram:
$\widetilde {U}_1\cap \widetilde {U}_2$
.Footnote
7
We display the situation in the following diagram:

Note also that
![]() ${\varphi }_U(U)$
intersects trivially with
${\varphi }_U(U)$
intersects trivially with
![]() $\iota _{{\overline {{D}}}_1,{\overline {{D}}}_1}(\Delta _{{\overline {{D}}}_1}^{\operatorname {univ}})$
if
$\iota _{{\overline {{D}}}_1,{\overline {{D}}}_1}(\Delta _{{\overline {{D}}}_1}^{\operatorname {univ}})$
if
![]() ${\overline {{D}}}_1={\overline {{D}}}_2$
. Hence, in all cases, the morphism
${\overline {{D}}}_1={\overline {{D}}}_2$
. Hence, in all cases, the morphism
![]() ${{\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_1}}}}\widehat {\times }_{{\mathbb {F}}\,\!{}} {{\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_2}}}} \to {{\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_1,{\overline {{D}}}_2}}}}$
is an étale Galois cover above
${{\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_1}}}}\widehat {\times }_{{\mathbb {F}}\,\!{}} {{\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_2}}}} \to {{\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_1,{\overline {{D}}}_2}}}}$
is an étale Galois cover above
![]() $\widetilde {U}_1\cap \widetilde {U}_2$
with group
$\widetilde {U}_1\cap \widetilde {U}_2$
with group
![]() ${\mathbb {Z}}/2$
or trivial group.
${\mathbb {Z}}/2$
or trivial group.
Let
![]() $w\in W$
be the point corresponding to
$w\in W$
be the point corresponding to
![]() $u\in U$
under the homeomorphism
$u\in U$
under the homeomorphism
![]() $W\to U$
. We complete at w and its images and pass to nil reductions. This gives
$W\to U$
. We complete at w and its images and pass to nil reductions. This gives
By Lemma A.1.14, the maps
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are finite étale. The completion
$\beta $
are finite étale. The completion
![]() $\widehat {{\cal O}}_{\widetilde {U}_1\cap \widetilde {U}_2,(x_1,x_2),{\operatorname {red}}} $
can be compared with the deformation ring
$\widehat {{\cal O}}_{\widetilde {U}_1\cap \widetilde {U}_2,(x_1,x_2),{\operatorname {red}}} $
can be compared with the deformation ring
![]() ${R^{\operatorname {univ}}_{L,(\rho _1,\rho _2)}}$
; using Proposition 4.8.11, it follows that the ring
${R^{\operatorname {univ}}_{L,(\rho _1,\rho _2)}}$
; using Proposition 4.8.11, it follows that the ring
![]() $\widehat {{\cal O}}_{\widetilde {U}_1\cap \widetilde {U}_2,(x_1,x_2),{\operatorname {red}}} $
is formally smooth over L of dimension
$\widehat {{\cal O}}_{\widetilde {U}_1\cap \widetilde {U}_2,(x_1,x_2),{\operatorname {red}}} $
is formally smooth over L of dimension
![]() $d(n_1^2+n_2^2)+1$
, because by Lemma 5.1.6 and by hypothesis Theorem 5.2.1
(a) the rings
$d(n_1^2+n_2^2)+1$
, because by Lemma 5.1.6 and by hypothesis Theorem 5.2.1
(a) the rings
![]() ${R^{\operatorname {univ}}_{\rho _1,{\operatorname {red}}}}$
are formally smooth over L of dimension
${R^{\operatorname {univ}}_{\rho _1,{\operatorname {red}}}}$
are formally smooth over L of dimension
![]() $dn_i^2+1$
. Hence, by Lemma A.1.14 all local rings in the above diagram will be formally smooth over L of dimension
$dn_i^2+1$
. Hence, by Lemma A.1.14 all local rings in the above diagram will be formally smooth over L of dimension
![]() $d(n_1^2+n_2^2)+1$
.
$d(n_1^2+n_2^2)+1$
.
Let now
![]() $\rho \colon G_K\to {\mathrm {GL}}_n(L)$
be a nontrivial extension of
$\rho \colon G_K\to {\mathrm {GL}}_n(L)$
be a nontrivial extension of
![]() $\rho _2$
by
$\rho _2$
by
![]() $\rho _1$
for
$\rho _1$
for
![]() $n=n_1+n_2$
as constructed in Lemma 5.1.7 (a). It possesses a universal deformation ring
$n=n_1+n_2$
as constructed in Lemma 5.1.7 (a). It possesses a universal deformation ring
![]() ${R^{\operatorname {univ}}_{\rho }}$
for deformation to
${R^{\operatorname {univ}}_{\rho }}$
for deformation to
![]() ${\mathcal {A}r}_L$
, because
${\mathcal {A}r}_L$
, because
![]() $L=H^0(G_K,{\operatorname {ad}_{{\rho }}} )$
. Let also
$L=H^0(G_K,{\operatorname {ad}_{{\rho }}} )$
. Let also
![]() $\widehat {R}$
be the universal pseudodeformation ring for
$\widehat {R}$
be the universal pseudodeformation ring for
![]() ${D}_\rho $
, and write
${D}_\rho $
, and write
![]() ${\varphi }$
for the natural morphism between associated space:
${\varphi }$
for the natural morphism between associated space:
The relation to the above is given by the following isomorphism obtained by combining Corollary 4.8.8 and Lemma 3.3.5
We now consider the map
![]() $\operatorname {d}\varphi \colon {\mathbf {t}_{{X^{\mathrm {univ}}_\rho} ,\rho }}\rightarrow {\mathbf {t}_{\widehat {X},x}}$
induced from
$\operatorname {d}\varphi \colon {\mathbf {t}_{{X^{\mathrm {univ}}_\rho} ,\rho }}\rightarrow {\mathbf {t}_{\widehat {X},x}}$
induced from
![]() ${\varphi }$
on tangent spaces at
${\varphi }$
on tangent spaces at
![]() $\rho $
and
$\rho $
and
![]() ${D}_\rho $
, respectively, or rather the induced map on nil-reductions
${D}_\rho $
, respectively, or rather the induced map on nil-reductions
By Lemma 5.1.7 (c) and (d) we have
![]() $\delta \in \{0,1\}$
(and
$\delta \in \{0,1\}$
(and
![]() $\delta =0$
if
$\delta =0$
if
![]() $\zeta _p\notin K$
) such that
$\zeta _p\notin K$
) such that
From (34) and the dimension found for
![]() $\widehat {{\cal O}}_{V,x}$
, we have
$\widehat {{\cal O}}_{V,x}$
, we have
![]() $\dim {\mathbf {t}_{\widehat {X}_{\operatorname {red}},x}}= 1+d(n_1^2+n_2^2)$
. This gives the inequality
$\dim {\mathbf {t}_{\widehat {X}_{\operatorname {red}},x}}= 1+d(n_1^2+n_2^2)$
. This gives the inequality
Using
![]() $n=n_1+n_2$
, we deduce
$n=n_1+n_2$
, we deduce
![]() $dn_1n_2+\delta \le 0$
, which is absurd since both
$dn_1n_2+\delta \le 0$
, which is absurd since both
![]() $n_i>0$
.
$n_i>0$
.
5.3 Alternative proof of Theorem 5.2.1
Following a suggestion of the referee, we now present a second proof of Theorem 5.2.1. It is technically easier than the proof given above, and might be of independent interest. The approach makes no assertion on the geometry of
![]() $ {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
near a reducible point x as in Lemma 5.2.2 but focuses directly on the completed deformation ring at such an x and a dimension estimate.
$ {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
near a reducible point x as in Lemma 5.2.2 but focuses directly on the completed deformation ring at such an x and a dimension estimate.
Let R be a Noetherian
![]() ${{\mathbb {F}}\,\!{}}$
-algebra, and let A be an associative (possible noncommutative) unital R-algebra, which is finitely generated as an R-module. For
${{\mathbb {F}}\,\!{}}$
-algebra, and let A be an associative (possible noncommutative) unital R-algebra, which is finitely generated as an R-module. For
![]() $x\in {\mathrm {Spec}}\ R$
, write
$x\in {\mathrm {Spec}}\ R$
, write
![]() $A_x:= A\otimes _R {\kappa ({x})} $
, where
$A_x:= A\otimes _R {\kappa ({x})} $
, where
![]() ${\kappa ({x})} $
is the residue field of x; that is,
${\kappa ({x})} $
is the residue field of x; that is,
![]() $A_x$
is the fiber at x and not a localization. Let
$A_x$
is the fiber at x and not a localization. Let
be the Azumaya locus of A in
![]() ${\mathrm {Spec}}\ R$
.
${\mathrm {Spec}}\ R$
.
Lemma 5.3.1. The Azumaya locus U is a constructible subset of
![]() ${\mathrm {Spec}}\ R$
.
${\mathrm {Spec}}\ R$
.
Proof. By [Reference StacksSta18, Lemma 051Z] and Noetherian induction, we can find a flattening stratification of A as an R-module, that is, a finite increasing chain of open subsets
![]() $U_0\subset \ldots \subset U_n={\mathrm {Spec}}\ R$
such that if
$U_0\subset \ldots \subset U_n={\mathrm {Spec}}\ R$
such that if
![]() $R_i$
is the reduced quotient of R with
$R_i$
is the reduced quotient of R with
![]() ${\mathrm {Spec}}\ R_i={\mathrm {Spec}}\ R{\smallsetminus } U_i$
, then
${\mathrm {Spec}}\ R_i={\mathrm {Spec}}\ R{\smallsetminus } U_i$
, then
![]() $U_{i+1}{\smallsetminus } U_i={\mathrm {Spec}}\ (R_i)_{f_i}$
for some
$U_{i+1}{\smallsetminus } U_i={\mathrm {Spec}}\ (R_i)_{f_i}$
for some
![]() $f_i\in R_i$
and
$f_i\in R_i$
and
![]() $A\otimes _R(R_i)_{f_1}$
is finite flat over
$A\otimes _R(R_i)_{f_1}$
is finite flat over
![]() ${\mathrm {Spec}}\ (R_i)_{f_i}$
. Hence, to prove the assertion on U, we may assume that A is finite flat over R.
${\mathrm {Spec}}\ (R_i)_{f_i}$
. Hence, to prove the assertion on U, we may assume that A is finite flat over R.
Now, let C and K be R-modules fitting in the exact sequence
Because C and K are finitely generated modules over the Noetherian ring R, their support is closed, and we deduce that
![]() $U = {\mathrm {Spec}}\ R{\smallsetminus } ({\mathop {\mathrm Supp}\nolimits } C\cup {\mathop {\mathrm Supp}\nolimits } K)$
is open in
$U = {\mathrm {Spec}}\ R{\smallsetminus } ({\mathop {\mathrm Supp}\nolimits } C\cup {\mathop {\mathrm Supp}\nolimits } K)$
is open in
![]() ${\mathrm {Spec}}\ R$
and hence constructible.
${\mathrm {Spec}}\ R$
and hence constructible.
Lemma 5.3.2. Let x be in
![]() ${\mathrm {Spec}}\ R$
, let
${\mathrm {Spec}}\ R$
, let
![]() $\widehat {R}$
be the completion of
$\widehat {R}$
be the completion of
![]() ${\kappa ({x})} \otimes _{{\mathbb {F}}\,\!{}} R$
at the kernel of the natural map
${\kappa ({x})} \otimes _{{\mathbb {F}}\,\!{}} R$
at the kernel of the natural map
![]() ${\kappa ({x})} \otimes _{{\mathbb {F}}\,\!{}} R\to {\kappa ({x})} $
and let
${\kappa ({x})} \otimes _{{\mathbb {F}}\,\!{}} R\to {\kappa ({x})} $
and let
![]() $\widehat {A}=A\otimes _R\widehat {R}$
. Let
$\widehat {A}=A\otimes _R\widehat {R}$
. Let
![]() $y\in {\mathrm {Spec}}\ \widehat {R}$
be such that
$y\in {\mathrm {Spec}}\ \widehat {R}$
be such that
![]() $\widehat {A}_y$
is an Azumaya algebra. Then U is nonempty and x lies in the closure of U in
$\widehat {A}_y$
is an Azumaya algebra. Then U is nonempty and x lies in the closure of U in
![]() ${\mathrm {Spec}}\ R$
.
${\mathrm {Spec}}\ R$
.
Proof. Let z be the image of y under
![]() ${\mathrm {Spec}}\ \widehat {R}\to {\mathrm {Spec}}\ R$
, and note that we have induced maps
${\mathrm {Spec}}\ \widehat {R}\to {\mathrm {Spec}}\ R$
, and note that we have induced maps
![]() $\iota \colon R/{\mathfrak {p}}_z\to \widehat {R}/{\mathfrak {p}}_y$
and
$\iota \colon R/{\mathfrak {p}}_z\to \widehat {R}/{\mathfrak {p}}_y$
and
![]() ${\kappa ({z})} \to {\kappa ({y})}$
for
${\kappa ({z})} \to {\kappa ({y})}$
for
![]() ${\mathfrak {p}}_z\subset R$
and
${\mathfrak {p}}_z\subset R$
and
![]() ${\mathfrak {p}}_y\subset \widehat {R}$
the primes corresponding to z and y, respectively. Since
${\mathfrak {p}}_y\subset \widehat {R}$
the primes corresponding to z and y, respectively. Since
![]() $\widehat {A}_y=A_z\otimes _{{\kappa ({z})} }{\kappa ({y})}$
, and
$\widehat {A}_y=A_z\otimes _{{\kappa ({z})} }{\kappa ({y})}$
, and
![]() ${\kappa ({z})} \to {\kappa ({y})}$
is faithfully flat, the diagram (35) with
${\kappa ({z})} \to {\kappa ({y})}$
is faithfully flat, the diagram (35) with
![]() $A_z$
and
$A_z$
and
![]() ${\kappa ({z})}$
in place of A and R, respectively, implies
${\kappa ({z})}$
in place of A and R, respectively, implies
![]() $z\in U$
so that U is nonempty.
$z\in U$
so that U is nonempty.
Moreover, by our definitions, the residue map
![]() $R\to \widehat {R} \to {\kappa ({x})} $
factors via
$R\to \widehat {R} \to {\kappa ({x})} $
factors via
![]() $R/{\mathfrak {p}}_z\stackrel \iota \to \widehat {R}/{\mathfrak {p}}_y\to {\kappa ({x})} $
with
$R/{\mathfrak {p}}_z\stackrel \iota \to \widehat {R}/{\mathfrak {p}}_y\to {\kappa ({x})} $
with
![]() $\iota $
injective. Hence,
$\iota $
injective. Hence,
![]() $x\in {\mathrm {Spec}}\ R/{\mathfrak {p}}_z=\overline { \{z\}}\subset {\mathrm {Spec}}\ R$
so that x lies in the closure of
$x\in {\mathrm {Spec}}\ R/{\mathfrak {p}}_z=\overline { \{z\}}\subset {\mathrm {Spec}}\ R$
so that x lies in the closure of
![]() $\{z\}$
and hence in the closure of
$\{z\}$
and hence in the closure of
![]() $U\supset \{z\}$
.
$U\supset \{z\}$
.
Let now
![]() $R:= {\overline {R}^{\operatorname {univ}}_{{\overline {{D}}}}}$
be the special fiber of the universal deformation ring for
$R:= {\overline {R}^{\operatorname {univ}}_{{\overline {{D}}}}}$
be the special fiber of the universal deformation ring for
![]() ${\overline {{D}}}$
so that R is complete Noetherian local with finite residue field. Let
${\overline {{D}}}$
so that R is complete Noetherian local with finite residue field. Let
![]() $A={\overline {{S}}^{{\operatorname {CH-univ}}}_{{\overline {{D}}}}}$
be the corresponding Cayley–Hamilton R-algebra so that by Proposition 4.7.11 the ring A is finitely generated as an R-module and hence Noetherian. In this setting, U is precisely the absolutely irreducible locus of
$A={\overline {{S}}^{{\operatorname {CH-univ}}}_{{\overline {{D}}}}}$
be the corresponding Cayley–Hamilton R-algebra so that by Proposition 4.7.11 the ring A is finitely generated as an R-module and hence Noetherian. In this setting, U is precisely the absolutely irreducible locus of
![]() ${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
as explained in [Reference ChenevierChe14, Corollary 2.23]; see also Proposition 4.7.18.
${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
as explained in [Reference ChenevierChe14, Corollary 2.23]; see also Proposition 4.7.18.
Proposition 5.3.3. In the setting just described, the closure of U in
![]() ${\mathrm {Spec}}\ R$
contains all points
${\mathrm {Spec}}\ R$
contains all points
![]() $x\in {\mathrm {Spec}}\ R$
of dimension
$x\in {\mathrm {Spec}}\ R$
of dimension
![]() $1$
such that
$1$
such that
![]() ${D}_x={D}_{1}+{D}_{2}$
, where the
${D}_x={D}_{1}+{D}_{2}$
, where the
![]() ${D}_i$
are nonspecial pseudocharacters of absolutely irreducible representations
${D}_i$
are nonspecial pseudocharacters of absolutely irreducible representations
![]() $\rho _i$
,
$\rho _i$
,
![]() $i=1,2$
such that
$i=1,2$
such that
![]() $\rho _1\not \cong \rho _2(j)$
for
$\rho _1\not \cong \rho _2(j)$
for
![]() $j\in \{0,\pm 1\}$
.
$j\in \{0,\pm 1\}$
.
Proof. In view of Lemma 5.3.2, we only have to explain how to find y. By Corollary 4.8.8 the ring
![]() $\widehat {R}$
can be identified with the universal pseudodeformation ring of
$\widehat {R}$
can be identified with the universal pseudodeformation ring of
![]() ${D}_x$
, and we need to show that the reducible locus in
${D}_x$
, and we need to show that the reducible locus in
![]() ${\mathrm {Spec}}\ \widehat {R}$
is not the whole of
${\mathrm {Spec}}\ \widehat {R}$
is not the whole of
![]() ${\mathrm {Spec}}\ \widehat {R}$
.
${\mathrm {Spec}}\ \widehat {R}$
.
To show this, we compare
![]() $\widehat {R}$
with the universal deformation ring
$\widehat {R}$
with the universal deformation ring
![]() $\overline R^{\operatorname {univ}}_{\rho }$
, where
$\overline R^{\operatorname {univ}}_{\rho }$
, where
![]() $\rho $
is a nonsplit extension of
$\rho $
is a nonsplit extension of
![]() $\rho _2$
by
$\rho _2$
by
![]() $\rho _1$
. The existence of
$\rho _1$
. The existence of
![]() $\rho $
and of
$\rho $
and of
![]() $\overline R^{\operatorname {univ}}_{\rho }$
was established in Lemma 5.1.7
(a). Moreover, by Lemma 5.1.7
(c) and (d), respectively, the ring
$\overline R^{\operatorname {univ}}_{\rho }$
was established in Lemma 5.1.7
(a). Moreover, by Lemma 5.1.7
(c) and (d), respectively, the ring
![]() $R':=(\overline R^{\operatorname {univ}}_{\rho })_{\operatorname {red}}$
is formally smooth over
$R':=(\overline R^{\operatorname {univ}}_{\rho })_{\operatorname {red}}$
is formally smooth over
![]() $\kappa (x)$
of dimension
$\kappa (x)$
of dimension
![]() $dn^2 +1$
. The map that sends a representation to its associated pseudocharacter induces a map
$dn^2 +1$
. The map that sends a representation to its associated pseudocharacter induces a map
![]() ${\mathrm {Spec}}\ \overline R^{\operatorname {univ}}_{\rho }\to {\mathrm {Spec}}\widehat {R}$
, and it will suffice to show that the generic point of
${\mathrm {Spec}}\ \overline R^{\operatorname {univ}}_{\rho }\to {\mathrm {Spec}}\widehat {R}$
, and it will suffice to show that the generic point of
![]() $R'=(\overline R^{\operatorname {univ}}_{\rho })_{\operatorname {red}}$
gives rise to an absolutely irreducible representation of
$R'=(\overline R^{\operatorname {univ}}_{\rho })_{\operatorname {red}}$
gives rise to an absolutely irreducible representation of
![]() $G_K$
. Let
$G_K$
. Let
![]() ${\mathfrak {m}}'\subset R'$
be its maximal ideal.
${\mathfrak {m}}'\subset R'$
be its maximal ideal.
Denote by
![]() $\rho '\colon G_K\to {\mathrm {GL}}_n(R')$
a representation corresponding to
$\rho '\colon G_K\to {\mathrm {GL}}_n(R')$
a representation corresponding to
![]() $R'$
. Because
$R'$
. Because
![]() ${D}_\rho $
is multiplicity free, by Theorem 4.3.10(b) the linearization of
${D}_\rho $
is multiplicity free, by Theorem 4.3.10(b) the linearization of
![]() $\rho '$
factors via a GMA of type
$\rho '$
factors via a GMA of type
![]() $(n_1,n_2)$
inside
$(n_1,n_2)$
inside
![]() ${\mathrm {Mat}}_{n\times n}(R')$
and thus gives a continuous surjective homomorphism
${\mathrm {Mat}}_{n\times n}(R')$
and thus gives a continuous surjective homomorphism
 $$ \begin{align*}R'[G_K]\,{\longrightarrow}\, \left(\begin{array}{cc} {\mathrm{Mat}}_{n_1\times n_1}(R')&{\mathrm{Mat}}_{n_1\times n_2}(J')\\ {\mathrm{Mat}}_{n_2\times n_1}(I')&{\mathrm{Mat}}_{n_2\times n_2}(R') \end{array}\right) \end{align*} $$
$$ \begin{align*}R'[G_K]\,{\longrightarrow}\, \left(\begin{array}{cc} {\mathrm{Mat}}_{n_1\times n_1}(R')&{\mathrm{Mat}}_{n_1\times n_2}(J')\\ {\mathrm{Mat}}_{n_2\times n_1}(I')&{\mathrm{Mat}}_{n_2\times n_2}(R') \end{array}\right) \end{align*} $$
for suitable ideals
![]() $I',J'$
of
$I',J'$
of
![]() $R'$
. The reduction modulo
$R'$
. The reduction modulo
![]() ${\mathfrak {m}}'$
of the right-hand side arises from the nonsplit extension
${\mathfrak {m}}'$
of the right-hand side arises from the nonsplit extension
![]() $\rho $
of
$\rho $
of
![]() $\rho _2$
by
$\rho _2$
by
![]() $\rho _1$
so that we must have
$\rho _1$
so that we must have
![]() $J'=R'$
, and
$J'=R'$
, and
![]() $I'\subset {\mathfrak {m}}'$
.
$I'\subset {\mathfrak {m}}'$
.
If
![]() $I'$
is nonzero, then after passing from the regular local ring
$I'$
is nonzero, then after passing from the regular local ring
![]() $R'$
to its fraction field, say
$R'$
to its fraction field, say
![]() $E'$
, we obtain
$E'$
, we obtain
![]() ${\mathrm {Mat}}_{n\times n}(E')$
as the image of the linearization map, and by the theorem of Burnside the corresponding representation is absolutely irreducible. If on the other hand
${\mathrm {Mat}}_{n\times n}(E')$
as the image of the linearization map, and by the theorem of Burnside the corresponding representation is absolutely irreducible. If on the other hand
![]() $I'=0$
, then
$I'=0$
, then
![]() $\rho '$
is reducible and we apply Proposition 3.4.6 and the discussion preceding it. It follows that
$\rho '$
is reducible and we apply Proposition 3.4.6 and the discussion preceding it. It follows that
![]() $\dim (R^{\operatorname {univ}}_{\rho _1\subset \rho })_{\operatorname {red}}=d(n^2-n_1n_2)+1$
and that the induced map of reduced rings
$\dim (R^{\operatorname {univ}}_{\rho _1\subset \rho })_{\operatorname {red}}=d(n^2-n_1n_2)+1$
and that the induced map of reduced rings
![]() $R'\to (R^{\operatorname {univ}}_{\rho _1\subset \rho })_{\operatorname {red}}$
is an isomorphism. This contradicts
$R'\to (R^{\operatorname {univ}}_{\rho _1\subset \rho })_{\operatorname {red}}$
is an isomorphism. This contradicts
![]() $\dim R'=dn^2+1$
found above, and so the case
$\dim R'=dn^2+1$
found above, and so the case
![]() $I'=0$
cannot occur.
$I'=0$
cannot occur.
Proof (Second proof of Theorem 5.2.1).
Let
![]() $U=({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{{\operatorname {irr}}}$
be the open locus of irreducible points on
$U=({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{{\operatorname {irr}}}$
be the open locus of irreducible points on
![]() ${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
. We need to show that the closure of U is the whole space. By the reduction steps given in the first two paragraphs of the first proof of Theorem 5.2.1 on page 68, it suffices to show that all points
${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
. We need to show that the closure of U is the whole space. By the reduction steps given in the first two paragraphs of the first proof of Theorem 5.2.1 on page 68, it suffices to show that all points
![]() $x\in {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
of dimension
$x\in {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
of dimension
![]() $1$
such that
$1$
such that
![]() $D_x=D_1+D_2$
with
$D_x=D_1+D_2$
with
![]() $D_i$
irreducible nonspecial and
$D_i$
irreducible nonspecial and
![]() $D_2\neq D_1(j)$
for
$D_2\neq D_1(j)$
for
![]() $j\in \{0,\pm 1\}$
lie in the closure of U. This follows from Proposition 5.3.3.
$j\in \{0,\pm 1\}$
lie in the closure of U. This follows from Proposition 5.3.3.
5.4 A dimension bound for the special locus
As before, we denote by
![]() ${\overline {{D}}}\colon G_K\to {{\mathbb {F}}\,\!{}}$
a residual pseudocharacter on
${\overline {{D}}}\colon G_K\to {{\mathbb {F}}\,\!{}}$
a residual pseudocharacter on
![]() $G_K$
, and we let n be its dimension. Theorem 5.2.1 of the previous subsection provided part of an inductive procedure to prove the equidimensionality of
$G_K$
, and we let n be its dimension. Theorem 5.2.1 of the previous subsection provided part of an inductive procedure to prove the equidimensionality of
![]() ${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}}$
for the dimension
${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}}$
for the dimension
![]() $[K:{\mathbb {Q}}_p]\cdot n^2+1$
. It remains to be proved that
$[K:{\mathbb {Q}}_p]\cdot n^2+1$
. It remains to be proved that
![]() $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}})^{{\mathrm {n}\textrm {-}\mathrm {spcl}}}\subset ({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}})^{\operatorname {irr}}$
is Zariski dense. In this subsection, we shall prove the following result.
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}})^{{\mathrm {n}\textrm {-}\mathrm {spcl}}}\subset ({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}})^{\operatorname {irr}}$
is Zariski dense. In this subsection, we shall prove the following result.
Theorem 5.4.1. Let
![]() $n\ge 2$
be an integer. Suppose that for all pseudocharacters
$n\ge 2$
be an integer. Suppose that for all pseudocharacters
![]() ${\overline {{D}}}'\colon G_{K'}\to {{\mathbb {F}}\,\!{}}$
on
${\overline {{D}}}'\colon G_{K'}\to {{\mathbb {F}}\,\!{}}$
on
![]() $G_K$
of dimension
$G_K$
of dimension
![]() $n'<n$
with
$n'<n$
with
![]() $K'$
a p-adic field the Krull dimension of the space
$K'$
a p-adic field the Krull dimension of the space
![]() ${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K',{\overline {{D}}}'}}}$
is bounded by
${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K',{\overline {{D}}}'}}}$
is bounded by
![]() $[K':{\mathbb {Q}}_p](n')^2+1$
, Then for all n-dimensional pseudocharacters
$[K':{\mathbb {Q}}_p](n')^2+1$
, Then for all n-dimensional pseudocharacters
![]() ${\overline {{D}}} \colon G_K\to {{\mathbb {F}}\,\!{}}$
on
${\overline {{D}}} \colon G_K\to {{\mathbb {F}}\,\!{}}$
on
![]() $G_K$
one has:
$G_K$
one has:
-
(a) The Zariski closure of
 $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}})^{\mathrm {spcl}}$
has dimension at most
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}})^{\mathrm {spcl}}$
has dimension at most
 $\frac 12 [K:{\mathbb {Q}}_p]n^2+1$
.
$\frac 12 [K:{\mathbb {Q}}_p]n^2+1$
. -
(b)
 $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}})^{{\mathrm {n}\textrm {-}\mathrm {spcl}}}\subset ({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}})^{\operatorname {irr}}$
is Zariski dense.
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}})^{{\mathrm {n}\textrm {-}\mathrm {spcl}}}\subset ({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}})^{\operatorname {irr}}$
is Zariski dense.
Before giving the proof, we need the following auxiliary result.
Lemma 5.4.2. Let
![]() $\overline {{R}}_{G,{{\mathbb {F}}\,\!{}},{\overline {{D}}}}\to A$
be a surjective homomorphism such that A is a domain with field of fractions
$\overline {{R}}_{G,{{\mathbb {F}}\,\!{}},{\overline {{D}}}}\to A$
be a surjective homomorphism such that A is a domain with field of fractions
![]() ${\mathbb {K}}$
, and set
${\mathbb {K}}$
, and set
![]() ${D}_A:={{D}^{\operatorname {univ}}_{{\overline {{D}}}}}\otimes _{\overline {{R}}_{G,{{\mathbb {F}}\,\!{}},{\overline {{D}}}}}A $
. Let
${D}_A:={{D}^{\operatorname {univ}}_{{\overline {{D}}}}}\otimes _{\overline {{R}}_{G,{{\mathbb {F}}\,\!{}},{\overline {{D}}}}}A $
. Let
![]() $H\subset G$
be an open normal subgroup and suppose the following hold:
$H\subset G$
be an open normal subgroup and suppose the following hold:
-
(i)
 ${\overline {{D}}}|_H$
is split over
${\overline {{D}}}|_H$
is split over
 ${{\mathbb {F}}\,\!{}}$
and condition
${{\mathbb {F}}\,\!{}}$
and condition
 $\Phi _{{\overline {{D}}}_H}$
is satisfied.
$\Phi _{{\overline {{D}}}_H}$
is satisfied. -
(ii)
 ${D}_{\mathbb {K}}:={D}_A\otimes _A{\mathbb {K}}$
is irreducible and
${D}_{\mathbb {K}}:={D}_A\otimes _A{\mathbb {K}}$
is irreducible and
 $\rho :=\rho _{{D}_{\mathbb {K}}\otimes {{{{\mathbb {K}}}}^{\mathrm {alg}}} }$
is induced from H.
$\rho :=\rho _{{D}_{\mathbb {K}}\otimes {{{{\mathbb {K}}}}^{\mathrm {alg}}} }$
is induced from H.
Then there exist a domain
![]() $A'\in {\widehat {\mathcal {A}}r}_{{\mathbb {F}}\,\!{}}$
that contains A and is finite over A, and a continuous irreducible pseudocharacter
$A'\in {\widehat {\mathcal {A}}r}_{{\mathbb {F}}\,\!{}}$
that contains A and is finite over A, and a continuous irreducible pseudocharacter
![]() ${D}'\colon A'[H]\to A'$
that is residually equal to a direct summand
${D}'\colon A'[H]\to A'$
that is residually equal to a direct summand
![]() ${\overline {{D}}}{}'$
of
${\overline {{D}}}{}'$
of
![]() ${\overline {{D}}}_H$
such that the following hold:
${\overline {{D}}}_H$
such that the following hold:
-
(a)
 ${\mathrm {Ind}}_H^G{D}'={D}_A\otimes _AA'$
${\mathrm {Ind}}_H^G{D}'={D}_A\otimes _AA'$
-
(b) The homomorphism
 $\overline {{R}}_{H,{{\mathbb {F}}\,\!{}},{\overline {{D}}}'}\to A'$
that results from
$\overline {{R}}_{H,{{\mathbb {F}}\,\!{}},{\overline {{D}}}'}\to A'$
that results from
 ${D}'$
is surjective.
${D}'$
is surjective.
In particular,
![]() $\dim A=\dim A'\le \dim \overline {{R}}_{H,{{\mathbb {F}}\,\!{}},{\overline {{D}}}'}$
.
$\dim A=\dim A'\le \dim \overline {{R}}_{H,{{\mathbb {F}}\,\!{}},{\overline {{D}}}'}$
.
Proof. Note first by Lemma 2.1.4
(b) and (f) that
![]() $\rho ={\mathrm {Ind}}_H^G\rho '$
for some irreducible representation
$\rho ={\mathrm {Ind}}_H^G\rho '$
for some irreducible representation
![]() $\rho '\colon H\to {\mathrm {GL}}_{n'}({{{{{\mathbb {K}}}}^{\mathrm {alg}}} })$
such that the representations
$\rho '\colon H\to {\mathrm {GL}}_{n'}({{{{{\mathbb {K}}}}^{\mathrm {alg}}} })$
such that the representations
![]() $(\rho ')^g$
,
$(\rho ')^g$
,
![]() $g\in G/H$
, are pairwise nonisomorphic, and that
$g\in G/H$
, are pairwise nonisomorphic, and that
![]() ${\mathrm {Res}}_H^G\rho =\bigoplus _{g\in G/H} (\rho ')^g$
. Hence,
${\mathrm {Res}}_H^G\rho =\bigoplus _{g\in G/H} (\rho ')^g$
. Hence,
![]() ${D}_{\mathbb {K}}|_H$
is multiplicity free so that we can apply Proposition 4.8.6 to it.
${D}_{\mathbb {K}}|_H$
is multiplicity free so that we can apply Proposition 4.8.6 to it.
By what we just observed, conjugation by
![]() $G/H$
acts simply transitively on the continuous pseudocharacters
$G/H$
acts simply transitively on the continuous pseudocharacters
![]() ${D}_i^{\prime }$
from Proposition 4.8.6, and so the
${D}_i^{\prime }$
from Proposition 4.8.6, and so the
![]() $A_i$
from Proposition 4.8.6 are independent of i. Define
$A_i$
from Proposition 4.8.6 are independent of i. Define
![]() $A'$
as any of the
$A'$
as any of the
![]() $A_i$
, and let
$A_i$
, and let
![]() ${D}'\colon A'[H]\to A'$
be that pseudocharacter
${D}'\colon A'[H]\to A'$
be that pseudocharacter
![]() ${D}^{\prime }_i$
for which
${D}^{\prime }_i$
for which
![]() ${D}^{\prime }_i\otimes _{A'}{{{{\mathbb {K}}}}^{\mathrm {alg}}} $
is the pseudocharacter attached to
${D}^{\prime }_i\otimes _{A'}{{{{\mathbb {K}}}}^{\mathrm {alg}}} $
is the pseudocharacter attached to
![]() $\rho '$
. Then
$\rho '$
. Then
![]() ${\mathrm {Ind}}_H^G{D}'\otimes _{A'}{{{{\mathbb {K}}}}^{\mathrm {alg}}} ={D}_A\otimes _A{{{{\mathbb {K}}}}^{\mathrm {alg}}} $
. Now,
${\mathrm {Ind}}_H^G{D}'\otimes _{A'}{{{{\mathbb {K}}}}^{\mathrm {alg}}} ={D}_A\otimes _A{{{{\mathbb {K}}}}^{\mathrm {alg}}} $
. Now,
![]() ${\mathrm {Ind}}_H^G{D}'$
is defined over
${\mathrm {Ind}}_H^G{D}'$
is defined over
![]() $A'$
and A is the minimal field of definition of
$A'$
and A is the minimal field of definition of
![]() ${D}_A$
by Corollary 4.7.13. Hence, A is contained in
${D}_A$
by Corollary 4.7.13. Hence, A is contained in
![]() $A'$
. By Proposition 4.8.6 it is then clear that
$A'$
. By Proposition 4.8.6 it is then clear that
![]() $A'$
is finite integral over A and lies in
$A'$
is finite integral over A and lies in
![]() ${\widehat {\mathcal {A}}r}_{{\mathbb {F}}\,\!{}}$
, and moreover that
${\widehat {\mathcal {A}}r}_{{\mathbb {F}}\,\!{}}$
, and moreover that
![]() $\oplus _{g\in G/H}({\overline {{D}}}{}')^g={\overline {{D}}}$
for
$\oplus _{g\in G/H}({\overline {{D}}}{}')^g={\overline {{D}}}$
for
![]() ${D}{}':={D}'\otimes _{A'}{\kappa ({A'})}$
. Part (a) is now clear.
${D}{}':={D}'\otimes _{A'}{\kappa ({A'})}$
. Part (a) is now clear.
It is also clear that
![]() ${D}'$
is a deformation of
${D}'$
is a deformation of
![]() ${\overline {{D}}}{}'$
. Since
${\overline {{D}}}{}'$
. Since
![]() $A'\in {\widehat {\mathcal {A}}r}_{{\mathbb {F}}\,\!{}}$
, we have a corresponding homomorphism
$A'\in {\widehat {\mathcal {A}}r}_{{\mathbb {F}}\,\!{}}$
, we have a corresponding homomorphism
![]() $\overline {{R}}_{H,{{\mathbb {F}}\,\!{}},{\overline {{D}}}'}\to A'$
, and the latter must be surjective by Corollary 4.7.13 since
$\overline {{R}}_{H,{{\mathbb {F}}\,\!{}},{\overline {{D}}}'}\to A'$
, and the latter must be surjective by Corollary 4.7.13 since
![]() $A'$
is the ring of definition of
$A'$
is the ring of definition of
![]() ${D}'$
. Now, by Lemma A.1.2 we have
${D}'$
. Now, by Lemma A.1.2 we have
![]() $\dim A'=\dim A$
, and the inequality
$\dim A'=\dim A$
, and the inequality
![]() $\dim A'\le \dim \overline {{R}}_{H,{{\mathbb {F}}\,\!{}},{\overline {{D}}}'}$
is trivial.
$\dim A'\le \dim \overline {{R}}_{H,{{\mathbb {F}}\,\!{}},{\overline {{D}}}'}$
is trivial.
Proof of Theorem 5.4.1.
By Lemma 3.2.6, by possibly enlarging
![]() ${{\mathbb {F}}\,\!{}}$
, we may assume that
${{\mathbb {F}}\,\!{}}$
, we may assume that
![]() ${\overline {{D}}}$
is split over
${\overline {{D}}}$
is split over
![]() ${{\mathbb {F}}\,\!{}}$
. Since the number of Galois extensions
${{\mathbb {F}}\,\!{}}$
. Since the number of Galois extensions
![]() $K'$
of K of degree p is finite, we may, by the same reasoning, also assume that
$K'$
of K of degree p is finite, we may, by the same reasoning, also assume that
![]() ${D}|_{G_K'}$
is split for any such
${D}|_{G_K'}$
is split for any such
![]() $K'$
and for
$K'$
and for
![]() $K'=K(\zeta _p)$
. It is also clear that Mazur’s condition
$K'=K(\zeta _p)$
. It is also clear that Mazur’s condition
![]() $\Phi _p$
holds over any such
$\Phi _p$
holds over any such
![]() $K'$
and hence
$K'$
and hence
![]() $\Phi _{{\overline {{D}}}|_{G_{K'}}}$
holds.
$\Phi _{{\overline {{D}}}|_{G_{K'}}}$
holds.
To prove (a), let
![]() $\eta $
be any generic point of
$\eta $
be any generic point of
![]() $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\mathrm {spcl}}$
. Let
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\mathrm {spcl}}$
. Let
be the corresponding surjective ring homomorphism so that
![]() $\eta ={\mathop {\mathrm{Ker}}\nolimits }(\varphi )$
. Because
$\eta ={\mathop {\mathrm{Ker}}\nolimits }(\varphi )$
. Because
![]() ${D}_\eta $
is irreducible,
${D}_\eta $
is irreducible,
![]() $\rho :=\rho _{{D}_\eta \otimes _{{\kappa ({\eta })}}{{{{\kappa ({\eta })}}}^{\mathrm {alg}}} }$
is defined. Since
$\rho :=\rho _{{D}_\eta \otimes _{{\kappa ({\eta })}}{{{{\kappa ({\eta })}}}^{\mathrm {alg}}} }$
is defined. Since
![]() $\eta $
is special, there exists a Galois extension
$\eta $
is special, there exists a Galois extension
![]() $K'$
of K such that either
$K'$
of K such that either
![]() $K'=K(\zeta _p)$
or
$K'=K(\zeta _p)$
or
![]() $K'$
has degree p over K and such that
$K'$
has degree p over K and such that
![]() $\rho $
is induced from
$\rho $
is induced from
![]() $G_{K'}$
. From Lemma 5.4.2, we deduce
$G_{K'}$
. From Lemma 5.4.2, we deduce
As the schemes
![]() ${\mathrm {Spec}}\ A$
cover
${\mathrm {Spec}}\ A$
cover
![]() $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}})^{\mathrm {spcl}}$
and as
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}})^{\mathrm {spcl}}$
and as
![]() $[K':K]\ge 2$
, the proof of (a) is complete.
$[K':K]\ge 2$
, the proof of (a) is complete.
To prove (b), we argue by contradiction and assume that there exists an open subset
![]() $V\subset {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}}$
that is entirely contained in
$V\subset {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}}$
that is entirely contained in
![]() $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}})^{\mathrm {spcl}}$
. Then
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{K,{\overline {{D}}}}}})^{\mathrm {spcl}}$
. Then
![]() $\dim \overline V\le \frac 12 [K:{\mathbb {Q}}_p]n^2 +1$
by (b), for
$\dim \overline V\le \frac 12 [K:{\mathbb {Q}}_p]n^2 +1$
by (b), for
![]() $\overline V$
the Zariski closure of V. Let x be any dimension
$\overline V$
the Zariski closure of V. Let x be any dimension
![]() $1$
point of V, and let
$1$
point of V, and let
![]() $\rho \colon G_K\to {\mathrm {GL}}_n(L)$
be an absolutely irreducible representation over a local field L containing
$\rho \colon G_K\to {\mathrm {GL}}_n(L)$
be an absolutely irreducible representation over a local field L containing
![]() ${\kappa ({x})} $
such that
${\kappa ({x})} $
such that
![]() ${D}_\rho ={D}_x\otimes _{{\kappa ({x})} }L$
. Let
${D}_\rho ={D}_x\otimes _{{\kappa ({x})} }L$
. Let
![]() ${R^{\operatorname {univ}}_{\rho }}$
be the universal ring for deformations of
${R^{\operatorname {univ}}_{\rho }}$
be the universal ring for deformations of
![]() $\rho $
to
$\rho $
to
![]() ${\mathcal {A}r}_L$
. Then
${\mathcal {A}r}_L$
. Then
![]() $\widehat {{\cal O}}_{\overline {V},x}[[T]]\cong {R^{\operatorname {univ}}_{\rho }}$
by Corollary 4.8.8 and Lemma 3.3.5. On the other hand,
$\widehat {{\cal O}}_{\overline {V},x}[[T]]\cong {R^{\operatorname {univ}}_{\rho }}$
by Corollary 4.8.8 and Lemma 3.3.5. On the other hand,
![]() $\dim {R^{\operatorname {univ}}_{\rho }}\ge [K:{\mathbb {Q}}_p]n^2+1$
by a standard argument using Theorem 3.4.1. It follows that
$\dim {R^{\operatorname {univ}}_{\rho }}\ge [K:{\mathbb {Q}}_p]n^2+1$
by a standard argument using Theorem 3.4.1. It follows that
and hence
![]() $2\ge [K:{\mathbb {Q}}_p]n^2$
, which implies
$2\ge [K:{\mathbb {Q}}_p]n^2$
, which implies
![]() $n=1$
. But then x cannot be induced, and hence not special, and we reach a contradiction.
$n=1$
. But then x cannot be induced, and hence not special, and we reach a contradiction.
5.5 Main results
Let K be a p-adic field, let
![]() ${\overline {{D}}}\colon G_K\to {{\mathbb {F}}\,\!{}}$
be a residual pseudocharacter on
${\overline {{D}}}\colon G_K\to {{\mathbb {F}}\,\!{}}$
be a residual pseudocharacter on
![]() $G_K$
, and set
$G_K$
, and set
![]() $n\!:=\!\dim {\overline {{D}}}$
.
$n\!:=\!\dim {\overline {{D}}}$
.
Theorem 5.5.1 (Theorem 1].
The following assertions hold:
-
(a)
 ${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
is equidimensional of dimension
${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
is equidimensional of dimension
 $[K:{\mathbb {Q}}_p] n^2+1$
.
$[K:{\mathbb {Q}}_p] n^2+1$
. -
(b)
 $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{{{\mathrm {n}\textrm {-}\mathrm {spcl}}}}\subset {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
is open and Zariski dense.
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{{{\mathrm {n}\textrm {-}\mathrm {spcl}}}}\subset {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
is open and Zariski dense. -
(c) If
 $\zeta _p\notin K$
, then
$\zeta _p\notin K$
, then
 $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{{{\mathrm {n}\textrm {-}\mathrm {spcl}}}}$
is regular.
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{{{\mathrm {n}\textrm {-}\mathrm {spcl}}}}$
is regular. -
(d) If
 $\zeta _p\in K$
, then
$\zeta _p\in K$
, then
 $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})_{\operatorname {red}}^{{{\mathrm {n}\textrm {-}\mathrm {spcl}}}}$
is regular, and
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})_{\operatorname {red}}^{{{\mathrm {n}\textrm {-}\mathrm {spcl}}}}$
is regular, and
 $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{{\operatorname {reg}}}$
is empty.
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{{\operatorname {reg}}}$
is empty.
Proof. Part (a) follows from Corollary 3.4.3, Theorem 5.2.1 and Theorem 5.4.1 by induction on
![]() $\dim {\overline {{D}}}$
and
$\dim {\overline {{D}}}$
and
![]() $[K:{\mathbb {Q}}_p]$
. The same results also prove (b). Parts (c) and (d) follow from Lemma 5.1.6; the last part of (d) uses Corollary 3.4.3(a).
$[K:{\mathbb {Q}}_p]$
. The same results also prove (b). Parts (c) and (d) follow from Lemma 5.1.6; the last part of (d) uses Corollary 3.4.3(a).
Lemma 5.5.2. One has the following estimates:
-
(a) If
 $n>1$
, then and in particular
$n>1$
, then and in particular $$ \begin{align*}\dim({\overline{X}{{\phantom{\overline{\overline m}}}}^{\operatorname{univ}}_{{{\overline{{D}}}}}})^{\operatorname{red}} = \dim {\overline{X}{{\phantom{\overline{\overline m}}}}^{\operatorname{univ}}_{{{\overline{{D}}}}}} - 2[K:{\mathbb{Q}}_p](n-1)+1, \end{align*} $$
$$ \begin{align*}\dim({\overline{X}{{\phantom{\overline{\overline m}}}}^{\operatorname{univ}}_{{{\overline{{D}}}}}})^{\operatorname{red}} = \dim {\overline{X}{{\phantom{\overline{\overline m}}}}^{\operatorname{univ}}_{{{\overline{{D}}}}}} - 2[K:{\mathbb{Q}}_p](n-1)+1, \end{align*} $$
 $ \dim ({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\operatorname {red}} \le \dim {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}} - 2$
unless
$ \dim ({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\operatorname {red}} \le \dim {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}} - 2$
unless
 $n=2$
and
$n=2$
and
 $K={\mathbb {Q}}_p$
. In the latter case
$K={\mathbb {Q}}_p$
. In the latter case
 $\dim ({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\operatorname {red}} = \dim {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}} - 1$
.
$\dim ({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\operatorname {red}} = \dim {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}} - 1$
.
-
(b)
 $\dim ({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\mathrm {spcl}} \le \dim {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}} - 2$
.
$\dim ({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\mathrm {spcl}} \le \dim {\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}} - 2$
.
Proof. Since
![]() $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\mathrm {spcl}} $
is empty for
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\mathrm {spcl}} $
is empty for
![]() $n=1$
, because nontrivially induced representations have dimension at least
$n=1$
, because nontrivially induced representations have dimension at least
![]() $2$
, Part (b) is immediate from Theorem 5.4.1. For Part (a), we may assume that
$2$
, Part (b) is immediate from Theorem 5.4.1. For Part (a), we may assume that
![]() ${\overline {{D}}}$
is split by Lemma 5.2.6. Then
${\overline {{D}}}$
is split by Lemma 5.2.6. Then
![]() $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\operatorname {red}}\subset \bigcup _{{\overline {{D}}}_1\oplus {\overline {{D}}}_2={\overline {{D}}}} \ \iota _{{\overline {{D}}}_1,{\overline {{D}}}_2}({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_1,{\overline {{D}}}_2}}})$
, and now Theorem 5.5.1
(a) yields
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\operatorname {red}}\subset \bigcup _{{\overline {{D}}}_1\oplus {\overline {{D}}}_2={\overline {{D}}}} \ \iota _{{\overline {{D}}}_1,{\overline {{D}}}_2}({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_1,{\overline {{D}}}_2}}})$
, and now Theorem 5.5.1
(a) yields
 $$ \begin{align*}\dim ({\overline{X}{{\phantom{\overline{\overline m}}}}^{\operatorname{univ}}_{{{\overline{{D}}}}}})^{\operatorname{red}}= \max_{\genfrac{}{}{0pt}{}{n_1+n_2=n}{n_1,n_2>0}}\dim{\overline{X}}_{n_1}+\dim{\overline{X}}_{n_2}=\max_{\genfrac{}{}{0pt}{}{n_1+n_2=n}{n_1,n_2>0}}d(n_1^2+n_2^2)+2=d((n-1)^2+1)+2.\end{align*} $$
$$ \begin{align*}\dim ({\overline{X}{{\phantom{\overline{\overline m}}}}^{\operatorname{univ}}_{{{\overline{{D}}}}}})^{\operatorname{red}}= \max_{\genfrac{}{}{0pt}{}{n_1+n_2=n}{n_1,n_2>0}}\dim{\overline{X}}_{n_1}+\dim{\overline{X}}_{n_2}=\max_{\genfrac{}{}{0pt}{}{n_1+n_2=n}{n_1,n_2>0}}d(n_1^2+n_2^2)+2=d((n-1)^2+1)+2.\end{align*} $$
The wanted estimate in (a) is immediate. For the remaining assertion note that
![]() $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\operatorname {red}} $
is empty when
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\operatorname {red}} $
is empty when
![]() $n=1$
.
$n=1$
.
Corollary 5.5.3. Suppose that
![]() $\zeta _p\notin K$
and that
$\zeta _p\notin K$
and that
![]() $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\mathrm {spcl}}$
is nonempty so that
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\mathrm {spcl}}$
is nonempty so that
![]() $e:=[K':K]$
divides n, for
$e:=[K':K]$
divides n, for
![]() $K'=K(\zeta _p)$
. Then the Zariski closure of
$K'=K(\zeta _p)$
. Then the Zariski closure of
![]() $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\mathrm {spcl}}$
has dimension
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\mathrm {spcl}}$
has dimension
![]() $\frac 1e[K:{\mathbb {Q}}_p]n^2+1$
.
$\frac 1e[K:{\mathbb {Q}}_p]n^2+1$
.
Proof. Let
![]() ${\mathfrak {p}}\in \operatorname {Spec}{\overline {R}^{\operatorname {univ}}_{{\overline {{D}}}}}$
be a generic point of
${\mathfrak {p}}\in \operatorname {Spec}{\overline {R}^{\operatorname {univ}}_{{\overline {{D}}}}}$
be a generic point of
![]() $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\mathrm {spcl}}$
, let
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\mathrm {spcl}}$
, let
![]() $A= \operatorname {Spec}{\overline {R}^{\operatorname {univ}}_{{\overline {{D}}}}}/{\mathfrak {p}}$
with fraction field
$A= \operatorname {Spec}{\overline {R}^{\operatorname {univ}}_{{\overline {{D}}}}}/{\mathfrak {p}}$
with fraction field
![]() ${\mathbb {K}}$
and let
${\mathbb {K}}$
and let
![]() ${D}_A$
be the corresponding pseudocharacter. Then
${D}_A$
be the corresponding pseudocharacter. Then
![]() ${\mathrm {Spec}}\ A$
contains a dense subset of dimension
${\mathrm {Spec}}\ A$
contains a dense subset of dimension
![]() $1$
points at which
$1$
points at which
![]() ${D}_A$
is irreducible and special. But then
${D}_A$
is irreducible and special. But then
![]() ${D}_A\otimes _A{\mathbb {K}}$
must be irreducible and it also must be special, that is, it is invariant under twisting by the mod p cyclotomic character
${D}_A\otimes _A{\mathbb {K}}$
must be irreducible and it also must be special, that is, it is invariant under twisting by the mod p cyclotomic character
![]() $\chi \colon {\mathrm {Gal}}(K'/K)\to {{\mathbb {F}}\,\!{}}_p^\times $
.
$\chi \colon {\mathrm {Gal}}(K'/K)\to {{\mathbb {F}}\,\!{}}_p^\times $
.
Let
![]() ${\mathbb {K}}'\supset {\mathbb {K}}$
be a finite extension over which there is an absolutely irreducible representation
${\mathbb {K}}'\supset {\mathbb {K}}$
be a finite extension over which there is an absolutely irreducible representation
![]() $\rho \colon G_K\to {\mathrm {GL}}_n({\mathbb {K}}')$
such that
$\rho \colon G_K\to {\mathrm {GL}}_n({\mathbb {K}}')$
such that
![]() ${D}_A\otimes _A{\mathbb {K}}'={D}_\rho $
, and so that
${D}_A\otimes _A{\mathbb {K}}'={D}_\rho $
, and so that
![]() $\rho \cong \rho \otimes \chi $
. Then by Theorem 2.2.1 we have
$\rho \cong \rho \otimes \chi $
. Then by Theorem 2.2.1 we have
![]() $e|n$
and after possibly enlarging
$e|n$
and after possibly enlarging
![]() ${\mathbb {K}}'$
there exists an absolutely irreducible representation
${\mathbb {K}}'$
there exists an absolutely irreducible representation
![]() $\rho '\colon G_{K'}\to {\mathrm {GL}}_{n'}({\mathbb {K}}')$
with
$\rho '\colon G_{K'}\to {\mathrm {GL}}_{n'}({\mathbb {K}}')$
with
![]() $n'=n/e$
such that
$n'=n/e$
such that
![]() ${\mathrm {Ind}}_{G_{K'}}^{G_K}\rho '\cong \rho $
. Moreover, letting
${\mathrm {Ind}}_{G_{K'}}^{G_K}\rho '\cong \rho $
. Moreover, letting
![]() ${D}'={D}_{\rho '}$
, the pseudocharacters
${D}'={D}_{\rho '}$
, the pseudocharacters
![]() $({D}')^g$
,
$({D}')^g$
,
![]() $g\in G_K/G_{K'}$
are pairwise nonisomorphic and
$g\in G_K/G_{K'}$
are pairwise nonisomorphic and
![]() ${\mathrm {Res}}_{G_K}^{G_{K'}}{D}=\oplus _{g\in G_K/G_{K'}} ({D}')^g$
. In particular,
${\mathrm {Res}}_{G_K}^{G_{K'}}{D}=\oplus _{g\in G_K/G_{K'}} ({D}')^g$
. In particular,
![]() ${\mathrm {Res}}_{G_K}^{G_{K'}}{D}$
is multiplicity free. Moreover,
${\mathrm {Res}}_{G_K}^{G_{K'}}{D}$
is multiplicity free. Moreover,
![]() $({D}_A)_{|G_{K'}}$
is a continuous pseudodeformation of
$({D}_A)_{|G_{K'}}$
is a continuous pseudodeformation of
![]() ${\overline {{D}}}_{|G_{K'}}$
, and so it arises from a map
${\overline {{D}}}_{|G_{K'}}$
, and so it arises from a map
![]() ${\overline {R}^{\operatorname {univ}}_{K^{\prime },{\overline {{D}}}}}\rightarrow A$
in
${\overline {R}^{\operatorname {univ}}_{K^{\prime },{\overline {{D}}}}}\rightarrow A$
in
![]() ${\widehat {\mathcal {A}}r}_{{\mathbb {F}}\,\!{}}$
.
${\widehat {\mathcal {A}}r}_{{\mathbb {F}}\,\!{}}$
.
We deduce from Proposition 4.8.6 (and its proof) that after possibly enlarging
![]() ${\mathbb {K}}'$
again there is a continuous pseudocharacter
${\mathbb {K}}'$
again there is a continuous pseudocharacter
![]() ${D}^{\prime }_{A'}\colon G_{K'}\to A'$
on
${D}^{\prime }_{A'}\colon G_{K'}\to A'$
on
![]() $G_K$
for
$G_K$
for
![]() $A'$
the integral closure of A in
$A'$
the integral closure of A in
![]() ${\mathbb {K}}'$
and with
${\mathbb {K}}'$
and with
![]() ${D}^{\prime }_{A'}\otimes _{A'}{\mathbb {K}}'={D}_{\rho '}$
, and moreover
${D}^{\prime }_{A'}\otimes _{A'}{\mathbb {K}}'={D}_{\rho '}$
, and moreover
![]() $A'$
lies in
$A'$
lies in
![]() ${\widehat {\mathcal {A}}r}_{{{\mathbb {F}}\,\!{}}'}$
for a finite extension
${\widehat {\mathcal {A}}r}_{{{\mathbb {F}}\,\!{}}'}$
for a finite extension
![]() ${{\mathbb {F}}\,\!{}}'$
of
${{\mathbb {F}}\,\!{}}'$
of
![]() ${{\mathbb {F}}\,\!{}}$
. Letting
${{\mathbb {F}}\,\!{}}$
. Letting
![]() ${\overline {{D}}}'={D}^{\prime }_{A'}\pmod {{\mathfrak {m}}_{A'}}$
, there is a map
${\overline {{D}}}'={D}^{\prime }_{A'}\pmod {{\mathfrak {m}}_{A'}}$
, there is a map
![]() $\alpha ^{\prime }\colon {\overline {R}^{\operatorname {univ}}_{K^{\prime },{\overline {{D}}}^{\prime }}}\rightarrow A^{\prime }$
in
$\alpha ^{\prime }\colon {\overline {R}^{\operatorname {univ}}_{K^{\prime },{\overline {{D}}}^{\prime }}}\rightarrow A^{\prime }$
in
![]() ${\widehat {\mathcal {A}}r}_{{{\mathbb {F}}\,\!{}}'}$
inducing
${\widehat {\mathcal {A}}r}_{{{\mathbb {F}}\,\!{}}'}$
inducing
![]() ${D}^{\prime }_{A'}$
. Moreover, the pseudocharacters
${D}^{\prime }_{A'}$
. Moreover, the pseudocharacters
![]() $({D}^{\prime }_{A'})^g$
,
$({D}^{\prime }_{A'})^g$
,
![]() $g\in G_K/G_{K'}$
are pairwise distinct.
$g\in G_K/G_{K'}$
are pairwise distinct.
Let
![]() ${\mathfrak {q}}$
be a generic point of
${\mathfrak {q}}$
be a generic point of
![]() ${\overline {R}^{\operatorname {univ}}_{K^{\prime },{\overline {{D}}}^{\prime }}}$
that lies in the kernel of
${\overline {R}^{\operatorname {univ}}_{K^{\prime },{\overline {{D}}}^{\prime }}}$
that lies in the kernel of
![]() $\alpha '$
, let
$\alpha '$
, let
![]() $B={\overline {R}^{\operatorname {univ}}_{K^{\prime },{\overline {{D}}}^{\prime }}}/{\mathfrak {q}}$
with quotient field L, and let
$B={\overline {R}^{\operatorname {univ}}_{K^{\prime },{\overline {{D}}}^{\prime }}}/{\mathfrak {q}}$
with quotient field L, and let
![]() ${D}^{\prime }_B$
be the associated pseudocharacter. Then
${D}^{\prime }_B$
be the associated pseudocharacter. Then
![]() ${D}_B\otimes _BL$
is irreducible and the pseudocharacters
${D}_B\otimes _BL$
is irreducible and the pseudocharacters
![]() $({D}^{\prime }_B)^g$
,
$({D}^{\prime }_B)^g$
,
![]() $g\in G_K/G_{K'}$
are pairwise distinct. Then by Theorem 4.6.7,
$g\in G_K/G_{K'}$
are pairwise distinct. Then by Theorem 4.6.7,
![]() ${D}_B={\mathrm {Ind}}_{G_{K'}}^{G_K}{D}^{\prime }_B\colon B[G]\to B$
is a continuous pseudodeformation of
${D}_B={\mathrm {Ind}}_{G_{K'}}^{G_K}{D}^{\prime }_B\colon B[G]\to B$
is a continuous pseudodeformation of
![]() ${\mathrm {Ind}}_{G_{K'}}^{G_K}{\overline {{D}}}'={\overline {{D}}}\otimes _{{\mathbb {F}}\,\!{}}{{\mathbb {F}}\,\!{}}'$
such that
${\mathrm {Ind}}_{G_{K'}}^{G_K}{\overline {{D}}}'={\overline {{D}}}\otimes _{{\mathbb {F}}\,\!{}}{{\mathbb {F}}\,\!{}}'$
such that
![]() ${D}_B\otimes _B{\mathrm {Quot}}(B)$
is irreducible and special (invariant by the twist with
${D}_B\otimes _B{\mathrm {Quot}}(B)$
is irreducible and special (invariant by the twist with
![]() $\chi $
). In particular,
$\chi $
). In particular,
![]() ${D}_B$
arises from a homomorphism
${D}_B$
arises from a homomorphism
![]() $\alpha \colon {\overline {R}^{\operatorname {univ}}_{K,{\overline {{D}}}\otimes _{{\mathbb {F}}\,\!{}}{{\mathbb {F}}\,\!{}}^{\prime }}}\rightarrow B$
and the point
$\alpha \colon {\overline {R}^{\operatorname {univ}}_{K,{\overline {{D}}}\otimes _{{\mathbb {F}}\,\!{}}{{\mathbb {F}}\,\!{}}^{\prime }}}\rightarrow B$
and the point
![]() ${\mathop {\mathrm{Ker}}\nolimits }\,\alpha $
of
${\mathop {\mathrm{Ker}}\nolimits }\,\alpha $
of
![]() ${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{{\mathbb {F}}\,\!{}}',{\overline {{D}}}\otimes _{{\mathbb {F}}\,\!{}}{{\mathbb {F}}\,\!{}}'}}}$
must be special. By our construction we have a commutative diagram
${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{{\mathbb {F}}\,\!{}}',{\overline {{D}}}\otimes _{{\mathbb {F}}\,\!{}}{{\mathbb {F}}\,\!{}}'}}}$
must be special. By our construction we have a commutative diagram

where we write
![]() $A{{\mathbb {F}}\,\!{}}'$
for the
$A{{\mathbb {F}}\,\!{}}'$
for the
![]() ${{\mathbb {F}}\,\!{}}'$
subalgebra of
${{\mathbb {F}}\,\!{}}'$
subalgebra of
![]() $A'$
generated by
$A'$
generated by
![]() ${{\mathbb {F}}\,\!{}}'$
and A, and initially without the dashed arrow. We deduce that
${{\mathbb {F}}\,\!{}}'$
and A, and initially without the dashed arrow. We deduce that
![]() ${\mathop {\mathrm{Ker}}\nolimits }\,\alpha $
is also the kernel of the map to
${\mathop {\mathrm{Ker}}\nolimits }\,\alpha $
is also the kernel of the map to
![]() $A{{\mathbb {F}}\,\!{}}'$
, and so the dashed arrow exists and is injective (by the definition of A). But then restricting the corresponding pseudocharacters to
$A{{\mathbb {F}}\,\!{}}'$
, and so the dashed arrow exists and is injective (by the definition of A). But then restricting the corresponding pseudocharacters to
![]() $G_{K'}$
, one deduces that the maps from
$G_{K'}$
, one deduces that the maps from
![]() ${\overline {R}^{\operatorname {univ}}_{K,{\overline {{D}}}^{\prime }}}$
to B and to a finite extension of
${\overline {R}^{\operatorname {univ}}_{K,{\overline {{D}}}^{\prime }}}$
to B and to a finite extension of
![]() $A{{\mathbb {F}}\,\!{}}$
have the same kernel, and so B and
$A{{\mathbb {F}}\,\!{}}$
have the same kernel, and so B and
![]() $A'$
, and hence A must have the same dimension. But
$A'$
, and hence A must have the same dimension. But
![]() $\dim B=\frac 1e[K:{\mathbb {Q}}_p]n^2+1$
by Theorem 5.5.1, and this concludes the proof.
$\dim B=\frac 1e[K:{\mathbb {Q}}_p]n^2+1$
by Theorem 5.5.1, and this concludes the proof.
Lemma 5.5.4. Let
![]() ${\kappa }$
be a local or a finite field. Suppose
${\kappa }$
be a local or a finite field. Suppose
![]() $p>2$
. Let
$p>2$
. Let
![]() ${D}_i\colon G_{{\mathbb {Q}}_p}\to {\kappa }$
,
${D}_i\colon G_{{\mathbb {Q}}_p}\to {\kappa }$
,
![]() $i=1,2$
, be continuous pseudocharacters on
$i=1,2$
, be continuous pseudocharacters on
![]() $G_{{\mathbb {Q}}_p}$
of dimension
$G_{{\mathbb {Q}}_p}$
of dimension
![]() $1$
, and let
$1$
, and let
![]() ${D}={D}_1\oplus {D}_2$
. Then
${D}={D}_1\oplus {D}_2$
. Then
-
(a) If
 ${D}_1\neq {D}_2(m)$
for
${D}_1\neq {D}_2(m)$
for
 $m\in \{0,\pm 1\}$
, then
$m\in \{0,\pm 1\}$
, then-
(1) there exists a unique nontrivial extension
 $\rho \colon G_{{\mathbb {Q}}_p}\to {\mathrm {GL}}_2({\kappa })$
of
$\rho \colon G_{{\mathbb {Q}}_p}\to {\mathrm {GL}}_2({\kappa })$
of
 ${D}_2$
by
${D}_2$
by
 ${D}_1$
,
${D}_1$
, -
(2) the natural map
 ${\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{D}}}}\to {\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{\rho }}}$
is an isomorphism,
${\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{D}}}}\to {\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{\rho }}}$
is an isomorphism, -
(3) and both rings are formally smooth over
 ${\kappa }$
of dimension
${\kappa }$
of dimension
 $5$
.
$5$
.
-
-
(b) If
 ${D}_1={D}_2(m)$
for some
${D}_1={D}_2(m)$
for some
 $m\in \{\pm 1\}$
, then
$m\in \{\pm 1\}$
, then
 ${\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{D}}}}$
is not regular.
${\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{D}}}}$
is not regular. -
(c) If
 ${D}_1={D}_2$
, then
${D}_1={D}_2$
, then
 ${\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{D}}}}$
is regular.
${\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{D}}}}$
is regular.
Proof. The idea for (a) stems from the proof of [Reference ChenevierChe11, Corollary 4.4] and goes back to Kisin. We regard the
![]() ${D}_i$
exchangeably as pseudocharacters or as representations because they are of dimension
${D}_i$
exchangeably as pseudocharacters or as representations because they are of dimension
![]() $1$
. Lemma 5.1.7
(a) guarantees the existence of
$1$
. Lemma 5.1.7
(a) guarantees the existence of
![]() $\rho $
as in (1). Since
$\rho $
as in (1). Since
![]() ${D}_1\notin \{{D}_2,{D}_2(\pm 1)\}$
, Theorem 3.4.1 yields
${D}_1\notin \{{D}_2,{D}_2(\pm 1)\}$
, Theorem 3.4.1 yields
![]() $\dim {\mathrm {Ext}}^1_{G_{{\mathbb {Q}}_p}}({D}_i,{D}_j)=1$
for
$\dim {\mathrm {Ext}}^1_{G_{{\mathbb {Q}}_p}}({D}_i,{D}_j)=1$
for
![]() $i\neq j$
, and this implies the uniqueness of
$i\neq j$
, and this implies the uniqueness of
![]() $\rho $
up to isomorphism. Note that once (2) is proved, Part (3) follows from Lemma 5.1.7
(c). To see (2), let
$\rho $
up to isomorphism. Note that once (2) is proved, Part (3) follows from Lemma 5.1.7
(c). To see (2), let
![]() $X_\rho :={\mathrm {Spec}}\ {\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{\rho }}}$
,
$X_\rho :={\mathrm {Spec}}\ {\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{\rho }}}$
,
![]() $X_{D}:={\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{D}}}}$
for
$X_{D}:={\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{D}}}}$
for
![]() ${D}:={D}_1\oplus {D}_2$
, write
${D}:={D}_1\oplus {D}_2$
, write
![]() $\varphi $
for the map in Part (1), and denote by
$\varphi $
for the map in Part (1), and denote by
the induced map on tangent spaces. By the formula in Lemma 5.1.7
(c), the kernel of
![]() ${\mathrm {d}}\varphi $
is zero. Because
${\mathrm {d}}\varphi $
is zero. Because
![]() $p>2$
, we also have
$p>2$
, we also have
![]() $\dim {\mathrm {Ext}}^1_{G_{{\mathbb {Q}}_p}}({D}_i,{D}_i)=2$
for
$\dim {\mathrm {Ext}}^1_{G_{{\mathbb {Q}}_p}}({D}_i,{D}_i)=2$
for
![]() $i=1,2$
. Consider now the following exact sequence from [Reference BellaïcheBel12, Theorem 2] with
$i=1,2$
. Consider now the following exact sequence from [Reference BellaïcheBel12, Theorem 2] with
![]() $\rho _i={D}_i$
$\rho _i={D}_i$
 $$\begin{align*} &{\longrightarrow } \operatorname{Ext}^1_{G_K}(\rho _{1} , \rho _{2} ) \otimes \operatorname{Ext}^1_{G_K}(\rho _{2}, \rho _1 ) \stackrel{h}{{\longrightarrow } } \bigoplus _{i=1,2} \operatorname{Ext}^2_{G_K} (\rho _{i}, \rho _{i}). \end{align*}$$
$$\begin{align*} &{\longrightarrow } \operatorname{Ext}^1_{G_K}(\rho _{1} , \rho _{2} ) \otimes \operatorname{Ext}^1_{G_K}(\rho _{2}, \rho _1 ) \stackrel{h}{{\longrightarrow } } \bigoplus _{i=1,2} \operatorname{Ext}^2_{G_K} (\rho _{i}, \rho _{i}). \end{align*}$$
It implies
![]() $\dim {\mathbf {t}_{X_{D},D}}\le 5$
. Hence,
$\dim {\mathbf {t}_{X_{D},D}}\le 5$
. Hence,
![]() ${\mathrm {d}}\varphi $
must be an isomorphism and
${\mathrm {d}}\varphi $
must be an isomorphism and
![]() $\dim {\mathbf {t}_{X_{D},D}}=5$
. This implies that
$\dim {\mathbf {t}_{X_{D},D}}=5$
. This implies that
![]() $\varphi $
must be surjective, and hence an isomorphism since the target is formally smooth over
$\varphi $
must be surjective, and hence an isomorphism since the target is formally smooth over
![]() ${\kappa }$
.
${\kappa }$
.
To prove (b), note that we have
![]() ${\mathrm {Ext}}^2(\rho _i,\rho _i)=0$
and
${\mathrm {Ext}}^2(\rho _i,\rho _i)=0$
and
![]() ${\mathrm {Ext}}^1(\rho _i,\rho _i)$
is of dimension
${\mathrm {Ext}}^1(\rho _i,\rho _i)$
is of dimension
![]() $1$
, while
$1$
, while
![]() ${\mathrm {Ext}}^1(\rho _i,\rho _i(m))$
is
${\mathrm {Ext}}^1(\rho _i,\rho _i(m))$
is
![]() $2$
for
$2$
for
![]() $m=1$
and
$m=1$
and
![]() $1$
for
$1$
for
![]() $m=-1$
. Hence, diagram (36) yields
$m=-1$
. Hence, diagram (36) yields
![]() $\dim _{\kappa } {\mathbf {t}_{X_{D},D}}=6$
. However,
$\dim _{\kappa } {\mathbf {t}_{X_{D},D}}=6$
. However,
![]() $\dim X_{D}=5$
by Theorem 5.5.1, and hence
$\dim X_{D}=5$
by Theorem 5.5.1, and hence
![]() ${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{D}}$
is not regular.
${R{{\phantom {\overline {m}}}}^{\operatorname {univ}}_{D}}$
is not regular.
Finally, we show (c). Because
![]() $p>2$
, we may apply [Reference ChenevierChe11, Théorème 3.1] in exactly the same way, as done in [Reference ChenevierChe11, Lemme 2.5]: Using that the mod p reduction of
$p>2$
, we may apply [Reference ChenevierChe11, Théorème 3.1] in exactly the same way, as done in [Reference ChenevierChe11, Lemme 2.5]: Using that the mod p reduction of
![]() $G_{{\mathbb {Q}}_p}^{\operatorname {ab}}$
is isomorphic to
$G_{{\mathbb {Q}}_p}^{\operatorname {ab}}$
is isomorphic to
![]() $({\mathbb {Z}}/p)^2$
, one has
$({\mathbb {Z}}/p)^2$
, one has
![]() $\dim _{\kappa } {\mathrm {Hom}}(G_{{\mathbb {Q}}_p},{\kappa })=2$
,
$\dim _{\kappa } {\mathrm {Hom}}(G_{{\mathbb {Q}}_p},{\kappa })=2$
,
![]() $\dim _{\kappa } {\mathrm {Sym}}(G_{{\mathbb {Q}}_p},{\kappa })=3$
and
$\dim _{\kappa } {\mathrm {Sym}}(G_{{\mathbb {Q}}_p},{\kappa })=3$
and
![]() $\dim _{\kappa } {\mathrm {Alt}}(G_{{\mathbb {Q}}_p},{\kappa })=0$
, and hence
$\dim _{\kappa } {\mathrm {Alt}}(G_{{\mathbb {Q}}_p},{\kappa })=0$
, and hence
![]() $\dim _{\kappa } {\mathbf {t}_{X_{D},D}}=5$
. We now conclude using
$\dim _{\kappa } {\mathbf {t}_{X_{D},D}}=5$
. We now conclude using
![]() $\dim X_{D}=5$
by Theorem 5.5.1.
$\dim X_{D}=5$
by Theorem 5.5.1.
We now characterize the singular locus when
![]() $\zeta _p\notin K$
.
$\zeta _p\notin K$
.
Theorem 5.5.5 (Theorem 2, [Reference ChenevierChe11, Théorème 2.3]).
If
![]() $\zeta _p\notin K$
, then the following hold:
$\zeta _p\notin K$
, then the following hold:
-
(a) The closure of
 $X_1:=({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\mathrm {spcl}}$
in
$X_1:=({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\mathrm {spcl}}$
in
 ${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
lies in
${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
lies in
 $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\operatorname {sing}}$
.
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\operatorname {sing}}$
. -
(b) If
 $n>2$
or
$n>2$
or
 $[K:{\mathbb {Q}}_p]>1$
, then
$[K:{\mathbb {Q}}_p]>1$
, then
 $X_2:=({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{{\operatorname {red}}}\subset ({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\operatorname {sing}}$
.
$X_2:=({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{{\operatorname {red}}}\subset ({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\operatorname {sing}}$
. -
(c) If
 $n=2$
,
$n=2$
,
 $K={\mathbb {Q}}_p$
, and
$K={\mathbb {Q}}_p$
, and
 $x\in X_2$
corresponds to a pair
$x\in X_2$
corresponds to a pair
 $({D}_1,{D}_2)$
of one-dimensional pseudocharacters, then
$({D}_1,{D}_2)$
of one-dimensional pseudocharacters, then
 $x\in ({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\operatorname {sing}}$
if and only if
$x\in ({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{\operatorname {sing}}$
if and only if
 ${D}_2={D}_1(m)$
for
${D}_2={D}_1(m)$
for
 $m\in \{\pm 1\}$
.
$m\in \{\pm 1\}$
.
Proof. We know from Proposition 4.7.11 that
![]() ${\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
is a complete Noetherian local ring so that by Lemma A.1.1(a),
${\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
is a complete Noetherian local ring so that by Lemma A.1.1(a),
![]() $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{{\operatorname {sing}}}$
is closed in
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{{\operatorname {sing}}}$
is closed in
![]() ${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
. Observe that if
${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
. Observe that if
![]() $X_i\neq \emptyset $
, then its Zariski closure
$X_i\neq \emptyset $
, then its Zariski closure
![]() $\overline X_i$
has dimension at least
$\overline X_i$
has dimension at least
![]() $2$
: for
$2$
: for
![]() $X_2$
, this is clear from Lemma 5.5.2
(a), for
$X_2$
, this is clear from Lemma 5.5.2
(a), for
![]() $X_1$
from Corollary 5.5.3. Hence, Proposition A.1.11 shows that the points of
$X_1$
from Corollary 5.5.3. Hence, Proposition A.1.11 shows that the points of
![]() $X_i$
of dimension
$X_i$
of dimension
![]() $1$
are dense in
$1$
are dense in
![]() $X_i$
.
$X_i$
.
To prove (a), let
![]() $x\in X_1$
be of dimension
$x\in X_1$
be of dimension
![]() $1$
. A standard computation of tangent spaces as in the proof of Lemma 5.1.7
(c) shows
$1$
. A standard computation of tangent spaces as in the proof of Lemma 5.1.7
(c) shows
![]() $\dim H^1(G_K,{\operatorname {ad}_{{\rho _x}}})=dn^2+2$
, while
$\dim H^1(G_K,{\operatorname {ad}_{{\rho _x}}})=dn^2+2$
, while
![]() $\dim {R^{\operatorname {univ}}_{\rho _x}}=dn^2+1$
. It follows from Lemma 3.3.5 that x is not regular on
$\dim {R^{\operatorname {univ}}_{\rho _x}}=dn^2+1$
. It follows from Lemma 3.3.5 that x is not regular on
![]() ${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
.
${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
.
For the proof of (b), we assume without loss of generality that
![]() ${\overline {{D}}}$
is split. Then
${\overline {{D}}}$
is split. Then
![]() $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{{\operatorname {red}}}$
is the image of the maps
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{{\operatorname {red}}}$
is the image of the maps
![]() $\iota _{{\overline {{D}}}_1,{\overline {{D}}}_2}$
from (32) for all
$\iota _{{\overline {{D}}}_1,{\overline {{D}}}_2}$
from (32) for all
![]() ${\overline {{D}}}_1$
,
${\overline {{D}}}_1$
,
![]() ${\overline {{D}}}_2$
such that
${\overline {{D}}}_2$
such that
![]() ${\overline {{D}}}={\overline {{D}}}_1\oplus {\overline {{D}}}_2$
. Fix such a pair, and let
${\overline {{D}}}={\overline {{D}}}_1\oplus {\overline {{D}}}_2$
. Fix such a pair, and let
![]() $n_i$
be the dimension of
$n_i$
be the dimension of
![]() ${\overline {{D}}}_i$
. Because of Theorem 5.5.1 it suffices to consider pairs
${\overline {{D}}}_i$
. Because of Theorem 5.5.1 it suffices to consider pairs
![]() $x=(x_1,x_2)$
with
$x=(x_1,x_2)$
with
![]() $x_i \in ({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_i}}})^{{{\mathrm {n}\textrm {-}\mathrm {spcl}}}}$
; and we may also assume that
$x_i \in ({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_i}}})^{{{\mathrm {n}\textrm {-}\mathrm {spcl}}}}$
; and we may also assume that
![]() ${D}_{x_1}$
is distinct from the finitely many
${D}_{x_1}$
is distinct from the finitely many
![]() ${D}_{x_2}(m)$
,
${D}_{x_2}(m)$
,
![]() $m\in \{1,\ldots ,p-1\}$
. We compute the tangent space dimension of
$m\in \{1,\ldots ,p-1\}$
. We compute the tangent space dimension of
![]() ${\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{D}_x}}}$
this time, using (36) from [Reference BellaïcheBel12, Theorem A] which also holds for
${\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{D}_x}}}$
this time, using (36) from [Reference BellaïcheBel12, Theorem A] which also holds for
![]() $\rho _{x_i}$
in place of
$\rho _{x_i}$
in place of
![]() $\rho _i$
. We conclude as in the proof of [Reference ChenevierChe11, Lemme 2.4]:
$\rho _i$
. We conclude as in the proof of [Reference ChenevierChe11, Lemme 2.4]:
![]() $\dim _L H^1(G_K,{\operatorname {ad}_{{\rho _{x_i}}}} )\ge 1+dn_i^2$
,
$\dim _L H^1(G_K,{\operatorname {ad}_{{\rho _{x_i}}}} )\ge 1+dn_i^2$
,
![]() $\dim _L {\mathrm {Ext}}^1_{G_K}(\rho _{x_i}, \rho _{x_{3-i}} )=dn_1n_2$
, and the second extension groups vanish since the
$\dim _L {\mathrm {Ext}}^1_{G_K}(\rho _{x_i}, \rho _{x_{3-i}} )=dn_1n_2$
, and the second extension groups vanish since the
![]() $D_{x_i}$
satisfy
$D_{x_i}$
satisfy
![]() $D_{x_i}\neq D_{x_i}(1)$
. Hence,
$D_{x_i}\neq D_{x_i}(1)$
. Hence,
This dimension is strictly larger than
![]() $dn^2+1$
, unless
$dn^2+1$
, unless
![]() $dn_1n_2=1$
, that is,
$dn_1n_2=1$
, that is,
![]() $n_1=n_2=1$
and
$n_1=n_2=1$
and
![]() $K={\mathbb {Q}}_p$
. However,
$K={\mathbb {Q}}_p$
. However,
![]() $\dim {\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{D}_x}}}=dn^2+1$
by Lemma 3.3.5 and Theorem 5.5.1, and it follows that x cannot be regular, proving (b).
$\dim {\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{D}_x}}}=dn^2+1$
by Lemma 3.3.5 and Theorem 5.5.1, and it follows that x cannot be regular, proving (b).
Concerning (c), note that if
![]() $x=({D}_1,{D}_2)$
is any point of dimension at most
$x=({D}_1,{D}_2)$
is any point of dimension at most
![]() $1$
, then the assertion follows from Lemma 5.5.4. Since such points are Zariski dense in the closure of any point of dimension at least
$1$
, then the assertion follows from Lemma 5.5.4. Since such points are Zariski dense in the closure of any point of dimension at least
![]() $2$
, the assertion in (c) follows in general.
$2$
, the assertion in (c) follows in general.
Remark 5.5.6. Note that Theorem 5.5.5 reproves a result of Paškūnas, namely [Reference PaškūnasPaš13, Proposition B.17]: suppose that
![]() $n=2$
,
$n=2$
,
![]() $p>2$
,
$p>2$
,
![]() $K={\mathbb {Q}}_p$
, and
$K={\mathbb {Q}}_p$
, and
![]() ${\overline {{D}}}\colon G_{{\mathbb {Q}}_p}\to {{\mathbb {F}}\,\!{}} $
is a direct sum
${\overline {{D}}}\colon G_{{\mathbb {Q}}_p}\to {{\mathbb {F}}\,\!{}} $
is a direct sum
![]() ${\overline {{D}}}_1\oplus {\overline {{D}}}_2$
of one-dimensional characters
${\overline {{D}}}_1\oplus {\overline {{D}}}_2$
of one-dimensional characters
![]() ${\overline {{D}}}_i$
sucht that
${\overline {{D}}}_i$
sucht that
![]() ${\overline {{D}}}_2\neq {\overline {{D}}}_1(m)$
for
${\overline {{D}}}_2\neq {\overline {{D}}}_1(m)$
for
![]() $m=0,\pm 1$
. Then
$m=0,\pm 1$
. Then
![]() ${\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}\cong {{\mathbb {F}}\,\!{}}_q[[X_1,\ldots ,X_5]]$
.
${\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}\cong {{\mathbb {F}}\,\!{}}_q[[X_1,\ldots ,X_5]]$
.
Theorem 5.5.7 (Theorem 3).
The ring
![]() ${\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}},{\operatorname {red}}}}}$
satisfies Serre’s condition
${\overline {R}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}},{\operatorname {red}}}}}$
satisfies Serre’s condition
![]() $(R_2)$
, unless
$(R_2)$
, unless
![]() $n=2$
,
$n=2$
,
![]() $K={\mathbb {Q}}_2$
and
$K={\mathbb {Q}}_2$
and
![]() ${\overline {{D}}}$
is trivial.
${\overline {{D}}}$
is trivial.
Proof. By Theorem 5.5.1 and Lemma 5.1.6, the subset
![]() $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}},{\operatorname {red}}}}})^{{\mathrm {n}\textrm {-}\mathrm {spcl}}}$
is regular, open and Zariski dense in
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}},{\operatorname {red}}}}})^{{\mathrm {n}\textrm {-}\mathrm {spcl}}}$
is regular, open and Zariski dense in
![]() ${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}},{\operatorname {red}}}}}$
. Thus, Lemma 5.5.2 implies the theorem unless
${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}},{\operatorname {red}}}}}$
. Thus, Lemma 5.5.2 implies the theorem unless
![]() $n=2$
and
$n=2$
and
![]() $K={\mathbb {Q}}_p$
. Also, if
$K={\mathbb {Q}}_p$
. Also, if
![]() ${\overline {{D}}}$
is irreducible, then so is any lift, and so
${\overline {{D}}}$
is irreducible, then so is any lift, and so
![]() $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}},{\operatorname {red}}}}})^{\operatorname {red}}$
is empty. Now, again we conclude by Lemma 5.5.2. Suppose from now on that
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}},{\operatorname {red}}}}})^{\operatorname {red}}$
is empty. Now, again we conclude by Lemma 5.5.2. Suppose from now on that
![]() $K={\mathbb {Q}}_p$
and
$K={\mathbb {Q}}_p$
and
![]() ${\overline {{D}}}={\overline {{D}}}_1\oplus {\overline {{D}}}_2$
for one-dimensional pseudocharacters
${\overline {{D}}}={\overline {{D}}}_1\oplus {\overline {{D}}}_2$
for one-dimensional pseudocharacters
![]() ${\overline {{D}}}_i\colon G_{{\mathbb {Q}}_p}\to {{\mathbb {F}}\,\!{}}$
on
${\overline {{D}}}_i\colon G_{{\mathbb {Q}}_p}\to {{\mathbb {F}}\,\!{}}$
on
![]() $G_{{\mathbb {Q}}_p}$
, and suppose now also
$G_{{\mathbb {Q}}_p}$
, and suppose now also
![]() $p>2$
which was excluded in this case.
$p>2$
which was excluded in this case.
The locus of
![]() $x\in X_2:=({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{{\operatorname {red}}}$
corresponding to a pair
$x\in X_2:=({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{{\operatorname {red}}}$
corresponding to a pair
![]() $({D}_1,{D}_2)$
of one-dimensional pseudocharacters such that
$({D}_1,{D}_2)$
of one-dimensional pseudocharacters such that
![]() ${D}_2={D}_1(m)$
for
${D}_2={D}_1(m)$
for
![]() $m\in \{\pm 1\}$
, can be realized as the image of
$m\in \{\pm 1\}$
, can be realized as the image of
![]() ${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_1}}}$
. Hence, it has dimension at most
${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}_1}}}$
. Hence, it has dimension at most
![]() $2$
because of Corollary 3.4.3. Outside this, locus points are smooth by Theorem 5.5.5 (and the density of points of dimension
$2$
because of Corollary 3.4.3. Outside this, locus points are smooth by Theorem 5.5.5 (and the density of points of dimension
![]() $1$
). It follows that
$1$
). It follows that
![]() $({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{{\operatorname {red}},{\operatorname {sing}}}$
has dimension at most
$({\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}})^{{\operatorname {red}},{\operatorname {sing}}}$
has dimension at most
![]() $2$
which is less than
$2$
which is less than
![]() $5-2=3$
so that then
$5-2=3$
so that then
![]() ${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
satisfies
${\overline {X}{{\phantom {\overline {\overline m}}}}^{\operatorname {univ}}_{{{\overline {{D}}}}}}$
satisfies
![]() $(R_2)$
, also.
$(R_2)$
, also.
A Appendix. Auxiliary results on rings, algebras and representations
In this appendix, we collect some results used in various parts of this work. We also prove some minor facts that could not be found directly in the literature.
A.1 Commutative algebra
Complete local rings, integral extensions and regularity
A domain B with quotient field
![]() ${\mathbb {K}}$
is said to satisfy N-2 if for any finite field extension L of
${\mathbb {K}}$
is said to satisfy N-2 if for any finite field extension L of
![]() ${\mathbb {K}}$
, the integral closure of B in L is a finite over B. A ring A is called a Nagata ring if A is Noetherian and for every prime ideal
${\mathbb {K}}$
, the integral closure of B in L is a finite over B. A ring A is called a Nagata ring if A is Noetherian and for every prime ideal
![]() ${\mathfrak {p}}$
of A the ring
${\mathfrak {p}}$
of A the ring
![]() $A/{\mathfrak {p}}$
satisfies N-2; see [Reference StacksSta18, §032E].
$A/{\mathfrak {p}}$
satisfies N-2; see [Reference StacksSta18, §032E].
Lemma A.1.1. If A is complete Noetherian local ring, then the following hold:
-
(a) A is a Nagata ring, and hence the set of regular points of
 ${\mathrm {Spec}}\ A$
is open in
${\mathrm {Spec}}\ A$
is open in
 ${\mathrm {Spec}}\ A$
.
${\mathrm {Spec}}\ A$
. -
(b) If A is a domain with fraction field
 ${\mathbb {K}}$
and perfect residue field, then
${\mathbb {K}}$
and perfect residue field, then
 $[{\mathbb {K}}:{\mathbb {K}}^p]<\infty $
.
$[{\mathbb {K}}:{\mathbb {K}}^p]<\infty $
.
Proof. Part (a) is [Reference StacksSta18, §032W] combined with [Reference GrothendieckGro65, Théorème (6.12.7)]. Part (b) is proved in [Reference HochsterHoc07, Proposition (d), (g)].
Lemma A.1.2 [Reference MatsumuraMat80, 13.C, Theorem 20].
If B is a domain and if
![]() $B'\subset B$
is a subring such that B if finite over
$B'\subset B$
is a subring such that B if finite over
![]() $B'$
, then
$B'$
, then
![]() $\dim B= \dim B'$
.
$\dim B= \dim B'$
.
Recall that for a prime
![]() ${\mathfrak {p}}$
of A, the height of
${\mathfrak {p}}$
of A, the height of
![]() ${\mathfrak {p}}$
is defined as
${\mathfrak {p}}$
is defined as
![]() ${\operatorname {ht}{{{\mathfrak {p}}}}} =\dim R_{\mathfrak {p}}$
.
${\operatorname {ht}{{{\mathfrak {p}}}}} =\dim R_{\mathfrak {p}}$
.
Definition A.1.3. A commutative ring A is said to satisfy (Serre’s) condition
![]() $(R_i)$
, if A is regular in codimension at most i, that is, if the local ring
$(R_i)$
, if A is regular in codimension at most i, that is, if the local ring
![]() $A_{\mathfrak {p}}$
is regular for every prime
$A_{\mathfrak {p}}$
is regular for every prime
![]() ${\mathfrak {p}}$
of height
${\mathfrak {p}}$
of height
![]() $\leq i$
.
$\leq i$
.
Density of points of dimension one
The next series of results stems from [Reference GrothendieckGro66, §10.1–10.5], except in one case where we give a direct reference. Let X be a topological space. It is called Noetherian if every descending chain of closed subsets becomes stationary. It is called irreducible if it is not the union of two proper closed subsets. If X is Noetherian, a subset is called constructible if it is a finite union of locally closed subsets of X, that is, of subsets that are the intersection of an open and a closed subset of X. The closure of a subset
![]() $Z\subset X$
is denoted by
$Z\subset X$
is denoted by
![]() $\overline Z$
. For a subset Z of X, its dimension
$\overline Z$
. For a subset Z of X, its dimension
![]() $\dim Z\in {\mathbb {N}}\cup \{\infty \}$
is the maximal length n of a chain
$\dim Z\in {\mathbb {N}}\cup \{\infty \}$
is the maximal length n of a chain
![]() $Y_0\subsetneq Y_1\subsetneq \ldots \subsetneq Y_n\subset \overline Z$
of irreducible closed subsets
$Y_0\subsetneq Y_1\subsetneq \ldots \subsetneq Y_n\subset \overline Z$
of irreducible closed subsets
![]() $Y_i$
in X.
$Y_i$
in X.
Definition A.1.4. A subset
![]() $X_0$
of X is called very dense in X if every nonempty locally closed subset
$X_0$
of X is called very dense in X if every nonempty locally closed subset
![]() $Z\subset X$
satisfies
$Z\subset X$
satisfies
![]() $Z\cap X_0\neq \emptyset $
.
$Z\cap X_0\neq \emptyset $
.
If
![]() $X_0$
is very dense in X, it is clearly dense in X.
$X_0$
is very dense in X, it is clearly dense in X.
Lemma A.1.5. If
![]() $X_0$
is very dense in X, then
$X_0$
is very dense in X, then
![]() $X_0\cap Z$
is very dense in Z and dense in
$X_0\cap Z$
is very dense in Z and dense in
![]() $\overline Z$
for any locally closed set Z in X.
$\overline Z$
for any locally closed set Z in X.
Proposition A.1.6. For a subset
![]() $X_0$
of X, the following conditions are equivalent:
$X_0$
of X, the following conditions are equivalent:
-
(a)
 $X_0$
is very dense in X;
$X_0$
is very dense in X; -
(b) Under
 $X'\mapsto X_0\cap X'$
, the open subsets in X are in bijection to those in
$X'\mapsto X_0\cap X'$
, the open subsets in X are in bijection to those in
 $X_0$
.
$X_0$
. -
(c) Under
 $X'\mapsto X_0\cap X'$
, the closed subsets in X are in bijection to those in
$X'\mapsto X_0\cap X'$
, the closed subsets in X are in bijection to those in
 $X_0$
.
$X_0$
.
In the following, we set
![]() $X_{\le 1}:=\{x \in X{\>:\>} \dim x \le 1\}$
. Since the union of finitely many irreducible subsets of dimension at most i has dimension at most i, we find:
$X_{\le 1}:=\{x \in X{\>:\>} \dim x \le 1\}$
. Since the union of finitely many irreducible subsets of dimension at most i has dimension at most i, we find:
Lemma A.1.7. If
![]() $U\subset X$
satisfies
$U\subset X$
satisfies
![]() $\dim U\ge 2$
, then no finite subset of
$\dim U\ge 2$
, then no finite subset of
![]() $U_{\le 1}$
is dense in U.
$U_{\le 1}$
is dense in U.
An important source for very dense subset of schemes comes from the following result:
Lemma A.1.8 [Reference MatsumuraMat80, (33.F) Lemma 5].
Let
![]() $X={\mathrm {Spec}}\ A$
for a Noetherian ring A. Then the set
$X={\mathrm {Spec}}\ A$
for a Noetherian ring A. Then the set
![]() $X_{\le 1}$
is very dense in X.
$X_{\le 1}$
is very dense in X.
From Lemma A.1.8 and Lemma A.1.5, one deduces:
Corollary A.1.9. Let
![]() $X={\mathrm {Spec}}\ A$
for a Noetherian ring A, and let
$X={\mathrm {Spec}}\ A$
for a Noetherian ring A, and let
![]() $Z\subset X$
be constructible. Then
$Z\subset X$
be constructible. Then
![]() $X_{\le 1}\cap Z$
is very dense in Z and dense in
$X_{\le 1}\cap Z$
is very dense in Z and dense in
![]() $\overline Z$
.
$\overline Z$
.
Definition A.1.10. The space X is called Jacobson if
![]() $\{x\in X{\>:\>} \dim x=0\}$
is very dense in X.
$\{x\in X{\>:\>} \dim x=0\}$
is very dense in X.
A scheme is called Jacobson if the underlying topological space is Jacobson; a ring A is called Jacobson if the scheme
![]() ${\mathrm {Spec}}\ A$
is Jacobson. For us, the following result is of importance:
${\mathrm {Spec}}\ A$
is Jacobson. For us, the following result is of importance:
Proposition A.1.11. For a Noetherian local ring with A maximal ideal
![]() $\mathfrak {m}_A$
, the scheme
$\mathfrak {m}_A$
, the scheme
![]() ${\mathrm {Spec}}\ A{\smallsetminus } \{\mathfrak {m}_A\}$
is Jacobson.
${\mathrm {Spec}}\ A{\smallsetminus } \{\mathfrak {m}_A\}$
is Jacobson.
Besides our reference to [Reference GrothendieckGro66], Proposition A.1.11 can also be found in [Reference StacksSta18, 02IM]
Étale morphisms and étale neighborhoods
We recall some terminology and a result on étale morphisms to be used in Section 5.
Definition A.1.12 [Reference StacksSta18, §00U0 and Definition 02GI].
-
(a) A ring map
 $A \to B$
is called étale if it is a smooth ring map of relative dimension zero.
$A \to B$
is called étale if it is a smooth ring map of relative dimension zero. -
(b) A morphism
 $f : X \to Y$
of schemes is called étale at
$f : X \to Y$
of schemes is called étale at
 $x \in X$
if there is an affine open neighborhood
$x \in X$
if there is an affine open neighborhood
 ${\mathrm {Spec}}(B) = U \subset X$
of x and an affine open
${\mathrm {Spec}}(B) = U \subset X$
of x and an affine open
 ${\mathrm {Spec}}(A) = V \subset Y$
with
${\mathrm {Spec}}(A) = V \subset Y$
with
 $f(U) \subset V$
so that the corresponding ring map
$f(U) \subset V$
so that the corresponding ring map
 $A \to B$
is étale. We say that f is étale if it is étale at each point
$A \to B$
is étale. We say that f is étale if it is étale at each point
 $x\in X$
.
$x\in X$
.
Definition A.1.13 [Reference StacksSta18, Definition 03PO]. Let X be a scheme.
-
(a) A geometric point of X is a morphism
 $\overline {x}\colon {\mathrm {Spec}}\ k \to X$
, where k is an algebraically closed field.
$\overline {x}\colon {\mathrm {Spec}}\ k \to X$
, where k is an algebraically closed field. -
(b) One says that
 $\overline {x}$
is lies over
$\overline {x}$
is lies over
 $x\in X$
to indicate that x is the image of
$x\in X$
to indicate that x is the image of
 $\overline {x}$
.
$\overline {x}$
. -
(c) An étale neighborhood
 $(U, \overline {u},{\varphi })$
of a geometric point
$(U, \overline {u},{\varphi })$
of a geometric point
 $\overline {x}\in X$
is a commutative diagram where
$\overline {x}\in X$
is a commutative diagram where
 ${\varphi }$
is an étale morphism of schemes and
${\varphi }$
is an étale morphism of schemes and
 $\overline u$
is a geometric point of U.
$\overline u$
is a geometric point of U.
Lemma A.1.14. Let
![]() ${\varphi }\colon U\to X$
be an étale morphism between schemes U and X. Let u be a point of U and denote by x its image
${\varphi }\colon U\to X$
be an étale morphism between schemes U and X. Let u be a point of U and denote by x its image
![]() ${\varphi }(u)$
. Consider the local homomorphism
${\varphi }(u)$
. Consider the local homomorphism
![]() ${\varphi }_u\colon {\cal O}_{X,x}\to {\cal O}_{U,u}$
induced from
${\varphi }_u\colon {\cal O}_{X,x}\to {\cal O}_{U,u}$
induced from
![]() ${\varphi }$
. Then
${\varphi }$
. Then
-
(a) The completion
 $\widehat {{\varphi }_u} \colon \widehat {{\cal O}}_{X,x}\to \widehat {{\cal O}}_{U,u}$
of
$\widehat {{\varphi }_u} \colon \widehat {{\cal O}}_{X,x}\to \widehat {{\cal O}}_{U,u}$
of
 ${{\varphi }_u}$
is finite étale; its degree is equal to
${{\varphi }_u}$
is finite étale; its degree is equal to
 $[{\kappa ({u})} :{\kappa ({x})} ]$
.
$[{\kappa ({u})} :{\kappa ({x})} ]$
. -
(b) The ring
 $\widehat {{\cal O}}_{X,x}$
is regular if and only if
$\widehat {{\cal O}}_{X,x}$
is regular if and only if
 $\widehat {{\cal O}}_{U,u}$
is regular, and in this case both have the same dimension.
$\widehat {{\cal O}}_{U,u}$
is regular, and in this case both have the same dimension.
Proof. Part (a) is [Reference StacksSta18, Lemma 039M] and the remark following it. For Part (b), note that by étaleness the tangent spaces at the closed point have the same dimension, and by finite étaleness the ring
![]() $ \widehat {{\cal O}}_{U,u}$
is free of finite rank over
$ \widehat {{\cal O}}_{U,u}$
is free of finite rank over
![]() $\widehat {{\cal O}}_{X,x}$
and hence they have the same dimension. From this, (b) follows easily.
$\widehat {{\cal O}}_{X,x}$
and hence they have the same dimension. From this, (b) follows easily.
A.2 Finite-dimensional algebras and modules
Let
![]() ${\mathbb {K}}$
be a field. We gather some results, mostly from [Reference Curtis and ReinerCR62], on not necessarily commutative
${\mathbb {K}}$
be a field. We gather some results, mostly from [Reference Curtis and ReinerCR62], on not necessarily commutative
![]() ${\mathbb {K}}$
-algebras
${\mathbb {K}}$
-algebras
![]() ${S}$
and modules M over them, assuming that either the algebra or the module have finite
${S}$
and modules M over them, assuming that either the algebra or the module have finite
![]() ${\mathbb {K}}$
-dimension. Our intended applications are to
${\mathbb {K}}$
-dimension. Our intended applications are to
![]() ${S}={\mathbb {K}}[G]$
for a possibly infinite group G, or to G-modules of finite
${S}={\mathbb {K}}[G]$
for a possibly infinite group G, or to G-modules of finite
![]() ${\mathbb {K}}$
-dimension; note that if G is profinite,
${\mathbb {K}}$
-dimension; note that if G is profinite,
![]() ${\mathbb {K}}$
is a topological field and M is a
${\mathbb {K}}$
is a topological field and M is a
![]() ${\mathbb {K}}[G]$
-module of finite
${\mathbb {K}}[G]$
-module of finite
![]() ${\mathbb {K}}$
-dimension with a continuous G-action, then all G-subquotients of M carry a continuous action. So we need not worry about continuity in the following.
${\mathbb {K}}$
-dimension with a continuous G-action, then all G-subquotients of M carry a continuous action. So we need not worry about continuity in the following.
Let first
![]() ${S}$
be a
${S}$
be a
![]() ${\mathbb {K}}$
-algebra of finite
${\mathbb {K}}$
-algebra of finite
![]() ${\mathbb {K}}$
-dimension. In this case, the sum of all nilpotent left ideals of
${\mathbb {K}}$
-dimension. In this case, the sum of all nilpotent left ideals of
![]() ${S}$
is a two-sided ideal of
${S}$
is a two-sided ideal of
![]() ${S}$
, the radical of
${S}$
, the radical of
![]() ${S}$
and denoted
${S}$
and denoted
![]() ${\mathrm {Rad}}({S})$
, see [Reference Curtis and ReinerCR62, § 24]. It is the maximal nilpotent two-sided ideal of
${\mathrm {Rad}}({S})$
, see [Reference Curtis and ReinerCR62, § 24]. It is the maximal nilpotent two-sided ideal of
![]() ${S}$
. The radical is zero if and only if
${S}$
. The radical is zero if and only if
![]() ${S}$
is semisimple; in this case,
${S}$
is semisimple; in this case,
![]() ${S}$
is the product of simple
${S}$
is the product of simple
![]() ${\mathbb {K}}$
-algebras (of finite
${\mathbb {K}}$
-algebras (of finite
![]() ${\mathbb {K}}$
-dimension). If
${\mathbb {K}}$
-dimension). If
![]() ${\mathbb {K}}'$
is any field extension of
${\mathbb {K}}'$
is any field extension of
![]() ${\mathbb {K}}$
, then
${\mathbb {K}}$
, then
Definition A.2.1. We call a
![]() ${\mathbb {K}}$
-algebra
${\mathbb {K}}$
-algebra
![]() ${S}$
of finite
${S}$
of finite
![]() ${\mathbb {K}}$
–dimension absolutely semisimple if
${\mathbb {K}}$
–dimension absolutely semisimple if
![]() ${S}\otimes _{\mathbb {K}}{{{{\mathbb {K}}}}^{\mathrm {alg}}} $
is semisimple.
${S}\otimes _{\mathbb {K}}{{{{\mathbb {K}}}}^{\mathrm {alg}}} $
is semisimple.
Remark A.2.2. Suppose that
![]() ${S}$
is absolutely semisimple. Then by the containment (37) it is semisimple. By the theorem of Artin–Wedderburn, the algebra
${S}$
is absolutely semisimple. Then by the containment (37) it is semisimple. By the theorem of Artin–Wedderburn, the algebra
![]() ${S}\otimes _{\mathbb {K}}{{{{\mathbb {K}}}}^{\mathrm {alg}}} $
is a product of matrix algebras over
${S}\otimes _{\mathbb {K}}{{{{\mathbb {K}}}}^{\mathrm {alg}}} $
is a product of matrix algebras over
![]() ${{{{\mathbb {K}}}}^{\mathrm {alg}}} $
. From this one deduces, by repeated application of the inclusion (37), that
${{{{\mathbb {K}}}}^{\mathrm {alg}}} $
. From this one deduces, by repeated application of the inclusion (37), that
![]() ${S}\otimes _{\mathbb {K}}{\mathbb {K}}'$
is semisimple for any field extension
${S}\otimes _{\mathbb {K}}{\mathbb {K}}'$
is semisimple for any field extension
![]() ${\mathbb {K}}'$
of
${\mathbb {K}}'$
of
![]() ${\mathbb {K}}$
. Suppose now that
${\mathbb {K}}$
. Suppose now that
![]() ${S}$
is only semisimple. By considering simple factors
${S}$
is only semisimple. By considering simple factors
![]() $D_i$
of
$D_i$
of
![]() ${S}$
, one shows that
${S}$
, one shows that
![]() ${S}$
is absolutely semisimple if and only if the center of each
${S}$
is absolutely semisimple if and only if the center of each
![]() $D_i$
is separable over
$D_i$
is separable over
![]() ${\mathbb {K}}$
.
${\mathbb {K}}$
.
Lemma A.2.3. Let
![]() ${S}$
a
${S}$
a
![]() ${\mathbb {K}}$
-algebra of finite
${\mathbb {K}}$
-algebra of finite
![]() ${\mathbb {K}}$
-dimension, and write
${\mathbb {K}}$
-dimension, and write
![]() ${S}'$
for
${S}'$
for
![]() ${S}\otimes _{\mathbb {K}}{\mathbb {K}}'$
and any field extension
${S}\otimes _{\mathbb {K}}{\mathbb {K}}'$
and any field extension
![]() ${\mathbb {K}}'$
of
${\mathbb {K}}'$
of
![]() ${\mathbb {K}}$
.
${\mathbb {K}}$
.
-
(a) There exists a finite extension
 ${\mathbb {K}}'$
of
${\mathbb {K}}'$
of
 ${\mathbb {K}}$
such that
${\mathbb {K}}$
such that
 ${S}'/{\mathrm {Rad}}({S}')$
is absolutely semisimple.
${S}'/{\mathrm {Rad}}({S}')$
is absolutely semisimple. -
(b) If
 ${S}/{\mathrm {Rad}}({S})$
is absolutely semisimple over
${S}/{\mathrm {Rad}}({S})$
is absolutely semisimple over
 ${\mathbb {K}}$
, then there exists an extension
${\mathbb {K}}$
, then there exists an extension
 ${\mathbb {K}}'$
of
${\mathbb {K}}'$
of
 ${\mathbb {K}}$
with
${\mathbb {K}}$
with
 $[{\mathbb {K}}':{\mathbb {K}}]\le (\dim _{\mathbb {K}} {S})!$
such that
$[{\mathbb {K}}':{\mathbb {K}}]\le (\dim _{\mathbb {K}} {S})!$
such that
 ${S}'/{\mathrm {Rad}}({S}')$
is a product of matrix algebras over
${S}'/{\mathrm {Rad}}({S}')$
is a product of matrix algebras over
 ${\mathbb {K}}'$
.
${\mathbb {K}}'$
. -
(c) If
 ${\mathbb {K}}$
is finite, and if we write
${\mathbb {K}}$
is finite, and if we write
 ${S}/{\mathrm {Rad}} ({S})\cong \prod _i {\mathrm {Mat}}_{d_i\times d_i}({\mathbb {K}}_i)$
for
${S}/{\mathrm {Rad}} ({S})\cong \prod _i {\mathrm {Mat}}_{d_i\times d_i}({\mathbb {K}}_i)$
for
 $d_i\ge 1$
and
$d_i\ge 1$
and
 ${\mathbb {K}}_i$
finite over
${\mathbb {K}}_i$
finite over
 ${\mathbb {K}}$
, then we may find
${\mathbb {K}}$
, then we may find
 ${\mathbb {K}}'$
as in (b) so that
${\mathbb {K}}'$
as in (b) so that
 $[{\mathbb {K}}':{\mathbb {K}}]$
divides
$[{\mathbb {K}}':{\mathbb {K}}]$
divides
 $\prod _{i}[{\mathbb {K}}_i:{\mathbb {K}}]$
.
$\prod _{i}[{\mathbb {K}}_i:{\mathbb {K}}]$
.
Proof. For (a) note first that for
![]() ${{{{S}}}^{\mathrm {alg}}}:={S}\otimes _{\mathbb {K}}{{{{\mathbb {K}}}}^{\mathrm {alg}}} $
the ring
${{{{S}}}^{\mathrm {alg}}}:={S}\otimes _{\mathbb {K}}{{{{\mathbb {K}}}}^{\mathrm {alg}}} $
the ring
![]() ${{{{S}}}^{\mathrm {alg}}}/{\mathrm {Rad}}({{{{S}}}^{\mathrm {alg}}})$
is semisimple and trivially absolutely semisimple. Let
${{{{S}}}^{\mathrm {alg}}}/{\mathrm {Rad}}({{{{S}}}^{\mathrm {alg}}})$
is semisimple and trivially absolutely semisimple. Let
![]() ${\mathbb {K}}'$
be a finite extension of
${\mathbb {K}}'$
be a finite extension of
![]() ${\mathbb {K}}$
over which
${\mathbb {K}}$
over which
![]() ${S}':={S}\otimes _{\mathbb {K}}{\mathbb {K}}'$
contains a sub-
${S}':={S}\otimes _{\mathbb {K}}{\mathbb {K}}'$
contains a sub-
![]() ${\mathbb {K}}'$
vector space I with
${\mathbb {K}}'$
vector space I with
![]() $I\otimes _{{\mathbb {K}}'}{{{{\mathbb {K}}}}^{\mathrm {alg}}} ={\mathrm {Rad}}({{{{S}}}^{\mathrm {alg}}})$
. Considering I inside
$I\otimes _{{\mathbb {K}}'}{{{{\mathbb {K}}}}^{\mathrm {alg}}} ={\mathrm {Rad}}({{{{S}}}^{\mathrm {alg}}})$
. Considering I inside
![]() ${\mathrm {Rad}}({{{{S}}}^{\mathrm {alg}}})$
, it follows that I is a nilpotent ideal of
${\mathrm {Rad}}({{{{S}}}^{\mathrm {alg}}})$
, it follows that I is a nilpotent ideal of
![]() ${S}'$
so that
${S}'$
so that
![]() $I\subset {\mathrm {Rad}}({S}')$
. But then using the inclusion (37) and the faithful flatness of
$I\subset {\mathrm {Rad}}({S}')$
. But then using the inclusion (37) and the faithful flatness of
![]() ${\mathbb {K}}'\to {{{{\mathbb {K}}}}^{\mathrm {alg}}} $
, it is straightforward to see that
${\mathbb {K}}'\to {{{{\mathbb {K}}}}^{\mathrm {alg}}} $
, it is straightforward to see that
![]() $I={\mathrm {Rad}}({S}')$
and that
$I={\mathrm {Rad}}({S}')$
and that
![]() ${S}'/I$
is absolutely simple.
${S}'/I$
is absolutely simple.
To prove (b), note first that we may replace
![]() ${S}$
by
${S}$
by
![]() ${S}/{\mathrm {Rad}}({S})$
, again by the inclusion (37) so that we may assume that
${S}/{\mathrm {Rad}}({S})$
, again by the inclusion (37) so that we may assume that
![]() ${S}$
is absolutely semisimple. Write
${S}$
is absolutely semisimple. Write
![]() ${S}$
as a product of division algebras
${S}$
as a product of division algebras
![]() $D_i$
, for i in a finite index set I, and write
$D_i$
, for i in a finite index set I, and write
![]() ${\mathbb {K}}_i$
for the center of
${\mathbb {K}}_i$
for the center of
![]() $D_i$
and let
$D_i$
and let
![]() $d_i\in {\mathbb {N}}$
be such that
$d_i\in {\mathbb {N}}$
be such that
![]() $d_i^2=\dim _{{\mathbb {K}}_i}D_i$
. We consider all finite field extensions of
$d_i^2=\dim _{{\mathbb {K}}_i}D_i$
. We consider all finite field extensions of
![]() ${\mathbb {K}}$
as subfields of a fixed algebraic closure
${\mathbb {K}}$
as subfields of a fixed algebraic closure
![]() ${{{{\mathbb {K}}}}^{\mathrm {alg}}} $
of
${{{{\mathbb {K}}}}^{\mathrm {alg}}} $
of
![]() ${\mathbb {K}}$
. Let
${\mathbb {K}}$
. Let
![]() ${\mathbb {K}}'\subset {{{{\mathbb {K}}}}^{\mathrm {alg}}} $
be the join of the normal hull of all
${\mathbb {K}}'\subset {{{{\mathbb {K}}}}^{\mathrm {alg}}} $
be the join of the normal hull of all
![]() ${\mathbb {K}}_i$
. By Remark A.2.2,
${\mathbb {K}}_i$
. By Remark A.2.2,
![]() ${\mathbb {K}}'$
is separable over
${\mathbb {K}}'$
is separable over
![]() ${\mathbb {K}}$
and for each i we have
${\mathbb {K}}$
and for each i we have
![]() ${\mathbb {K}}_i\otimes _{\mathbb {K}}{\mathbb {K}}'\cong ({\mathbb {K}}')^{m_i}$
for
${\mathbb {K}}_i\otimes _{\mathbb {K}}{\mathbb {K}}'\cong ({\mathbb {K}}')^{m_i}$
for
![]() $m_i=[{\mathbb {K}}_i:{\mathbb {K}}]$
. Note also that
$m_i=[{\mathbb {K}}_i:{\mathbb {K}}]$
. Note also that
![]() $[{\mathbb {K}}':{\mathbb {K}}]\le \prod _{i\in I}m_i!$
. Let
$[{\mathbb {K}}':{\mathbb {K}}]\le \prod _{i\in I}m_i!$
. Let
![]() ${\mathbb {E}}_i\subset D_i$
be a maximal subfield over
${\mathbb {E}}_i\subset D_i$
be a maximal subfield over
![]() ${\mathbb {K}}_i$
so that
${\mathbb {K}}_i$
so that
![]() $D_i\otimes _{{\mathbb {K}}_i}{\mathbb {E}}_i\cong {\mathrm {Mat}}_{d_i\times d_i}({\mathbb {E}}_i)$
. Let
$D_i\otimes _{{\mathbb {K}}_i}{\mathbb {E}}_i\cong {\mathrm {Mat}}_{d_i\times d_i}({\mathbb {E}}_i)$
. Let
![]() ${\mathbb {E}}'\supset {{{{\mathbb {K}}}}^{\mathrm {alg}}} $
be the join of
${\mathbb {E}}'\supset {{{{\mathbb {K}}}}^{\mathrm {alg}}} $
be the join of
![]() ${\mathbb {K}}'$
and the fields
${\mathbb {K}}'$
and the fields
![]() ${\mathbb {E}}_i$
,
${\mathbb {E}}_i$
,
![]() $i\in I$
. Then
$i\in I$
. Then
 $$ \begin{align} {S}\otimes_{\mathbb{K}}{\mathbb{E}}'\cong\prod_{i\in I} (D_i\otimes_{{\mathbb{K}}_i} ({\mathbb{K}}_i\otimes_{\mathbb{K}} {\mathbb{K}}')\otimes_{{\mathbb{K}}'}{\mathbb{E}}') \cong \prod_{i\in I} (D_i\otimes_{{\mathbb{K}}_i} {\mathbb{E}}')^{m_i}\stackrel{{\mathbb{E}}'\supset{\mathbb{E}}_i}{\cong} \prod_{i\in I} ({\mathrm{Mat}}_{d_i\times d_i}({\mathbb{E}}'))^{m_i}. \end{align} $$
$$ \begin{align} {S}\otimes_{\mathbb{K}}{\mathbb{E}}'\cong\prod_{i\in I} (D_i\otimes_{{\mathbb{K}}_i} ({\mathbb{K}}_i\otimes_{\mathbb{K}} {\mathbb{K}}')\otimes_{{\mathbb{K}}'}{\mathbb{E}}') \cong \prod_{i\in I} (D_i\otimes_{{\mathbb{K}}_i} {\mathbb{E}}')^{m_i}\stackrel{{\mathbb{E}}'\supset{\mathbb{E}}_i}{\cong} \prod_{i\in I} ({\mathrm{Mat}}_{d_i\times d_i}({\mathbb{E}}'))^{m_i}. \end{align} $$
Hence,
![]() ${\mathbb {E}}'$
is a field as in (a). Moreover,
${\mathbb {E}}'$
is a field as in (a). Moreover,
![]() $[{\mathbb {E}}':{\mathbb {K}}]\le \prod _{i\in I} (d_i \cdot m_i!) \le \prod _{i\in I} (d_i \cdot [{\mathbb {K}}_i:{\mathbb {K}}])!$
. Since
$[{\mathbb {E}}':{\mathbb {K}}]\le \prod _{i\in I} (d_i \cdot m_i!) \le \prod _{i\in I} (d_i \cdot [{\mathbb {K}}_i:{\mathbb {K}}])!$
. Since
![]() $ \sum _{i\in I} (d_i [{\mathbb {K}}_i:{\mathbb {K}}])\le \sum _{i\in I} d_i^2\cdot m_i= n$
, using that multinomials are integers, we deduce
$ \sum _{i\in I} (d_i [{\mathbb {K}}_i:{\mathbb {K}}])\le \sum _{i\in I} d_i^2\cdot m_i= n$
, using that multinomials are integers, we deduce
![]() $[{\mathbb {E}}':{\mathbb {K}}]\le n!$
, and this proves (b).
$[{\mathbb {E}}':{\mathbb {K}}]\le n!$
, and this proves (b).
To see (c) note that each
![]() ${\mathbb {K}}_i$
is normal over
${\mathbb {K}}_i$
is normal over
![]() ${\mathbb {K}}$
and for each degree there is a unique extension of
${\mathbb {K}}$
and for each degree there is a unique extension of
![]() ${\mathbb {K}}$
of that degree in a fixed choice
${\mathbb {K}}$
of that degree in a fixed choice
![]() ${{{{\mathbb {K}}}}^{\mathrm {alg}}} $
. Hence, in the proof of (b) we find
${{{{\mathbb {K}}}}^{\mathrm {alg}}} $
. Hence, in the proof of (b) we find
![]() $[{\mathbb {K}}':{\mathbb {K}}]\le {\mathrm {lcm}}_{i\in I}[{\mathbb {K}}_i:{\mathbb {K}}]$
. Moreover, over
$[{\mathbb {K}}':{\mathbb {K}}]\le {\mathrm {lcm}}_{i\in I}[{\mathbb {K}}_i:{\mathbb {K}}]$
. Moreover, over
![]() ${\mathbb {K}}_i$
the ring
${\mathbb {K}}_i$
the ring
![]() $D_i$
is already split, and so we can take
$D_i$
is already split, and so we can take
![]() ${\mathbb {E}}'={\mathbb {K}}'$
. The assertion now is clear.
${\mathbb {E}}'={\mathbb {K}}'$
. The assertion now is clear.
Remark A.2.4.
-
(a) Note that the hypothesis in Lemma A.2.3(b) holds whenever
 ${\mathbb {K}}$
is perfect.
${\mathbb {K}}$
is perfect. -
(b) A version of Lemma A.2.3(a) only under algebraicity hypotheses for
 ${S}$
over
${S}$
over
 ${\mathbb {K}}$
can be found in [Reference ChenevierChe14, Lemma 2.14].
${\mathbb {K}}$
can be found in [Reference ChenevierChe14, Lemma 2.14]. -
(c) It is possible to give effective bounds in Lemma A.2.3(b) also without any separability hypotheses. But the proof is longer and we do not need the result.
Let now
![]() ${S}$
be any
${S}$
be any
![]() ${\mathbb {K}}$
-algebra, not necessarily of finite
${\mathbb {K}}$
-algebra, not necessarily of finite
![]() ${\mathbb {K}}$
-dimension. Let M be an
${\mathbb {K}}$
-dimension. Let M be an
![]() ${S}$
-module of finite
${S}$
-module of finite
![]() ${\mathbb {K}}$
-dimension. If M is semisimple, the representation
${\mathbb {K}}$
-dimension. If M is semisimple, the representation
![]() $M\otimes _{\mathbb {K}}{{{{\mathbb {K}}}}^{\mathrm {alg}}} $
need in general not be semisimple over
$M\otimes _{\mathbb {K}}{{{{\mathbb {K}}}}^{\mathrm {alg}}} $
need in general not be semisimple over
![]() ${{{{S}}}^{\mathrm {alg}}}:={S}\otimes _{\mathbb {K}}{{{{\mathbb {K}}}}^{\mathrm {alg}}} $
.Footnote
8
${{{{S}}}^{\mathrm {alg}}}:={S}\otimes _{\mathbb {K}}{{{{\mathbb {K}}}}^{\mathrm {alg}}} $
.Footnote
8
Definition A.2.5. We call M absolutely semisimple, if
![]() $M\otimes _{\mathbb {K}}{{{{\mathbb {K}}}}^{\mathrm {alg}}} $
is semisimple as an
$M\otimes _{\mathbb {K}}{{{{\mathbb {K}}}}^{\mathrm {alg}}} $
is semisimple as an
![]() ${{{{S}}}^{\mathrm {alg}}}$
-module.
${{{{S}}}^{\mathrm {alg}}}$
-module.
We call M absolutely completely reducible if it is semisimple and all its irreducible summands are absolutely irreducible.
Remark A.2.6. If M is absolutely completely reducible, it is clearly absolutely semisimple. If M is absolutely semisimple, it is absolutely completely reducible if and only if for each irreducible summand N of M the natural map
![]() ${\mathbb {K}}\to {\mathrm {End}}_{S}(N)$
is an isomorphism, see [Reference Curtis and ReinerCR62, 29.13]; the latter condition is equivalent to
${\mathbb {K}}\to {\mathrm {End}}_{S}(N)$
is an isomorphism, see [Reference Curtis and ReinerCR62, 29.13]; the latter condition is equivalent to
![]() ${\mathrm {End}}_{S}(M)$
being a product of matrix algebras over
${\mathrm {End}}_{S}(M)$
being a product of matrix algebras over
![]() ${\mathbb {K}}$
.
${\mathbb {K}}$
.
For the following note, that if N is a second
![]() ${S}$
-modulo of finite
${S}$
-modulo of finite
![]() ${\mathbb {K}}$
-dimension and
${\mathbb {K}}$
-dimension and
![]() ${\mathbb {K}}'$
is any field extension of
${\mathbb {K}}'$
is any field extension of
![]() ${\mathbb {K}}$
, then by [Reference Curtis and ReinerCR62, 29.2] one has
${\mathbb {K}}$
, then by [Reference Curtis and ReinerCR62, 29.2] one has
Lemma A.2.7. Suppose M is absolutely semisimple. Then the following hold:
-
(a) The
 ${\mathbb {K}}$
-algebra
${\mathbb {K}}$
-algebra
 ${\mathrm {End}}_{S}(M)$
is absolutely semisimple.
${\mathrm {End}}_{S}(M)$
is absolutely semisimple. -
(b) If
 ${\mathbb {K}}'\supset {\mathbb {K}}$
is an extension such that
${\mathbb {K}}'\supset {\mathbb {K}}$
is an extension such that
 ${\mathrm {End}}_{S}(M)\otimes _{\mathbb {K}}{\mathbb {K}}'$
is a product of matrix algebras, then
${\mathrm {End}}_{S}(M)\otimes _{\mathbb {K}}{\mathbb {K}}'$
is a product of matrix algebras, then
 $M\otimes _{\mathbb {K}}{\mathbb {K}}'$
is absolutely completely reducible.
$M\otimes _{\mathbb {K}}{\mathbb {K}}'$
is absolutely completely reducible.
Proof. To prove (a) it suffices to assume that M is irreducible. Then
![]() $D:={\mathrm {End}}_{S}(M)$
is a skew field of finite dimension over
$D:={\mathrm {End}}_{S}(M)$
is a skew field of finite dimension over
![]() ${\mathbb {K}}$
. By the isomorphism (39), we have
${\mathbb {K}}$
. By the isomorphism (39), we have
By hypothesis,
![]() $M\otimes _{\mathbb {K}}{{{{\mathbb {K}}}}^{\mathrm {alg}}} $
is semisimple over
$M\otimes _{\mathbb {K}}{{{{\mathbb {K}}}}^{\mathrm {alg}}} $
is semisimple over
![]() ${S}\otimes _{\mathbb {K}}{{{{\mathbb {K}}}}^{\mathrm {alg}}} $
. By Remark A.2.6,
${S}\otimes _{\mathbb {K}}{{{{\mathbb {K}}}}^{\mathrm {alg}}} $
. By Remark A.2.6,
![]() $D\otimes _{\mathbb {K}}{{{{\mathbb {K}}}}^{\mathrm {alg}}} $
is then a product of matrix algebras over
$D\otimes _{\mathbb {K}}{{{{\mathbb {K}}}}^{\mathrm {alg}}} $
is then a product of matrix algebras over
![]() ${{{{\mathbb {K}}}}^{\mathrm {alg}}} $
. This proves (a). Part (b) is immediate from the isomorphism (39) since it implies
${{{{\mathbb {K}}}}^{\mathrm {alg}}} $
. This proves (a). Part (b) is immediate from the isomorphism (39) since it implies
![]() ${\mathbb {K}}'\cong {\mathrm {End}}_{{S}\otimes _{\mathbb {K}}{\mathbb {K}}'}(N)$
for every irreducible summand of
${\mathbb {K}}'\cong {\mathrm {End}}_{{S}\otimes _{\mathbb {K}}{\mathbb {K}}'}(N)$
for every irreducible summand of
![]() $M\otimes _{\mathbb {K}}{\mathbb {K}}'$
.
$M\otimes _{\mathbb {K}}{\mathbb {K}}'$
.
A.3 Absolutely irreducible mod p representations of the absolute Galois group of a p-adic field
This subsection gives the proof of the classification of irreducible finite-dimensional representations of
![]() $G_K$
for a p-adic field K over a finite field of characteristic p, and some complements.
$G_K$
for a p-adic field K over a finite field of characteristic p, and some complements.
We begin with some preparations and reminders: Recall the classification of tame characters of the inertia group
![]() $I_K$
of
$I_K$
of
![]() $G_K$
from [Reference SerreSer72]: Let m denote some natural number. Let
$G_K$
from [Reference SerreSer72]: Let m denote some natural number. Let
![]() ${{{k}}^{\mathrm {alg}}} $
be the residue field of
${{{k}}^{\mathrm {alg}}} $
be the residue field of
![]() ${{K}^{\mathrm {alg}}}$
and set
${{K}^{\mathrm {alg}}}$
and set
![]() $q:=|k|$
. Let in the following
$q:=|k|$
. Let in the following
![]() $\sigma \in G_K$
be any element that maps to Frobenius in
$\sigma \in G_K$
be any element that maps to Frobenius in
![]() $G_k$
. Let
$G_k$
. Let
![]() $K^{\operatorname {nr}}\subset K^{\operatorname {t}}\subset {{K}^{\mathrm {alg}}}$
denote the maximal unramified and maximal tamely ramified extensions of K, respectively. Denote by
$K^{\operatorname {nr}}\subset K^{\operatorname {t}}\subset {{K}^{\mathrm {alg}}}$
denote the maximal unramified and maximal tamely ramified extensions of K, respectively. Denote by
![]() $K_m\subset K^{\operatorname {nr}}$
the unique extension of K of degree m and by
$K_m\subset K^{\operatorname {nr}}$
the unique extension of K of degree m and by
![]() $k_m\subset {{{k}}^{\mathrm {alg}}} $
its residue field. If
$k_m\subset {{{k}}^{\mathrm {alg}}} $
its residue field. If
![]() $\varpi $
is a fixed choice of uniformizer of K and
$\varpi $
is a fixed choice of uniformizer of K and
![]() $K_m^t=K^{\operatorname {nr}}(\sqrt [q^m-1]{\varpi })$
, then
$K_m^t=K^{\operatorname {nr}}(\sqrt [q^m-1]{\varpi })$
, then
![]() . The characters
. The characters
 $$ \begin{align*}\omega_m\colon I_{\operatorname{t}}\!:=\!{\mathrm{Gal}}(K^{\operatorname{t}}/K^{\operatorname{nr}})\to {\mathrm{Gal}}(K_m^t/K^{\operatorname{nr}})\stackrel{\sim}{\to}\mu_{q^m-1}(K^{\operatorname{nr}})\!\cong\!\mu_{q^m-1}({{{k}}^{\mathrm{alg}}} )\!=\!k_m^\times, \sigma\mapsto\frac{\sigma(\sqrt[q^m-1]{\varpi})}{\sqrt[q^m-1]{\varpi}}, \end{align*} $$
$$ \begin{align*}\omega_m\colon I_{\operatorname{t}}\!:=\!{\mathrm{Gal}}(K^{\operatorname{t}}/K^{\operatorname{nr}})\to {\mathrm{Gal}}(K_m^t/K^{\operatorname{nr}})\stackrel{\sim}{\to}\mu_{q^m-1}(K^{\operatorname{nr}})\!\cong\!\mu_{q^m-1}({{{k}}^{\mathrm{alg}}} )\!=\!k_m^\times, \sigma\mapsto\frac{\sigma(\sqrt[q^m-1]{\varpi})}{\sqrt[q^m-1]{\varpi}}, \end{align*} $$
form an inverse system,
![]() $I_{\operatorname {t}}\cong \varprojlim \{k_m^\times \!:\!{m\!\in \!{\mathbb {N}}} \}$
is pro-cyclic and
$I_{\operatorname {t}}\cong \varprojlim \{k_m^\times \!:\!{m\!\in \!{\mathbb {N}}} \}$
is pro-cyclic and
![]() $I^p_{\operatorname {t}}=I_{\operatorname {t}}$
; see [Reference SerreSer72, Propositions 1 and 2].
$I^p_{\operatorname {t}}=I_{\operatorname {t}}$
; see [Reference SerreSer72, Propositions 1 and 2].
A continuous character
![]() $\omega \colon I_{\operatorname {t}}\to ({{{k}}^{\mathrm {alg}}} )^\times $
is called of level m (with respect to k) if m is the smallest integer such that
$\omega \colon I_{\operatorname {t}}\to ({{{k}}^{\mathrm {alg}}} )^\times $
is called of level m (with respect to k) if m is the smallest integer such that
![]() $\omega $
factors as
$\omega $
factors as
![]() $\omega ={\varphi }\circ \omega _m$
for some homomorphism
$\omega ={\varphi }\circ \omega _m$
for some homomorphism
![]() ${\varphi }\colon k_m^\times \to ({{{{{\mathbb {F}}\,\!{}}}}^{\mathrm {alg}} _p})^\times $
; since
${\varphi }\colon k_m^\times \to ({{{{{\mathbb {F}}\,\!{}}}}^{\mathrm {alg}} _p})^\times $
; since
![]() $I_{\operatorname {t}}$
is procyclic this is equivalent to
$I_{\operatorname {t}}$
is procyclic this is equivalent to
![]() $\omega $
having order a divisor of
$\omega $
having order a divisor of
![]() $q^m-1$
with m minimal; in particular, the number of such characters is finite. For any
$q^m-1$
with m minimal; in particular, the number of such characters is finite. For any
![]() $m\ge 1$
, let
$m\ge 1$
, let
![]() ${\cal P}_{m}:={\mathrm {Hom}}_{k}(k_m,{{{{{\mathbb {F}}\,\!{}}}}^{\mathrm {alg}} _p})$
, and set
${\cal P}_{m}:={\mathrm {Hom}}_{k}(k_m,{{{{{\mathbb {F}}\,\!{}}}}^{\mathrm {alg}} _p})$
, and set
![]() $\omega _{m,\tau }:=\tau \circ \omega _m$
for
$\omega _{m,\tau }:=\tau \circ \omega _m$
for
![]() $\tau \in {\cal P}_{m}$
. For any
$\tau \in {\cal P}_{m}$
. For any
![]() $\tau \in {\cal P}_m$
we have
$\tau \in {\cal P}_m$
we have
![]() ${\cal P}_m=\{\tau ^{q^i}\mid i=0,\ldots ,m-1\}$
. Moreover,
${\cal P}_m=\{\tau ^{q^i}\mid i=0,\ldots ,m-1\}$
. Moreover,
![]() $\sigma \in G_K$
as fixed above satisfies
$\sigma \in G_K$
as fixed above satisfies
![]() $\sigma \tau \sigma ^{-1}=\tau ^q$
.
$\sigma \tau \sigma ^{-1}=\tau ^q$
.
If
![]() $\omega $
is of level dividing m, it can be written as
$\omega $
is of level dividing m, it can be written as
![]() $\omega =\omega _{m,\tau }^r$
for any
$\omega =\omega _{m,\tau }^r$
for any
![]() $\tau \in {\cal P}_{m}$
and some
$\tau \in {\cal P}_{m}$
and some
![]() $r\in \{1,\ldots ,q^m-2\}$
(that depends on
$r\in \{1,\ldots ,q^m-2\}$
(that depends on
![]() $\tau $
). Call
$\tau $
). Call
![]() $r\in \{1,2,\ldots ,q^{m}-2\}$
primitive for m (and q) if there is no proper divisor d of m such that r is a multiple of
$r\in \{1,2,\ldots ,q^{m}-2\}$
primitive for m (and q) if there is no proper divisor d of m such that r is a multiple of
![]() $(q^m-1)/(q^d-1)$
; equivalently, r is primitive, if its base q expansion
$(q^m-1)/(q^d-1)$
; equivalently, r is primitive, if its base q expansion
![]() $r=[e_{m-1}e_{n-2}\ldots e_1e_0]_q$
, with digits
$r=[e_{m-1}e_{n-2}\ldots e_1e_0]_q$
, with digits
![]() $e_j\in \{0,\ldots ,q-1\}$
, is preserved under no cyclic digit permutation but the identity. Then the level m is minimal for
$e_j\in \{0,\ldots ,q-1\}$
, is preserved under no cyclic digit permutation but the identity. Then the level m is minimal for
![]() $\omega =\omega _{m,\tau }^r$
if and only if r is primitive for m. In the latter case, the orbit of
$\omega =\omega _{m,\tau }^r$
if and only if r is primitive for m. In the latter case, the orbit of
![]() $\omega $
under conjugation by
$\omega $
under conjugation by
![]() $\sigma $
has exact length m.
$\sigma $
has exact length m.
To extend
![]() $\omega _{m,\tau }$
to
$\omega _{m,\tau }$
to
![]() $G_{K_m}$
, recall that the local Artin map is an isomorphism
$G_{K_m}$
, recall that the local Artin map is an isomorphism
![]() $\widehat {K}_m^\times \stackrel \sim {\longrightarrow } G_{K_m}^{\operatorname {ab}}$
that maps
$\widehat {K}_m^\times \stackrel \sim {\longrightarrow } G_{K_m}^{\operatorname {ab}}$
that maps
![]() ${\cal O}_{K_m}^\times $
to the inertia subgroup of
${\cal O}_{K_m}^\times $
to the inertia subgroup of
![]() $G_{K_m}^{\operatorname {ab}}$
; the latter surjects onto
$G_{K_m}^{\operatorname {ab}}$
; the latter surjects onto
![]() $I_{\operatorname {t}}/(I_{\operatorname {t}})^{q^m-1}$
. The choice of
$I_{\operatorname {t}}/(I_{\operatorname {t}})^{q^m-1}$
. The choice of
![]() $\varpi $
gives an isomorphism
$\varpi $
gives an isomorphism
![]() $\widehat {K}_m^\times \cong \widehat {{\mathbb {Z}}}\times \mathcal {O}_{K_m}^\times $
; it induces a homomorphism
$\widehat {K}_m^\times \cong \widehat {{\mathbb {Z}}}\times \mathcal {O}_{K_m}^\times $
; it induces a homomorphism
![]() ${\mathrm {pr}}_2\colon G_{K_m}\to I_{\operatorname {t}}/(I_{\operatorname {t}})^{q^m-1}$
. We define
${\mathrm {pr}}_2\colon G_{K_m}\to I_{\operatorname {t}}/(I_{\operatorname {t}})^{q^m-1}$
. We define
Finally, for
![]() $\lambda \in ({{{k}}^{\mathrm {alg}}} )^\times $
and a finite extension field
$\lambda \in ({{{k}}^{\mathrm {alg}}} )^\times $
and a finite extension field
![]() $K'\supset K$
, we write
$K'\supset K$
, we write
![]() $\overline {\mu }_{K',\lambda }\colon G_{K'}\to ({{{k}}^{\mathrm {alg}}} )^\times $
for the unramified character of
$\overline {\mu }_{K',\lambda }\colon G_{K'}\to ({{{k}}^{\mathrm {alg}}} )^\times $
for the unramified character of
![]() $G_{K'}$
that sends a Frobenius automorphism to
$G_{K'}$
that sends a Frobenius automorphism to
![]() $\lambda ^{-1}\in {{{k}}^{\mathrm {alg}}} $
.
$\lambda ^{-1}\in {{{k}}^{\mathrm {alg}}} $
.
The following is the main result of this subsection.
Lemma A.3.1 (Berger, Muller).
Let
![]() ${\overline {\rho }}\colon G_K\to {\mathrm {GL}}_n({{{k}}^{\mathrm {alg}}} )$
be an n-dimensional irreducible continuous representation. Let
${\overline {\rho }}\colon G_K\to {\mathrm {GL}}_n({{{k}}^{\mathrm {alg}}} )$
be an n-dimensional irreducible continuous representation. Let
![]() ${{\mathbb {F}}\,\!{}}\subset {{{k}}^{\mathrm {alg}}} $
be a finite field that contains
${{\mathbb {F}}\,\!{}}\subset {{{k}}^{\mathrm {alg}}} $
be a finite field that contains
![]() $k_n$
. Then the following hold:
$k_n$
. Then the following hold:
-
(a) There exists
 $\lambda \in ({{{k}}^{\mathrm {alg}}} )^\times $
,
$\lambda \in ({{{k}}^{\mathrm {alg}}} )^\times $
,
 $\tau \in {\cal P}_{n}$
and a primitive number
$\tau \in {\cal P}_{n}$
and a primitive number
 $r\in \{ 1,2,\ldots ,q^n-2\}$
such that
$r\in \{ 1,2,\ldots ,q^n-2\}$
such that  $$ \begin{align*}{\overline{\rho}} \cong \overline{\mu}_{K,\lambda}\otimes {\mathrm{Ind}}^{G_K}_{G_{K_n}}\widehat{\omega_{n,\tau}}^r. \end{align*} $$
$$ \begin{align*}{\overline{\rho}} \cong \overline{\mu}_{K,\lambda}\otimes {\mathrm{Ind}}^{G_K}_{G_{K_n}}\widehat{\omega_{n,\tau}}^r. \end{align*} $$
-
(b)
 $\bar \rho $
can be defined over
$\bar \rho $
can be defined over
 ${{\mathbb {F}}\,\!{}}$
if and only if
${{\mathbb {F}}\,\!{}}$
if and only if
 $\lambda ^n\in {{\mathbb {F}}\,\!{}}$
.
$\lambda ^n\in {{\mathbb {F}}\,\!{}}$
.
In particular, given n there are only finitely many isomorphism classes of absolutely irreducible representations
![]() $G_K\to {\mathrm {GL}}_n({{\mathbb {F}}\,\!{}})$
.
$G_K\to {\mathrm {GL}}_n({{\mathbb {F}}\,\!{}})$
.
Proof. The proof of (a) is essentially that of [Reference BergerBer10, Corollary 2.1.5] for
![]() $K={\mathbb {Q}}_p$
as extended in [Reference MullerMul13, Proposition 2.1.1] to any K. We give a complete proof of (a), since it also serves to prove (b). Note that the last assertion is immediate from (a) and (b).
$K={\mathbb {Q}}_p$
as extended in [Reference MullerMul13, Proposition 2.1.1] to any K. We give a complete proof of (a), since it also serves to prove (b). Note that the last assertion is immediate from (a) and (b).
To prove (a), let
![]() ${\overline {\rho }}\colon G_K\to {\mathrm {GL}}_n({{{{{\mathbb {F}}\,\!{}}}}^{\mathrm {alg}}} )$
be irreducible. Then the wild ramification subgroup
${\overline {\rho }}\colon G_K\to {\mathrm {GL}}_n({{{{{\mathbb {F}}\,\!{}}}}^{\mathrm {alg}}} )$
be irreducible. Then the wild ramification subgroup
![]() $P_K$
of
$P_K$
of
![]() $G_K$
acts trivially via
$G_K$
acts trivially via
![]() $\bar \rho $
: the group
$\bar \rho $
: the group
![]() $P_K$
is normal in
$P_K$
is normal in
![]() $G_K$
and a pro-p subgroup. If its action on
$G_K$
and a pro-p subgroup. If its action on
![]() $({{{{{\mathbb {F}}\,\!{}}}}^{\mathrm {alg}}} )^n$
was not trivial, then the invariants
$({{{{{\mathbb {F}}\,\!{}}}}^{\mathrm {alg}}} )^n$
was not trivial, then the invariants
![]() $(({{{{{\mathbb {F}}\,\!{}}}}^{\mathrm {alg}}} )^n)^{P_K}$
would be a nontrivial proper subrepresentation of
$(({{{{{\mathbb {F}}\,\!{}}}}^{\mathrm {alg}}} )^n)^{P_K}$
would be a nontrivial proper subrepresentation of
![]() $G_K$
. But this is impossible, since
$G_K$
. But this is impossible, since
![]() ${\bar \rho }$
is irreducible.
${\bar \rho }$
is irreducible.
We deduce that the restriction
![]() ${\bar \rho }|_{I_K}$
factors via
${\bar \rho }|_{I_K}$
factors via
![]() $I_{\operatorname {t}}$
, and hence is a direct sum of one-dimensional continuous characters of
$I_{\operatorname {t}}$
, and hence is a direct sum of one-dimensional continuous characters of
![]() $I_{\operatorname {t}}$
. Fix one such character
$I_{\operatorname {t}}$
. Fix one such character
![]() $\omega $
and write
$\omega $
and write
![]() $\omega =\omega _{m,\tau }^r$
for m the level of
$\omega =\omega _{m,\tau }^r$
for m the level of
![]() $\omega $
, some
$\omega $
, some
![]() $\tau \in {\cal P}_{m}$
and
$\tau \in {\cal P}_{m}$
and
![]() $r\in \{1,\ldots ,q^m-2\}$
primitive, and let
$r\in \{1,\ldots ,q^m-2\}$
primitive, and let
![]() $\widehat {\omega }:= \widehat {\omega }_{m,\tau }^r$
. It follows that
$\widehat {\omega }:= \widehat {\omega }_{m,\tau }^r$
. It follows that
![]() $0\neq ({\bar \rho }|_{G_{K_m}}\otimes \widehat {\omega }^{-1})^{I_K}$
, and hence we can find
$0\neq ({\bar \rho }|_{G_{K_m}}\otimes \widehat {\omega }^{-1})^{I_K}$
, and hence we can find
![]() $\lambda '\in ({{{k}}^{\mathrm {alg}}} )^\times $
such that
$\lambda '\in ({{{k}}^{\mathrm {alg}}} )^\times $
such that
![]() $\bar \mu _{K_m,\lambda '}\otimes \widehat {\omega }$
is a subrepresentation of
$\bar \mu _{K_m,\lambda '}\otimes \widehat {\omega }$
is a subrepresentation of
![]() ${\bar \rho }|_{G_{K_m}}$
. Let
${\bar \rho }|_{G_{K_m}}$
. Let
![]() $\lambda \in {{{k}}^{\mathrm {alg}}} $
be such that
$\lambda \in {{{k}}^{\mathrm {alg}}} $
be such that
![]() $\lambda ^m=\lambda '$
so that
$\lambda ^m=\lambda '$
so that
![]() $\bar \mu _{K_m,\lambda '}=\bar \mu _{K,\lambda }|_{G_{K_m}}$
. Then by Frobenius reciprocity
$\bar \mu _{K_m,\lambda '}=\bar \mu _{K,\lambda }|_{G_{K_m}}$
. Then by Frobenius reciprocity
admits a nonzero homomorphism to the irreducible representation
![]() ${\bar \rho }$
. By the primitivity of r, the orbit of
${\bar \rho }$
. By the primitivity of r, the orbit of
![]() $\omega $
under conjugation by
$\omega $
under conjugation by
![]() $\sigma $
has length
$\sigma $
has length
![]() $m=[G_K:G_{K_m}]$
, and it follows that
$m=[G_K:G_{K_m}]$
, and it follows that
![]() ${\mathrm {Ind}}_{G_{K_m}}^{G_K}\widehat {\omega }$
is irreducible by the criterion of Mackey, see Lemma 2.1.4
(e). This yields the isomorphism
${\mathrm {Ind}}_{G_{K_m}}^{G_K}\widehat {\omega }$
is irreducible by the criterion of Mackey, see Lemma 2.1.4
(e). This yields the isomorphism
and moreover that
![]() $m=n$
, proving (a).
$m=n$
, proving (a).
For (b), assume first that
![]() $\bar \rho $
is defined over
$\bar \rho $
is defined over
![]() ${{\mathbb {F}}\,\!{}}$
. From our definitions and our hypothesis on
${{\mathbb {F}}\,\!{}}$
. From our definitions and our hypothesis on
![]() $|{{\mathbb {F}}\,\!{}}|$
is it clear that
$|{{\mathbb {F}}\,\!{}}|$
is it clear that
![]() ${\bar \rho }':={\mathrm {Ind}}^{G_K}_{G_{K_m}}\widehat {\omega }_{m,\tau }^r$
is defined over
${\bar \rho }':={\mathrm {Ind}}^{G_K}_{G_{K_m}}\widehat {\omega }_{m,\tau }^r$
is defined over
![]() $k_n\subset {{\mathbb {F}}\,\!{}}$
. It follows that
$k_n\subset {{\mathbb {F}}\,\!{}}$
. It follows that
![]() ${\mathrm {det}}{\bar \rho }'(\sigma ),{\mathrm {det}}{\bar \rho }(\sigma )\in {{\mathbb {F}}\,\!{}}^\times $
. Since
${\mathrm {det}}{\bar \rho }'(\sigma ),{\mathrm {det}}{\bar \rho }(\sigma )\in {{\mathbb {F}}\,\!{}}^\times $
. Since
![]() ${\mathrm {det}}{\bar \rho }(\sigma )=\lambda ^n\cdot {\mathrm {det}}{\bar \rho }'(\sigma )$
, we deduce
${\mathrm {det}}{\bar \rho }(\sigma )=\lambda ^n\cdot {\mathrm {det}}{\bar \rho }'(\sigma )$
, we deduce
![]() $\lambda ^n\in {{\mathbb {F}}\,\!{}}$
. For the converse, let
$\lambda ^n\in {{\mathbb {F}}\,\!{}}$
. For the converse, let
![]() $\lambda \in ({{{{{\mathbb {F}}\,\!{}}}}^{\mathrm {alg}} _p})^\times $
satisfy
$\lambda \in ({{{{{\mathbb {F}}\,\!{}}}}^{\mathrm {alg}} _p})^\times $
satisfy
![]() $\lambda ^n\in {{\mathbb {F}}\,\!{}}$
. From Lemma 4.6.6, one deduces that the characteristic polynomial of any
$\lambda ^n\in {{\mathbb {F}}\,\!{}}$
. From Lemma 4.6.6, one deduces that the characteristic polynomial of any
![]() $\sigma \in G_K$
acting via
$\sigma \in G_K$
acting via
![]() ${\bar \rho }$
lies in
${\bar \rho }$
lies in
![]() ${{\mathbb {F}}\,\!{}}[t]$
. It follows from the triviality of the Brauer group of a finite field and [Reference Curtis and ReinerCR62, Section 70] that the representation
${{\mathbb {F}}\,\!{}}[t]$
. It follows from the triviality of the Brauer group of a finite field and [Reference Curtis and ReinerCR62, Section 70] that the representation
![]() ${\bar \rho }$
can be defined over
${\bar \rho }$
can be defined over
![]() ${{\mathbb {F}}\,\!{}}$
.
${{\mathbb {F}}\,\!{}}$
.
A.4 A variant of a result of Vaccarino
In Theorem A.4.4 of this subsection, we prove a variant of the main theorem of Vaccarino from [Reference VaccarinoVac09] for group rings of free groups instead of free associative algebras. We use this result in the construction of induction for general pseudocharacters in Theorem 4.6.7.
Let us first introduce some notation. For a set
![]() ${X}$
, let
${X}$
, let
![]() ${\mathrm {FM}}({X})$
be the free monoid over
${\mathrm {FM}}({X})$
be the free monoid over
![]() ${X}$
and let
${X}$
and let
![]() ${\mathrm {FG}}({X})$
be the free group over
${\mathrm {FG}}({X})$
be the free group over
![]() ${X}$
; we regard
${X}$
; we regard
![]() ${\mathrm {FM}}({X})$
as a submonoid of
${\mathrm {FM}}({X})$
as a submonoid of
![]() ${\mathrm {FG}}({X})$
. We define
${\mathrm {FG}}({X})$
. We define
![]() ${\mathbb {Z}}\{{X}\}:={\mathbb {Z}}[{\mathrm {FM}}({X})]$
as the monoid ring of
${\mathbb {Z}}\{{X}\}:={\mathbb {Z}}[{\mathrm {FM}}({X})]$
as the monoid ring of
![]() ${\mathrm {FM}}({X})$
over
${\mathrm {FM}}({X})$
over
![]() ${\mathbb {Z}}$
; in other words,
${\mathbb {Z}}$
; in other words,
![]() ${\mathbb {Z}}\{{X}\}$
is the free associative
${\mathbb {Z}}\{{X}\}$
is the free associative
![]() ${\mathbb {Z}}$
-algebra in the indeterminates
${\mathbb {Z}}$
-algebra in the indeterminates
![]() ${x}\in {X}$
. We also define
${x}\in {X}$
. We also define
![]() ${\mathbb {Z}}\{{X}^{\pm }\}:={\mathbb {Z}}[{\mathrm {FG}}({X})]$
as the group ring of
${\mathbb {Z}}\{{X}^{\pm }\}:={\mathbb {Z}}[{\mathrm {FG}}({X})]$
as the group ring of
![]() ${\mathrm {FG}}({X})$
over
${\mathrm {FG}}({X})$
over
![]() ${\mathbb {Z}}$
and note that
${\mathbb {Z}}$
and note that
![]() ${\mathbb {Z}}\{{X}\}$
is a subring of
${\mathbb {Z}}\{{X}\}$
is a subring of
![]() ${\mathbb {Z}}\{{X}^{\pm }\}$
via the inclusion
${\mathbb {Z}}\{{X}^{\pm }\}$
via the inclusion
![]() ${\mathrm {FM}}({X})\subset {\mathrm {FG}}({X})$
. Let further
${\mathrm {FM}}({X})\subset {\mathrm {FG}}({X})$
. Let further
![]() $F_{{X}}(n)$
be the polynomial ring
$F_{{X}}(n)$
be the polynomial ring
![]() ${\mathbb {Z}}[\xi _{{x},i,j}: {x}\in {X}, 1\le i,j\le n]$
in indeterminates
${\mathbb {Z}}[\xi _{{x},i,j}: {x}\in {X}, 1\le i,j\le n]$
in indeterminates
![]() $\xi _{{x},i,j}$
, that is, the commutative ring of matrix coefficients of generic
$\xi _{{x},i,j}$
, that is, the commutative ring of matrix coefficients of generic
![]() $n\times n$
-matrices over
$n\times n$
-matrices over
![]() ${X}$
. Then one has the natural generic matrices representation
${X}$
. Then one has the natural generic matrices representation
Let
![]() $E_{X}(n)\subset F_{X}(n)$
be the subring generated by the coefficients of the characteristic polynomials of the matrices
$E_{X}(n)\subset F_{X}(n)$
be the subring generated by the coefficients of the characteristic polynomials of the matrices
![]() $\rho _{{X}}(w)$
,
$\rho _{{X}}(w)$
,
![]() $w\in {\mathrm {FM}}({X})$
. The associated degree n pseudocharacter
$w\in {\mathrm {FM}}({X})$
. The associated degree n pseudocharacter
![]() ${D}_{\rho _{{X}}}$
, cf. Definition 4.1.4, factors through a unique
${D}_{\rho _{{X}}}$
, cf. Definition 4.1.4, factors through a unique
![]() $E_{X}(n)$
-valued pseudocharacter
$E_{X}(n)$
-valued pseudocharacter
as follows for instance from [Reference ChenevierChe14, Corollary 1.14] using Amitsur’s formula.
Let
![]() $D_{{X}}^u\colon {\mathbb {Z}}\lbrace {X}\rbrace \rightarrow {R^{\operatorname {univ}}_{{\mathbb {Z}}\lbrace {X}\rbrace ,n}}$
be the universal n-dimensional pseudocharacter of
$D_{{X}}^u\colon {\mathbb {Z}}\lbrace {X}\rbrace \rightarrow {R^{\operatorname {univ}}_{{\mathbb {Z}}\lbrace {X}\rbrace ,n}}$
be the universal n-dimensional pseudocharacter of
![]() ${\mathbb {Z}}\{{X}\}$
from Proposition 4.2.1 so that one has a unique homomorphism
${\mathbb {Z}}\{{X}\}$
from Proposition 4.2.1 so that one has a unique homomorphism
![]() $\alpha _{{X}}\colon {R^{\operatorname {univ}}_{{\mathbb {Z}}\lbrace {X}\rbrace ,n}}\rightarrow E_{{X}}(n)$
in
$\alpha _{{X}}\colon {R^{\operatorname {univ}}_{{\mathbb {Z}}\lbrace {X}\rbrace ,n}}\rightarrow E_{{X}}(n)$
in
![]() ${\mathcal {CA}lg}_{\mathbb {Z}}$
with
${\mathcal {CA}lg}_{\mathbb {Z}}$
with
![]() $\alpha _{{X}}\circ D_{{X}}^u=D_{{X}}$
. The following result is an important theorem of Vaccarino.
$\alpha _{{X}}\circ D_{{X}}^u=D_{{X}}$
. The following result is an important theorem of Vaccarino.
Theorem A.4.1 (Vaccarino; [Reference VaccarinoVac09, Theorem 28]).
The map
![]() $\alpha _{{X}}\colon {R^{\operatorname {univ}}_{{\mathbb {Z}}\lbrace {X}\rbrace ,n}}\rightarrow E_{{X}}(n)$
is an isomorphism, and in particular
$\alpha _{{X}}\colon {R^{\operatorname {univ}}_{{\mathbb {Z}}\lbrace {X}\rbrace ,n}}\rightarrow E_{{X}}(n)$
is an isomorphism, and in particular
![]() ${R^{\operatorname {univ}}_{{\mathbb {Z}}\lbrace {X}\rbrace ,n}}$
is a domain and a free
${R^{\operatorname {univ}}_{{\mathbb {Z}}\lbrace {X}\rbrace ,n}}$
is a domain and a free
![]() ${\mathbb {Z}}$
-module.
${\mathbb {Z}}$
-module.
In the remainder of this section, we shall extend the pseudocharacter
![]() ${D}_{{X}}\colon {\mathbb {Z}}[{\mathrm {FM}}({X})]\to E_{{X}}(n)$
to an explicit pseudocharacter
${D}_{{X}}\colon {\mathbb {Z}}[{\mathrm {FM}}({X})]\to E_{{X}}(n)$
to an explicit pseudocharacter
![]() ${D}_{{X}^\pm }\colon {\mathrm {FG}}({X})\to E_{{X}^{\pm }}(n)$
on
${D}_{{X}^\pm }\colon {\mathrm {FG}}({X})\to E_{{X}^{\pm }}(n)$
on
![]() $ {\mathrm {FG}}({X})$
and prove that the extension has again a universal property. The following lemma provides some required auxiliary results.
$ {\mathrm {FG}}({X})$
and prove that the extension has again a universal property. The following lemma provides some required auxiliary results.
Lemma A.4.2. Let G be a group and let
![]() $M\subset G$
be a submonoid that is also a generating set of G (as a group). Let A be in
$M\subset G$
be a submonoid that is also a generating set of G (as a group). Let A be in
![]() ${\mathcal {CA}lg}_{\mathbb {Z}}$
. Then the following hold:
${\mathcal {CA}lg}_{\mathbb {Z}}$
. Then the following hold:
-
(a) If
 ${D} \colon A[M]\to A$
is a pseudocharacter of degree n and if
${D} \colon A[M]\to A$
is a pseudocharacter of degree n and if
 $m\in M$
is an element such that
$m\in M$
is an element such that
 $\Lambda _{{D},n}(m)\in A^\times $
, then the class of m is a unit of
$\Lambda _{{D},n}(m)\in A^\times $
, then the class of m is a unit of
 $A[M]/{\mathrm {CH}}({D})$
and its inverse is the class of
$A[M]/{\mathrm {CH}}({D})$
and its inverse is the class of  $$ \begin{align*}q_{{D},m}:=\Lambda_{{D},n}(m)^{-1}\cdot \sum_{i=0}^{n-1}(-1)^{n-1-i}\Lambda_{{D},i}(m) \, m^{n-i-1}.\end{align*} $$
$$ \begin{align*}q_{{D},m}:=\Lambda_{{D},n}(m)^{-1}\cdot \sum_{i=0}^{n-1}(-1)^{n-1-i}\Lambda_{{D},i}(m) \, m^{n-i-1}.\end{align*} $$
-
(b) Let
 ${D},{D}' \colon A[G]\to A$
be pseudocharacters of degree n. Then we have:
${D},{D}' \colon A[G]\to A$
be pseudocharacters of degree n. Then we have: -
(1) The canonical map
 $A[M]\to A[G]/{\mathrm {CH}}({D})$
is surjective.
$A[M]\to A[G]/{\mathrm {CH}}({D})$
is surjective. -
(2) If
 $B\subset A$
is a subring such that
$B\subset A$
is a subring such that
 ${D}(B[M])\subset B$
and
${D}(B[M])\subset B$
and
 $\Lambda _{{D},n}(M)\subset B^\times $
, then
$\Lambda _{{D},n}(M)\subset B^\times $
, then
 ${D}(B[G])\subset B$
.
${D}(B[G])\subset B$
. -
(3) If
 ${D}|_{A[M]}={D}^{\prime }_{A[M]}$
, then
${D}|_{A[M]}={D}^{\prime }_{A[M]}$
, then
 ${D}={D}'$
.
${D}={D}'$
.
-
Proof. For (a), simply note that the Cayley–Hamilton identity
![]() $\chi _{D}(m,t)|_{t=m}=0$
holds in the ring
$\chi _{D}(m,t)|_{t=m}=0$
holds in the ring
![]() $A[M]/{\mathrm {CH}}({D})$
. Because
$A[M]/{\mathrm {CH}}({D})$
. Because
![]() $1-m\cdot q_{{D},m}=(-1)^n\Lambda _{{D},n}(m)^{-1} \cdot \chi _{D}(m,t)|_{t=m}$
, Part (a) follows.
$1-m\cdot q_{{D},m}=(-1)^n\Lambda _{{D},n}(m)^{-1} \cdot \chi _{D}(m,t)|_{t=m}$
, Part (a) follows.
To see (b)(1), it suffices to show that the class of any
![]() $g\in G$
in
$g\in G$
in
![]() $A[G]/{\mathrm {CH}}({D})$
lies in the image of
$A[G]/{\mathrm {CH}}({D})$
lies in the image of
![]() $A[M]$
. Because M generates G, we can write
$A[M]$
. Because M generates G, we can write
![]() $g=m_1^{\varepsilon _1}\cdot m_2^{\varepsilon _2}\cdot \ldots \cdot m_r^{\varepsilon _r}$
for suitable
$g=m_1^{\varepsilon _1}\cdot m_2^{\varepsilon _2}\cdot \ldots \cdot m_r^{\varepsilon _r}$
for suitable
![]() $m_1,\ldots ,m_r\in M$
and
$m_1,\ldots ,m_r\in M$
and
![]() $\varepsilon _1,\ldots ,\varepsilon _r\in \{\pm 1\}$
. Note that
$\varepsilon _1,\ldots ,\varepsilon _r\in \{\pm 1\}$
. Note that
![]() $\Lambda _{{D},n}(m_i)\in A^\times $
as observed before Definition 4.1.5. So in the formula for g we can by (a), whenever
$\Lambda _{{D},n}(m_i)\in A^\times $
as observed before Definition 4.1.5. So in the formula for g we can by (a), whenever
![]() $\varepsilon _i=-1$
, replace the occurring
$\varepsilon _i=-1$
, replace the occurring
![]() $m_i^{-1}$
by
$m_i^{-1}$
by
![]() $q_{{D},m_i}\in A[M]$
, and this shows
$q_{{D},m_i}\in A[M]$
, and this shows
![]() $g\in A[M]+{\mathrm {CH}}({D})$
.
$g\in A[M]+{\mathrm {CH}}({D})$
.
We turn to (b)(2). As we assume
![]() $\Lambda _{{D},n}(M)\subset B^\times $
, the argument in the previous paragraph now shows that
$\Lambda _{{D},n}(M)\subset B^\times $
, the argument in the previous paragraph now shows that
![]() $B[G]\subset B[M]+{\mathrm {CH}}({D})$
. By the further hypothesis
$B[G]\subset B[M]+{\mathrm {CH}}({D})$
. By the further hypothesis
![]() ${D}(B[M])\subset B$
we deduce that all characteristic polynomial coefficients of any
${D}(B[M])\subset B$
we deduce that all characteristic polynomial coefficients of any
![]() $g\in G$
lie in B, and Part (b)(2) now follows from Proposition 4.1.10 quoted from [Reference ChenevierChe14].
$g\in G$
lie in B, and Part (b)(2) now follows from Proposition 4.1.10 quoted from [Reference ChenevierChe14].
Finally, we prove (b)(3). Let us go back to the argument for (b)(1). It replaces an element x of
![]() $A[G]$
by using the Cayley–Hamilton identity by an element
$A[G]$
by using the Cayley–Hamilton identity by an element
![]() $x'$
in
$x'$
in
![]() $A[M]$
in such a way that in the replacement, which used
$A[M]$
in such a way that in the replacement, which used
![]() $q_{{D},m}$
from (a), only values involving
$q_{{D},m}$
from (a), only values involving
![]() ${D}|_{A[M]}$
were used. It follows that the construction of
${D}|_{A[M]}$
were used. It follows that the construction of
![]() $x'$
from x is the same whether we use
$x'$
from x is the same whether we use
![]() ${D}$
or
${D}$
or
![]() ${D}'$
since we assume
${D}'$
since we assume
![]() ${D}|_{A[M]}={D}'|_{A[M]}$
. Therefore, we have
${D}|_{A[M]}={D}'|_{A[M]}$
. Therefore, we have
![]() ${D}(x)={D}(x')={D}'(x')={D}(x)$
for all
${D}(x)={D}(x')={D}'(x')={D}(x)$
for all
![]() $x\in A[G]$
, and we are done.
$x\in A[G]$
, and we are done.
Let us now turn to the construction of
![]() $\rho _{{X}^\pm }$
and its properties. To extend
$\rho _{{X}^\pm }$
and its properties. To extend
![]() $\rho _{{X}}$
to
$\rho _{{X}}$
to
![]() ${\mathrm {FG}}({X})$
, we wish to invert
${\mathrm {FG}}({X})$
, we wish to invert
![]() $\xi _{{x}}\in {\mathrm {Mat}}_{d\times d}(F_{{X}}(n))$
, and so we need
$\xi _{{x}}\in {\mathrm {Mat}}_{d\times d}(F_{{X}}(n))$
, and so we need
![]() ${\mathrm {det}}(\xi _{{x}})$
to be a unit; observe that
${\mathrm {det}}(\xi _{{x}})$
to be a unit; observe that
![]() ${\mathrm {det}}(\xi _{{x}})$
is a coefficient of the characteristic polynomial of
${\mathrm {det}}(\xi _{{x}})$
is a coefficient of the characteristic polynomial of
![]() $\rho _{{X}}({x})$
and hence lies in
$\rho _{{X}}({x})$
and hence lies in
![]() $E_{{X}}(n)$
. We define the subrings
$E_{{X}}(n)$
. We define the subrings
![]() $F_{{X}^{\pm }}(n)=F_{{X}}(n)[{\mathrm {det}}(\xi _{x})^{-1}:{x}\in {X}]$
and
$F_{{X}^{\pm }}(n)=F_{{X}}(n)[{\mathrm {det}}(\xi _{x})^{-1}:{x}\in {X}]$
and
![]() $E_{{X}^{\pm }}(n)=E_{{X}}(n)[{\mathrm {det}}(\xi _{x})^{-1}:{x}\in {X}]$
of the fraction field of the integral domain
$E_{{X}^{\pm }}(n)=E_{{X}}(n)[{\mathrm {det}}(\xi _{x})^{-1}:{x}\in {X}]$
of the fraction field of the integral domain
![]() $F_{{X}}(n)$
by adjoining the inverses of
$F_{{X}}(n)$
by adjoining the inverses of
![]() ${\mathrm {det}}(\xi _{x})$
for all
${\mathrm {det}}(\xi _{x})$
for all
![]() ${x}\in {X}$
to
${x}\in {X}$
to
![]() $F_{{X}}(n)$
and to
$F_{{X}}(n)$
and to
![]() $E_{{X}}(n)$
, respectively. It is now clear that the representation
$E_{{X}}(n)$
, respectively. It is now clear that the representation
![]() $\rho _{{X}}$
has a canonical extension to a representation
$\rho _{{X}}$
has a canonical extension to a representation
Proposition A.4.3. The pseudocharacter
associated to
![]() $ {\rho _{{X}^{\pm }}}$
takes values in
$ {\rho _{{X}^{\pm }}}$
takes values in
![]() $E_{{X}^{\pm }}(n)\subset F_{{X}^{\pm }}(n)$
, and
$E_{{X}^{\pm }}(n)\subset F_{{X}^{\pm }}(n)$
, and
![]() $E_{{X}^{\pm }}(n)$
is the minimal such ring.
$E_{{X}^{\pm }}(n)$
is the minimal such ring.
Proof. Let
![]() $M={\mathrm {FM}}({X})\subset G={\mathrm {FG}}({X})$
,
$M={\mathrm {FM}}({X})\subset G={\mathrm {FG}}({X})$
,
![]() $B=E_{{X}^{\pm }}(n)\subset A=F_{{X}^{\pm }}(n)$
and
$B=E_{{X}^{\pm }}(n)\subset A=F_{{X}^{\pm }}(n)$
and
![]() ${D}={D}_{{X}^{\pm }}$
so that
${D}={D}_{{X}^{\pm }}$
so that
![]() ${D}|_{B[M]}={D}_{{X}}\otimes _{E_{{X}}(n)}E_{{X}^{\pm }}(n)$
. Since
${D}|_{B[M]}={D}_{{X}}\otimes _{E_{{X}}(n)}E_{{X}^{\pm }}(n)$
. Since
![]() ${D}_{{X}}$
is defined over
${D}_{{X}}$
is defined over
![]() $E_{{X}}(n)$
we have
$E_{{X}}(n)$
we have
![]() ${D}(B[M])\subset B$
, and by definition of
${D}(B[M])\subset B$
, and by definition of
![]() $E_{{X}^{\pm }}(n)$
we have
$E_{{X}^{\pm }}(n)$
we have
![]() $\Lambda _{{D}_{{X}},n}({X})\subset B^\times $
and hence by multiplicativity of
$\Lambda _{{D}_{{X}},n}({X})\subset B^\times $
and hence by multiplicativity of
![]() ${D}$
also
${D}$
also
![]() $\Lambda _{{D}_{{X}},n}(M)\subset B^\times $
. The first assertion on
$\Lambda _{{D}_{{X}},n}(M)\subset B^\times $
. The first assertion on
![]() $D_{{X}^{\pm }}$
now follows by applying Lemma A.4.2(b)(2).
$D_{{X}^{\pm }}$
now follows by applying Lemma A.4.2(b)(2).
The minimality of
![]() $E_{{X}^{\pm }}(n)$
is straightforward: By Theorem A.4.1, the target ring has to contain
$E_{{X}^{\pm }}(n)$
is straightforward: By Theorem A.4.1, the target ring has to contain
![]() $E_{{X}}(n)$
, but it also has to contain the elements
$E_{{X}}(n)$
, but it also has to contain the elements
![]() $D_{{X}^{\pm }}({x}^{-1})={\mathrm {det}}(\xi _{x})^{-1}$
for all
$D_{{X}^{\pm }}({x}^{-1})={\mathrm {det}}(\xi _{x})^{-1}$
for all
![]() ${x}\in {X}$
.
${x}\in {X}$
.
From now on, we regard
![]() $D_{{X}^{\pm }}$
as a pseudocharacter
$D_{{X}^{\pm }}$
as a pseudocharacter
Let
![]() ${D}_{{X}^\pm }^u\colon {\mathbb {Z}}\lbrace {X}^\pm \rbrace \rightarrow {R^{\operatorname {univ}}_{{\mathbb {Z}}\lbrace {X}^\pm \rbrace ,n}}$
be the universal n-dimensional pseudocharacter from Proposition 4.2.1. By the universal property of
${D}_{{X}^\pm }^u\colon {\mathbb {Z}}\lbrace {X}^\pm \rbrace \rightarrow {R^{\operatorname {univ}}_{{\mathbb {Z}}\lbrace {X}^\pm \rbrace ,n}}$
be the universal n-dimensional pseudocharacter from Proposition 4.2.1. By the universal property of
![]() ${R^{\operatorname {univ}}_{{\mathbb {Z}}\lbrace {X}^{\pm }\rbrace ,n}}$
, there is a unique homomorphism
${R^{\operatorname {univ}}_{{\mathbb {Z}}\lbrace {X}^{\pm }\rbrace ,n}}$
, there is a unique homomorphism
such that
![]() $D_{{X}^{\pm }}=\alpha _{{X}^{\pm }}\circ {D}_{{X}^\pm }^u$
. The following variant of Theorem A.4.1 is the main result in this subsection.
$D_{{X}^{\pm }}=\alpha _{{X}^{\pm }}\circ {D}_{{X}^\pm }^u$
. The following variant of Theorem A.4.1 is the main result in this subsection.
Theorem A.4.4. The map
![]() $\alpha _{{X}^{\pm }}$
is an isomorphism, and in particular:
$\alpha _{{X}^{\pm }}$
is an isomorphism, and in particular:
-
(a)
 ${R^{\operatorname {univ}}_{{\mathbb {Z}}\lbrace {X}^{\pm }\rbrace ,n}}$
is a domain and a free
${R^{\operatorname {univ}}_{{\mathbb {Z}}\lbrace {X}^{\pm }\rbrace ,n}}$
is a domain and a free
 ${\mathbb {Z}}$
-module.
${\mathbb {Z}}$
-module. -
(b) The pseudocharacter
 $D^u_{{X}^{\pm }}$
is associated to the genuine representation
$D^u_{{X}^{\pm }}$
is associated to the genuine representation
 $\rho _{{X}^{\pm }}$
of
$\rho _{{X}^{\pm }}$
of
 ${\mathrm {FG}}(X)$
.
${\mathrm {FG}}(X)$
.
Proof. We directly prove that the pair
![]() $( E_{{X}^{\pm }}(n), {D}_{{X}^{\pm }})$
has the universal property of the pair
$( E_{{X}^{\pm }}(n), {D}_{{X}^{\pm }})$
has the universal property of the pair
![]() $( {R^{\operatorname {univ}}_{{\mathbb {Z}}\lbrace {X}^\pm \rbrace ,n}},{D}_{{X}^\pm }^u )$
. So let
$( {R^{\operatorname {univ}}_{{\mathbb {Z}}\lbrace {X}^\pm \rbrace ,n}},{D}_{{X}^\pm }^u )$
. So let
![]() ${D}^\pm \colon A[{\mathrm {FG}}({X})]\to A$
be a pseudocharacter of degree n. Its restriction
${D}^\pm \colon A[{\mathrm {FG}}({X})]\to A$
be a pseudocharacter of degree n. Its restriction
![]() ${D}:={D}^\pm |_{A[{\mathrm {FM}}({X})]}$
is an A-valued pseudocharacter on
${D}:={D}^\pm |_{A[{\mathrm {FM}}({X})]}$
is an A-valued pseudocharacter on
![]() $ {\mathrm {FM}}({X})$
. Hence, by the universal property of
$ {\mathrm {FM}}({X})$
. Hence, by the universal property of
![]() $E_{{X}}(n)$
from Theorem A.4.1 there is a unique homomorphism
$E_{{X}}(n)$
from Theorem A.4.1 there is a unique homomorphism
![]() $\alpha \colon E_{{X}}(n)\to A$
such that
$\alpha \colon E_{{X}}(n)\to A$
such that
![]() ${D}=\alpha \circ {D}_{{X}}$
.
${D}=\alpha \circ {D}_{{X}}$
.
Now,
![]() $\Lambda _{{D}^\pm ,n}(g)\in A^\times $
for all
$\Lambda _{{D}^\pm ,n}(g)\in A^\times $
for all
![]() $g\in {\mathrm {FG}}({X})$
as noted above Definition 4.1.5. So for
$g\in {\mathrm {FG}}({X})$
as noted above Definition 4.1.5. So for
![]() ${x}\in {X}$
the image of
${x}\in {X}$
the image of
![]() ${\mathrm {det}}(\xi _x)=\Lambda _{{D}_{{X}},n}(x)$
under
${\mathrm {det}}(\xi _x)=\Lambda _{{D}_{{X}},n}(x)$
under
![]() $\alpha $
is the unit
$\alpha $
is the unit
![]() $\Lambda _{{D}^\pm ,n}(x)\in A^\times $
. Therefore,
$\Lambda _{{D}^\pm ,n}(x)\in A^\times $
. Therefore,
![]() $\alpha $
has a unique extension
$\alpha $
has a unique extension
![]() $\alpha ^\pm \colon E_{{X}^{\pm }}(n)\to A$
. Let
$\alpha ^\pm \colon E_{{X}^{\pm }}(n)\to A$
. Let
![]() ${D}'$
be the A-valued degree n pseudocharacter
${D}'$
be the A-valued degree n pseudocharacter
![]() $\alpha ^\pm \circ {D}_{{X}^\pm }$
on
$\alpha ^\pm \circ {D}_{{X}^\pm }$
on
![]() ${\mathrm {FG}}({X})$
.
${\mathrm {FG}}({X})$
.
By construction,
![]() ${D}'$
and
${D}'$
and
![]() ${D}^\pm $
agree when restricted to
${D}^\pm $
agree when restricted to
![]() $A[{\mathrm {FM}}({X})]$
. From Lemma A.4.2(b)(3) we conclude that
$A[{\mathrm {FM}}({X})]$
. From Lemma A.4.2(b)(3) we conclude that
![]() ${D}'={D}^\pm $
, that is, that
${D}'={D}^\pm $
, that is, that
![]() ${D}^\pm =\alpha ^\pm \circ {D}_{{X}^\pm }$
, and this shows the existence of an
${D}^\pm =\alpha ^\pm \circ {D}_{{X}^\pm }$
, and this shows the existence of an
![]() $\alpha ^\pm $
as required for the universal property of
$\alpha ^\pm $
as required for the universal property of
![]() $( E_{{X}^{\pm }}(n), {D}_{{X}^{\pm }})$
. The uniqueness of
$( E_{{X}^{\pm }}(n), {D}_{{X}^{\pm }})$
. The uniqueness of
![]() $\alpha ^\pm $
is clear, because its restriction to
$\alpha ^\pm $
is clear, because its restriction to
![]() $E_{{X}}(n)$
, that is, the map
$E_{{X}}(n)$
, that is, the map
![]() $\alpha $
, is unique, and the extension from
$\alpha $
, is unique, and the extension from
![]() $\alpha $
to
$\alpha $
to
![]() $\alpha ^\pm $
is also unique.
$\alpha ^\pm $
is also unique.
Acknowledgments
We would like to thank very much G. Chenevier for an enlightening discussion and some suggestions regarding his results in [Reference ChenevierChe11] on the generic fiber which led to the present work. This suggested that at least large parts of the present work should be possible. It should also be clear to the reader that this work crucially relies on the pioneering ideas in [Reference ChenevierChe11] and [Reference ChenevierChe14]. Part of this work is contained in the PhD thesis of A.-K.J. We thank A. Conti, A. Iyengar and in particular V. Paškūnas for many valuable comments on this work. We also thank the referee for a very careful reading of this work and moreover for giving us a concrete idea for the general construction of induction for pseudocharacters that we now present in Subsection 4.6, and for suggesting to us a second independent proof of Theorem 5.2.1 that we present in Subsection 5.3.
Competing interest
The authors have no competing interest to declare.
Funding statement
G.B. acknowledges support by Deutsche Forschungsgemeinschaft (DFG) through the Collaborative Research Centre TRR 326 Geometry and Arithmetic of Uniformized Structures, project number 444845124.