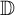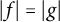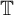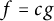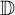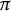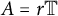1 Background
A fundamental question of phase retrieval is the following: For which measurable sets
![]() $A \subset \overline {\mathbb D}$
is an analytic function
$A \subset \overline {\mathbb D}$
is an analytic function
![]() $f \in H^1$
determined uniquely to within a unimodular constant by the values of
$f \in H^1$
determined uniquely to within a unimodular constant by the values of
![]() $|f|$
on A? Here,
$|f|$
on A? Here,
![]() ${\mathbb D}$
denotes the unit disk and
${\mathbb D}$
denotes the unit disk and
![]() $H^1=H^1({\mathbb D})$
the associated Hardy class of analytic functions. Such questions arise in signal processing, crystallography, quantum mechanics, microscopy, and many other applications.
$H^1=H^1({\mathbb D})$
the associated Hardy class of analytic functions. Such questions arise in signal processing, crystallography, quantum mechanics, microscopy, and many other applications.
In [Reference Pohl, Li, Boche and Tarnberg8], Pohl, Li, and Boche worked with the class
![]() $H^1_R$
of functions in
$H^1_R$
of functions in
![]() $H^1=H^1({\mathbb D})$
such that the inner factor is a Blaschke product (no singular part). They showed (their Theorem 3) that any such function f is determined to within a unimodular constant by the values of
$H^1=H^1({\mathbb D})$
such that the inner factor is a Blaschke product (no singular part). They showed (their Theorem 3) that any such function f is determined to within a unimodular constant by the values of
![]() $|f|$
on
$|f|$
on
![]() ${\mathbb T}$
and
${\mathbb T}$
and
![]() $r{\mathbb T}$
for any
$r{\mathbb T}$
for any
![]() $0<r<1$
. This restriction on the inner factor was removed by Perez [Reference Perez7].
$0<r<1$
. This restriction on the inner factor was removed by Perez [Reference Perez7].
Then in [Reference Jaming, Kellay and Perez2], Jaming, Kellay, and Perez solved a phase retrieval problem in
![]() $L^2({\mathbb R}, e^{2c|x|} \, dx)$
for
$L^2({\mathbb R}, e^{2c|x|} \, dx)$
for
![]() $c>0$
. This is isometric by the Fourier transform to the Hardy space of a strip
$c>0$
. This is isometric by the Fourier transform to the Hardy space of a strip
![]() ${\mathcal S} = \{z \in {\mathbb C}: | {\mathrm {Im}\ z}| < c \}$
(similar calculations occur in [Reference Smith9]).
${\mathcal S} = \{z \in {\mathbb C}: | {\mathrm {Im}\ z}| < c \}$
(similar calculations occur in [Reference Smith9]).
By conformal mapping, the phase retrieval problem can then be reformulated on
![]() $H^2({\mathbb D})$
in terms of finding an expression for all pairs
$H^2({\mathbb D})$
in terms of finding an expression for all pairs
![]() $F,G \in H^2$
such that
$F,G \in H^2$
such that
![]() $|F|=|G|$
on
$|F|=|G|$
on
![]() $(-1,1)$
. For example, with the notation
$(-1,1)$
. For example, with the notation
![]() $F^*$
for the function defined by
$F^*$
for the function defined by
![]() $F^*(z)=\overline {F(\bar z)}$
, they showed that for
$F^*(z)=\overline {F(\bar z)}$
, they showed that for
![]() $F,G \in H^2$
one has
$F,G \in H^2$
one has
![]() $|F|=|G|$
on
$|F|=|G|$
on
![]() $(-1,1)$
if and only if there exist
$(-1,1)$
if and only if there exist
![]() $u,v \in \mathrm {Hol}({\mathbb D})$
(the space of all holomorphic functions on
$u,v \in \mathrm {Hol}({\mathbb D})$
(the space of all holomorphic functions on
![]() ${\mathbb D}$
) such that
${\mathbb D}$
) such that
![]() $F=uv$
and
$F=uv$
and
![]() $G=uv^*$
.
$G=uv^*$
.
Earlier results along similar lines are due to McDonald [Reference McDonald5], who studied the problem of determining an entire function f when
![]() $|f (x)|$
is known for every real x.
$|f (x)|$
is known for every real x.
Finally, a recent paper of Liehr [Reference Liehr4] looks at Gabor phase retrieval and Pauli-type uniqueness problems.
This paper deals with several cases, for which it provides positive and negative results: intersecting curves, disjoint circles, disjoint lines, and a full analysis of the two-circle situation. We also show that many results have sequential counterparts, thus extending and generalizing the work of [Reference Perez7].
2 Results
2.1 Intersecting curves
Perez [Reference Perez7] proved a version of the following result, which generalizes [Reference Jaming, Kellay and Perez2, Lemma 4.5]. We give an independent proof, introducing a method that allows us to provide further extensions.
Theorem 2.1 Let
![]() $f, g: {\mathbb D} \to {\mathbb C}$
be analytic functions and
$f, g: {\mathbb D} \to {\mathbb C}$
be analytic functions and
![]() $L_1$
,
$L_1$
,
![]() $L_2$
two line segments in
$L_2$
two line segments in
![]() ${\mathbb D}$
, intersecting at an angle
${\mathbb D}$
, intersecting at an angle
![]() $\theta \in (0, \pi /2)\,{\backslash}\, \pi {\mathbb Q}$
, such that
$\theta \in (0, \pi /2)\,{\backslash}\, \pi {\mathbb Q}$
, such that
![]() $|f(z)|=|g(z)|$
for all
$|f(z)|=|g(z)|$
for all
![]() $z \in L_1 \cup L_2$
. Then
$z \in L_1 \cup L_2$
. Then
![]() $f=\beta g$
for some constant
$f=\beta g$
for some constant
![]() $\beta \in {\mathbb T}$
.
$\beta \in {\mathbb T}$
.
Proof Clearly by considering the functions on a small disk
![]() $\{z \in {\mathbb C}: |z-a| \le r \}$
, where a is the intersection point of
$\{z \in {\mathbb C}: |z-a| \le r \}$
, where a is the intersection point of
![]() $L_1$
and
$L_1$
and
![]() $L_2$
, and by translating and rescaling as necessary, we may suppose that f and g lie in the disk algebra and the two lines intersect at
$L_2$
, and by translating and rescaling as necessary, we may suppose that f and g lie in the disk algebra and the two lines intersect at
![]() $0$
.
$0$
.
We may also suppose that the functions are nonvanishing except possibly at
![]() $0$
.
$0$
.
If they do vanish at
![]() $0$
, then the orders of the zeros are equal, since for some N
$0$
, then the orders of the zeros are equal, since for some N
![]() $\lim _{z \to 0} |f(z)|/|z|^N $
exists and is nonzero, and the same for g. So by dividing out any the zeros at
$\lim _{z \to 0} |f(z)|/|z|^N $
exists and is nonzero, and the same for g. So by dividing out any the zeros at
![]() $0$
, and restricting to a smaller disk if necessary, we may suppose that f and g are invertible functions in the disk algebra.
$0$
, and restricting to a smaller disk if necessary, we may suppose that f and g are invertible functions in the disk algebra.
Now
![]() $h:=f/g$
is also in the disk algebra and it has modulus
$h:=f/g$
is also in the disk algebra and it has modulus
![]() $1$
on both lines
$1$
on both lines
![]() $L_1$
and
$L_1$
and
![]() $L_2$
. Thus, h maps
$L_2$
. Thus, h maps
![]() $L_1$
and
$L_1$
and
![]() $L_2$
into the unit circle in the complex plane.
$L_2$
into the unit circle in the complex plane.
Suppose that for some
![]() $k \ge 1$
, we have
$k \ge 1$
, we have
near
![]() $0$
, with
$0$
, with
![]() $|c_0|=1$
and
$|c_0|=1$
and
![]() $c_k \ne 0$
; then near to
$c_k \ne 0$
; then near to
![]() $0$
, it magnifies angles by a factor of k, and so if h is nonconstant, then
$0$
, it magnifies angles by a factor of k, and so if h is nonconstant, then
![]() $k \theta $
must be an integer multiple of
$k \theta $
must be an integer multiple of
![]() $\pi $
.
$\pi $
.
Example 2.2 Take
![]() $L_1=[-1,1]$
and
$L_1=[-1,1]$
and
![]() $L_2=i[-1,1]$
. Then
$L_2=i[-1,1]$
. Then
are both unimodular on
![]() $L_1 \cup L_2$
. Similar examples can be constructed for other rational multiples of
$L_1 \cup L_2$
. Similar examples can be constructed for other rational multiples of
![]() $\pi $
.
$\pi $
.
Corollary 2.3 The conclusions of Theorem 2.1 also hold if
![]() $L_1$
and
$L_1$
and
![]() $L_2$
are two
$L_2$
are two
![]() $C^1$
curves intersecting at an angle
$C^1$
curves intersecting at an angle
![]() $\theta \in (0, \pi /2]\,{\backslash}\, \pi {\mathbb Q}$
.
$\theta \in (0, \pi /2]\,{\backslash}\, \pi {\mathbb Q}$
.
Proof The conformality argument works with minor changes.
We may prove sequential versions of the above results with the aid of the following easy lemma.
Lemma 2.4 Let h be a function holomorphic on a neighborhood of
![]() $0$
,
$0$
,
![]() $\theta \in [0,2\pi ]$
and
$\theta \in [0,2\pi ]$
and
![]() $(a_n)$
a real sequence such that
$(a_n)$
a real sequence such that
![]() $a_n \to 0$
and
$a_n \to 0$
and
![]() $h(a_n e^{i\theta })$
is real for all n. Then all the derivatives of the function
$h(a_n e^{i\theta })$
is real for all n. Then all the derivatives of the function
![]() $z \mapsto h(z e^{-i\theta })$
at
$z \mapsto h(z e^{-i\theta })$
at
![]() $0$
are real.
$0$
are real.
Proof Clearly, we may assume without loss of generality that
![]() $\theta =0$
. Then
$\theta =0$
. Then
![]() $h'(0) = \lim _{n \to \infty } h(a_n)/a_n \in {\mathbb R}$
. The map
$h'(0) = \lim _{n \to \infty } h(a_n)/a_n \in {\mathbb R}$
. The map
![]() $h_1 : z \mapsto h(z)/z - h'(0)$
is also holomorphic around
$h_1 : z \mapsto h(z)/z - h'(0)$
is also holomorphic around
![]() $0$
, and satisfies
$0$
, and satisfies
![]() $h_1(a_n) \in {\mathbb R}$
. Then, in a same way, we get
$h_1(a_n) \in {\mathbb R}$
. Then, in a same way, we get
![]() $h_1'(0) = h"(0) \in {\mathbb R}$
. Iterating this reasoning, we see that all the derivatives of h at
$h_1'(0) = h"(0) \in {\mathbb R}$
. Iterating this reasoning, we see that all the derivatives of h at
![]() $0$
must be real.
$0$
must be real.
Corollary 2.5 Let
![]() $f, g: {\mathbb D} \to {\mathbb C}$
be analytic functions and
$f, g: {\mathbb D} \to {\mathbb C}$
be analytic functions and
![]() $L_1$
,
$L_1$
,
![]() $L_2$
two line segments in
$L_2$
two line segments in
![]() ${\mathbb D}$
, intersecting at a point p, at an angle
${\mathbb D}$
, intersecting at a point p, at an angle
![]() $\theta \in (0, \pi /2)\,{\backslash}\, \pi {\mathbb Q}$
, such that there are sequences
$\theta \in (0, \pi /2)\,{\backslash}\, \pi {\mathbb Q}$
, such that there are sequences
![]() $(a_n) \subset L_1$
and
$(a_n) \subset L_1$
and
![]() $(b_n) \subset L_2$
tending to p such that
$(b_n) \subset L_2$
tending to p such that
![]() $|f(a_n)|=|g(a_n)|$
and
$|f(a_n)|=|g(a_n)|$
and
![]() $|f(b_n)|=|g(b_n)|$
for all n. Then
$|f(b_n)|=|g(b_n)|$
for all n. Then
![]() $f=\beta g$
for some constant
$f=\beta g$
for some constant
![]() $\beta \in {\mathbb T}$
.
$\beta \in {\mathbb T}$
.
Proof We use the argument of the proof of Theorem 2.1 up to the point where we have that
![]() $h(a_n)$
and
$h(a_n)$
and
![]() $h(b_n)$
lie in
$h(b_n)$
lie in
![]() ${\mathbb T}$
for all n. By composing with suitable bilinear transformations, we can construct a function
${\mathbb T}$
for all n. By composing with suitable bilinear transformations, we can construct a function
![]() $\tilde h$
holomorphic near
$\tilde h$
holomorphic near
![]() $0$
with sequences
$0$
with sequences
![]() $c_n \to 0$
and
$c_n \to 0$
and
![]() $d_n \to 0$
such that the
$d_n \to 0$
such that the
![]() $c_n$
are real and the
$c_n$
are real and the
![]() $d_n$
have argument
$d_n$
have argument
![]() $\theta $
, but with
$\theta $
, but with
![]() $\tilde h(c_n)$
and
$\tilde h(c_n)$
and
![]() $\tilde h(d_n)$
both real for each n. By Lemma 2.4, we conclude that all the derivatives of
$\tilde h(d_n)$
both real for each n. By Lemma 2.4, we conclude that all the derivatives of
![]() $z \mapsto \tilde h(z)$
and
$z \mapsto \tilde h(z)$
and
![]() $z \mapsto \tilde h(ze^{i\theta })$
are real. By looking at the Taylor series, we see that either
$z \mapsto \tilde h(ze^{i\theta })$
are real. By looking at the Taylor series, we see that either
![]() $\tilde h$
is constant (and thus h is constant) or
$\tilde h$
is constant (and thus h is constant) or
![]() $e^{in\theta }=1$
for some
$e^{in\theta }=1$
for some
![]() $n>0$
.
$n>0$
.
Clearly, a similar generalization of Corollary 2.3 can be derived.
2.2 Disjoint circles
As described in the introduction to this paper, Perez [Reference Perez7] proved a more general version of the main result from [Reference Pohl, Li, Boche and Tarnberg8], removing the restriction on the singular factor. We give an alternative proof, which leads us to more general results in the same area.
Recall that the Nevanlinna class
![]() ${\mathcal N}$
consists of those holomorphic functions in the unit disk
${\mathcal N}$
consists of those holomorphic functions in the unit disk
![]() ${\mathbb D}$
that are expressible as the ratio of two
${\mathbb D}$
that are expressible as the ratio of two
![]() $H^1$
functions.
$H^1$
functions.
Theorem 2.6 Let
![]() $f,g \in {\mathcal N}$
satisfy
$f,g \in {\mathcal N}$
satisfy
![]() $|f|=|g|$
a.e. on
$|f|=|g|$
a.e. on
![]() ${\mathbb T}$
and
${\mathbb T}$
and
![]() $r{\mathbb T}$
for some
$r{\mathbb T}$
for some
![]() $0<r<1$
. Then
$0<r<1$
. Then
![]() $f=\lambda g$
for some
$f=\lambda g$
for some
![]() $\lambda \in {\mathbb T}$
.
$\lambda \in {\mathbb T}$
.
Proof By dividing out by the common outer factor u given by
 $$\begin{align*}u(z) = \exp \left( \frac{1}{2\pi} \int_0^{2\pi} \frac{e^{it}+z}{e^{it}-z} \log |f(e^{it})| \, dt \right), \end{align*}$$
$$\begin{align*}u(z) = \exp \left( \frac{1}{2\pi} \int_0^{2\pi} \frac{e^{it}+z}{e^{it}-z} \log |f(e^{it})| \, dt \right), \end{align*}$$
we may suppose without loss of generality that f and g are inner functions.
Now, if there are any zeros of f or g on
![]() $r{\mathbb T}$
, they are at the same points, and finite in number. By dividing out a finite Blaschke product, we may suppose without loss of generality that f and g have no zeros on
$r{\mathbb T}$
, they are at the same points, and finite in number. By dividing out a finite Blaschke product, we may suppose without loss of generality that f and g have no zeros on
![]() $r{\mathbb T}$
, so indeed
$r{\mathbb T}$
, so indeed
![]() $f/g$
is analytic on an annulus
$f/g$
is analytic on an annulus
![]() $\{z: r-\delta < |z| < r+\delta \}$
for some
$\{z: r-\delta < |z| < r+\delta \}$
for some
![]() $\delta>0$
and unimodular on
$\delta>0$
and unimodular on
![]() $r{\mathbb T}$
.
$r{\mathbb T}$
.
Indeed,
![]() $f/g$
has finitely many poles in
$f/g$
has finitely many poles in
![]() $\{z: |z| < r+\delta \}$
so, multiplying by a function h such that
$\{z: |z| < r+\delta \}$
so, multiplying by a function h such that
![]() $h(z/r)$
is a finite Blaschke product
$h(z/r)$
is a finite Blaschke product
![]() $B_1(z)$
,
$B_1(z)$
,
![]() $fh/g$
is a function k such that
$fh/g$
is a function k such that
![]() $k(z/r)$
is also a finite Blaschke product
$k(z/r)$
is also a finite Blaschke product
![]() $B_2(z)$
since it is analytic in a neighborhood of the disk
$B_2(z)$
since it is analytic in a neighborhood of the disk
![]() $r{\mathbb T}$
.
$r{\mathbb T}$
.
Our conclusion is that
![]() $f/g$
is a rational function
$f/g$
is a rational function
![]() $F(z)=B_2(rz)/B_1(rz)$
in
$F(z)=B_2(rz)/B_1(rz)$
in
![]() $r{\mathbb D}$
; by analytic continuation (and removing any isolated singularities)
$r{\mathbb D}$
; by analytic continuation (and removing any isolated singularities)
![]() $f=F g$
throughout the whole disk. But if F is nonconstant, then it is not unimodular on
$f=F g$
throughout the whole disk. But if F is nonconstant, then it is not unimodular on
![]() ${\mathbb T}$
as the zeros and poles are not placed at inverse points.
${\mathbb T}$
as the zeros and poles are not placed at inverse points.
With the aid of the following lemma, which gives a slight extension of [Reference Kamowitz3, Lemma 1.3], we can prove a stronger result.
Lemma 2.7 Let F be a function meromorphic on an open set containing the unit circle
![]() ${\mathbb T}$
and suppose that
${\mathbb T}$
and suppose that
![]() $|F(z)|=1$
for infinitely many
$|F(z)|=1$
for infinitely many
![]() $z \in {\mathbb T}$
. Then
$z \in {\mathbb T}$
. Then
![]() $|F(z)|=1$
for all
$|F(z)|=1$
for all
![]() $z \in {\mathbb T}$
.
$z \in {\mathbb T}$
.
Proof This result uses a modification of an argument introduced in [Reference Chalendar, Oger and Partington1, Theorem 1.4]. Namely, we restrict F to a continuous map from
![]() ${\mathbb T}$
to the Riemann sphere
${\mathbb T}$
to the Riemann sphere
![]() ${\mathbb C} \cup \{\infty \}$
, which we continue to denote by F. Then
${\mathbb C} \cup \{\infty \}$
, which we continue to denote by F. Then
![]() $X = F^{-1}({\mathbb T})$
is a closed subset of
$X = F^{-1}({\mathbb T})$
is a closed subset of
![]() ${\mathbb T}$
.
${\mathbb T}$
.
If X is an infinite proper subset of
![]() ${\mathbb T}$
, we claim that X contains a point that is a limit of two sequences, one in X and one in
${\mathbb T}$
, we claim that X contains a point that is a limit of two sequences, one in X and one in
![]() ${\mathbb T} \,{\backslash}\, X$
. This is clear if
${\mathbb T} \,{\backslash}\, X$
. This is clear if
![]() ${\mathbb T} \,{\backslash}\, X$
consists of a finite number of intervals. If there are infinitely many intervals, then their endpoints lie in X and accumulate at a point
${\mathbb T} \,{\backslash}\, X$
consists of a finite number of intervals. If there are infinitely many intervals, then their endpoints lie in X and accumulate at a point
![]() $z_0 \in X$
with the required property.
$z_0 \in X$
with the required property.
This point satisfies
![]() $|g(z_0)| = 1$
, and there exist two sequences
$|g(z_0)| = 1$
, and there exist two sequences
![]() $(u_n) \subset X$
and
$(u_n) \subset X$
and
![]() $(v_n) \subset {\mathbb T} \backslash X$
which tend to
$(v_n) \subset {\mathbb T} \backslash X$
which tend to
![]() $z_0$
, such that
$z_0$
, such that
![]() $|F(u_n)| = 1$
and
$|F(u_n)| = 1$
and
![]() $|F(v_n)| \ne 1$
(by passing to a subsequence, we may avoid any poles of F).
$|F(v_n)| \ne 1$
(by passing to a subsequence, we may avoid any poles of F).
By composing F with conformal mappings between
![]() ${\mathbb T}$
and
${\mathbb T}$
and
![]() ${\mathbb R} \cup \{\infty \}$
, we obtain a function h holomorphic around
${\mathbb R} \cup \{\infty \}$
, we obtain a function h holomorphic around
![]() $0$
, and two sequences
$0$
, and two sequences
![]() $(a_n), (b_n) \subset {\mathbb R}$
such that
$(a_n), (b_n) \subset {\mathbb R}$
such that
![]() $a_n \to 0$
,
$a_n \to 0$
,
![]() $b_n \to 0$
,
$b_n \to 0$
,
![]() $h(a_n) \in {\mathbb R}$
and
$h(a_n) \in {\mathbb R}$
and
![]() $h(b_n) \not \in {\mathbb R}$
. By Lemma 2.4, we have that all the derivatives of h at
$h(b_n) \not \in {\mathbb R}$
. By Lemma 2.4, we have that all the derivatives of h at
![]() $0$
must be real, so
$0$
must be real, so
![]() $h(b_n) \in {\mathbb R}$
(since
$h(b_n) \in {\mathbb R}$
(since
![]() $b_n \in {\mathbb R}$
). This contradiction shows that X cannot be an infinite proper subset of
$b_n \in {\mathbb R}$
). This contradiction shows that X cannot be an infinite proper subset of
![]() ${\mathbb T}$
.
${\mathbb T}$
.
Theorem 2.8 Let
![]() $f,g \in H^1({\mathbb D})$
satisfy
$f,g \in H^1({\mathbb D})$
satisfy
![]() $|f|=|g|$
a.e. on
$|f|=|g|$
a.e. on
![]() ${\mathbb T}$
and on an infinite subset
${\mathbb T}$
and on an infinite subset
![]() $X \subset r{\mathbb T}$
for some
$X \subset r{\mathbb T}$
for some
![]() $0<r<1$
. Then
$0<r<1$
. Then
![]() $f=\lambda g$
for some
$f=\lambda g$
for some
![]() $\lambda \in {\mathbb T}$
.
$\lambda \in {\mathbb T}$
.
Proof Let f and g have inner–outer factorizations
![]() $f=u_1 v_1$
,
$f=u_1 v_1$
,
![]() $g=u_2v_2$
, where
$g=u_2v_2$
, where
![]() $u_1$
and
$u_1$
and
![]() $u_2$
are inner and
$u_2$
are inner and
![]() $v_1$
are
$v_1$
are
![]() $v_2$
outer with
$v_2$
outer with
![]() $v_1(0)>0$
and
$v_1(0)>0$
and
![]() $v_2(0)>0$
. Since
$v_2(0)>0$
. Since
![]() $|f|=|g|$
on
$|f|=|g|$
on
![]() ${\mathbb T}$
, we have
${\mathbb T}$
, we have
![]() $v_1=v_2$
. We may therefore suppose without loss of generality that f and g are inner.
$v_1=v_2$
. We may therefore suppose without loss of generality that f and g are inner.
Note that the function
![]() $F:=f/g$
is meromorphic in the disk and
$F:=f/g$
is meromorphic in the disk and
![]() $|F(z)|=1$
for an infinite subset of
$|F(z)|=1$
for an infinite subset of
![]() ${\mathbb T}$
.
${\mathbb T}$
.
By Lemma 2.7,
![]() $|F|=1$
on
$|F|=1$
on
![]() ${\mathbb T}$
and so
${\mathbb T}$
and so
![]() $|f|=|g|$
on
$|f|=|g|$
on
![]() $r{\mathbb T}$
. The result now follows from Theorem 2.6.
$r{\mathbb T}$
. The result now follows from Theorem 2.6.
Corollary 2.9 Let
![]() $f,g \in H^1({\mathbb D})$
(or more generally in the Nevanlinna class) satisfy
$f,g \in H^1({\mathbb D})$
(or more generally in the Nevanlinna class) satisfy
![]() $|f|=|g|$
a.e. on
$|f|=|g|$
a.e. on
![]() ${\mathbb T}$
and on an infinite subset
${\mathbb T}$
and on an infinite subset
![]() $X \subset \Psi _{\omega ,\alpha } (r{\mathbb T})$
for some
$X \subset \Psi _{\omega ,\alpha } (r{\mathbb T})$
for some
![]() $0<r<1$
, where
$0<r<1$
, where
![]() $\omega \in {\mathbb T}$
,
$\omega \in {\mathbb T}$
,
![]() $\alpha \in {\mathbb D}$
, and
$\alpha \in {\mathbb D}$
, and
![]() $\Psi _{\omega ,\alpha }(z):=\omega \frac {\alpha -z}{1-\overline {\alpha }z}$
. Then
$\Psi _{\omega ,\alpha }(z):=\omega \frac {\alpha -z}{1-\overline {\alpha }z}$
. Then
![]() $f=\lambda g$
for some
$f=\lambda g$
for some
![]() $\lambda \in {\mathbb T}$
.
$\lambda \in {\mathbb T}$
.
Proof We apply Theorem 2.8 to
![]() $f\circ \Psi _{\omega ,\alpha }$
and
$f\circ \Psi _{\omega ,\alpha }$
and
![]() $g\circ \Psi _{\omega ,\alpha }$
, which implies that
$g\circ \Psi _{\omega ,\alpha }$
, which implies that
![]() $f\circ \Psi _{\omega ,\alpha } =g\circ \Psi _{\omega ,\alpha }$
, and thus
$f\circ \Psi _{\omega ,\alpha } =g\circ \Psi _{\omega ,\alpha }$
, and thus
![]() $f=g$
since
$f=g$
since
![]() $ \Psi _{\omega ,\alpha }$
is an automorphism of the open unit disk.
$ \Psi _{\omega ,\alpha }$
is an automorphism of the open unit disk.
Note that every circle contained in
![]() ${\mathbb D}$
can be written as
${\mathbb D}$
can be written as
![]() $ \Psi _{\omega ,\alpha }(r{\mathbb T})$
for a suitable choice of
$ \Psi _{\omega ,\alpha }(r{\mathbb T})$
for a suitable choice of
![]() $\omega \in {\mathbb T}$
,
$\omega \in {\mathbb T}$
,
![]() $\alpha \in {\mathbb D}$
, and
$\alpha \in {\mathbb D}$
, and
![]() $0<r<1$
.
$0<r<1$
.
Remark 2.10 It is clearly not enough to suppose that
![]() $|f|=|g|$
a.e. on
$|f|=|g|$
a.e. on
![]() ${\mathbb T}$
and on some finite subset
${\mathbb T}$
and on some finite subset
![]() $X \subset r{\mathbb T}$
. For example, we can let f and g be two different inner functions constructed in the following way:
$X \subset r{\mathbb T}$
. For example, we can let f and g be two different inner functions constructed in the following way:
where B is the finite Blaschke product associated with the finite set X, u and v are inner functions with
![]() $u\neq cv$
for any
$u\neq cv$
for any
![]() $c\in {\mathbb T}$
and
$c\in {\mathbb T}$
and
![]() $\Psi _\alpha (z):=\frac {\alpha -z}{1-\overline {\alpha }z}$
for an arbitrary
$\Psi _\alpha (z):=\frac {\alpha -z}{1-\overline {\alpha }z}$
for an arbitrary
![]() $\alpha \in {\mathbb D}$
. Since f and g are inner, their radial limits are of modulus one almost everywhere on
$\alpha \in {\mathbb D}$
. Since f and g are inner, their radial limits are of modulus one almost everywhere on
![]() ${\mathbb T}$
,
${\mathbb T}$
,
![]() $f(z)=\alpha =g(z)$
for all
$f(z)=\alpha =g(z)$
for all
![]() $z\in X$
. The choice of u and v implies that there is no
$z\in X$
. The choice of u and v implies that there is no
![]() $c\in {\mathbb T}$
such that
$c\in {\mathbb T}$
such that
![]() $f=cg$
.
$f=cg$
.
If the inner parts of f and g are finite Blaschke products
![]() $B_1$
and
$B_1$
and
![]() $B_2$
, then, depending on their degrees,
$B_2$
, then, depending on their degrees,
![]() $|f|=|g|$
a.e. on
$|f|=|g|$
a.e. on
![]() ${\mathbb T}$
and at only finitely many points on
${\mathbb T}$
and at only finitely many points on
![]() $r{\mathbb T}$
is a sufficient condition for Theorem 2.8 to hold.
$r{\mathbb T}$
is a sufficient condition for Theorem 2.8 to hold.
Theorem 2.11 Let
![]() $B_1$
and
$B_1$
and
![]() $B_2$
be Blaschke products of degrees M and N, respectively, and take
$B_2$
be Blaschke products of degrees M and N, respectively, and take
![]() $0<r<1$
. If
$0<r<1$
. If
![]() $|B_1(z)|=|B_2(z)|$
for more than
$|B_1(z)|=|B_2(z)|$
for more than
![]() $2N+2M-1$
distinct points on
$2N+2M-1$
distinct points on
![]() $r{\mathbb T}$
, then
$r{\mathbb T}$
, then
![]() $B_2$
is a constant multiple of
$B_2$
is a constant multiple of
![]() $B_1$
.
$B_1$
.
Proof Note that on
![]() $r{\mathbb T}$
, we have
$r{\mathbb T}$
, we have
![]() $\bar z=r^2/z$
; so for an elementary Blaschke factor with
$\bar z=r^2/z$
; so for an elementary Blaschke factor with
![]() $a \in {\mathbb D}$
, we have
$a \in {\mathbb D}$
, we have
 $$\begin{align*}\frac{z-a}{1-\bar a z}\frac{\bar z-\bar a}{1-a\bar z}= \frac{(z-a)(r^2-\bar a z)}{(1-\bar a z)(z-r^2 a)}, \end{align*}$$
$$\begin{align*}\frac{z-a}{1-\bar a z}\frac{\bar z-\bar a}{1-a\bar z}= \frac{(z-a)(r^2-\bar a z)}{(1-\bar a z)(z-r^2 a)}, \end{align*}$$
and thus the equation
can be rewritten as
![]() $ R_1(z)=R_2(z)$
, where
$ R_1(z)=R_2(z)$
, where
![]() $R_1$
and
$R_1$
and
![]() $R_2$
are rational functions of degrees
$R_2$
are rational functions of degrees
![]() $2M$
and
$2M$
and
![]() $2N$
, respectively. If
$2N$
, respectively. If
![]() $\alpha _1,\ldots , \alpha _M$
are the zeros of
$\alpha _1,\ldots , \alpha _M$
are the zeros of
![]() $B_1$
and
$B_1$
and
![]() $\beta _1,\dots , \beta _N$
are the zeros of
$\beta _1,\dots , \beta _N$
are the zeros of
![]() $B_2$
, we get
$B_2$
, we get
 $$\begin{align*}R_1(z)=\left(\frac{z-\alpha_1}{1-\overline{\alpha_1} z}\right) \cdots \left( \frac{z-\alpha_M}{1-\overline{\alpha_M} z}\right) \left( \frac{r^2-\overline{\alpha_1}z}{z-\alpha_1 r^2}\right) \cdots \left( \frac{r^2-\overline{\alpha_M}z}{z-\alpha_M r^2}\right) \end{align*}$$
$$\begin{align*}R_1(z)=\left(\frac{z-\alpha_1}{1-\overline{\alpha_1} z}\right) \cdots \left( \frac{z-\alpha_M}{1-\overline{\alpha_M} z}\right) \left( \frac{r^2-\overline{\alpha_1}z}{z-\alpha_1 r^2}\right) \cdots \left( \frac{r^2-\overline{\alpha_M}z}{z-\alpha_M r^2}\right) \end{align*}$$
and
 $$\begin{align*}R_2(z)=\left(\frac{z-\beta_1}{1-\overline{\beta_1} z}\right) \cdots \left( \frac{z-\beta_N}{1-\overline{\beta_N} z}\right) \left( \frac{r^2-\overline{\beta_1}z}{z-\beta_1 r^2}\right) \cdots \left( \frac{r^2-\overline{\beta_N}z}{z-\beta_N r^2}\right).\end{align*}$$
$$\begin{align*}R_2(z)=\left(\frac{z-\beta_1}{1-\overline{\beta_1} z}\right) \cdots \left( \frac{z-\beta_N}{1-\overline{\beta_N} z}\right) \left( \frac{r^2-\overline{\beta_1}z}{z-\beta_1 r^2}\right) \cdots \left( \frac{r^2-\overline{\beta_N}z}{z-\beta_N r^2}\right).\end{align*}$$
Denote by
![]() $P_1(z)$
(resp.
$P_1(z)$
(resp.
![]() $P_2(z)$
) the numerator of
$P_2(z)$
) the numerator of
![]() $R_1(z)$
(resp.
$R_1(z)$
(resp.
![]() $R_2(z)$
) and
$R_2(z)$
) and
![]() $Q_1(z)$
(resp.
$Q_1(z)$
(resp.
![]() $Q_2(z)$
) the denominator of
$Q_2(z)$
) the denominator of
![]() $R_1(z)$
(resp.
$R_1(z)$
(resp.
![]() $R_2(z)$
). This reduces to a polynomial equation of degree at most
$R_2(z)$
). This reduces to a polynomial equation of degree at most
![]() $2N+2M-1$
, noting that the coefficient of
$2N+2M-1$
, noting that the coefficient of
![]() $z^{2N+2M}$
of the polynomial
$z^{2N+2M}$
of the polynomial
![]() $P_1Q_2$
is
$P_1Q_2$
is
![]() $(-1)^{N+M} \prod _{i=1}^{M} \overline {\alpha _i }\prod _{j=1}^N \overline {\beta _j}$
, which coincide with the coefficient of
$(-1)^{N+M} \prod _{i=1}^{M} \overline {\alpha _i }\prod _{j=1}^N \overline {\beta _j}$
, which coincide with the coefficient of
![]() $z^{2N+2M}$
of the polynomial
$z^{2N+2M}$
of the polynomial
![]() $P_2Q_1$
. Therefore, if
$P_2Q_1$
. Therefore, if
![]() $P_1Q_2-P_2 Q_1$
it has more than
$P_1Q_2-P_2 Q_1$
it has more than
![]() $2N+2M-1$
roots, then it is identically zero. That is,
$2N+2M-1$
roots, then it is identically zero. That is,
![]() $|B_1|=|B_2|$
on the whole of
$|B_1|=|B_2|$
on the whole of
![]() $r{\mathbb T}$
and thus the result follows from the previous discussions.
$r{\mathbb T}$
and thus the result follows from the previous discussions.
In general, we have the following parameterization of functions of equal modulus on
![]() $r{\mathbb T}$
.
$r{\mathbb T}$
.
Theorem 2.12 Suppose that
![]() $f,g \in \mathrm {Hol}({\mathbb D})$
and
$f,g \in \mathrm {Hol}({\mathbb D})$
and
![]() $|f|=|g|$
on
$|f|=|g|$
on
![]() $r{\mathbb T}$
for some
$r{\mathbb T}$
for some
![]() $0<r<1$
. Then there exist finite Blaschke products
$0<r<1$
. Then there exist finite Blaschke products
![]() $B_1,B_2$
such that
$B_1,B_2$
such that
Proof We have that
![]() $f/g$
is meromorphic on a neighborhood of
$f/g$
is meromorphic on a neighborhood of
![]() $r\overline {\mathbb D}$
and
$r\overline {\mathbb D}$
and
![]() $|f/g|=1$
on
$|f/g|=1$
on
![]() $r{\mathbb T}$
. By choosing a suitable finite Blaschke product
$r{\mathbb T}$
. By choosing a suitable finite Blaschke product
![]() $B_1$
and writing
$B_1$
and writing
![]() $\tilde B_1(z)=B_1(z/r)$
, we have that
$\tilde B_1(z)=B_1(z/r)$
, we have that
![]() $\tilde B_1 f/g$
is still unimodular on
$\tilde B_1 f/g$
is still unimodular on
![]() $r{\mathbb T}$
and holomorphic on a neighborhood of
$r{\mathbb T}$
and holomorphic on a neighborhood of
![]() $r\overline {\mathbb D}$
. Thus, it has the form
$r\overline {\mathbb D}$
. Thus, it has the form
![]() $\tilde B_2$
, where
$\tilde B_2$
, where
![]() $\tilde B_2(z)=B_2(z/r)$
for some finite Blaschke product
$\tilde B_2(z)=B_2(z/r)$
for some finite Blaschke product
![]() $B_2$
.
$B_2$
.
2.3 Disjoint lines
In [Reference Pohl, Li, Boche and Tarnberg8], it is claimed that a similar result to Theorem 2.6 can be proved for the corresponding space
![]() $H^1_R({\mathbb C}^+)$
of analytic functions in the upper half-plane
$H^1_R({\mathbb C}^+)$
of analytic functions in the upper half-plane
![]() ${\mathbb C}^+$
, considering the values on
${\mathbb C}^+$
, considering the values on
![]() ${\mathbb R}$
and
${\mathbb R}$
and
![]() $i+{\mathbb R}$
, although no proof is given. The result cannot be deduced directly from the disk result as this strip
$i+{\mathbb R}$
, although no proof is given. The result cannot be deduced directly from the disk result as this strip
![]() $\mathbb S=\{s \in {\mathbb C}: 0 < {\mathrm {Re} s} < 1\}$
is not conformally equivalent to the annulus.
$\mathbb S=\{s \in {\mathbb C}: 0 < {\mathrm {Re} s} < 1\}$
is not conformally equivalent to the annulus.
We note also that there are nonconstant meromorphic functions F defined on
![]() ${\mathbb C}^+$
such that
${\mathbb C}^+$
such that
![]() $|F|=1$
on both
$|F|=1$
on both
![]() ${\mathbb R}$
and
${\mathbb R}$
and
![]() $i+{\mathbb R}$
. One example is
$i+{\mathbb R}$
. One example is
which provides a conformal map of the strip
![]() $\mathbb S$
onto the unit disk. However, the function does not extend to a quotient of
$\mathbb S$
onto the unit disk. However, the function does not extend to a quotient of
![]() $H^p$
functions, since its zeros
$H^p$
functions, since its zeros
![]() $\{i(\frac 12+2n): n \ge 0\}$
do not form a Blaschke sequence.
$\{i(\frac 12+2n): n \ge 0\}$
do not form a Blaschke sequence.
By means of the Weierstrass factorization theorem, F can be modified to give distinct analytic functions G and H on
![]() ${\mathbb C}^+$
such that
${\mathbb C}^+$
such that
![]() $|G|=|H|$
on
$|G|=|H|$
on
![]() ${\mathbb R}$
and
${\mathbb R}$
and
![]() $1+i{\mathbb R}$
.
$1+i{\mathbb R}$
.
In fact, the result we require does hold for the half-plane. It will be convenient to work with the right half-plane
![]() ${\mathbb C}_+$
.
${\mathbb C}_+$
.
Theorem 2.13 Suppose that
![]() $f,g \in H^1({\mathbb C}_+)$
and
$f,g \in H^1({\mathbb C}_+)$
and
![]() $|f|=|g|$
a.e. on
$|f|=|g|$
a.e. on
![]() $i{\mathbb R}$
, while
$i{\mathbb R}$
, while
![]() $|f|=|g|$
on
$|f|=|g|$
on
![]() $1+i{\mathbb R}$
. Then
$1+i{\mathbb R}$
. Then
![]() $f=cg$
for some unimodular constant c.
$f=cg$
for some unimodular constant c.
Proof We may assume without loss of generality that
![]() $f,g$
are inner.
$f,g$
are inner.
Now, the functions F and G defined by
![]() $F(s)=f(1+s)$
and
$F(s)=f(1+s)$
and
![]() $G(s)=g(1+s)$
satisfy
$G(s)=g(1+s)$
satisfy
![]() $|F|=|G|$
on
$|F|=|G|$
on
![]() $ i{\mathbb R}$
; and these functions are also in
$ i{\mathbb R}$
; and these functions are also in
![]() $H^1({\mathbb C}_+)$
, and holomorphic in a neighborhood of
$H^1({\mathbb C}_+)$
, and holomorphic in a neighborhood of
![]() $i{\mathbb R}$
. Let us consider the inner–outer factorization
$i{\mathbb R}$
. Let us consider the inner–outer factorization
![]() $F=uh$
, say.
$F=uh$
, say.
Clearly, the inner factor u has no zeros accumulating at a point on
![]() $i{\mathbb R}$
. Moreover, the outer factor h is continuous on the closed half-plane
$i{\mathbb R}$
. Moreover, the outer factor h is continuous on the closed half-plane
![]() ${\mathbb C}_+$
(see, for example, the arguments in [Reference Nikolski6, Section 4.3.8]), which means that the inner factor u is also continuous except possibly at the discrete set consisting of the zeros of
${\mathbb C}_+$
(see, for example, the arguments in [Reference Nikolski6, Section 4.3.8]), which means that the inner factor u is also continuous except possibly at the discrete set consisting of the zeros of
![]() $uh$
on
$uh$
on
![]() $i{\mathbb R}$
. On factoring out a zero at
$i{\mathbb R}$
. On factoring out a zero at
![]() $iy_0$
, by considering
$iy_0$
, by considering
![]() $uh/b$
, where
$uh/b$
, where
![]() $b(s)= \dfrac {s-iy_0}{1+s}$
(an outer function) we see that u is also continuous at the zeros of
$b(s)= \dfrac {s-iy_0}{1+s}$
(an outer function) we see that u is also continuous at the zeros of
![]() $uh$
. Thus, u has no singular part except possibly an exponential factor
$uh$
. Thus, u has no singular part except possibly an exponential factor
![]() $e^{-\alpha s}$
for some
$e^{-\alpha s}$
for some
![]() $\alpha \ge 0$
. We conclude that
$\alpha \ge 0$
. We conclude that
![]() $u(s)=B_1(s)e^{-\alpha s}$
, where
$u(s)=B_1(s)e^{-\alpha s}$
, where
![]() $B_1$
is a Blaschke product whose zeros do not accumulate at any point in
$B_1$
is a Blaschke product whose zeros do not accumulate at any point in
![]() $\overline {{\mathbb C}_+}$
. The function
$\overline {{\mathbb C}_+}$
. The function
![]() $B_1$
, which is a product of factors of the form
$B_1$
, which is a product of factors of the form
![]() $\dfrac {s-a_n}{s+ \overline {a_n}}$
, therefore has a meromorphic extension to
$\dfrac {s-a_n}{s+ \overline {a_n}}$
, therefore has a meromorphic extension to
![]() ${\mathbb C}$
.
${\mathbb C}$
.
So suppose that
![]() $B_1$
has a zero at w. Then the Blaschke factor of f, say,
$B_1$
has a zero at w. Then the Blaschke factor of f, say,
![]() $b_1$
, has a zero at
$b_1$
, has a zero at
![]() $w+1$
, and hence a pole at
$w+1$
, and hence a pole at
![]() $-\overline w-1$
. Thus
$-\overline w-1$
. Thus
![]() $B_1$
has a pole at
$B_1$
has a pole at
![]() $ -\overline w-2$
and hence a zero at
$ -\overline w-2$
and hence a zero at
![]() $w+2$
.
$w+2$
.
Repeating this argument, we find that
![]() $B_1$
has zeros at
$B_1$
has zeros at
![]() $w_n:=w+2n$
,
$w_n:=w+2n$
,
![]() $n \in {\mathbb N}$
. But these do not satisfy the Blaschke condition
$n \in {\mathbb N}$
. But these do not satisfy the Blaschke condition
![]() $\sum _{n=0}^\infty \frac {{\mathrm {Re}w}_n}{1+|w_n|^2} < \infty $
, and that is a contradiction.
$\sum _{n=0}^\infty \frac {{\mathrm {Re}w}_n}{1+|w_n|^2} < \infty $
, and that is a contradiction.
So
![]() $B_1$
is a unimodular constant and we may apply a similar argument to the inner function v. We conclude that
$B_1$
is a unimodular constant and we may apply a similar argument to the inner function v. We conclude that
![]() $f(s)/g(s)= c\exp (\lambda (s-1))$
, for a unimodular constant c, which, since f and g are inner, means that
$f(s)/g(s)= c\exp (\lambda (s-1))$
, for a unimodular constant c, which, since f and g are inner, means that
![]() $|\exp (\lambda (iy-1))|=1$
a.e., and
$|\exp (\lambda (iy-1))|=1$
a.e., and
![]() $\lambda =0$
.
$\lambda =0$
.
The translation of the previous theorem into the open unit disk via a standard conformal map between the unit disk and the right half-plane is the following.
Corollary 2.14 Suppose that
![]() $f,g \in H^1({\mathbb D})$
and
$f,g \in H^1({\mathbb D})$
and
![]() $|f|=|g|$
a.e. on
$|f|=|g|$
a.e. on
![]() ${\mathbb T}$
, while
${\mathbb T}$
, while
![]() $|f|=|g|$
on
$|f|=|g|$
on
![]() $\{z\in {\mathbb C}: |z-r|=1-r\}$
for some
$\{z\in {\mathbb C}: |z-r|=1-r\}$
for some
![]() $r\in (0,1)$
. Then
$r\in (0,1)$
. Then
![]() $f=cg$
for some unimodular constant c.
$f=cg$
for some unimodular constant c.
Remark 2.15 Corollary 2.14 also holds when f and g are in thee Nevalinna class
![]() $\mathcal N$
and when
$\mathcal N$
and when
![]() $|f|=|g|$
on
$|f|=|g|$
on
![]() ${\mathbb T}$
and on a sequence included in
${\mathbb T}$
and on a sequence included in
![]() $\{z\in {\mathbb C}: |z-r|=1-r\}$
.
$\{z\in {\mathbb C}: |z-r|=1-r\}$
.
2.4 Two circles contained in the unit disk
Suppose now that f and g are holomorphic on
![]() ${\mathbb D}$
and
${\mathbb D}$
and
![]() $|f|=|g|$
on two distinct circles
$|f|=|g|$
on two distinct circles
![]() $C_1,C_2$
contained in
$C_1,C_2$
contained in
![]() ${\mathbb D}$
, which bound open disks
${\mathbb D}$
, which bound open disks
![]() $D_1$
and
$D_1$
and
![]() $D_2$
, respectively. There are five cases to consider (we can of course swap the roles of
$D_2$
, respectively. There are five cases to consider (we can of course swap the roles of
![]() $C_1$
and
$C_1$
and
![]() $C_2$
if we wish):
$C_2$
if we wish):
-
(1)
 $C_1$
and
$C_1$
and
 $C_2$
are “internally” disjoint with
$C_2$
are “internally” disjoint with
 $C_2 \subset D_1$
;
$C_2 \subset D_1$
; -
(2)
 $C_1$
and
$C_1$
and
 $C_2$
are “externally” disjoint with
$C_2$
are “externally” disjoint with
 $C_2 \subset {\mathbb D} \,{\backslash}\, \overline {D_1}$
;
$C_2 \subset {\mathbb D} \,{\backslash}\, \overline {D_1}$
; -
(3)
 $C_1$
and
$C_1$
and
 $C_2$
are “internally” tangential with
$C_2$
are “internally” tangential with
 $C_2 \subset \overline {D_1}$
;
$C_2 \subset \overline {D_1}$
; -
(4)
 $C_1$
and
$C_1$
and
 $C_2$
are “externally” tangential with
$C_2$
are “externally” tangential with
 $C_2 \subset {\mathbb D} \,{\backslash}\, D_1$
;
$C_2 \subset {\mathbb D} \,{\backslash}\, D_1$
; -
(5)
 $C_1$
and
$C_1$
and
 $C_2$
intersect in two points, at which they make an angle
$C_2$
intersect in two points, at which they make an angle
 $\theta \in (0,\pi /2]$
.
$\theta \in (0,\pi /2]$
.

Theorem 2.16 Suppose that
![]() $C_1$
and
$C_1$
and
![]() $C_2$
satisfy one of the five conditions listed above and that
$C_2$
satisfy one of the five conditions listed above and that
![]() $|f|=|g|$
on
$|f|=|g|$
on
![]() $C_1 \cup C_2$
. Then in cases (1)–(4)
$C_1 \cup C_2$
. Then in cases (1)–(4)
![]() $f=cg$
for some c with
$f=cg$
for some c with
![]() $|c|=1$
. The same holds in case (5) if
$|c|=1$
. The same holds in case (5) if
![]() $\theta $
is an irrational multiple of
$\theta $
is an irrational multiple of
![]() $\pi $
, but need not hold if
$\pi $
, but need not hold if
![]() $\theta $
is a rational multiple of
$\theta $
is a rational multiple of
![]() $\pi $
.
$\pi $
.
Proof For parts (1)–(4), we may suppose without loss of generality, by composing with an automorphism, that
![]() $C_1$
is the circle
$C_1$
is the circle
![]() $r{\mathbb T}$
centered at
$r{\mathbb T}$
centered at
![]() $0$
with radius r for some
$0$
with radius r for some
![]() $0<r<1$
. For (1), we now consider
$0<r<1$
. For (1), we now consider
![]() $f_r$
and
$f_r$
and
![]() $g_r$
defined by
$g_r$
defined by
![]() $f_r(z)=f(z/r)$
and
$f_r(z)=f(z/r)$
and
![]() $g_r(z)=g(z/r)$
. Then, (1) follows easily from Corollary 2.9 and the comment following it.
$g_r(z)=g(z/r)$
. Then, (1) follows easily from Corollary 2.9 and the comment following it.
For (2) with
![]() $C_1=r{\mathbb T}$
, we note from Theorem 2.12 that
$C_1=r{\mathbb T}$
, we note from Theorem 2.12 that
![]() $f(z)/g(z)$
is a rational function of the form
$f(z)/g(z)$
is a rational function of the form
![]() $B_2(z/r)/B_1(z/r)$
and hence meromorphic on
$B_2(z/r)/B_1(z/r)$
and hence meromorphic on
![]() ${\mathbb C} \cup \{\infty \}$
. With the change of variable
${\mathbb C} \cup \{\infty \}$
. With the change of variable
![]() $w=z/r$
, we have a meromorphic function
$w=z/r$
, we have a meromorphic function
![]() $B_2(w)/B_1(w)$
that is unimodular on a smaller circle contained in
$B_2(w)/B_1(w)$
that is unimodular on a smaller circle contained in
![]() ${\mathbb D}$
. By composition with an automorphism, we may supposed that the smaller circle is centered at
${\mathbb D}$
. By composition with an automorphism, we may supposed that the smaller circle is centered at
![]() $0$
. But now the fact that
$0$
. But now the fact that
![]() $f/g$
is a constant follows an argument similar to that used in the proof of Theorem 2.6 (specifically, that poles and zeros occur in pairs of inverse points with respect to one circle, which means that they cannot occur at inverse points with respect to the other circle).
$f/g$
is a constant follows an argument similar to that used in the proof of Theorem 2.6 (specifically, that poles and zeros occur in pairs of inverse points with respect to one circle, which means that they cannot occur at inverse points with respect to the other circle).
(3) is easily derived from Corollary 2.14.
For (4), we may again suppose that
![]() $C_1=r{\mathbb T}$
and that
$C_1=r{\mathbb T}$
and that
![]() $f(z)/g(z)=B_2(z/r)/B_1(z/r)$
. Now we take
$f(z)/g(z)=B_2(z/r)/B_1(z/r)$
. Now we take
![]() $w=z/r$
again, reducing to the case when a function of the form
$w=z/r$
again, reducing to the case when a function of the form
![]() $B_2(w)/B_1(w)$
is of modulus 1 on a circle internally tangential to
$B_2(w)/B_1(w)$
is of modulus 1 on a circle internally tangential to
![]() ${\mathbb T}$
. By means of a conformal mapping, we can transform this to the half-plane, producing a rational function that has absolute value 1 on the lines
${\mathbb T}$
. By means of a conformal mapping, we can transform this to the half-plane, producing a rational function that has absolute value 1 on the lines
![]() $i{\mathbb R}$
and
$i{\mathbb R}$
and
![]() $1+i{\mathbb R}$
. Finally, an argument based on the fact that zeros and poles must occur at pairs of inverse points a and
$1+i{\mathbb R}$
. Finally, an argument based on the fact that zeros and poles must occur at pairs of inverse points a and
![]() $-\overline a$
with respect to
$-\overline a$
with respect to
![]() $i{\mathbb R}$
as well as inverse points
$i{\mathbb R}$
as well as inverse points
![]() $ a$
and
$ a$
and
![]() $-\overline a+2$
with respect to
$-\overline a+2$
with respect to
![]() $1+i{\mathbb R}$
(cf. the proof of Theorem 2.13) leads to a contradiction unless
$1+i{\mathbb R}$
(cf. the proof of Theorem 2.13) leads to a contradiction unless
![]() $f/g$
is constant.
$f/g$
is constant.
For (5), suppose that the two intersection points of
![]() $C_1$
and
$C_1$
and
![]() $C_2$
are a and b. By changing the variable to
$C_2$
are a and b. By changing the variable to
![]() $w=1/(z-a)$
, we transform the circles into straight lines, which meet at
$w=1/(z-a)$
, we transform the circles into straight lines, which meet at
![]() $1/(b-a)$
, still at an angle
$1/(b-a)$
, still at an angle
![]() $\theta $
. The result for irrational
$\theta $
. The result for irrational
![]() $\theta /\pi $
now follows from Theorem 2.1, applied to a small disk centered at
$\theta /\pi $
now follows from Theorem 2.1, applied to a small disk centered at
![]() $1/(b-a)$
.
$1/(b-a)$
.
We may similarly construct counterexamples for rational
![]() $\theta /\pi $
. Let
$\theta /\pi $
. Let
![]() $C_1$
and
$C_1$
and
![]() $C_2$
be circles of radius
$C_2$
be circles of radius
![]() $1/3$
centered at
$1/3$
centered at
![]() $\pm 1/(3\sqrt {2})$
. Then they meet at
$\pm 1/(3\sqrt {2})$
. Then they meet at
![]() $\pm a$
, where
$\pm a$
, where
![]() $a=i/(3\sqrt 2)$
. The angle between them is a right angle. The transformation
$a=i/(3\sqrt 2)$
. The angle between them is a right angle. The transformation
![]() $w= \dfrac {z+a}{z-a}$
sends the circles to two perpendicular lines, meeting at
$w= \dfrac {z+a}{z-a}$
sends the circles to two perpendicular lines, meeting at
![]() $0$
, from which examples similar to those in Example 2.2 can be constructed easily.
$0$
, from which examples similar to those in Example 2.2 can be constructed easily.
Example 2.17 There are limitations to the “inverse points” argument above if two circles are not concentric. For example, let
![]() $C_1=\{z \in {\mathbb C}: |z-3/5|=1/5\}$
and
$C_1=\{z \in {\mathbb C}: |z-3/5|=1/5\}$
and
![]() $C_2=\{z \in {\mathbb C}: |z+3/5|=1/5\}$
. Then the points
$C_2=\{z \in {\mathbb C}: |z+3/5|=1/5\}$
. Then the points
![]() $z_\pm :=\pm \sqrt {8}/5$
are inverse with respect to both circles, and one can construct rational functions of the form
$z_\pm :=\pm \sqrt {8}/5$
are inverse with respect to both circles, and one can construct rational functions of the form
![]() $c \dfrac {z-z_+}{z-z_-}$
that have constant absolute values on both circles. However, they do not have the same absolute values on
$c \dfrac {z-z_+}{z-z_-}$
that have constant absolute values on both circles. However, they do not have the same absolute values on
![]() $C_1$
and
$C_1$
and
![]() $C_2$
, so do not provide a counterexample to the above result.
$C_2$
, so do not provide a counterexample to the above result.
Finally, we note that Theorem 2.16 has sequential counterparts, which may be proved using the methods of Section 2.1. We omit the details.