1 Introduction
The interaction between solid-state matter and very intense lasers in the relativistic regime (
![]() $I_{L}>10^{18}~\text{W}/\text{cm}^{2}$
) has been widely investigated in the past two decades, mainly aiming to probe the feasibility of completely new, extremely compact proton accelerators thanks to the high electric fields generated (
$I_{L}>10^{18}~\text{W}/\text{cm}^{2}$
) has been widely investigated in the past two decades, mainly aiming to probe the feasibility of completely new, extremely compact proton accelerators thanks to the high electric fields generated (
![]() ${>}\text{TV}/\text{m}$
) in very short distances on the
${>}\text{TV}/\text{m}$
) in very short distances on the
![]() ${\sim}\unicode[STIX]{x03BC}\text{m}$
scale. Although the theory of laser–plasma acceleration was given during the seventies, only the great technological achievement of chirped pulse amplification (CPA)[Reference Strickland and Mourou1] in a laser field gave the needed boost for a series of experimental confirmations. Nevertheless, the physical mechanism is still not completely clear, due to the fast temporal evolution of this phenomenon, on the sub-picosecond time scale.
${\sim}\unicode[STIX]{x03BC}\text{m}$
scale. Although the theory of laser–plasma acceleration was given during the seventies, only the great technological achievement of chirped pulse amplification (CPA)[Reference Strickland and Mourou1] in a laser field gave the needed boost for a series of experimental confirmations. Nevertheless, the physical mechanism is still not completely clear, due to the fast temporal evolution of this phenomenon, on the sub-picosecond time scale.
During this process, beams in the multi-MeV range[Reference Clark, Krushelnick, Zepf, Beg, Tatarakis, Machacek, Santala, Watts, Norreys and Dangor2–Reference Mackinnon, Sentoku, Patel, Price, Hatchett, Key, Andersen, Snavely and Freeman4], tightly confined in time (ps scale) and space (few
![]() $\unicode[STIX]{x03BC}\text{m}$
radius), are produced. The physical picture of the interaction process is the following. Electron jets are produced at the early stages of the interaction[Reference Singh, Cui, Chatterjee, Adak, Wang, Ahmed, Lad, Sheng and Kumar5] with the focused laser generating a ‘hot’ electron cloud. A small fraction of them are energetic enough to escape the solid target, while the remaining fraction stays in the vicinity of its rear surface, hitting it again and ejecting secondary electrons[Reference Poyé, Hulin, Bailly-Grandvaux, Dubois, Ribolzi, Raffestin, Bardon, Lubrano-Lavaderci, D’Humières, Santos, Nicolaï and Tikhonchuk6, Reference Poyé, Hulin, Bailly-Grandvaux, Dubois, Ribolzi, Raffestin, Bardon, Lubrano-Lavaderci, D’Humières, Santos, Nicolaï and Tikhonchuk7]. This process is responsible for building up the electrostatic potential, which in turn governs the ion acceleration[Reference Krygier, Schumacher and Freeman8, Reference Macchi, Borghesi and Passoni9]. During the buildup of the potential, the electronic cloud locked near the target is thermalizing and some energetic electrons are still escaping from the target. Finally, this process ends when electrons can no longer overcome the electrostatic potential induced near the target surface, at which point a second slower expansion–relaxation process takes over[Reference Dubois, Lubrano-Lavaderci, Raffestin, Ribolzi, Gazave, La Fontaine, d’Humières, Hulin, Nicolaï, Poyé and Tikhonchuk10].
$\unicode[STIX]{x03BC}\text{m}$
radius), are produced. The physical picture of the interaction process is the following. Electron jets are produced at the early stages of the interaction[Reference Singh, Cui, Chatterjee, Adak, Wang, Ahmed, Lad, Sheng and Kumar5] with the focused laser generating a ‘hot’ electron cloud. A small fraction of them are energetic enough to escape the solid target, while the remaining fraction stays in the vicinity of its rear surface, hitting it again and ejecting secondary electrons[Reference Poyé, Hulin, Bailly-Grandvaux, Dubois, Ribolzi, Raffestin, Bardon, Lubrano-Lavaderci, D’Humières, Santos, Nicolaï and Tikhonchuk6, Reference Poyé, Hulin, Bailly-Grandvaux, Dubois, Ribolzi, Raffestin, Bardon, Lubrano-Lavaderci, D’Humières, Santos, Nicolaï and Tikhonchuk7]. This process is responsible for building up the electrostatic potential, which in turn governs the ion acceleration[Reference Krygier, Schumacher and Freeman8, Reference Macchi, Borghesi and Passoni9]. During the buildup of the potential, the electronic cloud locked near the target is thermalizing and some energetic electrons are still escaping from the target. Finally, this process ends when electrons can no longer overcome the electrostatic potential induced near the target surface, at which point a second slower expansion–relaxation process takes over[Reference Dubois, Lubrano-Lavaderci, Raffestin, Ribolzi, Gazave, La Fontaine, d’Humières, Hulin, Nicolaï, Poyé and Tikhonchuk10].
At SPARC_LAB[Reference Ferrario, Alesini, Anania, Bacci, Bellaveglia, Bogdanov, Boni, Castellano, Chiadroni, Cianchi, Dabagov, De Martinis, Di Giovenale, Di Pirro, Dosselli, Drago, Esposito, Faccini, Gallo, Gambaccini, Gatti, Gatti, Ghigo, Giulietti, Ligidov, Londrillo, Lupi, Mostacci, Pace, Palumbo, Petrillo, Pompili, Rossi, Serafini, Spataro, Tomassini, Turchetti, Vaccarezza, Villa, Dattoli, Di Palma, Giannessi, Petralia, Ronsivalle, Spassovsky, Surrenti, Gizzi, Labate, Levato and Rau11], the high-power laser FLAME[Reference Bisesto, Anania, Bellaveglia, Chiadroni, Cianchi, Costa, Curcio, Di Giovenale, Di Pirro, Ferrario, Filippi, Gallo, Marocchino, Pompili, Zigler and Vaccarezza12] is currently employed in pump-and-probe experiments, in which it is made to interact with solid-state targets. The main purpose of this is to carry out temporal characterization of the charged particles emitted during the interaction. For this reason two main diagnostic lines have been set up in the target area: an electro-optic sampling (EOS)[Reference van Tilborg13, Reference Pompili, Anania, Bellaveglia, Bisesto, Chiadroni, Cianchi, Curcio, Di Giovenale, Di Pirro, Ferrario, Cianchi and Zigler14] line to measure, with sub-picosecond resolution, the temporal distribution of fast electrons leaving the target, and a time-of-flight (TOF) detector to measure the longitudinal profile of the emitted protons/ions, and their energy spectrum and charge after the acceleration process[Reference Margarone, Krasa, Giuffrida, Picciotto, Torrisi, Nowak, Musumeci, Velyhan, Prokuupek, Laska, Mocek, Ullschmied and Rus15–Reference Cipriani, Consoli, Andreoli, Batani, Bonasera, Boutoux, Burgy, Cristofari, De Angelis, Di Giorgio, Ducret, Flamigni, Giulietti, Jakubowska, Verona and Verona-Rinati19]. In this work, preliminary results obtained with these two online temporal diagnostics will be presented.
2 Experimental setup
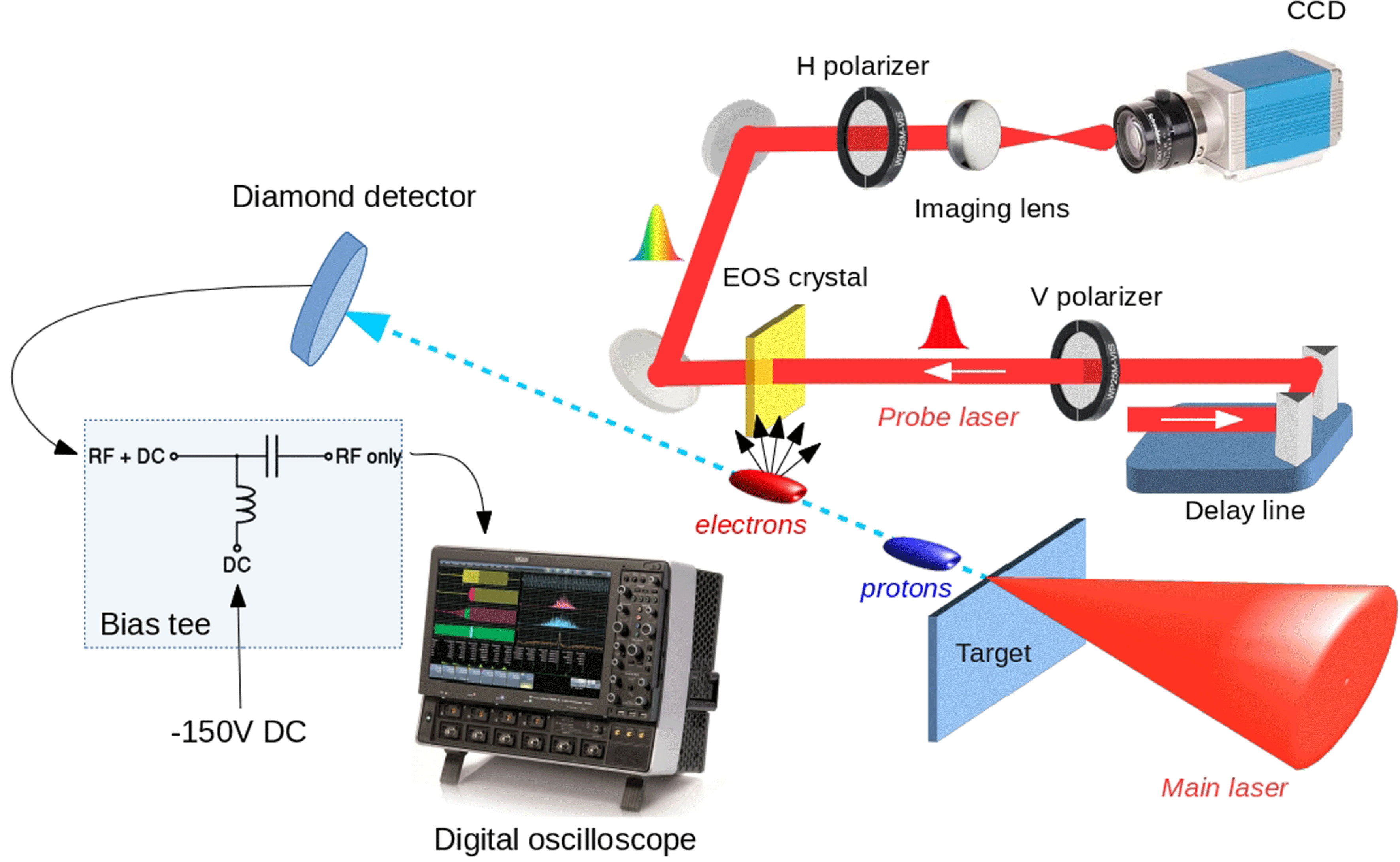
Figure 1. Experimental setup. The FLAME laser is sent to a stainless steel target. The charged particles emitted during this interaction are revealed by two single-shot time-resolved measurements: an electro-optical sampling diagnostic, able to measure the electric field carried by relativistic fast electrons, and a time-of-flight diamond detector, used to measure the temporal distribution of protons arriving on it and retrieve their energy spectra.
The high-power laser FLAME[Reference Bisesto, Anania, Bellaveglia, Chiadroni, Cianchi, Costa, Curcio, Di Giovenale, Di Pirro, Ferrario, Filippi, Gallo, Marocchino, Pompili, Zigler and Vaccarezza12] has been employed for this experiment. It consists of a CPA chain[Reference Strickland and Mourou1] delivering more than 6 J at the final cryo-amplifier output at a 10 Hz repetition rate. After optical compression down to 25 fs, the laser beam is focused by means of a
![]() $f/10$
off-axis parabolic mirror, reaching a final spot size of
$f/10$
off-axis parabolic mirror, reaching a final spot size of
![]() $15~\unicode[STIX]{x03BC}\text{m}$
$15~\unicode[STIX]{x03BC}\text{m}$
![]() $1/e^{2}$
radius. The total energy transport efficiency being 50%, a peak intensity greater than
$1/e^{2}$
radius. The total energy transport efficiency being 50%, a peak intensity greater than
![]() $10^{19}~\text{W}/\text{cm}^{2}$
is achieved in the target area, which is held in a high-vacuum environment (
$10^{19}~\text{W}/\text{cm}^{2}$
is achieved in the target area, which is held in a high-vacuum environment (
![]() $10^{-6}~\text{mbar}$
,
$10^{-6}~\text{mbar}$
,
![]() $1~\text{bar}=0.1~\text{MPa}$
), corresponding to a normalized intensity
$1~\text{bar}=0.1~\text{MPa}$
), corresponding to a normalized intensity
![]() $a_{0}>3$
.
$a_{0}>3$
.
The experimental setup is shown in Figure 1. The high-intensity FLAME laser beam is sent to a 5-
![]() $\unicode[STIX]{x03BC}\text{m}$
-thick stainless steel target. The fast electrons, able to escape the target, are detected by an electro-optic ZnTe crystal. Here, their electric field can induce a local birefringence that, in turn, can be probed by a laser beam. Previous works have shown the feasibility of this diagnostic as a fast electron monitor[Reference Pompili, Anania, Bisesto, Botton, Castellano, Chiadroni, Cianchi, Curcio, Ferrario, Galletti, Henis, Petrarca, Schleifer and Zigler20, Reference Bisesto, Anania, Botton, Chiadroni, Cianchi, Curcio, Ferrario, Galletti, Pompili, Schleifer and Zigler21] and that electro-magnetic pulses are generated in this kind of interaction[Reference Pompili, Anania, Bisesto, Botton, Chiadroni, Cianchi, Curcio, Ferrario, Galletti, Henis, Petrarca, Schleifer and Zigler22]. In particular, in the spatial encoding scheme[Reference Cavalieri23], the longitudinal distribution of the electrons can be mapped in the transverse profile of the probe laser. For this purpose, a small portion of the main beam is split and used as a completely jitter-free probe laser line. The two laser beams are synchronized at the femtosecond level in the interaction point by means of an autocorrelator, consisting of an
$\unicode[STIX]{x03BC}\text{m}$
-thick stainless steel target. The fast electrons, able to escape the target, are detected by an electro-optic ZnTe crystal. Here, their electric field can induce a local birefringence that, in turn, can be probed by a laser beam. Previous works have shown the feasibility of this diagnostic as a fast electron monitor[Reference Pompili, Anania, Bisesto, Botton, Castellano, Chiadroni, Cianchi, Curcio, Ferrario, Galletti, Henis, Petrarca, Schleifer and Zigler20, Reference Bisesto, Anania, Botton, Chiadroni, Cianchi, Curcio, Ferrario, Galletti, Pompili, Schleifer and Zigler21] and that electro-magnetic pulses are generated in this kind of interaction[Reference Pompili, Anania, Bisesto, Botton, Chiadroni, Cianchi, Curcio, Ferrario, Galletti, Henis, Petrarca, Schleifer and Zigler22]. In particular, in the spatial encoding scheme[Reference Cavalieri23], the longitudinal distribution of the electrons can be mapped in the transverse profile of the probe laser. For this purpose, a small portion of the main beam is split and used as a completely jitter-free probe laser line. The two laser beams are synchronized at the femtosecond level in the interaction point by means of an autocorrelator, consisting of an
![]() $\unicode[STIX]{x03B1}$
-BBO crystal and a delay line. The latter is also used to perform temporal scans of the interaction in a range of
$\unicode[STIX]{x03B1}$
-BBO crystal and a delay line. The latter is also used to perform temporal scans of the interaction in a range of
![]() $\pm 250~\text{ps}$
.
$\pm 250~\text{ps}$
.
After the fast electrons, protons are also emitted in the MeV energy range, thanks to the extremely high (
![]() ${\sim}\text{TV}/\text{m}$
) quasi-static electric field present on the target rear surface. The temporal structure of the positively charged beam has been measured by means of a TOF diamond detector[Reference Marinelli, Milani, Prestopino, Verona, Verona-Rinati, Cutroneo, Torrisi, Margarone, Velyhan, Krasa and Krousky24, Reference De Angelis, Consoli, Verona, Di Giorgio, Andreoli, Cristofari, Cipriani, Ingenito, Marinelli and Verona-Rinati25]. The superficial and interdigital geometry employed to realize it, made by several electrodes in the detector active area, as shown in Figure 2, separated by
${\sim}\text{TV}/\text{m}$
) quasi-static electric field present on the target rear surface. The temporal structure of the positively charged beam has been measured by means of a TOF diamond detector[Reference Marinelli, Milani, Prestopino, Verona, Verona-Rinati, Cutroneo, Torrisi, Margarone, Velyhan, Krasa and Krousky24, Reference De Angelis, Consoli, Verona, Di Giorgio, Andreoli, Cristofari, Cipriani, Ingenito, Marinelli and Verona-Rinati25]. The superficial and interdigital geometry employed to realize it, made by several electrodes in the detector active area, as shown in Figure 2, separated by
![]() $20~\unicode[STIX]{x03BC}\text{m}$
from each other, allows one to reach a temporal resolution of around 800 ps. This is well below that achievable by commercial detectors using only two electrodes placed on opposite sides of the active area (of the order of 6–8 ns). In turn, the resulting energy resolution is generally very high and, as shown in Figure 7, it achieves up to around 3% in the MeV range, for a 1 m distance of the detector from the target. The detector is biased at
$20~\unicode[STIX]{x03BC}\text{m}$
from each other, allows one to reach a temporal resolution of around 800 ps. This is well below that achievable by commercial detectors using only two electrodes placed on opposite sides of the active area (of the order of 6–8 ns). In turn, the resulting energy resolution is generally very high and, as shown in Figure 7, it achieves up to around 3% in the MeV range, for a 1 m distance of the detector from the target. The detector is biased at
![]() $-150~\text{V}$
and a custom high-frequency Millimetrica bias-tee is employed to separate the DC input from the AC output, due to electron–hole pairs produced by a charged particle leaving energy in the diamond. Electro-magnetic pulses (EMPs) usually represent a source of noise when this kind of detector is placed inside the interaction chamber[Reference Consoli, De Angelis, De Marco, Krasa, Cikhardt, Pfeifer, Margarone, Klir and Dudzak26]. Nevertheless, thanks to the specialized assembly design[Reference De Angelis, Consoli, Verona, Di Giorgio, Andreoli, Cristofari, Cipriani, Ingenito, Marinelli and Verona-Rinati25] and optimization of the readout system[Reference Consoli, De Angelis, De Marco, Krasa, Cikhardt, Pfeifer, Margarone, Klir and Dudzak26], signals with negligible EMP contributions have been measured.
$-150~\text{V}$
and a custom high-frequency Millimetrica bias-tee is employed to separate the DC input from the AC output, due to electron–hole pairs produced by a charged particle leaving energy in the diamond. Electro-magnetic pulses (EMPs) usually represent a source of noise when this kind of detector is placed inside the interaction chamber[Reference Consoli, De Angelis, De Marco, Krasa, Cikhardt, Pfeifer, Margarone, Klir and Dudzak26]. Nevertheless, thanks to the specialized assembly design[Reference De Angelis, Consoli, Verona, Di Giorgio, Andreoli, Cristofari, Cipriani, Ingenito, Marinelli and Verona-Rinati25] and optimization of the readout system[Reference Consoli, De Angelis, De Marco, Krasa, Cikhardt, Pfeifer, Margarone, Klir and Dudzak26], signals with negligible EMP contributions have been measured.

Figure 2. Time-of-flight detector geometry. Schematic representation of the device layer structure (left) and picture of the surface Al interdigitated electrodes (right). The metal fingers were processed to
![]() $20~\unicode[STIX]{x03BC}\text{m}$
in width, with a spacing between the electrodes of
$20~\unicode[STIX]{x03BC}\text{m}$
in width, with a spacing between the electrodes of
![]() $20~\unicode[STIX]{x03BC}\text{m}$
. The detector active area was approximately
$20~\unicode[STIX]{x03BC}\text{m}$
. The detector active area was approximately
![]() $2~\text{mm}^{2}$
.
$2~\text{mm}^{2}$
.
3 Experimental results
The EOS diagnostic has been employed to study the fast electrons emitted during the interaction. In particular, from the longitudinal profile of the electric field carried by fast electrons, their temporal charge distribution has been retrieved, within a 8 ps temporal window with
![]() ${\sim}100~\text{fs}$
resolution, limited by the crystal thickness. Figure 3 shows a typical measurement performed by means of our diagnostic. The curved shape is due to the geometry employed in our setup[Reference Pompili, Anania, Bisesto, Botton, Castellano, Chiadroni, Cianchi, Curcio, Ferrario, Galletti, Henis, Petrarca, Schleifer and Zigler27]. By tracing a line profile along the signal thickness, directly related to its temporal duration, the temporal distribution of the electric field can be retrieved, as reported in Figure 4. From this, the temporal duration in terms of the full-width at half-maximum (FWHM) and peak value have been found to be
${\sim}100~\text{fs}$
resolution, limited by the crystal thickness. Figure 3 shows a typical measurement performed by means of our diagnostic. The curved shape is due to the geometry employed in our setup[Reference Pompili, Anania, Bisesto, Botton, Castellano, Chiadroni, Cianchi, Curcio, Ferrario, Galletti, Henis, Petrarca, Schleifer and Zigler27]. By tracing a line profile along the signal thickness, directly related to its temporal duration, the temporal distribution of the electric field can be retrieved, as reported in Figure 4. From this, the temporal duration in terms of the full-width at half-maximum (FWHM) and peak value have been found to be
![]() $\unicode[STIX]{x1D70F}=0.5$
ps and
$\unicode[STIX]{x1D70F}=0.5$
ps and
![]() $E_{0}=1.5~\text{MV}/\text{m}$
, respectively. Moreover, the electric field generated by the bunch, inducing the electro-optic effect, is proportional to its charge. Therefore, the latter can be estimated from the signal intensity, making our EOS diagnostic act as a temporally resolved charge measurement with femtosecond resolution. Indeed, from the measured electric field value, the charge has been retrieved as having a value
$E_{0}=1.5~\text{MV}/\text{m}$
, respectively. Moreover, the electric field generated by the bunch, inducing the electro-optic effect, is proportional to its charge. Therefore, the latter can be estimated from the signal intensity, making our EOS diagnostic act as a temporally resolved charge measurement with femtosecond resolution. Indeed, from the measured electric field value, the charge has been retrieved as having a value
![]() $Q=6$
nC.
$Q=6$
nC.

Figure 3. Typical 2D electric field carried by fast electrons as seen by our EOS diagnostic tool. The signal thickness is related to the temporal duration of the electric field. The typical shape is a direct consequence of our setup geometry[Reference Pompili, Anania, Bisesto, Botton, Castellano, Chiadroni, Cianchi, Curcio, Ferrario, Galletti, Henis, Petrarca, Schleifer and Zigler27].

Figure 4. Line profile traced along the signal in Figure 3. The measured electric field shows a peak value
![]() $E_{0}=1.5~\text{MV}/\text{m}$
and a temporal duration
$E_{0}=1.5~\text{MV}/\text{m}$
and a temporal duration
![]() $\unicode[STIX]{x1D70F}=0.5$
ps FWHM. The fast electron charge also has been retrieved with a value of
$\unicode[STIX]{x1D70F}=0.5$
ps FWHM. The fast electron charge also has been retrieved with a value of
![]() $Q=6$
nC.
$Q=6$
nC.
Simultaneously, the proton energy spectra have also been recorded, thanks to the sub-ns resolution TOF diamond detector installed in our setup. Placed 1 m behind the target, with respect to the incoming laser beam, and along the same laser direction, it can provide temporal measurements with 800 ps resolution, thanks to the superficial interdigital structure shown in Figure 2. Figure 5 shows a typical signal received by our 2 GHz Lecroy 620ZI oscilloscope from the bias-tee AC output. Here, one can distinguish two different peaks: the first one represents X-rays and low-energy electrons coming to the detector much earlier than the protons, which in turn compose the second peak. In this way, by choosing the rising front of the first peak as the reference time, the temporal distribution of the protons has been retrieved. From this, the energy spectrum can be reconstructed, simply by transforming the temporal axis as
![]() $t\rightarrow E_{\text{ions}}=m_{\text{ion}}\times c^{2}(\unicode[STIX]{x1D6FE}-1)$
, with
$t\rightarrow E_{\text{ions}}=m_{\text{ion}}\times c^{2}(\unicode[STIX]{x1D6FE}-1)$
, with
![]() $\unicode[STIX]{x1D6FE}=1/\sqrt{1-\unicode[STIX]{x1D6FD}^{2}}$
being the Lorentz relativistic factor,
$\unicode[STIX]{x1D6FE}=1/\sqrt{1-\unicode[STIX]{x1D6FD}^{2}}$
being the Lorentz relativistic factor,
![]() $m_{\text{ion}}$
the ion rest mass and
$m_{\text{ion}}$
the ion rest mass and
![]() $\unicode[STIX]{x1D6FD}=v/c=L/[c\times (\unicode[STIX]{x0394}t+t_{0})]$
, where
$\unicode[STIX]{x1D6FD}=v/c=L/[c\times (\unicode[STIX]{x0394}t+t_{0})]$
, where
![]() $L=1$
m is the TOF detector distance from the source,
$L=1$
m is the TOF detector distance from the source,
![]() $\unicode[STIX]{x0394}t$
is the time difference with respect to the beginning of the rising edge of the photopeak and
$\unicode[STIX]{x0394}t$
is the time difference with respect to the beginning of the rising edge of the photopeak and
![]() $t_{0}=L/c=3.3$
ns is the time needed by X-rays to reach the diamond detector.
$t_{0}=L/c=3.3$
ns is the time needed by X-rays to reach the diamond detector.

Figure 5. Typical signal provided by the TOF detector as seen by our 2 GHz Lecroy 620ZI oscilloscope. As one can see, it is possible to distinguish between two different signals arriving at different times: the first is associated with X-rays and low-energy electrons coming at the early stage of the interaction; the second is related to protons accelerated through the TNSA mechanism.

Figure 6. Monte Carlo simulations by the SRIM code results for
![]() $10~\unicode[STIX]{x03BC}\text{m}$
of aluminium.
$10~\unicode[STIX]{x03BC}\text{m}$
of aluminium.
The TOF detector was covered by a 10-
![]() $\unicode[STIX]{x03BC}\text{m}$
-thick aluminium foil to reduce deposition of debris coming from the target and to minimize the EMP coupling to the detector. Monte Carlo simulations by the SRIM code have been performed to take into account the effect of energy attenuation due to the foil. Figure 6(a) shows the simulated energy outcome, as seen by the detector, as a function of the initial proton energy before crossing the aluminium foil, considering that the proton beam was monochromatic before passing through it. We show, for each set of simulations, the average value for the energy of protons able to get across the Al filter, together with the related standard deviation. The energy attenuation depends upon the initial proton energy, as reported in Figure 6(b). The threshold is around 750 keV: when protons approach this value the standard deviation becomes comparable to the average value. For this reason we estimate that reliable results are achieved for energies higher than 840 keV, and this lower limit is used in Figure 7, showing the proton energy spectrum, referring to the signal as acquired in Figure 5. Here, the proton spectra both with (black) and without (red) the effect of the aluminium foil are reported. The vertical axis represents the number of particles per energy unit (MeV) and steradian (that is,
$\unicode[STIX]{x03BC}\text{m}$
-thick aluminium foil to reduce deposition of debris coming from the target and to minimize the EMP coupling to the detector. Monte Carlo simulations by the SRIM code have been performed to take into account the effect of energy attenuation due to the foil. Figure 6(a) shows the simulated energy outcome, as seen by the detector, as a function of the initial proton energy before crossing the aluminium foil, considering that the proton beam was monochromatic before passing through it. We show, for each set of simulations, the average value for the energy of protons able to get across the Al filter, together with the related standard deviation. The energy attenuation depends upon the initial proton energy, as reported in Figure 6(b). The threshold is around 750 keV: when protons approach this value the standard deviation becomes comparable to the average value. For this reason we estimate that reliable results are achieved for energies higher than 840 keV, and this lower limit is used in Figure 7, showing the proton energy spectrum, referring to the signal as acquired in Figure 5. Here, the proton spectra both with (black) and without (red) the effect of the aluminium foil are reported. The vertical axis represents the number of particles per energy unit (MeV) and steradian (that is,
![]() $\text{d}^{2}N_{\text{particles}}/\text{d}E\text{d}\unicode[STIX]{x1D6FA}$
), on a log scale, reaching the TOF detector. In particular, in the black curve we consider only the tolerances due to the energy spread of the proton beam caused by the aluminium foil. For this shot, the maximum proton energy measured is equal to 1.37 MeV.
$\text{d}^{2}N_{\text{particles}}/\text{d}E\text{d}\unicode[STIX]{x1D6FA}$
), on a log scale, reaching the TOF detector. In particular, in the black curve we consider only the tolerances due to the energy spread of the proton beam caused by the aluminium foil. For this shot, the maximum proton energy measured is equal to 1.37 MeV.
![]() $\text{d}N_{\text{corrected}}/\text{d}\unicode[STIX]{x1D6FA}$
being the number of particles per steradian associated with the black curve, taking into account the aluminium foil, and
$\text{d}N_{\text{corrected}}/\text{d}\unicode[STIX]{x1D6FA}$
being the number of particles per steradian associated with the black curve, taking into account the aluminium foil, and
![]() $\text{d}N_{\text{not corrected}}/\text{d}\unicode[STIX]{x1D6FA}$
that associated with the red curve, yields
$\text{d}N_{\text{not corrected}}/\text{d}\unicode[STIX]{x1D6FA}$
that associated with the red curve, yields
![]() $\text{d}N_{\text{corrected}}/\text{d}\unicode[STIX]{x1D6FA}=2.63\times \text{d}N_{\text{not corrected}}/\text{d}\unicode[STIX]{x1D6FA}$
. In order to obtain the absolute particle spectra and the related number of particles from the measurements of Figure 5, a careful de-embedding of the readout system and a single-particle calibration of the diamond detector are needed (a paper is in preparation on this topic).
$\text{d}N_{\text{corrected}}/\text{d}\unicode[STIX]{x1D6FA}=2.63\times \text{d}N_{\text{not corrected}}/\text{d}\unicode[STIX]{x1D6FA}$
. In order to obtain the absolute particle spectra and the related number of particles from the measurements of Figure 5, a careful de-embedding of the readout system and a single-particle calibration of the diamond detector are needed (a paper is in preparation on this topic).
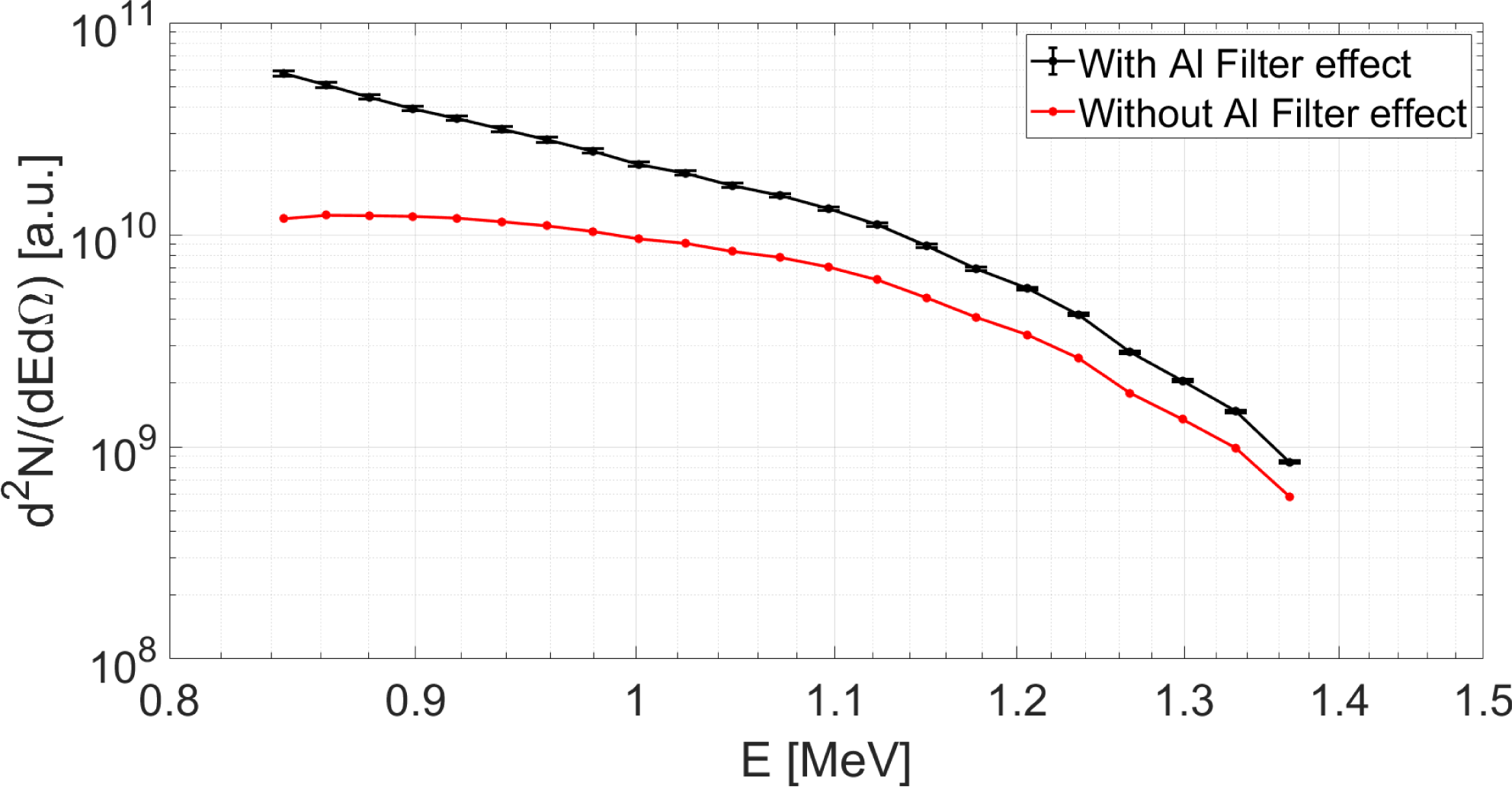
Figure 7. Proton energy spectra retrieved from the data in Figure 5 with (black line) and without (red line) taking into account the aluminium filter. Tolerances present in the black curve are only due to the energy spread of the incoming proton beam caused by crossing the foil.
4 Conclusions
In this work, we have shown typical experimental results provided by our temporally resolved diagnostics, detecting, simultaneously, both fast electrons and protons generated during FLAME laser–solid matter interactions. In this case, the target was made from 10-
![]() $\unicode[STIX]{x03BC}\text{m}$
-thick stainless steel. In detail, we have reported direct measurement of the electric field carried by fast electrons, characterized by a peak value
$\unicode[STIX]{x03BC}\text{m}$
-thick stainless steel. In detail, we have reported direct measurement of the electric field carried by fast electrons, characterized by a peak value
![]() $E_{0}=1.5~\text{MV}/\text{m}$
and a temporal duration
$E_{0}=1.5~\text{MV}/\text{m}$
and a temporal duration
![]() $\unicode[STIX]{x1D70F}=0.5$
ps FWHM. From these data, we were also able to measure the fast electron charge, which had a value
$\unicode[STIX]{x1D70F}=0.5$
ps FWHM. From these data, we were also able to measure the fast electron charge, which had a value
![]() $Q=6$
nC. At the same time, protons beams, accelerated through the TNSA mechanism, were detected by a diamond TOF diagnostic. By analysing the electric signal captured by our oscilloscope, we were able to resolve the proton energy spectrum. By means of Monte Carlo simulations performed by the SRIM code, we were able to correct our experimental data, taking into account a 10-
$Q=6$
nC. At the same time, protons beams, accelerated through the TNSA mechanism, were detected by a diamond TOF diagnostic. By analysing the electric signal captured by our oscilloscope, we were able to resolve the proton energy spectrum. By means of Monte Carlo simulations performed by the SRIM code, we were able to correct our experimental data, taking into account a 10-
![]() $\unicode[STIX]{x03BC}\text{m}$
-thick aluminium foil covering the detector. In detail, we found the maximum proton energy
$\unicode[STIX]{x03BC}\text{m}$
-thick aluminium foil covering the detector. In detail, we found the maximum proton energy
![]() $E_{\text{max}}=1.37$
MeV. These preliminary results show the feasibility of using our diagnostic tool to retrieve a complete picture of laser–target interactions, detecting at the same time both fast electrons and protons. In the near future, we plan to study possible correlations existing between these two interaction products.
$E_{\text{max}}=1.37$
MeV. These preliminary results show the feasibility of using our diagnostic tool to retrieve a complete picture of laser–target interactions, detecting at the same time both fast electrons and protons. In the near future, we plan to study possible correlations existing between these two interaction products.










