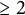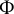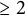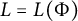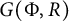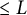Introduction and State of Art
In the present paper, we consider Chevalley groups
![]() $G=G(\Phi ,R)$
and their elementary subgroups
$G=G(\Phi ,R)$
and their elementary subgroups
![]() $E(\Phi ,R)$
over Dedekind rings of arithmetic type. Usually, it is more convenient to speak of the simply connected group
$E(\Phi ,R)$
over Dedekind rings of arithmetic type. Usually, it is more convenient to speak of the simply connected group
![]() $G_{\mathrm {sc}}(\Phi ,R)$
. In most of the cases we are interested in, it coincides with the elementary group
$G_{\mathrm {sc}}(\Phi ,R)$
. In most of the cases we are interested in, it coincides with the elementary group
![]() $E_{\mathrm {sc}}(\Phi ,R)$
. When there is no danger of confusion, we drop any indication of the weight lattice.
$E_{\mathrm {sc}}(\Phi ,R)$
. When there is no danger of confusion, we drop any indication of the weight lattice.
Our ring R is an arbitrary Dedekind ring of arithmetic type, which means that throughout the paper, one has to distinguish the corresponding number and function cases.
We occupy ourselves with the classical problem of estimating the width of
![]() $E(\Phi ,R)$
with respect to the elementary generators
$E(\Phi ,R)$
with respect to the elementary generators
![]() $x_{\alpha }(\xi )$
,
$x_{\alpha }(\xi )$
,
![]() $\alpha \in \Phi $
,
$\alpha \in \Phi $
,
![]() $\xi \in R$
. We consider the subset
$\xi \in R$
. We consider the subset
![]() $E^L(\Phi ,R)$
consisting of products of
$E^L(\Phi ,R)$
consisting of products of
![]() $\le L$
such elementary generators. The elementary width is defined as the smallest L such that each element of
$\le L$
such elementary generators. The elementary width is defined as the smallest L such that each element of
![]() $E(\Phi ,R)$
can be represented as a product of
$E(\Phi ,R)$
can be represented as a product of
![]() $\le L$
elementary generators
$\le L$
elementary generators
![]() $x_{\alpha }(\xi )$
; in other words,
$x_{\alpha }(\xi )$
; in other words,
If there is no such L, we say that the width is infinite. If the width is finite, we say that G is boundedly elementarily generated.
Let us start with a short review of early works on the topic. Most of them, and many papers even today, only treat the special case of
![]() $\mathrm {SL}(n,R)$
. The pioneering 1975 paper by George Cooke and Peter Weinberger [Reference Cooke and WeinbergerCW] showed that, with the exception of
$\mathrm {SL}(n,R)$
. The pioneering 1975 paper by George Cooke and Peter Weinberger [Reference Cooke and WeinbergerCW] showed that, with the exception of
![]() $\mathrm {SL}(2,R)$
over very meagre rings, such as
$\mathrm {SL}(2,R)$
over very meagre rings, such as
![]() $R={\mathbb Z}, {\mathbb F}_{\!q}[t]$
, or other arithmetic rings with the finite multiplicative group, the problem of bounded elementary generation admits a positive uniform solution. In other words, in this case, there exists a bound
$R={\mathbb Z}, {\mathbb F}_{\!q}[t]$
, or other arithmetic rings with the finite multiplicative group, the problem of bounded elementary generation admits a positive uniform solution. In other words, in this case, there exists a bound
![]() $L=L(\Phi )$
depending solely on
$L=L(\Phi )$
depending solely on
![]() $\Phi $
such that the elementary width of
$\Phi $
such that the elementary width of
![]() $G(\Phi ,R)$
over all Dedekind rings R of arithmetic type does not exceed L.
$G(\Phi ,R)$
over all Dedekind rings R of arithmetic type does not exceed L.
However, their actual proofs were conditional; they depended on a very strong form of the GRH = Generalized Riemann Hypothesis. The most important early contributions toward obtaining unconditional proofs of such results over number rings are due to David Carter and Gordon Keller, 1983–1985.
![]() $\bullet $
The arithmetic proofs for
$\bullet $
The arithmetic proofs for
![]() $\mathrm {SL}(n,R)$
,
$\mathrm {SL}(n,R)$
,
![]() $n\geq 3$
, with explicit bounds depending not only on
$n\geq 3$
, with explicit bounds depending not only on
![]() $\Phi $
but also on some arithmetic invariants of R, were obtained in [Reference Carter and KellerCK1, Reference Carter and KellerCK2],
$\Phi $
but also on some arithmetic invariants of R, were obtained in [Reference Carter and KellerCK1, Reference Carter and KellerCK2],
![]() $\bullet $
For the model theoretic proofs in the number case, which yield the existence of bounds
$\bullet $
For the model theoretic proofs in the number case, which yield the existence of bounds
![]() $L=L(\Phi ,d)$
depending on
$L=L(\Phi ,d)$
depending on
![]() $\Phi $
and the degree
$\Phi $
and the degree
![]() $d=[K:{\mathbb Q}]$
, non-constructive, without presenting any actual bounds, see, for instance, the truly remarkable [but unfortunately still unpublished] preprint by Carter and Keller with Eugene Paige [Reference Carter, Keller and PaigeCKP], and its re-exposition by Dave Morris [Reference MorrisMo].
$d=[K:{\mathbb Q}]$
, non-constructive, without presenting any actual bounds, see, for instance, the truly remarkable [but unfortunately still unpublished] preprint by Carter and Keller with Eugene Paige [Reference Carter, Keller and PaigeCKP], and its re-exposition by Dave Morris [Reference MorrisMo].
![]() $\bullet $
Around 1990, Oleg Tavgen [Reference TavgenTa1, Reference TavgenTa2, Reference TavgenTa3] succeeded in generalizing these results to all Chevalley groups of normal types, and to most twisted Chevalley groups. With this end, he invented a very slick reduction trick, which reduced the study of bounded generation to rank 2 cases, essentially to
$\bullet $
Around 1990, Oleg Tavgen [Reference TavgenTa1, Reference TavgenTa2, Reference TavgenTa3] succeeded in generalizing these results to all Chevalley groups of normal types, and to most twisted Chevalley groups. With this end, he invented a very slick reduction trick, which reduced the study of bounded generation to rank 2 cases, essentially to
![]() $\mathrm {SL}(3,R)$
and
$\mathrm {SL}(3,R)$
and
![]() $\mathrm {Sp}(4,R)$
, and was able to solve the cases of
$\mathrm {Sp}(4,R)$
, and was able to solve the cases of
![]() $\mathrm {Sp}(4,R)$
and
$\mathrm {Sp}(4,R)$
and
![]() $G(\mathsf G_2,R)$
by direct matrix computations imitating the arithmetic proof by Carter and Keller. As the Carter–Keller bounds, Tavgen’s ones depended on arithmetic invariants of R.
$G(\mathsf G_2,R)$
by direct matrix computations imitating the arithmetic proof by Carter and Keller. As the Carter–Keller bounds, Tavgen’s ones depended on arithmetic invariants of R.
![]() $\bullet $
The only published result for the function case until rather recently was the very early 1975 paper by Clifford Queen [Reference QueenQu], who established the best possible absolute bound
$\bullet $
The only published result for the function case until rather recently was the very early 1975 paper by Clifford Queen [Reference QueenQu], who established the best possible absolute bound
![]() $L=5$
, but only for some function rings with infinite multiplicative group subject to further arithmetic conditions. Even the case of
$L=5$
, but only for some function rings with infinite multiplicative group subject to further arithmetic conditions. Even the case of
![]() $R={\mathbb F}_{\!q}[t]$
remained open at that stage.
$R={\mathbb F}_{\!q}[t]$
remained open at that stage.
Such was the state of art around 1990, and the results listed above remained almost unrivaled for about two more decades. There were some interesting attempts to come up with explicit bounds (compare, for instance, [Reference LiehlLi, Reference Loukanidis and MurtyLM, Reference MurtyMu]), but the resulting bounds always depended on some further arithmetic invariants and/or worked only under some severe restrictions on R.
However, there were many reasons which eventually led to a new surge of activity in this direction starting around 2010.Footnote 1 Let us mention relations with the congruence subgroup property, Kazhdan property T, Waring-type problems for groups, model theoretic applications, and so on.
An important initial breakthrough, the first unconditional proof of the bounded generation of
![]() $\mathrm {SL}\Big (2,{\mathbb Z}\Big [\displaystyle {\frac 1p}\Big ]\Big )$
with an explicit bound, and at that the best possible one,
$\mathrm {SL}\Big (2,{\mathbb Z}\Big [\displaystyle {\frac 1p}\Big ]\Big )$
with an explicit bound, and at that the best possible one,
![]() $L=5$
, was achieved by Maxim Vsemirnov [Reference VsemirnovVs].
$L=5$
, was achieved by Maxim Vsemirnov [Reference VsemirnovVs].
Let us list the key contributions of the last five years which together essentially amount to the complete solution of the problem.
![]() $\bullet $
For the number case, when
$\bullet $
For the number case, when
![]() $R^*$
is infinite, there is a definitive result for
$R^*$
is infinite, there is a definitive result for
![]() $\mathrm {SL}(2,R)$
by Morgan, Rapinchuk, and Sury [Reference Morgan, Rapinchuk and SuryMRS] in 2018, with a small uniform bound
$\mathrm {SL}(2,R)$
by Morgan, Rapinchuk, and Sury [Reference Morgan, Rapinchuk and SuryMRS] in 2018, with a small uniform bound
![]() $L\le 9$
, which can be improved [and was improved!] in some cases. Thus, Bruce Jordan and Yevgeny Zaytman [Reference Jordan and ZaytmanJZ] improved it to
$L\le 9$
, which can be improved [and was improved!] in some cases. Thus, Bruce Jordan and Yevgeny Zaytman [Reference Jordan and ZaytmanJZ] improved it to
![]() $L\le 8$
(and further improved to
$L\le 8$
(and further improved to
![]() $L\le 7$
or
$L\le 7$
or
![]() $L\le 6$
in the presence of finite or real valuations in S).
$L\le 6$
in the presence of finite or real valuations in S).
![]() $\bullet $
In the same 2018, Bogdan Nica [Reference NicaNi] has finally established bounded elementary generation of
$\bullet $
In the same 2018, Bogdan Nica [Reference NicaNi] has finally established bounded elementary generation of
![]() $\mathrm {SL}(n,{\mathbb F}_{\!q}[t])$
,
$\mathrm {SL}(n,{\mathbb F}_{\!q}[t])$
,
![]() $n\ge 3$
. He proposed a slight variation of Carter–Keller’s approach, replacing the full multiplicativity of Mennicke symbol by a weaker form, “swindling lemma.” This is where we jumped in. In [Reference Kunyavskiĭ, Plotkin and VavilovKPV], we developed reductions of all non-symplectic Chevalley groups to
$n\ge 3$
. He proposed a slight variation of Carter–Keller’s approach, replacing the full multiplicativity of Mennicke symbol by a weaker form, “swindling lemma.” This is where we jumped in. In [Reference Kunyavskiĭ, Plotkin and VavilovKPV], we developed reductions of all non-symplectic Chevalley groups to
![]() $\mathrm {SL}(3,{\mathbb F}_{\!q}[t])$
and devised a similar proof for
$\mathrm {SL}(3,{\mathbb F}_{\!q}[t])$
and devised a similar proof for
![]() $\mathrm {Sp}(4,{\mathbb F}_{\!q}[t])$
.
$\mathrm {Sp}(4,{\mathbb F}_{\!q}[t])$
.
![]() $\bullet $
The decisive contributions in the function case are due to Alexander Trost [Reference TrostTr1, Reference TrostTr2], who succeeded in proving versions of all necessary arithmetic lemmas in the function case. Actually, his versions are better than the corresponding results in the number case.Footnote
2
In particular, he gave an explicit uniform bound for the bounded elementary generation of
$\bullet $
The decisive contributions in the function case are due to Alexander Trost [Reference TrostTr1, Reference TrostTr2], who succeeded in proving versions of all necessary arithmetic lemmas in the function case. Actually, his versions are better than the corresponding results in the number case.Footnote
2
In particular, he gave an explicit uniform bound for the bounded elementary generation of
![]() $\mathrm {SL}(n,R)$
,
$\mathrm {SL}(n,R)$
,
![]() $n\ge 3$
, which does not depend on the degree
$n\ge 3$
, which does not depend on the degree
![]() $d=[K:{\mathbb F}_{\!q}(t)]$
.
$d=[K:{\mathbb F}_{\!q}(t)]$
.
![]() $\bullet $
Finally, the recent paper by Kunyavskii, Morris, and Rapinchuk [Reference Kunyavskiĭ, Morris and RapinchukKMR] improves the uniform bound for
$\bullet $
Finally, the recent paper by Kunyavskii, Morris, and Rapinchuk [Reference Kunyavskiĭ, Morris and RapinchukKMR] improves the uniform bound for
![]() $\mathrm {SL}(2,R)$
for rings R with infinite multiplicative group
$\mathrm {SL}(2,R)$
for rings R with infinite multiplicative group
![]() $R^*$
to
$R^*$
to
![]() $L\le 7$
in the number case and establishes a similar result with the bound
$L\le 7$
in the number case and establishes a similar result with the bound
![]() $L\le 8$
in the function case.
$L\le 8$
in the function case.
Thus, the results of [Reference Carter, Keller and PaigeCKP, Reference MorrisMo, Reference Morgan, Rapinchuk and SuryMRS, Reference TrostTr2, Reference Kunyavskiĭ, Morris and RapinchukKMR] completely solve the problem of the uniform bounded elementary generation for the special linear groups
![]() $\mathrm {SL}(n,R)$
,
$\mathrm {SL}(n,R)$
,
![]() $n\ge 3$
– and when
$n\ge 3$
– and when
![]() $R^*$
is infinite, even for
$R^*$
is infinite, even for
![]() $\mathrm {SL}(2,R)$
.
$\mathrm {SL}(2,R)$
.
The methods of our previous paper [Reference Kunyavskiĭ, Plotkin and VavilovKPV] completely reduce the proof of a similar result for almost all other Chevalley groups, including even the symplectic groups
![]() $\mathrm {Sp}(2l,R)$
,
$\mathrm {Sp}(2l,R)$
,
![]() $l\ge 3$
to the case of
$l\ge 3$
to the case of
![]() $\Phi =\mathsf {A}_2$
. The only case that does not follow right away by combining results of the above papers is that of
$\Phi =\mathsf {A}_2$
. The only case that does not follow right away by combining results of the above papers is that of
![]() $\mathrm {Sp}(4,R)$
.
$\mathrm {Sp}(4,R)$
.
Here, we solve the remaining case of
![]() $\mathrm {Sp}(4,R)$
and thus come up with a complete solution of uniform bounded generation for Chevalley groups in the general case.
$\mathrm {Sp}(4,R)$
and thus come up with a complete solution of uniform bounded generation for Chevalley groups in the general case.
Theorem A Let
![]() $\Phi $
be a reduced irreducible root system of rank
$\Phi $
be a reduced irreducible root system of rank
![]() $l\ge 2$
. Then there exists a constant
$l\ge 2$
. Then there exists a constant
![]() $L=L(\Phi )$
, depending on
$L=L(\Phi )$
, depending on
![]() $\Phi $
alone, such that for any Dedekind ring of arithmetic type R, any element in
$\Phi $
alone, such that for any Dedekind ring of arithmetic type R, any element in
![]() $G_{\mathrm {sc}}(\Phi ,R)$
is a product of at most L elementary root unipotents,
$G_{\mathrm {sc}}(\Phi ,R)$
is a product of at most L elementary root unipotents,
Remark 0.1 The bounds obtained in Theorem A are uniform with respect to R, both in the number and function cases. What is important – and unexpected! – is that in the function case, they are explicit.
Remark 0.2 In the number case, explicit bounds are only available when
![]() $R^*$
is infinite.
$R^*$
is infinite.
Remark 0.3 Theorem A was already announced in [Reference Kunyavskiĭ, Lavrenov, Plotkin and VavilovKLPV], with a sketch of proof. However, since [Reference Kunyavskiĭ, Lavrenov, Plotkin and VavilovKLPV] is focused on bounded generation for the Steinberg groups, it would be unreasonable to provide their tedious computational aspects of the proof for Chevalley groups. Therefore, the most tricky case of
![]() $\mathrm {Sp}(4,R)$
was skipped there; in several cases not needed for the treatment of Steinberg groups, the arguments were only briefly sketched, and no care of explicit numerical bounds was taken. Here, we supply all the details for the case of
$\mathrm {Sp}(4,R)$
was skipped there; in several cases not needed for the treatment of Steinberg groups, the arguments were only briefly sketched, and no care of explicit numerical bounds was taken. Here, we supply all the details for the case of
![]() $\mathrm {Sp} (4,R)$
. Moreover, we redo the case
$\mathrm {Sp} (4,R)$
. Moreover, we redo the case
![]() $\mathrm {SL}(3,R)$
for the function rings, which was already solved in [Reference TrostTr2]. However, we do it in the style of [Reference NicaNi] rather than [Reference Carter and KellerCK1], which allows us to improve the estimate for L from
$\mathrm {SL}(3,R)$
for the function rings, which was already solved in [Reference TrostTr2]. However, we do it in the style of [Reference NicaNi] rather than [Reference Carter and KellerCK1], which allows us to improve the estimate for L from
![]() $L\le 65$
to
$L\le 65$
to
![]() $L\le 44$
. This improvement then gives slightly better bounds in all explicit estimates for all other Chevalley groups in the function case.
$L\le 44$
. This improvement then gives slightly better bounds in all explicit estimates for all other Chevalley groups in the function case.
Remark 0.4 Note that uniform estimates, being interesting in their own right, are indispensable for some applications – for example, for estimating Kazhdan constants of arithmetic groups; see [Reference HadadHa].
Roughly, the ingredients of the proof are as follows.
![]() $\bullet $
We consider the case where
$\bullet $
We consider the case where
![]() $R^*$
is infinite separately and prove the following statement.
$R^*$
is infinite separately and prove the following statement.
Theorem B For any Dedekind ring of arithmetic type R with the infinite multiplicative group
![]() $R^*$
, any element in
$R^*$
, any element in
![]() $G_{\mathrm {sc}}(\Phi ,R)$
is a product of at most
$G_{\mathrm {sc}}(\Phi ,R)$
is a product of at most
![]() $L=7N$
elementary unipotents in the number case or
$L=7N$
elementary unipotents in the number case or
![]() $L=8N$
elementary unipotents in the function case, where
$L=8N$
elementary unipotents in the function case, where
![]() $N=|\Phi ^+|$
is the number of positive roots of
$N=|\Phi ^+|$
is the number of positive roots of
![]() $\Phi $
.
$\Phi $
.
The proof of Theorem B is cheap modulo deep results for rank 1 case and requires Tavgen’s reduction trick. This is done in Section 3. Thus, in the proof of Theorem A, we may assume that
![]() $R^*$
is finite. This is important in the number case.
$R^*$
is finite. This is important in the number case.
![]() $\bullet $
In the function case, our proofs in this paper have almost zero arithmetic components. Namely, all arithmetic results we need are taken essentially as is from the paper by Trost [Reference TrostTr2, Lemma 3.1 and Lemma 3.3]. After that, the rest of the proof is a pure theory of algebraic groups and some stability theorems from algebraic K-theory.
$\bullet $
In the function case, our proofs in this paper have almost zero arithmetic components. Namely, all arithmetic results we need are taken essentially as is from the paper by Trost [Reference TrostTr2, Lemma 3.1 and Lemma 3.3]. After that, the rest of the proof is a pure theory of algebraic groups and some stability theorems from algebraic K-theory.
More precisely, we show – this part is indeed essentially contained already in [Reference Kunyavskiĭ, Plotkin and VavilovKPV] – that for all non-symplectic Chevalley groups, bounded generation is reduced to that for
![]() $\mathrm {SL}(3,R)$
. What has been overlooked in [Reference Kunyavskiĭ, Plotkin and VavilovKPV], though, is that bounded generation of
$\mathrm {SL}(3,R)$
. What has been overlooked in [Reference Kunyavskiĭ, Plotkin and VavilovKPV], though, is that bounded generation of
![]() $\mathrm {Sp}(2l,R)$
,
$\mathrm {Sp}(2l,R)$
,
![]() $l\ge 3$
, also reduces to
$l\ge 3$
, also reduces to
![]() $\mathrm {SL}(3,R)$
, with the help of the symplectic lemmas on switching long and short roots [Reference Kunyavskiĭ, Plotkin and VavilovKPV]. Only after rediscovering this trick ourselves in March 2023, we noticed that a similar approach has been used by Kairat Zakiryanov [Reference ZakiryanovZa], and this reference should have been included in [Reference Kunyavskiĭ, Plotkin and VavilovKPV].
$\mathrm {SL}(3,R)$
, with the help of the symplectic lemmas on switching long and short roots [Reference Kunyavskiĭ, Plotkin and VavilovKPV]. Only after rediscovering this trick ourselves in March 2023, we noticed that a similar approach has been used by Kairat Zakiryanov [Reference ZakiryanovZa], and this reference should have been included in [Reference Kunyavskiĭ, Plotkin and VavilovKPV].
For the only remaining case
![]() $\mathrm {Sp}(4,R)$
, we can also obtain an explicit uniform bound by combining the arithmetic lemmas of Trost [Reference TrostTr2] with our
$\mathrm {Sp}(4,R)$
, we can also obtain an explicit uniform bound by combining the arithmetic lemmas of Trost [Reference TrostTr2] with our
![]() $\mathrm {Sp}_4$
-lemmas from [Reference Kunyavskiĭ, Plotkin and VavilovKPV], in exactly the same style as in [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Section 6], and that is by far the most difficult part of the proof. Namely, Trost’s Lemma 3.1 is essentially a generalization of our Lemma 6.4; we only have to supplement it slightly in characteristic 2. Trost’s Lemma 3.3 shows that – unlike for the number fields! – the case of a general function ring R is not much different from the case when R is a PID (and, in particular, there is no dependence on degree or other invariants).
$\mathrm {Sp}_4$
-lemmas from [Reference Kunyavskiĭ, Plotkin and VavilovKPV], in exactly the same style as in [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Section 6], and that is by far the most difficult part of the proof. Namely, Trost’s Lemma 3.1 is essentially a generalization of our Lemma 6.4; we only have to supplement it slightly in characteristic 2. Trost’s Lemma 3.3 shows that – unlike for the number fields! – the case of a general function ring R is not much different from the case when R is a PID (and, in particular, there is no dependence on degree or other invariants).
Note that in a more recent preprint, Trost established the uniformly bounded generation in the symplectic case (with weaker estimates); see [Reference TrostTr3, Corollary 3.11].
![]() $\bullet $
The number case is very different. Our general strategy is similar to the proof of [Reference TrostTr2, Theorem 4.1]. Namely, we use very deep arithmetic results of [Reference Morgan, Rapinchuk and SuryMRS] (or any of their improvements in [Reference Jordan and ZaytmanJZ, Reference Kunyavskiĭ, Morris and RapinchukKMR]) pertaining to
$\bullet $
The number case is very different. Our general strategy is similar to the proof of [Reference TrostTr2, Theorem 4.1]. Namely, we use very deep arithmetic results of [Reference Morgan, Rapinchuk and SuryMRS] (or any of their improvements in [Reference Jordan and ZaytmanJZ, Reference Kunyavskiĭ, Morris and RapinchukKMR]) pertaining to
![]() $\mathrm {SL}(2,R)$
to prove Theorem B asserting that there is an explicit uniform bound when
$\mathrm {SL}(2,R)$
to prove Theorem B asserting that there is an explicit uniform bound when
![]() $R^*$
is infinite. Some such bounds can be easily derived by a version of the Tavgen’s trick [Reference TavgenTa2, Theorem 1], as described and generalized in [Reference Vavilov, Smolensky and SuryVSS, Reference Smolensky, Sury and VavilovSSV] and [Reference Kunyavskiĭ, Plotkin and VavilovKPV].
$R^*$
is infinite. Some such bounds can be easily derived by a version of the Tavgen’s trick [Reference TavgenTa2, Theorem 1], as described and generalized in [Reference Vavilov, Smolensky and SuryVSS, Reference Smolensky, Sury and VavilovSSV] and [Reference Kunyavskiĭ, Plotkin and VavilovKPV].
We are left with the rings of integers of the imaginary quadratic fields K, and thus with a single degree
![]() $d=2$
. Since this class is contained in a class defined by the first-order conditions and sharing uniform estimates of the congruence kernel, using nonstandard models (alias ultrafilters, alias compactness theorem in the first-order logic, alias…), one can then prove the following: if all
$d=2$
. Since this class is contained in a class defined by the first-order conditions and sharing uniform estimates of the congruence kernel, using nonstandard models (alias ultrafilters, alias compactness theorem in the first-order logic, alias…), one can then prove the following: if all
![]() $\mathrm {SL}(3,R)$
are boundedly elementarily generated, they are uniformly boundedly elementarily generated. This argument was devised by Carter–Keller–Paige [Reference Carter, Keller and PaigeCKP] and then rephrased slightly differently by Morris [Reference MorrisMo] (see also the discussion in [Reference TrostTr1, Reference TrostTr2]).
$\mathrm {SL}(3,R)$
are boundedly elementarily generated, they are uniformly boundedly elementarily generated. This argument was devised by Carter–Keller–Paige [Reference Carter, Keller and PaigeCKP] and then rephrased slightly differently by Morris [Reference MorrisMo] (see also the discussion in [Reference TrostTr1, Reference TrostTr2]).
Since all other cases, except
![]() $\mathrm {Sp}(4,R)$
, are reduced to
$\mathrm {Sp}(4,R)$
, are reduced to
![]() $\mathrm {SL}(3,R)$
by the standard tricks collected in [Reference Kunyavskiĭ, Plotkin and VavilovKPV], we are again left with
$\mathrm {SL}(3,R)$
by the standard tricks collected in [Reference Kunyavskiĭ, Plotkin and VavilovKPV], we are again left with
![]() $\mathrm {Sp}(4,R)$
alone. Of course, in the number case, the bound given for
$\mathrm {Sp}(4,R)$
alone. Of course, in the number case, the bound given for
![]() $\mathrm {Sp}(4,R)$
by Tavgen [Reference TavgenTa2] is not uniform; it depends on the degree and the discriminant of the number field K. However, since
$\mathrm {Sp}(4,R)$
by Tavgen [Reference TavgenTa2] is not uniform; it depends on the degree and the discriminant of the number field K. However, since
![]() $\mathrm {Sp}(4,R)$
and its elementary generators are described by first order relations, we can again use exactly the same argument of [Reference Carter, Keller and PaigeCKP, Reference MorrisMo] to conclude that there exists an absolute constant as an upper bound for the width of all
$\mathrm {Sp}(4,R)$
and its elementary generators are described by first order relations, we can again use exactly the same argument of [Reference Carter, Keller and PaigeCKP, Reference MorrisMo] to conclude that there exists an absolute constant as an upper bound for the width of all
![]() $\mathrm {Sp}(4,R)$
, where R is the ring of integers of an imaginary quadratic number field. Of course, now we know only that some such constant exists; it is by no means explicit.
$\mathrm {Sp}(4,R)$
, where R is the ring of integers of an imaginary quadratic number field. Of course, now we know only that some such constant exists; it is by no means explicit.
Remark 0.5 As the reader may have noticed, there is a significant overlap between our research and the recent works of Alexander Trost. Below, for the reader’s convenience, following the referee’s suggestion, we present a brief summary of the main common points. Some more detailed explanations can be found in the relevant parts of the paper.
![]() $\bullet $
In the number field case, our general strategy is based on focusing on the case of imaginary quadratic fields. This approach, in the setup of elementary bounded generation problems, was first applied by Trost; see [Reference TrostTr2, Theorem 4.1].Footnote
3
$\bullet $
In the number field case, our general strategy is based on focusing on the case of imaginary quadratic fields. This approach, in the setup of elementary bounded generation problems, was first applied by Trost; see [Reference TrostTr2, Theorem 4.1].Footnote
3
![]() $\bullet $
Arithmetical lemmas, indispensable for the proofs, can be viewed as variations on the Carter–Keller theme; see [Reference Carter and KellerCK1]. All such variations use some generalized form of Dirichlet’s theorem on primes in an arithmetic progression (see [Reference Bass, Milnor and SerreBMS]) along with certain specific arguments (see, for example, [Reference Morgan, Rapinchuk and SuryMRS]). In the present paper, our main arithmetic tools in the function field case are Trost’s Lemmas 3.1 and 3.3 from [Reference TrostTr2]. Lemma 3.1 provides an explicit procedure for extracting
$\bullet $
Arithmetical lemmas, indispensable for the proofs, can be viewed as variations on the Carter–Keller theme; see [Reference Carter and KellerCK1]. All such variations use some generalized form of Dirichlet’s theorem on primes in an arithmetic progression (see [Reference Bass, Milnor and SerreBMS]) along with certain specific arguments (see, for example, [Reference Morgan, Rapinchuk and SuryMRS]). In the present paper, our main arithmetic tools in the function field case are Trost’s Lemmas 3.1 and 3.3 from [Reference TrostTr2]. Lemma 3.1 provides an explicit procedure for extracting
![]() $(q-1)^{\mathrm {th}}$
roots of Mennicke symbols, generalizing the main content of our Lemma 6.4 from [Reference Kunyavskiĭ, Plotkin and VavilovKPV]. The latter lemma also contains a treatment of square roots of Mennicke symbols requiring a separate argument in characteristic 2. This is used in the present paper and in the proof of Claim 3 in [Reference TrostTr3].
$(q-1)^{\mathrm {th}}$
roots of Mennicke symbols, generalizing the main content of our Lemma 6.4 from [Reference Kunyavskiĭ, Plotkin and VavilovKPV]. The latter lemma also contains a treatment of square roots of Mennicke symbols requiring a separate argument in characteristic 2. This is used in the present paper and in the proof of Claim 3 in [Reference TrostTr3].
![]() $\bullet $
Uniform bounds for the symplectic groups in the function field case were obtained by Trost in [Reference TrostTr3, Corollary 3.11], generalizing our earlier results in [Reference Kunyavskiĭ, Plotkin and VavilovKPV]. In the present paper, we achieve better constants with the help of the swindling method.
$\bullet $
Uniform bounds for the symplectic groups in the function field case were obtained by Trost in [Reference TrostTr3, Corollary 3.11], generalizing our earlier results in [Reference Kunyavskiĭ, Plotkin and VavilovKPV]. In the present paper, we achieve better constants with the help of the swindling method.
![]() $\bullet $
Our proof of the uniform boundedness of
$\bullet $
Our proof of the uniform boundedness of
![]() $\mathrm {Sp}_4$
in the number case, given in Section 8 of the present paper, and Trost’s proof in [Reference TrostTr1] are essentially of the same model-theoretic nature, as the prototypical proof for
$\mathrm {Sp}_4$
in the number case, given in Section 8 of the present paper, and Trost’s proof in [Reference TrostTr1] are essentially of the same model-theoretic nature, as the prototypical proof for
![]() $\mathrm {SL}_n$
of Carter–Keller–Paige (and Morris). More precisely, Trost’s arguments, based on a quite technical Theorem 3.16 from [Reference TrostTr1], use the compactness theorem of the first-order logic, whereas ours employ nonstandard models.
$\mathrm {SL}_n$
of Carter–Keller–Paige (and Morris). More precisely, Trost’s arguments, based on a quite technical Theorem 3.16 from [Reference TrostTr1], use the compactness theorem of the first-order logic, whereas ours employ nonstandard models.
The paper is organized as follows. In Section 1, we recall notation and collect some preliminary results. In Section 2, we recall some important arithmetic lemmas. In Section 3, we prove Theorem B and also the cases of Theorem A corresponding to the simply laced root systems
![]() $\Phi $
and
$\Phi $
and
![]() $\Phi =\mathsf F_4$
(we collect these cases in Theorem C). Section 4 deals with surjective stability of K
$\Phi =\mathsf F_4$
(we collect these cases in Theorem C). Section 4 deals with surjective stability of K
![]() $_1$
-functor and consequences. In Section 5, we prove a swindling lemma for the groups
$_1$
-functor and consequences. In Section 5, we prove a swindling lemma for the groups
![]() $\mathrm {SL}(3,R)$
and
$\mathrm {SL}(3,R)$
and
![]() $\mathrm {Sp}(4,R)$
. In Section 6 and 7, we establish new bounds for the width of
$\mathrm {Sp}(4,R)$
. In Section 6 and 7, we establish new bounds for the width of
![]() $\mathrm {SL}(3,R)$
and
$\mathrm {SL}(3,R)$
and
![]() $\mathrm {Sp}(4,R)$
in the function case. Section 8 is devoted to
$\mathrm {Sp}(4,R)$
in the function case. Section 8 is devoted to
![]() $\mathrm {Sp}(4,R)$
in the number case. Finally, Section 9 contains some concluding remarks and open problems.
$\mathrm {Sp}(4,R)$
in the number case. Finally, Section 9 contains some concluding remarks and open problems.
1 Notation and preliminaries
In this section, we briefly recall the notation, mainly taken from [Reference Kunyavskiĭ, Lavrenov, Plotkin and VavilovKLPV], that will be used throughout the paper and some background facts. For more details on Chevalley groups over rings, see [Reference VavilovVa1] or [Reference Vavilov and PlotkinVP], where one can find many further references.
1.1 Chevalley groups
Given a reduced root system
![]() $\Phi $
(usually assumed irreducible), we denote by
$\Phi $
(usually assumed irreducible), we denote by
![]() $\Phi ^+$
,
$\Phi ^+$
,
![]() $\Phi ^{-}$
, and
$\Phi ^{-}$
, and
![]() $\Pi =\big \{\alpha _1,\ldots ,\alpha _l\big \}$
the sets of positive, negative, and fundamental roots with respect to a chosen order. Throughout, we denote
$\Pi =\big \{\alpha _1,\ldots ,\alpha _l\big \}$
the sets of positive, negative, and fundamental roots with respect to a chosen order. Throughout, we denote
![]() $N=|\Phi ^+|$
.
$N=|\Phi ^+|$
.
For a lattice
![]() ${\mathcal P}$
intermediate between the root lattice
${\mathcal P}$
intermediate between the root lattice
![]() ${\mathcal Q}(\Phi )$
and the weight lattice
${\mathcal Q}(\Phi )$
and the weight lattice
![]() ${\mathcal P}(\Phi )$
and any commutative unital ring R with the multiplicative group
${\mathcal P}(\Phi )$
and any commutative unital ring R with the multiplicative group
![]() $R^*$
, we denote by
$R^*$
, we denote by
![]() $G=G_{{\mathcal P}}(\Phi ,R)$
the Chevalley group of type
$G=G_{{\mathcal P}}(\Phi ,R)$
the Chevalley group of type
![]() $(\Phi ,{\mathcal P})$
over R. In the case
$(\Phi ,{\mathcal P})$
over R. In the case
![]() ${\mathcal P}={\mathcal P}(\Phi )$
, the group G is called simply connected and is denoted by
${\mathcal P}={\mathcal P}(\Phi )$
, the group G is called simply connected and is denoted by
![]() $G_{\mathrm {sc}}(\Phi ,R)$
. In another extreme case
$G_{\mathrm {sc}}(\Phi ,R)$
. In another extreme case
![]() ${\mathcal P}={\mathcal Q}(\Phi )$
, the group G is called adjoint and is denoted by
${\mathcal P}={\mathcal Q}(\Phi )$
, the group G is called adjoint and is denoted by
![]() $G_{\mathrm {ad}}(\Phi ,R)$
.
$G_{\mathrm {ad}}(\Phi ,R)$
.
Many results do not depend on the lattice
![]() ${\mathcal P}$
, and we often omit any reference to
${\mathcal P}$
, and we often omit any reference to
![]() ${\mathcal P}$
in the notation and denote by
${\mathcal P}$
in the notation and denote by
![]() $G(\Phi ,R)$
any Chevalley group of type
$G(\Phi ,R)$
any Chevalley group of type
![]() $\Phi $
over R. Usually, by default, we assume that
$\Phi $
over R. Usually, by default, we assume that
![]() $G(\Phi ,R)$
is simply connected, but in some cases, it is convenient to work with the adjoint group, which is then reflected in the notation.
$G(\Phi ,R)$
is simply connected, but in some cases, it is convenient to work with the adjoint group, which is then reflected in the notation.
Fixing a split maximal torus
![]() $T=T(\Phi ,R)$
in
$T=T(\Phi ,R)$
in
![]() $G=G(\Phi ,R)$
and identifying
$G=G(\Phi ,R)$
and identifying
![]() $\Phi $
with
$\Phi $
with
![]() $\Phi (G,T)$
, we denote by
$\Phi (G,T)$
, we denote by
![]() $X_{\alpha }$
,
$X_{\alpha }$
,
![]() $\alpha \in \Phi $
, the unipotent root subgroups in G, elementary with respect to T. We fix maps
$\alpha \in \Phi $
, the unipotent root subgroups in G, elementary with respect to T. We fix maps
![]() $x_{\alpha }\colon R\mapsto X_{\alpha }$
, so that
$x_{\alpha }\colon R\mapsto X_{\alpha }$
, so that
![]() $X_{\alpha }=\{x_{\alpha }(\xi )\mid \xi \in R\}$
, and require that these parametrizations are interrelated by the Chevalley commutator formula with integer coefficients; see [Reference CarterCa], [Reference SteinbergSteinb]. The above unipotent elements
$X_{\alpha }=\{x_{\alpha }(\xi )\mid \xi \in R\}$
, and require that these parametrizations are interrelated by the Chevalley commutator formula with integer coefficients; see [Reference CarterCa], [Reference SteinbergSteinb]. The above unipotent elements
![]() $x_{\alpha }(\xi )$
, where
$x_{\alpha }(\xi )$
, where
![]() ${\alpha \in \Phi} $
,
${\alpha \in \Phi} $
,
![]() $\xi \in R$
, elementary with respect to
$\xi \in R$
, elementary with respect to
![]() $T(\Phi ,R)$
, are also called [elementary] unipotent root elements or, for short, simply root unipotents.
$T(\Phi ,R)$
, are also called [elementary] unipotent root elements or, for short, simply root unipotents.
Further,
denotes the absolute elementary subgroup of
![]() $G(\Phi ,R)$
, spanned by all elementary root unipotents, or, what is the same, by all [elementary] root subgroups
$G(\Phi ,R)$
, spanned by all elementary root unipotents, or, what is the same, by all [elementary] root subgroups
![]() $X_{\alpha }$
,
$X_{\alpha }$
,
![]() $\alpha \in \Phi $
. For
$\alpha \in \Phi $
. For
![]() $\epsilon \in \{+,-\}$
, denote
$\epsilon \in \{+,-\}$
, denote
1.2 Relative groups
Let
![]() ${\mathfrak q}\unlhd R$
be an ideal of R, and let
${\mathfrak q}\unlhd R$
be an ideal of R, and let
![]() $\rho _{\mathfrak q}\colon R\longrightarrow R/{\mathfrak q}$
be the reduction modulo
$\rho _{\mathfrak q}\colon R\longrightarrow R/{\mathfrak q}$
be the reduction modulo
![]() ${\mathfrak q}$
. By functoriality, it defines the reduction homomorphism of Chevalley groups
${\mathfrak q}$
. By functoriality, it defines the reduction homomorphism of Chevalley groups
![]() $\rho _{\mathfrak q}\colon G(\Phi ,R)\longrightarrow G(\Phi ,R/{\mathfrak q})$
. The kernel of
$\rho _{\mathfrak q}\colon G(\Phi ,R)\longrightarrow G(\Phi ,R/{\mathfrak q})$
. The kernel of
![]() $\rho _{\mathfrak q}$
is denoted by
$\rho _{\mathfrak q}$
is denoted by
![]() $G(\Phi ,R,{\mathfrak q})$
and is called the principal congruence subgroup of
$G(\Phi ,R,{\mathfrak q})$
and is called the principal congruence subgroup of
![]() $G(\Phi ,R)$
of level
$G(\Phi ,R)$
of level
![]() ${\mathfrak q}$
. We denote by
${\mathfrak q}$
. We denote by
![]() $X_{\alpha }({\mathfrak q})$
the intersection of
$X_{\alpha }({\mathfrak q})$
the intersection of
![]() $X_{\alpha }$
with the principal congruence subgroup
$X_{\alpha }$
with the principal congruence subgroup
![]() $G(\Phi ,R,{\mathfrak q})$
. Clearly,
$G(\Phi ,R,{\mathfrak q})$
. Clearly,
![]() $X_{\alpha }({\mathfrak q})$
consists of all elementary root elements
$X_{\alpha }({\mathfrak q})$
consists of all elementary root elements
![]() $x_{\alpha }(\xi )$
,
$x_{\alpha }(\xi )$
,
![]() $\alpha \in \Phi $
,
$\alpha \in \Phi $
,
![]() $\xi \in {\mathfrak q}$
, of level
$\xi \in {\mathfrak q}$
, of level
![]() ${\mathfrak q}$
:
${\mathfrak q}$
:
By definition,
![]() $E(\Phi ,{\mathfrak q})$
is generated by
$E(\Phi ,{\mathfrak q})$
is generated by
![]() $X_{\alpha }({\mathfrak q})$
, for all roots
$X_{\alpha }({\mathfrak q})$
, for all roots
![]() $\alpha \in \Phi $
. The same subgroups generate
$\alpha \in \Phi $
. The same subgroups generate
![]() $E(\Phi ,R,{\mathfrak q})$
as a normal subgroup of the absolute elementary group
$E(\Phi ,R,{\mathfrak q})$
as a normal subgroup of the absolute elementary group
![]() $E(\Phi ,R)$
.
$E(\Phi ,R)$
.
The classical Suslin–Kopeiko–Taddei theorem asserts that for
![]() $\mathrm {rk}(\Phi )\ge 2$
, one has
$\mathrm {rk}(\Phi )\ge 2$
, one has
![]() $E(\Phi ,R,{\mathfrak q})\unlhd G(\Phi ,R)$
. The quotient
$E(\Phi ,R,{\mathfrak q})\unlhd G(\Phi ,R)$
. The quotient
is called the [relative] K
![]() $_1$
-functor. The absolute case corresponds to
$_1$
-functor. The absolute case corresponds to
![]() ${\mathfrak q}=R$
,
${\mathfrak q}=R$
,
Observe
so that our K
![]() $_1$
-functor corresponds rather to the
$_1$
-functor corresponds rather to the
![]() $\mathrm {SK}_1$
of the classical theory.
$\mathrm {SK}_1$
of the classical theory.
1.3 Arithmetic case
For a global field K and a finite nonempty set S of places of K (containing all archimedean places when K is a number field), let
It is a Dedekind domain whose maximal ideals can be canonically identified with the places outside S. Following [Reference Bass, Milnor and SerreBMS], we say that R is the Dedekind ring of arithmetic type defined by the set S (or, for short, an arithmetic ring).
For the arithmetic rings Bass, Milnor, and Serre [Reference Bass, Milnor and SerreBMS] have explicitly calculated
![]() $K_1(\Phi ,R,{\mathfrak q})$
,
$K_1(\Phi ,R,{\mathfrak q})$
,
![]() $\Phi =\mathsf A_l,\mathsf C_l$
,
$\Phi =\mathsf A_l,\mathsf C_l$
,
![]() $l\ge 2$
, in terms of Mennicke symbols. Namely, they have proven that
$l\ge 2$
, in terms of Mennicke symbols. Namely, they have proven that
![]() ${\mathrm K}_1(\mathsf A_l,R,{\mathfrak q})\cong C({\mathfrak q})$
and
${\mathrm K}_1(\mathsf A_l,R,{\mathfrak q})\cong C({\mathfrak q})$
and
![]() ${\mathrm K}_1(\mathsf C_l,R,{\mathfrak q})\cong \mathrm {Cp}({\mathfrak q})$
(the universal Mennicke groups), which in turn are then identified via reciprocity laws with certain groups of roots of 1 in R.
${\mathrm K}_1(\mathsf C_l,R,{\mathfrak q})\cong \mathrm {Cp}({\mathfrak q})$
(the universal Mennicke groups), which in turn are then identified via reciprocity laws with certain groups of roots of 1 in R.
The [almost] positive solution of the congruence subgroup problem for these groups amounts to the fact that the congruence kernel
taken over all nonzero ideals
![]() ${\mathfrak q}\unlhd R$
is finite. Actually, it is trivial, apart from the case when R is the ring of integers
${\mathfrak q}\unlhd R$
is finite. Actually, it is trivial, apart from the case when R is the ring of integers
![]() $\mathcal O_K$
in a purely imaginary number field K, when
$\mathcal O_K$
in a purely imaginary number field K, when
![]() $C(G)\cong \mu (K)$
is the group of all roots of 1 in K.
$C(G)\cong \mu (K)$
is the group of all roots of 1 in K.
Later, their results were generalized to all Chevalley groups by Hideya Matsumoto [Reference MatsumotoMa]. The following special case of his results [Reference MatsumotoMa, Théorème 12.7] explains why we usually prefer to work with simply connected groups.
Lemma 1.1 Let R be a Dedekind ring of arithmetic type and
![]() $\Phi $
a reduced irreducible root system of rank at least
$\Phi $
a reduced irreducible root system of rank at least
![]() $2$
. Then
$2$
. Then
2 Supporting statements
2.1 Reduction to the ring of integers
The following result is a combination of [Reference Bass, Milnor and SerreBMS, Lemma 2.1] and [Reference Bass, Milnor and SerreBMS, Lemma 5.3]. The same proof, with several successful deteriorations, is reproduced on page 685 of [Reference Carter and KellerCK1].
Lemma 2.1 Let R be a Dedekind ring,
![]() $s\in R$
,
$s\in R$
,
![]() $s\neq 0$
. Then
$s\neq 0$
. Then
In other words, every
![]() $2\times 2$
matrix with entries in
$2\times 2$
matrix with entries in
![]() $R\big [{\frac 1s}\big ]$
can be reduced to a matrix with entries in R by
$R\big [{\frac 1s}\big ]$
can be reduced to a matrix with entries in R by
![]() $\le 3$
elementary moves with parameters in
$\le 3$
elementary moves with parameters in
![]() $R\big [{\frac 1s}\big ]$
. Since the number of elementary moves during the rank reduction does not depend on the ring R, and the only such dependence occurs at the base of induction, we immediately get the following corollary.
$R\big [{\frac 1s}\big ]$
. Since the number of elementary moves during the rank reduction does not depend on the ring R, and the only such dependence occurs at the base of induction, we immediately get the following corollary.
Lemma 2.2 Let R be a Dedekind ring such that any element of
![]() $\mathrm {G_{sc}}(\Phi ,\,R)$
is a product of L elementary root unipotents. Then for any
$\mathrm {G_{sc}}(\Phi ,\,R)$
is a product of L elementary root unipotents. Then for any
![]() $s\in R$
,
$s\in R$
,
![]() $s\neq 0$
, any element of
$s\neq 0$
, any element of
![]() $\mathrm {G_{sc}}(\Phi ,\,R\big [{\frac 1s}\big ])$
is a product of at most
$\mathrm {G_{sc}}(\Phi ,\,R\big [{\frac 1s}\big ])$
is a product of at most
![]() $L+3$
elementary root unipotents.
$L+3$
elementary root unipotents.
2.2 Arithmetic lemmas
The following lemma is the arithmetic heart of the whole proof. In the number case, it is [Reference Carter and KellerCK1, Lemma 1], and in the function case, it was first proven in full generality in [Reference TrostTr2, Lemma 3.1] (before that, only a special case
![]() $R={\mathbb F}_{\!q}[t]$
was established as [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Lemma 6.4]).
$R={\mathbb F}_{\!q}[t]$
was established as [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Lemma 6.4]).
Lemma 2.3 Let
![]() $\mathcal O_K$
be the ring of integers of a global field K, and let
$\mathcal O_K$
be the ring of integers of a global field K, and let
![]() $x\in \mathrm {SL}(2,\mathcal O_K)$
. Let m be the number of roots of
$x\in \mathrm {SL}(2,\mathcal O_K)$
. Let m be the number of roots of
![]() $1$
in K in the number case, respectively
$1$
in K in the number case, respectively
![]() $m=q-1$
, where
$m=q-1$
, where
![]() ${\mathbb F}_{\!q}$
is the field of constants of K in the function case. Then for any matrix
${\mathbb F}_{\!q}$
is the field of constants of K in the function case. Then for any matrix
![]() $A\in \mathrm {SL}(2,\mathcal O_K)$
, there exist nonzero elements
$A\in \mathrm {SL}(2,\mathcal O_K)$
, there exist nonzero elements
![]() $a,b\in \mathcal O_K$
with the following properties:
$a,b\in \mathcal O_K$
with the following properties:
![]() $\bullet $
$\bullet $
![]() $b\mathcal O_K$
is a prime ideal, and, moreover, in the number case,
$b\mathcal O_K$
is a prime ideal, and, moreover, in the number case,
![]() $b\mathcal O_K$
is unramified in
$b\mathcal O_K$
is unramified in
![]() $K/\mathbb Q$
and does not contain m.
$K/\mathbb Q$
and does not contain m.
![]() $\bullet $
A can be transformed to a matrix with the first row
$\bullet $
A can be transformed to a matrix with the first row
![]() $(a^m,b)$
by means of not more than
$(a^m,b)$
by means of not more than
![]() $4$
elementary moves in the number case, or
$4$
elementary moves in the number case, or
![]() $3$
elementary moves in the function case.
$3$
elementary moves in the function case.
Remark 2.4 In the function case, in addition to Lemma 2.3, we shall need its version with
![]() $m=2$
to be able to extract square roots of Mennicke symbols. If q is odd, such a version follows automatically because we then have
$m=2$
to be able to extract square roots of Mennicke symbols. If q is odd, such a version follows automatically because we then have
![]() $a^{q-1}=(a^{(q-1)/2)})^2.$
If q is even, to adjust the proof of Lemma 2.3 to the case
$a^{q-1}=(a^{(q-1)/2)})^2.$
If q is even, to adjust the proof of Lemma 2.3 to the case
![]() $m=2$
, an additional argument is needed. Similar to Trost’s proof of [Reference TrostTr3, Claim 3], we apply our argument from the end of the proof of [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Lemma 6.4]. Namely, if K is a global function field of characteristic 2 and
$m=2$
, an additional argument is needed. Similar to Trost’s proof of [Reference TrostTr3, Claim 3], we apply our argument from the end of the proof of [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Lemma 6.4]. Namely, if K is a global function field of characteristic 2 and
![]() $f\in \mathcal O_K$
is such that the principal ideal
$f\in \mathcal O_K$
is such that the principal ideal
![]() $f\mathcal O_K$
is prime, any
$f\mathcal O_K$
is prime, any
![]() $g\in \mathcal O_K$
is a square modulo
$g\in \mathcal O_K$
is a square modulo
![]() $f\mathcal O_K$
because its image
$f\mathcal O_K$
because its image
![]() $\bar g$
in the residue field
$\bar g$
in the residue field
![]() $\mathcal O_K/(f)$
of characteristic 2 is a square, as any other element of a finite field of characteristic 2. This makes the argument significantly shorter: one only has to take care of the primality of the ideals
$\mathcal O_K/(f)$
of characteristic 2 is a square, as any other element of a finite field of characteristic 2. This makes the argument significantly shorter: one only has to take care of the primality of the ideals
![]() $a_2\mathcal O$
and
$a_2\mathcal O$
and
![]() $b_2\mathcal O$
(in the notation of [Reference TrostTr2, Lemma 3.1]), which is achieved by applying the Dirichlet theorem.
$b_2\mathcal O$
(in the notation of [Reference TrostTr2, Lemma 3.1]), which is achieved by applying the Dirichlet theorem.
For a global function field K with the field of constants
![]() ${\mathbb F}_{\!q}$
and
${\mathbb F}_{\!q}$
and
![]() $b\in \mathcal O_K$
,
$b\in \mathcal O_K$
,
![]() $b\neq 0$
, we denote by
$b\neq 0$
, we denote by
![]() $\epsilon (b)$
the exponent of the [finite] multiplicative group
$\epsilon (b)$
the exponent of the [finite] multiplicative group
![]() $(\mathcal O_K/b\mathcal O_K)^*$
and set
$(\mathcal O_K/b\mathcal O_K)^*$
and set
![]() $\delta (b)=\varepsilon (b)/(q-1)$
. The following result is due to Trost [Reference TrostTr2, Lemma 3.3].
$\delta (b)=\varepsilon (b)/(q-1)$
. The following result is due to Trost [Reference TrostTr2, Lemma 3.3].
Lemma 2.5 Let K be a global function field with the field of constants
![]() ${\mathbb F}_{\!q}$
,
${\mathbb F}_{\!q}$
,
![]() $a,b\in {\mathcal O}_K\setminus \{0\}$
, such that
$a,b\in {\mathcal O}_K\setminus \{0\}$
, such that
![]() $b{\mathcal O}_K$
is prime and a and b are comaximal,
$b{\mathcal O}_K$
is prime and a and b are comaximal,
![]() $a{\mathcal O}_K+b{\mathcal O}_K={\mathcal O}_K$
. Then for every unit
$a{\mathcal O}_K+b{\mathcal O}_K={\mathcal O}_K$
. Then for every unit
![]() $u\in {\mathcal O}_K^*$
, there exists
$u\in {\mathcal O}_K^*$
, there exists
![]() $c\in {\mathcal O}_K$
such that
$c\in {\mathcal O}_K$
such that
![]() $\bullet $
$\bullet $
![]() $bc\equiv u\ \ \pmod a$
,
$bc\equiv u\ \ \pmod a$
,
![]() $\bullet $
$\bullet $
![]() $\delta (b)$
and
$\delta (b)$
and
![]() $\delta (c)$
are coprime.
$\delta (c)$
are coprime.
3 Tavgen rank reduction theorem and applications
3.1 Tavgen rank reduction theorem
In this section, we prove Theorem B and establish some other useful consequences of Tavgen’s reduction theorem.
The following trick allowing one to reduce the rank of a root system under consideration was invented by Tavgen [Reference TavgenTa2] (and then generalized in [Reference Vavilov, Smolensky and SuryVSS] and [Reference Smolensky, Sury and VavilovSSV]). The following final form is proven in [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Theorem 4.2].
Lemma 3.1 Let
![]() $\Phi $
be a reduced irreducible root system of rank
$\Phi $
be a reduced irreducible root system of rank
![]() $l\geq 2$
, and R be a commutative ring. Let
$l\geq 2$
, and R be a commutative ring. Let
![]() $\Delta _1,\ldots ,\Delta _t$
be some subsystems of
$\Delta _1,\ldots ,\Delta _t$
be some subsystems of
![]() $\Phi $
, whose union contains all fundamental roots of
$\Phi $
, whose union contains all fundamental roots of
![]() $\Phi $
. Suppose that for all
$\Phi $
. Suppose that for all
![]() $\Delta _i$
, the elementary Chevalley group
$\Delta _i$
, the elementary Chevalley group
![]() $\mathrm {E_{sc}}(\Delta _i,\,R)$
admits a unitriangular factorization
$\mathrm {E_{sc}}(\Delta _i,\,R)$
admits a unitriangular factorization
of length N (not depending on i). Then the elementary group
![]() $\mathrm {E_{sc}}(\Phi ,\,R)$
itself admits unitriangular factorization
$\mathrm {E_{sc}}(\Phi ,\,R)$
itself admits unitriangular factorization
of the same length N.
It is used below in two cases, when all
![]() $\Delta _i$
’s are
$\Delta _i$
’s are
![]() $\mathsf {A}_1$
, and when all of them are
$\mathsf {A}_1$
, and when all of them are
![]() $\mathsf {A}_2$
.
$\mathsf {A}_2$
.
3.2 The case when
 $R^*$
is infinite
$R^*$
is infinite
The case where a Dedekind ring R of arithmetic type has infinitely many units is now completely solved, with very small absolute constant. Here is a brief account of main steps along this route. Vsemirnov [Reference VsemirnovVs] established a first unconditional result of this sort, not depending on the GRH; Morgan, Rapinchuk, and Sury [Reference Morgan, Rapinchuk and SuryMRS] proved that
![]() $\mathrm {SL}(2,R)$
is boundedly elementarily generated in number case for an arbitrary R with infinite
$\mathrm {SL}(2,R)$
is boundedly elementarily generated in number case for an arbitrary R with infinite
![]() $R^{\ast }$
. The absolute bound obtained in their paper is
$R^{\ast }$
. The absolute bound obtained in their paper is
![]() $L=9$
.
$L=9$
.
In the paper presently under way, the first author, Morris, and Rapinchuk [Reference Kunyavskiĭ, Morris and RapinchukKMR] improved the bound to
![]() $L=7$
in the number case (which we believe is the best possible and cannot be further improved, in general). A similar result holds in the function case, with the bound
$L=7$
in the number case (which we believe is the best possible and cannot be further improved, in general). A similar result holds in the function case, with the bound
![]() $L=8$
(which, we believe, can be further improved to
$L=8$
(which, we believe, can be further improved to
![]() $L=7$
).
$L=7$
).
Lemma 3.2 [Reference Kunyavskiĭ, Morris and RapinchukKMR]
For any Dedekind ring of arithmetic type R with the infinite multiplicative group
![]() $R^*$
, any element in
$R^*$
, any element in
![]() $\mathrm {SL}(2,R)$
is a product of at most
$\mathrm {SL}(2,R)$
is a product of at most
![]() $7$
elementary transvections in the number case or at most
$7$
elementary transvections in the number case or at most
![]() $8$
elementary transvections in the function case.
$8$
elementary transvections in the function case.
Together with Lemma 3.1, this immediately implies Theorem B: it covers the case
![]() $\Delta =\mathsf A_1$
, and all higher rank cases are reduced to rank one by putting
$\Delta =\mathsf A_1$
, and all higher rank cases are reduced to rank one by putting
![]() $\Delta _i=\mathsf A_1$
in Lemma 3.1.
$\Delta _i=\mathsf A_1$
in Lemma 3.1.
Thus, the condition
![]() $|R^*|=\infty $
makes a huge relief. Essentially, no extra work is needed to treat the general case with not the best possible but still rather plausible bounds (anyway, asymptotically, L cannot be smaller than something like
$|R^*|=\infty $
makes a huge relief. Essentially, no extra work is needed to treat the general case with not the best possible but still rather plausible bounds (anyway, asymptotically, L cannot be smaller than something like
![]() $3N$
to
$3N$
to
![]() $4N$
).
$4N$
).
So, if we are not interested in actual bounds, but just in uniform boundedness, the rest of the exposition is formally dedicated to the Dedekind rings of arithmetic type with finite multiplicative groups. Thus, in the number case, we restrict our attention to the rings of integers in imaginary quadratic number fields (since
![]() $\mathbb Z$
is already covered). In the function case, as discovered by Trost [Reference TrostTr2], for ranks
$\mathbb Z$
is already covered). In the function case, as discovered by Trost [Reference TrostTr2], for ranks
![]() $\ge 2$
, we do not have to distinguish between rings with finite and infinite multiplicative group, so that the rest of this section does not depend on [Reference Kunyavskiĭ, Morris and RapinchukKMR] (but does depend on [Reference Morgan, Rapinchuk and SuryMRS]).
$\ge 2$
, we do not have to distinguish between rings with finite and infinite multiplicative group, so that the rest of this section does not depend on [Reference Kunyavskiĭ, Morris and RapinchukKMR] (but does depend on [Reference Morgan, Rapinchuk and SuryMRS]).
3.3 The simply laced case and
 $\Phi =\mathsf F_4$
$\Phi =\mathsf F_4$
In this section, we prove the statement of Theorem A for the simply laced root systems and also for
![]() $\Phi =\mathsf F_4$
.
$\Phi =\mathsf F_4$
.
By a theorem of Carter–Keller–Paige (see [Reference Carter, Keller and PaigeCKP], (2.4)) (rewritten and explained by Morris [Reference MorrisMo]), bounded generation for groups of type
![]() $\mathsf A_{l}$
,
$\mathsf A_{l}$
,
![]() $l\ge 2$
, holds for all Dedekind rings R in number fields K, with a bound depending on l and also on the degree d of K. But since for all degrees
$l\ge 2$
, holds for all Dedekind rings R in number fields K, with a bound depending on l and also on the degree d of K. But since for all degrees
![]() $d\ge 3$
the existence of uniform bound already follows from Theorem B, we only need to take maximum of that, and the universal bound for
$d\ge 3$
the existence of uniform bound already follows from Theorem B, we only need to take maximum of that, and the universal bound for
![]() $d=2$
.
$d=2$
.
Combining this result with the subsequent work of Trost [Reference TrostTr2] on the function field case, one obtains the following result; see [Reference TrostTr2, Theorem 4.1].
Lemma 3.3 [Reference TrostTr2]
For each
![]() $l\ge 2$
, there exists a constant
$l\ge 2$
, there exists a constant
![]() $L=L(l)\in \mathbb N$
such that for any Dedekind ring of arithmetic type R, any element in
$L=L(l)\in \mathbb N$
such that for any Dedekind ring of arithmetic type R, any element in
![]() $\mathrm {G}_{\mathrm {sc}}(\mathsf A_{l},\,R)$
is a product of at most L elementary root unipotents.
$\mathrm {G}_{\mathrm {sc}}(\mathsf A_{l},\,R)$
is a product of at most L elementary root unipotents.
In fact, in the sequel, we only need the special case of the above result pertaining to
![]() $\mathrm {SL}(3,R)$
, which corresponds to
$\mathrm {SL}(3,R)$
, which corresponds to
![]() $\mathsf A_2$
. Indeed, by stability arguments, one has
$\mathsf A_2$
. Indeed, by stability arguments, one has
![]() $L(l)\le L(l-1)+3l+1$
for all
$L(l)\le L(l-1)+3l+1$
for all
![]() $l\ge 2$
, so that all
$l\ge 2$
, so that all
![]() $L(l)$
,
$L(l)$
,
![]() $l\ge 3$
can be expressed in terms of the constant
$l\ge 3$
can be expressed in terms of the constant
![]() $L(2)$
. In the function case, Trost [Reference TrostTr2] gave the estimate
$L(2)$
. In the function case, Trost [Reference TrostTr2] gave the estimate
![]() $L(2)\le 65$
. No such explicit estimate is available in the number case because the uniform boundedness was established by model-theoretic arguments.
$L(2)\le 65$
. No such explicit estimate is available in the number case because the uniform boundedness was established by model-theoretic arguments.
Now we are in a position to get a particular case of Theorem A.
Theorem C Let
![]() $\Phi $
be simply laced of rank
$\Phi $
be simply laced of rank
![]() $\ge 2$
or
$\ge 2$
or
![]() $\Phi =\mathsf F_4$
, and R be any Dedekind ring of arithmetic type. Then
$\Phi =\mathsf F_4$
, and R be any Dedekind ring of arithmetic type. Then
![]() $G_{\mathrm {sc}}(\Phi ,R)$
is a product of at most
$G_{\mathrm {sc}}(\Phi ,R)$
is a product of at most
![]() $L=L(2)N$
elementary unipotents.
$L=L(2)N$
elementary unipotents.
Proof Since the fundamental root systems of the simply laced systems and
![]() $\operatorname {\mathrm {\mathsf {F}}}_4$
are covered by copies of
$\operatorname {\mathrm {\mathsf {F}}}_4$
are covered by copies of
![]() $\mathsf {A}_2$
, one can take
$\mathsf {A}_2$
, one can take
![]() $\Delta _i=\mathsf A_2$
in Lemma 3.1 and then apply Lemma 3.3 to the
$\Delta _i=\mathsf A_2$
in Lemma 3.1 and then apply Lemma 3.3 to the
![]() $\mathsf A_2$
case.
$\mathsf A_2$
case.
Thus, in addition to Theorem B, we obtain another stronger form of Theorem A, now without the assumption that
![]() $R^*$
is infinite, but only in the special case of simply laced systems of rank
$R^*$
is infinite, but only in the special case of simply laced systems of rank
![]() $\ge 2$
and
$\ge 2$
and
![]() $\mathsf F_4$
. The bound here is very rough, since
$\mathsf F_4$
. The bound here is very rough, since
![]() $L(2)$
is the number of elementary factors; the number of unitriangular ones can be much smaller. Also, the use of stability arguments allows one to get much better bounds, of the type
$L(2)$
is the number of elementary factors; the number of unitriangular ones can be much smaller. Also, the use of stability arguments allows one to get much better bounds, of the type
![]() $L=L(2)+M$
, with
$L=L(2)+M$
, with
![]() $3N\le M\le 4N$
, where some multiple of N occurs as a summand, not as a factor.
$3N\le M\le 4N$
, where some multiple of N occurs as a summand, not as a factor.
4 Stability of K
 $_1$
-functor and flipping long and short roots
$_1$
-functor and flipping long and short roots
Another way to reduce bounded generation of
![]() $G(\Phi ,R)$
to bounded generation of
$G(\Phi ,R)$
to bounded generation of
![]() $G(\Delta ,R)$
, where
$G(\Delta ,R)$
, where
![]() $\Delta \subset \Phi $
, is called surjective stability of K
$\Delta \subset \Phi $
, is called surjective stability of K
![]() $_1$
-functor. Recall that K
$_1$
-functor. Recall that K
![]() $_1(\Phi ,R)=G(\Phi ,R)/E(\Phi ,R)$
. Let the root embedding
$_1(\Phi ,R)=G(\Phi ,R)/E(\Phi ,R)$
. Let the root embedding
![]() $\Delta \subset \Phi $
be given. Surjective stability of K
$\Delta \subset \Phi $
be given. Surjective stability of K
![]() $_1$
-functor tells us that
$_1$
-functor tells us that
![]() $G(\Phi ,R)=E(\Phi ,R)G(\Delta ,R)$
; see, for example, [Reference SteinSt], [Reference PlotkinPl]. Moreover, it provides a reduction from
$G(\Phi ,R)=E(\Phi ,R)G(\Delta ,R)$
; see, for example, [Reference SteinSt], [Reference PlotkinPl]. Moreover, it provides a reduction from
![]() $G(\Phi ,R)$
to
$G(\Phi ,R)$
to
![]() $G(\Delta ,R)$
by a bounded number of steps, with a bound depending on R and the root embedding. Here is the main observation we use (see [Reference Kunyavskiĭ, Plotkin and VavilovKPV]).
$G(\Delta ,R)$
by a bounded number of steps, with a bound depending on R and the root embedding. Here is the main observation we use (see [Reference Kunyavskiĭ, Plotkin and VavilovKPV]).
Lemma 4.1 Let R be a Dedekind ring of arithmetic type. Then (uniform) bounded generation of the groups
![]() $G(\Phi ,R)$
,
$G(\Phi ,R)$
,
![]() $\Phi \neq \mathsf C_2$
, follows from (uniform) bounded generation of the group
$\Phi \neq \mathsf C_2$
, follows from (uniform) bounded generation of the group
![]() $G(\mathsf A_2,R)$
.
$G(\mathsf A_2,R)$
.
We illustrate Lemma 4.1 by two examples of the Chevalley groups of types
![]() $\Phi ={\mathsf B}_l$
,
$\Phi ={\mathsf B}_l$
,
![]() $l\ge 3$
, and
$l\ge 3$
, and
![]() $\Phi =\mathsf G_2$
with explicit bounds for reduction. Of course, by stability arguments, one can assume that
$\Phi =\mathsf G_2$
with explicit bounds for reduction. Of course, by stability arguments, one can assume that
![]() $G(\mathsf B_l,R)$
is already reduced to
$G(\mathsf B_l,R)$
is already reduced to
![]() $G(\mathsf B_3,R)$
.
$G(\mathsf B_3,R)$
.
Proposition 4.2 Let R be a Dedekind ring and assume that any element of
![]() $\mathrm {G}(\mathsf A_2,\,R)$
is a product of at most L elementary root unipotents. Then any element of
$\mathrm {G}(\mathsf A_2,\,R)$
is a product of at most L elementary root unipotents. Then any element of
![]() $\mathrm {G}(\mathsf G_2,\,R)$
is a product of at most
$\mathrm {G}(\mathsf G_2,\,R)$
is a product of at most
![]() $L+20$
elementary root unipotents.
$L+20$
elementary root unipotents.
Proof From [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Proposition 5.3], we obtain the universal bound
![]() $L(2)+20$
for the elementary generation of
$L(2)+20$
for the elementary generation of
![]() $\mathrm E_{\mathrm {sc}}(\mathsf G_2,\,R)$
over all Dedekind rings of arithmetic type.
$\mathrm E_{\mathrm {sc}}(\mathsf G_2,\,R)$
over all Dedekind rings of arithmetic type.
Proposition 4.3 Let R be a Dedekind ring and assume that any element of
![]() $\mathrm {G_{sc}}(\mathsf A_2,\,R)$
is a product of L elementary root unipotents. Then any element of
$\mathrm {G_{sc}}(\mathsf A_2,\,R)$
is a product of L elementary root unipotents. Then any element of
![]() $\mathrm {E_{ad}}(\mathsf B_3,\,R)$
is a product of at most
$\mathrm {E_{ad}}(\mathsf B_3,\,R)$
is a product of at most
![]() $L+31$
elementary root unipotents.
$L+31$
elementary root unipotents.
Proof First, observe that [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Lemmas 7.3 and 6.1] are valid for any Dedekind ring R (although they are formally stated under the assumption
![]() $R=\mathbb F_q[t]$
).
$R=\mathbb F_q[t]$
).
By [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Lemma 7.3], each element
![]() $x\in \mathrm {E_{ad}}(\mathsf B_3,\,R)$
is a product of an image of
$x\in \mathrm {E_{ad}}(\mathsf B_3,\,R)$
is a product of an image of
![]() $y\in \mathrm {G_{ad}}(\mathsf B_2,\,R)$
and at most
$y\in \mathrm {G_{ad}}(\mathsf B_2,\,R)$
and at most
![]() $21$
elementary root unipotents. However, since the image of y in
$21$
elementary root unipotents. However, since the image of y in
![]() $\mathrm {G_{ad}}(\mathsf B_3,\,R)$
is elementary and, in particular, lies in the kernel of the spinor norm, we conclude that y itself lies in the kernel of the spinor norm [Reference BassBa, Proposition 3.4.1], and therefore, y is the image of some
$\mathrm {G_{ad}}(\mathsf B_3,\,R)$
is elementary and, in particular, lies in the kernel of the spinor norm, we conclude that y itself lies in the kernel of the spinor norm [Reference BassBa, Proposition 3.4.1], and therefore, y is the image of some
![]() $z\in \mathrm {G_{sc}}(\mathsf B_2,\,R)$
[Reference BassBa, (3.3.4)].
$z\in \mathrm {G_{sc}}(\mathsf B_2,\,R)$
[Reference BassBa, (3.3.4)].
Next, by [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Lemma 6.1], z is equal to a product of the image of some
![]() $w\in \mathrm {G_{sc}}(\mathsf A_1,\,R)$
and at most
$w\in \mathrm {G_{sc}}(\mathsf A_1,\,R)$
and at most
![]() $10$
elementary root unipotents (where
$10$
elementary root unipotents (where
![]() $\mathsf A_1\subset \mathsf B_2$
is the inclusion on long roots). Therefore, x is the product of the image of w in
$\mathsf A_1\subset \mathsf B_2$
is the inclusion on long roots). Therefore, x is the product of the image of w in
![]() $\mathrm {G_{ad}}(\mathsf B_3,\,R)$
and at most
$\mathrm {G_{ad}}(\mathsf B_3,\,R)$
and at most
![]() $31$
elementary root unipotents.
$31$
elementary root unipotents.
However, since the inclusion
![]() $\mathsf A_1\subset \mathsf B_3$
factors through
$\mathsf A_1\subset \mathsf B_3$
factors through
![]() $\mathsf A_2$
, we conclude that x is a product of an image of some element from
$\mathsf A_2$
, we conclude that x is a product of an image of some element from
![]() $\mathrm {G_{sc}}(\mathsf A_2,\,R)$
and at most
$\mathrm {G_{sc}}(\mathsf A_2,\,R)$
and at most
![]() $31$
elementary root unipotents. The claim follows.
$31$
elementary root unipotents. The claim follows.
Corollary 4.4 For any Dedekind ring of arithmetic type R, any element of
![]() $\mathrm {G_{sc}}(\mathsf B_3,\,R)$
is a product of at most
$\mathrm {G_{sc}}(\mathsf B_3,\,R)$
is a product of at most
![]() $L(2)+41$
elementary root unipotents.
$L(2)+41$
elementary root unipotents.
Proof Any element of
![]() $\mathrm {G_{sc}}(\mathsf B_3,\,R)$
is elementary by Lemma 1.1, and therefore, its image in
$\mathrm {G_{sc}}(\mathsf B_3,\,R)$
is elementary by Lemma 1.1, and therefore, its image in
![]() $\mathrm {G_{ad}}(\mathsf B_3,\,R)$
is a product of at most
$\mathrm {G_{ad}}(\mathsf B_3,\,R)$
is a product of at most
![]() $L(2)+31$
elementary root unipotents by Proposition 4.3. However,
$L(2)+31$
elementary root unipotents by Proposition 4.3. However,
![]() $\mathrm {G_{sc}}(\mathsf B_3,\,R)$
is a central extension of
$\mathrm {G_{sc}}(\mathsf B_3,\,R)$
is a central extension of
![]() $\mathrm {G_{ad}}(\mathsf B_3,\,R)$
with the kernel cyclic of order
$\mathrm {G_{ad}}(\mathsf B_3,\,R)$
with the kernel cyclic of order
![]() $2$
. The generator of the kernel comes from
$2$
. The generator of the kernel comes from
![]() $\mathrm {G_{sc}}(\mathsf D_3,\,R)$
[Reference BassBa, (3.4)], where it can be expressed as a product of at most
$\mathrm {G_{sc}}(\mathsf D_3,\,R)$
[Reference BassBa, (3.4)], where it can be expressed as a product of at most
![]() $10$
elementary root unipotents by [Reference Hahn and O’MearaHO, Theorem 7.2.12].
$10$
elementary root unipotents by [Reference Hahn and O’MearaHO, Theorem 7.2.12].
4.1 The case of
 $\mathrm {Sp}(2l,R)$
,
$\mathrm {Sp}(2l,R)$
,
 $l\ge 3$
$l\ge 3$
Thus, we are left with the analysis of the the symplectic groups
![]() $\mathrm {Sp}(2l,R)$
,
$\mathrm {Sp}(2l,R)$
,
![]() $l\ge 2$
. Quite amazingly, the results of [Reference Kunyavskiĭ, Plotkin and VavilovKPV] and [Reference TrostTr2] allow to reduce
$l\ge 2$
. Quite amazingly, the results of [Reference Kunyavskiĭ, Plotkin and VavilovKPV] and [Reference TrostTr2] allow to reduce
![]() $\mathrm {Sp}(6,R)$
to
$\mathrm {Sp}(6,R)$
to
![]() $\mathrm {SL}(3,R)$
as well. As mentioned in [Reference Kunyavskiĭ, Lavrenov, Plotkin and VavilovKLPV], the idea of such a reduction was contained already in Zakiryanov’s thesis; see [Reference ZakiryanovZa]. Of course, as above, the case
$\mathrm {SL}(3,R)$
as well. As mentioned in [Reference Kunyavskiĭ, Lavrenov, Plotkin and VavilovKLPV], the idea of such a reduction was contained already in Zakiryanov’s thesis; see [Reference ZakiryanovZa]. Of course, as above, the case
![]() $\Phi ={\mathsf C}_l$
,
$\Phi ={\mathsf C}_l$
,
![]() $l\ge 3$
is immediately reduced to
$l\ge 3$
is immediately reduced to
![]() $\Phi =\mathsf C_3$
by stability.
$\Phi =\mathsf C_3$
by stability.
Proposition 4.5 Let R be a Dedekind ring and assume that any element of
![]() $\mathrm {G_{sc}}(\mathsf A_2,\,R)$
is a product of L elementary root unipotents. Then any element of
$\mathrm {G_{sc}}(\mathsf A_2,\,R)$
is a product of L elementary root unipotents. Then any element of
![]() $\mathrm {E_{sc}}(\mathsf C_3,\,R)$
is a product of at most
$\mathrm {E_{sc}}(\mathsf C_3,\,R)$
is a product of at most
![]() $L+40$
elementary root unipotents.
$L+40$
elementary root unipotents.
Proof As in the case of
![]() $\Phi =\mathsf B_3$
, we first invoke [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Lemma 7.1] to reduce a matrix from
$\Phi =\mathsf B_3$
, we first invoke [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Lemma 7.1] to reduce a matrix from
![]() $\mathrm {Sp}(6,R)$
to a matrix from
$\mathrm {Sp}(6,R)$
to a matrix from
![]() $\mathrm {Sp}(4,R)$
by 16 elementary transformations. Then we invoke [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Lemma 6.1] to reduce a matrix from
$\mathrm {Sp}(4,R)$
by 16 elementary transformations. Then we invoke [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Lemma 6.1] to reduce a matrix from
![]() $\mathrm {Sp}(4,R)$
to a matrix from
$\mathrm {Sp}(4,R)$
to a matrix from
![]() $\mathrm {Sp}(2,R)=\mathrm {SL}(2,R)$
in long root position by 10 elementary transformations. After that, we invoke Lemma 2.3 to get a square in the nondiagonal position by 4 elementary transformations in the number case or to do the same in the function case by 3 elementary transformations. Now, we can invoke [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Lemma 6.15] to move such a matrix in the long root fundamental position to a matrix in the short root fundamental position by 10 elementary transformations. At this stage, we can apply Lemma 3.3 to the short root
$\mathrm {Sp}(2,R)=\mathrm {SL}(2,R)$
in long root position by 10 elementary transformations. After that, we invoke Lemma 2.3 to get a square in the nondiagonal position by 4 elementary transformations in the number case or to do the same in the function case by 3 elementary transformations. Now, we can invoke [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Lemma 6.15] to move such a matrix in the long root fundamental position to a matrix in the short root fundamental position by 10 elementary transformations. At this stage, we can apply Lemma 3.3 to the short root
![]() $\widetilde {\mathsf A}_2\le \mathsf C_3$
, which gives us
$\widetilde {\mathsf A}_2\le \mathsf C_3$
, which gives us
![]() $\le 16+10+4+10+L$
elementary moves in all cases.
$\le 16+10+4+10+L$
elementary moves in all cases.
So, we have two remaining tasks. First of all, we have to prove Theorem A in the
![]() $\mathsf C_2=\mathrm {Sp}(4,R)$
case, which is not covered by our previous considerations. Second, we want to make the number
$\mathsf C_2=\mathrm {Sp}(4,R)$
case, which is not covered by our previous considerations. Second, we want to make the number
![]() $L(2)$
, which is a crucial constituent in all estimates, as small as we can.
$L(2)$
, which is a crucial constituent in all estimates, as small as we can.
5 Swindling lemma
We concentrate now on minimizing estimates for bounded generation. As we know, this problem depends severely on the number of moves which are necessary in order to move any matrix from
![]() $\mathrm {SL}(3,R$
), where R is a Dedekind ring of arithmetic type, to the identity matrix.
$\mathrm {SL}(3,R$
), where R is a Dedekind ring of arithmetic type, to the identity matrix.
In this section, we establish what Nica [Reference NicaNi] calls “swindling lemma,” which is essentially a very weak form of multiplicativity of Mennicke symbols, sufficient for our purposes and cheaper than the form used in [Reference Carter and KellerCK1] in terms of the number of elementary moves. For the symplectic case, such a lemma in full generality is already contained in [Reference Kunyavskiĭ, Plotkin and VavilovKPV]. Here, we come up with a reverse engineering version of Nica’s lemma [Reference NicaNi, Lemma 4] in the linear case. The proof itself is organized in the same style as the proofs in [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Section 6.3].
5.1 Swindling lemma for
 $\mathrm {SL}(3,R)$
$\mathrm {SL}(3,R)$
The following result is essentially [Reference NicaNi, Lemma 4]. Of course, formally Nica assumes that R is a PID, to conclude that all s have the desired factorizations. But calculations with Mennicke symbols [Reference Bass, Milnor and SerreBMS] show that his result holds [at least] for all Dedekind rings. Below, we extract the rationale behind his proof to apply it in the only situation we need. Namely, we stipulate that the desired factorization of s does exist.
Lemma 5.1 Let R be any commutative ring. Assume that
 $$ \begin{align*}A=\left(\begin{array}{ccc} a&b&0 \\ sc&d&0 \\ 0&0&1 \end{array}\right) \in\mathrm{SL}(3,R),\end{align*} $$
$$ \begin{align*}A=\left(\begin{array}{ccc} a&b&0 \\ sc&d&0 \\ 0&0&1 \end{array}\right) \in\mathrm{SL}(3,R),\end{align*} $$
where s admits factorization
![]() $s=s_1s_2$
such that
$s=s_1s_2$
such that
Then A can be transformed to
 $$ \begin{align*}A=\left(\begin{array}{ccc} \pm a&-sb&0 \\ c&\mp d&0\\ 0&0&-1 \end{array}\right) \in\mathrm{SL}(3,R)\end{align*} $$
$$ \begin{align*}A=\left(\begin{array}{ccc} \pm a&-sb&0 \\ c&\mp d&0\\ 0&0&-1 \end{array}\right) \in\mathrm{SL}(3,R)\end{align*} $$
by
![]() $\le 11$
elementary moves.
$\le 11$
elementary moves.
Proof Let
![]() $t_1,t_2\in R$
be such that
$t_1,t_2\in R$
be such that
Below, we use programmers’ notation style to describe elementary moves, keeping the letter A to denote all matrices appearing along the way.
![]() $\bullet $
Step 1
$\bullet $
Step 1
 $$ \begin{align*}A=At_{31}(s_1)=\left(\begin{array}{ccc} a&b&0 \\ sc&d&0 \\ s_1&0&1 \end{array}\right).\end{align*} $$
$$ \begin{align*}A=At_{31}(s_1)=\left(\begin{array}{ccc} a&b&0 \\ sc&d&0 \\ s_1&0&1 \end{array}\right).\end{align*} $$
![]() $\bullet $
Step 2+3
$\bullet $
Step 2+3
 $$ \begin{align*}A=t_{13}(-t_1)t_{23}(-s_2c)A=\left(\begin{array}{ccc} 1&b&-t_1 \\ 0&d&-s_2c \\ s_1&0&1 \end{array}\right).\end{align*} $$
$$ \begin{align*}A=t_{13}(-t_1)t_{23}(-s_2c)A=\left(\begin{array}{ccc} 1&b&-t_1 \\ 0&d&-s_2c \\ s_1&0&1 \end{array}\right).\end{align*} $$
![]() $\bullet $
Step 4
$\bullet $
Step 4
 $$ \begin{align*}A=t_{31}(-s_1)A=\left(\begin{array}{ccc} 1&b&-t_1 \\ 0&d&-s_2c \\ 0&-s_1b&a \end{array}\right).\end{align*} $$
$$ \begin{align*}A=t_{31}(-s_1)A=\left(\begin{array}{ccc} 1&b&-t_1 \\ 0&d&-s_2c \\ 0&-s_1b&a \end{array}\right).\end{align*} $$
At this stage, we have rolled
![]() $s_1$
over the diagonal by simultaneously moving the
$s_1$
over the diagonal by simultaneously moving the
![]() $2\times 2$
matrix from the NW-corner to the SE-corner. Now we have to roll over
$2\times 2$
matrix from the NW-corner to the SE-corner. Now we have to roll over
![]() $s_2$
by simultaneously returning our
$s_2$
by simultaneously returning our
![]() $2\times 2$
matrix back to the NW-corner.
$2\times 2$
matrix back to the NW-corner.
![]() $\bullet $
Step 5+6
$\bullet $
Step 5+6
 $$ \begin{align*}A=At_{12}(-b)t_{13}(t_1+s_2)=\left(\begin{array}{ccc} 1&0&s_2 \\ 0&d&-s_2c \\ 0&-s_1b&a \end{array}\right).\end{align*} $$
$$ \begin{align*}A=At_{12}(-b)t_{13}(t_1+s_2)=\left(\begin{array}{ccc} 1&0&s_2 \\ 0&d&-s_2c \\ 0&-s_1b&a \end{array}\right).\end{align*} $$
Now we are in exactly the same position as we were after the first move and can start rolling back.
![]() $\bullet $
Step 7+8
$\bullet $
Step 7+8
 $$ \begin{align*}A=t_{21}(c)t_{31}(-t_2)A=\left(\begin{array}{ccc} 1&0&s_2 \\ c&d&0 \\ -t_2&-s_1b&-1 \end{array}\right).\end{align*} $$
$$ \begin{align*}A=t_{21}(c)t_{31}(-t_2)A=\left(\begin{array}{ccc} 1&0&s_2 \\ c&d&0 \\ -t_2&-s_1b&-1 \end{array}\right).\end{align*} $$
![]() $\bullet $
Step 9
$\bullet $
Step 9
 $$ \begin{align*}A=t_{13}(s_2)A=\left(\begin{array}{ccc} -a&-sb&0 \\ c&d&0 \\ -t_2&-s_1b&-1 \end{array}\right).\end{align*} $$
$$ \begin{align*}A=t_{13}(s_2)A=\left(\begin{array}{ccc} -a&-sb&0 \\ c&d&0 \\ -t_2&-s_1b&-1 \end{array}\right).\end{align*} $$
![]() $\bullet $
Step 10+11
$\bullet $
Step 10+11
 $$ \begin{align*}A=At_{31}(-t_2)t_{32}(-s_1b)=\left(\begin{array}{ccc} -a&-sb&0 \\ c&d&0 \\ 0&0&-1 \end{array}\right).\end{align*} $$
$$ \begin{align*}A=At_{31}(-t_2)t_{32}(-s_1b)=\left(\begin{array}{ccc} -a&-sb&0 \\ c&d&0 \\ 0&0&-1 \end{array}\right).\end{align*} $$
For the other choice of signs, one should start rolling over the other way, say, with moving A to
![]() $At_{32}(s_2)$
.
$At_{32}(s_2)$
.
Remark 5.2 Below, we state a stronger form of the swindling lemma for short roots in
![]() $\mathrm {Sp}(4,R)$
, Lemma 5.3 = [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Proposition 6.10], where an arbitrary s is rolled over from c to b. One could ask, how is it possible that the symplectic result is more general than the linear one? The answer is very easy. What we do here is the linear prototype of the swindling lemma for long roots in
$\mathrm {Sp}(4,R)$
, Lemma 5.3 = [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Proposition 6.10], where an arbitrary s is rolled over from c to b. One could ask, how is it possible that the symplectic result is more general than the linear one? The answer is very easy. What we do here is the linear prototype of the swindling lemma for long roots in
![]() $\mathrm {Sp}(4,R)$
, Lemma 5.4 = [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Lemma 6.7], where a square
$\mathrm {Sp}(4,R)$
, Lemma 5.4 = [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Lemma 6.7], where a square
![]() $s^2$
is rolled over from c to b. Of course, we could do the same here, but then to apply it, we would have to use the deep arithmetic Lemma 2.3 on the extraction of square roots of Mennicke symbols, which would increase the number of elementary moves.
$s^2$
is rolled over from c to b. Of course, we could do the same here, but then to apply it, we would have to use the deep arithmetic Lemma 2.3 on the extraction of square roots of Mennicke symbols, which would increase the number of elementary moves.
5.2 Swindling lemma for
 $\mathrm {Sp}(4,R)$
$\mathrm {Sp}(4,R)$
In what concerns
![]() $\mathrm {Sp}(4,R)$
, we keep the notation and conventions of [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Section 6]. In particular,
$\mathrm {Sp}(4,R)$
, we keep the notation and conventions of [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Section 6]. In particular,
![]() $\mathrm {Sp}(4,R)$
preserves the symplectic form with Gram matrix
$\mathrm {Sp}(4,R)$
preserves the symplectic form with Gram matrix
 $$ \begin{align*}\begin{pmatrix} 0&0&0&1\\ 0&0&1&0\\ 0&-1&0&0\\ -1&0&0&0\\ \end{pmatrix}.\end{align*} $$
$$ \begin{align*}\begin{pmatrix} 0&0&0&1\\ 0&0&1&0\\ 0&-1&0&0\\ -1&0&0&0\\ \end{pmatrix}.\end{align*} $$
Further,
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are fundamental roots of
$\beta $
are fundamental roots of
![]() $\mathsf C_2$
, and the corresponding root unipotents are
$\mathsf C_2$
, and the corresponding root unipotents are
 $$ \begin{align*}x_{\alpha}(\xi)=\begin{pmatrix} 1&\xi&0&0\\ 0&1&0&0\\ 0&0&1&-\xi\\ 0&0&0&1\\ \end{pmatrix},\qquad x_{\beta}(\xi)= \begin{pmatrix} 1&0&0&0\\ 0&1&\xi&0\\ 0&0&1&0\\ 0&0&0&1\\ \end{pmatrix},\end{align*} $$
$$ \begin{align*}x_{\alpha}(\xi)=\begin{pmatrix} 1&\xi&0&0\\ 0&1&0&0\\ 0&0&1&-\xi\\ 0&0&0&1\\ \end{pmatrix},\qquad x_{\beta}(\xi)= \begin{pmatrix} 1&0&0&0\\ 0&1&\xi&0\\ 0&0&1&0\\ 0&0&0&1\\ \end{pmatrix},\end{align*} $$
while
![]() $x_{-\alpha }(\xi )$
and
$x_{-\alpha }(\xi )$
and
![]() $x_{-\beta }(\xi )$
are their transposes. Together, they generate the elementary symplectic group
$x_{-\beta }(\xi )$
are their transposes. Together, they generate the elementary symplectic group
![]() $\mathrm {Ep}(4,R)$
which for Dedekind rings of arithmetic type coincides with
$\mathrm {Ep}(4,R)$
which for Dedekind rings of arithmetic type coincides with
![]() $\mathrm {Sp}(4,R)$
.
$\mathrm {Sp}(4,R)$
.
There are two natural embeddings of
![]() $\mathrm {SL}(2,R)$
into
$\mathrm {SL}(2,R)$
into
![]() $\mathrm {Sp}(4,R)$
, the short root embedding
$\mathrm {Sp}(4,R)$
, the short root embedding
![]() $\phi _{\alpha }$
$\phi _{\alpha }$
 $$ \begin{align*}\phi_{\alpha} \begin{pmatrix}1&\xi\\0&1\\ \end{pmatrix} =x_{\alpha}(\xi),\qquad \phi_{\alpha} \begin{pmatrix}1&0\\\xi&1\\ \end{pmatrix} =x_{-\alpha}(\xi),\end{align*} $$
$$ \begin{align*}\phi_{\alpha} \begin{pmatrix}1&\xi\\0&1\\ \end{pmatrix} =x_{\alpha}(\xi),\qquad \phi_{\alpha} \begin{pmatrix}1&0\\\xi&1\\ \end{pmatrix} =x_{-\alpha}(\xi),\end{align*} $$
and the long root embedding
![]() $\phi _{\beta }$
$\phi _{\beta }$
 $$ \begin{align*}\phi_{\beta} \begin{pmatrix}1&\xi\\0&1\\ \end{pmatrix} =x_{\beta}(\xi),\qquad \phi_{\beta} \begin{pmatrix}1&0\\\xi&1\\ \end{pmatrix} =x_{-\beta}(\xi),\end{align*} $$
$$ \begin{align*}\phi_{\beta} \begin{pmatrix}1&\xi\\0&1\\ \end{pmatrix} =x_{\beta}(\xi),\qquad \phi_{\beta} \begin{pmatrix}1&0\\\xi&1\\ \end{pmatrix} =x_{-\beta}(\xi),\end{align*} $$
and unlike groups of other types in the symplectic case, they behave very differently.
The following swindling lemma for the short root embedding that we use in the sequel seems to be stronger than the linear swindling lemma. But this is because, morally, the Mennicke symbol constructed via
![]() $\phi _{\alpha }$
is the square root of the Mennicke symbol constructed via
$\phi _{\alpha }$
is the square root of the Mennicke symbol constructed via
![]() $\phi _{\beta }$
. At the same time, stability reduction (see, for instance, [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Lemma 6.1]) reduces a symplectic matrix to an element of
$\phi _{\beta }$
. At the same time, stability reduction (see, for instance, [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Lemma 6.1]) reduces a symplectic matrix to an element of
![]() $\mathrm {SL}(2,R)$
in the long root embedding. Thus, to be able to use this [seemingly] stronger form of swindling, we should be able to extract square roots of Mennicke symbols anyway.
$\mathrm {SL}(2,R)$
in the long root embedding. Thus, to be able to use this [seemingly] stronger form of swindling, we should be able to extract square roots of Mennicke symbols anyway.
Lemma 5.3 [Reference Kunyavskiĭ, Plotkin and VavilovKPV]
Let
![]() $a,b,c,d,s\in R$
,
$a,b,c,d,s\in R$
,
![]() $ad-bcs=1$
, and, moreover,
$ad-bcs=1$
, and, moreover,
![]() $a\equiv d\ \ \pmod s$
. Then
$a\equiv d\ \ \pmod s$
. Then
 $$ \begin{align*}\phi_{\alpha} \begin{pmatrix} a&b\\ cs&d\\ \end{pmatrix}= \begin{pmatrix} a&b&0&0\\ cs&d&0&0\\ 0&0&a&-b\\ 0&0&-cs&d\\ \end{pmatrix}\end{align*} $$
$$ \begin{align*}\phi_{\alpha} \begin{pmatrix} a&b\\ cs&d\\ \end{pmatrix}= \begin{pmatrix} a&b&0&0\\ cs&d&0&0\\ 0&0&a&-b\\ 0&0&-cs&d\\ \end{pmatrix}\end{align*} $$
can be moved to
 $$ \begin{align*}\phi_{\alpha} \begin{pmatrix} d&c\\ bs&a\\ \end{pmatrix}=\begin{pmatrix} d&c&0&0\\ bs&a&0&0\\ 0&0&d&-c\\ 0&0&-bs&a\\ \end{pmatrix}\end{align*} $$
$$ \begin{align*}\phi_{\alpha} \begin{pmatrix} d&c\\ bs&a\\ \end{pmatrix}=\begin{pmatrix} d&c&0&0\\ bs&a&0&0\\ 0&0&d&-c\\ 0&0&-bs&a\\ \end{pmatrix}\end{align*} $$
by
![]() $\le 26$
elementary transformations.
$\le 26$
elementary transformations.
We do not use it here, but to put things in the right prospective, let us reproduce the swindling lemma for long roots [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Lemma 6.7], on which the proof of Lemma 5.3 hinges, and which is a true analogue of Lemma 5.1 valid for all commutative rings. The number of moves in Lemma 5.4 seems to be smaller than in Lemma 5.1. The reason is that we do not return the element of
![]() $\mathrm {SL}(2,R)$
to the initial position, corresponding to the long root
$\mathrm {SL}(2,R)$
to the initial position, corresponding to the long root
![]() $\beta $
, but leave it in another embedding, corresponding to another long root
$\beta $
, but leave it in another embedding, corresponding to another long root
![]() $2\alpha +\beta $
. This “half-swindling” in the long root embedding was followed by returning to the embedding
$2\alpha +\beta $
. This “half-swindling” in the long root embedding was followed by returning to the embedding
![]() $\varphi _{\alpha }$
corresponding to the short root
$\varphi _{\alpha }$
corresponding to the short root
![]() $\alpha $
(see [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Lemma 6.9]). This was sufficient for the proof of the key Proposition 6.10 in [Reference Kunyavskiĭ, Plotkin and VavilovKPV]
$\alpha $
(see [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Lemma 6.9]). This was sufficient for the proof of the key Proposition 6.10 in [Reference Kunyavskiĭ, Plotkin and VavilovKPV]
Lemma 5.4 [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Lemma 6.7]
Let
![]() $a,b,c,d,s\in R$
,
$a,b,c,d,s\in R$
,
![]() $ad-bcs^2=1$
, and, moreover,
$ad-bcs^2=1$
, and, moreover,
![]() $a\equiv d\equiv 1\ \ \pmod s$
. Then
$a\equiv d\equiv 1\ \ \pmod s$
. Then
 $$ \begin{align*}\phi_{\beta} \begin{pmatrix} a&b\\ cs^2&d\\ \end{pmatrix} =\begin{pmatrix} 1&0&0&0\\ 0&a&b&0\\ 0&cs^2&d&0\\ 0&0&0&1\\ \end{pmatrix}\end{align*} $$
$$ \begin{align*}\phi_{\beta} \begin{pmatrix} a&b\\ cs^2&d\\ \end{pmatrix} =\begin{pmatrix} 1&0&0&0\\ 0&a&b&0\\ 0&cs^2&d&0\\ 0&0&0&1\\ \end{pmatrix}\end{align*} $$
can be moved to
 $$ \begin{align*}\phi_{2\alpha+\beta} \begin{pmatrix} d&-c\\ -bs^2&a\\ \end{pmatrix}= \begin{pmatrix} d&0&0&-c\\ 0&1&0&0\\ 0&0&1&0\\ -bs^2&0&0&a\\ \end{pmatrix}\end{align*} $$
$$ \begin{align*}\phi_{2\alpha+\beta} \begin{pmatrix} d&-c\\ -bs^2&a\\ \end{pmatrix}= \begin{pmatrix} d&0&0&-c\\ 0&1&0&0\\ 0&0&1&0\\ -bs^2&0&0&a\\ \end{pmatrix}\end{align*} $$
by
![]() $\le 8$
elementary transformations.
$\le 8$
elementary transformations.
6
 $\mathrm {SL}(3,R)$
: function case
$\mathrm {SL}(3,R)$
: function case
Here, we prove that in the function case
![]() $L(2)\le 44$
. This allows us to calculate explicit uniform bounds for the width of all Chevalley groups of rank
$L(2)\le 44$
. This allows us to calculate explicit uniform bounds for the width of all Chevalley groups of rank
![]() $\ge 2$
, with the sole exception of
$\ge 2$
, with the sole exception of
![]() $\mathrm {Sp}(4,R)$
. This last case cannot be reduced to
$\mathrm {Sp}(4,R)$
. This last case cannot be reduced to
![]() $\mathrm {SL}(3,R)$
but can be treated similarly – and, in fact, nominally
Footnote
4
easier, since there we have swindling lemma for short roots in full generality, Lemma 5.3 = [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Proposition 6.10].
$\mathrm {SL}(3,R)$
but can be treated similarly – and, in fact, nominally
Footnote
4
easier, since there we have swindling lemma for short roots in full generality, Lemma 5.3 = [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Proposition 6.10].
With the bound
![]() $L\le 65$
, the following result was already established by Trost [Reference TrostTr2, Theorem 1.3]. We use his arithmetic lemmas, but to derive the bounded generation, we adopt the strategy of Nica [Reference NicaNi], with some improvements suggested in our previous paper [Reference Kunyavskiĭ, Plotkin and VavilovKPV].
$L\le 65$
, the following result was already established by Trost [Reference TrostTr2, Theorem 1.3]. We use his arithmetic lemmas, but to derive the bounded generation, we adopt the strategy of Nica [Reference NicaNi], with some improvements suggested in our previous paper [Reference Kunyavskiĭ, Plotkin and VavilovKPV].
Lemma 6.1 For any Dedekind ring of arithmetic type R in a global function field K, any element in
![]() $\mathrm {SL}(3,R)$
is a product of
$\mathrm {SL}(3,R)$
is a product of
![]() $L\le 44$
elementary root unipotents.
$L\le 44$
elementary root unipotents.
Proof Let, as always, K be a global function field with the field of constants
![]() ${\mathbb F}_{\!q}$
and
${\mathbb F}_{\!q}$
and
![]() $R=\mathcal O_{K,S}$
be any ring of arithmetic type with the quotient field K.
$R=\mathcal O_{K,S}$
be any ring of arithmetic type with the quotient field K.
![]() $\bullet $
We start with any matrix
$\bullet $
We start with any matrix
![]() $A\in \mathrm {SL}(3,R)$
and reduce it to a matrix
$A\in \mathrm {SL}(3,R)$
and reduce it to a matrix
 $$ \begin{align*}A=\left(\begin{array}{cc} a&b \\ c&d \\ \end{array}\right) \in \mathrm{SL}(2,R)\le\mathrm{SL}(3,R)\end{align*} $$
$$ \begin{align*}A=\left(\begin{array}{cc} a&b \\ c&d \\ \end{array}\right) \in \mathrm{SL}(2,R)\le\mathrm{SL}(3,R)\end{align*} $$
by
![]() $\le 7$
elementary moves.
$\le 7$
elementary moves.
![]() $\bullet $
Now by Lemma 2.1, any matrix in
$\bullet $
Now by Lemma 2.1, any matrix in
![]() $A\in \mathrm {SL}(2,\mathcal O_{K,S})$
can be reduced to a matrix
$A\in \mathrm {SL}(2,\mathcal O_{K,S})$
can be reduced to a matrix
![]() $A\in \mathrm {SL}(2,\mathcal O_{K})$
at the cost of
$A\in \mathrm {SL}(2,\mathcal O_{K})$
at the cost of
![]() $\le 3$
elementary moves. Thus, we can from the very start assume that
$\le 3$
elementary moves. Thus, we can from the very start assume that
![]() $A\in \mathrm {SL}(2,\mathcal O_{K})$
– in other words, that
$A\in \mathrm {SL}(2,\mathcal O_{K})$
– in other words, that
![]() $R=\mathcal O_{K}$
is precisely the ring of integers of K.
$R=\mathcal O_{K}$
is precisely the ring of integers of K.
![]() $\bullet $
Using a version of Dirichlet theorem (= Kornblum–Landau–Artin theorem in the function case) on primes in arithmetic progressions, we can assume that
$\bullet $
Using a version of Dirichlet theorem (= Kornblum–Landau–Artin theorem in the function case) on primes in arithmetic progressions, we can assume that
![]() $bR$
is a prime ideal at the cost of 1 elementary move.
$bR$
is a prime ideal at the cost of 1 elementary move.
Now Lemma 2.5 implies that there exists
![]() $c\in R$
such that
$c\in R$
such that
![]() $bc\equiv -1\ \ \pmod a$
and
$bc\equiv -1\ \ \pmod a$
and
![]() $\delta (b)$
and
$\delta (b)$
and
![]() $\delta (c)$
are coprime. The first of these conditions guarantees the existence of
$\delta (c)$
are coprime. The first of these conditions guarantees the existence of
![]() $d\in R$
such that
$d\in R$
such that
![]() $ad-bc=1$
. Since modulo the root subgroup
$ad-bc=1$
. Since modulo the root subgroup
![]() $X_{21}=\big \{ t_{21}(\xi ),\ \xi \in R\big \}$
a matrix
$X_{21}=\big \{ t_{21}(\xi ),\ \xi \in R\big \}$
a matrix
![]() $A\in \mathrm {SL}(2,R)$
only depends on its first row, by another 1 elementary move, we can assume that the entries of our A themselves have this last property. At this step, we have used 2 elementary moves.
$A\in \mathrm {SL}(2,R)$
only depends on its first row, by another 1 elementary move, we can assume that the entries of our A themselves have this last property. At this step, we have used 2 elementary moves.
![]() $\bullet $
Let
$\bullet $
Let
![]() $u,v\in {\mathbb N}$
be such that
$u,v\in {\mathbb N}$
be such that
![]() $u\delta (b)-v\delta (c)=1$
. It follows that
$u\delta (b)-v\delta (c)=1$
. It follows that
 $$ \begin{align*}\begin{pmatrix} a&b\\ c&d\\ \end{pmatrix}= {\begin{pmatrix} a&b\\ c&d\\ \end{pmatrix}}^{u\delta(b)}\cdot \begin{pmatrix} a&b\\ c&d\\ \end{pmatrix}^{-v\delta(c)},\end{align*} $$
$$ \begin{align*}\begin{pmatrix} a&b\\ c&d\\ \end{pmatrix}= {\begin{pmatrix} a&b\\ c&d\\ \end{pmatrix}}^{u\delta(b)}\cdot \begin{pmatrix} a&b\\ c&d\\ \end{pmatrix}^{-v\delta(c)},\end{align*} $$
and we reduce the factors independently.
With this end, we proceed exactly as Carter and Keller do in [Reference Carter and KellerCK1], and as everybody after them. Namely, we invoke the Cayley–Hamilton theorem, which asserts that
![]() $A^2=\mathrm {tr}(A)A-I$
so that
$A^2=\mathrm {tr}(A)A-I$
so that
where I stands for the identity matrix and X, Y are polynomials in
![]() ${\mathbb Z}[t]$
.
${\mathbb Z}[t]$
.
It is well known that X divides
![]() $Y^2-1$
or, what is the same, Y divides
$Y^2-1$
or, what is the same, Y divides
![]() $X^2-1$
; see the proof of [Reference Carter and KellerCK1, Lemma 1]. Since
$X^2-1$
; see the proof of [Reference Carter and KellerCK1, Lemma 1]. Since
![]() ${\mathbb Z}[t]$
is a unique factorization domain, there exists a factorization
${\mathbb Z}[t]$
is a unique factorization domain, there exists a factorization
Remark 6.2 In fact, X and Y are explicitly known; morally, they are the values of two consecutive Chebyshev polynomials
![]() $U_{m-1}$
and
$U_{m-1}$
and
![]() $U_m$
at
$U_m$
at
![]() $\mathrm {tr}(A)/2=(a+d)/2$
, which allows one to argue inductively, without swindling. This is essentially the approach taken by Sergei Adian and Jens Mennicke [Reference Adian and MennickeAM], only that they are not aware these are Chebyshev polynomials and have to establish their properties from scratch. We do not follow this path here since it would require considerably more elementary moves.
$\mathrm {tr}(A)/2=(a+d)/2$
, which allows one to argue inductively, without swindling. This is essentially the approach taken by Sergei Adian and Jens Mennicke [Reference Adian and MennickeAM], only that they are not aware these are Chebyshev polynomials and have to establish their properties from scratch. We do not follow this path here since it would require considerably more elementary moves.
![]() $\bullet $
Thus, for an arbitrary m, one has
$\bullet $
Thus, for an arbitrary m, one has
 $$ \begin{align*}\begin{pmatrix} a&b\\ c&d\\ \end{pmatrix}^m =x\begin{pmatrix} 1&0\\0&1\\ \end{pmatrix}+ y\begin{pmatrix} a&b\\ c&d\\ \end{pmatrix}= \begin{pmatrix} x+ya&yb\\ yc&x+yd\\ \end{pmatrix},\end{align*} $$
$$ \begin{align*}\begin{pmatrix} a&b\\ c&d\\ \end{pmatrix}^m =x\begin{pmatrix} 1&0\\0&1\\ \end{pmatrix}+ y\begin{pmatrix} a&b\\ c&d\\ \end{pmatrix}= \begin{pmatrix} x+ya&yb\\ yc&x+yd\\ \end{pmatrix},\end{align*} $$
where
![]() $x=X(a+d)$
,
$x=X(a+d)$
,
![]() $y=X(a+d)$
. An explicit calculation shows that
$y=X(a+d)$
. An explicit calculation shows that
Substituting
![]() $a+d$
into the decomposition
$a+d$
into the decomposition
![]() $Y=Y_1Y_2$
, we get
$Y=Y_1Y_2$
, we get
By the very definition of
![]() $y_1$
and
$y_1$
and
![]() $y_2$
, one has
$y_2$
, one has
now as congruences in R. Thus,
and we are in a position to apply swindling, as stated in Lemma 5.1.
![]() $\bullet $
Now, applying Lemma 5.1 we reduce
$\bullet $
Now, applying Lemma 5.1 we reduce
 $$ \begin{align*}A^m=\begin{pmatrix} x+ya&yb\\ yc&x+yd\\ \end{pmatrix}\end{align*} $$
$$ \begin{align*}A^m=\begin{pmatrix} x+ya&yb\\ yc&x+yd\\ \end{pmatrix}\end{align*} $$
to either
 $$ \begin{align*}B=\begin{pmatrix} x+ya&y^2b\\ c&x+yd\\ \end{pmatrix}\end{align*} $$
$$ \begin{align*}B=\begin{pmatrix} x+ya&y^2b\\ c&x+yd\\ \end{pmatrix}\end{align*} $$
or
 $$ \begin{align*}C=\begin{pmatrix} x+ya&b\\ y^2c&x+yd\\ \end{pmatrix}\end{align*} $$
$$ \begin{align*}C=\begin{pmatrix} x+ya&b\\ y^2c&x+yd\\ \end{pmatrix}\end{align*} $$
depending on whether we argue modulo c or modulo b, both in
![]() $\le 11$
elementary moves.
$\le 11$
elementary moves.
![]() $\bullet $
In the first case,
$\bullet $
In the first case,
![]() $A^m$
,
$A^m$
,
![]() $m=-v\delta (c)$
, by one appropriate row transformation, we get
$m=-v\delta (c)$
, by one appropriate row transformation, we get
 $$ \begin{align*}t_{12}(*)B=\begin{pmatrix} \big(a^{\delta(c)}\big)^{-v}&*\\ c&x+yd\\ \end{pmatrix},\end{align*} $$
$$ \begin{align*}t_{12}(*)B=\begin{pmatrix} \big(a^{\delta(c)}\big)^{-v}&*\\ c&x+yd\\ \end{pmatrix},\end{align*} $$
where
![]() $a^{\delta (c)}$
, and hence,
$a^{\delta (c)}$
, and hence,
![]() $\big (a^{\delta (c)}\big )^{-v}$
, is congruent to an element of
$\big (a^{\delta (c)}\big )^{-v}$
, is congruent to an element of
![]() ${\mathbb F}_{\!q}$
modulo c. Thus, changing the parameter of the elementary move, we may from the very start assume that
${\mathbb F}_{\!q}$
modulo c. Thus, changing the parameter of the elementary move, we may from the very start assume that
 $$ \begin{align*}t_{12}(*)B=\begin{pmatrix} e&*\\ c&x+yd\\ \end{pmatrix},\end{align*} $$
$$ \begin{align*}t_{12}(*)B=\begin{pmatrix} e&*\\ c&x+yd\\ \end{pmatrix},\end{align*} $$
with
![]() $f\in {\mathbb F}_{\!q}^*$
. Two more moves make this matrix diagonal
$f\in {\mathbb F}_{\!q}^*$
. Two more moves make this matrix diagonal
Altogether, we have spent
![]() $\le 14=11+3$
elementary moves to reduce
$\le 14=11+3$
elementary moves to reduce
![]() $A^m$
to a semisimple root element in this case.
$A^m$
to a semisimple root element in this case.
![]() $\bullet $
The analysis of the second case,
$\bullet $
The analysis of the second case,
![]() $A^m$
,
$A^m$
,
![]() $m=u\delta (b)$
, is similar. As above, by one appropriate column transformation, we get
$m=u\delta (b)$
, is similar. As above, by one appropriate column transformation, we get
 $$ \begin{align*}Ct_{21}(*)=\begin{pmatrix} \big(a^{\delta(b)}\big)^{u}&b\\ *&x+yd\\ \end{pmatrix},\end{align*} $$
$$ \begin{align*}Ct_{21}(*)=\begin{pmatrix} \big(a^{\delta(b)}\big)^{u}&b\\ *&x+yd\\ \end{pmatrix},\end{align*} $$
where
![]() $a^{\delta (b)}$
, and thus also
$a^{\delta (b)}$
, and thus also
![]() $\big (a^{\delta (b)}\big )^{u}$
, is congruent to an element of
$\big (a^{\delta (b)}\big )^{u}$
, is congruent to an element of
![]() ${\mathbb F}_{\!q}$
modulo c. Thus, changing the parameter of the elementary move, we may from the very start assume that
${\mathbb F}_{\!q}$
modulo c. Thus, changing the parameter of the elementary move, we may from the very start assume that
 $$ \begin{align*}t_{12}(*)B=\begin{pmatrix} g&b\\ *&x+yd\\ \end{pmatrix},\end{align*} $$
$$ \begin{align*}t_{12}(*)B=\begin{pmatrix} g&b\\ *&x+yd\\ \end{pmatrix},\end{align*} $$
with
![]() $g\in {\mathbb F}_{\!q}^*$
. Two more moves make this matrix diagonal
$g\in {\mathbb F}_{\!q}^*$
. Two more moves make this matrix diagonal
As above, we have spent
![]() $\le 14=11+3$
elementary moves to reduce
$\le 14=11+3$
elementary moves to reduce
![]() $A^m$
to a semisimple root element in this case as well.
$A^m$
to a semisimple root element in this case as well.
![]() $\bullet $
As is classically known (see, for instance, [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Corollary 2.2]), the semisimple root element
$\bullet $
As is classically known (see, for instance, [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Corollary 2.2]), the semisimple root element
![]() $h_{12}(fg)=h_{12}(f)h_{21}(g)$
can be expressed as a product of
$h_{12}(fg)=h_{12}(f)h_{21}(g)$
can be expressed as a product of
![]() $\le 4$
elementary transformations.
$\le 4$
elementary transformations.
Altogether, this gives us
![]() $\le 7+3+2+11+11+3+3+4=44$
elementary moves. A reference to Trost would give 65.
$\le 7+3+2+11+11+3+3+4=44$
elementary moves. A reference to Trost would give 65.
Remark 6.3 The estimate in Lemma 6.1 can eventually be slightly improved. Namely, instead of appealing to Lemma 2.1 at the second step of the proof, we could proceed as in [Reference TrostTr2, Remark 2.5]. More precisely, in our setup, there exists an element
![]() $x\in K$
, transcendental over
$x\in K$
, transcendental over
![]() $\mathbb F_q$
, such that the integral closure of
$\mathbb F_q$
, such that the integral closure of
![]() $\mathbb F_q[x]$
in K is isomorphic to
$\mathbb F_q[x]$
in K is isomorphic to
![]() $\mathcal {O}_{K,S}$
; see [Reference GersteinGe, Example (ii)] or [Reference RosenRo, Proposition 7]. More explicitly, according to Proposition 6 and the subsequent lemma in [Reference RosenRo], if
$\mathcal {O}_{K,S}$
; see [Reference GersteinGe, Example (ii)] or [Reference RosenRo, Proposition 7]. More explicitly, according to Proposition 6 and the subsequent lemma in [Reference RosenRo], if
![]() $S=\{P_1,\dots ,P_s\}$
and
$S=\{P_1,\dots ,P_s\}$
and
![]() $D=a_1P_1+\dots a_sP_s$
is a positive divisor of sufficiently large degree, then D appears as the polar divisor
$D=a_1P_1+\dots a_sP_s$
is a positive divisor of sufficiently large degree, then D appears as the polar divisor
![]() $D_{\infty }$
of some x, so that
$D_{\infty }$
of some x, so that
![]() ${\mathrm {div}} (x)=D_0-D_{\infty }$
.
${\mathrm {div}} (x)=D_0-D_{\infty }$
.
This argument allows one to justify the proof of [Reference TrostTr2, Lemma 3.1] over an arbitrary
![]() $R=\mathcal O_{K,S}$
; see [Reference Kunyavskiĭ, Morris and RapinchukKMR]. However, we do not know whether this is enough to streamline all steps of our proof, particularly the third one where we use Lemma 2.5. If yes, this would save us three elementary moves and give the estimate
$R=\mathcal O_{K,S}$
; see [Reference Kunyavskiĭ, Morris and RapinchukKMR]. However, we do not know whether this is enough to streamline all steps of our proof, particularly the third one where we use Lemma 2.5. If yes, this would save us three elementary moves and give the estimate
![]() $L\le 41$
.
$L\le 41$
.
7
 $\mathrm {Sp}(4,R)$
: function case
$\mathrm {Sp}(4,R)$
: function case
Here, we prove that for the group
![]() $\mathrm {Sp}(4,R)$
in the function case, the uniform bound is
$\mathrm {Sp}(4,R)$
in the function case, the uniform bound is
![]() $\le 90$
. Modulo Lemma 2.5 = [Reference TrostTr2, Lemma 3.3], it is essentially the same proof as the one given in [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Section 6.4], which from the very start uses extraction of square roots of Mennicke symbols – thus, Lemma 2.3 = [Reference TrostTr2, Lemma 3.1]. Since the swindling in short root position established in [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Proposition 6.10] is already quite general, the only difference with the proof in [Reference Kunyavskiĭ, Plotkin and VavilovKPV] is the necessity to invoke Lemma 2.1 to reduce to a matrix with entries in
$\le 90$
. Modulo Lemma 2.5 = [Reference TrostTr2, Lemma 3.3], it is essentially the same proof as the one given in [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Section 6.4], which from the very start uses extraction of square roots of Mennicke symbols – thus, Lemma 2.3 = [Reference TrostTr2, Lemma 3.1]. Since the swindling in short root position established in [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Proposition 6.10] is already quite general, the only difference with the proof in [Reference Kunyavskiĭ, Plotkin and VavilovKPV] is the necessity to invoke Lemma 2.1 to reduce to a matrix with entries in
![]() $\mathcal O_K$
, which costs 3 extra moves.
$\mathcal O_K$
, which costs 3 extra moves.
Lemma 7.1 For any Dedekind ring of arithmetic type R in a global function field K, any element in
![]() $\mathrm {Sp}(4,R)$
is a product of
$\mathrm {Sp}(4,R)$
is a product of
![]() $L\le 90$
elementary root unipotents.
$L\le 90$
elementary root unipotents.
Proof Essentially, we argue exactly as in the proof of Lemma 6.1, but now relying on the symplectic versions of the main lemmas from [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Section 6], the
![]() $\mathrm {SL}_2$
-part of the argument will be exactly the same, so we only indicate differences.
$\mathrm {SL}_2$
-part of the argument will be exactly the same, so we only indicate differences.
As above, we start with a global function field K with the field of constants
![]() ${\mathbb F}_{\!q}$
, and any ring of arithmetic type
${\mathbb F}_{\!q}$
, and any ring of arithmetic type
![]() $R=\mathcal O_{K,S}$
therein.
$R=\mathcal O_{K,S}$
therein.
![]() $\bullet $
We start with any matrix
$\bullet $
We start with any matrix
![]() $A\in \mathrm {Sp}(4,R)$
and reduce it to a matrix
$A\in \mathrm {Sp}(4,R)$
and reduce it to a matrix
 $$ \begin{align*}A=\phi_{\beta} \begin{pmatrix} a&b\\ c&d\\ \end{pmatrix} =\begin{pmatrix} 1&0&0&0\\ 0&a&b&0\\ 0&c&d&0\\ 0&0&0&1\\ \end{pmatrix} \in \mathrm{SL}^{\beta}(2,R)\le\mathrm{Sp}(4,R)\end{align*} $$
$$ \begin{align*}A=\phi_{\beta} \begin{pmatrix} a&b\\ c&d\\ \end{pmatrix} =\begin{pmatrix} 1&0&0&0\\ 0&a&b&0\\ 0&c&d&0\\ 0&0&0&1\\ \end{pmatrix} \in \mathrm{SL}^{\beta}(2,R)\le\mathrm{Sp}(4,R)\end{align*} $$
in the long root embedding of
![]() $\mathrm {SL}(2,R)$
by
$\mathrm {SL}(2,R)$
by
![]() $\le 10$
elementary moves, [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Lemma 6.1].
$\le 10$
elementary moves, [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Lemma 6.1].
![]() $\bullet $
Now by Lemma 2.1, any matrix in
$\bullet $
Now by Lemma 2.1, any matrix in
![]() $A\in \mathrm {SL}^{\beta }(2,\mathcal O_{K,S})$
can be reduced to a matrix
$A\in \mathrm {SL}^{\beta }(2,\mathcal O_{K,S})$
can be reduced to a matrix
![]() $A\in \mathrm {SL}^{\beta }(2,\mathcal O_{K})$
at the cost of
$A\in \mathrm {SL}^{\beta }(2,\mathcal O_{K})$
at the cost of
![]() $\le 3$
elementary moves so that we can from the very start assume that
$\le 3$
elementary moves so that we can from the very start assume that
![]() $R=\mathcal O_K$
is the full ring of integers of K.
$R=\mathcal O_K$
is the full ring of integers of K.
The next step does not have analogues for
![]() $\mathrm {SL}(3,R)$
.
$\mathrm {SL}(3,R)$
.
![]() $\bullet $
Now, being inside
$\bullet $
Now, being inside
![]() $\mathrm {SL}(2,\mathcal O_K)$
, we can invoke Lemma 2.3 to transform our A to another
$\mathrm {SL}(2,\mathcal O_K)$
, we can invoke Lemma 2.3 to transform our A to another
 $$ \begin{align*}A=\phi_{\beta} \begin{pmatrix} a&b^2\\ *&*\\ \end{pmatrix} \in \mathrm{SL}^{\beta}(2,R)\le\mathrm{Sp}(4,R),\end{align*} $$
$$ \begin{align*}A=\phi_{\beta} \begin{pmatrix} a&b^2\\ *&*\\ \end{pmatrix} \in \mathrm{SL}^{\beta}(2,R)\le\mathrm{Sp}(4,R),\end{align*} $$
with different a and b, at a cost of
![]() $\le 3$
elementary moves.
$\le 3$
elementary moves.
![]() $\bullet $
Next, we can move such an A to a matrix of the shape
$\bullet $
Next, we can move such an A to a matrix of the shape
 $$ \begin{align*}A=\phi_{\beta} \begin{pmatrix} a&b^2\\ -c^2&*\\ \end{pmatrix} \in \mathrm{SL}^{\beta}(2,R)\le\mathrm{Sp}(4,R),\end{align*} $$
$$ \begin{align*}A=\phi_{\beta} \begin{pmatrix} a&b^2\\ -c^2&*\\ \end{pmatrix} \in \mathrm{SL}^{\beta}(2,R)\le\mathrm{Sp}(4,R),\end{align*} $$
by
![]() $\le 1$
elementary move [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Lemma 6.14], which, in turn, can be moved to a short root position
$\le 1$
elementary move [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Lemma 6.14], which, in turn, can be moved to a short root position
 $$ \begin{align*}\phi_{\alpha}\begin{pmatrix} a&b\\ c&d\\ \end{pmatrix}= \begin{pmatrix} a&b&0&0\\ c&d&0&0\\ 0&0&a&-b\\ 0&0&-c&d\\ \end{pmatrix}\in \mathrm{SL}^{\alpha}(2,R)\le\mathrm{Sp}(4,R),\end{align*} $$
$$ \begin{align*}\phi_{\alpha}\begin{pmatrix} a&b\\ c&d\\ \end{pmatrix}= \begin{pmatrix} a&b&0&0\\ c&d&0&0\\ 0&0&a&-b\\ 0&0&-c&d\\ \end{pmatrix}\in \mathrm{SL}^{\alpha}(2,R)\le\mathrm{Sp}(4,R),\end{align*} $$
at a cost of
![]() $\le 9$
elementary moves; see [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Lemma 6.9]. Altogether, this gives us
$\le 9$
elementary moves; see [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Lemma 6.9]. Altogether, this gives us
![]() $\le 10$
elementary moves at this step; compare [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Lemma 6.15].
$\le 10$
elementary moves at this step; compare [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Lemma 6.15].
At this stage, we are in the same situation as in the proof of Lemma 6.1 and can return to its third step repeating the proof from that point on almost verbatim. Of course, now we have a stronger and more general version of swindling, Lemma 5.3 instead of Lemma 5.1, but on the other hand, since it involves switching to long root embeddings, and then back again, it requires many more elementary moves than in the linear case. Let us list the steps to specify the number of elementary moves.
![]() $\bullet $
Again, using a version of the Dirichlet theorem and Lemma 2.5 =[Reference TrostTr2, Lemma 3.3], we can assume that b is prime and c is such that
$\bullet $
Again, using a version of the Dirichlet theorem and Lemma 2.5 =[Reference TrostTr2, Lemma 3.3], we can assume that b is prime and c is such that
![]() $\delta (b)$
and
$\delta (b)$
and
![]() $\delta (c)$
are coprime. This requires
$\delta (c)$
are coprime. This requires
![]() $\le 2$
elementary moves.
$\le 2$
elementary moves.
![]() $\bullet $
After that, it is exactly the same proof as that of Lemma 6.1, with reference to Lemma 5.3 instead of Lemma 5.1, which uses 26 elementary moves instead of 11 in the linear case.
$\bullet $
After that, it is exactly the same proof as that of Lemma 6.1, with reference to Lemma 5.3 instead of Lemma 5.1, which uses 26 elementary moves instead of 11 in the linear case.
![]() $\bullet $
The last three steps are now literally the same as in the proof of Lemma 6.1, adding 3+3+4 elementary moves to reduce A to the identity matrix.
$\bullet $
The last three steps are now literally the same as in the proof of Lemma 6.1, adding 3+3+4 elementary moves to reduce A to the identity matrix.
This finishes the proof of Lemma 7.1. Altogether, we have used
elementary moves, as claimed.
Remark 7.2 In the spirit of Remark 6.3, one can eventually improve the estimate in Lemma 7.1 to
![]() $L\le 87$
by circumventing the use of Lemma 2.1.
$L\le 87$
by circumventing the use of Lemma 2.1.
Remark 7.3 The 6 elementary moves needed to diagonalize the matrix at the end of the proof of Lemmas 6.1 and 7.1 have been forgotten in the proof of [Reference Kunyavskiĭ, Plotkin and VavilovKPV, Theorem 6.18]. This corrigendum worsens the estimate in that theorem to
![]() $w_E(\mathrm {Sp}(4,\mathbb F_q[t])\le 85$
.
$w_E(\mathrm {Sp}(4,\mathbb F_q[t])\le 85$
.
8
 $\mathrm {Sp}(4,R)$
: number case
$\mathrm {Sp}(4,R)$
: number case
Thus, the only piece that is lacking at this point is a uniform bound for Dedekind rings R of number type with finite multiplicative group
![]() $R^*$
. Since
$R^*$
. Since
![]() $G_{\mathrm {sc}}(\Phi ,{\mathbb Z})$
,
$G_{\mathrm {sc}}(\Phi ,{\mathbb Z})$
,
![]() $\mathrm {rk}(\Phi )\ge 2$
, are boundedly generated [Reference TavgenTa2], we can henceforth assume that
$\mathrm {rk}(\Phi )\ge 2$
, are boundedly generated [Reference TavgenTa2], we can henceforth assume that
![]() $R=\mathcal O_K$
is the ring of integers of an imaginary quadratic field K,
$R=\mathcal O_K$
is the ring of integers of an imaginary quadratic field K,
![]() $[K:{\mathbb Q}]=2$
.
$[K:{\mathbb Q}]=2$
.
The existence of a uniform elementary width bound
![]() $L=L(2,2)$
for
$L=L(2,2)$
for
![]() $\mathrm {SL}(3,R)$
,
$\mathrm {SL}(3,R)$
,
![]() $R=\mathcal O_K$
,
$R=\mathcal O_K$
,
![]() $[K:{\mathbb Q}]=2$
was established by Carter, Keller, and Paige [Reference Carter, Keller and PaigeCKP] in the language of model theory/nonstandard analysisFootnote
5
and then presented slightly differently, in more traditional logical terms, by Morris [Reference MorrisMo]. Observe, though, that their bound is uniform but not explicit.
$[K:{\mathbb Q}]=2$
was established by Carter, Keller, and Paige [Reference Carter, Keller and PaigeCKP] in the language of model theory/nonstandard analysisFootnote
5
and then presented slightly differently, in more traditional logical terms, by Morris [Reference MorrisMo]. Observe, though, that their bound is uniform but not explicit.
As we know from Sections 2 and 3, the existence of a uniform bound for
![]() $\mathrm {SL}(3,R)$
implies the existence of uniform bounds for all
$\mathrm {SL}(3,R)$
implies the existence of uniform bounds for all
![]() $G_{\mathrm {sc}}(\Phi ,{\mathbb Z})$
,
$G_{\mathrm {sc}}(\Phi ,{\mathbb Z})$
,
![]() $\mathrm {rk}(\Phi )\ge 2$
, with the sole exception of
$\mathrm {rk}(\Phi )\ge 2$
, with the sole exception of
![]() $\mathrm {Sp}(4,R)$
.
$\mathrm {Sp}(4,R)$
.
However, using the results of Bass, Milnor, and Serre [Reference Bass, Milnor and SerreBMS], the existence of a uniform bound for elementary width of
![]() $\mathrm {Sp}(4,R)$
,
$\mathrm {Sp}(4,R)$
,
![]() $R=\mathcal O_K$
,
$R=\mathcal O_K$
,
![]() $[K:{\mathbb Q}]=2$
can be easily derived by exactly the same methods as in [Reference Carter, Keller and PaigeCKP], [Reference MorrisMo]. Below, we sketch a proof of the following result.
$[K:{\mathbb Q}]=2$
can be easily derived by exactly the same methods as in [Reference Carter, Keller and PaigeCKP], [Reference MorrisMo]. Below, we sketch a proof of the following result.
Lemma 8.1 There exists a uniform bound
![]() $L=L'(2,2)$
such that the width of all groups
$L=L'(2,2)$
such that the width of all groups
![]() $\mathrm {Sp}(4,R)$
, where
$\mathrm {Sp}(4,R)$
, where
![]() $R=\mathcal O_K$
is the ring of integers in a quadratic number field
$R=\mathcal O_K$
is the ring of integers in a quadratic number field
![]() $[K:{\mathbb Q}]=2$
, does not exceed L.
$[K:{\mathbb Q}]=2$
, does not exceed L.
With this end, we have to briefly recall parts of its general context.
8.1 Bounded generation of ultrapowers
First, recall that being algebraic groups Chevalley groups themselves commute with direct products:
However, elementary groups do not, in general, commute with direct products, which is due to the lack of the uniform elementary generation. Namely, Wilberd van der Kallen noticed that the quotient
(countably many copies) is precisely the obstruction to the bounded generation of
![]() $E(\Phi ,R)$
. This easily ensues from the following obvious observation. In the case of
$E(\Phi ,R)$
. This easily ensues from the following obvious observation. In the case of
![]() $\mathrm {SL}(n,R)$
the following result is [Reference Carter, Keller and PaigeCKP, Theorem 2.8]; generalization to all Chevalley groups is immediate.
$\mathrm {SL}(n,R)$
the following result is [Reference Carter, Keller and PaigeCKP, Theorem 2.8]; generalization to all Chevalley groups is immediate.
Lemma 8.2 Let I be any index set and
![]() $R_i$
,
$R_i$
,
![]() $i\in I$
be a family of commutative rings. Suppose all
$i\in I$
be a family of commutative rings. Suppose all
![]() $E(\Phi ,R_i)$
have elementary width
$E(\Phi ,R_i)$
have elementary width
![]() $\le L$
,
$\le L$
,
Then the elementary width of
does not exceed
![]() $2LN$
. Conversely, the above equality implies that all
$2LN$
. Conversely, the above equality implies that all
![]() $E(\Phi ,R_i)$
are uniformly elementarily boundedly generated.
$E(\Phi ,R_i)$
are uniformly elementarily boundedly generated.
Proof Take
![]() $g_i\in E(\Phi ,R_i)$
,
$g_i\in E(\Phi ,R_i)$
,
![]() $i\in I$
, and for each
$i\in I$
, and for each
![]() $i\in I$
, choose an elementary expression of
$i\in I$
, choose an elementary expression of
![]() $g_i$
of length
$g_i$
of length
![]() $\le L$
, say
$\le L$
, say
 $$ \begin{align*}g_i=x_{\beta(i)_1}(\xi(i)^1)\ldots x_{\beta(i)_L}(\xi(i)^L)=\prod_{j=1}^L x_{\beta(i)^j}(\xi(i)_j)\in E(\Phi,R_i).\end{align*} $$
$$ \begin{align*}g_i=x_{\beta(i)_1}(\xi(i)^1)\ldots x_{\beta(i)_L}(\xi(i)^L)=\prod_{j=1}^L x_{\beta(i)^j}(\xi(i)_j)\in E(\Phi,R_i).\end{align*} $$
If an actual expression of
![]() $g_i$
is shorter than L, just set the remaining
$g_i$
is shorter than L, just set the remaining
![]() $\beta (i)_j$
to the maximal root of
$\beta (i)_j$
to the maximal root of
![]() $\Phi $
and
$\Phi $
and
![]() $\xi (i)_j$
to
$\xi (i)_j$
to
![]() $0$
.
$0$
.
Now consider any ordering of roots in
![]() $\Phi =\{\gamma _1,\ldots ,\gamma _{2N}\}$
and form products
$\Phi =\{\gamma _1,\ldots ,\gamma _{2N}\}$
and form products
 $$ \begin{align*}u(i)^j=x_{\gamma_1}(\xi(i)^j_{1})\ldots x_{\gamma_{2N}}(\xi(i)^j_{2N})=\prod_{h=1}^{2N} x_{\gamma_h}(\xi(i)^j_{h})\in E(\Phi,R_i),\qquad 1\le j\le L\end{align*} $$
$$ \begin{align*}u(i)^j=x_{\gamma_1}(\xi(i)^j_{1})\ldots x_{\gamma_{2N}}(\xi(i)^j_{2N})=\prod_{h=1}^{2N} x_{\gamma_h}(\xi(i)^j_{h})\in E(\Phi,R_i),\qquad 1\le j\le L\end{align*} $$
by the following rule:
 $$ \begin{align*}\xi(i)^j_h= \begin{cases} \xi(i)^j,&\text{if } \beta(i)_j=\gamma_h,\\ 0,&\text{otherwise.} \end{cases}.\end{align*} $$
$$ \begin{align*}\xi(i)^j_h= \begin{cases} \xi(i)^j,&\text{if } \beta(i)_j=\gamma_h,\\ 0,&\text{otherwise.} \end{cases}.\end{align*} $$
Then clearly
Thus, every element
can be expressed as
![]() $g=u^1\ldots u^L$
, where each of the L factors
$g=u^1\ldots u^L$
, where each of the L factors
can be expressed as a product of
![]() $2N$
elementary generators
$2N$
elementary generators
with parameters in
![]() $\displaystyle {\prod _{i\in I}R_i}$
.
$\displaystyle {\prod _{i\in I}R_i}$
.
Conversely, an element
![]() $g=(g_i)_{i\in I}$
, where
$g=(g_i)_{i\in I}$
, where
![]() $g_i\in E(\Phi ,R_i)$
, such that the length of its components
$g_i\in E(\Phi ,R_i)$
, such that the length of its components
![]() $g_i$
is unbounded, cannot possibly belong to
$g_i$
is unbounded, cannot possibly belong to
![]() $E(\Phi ,\displaystyle {\prod _{i\in I}R_i})$
.
$E(\Phi ,\displaystyle {\prod _{i\in I}R_i})$
.
Since bounded generation is inherited by factors, any ultraproduct
![]() $R=\prod _{\mathcal U} R_i$
of rings
$R=\prod _{\mathcal U} R_i$
of rings
![]() $R_i$
for which the elementary groups
$R_i$
for which the elementary groups
![]() $E(\Phi ,R_i)$
are uniformly boundedly generated enjoys the property that
$E(\Phi ,R_i)$
are uniformly boundedly generated enjoys the property that
![]() $E(\Phi ,R)$
is boundedly generated. In particular, this applies to ultrapowers
$E(\Phi ,R)$
is boundedly generated. In particular, this applies to ultrapowers
![]() ${}^*R$
, also known as nonstandard models of R. In other words, we have the following result.
${}^*R$
, also known as nonstandard models of R. In other words, we have the following result.
Lemma 8.3 Bounded elementary generation of the elementary group
![]() $E(\Phi ,R)$
is equivalent to the equality
$E(\Phi ,R)$
is equivalent to the equality
for all nonstandard models
![]() ${}^*R$
of R.
${}^*R$
of R.
Proof By the remark preceding the statement of this lemma, we only need to check the inverse implication. Denote by F the Fréchet filter on
![]() $ {\mathbb N}$
. Assume that
$ {\mathbb N}$
. Assume that
![]() $E(\Phi ,R)$
is not boundedly generated, or, what is the same, there exists a sequence
$E(\Phi ,R)$
is not boundedly generated, or, what is the same, there exists a sequence
![]() $g_i\in E(\Phi ,R)$
,
$g_i\in E(\Phi ,R)$
,
![]() $i\in {\mathbb N}$
of matrices from
$i\in {\mathbb N}$
of matrices from
![]() $E(\Phi ,R)$
with infinitely growing lengths. Then the element
$E(\Phi ,R)$
with infinitely growing lengths. Then the element
![]() $g=(g_1,g_2,g_3,\dots )$
has infinite length in
$g=(g_1,g_2,g_3,\dots )$
has infinite length in
![]() $E(\Phi ,R)^{\infty }$
and, by the very definition of F, also in
$E(\Phi ,R)^{\infty }$
and, by the very definition of F, also in
![]() $E(\Phi ,R)^{\infty }/F$
. In other words,
$E(\Phi ,R)^{\infty }/F$
. In other words,
![]() $g\notin E(\Phi ,R^{\infty }/F)$
.
$g\notin E(\Phi ,R^{\infty }/F)$
.
Since F is the intersection of all nonprincipal ultrafilters, there exists a nonprincipal ultrafilter
![]() $\mathcal U$
such that the image of g in the ultrapower
$\mathcal U$
such that the image of g in the ultrapower
![]() $^{\ast }E(\Phi ,R)=E(\Phi ,R)^{\infty }/{\mathcal U}$
does not belong to
$^{\ast }E(\Phi ,R)=E(\Phi ,R)^{\infty }/{\mathcal U}$
does not belong to
![]() $E(\Phi ,^{\ast }\!R)= E(\Phi ,R^{\infty }/{\mathcal U})$
. Thus, for this particular
$E(\Phi ,^{\ast }\!R)= E(\Phi ,R^{\infty }/{\mathcal U})$
. Thus, for this particular
![]() ${\mathcal U}$
, we have
${\mathcal U}$
, we have
![]() $^{\ast }E(\Phi ,R) \neq E(\Phi ,^{\ast }\!R)$
.
$^{\ast }E(\Phi ,R) \neq E(\Phi ,^{\ast }\!R)$
.
Remark 8.4 Assuming the Continuum Hypothesis, all
![]() ${}^\ast \!R$
are isomorphic and one has to require the equality
${}^\ast \!R$
are isomorphic and one has to require the equality
![]() $^{\ast }E(\Phi ,R)=E(\Phi ,^{\ast }\!R)$
for one nonstandard model. Otherwise, there are
$^{\ast }E(\Phi ,R)=E(\Phi ,^{\ast }\!R)$
for one nonstandard model. Otherwise, there are
![]() $2^{2^{\aleph _0}}$
ultrafilters that lead to non-isomorphic
$2^{2^{\aleph _0}}$
ultrafilters that lead to non-isomorphic
![]() ${}^\ast \!R$
, and to be on the safe side, one has to stipulate this equality for all of them.
${}^\ast \!R$
, and to be on the safe side, one has to stipulate this equality for all of them.
8.2 Congruence subgroup problem for nonstandard models
However, Carter, Keller, and Paige [Reference Carter, Keller and PaigeCKP] made this observation quite a bit more precise. Namely (see [Reference Carter, Keller and PaigeCKP, 2.1] or [Reference MorrisMo, Lemma 2.29]), they established the following fact.
Lemma 8.5 Bounded elementary generation of the elementary group
![]() $E(\Phi ,R)$
is equivalent to the condition
$E(\Phi ,R)$
is equivalent to the condition
for all nonstandard models
![]() ${}^*R$
of R.
${}^*R$
of R.
In fact, they proved that bounded elementary generation of the elementary group
![]() $E(\Phi ,R)$
is equivalent to the almost positive solution of the congruence subgroup problem for all nonstandard models
$E(\Phi ,R)$
is equivalent to the almost positive solution of the congruence subgroup problem for all nonstandard models
![]() ${}^*R$
of R.
${}^*R$
of R.
More precisely, [Reference Carter, Keller and PaigeCKP, 2.3] and [Reference MorrisMo] apply the whole machinery not just to the bounded generation of
![]() $\mathrm {SL}(n,R)$
but also to the bounded generation of
$\mathrm {SL}(n,R)$
but also to the bounded generation of
![]() $E(n,R,{\mathfrak q})$
in terms of the conjugates of elementary generators of level
$E(n,R,{\mathfrak q})$
in terms of the conjugates of elementary generators of level
![]() ${\mathfrak q}$
. They consider groups
${\mathfrak q}$
. They consider groups
![]() $ \mathrm {SL}(n,R,{\mathfrak q})/E(n,R,{\mathfrak q})$
which are isomorphic to quotients of universal Mennicke groups
$ \mathrm {SL}(n,R,{\mathfrak q})/E(n,R,{\mathfrak q})$
which are isomorphic to quotients of universal Mennicke groups
![]() $C({\mathfrak q})$
for all nonzero ideals
$C({\mathfrak q})$
for all nonzero ideals
![]() ${\mathfrak q}\unlhd R$
and restate bounded elementary generation of
${\mathfrak q}\unlhd R$
and restate bounded elementary generation of
![]() $E(n,R,{\mathfrak q})$
as the almost positive solution of the congruence subgroup problem for
$E(n,R,{\mathfrak q})$
as the almost positive solution of the congruence subgroup problem for
![]() $\mathrm {SL}(n,{}^*R)$
.
$\mathrm {SL}(n,{}^*R)$
.
Recall that we need a universal bound that depends only on the root system
![]() $\Phi $
and the degree of K. Since we reduce the problem to the congruence subgroup problem for
$\Phi $
and the degree of K. Since we reduce the problem to the congruence subgroup problem for
![]() $\mathrm {SL}(n,{}^*R)$
, we are very close to that.
$\mathrm {SL}(n,{}^*R)$
, we are very close to that.
8.3 Universal bound
Before going to
![]() $\mathrm {Sp} (4,R)$
we shall recall one more principal invention of Carter, Keller, and Paige [Reference Carter, Keller and PaigeCKP]. We need to pass from the ring of integers
$\mathrm {Sp} (4,R)$
we shall recall one more principal invention of Carter, Keller, and Paige [Reference Carter, Keller and PaigeCKP]. We need to pass from the ring of integers
![]() $R=\mathcal O_K$
in an algebraic number field to the ring
$R=\mathcal O_K$
in an algebraic number field to the ring
![]() ${}^*R$
. The ring
${}^*R$
. The ring
![]() ${}^*R$
is a nonstandard model of R; that is,
${}^*R$
is a nonstandard model of R; that is,
![]() ${}^*R$
equals to an ultrapower
${}^*R$
equals to an ultrapower
![]() $\prod _{\mathcal U} R$
along the ultrafilter
$\prod _{\mathcal U} R$
along the ultrafilter
![]() $\mathcal U$
. The good point is that thanks to Łoś’s theorem [Reference Chang and KeislerChKe, Theorem 4.1.9] ultrapowers keep first-order properties of structures unchanged. The bad point is that other properties do not survive, and in many senses,
$\mathcal U$
. The good point is that thanks to Łoś’s theorem [Reference Chang and KeislerChKe, Theorem 4.1.9] ultrapowers keep first-order properties of structures unchanged. The bad point is that other properties do not survive, and in many senses,
![]() ${}^*R$
is far away from the ring of integers R.
${}^*R$
is far away from the ring of integers R.
With this end, Carter, Keller, and Paige [Reference Carter, Keller and PaigeCKP] introduce arithmetic conditions
![]() $\mathrm {Gen}(t,r)$
and
$\mathrm {Gen}(t,r)$
and
![]() $\mathrm {Exp}(t,s)$
on a ring R that depend on natural parameters
$\mathrm {Exp}(t,s)$
on a ring R that depend on natural parameters
![]() $r,s$
, and t, which are too technical to describe them here in full. Morally,
$r,s$
, and t, which are too technical to describe them here in full. Morally,
![]() $\mathrm {Gen}(t,r)$
allows to uniformly bound the number of generators of the abelian groups
$\mathrm {Gen}(t,r)$
allows to uniformly bound the number of generators of the abelian groups
![]() $C({\mathfrak q})$
, while
$C({\mathfrak q})$
, while
![]() $\mathrm {Exp}(t,s)$
allows to uniformly bound their exponent. Besides, [Reference Carter, Keller and PaigeCKP] constantly used the fact that the stable rank of R is 1.5.
$\mathrm {Exp}(t,s)$
allows to uniformly bound their exponent. Besides, [Reference Carter, Keller and PaigeCKP] constantly used the fact that the stable rank of R is 1.5.
The importance of these conditions consists in the following pivotal observations. First of all, conditions
![]() $\mathrm {Gen}(t,r)$
,
$\mathrm {Gen}(t,r)$
,
![]() $\mathrm {Exp}(t,s)$
, and
$\mathrm {Exp}(t,s)$
, and
![]() $\mathrm {sr}(R)=1.5$
are stated in the first-order language of ring theory; see [Reference Carter, Keller and PaigeCKP, 2.2] or [Reference MorrisMo, Sections 3A and 3B]. Hence, the characteristic property of ultraproducts imply the following:
$\mathrm {sr}(R)=1.5$
are stated in the first-order language of ring theory; see [Reference Carter, Keller and PaigeCKP, 2.2] or [Reference MorrisMo, Sections 3A and 3B]. Hence, the characteristic property of ultraproducts imply the following:
Lemma 8.6 A commutative ring R satisfies conditions
![]() $\mathrm {Gen}(t,r)$
and
$\mathrm {Gen}(t,r)$
and
![]() $\mathrm {Exp}(t,s)$
with specific parameters if and only if
$\mathrm {Exp}(t,s)$
with specific parameters if and only if
![]() ${}^*R$
satisfies these conditions with the same parameters. Besides,
${}^*R$
satisfies these conditions with the same parameters. Besides,
![]() $\mathrm {sr}({}^*R)$
is 1.5.
$\mathrm {sr}({}^*R)$
is 1.5.
Most importantly, these conditions allow to bound uniformly the universal Mennicke groups
![]() $C({\mathfrak q})$
for all ideals
$C({\mathfrak q})$
for all ideals
![]() ${\mathfrak q}\unlhd R$
– and thus to get the finite congruence kernel of
${\mathfrak q}\unlhd R$
– and thus to get the finite congruence kernel of
![]() $G(\Phi ,{}^*R)$
. Indeed, the main (difficult!) step in obtaining a uniform bound in the number case is the following result; see [Reference Carter, Keller and PaigeCKP, Theorem 1.8] or [Reference MorrisMo, Theorem 3.11].
$G(\Phi ,{}^*R)$
. Indeed, the main (difficult!) step in obtaining a uniform bound in the number case is the following result; see [Reference Carter, Keller and PaigeCKP, Theorem 1.8] or [Reference MorrisMo, Theorem 3.11].
Lemma 8.7 Let
![]() $r,s,t$
be positive integers, and let R be an integral domain subject to the conditions
$r,s,t$
be positive integers, and let R be an integral domain subject to the conditions
![]() $\bullet $
$\bullet $
![]() $\mathrm {sr}(R)=1.5$
,
$\mathrm {sr}(R)=1.5$
,
![]() $\bullet $
$\bullet $
![]() $\mathrm {Gen}(t,r)$
,
$\mathrm {Gen}(t,r)$
,
![]() $\bullet $
$\bullet $
![]() $\mathrm {Exp}(t,s)$
.
$\mathrm {Exp}(t,s)$
.
Then for all ideals
![]() ${\mathfrak q}$
, the universal Mennicke group
${\mathfrak q}$
, the universal Mennicke group
![]() $C({\mathfrak q})$
is finite and its order is uniformly bounded by
$C({\mathfrak q})$
is finite and its order is uniformly bounded by
![]() $t^r$
.
$t^r$
.
Finally, the rings of integers of the number fields of bounded degree
![]() $[K:{\mathbb Q}]\le d$
satisfy these conditions for some values of parameters (which depend on d and which we do not wish to specify here). This result depends on [a very strong form of] the Dirichlet theorem on primes in arithmetic progressions. The following lemma is a [weaker form of the] conjunction of [Reference Carter, Keller and PaigeCKP, Lemmas 4.4 and 4.5] or [Reference MorrisMo, Corollary 3.5 and Theorem 3.9]; the proof thereof requires subtle arithmetic properties of norm maps on the groups of units that are based on the aforementioned Dirichlet theorem (see [Reference Carter, Keller and PaigeCKP, Lemma 4.3] or [Reference MorrisMo, Lemma 3.8]).
$[K:{\mathbb Q}]\le d$
satisfy these conditions for some values of parameters (which depend on d and which we do not wish to specify here). This result depends on [a very strong form of] the Dirichlet theorem on primes in arithmetic progressions. The following lemma is a [weaker form of the] conjunction of [Reference Carter, Keller and PaigeCKP, Lemmas 4.4 and 4.5] or [Reference MorrisMo, Corollary 3.5 and Theorem 3.9]; the proof thereof requires subtle arithmetic properties of norm maps on the groups of units that are based on the aforementioned Dirichlet theorem (see [Reference Carter, Keller and PaigeCKP, Lemma 4.3] or [Reference MorrisMo, Lemma 3.8]).
Lemma 8.8 The ring of integers
![]() $R=\mathcal O_K$
in an algebraic number field K satisfies
$R=\mathcal O_K$
in an algebraic number field K satisfies
![]() $\mathrm {Gen}(t,1)$
for every positive integer t and
$\mathrm {Gen}(t,1)$
for every positive integer t and
![]() $\mathrm {Exp}(t,2)$
for some t depending on the degree
$\mathrm {Exp}(t,2)$
for some t depending on the degree
![]() $d=[K:{\mathbb Q}]$
.
$d=[K:{\mathbb Q}]$
.
Hence, one can take
![]() $R={}^*R$
in Lemma 8.7 and arrive at the almost positive solution of the congruence problem in
$R={}^*R$
in Lemma 8.7 and arrive at the almost positive solution of the congruence problem in
![]() $\mathrm {SL}(n,{}^*R)$
, as required.
$\mathrm {SL}(n,{}^*R)$
, as required.
To use the above fact for
![]() $\mathrm {SL}(n,{}^*R)=\mathrm {SL}(n,\prod _{\mathcal U} R)$
is the same as to use the Compactness Theorem as is in [Reference Carter, Keller and PaigeCKP] or [Reference MorrisMo, Theorem 2.7]. In any case (cf. [Reference Carter, Keller and PaigeCKP, Theorem 2.4] or [Reference MorrisMo, Corollary 3.13]), we get bounded elementary generation of
$\mathrm {SL}(n,{}^*R)=\mathrm {SL}(n,\prod _{\mathcal U} R)$
is the same as to use the Compactness Theorem as is in [Reference Carter, Keller and PaigeCKP] or [Reference MorrisMo, Theorem 2.7]. In any case (cf. [Reference Carter, Keller and PaigeCKP, Theorem 2.4] or [Reference MorrisMo, Corollary 3.13]), we get bounded elementary generation of
![]() $\mathrm {SL}(n,R)$
with the bound that only depends on the root system
$\mathrm {SL}(n,R)$
with the bound that only depends on the root system
![]() $\Phi $
and the degree of K.
$\Phi $
and the degree of K.
At this point, [Reference Carter, Keller and PaigeCKP, 2.5] use a standard argument from nonstandard analysis. Since the elementary width
![]() $w(G)\in {}^*{\mathbb N}$
of
$w(G)\in {}^*{\mathbb N}$
of
![]() $G=\mathrm {SL}(n,R)$
on this class of rings R is internally defined, everywhere finite, and bounded (by any infinite natural number), it must attain maximal value, which is obviously finite (all of them are!).
$G=\mathrm {SL}(n,R)$
on this class of rings R is internally defined, everywhere finite, and bounded (by any infinite natural number), it must attain maximal value, which is obviously finite (all of them are!).
The proof of the uniform bounded generation for Chevalley groups will be completed if we cover the case of symplectic groups. The standard reasoning says that it is enough to prove the fact for the rank 2 case – that is, for
![]() $\mathrm {Sp}(4,R)$
. The proof basically follows the line depicted above for
$\mathrm {Sp}(4,R)$
. The proof basically follows the line depicted above for
![]() $G=\mathrm {SL}(n,R)$
.
$G=\mathrm {SL}(n,R)$
.
Passing from
![]() $\mathrm {SL}(n,R)$
to
$\mathrm {SL}(n,R)$
to
![]() $\mathrm {Sp}(2l,R)$
(
$\mathrm {Sp}(2l,R)$
(
![]() $l\ge 2$
), we have to consider the group
$l\ge 2$
), we have to consider the group
![]() $\mathrm {Cp}({\mathfrak q}):=\mathrm {Sp}(2l,{\mathfrak q})/\mathrm {Ep}(2l,{\mathfrak q})$
in place of
$\mathrm {Cp}({\mathfrak q}):=\mathrm {Sp}(2l,{\mathfrak q})/\mathrm {Ep}(2l,{\mathfrak q})$
in place of
![]() $C({\mathfrak q})$
(recall that the group
$C({\mathfrak q})$
(recall that the group
![]() $\mathrm {Cp}({\mathfrak q})$
is well defined, finite, and independent of l; see [Reference Bass, Milnor and SerreBMS, Theorem 12.4 and Corollary 12.5]).
$\mathrm {Cp}({\mathfrak q})$
is well defined, finite, and independent of l; see [Reference Bass, Milnor and SerreBMS, Theorem 12.4 and Corollary 12.5]).
The case
![]() $\mathrm {Sp}(4,R)$
is similar but much more difficult than the one of
$\mathrm {Sp}(4,R)$
is similar but much more difficult than the one of
![]() $\mathrm {SL}(3,R)$
. The point is that there are two embeddings
$\mathrm {SL}(3,R)$
. The point is that there are two embeddings
![]() $\mathsf A_1\to \mathsf C_2$
and
$\mathsf A_1\to \mathsf C_2$
and
![]() $\widetilde {\mathsf {A}}_1\to \mathsf C_2$
, on long and short roots, respectively. This results in a more complicated structure of the universal Mennicke group (cf. [Reference Bass, Milnor and SerreBMS, Lemma 13.3]). The decisive role is played by the following quite technical theorem proven by Trost. It serves as a symplectic analogue of Lemma 8.7.
$\widetilde {\mathsf {A}}_1\to \mathsf C_2$
, on long and short roots, respectively. This results in a more complicated structure of the universal Mennicke group (cf. [Reference Bass, Milnor and SerreBMS, Lemma 13.3]). The decisive role is played by the following quite technical theorem proven by Trost. It serves as a symplectic analogue of Lemma 8.7.
Lemma 8.9 [Reference TrostTr1, Theorem 3.16]
Let
![]() $s,t$
be positive integers, and let R be a commutative ring with 1 subject to the conditions
$s,t$
be positive integers, and let R be a commutative ring with 1 subject to the conditions
![]() $\bullet $
$\bullet $
![]() $\mathrm {sr}(R)=1.5$
,
$\mathrm {sr}(R)=1.5$
,
![]() $\bullet $
$\bullet $
![]() $\mathrm {Gen}(2,1)$
,
$\mathrm {Gen}(2,1)$
,
![]() $\bullet $
$\bullet $
![]() $\mathrm {Gen}(t,1)$
,
$\mathrm {Gen}(t,1)$
,
![]() $\bullet $
$\bullet $
![]() $\mathrm {Exp}(t,s)$
.
$\mathrm {Exp}(t,s)$
.
Then for all ideals
![]() ${\mathfrak q}$
, the group
${\mathfrak q}$
, the group
![]() $\mathrm {Cp}({\mathfrak q})$
is finite and its order is uniformly bounded by
$\mathrm {Cp}({\mathfrak q})$
is finite and its order is uniformly bounded by
![]() $2t$
.
$2t$
.
This parallelism can now be used to conclude that
![]() $\mathrm {Sp} (4,R)$
is uniformly elementarily boundedly generated, with a universal bound that only depends on the degree of K (which is equal to 2 in the case under consideration), and is thus an absolute constant (see [Reference TrostTr1, Theorem 3.20 and Section 3.3] for details of the proof). This concludes the proof of Lemma 8.1.
$\mathrm {Sp} (4,R)$
is uniformly elementarily boundedly generated, with a universal bound that only depends on the degree of K (which is equal to 2 in the case under consideration), and is thus an absolute constant (see [Reference TrostTr1, Theorem 3.20 and Section 3.3] for details of the proof). This concludes the proof of Lemma 8.1.
Remark 8.10 The arguments presented above can be rephrased in a more traditional logical language, in the form of the compactness theorem of the first-order logic, as was done by Morris [Reference MorrisMo, Proposition 1.5] and Trost [Reference TrostTr1, Theorem 3.1].
9 Concluding remarks
Here, we mention a couple of eventual generalizations of our results.
![]() $\bullet $
In the number case, the bounds for
$\bullet $
In the number case, the bounds for
![]() $L(2,2)$
and
$L(2,2)$
and
![]() $L'(2,2)$
are not explicit at all. It seems that it might be quite a challenge to obtain any explicit bounds. Our impression is that it cannot be easily done at the level of the groups; one should invoke much more arithmetics.
$L'(2,2)$
are not explicit at all. It seems that it might be quite a challenge to obtain any explicit bounds. Our impression is that it cannot be easily done at the level of the groups; one should invoke much more arithmetics.
![]() $\bullet $
However, we do not claim that the bounds obtained in the present paper in the function case are sharp in any sense. It is another, maybe even a greater, challenge to obtain such sharp bounds. It is usually very hard to estimate width from above, but still harder to estimate it from below.
$\bullet $
However, we do not claim that the bounds obtained in the present paper in the function case are sharp in any sense. It is another, maybe even a greater, challenge to obtain such sharp bounds. It is usually very hard to estimate width from above, but still harder to estimate it from below.
![]() $\bullet $
Let
$\bullet $
Let
![]() ${\mathfrak q}\unlhd R$
be an ideal of R. In the present paper, we addressed the absolute case
${\mathfrak q}\unlhd R$
be an ideal of R. In the present paper, we addressed the absolute case
![]() ${\mathfrak q}=R$
alone. However, it makes sense to ask similar questions for the relative case; in other words, we believe there are uniform width bounds for the true elementary subgroup
${\mathfrak q}=R$
alone. However, it makes sense to ask similar questions for the relative case; in other words, we believe there are uniform width bounds for the true elementary subgroup
![]() $E(\Phi ,{\mathfrak q})$
and the relative elementary subgroups
$E(\Phi ,{\mathfrak q})$
and the relative elementary subgroups
![]() $E(\Phi ,R,{\mathfrak q})$
of level
$E(\Phi ,R,{\mathfrak q})$
of level
![]() ${\mathfrak q}\unlhd R$
in terms of elementary generators, or elementary conjugates of level
${\mathfrak q}\unlhd R$
in terms of elementary generators, or elementary conjugates of level
![]() ${\mathfrak q}$
.
${\mathfrak q}$
.
There are some partial results in this direction for classical groups, but some of them use larger sets of generators. The results by Tavgen [Reference TavgenTa2], Sergei Sinchuk, and Andrei Smolensky [Reference Sinchuk and SmolenskySiSm] and by Pavel Gvozdevsky [Reference GvozdevskyGv] use correct sets of generators (so-called Tits–Vaserstein generators), but their bounds are not uniform. Recently, the third author established the conclusive result in this direction [Reference VavilovVa2]: Theorem B in that paper states that given a reduced irreducible root system
![]() $\Phi $
of rank
$\Phi $
of rank
![]() $ \ge 2$
, a Dedekind ring R of arithmetic type, and an ideal
$ \ge 2$
, a Dedekind ring R of arithmetic type, and an ideal
![]() $\mathfrak q$
of R, there exists a constant
$\mathfrak q$
of R, there exists a constant
![]() $M = M(\Phi , R, \mathfrak q)$
such that any element in
$M = M(\Phi , R, \mathfrak q)$
such that any element in
![]() $E_{\textrm {sc}}(\Phi , R, \mathfrak q)$
is a product of at most M Tits–Vaserstein generators. Note that as in the works cited above, M depends on the ring and the ideal. In comparison, in the function case, Trost [Reference TrostTr3] produced uniform bounds for all types of irreducible root systems except
$E_{\textrm {sc}}(\Phi , R, \mathfrak q)$
is a product of at most M Tits–Vaserstein generators. Note that as in the works cited above, M depends on the ring and the ideal. In comparison, in the function case, Trost [Reference TrostTr3] produced uniform bounds for all types of irreducible root systems except
![]() $\mathsf B_n$
and
$\mathsf B_n$
and
![]() $\mathsf D_n$
.Footnote
6
$\mathsf D_n$
.Footnote
6
Acknowledgements
We are grateful to Nikolai Bazhenov, Sergei Gorchinsky, Pavel Gvozdevsky, Andrei Lavrenov, Alexei Myasnikov, Denis Osipov, Ivan Panin, Victor Selivanov, and Dmitry Timashev for useful discussions of various aspects of this work [and [Reference Kunyavskiĭ, Lavrenov, Plotkin and VavilovKLPV]]. Our special thanks go to Alexander Trost whose thoughtful comments on an earlier version of this paper allowed us to considerably improve the exposition. We thank the referee for careful reading and important remarks.