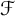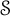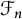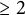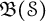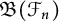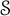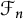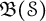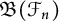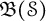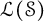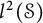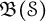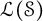1 Introduction
The cohomology theory of associative algebras was initiated by Hochschild [Reference Hochschild10–Reference Hochschild12] in 1945 in terms of multilinear maps into a bimodule and coboundary operators. In 1953, after discussing with Singer at a conference, Kaplansky went on from there to write his paper [Reference Kaplansky21] proposing some problems about derivations on
![]() $C^*$
-algebras and von Neumann algebras. He showed that every derivation on a von Neumann algebra
$C^*$
-algebras and von Neumann algebras. He showed that every derivation on a von Neumann algebra
![]() $\mathcal {M}$
of type I is inner, which may be restated in cohomological terms that the first continuous cohomology group of
$\mathcal {M}$
of type I is inner, which may be restated in cohomological terms that the first continuous cohomology group of
![]() $\mathcal {M}$
with coefficients in itself vanishes.
$\mathcal {M}$
with coefficients in itself vanishes.
Recall that a derivation of a Banach algebra
![]() $\mathcal {A}$
(over the complex field
$\mathcal {A}$
(over the complex field
![]() $\mathbb {C}$
) with coefficients in a Banach
$\mathbb {C}$
) with coefficients in a Banach
![]() $\mathcal {A}$
-bimodule
$\mathcal {A}$
-bimodule
![]() $\mathcal {X}$
is a linear map D from
$\mathcal {X}$
is a linear map D from
![]() $\mathcal {A}$
into
$\mathcal {A}$
into
![]() $\mathcal {X}$
satisfying the Leibniz rule, i.e.,
$\mathcal {X}$
satisfying the Leibniz rule, i.e.,
![]() $D(AB)=AD(B)+D(A)B$
for all A, B in
$D(AB)=AD(B)+D(A)B$
for all A, B in
![]() $\mathcal {A}$
. We say that D is inner if there is an element T in
$\mathcal {A}$
. We say that D is inner if there is an element T in
![]() $\mathcal {X}$
such that
$\mathcal {X}$
such that
![]() $D(A)=AT-TA$
for each A in
$D(A)=AT-TA$
for each A in
![]() $\mathcal {A}$
. Let
$\mathcal {A}$
. Let
![]() $\mathcal {Z}^1(\mathcal {A},\mathcal {X})$
denote the space of all (continuous) derivations from
$\mathcal {Z}^1(\mathcal {A},\mathcal {X})$
denote the space of all (continuous) derivations from
![]() $\mathcal {A}$
into
$\mathcal {A}$
into
![]() $\mathcal {X}$
and
$\mathcal {X}$
and
![]() $\mathcal {B}^1(\mathcal {A},\mathcal {X})$
the space of all inner derivations. It is clear that
$\mathcal {B}^1(\mathcal {A},\mathcal {X})$
the space of all inner derivations. It is clear that
![]() $\mathcal {B}^1(\mathcal {A},\mathcal {X})$
is a linear subspace of
$\mathcal {B}^1(\mathcal {A},\mathcal {X})$
is a linear subspace of
![]() $\mathcal {Z}^1(\mathcal {A},\mathcal {X})$
. The first (continuous) Hochschild cohomology group of
$\mathcal {Z}^1(\mathcal {A},\mathcal {X})$
. The first (continuous) Hochschild cohomology group of
![]() $\mathcal {A}$
with coefficients in
$\mathcal {A}$
with coefficients in
![]() $\mathcal {X}$
is then defined to be the following quotient vector space:
$\mathcal {X}$
is then defined to be the following quotient vector space:
 $$\begin{align*}H^1(\mathcal{A},\mathcal{X})=\frac{\mathcal{Z}^1(\mathcal{A},\mathcal{X})}{\mathcal{B}^1(\mathcal{A},\mathcal{X})}.\end{align*}$$
$$\begin{align*}H^1(\mathcal{A},\mathcal{X})=\frac{\mathcal{Z}^1(\mathcal{A},\mathcal{X})}{\mathcal{B}^1(\mathcal{A},\mathcal{X})}.\end{align*}$$
The study of cohomology groups of operator algebras started with the Kadison–Sakai theorem [Reference Kadison18, Reference Sakai24]: Every derivation on a von Neumann algebra
![]() $\mathcal {M}$
is inner, i.e.,
$\mathcal {M}$
is inner, i.e.,
![]() $H^{1}(\mathcal {M},\mathcal {M})=0$
. Whether every derivation of a von Neumann algebra
$H^{1}(\mathcal {M},\mathcal {M})=0$
. Whether every derivation of a von Neumann algebra
![]() $\mathcal {M}$
into
$\mathcal {M}$
into
![]() $B(\mathcal {H})$
is always inner is still an open problem, which is equivalent to several open problems in operator algebras. One of such problems is Kadison’s similarity problem [Reference Kadison17], which asks if every bounded representation of a
$B(\mathcal {H})$
is always inner is still an open problem, which is equivalent to several open problems in operator algebras. One of such problems is Kadison’s similarity problem [Reference Kadison17], which asks if every bounded representation of a
![]() $C^*$
-algebra into
$C^*$
-algebra into
![]() $B(\mathcal {H})$
is always similar to a
$B(\mathcal {H})$
is always similar to a
![]() $*$
-representation. To study the classification of von Neumann algebras, from 1968 to 1972, Johnson, Kadison, and Ringrose [Reference Johnson14, Reference Johnson, Kadison and Ringrose15, Reference Kadison and Ringrose19, Reference Kadison and Ringrose20] proved a series of technical results of the cohomology groups of von Neumann algebras. In particular, they showed that
$*$
-representation. To study the classification of von Neumann algebras, from 1968 to 1972, Johnson, Kadison, and Ringrose [Reference Johnson14, Reference Johnson, Kadison and Ringrose15, Reference Kadison and Ringrose19, Reference Kadison and Ringrose20] proved a series of technical results of the cohomology groups of von Neumann algebras. In particular, they showed that
![]() $H^{n}(\mathcal {M},\mathcal {M})=0$
for all
$H^{n}(\mathcal {M},\mathcal {M})=0$
for all
![]() $n\geq 1$
when
$n\geq 1$
when
![]() $\mathcal {M}$
is a hyperfinite von Neumann algebra. Due to this fact, Kadison and Ringrose conjectured that these cohomology groups are zero for all von Neumann algebras. With the aid of the theory of completely bounded cohomology groups, this conjecture can be ultimately reduced to the case when
$\mathcal {M}$
is a hyperfinite von Neumann algebra. Due to this fact, Kadison and Ringrose conjectured that these cohomology groups are zero for all von Neumann algebras. With the aid of the theory of completely bounded cohomology groups, this conjecture can be ultimately reduced to the case when
![]() $\mathcal {M}$
is a factor of type II
$\mathcal {M}$
is a factor of type II
![]() $_1$
with separable predual. In [Reference Sinclair and Smith26], Sinclair and Smith showed that the conjecture holds for von Neumann algebras with Cartan subalgebras and separable preduals. Later in 2003, Christensen et al. [Reference Christensen, Pop, Sinclair and Smith4] proved that the continuous cohomology groups
$_1$
with separable predual. In [Reference Sinclair and Smith26], Sinclair and Smith showed that the conjecture holds for von Neumann algebras with Cartan subalgebras and separable preduals. Later in 2003, Christensen et al. [Reference Christensen, Pop, Sinclair and Smith4] proved that the continuous cohomology groups
![]() $H^n(\mathcal {M},\mathcal {M})$
and
$H^n(\mathcal {M},\mathcal {M})$
and
![]() $H^n(\mathcal {M}, B(\mathcal {H})) $
of a factor
$H^n(\mathcal {M}, B(\mathcal {H})) $
of a factor
![]() $\mathcal {M} \subseteq B(\mathcal {H})$
of type II
$\mathcal {M} \subseteq B(\mathcal {H})$
of type II
![]() $_1$
with property
$_1$
with property
![]() $\Gamma $
are zero for all
$\Gamma $
are zero for all
![]() $n\geq 1$
. The latest result was proved by Pop and Smith [Reference Pop and Smith22]. They showed that the second cohomology group
$n\geq 1$
. The latest result was proved by Pop and Smith [Reference Pop and Smith22]. They showed that the second cohomology group
![]() $H^{2}(\mathcal {M} \overline {\otimes } \mathcal {N},\mathcal {M} \overline {\otimes } \mathcal {N})$
vanishes for arbitrary type II
$H^{2}(\mathcal {M} \overline {\otimes } \mathcal {N},\mathcal {M} \overline {\otimes } \mathcal {N})$
vanishes for arbitrary type II
![]() $_1$
von Neumann algebras
$_1$
von Neumann algebras
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathcal {N}$
. Note that the free group factor
$\mathcal {N}$
. Note that the free group factor
![]() $\mathcal {L}(\mathcal {F}_2)$
satisfies none of the above cases and the higher order cohomology groups of
$\mathcal {L}(\mathcal {F}_2)$
satisfies none of the above cases and the higher order cohomology groups of
![]() $\mathcal {L}(\mathcal {F}_2)$
are still unknown.
$\mathcal {L}(\mathcal {F}_2)$
are still unknown.
Cohomology groups of Banach algebras are different from that of von Neumann algebras in two main aspects: the automatic continuity of derivations and the cohomology groups. It was conjectured by Kaplansky in [Reference Kaplansky21] (which was finally proved by Sakai in [Reference Sakai23]) that every derivation on a C
![]() $^*$
-algebra is continuous. While, derivations on a Banach algebra are not necessarily continuous. In [Reference Bade and Curtis1], Bade and Curtis constructed several examples of Banach algebras on which not all derivations are continuous. On the other hand, Johnson and Sinclair [Reference Johnson and Sinclair16] showed that the continuity of derivations still holds for semisimple Banach algebras. Up to now, there are no examples showing that the cohomology groups of a von Neumann algebra are nontrivial. Let
$^*$
-algebra is continuous. While, derivations on a Banach algebra are not necessarily continuous. In [Reference Bade and Curtis1], Bade and Curtis constructed several examples of Banach algebras on which not all derivations are continuous. On the other hand, Johnson and Sinclair [Reference Johnson and Sinclair16] showed that the continuity of derivations still holds for semisimple Banach algebras. Up to now, there are no examples showing that the cohomology groups of a von Neumann algebra are nontrivial. Let
![]() $\mathcal {A}(\mathbb {D})$
be the set of all complex-valued functions that are continuous on the closed unit disk and analytic in the interior. Then
$\mathcal {A}(\mathbb {D})$
be the set of all complex-valued functions that are continuous on the closed unit disk and analytic in the interior. Then
![]() $\mathcal {A}(\mathbb {D})$
endowed with the supremum norm is a unital Banach algebra. The second cohomology group of
$\mathcal {A}(\mathbb {D})$
endowed with the supremum norm is a unital Banach algebra. The second cohomology group of
![]() $\mathcal {A}(\mathbb {D})$
(with coefficients in itself) is nontrivial [Reference Johnson13, Proposition 9.1].
$\mathcal {A}(\mathbb {D})$
(with coefficients in itself) is nontrivial [Reference Johnson13, Proposition 9.1].
Thompson’s group
![]() $\mathcal {F}=\langle X_0,X_1,X_2,\ldots \ |\ X_{i}^{-1}X_{j}X_{i}=X_{j+1},\ j>i\ \rangle $
was introduced by Richard Thompson in 1965 [Reference Cannon, Floyd and Parry3]. It was conjectured by Geoghegan around 1979 that: (i) the group
$\mathcal {F}=\langle X_0,X_1,X_2,\ldots \ |\ X_{i}^{-1}X_{j}X_{i}=X_{j+1},\ j>i\ \rangle $
was introduced by Richard Thompson in 1965 [Reference Cannon, Floyd and Parry3]. It was conjectured by Geoghegan around 1979 that: (i) the group
![]() $\mathcal {F}$
contains no non-abelian free groups; (
$\mathcal {F}$
contains no non-abelian free groups; (
![]() $ii$
)
$ii$
)
![]() $\mathcal {F}$
is not amenable. Statement (i) was obtained by Brin and Squier [Reference Brin and Squier2] in 1985 while (
$\mathcal {F}$
is not amenable. Statement (i) was obtained by Brin and Squier [Reference Brin and Squier2] in 1985 while (
![]() $ii$
) still remains unknown. Many research works nowadays are developed to answer this question due to two main reasons:
$ii$
) still remains unknown. Many research works nowadays are developed to answer this question due to two main reasons:
![]() $(1)$
$(1)$
![]() $\mathcal {F}$
is related to many branches of mathematics such as geometric group theory;
$\mathcal {F}$
is related to many branches of mathematics such as geometric group theory;
![]() $(2)$
the amenability problem is one of the most significant research areas in mathematics. Every non-unital element in
$(2)$
the amenability problem is one of the most significant research areas in mathematics. Every non-unital element in
![]() $\mathcal {F}$
has as a unique normal form:
$\mathcal {F}$
has as a unique normal form:
![]() $X_{0}^{\alpha _0}X_{1}^{\alpha _1}\dots X_{n}^{\alpha _n}X_{n}^{-\beta _n}\dots X_{0}^{-\beta _0}$
, where
$X_{0}^{\alpha _0}X_{1}^{\alpha _1}\dots X_{n}^{\alpha _n}X_{n}^{-\beta _n}\dots X_{0}^{-\beta _0}$
, where
![]() $\alpha _{0}$
,
$\alpha _{0}$
,
![]() $\ldots $
,
$\ldots $
,
![]() $\alpha _{n}$
,
$\alpha _{n}$
,
![]() $\beta _{0}$
,
$\beta _{0}$
,
![]() $\ldots $
,
$\ldots $
,
![]() $\beta _{n}$
, and n are natural numbers such that (i) exactly one of
$\beta _{n}$
, and n are natural numbers such that (i) exactly one of
![]() $\alpha _n$
and
$\alpha _n$
and
![]() $\beta _n$
is nonzero and (
$\beta _n$
is nonzero and (
![]() $ii$
) if
$ii$
) if
![]() $\alpha _k>0$
and
$\alpha _k>0$
and
![]() $\beta _k>0$
for some integer k with
$\beta _k>0$
for some integer k with
![]() $0 < k < n$
, then
$0 < k < n$
, then
![]() $\alpha _{k+1}> 0$
or
$\alpha _{k+1}> 0$
or
![]() $\beta _{k+1}> 0$
. For example,
$\beta _{k+1}> 0$
. For example,
![]() $X_0X_1X_{0}^{-1}$
and
$X_0X_1X_{0}^{-1}$
and
![]() $X_0X_1X_{2}^{-1}X_{0}^{-1}$
are two normal forms while
$X_0X_1X_{2}^{-1}X_{0}^{-1}$
are two normal forms while
![]() $X_0X_2X_{3}^{-1}X_{0}^{-1}$
is not. The amenability of Thompson’s group
$X_0X_2X_{3}^{-1}X_{0}^{-1}$
is not. The amenability of Thompson’s group
![]() $\mathcal {F}$
has been an open problem for more than 40 years. We refer to a nice survey paper [Reference Cannon, Floyd and Parry3] for more details.
$\mathcal {F}$
has been an open problem for more than 40 years. We refer to a nice survey paper [Reference Cannon, Floyd and Parry3] for more details.
The notion of amenability of a group is introduced by von Neumann. Let G be a discrete group and
![]() $l^{\infty }(G)$
the space of all bounded complex-valued functions on G. Then
$l^{\infty }(G)$
the space of all bounded complex-valued functions on G. Then
![]() $l^{\infty }(G)$
is a commutative
$l^{\infty }(G)$
is a commutative
![]() $C^{*}$
-algebra. The group G is said to be amenable if there is a state
$C^{*}$
-algebra. The group G is said to be amenable if there is a state
![]() $\mu $
on
$\mu $
on
![]() $l^{\infty }(G)$
such that
$l^{\infty }(G)$
such that
![]() $\mu (g\varphi )=\mu (\varphi )$
, where
$\mu (g\varphi )=\mu (\varphi )$
, where
![]() $\varphi \in l^{\infty }(G)$
,
$\varphi \in l^{\infty }(G)$
,
![]() $g\in G$
, and
$g\in G$
, and
![]() $g\varphi $
is defined by
$g\varphi $
is defined by
![]() $(g\varphi )(h)=\varphi (g^{-1}h)$
for each h in G. The state
$(g\varphi )(h)=\varphi (g^{-1}h)$
for each h in G. The state
![]() $\mu $
is then called (by von Neumann) a left invariant mean on
$\mu $
is then called (by von Neumann) a left invariant mean on
![]() $l^{\infty }(G)$
. The additive group of integers
$l^{\infty }(G)$
. The additive group of integers
![]() $(\mathbb {Z},+)$
is amenable while the free group
$(\mathbb {Z},+)$
is amenable while the free group
![]() $\mathcal {F}_2$
on two generators is not. In [Reference Johnson13], Johnson characterized the amenable group G through the first Hochschild cohomology groups of
$\mathcal {F}_2$
on two generators is not. In [Reference Johnson13], Johnson characterized the amenable group G through the first Hochschild cohomology groups of
![]() $l^{1}(G)$
, the space of all absolute-summable complex-valued functions on G, with coefficients in dual Banach
$l^{1}(G)$
, the space of all absolute-summable complex-valued functions on G, with coefficients in dual Banach
![]() $l^{1}(G)$
-bimodules: Let G be a discrete group. Then G is amenable if and only if
$l^{1}(G)$
-bimodules: Let G be a discrete group. Then G is amenable if and only if
![]() $H^{1}(l^{1}(G), \mathcal {X}^{*})=0$
for each Banach
$H^{1}(l^{1}(G), \mathcal {X}^{*})=0$
for each Banach
![]() $l^{1}(G)$
-bimodule
$l^{1}(G)$
-bimodule
![]() $\mathcal {X}$
. This statement is also true for locally compact groups by [Reference Johnson13].
$\mathcal {X}$
. This statement is also true for locally compact groups by [Reference Johnson13].
In this paper, we shall apply the theory of cohomology to study the amenability of
![]() $\mathcal {F}$
. Let
$\mathcal {F}$
. Let
![]() $\mathcal {S}$
be the subset
$\mathcal {S}$
be the subset
![]() $\{X_0^{i_0}\dots X_n^{i_n}\in \mathcal {F}\,:\, i_j\in \mathbb {N},\ 1\leq j \leq n \} $
of
$\{X_0^{i_0}\dots X_n^{i_n}\in \mathcal {F}\,:\, i_j\in \mathbb {N},\ 1\leq j \leq n \} $
of
![]() $\mathcal {F}$
. Then
$\mathcal {F}$
. Then
![]() $\mathcal {S}=\langle X_0,X_1,X_2,\ldots \ |\ X_{j}X_{i}=X_{i} X_{j+1},\ j>i\ \rangle ^+$
is a discrete cancellative semigroup. We call it Thompson’s semigroup. The structure of
$\mathcal {S}=\langle X_0,X_1,X_2,\ldots \ |\ X_{j}X_{i}=X_{i} X_{j+1},\ j>i\ \rangle ^+$
is a discrete cancellative semigroup. We call it Thompson’s semigroup. The structure of
![]() $\mathcal {F}$
is inherited by
$\mathcal {F}$
is inherited by
![]() $\mathcal {S}$
as well. It was proved by Grigorchuk in 1990 that Thompson’s group
$\mathcal {S}$
as well. It was proved by Grigorchuk in 1990 that Thompson’s group
![]() $\mathcal {F}$
is amenable if and only if Thompson’s semigroup
$\mathcal {F}$
is amenable if and only if Thompson’s semigroup
![]() $\mathcal {S}$
is left amenable. It is clear that every non-unital element in
$\mathcal {S}$
is left amenable. It is clear that every non-unital element in
![]() $\mathcal {S}$
can be uniquely written as
$\mathcal {S}$
can be uniquely written as
![]() $X_{i_1}^{\alpha _1}\dots X_{i_n}^{\alpha _n}$
(
$X_{i_1}^{\alpha _1}\dots X_{i_n}^{\alpha _n}$
(
![]() $i_1<\cdots <i_n$
) for some positive integers
$i_1<\cdots <i_n$
) for some positive integers
![]() $\alpha _j$
(
$\alpha _j$
(
![]() $1\leq j\leq n$
). This property is similar to the fundamental theorem of arithmetic which states that every natural number (
$1\leq j\leq n$
). This property is similar to the fundamental theorem of arithmetic which states that every natural number (
![]() $\geq 2$
) can be uniquely written as the product of primes up to reorder. Moreover, classical arithmetic functions, such as the Möbius function and divisor function, can be generalized on
$\geq 2$
) can be uniquely written as the product of primes up to reorder. Moreover, classical arithmetic functions, such as the Möbius function and divisor function, can be generalized on
![]() $\mathcal {S}$
[Reference Xue27]. Ge, Ma, and Qi introduced
$\mathcal {S}$
[Reference Xue27]. Ge, Ma, and Qi introduced
![]() $\zeta $
-functions on Thompson’s semigroup and studied the analytic structures [Reference Ge, Ma and Qi9]. These properties can help us to understand the structure of
$\zeta $
-functions on Thompson’s semigroup and studied the analytic structures [Reference Ge, Ma and Qi9]. These properties can help us to understand the structure of
![]() $\mathcal {S}$
better. Therefore, studying
$\mathcal {S}$
better. Therefore, studying
![]() $\mathcal {S}$
may bring more useful tools to study the amenability of
$\mathcal {S}$
may bring more useful tools to study the amenability of
![]() $\mathcal {F}$
.
$\mathcal {F}$
.
Let
![]() $\mathfrak {B}(\mathcal {S})$
be the Banach algebra generated by the left regular representation of
$\mathfrak {B}(\mathcal {S})$
be the Banach algebra generated by the left regular representation of
![]() $\mathcal {S}$
, and let
$\mathcal {S}$
, and let
![]() $\mathcal {X}$
be a Banach
$\mathcal {X}$
be a Banach
![]() $\mathfrak {B}(\mathcal {S})$
-bimodule. The Banach algebras
$\mathfrak {B}(\mathcal {S})$
-bimodule. The Banach algebras
![]() $\mathfrak {B}(\mathcal {S})$
and
$\mathfrak {B}(\mathcal {S})$
and
![]() $\mathcal {L}(\mathcal {S})$
(see Section 2) are two important Banach
$\mathcal {L}(\mathcal {S})$
(see Section 2) are two important Banach
![]() $\mathfrak {B}(\mathcal {S})$
-bimodules. We strongly believe that if
$\mathfrak {B}(\mathcal {S})$
-bimodules. We strongly believe that if
![]() $H^{n}(\mathfrak {B}(\mathcal {S}),\mathcal {X})\neq 0$
or
$H^{n}(\mathfrak {B}(\mathcal {S}),\mathcal {X})\neq 0$
or
![]() $H^{n}(\mathfrak {B}(\mathcal {S}),\mathcal {X}^*)\neq 0$
for some
$H^{n}(\mathfrak {B}(\mathcal {S}),\mathcal {X}^*)\neq 0$
for some
![]() $n\geq 1$
and bimodule
$n\geq 1$
and bimodule
![]() $\mathcal {X}$
or its dual
$\mathcal {X}$
or its dual
![]() $\mathcal {X}^*$
, then
$\mathcal {X}^*$
, then
![]() $\mathcal {S}$
is not left amenable. The main topic of this paper is to study the cohomology groups of
$\mathcal {S}$
is not left amenable. The main topic of this paper is to study the cohomology groups of
![]() $\mathfrak {B}(\mathcal {S})$
. The basic idea behind the calculation of cohomology groups is to take an average in a suitable way [Reference Sinclair and Smith25]. In most cases, averages are taken on amenable groups. In this article, we shall extend it to
$\mathfrak {B}(\mathcal {S})$
. The basic idea behind the calculation of cohomology groups is to take an average in a suitable way [Reference Sinclair and Smith25]. In most cases, averages are taken on amenable groups. In this article, we shall extend it to
![]() $\mathcal {S}$
.
$\mathcal {S}$
.
The following sections are organized as follows: In Section 2, we provide some basic definitions related to semigroup algebras and amenable semigroups. In Section 3, we introduce the notion of unique factorization semigroup and give three classical examples: Thompson’s semigroup, free semigroups, and the amenable semigroup
![]() $\mathcal {T}$
(see Example 3.12). The continuity of derivations (see Proposition 4.1) and the cohomology groups of
$\mathcal {T}$
(see Example 3.12). The continuity of derivations (see Proposition 4.1) and the cohomology groups of
![]() $\mathfrak {B}(\mathcal {S})$
(see Theorems 5.8 and 5.10) are the main results of this paper and are discussed in Sections 4 and 5. We end this paper with some further discussions and open questions.
$\mathfrak {B}(\mathcal {S})$
(see Theorems 5.8 and 5.10) are the main results of this paper and are discussed in Sections 4 and 5. We end this paper with some further discussions and open questions.
2 Preliminaries
Group algebras and group actions on manifolds are two major sources for the construction of operator algebras. In applications, generalizations of groups (group algebras), such as semigroups (semigroup algebras), are also used. A brief description of semigroup algebras follows.
The Hilbert space
![]() $\mathcal {H}$
is
$\mathcal {H}$
is
![]() $l^{2}(S)$
, the space of all square-summable complex valued functions on a cancellative semigroup S. The semigroup S (with unit e) is assumed to be discrete and countable. Hence
$l^{2}(S)$
, the space of all square-summable complex valued functions on a cancellative semigroup S. The semigroup S (with unit e) is assumed to be discrete and countable. Hence
![]() $\mathcal {H}$
is separable. The family of functions
$\mathcal {H}$
is separable. The family of functions
![]() $(\delta _s)_{s\in S}$
forms an orthonormal basis of
$(\delta _s)_{s\in S}$
forms an orthonormal basis of
![]() $\mathcal {H}$
, where
$\mathcal {H}$
, where
![]() $\delta _s(s)=1$
and
$\delta _s(s)=1$
and
![]() $\delta _s(t)=0$
for any
$\delta _s(t)=0$
for any
![]() $t\in S$
,
$t\in S$
,
![]() $t\neq s$
. For each f and g in
$t\neq s$
. For each f and g in
![]() $\mathcal {H}$
, let
$\mathcal {H}$
, let
![]() $L_f$
be the left convolution operator defined as
$L_f$
be the left convolution operator defined as
![]() $L_fg= f\ast g$
, where
$L_fg= f\ast g$
, where
![]() $ f\ast g(s)=\sum _{uv=s}f(u)g(v)$
for each s in S. Note that the convolution operators may be unbounded. We denote by
$ f\ast g(s)=\sum _{uv=s}f(u)g(v)$
for each s in S. Note that the convolution operators may be unbounded. We denote by
![]() $\mathcal {L}(S)$
the set of all bounded left convolution operators on
$\mathcal {L}(S)$
the set of all bounded left convolution operators on
![]() $\mathcal {H}$
. Then
$\mathcal {H}$
. Then
![]() $\mathcal {L}(S)$
is a subalgebra of
$\mathcal {L}(S)$
is a subalgebra of
![]() $B(\mathcal {H})$
. In general,
$B(\mathcal {H})$
. In general,
![]() $\mathcal {L}(S)$
is not a
$\mathcal {L}(S)$
is not a
![]() $*$
-algebra. Similarly, we denote by
$*$
-algebra. Similarly, we denote by
![]() $\mathcal {R}(S)$
the subalgebra of
$\mathcal {R}(S)$
the subalgebra of
![]() $B(\mathcal {H})$
consisting of all bounded right convolution operators. Then
$B(\mathcal {H})$
consisting of all bounded right convolution operators. Then
![]() $\mathcal {L}(S)'=\mathcal {R}(S)$
and
$\mathcal {L}(S)'=\mathcal {R}(S)$
and
![]() $\mathcal {R}(S)'=\mathcal {L}(S)$
, which implies that
$\mathcal {R}(S)'=\mathcal {L}(S)$
, which implies that
![]() $\mathcal {L}(S)$
and
$\mathcal {L}(S)$
and
![]() $\mathcal {R}(S)$
are both weak-operator closed algebras. For each s in S, the operator
$\mathcal {R}(S)$
are both weak-operator closed algebras. For each s in S, the operator
![]() $L_{\delta _s}$
is an isometry on
$L_{\delta _s}$
is an isometry on
![]() $\mathcal {H}$
and is denoted by
$\mathcal {H}$
and is denoted by
![]() $L_s$
in this paper for convenience. We denote by
$L_s$
in this paper for convenience. We denote by
![]() $\mathfrak {B}(S)$
the Banach algebra generated by
$\mathfrak {B}(S)$
the Banach algebra generated by
![]() $\{L_s:\ s\in S \}$
in norm topology in
$\{L_s:\ s\in S \}$
in norm topology in
![]() $B(\mathcal {H})$
. Then
$B(\mathcal {H})$
. Then
![]() $\mathfrak {B}(S)$
is a Banach subalgebra of
$\mathfrak {B}(S)$
is a Banach subalgebra of
![]() $\mathcal {L}(S)$
.
$\mathcal {L}(S)$
.
Specific examples for such Banach algebras result from choosing for S any of the free semigroup
![]() $\mathcal {F}_n$
on n (
$\mathcal {F}_n$
on n (
![]() $\geq 2$
) generators, Thompson’s semigroup
$\geq 2$
) generators, Thompson’s semigroup
![]() $\mathcal {S}$
, or the multiplicative semigroup of natural numbers
$\mathcal {S}$
, or the multiplicative semigroup of natural numbers
![]() $(\mathbb {N},\star )$
. The algebraic structure of
$(\mathbb {N},\star )$
. The algebraic structure of
![]() $\mathfrak {B}(S)$
can reflect the structure of S. In [Reference Dong, Huang and Xue5], Dong, Huang, and Xue proved that the maximal ideal space of the commutative Banach algebra
$\mathfrak {B}(S)$
can reflect the structure of S. In [Reference Dong, Huang and Xue5], Dong, Huang, and Xue proved that the maximal ideal space of the commutative Banach algebra
![]() $\mathfrak {B}(\mathbb {N})$
is homeomorphic to the Cartesian product of unit closed disk indexed by primes (see [Reference Dong, Huang and Xue5, Theorem 1.1]). They pointed out that this result implies the fundamental theorem of arithmetic. Analogously, studying the cohomology of the Banach algebras
$\mathfrak {B}(\mathbb {N})$
is homeomorphic to the Cartesian product of unit closed disk indexed by primes (see [Reference Dong, Huang and Xue5, Theorem 1.1]). They pointed out that this result implies the fundamental theorem of arithmetic. Analogously, studying the cohomology of the Banach algebras
![]() $\mathfrak {B}(\mathcal {S})$
,
$\mathfrak {B}(\mathcal {S})$
,
![]() $\mathfrak {B}(\mathcal {F}_n)$
, and
$\mathfrak {B}(\mathcal {F}_n)$
, and
![]() $\mathfrak {B}(\mathcal {T})$
can help us to understand the properties of the corresponding semigroups.
$\mathfrak {B}(\mathcal {T})$
can help us to understand the properties of the corresponding semigroups.
In this paper, we will prove that derivations on
![]() $\mathfrak {B}(\mathcal {S})$
,
$\mathfrak {B}(\mathcal {S})$
,
![]() $\mathfrak {B}(\mathcal {F}_n),$
and
$\mathfrak {B}(\mathcal {F}_n),$
and
![]() $\mathfrak {B}(\mathcal {T})$
are automatically continuous, and every derivation on
$\mathfrak {B}(\mathcal {T})$
are automatically continuous, and every derivation on
![]() $\mathfrak {B}(\mathcal {S})$
is spatial and induced by an operator in
$\mathfrak {B}(\mathcal {S})$
is spatial and induced by an operator in
![]() $\mathcal {L}(\mathcal {S})$
. Comparing with a result of Kadison [Reference Kadison18, Theorem 4] that every derivation on a
$\mathcal {L}(\mathcal {S})$
. Comparing with a result of Kadison [Reference Kadison18, Theorem 4] that every derivation on a
![]() $C^*$
-algebra is spatial, we give a nontrivial example in the case of Banach algebras. Moreover, we prove that the first cohomology group of
$C^*$
-algebra is spatial, we give a nontrivial example in the case of Banach algebras. Moreover, we prove that the first cohomology group of
![]() $\mathfrak {B}(\mathcal {S})$
with coefficients in
$\mathfrak {B}(\mathcal {S})$
with coefficients in
![]() $\mathcal {L}(\mathcal {S})$
is zero, which gives a positive indication for the left amenability of Thompson’s semigroup.
$\mathcal {L}(\mathcal {S})$
is zero, which gives a positive indication for the left amenability of Thompson’s semigroup.
In the following, we recall several concepts and results about amenable semigroups. We say that a discrete cancellative semigroup S is left (resp. right) amenable if there exists a left (resp. right) invariant mean on
![]() $l^{\infty }(S)$
. For example, the additive semigroup of natural numbers is amenable while the free semigroup on n (
$l^{\infty }(S)$
. For example, the additive semigroup of natural numbers is amenable while the free semigroup on n (
![]() $\geq 2$
) generators is not. A left (resp. right) Følner net of S is a net of non-empty finite subsets
$\geq 2$
) generators is not. A left (resp. right) Følner net of S is a net of non-empty finite subsets
![]() $\{F_{\alpha }\}$
in S such that for any
$\{F_{\alpha }\}$
in S such that for any
![]() $s\in S$
,
$s\in S$
,
 $$\begin{align*}\lim_{\alpha}\frac{|sF_{\alpha}\Delta F_{\alpha}|}{|F_{\alpha}|}=0\ \left( \text{resp}.\ \lim_{\alpha}\frac{|F_{\alpha}s\Delta F_{\alpha}|}{|F_{\alpha}|}=0\right). \end{align*}$$
$$\begin{align*}\lim_{\alpha}\frac{|sF_{\alpha}\Delta F_{\alpha}|}{|F_{\alpha}|}=0\ \left( \text{resp}.\ \lim_{\alpha}\frac{|F_{\alpha}s\Delta F_{\alpha}|}{|F_{\alpha}|}=0\right). \end{align*}$$
It was proved for groups by Følner, and then generalized to discrete cancellative semigroups by Frey [Reference Frey7] that S is left (resp. right) amenable if and only if S has a left (resp. right) Følner net. In [Reference Følner6], Følner proved that every subgroup of an amenable group is still amenable. For semigroups, it is not always true. In [Reference Frey7], Frey gave an example of a left amenable semigroup which contains a non-amenable semigroup.
3 Unique factorization semigroup
Definition 3.1 Let S be a discrete semigroup. We say that S is a unique factorization semigroup if there exists a subset
![]() $\{X_1,X_2,X_3,\ldots \}$
of S such that:
$\{X_1,X_2,X_3,\ldots \}$
of S such that:
(i) every non-unital element in S can be uniquely written as
![]() $X_{i_1}^{\alpha _1}\dots X_{i_n}^{\alpha _n}$
, where
$X_{i_1}^{\alpha _1}\dots X_{i_n}^{\alpha _n}$
, where
![]() $\alpha _i$
(
$\alpha _i$
(
![]() $1\leq i\leq n$
) are positive integers and
$1\leq i\leq n$
) are positive integers and
![]() $i_1<\cdots <i_n$
.
$i_1<\cdots <i_n$
.
(
![]() $\mathrm{ii}$
) If
$\mathrm{ii}$
) If
![]() $e=X_{1}^{\beta _1}\dots X_{n}^{\beta _n}$
for some nonnegative integers
$e=X_{1}^{\beta _1}\dots X_{n}^{\beta _n}$
for some nonnegative integers
![]() $\beta _i$
(
$\beta _i$
(
![]() $1\leq i\leq n$
), then
$1\leq i\leq n$
), then
![]() $\beta _i=0$
. The subset
$\beta _i=0$
. The subset
![]() $\{X_1,X_2,X_3,\ldots \}$
is called a basis of S.
$\{X_1,X_2,X_3,\ldots \}$
is called a basis of S.
For example, the multiplicative semigroup of natural numbers is a unique factorization semigroup and the set of all primes is the unique basis up to reorder. It is also clear that Thompson’s semigroup
![]() $\mathcal {S}=\langle X_0, X_1,\ldots \ |\ X_jX_i=X_iX_{j+1},\ i<j \rangle ^+$
is a unique factorization semigroup with the basis
$\mathcal {S}=\langle X_0, X_1,\ldots \ |\ X_jX_i=X_iX_{j+1},\ i<j \rangle ^+$
is a unique factorization semigroup with the basis
![]() $\{X_n\in \mathcal {S}:\ n\in \mathbb {N}\}$
.
$\{X_n\in \mathcal {S}:\ n\in \mathbb {N}\}$
.
Next, we introduce some properties of
![]() $\mathcal {S}$
that will be frequently used in Sections 4 and 5.
$\mathcal {S}$
that will be frequently used in Sections 4 and 5.
Definition 3.2 Let
![]() $X=X_{0}^{\alpha _0}X_{1}^{\alpha _1}\dots X_{n}^{\alpha _n}$
be an element in
$X=X_{0}^{\alpha _0}X_{1}^{\alpha _1}\dots X_{n}^{\alpha _n}$
be an element in
![]() $\mathcal {S}$
, where
$\mathcal {S}$
, where
![]() $\alpha _i$
(
$\alpha _i$
(
![]() $0\leq i\leq n$
) are nonnegative integers. We define the index of X at the
$0\leq i\leq n$
) are nonnegative integers. We define the index of X at the
![]() $i\mathrm {th}$
position as
$i\mathrm {th}$
position as
![]() $\mathsf {ind}_i(X):=\alpha _i$
and the index of X as
$\mathsf {ind}_i(X):=\alpha _i$
and the index of X as
![]() $\mathsf {ind}(X):=\sum _{i=0}^{n}\mathsf {ind}_i(X)$
. The index of the unit element e is zero.
$\mathsf {ind}(X):=\sum _{i=0}^{n}\mathsf {ind}_i(X)$
. The index of the unit element e is zero.
It is clear that
![]() $\mathsf {ind}_{0}(uv)=\mathsf {ind}_{0}(u)+\mathsf {ind}_{0}(v)=\mathsf {ind}_0(vu)$
and
$\mathsf {ind}_{0}(uv)=\mathsf {ind}_{0}(u)+\mathsf {ind}_{0}(v)=\mathsf {ind}_0(vu)$
and
![]() $\mathsf {ind}(uv)=\mathsf {ind}(u)+\mathsf {ind}(v)=\mathsf {ind}(vu)$
for all u and v in
$\mathsf {ind}(uv)=\mathsf {ind}(u)+\mathsf {ind}(v)=\mathsf {ind}(vu)$
for all u and v in
![]() $\mathcal {S}$
. In general,
$\mathcal {S}$
. In general,
![]() $\mathsf {ind}_i(uv)\neq \mathsf {ind}_i(u)+\mathsf {ind}_i(v)$
for
$\mathsf {ind}_i(uv)\neq \mathsf {ind}_i(u)+\mathsf {ind}_i(v)$
for
![]() $i{\kern-1pt}\geq{\kern-1pt} 1$
. For example,
$i{\kern-1pt}\geq{\kern-1pt} 1$
. For example,
![]() $\mathsf {ind}_2(X_0X_2X_1){\kern-1pt}={\kern-1pt}\mathsf {ind}_2(X_0X_1X_3){\kern-1pt}={\kern-1pt}0{\kern-1pt}\neq{\kern-1pt} 1{\kern-1pt}={\kern-1pt} \mathsf {ind}_2(X_0X_2)+\mathsf {ind}_2(X_1)$
.
$\mathsf {ind}_2(X_0X_2X_1){\kern-1pt}={\kern-1pt}\mathsf {ind}_2(X_0X_1X_3){\kern-1pt}={\kern-1pt}0{\kern-1pt}\neq{\kern-1pt} 1{\kern-1pt}={\kern-1pt} \mathsf {ind}_2(X_0X_2)+\mathsf {ind}_2(X_1)$
.
Definition 3.3 [Reference Xue27]
Let u, v, w
![]() $\in $
$\in $
![]() $\mathcal {S}$
. We call u a divisor of v if
$\mathcal {S}$
. We call u a divisor of v if
![]() $v=uw$
and we denote by
$v=uw$
and we denote by
![]() $u|v$
.
$u|v$
.
For example,
![]() $X_1|X_0X_2=X_1X_0$
while
$X_1|X_0X_2=X_1X_0$
while
![]() $X_2\nmid X_0X_2$
. It is clear that if
$X_2\nmid X_0X_2$
. It is clear that if
![]() $u|v$
then
$u|v$
then
![]() $\mathsf {ind}(u)\leq \mathsf {ind}(v)$
.
$\mathsf {ind}(u)\leq \mathsf {ind}(v)$
.
Lemma 3.4 [Reference Xue27]
The relation “
![]() $|$
” is a partial order on
$|$
” is a partial order on
![]() $\mathcal {S}$
.
$\mathcal {S}$
.
Proof Let u, v, w
![]() $\in $
$\in $
![]() $\mathcal {S}$
. We verify the following three axioms of the partial order.
$\mathcal {S}$
. We verify the following three axioms of the partial order.
-
(1) (Reflexivity.)
 $u=ue$
implies
$u=ue$
implies
 $u|u$
.
$u|u$
. -
(2) (Antisymmetry.) If
 $u|v$
and
$u|v$
and
 $v|u$
, then
$v|u$
, then
 $u=vw_1$
and
$u=vw_1$
and
 $v=uw_2$
for some
$v=uw_2$
for some
 $w_1$
,
$w_1$
,
 $w_2$
in
$w_2$
in
 $\mathcal {S}$
. Then we have
$\mathcal {S}$
. Then we have
 $w_2w_1=e$
, which implies
$w_2w_1=e$
, which implies
 $w_1=w_2=e$
. Thus
$w_1=w_2=e$
. Thus
 $u=v$
.
$u=v$
. -
(3) (Transitivity.) Suppose that
 $u|v$
and
$u|v$
and
 $v|w$
, then
$v|w$
, then
 $v=uw_1$
and
$v=uw_1$
and
 $w=vw_2$
for some
$w=vw_2$
for some
 $w_1$
,
$w_1$
,
 $w_2$
in
$w_2$
in
 $\mathcal {S}$
. We have
$\mathcal {S}$
. We have
 $w=uw_1w_2$
. Thus
$w=uw_1w_2$
. Thus
 $u|w$
.
$u|w$
.
As a result, we conclude that “
![]() $|$
” is a partial order.
$|$
” is a partial order.
Lemma 3.5 Let X be an element in
![]() $\mathcal {S}$
such that
$\mathcal {S}$
such that
![]() $X_0|X$
. Then for each
$X_0|X$
. Then for each
![]() $n\in \mathbb {N}$
, we have:
$n\in \mathbb {N}$
, we have:
(i)
![]() $X_{1}^{-n}XX_{1}^{n}\in \mathcal {S}$
if and only if
$X_{1}^{-n}XX_{1}^{n}\in \mathcal {S}$
if and only if
![]() $X_{1}^{n}|X$
;
$X_{1}^{n}|X$
;
![]() $(\mathrm{ii})$
$(\mathrm{ii})$
![]() $X_{1}^{n}XX_{1}^{-n}\in \mathcal {S} $
if and only if
$X_{1}^{n}XX_{1}^{-n}\in \mathcal {S} $
if and only if
![]() $X=YX_{1}^{n}$
for some
$X=YX_{1}^{n}$
for some
![]() $Y\in \mathcal {S}$
.
$Y\in \mathcal {S}$
.
Proof (i) If
![]() $X_{1}^{n}|X$
, then it is clear that
$X_{1}^{n}|X$
, then it is clear that
![]() $X_{1}^{-n}XX_{1}^{n}\in \mathcal {S}$
. Conversely, we have
$X_{1}^{-n}XX_{1}^{n}\in \mathcal {S}$
. Conversely, we have
![]() $X_1^n|XX_1^n$
. If
$X_1^n|XX_1^n$
. If
![]() $X_1^n$
is not a divisor of X, since
$X_1^n$
is not a divisor of X, since
![]() $X_1^{-n}X_0=X_0X_2^{-n}$
, we have that the normal form of
$X_1^{-n}X_0=X_0X_2^{-n}$
, we have that the normal form of
![]() $X_{1}^{-n}XX_{1}^{n}$
in Thompson’s group is
$X_{1}^{-n}XX_{1}^{n}$
in Thompson’s group is
![]() $ZX_j^{-m}$
for some
$ZX_j^{-m}$
for some
![]() $Z\in \mathcal {S}$
and
$Z\in \mathcal {S}$
and
![]() $j\geq 2$
,
$j\geq 2$
,
![]() $m\geq 1$
. This leads to a contradiction. Thus
$m\geq 1$
. This leads to a contradiction. Thus
![]() $X_1^n|X$
. (
$X_1^n|X$
. (
![]() $ii$
) Assume that
$ii$
) Assume that
![]() $W=X_{1}^{n}XX_{1}^{-n}\in \mathcal {S} $
, then we have
$W=X_{1}^{n}XX_{1}^{-n}\in \mathcal {S} $
, then we have
![]() $X_0|W$
and
$X_0|W$
and
![]() $X=X_1^{-n}WX_1^{n}\in \mathcal {S}$
. From (i), we have
$X=X_1^{-n}WX_1^{n}\in \mathcal {S}$
. From (i), we have
![]() $X_1^n|W$
. Let
$X_1^n|W$
. Let
![]() $Y= X_1^{-n}W$
, then
$Y= X_1^{-n}W$
, then
![]() $X=YX_1^n$
. The other direction is obvious. We complete the proof.
$X=YX_1^n$
. The other direction is obvious. We complete the proof.
With the aid of the index function we introduce a total order on
![]() $\mathcal {S}$
which plays an important role in Sections 4 and 5.
$\mathcal {S}$
which plays an important role in Sections 4 and 5.
Definition 3.6 Let u, v
![]() $\in $
$\in $
![]() $\mathcal {S}$
. We say
$\mathcal {S}$
. We say
![]() $u\prec v$
if one of the following conditions holds:
$u\prec v$
if one of the following conditions holds:
(i)
![]() $\mathsf {ind}(u)<\mathsf {ind}(v)$
;
$\mathsf {ind}(u)<\mathsf {ind}(v)$
;
(
![]() $\mathrm{ii}$
)
$\mathrm{ii}$
)
![]() $\mathsf {ind}(u)=\mathsf {ind}(v)$
and
$\mathsf {ind}(u)=\mathsf {ind}(v)$
and
![]() $\mathsf {ind}_{0}(u)>\mathsf {ind}_{0}(v)$
;
$\mathsf {ind}_{0}(u)>\mathsf {ind}_{0}(v)$
;
(
![]() $\mathrm{iii}$
)
$\mathrm{iii}$
)
![]() $\mathsf {ind}(u)=\mathsf {ind}(v)$
,
$\mathsf {ind}(u)=\mathsf {ind}(v)$
,
![]() $\mathsf {ind}_{0}(u)=\mathsf {ind}_{0}(v)$
, and there exists a positive integer i such that
$\mathsf {ind}_{0}(u)=\mathsf {ind}_{0}(v)$
, and there exists a positive integer i such that
![]() $\mathsf {ind}_{i}(u)>\mathsf {ind}_{i}(v)$
and
$\mathsf {ind}_{i}(u)>\mathsf {ind}_{i}(v)$
and
![]() $\mathsf {ind}_{j}(u)=\mathsf {ind}_{j}(v)$
whenever
$\mathsf {ind}_{j}(u)=\mathsf {ind}_{j}(v)$
whenever
![]() $j<i$
.
$j<i$
.
We use
![]() $u\preceq v$
to denote
$u\preceq v$
to denote
![]() $u\prec v$
or
$u\prec v$
or
![]() $u=v$
.
$u=v$
.
For example,
![]() $X_0\prec X_1\prec X_0X_1\prec X_0X_2 \prec X_1X_2$
. The relation “
$X_0\prec X_1\prec X_0X_1\prec X_0X_2 \prec X_1X_2$
. The relation “
![]() $\preceq $
” is a total order on
$\preceq $
” is a total order on
![]() $\mathcal {S}$
with the well-ordered properties.
$\mathcal {S}$
with the well-ordered properties.
Lemma 3.7 We have the following statements:
(i) There exists a unique minimal element in every non-empty subset of
![]() $\mathcal {S}$
under the total order.
$\mathcal {S}$
under the total order.
![]() $(\mathrm{ii})$
Let
$(\mathrm{ii})$
Let
![]() $u_i$
and
$u_i$
and
![]() $v_i$
(
$v_i$
(
![]() $1\leq i\leq n$
) be
$1\leq i\leq n$
) be
![]() $2n$
elements in
$2n$
elements in
![]() $\mathcal {S}$
. If
$\mathcal {S}$
. If
![]() $u_{i}\preceq v_{i}$
for each
$u_{i}\preceq v_{i}$
for each
![]() $1\leq i\leq n$
, then
$1\leq i\leq n$
, then
![]() $\Pi _{i=1}^{n}u_{i}\preceq \Pi _{i=1}^{n}v_{i}$
. The equality holds if and only if
$\Pi _{i=1}^{n}u_{i}\preceq \Pi _{i=1}^{n}v_{i}$
. The equality holds if and only if
![]() $u_{i}=v_{i}$
for each
$u_{i}=v_{i}$
for each
![]() $1\leq i\leq n$
.
$1\leq i\leq n$
.
Proof It is clear that (i) holds. We now give the proof of (
![]() $ii$
). First, we consider the case when
$ii$
). First, we consider the case when
![]() $n=2$
. If
$n=2$
. If
![]() $\mathsf {ind}(u_{1})<\mathsf {ind}(v_{1})$
or
$\mathsf {ind}(u_{1})<\mathsf {ind}(v_{1})$
or
![]() $\mathsf {ind}(u_{2})<\mathsf {ind}(v_{2})$
, then
$\mathsf {ind}(u_{2})<\mathsf {ind}(v_{2})$
, then
![]() $\mathsf {ind}(u_{1}u_{2})=\mathsf {ind}(u_{1})+\mathsf {ind}(u_{2})<\mathsf {ind}(v_{1})+\mathsf {ind}(v_{2})=\mathsf {ind}(v_{1}v_{2})$
. This implies
$\mathsf {ind}(u_{1}u_{2})=\mathsf {ind}(u_{1})+\mathsf {ind}(u_{2})<\mathsf {ind}(v_{1})+\mathsf {ind}(v_{2})=\mathsf {ind}(v_{1}v_{2})$
. This implies
![]() $u_{1}u_{2}\prec v_{1}v_{2}$
. In the case that
$u_{1}u_{2}\prec v_{1}v_{2}$
. In the case that
![]() $\mathsf {ind}(u_{1})=\mathsf {ind}(v_{1})$
and
$\mathsf {ind}(u_{1})=\mathsf {ind}(v_{1})$
and
![]() $\mathsf {ind}(u_{2})=\mathsf {ind}(v_{2})$
, if
$\mathsf {ind}(u_{2})=\mathsf {ind}(v_{2})$
, if
![]() $\mathsf {ind}_{0}(u_{1})>\mathsf {ind}_{0}(v_{1})$
or
$\mathsf {ind}_{0}(u_{1})>\mathsf {ind}_{0}(v_{1})$
or
![]() $\mathsf {ind}_{0}(u_{2})>\mathsf {ind}_{0}(v_{2})$
, then
$\mathsf {ind}_{0}(u_{2})>\mathsf {ind}_{0}(v_{2})$
, then
![]() $\mathsf {ind}_{0}(u_{1}u_{2})=\mathsf {ind}_{0}(u_{1})+\mathsf {ind}_{0}(u_{2})>\mathsf {ind}_{0}(v_{1})+\mathsf {ind}_{0}(v_{2})=\mathsf {ind}_{0}(v_{1}v_{2})$
. This also implies
$\mathsf {ind}_{0}(u_{1}u_{2})=\mathsf {ind}_{0}(u_{1})+\mathsf {ind}_{0}(u_{2})>\mathsf {ind}_{0}(v_{1})+\mathsf {ind}_{0}(v_{2})=\mathsf {ind}_{0}(v_{1}v_{2})$
. This also implies
![]() $u_{1}u_{2}\prec v_{1}v_{2}$
. Hence, we assume that
$u_{1}u_{2}\prec v_{1}v_{2}$
. Hence, we assume that
![]() $\mathsf {ind}_{0}(u_{1})=\mathsf {ind}_{0}(v_{1})$
and
$\mathsf {ind}_{0}(u_{1})=\mathsf {ind}_{0}(v_{1})$
and
![]() $\mathsf {ind}_{0}(u_{2})=\mathsf {ind}_{0}(v_{2})$
. If either
$\mathsf {ind}_{0}(u_{2})=\mathsf {ind}_{0}(v_{2})$
. If either
![]() $\mathsf {ind}(u_{1})$
or
$\mathsf {ind}(u_{1})$
or
![]() $\mathsf {ind}(u_{2})$
is zero, then it is trivial. Thus we may further assume that
$\mathsf {ind}(u_{2})$
is zero, then it is trivial. Thus we may further assume that
![]() $\mathsf {ind}(u_{1})=\mathsf {ind}(v_{1})\geq 1$
and
$\mathsf {ind}(u_{1})=\mathsf {ind}(v_{1})\geq 1$
and
![]() $\mathsf {ind}(u_{2})=\mathsf {ind}(v_{2})\geq 1$
.
$\mathsf {ind}(u_{2})=\mathsf {ind}(v_{2})\geq 1$
.
Case I:
![]() $u_{2}=v_{2}$
. If
$u_{2}=v_{2}$
. If
![]() $u_{1}=v_{1}$
, then it is obvious. Otherwise, let
$u_{1}=v_{1}$
, then it is obvious. Otherwise, let
![]() $u_{1}=X_{0}^{\alpha _{0}}\dots X_{n}^{\alpha _{n}}$
and
$u_{1}=X_{0}^{\alpha _{0}}\dots X_{n}^{\alpha _{n}}$
and
![]() $v_{1}=X_{0}^{\beta _{0}}\dots X_{m}^{\beta _{m}}$
. By the definition of the total order, there exists an integer
$v_{1}=X_{0}^{\beta _{0}}\dots X_{m}^{\beta _{m}}$
. By the definition of the total order, there exists an integer
![]() $i>0$
such that
$i>0$
such that
![]() $\alpha _{j}=\beta _{j}$
whenever
$\alpha _{j}=\beta _{j}$
whenever
![]() $j<i$
and
$j<i$
and
![]() $\alpha _{i}>\beta _{i}$
. Since
$\alpha _{i}>\beta _{i}$
. Since
![]() $\{X_l\in \mathcal {S}:\ l\in \mathbb {N}\}$
is a basis of
$\{X_l\in \mathcal {S}:\ l\in \mathbb {N}\}$
is a basis of
![]() $\mathcal {S}$
, it only needs to prove
$\mathcal {S}$
, it only needs to prove
![]() $u_{1}X_{l}\prec v_{1}X_{l}$
for each
$u_{1}X_{l}\prec v_{1}X_{l}$
for each
![]() $X_{l}\in \mathcal {S}$
. In fact, we have
$X_{l}\in \mathcal {S}$
. In fact, we have
 $$ \begin{align} u_{1}X_{l}= \begin{cases} X_{0}^{\alpha_{0}}\dots X_{l-1}^{\alpha_{l-1}}X_{l}^{\alpha_{l}+1} X_{l+2}^{\alpha_{l+1}}\dots X_{i+1}^{\alpha_{i}} \dots X_{n+1}^{\alpha_{n}},&l<i, \cr X_{0}^{\alpha_{0}}\dots X_{i-1}^{\alpha_{i-1}}X_{i}^{\alpha_{i}+1} X_{i+2}^{\alpha_{i+1}}\dots X_{n+1}^{\alpha_{n}},&l=i, \cr X_{0}^{\alpha_{0}}\dots X_{i-1}^{\alpha_{i-1}}X_{i}^{\alpha_{i}} X_{i_{1}}^{\alpha^{\prime}_{i_{1}}}\dots X_{i_{t}}^{\alpha^{\prime}_{i_{t}}},&l>i, \end{cases} \end{align} $$
$$ \begin{align} u_{1}X_{l}= \begin{cases} X_{0}^{\alpha_{0}}\dots X_{l-1}^{\alpha_{l-1}}X_{l}^{\alpha_{l}+1} X_{l+2}^{\alpha_{l+1}}\dots X_{i+1}^{\alpha_{i}} \dots X_{n+1}^{\alpha_{n}},&l<i, \cr X_{0}^{\alpha_{0}}\dots X_{i-1}^{\alpha_{i-1}}X_{i}^{\alpha_{i}+1} X_{i+2}^{\alpha_{i+1}}\dots X_{n+1}^{\alpha_{n}},&l=i, \cr X_{0}^{\alpha_{0}}\dots X_{i-1}^{\alpha_{i-1}}X_{i}^{\alpha_{i}} X_{i_{1}}^{\alpha^{\prime}_{i_{1}}}\dots X_{i_{t}}^{\alpha^{\prime}_{i_{t}}},&l>i, \end{cases} \end{align} $$
and
 $$ \begin{align} v_{1}X_{l}= \begin{cases} X_{0}^{\beta_{0}}\dots X_{l-1}^{\beta_{l-1}}X_{l}^{\beta_{l}+1} X_{l+2}^{\beta_{l+1}}\dots X_{i+1}^{\beta_{i}} \dots X_{m+1}^{\beta_{m}},&l<i, \cr X_{0}^{\beta_{0}}\dots X_{i-1}^{\beta_{i-1}}X_{i}^{\beta_{i}+1} X_{i+2}^{\beta_{i+1}}\dots X_{m+1}^{\beta_{m}},&l=i, \cr X_{0}^{\beta_{0}}\dots X_{i-1}^{\beta_{i-1}}X_{i}^{\beta_{i}} X_{j_{1}}^{\beta^{\prime}_{j_{1}}}\dots X_{j_{s}}^{\beta^{\prime}_{j_{s}}},&l>i, \end{cases} \end{align} $$
$$ \begin{align} v_{1}X_{l}= \begin{cases} X_{0}^{\beta_{0}}\dots X_{l-1}^{\beta_{l-1}}X_{l}^{\beta_{l}+1} X_{l+2}^{\beta_{l+1}}\dots X_{i+1}^{\beta_{i}} \dots X_{m+1}^{\beta_{m}},&l<i, \cr X_{0}^{\beta_{0}}\dots X_{i-1}^{\beta_{i-1}}X_{i}^{\beta_{i}+1} X_{i+2}^{\beta_{i+1}}\dots X_{m+1}^{\beta_{m}},&l=i, \cr X_{0}^{\beta_{0}}\dots X_{i-1}^{\beta_{i-1}}X_{i}^{\beta_{i}} X_{j_{1}}^{\beta^{\prime}_{j_{1}}}\dots X_{j_{s}}^{\beta^{\prime}_{j_{s}}},&l>i, \end{cases} \end{align} $$
where
![]() $i<i_{1}<\cdots <i_{t}$
and
$i<i_{1}<\cdots <i_{t}$
and
![]() $i<j_{1}<\cdots <j_{s}$
. By comparing equation (1) with (2), we have
$i<j_{1}<\cdots <j_{s}$
. By comparing equation (1) with (2), we have
![]() $u_{1}X_{l}\prec u_{2}X_{l}$
.
$u_{1}X_{l}\prec u_{2}X_{l}$
.
Case II:
![]() $u_{2}\prec v_{2}$
. Let
$u_{2}\prec v_{2}$
. Let
![]() $u_{2}=X_{0}^{\gamma _{0}}\dots X_{k}^{\gamma _{k}}$
and
$u_{2}=X_{0}^{\gamma _{0}}\dots X_{k}^{\gamma _{k}}$
and
![]() $v_{2}=X_{0}^{\omega _{0}}\dots X_{l}^{\omega _{l}}$
, then there exists an integer
$v_{2}=X_{0}^{\omega _{0}}\dots X_{l}^{\omega _{l}}$
, then there exists an integer
![]() $h>0$
such that
$h>0$
such that
![]() $\gamma _{j}=\omega _{j}$
whenever
$\gamma _{j}=\omega _{j}$
whenever
![]() $j<h$
and
$j<h$
and
![]() $\gamma _{h}>\omega _{h}$
. By the first case, it can be reduced to the case when
$\gamma _{h}>\omega _{h}$
. By the first case, it can be reduced to the case when
![]() $u_{2}=X_{h}^{\gamma _{h}}\dots X_{k}^{\gamma _{k}}$
and
$u_{2}=X_{h}^{\gamma _{h}}\dots X_{k}^{\gamma _{k}}$
and
![]() $v_{2}=X_{h}^{\omega _{h}}\dots X_{l}^{\omega _{l}}$
. If
$v_{2}=X_{h}^{\omega _{h}}\dots X_{l}^{\omega _{l}}$
. If
![]() $u_{1}=v_{1}=X_{0}^{\alpha _{0}}\dots X_{n}^{\alpha _{n}}$
, then
$u_{1}=v_{1}=X_{0}^{\alpha _{0}}\dots X_{n}^{\alpha _{n}}$
, then
 $$ \begin{align} u_{1}u_{2}= \begin{cases} X_{0}^{\alpha_{0}}\dots X_{n}^{\alpha_{n}}X_{h}^{\gamma_{h}}\dots X_{l}^{\gamma_{l}},&h>n, \cr X_{0}^{\alpha_{0}}\dots X_{h-1}^{\alpha_{h-1}}X_{h}^{\alpha_{h}+\gamma_{h}} X_{h_{1}}^{\alpha^{\prime}_{h_{1}}}\dots X_{h_{t}}^{\alpha^{\prime}_{h_{t}}},&h\leq n, \end{cases} \end{align} $$
$$ \begin{align} u_{1}u_{2}= \begin{cases} X_{0}^{\alpha_{0}}\dots X_{n}^{\alpha_{n}}X_{h}^{\gamma_{h}}\dots X_{l}^{\gamma_{l}},&h>n, \cr X_{0}^{\alpha_{0}}\dots X_{h-1}^{\alpha_{h-1}}X_{h}^{\alpha_{h}+\gamma_{h}} X_{h_{1}}^{\alpha^{\prime}_{h_{1}}}\dots X_{h_{t}}^{\alpha^{\prime}_{h_{t}}},&h\leq n, \end{cases} \end{align} $$
and
 $$ \begin{align} v_{1}v_{2}= \begin{cases} X_{0}^{\alpha_{0}}\dots X_{n}^{\alpha_{n}}X_{h}^{\omega_{h}}\dots X_{l}^{\omega_{l}},&h>n, \cr X_{0}^{\alpha_{0}}\dots X_{h-1}^{\alpha_{h-1}}X_{h}^{\alpha_{h}+\omega_{h}} X_{h_{1}}^{\alpha^{\prime\prime}_{h_{1}}}\dots X_{h_{s}}^{\alpha^{\prime\prime}_{h_{s}}},&h\leq n, \end{cases} \end{align} $$
$$ \begin{align} v_{1}v_{2}= \begin{cases} X_{0}^{\alpha_{0}}\dots X_{n}^{\alpha_{n}}X_{h}^{\omega_{h}}\dots X_{l}^{\omega_{l}},&h>n, \cr X_{0}^{\alpha_{0}}\dots X_{h-1}^{\alpha_{h-1}}X_{h}^{\alpha_{h}+\omega_{h}} X_{h_{1}}^{\alpha^{\prime\prime}_{h_{1}}}\dots X_{h_{s}}^{\alpha^{\prime\prime}_{h_{s}}},&h\leq n, \end{cases} \end{align} $$
where
![]() $h<h_{1}<\cdots <h_{\max \{t,s\}}$
. Comparing equation (3) with (4), we have
$h<h_{1}<\cdots <h_{\max \{t,s\}}$
. Comparing equation (3) with (4), we have
![]() $u_{1}u_{2}\prec v_{1}v_{2}$
. The proof of the case that
$u_{1}u_{2}\prec v_{1}v_{2}$
. The proof of the case that
![]() $u_{1}\prec v_{1}$
is similar, we omit it here. Moreover, we can obtain from the above process directly that
$u_{1}\prec v_{1}$
is similar, we omit it here. Moreover, we can obtain from the above process directly that
![]() $u_1u_2=v_1v_2$
if and only if
$u_1u_2=v_1v_2$
if and only if
![]() $u_1=v_1$
and
$u_1=v_1$
and
![]() $u_2=v_2$
.
$u_2=v_2$
.
The general case when
![]() $n>2$
can be obtained by induction.
$n>2$
can be obtained by induction.
We now turn to the free semigroup
![]() $\mathcal {F}_n$
on n (
$\mathcal {F}_n$
on n (
![]() $\geq 2$
) generators
$\geq 2$
) generators
![]() $a_i$
(
$a_i$
(
![]() $1\leq i \leq n$
). The following two definitions on
$1\leq i \leq n$
). The following two definitions on
![]() $\mathcal {F}_n$
are parallel to Definitions 3.2 and 3.6, and Lemma 3.10 is parallel to Lemma 3.7.
$\mathcal {F}_n$
are parallel to Definitions 3.2 and 3.6, and Lemma 3.10 is parallel to Lemma 3.7.
Definition 3.8 Let
![]() $g=\prod _{j=1}^m \prod _{k=1}^{n}a_k^{i_{jk}}$
be an element in
$g=\prod _{j=1}^m \prod _{k=1}^{n}a_k^{i_{jk}}$
be an element in
![]() $\mathcal {F}_n$
, where
$\mathcal {F}_n$
, where
![]() $i_{jk}$
(
$i_{jk}$
(
![]() $1\leq j \leq m$
,
$1\leq j \leq m$
,
![]() $1\leq k\leq n$
) are nonnegative integers. The index of g is defined as
$1\leq k\leq n$
) are nonnegative integers. The index of g is defined as
![]() $ \mathsf {ind}(g):= \sum _{j=1}^m \sum _{k=1}^{n}i_{jk}$
.
$ \mathsf {ind}(g):= \sum _{j=1}^m \sum _{k=1}^{n}i_{jk}$
.
It is clear that
![]() $\mathsf {ind}(gh)=\mathsf {ind}(g)+\mathsf {ind}(h)$
for all g and h in
$\mathsf {ind}(gh)=\mathsf {ind}(g)+\mathsf {ind}(h)$
for all g and h in
![]() $\mathcal {F}_n$
.
$\mathcal {F}_n$
.
Definition 3.9 Let
![]() $g=\prod _{j=1}^m \prod _{k=1}^{n}a_k^{i_{jk}}$
and
$g=\prod _{j=1}^m \prod _{k=1}^{n}a_k^{i_{jk}}$
and
![]() $h=\prod _{j=1}^m \prod _{k=1}^{n}a_k^{i^{\prime }_{jk}}$
be two elements in
$h=\prod _{j=1}^m \prod _{k=1}^{n}a_k^{i^{\prime }_{jk}}$
be two elements in
![]() $\mathcal {F}_n$
. We say
$\mathcal {F}_n$
. We say
![]() $g\prec h$
if one of the following conditions holds:
$g\prec h$
if one of the following conditions holds:
(i)
![]() $\mathsf {ind}(g)<\mathsf {ind}(h)$
;
$\mathsf {ind}(g)<\mathsf {ind}(h)$
;
![]() $(\mathrm{ii})$
$(\mathrm{ii})$
![]() $\mathsf {ind}(g)=\mathsf {ind}(h)$
and there exist some
$\mathsf {ind}(g)=\mathsf {ind}(h)$
and there exist some
![]() $j_0$
(
$j_0$
(
![]() $1\leq j_0\leq m$
) and
$1\leq j_0\leq m$
) and
![]() $k_0$
(
$k_0$
(
![]() $1\leq k_0\leq n$
) such that
$1\leq k_0\leq n$
) such that
![]() $i_{j_0k_0}> i^{\prime }_{j_0k_0}$
and
$i_{j_0k_0}> i^{\prime }_{j_0k_0}$
and
![]() $i_{jk}= i^{\prime }_{jk}$
whenever
$i_{jk}= i^{\prime }_{jk}$
whenever
![]() $j< j_0$
or
$j< j_0$
or
![]() $j= j_0$
and
$j= j_0$
and
![]() $k<k_0$
.
$k<k_0$
.
We use
![]() $g\preceq h$
to denote
$g\preceq h$
to denote
![]() $g\prec h$
or
$g\prec h$
or
![]() $g=h$
.
$g=h$
.
The relation “
![]() $\preceq $
” is a total order on
$\preceq $
” is a total order on
![]() $\mathcal {F}_n$
.
$\mathcal {F}_n$
.
Lemma 3.10 We have the following statements:
(i) There exists a unique minimal element in each subset of
![]() $\mathcal {F}_n$
under the total order.
$\mathcal {F}_n$
under the total order.
![]() $(\mathrm{ii})$
Let
$(\mathrm{ii})$
Let
![]() $g_i$
and
$g_i$
and
![]() $h_i$
(
$h_i$
(
![]() $1\leq i\leq m$
) be
$1\leq i\leq m$
) be
![]() $2m$
elements in
$2m$
elements in
![]() $\mathcal {F}_n$
. If
$\mathcal {F}_n$
. If
![]() $g_{i}\preceq h_{i}$
for each i (
$g_{i}\preceq h_{i}$
for each i (
![]() $1\leq i\leq m$
), then
$1\leq i\leq m$
), then
![]() $\Pi _{i=1}^{m}g_{i}\preceq \Pi _{i=1}^{m}h_{i}$
. Moreover, the equality holds if and only if
$\Pi _{i=1}^{m}g_{i}\preceq \Pi _{i=1}^{m}h_{i}$
. Moreover, the equality holds if and only if
![]() $g_{i}=h_{i}$
for each i (
$g_{i}=h_{i}$
for each i (
![]() $1\leq i\leq m$
).
$1\leq i\leq m$
).
Proposition 3.11 For
![]() $n\geq 2$
, the free semigroup
$n\geq 2$
, the free semigroup
![]() $\mathcal {F}_n$
on n generators
$\mathcal {F}_n$
on n generators
![]() $a_i$
(
$a_i$
(
![]() $1\leq i \leq n$
) is a unique factorization semigroup.Footnote
1
$1\leq i \leq n$
) is a unique factorization semigroup.Footnote
1
Proof Let
![]() $X_i=a_i$
(
$X_i=a_i$
(
![]() $1\leq i\leq n$
), then
$1\leq i\leq n$
), then
![]() $X_1\prec X_2 \prec \cdots \prec X_n$
. Let
$X_1\prec X_2 \prec \cdots \prec X_n$
. Let
![]() $X_{n+1}$
be the minimal element of
$X_{n+1}$
be the minimal element of
![]() $\mathcal {F}$
such that
$\mathcal {F}$
such that
![]() $X_{n+1}$
cannot be represented as
$X_{n+1}$
cannot be represented as
![]() $X_1^{i_1}\dots X_n^{i_n}$
for any nonnegative integers
$X_1^{i_1}\dots X_n^{i_n}$
for any nonnegative integers
![]() $i_j$
(
$i_j$
(
![]() $1\leq j\leq n$
). Then
$1\leq j\leq n$
). Then
![]() $X_n\prec X_{n+1}$
. Let
$X_n\prec X_{n+1}$
. Let
![]() $X_{n+2}$
be the minimal element of
$X_{n+2}$
be the minimal element of
![]() $\mathcal {F}$
such that
$\mathcal {F}$
such that
![]() $X_{n+2}$
cannot be represented as
$X_{n+2}$
cannot be represented as
![]() $X_1^{i_1}\dots X_{n+1}^{i_{n+1}}$
for any nonnegative integers
$X_1^{i_1}\dots X_{n+1}^{i_{n+1}}$
for any nonnegative integers
![]() $i_j$
(
$i_j$
(
![]() $1\leq j\leq n+1$
). Then
$1\leq j\leq n+1$
). Then
![]() $X_{n+1}\prec X_{n+2}$
. Continuing this process, we can obtain a subset
$X_{n+1}\prec X_{n+2}$
. Continuing this process, we can obtain a subset
![]() $\{X_1,X_2,\ldots \}$
of
$\{X_1,X_2,\ldots \}$
of
![]() $\mathcal {F}_n$
such that
$\mathcal {F}_n$
such that
![]() $X_i\prec X_{i+1}$
for each i (
$X_i\prec X_{i+1}$
for each i (
![]() $\geq 1$
). Then every element can be written as the product
$\geq 1$
). Then every element can be written as the product
![]() $X_1^{i_1}\dots X_n^{i_n}$
for some nonnegative integers
$X_1^{i_1}\dots X_n^{i_n}$
for some nonnegative integers
![]() $i_j$
(
$i_j$
(
![]() $1\leq j\leq n$
). We next show the uniqueness by induction on the index. It is clear that the uniqueness holds for index
$1\leq j\leq n$
). We next show the uniqueness by induction on the index. It is clear that the uniqueness holds for index
![]() $\leq 1$
. Assume that the uniqueness holds for index
$\leq 1$
. Assume that the uniqueness holds for index
![]() $\leq k$
(
$\leq k$
(
![]() $k\geq 1$
). Let
$k\geq 1$
). Let
![]() $g\in \mathcal {F}_n$
and
$g\in \mathcal {F}_n$
and
![]() $\mathsf {ind}(g)= k+1$
. Suppose that g has two different forms:
$\mathsf {ind}(g)= k+1$
. Suppose that g has two different forms:
where
![]() $\alpha _i$
(
$\alpha _i$
(
![]() $1\leq i\leq n$
) and
$1\leq i\leq n$
) and
![]() $\beta _j$
(
$\beta _j$
(
![]() $1\leq j\leq m$
) are positive integers,
$1\leq j\leq m$
) are positive integers,
![]() $i_1<\cdots <i_n$
and
$i_1<\cdots <i_n$
and
![]() $j_1<\cdots <j_m$
. If
$j_1<\cdots <j_m$
. If
![]() $i_1=j_1$
, then
$i_1=j_1$
, then
which implies that
![]() $n=m$
,
$n=m$
,
![]() $i_t=j_t$
and
$i_t=j_t$
and
![]() $\alpha _t=\beta _t$
(
$\alpha _t=\beta _t$
(
![]() $1\leq t\leq n$
). This leads to a contradiction.
$1\leq t\leq n$
). This leads to a contradiction.
We assume that
![]() $i_1<j_1$
. Then there exists some l (
$i_1<j_1$
. Then there exists some l (
![]() $1\leq l\leq n-1$
) such that
$1\leq l\leq n-1$
) such that
![]() $(X_{i_1}^{\alpha _1}\dots X_{i_l}^{\alpha _l})^{-1}X_{j_1}$
belongs to
$(X_{i_1}^{\alpha _1}\dots X_{i_l}^{\alpha _l})^{-1}X_{j_1}$
belongs to
![]() $\mathcal {F}_n$
and
$\mathcal {F}_n$
and
![]() $1\leq \mathsf {ind}((X_{i_1}^{\alpha _1}\dots X_{i_l}^{\alpha _l})^{-1}X_{j_1})< \mathsf {ind}(X_{i_{l+1}})$
, or
$1\leq \mathsf {ind}((X_{i_1}^{\alpha _1}\dots X_{i_l}^{\alpha _l})^{-1}X_{j_1})< \mathsf {ind}(X_{i_{l+1}})$
, or
![]() $(X_{i_1}^{\alpha _1}\dots X_{i_{l-1}}^{\alpha _{l-1}}$
$(X_{i_1}^{\alpha _1}\dots X_{i_{l-1}}^{\alpha _{l-1}}$
![]() $X_{i_l}^{\alpha ^{\prime }_l})^{-1}X_{j_1}$
(
$X_{i_l}^{\alpha ^{\prime }_l})^{-1}X_{j_1}$
(
![]() $1\leq l\leq n$
) belongs to
$1\leq l\leq n$
) belongs to
![]() $\mathcal {F}_n$
for some
$\mathcal {F}_n$
for some
![]() $\alpha ^{\prime }_l$
(
$\alpha ^{\prime }_l$
(
![]() $1\leq \alpha ^{\prime }_l< \alpha _l$
) and
$1\leq \alpha ^{\prime }_l< \alpha _l$
) and
![]() $1\leq \mathsf {ind}((X_{i_1}^{\alpha _1}\dots X_{i_{l-1}}^{\alpha _{l-1}}X_{i_l}^{\alpha ^{\prime }_l})^{-1}$
$1\leq \mathsf {ind}((X_{i_1}^{\alpha _1}\dots X_{i_{l-1}}^{\alpha _{l-1}}X_{i_l}^{\alpha ^{\prime }_l})^{-1}$
![]() $X_{j_1})< \mathsf {ind}(X_{i_l})$
. In the first case, we have
$X_{j_1})< \mathsf {ind}(X_{i_l})$
. In the first case, we have
![]() $(X_{i_1}^{\alpha _1}\dots X_{i_l}^{\alpha _l})^{-1}X_{j_1}=X_{s_1}^{\gamma _1}\dots X_{s_t}^{\gamma _t}$
for some positive integers
$(X_{i_1}^{\alpha _1}\dots X_{i_l}^{\alpha _l})^{-1}X_{j_1}=X_{s_1}^{\gamma _1}\dots X_{s_t}^{\gamma _t}$
for some positive integers
![]() $\gamma _1,\ldots ,\gamma _t$
and
$\gamma _1,\ldots ,\gamma _t$
and
![]() $s_1<\cdots <s_t<\min \{ i_{l+1},j_1\}$
. Then
$s_1<\cdots <s_t<\min \{ i_{l+1},j_1\}$
. Then
which leads to a contradiction. In the second case, we have
![]() $(X_{i_1}^{\alpha _1}\dots X_{i_l}^{\alpha ^{\prime }_l})^{-1}X_{j_1}=X_{s_1}^{\gamma _1}\dots X_{s_t}^{\gamma _t}$
for some positive integers
$(X_{i_1}^{\alpha _1}\dots X_{i_l}^{\alpha ^{\prime }_l})^{-1}X_{j_1}=X_{s_1}^{\gamma _1}\dots X_{s_t}^{\gamma _t}$
for some positive integers
![]() $\gamma _1,\ldots ,\gamma _t$
and
$\gamma _1,\ldots ,\gamma _t$
and
![]() $s_1<\cdots <s_t<\min \{ i_{l},j_1\}$
. Then
$s_1<\cdots <s_t<\min \{ i_{l},j_1\}$
. Then
which also leads to a contradiction. Above all, we complete the proof.
Free semigroups
![]() $\mathcal {F}_n$
(
$\mathcal {F}_n$
(
![]() $n\geq 2$
) are neither left nor right amenable. Thompson’s semigroup is not right amenable and whether it is left amenable is still unknown. For completeness, we construct the following both left and right amenable semigroup.
$n\geq 2$
) are neither left nor right amenable. Thompson’s semigroup is not right amenable and whether it is left amenable is still unknown. For completeness, we construct the following both left and right amenable semigroup.
Proposition 3.12 Let
![]() $\mathcal {T}$
be the semigroup generated by
$\mathcal {T}$
be the semigroup generated by
 $$ \begin{align*} A= \begin{pmatrix} 1 & 0 \\ 0 & 2 \end{pmatrix},\ B= \begin{pmatrix} 2 & 0 \\ 0 & 1 \end{pmatrix},\ C= \begin{pmatrix} 0 & 2 \\ 3 & 0 \end{pmatrix} \end{align*} $$
$$ \begin{align*} A= \begin{pmatrix} 1 & 0 \\ 0 & 2 \end{pmatrix},\ B= \begin{pmatrix} 2 & 0 \\ 0 & 1 \end{pmatrix},\ C= \begin{pmatrix} 0 & 2 \\ 3 & 0 \end{pmatrix} \end{align*} $$
in
![]() $GL_{2}(\mathbb {Z})$
. Then
$GL_{2}(\mathbb {Z})$
. Then
![]() $\mathcal {T}$
is a non-commutative unique factorization semigroup. Moreover,
$\mathcal {T}$
is a non-commutative unique factorization semigroup. Moreover,
![]() $\mathcal {T}$
is both left and right amenable.
$\mathcal {T}$
is both left and right amenable.
Proof It can be verified directly that
![]() $AB=BA$
,
$AB=BA$
,
![]() $AC=CB$
,
$AC=CB$
,
![]() $BC=CA$
. Hence,
$BC=CA$
. Hence,
![]() $\mathcal {T}$
is non-commutative and every element in
$\mathcal {T}$
is non-commutative and every element in
![]() $\mathcal {T}$
can be written as
$\mathcal {T}$
can be written as
![]() $A^{\alpha _1}B^{\alpha _2}C^{\alpha _3}$
for some natural numbers
$A^{\alpha _1}B^{\alpha _2}C^{\alpha _3}$
for some natural numbers
![]() $\alpha _1$
,
$\alpha _1$
,
![]() $\alpha _2$
, and
$\alpha _2$
, and
![]() $\alpha _3$
. Let X be a matrix in
$\alpha _3$
. Let X be a matrix in
![]() $\mathcal {T}$
with two different representations:
$\mathcal {T}$
with two different representations:
![]() $X=A^{\alpha _{1}}B^{\alpha _{2}}C^{\alpha _{3}}=A^{\beta _{1}}B^{\beta _{2}}C^{\beta _{3}}$
, where
$X=A^{\alpha _{1}}B^{\alpha _{2}}C^{\alpha _{3}}=A^{\beta _{1}}B^{\beta _{2}}C^{\beta _{3}}$
, where
![]() $\alpha _i$
and
$\alpha _i$
and
![]() $\beta _i$
(
$\beta _i$
(
![]() $1\leq i\leq 3$
) are natural numbers. Taking the determinant at the both sides, we have
$1\leq i\leq 3$
) are natural numbers. Taking the determinant at the both sides, we have
![]() $2^{\alpha _{1}}\dot 2^{\alpha _{2}}\dot (-6)^{\alpha _{3}}=2^{\beta _{1}}\dot 2^{\beta _{2}}\dot (-6)^{\beta _{3}}$
. Hence
$2^{\alpha _{1}}\dot 2^{\alpha _{2}}\dot (-6)^{\alpha _{3}}=2^{\beta _{1}}\dot 2^{\beta _{2}}\dot (-6)^{\beta _{3}}$
. Hence
![]() $\alpha _{3}=\beta _{3}$
and
$\alpha _{3}=\beta _{3}$
and
![]() $\alpha _{1}+\alpha _{2}=\beta _{1}+\beta _{2}$
. Then we have
$\alpha _{1}+\alpha _{2}=\beta _{1}+\beta _{2}$
. Then we have
![]() $A^{\alpha _{1}-\beta _{1}}=B^{\beta _{2}-\alpha _{2}}$
, which implies
$A^{\alpha _{1}-\beta _{1}}=B^{\beta _{2}-\alpha _{2}}$
, which implies
![]() $\alpha _{1}=\beta _{1}$
and
$\alpha _{1}=\beta _{1}$
and
![]() $\alpha _{2}=\beta _{2}$
. Thus
$\alpha _{2}=\beta _{2}$
. Thus
![]() $\mathcal {T}$
is a unique factorization semigroup. For each positive integer N (
$\mathcal {T}$
is a unique factorization semigroup. For each positive integer N (
![]() $\geq 2$
), let
$\geq 2$
), let
![]() $F_{N}=\{A^{\alpha _{1}}B^{\alpha _{2}}C^{\alpha _{3}}\in \mathcal {T}\ |\ 0\leq \alpha _{i}\leq N,\ i=1,2,3\}$
, we have
$F_{N}=\{A^{\alpha _{1}}B^{\alpha _{2}}C^{\alpha _{3}}\in \mathcal {T}\ |\ 0\leq \alpha _{i}\leq N,\ i=1,2,3\}$
, we have
 $$ \begin{align*} AF_{N}\cap F_{N}=\{A^{\alpha_{1}}B^{\alpha_{2}}C^{\alpha_{3}}\in \mathcal{T}\ |\ 1\leq \alpha_{1}\leq N,\ 0\leq \alpha_{i}\leq N,\ i=2,3\},\\ BF_{N}\cap F_{N}=\{A^{\alpha_{1}}B^{\alpha_{2}}C^{\alpha_{3}}\in \mathcal{T}\ |\ 1\leq \alpha_{2}\leq N,\ 0\leq \alpha_{i}\leq N,\ i=1,3\},\\ CF_{N}\cap F_{N}=\{A^{\alpha_{1}}B^{\alpha_{2}}C^{\alpha_{3}}\in \mathcal{T}\ |\ 1\leq \alpha_{3}\leq N,\ 0\leq \alpha_{i}\leq N,\ i=1,2\} \end{align*} $$
$$ \begin{align*} AF_{N}\cap F_{N}=\{A^{\alpha_{1}}B^{\alpha_{2}}C^{\alpha_{3}}\in \mathcal{T}\ |\ 1\leq \alpha_{1}\leq N,\ 0\leq \alpha_{i}\leq N,\ i=2,3\},\\ BF_{N}\cap F_{N}=\{A^{\alpha_{1}}B^{\alpha_{2}}C^{\alpha_{3}}\in \mathcal{T}\ |\ 1\leq \alpha_{2}\leq N,\ 0\leq \alpha_{i}\leq N,\ i=1,3\},\\ CF_{N}\cap F_{N}=\{A^{\alpha_{1}}B^{\alpha_{2}}C^{\alpha_{3}}\in \mathcal{T}\ |\ 1\leq \alpha_{3}\leq N,\ 0\leq \alpha_{i}\leq N,\ i=1,2\} \end{align*} $$
and
![]() $|AF_{N}\cap F_{N}|=|BF_{N}\cap F_{N}|=|CF_{N}\cap F_{N}|=N(N+1)^2$
. Then
$|AF_{N}\cap F_{N}|=|BF_{N}\cap F_{N}|=|CF_{N}\cap F_{N}|=N(N+1)^2$
. Then
 $$\begin{align*}\lim_{N\rightarrow\infty}\frac{|AF_{N}\cap F_{N}|}{|F_{N}|}=\lim_{N\rightarrow\infty}\frac{|BF_{N}\cap F_{N}|}{|F_{N}|}=\lim_{N\rightarrow\infty}\frac{|CF_{N}\cap F_{N}|}{|F_{N}|}=\lim_{N\rightarrow\infty}\frac{N(N+1)^2}{(N+1)^{3}}=1.\end{align*}$$
$$\begin{align*}\lim_{N\rightarrow\infty}\frac{|AF_{N}\cap F_{N}|}{|F_{N}|}=\lim_{N\rightarrow\infty}\frac{|BF_{N}\cap F_{N}|}{|F_{N}|}=\lim_{N\rightarrow\infty}\frac{|CF_{N}\cap F_{N}|}{|F_{N}|}=\lim_{N\rightarrow\infty}\frac{N(N+1)^2}{(N+1)^{3}}=1.\end{align*}$$
Since A, B, and C are generators of
![]() $\mathcal {T}$
,
$\mathcal {T}$
,
![]() $(F_N)_{N\in \mathbb {N}}$
is a left Følner sequence of
$(F_N)_{N\in \mathbb {N}}$
is a left Følner sequence of
![]() $\mathcal {T}$
. Thus
$\mathcal {T}$
. Thus
![]() $\mathcal {T}$
is left amenable. On the other hand, we have
$\mathcal {T}$
is left amenable. On the other hand, we have
 $$ \begin{align*} F_{N}A\cap F_{N}=&\{A^{\alpha_{1}}B^{\alpha_{2}}C^{\alpha_{3}}\in \mathcal{T}\ |\ 1\leq \alpha_{1}\leq N,\ 0\leq \alpha_{i}\leq N,\ i=2,3,\ \alpha_{3}\ \text{is even}\}\\ \cup&\{A^{\alpha_{1}}B^{\alpha_{2}}C^{\alpha_{3}}\in \mathcal{T}\ |\ 1\leq \alpha_{2}\leq N,\ 0\leq \alpha_{i}\leq N,\ i=1,3,\ \alpha_{3}\ \text{is odd}\},\\ F_{N}B\cap F_{N}=&\{A^{\alpha_{1}}B^{\alpha_{2}}C^{\alpha_{3}}\in \mathcal{T}\ |\ 1\leq \alpha_{2}\leq N,\ 0\leq \alpha_{i}\leq N,\ i=1,3,\ \alpha_{3}\ \text{is even}\}\\ \cup&\{A^{\alpha_{1}}B^{\alpha_{2}}C^{\alpha_{3}}\in \mathcal{T}\ |\ 1\leq \alpha_{1}\leq N,\ 0\leq \alpha_{i}\leq N,\ i=2,3,\ \alpha_{3}\ \text{is odd}\},\\ F_{N}C\cap F_{N}=&\{A^{\alpha_{1}}B^{\alpha_{2}}C^{\alpha_{3}}\in \mathcal{T}\ |\ 1\leq \alpha_{3}\leq N,\ 0\leq \alpha_{i}\leq N,\ i=1,2\}. \end{align*} $$
$$ \begin{align*} F_{N}A\cap F_{N}=&\{A^{\alpha_{1}}B^{\alpha_{2}}C^{\alpha_{3}}\in \mathcal{T}\ |\ 1\leq \alpha_{1}\leq N,\ 0\leq \alpha_{i}\leq N,\ i=2,3,\ \alpha_{3}\ \text{is even}\}\\ \cup&\{A^{\alpha_{1}}B^{\alpha_{2}}C^{\alpha_{3}}\in \mathcal{T}\ |\ 1\leq \alpha_{2}\leq N,\ 0\leq \alpha_{i}\leq N,\ i=1,3,\ \alpha_{3}\ \text{is odd}\},\\ F_{N}B\cap F_{N}=&\{A^{\alpha_{1}}B^{\alpha_{2}}C^{\alpha_{3}}\in \mathcal{T}\ |\ 1\leq \alpha_{2}\leq N,\ 0\leq \alpha_{i}\leq N,\ i=1,3,\ \alpha_{3}\ \text{is even}\}\\ \cup&\{A^{\alpha_{1}}B^{\alpha_{2}}C^{\alpha_{3}}\in \mathcal{T}\ |\ 1\leq \alpha_{1}\leq N,\ 0\leq \alpha_{i}\leq N,\ i=2,3,\ \alpha_{3}\ \text{is odd}\},\\ F_{N}C\cap F_{N}=&\{A^{\alpha_{1}}B^{\alpha_{2}}C^{\alpha_{3}}\in \mathcal{T}\ |\ 1\leq \alpha_{3}\leq N,\ 0\leq \alpha_{i}\leq N,\ i=1,2\}. \end{align*} $$
Similarly,
![]() $(F_N)_{N\in \mathbb {N}}$
is also a right Følner sequence of
$(F_N)_{N\in \mathbb {N}}$
is also a right Følner sequence of
![]() $\mathcal {T}$
. Thus
$\mathcal {T}$
. Thus
![]() $\mathcal {T}$
is both left and right amenable. We complete the proof.
$\mathcal {T}$
is both left and right amenable. We complete the proof.
4 The continuity of derivations
In this section, we will prove the following theorem.
Theorem 4.1 Derivations on the Banach algebras
![]() $\mathfrak {B}(\mathcal {S})$
and
$\mathfrak {B}(\mathcal {S})$
and
![]() $\mathfrak {B}(\mathcal {F}_n)$
are continuous.
$\mathfrak {B}(\mathcal {F}_n)$
are continuous.
Before proving Theorem 4.1, we introduce the following definition.
Definition 4.2 A discrete semigroup S is said to be lower stable if there exists a total order “
![]() $\preceq $
” on S such that:
$\preceq $
” on S such that:
(i) There exists a unique minimal element in each non-empty subset of S under the total order.
![]() $\mathrm{(ii)}$
Let
$\mathrm{(ii)}$
Let
![]() $u_i$
and
$u_i$
and
![]() $v_i$
(
$v_i$
(
![]() $1\leq i\leq n$
) be
$1\leq i\leq n$
) be
![]() $2n$
elements in S. If
$2n$
elements in S. If
![]() $u_{i}\preceq v_{i}$
for each
$u_{i}\preceq v_{i}$
for each
![]() $1\leq i\leq n$
, then
$1\leq i\leq n$
, then
![]() $\Pi _{i=1}^{n}u_{i}\preceq \Pi _{i=1}^{n}v_{i}$
. Moreover, the equality holds if and only if
$\Pi _{i=1}^{n}u_{i}\preceq \Pi _{i=1}^{n}v_{i}$
. Moreover, the equality holds if and only if
![]() $u_{i}=v_{i}$
for each
$u_{i}=v_{i}$
for each
![]() $1\leq i\leq n$
.
$1\leq i\leq n$
.
By Lemmas 3.7 and 3.10, Thompson’s semigroup
![]() $\mathcal {S}$
and free semigroups
$\mathcal {S}$
and free semigroups
![]() $\mathcal {F}_n$
(
$\mathcal {F}_n$
(
![]() $n\geq 2$
) are both lower stable.
$n\geq 2$
) are both lower stable.
Definition 4.3 A Banach algebra
![]() $\mathcal {A}$
is said to be semisimple if its Jacobson radical
$\mathcal {A}$
is said to be semisimple if its Jacobson radical
![]() $\mathcal {J}$
equals zero, where
$\mathcal {J}$
equals zero, where
The following lemma is a characterization of semisimple Banach algebras.
Lemma 4.4 Let
![]() $\mathcal {A}$
be a Banach algebra with the unit I. If
$\mathcal {A}$
be a Banach algebra with the unit I. If
![]() $\mathcal {A}$
contains no nonzero quasi-nilpotent operators, then
$\mathcal {A}$
contains no nonzero quasi-nilpotent operators, then
![]() $\mathcal {A}$
is semisimple.
$\mathcal {A}$
is semisimple.
Proof Let T be a nonzero element in
![]() $\mathcal {A}$
. Let
$\mathcal {A}$
. Let
![]() $\lambda $
be a nonzero point of the spectrum of T, then at least one of
$\lambda $
be a nonzero point of the spectrum of T, then at least one of
![]() $(\lambda I-T)\mathcal {A}$
and
$(\lambda I-T)\mathcal {A}$
and
![]() $\mathcal {A}(\lambda I-T)$
is properly contained in
$\mathcal {A}(\lambda I-T)$
is properly contained in
![]() $\mathcal {A}$
. We assume that the right ideal
$\mathcal {A}$
. We assume that the right ideal
![]() $(\lambda I-T)\mathcal {A}$
is properly contained in
$(\lambda I-T)\mathcal {A}$
is properly contained in
![]() $\mathcal {A}$
. Then there exists a maximal right ideal
$\mathcal {A}$
. Then there exists a maximal right ideal
![]() $\mathcal {I}_r$
of
$\mathcal {I}_r$
of
![]() $\mathcal {A}$
such that
$\mathcal {A}$
such that
![]() $(\lambda I-T)\mathcal {A}\subseteq \mathcal {I}_r\subset \mathcal {A}$
. Thus T does not belong to
$(\lambda I-T)\mathcal {A}\subseteq \mathcal {I}_r\subset \mathcal {A}$
. Thus T does not belong to
![]() $\mathcal {I}_r$
. This implies T is not in the Jacobson radical
$\mathcal {I}_r$
. This implies T is not in the Jacobson radical
![]() $\mathcal {J}$
of
$\mathcal {J}$
of
![]() $\mathcal {A}$
. Consequently, we have
$\mathcal {A}$
. Consequently, we have
![]() $\mathcal {J}=0$
. This completes the proof.
$\mathcal {J}=0$
. This completes the proof.
Lemma 4.5 Let S be a lower stable discrete semigroup and
![]() $\mathfrak {B}(S)$
the Banach algebra generated by
$\mathfrak {B}(S)$
the Banach algebra generated by
![]() $\{L_s:\ s\in S\}$
in
$\{L_s:\ s\in S\}$
in
![]() $B(l^2(S))$
. Then
$B(l^2(S))$
. Then
![]() $\mathfrak {B}(S)$
is semisimple.
$\mathfrak {B}(S)$
is semisimple.
Proof Let
![]() $L_f$
be a nonzero element in
$L_f$
be a nonzero element in
![]() $\mathfrak {B}(S)$
. We claim that the spectral radius
$\mathfrak {B}(S)$
. We claim that the spectral radius
![]() $r(L_f)>0$
. By the definition of lower stable semigroup, there is a unique minimal element X of the subset
$r(L_f)>0$
. By the definition of lower stable semigroup, there is a unique minimal element X of the subset
![]() $\{X\in S:f(X)\neq 0\}$
under the total order. Then we have
$\{X\in S:f(X)\neq 0\}$
under the total order. Then we have
 $$\begin{align*}\underbrace{f\ast\cdots \ast f}_{n}(X^{n})=f(X)^{n}\end{align*}$$
$$\begin{align*}\underbrace{f\ast\cdots \ast f}_{n}(X^{n})=f(X)^{n}\end{align*}$$
for each
![]() $n\geq 1$
. Therefore,
$n\geq 1$
. Therefore,
 $$ \begin{align*} r(L_{f})=\lim_{n\rightarrow\infty}\|L_{f}^{n}\|^{1/n}&\geq \lim_{n\rightarrow\infty}\|\underbrace{f\ast\cdots \ast f}_{n}\|_{2}^{1/n}\\ &\geq \lim_{n\rightarrow\infty}|\underbrace{f\ast\cdots \ast f}_{n}(X^{n})|^{1/n}=|f(X)|>0. \end{align*} $$
$$ \begin{align*} r(L_{f})=\lim_{n\rightarrow\infty}\|L_{f}^{n}\|^{1/n}&\geq \lim_{n\rightarrow\infty}\|\underbrace{f\ast\cdots \ast f}_{n}\|_{2}^{1/n}\\ &\geq \lim_{n\rightarrow\infty}|\underbrace{f\ast\cdots \ast f}_{n}(X^{n})|^{1/n}=|f(X)|>0. \end{align*} $$
By Lemma 4.4, we obtain that
![]() $\mathfrak {B}(S)$
is semisimple.
$\mathfrak {B}(S)$
is semisimple.
Corollary 4.6 The Banach algebras
![]() $\mathfrak {B}(\mathcal {S})$
and
$\mathfrak {B}(\mathcal {S})$
and
![]() $\mathfrak {B}(\mathcal {F}_n)$
are semisimple.
$\mathfrak {B}(\mathcal {F}_n)$
are semisimple.
In the semigroup
![]() $\mathcal {T}$
, if
$\mathcal {T}$
, if
![]() $A \prec B$
, then
$A \prec B$
, then
![]() $AC \prec BC = CA \prec CB = AC.$
Hence, we cannot have
$AC \prec BC = CA \prec CB = AC.$
Hence, we cannot have
![]() $A \prec B$
. Similarly,
$A \prec B$
. Similarly,
![]() $B \prec A$
is not allowed. Therefore, the semigroup
$B \prec A$
is not allowed. Therefore, the semigroup
![]() $\mathcal {T}$
in Example 3.12 is not lower stable. The Banach algebra
$\mathcal {T}$
in Example 3.12 is not lower stable. The Banach algebra
![]() $\mathfrak {B}(\mathcal {T})$
is also semisimple. The proof is similar to that of Lemma 4.5, we omit it here. Now, we prove Theorem 4.1.
$\mathfrak {B}(\mathcal {T})$
is also semisimple. The proof is similar to that of Lemma 4.5, we omit it here. Now, we prove Theorem 4.1.
Proof of Theorem 4.1
Theorem 4.1 of [Reference Johnson and Sinclair16] states that derivations on a semisimple Banach algebra are continuous, then by Corollary 4.6, we can obtain the conclusion.
5 The first cohomology group of
 $\mathfrak {B}(\mathcal {S})$
$\mathfrak {B}(\mathcal {S})$
A derivation D on a Banach algebra
![]() $\mathfrak {B}\subseteq B(\mathcal {H})$
is said to be spatial if there exists a bounded operator T in
$\mathfrak {B}\subseteq B(\mathcal {H})$
is said to be spatial if there exists a bounded operator T in
![]() $B(\mathcal {H})$
such that
$B(\mathcal {H})$
such that
![]() $D(A)=TA-AT$
for each A in
$D(A)=TA-AT$
for each A in
![]() $\mathfrak {B}$
. In [Reference Kadison18], Kadison proved that all derivations on a
$\mathfrak {B}$
. In [Reference Kadison18], Kadison proved that all derivations on a
![]() $C^{*}$
-algebra are spatial. In this section, we will prove that all derivations on the Banach algebra
$C^{*}$
-algebra are spatial. In this section, we will prove that all derivations on the Banach algebra
![]() $\mathfrak {B}(\mathcal {S})$
are spatial and induced by bounded operators in
$\mathfrak {B}(\mathcal {S})$
are spatial and induced by bounded operators in
![]() $\mathcal {L}(\mathcal {S})$
. Moreover, we prove that the first continuous cohomology group of
$\mathcal {L}(\mathcal {S})$
. Moreover, we prove that the first continuous cohomology group of
![]() $\mathfrak {B}(\mathcal {S})$
with coefficients in
$\mathfrak {B}(\mathcal {S})$
with coefficients in
![]() $\mathcal {L}(\mathcal {S})$
is zero (see Theorem 5.8).
$\mathcal {L}(\mathcal {S})$
is zero (see Theorem 5.8).
The Hilbert space
![]() $\mathcal {H}$
is
$\mathcal {H}$
is
![]() $l^2(\mathcal {S})$
. Recall that
$l^2(\mathcal {S})$
. Recall that
![]() $\mathfrak {B}(\mathcal {S})$
is the Banach algebra generated by
$\mathfrak {B}(\mathcal {S})$
is the Banach algebra generated by
![]() $\{L_s:s\in \mathcal {S} \}$
in
$\{L_s:s\in \mathcal {S} \}$
in
![]() $B(\mathcal {H})$
and
$B(\mathcal {H})$
and
![]() $\mathcal {L}(\mathcal {S})=\left \{L_{f}\in B(\mathcal {H}):f\in \mathcal {H}\right \}$
. We use
$\mathcal {L}(\mathcal {S})=\left \{L_{f}\in B(\mathcal {H}):f\in \mathcal {H}\right \}$
. We use
![]() $\sum _{X\in \mathcal {S}}f(X)X$
and
$\sum _{X\in \mathcal {S}}f(X)X$
and
![]() $\sum _{X\in \mathcal {S}}\overline {f(X)}X^{*}$
to denote
$\sum _{X\in \mathcal {S}}\overline {f(X)}X^{*}$
to denote
![]() $L_{f}$
and its adjoint operator
$L_{f}$
and its adjoint operator
![]() $L_f^*$
for convenience. It is clear that
$L_f^*$
for convenience. It is clear that
![]() $XX^{*}$
is the projection from
$XX^{*}$
is the projection from
![]() $\mathcal {H}$
onto the closure of the subspace span
$\mathcal {H}$
onto the closure of the subspace span
![]() $\{\delta _Y:\ Y\in \mathcal {S},\ X|Y\}$
and
$\{\delta _Y:\ Y\in \mathcal {S},\ X|Y\}$
and
![]() $X^{*}X=I$
(the identity map). Recall that “
$X^{*}X=I$
(the identity map). Recall that “
![]() $|$
” is the partial order of Thompson’s semigroup introduced in Section 3 and “
$|$
” is the partial order of Thompson’s semigroup introduced in Section 3 and “
![]() $X|Y$
” means that there exists an element Z in
$X|Y$
” means that there exists an element Z in
![]() $\mathcal {S}$
such that
$\mathcal {S}$
such that
![]() $Y=XZ$
.
$Y=XZ$
.
Let
![]() $(\mathbb {N},+)$
be the additive semigroup of natural numbers. The notation
$(\mathbb {N},+)$
be the additive semigroup of natural numbers. The notation
![]() $\beta \mathbb {N}$
denotes the maximal ideal space of the commutative
$\beta \mathbb {N}$
denotes the maximal ideal space of the commutative
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $l^{\infty }(\mathbb {N})$
. The elements in
$l^{\infty }(\mathbb {N})$
. The elements in
![]() $\beta \mathbb {N} \setminus \mathbb {N}$
are called free ultrafilters. Let
$\beta \mathbb {N} \setminus \mathbb {N}$
are called free ultrafilters. Let
![]() $\omega \in \beta \mathbb {N} \setminus \mathbb {N}$
be a free ultrafilter. For any n in
$\omega \in \beta \mathbb {N} \setminus \mathbb {N}$
be a free ultrafilter. For any n in
![]() $\mathbb {N} $
and any f in
$\mathbb {N} $
and any f in
![]() $l^{\infty }(\mathbb {N})$
, we define
$l^{\infty }(\mathbb {N})$
, we define
![]() $E_n(f) =\frac {1}{n} \sum _{i=0}^{n-1} f(i)$
. Then for each f, the function
$E_n(f) =\frac {1}{n} \sum _{i=0}^{n-1} f(i)$
. Then for each f, the function
![]() $n\mapsto E_n(f)$
is in
$n\mapsto E_n(f)$
is in
![]() $l^{\infty }(\mathbb {N})$
. By Gelfand–Naimark theorem, we have
$l^{\infty }(\mathbb {N})$
. By Gelfand–Naimark theorem, we have
![]() $l^{\infty }(\mathbb {N})\cong C(\beta \mathbb {N})$
. Thus
$l^{\infty }(\mathbb {N})\cong C(\beta \mathbb {N})$
. Thus
![]() $E_n(f)$
is a continuous function on
$E_n(f)$
is a continuous function on
![]() $\beta \mathbb {N}$
. We use
$\beta \mathbb {N}$
. We use
![]() $E_{\omega }(f)$
or the integral
$E_{\omega }(f)$
or the integral
![]() $\int _{\mathbb {N}} f(n) dE_{\omega }(n)$
to denote the limit of
$\int _{\mathbb {N}} f(n) dE_{\omega }(n)$
to denote the limit of
![]() $E_n(f)$
at
$E_n(f)$
at
![]() $\omega $
. Then
$\omega $
. Then
![]() $E_{\omega }$
is an invariant mean on
$E_{\omega }$
is an invariant mean on
![]() $l^{\infty }(\mathbb {N})$
, i.e.,
$l^{\infty }(\mathbb {N})$
, i.e.,
for each
![]() $m\geq 1$
. Moreover,
$m\geq 1$
. Moreover,
![]() $E_{\omega }$
satisfies that
$E_{\omega }$
satisfies that
![]() $E_{\omega }(f)=\lim _{n\rightarrow \infty }f(n)$
if the limit exists. The invariant mean
$E_{\omega }(f)=\lim _{n\rightarrow \infty }f(n)$
if the limit exists. The invariant mean
![]() $E_{\omega }$
is also called a Banach limit.
$E_{\omega }$
is also called a Banach limit.
Let D be a continuous derivation from the Banach algebra
![]() $\mathfrak {B}(\mathcal {S})$
into
$\mathfrak {B}(\mathcal {S})$
into
![]() $\mathcal {L}(\mathcal {S})$
. For each
$\mathcal {L}(\mathcal {S})$
. For each
![]() $\xi ,\eta \in \mathcal {H}$
, we define
$\xi ,\eta \in \mathcal {H}$
, we define
Then A is a bounded linear operator on
![]() $\mathcal {H}$
. Moreover, we have
$\mathcal {H}$
. Moreover, we have
 $$ \begin{align*} \langle A\xi,\eta\rangle&=\int_{\mathbb{N}} \langle (X_{0}^{*})^{n+1}D(X_{0}^{n+2})\xi,\eta \rangle dE_{\omega}(n)\\ &=\int_{\mathbb{N}} \langle D(X_{0})\xi,\eta \rangle dE_{\omega}(n)+ \int_{\mathbb{N}} \langle (X_{0}^{*})^{n+1}D(X_{0}^{n+1})X_0\xi,\eta \rangle dE_{\omega}(n)\\ &=\langle D(X_{0})\xi,\eta \rangle+ \langle X_{0}^{*}AX_0\xi,\eta \rangle, \end{align*} $$
$$ \begin{align*} \langle A\xi,\eta\rangle&=\int_{\mathbb{N}} \langle (X_{0}^{*})^{n+1}D(X_{0}^{n+2})\xi,\eta \rangle dE_{\omega}(n)\\ &=\int_{\mathbb{N}} \langle D(X_{0})\xi,\eta \rangle dE_{\omega}(n)+ \int_{\mathbb{N}} \langle (X_{0}^{*})^{n+1}D(X_{0}^{n+1})X_0\xi,\eta \rangle dE_{\omega}(n)\\ &=\langle D(X_{0})\xi,\eta \rangle+ \langle X_{0}^{*}AX_0\xi,\eta \rangle, \end{align*} $$
which follows that
Similarly, we define
We have
![]() $B \in B(\mathcal {H})$
and
$B \in B(\mathcal {H})$
and
5.1 The case of
 $X_0$
$X_0$
We prove the following local inner derivative property for
![]() $X_0$
in this subsection. A similar result for
$X_0$
in this subsection. A similar result for
![]() $X_1$
will be given later.
$X_1$
will be given later.
Lemma 5.1 There exists some
![]() $\widehat {A}$
in
$\widehat {A}$
in
![]() $\mathcal {L}(\mathcal {S})$
such that
$\mathcal {L}(\mathcal {S})$
such that
![]() $D(X_0)=\widehat {A}X_0-X_0\widehat {A}$
.
$D(X_0)=\widehat {A}X_0-X_0\widehat {A}$
.
Proof Let
By the fact that
![]() $X_{1}X_{0}=X_{0}X_{2}$
, we have
$X_{1}X_{0}=X_{0}X_{2}$
, we have
It follows that
Since
![]() $X_{1}X\prec XX_{2}$
when
$X_{1}X\prec XX_{2}$
when
![]() $X_{0}\nmid X$
, hence
$X_{0}\nmid X$
, hence
![]() $f(X)=0$
in this case. Therefore,
$f(X)=0$
in this case. Therefore,
for some
![]() $L_{f_1}$
in
$L_{f_1}$
in
![]() $\mathcal {L}(\mathcal {S})$
. By the Leibniz rule and induction, we can obtain that
$\mathcal {L}(\mathcal {S})$
. By the Leibniz rule and induction, we can obtain that
for some
![]() $L_{f_n}$
in
$L_{f_n}$
in
![]() $\mathcal {L}(\mathcal {S})$
. We define
$\mathcal {L}(\mathcal {S})$
. We define
Then
![]() $\widehat {A}\in B(\mathcal {H})$
. For each T in
$\widehat {A}\in B(\mathcal {H})$
. For each T in
![]() $\mathcal {R}(\mathcal {S})$
, we have
$\mathcal {R}(\mathcal {S})$
, we have
 $$ \begin{align*} \langle T\widehat{A}\xi,\eta\rangle&=-\int_{\mathbb{N}} \langle (X_{0}^{*})^{n+1}D(X_{0}^{n+1})\xi,T^*\eta \rangle dE_{\omega}(n)\\ &=-\int_{\mathbb{N}} \langle (X_{0}^{*})^{n+1}D(X_{0}^{n+1})T\xi, \eta \rangle dE_{\omega}(n)\\ &=\langle \widehat{A}T\xi,\eta\rangle. \end{align*} $$
$$ \begin{align*} \langle T\widehat{A}\xi,\eta\rangle&=-\int_{\mathbb{N}} \langle (X_{0}^{*})^{n+1}D(X_{0}^{n+1})\xi,T^*\eta \rangle dE_{\omega}(n)\\ &=-\int_{\mathbb{N}} \langle (X_{0}^{*})^{n+1}D(X_{0}^{n+1})T\xi, \eta \rangle dE_{\omega}(n)\\ &=\langle \widehat{A}T\xi,\eta\rangle. \end{align*} $$
The second equality is due to equation (9). It follows that
![]() $\widehat {A}\in \mathcal {R}(\mathcal {S})'=\mathcal {L}(\mathcal {S})$
. By equation (5), we have
$\widehat {A}\in \mathcal {R}(\mathcal {S})'=\mathcal {L}(\mathcal {S})$
. By equation (5), we have
 $$ \begin{align*} \langle A\xi,\eta\rangle&=\int_{\mathbb{N}} \langle (X_{0}^{*})^{n}D(X_{0}^{n+1})\xi,\eta \rangle dE_{\omega}(n)\\ &=\int_{\mathbb{N}} \langle (X_{0}^{*})^{n+1}D(X_{0}^{n+1})\xi,X_0^*\eta \rangle dE_{\omega}(n)\\ &= \langle -\widehat{A}\xi,X_0^*\eta \rangle, \end{align*} $$
$$ \begin{align*} \langle A\xi,\eta\rangle&=\int_{\mathbb{N}} \langle (X_{0}^{*})^{n}D(X_{0}^{n+1})\xi,\eta \rangle dE_{\omega}(n)\\ &=\int_{\mathbb{N}} \langle (X_{0}^{*})^{n+1}D(X_{0}^{n+1})\xi,X_0^*\eta \rangle dE_{\omega}(n)\\ &= \langle -\widehat{A}\xi,X_0^*\eta \rangle, \end{align*} $$
which implies
![]() $A=-X_0\widehat {A}$
. The second equality is due to equation (9). Then by equation (6), we have
$A=-X_0\widehat {A}$
. The second equality is due to equation (9). Then by equation (6), we have
![]() $D(X_0)=\widehat {A}X_0-X_0\widehat {A}$
. This completes the proof.
$D(X_0)=\widehat {A}X_0-X_0\widehat {A}$
. This completes the proof.
5.2 The case of
 $X_1$
$X_1$
The following lemma is the main conclusion of this subsection.
Lemma 5.2 There exists some
![]() $\widehat {B}$
in
$\widehat {B}$
in
![]() $\mathcal {L}(\mathcal {S})$
such that
$\mathcal {L}(\mathcal {S})$
such that
![]() $D(X_{1})=\widehat {B}X_{1}-X_{1}\widehat {B}$
.
$D(X_{1})=\widehat {B}X_{1}-X_{1}\widehat {B}$
.
We need Lemmas 5.3 and 5.4 to obtain Lemma 5.2.
Lemma 5.3 There exists some B in
![]() $\mathcal {L}(\mathcal {S})$
such that
$\mathcal {L}(\mathcal {S})$
such that
![]() $D(X_{1})=B-X_{1}^{*}BX_{1}$
.
$D(X_{1})=B-X_{1}^{*}BX_{1}$
.
Proof Let
![]() $D(X_{1})=L_{f}$
in
$D(X_{1})=L_{f}$
in
![]() $\mathcal {L}(\mathcal {S})$
. By the continuity of D, we have
$\mathcal {L}(\mathcal {S})$
. By the continuity of D, we have
![]() $f(X_{1}^{n})=0$
for each
$f(X_{1}^{n})=0$
for each
![]() $n\in \mathbb {N}$
. For each
$n\in \mathbb {N}$
. For each
![]() $m\geq 1$
, we have
$m\geq 1$
, we have
 $$\begin{align*}(X_{1}^{*})^{m-1}D(X_{1}^{m})=\sum_{i=0}^{m-1}(X_1^*)^iL_fX_1^{i}\end{align*}$$
$$\begin{align*}(X_{1}^{*})^{m-1}D(X_{1}^{m})=\sum_{i=0}^{m-1}(X_1^*)^iL_fX_1^{i}\end{align*}$$
and
Let
![]() $h_{1}$
and
$h_{1}$
and
![]() $ h_{2}$
be two elements in
$ h_{2}$
be two elements in
![]() $\mathcal {S}$
. If
$\mathcal {S}$
. If
![]() $h_{2}h_{1}^{-1}= X_{1}^{k}$
for some
$h_{2}h_{1}^{-1}= X_{1}^{k}$
for some
![]() $k\in \mathbb {N}$
, then
$k\in \mathbb {N}$
, then
 $$\begin{align*}\lim_{n,m\rightarrow\infty}\left\langle\bigg((X_{1}^{*})^{m-1}D(X_{1}^{m})-(X_{1}^{*})^{n-1}D(X_{1}^{n})\bigg)\delta_{h_{1}},\delta_{h_{2}}\right\rangle=\lim_{n,m\rightarrow\infty}\sum_{i=n+1}^{m}f(X_{1}^{i}h_{2}h_{1}^{-1}X_{1}^{-i})=0.\end{align*}$$
$$\begin{align*}\lim_{n,m\rightarrow\infty}\left\langle\bigg((X_{1}^{*})^{m-1}D(X_{1}^{m})-(X_{1}^{*})^{n-1}D(X_{1}^{n})\bigg)\delta_{h_{1}},\delta_{h_{2}}\right\rangle=\lim_{n,m\rightarrow\infty}\sum_{i=n+1}^{m}f(X_{1}^{i}h_{2}h_{1}^{-1}X_{1}^{-i})=0.\end{align*}$$
If
![]() $h_{2}h_{1}^{-1}\neq X_{1}^{k}$
for any
$h_{2}h_{1}^{-1}\neq X_{1}^{k}$
for any
![]() $k\in \mathbb {N}$
, then
$k\in \mathbb {N}$
, then
![]() $X_{1}^{i}h_{2}h_{1}^{-1}X_{1}^{-i}\notin \mathcal {S}$
when i is sufficiently large. Therefore,
$X_{1}^{i}h_{2}h_{1}^{-1}X_{1}^{-i}\notin \mathcal {S}$
when i is sufficiently large. Therefore,
 $$\begin{align*}\lim_{n,m\rightarrow\infty}\left\langle\bigg((X_{1}^{*})^{m-1}D(X_{1}^{m})-(X_{1}^{*})^{n-1}D(X_{1}^{n})\bigg)\delta_{h_{1}},\delta_{h_{2}}\right\rangle=\lim_{n,m\rightarrow\infty}\sum_{i=n+1}^{m}f(X_{1}^{i}h_{2}h_{1}^{-1}X_{1}^{-i})=0.\end{align*}$$
$$\begin{align*}\lim_{n,m\rightarrow\infty}\left\langle\bigg((X_{1}^{*})^{m-1}D(X_{1}^{m})-(X_{1}^{*})^{n-1}D(X_{1}^{n})\bigg)\delta_{h_{1}},\delta_{h_{2}}\right\rangle=\lim_{n,m\rightarrow\infty}\sum_{i=n+1}^{m}f(X_{1}^{i}h_{2}h_{1}^{-1}X_{1}^{-i})=0.\end{align*}$$
We define
Then T is the weak-operator limit of
![]() $(X_{1}^{*})^{m-1}D(X_{1}^{m})$
in
$(X_{1}^{*})^{m-1}D(X_{1}^{m})$
in
![]() $B(\mathcal {H})$
.
$B(\mathcal {H})$
.
Claim
![]() $T=L_{T\delta _{e}}\in \mathcal {L}(\mathcal {S})$
.
$T=L_{T\delta _{e}}\in \mathcal {L}(\mathcal {S})$
.
To prove this claim, we distinguish two cases:
Case I:
![]() $h_{2}h_{1}^{-1}\in \mathcal {S}$
. We have
$h_{2}h_{1}^{-1}\in \mathcal {S}$
. We have
Case II:
![]() $h_{2}h_{1}^{-1}\notin \mathcal {S}$
. If
$h_{2}h_{1}^{-1}\notin \mathcal {S}$
. If
![]() $X_{1}^{n}h_{2}h_{1}^{-1}X_{1}^{-n}\notin \mathcal {S}$
for any
$X_{1}^{n}h_{2}h_{1}^{-1}X_{1}^{-n}\notin \mathcal {S}$
for any
![]() $n\in \mathbb {N}$
, then
$n\in \mathbb {N}$
, then
On the other hand, there exists a natural number n such that
![]() $X_{1}^{n+1}h_{2}h_{1}^{-1}X_{1}^{-n-1}\in \mathcal {S}$
and
$X_{1}^{n+1}h_{2}h_{1}^{-1}X_{1}^{-n-1}\in \mathcal {S}$
and
![]() $X_{1}^{i}h_{2}h_{1}^{-1}X_{1}^{-i}\notin \mathcal {S}$
whenever
$X_{1}^{i}h_{2}h_{1}^{-1}X_{1}^{-i}\notin \mathcal {S}$
whenever
![]() $i\leq n$
. Let
$i\leq n$
. Let
![]() $X=X_{1}^{n+1}h_{2}h_{1}^{-1}X_{1}^{-n-1}$
, then
$X=X_{1}^{n+1}h_{2}h_{1}^{-1}X_{1}^{-n-1}$
, then
![]() $X_{0}|X$
. By Lemma 3.5, we have that
$X_{0}|X$
. By Lemma 3.5, we have that
![]() $X_{1}^{-k}XX_{1}^{k}\notin \mathcal {S}$
for any
$X_{1}^{-k}XX_{1}^{k}\notin \mathcal {S}$
for any
![]() $k\geq 1$
and
$k\geq 1$
and
![]() $X_{1}^{k}XX_{1}^{-k}\notin \mathcal {S}$
when
$X_{1}^{k}XX_{1}^{-k}\notin \mathcal {S}$
when
![]() $k>\mathsf {ind}(X)$
. Let m be an even integer such that m is sufficiently lager than
$k>\mathsf {ind}(X)$
. Let m be an even integer such that m is sufficiently lager than
![]() $\mathsf {ind}(X)$
. Then we have
$\mathsf {ind}(X)$
. Then we have
 $$ \begin{align*} \sum_{i=1}^{m}\left|\langle D(X_1^{2m})\delta_e,\delta_{X_1^{2m-i}XX_1^{i-1}}\rangle \right|^2= \sum_{i=1}^{m}\left|\sum_{j=-(i-1)}^{2m-i}f(X_1^{j}XX_1^{-j})\right|^2= \sum_{i=1}^{m}\left|\sum_{j=0}^{\mathsf{ind}(X)}f(X_1^{j}XX_1^{-j})\right|^2. \end{align*} $$
$$ \begin{align*} \sum_{i=1}^{m}\left|\langle D(X_1^{2m})\delta_e,\delta_{X_1^{2m-i}XX_1^{i-1}}\rangle \right|^2= \sum_{i=1}^{m}\left|\sum_{j=-(i-1)}^{2m-i}f(X_1^{j}XX_1^{-j})\right|^2= \sum_{i=1}^{m}\left|\sum_{j=0}^{\mathsf{ind}(X)}f(X_1^{j}XX_1^{-j})\right|^2. \end{align*} $$
Note that
![]() $X_{1}^{2m-i}XX_{1}^{i-1}\neq X_{1}^{2m-j}XX_{1}^{j-1}$
when
$X_{1}^{2m-i}XX_{1}^{i-1}\neq X_{1}^{2m-j}XX_{1}^{j-1}$
when
![]() $1\leq i< j\leq m$
, then we have
$1\leq i< j\leq m$
, then we have
 $$\begin{align*}\sum_{i=1}^{m}\left|\sum_{j=0}^{\mathsf{ind}(X)}f(X_1^{j}XX_1^{-j})\right|^2 \leq \left\|D(X_{1}^{2m})\delta_{e}\right\|_{2}^{2} \leq\left\|D\right\|^{2} \end{align*}$$
$$\begin{align*}\sum_{i=1}^{m}\left|\sum_{j=0}^{\mathsf{ind}(X)}f(X_1^{j}XX_1^{-j})\right|^2 \leq \left\|D(X_{1}^{2m})\delta_{e}\right\|_{2}^{2} \leq\left\|D\right\|^{2} \end{align*}$$
for any sufficiently large even integer m. This implies that
 $$\begin{align*}\sum_{j=0}^{\mathsf{ind}(X)}f(X_1^{j}XX_1^{-j})=0.\end{align*}$$
$$\begin{align*}\sum_{j=0}^{\mathsf{ind}(X)}f(X_1^{j}XX_1^{-j})=0.\end{align*}$$
Therefore,
 $$\begin{align*}\langle T\delta_{h_{1}},\delta_{h_{2}}\rangle=\sum_{j=0}^{\infty}f(X_{1}^{j}h_{2}h_{1}^{-1}X_{1}^{-j}) =\sum_{j=0}^{\mathsf{ind}(X)}f(X_{1}^{j}XX_{1}^{-j})=0.\end{align*}$$
$$\begin{align*}\langle T\delta_{h_{1}},\delta_{h_{2}}\rangle=\sum_{j=0}^{\infty}f(X_{1}^{j}h_{2}h_{1}^{-1}X_{1}^{-j}) =\sum_{j=0}^{\mathsf{ind}(X)}f(X_{1}^{j}XX_{1}^{-j})=0.\end{align*}$$
From the above discussion, we have
![]() $\langle T\delta _{h_{1}},\delta _{h_{2}}\rangle =\langle T\delta _{e}\ast \delta _{h_{1}},\delta _{h_{2}}\rangle $
for all
$\langle T\delta _{h_{1}},\delta _{h_{2}}\rangle =\langle T\delta _{e}\ast \delta _{h_{1}},\delta _{h_{2}}\rangle $
for all
![]() $h_{1}$
and
$h_{1}$
and
![]() $h_{2}$
in
$h_{2}$
in
![]() $\mathcal {S}$
. Thus the claim holds.
$\mathcal {S}$
. Thus the claim holds.
By equations (7) and (10), we have
 $$ \begin{align*} \langle T\delta_{h_1},\delta_{h_2}\rangle&= \lim_{m\rightarrow\infty}\big\langle(X_{1}^{*})^{m-1}D(X_{1}^{m})\delta_{h_{1}},\delta_{h_{2}}\big\rangle\\ &=\int_{\mathbb{N}}\big\langle(X_{1}^{*})^{m-1}D(X_{1}^{m})\delta_{h_{1}},\delta_{h_{2}}\big\rangle dE_{\omega}(m)\\ &= \langle B\delta_{h_1},\delta_{h_2}\rangle, \end{align*} $$
$$ \begin{align*} \langle T\delta_{h_1},\delta_{h_2}\rangle&= \lim_{m\rightarrow\infty}\big\langle(X_{1}^{*})^{m-1}D(X_{1}^{m})\delta_{h_{1}},\delta_{h_{2}}\big\rangle\\ &=\int_{\mathbb{N}}\big\langle(X_{1}^{*})^{m-1}D(X_{1}^{m})\delta_{h_{1}},\delta_{h_{2}}\big\rangle dE_{\omega}(m)\\ &= \langle B\delta_{h_1},\delta_{h_2}\rangle, \end{align*} $$
which follows that
![]() $B=T$
. This completes the proof.
$B=T$
. This completes the proof.
Lemma 5.4 Let
![]() $D(X_{1})=L_{f}\in \mathcal {L}(\mathcal {S})$
. Then
$D(X_{1})=L_{f}\in \mathcal {L}(\mathcal {S})$
. Then
Proof Let
By the fact that
![]() $X_{1}X_{3}=X_{2}X_{1}$
, we have
$X_{1}X_{3}=X_{2}X_{1}$
, we have
Then
Let X be the minimal element of the set
![]() $\{X\in \mathcal {S}:\ X_{0}\nmid X,\ X_{1}\nmid X,\ f(X)\neq 0\}$
. Then
$\{X\in \mathcal {S}:\ X_{0}\nmid X,\ X_{1}\nmid X,\ f(X)\neq 0\}$
. Then
![]() $X_2X\prec XX_3$
. It follows that
$X_2X\prec XX_3$
. It follows that
![]() $f(X)=0$
when
$f(X)=0$
when
![]() $X_{0}\nmid X$
and
$X_{0}\nmid X$
and
![]() $X_{1}\nmid X$
. This completes the proof.
$X_{1}\nmid X$
. This completes the proof.
Now, we are ready to prove Lemma 5.2.
Proof of Lemma 5.2
By Lemma 5.3, we have
![]() $D(X_{1})=B-X_{1}^{*}BX_{1}$
for some
$D(X_{1})=B-X_{1}^{*}BX_{1}$
for some
![]() $B=L_{g}\in \mathcal {L}(\mathcal {S})$
. We assume that
$B=L_{g}\in \mathcal {L}(\mathcal {S})$
. We assume that
![]() $g(e)=0$
, where e is the unit element of
$g(e)=0$
, where e is the unit element of
![]() $\mathcal {S}$
. Let
$\mathcal {S}$
. Let
Then
Since
![]() $D(X_{1})\in \mathcal {L}(\mathcal {S})$
and
$D(X_{1})\in \mathcal {L}(\mathcal {S})$
and
![]() $X_1^{-1}XX_1\notin \mathcal {S}$
when
$X_1^{-1}XX_1\notin \mathcal {S}$
when
![]() $X_{1}\nmid X$
and
$X_{1}\nmid X$
and
![]() $X_{0}|X$
, we have
$X_{0}|X$
, we have
For
![]() $X\in \mathcal {S}$
with
$X\in \mathcal {S}$
with
![]() $X_{1}\nmid X$
and
$X_{1}\nmid X$
and
![]() $X_{0}|X$
, let
$X_{0}|X$
, let
![]() $X_1^{-1}XX_1=UV^{-1}$
, where
$X_1^{-1}XX_1=UV^{-1}$
, where
![]() $U,V\in \mathcal {S}$
. Then
$U,V\in \mathcal {S}$
. Then
 $$ \begin{align*} g(X)=\left\langle X_1^*\sum_{X_{1}\nmid X,X_{0}|X}g(X)XX_1\delta_V,\delta_U \right\rangle=0. \end{align*} $$
$$ \begin{align*} g(X)=\left\langle X_1^*\sum_{X_{1}\nmid X,X_{0}|X}g(X)XX_1\delta_V,\delta_U \right\rangle=0. \end{align*} $$
It follows that
Therefore,
By Lemma 5.4, we have
Let X be the minimal element of the set
![]() $\{X\in \mathcal {S}:\ X_{1}\nmid X,\ X_{0}\nmid X,\ g(X)\neq 0\}$
. Then
$\{X\in \mathcal {S}:\ X_{1}\nmid X,\ X_{0}\nmid X,\ g(X)\neq 0\}$
. Then
![]() $X\prec X_1^{-1}XX_1$
since
$X\prec X_1^{-1}XX_1$
since
![]() $X\neq e$
. It follows that
$X\neq e$
. It follows that
![]() $g(X)=0$
when
$g(X)=0$
when
![]() $X_{1}\nmid X$
and
$X_{1}\nmid X$
and
![]() $X_{0}\nmid X$
. Thus
$X_{0}\nmid X$
. Thus
![]() $B=\sum _{X_{1}|X}g(X)X$
. Let
$B=\sum _{X_{1}|X}g(X)X$
. Let
![]() $\widehat {B}=-X_{1}^{*}B$
, then
$\widehat {B}=-X_{1}^{*}B$
, then
![]() $\widehat {B}\in \mathcal {L}(S)$
and
$\widehat {B}\in \mathcal {L}(S)$
and
We complete the proof.
5.3 Conditional expectation
Definition 5.5 Let
![]() $\mathfrak {B}$
be a Banach algebra, and let
$\mathfrak {B}$
be a Banach algebra, and let
![]() $\mathcal {A}$
be a Banach subalgebra of
$\mathcal {A}$
be a Banach subalgebra of
![]() $\mathfrak {B}$
. Let E:
$\mathfrak {B}$
. Let E:
![]() $\mathfrak {B}\rightarrow \mathcal {A}$
be a contraction such that:
$\mathfrak {B}\rightarrow \mathcal {A}$
be a contraction such that:
(i)
![]() $E(I)=I$
;
$E(I)=I$
;
(
![]() $\mathrm{ii}$
)
$\mathrm{ii}$
)
![]() $E(A_1BA_2)=A_1E(B)A_2$
whenever
$E(A_1BA_2)=A_1E(B)A_2$
whenever
![]() $A_1$
,
$A_1$
,
![]() $A_2$
$A_2$
![]() $\in \mathcal {A}$
and B
$\in \mathcal {A}$
and B
![]() $\in \mathfrak {B}$
.
$\in \mathfrak {B}$
.
Then E is described as a conditional expectation from
![]() $\mathfrak {B}$
onto
$\mathfrak {B}$
onto
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
Definition 5.6 We denote by
![]() $\mathcal {L}_0(\mathcal {S})$
the subset of
$\mathcal {L}_0(\mathcal {S})$
the subset of
![]() $\mathcal {L}(\mathcal {S})$
such that for each
$\mathcal {L}(\mathcal {S})$
such that for each
![]() $L_f$
in
$L_f$
in
![]() $\mathcal {L}_0(\mathcal {S})$
,
$\mathcal {L}_0(\mathcal {S})$
,
![]() $f(X)=0$
if X is not in the semigroup generated by
$f(X)=0$
if X is not in the semigroup generated by
![]() $X_0$
.
$X_0$
.
It is not difficult to check that
![]() $\mathcal {L}_0(\mathcal {S})$
is a Banach subalgebra of
$\mathcal {L}_0(\mathcal {S})$
is a Banach subalgebra of
![]() $\mathcal {L}(\mathcal {S})$
. We have the following theorem.
$\mathcal {L}(\mathcal {S})$
. We have the following theorem.
Theorem 5.7 Let E be the map:
![]() $\mathcal {L}(\mathcal {S})$
$\mathcal {L}(\mathcal {S})$
![]() $\rightarrow $
$\rightarrow $
![]() $\mathcal {L}_0(\mathcal {S})$
,
$\mathcal {L}_0(\mathcal {S})$
,
![]() $\sum _{X\in \mathcal {S}} f(X)X$
$\sum _{X\in \mathcal {S}} f(X)X$
![]() $\mapsto $
$\mapsto $
![]() $\sum _{n=0}^{\infty } f(X_0^n)X_0^n$
. Then E is a well-defined conditional expectation from
$\sum _{n=0}^{\infty } f(X_0^n)X_0^n$
. Then E is a well-defined conditional expectation from
![]() $\mathcal {L}(\mathcal {S})$
onto
$\mathcal {L}(\mathcal {S})$
onto
![]() $\mathcal {L}_0(\mathcal {S})$
.
$\mathcal {L}_0(\mathcal {S})$
.
Proof For each
![]() $g\in l^2(\mathcal {S})$
such that
$g\in l^2(\mathcal {S})$
such that
![]() $g(X)=0$
when
$g(X)=0$
when
![]() $X\neq X_0^n$
, we have
$X\neq X_0^n$
, we have
 $$ \begin{align*} \bigg\|\sum_{n=0}^{\infty} f(X_0^n)X_0^n \sum_{n=0}^{\infty}g(X_0^n)\delta_{X_0^n} \bigg\|_2^2\leq \|L_fg\|_2^2\leq \|L_f\|^2\|g\|_2^2. \end{align*} $$
$$ \begin{align*} \bigg\|\sum_{n=0}^{\infty} f(X_0^n)X_0^n \sum_{n=0}^{\infty}g(X_0^n)\delta_{X_0^n} \bigg\|_2^2\leq \|L_fg\|_2^2\leq \|L_f\|^2\|g\|_2^2. \end{align*} $$
This implies that
![]() $\sum _{n=0}^{\infty } f(X_0^n)X_0^n$
is bounded on the Hilbert subspace
$\sum _{n=0}^{\infty } f(X_0^n)X_0^n$
is bounded on the Hilbert subspace
![]() $l^2(\mathcal {S}_0)$
, where
$l^2(\mathcal {S}_0)$
, where
![]() $\mathcal {S}_0$
is the subsemigroup of
$\mathcal {S}_0$
is the subsemigroup of
![]() $\mathcal {S}$
generated by
$\mathcal {S}$
generated by
![]() $X_0$
. The norm of
$X_0$
. The norm of
![]() $\sum _{n=0}^{\infty } f(X_0^n)X_0^n$
is bounded by
$\sum _{n=0}^{\infty } f(X_0^n)X_0^n$
is bounded by
![]() $\|L_f\|$
. Let
$\|L_f\|$
. Let
![]() $\mathscr {F}$
be the Fourier transform:
$\mathscr {F}$
be the Fourier transform:
![]() $\mathbb {Z}\rightarrow \mathbb {S}^1$
,
$\mathbb {Z}\rightarrow \mathbb {S}^1$
,
![]() $n\mapsto e^{2\pi i n\theta }$
,
$n\mapsto e^{2\pi i n\theta }$
,
![]() $\theta \in [0,1)$
. This induces the following isomorphisms [Reference Ge and Xi8]:
$\theta \in [0,1)$
. This induces the following isomorphisms [Reference Ge and Xi8]:
 $$ \begin{align*} &\mathbb{Z}\quad \subseteq\quad\ \ \mathbb{C}\mathbb{Z}\quad\quad \subseteq \quad l^1(\mathbb{Z})\ \quad \subseteq \quad C^*(\mathbb{Z})\quad \subseteq \quad\ \mathcal{L}(\mathbb{Z})\quad\ \ \subseteq\quad l^2(\mathbb{Z})\quad\ \subseteq\quad \cdots\\ &\updownarrow \quad\quad\quad\quad\ \updownarrow \quad\quad\quad\quad\quad\ \updownarrow \quad\quad\quad\quad\quad\quad \updownarrow \quad\quad\quad\quad\quad\ \updownarrow \quad\quad\quad\quad\quad\ \ \updownarrow \\ &\mathbb{S}^1\quad \subseteq\quad \mathbb{C}[\mathbb{Z}]_{\mathbb{S}^1}\quad \subseteq \quad R(\mathbb{S}^1)\quad \subseteq \quad C(\mathbb{S}^1)\quad \subseteq \quad L^{\infty}(\mathbb{S}^1)\quad \subseteq\quad l^2(\mathbb{S}^1)\quad \subseteq\quad \cdots \end{align*} $$
$$ \begin{align*} &\mathbb{Z}\quad \subseteq\quad\ \ \mathbb{C}\mathbb{Z}\quad\quad \subseteq \quad l^1(\mathbb{Z})\ \quad \subseteq \quad C^*(\mathbb{Z})\quad \subseteq \quad\ \mathcal{L}(\mathbb{Z})\quad\ \ \subseteq\quad l^2(\mathbb{Z})\quad\ \subseteq\quad \cdots\\ &\updownarrow \quad\quad\quad\quad\ \updownarrow \quad\quad\quad\quad\quad\ \updownarrow \quad\quad\quad\quad\quad\quad \updownarrow \quad\quad\quad\quad\quad\ \updownarrow \quad\quad\quad\quad\quad\ \ \updownarrow \\ &\mathbb{S}^1\quad \subseteq\quad \mathbb{C}[\mathbb{Z}]_{\mathbb{S}^1}\quad \subseteq \quad R(\mathbb{S}^1)\quad \subseteq \quad C(\mathbb{S}^1)\quad \subseteq \quad L^{\infty}(\mathbb{S}^1)\quad \subseteq\quad l^2(\mathbb{S}^1)\quad \subseteq\quad \cdots \end{align*} $$
Restricting the Fourier transform on
![]() $\mathbb {N}$
, we have
$\mathbb {N}$
, we have
 $$ \begin{align*} &\mathbb{C}\mathbb{N}\quad\quad \subseteq \quad\ l^1(\mathbb{N})\quad\ \subseteq \quad B(\mathbb{N})\quad\ \subseteq \quad\ \ \mathcal{L}(\mathbb{N})\quad\ \subseteq\quad\ l^2(\mathbb{N})\quad\ \subseteq\quad \cdots\\ &\ \updownarrow \quad\quad\quad\quad\quad\quad \updownarrow \quad\quad\quad\quad\quad\ \updownarrow \quad\quad\quad\quad\quad\quad \updownarrow \quad\quad\quad\quad\quad\ \ \updownarrow \\ &\mathbb{C}[\mathbb{Z}]_{\mathbb{D}}\quad \subseteq \quad H^1(\mathbb{D})\quad \subseteq \quad H_c(\mathbb{D})\quad \subseteq \quad H^{\infty}(\mathbb{D})\quad \subseteq\quad H^2(\mathbb{D})\quad \subseteq\quad \cdots \end{align*} $$
$$ \begin{align*} &\mathbb{C}\mathbb{N}\quad\quad \subseteq \quad\ l^1(\mathbb{N})\quad\ \subseteq \quad B(\mathbb{N})\quad\ \subseteq \quad\ \ \mathcal{L}(\mathbb{N})\quad\ \subseteq\quad\ l^2(\mathbb{N})\quad\ \subseteq\quad \cdots\\ &\ \updownarrow \quad\quad\quad\quad\quad\quad \updownarrow \quad\quad\quad\quad\quad\ \updownarrow \quad\quad\quad\quad\quad\quad \updownarrow \quad\quad\quad\quad\quad\ \ \updownarrow \\ &\mathbb{C}[\mathbb{Z}]_{\mathbb{D}}\quad \subseteq \quad H^1(\mathbb{D})\quad \subseteq \quad H_c(\mathbb{D})\quad \subseteq \quad H^{\infty}(\mathbb{D})\quad \subseteq\quad H^2(\mathbb{D})\quad \subseteq\quad \cdots \end{align*} $$
Since
![]() $\mathcal {S}_0$
is isomorphic to (
$\mathcal {S}_0$
is isomorphic to (
![]() $\mathbb {N},+$
),
$\mathbb {N},+$
),
![]() $\sum _{n=0}^{\infty } f(X_0^n)\delta _{n}$
belongs to
$\sum _{n=0}^{\infty } f(X_0^n)\delta _{n}$
belongs to
![]() $\mathcal {L}(\mathbb {N})$
and
$\mathcal {L}(\mathbb {N})$
and
![]() $\mathscr {F}(\sum _{n=0}^{\infty } f(X_0^n)\delta _{n})$
is in
$\mathscr {F}(\sum _{n=0}^{\infty } f(X_0^n)\delta _{n})$
is in
![]() $H^{\infty }(\mathbb {D})$
. It follows that
$H^{\infty }(\mathbb {D})$
. It follows that
![]() $\mathscr {F}(\sum _{n=0}^{\infty } f(X_0^n)\delta _{n})$
belongs to
$\mathscr {F}(\sum _{n=0}^{\infty } f(X_0^n)\delta _{n})$
belongs to
![]() $L^{\infty }(\mathbb {S}^1)$
. Thus
$L^{\infty }(\mathbb {S}^1)$
. Thus
![]() $\sum _{n=0}^{\infty } f(X_0^n)\delta _{n}$
is a bounded operator on
$\sum _{n=0}^{\infty } f(X_0^n)\delta _{n}$
is a bounded operator on
![]() $l^2(\mathbb {Z})$
and belongs to
$l^2(\mathbb {Z})$
and belongs to
![]() $\mathcal {L}(\mathbb {Z})$
. Since the subgroup
$\mathcal {L}(\mathbb {Z})$
. Since the subgroup
![]() $H=\left \langle X_0\right \rangle $
of Thompson’s group
$H=\left \langle X_0\right \rangle $
of Thompson’s group
![]() $\mathcal {F}$
is isomorphic to
$\mathcal {F}$
is isomorphic to
![]() $\mathbb {Z}$
, we have that
$\mathbb {Z}$
, we have that
![]() $\sum _{n=0}^{\infty } f(X_0^n)X_0^n$
is bounded on
$\sum _{n=0}^{\infty } f(X_0^n)X_0^n$
is bounded on
![]() $l^2(H)$
. Let
$l^2(H)$
. Let
![]() $\{H_n\}_{n=1}^{\infty }$
be all right cosets of H in Thompson’s group
$\{H_n\}_{n=1}^{\infty }$
be all right cosets of H in Thompson’s group
![]() $\mathcal {F}$
such that
$\mathcal {F}$
such that
![]() $\mathcal {F}=\sqcup H_n$
. Then
$\mathcal {F}=\sqcup H_n$
. Then
Moreover,
![]() $l^2(H_n)$
are invariant subspaces of
$l^2(H_n)$
are invariant subspaces of
![]() $\sum _{n=0}^{\infty } f(X_0^n)X_0^n$
and the operator norms on each subspace are same. Hence
$\sum _{n=0}^{\infty } f(X_0^n)X_0^n$
and the operator norms on each subspace are same. Hence
![]() $\sum _{n=0}^{\infty } f(X_0^n)X_0^n$
is bounded on
$\sum _{n=0}^{\infty } f(X_0^n)X_0^n$
is bounded on
![]() $l^2(\mathcal {F})$
. Thus
$l^2(\mathcal {F})$
. Thus
![]() $\sum _{n=0}^{\infty } f(X_0^n)X_0^n$
is in
$\sum _{n=0}^{\infty } f(X_0^n)X_0^n$
is in
![]() $\mathcal {L}_0(\mathcal {S})$
. Then E is well-defined. It is clear that conditions (i) and (
$\mathcal {L}_0(\mathcal {S})$
. Then E is well-defined. It is clear that conditions (i) and (
![]() $ii$
) in Definition 5.5 hold for E. We complete the proof.
$ii$
) in Definition 5.5 hold for E. We complete the proof.
5.4 Proof of main results
In this subsection, we will prove the main results of this paper (see Theorems 5.8 and 5.10). When the
![]() $\mathfrak {B}(\mathcal {S})$
-bimodule is
$\mathfrak {B}(\mathcal {S})$
-bimodule is
![]() $\mathcal {L}(\mathcal {S})$
, the first continuous cohomology group of
$\mathcal {L}(\mathcal {S})$
, the first continuous cohomology group of
![]() $\mathfrak {B}(\mathcal {S})$
vanishes.
$\mathfrak {B}(\mathcal {S})$
vanishes.
Theorem 5.8 The first continuous cohomology group
![]() $H^1(\mathfrak {B}(\mathcal {S}),\mathcal {L}(\mathcal {S}))=0$
.
$H^1(\mathfrak {B}(\mathcal {S}),\mathcal {L}(\mathcal {S}))=0$
.
The following result is an immediate corollary of Theorems 4.1 and 5.8.
Corollary 5.9 Derivations on the Banach algebra
![]() $\mathfrak {B}(\mathcal {S})$
are spatial and induced by operators in
$\mathfrak {B}(\mathcal {S})$
are spatial and induced by operators in
![]() $\mathcal {L}(\mathcal {S})$
.
$\mathcal {L}(\mathcal {S})$
.
Let
![]() $\mathcal {M}(\mathcal {S})$
be the set of all
$\mathcal {M}(\mathcal {S})$
be the set of all
![]() $T\in \mathcal {L}(\mathcal {S})$
such that
$T\in \mathcal {L}(\mathcal {S})$
such that
![]() $[T,A]\in \mathfrak {B}(\mathcal {S})$
for each
$[T,A]\in \mathfrak {B}(\mathcal {S})$
for each
![]() $A\in \mathfrak {B}(\mathcal {S})$
, where
$A\in \mathfrak {B}(\mathcal {S})$
, where
![]() $[T,A]=TA-AT$
. Then
$[T,A]=TA-AT$
. Then
![]() $\mathcal {M}(\mathcal {S})$
is a norm closed linear subspace of
$\mathcal {M}(\mathcal {S})$
is a norm closed linear subspace of
![]() $\mathcal {L}(\mathcal {S})$
containing
$\mathcal {L}(\mathcal {S})$
containing
![]() $\mathfrak {B}(\mathcal {S})$
. The first cohomology group of
$\mathfrak {B}(\mathcal {S})$
. The first cohomology group of
![]() $\mathfrak {B}(\mathcal {S})$
is characterized as the linear space
$\mathfrak {B}(\mathcal {S})$
is characterized as the linear space
![]() $\mathcal {M}(\mathcal {S})$
module
$\mathcal {M}(\mathcal {S})$
module
![]() $\mathfrak {B}(\mathcal {S})$
.
$\mathfrak {B}(\mathcal {S})$
.
Theorem 5.10 The first continuous cohomology group
 $H^{1}(\mathfrak {B}(\mathcal {S}),\mathfrak {B}(\mathcal {S}))=\dfrac {\mathcal {M}(\mathcal {S})}{\mathfrak {B}(\mathcal {S})}$
.
$H^{1}(\mathfrak {B}(\mathcal {S}),\mathfrak {B}(\mathcal {S}))=\dfrac {\mathcal {M}(\mathcal {S})}{\mathfrak {B}(\mathcal {S})}$
.
The following two lemmas are crucial to obtain the above results.
Lemma 5.11 Let D be a continuous derivation from the Banach algebra
![]() $\mathfrak {B}(\mathcal {S})$
into
$\mathfrak {B}(\mathcal {S})$
into
![]() $\mathcal {L}(\mathcal {S})$
. If
$\mathcal {L}(\mathcal {S})$
. If
![]() $D(X_0)=AX_{0}-X_{0}A$
and
$D(X_0)=AX_{0}-X_{0}A$
and
![]() $D(X_{1})=AX_{1}-X_{1}A$
for some A in
$D(X_{1})=AX_{1}-X_{1}A$
for some A in
![]() $B(l^{2}(\mathcal {S}))$
, then
$B(l^{2}(\mathcal {S}))$
, then
![]() $D(T)=AT-TA$
for each T in
$D(T)=AT-TA$
for each T in
![]() $\mathfrak {B}(\mathcal {S})$
.
$\mathfrak {B}(\mathcal {S})$
.
Proof For each
![]() $n\geq 1$
, if
$n\geq 1$
, if
![]() $D(X_{0}^{n})=AX_{0}^{n}-X_{0}^{n}A$
, then
$D(X_{0}^{n})=AX_{0}^{n}-X_{0}^{n}A$
, then
Therefore, by induction, we have
![]() $D(X_{0}^{n})=AX_{0}^{n}-X_{0}^{n}A$
for any
$D(X_{0}^{n})=AX_{0}^{n}-X_{0}^{n}A$
for any
![]() $n\geq 1$
. By the definition of Thompson’s semigroup, we have
$n\geq 1$
. By the definition of Thompson’s semigroup, we have
![]() $X_{1}X_{0}^{m}=X_{0}^{m}X_{m+1}$
for any
$X_{1}X_{0}^{m}=X_{0}^{m}X_{m+1}$
for any
![]() $m\geq 1$
. Then
$m\geq 1$
. Then
We have
 $$ \begin{align*} D(X_{m+1})&=X_0^{*m}(D(X_{1})X_{0}^{m}+X_{1}D(X_{0}^{m})-D(X_{0}^{m})X_{m+1})\\ &=X_0^{*m}(AX_1X_{0}^{m}-X_1AX_{0}^{m}+ X_1AX_0^m-X_1X_0^mA-AX_0^mX_{m+1}+ X_0^mAX_{m+1})\\ &=X_0^{*m}(X_0^mAX_{m+1}- X_1X_0^mA)\\ &=AX_{m+1}-X_{m+1}A. \end{align*} $$
$$ \begin{align*} D(X_{m+1})&=X_0^{*m}(D(X_{1})X_{0}^{m}+X_{1}D(X_{0}^{m})-D(X_{0}^{m})X_{m+1})\\ &=X_0^{*m}(AX_1X_{0}^{m}-X_1AX_{0}^{m}+ X_1AX_0^m-X_1X_0^mA-AX_0^mX_{m+1}+ X_0^mAX_{m+1})\\ &=X_0^{*m}(X_0^mAX_{m+1}- X_1X_0^mA)\\ &=AX_{m+1}-X_{m+1}A. \end{align*} $$
Similarly, we can prove that
![]() $D(X)=AX-XA$
for any X in
$D(X)=AX-XA$
for any X in
![]() $\mathcal {S}$
. By linearity, we have
$\mathcal {S}$
. By linearity, we have
![]() $D(T)=AT-TA$
for each T in the semigroup algebra
$D(T)=AT-TA$
for each T in the semigroup algebra
![]() $\mathbb {C}[\mathcal {S}]$
. Since
$\mathbb {C}[\mathcal {S}]$
. Since
![]() $\mathbb {C}[\mathcal {S}]$
is a dense subalgebra of
$\mathbb {C}[\mathcal {S}]$
is a dense subalgebra of
![]() $\mathfrak {B}(\mathcal {S})$
, we obtain that
$\mathfrak {B}(\mathcal {S})$
, we obtain that
![]() $D(T)=AT-TA$
for each T in
$D(T)=AT-TA$
for each T in
![]() $\mathfrak {B}(\mathcal {S})$
by the continuity of D.
$\mathfrak {B}(\mathcal {S})$
by the continuity of D.
The following lemma is a generalization of the above conclusion.
Lemma 5.12 Let D be a continuous derivation from the Banach algebra
![]() $\mathfrak {B}(\mathcal {S})$
into
$\mathfrak {B}(\mathcal {S})$
into
![]() $\mathcal {L}(\mathcal {S})$
. If
$\mathcal {L}(\mathcal {S})$
. If
![]() $D(X_0)=AX_{0}-X_{0}A$
and
$D(X_0)=AX_{0}-X_{0}A$
and
![]() $D(X_{1})=BX_{1}-X_{1}B$
for some A and B in
$D(X_{1})=BX_{1}-X_{1}B$
for some A and B in
![]() $\mathcal {L}(\mathcal {S})$
, then there exists an operator C in
$\mathcal {L}(\mathcal {S})$
, then there exists an operator C in
![]() $\mathcal {L}(\mathcal {S})$
such that
$\mathcal {L}(\mathcal {S})$
such that
![]() $D(T)=CT-TC$
for each T in
$D(T)=CT-TC$
for each T in
![]() $\mathfrak {B}(\mathcal {S})$
.
$\mathfrak {B}(\mathcal {S})$
.
Proof By the definitions of Thompson’s semigroup and derivation, we have
and
 $$ \begin{align*} D(X_{1})X_{0}+X_{1}D(X_{0})&=D(X_{0})X_{2}+X_{0}D(X_{2}),\\ D(X_{2})X_{0}+X_{2}D(X_{0})&=D(X_{0})X_{3}+X_{0}D(X_{3}),\\ D(X_{2})X_{1}+X_{2}D(X_{1})&=D(X_{1})X_{3}+X_{1}D(X_{3}). \end{align*} $$
$$ \begin{align*} D(X_{1})X_{0}+X_{1}D(X_{0})&=D(X_{0})X_{2}+X_{0}D(X_{2}),\\ D(X_{2})X_{0}+X_{2}D(X_{0})&=D(X_{0})X_{3}+X_{0}D(X_{3}),\\ D(X_{2})X_{1}+X_{2}D(X_{1})&=D(X_{1})X_{3}+X_{1}D(X_{3}). \end{align*} $$
By the above equations, we have
 $$ \begin{align*} D(X_{2})&=X_{0}^{*}X_{1}(A-B)X_{0}+X_{0}^{*}(B-A)X_{1}X_{0}+(AX_{2}-X_{2}A),\\D(X_{3})&=(X_{0}^{*})^{2}X_{1}(A-B)X_{0}^{2}+(X_{0}^{*})^{2}(B-A)X_{1}X_{0}^{2}+(AX_{3}-X_{3}A),\\D(X_{3})&=X_{1}^{*}X_{0}^{*}X_{1}(A-B)X_{0}X_{1}+X_{1}^{*}X_{0}^{*}(B-A)X_{1}X_{0}X_{1} +X_{1}^{*}(A-B)X_{2}X_{1}\\& \quad +X_{1}^{*}X_{2}(B-A)X_{1}+(BX_{3}-X_{3}B). \end{align*} $$
$$ \begin{align*} D(X_{2})&=X_{0}^{*}X_{1}(A-B)X_{0}+X_{0}^{*}(B-A)X_{1}X_{0}+(AX_{2}-X_{2}A),\\D(X_{3})&=(X_{0}^{*})^{2}X_{1}(A-B)X_{0}^{2}+(X_{0}^{*})^{2}(B-A)X_{1}X_{0}^{2}+(AX_{3}-X_{3}A),\\D(X_{3})&=X_{1}^{*}X_{0}^{*}X_{1}(A-B)X_{0}X_{1}+X_{1}^{*}X_{0}^{*}(B-A)X_{1}X_{0}X_{1} +X_{1}^{*}(A-B)X_{2}X_{1}\\& \quad +X_{1}^{*}X_{2}(B-A)X_{1}+(BX_{3}-X_{3}B). \end{align*} $$
It follows that
 $$ \begin{align*} &(X_{0}^{*})^{2}X_{1}(A-B)X_{0}^{2}+(X_{0}^{*})^{2}(B-A)X_{1}X_{0}^{2}+(A-B)X_{3}+X_{3}(B-A)\\& \quad = X_{1}^{*}X_{0}^{*}X_{1}(A-B)X_{0}X_{1}+X_{1}^{*}X_{0}^{*}(B-A)X_{1}X_{0}X_{1}+X_{1}^{*}(A-B)X_{2}X_{1}\\& \qquad +X_{1}^{*}X_{2}(B-A)X_{1}. \end{align*} $$
$$ \begin{align*} &(X_{0}^{*})^{2}X_{1}(A-B)X_{0}^{2}+(X_{0}^{*})^{2}(B-A)X_{1}X_{0}^{2}+(A-B)X_{3}+X_{3}(B-A)\\& \quad = X_{1}^{*}X_{0}^{*}X_{1}(A-B)X_{0}X_{1}+X_{1}^{*}X_{0}^{*}(B-A)X_{1}X_{0}X_{1}+X_{1}^{*}(A-B)X_{2}X_{1}\\& \qquad +X_{1}^{*}X_{2}(B-A)X_{1}. \end{align*} $$
Let
![]() $A-B=L_{f}\in \mathcal {L}(\mathcal {S})$
and
$A-B=L_{f}\in \mathcal {L}(\mathcal {S})$
and
![]() $L_{g}=L_{f}-f(e)I-\sum _{n\geq 0}\sum _{m\geq 1}f(X_{n}^{m})X_{n}^{m}$
. Then we have
$L_{g}=L_{f}-f(e)I-\sum _{n\geq 0}\sum _{m\geq 1}f(X_{n}^{m})X_{n}^{m}$
. Then we have
 $$ \begin{align} &(X_{0}^{*})^{2}X_{1}L_{g}X_{0}^{2}-(X_{0}^{*})^{2}L_{g}X_{1}X_{0}^{2}+L_{g}X_{3} - X_{3}L_{g}=X_{1}^{*}X_{0}^{*}X_{1}L_{g}X_{0}X_{1}-X_{1}^{*}X_{0}^{*}L_{g}X_{1}X_{0}X_{1}\nonumber\\& \quad +X_{1}^{*}L_{g}X_{2}X_{1}-X_{1}^{*}X_{2}L_{g}X_{1}+\left(\sum_{n\geq2}\sum_{m\geq1} f(X_{n}^{m})X_{n+1}^{m}\right)X_{3}- X_{3}\left(\sum_{n\geq2}\sum_{m\geq1}f(X_{n}^{m})X_{n+1}^{m}\right)\nonumber \\& \quad +X_{3}\left(\sum_{n\geq2}\sum_{m\geq1}f(X_{n}^{m})X_{n}^{m}\right)-\left(\sum_{n\geq2}\sum_{m\geq1}f(X_{n}^{m})X_{n}^{m}\right)X_{3}. \end{align} $$
$$ \begin{align} &(X_{0}^{*})^{2}X_{1}L_{g}X_{0}^{2}-(X_{0}^{*})^{2}L_{g}X_{1}X_{0}^{2}+L_{g}X_{3} - X_{3}L_{g}=X_{1}^{*}X_{0}^{*}X_{1}L_{g}X_{0}X_{1}-X_{1}^{*}X_{0}^{*}L_{g}X_{1}X_{0}X_{1}\nonumber\\& \quad +X_{1}^{*}L_{g}X_{2}X_{1}-X_{1}^{*}X_{2}L_{g}X_{1}+\left(\sum_{n\geq2}\sum_{m\geq1} f(X_{n}^{m})X_{n+1}^{m}\right)X_{3}- X_{3}\left(\sum_{n\geq2}\sum_{m\geq1}f(X_{n}^{m})X_{n+1}^{m}\right)\nonumber \\& \quad +X_{3}\left(\sum_{n\geq2}\sum_{m\geq1}f(X_{n}^{m})X_{n}^{m}\right)-\left(\sum_{n\geq2}\sum_{m\geq1}f(X_{n}^{m})X_{n}^{m}\right)X_{3}. \end{align} $$
If
![]() $g\neq 0$
, then we take the minimal element X of the set
$g\neq 0$
, then we take the minimal element X of the set
![]() $\{X\in \mathcal {S}\ |\ g(X)\neq 0\}$
under the total order. By the definition of
$\{X\in \mathcal {S}\ |\ g(X)\neq 0\}$
under the total order. By the definition of
![]() $L_{g}$
, we have
$L_{g}$
, we have
![]() $X=X_{i_{1}}^{\alpha _{i_{1}}}\dots X_{i_{t}}^{\alpha _{i_{t}}}$
, where
$X=X_{i_{1}}^{\alpha _{i_{1}}}\dots X_{i_{t}}^{\alpha _{i_{t}}}$
, where
![]() $i_{1}<i_{2}<\cdots <i_{t}$
and
$i_{1}<i_{2}<\cdots <i_{t}$
and
![]() $\alpha _{i_{1}},\ldots ,\alpha _{i_{t}}\geq 1$
,
$\alpha _{i_{1}},\ldots ,\alpha _{i_{t}}\geq 1$
,
![]() $t\geq 2$
.
$t\geq 2$
.
Case I:
![]() $i_{1}\geq 3$
. We have
$i_{1}\geq 3$
. We have
![]() $X_{3}X\prec XX_{3}$
. Taking
$X_{3}X\prec XX_{3}$
. Taking
![]() $\langle \cdot \ \delta _{e},\delta _{X_{3}X}\rangle $
on the both sides of equation (11), we obtain that
$\langle \cdot \ \delta _{e},\delta _{X_{3}X}\rangle $
on the both sides of equation (11), we obtain that
![]() $g(X)=0$
.
$g(X)=0$
.
Case II:
![]() $i_{1}=1$
or
$i_{1}=1$
or
![]() $2$
. We have
$2$
. We have
![]() $ XX_{3}\prec X_{3}X$
. Analogously, taking
$ XX_{3}\prec X_{3}X$
. Analogously, taking
![]() $\langle \cdot \ \delta _{e},\delta _{XX_{3}}\rangle $
on the both sides of equation (11), we also have
$\langle \cdot \ \delta _{e},\delta _{XX_{3}}\rangle $
on the both sides of equation (11), we also have
![]() $g(X)=0$
.
$g(X)=0$
.
Case III:
![]() $i_{1}=0$
. If
$i_{1}=0$
. If
![]() $X_1|XX_{2}X_{1}$
, then taking
$X_1|XX_{2}X_{1}$
, then taking
![]() $\langle \cdot \ \delta _{e},\delta _{X_{1}^{-1}XX_{2}X_{1}}\rangle $
, we can obtain that
$\langle \cdot \ \delta _{e},\delta _{X_{1}^{-1}XX_{2}X_{1}}\rangle $
, we can obtain that
![]() $g(X)=0$
. If
$g(X)=0$
. If
![]() $X_1\nmid XX_{2}X_{1}$
, by the normal form (of elements) in Thompson”s group
$X_1\nmid XX_{2}X_{1}$
, by the normal form (of elements) in Thompson”s group
![]() $\mathcal {F}$
, there exist Y and
$\mathcal {F}$
, there exist Y and
![]() $X_{k}$
in
$X_{k}$
in
![]() $\mathcal {S}$
such that
$\mathcal {S}$
such that
![]() $X_{1}^{-1}XX_{2}X_{1}=YX_{k}^{-1}$
, where
$X_{1}^{-1}XX_{2}X_{1}=YX_{k}^{-1}$
, where
![]() $X_{1}^{-1}$
and
$X_{1}^{-1}$
and
![]() $X_{k}^{-1}$
are in
$X_{k}^{-1}$
are in
![]() $\mathcal {F}$
. Then taking
$\mathcal {F}$
. Then taking
![]() $\langle \cdot \ \delta _{X_{k}},\delta _{Y}\rangle $
, we can also obtain that
$\langle \cdot \ \delta _{X_{k}},\delta _{Y}\rangle $
, we can also obtain that
![]() $g(X)=0$
.
$g(X)=0$
.
It follows from the above discussion that
![]() $g=0$
. This leads to
$g=0$
. This leads to
 $$ \begin{align*} \left(\sum_{n\geq2}\sum_{m\geq1}f(X_{n}^{m})X_{n+1}^{m}\right)X_{3}-&X_{3}\left(\sum_{n\geq2}\sum_{m\geq1}f(X_{n}^{m})X_{n+1}^{m}\right)\\ +&X_{3}\left(\sum_{n\geq2}\sum_{m\geq1}f(X_{n}^{m})X_{n}^{m}\right)-\left(\sum_{n\geq2}\sum_{m\geq1}f(X_{n}^{m})X_{n}^{m}\right)X_{3}\\ =&\ 0. \end{align*} $$
$$ \begin{align*} \left(\sum_{n\geq2}\sum_{m\geq1}f(X_{n}^{m})X_{n+1}^{m}\right)X_{3}-&X_{3}\left(\sum_{n\geq2}\sum_{m\geq1}f(X_{n}^{m})X_{n+1}^{m}\right)\\ +&X_{3}\left(\sum_{n\geq2}\sum_{m\geq1}f(X_{n}^{m})X_{n}^{m}\right)-\left(\sum_{n\geq2}\sum_{m\geq1}f(X_{n}^{m})X_{n}^{m}\right)X_{3}\\ =&\ 0. \end{align*} $$
It is not difficult to verify that
![]() $f(X_2^m)=0$
and
$f(X_2^m)=0$
and
![]() $f(X_n^m)=f(X_3^m)$
for all
$f(X_n^m)=f(X_3^m)$
for all
![]() $n \geq 4$
and
$n \geq 4$
and
![]() $m\geq 1$
. Since
$m\geq 1$
. Since
![]() $f\in l^2(\mathcal {S})$
, we have
$f\in l^2(\mathcal {S})$
, we have
![]() $f(X_{n}^{m})=0$
for any
$f(X_{n}^{m})=0$
for any
![]() $n\geq 2$
and
$n\geq 2$
and
![]() $m\geq 1$
. Therefore,
$m\geq 1$
. Therefore,
Let
Then by Theorem 5.7, we have
![]() $C\in \mathcal {L}(\mathcal {S})$
and
$C\in \mathcal {L}(\mathcal {S})$
and
By Lemma 5.11, we have
![]() $D(T)=CT-TC$
for each T in
$D(T)=CT-TC$
for each T in
![]() $\mathfrak {B}(\mathcal {S})$
.
$\mathfrak {B}(\mathcal {S})$
.
Proof of Theorem 5.8
Let D be a continuous derivation from
![]() $\mathfrak {B}(\mathcal {S})$
into
$\mathfrak {B}(\mathcal {S})$
into
![]() $\mathcal {L}(\mathcal {S})$
. By Lemma 5.1, Lemma 5.2 and Lemma 5.12, there exits an operator C in
$\mathcal {L}(\mathcal {S})$
. By Lemma 5.1, Lemma 5.2 and Lemma 5.12, there exits an operator C in
![]() $\mathcal {L}(S)$
such that
$\mathcal {L}(S)$
such that
![]() $D(T)=CT-TC$
for each T in
$D(T)=CT-TC$
for each T in
![]() $\mathfrak {B}(\mathcal {S})$
. Thus D is an inner derivation and then
$\mathfrak {B}(\mathcal {S})$
. Thus D is an inner derivation and then
![]() $H^1(\mathfrak {B}(\mathcal {S}),\mathcal {L}(\mathcal {S}))=0$
. We complete the proof.
$H^1(\mathfrak {B}(\mathcal {S}),\mathcal {L}(\mathcal {S}))=0$
. We complete the proof.
Let us see the following lemma before proving Theorem 5.10.
Lemma 5.13 The intersection
![]() $\mathcal {L}(\mathcal {S})\cap \mathcal {R}(\mathcal {S})=\mathbb {C}I$
.
$\mathcal {L}(\mathcal {S})\cap \mathcal {R}(\mathcal {S})=\mathbb {C}I$
.
Proof For any
![]() $L_f\in \mathcal {L}(\mathcal {S})\cap \mathcal {R}(\mathcal {S}) $
, there exists an operator
$L_f\in \mathcal {L}(\mathcal {S})\cap \mathcal {R}(\mathcal {S}) $
, there exists an operator
![]() $R_g\in \mathcal {R}(\mathcal {S}) $
such that
$R_g\in \mathcal {R}(\mathcal {S}) $
such that
![]() $L_f=R_g$
. Hence
$L_f=R_g$
. Hence
![]() $f=L_f\delta _e=R_g\delta _e=g$
. Moreover,
$f=L_f\delta _e=R_g\delta _e=g$
. Moreover,
It is not hard to check that
![]() $f=\sum _{n=0}^{\infty }f(X_0^n)\delta _{X_0^n}$
using Lemma 3.7. Similarly,
$f=\sum _{n=0}^{\infty }f(X_0^n)\delta _{X_0^n}$
using Lemma 3.7. Similarly,
Hence
![]() $f=f(e)\delta _e$
. This completes the proof.
$f=f(e)\delta _e$
. This completes the proof.
Proof of Theorem 5.10
Let D be a derivation on the Banach algebra
![]() $\mathfrak {B}(\mathcal {S})$
then D is continuous. By Lemmas 5.1, 5.2, and 5.12, there exists an operator C in
$\mathfrak {B}(\mathcal {S})$
then D is continuous. By Lemmas 5.1, 5.2, and 5.12, there exists an operator C in
![]() $\mathcal {L}(\mathcal {S})$
such that
$\mathcal {L}(\mathcal {S})$
such that
![]() $D(T)=CT-TC$
for each T in
$D(T)=CT-TC$
for each T in
![]() $\mathfrak {B}(\mathcal {S})$
. This induces the following map:
$\mathfrak {B}(\mathcal {S})$
. This induces the following map:
 $$ \begin{align*} \pi:\quad H^{1}(\mathfrak{B}(\mathcal{S}),\mathfrak{B}(\mathcal{S}))\quad&\longrightarrow\qquad \frac{ \mathcal{M}(\mathcal{S})}{\mathfrak{B}(\mathcal{S})}\\ \overline{D}\qquad\qquad&\longrightarrow\quad\ C+\mathfrak{B}(\mathcal{S}). \end{align*} $$
$$ \begin{align*} \pi:\quad H^{1}(\mathfrak{B}(\mathcal{S}),\mathfrak{B}(\mathcal{S}))\quad&\longrightarrow\qquad \frac{ \mathcal{M}(\mathcal{S})}{\mathfrak{B}(\mathcal{S})}\\ \overline{D}\qquad\qquad&\longrightarrow\quad\ C+\mathfrak{B}(\mathcal{S}). \end{align*} $$
We will show that
![]() $\pi $
is well-defined. If there exist two operators
$\pi $
is well-defined. If there exist two operators
![]() $C_1$
and
$C_1$
and
![]() $C_2$
in
$C_2$
in
![]() $\mathcal {L}(\mathcal {S})$
such that
$\mathcal {L}(\mathcal {S})$
such that
![]() $D(T)=C_1T-TC_1=C_2T-TC_2$
for each T in
$D(T)=C_1T-TC_1=C_2T-TC_2$
for each T in
![]() $\mathfrak {B}(\mathcal {S})$
, then
$\mathfrak {B}(\mathcal {S})$
, then
![]() $C_1-C_2\in \mathcal {L}(\mathcal {S}) \cap \mathfrak {B}(\mathcal {S})'=\mathcal {L}(\mathcal {S}) \cap \mathcal {R}(\mathcal {S})=\mathbb {C}I$
from Lemma 5.13. Thus
$C_1-C_2\in \mathcal {L}(\mathcal {S}) \cap \mathfrak {B}(\mathcal {S})'=\mathcal {L}(\mathcal {S}) \cap \mathcal {R}(\mathcal {S})=\mathbb {C}I$
from Lemma 5.13. Thus
![]() $C_1+\mathfrak {B}(\mathcal {S})=C_2+\mathfrak {B}(\mathcal {S})$
. Now, if
$C_1+\mathfrak {B}(\mathcal {S})=C_2+\mathfrak {B}(\mathcal {S})$
. Now, if
![]() $\overline {D_1}=\overline {D_2}$
, then
$\overline {D_1}=\overline {D_2}$
, then
![]() $D_1-D_2$
is an inner derivation of
$D_1-D_2$
is an inner derivation of
![]() $\mathfrak {B}(\mathcal {S})$
. There exists an operator
$\mathfrak {B}(\mathcal {S})$
. There exists an operator
![]() $C_3$
in
$C_3$
in
![]() $\mathfrak {B}(\mathcal {S})$
such that
$\mathfrak {B}(\mathcal {S})$
such that
![]() $(D_1-D_2)(T)=C_3T-TC_3$
for each T in
$(D_1-D_2)(T)=C_3T-TC_3$
for each T in
![]() $\mathfrak {B}(\mathcal {S})$
. Assume that
$\mathfrak {B}(\mathcal {S})$
. Assume that
![]() $D_1(T)=C_1^{\prime }T-TC_1^{\prime }$
and
$D_1(T)=C_1^{\prime }T-TC_1^{\prime }$
and
![]() $D_2(T)=C_2^{\prime }T-TC_2^{\prime }$
, where
$D_2(T)=C_2^{\prime }T-TC_2^{\prime }$
, where
![]() $C_1^{\prime }$
and
$C_1^{\prime }$
and
![]() $C_2^{\prime }$
are in
$C_2^{\prime }$
are in
![]() $\mathcal {L}(\mathcal {S})$
, then
$\mathcal {L}(\mathcal {S})$
, then
![]() $(C_1^{\prime }-C_2^{\prime })T-T(C_1^{\prime }-C_2^{\prime })=C_3T-TC_3$
. It follows that
$(C_1^{\prime }-C_2^{\prime })T-T(C_1^{\prime }-C_2^{\prime })=C_3T-TC_3$
. It follows that
![]() $C_1^{\prime }-C_2^{\prime }-C_3$
belongs to
$C_1^{\prime }-C_2^{\prime }-C_3$
belongs to
![]() $\mathcal {L}(\mathcal {S}) \cap \mathfrak {B}(\mathcal {S})'=\mathbb {C}I$
. Thus
$\mathcal {L}(\mathcal {S}) \cap \mathfrak {B}(\mathcal {S})'=\mathbb {C}I$
. Thus
![]() $C_1^{\prime }-C_2^{\prime }$
belongs to
$C_1^{\prime }-C_2^{\prime }$
belongs to
![]() $ \mathfrak {B}(\mathcal {S})$
, that is
$ \mathfrak {B}(\mathcal {S})$
, that is
![]() $C_1^{\prime }+\mathfrak {B}(\mathcal {S})=C_2^{\prime }+\mathfrak {B}(\mathcal {S})$
. The map
$C_1^{\prime }+\mathfrak {B}(\mathcal {S})=C_2^{\prime }+\mathfrak {B}(\mathcal {S})$
. The map
![]() $\pi $
is a well-defined group homomorphism. If
$\pi $
is a well-defined group homomorphism. If
![]() $\pi (\overline {D})=0$
, then there exists an operator
$\pi (\overline {D})=0$
, then there exists an operator
![]() $C'$
in
$C'$
in
![]() $\mathfrak {B}(\mathcal {S})$
such that
$\mathfrak {B}(\mathcal {S})$
such that
![]() $D(T)=C'T-TC'$
, which means that D is an inner derivation. The map
$D(T)=C'T-TC'$
, which means that D is an inner derivation. The map
![]() $\pi $
is injective. The surjectivity of
$\pi $
is injective. The surjectivity of
![]() $\pi $
is obvious. It follows from the above discussion that
$\pi $
is obvious. It follows from the above discussion that
![]() $\pi $
is a group isomorphism. We complete the proof.
$\pi $
is a group isomorphism. We complete the proof.
6 Further discussions
We now recall the definition of higher order continuous Hochschild cohomology for Banach algebras. Let
![]() $\mathcal {M}$
be a Banach algebra, and let
$\mathcal {M}$
be a Banach algebra, and let
![]() $\mathcal {X}$
be a Banach
$\mathcal {X}$
be a Banach
![]() $\mathcal {M}$
-bimodule. The space of all n-linear (continuous) maps from n-fold Cartesian product
$\mathcal {M}$
-bimodule. The space of all n-linear (continuous) maps from n-fold Cartesian product
![]() $\mathcal {M}^n=\mathcal {M}\times \cdots \times \mathcal {M}$
into
$\mathcal {M}^n=\mathcal {M}\times \cdots \times \mathcal {M}$
into
![]() $\mathcal {X}$
is denoted by
$\mathcal {X}$
is denoted by
![]() $L^{n}(\mathcal {M},\mathcal {X})$
for
$L^{n}(\mathcal {M},\mathcal {X})$
for
![]() $n\geq 1$
, while
$n\geq 1$
, while
![]() $L^{0}(\mathcal {M},\mathcal {X})$
is defined to be
$L^{0}(\mathcal {M},\mathcal {X})$
is defined to be
![]() $\mathcal {X}$
.
$\mathcal {X}$
.
The coboundary operator
![]() $\partial ^n$
:
$\partial ^n$
:
![]() $L^{n}(\mathcal {M},\mathcal {X})\rightarrow L^{n+1}(\mathcal {M},\mathcal {X})$
is defined, for
$L^{n}(\mathcal {M},\mathcal {X})\rightarrow L^{n+1}(\mathcal {M},\mathcal {X})$
is defined, for
![]() $n\geq 1$
, by
$n\geq 1$
, by
 $$ \begin{align*} \partial^n\phi(a_{1},a_{2},\ldots,a_{n+1})&=a_{1}\phi(a_{2},\ldots,a_{n+1})\\ &\quad+\sum_{i=1}^{n}(-1)^{i}\phi(a_1,\ldots,a_{i-1},a_ia_{i+1},a_{i+2},\ldots,a_{n+1})\\ &\quad+(-1)^{n+1}\phi(a_{1},\ldots,a_{n})a_{n+1}, \end{align*} $$
$$ \begin{align*} \partial^n\phi(a_{1},a_{2},\ldots,a_{n+1})&=a_{1}\phi(a_{2},\ldots,a_{n+1})\\ &\quad+\sum_{i=1}^{n}(-1)^{i}\phi(a_1,\ldots,a_{i-1},a_ia_{i+1},a_{i+2},\ldots,a_{n+1})\\ &\quad+(-1)^{n+1}\phi(a_{1},\ldots,a_{n})a_{n+1}, \end{align*} $$
where
![]() $\phi \in L^{n}(\mathcal {M},\mathcal {X})$
and
$\phi \in L^{n}(\mathcal {M},\mathcal {X})$
and
![]() $a_1,\ a_2,\ldots ,\ a_{n+1}\in \mathcal {M}$
. When
$a_1,\ a_2,\ldots ,\ a_{n+1}\in \mathcal {M}$
. When
![]() $n=0$
, we define
$n=0$
, we define
![]() $\partial ^0$
by
$\partial ^0$
by
It is routine to check that
![]() $\partial ^{n}\partial ^{n-1}$
:
$\partial ^{n}\partial ^{n-1}$
:
![]() $L^{n-1}(\mathcal {M},\mathcal {X})$
$L^{n-1}(\mathcal {M},\mathcal {X})$
![]() $\rightarrow $
$\rightarrow $
![]() $L^{n+1}(\mathcal {M},\mathcal {X})$
is zero for all
$L^{n+1}(\mathcal {M},\mathcal {X})$
is zero for all
![]() $n\geq 1$
, and so
$n\geq 1$
, and so
![]() $\mathrm {Im}(\partial ^{n-1})$
is a linear subspace of
$\mathrm {Im}(\partial ^{n-1})$
is a linear subspace of
![]() $\mathrm {Ker}(\partial ^n)$
. The
$\mathrm {Ker}(\partial ^n)$
. The
![]() $n\mathrm {th}$
Hochschild cohomology group
$n\mathrm {th}$
Hochschild cohomology group
![]() $H^{n}(\mathcal {M},\mathcal {X})$
is then defined to be the following quotient space:
$H^{n}(\mathcal {M},\mathcal {X})$
is then defined to be the following quotient space:
 $$\begin{align*}\frac{\mathrm{Ker}(\partial^n:\ L^{n}(\mathcal{M},\mathcal{X})\rightarrow L^{n+1}(\mathcal{M},\mathcal{X}))}{\mathrm{Im}(\partial^{n-1}:\ L^{n-1}(\mathcal{M},\mathcal{X})\rightarrow L^{n}(\mathcal{M},\mathcal{X}))}\end{align*}$$
$$\begin{align*}\frac{\mathrm{Ker}(\partial^n:\ L^{n}(\mathcal{M},\mathcal{X})\rightarrow L^{n+1}(\mathcal{M},\mathcal{X}))}{\mathrm{Im}(\partial^{n-1}:\ L^{n-1}(\mathcal{M},\mathcal{X})\rightarrow L^{n}(\mathcal{M},\mathcal{X}))}\end{align*}$$
for
![]() $n\geq 1$
. We end this paper by proposing some problems for future study:
$n\geq 1$
. We end this paper by proposing some problems for future study:
-
• What are the higher order cohomology groups
 $H^{n}(\mathfrak {B}(S),\mathfrak {B}(S))$
for
$H^{n}(\mathfrak {B}(S),\mathfrak {B}(S))$
for
 $n\geq 2$
?
$n\geq 2$
? -
• When
 $n\geq 2$
, does
$n\geq 2$
, does
 $H^n(\mathfrak {B}(\mathcal {S}),\mathcal {L}(\mathcal {S}))=0$
? The first step to calculate the high order cohomology groups should be the following. Given a 2-cocycle
$H^n(\mathfrak {B}(\mathcal {S}),\mathcal {L}(\mathcal {S}))=0$
? The first step to calculate the high order cohomology groups should be the following. Given a 2-cocycle
 $\phi $
, we need to modify it by a 1-coboundary such that
$\phi $
, we need to modify it by a 1-coboundary such that
 $\phi $
is
$\phi $
is
 $X_0$
-multimodular, i.e.,
$X_0$
-multimodular, i.e.,
 $\phi (X_0A,B)= X_0\phi (A,B)$
,
$\phi (X_0A,B)= X_0\phi (A,B)$
,
 $\phi (AX_0,B)= \phi (A,X_0B)$
, and
$\phi (AX_0,B)= \phi (A,X_0B)$
, and
 $\phi (A,BX_0)= \phi (A,B)X_0$
for all
$\phi (A,BX_0)= \phi (A,B)X_0$
for all
 $A,B\in \mathfrak {B}(\mathcal {S})$
.
$A,B\in \mathfrak {B}(\mathcal {S})$
. -
• What are the cohomology groups of
 $\mathfrak {B}(\mathcal {F}_n)$
and
$\mathfrak {B}(\mathcal {F}_n)$
and
 $\mathfrak {B}(\mathcal {T})$
?
$\mathfrak {B}(\mathcal {T})$
?
Acknowledgments
The author wishes to thank Professor Liming Ge for all his long-term help and encouragement. He would like to thank Boqing Xue and Yongle Jiang for helpful discussions. He heartly thanks Hanbin Zhang for valuable suggestions on the manuscript. He also thanks anonymous referee’s comments and suggestions.