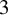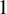1 Introduction
1.1 Main results
A Postnikov diagram, or alternating strand diagram [Reference Postnikov41], is a combinatorial object consisting of a collection of strands in the disc. It encodes a great deal of further combinatorial, algebraic and geometric data, mostly connected to questions regarding total positivity in the Grassmannian. From the point of view of this paper, the key piece of data encoded by a Postnikov diagram D is that of an ice quiver with potential
![]() $(Q_D,F_D,W_D)$
. Here
$(Q_D,F_D,W_D)$
. Here
![]() $Q_D$
is a quiver with a distinguished subquiver
$Q_D$
is a quiver with a distinguished subquiver
![]() $F_D$
, which we call frozen, so that the pair
$F_D$
, which we call frozen, so that the pair
![]() $(Q_D,F_D)$
is an ice quiver, and the potential
$(Q_D,F_D)$
is an ice quiver, and the potential
![]() $W_D$
is, loosely speaking, a linear combination of cycles in
$W_D$
is, loosely speaking, a linear combination of cycles in
![]() $Q_D$
(see Definition 2.3 for a precise definition). The quiver
$Q_D$
(see Definition 2.3 for a precise definition). The quiver
![]() $Q_D$
and the vertex set of
$Q_D$
and the vertex set of
![]() $F_D$
determine a cluster algebra
$F_D$
determine a cluster algebra
![]() $\mathscr {A}_{D}$
with frozen variables; the reader unfamiliar with this construction can find details in, for example, Keller’s survey [Reference Keller29]. In this paper, we will explain how to use the triple
$\mathscr {A}_{D}$
with frozen variables; the reader unfamiliar with this construction can find details in, for example, Keller’s survey [Reference Keller29]. In this paper, we will explain how to use the triple
![]() $(Q_D,F_D,W_D)$
to construct an additive categorification of this cluster algebra, in the case that D is connected.
$(Q_D,F_D,W_D)$
to construct an additive categorification of this cluster algebra, in the case that D is connected.
The construction proceeds via the frozen Jacobian algebra
![]() $A_D$
associated to
$A_D$
associated to
![]() $(Q_D,F_D,W_D)$
, also known as the dimer algebra of D. This algebra is a quotient of the complete path algebra of
$(Q_D,F_D,W_D)$
, also known as the dimer algebra of D. This algebra is a quotient of the complete path algebra of
![]() $Q_D$
by the closure of an ideal generated by relations computed using the data of the arrow set of
$Q_D$
by the closure of an ideal generated by relations computed using the data of the arrow set of
![]() $F_D$
(or, more directly, the complement of this set) and the potential
$F_D$
(or, more directly, the complement of this set) and the potential
![]() $W_D$
; again, precise definitions are found in Definition 2.3. This algebra has a distinguished idempotent e, given by the sum of vertex idempotents over the vertices of
$W_D$
; again, precise definitions are found in Definition 2.3. This algebra has a distinguished idempotent e, given by the sum of vertex idempotents over the vertices of
![]() $F_D$
, from which we obtain a boundary algebra
$F_D$
, from which we obtain a boundary algebra
![]() $B_D=eA_De$
. We will show that the category
$B_D=eA_De$
. We will show that the category
![]() $\operatorname {\mathrm {GP}}(B_D)$
of Gorenstein projective
$\operatorname {\mathrm {GP}}(B_D)$
of Gorenstein projective
![]() $B_D$
-modules is our desired categorification.
$B_D$
-modules is our desired categorification.
Theorem 1 (compare to Theorem 4.3 and Theorem 6.11)
Let D be a connected Postnikov diagram, and let
![]() $B_D=eA_De$
be the boundary algebra of its dimer algebra. Then the category
$B_D=eA_De$
be the boundary algebra of its dimer algebra. Then the category
![]() $\operatorname {\mathrm {GP}}(B_D)$
is an additive categorification of the cluster algebra
$\operatorname {\mathrm {GP}}(B_D)$
is an additive categorification of the cluster algebra
![]() $\mathscr {A}_{D}$
.
$\mathscr {A}_{D}$
.
While we use the term ‘additive categorification’ for brevity in the introduction, we acknowledge that it does not have a widely accepted formal definition in this context and refer the reader to the more precise statements below, which we hope justify our use of this terminology.
The main step in proving Theorem 1 is to establish a certain Calabi–Yau property for the algebra
![]() $A_D$
, relative to the boundary idempotent e, as referred to in the title. This result is likely to be of independent interest and is analogous to Broomhead’s theorem [Reference Broomhead3, Thm. 7.1] concerning Calabi–Yau properties of algebraically consistent dimer models on the torus (see also Davison [Reference Davison13] for higher genus closed surfaces).
$A_D$
, relative to the boundary idempotent e, as referred to in the title. This result is likely to be of independent interest and is analogous to Broomhead’s theorem [Reference Broomhead3, Thm. 7.1] concerning Calabi–Yau properties of algebraically consistent dimer models on the torus (see also Davison [Reference Davison13] for higher genus closed surfaces).
Theorem 2 (compare to Theorem 3.7)
Let D be a connected Postnikov diagram with dimer algebra
![]() $A_D$
. Then
$A_D$
. Then
![]() $A_D$
is bimodule internally
$A_D$
is bimodule internally
![]() $3$
-Calabi–Yau with respect to the idempotent e given by summing the vertex idempotents for the vertices of
$3$
-Calabi–Yau with respect to the idempotent e given by summing the vertex idempotents for the vertices of
![]() $F_D$
.
$F_D$
.
The general definition of a bimodule internally
![]() $3$
-Calabi–Yau algebra, and the role of this property in constructing categorifications, is explained in [Reference Pressland43]. We will not give this general definition here; since
$3$
-Calabi–Yau algebra, and the role of this property in constructing categorifications, is explained in [Reference Pressland43]. We will not give this general definition here; since
![]() $A_D$
is presented as a frozen Jacobian algebra, we can work instead with a sufficient condition implying the Calabi–Yau property, which appears in Theorem 3.7.
$A_D$
is presented as a frozen Jacobian algebra, we can work instead with a sufficient condition implying the Calabi–Yau property, which appears in Theorem 3.7.
1.2 Positroid varieties
Postnikov diagrams and their associated cluster algebras are important in studying positroid varieties in the Grassmannian—while this connection has only a minor logical role in the paper, we recall it here to help contextualise and motivate our results. Positroid varieties were introduced by Knutson, Lam and Speyer [Reference Knutson, Lam and Speyer32] and are closely related to various stratifications of the Grassmannian [Reference Brown, Goodearl and Yakimov4, Reference Goodearl and Yakimov21, Reference Lusztig36, Reference Rietsch46]; see [Reference Knutson, Lam and Speyer32, §5.3] for a discussion of this relationship. Intersecting a positroid variety with the totally nonnegative Grassmannian produces a cell in Postnikov’s decomposition of this space, the study of which is one of the main motivations of the work in [Reference Postnikov41].
In this context, a positroid is a subset
![]() $\mathcal {P}$
of the set
$\mathcal {P}$
of the set
![]() $\binom {[n]}{k}$
of k-element subsets of
$\binom {[n]}{k}$
of k-element subsets of
![]() $\left \{1,\dotsc ,n\right \}$
(see [Reference Muller and Speyer38, §1.4] for the defining properties). Each positroid is uniquely determined by a necklace, a cyclically ordered set of n elements of
$\left \{1,\dotsc ,n\right \}$
(see [Reference Muller and Speyer38, §1.4] for the defining properties). Each positroid is uniquely determined by a necklace, a cyclically ordered set of n elements of
![]() $\binom {[n]}{k}$
(see [Reference Oh, Postnikov and Speyer39, Defn. 4.2]). Strictly speaking, it is more compatible with our conventions to use the reverse necklace (see [Reference Muller and Speyer38, §2.1] and [Reference Çanakçı, King and Pressland11, §8]), but we will abuse terminology by referring to the set
$\binom {[n]}{k}$
(see [Reference Oh, Postnikov and Speyer39, Defn. 4.2]). Strictly speaking, it is more compatible with our conventions to use the reverse necklace (see [Reference Muller and Speyer38, §2.1] and [Reference Çanakçı, King and Pressland11, §8]), but we will abuse terminology by referring to the set
![]() $\mathcal {I}\subseteq \mathcal {P}$
of elements of this reverse necklace as simply ‘the necklace
$\mathcal {I}\subseteq \mathcal {P}$
of elements of this reverse necklace as simply ‘the necklace
![]() $\mathcal {I}$
of
$\mathcal {I}$
of
![]() $\mathcal {P}$
’. Recall that the Grassmannian
$\mathcal {P}$
’. Recall that the Grassmannian
![]() $\mathrm {Gr}_{k}^{n}$
of k-dimensional subspaces of
$\mathrm {Gr}_{k}^{n}$
of k-dimensional subspaces of
![]() $\mathbb {C}^n$
has as a standard generating set of homogeneous coordinates the Plücker coordinates
$\mathbb {C}^n$
has as a standard generating set of homogeneous coordinates the Plücker coordinates
![]() $\Delta _{I}$
for
$\Delta _{I}$
for
![]() $I\in \binom {[n]}{k}$
.
$I\in \binom {[n]}{k}$
.
Definition 1.1. Given a positroid
![]() $\mathcal {P}\subseteq \binom {[n]}{k}$
, the (closed) positroid variety
$\mathcal {P}\subseteq \binom {[n]}{k}$
, the (closed) positroid variety
![]() $\Pi (\mathcal {P})$
is the subvariety of the Grassmannian
$\Pi (\mathcal {P})$
is the subvariety of the Grassmannian
![]() $\mathrm {Gr}_{k}^{n}$
on which
$\mathrm {Gr}_{k}^{n}$
on which
![]() $\Delta _{I}=0$
for
$\Delta _{I}=0$
for
![]() $I\notin \mathcal {P}$
. The open positroid variety
$I\notin \mathcal {P}$
. The open positroid variety
![]() $\Pi ^\circ (\mathcal {P})$
is the subvariety of
$\Pi ^\circ (\mathcal {P})$
is the subvariety of
![]() $\Pi (\mathcal {P})$
on which additionally
$\Pi (\mathcal {P})$
on which additionally
![]() $\Delta _{I}\ne 0$
for
$\Delta _{I}\ne 0$
for
![]() $I\in \mathcal {I}$
. We denote the cones on these varieties, which are defined by the same conditions inside the affine cone
$I\in \mathcal {I}$
. We denote the cones on these varieties, which are defined by the same conditions inside the affine cone
![]() $\widehat {\mathrm {Gr}}{\vphantom {\mathrm {Gr}}}_{k}^{n}$
on the Grassmannian, by
$\widehat {\mathrm {Gr}}{\vphantom {\mathrm {Gr}}}_{k}^{n}$
on the Grassmannian, by
![]() $\widehat {\Pi }(\mathcal {P})$
and
$\widehat {\Pi }(\mathcal {P})$
and
![]() $\widehat {\Pi }^\circ (\mathcal {P})$
, respectively.
$\widehat {\Pi }^\circ (\mathcal {P})$
, respectively.
A Postnikov diagram D determines a positroid
![]() $\mathcal {P}_D$
with necklace
$\mathcal {P}_D$
with necklace
![]() $\mathcal {I}_D$
and a maximal weakly separated (or maximal noncrossing) collection [Reference Oh, Postnikov and Speyer39, Defn. 4.3]
$\mathcal {I}_D$
and a maximal weakly separated (or maximal noncrossing) collection [Reference Oh, Postnikov and Speyer39, Defn. 4.3]
![]() $\mathcal {C}_D$
with
$\mathcal {C}_D$
with
![]() $\mathcal {I}_D\subseteq \mathcal {C}_D\subseteq \mathcal {P}_D$
. In particular, D determines the numbers k and n such that
$\mathcal {I}_D\subseteq \mathcal {C}_D\subseteq \mathcal {P}_D$
. In particular, D determines the numbers k and n such that
![]() $\mathcal {P}_D$
,
$\mathcal {P}_D$
,
![]() $\mathcal {I}_D$
and
$\mathcal {I}_D$
and
![]() $\mathcal {C}_D$
consist of k-element subsets of
$\mathcal {C}_D$
consist of k-element subsets of
![]() $\left \{1,\dotsc ,n\right \}$
; see Definition 2.1. The elements of
$\left \{1,\dotsc ,n\right \}$
; see Definition 2.1. The elements of
![]() $\mathcal {C}_D$
are attached to the alternating regions of D, or equivalently to the vertices of the associated ice quiver
$\mathcal {C}_D$
are attached to the alternating regions of D, or equivalently to the vertices of the associated ice quiver
![]() $Q_D$
; the precise construction is given in Remark 2.7. While many different Postnikov diagrams can determine the same positroid and necklace, it is rarer for two diagrams to determine the same weakly separated collection—indeed, given a positroid
$Q_D$
; the precise construction is given in Remark 2.7. While many different Postnikov diagrams can determine the same positroid and necklace, it is rarer for two diagrams to determine the same weakly separated collection—indeed, given a positroid
![]() $\mathcal {P}$
with necklace
$\mathcal {P}$
with necklace
![]() $\mathcal {I}$
, Oh–Postnikov–Speyer [Reference Oh, Postnikov and Speyer39, Thm. 1.5] show that the maximal weakly separated collections
$\mathcal {I}$
, Oh–Postnikov–Speyer [Reference Oh, Postnikov and Speyer39, Thm. 1.5] show that the maximal weakly separated collections
![]() $\mathcal {C}$
with
$\mathcal {C}$
with
![]() $\mathcal {I}\subseteq \mathcal {C}\subseteq \mathcal {P}$
are in bijection with Postnikov diagrams D such that
$\mathcal {I}\subseteq \mathcal {C}\subseteq \mathcal {P}$
are in bijection with Postnikov diagrams D such that
![]() $\mathcal {P}_D=\mathcal {P}$
(equivalently,
$\mathcal {P}_D=\mathcal {P}$
(equivalently,
![]() $\mathcal {I}_D=\mathcal {I}$
), up to isotopy and certain moves (see Figure 4).
$\mathcal {I}_D=\mathcal {I}$
), up to isotopy and certain moves (see Figure 4).
We may interpret the collection
![]() $\mathcal {C}_D$
as a set of functions on
$\mathcal {C}_D$
as a set of functions on
![]() $\widehat {\Pi }^\circ (\mathcal {P}_D)$
by restricting the Plücker coordinates
$\widehat {\Pi }^\circ (\mathcal {P}_D)$
by restricting the Plücker coordinates
![]() $\Delta _I$
for
$\Delta _I$
for
![]() $I\in \mathcal {C}_D$
to this subvariety of
$I\in \mathcal {C}_D$
to this subvariety of
![]() $\widehat {\mathrm {Gr}}{\vphantom {\mathrm {Gr}}}_{k}^{n}$
. Since these functions are attached to the vertices of
$\widehat {\mathrm {Gr}}{\vphantom {\mathrm {Gr}}}_{k}^{n}$
. Since these functions are attached to the vertices of
![]() $Q_D$
, we thus obtain a map
$Q_D$
, we thus obtain a map
![]() $\mathscr {A}_{D}\to \mathbb {C}(\widehat {\Pi }^\circ (\mathcal {P}_D))$
, from the abstract cluster algebra
$\mathscr {A}_{D}\to \mathbb {C}(\widehat {\Pi }^\circ (\mathcal {P}_D))$
, from the abstract cluster algebra
![]() $\mathscr {A}_{D}$
associated to D to the ring of rational functions on
$\mathscr {A}_{D}$
associated to D to the ring of rational functions on
![]() $\widehat {\Pi }^\circ (\mathcal {P}_D)$
, sending each initial cluster variable to the restricted Plücker coordinate corresponding to the same quiver vertex. A long-standing conjecture, formalised by Muller and Speyer [Reference Muller and Speyer37, Conj. 3.4] and recently verified by Galashin and Lam [Reference Galashin and Lam18] (see also [Reference Serhiyenko, Sherman-Bennett and Williams48] for the special case of Schubert varieties), is the following.
$\widehat {\Pi }^\circ (\mathcal {P}_D)$
, sending each initial cluster variable to the restricted Plücker coordinate corresponding to the same quiver vertex. A long-standing conjecture, formalised by Muller and Speyer [Reference Muller and Speyer37, Conj. 3.4] and recently verified by Galashin and Lam [Reference Galashin and Lam18] (see also [Reference Serhiyenko, Sherman-Bennett and Williams48] for the special case of Schubert varieties), is the following.
Theorem 1.2 [Reference Galashin and Lam18]
The specialisation map
![]() $\mathscr {A}_{D}\to \mathbb {C}(\widehat {\Pi }^\circ (\mathcal {P}_D))$
above is injective, and its image is precisely the coordinate ring
$\mathscr {A}_{D}\to \mathbb {C}(\widehat {\Pi }^\circ (\mathcal {P}_D))$
above is injective, and its image is precisely the coordinate ring
![]() $\mathbb {C}[\widehat {\Pi }^\circ (\mathcal {P}_D)]$
.
$\mathbb {C}[\widehat {\Pi }^\circ (\mathcal {P}_D)]$
.
Thus the coordinate ring
![]() $\mathbb {C}[\widehat {\Pi }^\circ (\mathcal {P}_D)]$
has a cluster algebra structure, with initial seed
$\mathbb {C}[\widehat {\Pi }^\circ (\mathcal {P}_D)]$
has a cluster algebra structure, with initial seed
![]() $(Q_D,\mathcal {C}_D)$
, isomorphic to the cluster algebra we categorify in Theorem 1. While
$(Q_D,\mathcal {C}_D)$
, isomorphic to the cluster algebra we categorify in Theorem 1. While
![]() $\Pi ^\circ (\mathcal {P}_D)$
is an affine variety, and so it is slightly unusual to consider its affine cone, it is this cone on which restricted Plücker coordinates are functions. By contrast, the coordinate ring
$\Pi ^\circ (\mathcal {P}_D)$
is an affine variety, and so it is slightly unusual to consider its affine cone, it is this cone on which restricted Plücker coordinates are functions. By contrast, the coordinate ring
![]() $\mathbb {C}[\Pi ^\circ (\mathcal {P}_D)]$
is the degree zero part of
$\mathbb {C}[\Pi ^\circ (\mathcal {P}_D)]$
is the degree zero part of
![]() $\mathbb {C}[\widehat {\Pi }^\circ (\mathcal {P}_D)]$
in the
$\mathbb {C}[\widehat {\Pi }^\circ (\mathcal {P}_D)]$
in the
![]() $\mathbb {Z}$
-grading in which Plücker coordinates have degree
$\mathbb {Z}$
-grading in which Plücker coordinates have degree
![]() $1$
. Said differently, the grading determines a
$1$
. Said differently, the grading determines a
![]() $\mathbb {C}^\times $
-action on
$\mathbb {C}^\times $
-action on
![]() $\mathbb {C}[\widehat {\Pi }^\circ (\mathcal {P}_D)]$
by
$\mathbb {C}[\widehat {\Pi }^\circ (\mathcal {P}_D)]$
by
![]() $\lambda \cdot f=\lambda ^df$
when f has degree d, and
$\lambda \cdot f=\lambda ^df$
when f has degree d, and
![]() $\mathbb {C}[\Pi ^\circ (\mathcal {P}_D)]$
is the invariant subring
$\mathbb {C}[\Pi ^\circ (\mathcal {P}_D)]$
is the invariant subring
![]() $\mathbb {C}[\widehat {\Pi }^\circ (\mathcal {P}_D)]^{\mathbb {C}^\times }$
for this action.
$\mathbb {C}[\widehat {\Pi }^\circ (\mathcal {P}_D)]^{\mathbb {C}^\times }$
for this action.
Remark 1.3. For Theorem 1.2, it is necessary to adopt the convention that the frozen variables of
![]() $\mathscr {A}_{D}$
are invertible, since the images of these frozen variables in
$\mathscr {A}_{D}$
are invertible, since the images of these frozen variables in
![]() $\mathbb {C}[\widehat {\Pi }^\circ (\mathcal {P}_D)]$
are precisely the Plücker coordinates
$\mathbb {C}[\widehat {\Pi }^\circ (\mathcal {P}_D)]$
are precisely the Plücker coordinates
![]() $\Delta _{I}$
for
$\Delta _{I}$
for
![]() $I\in \mathcal {I}_D$
, which are nonzero on
$I\in \mathcal {I}_D$
, which are nonzero on
![]() $\widehat {\Pi }^\circ (\mathcal {P}_D)$
by definition. This convention is not relevant to Theorem 1, however, so we will freely compare our results with those of authors who do not invert frozen variables, such as [Reference Jensen, King and Su28].
$\widehat {\Pi }^\circ (\mathcal {P}_D)$
by definition. This convention is not relevant to Theorem 1, however, so we will freely compare our results with those of authors who do not invert frozen variables, such as [Reference Jensen, King and Su28].
As already observed, the positroid
![]() $\mathcal {P}_D$
and its corresponding variety
$\mathcal {P}_D$
and its corresponding variety
![]() $\Pi ^\circ (\mathcal {P}_D)$
do not determine D uniquely; choosing a different Postnikov diagram with positroid
$\Pi ^\circ (\mathcal {P}_D)$
do not determine D uniquely; choosing a different Postnikov diagram with positroid
![]() $\mathcal {P}_D$
amounts to choosing a different initial seed in the cluster algebra structure on
$\mathcal {P}_D$
amounts to choosing a different initial seed in the cluster algebra structure on
![]() $\mathbb {C}[\widehat {\Pi }^\circ (\mathcal {P}_D)]$
. This is reflected in our categorical picture by the fact (Corollary 4.7) that if
$\mathbb {C}[\widehat {\Pi }^\circ (\mathcal {P}_D)]$
. This is reflected in our categorical picture by the fact (Corollary 4.7) that if
![]() $\mathcal {P}_D=\mathcal {P}_{D'}$
for two connected Postnikov diagrams D and
$\mathcal {P}_D=\mathcal {P}_{D'}$
for two connected Postnikov diagrams D and
![]() $D'$
, then the two algebras
$D'$
, then the two algebras
![]() $B_D$
and
$B_D$
and
![]() $B_D'$
are isomorphic, and hence the categories
$B_D'$
are isomorphic, and hence the categories
![]() $\operatorname {\mathrm {GP}}(B_D)$
and
$\operatorname {\mathrm {GP}}(B_D)$
and
![]() $\operatorname {\mathrm {GP}}(B_{D'})$
from Theorem 1 are equivalent.
$\operatorname {\mathrm {GP}}(B_{D'})$
from Theorem 1 are equivalent.
The best understood case of these constructions is that in which
![]() $\mathcal {P}_D=\binom {[n]}{k}$
is the uniform positroid, in which the notion of a maximal weakly separated collection from [Reference Oh, Postnikov and Speyer39] coincides with that of Leclerc–Zelevinsky [Reference Leclerc and Zelevinsky34]. In this case, we have
$\mathcal {P}_D=\binom {[n]}{k}$
is the uniform positroid, in which the notion of a maximal weakly separated collection from [Reference Oh, Postnikov and Speyer39] coincides with that of Leclerc–Zelevinsky [Reference Leclerc and Zelevinsky34]. In this case, we have
![]() $\Pi (\mathcal {P}_D)=\mathrm {Gr}_{k}^{n}$
, the open subvariety
$\Pi (\mathcal {P}_D)=\mathrm {Gr}_{k}^{n}$
, the open subvariety
![]() $\Pi ^\circ (\mathcal {P}_D)$
is determined by the nonvanishing of those Plücker coordinates labelled by cyclic intervals, and Muller–Speyer’s conjecture was verified much earlier by Scott [Reference Scott47]. (The case
$\Pi ^\circ (\mathcal {P}_D)$
is determined by the nonvanishing of those Plücker coordinates labelled by cyclic intervals, and Muller–Speyer’s conjecture was verified much earlier by Scott [Reference Scott47]. (The case
![]() $k=2$
even appears in Fomin–Zelevinsky’s first paper on cluster algebras [Reference Fomin and Zelevinsky16].) Scott in fact proves more, namely that a completely analogous specialisation map to that of Theorem 1.2 is an isomorphism from the cluster algebra with noninvertible frozen variables determined by
$k=2$
even appears in Fomin–Zelevinsky’s first paper on cluster algebras [Reference Fomin and Zelevinsky16].) Scott in fact proves more, namely that a completely analogous specialisation map to that of Theorem 1.2 is an isomorphism from the cluster algebra with noninvertible frozen variables determined by
![]() $Q_D$
to the homogeneous coordinate ring of
$Q_D$
to the homogeneous coordinate ring of
![]() $\mathrm {Gr}_{k}^{n}$
. However, this depends on special properties of the uniform positroid, and there is no corresponding result for arbitrary Postnikov diagrams.
$\mathrm {Gr}_{k}^{n}$
. However, this depends on special properties of the uniform positroid, and there is no corresponding result for arbitrary Postnikov diagrams.
1.3 The Grassmannian cluster category
When
![]() $\mathcal {P}_D$
is the uniform positroid, a categorification of
$\mathcal {P}_D$
is the uniform positroid, a categorification of
![]() $\mathscr {A}_{D}$
is provided by Jensen–King–Su [Reference Jensen, King and Su28] (see also Demonet–Luo [Reference Demonet and Luo14] for
$\mathscr {A}_{D}$
is provided by Jensen–King–Su [Reference Jensen, King and Su28] (see also Demonet–Luo [Reference Demonet and Luo14] for
![]() $k=2$
). This Grassmannian cluster category, denoted
$k=2$
). This Grassmannian cluster category, denoted
![]() $\operatorname {\mathrm {CM}}(C)$
, consists of Cohen–Macaulay modules over a certain algebra C (depending on k and n), defined directly via a quiver with relations. Some of the results in [Reference Jensen, King and Su28] rely on the categorification by Geiß–Leclerc–Schröer [Reference Geiß, Leclerc and Schröer19] of a cluster algebra obtained from
$\operatorname {\mathrm {CM}}(C)$
, consists of Cohen–Macaulay modules over a certain algebra C (depending on k and n), defined directly via a quiver with relations. Some of the results in [Reference Jensen, King and Su28] rely on the categorification by Geiß–Leclerc–Schröer [Reference Geiß, Leclerc and Schröer19] of a cluster algebra obtained from
![]() $\mathscr {A}_{D}$
by specialising a single frozen variable to
$\mathscr {A}_{D}$
by specialising a single frozen variable to
![]() $1$
or, equivalently, removing a frozen vertex and all adjacent arrows from the quiver.
$1$
or, equivalently, removing a frozen vertex and all adjacent arrows from the quiver.
Jensen–King–Su’s categorification is connected back to the combinatorics of Postnikov diagrams by work of Baur–King–Marsh [Reference Baur, King and Marsh2], which is our main inspiration. They show [Reference Baur, King and Marsh2, Cor. 10.4] that for any Postnikov diagram D for which
![]() $\mathcal {P}_D$
is the uniform positroid, there is an isomorphism
$\mathcal {P}_D$
is the uniform positroid, there is an isomorphism
![]() $B_D\cong C$
between the boundary algebra of D, with which we describe our categorification, and the algebra C describing the Grassmannian cluster category. Since C has the property that
$B_D\cong C$
between the boundary algebra of D, with which we describe our categorification, and the algebra C describing the Grassmannian cluster category. Since C has the property that
![]() $\operatorname {\mathrm {CM}}(C)=\operatorname {\mathrm {GP}}(C)$
, our categorification coincides with Jensen–King–Su’s in this case.
$\operatorname {\mathrm {CM}}(C)=\operatorname {\mathrm {GP}}(C)$
, our categorification coincides with Jensen–King–Su’s in this case.
In our more general situation, because
![]() $B_D$
is defined as an idempotent subalgebra of the dimer algebra
$B_D$
is defined as an idempotent subalgebra of the dimer algebra
![]() $A_D$
, we do not typically know a presentation of
$A_D$
, we do not typically know a presentation of
![]() $B_D$
via a quiver with relations. Our approach therefore differs significantly from that of Jensen–King–Su, since we must deduce properties of the category
$B_D$
via a quiver with relations. Our approach therefore differs significantly from that of Jensen–King–Su, since we must deduce properties of the category
![]() $\operatorname {\mathrm {GP}}(B_D)$
from the combinatorics of the diagram D and the representation theory of
$\operatorname {\mathrm {GP}}(B_D)$
from the combinatorics of the diagram D and the representation theory of
![]() $A_D$
, for which we do have such a presentation. This is done primarily via the internal Calabi–Yau property of Theorem 3.7, which, in the full strength established here, is also a new result in the case that
$A_D$
, for which we do have such a presentation. This is done primarily via the internal Calabi–Yau property of Theorem 3.7, which, in the full strength established here, is also a new result in the case that
![]() $\mathcal {P}_D$
is the uniform positroid.
$\mathcal {P}_D$
is the uniform positroid.
For more general Postnikov diagrams D, a categorification analogous to that of Geiß–Leclerc–Schröer’s in the uniform case is provided by Leclerc [Reference Leclerc33] in work on Richardson varieties; again, he categorifies a cluster algebra obtained from
![]() $\mathscr {A}_{D}$
by specialising a frozen variable to
$\mathscr {A}_{D}$
by specialising a frozen variable to
![]() $1$
. Leclerc’s category plays a crucial role in the construction of a cluster structure on
$1$
. Leclerc’s category plays a crucial role in the construction of a cluster structure on
![]() $\mathbb {C}[\widehat {\Pi }^\circ (\mathcal {P}_D)]$
in [Reference Galashin and Lam18, Reference Serhiyenko, Sherman-Bennett and Williams48]. In this paper, we will always consider the full quiver
$\mathbb {C}[\widehat {\Pi }^\circ (\mathcal {P}_D)]$
in [Reference Galashin and Lam18, Reference Serhiyenko, Sherman-Bennett and Williams48]. In this paper, we will always consider the full quiver
![]() $Q_D$
and its associated cluster algebra—in particular, this means that in the case of the uniform positroid, Theorem 1 recovers Jensen–King–Su’s category [Reference Jensen, King and Su28], not Geiß–Leclerc–Schröer’s [Reference Geiß, Leclerc and Schröer19].
$Q_D$
and its associated cluster algebra—in particular, this means that in the case of the uniform positroid, Theorem 1 recovers Jensen–King–Su’s category [Reference Jensen, King and Su28], not Geiß–Leclerc–Schröer’s [Reference Geiß, Leclerc and Schröer19].
Our category
![]() $\operatorname {\mathrm {GP}}(B_D)$
is closely connected to the coordinate ring
$\operatorname {\mathrm {GP}}(B_D)$
is closely connected to the coordinate ring
![]() $\mathbb {C}[\widehat {\Pi }^\circ (\mathcal {P}_D)]$
(and its cluster algebra structure). To demonstrate this, we exhibit a cluster character on
$\mathbb {C}[\widehat {\Pi }^\circ (\mathcal {P}_D)]$
(and its cluster algebra structure). To demonstrate this, we exhibit a cluster character on
![]() $\operatorname {\mathrm {GP}}(B_D)$
, in the sense of Fu–Keller [Reference Fu and Keller17], providing a bijection between reachable rigid indecomposable objects of
$\operatorname {\mathrm {GP}}(B_D)$
, in the sense of Fu–Keller [Reference Fu and Keller17], providing a bijection between reachable rigid indecomposable objects of
![]() $\operatorname {\mathrm {GP}}(B_D)$
and cluster variables of
$\operatorname {\mathrm {GP}}(B_D)$
and cluster variables of
![]() $\mathbb {C}[\widehat {\Pi }^\circ (\mathcal {P}_D)]$
, and a bijection between reachable cluster-tilting objects of
$\mathbb {C}[\widehat {\Pi }^\circ (\mathcal {P}_D)]$
, and a bijection between reachable cluster-tilting objects of
![]() $\operatorname {\mathrm {GP}}(B_D)$
and clusters of
$\operatorname {\mathrm {GP}}(B_D)$
and clusters of
![]() $\mathbb {C}[\widehat {\Pi }^\circ (\mathcal {P}_D)]$
. We also recall results from joint work with Çanakçı and King [Reference Çanakçı, King and Pressland11] demonstrating even stronger combinatorial connections between the representation theory of
$\mathbb {C}[\widehat {\Pi }^\circ (\mathcal {P}_D)]$
. We also recall results from joint work with Çanakçı and King [Reference Çanakçı, King and Pressland11] demonstrating even stronger combinatorial connections between the representation theory of
![]() $B_D$
and the geometry of
$B_D$
and the geometry of
![]() $\widehat {\Pi }^\circ (\mathcal {P}_D)$
. Precisely, there is a fully faithful functor
$\widehat {\Pi }^\circ (\mathcal {P}_D)$
. Precisely, there is a fully faithful functor
![]() $\rho \colon \operatorname {\mathrm {GP}}(B_D)\to \operatorname {\mathrm {CM}}(C)$
from the categorification described here to the Grassmannian cluster category (for the appropriate Grassmannian). For each
$\rho \colon \operatorname {\mathrm {GP}}(B_D)\to \operatorname {\mathrm {CM}}(C)$
from the categorification described here to the Grassmannian cluster category (for the appropriate Grassmannian). For each
![]() $I\in \binom {[n]}{k}$
, there is a combinatorially defined C-module
$I\in \binom {[n]}{k}$
, there is a combinatorially defined C-module
![]() $M_I$
corresponding to the Plücker coordinate
$M_I$
corresponding to the Plücker coordinate
![]() $\Delta _{I}$
, and we show (Theorem 7.6) that if
$\Delta _{I}$
, and we show (Theorem 7.6) that if
![]() $\rho (M)=M_I$
, then the cluster character on
$\rho (M)=M_I$
, then the cluster character on
![]() $\operatorname {\mathrm {GP}}(B_D)$
takes M to the restriction of
$\operatorname {\mathrm {GP}}(B_D)$
takes M to the restriction of
![]() $\Delta _{I}$
to
$\Delta _{I}$
to
![]() $\widehat {\Pi }^\circ (\mathcal {P}_D)$
.
$\widehat {\Pi }^\circ (\mathcal {P}_D)$
.
Remark 1.4. Leclerc’s categories [Reference Leclerc33] can be used to categorify a cluster algebra structure on
![]() $\mathbb {C}[\Pi ^\circ (\mathcal {P}_D)]$
—that is, on the coordinate ring of the open positroid variety itself rather than its affine cone—but in a way that depends on choosing a frozen variable
$\mathbb {C}[\Pi ^\circ (\mathcal {P}_D)]$
—that is, on the coordinate ring of the open positroid variety itself rather than its affine cone—but in a way that depends on choosing a frozen variable
![]() $\Delta _{I}$
with
$\Delta _{I}$
with
![]() $I\in \mathcal {I}_D$
. Indeed, the construction involves an isomorphism of
$I\in \mathcal {I}_D$
. Indeed, the construction involves an isomorphism of
![]() $\Pi ^\circ (\mathcal {P}_D)$
with the subvariety of
$\Pi ^\circ (\mathcal {P}_D)$
with the subvariety of
![]() $\widehat {\Pi }^\circ (\mathcal {P}_D)$
on which
$\widehat {\Pi }^\circ (\mathcal {P}_D)$
on which
![]() $\Delta _{I}=1$
; this is the graph of a global section of the line bundle
$\Delta _{I}=1$
; this is the graph of a global section of the line bundle
![]() $\widehat {\Pi }^\circ (\mathcal {P}_D)\to \Pi ^\circ (\mathcal {P}_D)$
. In ring-theoretic terms, this isomorphism corresponds to splitting the inclusion
$\widehat {\Pi }^\circ (\mathcal {P}_D)\to \Pi ^\circ (\mathcal {P}_D)$
. In ring-theoretic terms, this isomorphism corresponds to splitting the inclusion
using the map taking
![]() $f\in \mathbb {C}[\widehat {\Pi }^\circ (\mathcal {P}_D)]$
of degree d to the
$f\in \mathbb {C}[\widehat {\Pi }^\circ (\mathcal {P}_D)]$
of degree d to the
![]() $\mathbb {C}^\times $
-invariant function
$\mathbb {C}^\times $
-invariant function
![]() $f\Delta _{I}^{-d}$
, recalling that
$f\Delta _{I}^{-d}$
, recalling that
![]() $\Delta _{I}$
is invertible on
$\Delta _{I}$
is invertible on
![]() $\Pi ^\circ (\mathcal {P}_D)$
.
$\Pi ^\circ (\mathcal {P}_D)$
.
By avoiding this arbitrary choice, our categorification better reflects the symmetries of
![]() $\Pi ^\circ (\mathcal {P}_D)$
. For example, in the case of the uniform positroid, both
$\Pi ^\circ (\mathcal {P}_D)$
. For example, in the case of the uniform positroid, both
![]() $\Pi ^\circ (\mathcal {P}_D)$
and our category (which coincides with Jensen–King–Su’s [Reference Jensen, King and Su28] in this case) carry an action of the order n cyclic group coming from natural action of this group on the cyclically ordered set
$\Pi ^\circ (\mathcal {P}_D)$
and our category (which coincides with Jensen–King–Su’s [Reference Jensen, King and Su28] in this case) carry an action of the order n cyclic group coming from natural action of this group on the cyclically ordered set
![]() $[n]$
, and by extension on the set
$[n]$
, and by extension on the set
![]() $\binom {[n]}{k}$
labelling Plücker coordinates. Since this action does not fix the frozen variables, but rather cyclically permutes them, choosing a frozen vertex breaks the symmetry, which indeed is no longer present in Geiß–Leclerc–Schröer’s category [Reference Geiß, Leclerc and Schröer19].
$\binom {[n]}{k}$
labelling Plücker coordinates. Since this action does not fix the frozen variables, but rather cyclically permutes them, choosing a frozen vertex breaks the symmetry, which indeed is no longer present in Geiß–Leclerc–Schröer’s category [Reference Geiß, Leclerc and Schröer19].
In the case of the uniform positroid, the distinction between Jensen–King–Su’s category and Geiß–Leclerc–Schröer’s is even more critical, since in this case the homogeneous coordinate ring
![]() $\mathbb {C}[\widehat {\Pi }(\mathcal {P}_D)]=\mathbb {C}[\widehat {\mathrm {Gr}}{\vphantom {\mathrm {Gr}}}_{k}^{n}]$
of the closed positroid variety carries its own cluster algebra structure, in which the n frozen variables are noninvertible. For more general positroids
$\mathbb {C}[\widehat {\Pi }(\mathcal {P}_D)]=\mathbb {C}[\widehat {\mathrm {Gr}}{\vphantom {\mathrm {Gr}}}_{k}^{n}]$
of the closed positroid variety carries its own cluster algebra structure, in which the n frozen variables are noninvertible. For more general positroids
![]() $\mathcal {P}$
, the ring
$\mathcal {P}$
, the ring
![]() $\mathbb {C}[\widehat {\Pi }(\mathcal {P})]$
is not a cluster algebra, but we still hope that the avoidance of symmetry-breaking in our constructions will allow us to use the algebra
$\mathbb {C}[\widehat {\Pi }(\mathcal {P})]$
is not a cluster algebra, but we still hope that the avoidance of symmetry-breaking in our constructions will allow us to use the algebra
![]() $B_D$
constructed here, and its category of Cohen–Macaulay modules, to study the closed varieties
$B_D$
constructed here, and its category of Cohen–Macaulay modules, to study the closed varieties
![]() $\Pi (\mathcal {P})$
and
$\Pi (\mathcal {P})$
and
![]() $\widehat {\Pi }(\mathcal {P})$
—see [Reference Çanakçı, King and Pressland11, Prop. 8.6] for a first step in this direction.
$\widehat {\Pi }(\mathcal {P})$
—see [Reference Çanakçı, King and Pressland11, Prop. 8.6] for a first step in this direction.
The structure of the paper is as follows. In Section 2, we recall the definition of a Postnikov diagram and the construction of its dimer algebra. The necessary Calabi–Yau property of this algebra is established in Section 3 and used to construct the categorification
![]() $\operatorname {\mathrm {GP}}(B_D)$
in Section 4. In Section 5, we show that
$\operatorname {\mathrm {GP}}(B_D)$
in Section 4. In Section 5, we show that
![]() $\operatorname {\mathrm {GP}}(B_D)$
has a mutation class of cluster-tilting objects, again determined by D, whose quivers have no loops or
$\operatorname {\mathrm {GP}}(B_D)$
has a mutation class of cluster-tilting objects, again determined by D, whose quivers have no loops or
![]() $2$
-cycles. This allows us to show in Section 6 that there is a cluster character on
$2$
-cycles. This allows us to show in Section 6 that there is a cluster character on
![]() $\operatorname {\mathrm {GP}}(B_D)$
inducing bijections between the cluster-tilting objects in this class and the clusters of
$\operatorname {\mathrm {GP}}(B_D)$
inducing bijections between the cluster-tilting objects in this class and the clusters of
![]() $\mathscr {A}_{D}$
, and between their indecomposable summands and the cluster (and frozen) variables of
$\mathscr {A}_{D}$
, and between their indecomposable summands and the cluster (and frozen) variables of
![]() $\mathscr {A}_{D}$
. We close in Section 7 by explaining how our categorification is related to Jensen–King–Su’s Grassmannian cluster category [Reference Jensen, King and Su28] and how its cluster character relates to Galashin and Lam’s isomorphism of
$\mathscr {A}_{D}$
. We close in Section 7 by explaining how our categorification is related to Jensen–King–Su’s Grassmannian cluster category [Reference Jensen, King and Su28] and how its cluster character relates to Galashin and Lam’s isomorphism of
![]() $\mathscr {A}_{D}$
with the coordinate ring
$\mathscr {A}_{D}$
with the coordinate ring
![]() $\mathbb {C}[\widehat {\Pi }^\circ (\mathcal {P}_D)]$
.
$\mathbb {C}[\widehat {\Pi }^\circ (\mathcal {P}_D)]$
.
2 Postnikov diagrams and their dimer algebras
In this section, we introduce Postnikov diagrams in the disc and their associated dimer algebras, which will be defined over a field
![]() $\mathbb {K}$
of characteristic zero.
$\mathbb {K}$
of characteristic zero.
Definition 2.1 [Reference Postnikov41, §14] (see also [Reference Scott47, §3] and [Reference Baur, King and Marsh2, §2])
Let
![]() $\Sigma $
be an oriented disc, with
$\Sigma $
be an oriented disc, with
![]() $n\geq 3$
marked points on its boundary. A Postnikov diagram D in
$n\geq 3$
marked points on its boundary. A Postnikov diagram D in
![]() $\Sigma $
consists of n oriented strands in
$\Sigma $
consists of n oriented strands in
![]() $\Sigma $
, starting and ending at the boundary marked points, subject to the following constraints:
$\Sigma $
, starting and ending at the boundary marked points, subject to the following constraints:
-
(P0) Each boundary marked point is the start point of exactly one strand and the end point of exactly one strand.
-
(P1) The strands intersect in finitely many points, and each such crossing is transverse and involves only two strands.
-
(P2) Moving along a strand, the signs of its crossings with other strands alternate.

-
(P3) A strand may not intersect itself in the interior of the disc.
-
(P4) If two strands intersect twice, the strands are oriented in opposite directions between these intersection points. In other words, the configuration
is not permitted, but the configuration obtained from this by reversing the orientation of one of the strands is legal.
For axioms (P2) and (P4), the intersection of two strands at the boundary, with its natural sign, is also treated as a crossing.
The diagram D divides
![]() $\Sigma $
into regions, the connected components of the complement of the strands, which have three types: the orientations of the strands around the boundary of such a region can be inconsistent (in which case we call the region alternating), oriented anticlockwise (i.e. consistent with the orientation of
$\Sigma $
into regions, the connected components of the complement of the strands, which have three types: the orientations of the strands around the boundary of such a region can be inconsistent (in which case we call the region alternating), oriented anticlockwise (i.e. consistent with the orientation of
![]() $\Sigma $
) or oriented clockwise. We will use the terminology anticlockwise and clockwise for regions with these boundary orientations. The alternating regions are further subdivided into boundary regions, those incident with the boundary of
$\Sigma $
) or oriented clockwise. We will use the terminology anticlockwise and clockwise for regions with these boundary orientations. The alternating regions are further subdivided into boundary regions, those incident with the boundary of
![]() $\Sigma $
, and internal regions.
$\Sigma $
, and internal regions.
We say that D is connected if the union of its strands is connected. This forces each boundary region to meet the boundary of
![]() $\Sigma $
in a single arc, so there are exactly n such regions.
$\Sigma $
in a single arc, so there are exactly n such regions.
There is an integer
![]() $k\in \{1,\dotsc ,n\}$
such that each alternating region of D is on the left of exactly k strands. We say that the type of D is
$k\in \{1,\dotsc ,n\}$
such that each alternating region of D is on the left of exactly k strands. We say that the type of D is
![]() $(k,n)$
, recalling that n is the number of strands. One can also compute k as the average number of boundary regions to the left of a strand. If D has the property that every strand has exactly k boundary regions on its left, then each strand must terminate at a marked point k steps clockwise from its source, and in this case D is sometimes [Reference Baur, King and Marsh2] called a
$(k,n)$
, recalling that n is the number of strands. One can also compute k as the average number of boundary regions to the left of a strand. If D has the property that every strand has exactly k boundary regions on its left, then each strand must terminate at a marked point k steps clockwise from its source, and in this case D is sometimes [Reference Baur, King and Marsh2] called a
![]() $(k,n)$
-diagram. Diagrams of this kind are always connected.
$(k,n)$
-diagram. Diagrams of this kind are always connected.
Remark 2.2. It is possible to consider Postnikov diagrams on
![]() $n<3$
strands, but they do not lead to interesting cluster algebras. For example, their associated ice quivers (see Definition 2.4 below) have only frozen vertices and so describe a cluster algebra with only frozen variables: that is, a polynomial ring. Thus the assumption that
$n<3$
strands, but they do not lead to interesting cluster algebras. For example, their associated ice quivers (see Definition 2.4 below) have only frozen vertices and so describe a cluster algebra with only frozen variables: that is, a polynomial ring. Thus the assumption that
![]() $n\geq 3$
, which will be useful in Section 5, only excludes a small number of highly degenerate examples. Both Theorems 1 and 2 do hold when
$n\geq 3$
, which will be useful in Section 5, only excludes a small number of highly degenerate examples. Both Theorems 1 and 2 do hold when
![]() $n<3$
, but they reduce to the claim that
$n<3$
, but they reduce to the claim that
![]() $B_D$
is an algebra of global dimension at most
$B_D$
is an algebra of global dimension at most
![]() $3$
with n indecomposable projective modules up to isomorphism, which follows immediately from observing that
$3$
with n indecomposable projective modules up to isomorphism, which follows immediately from observing that
![]() $B_D$
is the complete path algebra of an n-cycle in this case (or from the results of Section 3, which do not use the assumption
$B_D$
is the complete path algebra of an n-cycle in this case (or from the results of Section 3, which do not use the assumption
![]() $n\geq 3$
).
$n\geq 3$
).
A Postnikov diagram in the disc has an associated algebra called its dimer algebra, which, when D is connected, is an instance of a frozen Jacobian algebra defined via an ice quiver with potential. We first give the necessary definitions for this general construction and then explain how to read off the relevant data from a Postnikov diagram.
Definition 2.3 (compare to [Reference Pressland44, §2])
An ice quiver is a pair
![]() $(Q,F)$
, where Q is a quiver and F is a (not necessarily full) subquiver of Q. We call
$(Q,F)$
, where Q is a quiver and F is a (not necessarily full) subquiver of Q. We call
![]() $F_0$
,
$F_0$
,
![]() $F_1$
and F the frozen vertices, arrows and subquiver, respectively. Vertices in
$F_1$
and F the frozen vertices, arrows and subquiver, respectively. Vertices in
![]() $Q_0^{\mathrm {m}}:=Q_0\setminus F_0$
will be called mutable, whereas arrows in
$Q_0^{\mathrm {m}}:=Q_0\setminus F_0$
will be called mutable, whereas arrows in
![]() $Q_1^{\mathrm {m}}:=Q_1\setminus F_1$
will be simply called unfrozen. We assume for simplicity that Q has no loops.
$Q_1^{\mathrm {m}}:=Q_1\setminus F_1$
will be simply called unfrozen. We assume for simplicity that Q has no loops.
Let
![]() $\mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle $
denote the complete path algebra of Q (see [Reference Pressland44, Defn. 2.6]). This algebra is graded by path length, which makes its quotient
$\mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle $
denote the complete path algebra of Q (see [Reference Pressland44, Defn. 2.6]). This algebra is graded by path length, which makes its quotient
![]() $\mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle _{\mathrm {cyc}}$
by the vector subspace spanned by commutators into a graded vector space. A potential on Q is an element
$\mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle _{\mathrm {cyc}}$
by the vector subspace spanned by commutators into a graded vector space. A potential on Q is an element
![]() $W\in \mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle _{\mathrm {cyc}}$
expressible as a linear combination of homogeneous elements of degree at least
$W\in \mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle _{\mathrm {cyc}}$
expressible as a linear combination of homogeneous elements of degree at least
![]() $2$
. We usually think of W as a linear combination of cyclic paths in Q (of length at least
$2$
. We usually think of W as a linear combination of cyclic paths in Q (of length at least
![]() $2$
), considered up to cyclic equivalence: that is, the finest equivalence relation on such paths such that
$2$
), considered up to cyclic equivalence: that is, the finest equivalence relation on such paths such that
We call the triple
![]() $(Q,F,W)$
an ice quiver with potential.
$(Q,F,W)$
an ice quiver with potential.
Let
![]() $p=a_n\dotsm a_1$
be a cyclic path, with each
$p=a_n\dotsm a_1$
be a cyclic path, with each
![]() $a_i\in Q_1$
, and let
$a_i\in Q_1$
, and let
![]() $a\in Q_1$
be any arrow. Then the cyclic derivative of p with respect to a is
$a\in Q_1$
be any arrow. Then the cyclic derivative of p with respect to a is
Extending
![]() $\partial _{a}{}$
by linearity and continuity, we obtain a map
$\partial _{a}{}$
by linearity and continuity, we obtain a map
![]() $\mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle _{\mathrm {cyc}}\to \mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle $
. For an ice quiver with potential
$\mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle _{\mathrm {cyc}}\to \mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle $
. For an ice quiver with potential
![]() $(Q,F,W)$
, we define the frozen Jacobian algebra
$(Q,F,W)$
, we define the frozen Jacobian algebra
Here the closure is taken in the J-adic topology on
![]() $\mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle $
, where J is the ideal generated by arrows.
$\mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle $
, where J is the ideal generated by arrows.
Definition 2.4. Let D be a Postnikov diagram in the disc. We associate to D an ice quiver
![]() $(Q_D,F_D)$
as follows. The vertices of
$(Q_D,F_D)$
as follows. The vertices of
![]() $Q_D$
are the alternating regions of D, as in Definition 2.1. When the closures of two different alternating regions
$Q_D$
are the alternating regions of D, as in Definition 2.1. When the closures of two different alternating regions
![]() $v_1$
and
$v_1$
and
![]() $v_2$
meet in a crossing point between strands of D, or at one of the boundary marked points, we draw an arrow between
$v_2$
meet in a crossing point between strands of D, or at one of the boundary marked points, we draw an arrow between
![]() $v_1$
and
$v_1$
and
![]() $v_2$
, oriented in a way consistent with these strands, as shown in Figure 1.
$v_2$
, oriented in a way consistent with these strands, as shown in Figure 1.

Figure 1 Arrows associated to strand crossings.
The vertices of
![]() $F_D$
are the boundary regions, and the arrows of
$F_D$
are the boundary regions, and the arrows of
![]() $F_D$
are those corresponding to boundary marked points, as on the right in Figure 1.
$F_D$
are those corresponding to boundary marked points, as on the right in Figure 1.
Each clockwise or anticlockwise region f of D determines a fundamental cycle
![]() $C_f$
in Q, by following the arrows corresponding to the crossing points in the boundary of the region, as shown in Figure 2 for a quadrilateral anticlockwise region.
$C_f$
in Q, by following the arrows corresponding to the crossing points in the boundary of the region, as shown in Figure 2 for a quadrilateral anticlockwise region.

Figure 2 A fundamental cycle around an oriented region.
Thus we may define a potential
 $$\begin{align*}W_D=\sum_{f \text{ anticlockwise}}C_f-\sum_{f \text{ clockwise}}C_f\end{align*}$$
$$\begin{align*}W_D=\sum_{f \text{ anticlockwise}}C_f-\sum_{f \text{ clockwise}}C_f\end{align*}$$
on
![]() $Q_D$
, and we call
$Q_D$
, and we call
![]() $A_D:=\mathcal {J}(Q_D,F_D,W_D)$
the dimer algebra of D.
$A_D:=\mathcal {J}(Q_D,F_D,W_D)$
the dimer algebra of D.
Remark 2.5. While it is straightforward to describe the defining relations of
![]() $A_D$
directly without using a potential (see, e.g., [Reference Çanakçı, King and Pressland11, Def. 2.11]), results on frozen Jacobian algebras will play a crucial role for us in Section 3, making it important that
$A_D$
directly without using a potential (see, e.g., [Reference Çanakçı, King and Pressland11, Def. 2.11]), results on frozen Jacobian algebras will play a crucial role for us in Section 3, making it important that
![]() $A_D$
has this structure.
$A_D$
has this structure.
Proposition 2.6 (compare to [Reference Baur, King and Marsh2, Rem. 3.3])
The quiver
![]() $Q_D$
is strongly connected: that is, any two vertices are connected by a directed path.
$Q_D$
is strongly connected: that is, any two vertices are connected by a directed path.
Proof. Since the regions of D cover the disc, the underlying graph of
![]() $Q_D$
is connected. Moreover, every arrow a of
$Q_D$
is connected. Moreover, every arrow a of
![]() $Q_D$
is contained in at least one fundamental cycle—exactly one if a is frozen, and exactly two otherwise. Thus every arrow has a path from its head to its tail, so
$Q_D$
is contained in at least one fundamental cycle—exactly one if a is frozen, and exactly two otherwise. Thus every arrow has a path from its head to its tail, so
![]() $Q_D$
is even strongly connected.
$Q_D$
is even strongly connected.
Remark 2.7. Having now defined Postnikov diagrams and their associated quivers and algebras more precisely, we may provide a few more details on the relationship to positroid varieties discussed in Section 1.2.
Label the boundary marked points of
![]() $\Sigma $
by
$\Sigma $
by
![]() $\{1,\dotsc ,n\}$
, in the clockwise direction. These labels can be transferred first to the strands, by giving a strand the label of its source, and then to the alternating regions, by applying the label of a strand to every alternating region on its left. By the definition of k, this process labels each alternating region v of D by a k-label
$\{1,\dotsc ,n\}$
, in the clockwise direction. These labels can be transferred first to the strands, by giving a strand the label of its source, and then to the alternating regions, by applying the label of a strand to every alternating region on its left. By the definition of k, this process labels each alternating region v of D by a k-label
![]() $I_v\in \binom {[n]}{k}$
, and it turns out [Reference Oh, Postnikov and Speyer39, Thm. 6.6] that the collection
$I_v\in \binom {[n]}{k}$
, and it turns out [Reference Oh, Postnikov and Speyer39, Thm. 6.6] that the collection
![]() $\mathcal {C}_D$
of these labels is a maximal weakly separated collection in the positroid
$\mathcal {C}_D$
of these labels is a maximal weakly separated collection in the positroid
![]() $\mathcal {P}_D$
. We note here that
$\mathcal {P}_D$
. We note here that
![]() $\mathcal {P}_D=\binom {[n]}{k}$
(i.e.
$\mathcal {P}_D=\binom {[n]}{k}$
(i.e.
![]() $\mathcal {P}_D$
is the uniform positroid) if and only if D is a
$\mathcal {P}_D$
is the uniform positroid) if and only if D is a
![]() $(k,n)$
-diagram.
$(k,n)$
-diagram.
The cluster algebra
![]() $\mathscr {A}_{D}$
has initial cluster variables
$\mathscr {A}_{D}$
has initial cluster variables
![]() $x_v$
indexed by the vertices of
$x_v$
indexed by the vertices of
![]() $Q_D$
. By construction, these vertices are the alternating regions of
$Q_D$
. By construction, these vertices are the alternating regions of
![]() $D$
, so each v has an attached k-label
$D$
, so each v has an attached k-label
![]() $I_v\in \binom {[n]}{k}$
and Plücker coordinate
$I_v\in \binom {[n]}{k}$
and Plücker coordinate
![]() $\Delta _{I_v}$
. The assignment
$\Delta _{I_v}$
. The assignment
![]() $x_v\mapsto \Delta _{I_v}$
induces Galashin and Lam’s isomorphism
$x_v\mapsto \Delta _{I_v}$
induces Galashin and Lam’s isomorphism
![]() $\mathscr {A}_{D}\to \mathbb {C}[\widehat {\Pi }^\circ (\mathcal {P}_D)]$
[Reference Galashin and Lam18]. (Strictly speaking, Galashin and Lam use the complementary set of
$\mathscr {A}_{D}\to \mathbb {C}[\widehat {\Pi }^\circ (\mathcal {P}_D)]$
[Reference Galashin and Lam18]. (Strictly speaking, Galashin and Lam use the complementary set of
![]() $(n-k)$
-labels obtained by labelling regions to the right of each strand, so they put a cluster structure on the coordinate ring of an isomorphic positroid variety in
$(n-k)$
-labels obtained by labelling regions to the right of each strand, so they put a cluster structure on the coordinate ring of an isomorphic positroid variety in
![]() $\mathrm {Gr}_{n-k}^{n}$
. Our isomorphism is obtained from theirs using the natural isomorphism
$\mathrm {Gr}_{n-k}^{n}$
. Our isomorphism is obtained from theirs using the natural isomorphism
![]() $\mathbb {C}[\mathrm {Gr}_{n-k}^{n}]\stackrel {\sim }{\to }\mathbb {C}[\mathrm {Gr}_{k}^{n}]$
with
$\mathbb {C}[\mathrm {Gr}_{n-k}^{n}]\stackrel {\sim }{\to }\mathbb {C}[\mathrm {Gr}_{k}^{n}]$
with
![]() $\Delta _{I}\mapsto \Delta _{I^c}$
.)
$\Delta _{I}\mapsto \Delta _{I^c}$
.)
We note that we could have obtained a different set of k-labels, and hence a different specialisation map
![]() $\mathscr {A}_{D}\to \mathbb {C}(\widehat {\Pi }^\circ (\mathcal {P}_D))$
, by instead giving the strands of D the labels of their targets. This can produce a different cluster algebra structure (in the sense that different functions are cluster variables) on
$\mathscr {A}_{D}\to \mathbb {C}(\widehat {\Pi }^\circ (\mathcal {P}_D))$
, by instead giving the strands of D the labels of their targets. This can produce a different cluster algebra structure (in the sense that different functions are cluster variables) on
![]() $\mathbb {C}[\widehat {\Pi }^\circ (\mathcal {P}_D)]$
, isomorphic to the same abstract cluster algebra
$\mathbb {C}[\widehat {\Pi }^\circ (\mathcal {P}_D)]$
, isomorphic to the same abstract cluster algebra
![]() $\mathscr {A}_{D}$
. While this paper is mostly concerned with categorifying
$\mathscr {A}_{D}$
. While this paper is mostly concerned with categorifying
![]() $\mathscr {A}_{D}$
, and so is insensitive to such labelling conventions, they will reappear in Section 7 when we use results of the author with Çanakçı and King [Reference Çanakçı, King and Pressland11] to relate our categories more directly with the coordinate rings
$\mathscr {A}_{D}$
, and so is insensitive to such labelling conventions, they will reappear in Section 7 when we use results of the author with Çanakçı and King [Reference Çanakçı, King and Pressland11] to relate our categories more directly with the coordinate rings
![]() $\mathbb {C}[\widehat {\Pi }^\circ (\mathcal {P}_D)]$
. In particular, it will turn out to be the source labelling convention that is most compatible with our categorification and its relationship to Jensen–King–Su’s Grassmannian cluster category
$\mathbb {C}[\widehat {\Pi }^\circ (\mathcal {P}_D)]$
. In particular, it will turn out to be the source labelling convention that is most compatible with our categorification and its relationship to Jensen–King–Su’s Grassmannian cluster category
![]() $\operatorname {\mathrm {CM}}(C)$
[Reference Jensen, King and Su28].
$\operatorname {\mathrm {CM}}(C)$
[Reference Jensen, King and Su28].
Remark 2.8. Given a Postnikov diagram D in the disc
![]() $\Sigma $
, we can construct from D a bipartite graph G as follows. The vertices of G are given by the anticlockwise and clockwise regions of D, and two such vertices are connected by an edge if the the closures of the regions meet at a crossing of strands in the interior of
$\Sigma $
, we can construct from D a bipartite graph G as follows. The vertices of G are given by the anticlockwise and clockwise regions of D, and two such vertices are connected by an edge if the the closures of the regions meet at a crossing of strands in the interior of
![]() $\Sigma $
. The graph G is connected if and only if D is connected. Adding to G the data of half-edges, which connect the vertex corresponding to a region to any boundary marked points in its closure, we obtain a dimer model in
$\Sigma $
. The graph G is connected if and only if D is connected. Adding to G the data of half-edges, which connect the vertex corresponding to a region to any boundary marked points in its closure, we obtain a dimer model in
![]() $\Sigma $
in the sense of [Reference Pressland44, Ex. 2.5]. This construction appears in [Reference Postnikov41, §14], where the dimer model is called a plabic graph. The dimer algebra
$\Sigma $
in the sense of [Reference Pressland44, Ex. 2.5]. This construction appears in [Reference Postnikov41, §14], where the dimer model is called a plabic graph. The dimer algebra
![]() $A_D$
is precisely the dimer algebra of
$A_D$
is precisely the dimer algebra of
![]() $(\Sigma ,G)$
, as defined in [Reference Pressland44, Ex. 2.12]. An example of a Postnikov diagram, its corresponding dimer model and the ice quiver of its dimer algebra is shown in Figure 3.
$(\Sigma ,G)$
, as defined in [Reference Pressland44, Ex. 2.12]. An example of a Postnikov diagram, its corresponding dimer model and the ice quiver of its dimer algebra is shown in Figure 3.

Figure 3 A Postnikov diagram (left), its corresponding dimer model (centre) and the ice quiver of its dimer algebra (right). The frozen vertices of this ice quiver are shown as white diamonds, and the frozen arrows are drawn in bold.

Figure 4 Twisting (right-to-left) and untwisting (left-to-right) moves for a Postnikov diagram, in the interior (above) and at the boundary (below). The reflections of these figures in a horizontal line also show twisting and untwisting moves.
Given the data of a dimer model G in the disc, or indeed in any oriented surface
![]() $\Sigma $
with or without boundary, it is always possible to produce a collection of strands, dividing
$\Sigma $
with or without boundary, it is always possible to produce a collection of strands, dividing
![]() $\Sigma $
into alternating, clockwise and anticlockwise regions, from which G may be recovered by the above rules. These strands are usually called the zig-zag paths or flows of G [Reference Broomhead3, §3.3]. Note that in general these strands can either travel between points on the boundary of
$\Sigma $
into alternating, clockwise and anticlockwise regions, from which G may be recovered by the above rules. These strands are usually called the zig-zag paths or flows of G [Reference Broomhead3, §3.3]. Note that in general these strands can either travel between points on the boundary of
![]() $\Sigma $
, as in Definition 2.1, or be closed curves in the interior. In the case that
$\Sigma $
, as in Definition 2.1, or be closed curves in the interior. In the case that
![]() $\Sigma $
is a disc, these strands will always satisfy conditions (P0)–(P2) from Definition 2.1. Requiring that they also satisfy (P3) and (P4)—which in particular rules out any closed curves in the interior—places an extra condition on the dimer model G, the analogue of Broomhead’s geometric consistency [Reference Broomhead3, Prop. 3.12]. Since these conditions, particularly (P4), will be important for us, we prefer to start from the data of a Postnikov diagram.
$\Sigma $
is a disc, these strands will always satisfy conditions (P0)–(P2) from Definition 2.1. Requiring that they also satisfy (P3) and (P4)—which in particular rules out any closed curves in the interior—places an extra condition on the dimer model G, the analogue of Broomhead’s geometric consistency [Reference Broomhead3, Prop. 3.12]. Since these conditions, particularly (P4), will be important for us, we prefer to start from the data of a Postnikov diagram.
Postnikov diagrams are typically considered up to isotopy fixing the boundary, which does not affect the construction of the dimer algebra at all, and certain twisting and untwisting moves shown in Figure 4. These moves do affect the construction of the dimer algebra, in the sense that two Postnikov diagrams related by such a move determine different ice quivers with potential, as shown in Figure 5 (compare to [Reference Pressland44, Ex. 4.5]). However, the frozen Jacobian algebras of these two quivers with potential—that is, the dimer algebras of the two Postnikov diagrams—are isomorphic in a natural way. These moves also do not affect the k-labels attached to the quiver vertices.

Figure 5 The effect on the quiver of applying a twisting or untwisting move in the interior (left) or at the boundary (right). Bold arrows are frozen.
Proposition 2.9 (compare to [Reference Baur, King and Marsh2, Lem. 12.1])
Let D and
![]() $D'$
be Postnikov diagrams such that
$D'$
be Postnikov diagrams such that
![]() $D'$
is obtained from D via an untwisting move. Then the dimer algebras
$D'$
is obtained from D via an untwisting move. Then the dimer algebras
![]() $A_D$
and
$A_D$
and
![]() $A_{D'}$
are isomorphic.
$A_{D'}$
are isomorphic.
Proof. First we consider the case that the untwisting move happens in the interior, as in the upper part of Figure 4. Then
![]() $Q_{D'}$
is obtained from
$Q_{D'}$
is obtained from
![]() $Q_D$
by removing two arrows a and b, which form a fundamental cycle, as in the left-hand side of Figure 5. Since these arrows are unfrozen, they are each contained in a second fundamental cycle, and we write these cycles as
$Q_D$
by removing two arrows a and b, which form a fundamental cycle, as in the left-hand side of Figure 5. Since these arrows are unfrozen, they are each contained in a second fundamental cycle, and we write these cycles as
![]() $ap$
and
$ap$
and
![]() $bq$
for some paths p and q, respectively. Since these paths do not contain the arrows a or b, they are also paths in
$bq$
for some paths p and q, respectively. Since these paths do not contain the arrows a or b, they are also paths in
![]() $Q_{D'}$
. Moreover, the relation
$Q_{D'}$
. Moreover, the relation
![]() $\partial _{a}{W_D}=0$
implies that
$\partial _{a}{W_D}=0$
implies that
![]() $b=p$
in
$b=p$
in
![]() $A_D$
, and the relation
$A_D$
, and the relation
![]() $\partial _{b}{W_D}=0$
that
$\partial _{b}{W_D}=0$
that
![]() $a=q$
in
$a=q$
in
![]() $A_D$
. Define a map
$A_D$
. Define a map
![]() $\varphi \colon \mathbb {K}\langle \hspace {-0.1em}\langle Q_D\rangle \hspace {-0.1em}\rangle \to \mathbb {K}\langle \hspace {-0.1em}\langle Q_{D'}\rangle \hspace {-0.1em}\rangle $
, fixing all vertex idempotents (the two quivers having the same vertex set) and all arrows different from a and b, and with
$\varphi \colon \mathbb {K}\langle \hspace {-0.1em}\langle Q_D\rangle \hspace {-0.1em}\rangle \to \mathbb {K}\langle \hspace {-0.1em}\langle Q_{D'}\rangle \hspace {-0.1em}\rangle $
, fixing all vertex idempotents (the two quivers having the same vertex set) and all arrows different from a and b, and with
![]() $\varphi (a)=q$
and
$\varphi (a)=q$
and
![]() $\varphi (b)=p$
. This map induces a homomorphism
$\varphi (b)=p$
. This map induces a homomorphism
![]() $A_D\to A_{D'}$
inverse to that induced by the map
$A_D\to A_{D'}$
inverse to that induced by the map
![]() $\mathbb {K}\langle \hspace {-0.1em}\langle Q_{D'}\rangle \hspace {-0.1em}\rangle \to \mathbb {K}\langle \hspace {-0.1em}\langle Q_D\rangle \hspace {-0.1em}\rangle $
arising from the inclusion map between arrow sets.
$\mathbb {K}\langle \hspace {-0.1em}\langle Q_{D'}\rangle \hspace {-0.1em}\rangle \to \mathbb {K}\langle \hspace {-0.1em}\langle Q_D\rangle \hspace {-0.1em}\rangle $
arising from the inclusion map between arrow sets.
On the other hand, if the untwisting move takes place at the boundary, then
![]() $Q_{D'}$
is obtained from
$Q_{D'}$
is obtained from
![]() $Q_D$
by removing a frozen arrow a lying in a fundamental
$Q_D$
by removing a frozen arrow a lying in a fundamental
![]() $2$
-cycle, and
$2$
-cycle, and
![]() $F_{D'}$
is obtained from
$F_{D'}$
is obtained from
![]() $F_D$
by replacing a by the other arrow b in this
$F_D$
by replacing a by the other arrow b in this
![]() $2$
-cycle. As before, since b is unfrozen it lies in a second fundamental cycle
$2$
-cycle. As before, since b is unfrozen it lies in a second fundamental cycle
![]() $bq$
for some path q not involving a, and it follows from the relation
$bq$
for some path q not involving a, and it follows from the relation
![]() $\partial _{b}{W_D}=0$
that
$\partial _{b}{W_D}=0$
that
![]() $a=q$
in
$a=q$
in
![]() $A_D$
. Thus defining
$A_D$
. Thus defining
![]() $\varphi $
as in the first case except for
$\varphi $
as in the first case except for
![]() $\varphi (b)=b$
provides an isomorphism of dimer algebras in an analogous way.
$\varphi (b)=b$
provides an isomorphism of dimer algebras in an analogous way.
We call a Postnikov diagram reduced if no untwisting moves can be applied to it; any Postnikov diagram D is equivalent under untwisting moves to a reduced diagram
![]() $D'$
, unique up to isotopy fixing the boundary. The reader is warned that this does not correspond to Postnikov’s definition of reducedness for plabic graphs [Reference Postnikov41, §12] but rather is compatible with terminology for quivers with potential: the ice quiver with potential
$D'$
, unique up to isotopy fixing the boundary. The reader is warned that this does not correspond to Postnikov’s definition of reducedness for plabic graphs [Reference Postnikov41, §12] but rather is compatible with terminology for quivers with potential: the ice quiver with potential
![]() $(Q_{D'},F_{D'},W_{D'})$
is the reduction of
$(Q_{D'},F_{D'},W_{D'})$
is the reduction of
![]() $(Q_D,F_D,W_D)$
, in the sense of [Reference Pressland44, §3]. Indeed, the above isomorphisms of dimer algebras in the proof of Proposition 2.9 are local versions of the reduction isomorphism given at the end of the proof of [Reference Pressland44, Thm. 3.6].
$(Q_D,F_D,W_D)$
, in the sense of [Reference Pressland44, §3]. Indeed, the above isomorphisms of dimer algebras in the proof of Proposition 2.9 are local versions of the reduction isomorphism given at the end of the proof of [Reference Pressland44, Thm. 3.6].
Proposition 2.10. If D is reduced, the quiver
![]() $Q_D$
has no
$Q_D$
has no
![]() $2$
-cycles.
$2$
-cycles.
Proof. A
![]() $2$
-cycle in
$2$
-cycle in
![]() $Q_D$
containing at least one unfrozen arrow corresponds to a possible untwisting move (see Figures 4 and 5) and so does not occur when D is reduced. A
$Q_D$
containing at least one unfrozen arrow corresponds to a possible untwisting move (see Figures 4 and 5) and so does not occur when D is reduced. A
![]() $2$
-cycle consisting only of frozen arrows would correspond to a pair of boundary regions meeting at two points on the boundary of the disc, which must then be the only boundary regions. But D has at least
$2$
-cycle consisting only of frozen arrows would correspond to a pair of boundary regions meeting at two points on the boundary of the disc, which must then be the only boundary regions. But D has at least
![]() $3$
boundary regions, so this is also impossible.
$3$
boundary regions, so this is also impossible.
Before moving on to the homological part of the paper, we discuss one additional feature of the dimer algebra
![]() $A_D$
of a connected Postnikov diagram D. For each vertex v of
$A_D$
of a connected Postnikov diagram D. For each vertex v of
![]() $Q_D$
, choose a path
$Q_D$
, choose a path
![]() $t_v\colon v\to v$
representing a fundamental cycle. Writing
$t_v\colon v\to v$
representing a fundamental cycle. Writing
![]() $t=\sum _{v\in Q_0}t_v\in A_D$
, it follows from connectedness of D that t does not depend on the choices of paths
$t=\sum _{v\in Q_0}t_v\in A_D$
, it follows from connectedness of D that t does not depend on the choices of paths
![]() $t_v$
. Moreover, t is a central element of the algebra. Thus
$t_v$
. Moreover, t is a central element of the algebra. Thus
![]() $A_D$
has the structure of an algebra over
$A_D$
has the structure of an algebra over
![]() $Z=\mathbb {K}[\hspace {-0.1em}[t]\hspace {-0.1em}]$
; the abuse of notation in identifying the abstract generator of Z with the element
$Z=\mathbb {K}[\hspace {-0.1em}[t]\hspace {-0.1em}]$
; the abuse of notation in identifying the abstract generator of Z with the element
![]() $t\in A_D$
, thus making the Z-action clear, is justified by the following result, which is also fundamental to the arguments in Section 3. The proof is close to that of Baur–King–Marsh [Reference Baur, King and Marsh2] for the case that D is a
$t\in A_D$
, thus making the Z-action clear, is justified by the following result, which is also fundamental to the arguments in Section 3. The proof is close to that of Baur–King–Marsh [Reference Baur, King and Marsh2] for the case that D is a
![]() $(k,n)$
-diagram, and we refer to their paper when the arguments apply without change to our more general setting.
$(k,n)$
-diagram, and we refer to their paper when the arguments apply without change to our more general setting.
Proposition 2.11. The dimer algebra
![]() $A_D$
of a connected Postnikov diagram D is thin, meaning that for any vertices v and w, there is some
$A_D$
of a connected Postnikov diagram D is thin, meaning that for any vertices v and w, there is some
![]() $p\in e_{w}A_De_{v}$
such that
$p\in e_{w}A_De_{v}$
such that
and moreover that
![]() $Zp$
is a free Z-module of rank
$Zp$
is a free Z-module of rank
![]() $1$
. Moreover, there is a unique such p expressible as the image of a path from v to w under the projection
$1$
. Moreover, there is a unique such p expressible as the image of a path from v to w under the projection
![]() $\mathbb {K}\langle \hspace {-0.1em}\langle Q_D\rangle \hspace {-0.1em}\rangle \to A_D$
.
$\mathbb {K}\langle \hspace {-0.1em}\langle Q_D\rangle \hspace {-0.1em}\rangle \to A_D$
.
Proof. As in [Reference Baur, King and Marsh2, §4], we may weight the arrows of
![]() $Q=Q_D$
by elements of the set
$Q=Q_D$
by elements of the set
![]() $\left \{1,\dotsc ,n\right \}$
, labelling the boundary marked points of
$\left \{1,\dotsc ,n\right \}$
, labelling the boundary marked points of
![]() $\Sigma $
. An arrow a of Q is crossed by two strands of D, say that starting at marked point i from right to left and that starting at j from left to right. We then weight a by the (indicator function of) the cyclic interval
$\Sigma $
. An arrow a of Q is crossed by two strands of D, say that starting at marked point i from right to left and that starting at j from left to right. We then weight a by the (indicator function of) the cyclic interval
![]() $[i,j-1]$
(compare to [Reference Baur, King and Marsh2, Defn. 4.1]). A path in Q is weighted by the sum
$[i,j-1]$
(compare to [Reference Baur, King and Marsh2, Defn. 4.1]). A path in Q is weighted by the sum
![]() $\mathrm {wt}_p$
of weights of its arrows, and its total weight is defined to be
$\mathrm {wt}_p$
of weights of its arrows, and its total weight is defined to be
![]() $\sum _{i=1}^n\mathrm {wt}_p(i)$
, which is always at least
$\sum _{i=1}^n\mathrm {wt}_p(i)$
, which is always at least
![]() $1$
if the path has nonzero length.
$1$
if the path has nonzero length.
The proof of [Reference Baur, King and Marsh2, Cor. 4.4], stated for
![]() $(k,n)$
-Postnikov diagrams, remains valid in our more general setting to show that every fundamental cycle has constant weight
$(k,n)$
-Postnikov diagrams, remains valid in our more general setting to show that every fundamental cycle has constant weight
![]() $w(i)=1$
for all
$w(i)=1$
for all
![]() $1\leq i\leq n$
. If
$1\leq i\leq n$
. If
![]() $p_+=p_-$
is one of the defining relations of
$p_+=p_-$
is one of the defining relations of
![]() $A_D$
, then there is an arrow
$A_D$
, then there is an arrow
![]() $a\in Q_1$
such that both
$a\in Q_1$
such that both
![]() $a p_+$
and
$a p_+$
and
![]() $a p_-$
are fundamental cycles, from which it follows that the weights of
$a p_-$
are fundamental cycles, from which it follows that the weights of
![]() $p_+$
and
$p_+$
and
![]() $p_-$
agree. It follows that the weight, and hence the total weight, descends to a grading of A.
$p_-$
agree. It follows that the weight, and hence the total weight, descends to a grading of A.
Now let
![]() $v,w\in Q_0$
. Since Q is strongly connected as in Proposition 2.6, there is some path from v to w in Q, and we choose p to be such a path with minimal total weight. If q is any other path from v to w, then [Reference Baur, King and Marsh2, Prop. 9.3] applies to show that there is a path
$v,w\in Q_0$
. Since Q is strongly connected as in Proposition 2.6, there is some path from v to w in Q, and we choose p to be such a path with minimal total weight. If q is any other path from v to w, then [Reference Baur, King and Marsh2, Prop. 9.3] applies to show that there is a path
![]() $r\colon v\to w$
and nonnegative integers
$r\colon v\to w$
and nonnegative integers
![]() $N_p$
and
$N_p$
and
![]() $N_q$
such that
$N_q$
such that
in
![]() $A_D$
. As before, this proposition is stated only in the case that D is a
$A_D$
. As before, this proposition is stated only in the case that D is a
![]() $(k,n)$
-Postnikov diagram, but its proof is still valid under our weaker assumptions—the key property of D here is (P4).
$(k,n)$
-Postnikov diagram, but its proof is still valid under our weaker assumptions—the key property of D here is (P4).
Since the total weight of t is nonzero, and p has minimal total weight among paths from v to w, we must have
![]() $N_p=0$
and
$N_p=0$
and
![]() $p=r$
in
$p=r$
in
![]() $A_D$
. Thus
$A_D$
. Thus
![]() $q=t^{N_q}p$
, and we see that
$q=t^{N_q}p$
, and we see that
![]() $e_wAe_v$
is generated over Z by p. It is moreover freely generated since each element of
$e_wAe_v$
is generated over Z by p. It is moreover freely generated since each element of
![]() $\{t^Np:N\geq 0\}$
has a different total weight, which implies that these elements are linearly independent in
$\{t^Np:N\geq 0\}$
has a different total weight, which implies that these elements are linearly independent in
![]() $A_D$
.
$A_D$
.
Definition 2.12. We call a path
![]() $p\colon v\to w$
in
$p\colon v\to w$
in
![]() $Q_D$
a minimal path if
$Q_D$
a minimal path if
![]() $e_{w}A_De_{v}=Zp$
. Proposition 2.11 then states that there is a minimal path between any pair of vertices in
$e_{w}A_De_{v}=Zp$
. Proposition 2.11 then states that there is a minimal path between any pair of vertices in
![]() $Q_D$
and that any two such paths define the same element of
$Q_D$
and that any two such paths define the same element of
![]() $A_D$
. We write
$A_D$
. We write
![]() $p_{wv}$
for the class in
$p_{wv}$
for the class in
![]() $A_D$
of any minimal path from v to w.
$A_D$
of any minimal path from v to w.
Thinness of
![]() $A_D$
, as in Proposition 2.11, is the analogue of algebraic consistency for dimer models on the torus, as described by Broomhead [Reference Broomhead3, Def. 5.12] (the analogue of geometric consistency, compare to [Reference Broomhead3, Prop. 3.12], being conditions (P3) and (P4) in the definition of a Postnikov diagram). The following observation about minimal paths is straightforward but useful.
$A_D$
, as in Proposition 2.11, is the analogue of algebraic consistency for dimer models on the torus, as described by Broomhead [Reference Broomhead3, Def. 5.12] (the analogue of geometric consistency, compare to [Reference Broomhead3, Prop. 3.12], being conditions (P3) and (P4) in the definition of a Postnikov diagram). The following observation about minimal paths is straightforward but useful.
Lemma 2.13. Let D be a connected Postnikov diagram, and let
![]() $p\colon u\to v$
and
$p\colon u\to v$
and
![]() $q\colon v\to w$
be paths in
$q\colon v\to w$
be paths in
![]() $Q_D$
. If the composition
$Q_D$
. If the composition
![]() $qp$
is a minimal path, then both p and q are minimal paths.
$qp$
is a minimal path, then both p and q are minimal paths.
Proof. By Proposition 2.11, there are
![]() $m,n\geq 0$
such that
$m,n\geq 0$
such that
![]() $p=t^mp_{vu}$
and
$p=t^mp_{vu}$
and
![]() $q=t^np_{wv}$
in
$q=t^np_{wv}$
in
![]() $A_D$
. Thus
$A_D$
. Thus
![]() $qp=t^{m+n}p_{wv}p_{vu}=t^{m+n+\delta }p_{wu}$
for some
$qp=t^{m+n}p_{wv}p_{vu}=t^{m+n+\delta }p_{wu}$
for some
![]() $\delta \geq 0$
. But
$\delta \geq 0$
. But
![]() $qp$
is minimal, so by Proposition 2.11 again we must have
$qp$
is minimal, so by Proposition 2.11 again we must have
![]() $m+n+\delta =0$
, and so in particular
$m+n+\delta =0$
, and so in particular
![]() $m=n=0$
. Hence both p and q are minimal paths.
$m=n=0$
. Hence both p and q are minimal paths.
3 The Calabi–Yau property
Let
![]() $A=A_D$
be the dimer algebra of a connected Postnikov diagram D. In this section, we show that this algebra is bimodule internally
$A=A_D$
be the dimer algebra of a connected Postnikov diagram D. In this section, we show that this algebra is bimodule internally
![]() $3$
-Calabi–Yau, in the sense of [Reference Pressland43], with respect to the idempotent corresponding to the boundary regions of D, thus proving Theorem 2. Since A is presented as a frozen Jacobian algebra, we will prove this statement via [Reference Pressland43, Thm. 5.6], which tells us that it is enough to check the exactness of a certain complex of A-bimodules.
$3$
-Calabi–Yau, in the sense of [Reference Pressland43], with respect to the idempotent corresponding to the boundary regions of D, thus proving Theorem 2. Since A is presented as a frozen Jacobian algebra, we will prove this statement via [Reference Pressland43, Thm. 5.6], which tells us that it is enough to check the exactness of a certain complex of A-bimodules.
Throughout the proof, we will write
for the set of arrows with head, respectively tail, at
![]() $v\in Q_0$
, and
$v\in Q_0$
, and
for their intersections with the set
![]() $Q_1^{\mathrm {m}}$
of unfrozen arrows.
$Q_1^{\mathrm {m}}$
of unfrozen arrows.
As well as using the fact that A is thin, as in Proposition 2.11, we will also rely on the following gradability property of A, which allows us to deduce exactness of the relevant complex of bimodules from the exactness of certain complexes of (one-sided) A-modules.
Proposition 3.1. The dimer algebra
![]() $A_D$
of a connected Postnikov diagram D admits a grading in which all arrows have positive degrees.
$A_D$
of a connected Postnikov diagram D admits a grading in which all arrows have positive degrees.
Proof. The algebra
![]() $A_D$
may be graded by total weights of paths, as discussed in the proof of Proposition 2.11. As already mentioned in that proof, each arrow has positive total weight.
$A_D$
may be graded by total weights of paths, as discussed in the proof of Proposition 2.11. As already mentioned in that proof, each arrow has positive total weight.
Most of the arguments in this section will depend on the fact that A is thin, as in Proposition 2.11, so that each piece
![]() $e_{w}Ae_{v}$
is freely generated over
$e_{w}Ae_{v}$
is freely generated over
![]() $Z=\mathbb {K}[\hspace {-0.1em}[t]\hspace {-0.1em}]$
by a minimal path. Before introducing the complexes of A-modules whose exactness implies the required
$Z=\mathbb {K}[\hspace {-0.1em}[t]\hspace {-0.1em}]$
by a minimal path. Before introducing the complexes of A-modules whose exactness implies the required
![]() $3$
-Calabi–Yau property of A, we give one more lemma concerning these paths.
$3$
-Calabi–Yau property of A, we give one more lemma concerning these paths.
Lemma 3.2. Let
![]() $v,w\in Q_0$
with v mutable, and consider a minimal path
$v,w\in Q_0$
with v mutable, and consider a minimal path
![]() $p_{wv}\colon v\to w$
. Then there is some
$p_{wv}\colon v\to w$
. Then there is some
![]() $a\in \mathrm {H}_{v}$
such that
$a\in \mathrm {H}_{v}$
such that
![]() $p_{wv}a=p_{w,ta}$
in A.
$p_{wv}a=p_{w,ta}$
in A.
Proof. We first observe that if
![]() $p\colon u\to w$
is a minimal path in Q passing through the vertex v, then p includes our desired arrow as follows. Write
$p\colon u\to w$
is a minimal path in Q passing through the vertex v, then p includes our desired arrow as follows. Write
![]() $p=p_2ap_1$
for some
$p=p_2ap_1$
for some
![]() $a\in \mathrm {H}_{v}$
. Then by Lemma 2.13, each subpath of p is also minimal, so in A we have
$a\in \mathrm {H}_{v}$
. Then by Lemma 2.13, each subpath of p is also minimal, so in A we have
![]() $p_2=p_{wv}$
and
$p_2=p_{wv}$
and
![]() $p_2a=p_{w,ta}$
, and hence a is our desired arrow.
$p_2a=p_{w,ta}$
, and hence a is our desired arrow.
Now for each
![]() $a\in \mathrm {H}_{v}$
, choose a minimal path
$a\in \mathrm {H}_{v}$
, choose a minimal path
![]() $m_a\colon ta\to w$
. If any of these paths passes through v, then we find our desired arrow as above, so we assume the contrary. Since v is mutable, each
$m_a\colon ta\to w$
. If any of these paths passes through v, then we find our desired arrow as above, so we assume the contrary. Since v is mutable, each
![]() $b\in \mathrm {T}_{v}$
is involved in two fundamental cycles
$b\in \mathrm {T}_{v}$
is involved in two fundamental cycles
![]() $a_+pb$
and
$a_+pb$
and
![]() $a_-qb$
with
$a_-qb$
with
![]() $a_{\pm }\in \mathrm {H}_{v}$
, and we can write
$a_{\pm }\in \mathrm {H}_{v}$
, and we can write
![]() $p'=m_{a_+}p$
and
$p'=m_{a_+}p$
and
![]() $q'=m_{a_-}q$
. By our assumption on the
$q'=m_{a_-}q$
. By our assumption on the
![]() $m_a$
, neither
$m_a$
, neither
![]() $p'$
nor
$p'$
nor
![]() $q'$
passes through v.
$q'$
passes through v.
Using again that v is mutable, the union of fundamental cycles containing v is a disc with v in the interior, so there must be some b for which the paths
![]() $p'$
and
$p'$
and
![]() $q'$
are two sides of a digon containing v (compare to the argument in [Reference Broomhead3, Lem. 6.17]). From now on, we assume that we are in this situation, shown in Figure 6.
$q'$
are two sides of a digon containing v (compare to the argument in [Reference Broomhead3, Lem. 6.17]). From now on, we assume that we are in this situation, shown in Figure 6.

Figure 6 Fundamental cycles
![]() $a_+pb$
and
$a_+pb$
and
![]() $a_-qb$
together with minimal paths
$a_-qb$
together with minimal paths
![]() $m_{a_{\pm }}\colon ta_{\pm }\to w$
such that
$m_{a_{\pm }}\colon ta_{\pm }\to w$
such that
![]() $p'=m_{a_+}p$
and
$p'=m_{a_+}p$
and
![]() $q'=m_{a_-}q$
form a digon containing v. Solid arrows represent arrows in Q, whereas dashed arrows represent paths.
$q'=m_{a_-}q$
form a digon containing v. Solid arrows represent arrows in Q, whereas dashed arrows represent paths.
Observe that
![]() $p_{wv}a_+=t^{\delta }p_{w,ta_+}$
for some
$p_{wv}a_+=t^{\delta }p_{w,ta_+}$
for some
![]() $\delta \geq 0$
by Proposition 2.11. If
$\delta \geq 0$
by Proposition 2.11. If
![]() $\delta =0$
, then
$\delta =0$
, then
![]() $a_+$
was our desired arrow, so assume
$a_+$
was our desired arrow, so assume
![]() $\delta>0$
. In a similar way, we find
$\delta>0$
. In a similar way, we find
![]() $m,n\geq 0$
such that
$m,n\geq 0$
such that
![]() $p_{w,ta_+}p=t^mp_{w,hb}$
and
$p_{w,ta_+}p=t^mp_{w,hb}$
and
![]() $p_{w,hb}b=t^np_{wv}$
. Since
$p_{w,hb}b=t^np_{wv}$
. Since
![]() $pba_+$
is a fundamental cycle, we must have
$pba_+$
is a fundamental cycle, we must have
By Proposition 2.11 again, we must have
![]() $m+n+\delta =1$
, so we conclude from positivity of
$m+n+\delta =1$
, so we conclude from positivity of
![]() $\delta $
that
$\delta $
that
![]() $m=n=0$
(and
$m=n=0$
(and
![]() $\delta =1$
). In particular, this means
$\delta =1$
). In particular, this means
![]() $p'=m_{a_+}p$
is a minimal path, representing
$p'=m_{a_+}p$
is a minimal path, representing
![]() $p_{w,hb}$
. Repeating the argument with
$p_{w,hb}$
. Repeating the argument with
![]() $a_-$
and q replacing
$a_-$
and q replacing
![]() $a_+$
and p, we see that either
$a_+$
and p, we see that either
![]() $a_-$
is our desired arrow or
$a_-$
is our desired arrow or
![]() $q'=m_{a_-}q$
is also a minimal path representing
$q'=m_{a_-}q$
is also a minimal path representing
![]() $p_{w,hb}$
.
$p_{w,hb}$
.
In the latter case,
![]() $p'$
and
$p'$
and
![]() $q'$
are paths from
$q'$
are paths from
![]() $hb$
to w defining the same element of A, namely
$hb$
to w defining the same element of A, namely
![]() $p_{w,hb}$
, and bounding a digon containing v. It is then a consequence of [Reference Broomhead3, Lem. 6.17] that there is a path
$p_{w,hb}$
, and bounding a digon containing v. It is then a consequence of [Reference Broomhead3, Lem. 6.17] that there is a path
![]() $r\colon hb\to w$
passing through v and also defining
$r\colon hb\to w$
passing through v and also defining
![]() $p_{w,hb}$
in A. In particular, r is a minimal path passing through v, so we may find our desired arrow as in the first paragraph of the proof.
$p_{w,hb}$
in A. In particular, r is a minimal path passing through v, so we may find our desired arrow as in the first paragraph of the proof.
We now turn to the main part of the argument. In [Reference Pressland43, §5], it is explained how an ice quiver with potential
![]() $(Q,F,W)$
determines a complex of projective bimodules for the associated frozen Jacobian algebra
$(Q,F,W)$
determines a complex of projective bimodules for the associated frozen Jacobian algebra
![]() $A=\mathcal {J}(Q,F,W)$
; we will denote this complex by
$A=\mathcal {J}(Q,F,W)$
; we will denote this complex by
![]() $\mathbf {P}(A)$
, although strictly it depends on the presentation of A determined by
$\mathbf {P}(A)$
, although strictly it depends on the presentation of A determined by
![]() $(Q,F,W)$
. For the convenience of the reader, we repeat its definition here, following [Reference Pressland42, §4].
$(Q,F,W)$
. For the convenience of the reader, we repeat its definition here, following [Reference Pressland42, §4].
Let
![]() $S=A/\overline {J}$
, where J is the the ideal generated by arrows. As a left A-module, S is the direct sum of the vertex simple modules and has a basis consisting of the vertex idempotents
$S=A/\overline {J}$
, where J is the the ideal generated by arrows. As a left A-module, S is the direct sum of the vertex simple modules and has a basis consisting of the vertex idempotents
![]() $e_v$
. For the remainder of this section, we write
$e_v$
. For the remainder of this section, we write
![]() $\mathbin {\otimes }=\mathbin {\otimes }_S$
.
$\mathbin {\otimes }=\mathbin {\otimes }_S$
.
Introduce formal symbols
![]() $\rho _a$
for each
$\rho _a$
for each
![]() $a\in Q_1$
and
$a\in Q_1$
and
![]() $\omega _v$
for each
$\omega _v$
for each
![]() $v\in Q_0$
, and define S-bimodule structures on the vector spaces
$v\in Q_0$
, and define S-bimodule structures on the vector spaces
 $$ \begin{align*} \mathbb{K} Q_0&=\bigoplus_{v\in Q_0}\mathbb{K}e_{v},& \mathbb{K} Q_1&=\bigoplus_{a\in Q_1}\mathbb{K} a,& \mathbb{K} Q_2^{\mathrm{m}}&=\bigoplus_{a\in Q_1^{\mathrm{m}}}\mathbb{K}\rho_{a},& \mathbb{K} Q_3^{\mathrm{m}}&=\bigoplus_{v\in Q_0^{\mathrm{m}}}\mathbb{K}\omega_v, \end{align*} $$
$$ \begin{align*} \mathbb{K} Q_0&=\bigoplus_{v\in Q_0}\mathbb{K}e_{v},& \mathbb{K} Q_1&=\bigoplus_{a\in Q_1}\mathbb{K} a,& \mathbb{K} Q_2^{\mathrm{m}}&=\bigoplus_{a\in Q_1^{\mathrm{m}}}\mathbb{K}\rho_{a},& \mathbb{K} Q_3^{\mathrm{m}}&=\bigoplus_{v\in Q_0^{\mathrm{m}}}\mathbb{K}\omega_v, \end{align*} $$
via the formulae
We recall here that
![]() $Q_0^{\mathrm {m}}=Q_0\setminus F_0$
and
$Q_0^{\mathrm {m}}=Q_0\setminus F_0$
and
![]() $Q_1^{\mathrm {m}}=Q_1\setminus F_1$
are the sets of mutable vertices and unfrozen arrows, respectively.
$Q_1^{\mathrm {m}}=Q_1\setminus F_1$
are the sets of mutable vertices and unfrozen arrows, respectively.
Since
![]() $\mathbb {K} Q_0$
is naturally isomorphic to S as a bimodule, there is a natural isomorphism
$\mathbb {K} Q_0$
is naturally isomorphic to S as a bimodule, there is a natural isomorphism
which we can compose with the multiplication map for A to obtain a map
![]() $\mu _0\colon A\mathbin {\otimes }\mathbb {K} Q_0\mathbin {\otimes } A\to A$
. Define
$\mu _0\colon A\mathbin {\otimes }\mathbb {K} Q_0\mathbin {\otimes } A\to A$
. Define
![]() $\mu _1\colon A\mathbin {\otimes }\mathbb {K} Q_1\mathbin {\otimes } A\to A\mathbin {\otimes }\mathbb {K} Q_0\mathbin {\otimes } A$
by
$\mu _1\colon A\mathbin {\otimes }\mathbb {K} Q_1\mathbin {\otimes } A\to A\mathbin {\otimes }\mathbb {K} Q_0\mathbin {\otimes } A$
by
For any path
![]() $p=a_m\dotsm a_1$
in Q, we may define
$p=a_m\dotsm a_1$
in Q, we may define
and extend by linearity and continuity to obtain a map
![]() $\Delta _a\colon \mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle \to A\mathbin {\otimes }\mathbb {K} Q_1\mathbin {\otimes } A$
. We then define
$\Delta _a\colon \mathbb {K}\langle \hspace {-0.1em}\langle Q\rangle \hspace {-0.1em}\rangle \to A\mathbin {\otimes }\mathbb {K} Q_1\mathbin {\otimes } A$
. We then define
![]() $\mu _2\colon A\mathbin {\otimes }\mathbb {K} Q_2^{\mathrm {m}}\mathbin {\otimes } A\to A\mathbin {\otimes } \mathbb {K} Q_1\mathbin {\otimes } A$
by
$\mu _2\colon A\mathbin {\otimes }\mathbb {K} Q_2^{\mathrm {m}}\mathbin {\otimes } A\to A\mathbin {\otimes } \mathbb {K} Q_1\mathbin {\otimes } A$
by
Finally, define
![]() $\mu _3\colon A\mathbin {\otimes } \mathbb {K} Q_3^{\mathrm {m}}\mathbin {\otimes } A\to A\mathbin {\otimes } \mathbb {K} Q_2^{\mathrm {m}}\mathbin {\otimes } A$
by
$\mu _3\colon A\mathbin {\otimes } \mathbb {K} Q_3^{\mathrm {m}}\mathbin {\otimes } A\to A\mathbin {\otimes } \mathbb {K} Q_2^{\mathrm {m}}\mathbin {\otimes } A$
by
As
![]() $\mathrm {T}_{v}\cup \mathrm {H}_{v}\subseteq Q_1^{\mathrm {m}}$
for any
$\mathrm {T}_{v}\cup \mathrm {H}_{v}\subseteq Q_1^{\mathrm {m}}$
for any
![]() $v\in Q_0^{\mathrm {m}}$
, this map has the claimed codomain.
$v\in Q_0^{\mathrm {m}}$
, this map has the claimed codomain.
Definition 3.3. For an ice quiver with potential
![]() $(Q,F,W)$
, with frozen Jacobian algebra
$(Q,F,W)$
, with frozen Jacobian algebra
![]() $A=\mathcal {J}(Q,F,W)$
, let
$A=\mathcal {J}(Q,F,W)$
, let
![]() $\mathbf {P}(A)$
be the complex of A-bimodules with nonzero terms
$\mathbf {P}(A)$
be the complex of A-bimodules with nonzero terms
and
![]() $A\mathbin {\otimes }\mathbb {K} Q_0\mathbin {\otimes } A$
in degree
$A\mathbin {\otimes }\mathbb {K} Q_0\mathbin {\otimes } A$
in degree
![]() $0$
.
$0$
.
Using this complex, we can give a sufficient condition for the frozen Jacobian algebra to be bimodule internally
![]() $3$
-Calabi–Yau [Reference Pressland43, Defn. 2.4] with respect to the idempotent determined by the vertices of F. This condition will suffice as a definition for the purposes of the present paper.
$3$
-Calabi–Yau [Reference Pressland43, Defn. 2.4] with respect to the idempotent determined by the vertices of F. This condition will suffice as a definition for the purposes of the present paper.
Theorem 3.4 [Reference Pressland43, Thm. 5.7]
If A is a frozen Jacobian algebra such that
is exact, then A is bimodule internally
![]() $3$
-Calabi–Yau with respect to the idempotent
$3$
-Calabi–Yau with respect to the idempotent
![]() $e=\sum _{v\in F_0}e_{v}$
.
$e=\sum _{v\in F_0}e_{v}$
.
Remark 3.5. By standard results on presentations of algebras, as in Butler–King [Reference Butler and King9], we need only check exactness at the two left-most nonzero terms of
![]() $\mathbf {P}(A)$
(in degrees
$\mathbf {P}(A)$
(in degrees
![]() $-3$
and
$-3$
and
![]() $-2$
), since the rest of the complex in equation (3.1) is the standard projective bimodule presentation of an algebra defined by a quiver with relations.
$-2$
), since the rest of the complex in equation (3.1) is the standard projective bimodule presentation of an algebra defined by a quiver with relations.
Proposition 3.6. For
![]() $A=A_D$
the dimer algebra of a connected Postnikov diagram, the complex in equation (3.1) is exact in degree d if and only if the complex
$A=A_D$
the dimer algebra of a connected Postnikov diagram, the complex in equation (3.1) is exact in degree d if and only if the complex
is exact in degree d, if and only if the complex
is exact in degree d for any
![]() $v\in Q_0$
, where
$v\in Q_0$
, where
![]() $S_{v}$
denotes the simple left A-module at v.
$S_{v}$
denotes the simple left A-module at v.
Proof. Exactness of equation (3.1) and equation (3.2) are equivalent because of the existence of a grading as in Proposition 3.1, by an argument that is essentially due to Broomhead [Reference Broomhead3, Prop. 7.5]. The reader can find an explanation of how this argument extends to the case of frozen Jacobian algebras in [Reference Pressland42, §4]. The second equivalence is simply the observation that the complex in equation (3.2) is the direct sum of the complexes in equation (3.3).
It will be useful to introduce some notation for elements of terms of
![]() $\mathbf {P}(A)\mathbin {\otimes }_AS_{v}$
, following [Reference Pressland42, §4]. First note that we have isomorphisms
$\mathbf {P}(A)\mathbin {\otimes }_AS_{v}$
, following [Reference Pressland42, §4]. First note that we have isomorphisms
 $$ \begin{align} \begin{split} A\mathbin{\otimes}\mathbb{K} Q_1\mathbin{\otimes} A\mathbin{\otimes}_AS_{v}&\cong\bigoplus_{b\in\mathrm{T}_{v}}Ae_{hb},\\ A\mathbin{\otimes}\mathbb{K} Q_2^{\mathrm{m}}\mathbin{\otimes} A\mathbin{\otimes}_AS_{v}&\cong\bigoplus_{a\in\mathrm{H}_{v}^{\mathrm{m}}}Ae_{ta},\\ A\mathbin{\otimes}\mathbb{K} Q_3^{\mathrm{m}}\mathbin{\otimes} A\mathbin{\otimes}_AS_{v}&\cong{\begin{cases}Ae_{v},&v\in Q_0^{\mathrm{m}},\\0,&v\in F_0.\end{cases}} \end{split} \end{align} $$
$$ \begin{align} \begin{split} A\mathbin{\otimes}\mathbb{K} Q_1\mathbin{\otimes} A\mathbin{\otimes}_AS_{v}&\cong\bigoplus_{b\in\mathrm{T}_{v}}Ae_{hb},\\ A\mathbin{\otimes}\mathbb{K} Q_2^{\mathrm{m}}\mathbin{\otimes} A\mathbin{\otimes}_AS_{v}&\cong\bigoplus_{a\in\mathrm{H}_{v}^{\mathrm{m}}}Ae_{ta},\\ A\mathbin{\otimes}\mathbb{K} Q_3^{\mathrm{m}}\mathbin{\otimes} A\mathbin{\otimes}_AS_{v}&\cong{\begin{cases}Ae_{v},&v\in Q_0^{\mathrm{m}},\\0,&v\in F_0.\end{cases}} \end{split} \end{align} $$
In the first two cases, the right-hand sides are of the form
![]() $\bigoplus _{a\in S}Ae_{\delta a}$
, where S is a set of arrows and
$\bigoplus _{a\in S}Ae_{\delta a}$
, where S is a set of arrows and
![]() $\delta \colon S\to Q_0$
. The map
$\delta \colon S\to Q_0$
. The map
![]() $Ae_{\delta a}\to \bigoplus _{a\in S}Ae_{\delta a}$
including the domain as the summand indexed by a will be denoted by
$Ae_{\delta a}\to \bigoplus _{a\in S}Ae_{\delta a}$
including the domain as the summand indexed by a will be denoted by
![]() $x\mapsto x\otimes [a]$
; this helps us to distinguish these various inclusions when
$x\mapsto x\otimes [a]$
; this helps us to distinguish these various inclusions when
![]() $\delta $
is not injective. As a consequence, a general element of the direct sum is
$\delta $
is not injective. As a consequence, a general element of the direct sum is
with
![]() $x_a\in Ae_{\delta a}$
.
$x_a\in Ae_{\delta a}$
.
The most complicated map in the complex
![]() $\mathbf {P}(A)$
is
$\mathbf {P}(A)$
is
![]() $\mu _2$
, so we will spell out
$\mu _2$
, so we will spell out
![]() $\mu _2\mathbin {\otimes }_AS_{v}$
explicitly. Using the isomorphisms from equation (3.4) and our notation for elements of the direct sums, we have
$\mu _2\mathbin {\otimes }_AS_{v}$
explicitly. Using the isomorphisms from equation (3.4) and our notation for elements of the direct sums, we have
 $$\begin{align*}(\mu_2\mathbin{\otimes}_AS_{v})(x)=\sum_{b\in\mathrm{T}_{v}}\bigg(\sum_{a\in\mathrm{H}_{v}^{\mathrm{m}}}x_a\partial^r_{b}{\partial_{a}{W}}\bigg)\mathbin{\otimes}[b],\end{align*}$$
$$\begin{align*}(\mu_2\mathbin{\otimes}_AS_{v})(x)=\sum_{b\in\mathrm{T}_{v}}\bigg(\sum_{a\in\mathrm{H}_{v}^{\mathrm{m}}}x_a\partial^r_{b}{\partial_{a}{W}}\bigg)\mathbin{\otimes}[b],\end{align*}$$
where
![]() $\partial ^r_{b}$
, called the right derivative with respect to b, is defined on paths by
$\partial ^r_{b}$
, called the right derivative with respect to b, is defined on paths by
 $$ \begin{align} \partial^r_{b}(a_k\dotsm a_1)=\begin{cases}a_k\dotsm a_2,&a_1=b,\\0,&a_1\ne b\end{cases} \end{align} $$
$$ \begin{align} \partial^r_{b}(a_k\dotsm a_1)=\begin{cases}a_k\dotsm a_2,&a_1=b,\\0,&a_1\ne b\end{cases} \end{align} $$
and extended linearly and continuously. Similarly, there is a left derivative, defined on paths by
 $$ \begin{align} \partial^l_{b}(a_k\dotsm a_1)=\begin{cases}a_{k-1}\dotsm a_1,&a_k=b,\\0,&a_k\ne b.\end{cases} \end{align} $$
$$ \begin{align} \partial^l_{b}(a_k\dotsm a_1)=\begin{cases}a_{k-1}\dotsm a_1,&a_k=b,\\0,&a_k\ne b.\end{cases} \end{align} $$
Given a Postnikov diagram D and two arrows a and b of
![]() $Q_D$
, we may observe that
$Q_D$
, we may observe that
Indeed, there are at most two fundamental cycles in
![]() $Q_D$
containing a, so the part of W consisting of terms containing both a and b is of the form
$Q_D$
containing a, so the part of W consisting of terms containing both a and b is of the form
![]() $apb-aqb$
for some p and q, which are either paths, not containing the arrows a or b, or are zero. Thus one can directly calculate each side of equation (3.8), which both result in
$apb-aqb$
for some p and q, which are either paths, not containing the arrows a or b, or are zero. Thus one can directly calculate each side of equation (3.8), which both result in
![]() $p-q$
.
$p-q$
.
We are now ready to prove our main theorem.
Theorem 3.7. For
![]() $A=A_D$
the dimer algebra of a connected Postnikov diagram D, the complex in equation (3.1) is exact, and hence A is bimodule internally
$A=A_D$
the dimer algebra of a connected Postnikov diagram D, the complex in equation (3.1) is exact, and hence A is bimodule internally
![]() $3$
-Calabi–Yau with respect to the idempotent determined by the boundary vertices.
$3$
-Calabi–Yau with respect to the idempotent determined by the boundary vertices.
Proof. As already noted in Remark 3.5, the complex in equation (3.1) can only fail to be exact in degrees
![]() $-2$
and
$-2$
and
![]() $-3$
, so, by Proposition 3.6, we need only check that the complex in equation (3.3) is exact at the terms
$-3$
, so, by Proposition 3.6, we need only check that the complex in equation (3.3) is exact at the terms
![]() $A\mathbin {\otimes }\mathbb {K} Q_3^{\mathrm {m}}\mathbin {\otimes }S_{v}$
and
$A\mathbin {\otimes }\mathbb {K} Q_3^{\mathrm {m}}\mathbin {\otimes }S_{v}$
and
![]() $A\mathbin {\otimes }\mathbb {K} Q_2^{\mathrm {m}}\mathbin {\otimes }S_{v}$
for each
$A\mathbin {\otimes }\mathbb {K} Q_2^{\mathrm {m}}\mathbin {\otimes }S_{v}$
for each
![]() $v\in Q_0$
.
$v\in Q_0$
.
We first deal with exactness at
![]() $A\mathbin {\otimes }\mathbb {K} Q_3^{\mathrm {m}}\mathbin {\otimes }S_{v}$
. This term is zero unless
$A\mathbin {\otimes }\mathbb {K} Q_3^{\mathrm {m}}\mathbin {\otimes }S_{v}$
. This term is zero unless
![]() $v\in Q_0^{\mathrm {m}}$
, so we may additionally assume this. By the third isomorphism in equation (3.4), we then have
$v\in Q_0^{\mathrm {m}}$
, so we may additionally assume this. By the third isomorphism in equation (3.4), we then have
![]() $A\mathbin {\otimes }\mathbb {K} Q_3^{\mathrm {m}}\mathbin {\otimes }S_{v}\cong Ae_{v}$
, so let
$A\mathbin {\otimes }\mathbb {K} Q_3^{\mathrm {m}}\mathbin {\otimes }S_{v}\cong Ae_{v}$
, so let
![]() $x\in Ae_{v}$
. We calculate
$x\in Ae_{v}$
. We calculate
 $$\begin{align*}(\mu_3\otimes S_{v})(x)=\sum_{a\in\mathrm{H}_{v}^{\mathrm{m}}}xa\otimes[a],\end{align*}$$
$$\begin{align*}(\mu_3\otimes S_{v})(x)=\sum_{a\in\mathrm{H}_{v}^{\mathrm{m}}}xa\otimes[a],\end{align*}$$
using the notation in (3.5) for elements of
![]() $A\mathbin {\otimes }\mathbb {K} Q_2^{\mathrm {m}}\mathbin {\otimes }S_{v}\cong \bigoplus _{a\in \mathrm {H}_{v}^{\mathrm {m}}}Ae_{ta}$
. Thus
$A\mathbin {\otimes }\mathbb {K} Q_2^{\mathrm {m}}\mathbin {\otimes }S_{v}\cong \bigoplus _{a\in \mathrm {H}_{v}^{\mathrm {m}}}Ae_{ta}$
. Thus
![]() $x\in \ker (\mu _3\otimes S_{v})$
if and only if
$x\in \ker (\mu _3\otimes S_{v})$
if and only if
![]() $xa=0$
for all
$xa=0$
for all
![]() $a\in \mathrm {H}_{v}^{\mathrm {m}}$
. Note that since v is mutable,
$a\in \mathrm {H}_{v}^{\mathrm {m}}$
. Note that since v is mutable,
![]() $\mathrm {H}_{v}^{\mathrm {m}}=\mathrm {H}_{v}\neq \varnothing $
.
$\mathrm {H}_{v}^{\mathrm {m}}=\mathrm {H}_{v}\neq \varnothing $
.
Let
![]() $w\in Q_0$
, so
$w\in Q_0$
, so
![]() $e_{w}x\in e_{w}Ae_{v}$
. Since A is thin by Proposition 2.11, we have
$e_{w}x\in e_{w}Ae_{v}$
. Since A is thin by Proposition 2.11, we have
![]() $e_{w}Ae_{v}=Zp_{wv}$
, so we may write
$e_{w}Ae_{v}=Zp_{wv}$
, so we may write
![]() $e_{w}x=\sum _{n\in \mathbb {N}}z_nt^n\cdot p_{wv}$
for some sequence of scalars
$e_{w}x=\sum _{n\in \mathbb {N}}z_nt^n\cdot p_{wv}$
for some sequence of scalars
![]() $z_n\in \mathbb {K}$
. Using thinness again, for any
$z_n\in \mathbb {K}$
. Using thinness again, for any
![]() $a\in \mathrm {H}_{v}^{\mathrm {m}}$
, there is some
$a\in \mathrm {H}_{v}^{\mathrm {m}}$
, there is some
![]() $\delta _a\in \mathbb {N}$
such that
$\delta _a\in \mathbb {N}$
such that
![]() $p_{wv}a=t^{\delta _a}p_{w,ta}$
. It then follows that
$p_{wv}a=t^{\delta _a}p_{w,ta}$
. It then follows that
Thus if
![]() $xa=0$
, we have
$xa=0$
, we have
![]() $z_n=0$
for all n, and so
$z_n=0$
for all n, and so
![]() $e_{w}x=0$
. Since w was chosen arbitrarily, we conclude that
$e_{w}x=0$
. Since w was chosen arbitrarily, we conclude that
![]() $x=0$
, and so the kernel of
$x=0$
, and so the kernel of
![]() $\mu _3\otimes S_{v}$
is trivial. This establishes exactness of equation (3.3) at the term
$\mu _3\otimes S_{v}$
is trivial. This establishes exactness of equation (3.3) at the term
![]() $A\mathbin {\otimes }\mathbb {K} Q_3^{\mathrm {m}}\mathbin {\otimes }S_{v}$
.
$A\mathbin {\otimes }\mathbb {K} Q_3^{\mathrm {m}}\mathbin {\otimes }S_{v}$
.
We now move to the term
![]() $A\mathbin {\otimes }\mathbb {K} Q_2^{\mathrm {m}}\mathbin {\otimes }S_{v}$
. Using the relevant isomorphisms in equation (3.4) and the notation of equation (3.5), a general element of this term is of the form
$A\mathbin {\otimes }\mathbb {K} Q_2^{\mathrm {m}}\mathbin {\otimes }S_{v}$
. Using the relevant isomorphisms in equation (3.4) and the notation of equation (3.5), a general element of this term is of the form
![]() $\phi =\sum _{a\in \mathrm {H}_{v}^{\mathrm {m}}}x_a\mathbin {\otimes }[a]$
for
$\phi =\sum _{a\in \mathrm {H}_{v}^{\mathrm {m}}}x_a\mathbin {\otimes }[a]$
for
![]() $x\in Ae_{ta}$
, and its image under
$x\in Ae_{ta}$
, and its image under
![]() $\mu _2\mathbin {\otimes }S_{v}$
is
$\mu _2\mathbin {\otimes }S_{v}$
is
 $$\begin{align*}(\mu_2\mathbin{\otimes}S_{v})(\phi)=\sum_{b\in\mathrm{T}_{v}}\Bigg(\sum_{a\in\mathrm{H}_{v}^{\mathrm{m}}}x_a\partial^r_{b}{\partial_{a}{W}}\Bigg)\mathbin{\otimes}[b]=\sum_{b\in\mathrm{T}_{v}}\Bigg(\sum_{a\in\mathrm{H}_{v}^{\mathrm{m}}}x_a\partial^l_{a}{\partial_{b}{W}}\Bigg)\mathbin{\otimes}[b],\end{align*}$$
$$\begin{align*}(\mu_2\mathbin{\otimes}S_{v})(\phi)=\sum_{b\in\mathrm{T}_{v}}\Bigg(\sum_{a\in\mathrm{H}_{v}^{\mathrm{m}}}x_a\partial^r_{b}{\partial_{a}{W}}\Bigg)\mathbin{\otimes}[b]=\sum_{b\in\mathrm{T}_{v}}\Bigg(\sum_{a\in\mathrm{H}_{v}^{\mathrm{m}}}x_a\partial^l_{a}{\partial_{b}{W}}\Bigg)\mathbin{\otimes}[b],\end{align*}$$
where the second equality follows from equation (3.8). The reader is warned that since
![]() $b\in \mathrm {T}_{v}$
may be frozen, the derivative
$b\in \mathrm {T}_{v}$
may be frozen, the derivative
![]() $\partial _{b}{W}$
is not necessarily zero in A.
$\partial _{b}{W}$
is not necessarily zero in A.
Now assume that
![]() $(\mu _2\mathbin {\otimes }S_{v})(\phi )=0$
or, equivalently by the above calculation, that
$(\mu _2\mathbin {\otimes }S_{v})(\phi )=0$
or, equivalently by the above calculation, that
 $$ \begin{align} \sum_{a\in\mathrm{H}_{v}^{\mathrm{m}}}x_a\partial^l_{a}{\partial_{b}{W}}=0 \end{align} $$
$$ \begin{align} \sum_{a\in\mathrm{H}_{v}^{\mathrm{m}}}x_a\partial^l_{a}{\partial_{b}{W}}=0 \end{align} $$
for all
![]() $b\in \mathrm {T}_{v}$
. Picking
$b\in \mathrm {T}_{v}$
. Picking
![]() $w\in Q_0$
and multiplying by
$w\in Q_0$
and multiplying by
![]() $e_{w}$
on the left, we obtain elements
$e_{w}$
on the left, we obtain elements
![]() $e_{w}x_a\in e_{w}Ae_{ta}$
for each
$e_{w}x_a\in e_{w}Ae_{ta}$
for each
![]() $a\in \mathrm {H}_{v}^{\mathrm {m}}$
.
$a\in \mathrm {H}_{v}^{\mathrm {m}}$
.
As in the first part of the proof, we will now use thinness of A to write the elements
![]() $e_{w}x_a$
as the product of a power series in t with
$e_{w}x_a$
as the product of a power series in t with
![]() $p_{w,ta}$
, but in order to keep the notation clean in the subsequent argument, we will do this in a slightly unusual way. First, note that, having fixed the vertex w, any path p determines
$p_{w,ta}$
, but in order to keep the notation clean in the subsequent argument, we will do this in a slightly unusual way. First, note that, having fixed the vertex w, any path p determines
![]() $\delta _p\in \mathbb {N}$
with the property that
$\delta _p\in \mathbb {N}$
with the property that
![]() $p_{w,hp}p=t^{\delta _p}p_{w,tp}$
. Since this equality is formulated in the algebra A, the quantity
$p_{w,hp}p=t^{\delta _p}p_{w,tp}$
. Since this equality is formulated in the algebra A, the quantity
![]() $\delta _p$
depends only on the class of p in the algebra.
$\delta _p$
depends only on the class of p in the algebra.
Using this notation, we can write
for some scalars
![]() $z_n^{w,a}\in \mathbb {K}$
. Since the right-hand side of this expression may only involve nonnegative powers of t, we have
$z_n^{w,a}\in \mathbb {K}$
. Since the right-hand side of this expression may only involve nonnegative powers of t, we have
![]() $z_n^{w,a}=0$
whenever
$z_n^{w,a}=0$
whenever
![]() $n<-\delta _a$
.
$n<-\delta _a$
.
The key step in the argument is to show, under our assumption that
![]() $(\mu _2\mathbin {\otimes }S_{v})(\phi )=0$
, that the coefficient
$(\mu _2\mathbin {\otimes }S_{v})(\phi )=0$
, that the coefficient
![]() $z_n^{w,a}$
depends only on n and w, and not on
$z_n^{w,a}$
depends only on n and w, and not on
![]() $a\in \mathrm {H}_{v}^{\mathrm {m}}$
. We consider the configuration
$a\in \mathrm {H}_{v}^{\mathrm {m}}$
. We consider the configuration

Here solid arrows represent arrows in
![]() $Q_1$
, dashed arrows represent paths in Q and dotted arrows represent linear combinations of paths. Our assumption is that
$Q_1$
, dashed arrows represent paths in Q and dotted arrows represent linear combinations of paths. Our assumption is that
![]() $a_+$
and
$a_+$
and
![]() $a_-$
are unfrozen arrows, with head at v as depicted, which appear in the two fundamental cycles
$a_-$
are unfrozen arrows, with head at v as depicted, which appear in the two fundamental cycles
![]() $a_+pb$
and
$a_+pb$
and
![]() $a_-qb$
containing the arrow b, also unfrozen, with tail at v. As indicated by the notation in equation (3.11), we will usually omit the letter a when
$a_-qb$
containing the arrow b, also unfrozen, with tail at v. As indicated by the notation in equation (3.11), we will usually omit the letter a when
![]() $a_+$
or
$a_+$
or
![]() $a_-$
appears in subscripts or superscripts in the following argument—for example, this means
$a_-$
appears in subscripts or superscripts in the following argument—for example, this means
![]() $x_+:=x_{a_+}$
. Our aim is to show that
$x_+:=x_{a_+}$
. Our aim is to show that
![]() $z_n^{w,+}=z_n^{w,-}$
for all
$z_n^{w,+}=z_n^{w,-}$
for all
![]() $n\in \mathbb {Z}$
; it will then follow from the way the quiver Q is embedded in the disc that
$n\in \mathbb {Z}$
; it will then follow from the way the quiver Q is embedded in the disc that
![]() $z_n^{w,a}$
is independent of
$z_n^{w,a}$
is independent of
![]() $a\in \mathrm {H}_{v}^{\mathrm {m}}$
, since if
$a\in \mathrm {H}_{v}^{\mathrm {m}}$
, since if
![]() $a,a'\in \mathrm {H}_{v}^{\mathrm {m}}$
, we can find sequences
$a,a'\in \mathrm {H}_{v}^{\mathrm {m}}$
, we can find sequences
![]() $a_0,\dotsc ,a_k$
and
$a_0,\dotsc ,a_k$
and
![]() $b_1\cdots b_k$
such that
$b_1\cdots b_k$
such that
![]() $a_0=a$
,
$a_0=a$
,
![]() $a_k=a'$
, and for all
$a_k=a'$
, and for all
![]() $1\leq i\leq k$
the triple of arrows
$1\leq i\leq k$
the triple of arrows
![]() $(a_{i-1},b_i,a_i)$
has the same configuration as
$(a_{i-1},b_i,a_i)$
has the same configuration as
![]() $(a_-,b,a_+)$
in equation (3.11) (or its mirror image), so that
$(a_-,b,a_+)$
in equation (3.11) (or its mirror image), so that
![]() $z_n^{w,a_{i-1}}=z_n^{w,a_i}$
.
$z_n^{w,a_{i-1}}=z_n^{w,a_i}$
.
So consider the configuration shown in equation (3.11). We see from the figure that
![]() $\partial _{b}{W}=a_+p-a_-q$
. While it can happen that
$\partial _{b}{W}=a_+p-a_-q$
. While it can happen that
![]() $a_+=a_-$
(if and only if v is a bivalent vertex of Q), in this case there is nothing to prove, so we may assume
$a_+=a_-$
(if and only if v is a bivalent vertex of Q), in this case there is nothing to prove, so we may assume
![]() $a_+\ne a_-$
. Then for
$a_+\ne a_-$
. Then for
![]() $a\in \mathrm {H}_{v}^{\mathrm {m}}$
, we have
$a\in \mathrm {H}_{v}^{\mathrm {m}}$
, we have
 $$\begin{align*}\partial^l_{a}{\partial_{b}{W}}=\begin{cases}p,&a=a_+,\\-q,&a=a_-,\\0,&\text{otherwise}.\end{cases}\end{align*}$$
$$\begin{align*}\partial^l_{a}{\partial_{b}{W}}=\begin{cases}p,&a=a_+,\\-q,&a=a_-,\\0,&\text{otherwise}.\end{cases}\end{align*}$$
Thus
 $$\begin{align*}\sum_{a\in\mathrm{H}_{v}^{\mathrm{m}}}x_a\partial^l_{a}{\partial_{b}{W}}=x_+p-x_-q.\end{align*}$$
$$\begin{align*}\sum_{a\in\mathrm{H}_{v}^{\mathrm{m}}}x_a\partial^l_{a}{\partial_{b}{W}}=x_+p-x_-q.\end{align*}$$
Since
![]() $\phi =\sum _{a\in \mathrm {H}_{v}^{\mathrm {m}}}x_a\mathbin {\otimes }[a]$
is in the kernel of
$\phi =\sum _{a\in \mathrm {H}_{v}^{\mathrm {m}}}x_a\mathbin {\otimes }[a]$
is in the kernel of
![]() $\mu _2\mathbin {\otimes }S_{v}$
, this quantity is zero by equation (3.9), so
$\mu _2\mathbin {\otimes }S_{v}$
, this quantity is zero by equation (3.9), so
![]() $x_+p=x_-q$
. It follows that
$x_+p=x_-q$
. It follows that
 $$ \begin{align*} e_{w}x_+p&=t^{\delta_+}\sum_{n\in\mathbb{Z}}z_n^{w,+}t^n\cdot p_{w,ta_+}p=t^{\delta_++\delta_p}\sum_{n\in\mathbb{Z}}z_n^{w,+}t^n\cdot p_{w,hb},\\ e_{w}x_-q&=t^{\delta_-}\sum_{n\in\mathbb{Z}}z_n^{w,-}t^n\cdot p_{w,ta_-}q=t^{\delta_-+\delta_q}\sum_{n\in\mathbb{Z}}z_n^{w,-}t^n\cdot p_{w,hb}, \end{align*} $$
$$ \begin{align*} e_{w}x_+p&=t^{\delta_+}\sum_{n\in\mathbb{Z}}z_n^{w,+}t^n\cdot p_{w,ta_+}p=t^{\delta_++\delta_p}\sum_{n\in\mathbb{Z}}z_n^{w,+}t^n\cdot p_{w,hb},\\ e_{w}x_-q&=t^{\delta_-}\sum_{n\in\mathbb{Z}}z_n^{w,-}t^n\cdot p_{w,ta_-}q=t^{\delta_-+\delta_q}\sum_{n\in\mathbb{Z}}z_n^{w,-}t^n\cdot p_{w,hb}, \end{align*} $$
must also be equal. Since
![]() $a_+p=a_-q$
in A (because of the relation
$a_+p=a_-q$
in A (because of the relation
![]() $\partial _{b}{W}$
), we must have
$\partial _{b}{W}$
), we must have
![]() $\delta _++\delta _p=\delta _-+\delta _q$
, so we can conclude, for any
$\delta _++\delta _p=\delta _-+\delta _q$
, so we can conclude, for any
![]() $n\in \mathbb {Z}$
, that
$n\in \mathbb {Z}$
, that
![]() $z_n^{w,+}=z_n^{w,-}$
, and further that
$z_n^{w,+}=z_n^{w,-}$
, and further that
![]() $z_n^{w,a}$
is independent of
$z_n^{w,a}$
is independent of
![]() $a\in \mathrm {H}_{v}^{\mathrm {m}}$
, as required. From now on, we abbreviate
$a\in \mathrm {H}_{v}^{\mathrm {m}}$
, as required. From now on, we abbreviate
![]() $z_n^w:=z_n^{w,a}$
, and for any
$z_n^w:=z_n^{w,a}$
, and for any
![]() $a\in \mathrm {H}_{v}^{\mathrm {m}}$
, we have
$a\in \mathrm {H}_{v}^{\mathrm {m}}$
, we have
We now return to our main purpose, to show that the complex in equation (3.1) is exact. We recall that we are assuming that
![]() $\phi =\sum _{a\in \mathrm {H}_{v}^{\mathrm {m}}}x_a\mathbin {\otimes }[a]$
satisfies
$\phi =\sum _{a\in \mathrm {H}_{v}^{\mathrm {m}}}x_a\mathbin {\otimes }[a]$
satisfies
![]() $(\mu _2\mathbin {\otimes }S_{v})(\phi )=0$
and wish to show that
$(\mu _2\mathbin {\otimes }S_{v})(\phi )=0$
and wish to show that
![]() $\phi $
is in the image of
$\phi $
is in the image of
![]() $\mu _3\mathbin {\otimes }S_{v}$
.
$\mu _3\mathbin {\otimes }S_{v}$
.
First we deal with the case that v is a frozen vertex, in which case
![]() $\mu _3\mathbin {\otimes }S_{v}=0$
, and we wish to conclude that
$\mu _3\mathbin {\otimes }S_{v}=0$
, and we wish to conclude that
![]() $x_a=0$
for all
$x_a=0$
for all
![]() $a\in \mathrm {H}_{v}^{\mathrm {m}}$
. This is equivalent to showing that the complex numbers
$a\in \mathrm {H}_{v}^{\mathrm {m}}$
. This is equivalent to showing that the complex numbers
![]() $z_n^w$
appearing in equation (3.12) are zero for all n and all w.
$z_n^w$
appearing in equation (3.12) are zero for all n and all w.
It follows from the construction of
![]() $(Q_D,F_D)$
that, since v is frozen, it is incident with a frozen arrow. If
$(Q_D,F_D)$
that, since v is frozen, it is incident with a frozen arrow. If
![]() $\mathrm {H}_{v}^{\mathrm {m}}=\varnothing $
, then we have nothing to show, and otherwise there is an arrow
$\mathrm {H}_{v}^{\mathrm {m}}=\varnothing $
, then we have nothing to show, and otherwise there is an arrow
![]() $a\in \mathrm {H}_{v}^{\mathrm {m}}$
as in one of the following configurations
$a\in \mathrm {H}_{v}^{\mathrm {m}}$
as in one of the following configurations

in which
![]() $apb$
and
$apb$
and
![]() $cqb$
are fundamental cycles. As earlier in the paper, the bold arrows are frozen, and the dashed arrows represent paths. The vertices indicated by diamonds are frozen, like the vertex v, whereas the others may be mutable or frozen.
$cqb$
are fundamental cycles. As earlier in the paper, the bold arrows are frozen, and the dashed arrows represent paths. The vertices indicated by diamonds are frozen, like the vertex v, whereas the others may be mutable or frozen.
In the two configurations in equation (3.13), we have
![]() $\partial _{b}{W}=\pm ap$
and
$\partial _{b}{W}=\pm ap$
and
![]() $\partial _{b}{W}=\pm (ap-cq)$
, respectively. Thus in either case we calculate for
$\partial _{b}{W}=\pm (ap-cq)$
, respectively. Thus in either case we calculate for
![]() $a'\in \mathrm {H}_{v}^{\mathrm {m}}$
that
$a'\in \mathrm {H}_{v}^{\mathrm {m}}$
that
 $$\begin{align*}\partial^l_{a'}{\partial_{b}{W}}=\begin{cases}\pm p,&a'=a,\\0,&\text{otherwise}.\end{cases}\end{align*}$$
$$\begin{align*}\partial^l_{a'}{\partial_{b}{W}}=\begin{cases}\pm p,&a'=a,\\0,&\text{otherwise}.\end{cases}\end{align*}$$
Since
![]() $(\mu _2\mathbin {\otimes }S_{v})(\phi )=0$
, we deduce from equation (3.9) that
$(\mu _2\mathbin {\otimes }S_{v})(\phi )=0$
, we deduce from equation (3.9) that
 $$\begin{align*}x_ap=\pm\sum_{a'\in\mathrm{H}_{v}^{\mathrm{m}}}x_a\partial^l_{a'}\partial_{b}{W}=0.\end{align*}$$
$$\begin{align*}x_ap=\pm\sum_{a'\in\mathrm{H}_{v}^{\mathrm{m}}}x_a\partial^l_{a'}\partial_{b}{W}=0.\end{align*}$$
Multiplying on the left by
![]() $e_{w}$
and using that A is thin, we see that
$e_{w}$
and using that A is thin, we see that
so
![]() $z_n^w=0$
for all n and w, as required.
$z_n^w=0$
for all n and w, as required.
Now we treat the case that v is a mutable vertex; in this case,
![]() $\mathrm {H}_{v}^{\mathrm {m}}=\mathrm {H}_{v}$
and we use the latter to keep the notation simpler. In this case, we want to construct
$\mathrm {H}_{v}^{\mathrm {m}}=\mathrm {H}_{v}$
and we use the latter to keep the notation simpler. In this case, we want to construct
![]() $y\in Ae_{v}$
such that
$y\in Ae_{v}$
such that
Using the sequence of complex numbers
![]() $z_n^w$
appearing in equation (3.12), we write
$z_n^w$
appearing in equation (3.12), we write
For this to be a well-defined element of
![]() $e_{w}Ae_{v}$
, we need
$e_{w}Ae_{v}$
, we need
![]() $z_n^w=0$
for all
$z_n^w=0$
for all
![]() $n<0$
. Choosing any
$n<0$
. Choosing any
![]() $a\in \mathrm {H}_{v}$
, we have that
$a\in \mathrm {H}_{v}$
, we have that
![]() $z_n^w=z_n^{w,a}$
is zero whenever
$z_n^w=z_n^{w,a}$
is zero whenever
![]() $n<-\delta _a$
, as in equation (3.10). But by Lemma 3.2, there is some
$n<-\delta _a$
, as in equation (3.10). But by Lemma 3.2, there is some
![]() $a\in \mathrm {H}_{v}$
such that
$a\in \mathrm {H}_{v}$
such that
![]() $\delta _a=0$
, so
$\delta _a=0$
, so
![]() $y_w\in e_{w}Ae_{v}$
as required.
$y_w\in e_{w}Ae_{v}$
as required.
Now, letting
![]() $y=\sum _{w\in Q_0}y_w\in Ae_{v}\cong A\mathbin {\otimes }\mathbb {K} Q_3^{\mathrm {m}}\mathbin {\otimes }S_{v}$
, we can calculate
$y=\sum _{w\in Q_0}y_w\in Ae_{v}\cong A\mathbin {\otimes }\mathbb {K} Q_3^{\mathrm {m}}\mathbin {\otimes }S_{v}$
, we can calculate
 $$ \begin{align*} (\mu_3\mathbin{\otimes}S_{v})(y)=\sum_{w\in Q_0}\sum_{a\in\mathrm{H}_{v}}y_wa\mathbin{\otimes}[a]&=\sum_{w\in Q_0}\sum_{a\in\mathrm{H}_{v}}\Bigg(\sum_{n\in\mathbb{N}}z_n^wt^n\cdot p_{wv}a\Bigg)\mathbin{\otimes}[a]\\ &=\sum_{w\in Q_0}\sum_{a\in\mathrm{H}_{v}}\Bigg(\sum_{n\in\mathbb{N}}z_n^wt^{n+\delta_a}\cdot p_{w,ta}\Bigg)\mathbin{\otimes}[a]\\ &=\sum_{w\in Q_0}\sum_{a\in\mathrm{H}_{v}}e_{w}x_a\mathbin{\otimes}[a]=\sum_{a\in\mathrm{H}_{v}}x_a\mathbin{\otimes}[a]=\phi, \end{align*} $$
$$ \begin{align*} (\mu_3\mathbin{\otimes}S_{v})(y)=\sum_{w\in Q_0}\sum_{a\in\mathrm{H}_{v}}y_wa\mathbin{\otimes}[a]&=\sum_{w\in Q_0}\sum_{a\in\mathrm{H}_{v}}\Bigg(\sum_{n\in\mathbb{N}}z_n^wt^n\cdot p_{wv}a\Bigg)\mathbin{\otimes}[a]\\ &=\sum_{w\in Q_0}\sum_{a\in\mathrm{H}_{v}}\Bigg(\sum_{n\in\mathbb{N}}z_n^wt^{n+\delta_a}\cdot p_{w,ta}\Bigg)\mathbin{\otimes}[a]\\ &=\sum_{w\in Q_0}\sum_{a\in\mathrm{H}_{v}}e_{w}x_a\mathbin{\otimes}[a]=\sum_{a\in\mathrm{H}_{v}}x_a\mathbin{\otimes}[a]=\phi, \end{align*} $$
so we conclude that
![]() $\phi \in \operatorname {\mathrm {im}}(\mu _3\mathbin {\otimes }S_{v})$
, as required.
$\phi \in \operatorname {\mathrm {im}}(\mu _3\mathbin {\otimes }S_{v})$
, as required.
4 Categorification
Given a suitable algebra A, which is bimodule internally
![]() $3$
-Calabi–Yau with respect to an idempotent e, one can construct from A and e a Frobenius category having many desirable properties from the point of view of categorifying cluster algebras. This is done via the main result of [Reference Pressland43] (specialised to the case that the Calabi–Yau dimension is
$3$
-Calabi–Yau with respect to an idempotent e, one can construct from A and e a Frobenius category having many desirable properties from the point of view of categorifying cluster algebras. This is done via the main result of [Reference Pressland43] (specialised to the case that the Calabi–Yau dimension is
![]() $3$
), which we will recall after collecting the necessary algebraic definitions. Applied to the dimer algebra
$3$
), which we will recall after collecting the necessary algebraic definitions. Applied to the dimer algebra
![]() $A_D$
of a connected Postnikov diagram D, this will allow us to show (Theorem 4.5) that the category
$A_D$
of a connected Postnikov diagram D, this will allow us to show (Theorem 4.5) that the category
![]() $\operatorname {\mathrm {GP}}(B_D)$
appearing in Theorem 1 has many of the properties required of an additive categorification of the cluster algebra
$\operatorname {\mathrm {GP}}(B_D)$
appearing in Theorem 1 has many of the properties required of an additive categorification of the cluster algebra
![]() $\mathscr {A}_{D}$
. Further such properties will be proved in Section 6.
$\mathscr {A}_{D}$
. Further such properties will be proved in Section 6.
Definition 4.1. Let
![]() $\mathcal {E}$
be an exact
$\mathcal {E}$
be an exact
![]() $\mathbb {K}$
-linear category, as in [Reference Bühler8]. We do not recall the full definition of this structure here but simply note that any full extension-closed subcategory
$\mathbb {K}$
-linear category, as in [Reference Bühler8]. We do not recall the full definition of this structure here but simply note that any full extension-closed subcategory
![]() $\mathcal {E}$
of an abelian category
$\mathcal {E}$
of an abelian category
![]() $\mathcal {A}$
has a natural structure of an exact category, by taking the class of short exact sequences to be the short exact sequences of
$\mathcal {A}$
has a natural structure of an exact category, by taking the class of short exact sequences to be the short exact sequences of
![]() $\mathcal {A}$
with terms in
$\mathcal {A}$
with terms in
![]() $\mathcal {E}$
.
$\mathcal {E}$
.
We say
![]() $\mathcal {E}$
is a Frobenius category if it has enough projective objects and enough injective objects, and these two classes of objects coincide. The stable category
$\mathcal {E}$
is a Frobenius category if it has enough projective objects and enough injective objects, and these two classes of objects coincide. The stable category
![]() $\underline {\mathcal {E}}$
is obtained from
$\underline {\mathcal {E}}$
is obtained from
![]() $\mathcal {E}$
by factoring out the ideal of morphisms that factor over a projective (equivalently injective) object and has a natural triangulated structure [Reference Happel22, §I.2]. We say that
$\mathcal {E}$
by factoring out the ideal of morphisms that factor over a projective (equivalently injective) object and has a natural triangulated structure [Reference Happel22, §I.2]. We say that
![]() $\underline {\mathcal {E}}$
is
$\underline {\mathcal {E}}$
is
![]() $2$
-Calabi–Yau, and
$2$
-Calabi–Yau, and
![]() $\mathcal {E}$
is stably
$\mathcal {E}$
is stably
![]() $2$
-Calabi–Yau, if
$2$
-Calabi–Yau, if
![]() $\underline {\mathcal {E}}$
is Hom-finite and there is a functorial isomorphism
$\underline {\mathcal {E}}$
is Hom-finite and there is a functorial isomorphism
for any two objects X and Y of
![]() $\underline {\mathcal {E}}$
, where
$\underline {\mathcal {E}}$
, where
![]() $\Sigma $
is the shift functor in the triangulated structure of
$\Sigma $
is the shift functor in the triangulated structure of
![]() $\underline {\mathcal {E}}$
(computed by taking the cokernel of an injective envelope) and
$\underline {\mathcal {E}}$
(computed by taking the cokernel of an injective envelope) and
![]() $\mathrm {D}$
is duality over the ground field
$\mathrm {D}$
is duality over the ground field
![]() $\mathbb {K}$
.
$\mathbb {K}$
.
A full subcategory
![]() $\mathcal {T}\subseteq \mathcal {E}$
is called cluster-tilting if it is functorially finite and
$\mathcal {T}\subseteq \mathcal {E}$
is called cluster-tilting if it is functorially finite and
Note that cluster-tilting subcategories are necessarily additively closed: that is, closed under direct sums and summands. We can make the same definition in
![]() $\underline {\mathcal {E}}$
, using the usual definition
$\underline {\mathcal {E}}$
, using the usual definition
![]() $\operatorname {\mathrm {Ext}}^1_{\underline {\mathcal {E}}}(M,N)=\operatorname {\mathrm {Hom}}_{\underline {\mathcal {E}}}(M,\Sigma N)$
for triangulated categories, and observe that a subcategory
$\operatorname {\mathrm {Ext}}^1_{\underline {\mathcal {E}}}(M,N)=\operatorname {\mathrm {Hom}}_{\underline {\mathcal {E}}}(M,\Sigma N)$
for triangulated categories, and observe that a subcategory
![]() $\mathcal {T}\subseteq \mathcal {E}$
containing all projective objects is cluster-tilting if and only if its image in the stable category
$\mathcal {T}\subseteq \mathcal {E}$
containing all projective objects is cluster-tilting if and only if its image in the stable category
![]() $\underline {\mathcal {E}}$
(i.e., the full subcategory of
$\underline {\mathcal {E}}$
(i.e., the full subcategory of
![]() $\underline {\mathcal {E}}$
on the same set of objects as
$\underline {\mathcal {E}}$
on the same set of objects as
![]() $\mathcal {T}$
) is cluster-tilting. When
$\mathcal {T}$
) is cluster-tilting. When
![]() $\mathcal {E}$
is stably
$\mathcal {E}$
is stably
![]() $2$
-Calabi–Yau, the second equality in the definition of a cluster-tilting subcategory is automatic. An object
$2$
-Calabi–Yau, the second equality in the definition of a cluster-tilting subcategory is automatic. An object
![]() $T\in \mathcal {E}$
is a cluster-tilting object if its additive closure
$T\in \mathcal {E}$
is a cluster-tilting object if its additive closure
![]() $\operatorname {\mathrm {add}}{T}$
is a cluster-tilting subcategory.
$\operatorname {\mathrm {add}}{T}$
is a cluster-tilting subcategory.
An algebra B is called Iwanaga–Gorenstein if it is Noetherian and has finite injective dimension both as a left and as a right module over itself. In this case these two injective dimensions coincide [Reference Iwanaga25], and we call this number the Gorenstein dimension of B. For an Iwanaga–Gorenstein algebra B, we define the category of Gorenstein projective B-modules to be the full subcategory
of the abelian category of finitely generated B-modules. This is a Frobenius category; see for example [Reference Buchweitz, Avramov, Briggs, Iyengar and Letz7, §4], where this category is denoted by
![]() $\operatorname {\mathrm {MCM}}(B)$
and its objects called maximal Cohen–Macaulay modules.
$\operatorname {\mathrm {MCM}}(B)$
and its objects called maximal Cohen–Macaulay modules.
Remark 4.2. The reader is warned that when B is free and finitely generated over
![]() $Z=\mathbb {K}[\hspace {-0.1em}[t]\hspace {-0.1em}]$
, as will be the case in our examples, one can define the (maximal) Cohen–Macaulay B-modules to be those B-modules that are free and finitely generated over Z, as in [Reference Jensen, King and Su28, §3]. While a module for the algebra C defining the Grassmannian cluster category is Gorenstein projective if and only if it is Cohen–Macaulay [Reference Jensen, King and Su28, Cor. 3.7], this will not be the case for B in general (see Example 4.8). To avoid having two nonequivalent definitions of Cohen–Macaulay B-modules, we prefer the terminology ‘Gorenstein projective’ for the homological condition. The reader is, however, further warned that Gorenstein projective modules are defined over an arbitrary ring (as in [Reference Holm23, Defn. 2.1] for example), but in a way that need not be equivalent to Definition 4.1 if the ring is not Iwanaga–Gorenstein.
$Z=\mathbb {K}[\hspace {-0.1em}[t]\hspace {-0.1em}]$
, as will be the case in our examples, one can define the (maximal) Cohen–Macaulay B-modules to be those B-modules that are free and finitely generated over Z, as in [Reference Jensen, King and Su28, §3]. While a module for the algebra C defining the Grassmannian cluster category is Gorenstein projective if and only if it is Cohen–Macaulay [Reference Jensen, King and Su28, Cor. 3.7], this will not be the case for B in general (see Example 4.8). To avoid having two nonequivalent definitions of Cohen–Macaulay B-modules, we prefer the terminology ‘Gorenstein projective’ for the homological condition. The reader is, however, further warned that Gorenstein projective modules are defined over an arbitrary ring (as in [Reference Holm23, Defn. 2.1] for example), but in a way that need not be equivalent to Definition 4.1 if the ring is not Iwanaga–Gorenstein.
Theorem 4.3 [Reference Pressland43, Thm. 4.1, Thm. 4.10]
Let A be an algebra and
![]() $e\in A$
an idempotent. If A is Noetherian,
$e\in A$
an idempotent. If A is Noetherian,
![]() $\underline {A}=A/\langle e\rangle $
is finite-dimensional and A is bimodule internally
$\underline {A}=A/\langle e\rangle $
is finite-dimensional and A is bimodule internally
![]() $3$
-Calabi–Yau with respect to e, then
$3$
-Calabi–Yau with respect to e, then
-
(1)
 $B=eAe$
is Iwanaga–Gorenstein with Gorenstein dimension at most
$B=eAe$
is Iwanaga–Gorenstein with Gorenstein dimension at most
 $3$
,
$3$
, -
(2)
 $eA$
is a cluster-tilting object in the Frobenius category
$eA$
is a cluster-tilting object in the Frobenius category
 $\operatorname {\mathrm {GP}}(B)$
,
$\operatorname {\mathrm {GP}}(B)$
, -
(3) the stable category
 $\operatorname {\mathrm {\underline {GP}}}(B)$
is a
$\operatorname {\mathrm {\underline {GP}}}(B)$
is a
 $2$
-Calabi–Yau triangulated category, and
$2$
-Calabi–Yau triangulated category, and -
(4) the natural maps
 $A\to \operatorname {\mathrm {End}}_{B}(eA)^{\mathrm {op}}$
and
$A\to \operatorname {\mathrm {End}}_{B}(eA)^{\mathrm {op}}$
and
 $\underline {A}\to \operatorname {\mathrm {\underline {End}}}_{B}(eA)^{\mathrm {op}}$
are isomorphisms.
$\underline {A}\to \operatorname {\mathrm {\underline {End}}}_{B}(eA)^{\mathrm {op}}$
are isomorphisms.
We already saw in Theorem 3.7 that the dimer algebra
![]() $A_D$
of a connected Postnikov diagram D is bimodule internally
$A_D$
of a connected Postnikov diagram D is bimodule internally
![]() $3$
-Calabi–Yau with respect to its boundary idempotent. Checking the other conditions needed to apply Theorem 4.3 to
$3$
-Calabi–Yau with respect to its boundary idempotent. Checking the other conditions needed to apply Theorem 4.3 to
![]() $A_D$
is comparatively straightforward, although we note that we once again rely heavily on Proposition 2.11.
$A_D$
is comparatively straightforward, although we note that we once again rely heavily on Proposition 2.11.
Proposition 4.4. Let D be a connected Postnikov diagram with dimer algebra
![]() $A_D$
, and let e be the boundary idempotent of this algebra. Then
$A_D$
, and let e be the boundary idempotent of this algebra. Then
![]() $A_D$
is Noetherian and
$A_D$
is Noetherian and
![]() $A_D/\langle e\rangle $
is finite-dimensional.
$A_D/\langle e\rangle $
is finite-dimensional.
Proof. Since
![]() $A_D$
is thin, as in Proposition 2.11, it is finitely generated as a module over the commutative Noetherian ring
$A_D$
is thin, as in Proposition 2.11, it is finitely generated as a module over the commutative Noetherian ring
![]() $\mathbb {K}[\hspace {-0.1em}[t]\hspace {-0.1em}]$
and so is Noetherian.
$\mathbb {K}[\hspace {-0.1em}[t]\hspace {-0.1em}]$
and so is Noetherian.
By thinness again,
![]() $A_D$
has a basis
$A_D$
has a basis
![]() $\{t^np_{wv}:v,w\in Q_0,n\in \mathbb {N}\}$
. To see that
$\{t^np_{wv}:v,w\in Q_0,n\in \mathbb {N}\}$
. To see that
![]() $A_D/\langle e\rangle $
is finite-dimensional, we show that all but finitely many of these basis vectors are zero in the quotient. Picking any
$A_D/\langle e\rangle $
is finite-dimensional, we show that all but finitely many of these basis vectors are zero in the quotient. Picking any
![]() $v,w\in Q_0$
, let c be any cycle at w passing through a boundary vertex, which exists since
$v,w\in Q_0$
, let c be any cycle at w passing through a boundary vertex, which exists since
![]() $Q_D$
is strongly connected as in Proposition 2.6. Then since
$Q_D$
is strongly connected as in Proposition 2.6. Then since
![]() $A_D$
is thin, we have
$A_D$
is thin, we have
![]() $cp_{wv}=t^Np_{wv}$
for some
$cp_{wv}=t^Np_{wv}$
for some
![]() $N\in \mathbb {N}$
. By construction, this element is zero in the quotient
$N\in \mathbb {N}$
. By construction, this element is zero in the quotient
![]() $A_D/\langle e\rangle $
, and thus
$A_D/\langle e\rangle $
, and thus
![]() $t^np_{wv}=0$
in this quotient algebra for all
$t^np_{wv}=0$
in this quotient algebra for all
![]() $n\geq N$
. Running over all pairs
$n\geq N$
. Running over all pairs
![]() $v,w\in Q_0$
completes the proof.
$v,w\in Q_0$
completes the proof.
Recall that we write
![]() $\mathscr {A}_{D}$
for the cluster algebra with frozen variables determined by the ice quiver
$\mathscr {A}_{D}$
for the cluster algebra with frozen variables determined by the ice quiver
![]() $(Q_D,F_D)$
of a Postnikov diagram D. Note that arrows between frozen vertices play no role in the construction of this cluster algebra. Since
$(Q_D,F_D)$
of a Postnikov diagram D. Note that arrows between frozen vertices play no role in the construction of this cluster algebra. Since
![]() $Q_D$
may contain
$Q_D$
may contain
![]() $2$
-cycles, we are committing a small abuse of notation here; really,
$2$
-cycles, we are committing a small abuse of notation here; really,
![]() $\mathscr {A}_{D}$
is the cluster algebra determined by the quiver
$\mathscr {A}_{D}$
is the cluster algebra determined by the quiver
![]() $Q'$
of the unique reduced Postnikov diagram obtained from D by untwisting moves, as in Figure 4. Equivalently,
$Q'$
of the unique reduced Postnikov diagram obtained from D by untwisting moves, as in Figure 4. Equivalently,
![]() $Q'$
is obtained from
$Q'$
is obtained from
![]() $Q_D$
by removing a maximal collection of
$Q_D$
by removing a maximal collection of
![]() $2$
-cycles incident with unfrozen vertices. Using the description via untwisting and Proposition 2.9, we see that
$2$
-cycles incident with unfrozen vertices. Using the description via untwisting and Proposition 2.9, we see that
![]() $Q'$
has a potential
$Q'$
has a potential
![]() $W'$
such that
$W'$
such that
![]() $\mathcal {J}(Q',F_D,W')\cong A_D$
is the dimer algebra of the original diagram D.
$\mathcal {J}(Q',F_D,W')\cong A_D$
is the dimer algebra of the original diagram D.
By Theorem 3.7 and Proposition 4.4, we may apply Theorem 4.3 to the dimer algebra
![]() $A_D$
of a connected Postnikov diagram, to obtain the following.
$A_D$
of a connected Postnikov diagram, to obtain the following.
Theorem 4.5. Let D be a connected Postnikov diagram with dimer algebra
![]() $A_D$
. Let e be the boundary idempotent of this algebra, and write
$A_D$
. Let e be the boundary idempotent of this algebra, and write
![]() $B_D=eA_De$
. Then
$B_D=eA_De$
. Then
-
(1)
 $B_D$
is Iwanaga–Gorenstein of Gorenstein dimension at most
$B_D$
is Iwanaga–Gorenstein of Gorenstein dimension at most
 $3$
,
$3$
, -
(2)
 $\operatorname {\mathrm {GP}}(B_D)$
is a stably
$\operatorname {\mathrm {GP}}(B_D)$
is a stably
 $2$
-Calabi–Yau Frobenius category,
$2$
-Calabi–Yau Frobenius category, -
(3)
 $T_D=eA_D\in \operatorname {\mathrm {GP}}(B_D)$
is cluster-tilting, and
$T_D=eA_D\in \operatorname {\mathrm {GP}}(B_D)$
is cluster-tilting, and -
(4)
 $\operatorname {\mathrm {End}}_{B_D}(T_D)^{\mathrm {op}}\cong A_D$
.
$\operatorname {\mathrm {End}}_{B_D}(T_D)^{\mathrm {op}}\cong A_D$
.
In particular, it follows from (4) that the Gabriel quiver of
![]() $\operatorname {\mathrm {End}}_{B_D}(T_D)^{\mathrm {op}}$
is, up to arrows between frozen vertices, the quiver of a seed in the cluster algebra
$\operatorname {\mathrm {End}}_{B_D}(T_D)^{\mathrm {op}}$
is, up to arrows between frozen vertices, the quiver of a seed in the cluster algebra
![]() $\mathscr {A}_{D}$
.
$\mathscr {A}_{D}$
.
We note that if the full subquiver of
![]() $Q_D$
on the mutable vertices is, after removing
$Q_D$
on the mutable vertices is, after removing
![]() $2$
-cycles, mutation-equivalent to an acyclic quiver
$2$
-cycles, mutation-equivalent to an acyclic quiver
![]() $\underline {Q}$
, it follows from a result of Keller and Reiten [Reference Keller and Reiten30, Thm. 2.1] that the stable category
$\underline {Q}$
, it follows from a result of Keller and Reiten [Reference Keller and Reiten30, Thm. 2.1] that the stable category
![]() $\operatorname {\mathrm {\underline {GP}}}(B_D)$
of our categorification is equivalent to the cluster category
$\operatorname {\mathrm {\underline {GP}}}(B_D)$
of our categorification is equivalent to the cluster category
![]() $\mathcal {C}_{\underline {Q}}$
[Reference Buan, Iyama, Reiten and Scott5]. This mutation-acyclicity assumption does not hold for most Postnikov diagrams, however. We conjecture that
$\mathcal {C}_{\underline {Q}}$
[Reference Buan, Iyama, Reiten and Scott5]. This mutation-acyclicity assumption does not hold for most Postnikov diagrams, however. We conjecture that
![]() $\operatorname {\mathrm {\underline {GP}}}(B_D)$
is always equivalent to Amiot’s cluster category [Reference Amiot1] for the quiver with potential obtained from
$\operatorname {\mathrm {\underline {GP}}}(B_D)$
is always equivalent to Amiot’s cluster category [Reference Amiot1] for the quiver with potential obtained from
![]() $(Q_D,F_D,W_D)$
by deleting the frozen vertices and all incident arrows from
$(Q_D,F_D,W_D)$
by deleting the frozen vertices and all incident arrows from
![]() $Q_D$
and removing terms passing through these vertices from
$Q_D$
and removing terms passing through these vertices from
![]() $W_D$
.
$W_D$
.
If D is a
![]() $(k,n)$
-diagram, as in Definition 2.1, it follows from [Reference Baur, King and Marsh2, Cor. 10.4] that the boundary algebra
$(k,n)$
-diagram, as in Definition 2.1, it follows from [Reference Baur, King and Marsh2, Cor. 10.4] that the boundary algebra
![]() $B_D=eA_De$
does not depend on the choice of D within this class, up to isomorphism, and the category
$B_D=eA_De$
does not depend on the choice of D within this class, up to isomorphism, and the category
![]() $\operatorname {\mathrm {GP}}(B_D)$
is equivalent to Jensen–King–Su’s categorification of the cluster algebra structure on the whole Grassmannian [Reference Jensen, King and Su28].
$\operatorname {\mathrm {GP}}(B_D)$
is equivalent to Jensen–King–Su’s categorification of the cluster algebra structure on the whole Grassmannian [Reference Jensen, King and Su28].
In general, we can consider two Postnikov diagrams D and
![]() $D'$
related by geometric exchange as shown in Figure 7. Combining [Reference Postnikov41, Thm. 13.4] and [Reference Postnikov41, Thm. 17.1], we see that these diagrams determine the same positroid and hence the same positroid varieties. Moreover, the quivers
$D'$
related by geometric exchange as shown in Figure 7. Combining [Reference Postnikov41, Thm. 13.4] and [Reference Postnikov41, Thm. 17.1], we see that these diagrams determine the same positroid and hence the same positroid varieties. Moreover, the quivers
![]() $Q_D$
and
$Q_D$
and
![]() $Q_{D'}$
are related by a mutation, so the cluster algebras
$Q_{D'}$
are related by a mutation, so the cluster algebras
![]() $\mathscr {A}_{D}$
and
$\mathscr {A}_{D}$
and
![]() $\mathscr {A}_{Q_{D'}}$
are isomorphic. Thus we would like both D and
$\mathscr {A}_{Q_{D'}}$
are isomorphic. Thus we would like both D and
![]() $D'$
to give rise to the same category of Gorenstein projective modules in Theorem 4.5. This is indeed the case, as follows.
$D'$
to give rise to the same category of Gorenstein projective modules in Theorem 4.5. This is indeed the case, as follows.

Figure 7 A geometric exchange of a Postnikov diagram transforms the local configuration of a quadrilateral alternating region, shown on the left, to that shown on the right. The effect on the quiver with potential is a mutation [Reference Derksen, Weyman and Zelevinsky15, §5] at the vertex corresponding to the quadrilateral alternating region (compare to [Reference Vitória49]).
Proposition 4.6. Let D and
![]() $D'$
be Postnikov diagrams related by geometric exchange. Then the boundary algebras
$D'$
be Postnikov diagrams related by geometric exchange. Then the boundary algebras
![]() $B_D$
and
$B_D$
and
![]() $B_{D'}$
are isomorphic, and hence the categories
$B_{D'}$
are isomorphic, and hence the categories
![]() $\operatorname {\mathrm {GP}}(B_D)$
and
$\operatorname {\mathrm {GP}}(B_D)$
and
![]() $\operatorname {\mathrm {GP}}(B_{D'})$
are equivalent.
$\operatorname {\mathrm {GP}}(B_{D'})$
are equivalent.
Proof. This can be proved exactly as in [Reference Baur, King and Marsh2, Prop. 12.2]; while this proposition is stated only for
![]() $(k,n)$
-diagrams, the proof does not use the extra assumption on the strand permutation.
$(k,n)$
-diagrams, the proof does not use the extra assumption on the strand permutation.
Corollary 4.7. Given a Postnikov diagram D, the algebra
![]() $B_D$
is determined up to isomorphism by the positroid
$B_D$
is determined up to isomorphism by the positroid
![]() $\mathcal {P}_D$
.
$\mathcal {P}_D$
.
Proof. Again combining [Reference Postnikov41, Thm. 13.4] and [Reference Postnikov41, Thm. 17.1], any two diagrams determining the same positroid are connected by a sequence of geometric exchanges, so the result follows from Proposition 4.6.
One consequence of the general results in Theorem 4.3 on bimodule internally
![]() $3$
-Calabi–Yau algebras is that the Gorenstein dimension of
$3$
-Calabi–Yau algebras is that the Gorenstein dimension of
![]() $B_D$
is at most
$B_D$
is at most
![]() $3$
for any connected Postnikov diagram D. In fact, this Gorenstein dimension never exceeds
$3$
for any connected Postnikov diagram D. In fact, this Gorenstein dimension never exceeds
![]() $2$
by [Reference Çanakçı, King and Pressland11, Cor. 10.5]. When D is a
$2$
by [Reference Çanakçı, King and Pressland11, Cor. 10.5]. When D is a
![]() $(k,n)$
-diagram,
$(k,n)$
-diagram,
![]() $B_D$
even has Gorenstein dimension
$B_D$
even has Gorenstein dimension
![]() $1$
, as in the proof of [Reference Jensen, King and Su28, Cor. 3.7]. Since
$1$
, as in the proof of [Reference Jensen, King and Su28, Cor. 3.7]. Since
![]() $1$
is also the Krull dimension of
$1$
is also the Krull dimension of
![]() $Z=\mathbb {K}[\hspace {-0.1em}[t]\hspace {-0.1em}]$
, in this case the category
$Z=\mathbb {K}[\hspace {-0.1em}[t]\hspace {-0.1em}]$
, in this case the category
![]() $\operatorname {\mathrm {GP}}(B_D)$
coincides with the category of Cohen–Macaulay
$\operatorname {\mathrm {GP}}(B_D)$
coincides with the category of Cohen–Macaulay
![]() $B_D$
-modules, meaning those
$B_D$
-modules, meaning those
![]() $B_D$
-modules free and finitely generated over Z. However, the Gorenstein dimension of
$B_D$
-modules free and finitely generated over Z. However, the Gorenstein dimension of
![]() $B_D$
can be equal to
$B_D$
can be equal to
![]() $2$
, and the inclusion
$2$
, and the inclusion
![]() $\operatorname {\mathrm {GP}}(B_D)\to \operatorname {\mathrm {CM}}(B_D)$
can be proper, as the following example shows.
$\operatorname {\mathrm {GP}}(B_D)\to \operatorname {\mathrm {CM}}(B_D)$
can be proper, as the following example shows.
Example 4.8. Consider the Postnikov diagram D shown in Figure 8 and its dimer algebra
![]() $A_D$
, the quiver of which is shown in the same figure. Since every alternating region of D is on the boundary (equivalently, every vertex of the quiver is frozen), we have
$A_D$
, the quiver of which is shown in the same figure. Since every alternating region of D is on the boundary (equivalently, every vertex of the quiver is frozen), we have
![]() $B_D=A_D$
, which has finite global dimension by Theorem 3.7. In fact, since the left-most term of
$B_D=A_D$
, which has finite global dimension by Theorem 3.7. In fact, since the left-most term of
![]() $\mathbf {P}(A_D)$
is zero in this case, again because all vertices are frozen, the global dimension of
$\mathbf {P}(A_D)$
is zero in this case, again because all vertices are frozen, the global dimension of
![]() $B_D$
is
$B_D$
is
![]() $2$
.
$2$
.

Figure 8 A Postnikov diagram D of type
![]() $(2,4)$
giving rise to a boundary algebra
$(2,4)$
giving rise to a boundary algebra
![]() $B_D$
for which not all Cohen–Macaulay modules are Gorenstein projective. The right-hand figure shows the quiver
$B_D$
for which not all Cohen–Macaulay modules are Gorenstein projective. The right-hand figure shows the quiver
![]() $Q_D$
, with frozen arrows marked in bold as usual, which is the Gabriel quiver of
$Q_D$
, with frozen arrows marked in bold as usual, which is the Gabriel quiver of
![]() $A_D=B_D$
.
$A_D=B_D$
.
As is the case for any algebra of finite global dimension,
![]() $B_D$
is Iwanaga–Gorenstein (of Gorenstein dimension equal to the global dimension, so in this case
$B_D$
is Iwanaga–Gorenstein (of Gorenstein dimension equal to the global dimension, so in this case
![]() $2$
), and a
$2$
), and a
![]() $B_D$
-module is Gorenstein projective if and only if it is projective. However, one can observe that the radical of the projective
$B_D$
-module is Gorenstein projective if and only if it is projective. However, one can observe that the radical of the projective
![]() $B_D$
-module at the lowest vertex (the head of the unfrozen arrow) is not projective, but it is free and finitely generated over Z: that is, Cohen–Macaulay, since it is a submodule of a projective
$B_D$
-module at the lowest vertex (the head of the unfrozen arrow) is not projective, but it is free and finitely generated over Z: that is, Cohen–Macaulay, since it is a submodule of a projective
![]() $B_D$
-module, which is Cohen–Macaulay by Proposition 2.11. Hence in this case the category of Gorenstein projective modules for
$B_D$
-module, which is Cohen–Macaulay by Proposition 2.11. Hence in this case the category of Gorenstein projective modules for
![]() $B_D$
is a proper subcategory of the category of Cohen–Macaulay modules.
$B_D$
is a proper subcategory of the category of Cohen–Macaulay modules.
5 Loops and
 $2$
-cycles
$2$
-cycles
Let
![]() $B=B_D$
be the boundary algebra of a connected Postnikov diagram D, and let
$B=B_D$
be the boundary algebra of a connected Postnikov diagram D, and let
![]() $T_D=eA_D\in \operatorname {\mathrm {GP}}(B)$
be the cluster-tilting object from Theorem 4.5. In this section, we show that the quiver of
$T_D=eA_D\in \operatorname {\mathrm {GP}}(B)$
be the cluster-tilting object from Theorem 4.5. In this section, we show that the quiver of
![]() $\operatorname {\mathrm {End}}_{B}(T)^{\mathrm {op}}$
has no loops or
$\operatorname {\mathrm {End}}_{B}(T)^{\mathrm {op}}$
has no loops or
![]() $2$
-cycles for any cluster-tilting object
$2$
-cycles for any cluster-tilting object
![]() $T\in \operatorname {\mathrm {GP}}(B)$
mutation equivalent to
$T\in \operatorname {\mathrm {GP}}(B)$
mutation equivalent to
![]() $T_D$
—so far, we know this only for the relatively small number of such objects arising from the Postnikov diagrams related to D by sequences of geometric exchanges. This will allow us to complete the proof of Theorem 1 in the next section by giving us access to results of Fu and Keller [Reference Fu and Keller17]. The statement requires our nondegeneracy assumption that D has at least
$T_D$
—so far, we know this only for the relatively small number of such objects arising from the Postnikov diagrams related to D by sequences of geometric exchanges. This will allow us to complete the proof of Theorem 1 in the next section by giving us access to results of Fu and Keller [Reference Fu and Keller17]. The statement requires our nondegeneracy assumption that D has at least
![]() $3$
strands (compare to [Reference Pressland44, Prop. 5.17]).
$3$
strands (compare to [Reference Pressland44, Prop. 5.17]).
For the remainder of the section, we fix a cluster-tilting object
![]() $T_0\in \operatorname {\mathrm {GP}}(B)$
and write
$T_0\in \operatorname {\mathrm {GP}}(B)$
and write
![]() $A_0=\operatorname {\mathrm {End}}_{B}(T_0)^{\mathrm {op}}$
. We assume that
$A_0=\operatorname {\mathrm {End}}_{B}(T_0)^{\mathrm {op}}$
. We assume that
-
(1)
 $A_0$
is isomorphic to the frozen Jacobian algebra of an ice quiver with potential
$A_0$
is isomorphic to the frozen Jacobian algebra of an ice quiver with potential
 $(Q,F,W)$
in such a way that the vertices of F correspond to projection onto indecomposable projective summands of
$(Q,F,W)$
in such a way that the vertices of F correspond to projection onto indecomposable projective summands of
 $T_0$
,
$T_0$
, -
(2) the quiver Q has no loops or
 $2$
-cycles, and
$2$
-cycles, and -
(3)
 $A_0/\langle e_{i}\rangle $
is finite-dimensional whenever
$A_0/\langle e_{i}\rangle $
is finite-dimensional whenever
 $i\in F_0$
.
$i\in F_0$
.
All of these assumptions hold if
![]() $T_0=eA_D$
is the initial cluster-tilting object from Theorem 4.5—the absence of loops and
$T_0=eA_D$
is the initial cluster-tilting object from Theorem 4.5—the absence of loops and
![]() $2$
-cycles in
$2$
-cycles in
![]() $Q_D$
(after replacing D by a reduced diagram if necessary) follows from Proposition 2.10, and finite-dimensionality in (3) follows from Proposition 2.11 via an exactly analogous argument to that in the proof of Proposition 4.4. Our goal is to show that these properties are preserved by mutations and so hold in the entire mutation class of those cluster-tilting objects coming from Postnikov diagrams.
$Q_D$
(after replacing D by a reduced diagram if necessary) follows from Proposition 2.10, and finite-dimensionality in (3) follows from Proposition 2.11 via an exactly analogous argument to that in the proof of Proposition 4.4. Our goal is to show that these properties are preserved by mutations and so hold in the entire mutation class of those cluster-tilting objects coming from Postnikov diagrams.
With this in mind, we additionally fix for the rest of the section a cluster-tilting object T obtained from
![]() $T_0$
by mutation at a nonprojective indecomposable summand and write
$T_0$
by mutation at a nonprojective indecomposable summand and write
![]() $A=\operatorname {\mathrm {End}}_{B}(T)^{\mathrm {op}}$
. By [Reference Pressland44, Thm. 5.14], the algebra A again satisfies (1), with the required ice quiver with potential being the mutation
$A=\operatorname {\mathrm {End}}_{B}(T)^{\mathrm {op}}$
. By [Reference Pressland44, Thm. 5.14], the algebra A again satisfies (1), with the required ice quiver with potential being the mutation
![]() $\mu _k(Q,F,W)=(Q',F',W')$
at an appropriate vertex k. Thus
$\mu _k(Q,F,W)=(Q',F',W')$
at an appropriate vertex k. Thus
![]() $Q'$
has no loops and no
$Q'$
has no loops and no
![]() $2$
-cycles incident with k, but a priori it may have other
$2$
-cycles incident with k, but a priori it may have other
![]() $2$
-cycles. The algebra A satisfies (3), as the following lemma shows.
$2$
-cycles. The algebra A satisfies (3), as the following lemma shows.
Lemma 5.1. Let
![]() $A_0$
be the frozen Jacobian algebra of an ice quiver with potential
$A_0$
be the frozen Jacobian algebra of an ice quiver with potential
![]() $(Q,F,W)$
, and assume i is a frozen vertex such that
$(Q,F,W)$
, and assume i is a frozen vertex such that
![]() $A_0/\langle e_{i}\rangle $
is finite-dimensional. If A is the frozen Jacobian algebra of
$A_0/\langle e_{i}\rangle $
is finite-dimensional. If A is the frozen Jacobian algebra of
![]() $\mu _k(Q,F,W)$
for some mutable vertex k, then
$\mu _k(Q,F,W)$
for some mutable vertex k, then
![]() $A/\langle e_{i}\rangle $
is again finite-dimensional.
$A/\langle e_{i}\rangle $
is again finite-dimensional.
Proof. Note that the quivers Q and
![]() $\mu _kQ$
have the same set of frozen vertices, so the statement makes sense. It is straightforward to check that
$\mu _kQ$
have the same set of frozen vertices, so the statement makes sense. It is straightforward to check that
![]() $A_0/\langle e_{i}\rangle $
and
$A_0/\langle e_{i}\rangle $
and
![]() $A/\langle e_{i}\rangle $
are, like
$A/\langle e_{i}\rangle $
are, like
![]() $A_0$
and A, frozen Jacobian algebras of ice quivers with potential related by mutation at k. (The required ice quivers with potential are obtained from those of
$A_0$
and A, frozen Jacobian algebras of ice quivers with potential related by mutation at k. (The required ice quivers with potential are obtained from those of
![]() $A_0$
and A by removing the vertex i and all incident arrows from the quiver, and removing from the potential all terms given by cycles through i.) That mutations preserve finite dimensionality of frozen Jacobian algebras follows via a straightforward adaptation of the proof of [Reference Derksen, Weyman and Zelevinsky15, Cor. 6.6] for ordinary Jacobian algebras.
$A_0$
and A by removing the vertex i and all incident arrows from the quiver, and removing from the potential all terms given by cycles through i.) That mutations preserve finite dimensionality of frozen Jacobian algebras follows via a straightforward adaptation of the proof of [Reference Derksen, Weyman and Zelevinsky15, Cor. 6.6] for ordinary Jacobian algebras.
Thus it remains to show that the quiver
![]() $Q'$
has no
$Q'$
has no
![]() $2$
-cycles. We start by showing that
$2$
-cycles. We start by showing that
![]() $A/\langle e_{i}\rangle $
has finite global dimension for any frozen vertex i.
$A/\langle e_{i}\rangle $
has finite global dimension for any frozen vertex i.
Proposition 5.2. Let i be a frozen vertex. Then
![]() $e_{i}Ae_{i}\cong Z$
.
$e_{i}Ae_{i}\cong Z$
.
Proof. Since
![]() $e_{i}$
corresponds to projection onto an indecomposable projective summand
$e_{i}$
corresponds to projection onto an indecomposable projective summand
![]() $P_i$
of T, we have
$P_i$
of T, we have
![]() $e_{i}Ae_{i}=\operatorname {\mathrm {End}}_{B}(P_i)^{\mathrm {op}}$
. Since
$e_{i}Ae_{i}=\operatorname {\mathrm {End}}_{B}(P_i)^{\mathrm {op}}$
. Since
![]() $P_i$
is an indecomposable summand of every cluster-tilting object of
$P_i$
is an indecomposable summand of every cluster-tilting object of
![]() $\operatorname {\mathrm {GP}}(B)$
, including
$\operatorname {\mathrm {GP}}(B)$
, including
![]() $T_D$
, this endomorphism algebra is isomorphic to Z by Proposition 2.11 and Theorem 4.5.
$T_D$
, this endomorphism algebra is isomorphic to Z by Proposition 2.11 and Theorem 4.5.
In the setting of Proposition 5.2, we thus have a recollement

of abelian categories, in which
![]() $\iota $
is the natural inclusion,
$\iota $
is the natural inclusion,
![]() $e_{i}\colon X\mapsto e_{i}X$
and
$e_{i}\colon X\mapsto e_{i}X$
and
![]() $\ell =Ae_{i}\mathbin {\otimes }_Z-$
is left adjoint to
$\ell =Ae_{i}\mathbin {\otimes }_Z-$
is left adjoint to
![]() $e_{i}$
.
$e_{i}$
.
Lemma 5.3. In the recollement in equation (5.1), the functor
![]() $\iota $
is a homological embedding, meaning it induces isomorphisms on all extension groups. As a consequence,
$\iota $
is a homological embedding, meaning it induces isomorphisms on all extension groups. As a consequence,
![]() $\operatorname {\mathrm {gldim}}{A/\langle e_{i}\rangle }\leq \operatorname {\mathrm {gldim}}{A}\leq 3$
.
$\operatorname {\mathrm {gldim}}{A/\langle e_{i}\rangle }\leq \operatorname {\mathrm {gldim}}{A}\leq 3$
.
Proof. We use a result of Psaroudakis [Reference Psaroudakis45, Prop. 4.15], implying that it is enough to check that the image, denoted by
![]() $\mathsf {F}(P)$
in [Reference Psaroudakis45], of the counit
$\mathsf {F}(P)$
in [Reference Psaroudakis45], of the counit
is projective for all projective
![]() $P\in \operatorname {\mathrm {mod}}{A}$
. We may write
$P\in \operatorname {\mathrm {mod}}{A}$
. We may write
![]() $P=\operatorname {\mathrm {Hom}}_{B}(T,T')$
for
$P=\operatorname {\mathrm {Hom}}_{B}(T,T')$
for
![]() $T'\in \operatorname {\mathrm {add}}{T}\subseteq \operatorname {\mathrm {GP}}(B)\subseteq \operatorname {\mathrm {CM}}(B)$
so that
$T'\in \operatorname {\mathrm {add}}{T}\subseteq \operatorname {\mathrm {GP}}(B)\subseteq \operatorname {\mathrm {CM}}(B)$
so that
![]() $e_{i}P=\operatorname {\mathrm {Hom}}_B(P_i,T')$
is a free Z-module. Thus
$e_{i}P=\operatorname {\mathrm {Hom}}_B(P_i,T')$
is a free Z-module. Thus
![]() $Ae_{i}\mathbin {\otimes }_Ze_{i}P\cong (Ae_{i})^n$
, where n is the rank of the Z-module
$Ae_{i}\mathbin {\otimes }_Ze_{i}P\cong (Ae_{i})^n$
, where n is the rank of the Z-module
![]() $e_{i}P$
, is projective. We claim that the counit
$e_{i}P$
, is projective. We claim that the counit
![]() $\varepsilon $
is injective so that its image is isomorphic to the projective module
$\varepsilon $
is injective so that its image is isomorphic to the projective module
![]() $(Ae_{i})^n$
.
$(Ae_{i})^n$
.
To see this, observe that
![]() $Ae_{i}\mathbin {\otimes }_Ze_{i}P\cong (Ae_{i})^n$
and P are Cohen–Macaulay A-modules—that is, they are free and finitely generated over Z—so this property is inherited by the kernel K of
$Ae_{i}\mathbin {\otimes }_Ze_{i}P\cong (Ae_{i})^n$
and P are Cohen–Macaulay A-modules—that is, they are free and finitely generated over Z—so this property is inherited by the kernel K of
![]() $\varepsilon $
. On the other hand,
$\varepsilon $
. On the other hand,
![]() $e_{i}\varepsilon \colon e_{i}Ae_{i}\mathbin {\otimes }_Z e_{i}P\to e_{i}P$
is an isomorphism by Proposition 5.2, so
$e_{i}\varepsilon \colon e_{i}Ae_{i}\mathbin {\otimes }_Z e_{i}P\to e_{i}P$
is an isomorphism by Proposition 5.2, so
![]() $e_{i}K=0$
. Thus K is a finitely generated
$e_{i}K=0$
. Thus K is a finitely generated
![]() $A/\langle e_{i}\rangle $
-module and hence finite-dimensional by Lemma 5.1. Since the only finite-dimensional Cohen–Macaulay A-module is
$A/\langle e_{i}\rangle $
-module and hence finite-dimensional by Lemma 5.1. Since the only finite-dimensional Cohen–Macaulay A-module is
![]() $0$
, we have the result.
$0$
, we have the result.
Having established that
![]() $\iota $
is a homological embedding, it is then immediate that
$\iota $
is a homological embedding, it is then immediate that
![]() $\operatorname {\mathrm {gldim}}{A/\langle e_{i}\rangle }\leq \operatorname {\mathrm {gldim}}{A}$
. That
$\operatorname {\mathrm {gldim}}{A/\langle e_{i}\rangle }\leq \operatorname {\mathrm {gldim}}{A}$
. That
![]() $\operatorname {\mathrm {gldim}}{A}\leq 3$
is a consequence of [Reference Pressland43, Prop. 3.7], since A is the endomorphism algebra of the (
$\operatorname {\mathrm {gldim}}{A}\leq 3$
is a consequence of [Reference Pressland43, Prop. 3.7], since A is the endomorphism algebra of the (
![]() $2$
-)cluster-tilting object
$2$
-)cluster-tilting object
![]() $T\in \operatorname {\mathrm {GP}}(B)$
, and
$T\in \operatorname {\mathrm {GP}}(B)$
, and
![]() $\operatorname {\mathrm {GP}}(B)\subseteq \operatorname {\mathrm {mod}}(B)$
is the category of third syzygy modules since B has Gorenstein dimension at most
$\operatorname {\mathrm {GP}}(B)\subseteq \operatorname {\mathrm {mod}}(B)$
is the category of third syzygy modules since B has Gorenstein dimension at most
![]() $3$
by Theorem 4.5(1).
$3$
by Theorem 4.5(1).
Proposition 5.4. Let
![]() $J=\mathcal {J}(Q,F,W)$
be the frozen Jacobian algebra of a reduced ice quiver with potential
$J=\mathcal {J}(Q,F,W)$
be the frozen Jacobian algebra of a reduced ice quiver with potential
![]() $(Q,F,W)$
. If J is finite-dimensional and
$(Q,F,W)$
. If J is finite-dimensional and
![]() $\operatorname {\mathrm {gldim}}{J}<\infty $
, then Q has no loops or
$\operatorname {\mathrm {gldim}}{J}<\infty $
, then Q has no loops or
![]() $2$
-cycles.
$2$
-cycles.
Proof. Since
![]() $(Q,F,W)$
is reduced, Q is the Gabriel quiver of J [Reference Pressland44, Rem. 3.4]. That Q has no loops then follows from the no-loops theorem [Reference Igusa24, Reference Lenzing35], without using that J is a frozen Jacobian algebra. However, this latter assumption means that for each
$(Q,F,W)$
is reduced, Q is the Gabriel quiver of J [Reference Pressland44, Rem. 3.4]. That Q has no loops then follows from the no-loops theorem [Reference Igusa24, Reference Lenzing35], without using that J is a frozen Jacobian algebra. However, this latter assumption means that for each
![]() $i\in Q_0$
, there is an exact sequence
$i\in Q_0$
, there is an exact sequence
 $$\begin{align*}\bigoplus_{b\in\mathrm{H}_{i}^{\mathrm{m}}}Je_{tb}\to\bigoplus_{a\in\mathrm{T}_{i}}Je_{ha}\to Je_{i}\to S_i\to 0\end{align*}$$
$$\begin{align*}\bigoplus_{b\in\mathrm{H}_{i}^{\mathrm{m}}}Je_{tb}\to\bigoplus_{a\in\mathrm{T}_{i}}Je_{ha}\to Je_{i}\to S_i\to 0\end{align*}$$
for
![]() $S_i=Je_{i}/\operatorname {rad}(J)e_{i}$
, the simple J-module supported at vertex i, and this sequence is the start of a projective resolution of
$S_i=Je_{i}/\operatorname {rad}(J)e_{i}$
, the simple J-module supported at vertex i, and this sequence is the start of a projective resolution of
![]() $S_i$
[Reference Buan, Iyama, Reiten and Smith6, Prop. 3.3(b)]. Since Q has no loops,
$S_i$
[Reference Buan, Iyama, Reiten and Smith6, Prop. 3.3(b)]. Since Q has no loops,
![]() $tb\ne i$
for all
$tb\ne i$
for all
![]() $b\in \mathrm {H}_{i}^{\mathrm {m}}$
, so
$b\in \mathrm {H}_{i}^{\mathrm {m}}$
, so
 $$\begin{align*}\operatorname{\mathrm{Hom}}_J\Bigg(\bigoplus_{b\in\mathrm{H}_{i}^{\mathrm{m}}}Je_{tb},S_i\Bigg)=0.\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Hom}}_J\Bigg(\bigoplus_{b\in\mathrm{H}_{i}^{\mathrm{m}}}Je_{tb},S_i\Bigg)=0.\end{align*}$$
It follows that
![]() $\operatorname {\mathrm {Ext}}^2_J(S_i,S_i)$
, which is a subquotient of this space, is also zero. That Q has no
$\operatorname {\mathrm {Ext}}^2_J(S_i,S_i)$
, which is a subquotient of this space, is also zero. That Q has no
![]() $2$
-cycles then follows from [Reference Geiß, Leclerc and Schröer20, Prop. 3.11].
$2$
-cycles then follows from [Reference Geiß, Leclerc and Schröer20, Prop. 3.11].
We now return to
![]() $A=\operatorname {\mathrm {End}}_B(T)^{\mathrm {op}}$
for T obtained from
$A=\operatorname {\mathrm {End}}_B(T)^{\mathrm {op}}$
for T obtained from
![]() $T_0$
by a mutation at a nonprojective indecomposable summand. Recall that
$T_0$
by a mutation at a nonprojective indecomposable summand. Recall that
![]() $A\cong \mathcal {J}(Q',F',W')$
, where
$A\cong \mathcal {J}(Q',F',W')$
, where
![]() $(Q',F',W')$
is obtained by mutation from
$(Q',F',W')$
is obtained by mutation from
![]() $(Q,F,W)$
and is thus reduced by definition.
$(Q,F,W)$
and is thus reduced by definition.
Proposition 5.5. The quiver
![]() $Q'$
has no
$Q'$
has no
![]() $2$
-cycles.
$2$
-cycles.
Proof. Let i be a frozen vertex and
![]() $e_{i}\in A$
the corresponding idempotent. As in the proof of Lemma 5.1, the algebra
$e_{i}\in A$
the corresponding idempotent. As in the proof of Lemma 5.1, the algebra
![]() $A/\langle e_{i}\rangle $
is again a frozen Jacobian algebra. It is finite-dimensional by the same lemma and has finite global dimension by Lemma 5.3. Thus by Proposition 5.4, its quiver has no
$A/\langle e_{i}\rangle $
is again a frozen Jacobian algebra. It is finite-dimensional by the same lemma and has finite global dimension by Lemma 5.3. Thus by Proposition 5.4, its quiver has no
![]() $2$
-cycles. Since this quiver is obtained from
$2$
-cycles. Since this quiver is obtained from
![]() $Q'$
by deleting the vertex i and all incident arrows, there are no
$Q'$
by deleting the vertex i and all incident arrows, there are no
![]() $2$
-cycles in
$2$
-cycles in
![]() $Q'$
incident with i. Since D has at least
$Q'$
incident with i. Since D has at least
![]() $3$
boundary regions,
$3$
boundary regions,
![]() $Q'$
has at least three frozen vertices, and by repeating this process we rule out
$Q'$
has at least three frozen vertices, and by repeating this process we rule out
![]() $2$
-cycles in
$2$
-cycles in
![]() $Q'$
altogether.
$Q'$
altogether.
Remark 5.6. Our standing assumption that Postnikov diagrams have at least
![]() $3$
strands is only used here to rule out loops and
$3$
strands is only used here to rule out loops and
![]() $2$
-cycles incident only with frozen vertices. It is not needed to rule out loops and
$2$
-cycles incident only with frozen vertices. It is not needed to rule out loops and
![]() $2$
-cycles incident with mutable vertices—indeed, if there are fewer than
$2$
-cycles incident with mutable vertices—indeed, if there are fewer than
![]() $3$
strands, there are no mutable vertices anyway.
$3$
strands, there are no mutable vertices anyway.
We sum up our arguments in the following theorem.
Theorem 5.7. Let D be a reduced and connected Postnikov diagram. Let B be the boundary algebra of D, and let
![]() $T_D\in \operatorname {\mathrm {GP}}(B)$
be the initial cluster-tilting object from Theorem 4.5. If
$T_D\in \operatorname {\mathrm {GP}}(B)$
be the initial cluster-tilting object from Theorem 4.5. If
![]() $T\in \operatorname {\mathrm {GP}}(B)$
is a cluster-tilting object obtained from
$T\in \operatorname {\mathrm {GP}}(B)$
is a cluster-tilting object obtained from
![]() $T_D$
by a sequence of mutations, then
$T_D$
by a sequence of mutations, then
![]() $\operatorname {\mathrm {End}}_{B}(T)^{\mathrm {op}}$
is isomorphic to the frozen Jacobian algebra of an ice quiver with potential
$\operatorname {\mathrm {End}}_{B}(T)^{\mathrm {op}}$
is isomorphic to the frozen Jacobian algebra of an ice quiver with potential
![]() $(Q,F,W)$
such that Q has no loops and no
$(Q,F,W)$
such that Q has no loops and no
![]() $2$
-cycles.
$2$
-cycles.
Proof. The results of this section show that the desired properties of T are preserved by mutations. Since they hold in the case
![]() $T=T_D$
by Theorem 4.5—reducedness of D implying that
$T=T_D$
by Theorem 4.5—reducedness of D implying that
![]() $Q_D$
has no loops or
$Q_D$
has no loops or
![]() $2$
-cycles—we obtain the result by induction.
$2$
-cycles—we obtain the result by induction.
6 Cluster structures and cluster characters
In this section, we recall definitions and results of Buan–Iyama–Reiten–Scott [Reference Buan, Iyama, Reiten and Scott5] and Fu–Keller [Reference Fu and Keller17] on cluster structures and cluster characters. For our applications here, we need to weaken some definitions slightly, since the conclusions of Theorem 5.7 hold only for one mutation class of cluster-tilting objects in the category
![]() $\operatorname {\mathrm {GP}}(B_D)$
for a suitable Postnikov diagram D, whereas the original definition of a cluster structure requires these properties for all cluster-tilting objects. However, we will see in this section that (unsurprisingly) Fu–Keller’s cluster character [Reference Fu and Keller17] still provides a bijection between the cluster-tilting objects in this mutation class and the clusters of
$\operatorname {\mathrm {GP}}(B_D)$
for a suitable Postnikov diagram D, whereas the original definition of a cluster structure requires these properties for all cluster-tilting objects. However, we will see in this section that (unsurprisingly) Fu–Keller’s cluster character [Reference Fu and Keller17] still provides a bijection between the cluster-tilting objects in this mutation class and the clusters of
![]() $\mathscr {A}_{D}$
, and between their indecomposable summands and the cluster variables of
$\mathscr {A}_{D}$
, and between their indecomposable summands and the cluster variables of
![]() $\mathscr {A}_{D}$
.
$\mathscr {A}_{D}$
.
All categories in this section are assumed to be
![]() $\mathbb {K}$
-linear for a field
$\mathbb {K}$
-linear for a field
![]() $\mathbb {K}$
, which is of characteristic zero (as above) and now additionally algebraically closed. Note that the category
$\mathbb {K}$
, which is of characteristic zero (as above) and now additionally algebraically closed. Note that the category
![]() $\operatorname {\mathrm {GP}}(B_D)$
constructed above from a Postnikov diagram has this property for
$\operatorname {\mathrm {GP}}(B_D)$
constructed above from a Postnikov diagram has this property for
![]() $\mathbb {K}$
the field over which the dimer algebra is defined.
$\mathbb {K}$
the field over which the dimer algebra is defined.
Definition 6.1. Let
![]() $\mathcal {E}$
be a Krull–Schmidt category, and let
$\mathcal {E}$
be a Krull–Schmidt category, and let
![]() $\mathcal {T}\subseteq \mathcal {E}$
be a full and additively closed subcategory. The quiver
$\mathcal {T}\subseteq \mathcal {E}$
be a full and additively closed subcategory. The quiver
![]() $Q(\mathcal {T}\kern1.5pt)$
has vertices given by the set
$Q(\mathcal {T}\kern1.5pt)$
has vertices given by the set
![]() $\operatorname {\mathrm {indec}}{\mathcal {T}}$
of isomorphism classes of indecomposable objects in
$\operatorname {\mathrm {indec}}{\mathcal {T}}$
of isomorphism classes of indecomposable objects in
![]() $\mathcal {T}$
, and
$\mathcal {T}$
, and
![]() $\dim (\operatorname {\mathrm {Rad}}_{\mathcal {T}}(T,U)/\operatorname {\mathrm {Rad}}^2_{\mathcal {T}}(T,U))$
arrows from U to T for each
$\dim (\operatorname {\mathrm {Rad}}_{\mathcal {T}}(T,U)/\operatorname {\mathrm {Rad}}^2_{\mathcal {T}}(T,U))$
arrows from U to T for each
![]() $T,U\in \operatorname {\mathrm {indec}}{\mathcal {T}}$
. Here
$T,U\in \operatorname {\mathrm {indec}}{\mathcal {T}}$
. Here
![]() $\operatorname {\mathrm {Rad}}_{\mathcal {T}}(T,U)$
consists of nonisomorphisms
$\operatorname {\mathrm {Rad}}_{\mathcal {T}}(T,U)$
consists of nonisomorphisms
![]() $T\to U$
, and
$T\to U$
, and
![]() $\operatorname {\mathrm {Rad}}_{\mathcal {T}}^2(T,U)$
is the subspace consisting of those expressible as a composition
$\operatorname {\mathrm {Rad}}_{\mathcal {T}}^2(T,U)$
is the subspace consisting of those expressible as a composition
![]() $T\stackrel {f}{\longrightarrow } V\stackrel {g}{\longrightarrow } U$
, where f is not a split monomorphism, g is not a split epimorphism and
$T\stackrel {f}{\longrightarrow } V\stackrel {g}{\longrightarrow } U$
, where f is not a split monomorphism, g is not a split epimorphism and
![]() $V\in \mathcal {T}$
. We treat
$V\in \mathcal {T}$
. We treat
![]() $Q(\mathcal {T}\kern1.5pt)$
as an ice quiver whose frozen vertices are those corresponding to indecomposable projective objects of
$Q(\mathcal {T}\kern1.5pt)$
as an ice quiver whose frozen vertices are those corresponding to indecomposable projective objects of
![]() $\mathcal {E}$
, which lie in
$\mathcal {E}$
, which lie in
![]() $\mathcal {T}$
.
$\mathcal {T}$
.
If
![]() $T\in \mathcal {E}$
is an object, we write
$T\in \mathcal {E}$
is an object, we write
![]() $Q(T):=Q(\operatorname {\mathrm {add}}{T})$
, noting that this is the ordinary quiver of the semi-perfect algebra
$Q(T):=Q(\operatorname {\mathrm {add}}{T})$
, noting that this is the ordinary quiver of the semi-perfect algebra
![]() $\operatorname {\mathrm {End}}_{\mathcal {E}}(T)^{\mathrm {op}}$
.
$\operatorname {\mathrm {End}}_{\mathcal {E}}(T)^{\mathrm {op}}$
.
Definition 6.2 (compare to [Reference Buan, Iyama, Reiten and Scott5, §II.1], [Reference Fu and Keller17, Def. 2.4])
Let
![]() $\mathcal {E}$
be a Krull–Schmidt stably
$\mathcal {E}$
be a Krull–Schmidt stably
![]() $2$
-Calabi–Yau Frobenius category, and let
$2$
-Calabi–Yau Frobenius category, and let
![]() $\mathcal {T}_0\subseteq \mathcal {E}$
be a cluster-tilting subcategory. We say that
$\mathcal {T}_0\subseteq \mathcal {E}$
be a cluster-tilting subcategory. We say that
![]() $(\mathcal {E},\mathcal {T}_0)$
has a cluster structure if
$(\mathcal {E},\mathcal {T}_0)$
has a cluster structure if
-
(1) for each cluster-tilting subcategory
 $\mathcal {T}$
of
$\mathcal {T}$
of
 $\mathcal {E}$
and each nonprojective indecomposable
$\mathcal {E}$
and each nonprojective indecomposable
 $X\in \mathcal {T}$
, there is a nonprojective indecomposable object
$X\in \mathcal {T}$
, there is a nonprojective indecomposable object
 $X^*$
, unique up to isomorphism, such that the full and additively closed subcategory
$X^*$
, unique up to isomorphism, such that the full and additively closed subcategory
 $\mathcal {T}'=\mu _X\mathcal {T}$
, called the mutation of
$\mathcal {T}'=\mu _X\mathcal {T}$
, called the mutation of
 $\mathcal {T}$
at X and having indecomposable objects is cluster-tilting;
$\mathcal {T}$
at X and having indecomposable objects is cluster-tilting; $$\begin{align*}\operatorname{\mathrm{indec}}{\mathcal{T}'}=\operatorname{\mathrm{indec}}{\mathcal{T}}\setminus\{X\}\cup\{X^*\},\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{indec}}{\mathcal{T}'}=\operatorname{\mathrm{indec}}{\mathcal{T}}\setminus\{X\}\cup\{X^*\},\end{align*}$$
-
(2) in the situation of (1), there are short exact sequences
in which the nonzero maps are minimal
 $(\mathcal {T}\cap \mathcal {T}')$
-approximations (on the left or the right as appropriate);
$(\mathcal {T}\cap \mathcal {T}')$
-approximations (on the left or the right as appropriate);
-
(3) for any cluster-tilting subcategory
 $\mathcal {T}$
in the mutation class of
$\mathcal {T}$
in the mutation class of
 $\mathcal {T}_0$
(i.e., related to
$\mathcal {T}_0$
(i.e., related to
 $\mathcal {T}_0$
by a sequence of mutations as in (1)), the quiver
$\mathcal {T}_0$
by a sequence of mutations as in (1)), the quiver
 $Q(\mathcal {T}\kern1.5pt)$
has no loops or
$Q(\mathcal {T}\kern1.5pt)$
has no loops or
 $2$
-cycles; and
$2$
-cycles; and -
(4) for
 $\mathcal {T}$
as in (3) and
$\mathcal {T}$
as in (3) and
 $X\in \mathcal {T}$
nonprojective, the quiver
$X\in \mathcal {T}$
nonprojective, the quiver
 $Q(\mu _X\mathcal {T}\kern1.5pt)$
agrees, up to arrows between frozen vertices, with the Fomin–Zelevinsky mutation
$Q(\mu _X\mathcal {T}\kern1.5pt)$
agrees, up to arrows between frozen vertices, with the Fomin–Zelevinsky mutation
 $\mu _XQ(\mathcal {T}\kern1.5pt)$
.
$\mu _XQ(\mathcal {T}\kern1.5pt)$
.
If
![]() $T_0$
is a cluster-tilting object, then the additive closure
$T_0$
is a cluster-tilting object, then the additive closure
![]() $\operatorname {\mathrm {add}}{T_0}$
is a cluster-tilting subcategory, and we say that
$\operatorname {\mathrm {add}}{T_0}$
is a cluster-tilting subcategory, and we say that
![]() $(\mathcal {E},T_0)$
has a cluster structure if
$(\mathcal {E},T_0)$
has a cluster structure if
![]() $(\mathcal {E},\operatorname {\mathrm {add}}{T_0})$
does. Cluster-tilting subcategories
$(\mathcal {E},\operatorname {\mathrm {add}}{T_0})$
does. Cluster-tilting subcategories
![]() $\mathcal {T}$
in the mutation class of
$\mathcal {T}$
in the mutation class of
![]() $\mathcal {T}_0$
, and their objects, are said to be reachable from
$\mathcal {T}_0$
, and their objects, are said to be reachable from
![]() $\mathcal {T}_0$
.
$\mathcal {T}_0$
.
Under our assumptions on
![]() $\mathcal {E}$
, conditions (1) and (2) of this definition are automatic by [Reference Buan, Iyama, Reiten and Scott5, Thm. II.1.10(a)] (see also [Reference Iyama and Yoshino26, Thms. 5.1, 5.3]), but we include them in the definition anyway to aid comparison with [Reference Buan, Iyama, Reiten and Scott5].
$\mathcal {E}$
, conditions (1) and (2) of this definition are automatic by [Reference Buan, Iyama, Reiten and Scott5, Thm. II.1.10(a)] (see also [Reference Iyama and Yoshino26, Thms. 5.1, 5.3]), but we include them in the definition anyway to aid comparison with [Reference Buan, Iyama, Reiten and Scott5].
Remark 6.3. In making Definition 6.2, we follow [Reference Fu and Keller17], weakening conditions (3) and (4) to restrict to a single mutation class of cluster-tilting subcategories. Thus
![]() $\mathcal {E}$
has a cluster structure, in the sense of [Reference Fu and Keller17, Def. 2.4], if and only if
$\mathcal {E}$
has a cluster structure, in the sense of [Reference Fu and Keller17, Def. 2.4], if and only if
![]() $\mathcal {E}$
has a cluster-tilting subcategory and
$\mathcal {E}$
has a cluster-tilting subcategory and
![]() $(\mathcal {E},\mathcal {T}\kern1.5pt)$
has a cluster structure for all such subcategories
$(\mathcal {E},\mathcal {T}\kern1.5pt)$
has a cluster structure for all such subcategories
![]() $\mathcal {T}$
. In principle, one could weaken conditions (1) and (2) in a similar way, but this seems to be less useful since these conditions are known to hold as stated in wide generality. The original definition from [Reference Buan, Iyama, Reiten and Scott5] applies to a larger class of categories, but we will not need this generality here.
$\mathcal {T}$
. In principle, one could weaken conditions (1) and (2) in a similar way, but this seems to be less useful since these conditions are known to hold as stated in wide generality. The original definition from [Reference Buan, Iyama, Reiten and Scott5] applies to a larger class of categories, but we will not need this generality here.
Lemma 6.4. Assume that
![]() $(\mathcal {E},\mathcal {T}_0)$
has a cluster structure. If
$(\mathcal {E},\mathcal {T}_0)$
has a cluster structure. If
![]() $\mathcal {T}$
is reachable, and
$\mathcal {T}$
is reachable, and
![]() $X\in \mathcal {T}$
is indecomposable and nonprojective, then the object
$X\in \mathcal {T}$
is indecomposable and nonprojective, then the object
![]() $X^*$
as in Definition 6.2(1) satisfies
$X^*$
as in Definition 6.2(1) satisfies
and the exact sequences in Definition 6.2(2) are not split. Moreover, if we write
![]() $B(X,Y)$
for the number of arrows
$B(X,Y)$
for the number of arrows
![]() $X\to Y$
in
$X\to Y$
in
![]() $Q(\mathcal {T}\kern1.5pt)$
, the middle terms of the exact sequences in Definition 6.2(2) are
$Q(\mathcal {T}\kern1.5pt)$
, the middle terms of the exact sequences in Definition 6.2(2) are
Proof. This is proved in exactly the same way as [Reference Fu and Keller17, Lem. 2.2] (in particular, using the assumption that
![]() $\mathbb {K}$
is algebraically closed), noting that
$\mathbb {K}$
is algebraically closed), noting that
![]() $Q(\mathcal {T}\kern1.5pt)$
has no loops by Definition 6.2(3) and the assumption that
$Q(\mathcal {T}\kern1.5pt)$
has no loops by Definition 6.2(3) and the assumption that
![]() $\mathcal {T}$
is reachable.
$\mathcal {T}$
is reachable.
Definition 6.5 (compare to [Reference Fu and Keller17, Def. 3.1])
Let
![]() $\mathcal {E}$
be a Krull–Schmidt stably
$\mathcal {E}$
be a Krull–Schmidt stably
![]() $2$
-Calabi–Yau Frobenius category, and let R be a commutative ring. A cluster character is a map
$2$
-Calabi–Yau Frobenius category, and let R be a commutative ring. A cluster character is a map
![]() $\Phi \colon \operatorname {\mathrm {Ob}}(\mathcal {E})\to R$
such that
$\Phi \colon \operatorname {\mathrm {Ob}}(\mathcal {E})\to R$
such that
-
(1) if
 $X\cong X'$
, then
$X\cong X'$
, then
 $\Phi (X)=\Phi (X')$
,
$\Phi (X)=\Phi (X')$
, -
(2) we have
 $\Phi (X\oplus Y)=\Phi (X)\Phi (Y)$
for all
$\Phi (X\oplus Y)=\Phi (X)\Phi (Y)$
for all
 $X,Y\in \operatorname {\mathrm {Ob}}(\mathcal {E})$
, and
$X,Y\in \operatorname {\mathrm {Ob}}(\mathcal {E})$
, and -
(3) if
 $X,Y\in \operatorname {\mathrm {Ob}}(\mathcal {E})$
satisfy
$X,Y\in \operatorname {\mathrm {Ob}}(\mathcal {E})$
satisfy
 $\dim \operatorname {\mathrm {Ext}}^1_{\mathcal {E}}(X,Y)=1$
(and hence
$\dim \operatorname {\mathrm {Ext}}^1_{\mathcal {E}}(X,Y)=1$
(and hence
 $\dim \operatorname {\mathrm {Ext}}^1_{\mathcal {E}}(Y,X)=1$
by the Calabi–Yau property) and are nonsplit sequences, then
$\dim \operatorname {\mathrm {Ext}}^1_{\mathcal {E}}(Y,X)=1$
by the Calabi–Yau property) and are nonsplit sequences, then
 $$\begin{align*}\Phi(X)\Phi(Y)=\Phi(E^+)+\Phi(E^-).\end{align*}$$
$$\begin{align*}\Phi(X)\Phi(Y)=\Phi(E^+)+\Phi(E^-).\end{align*}$$
Below, we will often employ a standard abuse of notation and write
![]() $\Phi \colon \mathcal {E}\to R$
.
$\Phi \colon \mathcal {E}\to R$
.
The next definition is due to Fu and Keller [Reference Fu and Keller17], following Palu [Reference Palu40] and Caldero–Chapoton [Reference Caldero and Chapoton10] for triangulated categories, and describes a standard cluster character on a suitable Frobenius category with a cluster-tilting object.
Definition 6.6 (compare to [Reference Fu and Keller17, Rem. 3.5])
Let
![]() $\mathcal {E}$
be a Krull–Schmidt stably
$\mathcal {E}$
be a Krull–Schmidt stably
![]() $2$
-Calabi–Yau Frobenius category. Assume
$2$
-Calabi–Yau Frobenius category. Assume
![]() $T\in \mathcal {E}$
is a cluster-tilting object such that
$T\in \mathcal {E}$
is a cluster-tilting object such that
![]() $A=\operatorname {\mathrm {End}}_{\mathcal {E}}(T)^{\mathrm {op}}$
is a Noetherian algebra of finite global dimension. The stable endomorphism algebra
$A=\operatorname {\mathrm {End}}_{\mathcal {E}}(T)^{\mathrm {op}}$
is a Noetherian algebra of finite global dimension. The stable endomorphism algebra
![]() $\underline {A}=\operatorname {\mathrm {\underline {End}}}_{\mathcal {E}}(T)^{\mathrm {op}}$
is finite-dimensional since
$\underline {A}=\operatorname {\mathrm {\underline {End}}}_{\mathcal {E}}(T)^{\mathrm {op}}$
is finite-dimensional since
![]() $\mathcal {E}$
is stably
$\mathcal {E}$
is stably
![]() $2$
-Calabi–Yau, and we view
$2$
-Calabi–Yau, and we view
![]() $\operatorname {\mathrm {mod}}{\underline {A}}$
as a subcategory of
$\operatorname {\mathrm {mod}}{\underline {A}}$
as a subcategory of
![]() $\operatorname {\mathrm {mod}}{A}$
via the quotient map. Writing
$\operatorname {\mathrm {mod}}{A}$
via the quotient map. Writing
 $$ \begin{align*} F&=\operatorname{\mathrm{Hom}}_{\mathcal{E}}(T,-)\colon\mathcal{E}\to\operatorname{\mathrm{mod}} A,\\ G&=\operatorname{\mathrm{Ext}}^1_{\mathcal{E}}(T,-)\colon\mathcal{E}\to\operatorname{\mathrm{mod}}\underline{A}, \end{align*} $$
$$ \begin{align*} F&=\operatorname{\mathrm{Hom}}_{\mathcal{E}}(T,-)\colon\mathcal{E}\to\operatorname{\mathrm{mod}} A,\\ G&=\operatorname{\mathrm{Ext}}^1_{\mathcal{E}}(T,-)\colon\mathcal{E}\to\operatorname{\mathrm{mod}}\underline{A}, \end{align*} $$
we define, for each
![]() $X\in \mathcal {E}$
,
$X\in \mathcal {E}$
,
Here the sum is taken over possible dimension vectors d of
![]() $\underline {A}$
-modules,
$\underline {A}$
-modules,
![]() $\mathrm {Gr}_{e}(GX)$
denotes the Grassmannian of submodules of
$\mathrm {Gr}_{e}(GX)$
denotes the Grassmannian of submodules of
![]() $GX$
of dimension vector d, and
$GX$
of dimension vector d, and
![]() $\chi $
denotes the Euler characteristic. Moreover,
$\chi $
denotes the Euler characteristic. Moreover,
![]() $[M]$
denotes the class of an A-module M in the Grothendieck group
$[M]$
denotes the class of an A-module M in the Grothendieck group
![]() $\mathrm {K}_0(\operatorname {\mathrm {per}}{A})=\mathrm {K}_0(\operatorname {\mathrm {mod}}{A})$
, and
$\mathrm {K}_0(\operatorname {\mathrm {per}}{A})=\mathrm {K}_0(\operatorname {\mathrm {mod}}{A})$
, and
![]() $[d]=[N]\in \mathrm {K}_0(\operatorname {\mathrm {per}}{A})$
for any module N of dimension vector d, this class being independent of the choice of N as in the proof of [Reference Fu and Keller17, Prop. 3.2].
$[d]=[N]\in \mathrm {K}_0(\operatorname {\mathrm {per}}{A})$
for any module N of dimension vector d, this class being independent of the choice of N as in the proof of [Reference Fu and Keller17, Prop. 3.2].
Remark 6.7. We may assume T is basic and choose a decomposition
![]() $T=\bigoplus _{i=1}^nT_i$
of T into indecomposable direct summands. This yields a basis (strictly speaking, a free generating set)
$T=\bigoplus _{i=1}^nT_i$
of T into indecomposable direct summands. This yields a basis (strictly speaking, a free generating set)
![]() $[P_i]=[FT_i]$
of
$[P_i]=[FT_i]$
of
![]() $\mathrm {K}_0(\operatorname {\mathrm {per}}{A})$
consisting of the classes of indecomposable projective A-modules and allows us to write
$\mathrm {K}_0(\operatorname {\mathrm {per}}{A})$
consisting of the classes of indecomposable projective A-modules and allows us to write
![]() $\varphi ^{T}(X)$
as a Laurent polynomial in the variables
$\varphi ^{T}(X)$
as a Laurent polynomial in the variables
![]() $x_i=x^{[P_i]}$
. Since
$x_i=x^{[P_i]}$
. Since
![]() $GT_i=0$
, it follows immediately that
$GT_i=0$
, it follows immediately that
![]() $\varphi ^{T}(T_i)=x_i$
. This preference for the basis of indecomposable projectives is why we usually write
$\varphi ^{T}(T_i)=x_i$
. This preference for the basis of indecomposable projectives is why we usually write
![]() $\mathrm {K}_0(\operatorname {\mathrm {per}}{A})$
instead of
$\mathrm {K}_0(\operatorname {\mathrm {per}}{A})$
instead of
![]() $\mathrm {K}_0(\operatorname {\mathrm {mod}}{A})$
for the lattice of exponents.
$\mathrm {K}_0(\operatorname {\mathrm {mod}}{A})$
for the lattice of exponents.
However, thinking instead in terms of
![]() $\mathrm {K}_0(\operatorname {\mathrm {mod}}{A})$
, we may use the nondegenerate Euler pairing
$\mathrm {K}_0(\operatorname {\mathrm {mod}}{A})$
, we may use the nondegenerate Euler pairing
 $$\begin{align*}\mathrm{K}_0(\operatorname{\mathrm{mod}}{A})\times\mathrm{K}_0(\operatorname{\mathrm{fd}}{A})\to\mathbb{Z}:([M],[N])\mapsto\langle M,N\rangle:=\sum_{j\geq0}\dim\operatorname{\mathrm{Ext}}^j_A(M,N)\end{align*}$$
$$\begin{align*}\mathrm{K}_0(\operatorname{\mathrm{mod}}{A})\times\mathrm{K}_0(\operatorname{\mathrm{fd}}{A})\to\mathbb{Z}:([M],[N])\mapsto\langle M,N\rangle:=\sum_{j\geq0}\dim\operatorname{\mathrm{Ext}}^j_A(M,N)\end{align*}$$
between the Grothendieck groups of finitely generated and finite-dimensional A-modules, well-defined since A has finite global dimension. This pairing exhibits the classes of simple modules
![]() $S_i=FT_i/\operatorname {\mathrm {Rad}}_{\mathcal {E}}(T,T_i)$
as a basis of
$S_i=FT_i/\operatorname {\mathrm {Rad}}_{\mathcal {E}}(T,T_i)$
as a basis of
![]() $\mathrm {K}_0(\operatorname {\mathrm {fd}}{A})$
dual to the basis of
$\mathrm {K}_0(\operatorname {\mathrm {fd}}{A})$
dual to the basis of
![]() $\mathrm {K}_0(\operatorname {\mathrm {mod}}{A})=\mathrm {K}_0(\operatorname {\mathrm {per}}{A})$
given by the classes of indecomposable projectives
$\mathrm {K}_0(\operatorname {\mathrm {mod}}{A})=\mathrm {K}_0(\operatorname {\mathrm {per}}{A})$
given by the classes of indecomposable projectives
![]() $P_i=FT_i$
. Thus we may write
$P_i=FT_i$
. Thus we may write
 $$\begin{align*}\varphi^{T}(X)=\prod_{i=1}^nx_i^{\langle FX,S_i\rangle}\sum_d\chi(\mathrm{Gr}_{d}(GX))\prod_{i=1}^nx_i^{-\langle d,S_i\rangle}.\end{align*}$$
$$\begin{align*}\varphi^{T}(X)=\prod_{i=1}^nx_i^{\langle FX,S_i\rangle}\sum_d\chi(\mathrm{Gr}_{d}(GX))\prod_{i=1}^nx_i^{-\langle d,S_i\rangle}.\end{align*}$$
Since d is a dimension vector for
![]() $\underline {A}$
, we have
$\underline {A}$
, we have
![]() $-\langle d,S_i\rangle =\langle S_i,d\rangle $
by the relative (or internal) Calabi–Yau property of A [Reference Keller and Reiten31]. In this way, we recover the formula as stated in [Reference Fu and Keller17, Rem. 3.5].
$-\langle d,S_i\rangle =\langle S_i,d\rangle $
by the relative (or internal) Calabi–Yau property of A [Reference Keller and Reiten31]. In this way, we recover the formula as stated in [Reference Fu and Keller17, Rem. 3.5].
Theorem 6.8 (compare to [Reference Fu and Keller17, Thm. 3.3])
For
![]() $\mathcal {E}$
and T as in Definition 6.6, the function
$\mathcal {E}$
and T as in Definition 6.6, the function
![]() $\varphi ^{T}\colon \mathcal {E}\to \mathbb {C}[\mathrm {K}_0(\operatorname {\mathrm {per}}{A})]$
is a cluster character on
$\varphi ^{T}\colon \mathcal {E}\to \mathbb {C}[\mathrm {K}_0(\operatorname {\mathrm {per}}{A})]$
is a cluster character on
![]() $\mathcal {E}$
in the sense of Definition 6.5.
$\mathcal {E}$
in the sense of Definition 6.5.
Proof. The argument given for [Reference Fu and Keller17, Thm. 3.3] applies equally well here; while Fu and Keller assume that
![]() $\mathcal {E}$
is Hom-finite, our assumption that
$\mathcal {E}$
is Hom-finite, our assumption that
![]() $A=\operatorname {\mathrm {End}}_{\mathcal {E}}(T)^{\mathrm {op}}$
is Noetherian is sufficient for their proof to go through. (For example, it is still the case that any finitely generated A-module, such as a finite-dimensional
$A=\operatorname {\mathrm {End}}_{\mathcal {E}}(T)^{\mathrm {op}}$
is Noetherian is sufficient for their proof to go through. (For example, it is still the case that any finitely generated A-module, such as a finite-dimensional
![]() $\underline {A}$
-module, is finitely presented.) Indeed, our additional assumption that
$\underline {A}$
-module, is finitely presented.) Indeed, our additional assumption that
![]() $\operatorname {\mathrm {gldim}}{A}<\infty $
even allows some parts of the proof in [Reference Fu and Keller17] to be simplified.
$\operatorname {\mathrm {gldim}}{A}<\infty $
even allows some parts of the proof in [Reference Fu and Keller17] to be simplified.
Definition 6.9 (compare to [Reference Fu and Keller17, Def. 5.1])
Let
![]() $\mathcal {E}$
be a Krull–Schmidt stably
$\mathcal {E}$
be a Krull–Schmidt stably
![]() $2$
-Calabi–Yau Frobenius category with cluster-tilting object T, and let
$2$
-Calabi–Yau Frobenius category with cluster-tilting object T, and let
![]() $\mathscr {A}_{Q}$
be the cluster algebra determined by an ice quiver Q. We say
$\mathscr {A}_{Q}$
be the cluster algebra determined by an ice quiver Q. We say
![]() $(\mathcal {E},T)$
is a Frobenius
$(\mathcal {E},T)$
is a Frobenius
![]() $2$
-Calabi–Yau realisation of
$2$
-Calabi–Yau realisation of
![]() $\mathscr {A}_{Q}$
if
$\mathscr {A}_{Q}$
if
![]() $(\mathcal {E},T)$
has a cluster structure in the sense of Definition 6.2 and the quiver
$(\mathcal {E},T)$
has a cluster structure in the sense of Definition 6.2 and the quiver
![]() $Q(T)$
is isomorphic to Q as an ice quiver, up to arrows between frozen vertices.
$Q(T)$
is isomorphic to Q as an ice quiver, up to arrows between frozen vertices.
Note that Definition 6.9 is slightly weaker than [Reference Fu and Keller17, Def. 5.1] since we have weakened the definition of a cluster structure. For example, we do not require that
![]() $Q(T')$
has no loops or
$Q(T')$
has no loops or
![]() $2$
-cycles if
$2$
-cycles if
![]() $T'$
is a nonreachable cluster-tilting object. However, we still have the following important result.
$T'$
is a nonreachable cluster-tilting object. However, we still have the following important result.
Theorem 6.10 (compare to [Reference Fu and Keller17, Thm. 5.4])
Let
![]() $\mathscr {A}_{Q}$
be a cluster algebra with Frobenius
$\mathscr {A}_{Q}$
be a cluster algebra with Frobenius
![]() $2$
-Calabi–Yau realisation
$2$
-Calabi–Yau realisation
![]() $(\mathcal {E},T)$
, and write
$(\mathcal {E},T)$
, and write
![]() $A=\operatorname {\mathrm {End}}_{\mathcal {E}}(T)^{\mathrm {op}}$
. The Grothendieck group
$A=\operatorname {\mathrm {End}}_{\mathcal {E}}(T)^{\mathrm {op}}$
. The Grothendieck group
![]() $\mathrm {K}_0(\operatorname {\mathrm {per}}{A})$
has a basis given by the classes
$\mathrm {K}_0(\operatorname {\mathrm {per}}{A})$
has a basis given by the classes
![]() $[P_i]$
, for
$[P_i]$
, for
![]() $i\in Q_0$
, of indecomposable projective A-modules, and so we may view
$i\in Q_0$
, of indecomposable projective A-modules, and so we may view
![]() $\mathscr {A}_{Q}$
as a subalgebra of the Laurent polynomial ring
$\mathscr {A}_{Q}$
as a subalgebra of the Laurent polynomial ring
![]() $\mathbb {C}[\mathrm {K}_0(\operatorname {\mathrm {per}}{A})]$
by identifying
$\mathbb {C}[\mathrm {K}_0(\operatorname {\mathrm {per}}{A})]$
by identifying
![]() $x_i=x^{[P_i]}$
with the initial cluster variables. Then the cluster character
$x_i=x^{[P_i]}$
with the initial cluster variables. Then the cluster character
![]() $\varphi ^{T}$
induces bijections
$\varphi ^{T}$
induces bijections
-
(1) from the set of isomorphism classes of indecomposable projective objects in
 $\mathcal {E}$
to the set of frozen variables of
$\mathcal {E}$
to the set of frozen variables of
 $\mathscr {A}_{Q}$
,
$\mathscr {A}_{Q}$
, -
(2) from the set of isomorphism classes of reachable rigid indecomposable nonprojective objects of
 $(\mathcal {E},T_0)$
to the set of nonfrozen cluster variables of
$(\mathcal {E},T_0)$
to the set of nonfrozen cluster variables of
 $\mathscr {A}_{Q}$
, and
$\mathscr {A}_{Q}$
, and -
(3) from the set of isomorphism classes of reachable cluster-tilting objects of
 $(\mathcal {E},T_0)$
to the set of clusters of
$(\mathcal {E},T_0)$
to the set of clusters of
 $\mathscr {A}_{Q}$
.
$\mathscr {A}_{Q}$
.
Proof. This is proved exactly as [Reference Fu and Keller17, Thm. 5.4], despite our weakening of the definition of a cluster structure. Indeed, the relevant maps are shown to be injective in [Reference Fu and Keller17, Lem. 4.2, Prop. 4.3] without assuming that
![]() $\mathcal {E}$
has a cluster structure in either sense. The proof of surjectivity (and that the maps are well-defined: that is, that they take values in the appropriate sets) uses an inductive argument. We have already seen in Remark 6.7 that
$\mathcal {E}$
has a cluster structure in either sense. The proof of surjectivity (and that the maps are well-defined: that is, that they take values in the appropriate sets) uses an inductive argument. We have already seen in Remark 6.7 that
![]() $\varphi ^{T}$
takes the indecomposable summands of T to the initial cluster variables
$\varphi ^{T}$
takes the indecomposable summands of T to the initial cluster variables
![]() $x_i$
of
$x_i$
of
![]() $\mathscr {A}_{Q}$
(and the indecomposable projective summands to the frozen variables, by the definition of the ice quiver structure on
$\mathscr {A}_{Q}$
(and the indecomposable projective summands to the frozen variables, by the definition of the ice quiver structure on
![]() $Q(T)=Q$
). The conclusion then follows by using compatibility between mutations of reachable cluster-tilting objects and mutations of clusters in
$Q(T)=Q$
). The conclusion then follows by using compatibility between mutations of reachable cluster-tilting objects and mutations of clusters in
![]() $\mathscr {A}_{Q}$
. For example, the quivers of endomorphism algebras transform correctly by parts (3) and (4) of Definition 6.2, and in the notation of Definition 6.2(2), we have
$\mathscr {A}_{Q}$
. For example, the quivers of endomorphism algebras transform correctly by parts (3) and (4) of Definition 6.2, and in the notation of Definition 6.2(2), we have
by Lemma 6.4 and Theorem 6.8, corresponding to an exchange relation in
![]() $\mathscr {A}_{Q}$
by Lemma 6.4 again. The inductive nature of the argument means we do not require any properties of nonreachable cluster-tilting objects, since these do not appear.
$\mathscr {A}_{Q}$
by Lemma 6.4 again. The inductive nature of the argument means we do not require any properties of nonreachable cluster-tilting objects, since these do not appear.
We close this section by applying our results to the category
![]() $\operatorname {\mathrm {GP}}(B_D)$
obtained from a suitable connected Postnikov diagram D. The resulting theorem justifies our description of
$\operatorname {\mathrm {GP}}(B_D)$
obtained from a suitable connected Postnikov diagram D. The resulting theorem justifies our description of
![]() $\operatorname {\mathrm {GP}}(B_D)$
, with its distinguished mutation class of cluster-tilting objects reachable from
$\operatorname {\mathrm {GP}}(B_D)$
, with its distinguished mutation class of cluster-tilting objects reachable from
![]() $T_D$
, as a categorification of the cluster algebra
$T_D$
, as a categorification of the cluster algebra
![]() $\mathscr {A}_{D}$
.
$\mathscr {A}_{D}$
.
Theorem 6.11. Let D be a connected Postnikov diagram, let
![]() $B_D$
be its boundary algebra (defined over an algebraically closed field
$B_D$
be its boundary algebra (defined over an algebraically closed field
![]() $\mathbb {K}$
of characteristic zero), and let
$\mathbb {K}$
of characteristic zero), and let
![]() $T_D\in \operatorname {\mathrm {GP}}(B_D)$
be the cluster-tilting object from Theorem 4.5. Then
$T_D\in \operatorname {\mathrm {GP}}(B_D)$
be the cluster-tilting object from Theorem 4.5. Then
![]() $(\operatorname {\mathrm {GP}}(B_D),T_D)$
is a Frobenius
$(\operatorname {\mathrm {GP}}(B_D),T_D)$
is a Frobenius
![]() $2$
-Calabi–Yau realisation of the cluster algebra
$2$
-Calabi–Yau realisation of the cluster algebra
![]() $\mathscr {A}_{D}$
.
$\mathscr {A}_{D}$
.
In particular, the Fu–Keller cluster character
![]() $\varphi ^{T_D}$
provides a bijection between rigid indecomposable objects reachable from
$\varphi ^{T_D}$
provides a bijection between rigid indecomposable objects reachable from
![]() $T_D$
and cluster variables of
$T_D$
and cluster variables of
![]() $\mathscr {A}_{D}$
(including a bijection between indecomposable projectives and frozen variables) and between cluster-tilting objects reachable from
$\mathscr {A}_{D}$
(including a bijection between indecomposable projectives and frozen variables) and between cluster-tilting objects reachable from
![]() $T_D$
and clusters of
$T_D$
and clusters of
![]() $\mathscr {A}_{D}$
.
$\mathscr {A}_{D}$
.
Proof. The category
![]() $\operatorname {\mathrm {GP}}(B_D)$
is a stably
$\operatorname {\mathrm {GP}}(B_D)$
is a stably
![]() $2$
-Calabi–Yau Frobenius category, and
$2$
-Calabi–Yau Frobenius category, and
![]() $T_D\in \operatorname {\mathrm {GP}}(B_D)$
a cluster-tilting object, by Theorem 4.5. It is idempotent complete and admits a fully faithful embedding to a Krull–Schmidt category by [Reference Çanakçı, King and Pressland11, Prop. 3.6] (see Proposition 7.1 below), so it is Krull–Schmidt. Moreover,
$T_D\in \operatorname {\mathrm {GP}}(B_D)$
a cluster-tilting object, by Theorem 4.5. It is idempotent complete and admits a fully faithful embedding to a Krull–Schmidt category by [Reference Çanakçı, King and Pressland11, Prop. 3.6] (see Proposition 7.1 below), so it is Krull–Schmidt. Moreover,
![]() $(\operatorname {\mathrm {GP}}(B_D),T_D)$
has a cluster structure as follows. Conditions (1) and (2) are automatic, as discussed in Definition 6.2. Condition (3) holds by Theorem 5.7, and as a consequence, condition (4) holds by [Reference Pressland44, Thm. 5.15]. Since
$(\operatorname {\mathrm {GP}}(B_D),T_D)$
has a cluster structure as follows. Conditions (1) and (2) are automatic, as discussed in Definition 6.2. Condition (3) holds by Theorem 5.7, and as a consequence, condition (4) holds by [Reference Pressland44, Thm. 5.15]. Since
![]() $Q(T_D)$
is isomorphic to
$Q(T_D)$
is isomorphic to
![]() $Q_D$
by Theorem 4.5 again,
$Q_D$
by Theorem 4.5 again,
![]() $(\operatorname {\mathrm {GP}}(B_D),T_D)$
is a Frobenius
$(\operatorname {\mathrm {GP}}(B_D),T_D)$
is a Frobenius
![]() $2$
-Calabi–Yau realisation of
$2$
-Calabi–Yau realisation of
![]() $\mathscr {A}_{D}$
, and the required bijections then follow from Theorem 6.10.
$\mathscr {A}_{D}$
, and the required bijections then follow from Theorem 6.10.
7 Relationship to the Grassmannian cluster category
Fix a connected Postnikov diagram D of type
![]() $(k,n)$
, and abbreviate
$(k,n)$
, and abbreviate
![]() $A=A_D$
,
$A=A_D$
,
![]() $B=B_D$
and
$B=B_D$
and
![]() $T=T_D$
. To be able to use the results of Section 6, we take the ground field for these algebras to be algebraically closed.
$T=T_D$
. To be able to use the results of Section 6, we take the ground field for these algebras to be algebraically closed.
Recall that D determines an ice quiver
![]() $Q=Q_D$
with cluster algebra
$Q=Q_D$
with cluster algebra
![]() $\mathscr {A}_{}=\mathscr {A}_{D}$
, a positroid
$\mathscr {A}_{}=\mathscr {A}_{D}$
, a positroid
![]() $\mathcal {P}=\mathcal {P}_D$
with necklace
$\mathcal {P}=\mathcal {P}_D$
with necklace
![]() $\mathcal {I}=\mathcal {I}_D$
and an open positroid variety
$\mathcal {I}=\mathcal {I}_D$
and an open positroid variety
![]() $\Pi ^\circ =\Pi ^\circ (\mathcal {P}_D)$
with cone
$\Pi ^\circ =\Pi ^\circ (\mathcal {P}_D)$
with cone
![]() $\widehat {\Pi }^\circ $
. In this final section, we explain the relationship between
$\widehat {\Pi }^\circ $
. In this final section, we explain the relationship between
![]() $\operatorname {\mathrm {GP}}(B)$
and the cluster category
$\operatorname {\mathrm {GP}}(B)$
and the cluster category
![]() $\operatorname {\mathrm {CM}}(C)$
for the Grassmannian
$\operatorname {\mathrm {CM}}(C)$
for the Grassmannian
![]() $\mathrm {Gr}_{k}^{n}$
introduced by Jensen, King and Su [Reference Jensen, King and Su28]. As a result, we will see that the composition of the Fu–Keller cluster character
$\mathrm {Gr}_{k}^{n}$
introduced by Jensen, King and Su [Reference Jensen, King and Su28]. As a result, we will see that the composition of the Fu–Keller cluster character
![]() $\varphi ^{T}$
on
$\varphi ^{T}$
on
![]() $\operatorname {\mathrm {GP}}(B)$
with Galashin–Lam’s isomorphism
$\operatorname {\mathrm {GP}}(B)$
with Galashin–Lam’s isomorphism
![]() $\mathscr {A}_{}\stackrel {\sim }{\to }\mathbb {C}[\widehat {\Pi }^\circ ]$
(modified as in Remark 2.7) is a representation-theoretically natural map.
$\mathscr {A}_{}\stackrel {\sim }{\to }\mathbb {C}[\widehat {\Pi }^\circ ]$
(modified as in Remark 2.7) is a representation-theoretically natural map.
Proposition 7.1 [Reference Çanakçı, King and Pressland11, Prop. 3.6]
Let
![]() $\operatorname {\mathrm {CM}}(C)$
be the Grassmannian cluster category for the
$\operatorname {\mathrm {CM}}(C)$
be the Grassmannian cluster category for the
![]() $(k,n)$
-Grassmannian. Then there is a fully faithful functor
$(k,n)$
-Grassmannian. Then there is a fully faithful functor
![]() $\rho \colon \operatorname {\mathrm {GP}}(B)\to \operatorname {\mathrm {CM}}(C)$
arising from an injective map
$\rho \colon \operatorname {\mathrm {GP}}(B)\to \operatorname {\mathrm {CM}}(C)$
arising from an injective map
![]() $C\to B$
of Z-orders that becomes an isomorphism under tensor product with
$C\to B$
of Z-orders that becomes an isomorphism under tensor product with
![]() $Z[t^{-1}]$
.
$Z[t^{-1}]$
.
Recall from Remark 2.7 that we can label each alternating region of D (or equivalently, each vertex
![]() $j\in Q_0$
) by
$j\in Q_0$
) by
![]() $I_j\in \binom {[n]}{k}$
. Precisely, the alternating region corresponding to j lies to the left of k strands, and
$I_j\in \binom {[n]}{k}$
. Precisely, the alternating region corresponding to j lies to the left of k strands, and
![]() $I_j$
consists of the labels of the start-points of these strands. This leads to the specialisation map
$I_j$
consists of the labels of the start-points of these strands. This leads to the specialisation map
![]() $\mathbb {C}[x_j^{\pm 1}:j \in Q_0]\to \mathbb {C}(\widehat {\Pi }^\circ )$
, taking each
$\mathbb {C}[x_j^{\pm 1}:j \in Q_0]\to \mathbb {C}(\widehat {\Pi }^\circ )$
, taking each
![]() $x_j$
to
$x_j$
to
![]() $\Delta _{I_j}|_{\widehat {\Pi }^\circ }$
, which restricts to an isomorphism
$\Delta _{I_j}|_{\widehat {\Pi }^\circ }$
, which restricts to an isomorphism
![]() $\mathscr {A}_{D}\to \mathbb {C}[\widehat {\Pi }^\circ ]$
[Reference Galashin and Lam18]. We write
$\mathscr {A}_{D}\to \mathbb {C}[\widehat {\Pi }^\circ ]$
[Reference Galashin and Lam18]. We write
![]() $\Phi \colon \operatorname {\mathrm {GP}}(B)\to \mathbb {C}[\widehat {\Pi }^\circ ]$
for the composition of the Fu–Keller cluster character
$\Phi \colon \operatorname {\mathrm {GP}}(B)\to \mathbb {C}[\widehat {\Pi }^\circ ]$
for the composition of the Fu–Keller cluster character
![]() $\varphi ^{T}\colon \operatorname {\mathrm {GP}}(B)\to \mathbb {C}[\mathrm {K}_0(\operatorname {\mathrm {per}}{A})]=\mathbb {C}[x_j^{\pm 1}:j \in Q_0]$
with this specialisation map. Since the indecomposable summand
$\varphi ^{T}\colon \operatorname {\mathrm {GP}}(B)\to \mathbb {C}[\mathrm {K}_0(\operatorname {\mathrm {per}}{A})]=\mathbb {C}[x_j^{\pm 1}:j \in Q_0]$
with this specialisation map. Since the indecomposable summand
![]() $T_j=eAe_j$
of T satisfies
$T_j=eAe_j$
of T satisfies
![]() $\varphi ^{T}(T_j)=x_j$
for each
$\varphi ^{T}(T_j)=x_j$
for each
![]() $j\in Q_0$
, we have
$j\in Q_0$
, we have
![]() $\Phi (T_j)=\Delta _{I_j}|_{\widehat {\Pi }^\circ }$
.
$\Phi (T_j)=\Delta _{I_j}|_{\widehat {\Pi }^\circ }$
.
For each
![]() $I\in \binom {[n]}{k}$
, Jensen, King and Su explicitly describe an indecomposable rigid module
$I\in \binom {[n]}{k}$
, Jensen, King and Su explicitly describe an indecomposable rigid module
![]() $M_I\in \operatorname {\mathrm {CM}}(C)$
. These objects categorify the Plücker coordinates
$M_I\in \operatorname {\mathrm {CM}}(C)$
. These objects categorify the Plücker coordinates
![]() $\Delta _{I}\in \mathbb {C}[\widehat {\mathrm {Gr}}{\vphantom {\mathrm {Gr}}}_{k}^{n}]$
, all of which are cluster variables. Over the course of this section, we will show that our cluster character
$\Delta _{I}\in \mathbb {C}[\widehat {\mathrm {Gr}}{\vphantom {\mathrm {Gr}}}_{k}^{n}]$
, all of which are cluster variables. Over the course of this section, we will show that our cluster character
![]() $\Phi $
is compatible with the embedding
$\Phi $
is compatible with the embedding
![]() $\rho $
. The next proposition is crucial for this.
$\rho $
. The next proposition is crucial for this.
Proposition 7.2 [Reference Jensen, King and Su27]
The natural map
is an isomorphism whenever
![]() $X\in \operatorname {\mathrm {CM}}(B)$
and
$X\in \operatorname {\mathrm {CM}}(B)$
and
![]() $Y\in \operatorname {\mathrm {GP}}(B)$
. In particular, the essential image of
$Y\in \operatorname {\mathrm {GP}}(B)$
. In particular, the essential image of
![]() $\rho $
is extension-closed.
$\rho $
is extension-closed.
Proof. The map is well-defined since
![]() $\rho $
is exact and injective since
$\rho $
is exact and injective since
![]() $\rho $
is fully faithful; these conclusions hold even under the weaker assumption
$\rho $
is fully faithful; these conclusions hold even under the weaker assumption
![]() $Y\in \operatorname {\mathrm {CM}}(B)$
. For surjectivity, let
$Y\in \operatorname {\mathrm {CM}}(B)$
. For surjectivity, let
![]() $P\to X$
be a projective cover of X, and consider the commutative diagram
$P\to X$
be a projective cover of X, and consider the commutative diagram

in which the lower row is an extension in
![]() $\operatorname {\mathrm {CM}}(C)$
and the right-hand square is a pull-back. Since
$\operatorname {\mathrm {CM}}(C)$
and the right-hand square is a pull-back. Since
![]() $\rho $
is fully faithful, to show that the the lower row comes from an extension of B-modules, it suffices to show that E is in the essential image of
$\rho $
is fully faithful, to show that the the lower row comes from an extension of B-modules, it suffices to show that E is in the essential image of
![]() $\rho $
.
$\rho $
.
Note that
![]() $\rho B$
is rigid, as follows. By [Reference Çanakçı, King and Pressland11, Prop. 8.2], we have
$\rho B$
is rigid, as follows. By [Reference Çanakçı, King and Pressland11, Prop. 8.2], we have
![]() $\rho B\cong \bigoplus _{I\in \mathcal {I}}M_I$
. Since the elements of
$\rho B\cong \bigoplus _{I\in \mathcal {I}}M_I$
. Since the elements of
![]() $\mathcal {I}$
are weakly separated [Reference Oh, Postnikov and Speyer39, Lem. 4.5], the required rigidity follows from [Reference Jensen, King and Su28, Prop. 5.6]. As a consequence, if
$\mathcal {I}$
are weakly separated [Reference Oh, Postnikov and Speyer39, Lem. 4.5], the required rigidity follows from [Reference Jensen, King and Su28, Prop. 5.6]. As a consequence, if
![]() $Y=B$
, then the upper row of equation (7.1) splits, since
$Y=B$
, then the upper row of equation (7.1) splits, since
![]() $P\in \operatorname {\mathrm {add}}(B)$
. It follows that E is a factor of
$P\in \operatorname {\mathrm {add}}(B)$
. It follows that E is a factor of
![]() $\rho B\oplus \rho P$
, so it lies in the essential image of
$\rho B\oplus \rho P$
, so it lies in the essential image of
![]() $\rho $
by [Reference Curtis12, §37, Ex. 10]; here we use the additional properties of
$\rho $
by [Reference Curtis12, §37, Ex. 10]; here we use the additional properties of
![]() $\rho $
from Proposition 7.1 to see that
$\rho $
from Proposition 7.1 to see that
![]() $\rho B\subseteq C$
and
$\rho B\subseteq C$
and
![]() $\rho B[t^{-1}]=C[t^{-1}]$
. Thus
$\rho B[t^{-1}]=C[t^{-1}]$
. Thus
Now, for general
![]() $Y\in \operatorname {\mathrm {GP}}(B)$
, the upper row of equation (7.1) is an element of
$Y\in \operatorname {\mathrm {GP}}(B)$
, the upper row of equation (7.1) is an element of
where the first equality is the
![]() $2$
-Calabi–Yau property of
$2$
-Calabi–Yau property of
![]() $\operatorname {\mathrm {CM}}(C)$
, the second follows from equation (7.2) since
$\operatorname {\mathrm {CM}}(C)$
, the second follows from equation (7.2) since
![]() $P\in \operatorname {\mathrm {add}}{B}$
, and the last uses that
$P\in \operatorname {\mathrm {add}}{B}$
, and the last uses that
![]() $P\in \operatorname {\mathrm {add}}(B)$
and
$P\in \operatorname {\mathrm {add}}(B)$
and
![]() $Y\in \operatorname {\mathrm {GP}}(B)$
. Thus this upper row once again splits, and we conclude as before that E is in the essential image of
$Y\in \operatorname {\mathrm {GP}}(B)$
. Thus this upper row once again splits, and we conclude as before that E is in the essential image of
![]() $\rho $
.
$\rho $
.
Proposition 7.3 [Reference Çanakçı, King and Pressland11, Prop. 8.2]
Let
![]() $j\in Q_0$
, and let
$j\in Q_0$
, and let
![]() $T_j=eAe_j\in \operatorname {\mathrm {GP}}(B)$
be the corresponding indecomposable summand of the initial cluster tilting object
$T_j=eAe_j\in \operatorname {\mathrm {GP}}(B)$
be the corresponding indecomposable summand of the initial cluster tilting object
![]() $T=eA$
. Then
$T=eA$
. Then
![]() $\rho T_j\cong M_{I_j}$
.
$\rho T_j\cong M_{I_j}$
.
Over the course of the next several results, we will show that
![]() $\Phi (M)=\Delta _{I}|_{\widehat {\Pi }^\circ }$
whenever
$\Phi (M)=\Delta _{I}|_{\widehat {\Pi }^\circ }$
whenever
![]() $\rho (M)\cong M_I$
. We begin by recalling Jensen–King–Su’s cluster character on
$\rho (M)\cong M_I$
. We begin by recalling Jensen–King–Su’s cluster character on
![]() $\operatorname {\mathrm {CM}}(C)$
and relating it to our cluster character on
$\operatorname {\mathrm {CM}}(C)$
and relating it to our cluster character on
![]() $\operatorname {\mathrm {GP}}(B)$
.
$\operatorname {\mathrm {GP}}(B)$
.
Proposition 7.4 [Reference Jensen, King and Su28, Eq. 9.4]
There is a cluster character
![]() $\Psi \colon \operatorname {\mathrm {CM}}(C)\to \mathbb {C}[\widehat {\mathrm {Gr}}{\vphantom {\mathrm {Gr}}}_{k}^{n}]$
such that
$\Psi \colon \operatorname {\mathrm {CM}}(C)\to \mathbb {C}[\widehat {\mathrm {Gr}}{\vphantom {\mathrm {Gr}}}_{k}^{n}]$
such that
![]() $\Psi (M_I)=\Delta _{I}$
for every k-subset I.
$\Psi (M_I)=\Delta _{I}$
for every k-subset I.
Proposition 7.5. For any reachable rigid object
![]() $X\in \operatorname {\mathrm {GP}}(B)$
, we have
$X\in \operatorname {\mathrm {GP}}(B)$
, we have
Proof. First, observe that
![]() $X\mapsto \Psi (\rho X)|_{\widehat {\Pi }^\circ }$
defines a cluster character
$X\mapsto \Psi (\rho X)|_{\widehat {\Pi }^\circ }$
defines a cluster character
![]() $\operatorname {\mathrm {GP}}(B)\to \mathbb {C}[\widehat {\Pi }^\circ ]$
since
$\operatorname {\mathrm {GP}}(B)\to \mathbb {C}[\widehat {\Pi }^\circ ]$
since
![]() $\Psi $
is a cluster character on
$\Psi $
is a cluster character on
![]() $\operatorname {\mathrm {CM}}(C)$
; this uses both Proposition 7.1 and, to see that the restricted map still satisfies the multiplication formula from Definition 6.5(3), Proposition 7.2.
$\operatorname {\mathrm {CM}}(C)$
; this uses both Proposition 7.1 and, to see that the restricted map still satisfies the multiplication formula from Definition 6.5(3), Proposition 7.2.
Thus it suffices to check the required equality on the indecomposable summands of a single reachable cluster-tilting object, which we may take to be the initial object T. For each
![]() $j\in Q_0$
, the summand
$j\in Q_0$
, the summand
![]() $T_j=eAe_j$
satisfies
$T_j=eAe_j$
satisfies
Theorem 7.6. If
![]() $M\in \operatorname {\mathrm {GP}}(B)$
satisfies
$M\in \operatorname {\mathrm {GP}}(B)$
satisfies
![]() $\rho M\cong M_I$
for some
$\rho M\cong M_I$
for some
![]() $I\in \binom {[n]}{k}$
, then
$I\in \binom {[n]}{k}$
, then
![]() $\Phi (M)=\Delta _{I}|_{\widehat {\Pi }^\circ }$
.
$\Phi (M)=\Delta _{I}|_{\widehat {\Pi }^\circ }$
.
Proof. By Proposition 7.4, we have
![]() $\Delta _{I}=\Psi (M_I)=\Psi (\rho M)$
. Thus by Proposition 7.5, it suffices to check that M is reachable—it is rigid by Proposition 7.2 (see also the proof of [Reference Çanakçı, King and Pressland11, Lem. 10.4]).
$\Delta _{I}=\Psi (M_I)=\Psi (\rho M)$
. Thus by Proposition 7.5, it suffices to check that M is reachable—it is rigid by Proposition 7.2 (see also the proof of [Reference Çanakçı, King and Pressland11, Lem. 10.4]).
Consider a geometric exchange at an alternating region j of D (corresponding to a mutation at the vertex j of Q), producing a new diagram
![]() $D'$
. By considering the exchange sequences as in Definition 6.2(2), we may see that the mutation
$D'$
. By considering the exchange sequences as in Definition 6.2(2), we may see that the mutation
![]() $T_j'$
of the direct summand
$T_j'$
of the direct summand
![]() $T_k$
of T satisfies
$T_k$
of T satisfies
![]() $\rho (T_j')=M_{I_j'}$
. Since
$\rho (T_j')=M_{I_j'}$
. Since
![]() $\rho $
is fully faithful,
$\rho $
is fully faithful,
![]() $T_j'$
is also the unique such object in
$T_j'$
is also the unique such object in
![]() $\operatorname {\mathrm {GP}}(B)$
up to isomorphism. Inductively, it follows that
$\operatorname {\mathrm {GP}}(B)$
up to isomorphism. Inductively, it follows that
![]() $M\in \operatorname {\mathrm {GP}}(B)$
with
$M\in \operatorname {\mathrm {GP}}(B)$
with
![]() $\rho (M)\cong M_I$
is reachable as long as I appears as a label in a Postnikov diagram related to D by a sequence of geometric exchanges. By [Reference Oh, Postnikov and Speyer39, Thm. 6.6], such subsets I are precisely those appearing in some maximal weakly separated collection
$\rho (M)\cong M_I$
is reachable as long as I appears as a label in a Postnikov diagram related to D by a sequence of geometric exchanges. By [Reference Oh, Postnikov and Speyer39, Thm. 6.6], such subsets I are precisely those appearing in some maximal weakly separated collection
![]() $\mathcal {C}$
with
$\mathcal {C}$
with
![]() $\mathcal {I}\subseteq \mathcal {C}\subseteq \mathcal {P}$
: that is, they are those
$\mathcal {I}\subseteq \mathcal {C}\subseteq \mathcal {P}$
: that is, they are those
![]() $I\in \mathcal {P}$
, which are weakly separated from every element of
$I\in \mathcal {P}$
, which are weakly separated from every element of
![]() $\mathcal {I}$
.
$\mathcal {I}$
.
So assume
![]() $M\in \operatorname {\mathrm {GP}}(B)$
has
$M\in \operatorname {\mathrm {GP}}(B)$
has
![]() $\rho (M)\cong M_I$
. Since
$\rho (M)\cong M_I$
. Since
![]() $M\in \operatorname {\mathrm {CM}}(B)$
, it follows from [Reference Çanakçı, King and Pressland11, Prop. 8.6] that
$M\in \operatorname {\mathrm {CM}}(B)$
, it follows from [Reference Çanakçı, King and Pressland11, Prop. 8.6] that
![]() $I\in \mathcal {P}_D$
. Since M is even Gorenstein projective, it follows from Proposition 7.2 that
$I\in \mathcal {P}_D$
. Since M is even Gorenstein projective, it follows from Proposition 7.2 that
for
![]() $T_j=eA_De_j$
with j a frozen vertex, these being precisely the indecomposable summands of B. By [Reference Jensen, King and Su28, Prop. 5.6], this means precisely that I and
$T_j=eA_De_j$
with j a frozen vertex, these being precisely the indecomposable summands of B. By [Reference Jensen, King and Su28, Prop. 5.6], this means precisely that I and
![]() $I_j$
are weakly separated. Since
$I_j$
are weakly separated. Since
![]() $\mathcal {I}$
is the set of labels
$\mathcal {I}$
is the set of labels
![]() $I_j$
of frozen vertices j, we have the result.
$I_j$
of frozen vertices j, we have the result.
Remark 7.7. We do not yet know whether
![]() $\Phi (X)=\Psi (\rho X)|_{\widehat {\Pi }^\circ }$
for all
$\Phi (X)=\Psi (\rho X)|_{\widehat {\Pi }^\circ }$
for all
![]() $X\in \operatorname {\mathrm {GP}}(B)$
. However, we expect that this equality does hold, even for all
$X\in \operatorname {\mathrm {GP}}(B)$
. However, we expect that this equality does hold, even for all
![]() $X\in \operatorname {\mathrm {CM}}(B)$
; note that the Fu–Keller cluster character
$X\in \operatorname {\mathrm {CM}}(B)$
; note that the Fu–Keller cluster character
![]() $\varphi ^{T}$
, and hence
$\varphi ^{T}$
, and hence
![]() $\Phi $
, may be defined on this larger category via the same formula in equation (6.1), although it is only a cluster character on the stably
$\Phi $
, may be defined on this larger category via the same formula in equation (6.1), although it is only a cluster character on the stably
![]() $2$
-Calabi–Yau Frobenius category
$2$
-Calabi–Yau Frobenius category
![]() $\operatorname {\mathrm {GP}}(B)$
. If this were the case, the conclusion of Theorem 7.6 would hold under the weaker assumption that
$\operatorname {\mathrm {GP}}(B)$
. If this were the case, the conclusion of Theorem 7.6 would hold under the weaker assumption that
![]() $M\in \operatorname {\mathrm {CM}}(B)$
. The k-subsets I appearing in the resulting statement would then be all of the elements of the positroid
$M\in \operatorname {\mathrm {CM}}(B)$
. The k-subsets I appearing in the resulting statement would then be all of the elements of the positroid
![]() $\mathcal {P}$
, including those not weakly separated from the necklace, by [Reference Çanakçı, King and Pressland11, Prop. 8.6].
$\mathcal {P}$
, including those not weakly separated from the necklace, by [Reference Çanakçı, King and Pressland11, Prop. 8.6].
Acknowledgements
Some important realisations concerning the results of this paper were made during discussions with İlke Çanakçı and Alastair King concerning our work in [Reference Çanakçı, King and Pressland11], and we are grateful to them for the inspiration. We also thank Chris Fraser, Bernt Tore Jensen, Andrea Pasquali, Khrystyna Serhiyenko, Melissa Sherman-Bennett and Lauren Williams for useful conversations. Additional thanks are due to Bernt Tore Jensen for informing us of the statement and proof of Proposition 7.2.
Conflicts of Interest
None.
Funding statement
The author was supported by the EPSRC postdoctoral fellowship EP/T001771/1 while expanding and revising this paper. The author would like to thank the Isaac Newton Institute for Mathematical Sciences, Cambridge, for support and hospitality during the programme Cluster Algebras and Representation Theory, supported by EPSRC grant no. EP/R014604/1, where some of these revisions were undertaken.