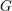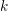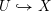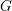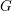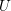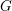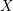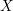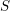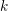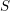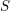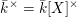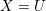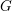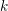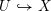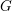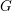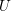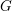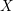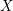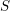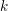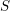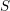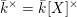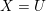1 Introduction
Soit
![]() $k$
un corps de nombres. On note
$k$
un corps de nombres. On note
![]() $\unicode[STIX]{x1D6FA}_{k}$
l’ensemble des places de
$\unicode[STIX]{x1D6FA}_{k}$
l’ensemble des places de
![]() $k$
et
$k$
et
![]() $\infty _{k}$
l’ensemble des places archimédiennes de
$\infty _{k}$
l’ensemble des places archimédiennes de
![]() $k$
. Notons
$k$
. Notons
![]() ${\mathcal{O}}_{k}$
l’anneau des entiers de
${\mathcal{O}}_{k}$
l’anneau des entiers de
![]() $k$
et
$k$
et
![]() ${\mathcal{O}}_{S}$
l’anneau des
${\mathcal{O}}_{S}$
l’anneau des
![]() $S$
-entiers de
$S$
-entiers de
![]() $k$
pour un sous-ensemble fini
$k$
pour un sous-ensemble fini
![]() $S$
de
$S$
de
![]() $\unicode[STIX]{x1D6FA}_{k}$
contenant
$\unicode[STIX]{x1D6FA}_{k}$
contenant
![]() $\infty _{k}$
. Pour chaque
$\infty _{k}$
. Pour chaque
![]() $v\in \unicode[STIX]{x1D6FA}_{k}$
, on note
$v\in \unicode[STIX]{x1D6FA}_{k}$
, on note
![]() $k_{v}$
le complété de
$k_{v}$
le complété de
![]() $k$
en
$k$
en
![]() $v$
et
$v$
et
 ${\mathcal{O}}_{v}\subset k_{v}$
l’anneau des entiers (
${\mathcal{O}}_{v}\subset k_{v}$
l’anneau des entiers (
 ${\mathcal{O}}_{v}=k_{v}$
pour
${\mathcal{O}}_{v}=k_{v}$
pour
![]() $v\in \infty _{k}$
). Soit
$v\in \infty _{k}$
). Soit
![]() $\mathbf{A}_{k}$
l’anneau des adèles de
$\mathbf{A}_{k}$
l’anneau des adèles de
![]() $k$
. Pour un sous-ensemble fini
$k$
. Pour un sous-ensemble fini
![]() $S\subset \unicode[STIX]{x1D6FA}_{k}$
, soit
$S\subset \unicode[STIX]{x1D6FA}_{k}$
, soit
![]() $\mathbf{A}_{k}^{S}$
l’anneau des adèles hors de
$\mathbf{A}_{k}^{S}$
l’anneau des adèles hors de
![]() $S$
et
$S$
et
 $k_{S}:=\prod _{v\in S}k_{v}$
. Par exemple, soit
$k_{S}:=\prod _{v\in S}k_{v}$
. Par exemple, soit
![]() $\mathbf{A}_{k}^{\infty }$
l’anneau des adèles finis et
$\mathbf{A}_{k}^{\infty }$
l’anneau des adèles finis et
 $k_{\infty }:=\prod _{v\in \infty _{k}}k_{v}$
.
$k_{\infty }:=\prod _{v\in \infty _{k}}k_{v}$
.
On rappelle les définitions de [Reference Colliot-Thélène and XuCX09], [Reference Colliot-Thélène and XuCX13, § 2], [Reference Borovoi and DemarcheBD13] et [Reference Cao and XuCX15].
Soit
![]() $X$
une
$X$
une
![]() $k$
-variété algébrique et
$k$
-variété algébrique et
![]() $\text{Br}(X)$
son groupe de Brauer. Pour
$\text{Br}(X)$
son groupe de Brauer. Pour
![]() $B$
sous-ensemble de
$B$
sous-ensemble de
![]() $\text{Br}(X)$
, on définit
$\text{Br}(X)$
, on définit
 $$\begin{eqnarray}X(\mathbf{A}_{k})^{B}=\biggl\{(x_{v})_{v\in \unicode[STIX]{x1D6FA}_{k}}\in X(\mathbf{A}_{k}):~~\mathop{\sum }_{v\in \unicode[STIX]{x1D6FA}_{k}}\,\text{inv}_{v}(\unicode[STIX]{x1D709}(x_{v}))=0\in \mathbb{Q}/\mathbb{Z},~\forall \unicode[STIX]{x1D709}\in B\biggr\}.\end{eqnarray}$$
$$\begin{eqnarray}X(\mathbf{A}_{k})^{B}=\biggl\{(x_{v})_{v\in \unicode[STIX]{x1D6FA}_{k}}\in X(\mathbf{A}_{k}):~~\mathop{\sum }_{v\in \unicode[STIX]{x1D6FA}_{k}}\,\text{inv}_{v}(\unicode[STIX]{x1D709}(x_{v}))=0\in \mathbb{Q}/\mathbb{Z},~\forall \unicode[STIX]{x1D709}\in B\biggr\}.\end{eqnarray}$$
Comme l’a remarqué Manin, la théorie du corps de classes donne
 $X(k)\subseteq X(\mathbf{A}_{k})^{B}$
.
$X(k)\subseteq X(\mathbf{A}_{k})^{B}$
.
Définissons
 $$\begin{eqnarray}X(\mathbf{A}_{k})_{\bullet }=\unicode[STIX]{x1D70B}_{0}(X(k_{\infty }))\times X(\mathbf{A}_{k}^{\infty })\end{eqnarray}$$
$$\begin{eqnarray}X(\mathbf{A}_{k})_{\bullet }=\unicode[STIX]{x1D70B}_{0}(X(k_{\infty }))\times X(\mathbf{A}_{k}^{\infty })\end{eqnarray}$$
la projection, où
 $\unicode[STIX]{x1D70B}_{0}(X(k_{\infty }))$
est l’ensemble des composantes connexes de
$\unicode[STIX]{x1D70B}_{0}(X(k_{\infty }))$
est l’ensemble des composantes connexes de
![]() $X(k_{\infty })$
.
$X(k_{\infty })$
.
Puisque, pour tout
![]() $v\in \infty _{k}$
, chaque élément de
$v\in \infty _{k}$
, chaque élément de
![]() $\text{Br}(X)$
prend une valeur constante sur chaque composante connexe de
$\text{Br}(X)$
prend une valeur constante sur chaque composante connexe de
 $\unicode[STIX]{x1D70B}_{0}(X(k_{v}))$
, pour tout sous-ensemble
$\unicode[STIX]{x1D70B}_{0}(X(k_{v}))$
, pour tout sous-ensemble
 $B\subset \text{Br}(X)$
on peut définir :
$B\subset \text{Br}(X)$
on peut définir :
 $$\begin{eqnarray}X(\mathbf{A}_{k})_{\bullet }^{B}=\biggl\{(x_{v})_{v\in \unicode[STIX]{x1D6FA}_{k}}\in X(\mathbf{A}_{k})_{\bullet }:~~\mathop{\sum }_{v\in \unicode[STIX]{x1D6FA}_{k}}\,\text{inv}_{v}(\unicode[STIX]{x1D709}(x_{v}))=0\in \mathbb{Q}/\mathbb{Z},~\forall \unicode[STIX]{x1D709}\in B\biggr\}.\end{eqnarray}$$
$$\begin{eqnarray}X(\mathbf{A}_{k})_{\bullet }^{B}=\biggl\{(x_{v})_{v\in \unicode[STIX]{x1D6FA}_{k}}\in X(\mathbf{A}_{k})_{\bullet }:~~\mathop{\sum }_{v\in \unicode[STIX]{x1D6FA}_{k}}\,\text{inv}_{v}(\unicode[STIX]{x1D709}(x_{v}))=0\in \mathbb{Q}/\mathbb{Z},~\forall \unicode[STIX]{x1D709}\in B\biggr\}.\end{eqnarray}$$
Définition 1.1. [Reference Colliot-Thélène and XuCX09, Reference Colliot-Thélène and XuCX13] Soient
![]() $k$
un corps de nombres,
$k$
un corps de nombres,
![]() $X$
une
$X$
une
![]() $k$
-variété et
$k$
-variété et
![]() $S\subset \unicode[STIX]{x1D6FA}_{k}$
un sous-ensemble fini. Notons
$S\subset \unicode[STIX]{x1D6FA}_{k}$
un sous-ensemble fini. Notons
 $Pr^{S}:X(\mathbf{A}_{k})\rightarrow X(\mathbf{A}_{k}^{S})$
la projection.
$Pr^{S}:X(\mathbf{A}_{k})\rightarrow X(\mathbf{A}_{k}^{S})$
la projection.
(1) Si
 $X(k)$
est dense dans
$X(k)$
est dense dans
 $Pr^{S}(X(\mathbf{A}_{k}))$
, on dit que
$Pr^{S}(X(\mathbf{A}_{k}))$
, on dit que
 $X$
satisfait l’approximation forte hors de
$X$
satisfait l’approximation forte hors de
 $S$
.
$S$
.(2) Si
 $X(k)$
est dense dans
$X(k)$
est dense dans
 $Pr^{S}(X(\mathbf{A}_{k})^{B})$
pour un sous-ensemble
$Pr^{S}(X(\mathbf{A}_{k})^{B})$
pour un sous-ensemble
 $B$
de
$B$
de
 $\text{Br}(X)$
, on dit que
$\text{Br}(X)$
, on dit que
 $X$
satisfait l’approximation forte par rapport à
$X$
satisfait l’approximation forte par rapport à
 $B$
hors de
$B$
hors de
 $S$
. On dit aussi alors que
$S$
. On dit aussi alors que
 $X$
satisfait l’approximation forte de Brauer–Manin par rapport à
$X$
satisfait l’approximation forte de Brauer–Manin par rapport à
 $B$
hors de
$B$
hors de
 $S$
.
$S$
.
Si
 $S=\infty _{k}$
, on peut s’intéresser à une question un peu plus précise tenant compte des composantes connexes réelles :
$S=\infty _{k}$
, on peut s’intéresser à une question un peu plus précise tenant compte des composantes connexes réelles :
![]() $X(k)$
est-il dense dans
$X(k)$
est-il dense dans
 $X(\mathbf{A}_{k})_{\bullet }^{B}$
pour un sous-groupe
$X(\mathbf{A}_{k})_{\bullet }^{B}$
pour un sous-groupe
 $B\subset \text{Br}(X)$
?
$B\subset \text{Br}(X)$
?
Pour les espaces homogènes de groupes algébriques connexes, ces questions ont fait ces dernières années l’objet d’une série de travaux [Reference Colliot-Thélène and XuCX09, Reference HarariHar08, Reference Borovoi and DemarcheBD13] prolongeant des travaux classiques.
Lorsqu’on cherche à étendre la classe des variétés satisfaisant les propriétés ci-dessus, il est naturel de poser les questions 1.2 et 1.3 suivantes.
Question 1.2. Soient
![]() $X$
une
$X$
une
![]() $k$
-variété lisse géométriquement intègre et
$k$
-variété lisse géométriquement intègre et
![]() $U$
un ouvert de
$U$
un ouvert de
![]() $X$
. Si
$X$
. Si
![]() $U(k)$
est dense dans
$U(k)$
est dense dans
 $U(\mathbf{A}_{k})_{\bullet }^{\text{Br}(U)}$
, sous quelles conditions peut-on établir que
$U(\mathbf{A}_{k})_{\bullet }^{\text{Br}(U)}$
, sous quelles conditions peut-on établir que
![]() $X(k)$
est dense dans
$X(k)$
est dense dans
 $X(\mathbf{A}_{k})_{\bullet }^{\text{Br}(X)}$
?
$X(\mathbf{A}_{k})_{\bullet }^{\text{Br}(X)}$
?
Le cas qui nous intéresse est celui où
![]() $G$
est un groupe linéaire connexe et
$G$
est un groupe linéaire connexe et
![]() $U$
est un
$U$
est un
![]() $G$
-espace homogène. En général, l’inclusion
$G$
-espace homogène. En général, l’inclusion
 $\bar{k}^{\times }\subset \bar{k}[U]^{\times }$
n’est pas un isomorphisme et, dans ce cas, il existe des exemples pour lesquels
$\bar{k}^{\times }\subset \bar{k}[U]^{\times }$
n’est pas un isomorphisme et, dans ce cas, il existe des exemples pour lesquels
![]() $U$
ne satisfait pas l’approximation forte par rapport à
$U$
ne satisfait pas l’approximation forte par rapport à
![]() $\text{Br}(U)$
hors d’un sous-ensemble fini
$\text{Br}(U)$
hors d’un sous-ensemble fini
![]() $S\subset \unicode[STIX]{x1D6FA}_{k}$
non vide donné (par exemple
$S\subset \unicode[STIX]{x1D6FA}_{k}$
non vide donné (par exemple
 $U\cong \mathbb{G}_{m}$
,
$U\cong \mathbb{G}_{m}$
,
![]() $k=\mathbb{Q}$
et
$k=\mathbb{Q}$
et
 $S=\{v_{0}\}$
avec
$S=\{v_{0}\}$
avec
![]() $v_{0}$
une place non archimédienne).
$v_{0}$
une place non archimédienne).
Question 1.3. Soit
![]() $S\subset \unicode[STIX]{x1D6FA}_{k}$
un sous-ensemble fini non vide. Soit
$S\subset \unicode[STIX]{x1D6FA}_{k}$
un sous-ensemble fini non vide. Soit
![]() $G$
un groupe linéaire connexe. Soient
$G$
un groupe linéaire connexe. Soient
![]() $X$
une
$X$
une
![]() $G$
-variété lisse géométriquement intègre et
$G$
-variété lisse géométriquement intègre et
![]() $U$
un
$U$
un
![]() $G$
-ouvert de
$G$
-ouvert de
![]() $X$
équipé d’un
$X$
équipé d’un
![]() $G$
-morphisme
$G$
-morphisme
 $X\rightarrow Z$
dans un
$X\rightarrow Z$
dans un
![]() $G$
-espace homogène
$G$
-espace homogène
![]() $Z$
. Si
$Z$
. Si
 $\bar{k}[X]^{\times }=\bar{k}^{\times }$
et toute fibre de
$\bar{k}[X]^{\times }=\bar{k}^{\times }$
et toute fibre de
![]() $U$
au-dessus d’un
$U$
au-dessus d’un
![]() $k$
-point de
$k$
-point de
![]() $Z$
satisfait l’approximation forte hors de
$Z$
satisfait l’approximation forte hors de
![]() $S$
, sous quelles conditions peut-on établir l’approximation forte pour
$S$
, sous quelles conditions peut-on établir l’approximation forte pour
![]() $X$
par rapport à
$X$
par rapport à
![]() $\text{Br}(X)$
hors de
$\text{Br}(X)$
hors de
![]() $S$
?
$S$
?
Le principal résultat de cet article est le théorème suivant.
Théorème 1.4 (Cf. Théorème 7.6). Soit
![]() $G$
un groupe linéaire connexe sur un corps de nombres
$G$
un groupe linéaire connexe sur un corps de nombres
![]() $k$
, et soit
$k$
, et soit
![]() $X$
une
$X$
une
![]() $G$
-variété lisse géométriquement intègre sur
$G$
-variété lisse géométriquement intègre sur
![]() $k$
. Supposons qu’il existe un
$k$
. Supposons qu’il existe un
![]() $G$
-ouvert
$G$
-ouvert
![]() $U\subset X$
tel que
$U\subset X$
tel que
 $U\cong G/G_{0}$
, où
$U\cong G/G_{0}$
, où
 $G_{0}\subset G$
est un sous-groupe fermé connexe. Soit
$G_{0}\subset G$
est un sous-groupe fermé connexe. Soit
![]() $S\subset \unicode[STIX]{x1D6FA}_{k}$
un sous-ensemble fini non vide. Supposons que
$S\subset \unicode[STIX]{x1D6FA}_{k}$
un sous-ensemble fini non vide. Supposons que
![]() $G^{\prime }(k_{S})$
est non compact pour chaque facteur simple
$G^{\prime }(k_{S})$
est non compact pour chaque facteur simple
![]() $G^{\prime }$
du groupe
$G^{\prime }$
du groupe
![]() $G^{\text{sc}}$
(cf. (1.4)).
$G^{\text{sc}}$
(cf. (1.4)).
(1) Si
 $S\subset \infty _{k}$
, alors
$S\subset \infty _{k}$
, alors
 $X(k)$
est dense dans
$X(k)$
est dense dans
 $X(\mathbf{A}_{k})_{\bullet }^{\text{Br}(X)}$
.
$X(\mathbf{A}_{k})_{\bullet }^{\text{Br}(X)}$
.(2) Si
 $\bar{k}^{\times }=\bar{k}[X]^{\times }$
, alors
$\bar{k}^{\times }=\bar{k}[X]^{\times }$
, alors
 $X$
satisfait l’approximation forte de Brauer–Manin par rapport à
$X$
satisfait l’approximation forte de Brauer–Manin par rapport à
 $\text{Br}(X)$
hors de
$\text{Br}(X)$
hors de
 $S$
.
$S$
.
Ce théorème est un cas spécial d’un résultat plus général mais d’énoncé technique (Théorème 7.6).
Le théorème 1.4(1) avait déjà été établi dans les cas suivants :
(i)
 $X$
est une variété torique, c’est-à-dire que
$X$
est une variété torique, c’est-à-dire que
 $G$
est un tore (Xu et l’auteur [Reference Cao and XuCX13]) ;
$G$
est un tore (Xu et l’auteur [Reference Cao and XuCX13]) ;(ii)
 $X$
est une variété groupique, c’est-à-dire que
$X$
est une variété groupique, c’est-à-dire que
 $G$
est un groupe linéaire connexe et que
$G$
est un groupe linéaire connexe et que
 $G_{0}=1$
(Xu et l’auteur [Reference Cao and XuCX15]) ;
$G_{0}=1$
(Xu et l’auteur [Reference Cao and XuCX15]) ;(iii)
 $X$
est comme dans le théorème, avec
$X$
est comme dans le théorème, avec
 $G_{0}$
résoluble connexe (résultat tout récent de Wei [Reference WeiWei16]).
$G_{0}$
résoluble connexe (résultat tout récent de Wei [Reference WeiWei16]).
Au § 4, on donne une démonstration totalement nouvelle du théorème 1.4(1), laquelle est plus simple que celles des trois travaux ci-dessus.
Le théorème 1.4(2) avait déjà été établi dans les cas suivants :
(iv)
 $X$
est une variété torique (Wei [Reference WeiWei14]) ;
$X$
est une variété torique (Wei [Reference WeiWei14]) ;
(v)
 $X$
est une variété groupique (Xu et l’auteur [Reference Cao and XuCX15]).
$X$
est une variété groupique (Xu et l’auteur [Reference Cao and XuCX15]).
Les démonstrations du théorème 1.4, comme celle de [Reference Cao and XuCX15], reposent d’une part sur des constructions géométriques sur un corps quelconque, d’autre part sur les théorèmes d’approximation forte avec condition de Brauer–Manin pour les espaces homogènes établis dans [Reference Colliot-Thélène and XuCX09, Reference HarariHar08, Reference Borovoi and DemarcheBD13]. Les constructions géométriques du présent article s’inspirent de celles de [Reference Cao and XuCX15] et la partie arithmétique du présent article utilise une généralisation de [Reference Cao, Demarche and XuCDX16] (cf. § 5).
Dans les quatre articles cités, on a la conclusion plus précise : dans les énoncés, on peut remplacer
![]() $\text{Br}(X)$
par le sous-groupe ‘algébrique’
$\text{Br}(X)$
par le sous-groupe ‘algébrique’
 $\text{Br}_{1}(X)\subset \text{Br}(X)$
, dont la définition est rappelée ci-dessous. Dans le cadre général où nous nous plaçons, il faut utiliser tout le groupe de Brauer
$\text{Br}_{1}(X)\subset \text{Br}(X)$
, dont la définition est rappelée ci-dessous. Dans le cadre général où nous nous plaçons, il faut utiliser tout le groupe de Brauer
![]() $\text{Br}(X)$
. L’idée clé est la notion de sous-groupe de Brauer invariant (cf. § 3), qui généralise [Reference Borovoi and DemarcheBD13, § 1.2].
$\text{Br}(X)$
. L’idée clé est la notion de sous-groupe de Brauer invariant (cf. § 3), qui généralise [Reference Borovoi and DemarcheBD13, § 1.2].
Soit
![]() $G$
un
$G$
un
![]() $k$
-groupe linéaire connexe. Le plan de l’article est le suivant :
$k$
-groupe linéaire connexe. Le plan de l’article est le suivant :

La section 2 est consacrée à divers préliminaires géométriques, notamment sur les
![]() $G$
-variétés et leurs torseurs sous un tore ou un groupe de type multiplicatif. Au § 2.3, on étudie les torseurs sous un groupe de type multiplicatif sur une
$G$
-variétés et leurs torseurs sous un tore ou un groupe de type multiplicatif. Au § 2.3, on étudie les torseurs sous un groupe de type multiplicatif sur une
![]() $G$
-variété. On montre que tout tel torseur peut être muni canoniquement d’une action d’un groupe linéaire
$G$
-variété. On montre que tout tel torseur peut être muni canoniquement d’une action d’un groupe linéaire
![]() $H$
qui s’envoie sur
$H$
qui s’envoie sur
![]() $G$
(Théorème 2.7). Pour cela, on utilise un théorème de Colliot-Thélène [Reference Colliot-ThélèneCol08, Thm. 5.6] sur les torseurs au-dessus d’un groupe linéaire connexe.
$G$
(Théorème 2.7). Pour cela, on utilise un théorème de Colliot-Thélène [Reference Colliot-ThélèneCol08, Thm. 5.6] sur les torseurs au-dessus d’un groupe linéaire connexe.
Au § 3, on définit la notion de sous-groupe de Brauer
![]() $G$
-invariant
$G$
-invariant
 $\text{Br}_{G}(X)$
d’une
$\text{Br}_{G}(X)$
d’une
![]() $G$
-variété lisse (cf. Définition 3.1). On donne des caractérisations équivalentes sur les sous-groupes de
$G$
-variété lisse (cf. Définition 3.1). On donne des caractérisations équivalentes sur les sous-groupes de
 $\text{Br}_{G}(X)$
(Proposition 3.4). Ensuite, on définit la notion d’homomorphisme de Sansuc (cf. Définition 3.8) et on généralise la suite exacte de Sansuc (cf. (3.6)). On étudie la propriété de
$\text{Br}_{G}(X)$
(Proposition 3.4). Ensuite, on définit la notion d’homomorphisme de Sansuc (cf. Définition 3.8) et on généralise la suite exacte de Sansuc (cf. (3.6)). On étudie la propriété de
 $\text{Br}_{G}(X)$
par rapport au passage à la fibre d’un
$\text{Br}_{G}(X)$
par rapport au passage à la fibre d’un
![]() $G$
-morphisme vers un tore (Proposition 3.13). On généralise la notion de
$G$
-morphisme vers un tore (Proposition 3.13). On généralise la notion de
![]() $G$
-espace homogène à stabilisateur géométrique connexe et on définit la notion de pseudo
$G$
-espace homogène à stabilisateur géométrique connexe et on définit la notion de pseudo
![]() $G$
-espace homogène (Définition 3.15) qui sera utilisée aux §§ 4 et 6.
$G$
-espace homogène (Définition 3.15) qui sera utilisée aux §§ 4 et 6.
La section 4 est consacrée à l’approximation forte hors des places archimédiennes. On établit le théorème 4.2 sur l’approximation d’un point adélique de
![]() $X$
satisfaisant une condition de Brauer–Manin par un tel point situé sur
$X$
satisfaisant une condition de Brauer–Manin par un tel point situé sur
![]() $U$
. Comme conséquence, on répond à la question 1.2 (Corollaire 4.5) dans ce cas. Ceci donne le théorème 1.4(1).
$U$
. Comme conséquence, on répond à la question 1.2 (Corollaire 4.5) dans ce cas. Ceci donne le théorème 1.4(1).
Au § 5, en utilisant la notion de sous-groupe
![]() $G$
-invariant du groupe de Brauer, on combine la suite exacte (3.6) et la méthode de [Reference Cao, Demarche and XuCDX16], et on généralise [Reference Cao, Demarche and XuCDX16, Thm. 1.2]. On établit un théorème de descente pour un torseur sous un groupe linéaire connexe quelconque (Théorème 5.9). Comme conséquence, on établit une formule sur les points adéliques d’un certain
$G$
-invariant du groupe de Brauer, on combine la suite exacte (3.6) et la méthode de [Reference Cao, Demarche and XuCDX16], et on généralise [Reference Cao, Demarche and XuCDX16, Thm. 1.2]. On établit un théorème de descente pour un torseur sous un groupe linéaire connexe quelconque (Théorème 5.9). Comme conséquence, on établit une formule sur les points adéliques d’un certain
![]() $G$
-espace homogène satisfaisant une condition de Brauer–Manin (Corollaire 5.13).
$G$
-espace homogène satisfaisant une condition de Brauer–Manin (Corollaire 5.13).
Au § 6, pour une
![]() $G$
-variété
$G$
-variété
![]() $X$
munie d’un
$X$
munie d’un
![]() $G$
-ouvert
$G$
-ouvert
![]() $U$
équipé d’un
$U$
équipé d’un
![]() $G$
-morphisme vers une
$G$
-morphisme vers une
![]() $G$
-variété
$G$
-variété
![]() $Z$
, on considère l’approximation d’un point adélique de
$Z$
, on considère l’approximation d’un point adélique de
![]() $X$
satisfaisant une condition de Brauer–Manin par un tel point situé dans la fibre au-dessus d’un point rationnel de
$X$
satisfaisant une condition de Brauer–Manin par un tel point situé dans la fibre au-dessus d’un point rationnel de
![]() $Z$
(Question 6.1). Pour répondre à la question 6.1, on généralise [Reference Cao and XuCX15, Prop. 3.6] et on établit au § 6.1 un théorème plus fin sur l’approximation forte d’un espace affine (Théorème 6.2). Ensuite, on combine ce théorème et l’étude du sous-groupe de Brauer
$Z$
(Question 6.1). Pour répondre à la question 6.1, on généralise [Reference Cao and XuCX15, Prop. 3.6] et on établit au § 6.1 un théorème plus fin sur l’approximation forte d’un espace affine (Théorème 6.2). Ensuite, on combine ce théorème et l’étude du sous-groupe de Brauer
![]() $G$
-invariant (§ 3) avec la méthode de fibration de Colliot-Thélène et Harari [Reference Colliot-Thélène and HarariCH16] et les constructions géométriques de [Reference Cao and XuCX15], et on répond à la question 6.1 dans le cas où
$G$
-invariant (§ 3) avec la méthode de fibration de Colliot-Thélène et Harari [Reference Colliot-Thélène and HarariCH16] et les constructions géométriques de [Reference Cao and XuCX15], et on répond à la question 6.1 dans le cas où
![]() $Z$
est un certain tore (Théorèmes 6.7 et 6.9). Dans le cas où
$Z$
est un certain tore (Théorèmes 6.7 et 6.9). Dans le cas où
![]() $Z$
est un pseudo
$Z$
est un pseudo
![]() $G$
-espace homogène, on résoud la question 6.1 (Théorème 6.11) à l’aide de tous les résultats ci-dessus (sauf ceux du § 4).
$G$
-espace homogène, on résoud la question 6.1 (Théorème 6.11) à l’aide de tous les résultats ci-dessus (sauf ceux du § 4).
Au § 7, en utilisant la descente (§ 5), on établit d’abord un résultat (Proposition 7.4) sur l’approximation forte pour les
![]() $G$
-espaces homogènes à stabilisateur géométrique connexe, ce qui généralise un résultat de Borovoi et Demarche [Reference Borovoi and DemarcheBD13, Thm. 1.4]. Ensuite, on combine ce résultat avec les résultats des § 4 et § 6, et on établit le théorème général (Théorème 7.6) sur l’approximation forte d’une
$G$
-espaces homogènes à stabilisateur géométrique connexe, ce qui généralise un résultat de Borovoi et Demarche [Reference Borovoi and DemarcheBD13, Thm. 1.4]. Ensuite, on combine ce résultat avec les résultats des § 4 et § 6, et on établit le théorème général (Théorème 7.6) sur l’approximation forte d’une
![]() $G$
-variété munie d’un
$G$
-variété munie d’un
![]() $G$
-ouvert fibré sur un certain
$G$
-ouvert fibré sur un certain
![]() $G$
-espace homogène. Le théorème 1.4 est un cas particulier du théorème 7.6.
$G$
-espace homogène. Le théorème 1.4 est un cas particulier du théorème 7.6.
Conventions et notations. Soit
![]() $k$
un corps quelconque de caractéristique
$k$
un corps quelconque de caractéristique
![]() $0$
. On note
$0$
. On note
![]() $\overline{k}$
une clôture algébrique et
$\overline{k}$
une clôture algébrique et
 $\unicode[STIX]{x1D6E4}_{k}:=\text{Gal}(\bar{k}/k)$
.
$\unicode[STIX]{x1D6E4}_{k}:=\text{Gal}(\bar{k}/k)$
.
Tous les groupes de cohomologie sont des groupes de cohomologie étale. Soit
![]() $X$
un schéma intègre. On note
$X$
un schéma intègre. On note
![]() $\unicode[STIX]{x1D702}_{X}$
le point générique de
$\unicode[STIX]{x1D702}_{X}$
le point générique de
![]() $X$
.
$X$
.
Une
![]() $k$
-variété
$k$
-variété
![]() $X$
est un
$X$
est un
![]() $k$
-schéma séparé de type fini. Pour
$k$
-schéma séparé de type fini. Pour
![]() $X$
une telle variété, on note
$X$
une telle variété, on note
![]() $k[X]$
son anneau des fonctions globales,
$k[X]$
son anneau des fonctions globales,
![]() $k[X]^{\times }$
son groupe des fonctions inversibles,
$k[X]^{\times }$
son groupe des fonctions inversibles,
 $\text{Pic}(X):=H_{\acute{\text{e}}\text{t}}^{1}(X,\mathbb{G}_{m})$
son groupe de Picard et
$\text{Pic}(X):=H_{\acute{\text{e}}\text{t}}^{1}(X,\mathbb{G}_{m})$
son groupe de Picard et
 $\text{Br}(X):=H_{\acute{\text{e}}\text{t}}^{2}(X,\mathbb{G}_{m})$
son groupe de Brauer. Notons
$\text{Br}(X):=H_{\acute{\text{e}}\text{t}}^{2}(X,\mathbb{G}_{m})$
son groupe de Brauer. Notons
 $$\begin{eqnarray}\text{Br}_{1}(X):=\text{Ker}[\text{Br}(X)\rightarrow \text{Br}(X_{\bar{k}})]~~\text{ et}~~\text{Br}_{a}(X):=\text{Br}_{1}(X)/\text{Im}\,\text{Br}(k).\end{eqnarray}$$
$$\begin{eqnarray}\text{Br}_{1}(X):=\text{Ker}[\text{Br}(X)\rightarrow \text{Br}(X_{\bar{k}})]~~\text{ et}~~\text{Br}_{a}(X):=\text{Br}_{1}(X)/\text{Im}\,\text{Br}(k).\end{eqnarray}$$
Le groupe
![]() $\text{Br}_{1}(X)$
est le sous-groupe ‘algébrique’ du groupe de Brauer de
$\text{Br}_{1}(X)$
est le sous-groupe ‘algébrique’ du groupe de Brauer de
![]() $X$
. Si
$X$
. Si
![]() $X$
est intègre, on note
$X$
est intègre, on note
![]() $k(X)$
son corps des fonctions rationnelles.
$k(X)$
son corps des fonctions rationnelles.
Pour tout sous-groupe
![]() $B$
de
$B$
de
![]() $\text{Br}(X)$
(ou de
$\text{Br}(X)$
(ou de
 $\text{Br}(X)/\text{Im}(\text{Br}(k))$
), notons
$\text{Br}(X)/\text{Im}(\text{Br}(k))$
), notons
 $$\begin{eqnarray}B^{D}:=\text{Hom}(B,\mathbb{Q}/\mathbb{Z})\end{eqnarray}$$
$$\begin{eqnarray}B^{D}:=\text{Hom}(B,\mathbb{Q}/\mathbb{Z})\end{eqnarray}$$
le groupe des homomorphismes. On munit
![]() $B$
de la topologie discrète et
$B$
de la topologie discrète et
![]() $B^{D}$
de la topologie compacte-ouverte.
$B^{D}$
de la topologie compacte-ouverte.
On note
![]() $X_{\text{sing}}$
le lieu singulier de
$X_{\text{sing}}$
le lieu singulier de
![]() $X$
, et pour un sous-ensemble fermé
$X$
, et pour un sous-ensemble fermé
![]() $D\subset X$
, on note
$D\subset X$
, on note
![]() $D_{\text{sing}}$
le lieu singulier de
$D_{\text{sing}}$
le lieu singulier de
![]() $D$
comme sous-variété fermée réduite.
$D$
comme sous-variété fermée réduite.
Un
![]() $k$
-groupe algébrique
$k$
-groupe algébrique
![]() $G$
est une
$G$
est une
![]() $k$
-variété qui est un
$k$
-variété qui est un
![]() $k$
-schéma en groupes. On note
$k$
-schéma en groupes. On note
![]() $e_{G}$
l’unité de
$e_{G}$
l’unité de
![]() $G$
et
$G$
et
![]() $G^{\ast }$
le groupe des caractères de
$G^{\ast }$
le groupe des caractères de
![]() $G_{\bar{k}}$
. C’est un module galoisien de type fini. Si
$G_{\bar{k}}$
. C’est un module galoisien de type fini. Si
![]() $G$
est connexe, on note
$G$
est connexe, on note
 $$\begin{eqnarray}\text{Br}_{e}(G):=\text{Ker}(\text{Br}_{1}(G)\xrightarrow[{}]{e_{G}^{\ast }}\text{Br}(k))\cong \text{Br}_{a}(G).\end{eqnarray}$$
$$\begin{eqnarray}\text{Br}_{e}(G):=\text{Ker}(\text{Br}_{1}(G)\xrightarrow[{}]{e_{G}^{\ast }}\text{Br}(k))\cong \text{Br}_{a}(G).\end{eqnarray}$$
Soit
![]() $G$
un
$G$
un
![]() $k$
-groupe linéaire connexe. On note
$k$
-groupe linéaire connexe. On note
![]() $G^{\text{tor}}$
son quotient torique maximal,
$G^{\text{tor}}$
son quotient torique maximal,
![]() $G^{u}$
son radical unipotent,
$G^{u}$
son radical unipotent,
 $G^{\text{red}}:=G/G^{u}$
son quotient réductif maximal,
$G^{\text{red}}:=G/G^{u}$
son quotient réductif maximal,
 $G^{\text{ssu}}:=\text{Ker}(G\rightarrow G^{\text{tor}})$
,
$G^{\text{ssu}}:=\text{Ker}(G\rightarrow G^{\text{tor}})$
,
 $G^{\text{ss}}:=G^{\text{ssu}}/G^{u}$
et
$G^{\text{ss}}:=G^{\text{ssu}}/G^{u}$
et
![]() $G^{\text{sc}}$
le revêtement simplement connexe du groupe semi-simple
$G^{\text{sc}}$
le revêtement simplement connexe du groupe semi-simple
![]() $G^{\text{ss}}$
. Alors on a
$G^{\text{ss}}$
. Alors on a
 $G^{\ast }=(G^{\text{tor}})^{\ast }$
et un diagramme commutatif :
$G^{\ast }=(G^{\text{tor}})^{\ast }$
et un diagramme commutatif :

Soit
![]() $G$
un
$G$
un
![]() $k$
-groupe algébrique. Une
$k$
-groupe algébrique. Une
![]() $G$
-variété
$G$
-variété
![]() $(X,\unicode[STIX]{x1D70C})$
(ou
$(X,\unicode[STIX]{x1D70C})$
(ou
![]() $X$
) est une
$X$
) est une
![]() $k$
-variété
$k$
-variété
![]() $X$
munie d’une action à gauche
$X$
munie d’une action à gauche
 $G\times _{k}X\xrightarrow[{}]{\unicode[STIX]{x1D70C}}X$
. Un ouvert
$G\times _{k}X\xrightarrow[{}]{\unicode[STIX]{x1D70C}}X$
. Un ouvert
![]() $U\subset X$
est un
$U\subset X$
est un
![]() $G$
-ouvert si
$G$
-ouvert si
![]() $U$
est invariant sous l’action de
$U$
est invariant sous l’action de
![]() $G$
. Un
$G$
. Un
![]() $k$
-morphisme de
$k$
-morphisme de
![]() $G$
-variétés est appelé
$G$
-variétés est appelé
![]() $G$
-morphisme s’il est compatible avec l’action de
$G$
-morphisme s’il est compatible avec l’action de
![]() $G$
. Sauf mention explicite du contraire, un
$G$
. Sauf mention explicite du contraire, un
![]() $G$
-torseur est un
$G$
-torseur est un
![]() $G$
-torseur à gauche.
$G$
-torseur à gauche.
Soit
![]() $G$
un
$G$
un
![]() $k$
-groupe algébrique connexe et
$k$
-groupe algébrique connexe et
![]() $X$
une
$X$
une
![]() $G$
-variété lisse géométriquement intègre. Notons
$G$
-variété lisse géométriquement intègre. Notons
 $\text{Br}_{G}(X)$
le sous-groupe de Brauer
$\text{Br}_{G}(X)$
le sous-groupe de Brauer
![]() $G$
-invariant (cf. Définition 3.1). Dans le cas où
$G$
-invariant (cf. Définition 3.1). Dans le cas où
 $X\cong G/G_{0}$
avec
$X\cong G/G_{0}$
avec
![]() $G$
linéaire et
$G$
linéaire et
 $G_{0}\subset G$
un sous-groupe fermé connexe, Borovoi et Demarche ont défini
$G_{0}\subset G$
un sous-groupe fermé connexe, Borovoi et Demarche ont défini
 $\text{Br}_{1}(X,G):=\text{Ker}(\text{Br}(X)\rightarrow \text{Br}(G_{\bar{k}}))$
[Reference Borovoi and DemarcheBD13, § 1.2] En fait, on a (Proposition 3.9) :
$\text{Br}_{1}(X,G):=\text{Ker}(\text{Br}(X)\rightarrow \text{Br}(G_{\bar{k}}))$
[Reference Borovoi and DemarcheBD13, § 1.2] En fait, on a (Proposition 3.9) :
 $\text{Br}_{G}(X)\cong \text{Br}_{1}(X,G)$
.
$\text{Br}_{G}(X)\cong \text{Br}_{1}(X,G)$
.
Soit
![]() $T$
un tore. Une variété torique
$T$
un tore. Une variété torique
 $(T{\hookrightarrow}X)$
est une
$(T{\hookrightarrow}X)$
est une
![]() $T$
-variété lisse intègre
$T$
-variété lisse intègre
![]() $X$
munie d’une immersion ouverte fixée
$X$
munie d’une immersion ouverte fixée
 $T{\hookrightarrow}X$
de
$T{\hookrightarrow}X$
de
![]() $T$
-variétés. Pour une
$T$
-variétés. Pour une
![]() $k$
-algèbre finie séparable
$k$
-algèbre finie séparable
![]() $K$
, on a une variété torique canonique :
$K$
, on a une variété torique canonique :
 $(\text{Res}_{K/k}\,\mathbb{G}_{m}{\hookrightarrow}\text{Res}_{K/k}\,\mathbb{A}^{1}).$
$(\text{Res}_{K/k}\,\mathbb{G}_{m}{\hookrightarrow}\text{Res}_{K/k}\,\mathbb{A}^{1}).$
Soit
![]() $k$
un corps de nombres. Soit
$k$
un corps de nombres. Soit
![]() $X$
une
$X$
une
![]() $k$
-variété. On note
$k$
-variété. On note
![]() $X(\mathbf{A}_{k})$
l’ensemble des points adéliques de
$X(\mathbf{A}_{k})$
l’ensemble des points adéliques de
![]() $X$
et on note
$X$
et on note
 $X(\mathbf{A}_{k})_{\bullet }$
comme en (1.1). Soit
$X(\mathbf{A}_{k})_{\bullet }$
comme en (1.1). Soit
![]() $G$
un
$G$
un
![]() $k$
-groupe algébrique. On note
$k$
-groupe algébrique. On note
 $G(k_{\infty })^{+}$
la composante connexe de l’identité de
$G(k_{\infty })^{+}$
la composante connexe de l’identité de
 $G(k_{\infty }):=\prod _{v\in \infty _{k}}G(k_{v})$
.
$G(k_{\infty }):=\prod _{v\in \infty _{k}}G(k_{v})$
.
2 Préliminaires sur les
 $G$
-variétés et les torseurs
$G$
-variétés et les torseurs
Dans toute cette section,
![]() $k$
est un corps quelconque de caractéristique
$k$
est un corps quelconque de caractéristique
![]() $0$
. Sauf mention explicite du contraire, une variété est une
$0$
. Sauf mention explicite du contraire, une variété est une
![]() $k$
-variété. Dans [Reference Cao and XuCX15], le résultat de structure géométrique est [Reference Cao and XuCX15, Prop. 3.12]. On en donne une généralisation (Propositions 2.2 et 2.3). Dans [Reference Colliot-Thélène and SansucCS87b, Lem. 1.6.2], Colliot-Thélène et Sansuc ont étudié la structure des torseurs
$k$
-variété. Dans [Reference Cao and XuCX15], le résultat de structure géométrique est [Reference Cao and XuCX15, Prop. 3.12]. On en donne une généralisation (Propositions 2.2 et 2.3). Dans [Reference Colliot-Thélène and SansucCS87b, Lem. 1.6.2], Colliot-Thélène et Sansuc ont étudié la structure des torseurs
 $Y\rightarrow X$
sous un tore et obtenu la suite exacte (2.2). On précise ici les morphismes de la suite exacte (2.2) (Proposition 2.5). Colliot-Thélène [Reference Colliot-ThélèneCol08, Thm. 5.6] a étudié la structure des torseurs
$Y\rightarrow X$
sous un tore et obtenu la suite exacte (2.2). On précise ici les morphismes de la suite exacte (2.2) (Proposition 2.5). Colliot-Thélène [Reference Colliot-ThélèneCol08, Thm. 5.6] a étudié la structure des torseurs
 $Y\rightarrow X$
sous un groupe de type mutiplicatif lorque la base
$Y\rightarrow X$
sous un groupe de type mutiplicatif lorque la base
![]() $X$
est un groupe linéaire connexe. On considère ici le cas plus général des torseurs sur une variété
$X$
est un groupe linéaire connexe. On considère ici le cas plus général des torseurs sur une variété
![]() $X$
munie d’une action d’un groupe
$X$
munie d’une action d’un groupe
![]() $G$
. On établit un théorème général (Théorème 2.7) sur la structure de ces torseurs.
$G$
. On établit un théorème général (Théorème 2.7) sur la structure de ces torseurs.
2.1 Préliminaires sur les
 $G$
-variétés
$G$
-variétés
On rappelle un résultat pour les variétés toriques lisses [Reference Cao and XuCX13, Prop. 2.10].
Lemme 2.1. Soient
![]() $T$
un tore et
$T$
un tore et
 $(T{\hookrightarrow}Z)$
une variété torique lisse. Soit
$(T{\hookrightarrow}Z)$
une variété torique lisse. Soit
 $Z_{1}:=Z\setminus [(Z\setminus T)_{\text{sing}}]$
. Alors
$Z_{1}:=Z\setminus [(Z\setminus T)_{\text{sing}}]$
. Alors
 $(T{\hookrightarrow}Z_{1})$
est une variété torique,
$(T{\hookrightarrow}Z_{1})$
est une variété torique,
 $\text{codim}(Z\setminus Z_{1},Z)\geqslant 2$
et chaque
$\text{codim}(Z\setminus Z_{1},Z)\geqslant 2$
et chaque
![]() $T_{\bar{k}}$
-orbite de
$T_{\bar{k}}$
-orbite de
 $(Z_{1}\setminus T)_{\bar{k}}$
est de codimension
$(Z_{1}\setminus T)_{\bar{k}}$
est de codimension
![]() $1$
et son stabilisateur géométrique est isomorphe à
$1$
et son stabilisateur géométrique est isomorphe à
![]() $\mathbb{G}_{m,\bar{k}}$
.
$\mathbb{G}_{m,\bar{k}}$
.
Démonstration.
Puisque
 $(Z\setminus T)_{\text{sing}}$
est
$(Z\setminus T)_{\text{sing}}$
est
![]() $T$
-invariant et
$T$
-invariant et
 $\dim ((Z\setminus T)_{\text{sing}})<\dim (Z\setminus T)$
, la variété
$\dim ((Z\setminus T)_{\text{sing}})<\dim (Z\setminus T)$
, la variété
 $(T{\hookrightarrow}Z_{1})$
est une variété torique et
$(T{\hookrightarrow}Z_{1})$
est une variété torique et
 $\text{codim}(Z\setminus Z_{1},Z)\geqslant 2$
.
$\text{codim}(Z\setminus Z_{1},Z)\geqslant 2$
.
Supposons que
![]() $k=\bar{k}$
. Dans ce cas, toutes les variétés toriques lisses de dimension
$k=\bar{k}$
. Dans ce cas, toutes les variétés toriques lisses de dimension
![]() $d$
ont un recouvrement par des variétés toriques
$d$
ont un recouvrement par des variétés toriques
 $(\mathbb{G}_{m}^{n}{\hookrightarrow}\mathbb{G}_{m}^{i}\times \mathbb{A}^{n-i})_{i}$
(cf. [Reference Cao and XuCX13, Lem. 2.1]), et donc
$(\mathbb{G}_{m}^{n}{\hookrightarrow}\mathbb{G}_{m}^{i}\times \mathbb{A}^{n-i})_{i}$
(cf. [Reference Cao and XuCX13, Lem. 2.1]), et donc
![]() $Z_{1}$
admet un recouvrement par des variétés toriques
$Z_{1}$
admet un recouvrement par des variétés toriques
 $\mathbb{G}_{m}^{\dim (Z)-1}\times \mathbb{A}^{1}$
et
$\mathbb{G}_{m}^{\dim (Z)-1}\times \mathbb{A}^{1}$
et
![]() $\mathbb{G}_{m}^{\dim (Z)}$
. Le résultat en découle.◻
$\mathbb{G}_{m}^{\dim (Z)}$
. Le résultat en découle.◻
Proposition 2.2. Soient
 $T\subset Z_{1}\subset Z$
comme dans le lemme 2.1. Soit
$T\subset Z_{1}\subset Z$
comme dans le lemme 2.1. Soit
![]() $G$
un groupe linéaire connexe muni d’un homomorphisme surjectif
$G$
un groupe linéaire connexe muni d’un homomorphisme surjectif
![]() $G\xrightarrow[{}]{\unicode[STIX]{x1D711}}T$
de noyau connexe. Soit
$G\xrightarrow[{}]{\unicode[STIX]{x1D711}}T$
de noyau connexe. Soit
![]() $X$
une
$X$
une
![]() $G$
-variété lisse géométriquement intègre munie d’un
$G$
-variété lisse géométriquement intègre munie d’un
![]() $G$
-morphisme dominant
$G$
-morphisme dominant
 $X\xrightarrow[{}]{f}Z$
. Soit
$X\xrightarrow[{}]{f}Z$
. Soit
![]() $U$
un
$U$
un
![]() $G$
-ouvert de
$G$
-ouvert de
![]() $X$
tel que
$X$
tel que
 $f(U)\subset T$
. On a :
$f(U)\subset T$
. On a :
(1) le morphisme
 $f^{-1}(Z_{1})\xrightarrow[{}]{f|_{Z_{1}}}Z_{1}$
est plat ;
$f^{-1}(Z_{1})\xrightarrow[{}]{f|_{Z_{1}}}Z_{1}$
est plat ;(2) si
 $f$
induit un isomorphisme
$f$
induit un isomorphisme
 $\text{Div}_{Z_{\bar{k}}\setminus T_{\bar{k}}}(Z_{\bar{k}})\xrightarrow[{}]{f_{\text{Div}}^{\ast }}\text{Div}_{X_{\bar{k}}\setminus U_{\bar{k}}}(X_{\bar{k}})$
, alors il existe un
$\text{Div}_{Z_{\bar{k}}\setminus T_{\bar{k}}}(Z_{\bar{k}})\xrightarrow[{}]{f_{\text{Div}}^{\ast }}\text{Div}_{X_{\bar{k}}\setminus U_{\bar{k}}}(X_{\bar{k}})$
, alors il existe un
 $G$
-ouvert
$G$
-ouvert
 $X_{1}$
de
$X_{1}$
de
 $X$
tel que
$X$
tel que
 $f(X_{1})\subset Z_{1}$
,
$f(X_{1})\subset Z_{1}$
,
 $X_{1}\cap f^{-1}(T)=U$
,
$X_{1}\cap f^{-1}(T)=U$
,
 $\text{codim}(X\setminus X_{1},X)\geqslant 2$
et
$\text{codim}(X\setminus X_{1},X)\geqslant 2$
et
 $X_{1}\xrightarrow[{}]{f|_{X_{1}}}Z_{1}$
soit lisse, surjectif à fibres géométriquement intègres.
$X_{1}\xrightarrow[{}]{f|_{X_{1}}}Z_{1}$
soit lisse, surjectif à fibres géométriquement intègres.
Démonstration.
Par le lemme 2.1,
![]() $Z_{1}$
est
$Z_{1}$
est
![]() $T$
-invariant,
$T$
-invariant,
 $\text{codim}(Z\setminus Z_{1},Z)\geqslant 2$
et
$\text{codim}(Z\setminus Z_{1},Z)\geqslant 2$
et
 $(Z_{1}\setminus T)_{\bar{k}}=\coprod _{i}F_{i}$
, où
$(Z_{1}\setminus T)_{\bar{k}}=\coprod _{i}F_{i}$
, où
![]() $F_{i}$
est
$F_{i}$
est
![]() $T_{\bar{k}}$
-orbite de codimension
$T_{\bar{k}}$
-orbite de codimension
![]() $1$
. Donc
$1$
. Donc
 $f^{-1}(Z_{1})$
et
$f^{-1}(Z_{1})$
et
 $\overline{f^{-1}(T)\setminus U}\subset X$
sont
$\overline{f^{-1}(T)\setminus U}\subset X$
sont
![]() $G$
-invariants.
$G$
-invariants.
Pour (1), on peut supposer que
 $X=f^{-1}(Z_{1})$
et
$X=f^{-1}(Z_{1})$
et
![]() $k=\bar{k}$
. Puisque
$k=\bar{k}$
. Puisque
![]() $Z_{1}$
est lisse,
$Z_{1}$
est lisse,
![]() $X$
est intègre et
$X$
est intègre et
![]() $f$
est dominant, il existe un ouvert
$f$
est dominant, il existe un ouvert
![]() $V\subset Z_{1}$
tel que
$V\subset Z_{1}$
tel que
 $\text{codim}(Z_{1}\setminus V,Z_{1})\geqslant 2$
et
$\text{codim}(Z_{1}\setminus V,Z_{1})\geqslant 2$
et
 $f^{-1}(V)\rightarrow V$
soit plat. Donc pour chaque
$f^{-1}(V)\rightarrow V$
soit plat. Donc pour chaque
![]() $i$
,
$i$
,
 $V\cap F_{i}\neq \emptyset$
. En utilisant l’action de
$V\cap F_{i}\neq \emptyset$
. En utilisant l’action de
![]() $G$
, on voit que
$G$
, on voit que
![]() $f|_{Z_{1}}$
est plat.
$f|_{Z_{1}}$
est plat.
Pour (2), puisque
![]() $f_{\text{Div}}^{\ast }$
est un isomorphisme, on a
$f_{\text{Div}}^{\ast }$
est un isomorphisme, on a
 $$\begin{eqnarray}\text{codim}(\overline{f^{-1}(T)\setminus U},X)\geqslant 2~~~\text{ et}~~~\text{codim}(f^{-1}(Z\setminus Z_{1}),X)\geqslant 2.\end{eqnarray}$$
$$\begin{eqnarray}\text{codim}(\overline{f^{-1}(T)\setminus U},X)\geqslant 2~~~\text{ et}~~~\text{codim}(f^{-1}(Z\setminus Z_{1}),X)\geqslant 2.\end{eqnarray}$$
On note
 $X_{2}:=f^{-1}(Z_{1})\setminus \overline{f^{-1}(T)\setminus U}$
et
$X_{2}:=f^{-1}(Z_{1})\setminus \overline{f^{-1}(T)\setminus U}$
et
 $X_{3}:=X_{2}\setminus (X_{2}\setminus U)_{\text{sing}}$
. Alors
$X_{3}:=X_{2}\setminus (X_{2}\setminus U)_{\text{sing}}$
. Alors
 $(X_{3}\setminus U)=D\coprod E$
avec
$(X_{3}\setminus U)=D\coprod E$
avec
 $\text{codim}(E,X_{3})\geqslant 2$
et toutes les composantes connexes de
$\text{codim}(E,X_{3})\geqslant 2$
et toutes les composantes connexes de
![]() $D$
sont de dimension
$D$
sont de dimension
 $\dim (X)-1$
. On note
$\dim (X)-1$
. On note
 $X_{1}:=X_{3}\setminus E$
. Alors
$X_{1}:=X_{3}\setminus E$
. Alors
![]() $X_{1}$
est
$X_{1}$
est
![]() $G$
-invariant,
$G$
-invariant,
 $f(X_{1})\subset Z_{1}$
,
$f(X_{1})\subset Z_{1}$
,
 $X_{1}\cap f^{-1}(T)=U$
,
$X_{1}\cap f^{-1}(T)=U$
,
 $\text{codim}(X\setminus X_{1},X)\geqslant 2$
et chaque composante connexe de
$\text{codim}(X\setminus X_{1},X)\geqslant 2$
et chaque composante connexe de
 $(X_{1}\setminus U)_{\bar{k}}$
est lisse, intègre de dimension
$(X_{1}\setminus U)_{\bar{k}}$
est lisse, intègre de dimension
 $\dim (X)-1$
.
$\dim (X)-1$
.
Puisque
![]() $f_{\text{Div}}^{\ast }$
est un isomorphisme,
$f_{\text{Div}}^{\ast }$
est un isomorphisme,
 $(X_{1}\setminus U)_{\bar{k}}\cong \coprod _{i}D_{i}$
avec
$(X_{1}\setminus U)_{\bar{k}}\cong \coprod _{i}D_{i}$
avec
 $D_{i}=f^{-1}(F_{i})\cap X_{1}$
. Alors chaque
$D_{i}=f^{-1}(F_{i})\cap X_{1}$
. Alors chaque
![]() $D_{i}$
est une
$D_{i}$
est une
![]() $G_{\bar{k}}$
-variété lisse intègre de dimension
$G_{\bar{k}}$
-variété lisse intègre de dimension
 $\dim (X)-1$
. Puisque
$\dim (X)-1$
. Puisque
![]() $\text{Ker}(\unicode[STIX]{x1D711})$
est connexe, le stabilisateur de
$\text{Ker}(\unicode[STIX]{x1D711})$
est connexe, le stabilisateur de
![]() $F_{i}$
comme
$F_{i}$
comme
![]() $G_{\bar{k}}$
-variété est connexe. Par [Reference Cao and XuCX15, Prop. 2.2], les morphismes
$G_{\bar{k}}$
-variété est connexe. Par [Reference Cao and XuCX15, Prop. 2.2], les morphismes
![]() $U\rightarrow T$
et
$U\rightarrow T$
et
 $D_{i}\rightarrow F_{i}$
sont lisses surjectifs à fibres géométriquement intègres. Le résultat en découle.◻
$D_{i}\rightarrow F_{i}$
sont lisses surjectifs à fibres géométriquement intègres. Le résultat en découle.◻
Proposition 2.3. Soient
![]() $T$
et
$T$
et
![]() $T_{0}$
deux tores avec
$T_{0}$
deux tores avec
![]() $T_{0}$
quasi-trivial. Soient
$T_{0}$
quasi-trivial. Soient
![]() $X$
une variété lisse géométriquement intègre et
$X$
une variété lisse géométriquement intègre et
![]() $U\subset X$
un ouvert muni d’un morphisme
$U\subset X$
un ouvert muni d’un morphisme
 $U\xrightarrow[{}]{f}T_{0}\times T$
. Supposons que la composition
$U\xrightarrow[{}]{f}T_{0}\times T$
. Supposons que la composition
 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}:~T_{0}^{\ast }\xrightarrow[{}]{p_{1}^{\ast }}T_{0}^{\ast }\times T^{\ast }\xrightarrow[{}]{f^{\ast }}\bar{k}[U]^{\times }/\bar{k}^{\times }\xrightarrow[{}]{\text{div}_{X}}\text{Div}_{X_{\bar{k}}\setminus U_{\bar{k}}}(X_{\bar{k}})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}:~T_{0}^{\ast }\xrightarrow[{}]{p_{1}^{\ast }}T_{0}^{\ast }\times T^{\ast }\xrightarrow[{}]{f^{\ast }}\bar{k}[U]^{\times }/\bar{k}^{\times }\xrightarrow[{}]{\text{div}_{X}}\text{Div}_{X_{\bar{k}}\setminus U_{\bar{k}}}(X_{\bar{k}})\end{eqnarray}$$
est un isomorphisme de modules galoisiens.
(1) Alors il existe un homomorphisme
 $T_{0}\xrightarrow[{}]{\unicode[STIX]{x1D719}}T$
et une variété torique
$T_{0}\xrightarrow[{}]{\unicode[STIX]{x1D719}}T$
et une variété torique
 $(T_{0}{\hookrightarrow}\mathbb{A}^{l})$
tels que :
$(T_{0}{\hookrightarrow}\mathbb{A}^{l})$
tels que :(a) il existe une
 $k$
-algèbre finie séparable
$k$
-algèbre finie séparable
 $K$
et un isomorphisme de variétés toriques : (2.1)
$K$
et un isomorphisme de variétés toriques : (2.1) $$\begin{eqnarray}(T_{0}{\hookrightarrow}\mathbb{A}^{l})\cong (\text{Res}_{K/k}\,\mathbb{G}_{m}{\hookrightarrow}\text{Res}_{K/k}\,\mathbb{A}_{K}^{1});\end{eqnarray}$$
$$\begin{eqnarray}(T_{0}{\hookrightarrow}\mathbb{A}^{l})\cong (\text{Res}_{K/k}\,\mathbb{G}_{m}{\hookrightarrow}\text{Res}_{K/k}\,\mathbb{A}_{K}^{1});\end{eqnarray}$$
(b) si l’on note
alors le morphisme $$\begin{eqnarray}T_{0}\times T\xrightarrow[{}]{\widetilde{\unicode[STIX]{x1D719}}}T_{0}\times T:~(t_{0},t)\mapsto (t_{0},t\cdot \unicode[STIX]{x1D719}(t_{0})^{-1}),\end{eqnarray}$$
$$\begin{eqnarray}T_{0}\times T\xrightarrow[{}]{\widetilde{\unicode[STIX]{x1D719}}}T_{0}\times T:~(t_{0},t)\mapsto (t_{0},t\cdot \unicode[STIX]{x1D719}(t_{0})^{-1}),\end{eqnarray}$$
 $\widetilde{\unicode[STIX]{x1D719}}\circ f$
peut être étendu à un unique morphisme
$\widetilde{\unicode[STIX]{x1D719}}\circ f$
peut être étendu à un unique morphisme
 $X\xrightarrow[{}]{f^{\prime }}\mathbb{A}^{l}\times T$
;
$X\xrightarrow[{}]{f^{\prime }}\mathbb{A}^{l}\times T$
;(c) on a un isomorphisme
 ${f^{\prime }}^{\ast }:\text{Div}_{(\mathbb{A}^{l}\times T)_{\bar{k}}\setminus (T_{0}\times T)_{\bar{k}}}((\mathbb{A}^{l}\times T)_{\bar{k}})\stackrel{{\sim}}{\rightarrow }\text{Div}_{X_{\bar{k}}\setminus U_{\bar{k}}}(X_{\bar{k}}).$
${f^{\prime }}^{\ast }:\text{Div}_{(\mathbb{A}^{l}\times T)_{\bar{k}}\setminus (T_{0}\times T)_{\bar{k}}}((\mathbb{A}^{l}\times T)_{\bar{k}})\stackrel{{\sim}}{\rightarrow }\text{Div}_{X_{\bar{k}}\setminus U_{\bar{k}}}(X_{\bar{k}}).$
(2) Soit
 $G$
un groupe linéaire muni d’un homomorphisme
$G$
un groupe linéaire muni d’un homomorphisme
 $G\xrightarrow[{}]{\unicode[STIX]{x1D711}}T_{0}\times T$
. Supposons que
$G\xrightarrow[{}]{\unicode[STIX]{x1D711}}T_{0}\times T$
. Supposons que
 $X$
est une
$X$
est une
 $G$
-variété,
$G$
-variété,
 $U\subset X$
est un
$U\subset X$
est un
 $G$
-ouvert et
$G$
-ouvert et
 $f$
est un
$f$
est un
 $G$
-morphisme. Alors le morphisme
$G$
-morphisme. Alors le morphisme
 $f^{\prime }$
est un
$f^{\prime }$
est un
 $G$
-morphisme, où l’action de
$G$
-morphisme, où l’action de
 $G$
sur
$G$
sur
 $\mathbb{A}^{l}\times T$
est induite par
$\mathbb{A}^{l}\times T$
est induite par
 $\widetilde{\unicode[STIX]{x1D719}}\circ \unicode[STIX]{x1D711}$
.
$\widetilde{\unicode[STIX]{x1D719}}\circ \unicode[STIX]{x1D711}$
.
Démonstration.
Soient
 $\{D_{i}\}_{i=1}^{l}$
les composantes irréductibles de
$\{D_{i}\}_{i=1}^{l}$
les composantes irréductibles de
 $(X\setminus U)_{\bar{k}}$
dont la dimension est
$(X\setminus U)_{\bar{k}}$
dont la dimension est
 $\dim (X)-1$
. Alors
$\dim (X)-1$
. Alors
 $\text{Div}_{X_{\bar{k}}\setminus U_{\bar{k}}}(X_{\bar{k}})\cong \bigoplus _{i}\mathbb{Z}\cdot [D_{i}]$
. Puisque
$\text{Div}_{X_{\bar{k}}\setminus U_{\bar{k}}}(X_{\bar{k}})\cong \bigoplus _{i}\mathbb{Z}\cdot [D_{i}]$
. Puisque
![]() $\unicode[STIX]{x1D6EC}$
est un isomorphisme, il existe une base
$\unicode[STIX]{x1D6EC}$
est un isomorphisme, il existe une base
![]() $\{x_{i}\}$
de
$\{x_{i}\}$
de
![]() $T_{0}^{\ast }$
telle que
$T_{0}^{\ast }$
telle que
 $\unicode[STIX]{x1D6EC}(x_{i})=D_{i}$
. Puisque
$\unicode[STIX]{x1D6EC}(x_{i})=D_{i}$
. Puisque
 $\bar{k}[T_{0}]^{\times }=\bar{k}^{\times }\oplus T_{0}^{\ast }$
, on peut supposer que
$\bar{k}[T_{0}]^{\times }=\bar{k}^{\times }\oplus T_{0}^{\ast }$
, on peut supposer que
 $x_{i}\in \bar{k}[T_{0}]^{\times }$
et
$x_{i}\in \bar{k}[T_{0}]^{\times }$
et
![]() $\{x_{i}\}_{i=1}^{l}$
est globalement
$\{x_{i}\}_{i=1}^{l}$
est globalement
 $\text{Gal}(\bar{k}/k)$
-invariant. Soit
$\text{Gal}(\bar{k}/k)$
-invariant. Soit
![]() $K$
la
$K$
la
![]() $k$
-algèbre finie séparable qui correspond au
$k$
-algèbre finie séparable qui correspond au
 $\text{Gal}(\bar{k}/k)$
-ensemble
$\text{Gal}(\bar{k}/k)$
-ensemble
![]() $\{x_{i}\}_{i=1}^{l}$
. Alors
$\{x_{i}\}_{i=1}^{l}$
. Alors
 $T_{0}\cong \text{Res}_{K/k}\,\mathbb{G}_{m,K}$
, et l’immersion ouverte
$T_{0}\cong \text{Res}_{K/k}\,\mathbb{G}_{m,K}$
, et l’immersion ouverte
 $$\begin{eqnarray}T_{0,\bar{k}}\cong \text{Spec}\,\bar{k}[x_{1},x_{1}^{-1},\ldots ,x_{l},x_{l}^{-1}]{\hookrightarrow}\text{Spec}\,\bar{k}[x_{1},\ldots ,x_{l}]\cong \mathbb{A}_{\bar{k}}^{l}\cong (\text{Res}_{K/k}\,\mathbb{A}_{K}^{1})_{\bar{k}}\end{eqnarray}$$
$$\begin{eqnarray}T_{0,\bar{k}}\cong \text{Spec}\,\bar{k}[x_{1},x_{1}^{-1},\ldots ,x_{l},x_{l}^{-1}]{\hookrightarrow}\text{Spec}\,\bar{k}[x_{1},\ldots ,x_{l}]\cong \mathbb{A}_{\bar{k}}^{l}\cong (\text{Res}_{K/k}\,\mathbb{A}_{K}^{1})_{\bar{k}}\end{eqnarray}$$
est exactement l’immersion ouverte
 $(\text{Res}_{K/k}\,\mathbb{G}_{m,K}{\hookrightarrow}\text{Res}_{K/k}\,\mathbb{A}_{K}^{1})_{\bar{k}}$
. Puisque
$(\text{Res}_{K/k}\,\mathbb{G}_{m,K}{\hookrightarrow}\text{Res}_{K/k}\,\mathbb{A}_{K}^{1})_{\bar{k}}$
. Puisque
 $\mathbb{A}^{l}\cong \text{Res}_{K/k}\,\mathbb{A}_{K}^{1}$
, on obtient canoniquement une variété torique
$\mathbb{A}^{l}\cong \text{Res}_{K/k}\,\mathbb{A}_{K}^{1}$
, on obtient canoniquement une variété torique
 $T_{0}{\hookrightarrow}\mathbb{A}^{l}$
.
$T_{0}{\hookrightarrow}\mathbb{A}^{l}$
.
Notons
 $T_{\bar{k}}\cong \text{Spec}\,\bar{k}[t_{1},t_{1}^{-1},\ldots ,t_{n},t_{n}^{-1}]$
et donc
$T_{\bar{k}}\cong \text{Spec}\,\bar{k}[t_{1},t_{1}^{-1},\ldots ,t_{n},t_{n}^{-1}]$
et donc
 $$\begin{eqnarray}(\mathbb{A}^{l}\times T)_{\bar{k}}\cong \text{Spec}\,\bar{k}[x_{1},\ldots ,x_{l},t_{1},t_{1}^{-1},\ldots ,t_{n},t_{n}^{-1}].\end{eqnarray}$$
$$\begin{eqnarray}(\mathbb{A}^{l}\times T)_{\bar{k}}\cong \text{Spec}\,\bar{k}[x_{1},\ldots ,x_{l},t_{1},t_{1}^{-1},\ldots ,t_{n},t_{n}^{-1}].\end{eqnarray}$$
Soit
 $T_{0}\xrightarrow[{}]{\unicode[STIX]{x1D719}}T$
l’homomorphisme correspondant à la composition
$T_{0}\xrightarrow[{}]{\unicode[STIX]{x1D719}}T$
l’homomorphisme correspondant à la composition

Puisque l’homomorphisme
 $T_{0}^{\ast }\times T^{\ast }\xrightarrow[{}]{\widetilde{\unicode[STIX]{x1D719}}^{\ast }}T_{0}^{\ast }\times T^{\ast }$
est défini par
$T_{0}^{\ast }\times T^{\ast }\xrightarrow[{}]{\widetilde{\unicode[STIX]{x1D719}}^{\ast }}T_{0}^{\ast }\times T^{\ast }$
est défini par
 $~(t_{0},t)\mapsto (t_{0}-\unicode[STIX]{x1D719}^{\ast }(t),t)$
, on a
$~(t_{0},t)\mapsto (t_{0}-\unicode[STIX]{x1D719}^{\ast }(t),t)$
, on a
 $$\begin{eqnarray}(\text{div}_{X}\circ f^{\ast }\circ \widetilde{\unicode[STIX]{x1D719}}^{\ast })(x_{i})=(\text{div}_{X}\circ f^{\ast })(x_{i})=\unicode[STIX]{x1D6EC}(x_{i})=D_{i}\end{eqnarray}$$
$$\begin{eqnarray}(\text{div}_{X}\circ f^{\ast }\circ \widetilde{\unicode[STIX]{x1D719}}^{\ast })(x_{i})=(\text{div}_{X}\circ f^{\ast })(x_{i})=\unicode[STIX]{x1D6EC}(x_{i})=D_{i}\end{eqnarray}$$
et
 $$\begin{eqnarray}(\text{div}_{X}\circ f^{\ast }\circ \widetilde{\unicode[STIX]{x1D719}}^{\ast })(t_{i})=((\text{div}_{X}\circ f^{\ast })-(\text{div}_{X}\circ f^{\ast }\circ p_{1}^{\ast }\circ \unicode[STIX]{x1D719}^{\ast }))(t_{i})=((\text{div}_{X}\circ f^{\ast })-(\unicode[STIX]{x1D6EC}\circ \unicode[STIX]{x1D719}^{\ast }))(t_{i})=0.\end{eqnarray}$$
$$\begin{eqnarray}(\text{div}_{X}\circ f^{\ast }\circ \widetilde{\unicode[STIX]{x1D719}}^{\ast })(t_{i})=((\text{div}_{X}\circ f^{\ast })-(\text{div}_{X}\circ f^{\ast }\circ p_{1}^{\ast }\circ \unicode[STIX]{x1D719}^{\ast }))(t_{i})=((\text{div}_{X}\circ f^{\ast })-(\unicode[STIX]{x1D6EC}\circ \unicode[STIX]{x1D719}^{\ast }))(t_{i})=0.\end{eqnarray}$$
Puisque
![]() $X$
est lisse, et donc normale, on a
$X$
est lisse, et donc normale, on a
 $$\begin{eqnarray}(\widetilde{\unicode[STIX]{x1D719}}\circ f)^{\ast }(\bar{k}[\mathbb{A}^{l}\times T])\subset \bar{k}[X]~~~\text{et donc}~(\widetilde{\unicode[STIX]{x1D719}}\circ f)^{\ast }(k[\mathbb{A}^{l}\times T])\subset k[X].\end{eqnarray}$$
$$\begin{eqnarray}(\widetilde{\unicode[STIX]{x1D719}}\circ f)^{\ast }(\bar{k}[\mathbb{A}^{l}\times T])\subset \bar{k}[X]~~~\text{et donc}~(\widetilde{\unicode[STIX]{x1D719}}\circ f)^{\ast }(k[\mathbb{A}^{l}\times T])\subset k[X].\end{eqnarray}$$
Alors
![]() $\widetilde{\unicode[STIX]{x1D719}}\circ f$
s’étend en un morphisme
$\widetilde{\unicode[STIX]{x1D719}}\circ f$
s’étend en un morphisme
 $X\xrightarrow[{}]{f^{\prime }}\mathbb{A}^{l}\times T$
. Un tel morphisme
$X\xrightarrow[{}]{f^{\prime }}\mathbb{A}^{l}\times T$
. Un tel morphisme
![]() $f^{\prime }$
est unique [Reference HartshorneHar77, II. Exer. 4.2].
$f^{\prime }$
est unique [Reference HartshorneHar77, II. Exer. 4.2].
Pour (c), puisque dans le diagramme commutatif

les compositions horizontales sont des isomorphismes,
![]() $(f^{\prime })^{\ast }$
est un isomorphisme.
$(f^{\prime })^{\ast }$
est un isomorphisme.
Pour (2), puisque le diagramme

est commutatif en
![]() $G\times U$
, ce diagramme est commutatif et
$G\times U$
, ce diagramme est commutatif et
![]() $f^{\prime }$
est un
$f^{\prime }$
est un
![]() $G$
-morphisme. ◻
$G$
-morphisme. ◻
2.2 Trivialisation d’un torseur
Les torseurs sous un tore ou sous un groupe de type multiplicatif sont étudiés par Colliot-Thélène et Sansuc [Reference Colliot-Thélène and SansucCS87b]. Soit
![]() $T$
un tore. Soient
$T$
un tore. Soient
![]() $X$
une variété lisse géométriquement intègre et
$X$
une variété lisse géométriquement intègre et
![]() $U\subset X$
un ouvert. Par [Reference Colliot-Thélène and SansucCS87b, Lem. 1.6.2], on a une suite exacte canonique :
$U\subset X$
un ouvert. Par [Reference Colliot-Thélène and SansucCS87b, Lem. 1.6.2], on a une suite exacte canonique :

et pour chaque
 $\unicode[STIX]{x1D712}\in H^{0}(U,T)=\text{Mor}(U,T)$
, on a
$\unicode[STIX]{x1D712}\in H^{0}(U,T)=\text{Mor}(U,T)$
, on a
 $\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D712}):T^{\ast }\xrightarrow[{}]{\unicode[STIX]{x1D712}^{\ast }}\bar{k}[U]^{\times }/\bar{k}^{\times }\xrightarrow[{}]{\text{div}_{X}}\text{Div}_{X_{\bar{k}}\setminus U_{\bar{k}}}(X_{\bar{k}})$
.
$\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D712}):T^{\ast }\xrightarrow[{}]{\unicode[STIX]{x1D712}^{\ast }}\bar{k}[U]^{\times }/\bar{k}^{\times }\xrightarrow[{}]{\text{div}_{X}}\text{Div}_{X_{\bar{k}}\setminus U_{\bar{k}}}(X_{\bar{k}})$
.
Pour un
![]() $T$
-torseur
$T$
-torseur
 $Y\xrightarrow[{}]{p}X$
tel que
$Y\xrightarrow[{}]{p}X$
tel que
![]() $Y|_{U}$
soit trivial, on note
$Y|_{U}$
soit trivial, on note
 $V:=Y\times _{X}U$
et
$V:=Y\times _{X}U$
et
 $\text{Triv}_{U}(V,T)$
l’ensemble des trivialisations
$\text{Triv}_{U}(V,T)$
l’ensemble des trivialisations
 $\unicode[STIX]{x1D70F}:V\stackrel{{\sim}}{\rightarrow }T\times U$
(un
$\unicode[STIX]{x1D70F}:V\stackrel{{\sim}}{\rightarrow }T\times U$
(un
![]() $T$
-isomorphisme au-dessus de
$T$
-isomorphisme au-dessus de
![]() $U$
). On a une application canonique
$U$
). On a une application canonique
 $$\begin{eqnarray}\text{Triv}_{U}(V,T)\xrightarrow[{}]{\unicode[STIX]{x1D6F6}}\text{Hom}_{k}(T^{\ast },\text{Div}_{X_{\bar{k}}\setminus U_{\bar{k}}}(X_{\bar{k}}))\end{eqnarray}$$
$$\begin{eqnarray}\text{Triv}_{U}(V,T)\xrightarrow[{}]{\unicode[STIX]{x1D6F6}}\text{Hom}_{k}(T^{\ast },\text{Div}_{X_{\bar{k}}\setminus U_{\bar{k}}}(X_{\bar{k}}))\end{eqnarray}$$
définie par : pour chaque
 $\unicode[STIX]{x1D70F}\in \text{Triv}_{U}(V,T)$
, le morphisme
$\unicode[STIX]{x1D70F}\in \text{Triv}_{U}(V,T)$
, le morphisme
![]() $\unicode[STIX]{x1D6F6}(\unicode[STIX]{x1D70F})$
est la composition :
$\unicode[STIX]{x1D6F6}(\unicode[STIX]{x1D70F})$
est la composition :
 $$\begin{eqnarray}T^{\ast }\xrightarrow[{}]{p_{1}^{\ast }}\bar{k}[T\times U]^{\times }/\bar{k}^{\times }\xrightarrow[{}]{\unicode[STIX]{x1D70F}^{\ast }}\bar{k}[V]^{\times }/\bar{k}^{\times }\xrightarrow[{}]{\text{div}_{Y}}\text{Div}_{Y_{\bar{k}}\setminus V_{\bar{k}}}(Y_{\bar{k}})\xrightarrow[{}]{(p^{\ast })^{-1}}\text{Div}_{X_{\bar{k}}\setminus U_{\bar{k}}}(X_{\bar{k}}),\end{eqnarray}$$
$$\begin{eqnarray}T^{\ast }\xrightarrow[{}]{p_{1}^{\ast }}\bar{k}[T\times U]^{\times }/\bar{k}^{\times }\xrightarrow[{}]{\unicode[STIX]{x1D70F}^{\ast }}\bar{k}[V]^{\times }/\bar{k}^{\times }\xrightarrow[{}]{\text{div}_{Y}}\text{Div}_{Y_{\bar{k}}\setminus V_{\bar{k}}}(Y_{\bar{k}})\xrightarrow[{}]{(p^{\ast })^{-1}}\text{Div}_{X_{\bar{k}}\setminus U_{\bar{k}}}(X_{\bar{k}}),\end{eqnarray}$$
où
 $\text{Div}_{X_{\bar{k}}\setminus U_{\bar{k}}}(X_{\bar{k}})\xrightarrow[{}]{p^{\ast }}\text{Div}_{Y_{\bar{k}}\setminus V_{\bar{k}}}(Y_{\bar{k}})$
est un isomorphisme par [Reference Colliot-ThélèneCol08, Lem. B.1]. On a aussi une application canonique
$\text{Div}_{X_{\bar{k}}\setminus U_{\bar{k}}}(X_{\bar{k}})\xrightarrow[{}]{p^{\ast }}\text{Div}_{Y_{\bar{k}}\setminus V_{\bar{k}}}(Y_{\bar{k}})$
est un isomorphisme par [Reference Colliot-ThélèneCol08, Lem. B.1]. On a aussi une application canonique
 $$\begin{eqnarray}H^{0}(U,T)\times \text{Triv}_{U}(V,T)\xrightarrow[{}]{\unicode[STIX]{x1D6E9}}\text{Triv}_{U}(V,T):(\unicode[STIX]{x1D712},\unicode[STIX]{x1D70F})\mapsto \widehat{\unicode[STIX]{x1D712}}\circ \unicode[STIX]{x1D70F}\end{eqnarray}$$
$$\begin{eqnarray}H^{0}(U,T)\times \text{Triv}_{U}(V,T)\xrightarrow[{}]{\unicode[STIX]{x1D6E9}}\text{Triv}_{U}(V,T):(\unicode[STIX]{x1D712},\unicode[STIX]{x1D70F})\mapsto \widehat{\unicode[STIX]{x1D712}}\circ \unicode[STIX]{x1D70F}\end{eqnarray}$$
où
 $T\times U\xrightarrow[{}]{\widehat{\unicode[STIX]{x1D712}}}T\times U:(t,u)\mapsto (t+\unicode[STIX]{x1D712}(u),u)$
.
$T\times U\xrightarrow[{}]{\widehat{\unicode[STIX]{x1D712}}}T\times U:(t,u)\mapsto (t+\unicode[STIX]{x1D712}(u),u)$
.
Lemme 2.4. L’application
![]() $\unicode[STIX]{x1D6E9}$
induit une action transitive de
$\unicode[STIX]{x1D6E9}$
induit une action transitive de
 $H^{0}(U,T)$
sur
$H^{0}(U,T)$
sur
 $\text{Triv}_{U}(V,T)$
, et pour chaque
$\text{Triv}_{U}(V,T)$
, et pour chaque
 $\unicode[STIX]{x1D70F}\in \text{Triv}_{U}(V,T)$
,
$\unicode[STIX]{x1D70F}\in \text{Triv}_{U}(V,T)$
,
 $\unicode[STIX]{x1D712}\in H^{0}(U,T)$
, on a
$\unicode[STIX]{x1D712}\in H^{0}(U,T)$
, on a
 $\unicode[STIX]{x1D6F6}(\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D712},\unicode[STIX]{x1D70F}))=\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D712})+\unicode[STIX]{x1D6F6}(\unicode[STIX]{x1D70F})$
.
$\unicode[STIX]{x1D6F6}(\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D712},\unicode[STIX]{x1D70F}))=\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D712})+\unicode[STIX]{x1D6F6}(\unicode[STIX]{x1D70F})$
.
Démonstration.
Pour
 $\unicode[STIX]{x1D712}_{1},\unicode[STIX]{x1D712}_{2}\in H^{0}(U,T)$
, on a
$\unicode[STIX]{x1D712}_{1},\unicode[STIX]{x1D712}_{2}\in H^{0}(U,T)$
, on a
 $\widehat{\unicode[STIX]{x1D712}_{1}+\unicode[STIX]{x1D712}_{2}}=\widehat{\unicode[STIX]{x1D712}_{2}}\circ \widehat{\unicode[STIX]{x1D712}_{1}}$
, et donc
$\widehat{\unicode[STIX]{x1D712}_{1}+\unicode[STIX]{x1D712}_{2}}=\widehat{\unicode[STIX]{x1D712}_{2}}\circ \widehat{\unicode[STIX]{x1D712}_{1}}$
, et donc
![]() $\unicode[STIX]{x1D6E9}$
est une action.
$\unicode[STIX]{x1D6E9}$
est une action.
Notons
 $T\times U\xrightarrow[{}]{p_{1}}T$
. Pour deux trivialisations
$T\times U\xrightarrow[{}]{p_{1}}T$
. Pour deux trivialisations
 $\unicode[STIX]{x1D70F}_{1},\unicode[STIX]{x1D70F}_{2}\in \text{Triv}_{U}(V,T)$
, le morphisme
$\unicode[STIX]{x1D70F}_{1},\unicode[STIX]{x1D70F}_{2}\in \text{Triv}_{U}(V,T)$
, le morphisme
 $\unicode[STIX]{x1D70F}_{2}\circ \unicode[STIX]{x1D70F}_{1}^{-1}$
est un
$\unicode[STIX]{x1D70F}_{2}\circ \unicode[STIX]{x1D70F}_{1}^{-1}$
est un
![]() $T$
-morphisme au-dessus de
$T$
-morphisme au-dessus de
![]() $U$
, i.e. pour chaque
$U$
, i.e. pour chaque
![]() $t\in T$
et
$t\in T$
et
![]() $u\in U$
, on a
$u\in U$
, on a
 $$\begin{eqnarray}(\unicode[STIX]{x1D70F}_{2}\circ \unicode[STIX]{x1D70F}_{1}^{-1})(t,u)=((p_{1}\circ \unicode[STIX]{x1D70F}_{2}\circ \unicode[STIX]{x1D70F}_{1}^{-1})(t,u),u)=(t+(p_{1}\circ \unicode[STIX]{x1D70F}_{2}\circ \unicode[STIX]{x1D70F}_{1}^{-1})(e_{T},u),u).\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D70F}_{2}\circ \unicode[STIX]{x1D70F}_{1}^{-1})(t,u)=((p_{1}\circ \unicode[STIX]{x1D70F}_{2}\circ \unicode[STIX]{x1D70F}_{1}^{-1})(t,u),u)=(t+(p_{1}\circ \unicode[STIX]{x1D70F}_{2}\circ \unicode[STIX]{x1D70F}_{1}^{-1})(e_{T},u),u).\end{eqnarray}$$
Notons
 $\unicode[STIX]{x1D712}:=(p_{1}\circ \unicode[STIX]{x1D70F}_{2}\circ \unicode[STIX]{x1D70F}_{1}^{-1})(e_{T},-)\in H^{0}(U,T)$
, alors
$\unicode[STIX]{x1D712}:=(p_{1}\circ \unicode[STIX]{x1D70F}_{2}\circ \unicode[STIX]{x1D70F}_{1}^{-1})(e_{T},-)\in H^{0}(U,T)$
, alors
 $\unicode[STIX]{x1D70F}_{2}=\widehat{\unicode[STIX]{x1D712}}\circ \unicode[STIX]{x1D70F}_{1}$
et donc
$\unicode[STIX]{x1D70F}_{2}=\widehat{\unicode[STIX]{x1D712}}\circ \unicode[STIX]{x1D70F}_{1}$
et donc
![]() $\unicode[STIX]{x1D6E9}$
est transitive.
$\unicode[STIX]{x1D6E9}$
est transitive.
Notons
 $T\times U\xrightarrow[{}]{p_{2}}U$
. Pour tout
$T\times U\xrightarrow[{}]{p_{2}}U$
. Pour tout
 $\unicode[STIX]{x1D70F}\in \text{Triv}_{U}(V,T)$
et tout
$\unicode[STIX]{x1D70F}\in \text{Triv}_{U}(V,T)$
et tout
 $\unicode[STIX]{x1D712}\in H^{0}(U,T)$
, on a
$\unicode[STIX]{x1D712}\in H^{0}(U,T)$
, on a
 $$\begin{eqnarray}p_{1}\circ \unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D712},\unicode[STIX]{x1D70F})=p_{1}\circ \widehat{\unicode[STIX]{x1D712}}\circ \unicode[STIX]{x1D70F}=(p_{1}+\unicode[STIX]{x1D712}\circ p_{2})\circ \unicode[STIX]{x1D70F}=p_{1}\circ \unicode[STIX]{x1D70F}+\unicode[STIX]{x1D712}\circ p_{2}\circ \unicode[STIX]{x1D70F}=p_{1}\circ \unicode[STIX]{x1D70F}+\unicode[STIX]{x1D712}\circ p|_{U}\end{eqnarray}$$
$$\begin{eqnarray}p_{1}\circ \unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D712},\unicode[STIX]{x1D70F})=p_{1}\circ \widehat{\unicode[STIX]{x1D712}}\circ \unicode[STIX]{x1D70F}=(p_{1}+\unicode[STIX]{x1D712}\circ p_{2})\circ \unicode[STIX]{x1D70F}=p_{1}\circ \unicode[STIX]{x1D70F}+\unicode[STIX]{x1D712}\circ p_{2}\circ \unicode[STIX]{x1D70F}=p_{1}\circ \unicode[STIX]{x1D70F}+\unicode[STIX]{x1D712}\circ p|_{U}\end{eqnarray}$$
dans
 $\text{Mor}(V,T)$
. Puisque les deux morphismes composés
$\text{Mor}(V,T)$
. Puisque les deux morphismes composés
 $$\begin{eqnarray}\bar{k}[U]^{\times }/\bar{k}^{\times }\xrightarrow[{}]{p|_{U}^{\ast }}\bar{k}[V]^{\times }/\bar{k}^{\times }\xrightarrow[{}]{\text{div}_{Y}}\text{Div}_{Y_{\bar{k}}\setminus V_{\bar{k}}}(Y_{\bar{k}})~~~\text{et}~~~\bar{k}[U]^{\times }/\bar{k}^{\times }\xrightarrow[{}]{\text{div}_{X}}\text{Div}_{X_{\bar{k}}\setminus U_{\bar{k}}}(X_{\bar{k}})\xrightarrow[{}]{p^{\ast }}\text{Div}_{Y_{\bar{k}}\setminus V_{\bar{k}}}(Y_{\bar{k}})\end{eqnarray}$$
$$\begin{eqnarray}\bar{k}[U]^{\times }/\bar{k}^{\times }\xrightarrow[{}]{p|_{U}^{\ast }}\bar{k}[V]^{\times }/\bar{k}^{\times }\xrightarrow[{}]{\text{div}_{Y}}\text{Div}_{Y_{\bar{k}}\setminus V_{\bar{k}}}(Y_{\bar{k}})~~~\text{et}~~~\bar{k}[U]^{\times }/\bar{k}^{\times }\xrightarrow[{}]{\text{div}_{X}}\text{Div}_{X_{\bar{k}}\setminus U_{\bar{k}}}(X_{\bar{k}})\xrightarrow[{}]{p^{\ast }}\text{Div}_{Y_{\bar{k}}\setminus V_{\bar{k}}}(Y_{\bar{k}})\end{eqnarray}$$
coïncident, on a
 $\text{div}_{Y}\circ (\unicode[STIX]{x1D712}\circ p|_{U})^{\ast }=p^{\ast }\circ \text{div}_{X}\circ \unicode[STIX]{x1D712}^{\ast }$
et le résultat en découle.◻
$\text{div}_{Y}\circ (\unicode[STIX]{x1D712}\circ p|_{U})^{\ast }=p^{\ast }\circ \text{div}_{X}\circ \unicode[STIX]{x1D712}^{\ast }$
et le résultat en découle.◻
Proposition 2.5. Avec les notations des (2.2) et (2.3), pour un
 $\unicode[STIX]{x1D719}\in \text{Hom}_{k}(T^{\ast },\text{Div}_{X_{\bar{k}}\setminus U_{\bar{k}}}(X_{\bar{k}}))$
, soit
$\unicode[STIX]{x1D719}\in \text{Hom}_{k}(T^{\ast },\text{Div}_{X_{\bar{k}}\setminus U_{\bar{k}}}(X_{\bar{k}}))$
, soit
 $Y\rightarrow X$
un torseur correspondant à
$Y\rightarrow X$
un torseur correspondant à
![]() $\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D719})$
et soit
$\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D719})$
et soit
 $V:=Y\times _{X}U$
. Alors, après avoir bien choisi le signe de
$V:=Y\times _{X}U$
. Alors, après avoir bien choisi le signe de
![]() $\unicode[STIX]{x1D6F9}$
, il existe une trivialisation
$\unicode[STIX]{x1D6F9}$
, il existe une trivialisation
 $\unicode[STIX]{x1D70F}\in \text{Triv}_{U}(V,T)$
telle que
$\unicode[STIX]{x1D70F}\in \text{Triv}_{U}(V,T)$
telle que
 $\unicode[STIX]{x1D6F6}(\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D719}$
et que, pour chaque
$\unicode[STIX]{x1D6F6}(\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D719}$
et que, pour chaque
 $\unicode[STIX]{x1D70F}^{\prime }\in \text{Triv}_{U}(V,T)$
, on ait
$\unicode[STIX]{x1D70F}^{\prime }\in \text{Triv}_{U}(V,T)$
, on ait
 $\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D6F6}(\unicode[STIX]{x1D70F}^{\prime }))=[Y]$
.
$\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D6F6}(\unicode[STIX]{x1D70F}^{\prime }))=[Y]$
.
Démonstration.
D’après le lemme 2.4, l’énoncé est équivalent à l’existence d’une trivialisation
 $\unicode[STIX]{x1D70F}\in \text{Triv}_{U}(V,T)$
telle que
$\unicode[STIX]{x1D70F}\in \text{Triv}_{U}(V,T)$
telle que
 $\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D6F6}(\unicode[STIX]{x1D70F}))=[Y]$
.
$\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D6F6}(\unicode[STIX]{x1D70F}))=[Y]$
.
Étape (1). Supposons que
![]() $k=\bar{k}$
et
$k=\bar{k}$
et
 $T=\mathbb{G}_{m}$
. Dans ce cas,
$T=\mathbb{G}_{m}$
. Dans ce cas,
![]() $T^{\ast }\cong \mathbb{Z}$
. La suite exacte (2.2) est obtenue en appliquant
$T^{\ast }\cong \mathbb{Z}$
. La suite exacte (2.2) est obtenue en appliquant
 $H^{i}(X,-)=Ext_{X_{\acute{\text{e}}\text{t}}}^{i}(\mathbb{Z},-)$
à la suite exacte de faisceaux (cf. [Reference Colliot-Thélène and SansucCS87b, Lem. 1.6.2])
$H^{i}(X,-)=Ext_{X_{\acute{\text{e}}\text{t}}}^{i}(\mathbb{Z},-)$
à la suite exacte de faisceaux (cf. [Reference Colliot-Thélène and SansucCS87b, Lem. 1.6.2])
 $$\begin{eqnarray}0\rightarrow \mathbb{G}_{m,X}\rightarrow j_{\ast }\mathbb{G}_{m,U}\rightarrow \text{}\text{Div}_{X\setminus U}(X)\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow \mathbb{G}_{m,X}\rightarrow j_{\ast }\mathbb{G}_{m,U}\rightarrow \text{}\text{Div}_{X\setminus U}(X)\rightarrow 0\end{eqnarray}$$
où
 $U\xrightarrow[{}]{j}X$
. Donc, après avoir choisi
$U\xrightarrow[{}]{j}X$
. Donc, après avoir choisi
 $1_{T^{\ast }}\in T^{\ast }$
, le morphisme
$1_{T^{\ast }}\in T^{\ast }$
, le morphisme
 $$\begin{eqnarray}\text{Div}_{X\setminus U}(X)\xleftarrow[{}]{{\sim}}\text{Hom}_{k}(T^{\ast },\text{Div}_{X\setminus U}(X))\xrightarrow[{}]{\unicode[STIX]{x1D6F9}}H^{1}(X,T)\stackrel{{\sim}}{\rightarrow }\text{Pic}(X)\end{eqnarray}$$
$$\begin{eqnarray}\text{Div}_{X\setminus U}(X)\xleftarrow[{}]{{\sim}}\text{Hom}_{k}(T^{\ast },\text{Div}_{X\setminus U}(X))\xrightarrow[{}]{\unicode[STIX]{x1D6F9}}H^{1}(X,T)\stackrel{{\sim}}{\rightarrow }\text{Pic}(X)\end{eqnarray}$$
est le morphisme canonique
 $\text{Div}_{X\setminus U}(X)\rightarrow \text{Pic}(X)$
. Par [Reference Colliot-ThélèneCol08, Lem. B.1], pour chaque trivialisation
$\text{Div}_{X\setminus U}(X)\rightarrow \text{Pic}(X)$
. Par [Reference Colliot-ThélèneCol08, Lem. B.1], pour chaque trivialisation
![]() $\unicode[STIX]{x1D70F}$
, on a un diagramme commutatif :
$\unicode[STIX]{x1D70F}$
, on a un diagramme commutatif :

Puisque
 $type(1_{T^{\ast }})=[Y]$
, le résultat en découle.
$type(1_{T^{\ast }})=[Y]$
, le résultat en découle.
Étape (2). Supposons
![]() $k=\bar{k}$
. Notons
$k=\bar{k}$
. Notons
 $n=\dim (T)$
. Alors
$n=\dim (T)$
. Alors
 $T\cong \mathbb{G}_{m}^{n}$
,
$T\cong \mathbb{G}_{m}^{n}$
,
 $T^{\ast }\cong \mathbb{Z}^{n}$
,
$T^{\ast }\cong \mathbb{Z}^{n}$
,
 $H^{1}(X,T)\cong \text{Pic}(X)^{\oplus n}$
et
$H^{1}(X,T)\cong \text{Pic}(X)^{\oplus n}$
et
 $\text{Hom}(T^{\ast },\text{Div}_{X\setminus U}(X))\cong \text{Div}_{X\setminus U}(X)^{\oplus n}$
. On se réduit ainsi à l’étape (1).
$\text{Hom}(T^{\ast },\text{Div}_{X\setminus U}(X))\cong \text{Div}_{X\setminus U}(X)^{\oplus n}$
. On se réduit ainsi à l’étape (1).
Étape (3). Supposons que
![]() $T$
est quasi-trivial et
$T$
est quasi-trivial et
![]() $X$
est projective. Dans ce cas, le morphisme
$X$
est projective. Dans ce cas, le morphisme
 $H^{1}(X,T)\rightarrow H^{1}(X_{\bar{k}},T)$
est injectif (une conséquence de [Reference Colliot-Thélène and SansucCS87b, (2.0.2)]). Par l’étape (2), pour chaque
$H^{1}(X,T)\rightarrow H^{1}(X_{\bar{k}},T)$
est injectif (une conséquence de [Reference Colliot-Thélène and SansucCS87b, (2.0.2)]). Par l’étape (2), pour chaque
 $\unicode[STIX]{x1D70F}\in \text{Triv}_{U}(V,T)$
, on a
$\unicode[STIX]{x1D70F}\in \text{Triv}_{U}(V,T)$
, on a
 $\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D6F6}(\unicode[STIX]{x1D70F}))|_{\bar{k}}=[Y_{\bar{k}}]$
, et donc
$\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D6F6}(\unicode[STIX]{x1D70F}))|_{\bar{k}}=[Y_{\bar{k}}]$
, et donc
 $\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D6F6}(\unicode[STIX]{x1D70F}))=[Y]$
.
$\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D6F6}(\unicode[STIX]{x1D70F}))=[Y]$
.
Étape (4). En général, soit
![]() $X^{c}$
une compactification lisse de
$X^{c}$
une compactification lisse de
![]() $X$
et soit
$X$
et soit
![]() $T_{0}$
un tore avec un isomorphisme
$T_{0}$
un tore avec un isomorphisme
 $T_{0}^{\ast }\xrightarrow[{}]{\unicode[STIX]{x1D704}}\text{Div}_{X_{\bar{k}}\setminus U_{\bar{k}}}(X_{\bar{k}})$
. Notons
$T_{0}^{\ast }\xrightarrow[{}]{\unicode[STIX]{x1D704}}\text{Div}_{X_{\bar{k}}\setminus U_{\bar{k}}}(X_{\bar{k}})$
. Notons
 $\unicode[STIX]{x1D70E}^{\ast }:=\unicode[STIX]{x1D704}^{-1}\circ \unicode[STIX]{x1D719}$
et
$\unicode[STIX]{x1D70E}^{\ast }:=\unicode[STIX]{x1D704}^{-1}\circ \unicode[STIX]{x1D719}$
et
 $T_{0}\xrightarrow[{}]{\unicode[STIX]{x1D70E}}T$
le morphisme correspondant de tores. L’égalité
$T_{0}\xrightarrow[{}]{\unicode[STIX]{x1D70E}}T$
le morphisme correspondant de tores. L’égalité
 $\text{Div}_{X_{\bar{k}}^{c}\setminus U_{\bar{k}}}(X_{\bar{k}}^{c})\cong \text{Div}_{X_{\bar{k}}^{c}\setminus X_{\bar{k}}}(X_{\bar{k}}^{c})\oplus \text{Div}_{X_{\bar{k}}\setminus U_{\bar{k}}}(X_{\bar{k}})$
donne des morphismes
$\text{Div}_{X_{\bar{k}}^{c}\setminus U_{\bar{k}}}(X_{\bar{k}}^{c})\cong \text{Div}_{X_{\bar{k}}^{c}\setminus X_{\bar{k}}}(X_{\bar{k}}^{c})\oplus \text{Div}_{X_{\bar{k}}\setminus U_{\bar{k}}}(X_{\bar{k}})$
donne des morphismes
 $$\begin{eqnarray}\unicode[STIX]{x1D704}_{c}:T_{0}^{\ast }\xrightarrow[{}]{\unicode[STIX]{x1D704}}\text{Div}_{X_{\bar{k}}\setminus U_{\bar{k}}}(X_{\bar{k}}){\hookrightarrow}\text{Div}_{X_{\bar{k}}^{c}\setminus U_{\bar{k}}}(X_{\bar{k}}^{c})~~~\text{et}~~~\unicode[STIX]{x1D70B}:\text{Div}_{X_{\bar{k}}^{c}\setminus U_{\bar{k}}}(X_{\bar{k}}^{c})\rightarrow \text{Div}_{X_{\bar{k}}\setminus U_{\bar{k}}}(X_{\bar{k}})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D704}_{c}:T_{0}^{\ast }\xrightarrow[{}]{\unicode[STIX]{x1D704}}\text{Div}_{X_{\bar{k}}\setminus U_{\bar{k}}}(X_{\bar{k}}){\hookrightarrow}\text{Div}_{X_{\bar{k}}^{c}\setminus U_{\bar{k}}}(X_{\bar{k}}^{c})~~~\text{et}~~~\unicode[STIX]{x1D70B}:\text{Div}_{X_{\bar{k}}^{c}\setminus U_{\bar{k}}}(X_{\bar{k}}^{c})\rightarrow \text{Div}_{X_{\bar{k}}\setminus U_{\bar{k}}}(X_{\bar{k}})\end{eqnarray}$$
tels que
 $\unicode[STIX]{x1D70B}\circ \unicode[STIX]{x1D704}_{c}=\unicode[STIX]{x1D704}$
. Par la suite exacte (2.2), on a le diagramme commutatif suivant.
$\unicode[STIX]{x1D70B}\circ \unicode[STIX]{x1D704}_{c}=\unicode[STIX]{x1D704}$
. Par la suite exacte (2.2), on a le diagramme commutatif suivant.

Alors
![]() $\unicode[STIX]{x1D6F9}_{c}(\unicode[STIX]{x1D704}_{c})$
donne un
$\unicode[STIX]{x1D6F9}_{c}(\unicode[STIX]{x1D704}_{c})$
donne un
![]() $T_{0}$
-torseur
$T_{0}$
-torseur
![]() $Y_{0}^{c}$
sur
$Y_{0}^{c}$
sur
![]() $X^{c}$
tel que
$X^{c}$
tel que
 $\unicode[STIX]{x1D70B}\circ \unicode[STIX]{x1D704}_{c}\circ \unicode[STIX]{x1D70E}^{\ast }=\unicode[STIX]{x1D719}$
,
$\unicode[STIX]{x1D70B}\circ \unicode[STIX]{x1D704}_{c}\circ \unicode[STIX]{x1D70E}^{\ast }=\unicode[STIX]{x1D719}$
,
 $\unicode[STIX]{x1D70E}_{\ast }[Y_{0}^{c}|_{X}]=[Y]\in H^{1}(X,T)$
et que
$\unicode[STIX]{x1D70E}_{\ast }[Y_{0}^{c}|_{X}]=[Y]\in H^{1}(X,T)$
et que
 $V_{0}:=Y_{0}^{c}|_{U}\cong T_{0}\times U$
. Ceci donne un diagramme commutatif :
$V_{0}:=Y_{0}^{c}|_{U}\cong T_{0}\times U$
. Ceci donne un diagramme commutatif :

et le résultat découle de l’étape (3). ◻
2.3 L’action d’un groupe sur un torseur
Soit
![]() $S$
un groupe de type multiplicatif et soit
$S$
un groupe de type multiplicatif et soit
![]() $G$
un groupe linéaire connexe. Colliot-Thélène a montré que tout
$G$
un groupe linéaire connexe. Colliot-Thélène a montré que tout
![]() $S$
-torseur
$S$
-torseur
![]() $H$
sur
$H$
sur
![]() $G$
avec
$G$
avec
 $H(k)\neq \emptyset$
peut être muni d’une structure de groupe telle que
$H(k)\neq \emptyset$
peut être muni d’une structure de groupe telle que
 $H\rightarrow G$
soit un homomorphisme de groupes, s’il possède un point rationnel au-dessus de
$H\rightarrow G$
soit un homomorphisme de groupes, s’il possède un point rationnel au-dessus de
![]() $e_{G}$
(cf. [Reference Colliot-ThélèneCol08, Thm. 5.6]). On donne une généralisation de ce résultat (Théorème 2.7).
$e_{G}$
(cf. [Reference Colliot-ThélèneCol08, Thm. 5.6]). On donne une généralisation de ce résultat (Théorème 2.7).
On commence par une généralisation de [Reference Colliot-ThélèneCol08, Lem. 5.5].
Lemme 2.6. Soient
![]() $X_{1}$
,
$X_{1}$
,
![]() $X_{2}$
deux variétés lisses géométriquement intègres. Soit
$X_{2}$
deux variétés lisses géométriquement intègres. Soit
![]() $S$
un groupe de type multiplicatif. Supposons que
$S$
un groupe de type multiplicatif. Supposons que
![]() $X_{1}$
est géométriquement rationnelle et
$X_{1}$
est géométriquement rationnelle et
 $X_{1}(k)\neq \emptyset$
. Alors pour chaque
$X_{1}(k)\neq \emptyset$
. Alors pour chaque
 $e\in X_{1}(k)$
et
$e\in X_{1}(k)$
et
![]() $i=0$
ou
$i=0$
ou
![]() $1$
, on a un isomorphisme canonique :
$1$
, on a un isomorphisme canonique :
 $$\begin{eqnarray}H_{e}^{i}(X_{1},S)\oplus H^{i}(X_{2},S)\stackrel{{\sim}}{\rightarrow }H^{i}(X_{1}\times X_{2},S)\end{eqnarray}$$
$$\begin{eqnarray}H_{e}^{i}(X_{1},S)\oplus H^{i}(X_{2},S)\stackrel{{\sim}}{\rightarrow }H^{i}(X_{1}\times X_{2},S)\end{eqnarray}$$
où
 $H_{e}^{i}(X_{1},S):=\text{Ker}(H^{i}(X_{1},S)\xrightarrow[{}]{e^{\ast }}H^{i}(k,S))$
.
$H_{e}^{i}(X_{1},S):=\text{Ker}(H^{i}(X_{1},S)\xrightarrow[{}]{e^{\ast }}H^{i}(k,S))$
.
Démonstration.
Si
 $S=\mathbb{G}_{m}$
, l’énoncé découle de [Reference SansucSan81, Lem. 6.5 et Lem. 6.6]. Si
$S=\mathbb{G}_{m}$
, l’énoncé découle de [Reference SansucSan81, Lem. 6.5 et Lem. 6.6]. Si
![]() $S$
est quasi-trivial, i.e. il existe une
$S$
est quasi-trivial, i.e. il existe une
![]() $k$
-algèbre finie étale
$k$
-algèbre finie étale
![]() $K$
tel que
$K$
tel que
 $S=\text{Res}_{K/k}\,\mathbb{G}_{m}$
, l’énoncé découle du fait
$S=\text{Res}_{K/k}\,\mathbb{G}_{m}$
, l’énoncé découle du fait
 $H^{i}(-,S)\cong H^{i}((-)_{K},\mathbb{G}_{m})$
.
$H^{i}(-,S)\cong H^{i}((-)_{K},\mathbb{G}_{m})$
.
En général, on note
 $H_{1}^{i}(S):=H_{e}^{i}(X_{1},S)\oplus H^{i}(X_{2},S)$
et
$H_{1}^{i}(S):=H_{e}^{i}(X_{1},S)\oplus H^{i}(X_{2},S)$
et
 $H_{2}^{i}(S):=H^{i}(X_{1}\times X_{2},S)$
pour
$H_{2}^{i}(S):=H^{i}(X_{1}\times X_{2},S)$
pour
![]() $i=0$
ou
$i=0$
ou
![]() $1$
. Il existe un tore
$1$
. Il existe un tore
![]() $T$
, un tore quasi-trivial
$T$
, un tore quasi-trivial
![]() $T_{0}$
et une suite exacte :
$T_{0}$
et une suite exacte :
 $$\begin{eqnarray}0\rightarrow S\rightarrow T_{0}\rightarrow T\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow S\rightarrow T_{0}\rightarrow T\rightarrow 0.\end{eqnarray}$$
Elle induit le diagramme suivant commutatif de suites exactes.

Alors
![]() $\unicode[STIX]{x1D719}_{S}^{0}$
est injectif pour tout groupe de type multaplicatif
$\unicode[STIX]{x1D719}_{S}^{0}$
est injectif pour tout groupe de type multaplicatif
![]() $S$
. Donc
$S$
. Donc
![]() $\unicode[STIX]{x1D719}_{T}^{0}$
est injectif. Par le lemme des cinq,
$\unicode[STIX]{x1D719}_{T}^{0}$
est injectif. Par le lemme des cinq,
![]() $\unicode[STIX]{x1D719}_{S}^{0}$
est isomorphe pour tout groupe de type multiplicatif
$\unicode[STIX]{x1D719}_{S}^{0}$
est isomorphe pour tout groupe de type multiplicatif
![]() $S$
. Par la même méthode,
$S$
. Par la même méthode,
![]() $\unicode[STIX]{x1D719}_{T}^{0}$
et
$\unicode[STIX]{x1D719}_{T}^{0}$
et
![]() $\unicode[STIX]{x1D719}_{S}^{1}$
sont isomorphes.◻
$\unicode[STIX]{x1D719}_{S}^{1}$
sont isomorphes.◻
Théorème 2.7. Soient
![]() $G$
un groupe linéaire connexe et
$G$
un groupe linéaire connexe et
![]() $(X,\unicode[STIX]{x1D70C})$
une
$(X,\unicode[STIX]{x1D70C})$
une
![]() $G$
-variété lisse géométriquement intègre. Soient
$G$
-variété lisse géométriquement intègre. Soient
![]() $S$
un groupe de type multiplicatif et
$S$
un groupe de type multiplicatif et
 $Y\xrightarrow[{}]{p}X$
un
$Y\xrightarrow[{}]{p}X$
un
![]() $S$
-torseur. Alors il existe un groupe linéaire
$S$
-torseur. Alors il existe un groupe linéaire
![]() $H$
et un homomorphisme
$H$
et un homomorphisme
 $H\xrightarrow[{}]{\unicode[STIX]{x1D713}}G$
tels que
$H\xrightarrow[{}]{\unicode[STIX]{x1D713}}G$
tels que
![]() $\unicode[STIX]{x1D713}$
soit surjectif de noyau
$\unicode[STIX]{x1D713}$
soit surjectif de noyau
![]() $S$
central et que l’action
$S$
central et que l’action
![]() $\unicode[STIX]{x1D70C}_{S}$
de
$\unicode[STIX]{x1D70C}_{S}$
de
![]() $S$
sur
$S$
sur
![]() $Y$
s’étende une action
$Y$
s’étende une action
![]() $\unicode[STIX]{x1D70C}_{H}$
de
$\unicode[STIX]{x1D70C}_{H}$
de
![]() $H$
sur
$H$
sur
![]() $Y$
qui fait de
$Y$
qui fait de
![]() $p$
un
$p$
un
![]() $H$
-morphisme.
$H$
-morphisme.
De plus :
![]() $(1)$
le groupe
$(1)$
le groupe
![]() $H$
est unique, i.e. si
$H$
est unique, i.e. si
 $H_{1}\xrightarrow[{}]{\unicode[STIX]{x1D713}_{1}}G$
satisfait les conditions ci-dessus, alors il existe un isomorphisme de
$H_{1}\xrightarrow[{}]{\unicode[STIX]{x1D713}_{1}}G$
satisfait les conditions ci-dessus, alors il existe un isomorphisme de
![]() $k$
-groupes
$k$
-groupes
 $\unicode[STIX]{x1D717}:H_{1}\stackrel{{\sim}}{\rightarrow }H$
tel que l’on ait un diagramme commutatif :
$\unicode[STIX]{x1D717}:H_{1}\stackrel{{\sim}}{\rightarrow }H$
tel que l’on ait un diagramme commutatif :

![]() $(2)$
si
$(2)$
si
 $\unicode[STIX]{x1D70C}^{\ast }[Y]=p_{2}^{\ast }[Y]$
dans
$\unicode[STIX]{x1D70C}^{\ast }[Y]=p_{2}^{\ast }[Y]$
dans
 $H^{1}(G\times X,S)$
, alors
$H^{1}(G\times X,S)$
, alors
 $H\cong S\times G$
;
$H\cong S\times G$
;
![]() $(3)$
pour chaque choix d’une action
$(3)$
pour chaque choix d’une action
![]() $\unicode[STIX]{x1D70C}_{H}$
, chaque homomorphisme
$\unicode[STIX]{x1D70C}_{H}$
, chaque homomorphisme
![]() $G\xrightarrow[{}]{\unicode[STIX]{x1D719}}S$
induit une nouvelle action
$G\xrightarrow[{}]{\unicode[STIX]{x1D719}}S$
induit une nouvelle action
 $H\times Y\xrightarrow[{}]{\unicode[STIX]{x1D70C}_{H,\unicode[STIX]{x1D719}}}Y$
satisfaisant les conditions ci-dessus, où
$H\times Y\xrightarrow[{}]{\unicode[STIX]{x1D70C}_{H,\unicode[STIX]{x1D719}}}Y$
satisfaisant les conditions ci-dessus, où
 $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{H,\unicode[STIX]{x1D719}}(h,y)=(\unicode[STIX]{x1D719}\circ \unicode[STIX]{x1D713})(h)\cdot \unicode[STIX]{x1D70C}_{H}(h,y)~~~\text{pour chaque}~h\in H,~y\in Y,\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{H,\unicode[STIX]{x1D719}}(h,y)=(\unicode[STIX]{x1D719}\circ \unicode[STIX]{x1D713})(h)\cdot \unicode[STIX]{x1D70C}_{H}(h,y)~~~\text{pour chaque}~h\in H,~y\in Y,\end{eqnarray}$$
et toutes les actions satisfaisant les conditions ci-dessus sont obtenues de cette façon.
Démonstration.
On suit la démonstration de Colliot-Thélène [Reference Colliot-ThélèneCol08, Thm. 5.6]. D’après le lemme 2.6, pour chaque élément
 $\unicode[STIX]{x1D6FC}\in H^{1}(X,S)$
, puisque
$\unicode[STIX]{x1D6FC}\in H^{1}(X,S)$
, puisque
 $\unicode[STIX]{x1D70C}^{\ast }(\unicode[STIX]{x1D6FC})|_{e_{G}\times X}=\unicode[STIX]{x1D6FC}$
, il existe un unique
$\unicode[STIX]{x1D70C}^{\ast }(\unicode[STIX]{x1D6FC})|_{e_{G}\times X}=\unicode[STIX]{x1D6FC}$
, il existe un unique
 $\unicode[STIX]{x1D6FD}\in H_{e_{G}}^{1}(G,S)$
tel que
$\unicode[STIX]{x1D6FD}\in H_{e_{G}}^{1}(G,S)$
tel que
 $\unicode[STIX]{x1D70C}^{\ast }(\unicode[STIX]{x1D6FC})=p_{2}^{\ast }(\unicode[STIX]{x1D6FC})+p_{1}^{\ast }(\unicode[STIX]{x1D6FD})$
, où
$\unicode[STIX]{x1D70C}^{\ast }(\unicode[STIX]{x1D6FC})=p_{2}^{\ast }(\unicode[STIX]{x1D6FC})+p_{1}^{\ast }(\unicode[STIX]{x1D6FD})$
, où
![]() $p_{1},~p_{2}$
sont les projections. Si
$p_{1},~p_{2}$
sont les projections. Si
 $\unicode[STIX]{x1D6FC}=[Y]$
, on note
$\unicode[STIX]{x1D6FC}=[Y]$
, on note
 $\unicode[STIX]{x1D6FD}=(H\xrightarrow[{}]{\unicode[STIX]{x1D713}}G)$
. Par [Reference Colliot-ThélèneCol08, Thm. 5.6 et Cor. 5.7], il existe une structure unique de
$\unicode[STIX]{x1D6FD}=(H\xrightarrow[{}]{\unicode[STIX]{x1D713}}G)$
. Par [Reference Colliot-ThélèneCol08, Thm. 5.6 et Cor. 5.7], il existe une structure unique de
![]() $k$
-groupe linéaire sur
$k$
-groupe linéaire sur
![]() $H$
(à (2.5) près) telle que
$H$
(à (2.5) près) telle que
![]() $\unicode[STIX]{x1D713}$
soit un homomorphisme de noyau
$\unicode[STIX]{x1D713}$
soit un homomorphisme de noyau
![]() $S$
central.
$S$
central.
Notons
 $S\xrightarrow[{}]{i}H$
l’immersion. L’égalité
$S\xrightarrow[{}]{i}H$
l’immersion. L’égalité
 $\unicode[STIX]{x1D70C}^{\ast }[Y]=p_{1}^{\ast }[H]+p_{2}^{\ast }[Y]$
donne un diagramme commutatif :
$\unicode[STIX]{x1D70C}^{\ast }[Y]=p_{1}^{\ast }[H]+p_{2}^{\ast }[Y]$
donne un diagramme commutatif :

tel que
![]() $\unicode[STIX]{x1D70C}_{+}$
induise un isomorphisme
$\unicode[STIX]{x1D70C}_{+}$
induise un isomorphisme
 $H\times ^{S}Y\stackrel{{\sim}}{\rightarrow }\unicode[STIX]{x1D70C}^{\ast }Y$
et
$H\times ^{S}Y\stackrel{{\sim}}{\rightarrow }\unicode[STIX]{x1D70C}^{\ast }Y$
et
 $\unicode[STIX]{x1D70C}_{H}:=\unicode[STIX]{x1D70C}_{Y}\circ \unicode[STIX]{x1D70C}_{+}$
soit un
$\unicode[STIX]{x1D70C}_{H}:=\unicode[STIX]{x1D70C}_{Y}\circ \unicode[STIX]{x1D70C}_{+}$
soit un
![]() $S\times S$
-morphisme, où l’action
$S\times S$
-morphisme, où l’action
 $S\times S\curvearrowright Y:(s_{1},s_{2},y)\mapsto \unicode[STIX]{x1D70C}_{S}(s_{1}\cdot s_{2},y)$
. Donc
$S\times S\curvearrowright Y:(s_{1},s_{2},y)\mapsto \unicode[STIX]{x1D70C}_{S}(s_{1}\cdot s_{2},y)$
. Donc
 $\unicode[STIX]{x1D70C}_{H}|_{e_{S}\times Y}\in \text{Hom}_{X}(Y,Y)$
est un
$\unicode[STIX]{x1D70C}_{H}|_{e_{S}\times Y}\in \text{Hom}_{X}(Y,Y)$
est un
![]() $S$
-morphisme, et donc un isomorphisme. Remplaçant
$S$
-morphisme, et donc un isomorphisme. Remplaçant
![]() $\unicode[STIX]{x1D70C}_{Y}$
par
$\unicode[STIX]{x1D70C}_{Y}$
par
 $(\unicode[STIX]{x1D70C}_{H}|_{e_{S}\times Y})^{-1}\circ \unicode[STIX]{x1D70C}_{Y}$
, on peut supposer que
$(\unicode[STIX]{x1D70C}_{H}|_{e_{S}\times Y})^{-1}\circ \unicode[STIX]{x1D70C}_{Y}$
, on peut supposer que
 $\unicode[STIX]{x1D70C}_{H}|_{e_{S}\times Y}$
est l’identité, et donc
$\unicode[STIX]{x1D70C}_{H}|_{e_{S}\times Y}$
est l’identité, et donc
 $\unicode[STIX]{x1D70C}_{S}=\unicode[STIX]{x1D70C}_{H}\circ (i\times \text{id}_{Y})$
.
$\unicode[STIX]{x1D70C}_{S}=\unicode[STIX]{x1D70C}_{H}\circ (i\times \text{id}_{Y})$
.
Montrons que
![]() $\unicode[STIX]{x1D70C}_{H}$
est une action. Notons
$\unicode[STIX]{x1D70C}_{H}$
est une action. Notons
![]() $m_{H}$
la multiplication sur
$m_{H}$
la multiplication sur
![]() $H$
. Puisque
$H$
. Puisque
![]() $\unicode[STIX]{x1D70C}$
est une action, les morphismes
$\unicode[STIX]{x1D70C}$
est une action, les morphismes
 $\unicode[STIX]{x1D70C}_{1}:=\unicode[STIX]{x1D70C}_{H}\circ (m_{H}\times \text{id}_{Y})$
et
$\unicode[STIX]{x1D70C}_{1}:=\unicode[STIX]{x1D70C}_{H}\circ (m_{H}\times \text{id}_{Y})$
et
 $\unicode[STIX]{x1D70C}_{2}:=\unicode[STIX]{x1D70C}_{H}\circ (\text{id}_{H}\times \unicode[STIX]{x1D70C}_{H})$
induisent un morphisme
$\unicode[STIX]{x1D70C}_{2}:=\unicode[STIX]{x1D70C}_{H}\circ (\text{id}_{H}\times \unicode[STIX]{x1D70C}_{H})$
induisent un morphisme
 $$\begin{eqnarray}\unicode[STIX]{x1D6F9}:H\times H\times Y\xrightarrow[{}]{(\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D70C}_{2})}Y\times _{X}Y\stackrel{{\sim}}{\rightarrow }Y\times S\xrightarrow[{}]{p_{2}}S,~~~\text{i.e.}~~~\unicode[STIX]{x1D70C}_{H}(h_{1}\cdot h_{2},y)=\unicode[STIX]{x1D6F9}(h_{1},h_{2},y)\cdot \unicode[STIX]{x1D70C}_{H}(h_{1},\unicode[STIX]{x1D70C}_{H}(h_{2},y))\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}:H\times H\times Y\xrightarrow[{}]{(\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D70C}_{2})}Y\times _{X}Y\stackrel{{\sim}}{\rightarrow }Y\times S\xrightarrow[{}]{p_{2}}S,~~~\text{i.e.}~~~\unicode[STIX]{x1D70C}_{H}(h_{1}\cdot h_{2},y)=\unicode[STIX]{x1D6F9}(h_{1},h_{2},y)\cdot \unicode[STIX]{x1D70C}_{H}(h_{1},\unicode[STIX]{x1D70C}_{H}(h_{2},y))\end{eqnarray}$$
pour chaque
 $h_{1},h_{2}\in H$
et
$h_{1},h_{2}\in H$
et
![]() $y\in Y$
. Puisque
$y\in Y$
. Puisque
![]() $\unicode[STIX]{x1D70C}_{H}$
est un
$\unicode[STIX]{x1D70C}_{H}$
est un
![]() $S\times S$
-morphisme et
$S\times S$
-morphisme et
![]() $S$
est central dans
$S$
est central dans
![]() $H$
, il existe un morphisme
$H$
, il existe un morphisme
 $G\times G\times X\xrightarrow[{}]{\unicode[STIX]{x1D6F9}_{1}}S$
tel que
$G\times G\times X\xrightarrow[{}]{\unicode[STIX]{x1D6F9}_{1}}S$
tel que
 $\unicode[STIX]{x1D6F9}=\unicode[STIX]{x1D6F9}_{1}\circ (\unicode[STIX]{x1D713}\times \unicode[STIX]{x1D713}\times p)$
. Par le lemme de Rosenlicht (voir [Reference SansucSan81, Lem. 6.5]), il existe des homomorphismes
$\unicode[STIX]{x1D6F9}=\unicode[STIX]{x1D6F9}_{1}\circ (\unicode[STIX]{x1D713}\times \unicode[STIX]{x1D713}\times p)$
. Par le lemme de Rosenlicht (voir [Reference SansucSan81, Lem. 6.5]), il existe des homomorphismes
 $\unicode[STIX]{x1D712}_{1},\unicode[STIX]{x1D712}_{2}:G\rightarrow S$
et un morphisme
$\unicode[STIX]{x1D712}_{1},\unicode[STIX]{x1D712}_{2}:G\rightarrow S$
et un morphisme
 $X\xrightarrow[{}]{\unicode[STIX]{x1D712}_{0}}S$
tels que
$X\xrightarrow[{}]{\unicode[STIX]{x1D712}_{0}}S$
tels que
 $$\begin{eqnarray}\unicode[STIX]{x1D6F9}_{1}(g_{1},g_{2},x)=\unicode[STIX]{x1D712}_{1}(g_{1})\cdot \unicode[STIX]{x1D712}_{2}(g_{2})\cdot \unicode[STIX]{x1D712}_{0}(x)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}_{1}(g_{1},g_{2},x)=\unicode[STIX]{x1D712}_{1}(g_{1})\cdot \unicode[STIX]{x1D712}_{2}(g_{2})\cdot \unicode[STIX]{x1D712}_{0}(x)\end{eqnarray}$$
pour chaque
 $g_{1},g_{2}\in G$
et
$g_{1},g_{2}\in G$
et
![]() $x\in X$
. Puisque
$x\in X$
. Puisque
 $\unicode[STIX]{x1D70C}_{H}(e_{H},y)=y$
pour chaque
$\unicode[STIX]{x1D70C}_{H}(e_{H},y)=y$
pour chaque
![]() $y\in Y$
, on a
$y\in Y$
, on a
 $$\begin{eqnarray}\unicode[STIX]{x1D712}_{1}(g)=\unicode[STIX]{x1D712}_{2}(g)=\unicode[STIX]{x1D712}_{0}(x)=e_{S}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D712}_{1}(g)=\unicode[STIX]{x1D712}_{2}(g)=\unicode[STIX]{x1D712}_{0}(x)=e_{S}\end{eqnarray}$$
pour tout
![]() $x\in X$
et tout
$x\in X$
et tout
![]() $g\in G$
. Donc
$g\in G$
. Donc
![]() $\unicode[STIX]{x1D70C}_{H}$
est une action.
$\unicode[STIX]{x1D70C}_{H}$
est une action.
Pour (1), s’il existe un groupe linéaire
![]() $H$
qui satisfait l’énoncé du théorème, alors
$H$
qui satisfait l’énoncé du théorème, alors
![]() $H$
et l’action
$H$
et l’action
![]() $\unicode[STIX]{x1D70C}_{H}$
sur
$\unicode[STIX]{x1D70C}_{H}$
sur
![]() $Y$
induisent le diagramme (2.6) tel que
$Y$
induisent le diagramme (2.6) tel que
 $\unicode[STIX]{x1D70C}_{H}:=\unicode[STIX]{x1D70C}_{Y}\circ \unicode[STIX]{x1D70C}_{+}$
et
$\unicode[STIX]{x1D70C}_{H}:=\unicode[STIX]{x1D70C}_{Y}\circ \unicode[STIX]{x1D70C}_{+}$
et
 $H\times ^{S}Y\stackrel{{\sim}}{\rightarrow }\unicode[STIX]{x1D70C}^{\ast }Y$
. Alors dans
$H\times ^{S}Y\stackrel{{\sim}}{\rightarrow }\unicode[STIX]{x1D70C}^{\ast }Y$
. Alors dans
 $H^{1}(G\times X,S)$
, on a
$H^{1}(G\times X,S)$
, on a
 $p_{1}^{\ast }[H]+p_{2}^{\ast }[Y]=\unicode[STIX]{x1D70C}^{\ast }[Y]$
, ce qui détermine uniquement
$p_{1}^{\ast }[H]+p_{2}^{\ast }[Y]=\unicode[STIX]{x1D70C}^{\ast }[Y]$
, ce qui détermine uniquement
![]() $H$
par l’argument ci-dessus.
$H$
par l’argument ci-dessus.
Pour (2), si
 $\unicode[STIX]{x1D70C}^{\ast }[Y]=p_{2}^{\ast }[Y]$
, on a
$\unicode[STIX]{x1D70C}^{\ast }[Y]=p_{2}^{\ast }[Y]$
, on a
![]() $[H]=0$
et, d’après (1), on a
$[H]=0$
et, d’après (1), on a
 $H\cong S\times G$
.
$H\cong S\times G$
.
Pour (3), il est clair que
 $\unicode[STIX]{x1D70C}_{H,\unicode[STIX]{x1D719}}|_{S\times Y}=\unicode[STIX]{x1D70C}_{S}$
et
$\unicode[STIX]{x1D70C}_{H,\unicode[STIX]{x1D719}}|_{S\times Y}=\unicode[STIX]{x1D70C}_{S}$
et
 $p\circ \unicode[STIX]{x1D70C}_{H,\unicode[STIX]{x1D719}}=\unicode[STIX]{x1D70C}\circ (\unicode[STIX]{x1D713}\times p)$
. Par ailleurs, soit
$p\circ \unicode[STIX]{x1D70C}_{H,\unicode[STIX]{x1D719}}=\unicode[STIX]{x1D70C}\circ (\unicode[STIX]{x1D713}\times p)$
. Par ailleurs, soit
![]() $\unicode[STIX]{x1D70C}_{H}^{\prime }$
une action satisfaisant les conditions. Alors on a un morphisme
$\unicode[STIX]{x1D70C}_{H}^{\prime }$
une action satisfaisant les conditions. Alors on a un morphisme
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}:H\times Y\xrightarrow[{}]{(\unicode[STIX]{x1D70C}_{H},\unicode[STIX]{x1D70C}_{H}^{\prime })}Y\times _{X}Y\stackrel{{\sim}}{\rightarrow }Y\times S\xrightarrow[{}]{p_{2}}S~~~\text{i.e.}~~~\unicode[STIX]{x1D70C}_{H}^{\prime }(h,y)=\unicode[STIX]{x1D6F7}(y,h)\cdot \unicode[STIX]{x1D70C}_{H}(h,y)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}:H\times Y\xrightarrow[{}]{(\unicode[STIX]{x1D70C}_{H},\unicode[STIX]{x1D70C}_{H}^{\prime })}Y\times _{X}Y\stackrel{{\sim}}{\rightarrow }Y\times S\xrightarrow[{}]{p_{2}}S~~~\text{i.e.}~~~\unicode[STIX]{x1D70C}_{H}^{\prime }(h,y)=\unicode[STIX]{x1D6F7}(y,h)\cdot \unicode[STIX]{x1D70C}_{H}(h,y)\end{eqnarray}$$
pour chaque
![]() $h\in H$
et
$h\in H$
et
![]() $y\in Y$
. Puisque
$y\in Y$
. Puisque
 $\unicode[STIX]{x1D70C}_{H}^{\prime }|_{S\times Y}=\unicode[STIX]{x1D70C}_{S}$
, il existe
$\unicode[STIX]{x1D70C}_{H}^{\prime }|_{S\times Y}=\unicode[STIX]{x1D70C}_{S}$
, il existe
 $G\times X\xrightarrow[{}]{\unicode[STIX]{x1D6F7}_{1}}S$
tel que
$G\times X\xrightarrow[{}]{\unicode[STIX]{x1D6F7}_{1}}S$
tel que
 $\unicode[STIX]{x1D6F7}=\unicode[STIX]{x1D6F7}_{1}\circ (\unicode[STIX]{x1D713}\times p)$
. Par le lemme de Rosenlicht (voir [Reference SansucSan81, Lem. 6.5]), il existe un homomorphisme
$\unicode[STIX]{x1D6F7}=\unicode[STIX]{x1D6F7}_{1}\circ (\unicode[STIX]{x1D713}\times p)$
. Par le lemme de Rosenlicht (voir [Reference SansucSan81, Lem. 6.5]), il existe un homomorphisme
![]() $G\xrightarrow[{}]{\unicode[STIX]{x1D719}}S$
et un morphisme
$G\xrightarrow[{}]{\unicode[STIX]{x1D719}}S$
et un morphisme
![]() $X\xrightarrow[{}]{\unicode[STIX]{x1D712}}S$
tels que
$X\xrightarrow[{}]{\unicode[STIX]{x1D712}}S$
tels que
 $\unicode[STIX]{x1D6F7}_{1}(g,x)=\unicode[STIX]{x1D719}(g)\cdot \unicode[STIX]{x1D712}(x)$
pour chaque
$\unicode[STIX]{x1D6F7}_{1}(g,x)=\unicode[STIX]{x1D719}(g)\cdot \unicode[STIX]{x1D712}(x)$
pour chaque
![]() $g\in G$
et
$g\in G$
et
![]() $x\in X$
. Puisque
$x\in X$
. Puisque
 $\unicode[STIX]{x1D70C}_{H}^{\prime }(e_{H},y)=y$
pour chaque
$\unicode[STIX]{x1D70C}_{H}^{\prime }(e_{H},y)=y$
pour chaque
![]() $y\in Y$
, on a
$y\in Y$
, on a
 $\unicode[STIX]{x1D712}(x)=e_{S}$
pour tout
$\unicode[STIX]{x1D712}(x)=e_{S}$
pour tout
![]() $x\in X$
. Donc
$x\in X$
. Donc
 $\unicode[STIX]{x1D70C}_{H}^{\prime }=\unicode[STIX]{x1D70C}_{H,\unicode[STIX]{x1D719}}$
.◻
$\unicode[STIX]{x1D70C}_{H}^{\prime }=\unicode[STIX]{x1D70C}_{H,\unicode[STIX]{x1D719}}$
.◻
Corollaire 2.8. Soient
![]() $G$
un
$G$
un
![]() $k$
-groupe linéaire connexe et
$k$
-groupe linéaire connexe et
![]() $X_{1},$
$X_{1},$
![]() $X_{2}$
deux
$X_{2}$
deux
![]() $G$
-variétés lisses géométriquement intègres munies d’un
$G$
-variétés lisses géométriquement intègres munies d’un
![]() $G$
-morphisme
$G$
-morphisme
 $X_{1}\rightarrow X_{2}$
. Soit
$X_{1}\rightarrow X_{2}$
. Soit
![]() $S$
un groupe de type multiplicatif. Pour
$S$
un groupe de type multiplicatif. Pour
![]() $i=1,2$
, soient
$i=1,2$
, soient
 $Y_{i}\rightarrow X_{i}$
un
$Y_{i}\rightarrow X_{i}$
un
![]() $S$
-torseur et
$S$
-torseur et
![]() $H_{i}$
le groupe linéaire donné par le théorème 2.7. Si
$H_{i}$
le groupe linéaire donné par le théorème 2.7. Si
 $Y_{1}\cong Y_{2}\times _{X_{2}}X_{1}$
comme
$Y_{1}\cong Y_{2}\times _{X_{2}}X_{1}$
comme
![]() $S$
-torseurs, alors
$S$
-torseurs, alors
 $H_{1}\cong H_{2}$
et, après avoir changé l’action de
$H_{1}\cong H_{2}$
et, après avoir changé l’action de
![]() $H_{1}$
sur
$H_{1}$
sur
![]() $Y_{1}$
ou l’action de
$Y_{1}$
ou l’action de
![]() $H_{2}$
sur
$H_{2}$
sur
![]() $Y_{2}$
, on peut imposer que
$Y_{2}$
, on peut imposer que
 $Y_{1}\cong Y_{2}\times _{X_{2}}X_{1}\rightarrow Y_{2}$
soit un
$Y_{1}\cong Y_{2}\times _{X_{2}}X_{1}\rightarrow Y_{2}$
soit un
![]() $H_{1}$
-morphisme.
$H_{1}$
-morphisme.
Démonstration.
L’action de
![]() $H_{2}$
sur
$H_{2}$
sur
![]() $Y_{2}$
induit canoniquement une action de
$Y_{2}$
induit canoniquement une action de
![]() $H_{2}$
sur
$H_{2}$
sur
 $Y_{2}\times _{X_{2}}X_{1}$
telle que
$Y_{2}\times _{X_{2}}X_{1}$
telle que
 $Y_{2}\times _{X_{2}}X_{1}\rightarrow X_{1}$
soit un
$Y_{2}\times _{X_{2}}X_{1}\rightarrow X_{1}$
soit un
![]() $H_{2}$
-morphisme. Par l’unicité dans le théorème 2.7,
$H_{2}$
-morphisme. Par l’unicité dans le théorème 2.7,
 $H_{1}\cong H_{2}$
. Le résultat découle du fait que la différence de deux actions est un homomorphisme
$H_{1}\cong H_{2}$
. Le résultat découle du fait que la différence de deux actions est un homomorphisme
![]() $G\rightarrow S$
, qui ne dépend pas de
$G\rightarrow S$
, qui ne dépend pas de
![]() $X_{i}$
.◻
$X_{i}$
.◻
Corollaire 2.9. Sous les hypothèses du théorème 2.7, si le
![]() $S$
-torseur
$S$
-torseur
![]() $[Y]$
est trivial sur un
$[Y]$
est trivial sur un
![]() $G$
-ouvert
$G$
-ouvert
![]() $U$
de
$U$
de
![]() $X$
, alors
$X$
, alors
 $H\cong S\times G$
.
$H\cong S\times G$
.
Démonstration.
En appliquant le théorème 2.7(2) à
![]() $U$
et le corollaire 2.8 à
$U$
et le corollaire 2.8 à
![]() $U\rightarrow X$
, on obtient le résultat.◻
$U\rightarrow X$
, on obtient le résultat.◻
Corollaire 2.10. Sous les hypothèses du théorème 2.7, supposons que
 $X\cong G/G_{0}$
, où
$X\cong G/G_{0}$
, où
 $G_{0}\subset G$
est un sous-groupe fermé connexe. Si
$G_{0}\subset G$
est un sous-groupe fermé connexe. Si
 $Y(k)\neq \emptyset$
, alors il existe un sous-groupe connexe fermé
$Y(k)\neq \emptyset$
, alors il existe un sous-groupe connexe fermé
![]() $H_{0}$
de
$H_{0}$
de
![]() $H$
tel que
$H$
tel que
 $Y\cong H/H_{0}$
et
$Y\cong H/H_{0}$
et
 $H_{0}\cong G_{0}$
.
$H_{0}\cong G_{0}$
.
Démonstration.
Soient
 $y\in Y(k)$
,
$y\in Y(k)$
,
 $x:=p(y)$
et
$x:=p(y)$
et
 $G\xrightarrow[{}]{\unicode[STIX]{x1D70B}}X$
le morphisme induit par
$G\xrightarrow[{}]{\unicode[STIX]{x1D70B}}X$
le morphisme induit par
![]() $x$
. Alors
$x$
. Alors
 $Y_{G}:=Y\times _{X}G$
a un
$Y_{G}:=Y\times _{X}G$
a un
![]() $k$
-point sur
$k$
-point sur
![]() $e_{G}$
. Par [Reference Colliot-ThélèneCol08, Thm. 5.6],
$e_{G}$
. Par [Reference Colliot-ThélèneCol08, Thm. 5.6],
![]() $Y_{G}$
est un groupe satisfaisant les conditions du théorème 2.7. Par le corollaire 2.8,
$Y_{G}$
est un groupe satisfaisant les conditions du théorème 2.7. Par le corollaire 2.8,
 $Y_{G}\cong H$
et
$Y_{G}\cong H$
et
 $H\xrightarrow[{}]{\unicode[STIX]{x1D70B}_{Y}}Y$
est un
$H\xrightarrow[{}]{\unicode[STIX]{x1D70B}_{Y}}Y$
est un
![]() $H$
-morphisme. Donc
$H$
-morphisme. Donc
 $H_{0}:=\unicode[STIX]{x1D70B}_{Y}^{-1}(y)\cong \unicode[STIX]{x1D70B}^{-1}(x)\cong G_{0}$
.◻
$H_{0}:=\unicode[STIX]{x1D70B}_{Y}^{-1}(y)\cong \unicode[STIX]{x1D70B}^{-1}(x)\cong G_{0}$
.◻
3 Groupe de Brauer invariant
Dans toute cette section,
![]() $k$
est un corps quelconque de caractéristique
$k$
est un corps quelconque de caractéristique
![]() $0$
. Sauf mention explicite, une variété est une
$0$
. Sauf mention explicite, une variété est une
![]() $k$
-variété et les morphismes sont les
$k$
-variété et les morphismes sont les
![]() $k$
-morphismes. Soit
$k$
-morphismes. Soit
![]() $G$
un groupe linéaire et soit
$G$
un groupe linéaire et soit
![]() $X$
une
$X$
une
![]() $G$
-variété lisse. On définit la notion de sous-groupe
$G$
-variété lisse. On définit la notion de sous-groupe
![]() $G$
-invariant de
$G$
-invariant de
![]() $\text{Br}(X)$
(Définition 3.1). Ensuite on établit ‘l’algébricité’ de
$\text{Br}(X)$
(Définition 3.1). Ensuite on établit ‘l’algébricité’ de
 $\text{Br}_{G}(X)$
(Proposition 3.7). On définit la notion d’homomorphisme de Sansuc (cf. Définition 3.8) et on obtient un diagramme commutatif canonique de suites exactes de Sansuc (Théorème 3.10).
$\text{Br}_{G}(X)$
(Proposition 3.7). On définit la notion d’homomorphisme de Sansuc (cf. Définition 3.8) et on obtient un diagramme commutatif canonique de suites exactes de Sansuc (Théorème 3.10).
3.1 Définitions et propriétés
Définition 3.1. Soient
![]() $G$
un groupe linéaire connexe et
$G$
un groupe linéaire connexe et
![]() $(X,\unicode[STIX]{x1D70C})$
une
$(X,\unicode[STIX]{x1D70C})$
une
![]() $G$
-variété lisse géométriquement intègre. Le sous-groupe de Brauer
$G$
-variété lisse géométriquement intègre. Le sous-groupe de Brauer
![]() $G$
-invariant de
$G$
-invariant de
![]() $X$
est le sous-groupe
$X$
est le sous-groupe
 $$\begin{eqnarray}\text{Br}_{G}(X):=\{b\in \text{Br}(X):(\unicode[STIX]{x1D70C}^{\ast }(b)-p_{2}^{\ast }(b))\in p_{1}^{\ast }\,\text{Br}(G)\}\end{eqnarray}$$
$$\begin{eqnarray}\text{Br}_{G}(X):=\{b\in \text{Br}(X):(\unicode[STIX]{x1D70C}^{\ast }(b)-p_{2}^{\ast }(b))\in p_{1}^{\ast }\,\text{Br}(G)\}\end{eqnarray}$$
de
![]() $\text{Br}(X)$
, où
$\text{Br}(X)$
, où
 $G\times X\xrightarrow[{}]{p_{1}}G$
,
$G\times X\xrightarrow[{}]{p_{1}}G$
,
 $G\times X\xrightarrow[{}]{p_{2}}X$
sont les projections.
$G\times X\xrightarrow[{}]{p_{2}}X$
sont les projections.
Dans la proposition 3.4, pour un sous-groupe
 $B\subset \text{Br}(X)$
, on montre que
$B\subset \text{Br}(X)$
, on montre que
 $B\subset \text{Br}_{G}(X)$
si et seulement si
$B\subset \text{Br}_{G}(X)$
si et seulement si
![]() $B$
est ‘
$B$
est ‘
![]() $G$
-invariant’.
$G$
-invariant’.
Proposition 3.2. Sous les hypothèses de la Définition 3.1, alors :
(1) pour toute extension de corps
 $K/k$
, l’homomorphisme
$K/k$
, l’homomorphisme
 $\unicode[STIX]{x1D70B}^{\ast }:\text{Br}(X)\rightarrow \text{Br}(X_{K})$
induit par
$\unicode[STIX]{x1D70B}^{\ast }:\text{Br}(X)\rightarrow \text{Br}(X_{K})$
induit par
 $\unicode[STIX]{x1D70B}:X_{K}\rightarrow X$
vérifie
$\unicode[STIX]{x1D70B}:X_{K}\rightarrow X$
vérifie
 $\unicode[STIX]{x1D70B}^{\ast }(\text{Br}_{G}(X))\subset \text{Br}_{G_{K}}(X_{K})$
;
$\unicode[STIX]{x1D70B}^{\ast }(\text{Br}_{G}(X))\subset \text{Br}_{G_{K}}(X_{K})$
;(2) pour tout groupe linéaire connexe
 $H$
, tout homomorphisme
$H$
, tout homomorphisme
 $H\xrightarrow[{}]{\unicode[STIX]{x1D713}}G$
, toute
$H\xrightarrow[{}]{\unicode[STIX]{x1D713}}G$
, toute
 $H$
-variété
$H$
-variété
 $Y$
et tout
$Y$
et tout
 $H$
-morphisme
$H$
-morphisme
 $p:Y\rightarrow X$
(compatible avec
$p:Y\rightarrow X$
(compatible avec
 $\unicode[STIX]{x1D713}$
) on a
$\unicode[STIX]{x1D713}$
) on a
 $p^{\ast }(\text{Br}_{G}(X))\subset \text{Br}_{H}(Y)$
;
$p^{\ast }(\text{Br}_{G}(X))\subset \text{Br}_{H}(Y)$
;(3) pour tout
 $G$
-ouvert dense
$G$
-ouvert dense
 $U\subset X$
, on a
$U\subset X$
, on a
 $\text{Br}_{G}(X)=\text{Br}_{G}(U)\cap \text{Br}(X)$
;
$\text{Br}_{G}(X)=\text{Br}_{G}(U)\cap \text{Br}(X)$
;(4) on a
 $\text{Br}_{1}(X)\subset \text{Br}_{G}(X)$
;
$\text{Br}_{1}(X)\subset \text{Br}_{G}(X)$
;(5) pour toute
 $G$
-variété
$G$
-variété
 $Y$
munie d’un
$Y$
munie d’un
 $G$
-morphisme
$G$
-morphisme
 $Y\xrightarrow[{}]{p}X$
, si
$Y\xrightarrow[{}]{p}X$
, si
 $p$
est un torseur sous un groupe linéaire connexe
$p$
est un torseur sous un groupe linéaire connexe
 $H$
, on a
$H$
, on a
 $(p^{\ast })^{-1}\,\text{Br}_{G}(Y)=\text{Br}_{G}(X)$
, où
$(p^{\ast })^{-1}\,\text{Br}_{G}(Y)=\text{Br}_{G}(X)$
, où
 $\text{Br}(X)\xrightarrow[{}]{p^{\ast }}\text{Br}(Y)$
;
$\text{Br}(X)\xrightarrow[{}]{p^{\ast }}\text{Br}(Y)$
;(6) sous les hypothèses de (5), on a
 $$\begin{eqnarray}\text{Br}_{1}(X,Y):=\text{Ker}(\text{Br}(X)\rightarrow \text{Br}(Y_{\bar{k}}))\subset \text{Br}_{G}(X).\end{eqnarray}$$
$$\begin{eqnarray}\text{Br}_{1}(X,Y):=\text{Ker}(\text{Br}(X)\rightarrow \text{Br}(Y_{\bar{k}}))\subset \text{Br}_{G}(X).\end{eqnarray}$$
Démonstration.
Les énoncés (1), (2) et (3) découlent de la définition.
Pour (4), par [Reference SansucSan81, Lem. 6.6],
 $\text{Br}_{1}(G\times X)=\text{Br}_{a}(G)\oplus \text{Br}_{1}(X)=p_{1}^{\ast }\,\text{Br}_{1}(G)+p_{2}^{\ast }\,\text{Br}_{1}(X).$
Pour tout
$\text{Br}_{1}(G\times X)=\text{Br}_{a}(G)\oplus \text{Br}_{1}(X)=p_{1}^{\ast }\,\text{Br}_{1}(G)+p_{2}^{\ast }\,\text{Br}_{1}(X).$
Pour tout
 $\unicode[STIX]{x1D6FC}\in \text{Br}_{1}(X)$
, on a
$\unicode[STIX]{x1D6FC}\in \text{Br}_{1}(X)$
, on a
 $(\unicode[STIX]{x1D70C}^{\ast }(\unicode[STIX]{x1D6FC})-p_{2}^{\ast }(\unicode[STIX]{x1D6FC}))|_{e_{G}\times X}=0$
et donc
$(\unicode[STIX]{x1D70C}^{\ast }(\unicode[STIX]{x1D6FC})-p_{2}^{\ast }(\unicode[STIX]{x1D6FC}))|_{e_{G}\times X}=0$
et donc
 $(\unicode[STIX]{x1D70C}^{\ast }(\unicode[STIX]{x1D6FC})-p_{2}^{\ast }(\unicode[STIX]{x1D6FC}))\subset p_{1}^{\ast }\,\text{Br}_{1}(G)$
.
$(\unicode[STIX]{x1D70C}^{\ast }(\unicode[STIX]{x1D6FC})-p_{2}^{\ast }(\unicode[STIX]{x1D6FC}))\subset p_{1}^{\ast }\,\text{Br}_{1}(G)$
.
Pour (5), puisque
 $G\times Y\xrightarrow[{}]{\text{id}_{G}\times p}G\times X$
est aussi un
$G\times Y\xrightarrow[{}]{\text{id}_{G}\times p}G\times X$
est aussi un
![]() $H$
-torseur, par la suite exacte de Sansuc [Reference SansucSan81, Prop. 6.10], on a le diagramme suivant commutatif de suites exactes.
$H$
-torseur, par la suite exacte de Sansuc [Reference SansucSan81, Prop. 6.10], on a le diagramme suivant commutatif de suites exactes.

Donc, pour tout
 $\unicode[STIX]{x1D6FC}\in (p^{\ast })^{-1}\,\text{Br}_{G}(Y)$
, on a
$\unicode[STIX]{x1D6FC}\in (p^{\ast })^{-1}\,\text{Br}_{G}(Y)$
, on a
 $$\begin{eqnarray}\unicode[STIX]{x1D70C}^{\ast }(\unicode[STIX]{x1D6FC})-p_{2}^{\ast }(\unicode[STIX]{x1D6FC})\in p_{1}^{\ast }\,\text{Br}(G)+\text{Im}\,\text{Pic}(H)\subset p_{1}^{\ast }\,\text{Br}(G)+p_{2}^{\ast }\,\text{Br}(X).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}^{\ast }(\unicode[STIX]{x1D6FC})-p_{2}^{\ast }(\unicode[STIX]{x1D6FC})\in p_{1}^{\ast }\,\text{Br}(G)+\text{Im}\,\text{Pic}(H)\subset p_{1}^{\ast }\,\text{Br}(G)+p_{2}^{\ast }\,\text{Br}(X).\end{eqnarray}$$
Puisque
 $(\unicode[STIX]{x1D70C}^{\ast }(\unicode[STIX]{x1D6FC})-p_{2}^{\ast }(\unicode[STIX]{x1D6FC}))|_{e_{G}\times X}=0$
, on peut voir que
$(\unicode[STIX]{x1D70C}^{\ast }(\unicode[STIX]{x1D6FC})-p_{2}^{\ast }(\unicode[STIX]{x1D6FC}))|_{e_{G}\times X}=0$
, on peut voir que
 $\unicode[STIX]{x1D70C}^{\ast }(\unicode[STIX]{x1D6FC})-p_{2}^{\ast }(\unicode[STIX]{x1D6FC})\in p_{1}^{\ast }\,\text{Br}(G)$
.
$\unicode[STIX]{x1D70C}^{\ast }(\unicode[STIX]{x1D6FC})-p_{2}^{\ast }(\unicode[STIX]{x1D6FC})\in p_{1}^{\ast }\,\text{Br}(G)$
.
Par (4) et (5),
 $\text{Br}_{1}(X,Y)\subset \text{Br}_{G}(X)$
.◻
$\text{Br}_{1}(X,Y)\subset \text{Br}_{G}(X)$
.◻
Le lemme suivant est bien connu.
Lemme 3.3. Soient
![]() $X$
,
$X$
,
![]() $Y$
deux variétés lisses intègres et
$Y$
deux variétés lisses intègres et
 $Y\xrightarrow[{}]{p}X$
un morphisme fidèlement plat à fibres géométriquement intègres. Soit
$Y\xrightarrow[{}]{p}X$
un morphisme fidèlement plat à fibres géométriquement intègres. Soit
 $B\subset \text{Br}(k(X))$
(resp.
$B\subset \text{Br}(k(X))$
(resp.
 $B\subset \text{Br}(U)$
avec
$B\subset \text{Br}(U)$
avec
![]() $U\subset X$
un ouvert) un sous-groupe. Alors
$U\subset X$
un ouvert) un sous-groupe. Alors
 $$\begin{eqnarray}p^{\ast }(B\cap \text{Br}(X))=(p^{\ast }B)\cap \text{Br}(Y).\end{eqnarray}$$
$$\begin{eqnarray}p^{\ast }(B\cap \text{Br}(X))=(p^{\ast }B)\cap \text{Br}(Y).\end{eqnarray}$$
Démonstration.
Pour tout
![]() $x\in X$
, la fibre
$x\in X$
, la fibre
![]() $Y_{x}$
est intègre et
$Y_{x}$
est intègre et
 $H^{1}(k(x),\mathbb{Q}/\mathbb{Z})\rightarrow H^{1}(k(Y_{x}),\mathbb{Q}/\mathbb{Z})$
est injectif. En appliquant la suite exacte naturelle [Reference Colliot-Thélène, Jacob and RosenbergCol95, (3.9)] à
$H^{1}(k(x),\mathbb{Q}/\mathbb{Z})\rightarrow H^{1}(k(Y_{x}),\mathbb{Q}/\mathbb{Z})$
est injectif. En appliquant la suite exacte naturelle [Reference Colliot-Thélène, Jacob and RosenbergCol95, (3.9)] à
![]() $X$
et à
$X$
et à
![]() $Y$
, on obtient le résultat.◻
$Y$
, on obtient le résultat.◻
Proposition 3.4. Sous les hypothèses de la Définition 3.1, pour un sous-groupe
 $B\subset \text{Br}(X)$
, les énoncés ci-dessous sont équivalents :
$B\subset \text{Br}(X)$
, les énoncés ci-dessous sont équivalents :
(1)
 $B\subset \text{Br}_{G}(X)$
;
$B\subset \text{Br}_{G}(X)$
;(2)
 $\unicode[STIX]{x1D70C}^{\ast }B+p_{1}^{\ast }\,\text{Br}(G)=p_{2}^{\ast }B+p_{1}^{\ast }\,\text{Br}(G)$
;
$\unicode[STIX]{x1D70C}^{\ast }B+p_{1}^{\ast }\,\text{Br}(G)=p_{2}^{\ast }B+p_{1}^{\ast }\,\text{Br}(G)$
;(3) pour toute extension de corps
 $K/k$
et tout
$K/k$
et tout
 $g\in G(K)$
, l’action
$g\in G(K)$
, l’action
 $\unicode[STIX]{x1D70C}_{g}:X_{K}\xrightarrow[{}]{g\cdot (-)}X_{K}$
induit un morphisme
$\unicode[STIX]{x1D70C}_{g}:X_{K}\xrightarrow[{}]{g\cdot (-)}X_{K}$
induit un morphisme
 $\text{Br}(X_{K})\xrightarrow[{}]{\unicode[STIX]{x1D70C}_{g}^{\ast }}\text{Br}(X_{K})$
tel que (3.2)où
$\text{Br}(X_{K})\xrightarrow[{}]{\unicode[STIX]{x1D70C}_{g}^{\ast }}\text{Br}(X_{K})$
tel que (3.2)où $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{g}^{\ast }\unicode[STIX]{x1D70B}^{\ast }B+\text{Im}\,\text{Br}(K)=\unicode[STIX]{x1D70B}^{\ast }B+\text{Im}\,\text{Br}(K),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{g}^{\ast }\unicode[STIX]{x1D70B}^{\ast }B+\text{Im}\,\text{Br}(K)=\unicode[STIX]{x1D70B}^{\ast }B+\text{Im}\,\text{Br}(K),\end{eqnarray}$$
 $X_{K}\xrightarrow[{}]{\unicode[STIX]{x1D70B}}X$
;
$X_{K}\xrightarrow[{}]{\unicode[STIX]{x1D70B}}X$
;(4) pour tout
 $b\in B$
, toute extension de corps
$b\in B$
, toute extension de corps
 $K/k$
et tout
$K/k$
et tout
 $g\in G(K)$
, on a où
$g\in G(K)$
, on a où $$\begin{eqnarray}(\unicode[STIX]{x1D70C}_{g}^{\ast }\unicode[STIX]{x1D70B}^{\ast }(b)-\unicode[STIX]{x1D70B}^{\ast }(b))\in \text{Im}\,\text{Br}(K),\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D70C}_{g}^{\ast }\unicode[STIX]{x1D70B}^{\ast }(b)-\unicode[STIX]{x1D70B}^{\ast }(b))\in \text{Im}\,\text{Br}(K),\end{eqnarray}$$
 $\unicode[STIX]{x1D70B}$
et
$\unicode[STIX]{x1D70B}$
et
 $\unicode[STIX]{x1D70C}_{g}^{\ast }$
sont définis dans (3) ;
$\unicode[STIX]{x1D70C}_{g}^{\ast }$
sont définis dans (3) ;(5) pour toute extension de corps
 $K/k$
telle que
$K/k$
telle que
 $k$
soit algébriquement clos dans
$k$
soit algébriquement clos dans
 $K$
, et tout
$K$
, et tout
 $g\in G(K)$
, on a (3.2), où
$g\in G(K)$
, on a (3.2), où
 $\unicode[STIX]{x1D70B}$
et
$\unicode[STIX]{x1D70B}$
et
 $\unicode[STIX]{x1D70C}_{g}^{\ast }$
sont définis dans (3).
$\unicode[STIX]{x1D70C}_{g}^{\ast }$
sont définis dans (3).
Démonstration.
Les implications
 $(4)\Rightarrow (3)$
,
$(4)\Rightarrow (3)$
,
 $(3)\Rightarrow (5)$
sont claires.
$(3)\Rightarrow (5)$
sont claires.
Pour
 $(2)\Rightarrow (1)$
, on note
$(2)\Rightarrow (1)$
, on note
 $i_{e}:X\xrightarrow[{}]{e_{G}\times \text{id}_{X}}G\times X$
l’immersion fermée. Pour
$i_{e}:X\xrightarrow[{}]{e_{G}\times \text{id}_{X}}G\times X$
l’immersion fermée. Pour
![]() $b\in B$
, il existe
$b\in B$
, il existe
![]() $b^{\prime }\in B$
et
$b^{\prime }\in B$
et
 $a\in \text{Br}(G)$
tels que
$a\in \text{Br}(G)$
tels que
 $\unicode[STIX]{x1D70C}^{\ast }(b)=p_{2}^{\ast }(b^{\prime })+p_{1}^{\ast }(a)$
. Puisque
$\unicode[STIX]{x1D70C}^{\ast }(b)=p_{2}^{\ast }(b^{\prime })+p_{1}^{\ast }(a)$
. Puisque
 $\unicode[STIX]{x1D70C}\circ i_{e}=p_{2}\circ i_{e}=\text{id}_{X}$
et que
$\unicode[STIX]{x1D70C}\circ i_{e}=p_{2}\circ i_{e}=\text{id}_{X}$
et que
![]() $p_{1}\circ i_{e}$
se factorise par
$p_{1}\circ i_{e}$
se factorise par
![]() $\text{Spec}\,k$
, on a
$\text{Spec}\,k$
, on a
 $b-b^{\prime }\in \text{Im}\,\text{Br}(k)$
et donc
$b-b^{\prime }\in \text{Im}\,\text{Br}(k)$
et donc
 $$\begin{eqnarray}(\unicode[STIX]{x1D70C}^{\ast }(b)-p_{2}^{\ast }(b))\in (p_{1}^{\ast }\,\text{Br}(G)+\text{Im}\,\text{Br}(k))=p_{1}^{\ast }\,\text{Br}(G).\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D70C}^{\ast }(b)-p_{2}^{\ast }(b))\in (p_{1}^{\ast }\,\text{Br}(G)+\text{Im}\,\text{Br}(k))=p_{1}^{\ast }\,\text{Br}(G).\end{eqnarray}$$
Pour
 $(1)\Rightarrow (4)$
, on note
$(1)\Rightarrow (4)$
, on note
 $i_{g}:X_{K}\xrightarrow[{}]{g\times \text{id}_{X}}G\times X$
le morphisme et
$i_{g}:X_{K}\xrightarrow[{}]{g\times \text{id}_{X}}G\times X$
le morphisme et
 $A:=\text{Im}\,\text{Br}(K)$
. Alors
$A:=\text{Im}\,\text{Br}(K)$
. Alors
 $\unicode[STIX]{x1D70B}\circ \unicode[STIX]{x1D70C}_{g}=\unicode[STIX]{x1D70C}\circ i_{g}$
et
$\unicode[STIX]{x1D70B}\circ \unicode[STIX]{x1D70C}_{g}=\unicode[STIX]{x1D70C}\circ i_{g}$
et
 $\unicode[STIX]{x1D70B}=p_{2}\circ i_{g}$
. Puisque
$\unicode[STIX]{x1D70B}=p_{2}\circ i_{g}$
. Puisque
 $i_{g}^{\ast }(p_{1}^{\ast }\,\text{Br}(G))\subset A$
, on a
$i_{g}^{\ast }(p_{1}^{\ast }\,\text{Br}(G))\subset A$
, on a
 $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{g}^{\ast }\unicode[STIX]{x1D70B}^{\ast }(b)+A=i_{g}^{\ast }(p_{1}^{\ast }\,\text{Br}(G)+\unicode[STIX]{x1D70C}^{\ast }(b))+A=i_{g}^{\ast }(p_{1}^{\ast }\,\text{Br}(G)+p_{2}^{\ast }(b))+A=\unicode[STIX]{x1D70B}^{\ast }(b)+A.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{g}^{\ast }\unicode[STIX]{x1D70B}^{\ast }(b)+A=i_{g}^{\ast }(p_{1}^{\ast }\,\text{Br}(G)+\unicode[STIX]{x1D70C}^{\ast }(b))+A=i_{g}^{\ast }(p_{1}^{\ast }\,\text{Br}(G)+p_{2}^{\ast }(b))+A=\unicode[STIX]{x1D70B}^{\ast }(b)+A.\end{eqnarray}$$
Pour
 $(5)\Rightarrow (2)$
, notons
$(5)\Rightarrow (2)$
, notons
 $X_{\unicode[STIX]{x1D702}_{G}}\xrightarrow[{}]{\unicode[STIX]{x1D70B}}X$
la projection et
$X_{\unicode[STIX]{x1D702}_{G}}\xrightarrow[{}]{\unicode[STIX]{x1D70B}}X$
la projection et
 $X_{\unicode[STIX]{x1D702}_{G}}\xrightarrow[{}]{i_{\unicode[STIX]{x1D702}}}G\times X$
l’immersion canonique. Alors
$X_{\unicode[STIX]{x1D702}_{G}}\xrightarrow[{}]{i_{\unicode[STIX]{x1D702}}}G\times X$
l’immersion canonique. Alors
 $\text{Br}(G\times X)\rightarrow \text{Br}(X_{\unicode[STIX]{x1D702}_{G}})$
est injectif. Par le lemme 3.3,
$\text{Br}(G\times X)\rightarrow \text{Br}(X_{\unicode[STIX]{x1D702}_{G}})$
est injectif. Par le lemme 3.3,
 $p_{1}^{\ast }\,\text{Br}(\unicode[STIX]{x1D702}_{G})\cap \text{Br}(G\times X)=p_{1}^{\ast }\,\text{Br}(G)$
. Donc il suffit de montrer que :
$p_{1}^{\ast }\,\text{Br}(\unicode[STIX]{x1D702}_{G})\cap \text{Br}(G\times X)=p_{1}^{\ast }\,\text{Br}(G)$
. Donc il suffit de montrer que :
 $$\begin{eqnarray}(i_{\unicode[STIX]{x1D702}}^{\ast }\unicode[STIX]{x1D70C}^{\ast })B+\text{Im}\,\text{Br}(\unicode[STIX]{x1D702}_{G})=(i_{\unicode[STIX]{x1D702}}^{\ast }p_{2}^{\ast })B+\text{Im}\,\text{Br}(\unicode[STIX]{x1D702}_{G}).\end{eqnarray}$$
$$\begin{eqnarray}(i_{\unicode[STIX]{x1D702}}^{\ast }\unicode[STIX]{x1D70C}^{\ast })B+\text{Im}\,\text{Br}(\unicode[STIX]{x1D702}_{G})=(i_{\unicode[STIX]{x1D702}}^{\ast }p_{2}^{\ast })B+\text{Im}\,\text{Br}(\unicode[STIX]{x1D702}_{G}).\end{eqnarray}$$
Le résultat découle de
 $p_{2}\circ i_{\unicode[STIX]{x1D702}}=\unicode[STIX]{x1D70B}$
et
$p_{2}\circ i_{\unicode[STIX]{x1D702}}=\unicode[STIX]{x1D70B}$
et
 $\unicode[STIX]{x1D70C}\circ i_{\unicode[STIX]{x1D702}}=\unicode[STIX]{x1D70B}\circ \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D702}_{G}}$
.◻
$\unicode[STIX]{x1D70C}\circ i_{\unicode[STIX]{x1D702}}=\unicode[STIX]{x1D70B}\circ \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D702}_{G}}$
.◻
Soient
![]() $X$
une variété lisse géométriquement intègre et
$X$
une variété lisse géométriquement intègre et
![]() $U\subset X$
un ouvert non vide. Supposons que
$U\subset X$
un ouvert non vide. Supposons que
 $D:=(X\setminus U)$
est lisse de codimension
$D:=(X\setminus U)$
est lisse de codimension
![]() $1$
. Par le théorème de pureté pour la cohomologie étale à support dans un fermé lisse (cf. [Reference MilneMil80, § VI.5]), on a une suite exacte :
$1$
. Par le théorème de pureté pour la cohomologie étale à support dans un fermé lisse (cf. [Reference MilneMil80, § VI.5]), on a une suite exacte :
 $$\begin{eqnarray}H^{2}(X,\mathbb{Q}/\mathbb{Z}(1))\rightarrow H^{2}(U,\mathbb{Q}/\mathbb{Z}(1))\rightarrow H^{1}(D,\mathbb{Q}/\mathbb{Z})\rightarrow H^{3}(X,\mathbb{Q}/\mathbb{Z}(1))\rightarrow H^{3}(U,\mathbb{Q}/\mathbb{Z}(1)).\end{eqnarray}$$
$$\begin{eqnarray}H^{2}(X,\mathbb{Q}/\mathbb{Z}(1))\rightarrow H^{2}(U,\mathbb{Q}/\mathbb{Z}(1))\rightarrow H^{1}(D,\mathbb{Q}/\mathbb{Z})\rightarrow H^{3}(X,\mathbb{Q}/\mathbb{Z}(1))\rightarrow H^{3}(U,\mathbb{Q}/\mathbb{Z}(1)).\end{eqnarray}$$
Puisque
 $\text{Pic}(X)\rightarrow \text{Pic}(U)$
est surjectif et
$\text{Pic}(X)\rightarrow \text{Pic}(U)$
est surjectif et
 $\text{Br}(X)\rightarrow \text{Br}(U)$
est injectif, d’après la suite exacte de Kummer, on a la suite exacte (cf. Grothendieck [Reference GrothendieckGro68])
$\text{Br}(X)\rightarrow \text{Br}(U)$
est injectif, d’après la suite exacte de Kummer, on a la suite exacte (cf. Grothendieck [Reference GrothendieckGro68])
 $$\begin{eqnarray}0\rightarrow \text{Br}(X)\rightarrow \text{Br}(U)\xrightarrow[{}]{\unicode[STIX]{x2202}}H^{1}(D,\mathbb{Q}/\mathbb{Z})\rightarrow H^{3}(X,\mathbb{Q}/\mathbb{Z}(1))\rightarrow H^{3}(U,\mathbb{Q}/\mathbb{Z}(1)).\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow \text{Br}(X)\rightarrow \text{Br}(U)\xrightarrow[{}]{\unicode[STIX]{x2202}}H^{1}(D,\mathbb{Q}/\mathbb{Z})\rightarrow H^{3}(X,\mathbb{Q}/\mathbb{Z}(1))\rightarrow H^{3}(U,\mathbb{Q}/\mathbb{Z}(1)).\end{eqnarray}$$
Soit
![]() $G$
un groupe linéaire connexe. Si
$G$
un groupe linéaire connexe. Si
![]() $X$
est munie d’une
$X$
est munie d’une
![]() $G$
-action
$G$
-action
 $\unicode[STIX]{x1D70C}:G\times X\rightarrow X$
respectant
$\unicode[STIX]{x1D70C}:G\times X\rightarrow X$
respectant
![]() $U$
, on a un diagramme de suites exactes :
$U$
, on a un diagramme de suites exactes :

où
 $G\times X\xrightarrow[{}]{\unicode[STIX]{x1D703}}X$
est soit
$G\times X\xrightarrow[{}]{\unicode[STIX]{x1D703}}X$
est soit
![]() $p_{2}$
soit
$p_{2}$
soit
![]() $\unicode[STIX]{x1D70C}$
. On a le lemme suivant.
$\unicode[STIX]{x1D70C}$
. On a le lemme suivant.
Lemme 3.5. Avec les notations et hypothèses ci-dessus, on a :
(1)
 $p_{2,D}^{\ast }|_{\unicode[STIX]{x2202}(\text{Br}_{G}(U))}=\unicode[STIX]{x1D70C}_{D}^{\ast }|_{\unicode[STIX]{x2202}(\text{Br}_{G}(U))}$
;
$p_{2,D}^{\ast }|_{\unicode[STIX]{x2202}(\text{Br}_{G}(U))}=\unicode[STIX]{x1D70C}_{D}^{\ast }|_{\unicode[STIX]{x2202}(\text{Br}_{G}(U))}$
;(2) pour tout
 $b\in \text{Br}_{G}(U)$
, il existe un revêtement fini étale galoisien abélien
$b\in \text{Br}_{G}(U)$
, il existe un revêtement fini étale galoisien abélien
 $D^{\prime }\xrightarrow[{}]{\unicode[STIX]{x1D70B}}D$
tel que
$D^{\prime }\xrightarrow[{}]{\unicode[STIX]{x1D70B}}D$
tel que
 $D^{\prime }$
soit une
$D^{\prime }$
soit une
 $G$
-variété,
$G$
-variété,
 $\unicode[STIX]{x1D70B}$
soit un
$\unicode[STIX]{x1D70B}$
soit un
 $G$
-morphisme et que
$G$
-morphisme et que
 $\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x2202}(b))=0\in H^{1}(D^{\prime },\mathbb{Q}/\mathbb{Z})$
.
$\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x2202}(b))=0\in H^{1}(D^{\prime },\mathbb{Q}/\mathbb{Z})$
.
Démonstration.
Puisque
 $p_{1,U}^{\ast }\,\text{Br}(G)\subset \text{Im}(\text{Res})$
, l’énoncé (1) découle de la proposition 3.4(2). Pour
$p_{1,U}^{\ast }\,\text{Br}(G)\subset \text{Im}(\text{Res})$
, l’énoncé (1) découle de la proposition 3.4(2). Pour
 $b\in \text{Br}_{G}(U)$
, soit
$b\in \text{Br}_{G}(U)$
, soit
![]() $n\in \mathbb{Z}$
l’ordre de
$n\in \mathbb{Z}$
l’ordre de
![]() $\unicode[STIX]{x2202}(b)$
. Alors
$\unicode[STIX]{x2202}(b)$
. Alors
 $\unicode[STIX]{x2202}(b)\in H^{1}(D,\mathbb{Z}/n)$
. Soit
$\unicode[STIX]{x2202}(b)\in H^{1}(D,\mathbb{Z}/n)$
. Soit
 $D^{\prime }\xrightarrow[{}]{\unicode[STIX]{x1D70B}}D$
un
$D^{\prime }\xrightarrow[{}]{\unicode[STIX]{x1D70B}}D$
un
![]() $\mathbb{Z}/n$
-torseur tel que
$\mathbb{Z}/n$
-torseur tel que
 $[D^{\prime }]=\unicode[STIX]{x2202}(b)$
. Par (1),
$[D^{\prime }]=\unicode[STIX]{x2202}(b)$
. Par (1),
 $p_{2,D}^{\ast }[D^{\prime }]=\unicode[STIX]{x1D70C}_{D}^{\ast }[D^{\prime }]\in H^{1}(G\times D,\mathbb{Z}/n)$
. D’après le théorème 2.7(2),
$p_{2,D}^{\ast }[D^{\prime }]=\unicode[STIX]{x1D70C}_{D}^{\ast }[D^{\prime }]\in H^{1}(G\times D,\mathbb{Z}/n)$
. D’après le théorème 2.7(2),
![]() $D^{\prime }$
est une
$D^{\prime }$
est une
![]() $G$
-variété.◻
$G$
-variété.◻
Lemme 3.6. Soient
![]() $G$
un groupe linéaire connexe et
$G$
un groupe linéaire connexe et
![]() $P$
un
$P$
un
![]() $G$
-torseur. Alors
$G$
-torseur. Alors
 $\text{Br}_{G}(P)=\text{Br}_{1}(P)$
.
$\text{Br}_{G}(P)=\text{Br}_{1}(P)$
.
Démonstration.
D’après la proposition 3.2(1) et (4), il suffit de montrer que
 $\text{Br}_{G}(P_{\bar{k}})=0$
. On peut supposer
$\text{Br}_{G}(P_{\bar{k}})=0$
. On peut supposer
![]() $k=\bar{k}$
et
$k=\bar{k}$
et
![]() $P\cong G$
.
$P\cong G$
.
Si
![]() $G$
est un tore de dimension
$G$
est un tore de dimension
![]() $n$
, alors
$n$
, alors
 $G\cong \mathbb{G}_{m}^{n}$
est un ouvert de
$G\cong \mathbb{G}_{m}^{n}$
est un ouvert de
![]() $\mathbb{A}^{n}$
canoniquement. Soit
$\mathbb{A}^{n}$
canoniquement. Soit
 $X:=\mathbb{A}^{n}\setminus [(\mathbb{A}^{n}\setminus G)_{\text{sing}}]$
. Alors
$X:=\mathbb{A}^{n}\setminus [(\mathbb{A}^{n}\setminus G)_{\text{sing}}]$
. Alors
 $\text{codim}(\mathbb{A}^{n}\setminus X,\mathbb{A}^{n})\geqslant 2$
,
$\text{codim}(\mathbb{A}^{n}\setminus X,\mathbb{A}^{n})\geqslant 2$
,
 $\text{Br}(X)=0$
,
$\text{Br}(X)=0$
,
![]() $G$
est un ouvert de
$G$
est un ouvert de
![]() $X$
et
$X$
et
 $X\setminus G=\bigsqcup _{i=1}^{n}D_{i}$
, chaque
$X\setminus G=\bigsqcup _{i=1}^{n}D_{i}$
, chaque
![]() $D_{i}$
étant un
$D_{i}$
étant un
![]() $G$
-espace homogène de stabilisateur
$G$
-espace homogène de stabilisateur
![]() $\mathbb{G}_{m}$
. D’après [Reference Cao and XuCX15, Prop. 2.2], pour tout revêtement fini étale galoisien
$\mathbb{G}_{m}$
. D’après [Reference Cao and XuCX15, Prop. 2.2], pour tout revêtement fini étale galoisien
 $D_{i}^{\prime }\xrightarrow[{}]{\unicode[STIX]{x1D70B}_{i}}D_{i}$
tel que
$D_{i}^{\prime }\xrightarrow[{}]{\unicode[STIX]{x1D70B}_{i}}D_{i}$
tel que
![]() $D_{i}^{\prime }$
soit une
$D_{i}^{\prime }$
soit une
![]() $G$
-variété intègre et que
$G$
-variété intègre et que
![]() $\unicode[STIX]{x1D70B}_{i}$
soit un
$\unicode[STIX]{x1D70B}_{i}$
soit un
![]() $G$
-morphisme, le morphisme
$G$
-morphisme, le morphisme
![]() $\unicode[STIX]{x1D70B}_{i}$
est un isomorphisme. D’après le lemme 3.5(2) et (3.3),
$\unicode[STIX]{x1D70B}_{i}$
est un isomorphisme. D’après le lemme 3.5(2) et (3.3),
 $\text{Br}_{G}(G)\subset \text{Br}(X)=0$
.
$\text{Br}_{G}(G)\subset \text{Br}(X)=0$
.
Si
![]() $G$
est réductif, soit
$G$
est réductif, soit
![]() $T$
le tore maximal de
$T$
le tore maximal de
![]() $G$
. Par la décomposition de Bruhat, il existe un ouvert
$G$
. Par la décomposition de Bruhat, il existe un ouvert
![]() $U$
de
$U$
de
![]() $G$
tel que
$G$
tel que
 $U\cong \mathbb{A}^{n}\times T\times \mathbb{A}^{n}$
, où
$U\cong \mathbb{A}^{n}\times T\times \mathbb{A}^{n}$
, où
 $2n=\dim (U)-\dim (T)$
(voir la démonstration de [Reference Colliot-ThélèneCol07, Prop. 4.2]). Donc
$2n=\dim (U)-\dim (T)$
(voir la démonstration de [Reference Colliot-ThélèneCol07, Prop. 4.2]). Donc
 $\text{Br}(G)\rightarrow \text{Br}(T)$
est injectif. Le résultat découle de la proposition 3.2(2).
$\text{Br}(G)\rightarrow \text{Br}(T)$
est injectif. Le résultat découle de la proposition 3.2(2).
En général, par [Reference Cao, Demarche and XuCDX16, Lem. 2.1], le morphisme
 $\text{Br}(G^{\text{red}})\rightarrow \text{Br}(G)$
est un isomorphisme. Le résultat découle de la proposition 3.2(2).◻
$\text{Br}(G^{\text{red}})\rightarrow \text{Br}(G)$
est un isomorphisme. Le résultat découle de la proposition 3.2(2).◻
Proposition 3.7. Soient
![]() $G$
un groupe linéaire connexe et
$G$
un groupe linéaire connexe et
![]() $(X,\unicode[STIX]{x1D70C})$
une
$(X,\unicode[STIX]{x1D70C})$
une
![]() $G$
-variété lisse géométriquement intègre. Pour tout
$G$
-variété lisse géométriquement intègre. Pour tout
 $b\in \text{Br}_{G}(X)$
, on a
$b\in \text{Br}_{G}(X)$
, on a
 $(\unicode[STIX]{x1D70C}^{\ast }(b)-p_{2}^{\ast }(b))\in p_{1}^{\ast }\,\text{Br}_{e}(G).$
$(\unicode[STIX]{x1D70C}^{\ast }(b)-p_{2}^{\ast }(b))\in p_{1}^{\ast }\,\text{Br}_{e}(G).$
Démonstration.
Pour la définition de
![]() $\text{Br}_{e}(G)$
, voir (1.3). Notons
$\text{Br}_{e}(G)$
, voir (1.3). Notons
 $X\xrightarrow[{}]{e_{G}\times \text{id}_{X}}G\times X$
. Puisque
$X\xrightarrow[{}]{e_{G}\times \text{id}_{X}}G\times X$
. Puisque
 $p_{2}\circ (e_{G}\times \text{id}_{X})=\unicode[STIX]{x1D70C}\circ (e_{G}\times \text{id}_{X})$
, il suffit de montrer que, pour tout
$p_{2}\circ (e_{G}\times \text{id}_{X})=\unicode[STIX]{x1D70C}\circ (e_{G}\times \text{id}_{X})$
, il suffit de montrer que, pour tout
 $b\in \text{Br}_{G}(X)$
, on a
$b\in \text{Br}_{G}(X)$
, on a
 $(\unicode[STIX]{x1D70C}^{\ast }(b)-p_{2}^{\ast }(b))\in p_{1}^{\ast }\,\text{Br}_{1}(G)$
.
$(\unicode[STIX]{x1D70C}^{\ast }(b)-p_{2}^{\ast }(b))\in p_{1}^{\ast }\,\text{Br}_{1}(G)$
.
On peut supposer
![]() $k=\bar{k}$
. Un point
$k=\bar{k}$
. Un point
 $x\in X(k)$
induit un morphisme
$x\in X(k)$
induit un morphisme
 $G\xrightarrow[{}]{i_{x}}X$
. Notons
$G\xrightarrow[{}]{i_{x}}X$
. Notons
![]() $m$
la multiplication sur
$m$
la multiplication sur
![]() $G$
. Alors on a le diagramme suivant commutatif.
$G$
. Alors on a le diagramme suivant commutatif.

Le résultat découle du lemme 3.6, de la proposition 3.2(2) et de l’injectivité de
![]() $p_{1}^{\ast }$
.◻
$p_{1}^{\ast }$
.◻
3.2 L’homomorphisme de Sansuc
Soient
![]() $G$
un groupe algébrique connexe et
$G$
un groupe algébrique connexe et
![]() $(X,\unicode[STIX]{x1D70C})$
une
$(X,\unicode[STIX]{x1D70C})$
une
![]() $G$
-variété lisse géométriquement intègre. Notons
$G$
-variété lisse géométriquement intègre. Notons
 $G\times X\xrightarrow[{}]{p_{1}}G$
,
$G\times X\xrightarrow[{}]{p_{1}}G$
,
 $G\times X\xrightarrow[{}]{p_{2}}X$
les deux projections. Soit
$G\times X\xrightarrow[{}]{p_{2}}X$
les deux projections. Soit
 $\text{Br}_{G}(X)$
le sous-groupe de Brauer
$\text{Br}_{G}(X)$
le sous-groupe de Brauer
![]() $G$
-invariant de
$G$
-invariant de
![]() $X$
(Définition 3.1). Pour la définition de
$X$
(Définition 3.1). Pour la définition de
![]() $\text{Br}_{e}(G)$
, voir (1.3).
$\text{Br}_{e}(G)$
, voir (1.3).
Par [Reference SansucSan81, Lem. 6.6], on a
 $\text{Br}_{a}(G\times X)=\text{Br}_{a}(G)\oplus \text{Br}_{a}(X)$
, et donc
$\text{Br}_{a}(G\times X)=\text{Br}_{a}(G)\oplus \text{Br}_{a}(X)$
, et donc
 $p_{1}^{\ast }|_{\text{Br}_{e}(G)}$
est injectif. Par la proposition 3.7, il existe un unique homomorphisme
$p_{1}^{\ast }|_{\text{Br}_{e}(G)}$
est injectif. Par la proposition 3.7, il existe un unique homomorphisme
 $\text{Br}_{G}(X)\xrightarrow[{}]{\unicode[STIX]{x1D706}}\text{Br}_{e}(G)$
tel que
$\text{Br}_{G}(X)\xrightarrow[{}]{\unicode[STIX]{x1D706}}\text{Br}_{e}(G)$
tel que
 $$\begin{eqnarray}p_{1}^{\ast }\circ \unicode[STIX]{x1D706}=\unicode[STIX]{x1D70C}^{\ast }-p_{2}^{\ast }:\text{Br}_{G}(X)\rightarrow \text{Br}(G\times X).\end{eqnarray}$$
$$\begin{eqnarray}p_{1}^{\ast }\circ \unicode[STIX]{x1D706}=\unicode[STIX]{x1D70C}^{\ast }-p_{2}^{\ast }:\text{Br}_{G}(X)\rightarrow \text{Br}(G\times X).\end{eqnarray}$$
Définition 3.8. Soient
![]() $G$
un groupe linéaire connexe et
$G$
un groupe linéaire connexe et
![]() $(X,\unicode[STIX]{x1D70C})$
une
$(X,\unicode[STIX]{x1D70C})$
une
![]() $G$
-variété lisse géométriquement intègre. L’unique homomorphisme
$G$
-variété lisse géométriquement intègre. L’unique homomorphisme
 $\text{Br}_{G}(X)\xrightarrow[{}]{\unicode[STIX]{x1D706}}\text{Br}_{e}(G)$
satisfaisant (3.4) est appelé l’homomorphisme de Sansuc.
$\text{Br}_{G}(X)\xrightarrow[{}]{\unicode[STIX]{x1D706}}\text{Br}_{e}(G)$
satisfaisant (3.4) est appelé l’homomorphisme de Sansuc.
Proposition 3.9. Sous les hypothèses de la définition 3.8, on a :
(1) pour toute extension de corps
 $K/k$
, et tous
$K/k$
, et tous
 $x\in X(K)$
,
$x\in X(K)$
,
 $g\in G(K)$
,
$g\in G(K)$
,
 $\unicode[STIX]{x1D6FC}\in \text{Br}_{G}(X)$
, on a
$\unicode[STIX]{x1D6FC}\in \text{Br}_{G}(X)$
, on a  $$\begin{eqnarray}(g\cdot x)^{\ast }(\unicode[STIX]{x1D6FC})=g^{\ast }(\unicode[STIX]{x1D706}(\unicode[STIX]{x1D6FC}))+x^{\ast }(\unicode[STIX]{x1D6FC})\in \text{Br}(K);\end{eqnarray}$$
$$\begin{eqnarray}(g\cdot x)^{\ast }(\unicode[STIX]{x1D6FC})=g^{\ast }(\unicode[STIX]{x1D706}(\unicode[STIX]{x1D6FC}))+x^{\ast }(\unicode[STIX]{x1D6FC})\in \text{Br}(K);\end{eqnarray}$$
(2) si
 $X(k)\neq \emptyset$
, alors, pour tout
$X(k)\neq \emptyset$
, alors, pour tout
 $x\in X(k)$
, on a (3.5)où
$x\in X(k)$
, on a (3.5)où $$\begin{eqnarray}\unicode[STIX]{x1D706}=\unicode[STIX]{x1D70C}_{x}^{\ast }-x^{\ast },\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D706}=\unicode[STIX]{x1D70C}_{x}^{\ast }-x^{\ast },\end{eqnarray}$$
 $G\xrightarrow[{}]{\unicode[STIX]{x1D70C}_{x}}X:g\mapsto g\cdot x$
,
$G\xrightarrow[{}]{\unicode[STIX]{x1D70C}_{x}}X:g\mapsto g\cdot x$
,
 $\text{Spec}\,k\xrightarrow[{}]{x}X$
est le point
$\text{Spec}\,k\xrightarrow[{}]{x}X$
est le point
 $x$
et
$x$
et
 $\text{Br}(X)\xrightarrow[{}]{x^{\ast }}\text{Br}(k)\subset \text{Br}(G)$
.
$\text{Br}(X)\xrightarrow[{}]{x^{\ast }}\text{Br}(k)\subset \text{Br}(G)$
.(3) si
 $X\cong G/G_{0}$
avec
$X\cong G/G_{0}$
avec
 $G_{0}\subset G$
un sous-groupe fermé connexe, alors
$G_{0}\subset G$
un sous-groupe fermé connexe, alors  $$\begin{eqnarray}\text{Br}_{G}(X)\cong \text{Br}_{1}(X,G):=\text{Ker}(\text{Br}(X)\rightarrow \text{Br}(G_{\bar{k}})).\end{eqnarray}$$
$$\begin{eqnarray}\text{Br}_{G}(X)\cong \text{Br}_{1}(X,G):=\text{Ker}(\text{Br}(X)\rightarrow \text{Br}(G_{\bar{k}})).\end{eqnarray}$$
Démonstration.
Pour (1), on a
 $$\begin{eqnarray}(g\cdot x)^{\ast }(\unicode[STIX]{x1D6FC})=(g,x)^{\ast }(\unicode[STIX]{x1D70C}^{\ast }(\unicode[STIX]{x1D6FC}))=(g,x)^{\ast }(p_{2}^{\ast }(\unicode[STIX]{x1D6FC})+p_{1}^{\ast }(\unicode[STIX]{x1D706}(\unicode[STIX]{x1D6FC})))=g^{\ast }(\unicode[STIX]{x1D706}(\unicode[STIX]{x1D6FC}))+x^{\ast }(\unicode[STIX]{x1D6FC})\in \text{Br}(K).\end{eqnarray}$$
$$\begin{eqnarray}(g\cdot x)^{\ast }(\unicode[STIX]{x1D6FC})=(g,x)^{\ast }(\unicode[STIX]{x1D70C}^{\ast }(\unicode[STIX]{x1D6FC}))=(g,x)^{\ast }(p_{2}^{\ast }(\unicode[STIX]{x1D6FC})+p_{1}^{\ast }(\unicode[STIX]{x1D706}(\unicode[STIX]{x1D6FC})))=g^{\ast }(\unicode[STIX]{x1D706}(\unicode[STIX]{x1D6FC}))+x^{\ast }(\unicode[STIX]{x1D6FC})\in \text{Br}(K).\end{eqnarray}$$
Dans le cas (2), pour tout
 $\unicode[STIX]{x1D6FC}\in \text{Br}_{G}(X)$
, on obtient
$\unicode[STIX]{x1D6FC}\in \text{Br}_{G}(X)$
, on obtient
 $(\unicode[STIX]{x1D70C}^{\ast }-p_{2}^{\ast })(\unicode[STIX]{x1D6FC})|_{G\times x}=(\unicode[STIX]{x1D70C}_{x}^{\ast }-x^{\ast })(\unicode[STIX]{x1D6FC})$
.
$(\unicode[STIX]{x1D70C}^{\ast }-p_{2}^{\ast })(\unicode[STIX]{x1D6FC})|_{G\times x}=(\unicode[STIX]{x1D70C}_{x}^{\ast }-x^{\ast })(\unicode[STIX]{x1D6FC})$
.
L’énoncé (3) résulte de la proposition 3.2(2) (5) et du lemme 3.6. ◻
Si
 $X\xrightarrow[{}]{f}Z$
est un
$X\xrightarrow[{}]{f}Z$
est un
![]() $G$
-torseur, par définition, l’homomorphisme de Sansuc
$G$
-torseur, par définition, l’homomorphisme de Sansuc
 $\unicode[STIX]{x1D706}|_{\text{Br}_{1}(X)}$
est exactement le morphisme dans la suite exacte de Sansuc à isomorphisme canonique
$\unicode[STIX]{x1D706}|_{\text{Br}_{1}(X)}$
est exactement le morphisme dans la suite exacte de Sansuc à isomorphisme canonique
 $\text{Br}_{e}(G)\cong \text{Br}_{a}(G)$
près (cf. [Reference Borovoi and DemarcheBD13, Thm. 2.8]).
$\text{Br}_{e}(G)\cong \text{Br}_{a}(G)$
près (cf. [Reference Borovoi and DemarcheBD13, Thm. 2.8]).
Théorème 3.10. Soient
![]() $G$
un groupe linéaire connexe,
$G$
un groupe linéaire connexe,
![]() $Z$
une variété lisse géométriquement intègre et
$Z$
une variété lisse géométriquement intègre et
 $X\xrightarrow[{}]{f}Z$
un
$X\xrightarrow[{}]{f}Z$
un
![]() $G$
-torseur. Notons
$G$
-torseur. Notons
 $G\times X\xrightarrow[{}]{\unicode[STIX]{x1D70C}}X$
l’action de
$G\times X\xrightarrow[{}]{\unicode[STIX]{x1D70C}}X$
l’action de
![]() $G$
. Alors l’homomorphisme de Sansuc
$G$
. Alors l’homomorphisme de Sansuc
![]() $\unicode[STIX]{x1D706}$
induit le diagramme suivant commutatif de suites exactes, fonctoriel en
$\unicode[STIX]{x1D706}$
induit le diagramme suivant commutatif de suites exactes, fonctoriel en
 $(X,Z,f,G)$
.
$(X,Z,f,G)$
.

Démonstration.
D’après Borovoi et Demarche [Reference Borovoi and DemarcheBD13, Thm. 2.8], on a une suite exacte
 $$\begin{eqnarray}\text{Pic}(X)\rightarrow \text{Pic}(G)\rightarrow \text{Br}(Z)\xrightarrow[{}]{f^{\ast }}\text{Br}(X)\xrightarrow[{}]{\unicode[STIX]{x1D70C}^{\ast }-p_{2}^{\ast }}\text{Br}(G\times X)\end{eqnarray}$$
$$\begin{eqnarray}\text{Pic}(X)\rightarrow \text{Pic}(G)\rightarrow \text{Br}(Z)\xrightarrow[{}]{f^{\ast }}\text{Br}(X)\xrightarrow[{}]{\unicode[STIX]{x1D70C}^{\ast }-p_{2}^{\ast }}\text{Br}(G\times X)\end{eqnarray}$$
fonctoriel en
 $(X,Z,f,G)$
, telle que
$(X,Z,f,G)$
, telle que
 $(\unicode[STIX]{x1D70C}^{\ast }-p_{2}^{\ast })(\text{Br}_{1}(X))\subset p_{1}^{\ast }\,\text{Br}_{e}(G)$
. Le résultat découle de la proposition 3.7.◻
$(\unicode[STIX]{x1D70C}^{\ast }-p_{2}^{\ast })(\text{Br}_{1}(X))\subset p_{1}^{\ast }\,\text{Br}_{e}(G)$
. Le résultat découle de la proposition 3.7.◻
Corollaire 3.11. Soient
 $1\rightarrow N\rightarrow H\xrightarrow[{}]{\unicode[STIX]{x1D713}}G\rightarrow 1$
une suite exacte de groupes linéaires connexes et
$1\rightarrow N\rightarrow H\xrightarrow[{}]{\unicode[STIX]{x1D713}}G\rightarrow 1$
une suite exacte de groupes linéaires connexes et
![]() $(X,\unicode[STIX]{x1D70C})$
une
$(X,\unicode[STIX]{x1D70C})$
une
![]() $G$
-variété lisse géométriquement intègre.
$G$
-variété lisse géométriquement intègre.
(1) On a
 $\text{Br}_{G}(X)=\text{Br}_{H}(X)$
.
$\text{Br}_{G}(X)=\text{Br}_{H}(X)$
.(2) S’il existe une
 $H$
-variété
$H$
-variété
 $Y$
et un
$Y$
et un
 $H$
-morphisme
$H$
-morphisme
 $Y\xrightarrow[{}]{p}X$
tels que
$Y\xrightarrow[{}]{p}X$
tels que
 $Y\rightarrow X$
soit un
$Y\rightarrow X$
soit un
 $N$
-torseur, alors
$N$
-torseur, alors
 $\text{Br}(X)\xrightarrow[{}]{p^{\ast }}\text{Br}(Y)$
satisfait
$\text{Br}(X)\xrightarrow[{}]{p^{\ast }}\text{Br}(Y)$
satisfait
 $(p^{\ast })^{-1}\,\text{Br}_{H}(Y)=\text{Br}_{G}(X)$
et on a une suite exacte (où
$(p^{\ast })^{-1}\,\text{Br}_{H}(Y)=\text{Br}_{G}(X)$
et on a une suite exacte (où
 $\unicode[STIX]{x1D706}$
est l’homomorphisme de Sansuc), fonctorielle en
$\unicode[STIX]{x1D706}$
est l’homomorphisme de Sansuc), fonctorielle en
 $(X,Y,p,N)$
:
$(X,Y,p,N)$
:  $$\begin{eqnarray}\text{Pic}(Y)\rightarrow \text{Pic}(N)\xrightarrow[{}]{\unicode[STIX]{x1D712}}\text{Br}_{G}(X)\xrightarrow[{}]{p^{\ast }}\text{Br}_{H}(Y)\xrightarrow[{}]{\unicode[STIX]{x1D706}}\text{Br}_{e}(N).\end{eqnarray}$$
$$\begin{eqnarray}\text{Pic}(Y)\rightarrow \text{Pic}(N)\xrightarrow[{}]{\unicode[STIX]{x1D712}}\text{Br}_{G}(X)\xrightarrow[{}]{p^{\ast }}\text{Br}_{H}(Y)\xrightarrow[{}]{\unicode[STIX]{x1D706}}\text{Br}_{e}(N).\end{eqnarray}$$
Démonstration.
Puisque
 $H\times X\xrightarrow[{}]{\unicode[STIX]{x1D713}_{X}}G\times X$
est un
$H\times X\xrightarrow[{}]{\unicode[STIX]{x1D713}_{X}}G\times X$
est un
![]() $N$
-torseur, par le diagramme (3.6), on a le diagramme suivant commutatif de suites exactes.
$N$
-torseur, par le diagramme (3.6), on a le diagramme suivant commutatif de suites exactes.

Donc
 $(\unicode[STIX]{x1D713}_{X}^{\ast })^{-1}(p_{1}^{\ast }\,\text{Br}_{N}(H))=p_{1}^{\ast }\,\text{Br}(G)$
. Puisque
$(\unicode[STIX]{x1D713}_{X}^{\ast })^{-1}(p_{1}^{\ast }\,\text{Br}_{N}(H))=p_{1}^{\ast }\,\text{Br}(G)$
. Puisque
 $\text{Br}_{e}(H)\subset \text{Br}_{1}(H)\subset \text{Br}_{N}(H)$
(Proposition 3.2(4)), la proposition 3.7 donne (1).
$\text{Br}_{e}(H)\subset \text{Br}_{1}(H)\subset \text{Br}_{N}(H)$
(Proposition 3.2(4)), la proposition 3.7 donne (1).
Appliquons la proposition 3.2(5) au
![]() $N$
-torseur
$N$
-torseur
 $p:Y\rightarrow X$
(avec l’action de
$p:Y\rightarrow X$
(avec l’action de
![]() $H$
). On a (en utilisant (1))
$H$
). On a (en utilisant (1))
 $$\begin{eqnarray}\unicode[STIX]{x1D712}(\text{Pic}(N))\subset (p^{\ast })^{-1}(0)\subset (p^{\ast })^{-1}(\text{Br}_{H}(Y))=\text{Br}_{H}(X)=\text{Br}_{G}(X).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D712}(\text{Pic}(N))\subset (p^{\ast })^{-1}(0)\subset (p^{\ast })^{-1}(\text{Br}_{H}(Y))=\text{Br}_{H}(X)=\text{Br}_{G}(X).\end{eqnarray}$$
Une application du diagramme (3.6) au
![]() $N$
-torseur
$N$
-torseur
 $Y\rightarrow X$
donne (2).◻
$Y\rightarrow X$
donne (2).◻
Comme conséquence, par le lemme 3.6, on a une suite exacte [Reference SansucSan81, Cor. 6.11] :
 $$\begin{eqnarray}\text{Pic}(N)\rightarrow \text{Br}_{1}(G)\rightarrow \text{Br}_{1}(H)\rightarrow \text{Br}_{e}(N).\end{eqnarray}$$
$$\begin{eqnarray}\text{Pic}(N)\rightarrow \text{Br}_{1}(G)\rightarrow \text{Br}_{1}(H)\rightarrow \text{Br}_{e}(N).\end{eqnarray}$$
Lemme 3.12. Soient
![]() $G$
,
$G$
,
![]() $N$
deux groupes linéaires connexes et
$N$
deux groupes linéaires connexes et
![]() $X$
une
$X$
une
![]() $G$
-variété lisse géométriquement intègre. Soient
$G$
-variété lisse géométriquement intègre. Soient
 $H:=N\times G$
et
$H:=N\times G$
et
![]() $P$
une
$P$
une
![]() $H$
-variété telle que
$H$
-variété telle que
![]() $P$
soit un
$P$
soit un
![]() $N$
-torseur sur
$N$
-torseur sur
![]() $k$
. Soient
$k$
. Soient
 $Y:=P\times X$
et
$Y:=P\times X$
et
 $Y\xrightarrow[{}]{p_{1}}P$
,
$Y\xrightarrow[{}]{p_{1}}P$
,
 $Y\xrightarrow[{}]{p_{2}}X$
les deux projections. Si
$Y\xrightarrow[{}]{p_{2}}X$
les deux projections. Si
 $P(k)\neq \emptyset$
ou
$P(k)\neq \emptyset$
ou
 $H^{3}(k,\bar{k}^{\times })=0$
, on a un isomorphisme :
$H^{3}(k,\bar{k}^{\times })=0$
, on a un isomorphisme :
 $$\begin{eqnarray}(p_{1}^{\ast },p_{2}^{\ast }):\text{Br}_{a}(P)\oplus \text{Br}_{G}(X)/\text{Im}\,\text{Br}(k)\stackrel{{\sim}}{\rightarrow }\text{Br}_{H}(Y)/\text{Im}\,\text{Br}(k).\end{eqnarray}$$
$$\begin{eqnarray}(p_{1}^{\ast },p_{2}^{\ast }):\text{Br}_{a}(P)\oplus \text{Br}_{G}(X)/\text{Im}\,\text{Br}(k)\stackrel{{\sim}}{\rightarrow }\text{Br}_{H}(Y)/\text{Im}\,\text{Br}(k).\end{eqnarray}$$
De plus, cet isomorphisme induit un isomorphisme :
 $(p_{1}^{\ast },p_{2}^{\ast }):\text{Br}_{a}(P)\oplus \text{Br}_{a}(X)\stackrel{{\sim}}{\rightarrow }\text{Br}_{a}(Y)$
.
$(p_{1}^{\ast },p_{2}^{\ast }):\text{Br}_{a}(P)\oplus \text{Br}_{a}(X)\stackrel{{\sim}}{\rightarrow }\text{Br}_{a}(Y)$
.
Démonstration.
Par la proposition 3.2(1) et le lemme 3.6, on a
 $\text{Br}_{H}(P)=\text{Br}_{1}(P)$
. D’après le corollaire 3.11(2) et l’isomorphisme
$\text{Br}_{H}(P)=\text{Br}_{1}(P)$
. D’après le corollaire 3.11(2) et l’isomorphisme
 $\text{Br}_{e}(N)\cong \text{Br}_{a}(N)$
, on a le diagramme suivant commutatif de suites exactes.
$\text{Br}_{e}(N)\cong \text{Br}_{a}(N)$
, on a le diagramme suivant commutatif de suites exactes.

Puisque
 $P(k)\neq \emptyset$
ou
$P(k)\neq \emptyset$
ou
 $H^{3}(k,\bar{k}^{\times })=0$
, par [Reference SansucSan81, Lem. 6.7 et 6.8],
$H^{3}(k,\bar{k}^{\times })=0$
, par [Reference SansucSan81, Lem. 6.7 et 6.8],
![]() $\unicode[STIX]{x1D717}_{1}$
et
$\unicode[STIX]{x1D717}_{1}$
et
![]() $\unicode[STIX]{x1D717}_{2}$
sont surjectifs. Alors on a une suite exacte
$\unicode[STIX]{x1D717}_{2}$
sont surjectifs. Alors on a une suite exacte
 $$\begin{eqnarray}0\rightarrow \text{Br}(k)\rightarrow \text{Br}_{1}(P)\oplus \text{Br}_{G}(X)\xrightarrow[{}]{(p_{1}^{\ast },p_{2}^{\ast })}\text{Br}_{H}(Y)\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow \text{Br}(k)\rightarrow \text{Br}_{1}(P)\oplus \text{Br}_{G}(X)\xrightarrow[{}]{(p_{1}^{\ast },p_{2}^{\ast })}\text{Br}_{H}(Y)\rightarrow 0.\end{eqnarray}$$
Puisque le morphisme
 $\text{Br}(X_{\bar{k}})\rightarrow \text{Br}((P\times X)_{\bar{k}})\cong \text{Br}(Y_{\bar{k}})$
est injectif, on a une suite exacte :
$\text{Br}(X_{\bar{k}})\rightarrow \text{Br}((P\times X)_{\bar{k}})\cong \text{Br}(Y_{\bar{k}})$
est injectif, on a une suite exacte :
 $$\begin{eqnarray}0\rightarrow \text{Br}(k)\rightarrow \text{Br}_{1}(P)\oplus \text{Br}_{1}(X)\xrightarrow[{}]{(p_{1}^{\ast },p_{2}^{\ast })}\text{Br}_{1}(Y)\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow \text{Br}(k)\rightarrow \text{Br}_{1}(P)\oplus \text{Br}_{1}(X)\xrightarrow[{}]{(p_{1}^{\ast },p_{2}^{\ast })}\text{Br}_{1}(Y)\rightarrow 0.\end{eqnarray}$$
Le résultat en découle. ◻
Proposition 3.13. Soient
![]() $T$
un tore et
$T$
un tore et
 $1\rightarrow G_{0}\rightarrow G\xrightarrow[{}]{\unicode[STIX]{x1D713}}T\rightarrow 1$
une suite exacte de groupes linéaires connexes. Soient
$1\rightarrow G_{0}\rightarrow G\xrightarrow[{}]{\unicode[STIX]{x1D713}}T\rightarrow 1$
une suite exacte de groupes linéaires connexes. Soient
![]() $X$
une
$X$
une
![]() $G$
-variété lisse, géométriquement intègre et
$G$
-variété lisse, géométriquement intègre et
 $X\xrightarrow[{}]{f}T$
un
$X\xrightarrow[{}]{f}T$
un
![]() $G$
-morphisme. Notons
$G$
-morphisme. Notons
 $\text{Br}_{a}(G)\xrightarrow[{}]{\unicode[STIX]{x1D717}}\text{Br}_{a}(G_{0})$
l’homomorphisme induit par
$\text{Br}_{a}(G)\xrightarrow[{}]{\unicode[STIX]{x1D717}}\text{Br}_{a}(G_{0})$
l’homomorphisme induit par
 $G_{0}\subset G$
. Alors, pour tout
$G_{0}\subset G$
. Alors, pour tout
 $t\in T(k)$
, la fibre
$t\in T(k)$
, la fibre
![]() $X_{t}$
est
$X_{t}$
est
![]() $G_{0}$
-invariante et on a un isomorphisme naturel
$G_{0}$
-invariante et on a un isomorphisme naturel
 $\text{Pic}(X_{\bar{k}})\cong \text{Pic}(X_{t,\bar{k}})$
et deux suites exactes naturelles
$\text{Pic}(X_{\bar{k}})\cong \text{Pic}(X_{t,\bar{k}})$
et deux suites exactes naturelles
 $$\begin{eqnarray}0\rightarrow T^{\ast }\xrightarrow[{}]{f^{\ast }}\bar{k}[X]^{\times }/\bar{k}^{\times }\rightarrow \bar{k}[X_{t}]^{\times }/\bar{k}^{\times }\rightarrow 0~~~\text{et}~~~\text{Br}_{e}(T)\rightarrow \text{Br}_{G}(X)\rightarrow \text{Br}_{G_{0}}(X_{t})\rightarrow \text{coker}(\unicode[STIX]{x1D717}).\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow T^{\ast }\xrightarrow[{}]{f^{\ast }}\bar{k}[X]^{\times }/\bar{k}^{\times }\rightarrow \bar{k}[X_{t}]^{\times }/\bar{k}^{\times }\rightarrow 0~~~\text{et}~~~\text{Br}_{e}(T)\rightarrow \text{Br}_{G}(X)\rightarrow \text{Br}_{G_{0}}(X_{t})\rightarrow \text{coker}(\unicode[STIX]{x1D717}).\end{eqnarray}$$
Démonstration.
D’après [Reference Cao and XuCX15, Prop. 2.2],
![]() $X_{t}$
est lisse, géométriquement intègre. Puisque
$X_{t}$
est lisse, géométriquement intègre. Puisque
![]() $T$
est commutatif,
$T$
est commutatif,
![]() $X_{t}$
est
$X_{t}$
est
![]() $G_{0}$
-invariant. Notons :
$G_{0}$
-invariant. Notons :
 $$\begin{eqnarray}X_{t}\xrightarrow[{}]{i}G\times X_{t}:x\mapsto (e_{G},x)~~~\text{et}~~~G\times X_{t}\xrightarrow[{}]{\unicode[STIX]{x1D70C}}X:(g,x)\mapsto g\cdot x.\end{eqnarray}$$
$$\begin{eqnarray}X_{t}\xrightarrow[{}]{i}G\times X_{t}:x\mapsto (e_{G},x)~~~\text{et}~~~G\times X_{t}\xrightarrow[{}]{\unicode[STIX]{x1D70C}}X:(g,x)\mapsto g\cdot x.\end{eqnarray}$$
Alors
![]() $\unicode[STIX]{x1D70C}\circ i$
est l’immersion
$\unicode[STIX]{x1D70C}\circ i$
est l’immersion
 $X_{t}\subset X$
. On fixe des actions
$X_{t}\subset X$
. On fixe des actions
 $$\begin{eqnarray}G\times G_{0}\curvearrowright G\times X_{t}:(g,g_{0})\times (g^{\prime },x)\mapsto (gg^{\prime }g_{0}^{-1},g_{0}\cdot x)~~~\text{et}~~~G\times G_{0}\curvearrowright G:(g,g_{0})\times g^{\prime }\mapsto gg^{\prime }g_{0}^{-1}.\end{eqnarray}$$
$$\begin{eqnarray}G\times G_{0}\curvearrowright G\times X_{t}:(g,g_{0})\times (g^{\prime },x)\mapsto (gg^{\prime }g_{0}^{-1},g_{0}\cdot x)~~~\text{et}~~~G\times G_{0}\curvearrowright G:(g,g_{0})\times g^{\prime }\mapsto gg^{\prime }g_{0}^{-1}.\end{eqnarray}$$
Par définition,
 $X\cong G\times ^{G_{0}}X_{t}$
et on a un diagramme commutatif de
$X\cong G\times ^{G_{0}}X_{t}$
et on a un diagramme commutatif de
![]() $G\times G_{0}$
-morphismes
$G\times G_{0}$
-morphismes

tel que les colonnes soient des
![]() $G_{0}$
-torseurs.
$G_{0}$
-torseurs.
D’après [Reference SansucSan81, Lem. 6.5 et Lem. 6.6], on a
 $$\begin{eqnarray}\bar{k}[G\times X_{t}]^{\times }/\bar{k}^{\times }\cong \bar{k}[G]^{\times }/\bar{k}^{\times }\oplus \bar{k}[X_{t}]^{\times }/\bar{k}^{\times }~~~\text{et}~~~\text{Pic}(G_{\bar{k}}\times X_{t,\bar{k}})\cong \text{Pic}(G_{\bar{k}})\oplus \text{Pic}(X_{t,\bar{k}}).\end{eqnarray}$$
$$\begin{eqnarray}\bar{k}[G\times X_{t}]^{\times }/\bar{k}^{\times }\cong \bar{k}[G]^{\times }/\bar{k}^{\times }\oplus \bar{k}[X_{t}]^{\times }/\bar{k}^{\times }~~~\text{et}~~~\text{Pic}(G_{\bar{k}}\times X_{t,\bar{k}})\cong \text{Pic}(G_{\bar{k}})\oplus \text{Pic}(X_{t,\bar{k}}).\end{eqnarray}$$
Par la suite exacte de Sansuc [Reference SansucSan81, Prop. 6.10 et Cor. 6.11], on a le diagramme suivant commutatif de suites exactes.

Puisque
 $\text{Pic}(T_{\bar{k}})=0$
, une application du lemme du serpent donne l’isomorphisme et la première suite exacte de l’énoncé.
$\text{Pic}(T_{\bar{k}})=0$
, une application du lemme du serpent donne l’isomorphisme et la première suite exacte de l’énoncé.
D’après (3.8), on a un isomorphisme :
 $\text{Br}_{e}(G)\oplus \text{Br}_{G_{0}}(X_{t})\xrightarrow[{}]{(p_{1}^{\ast },p_{2}^{\ast })}\text{Br}_{G\times G_{0}}(G\times X_{t})$
. Le corollaire 3.11 donne le diagramme suivant commutatif de suites exactes.
$\text{Br}_{e}(G)\oplus \text{Br}_{G_{0}}(X_{t})\xrightarrow[{}]{(p_{1}^{\ast },p_{2}^{\ast })}\text{Br}_{G\times G_{0}}(G\times X_{t})$
. Le corollaire 3.11 donne le diagramme suivant commutatif de suites exactes.

D’après la proposition 3.9(2),
 $\text{Coker}(\unicode[STIX]{x1D717})\cong \text{Coker}(\unicode[STIX]{x1D706}_{G})$
. Puisque
$\text{Coker}(\unicode[STIX]{x1D717})\cong \text{Coker}(\unicode[STIX]{x1D706}_{G})$
. Puisque
 $p_{2}\circ i=\text{id}$
et
$p_{2}\circ i=\text{id}$
et
 $i^{\ast }\circ p_{1}^{\ast }=0$
, on a
$i^{\ast }\circ p_{1}^{\ast }=0$
, on a
 $\text{Br}_{G_{0}}(X_{t})=\text{Im}(i^{\ast })\cong \text{coker}(p_{1}^{\ast })$
. Une chasse au diagramme donne l’énoncé.◻
$\text{Br}_{G_{0}}(X_{t})=\text{Im}(i^{\ast })\cong \text{coker}(p_{1}^{\ast })$
. Une chasse au diagramme donne l’énoncé.◻
Corollaire 3.14. Sous les hypothèses de la proposition 3.13, soient
![]() $U\subset X$
un
$U\subset X$
un
![]() $G$
-ouvert et
$G$
-ouvert et
 $B\subset \text{Br}_{G}(U)$
un sous-groupe. Alors, pour tout
$B\subset \text{Br}_{G}(U)$
un sous-groupe. Alors, pour tout
 $t\in T(k)$
, de fibre
$t\in T(k)$
, de fibre
 $U_{t}\subset X_{t}\stackrel{i_{t}}{{\hookrightarrow}}X$
, on a :
$U_{t}\subset X_{t}\stackrel{i_{t}}{{\hookrightarrow}}X$
, on a :
 $$\begin{eqnarray}i_{t}^{\ast }(B\cap \text{Br}(X))=(i_{t}^{\ast }(B)\cap \text{Br}(X_{t})).\end{eqnarray}$$
$$\begin{eqnarray}i_{t}^{\ast }(B\cap \text{Br}(X))=(i_{t}^{\ast }(B)\cap \text{Br}(X_{t})).\end{eqnarray}$$
Démonstration.
D’après la proposition 3.13, on a le diagramme suivant de suites exactes.

Une chasse au diagramme donne l’énoncé. ◻
3.3 Pseudo espace homogène
Soit
![]() $G$
un groupe linéaire connexe. Pour les besoins de cet article, on introduit la notion de pseudo
$G$
un groupe linéaire connexe. Pour les besoins de cet article, on introduit la notion de pseudo
![]() $G$
-espace homogène. Elle généralise la notion de
$G$
-espace homogène. Elle généralise la notion de
![]() $G$
-espace homogène avec un
$G$
-espace homogène avec un
![]() $k$
-point à stabilisateur géométrique connexe (cf. exemple 3.16(1)).
$k$
-point à stabilisateur géométrique connexe (cf. exemple 3.16(1)).
Définition 3.15. Soit
![]() $G$
un groupe linéaire connexe. Une
$G$
un groupe linéaire connexe. Une
![]() $G$
-variété
$G$
-variété
![]() $Z$
est appelée pseudo
$Z$
est appelée pseudo
![]() $G$
-espace homogène si
$G$
-espace homogène si
![]() $Z$
est lisse, géométriquement intègre,
$Z$
est lisse, géométriquement intègre,
 $\text{Pic}(Z_{\bar{k}})$
est de type fini,
$\text{Pic}(Z_{\bar{k}})$
est de type fini,
 $Z(k)\neq \emptyset$
et
$Z(k)\neq \emptyset$
et
 $\text{Ker}(\unicode[STIX]{x1D706})/\text{Br}(k),\text{Br}_{G_{\bar{k}}}(Z_{\bar{k}})$
sont finis, où
$\text{Ker}(\unicode[STIX]{x1D706})/\text{Br}(k),\text{Br}_{G_{\bar{k}}}(Z_{\bar{k}})$
sont finis, où
 $\unicode[STIX]{x1D706}:\text{Br}_{G}(Z)\rightarrow \text{Br}_{e}(G)$
est l’homomorphisme de Sansuc (cf. Définition 3.8).
$\unicode[STIX]{x1D706}:\text{Br}_{G}(Z)\rightarrow \text{Br}_{e}(G)$
est l’homomorphisme de Sansuc (cf. Définition 3.8).
Fixons
 $z\in Z(k)$
et notons
$z\in Z(k)$
et notons
 $\unicode[STIX]{x1D70C}_{z}:G\rightarrow Z:g\mapsto g\cdot z$
. D’après (3.5), le groupe
$\unicode[STIX]{x1D70C}_{z}:G\rightarrow Z:g\mapsto g\cdot z$
. D’après (3.5), le groupe
 $\text{Ker}(\unicode[STIX]{x1D706})/\text{Br}(k)$
est fini si et seulement si
$\text{Ker}(\unicode[STIX]{x1D706})/\text{Br}(k)$
est fini si et seulement si
 $\text{Ker}(\unicode[STIX]{x1D70C}_{z}^{\ast })\cap \text{Br}_{G}(Z)$
est fini, où
$\text{Ker}(\unicode[STIX]{x1D70C}_{z}^{\ast })\cap \text{Br}_{G}(Z)$
est fini, où
 $\text{Br}(Z)\xrightarrow[{}]{\unicode[STIX]{x1D70C}_{z}^{\ast }}\text{Br}(G)$
.
$\text{Br}(Z)\xrightarrow[{}]{\unicode[STIX]{x1D70C}_{z}^{\ast }}\text{Br}(G)$
.
Example 3.16. Soit
![]() $G$
un groupe linéaire connexe.
$G$
un groupe linéaire connexe.
(1) Soit
 $G_{0}\subset G$
un sous-groupe fermé connexe. Alors
$G_{0}\subset G$
un sous-groupe fermé connexe. Alors
 $G/G_{0}$
est un pseudo
$G/G_{0}$
est un pseudo
 $G$
-espace homogène.
$G$
-espace homogène.(2) Soient
 $W$
une variété lisse géométriquement intègre et
$W$
une variété lisse géométriquement intègre et
 $Z\rightarrow W$
un
$Z\rightarrow W$
un
 $G$
-torseur. Si
$G$
-torseur. Si
 $\text{Pic}(W)$
est de type fini,
$\text{Pic}(W)$
est de type fini,
 $\text{Br}(W)/\text{Br}(k),\text{Br}(W_{\bar{k}})$
sont finis et
$\text{Br}(W)/\text{Br}(k),\text{Br}(W_{\bar{k}})$
sont finis et
 $Z(k)\neq \emptyset$
, alors
$Z(k)\neq \emptyset$
, alors
 $Z$
est un pseudo
$Z$
est un pseudo
 $G$
-espace homogène.
$G$
-espace homogène.
Démonstration.
L’énoncé (1) résulte de [Reference Borovoi and DemarcheBD13, Thm. 2.8] et de la proposition 3.9(3). L’énoncé (2) résulte du corollaire 3.11(2). ◻
Proposition 3.17. Soient
![]() $G$
un groupe linéaire connexe et
$G$
un groupe linéaire connexe et
![]() $Z$
un pseudo
$Z$
un pseudo
![]() $G$
-espace homogène. Soient
$G$
-espace homogène. Soient
![]() $T$
un tore,
$T$
un tore,
 $Z^{\prime }\rightarrow Z$
un
$Z^{\prime }\rightarrow Z$
un
![]() $T$
-torseur et
$T$
-torseur et
![]() $H$
le groupe linéaire connexe déterminé dans le théorème 2.7. Si
$H$
le groupe linéaire connexe déterminé dans le théorème 2.7. Si
 $Z^{\prime }(k)\neq \emptyset$
, alors
$Z^{\prime }(k)\neq \emptyset$
, alors
![]() $Z^{\prime }$
est un pseudo
$Z^{\prime }$
est un pseudo
![]() $H$
-espace homogène.
$H$
-espace homogène.
Démonstration.
Fixons
 $z^{\prime }\in Z^{\prime }(k)$
et
$z^{\prime }\in Z^{\prime }(k)$
et
 $z\in Z(k)$
l’image de
$z\in Z(k)$
l’image de
![]() $z$
. Notons
$z$
. Notons
 $\unicode[STIX]{x1D70C}_{z^{\prime }}:H\rightarrow Z^{\prime }:h\mapsto h\cdot z^{\prime }$
et
$\unicode[STIX]{x1D70C}_{z^{\prime }}:H\rightarrow Z^{\prime }:h\mapsto h\cdot z^{\prime }$
et
 $\unicode[STIX]{x1D70C}_{z}:G\rightarrow Z:g\mapsto g\cdot z$
. D’après la suite exacte de Sansuc [Reference SansucSan81, Prop. 6.10],
$\unicode[STIX]{x1D70C}_{z}:G\rightarrow Z:g\mapsto g\cdot z$
. D’après la suite exacte de Sansuc [Reference SansucSan81, Prop. 6.10],
 $\text{Pic}({Z^{\prime }}_{\bar{k}})$
est de type fini. Par le corollaire 3.11(2) et (3.7), on a un diagramme commutatif de suites exactes :
$\text{Pic}({Z^{\prime }}_{\bar{k}})$
est de type fini. Par le corollaire 3.11(2) et (3.7), on a un diagramme commutatif de suites exactes :

et un isomorphisme
 $\text{Br}_{G_{\bar{k}}}(Z_{\bar{k}})\rightarrow \text{Br}_{H_{\bar{k}}}(Z_{\bar{k}}^{\prime })$
. Ainsi
$\text{Br}_{G_{\bar{k}}}(Z_{\bar{k}})\rightarrow \text{Br}_{H_{\bar{k}}}(Z_{\bar{k}}^{\prime })$
. Ainsi
 $\text{Br}_{H_{\bar{k}}}(Z_{\bar{k}}^{\prime })$
est fini. Puisque
$\text{Br}_{H_{\bar{k}}}(Z_{\bar{k}}^{\prime })$
est fini. Puisque
 $\text{Ker}(\unicode[STIX]{x1D70C}_{z}^{\ast })$
est fini, le groupe
$\text{Ker}(\unicode[STIX]{x1D70C}_{z}^{\ast })$
est fini, le groupe
 $\text{Ker}(\unicode[STIX]{x1D70C}_{z^{\prime }}^{\ast })$
est fini et
$\text{Ker}(\unicode[STIX]{x1D70C}_{z^{\prime }}^{\ast })$
est fini et
![]() $Z^{\prime }$
est un pseudo
$Z^{\prime }$
est un pseudo
![]() $H$
-espace homogène.◻
$H$
-espace homogène.◻
Proposition 3.18. Soient
![]() $G$
un groupe linéaire connexe et
$G$
un groupe linéaire connexe et
![]() $Z$
un pseudo
$Z$
un pseudo
![]() $G$
-espace homogène. Alors
$G$
-espace homogène. Alors
 $\text{Br}_{G}(Z)/\text{Br}_{1}(Z)$
est fini.
$\text{Br}_{G}(Z)/\text{Br}_{1}(Z)$
est fini.
Démonstration.
Ceci vaut car
 $\text{Br}_{G}(Z)/\text{Br}_{1}(Z)$
est un sous-groupe de
$\text{Br}_{G}(Z)/\text{Br}_{1}(Z)$
est un sous-groupe de
 $\text{Br}_{G_{\bar{k}}}(Z_{\bar{k}})$
.◻
$\text{Br}_{G_{\bar{k}}}(Z_{\bar{k}})$
.◻
Pour un corps de nombres, le lemme suivant est bien connu.
Lemme 3.19. Supposons que
![]() $k$
est un corps de nombres. Soit
$k$
est un corps de nombres. Soit
![]() $M$
un
$M$
un
![]() $\unicode[STIX]{x1D6E4}_{k}$
-module de type fini avec
$\unicode[STIX]{x1D6E4}_{k}$
-module de type fini avec
![]() $M\neq 0$
. On a :
$M\neq 0$
. On a :
(i) si
 $M$
est sans torsion, alors
$M$
est sans torsion, alors
 $H^{2}(k,M)$
est infini ;
$H^{2}(k,M)$
est infini ;(ii)
 $M$
est sans torsion ssi
$M$
est sans torsion ssi
 $H^{1}(k,M)$
est fini.
$H^{1}(k,M)$
est fini.
Démonstration.
Si
![]() $M$
est fini, par l’approximation très faible de
$M$
est fini, par l’approximation très faible de
![]() $M$
(cf. le cas
$M$
(cf. le cas
![]() $G=1$
de [Reference HarariHar07, Thm. 1]), il existe un sous-ensemble fini
$G=1$
de [Reference HarariHar07, Thm. 1]), il existe un sous-ensemble fini
![]() $S_{0}\subset \unicode[STIX]{x1D6FA}$
tel que, pour tout sous-ensemble fini
$S_{0}\subset \unicode[STIX]{x1D6FA}$
tel que, pour tout sous-ensemble fini
![]() $S\subset \unicode[STIX]{x1D6FA}_{k}$
avec
$S\subset \unicode[STIX]{x1D6FA}_{k}$
avec
 $S\cap S_{0}=\emptyset$
, l’homomorphisme
$S\cap S_{0}=\emptyset$
, l’homomorphisme
 $H^{1}(k,M)\rightarrow \bigoplus _{v\in S}H^{1}(k_{v},M)$
soit surjectif. Il existe un nombre infini de
$H^{1}(k,M)\rightarrow \bigoplus _{v\in S}H^{1}(k_{v},M)$
soit surjectif. Il existe un nombre infini de
![]() $v\in \unicode[STIX]{x1D6FA}_{k}$
tel que l’action de
$v\in \unicode[STIX]{x1D6FA}_{k}$
tel que l’action de
![]() $\unicode[STIX]{x1D6E4}_{k_{v}}$
sur
$\unicode[STIX]{x1D6E4}_{k_{v}}$
sur
![]() $M$
soit triviale. Dans ce cas,
$M$
soit triviale. Dans ce cas,
 $H^{1}(k_{v},M)\neq 0$
. Donc
$H^{1}(k_{v},M)\neq 0$
. Donc
 $H^{1}(k,M)$
est infini.
$H^{1}(k,M)$
est infini.
En général, la suite exacte
 $0\rightarrow M_{\text{tor}}\rightarrow M\rightarrow M_{\text{free}}\rightarrow 0$
induit une suite exacte
$0\rightarrow M_{\text{tor}}\rightarrow M\rightarrow M_{\text{free}}\rightarrow 0$
induit une suite exacte
 $$\begin{eqnarray}M_{\text{free}}^{\unicode[STIX]{x1D6E4}_{k}}\xrightarrow[{}]{\unicode[STIX]{x1D717}}H^{1}(k,M_{\text{tor}})\rightarrow H^{1}(k,M),\end{eqnarray}$$
$$\begin{eqnarray}M_{\text{free}}^{\unicode[STIX]{x1D6E4}_{k}}\xrightarrow[{}]{\unicode[STIX]{x1D717}}H^{1}(k,M_{\text{tor}})\rightarrow H^{1}(k,M),\end{eqnarray}$$
où
 $M_{\text{tor}}\subset M$
est le sous-module torsion maximal et
$M_{\text{tor}}\subset M$
est le sous-module torsion maximal et
 $M_{\text{free}}:=M/M_{\text{tor}}$
. Ainsi
$M_{\text{free}}:=M/M_{\text{tor}}$
. Ainsi
![]() $M_{\text{free}}$
est de type fini et donc
$M_{\text{free}}$
est de type fini et donc
![]() $\text{Im}(\unicode[STIX]{x1D717})$
est fini. Si
$\text{Im}(\unicode[STIX]{x1D717})$
est fini. Si
 $H^{1}(k,M)$
est fini,
$H^{1}(k,M)$
est fini,
![]() $M$
est donc sans torsion. Par ailleurs, si
$M$
est donc sans torsion. Par ailleurs, si
![]() $M$
est sans torsion,
$M$
est sans torsion,
 $H^{1}(k,M)$
est fini. Ceci donne (ii).
$H^{1}(k,M)$
est fini. Ceci donne (ii).
Si
![]() $M$
est sans torsion, la suite exacte
$M$
est sans torsion, la suite exacte
 $0\rightarrow M\xrightarrow[{}]{n\cdot }M\rightarrow M/n\rightarrow 0$
(
$0\rightarrow M\xrightarrow[{}]{n\cdot }M\rightarrow M/n\rightarrow 0$
(
 $n\in \mathbb{Z}_{{\geqslant}2}$
) induit une suite exacte :
$n\in \mathbb{Z}_{{\geqslant}2}$
) induit une suite exacte :
 $H^{1}(k,M)\rightarrow H^{1}(k,M/n)\rightarrow H^{2}(k,M)\xrightarrow[{}]{n\cdot }H^{2}(k,M)$
. Alors
$H^{1}(k,M)\rightarrow H^{1}(k,M/n)\rightarrow H^{2}(k,M)\xrightarrow[{}]{n\cdot }H^{2}(k,M)$
. Alors
 $H^{1}(k,M/n)$
est infini et (ii) implique (i).◻
$H^{1}(k,M/n)$
est infini et (ii) implique (i).◻
Lemme 3.20. Supposons que
![]() $k$
est un corps de nombres. Soit
$k$
est un corps de nombres. Soit
 $\unicode[STIX]{x1D719}:M\rightarrow N$
un homomorphisme de
$\unicode[STIX]{x1D719}:M\rightarrow N$
un homomorphisme de
![]() $\unicode[STIX]{x1D6E4}_{k}$
-modules de type fini sans torsion. Si
$\unicode[STIX]{x1D6E4}_{k}$
-modules de type fini sans torsion. Si
 $\text{Ker}(H^{2}(k,M)\xrightarrow[{}]{\unicode[STIX]{x1D719}_{\ast }}H^{2}(k,N))$
est fini, alors
$\text{Ker}(H^{2}(k,M)\xrightarrow[{}]{\unicode[STIX]{x1D719}_{\ast }}H^{2}(k,N))$
est fini, alors
![]() $\unicode[STIX]{x1D719}$
est injectif et
$\unicode[STIX]{x1D719}$
est injectif et
 $\text{coker}(\unicode[STIX]{x1D719})$
est sans torsion.
$\text{coker}(\unicode[STIX]{x1D719})$
est sans torsion.
Démonstration.
Notons
 $I:=\text{Im}(\unicode[STIX]{x1D719})$
,
$I:=\text{Im}(\unicode[STIX]{x1D719})$
,
 $K:=\text{Ker}(\unicode[STIX]{x1D719})$
et
$K:=\text{Ker}(\unicode[STIX]{x1D719})$
et
 $C:=\text{coker}(\unicode[STIX]{x1D719})$
. Alors
$C:=\text{coker}(\unicode[STIX]{x1D719})$
. Alors
![]() $I$
et
$I$
et
![]() $K$
sont de type fini sans torsion et on a deux suites exactes :
$K$
sont de type fini sans torsion et on a deux suites exactes :
 $$\begin{eqnarray}H^{1}(k,I)\rightarrow H^{2}(k,K)\rightarrow H^{2}(k,M)\xrightarrow[{}]{\unicode[STIX]{x1D703}_{1}}H^{2}(k,I)\end{eqnarray}$$
$$\begin{eqnarray}H^{1}(k,I)\rightarrow H^{2}(k,K)\rightarrow H^{2}(k,M)\xrightarrow[{}]{\unicode[STIX]{x1D703}_{1}}H^{2}(k,I)\end{eqnarray}$$
et
 $$\begin{eqnarray}H^{1}(k,N)\rightarrow H^{1}(k,C)\rightarrow H^{2}(k,I)\xrightarrow[{}]{\unicode[STIX]{x1D703}_{2}}H^{2}(k,N).\end{eqnarray}$$
$$\begin{eqnarray}H^{1}(k,N)\rightarrow H^{1}(k,C)\rightarrow H^{2}(k,I)\xrightarrow[{}]{\unicode[STIX]{x1D703}_{2}}H^{2}(k,N).\end{eqnarray}$$
Ainsi
 $H^{1}(k,I)$
,
$H^{1}(k,I)$
,
 $H^{1}(k,N)$
et
$H^{1}(k,N)$
et
![]() $\text{Ker}(\unicode[STIX]{x1D703}_{1})$
sont finis. Alors
$\text{Ker}(\unicode[STIX]{x1D703}_{1})$
sont finis. Alors
 $H^{2}(k,K)$
est fini et donc
$H^{2}(k,K)$
est fini et donc
![]() $K=0$
(Lemme 3.19). Ainsi
$K=0$
(Lemme 3.19). Ainsi
![]() $\text{Ker}(\unicode[STIX]{x1D703}_{2})$
est fini. Alors
$\text{Ker}(\unicode[STIX]{x1D703}_{2})$
est fini. Alors
 $H^{1}(k,C)$
est fini et donc
$H^{1}(k,C)$
est fini et donc
![]() $C$
est sans torsion (Lemme 3.19).◻
$C$
est sans torsion (Lemme 3.19).◻
Lemme 3.21. Supposons que
![]() $k$
est un corps de nombres. Soient
$k$
est un corps de nombres. Soient
![]() $G$
un groupe linéaire connexe,
$G$
un groupe linéaire connexe,
![]() $T$
un tore et
$T$
un tore et
![]() $G\xrightarrow[{}]{\unicode[STIX]{x1D713}}T$
un homomorphisme. Alors les énoncés suivants sont équivalents :
$G\xrightarrow[{}]{\unicode[STIX]{x1D713}}T$
un homomorphisme. Alors les énoncés suivants sont équivalents :
(i) le groupe
 $\text{Ker}(\text{Br}_{1}(T)\xrightarrow[{}]{\unicode[STIX]{x1D713}^{\ast }}\text{Br}_{1}(G))$
est fini ;
$\text{Ker}(\text{Br}_{1}(T)\xrightarrow[{}]{\unicode[STIX]{x1D713}^{\ast }}\text{Br}_{1}(G))$
est fini ;(ii) le morphisme
 $\unicode[STIX]{x1D713}$
est surjectif de noyau connexe ;
$\unicode[STIX]{x1D713}$
est surjectif de noyau connexe ;(iii) la
 $G$
-variété
$G$
-variété
 $T$
est un pseudo
$T$
est un pseudo
 $G$
-espace homogène.
$G$
-espace homogène.
Démonstration.
D’après l’exemple 3.16(1), on a (ii)
![]() $\Rightarrow$
(iii). Par la phrase après la définition 3.15, on a (iii)
$\Rightarrow$
(iii). Par la phrase après la définition 3.15, on a (iii)
![]() $\Rightarrow$
(i). Pour (i)
$\Rightarrow$
(i). Pour (i)
![]() $\Rightarrow$
(ii), puisque
$\Rightarrow$
(ii), puisque
![]() $\unicode[STIX]{x1D713}$
se factorise par
$\unicode[STIX]{x1D713}$
se factorise par
![]() $G^{\text{tor}}$
, on peut remplacer
$G^{\text{tor}}$
, on peut remplacer
![]() $G$
par
$G$
par
![]() $G^{\text{tor}}$
et supposer que
$G^{\text{tor}}$
et supposer que
![]() $G$
est un tore. Dans ce cas, puisque
$G$
est un tore. Dans ce cas, puisque
 $\text{Br}_{a}(T)\cong H^{2}(k,T^{\ast })$
, le noyau de
$\text{Br}_{a}(T)\cong H^{2}(k,T^{\ast })$
, le noyau de
 $H^{2}(k,T^{\ast })\xrightarrow[{}]{\unicode[STIX]{x1D713}^{\ast }}H^{2}(k,G^{\ast })$
est fini. Le lemme 3.20 ci-dessus donne (ii).◻
$H^{2}(k,T^{\ast })\xrightarrow[{}]{\unicode[STIX]{x1D713}^{\ast }}H^{2}(k,G^{\ast })$
est fini. Le lemme 3.20 ci-dessus donne (ii).◻
Soient
![]() $G$
un groupe linéaire connexe et
$G$
un groupe linéaire connexe et
![]() $Z$
un pseudo
$Z$
un pseudo
![]() $G$
-espace homogène (cf. Définition 3.15). Soient
$G$
-espace homogène (cf. Définition 3.15). Soient
 $(Z^{\text{tor}})^{\ast }:=\bar{k}[Z]^{\times }/\bar{k}^{\times }$
un
$(Z^{\text{tor}})^{\ast }:=\bar{k}[Z]^{\times }/\bar{k}^{\times }$
un
![]() $\unicode[STIX]{x1D6E4}_{k}$
-module libre de type fini et
$\unicode[STIX]{x1D6E4}_{k}$
-module libre de type fini et
![]() $Z^{\text{tor}}$
le tore correspondant. Pour tout
$Z^{\text{tor}}$
le tore correspondant. Pour tout
 $z\in Z(k)$
, on a un morphisme canonique
$z\in Z(k)$
, on a un morphisme canonique
 $Z\xrightarrow[{}]{\unicode[STIX]{x1D70B}_{z}}Z^{\text{tor}}$
tel que
$Z\xrightarrow[{}]{\unicode[STIX]{x1D70B}_{z}}Z^{\text{tor}}$
tel que
 $\unicode[STIX]{x1D70B}_{z}(z)=e_{Z^{\text{tor}}}$
(Rosenlicht). Soit
$\unicode[STIX]{x1D70B}_{z}(z)=e_{Z^{\text{tor}}}$
(Rosenlicht). Soit
![]() $\unicode[STIX]{x1D713}_{z}$
la composition
$\unicode[STIX]{x1D713}_{z}$
la composition
 $G\rightarrow G\cdot z{\hookrightarrow}Z\xrightarrow[{}]{\unicode[STIX]{x1D70B}_{z}}Z^{\text{tor}}$
.
$G\rightarrow G\cdot z{\hookrightarrow}Z\xrightarrow[{}]{\unicode[STIX]{x1D70B}_{z}}Z^{\text{tor}}$
.
Proposition 3.22. Le morphisme
![]() $\unicode[STIX]{x1D713}_{z}$
ne dépend pas du choix de
$\unicode[STIX]{x1D713}_{z}$
ne dépend pas du choix de
![]() $z$
, et c’est un homomorphisme tel que
$z$
, et c’est un homomorphisme tel que
![]() $Z^{\text{tor}}$
soit une
$Z^{\text{tor}}$
soit une
![]() $G$
-variété et
$G$
-variété et
![]() $\unicode[STIX]{x1D70B}_{z}$
soit un
$\unicode[STIX]{x1D70B}_{z}$
soit un
![]() $G$
-morphisme.
$G$
-morphisme.
De plus, si
![]() $k$
est un corps de nombres, la
$k$
est un corps de nombres, la
![]() $G$
-variété
$G$
-variété
![]() $Z^{\text{tor}}$
est un pseudo
$Z^{\text{tor}}$
est un pseudo
![]() $G$
-espace homogène.
$G$
-espace homogène.
Démonstration.
Notons
 $\unicode[STIX]{x1D70C}:G\times Z\rightarrow Z$
l’action de
$\unicode[STIX]{x1D70C}:G\times Z\rightarrow Z$
l’action de
![]() $G$
. Par le lemme de Rosenlicht,
$G$
. Par le lemme de Rosenlicht,
![]() $\unicode[STIX]{x1D713}_{z}$
est un homomorphisme. D’après le lemme 2.6, on a un isomorphisme canonique
$\unicode[STIX]{x1D713}_{z}$
est un homomorphisme. D’après le lemme 2.6, on a un isomorphisme canonique

tel que
 $\unicode[STIX]{x1D703}(\unicode[STIX]{x1D70B}_{z}\circ \unicode[STIX]{x1D70C})=((\unicode[STIX]{x1D70B}_{z}\circ \unicode[STIX]{x1D70C})|_{G\times z},(\unicode[STIX]{x1D70B}_{z}\circ \unicode[STIX]{x1D70C})|_{e_{G}\times Z})=(\unicode[STIX]{x1D713}_{z},\unicode[STIX]{x1D70B}_{z})$
. Alors
$\unicode[STIX]{x1D703}(\unicode[STIX]{x1D70B}_{z}\circ \unicode[STIX]{x1D70C})=((\unicode[STIX]{x1D70B}_{z}\circ \unicode[STIX]{x1D70C})|_{G\times z},(\unicode[STIX]{x1D70B}_{z}\circ \unicode[STIX]{x1D70C})|_{e_{G}\times Z})=(\unicode[STIX]{x1D713}_{z},\unicode[STIX]{x1D70B}_{z})$
. Alors
 $\unicode[STIX]{x1D70B}_{z}\circ \unicode[STIX]{x1D70C}=\unicode[STIX]{x1D713}_{z}\cdot \unicode[STIX]{x1D70B}_{z}$
et
$\unicode[STIX]{x1D70B}_{z}\circ \unicode[STIX]{x1D70C}=\unicode[STIX]{x1D713}_{z}\cdot \unicode[STIX]{x1D70B}_{z}$
et
![]() $\unicode[STIX]{x1D70B}_{z}$
est un
$\unicode[STIX]{x1D70B}_{z}$
est un
![]() $G$
-morphisme.
$G$
-morphisme.
Pour tout
 $z^{\prime }\in Z(k)$
, on a
$z^{\prime }\in Z(k)$
, on a
 $\unicode[STIX]{x1D70B}_{z^{\prime }}=\unicode[STIX]{x1D70B}_{z}(z^{\prime })^{-1}\cdot \unicode[STIX]{x1D70B}_{z}$
et donc
$\unicode[STIX]{x1D70B}_{z^{\prime }}=\unicode[STIX]{x1D70B}_{z}(z^{\prime })^{-1}\cdot \unicode[STIX]{x1D70B}_{z}$
et donc
 $\unicode[STIX]{x1D703}(\unicode[STIX]{x1D70B}_{z^{\prime }}\circ \unicode[STIX]{x1D70C})=(\unicode[STIX]{x1D713}_{z},\unicode[STIX]{x1D70B}_{z}(z^{\prime })^{-1}\cdot \unicode[STIX]{x1D70B}_{z})$
. Ainsi
$\unicode[STIX]{x1D703}(\unicode[STIX]{x1D70B}_{z^{\prime }}\circ \unicode[STIX]{x1D70C})=(\unicode[STIX]{x1D713}_{z},\unicode[STIX]{x1D70B}_{z}(z^{\prime })^{-1}\cdot \unicode[STIX]{x1D70B}_{z})$
. Ainsi
 $\unicode[STIX]{x1D713}_{z^{\prime }}=\unicode[STIX]{x1D713}_{z}$
.
$\unicode[STIX]{x1D713}_{z^{\prime }}=\unicode[STIX]{x1D713}_{z}$
.
La suite spectrale de Hochschild–Serre donne une suite exacte
 $$\begin{eqnarray}\text{Pic}(Z)\rightarrow \text{Pic}(Z_{\bar{k}})^{\unicode[STIX]{x1D6E4}_{k}}\rightarrow \text{Br}_{1}(Z^{\text{tor}})\xrightarrow[{}]{\unicode[STIX]{x1D70B}_{z}^{\ast }|_{\text{Br}_{1}}}\text{Br}(Z).\end{eqnarray}$$
$$\begin{eqnarray}\text{Pic}(Z)\rightarrow \text{Pic}(Z_{\bar{k}})^{\unicode[STIX]{x1D6E4}_{k}}\rightarrow \text{Br}_{1}(Z^{\text{tor}})\xrightarrow[{}]{\unicode[STIX]{x1D70B}_{z}^{\ast }|_{\text{Br}_{1}}}\text{Br}(Z).\end{eqnarray}$$
Puisque
 $\text{Pic}(Z_{\bar{k}})$
est de type fini et
$\text{Pic}(Z_{\bar{k}})$
est de type fini et
 $\text{Br}_{1}(Z^{\text{tor}})$
est de torsion, le groupe
$\text{Br}_{1}(Z^{\text{tor}})$
est de torsion, le groupe
 $\text{Ker}(\unicode[STIX]{x1D70B}_{z}^{\ast }|_{\text{Br}_{1}})$
est fini. Puisque
$\text{Ker}(\unicode[STIX]{x1D70B}_{z}^{\ast }|_{\text{Br}_{1}})$
est fini. Puisque
 $\text{Ker}(\text{Br}_{G}(Z)\xrightarrow[{}]{\unicode[STIX]{x1D70C}_{z}^{\ast }}\text{Br}(G))$
est fini, le groupe
$\text{Ker}(\text{Br}_{G}(Z)\xrightarrow[{}]{\unicode[STIX]{x1D70C}_{z}^{\ast }}\text{Br}(G))$
est fini, le groupe
 $\text{Ker}(\text{Br}_{1}(Z^{\text{tor}})\xrightarrow[{}]{\unicode[STIX]{x1D713}_{z}^{\ast }|_{\text{Br}_{1}}}\text{Br}(G))$
est fini. Si
$\text{Ker}(\text{Br}_{1}(Z^{\text{tor}})\xrightarrow[{}]{\unicode[STIX]{x1D713}_{z}^{\ast }|_{\text{Br}_{1}}}\text{Br}(G))$
est fini. Si
![]() $k$
est un corps de nombres, une application du lemme 3.21 donne l’énoncé.◻
$k$
est un corps de nombres, une application du lemme 3.21 donne l’énoncé.◻
Définition 3.23. Dans la proposition 3.22, une fois qu’on a choisi
 $z\in Z(k)$
, le morphisme
$z\in Z(k)$
, le morphisme
 $Z\xrightarrow[{}]{\unicode[STIX]{x1D70B}}Z^{\text{tor}}$
est appelé le quotient torique maximal. Il ne dépend du choix de
$Z\xrightarrow[{}]{\unicode[STIX]{x1D70B}}Z^{\text{tor}}$
est appelé le quotient torique maximal. Il ne dépend du choix de
![]() $z$
qu’à translation près. Si
$z$
qu’à translation près. Si
![]() $k$
est un corps de nombres, le morphisme
$k$
est un corps de nombres, le morphisme
 $G\rightarrow Z^{\text{tor}}$
dans la proposition 3.22 est surjectif de noyau
$G\rightarrow Z^{\text{tor}}$
dans la proposition 3.22 est surjectif de noyau
![]() $G_{0}$
connexe. Le groupe
$G_{0}$
connexe. Le groupe
![]() $G_{0}$
est appelé le stabilisateur de
$G_{0}$
est appelé le stabilisateur de
![]() $G$
sur
$G$
sur
![]() $Z^{\text{tor}}$
.
$Z^{\text{tor}}$
.
4 L’approximation forte hors des places archimédiennes et la question 1.2
Dans toute cette section,
![]() $k$
est un corps de nombres. Sauf mention explicite, une variété est une
$k$
est un corps de nombres. Sauf mention explicite, une variété est une
![]() $k$
-variété. Soit
$k$
-variété. Soit
![]() $G$
un groupe linéaire connexe. Pour répondre à la question 1.2, on établit le théorème 4.2. Comme conséquence, on montre le théorème 1.4(1).
$G$
un groupe linéaire connexe. Pour répondre à la question 1.2, on établit le théorème 4.2. Comme conséquence, on montre le théorème 1.4(1).
Rappelons la notion de sous-groupe de Brauer invariant (cf. Définition 3.1).
Lemme 4.1. Soit
![]() $G$
un groupe linéaire connexe. Alors l’homomorphisme induit par l’accouplement de Brauer–Manin
$G$
un groupe linéaire connexe. Alors l’homomorphisme induit par l’accouplement de Brauer–Manin
 $G(\mathbf{A}_{k})_{\bullet }\xrightarrow[{}]{\unicode[STIX]{x1D703}_{G}}\text{Br}_{a}(G)^{D}$
est ouvert, où
$G(\mathbf{A}_{k})_{\bullet }\xrightarrow[{}]{\unicode[STIX]{x1D703}_{G}}\text{Br}_{a}(G)^{D}$
est ouvert, où
 $(-)^{D}:=\text{Hom}(-,\mathbb{Q}/\mathbb{Z})$
(cf. (1.2)).
$(-)^{D}:=\text{Hom}(-,\mathbb{Q}/\mathbb{Z})$
(cf. (1.2)).
Démonstration.
Dans
 $G(\mathbf{A}_{k})_{\bullet }$
, les sous-groupes ouverts compacts forment une base topologique de
$G(\mathbf{A}_{k})_{\bullet }$
, les sous-groupes ouverts compacts forment une base topologique de
![]() $e_{G}$
. Pour tout tel sous-groupe
$e_{G}$
. Pour tout tel sous-groupe
![]() $C$
, l’image
$C$
, l’image
 $\unicode[STIX]{x1D703}_{G}(C)\subset \text{Br}_{a}(G)^{D}$
est compacte, et donc fermée. Il suffit alors de montrer que cette image est d’indice fini. Par la finitude du nombre de classes de
$\unicode[STIX]{x1D703}_{G}(C)\subset \text{Br}_{a}(G)^{D}$
est compacte, et donc fermée. Il suffit alors de montrer que cette image est d’indice fini. Par la finitude du nombre de classes de
![]() $G$
[Reference Platonov and RapinchukPR94, Thm. 5.1], il existe un tel sous-groupe
$G$
[Reference Platonov and RapinchukPR94, Thm. 5.1], il existe un tel sous-groupe
![]() $C_{0}$
tel que le double quotient
$C_{0}$
tel que le double quotient
 $C_{0}\backslash G(\mathbf{A}_{k})_{\bullet }/G(k)$
soit finie. Puisque
$C_{0}\backslash G(\mathbf{A}_{k})_{\bullet }/G(k)$
soit finie. Puisque
![]() $\unicode[STIX]{x0428}^{1}(G)$
est fini, d’après [Reference DemarcheDem11, Thm. 5.1],
$\unicode[STIX]{x0428}^{1}(G)$
est fini, d’après [Reference DemarcheDem11, Thm. 5.1],
![]() $\unicode[STIX]{x1D703}_{G}(C_{0})$
est d’indice fini. Pour tout tel sous-groupe
$\unicode[STIX]{x1D703}_{G}(C_{0})$
est d’indice fini. Pour tout tel sous-groupe
![]() $C$
, le quotient
$C$
, le quotient
 $C_{0}/(C\cap C_{0})$
est fini, car
$C_{0}/(C\cap C_{0})$
est fini, car
![]() $C_{0}$
est compact. Donc
$C_{0}$
est compact. Donc
![]() $\unicode[STIX]{x1D703}_{G}(C)$
est d’indice fini.◻
$\unicode[STIX]{x1D703}_{G}(C)$
est d’indice fini.◻
Théorème 4.2. Soient
![]() $G$
un groupe linéaire connexe,
$G$
un groupe linéaire connexe,
![]() $X$
une
$X$
une
![]() $G$
-variété lisse géométriquement intègre et
$G$
-variété lisse géométriquement intègre et
![]() $U\subset X$
un
$U\subset X$
un
![]() $G$
-ouvert. Soient
$G$
-ouvert. Soient
 $A\subset \text{Br}(X)$
un sous-groupe fini et
$A\subset \text{Br}(X)$
un sous-groupe fini et
 $B\subset \text{Br}_{G}(U)$
(cf. (3.1)) un sous-groupe. Supposons que
$B\subset \text{Br}_{G}(U)$
(cf. (3.1)) un sous-groupe. Supposons que
 $(B\cap \text{Ker}(\unicode[STIX]{x1D706}))/(B\cap \text{Im}\,\text{Br}(k))$
est fini, où
$(B\cap \text{Ker}(\unicode[STIX]{x1D706}))/(B\cap \text{Im}\,\text{Br}(k))$
est fini, où
 $\text{Br}_{G}(U)\xrightarrow[{}]{\unicode[STIX]{x1D706}}\text{Br}_{e}(G)$
est l’homomorphisme de Sansuc (Définition 3.8). Alors, pour tout ouvert
$\text{Br}_{G}(U)\xrightarrow[{}]{\unicode[STIX]{x1D706}}\text{Br}_{e}(G)$
est l’homomorphisme de Sansuc (Définition 3.8). Alors, pour tout ouvert
 $W\subset X(\mathbf{A}_{k})$
satisfaisant
$W\subset X(\mathbf{A}_{k})$
satisfaisant
 $W^{(A+B)\cap \text{Br}(X)}\neq \emptyset$
, on a
$W^{(A+B)\cap \text{Br}(X)}\neq \emptyset$
, on a
 $W\cap U(\mathbf{A}_{k})^{A+B}\neq \emptyset$
.
$W\cap U(\mathbf{A}_{k})^{A+B}\neq \emptyset$
.
Démonstration.
On peut supposer que
 $\text{Im}\,\text{Br}(k)\subset B$
. Après avoir rétréci
$\text{Im}\,\text{Br}(k)\subset B$
. Après avoir rétréci
![]() $W$
, on peut supposer que tout élément de
$W$
, on peut supposer que tout élément de
![]() $A$
s’annule sur
$A$
s’annule sur
![]() $W$
et
$W$
et
 $W\cong W_{\infty }\times W_{f}$
avec
$W\cong W_{\infty }\times W_{f}$
avec
 $W_{\infty }\subset X(k_{\infty })$
,
$W_{\infty }\subset X(k_{\infty })$
,
 $W_{f}\subset X(\mathbf{A}_{k}^{\infty })$
tel que
$W_{f}\subset X(\mathbf{A}_{k}^{\infty })$
tel que
![]() $W_{f}$
soit compact.
$W_{f}$
soit compact.
Pour tout
 $w\in W_{f}$
, il existe un ouvert
$w\in W_{f}$
, il existe un ouvert
 $W_{w}\subset W_{f}$
contenant
$W_{w}\subset W_{f}$
contenant
![]() $w$
et un ouvert
$w$
et un ouvert
 $C_{w}\subset G(\mathbf{A}^{\infty })$
tel que
$C_{w}\subset G(\mathbf{A}^{\infty })$
tel que
 $C_{w}\cdot W_{w}\subset W_{f}$
. Puisque
$C_{w}\cdot W_{w}\subset W_{f}$
. Puisque
![]() $W_{f}$
est compact, il existe un sous-ensemble fini
$W_{f}$
est compact, il existe un sous-ensemble fini
![]() $I\subset W_{f}$
tel que
$I\subset W_{f}$
tel que
 $\bigcup _{w\in I}W_{w}=W_{f}$
. Soit
$\bigcup _{w\in I}W_{w}=W_{f}$
. Soit
![]() $C_{f}$
le sous-groupe de
$C_{f}$
le sous-groupe de
![]() $G(\mathbf{A}^{\infty })$
engendré par
$G(\mathbf{A}^{\infty })$
engendré par
 $\bigcap _{w\in I}C_{w}$
. Alors
$\bigcap _{w\in I}C_{w}$
. Alors
 $C_{f}\cdot W_{f}\subset W_{f}$
et
$C_{f}\cdot W_{f}\subset W_{f}$
et
![]() $C_{f}$
est ouvert dans
$C_{f}$
est ouvert dans
![]() $G(\mathbf{A}^{\infty })$
. Soit
$G(\mathbf{A}^{\infty })$
. Soit
 $C:=(e_{G})_{\infty }\times C_{f}\subset G(\mathbf{A}_{k})$
. Alors
$C:=(e_{G})_{\infty }\times C_{f}\subset G(\mathbf{A}_{k})$
. Alors
 $C\cdot W=W$
et l’image de
$C\cdot W=W$
et l’image de
![]() $C$
dans
$C$
dans
 $G(\mathbf{A}_{k})_{\bullet }$
est ouvert.
$G(\mathbf{A}_{k})_{\bullet }$
est ouvert.
Notons
 $G(\mathbf{A}_{k})\xrightarrow[{}]{\unicode[STIX]{x1D703}_{G}}\text{Br}_{a}(G)^{D}$
et
$G(\mathbf{A}_{k})\xrightarrow[{}]{\unicode[STIX]{x1D703}_{G}}\text{Br}_{a}(G)^{D}$
et
 $U(\mathbf{A}_{k})\xrightarrow[{}]{\unicode[STIX]{x1D703}_{U}}B^{D}$
les applications induites par l’accouplement de Brauer–Manin, où
$U(\mathbf{A}_{k})\xrightarrow[{}]{\unicode[STIX]{x1D703}_{U}}B^{D}$
les applications induites par l’accouplement de Brauer–Manin, où
 $(-)^{D}:=\text{Hom}(-,\mathbb{Q}/\mathbb{Z})$
(cf. (1.2)). D’après le lemme 4.1,
$(-)^{D}:=\text{Hom}(-,\mathbb{Q}/\mathbb{Z})$
(cf. (1.2)). D’après le lemme 4.1,
 $\unicode[STIX]{x1D703}_{G}(C)\subset \text{Br}_{a}(G)^{D}$
est un sous-groupe ouvert d’indice fini. Puisque
$\unicode[STIX]{x1D703}_{G}(C)\subset \text{Br}_{a}(G)^{D}$
est un sous-groupe ouvert d’indice fini. Puisque
 $(B\cap \text{Ker}(\unicode[STIX]{x1D706}))/(\text{Im}\,\text{Br}(k))$
est fini,
$(B\cap \text{Ker}(\unicode[STIX]{x1D706}))/(\text{Im}\,\text{Br}(k))$
est fini,
 $(\unicode[STIX]{x1D706}^{D}\circ \unicode[STIX]{x1D703}_{G})(C)\subset (B/\text{Im}\,\text{Br}(k))^{D}$
est un sous-groupe ouvert d’indice fini, où l’homomorphisme
$(\unicode[STIX]{x1D706}^{D}\circ \unicode[STIX]{x1D703}_{G})(C)\subset (B/\text{Im}\,\text{Br}(k))^{D}$
est un sous-groupe ouvert d’indice fini, où l’homomorphisme
 $$\begin{eqnarray}\unicode[STIX]{x1D706}:B\subset \text{Br}_{G}(U)\rightarrow \text{Br}_{e}(G)=\text{Br}_{a}(G)~~~\text{induit}~\unicode[STIX]{x1D706}^{D}:=\text{Hom}(\unicode[STIX]{x1D706},\mathbb{Q}/\mathbb{Z}):\text{Br}_{a}(G)^{D}\rightarrow (B/\text{Im}\,\text{Br}(k))^{D}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D706}:B\subset \text{Br}_{G}(U)\rightarrow \text{Br}_{e}(G)=\text{Br}_{a}(G)~~~\text{induit}~\unicode[STIX]{x1D706}^{D}:=\text{Hom}(\unicode[STIX]{x1D706},\mathbb{Q}/\mathbb{Z}):\text{Br}_{a}(G)^{D}\rightarrow (B/\text{Im}\,\text{Br}(k))^{D}.\end{eqnarray}$$
Donc il existe un sous-groupe fini
 $B_{1}\subset B$
tel que
$B_{1}\subset B$
tel que
 $$\begin{eqnarray}\text{Ker}((B/\text{Im}\,\text{Br}(k))^{D}\xrightarrow[{}]{\unicode[STIX]{x1D717}}(B_{1})^{D})\subset (\unicode[STIX]{x1D706}^{D}\circ \unicode[STIX]{x1D703}_{G})(C),\end{eqnarray}$$
$$\begin{eqnarray}\text{Ker}((B/\text{Im}\,\text{Br}(k))^{D}\xrightarrow[{}]{\unicode[STIX]{x1D717}}(B_{1})^{D})\subset (\unicode[STIX]{x1D706}^{D}\circ \unicode[STIX]{x1D703}_{G})(C),\end{eqnarray}$$
où
![]() $\unicode[STIX]{x1D717}$
est induit par
$\unicode[STIX]{x1D717}$
est induit par
 $B_{1}\subset B\rightarrow B/\text{Im}\,\text{Br}(k)$
.
$B_{1}\subset B\rightarrow B/\text{Im}\,\text{Br}(k)$
.
D’après le lemme formel d’Harari [Reference HarariHar94, Cor. 2.6.1],
 $W\cap U(\mathbf{A}_{k})^{B_{1}}\neq \emptyset$
. On a le diagramme suivant.
$W\cap U(\mathbf{A}_{k})^{B_{1}}\neq \emptyset$
. On a le diagramme suivant.

Soit
 $u\in W\cap U(\mathbf{A}_{k})^{B_{1}}$
, alors
$u\in W\cap U(\mathbf{A}_{k})^{B_{1}}$
, alors
 $\unicode[STIX]{x1D717}(\unicode[STIX]{x1D703}_{U}(u))=0$
et, d’après (4.1), il existe
$\unicode[STIX]{x1D717}(\unicode[STIX]{x1D703}_{U}(u))=0$
et, d’après (4.1), il existe
![]() $g\in C$
tel que
$g\in C$
tel que
 $g^{-1}\cdot u\in W$
et
$g^{-1}\cdot u\in W$
et
 $(\unicode[STIX]{x1D706}^{D}\circ \unicode[STIX]{x1D703}_{G})(g)=\unicode[STIX]{x1D703}_{U}(u)$
. D’après la proposition 3.9(1), on a
$(\unicode[STIX]{x1D706}^{D}\circ \unicode[STIX]{x1D703}_{G})(g)=\unicode[STIX]{x1D703}_{U}(u)$
. D’après la proposition 3.9(1), on a
 $\unicode[STIX]{x1D703}_{U}(g^{-1}\cdot u)=0$
.◻
$\unicode[STIX]{x1D703}_{U}(g^{-1}\cdot u)=0$
.◻
Remarque 4.3. Dans le théorème 4.2, si
![]() $G=1$
, alors ce théorème est équivalent au lemme formel d’Harari [Reference HarariHar94, Cor. 2.6.1].
$G=1$
, alors ce théorème est équivalent au lemme formel d’Harari [Reference HarariHar94, Cor. 2.6.1].
Comme conséquence directe, on a le suivant.
Corollaire 4.4. Avec les hypothèses et notations du théorème 4.2, pour tout sous-ensemble fini
![]() $S\subset \unicode[STIX]{x1D6FA}_{k}$
, s’il existe un ouvert
$S\subset \unicode[STIX]{x1D6FA}_{k}$
, s’il existe un ouvert
![]() $X_{1}$
de
$X_{1}$
de
![]() $X$
tel que
$X$
tel que
![]() $U\subset X_{1}$
et
$U\subset X_{1}$
et
![]() $X_{1}$
satisfasse l’approximation forte par rapport à
$X_{1}$
satisfasse l’approximation forte par rapport à
 $\text{Br}(X_{1})\cap (A+B)$
hors de
$\text{Br}(X_{1})\cap (A+B)$
hors de
![]() $S$
, alors
$S$
, alors
![]() $X$
satisfait l’approximation forte par rapport à
$X$
satisfait l’approximation forte par rapport à
 $\text{Br}(X)\cap (A+B)$
hors de
$\text{Br}(X)\cap (A+B)$
hors de
![]() $S$
.
$S$
.
Corollaire 4.5. Avec les hypothèses et notations du théorème 4.2, s’il existe un ouvert
![]() $X_{1}$
de
$X_{1}$
de
![]() $X$
tel que
$X$
tel que
 $U\subset X_{1}$
et
$U\subset X_{1}$
et
![]() $X_{1}(k)$
soit dense dans
$X_{1}(k)$
soit dense dans
 $X_{1}(\mathbf{A}_{k})_{\bullet }^{\text{Br}(X_{1})\cap (A+B)}$
, alors
$X_{1}(\mathbf{A}_{k})_{\bullet }^{\text{Br}(X_{1})\cap (A+B)}$
, alors
![]() $X(k)$
est dense dans
$X(k)$
est dense dans
 $X(\mathbf{A}_{k})_{\bullet }^{\text{Br}(X)\cap (A+B)}$
.
$X(\mathbf{A}_{k})_{\bullet }^{\text{Br}(X)\cap (A+B)}$
.
Soit
![]() $G$
un groupe linéaire connexe. Pour la notion de pseudo
$G$
un groupe linéaire connexe. Pour la notion de pseudo
![]() $G$
-espace homogène, voir la Définition 3.15.
$G$
-espace homogène, voir la Définition 3.15.
Théorème 4.6. Soient
![]() $G$
un groupe linéaire connexe et
$G$
un groupe linéaire connexe et
![]() $Z$
un pseudo
$Z$
un pseudo
![]() $G$
-espace homogène. Soient
$G$
-espace homogène. Soient
![]() $X$
une
$X$
une
![]() $G$
-variété lisse, géométriquement intègre et
$G$
-variété lisse, géométriquement intègre et
![]() $U\subset X$
un
$U\subset X$
un
![]() $G$
-ouvert muni d’un
$G$
-ouvert muni d’un
![]() $G$
-morphisme
$G$
-morphisme
![]() $U\xrightarrow[{}]{f}Z$
. Soient
$U\xrightarrow[{}]{f}Z$
. Soient
 $A\subset \text{Br}(X)$
et
$A\subset \text{Br}(X)$
et
 $B\subset \text{Br}_{G}(U)$
(cf. (3.1)) deux sous-groupes finis. Alors, pour tout ouvert
$B\subset \text{Br}_{G}(U)$
(cf. (3.1)) deux sous-groupes finis. Alors, pour tout ouvert
 $W\subset X(\mathbf{A}_{k})$
satisfaisant
$W\subset X(\mathbf{A}_{k})$
satisfaisant
 $W^{\text{Br}(X)\cap (A+B+f^{\ast }\,\text{Br}_{G}(Z))}\neq \emptyset$
:
$W^{\text{Br}(X)\cap (A+B+f^{\ast }\,\text{Br}_{G}(Z))}\neq \emptyset$
:
(1) on a
 $W\cap U(\mathbf{A}_{k})^{A+B+f^{\ast }\,\text{Br}_{G}(Z)}\neq \emptyset$
;
$W\cap U(\mathbf{A}_{k})^{A+B+f^{\ast }\,\text{Br}_{G}(Z)}\neq \emptyset$
;(2) si
 $G(k_{\infty })^{+}\cdot Z(k)$
est dense dans
$G(k_{\infty })^{+}\cdot Z(k)$
est dense dans
 $Z(\mathbf{A}_{k})^{\text{Br}_{G}(Z)}$
, il existe
$Z(\mathbf{A}_{k})^{\text{Br}_{G}(Z)}$
, il existe
 $z\in Z(k)$
de fibre
$z\in Z(k)$
de fibre
 $U_{z}$
tel que
$U_{z}$
tel que  $$\begin{eqnarray}(G(k_{\infty })^{+}\cdot W)\cap U_{z}(\mathbf{A}_{k})^{A+B}\neq \emptyset .\end{eqnarray}$$
$$\begin{eqnarray}(G(k_{\infty })^{+}\cdot W)\cap U_{z}(\mathbf{A}_{k})^{A+B}\neq \emptyset .\end{eqnarray}$$
Démonstration.
Notons
 $\text{Br}_{G}(Z)\xrightarrow[{}]{\unicode[STIX]{x1D706}_{Z}}\text{Br}_{a}(G)$
,
$\text{Br}_{G}(Z)\xrightarrow[{}]{\unicode[STIX]{x1D706}_{Z}}\text{Br}_{a}(G)$
,
 $\text{Br}_{G}(U)\xrightarrow[{}]{\unicode[STIX]{x1D706}_{U}}\text{Br}_{a}(G)$
les homomorphismes de Sansuc (cf. Définition 3.8). Puisque
$\text{Br}_{G}(U)\xrightarrow[{}]{\unicode[STIX]{x1D706}_{U}}\text{Br}_{a}(G)$
les homomorphismes de Sansuc (cf. Définition 3.8). Puisque
 $\text{Ker}(\unicode[STIX]{x1D706}_{Z})/(\text{Im}\,\text{Br}(k))$
est fini et
$\text{Ker}(\unicode[STIX]{x1D706}_{Z})/(\text{Im}\,\text{Br}(k))$
est fini et
 $\unicode[STIX]{x1D706}_{Z}=\unicode[STIX]{x1D706}_{U}\circ f^{\ast }$
, le quotient
$\unicode[STIX]{x1D706}_{Z}=\unicode[STIX]{x1D706}_{U}\circ f^{\ast }$
, le quotient
 $(\text{Ker}(\unicode[STIX]{x1D706}_{U})\cap (B+f^{\ast }\,\text{Br}_{G}(Z)))/\text{Im}\,\text{Br}(k)$
est fini. Une application du théorème 4.2 donne (1).
$(\text{Ker}(\unicode[STIX]{x1D706}_{U})\cap (B+f^{\ast }\,\text{Br}_{G}(Z)))/\text{Im}\,\text{Br}(k)$
est fini. Une application du théorème 4.2 donne (1).
D’après [Reference ConradCon12, Thm. 4.5], l’application
 $U(\mathbf{A}_{k})\rightarrow Z(\mathbf{A}_{k})$
est ouverte et on obtient (2).◻
$U(\mathbf{A}_{k})\rightarrow Z(\mathbf{A}_{k})$
est ouverte et on obtient (2).◻
Démonstration du théorème 1.4(1).
D’après un théorème de Kneser et Platonov (cf. [Reference Platonov and RapinchukPR94, Thm. 7.12]),
![]() $G^{\text{sc}}(k)$
est dense dans
$G^{\text{sc}}(k)$
est dense dans
 $G^{\text{sc}}(\mathbf{A}_{k}^{\infty _{k}})$
. Par la proposition 3.9(3) et l’approximation forte pour les espaces homogènes à stabilisateur géométrique connexe (Borovoi et Demarche [Reference Borovoi and DemarcheBD13, Thm. 1.4]),
$G^{\text{sc}}(\mathbf{A}_{k}^{\infty _{k}})$
. Par la proposition 3.9(3) et l’approximation forte pour les espaces homogènes à stabilisateur géométrique connexe (Borovoi et Demarche [Reference Borovoi and DemarcheBD13, Thm. 1.4]),
![]() $U(k)$
est dense dans
$U(k)$
est dense dans
 $U(\mathbf{A}_{k})_{\bullet }^{\text{Br}_{G}(U)}$
. Une application du théorème 4.6(2) au quintuple
$U(\mathbf{A}_{k})_{\bullet }^{\text{Br}_{G}(U)}$
. Une application du théorème 4.6(2) au quintuple
 $$\begin{eqnarray}(G,U\subset X,U\xrightarrow[{}]{f=\text{id}_{U}}U,0\subset \text{Br}(X),0\subset \text{Br}_{G}(U))\end{eqnarray}$$
$$\begin{eqnarray}(G,U\subset X,U\xrightarrow[{}]{f=\text{id}_{U}}U,0\subset \text{Br}(X),0\subset \text{Br}_{G}(U))\end{eqnarray}$$
donne l’énoncé. ◻
5 La descente par rapport au groupe de Brauer invariant
Dans toute cette section,
![]() $k$
est un corps de nombres. Sauf mention explicite du contraire, une variété est une
$k$
est un corps de nombres. Sauf mention explicite du contraire, une variété est une
![]() $k$
-variété. La méthode de descente des points adéliques est établie par Colliot and Thélène et Sansuc dans [Reference Colliot-Thélène and SansucCS87b]. Dans [Reference Cao, Demarche and XuCDX16], Demarche, Xu et l’auteur étudient la méthode de descente des points adéliques orthogonaux à certains groupes de Brauer dans le cas des torseurs sous un tore. On suit leur méthode et considère ici le cas plus général des torseurs sous un groupe linéaire connexe (Théorème 5.9).
$k$
-variété. La méthode de descente des points adéliques est établie par Colliot and Thélène et Sansuc dans [Reference Colliot-Thélène and SansucCS87b]. Dans [Reference Cao, Demarche and XuCDX16], Demarche, Xu et l’auteur étudient la méthode de descente des points adéliques orthogonaux à certains groupes de Brauer dans le cas des torseurs sous un tore. On suit leur méthode et considère ici le cas plus général des torseurs sous un groupe linéaire connexe (Théorème 5.9).
Pour la notion de sous-groupe de Brauer invariant, voir la définition 3.1.
5.1 Un cas spécial (
 $\unicode[STIX]{x0428}^{1}(G)=1$
)
$\unicode[STIX]{x0428}^{1}(G)=1$
)
Soient
![]() $G$
un groupe linéaire connexe,
$G$
un groupe linéaire connexe,
![]() $X$
une variété lisse géométriquement intègre et
$X$
une variété lisse géométriquement intègre et
 $Y\xrightarrow[{}]{p}X$
un
$Y\xrightarrow[{}]{p}X$
un
![]() $G$
-torseur (à gauche). Pour tout
$G$
-torseur (à gauche). Pour tout
 $\unicode[STIX]{x1D70E}\in Z^{1}(k,G)$
, soient
$\unicode[STIX]{x1D70E}\in Z^{1}(k,G)$
, soient
![]() $P_{\unicode[STIX]{x1D70E}}$
le
$P_{\unicode[STIX]{x1D70E}}$
le
![]() $G$
-torseur à droite correspondant et
$G$
-torseur à droite correspondant et
![]() $G_{\unicode[STIX]{x1D70E}}$
le tordu par 1-cocycle
$G_{\unicode[STIX]{x1D70E}}$
le tordu par 1-cocycle
![]() $\unicode[STIX]{x1D70E}$
. Alors
$\unicode[STIX]{x1D70E}$
. Alors
![]() $P_{\unicode[STIX]{x1D70E}}$
est un
$P_{\unicode[STIX]{x1D70E}}$
est un
![]() $G_{\unicode[STIX]{x1D70E}}$
-torseur à gauche. Soit
$G_{\unicode[STIX]{x1D70E}}$
-torseur à gauche. Soit
 $Y_{\unicode[STIX]{x1D70E}}\xrightarrow[{}]{p_{\unicode[STIX]{x1D70E}}}X$
le tordu de
$Y_{\unicode[STIX]{x1D70E}}\xrightarrow[{}]{p_{\unicode[STIX]{x1D70E}}}X$
le tordu de
![]() $Y$
, i.e.
$Y$
, i.e.
 $Y_{\unicode[STIX]{x1D70E}}=P_{\unicode[STIX]{x1D70E}}\times ^{G}Y$
. Alors
$Y_{\unicode[STIX]{x1D70E}}=P_{\unicode[STIX]{x1D70E}}\times ^{G}Y$
. Alors
![]() $Y_{\unicode[STIX]{x1D70E}}$
est un
$Y_{\unicode[STIX]{x1D70E}}$
est un
![]() $G_{\unicode[STIX]{x1D70E}}$
-torseur à gauche sur
$G_{\unicode[STIX]{x1D70E}}$
-torseur à gauche sur
![]() $X$
. Soit
$X$
. Soit
 $\text{Br}_{G_{\unicode[STIX]{x1D70E}}}(Y_{\unicode[STIX]{x1D70E}})$
le sous-groupe de Brauer
$\text{Br}_{G_{\unicode[STIX]{x1D70E}}}(Y_{\unicode[STIX]{x1D70E}})$
le sous-groupe de Brauer
![]() $G_{\unicode[STIX]{x1D70E}}$
-invariant de
$G_{\unicode[STIX]{x1D70E}}$
-invariant de
![]() $Y_{\unicode[STIX]{x1D70E}}$
(Définition 3.1).
$Y_{\unicode[STIX]{x1D70E}}$
(Définition 3.1).
Lemme 5.1. Supposons que
 $\unicode[STIX]{x0428}^{1}(G)=1$
. Alors pour tout sous-groupe
$\unicode[STIX]{x0428}^{1}(G)=1$
. Alors pour tout sous-groupe
 $B\subset \text{Br}_{G}(Y)$
, on a :
$B\subset \text{Br}_{G}(Y)$
, on a :
 $$\begin{eqnarray}p(Y(\mathbf{A}_{k})^{p^{\ast }((p^{\ast })^{-1}B)})=p(Y(\mathbf{A}_{k})^{B}),\end{eqnarray}$$
$$\begin{eqnarray}p(Y(\mathbf{A}_{k})^{p^{\ast }((p^{\ast })^{-1}B)})=p(Y(\mathbf{A}_{k})^{B}),\end{eqnarray}$$
où
 $\text{Br}(X)\xrightarrow[{}]{p^{\ast }}\text{Br}(Y)$
.
$\text{Br}(X)\xrightarrow[{}]{p^{\ast }}\text{Br}(Y)$
.
Démonstration.
Puisque
 $p^{\ast }((p^{\ast })^{-1}B)\subset B$
, on a
$p^{\ast }((p^{\ast })^{-1}B)\subset B$
, on a
 $p(Y(\mathbf{A}_{k})^{B})\subset p(Y(\mathbf{A}_{k})^{p^{\ast }((p^{\ast })^{-1}B)}).$
$p(Y(\mathbf{A}_{k})^{B})\subset p(Y(\mathbf{A}_{k})^{p^{\ast }((p^{\ast })^{-1}B)}).$
Par le théorème 3.10, on a le diagramme suivant commutatif de suites exactes.

Il induit un diagramme commutatif avec suite exacte :

où
 $(-)^{D}:=\text{Hom}(-,\mathbb{Q}/\mathbb{Z})$
(cf. (1.2)) et
$(-)^{D}:=\text{Hom}(-,\mathbb{Q}/\mathbb{Z})$
(cf. (1.2)) et
![]() $a_{G}$
,
$a_{G}$
,
![]() $a_{Y}$
,
$a_{Y}$
,
![]() $a_{X}$
sont induits par l’accouplement de Brauer–Manin. Par la proposition 3.9, pour tout
$a_{X}$
sont induits par l’accouplement de Brauer–Manin. Par la proposition 3.9, pour tout
 $y\in Y(\mathbf{A}_{k})$
et tout
$y\in Y(\mathbf{A}_{k})$
et tout
 $g\in G(\mathbf{A}_{k})$
, on a
$g\in G(\mathbf{A}_{k})$
, on a
 $$\begin{eqnarray}a_{Y}(g\cdot y)=(\unicode[STIX]{x1D706}^{D}\circ a_{G})(g)+a_{Y}(y).\end{eqnarray}$$
$$\begin{eqnarray}a_{Y}(g\cdot y)=(\unicode[STIX]{x1D706}^{D}\circ a_{G})(g)+a_{Y}(y).\end{eqnarray}$$
Puisque
 $\unicode[STIX]{x0428}^{1}(G)=1$
, par la suite exacte de Poitou-Tate de
$\unicode[STIX]{x0428}^{1}(G)=1$
, par la suite exacte de Poitou-Tate de
![]() $G$
(Demarche [Reference DemarcheDem11, Thm. 5.1]),
$G$
(Demarche [Reference DemarcheDem11, Thm. 5.1]),
![]() $a_{G}$
est surjectif. Pour tout
$a_{G}$
est surjectif. Pour tout
 $y\in Y(\mathbf{A}_{k})^{p^{\ast }((p^{\ast })^{-1}B)}$
, on a
$y\in Y(\mathbf{A}_{k})^{p^{\ast }((p^{\ast })^{-1}B)}$
, on a
 $x:=p(y)\in X(\mathbf{A}_{k})^{(p^{\ast })^{-1}B}$
. Alors
$x:=p(y)\in X(\mathbf{A}_{k})^{(p^{\ast })^{-1}B}$
. Alors
 $(p^{\ast D}\circ a_{Y})(y)=a_{X}(x)=0$
et il existe
$(p^{\ast D}\circ a_{Y})(y)=a_{X}(x)=0$
et il existe
 $g\in G(\mathbf{A}_{k})$
tel que
$g\in G(\mathbf{A}_{k})$
tel que
 $(\unicode[STIX]{x1D706}^{D}\circ a_{G})(g)=a_{Y}(y)$
. Donc
$(\unicode[STIX]{x1D706}^{D}\circ a_{G})(g)=a_{Y}(y)$
. Donc
 $a_{Y}(g^{-1}\cdot y)=0$
et
$a_{Y}(g^{-1}\cdot y)=0$
et
 $p(g^{-1}\cdot y)=x$
.◻
$p(g^{-1}\cdot y)=x$
.◻
Proposition 5.2. Soient
![]() $G$
un groupe linéaire connexe,
$G$
un groupe linéaire connexe,
![]() $X$
une variété lisse géométriquement intègre et
$X$
une variété lisse géométriquement intègre et
 $Y\xrightarrow[{}]{p}X$
un
$Y\xrightarrow[{}]{p}X$
un
![]() $G$
-torseur. Soit
$G$
-torseur. Soit
 $A\subset \text{Br}(X)$
un sous-groupe et, pour chaque
$A\subset \text{Br}(X)$
un sous-groupe et, pour chaque
 $\unicode[STIX]{x1D70E}\in H^{1}(k,G)$
, soit
$\unicode[STIX]{x1D70E}\in H^{1}(k,G)$
, soit
 $B_{\unicode[STIX]{x1D70E}}\subset \text{Br}_{G_{\unicode[STIX]{x1D70E}}}(Y_{\unicode[STIX]{x1D70E}})$
un sous-groupe. Supposons que
$B_{\unicode[STIX]{x1D70E}}\subset \text{Br}_{G_{\unicode[STIX]{x1D70E}}}(Y_{\unicode[STIX]{x1D70E}})$
un sous-groupe. Supposons que
 $\unicode[STIX]{x0428}^{1}(G)=1$
et que, pour tout
$\unicode[STIX]{x0428}^{1}(G)=1$
et que, pour tout
 $\unicode[STIX]{x1D70E}\in H^{1}(k,G)$
, on a
$\unicode[STIX]{x1D70E}\in H^{1}(k,G)$
, on a
 $(p_{\unicode[STIX]{x1D70E}}^{\ast })^{-1}(B_{\unicode[STIX]{x1D70E}})\subset A$
, où
$(p_{\unicode[STIX]{x1D70E}}^{\ast })^{-1}(B_{\unicode[STIX]{x1D70E}})\subset A$
, où
 $\text{Br}(X)\xrightarrow[{}]{p_{\unicode[STIX]{x1D70E}}^{\ast }}\text{Br}(Y_{\unicode[STIX]{x1D70E}})$
. Alors on a :
$\text{Br}(X)\xrightarrow[{}]{p_{\unicode[STIX]{x1D70E}}^{\ast }}\text{Br}(Y_{\unicode[STIX]{x1D70E}})$
. Alors on a :
 $$\begin{eqnarray}X(\mathbf{A}_{k})^{A}=\mathop{\bigcup }_{\unicode[STIX]{x1D70E}\in H^{1}(k,G)}p_{\unicode[STIX]{x1D70E}}(Y_{\unicode[STIX]{x1D70E}}(\mathbf{A}_{k})^{B_{\unicode[STIX]{x1D70E}}+p_{\unicode[STIX]{x1D70E}}^{\ast }A}).\end{eqnarray}$$
$$\begin{eqnarray}X(\mathbf{A}_{k})^{A}=\mathop{\bigcup }_{\unicode[STIX]{x1D70E}\in H^{1}(k,G)}p_{\unicode[STIX]{x1D70E}}(Y_{\unicode[STIX]{x1D70E}}(\mathbf{A}_{k})^{B_{\unicode[STIX]{x1D70E}}+p_{\unicode[STIX]{x1D70E}}^{\ast }A}).\end{eqnarray}$$
Démonstration.
Le résultat découle de [Reference Cao, Demarche and XuCDX16, Thm. 1.1] et du lemme 5.1. ◻
Corollaire 5.3. Soit
![]() $T$
un tore quasi-trivial. Soient
$T$
un tore quasi-trivial. Soient
![]() $X$
une variété lisse, géométriquement intègre et
$X$
une variété lisse, géométriquement intègre et
 $Y\xrightarrow[{}]{p}X$
un
$Y\xrightarrow[{}]{p}X$
un
![]() $T$
-torseur. Soient
$T$
-torseur. Soient
![]() $U\subset X$
un ouvert et
$U\subset X$
un ouvert et
 $V=p^{-1}(U)$
. Alors pour tous sous-groupes
$V=p^{-1}(U)$
. Alors pour tous sous-groupes
 $A\subset \text{Br}(U)$
,
$A\subset \text{Br}(U)$
,
 $B\subset \text{Br}_{T}(V)$
, si
$B\subset \text{Br}_{T}(V)$
, si
 $(p^{\ast })^{-1}(B)\subset A$
, où
$(p^{\ast })^{-1}(B)\subset A$
, où
 $\text{Br}(U)\xrightarrow[{}]{p^{\ast }}\text{Br}(V)$
, on a
$\text{Br}(U)\xrightarrow[{}]{p^{\ast }}\text{Br}(V)$
, on a
 $$\begin{eqnarray}X(\mathbf{A}_{k})^{\text{Br}(X)\cap A}=p(Y(\mathbf{A}_{k})^{\text{Br}(Y)\cap (B+p^{\ast }A)}).\end{eqnarray}$$
$$\begin{eqnarray}X(\mathbf{A}_{k})^{\text{Br}(X)\cap A}=p(Y(\mathbf{A}_{k})^{\text{Br}(Y)\cap (B+p^{\ast }A)}).\end{eqnarray}$$
5.2 Applications des résolutions coflasques
Par [Reference Colliot-Thélène and SansucCS87a], un
![]() $\unicode[STIX]{x1D6E4}_{k}$
-module
$\unicode[STIX]{x1D6E4}_{k}$
-module
![]() $M$
de type fini est appelé coflasque si
$M$
de type fini est appelé coflasque si
![]() $M$
est sans torsion et, pour tout sous-groupe fermé
$M$
est sans torsion et, pour tout sous-groupe fermé
![]() $\unicode[STIX]{x1D6E4}\subset \unicode[STIX]{x1D6E4}_{k}$
, on a
$\unicode[STIX]{x1D6E4}\subset \unicode[STIX]{x1D6E4}_{k}$
, on a
 $H^{1}(\unicode[STIX]{x1D6E4},M)=0$
. Un
$H^{1}(\unicode[STIX]{x1D6E4},M)=0$
. Un
![]() $k$
-tore
$k$
-tore
![]() $T$
est appelé coflasque si
$T$
est appelé coflasque si
![]() $T^{\ast }$
est coflasque. Alors
$T^{\ast }$
est coflasque. Alors
 $H^{1}(k,T^{\ast })=0$
et, pour tout
$H^{1}(k,T^{\ast })=0$
et, pour tout
![]() $v\in \unicode[STIX]{x1D6FA}_{k}$
, on a
$v\in \unicode[STIX]{x1D6FA}_{k}$
, on a
 $H^{1}(k_{v},T^{\ast })=0$
. On renvoie à [Reference Colliot-Thélène and SansucCS87a, Prop. 1.3] pour les résolutions par tores coflasque et tores quasi-triviaux.
$H^{1}(k_{v},T^{\ast })=0$
. On renvoie à [Reference Colliot-Thélène and SansucCS87a, Prop. 1.3] pour les résolutions par tores coflasque et tores quasi-triviaux.
Lemme 5.4. Soit
![]() $T$
un tore. Alors
$T$
un tore. Alors
 $H^{3}(k,T^{\ast })\cong \prod _{v\in \infty _{k}}H^{3}(k_{v},T^{\ast })\cong \prod _{v\in \infty _{k}}H^{1}(k_{v},T^{\ast })$
.
$H^{3}(k,T^{\ast })\cong \prod _{v\in \infty _{k}}H^{3}(k_{v},T^{\ast })\cong \prod _{v\in \infty _{k}}H^{1}(k_{v},T^{\ast })$
.
Démonstration.
Pour tout
![]() $v\in \infty _{k}$
, puisque
$v\in \infty _{k}$
, puisque
 $\unicode[STIX]{x1D6E4}_{k_{v}}\cong \mathbb{Z}/2$
, on a
$\unicode[STIX]{x1D6E4}_{k_{v}}\cong \mathbb{Z}/2$
, on a
 $H^{3}(k_{v},T^{\ast })=H^{1}(k_{v},T^{\ast })$
. Par la ligne 3 de la démonstration de [Reference Harari and SzamuelyHS05, Prop. 5.9], on a
$H^{3}(k_{v},T^{\ast })=H^{1}(k_{v},T^{\ast })$
. Par la ligne 3 de la démonstration de [Reference Harari and SzamuelyHS05, Prop. 5.9], on a
 $H^{3}(k,T^{\ast })=\prod _{v\in \infty _{k}}H^{3}(k_{v},T^{\ast })$
. Le résultat en découle.◻
$H^{3}(k,T^{\ast })=\prod _{v\in \infty _{k}}H^{3}(k_{v},T^{\ast })$
. Le résultat en découle.◻
Lemme 5.5. Soit
 $$\begin{eqnarray}1\rightarrow G\xrightarrow[{}]{\unicode[STIX]{x1D713}}H\xrightarrow[{}]{\unicode[STIX]{x1D719}}T\rightarrow 1\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow G\xrightarrow[{}]{\unicode[STIX]{x1D713}}H\xrightarrow[{}]{\unicode[STIX]{x1D719}}T\rightarrow 1\end{eqnarray}$$
une suite exacte de groupes linéaires connexes avec
![]() $T$
un tore.
$T$
un tore.
(1) Si
 $H^{3}(k,T^{\ast })=0$
, alors l’homomorphisme
$H^{3}(k,T^{\ast })=0$
, alors l’homomorphisme
 $\text{Br}_{a}(H)\xrightarrow[{}]{\unicode[STIX]{x1D713}^{\ast }}\text{Br}_{a}(G)$
est surjectif.
$\text{Br}_{a}(H)\xrightarrow[{}]{\unicode[STIX]{x1D713}^{\ast }}\text{Br}_{a}(G)$
est surjectif.(2) Si
 $G$
est réductif, alors l’homomorphisme
$G$
est réductif, alors l’homomorphisme
 $\unicode[STIX]{x2202}:T(k)\rightarrow H^{1}(k,G)$
induit par cette suite exacte vérifie
$\unicode[STIX]{x2202}:T(k)\rightarrow H^{1}(k,G)$
induit par cette suite exacte vérifie
 $\text{Im}(\unicode[STIX]{x2202})\subset \text{Im}(H^{1}(k,Z(G))\rightarrow H^{1}(k,G))$
, où
$\text{Im}(\unicode[STIX]{x2202})\subset \text{Im}(H^{1}(k,Z(G))\rightarrow H^{1}(k,G))$
, où
 $Z(G)$
est le centre de
$Z(G)$
est le centre de
 $G$
.
$G$
.
Démonstration.
Par la suite exacte de Sansuc [Reference SansucSan81, Cor. 6.11], on a une suite exacte de
![]() $\unicode[STIX]{x1D6E4}_{k}$
-modules
$\unicode[STIX]{x1D6E4}_{k}$
-modules
 $$\begin{eqnarray}0\rightarrow T^{\ast }\rightarrow H^{\ast }\rightarrow G^{\ast }\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow T^{\ast }\rightarrow H^{\ast }\rightarrow G^{\ast }\rightarrow 0\end{eqnarray}$$
et un isomorphisme de
![]() $\unicode[STIX]{x1D6E4}_{k}$
-modules
$\unicode[STIX]{x1D6E4}_{k}$
-modules
 $\text{Pic}(H_{\bar{k}})\stackrel{{\sim}}{\rightarrow }\text{Pic}(G_{\bar{k}})$
. Par [Reference Colliot-Thélène and XuCX09, Lem. 2.1] (modulo
$\text{Pic}(H_{\bar{k}})\stackrel{{\sim}}{\rightarrow }\text{Pic}(G_{\bar{k}})$
. Par [Reference Colliot-Thélène and XuCX09, Lem. 2.1] (modulo
 $H^{2}(k,\bar{k}^{\times })\cong \text{Br}(k)$
), on a le diagramme suivant commutatif de suites exactes.
$H^{2}(k,\bar{k}^{\times })\cong \text{Br}(k)$
), on a le diagramme suivant commutatif de suites exactes.

Si
 $H^{3}(k,T^{\ast })=0$
, alors
$H^{3}(k,T^{\ast })=0$
, alors
![]() $\unicode[STIX]{x1D713}_{1}$
est surjectif et
$\unicode[STIX]{x1D713}_{1}$
est surjectif et
![]() $\unicode[STIX]{x1D713}_{2}$
est injectif. Ceci donne (1).
$\unicode[STIX]{x1D713}_{2}$
est injectif. Ceci donne (1).
Pour (2), puisque
![]() $G$
est réductif,
$G$
est réductif,
![]() $H$
est réductif et l’homomorphisme
$H$
est réductif et l’homomorphisme
 $Z(H)\rightarrow H^{\text{tor}}$
est surjectif. Donc la composition
$Z(H)\rightarrow H^{\text{tor}}$
est surjectif. Donc la composition
 $Z(H)\rightarrow H\rightarrow T$
est surjective. Soit
$Z(H)\rightarrow H\rightarrow T$
est surjective. Soit
 $S:=Z(H)\cap G\subset Z(G)$
. Ceci induit le diagramme suivant commutatif de suites exactes.
$S:=Z(H)\cap G\subset Z(G)$
. Ceci induit le diagramme suivant commutatif de suites exactes.

Ainsi
 $\text{Im}(\unicode[STIX]{x2202})\subset \text{Im}(H^{1}(k,S)\rightarrow H^{1}(k,G))$
et on a (2).◻
$\text{Im}(\unicode[STIX]{x2202})\subset \text{Im}(H^{1}(k,S)\rightarrow H^{1}(k,G))$
et on a (2).◻
Proposition 5.6. Soit
![]() $G$
un groupe réductif connexe. Alors il existe un groupe réductif connexe
$G$
un groupe réductif connexe. Alors il existe un groupe réductif connexe
![]() $H$
, un tore
$H$
, un tore
![]() $T$
et une suite exacte :
$T$
et une suite exacte :
 $$\begin{eqnarray}1\rightarrow G\xrightarrow[{}]{\unicode[STIX]{x1D713}}H\xrightarrow[{}]{\unicode[STIX]{x1D719}}T\rightarrow 1\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow G\xrightarrow[{}]{\unicode[STIX]{x1D713}}H\xrightarrow[{}]{\unicode[STIX]{x1D719}}T\rightarrow 1\end{eqnarray}$$
tels que
 $\unicode[STIX]{x0428}^{1}(H)=0$
,
$\unicode[STIX]{x0428}^{1}(H)=0$
,
 $H^{3}(k,T^{\ast })=0$
et
$H^{3}(k,T^{\ast })=0$
et
 $\text{Br}_{a}(H)\xrightarrow[{}]{\unicode[STIX]{x1D713}^{\ast }}\text{Br}_{a}(G)$
soit surjectif.
$\text{Br}_{a}(H)\xrightarrow[{}]{\unicode[STIX]{x1D713}^{\ast }}\text{Br}_{a}(G)$
soit surjectif.
De plus, si
![]() $G$
est un tore, on peut imposer que
$G$
est un tore, on peut imposer que
![]() $H$
soit un tore quasi-trivial.
$H$
soit un tore quasi-trivial.
Démonstration.
Puisque
![]() $G$
est réductif, il existe une suite exacte
$G$
est réductif, il existe une suite exacte
 $0\rightarrow S\rightarrow G\rightarrow G^{\text{ad}}\rightarrow 0$
telle que
$0\rightarrow S\rightarrow G\rightarrow G^{\text{ad}}\rightarrow 0$
telle que
![]() $S$
soit le centre de
$S$
soit le centre de
![]() $G$
et
$G$
et
![]() $G^{\text{ad}}$
soit le groupe adjoint de
$G^{\text{ad}}$
soit le groupe adjoint de
![]() $G$
. Alors
$G$
. Alors
![]() $S$
est un groupe de type multiplicatif. Par [Reference Colliot-Thélène and SansucCS87a, Prop. 1.3], il existe un tore quasi-trivial
$S$
est un groupe de type multiplicatif. Par [Reference Colliot-Thélène and SansucCS87a, Prop. 1.3], il existe un tore quasi-trivial
![]() $T_{0}$
et un homomorphisme injectif
$T_{0}$
et un homomorphisme injectif
 $S\xrightarrow[{}]{\unicode[STIX]{x1D712}}T_{0}$
tels que
$S\xrightarrow[{}]{\unicode[STIX]{x1D712}}T_{0}$
tels que
 $T:=T_{0}/S$
soit un tore coflasque. Alors, pour tout
$T:=T_{0}/S$
soit un tore coflasque. Alors, pour tout
![]() $v\in \infty _{k}$
, on a
$v\in \infty _{k}$
, on a
 $H^{1}(k_{v},T^{\ast })=0$
. Par le lemme 5.4, on a
$H^{1}(k_{v},T^{\ast })=0$
. Par le lemme 5.4, on a
 $H^{3}(k,T^{\ast })=0$
.
$H^{3}(k,T^{\ast })=0$
.
Soit
 $H:=G\times ^{S}T_{0}$
. Alors
$H:=G\times ^{S}T_{0}$
. Alors
![]() $H$
est un groupe linéaire et on a deux suites exactes
$H$
est un groupe linéaire et on a deux suites exactes
 $$\begin{eqnarray}1\rightarrow G\xrightarrow[{}]{\unicode[STIX]{x1D713}}H\xrightarrow[{}]{\unicode[STIX]{x1D719}}T\rightarrow 1~~~\text{et}~~~1\rightarrow T_{0}\rightarrow H\rightarrow G^{\text{ad}}\rightarrow 1.\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow G\xrightarrow[{}]{\unicode[STIX]{x1D713}}H\xrightarrow[{}]{\unicode[STIX]{x1D719}}T\rightarrow 1~~~\text{et}~~~1\rightarrow T_{0}\rightarrow H\rightarrow G^{\text{ad}}\rightarrow 1.\end{eqnarray}$$
Par le lemme 5.5(1), le morphisme
 $\text{Br}_{a}(H)\xrightarrow[{}]{\unicode[STIX]{x1D713}^{\ast }}\text{Br}_{a}(G)$
est surjectif. Par [Reference SansucSan81, Cor. 5.4], on a
$\text{Br}_{a}(H)\xrightarrow[{}]{\unicode[STIX]{x1D713}^{\ast }}\text{Br}_{a}(G)$
est surjectif. Par [Reference SansucSan81, Cor. 5.4], on a
 $\unicode[STIX]{x0428}^{1}(G^{\text{ad}})=0$
. Puisque
$\unicode[STIX]{x0428}^{1}(G^{\text{ad}})=0$
. Puisque
![]() $T_{0}$
est quasi-trivial, on a
$T_{0}$
est quasi-trivial, on a
 $\unicode[STIX]{x0428}^{1}(H)=0$
.◻
$\unicode[STIX]{x0428}^{1}(H)=0$
.◻
Proposition 5.7. Soit
![]() $X$
une variété lisse géométriquement intègre. Supposons que
$X$
une variété lisse géométriquement intègre. Supposons que
 $X(k)\neq \emptyset$
et que
$X(k)\neq \emptyset$
et que
 $\text{Pic}(X_{\bar{k}})$
est de type fini. Alors il existe un tore quasi-trivial
$\text{Pic}(X_{\bar{k}})$
est de type fini. Alors il existe un tore quasi-trivial
![]() $T$
et un
$T$
et un
![]() $T$
-torseur
$T$
-torseur
 $Y\rightarrow X$
tels que
$Y\rightarrow X$
tels que
 $\text{Pic}(Y_{\bar{k}})=0$
et
$\text{Pic}(Y_{\bar{k}})=0$
et
 $H^{3}(k,\bar{k}[Y]^{\times }/\bar{k}^{\times })=0$
.
$H^{3}(k,\bar{k}[Y]^{\times }/\bar{k}^{\times })=0$
.
Démonstration.
Il existe un ouvert
![]() $U\subset X$
tel que
$U\subset X$
tel que
 $\text{Pic}(U_{\bar{k}})=0$
. Soient
$\text{Pic}(U_{\bar{k}})=0$
. Soient
![]() $T_{0}$
un tore tel que
$T_{0}$
un tore tel que
 $T_{0}^{\ast }:=\text{Div}_{X_{\bar{k}}\setminus U_{\bar{k}}}(X_{\bar{k}})$
et
$T_{0}^{\ast }:=\text{Div}_{X_{\bar{k}}\setminus U_{\bar{k}}}(X_{\bar{k}})$
et
 $Y_{0}\rightarrow X$
le
$Y_{0}\rightarrow X$
le
![]() $T_{0}$
-torseur induit par l’homomorphisme
$T_{0}$
-torseur induit par l’homomorphisme
![]() $\unicode[STIX]{x1D6F9}$
de la suite exacte (2.2). Par la suite exacte de Sansuc [Reference SansucSan81, Prop. 6.10],
$\unicode[STIX]{x1D6F9}$
de la suite exacte (2.2). Par la suite exacte de Sansuc [Reference SansucSan81, Prop. 6.10],
 $\text{Pic}(Y_{0,\bar{k}})=0$
. Soit
$\text{Pic}(Y_{0,\bar{k}})=0$
. Soit
![]() $T_{1}$
le tore tel que
$T_{1}$
le tore tel que
 $T_{1}^{\ast }\cong \bar{k}[Y_{0}]^{\times }/\bar{k}^{\times }$
. Puisque
$T_{1}^{\ast }\cong \bar{k}[Y_{0}]^{\times }/\bar{k}^{\times }$
. Puisque
 $X(k)\neq \emptyset$
et que
$X(k)\neq \emptyset$
et que
![]() $T_{0}$
est quasi-trivial, on a
$T_{0}$
est quasi-trivial, on a
 $Y_{0}(k)\neq \emptyset$
. À un point de
$Y_{0}(k)\neq \emptyset$
. À un point de
![]() $Y_{0}(k)$
on associe un morphisme
$Y_{0}(k)$
on associe un morphisme
 $Y_{0}\xrightarrow[{}]{\unicode[STIX]{x1D70B}}T_{1}$
(envoyant ce point sur
$Y_{0}\xrightarrow[{}]{\unicode[STIX]{x1D70B}}T_{1}$
(envoyant ce point sur
![]() $e_{T_{1}}$
) tel que
$e_{T_{1}}$
) tel que
 $T_{1}^{\ast }\xrightarrow[{}]{\unicode[STIX]{x1D70B}^{\ast }}\bar{k}[Y_{0}]^{\times }/\bar{k}^{\times }$
soit un isomorphisme.
$T_{1}^{\ast }\xrightarrow[{}]{\unicode[STIX]{x1D70B}^{\ast }}\bar{k}[Y_{0}]^{\times }/\bar{k}^{\times }$
soit un isomorphisme.
D’après [Reference Colliot-Thélène and SansucCS87a, Prop. 1.3], il existe une suite exacte
 $0\rightarrow T_{2}\rightarrow T_{3}\rightarrow T_{1}\rightarrow 0$
telle que
$0\rightarrow T_{2}\rightarrow T_{3}\rightarrow T_{1}\rightarrow 0$
telle que
![]() $T_{2}$
soit quasi-trivial et que
$T_{2}$
soit quasi-trivial et que
![]() $T_{3}$
soit coflasque. Soit
$T_{3}$
soit coflasque. Soit
 $Y:=Y_{0}\times _{T_{1}}T_{3}$
un
$Y:=Y_{0}\times _{T_{1}}T_{3}$
un
![]() $T_{2}$
torseur sur
$T_{2}$
torseur sur
![]() $Y_{0}$
. Par la suite exacte de Sansuc [Reference SansucSan81, Prop. 6.10],
$Y_{0}$
. Par la suite exacte de Sansuc [Reference SansucSan81, Prop. 6.10],
 $\text{Pic}(Y_{\bar{k}})=0$
,
$\text{Pic}(Y_{\bar{k}})=0$
,
 $\bar{k}[Y]^{\times }/\bar{k}^{\times }=T_{3}^{\ast }$
et, d’après le lemme 5.4, on a
$\bar{k}[Y]^{\times }/\bar{k}^{\times }=T_{3}^{\ast }$
et, d’après le lemme 5.4, on a
 $H^{3}(k,\bar{k}[Y]^{\times }/\bar{k}^{\times })=0$
.
$H^{3}(k,\bar{k}[Y]^{\times }/\bar{k}^{\times })=0$
.
Soit
 $T:=T_{0}\times T_{2}$
. Puisque
$T:=T_{0}\times T_{2}$
. Puisque
![]() $T_{0},T_{2}$
sont quasi-triviaux, on a
$T_{0},T_{2}$
sont quasi-triviaux, on a
 $H^{1}(T_{0},T_{2})=0$
et, d’après [Reference Colliot-ThélèneCol08, Cor. 5.7], toute extension centrale de
$H^{1}(T_{0},T_{2})=0$
et, d’après [Reference Colliot-ThélèneCol08, Cor. 5.7], toute extension centrale de
![]() $T_{0}$
par
$T_{0}$
par
![]() $T_{2}$
est isomorphe à
$T_{2}$
est isomorphe à
![]() $T_{0}\times T_{2}$
. D’après le théorème 2.7, il existe une action de
$T_{0}\times T_{2}$
. D’après le théorème 2.7, il existe une action de
![]() $T$
sur
$T$
sur
![]() $Y$
compatible avec les actions
$Y$
compatible avec les actions
![]() $T_{2}$
sur
$T_{2}$
sur
![]() $Y$
et
$Y$
et
![]() $T_{0}$
sur
$T_{0}$
sur
![]() $Y_{0}$
. Alors
$Y_{0}$
. Alors
![]() $Y$
est un
$Y$
est un
![]() $T$
-torseur sur
$T$
-torseur sur
![]() $X$
.◻
$X$
.◻
5.3 Le cas général
Soient
![]() $G$
un groupe linéaire connexe,
$G$
un groupe linéaire connexe,
![]() $X$
une variété lisse géométriquement intègre et
$X$
une variété lisse géométriquement intègre et
 $Y\xrightarrow[{}]{p}X$
un
$Y\xrightarrow[{}]{p}X$
un
![]() $G$
-torseur (à gauche). Pour tout
$G$
-torseur (à gauche). Pour tout
 $\unicode[STIX]{x1D70E}\in Z^{1}(k,G)$
, soient
$\unicode[STIX]{x1D70E}\in Z^{1}(k,G)$
, soient
![]() $P_{\unicode[STIX]{x1D70E}}$
le
$P_{\unicode[STIX]{x1D70E}}$
le
![]() $G$
-torseur à droite correspondant et
$G$
-torseur à droite correspondant et
![]() $G_{\unicode[STIX]{x1D70E}}$
le tordu par le 1-cocycle
$G_{\unicode[STIX]{x1D70E}}$
le tordu par le 1-cocycle
![]() $\unicode[STIX]{x1D70E}$
. Alors
$\unicode[STIX]{x1D70E}$
. Alors
![]() $P_{\unicode[STIX]{x1D70E}}$
est un
$P_{\unicode[STIX]{x1D70E}}$
est un
![]() $G_{\unicode[STIX]{x1D70E}}$
-torseur à gauche. Soit
$G_{\unicode[STIX]{x1D70E}}$
-torseur à gauche. Soit
 $Y_{\unicode[STIX]{x1D70E}}\xrightarrow[{}]{p_{\unicode[STIX]{x1D70E}}}X$
le tordu de
$Y_{\unicode[STIX]{x1D70E}}\xrightarrow[{}]{p_{\unicode[STIX]{x1D70E}}}X$
le tordu de
![]() $Y$
, i.e.
$Y$
, i.e.
 $Y_{\unicode[STIX]{x1D70E}}=P_{\unicode[STIX]{x1D70E}}\times ^{G}Y$
. Alors
$Y_{\unicode[STIX]{x1D70E}}=P_{\unicode[STIX]{x1D70E}}\times ^{G}Y$
. Alors
![]() $Y_{\unicode[STIX]{x1D70E}}$
est un
$Y_{\unicode[STIX]{x1D70E}}$
est un
![]() $G_{\unicode[STIX]{x1D70E}}$
-torseur à gauche sur
$G_{\unicode[STIX]{x1D70E}}$
-torseur à gauche sur
![]() $X$
. Soit
$X$
. Soit
 $\text{Br}_{G_{\unicode[STIX]{x1D70E}}}(Y_{\unicode[STIX]{x1D70E}})$
le sous-groupe de Brauer
$\text{Br}_{G_{\unicode[STIX]{x1D70E}}}(Y_{\unicode[STIX]{x1D70E}})$
le sous-groupe de Brauer
![]() $G_{\unicode[STIX]{x1D70E}}$
-invariant de
$G_{\unicode[STIX]{x1D70E}}$
-invariant de
![]() $Y_{\unicode[STIX]{x1D70E}}$
(Définition 3.1).
$Y_{\unicode[STIX]{x1D70E}}$
(Définition 3.1).
Notons
 $\unicode[STIX]{x1D703}_{Y}^{\unicode[STIX]{x1D70E}}:P_{\unicode[STIX]{x1D70E}}\times Y\rightarrow Y_{\unicode[STIX]{x1D70E}}$
. Le lemme 3.12 donne un isomorphisme canonique :
$\unicode[STIX]{x1D703}_{Y}^{\unicode[STIX]{x1D70E}}:P_{\unicode[STIX]{x1D70E}}\times Y\rightarrow Y_{\unicode[STIX]{x1D70E}}$
. Le lemme 3.12 donne un isomorphisme canonique :
 $$\begin{eqnarray}(p_{1}^{\ast },p_{2}^{\ast }):~\text{Br}_{a}(P_{\unicode[STIX]{x1D70E}})\oplus \text{Br}_{G}(Y)/\text{Im}\,\text{Br}(k)\stackrel{{\sim}}{\rightarrow }\text{Br}_{G_{\unicode[STIX]{x1D70E}}\times G}(P_{\unicode[STIX]{x1D70E}}\times Y)/\text{Im}\,\text{Br}(k).\end{eqnarray}$$
$$\begin{eqnarray}(p_{1}^{\ast },p_{2}^{\ast }):~\text{Br}_{a}(P_{\unicode[STIX]{x1D70E}})\oplus \text{Br}_{G}(Y)/\text{Im}\,\text{Br}(k)\stackrel{{\sim}}{\rightarrow }\text{Br}_{G_{\unicode[STIX]{x1D70E}}\times G}(P_{\unicode[STIX]{x1D70E}}\times Y)/\text{Im}\,\text{Br}(k).\end{eqnarray}$$
Ceci induit un morphisme canonique
 $$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{Y}^{\unicode[STIX]{x1D70E}}:~\text{Br}_{G_{\unicode[STIX]{x1D70E}}}(Y_{\unicode[STIX]{x1D70E}})/\text{Im}\,\text{Br}(k)\xrightarrow[{}]{(\unicode[STIX]{x1D703}_{Y}^{\unicode[STIX]{x1D70E}})^{\ast }}\text{Br}_{G_{\unicode[STIX]{x1D70E}}\times G}(P_{\unicode[STIX]{x1D70E}}\times Y)/\text{Im}\,\text{Br}(k)\rightarrow \text{Br}_{G}(Y)/\text{Im}\,\text{Br}(k).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{Y}^{\unicode[STIX]{x1D70E}}:~\text{Br}_{G_{\unicode[STIX]{x1D70E}}}(Y_{\unicode[STIX]{x1D70E}})/\text{Im}\,\text{Br}(k)\xrightarrow[{}]{(\unicode[STIX]{x1D703}_{Y}^{\unicode[STIX]{x1D70E}})^{\ast }}\text{Br}_{G_{\unicode[STIX]{x1D70E}}\times G}(P_{\unicode[STIX]{x1D70E}}\times Y)/\text{Im}\,\text{Br}(k)\rightarrow \text{Br}_{G}(Y)/\text{Im}\,\text{Br}(k).\end{eqnarray}$$
Soit
![]() $Q_{\unicode[STIX]{x1D70E}^{-1}}$
le torseur inverse de
$Q_{\unicode[STIX]{x1D70E}^{-1}}$
le torseur inverse de
![]() $P_{\unicode[STIX]{x1D70E}}$
(cf. [Reference SkorobogatovSko01, p. 20, Exemple 2]). Alors
$P_{\unicode[STIX]{x1D70E}}$
(cf. [Reference SkorobogatovSko01, p. 20, Exemple 2]). Alors
![]() $Q_{\unicode[STIX]{x1D70E}^{-1}}$
est un
$Q_{\unicode[STIX]{x1D70E}^{-1}}$
est un
![]() $G_{\unicode[STIX]{x1D70E}}$
-torseur à droite et aussi un
$G_{\unicode[STIX]{x1D70E}}$
-torseur à droite et aussi un
![]() $G$
-torseur à gauche. Notons
$G$
-torseur à gauche. Notons
 $\unicode[STIX]{x1D70E}^{-1}:=[Q_{\unicode[STIX]{x1D70E}^{-1}}]\in H^{1}(k,G_{\unicode[STIX]{x1D70E}})$
. Pour tout
$\unicode[STIX]{x1D70E}^{-1}:=[Q_{\unicode[STIX]{x1D70E}^{-1}}]\in H^{1}(k,G_{\unicode[STIX]{x1D70E}})$
. Pour tout
![]() $G_{\unicode[STIX]{x1D70E}}$
-torseur à gauche
$G_{\unicode[STIX]{x1D70E}}$
-torseur à gauche
 $Y^{\prime }\rightarrow X$
, soit
$Y^{\prime }\rightarrow X$
, soit
 $Y_{\unicode[STIX]{x1D70E}^{-1}}^{\prime }:=Y^{\prime }\times ^{G_{\unicode[STIX]{x1D70E}}}Q_{\unicode[STIX]{x1D70E}^{-1}}$
(un
$Y_{\unicode[STIX]{x1D70E}^{-1}}^{\prime }:=Y^{\prime }\times ^{G_{\unicode[STIX]{x1D70E}}}Q_{\unicode[STIX]{x1D70E}^{-1}}$
(un
![]() $G$
-torseur à gauche sur
$G$
-torseur à gauche sur
![]() $X$
).
$X$
).
Lemme 5.8. On a
 $Y\cong (Y_{\unicode[STIX]{x1D70E}})_{\unicode[STIX]{x1D70E}^{-1}}$
et l’homomorphisme
$Y\cong (Y_{\unicode[STIX]{x1D70E}})_{\unicode[STIX]{x1D70E}^{-1}}$
et l’homomorphisme
![]() $\unicode[STIX]{x1D6E9}_{Y}^{\unicode[STIX]{x1D70E}}$
est un isomorphisme d’inverse
$\unicode[STIX]{x1D6E9}_{Y}^{\unicode[STIX]{x1D70E}}$
est un isomorphisme d’inverse
![]() $\unicode[STIX]{x1D6E9}_{Y_{\unicode[STIX]{x1D70E}}}^{(\unicode[STIX]{x1D70E}^{-1})}$
.
$\unicode[STIX]{x1D6E9}_{Y_{\unicode[STIX]{x1D70E}}}^{(\unicode[STIX]{x1D70E}^{-1})}$
.
Démonstration.
On a
 $(Y_{\unicode[STIX]{x1D70E}})_{\unicode[STIX]{x1D70E}^{-1}}=P_{\unicode[STIX]{x1D70E}}\times ^{G_{\unicode[STIX]{x1D70E}}}P_{\unicode[STIX]{x1D70E}}\times ^{G}Y\cong G\times ^{G}Y\cong Y$
. On a un isomorphisme canonique
$(Y_{\unicode[STIX]{x1D70E}})_{\unicode[STIX]{x1D70E}^{-1}}=P_{\unicode[STIX]{x1D70E}}\times ^{G_{\unicode[STIX]{x1D70E}}}P_{\unicode[STIX]{x1D70E}}\times ^{G}Y\cong G\times ^{G}Y\cong Y$
. On a un isomorphisme canonique
 $P_{\unicode[STIX]{x1D70E}}\times Y\xrightarrow[{}]{p_{1}\times \unicode[STIX]{x1D703}_{Y}^{\unicode[STIX]{x1D70E}}}P_{\unicode[STIX]{x1D70E}}\times Y_{\unicode[STIX]{x1D70E}}$
d’inverse
$P_{\unicode[STIX]{x1D70E}}\times Y\xrightarrow[{}]{p_{1}\times \unicode[STIX]{x1D703}_{Y}^{\unicode[STIX]{x1D70E}}}P_{\unicode[STIX]{x1D70E}}\times Y_{\unicode[STIX]{x1D70E}}$
d’inverse
 $p_{1}\times \unicode[STIX]{x1D703}_{Y_{\unicode[STIX]{x1D70E}}}^{(\unicode[STIX]{x1D70E}^{-1})}$
. Par le lemme 3.12, on a :
$p_{1}\times \unicode[STIX]{x1D703}_{Y_{\unicode[STIX]{x1D70E}}}^{(\unicode[STIX]{x1D70E}^{-1})}$
. Par le lemme 3.12, on a :
 $$\begin{eqnarray}\text{Br}_{a}(P_{\unicode[STIX]{x1D70E}})\oplus \text{Br}_{G}(Y)/\text{Im}\,\text{Br}(k)\cong \text{Br}_{G_{\unicode[STIX]{x1D70E}}\times G}(P_{\unicode[STIX]{x1D70E}}\times Y)/\text{Im}\,\text{Br}(k)\end{eqnarray}$$
$$\begin{eqnarray}\text{Br}_{a}(P_{\unicode[STIX]{x1D70E}})\oplus \text{Br}_{G}(Y)/\text{Im}\,\text{Br}(k)\cong \text{Br}_{G_{\unicode[STIX]{x1D70E}}\times G}(P_{\unicode[STIX]{x1D70E}}\times Y)/\text{Im}\,\text{Br}(k)\end{eqnarray}$$
et
 $$\begin{eqnarray}\text{Br}_{a}(P_{\unicode[STIX]{x1D70E}})\oplus \text{Br}_{G_{\unicode[STIX]{x1D70E}}}(Y_{\unicode[STIX]{x1D70E}})/\text{Im}\,\text{Br}(k)\cong \text{Br}_{G_{\unicode[STIX]{x1D70E}}\times G}(P_{\unicode[STIX]{x1D70E}}\times Y_{\unicode[STIX]{x1D70E}})/\text{Im}\,\text{Br}(k).\end{eqnarray}$$
$$\begin{eqnarray}\text{Br}_{a}(P_{\unicode[STIX]{x1D70E}})\oplus \text{Br}_{G_{\unicode[STIX]{x1D70E}}}(Y_{\unicode[STIX]{x1D70E}})/\text{Im}\,\text{Br}(k)\cong \text{Br}_{G_{\unicode[STIX]{x1D70E}}\times G}(P_{\unicode[STIX]{x1D70E}}\times Y_{\unicode[STIX]{x1D70E}})/\text{Im}\,\text{Br}(k).\end{eqnarray}$$
Le résultat en découle. ◻
Pour un sous-groupe
 $B_{\unicode[STIX]{x1D70E}}\subset \text{Br}_{G_{\unicode[STIX]{x1D70E}}}(Y_{\unicode[STIX]{x1D70E}})$
contenant
$B_{\unicode[STIX]{x1D70E}}\subset \text{Br}_{G_{\unicode[STIX]{x1D70E}}}(Y_{\unicode[STIX]{x1D70E}})$
contenant
 $\text{Im}\,\text{Br}(k)$
, on note
$\text{Im}\,\text{Br}(k)$
, on note
 $\widetilde{\unicode[STIX]{x1D6E9}_{Y}^{\unicode[STIX]{x1D70E}}}(B_{\unicode[STIX]{x1D70E}})\subset \text{Br}_{G}(Y)$
l’image inverse de
$\widetilde{\unicode[STIX]{x1D6E9}_{Y}^{\unicode[STIX]{x1D70E}}}(B_{\unicode[STIX]{x1D70E}})\subset \text{Br}_{G}(Y)$
l’image inverse de
 $\unicode[STIX]{x1D6E9}_{Y}^{\unicode[STIX]{x1D70E}}(B_{\unicode[STIX]{x1D70E}})$
. Alors
$\unicode[STIX]{x1D6E9}_{Y}^{\unicode[STIX]{x1D70E}}(B_{\unicode[STIX]{x1D70E}})$
. Alors
 $\widetilde{\unicode[STIX]{x1D6E9}_{Y_{\unicode[STIX]{x1D70E}}}^{(\unicode[STIX]{x1D70E}^{-1})}}(\widetilde{\unicode[STIX]{x1D6E9}_{Y}^{\unicode[STIX]{x1D70E}}}(B_{\unicode[STIX]{x1D70E}}))=B_{\unicode[STIX]{x1D70E}}$
.
$\widetilde{\unicode[STIX]{x1D6E9}_{Y_{\unicode[STIX]{x1D70E}}}^{(\unicode[STIX]{x1D70E}^{-1})}}(\widetilde{\unicode[STIX]{x1D6E9}_{Y}^{\unicode[STIX]{x1D70E}}}(B_{\unicode[STIX]{x1D70E}}))=B_{\unicode[STIX]{x1D70E}}$
.
Théorème 5.9. Soient
![]() $G$
un groupe linéaire connexe,
$G$
un groupe linéaire connexe,
![]() $X$
une variété lisse géométriquement intègre et
$X$
une variété lisse géométriquement intègre et
 $Y\xrightarrow[{}]{p}X$
un
$Y\xrightarrow[{}]{p}X$
un
![]() $G$
-torseur. Soit
$G$
-torseur. Soit
 $A\subset \text{Br}(X)$
un sous-groupe et, pour chaque
$A\subset \text{Br}(X)$
un sous-groupe et, pour chaque
 $\unicode[STIX]{x1D70E}\in H^{1}(k,G)$
, soit
$\unicode[STIX]{x1D70E}\in H^{1}(k,G)$
, soit
 $B_{\unicode[STIX]{x1D70E}}\subset \text{Br}_{G_{\unicode[STIX]{x1D70E}}}(Y_{\unicode[STIX]{x1D70E}})$
un sous-groupe contenant
$B_{\unicode[STIX]{x1D70E}}\subset \text{Br}_{G_{\unicode[STIX]{x1D70E}}}(Y_{\unicode[STIX]{x1D70E}})$
un sous-groupe contenant
 $\text{Im}\,\text{Br}(k)$
. Supposons que, pour tout
$\text{Im}\,\text{Br}(k)$
. Supposons que, pour tout
 $\unicode[STIX]{x1D70E}\in H^{1}(k,G)$
, on a
$\unicode[STIX]{x1D70E}\in H^{1}(k,G)$
, on a
 $$\begin{eqnarray}(p_{\unicode[STIX]{x1D70E}}^{\ast })^{-1}\biggl(\mathop{\sum }_{\unicode[STIX]{x1D70E}^{\prime }\in \unicode[STIX]{x0428}^{1}(G_{\unicode[STIX]{x1D70E}})}\widetilde{\unicode[STIX]{x1D6E9}_{Y_{\unicode[STIX]{x1D70E}}}^{\unicode[STIX]{x1D70E}^{\prime }}}(B_{\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D70E}^{\prime }})\biggr)\subset A\end{eqnarray}$$
$$\begin{eqnarray}(p_{\unicode[STIX]{x1D70E}}^{\ast })^{-1}\biggl(\mathop{\sum }_{\unicode[STIX]{x1D70E}^{\prime }\in \unicode[STIX]{x0428}^{1}(G_{\unicode[STIX]{x1D70E}})}\widetilde{\unicode[STIX]{x1D6E9}_{Y_{\unicode[STIX]{x1D70E}}}^{\unicode[STIX]{x1D70E}^{\prime }}}(B_{\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D70E}^{\prime }})\biggr)\subset A\end{eqnarray}$$
où
 $\text{Br}(X)\xrightarrow[{}]{p_{\unicode[STIX]{x1D70E}}^{\ast }}\text{Br}(Y_{\unicode[STIX]{x1D70E}})$
et
$\text{Br}(X)\xrightarrow[{}]{p_{\unicode[STIX]{x1D70E}}^{\ast }}\text{Br}(Y_{\unicode[STIX]{x1D70E}})$
et
 $Y_{\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D70E}^{\prime }}:=(Y_{\unicode[STIX]{x1D70E}})_{\unicode[STIX]{x1D70E}^{\prime }}$
. Alors on a :
$Y_{\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D70E}^{\prime }}:=(Y_{\unicode[STIX]{x1D70E}})_{\unicode[STIX]{x1D70E}^{\prime }}$
. Alors on a :
 $$\begin{eqnarray}X(\mathbf{A}_{k})^{A}=\mathop{\bigcup }_{\unicode[STIX]{x1D70E}\in H^{1}(k,G)}p_{\unicode[STIX]{x1D70E}}(Y_{\unicode[STIX]{x1D70E}}(\mathbf{A}_{k})^{B_{\unicode[STIX]{x1D70E}}+p_{\unicode[STIX]{x1D70E}}^{\ast }A}).\end{eqnarray}$$
$$\begin{eqnarray}X(\mathbf{A}_{k})^{A}=\mathop{\bigcup }_{\unicode[STIX]{x1D70E}\in H^{1}(k,G)}p_{\unicode[STIX]{x1D70E}}(Y_{\unicode[STIX]{x1D70E}}(\mathbf{A}_{k})^{B_{\unicode[STIX]{x1D70E}}+p_{\unicode[STIX]{x1D70E}}^{\ast }A}).\end{eqnarray}$$
Démonstration.
La démonstraction ci-dessous suit celle de [Reference Cao, Demarche and XuCDX16, Thm. 4.1].
Par [Reference Cao, Demarche and XuCDX16, Thm. 1.1], il suffit de montrer que, pour tout
 $\unicode[STIX]{x1D70E}\in H^{1}(k,G)$
, on a :
$\unicode[STIX]{x1D70E}\in H^{1}(k,G)$
, on a :
 $$\begin{eqnarray}p_{\unicode[STIX]{x1D70E}}(Y_{\unicode[STIX]{x1D70E}}(\mathbf{A}_{k})^{p_{\unicode[STIX]{x1D70E}}^{\ast }A})\subset \mathop{\bigcup }_{\unicode[STIX]{x1D70E}^{\prime }\in \unicode[STIX]{x0428}^{1}(G_{\unicode[STIX]{x1D70E}})}p_{\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D70E}^{\prime }}(Y_{\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D70E}^{\prime }}(\mathbf{A}_{k})^{B_{\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D70E}^{\prime }}+p_{\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D70E}^{\prime }}^{\ast }A}).\end{eqnarray}$$
$$\begin{eqnarray}p_{\unicode[STIX]{x1D70E}}(Y_{\unicode[STIX]{x1D70E}}(\mathbf{A}_{k})^{p_{\unicode[STIX]{x1D70E}}^{\ast }A})\subset \mathop{\bigcup }_{\unicode[STIX]{x1D70E}^{\prime }\in \unicode[STIX]{x0428}^{1}(G_{\unicode[STIX]{x1D70E}})}p_{\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D70E}^{\prime }}(Y_{\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D70E}^{\prime }}(\mathbf{A}_{k})^{B_{\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D70E}^{\prime }}+p_{\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D70E}^{\prime }}^{\ast }A}).\end{eqnarray}$$
On peut supposer que
![]() $\unicode[STIX]{x1D70E}=0$
. Pour tout
$\unicode[STIX]{x1D70E}=0$
. Pour tout
![]() $v$
, puisque
$v$
, puisque
 $H^{1}(k_{v},G^{u})=0$
, le morphisme
$H^{1}(k_{v},G^{u})=0$
, le morphisme
 $Y(k_{v})\rightarrow (G^{\text{red}}\times ^{G}Y)(k_{v})$
est surjectif. Puisque
$Y(k_{v})\rightarrow (G^{\text{red}}\times ^{G}Y)(k_{v})$
est surjectif. Puisque
 $\unicode[STIX]{x0428}^{1}(G)\cong \unicode[STIX]{x0428}^{1}(G^{\text{red}})$
[Reference SansucSan81, Prop. 4.1] et que l’on a
$\unicode[STIX]{x0428}^{1}(G)\cong \unicode[STIX]{x0428}^{1}(G^{\text{red}})$
[Reference SansucSan81, Prop. 4.1] et que l’on a
 $\text{Br}(Y)\cong \text{Br}(G^{\text{red}}\times ^{G}Y)$
[Reference Cao, Demarche and XuCDX16, Lem. 2.1], on peut supposer que
$\text{Br}(Y)\cong \text{Br}(G^{\text{red}}\times ^{G}Y)$
[Reference Cao, Demarche and XuCDX16, Lem. 2.1], on peut supposer que
![]() $G$
est réductif.
$G$
est réductif.
Par la proposition 5.6, il existe un groupe linéaire connexe
![]() $H$
, un tore
$H$
, un tore
![]() $T$
et une suite exacte :
$T$
et une suite exacte :
 $$\begin{eqnarray}1\rightarrow G\xrightarrow[{}]{\unicode[STIX]{x1D713}}H\xrightarrow[{}]{\unicode[STIX]{x1D719}}T\rightarrow 1\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow G\xrightarrow[{}]{\unicode[STIX]{x1D713}}H\xrightarrow[{}]{\unicode[STIX]{x1D719}}T\rightarrow 1\end{eqnarray}$$
tels que
 $\unicode[STIX]{x0428}^{1}(H)=0$
,
$\unicode[STIX]{x0428}^{1}(H)=0$
,
 $H^{3}(k,T^{\ast })=0$
et
$H^{3}(k,T^{\ast })=0$
et
 $\text{Br}_{a}(H)\xrightarrow[{}]{\unicode[STIX]{x1D713}^{\ast }}\text{Br}_{a}(G)$
soit surjectif. Par [Reference SerreSer65, Prop. 36 du Chapitre 1], on a une suite exacte d’ensembles pointés :
$\text{Br}_{a}(H)\xrightarrow[{}]{\unicode[STIX]{x1D713}^{\ast }}\text{Br}_{a}(G)$
soit surjectif. Par [Reference SerreSer65, Prop. 36 du Chapitre 1], on a une suite exacte d’ensembles pointés :
 $$\begin{eqnarray}1\rightarrow G(k)\rightarrow H(k)\rightarrow T(k)\xrightarrow[{}]{\unicode[STIX]{x2202}}H^{1}(k,G)\rightarrow H^{1}(k,H),\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow G(k)\rightarrow H(k)\rightarrow T(k)\xrightarrow[{}]{\unicode[STIX]{x2202}}H^{1}(k,G)\rightarrow H^{1}(k,H),\end{eqnarray}$$
telle que, pour tout
![]() $t\in T$
, on ait
$t\in T$
, on ait
 $\unicode[STIX]{x2202}(t):=[\unicode[STIX]{x1D719}^{-1}(t)]$
. Alors
$\unicode[STIX]{x2202}(t):=[\unicode[STIX]{x1D719}^{-1}(t)]$
. Alors
 $\unicode[STIX]{x0428}^{1}(G)\subset \text{Im}(\unicode[STIX]{x2202})$
et, pour tout
$\unicode[STIX]{x0428}^{1}(G)\subset \text{Im}(\unicode[STIX]{x2202})$
et, pour tout
 $t\in T(k)$
, on a
$t\in T(k)$
, on a
 $G_{\unicode[STIX]{x2202}(t)}\cong G$
(Lemme 5.5(2)).
$G_{\unicode[STIX]{x2202}(t)}\cong G$
(Lemme 5.5(2)).
Soient
 $Y_{H}:=H\times ^{G}Y$
et
$Y_{H}:=H\times ^{G}Y$
et
 $Y\xrightarrow[{}]{i}Y_{H}$
le morphisme canonique. Alors
$Y\xrightarrow[{}]{i}Y_{H}$
le morphisme canonique. Alors
 $Y_{H}\xrightarrow[{}]{p_{H}}X$
est un
$Y_{H}\xrightarrow[{}]{p_{H}}X$
est un
![]() $H$
-torseur sur
$H$
-torseur sur
![]() $X$
et
$X$
et
 $T\times ^{H}Y_{H}\cong T\times X$
. Alors on a un morphisme canonique
$T\times ^{H}Y_{H}\cong T\times X$
. Alors on a un morphisme canonique
 $Y_{H}\xrightarrow[{}]{\unicode[STIX]{x1D707}}T$
tel que, pour tout
$Y_{H}\xrightarrow[{}]{\unicode[STIX]{x1D707}}T$
tel que, pour tout
 $t\in T(k)$
, on a
$t\in T(k)$
, on a
 $\unicode[STIX]{x1D707}^{-1}(t)\cong \unicode[STIX]{x1D719}^{-1}(t)\times ^{G}Y\cong Y_{\unicode[STIX]{x2202}(t)}$
. Notons
$\unicode[STIX]{x1D707}^{-1}(t)\cong \unicode[STIX]{x1D719}^{-1}(t)\times ^{G}Y\cong Y_{\unicode[STIX]{x2202}(t)}$
. Notons
 $\unicode[STIX]{x1D707}^{-1}(t)\xrightarrow[{}]{i_{t}}Y_{H}$
. Par la définition de
$\unicode[STIX]{x1D707}^{-1}(t)\xrightarrow[{}]{i_{t}}Y_{H}$
. Par la définition de
![]() $\unicode[STIX]{x1D6E9}_{Y}^{\unicode[STIX]{x2202}(t)}$
, on a :
$\unicode[STIX]{x1D6E9}_{Y}^{\unicode[STIX]{x2202}(t)}$
, on a :
 $\unicode[STIX]{x1D6E9}_{Y}^{\unicode[STIX]{x2202}(t)}\circ i_{t}^{\ast }=i^{\ast }$
. Par la proposition 3.13, le lemme 5.8 et la surjectivité de
$\unicode[STIX]{x1D6E9}_{Y}^{\unicode[STIX]{x2202}(t)}\circ i_{t}^{\ast }=i^{\ast }$
. Par la proposition 3.13, le lemme 5.8 et la surjectivité de
![]() $\unicode[STIX]{x1D713}^{\ast }$
, les morphismes
$\unicode[STIX]{x1D713}^{\ast }$
, les morphismes
 $\text{Br}_{H}(Y_{H})\xrightarrow[{}]{i^{\ast }}\text{Br}_{G}(Y)$
et
$\text{Br}_{H}(Y_{H})\xrightarrow[{}]{i^{\ast }}\text{Br}_{G}(Y)$
et
 $\text{Br}_{H}(Y_{H})\xrightarrow[{}]{i_{t}^{\ast }}\text{Br}_{G}(\unicode[STIX]{x1D707}^{-1}(t))$
sont surjectifs.
$\text{Br}_{H}(Y_{H})\xrightarrow[{}]{i_{t}^{\ast }}\text{Br}_{G}(\unicode[STIX]{x1D707}^{-1}(t))$
sont surjectifs.
Notons
 $$\begin{eqnarray}B:=\text{Br}_{H}(Y_{H})\cap (i^{\ast })^{-1}\biggl(\mathop{\sum }_{\unicode[STIX]{x1D70E}\in \unicode[STIX]{x0428}^{1}(G)}\widetilde{\unicode[STIX]{x1D6E9}_{Y}^{\unicode[STIX]{x1D70E}}}(B_{\unicode[STIX]{x1D70E}})\biggr)\subset \text{Br}_{H}(Y_{H}).\end{eqnarray}$$
$$\begin{eqnarray}B:=\text{Br}_{H}(Y_{H})\cap (i^{\ast })^{-1}\biggl(\mathop{\sum }_{\unicode[STIX]{x1D70E}\in \unicode[STIX]{x0428}^{1}(G)}\widetilde{\unicode[STIX]{x1D6E9}_{Y}^{\unicode[STIX]{x1D70E}}}(B_{\unicode[STIX]{x1D70E}})\biggr)\subset \text{Br}_{H}(Y_{H}).\end{eqnarray}$$
Alors
 $(p_{H}^{\ast })^{-1}(B)\subset A$
et
$(p_{H}^{\ast })^{-1}(B)\subset A$
et
 $B_{\unicode[STIX]{x2202}(t)}\subset i_{t}^{\ast }B$
. Puisque
$B_{\unicode[STIX]{x2202}(t)}\subset i_{t}^{\ast }B$
. Puisque
![]() $\unicode[STIX]{x1D707}\circ i$
se factorise par
$\unicode[STIX]{x1D707}\circ i$
se factorise par
![]() $\text{Spec}\,k$
, on a
$\text{Spec}\,k$
, on a
 $\unicode[STIX]{x1D707}^{\ast }\,\text{Br}_{1}(T)\subset B.$
$\unicode[STIX]{x1D707}^{\ast }\,\text{Br}_{1}(T)\subset B.$
Pour un
 $y\in Y(\mathbf{A}_{k})^{p^{\ast }A}$
, par le lemme 5.1, il existe
$y\in Y(\mathbf{A}_{k})^{p^{\ast }A}$
, par le lemme 5.1, il existe
 $y_{1}\in Y_{H}(\mathbf{A}_{k})^{B+p_{H}^{\ast }A}$
tel que
$y_{1}\in Y_{H}(\mathbf{A}_{k})^{B+p_{H}^{\ast }A}$
tel que
 $p_{H}(y_{1})=p(y)$
. Alors il existe
$p_{H}(y_{1})=p(y)$
. Alors il existe
 $h\in H(\mathbf{A}_{k})$
tel que
$h\in H(\mathbf{A}_{k})$
tel que
 $y_{1}=h\cdot y$
. Donc
$y_{1}=h\cdot y$
. Donc
 $\unicode[STIX]{x1D707}(y_{1})\in \unicode[STIX]{x1D719}(H(\mathbf{A}_{k}))\cap T(\mathbf{A}_{k})^{\text{Br}_{1}(T)}$
.
$\unicode[STIX]{x1D707}(y_{1})\in \unicode[STIX]{x1D719}(H(\mathbf{A}_{k}))\cap T(\mathbf{A}_{k})^{\text{Br}_{1}(T)}$
.
Par [Reference Cao, Demarche and XuCDX16, Prop. 3.3], on a :
 $$\begin{eqnarray}T(\mathbf{A}_{k})^{\text{Br}_{1}(T)}=T(k)\cdot \unicode[STIX]{x1D719}(H(\mathbf{A}_{k})^{\text{Br}_{1}(H)}).\end{eqnarray}$$
$$\begin{eqnarray}T(\mathbf{A}_{k})^{\text{Br}_{1}(T)}=T(k)\cdot \unicode[STIX]{x1D719}(H(\mathbf{A}_{k})^{\text{Br}_{1}(H)}).\end{eqnarray}$$
Donc il existe
 $h_{1}\in H(\mathbf{A}_{k})^{\text{Br}_{1}(H)}$
tel que
$h_{1}\in H(\mathbf{A}_{k})^{\text{Br}_{1}(H)}$
tel que
 $$\begin{eqnarray}t:=\unicode[STIX]{x1D707}(h_{1}\cdot y_{1})\in T(k)\cap \unicode[STIX]{x1D719}(H(\mathbf{A}_{k})).\end{eqnarray}$$
$$\begin{eqnarray}t:=\unicode[STIX]{x1D707}(h_{1}\cdot y_{1})\in T(k)\cap \unicode[STIX]{x1D719}(H(\mathbf{A}_{k})).\end{eqnarray}$$
Donc
 $\unicode[STIX]{x2202}(t)\subset \unicode[STIX]{x0428}^{1}(G)$
. Puisque
$\unicode[STIX]{x2202}(t)\subset \unicode[STIX]{x0428}^{1}(G)$
. Puisque
 $\text{Br}_{H}(H)=\text{Br}_{1}(H)$
(Lemme 3.6), par la proposition 3.9(1),
$\text{Br}_{H}(H)=\text{Br}_{1}(H)$
(Lemme 3.6), par la proposition 3.9(1),
 $$\begin{eqnarray}y_{2}:=h_{1}\cdot y_{1}\in Y_{H}(\mathbf{A}_{k})^{B+p_{H}^{\ast }A}~~~\text{et donc}~y_{2}\in \unicode[STIX]{x1D707}^{-1}(t)(\mathbf{A}_{k})^{B_{\unicode[STIX]{x2202}(t)}+p_{\unicode[STIX]{x2202}(t)}^{\ast }A}.\end{eqnarray}$$
$$\begin{eqnarray}y_{2}:=h_{1}\cdot y_{1}\in Y_{H}(\mathbf{A}_{k})^{B+p_{H}^{\ast }A}~~~\text{et donc}~y_{2}\in \unicode[STIX]{x1D707}^{-1}(t)(\mathbf{A}_{k})^{B_{\unicode[STIX]{x2202}(t)}+p_{\unicode[STIX]{x2202}(t)}^{\ast }A}.\end{eqnarray}$$
Le résultat découle de
 $p_{\unicode[STIX]{x2202}(t)}(y_{2})=p_{H}(y_{2})=p(y)$
.◻
$p_{\unicode[STIX]{x2202}(t)}(y_{2})=p_{H}(y_{2})=p(y)$
.◻
Corollaire 5.10. Sous les hypothèses du théorème 5.9, soit
 $$\begin{eqnarray}X(k)\xrightarrow[{}]{\unicode[STIX]{x2202}}H^{1}(k,G):~z\mapsto [p^{-1}(z)]\end{eqnarray}$$
$$\begin{eqnarray}X(k)\xrightarrow[{}]{\unicode[STIX]{x2202}}H^{1}(k,G):~z\mapsto [p^{-1}(z)]\end{eqnarray}$$
le morphisme canonique. Supposons que pour tout
 $\unicode[STIX]{x1D70E}\in H^{1}(k,G)$
, la variété
$\unicode[STIX]{x1D70E}\in H^{1}(k,G)$
, la variété
![]() $Y_{\unicode[STIX]{x1D70E}}$
satisfait le principe de Hasse par rapport à
$Y_{\unicode[STIX]{x1D70E}}$
satisfait le principe de Hasse par rapport à
 $B_{\unicode[STIX]{x1D70E}}+p_{\unicode[STIX]{x1D70E}}^{\ast }A$
. Alors
$B_{\unicode[STIX]{x1D70E}}+p_{\unicode[STIX]{x1D70E}}^{\ast }A$
. Alors
 $$\begin{eqnarray}X(\mathbf{A}_{k})^{A}=\mathop{\bigcup }_{\unicode[STIX]{x1D70E}\in \text{Im}(\unicode[STIX]{x2202})}p_{\unicode[STIX]{x1D70E}}(Y_{\unicode[STIX]{x1D70E}}(\mathbf{A}_{k})^{B_{\unicode[STIX]{x1D70E}}+p_{\unicode[STIX]{x1D70E}}^{\ast }A}).\end{eqnarray}$$
$$\begin{eqnarray}X(\mathbf{A}_{k})^{A}=\mathop{\bigcup }_{\unicode[STIX]{x1D70E}\in \text{Im}(\unicode[STIX]{x2202})}p_{\unicode[STIX]{x1D70E}}(Y_{\unicode[STIX]{x1D70E}}(\mathbf{A}_{k})^{B_{\unicode[STIX]{x1D70E}}+p_{\unicode[STIX]{x1D70E}}^{\ast }A}).\end{eqnarray}$$
Démonstration.
Pour tout
 $\unicode[STIX]{x1D70E}\in H^{1}(k,G)$
, si
$\unicode[STIX]{x1D70E}\in H^{1}(k,G)$
, si
 $Y_{\unicode[STIX]{x1D70E}}(\mathbf{A}_{k})^{B_{\unicode[STIX]{x1D70E}}+p_{\unicode[STIX]{x1D70E}}^{\ast }A}\neq \emptyset$
, alors on a
$Y_{\unicode[STIX]{x1D70E}}(\mathbf{A}_{k})^{B_{\unicode[STIX]{x1D70E}}+p_{\unicode[STIX]{x1D70E}}^{\ast }A}\neq \emptyset$
, alors on a
 $Y_{\unicode[STIX]{x1D70E}}(k)\neq \emptyset$
et donc
$Y_{\unicode[STIX]{x1D70E}}(k)\neq \emptyset$
et donc
 $\unicode[STIX]{x1D70E}\in \text{Im}(\unicode[STIX]{x2202})$
. Le résultat en découle.◻
$\unicode[STIX]{x1D70E}\in \text{Im}(\unicode[STIX]{x2202})$
. Le résultat en découle.◻
Corollaire 5.11. Soient
![]() $G$
un groupe linéaire connexe,
$G$
un groupe linéaire connexe,
![]() $X$
une variété lisse géométriquement intègre et
$X$
une variété lisse géométriquement intègre et
 $Y\xrightarrow[{}]{p}X$
un
$Y\xrightarrow[{}]{p}X$
un
![]() $G$
-torseur. Soit
$G$
-torseur. Soit
 $\text{Br}_{1}(X,Y):=\text{Ker}(\text{Br}(X)\rightarrow \text{Br}(Y_{\bar{k}})).$
Alors on a :
$\text{Br}_{1}(X,Y):=\text{Ker}(\text{Br}(X)\rightarrow \text{Br}(Y_{\bar{k}})).$
Alors on a :
 $$\begin{eqnarray}X(\mathbf{A}_{k})^{\text{Br}_{1}(X,Y)}=\mathop{\bigcup }_{\unicode[STIX]{x1D70E}\in H^{1}(k,G)}p_{\unicode[STIX]{x1D70E}}(Y_{\unicode[STIX]{x1D70E}}(\mathbf{A}_{k})^{\text{Br}_{1}(Y_{\unicode[STIX]{x1D70E}})}).\end{eqnarray}$$
$$\begin{eqnarray}X(\mathbf{A}_{k})^{\text{Br}_{1}(X,Y)}=\mathop{\bigcup }_{\unicode[STIX]{x1D70E}\in H^{1}(k,G)}p_{\unicode[STIX]{x1D70E}}(Y_{\unicode[STIX]{x1D70E}}(\mathbf{A}_{k})^{\text{Br}_{1}(Y_{\unicode[STIX]{x1D70E}})}).\end{eqnarray}$$
Démonstration.
Pour tout
 $\unicode[STIX]{x1D70E}\in H^{1}(k,G)$
, puisque le morphisme
$\unicode[STIX]{x1D70E}\in H^{1}(k,G)$
, puisque le morphisme
 $\text{Br}(Y_{\bar{k}})\rightarrow \text{Br}((P_{\unicode[STIX]{x1D70E}}\times Y)_{\bar{k}})$
est injectif, on a
$\text{Br}(Y_{\bar{k}})\rightarrow \text{Br}((P_{\unicode[STIX]{x1D70E}}\times Y)_{\bar{k}})$
est injectif, on a
 $\text{Br}_{1}(X,Y_{\unicode[STIX]{x1D70E}})\subset \text{Br}_{1}(X,Y)$
. Donc
$\text{Br}_{1}(X,Y_{\unicode[STIX]{x1D70E}})\subset \text{Br}_{1}(X,Y)$
. Donc
 $\text{Br}_{1}(X,Y_{\unicode[STIX]{x1D70E}})=\text{Br}_{1}(X,Y)=(p^{\ast })^{-1}\,\text{Br}_{1}(Y)$
.
$\text{Br}_{1}(X,Y_{\unicode[STIX]{x1D70E}})=\text{Br}_{1}(X,Y)=(p^{\ast })^{-1}\,\text{Br}_{1}(Y)$
.
Pour tout
 $\unicode[STIX]{x1D70E}\in H^{1}(k,G)$
, par le lemme 3.12 et le lemme 5.8, le morphisme
$\unicode[STIX]{x1D70E}\in H^{1}(k,G)$
, par le lemme 3.12 et le lemme 5.8, le morphisme
![]() $\unicode[STIX]{x1D6E9}_{Y}^{\unicode[STIX]{x1D70E}}$
induit un isomorphisme
$\unicode[STIX]{x1D6E9}_{Y}^{\unicode[STIX]{x1D70E}}$
induit un isomorphisme
 $\text{Br}_{a}(Y_{\unicode[STIX]{x1D70E}})\stackrel{{\sim}}{\rightarrow }\text{Br}_{a}(Y)$
. Donc
$\text{Br}_{a}(Y_{\unicode[STIX]{x1D70E}})\stackrel{{\sim}}{\rightarrow }\text{Br}_{a}(Y)$
. Donc
 $\widetilde{\unicode[STIX]{x1D6E9}_{Y}^{\unicode[STIX]{x1D70E}}}(\text{Br}_{1}(Y_{\unicode[STIX]{x1D70E}}))=\text{Br}_{1}(Y)$
. Le résultat découle du théorème 5.9.◻
$\widetilde{\unicode[STIX]{x1D6E9}_{Y}^{\unicode[STIX]{x1D70E}}}(\text{Br}_{1}(Y_{\unicode[STIX]{x1D70E}}))=\text{Br}_{1}(Y)$
. Le résultat découle du théorème 5.9.◻
Remarque 5.12. La démonstration du théorème 5.9 n’utilise pas l’approximation forte pour les espaces homogènes à stabilisateur géométrique connexe (Borovoi et Demarche [Reference Borovoi and DemarcheBD13, Thm. 1.4]), mais elle utilise [Reference Borovoi and DemarcheBD13, Thm. 2.8].
Corollaire 5.13. Soient
![]() $G$
un groupe linéaire connexe,
$G$
un groupe linéaire connexe,
 $G_{0}\subset G$
un sous groupe fermé connexe et
$G_{0}\subset G$
un sous groupe fermé connexe et
 $Z:=G_{0}\backslash G$
. Notons
$Z:=G_{0}\backslash G$
. Notons
![]() $G\xrightarrow[{}]{\unicode[STIX]{x1D70B}}Z$
la projection. Alors on a
$G\xrightarrow[{}]{\unicode[STIX]{x1D70B}}Z$
la projection. Alors on a
 $$\begin{eqnarray}Z(\mathbf{A}_{k})^{\text{Br}_{G}(Z)}=\unicode[STIX]{x1D70B}(G(\mathbf{A}_{k})^{\text{Br}_{1}(G)})\cdot Z(k).\end{eqnarray}$$
$$\begin{eqnarray}Z(\mathbf{A}_{k})^{\text{Br}_{G}(Z)}=\unicode[STIX]{x1D70B}(G(\mathbf{A}_{k})^{\text{Br}_{1}(G)})\cdot Z(k).\end{eqnarray}$$
Démonstration.
Puisque
![]() $G\xrightarrow[{}]{\unicode[STIX]{x1D70B}}Z$
est un
$G\xrightarrow[{}]{\unicode[STIX]{x1D70B}}Z$
est un
![]() $G_{0}$
-torseur à gauche, pour tout
$G_{0}$
-torseur à gauche, pour tout
 $P_{\unicode[STIX]{x1D70E}}\in H^{1}(k,G_{0})$
(un
$P_{\unicode[STIX]{x1D70E}}\in H^{1}(k,G_{0})$
(un
![]() $G_{0}$
-torseur à droite), le tordu
$G_{0}$
-torseur à droite), le tordu
 $P_{\unicode[STIX]{x1D70E}}\times ^{G_{0}}G$
est un
$P_{\unicode[STIX]{x1D70E}}\times ^{G_{0}}G$
est un
![]() $G$
torseur à droite. Donc
$G$
torseur à droite. Donc
 $P_{\unicode[STIX]{x1D70E}}\times ^{G_{0}}G$
satisfait le principe de Hasse par rapport à
$P_{\unicode[STIX]{x1D70E}}\times ^{G_{0}}G$
satisfait le principe de Hasse par rapport à
 $\text{Br}_{1}(P_{\unicode[STIX]{x1D70E}}\times ^{G_{0}}G)$
(Sansuc, cf. [Reference SkorobogatovSko01, Thm. 5.2.1]). Le résultat découle du corollaire 5.10.◻
$\text{Br}_{1}(P_{\unicode[STIX]{x1D70E}}\times ^{G_{0}}G)$
(Sansuc, cf. [Reference SkorobogatovSko01, Thm. 5.2.1]). Le résultat découle du corollaire 5.10.◻
C’est clair que le corollaire 5.13 vaut aussi pour
 $Z:=G/G_{0}$
.
$Z:=G/G_{0}$
.
6 La méthode de fibration et la question 1.3
Dans toute cette section,
![]() $k$
est un corps de nombres. Sauf mention explicite du contraire, une variété est une
$k$
est un corps de nombres. Sauf mention explicite du contraire, une variété est une
![]() $k$
-variété. Pour traiter la question 1.3, on est amené à étudier la question :
$k$
-variété. Pour traiter la question 1.3, on est amené à étudier la question :
Question 6.1. Soit
![]() $G$
un groupe linéaire. Soient
$G$
un groupe linéaire. Soient
![]() $X$
et
$X$
et
![]() $Z$
deux
$Z$
deux
![]() $G$
-variétés lisses géométriquement intègres. Soient
$G$
-variétés lisses géométriquement intègres. Soient
![]() $U\subset X$
un
$U\subset X$
un
![]() $G$
-ouvert et
$G$
-ouvert et
![]() $U\xrightarrow[{}]{f}Z$
un
$U\xrightarrow[{}]{f}Z$
un
![]() $G$
-morphisme. Soient
$G$
-morphisme. Soient
 $B\subset \text{Br}(U)$
un sous-groupe fini,
$B\subset \text{Br}(U)$
un sous-groupe fini,
![]() $S\subset \unicode[STIX]{x1D6FA}_{k}$
un sous-ensemble fini non vide et
$S\subset \unicode[STIX]{x1D6FA}_{k}$
un sous-ensemble fini non vide et
 $W\subset X(\mathbf{A}_{k})$
un ouvert. Sous quelles conditions peut-on montrer que, si
$W\subset X(\mathbf{A}_{k})$
un ouvert. Sous quelles conditions peut-on montrer que, si
 $W^{\text{Br}(U)\cap (B+f^{\ast }\,\text{Br}_{G}(Z))}\neq \emptyset$
, alors il existe
$W^{\text{Br}(U)\cap (B+f^{\ast }\,\text{Br}_{G}(Z))}\neq \emptyset$
, alors il existe
 $z\in Z(k)$
de fibre
$z\in Z(k)$
de fibre
![]() $U_{z}$
tel que
$U_{z}$
tel que
 $((G(k_{S})\cdot W)\cap U_{z}(\mathbf{A}_{k}))^{B}\neq \emptyset$
?
$((G(k_{S})\cdot W)\cap U_{z}(\mathbf{A}_{k}))^{B}\neq \emptyset$
?
Dans [Reference Colliot-Thélène and HarariCH16], Colliot-Thélène et Harari étudient la méthode de fibration au dessus de
![]() $\mathbb{A}^{1}$
. On suit leur méthode et répond à la question 6.1 d’abord dans le cas où
$\mathbb{A}^{1}$
. On suit leur méthode et répond à la question 6.1 d’abord dans le cas où
![]() $Z$
est un tore quasi-trivial et
$Z$
est un tore quasi-trivial et
![]() $f$
s’étend à un morphisme de
$f$
s’étend à un morphisme de
![]() $X$
vers une
$X$
vers une
![]() $Z$
-variété torique standard (Théorème 6.7). Ensuite, en utilisant ce résultat, on résoud cette question dans le cas où
$Z$
-variété torique standard (Théorème 6.7). Ensuite, en utilisant ce résultat, on résoud cette question dans le cas où
![]() $Z$
est un tore (Théorème 6.9). En utilisant la descente (§ 5.1), on établit le théorème 6.11 dans le cas plus général où
$Z$
est un tore (Théorème 6.9). En utilisant la descente (§ 5.1), on établit le théorème 6.11 dans le cas plus général où
![]() $Z$
est un pseudo
$Z$
est un pseudo
![]() $G$
-espace homogène. Ceci sera utilisé dans la § 7 pour traiter le cas d’un
$G$
-espace homogène. Ceci sera utilisé dans la § 7 pour traiter le cas d’un
![]() $G$
-espace homogène
$G$
-espace homogène
![]() $Z$
à stabilisateur géométrique connexe.
$Z$
à stabilisateur géométrique connexe.
6.1 L’approximation forte raffinée pour l’espace affine
Pour un ouvert
![]() $U$
d’un espace affine
$U$
d’un espace affine
![]() $\mathbb{A}^{n}$
satisfaisant
$\mathbb{A}^{n}$
satisfaisant
 $\text{codim}(\mathbb{A}^{n}\setminus U,\mathbb{A}^{n})\geqslant 2$
, l’approximation forte hors d’une place
$\text{codim}(\mathbb{A}^{n}\setminus U,\mathbb{A}^{n})\geqslant 2$
, l’approximation forte hors d’une place
![]() $v_{0}$
a été établie par Fei Xu et l’auteur dans [Reference Cao and XuCX13, Prop. 3.6], et raffinée lorsque la place
$v_{0}$
a été établie par Fei Xu et l’auteur dans [Reference Cao and XuCX13, Prop. 3.6], et raffinée lorsque la place
![]() $v_{0}$
est archimédienne dans [Reference Cao and XuCX15, Prop. 4.6 et Cor. 4.7 ], où l’on montre que
$v_{0}$
est archimédienne dans [Reference Cao and XuCX15, Prop. 4.6 et Cor. 4.7 ], où l’on montre que
 $U(k)\cap T(k_{v_{0}})^{+}\subset \mathbb{A}^{n}(k_{v_{0}})$
est dense dans
$U(k)\cap T(k_{v_{0}})^{+}\subset \mathbb{A}^{n}(k_{v_{0}})$
est dense dans
![]() $U(\mathbf{A}_{k}^{v_{0}})$
pour une variété torique
$U(\mathbf{A}_{k}^{v_{0}})$
pour une variété torique
 $(T{\hookrightarrow}\mathbb{A}^{n})$
comme (6.1) ci-dessous. On généralise maintenant ce résultat au cas où
$(T{\hookrightarrow}\mathbb{A}^{n})$
comme (6.1) ci-dessous. On généralise maintenant ce résultat au cas où
![]() $v_{0}$
est une place quelconque.
$v_{0}$
est une place quelconque.
Théorème 6.2. Soient
![]() $K$
une
$K$
une
![]() $k$
-algèbre finie séparable de degré
$k$
-algèbre finie séparable de degré
![]() $n$
et
$n$
et
 $$\begin{eqnarray}(T{\hookrightarrow}\mathbb{A}^{n}):=(\text{Res}_{K/k}\,\mathbb{G}_{m}{\hookrightarrow}\text{Res}_{K/k}\,\mathbb{A}^{1})\end{eqnarray}$$
$$\begin{eqnarray}(T{\hookrightarrow}\mathbb{A}^{n}):=(\text{Res}_{K/k}\,\mathbb{G}_{m}{\hookrightarrow}\text{Res}_{K/k}\,\mathbb{A}^{1})\end{eqnarray}$$
la variété torique correspondante. Soit
 $U\subset \mathbb{A}^{n}$
un ouvert tel que
$U\subset \mathbb{A}^{n}$
un ouvert tel que
 $\text{codim}(\mathbb{A}^{n}\setminus U,\mathbb{A}^{n})\geqslant 2$
. Soient
$\text{codim}(\mathbb{A}^{n}\setminus U,\mathbb{A}^{n})\geqslant 2$
. Soient
![]() $v_{0}$
une place et
$v_{0}$
une place et
 $D_{v_{0}}\subset T(k_{v_{0}})$
un sous-groupe ouvert d’indice fini. Alors, pour tout ouvert
$D_{v_{0}}\subset T(k_{v_{0}})$
un sous-groupe ouvert d’indice fini. Alors, pour tout ouvert
 $W\subset U(\mathbf{A}^{v_{0}})$
non vide et tout ouvert
$W\subset U(\mathbf{A}^{v_{0}})$
non vide et tout ouvert
 $W_{0}\subset \mathbb{A}^{n}(k_{v_{0}})$
non vide
$W_{0}\subset \mathbb{A}^{n}(k_{v_{0}})$
non vide
![]() $D_{v_{0}}$
-invariant, on a
$D_{v_{0}}$
-invariant, on a
 $$\begin{eqnarray}U(k)\cap (W_{0}\times W)\neq \emptyset .\end{eqnarray}$$
$$\begin{eqnarray}U(k)\cap (W_{0}\times W)\neq \emptyset .\end{eqnarray}$$
Démonstration.
Étape (0). Par approximation faible pour le tore quasi-trivial
![]() $T$
, il existe un
$T$
, il existe un
 $\unicode[STIX]{x1D6FC}\in T(k)\cap W_{0}$
. Ainsi on a
$\unicode[STIX]{x1D6FC}\in T(k)\cap W_{0}$
. Ainsi on a
 $D_{v_{0}}\subset \unicode[STIX]{x1D6FC}^{-1}\cdot W_{0}$
. En remplaçant
$D_{v_{0}}\subset \unicode[STIX]{x1D6FC}^{-1}\cdot W_{0}$
. En remplaçant
![]() $U$
par
$U$
par
![]() $\unicode[STIX]{x1D6FC}^{-1}U$
et
$\unicode[STIX]{x1D6FC}^{-1}U$
et
![]() $W$
par
$W$
par
![]() $\unicode[STIX]{x1D6FC}^{-1}W$
, on peut supposer que
$\unicode[STIX]{x1D6FC}^{-1}W$
, on peut supposer que
 $W_{0}=D_{v_{0}}$
. Si
$W_{0}=D_{v_{0}}$
. Si
![]() $v_{0}$
est complexe, on a
$v_{0}$
est complexe, on a
 $D_{v_{0}}=T(k_{v_{0}})$
et l’énoncé découle de [Reference Cao and XuCX13, Prop. 3.6]. On suppose que
$D_{v_{0}}=T(k_{v_{0}})$
et l’énoncé découle de [Reference Cao and XuCX13, Prop. 3.6]. On suppose que
![]() $v_{0}$
n’est pas complexe.
$v_{0}$
n’est pas complexe.
Étape (1). Supposons que
 $v_{0}\in \infty _{k}$
et
$v_{0}\in \infty _{k}$
et
 $T=\mathbb{G}_{m}^{n}$
. Puisque
$T=\mathbb{G}_{m}^{n}$
. Puisque
 $D_{v_{0}}\subset T(k_{v_{0}})$
est ouvert et donc fermé, le sous-groupe
$D_{v_{0}}\subset T(k_{v_{0}})$
est ouvert et donc fermé, le sous-groupe
![]() $D_{v_{0}}$
contient la composante connexe de l’identité de
$D_{v_{0}}$
contient la composante connexe de l’identité de
![]() $T(k_{v_{0}})$
. Ainsi l’énoncé est équivalent à [Reference Cao and XuCX15, Prop. 4.6].
$T(k_{v_{0}})$
. Ainsi l’énoncé est équivalent à [Reference Cao and XuCX15, Prop. 4.6].
Étape (2). Supposons que
 $v_{0}\notin \infty _{k}$
,
$v_{0}\notin \infty _{k}$
,
![]() $n=1$
et
$n=1$
et
 $T=\mathbb{G}_{m}$
. On a
$T=\mathbb{G}_{m}$
. On a
![]() $U=\mathbb{A}^{1}$
. Par définition, Il existe un sous-ensemble fini
$U=\mathbb{A}^{1}$
. Par définition, Il existe un sous-ensemble fini
 $S\subset \unicode[STIX]{x1D6FA}_{k}\setminus \{v_{0}\}$
contenant
$S\subset \unicode[STIX]{x1D6FA}_{k}\setminus \{v_{0}\}$
contenant
![]() $\infty _{k}$
, un élément
$\infty _{k}$
, un élément
![]() $a_{v}\in k_{v}$
pour chaque
$a_{v}\in k_{v}$
pour chaque
![]() $v\in S$
et
$v\in S$
et
 $0<\unicode[STIX]{x1D716}<1$
tels que
$0<\unicode[STIX]{x1D716}<1$
tels que
 $$\begin{eqnarray}\mathop{\prod }_{v\in S}\{x\in k_{v}:|x-a_{v}|<\unicode[STIX]{x1D716}\}\times \mathop{\prod }_{v\notin S\cup \{v_{0}\}}{\mathcal{O}}_{v}\subset W.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\prod }_{v\in S}\{x\in k_{v}:|x-a_{v}|<\unicode[STIX]{x1D716}\}\times \mathop{\prod }_{v\notin S\cup \{v_{0}\}}{\mathcal{O}}_{v}\subset W.\end{eqnarray}$$
On fixe une uniformisante
![]() $\unicode[STIX]{x1D70B}_{v_{0}}$
de
$\unicode[STIX]{x1D70B}_{v_{0}}$
de
![]() $k_{v_{0}}$
. Pour le sous-groupe d’indice fini
$k_{v_{0}}$
. Pour le sous-groupe d’indice fini
 $D_{v_{0}}\subset k_{v_{0}}^{\times }$
, il existe un entier
$D_{v_{0}}\subset k_{v_{0}}^{\times }$
, il existe un entier
![]() $N>0$
tel que
$N>0$
tel que
 $$\begin{eqnarray}\mathop{\bigcup }_{i\in \mathbb{Z}}(1+\unicode[STIX]{x1D70B}_{v_{0}}^{N}{\mathcal{O}}_{v_{0}})\cdot \unicode[STIX]{x1D70B}_{v_{0}}^{iN}\subset D_{v_{0}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\bigcup }_{i\in \mathbb{Z}}(1+\unicode[STIX]{x1D70B}_{v_{0}}^{N}{\mathcal{O}}_{v_{0}})\cdot \unicode[STIX]{x1D70B}_{v_{0}}^{iN}\subset D_{v_{0}}.\end{eqnarray}$$
Par approximation forte sur
![]() $\mathbb{A}^{1}$
, il existe
$\mathbb{A}^{1}$
, il existe
 $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in k^{\times }$
tels que
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in k^{\times }$
tels que
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}\in k_{v_{0}}\times \mathop{\prod }_{v\in S}\biggl\{x\in k_{v}:|x-a_{v}|<\frac{1}{2}\unicode[STIX]{x1D716}\biggr\}\times \mathop{\prod }_{v\notin S\cup \{v_{0}\}}{\mathcal{O}}_{v}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}\in k_{v_{0}}\times \mathop{\prod }_{v\in S}\biggl\{x\in k_{v}:|x-a_{v}|<\frac{1}{2}\unicode[STIX]{x1D716}\biggr\}\times \mathop{\prod }_{v\notin S\cup \{v_{0}\}}{\mathcal{O}}_{v}\end{eqnarray}$$
et
 $$\begin{eqnarray}\unicode[STIX]{x1D6FD}\in k_{v_{0}}\times \mathop{\prod }_{v\in S}\biggl\{x\in k_{v}:|x|<\frac{1}{2}\unicode[STIX]{x1D716}\biggr\}\times \mathop{\prod }_{v\notin S\cup \{v_{0}\}}{\mathcal{O}}_{v}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FD}\in k_{v_{0}}\times \mathop{\prod }_{v\in S}\biggl\{x\in k_{v}:|x|<\frac{1}{2}\unicode[STIX]{x1D716}\biggr\}\times \mathop{\prod }_{v\notin S\cup \{v_{0}\}}{\mathcal{O}}_{v}.\end{eqnarray}$$
D’après la formule du produit,
 $l:=-v_{0}(\unicode[STIX]{x1D6FD})>0$
et donc
$l:=-v_{0}(\unicode[STIX]{x1D6FD})>0$
et donc
 $\unicode[STIX]{x1D70B}_{v_{0}}^{l}\unicode[STIX]{x1D6FD}\in {\mathcal{O}}_{v_{0}}^{\times }$
. Alors il existe
$\unicode[STIX]{x1D70B}_{v_{0}}^{l}\unicode[STIX]{x1D6FD}\in {\mathcal{O}}_{v_{0}}^{\times }$
. Alors il existe
![]() $m\in \mathbb{Z}$
assez grand tel que
$m\in \mathbb{Z}$
assez grand tel que
 $$\begin{eqnarray}(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D70B}_{v_{0}}^{l})^{m}\in (1+\unicode[STIX]{x1D70B}_{v_{0}}^{N}{\mathcal{O}}_{v_{0}})~~~\text{et}~~~v_{0}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{-m})>N.\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D70B}_{v_{0}}^{l})^{m}\in (1+\unicode[STIX]{x1D70B}_{v_{0}}^{N}{\mathcal{O}}_{v_{0}})~~~\text{et}~~~v_{0}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{-m})>N.\end{eqnarray}$$
Ainsi
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}^{mN}=\unicode[STIX]{x1D70B}_{v_{0}}^{-mlN}(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D70B}_{v_{0}}^{l})^{mN}(1+\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{-mN})\in (1+\unicode[STIX]{x1D70B}_{v_{0}}^{N}{\mathcal{O}}_{v_{0}})\unicode[STIX]{x1D70B}_{v_{0}}^{-mlN}\subset D_{v_{0}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}^{mN}=\unicode[STIX]{x1D70B}_{v_{0}}^{-mlN}(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D70B}_{v_{0}}^{l})^{mN}(1+\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{-mN})\in (1+\unicode[STIX]{x1D70B}_{v_{0}}^{N}{\mathcal{O}}_{v_{0}})\unicode[STIX]{x1D70B}_{v_{0}}^{-mlN}\subset D_{v_{0}}.\end{eqnarray}$$
Ceci implique que
 $\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}^{mN}\in D_{v_{0}}\times W$
.
$\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}^{mN}\in D_{v_{0}}\times W$
.
Étape (3). Supposons que
 $v_{0}\notin \infty _{k}$
,
$v_{0}\notin \infty _{k}$
,
 $T\cong \mathbb{G}_{m}^{n}$
et, sous cet isomorphisme,
$T\cong \mathbb{G}_{m}^{n}$
et, sous cet isomorphisme,
 $D_{v_{0}}\cong \prod _{i=1}^{n}D_{i}$
avec
$D_{v_{0}}\cong \prod _{i=1}^{n}D_{i}$
avec
 $D_{i}\subset k_{v_{0}}^{\times }$
un sous-groupe ouvert d’indice fini. On établit le résultat en utilisant la projection
$D_{i}\subset k_{v_{0}}^{\times }$
un sous-groupe ouvert d’indice fini. On établit le résultat en utilisant la projection
 $\mathbb{A}^{n}\rightarrow \mathbb{A}^{1}$
sur le premier facteur. L’argument donné pour
$\mathbb{A}^{n}\rightarrow \mathbb{A}^{1}$
sur le premier facteur. L’argument donné pour
![]() $v_{0}$
réel dans [Reference Cao and XuCX15, Prop. 4.6] vaut pour tout
$v_{0}$
réel dans [Reference Cao and XuCX15, Prop. 4.6] vaut pour tout
![]() $v_{0}$
en remplaçant
$v_{0}$
en remplaçant
![]() $\mathbb{R}$
par
$\mathbb{R}$
par
![]() $D_{1}$
.
$D_{1}$
.
Étape (4). En général, d’après (1) et (3), il reste à montrer qu’il existe des sous-groupes ouverts
 $\{D_{i}\}_{i=1}^{n}$
de
$\{D_{i}\}_{i=1}^{n}$
de
![]() $k_{v_{0}}^{\times }$
d’indice fini et un isomorphisme
$k_{v_{0}}^{\times }$
d’indice fini et un isomorphisme
 $$\begin{eqnarray}\unicode[STIX]{x1D713}:~\text{Res}_{K/k}\,\mathbb{A}^{1}\stackrel{{\sim}}{\rightarrow }\mathbb{A}^{n}~~~\text{ tels que }\mathop{\prod }_{i=1}^{n}D_{i}\subset \unicode[STIX]{x1D713}(D_{v_{0}}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D713}:~\text{Res}_{K/k}\,\mathbb{A}^{1}\stackrel{{\sim}}{\rightarrow }\mathbb{A}^{n}~~~\text{ tels que }\mathop{\prod }_{i=1}^{n}D_{i}\subset \unicode[STIX]{x1D713}(D_{v_{0}}).\end{eqnarray}$$
Si
![]() $v_{0}$
est réel, ceci est établi dans la démonstration de [Reference Cao and XuCX15, Cor. 4.7]. On peut alors supposer que
$v_{0}$
est réel, ceci est établi dans la démonstration de [Reference Cao and XuCX15, Cor. 4.7]. On peut alors supposer que
 $v_{0}\notin \infty _{k}$
et
$v_{0}\notin \infty _{k}$
et
 $K=k(\unicode[STIX]{x1D703})$
soit un corps.
$K=k(\unicode[STIX]{x1D703})$
soit un corps.
Soit
![]() $\{w_{j}\}_{j}$
les places de
$\{w_{j}\}_{j}$
les places de
![]() $K$
au-dessus de
$K$
au-dessus de
![]() $v_{0}$
et, pour tout
$v_{0}$
et, pour tout
![]() $j$
, soient
$j$
, soient
![]() $\unicode[STIX]{x1D70B}_{j}$
une uniformisante de
$\unicode[STIX]{x1D70B}_{j}$
une uniformisante de
![]() $K_{w_{j}}$
et
$K_{w_{j}}$
et
![]() ${\mathcal{O}}_{j}$
l’anneau des entiers de
${\mathcal{O}}_{j}$
l’anneau des entiers de
![]() $K_{w_{j}}$
Pour
$K_{w_{j}}$
Pour
![]() $\unicode[STIX]{x1D70B}_{v_{0}}$
une uniformisante de
$\unicode[STIX]{x1D70B}_{v_{0}}$
une uniformisante de
![]() $k_{v_{0}}$
et pour chaque
$k_{v_{0}}$
et pour chaque
![]() $j$
, soit
$j$
, soit
 $e_{j}:=w_{j}(\unicode[STIX]{x1D70B}_{v_{0}})\leqslant n$
. Puisque
$e_{j}:=w_{j}(\unicode[STIX]{x1D70B}_{v_{0}})\leqslant n$
. Puisque
![]() $D_{v_{0}}$
est un sous-groupe ouvert de
$D_{v_{0}}$
est un sous-groupe ouvert de
 $T(k_{v_{0}})\cong \prod _{j}K_{w_{j}}^{\times }$
, il existe un entier
$T(k_{v_{0}})\cong \prod _{j}K_{w_{j}}^{\times }$
, il existe un entier
 $N\in \mathbb{Z}_{{>}0}$
tel que
$N\in \mathbb{Z}_{{>}0}$
tel que
 $$\begin{eqnarray}\mathop{\prod }_{j}\biggl[\mathop{\bigcup }_{l\in \mathbb{Z}}(1+\unicode[STIX]{x1D70B}_{j}^{N}{\mathcal{O}}_{j})\unicode[STIX]{x1D70B}_{j}^{lN}\biggr]\subset D_{v_{0}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\prod }_{j}\biggl[\mathop{\bigcup }_{l\in \mathbb{Z}}(1+\unicode[STIX]{x1D70B}_{j}^{N}{\mathcal{O}}_{j})\unicode[STIX]{x1D70B}_{j}^{lN}\biggr]\subset D_{v_{0}}.\end{eqnarray}$$
Après avoir remplacé
![]() $\unicode[STIX]{x1D703}$
par
$\unicode[STIX]{x1D703}$
par
 $\unicode[STIX]{x1D703}+\unicode[STIX]{x1D70B}_{v_{0}}^{-cN}$
avec
$\unicode[STIX]{x1D703}+\unicode[STIX]{x1D70B}_{v_{0}}^{-cN}$
avec
![]() $c\gg 0$
suffisamment divisible, on peut supposer que
$c\gg 0$
suffisamment divisible, on peut supposer que
 $$\begin{eqnarray}w_{j}(\unicode[STIX]{x1D703})=-e_{j}cN,~~~\unicode[STIX]{x1D703}\unicode[STIX]{x1D70B}_{j}^{e_{j}cN}\in (1+\unicode[STIX]{x1D70B}_{j}^{N}{\mathcal{O}}_{j})~~~\text{et}~~~(\unicode[STIX]{x1D70B}_{v_{0}}\unicode[STIX]{x1D70B}_{j}^{-e_{j}})^{c}\in (1+\unicode[STIX]{x1D70B}_{j}^{N}{\mathcal{O}}_{j}).\end{eqnarray}$$
$$\begin{eqnarray}w_{j}(\unicode[STIX]{x1D703})=-e_{j}cN,~~~\unicode[STIX]{x1D703}\unicode[STIX]{x1D70B}_{j}^{e_{j}cN}\in (1+\unicode[STIX]{x1D70B}_{j}^{N}{\mathcal{O}}_{j})~~~\text{et}~~~(\unicode[STIX]{x1D70B}_{v_{0}}\unicode[STIX]{x1D70B}_{j}^{-e_{j}})^{c}\in (1+\unicode[STIX]{x1D70B}_{j}^{N}{\mathcal{O}}_{j}).\end{eqnarray}$$
Soit
 $M:=cn^{2}N$
. Alors, pour tout
$M:=cn^{2}N$
. Alors, pour tout
![]() $j$
et tous entiers
$j$
et tous entiers
![]() $m,m^{\prime }$
avec
$m,m^{\prime }$
avec
 $0\leqslant m<m^{\prime }\leqslant n-1$
, on a
$0\leqslant m<m^{\prime }\leqslant n-1$
, on a
 $$\begin{eqnarray}|m^{\prime }-m||w_{j}(\unicode[STIX]{x1D703})|<ne_{j}cN\leqslant M~~~\text{et donc }0<(w_{j}(\unicode[STIX]{x1D703}^{m})-w_{j}(\unicode[STIX]{x1D703}^{m^{\prime }}))<M.\end{eqnarray}$$
$$\begin{eqnarray}|m^{\prime }-m||w_{j}(\unicode[STIX]{x1D703})|<ne_{j}cN\leqslant M~~~\text{et donc }0<(w_{j}(\unicode[STIX]{x1D703}^{m})-w_{j}(\unicode[STIX]{x1D703}^{m^{\prime }}))<M.\end{eqnarray}$$
Donc, pour tous
 $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FC}^{\prime }\in k_{v_{0}}^{\times }$
satisfaisant
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FC}^{\prime }\in k_{v_{0}}^{\times }$
satisfaisant
 $M|v_{0}(\unicode[STIX]{x1D6FC})$
et
$M|v_{0}(\unicode[STIX]{x1D6FC})$
et
 $M|v_{0}(\unicode[STIX]{x1D6FC}^{\prime })$
, on a
$M|v_{0}(\unicode[STIX]{x1D6FC}^{\prime })$
, on a
 $$\begin{eqnarray}w_{j}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D703}^{m})\neq w_{j}(\unicode[STIX]{x1D6FC}^{\prime }\unicode[STIX]{x1D703}^{m^{\prime }})~~~\text{et}~~~\left\{\begin{array}{@{}ll@{}}w_{j}(\unicode[STIX]{x1D6FC}^{\prime })>w_{j}(\unicode[STIX]{x1D6FC})\quad & \text{si}~w_{j}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D703}^{m})<w_{j}(\unicode[STIX]{x1D6FC}^{\prime }\unicode[STIX]{x1D703}^{m^{\prime }}),\\ w_{j}(\unicode[STIX]{x1D6FC})\geqslant w_{j}(\unicode[STIX]{x1D6FC}^{\prime })\quad & \text{si}~w_{j}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D703}^{m})>w_{j}(\unicode[STIX]{x1D6FC}^{\prime }\unicode[STIX]{x1D703}^{m^{\prime }}).\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}w_{j}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D703}^{m})\neq w_{j}(\unicode[STIX]{x1D6FC}^{\prime }\unicode[STIX]{x1D703}^{m^{\prime }})~~~\text{et}~~~\left\{\begin{array}{@{}ll@{}}w_{j}(\unicode[STIX]{x1D6FC}^{\prime })>w_{j}(\unicode[STIX]{x1D6FC})\quad & \text{si}~w_{j}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D703}^{m})<w_{j}(\unicode[STIX]{x1D6FC}^{\prime }\unicode[STIX]{x1D703}^{m^{\prime }}),\\ w_{j}(\unicode[STIX]{x1D6FC})\geqslant w_{j}(\unicode[STIX]{x1D6FC}^{\prime })\quad & \text{si}~w_{j}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D703}^{m})>w_{j}(\unicode[STIX]{x1D6FC}^{\prime }\unicode[STIX]{x1D703}^{m^{\prime }}).\end{array}\right.\end{eqnarray}$$
Donc
 $$\begin{eqnarray}\left\{\begin{array}{@{}ll@{}}w_{j}(\unicode[STIX]{x1D6FC}^{\prime }\unicode[STIX]{x1D703}^{m^{\prime }})-w_{j}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D703}^{m})>M-(m^{\prime }-m)(-w_{j}(\unicode[STIX]{x1D703}))\quad & \text{si}~w_{j}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D703}^{m})<w_{j}(\unicode[STIX]{x1D6FC}^{\prime }\unicode[STIX]{x1D703}^{m^{\prime }}),\\ w_{j}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D703}^{m})-w_{j}(\unicode[STIX]{x1D6FC}^{\prime }\unicode[STIX]{x1D703}^{m^{\prime }})>(m^{\prime }-m)(-w_{j}(\unicode[STIX]{x1D703}))\quad & \text{si}~w_{j}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D703}^{m})>w_{j}(\unicode[STIX]{x1D6FC}^{\prime }\unicode[STIX]{x1D703}^{m^{\prime }}).\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\left\{\begin{array}{@{}ll@{}}w_{j}(\unicode[STIX]{x1D6FC}^{\prime }\unicode[STIX]{x1D703}^{m^{\prime }})-w_{j}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D703}^{m})>M-(m^{\prime }-m)(-w_{j}(\unicode[STIX]{x1D703}))\quad & \text{si}~w_{j}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D703}^{m})<w_{j}(\unicode[STIX]{x1D6FC}^{\prime }\unicode[STIX]{x1D703}^{m^{\prime }}),\\ w_{j}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D703}^{m})-w_{j}(\unicode[STIX]{x1D6FC}^{\prime }\unicode[STIX]{x1D703}^{m^{\prime }})>(m^{\prime }-m)(-w_{j}(\unicode[STIX]{x1D703}))\quad & \text{si}~w_{j}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D703}^{m})>w_{j}(\unicode[STIX]{x1D6FC}^{\prime }\unicode[STIX]{x1D703}^{m^{\prime }}).\end{array}\right.\end{eqnarray}$$
L’élément
![]() $\unicode[STIX]{x1D703}$
induit un isomorphisme
$\unicode[STIX]{x1D703}$
induit un isomorphisme
 $\unicode[STIX]{x1D713}:\text{Res}_{K/k}\,\mathbb{A}^{1}\rightarrow \mathbb{A}^{n}$
, qui est défini par
$\unicode[STIX]{x1D713}:\text{Res}_{K/k}\,\mathbb{A}^{1}\rightarrow \mathbb{A}^{n}$
, qui est défini par
 $$\begin{eqnarray}\text{Res}_{K/k}\,\mathbb{A}^{1}(A)=\mathop{\sum }_{i=0}^{n-1}A\unicode[STIX]{x1D703}^{i}\xrightarrow[{}]{\unicode[STIX]{x1D713}}\mathbb{A}^{n}(A)=A^{n}:~~~\mathop{\sum }_{i=0}^{n-1}a_{i}\unicode[STIX]{x1D703}^{i}\mapsto (a_{0},\ldots ,a_{n-1})\end{eqnarray}$$
$$\begin{eqnarray}\text{Res}_{K/k}\,\mathbb{A}^{1}(A)=\mathop{\sum }_{i=0}^{n-1}A\unicode[STIX]{x1D703}^{i}\xrightarrow[{}]{\unicode[STIX]{x1D713}}\mathbb{A}^{n}(A)=A^{n}:~~~\mathop{\sum }_{i=0}^{n-1}a_{i}\unicode[STIX]{x1D703}^{i}\mapsto (a_{0},\ldots ,a_{n-1})\end{eqnarray}$$
pour toute
![]() $k$
-algèbre
$k$
-algèbre
![]() $A$
. Soit
$A$
. Soit
 $$\begin{eqnarray}D:=\mathop{\bigcup }_{l\in \mathbb{Z}}(1+\unicode[STIX]{x1D70B}_{v_{0}}^{N}{\mathcal{O}}_{v_{0}})\unicode[STIX]{x1D70B}_{v_{0}}^{lM}\subset k_{v_{0}}^{\times }\end{eqnarray}$$
$$\begin{eqnarray}D:=\mathop{\bigcup }_{l\in \mathbb{Z}}(1+\unicode[STIX]{x1D70B}_{v_{0}}^{N}{\mathcal{O}}_{v_{0}})\unicode[STIX]{x1D70B}_{v_{0}}^{lM}\subset k_{v_{0}}^{\times }\end{eqnarray}$$
un sous-groupe ouvert d’indice fini. D’après (6.3), on a
 $D\subset \bigcup _{l\in \mathbb{Z}}(1+\unicode[STIX]{x1D70B}_{j}^{N}{\mathcal{O}}_{j})\unicode[STIX]{x1D70B}_{j}^{lN}$
. Pour tout
$D\subset \bigcup _{l\in \mathbb{Z}}(1+\unicode[STIX]{x1D70B}_{j}^{N}{\mathcal{O}}_{j})\unicode[STIX]{x1D70B}_{j}^{lN}$
. Pour tout
![]() $j$
et tout
$j$
et tout
 $(x_{0},\ldots ,x_{n-1})\in D^{n}$
, il existe un
$(x_{0},\ldots ,x_{n-1})\in D^{n}$
, il existe un
 $0\leqslant i_{j}\leqslant n-1$
tel que
$0\leqslant i_{j}\leqslant n-1$
tel que
 $$\begin{eqnarray}w_{j}(x_{i_{j}}\unicode[STIX]{x1D703}^{i_{j}})=\min _{0\leqslant i\leqslant n-1}\{w_{j}(x_{i}\unicode[STIX]{x1D703}^{i})\}=w_{j}\biggl(\mathop{\sum }_{i=0}^{n-1}x_{i}\unicode[STIX]{x1D703}^{i}\biggr),\end{eqnarray}$$
$$\begin{eqnarray}w_{j}(x_{i_{j}}\unicode[STIX]{x1D703}^{i_{j}})=\min _{0\leqslant i\leqslant n-1}\{w_{j}(x_{i}\unicode[STIX]{x1D703}^{i})\}=w_{j}\biggl(\mathop{\sum }_{i=0}^{n-1}x_{i}\unicode[STIX]{x1D703}^{i}\biggr),\end{eqnarray}$$
où la deuxième égalité découle par (6.4). Pour
![]() $i\neq i_{j}$
, d’après (6.5), on a
$i\neq i_{j}$
, d’après (6.5), on a
 $$\begin{eqnarray}w_{j}(x_{i}\unicode[STIX]{x1D703}^{i})-w_{j}(x_{i_{j}}\unicode[STIX]{x1D703}^{i_{j}})\geqslant \left\{\begin{array}{@{}ll@{}}(i-i_{j})e_{j}cN\geqslant N\quad & \text{si}~i>i_{j},\\ M-(i_{j}-i)e_{j}cN\geqslant N\quad & \text{si}~i<i_{j}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}w_{j}(x_{i}\unicode[STIX]{x1D703}^{i})-w_{j}(x_{i_{j}}\unicode[STIX]{x1D703}^{i_{j}})\geqslant \left\{\begin{array}{@{}ll@{}}(i-i_{j})e_{j}cN\geqslant N\quad & \text{si}~i>i_{j},\\ M-(i_{j}-i)e_{j}cN\geqslant N\quad & \text{si}~i<i_{j}.\end{array}\right.\end{eqnarray}$$
Alors
 $$\begin{eqnarray}\unicode[STIX]{x1D713}^{-1}(x_{0},\ldots ,x_{n-1})=\mathop{\sum }_{i=0}^{n-1}x_{i}\unicode[STIX]{x1D703}^{i}\in x_{i_{j}}\unicode[STIX]{x1D703}^{i_{j}}(1+\unicode[STIX]{x1D70B}_{j}^{N}{\mathcal{O}}_{j})\subset \mathop{\bigcup }_{l\in \mathbb{Z}}(1+\unicode[STIX]{x1D70B}_{j}^{N}{\mathcal{O}}_{j})\unicode[STIX]{x1D70B}_{j}^{lN}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D713}^{-1}(x_{0},\ldots ,x_{n-1})=\mathop{\sum }_{i=0}^{n-1}x_{i}\unicode[STIX]{x1D703}^{i}\in x_{i_{j}}\unicode[STIX]{x1D703}^{i_{j}}(1+\unicode[STIX]{x1D70B}_{j}^{N}{\mathcal{O}}_{j})\subset \mathop{\bigcup }_{l\in \mathbb{Z}}(1+\unicode[STIX]{x1D70B}_{j}^{N}{\mathcal{O}}_{j})\unicode[STIX]{x1D70B}_{j}^{lN}.\end{eqnarray}$$
D’après (6.2), on a
 $D^{n}\subset \unicode[STIX]{x1D713}(D_{v_{0}})$
.◻
$D^{n}\subset \unicode[STIX]{x1D713}(D_{v_{0}})$
.◻
On rappelle la définition des variétés toriques standards [Reference Cao and XuCX13, Déf. 2.12].
Définition 6.3. Soit
![]() $K$
une
$K$
une
![]() $k$
-algèbre finie séparable. La variété torique standard par rapport à
$k$
-algèbre finie séparable. La variété torique standard par rapport à
![]() $K/k$
est la sous-variété torique
$K/k$
est la sous-variété torique
 $(\text{Res}_{K/k}\,\mathbb{G}_{m}{\hookrightarrow}Z)$
de
$(\text{Res}_{K/k}\,\mathbb{G}_{m}{\hookrightarrow}Z)$
de
 $(\text{Res}_{K/k}\,\mathbb{G}_{m}{\hookrightarrow}\text{Res}_{K/k}\,\mathbb{A}^{1})$
avec
$(\text{Res}_{K/k}\,\mathbb{G}_{m}{\hookrightarrow}\text{Res}_{K/k}\,\mathbb{A}^{1})$
avec
 $$\begin{eqnarray}Z:=\text{Res}_{K/k}\,\mathbb{A}^{1}\setminus [(\text{Res}_{K/k}\,\mathbb{A}^{1}\setminus \text{Res}_{K/k}\,\mathbb{G}_{m})_{\text{sing}}].\end{eqnarray}$$
$$\begin{eqnarray}Z:=\text{Res}_{K/k}\,\mathbb{A}^{1}\setminus [(\text{Res}_{K/k}\,\mathbb{A}^{1}\setminus \text{Res}_{K/k}\,\mathbb{G}_{m})_{\text{sing}}].\end{eqnarray}$$
Corollaire 6.4. Soit
 $(T{\hookrightarrow}Z)$
une variété torique standard. Soient
$(T{\hookrightarrow}Z)$
une variété torique standard. Soient
![]() $v_{0}$
une place de
$v_{0}$
une place de
![]() $k$
et
$k$
et
 $D_{v_{0}}\subset T(k_{v_{0}})$
un sous-groupe ouvert d’indice fini. Pour tout fermé
$D_{v_{0}}\subset T(k_{v_{0}})$
un sous-groupe ouvert d’indice fini. Pour tout fermé
![]() $F\subset Z$
de codimension
$F\subset Z$
de codimension
![]() ${\geqslant}2$
et tout ouvert non vide
${\geqslant}2$
et tout ouvert non vide
 $W\subset (Z\setminus F)(\mathbf{A}_{k})$
, si
$W\subset (Z\setminus F)(\mathbf{A}_{k})$
, si
 $(D_{v_{0}}\cdot W)\cap (Z\setminus F)(\mathbf{A}_{k})=W$
, alors on a
$(D_{v_{0}}\cdot W)\cap (Z\setminus F)(\mathbf{A}_{k})=W$
, alors on a
 $T(k)\cap W\neq \emptyset$
.
$T(k)\cap W\neq \emptyset$
.
Démonstration.
Puisque
 $\text{codim}(\text{Res}_{K/k}\,\mathbb{A}^{1}\setminus Z,\text{Res}_{K/k}\,\mathbb{A}^{1})\geqslant 2$
, une application du théorème 6.2 donne le résultat.◻
$\text{codim}(\text{Res}_{K/k}\,\mathbb{A}^{1}\setminus Z,\text{Res}_{K/k}\,\mathbb{A}^{1})\geqslant 2$
, une application du théorème 6.2 donne le résultat.◻
6.2 Fibration sur une variété torique standard
On a besoin d’une généralisation du théorème de Tchebotarev ‘géométrique’ (Ekedahl [Reference EkedahlEke90, Lem. 1.2]) :
Lemme 6.5. Soient
![]() $X$
,
$X$
,
![]() $Y$
,
$Y$
,
![]() $Z$
des schémas intègres de type fini sur
$Z$
des schémas intègres de type fini sur
![]() ${\mathcal{O}}_{k}$
, et
${\mathcal{O}}_{k}$
, et
 $Y\xrightarrow[{}]{p}X$
,
$Y\xrightarrow[{}]{p}X$
,
 $X\xrightarrow[{}]{f}Z$
deux
$X\xrightarrow[{}]{f}Z$
deux
![]() ${\mathcal{O}}_{k}$
-morphismes. Supposons que
${\mathcal{O}}_{k}$
-morphismes. Supposons que
![]() $f$
et
$f$
et
![]() $f\circ p$
sont lisses à fibres géométriquement intègres et
$f\circ p$
sont lisses à fibres géométriquement intègres et
![]() $p$
est fini étale galoisenne de groupe de Galois
$p$
est fini étale galoisenne de groupe de Galois
![]() $\unicode[STIX]{x1D6E4}$
. Soit
$\unicode[STIX]{x1D6E4}$
. Soit
![]() $C$
une classe de conjugaison de
$C$
une classe de conjugaison de
![]() $\unicode[STIX]{x1D6E4}$
et
$\unicode[STIX]{x1D6E4}$
et
 $c:=|C|/|\unicode[STIX]{x1D6E4}|$
. Pour chaque place
$c:=|C|/|\unicode[STIX]{x1D6E4}|$
. Pour chaque place
![]() $v\in \unicode[STIX]{x1D6FA}_{k}$
et chaque
$v\in \unicode[STIX]{x1D6FA}_{k}$
et chaque
 $z\in Z(k(v))$
, soit
$z\in Z(k(v))$
, soit
![]() $N_{C}(z)$
le nombre de
$N_{C}(z)$
le nombre de
 $x\in X_{z}(k(v))$
tel que le Frobenius
$x\in X_{z}(k(v))$
tel que le Frobenius
![]() $\text{Fr}_{x}$
de
$\text{Fr}_{x}$
de
![]() $x$
soit dans
$x$
soit dans
![]() $C$
. Alors
$C$
. Alors
 $$\begin{eqnarray}\frac{N_{C}(z)}{|X_{z}(k(v))|}-c=O(|k(v)|^{-1/2})\end{eqnarray}$$
$$\begin{eqnarray}\frac{N_{C}(z)}{|X_{z}(k(v))|}-c=O(|k(v)|^{-1/2})\end{eqnarray}$$
où la constante dans
![]() $O(-)$
ne dépend ni de
$O(-)$
ne dépend ni de
![]() $v$
ni de
$v$
ni de
![]() $z$
.
$z$
.
Démonstration.
Le résultat découle de la démonstration standard de [Reference EkedahlEke90, Lem. 1.2] avec la formule des traces de Lefschetz
 $$\begin{eqnarray}\mathop{\sum }_{x\in X_{z}(k(v))}\unicode[STIX]{x1D712}(\text{Fr}_{x})=\mathop{\sum }_{0\leqslant i\leqslant 2\dim (X_{z})}(-1)^{i}\,\text{Tr}(\text{Fr}^{\ast },H_{c}^{i}(X_{\bar{z}},V_{\unicode[STIX]{x1D712}})),\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{x\in X_{z}(k(v))}\unicode[STIX]{x1D712}(\text{Fr}_{x})=\mathop{\sum }_{0\leqslant i\leqslant 2\dim (X_{z})}(-1)^{i}\,\text{Tr}(\text{Fr}^{\ast },H_{c}^{i}(X_{\bar{z}},V_{\unicode[STIX]{x1D712}})),\end{eqnarray}$$
où
![]() $V_{\unicode[STIX]{x1D712}}$
est défini dans la démonstration de [Reference EkedahlEke90, Lem. 1.2]. Puisque
$V_{\unicode[STIX]{x1D712}}$
est défini dans la démonstration de [Reference EkedahlEke90, Lem. 1.2]. Puisque
![]() $R^{i}f_{!}V_{\unicode[STIX]{x1D712}}$
est constructible et
$R^{i}f_{!}V_{\unicode[STIX]{x1D712}}$
est constructible et
 $H_{c}^{i}(X_{\bar{z}},V_{\unicode[STIX]{x1D712}})=(R^{i}f_{!}V_{\unicode[STIX]{x1D712}})_{\bar{z}}$
, les dimensions des
$H_{c}^{i}(X_{\bar{z}},V_{\unicode[STIX]{x1D712}})=(R^{i}f_{!}V_{\unicode[STIX]{x1D712}})_{\bar{z}}$
, les dimensions des
 $H_{c}^{i}(X_{\bar{z}},V_{\unicode[STIX]{x1D712}})$
sont bornées uniformément. De plus, la valeur absolue de la valeur propre de
$H_{c}^{i}(X_{\bar{z}},V_{\unicode[STIX]{x1D712}})$
sont bornées uniformément. De plus, la valeur absolue de la valeur propre de
![]() $\text{Fr}^{\ast }$
en
$\text{Fr}^{\ast }$
en
 $H_{c}^{i}(X_{\bar{z}},V_{\unicode[STIX]{x1D712}})$
est inférieure ou égale à
$H_{c}^{i}(X_{\bar{z}},V_{\unicode[STIX]{x1D712}})$
est inférieure ou égale à
 $|k(v)|^{i/2}$
. Le reste de la démonstration est la même que celle de [Reference EkedahlEke90, Lem. 1.2].◻
$|k(v)|^{i/2}$
. Le reste de la démonstration est la même que celle de [Reference EkedahlEke90, Lem. 1.2].◻
Lemme 6.6. Soient
![]() $Z$
un ouvert de
$Z$
un ouvert de
![]() $\mathbb{A}^{n}$
satisfaisant
$\mathbb{A}^{n}$
satisfaisant
 $\text{codim}(\mathbb{A}^{n}\setminus Z,\mathbb{A}^{n})\geqslant 2$
et
$\text{codim}(\mathbb{A}^{n}\setminus Z,\mathbb{A}^{n})\geqslant 2$
et
![]() $V$
un ouvert de
$V$
un ouvert de
![]() $Z$
. Soient
$Z$
. Soient
![]() $\{C_{i}\}_{i\in I}$
les composantes connexes de
$\{C_{i}\}_{i\in I}$
les composantes connexes de
![]() $Z\setminus V$
et
$Z\setminus V$
et
![]() $k_{i}$
la fermeture intégrale de
$k_{i}$
la fermeture intégrale de
![]() $k$
dans
$k$
dans
![]() $k(C_{i})$
. Alors la suite exacte (3.3) induit un isomorphisme
$k(C_{i})$
. Alors la suite exacte (3.3) induit un isomorphisme
 $$\begin{eqnarray}\unicode[STIX]{x2202}:\text{Br}_{a}(V)\stackrel{{\sim}}{\rightarrow }\bigoplus _{i}H^{1}(k_{i},\mathbb{Q}/\mathbb{Z}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}:\text{Br}_{a}(V)\stackrel{{\sim}}{\rightarrow }\bigoplus _{i}H^{1}(k_{i},\mathbb{Q}/\mathbb{Z}).\end{eqnarray}$$
Démonstration.
On peut supposer que
![]() $Z\setminus V$
est lisse. Puisque
$Z\setminus V$
est lisse. Puisque
 $\text{codim}(\mathbb{A}^{n}\setminus Z,\mathbb{A}^{n})\geqslant 2$
, on a
$\text{codim}(\mathbb{A}^{n}\setminus Z,\mathbb{A}^{n})\geqslant 2$
, on a
 $\text{Br}(Z)\cong \text{Br}(k)$
et
$\text{Br}(Z)\cong \text{Br}(k)$
et
 $H^{i}(Z_{\bar{k}},\mathbb{Q}/\mathbb{Z}(1))=0$
pour
$H^{i}(Z_{\bar{k}},\mathbb{Q}/\mathbb{Z}(1))=0$
pour
![]() $i=1,2$
. Puisque
$i=1,2$
. Puisque
 $V(k)\neq \emptyset$
, le morphisme
$V(k)\neq \emptyset$
, le morphisme
 $$\begin{eqnarray}H^{3}(Z,\mathbb{Q}/\mathbb{Z}(1))\rightarrow H^{3}(V,\mathbb{Q}/\mathbb{Z}(1))\oplus H^{3}(Z_{\bar{k}},\mathbb{Q}/\mathbb{Z}(1))\end{eqnarray}$$
$$\begin{eqnarray}H^{3}(Z,\mathbb{Q}/\mathbb{Z}(1))\rightarrow H^{3}(V,\mathbb{Q}/\mathbb{Z}(1))\oplus H^{3}(Z_{\bar{k}},\mathbb{Q}/\mathbb{Z}(1))\end{eqnarray}$$
est donc injectif (suite spectrale de Hochschild–Serre). La suite exacte (3.3) induit un diagramme commutatif de suites exactes :

d’où le résultat. ◻
Théorème 6.7. Soient
 $(T{\hookrightarrow}Z)$
une variété torique standard,
$(T{\hookrightarrow}Z)$
une variété torique standard,
![]() $G$
un groupe linéaire connexe et
$G$
un groupe linéaire connexe et
![]() $G\xrightarrow[{}]{\unicode[STIX]{x1D711}}T$
un homomorphisme surjectif de noyau connexe. Soient
$G\xrightarrow[{}]{\unicode[STIX]{x1D711}}T$
un homomorphisme surjectif de noyau connexe. Soient
![]() $X$
une
$X$
une
![]() $G$
-variété lisse, géométriquement intègre et
$G$
-variété lisse, géométriquement intègre et
 $X\xrightarrow[{}]{f}Z$
un
$X\xrightarrow[{}]{f}Z$
un
![]() $G$
-morphisme lisse surjectif à fibres géométriquement intègres. Notons
$G$
-morphisme lisse surjectif à fibres géométriquement intègres. Notons
 $U:=X\times _{Z}T$
. Soit
$U:=X\times _{Z}T$
. Soit
 $B\subset \text{Br}_{G}(U)$
(cf. (3.1)) un sous-groupe fini. Soient
$B\subset \text{Br}_{G}(U)$
(cf. (3.1)) un sous-groupe fini. Soient
 $v_{0}\in \unicode[STIX]{x1D6FA}_{k}$
une place et
$v_{0}\in \unicode[STIX]{x1D6FA}_{k}$
une place et
 $G(k_{v_{0}})^{0}\subset G(k_{v_{0}})$
un sous-groupe d’indice fini. Alors, pour tout fermé
$G(k_{v_{0}})^{0}\subset G(k_{v_{0}})$
un sous-groupe d’indice fini. Alors, pour tout fermé
![]() $F\subset X$
de codimension
$F\subset X$
de codimension
![]() ${\geqslant}2$
et tout ouvert
${\geqslant}2$
et tout ouvert
![]() $W$
de
$W$
de
 $(X\setminus F)(\mathbf{A}_{k})$
satisfaisant
$(X\setminus F)(\mathbf{A}_{k})$
satisfaisant
 $W^{\text{Br}(X)\cap (B+f|_{U}^{\ast }\,\text{Br}_{e}(T))}\neq \emptyset$
, il existe
$W^{\text{Br}(X)\cap (B+f|_{U}^{\ast }\,\text{Br}_{e}(T))}\neq \emptyset$
, il existe
 $t\in T(k)$
de fibre
$t\in T(k)$
de fibre
 $F_{t}\subset X_{t}$
, tel que
$F_{t}\subset X_{t}$
, tel que
 $$\begin{eqnarray}\text{codim}(F_{t},X_{t})\geqslant 2~~~\text{et}~~~(X_{t}\setminus F_{t})(\mathbf{A}_{k})^{B}\cap (G(k_{v_{0}})^{0}\cdot W)\neq \emptyset .\end{eqnarray}$$
$$\begin{eqnarray}\text{codim}(F_{t},X_{t})\geqslant 2~~~\text{et}~~~(X_{t}\setminus F_{t})(\mathbf{A}_{k})^{B}\cap (G(k_{v_{0}})^{0}\cdot W)\neq \emptyset .\end{eqnarray}$$
Démonstration.
Puisque
![]() $f$
est lisse, il existe un fermé
$f$
est lisse, il existe un fermé
![]() $F_{1}\subset Z$
tel que
$F_{1}\subset Z$
tel que
 $f(X\setminus F)=Z\setminus F_{1}$
.
$f(X\setminus F)=Z\setminus F_{1}$
.
Soient
![]() $\{C_{i}\}_{i\in I}$
les composantes connexes de
$\{C_{i}\}_{i\in I}$
les composantes connexes de
![]() $Z\setminus T$
et
$Z\setminus T$
et
 $D_{i}:=X\times _{Z}C_{i}$
les composantes connexes de
$D_{i}:=X\times _{Z}C_{i}$
les composantes connexes de
![]() $X\setminus U$
. Par hypothèse, les variétés
$X\setminus U$
. Par hypothèse, les variétés
![]() $C_{i}$
et
$C_{i}$
et
![]() $D_{i}$
sont lisses intègres. D’après (3.3), on a une suite exacte :
$D_{i}$
sont lisses intègres. D’après (3.3), on a une suite exacte :
 $$\begin{eqnarray}0\rightarrow \text{Br}(X)\cap (B+f|_{U}^{\ast }\,\text{Br}_{e}(T))\rightarrow (B+f|_{U}^{\ast }\,\text{Br}_{e}(T))\mathop{\xrightarrow[{}]{\unicode[STIX]{x2202}}\bigoplus }\nolimits_{i}H^{1}(D_{i},\mathbb{Q}/\mathbb{Z}).\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow \text{Br}(X)\cap (B+f|_{U}^{\ast }\,\text{Br}_{e}(T))\rightarrow (B+f|_{U}^{\ast }\,\text{Br}_{e}(T))\mathop{\xrightarrow[{}]{\unicode[STIX]{x2202}}\bigoplus }\nolimits_{i}H^{1}(D_{i},\mathbb{Q}/\mathbb{Z}).\end{eqnarray}$$
Par le lemme 3.5, pour tout
![]() $i$
, il existe un revêtement fini étale galoisien abélien
$i$
, il existe un revêtement fini étale galoisien abélien
 $D_{i}^{\prime }\xrightarrow[{}]{\unicode[STIX]{x1D70B}_{i}}D_{i}$
tel que
$D_{i}^{\prime }\xrightarrow[{}]{\unicode[STIX]{x1D70B}_{i}}D_{i}$
tel que
![]() $D_{i}^{\prime }$
soit une
$D_{i}^{\prime }$
soit une
![]() $G$
-variété intègre,
$G$
-variété intègre,
![]() $\unicode[STIX]{x1D70B}_{i}$
soit un
$\unicode[STIX]{x1D70B}_{i}$
soit un
![]() $G$
-morphisme et
$G$
-morphisme et
 $\unicode[STIX]{x2202}(b)\in H^{1}(D_{i}^{\prime }/D_{i},\mathbb{Q}/\mathbb{Z})$
.
$\unicode[STIX]{x2202}(b)\in H^{1}(D_{i}^{\prime }/D_{i},\mathbb{Q}/\mathbb{Z})$
.
Soient
![]() $k_{i}$
la fermeture intégrale de
$k_{i}$
la fermeture intégrale de
![]() $k$
dans
$k$
dans
![]() $k(C_{i})$
et
$k(C_{i})$
et
![]() $k_{i}^{\prime }$
la fermeture intégrale de
$k_{i}^{\prime }$
la fermeture intégrale de
![]() $k$
dans
$k$
dans
![]() $k(D_{i}^{\prime })$
. Par hypothèse, la fermeture intégrale
$k(D_{i}^{\prime })$
. Par hypothèse, la fermeture intégrale
![]() $k$
dans
$k$
dans
![]() $k(D_{i})$
est
$k(D_{i})$
est
![]() $k_{i}$
. D’après [Reference Cao and XuCX15, Prop. 2.2], le morphisme
$k_{i}$
. D’après [Reference Cao and XuCX15, Prop. 2.2], le morphisme
 $D_{i}^{\prime }\rightarrow C_{i}\times _{k_{i}}k_{i}^{\prime }$
est lisse à fibres géométriquement intègres.
$D_{i}^{\prime }\rightarrow C_{i}\times _{k_{i}}k_{i}^{\prime }$
est lisse à fibres géométriquement intègres.
Soit
 $B_{X}:=\text{Br}(X)\cap (B+f|_{U}^{\ast }\,\text{Br}_{e}(T))$
. D’après le lemme 3.3,
$B_{X}:=\text{Br}(X)\cap (B+f|_{U}^{\ast }\,\text{Br}_{e}(T))$
. D’après le lemme 3.3,
 $(f|_{U}^{\ast }\,\text{Br}_{e}(T))\cap \text{Br}(X)=0$
et donc
$(f|_{U}^{\ast }\,\text{Br}_{e}(T))\cap \text{Br}(X)=0$
et donc
![]() $B_{X}$
est fini. D’après la proposition 3.2(2) et (3), on a
$B_{X}$
est fini. D’après la proposition 3.2(2) et (3), on a
 $B_{X}\subset \text{Br}_{G}(X)$
. D’après le lemme 6.6 pour
$B_{X}\subset \text{Br}_{G}(X)$
. D’après le lemme 6.6 pour
![]() $T$
et la suite exacte (3.3), on a le diagramme suivant commutatif de suites exactes.
$T$
et la suite exacte (3.3), on a le diagramme suivant commutatif de suites exactes.

Alors
 $\text{Im}(\unicode[STIX]{x2202}_{0})\subset \bigoplus _{i}H^{1}((D_{i}^{\prime }\times _{k_{i}^{\prime }}\bar{k})/D_{i},\mathbb{Q}/\mathbb{Z})$
. Ceci induit le diagramme suivant commutatif de suites exactes.
$\text{Im}(\unicode[STIX]{x2202}_{0})\subset \bigoplus _{i}H^{1}((D_{i}^{\prime }\times _{k_{i}^{\prime }}\bar{k})/D_{i},\mathbb{Q}/\mathbb{Z})$
. Ceci induit le diagramme suivant commutatif de suites exactes.

Soit
 $\text{Br}_{G}(X)\xrightarrow[{}]{\unicode[STIX]{x1D706}}\text{Br}_{e}(G)$
l’homomorphisme de Sansuc (cf. Définition 3.8). Après avoir rétréci le sous-groupe d’indice fini
$\text{Br}_{G}(X)\xrightarrow[{}]{\unicode[STIX]{x1D706}}\text{Br}_{e}(G)$
l’homomorphisme de Sansuc (cf. Définition 3.8). Après avoir rétréci le sous-groupe d’indice fini
 $G(k_{v_{0}})^{0}$
, on peut supposer que tout élément de
$G(k_{v_{0}})^{0}$
, on peut supposer que tout élément de
![]() $\unicode[STIX]{x1D706}(B_{X})$
s’annule sur
$\unicode[STIX]{x1D706}(B_{X})$
s’annule sur
 $G(k_{v_{0}})^{0}$
. Par la proposition 3.9, pour tout
$G(k_{v_{0}})^{0}$
. Par la proposition 3.9, pour tout
 $x\in X(\mathbf{A}_{k})$
, on a que tout élément de
$x\in X(\mathbf{A}_{k})$
, on a que tout élément de
![]() $B_{X}$
est constant sur
$B_{X}$
est constant sur
 $G(k_{v_{0}})^{0}\cdot x$
.
$G(k_{v_{0}})^{0}\cdot x$
.
Soient
 $l:=\dim (Z)$
,
$l:=\dim (Z)$
,
 $\unicode[STIX]{x1D6E4}_{i}:=\text{Gal}(D_{i}^{\prime }/k_{i}^{\prime }D_{i})$
et
$\unicode[STIX]{x1D6E4}_{i}:=\text{Gal}(D_{i}^{\prime }/k_{i}^{\prime }D_{i})$
et
 $W_{1}:=(G(k_{v_{0}})^{0}\cdot W)\cap (X\setminus F)(\mathbf{A}_{k})$
.
$W_{1}:=(G(k_{v_{0}})^{0}\cdot W)\cap (X\setminus F)(\mathbf{A}_{k})$
.
Puisque
![]() $T$
est quasi-trivial, il existe des extensions de corps
$T$
est quasi-trivial, il existe des extensions de corps
![]() $L_{j}/k$
telles que
$L_{j}/k$
telles que
 $T\cong \text{Res}_{\prod _{j}L_{j}/k}\,\mathbb{G}_{m}$
. En fait,
$T\cong \text{Res}_{\prod _{j}L_{j}/k}\,\mathbb{G}_{m}$
. En fait,
 $\prod _{j}L_{j}\cong \prod _{i}k_{i}$
, mais on ne l’utilise pas. Soit
$\prod _{j}L_{j}\cong \prod _{i}k_{i}$
, mais on ne l’utilise pas. Soit
![]() $\unicode[STIX]{x1D6FA}_{0}$
l’ensemble des places
$\unicode[STIX]{x1D6FA}_{0}$
l’ensemble des places
![]() $v\in \unicode[STIX]{x1D6FA}_{k}$
totalement décomposées dans la fermeture galoisienne de
$v\in \unicode[STIX]{x1D6FA}_{k}$
totalement décomposées dans la fermeture galoisienne de
![]() $k_{i}^{\prime }/k$
pour tout
$k_{i}^{\prime }/k$
pour tout
![]() $i$
et de
$i$
et de
![]() $L_{j}/k$
pour tout
$L_{j}/k$
pour tout
![]() $j$
. Alors
$j$
. Alors
![]() $\unicode[STIX]{x1D6FA}_{0}$
est infini et pour tout
$\unicode[STIX]{x1D6FA}_{0}$
est infini et pour tout
![]() $v\in \unicode[STIX]{x1D6FA}_{0}$
, on a
$v\in \unicode[STIX]{x1D6FA}_{0}$
, on a
 $T_{k_{v}}\cong \mathbb{G}_{m,k_{v}}^{l}$
. Par la définition 6.3, on a
$T_{k_{v}}\cong \mathbb{G}_{m,k_{v}}^{l}$
. Par la définition 6.3, on a
 $$\begin{eqnarray}Z_{k_{v}}\cong \text{Spec}\,k_{v}[t_{1},\ldots ,t_{l}]\bigg\backslash\mathop{\bigcup }_{n\neq m}V(t_{n},t_{m})~~~\text{et}~~~T_{k_{v}}\cong \text{Spec}\,k_{v}[t_{1},t_{1}^{-1},\ldots ,t_{l},t_{l}^{-1}].\end{eqnarray}$$
$$\begin{eqnarray}Z_{k_{v}}\cong \text{Spec}\,k_{v}[t_{1},\ldots ,t_{l}]\bigg\backslash\mathop{\bigcup }_{n\neq m}V(t_{n},t_{m})~~~\text{et}~~~T_{k_{v}}\cong \text{Spec}\,k_{v}[t_{1},t_{1}^{-1},\ldots ,t_{l},t_{l}^{-1}].\end{eqnarray}$$
Soit
![]() $S$
un sous-ensemble fini de
$S$
un sous-ensemble fini de
![]() $\unicode[STIX]{x1D6FA}_{k}$
tel que
$\unicode[STIX]{x1D6FA}_{k}$
tel que
 $v_{0}\cup \infty _{k}\subset S$
. On agrandit
$v_{0}\cup \infty _{k}\subset S$
. On agrandit
![]() $S$
de façon à avoir les propriétés suivantes :
$S$
de façon à avoir les propriétés suivantes :
(a) Le
![]() $k$
-morphisme
$k$
-morphisme
![]() $f$
s’étend en un
$f$
s’étend en un
![]() ${\mathcal{O}}_{S}$
-morphisme lisse à fibres géométriquement intègres
${\mathcal{O}}_{S}$
-morphisme lisse à fibres géométriquement intègres
 ${\mathcal{X}}\rightarrow {\mathcal{Z}}$
de
${\mathcal{X}}\rightarrow {\mathcal{Z}}$
de
![]() ${\mathcal{O}}_{S}$
-schémas lisses, tel que pour tout point fermé
${\mathcal{O}}_{S}$
-schémas lisses, tel que pour tout point fermé
 $z\in {\mathcal{Z}}\setminus {\mathcal{F}}_{1}$
, la fibre
$z\in {\mathcal{Z}}\setminus {\mathcal{F}}_{1}$
, la fibre
![]() $f^{-1}(z)$
possède un
$f^{-1}(z)$
possède un
![]() $k(z)$
-point
$k(z)$
-point
![]() $x\notin {\mathcal{F}}$
, où
$x\notin {\mathcal{F}}$
, où
![]() ${\mathcal{F}}$
est l’adhérence de
${\mathcal{F}}$
est l’adhérence de
![]() $F$
dans
$F$
dans
![]() ${\mathcal{X}}$
et
${\mathcal{X}}$
et
![]() ${\mathcal{F}}_{1}$
est l’adhérence de
${\mathcal{F}}_{1}$
est l’adhérence de
![]() $F_{1}$
dans
$F_{1}$
dans
![]() ${\mathcal{Z}}$
. Ceci est possible par les estimées de Lang-Weil [Reference SkorobogatovSko90, Thm. 1, étape 3]. Par le lemme de Hensel, pour tout
${\mathcal{Z}}$
. Ceci est possible par les estimées de Lang-Weil [Reference SkorobogatovSko90, Thm. 1, étape 3]. Par le lemme de Hensel, pour tout
![]() $v\notin S$
, l’application
$v\notin S$
, l’application
 $({\mathcal{X}}\setminus {\mathcal{F}})({\mathcal{O}}_{v})\rightarrow ({\mathcal{Z}}\setminus {\mathcal{F}}_{1})({\mathcal{O}}_{v})$
est donc surjective.
$({\mathcal{X}}\setminus {\mathcal{F}})({\mathcal{O}}_{v})\rightarrow ({\mathcal{Z}}\setminus {\mathcal{F}}_{1})({\mathcal{O}}_{v})$
est donc surjective.
(b) Les extensions
![]() $k_{i}/k$
et
$k_{i}/k$
et
![]() $k_{i}^{\prime }/k_{i}$
induisent des revêtements finis étales
$k_{i}^{\prime }/k_{i}$
induisent des revêtements finis étales
 ${\mathcal{O}}_{k_{i},S}/{\mathcal{O}}_{S}$
et
${\mathcal{O}}_{k_{i},S}/{\mathcal{O}}_{S}$
et
 ${\mathcal{O}}_{k_{i}^{\prime },S}/{\mathcal{O}}_{k_{i},S}$
.
${\mathcal{O}}_{k_{i}^{\prime },S}/{\mathcal{O}}_{k_{i},S}$
.
(c) Le sous-schéma
 ${\mathcal{C}}_{i}:=\overline{C_{i}}\subset {\mathcal{Z}}$
est lisse à fibres géométriquement intègres sur
${\mathcal{C}}_{i}:=\overline{C_{i}}\subset {\mathcal{Z}}$
est lisse à fibres géométriquement intègres sur
![]() ${\mathcal{O}}_{k_{i},S}$
. Soient
${\mathcal{O}}_{k_{i},S}$
. Soient
 ${\mathcal{D}}_{i}:={\mathcal{C}}_{i}\times _{{\mathcal{Z}}}{\mathcal{X}}$
,
${\mathcal{D}}_{i}:={\mathcal{C}}_{i}\times _{{\mathcal{Z}}}{\mathcal{X}}$
,
 ${\mathcal{T}}:={\mathcal{Z}}\setminus \bigcup _{i}{\mathcal{C}}_{i}$
et
${\mathcal{T}}:={\mathcal{Z}}\setminus \bigcup _{i}{\mathcal{C}}_{i}$
et
 ${\mathcal{U}}:={\mathcal{T}}\times _{{\mathcal{Z}}}{\mathcal{X}}$
.
${\mathcal{U}}:={\mathcal{T}}\times _{{\mathcal{Z}}}{\mathcal{X}}$
.
(d) Les éléments de
![]() $B_{X}$
appartiennent à
$B_{X}$
appartiennent à
![]() $\text{Br}({\mathcal{X}})$
et les éléments de
$\text{Br}({\mathcal{X}})$
et les éléments de
![]() $B$
appartiennent à
$B$
appartiennent à
![]() $\text{Br}({\mathcal{U}})$
.
$\text{Br}({\mathcal{U}})$
.
(e) Le revêtement
 $D_{i}^{\prime }\xrightarrow[{}]{\unicode[STIX]{x1D70B}_{i}}D_{i}$
s’étend en un
$D_{i}^{\prime }\xrightarrow[{}]{\unicode[STIX]{x1D70B}_{i}}D_{i}$
s’étend en un
![]() ${\mathcal{O}}_{S}$
-revêtement fini étale galoisien abélien
${\mathcal{O}}_{S}$
-revêtement fini étale galoisien abélien
 ${\mathcal{D}}_{i}^{\prime }\rightarrow {\mathcal{D}}_{i}$
tel que
${\mathcal{D}}_{i}^{\prime }\rightarrow {\mathcal{D}}_{i}$
tel que
![]() ${\mathcal{D}}_{i}^{\prime }$
soit un schéma sur
${\mathcal{D}}_{i}^{\prime }$
soit un schéma sur
![]() ${\mathcal{O}}_{k_{i}^{\prime },S}$
, les résidus des éléments de
${\mathcal{O}}_{k_{i}^{\prime },S}$
, les résidus des éléments de
![]() $B$
soient dans
$B$
soient dans
 $H^{1}({\mathcal{D}}_{i}^{\prime }/{\mathcal{D}}_{i},\mathbb{Q}/\mathbb{Z})$
et
$H^{1}({\mathcal{D}}_{i}^{\prime }/{\mathcal{D}}_{i},\mathbb{Q}/\mathbb{Z})$
et
 ${\mathcal{D}}_{i}^{\prime }\rightarrow {\mathcal{C}}_{i}\times _{{\mathcal{O}}_{k_{i},S}}{\mathcal{O}}_{k_{i}^{\prime },S}$
soit lisse à fibres géométriquement intègres.
${\mathcal{D}}_{i}^{\prime }\rightarrow {\mathcal{C}}_{i}\times _{{\mathcal{O}}_{k_{i},S}}{\mathcal{O}}_{k_{i}^{\prime },S}$
soit lisse à fibres géométriquement intègres.
(f) Il existe un ouvert
 $W_{2}\subset W_{1}\subset (X\setminus F)(\mathbf{A}_{k})$
tel que
$W_{2}\subset W_{1}\subset (X\setminus F)(\mathbf{A}_{k})$
tel que
 $$\begin{eqnarray}W_{2}^{B_{X}}=W_{2}\neq \emptyset ,~~~W_{2}=(G(k_{v_{0}})^{0}\cdot W_{2})\cap (X\setminus F)(\mathbf{A}_{k})~~~\text{et}~~~W_{2}=W_{v_{0}}\times W_{S\setminus v_{0}}\times \mathop{\prod }_{v\notin S}({\mathcal{X}}\setminus {\mathcal{F}})({\mathcal{O}}_{v})\end{eqnarray}$$
$$\begin{eqnarray}W_{2}^{B_{X}}=W_{2}\neq \emptyset ,~~~W_{2}=(G(k_{v_{0}})^{0}\cdot W_{2})\cap (X\setminus F)(\mathbf{A}_{k})~~~\text{et}~~~W_{2}=W_{v_{0}}\times W_{S\setminus v_{0}}\times \mathop{\prod }_{v\notin S}({\mathcal{X}}\setminus {\mathcal{F}})({\mathcal{O}}_{v})\end{eqnarray}$$
avec
 $W_{S\setminus v_{0}}\subset \prod _{v\in S\setminus \{v_{0}\}}(X\setminus F)(k_{v})$
un ouvert et
$W_{S\setminus v_{0}}\subset \prod _{v\in S\setminus \{v_{0}\}}(X\setminus F)(k_{v})$
un ouvert et
 $W_{v_{0}}\subset (X\setminus F)(k_{v_{0}})$
un ouvert.
$W_{v_{0}}\subset (X\setminus F)(k_{v_{0}})$
un ouvert.
(g) Pour tout
 $v\in \unicode[STIX]{x1D6FA}_{0}\setminus (\unicode[STIX]{x1D6FA}_{0}\cap S)$
, on note
$v\in \unicode[STIX]{x1D6FA}_{0}\setminus (\unicode[STIX]{x1D6FA}_{0}\cap S)$
, on note
 ${\mathcal{C}}_{i,v}:={\mathcal{C}}_{i}\times _{{\mathcal{O}}_{k_{i},S}}{\mathcal{O}}_{v}$
,
${\mathcal{C}}_{i,v}:={\mathcal{C}}_{i}\times _{{\mathcal{O}}_{k_{i},S}}{\mathcal{O}}_{v}$
,
 ${\mathcal{D}}_{i,v}:={\mathcal{D}}_{i}\times _{{\mathcal{O}}_{k_{i},S}}{\mathcal{O}}_{v}$
et
${\mathcal{D}}_{i,v}:={\mathcal{D}}_{i}\times _{{\mathcal{O}}_{k_{i},S}}{\mathcal{O}}_{v}$
et
 ${\mathcal{D}}_{i,v}^{\prime }:={\mathcal{D}}_{i}^{\prime }\times _{{\mathcal{O}}_{k_{i}^{\prime },S}}{\mathcal{O}}_{v}$
. On a un diagramme commutatif de schémas intègres :
${\mathcal{D}}_{i,v}^{\prime }:={\mathcal{D}}_{i}^{\prime }\times _{{\mathcal{O}}_{k_{i}^{\prime },S}}{\mathcal{O}}_{v}$
. On a un diagramme commutatif de schémas intègres :

De plus, on a
 $\unicode[STIX]{x1D6E4}_{i}\cong \text{Gal}({\mathcal{D}}_{i}^{\prime }/({\mathcal{D}}_{i}\times _{{\mathcal{O}}_{k_{i},S}}{\mathcal{O}}_{k_{i}^{\prime },S}))\cong \text{Gal}({\mathcal{D}}_{i,v}^{\prime }/{\mathcal{D}}_{i,v})$
.
$\unicode[STIX]{x1D6E4}_{i}\cong \text{Gal}({\mathcal{D}}_{i}^{\prime }/({\mathcal{D}}_{i}\times _{{\mathcal{O}}_{k_{i},S}}{\mathcal{O}}_{k_{i}^{\prime },S}))\cong \text{Gal}({\mathcal{D}}_{i,v}^{\prime }/{\mathcal{D}}_{i,v})$
.
(h) Pour tout
 $v\in \unicode[STIX]{x1D6FA}_{0}\setminus (\unicode[STIX]{x1D6FA}_{0}\cap S)$
, tout
$v\in \unicode[STIX]{x1D6FA}_{0}\setminus (\unicode[STIX]{x1D6FA}_{0}\cap S)$
, tout
![]() $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}_{i}$
et tout
$\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}_{i}$
et tout
 $c\in {\mathcal{C}}_{i,v}(k(v))$
avec
$c\in {\mathcal{C}}_{i,v}(k(v))$
avec
![]() $c\notin {\mathcal{F}}_{1}$
, la fibre
$c\notin {\mathcal{F}}_{1}$
, la fibre
![]() $({\mathcal{D}}_{i,v})_{c}$
possède un
$({\mathcal{D}}_{i,v})_{c}$
possède un
![]() $k(v)$
-point
$k(v)$
-point
![]() $d$
avec
$d$
avec
![]() $d\notin {\mathcal{F}}$
dont le Frobenius est
$d\notin {\mathcal{F}}$
dont le Frobenius est
![]() $\unicode[STIX]{x1D70E}$
. Ceci est possible en appliquant le lemme 6.5 à (6.8).
$\unicode[STIX]{x1D70E}$
. Ceci est possible en appliquant le lemme 6.5 à (6.8).
(i) Pour tout
 $v\in \unicode[STIX]{x1D6FA}_{0}\setminus (\unicode[STIX]{x1D6FA}_{0}\cap S)$
, on note
$v\in \unicode[STIX]{x1D6FA}_{0}\setminus (\unicode[STIX]{x1D6FA}_{0}\cap S)$
, on note
 $(-)_{{\mathcal{O}}_{v}}:=(-)\times _{{\mathcal{O}}_{k,S}}{\mathcal{O}}_{v}$
et on a
$(-)_{{\mathcal{O}}_{v}}:=(-)\times _{{\mathcal{O}}_{k,S}}{\mathcal{O}}_{v}$
et on a
 $$\begin{eqnarray}{\mathcal{Z}}_{{\mathcal{O}}_{v}}\cong \text{Spec}\,{\mathcal{O}}_{v}[t_{1},\ldots ,t_{l}]\bigg\backslash\mathop{\bigcup }_{n\neq m}V(t_{n},t_{m}),~~~{\mathcal{T}}_{{\mathcal{O}}_{v}}\cong \text{Spec}\,{\mathcal{O}}_{v}[t_{1},t_{1}^{-1},\ldots ,t_{l},t_{l}^{-1}]\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{Z}}_{{\mathcal{O}}_{v}}\cong \text{Spec}\,{\mathcal{O}}_{v}[t_{1},\ldots ,t_{l}]\bigg\backslash\mathop{\bigcup }_{n\neq m}V(t_{n},t_{m}),~~~{\mathcal{T}}_{{\mathcal{O}}_{v}}\cong \text{Spec}\,{\mathcal{O}}_{v}[t_{1},t_{1}^{-1},\ldots ,t_{l},t_{l}^{-1}]\end{eqnarray}$$
et il existe une partition
 $\{1,\ldots ,l\}=\coprod _{i}I_{i}$
telle que
$\{1,\ldots ,l\}=\coprod _{i}I_{i}$
telle que
 ${\mathcal{C}}_{i,{\mathcal{O}}_{v}}=\bigcup _{n\in I_{i}}V(t_{n})\subset {\mathcal{Z}}$
et que
${\mathcal{C}}_{i,{\mathcal{O}}_{v}}=\bigcup _{n\in I_{i}}V(t_{n})\subset {\mathcal{Z}}$
et que
 $V(t_{n})\cong {\mathcal{C}}_{i,v}$
.
$V(t_{n})\cong {\mathcal{C}}_{i,v}$
.
Pour chaque
![]() $i$
, on choisit une place
$i$
, on choisit une place
 $v_{i}\in \unicode[STIX]{x1D6FA}_{0}\setminus (\unicode[STIX]{x1D6FA}_{0}\cap S)$
et un
$v_{i}\in \unicode[STIX]{x1D6FA}_{0}\setminus (\unicode[STIX]{x1D6FA}_{0}\cap S)$
et un
![]() $n_{i}\in I_{i}$
tels que pour
$n_{i}\in I_{i}$
tels que pour
![]() $i\neq j$
, on ait
$i\neq j$
, on ait
![]() $v_{i}\neq v_{j}$
. Soient
$v_{i}\neq v_{j}$
. Soient
 ${\mathcal{C}}_{i,n_{i}}:=V(t_{n_{i}})\subset {\mathcal{C}}_{i,{\mathcal{O}}_{v_{i}}}$
,
${\mathcal{C}}_{i,n_{i}}:=V(t_{n_{i}})\subset {\mathcal{C}}_{i,{\mathcal{O}}_{v_{i}}}$
,
 ${\mathcal{D}}_{i,n_{i}}:={\mathcal{C}}_{i,n_{i}}\times _{{\mathcal{Z}}}{\mathcal{X}}$
et
${\mathcal{D}}_{i,n_{i}}:={\mathcal{C}}_{i,n_{i}}\times _{{\mathcal{Z}}}{\mathcal{X}}$
et
 $$\begin{eqnarray}E_{i}:=\{(t_{1},\ldots ,t_{l})\in {\mathcal{O}}_{v_{i}}^{l}:t_{n_{i}}\in m_{v_{i}}\setminus m_{v_{i}}^{2}\text{ et }t_{n}\in {\mathcal{O}}_{v_{i}}^{\times }\text{pour }n\neq n_{i}\}\end{eqnarray}$$
$$\begin{eqnarray}E_{i}:=\{(t_{1},\ldots ,t_{l})\in {\mathcal{O}}_{v_{i}}^{l}:t_{n_{i}}\in m_{v_{i}}\setminus m_{v_{i}}^{2}\text{ et }t_{n}\in {\mathcal{O}}_{v_{i}}^{\times }\text{pour }n\neq n_{i}\}\end{eqnarray}$$
un ouvert de
![]() ${\mathcal{Z}}({\mathcal{O}}_{v_{i}})$
. Alors
${\mathcal{Z}}({\mathcal{O}}_{v_{i}})$
. Alors
 ${\mathcal{C}}_{i,n_{i}}\cong {\mathcal{C}}_{i,v_{i}}$
,
${\mathcal{C}}_{i,n_{i}}\cong {\mathcal{C}}_{i,v_{i}}$
,
 ${\mathcal{D}}_{i,n_{i}}\cong {\mathcal{D}}_{i,v_{i}}$
et
${\mathcal{D}}_{i,n_{i}}\cong {\mathcal{D}}_{i,v_{i}}$
et
 ${\mathcal{D}}_{i}^{\prime }\times _{{\mathcal{D}}}{\mathcal{D}}_{i,n_{i}}\cong \bigsqcup _{[k_{i}^{\prime }:k_{i}]}{\mathcal{D}}_{i,v_{i}}^{\prime }$
. Donc le Frobenius en un point de
${\mathcal{D}}_{i}^{\prime }\times _{{\mathcal{D}}}{\mathcal{D}}_{i,n_{i}}\cong \bigsqcup _{[k_{i}^{\prime }:k_{i}]}{\mathcal{D}}_{i,v_{i}}^{\prime }$
. Donc le Frobenius en un point de
 ${\mathcal{D}}_{i,n_{i}}(k(v_{i}))$
pour le revêtement
${\mathcal{D}}_{i,n_{i}}(k(v_{i}))$
pour le revêtement
![]() ${\mathcal{D}}_{i}^{\prime }/{\mathcal{D}}_{i}$
est dans
${\mathcal{D}}_{i}^{\prime }/{\mathcal{D}}_{i}$
est dans
![]() $\unicode[STIX]{x1D6E4}_{i}$
.
$\unicode[STIX]{x1D6E4}_{i}$
.
Pour tout
![]() $b\in B$
et tout
$b\in B$
et tout
 $P_{i}\in {\mathcal{X}}({\mathcal{O}}_{v_{i}})$
avec
$P_{i}\in {\mathcal{X}}({\mathcal{O}}_{v_{i}})$
avec
 $f(P_{i})\in E_{i}$
, on a
$f(P_{i})\in E_{i}$
, on a
 $\bar{P_{i}}:=P_{i}(k(v_{i}))\in {\mathcal{D}}_{i,n_{i}}(k(v_{i}))$
. On a la formule [Reference HarariHar94, Cor. 2.4.3 et pp. 244–245] (voir [Reference Colliot-Thélène and HarariCH16, Formule (3.6)])
$\bar{P_{i}}:=P_{i}(k(v_{i}))\in {\mathcal{D}}_{i,n_{i}}(k(v_{i}))$
. On a la formule [Reference HarariHar94, Cor. 2.4.3 et pp. 244–245] (voir [Reference Colliot-Thélène and HarariCH16, Formule (3.6)])
 $$\begin{eqnarray}b(P_{i})=\unicode[STIX]{x2202}_{i}(b)(\text{Fr}_{\bar{P_{i}}})\in \mathbb{Q}/\mathbb{Z},\end{eqnarray}$$
$$\begin{eqnarray}b(P_{i})=\unicode[STIX]{x2202}_{i}(b)(\text{Fr}_{\bar{P_{i}}})\in \mathbb{Q}/\mathbb{Z},\end{eqnarray}$$
où
 $\text{Fr}_{\bar{P_{i}}}\in \unicode[STIX]{x1D6E4}_{i}\subset \text{Gal}({\mathcal{D}}_{i}^{\prime }/{\mathcal{D}}_{i})$
est le Frobenius en
$\text{Fr}_{\bar{P_{i}}}\in \unicode[STIX]{x1D6E4}_{i}\subset \text{Gal}({\mathcal{D}}_{i}^{\prime }/{\mathcal{D}}_{i})$
est le Frobenius en
![]() $\bar{P_{i}}$
pour le revêtement
$\bar{P_{i}}$
pour le revêtement
![]() ${\mathcal{D}}_{i}^{\prime }/{\mathcal{D}}_{i}$
et
${\mathcal{D}}_{i}^{\prime }/{\mathcal{D}}_{i}$
et
 $$\begin{eqnarray}\unicode[STIX]{x2202}_{i}:\text{Br}({\mathcal{U}})\xrightarrow[{}]{\unicode[STIX]{x2202}}H^{1}({\mathcal{D}}_{i}^{\prime }/{\mathcal{D}}_{i},\mathbb{Q}/\mathbb{Z})\rightarrow H^{1}({\mathcal{D}}_{i,v_{i}}^{\prime }/{\mathcal{D}}_{i,v_{i}},\mathbb{Q}/\mathbb{Z})=\text{Hom}(\unicode[STIX]{x1D6E4}_{i},\mathbb{Q}/\mathbb{Z}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}_{i}:\text{Br}({\mathcal{U}})\xrightarrow[{}]{\unicode[STIX]{x2202}}H^{1}({\mathcal{D}}_{i}^{\prime }/{\mathcal{D}}_{i},\mathbb{Q}/\mathbb{Z})\rightarrow H^{1}({\mathcal{D}}_{i,v_{i}}^{\prime }/{\mathcal{D}}_{i,v_{i}},\mathbb{Q}/\mathbb{Z})=\text{Hom}(\unicode[STIX]{x1D6E4}_{i},\mathbb{Q}/\mathbb{Z}).\end{eqnarray}$$
Par la fonctorialité du résidu, l’application
![]() $\bar{\unicode[STIX]{x2202}}$
de (6.7) satisfait
$\bar{\unicode[STIX]{x2202}}$
de (6.7) satisfait
 $\bar{\unicode[STIX]{x2202}}=\bigoplus _{i}\unicode[STIX]{x2202}_{i}$
.
$\bar{\unicode[STIX]{x2202}}=\bigoplus _{i}\unicode[STIX]{x2202}_{i}$
.
Notons
 $T(k_{v_{0}})^{0}:=\unicode[STIX]{x1D711}(G(k_{v_{0}})^{0})$
. Puisque
$T(k_{v_{0}})^{0}:=\unicode[STIX]{x1D711}(G(k_{v_{0}})^{0})$
. Puisque
 $H^{1}(k_{v_{0}},\text{Ker}(\unicode[STIX]{x1D711}))$
est fini [Reference Platonov and RapinchukPR94, Thm. 6.14], le sous-groupe
$H^{1}(k_{v_{0}},\text{Ker}(\unicode[STIX]{x1D711}))$
est fini [Reference Platonov and RapinchukPR94, Thm. 6.14], le sous-groupe
 $T(k_{v_{0}})^{0}\subset T(k_{v_{0}})$
est d’indice fini. D’après [Reference ConradCon12, Thm. 4.5],
$T(k_{v_{0}})^{0}\subset T(k_{v_{0}})$
est d’indice fini. D’après [Reference ConradCon12, Thm. 4.5],
![]() $f(W_{2})$
est un ouvert de
$f(W_{2})$
est un ouvert de
 $(Z\setminus F_{1})(\mathbf{A}_{k})$
. Pour tout
$(Z\setminus F_{1})(\mathbf{A}_{k})$
. Pour tout
 $z\in (Z\setminus F_{1})(k_{v_{0}})$
, l’ouvert
$z\in (Z\setminus F_{1})(k_{v_{0}})$
, l’ouvert
 $(X_{z}\setminus F_{z})(k_{v_{0}})$
est dense dans
$(X_{z}\setminus F_{z})(k_{v_{0}})$
est dense dans
 $X_{z}(k_{v_{0}})$
. Donc
$X_{z}(k_{v_{0}})$
. Donc
 $$\begin{eqnarray}(T(k_{v_{0}})^{0}\cdot f(W_{v_{0}}))\cap (Z\setminus F_{1})(k_{v_{0}})=f(W_{v_{0}})~~~\text{et}~~~(T(k_{v_{0}})^{0}\cdot f(W_{2}))\cap (Z\setminus F_{1})(\mathbf{A}_{k})=f(W_{2}).\end{eqnarray}$$
$$\begin{eqnarray}(T(k_{v_{0}})^{0}\cdot f(W_{v_{0}}))\cap (Z\setminus F_{1})(k_{v_{0}})=f(W_{v_{0}})~~~\text{et}~~~(T(k_{v_{0}})^{0}\cdot f(W_{2}))\cap (Z\setminus F_{1})(\mathbf{A}_{k})=f(W_{2}).\end{eqnarray}$$
Par le corollaire 6.4, il existe
 $t\in T(k)\cap f(W_{2})$
tel que
$t\in T(k)\cap f(W_{2})$
tel que
 $t|_{v_{i}}\in E_{i}$
pour tout
$t|_{v_{i}}\in E_{i}$
pour tout
![]() $i$
et que
$i$
et que
 $\text{codim}(F_{t},X_{t})\geqslant 2$
. Alors il existe
$\text{codim}(F_{t},X_{t})\geqslant 2$
. Alors il existe
 $(P_{v})\in W_{2}$
tel que
$(P_{v})\in W_{2}$
tel que
 $f(P_{v})=t$
.
$f(P_{v})=t$
.
Soit
 $t_{i}\in {\mathcal{Z}}(k(v_{i}))$
la spécialisation de
$t_{i}\in {\mathcal{Z}}(k(v_{i}))$
la spécialisation de
![]() $t$
, alors
$t$
, alors
 $t_{i}\in {\mathcal{C}}_{i,n_{i}}(k(v_{i}))$
et
$t_{i}\in {\mathcal{C}}_{i,n_{i}}(k(v_{i}))$
et
![]() $t_{i}\notin {\mathcal{F}}_{1}$
. D’après (6.7), on a un diagramme avec suite exacte :
$t_{i}\notin {\mathcal{F}}_{1}$
. D’après (6.7), on a un diagramme avec suite exacte :

où
![]() $a_{U}$
est l’accouplement de Brauer–Manin,
$a_{U}$
est l’accouplement de Brauer–Manin,
 $(-)^{D}:=\text{Hom}(-,\mathbb{Q}/\mathbb{Z})$
(cf. (1.2)) et, pour
$(-)^{D}:=\text{Hom}(-,\mathbb{Q}/\mathbb{Z})$
(cf. (1.2)) et, pour
 $u\in f^{-1}(t_{i})$
, l’élément
$u\in f^{-1}(t_{i})$
, l’élément
![]() $Fr(u)$
est son Frobenius. Donc
$Fr(u)$
est son Frobenius. Donc
![]() $Fr$
est surjectif par (h). Puisque
$Fr$
est surjectif par (h). Puisque
 $\text{Res}\circ a_{U}=0$
, il existe
$\text{Res}\circ a_{U}=0$
, il existe
 $\{\unicode[STIX]{x1D70E}_{i}\}_{i}\in \bigoplus _{i}\unicode[STIX]{x1D6E4}_{i}$
tel que
$\{\unicode[STIX]{x1D70E}_{i}\}_{i}\in \bigoplus _{i}\unicode[STIX]{x1D6E4}_{i}$
tel que
 $\bar{\unicode[STIX]{x2202}}^{D}(\{\unicode[STIX]{x1D70E}_{i}\})=a_{U}(\{P_{v}\})$
. Alors il existe
$\bar{\unicode[STIX]{x2202}}^{D}(\{\unicode[STIX]{x1D70E}_{i}\})=a_{U}(\{P_{v}\})$
. Alors il existe
 $u_{i}\in (({\mathcal{D}}_{i,n_{i}})_{t_{i}}\setminus {\mathcal{F}}_{t_{i}})(k(v_{i}))$
tel que
$u_{i}\in (({\mathcal{D}}_{i,n_{i}})_{t_{i}}\setminus {\mathcal{F}}_{t_{i}})(k(v_{i}))$
tel que
 $Fr(u_{i})=Fr(\bar{P_{v_{i}}})-\unicode[STIX]{x1D70E}_{i}$
. Par le lemme de Hensel, il existe un point
$Fr(u_{i})=Fr(\bar{P_{v_{i}}})-\unicode[STIX]{x1D70E}_{i}$
. Par le lemme de Hensel, il existe un point
 $Q_{v_{i}}\in ({\mathcal{X}}_{t}\setminus {\mathcal{F}}_{t})({\mathcal{O}}_{v_{i}})$
relevant
$Q_{v_{i}}\in ({\mathcal{X}}_{t}\setminus {\mathcal{F}}_{t})({\mathcal{O}}_{v_{i}})$
relevant
![]() $u_{i}$
. Soit
$u_{i}$
. Soit
 $Q_{v}:=P_{v}$
pour tout
$Q_{v}:=P_{v}$
pour tout
![]() $v$
distinct de l’un des
$v$
distinct de l’un des
![]() $v_{i}$
. Par (6.9),
$v_{i}$
. Par (6.9),
 $\{Q_{v}\}\in (X_{t}\setminus F_{t})(\mathbf{A}_{k})^{B}$
. Donc
$\{Q_{v}\}\in (X_{t}\setminus F_{t})(\mathbf{A}_{k})^{B}$
. Donc
 $\{Q_{v}\}\in (X_{t}\setminus F_{t})(\mathbf{A}_{k})^{B}\cap (G(k_{v_{0}})^{0}\cdot W)$
, d’où le résultat.◻
$\{Q_{v}\}\in (X_{t}\setminus F_{t})(\mathbf{A}_{k})^{B}\cap (G(k_{v_{0}})^{0}\cdot W)$
, d’où le résultat.◻
6.3 Fibration sur un tore
Lemme 6.8. Soient
![]() $X$
et
$X$
et
![]() $Z$
deux variétés lisses géométriquement intègres, et
$Z$
deux variétés lisses géométriquement intègres, et
 $X\xrightarrow[{}]{f}Z$
un morphisme lisse surjectif à fibres géométriquement intègres. Soit
$X\xrightarrow[{}]{f}Z$
un morphisme lisse surjectif à fibres géométriquement intègres. Soit
![]() $U\subset X$
un ouvert tel que
$U\subset X$
un ouvert tel que
![]() $f|_{U}$
soit surjectif. Soient
$f|_{U}$
soit surjectif. Soient
 $W\subset X(\mathbf{A}_{k})$
un ouvert et
$W\subset X(\mathbf{A}_{k})$
un ouvert et
![]() $x\in W$
. Alors il existe
$x\in W$
. Alors il existe
 $u\in W\cap U(\mathbf{A}_{k})$
tel que
$u\in W\cap U(\mathbf{A}_{k})$
tel que
 $f(u)=f(x)$
.
$f(u)=f(x)$
.
Démonstration.
Pour chaque
![]() $z\in Z$
, la fibre
$z\in Z$
, la fibre
![]() $X_{z}$
est lisse intègre et l’ouvert
$X_{z}$
est lisse intègre et l’ouvert
 $U_{z}\subset X_{z}$
est donc dense. Soit
$U_{z}\subset X_{z}$
est donc dense. Soit
 $\{z_{v}\}_{v}=f(x)$
. Pour chaque
$\{z_{v}\}_{v}=f(x)$
. Pour chaque
![]() $v$
, l’ouvert
$v$
, l’ouvert
![]() $U_{z_{v}}(k_{v})$
est dense en
$U_{z_{v}}(k_{v})$
est dense en
 $X_{z_{v}}(k_{v})$
. Puisque
$X_{z_{v}}(k_{v})$
. Puisque
![]() $f|_{U}$
est surjectif, le morphisme
$f|_{U}$
est surjectif, le morphisme
![]() $f|_{U}$
est lisse à fibres géométriquement intègres. Après avoir fixé un modèle entier
$f|_{U}$
est lisse à fibres géométriquement intègres. Après avoir fixé un modèle entier
 ${\mathcal{U}}\rightarrow {\mathcal{Z}}$
de
${\mathcal{U}}\rightarrow {\mathcal{Z}}$
de
![]() $f|_{U}$
, on a que, pour presque toute place
$f|_{U}$
, on a que, pour presque toute place
![]() $v$
, le morphisme
$v$
, le morphisme
 ${\mathcal{U}}({\mathcal{O}}_{v})\rightarrow {\mathcal{Z}}({\mathcal{O}}_{v})$
est surjectif (la démonstration de [Reference ConradCon12, Thm. 4.5]). Le résultat en découle.◻
${\mathcal{U}}({\mathcal{O}}_{v})\rightarrow {\mathcal{Z}}({\mathcal{O}}_{v})$
est surjectif (la démonstration de [Reference ConradCon12, Thm. 4.5]). Le résultat en découle.◻
Le théorème suivant, d’énoncé un peu technique, joue un rôle clé dans la démonstration du théorème 6.11.
Théorème 6.9. Soient
![]() $T$
,
$T$
,
![]() $T_{0}$
deux tores avec
$T_{0}$
deux tores avec
![]() $T_{0}$
quasi-trivial,
$T_{0}$
quasi-trivial,
![]() $G$
un groupe linéaire connexe,
$G$
un groupe linéaire connexe,
 $G\xrightarrow[{}]{\unicode[STIX]{x1D711}}T_{0}\times T$
un homomorphisme surjectif de noyau connexe et
$G\xrightarrow[{}]{\unicode[STIX]{x1D711}}T_{0}\times T$
un homomorphisme surjectif de noyau connexe et
 $G_{0}\subset G$
un sous-groupe fermé connexe. Soient
$G_{0}\subset G$
un sous-groupe fermé connexe. Soient
![]() $X$
une
$X$
une
![]() $G$
-variété lisse géométriquement intègre,
$G$
-variété lisse géométriquement intègre,
![]() $U\subset X$
un
$U\subset X$
un
![]() $G$
-ouvert et
$G$
-ouvert et
 $U\xrightarrow[{}]{f}T_{0}\times T$
un
$U\xrightarrow[{}]{f}T_{0}\times T$
un
![]() $G$
-morphisme. Soit
$G$
-morphisme. Soit
 $B\subset \text{Br}_{G}(U)$
(cf. (3.1)) un sous-groupe fini. Supposons que :
$B\subset \text{Br}_{G}(U)$
(cf. (3.1)) un sous-groupe fini. Supposons que :
(1) la composition
 $T_{0}^{\ast }\xrightarrow[{}]{p_{1}^{\ast }}T_{0}^{\ast }\times T^{\ast }\xrightarrow[{}]{f^{\ast }}\bar{k}[U]^{\times }/\bar{k}^{\times }\xrightarrow[{}]{\text{div}_{X}}\text{Div}_{X_{\bar{k}}\setminus U_{\bar{k}}}(X_{\bar{k}})$
est un isomorphisme ;
$T_{0}^{\ast }\xrightarrow[{}]{p_{1}^{\ast }}T_{0}^{\ast }\times T^{\ast }\xrightarrow[{}]{f^{\ast }}\bar{k}[U]^{\times }/\bar{k}^{\times }\xrightarrow[{}]{\text{div}_{X}}\text{Div}_{X_{\bar{k}}\setminus U_{\bar{k}}}(X_{\bar{k}})$
est un isomorphisme ;(2) pour l’action de
 $G_{0}$
sur
$G_{0}$
sur
 $X$
, le morphisme
$X$
, le morphisme
 $\bar{k}[X]^{\times }/\bar{k}^{\times }\rightarrow \bar{k}[G_{0}]^{\times }/\bar{k}^{\times }$
défini par Sansuc [Reference SansucSan81, (6.4.1)] est injectif.
$\bar{k}[X]^{\times }/\bar{k}^{\times }\rightarrow \bar{k}[G_{0}]^{\times }/\bar{k}^{\times }$
défini par Sansuc [Reference SansucSan81, (6.4.1)] est injectif.
Alors, pour tout
![]() $v_{0}\in \unicode[STIX]{x1D6FA}_{k}$
, tout sous-groupe ouvert d’indice fini
$v_{0}\in \unicode[STIX]{x1D6FA}_{k}$
, tout sous-groupe ouvert d’indice fini
 $G(k_{v_{0}})^{0}\subset G(k_{v_{0}})$
et tout ouvert
$G(k_{v_{0}})^{0}\subset G(k_{v_{0}})$
et tout ouvert
 $W\subset X(\mathbf{A}_{k})$
satisfaisant
$W\subset X(\mathbf{A}_{k})$
satisfaisant
 $W^{\text{Br}(X)\cap (B+f^{\ast }\,\text{Br}_{1}(T_{0}\times T))}\neq \emptyset$
, il existe
$W^{\text{Br}(X)\cap (B+f^{\ast }\,\text{Br}_{1}(T_{0}\times T))}\neq \emptyset$
, il existe
 $t\in (T_{0}\times T)(k)$
de fibre
$t\in (T_{0}\times T)(k)$
de fibre
![]() $U_{t}$
, tel que
$U_{t}$
, tel que
 $$\begin{eqnarray}(G(k_{v_{0}})^{0}\cdot G_{0}(k_{\infty })^{+}\cdot W)\cap U_{t}(\mathbf{A}_{k})^{B}\neq \emptyset .\end{eqnarray}$$
$$\begin{eqnarray}(G(k_{v_{0}})^{0}\cdot G_{0}(k_{\infty })^{+}\cdot W)\cap U_{t}(\mathbf{A}_{k})^{B}\neq \emptyset .\end{eqnarray}$$
Démonstration.
Par la proposition 2.3, après avoir remplacé
![]() $f$
par
$f$
par
![]() $\widetilde{\unicode[STIX]{x1D719}}\circ f$
et
$\widetilde{\unicode[STIX]{x1D719}}\circ f$
et
![]() $\unicode[STIX]{x1D711}$
par
$\unicode[STIX]{x1D711}$
par
![]() $\widetilde{\unicode[STIX]{x1D719}}\circ \unicode[STIX]{x1D711}$
avec
$\widetilde{\unicode[STIX]{x1D719}}\circ \unicode[STIX]{x1D711}$
avec
![]() $\widetilde{\unicode[STIX]{x1D719}}$
un automorphisme de
$\widetilde{\unicode[STIX]{x1D719}}$
un automorphisme de
![]() $T_{0}\times T$
, on peut supposer que :
$T_{0}\times T$
, on peut supposer que :
(i) il existe une variété torique
 $(T_{0}{\hookrightarrow}\mathbb{A}^{l})$
satisfaisant (2.1) ;
$(T_{0}{\hookrightarrow}\mathbb{A}^{l})$
satisfaisant (2.1) ;(ii) le morphisme
 $f$
s’étend en un
$f$
s’étend en un
 $G$
-morphisme
$G$
-morphisme
 $X\xrightarrow[{}]{f_{X}}Z$
où
$X\xrightarrow[{}]{f_{X}}Z$
où
 $Z:=\mathbb{A}^{l}\times T\supset T_{0}\times T$
;
$Z:=\mathbb{A}^{l}\times T\supset T_{0}\times T$
;(iii) on a
 $f_{X}(U)\subset T_{0}\times T$
et un isomorphisme
$f_{X}(U)\subset T_{0}\times T$
et un isomorphisme
 $\text{Div}_{Z_{\bar{k}}\setminus (T_{0}\times T)_{\bar{k}}}(Z_{\bar{k}})\xrightarrow[{}]{f_{X}^{\ast }}\text{Div}_{X_{\bar{k}}\setminus U_{\bar{k}}}(X_{\bar{k}}).$
$\text{Div}_{Z_{\bar{k}}\setminus (T_{0}\times T)_{\bar{k}}}(Z_{\bar{k}})\xrightarrow[{}]{f_{X}^{\ast }}\text{Div}_{X_{\bar{k}}\setminus U_{\bar{k}}}(X_{\bar{k}}).$
Soit
 $Z_{0}:=\mathbb{A}^{l}\setminus [(\mathbb{A}^{l}\setminus T_{0})_{\text{sing}}]$
. Alors
$Z_{0}:=\mathbb{A}^{l}\setminus [(\mathbb{A}^{l}\setminus T_{0})_{\text{sing}}]$
. Alors
 $(T_{0}{\hookrightarrow}Z_{0})$
est une variété torique standard et
$(T_{0}{\hookrightarrow}Z_{0})$
est une variété torique standard et
 $$\begin{eqnarray}Z_{1}:=Z_{0}\times T\cong Z\setminus [(Z\setminus T_{0}\times T)_{\text{sing}}].\end{eqnarray}$$
$$\begin{eqnarray}Z_{1}:=Z_{0}\times T\cong Z\setminus [(Z\setminus T_{0}\times T)_{\text{sing}}].\end{eqnarray}$$
D’après la proposition 2.2, il existe un
![]() $G$
-ouvert
$G$
-ouvert
 $X_{1}\subset X$
tel que
$X_{1}\subset X$
tel que
 $f(X_{1})\subset Z_{1}$
,
$f(X_{1})\subset Z_{1}$
,
 $X_{1}\cap f_{X}^{-1}(T)=U$
,
$X_{1}\cap f_{X}^{-1}(T)=U$
,
 $\text{codim}(X\setminus X_{1},X)\geqslant 2$
,
$\text{codim}(X\setminus X_{1},X)\geqslant 2$
,
 $\text{Br}(X)\cong \text{Br}(X_{1})$
et que le morphisme
$\text{Br}(X)\cong \text{Br}(X_{1})$
et que le morphisme
 $X_{1}\xrightarrow[{}]{f_{X}|_{X_{1}}}Z_{1}$
soit lisse surjectif à fibres géométriquement intègres.
$X_{1}\xrightarrow[{}]{f_{X}|_{X_{1}}}Z_{1}$
soit lisse surjectif à fibres géométriquement intègres.
Notons
 $\unicode[STIX]{x1D719}:X\xrightarrow[{}]{f_{X}}\mathbb{A}^{l}\times T\xrightarrow[{}]{p_{2}}T$
. Pour chaque
$\unicode[STIX]{x1D719}:X\xrightarrow[{}]{f_{X}}\mathbb{A}^{l}\times T\xrightarrow[{}]{p_{2}}T$
. Pour chaque
 $t\in T(k)$
, notons
$t\in T(k)$
, notons
 $X_{1,t}:=\unicode[STIX]{x1D719}^{-1}(t)\cap X_{1}$
,
$X_{1,t}:=\unicode[STIX]{x1D719}^{-1}(t)\cap X_{1}$
,
 $U_{t}:=U\cap X_{1,t}$
,
$U_{t}:=U\cap X_{1,t}$
,
 $X_{1,t}\xrightarrow[{}]{i_{t}}X_{1}$
et
$X_{1,t}\xrightarrow[{}]{i_{t}}X_{1}$
et
 $X_{1,t}\xrightarrow[{}]{f_{t}}Z_{0}$
. On a le diagramme suivant.
$X_{1,t}\xrightarrow[{}]{f_{t}}Z_{0}$
. On a le diagramme suivant.

On a les propriétés ci-dessous :
(a) le morphisme
 $f_{t}$
satisfait les hypothèses géométriques du théorème 6.7 par rapport à
$f_{t}$
satisfait les hypothèses géométriques du théorème 6.7 par rapport à
 $\text{Ker}(G\xrightarrow[{}]{p_{2}\circ \unicode[STIX]{x1D711}}T)\rightarrow T_{0}$
;
$\text{Ker}(G\xrightarrow[{}]{p_{2}\circ \unicode[STIX]{x1D711}}T)\rightarrow T_{0}$
;(b) l’homomorphisme
 $G_{0}\xrightarrow[{}]{p_{2}\circ \unicode[STIX]{x1D711}}T$
est surjectif et donc
$G_{0}\xrightarrow[{}]{p_{2}\circ \unicode[STIX]{x1D711}}T$
est surjectif et donc
 $(p_{2}\circ \unicode[STIX]{x1D711})(G_{0}(k_{\infty })^{+})=T(k_{\infty })^{+}$
;
$(p_{2}\circ \unicode[STIX]{x1D711})(G_{0}(k_{\infty })^{+})=T(k_{\infty })^{+}$
;(c) soient
 $B_{1}:=B+f^{\ast }\,\text{Br}_{1}(T_{0}\times T)$
et
$B_{1}:=B+f^{\ast }\,\text{Br}_{1}(T_{0}\times T)$
et
 $B_{2}\subset (\text{Br}(X)\cap B_{1})$
un sous-groupe fini tels que le morphisme
$B_{2}\subset (\text{Br}(X)\cap B_{1})$
un sous-groupe fini tels que le morphisme
 $B_{2}\rightarrow (\text{Br}(X)\cap B_{1})/(\text{Br}(X)\cap f^{\ast }\,\text{Br}_{1}(T_{0}\times T))$
soit surjectif, alors
$B_{2}\rightarrow (\text{Br}(X)\cap B_{1})/(\text{Br}(X)\cap f^{\ast }\,\text{Br}_{1}(T_{0}\times T))$
soit surjectif, alors
 $i_{t}^{\ast }B\cap \text{Br}(X_{1,t})\subset i_{t}^{\ast }B_{2}$
.
$i_{t}^{\ast }B\cap \text{Br}(X_{1,t})\subset i_{t}^{\ast }B_{2}$
.
L’énoncé (a) est clair.
Pour (b), d’après [Reference Cao and XuCX15, Prop. 2.2],
![]() $\unicode[STIX]{x1D719}$
est lisse surjectif à fibres géométriquement intègres. Donc
$\unicode[STIX]{x1D719}$
est lisse surjectif à fibres géométriquement intègres. Donc
 $\bar{k}[T]^{\times }/\bar{k}^{\times }\xrightarrow[{}]{\unicode[STIX]{x1D719}^{\ast }}\bar{k}[X]^{\times }/\bar{k}^{\times }$
est injectif. Notons
$\bar{k}[T]^{\times }/\bar{k}^{\times }\xrightarrow[{}]{\unicode[STIX]{x1D719}^{\ast }}\bar{k}[X]^{\times }/\bar{k}^{\times }$
est injectif. Notons
 $\bar{k}[X]^{\times }/\bar{k}^{\times }\xrightarrow[{}]{\unicode[STIX]{x1D703}_{X}}\bar{k}[G_{0}]^{\times }/\bar{k}^{\times }$
et
$\bar{k}[X]^{\times }/\bar{k}^{\times }\xrightarrow[{}]{\unicode[STIX]{x1D703}_{X}}\bar{k}[G_{0}]^{\times }/\bar{k}^{\times }$
et
 $\bar{k}[T]^{\times }/\bar{k}^{\times }\xrightarrow[{}]{\unicode[STIX]{x1D703}_{T}}\bar{k}[G_{0}]^{\times }/\bar{k}^{\times }$
les morphismes définis par Sansuc [Reference SansucSan81, (6.4.1)]. Ainsi
$\bar{k}[T]^{\times }/\bar{k}^{\times }\xrightarrow[{}]{\unicode[STIX]{x1D703}_{T}}\bar{k}[G_{0}]^{\times }/\bar{k}^{\times }$
les morphismes définis par Sansuc [Reference SansucSan81, (6.4.1)]. Ainsi
 $\unicode[STIX]{x1D703}_{T}=\unicode[STIX]{x1D703}_{X}\circ \unicode[STIX]{x1D719}^{\ast }$
est injectif. Par l’argument de Sansuc [Reference SansucSan81, p. 39],
$\unicode[STIX]{x1D703}_{T}=\unicode[STIX]{x1D703}_{X}\circ \unicode[STIX]{x1D719}^{\ast }$
est injectif. Par l’argument de Sansuc [Reference SansucSan81, p. 39],
 $\unicode[STIX]{x1D703}_{T}=((p_{2}\circ \unicode[STIX]{x1D711})|_{G_{0}})^{\ast }$
. Alors
$\unicode[STIX]{x1D703}_{T}=((p_{2}\circ \unicode[STIX]{x1D711})|_{G_{0}})^{\ast }$
. Alors
 $G_{0}\xrightarrow[{}]{p_{2}\circ \unicode[STIX]{x1D711}}T$
est surjectif.
$G_{0}\xrightarrow[{}]{p_{2}\circ \unicode[STIX]{x1D711}}T$
est surjectif.
Pour (c), d’après le lemme 3.3, on a
 $$\begin{eqnarray}\text{Br}(X_{1})\cap f^{\ast }\,\text{Br}_{1}(T_{0}\times T)\cong f_{X}^{\ast }\,\text{Br}_{1}(Z_{1})\cong \unicode[STIX]{x1D719}^{\ast }\,\text{Br}_{1}(T)~~~\text{et}~~~B_{1}\cap \text{Br}(X_{1})=B_{2}+\unicode[STIX]{x1D719}^{\ast }\,\text{Br}_{1}(T).\end{eqnarray}$$
$$\begin{eqnarray}\text{Br}(X_{1})\cap f^{\ast }\,\text{Br}_{1}(T_{0}\times T)\cong f_{X}^{\ast }\,\text{Br}_{1}(Z_{1})\cong \unicode[STIX]{x1D719}^{\ast }\,\text{Br}_{1}(T)~~~\text{et}~~~B_{1}\cap \text{Br}(X_{1})=B_{2}+\unicode[STIX]{x1D719}^{\ast }\,\text{Br}_{1}(T).\end{eqnarray}$$
Par le corollaire 3.14, on a
 $$\begin{eqnarray}i_{t}^{\ast }B_{2}=i_{t}^{\ast }(B_{2}+\unicode[STIX]{x1D719}^{\ast }\,\text{Br}_{1}(T))=i_{t}^{\ast }(B_{1}\cap \text{Br}(X_{1}))=i_{t}^{\ast }B_{1}\cap \text{Br}(X_{1,t})\supset i_{t}^{\ast }B\cap \text{Br}(X_{1,t}).\end{eqnarray}$$
$$\begin{eqnarray}i_{t}^{\ast }B_{2}=i_{t}^{\ast }(B_{2}+\unicode[STIX]{x1D719}^{\ast }\,\text{Br}_{1}(T))=i_{t}^{\ast }(B_{1}\cap \text{Br}(X_{1}))=i_{t}^{\ast }B_{1}\cap \text{Br}(X_{1,t})\supset i_{t}^{\ast }B\cap \text{Br}(X_{1,t}).\end{eqnarray}$$
Ceci donne (c).
On considère l’ouvert
![]() $W$
de l’énoncé. Après avoir rétréci
$W$
de l’énoncé. Après avoir rétréci
![]() $W$
, on peut supposer que tout élément de
$W$
, on peut supposer que tout élément de
![]() $B_{2}$
s’annule sur
$B_{2}$
s’annule sur
![]() $W$
.
$W$
.
On note
 $W_{1}:=W\cap X_{1}(\mathbf{A}_{k})$
. Soit
$W_{1}:=W\cap X_{1}(\mathbf{A}_{k})$
. Soit
 $x\in W^{\unicode[STIX]{x1D719}^{\ast }\,\text{Br}_{1}(T)}$
. En appliquant le lemme 6.8 au triple
$x\in W^{\unicode[STIX]{x1D719}^{\ast }\,\text{Br}_{1}(T)}$
. En appliquant le lemme 6.8 au triple
 $(X_{1}\subset X,X\xrightarrow[{}]{\unicode[STIX]{x1D719}}T,W)$
, on voit qu’il existe
$(X_{1}\subset X,X\xrightarrow[{}]{\unicode[STIX]{x1D719}}T,W)$
, on voit qu’il existe
 $x_{1}\in W_{1}$
, tel que
$x_{1}\in W_{1}$
, tel que
 $\unicode[STIX]{x1D719}(x_{1})=\unicode[STIX]{x1D719}(x)$
. Donc
$\unicode[STIX]{x1D719}(x_{1})=\unicode[STIX]{x1D719}(x)$
. Donc
 $W_{1}^{\unicode[STIX]{x1D719}^{\ast }\,\text{Br}_{1}(T)}\neq \emptyset$
et
$W_{1}^{\unicode[STIX]{x1D719}^{\ast }\,\text{Br}_{1}(T)}\neq \emptyset$
et
 $\unicode[STIX]{x1D719}(W_{1})^{\text{Br}_{1}(T)}\neq \emptyset$
.
$\unicode[STIX]{x1D719}(W_{1})^{\text{Br}_{1}(T)}\neq \emptyset$
.
Soit
 $W_{2}:=G_{0}(k_{\infty })^{+}\cdot W_{1}$
. D’après (b), on a
$W_{2}:=G_{0}(k_{\infty })^{+}\cdot W_{1}$
. D’après (b), on a
 $\unicode[STIX]{x1D719}(W_{2})=T(k_{\infty })^{+}\cdot \unicode[STIX]{x1D719}(W_{1})$
. Puisque
$\unicode[STIX]{x1D719}(W_{2})=T(k_{\infty })^{+}\cdot \unicode[STIX]{x1D719}(W_{1})$
. Puisque
![]() $T$
satisfait l’approximation forte par rapport à
$T$
satisfait l’approximation forte par rapport à
![]() $\text{Br}_{1}(T)$
hors de
$\text{Br}_{1}(T)$
hors de
![]() $\infty _{k}$
(Harari [Reference HarariHar08, Thm. 2]), il existe
$\infty _{k}$
(Harari [Reference HarariHar08, Thm. 2]), il existe
 $t\in T(k)\,\cap \,\unicode[STIX]{x1D719}(W_{2})$
. Donc
$t\in T(k)\,\cap \,\unicode[STIX]{x1D719}(W_{2})$
. Donc
 $X_{1,t}(\mathbf{A}_{k})\,\cap \,W_{2}\neq \emptyset$
. Puisque l’accouplement de Brauer–Manin est constant sur
$X_{1,t}(\mathbf{A}_{k})\,\cap \,W_{2}\neq \emptyset$
. Puisque l’accouplement de Brauer–Manin est constant sur
 $G_{0}(k_{\infty })^{+}$
, d’après (c),
$G_{0}(k_{\infty })^{+}$
, d’après (c),
 $(X_{1,t}(\mathbf{A}_{k})\cap W_{2})^{i_{t}^{\ast }B\cap \text{Br}(X_{1,t})}\neq \emptyset .$
$(X_{1,t}(\mathbf{A}_{k})\cap W_{2})^{i_{t}^{\ast }B\cap \text{Br}(X_{1,t})}\neq \emptyset .$
Soit
 $W_{3}:=G(k_{v_{0}})^{0}\cdot W_{2}\supset W_{2}$
. D’après le théorème 6.7, il existe
$W_{3}:=G(k_{v_{0}})^{0}\cdot W_{2}\supset W_{2}$
. D’après le théorème 6.7, il existe
 $u\in W_{3}\cap U_{t}(\mathbf{A}_{k})^{i_{t}^{\ast }B}$
tel que
$u\in W_{3}\cap U_{t}(\mathbf{A}_{k})^{i_{t}^{\ast }B}$
tel que
 $f_{t}(u)\in T_{0}(k)$
.◻
$f_{t}(u)\in T_{0}(k)$
.◻
Corollaire 6.10. Avec les hypothèses et notations du théorème 6.9, soit
![]() $F\subset X$
un sous-schéma fermé
$F\subset X$
un sous-schéma fermé
![]() $G_{0}$
-invariant de codimension
$G_{0}$
-invariant de codimension
![]() ${\geqslant}2$
. Alors, pour tout
${\geqslant}2$
. Alors, pour tout
 $v_{0}\in \unicode[STIX]{x1D6FA}_{k}$
et tout
$v_{0}\in \unicode[STIX]{x1D6FA}_{k}$
et tout
 $\tilde{W}\subset (X\setminus F)(\mathbf{A}_{k})$
satisfaisant
$\tilde{W}\subset (X\setminus F)(\mathbf{A}_{k})$
satisfaisant
 $\tilde{W}^{\text{Br}(X)\cap (B+f^{\ast }\,\text{Br}_{1}(T_{0}\times T))}\neq \emptyset$
, il existe un
$\tilde{W}^{\text{Br}(X)\cap (B+f^{\ast }\,\text{Br}_{1}(T_{0}\times T))}\neq \emptyset$
, il existe un
 $t\in (T_{0}\times T)(k)$
tel que
$t\in (T_{0}\times T)(k)$
tel que
 $$\begin{eqnarray}\text{codim}(F\cap U_{t},U_{t})\geqslant 2~~~\text{et}~~~(G(k_{v_{0}})^{0}\cdot G_{0}(k_{\infty })^{+}\cdot \tilde{W})\cap (U_{t}\setminus (F\cap U_{t}))(\mathbf{A}_{k})^{B}\neq \emptyset .\end{eqnarray}$$
$$\begin{eqnarray}\text{codim}(F\cap U_{t},U_{t})\geqslant 2~~~\text{et}~~~(G(k_{v_{0}})^{0}\cdot G_{0}(k_{\infty })^{+}\cdot \tilde{W})\cap (U_{t}\setminus (F\cap U_{t}))(\mathbf{A}_{k})^{B}\neq \emptyset .\end{eqnarray}$$
Démonstration.
Avec les constructions et notations de la démonstration du théorème 6.9, soit
 $$\begin{eqnarray}\tilde{W}_{1}:=\tilde{W}\cap (X_{1}\setminus F)(\mathbf{A}_{k}),~~~\tilde{W}_{2}:=G_{0}(k_{\infty })^{+}\cdot \tilde{W}_{1}~~~\text{et}~~~\tilde{W}_{3}:=(G(k_{v_{0}})^{0}\cdot \tilde{W}_{2})\cap (X_{1}\setminus F)(\mathbf{A}_{k}).\end{eqnarray}$$
$$\begin{eqnarray}\tilde{W}_{1}:=\tilde{W}\cap (X_{1}\setminus F)(\mathbf{A}_{k}),~~~\tilde{W}_{2}:=G_{0}(k_{\infty })^{+}\cdot \tilde{W}_{1}~~~\text{et}~~~\tilde{W}_{3}:=(G(k_{v_{0}})^{0}\cdot \tilde{W}_{2})\cap (X_{1}\setminus F)(\mathbf{A}_{k}).\end{eqnarray}$$
Le résultat découle du même argument que dans la démonstration du théorème 6.9, en remplaçant
 $W_{1},W_{2},W_{3}$
par
$W_{1},W_{2},W_{3}$
par
 $\tilde{W}_{1},\tilde{W}_{2},\tilde{W}_{3}$
.◻
$\tilde{W}_{1},\tilde{W}_{2},\tilde{W}_{3}$
.◻
6.4 Fibration sur un pseudo espace homogène
Soit
![]() $G$
un groupe linéaire connexe. Rappelons la notion de pseudo
$G$
un groupe linéaire connexe. Rappelons la notion de pseudo
![]() $G$
-espace homogène (cf. Définition 3.15). Soit
$G$
-espace homogène (cf. Définition 3.15). Soit
![]() $Z$
un pseudo
$Z$
un pseudo
![]() $G$
-espace homogène, on peut définir son quotient torique maximal
$G$
-espace homogène, on peut définir son quotient torique maximal
 $Z\xrightarrow[{}]{\unicode[STIX]{x1D70B}}Z^{\text{tor}}$
et le stabilisateur de
$Z\xrightarrow[{}]{\unicode[STIX]{x1D70B}}Z^{\text{tor}}$
et le stabilisateur de
![]() $G$
sur
$G$
sur
![]() $Z^{\text{tor}}$
(cf. Définition 3.23).
$Z^{\text{tor}}$
(cf. Définition 3.23).
Théorème 6.11. Soient
![]() $G$
un groupe linéaire connexe,
$G$
un groupe linéaire connexe,
![]() $Z$
un pseudo
$Z$
un pseudo
![]() $G$
-espace homogène,
$G$
-espace homogène,
 $Z\xrightarrow[{}]{\unicode[STIX]{x1D70B}}Z^{\text{tor}}$
le quotient torique maximal et
$Z\xrightarrow[{}]{\unicode[STIX]{x1D70B}}Z^{\text{tor}}$
le quotient torique maximal et
![]() $G_{0}$
le stabilisateur de
$G_{0}$
le stabilisateur de
![]() $G$
sur
$G$
sur
![]() $Z^{\text{tor}}$
. Soit
$Z^{\text{tor}}$
. Soit
![]() $X$
une
$X$
une
![]() $G$
-variété lisse géométriquement intègre telle que
$G$
-variété lisse géométriquement intègre telle que
 $\bar{k}[X]^{\times }/\bar{k}^{\times }=0$
. Soient
$\bar{k}[X]^{\times }/\bar{k}^{\times }=0$
. Soient
![]() $U\subset X$
un
$U\subset X$
un
![]() $G$
-ouvert et
$G$
-ouvert et
![]() $U\xrightarrow[{}]{f}Z$
un
$U\xrightarrow[{}]{f}Z$
un
![]() $G$
-morphisme. Soient
$G$
-morphisme. Soient
 $A\subset \text{Br}(X)$
,
$A\subset \text{Br}(X)$
,
 $B\subset \text{Br}_{G}(U)$
(cf. (3.1)) deux sous-groupes finis. Pour tout ouvert
$B\subset \text{Br}_{G}(U)$
(cf. (3.1)) deux sous-groupes finis. Pour tout ouvert
 $W\subset X(\mathbf{A}_{k})$
satisfaisant
$W\subset X(\mathbf{A}_{k})$
satisfaisant
 $W^{\text{Br}(X)\cap (A+B+f^{\ast }\,\text{Br}_{G}(Z))}\neq \emptyset$
, on a :
$W^{\text{Br}(X)\cap (A+B+f^{\ast }\,\text{Br}_{G}(Z))}\neq \emptyset$
, on a :
(1) pour toute place
 $v_{0}\in \unicode[STIX]{x1D6FA}_{k}$
et tout sous-groupe ouvert d’indice fini
$v_{0}\in \unicode[STIX]{x1D6FA}_{k}$
et tout sous-groupe ouvert d’indice fini
 $G(k_{v_{0}})^{0}\subset G(k_{v_{0}})$
, il existe un
$G(k_{v_{0}})^{0}\subset G(k_{v_{0}})$
, il existe un
 $t\in Z^{\text{tor}}(k)$
de fibre
$t\in Z^{\text{tor}}(k)$
de fibre
 $U_{t}\xrightarrow[{}]{f_{t}}Z_{t}$
, tel que
$U_{t}\xrightarrow[{}]{f_{t}}Z_{t}$
, tel que  $$\begin{eqnarray}(G(k_{v_{0}})^{0}\cdot W)\cap U_{t}(\mathbf{A}_{k})^{A+B+f_{t}^{\ast }\,\text{Br}_{G_{0}}(Z_{t})}\neq \emptyset ;\end{eqnarray}$$
$$\begin{eqnarray}(G(k_{v_{0}})^{0}\cdot W)\cap U_{t}(\mathbf{A}_{k})^{A+B+f_{t}^{\ast }\,\text{Br}_{G_{0}}(Z_{t})}\neq \emptyset ;\end{eqnarray}$$
(2) s’il existe un sous-ensemble fini non vide
 $S\subset \unicode[STIX]{x1D6FA}_{k}$
tel que, pour tout sous-groupe ouvert d’indice fini
$S\subset \unicode[STIX]{x1D6FA}_{k}$
tel que, pour tout sous-groupe ouvert d’indice fini
 $G_{0}(k_{S})^{0}\subset G_{0}(k_{S})$
et tout
$G_{0}(k_{S})^{0}\subset G_{0}(k_{S})$
et tout
 $t\in Z^{\text{tor}}(k)$
de fibre
$t\in Z^{\text{tor}}(k)$
de fibre
 $Z_{t}$
, l’adhérence
$Z_{t}$
, l’adhérence
 $\overline{G_{0}(k_{S})^{0}\cdot Z_{t}(k)}$
contient
$\overline{G_{0}(k_{S})^{0}\cdot Z_{t}(k)}$
contient
 $Z_{t}(\mathbf{A}_{k})^{\text{Br}_{G_{0}}(Z_{t})}$
, alors, pour tout sous-groupe ouvert d’indice fini
$Z_{t}(\mathbf{A}_{k})^{\text{Br}_{G_{0}}(Z_{t})}$
, alors, pour tout sous-groupe ouvert d’indice fini
 $G(k_{S})^{0}\subset G(k_{S})$
, il existe un
$G(k_{S})^{0}\subset G(k_{S})$
, il existe un
 $z\in Z(k)$
de fibre
$z\in Z(k)$
de fibre
 $U_{z}$
tel que
$U_{z}$
tel que
 $(G(k_{S})^{0}\cdot W)\cap U_{z}(\mathbf{A}_{k})^{A+B}\neq \emptyset .$
$(G(k_{S})^{0}\cdot W)\cap U_{z}(\mathbf{A}_{k})^{A+B}\neq \emptyset .$
Démonstration.
On considère (1).
Soient
![]() $T_{0}$
un tore tel que
$T_{0}$
un tore tel que
 $T_{0}^{\ast }\cong \text{Div}_{X_{\bar{k}}\setminus U_{\bar{k}}}(X_{\bar{k}})$
et
$T_{0}^{\ast }\cong \text{Div}_{X_{\bar{k}}\setminus U_{\bar{k}}}(X_{\bar{k}})$
et
 $Y_{0}\rightarrow X$
le
$Y_{0}\rightarrow X$
le
![]() $T_{0}$
-torseur induit par l’homomorphisme
$T_{0}$
-torseur induit par l’homomorphisme
![]() $\unicode[STIX]{x1D6F9}$
de la suite exacte (2.2).
$\unicode[STIX]{x1D6F9}$
de la suite exacte (2.2).
D’après la proposition 5.7, il existe un tore quasi-trivial
![]() $T_{1}$
et un
$T_{1}$
et un
![]() $T_{1}$
-torseur
$T_{1}$
-torseur
 $Z_{1}\xrightarrow[{}]{p_{1,Z}}Z$
tels que
$Z_{1}\xrightarrow[{}]{p_{1,Z}}Z$
tels que
 $\text{Pic}(Z_{1,\bar{k}})=0$
et
$\text{Pic}(Z_{1,\bar{k}})=0$
et
 $H^{3}(k,\bar{k}[Z_{1}]^{\times }/\bar{k}^{\times })=0$
. Par le théorème 2.7, il existe un groupe linéaire connexe
$H^{3}(k,\bar{k}[Z_{1}]^{\times }/\bar{k}^{\times })=0$
. Par le théorème 2.7, il existe un groupe linéaire connexe
![]() $H$
muni d’un homomorphisme surjectif
$H$
muni d’un homomorphisme surjectif
 $H\rightarrow G$
de noyau central
$H\rightarrow G$
de noyau central
![]() $T_{1}$
tel que
$T_{1}$
tel que
![]() $Z_{1}$
soit une
$Z_{1}$
soit une
![]() $H$
-variété et que
$H$
-variété et que
![]() $p_{1,Z}$
soit un
$p_{1,Z}$
soit un
![]() $H$
-morphisme. De plus,
$H$
-morphisme. De plus,
 $Z_{1}(k)\neq \emptyset$
et, d’après la proposition 3.17,
$Z_{1}(k)\neq \emptyset$
et, d’après la proposition 3.17,
![]() $Z_{1}$
est un pseudo
$Z_{1}$
est un pseudo
![]() $H$
-espace homogène.
$H$
-espace homogène.
Soient
 $T_{2}:=T_{0}\times T_{1}$
et
$T_{2}:=T_{0}\times T_{1}$
et
 $V_{1}:=U\times _{Z}Z_{1}$
un
$V_{1}:=U\times _{Z}Z_{1}$
un
![]() $T_{1}$
-torseur sur
$T_{1}$
-torseur sur
![]() $U$
. Puisque
$U$
. Puisque
![]() $T_{1}$
est quasi-trivial, d’après [Reference Colliot-Thélène and SansucCS87b, Rem. 1.6.3], l’homomorphisme
$T_{1}$
est quasi-trivial, d’après [Reference Colliot-Thélène and SansucCS87b, Rem. 1.6.3], l’homomorphisme
 $H^{1}(X,T_{1})\rightarrow H^{1}(U,T_{1})$
est surjectif. Ainsi il existe un
$H^{1}(X,T_{1})\rightarrow H^{1}(U,T_{1})$
est surjectif. Ainsi il existe un
![]() $T_{1}$
-torseur
$T_{1}$
-torseur
 $Y_{1}\rightarrow X$
tel que
$Y_{1}\rightarrow X$
tel que
 $[Y_{1}]_{U}=[V_{1}]$
. L’isomorphisme canonique
$[Y_{1}]_{U}=[V_{1}]$
. L’isomorphisme canonique
 $$\begin{eqnarray}\unicode[STIX]{x1D703}:H^{1}(X,T_{0})\oplus H^{1}(X,T_{1})\rightarrow H^{1}(X,T_{2})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}:H^{1}(X,T_{0})\oplus H^{1}(X,T_{1})\rightarrow H^{1}(X,T_{2})\end{eqnarray}$$
donne un
![]() $T_{2}$
-torseur
$T_{2}$
-torseur
 $Y\rightarrow X$
tel que
$Y\rightarrow X$
tel que
 $[Y]=\unicode[STIX]{x1D703}([Y_{0}],[Y_{1}])$
. Maintenant on obtient des
$[Y]=\unicode[STIX]{x1D703}([Y_{0}],[Y_{1}])$
. Maintenant on obtient des
![]() $T_{1}$
-torseurs
$T_{1}$
-torseurs
 $Z_{1}\rightarrow Z$
,
$Z_{1}\rightarrow Z$
,
 $V_{1}\rightarrow U$
et des
$V_{1}\rightarrow U$
et des
![]() $T_{2}$
-torseurs
$T_{2}$
-torseurs
 $Y\rightarrow X$
,
$Y\rightarrow X$
,
 $V\rightarrow U$
tels que
$V\rightarrow U$
tels que
 $f^{\ast }[Z_{1}]=[V_{1}]$
,
$f^{\ast }[Z_{1}]=[V_{1}]$
,
 $[Y]|_{U}=[V]$
et
$[Y]|_{U}=[V]$
et
 $[V]=[T_{0}\times V_{1}]$
.
$[V]=[T_{0}\times V_{1}]$
.
Par le théorème 2.7, le corollaire 2.8 et le corollaire 2.9, il existe un homomorphisme surjectif
 $T_{0}\times H\xrightarrow[{}]{\unicode[STIX]{x1D713}}G$
de noyau central
$T_{0}\times H\xrightarrow[{}]{\unicode[STIX]{x1D713}}G$
de noyau central
![]() $T_{2}$
et un diagramme commutatif de
$T_{2}$
et un diagramme commutatif de
![]() $T_{0}\times H$
-variétés et de
$T_{0}\times H$
-variétés et de
![]() $T_{0}\times H$
-morphismes :
$T_{0}\times H$
-morphismes :

où
![]() $\unicode[STIX]{x1D70F}$
est une trivialisation,
$\unicode[STIX]{x1D70F}$
est une trivialisation,
 $Z_{1}\xrightarrow[{}]{\unicode[STIX]{x1D70B}_{1}}Z_{1}^{\text{tor}}$
est le quotient torique maximal,
$Z_{1}\xrightarrow[{}]{\unicode[STIX]{x1D70B}_{1}}Z_{1}^{\text{tor}}$
est le quotient torique maximal,
 $f_{V}:=(\text{id}\times \unicode[STIX]{x1D70B}_{1})\circ f_{1}\circ \unicode[STIX]{x1D70F}$
est la composition et
$f_{V}:=(\text{id}\times \unicode[STIX]{x1D70B}_{1})\circ f_{1}\circ \unicode[STIX]{x1D70F}$
est la composition et
 $p_{Z}:=p_{1,Z}\circ p_{2}$
.
$p_{Z}:=p_{1,Z}\circ p_{2}$
.
Montrons :
(a) on peut supposer que la composition
est un isomorphisme ; $$\begin{eqnarray}T_{0}^{\ast }\xrightarrow[{}]{p_{1}^{\ast }}\bar{k}[T_{0}\times V_{1}]^{\times }/\bar{k}^{\times }\xrightarrow[{}]{\unicode[STIX]{x1D70F}^{\ast }}\bar{k}[V]^{\times }/\bar{k}^{\times }\xrightarrow[{}]{\text{div}}\text{Div}_{Y_{\bar{k}}\setminus V_{\bar{k}}}(Y_{\bar{k}})\end{eqnarray}$$
$$\begin{eqnarray}T_{0}^{\ast }\xrightarrow[{}]{p_{1}^{\ast }}\bar{k}[T_{0}\times V_{1}]^{\times }/\bar{k}^{\times }\xrightarrow[{}]{\unicode[STIX]{x1D70F}^{\ast }}\bar{k}[V]^{\times }/\bar{k}^{\times }\xrightarrow[{}]{\text{div}}\text{Div}_{Y_{\bar{k}}\setminus V_{\bar{k}}}(Y_{\bar{k}})\end{eqnarray}$$
(b) le stabilisateur
 $H_{0}$
de
$H_{0}$
de
 $H$
sur
$H$
sur
 $Z_{1}^{\text{tor}}$
est connexe et donc les morphismes
$Z_{1}^{\text{tor}}$
est connexe et donc les morphismes
 $f_{V}$
,
$f_{V}$
,
 $\unicode[STIX]{x1D70B}$
,
$\unicode[STIX]{x1D70B}$
,
 $\unicode[STIX]{x1D70B}_{1}$
et
$\unicode[STIX]{x1D70B}_{1}$
et
 $\unicode[STIX]{x1D70B}\circ f$
sont lisses à fibres géométriquement intègres [Reference Cao and XuCX15, Prop. 2.2] ;
$\unicode[STIX]{x1D70B}\circ f$
sont lisses à fibres géométriquement intègres [Reference Cao and XuCX15, Prop. 2.2] ;(c) on a
(6.11) $$\begin{eqnarray}X(\mathbf{A}_{k})^{\text{Br}(X)\cap (B+f^{\ast }\,\text{Br}_{G}(Z))}=p(Y(\mathbf{A}_{k})^{\text{Br}(Y)\cap [p^{\ast }B+(f_{1}\circ \unicode[STIX]{x1D70F})^{\ast }\,\text{Br}_{T_{0}\times H}(T_{0}\times Z_{1})]});\end{eqnarray}$$
$$\begin{eqnarray}X(\mathbf{A}_{k})^{\text{Br}(X)\cap (B+f^{\ast }\,\text{Br}_{G}(Z))}=p(Y(\mathbf{A}_{k})^{\text{Br}(Y)\cap [p^{\ast }B+(f_{1}\circ \unicode[STIX]{x1D70F})^{\ast }\,\text{Br}_{T_{0}\times H}(T_{0}\times Z_{1})]});\end{eqnarray}$$
(d) il existe un sous groupe fini
 $B_{1}\subset \text{Br}_{T_{0}\times H}(V)$
tel que
$B_{1}\subset \text{Br}_{T_{0}\times H}(V)$
tel que  $$\begin{eqnarray}B_{1}+f_{V}^{\ast }\,\text{Br}_{1}(T_{0}\times Z_{1}^{\text{tor}})=(f_{1}\circ \unicode[STIX]{x1D70F})^{\ast }\,\text{Br}_{T_{0}\times H}(T_{0}\times Z_{1})\subset \text{Br}(V);\end{eqnarray}$$
$$\begin{eqnarray}B_{1}+f_{V}^{\ast }\,\text{Br}_{1}(T_{0}\times Z_{1}^{\text{tor}})=(f_{1}\circ \unicode[STIX]{x1D70F})^{\ast }\,\text{Br}_{T_{0}\times H}(T_{0}\times Z_{1})\subset \text{Br}(V);\end{eqnarray}$$
(e) pour tout
 $(t_{0},t_{1})\in (T_{0}\times Z_{1}^{\text{tor}})(k)$
, la restriction
$(t_{0},t_{1})\in (T_{0}\times Z_{1}^{\text{tor}})(k)$
, la restriction
 $\text{Br}_{T_{0}\times H}(T_{0}\times Z_{1}){\twoheadrightarrow}\text{Br}_{H_{0}}(Z_{1,t_{1}})$
est surjective, où
$\text{Br}_{T_{0}\times H}(T_{0}\times Z_{1}){\twoheadrightarrow}\text{Br}_{H_{0}}(Z_{1,t_{1}})$
est surjective, où
 $V_{(t_{0},t_{1})}\xrightarrow[{}]{f_{1}|_{(t_{0},t_{1})}}t_{0}\times Z_{1,t_{1}}\rightarrow (t_{0},t_{1})$
est la fibre de
$V_{(t_{0},t_{1})}\xrightarrow[{}]{f_{1}|_{(t_{0},t_{1})}}t_{0}\times Z_{1,t_{1}}\rightarrow (t_{0},t_{1})$
est la fibre de
 $V\xrightarrow[{}]{f_{1}\circ \unicode[STIX]{x1D70F}}T_{0}\times Z_{1}\rightarrow T_{0}\times Z_{1}^{\text{tor}}$
.
$V\xrightarrow[{}]{f_{1}\circ \unicode[STIX]{x1D70F}}T_{0}\times Z_{1}\rightarrow T_{0}\times Z_{1}^{\text{tor}}$
.
L’énoncé (a) résulte de la proposition 2.5. La proposition 3.22 et le lemme 3.21 donnent(b).
Pour (c), puisque
 $\text{Pic}(T_{2})=0$
(car
$\text{Pic}(T_{2})=0$
(car
![]() $T_{2}$
est quasi-trivial), par le corollaire 3.11 et la suite exacte de Sansuc [Reference SansucSan81, Prop. 6.10], on a deux diagrammes commutatifs de suites exactes
$T_{2}$
est quasi-trivial), par le corollaire 3.11 et la suite exacte de Sansuc [Reference SansucSan81, Prop. 6.10], on a deux diagrammes commutatifs de suites exactes

et
 $(p^{\ast })^{-1}\,\text{Br}_{T_{0}\times H}(V)=\text{Br}_{G}(U)$
. Donc
$(p^{\ast })^{-1}\,\text{Br}_{T_{0}\times H}(V)=\text{Br}_{G}(U)$
. Donc
 $(p^{\ast })^{-1}((f_{1}\circ \unicode[STIX]{x1D70F})^{\ast }\,\text{Br}_{T_{0}\times H}(T_{0}\times Z_{1}))=f^{\ast }\,\text{Br}_{G}(Z).$
Une application du corollaire 5.3 au torseur
$(p^{\ast })^{-1}((f_{1}\circ \unicode[STIX]{x1D70F})^{\ast }\,\text{Br}_{T_{0}\times H}(T_{0}\times Z_{1}))=f^{\ast }\,\text{Br}_{G}(Z).$
Une application du corollaire 5.3 au torseur
 $Y\xrightarrow[{}]{p}X$
sous le tore quasi-trivial
$Y\xrightarrow[{}]{p}X$
sous le tore quasi-trivial
![]() $T_{2}$
et aux sous-groupes :
$T_{2}$
et aux sous-groupes :
 $$\begin{eqnarray}(B+f^{\ast }\,\text{Br}_{G}(Z))\subset \text{Br}(U)~~~\text{ et}~~~(f_{1}\circ \unicode[STIX]{x1D70F})^{\ast }\,\text{Br}_{T_{0}\times H}(T_{0}\times Z_{1})\subset \text{Br}_{T_{0}\times H}(V)\subset \text{Br}_{T_{2}}(V)\end{eqnarray}$$
$$\begin{eqnarray}(B+f^{\ast }\,\text{Br}_{G}(Z))\subset \text{Br}(U)~~~\text{ et}~~~(f_{1}\circ \unicode[STIX]{x1D70F})^{\ast }\,\text{Br}_{T_{0}\times H}(T_{0}\times Z_{1})\subset \text{Br}_{T_{0}\times H}(V)\subset \text{Br}_{T_{2}}(V)\end{eqnarray}$$
donne (c).
Pour (d), par la construction, on a
 $\bar{k}[Z_{1}^{\text{tor}}]^{\times }\cong \bar{k}[Z_{1}]^{\times }$
,
$\bar{k}[Z_{1}^{\text{tor}}]^{\times }\cong \bar{k}[Z_{1}]^{\times }$
,
 $\text{Pic}(Z_{1,\bar{k}})=0$
et
$\text{Pic}(Z_{1,\bar{k}})=0$
et
 $Z_{1}(k)\neq \emptyset$
. Par la suite spectrale de Hochschild–Serre et [Reference SansucSan81, Lem. 6.6], on a
$Z_{1}(k)\neq \emptyset$
. Par la suite spectrale de Hochschild–Serre et [Reference SansucSan81, Lem. 6.6], on a
 $\text{Br}_{1}(T_{0}\times Z_{1}^{\text{tor}})\cong \text{Br}_{1}(T_{0}\times Z_{1})$
. L’énoncé (d) découle de la proposition 3.18.
$\text{Br}_{1}(T_{0}\times Z_{1}^{\text{tor}})\cong \text{Br}_{1}(T_{0}\times Z_{1})$
. L’énoncé (d) découle de la proposition 3.18.
Pour (e), puisque
 $H^{3}(k,Z_{1}^{\text{tor},\ast })=0$
, d’après le lemme 5.5, le morphisme
$H^{3}(k,Z_{1}^{\text{tor},\ast })=0$
, d’après le lemme 5.5, le morphisme
 $\text{Br}_{a}(H)\rightarrow \text{Br}_{a}(H_{0})$
est surjectif. La proposition 3.13 donne (e).
$\text{Br}_{a}(H)\rightarrow \text{Br}_{a}(H_{0})$
est surjectif. La proposition 3.13 donne (e).
On considère l’ouvert
![]() $W$
de l’énoncé. Après avoir rétréci
$W$
de l’énoncé. Après avoir rétréci
![]() $W$
, on peut supposer que tout élément de
$W$
, on peut supposer que tout élément de
![]() $A$
s’annule sur
$A$
s’annule sur
![]() $W$
. D’après (c) et (d), on a
$W$
. D’après (c) et (d), on a
 $(p^{-1}(W))^{\text{Br}(Y)\cap (p^{\ast }B+B_{1}+f_{V}^{\ast }\,\text{Br}_{1}(T_{0}\times Z_{1}^{\text{tor}}))}\neq \emptyset$
.
$(p^{-1}(W))^{\text{Br}(Y)\cap (p^{\ast }B+B_{1}+f_{V}^{\ast }\,\text{Br}_{1}(T_{0}\times Z_{1}^{\text{tor}}))}\neq \emptyset$
.
Par la suite exacte de Sansuc [Reference SansucSan81, Prop. 6.10] et l’hypothèse
 $\bar{k}[X]^{\times }/\bar{k}^{\times }=0$
, le morphisme canonique
$\bar{k}[X]^{\times }/\bar{k}^{\times }=0$
, le morphisme canonique
 $\bar{k}[Y]^{\times }/\bar{k}^{\times }\rightarrow \bar{k}[T_{2}]^{\times }/\bar{k}^{\times }$
est injectif. Puisque
$\bar{k}[Y]^{\times }/\bar{k}^{\times }\rightarrow \bar{k}[T_{2}]^{\times }/\bar{k}^{\times }$
est injectif. Puisque
 $p^{\ast }B+B_{1}\subset \text{Br}_{T_{0}\times H}(V)$
est fini, une application du théorème 6.9 au quintuple
$p^{\ast }B+B_{1}\subset \text{Br}_{T_{0}\times H}(V)$
est fini, une application du théorème 6.9 au quintuple
 $$\begin{eqnarray}(T_{0}\times H\rightarrow T_{0}\times Z_{1}^{\text{tor}},T_{2}\subset T_{0}\times H,V\subset Y,V\xrightarrow[{}]{f_{V}}T_{0}\times Z_{1}^{\text{tor}},p^{\ast }B+B_{1})\end{eqnarray}$$
$$\begin{eqnarray}(T_{0}\times H\rightarrow T_{0}\times Z_{1}^{\text{tor}},T_{2}\subset T_{0}\times H,V\subset Y,V\xrightarrow[{}]{f_{V}}T_{0}\times Z_{1}^{\text{tor}},p^{\ast }B+B_{1})\end{eqnarray}$$
montre qu’il existe
 $$\begin{eqnarray}v\in [(T_{0}\times H)(k_{v_{0}})^{0}\cdot T_{2}(k_{\infty })^{+}\cdot p^{-1}(W)]\,\cap \,V(\mathbf{A}_{k})^{p^{\ast }B+B_{1}}~~~\text{tel que}~(t_{0},t_{1}):=f_{V}(v)\in (T_{0}\times Z_{1}^{\text{tor}})(k),\end{eqnarray}$$
$$\begin{eqnarray}v\in [(T_{0}\times H)(k_{v_{0}})^{0}\cdot T_{2}(k_{\infty })^{+}\cdot p^{-1}(W)]\,\cap \,V(\mathbf{A}_{k})^{p^{\ast }B+B_{1}}~~~\text{tel que}~(t_{0},t_{1}):=f_{V}(v)\in (T_{0}\times Z_{1}^{\text{tor}})(k),\end{eqnarray}$$
où
 $(T_{0}\times H)(k_{v_{0}})^{0}:=\unicode[STIX]{x1D713}^{-1}(G(k_{v_{0}})^{0})$
.
$(T_{0}\times H)(k_{v_{0}})^{0}:=\unicode[STIX]{x1D713}^{-1}(G(k_{v_{0}})^{0})$
.
D’après (d) et (e) on a
 $v\in V_{(t_{0},t_{1})}(\mathbf{A}_{k})^{p^{\ast }B+f_{1}|_{(t_{0},t_{1})}^{\ast }\,\text{Br}_{H_{0}}(Z_{1,t_{1}})}$
. Donc
$v\in V_{(t_{0},t_{1})}(\mathbf{A}_{k})^{p^{\ast }B+f_{1}|_{(t_{0},t_{1})}^{\ast }\,\text{Br}_{H_{0}}(Z_{1,t_{1}})}$
. Donc
 $t:=\unicode[STIX]{x1D70B}_{Z^{\text{tor}}}((t_{0},t_{1}))\in Z^{\text{tor}}(k)$
et
$t:=\unicode[STIX]{x1D70B}_{Z^{\text{tor}}}((t_{0},t_{1}))\in Z^{\text{tor}}(k)$
et
 $u:=p(v)\in (G(k_{v_{0}})^{0}\cdot W)\cap U_{t}(\mathbf{A}_{k})^{B+f^{\ast }\,\text{Br}_{G_{0}}(Z_{t})}.$
Ce qui donne (1).
$u:=p(v)\in (G(k_{v_{0}})^{0}\cdot W)\cap U_{t}(\mathbf{A}_{k})^{B+f^{\ast }\,\text{Br}_{G_{0}}(Z_{t})}.$
Ce qui donne (1).
On considère (2).
Fixons
![]() $v_{0}\in S$
. On a le plongement canonique de groupes
$v_{0}\in S$
. On a le plongement canonique de groupes
 $G(k_{v_{0}})\subset G(k_{S})$
. Puisque
$G(k_{v_{0}})\subset G(k_{S})$
. Puisque
 $G(k_{S})^{0}\subset G(k_{S})$
est ouvert d’indice fini, les sous-groupes
$G(k_{S})^{0}\subset G(k_{S})$
est ouvert d’indice fini, les sous-groupes
 $$\begin{eqnarray}G(k_{v_{0}})^{0}:=G(k_{S})^{0}\cap G(k_{v_{0}})\subset G(k_{v_{0}})~~~\text{et}~~~G_{0}(k_{S})^{0}:=G(k_{S})^{0}\cap G_{0}(k_{S})\subset G_{0}(k_{S})\end{eqnarray}$$
$$\begin{eqnarray}G(k_{v_{0}})^{0}:=G(k_{S})^{0}\cap G(k_{v_{0}})\subset G(k_{v_{0}})~~~\text{et}~~~G_{0}(k_{S})^{0}:=G(k_{S})^{0}\cap G_{0}(k_{S})\subset G_{0}(k_{S})\end{eqnarray}$$
sont ouverts d’indice fini. Pour tout
 $t\in Z^{\text{tor}}(k)$
, l’ensemble
$t\in Z^{\text{tor}}(k)$
, l’ensemble
 $W_{t}:=(G(k_{v_{0}})^{0}\cdot W)\cap U_{t}(\mathbf{A}_{k})^{A+B}$
est ouvert dans
$W_{t}:=(G(k_{v_{0}})^{0}\cdot W)\cap U_{t}(\mathbf{A}_{k})^{A+B}$
est ouvert dans
![]() $U_{t}(\mathbf{A}_{k})$
. D’après (1), il existe
$U_{t}(\mathbf{A}_{k})$
. D’après (1), il existe
 $t\in Z^{\text{tor}}(k)$
tel que
$t\in Z^{\text{tor}}(k)$
tel que
 $W_{t}^{f^{\ast }\,\text{Br}_{G_{0}}(Z_{t})}\neq \emptyset$
et donc
$W_{t}^{f^{\ast }\,\text{Br}_{G_{0}}(Z_{t})}\neq \emptyset$
et donc
 $f_{t}(W_{t})^{\text{Br}_{G_{0}}(Z_{t})}\neq \emptyset$
. D’après [Reference ConradCon12, Thm. 4.5],
$f_{t}(W_{t})^{\text{Br}_{G_{0}}(Z_{t})}\neq \emptyset$
. D’après [Reference ConradCon12, Thm. 4.5],
 $f_{t}(W_{t})\subset Z_{t}(\mathbf{A}_{k})$
est ouvert. Par hypothèse, il existe
$f_{t}(W_{t})\subset Z_{t}(\mathbf{A}_{k})$
est ouvert. Par hypothèse, il existe
 $z\in Z_{t}(k)\cap f_{t}(G_{0}(k_{S})^{0}\cdot W_{t})$
et ceci établit (2).◻
$z\in Z_{t}(k)\cap f_{t}(G_{0}(k_{S})^{0}\cdot W_{t})$
et ceci établit (2).◻
Remarque 6.12. On peut établir le théorème 4.6 par la méthode de la démonstration du théorème 6.11. Mais l’argument donné au § 4 est plus simple.
Corollaire 6.13. Avec les hypothèses et notations du théorème 6.11, soit
![]() $F\subset X$
un sous-schéma fermé de codimension
$F\subset X$
un sous-schéma fermé de codimension
![]() ${\geqslant}2$
. Alors, pour tout
${\geqslant}2$
. Alors, pour tout
![]() $v_{0}\in \unicode[STIX]{x1D6FA}_{k}$
, tout sous-groupe ouvert d’indice fini
$v_{0}\in \unicode[STIX]{x1D6FA}_{k}$
, tout sous-groupe ouvert d’indice fini
 $G(k_{v_{0}})^{0}\subset G(k_{v_{0}})$
et tout ouvert
$G(k_{v_{0}})^{0}\subset G(k_{v_{0}})$
et tout ouvert
 $\tilde{W}\subset (X\setminus F)(\mathbf{A}_{k})$
satisfaisant
$\tilde{W}\subset (X\setminus F)(\mathbf{A}_{k})$
satisfaisant
 $\tilde{W}^{\text{Br}(X)\cap (A+B+f^{\ast }\,\text{Br}_{G}(Z))}\neq \emptyset$
, il existe un
$\tilde{W}^{\text{Br}(X)\cap (A+B+f^{\ast }\,\text{Br}_{G}(Z))}\neq \emptyset$
, il existe un
 $t\in Z^{\text{tor}}(k)$
tel que
$t\in Z^{\text{tor}}(k)$
tel que
 $$\begin{eqnarray}\text{codim}(F\cap U_{t},U_{t})\geqslant 2~~~\text{et}~~~(G(k_{v_{0}})^{0}\cdot \tilde{W})\cap (U_{t}\setminus (F\cap U_{t}))(\mathbf{A}_{k})^{B+A+f_{t}^{\ast }\,\text{Br}_{G_{0}}(Z_{t})}\neq \emptyset .\end{eqnarray}$$
$$\begin{eqnarray}\text{codim}(F\cap U_{t},U_{t})\geqslant 2~~~\text{et}~~~(G(k_{v_{0}})^{0}\cdot \tilde{W})\cap (U_{t}\setminus (F\cap U_{t}))(\mathbf{A}_{k})^{B+A+f_{t}^{\ast }\,\text{Br}_{G_{0}}(Z_{t})}\neq \emptyset .\end{eqnarray}$$
Démonstration.
Avec les constructions et notations de la démonstration du théorème 6.11, d’après (6.11), on a
 $$\begin{eqnarray}(X\setminus F)(\mathbf{A}_{k})^{\text{Br}(X)\cap (B+f^{\ast }\,\text{Br}_{G}(Z))}=p((Y\setminus p^{-1}F)(\mathbf{A}_{k})^{\text{Br}(Y)\cap (p^{\ast }B+B_{1}+f_{V}^{\ast }\,\text{Br}_{1}(T_{0}\times Z_{1}^{\text{tor}}))}).\end{eqnarray}$$
$$\begin{eqnarray}(X\setminus F)(\mathbf{A}_{k})^{\text{Br}(X)\cap (B+f^{\ast }\,\text{Br}_{G}(Z))}=p((Y\setminus p^{-1}F)(\mathbf{A}_{k})^{\text{Br}(Y)\cap (p^{\ast }B+B_{1}+f_{V}^{\ast }\,\text{Br}_{1}(T_{0}\times Z_{1}^{\text{tor}}))}).\end{eqnarray}$$
Une application du corollaire 6.10 au quintuple (6.12) donne le résultat. ◻
7 Le résultat principal
Dans toute cette section,
![]() $k$
est un corps de nombres. Sauf mention explicite du contraire, une variété est une
$k$
est un corps de nombres. Sauf mention explicite du contraire, une variété est une
![]() $k$
-variété. Dans cette section, on établit le résultat principal : le théorème 7.6 (ou le théorème 7.5 sur la version de la fibration).
$k$
-variété. Dans cette section, on établit le résultat principal : le théorème 7.6 (ou le théorème 7.5 sur la version de la fibration).
Rappelons la notion de sous-groupe de Brauer invariant (cf. Définition 3.1).
Soit
![]() $G$
un groupe linéaire connexe. Soit
$G$
un groupe linéaire connexe. Soit
![]() $S\subset \unicode[STIX]{x1D6FA}_{k}$
un sous-ensemble fini. On considère tout sous-groupe ouvert d’indice fini
$S\subset \unicode[STIX]{x1D6FA}_{k}$
un sous-ensemble fini. On considère tout sous-groupe ouvert d’indice fini
![]() $G(k_{S})^{0}$
de
$G(k_{S})^{0}$
de
![]() $G(k_{S})$
. Alors
$G(k_{S})$
. Alors
![]() $G(k_{S})^{0}$
est fermé dans
$G(k_{S})^{0}$
est fermé dans
![]() $G(k_{S})$
et on a directement :
$G(k_{S})$
et on a directement :
Lemme 7.1. Si
 $S=\infty _{k}$
, alors
$S=\infty _{k}$
, alors
 $G(k_{\infty })^{+}\subset G(k_{\infty })$
est un sous-groupe ouvert d’indice fini et tout tel sous-groupe
$G(k_{\infty })^{+}\subset G(k_{\infty })$
est un sous-groupe ouvert d’indice fini et tout tel sous-groupe
![]() $G(k_{S})^{0}$
contient
$G(k_{S})^{0}$
contient
 $G(k_{\infty })^{+}$
.
$G(k_{\infty })^{+}$
.
Lemme 7.2. Soit
![]() $G$
un groupe linéaire connexe et simplement connexe. Soit
$G$
un groupe linéaire connexe et simplement connexe. Soit
![]() $v\in \unicode[STIX]{x1D6FA}_{k}$
une place. Supposons que
$v\in \unicode[STIX]{x1D6FA}_{k}$
une place. Supposons que
![]() $G$
est unipotent ou que
$G$
est unipotent ou que
![]() $G$
est semi-simple et absolument simple avec
$G$
est semi-simple et absolument simple avec
![]() $G(k_{v})$
non compact. Alors
$G(k_{v})$
non compact. Alors
![]() $G(k_{v})$
ne possède pas de sous-groupe ouvert d’indice fini non-trivial.
$G(k_{v})$
ne possède pas de sous-groupe ouvert d’indice fini non-trivial.
Démonstration.
Si
 $G\cong \mathbb{G}_{a}$
, ceci vaut car
$G\cong \mathbb{G}_{a}$
, ceci vaut car
 $G(k_{v})\cong k_{v}$
est uniquement divisible. Dans le cas où
$G(k_{v})\cong k_{v}$
est uniquement divisible. Dans le cas où
![]() $G$
est unipotent, ceci vaut car il existe une filtration de
$G$
est unipotent, ceci vaut car il existe une filtration de
![]() $G$
de facteurs
$G$
de facteurs
![]() $\mathbb{G}_{a}$
[Reference BorelBor91, Cor. 15.5(ii)]. Ceci vaut aussi pour tout tel
$\mathbb{G}_{a}$
[Reference BorelBor91, Cor. 15.5(ii)]. Ceci vaut aussi pour tout tel
![]() $G$
défini sur
$G$
défini sur
![]() $k_{v}$
.
$k_{v}$
.
Dans le cas où
![]() $G$
est semi-simple, simplement connexe et absolument simple avec
$G$
est semi-simple, simplement connexe et absolument simple avec
![]() $G(k_{v})$
non compact, si
$G(k_{v})$
non compact, si
![]() $v\in \infty _{k}$
, ceci vaut par E. Cartan (cf. [Reference Platonov and RapinchukPR94, Prop. 7.6]). Si
$v\in \infty _{k}$
, ceci vaut par E. Cartan (cf. [Reference Platonov and RapinchukPR94, Prop. 7.6]). Si
![]() $v\notin \infty _{k}$
, ceci vaut car
$v\notin \infty _{k}$
, ceci vaut car
![]() $G(k_{v})$
est engendré par les
$G(k_{v})$
est engendré par les
![]() $k_{v}$
-points des sous-groupes unipotents de
$k_{v}$
-points des sous-groupes unipotents de
![]() $G$
sur
$G$
sur
![]() $k_{v}$
(la conjecture de Kneser–Tits établie par Platonov, cf. [Reference Platonov and RapinchukPR94, Thm. 7.6]).◻
$k_{v}$
(la conjecture de Kneser–Tits établie par Platonov, cf. [Reference Platonov and RapinchukPR94, Thm. 7.6]).◻
Proposition 7.3. Soit
![]() $G$
un groupe linéaire connexe et simplement connexe. Soit
$G$
un groupe linéaire connexe et simplement connexe. Soit
![]() $S\subset \unicode[STIX]{x1D6FA}_{k}$
un sous-ensemble fini non vide tel que
$S\subset \unicode[STIX]{x1D6FA}_{k}$
un sous-ensemble fini non vide tel que
![]() $G^{\prime }(k_{S})$
soit non compact pour chaque facteur simple
$G^{\prime }(k_{S})$
soit non compact pour chaque facteur simple
![]() $G^{\prime }$
du groupe
$G^{\prime }$
du groupe
![]() $G^{\text{sc}}$
. Alors, pour tout sous-groupe ouvert d’indice fini
$G^{\text{sc}}$
. Alors, pour tout sous-groupe ouvert d’indice fini
 $G(k_{S})^{0}\subset G(k_{S})$
et tout
$G(k_{S})^{0}\subset G(k_{S})$
et tout
![]() $G$
-torseur
$G$
-torseur
![]() $P$
sur
$P$
sur
![]() $k$
, l’ensemble
$k$
, l’ensemble
 $G(k_{S})^{0}\cdot P(k)$
est dense dans
$G(k_{S})^{0}\cdot P(k)$
est dense dans
![]() $P(\mathbf{A}_{k})$
.
$P(\mathbf{A}_{k})$
.
Démonstration.
On peut supposer que
 $P(\mathbf{A}_{k})\neq \emptyset$
. Puisque
$P(\mathbf{A}_{k})\neq \emptyset$
. Puisque
 $\text{Br}_{a}(G)=0$
, par le principe de Hasse pour un
$\text{Br}_{a}(G)=0$
, par le principe de Hasse pour un
![]() $G$
-torseur (Kneser, Harder et Chernousov, cf. [Reference SkorobogatovSko01, Thm. 5.1.1(e)]), on a
$G$
-torseur (Kneser, Harder et Chernousov, cf. [Reference SkorobogatovSko01, Thm. 5.1.1(e)]), on a
 $P(k)\neq \emptyset$
. Alors on peut supposer que
$P(k)\neq \emptyset$
. Alors on peut supposer que
![]() $G\cong P$
.
$G\cong P$
.
Si
![]() $G$
est soit unipotent soit semi-simple, simplement connexe et absolument simple, par hypothèse il existe une place
$G$
est soit unipotent soit semi-simple, simplement connexe et absolument simple, par hypothèse il existe une place
![]() $v\in S$
tel que
$v\in S$
tel que
![]() $G(k_{v})$
soit non compact. D’après le lemme 7.2,
$G(k_{v})$
soit non compact. D’après le lemme 7.2,
 $G(k_{v})^{0}:=G(k_{S})^{0}\cap G(k_{v})$
est exactement
$G(k_{v})^{0}:=G(k_{S})^{0}\cap G(k_{v})$
est exactement
![]() $G(k_{v})$
. Une application de l’approximation forte de
$G(k_{v})$
. Une application de l’approximation forte de
![]() $G$
(Kneser, Platonov, cf. [Reference Platonov and RapinchukPR94, Thm. 7.12]) donne l’énoncé.
$G$
(Kneser, Platonov, cf. [Reference Platonov and RapinchukPR94, Thm. 7.12]) donne l’énoncé.
Si
![]() $G$
est semi-simple, simplement connexe et simple, il existe une extension fini
$G$
est semi-simple, simplement connexe et simple, il existe une extension fini
![]() $K/k$
et un
$K/k$
et un
![]() $K$
-groupe linéaire semi-simple, simplement connexe et absolument simple
$K$
-groupe linéaire semi-simple, simplement connexe et absolument simple
![]() $G^{\prime }$
tel que
$G^{\prime }$
tel que
 $G\cong \text{Res}_{K/k}\,G^{\prime }$
. L’énoncé en découle.
$G\cong \text{Res}_{K/k}\,G^{\prime }$
. L’énoncé en découle.
Pour une suite exacte de tels groupes
 $1\rightarrow G_{1}\rightarrow G_{2}\xrightarrow[{}]{\unicode[STIX]{x1D719}}G_{3}\rightarrow 1$
, si l’énoncé vaut pour
$1\rightarrow G_{1}\rightarrow G_{2}\xrightarrow[{}]{\unicode[STIX]{x1D719}}G_{3}\rightarrow 1$
, si l’énoncé vaut pour
![]() $G_{1}$
et
$G_{1}$
et
![]() $G_{3}$
, montrons qu’il vaut pour
$G_{3}$
, montrons qu’il vaut pour
![]() $G_{2}$
. Pour un tel
$G_{2}$
. Pour un tel
 $G_{2}(k_{S})^{0}$
, les sous-groupes
$G_{2}(k_{S})^{0}$
, les sous-groupes
 $$\begin{eqnarray}G_{3}(k_{S})^{0}:=\unicode[STIX]{x1D719}(G_{2}(k_{S})^{0})\subset G_{3}(k_{S})~~~\text{et}~~~G_{1}(k_{S})^{0}:=G_{2}(k_{S})^{0}\cap G_{1}(k_{S})\subset G_{1}(k_{S})\end{eqnarray}$$
$$\begin{eqnarray}G_{3}(k_{S})^{0}:=\unicode[STIX]{x1D719}(G_{2}(k_{S})^{0})\subset G_{3}(k_{S})~~~\text{et}~~~G_{1}(k_{S})^{0}:=G_{2}(k_{S})^{0}\cap G_{1}(k_{S})\subset G_{1}(k_{S})\end{eqnarray}$$
sont ouverts d’indice fini. Ainsi, pour tout ouvert
 $W\subset G_{2}(\mathbf{A}_{k})$
, l’image
$W\subset G_{2}(\mathbf{A}_{k})$
, l’image
 $\unicode[STIX]{x1D719}(W)\subset G_{3}(\mathbf{A}_{k})$
est ouvert [Reference ConradCon12, Thm. 4.5]. Donc il existe
$\unicode[STIX]{x1D719}(W)\subset G_{3}(\mathbf{A}_{k})$
est ouvert [Reference ConradCon12, Thm. 4.5]. Donc il existe
 $t\in G_{3}(k)$
tel que
$t\in G_{3}(k)$
tel que
 $(G_{2}(k_{S})^{0}\cdot W)\cap \unicode[STIX]{x1D719}^{-1}(t)\neq \emptyset$
. Puisque
$(G_{2}(k_{S})^{0}\cdot W)\cap \unicode[STIX]{x1D719}^{-1}(t)\neq \emptyset$
. Puisque
![]() $\unicode[STIX]{x1D719}^{-1}(t)$
est un torseur de
$\unicode[STIX]{x1D719}^{-1}(t)$
est un torseur de
![]() $G_{1}$
, on a
$G_{1}$
, on a
 $$\begin{eqnarray}(G_{2}(k_{S})^{0}\cdot W)\cap (G_{1}(k_{S})^{0}\cdot \unicode[STIX]{x1D719}^{-1}(t)(k))\neq \emptyset ,\end{eqnarray}$$
$$\begin{eqnarray}(G_{2}(k_{S})^{0}\cdot W)\cap (G_{1}(k_{S})^{0}\cdot \unicode[STIX]{x1D719}^{-1}(t)(k))\neq \emptyset ,\end{eqnarray}$$
d’où le résultat.
En général, le groupe
![]() $G$
possède une filtration de facteurs soit unipotents soit semi-simples simplement connexes et simples. Une application de la méthode de fibration ci-dessus donne l’énoncé.◻
$G$
possède une filtration de facteurs soit unipotents soit semi-simples simplement connexes et simples. Une application de la méthode de fibration ci-dessus donne l’énoncé.◻
Proposition 7.4. Soient
![]() $G$
un groupe linéaire connexe, et
$G$
un groupe linéaire connexe, et
![]() $Z$
un
$Z$
un
![]() $G$
-espace homogène à stabilisateur géométrique connexe. Soit
$G$
-espace homogène à stabilisateur géométrique connexe. Soit
![]() $S\subset \unicode[STIX]{x1D6FA}_{k}$
un sous-ensemble fini non vide tel que
$S\subset \unicode[STIX]{x1D6FA}_{k}$
un sous-ensemble fini non vide tel que
![]() $G^{\prime }(k_{S})$
soit non compact pour chaque facteur simple
$G^{\prime }(k_{S})$
soit non compact pour chaque facteur simple
![]() $G^{\prime }$
du groupe
$G^{\prime }$
du groupe
![]() $G^{\text{sc}}$
. Supposons que
$G^{\text{sc}}$
. Supposons que
 $S=\infty _{k}$
ou que
$S=\infty _{k}$
ou que
 $\bar{k}[Z]^{\times }=\bar{k}^{\times }$
. Alors, pour tout sous-groupe ouvert d’indice fini
$\bar{k}[Z]^{\times }=\bar{k}^{\times }$
. Alors, pour tout sous-groupe ouvert d’indice fini
 $G(k_{S})^{0}\subset G(k_{S})$
et tout ouvert
$G(k_{S})^{0}\subset G(k_{S})$
et tout ouvert
 $W\subset Z(\mathbf{A}_{k})$
satisfaisant
$W\subset Z(\mathbf{A}_{k})$
satisfaisant
 $W^{\text{Br}_{G}(Z)}\neq \emptyset$
, on a
$W^{\text{Br}_{G}(Z)}\neq \emptyset$
, on a
 $Z(k)\cap (G(k_{S})^{0}\cdot W)\neq \emptyset$
.
$Z(k)\cap (G(k_{S})^{0}\cdot W)\neq \emptyset$
.
Démonstration.
Le cas où
 $S=\infty _{k}$
a été établi par Borovoi et Demarche [Reference Borovoi and DemarcheBD13, Thm. 1.4]. Ici, on donne une démonstration unifiée des deux cas considérés.
$S=\infty _{k}$
a été établi par Borovoi et Demarche [Reference Borovoi and DemarcheBD13, Thm. 1.4]. Ici, on donne une démonstration unifiée des deux cas considérés.
Puisque l’obstruction de Brauer–Manin au principe de Hasse est la seule pour un espace homogène à stabilisateur géométrique connexe (Borovoi [Reference BorovoiBor96], cf. [Reference SkorobogatovSko01, Thm. 5.2.1(a)]), on a
 $Z(k)\neq \emptyset$
. Un
$Z(k)\neq \emptyset$
. Un
![]() $k$
-point de
$k$
-point de
![]() $Z$
permet de définir un
$Z$
permet de définir un
![]() $G$
-morphisme
$G$
-morphisme
 $\unicode[STIX]{x1D70B}:G\rightarrow Z$
tel que
$\unicode[STIX]{x1D70B}:G\rightarrow Z$
tel que
 $Z\cong G/G_{0}$
avec
$Z\cong G/G_{0}$
avec
 $G_{0}\subset G$
un sous-groupe fermé connexe.
$G_{0}\subset G$
un sous-groupe fermé connexe.
Par la résolution flasque [Reference Colliot-ThélèneCol08, Prop. 5.4], il existe un groupe linéaire connexe
![]() $H$
et un homomorphisme surjectif
$H$
et un homomorphisme surjectif
 $H\xrightarrow[{}]{\unicode[STIX]{x1D713}}G$
tels que
$H\xrightarrow[{}]{\unicode[STIX]{x1D713}}G$
tels que
![]() $\text{Ker}(\unicode[STIX]{x1D713})$
soit un tore et
$\text{Ker}(\unicode[STIX]{x1D713})$
soit un tore et
![]() $H$
soit quasi-trivial, i.e.
$H$
soit quasi-trivial, i.e.
![]() $H^{\text{tor}}$
soit quasi-trivial et
$H^{\text{tor}}$
soit quasi-trivial et
 $H^{\text{sc}}=H^{\text{ss}}$
. Alors
$H^{\text{sc}}=H^{\text{ss}}$
. Alors
![]() $Z$
est un
$Z$
est un
![]() $H$
-espace homogène à stabilisateur géométrique connexe,
$H$
-espace homogène à stabilisateur géométrique connexe,
 $H^{\text{sc}}\cong G^{\text{sc}}$
et, d’après le corollaire 3.11 et la proposition 3.9, on a :
$H^{\text{sc}}\cong G^{\text{sc}}$
et, d’après le corollaire 3.11 et la proposition 3.9, on a :
 $\text{Br}_{G}(Z)=\text{Br}_{H}(Z).$
Le sous-groupe
$\text{Br}_{G}(Z)=\text{Br}_{H}(Z).$
Le sous-groupe
 $H(k_{S})^{0}:=\unicode[STIX]{x1D713}^{-1}(G(k_{S})^{0})\subset H(k_{S})$
est ouvert d’indice fini. Alors on peut remplacer
$H(k_{S})^{0}:=\unicode[STIX]{x1D713}^{-1}(G(k_{S})^{0})\subset H(k_{S})$
est ouvert d’indice fini. Alors on peut remplacer
![]() $G$
par
$G$
par
![]() $H$
et supposer que
$H$
et supposer que
![]() $G$
est quasi-trivial.
$G$
est quasi-trivial.
Notons
 $G\xrightarrow[{}]{\unicode[STIX]{x1D719}}G^{\text{tor}}$
le quotient torique maximal. Alors
$G\xrightarrow[{}]{\unicode[STIX]{x1D719}}G^{\text{tor}}$
le quotient torique maximal. Alors
![]() $\unicode[STIX]{x1D719}$
est lisse à fibres géométriquement intègres et donc
$\unicode[STIX]{x1D719}$
est lisse à fibres géométriquement intègres et donc
 $G(\mathbf{A}_{k})\rightarrow G^{\text{tor}}(\mathbf{A}_{k})$
est ouvert [Reference ConradCon12, Thm. 4.5]. D’après le corollaire 5.13, il existe un ouvert
$G(\mathbf{A}_{k})\rightarrow G^{\text{tor}}(\mathbf{A}_{k})$
est ouvert [Reference ConradCon12, Thm. 4.5]. D’après le corollaire 5.13, il existe un ouvert
 $W_{1}\subset G(\mathbf{A}_{k})$
et un point
$W_{1}\subset G(\mathbf{A}_{k})$
et un point
 $z\in Z(k)$
tels que
$z\in Z(k)$
tels que
 $\unicode[STIX]{x1D70B}(W_{1})\cdot z\subset W$
et
$\unicode[STIX]{x1D70B}(W_{1})\cdot z\subset W$
et
 $W_{1}^{\text{Br}_{1}(G)}\neq \emptyset$
. Puisque
$W_{1}^{\text{Br}_{1}(G)}\neq \emptyset$
. Puisque
![]() $G^{\text{tor}}$
satisfait l’approximation forte par rapport à
$G^{\text{tor}}$
satisfait l’approximation forte par rapport à
 $\text{Br}_{1}(G^{\text{tor}})$
hors de
$\text{Br}_{1}(G^{\text{tor}})$
hors de
![]() $\infty _{k}$
(Harari [Reference HarariHar08, Thm. 2]), il existe
$\infty _{k}$
(Harari [Reference HarariHar08, Thm. 2]), il existe
 $$\begin{eqnarray}t\in G^{\text{tor}}(k)\cap (G^{\text{tor}}(k_{\infty })^{+}\cdot \unicode[STIX]{x1D719}(W_{1})).\end{eqnarray}$$
$$\begin{eqnarray}t\in G^{\text{tor}}(k)\cap (G^{\text{tor}}(k_{\infty })^{+}\cdot \unicode[STIX]{x1D719}(W_{1})).\end{eqnarray}$$
Notons
![]() $G_{t}$
la fibre de
$G_{t}$
la fibre de
![]() $\unicode[STIX]{x1D719}$
au-dessus de
$\unicode[STIX]{x1D719}$
au-dessus de
![]() $t$
et
$t$
et
 $G^{\text{ssu}}(k_{S})^{0}:=G(k_{S})^{0}\cap G^{\text{ssu}}(k_{S})$
. Ainsi
$G^{\text{ssu}}(k_{S})^{0}:=G(k_{S})^{0}\cap G^{\text{ssu}}(k_{S})$
. Ainsi
![]() $G_{t}$
est un
$G_{t}$
est un
![]() $G^{\text{ssu}}$
-torseur. D’après la proposition 7.3, l’ensemble
$G^{\text{ssu}}$
-torseur. D’après la proposition 7.3, l’ensemble
 $G^{\text{ssu}}(k_{S})^{0}\cdot G_{t}(k)$
est dense dans
$G^{\text{ssu}}(k_{S})^{0}\cdot G_{t}(k)$
est dense dans
![]() $G_{t}(\mathbf{A}_{k})$
.
$G_{t}(\mathbf{A}_{k})$
.
Dans le cas où
 $S=\infty _{k}$
, puisque l’homomorphisme
$S=\infty _{k}$
, puisque l’homomorphisme
 $G(k_{\infty })^{+}\rightarrow G^{\text{tor}}(k_{\infty })^{+}$
est surjectif, il existe
$G(k_{\infty })^{+}\rightarrow G^{\text{tor}}(k_{\infty })^{+}$
est surjectif, il existe
 $$\begin{eqnarray}a\in G_{t}(\mathbf{A}_{k})\cap (G(k_{\infty })^{+}\cdot W_{1})~~~\text{et donc}~g\in G_{t}(k)\cap (G^{\text{ssu}}(k_{S})^{0}\cdot G(k_{\infty })^{+}\cdot W_{1}).\end{eqnarray}$$
$$\begin{eqnarray}a\in G_{t}(\mathbf{A}_{k})\cap (G(k_{\infty })^{+}\cdot W_{1})~~~\text{et donc}~g\in G_{t}(k)\cap (G^{\text{ssu}}(k_{S})^{0}\cdot G(k_{\infty })^{+}\cdot W_{1}).\end{eqnarray}$$
Par le lemme 7.1, on a
 $G^{\text{ssu}}(k_{S})^{0}\cdot G(k_{\infty })^{+}\subset G(k_{S})^{0}$
et donc
$G^{\text{ssu}}(k_{S})^{0}\cdot G(k_{\infty })^{+}\subset G(k_{S})^{0}$
et donc
 $g\cdot z\in Z(k)\cap (G(k_{S})^{0}\cdot W)$
.
$g\cdot z\in Z(k)\cap (G(k_{S})^{0}\cdot W)$
.
Dans le cas où
 $\bar{k}[Z]^{\times }=\bar{k}^{\times }$
, par la suite exacte de Sansuc [Reference SansucSan81, Prop. 6.10],
$\bar{k}[Z]^{\times }=\bar{k}^{\times }$
, par la suite exacte de Sansuc [Reference SansucSan81, Prop. 6.10],
 $G_{0}^{\text{tor}}\rightarrow G^{\text{tor}}$
est surjectif et donc
$G_{0}^{\text{tor}}\rightarrow G^{\text{tor}}$
est surjectif et donc
 $G_{0}\rightarrow G\rightarrow G^{\text{tor}}$
est surjectif. Ainsi
$G_{0}\rightarrow G\rightarrow G^{\text{tor}}$
est surjectif. Ainsi
 $G_{0}(k_{\infty })^{+}\rightarrow G^{\text{tor}}(k_{\infty })^{+}$
est surjectif. Alors il existe
$G_{0}(k_{\infty })^{+}\rightarrow G^{\text{tor}}(k_{\infty })^{+}$
est surjectif. Alors il existe
 $a\in G_{t}(\mathbf{A}_{k})\cap (G_{0}(k_{\infty })^{+}\cdot W_{1})$
et donc
$a\in G_{t}(\mathbf{A}_{k})\cap (G_{0}(k_{\infty })^{+}\cdot W_{1})$
et donc
 $$\begin{eqnarray}g\in G_{t}(k)\cap (G^{\text{ssu}}(k_{S})^{0}\cdot G_{0}(k_{\infty })^{+}\cdot W_{1}).\end{eqnarray}$$
$$\begin{eqnarray}g\in G_{t}(k)\cap (G^{\text{ssu}}(k_{S})^{0}\cdot G_{0}(k_{\infty })^{+}\cdot W_{1}).\end{eqnarray}$$
Ainsi
 $g\cdot z\in Z(k)\cap (G(k_{S})^{0}\cdot W)$
.◻
$g\cdot z\in Z(k)\cap (G(k_{S})^{0}\cdot W)$
.◻
Théorème 7.5. Soient
![]() $G$
un groupe linéaire connexe,
$G$
un groupe linéaire connexe,
 $G_{0}\subset G$
un sous-groupe fermé connexe et
$G_{0}\subset G$
un sous-groupe fermé connexe et
 $Z:=G/G_{0}$
. Soient
$Z:=G/G_{0}$
. Soient
![]() $X$
une
$X$
une
![]() $G$
-variété lisse géométriquement intègre,
$G$
-variété lisse géométriquement intègre,
![]() $U\subset X$
un
$U\subset X$
un
![]() $G$
-ouvert et
$G$
-ouvert et
![]() $U\xrightarrow[{}]{f}Z$
un
$U\xrightarrow[{}]{f}Z$
un
![]() $G$
-morphisme. Soient
$G$
-morphisme. Soient
 $A\subset \text{Br}(X)$
et
$A\subset \text{Br}(X)$
et
 $B\subset \text{Br}_{G}(U)$
(cf. (3.1)) deux sous-groupes finis. Soit
$B\subset \text{Br}_{G}(U)$
(cf. (3.1)) deux sous-groupes finis. Soit
![]() $S\subset \unicode[STIX]{x1D6FA}_{k}$
un sous-ensemble fini non vide tel que
$S\subset \unicode[STIX]{x1D6FA}_{k}$
un sous-ensemble fini non vide tel que
![]() $G^{\prime }(k_{S})$
soit non compact pour chaque facteur simple
$G^{\prime }(k_{S})$
soit non compact pour chaque facteur simple
![]() $G^{\prime }$
du groupe
$G^{\prime }$
du groupe
![]() $G^{\text{sc}}$
. Supposons que
$G^{\text{sc}}$
. Supposons que
 $S=\infty _{k}$
ou que
$S=\infty _{k}$
ou que
 $\bar{k}[X]^{\times }/\bar{k}^{\times }=0$
. Alors, pour tout sous-groupe ouvert d’indice fini
$\bar{k}[X]^{\times }/\bar{k}^{\times }=0$
. Alors, pour tout sous-groupe ouvert d’indice fini
 $G(k_{S})^{0}\subset G(k_{S})$
et tout ouvert
$G(k_{S})^{0}\subset G(k_{S})$
et tout ouvert
 $W\subset X(\mathbf{A}_{k})$
satisfaisant
$W\subset X(\mathbf{A}_{k})$
satisfaisant
 $W^{\text{Br}(X)\cap (A+B+f^{\ast }\,\text{Br}_{G}(Z))}\neq \emptyset ,$
il existe un
$W^{\text{Br}(X)\cap (A+B+f^{\ast }\,\text{Br}_{G}(Z))}\neq \emptyset ,$
il existe un
 $z\in Z(k)$
de fibre
$z\in Z(k)$
de fibre
![]() $U_{z}$
, tel que
$U_{z}$
, tel que
 $$\begin{eqnarray}(G(k_{S})^{0}\cdot W)\cap U_{z}(\mathbf{A}_{k})^{B+A}\neq \emptyset .\end{eqnarray}$$
$$\begin{eqnarray}(G(k_{S})^{0}\cdot W)\cap U_{z}(\mathbf{A}_{k})^{B+A}\neq \emptyset .\end{eqnarray}$$
Démonstration.
Le cas où
 $S=\infty _{k}$
découle du théorème 4.6(2) et de la proposition 7.4.
$S=\infty _{k}$
découle du théorème 4.6(2) et de la proposition 7.4.
Soit
 $\unicode[STIX]{x1D70B}:Z\xrightarrow[{}]{\unicode[STIX]{x1D70B}}Z^{\text{tor}}$
le quotient torique maximal de
$\unicode[STIX]{x1D70B}:Z\xrightarrow[{}]{\unicode[STIX]{x1D70B}}Z^{\text{tor}}$
le quotient torique maximal de
![]() $Z$
et
$Z$
et
 $G_{1}\subset G$
le stabilisateur de
$G_{1}\subset G$
le stabilisateur de
![]() $G$
sur
$G$
sur
![]() $Z^{\text{tor}}$
(cf. Définition 3.23). Pour tout
$Z^{\text{tor}}$
(cf. Définition 3.23). Pour tout
 $t\in Z^{\text{tor}}(k)$
, notons
$t\in Z^{\text{tor}}(k)$
, notons
![]() $Z_{t}$
la fibre de
$Z_{t}$
la fibre de
![]() $\unicode[STIX]{x1D70B}$
au-dessus de
$\unicode[STIX]{x1D70B}$
au-dessus de
![]() $t$
. Alors
$t$
. Alors
![]() $Z_{t}$
est un
$Z_{t}$
est un
![]() $G_{1}$
-espace homogène à stabilisateur géométrique connexe. Par la proposition 3.13, on a
$G_{1}$
-espace homogène à stabilisateur géométrique connexe. Par la proposition 3.13, on a
 $\bar{k}[Z_{t}]^{\times }=\bar{k}^{\times }$
. D’après la proposition 7.4, l’adhérence
$\bar{k}[Z_{t}]^{\times }=\bar{k}^{\times }$
. D’après la proposition 7.4, l’adhérence
 $\overline{G_{0}(k_{S})^{0}\cdot Z_{t}(k)}$
contient
$\overline{G_{0}(k_{S})^{0}\cdot Z_{t}(k)}$
contient
 $Z_{t}(\mathbf{A}_{k})^{\text{Br}_{G_{0}}(Z_{t})}$
.
$Z_{t}(\mathbf{A}_{k})^{\text{Br}_{G_{0}}(Z_{t})}$
.
Le cas où
 $\bar{k}[X]^{\times }=\bar{k}^{\times }$
découle du théorème 6.11(2) (avec les même notations sauf remplacer
$\bar{k}[X]^{\times }=\bar{k}^{\times }$
découle du théorème 6.11(2) (avec les même notations sauf remplacer
![]() $G_{0}$
par
$G_{0}$
par
![]() $G_{1}$
).◻
$G_{1}$
).◻
Théorème 7.6. Soient
![]() $G$
un groupe linéaire connexe,
$G$
un groupe linéaire connexe,
 $G_{0}\subset G$
un sous-groupe fermé connexe et
$G_{0}\subset G$
un sous-groupe fermé connexe et
 $Z:=G/G_{0}$
. Soient
$Z:=G/G_{0}$
. Soient
![]() $X$
une
$X$
une
![]() $G$
-variété lisse géométriquement intègre,
$G$
-variété lisse géométriquement intègre,
![]() $U\subset X$
un
$U\subset X$
un
![]() $G$
-ouvert et
$G$
-ouvert et
![]() $U\xrightarrow[{}]{f}Z$
un
$U\xrightarrow[{}]{f}Z$
un
![]() $G$
-morphisme. Soient
$G$
-morphisme. Soient
 $A\subset \text{Br}(X)$
et
$A\subset \text{Br}(X)$
et
 $B\subset \text{Br}_{G}(U)$
(cf. (3.1)) deux sous-groupes finis. Soit
$B\subset \text{Br}_{G}(U)$
(cf. (3.1)) deux sous-groupes finis. Soit
![]() $S\subset \unicode[STIX]{x1D6FA}_{k}$
un sous-ensemble fini non vide tel que
$S\subset \unicode[STIX]{x1D6FA}_{k}$
un sous-ensemble fini non vide tel que
![]() $G^{\prime }(k_{S})$
soit non compact pour chaque facteur simple
$G^{\prime }(k_{S})$
soit non compact pour chaque facteur simple
![]() $G^{\prime }$
du groupe
$G^{\prime }$
du groupe
![]() $G^{\text{sc}}$
.
$G^{\text{sc}}$
.
(1) Si
 $S=\infty _{k}$
et, pour tout
$S=\infty _{k}$
et, pour tout
 $z\in Z(k)$
de fibre
$z\in Z(k)$
de fibre
 $U_{z}$
, l’ensemble
$U_{z}$
, l’ensemble
 $U_{z}(k)$
est dense dans
$U_{z}(k)$
est dense dans
 $U_{z}(\mathbf{A}_{k})_{\bullet }^{A+B}$
, alors
$U_{z}(\mathbf{A}_{k})_{\bullet }^{A+B}$
, alors
 $X(k)$
est dense dans
$X(k)$
est dense dans
 $X(\mathbf{A}_{k})_{\bullet }^{\text{Br}(X)\cap (A+B+f^{\ast }\,\text{Br}_{G}(Z))}$
.
$X(\mathbf{A}_{k})_{\bullet }^{\text{Br}(X)\cap (A+B+f^{\ast }\,\text{Br}_{G}(Z))}$
.(2) Si
 $\bar{k}[X]^{\times }=\bar{k}^{\times }$
et, pour tout
$\bar{k}[X]^{\times }=\bar{k}^{\times }$
et, pour tout
 $z\in Z(k)$
, la fibre
$z\in Z(k)$
, la fibre
 $U_{z}$
satisfait l’approximation forte de Brauer–Manin par rapport à
$U_{z}$
satisfait l’approximation forte de Brauer–Manin par rapport à
 $A+B$
hors de
$A+B$
hors de
 $S$
, alors
$S$
, alors
 $X$
satisfait l’approximation forte de Brauer–Manin par rapport à
$X$
satisfait l’approximation forte de Brauer–Manin par rapport à
 $\text{Br}(X)\cap (A+B+f^{\ast }\,\text{Br}_{G}(Z))$
hors de
$\text{Br}(X)\cap (A+B+f^{\ast }\,\text{Br}_{G}(Z))$
hors de
 $S$
.
$S$
.
Démonstration.
Ceci suit immédiatement du théorème 7.5. ◻
Le cas où
![]() $U\cong Z$
,
$U\cong Z$
,
![]() $f=\text{id}$
et
$f=\text{id}$
et
 $A=B=0$
donne le théorème 1.4.
$A=B=0$
donne le théorème 1.4.
Remerciements
Je remercie très chaleureusement Jean-Louis Colliot-Thélène et Fei Xu pour plusieurs discussions. Je remercie également Cyril Demarche, Qifeng Li et Giancarlo Lucchini Arteche pour leurs commentaires. Je remercie vivement les rapporteurs de Compositio Math. pour leurs commentaires. Projet soutenu par l’attribution d’une allocation de recherche Région Ile-de-France.