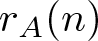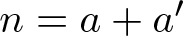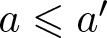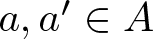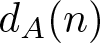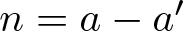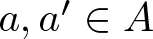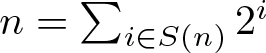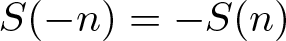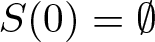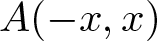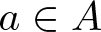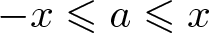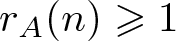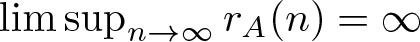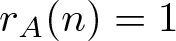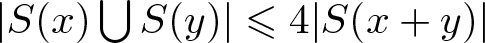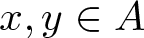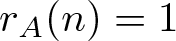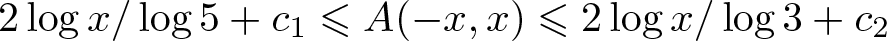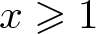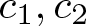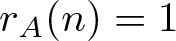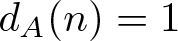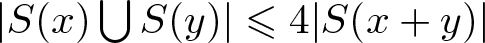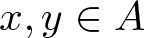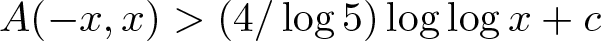1. Introduction
For nonempty sets ![]() $A,B$ of integers, define
$A,B$ of integers, define
Let ![]() $\mathbb{Z}$ be the set of integers and
$\mathbb{Z}$ be the set of integers and ![]() $\mathbb{N}$ the set of positive integers. For any integer n, let
$\mathbb{N}$ the set of positive integers. For any integer n, let ![]() $r_{A}(n)$ be the number of representations of n in the form
$r_{A}(n)$ be the number of representations of n in the form ![]() $n=a+a'$, where
$n=a+a'$, where ![]() $a\leqslant a'$ and
$a\leqslant a'$ and ![]() $a, a'\in A$, and
$a, a'\in A$, and ![]() $d_{A}(n)$ be the number of representations of n in the form
$d_{A}(n)$ be the number of representations of n in the form ![]() $n=a-a'$, where
$n=a-a'$, where ![]() $a, a'\in A$. Clearly,
$a, a'\in A$. Clearly, ![]() $d_{A}(-n)=d_{A}(n)$ for any positive integer n. Let
$d_{A}(-n)=d_{A}(n)$ for any positive integer n. Let ![]() $|A|$ be the cardinality of the set A and
$|A|$ be the cardinality of the set A and ![]() $\max A$ be the maximal element in A. For a real number x, denote
$\max A$ be the maximal element in A. For a real number x, denote ![]() $|x|$ by the absolute value of x,
$|x|$ by the absolute value of x, ![]() $\lfloor x\rfloor$ by the largest integer no larger than x,
$\lfloor x\rfloor$ by the largest integer no larger than x, ![]() $A+x=\{a+x:a\in A\}$, and
$A+x=\{a+x:a\in A\}$, and ![]() $A(-x,x)$ by the number of elements
$A(-x,x)$ by the number of elements ![]() $a\in A$ with
$a\in A$ with ![]() $-x\leqslant a\leqslant x$.
$-x\leqslant a\leqslant x$.
The famous Erdős-Turán Conjecture [Reference Erdős and Turán3] states that if A is a set of positive integers such that ![]() $r_A(n)\geqslant 1$ for all sufficiently large n, then
$r_A(n)\geqslant 1$ for all sufficiently large n, then
 \begin{equation*}\limsup_{n\rightarrow\infty}r_A(n)=\infty.\end{equation*}
\begin{equation*}\limsup_{n\rightarrow\infty}r_A(n)=\infty.\end{equation*} In 2004, Nešetřil and Serra [Reference Nešetřil and Serra6] initially introduced the notation of “bounded” property. For a positive integer n, denote the binary support of n by the subset S(n) of nonnegative integers consisting of the exponents in the binary expansion of n, i.e.,  $n=\sum_{i\in S(n)} 2^i$, and
$n=\sum_{i\in S(n)} 2^i$, and ![]() $S(-n)=-S(n)$. Define
$S(-n)=-S(n)$. Define ![]() $S(0)=\emptyset$. A set A of integers is called bounded if there is a function
$S(0)=\emptyset$. A set A of integers is called bounded if there is a function ![]() $f:\mathbb{N}\bigcup\{0\}\rightarrow \mathbb{N}\bigcup\{0\}$ such that
$f:\mathbb{N}\bigcup\{0\}\rightarrow \mathbb{N}\bigcup\{0\}$ such that ![]() $f(0)=0$ and for each
$f(0)=0$ and for each ![]() $n\in A+A$ there exists a pair
$n\in A+A$ there exists a pair ![]() $x,y\in A$ with
$x,y\in A$ with
 \begin{equation*}n=x+y,\hskip6mm|S(x)\bigcup S(y)|\leqslant f(|S(n)|).\end{equation*}
\begin{equation*}n=x+y,\hskip6mm|S(x)\bigcup S(y)|\leqslant f(|S(n)|).\end{equation*} Obviously, if A is a set of positive integers and the binary expansion of each element in A has no two consecutive 1’s, then A is a bounded set with ![]() $f(n)=n$. Nešetřil and Serra [Reference Nešetřil and Serra6] confirmed the Erdős-Turán conjecture for a class of “bounded” bases.
$f(n)=n$. Nešetřil and Serra [Reference Nešetřil and Serra6] confirmed the Erdős-Turán conjecture for a class of “bounded” bases.
For a set A of integers, A is a basis for ![]() $\mathbb{Z}$ if
$\mathbb{Z}$ if ![]() $r_A(n)\geqslant 1$ for all integers n and a unique representation basis for
$r_A(n)\geqslant 1$ for all integers n and a unique representation basis for ![]() $\mathbb{Z}$ if
$\mathbb{Z}$ if ![]() $r_A(n)=1$ for all integers n. For the unique representation basis for
$r_A(n)=1$ for all integers n. For the unique representation basis for ![]() $\mathbb{Z}$, by considering the bounded property, Nešetřil and Serra [Reference Nešetřil and Serra6] also obtained the following result:
$\mathbb{Z}$, by considering the bounded property, Nešetřil and Serra [Reference Nešetřil and Serra6] also obtained the following result:
Theorem A. ([Reference Nešetřil and Serra6, Theorem 5])
There is a bounded basis A of ![]() $\mathbb{Z}$ satisfying
$\mathbb{Z}$ satisfying ![]() $r_A(n)=1$ for each
$r_A(n)=1$ for each ![]() $n\in \mathbb{Z}$.
$n\in \mathbb{Z}$.
Recently, the author [Reference Fang4] generalized the above result by adding the restriction that ![]() $d_A(n)=1$ for all positive integers n. On the other hand, research on the density of basis also attracts much interest from experts. In 2003, Nathanson [Reference Nathanson5] considered the existence of unique representation basis A with logarithmic growth, that is:
$d_A(n)=1$ for all positive integers n. On the other hand, research on the density of basis also attracts much interest from experts. In 2003, Nathanson [Reference Nathanson5] considered the existence of unique representation basis A with logarithmic growth, that is:
Theorem B. ([Reference Nathanson5, Theorem 2])
There is a unique representation basis A for ![]() $\mathbb{Z}$ such that
$\mathbb{Z}$ such that
 \begin{eqnarray*}\frac{2\log x}{\log 5}+2(1-\frac{\log 3}{\log 5})\leqslant A(-x,x)\leqslant \frac{2\log x}{\log 3}+2 \end{eqnarray*}
\begin{eqnarray*}\frac{2\log x}{\log 5}+2(1-\frac{\log 3}{\log 5})\leqslant A(-x,x)\leqslant \frac{2\log x}{\log 3}+2 \end{eqnarray*}for all ![]() $x\geqslant 1$.
$x\geqslant 1$.
Afterwards, Xiong and Tang [Reference Xiong and Tang7] extended Theorem B by considering the structure of difference, and constructed a unique representation basis A of integers such that ![]() $d_A(n)=1$ for all positive integers n and
$d_A(n)=1$ for all positive integers n and
 \begin{equation*}\frac{4(\log x-\log 2)}{\log 15}-1 \lt A(-x,x) \lt \frac{4(\log x-\log 2)}{\log 3}+7\end{equation*}
\begin{equation*}\frac{4(\log x-\log 2)}{\log 15}-1 \lt A(-x,x) \lt \frac{4(\log x-\log 2)}{\log 3}+7\end{equation*}for all x > 1.
In this paper, based on the above results, we incorporate the bounded property and prove that:
Theorem 1.1. There exists a bounded basis A of integers such that ![]() $r_A(n)=1$ for all integers n and
$r_A(n)=1$ for all integers n and ![]() $d_A(n)=1$ for all positive integers n, and
$d_A(n)=1$ for all positive integers n, and
 \begin{equation*}A(-x,x) \gt \frac{4}{\log 5}\log\log x+c \hskip2mm \text{for all} \hskip2mm x\geqslant 1,\end{equation*}
\begin{equation*}A(-x,x) \gt \frac{4}{\log 5}\log\log x+c \hskip2mm \text{for all} \hskip2mm x\geqslant 1,\end{equation*}where c is an absolute constant.
On the other hand, similar to [Reference Nathanson5] and [Reference Xiong and Tang7], we also obtain the following result:
Theorem 1.2. Let f(x) be a function such that ![]() $\lim_{x\rightarrow\infty}f(x)=\infty$. Then there exists a bounded basis A of integers such that
$\lim_{x\rightarrow\infty}f(x)=\infty$. Then there exists a bounded basis A of integers such that ![]() $r_A(n)=1$ for all integers n and
$r_A(n)=1$ for all integers n and ![]() $d_A(n)=1$ for all positive integers n, and
$d_A(n)=1$ for all positive integers n, and
Furthermore, noting that if ![]() $r_{A}(n)=2$ for infinitely many integers, then
$r_{A}(n)=2$ for infinitely many integers, then ![]() $d_A(n)\geqslant 2$ for infinitely many integers n, Cilleruelo and Nathanson [Reference Cilleruelo and Nathanson2] posed the following problem:
$d_A(n)\geqslant 2$ for infinitely many integers n, Cilleruelo and Nathanson [Reference Cilleruelo and Nathanson2] posed the following problem:
Cilleruelo-Nathanson Problem. Give general conditions for functions f 1 and f 2 to assure that there exists a set A such that ![]() $d_A(n)\equiv f_1(n)$ and
$d_A(n)\equiv f_1(n)$ and ![]() $r_{A}(n)\equiv f_2(n)$. Is the condition
$r_{A}(n)\equiv f_2(n)$. Is the condition ![]() $\liminf_{u\rightarrow \infty}f_1(u)\geqslant 2$ and
$\liminf_{u\rightarrow \infty}f_1(u)\geqslant 2$ and ![]() $\liminf_{|u|\rightarrow \infty}f_2(u)\geqslant 2$ sufficient?
$\liminf_{|u|\rightarrow \infty}f_2(u)\geqslant 2$ sufficient?
In 2011, Y.G. Chen and the author [Reference Chen and Fang1] answered this problem affirmatively. In this paper, we also consider the bounded property and obtain that:
Theorem 1.3. If two functions ![]() $f_1:\mathbb{N}\rightarrow \mathbb{N}$ and
$f_1:\mathbb{N}\rightarrow \mathbb{N}$ and ![]() $f_2:\mathbb{Z}\rightarrow \mathbb{N}$ satisfy that
$f_2:\mathbb{Z}\rightarrow \mathbb{N}$ satisfy that ![]() $\liminf_{u\rightarrow \infty}f_1(u)\geqslant 2$ and
$\liminf_{u\rightarrow \infty}f_1(u)\geqslant 2$ and ![]() $\liminf_{|u|\rightarrow \infty}f_2(u)\geqslant 2$, then there exists a bounded set A of integers such that
$\liminf_{|u|\rightarrow \infty}f_2(u)\geqslant 2$, then there exists a bounded set A of integers such that ![]() $d_A(n)=f_1(n)$ for all
$d_A(n)=f_1(n)$ for all ![]() $n\in \mathbb{N}$ and
$n\in \mathbb{N}$ and ![]() $r_{A}(n)=f_2(n)$ for all
$r_{A}(n)=f_2(n)$ for all ![]() $n\in \mathbb{Z}$.
$n\in \mathbb{Z}$.
2. Proof of Theorem 1.1 and Theorem 1.2
The main idea is from [Reference Nathanson5]-[Reference Xiong and Tang7]. During the induction process, we focus on the choice of critical values. Denote ![]() $\sigma(n)$ by
$\sigma(n)$ by
and
It easily follows from the definition of ![]() $\sigma(n)$ that
$\sigma(n)$ that ![]() $|S(n+\sigma(n))|=|S(\sigma(n))|\leqslant |S(n)|$,
$|S(n+\sigma(n))|=|S(\sigma(n))|\leqslant |S(n)|$, ![]() $S(\sigma(n))$ and
$S(\sigma(n))$ and ![]() $S(n+\sigma(n))$ has no two consecutive integers.
$S(n+\sigma(n))$ has no two consecutive integers.
Lemma 2.1. ([Reference Fang4, Lemma 2.1])
Let ![]() $x,y,z$ be integers with yz > 0 such that
$x,y,z$ be integers with yz > 0 such that
(i)
 $|S(|y|)|\leqslant |S(|z|)|$;
$|S(|y|)|\leqslant |S(|z|)|$;(ii) a > b for any
 $a\in S(|z|)$ and
$a\in S(|z|)$ and  $b\in S(|x|)\bigcup S(|y|)$;
$b\in S(|x|)\bigcup S(|y|)$;(iii) each of S(x), S(y) and S(z) has no two consecutive integers.
Then
 \begin{equation*}|S(x)\bigcup S(y+z)|\leqslant 4|S(x+y+z)|.\end{equation*}
\begin{equation*}|S(x)\bigcup S(y+z)|\leqslant 4|S(x+y+z)|.\end{equation*} Proof of Theorem 1.1. We will construct finite sets of integers ![]() $A_1\subseteq A_2\subseteq\cdots\subseteq A_k\subseteq \cdots$ such that for any positive integer k, we have:
$A_1\subseteq A_2\subseteq\cdots\subseteq A_k\subseteq \cdots$ such that for any positive integer k, we have:
(i)
 $|A_k|=4k+3$;
$|A_k|=4k+3$;(ii)
 $r_{A_k}(n)\leqslant 1$ for all
$r_{A_k}(n)\leqslant 1$ for all  $n\in \mathbb{Z}$ and
$n\in \mathbb{Z}$ and  $d_{A_k}(n)\leqslant 1$ for all
$d_{A_k}(n)\leqslant 1$ for all  $n\in \mathbb{N}$;
$n\in \mathbb{N}$;(iii)
 $r_{A_{k}}(n)=1$ for all
$r_{A_{k}}(n)=1$ for all  $n\in \mathbb{Z}$ with
$n\in \mathbb{Z}$ with  $|n|\leqslant \lfloor\frac{k}{2}\rfloor$ and
$|n|\leqslant \lfloor\frac{k}{2}\rfloor$ and  $d_{A_k}(n)=1$ for all
$d_{A_k}(n)=1$ for all  $n\in \mathbb{N}$ with
$n\in \mathbb{N}$ with  $1\leqslant n\leqslant k$;
$1\leqslant n\leqslant k$;(iv)
 $|S(x)\bigcup S(y)|\leqslant 4|S(x+y)|$ for
$|S(x)\bigcup S(y)|\leqslant 4|S(x+y)|$ for  $x,y\in A_k$;
$x,y\in A_k$;(v) the binary support of each element in Ak has no two consecutive integers;
(vi)
 $d_{k} \lt 172d_{k-1}^5$, where
$d_{k} \lt 172d_{k-1}^5$, where  $d_k=\max\{|a|:a\in A_k\}$ and
$d_k=\max\{|a|:a\in A_k\}$ and  $d_0=1$.
$d_0=1$.
Let ![]() $A_1=\{-32,-10,0,9,33,128,129\}$. Then
$A_1=\{-32,-10,0,9,33,128,129\}$. Then ![]() $d_1=129$,
$d_1=129$, ![]() $r_{A_1}(0)=1$,
$r_{A_1}(0)=1$, ![]() $r_{A_1}(1)=r_{A_1}(-1)=d_{A_1}(1)=1$,
$r_{A_1}(1)=r_{A_1}(-1)=d_{A_1}(1)=1$, ![]() $r_{A_1}(n)\leqslant 1$ for all
$r_{A_1}(n)\leqslant 1$ for all ![]() $n\in \mathbb{Z}$ and
$n\in \mathbb{Z}$ and ![]() $d_{A_1}(n)\leqslant 1$ for all
$d_{A_1}(n)\leqslant 1$ for all ![]() $n\in \mathbb{N}$,
$n\in \mathbb{N}$, ![]() $|S(x)\bigcup S(y)|\leqslant 4|S(x+y)|$ for
$|S(x)\bigcup S(y)|\leqslant 4|S(x+y)|$ for ![]() $x,y\in A_1$, and the binary support of each element in A 1 has no two consecutive integers. Thus, (i)-(vi) hold for k = 1.
$x,y\in A_1$, and the binary support of each element in A 1 has no two consecutive integers. Thus, (i)-(vi) hold for k = 1.
Assume that we have already obtained a set Ak of integers satisfying (i)-(vi) for some positive integer k. By the definition of dk we know that ![]() $A_k\subseteq [-d_k,d_k]$. Since
$A_k\subseteq [-d_k,d_k]$. Since ![]() $r_{A_k}(0)\leqslant 1$, we have
$r_{A_k}(0)\leqslant 1$, we have ![]() $d_k\in A_k$ and
$d_k\in A_k$ and ![]() $-d_k\not\in A_k$, or
$-d_k\not\in A_k$, or ![]() $-d_k\in A_k$ and
$-d_k\in A_k$ and ![]() $d_k\not\in A_k$. Thus,
$d_k\not\in A_k$. Thus, ![]() $A_k+A_k\subseteq [-2d_k+2,2d_k]$ or
$A_k+A_k\subseteq [-2d_k+2,2d_k]$ or ![]() $[-2d_k,2d_k-2]$. In any case, we have
$[-2d_k,2d_k-2]$. In any case, we have ![]() $A_k-A_k\subseteq [-2d_k+1,2d_k-1]$. Write
$A_k-A_k\subseteq [-2d_k+1,2d_k-1]$. Write
It follows that
Let
 \begin{eqnarray} a_k=\lceil\max\{\log_2\left(\frac{3d_k+1-\sigma(u_k)}{4^{|S(u_k)|-1}}\right), \log_2d_k+1, \max S(u_k)+3\}\rceil,
\end{eqnarray}
\begin{eqnarray} a_k=\lceil\max\{\log_2\left(\frac{3d_k+1-\sigma(u_k)}{4^{|S(u_k)|-1}}\right), \log_2d_k+1, \max S(u_k)+3\}\rceil,
\end{eqnarray}where ![]() $\lceil x \rceil$ is the least integer no less than x. Then
$\lceil x \rceil$ is the least integer no less than x. Then
Take
Thus, ![]() $x_k-u_k\geqslant 3d_k+1$. Furthermore,
$x_k-u_k\geqslant 3d_k+1$. Furthermore,
 \begin{eqnarray}
x_k=u_k+\sigma(u_k)+2^{a_k}\frac{4^{|S(u_k)|}-1}{3} \lt 4d_k+\frac{1}{3}4^{|S(u_k)|}2^{a_k},
\end{eqnarray}
\begin{eqnarray}
x_k=u_k+\sigma(u_k)+2^{a_k}\frac{4^{|S(u_k)|}-1}{3} \lt 4d_k+\frac{1}{3}4^{|S(u_k)|}2^{a_k},
\end{eqnarray}where the last inequality is based on the facts that ![]() $\sigma(u_k)\leqslant u_k$ and
$\sigma(u_k)\leqslant u_k$ and ![]() $u_k\leqslant 2d_k-1$. If
$u_k\leqslant 2d_k-1$. If  $a_k=\lceil \log_2\left(\frac{3d_k+1-\sigma(u_k)}{4^{|S(u_k)|-1}}\right)\rceil$, then
$a_k=\lceil \log_2\left(\frac{3d_k+1-\sigma(u_k)}{4^{|S(u_k)|-1}}\right)\rceil$, then
 \begin{equation*}4d_k+\frac{1}{3}4^{|S(u_k)|}2^{a_k} \lt 4d_k+\frac{1}{3}4^{|S(u_k)|}(2\cdot\frac{3d_k}{4^{|S(u_k)|-1}})=12d_k.\end{equation*}
\begin{equation*}4d_k+\frac{1}{3}4^{|S(u_k)|}2^{a_k} \lt 4d_k+\frac{1}{3}4^{|S(u_k)|}(2\cdot\frac{3d_k}{4^{|S(u_k)|-1}})=12d_k.\end{equation*} If ![]() $a_k=\lceil \log_2d_k+1\rceil$, then by
$a_k=\lceil \log_2d_k+1\rceil$, then by ![]() $|S(u_k)|\leqslant \max S(u_k)+1$ and
$|S(u_k)|\leqslant \max S(u_k)+1$ and ![]() $2^{\max S(u_k)}\leqslant u_k$ we know that
$2^{\max S(u_k)}\leqslant u_k$ we know that
 \begin{eqnarray*}4d_k+\frac{1}{3}4^{|S(u_k)|}2^{a_k}
& \lt &4d_k+\frac{1}{3}4^{|S(u_k)|}(2\cdot2^{\log_2d_k+1})\\
&\leqslant &4d_k+\frac{4}{3}d_k4^{\max S(u_k)+1}\leqslant 4d_k+\frac{16}{3}d_ku_k^2\\
&\leqslant &4d_k+\frac{64}{3}d_k^3 \lt 22d_k^3.\end{eqnarray*}
\begin{eqnarray*}4d_k+\frac{1}{3}4^{|S(u_k)|}2^{a_k}
& \lt &4d_k+\frac{1}{3}4^{|S(u_k)|}(2\cdot2^{\log_2d_k+1})\\
&\leqslant &4d_k+\frac{4}{3}d_k4^{\max S(u_k)+1}\leqslant 4d_k+\frac{16}{3}d_ku_k^2\\
&\leqslant &4d_k+\frac{64}{3}d_k^3 \lt 22d_k^3.\end{eqnarray*} If ![]() $a_k=\max S(u_k)+3$, then
$a_k=\max S(u_k)+3$, then
 \begin{eqnarray*}4d_k+\frac{1}{3}4^{|S(u_k)|}2^{a_k}
&=&4d_k+\frac{8}{3}4^{|S(u_k)|}2^{\max S(u_k)}\leqslant 4d_k+\frac{32}{3}2^{3\max S(u_k)}\\
&\leqslant &4d_k+\frac{32}{3}u_k^3\leqslant 86d_k^3.\end{eqnarray*}
\begin{eqnarray*}4d_k+\frac{1}{3}4^{|S(u_k)|}2^{a_k}
&=&4d_k+\frac{8}{3}4^{|S(u_k)|}2^{\max S(u_k)}\leqslant 4d_k+\frac{32}{3}2^{3\max S(u_k)}\\
&\leqslant &4d_k+\frac{32}{3}u_k^3\leqslant 86d_k^3.\end{eqnarray*}In any case,
 \begin{eqnarray}
4d_k+\frac{1}{3}4^{|S(u_k)|}2^{a_k}\leqslant 86d_k^3.
\end{eqnarray}
\begin{eqnarray}
4d_k+\frac{1}{3}4^{|S(u_k)|}2^{a_k}\leqslant 86d_k^3.
\end{eqnarray}It infers from (2.1) and (2.3) that
Let
 \begin{eqnarray} b_k=\lceil\max\{\log_2\left(\frac{3x_k+2u_k-\sigma(v_k)}{4^{|S(v_k)|-1}}\right),\max S(v_k)+3, a_k+2|S(u_k)|-1\}\rceil.
\end{eqnarray}
\begin{eqnarray} b_k=\lceil\max\{\log_2\left(\frac{3x_k+2u_k-\sigma(v_k)}{4^{|S(v_k)|-1}}\right),\max S(v_k)+3, a_k+2|S(u_k)|-1\}\rceil.
\end{eqnarray}Then
Take
Thus, ![]() $y_k\geqslant3x_k+2u_k$. Furthermore,
$y_k\geqslant3x_k+2u_k$. Furthermore,
 \begin{eqnarray}
y_k+v_k=v_k+\sigma(v_k)+2^{b_k}\frac{4^{|S(v_k)|}-1}{3} \lt 4d_k+\frac{1}{3}4^{|S(v_k)|}2^{b_k},
\end{eqnarray}
\begin{eqnarray}
y_k+v_k=v_k+\sigma(v_k)+2^{b_k}\frac{4^{|S(v_k)|}-1}{3} \lt 4d_k+\frac{1}{3}4^{|S(v_k)|}2^{b_k},
\end{eqnarray}where the last inequality is based on the facts that ![]() $\sigma(v_k)\leqslant v_k$ and
$\sigma(v_k)\leqslant v_k$ and ![]() $v_k\leqslant 2d_k$. If
$v_k\leqslant 2d_k$. If  $b_k=\lceil \log_2\left(\frac{3x_k+2u_k-\sigma(v_k)}{4^{|S(v_k)|-1}}\right)\rceil$, then by
$b_k=\lceil \log_2\left(\frac{3x_k+2u_k-\sigma(v_k)}{4^{|S(v_k)|-1}}\right)\rceil$, then by ![]() $x_k \lt 86 d_k^3$ we know that
$x_k \lt 86 d_k^3$ we know that
 \begin{equation*}4d_k+\frac{1}{3}4^{|S(v_k)|}2^{b_k} \lt 4d_k+\frac{1}{3}4^{|S(v_k)|}(2\cdot\frac{3x_k+2u_k}{4^{|S(v_k)|-1}})
=4d_k+\frac{8}{3}(3x_k+2u_k) \lt 689d_k^3.\end{equation*}
\begin{equation*}4d_k+\frac{1}{3}4^{|S(v_k)|}2^{b_k} \lt 4d_k+\frac{1}{3}4^{|S(v_k)|}(2\cdot\frac{3x_k+2u_k}{4^{|S(v_k)|-1}})
=4d_k+\frac{8}{3}(3x_k+2u_k) \lt 689d_k^3.\end{equation*} If ![]() $b_k=\max S(v_k)+3$, then we could deduce from
$b_k=\max S(v_k)+3$, then we could deduce from ![]() $|S(v_k)|\leqslant \max S(v_k)+1$ and
$|S(v_k)|\leqslant \max S(v_k)+1$ and ![]() $2^{\max S(v_k)}\leqslant v_k$ that
$2^{\max S(v_k)}\leqslant v_k$ that
 \begin{eqnarray*}4d_k+\frac{1}{3}4^{|S(v_k)|}2^{b_k}
&=&4d_k+\frac{8}{3}4^{|S(v_k)|}2^{\max S(v_k)}\leqslant 4d_k+\frac{32}{3}2^{3\max S(v_k)}\\
&\leqslant &4d_k+\frac{32}{3}v_k^3\leqslant 86d_k^3.\end{eqnarray*}
\begin{eqnarray*}4d_k+\frac{1}{3}4^{|S(v_k)|}2^{b_k}
&=&4d_k+\frac{8}{3}4^{|S(v_k)|}2^{\max S(v_k)}\leqslant 4d_k+\frac{32}{3}2^{3\max S(v_k)}\\
&\leqslant &4d_k+\frac{32}{3}v_k^3\leqslant 86d_k^3.\end{eqnarray*} If ![]() $b_k=a_k+2|S(u_k)|-1$, then it infers from (2.4) that
$b_k=a_k+2|S(u_k)|-1$, then it infers from (2.4) that
 \begin{eqnarray*}4d_k+\frac{1}{3}4^{|S(v_k)|}2^{b_k}
&=&4d_k+\frac{1}{3}4^{|S(u_k)|}2^{a_k}\cdot\frac{1}{2}4^{|S(v_k)|}\leqslant 86d_k^3\cdot\frac{1}{2}4^{|S(v_k)|}\\
&\leqslant& 86d_k^3\cdot\frac{1}{2}(2d_k)^2=172d_k^5.
\end{eqnarray*}
\begin{eqnarray*}4d_k+\frac{1}{3}4^{|S(v_k)|}2^{b_k}
&=&4d_k+\frac{1}{3}4^{|S(u_k)|}2^{a_k}\cdot\frac{1}{2}4^{|S(v_k)|}\leqslant 86d_k^3\cdot\frac{1}{2}4^{|S(v_k)|}\\
&\leqslant& 86d_k^3\cdot\frac{1}{2}(2d_k)^2=172d_k^5.
\end{eqnarray*}In any case,
 \begin{eqnarray*}4d_k+\frac{1}{3}4^{|S(v_k)|}2^{b_k}\leqslant 172d_k^5.\end{eqnarray*}
\begin{eqnarray*}4d_k+\frac{1}{3}4^{|S(v_k)|}2^{b_k}\leqslant 172d_k^5.\end{eqnarray*}It infers from (2.5) and (2.7) that
To sum up,
Now we divide into the following two cases according to ![]() $u_k\not\in A_k+A_k$ or
$u_k\not\in A_k+A_k$ or ![]() $u_k\in A_k+A_k$.
$u_k\in A_k+A_k$.
Case 1. ![]() $u_k\not\in A_k+A_k$.
$u_k\not\in A_k+A_k$.
Let
 \begin{equation*}B_{k+1}=A_k\bigcup\{x_k,-x_k+u_k\} \hskip3mm \textrm{and} \hskip2mm A_{k+1}=B_{k+1}\bigcup\{y_k,y_k+v_k\}.\end{equation*}
\begin{equation*}B_{k+1}=A_k\bigcup\{x_k,-x_k+u_k\} \hskip3mm \textrm{and} \hskip2mm A_{k+1}=B_{k+1}\bigcup\{y_k,y_k+v_k\}.\end{equation*} It follows from ![]() $x_k \gt x_k-u_k \gt 3d_k$,
$x_k \gt x_k-u_k \gt 3d_k$, ![]() $3x_k+2u_k\leqslant y_k \lt y_k+v_k$ and the definitions of dk, xk, yk, we know that
$3x_k+2u_k\leqslant y_k \lt y_k+v_k$ and the definitions of dk, xk, yk, we know that  $r_{A_{k+1}}(u_k)=d_{A_{k+1}}(v_k)=1$,
$r_{A_{k+1}}(u_k)=d_{A_{k+1}}(v_k)=1$,  $r_{A_{k+1}}(n)\leqslant 1$ for all
$r_{A_{k+1}}(n)\leqslant 1$ for all ![]() $n\in \mathbb{Z}$ and
$n\in \mathbb{Z}$ and  $d_{A_{k+1}}(n)\leqslant 1$ for all
$d_{A_{k+1}}(n)\leqslant 1$ for all ![]() $n\in \mathbb{N}$. Thus, (ii) holds. By
$n\in \mathbb{N}$. Thus, (ii) holds. By ![]() $a_k\geqslant\max S(u_k)+3$,
$a_k\geqslant\max S(u_k)+3$, ![]() $b_k\geqslant\max S(v_k)+3$ and the definition of
$b_k\geqslant\max S(v_k)+3$ and the definition of ![]() $A_{k+1}$ we know that (i) and (v) hold. We will prove that
$A_{k+1}$ we know that (i) and (v) hold. We will prove that ![]() $|S(x)\bigcup S(y)|\leqslant 4|S(x+y)|$ for
$|S(x)\bigcup S(y)|\leqslant 4|S(x+y)|$ for ![]() $x,y\in A_{k+1}$. If x = y, then
$x,y\in A_{k+1}$. If x = y, then
 \begin{equation*}|S(x)\bigcup S(y)|=|S(x)|=|S(2x)|=|S(x+y)|\leqslant 4|S(x+y)|.\end{equation*}
\begin{equation*}|S(x)\bigcup S(y)|=|S(x)|=|S(2x)|=|S(x+y)|\leqslant 4|S(x+y)|.\end{equation*}So we only need to consider x ≠ y.
Firstly, we will prove that ![]() $|S(x)\bigcup S(y)|\leqslant 4|S(x+y)|$ for
$|S(x)\bigcup S(y)|\leqslant 4|S(x+y)|$ for ![]() $x,y\in B_{k+1}$ with x ≠ y. Noting that
$x,y\in B_{k+1}$ with x ≠ y. Noting that
 \begin{eqnarray*}|S(x_k)|&\leqslant& |S(u_k+\sigma(u_k))|+\left|S\left(2^{a_k}+2^{a_k+2}
+2^{a_k+4}+\cdots+2^{a_k+2(|S(u_k)|-1)}\right)\right|\\
&=&|S(\sigma(u_k))|+|S(u_k)|\leqslant 2|S(u_k)|\end{eqnarray*}
\begin{eqnarray*}|S(x_k)|&\leqslant& |S(u_k+\sigma(u_k))|+\left|S\left(2^{a_k}+2^{a_k+2}
+2^{a_k+4}+\cdots+2^{a_k+2(|S(u_k)|-1)}\right)\right|\\
&=&|S(\sigma(u_k))|+|S(u_k)|\leqslant 2|S(u_k)|\end{eqnarray*}and
 \begin{eqnarray*}|S(-x_k+u_k)|&=&\left|S\left(\sigma(u_k)+2^{a_k}+2^{a_k+2}
+2^{a_k+4}+\cdots+2^{a_k+2(|S(u_k)|-1)}\right)\right|\\
&\leqslant& |S(\sigma(u_k))|+|S(u_k)|\leqslant 2|S(u_k)|,\end{eqnarray*}
\begin{eqnarray*}|S(-x_k+u_k)|&=&\left|S\left(\sigma(u_k)+2^{a_k}+2^{a_k+2}
+2^{a_k+4}+\cdots+2^{a_k+2(|S(u_k)|-1)}\right)\right|\\
&\leqslant& |S(\sigma(u_k))|+|S(u_k)|\leqslant 2|S(u_k)|,\end{eqnarray*}we have
 \begin{equation*}|S(x_k)\bigcup S(-x_k+u_k)|\leqslant 4|S(u_k)|=4|S(x_k+(-x_k+u_k))|.\end{equation*}
\begin{equation*}|S(x_k)\bigcup S(-x_k+u_k)|\leqslant 4|S(u_k)|=4|S(x_k+(-x_k+u_k))|.\end{equation*} Let ![]() $x\in A_k$. By (2.1) we have
$x\in A_k$. By (2.1) we have ![]() $a_k\geqslant \log_2 d_k+1$, then
$a_k\geqslant \log_2 d_k+1$, then ![]() $a_k \gt \max S(|x|)$. Also by (2.1), we know that
$a_k \gt \max S(|x|)$. Also by (2.1), we know that ![]() $a_k\geqslant\max S(u_k)+3$. Taking
$a_k\geqslant\max S(u_k)+3$. Taking ![]() $y_1=u_k+\sigma(u_k)$ and
$y_1=u_k+\sigma(u_k)$ and ![]() $z_1=2^{a_k}+2^{a_k+2}+2^{a_k+4}+\cdots+2^{a_k+2(|S(u_k)|-1)}$ in Lemma 2.1, we have
$z_1=2^{a_k}+2^{a_k+2}+2^{a_k+4}+\cdots+2^{a_k+2(|S(u_k)|-1)}$ in Lemma 2.1, we have
 \begin{eqnarray*}|S(x)\bigcup S(x_k)|=|S(x)\bigcup S(y_1+z_1)|\leqslant 4|S(x+y_1+z_1)|=4|S(x+x_k)|.\end{eqnarray*}
\begin{eqnarray*}|S(x)\bigcup S(x_k)|=|S(x)\bigcup S(y_1+z_1)|\leqslant 4|S(x+y_1+z_1)|=4|S(x+x_k)|.\end{eqnarray*} Taking ![]() $y_2=-\sigma(u_k)$ and
$y_2=-\sigma(u_k)$ and ![]() $z_2=-(2^{a_k}+2^{a_k+2}+2^{a_k+4}+\cdots+2^{a_k+2(|S(u_k)|-1)})$ in Lemma 2.1, we have
$z_2=-(2^{a_k}+2^{a_k+2}+2^{a_k+4}+\cdots+2^{a_k+2(|S(u_k)|-1)})$ in Lemma 2.1, we have
 \begin{eqnarray*}|S(x)\bigcup S(-x_k+u_k)|=|S(x)\bigcup S(y_2+z_2)|\leqslant 4|S(x+y_2+z_2)|=4|S(x-x_k+u_k)|.\end{eqnarray*}
\begin{eqnarray*}|S(x)\bigcup S(-x_k+u_k)|=|S(x)\bigcup S(y_2+z_2)|\leqslant 4|S(x+y_2+z_2)|=4|S(x-x_k+u_k)|.\end{eqnarray*} Thus, ![]() $|S(x)\bigcup S(y)|\leqslant 4|S(x+y)|$ for
$|S(x)\bigcup S(y)|\leqslant 4|S(x+y)|$ for ![]() $x,y\in B_{k+1}$ with x ≠ y.
$x,y\in B_{k+1}$ with x ≠ y.
Now, we will prove that ![]() $|S(x)\bigcup S(y)|\leqslant 4|S(x+y)|$ for
$|S(x)\bigcup S(y)|\leqslant 4|S(x+y)|$ for ![]() $x,y\in A_{k+1}$ with x ≠ y. It follows from (2.6) that
$x,y\in A_{k+1}$ with x ≠ y. It follows from (2.6) that
 \begin{eqnarray*}|S(y_k)|&=&\left|S\left(\sigma(v_k)+2^{b_k}+2^{b_k+2}+2^{b_k+4}+\cdots
+2^{b_k+2(|S(v_k)|-1)}\right)\right|\\
&\leqslant& |S(\sigma(v_k))|+\left|S\left(2^{b_k}+2^{b_k+2}+2^{b_k+4}+\cdots
+2^{b_k+2(|S(v_k)|-1)}\right)\right|\\
&=&|S(\sigma(v_k))|+|S(v_k)|\leqslant 2|S(v_k)|\end{eqnarray*}
\begin{eqnarray*}|S(y_k)|&=&\left|S\left(\sigma(v_k)+2^{b_k}+2^{b_k+2}+2^{b_k+4}+\cdots
+2^{b_k+2(|S(v_k)|-1)}\right)\right|\\
&\leqslant& |S(\sigma(v_k))|+\left|S\left(2^{b_k}+2^{b_k+2}+2^{b_k+4}+\cdots
+2^{b_k+2(|S(v_k)|-1)}\right)\right|\\
&=&|S(\sigma(v_k))|+|S(v_k)|\leqslant 2|S(v_k)|\end{eqnarray*}and
 \begin{eqnarray*}|S(y_k+v_k)|&=&\left|S\left(v_k+\sigma(v_k)+2^{b_k}+2^{b_k+2}+2^{b_k+4}+\cdots
+2^{b_k+2(|S(v_k)|-1)}\right)\right|\\
&\leqslant&|S(v_k+\sigma(v_k))|+|S(v_k)|\leqslant 2|S(v_k)|,\end{eqnarray*}
\begin{eqnarray*}|S(y_k+v_k)|&=&\left|S\left(v_k+\sigma(v_k)+2^{b_k}+2^{b_k+2}+2^{b_k+4}+\cdots
+2^{b_k+2(|S(v_k)|-1)}\right)\right|\\
&\leqslant&|S(v_k+\sigma(v_k))|+|S(v_k)|\leqslant 2|S(v_k)|,\end{eqnarray*}we have
 \begin{equation*}|S(y_k)\bigcup S(y_k+v_k)|\leqslant 4|S(v_k)|.\end{equation*}
\begin{equation*}|S(y_k)\bigcup S(y_k+v_k)|\leqslant 4|S(v_k)|.\end{equation*} By ![]() $b_k\geqslant\max S(v_k)+3$ and
$b_k\geqslant\max S(v_k)+3$ and
 \begin{eqnarray*}S(2y_k+v_k)=S(2\sigma(v_k)+v_k+2\left(2^{b_k}+2^{b_k+2}+2^{b_k+4}+\cdots
+2^{b_k+2(|S(v_k)|-1)}\right)),\end{eqnarray*}
\begin{eqnarray*}S(2y_k+v_k)=S(2\sigma(v_k)+v_k+2\left(2^{b_k}+2^{b_k+2}+2^{b_k+4}+\cdots
+2^{b_k+2(|S(v_k)|-1)}\right)),\end{eqnarray*}we know that
 \begin{eqnarray*}|S(2y_k+v_k)|&=&|S(2\sigma(v_k)+v_k)|+\left|S\left(2^{b_k}+2^{b_k+2}+2^{b_k+4}+\cdots
+2^{b_k+2(|S(v_k)|-1)}\right)\right|\\
&\geqslant& \left|S\left(2^{b_k}+2^{b_k+2}+2^{b_k+4}+\cdots
+2^{b_k+2(|S(v_k)|-1)}\right)\right|=|S(v_k)|.\end{eqnarray*}
\begin{eqnarray*}|S(2y_k+v_k)|&=&|S(2\sigma(v_k)+v_k)|+\left|S\left(2^{b_k}+2^{b_k+2}+2^{b_k+4}+\cdots
+2^{b_k+2(|S(v_k)|-1)}\right)\right|\\
&\geqslant& \left|S\left(2^{b_k}+2^{b_k+2}+2^{b_k+4}+\cdots
+2^{b_k+2(|S(v_k)|-1)}\right)\right|=|S(v_k)|.\end{eqnarray*}Thus,
 \begin{equation*}|S(y_k)\bigcup S(y_k+v_k)|\leqslant 4|S(2y_k+v_k)|.\end{equation*}
\begin{equation*}|S(y_k)\bigcup S(y_k+v_k)|\leqslant 4|S(2y_k+v_k)|.\end{equation*} Let ![]() $x\in B_{k+1}$. By (2.5) we have
$x\in B_{k+1}$. By (2.5) we have ![]() $b_k\geqslant a_k+2|S(u_k)|-1$, namely,
$b_k\geqslant a_k+2|S(u_k)|-1$, namely, ![]() $b_k \gt a_k+2(|S(u_k)|-1)$. Then
$b_k \gt a_k+2(|S(u_k)|-1)$. Then ![]() $b_k \gt \max S(|x|)$. Also by (2.5), we know that
$b_k \gt \max S(|x|)$. Also by (2.5), we know that ![]() $b_k\geqslant\max S(v_k)+3$. Taking
$b_k\geqslant\max S(v_k)+3$. Taking ![]() $y_1=\sigma(v_k)$ and
$y_1=\sigma(v_k)$ and ![]() $z_1=2^{b_k}+2^{b_k+2}+2^{b_k+4}+\cdots
+2^{b_k+2(|S(v_k)|-1)}$ in Lemma 2.1, we have
$z_1=2^{b_k}+2^{b_k+2}+2^{b_k+4}+\cdots
+2^{b_k+2(|S(v_k)|-1)}$ in Lemma 2.1, we have
 \begin{eqnarray*}|S(x)\bigcup S(y_k)|=|S(x)\bigcup S(y_1+z_1)|\leqslant 4|S(x+y_1+z_1)|=4|S(x+y_k)|.\end{eqnarray*}
\begin{eqnarray*}|S(x)\bigcup S(y_k)|=|S(x)\bigcup S(y_1+z_1)|\leqslant 4|S(x+y_1+z_1)|=4|S(x+y_k)|.\end{eqnarray*} Taking ![]() $y_2=\sigma(v_k)+v_k$ and
$y_2=\sigma(v_k)+v_k$ and ![]() $z_2=2^{b_k}+2^{b_k+2}+2^{b_k+4}+\cdots
+2^{b_k+2(|S(v_k)|-1)}$ in Lemma 2.1, we have
$z_2=2^{b_k}+2^{b_k+2}+2^{b_k+4}+\cdots
+2^{b_k+2(|S(v_k)|-1)}$ in Lemma 2.1, we have
 \begin{eqnarray*}|S(x)\bigcup S(y_k+v_k)|=|S(x)\bigcup S(y_2+z_2)|\leqslant 4|S(x+y_2+z_2)|=4|S(x+y_k+v_k)|.\end{eqnarray*}
\begin{eqnarray*}|S(x)\bigcup S(y_k+v_k)|=|S(x)\bigcup S(y_2+z_2)|\leqslant 4|S(x+y_2+z_2)|=4|S(x+y_k+v_k)|.\end{eqnarray*} To sum up, ![]() $|S(x)\bigcup S(y)|\leqslant 4|S(x+y)|$ for
$|S(x)\bigcup S(y)|\leqslant 4|S(x+y)|$ for ![]() $x,y\in A_{k+1}$.
$x,y\in A_{k+1}$.
Case 2. ![]() $u_k\in A_k+A_k$. Then
$u_k\in A_k+A_k$. Then ![]() $-u_k\not\in A_k+A_k$.
$-u_k\not\in A_k+A_k$.
Let
where xk and yk are defined in (2.2) and (2.6). Similar to Case 1, we know that ![]() $A_{k+1}$ satisfies (i)-(ii), (iv)-(v) and
$A_{k+1}$ satisfies (i)-(ii), (iv)-(v) and  $r_{A_{k+1}}(-u_k)=d_{A_{k+1}}(v_k)=1$.
$r_{A_{k+1}}(-u_k)=d_{A_{k+1}}(v_k)=1$.
In both cases, it follows from (2.8) and the construction of ![]() $A_{k+1}$ that
$A_{k+1}$ that ![]() $d_{k+1} \lt 172d_k^5$. Thus, (vi) holds.
$d_{k+1} \lt 172d_k^5$. Thus, (vi) holds.
Now we will prove that (iii) holds. (The proof of (iii) is the same as in [Reference Xiong and Tang7, Theorem 1.1], we also give the details for the sake of completeness). If ![]() $u_k\not\in A_k+A_k$, then by Case 1 we know that
$u_k\not\in A_k+A_k$, then by Case 1 we know that ![]() $u_k\in A_{k+1}+A_{k+1}$, thus,
$u_k\in A_{k+1}+A_{k+1}$, thus, ![]() $u_{k+2}\geqslant u_{k+1} \gt u_k$ if
$u_{k+2}\geqslant u_{k+1} \gt u_k$ if ![]() $-u_k\in A_{k+1}+A_{k+1}$. Otherwise, if
$-u_k\in A_{k+1}+A_{k+1}$. Otherwise, if ![]() $-u_k\not\in A_{k+1}+A_{k+1}$, then
$-u_k\not\in A_{k+1}+A_{k+1}$, then ![]() $u_{k+1}=u_k\in A_{k+1}+A_{k+1}$ and
$u_{k+1}=u_k\in A_{k+1}+A_{k+1}$ and ![]() $-u_{k+1}\in A_{k+2}+A_{k+2}$ by Case 2, thus,
$-u_{k+1}\in A_{k+2}+A_{k+2}$ by Case 2, thus, ![]() $u_{k+2} \gt u_{k+1}=u_k$. If
$u_{k+2} \gt u_{k+1}=u_k$. If ![]() $u_k\in A_k+A_k$, then by Case 2 we know that
$u_k\in A_k+A_k$, then by Case 2 we know that ![]() $-u_k\in A_{k+1}+A_{k+1}$. It follows from
$-u_k\in A_{k+1}+A_{k+1}$. It follows from ![]() $u_k\in A_k+A_k\subseteq A_{k+1}+A_{k+1}$ that
$u_k\in A_k+A_k\subseteq A_{k+1}+A_{k+1}$ that ![]() $u_{k+2}\geqslant u_{k+1} \gt u_k$. In both cases,
$u_{k+2}\geqslant u_{k+1} \gt u_k$. In both cases, ![]() $u_{k+2} \gt u_k$. It follows from
$u_{k+2} \gt u_k$. It follows from ![]() $u_2\geqslant 2$ that
$u_2\geqslant 2$ that ![]() $u_{2k}\geqslant u_2+k-1\geqslant k+1$. Thus, for any positive integer k we have
$u_{2k}\geqslant u_2+k-1\geqslant k+1$. Thus, for any positive integer k we have
Similarly, ![]() $v_k \lt v_{k+1}$. It infers from
$v_k \lt v_{k+1}$. It infers from ![]() $v_1\geqslant 2$ that
$v_1\geqslant 2$ that ![]() $v_k\geqslant k+1$. Thus, for any positive integer k we have
$v_k\geqslant k+1$. Thus, for any positive integer k we have
Namely,  $r_{A_{k+1}}(n)=1$ for all
$r_{A_{k+1}}(n)=1$ for all ![]() $n\in \mathbb{Z}$ with
$n\in \mathbb{Z}$ with  $|n|\leqslant \lfloor\frac{k+1}{2}\rfloor$ and
$|n|\leqslant \lfloor\frac{k+1}{2}\rfloor$ and  $d_{A_{k+1}}(n)=1$ for all
$d_{A_{k+1}}(n)=1$ for all ![]() $n\in \mathbb{N}$ with
$n\in \mathbb{N}$ with ![]() $1\leqslant n\leqslant k+1$. Thus, (iii) holds.
$1\leqslant n\leqslant k+1$. Thus, (iii) holds.
Let
 \begin{equation*}A=\bigcup_{k=1}^{\infty} A_k.\end{equation*}
\begin{equation*}A=\bigcup_{k=1}^{\infty} A_k.\end{equation*} Then ![]() $r_A(n)=1$ for all
$r_A(n)=1$ for all ![]() $n\in \mathbb{Z}$ and
$n\in \mathbb{Z}$ and ![]() $d_A(n)=1$ for all
$d_A(n)=1$ for all ![]() $n\in \mathbb{N}$,
$n\in \mathbb{N}$, ![]() $|S(x)\bigcup S(y)|\leqslant 4|S(x+y)|$ for
$|S(x)\bigcup S(y)|\leqslant 4|S(x+y)|$ for ![]() $x,y\in A$. Furthermore, we could deduce from (vi) and
$x,y\in A$. Furthermore, we could deduce from (vi) and ![]() $d_0=1$ that
$d_0=1$ that
 \begin{eqnarray*} d_k\leqslant c_1^{5^k}, \hskip3mm \textrm{where} \hskip3mm c_1=\sqrt[4]{172}. \end{eqnarray*}
\begin{eqnarray*} d_k\leqslant c_1^{5^k}, \hskip3mm \textrm{where} \hskip3mm c_1=\sqrt[4]{172}. \end{eqnarray*} For sufficiently large x, there exists a positive integer k such that ![]() $d_k\leqslant x \lt d_{k+1}$. It follows from
$d_k\leqslant x \lt d_{k+1}$. It follows from ![]() $4k+3\leqslant A(-x,x)\leqslant 4k+7$ that
$4k+3\leqslant A(-x,x)\leqslant 4k+7$ that
 \begin{equation*}A(-x,x) \gt \frac{4}{\log 5}\log\log x+c, \hskip2mm\textrm{where}\hskip2mm c \hskip2mm\textrm{is an absolute constant}.\end{equation*}
\begin{equation*}A(-x,x) \gt \frac{4}{\log 5}\log\log x+c, \hskip2mm\textrm{where}\hskip2mm c \hskip2mm\textrm{is an absolute constant}.\end{equation*} This completes the proof of Theorem 1.1. ![]() $\Box$
$\Box$
Proof of Theorem 1.2. In the proof of Theorem 1.1, the only constraint on the choice of xk (resp. yk) is the size of the value ak (resp. bk). The following proof is similar to [Reference Nathanson5, Theorem 1] and [Reference Xiong and Tang7, Theorem 1.1]. We apply the method of Theorem 1.1 by replacing ak with ![]() $s_k(\geqslant a_k)$. Namely, take
$s_k(\geqslant a_k)$. Namely, take
Given a function f(x) tending to infinity, we shall take induction on k to construct a non-decreasing sequence of integers ![]() $\{h_k\}_{k=1}^\infty$ such that
$\{h_k\}_{k=1}^\infty$ such that ![]() $A(-x,x)\leqslant f(x)$ for all integers x with
$A(-x,x)\leqslant f(x)$ for all integers x with ![]() $h_1\leqslant x\leqslant d_k$. Firstly, choose
$h_1\leqslant x\leqslant d_k$. Firstly, choose ![]() $h_1\geqslant d_1$ so that
$h_1\geqslant d_1$ so that ![]() $f(x)\geqslant 11$ for
$f(x)\geqslant 11$ for ![]() $x\geqslant h_1$. Then
$x\geqslant h_1$. Then
Suppose that for some integer ![]() $k\geqslant 2$, we have already selected an integer
$k\geqslant 2$, we have already selected an integer ![]() $h_{k-1}\geqslant d_{k-1}$ such that
$h_{k-1}\geqslant d_{k-1}$ such that
Noting that f(x) tends to infinity, there exist positive integers hk and ![]() $s_{k+1}$ with
$s_{k+1}$ with ![]() $h_k\geqslant d_k$ and
$h_k\geqslant d_k$ and ![]() $h_k \lt x_{k+1}-u_{k+1}$ (taking large
$h_k \lt x_{k+1}-u_{k+1}$ (taking large ![]() $s_{k+1}$ in (2.9)) such that
$s_{k+1}$ in (2.9)) such that ![]() $f(x)\geqslant 4k+7$ for
$f(x)\geqslant 4k+7$ for ![]() $x\geqslant h_{k}$. It follows that
$x\geqslant h_{k}$. It follows that
For ![]() $d_k\leqslant x\leqslant h_k$, we could deduce from the construction of
$d_k\leqslant x\leqslant h_k$, we could deduce from the construction of ![]() $A_{k+1}\setminus A_k$ and the fact
$A_{k+1}\setminus A_k$ and the fact ![]() $h_k \lt x_{k+1}-u_{k+1}$ that
$h_k \lt x_{k+1}-u_{k+1}$ that
To sum up,
By the induction hypothesis we know that ![]() $A(-x,x)\leqslant f(x)$ for
$A(-x,x)\leqslant f(x)$ for ![]() $h_1\leqslant x\leqslant d_{k+1}$. It follows that
$h_1\leqslant x\leqslant d_{k+1}$. It follows that
This completes the proof of Theorem 1.2.
3. Proof of Theorem 1.3
To give the proof of Theorem 1.3, we need the following preliminary lemmas. The idea is from [Reference Chen and Fang1, Theorem 1.2], [Reference Fang4, Theorem 1.1] and [Reference Nešetřil and Serra6, Theorem 5].
Lemma 3.1. Let ![]() $f_1:\mathbb{N}\rightarrow \mathbb{N}$ and
$f_1:\mathbb{N}\rightarrow \mathbb{N}$ and ![]() $f_2:\mathbb{Z}\rightarrow \mathbb{N}$ be two functions such that
$f_2:\mathbb{Z}\rightarrow \mathbb{N}$ be two functions such that
 \begin{eqnarray}
\liminf_{u\rightarrow \infty}f_1(u)\geqslant 2 \hskip4mm \textrm{and} \hskip4mm \liminf_{|u|\rightarrow \infty}f_2(u)\geqslant 2.
\end{eqnarray}
\begin{eqnarray}
\liminf_{u\rightarrow \infty}f_1(u)\geqslant 2 \hskip4mm \textrm{and} \hskip4mm \liminf_{|u|\rightarrow \infty}f_2(u)\geqslant 2.
\end{eqnarray} Let ![]() $B\subseteq \mathbb{Z}$ be a finite set with
$B\subseteq \mathbb{Z}$ be a finite set with ![]() $|B|\geqslant 2$ such that:
$|B|\geqslant 2$ such that:
(i)
 $d_B(n)\leqslant f_1(n)$ for all
$d_B(n)\leqslant f_1(n)$ for all  $n\in \mathbb{N}$ and
$n\in \mathbb{N}$ and  $r_B(n)\leqslant f_2(n)$ for all
$r_B(n)\leqslant f_2(n)$ for all  $n\in \mathbb{Z}$;
$n\in \mathbb{Z}$;(ii)
 $|S(x)\bigcup S(y)|\leqslant 4|S(x+y)|$ for
$|S(x)\bigcup S(y)|\leqslant 4|S(x+y)|$ for  $x,y\in B$;
$x,y\in B$;(iii) the binary support of each element in B has no two consecutive integers.
If k is a positive integer with
 $d_B(k) \lt f_1(k)$, then there exists a finite set D with
$d_B(k) \lt f_1(k)$, then there exists a finite set D with  $B\subseteq D\subseteq \mathbb{Z}$ such that:
$B\subseteq D\subseteq \mathbb{Z}$ such that:(iv)
 $d_D(k)=d_B(k)+1$;
$d_D(k)=d_B(k)+1$;(v)
 $d_D(n)\leqslant f_1(n)$ for all
$d_D(n)\leqslant f_1(n)$ for all  $n\in \mathbb{N}$ and
$n\in \mathbb{N}$ and  $r_D(n)\leqslant f_2(n)$ for all
$r_D(n)\leqslant f_2(n)$ for all  $n\in \mathbb{Z}$;
$n\in \mathbb{Z}$;(vi)
 $|S(x)\bigcup S(y)|\leqslant 4|S(x+y)|$ for
$|S(x)\bigcup S(y)|\leqslant 4|S(x+y)|$ for  $x,y\in D$;
$x,y\in D$;(vii) the binary support of each element in D has no two consecutive integers.
Proof. Let ![]() $B=\{b_1,b_2,\cdots,b_s\}$, where
$B=\{b_1,b_2,\cdots,b_s\}$, where ![]() $b_1 \lt b_2 \lt \cdots \lt b_s$. Let
$b_1 \lt b_2 \lt \cdots \lt b_s$. Let ![]() $m=2\max_{1\leqslant j\leqslant s}|b_j|+k$. By (3.1), we could choose a subset Uk of positive integers such that:
$m=2\max_{1\leqslant j\leqslant s}|b_j|+k$. By (3.1), we could choose a subset Uk of positive integers such that:
(1)
 $|U_k|=|S(k)|$;
$|U_k|=|S(k)|$;(2)
 $\min U_k \gt k+3\max ||B||$, where
$\min U_k \gt k+3\max ||B||$, where  $||B||=\{|b|:b\in B\}$;
$||B||=\{|b|:b\in B\}$;(3) Uk has no two consecutive integers;
(4)
 $f_1(n)\geqslant 2$ and
$f_1(n)\geqslant 2$ and  $f_2(n)\geqslant 2$ for all integers
$f_2(n)\geqslant 2$ for all integers  $n\in [b-m,b+m]\bigcap \mathbb{Z}$, where
$n\in [b-m,b+m]\bigcap \mathbb{Z}$, where  $b=\sigma(k)+\sum_{i\in U_k} 2^i$.
$b=\sigma(k)+\sum_{i\in U_k} 2^i$.
Let
 \begin{equation*}D=B\bigcup \{b,b+k\}.\end{equation*}
\begin{equation*}D=B\bigcup \{b,b+k\}.\end{equation*}Then
 \begin{equation*}D+D=\{2b,2b+k,2b+2k\}\bigcup\{B+B\}\bigcup\{B+b\}\bigcup\{B+b+k\}\end{equation*}
\begin{equation*}D+D=\{2b,2b+k,2b+2k\}\bigcup\{B+B\}\bigcup\{B+b\}\bigcup\{B+b+k\}\end{equation*}and
 \begin{equation*}D-D=\pm\{\{k\}\bigcup\{B-B\}\bigcup\{B-b\}\bigcup\{B-b-k\}\}.\end{equation*}
\begin{equation*}D-D=\pm\{\{k\}\bigcup\{B-B\}\bigcup\{B-b\}\bigcup\{B-b-k\}\}.\end{equation*} We could deduce from (i)-(iii), the definition of D and the fact ![]() $b \gt 3\max ||B||+k$ that
$b \gt 3\max ||B||+k$ that ![]() $d_D(k)=d_B(k)+1$, and the binary support of each element in D has no two consecutive integers. Furthermore,
$d_D(k)=d_B(k)+1$, and the binary support of each element in D has no two consecutive integers. Furthermore, ![]() $r_D(2b)=r_D(2b+k)=r_D(2b+2k)=1$. It also follows from
$r_D(2b)=r_D(2b+k)=r_D(2b+2k)=1$. It also follows from
 \begin{eqnarray*}&&b-m \lt b+b_1 \lt b+b_2 \lt \cdots \lt b+b_s \lt b+m,\\
&&b-m \lt b+k+b_1 \lt b+k+b_2 \lt \cdots \lt b+k+b_s \lt b+m\end{eqnarray*}
\begin{eqnarray*}&&b-m \lt b+b_1 \lt b+b_2 \lt \cdots \lt b+b_s \lt b+m,\\
&&b-m \lt b+k+b_1 \lt b+k+b_2 \lt \cdots \lt b+k+b_s \lt b+m\end{eqnarray*}and (4) that ![]() $r_D(n)\leqslant 2\leqslant f_2(n)$ for each
$r_D(n)\leqslant 2\leqslant f_2(n)$ for each ![]() $n\in \{B+b\}\bigcup\{B+b+k\}$. Noting that the sets
$n\in \{B+b\}\bigcup\{B+b+k\}$. Noting that the sets ![]() $\{2b,2b+k,2b+2k\}$, B + B, B + b and
$\{2b,2b+k,2b+2k\}$, B + B, B + b and ![]() $B+b+k$ are pairwise disjoint, we know that
$B+b+k$ are pairwise disjoint, we know that ![]() $r_D(n)\leqslant f_2(n)$ for all integers n. Similarly, by
$r_D(n)\leqslant f_2(n)$ for all integers n. Similarly, by
 \begin{eqnarray*}&&b-m \lt b-b_s \lt b-b_{s-1} \lt \cdots \lt b-b_1 \lt b+m,\\
&&b-m \lt b+k-b_s \lt b+k-b_{s-1} \lt \cdots \lt b+k-b_1 \lt b+m,\end{eqnarray*}
\begin{eqnarray*}&&b-m \lt b-b_s \lt b-b_{s-1} \lt \cdots \lt b-b_1 \lt b+m,\\
&&b-m \lt b+k-b_s \lt b+k-b_{s-1} \lt \cdots \lt b+k-b_1 \lt b+m,\end{eqnarray*}and (4) we have ![]() $d_D(n)\leqslant 2\leqslant f_1(n)$ for each
$d_D(n)\leqslant 2\leqslant f_1(n)$ for each ![]() $n\in \{B-b\}\bigcup\{B-b-k\}$. Noting that the sets B − B, B − b and
$n\in \{B-b\}\bigcup\{B-b-k\}$. Noting that the sets B − B, B − b and ![]() $B-b-k$ are pairwise disjoint, we know that
$B-b-k$ are pairwise disjoint, we know that ![]() $d_D(n)\leqslant f_1(n)$ for all positive integers n. By the same proof as in Theorem 1.1, we know that
$d_D(n)\leqslant f_1(n)$ for all positive integers n. By the same proof as in Theorem 1.1, we know that ![]() $|S(x)\bigcup S(y)|\leqslant 4|S(x+y)|$ for
$|S(x)\bigcup S(y)|\leqslant 4|S(x+y)|$ for ![]() $x,y\in D$.
$x,y\in D$.
This completes the proof of Lemma 3.1.
Lemma 3.2. Let ![]() $f_1:\mathbb{N}\rightarrow \mathbb{N}$ and
$f_1:\mathbb{N}\rightarrow \mathbb{N}$ and ![]() $f_2:\mathbb{Z}\rightarrow \mathbb{N}$ be two functions such that (3.1) holds. Let
$f_2:\mathbb{Z}\rightarrow \mathbb{N}$ be two functions such that (3.1) holds. Let ![]() $B\subseteq \mathbb{Z}$ be a finite set with
$B\subseteq \mathbb{Z}$ be a finite set with ![]() $|B|\geqslant 2$ such that:
$|B|\geqslant 2$ such that:
(i)
 $d_B(n)\leqslant f_1(n)$ for all
$d_B(n)\leqslant f_1(n)$ for all  $n\in \mathbb{N}$ and
$n\in \mathbb{N}$ and  $r_B(n)\leqslant f_2(n)$ for all
$r_B(n)\leqslant f_2(n)$ for all  $n\in \mathbb{Z}$;
$n\in \mathbb{Z}$;(ii)
 $|S(x)\bigcup S(y)|\leqslant 4|S(x+y)|$ for
$|S(x)\bigcup S(y)|\leqslant 4|S(x+y)|$ for  $x,y\in B$;
$x,y\in B$;(iii) the binary support of each element in B has no two consecutive integers.
If k is an integer with
 $r_B(k) \lt f_2(k)$, then there exists a finite set D with
$r_B(k) \lt f_2(k)$, then there exists a finite set D with  $B\subseteq D\subseteq \mathbb{Z}$ such that:
$B\subseteq D\subseteq \mathbb{Z}$ such that:(iv)
 $r_D(k)=r_B(k)+1$;
$r_D(k)=r_B(k)+1$;(v)
 $d_D(n)\leqslant f_1(n)$ for all
$d_D(n)\leqslant f_1(n)$ for all  $n\in \mathbb{N}$ and
$n\in \mathbb{N}$ and  $r_D(n)\leqslant f_2(n)$ for all
$r_D(n)\leqslant f_2(n)$ for all  $n\in \mathbb{Z}$;
$n\in \mathbb{Z}$;(vi)
 $|S(x)\bigcup S(y)|\leqslant 4|S(x+y)|$ for
$|S(x)\bigcup S(y)|\leqslant 4|S(x+y)|$ for  $x,y\in D$;
$x,y\in D$;(vii) the binary support of each element in D has no two consecutive integers.
Proof. Let ![]() $B=\{b_1,b_2,\cdots,b_s\}$, where
$B=\{b_1,b_2,\cdots,b_s\}$, where ![]() $b_1 \lt b_2 \lt \cdots \lt b_s$. Let
$b_1 \lt b_2 \lt \cdots \lt b_s$. Let ![]() $m=2\max_{1\leqslant j\leqslant s}|b_j|+|k|$. By (3.1), we could choose a subset Uk of positive integers such that:
$m=2\max_{1\leqslant j\leqslant s}|b_j|+|k|$. By (3.1), we could choose a subset Uk of positive integers such that:
(1)
 $|U_k|=|S(k)|$;
$|U_k|=|S(k)|$;(2)
 $\min U_k \gt |k|+3\max ||B||$;
$\min U_k \gt |k|+3\max ||B||$;(3) Uk has no two consecutive integers;
(4)
 $f_1(n)\geqslant 2$ and
$f_1(n)\geqslant 2$ and  $f_2(n)\geqslant 2$ for all integers
$f_2(n)\geqslant 2$ for all integers  $n\in [b-m,b+m]\bigcap \mathbb{Z}$, where
$n\in [b-m,b+m]\bigcap \mathbb{Z}$, where
 \begin{eqnarray*}b=
\begin{cases}
k+\sigma(k)+\sum_{i\in U_k} 2^i, &\textrm{if}\hskip2mm k \gt 0,
\cr \sum_{i\in U_k} 2^i, & \textrm{if}\hskip2mm k=0,
\cr k+\sigma(k)+\sum_{i\in U_k} 2^{-i}, & \textrm{if}\hskip2mm k \lt 0.\end{cases}
\end{eqnarray*}
\begin{eqnarray*}b=
\begin{cases}
k+\sigma(k)+\sum_{i\in U_k} 2^i, &\textrm{if}\hskip2mm k \gt 0,
\cr \sum_{i\in U_k} 2^i, & \textrm{if}\hskip2mm k=0,
\cr k+\sigma(k)+\sum_{i\in U_k} 2^{-i}, & \textrm{if}\hskip2mm k \lt 0.\end{cases}
\end{eqnarray*}
Let
 \begin{equation*}D=B\bigcup \{b,-b+k\}.\end{equation*}
\begin{equation*}D=B\bigcup \{b,-b+k\}.\end{equation*}Then
 \begin{equation*}D+D=\{k,2b,-2b+2k\}\bigcup(B+B)\bigcup(B+b)\bigcup(B-b+k)\end{equation*}
\begin{equation*}D+D=\{k,2b,-2b+2k\}\bigcup(B+B)\bigcup(B+b)\bigcup(B-b+k)\end{equation*}and
 \begin{equation*}D-D=\pm\{\{2b-k\}\bigcup(B-B)\bigcup(B-b)\bigcup(B+b-k)\}.\end{equation*}
\begin{equation*}D-D=\pm\{\{2b-k\}\bigcup(B-B)\bigcup(B-b)\bigcup(B+b-k)\}.\end{equation*} We could deduce from (i)-(iii), the definition of D and the fact ![]() $b \gt 3\max ||B||+k$ that
$b \gt 3\max ||B||+k$ that ![]() $r_D(k)=r_B(k)+1$, and the binary support of each element in D has no two consecutive integers. Furthermore,
$r_D(k)=r_B(k)+1$, and the binary support of each element in D has no two consecutive integers. Furthermore, ![]() $r_D(2b)=r_D(-2b+2k)=1$. It also follows from
$r_D(2b)=r_D(-2b+2k)=1$. It also follows from
 \begin{eqnarray*}&&b-m \lt b+b_1 \lt b+b_2 \lt \cdots \lt b+b_s \lt b+m,\\
&&b-m \lt -b+k+b_1 \lt -b+k+b_2 \lt \cdots \lt -b+k+b_s \lt b+m\end{eqnarray*}
\begin{eqnarray*}&&b-m \lt b+b_1 \lt b+b_2 \lt \cdots \lt b+b_s \lt b+m,\\
&&b-m \lt -b+k+b_1 \lt -b+k+b_2 \lt \cdots \lt -b+k+b_s \lt b+m\end{eqnarray*}and (4) that ![]() $r_D(n)\leqslant 2\leqslant f_2(n)$ for each
$r_D(n)\leqslant 2\leqslant f_2(n)$ for each ![]() $n\in \{B+b\}\bigcup\{B-b+k\}$. Noting that the sets
$n\in \{B+b\}\bigcup\{B-b+k\}$. Noting that the sets ![]() $\{2b,-2b+2k\}$, B + B, B + b and
$\{2b,-2b+2k\}$, B + B, B + b and ![]() $B-b+k$ are pairwise disjoint, we know that
$B-b+k$ are pairwise disjoint, we know that ![]() $r_D(n)\leqslant f_2(n)$ for all integers n. Similarly, by
$r_D(n)\leqslant f_2(n)$ for all integers n. Similarly, by
 \begin{eqnarray*}&&-2b-k \lt b-m \lt b-b_s \lt b-b_{s-1} \lt \cdots \lt b-b_1 \lt b+m \lt 2b+k,\\
&&b-m \lt b-k+b_1 \lt b-k+b_2 \lt \cdots \lt b-k+b_s \lt b+m\end{eqnarray*}
\begin{eqnarray*}&&-2b-k \lt b-m \lt b-b_s \lt b-b_{s-1} \lt \cdots \lt b-b_1 \lt b+m \lt 2b+k,\\
&&b-m \lt b-k+b_1 \lt b-k+b_2 \lt \cdots \lt b-k+b_s \lt b+m\end{eqnarray*}and (4) we have ![]() $d_D(n)\leqslant 2\leqslant f_1(n)$ for each
$d_D(n)\leqslant 2\leqslant f_1(n)$ for each ![]() $n\in \{B-b\}\bigcup\{B+b-k\}$. Noting that the sets
$n\in \{B-b\}\bigcup\{B+b-k\}$. Noting that the sets ![]() $\{2b-k\}$, B − B, B − b and
$\{2b-k\}$, B − B, B − b and ![]() $B+b-k$ are pairwise disjoint, we know that
$B+b-k$ are pairwise disjoint, we know that ![]() $d_D(n)\leqslant f_1(n)$ for all positive integers n. By the same proof as in Theorem 1.1, we know that
$d_D(n)\leqslant f_1(n)$ for all positive integers n. By the same proof as in Theorem 1.1, we know that ![]() $|S(x)\bigcup S(y)|\leqslant 4|S(x+y)|$ for
$|S(x)\bigcup S(y)|\leqslant 4|S(x+y)|$ for ![]() $x,y\in D$.
$x,y\in D$.
This completes the proof of Lemma 3.2.
Remark 3.3. During the proof of Lemma 3.1 and Lemma 3.2, since we do not need accurate quantitative estimation for dk, we just choose sufficiently large b in each stage.
Proof of Theorem 1.3. Theorem 1.3 follows from Lemma 3.1 and Lemma 3.2. The proof is similar to Theorem 1.1, we omit the detail here.
Funding Statement
This work was supported by the National Natural Science Foundation of China, Grant No. 12171246 and the Natural Science Foundation of Jiangsu Province, Grant No. BK20211282.