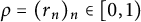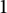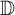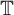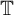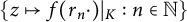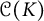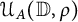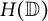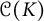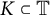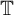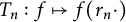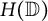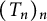1 Introduction
Let
![]() $\mathbb {D}:=\{z\in \mathbb {C}:\vert z\vert <1\}$
denote the open unit disk, let
$\mathbb {D}:=\{z\in \mathbb {C}:\vert z\vert <1\}$
denote the open unit disk, let
![]() ${\mathbb {T}}=\{z\in {\mathbb {C}}:\, \vert z\vert =1\}$
denote the unit circle, and let
${\mathbb {T}}=\{z\in {\mathbb {C}}:\, \vert z\vert =1\}$
denote the unit circle, and let
![]() $H(\mathbb {D})$
be the Fréchet space consisting of all holomorphic functions on
$H(\mathbb {D})$
be the Fréchet space consisting of all holomorphic functions on
![]() $\mathbb {D}$
endowed with the topology of uniform convergence on all compact subsets of
$\mathbb {D}$
endowed with the topology of uniform convergence on all compact subsets of
![]() $\mathbb {D}$
. When one is interested in the boundary behavior of a holomorphic function f in
$\mathbb {D}$
. When one is interested in the boundary behavior of a holomorphic function f in
![]() ${\mathbb {D}}$
, one can look at the behavior on
${\mathbb {D}}$
, one can look at the behavior on
![]() ${\mathbb {T}}$
of the partial sums of the Taylor expansion of f at
${\mathbb {T}}$
of the partial sums of the Taylor expansion of f at
![]() $0$
, or one can look at the behavior of
$0$
, or one can look at the behavior of
![]() $f(z)$
when z in
$f(z)$
when z in
![]() ${\mathbb {D}}$
approaches
${\mathbb {D}}$
approaches
![]() ${\mathbb {T}}$
. In the second case, the notion of cluster set of f at z comes naturally into play. Let us recall that if
${\mathbb {T}}$
. In the second case, the notion of cluster set of f at z comes naturally into play. Let us recall that if
![]() $\gamma :[0,1)\to {\mathbb {D}}$
is a continuous path to a boundary point of
$\gamma :[0,1)\to {\mathbb {D}}$
is a continuous path to a boundary point of
![]() ${\mathbb {D}}$
(that is,
${\mathbb {D}}$
(that is,
![]() $\gamma (r)\to z \in {\mathbb {T}}$
as
$\gamma (r)\to z \in {\mathbb {T}}$
as
![]() $r\to 1$
), the cluster set of f along
$r\to 1$
), the cluster set of f along
![]() $\gamma $
is defined as
$\gamma $
is defined as
In complex function theory, it is of great interest to distinguish and study classes of holomorphic functions with a regular boundary behavior. Regular boundary behavior at a point of
![]() ${\mathbb {T}}$
can mean, for instance, convergence, Cesàro summability, or Abel summability of the Taylor expansion at this point. We recall that a function f in
${\mathbb {T}}$
can mean, for instance, convergence, Cesàro summability, or Abel summability of the Taylor expansion at this point. We recall that a function f in
![]() $H({\mathbb {D}})$
is Abel summable at
$H({\mathbb {D}})$
is Abel summable at
![]() $\zeta \in {\mathbb {T}}$
if the quantity
$\zeta \in {\mathbb {T}}$
if the quantity
![]() $f(r\zeta )$
,
$f(r\zeta )$
,
![]() $r\in [0,1)$
, has a finite limit as
$r\in [0,1)$
, has a finite limit as
![]() $r\to 1$
. Note that in the latter case, the cluster set of f along the radius
$r\to 1$
. Note that in the latter case, the cluster set of f along the radius
![]() $\{r\zeta :\,r\in [0,1)\}$
is reduced to a single value. Yet, it is now well understood that nonregularity is a generic behavior. We say that a property is generic in a Baire space X if the set of those
$\{r\zeta :\,r\in [0,1)\}$
is reduced to a single value. Yet, it is now well understood that nonregularity is a generic behavior. We say that a property is generic in a Baire space X if the set of those
![]() $x\in X$
which satisfy this property contains a countable intersection of dense open sets. For example, it was already observed in 1933 that the set of functions whose cluster sets along any radius is equal to
$x\in X$
which satisfy this property contains a countable intersection of dense open sets. For example, it was already observed in 1933 that the set of functions whose cluster sets along any radius is equal to
![]() ${\mathbb {C}}$
, is residual in
${\mathbb {C}}$
, is residual in
![]() $H({\mathbb {D}})$
[Reference Kierst and Szpilrajn30]. In 2008, it was even shown that the set—denoted by
$H({\mathbb {D}})$
[Reference Kierst and Szpilrajn30]. In 2008, it was even shown that the set—denoted by
![]() ${\mathcal {U}}_C({\mathbb {D}})$
—of those functions
${\mathcal {U}}_C({\mathbb {D}})$
—of those functions
![]() $f\in H({\mathbb {D}})$
satisfying the previous property along any (continuous) path
$f\in H({\mathbb {D}})$
satisfying the previous property along any (continuous) path
![]() $\gamma :[0,1)\to {\mathbb {D}}$
having some limit
$\gamma :[0,1)\to {\mathbb {D}}$
having some limit
![]() $\zeta \in {\mathbb {T}}$
at
$\zeta \in {\mathbb {T}}$
at
![]() $1$
is residual in
$1$
is residual in
![]() $H({\mathbb {D}})$
[Reference Bernal-González, Calderón and Prado-Bassas8]. More recently, the first author exhibited in [Reference Charpentier12] another residual set of functions in
$H({\mathbb {D}})$
[Reference Bernal-González, Calderón and Prado-Bassas8]. More recently, the first author exhibited in [Reference Charpentier12] another residual set of functions in
![]() $H({\mathbb {D}})$
with a boundary behavior at least as wild as those of
$H({\mathbb {D}})$
with a boundary behavior at least as wild as those of
![]() ${\mathcal {U}}_C({\mathbb {D}})$
. Let
${\mathcal {U}}_C({\mathbb {D}})$
. Let
![]() $\varrho :=(r_n)_n \subset [0,1)$
be a sequence convergent to
$\varrho :=(r_n)_n \subset [0,1)$
be a sequence convergent to
![]() $1$
and denote by
$1$
and denote by
![]() ${\mathcal {U}}_A({\mathbb {D}},\varrho )$
the set of those
${\mathcal {U}}_A({\mathbb {D}},\varrho )$
the set of those
![]() $f\in H({\mathbb {D}})$
that satisfy the following property: for any compact set
$f\in H({\mathbb {D}})$
that satisfy the following property: for any compact set
![]() $K\subset {\mathbb {T}}$
different from
$K\subset {\mathbb {T}}$
different from
![]() ${\mathbb {T}}$
, the set
${\mathbb {T}}$
, the set
![]() $\{f_{r_n}|_K:\,n\in {\mathbb {N}}\}$
is dense in the space
$\{f_{r_n}|_K:\,n\in {\mathbb {N}}\}$
is dense in the space
![]() ${\mathcal {C}}(K)$
of all continuous functions on K endowed with the uniform topology. Here, for
${\mathcal {C}}(K)$
of all continuous functions on K endowed with the uniform topology. Here, for
![]() $r\in [0,1)$
, we denote by
$r\in [0,1)$
, we denote by
![]() $f_r$
the function given by
$f_r$
the function given by
![]() $f_r(z)=f(rz)$
,
$f_r(z)=f(rz)$
,
![]() $rz\in {\mathbb {D}}$
. It was then observed in [Reference Charpentier12] that
$rz\in {\mathbb {D}}$
. It was then observed in [Reference Charpentier12] that
![]() ${\mathcal {U}}_A({\mathbb {D}},\varrho )$
is residual in
${\mathcal {U}}_A({\mathbb {D}},\varrho )$
is residual in
![]() $H({\mathbb {D}})$
and that
$H({\mathbb {D}})$
and that
![]() ${\mathcal {U}}_A({\mathbb {D}},\varrho )\subset {\mathcal {U}}_C({\mathbb {D}})$
. At this point, we would like to introduce another natural class of universal functions, defined on the model of
${\mathcal {U}}_A({\mathbb {D}},\varrho )\subset {\mathcal {U}}_C({\mathbb {D}})$
. At this point, we would like to introduce another natural class of universal functions, defined on the model of
![]() ${\mathcal {U}}_A({\mathbb {D}},\varrho )$
but independent of the choice of a sequence
${\mathcal {U}}_A({\mathbb {D}},\varrho )$
but independent of the choice of a sequence
![]() $\varrho $
. Precisely, let
$\varrho $
. Precisely, let
![]() ${\mathcal {U}}_A({\mathbb {D}})$
denote the set of all functions f in
${\mathcal {U}}_A({\mathbb {D}})$
denote the set of all functions f in
![]() $H({\mathbb {D}})$
satisfying that, given any compact set
$H({\mathbb {D}})$
satisfying that, given any compact set
![]() $K\subset {\mathbb {T}}$
different from
$K\subset {\mathbb {T}}$
different from
![]() ${\mathbb {T}}$
and any
${\mathbb {T}}$
and any
![]() $h\in {\mathcal {C}}(K)$
, there exists
$h\in {\mathcal {C}}(K)$
, there exists
![]() $(r_n)_n\subset [0,1)$
tending to
$(r_n)_n\subset [0,1)$
tending to
![]() $1$
such that
$1$
such that
![]() $f_{r_n}$
approximates h uniformly on K. One can easily checks that
$f_{r_n}$
approximates h uniformly on K. One can easily checks that
In the whole paper, the elements of
![]() ${\mathcal {U}}_A({\mathbb {D}},\varrho )$
will be referred to as
${\mathcal {U}}_A({\mathbb {D}},\varrho )$
will be referred to as
![]() $\varrho $
-Abel universal functions, and those of
$\varrho $
-Abel universal functions, and those of
![]() ${\mathcal {U}}_A({\mathbb {D}})$
as Abel universal functions. For the interested readers, we should mention the papers [Reference Bayart2, Reference Charpentier and Kosiński14] where universal boundary phenomena for holomorphic functions in several complex variables are exhibited and [Reference Abakumov, Nestoridis and Picardello1] where universal boundary behavior for harmonic functions on trees are studied.
${\mathcal {U}}_A({\mathbb {D}})$
as Abel universal functions. For the interested readers, we should mention the papers [Reference Bayart2, Reference Charpentier and Kosiński14] where universal boundary phenomena for holomorphic functions in several complex variables are exhibited and [Reference Abakumov, Nestoridis and Picardello1] where universal boundary behavior for harmonic functions on trees are studied.
For those who are familiar with the topic, the property enjoyed by the functions in
![]() ${\mathcal {U}}_A({\mathbb {D}},\varrho )$
evokes that enjoyed by the well-studied universal Taylor series. In 1996, Nestoridis proved that there exists a residual set
${\mathcal {U}}_A({\mathbb {D}},\varrho )$
evokes that enjoyed by the well-studied universal Taylor series. In 1996, Nestoridis proved that there exists a residual set
![]() ${\mathcal {U}}({\mathbb {D}})$
of functions f in
${\mathcal {U}}({\mathbb {D}})$
of functions f in
![]() $H({\mathbb {D}})$
such that for any compact set
$H({\mathbb {D}})$
such that for any compact set
![]() $K\subset {\mathbb {C}}\setminus {\mathbb {D}}$
, with connected complement, the set
$K\subset {\mathbb {C}}\setminus {\mathbb {D}}$
, with connected complement, the set
![]() $\{S_n(f)|_K:\, n\in {\mathbb {N}}\}$
of all partial sums of the Taylor expansion of f at
$\{S_n(f)|_K:\, n\in {\mathbb {N}}\}$
of all partial sums of the Taylor expansion of f at
![]() $0$
is dense in
$0$
is dense in
![]() ${\mathcal {C}}(K)$
[Reference Nestoridis39]. Let us denote by
${\mathcal {C}}(K)$
[Reference Nestoridis39]. Let us denote by
![]() ${\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
the set of those functions
${\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
the set of those functions
![]() $f\in H({\mathbb {D}})$
satisfying the previous property not for any compact set
$f\in H({\mathbb {D}})$
satisfying the previous property not for any compact set
![]() $K\in {\mathbb {C}}\setminus {\mathbb {D}}$
with connected complement, but only for all compact sets
$K\in {\mathbb {C}}\setminus {\mathbb {D}}$
with connected complement, but only for all compact sets
![]() $K\subset {\mathbb {T}}$
different from
$K\subset {\mathbb {T}}$
different from
![]() ${\mathbb {T}}$
. Note that
${\mathbb {T}}$
. Note that
![]() ${\mathcal {U}}({\mathbb {D}})\subset {\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
. The functions in
${\mathcal {U}}({\mathbb {D}})\subset {\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
. The functions in
![]() ${\mathcal {U}}({\mathbb {D}})$
were extensively studied from many points of view. We refer to [Reference Bayart3, Reference Bayart, Grosse-Erdmann, Nestoridis and Papadimitropoulos6, Reference Charpentier and Mouze15, Reference Costakis, Jung and Müller22–Reference Gardiner and Manolaki25, Reference Melas and Nestoridis33, Reference Melas, Nestoridis and Papadoperakis34, Reference Mouze36] and the references therein for a nonexhaustive list of papers. In particular, some of these highlight the fact that functions in
${\mathcal {U}}({\mathbb {D}})$
were extensively studied from many points of view. We refer to [Reference Bayart3, Reference Bayart, Grosse-Erdmann, Nestoridis and Papadimitropoulos6, Reference Charpentier and Mouze15, Reference Costakis, Jung and Müller22–Reference Gardiner and Manolaki25, Reference Melas and Nestoridis33, Reference Melas, Nestoridis and Papadoperakis34, Reference Mouze36] and the references therein for a nonexhaustive list of papers. In particular, some of these highlight the fact that functions in
![]() ${\mathcal {U}}({\mathbb {D}})$
enjoy irregular boundary behavior, for example, along radii. In comparison, the recently introduced Abel universal functions were considered in two papers [Reference Charpentier12, Reference Maronikolakis32]. In [Reference Charpentier12], the first author sketched a comparison of the sets
${\mathcal {U}}({\mathbb {D}})$
enjoy irregular boundary behavior, for example, along radii. In comparison, the recently introduced Abel universal functions were considered in two papers [Reference Charpentier12, Reference Maronikolakis32]. In [Reference Charpentier12], the first author sketched a comparison of the sets
![]() ${\mathcal {U}}({\mathbb {D}})$
and
${\mathcal {U}}({\mathbb {D}})$
and
![]() ${\mathcal {U}}_A({\mathbb {D}},\varrho )$
and noticed that the main results of [Reference Costakis20, Reference Gehlen, Luh and Müller26] actually imply that none of them is included in the other. More precisely, the assertion
${\mathcal {U}}_A({\mathbb {D}},\varrho )$
and noticed that the main results of [Reference Costakis20, Reference Gehlen, Luh and Müller26] actually imply that none of them is included in the other. More precisely, the assertion
![]() ${\mathcal {U}}_A({\mathbb {D}},\varrho )\setminus {\mathcal {U}}({\mathbb {D}})\neq \emptyset $
was derived from the fact that the partial sums of the functions in
${\mathcal {U}}_A({\mathbb {D}},\varrho )\setminus {\mathcal {U}}({\mathbb {D}})\neq \emptyset $
was derived from the fact that the partial sums of the functions in
![]() ${\mathcal {U}}({\mathbb {D}})$
have to behave wild not only at the boundary of
${\mathcal {U}}({\mathbb {D}})$
have to behave wild not only at the boundary of
![]() ${\mathbb {D}}$
, but also on compact sets as far as possible from
${\mathbb {D}}$
, but also on compact sets as far as possible from
![]() $0$
. This thus leads to ask rather if
$0$
. This thus leads to ask rather if
![]() ${\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
and
${\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
and
![]() ${\mathcal {U}}_A({\mathbb {D}},\varrho )$
or
${\mathcal {U}}_A({\mathbb {D}},\varrho )$
or
![]() ${\mathcal {U}}_A({\mathbb {D}})$
are comparable. The question was explicitly stated in [Reference Charpentier12].
${\mathcal {U}}_A({\mathbb {D}})$
are comparable. The question was explicitly stated in [Reference Charpentier12].
The first goal of this paper is to show that neither
![]() ${\mathcal {U}}_A({\mathbb {D}})$
nor
${\mathcal {U}}_A({\mathbb {D}})$
nor
![]() ${\mathcal {U}}_A({\mathbb {D}},\varrho )$
is comparable to
${\mathcal {U}}_A({\mathbb {D}},\varrho )$
is comparable to
![]() ${\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
and that
${\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
and that
![]() ${\mathcal {U}}_C({\mathbb {D}})\setminus {\mathcal {U}}_A({\mathbb {D}})\neq \emptyset $
, making it interesting to study independently the functions in
${\mathcal {U}}_C({\mathbb {D}})\setminus {\mathcal {U}}_A({\mathbb {D}})\neq \emptyset $
, making it interesting to study independently the functions in
![]() ${\mathcal {U}}_A({\mathbb {D}},\varrho )$
or
${\mathcal {U}}_A({\mathbb {D}},\varrho )$
or
![]() ${\mathcal {U}}_A({\mathbb {D}})$
. It is worth mentioning that, whereas exhibiting generic functions with universal behavior is rather standard, building nongeneric functions that still enjoy some universal property can be very tricky. This is probably why there are very few results of this type. For example, in order to build up a function in
${\mathcal {U}}_A({\mathbb {D}})$
. It is worth mentioning that, whereas exhibiting generic functions with universal behavior is rather standard, building nongeneric functions that still enjoy some universal property can be very tricky. This is probably why there are very few results of this type. For example, in order to build up a function in
![]() ${\mathcal {U}}_A({\mathbb {D}},\varrho )$
which is not in
${\mathcal {U}}_A({\mathbb {D}},\varrho )$
which is not in
![]() ${\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
, we will make use of a purely constructive trick. In passing, we will observe that this trick can turn out to be useful in order to attack one of the most important open questions about universal series: does the derivative of a universal Taylor series remain a universal Taylor series? We will build functions in
${\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
, we will make use of a purely constructive trick. In passing, we will observe that this trick can turn out to be useful in order to attack one of the most important open questions about universal series: does the derivative of a universal Taylor series remain a universal Taylor series? We will build functions in
![]() ${\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
with partial sums simultaneously enjoying a universal property outside
${\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
with partial sums simultaneously enjoying a universal property outside
![]() $\overline {{\mathbb {D}}}$
, and whose derivative is not even in
$\overline {{\mathbb {D}}}$
, and whose derivative is not even in
![]() ${\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
. Let us observe that by Weierstrass’ theorem, it is easily seen that if
${\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
. Let us observe that by Weierstrass’ theorem, it is easily seen that if
![]() $\{S_n(f)|_K:\,n\in {\mathbb {N}}\}$
is dense in
$\{S_n(f)|_K:\,n\in {\mathbb {N}}\}$
is dense in
![]() ${\mathcal {C}}(K)$
for any
${\mathcal {C}}(K)$
for any
![]() $K\subset {\mathbb {C}}\setminus \overline {{\mathbb {D}}}$
, then so is
$K\subset {\mathbb {C}}\setminus \overline {{\mathbb {D}}}$
, then so is
![]() $\{S_n(f')|_K:\,n\in {\mathbb {N}}\}$
. The same question makes sense for
$\{S_n(f')|_K:\,n\in {\mathbb {N}}\}$
. The same question makes sense for
![]() $\varrho $
-Abel universal functions. In this context, we will be able to exhibit functions in
$\varrho $
-Abel universal functions. In this context, we will be able to exhibit functions in
![]() ${\mathcal {U}}_A({\mathbb {D}},\varrho )$
whose derivative is not in
${\mathcal {U}}_A({\mathbb {D}},\varrho )$
whose derivative is not in
![]() ${\mathcal {U}}_A({\mathbb {D}},\varrho )$
, answering a question also posed in [Reference Charpentier12].
${\mathcal {U}}_A({\mathbb {D}},\varrho )$
, answering a question also posed in [Reference Charpentier12].
Being now convinced that the notions of universal Taylor series and Abel universal functions are quite distinct, it is legitimate to consider the study of the second one for itself. Like universal Taylor series, Abel universal functions are natural examples within the large theory of universality in operator theory. Let us say that, given two Fréchet spaces X et Y, a family
![]() $(T_i)_{i\in I}$
of continuous operators from X to Y is universal if there exists
$(T_i)_{i\in I}$
of continuous operators from X to Y is universal if there exists
![]() $x\in X$
such that the set
$x\in X$
such that the set
is dense in Y. Such a vector x is said to be universal for
![]() $(T_i)_{i\in I}$
. Most of the concrete examples of universal families of operators fall into the situation where
$(T_i)_{i\in I}$
. Most of the concrete examples of universal families of operators fall into the situation where
![]() $I={\mathbb {N}}$
,
$I={\mathbb {N}}$
,
![]() $X=Y$
, and
$X=Y$
, and
![]() $T_n=T^n$
,
$T_n=T^n$
,
![]() $n\in {\mathbb {N}}$
, where T is a continuous operator from X to X. In this case, the operator T is called hypercyclic whenever
$n\in {\mathbb {N}}$
, where T is a continuous operator from X to X. In this case, the operator T is called hypercyclic whenever
![]() $(T^n)_n$
is universal and the notion lies within linear dynamics, a very active branch of operator theory. Apart from this setting, there are some other natural families of operators that are universal [Reference Bayart, Grosse-Erdmann, Nestoridis and Papadimitropoulos6, Reference Grosse Erdmann28]. By natural families of operators, we mean families of operators which naturally come into play in mathematical analysis. This is in particular the case of the family
$(T^n)_n$
is universal and the notion lies within linear dynamics, a very active branch of operator theory. Apart from this setting, there are some other natural families of operators that are universal [Reference Bayart, Grosse-Erdmann, Nestoridis and Papadimitropoulos6, Reference Grosse Erdmann28]. By natural families of operators, we mean families of operators which naturally come into play in mathematical analysis. This is in particular the case of the family
![]() ${\mathcal {T}}_{\varrho }^K:=\{T_{\varrho ,n}^K:\, n\in {\mathbb {N}}\}$
(resp.
${\mathcal {T}}_{\varrho }^K:=\{T_{\varrho ,n}^K:\, n\in {\mathbb {N}}\}$
(resp.
![]() $\mathcal {S} ^K:= \{S_n^K:\,n\in {\mathbb {N}}\}$
) defined, for a compact set
$\mathcal {S} ^K:= \{S_n^K:\,n\in {\mathbb {N}}\}$
) defined, for a compact set
![]() $K\subset {\mathbb {T}}$
(resp.
$K\subset {\mathbb {T}}$
(resp.
![]() $K\subset {\mathbb {C}}\setminus {\mathbb {D}}$
), by
$K\subset {\mathbb {C}}\setminus {\mathbb {D}}$
), by
 $$ \begin{align*} T_{\varrho,n}^K:\left\{\begin{array}{lll}H({\mathbb{D}}) & \to & {\mathcal{C}}(K)\\ f & \mapsto & f_{r_n}|_K \end{array} \right. \quad \left( \text{resp. } S_n^K:\left\{\begin{array}{lll}H({\mathbb{D}}) & \to & {\mathcal{C}}(K)\\ f=\sum_ka_kz^k & \mapsto & \sum_{k=0}^na_kz^k|_K \end{array} \right.\right)\!, \end{align*} $$
$$ \begin{align*} T_{\varrho,n}^K:\left\{\begin{array}{lll}H({\mathbb{D}}) & \to & {\mathcal{C}}(K)\\ f & \mapsto & f_{r_n}|_K \end{array} \right. \quad \left( \text{resp. } S_n^K:\left\{\begin{array}{lll}H({\mathbb{D}}) & \to & {\mathcal{C}}(K)\\ f=\sum_ka_kz^k & \mapsto & \sum_{k=0}^na_kz^k|_K \end{array} \right.\right)\!, \end{align*} $$
where
![]() $\varrho =(r_n)_n$
is a given sequence in
$\varrho =(r_n)_n$
is a given sequence in
![]() $[0,1)$
tending to
$[0,1)$
tending to
![]() $1$
. According to the definitions given in the first part of the introduction, the elements of
$1$
. According to the definitions given in the first part of the introduction, the elements of
![]() ${\mathcal {U}}_A({\mathbb {D}},\varrho )$
with
${\mathcal {U}}_A({\mathbb {D}},\varrho )$
with
![]() $\varrho =(r_n)_n$
(resp.
$\varrho =(r_n)_n$
(resp.
![]() ${\mathcal {U}}({\mathbb {D}})$
) appear as functions in
${\mathcal {U}}({\mathbb {D}})$
) appear as functions in
![]() $H({\mathbb {D}})$
that are universal for all families
$H({\mathbb {D}})$
that are universal for all families
![]() ${\mathcal {T}}_{\varrho }^K$
,
${\mathcal {T}}_{\varrho }^K$
,
![]() $K\subset {\mathbb {T}}$
different from
$K\subset {\mathbb {T}}$
different from
![]() ${\mathbb {T}}$
(resp.
${\mathbb {T}}$
(resp.
![]() $\mathcal {S}^K$
,
$\mathcal {S}^K$
,
![]() $K\subset {\mathbb {C}} \setminus {\mathbb {D}}$
with connected complement). Let us observe that the sequences
$K\subset {\mathbb {C}} \setminus {\mathbb {D}}$
with connected complement). Let us observe that the sequences
![]() $(T_{\varrho ,n}^K)_n$
are universal sequences of composition operators that fit within the framework of the recent paper [Reference Charpentier and Mouze16]. Furthermore, when I is not countable, standard examples of universal families
$(T_{\varrho ,n}^K)_n$
are universal sequences of composition operators that fit within the framework of the recent paper [Reference Charpentier and Mouze16]. Furthermore, when I is not countable, standard examples of universal families
![]() $(T_i)_{i\in I}$
are given by semigroups. Universality or hypercyclicity of semigroups has been a subject of interest during the last decade, and strong similarities with hypercyclicity of a single operator have been discovered (see [Reference Conejero, Peris and Müller18] and [Reference Bayart and Matheron7, Chapter 3]). In this context, Abel universal functions thus appear as singular and natural examples of objects that are universal for the nonsemigroup families
$(T_i)_{i\in I}$
are given by semigroups. Universality or hypercyclicity of semigroups has been a subject of interest during the last decade, and strong similarities with hypercyclicity of a single operator have been discovered (see [Reference Conejero, Peris and Müller18] and [Reference Bayart and Matheron7, Chapter 3]). In this context, Abel universal functions thus appear as singular and natural examples of objects that are universal for the nonsemigroup families
![]() ${\mathcal {T}}^K:=(T_r^K)_{r\in [0,1)}$
of operators, where K is any subset of
${\mathcal {T}}^K:=(T_r^K)_{r\in [0,1)}$
of operators, where K is any subset of
![]() ${\mathbb {T}}$
different from
${\mathbb {T}}$
different from
![]() ${\mathbb {T}}$
, and
${\mathbb {T}}$
, and
![]() $T_r^K$
is defined by
$T_r^K$
is defined by
 $$ \begin{align*} T_r^K:\left\{\begin{array}{lll}H({\mathbb{D}}) & \to & {\mathcal{C}}(K),\\ f & \mapsto & f_{r}|_K. \end{array} \right. \end{align*} $$
$$ \begin{align*} T_r^K:\left\{\begin{array}{lll}H({\mathbb{D}}) & \to & {\mathcal{C}}(K),\\ f & \mapsto & f_{r}|_K. \end{array} \right. \end{align*} $$
With all this in mind, it looks quite motivating to wonder which of the most interesting phenomena observed in linear dynamics can also be observed for the natural families of operators that are universal and do not fall into the concept of hypercyclicity. The remainder of this paper will focus on this program around the notion of Abel universal functions.
One of the most elegant results on hypercyclicity, due to Bourdon and Feldman [Reference Bourdon10], asserts that a vector
![]() $x\in X$
is hypercyclic for a bounded operator
$x\in X$
is hypercyclic for a bounded operator
![]() $T:X\to X$
whenever its orbit under T is somewhere dense in X. A straight consequence of this fact is a result, independently obtained earlier by Costakis [Reference Costakis21] and Peris [Reference Peris40], telling us that if for finitely many
$T:X\to X$
whenever its orbit under T is somewhere dense in X. A straight consequence of this fact is a result, independently obtained earlier by Costakis [Reference Costakis21] and Peris [Reference Peris40], telling us that if for finitely many
![]() $x_1,\ldots ,x_l\in X$
the set
$x_1,\ldots ,x_l\in X$
the set
![]() $\bigcup _{k=1}^l\{T^n (x_k):\,n\in {\mathbb {N}}\}$
is dense in X, then one of the
$\bigcup _{k=1}^l\{T^n (x_k):\,n\in {\mathbb {N}}\}$
is dense in X, then one of the
![]() $x_i$
’s is hypercyclic for T. Both results extend to the setting of semigroups [Reference Bayart and Matheron7]. One may now ask whether this property is also shared by sequences
$x_i$
’s is hypercyclic for T. Both results extend to the setting of semigroups [Reference Bayart and Matheron7]. One may now ask whether this property is also shared by sequences
![]() ${\mathcal {T}}^K$
or
${\mathcal {T}}^K$
or
![]() ${\mathcal {T}}_{\varrho }^K$
, for some
${\mathcal {T}}_{\varrho }^K$
, for some
![]() $\varrho =(r_n)_n \subset [0,1)$
tending to
$\varrho =(r_n)_n \subset [0,1)$
tending to
![]() $1$
and
$1$
and
![]() $K\subset {\mathbb {T}}$
different from
$K\subset {\mathbb {T}}$
different from
![]() ${\mathbb {T}}$
. In fact, we will constructively prove that this is not the case: given
${\mathbb {T}}$
. In fact, we will constructively prove that this is not the case: given
![]() $K_0\subset {\mathbb {T}}$
different from
$K_0\subset {\mathbb {T}}$
different from
![]() ${\mathbb {T}}$
and
${\mathbb {T}}$
and
![]() $\varrho =(r_n)_n$
, there exist two functions
$\varrho =(r_n)_n$
, there exist two functions
![]() $f_1,f_2\in H({\mathbb {D}})$
, none of them Abel universal for
$f_1,f_2\in H({\mathbb {D}})$
, none of them Abel universal for
![]() ${\mathcal {T}}^{K_0}$
, such that the set
${\mathcal {T}}^{K_0}$
, such that the set
![]() $\{T_{\varrho ,n}^{K}(f_i):\,n\in {\mathbb {N}}, i=1,2\}$
is dense in
$\{T_{\varrho ,n}^{K}(f_i):\,n\in {\mathbb {N}}, i=1,2\}$
is dense in
![]() ${\mathcal {C}}(K)$
for any compact set
${\mathcal {C}}(K)$
for any compact set
![]() $K\subset {\mathbb {T}}$
different from
$K\subset {\mathbb {T}}$
different from
![]() ${\mathbb {T}}$
. As a consequence, this will also show that the families
${\mathbb {T}}$
. As a consequence, this will also show that the families
![]() ${\mathcal {T}}^K$
and
${\mathcal {T}}^K$
and
![]() ${\mathcal {T}}_{\varrho }^{K}$
do not satisfy a Bourdon–Feldman-type property. We should mention that an analogue of those results was obtained by the second author for Fekete universal series, a real-analytic variant of universal Taylor series [Reference Mouze35]. However, the case of universal Taylor series—i.e., for the sequences
${\mathcal {T}}_{\varrho }^{K}$
do not satisfy a Bourdon–Feldman-type property. We should mention that an analogue of those results was obtained by the second author for Fekete universal series, a real-analytic variant of universal Taylor series [Reference Mouze35]. However, the case of universal Taylor series—i.e., for the sequences
![]() $\mathcal {S}^K$
,
$\mathcal {S}^K$
,
![]() $K\subset {\mathbb {C}} \setminus {\mathbb {D}}$
with connected complement—is still open.
$K\subset {\mathbb {C}} \setminus {\mathbb {D}}$
with connected complement—is still open.
In 2006, Bayart and Grivaux [Reference Bayart and Grivaux5] introduced the notion of frequent hypercyclicity, which quickly became central in linear dynamics (see the books [Reference Bayart and Matheron7, Reference Grosse-Erdmann and Peris Manguillot29] and the recent paper [Reference Grivaux, Matheron and Menet27]). It was extended to the larger setting of universality [Reference Bonilla and Grosse-Erdmann9]. A sequence
![]() $(T_n)_n$
of continuous operators from a Fréchet space X to another one Y is said to be frequently universal if there exists
$(T_n)_n$
of continuous operators from a Fréchet space X to another one Y is said to be frequently universal if there exists
![]() $x\in X$
such that the set
$x\in X$
such that the set
![]() $\{n\in {\mathbb {N}}: T_n(x) \in U\}$
has positive lower density for any nonempty open set U of Y. For the definition of the lower density, we refer to Section 6. Roughly speaking, it quantifies the proportion of elements in
$\{n\in {\mathbb {N}}: T_n(x) \in U\}$
has positive lower density for any nonempty open set U of Y. For the definition of the lower density, we refer to Section 6. Roughly speaking, it quantifies the proportion of elements in
![]() $\{n\in {\mathbb {N}}: T_n(x) \in U\}$
among all natural numbers. The same notion makes perfectly sense for a family
$\{n\in {\mathbb {N}}: T_n(x) \in U\}$
among all natural numbers. The same notion makes perfectly sense for a family
![]() $(T_i)_{i\in I}$
of operators when I is an interval in
$(T_i)_{i\in I}$
of operators when I is an interval in
![]() ${\mathbb {R}}$
, replacing the lower density by the uniform lower density (see Section 6 for the definition). As far as we know, nondiscrete frequent universality was only considered, rather briefly, for semigroups [Reference Grosse-Erdmann and Peris Manguillot29, Chapter 7]. On the contrary, several descriptions of frequently hypercyclic operators among classes of concrete operators have been obtained [Reference Bayart and Matheron7, Reference Grosse-Erdmann and Peris Manguillot29]. In [Reference Charpentier11, Reference Mouze and Munnier37], it was observed that there cannot exist functions in
${\mathbb {R}}$
, replacing the lower density by the uniform lower density (see Section 6 for the definition). As far as we know, nondiscrete frequent universality was only considered, rather briefly, for semigroups [Reference Grosse-Erdmann and Peris Manguillot29, Chapter 7]. On the contrary, several descriptions of frequently hypercyclic operators among classes of concrete operators have been obtained [Reference Bayart and Matheron7, Reference Grosse-Erdmann and Peris Manguillot29]. In [Reference Charpentier11, Reference Mouze and Munnier37], it was observed that there cannot exist functions in
![]() $H({\mathbb {D}})$
that are frequently universal for all sequences
$H({\mathbb {D}})$
that are frequently universal for all sequences
![]() $\mathcal {S}^K$
,
$\mathcal {S}^K$
,
![]() $K\subset {\mathbb {C}} \setminus {\mathbb {D}}$
with connected complement. Yet, if K is fixed outside
$K\subset {\mathbb {C}} \setminus {\mathbb {D}}$
with connected complement. Yet, if K is fixed outside
![]() ${\mathbb {D}}$
, it is still open whether there exist functions in
${\mathbb {D}}$
, it is still open whether there exist functions in
![]() $H({\mathbb {D}})$
frequently universal for
$H({\mathbb {D}})$
frequently universal for
![]() $\mathcal {S}^K$
. In a broad but different setting, we mention that the authors of [Reference Abakumov, Nestoridis and Picardello1] prove the existence of harmonic functions on trees with frequently universal boundary behavior.
$\mathcal {S}^K$
. In a broad but different setting, we mention that the authors of [Reference Abakumov, Nestoridis and Picardello1] prove the existence of harmonic functions on trees with frequently universal boundary behavior.
The last section of this paper is devoted to showing various results revolving around frequent Abel universality. For example, given
![]() $\varrho =(r_n)_n\subset [0,1)$
tending to
$\varrho =(r_n)_n\subset [0,1)$
tending to
![]() $1$
, we will prove a rather strong result implying that the set of all functions that are frequently universal for all sequences
$1$
, we will prove a rather strong result implying that the set of all functions that are frequently universal for all sequences
![]() ${\mathcal {T}}_{\varrho }^K$
,
${\mathcal {T}}_{\varrho }^K$
,
![]() $K\subset {\mathbb {T}}$
different from
$K\subset {\mathbb {T}}$
different from
![]() ${\mathbb {T}}$
(resp. for all families
${\mathbb {T}}$
(resp. for all families
![]() ${\mathcal {T}}^K$
,
${\mathcal {T}}^K$
,
![]() $K\subset {\mathbb {T}}$
different from
$K\subset {\mathbb {T}}$
different from
![]() ${\mathbb {T}}$
) is a dense meagre subset of
${\mathbb {T}}$
) is a dense meagre subset of
![]() $H(\mathbb {D})$
. We will even show that there exist functions in
$H(\mathbb {D})$
. We will even show that there exist functions in
![]() $H({\mathbb {D}})$
that are frequently universal for all families
$H({\mathbb {D}})$
that are frequently universal for all families
![]() ${\mathcal {T}}_{\varrho (\alpha )}^K$
,
${\mathcal {T}}_{\varrho (\alpha )}^K$
,
![]() $K\subset {\mathbb {T}}$
different from
$K\subset {\mathbb {T}}$
different from
![]() ${\mathbb {T}}$
, where
${\mathbb {T}}$
, where
![]() $(\varrho (\alpha ))_{\alpha \in A}$
is a countable collection of pairwise disjoint sequences in
$(\varrho (\alpha ))_{\alpha \in A}$
is a countable collection of pairwise disjoint sequences in
![]() $[0,1)$
tending to
$[0,1)$
tending to
![]() $1$
. These results thus lie within the newly active topic of common frequent universality (see [Reference Bayart4, Reference Charpentier, Ernst, Mestiri and Mouze13]).
$1$
. These results thus lie within the newly active topic of common frequent universality (see [Reference Bayart4, Reference Charpentier, Ernst, Mestiri and Mouze13]).
The paper is organized as follows. The next section gathers some basic materials and definitions that will be used all along the paper. In Section 3, we prove that all the classical notions of universal functions are distinct. Section 4 deals with the nonstability of the classes of Abel universal functions under the action of the differentiation operator. In Sections 5 and 6, we focus on the “dynamical” properties of the sequences
![]() ${\mathcal {T}}_{\varrho }^K$
and
${\mathcal {T}}_{\varrho }^K$
and
![]() ${\mathcal {T}}_{\varrho }$
with respect to the concept of multiuniversality and (common) frequent universality, respectively.
${\mathcal {T}}_{\varrho }$
with respect to the concept of multiuniversality and (common) frequent universality, respectively.
2 Preliminaries
The aim of this section is to introduce once and for all, the notations and objects that will be used often in the paper. We start with general notations. The letter
![]() ${\mathbb {N}}$
will stand for the set
${\mathbb {N}}$
will stand for the set
![]() $\{0,1,2,3,\ldots \}$
of all nonnegative integers. A sequence of general terms
$\{0,1,2,3,\ldots \}$
of all nonnegative integers. A sequence of general terms
![]() $u_n$
,
$u_n$
,
![]() $n\in {\mathbb {N}}$
, will be denoted by
$n\in {\mathbb {N}}$
, will be denoted by
![]() $(u_n)_n$
. If P is any polynomial, we will denote by
$(u_n)_n$
. If P is any polynomial, we will denote by
![]() $\text {deg}(P)$
its degree and by
$\text {deg}(P)$
its degree and by
![]() $\text {val}(P)$
its valuation. If
$\text {val}(P)$
its valuation. If
![]() $E\subset {\mathbb {C}}$
, the notation
$E\subset {\mathbb {C}}$
, the notation
![]() $\text {int}(E)$
will stand for the set of all interior points of E. For any
$\text {int}(E)$
will stand for the set of all interior points of E. For any
![]() $r\geq 0$
and
$r\geq 0$
and
![]() $E\subset {\mathbb {C}}$
, we will denote by
$E\subset {\mathbb {C}}$
, we will denote by
![]() $rE$
the set
$rE$
the set
![]() $\{rz:\, z\in E\}$
. For
$\{rz:\, z\in E\}$
. For
![]() $a\in {\mathbb {C}}$
and
$a\in {\mathbb {C}}$
and
![]() $r\geq 0$
, the open disk centered at a with radius r will be denoted by
$r\geq 0$
, the open disk centered at a with radius r will be denoted by
![]() $D(a,r)$
.
$D(a,r)$
.
Let us now focus on more specific notations. In the whole paper,
![]() $\varrho =(r_n)_n$
denotes an arbitrary sequence in
$\varrho =(r_n)_n$
denotes an arbitrary sequence in
![]() $[0,1)$
converging to
$[0,1)$
converging to
![]() $1$
. For
$1$
. For
![]() $r\in [0,1)$
we denote by
$r\in [0,1)$
we denote by
![]() $\phi _r$
the function defined by
$\phi _r$
the function defined by
![]() $z\mapsto rz$
,
$z\mapsto rz$
,
![]() $z\in \mathbb {C}$
. Without possible confusions, we will use the same notation to denote a function defined in a set
$z\in \mathbb {C}$
. Without possible confusions, we will use the same notation to denote a function defined in a set
![]() $E\subset {\mathbb {C}}$
and its restriction to a subset of E. Given a compact set
$E\subset {\mathbb {C}}$
and its restriction to a subset of E. Given a compact set
![]() $K\subset {\mathbb {T}}$
, different from
$K\subset {\mathbb {T}}$
, different from
![]() ${\mathbb {T}}$
, we will denote by
${\mathbb {T}}$
, we will denote by
![]() ${\mathcal {V}}(K)$
a countable set of nonempty open sets defining the topology of
${\mathcal {V}}(K)$
a countable set of nonempty open sets defining the topology of
![]() ${\mathcal {C}}(K)$
.
${\mathcal {C}}(K)$
.
With these notations, the definition of Abel universal functions can be reformulated as follows.
Definition 2.1 A function
![]() $f \in H({\mathbb {D}})$
is called
$f \in H({\mathbb {D}})$
is called
![]() $\varrho $
-Abel universal if for any compact set
$\varrho $
-Abel universal if for any compact set
![]() $K\subset {\mathbb {T}}$
different from
$K\subset {\mathbb {T}}$
different from
![]() ${\mathbb {T}}$
, and any
${\mathbb {T}}$
, and any
![]() $V\in {\mathcal {V}}(K)$
, the set
$V\in {\mathcal {V}}(K)$
, the set
is nonempty (or equivalently infinite), where
![]() $\phi _n:=\phi _{r_n}$
.
$\phi _n:=\phi _{r_n}$
.
We recall that the set
![]() ${\mathcal {U}}_A({\mathbb {D}},\varrho )$
of
${\mathcal {U}}_A({\mathbb {D}},\varrho )$
of
![]() $\varrho $
-Abel universal functions is a dense
$\varrho $
-Abel universal functions is a dense
![]() $G_{\delta }$
-subset of
$G_{\delta }$
-subset of
![]() $H({\mathbb {D}})$
[Reference Charpentier12]. Similarly, the definition of an Abel universal functions given in the introduction is equivalent to the following one.
$H({\mathbb {D}})$
[Reference Charpentier12]. Similarly, the definition of an Abel universal functions given in the introduction is equivalent to the following one.
Definition 2.2 A function
![]() $f\in H({\mathbb {D}})$
is called Abel universal if for any compact set
$f\in H({\mathbb {D}})$
is called Abel universal if for any compact set
![]() $K\subset {\mathbb {T}}$
different from
$K\subset {\mathbb {T}}$
different from
![]() ${\mathbb {T}}$
, and any
${\mathbb {T}}$
, and any
![]() $V\in {\mathcal {V}}(K)$
, the set
$V\in {\mathcal {V}}(K)$
, the set
is nonempty.
Clearly,
![]() ${\mathcal {U}}_A({\mathbb {D}},\varrho )\subset {\mathcal {U}}_A({\mathbb {D}})$
, where
${\mathcal {U}}_A({\mathbb {D}},\varrho )\subset {\mathcal {U}}_A({\mathbb {D}})$
, where
![]() ${\mathcal {U}}_A({\mathbb {D}})$
is the set of all Abel universal functions. Note also that if
${\mathcal {U}}_A({\mathbb {D}})$
is the set of all Abel universal functions. Note also that if
![]() $f\in {\mathcal {U}}_A({\mathbb {D}})$
, then
$f\in {\mathcal {U}}_A({\mathbb {D}})$
, then
![]() $1$
is a limit point of
$1$
is a limit point of
![]() $N_f(V,K)$
, for any V and K.
$N_f(V,K)$
, for any V and K.
We introduce the following technical notations that will be used in most of the proofs:
-
•
 $(\varphi _n)_n$
denotes an enumeration of all polynomials with coefficients whose real and imaginary parts are rational.
$(\varphi _n)_n$
denotes an enumeration of all polynomials with coefficients whose real and imaginary parts are rational. -
•
 $(K_n)_n$
denotes a sequence of compact subsets of
$(K_n)_n$
denotes a sequence of compact subsets of
 ${\mathbb {T}}$
, with connected complement, such that for any compact set
${\mathbb {T}}$
, with connected complement, such that for any compact set
 $K\subset {\mathbb {T}}$
, different from
$K\subset {\mathbb {T}}$
, different from
 ${\mathbb {T}}$
, there exists
${\mathbb {T}}$
, there exists
 $n\in {\mathbb {N}}$
such that
$n\in {\mathbb {N}}$
such that
 $K\subset K_n$
(see, e.g., [Reference Charpentier12] for the existence of such sequence).
$K\subset K_n$
(see, e.g., [Reference Charpentier12] for the existence of such sequence). -
•
 $(\varepsilon _n)_n$
denotes a decreasing sequence of positive real numbers such that
$(\varepsilon _n)_n$
denotes a decreasing sequence of positive real numbers such that
 $\sum _n\varepsilon _n < 1$
. The speed of decrease of
$\sum _n\varepsilon _n < 1$
. The speed of decrease of
 $(\varepsilon _n)_n$
may change from a proof to another, and will be specified if necessary.
$(\varepsilon _n)_n$
may change from a proof to another, and will be specified if necessary. -
•
 $\alpha ,\beta : {\mathbb {N}} \to {\mathbb {N}}$
denote two functions such that for any
$\alpha ,\beta : {\mathbb {N}} \to {\mathbb {N}}$
denote two functions such that for any
 $n,m\in {\mathbb {N}}$
, there exists an increasing sequence
$n,m\in {\mathbb {N}}$
, there exists an increasing sequence
 $(n_l)_l\subset {\mathbb {N}}$
such that
$(n_l)_l\subset {\mathbb {N}}$
such that
 $\alpha (n_l)=n$
and
$\alpha (n_l)=n$
and
 $\beta (n_l)=m$
for any
$\beta (n_l)=m$
for any
 $l\in {\mathbb {N}}$
.
$l\in {\mathbb {N}}$
.
All these notations will be tacitly used throughout the paper.
The purpose of the next sections is twofold: first, to compare the sets
![]() ${\mathcal {U}}_A({\mathbb {D}},\varrho )$
and
${\mathcal {U}}_A({\mathbb {D}},\varrho )$
and
![]() ${\mathcal {U}}_A({\mathbb {D}})$
with other classical sets of analytic functions in
${\mathcal {U}}_A({\mathbb {D}})$
with other classical sets of analytic functions in
![]() ${\mathbb {D}}$
with universal behavior at the boundary; second, to study Abel universal functions, in particular with respect to classical notions coming from linear dynamics.
${\mathbb {D}}$
with universal behavior at the boundary; second, to study Abel universal functions, in particular with respect to classical notions coming from linear dynamics.
3 Abel universal functions among universal holomorphic functions
For
![]() $f=\sum _ka_kz^k \in H({\mathbb {D}})$
and
$f=\sum _ka_kz^k \in H({\mathbb {D}})$
and
![]() $n\in {\mathbb {N}}$
, we denote by
$n\in {\mathbb {N}}$
, we denote by
![]() $S_n(f)$
the nth partial sum of the Taylor expansion of f at
$S_n(f)$
the nth partial sum of the Taylor expansion of f at
![]() $0$
, i.e.,
$0$
, i.e.,
![]() $S_n(f)=\sum _{k=0}^na_kz^k$
.
$S_n(f)=\sum _{k=0}^na_kz^k$
.
Let us recall more explicitly the definitions of the classes of universal holomorphic functions that we intend to compare with that of Abel universal functions. The first one consists of universal Taylor series.
Definition 3.1 (Universal Taylor series)
-
(1) We denote by
 ${\mathcal {U}}({\mathbb {D}})$
the set of those functions
${\mathcal {U}}({\mathbb {D}})$
the set of those functions
 $f \in H({\mathbb {D}})$
which satisfy the following property: for any compact set
$f \in H({\mathbb {D}})$
which satisfy the following property: for any compact set
 $K\subset {\mathbb {C}}\setminus {\mathbb {D}}$
with connected complement, and any function
$K\subset {\mathbb {C}}\setminus {\mathbb {D}}$
with connected complement, and any function
 $\varphi $
continuous on K and holomorphic in its interior, there exists an increasing sequence
$\varphi $
continuous on K and holomorphic in its interior, there exists an increasing sequence
 $(\lambda _n)_n$
of integers such that
$(\lambda _n)_n$
of integers such that  $$ \begin{align*} \sup_{\zeta \in K}\left\vert S_{\lambda_n}(f)(\zeta) -\varphi (\zeta) \right\vert \to 0 \quad \text{as }n\to \infty. \end{align*} $$
$$ \begin{align*} \sup_{\zeta \in K}\left\vert S_{\lambda_n}(f)(\zeta) -\varphi (\zeta) \right\vert \to 0 \quad \text{as }n\to \infty. \end{align*} $$
The elements of
 ${\mathcal {U}}({\mathbb {D}})$
are called universal Taylor series.
${\mathcal {U}}({\mathbb {D}})$
are called universal Taylor series. -
(2) We denote by
 ${\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
the set of those functions
${\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
the set of those functions
 $f \in H({\mathbb {D}})$
which satisfy the following property: for any compact set
$f \in H({\mathbb {D}})$
which satisfy the following property: for any compact set
 $K\subset {\mathbb {T}}$
, different from
$K\subset {\mathbb {T}}$
, different from
 ${\mathbb {T}}$
, and any function
${\mathbb {T}}$
, and any function
 $\varphi $
continuous on K, there exists an increasing sequence
$\varphi $
continuous on K, there exists an increasing sequence
 $(\lambda _n)_n$
of integers such that
$(\lambda _n)_n$
of integers such that  $$ \begin{align*} \sup_{\zeta \in K}\left\vert S_{\lambda_n}(f)(\zeta) -\varphi (\zeta) \right\vert \to 0 \quad \text{as }n\to \infty. \end{align*} $$
$$ \begin{align*} \sup_{\zeta \in K}\left\vert S_{\lambda_n}(f)(\zeta) -\varphi (\zeta) \right\vert \to 0 \quad \text{as }n\to \infty. \end{align*} $$
The elements of
 ${\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
will be called
${\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
will be called
 ${\mathbb {T}}$
-universal Taylor series.
${\mathbb {T}}$
-universal Taylor series.
As already said, the radial limit of a function holomorphic in
![]() $\mathbb {D}$
at a boundary point along an increasing sequence
$\mathbb {D}$
at a boundary point along an increasing sequence
![]() $(r_n)_n$
tending to
$(r_n)_n$
tending to
![]() $1$
can be seen as the operation on the Taylor partial sums at
$1$
can be seen as the operation on the Taylor partial sums at
![]() $0$
of this function by a regular process of summation. Indeed, one can write
$0$
of this function by a regular process of summation. Indeed, one can write
![]() $f(r_nz)=\sum _{k} a_kr_n^kz^k=\sum _{k} c_{n,k} S_k(f)$
with
$f(r_nz)=\sum _{k} a_kr_n^kz^k=\sum _{k} c_{n,k} S_k(f)$
with
![]() $c_{n,k}=r_n^k(1-r_n)$
. One can check that this process of summation is regular (see [Reference Zygmund42]). Now, it turns out that the universality of a holomorphic function in
$c_{n,k}=r_n^k(1-r_n)$
. One can check that this process of summation is regular (see [Reference Zygmund42]). Now, it turns out that the universality of a holomorphic function in
![]() ${\mathbb {D}}$
is often preserved by the action of a summation process. It is in particular the case that the Cesàro means of the Taylor partial sums of an analytic function in
${\mathbb {D}}$
is often preserved by the action of a summation process. It is in particular the case that the Cesàro means of the Taylor partial sums of an analytic function in
![]() ${\mathbb {D}}$
are universal if and only if the function is itself a universal Taylor series [Reference Bayart3] (see [Reference Charpentier and Mouze15, Reference Mouze and Munnier37] for more general summation processes). Let us then introduce the following definition.
${\mathbb {D}}$
are universal if and only if the function is itself a universal Taylor series [Reference Bayart3] (see [Reference Charpentier and Mouze15, Reference Mouze and Munnier37] for more general summation processes). Let us then introduce the following definition.
Definition 3.2 (Cesàro universal Taylor series)
-
(1) We denote by
 ${\mathcal {U}}_{Ces}({\mathbb {D}})$
the set of those functions
${\mathcal {U}}_{Ces}({\mathbb {D}})$
the set of those functions
 $f \in H({\mathbb {D}})$
which satisfy the following property: for any compact set
$f \in H({\mathbb {D}})$
which satisfy the following property: for any compact set
 $K\subset {\mathbb {C}}\setminus {\mathbb {D}}$
with connected complement, and any function
$K\subset {\mathbb {C}}\setminus {\mathbb {D}}$
with connected complement, and any function
 $\varphi $
continuous on K and holomorphic in its interior, there exists an increasing sequence
$\varphi $
continuous on K and holomorphic in its interior, there exists an increasing sequence
 $(\lambda _n)_n$
of integers such that
$(\lambda _n)_n$
of integers such that  $$ \begin{align*} \sup_{\zeta \in K}\left\vert \frac{1}{\lambda_n+1}\sum_{j=0}^{\lambda_n}S_{j}(f)(\zeta) -\varphi (\zeta) \right\vert \to 0 \quad \text{as }n\to \infty. \end{align*} $$
$$ \begin{align*} \sup_{\zeta \in K}\left\vert \frac{1}{\lambda_n+1}\sum_{j=0}^{\lambda_n}S_{j}(f)(\zeta) -\varphi (\zeta) \right\vert \to 0 \quad \text{as }n\to \infty. \end{align*} $$
The elements of
 ${\mathcal {U}}_{Ces}({\mathbb {D}})$
are called Cesàro universal Taylor series.
${\mathcal {U}}_{Ces}({\mathbb {D}})$
are called Cesàro universal Taylor series. -
(2) We denote by
 ${\mathcal {U}}_{Ces}({\mathbb {D}},{\mathbb {T}})$
the set of those functions
${\mathcal {U}}_{Ces}({\mathbb {D}},{\mathbb {T}})$
the set of those functions
 $f \in H({\mathbb {D}})$
which satisfy the following property: for any compact set
$f \in H({\mathbb {D}})$
which satisfy the following property: for any compact set
 $K\subset {\mathbb {T}}$
, different from
$K\subset {\mathbb {T}}$
, different from
 ${\mathbb {T}}$
, and any function
${\mathbb {T}}$
, and any function
 $\varphi $
continuous on K, there exists an increasing sequence
$\varphi $
continuous on K, there exists an increasing sequence
 $(\lambda _n)_n$
of integers such that
$(\lambda _n)_n$
of integers such that  $$ \begin{align*} \sup_{\zeta \in K}\left\vert \frac{1}{\lambda_n+1}\sum_{j=0}^{\lambda_n}S_{j}(f)(\zeta) -\varphi (\zeta) \right\vert \to 0 \quad \text{as }n\to \infty. \end{align*} $$
$$ \begin{align*} \sup_{\zeta \in K}\left\vert \frac{1}{\lambda_n+1}\sum_{j=0}^{\lambda_n}S_{j}(f)(\zeta) -\varphi (\zeta) \right\vert \to 0 \quad \text{as }n\to \infty. \end{align*} $$
The elements of
 ${\mathcal {U}}_{Ces}({\mathbb {D}},{\mathbb {T}})$
are called
${\mathcal {U}}_{Ces}({\mathbb {D}},{\mathbb {T}})$
are called
 ${\mathbb {T}}$
-Cesàro universal Taylor series.
${\mathbb {T}}$
-Cesàro universal Taylor series.
The last class of universal functions is that of functions with maximal cluster set along any path to
![]() ${\mathbb {T}}$
(by definition, a path to
${\mathbb {T}}$
(by definition, a path to
![]() ${\mathbb {T}}$
will always stand for a continuous function
${\mathbb {T}}$
will always stand for a continuous function
![]() $\gamma :[0,1)\to {\mathbb {D}}$
such that
$\gamma :[0,1)\to {\mathbb {D}}$
such that
![]() $\gamma (r)\to z$
for some
$\gamma (r)\to z$
for some
![]() $z\in {\mathbb {T}}$
).
$z\in {\mathbb {T}}$
).
Definition 3.3 (Functions with maximal cluster sets along every path)
We denote by
![]() ${\mathcal {U}}_C({\mathbb {D}})$
the set of those functions
${\mathcal {U}}_C({\mathbb {D}})$
the set of those functions
![]() $f \in H({\mathbb {D}})$
which satisfy the following property: for any path to
$f \in H({\mathbb {D}})$
which satisfy the following property: for any path to
![]() ${\mathbb {T}}$
, the cluster set
${\mathbb {T}}$
, the cluster set
![]() $C_{\gamma }(f)$
of f along
$C_{\gamma }(f)$
of f along
![]() $\gamma $
is maximal, i.e., equal to
$\gamma $
is maximal, i.e., equal to
![]() ${\mathbb {C}}$
.
${\mathbb {C}}$
.
All the sets introduced above are residual in
![]() $H({\mathbb {D}})$
, so that they intersect each other. It is natural to wonder whether some nonobvious inclusions may hold. So far, here is what is known (see, e.g., [Reference Bayart3, Reference Charpentier12, Reference Charpentier and Mouze15]): for any
$H({\mathbb {D}})$
, so that they intersect each other. It is natural to wonder whether some nonobvious inclusions may hold. So far, here is what is known (see, e.g., [Reference Bayart3, Reference Charpentier12, Reference Charpentier and Mouze15]): for any
![]() $\varrho =(r_n)_n$
,
$\varrho =(r_n)_n$
,
-
•
 ${\mathcal {U}}_{Ces}({\mathbb {D}})={\mathcal {U}}({\mathbb {D}}) \subsetneq {\mathcal {U}}({\mathbb {D}},{\mathbb {T}}) \subset {\mathcal {U}}_{Ces}({\mathbb {D}},{\mathbb {T}})$
;
${\mathcal {U}}_{Ces}({\mathbb {D}})={\mathcal {U}}({\mathbb {D}}) \subsetneq {\mathcal {U}}({\mathbb {D}},{\mathbb {T}}) \subset {\mathcal {U}}_{Ces}({\mathbb {D}},{\mathbb {T}})$
; -
•
 ${\mathcal {U}}_A({\mathbb {D}},\varrho ) \subset {\mathcal {U}}_A({\mathbb {D}}) \subset {\mathcal {U}}_C({\mathbb {D}})$
;
${\mathcal {U}}_A({\mathbb {D}},\varrho ) \subset {\mathcal {U}}_A({\mathbb {D}}) \subset {\mathcal {U}}_C({\mathbb {D}})$
; -
•
 ${\mathcal {U}}({\mathbb {D}})\setminus {\mathcal {U}}_A({\mathbb {D}})\neq \emptyset $
and
${\mathcal {U}}({\mathbb {D}})\setminus {\mathcal {U}}_A({\mathbb {D}})\neq \emptyset $
and
 ${\mathcal {U}}_A({\mathbb {D}},\varrho )\setminus {\mathcal {U}}({\mathbb {D}}) \neq \emptyset $
.
${\mathcal {U}}_A({\mathbb {D}},\varrho )\setminus {\mathcal {U}}({\mathbb {D}}) \neq \emptyset $
.
Note that the inclusions
![]() ${\mathcal {U}}({\mathbb {D}}) \subset {\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
and
${\mathcal {U}}({\mathbb {D}}) \subset {\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
and
![]() ${\mathcal {U}}_A({\mathbb {D}},\varrho ) \subset {\mathcal {U}}_A({\mathbb {D}}) \subset {\mathcal {U}}_C({\mathbb {D}})$
are either trivial or obvious. Moreover, that
${\mathcal {U}}_A({\mathbb {D}},\varrho ) \subset {\mathcal {U}}_A({\mathbb {D}}) \subset {\mathcal {U}}_C({\mathbb {D}})$
are either trivial or obvious. Moreover, that
![]() ${\mathcal {U}}({\mathbb {D}})\setminus {\mathcal {U}}_C({\mathbb {D}})\neq \emptyset $
is a consequence of the existence of universal Taylor series that are Abel summable at some boundary points [Reference Costakis20]. The assertion
${\mathcal {U}}({\mathbb {D}})\setminus {\mathcal {U}}_C({\mathbb {D}})\neq \emptyset $
is a consequence of the existence of universal Taylor series that are Abel summable at some boundary points [Reference Costakis20]. The assertion
![]() ${\mathcal {U}}_A({\mathbb {D}},\varrho )\setminus {\mathcal {U}}({\mathbb {D}})\neq \emptyset $
was observed in [Reference Charpentier12] using that functions in
${\mathcal {U}}_A({\mathbb {D}},\varrho )\setminus {\mathcal {U}}({\mathbb {D}})\neq \emptyset $
was observed in [Reference Charpentier12] using that functions in
![]() ${\mathcal {U}}({\mathbb {D}})$
possess Ostrowski gaps, whereas some functions in
${\mathcal {U}}({\mathbb {D}})$
possess Ostrowski gaps, whereas some functions in
![]() ${\mathcal {U}}_A({\mathbb {D}},\varrho )$
may not have Ostrowski gaps. We mention that functions in
${\mathcal {U}}_A({\mathbb {D}},\varrho )$
may not have Ostrowski gaps. We mention that functions in
![]() ${\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
may not have Ostrowski gaps in general [Reference Charpentier and Mouze15]. The aim of this section is to contribute in completing the description of the relationships between these classes. Precisely, we will prove the following.
${\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
may not have Ostrowski gaps in general [Reference Charpentier and Mouze15]. The aim of this section is to contribute in completing the description of the relationships between these classes. Precisely, we will prove the following.
Proposition 3.1 For any
![]() $\varrho =(r_n)_n$
, we have:
$\varrho =(r_n)_n$
, we have:
-
(1)
 ${\mathcal {U}}_A({\mathbb {D}},\varrho )\setminus {\mathcal {U}}_{Ces}({\mathbb {D}},{\mathbb {T}})\neq \emptyset $
;
${\mathcal {U}}_A({\mathbb {D}},\varrho )\setminus {\mathcal {U}}_{Ces}({\mathbb {D}},{\mathbb {T}})\neq \emptyset $
; -
(2)
 ${\mathcal {U}}_A({\mathbb {D}})\setminus {\mathcal {U}}_A({\mathbb {D}},\varrho )\neq \emptyset $
;
${\mathcal {U}}_A({\mathbb {D}})\setminus {\mathcal {U}}_A({\mathbb {D}},\varrho )\neq \emptyset $
; -
(3)
 ${\mathcal {U}}_C({\mathbb {D}})\setminus {\mathcal {U}}_A({\mathbb {D}})\neq \emptyset $
.
${\mathcal {U}}_C({\mathbb {D}})\setminus {\mathcal {U}}_A({\mathbb {D}})\neq \emptyset $
.
In particular, the sets
![]() ${\mathcal {U}}_A({\mathbb {D}},\varrho )$
and
${\mathcal {U}}_A({\mathbb {D}},\varrho )$
and
![]() ${\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
are incomparable.
${\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
are incomparable.
In passing, we can deduce (from (a) and
![]() ${\mathcal {U}}_A({\mathbb {D}})\subset {\mathcal {U}}_C({\mathbb {D}})$
) that
${\mathcal {U}}_A({\mathbb {D}})\subset {\mathcal {U}}_C({\mathbb {D}})$
) that
![]() ${\mathcal {U}}_C({\mathbb {D}})\setminus {\mathcal {U}}_{Ces}({\mathbb {D}},{\mathbb {T}})\neq \emptyset $
. However, it is still an open question whether
${\mathcal {U}}_C({\mathbb {D}})\setminus {\mathcal {U}}_{Ces}({\mathbb {D}},{\mathbb {T}})\neq \emptyset $
. However, it is still an open question whether
![]() ${\mathcal {U}}_{Ces}({\mathbb {D}},{\mathbb {T}})$
is included in
${\mathcal {U}}_{Ces}({\mathbb {D}},{\mathbb {T}})$
is included in
![]() ${\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
or not (i.e., whether
${\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
or not (i.e., whether
![]() ${\mathcal {U}}_{Ces}({\mathbb {D}},{\mathbb {T}})={\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
or not).
${\mathcal {U}}_{Ces}({\mathbb {D}},{\mathbb {T}})={\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
or not).
Proof of Proposition 3.1
We first prove (a). Let
![]() $(R_n)_n\subset [0,1)$
be such that
$(R_n)_n\subset [0,1)$
be such that
![]() $0<R_n<r_n<R_{n+1}<r_{n+1}<1$
,
$0<R_n<r_n<R_{n+1}<r_{n+1}<1$
,
![]() $n\in {\mathbb {N}}$
. Let us define, for every
$n\in {\mathbb {N}}$
. Let us define, for every
![]() $0<r<1$
and
$0<r<1$
and
![]() $k\geq 0$
,
$k\geq 0$
,
 $$ \begin{align} H_k(r)=\sum_{j\geq k}h_j(r)\quad \mbox{ where }\quad h_j(r):=\sum_{i=j}^{+\infty}2ir^i. \end{align} $$
$$ \begin{align} H_k(r)=\sum_{j\geq k}h_j(r)\quad \mbox{ where }\quad h_j(r):=\sum_{i=j}^{+\infty}2ir^i. \end{align} $$
Observe that
![]() $H_k(r)\rightarrow 0$
as k tends to infinity. We choose
$H_k(r)\rightarrow 0$
as k tends to infinity. We choose
![]() $u_1>0$
such that
$u_1>0$
such that
 $$ \begin{align*}\max\left(H_{u_{1}}(r_{1}),\frac{(r_1/R_{2})^{u_1}}{1-r_1/R_{2}}\right)\leq \varepsilon_1.\end{align*} $$
$$ \begin{align*}\max\left(H_{u_{1}}(r_{1}),\frac{(r_1/R_{2})^{u_1}}{1-r_1/R_{2}}\right)\leq \varepsilon_1.\end{align*} $$
By Mergelyan’s theorem, we find
![]() $P_1=\sum \limits _{i\geq u_1}a_{i,1}z^i$
so that
$P_1=\sum \limits _{i\geq u_1}a_{i,1}z^i$
so that
Let us build by induction sequences
![]() $(P_n)_n$
and
$(P_n)_n$
and
![]() $(Q_n)_n$
of polynomials and an increasing sequence
$(Q_n)_n$
of polynomials and an increasing sequence
![]() $(u_n)_n$
of integers as follows. Let
$(u_n)_n$
of integers as follows. Let
![]() $Q_0=0$
and suppose that
$Q_0=0$
and suppose that
![]() $P_1,\dots ,P_{n-1}$
,
$P_1,\dots ,P_{n-1}$
,
![]() $u_1,\dots ,u_{n-1}$
, and
$u_1,\dots ,u_{n-1}$
, and
![]() $Q_0,\dots ,Q_{n-2}$
have been chosen for
$Q_0,\dots ,Q_{n-2}$
have been chosen for
![]() $n\geq 2$
. We shall write these polynomials under the following form:
$n\geq 2$
. We shall write these polynomials under the following form:
 $$ \begin{align*}\mbox{for } k=2,\dots, n-2,\hspace{6pt} P_k=\sum_{i=u_k}^{u_{k+1}-1}a_{i,k}z^i,\hspace{6pt} Q_{k}=\sum_{i=u_{k}}^{u_{k+1}-1}b_{i,k}z^i,\hspace{6pt} \mbox{ with }u_k\geq\deg(P_{k-1})+1,\end{align*} $$
$$ \begin{align*}\mbox{for } k=2,\dots, n-2,\hspace{6pt} P_k=\sum_{i=u_k}^{u_{k+1}-1}a_{i,k}z^i,\hspace{6pt} Q_{k}=\sum_{i=u_{k}}^{u_{k+1}-1}b_{i,k}z^i,\hspace{6pt} \mbox{ with }u_k\geq\deg(P_{k-1})+1,\end{align*} $$
and
 $$ \begin{align*}P_{n-1}=\sum_{i=u_{n-1}}^{\deg(P_{n-1})}a_{i,n-1}z^i,\mbox{ with }u_{n-1}\geq\deg(P_{n-2})+1,\end{align*} $$
$$ \begin{align*}P_{n-1}=\sum_{i=u_{n-1}}^{\deg(P_{n-1})}a_{i,n-1}z^i,\mbox{ with }u_{n-1}\geq\deg(P_{n-2})+1,\end{align*} $$
where the coefficients
![]() $a_{i,j}$
and
$a_{i,j}$
and
![]() $b_{i,j}$
will satisfy suitable conditions that will be specified in the induction. We are going to construct
$b_{i,j}$
will satisfy suitable conditions that will be specified in the induction. We are going to construct
![]() $u_n$
,
$u_n$
,
![]() $Q_{n-1}$
, and
$Q_{n-1}$
, and
![]() $P_n$
in this order. First, choose
$P_n$
in this order. First, choose
![]() $u_n\geq 1+ \deg (P_{n-1})$
satisfying
$u_n\geq 1+ \deg (P_{n-1})$
satisfying
-
(1)
 $\max \left (H_{u_{n}}(r_{n}), \frac {(r_n/R_{n+1})^{u_n}}{1-r_n/R_{n+1}}\right )\leq \varepsilon _n$
.
$\max \left (H_{u_{n}}(r_{n}), \frac {(r_n/R_{n+1})^{u_n}}{1-r_n/R_{n+1}}\right )\leq \varepsilon _n$
.
Set
![]() $a_{i,n-1}=0$
for
$a_{i,n-1}=0$
for
![]() $i=\deg (P_{n-1})+1,\dots ,u_n-1$
, which implies that
$i=\deg (P_{n-1})+1,\dots ,u_n-1$
, which implies that
![]() $P_{n-1}=\sum \limits _{i=u_{n-1}}^{u_n-1}a_{i,n-1}z^i.$
Let us consider
$P_{n-1}=\sum \limits _{i=u_{n-1}}^{u_n-1}a_{i,n-1}z^i.$
Let us consider
![]() $w_{n-2}(z)=\sum \limits _{j=1}^{n-2}(P_j+Q_j)(z)$
,
$w_{n-2}(z)=\sum \limits _{j=1}^{n-2}(P_j+Q_j)(z)$
,
![]() $z\in {\mathbb {C}}$
. Then we define
$z\in {\mathbb {C}}$
. Then we define
![]() $Q_{n-1}=\sum \limits _{i= u_{n-1}}^{u_n-1}b_{i,n-1}z^i$
, where the coefficients
$Q_{n-1}=\sum \limits _{i= u_{n-1}}^{u_n-1}b_{i,n-1}z^i$
, where the coefficients
![]() $b_{i,n-1}$
for
$b_{i,n-1}$
for
![]() $u_{n-1}\leq i\leq u_n-1$
are built by induction as follows. We first set
$u_{n-1}\leq i\leq u_n-1$
are built by induction as follows. We first set
 $$ \begin{align*} b_{u_{n-1},n-1}:=\left\{\begin{array}{ll} 0, & \text{if } \vert \sum\limits_{l=1}^{u_{n-1}}S_l(w_{n-2})(1) + a_{u_{n-1},n-1}\vert \geq u_{n-1},\\ 2u_{n-1}, & \text{otherwise}. \end{array} \right. \end{align*} $$
$$ \begin{align*} b_{u_{n-1},n-1}:=\left\{\begin{array}{ll} 0, & \text{if } \vert \sum\limits_{l=1}^{u_{n-1}}S_l(w_{n-2})(1) + a_{u_{n-1},n-1}\vert \geq u_{n-1},\\ 2u_{n-1}, & \text{otherwise}. \end{array} \right. \end{align*} $$
Then, once
![]() $b_{u_{n-1},n-1},b_{u_{n-1}+1,n-1},\ldots , b_{k-1,n-1}$
have been built for some
$b_{u_{n-1},n-1},b_{u_{n-1}+1,n-1},\ldots , b_{k-1,n-1}$
have been built for some
![]() $u_{n-1}+1\leq k\leq u_n-1$
, we set:
$u_{n-1}+1\leq k\leq u_n-1$
, we set:
-
•
 $b_{k,n-1}=0$
if we have
$b_{k,n-1}=0$
if we have
 $\left \vert \sum \limits _{l=1}^{k}S_l(w_{n-2})(1) + \sum \limits _{l=u_{n-1}}^{k-1}\sum \limits _{i=u_{n-1}}^{l}(a_{i,n-1}+b_{i,n-1}) + \sum \limits _{i=u_{n-1}}^{k-1}(a_{i,n-1}+b_{i,n-1}) + a_{k,n-1}\right \vert \geq k,$
$\left \vert \sum \limits _{l=1}^{k}S_l(w_{n-2})(1) + \sum \limits _{l=u_{n-1}}^{k-1}\sum \limits _{i=u_{n-1}}^{l}(a_{i,n-1}+b_{i,n-1}) + \sum \limits _{i=u_{n-1}}^{k-1}(a_{i,n-1}+b_{i,n-1}) + a_{k,n-1}\right \vert \geq k,$
-
•
 $b_{k,n-1}=2k$
otherwise.
$b_{k,n-1}=2k$
otherwise.
Doing so, we obtain for all
![]() $n\geq 2$
and for all
$n\geq 2$
and for all
![]() $k=u_{n-1},\dots ,u_n-1$
,
$k=u_{n-1},\dots ,u_n-1$
,
-
(2)
 $\vert \sum _{l=1}^{k}S_l(\sum _{j=1}^{n-1}(P_j+Q_j))(1) \vert \geq k$
;
$\vert \sum _{l=1}^{k}S_l(\sum _{j=1}^{n-1}(P_j+Q_j))(1) \vert \geq k$
; -
(3)
 $|b_{k,n-1}|\leq 2k$
.
$|b_{k,n-1}|\leq 2k$
.
Then apply Mergelyan’s theorem to get
![]() $P_n=\sum \limits _{i\geq u_n}a_{i,n}z^i$
so that the following conditions hold:
$P_n=\sum \limits _{i\geq u_n}a_{i,n}z^i$
so that the following conditions hold:
-
(4)
 $\sup _{|z|\leq R_n} | P_n(z) | \leq \varepsilon _n$
;
$\sup _{|z|\leq R_n} | P_n(z) | \leq \varepsilon _n$
; -
(5)
 $\sup _{z\in K_{\alpha (n)}}|P_n(r_nz)-\left (\varphi _{\beta (n)}(z)-\sum _{0\leq j\leq n-1}(P_j+Q_j)(r_nz)\right )|\leq \varepsilon _n$
.
$\sup _{z\in K_{\alpha (n)}}|P_n(r_nz)-\left (\varphi _{\beta (n)}(z)-\sum _{0\leq j\leq n-1}(P_j+Q_j)(r_nz)\right )|\leq \varepsilon _n$
.
Finally, we set
![]() $f=\sum \limits _{n\geq 1}(P_n+Q_n)$
and get from (3) and (4) that
$f=\sum \limits _{n\geq 1}(P_n+Q_n)$
and get from (3) and (4) that
![]() $f\in H({\mathbb {D}})$
. Moreover, it is clear from (2) that
$f\in H({\mathbb {D}})$
. Moreover, it is clear from (2) that
![]() $|\sum \limits _{l=1}^{k}S_l(f)(1)|\geq k$
, for all
$|\sum \limits _{l=1}^{k}S_l(f)(1)|\geq k$
, for all
![]() $k\in {\mathbb {N}}$
, and therefore
$k\in {\mathbb {N}}$
, and therefore
![]() $f\not \in {\mathcal {U}}_{Ces}({\mathbb {D}},{\mathbb {T}})$
. The proof will be completed once we have proved that
$f\not \in {\mathcal {U}}_{Ces}({\mathbb {D}},{\mathbb {T}})$
. The proof will be completed once we have proved that
![]() $f\in {\mathcal {U}}_A({\mathbb {D}},\varrho )$
. To do this, we will use the equality (3.1). Let us fix
$f\in {\mathcal {U}}_A({\mathbb {D}},\varrho )$
. To do this, we will use the equality (3.1). Let us fix
![]() $n,m\in {\mathbb {N}}$
, and let
$n,m\in {\mathbb {N}}$
, and let
![]() $(n_l)_l\subset {\mathbb {N}}$
be such that for any
$(n_l)_l\subset {\mathbb {N}}$
be such that for any
![]() $l\in {\mathbb {N}}$
,
$l\in {\mathbb {N}}$
,
![]() $\alpha (n_l)=n$
and
$\alpha (n_l)=n$
and
![]() $\beta (n_l)=m$
. By (5), we have, for any
$\beta (n_l)=m$
. By (5), we have, for any
![]() $\zeta \in K_n$
,
$\zeta \in K_n$
,
 $$ \begin{align*} \left|f(r_{n_l}\zeta)-\varphi_m(\zeta)\right| \leq \varepsilon_{n_l} + \left|Q_{n_l}(r_{n_l}\zeta)\right| + \left|\sum _{j\geq n_l+1} \left(P_j(r_{n_l}\zeta)+Q_j(r_{n_l}\zeta)\right)\right|\!. \end{align*} $$
$$ \begin{align*} \left|f(r_{n_l}\zeta)-\varphi_m(\zeta)\right| \leq \varepsilon_{n_l} + \left|Q_{n_l}(r_{n_l}\zeta)\right| + \left|\sum _{j\geq n_l+1} \left(P_j(r_{n_l}\zeta)+Q_j(r_{n_l}\zeta)\right)\right|\!. \end{align*} $$
Moreover, it follows from (3), (3.1), and (1) that for any
![]() $\zeta \in K_{n}$
,
$\zeta \in K_{n}$
,
Now, let us observe by (4) and Cauchy’s inequalities that we have
![]() $\left |a_{i,j}\right |\leq \varepsilon _{j}R_{j}^{-i}$
for any
$\left |a_{i,j}\right |\leq \varepsilon _{j}R_{j}^{-i}$
for any
![]() $j\geq 1$
and any
$j\geq 1$
and any
![]() $u_j \leq i \leq u_{j+1}-1$
, whence by (1), (3.1), and (3),
$u_j \leq i \leq u_{j+1}-1$
, whence by (1), (3.1), and (3),
 $$ \begin{align*} \left|\sum_{j\geq n_l+1} \left(P_j(r_{n_l}\zeta)+Q_j(r_{n_l}\zeta)\right)\right| & \leq \sum_{j\geq n_l+1}\sum_{i\geq u_{j}}\varepsilon_{j}\left(\frac{r_{n_l}}{R_{j}}\right)^i+ \sum_{j\geq n_l+1}\sum_{i\geq u_{j}}2ir_{n_l}^i \\& \leq \sum_{j\geq n_l+1}\varepsilon_{j}\left(\frac{r_{n_l}}{R_{n_l+1}}\right)^{u_{n_l}}\frac{1}{1-r_{n_l}/R_{n_l+1}}+ \sum_{j\geq n_l+1} h_{u_j}(r_{n_l}) \\&\leq \sum_{j\geq n_l+1}\varepsilon_{j}+H_{u_{n_l}}(r_{n_l}) \\& \leq \sum_{j\geq n_l+1}\varepsilon_{j} + \varepsilon_{n_l}. \end{align*} $$
$$ \begin{align*} \left|\sum_{j\geq n_l+1} \left(P_j(r_{n_l}\zeta)+Q_j(r_{n_l}\zeta)\right)\right| & \leq \sum_{j\geq n_l+1}\sum_{i\geq u_{j}}\varepsilon_{j}\left(\frac{r_{n_l}}{R_{j}}\right)^i+ \sum_{j\geq n_l+1}\sum_{i\geq u_{j}}2ir_{n_l}^i \\& \leq \sum_{j\geq n_l+1}\varepsilon_{j}\left(\frac{r_{n_l}}{R_{n_l+1}}\right)^{u_{n_l}}\frac{1}{1-r_{n_l}/R_{n_l+1}}+ \sum_{j\geq n_l+1} h_{u_j}(r_{n_l}) \\&\leq \sum_{j\geq n_l+1}\varepsilon_{j}+H_{u_{n_l}}(r_{n_l}) \\& \leq \sum_{j\geq n_l+1}\varepsilon_{j} + \varepsilon_{n_l}. \end{align*} $$
Altogether we get
and thus
![]() $f\in {\mathcal {U}}_A({\mathbb {D}},\varrho )$
.
$f\in {\mathcal {U}}_A({\mathbb {D}},\varrho )$
.
Let us prove (b). Let
![]() $\varrho '=\left (r_n'\right )_n\subset [0,1)$
be an increasing sequence such that
$\varrho '=\left (r_n'\right )_n\subset [0,1)$
be an increasing sequence such that
![]() $r_n < r^{\prime }_n < r_{n+1}$
,
$r_n < r^{\prime }_n < r_{n+1}$
,
![]() $n\in {\mathbb {N}}$
. Using Runge’s theorem, we build by induction a sequence of polynomials
$n\in {\mathbb {N}}$
. Using Runge’s theorem, we build by induction a sequence of polynomials
![]() $P_n$
such that:
$P_n$
such that:
-
(1)
 $\sup _{|z|\leq r^{\prime }_{n-1}}\vert P_n(z)\vert \leq \varepsilon _n$
;
$\sup _{|z|\leq r^{\prime }_{n-1}}\vert P_n(z)\vert \leq \varepsilon _n$
; -
(2)
 $\vert P_n(r_n) + \sum _{0\leq j\leq n-1} P_j(r_n)\vert \leq \varepsilon _n$
;
$\vert P_n(r_n) + \sum _{0\leq j\leq n-1} P_j(r_n)\vert \leq \varepsilon _n$
; -
(3)
 $\sup _{\zeta \in K_{\alpha (n)}}\left \vert P_n(r^{\prime }_n\zeta ) - (\varphi _{\beta (n)}(\zeta ) - \sum _{0\leq j\leq n-1} P_j(r^{\prime }_n\zeta ))\right \vert \leq \varepsilon _n$
.
$\sup _{\zeta \in K_{\alpha (n)}}\left \vert P_n(r^{\prime }_n\zeta ) - (\varphi _{\beta (n)}(\zeta ) - \sum _{0\leq j\leq n-1} P_j(r^{\prime }_n\zeta ))\right \vert \leq \varepsilon _n$
.
Then we set
![]() $f=\sum _{j\geq 0}P_j$
. We get from (1) that
$f=\sum _{j\geq 0}P_j$
. We get from (1) that
![]() $f\in H({\mathbb {D}})$
. Let us now check that
$f\in H({\mathbb {D}})$
. Let us now check that
![]() $f\in {\mathcal {U}}_A({\mathbb {D}})\setminus {\mathcal {U}}_A({\mathbb {D}},\varrho )$
. It is first clear from (1) and (2) that
$f\in {\mathcal {U}}_A({\mathbb {D}})\setminus {\mathcal {U}}_A({\mathbb {D}},\varrho )$
. It is first clear from (1) and (2) that
![]() $f\not \in {\mathcal {U}}_A({\mathbb {D}},\varrho )$
since
$f\not \in {\mathcal {U}}_A({\mathbb {D}},\varrho )$
since
![]() $|f(r_n)|\leq \sum _k\varepsilon _k$
. Now, let us fix
$|f(r_n)|\leq \sum _k\varepsilon _k$
. Now, let us fix
![]() $n,m\in {\mathbb {N}}$
and let
$n,m\in {\mathbb {N}}$
and let
![]() $(n_l)_l\subset {\mathbb {N}}$
be increasing such that for any
$(n_l)_l\subset {\mathbb {N}}$
be increasing such that for any
![]() $l\in {\mathbb {N}}$
,
$l\in {\mathbb {N}}$
,
![]() $\alpha (n_l)=n$
and
$\alpha (n_l)=n$
and
![]() $\beta (n_l)=m$
for any
$\beta (n_l)=m$
for any
![]() $l\in {\mathbb {N}}$
. Then, by (1) and (3), for any
$l\in {\mathbb {N}}$
. Then, by (1) and (3), for any
![]() $l\in {\mathbb {N}}$
and any
$l\in {\mathbb {N}}$
and any
![]() $\zeta \in K_{n}$
,
$\zeta \in K_{n}$
,
which goes to
![]() $0$
as
$0$
as
![]() $l\to \infty $
. Thus,
$l\to \infty $
. Thus,
![]() $f\in {\mathcal {U}}_A({\mathbb {D}},\varrho ')\subset {\mathcal {U}}_A({\mathbb {D}})$
.
$f\in {\mathcal {U}}_A({\mathbb {D}},\varrho ')\subset {\mathcal {U}}_A({\mathbb {D}})$
.
We turn to proving (c). For
![]() $\zeta \in {\mathbb {T}}$
and
$\zeta \in {\mathbb {T}}$
and
![]() $A\subset [0,1)$
, we will denote by
$A\subset [0,1)$
, we will denote by
![]() $A\zeta $
the set
$A\zeta $
the set
![]() $\{r\zeta :\,r\in A\}$
. Let us fix
$\{r\zeta :\,r\in A\}$
. Let us fix
![]() $\zeta _1\neq \zeta _2$
in
$\zeta _1\neq \zeta _2$
in
![]() ${\mathbb {T}}$
, and let
${\mathbb {T}}$
, and let
![]() $(a_n)$
be an increasing sequence in
$(a_n)$
be an increasing sequence in
![]() $[0,1)$
, tending to
$[0,1)$
, tending to
![]() $1$
. Note that for any
$1$
. Note that for any
![]() $r\in [a_0,1)$
and any
$r\in [a_0,1)$
and any
![]() $K\subset {\mathbb {T}}$
containing
$K\subset {\mathbb {T}}$
containing
![]() $\zeta _1$
and
$\zeta _1$
and
![]() $\zeta _2$
, we have
$\zeta _2$
, we have
We also fix a sequence
![]() $(\eta _n)$
of positive real numbers such that
$(\eta _n)$
of positive real numbers such that
Remark that
![]() $\eta _n \to 0$
as
$\eta _n \to 0$
as
![]() $n\to \infty $
. Let us now consider, for
$n\to \infty $
. Let us now consider, for
![]() $n\in {\mathbb {N}}$
, the compact set
$n\in {\mathbb {N}}$
, the compact set
![]() $L_n$
defined by
$L_n$
defined by
The sequence
![]() $(L_n)$
is clearly an exhaustion of
$(L_n)$
is clearly an exhaustion of
![]() ${\mathbb {D}}$
by compact sets with connected complement. Moreover, we have, for any
${\mathbb {D}}$
by compact sets with connected complement. Moreover, we have, for any
![]() $n\in {\mathbb {N}}$
and any
$n\in {\mathbb {N}}$
and any
![]() $m>n$
,
$m>n$
,
and
Then, for any
![]() $I\subset {\mathbb {T}}$
, we denote by
$I\subset {\mathbb {T}}$
, we denote by
![]() $C(I)$
the cone
$C(I)$
the cone
![]() $\{r\zeta :\,r\in [0,1),\,\zeta \in I\}$
and by
$\{r\zeta :\,r\in [0,1),\,\zeta \in I\}$
and by
![]() $C_n(I)$
the set
$C_n(I)$
the set
![]() $C(I)\cap \partial L_n$
. Thus, for any
$C(I)\cap \partial L_n$
. Thus, for any
![]() $n\geq 1$
, the sets
$n\geq 1$
, the sets
![]() $L_{n-1}$
,
$L_{n-1}$
,
![]() $[a_{2n},a_{2n+1}]\zeta _1\cup [a_{2n+1},a_{2n+2}]\zeta _2$
, and
$[a_{2n},a_{2n+1}]\zeta _1\cup [a_{2n+1},a_{2n+2}]\zeta _2$
, and
![]() $C_n(K_{\alpha (n)})$
are pairwise disjoint (and with connected complement), so we can apply Runge’s theorem to build a sequence
$C_n(K_{\alpha (n)})$
are pairwise disjoint (and with connected complement), so we can apply Runge’s theorem to build a sequence
![]() $(P_n)$
of polynomials (with
$(P_n)$
of polynomials (with
![]() $P_0=0$
), satisfying for any
$P_0=0$
), satisfying for any
![]() $n\geq 1$
,
$n\geq 1$
,
-
(1)
 $\sup _{z\in L_{n-1}}\vert P_n(z)\vert \leq \varepsilon _n$
;
$\sup _{z\in L_{n-1}}\vert P_n(z)\vert \leq \varepsilon _n$
; -
(2)
 $\sup _{z\in [a_{2n},a_{2n+1}]\zeta _1\cup [a_{2n+1},a_{2n+2}]\zeta _2}\vert P_n (z) + \sum _{0\leq j\leq n-1} P_j(z)\vert \leq \varepsilon _n$
;
$\sup _{z\in [a_{2n},a_{2n+1}]\zeta _1\cup [a_{2n+1},a_{2n+2}]\zeta _2}\vert P_n (z) + \sum _{0\leq j\leq n-1} P_j(z)\vert \leq \varepsilon _n$
; -
(3)
 $\sup _{z\in C_n(K_{\alpha (n)})}\left \vert P_n(z) - (\varphi _{\beta (n)}(z/|z|) - \sum _{0\leq j\leq n-1} P_j(z))\right \vert \leq \varepsilon _n$
.
$\sup _{z\in C_n(K_{\alpha (n)})}\left \vert P_n(z) - (\varphi _{\beta (n)}(z/|z|) - \sum _{0\leq j\leq n-1} P_j(z))\right \vert \leq \varepsilon _n$
.
We set
![]() $f=\sum _{n\geq 0}P_n$
. By (1),
$f=\sum _{n\geq 0}P_n$
. By (1),
![]() $f\in H({\mathbb {D}})$
. Moreover,
$f\in H({\mathbb {D}})$
. Moreover,
![]() $f\not \in {\mathcal {U}}_A({\mathbb {D}})$
. Indeed, let us consider the compact set
$f\not \in {\mathcal {U}}_A({\mathbb {D}})$
. Indeed, let us consider the compact set
![]() $K=\{\zeta _1\}\cup \{\zeta _2\}$
and fix
$K=\{\zeta _1\}\cup \{\zeta _2\}$
and fix
![]() $r\in [0,1)$
. Then there exists
$r\in [0,1)$
. Then there exists
![]() $n\in {\mathbb {N}}$
such that
$n\in {\mathbb {N}}$
such that
So, by (1) and (2), there exists
![]() $i\in \{1,2\}$
such that
$i\in \{1,2\}$
such that
![]() $|f(r\zeta _i)|\leq \sum _k\varepsilon _k$
. This proves that
$|f(r\zeta _i)|\leq \sum _k\varepsilon _k$
. This proves that
![]() $f\not \in {\mathcal {U}}_A({\mathbb {D}})$
.
$f\not \in {\mathcal {U}}_A({\mathbb {D}})$
.
It remains to check that
![]() $f\in {\mathcal {U}}_C({\mathbb {D}})$
. To do so, we will first prove that f has some universality property at the boundary, with respect to
$f\in {\mathcal {U}}_C({\mathbb {D}})$
. To do so, we will first prove that f has some universality property at the boundary, with respect to
![]() $(\partial L_n)_n$
. More precisely, let us fix
$(\partial L_n)_n$
. More precisely, let us fix
![]() $n,m\in {\mathbb {N}}$
and let
$n,m\in {\mathbb {N}}$
and let
![]() $(n_l)_l\subset {\mathbb {N}}$
be increasing such that
$(n_l)_l\subset {\mathbb {N}}$
be increasing such that
![]() $\alpha (n_l)=n$
and
$\alpha (n_l)=n$
and
![]() $\beta (n_l)=m$
for any l. Then, by (1) and (3), for any
$\beta (n_l)=m$
for any l. Then, by (1) and (3), for any
![]() $l\in {\mathbb {N}}$
and any
$l\in {\mathbb {N}}$
and any
![]() $z \in C_{n_l}(K_n)$
,
$z \in C_{n_l}(K_n)$
,
 $$ \begin{align*} \left|f\left(z\right) - \varphi_m\left(\frac{z}{|z|}\right) \right| \leq \varepsilon_{n_l} + \sum _{j\geq n_l+1}\left|P_j(z)\right| \leq \sum _{j\geq n_l}\varepsilon_j, \end{align*} $$
$$ \begin{align*} \left|f\left(z\right) - \varphi_m\left(\frac{z}{|z|}\right) \right| \leq \varepsilon_{n_l} + \sum _{j\geq n_l+1}\left|P_j(z)\right| \leq \sum _{j\geq n_l}\varepsilon_j, \end{align*} $$
which goes to
![]() $0$
as
$0$
as
![]() $l\to \infty $
. Now, let
$l\to \infty $
. Now, let
![]() $\gamma $
be any continuous path to some
$\gamma $
be any continuous path to some
![]() $\zeta \in {\mathbb {T}}$
and let
$\zeta \in {\mathbb {T}}$
and let
![]() $c\in {\mathbb {C}}$
. By construction, if
$c\in {\mathbb {C}}$
. By construction, if
![]() $I\subset {\mathbb {T}}$
with
$I\subset {\mathbb {T}}$
with
![]() $\zeta \in I$
is an arc, then
$\zeta \in I$
is an arc, then
![]() $\gamma $
intersects all but finitely many
$\gamma $
intersects all but finitely many
![]() $C_k(I)$
. In particular,
$C_k(I)$
. In particular,
![]() $\gamma $
intersects all
$\gamma $
intersects all
![]() $C_{n_l}(K_n)$
,
$C_{n_l}(K_n)$
,
![]() $l\in {\mathbb {N}}$
, for some
$l\in {\mathbb {N}}$
, for some
![]() $n\in {\mathbb {N}}$
and some increasing sequence
$n\in {\mathbb {N}}$
and some increasing sequence
![]() $(n_l)_l\subset {\mathbb {N}}$
so that
$(n_l)_l\subset {\mathbb {N}}$
so that
Thus, if
![]() $(z_{n_l})_l$
is any sequence so that
$(z_{n_l})_l$
is any sequence so that
![]() $z_{n_l}\in \gamma \cap C_{n_l}(K_n)$
, we have
$z_{n_l}\in \gamma \cap C_{n_l}(K_n)$
, we have
![]() $z_{n_l}\to \zeta $
and
$z_{n_l}\to \zeta $
and
![]() $f(z_{n_l})\to c$
as
$f(z_{n_l})\to c$
as
![]() $l\to \infty $
. This completes the proof that
$l\to \infty $
. This completes the proof that
![]() $f\in {\mathcal {U}}_C({\mathbb {D}})$
.
$f\in {\mathcal {U}}_C({\mathbb {D}})$
.
Remark 3.2 The proof of (2) shows that if
![]() $\varrho =(r_n)_n$
and
$\varrho =(r_n)_n$
and
![]() $\varrho '=(r^{\prime }_n)_n$
are such that
$\varrho '=(r^{\prime }_n)_n$
are such that
![]() $r_n=r^{\prime }_n$
only for finitely many n, then the sets
$r_n=r^{\prime }_n$
only for finitely many n, then the sets
![]() ${\mathcal {U}}_A({\mathbb {D}},\varrho )$
and
${\mathcal {U}}_A({\mathbb {D}},\varrho )$
and
![]() ${\mathcal {U}}_A({\mathbb {D}},\varrho ')$
are incomparable.
${\mathcal {U}}_A({\mathbb {D}},\varrho ')$
are incomparable.
4 Derivatives of Abel universal functions
One of the most important open questions on universal Taylor series is to know whether
![]() $f'\in {\mathcal {U}}({\mathbb {D}})$
whenever
$f'\in {\mathcal {U}}({\mathbb {D}})$
whenever
![]() $f\in {\mathcal {U}}({\mathbb {D}})$
. In this section, we prove that the same question for Abel universal functions has a negative answer. Next, we also show that the answer to this question is “no” for a natural class of universal Taylor series which contains
$f\in {\mathcal {U}}({\mathbb {D}})$
. In this section, we prove that the same question for Abel universal functions has a negative answer. Next, we also show that the answer to this question is “no” for a natural class of universal Taylor series which contains
![]() ${\mathcal {U}}({\mathbb {D}})$
and is contained in
${\mathcal {U}}({\mathbb {D}})$
and is contained in
![]() ${\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
. In the next results, we denote by
${\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
. In the next results, we denote by
![]() $f^{(l)}$
the lth derivative of
$f^{(l)}$
the lth derivative of
![]() $f\in H({\mathbb {D}})$
.
$f\in H({\mathbb {D}})$
.
Theorem 4.1 For any
![]() $\varrho $
and any
$\varrho $
and any
![]() $l\geq 1$
, there exists
$l\geq 1$
, there exists
![]() $f\in {\mathcal {U}}_A({\mathbb {D}},\varrho )$
such that
$f\in {\mathcal {U}}_A({\mathbb {D}},\varrho )$
such that
![]() $f^{(l)}\not \in {\mathcal {U}}_A({\mathbb {D}},\varrho )$
.
$f^{(l)}\not \in {\mathcal {U}}_A({\mathbb {D}},\varrho )$
.
In order to make the presentation simple, we shall extract the main ingredient of the construction as an independent lemma.
Lemma 4.2 Let K be a compact subset of
![]() ${\mathbb {T}}$
, different from
${\mathbb {T}}$
, different from
![]() ${\mathbb {T}}$
, and let
${\mathbb {T}}$
, and let
![]() $\varphi $
be a polynomial. For any
$\varphi $
be a polynomial. For any
![]() $\varepsilon>0$
, any
$\varepsilon>0$
, any
![]() $l\geq 1$
, and any
$l\geq 1$
, and any
![]() $r'<r\in [0,1)$
, there exists a polynomial P such that:
$r'<r\in [0,1)$
, there exists a polynomial P such that:
-
(1)
 $\sup _{|z|\leq r'}|P(z)|\leq \varepsilon $
;
$\sup _{|z|\leq r'}|P(z)|\leq \varepsilon $
; -
(2)
 $\sup _{[0,r']\cup [r,1)}|P^{(l)}(z)|\leq \varepsilon $
;
$\sup _{[0,r']\cup [r,1)}|P^{(l)}(z)|\leq \varepsilon $
; -
(3)
 $\sup _{z\in rK}|P(z)-\varphi (z)|\leq \varepsilon $
.
$\sup _{z\in rK}|P(z)-\varphi (z)|\leq \varepsilon $
.
Proof If
![]() $rK\cap [0,1)=\emptyset $
, it is enough to apply Mergelyan’s theorem on
$rK\cap [0,1)=\emptyset $
, it is enough to apply Mergelyan’s theorem on
![]() $rK\cup \overline {V}\cup \overline {D(0,r')}$
, where V is any neighborhood of
$rK\cup \overline {V}\cup \overline {D(0,r')}$
, where V is any neighborhood of
![]() $[0,1]$
with
$[0,1]$
with
![]() $\overline {V}\cap rK=\emptyset $
, and then Weierstrass’ theorem.
$\overline {V}\cap rK=\emptyset $
, and then Weierstrass’ theorem.
Let us now focus on the case where
![]() $rK\cap [0,1)=\{r\}$
(note that this intersection cannot contain more than
$rK\cap [0,1)=\{r\}$
(note that this intersection cannot contain more than
![]() $1$
point). For
$1$
point). For
![]() $\delta>0$
, let us denote
$\delta>0$
, let us denote
![]() $C_{\delta }:=\{z\in {\mathbb {C}}:\,\text {dist}(z,[r,1])\leq \delta \}$
. Since
$C_{\delta }:=\{z\in {\mathbb {C}}:\,\text {dist}(z,[r,1])\leq \delta \}$
. Since
![]() $r'<r$
and by uniform continuity of
$r'<r$
and by uniform continuity of
![]() $\varphi $
on
$\varphi $
on
![]() $rK$
, there exist
$rK$
, there exist
![]() $\delta>0$
such that
$\delta>0$
such that
![]() $\overline {D(0,r'+\delta )}\cap C_\delta =\emptyset $
, and a function
$\overline {D(0,r'+\delta )}\cap C_\delta =\emptyset $
, and a function
![]() $\tilde {\varphi }$
continuous on
$\tilde {\varphi }$
continuous on
![]() $\overline {D(0,r'+\delta )}\cup rK\cup C_{\delta }$
, such that
$\overline {D(0,r'+\delta )}\cup rK\cup C_{\delta }$
, such that
 $$ \begin{align}\hspace{15pt} \sup_{z\in rK}|\varphi(z)-\tilde{\varphi}(z)|\leq \varepsilon/2 \quad \text{and} \quad \tilde{\varphi}(z)= \left\{\begin{array}{lll} \varphi(r), & \text{if } & z\in C_{\delta},\\ 0, & \text{if } & z\in \overline{D(0,r'+\delta)}. \end{array} \right. \end{align} $$
$$ \begin{align}\hspace{15pt} \sup_{z\in rK}|\varphi(z)-\tilde{\varphi}(z)|\leq \varepsilon/2 \quad \text{and} \quad \tilde{\varphi}(z)= \left\{\begin{array}{lll} \varphi(r), & \text{if } & z\in C_{\delta},\\ 0, & \text{if } & z\in \overline{D(0,r'+\delta)}. \end{array} \right. \end{align} $$
Note that
![]() $\overline {D(0,r'+\delta )}\cup rK\cup C_{\delta }$
has connected complement and that
$\overline {D(0,r'+\delta )}\cup rK\cup C_{\delta }$
has connected complement and that
![]() $\tilde {\varphi }$
is continuous on this set and holomorphic in its interior (since it is constant there). Now, by Mergelyan’s theorem, there exists a sequence
$\tilde {\varphi }$
is continuous on this set and holomorphic in its interior (since it is constant there). Now, by Mergelyan’s theorem, there exists a sequence
![]() $(P_n)_n$
of polynomials tending to
$(P_n)_n$
of polynomials tending to
![]() $\tilde {\varphi }$
uniformly on
$\tilde {\varphi }$
uniformly on
![]() $\overline {D(0,r'+\delta )}\cup rK\cup C_{\delta }$
. In particular, by Weierstrass’ theorem,
$\overline {D(0,r'+\delta )}\cup rK\cup C_{\delta }$
. In particular, by Weierstrass’ theorem,
![]() $P^{(l)}_n\to 0$
uniformly on
$P^{(l)}_n\to 0$
uniformly on
![]() $[0,r']\cup [r,1]$
, whence we conclude that there exists
$[0,r']\cup [r,1]$
, whence we conclude that there exists
![]() $n_0\in {\mathbb {N}}$
such that
$n_0\in {\mathbb {N}}$
such that
![]() $P_{n_0}$
satisfies (1)–(3) in the statement.
$P_{n_0}$
satisfies (1)–(3) in the statement.
Proof of Theorem 4.1
Let us fix
![]() $l\geq 1$
. We let
$l\geq 1$
. We let
![]() $\varrho =(r_n)_n$
and set
$\varrho =(r_n)_n$
and set
![]() $r_{-1}=0$
. Without loss of generality, we shall assume that
$r_{-1}=0$
. Without loss of generality, we shall assume that
![]() $(r_n)_n$
is increasing. We recall that the notation
$(r_n)_n$
is increasing. We recall that the notation
![]() $(\varepsilon _n)_n$
denotes a decreasing sequence of positive real numbers such that
$(\varepsilon _n)_n$
denotes a decreasing sequence of positive real numbers such that
![]() $\sum _n\varepsilon _n<1$
(see Section 2). Using Lemma 4.2, we build by induction polynomial
$\sum _n\varepsilon _n<1$
(see Section 2). Using Lemma 4.2, we build by induction polynomial
![]() $P_n$
,
$P_n$
,
![]() $n\in {\mathbb {N}}$
, such that:
$n\in {\mathbb {N}}$
, such that:
-
(1)
 $\sup _{|z|\leq r_{n-1}}\vert P_n (z) \vert \leq \varepsilon _n$
;
$\sup _{|z|\leq r_{n-1}}\vert P_n (z) \vert \leq \varepsilon _n$
; -
(2)
 $\sup _{z\in [0,r_{n-1}]\cup [r_n,1)}\vert P^{(l)}_n(z) \vert \leq \varepsilon _n$
;
$\sup _{z\in [0,r_{n-1}]\cup [r_n,1)}\vert P^{(l)}_n(z) \vert \leq \varepsilon _n$
; -
(3)
 $\sup _{z \in K_{\alpha (n)}}\left \vert P_n (r_nz)-(\varphi _{\beta (n)}(z) - \sum _{0\leq j\leq n-1} P_j(r_nz)) \right \vert \leq \varepsilon _n$
.
$\sup _{z \in K_{\alpha (n)}}\left \vert P_n (r_nz)-(\varphi _{\beta (n)}(z) - \sum _{0\leq j\leq n-1} P_j(r_nz)) \right \vert \leq \varepsilon _n$
.
By (1),
![]() $f:=\sum _nP_n \in H({\mathbb {D}})$
and, by (2), for any
$f:=\sum _nP_n \in H({\mathbb {D}})$
and, by (2), for any
![]() $n\in {\mathbb {N}}$
and any
$n\in {\mathbb {N}}$
and any
![]() $k\geq 0$
,
$k\geq 0$
,
![]() $\vert P_n^{(l)}(r_k)\vert \leq \varepsilon _n$
, so
$\vert P_n^{(l)}(r_k)\vert \leq \varepsilon _n$
, so
![]() $\vert f^{(l)}(r_k)\vert =\sum _n \vert P_n^{(l)}(r_k)\vert \leq \sum _n \varepsilon _n <1$
. In particular,
$\vert f^{(l)}(r_k)\vert =\sum _n \vert P_n^{(l)}(r_k)\vert \leq \sum _n \varepsilon _n <1$
. In particular,
![]() $f^{(l)} \not \in {\mathcal {U}}_A({\mathbb {D}},\varrho )$
. The proof that
$f^{(l)} \not \in {\mathcal {U}}_A({\mathbb {D}},\varrho )$
. The proof that
![]() $f\in {\mathcal {U}}_A({\mathbb {D}},\varrho )$
is now quite standard. We fix
$f\in {\mathcal {U}}_A({\mathbb {D}},\varrho )$
is now quite standard. We fix
![]() $n,m \in {\mathbb {N}}$
and let
$n,m \in {\mathbb {N}}$
and let
![]() $(n_k)_k\subset {\mathbb {N}}$
such that
$(n_k)_k\subset {\mathbb {N}}$
such that
![]() $\alpha (n_k)=n$
and
$\alpha (n_k)=n$
and
![]() $\beta (n_k)=m$
for any
$\beta (n_k)=m$
for any
![]() $k\in {\mathbb {N}}$
. By construction, we have
$k\in {\mathbb {N}}$
. By construction, we have
 $$ \begin{align*}\sup_{z\in K_n}|f(r_{n_k}z) - \varphi_m(z)| & \leq \varepsilon_{n_k} + \sum _{j>n_k} \vert P_j (r_{n_k}z)\vert \\ & \leq \varepsilon_{n_k} +\sum _{j>n_k}\varepsilon_j, \end{align*} $$
$$ \begin{align*}\sup_{z\in K_n}|f(r_{n_k}z) - \varphi_m(z)| & \leq \varepsilon_{n_k} + \sum _{j>n_k} \vert P_j (r_{n_k}z)\vert \\ & \leq \varepsilon_{n_k} +\sum _{j>n_k}\varepsilon_j, \end{align*} $$
which goes to
![]() $0$
as
$0$
as
![]() $k\to \infty $
.
$k\to \infty $
.
Let us come back to the original open question whether the derivatives of functions in
![]() ${\mathcal {U}}({\mathbb {D}})$
are also in
${\mathcal {U}}({\mathbb {D}})$
are also in
![]() ${\mathcal {U}}({\mathbb {D}})$
. This question is still open, but the following result asserts that there exist functions in
${\mathcal {U}}({\mathbb {D}})$
. This question is still open, but the following result asserts that there exist functions in
![]() ${\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
whose derivative is not in
${\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
whose derivative is not in
![]() ${\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
.
${\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
.
Theorem 4.3 For any
![]() $l\geq 1$
, there exists
$l\geq 1$
, there exists
![]() $f\in {\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
such that
$f\in {\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
such that
![]() $f^{(l)}\not \in {\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
.
$f^{(l)}\not \in {\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
.
Proof Let us first prove the result for
![]() $l=2$
. Let
$l=2$
. Let
![]() $f=\sum _ka_kz^k \in {\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
. For any k, let the real number
$f=\sum _ka_kz^k \in {\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
. For any k, let the real number
![]() $\alpha _k$
be such that for any
$\alpha _k$
be such that for any
![]() $k\geq 0$
,
$k\geq 0$
,
Then, for any
![]() $k\geq 2$
,
$k\geq 2$
,
In particular,
![]() $\sum _k \alpha _k\zeta ^k$
is uniformly convergent for any
$\sum _k \alpha _k\zeta ^k$
is uniformly convergent for any
![]() $\zeta \in {\mathbb {T}}$
, and thus the series
$\zeta \in {\mathbb {T}}$
, and thus the series
![]() $g:=\sum _k(a_k+\alpha _k)z^k$
still belongs to
$g:=\sum _k(a_k+\alpha _k)z^k$
still belongs to
![]() ${\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
. However,
${\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
. However,
![]() $g^{(2)}$
cannot be universal at
$g^{(2)}$
cannot be universal at
![]() $1$
, since
$1$
, since
![]() $S_n(g^{(2)})(1)\in \mathbb {Z}$
for any
$S_n(g^{(2)})(1)\in \mathbb {Z}$
for any
![]() $n\in {\mathbb {N}}$
.
$n\in {\mathbb {N}}$
.
We can proceed similarly for any
![]() $l\geq 3$
. The details are left to the reader. Now, if it were true that
$l\geq 3$
. The details are left to the reader. Now, if it were true that
![]() $f'\in {\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
whenever
$f'\in {\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
whenever
![]() $f\in {\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
, then
$f\in {\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
, then
![]() $f^{(2)}$
would also belong to
$f^{(2)}$
would also belong to
![]() ${\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
for any
${\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
for any
![]() $f\in {\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
. That would contradict the first part of the proof.
$f\in {\mathcal {U}}({\mathbb {D}},{\mathbb {T}})$
. That would contradict the first part of the proof.
In fact, the previous result can be improved a little bit. Let us introduce another type of universal Taylor series. We will denote by
![]() ${\mathbb {D}}_R$
the open disk
${\mathbb {D}}_R$
the open disk
![]() $D(0,R)$
.
$D(0,R)$
.
Definition 4.1 Let
![]() $R\geq 1$
. We denote by
$R\geq 1$
. We denote by
![]() ${\mathcal {U}}({\mathbb {D}},R)$
the set of those functions
${\mathcal {U}}({\mathbb {D}},R)$
the set of those functions
![]() $f\in H({\mathbb {D}})$
satisfying that, for any compact set
$f\in H({\mathbb {D}})$
satisfying that, for any compact set
![]() $K_1\subset {\mathbb {C}}\setminus \overline {{\mathbb {D}}_R}$
and any compact set
$K_1\subset {\mathbb {C}}\setminus \overline {{\mathbb {D}}_R}$
and any compact set
![]() $K_2 \subset \overline {{\mathbb {D}}_R}\setminus {\mathbb {D}}$
both with connected complement, and for any function
$K_2 \subset \overline {{\mathbb {D}}_R}\setminus {\mathbb {D}}$
both with connected complement, and for any function
![]() $\varphi \in A(K_1\cup K_2)$
, there exists an increasing sequence
$\varphi \in A(K_1\cup K_2)$
, there exists an increasing sequence
![]() $(\lambda _n)_n\subset {\mathbb {N}}$
such that
$(\lambda _n)_n\subset {\mathbb {N}}$
such that
Clearly, we have
for any
![]() $R\geq 1$
. Now, let us comment on the case
$R\geq 1$
. Now, let us comment on the case
![]() $R=1$
, which we think is of particular interest. Indeed, one can observe that
$R=1$
, which we think is of particular interest. Indeed, one can observe that
where
![]() ${\mathcal {U}}_0({\mathbb {D}})$
is the set consisting of those functions f in
${\mathcal {U}}_0({\mathbb {D}})$
is the set consisting of those functions f in
![]() $H({\mathbb {D}})$
that are universal for
$H({\mathbb {D}})$
that are universal for
![]() $\mathcal {S}^K$
for any compact set
$\mathcal {S}^K$
for any compact set
![]() $K\subset {\mathbb {C}}\setminus \overline {{\mathbb {D}}}$
with connected complement. The difference between
$K\subset {\mathbb {C}}\setminus \overline {{\mathbb {D}}}$
with connected complement. The difference between
![]() ${\mathcal {U}}({\mathbb {D}})$
and
${\mathcal {U}}({\mathbb {D}})$
and
![]() ${\mathcal {U}}_0({\mathbb {D}})$
is that universal approximation by partial Taylor sums of f in
${\mathcal {U}}_0({\mathbb {D}})$
is that universal approximation by partial Taylor sums of f in
![]() ${\mathcal {U}}_0({\mathbb {D}})$
are a priori valid only on compact subsets in
${\mathcal {U}}_0({\mathbb {D}})$
are a priori valid only on compact subsets in
![]() ${\mathbb {C}}\setminus {\mathbb {D}}$
that do not touch
${\mathbb {C}}\setminus {\mathbb {D}}$
that do not touch
![]() ${\mathbb {T}}$
. The class
${\mathbb {T}}$
. The class
![]() ${\mathcal {U}}({\mathbb {D}})$
is obviously contained in
${\mathcal {U}}({\mathbb {D}})$
is obviously contained in
![]() ${\mathcal {U}}_0({\mathbb {D}})$
, and it is also well known that both are distinct (e.g., [Reference Melas, Nestoridis and Papadoperakis34]). In fact, this class
${\mathcal {U}}_0({\mathbb {D}})$
, and it is also well known that both are distinct (e.g., [Reference Melas, Nestoridis and Papadoperakis34]). In fact, this class
![]() ${\mathcal {U}}_0({\mathbb {D}})$
was already shown to be nonempty in the early 1970s by Chui and Parnes [Reference Chui and Parnes17] (see also [Reference Luh31]). Using that the locally uniform convergence of a sequence of holomorphic functions implies the locally uniform convergence of the sequence of the derivatives, one can easily show that if f belongs to
${\mathcal {U}}_0({\mathbb {D}})$
was already shown to be nonempty in the early 1970s by Chui and Parnes [Reference Chui and Parnes17] (see also [Reference Luh31]). Using that the locally uniform convergence of a sequence of holomorphic functions implies the locally uniform convergence of the sequence of the derivatives, one can easily show that if f belongs to
![]() ${\mathcal {U}}_0({\mathbb {D}})$
, then so does
${\mathcal {U}}_0({\mathbb {D}})$
, then so does
![]() $f'$
(see also [Reference Costakis19, Proposition 3.5]). Thus,
$f'$
(see also [Reference Costakis19, Proposition 3.5]). Thus,
![]() ${\mathcal {U}}({\mathbb {D}},1)$
is the intersection of a class which is stable under differentiation and of a class that is not, according to Theorem 4.3. The following improvement tells us that the set
${\mathcal {U}}({\mathbb {D}},1)$
is the intersection of a class which is stable under differentiation and of a class that is not, according to Theorem 4.3. The following improvement tells us that the set
![]() ${\mathcal {U}}({\mathbb {D}},R)$
is not stable under differentiation either, for any
${\mathcal {U}}({\mathbb {D}},R)$
is not stable under differentiation either, for any
![]() $R\geq 1$
.
$R\geq 1$
.
Theorem 4.4 For any
![]() $R\geq 1$
and any
$R\geq 1$
and any
![]() $l\geq 1$
, there exists
$l\geq 1$
, there exists
![]() $f\in {\mathcal {U}}({\mathbb {D}},R)$
such that
$f\in {\mathcal {U}}({\mathbb {D}},R)$
such that
![]() $f^{(l)}\not \in {\mathcal {U}}({\mathbb {D}},R)$
.
$f^{(l)}\not \in {\mathcal {U}}({\mathbb {D}},R)$
.
We will make use of the following lemma.
Lemma 4.5 Let
![]() $R\geq 1$
,
$R\geq 1$
,
![]() $K\subset {\mathbb {C}}\setminus \overline {{\mathbb {D}}_R}$
with connected complement, and
$K\subset {\mathbb {C}}\setminus \overline {{\mathbb {D}}_R}$
with connected complement, and
![]() $\varphi \in A(K)$
. For any
$\varphi \in A(K)$
. For any
![]() $\varepsilon>0$
, any
$\varepsilon>0$
, any
![]() $l\in {\mathbb {N}}$
, and any
$l\in {\mathbb {N}}$
, and any
![]() $N\in {\mathbb {N}}$
, there exists a polynomial
$N\in {\mathbb {N}}$
, there exists a polynomial
![]() $P=\sum _{k\geq N} a_k z^k$
with
$P=\sum _{k\geq N} a_k z^k$
with
![]() $|a_k|R^k\leq k^{-(l+2)}$
such that
$|a_k|R^k\leq k^{-(l+2)}$
such that
Proof Let
![]() $\varepsilon $
, l, N, K, R, and
$\varepsilon $
, l, N, K, R, and
![]() $\varphi $
be fixed as in the lemma. Let
$\varphi $
be fixed as in the lemma. Let
![]() $\eta>0$
be such that
$\eta>0$
be such that
![]() $0<\eta < \text {dist}({\mathbb {D}}_R,K)$
, and let
$0<\eta < \text {dist}({\mathbb {D}}_R,K)$
, and let
![]() $M\geq N$
be an integer such that
$M\geq N$
be an integer such that
![]() $\frac {\varepsilon k^{l+2}R^k}{(R+\eta )^k}\leq 1$
for any
$\frac {\varepsilon k^{l+2}R^k}{(R+\eta )^k}\leq 1$
for any
![]() $k\geq M$
. Then Mergelyan’s theorem gives the existence of a polynomial
$k\geq M$
. Then Mergelyan’s theorem gives the existence of a polynomial
![]() $P=\sum _{k\geq M}a_kz^k$
such that
$P=\sum _{k\geq M}a_kz^k$
such that
By Cauchy’s inequalities, we deduce from the first inequality that for any
![]() $k\geq M$
,
$k\geq M$
,
This gives the conclusion by the choice of M.
Proof of Theorem 4.4
Let us first fix
![]() $R\geq 1$
and
$R\geq 1$
and
![]() $l\geq 2$
as in the statement. We keep the notations used in the previous proofs and let
$l\geq 2$
as in the statement. We keep the notations used in the previous proofs and let
![]() $(L_n)_n$
be an enumeration of compact sets in
$(L_n)_n$
be an enumeration of compact sets in
![]() $(\overline {{\mathbb {D}}_R}\setminus {\mathbb {D}})\cup ({\mathbb {C}}\setminus \overline {{\mathbb {D}}_R})$
, with connected complement, such that for any compact sets
$(\overline {{\mathbb {D}}_R}\setminus {\mathbb {D}})\cup ({\mathbb {C}}\setminus \overline {{\mathbb {D}}_R})$
, with connected complement, such that for any compact sets
![]() $K_1\subset \overline {{\mathbb {D}}_R}\setminus {\mathbb {D}}$
and any
$K_1\subset \overline {{\mathbb {D}}_R}\setminus {\mathbb {D}}$
and any
![]() $K_2\subset {\mathbb {C}}\setminus \overline {{\mathbb {D}}_R}$
, both with connected complement, there exists n such that
$K_2\subset {\mathbb {C}}\setminus \overline {{\mathbb {D}}_R}$
, both with connected complement, there exists n such that
![]() $K_1\cup K_2 \subset L_n$
(the proof of the existence of such sequence is straightforward and omitted). We also let
$K_1\cup K_2 \subset L_n$
(the proof of the existence of such sequence is straightforward and omitted). We also let
![]() $\psi _1:{\mathbb {N}}\to {\mathbb {N}}$
,
$\psi _1:{\mathbb {N}}\to {\mathbb {N}}$
,
![]() $\psi _2:{\mathbb {N}}\to {\mathbb {N}}$
and
$\psi _2:{\mathbb {N}}\to {\mathbb {N}}$
and
![]() $\psi _3:{\mathbb {N}}\to {\mathbb {N}}$
, such that for any
$\psi _3:{\mathbb {N}}\to {\mathbb {N}}$
, such that for any
![]() $n_1,n_2,m \in {\mathbb {N}}$
, there exist infinitely many
$n_1,n_2,m \in {\mathbb {N}}$
, there exist infinitely many
![]() $n\in {\mathbb {N}}$
such that
$n\in {\mathbb {N}}$
such that
![]() $(\varphi _{n_1},\varphi _{n_2},L_m)=(\varphi _{\psi _1(n)},\varphi _{\psi _2(n)},L_{\psi _3(n)})$
. Let
$(\varphi _{n_1},\varphi _{n_2},L_m)=(\varphi _{\psi _1(n)},\varphi _{\psi _2(n)},L_{\psi _3(n)})$
. Let
![]() $Q_0=P_0=0$
and
$Q_0=P_0=0$
and
![]() $R_0=0$
. We build by induction three sequences
$R_0=0$
. We build by induction three sequences
![]() $(P_n=\sum a_k(n)z^k)_n$
,
$(P_n=\sum a_k(n)z^k)_n$
,
![]() $(Q_n=\sum b_k(n)z^k)_n$
, and
$(Q_n=\sum b_k(n)z^k)_n$
, and
![]() $(R_n)_n$
of polynomials (using Runge’s theorem for
$(R_n)_n$
of polynomials (using Runge’s theorem for
![]() $(P_n)_n$
and Lemma 4.5 for
$(P_n)_n$
and Lemma 4.5 for
![]() $(Q_n)_n$
), in the following order
$(Q_n)_n$
), in the following order
![]() $Q_n\rightarrow P_n\rightarrow R_n$
, with
$Q_n\rightarrow P_n\rightarrow R_n$
, with
 $R_n=\sum \limits _{k=\text {val}(P_n)}^{\deg (P_n)}\alpha _k z^k$
, such that:
$R_n=\sum \limits _{k=\text {val}(P_n)}^{\deg (P_n)}\alpha _k z^k$
, such that:
-
(1)
 $\text {val}(Q_n)> \text {deg}(P_{n-1})$
;
$\text {val}(Q_n)> \text {deg}(P_{n-1})$
; -
(2)
 $\sup _{|z|\leq R}\vert Q_n(z) \vert \leq \varepsilon _n$
;
$\sup _{|z|\leq R}\vert Q_n(z) \vert \leq \varepsilon _n$
; -
(3)
 $\sup _{z\in L_{\psi _3(n)}\cap ({\mathbb {C}}\setminus \overline {{\mathbb {D}}_R})}\vert Q_n(z) - \left (\varphi _{\psi _2(n)}(z) - \sum _{k=0}^{n-1} (Q_k + P_k + R_k)(z) \right )\vert \leq \varepsilon _n$
;
$\sup _{z\in L_{\psi _3(n)}\cap ({\mathbb {C}}\setminus \overline {{\mathbb {D}}_R})}\vert Q_n(z) - \left (\varphi _{\psi _2(n)}(z) - \sum _{k=0}^{n-1} (Q_k + P_k + R_k)(z) \right )\vert \leq \varepsilon _n$
; -
(4)
 $|b_k(n)|\leq R^{-k}k^{-(l+2)}$
for any
$|b_k(n)|\leq R^{-k}k^{-(l+2)}$
for any
 $n,k$
;
$n,k$
; -
(5)
 $\sup _{|z|\leq 1-1/n}\vert P_n(z) \vert \leq \varepsilon _n$
;
$\sup _{|z|\leq 1-1/n}\vert P_n(z) \vert \leq \varepsilon _n$
; -
(6)
 $\sup _{z\in L_{\psi _3(n)}\cap (\overline {{\mathbb {D}}_R}\setminus {\mathbb {D}})}\vert P_n(z) - (\varphi _{\psi _1(n)}(z) - \sum _{k=0}^{n-1} P_k(z))\vert \leq \varepsilon _n$
;
$\sup _{z\in L_{\psi _3(n)}\cap (\overline {{\mathbb {D}}_R}\setminus {\mathbb {D}})}\vert P_n(z) - (\varphi _{\psi _1(n)}(z) - \sum _{k=0}^{n-1} P_k(z))\vert \leq \varepsilon _n$
; -
(7)
 $\text {val}(P_n)> \text {deg}(Q_n)$
;
$\text {val}(P_n)> \text {deg}(Q_n)$
; -
(8)
 $\Re (k(k-1)\ldots (k-l+2)(k-l+1)R^{k-l}(a_{k}(n)+\alpha _{k}))$
is the integer part of
$\Re (k(k-1)\ldots (k-l+2)(k-l+1)R^{k-l}(a_{k}(n)+\alpha _{k}))$
is the integer part of
 $\Re (k(k-1)\ldots (k-l+2)(k-l+1)R^{k-l}a_{k}(n))$
for
$\Re (k(k-1)\ldots (k-l+2)(k-l+1)R^{k-l}a_{k}(n))$
for
 $k=\text {val}(P_n),\dots ,\deg (P_n)$
.
$k=\text {val}(P_n),\dots ,\deg (P_n)$
.
We set
![]() $f=\sum _n Q_n +\sum _n P_n + \sum _{n} R_n$
. Because of (2), (5), and (8),
$f=\sum _n Q_n +\sum _n P_n + \sum _{n} R_n$
. Because of (2), (5), and (8),
![]() $f \in H({\mathbb {D}})$
and
$f \in H({\mathbb {D}})$
and
![]() $\sum _{n} R_n$
is absolutely convergent on
$\sum _{n} R_n$
is absolutely convergent on
![]() $\overline {{\mathbb {D}}_R}$
(indeed, (8) implies
$\overline {{\mathbb {D}}_R}$
(indeed, (8) implies
![]() $|\alpha _k|\leq R^{-k}(k(k-1))^{-1}$
).
$|\alpha _k|\leq R^{-k}(k(k-1))^{-1}$
).
Moreover, (6) implies that
![]() $\{S_j(\sum _n P_n)|_K:\,j\in {\mathbb {N}}\}$
is dense in
$\{S_j(\sum _n P_n)|_K:\,j\in {\mathbb {N}}\}$
is dense in
![]() $A(K)$
for any
$A(K)$
for any
![]() $K\subset \overline {{\mathbb {D}}_R}\setminus {\mathbb {D}}$
with connected complement. By (8) and (4), respectively,
$K\subset \overline {{\mathbb {D}}_R}\setminus {\mathbb {D}}$
with connected complement. By (8) and (4), respectively,
![]() $\sum _{n} R_n$
and the Taylor expansion at
$\sum _{n} R_n$
and the Taylor expansion at
![]() $0$
of
$0$
of
![]() $\sum _n Q_n$
are absolutely convergent on
$\sum _n Q_n$
are absolutely convergent on
![]() $\overline {{\mathbb {D}}_R}$
, so
$\overline {{\mathbb {D}}_R}$
, so
![]() $\{S_j(f)|_K:\,j\in {\mathbb {N}}\}$
is also dense in
$\{S_j(f)|_K:\,j\in {\mathbb {N}}\}$
is also dense in
![]() $A(K)$
for any
$A(K)$
for any
![]() $K\subset \overline {{\mathbb {D}}_R}\setminus {\mathbb {D}}$
with connected complement.
$K\subset \overline {{\mathbb {D}}_R}\setminus {\mathbb {D}}$
with connected complement.
Now, (3) and (7) imply that
![]() $\{S_j(f)|_K:\,j\in {\mathbb {N}}\}$
is dense in
$\{S_j(f)|_K:\,j\in {\mathbb {N}}\}$
is dense in
![]() $A(K)$
for any
$A(K)$
for any
![]() $K\subset {\mathbb {C}}\setminus \overline {{\mathbb {D}}_R}$
with connected complement.
$K\subset {\mathbb {C}}\setminus \overline {{\mathbb {D}}_R}$
with connected complement.
Last, let us observe that by (8) the set
![]() $\{S_j\left ((\sum _n P_n+\sum _n R_n)^{(l)}\right )(R):\,j\in {\mathbb {N}}\}$
is contained in
$\{S_j\left ((\sum _n P_n+\sum _n R_n)^{(l)}\right )(R):\,j\in {\mathbb {N}}\}$
is contained in
![]() ${\mathbb {Z}}$
. Now, since by (4) the Taylor series of the lth derivative of
${\mathbb {Z}}$
. Now, since by (4) the Taylor series of the lth derivative of
![]() $\sum Q_n$
is absolutely convergent on
$\sum Q_n$
is absolutely convergent on
![]() $\overline {{\mathbb {D}}_R}$
, the set
$\overline {{\mathbb {D}}_R}$
, the set
![]() $\{S_j(f^{(l)})(R):\,j\in {\mathbb {N}}\}$
cannot be dense in
$\{S_j(f^{(l)})(R):\,j\in {\mathbb {N}}\}$
cannot be dense in
![]() ${\mathbb {C}}$
. In particular,
${\mathbb {C}}$
. In particular,
![]() $f^{(l)}\not \in {\mathcal {U}}({\mathbb {D}},R)$
and, by induction, there must be some
$f^{(l)}\not \in {\mathcal {U}}({\mathbb {D}},R)$
and, by induction, there must be some
![]() $f\in {\mathcal {U}}({\mathbb {D}},R)$
such that
$f\in {\mathcal {U}}({\mathbb {D}},R)$
such that
![]() $f'\not \in {\mathcal {U}}({\mathbb {D}},R)$
.
$f'\not \in {\mathcal {U}}({\mathbb {D}},R)$
.
Since the important question whether
![]() ${\mathcal {U}}({\mathbb {D}})$
is invariant under differentiation is still open, the last result makes the following question interesting.
${\mathcal {U}}({\mathbb {D}})$
is invariant under differentiation is still open, the last result makes the following question interesting.
Question 4.6 Does the set
![]() ${\mathcal {U}}({\mathbb {D}})$
coincide with
${\mathcal {U}}({\mathbb {D}})$
coincide with
![]() ${\mathcal {U}}({\mathbb {D}},R)$
for some
${\mathcal {U}}({\mathbb {D}},R)$
for some
![]() $R\geq 1$
?
$R\geq 1$
?
5 Abel multiuniversality
In this section, we are interested in the concept of multiuniversality, which comes from that of multihypercyclicity. Given a Fréchet space X and a continuous operator
![]() $T:X\rightarrow X$
, a finite subset
$T:X\rightarrow X$
, a finite subset
![]() $\{x_1,\dots ,x_l\}$
of X is said to be multihypercyclic for T if the set
$\{x_1,\dots ,x_l\}$
of X is said to be multihypercyclic for T if the set
![]() $\bigcup _{k=1}^l\{T^nx_k:n\in \mathbb {N}\}$
is dense in X. Costakis [Reference Costakis21] and Peris [Reference Peris40] independently proved that if
$\bigcup _{k=1}^l\{T^nx_k:n\in \mathbb {N}\}$
is dense in X. Costakis [Reference Costakis21] and Peris [Reference Peris40] independently proved that if
![]() $\{x_1,\dots ,x_l\}$
is multihypercyclic for T, then one of the
$\{x_1,\dots ,x_l\}$
is multihypercyclic for T, then one of the
![]() $x_i$
’s is hypercyclic for T. Let us extend this notion to the setting of universality.
$x_i$
’s is hypercyclic for T. Let us extend this notion to the setting of universality.
Definition 5.1 Let X and Y be two Fréchet spaces, and let
![]() $T_n:X\rightarrow Y$
,
$T_n:X\rightarrow Y$
,
![]() $n\in \mathbb {N}$
, be continuous linear maps. A finite set
$n\in \mathbb {N}$
, be continuous linear maps. A finite set
![]() $\{x_1,\dots ,x_l\}$
of X is said to be multiuniversal for
$\{x_1,\dots ,x_l\}$
of X is said to be multiuniversal for
![]() $(T_n)_n$
if
$(T_n)_n$
if
![]() $\bigcup _{k=1}^l\{T_nx_k:n\in \mathbb {N}\}$
is dense in Y.
$\bigcup _{k=1}^l\{T_nx_k:n\in \mathbb {N}\}$
is dense in Y.
The concept of multiuniversality was recently studied in the case of Fekete universal series [Reference Mouze35]. In this section, we are going to investigate it for Abel universal functions. For
![]() $K\subset {\mathbb {T}}$
and
$K\subset {\mathbb {T}}$
and
![]() $\varrho =(r_n)_n \subset [0,1)$
increasing and converging to
$\varrho =(r_n)_n \subset [0,1)$
increasing and converging to
![]() $1$
, let us denote as in the introduction by
$1$
, let us denote as in the introduction by
![]() ${\mathcal {T}}_{\varrho }^K$
the sequence
${\mathcal {T}}_{\varrho }^K$
the sequence
![]() $(T_{\varrho ,n}^K)_n$
of continuous operators from
$(T_{\varrho ,n}^K)_n$
of continuous operators from
![]() $H({\mathbb {D}})$
to
$H({\mathbb {D}})$
to
![]() ${\mathcal {C}}(K)$
defined, for any
${\mathcal {C}}(K)$
defined, for any
![]() $n\in {\mathbb {N}}$
, by
$n\in {\mathbb {N}}$
, by
![]() $T_{\varrho ,n}^K(f)=f_{r_n}|_K$
.
$T_{\varrho ,n}^K(f)=f_{r_n}|_K$
.
Definition 5.2 A set
![]() $\{f_1,\dots ,f_l\}\in H({\mathbb {D}})$
is said to be
$\{f_1,\dots ,f_l\}\in H({\mathbb {D}})$
is said to be
![]() $\varrho $
-Abel multiuniversal if, for any
$\varrho $
-Abel multiuniversal if, for any
![]() $K\subset {\mathbb {T}}$
different from
$K\subset {\mathbb {T}}$
different from
![]() ${\mathbb {T}}$
, it is multiuniversal for the sequence
${\mathbb {T}}$
, it is multiuniversal for the sequence
![]() ${\mathcal {T}}_{\varrho }^K$
.
${\mathcal {T}}_{\varrho }^K$
.
Equivalently,
![]() $\{f_1,\dots ,f_l\}\in H({\mathbb {D}})$
is
$\{f_1,\dots ,f_l\}\in H({\mathbb {D}})$
is
![]() $\varrho $
-Abel multiuniversal if for any compact set
$\varrho $
-Abel multiuniversal if for any compact set
![]() $K\subset \mathbb {T}$
, different from
$K\subset \mathbb {T}$
, different from
![]() $\mathbb {T}$
, and any function
$\mathbb {T}$
, and any function
![]() $h\in {\mathcal {C}}({\mathbb {T}})$
, there exist
$h\in {\mathcal {C}}({\mathbb {T}})$
, there exist
![]() $i\in \{1,\dots ,l\}$
and an increasing sequence
$i\in \{1,\dots ,l\}$
and an increasing sequence
![]() $(\lambda _n)_n\subset {\mathbb {N}}$
such that
$(\lambda _n)_n\subset {\mathbb {N}}$
such that
In the same spirit, we can introduce the following definition.
Definition 5.3 A set
![]() $\{f_1,\dots ,f_l\}\in H({\mathbb {D}})$
is said to be Abel multiuniversal if for any compact set
$\{f_1,\dots ,f_l\}\in H({\mathbb {D}})$
is said to be Abel multiuniversal if for any compact set
![]() $K\subset \mathbb {T}$
, different from
$K\subset \mathbb {T}$
, different from
![]() $\mathbb {T}$
, and any function
$\mathbb {T}$
, and any function
![]() $h\in {\mathcal {C}}({\mathbb {T}})$
, there exist
$h\in {\mathcal {C}}({\mathbb {T}})$
, there exist
![]() $i\in \{1,\dots ,l\}$
and an increasing sequence of positive real numbers
$i\in \{1,\dots ,l\}$
and an increasing sequence of positive real numbers
![]() $(r_n)_n$
tending to
$(r_n)_n$
tending to
![]() $1$
such that
$1$
such that
![]() $\sup _{z\in K}\vert f_i(r_{n}z)-h(z)\vert \rightarrow 0,$
as
$\sup _{z\in K}\vert f_i(r_{n}z)-h(z)\vert \rightarrow 0,$
as
![]() $n\rightarrow +\infty $
.
$n\rightarrow +\infty $
.
The following question naturally arises.
Question 5.1 If
![]() $\{f_1,\dots ,f_l\}$
is
$\{f_1,\dots ,f_l\}$
is
![]() $\varrho $
-Abel multiuniversal (resp. Abel multiuniversal), does there exist
$\varrho $
-Abel multiuniversal (resp. Abel multiuniversal), does there exist
![]() $i\in \{1,\dots ,l\}$
such that
$i\in \{1,\dots ,l\}$
such that
![]() $f_i$
is a
$f_i$
is a
![]() $\varrho $
-Abel universal functions (resp. Abel universal functions)?
$\varrho $
-Abel universal functions (resp. Abel universal functions)?
We shall see that this question has a negative answer. To do this, inspired by [Reference Mouze35], we first construct a function f in
![]() $H(\mathbb {D})$
such that for any compact set
$H(\mathbb {D})$
such that for any compact set
![]() $K\subset {\mathbb {T}}$
containing
$K\subset {\mathbb {T}}$
containing
![]() $1$
and different from
$1$
and different from
![]() ${\mathbb {T}}$
, the following two conditions hold:
${\mathbb {T}}$
, the following two conditions hold:
-
(1)
 $T_{\varrho ,n}^K(f)(1)$
is off some nonempty disk.
$T_{\varrho ,n}^K(f)(1)$
is off some nonempty disk. -
(2) The closure of
 $\{T_{\varrho ,n}^K(f)|_K:\,n\in {\mathbb {N}}\}$
in
$\{T_{\varrho ,n}^K(f)|_K:\,n\in {\mathbb {N}}\}$
in
 ${\mathcal {C}}(K)$
contains all continuous function in
${\mathcal {C}}(K)$
contains all continuous function in
 ${\mathcal {C}}(K)$
whose value at
${\mathcal {C}}(K)$
whose value at
 $1$
is off some other nonempty disk.
$1$
is off some other nonempty disk.
More precisely, our key proposition states the following.
Proposition 5.2 Let
![]() $\varrho =(r_n)_n\subset [0,1)$
be an increasing sequence tending to
$\varrho =(r_n)_n\subset [0,1)$
be an increasing sequence tending to
![]() $1$
, and let
$1$
, and let
![]() $a\in \mathbb {C}$
. There exists a function
$a\in \mathbb {C}$
. There exists a function
![]() $f \in H(\mathbb {D})$
, which satisfies the following two properties:
$f \in H(\mathbb {D})$
, which satisfies the following two properties:
-
(1) For any
 $r_1<r<1$
,
$r_1<r<1$
,
 $f(r)\notin D(a,1/2)$
.
$f(r)\notin D(a,1/2)$
. -
(2) For any compact set
 $K\subset \mathbb {T}$
containing
$K\subset \mathbb {T}$
containing
 $1$
and different from
$1$
and different from
 $\mathbb {T}$
, and any function h continuous on K, with
$\mathbb {T}$
, and any function h continuous on K, with
 $ h (1) \notin \overline {D(a,1)}$
, there exists an increasing sequence
$ h (1) \notin \overline {D(a,1)}$
, there exists an increasing sequence
 $(\lambda _n)_n$
of integers such that
$(\lambda _n)_n$
of integers such that  $$ \begin{align*} \sup_{\zeta \in K}\left\vert f\left(r_{\lambda_n}\zeta \right) -h (\zeta) \right\vert \to 0 \quad \mbox{ as }n\to \infty. \end{align*} $$
$$ \begin{align*} \sup_{\zeta \in K}\left\vert f\left(r_{\lambda_n}\zeta \right) -h (\zeta) \right\vert \to 0 \quad \mbox{ as }n\to \infty. \end{align*} $$
Proof We assume that
![]() $\sum _n\varepsilon _n< 1/4$
. Let us set, for any
$\sum _n\varepsilon _n< 1/4$
. Let us set, for any
![]() $n\in {\mathbb {N}}$
,
$n\in {\mathbb {N}}$
,
![]() $I_n=K_n \cup \{1\}$
. Note that
$I_n=K_n \cup \{1\}$
. Note that
![]() $I_n$
is different from
$I_n$
is different from
![]() ${\mathbb {T}}$
for any
${\mathbb {T}}$
for any
![]() $n\in {\mathbb {N}}$
and that any compact subset of
$n\in {\mathbb {N}}$
and that any compact subset of
![]() ${\mathbb {T}}$
containing
${\mathbb {T}}$
containing
![]() $1$
and different from
$1$
and different from
![]() ${\mathbb {T}}$
is contained in some
${\mathbb {T}}$
is contained in some
![]() $I_n$
. Let us also denote by
$I_n$
. Let us also denote by
![]() $(\tilde {\varphi }_n)_n$
an enumeration of all polynomials with rational real and imaginary parts coefficients with value at
$(\tilde {\varphi }_n)_n$
an enumeration of all polynomials with rational real and imaginary parts coefficients with value at
![]() $1$
off
$1$
off
![]() $D(a,1)$
. Note that every continuous function on
$D(a,1)$
. Note that every continuous function on
![]() ${\mathbb {T}}$
with value at
${\mathbb {T}}$
with value at
![]() $1$
off
$1$
off
![]() $\overline {D(a,1)}$
can be uniformly approximated on every compact subset of
$\overline {D(a,1)}$
can be uniformly approximated on every compact subset of
![]() ${\mathbb {T}}$
containing
${\mathbb {T}}$
containing
![]() $1$
and different from
$1$
and different from
![]() ${\mathbb {T}}$
, by a subsequence of
${\mathbb {T}}$
, by a subsequence of
![]() $(\tilde {\varphi }_n)_n$
.
$(\tilde {\varphi }_n)_n$
.
Set
![]() $f_1(z)=\tilde {\varphi }_{\alpha (1)}\left (\frac {z}{r_{1}}\right )$
. Observe that
$f_1(z)=\tilde {\varphi }_{\alpha (1)}\left (\frac {z}{r_{1}}\right )$
. Observe that
![]() $f_1(r_1)\notin D(a,1)$
. Moreover, we can assume that, for all
$f_1(r_1)\notin D(a,1)$
. Moreover, we can assume that, for all
![]() $k\geq 2$
,
$k\geq 2$
,
![]() $\varepsilon _k<d(\tilde {\varphi }_{\alpha (k)}(1),D(a,1))$
, where d is the usual distance on
$\varepsilon _k<d(\tilde {\varphi }_{\alpha (k)}(1),D(a,1))$
, where d is the usual distance on
![]() $\mathbb {C}$
. Using Mergelyan’s theorem, we build by induction a sequence of polynomials
$\mathbb {C}$
. Using Mergelyan’s theorem, we build by induction a sequence of polynomials
![]() $f_k$
,
$f_k$
,
![]() $k\geq 2$
, such that, for any
$k\geq 2$
, such that, for any
![]() $k\geq 2$
,
$k\geq 2$
,
-
(1)
 $\sup _{z\in r_{k}I_{\beta (k)}}\left \vert f_{k}(z)-\tilde {\varphi }_{\alpha (k)}\left (\frac {z}{r_k}\right ) \right \vert <\varepsilon _k$
;
$\sup _{z\in r_{k}I_{\beta (k)}}\left \vert f_{k}(z)-\tilde {\varphi }_{\alpha (k)}\left (\frac {z}{r_k}\right ) \right \vert <\varepsilon _k$
; -
(2)
 $\sup _{\vert z\vert \leq r_{k-1}}\left \vert f_{k}(z)-f_{k-1}(z) \right \vert <\varepsilon _k$
;
$\sup _{\vert z\vert \leq r_{k-1}}\left \vert f_{k}(z)-f_{k-1}(z) \right \vert <\varepsilon _k$
; -
(3)
 $\sup _{r\in [r_{k-1},r_k]}\vert f_{k}(r)-h_k(r)\vert <\varepsilon _k$
, where
$\sup _{r\in [r_{k-1},r_k]}\vert f_{k}(r)-h_k(r)\vert <\varepsilon _k$
, where
 $h_k:[r_{k-1},r_k]\rightarrow \mathbb {C}$
is a continuous functions such that
$h_k:[r_{k-1},r_k]\rightarrow \mathbb {C}$
is a continuous functions such that
 $h_k(r_{k-1})=f_{k-1}(r_{k-1})$
,
$h_k(r_{k-1})=f_{k-1}(r_{k-1})$
,
 $h_{k}(r_k)=\tilde {\varphi }_{\alpha (k)}(1)$
and for all
$h_{k}(r_k)=\tilde {\varphi }_{\alpha (k)}(1)$
and for all
 $r_{k-1}\leq r\leq r_{k}$
,
$r_{k-1}\leq r\leq r_{k}$
,
 $h_k(r)\notin D(a,1)$
.
$h_k(r)\notin D(a,1)$
.
Observe that the choice of the sequence
![]() $(\varepsilon _k)_k$
and the property (1) ensure that
$(\varepsilon _k)_k$
and the property (1) ensure that
![]() $f_k(r_k)\notin D(a,1)$
.
$f_k(r_k)\notin D(a,1)$
.
Let us set
 $$ \begin{align*} f(z)=f_1(z)+\sum_{k=1}^{+\infty}(f_{k+1}(z)-f_k(z)). \end{align*} $$
$$ \begin{align*} f(z)=f_1(z)+\sum_{k=1}^{+\infty}(f_{k+1}(z)-f_k(z)). \end{align*} $$
From (2), we deduce that
![]() $f\in H(\mathbb {D})$
. Now, by (1) and (2), we have, for any
$f\in H(\mathbb {D})$
. Now, by (1) and (2), we have, for any
![]() $n\in {\mathbb {N}}$
and any
$n\in {\mathbb {N}}$
and any
![]() $z\in I_{\beta (n)}$
,
$z\in I_{\beta (n)}$
,
 $$ \begin{align} \begin{array}{lll} \left\vert f(r_{n}z)-\tilde{\varphi}_{\alpha(n)}\left(z\right) \right\vert & \leq & \displaystyle \left\vert f_n(r_{n}z)-\tilde{\varphi}_{\alpha(n)}\left(z\right)\right\vert+ \sum_{k=n}^{+\infty}\left\vert f_{k+1}(r_{n}z)-f_k(r_{n}z)\right\vert\\ & \leq & \displaystyle \left\vert f_n(r_{n}z)-\tilde{\varphi}_{\alpha(n)}\left(z\right)\right\vert+ \sum_{k=n}^{+\infty}\sup_{\vert z\vert \leq r_{k}}\left\vert f_{k+1}(z)-f_k(z)\right\vert\\ & < & \displaystyle \sum_{k=n}^{+\infty}\varepsilon_k.\end{array} \end{align} $$
$$ \begin{align} \begin{array}{lll} \left\vert f(r_{n}z)-\tilde{\varphi}_{\alpha(n)}\left(z\right) \right\vert & \leq & \displaystyle \left\vert f_n(r_{n}z)-\tilde{\varphi}_{\alpha(n)}\left(z\right)\right\vert+ \sum_{k=n}^{+\infty}\left\vert f_{k+1}(r_{n}z)-f_k(r_{n}z)\right\vert\\ & \leq & \displaystyle \left\vert f_n(r_{n}z)-\tilde{\varphi}_{\alpha(n)}\left(z\right)\right\vert+ \sum_{k=n}^{+\infty}\sup_{\vert z\vert \leq r_{k}}\left\vert f_{k+1}(z)-f_k(z)\right\vert\\ & < & \displaystyle \sum_{k=n}^{+\infty}\varepsilon_k.\end{array} \end{align} $$
This yields the point (2) of the proposition. Indeed, if
![]() $n,m\in {\mathbb {N}}$
are fixed and
$n,m\in {\mathbb {N}}$
are fixed and
![]() $(n_l)_l\subset {\mathbb {N}}$
is an increasing sequence such that
$(n_l)_l\subset {\mathbb {N}}$
is an increasing sequence such that
![]() $\alpha (n_l)=n$
and
$\alpha (n_l)=n$
and
![]() $\beta (n_l)=m$
for any
$\beta (n_l)=m$
for any
![]() $l\in {\mathbb {N}}$
, then by (5.1)
$l\in {\mathbb {N}}$
, then by (5.1)
![]() $f_{r_{n_l}}$
tends to
$f_{r_{n_l}}$
tends to
![]() $\tilde {\varphi }_{n}$
uniformly on
$\tilde {\varphi }_{n}$
uniformly on
![]() $I_m$
as
$I_m$
as
![]() $l\to \infty $
.
$l\to \infty $
.
For the proof of (1), let us fix
![]() $r\in [r_1,1)$
and let
$r\in [r_1,1)$
and let
![]() $n\geq 2$
be an integer such that
$n\geq 2$
be an integer such that
![]() $r_{n-1} \leq r\leq r_n$
. Since
$r_{n-1} \leq r\leq r_n$
. Since
![]() $\sum _k\varepsilon _k< 1/4$
, we deduce from (3) that
$\sum _k\varepsilon _k< 1/4$
, we deduce from (3) that
 $$ \begin{align*} \begin{array}{lll}\vert f(r)-h_n(r)\vert &\leq &\vert f(r)-f_n(r)\vert+\vert f_n(r)-h_n(r)\vert\\&\leq& \displaystyle\sum_{k\geq n}\vert f_{k+1}(r)-f_k(r)\vert +\vert f_n(r)-h_n(r)\vert\\ &<&\displaystyle\frac{1}{4} + \frac{1}{4}=\frac{1}{2}.\end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{lll}\vert f(r)-h_n(r)\vert &\leq &\vert f(r)-f_n(r)\vert+\vert f_n(r)-h_n(r)\vert\\&\leq& \displaystyle\sum_{k\geq n}\vert f_{k+1}(r)-f_k(r)\vert +\vert f_n(r)-h_n(r)\vert\\ &<&\displaystyle\frac{1}{4} + \frac{1}{4}=\frac{1}{2}.\end{array} \end{align*} $$
We conclude the proof thanks to the fact that
![]() $h_n(r)\in {\mathbb {C}}\setminus D(a,1)$
for any
$h_n(r)\in {\mathbb {C}}\setminus D(a,1)$
for any
![]() $r_{n-1}\leq r\leq r_{n}$
.
$r_{n-1}\leq r\leq r_{n}$
.
We can easily deduce the answer to Question 5.1.
Theorem 5.3 There exist two functions
![]() $f_1$
and
$f_1$
and
![]() $f_2$
in
$f_2$
in
![]() $H(\mathbb {D})$
such that the family
$H(\mathbb {D})$
such that the family
![]() $\{f_1,f_2\}$
is
$\{f_1,f_2\}$
is
![]() $\varrho $
-Abel multiuniversal (resp. Abel multiuniversal), but neither
$\varrho $
-Abel multiuniversal (resp. Abel multiuniversal), but neither
![]() $f_1$
nor
$f_1$
nor
![]() $f_2$
is
$f_2$
is
![]() $\varrho $
-Abel universal (resp. Abel universal).
$\varrho $
-Abel universal (resp. Abel universal).
Proof Let
![]() $a_1,a_2\in \mathbb {C}$
such that
$a_1,a_2\in \mathbb {C}$
such that
![]() $\vert a_1- a_2\vert>2$
. Let
$\vert a_1- a_2\vert>2$
. Let
![]() $f_1$
and
$f_1$
and
![]() $f_2$
in
$f_2$
in
![]() $H({\mathbb {D}})$
be given by Proposition 5.2 applied, respectively, with
$H({\mathbb {D}})$
be given by Proposition 5.2 applied, respectively, with
![]() $a=a_1$
and
$a=a_1$
and
![]() $a=a_2$
. Clearly, neither
$a=a_2$
. Clearly, neither
![]() $f_1$
nor
$f_1$
nor
![]() $f_2$
is Abel universal. Now, since
$f_2$
is Abel universal. Now, since
![]() $\overline {D(a_1,1)}\cap \overline {D(a_2,1)}=\emptyset $
, it is also clear that the family
$\overline {D(a_1,1)}\cap \overline {D(a_2,1)}=\emptyset $
, it is also clear that the family
![]() $\{f_1,f_2\}$
is
$\{f_1,f_2\}$
is
![]() $\varrho $
-Abel multiuniversal. To complete the proof, it is enough to observe that any
$\varrho $
-Abel multiuniversal. To complete the proof, it is enough to observe that any
![]() $\varrho $
-Abel multiuniversal set is Abel multiuniversal.
$\varrho $
-Abel multiuniversal set is Abel multiuniversal.
Remark 5.4 (1) In fact, Proposition 5.2 implies a result slightly stronger than Theorem 5.3. Indeed, it shows the existence of a set
![]() $\{f_1,f_2\}$
in
$\{f_1,f_2\}$
in
![]() $H({\mathbb {D}})\setminus {\mathcal {U}}_A({\mathbb {D}},\varrho )$
such that the following holds: for any function h continuous on
$H({\mathbb {D}})\setminus {\mathcal {U}}_A({\mathbb {D}},\varrho )$
such that the following holds: for any function h continuous on
![]() ${\mathbb {T}}$
, there exists
${\mathbb {T}}$
, there exists
![]() $i\in \{1,2\}$
such that for any compact set
$i\in \{1,2\}$
such that for any compact set
![]() $K\subset \mathbb {T}$
, different from
$K\subset \mathbb {T}$
, different from
![]() $\mathbb {T}$
, there exists an increasing sequence
$\mathbb {T}$
, there exists an increasing sequence
![]() $(\lambda _n)_n \subset {\mathbb {N}}$
so that
$(\lambda _n)_n \subset {\mathbb {N}}$
so that
![]() $T_{\varrho ,\lambda _n}^K(f) \to h$
in
$T_{\varrho ,\lambda _n}^K(f) \to h$
in
![]() ${\mathcal {C}}(K)$
as
${\mathcal {C}}(K)$
as
![]() $n\to \infty $
. Note that the latter property is stronger than that required in Definitions 5.1 and 5.2.
$n\to \infty $
. Note that the latter property is stronger than that required in Definitions 5.1 and 5.2.
(2) Assume that a set
![]() $\{f_1,f_2\} \in H({\mathbb {D}})$
satisfies the following property: for any compact set
$\{f_1,f_2\} \in H({\mathbb {D}})$
satisfies the following property: for any compact set
![]() $K\subset \mathbb {T}$
different from
$K\subset \mathbb {T}$
different from
![]() $\mathbb {T}$
, there exists
$\mathbb {T}$
, there exists
![]() $i\in \{1,2\}$
for which
$i\in \{1,2\}$
for which
![]() $f_i$
is universal for
$f_i$
is universal for
![]() ${\mathcal {T}}_{\varrho }^K$
. Note that this condition is stronger than that given in (1) and that there exist functions universal for
${\mathcal {T}}_{\varrho }^K$
. Note that this condition is stronger than that given in (1) and that there exist functions universal for
![]() ${\mathcal {T}}_{\varrho }^K$
which are not Abel universal. Then such a property now implies that at least one of the two functions
${\mathcal {T}}_{\varrho }^K$
which are not Abel universal. Then such a property now implies that at least one of the two functions
![]() $f_1$
or
$f_1$
or
![]() $f_2$
is
$f_2$
is
![]() $\varrho $
-Abel universal. Similarly, if we assume that for any compact set
$\varrho $
-Abel universal. Similarly, if we assume that for any compact set
![]() $K\subset \mathbb {T}$
different from
$K\subset \mathbb {T}$
different from
![]() $\mathbb {T}$
, there exists
$\mathbb {T}$
, there exists
![]() $i\in \{1,2\}$
for which there exists
$i\in \{1,2\}$
for which there exists
![]() $\varrho $
such that
$\varrho $
such that
![]() $f_i$
is universal for
$f_i$
is universal for
![]() ${\mathcal {T}}_{\varrho }^K$
, then
${\mathcal {T}}_{\varrho }^K$
, then
![]() $f_1$
or
$f_1$
or
![]() $f_2$
is Abel universal.
$f_2$
is Abel universal.
Let us only outline the proof in the case where
![]() $\varrho $
is fixed in advance. Thus, assume by contradiction that
$\varrho $
is fixed in advance. Thus, assume by contradiction that
![]() $\{f_1,f_2\}$
satisfies the above property, whereas neither
$\{f_1,f_2\}$
satisfies the above property, whereas neither
![]() $f_1$
nor
$f_1$
nor
![]() $f_2$
is
$f_2$
is
![]() $\varrho $
-Abel universal. Then, for each
$\varrho $
-Abel universal. Then, for each
![]() $i=1,2$
, one can find a compact set
$i=1,2$
, one can find a compact set
![]() $L_i\subset \mathbb {T}$
, different from
$L_i\subset \mathbb {T}$
, different from
![]() $\mathbb {T}$
, a polynomial
$\mathbb {T}$
, a polynomial
![]() $h_i$
, and
$h_i$
, and
![]() $\varepsilon _i>0$
such that for all positive integers n there exists
$\varepsilon _i>0$
such that for all positive integers n there exists
![]() $z_n^{(i)}\in L_i$
satisfying
$z_n^{(i)}\in L_i$
satisfying
Using the fact that
![]() $L_1$
and
$L_1$
and
![]() $L_2$
are compact sets, there exist increasing sequences of positive integers
$L_2$
are compact sets, there exist increasing sequences of positive integers
![]() $(\lambda _n^{(i)})$
and
$(\lambda _n^{(i)})$
and
![]() $z_{\infty }^{(i)}\in L_i$
,
$z_{\infty }^{(i)}\in L_i$
,
![]() $i=1,2$
, so that
$i=1,2$
, so that
![]() $z_{\lambda _n^{(i)}}^{(i)}\rightarrow z_{\infty }^{(i)}$
. We set, for
$z_{\lambda _n^{(i)}}^{(i)}\rightarrow z_{\infty }^{(i)}$
. We set, for
![]() $i=1,2$
,
$i=1,2$
,
![]() $K_i=\{z_{\infty }^{(i)}\}\cup \{z_{\lambda _n^{(i)}},n\geq 1\}$
. Clearly,
$K_i=\{z_{\infty }^{(i)}\}\cup \{z_{\lambda _n^{(i)}},n\geq 1\}$
. Clearly,
![]() $K_1$
and
$K_1$
and
![]() $K_2$
are compact subsets of
$K_2$
are compact subsets of
![]() $\mathbb {T}$
with
$\mathbb {T}$
with
![]() $K_1\cup K_2\ne \mathbb {T}$
. So, by assumption, one of the two functions
$K_1\cup K_2\ne \mathbb {T}$
. So, by assumption, one of the two functions
![]() $f_i$
is universal for
$f_i$
is universal for
![]() ${\mathcal {T}}_{\varrho }^{K_1\cup K_2}$
, a contradiction with (5.2).
${\mathcal {T}}_{\varrho }^{K_1\cup K_2}$
, a contradiction with (5.2).
To conclude this section, let us recall that one of the most elegant results in linear dynamics asserts that a vector x in some separable Fréchet space X is hypercyclic for some continuous operator
![]() $T:X\to X$
whenever the orbit
$T:X\to X$
whenever the orbit
![]() $\{T^n x:\, n\in {\mathbb {N}}\}$
of x under T is somewhere dense in X (see [Reference Bourdon10] or [Reference Grosse-Erdmann and Peris Manguillot29, Theorem 6.5]). Costakis and Peris’ result is a corollary of this result. The following proposition, which is a direct consequence of Proposition 5.2, shows that Bourdon–Feldman’s theorem does not extend to the concept of universality.
$\{T^n x:\, n\in {\mathbb {N}}\}$
of x under T is somewhere dense in X (see [Reference Bourdon10] or [Reference Grosse-Erdmann and Peris Manguillot29, Theorem 6.5]). Costakis and Peris’ result is a corollary of this result. The following proposition, which is a direct consequence of Proposition 5.2, shows that Bourdon–Feldman’s theorem does not extend to the concept of universality.
Proposition 5.5 For any
![]() $\varrho $
, there exists a function
$\varrho $
, there exists a function
![]() $f\in H({\mathbb {D}})$
that is
$f\in H({\mathbb {D}})$
that is
![]() ${\mathcal {T}}_{\varrho '}^{\{1\}}$
-universal for no sequence
${\mathcal {T}}_{\varrho '}^{\{1\}}$
-universal for no sequence
![]() $\varrho '$
, and that enjoys yet the property that given any compact set
$\varrho '$
, and that enjoys yet the property that given any compact set
![]() $K\subset \mathbb {T}$
different from
$K\subset \mathbb {T}$
different from
![]() $\mathbb {T}$
, the set
$\mathbb {T}$
, the set
![]() $\{T_{\varrho ,n}^K(f)|_K:\,n\in {\mathbb {N}}\}$
is somewhere dense in
$\{T_{\varrho ,n}^K(f)|_K:\,n\in {\mathbb {N}}\}$
is somewhere dense in
![]() ${\mathcal {C}}(K)$
.
${\mathcal {C}}(K)$
.
6 Abel universality: a very flexible notion
Paraphrasing Section 2, a function
![]() $f\in H({\mathbb {D}})$
is Abel universal (resp.
$f\in H({\mathbb {D}})$
is Abel universal (resp.
![]() $\varrho $
-Abel universal) if the set
$\varrho $
-Abel universal) if the set
![]() $N_{f}(V,K)$
(resp.
$N_{f}(V,K)$
(resp.
![]() $N_{f}(V,K,\varrho )$
) is nonempty (or equivalently infinite) for any compact set
$N_{f}(V,K,\varrho )$
) is nonempty (or equivalently infinite) for any compact set
![]() $K\subset {\mathbb {T}}$
, different from
$K\subset {\mathbb {T}}$
, different from
![]() ${\mathbb {T}}$
, and for any
${\mathbb {T}}$
, and for any
![]() $V\in {\mathcal {V}}(K)$
. It is natural to think of quantifying the size of these sets or, more generally, of understanding which “type” of sets they can be. The purpose of this section is to show that the notion of Abel universality is as flexible as one may think of, namely that the sets
$V\in {\mathcal {V}}(K)$
. It is natural to think of quantifying the size of these sets or, more generally, of understanding which “type” of sets they can be. The purpose of this section is to show that the notion of Abel universality is as flexible as one may think of, namely that the sets
![]() $N_{f}(V,K)$
can literally be “anything which makes sense.” In this context, “anything which makes sense” will refer to a locally finite countable family of compact subsets of
$N_{f}(V,K)$
can literally be “anything which makes sense.” In this context, “anything which makes sense” will refer to a locally finite countable family of compact subsets of
![]() $[r(V,K),1)$
for some
$[r(V,K),1)$
for some
![]() $r(V,K)\in [0,1)$
close enough to
$r(V,K)\in [0,1)$
close enough to
![]() $1$
(depending only on V and K) and where, by definition, a countable family
$1$
(depending only on V and K) and where, by definition, a countable family
![]() ${\mathcal {F}}$
of compact subsets of
${\mathcal {F}}$
of compact subsets of
![]() $[0,1)$
is locally finite if for any compact set
$[0,1)$
is locally finite if for any compact set
![]() $K\subset [0,1)$
, K intersects at most finitely many sets of
$K\subset [0,1)$
, K intersects at most finitely many sets of
![]() ${\mathcal {F}}$
.
${\mathcal {F}}$
.
For
![]() $l\in {\mathbb {N}}$
, let
$l\in {\mathbb {N}}$
, let
![]() $(V_n(l))_n$
be a sequence of nonempty open balls defining the topology of
$(V_n(l))_n$
be a sequence of nonempty open balls defining the topology of
![]() $\mathcal {C}(K_l)$
. Moreover, throughout this section by segment, we always mean a closed segment.
$\mathcal {C}(K_l)$
. Moreover, throughout this section by segment, we always mean a closed segment.
Proposition 6.1 Let
![]() $\{\Gamma (l,n,m):\, l,n,m\in {\mathbb {N}}\}$
be a locally finite infinite family of pairwise disjoint segments in
$\{\Gamma (l,n,m):\, l,n,m\in {\mathbb {N}}\}$
be a locally finite infinite family of pairwise disjoint segments in
![]() $[0,1)$
. Set
$[0,1)$
. Set
Let
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
![]() $g\in H({\mathbb {D}})$
, and let
$g\in H({\mathbb {D}})$
, and let
![]() $D\subset \mathbb {D}$
be a closed disk centered at
$D\subset \mathbb {D}$
be a closed disk centered at
![]() $0$
. There exist a family
$0$
. There exist a family
![]() $\{r(l,n):\,l,n\in {\mathbb {N}}\}$
in
$\{r(l,n):\,l,n\in {\mathbb {N}}\}$
in
![]() $[0,1)$
and a function
$[0,1)$
and a function
![]() $f\in H({\mathbb {D}})$
such that
$f\in H({\mathbb {D}})$
such that
![]() $\sup _D |f - g| < \varepsilon $
and such that for any
$\sup _D |f - g| < \varepsilon $
and such that for any
![]() $l,n\in {\mathbb {N}}$
and any
$l,n\in {\mathbb {N}}$
and any
![]() $r\in \Gamma (l,n)\cap [r(l,n),1)$
,
$r\in \Gamma (l,n)\cap [r(l,n),1)$
,
![]() $f\circ \phi _r \in V_n(l)$
.
$f\circ \phi _r \in V_n(l)$
.
This proposition is of interest if for some
![]() $(l,n)$
, the point
$(l,n)$
, the point
![]() $1$
is contained in the closure of
$1$
is contained in the closure of
![]() $\Gamma (l,n)$
(if there is no
$\Gamma (l,n)$
(if there is no
![]() $(l,n)$
for which it is the case, then
$(l,n)$
for which it is the case, then
![]() $r(l,n)$
can be chosen so that
$r(l,n)$
can be chosen so that
![]() $\Gamma (l,n)\cap [r(l,n),1)$
is empty). For our purpose, we are interested in applications where the sets
$\Gamma (l,n)\cap [r(l,n),1)$
is empty). For our purpose, we are interested in applications where the sets
![]() $\Gamma (l,n)$
are “big” near
$\Gamma (l,n)$
are “big” near
![]() $1$
, e.g., when
$1$
, e.g., when
![]() $1$
is a limit point of every set
$1$
is a limit point of every set
![]() $\Gamma (l,n)$
,
$\Gamma (l,n)$
,
![]() $l,n\in {\mathbb {N}}$
.
$l,n\in {\mathbb {N}}$
.
Proof By Mergelyan’s theorem, we may and shall assume that for any
![]() $l,n\in {\mathbb {N}}$
,
$l,n\in {\mathbb {N}}$
,
![]() $V_n(l)$
is centered at some entire function
$V_n(l)$
is centered at some entire function
![]() $g_{n,l}$
and has radius
$g_{n,l}$
and has radius
![]() $\delta _{n,l}$
, where
$\delta _{n,l}$
, where
![]() $(\delta _{n,l})_n$
,
$(\delta _{n,l})_n$
,
![]() $l\in \mathbb {N}$
, are some sequences of positive numbers. By uniform continuity, for any
$l\in \mathbb {N}$
, are some sequences of positive numbers. By uniform continuity, for any
![]() $l,n\in {\mathbb {N}}$
, we can define
$l,n\in {\mathbb {N}}$
, we can define
![]() $r(l,n)\in [0,1)$
such that
$r(l,n)\in [0,1)$
such that
 $$ \begin{align} \sup_{r\in [r(l,n),1]}\sup_{\zeta\in K_l}|g_{n,l}\circ \phi_r(\zeta)-g_{n,l}(\zeta)| < \frac{\delta_{n,l}}{4}. \end{align} $$
$$ \begin{align} \sup_{r\in [r(l,n),1]}\sup_{\zeta\in K_l}|g_{n,l}\circ \phi_r(\zeta)-g_{n,l}(\zeta)| < \frac{\delta_{n,l}}{4}. \end{align} $$
We shall also assume that
![]() $r(l,n)$
is larger than the radius of D for any
$r(l,n)$
is larger than the radius of D for any
![]() $l,n\in {\mathbb {N}}$
. For any
$l,n\in {\mathbb {N}}$
. For any
![]() $l,n,m\in {\mathbb {N}}$
, let us denote by
$l,n,m\in {\mathbb {N}}$
, let us denote by
![]() $\tilde {\Gamma }(l,n,m)$
the set
$\tilde {\Gamma }(l,n,m)$
the set
![]() $\Gamma (l,n,m)\cap [r(l,n),1)$
and by
$\Gamma (l,n,m)\cap [r(l,n),1)$
and by
![]() $\tilde {\Gamma }(l,n)$
the set
$\tilde {\Gamma }(l,n)$
the set
It may happen that the family
![]() $\{\tilde {\Gamma }(l,n,m):\, l,n,m\in {\mathbb {N}}\}$
is finite. In that case, we choose
$\{\tilde {\Gamma }(l,n,m):\, l,n,m\in {\mathbb {N}}\}$
is finite. In that case, we choose
![]() $r(n,l)$
larger than the largest element in these sets, so that nothing further needs to be proved. Let us then assume that the family
$r(n,l)$
larger than the largest element in these sets, so that nothing further needs to be proved. Let us then assume that the family
![]() $\{\tilde {\Gamma }(l,n,m):\, l,n,m\in {\mathbb {N}}\}$
is infinite. Furthermore, upon removing all the empty sets
$\{\tilde {\Gamma }(l,n,m):\, l,n,m\in {\mathbb {N}}\}$
is infinite. Furthermore, upon removing all the empty sets
![]() $\tilde {\Gamma }(l,n,m)$
and reordering the remaining nonempty ones, we may and shall assume that every
$\tilde {\Gamma }(l,n,m)$
and reordering the remaining nonempty ones, we may and shall assume that every
![]() $\tilde {\Gamma }(l,n,m)$
,
$\tilde {\Gamma }(l,n,m)$
,
![]() $l,n,m \in {\mathbb {N}}$
, is nonempty.
$l,n,m \in {\mathbb {N}}$
, is nonempty.
Since
![]() $\{\tilde {\Gamma }(l,n,m):\, l,n,m\in {\mathbb {N}}\}$
is locally finite, we can then find an ordering
$\{\tilde {\Gamma }(l,n,m):\, l,n,m\in {\mathbb {N}}\}$
is locally finite, we can then find an ordering
![]() $(\tilde {\Gamma }_i)_{i\in {\mathbb {N}}}$
of it and an increasing sequence
$(\tilde {\Gamma }_i)_{i\in {\mathbb {N}}}$
of it and an increasing sequence
![]() $(s_i)_{i\geq 1}$
in
$(s_i)_{i\geq 1}$
in
![]() $(0,1)$
, tending to
$(0,1)$
, tending to
![]() $1$
, such that for any
$1$
, such that for any
![]() $i\geq 1$
,
$i\geq 1$
,
Note that for any
![]() $i\in {\mathbb {N}}$
, there exists a unique pair
$i\in {\mathbb {N}}$
, there exists a unique pair
![]() $(l,n)$
such that
$(l,n)$
such that
![]() $\tilde {\Gamma }_{i}\subset \tilde {\Gamma }(l,n)$
. Let us write
$\tilde {\Gamma }_{i}\subset \tilde {\Gamma }(l,n)$
. Let us write
![]() $D_0=D$
and denote by
$D_0=D$
and denote by
![]() $D_i$
,
$D_i$
,
![]() $i\geq 1$
, the closed disk centered at
$i\geq 1$
, the closed disk centered at
![]() $0$
, with radius
$0$
, with radius
![]() $s_i$
. By induction, let us build a sequence
$s_i$
. By induction, let us build a sequence
![]() $(P_i)_i$
of polynomials as follows. If
$(P_i)_i$
of polynomials as follows. If
![]() $D_0=\emptyset $
, set
$D_0=\emptyset $
, set
![]() $P_0=0$
. If not, observe that by construction the real number
$P_0=0$
. If not, observe that by construction the real number
![]() $\min (\tilde {\Gamma }_{0})$
is larger than the radius of D and let us apply Runge’s theorem to define
$\min (\tilde {\Gamma }_{0})$
is larger than the radius of D and let us apply Runge’s theorem to define
![]() $P_0$
as any polynomial satisfying
$P_0$
as any polynomial satisfying
![]() $\sup _{D_0} |P_0-g| < \varepsilon /2$
and
$\sup _{D_0} |P_0-g| < \varepsilon /2$
and
 $$ \begin{align*} \sup_{\zeta\in K_l}|P_0\circ \phi_r(\zeta)-g_{n,l}\circ \phi_r(\zeta)| < \frac{\delta_{n,l}}{4} \end{align*} $$
$$ \begin{align*} \sup_{\zeta\in K_l}|P_0\circ \phi_r(\zeta)-g_{n,l}\circ \phi_r(\zeta)| < \frac{\delta_{n,l}}{4} \end{align*} $$
for any
![]() $r\in \tilde {\Gamma }_0$
, where
$r\in \tilde {\Gamma }_0$
, where
![]() $(l,n)$
is the only pair such that
$(l,n)$
is the only pair such that
![]() $\tilde {\Gamma }_{0}\subset \tilde {\Gamma }(l,n)$
. Then we build by induction positive real numbers
$\tilde {\Gamma }_{0}\subset \tilde {\Gamma }(l,n)$
. Then we build by induction positive real numbers
![]() $\eta _k$
,
$\eta _k$
,
![]() $k\geq 1$
, and by applying Runge’s theorem, polynomials
$k\geq 1$
, and by applying Runge’s theorem, polynomials
![]() $P_k$
,
$P_k$
,
![]() $k\geq 1$
, such that for any
$k\geq 1$
, such that for any
![]() $j\geq 1$
and any
$j\geq 1$
and any
![]() $0\leq i\leq j-1$
:
$0\leq i\leq j-1$
:
-
(1)
 $\sup _{K_l}\left \vert \sum _{k=0}^i P_k\circ \phi _r - g_{n,l}\circ \phi _r \right \vert + \sum _{k=i+1}^j \eta _k < \frac {\delta _{n,l}}{4}$
for any
$\sup _{K_l}\left \vert \sum _{k=0}^i P_k\circ \phi _r - g_{n,l}\circ \phi _r \right \vert + \sum _{k=i+1}^j \eta _k < \frac {\delta _{n,l}}{4}$
for any
 $r \in \tilde {\Gamma }_{i}$
where
$r \in \tilde {\Gamma }_{i}$
where
 $(l,n)$
is the only pair for which
$(l,n)$
is the only pair for which
 $\tilde {\Gamma }_{i}\subset \tilde {\Gamma }(l,n)$
;
$\tilde {\Gamma }_{i}\subset \tilde {\Gamma }(l,n)$
; -
(2)
 $\eta _j < \varepsilon /2^{j+1}$
;
$\eta _j < \varepsilon /2^{j+1}$
; -
(3)
 $\sup _{K_l}\left \vert \sum _{k=0}^j P_k\circ \phi _r - g_{n,l}\circ \phi _r \right \vert < \frac {\delta _{n,l}}{4}$
for any
$\sup _{K_l}\left \vert \sum _{k=0}^j P_k\circ \phi _r - g_{n,l}\circ \phi _r \right \vert < \frac {\delta _{n,l}}{4}$
for any
 $r \in \tilde {\Gamma }_{j}$
where
$r \in \tilde {\Gamma }_{j}$
where
 $(l,n)$
is the only pair for which
$(l,n)$
is the only pair for which
 $\tilde {\Gamma }_{j}\subset \tilde {\Gamma }(l,n)$
;
$\tilde {\Gamma }_{j}\subset \tilde {\Gamma }(l,n)$
; -
(4)
 $\sup _{D_{j}}|P_j|< \eta _{j}$
.
$\sup _{D_{j}}|P_j|< \eta _{j}$
.
Then we set
![]() $f=\sum _{i\geq 0} P_i$
. By (b) and (d) and the choice of
$f=\sum _{i\geq 0} P_i$
. By (b) and (d) and the choice of
![]() $P_0$
, we get
$P_0$
, we get
![]() $f\in H({\mathbb {D}})$
and
$f\in H({\mathbb {D}})$
and
![]() $\sup _{D} |f - g| < \varepsilon $
. Let us now check that f satisfies
$\sup _{D} |f - g| < \varepsilon $
. Let us now check that f satisfies
![]() $f\circ \phi _r \in V_n(l)$
for any
$f\circ \phi _r \in V_n(l)$
for any
![]() $l,n\in {\mathbb {N}}$
and any
$l,n\in {\mathbb {N}}$
and any
![]() $r\in \tilde {\Gamma }(l,n)$
. Fix
$r\in \tilde {\Gamma }(l,n)$
. Fix
![]() $l,n\in {\mathbb {N}}$
and
$l,n\in {\mathbb {N}}$
and
![]() $r\in \tilde {\Gamma }(l,n)$
. There exists a unique
$r\in \tilde {\Gamma }(l,n)$
. There exists a unique
![]() $i\in {\mathbb {N}}$
such that
$i\in {\mathbb {N}}$
such that
![]() $r\in \tilde {\Gamma }_i$
. We deduce from (a), (c), and (6.1) that
$r\in \tilde {\Gamma }_i$
. We deduce from (a), (c), and (6.1) that
 $$ \begin{align*} f\circ \phi_r = \sum_{k=0}^i P_k\circ \phi_r + \sum _{k\geq i+1}P_k\circ \phi_r \in V_n(l). \end{align*} $$
$$ \begin{align*} f\circ \phi_r = \sum_{k=0}^i P_k\circ \phi_r + \sum _{k\geq i+1}P_k\circ \phi_r \in V_n(l). \end{align*} $$
This gives the desired conclusion.
Remark 6.2 If we assume that the sets
![]() $\Gamma (l,n,m)$
all have empty interior, then Proposition 6.1 may be a little bit strengthened, using Mergelyan’s theorem instead of Runge’s theorem. In that case, one does not need inequality (6.1) and in the proof one can work with
$\Gamma (l,n,m)$
all have empty interior, then Proposition 6.1 may be a little bit strengthened, using Mergelyan’s theorem instead of Runge’s theorem. In that case, one does not need inequality (6.1) and in the proof one can work with
![]() $g_{n,l}$
instead of
$g_{n,l}$
instead of
![]() $g_{n,l}\circ \phi _r$
. More precisely, the reader may check that the following holds.
$g_{n,l}\circ \phi _r$
. More precisely, the reader may check that the following holds.
Proposition 6.3 Let
![]() $\{\Gamma (l,n,m):\, l,n,m\in {\mathbb {N}}\}$
be a locally finite infinite family of pairwise disjoint singletons in
$\{\Gamma (l,n,m):\, l,n,m\in {\mathbb {N}}\}$
be a locally finite infinite family of pairwise disjoint singletons in
![]() $[0,1)$
. Set
$[0,1)$
. Set
Let
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
![]() $g\in H({\mathbb {D}})$
, and let
$g\in H({\mathbb {D}})$
, and let
![]() $D\subset \mathbb {D}$
be a closed disk centered at
$D\subset \mathbb {D}$
be a closed disk centered at
![]() $0$
. There exists a function
$0$
. There exists a function
![]() $f\in H({\mathbb {D}})$
such that
$f\in H({\mathbb {D}})$
such that
![]() $\sup _D |f - g| < \varepsilon $
and such that for any
$\sup _D |f - g| < \varepsilon $
and such that for any
![]() $l,n\in {\mathbb {N}}$
and any
$l,n\in {\mathbb {N}}$
and any
![]() $r\in \Gamma (l,n)$
,
$r\in \Gamma (l,n)$
,
![]() $f\circ \phi _r \in V_n(l)$
.
$f\circ \phi _r \in V_n(l)$
.
This statement makes it appear that the sequence
![]() $T^K_{\varrho ,n}: f\in H({\mathbb {D}}) \mapsto f\circ \phi _{r_n} \in {\mathcal {C}}(K)$
is Runge transitive in a very strong sense, for any compact set
$T^K_{\varrho ,n}: f\in H({\mathbb {D}}) \mapsto f\circ \phi _{r_n} \in {\mathcal {C}}(K)$
is Runge transitive in a very strong sense, for any compact set
![]() $K\subset {\mathbb {T}}$
different from
$K\subset {\mathbb {T}}$
different from
![]() ${\mathbb {T}}$
. We refer to [Reference Bonilla and Grosse-Erdmann9, Definition 3.1] for the definition of Runge transitive operators, a definition that can easily be extended to general sequences of operators. Here, if X and Y were Banach spaces, we may say that a sequence
${\mathbb {T}}$
. We refer to [Reference Bonilla and Grosse-Erdmann9, Definition 3.1] for the definition of Runge transitive operators, a definition that can easily be extended to general sequences of operators. Here, if X and Y were Banach spaces, we may say that a sequence
![]() $(T_n)_n:X\to Y$
is Runge transitive “in a very strong sense” if it satisfies the following: given any nonempty open set
$(T_n)_n:X\to Y$
is Runge transitive “in a very strong sense” if it satisfies the following: given any nonempty open set
![]() $U\subset X$
, any nonempty open sets
$U\subset X$
, any nonempty open sets
![]() $V_1,V_2 \subset Y$
, and any finite sets
$V_1,V_2 \subset Y$
, and any finite sets
![]() $E_1\subset {\mathbb {N}}$
and
$E_1\subset {\mathbb {N}}$
and
![]() $E_2\subset {\mathbb {N}}$
with
$E_2\subset {\mathbb {N}}$
with
![]() $E_1\cap E_2=\emptyset $
, there exists
$E_1\cap E_2=\emptyset $
, there exists
![]() $x\in U$
such that for any
$x\in U$
such that for any
![]() $n_1\in E_1$
and any
$n_1\in E_1$
and any
![]() $n_2\in E_2$
,
$n_2\in E_2$
,
In view of the previous remark and [Reference Bonilla and Grosse-Erdmann9, Theorem 3.3], it is natural to expect the existence of frequently Abel universal functions. The rest of this section will confirm this. Let us recall that frequent universality is a generalization of the very important notion of frequent hypercyclicity, introduced by Bayart and Grivaux [Reference Bayart and Grivaux5]. Another important notion in linear dynamics is that of upper frequent universality, introduced by Shkarin [Reference Shkarin41], which also makes sense in the theory of universality. In order to give definitions, let us introduce some terminology. We define the lower density (resp. the upper density) of a subset E of
![]() ${\mathbb {N}}$
, denoted by
${\mathbb {N}}$
, denoted by
![]() $\underline {d}(E)$
(resp.
$\underline {d}(E)$
(resp.
![]() $\overline {d}(E)$
), as the quantity
$\overline {d}(E)$
), as the quantity
where the notation
![]() $|E|$
denotes the cardinality of E. Note that we have
$|E|$
denotes the cardinality of E. Note that we have
![]() $\overline {d}(E):=1-\underline {d}({\mathbb {N}}\setminus E)$
. Then a sequence
$\overline {d}(E):=1-\underline {d}({\mathbb {N}}\setminus E)$
. Then a sequence
![]() $(T_n)_n$
of continuous linear operators from one Fréchet space X to another Fréchet space Y is said to be frequently universal (resp. upper frequently universal) if there exists
$(T_n)_n$
of continuous linear operators from one Fréchet space X to another Fréchet space Y is said to be frequently universal (resp. upper frequently universal) if there exists
![]() $x\in X$
such that for any nonempty open set U of Y, the set
$x\in X$
such that for any nonempty open set U of Y, the set
has positive lower density (resp. positive upper density). Such a vector x is said to be frequently universal (resp. upper frequently universal) for
![]() $(T_n)_n$
.
$(T_n)_n$
.
As recalled in the introduction, many concrete examples of frequently universal sequences of iterates
![]() $(T^n)_n$
of a single continuous operator T from a Fréchet space to itself have been exhibited (we refer the reader to the books [Reference Bayart and Matheron7, Reference Grosse-Erdmann and Peris Manguillot29]). However, rather few (explicit and natural) examples of frequently universal sequences
$(T^n)_n$
of a single continuous operator T from a Fréchet space to itself have been exhibited (we refer the reader to the books [Reference Bayart and Matheron7, Reference Grosse-Erdmann and Peris Manguillot29]). However, rather few (explicit and natural) examples of frequently universal sequences
![]() $(T_n)_n$
, which are not iterates of a single operator, are known (see, e.g., [Reference Charpentier, Ernst, Mestiri and Mouze13]).
$(T_n)_n$
, which are not iterates of a single operator, are known (see, e.g., [Reference Charpentier, Ernst, Mestiri and Mouze13]).
Thus, it is natural to wonder whether Abel universal functions may be (upper) frequently universal. Let us specify what we mean by a (upper) frequently Abel universal functions.
Definition 6.1 Let
![]() $f\in H({\mathbb {D}})$
.
$f\in H({\mathbb {D}})$
.
-
(1) The function f is said to be
 $\varrho $
-frequently Abel universal if it satisfies the following property: for every compact set
$\varrho $
-frequently Abel universal if it satisfies the following property: for every compact set
 $K\subset {\mathbb {T}}$
different from
$K\subset {\mathbb {T}}$
different from
 ${\mathbb {T}}$
and any
${\mathbb {T}}$
and any
 $V\in {\mathcal {V}}(K)$
, the set
$V\in {\mathcal {V}}(K)$
, the set
 $N_{f}(V,K,\varrho )$
has positive lower density.
$N_{f}(V,K,\varrho )$
has positive lower density.We will denote by
 $\mathcal {FU}_A(\mathbb {D},\varrho )$
the set of all
$\mathcal {FU}_A(\mathbb {D},\varrho )$
the set of all
 $\varrho $
-frequently Abel universal functions.
$\varrho $
-frequently Abel universal functions. -
(2) The function f is said to be
 $\varrho $
-upper frequently Abel universal if it satisfies the following property: for every compact set
$\varrho $
-upper frequently Abel universal if it satisfies the following property: for every compact set
 $K\subset {\mathbb {T}}$
different from
$K\subset {\mathbb {T}}$
different from
 ${\mathbb {T}}$
and any
${\mathbb {T}}$
and any
 $V\in {\mathcal {V}}(K)$
, the set
$V\in {\mathcal {V}}(K)$
, the set
 $N_{f}(V,K,\varrho )$
has positive upper density.
$N_{f}(V,K,\varrho )$
has positive upper density.We will denote by
 $\mathcal {FU}^u_A(\mathbb {D},\varrho )$
the set of all
$\mathcal {FU}^u_A(\mathbb {D},\varrho )$
the set of all
 $\varrho $
-upper frequently Abel universal functions.
$\varrho $
-upper frequently Abel universal functions.
The definition of the set
![]() ${\mathcal {U}}_A({\mathbb {D}})$
invites us to propose a variant of the previous definitions. Indeed, there exist notions of lower and upper density for subsets of
${\mathcal {U}}_A({\mathbb {D}})$
invites us to propose a variant of the previous definitions. Indeed, there exist notions of lower and upper density for subsets of
![]() $[0,1)$
. Let
$[0,1)$
. Let
![]() $\Gamma \subset [0,1)$
be a measurable set. We call uniform lower density of
$\Gamma \subset [0,1)$
be a measurable set. We call uniform lower density of
![]() $\Gamma $
the quantity defined by
$\Gamma $
the quantity defined by
where
![]() $|E|$
denotes the Lebesgue measure of a set
$|E|$
denotes the Lebesgue measure of a set
![]() $E\subset [0,1)$
. Similarly, the uniform upper density of
$E\subset [0,1)$
. Similarly, the uniform upper density of
![]() $\Gamma $
is defined by
$\Gamma $
is defined by
![]() $\overline {d_u}(\Gamma )=1-\underline {d_u}([0,1)\setminus \Gamma )$
. It is also easily seen that
$\overline {d_u}(\Gamma )=1-\underline {d_u}([0,1)\setminus \Gamma )$
. It is also easily seen that
This leads us to the following definition.
Definition 6.2 Let
![]() $f\in H({\mathbb {D}})$
.
$f\in H({\mathbb {D}})$
.
-
(1) The function f is said to be frequently Abel universal if it satisfies the following property: for every compact set
 $K\subset {\mathbb {T}}$
different from
$K\subset {\mathbb {T}}$
different from
 ${\mathbb {T}}$
and any
${\mathbb {T}}$
and any
 $V\in {\mathcal {V}}(K)$
, the set
$V\in {\mathcal {V}}(K)$
, the set
 $N_{f}(V,K)$
has positive uniform lower density.
$N_{f}(V,K)$
has positive uniform lower density.We will denote by
 $\mathcal {FU}_A(\mathbb {D})$
the set of all frequently Abel universal functions.
$\mathcal {FU}_A(\mathbb {D})$
the set of all frequently Abel universal functions. -
(2) The function f is said to be upper frequently Abel universal if it satisfies the following property: for every compact set
 $K\subset {\mathbb {T}}$
different from
$K\subset {\mathbb {T}}$
different from
 ${\mathbb {T}}$
and any
${\mathbb {T}}$
and any
 $V\in {\mathcal {V}}(K)$
, the set
$V\in {\mathcal {V}}(K)$
, the set
 $N_{f}(V,K)$
has positive uniform upper density.
$N_{f}(V,K)$
has positive uniform upper density.We will denote by
 $\mathcal {FU}^u_A(\mathbb {D})$
the set of all frequently Abel universal functions.
$\mathcal {FU}^u_A(\mathbb {D})$
the set of all frequently Abel universal functions.
The following lemma gives examples of sets with positive lower or upper densities that are useful for our purpose.
Lemma 6.4
-
(1) There exist pairwise disjoint subsets
 $A(l,n)$
of
$A(l,n)$
of
 ${\mathbb {N}}$
such that
${\mathbb {N}}$
such that
 $\underline {d}(A(l,n))>0$
for any
$\underline {d}(A(l,n))>0$
for any
 $l,n\in {\mathbb {N}}$
.
$l,n\in {\mathbb {N}}$
. -
(2) There exist pairwise disjoint subsets
 $A(l,n)$
of
$A(l,n)$
of
 ${\mathbb {N}}$
such that
${\mathbb {N}}$
such that
 $\overline {d}(A(l,n))=1$
for any
$\overline {d}(A(l,n))=1$
for any
 $l,n\in {\mathbb {N}}$
.
$l,n\in {\mathbb {N}}$
. -
(3) There exist a locally finite family
 $\{\Gamma (l,n,m):\,l,n,m\in {\mathbb {N}}\}$
of pairwise disjoint segments in
$\{\Gamma (l,n,m):\,l,n,m\in {\mathbb {N}}\}$
of pairwise disjoint segments in
 $[0,1)$
such that
$[0,1)$
such that
 $\underline {d_u}(\Gamma (l,n))>0$
for any
$\underline {d_u}(\Gamma (l,n))>0$
for any
 $l,n\in {\mathbb {N}}$
.
$l,n\in {\mathbb {N}}$
. -
(4) There exist a locally finite family
 $\{\Gamma (l,n,m):\,l,n,m\in {\mathbb {N}}\}$
of pairwise disjoint segments in
$\{\Gamma (l,n,m):\,l,n,m\in {\mathbb {N}}\}$
of pairwise disjoint segments in
 $[0,1)$
such that
$[0,1)$
such that
 $\overline {d_u}(\Gamma (l,n))=1$
for any
$\overline {d_u}(\Gamma (l,n))=1$
for any
 $l,n\in {\mathbb {N}}$
.
$l,n\in {\mathbb {N}}$
.
Proof The assertion (1) is contained in [Reference Grosse-Erdmann and Peris Manguillot29, Lemma 9.5]. Let us prove (3). According to [Reference Grosse-Erdmann and Peris Manguillot29, Lemma 9.5], there exist pairwise disjoint subsets
![]() $A(l,n)$
,
$A(l,n)$
,
![]() $l,n\geq 1$
, of
$l,n\geq 1$
, of
![]() ${\mathbb {N}}$
, with positive lower density, such that for any
${\mathbb {N}}$
, with positive lower density, such that for any
![]() $j\in A(l,n)$
and
$j\in A(l,n)$
and
![]() $j'\in A(l',n')$
, one has
$j'\in A(l',n')$
, one has
For any
![]() $l,n\geq 1$
, let us write
$l,n\geq 1$
, let us write
where
![]() $(j_m^{l,n})_m$
is increasing. Now, for
$(j_m^{l,n})_m$
is increasing. Now, for
![]() $l,n,m\geq 1$
, we set
$l,n,m\geq 1$
, we set
 $$ \begin{align*} \Gamma(l,n,m):=\left[1-\frac{1}{j_m^{l,n}}-\frac{1}{3}\left(\frac{1}{j_m^{l,n}-1}-\frac{1}{j_m^{l,n}}\right), 1-\frac{1}{j_m^{l,n}}+\frac{1}{3}\left(\frac{1}{j_m^{l,n}}-\frac{1}{j_m^{l,n}+1}\right) \right] \end{align*} $$
$$ \begin{align*} \Gamma(l,n,m):=\left[1-\frac{1}{j_m^{l,n}}-\frac{1}{3}\left(\frac{1}{j_m^{l,n}-1}-\frac{1}{j_m^{l,n}}\right), 1-\frac{1}{j_m^{l,n}}+\frac{1}{3}\left(\frac{1}{j_m^{l,n}}-\frac{1}{j_m^{l,n}+1}\right) \right] \end{align*} $$
and for
![]() $l,n\geq 1$
,
$l,n\geq 1$
,
Using (6.2), it is not difficult to check that the sets
![]() $\Gamma (l,n)$
,
$\Gamma (l,n)$
,
![]() $l,n\geq 1$
, are pairwise disjoint and that
$l,n\geq 1$
, are pairwise disjoint and that
![]() $r\geq 1-\frac {1}{n-1}$
for any
$r\geq 1-\frac {1}{n-1}$
for any
![]() $r\in \Gamma (l,n)$
. This shows that the family
$r\in \Gamma (l,n)$
. This shows that the family
![]() $\{\Gamma (l,n,m):\,l,n,m\in {\mathbb {N}}\}$
is locally finite. Now, let us fix
$\{\Gamma (l,n,m):\,l,n,m\in {\mathbb {N}}\}$
is locally finite. Now, let us fix
![]() $l,n\geq 1$
and simply denote
$l,n\geq 1$
and simply denote
![]() $j_m^{l,n}=j_m$
,
$j_m^{l,n}=j_m$
,
![]() $m\geq 1$
. An easy calculation leads to
$m\geq 1$
. An easy calculation leads to
Now, taking into account that
![]() $A(l,n)$
has positive lower density, there exist
$A(l,n)$
has positive lower density, there exist
![]() $M>1$
such that
$M>1$
such that
![]() $m\leq j_m\leq Mm$
,
$m\leq j_m\leq Mm$
,
![]() $m\geq 1$
. Therefore, for any integer
$m\geq 1$
. Therefore, for any integer
![]() $N\geq 1$
, we get
$N\geq 1$
, we get
 $$ \begin{align*} N\left|\Gamma(l,n)\cap [1-1/N,1)\right| & \geq \frac{2N}{3}\sum_{\substack{m\geq 1\\j_m\geq N}}\frac{1}{j_m^2-1}\\ &\geq \frac{2N}{3}\sum_{m\geq N}\frac{1}{M^2m^2}\\ &\geq \frac{2N}{3M^2N}=\frac{2}{3M^2}. \end{align*} $$
$$ \begin{align*} N\left|\Gamma(l,n)\cap [1-1/N,1)\right| & \geq \frac{2N}{3}\sum_{\substack{m\geq 1\\j_m\geq N}}\frac{1}{j_m^2-1}\\ &\geq \frac{2N}{3}\sum_{m\geq N}\frac{1}{M^2m^2}\\ &\geq \frac{2N}{3M^2N}=\frac{2}{3M^2}. \end{align*} $$
This finishes the proof of (3).
The proof of (2) is standard and similar to that of (4), so we only check (4). By induction, one can build two increasing sequences
![]() $(N_i)_i$
and
$(N_i)_i$
and
![]() $(M_i)_i$
of positive integers such that
$(M_i)_i$
of positive integers such that
![]() $2^{N_i-M_i}\to 0$
as
$2^{N_i-M_i}\to 0$
as
![]() $i\to \infty $
and such that
$i\to \infty $
and such that
![]() $N_{i+1}>M_i$
,
$N_{i+1}>M_i$
,
![]() $i\in {\mathbb {N}}$
. Then we set
$i\in {\mathbb {N}}$
. Then we set
![]() $\Gamma _i=[1-2^{-N_i},1-2^{-M_i}]$
and fix increasing sequences
$\Gamma _i=[1-2^{-N_i},1-2^{-M_i}]$
and fix increasing sequences
![]() $(u_{m}(l,n))_m$
,
$(u_{m}(l,n))_m$
,
![]() $l,n\in {\mathbb {N}}$
, such that
$l,n\in {\mathbb {N}}$
, such that
![]() $u_m(l,n)\neq u_{m'}(l',n')$
whenever
$u_m(l,n)\neq u_{m'}(l',n')$
whenever
![]() $(m,l,n)\neq (m',l',n')$
. It is now easily checked that the family
$(m,l,n)\neq (m',l',n')$
. It is now easily checked that the family
![]() $\{\Gamma _{u_m(l,n)}:\,l,n,m\in {\mathbb {N}}\}$
is locally finite and that the sets
$\{\Gamma _{u_m(l,n)}:\,l,n,m\in {\mathbb {N}}\}$
is locally finite and that the sets
have upper density equal to
![]() $1$
.
$1$
.
Remark 6.5 We notice that if
![]() $\{\Gamma (l,n,m):\,l,n,m\in {\mathbb {N}}\}$
is a family of pairwise disjoint segments in
$\{\Gamma (l,n,m):\,l,n,m\in {\mathbb {N}}\}$
is a family of pairwise disjoint segments in
![]() $[0,1)$
such that
$[0,1)$
such that
![]() $\underline {d_u}(\Gamma (l,n))>0$
(resp.
$\underline {d_u}(\Gamma (l,n))>0$
(resp.
![]() $\overline {d_u}(\Gamma (l,n))>0$
) for any
$\overline {d_u}(\Gamma (l,n))>0$
) for any
![]() $l,n\in {\mathbb {N}}$
, then every set
$l,n\in {\mathbb {N}}$
, then every set
![]() $\Gamma (l,n)\cap [r,1)$
,
$\Gamma (l,n)\cap [r,1)$
,
![]() $l,n\in {\mathbb {N}}$
,
$l,n\in {\mathbb {N}}$
,
![]() $r\in [0,1)$
, also has positive uniform lower density (resp. uniform upper density; and is of course infinite).
$r\in [0,1)$
, also has positive uniform lower density (resp. uniform upper density; and is of course infinite).
We can immediately deduce from Proposition 6.1 and the previous lemma the existence of functions satisfying Definition 6.1 or 6.2. However, we can also say a bit more. We recall that a subset A of a Fréchet space is first category if it is contained in the complement of a residual set.
Corollary 6.6
-
(1) The sets
 $\mathcal {FU}^u_A(\mathbb {D},\varrho )$
and
$\mathcal {FU}^u_A(\mathbb {D},\varrho )$
and
 $\mathcal {FU}^u_A(\mathbb {D})$
are residual in
$\mathcal {FU}^u_A(\mathbb {D})$
are residual in
 $H({\mathbb {D}})$
.
$H({\mathbb {D}})$
. -
(2) The sets
 $\mathcal {FU}_A(\mathbb {D},\varrho )$
and
$\mathcal {FU}_A(\mathbb {D},\varrho )$
and
 $\mathcal {FU}_A(\mathbb {D})$
are dense and first category in
$\mathcal {FU}_A(\mathbb {D})$
are dense and first category in
 $H({\mathbb {D}})$
.
$H({\mathbb {D}})$
.
Proof Setting
![]() $\Gamma (l,n,m)=\{r_{j_m}\}$
,
$\Gamma (l,n,m)=\{r_{j_m}\}$
,
![]() $l,n,m\in \mathbb {N}$
, where
$l,n,m\in \mathbb {N}$
, where
![]() $(j_m)_m$
is the increasing sequence of elements of the set
$(j_m)_m$
is the increasing sequence of elements of the set
![]() $A(l,n)$
given by point (2) of Lemma 6.4, and applying Proposition 6.1, we get that the set
$A(l,n)$
given by point (2) of Lemma 6.4, and applying Proposition 6.1, we get that the set
![]() $\mathcal {FU}^{u=1}_A(\mathbb {D},\varrho )$
consisting of those
$\mathcal {FU}^{u=1}_A(\mathbb {D},\varrho )$
consisting of those
![]() $f\in H({\mathbb {D}})$
such that
$f\in H({\mathbb {D}})$
such that
![]() $\overline {d}(N_f(V,K,\varrho ))=1$
for any compact set
$\overline {d}(N_f(V,K,\varrho ))=1$
for any compact set
![]() $K\subset {\mathbb {T}}$
different from
$K\subset {\mathbb {T}}$
different from
![]() ${\mathbb {T}}$
and any
${\mathbb {T}}$
and any
![]() $V\in {\mathcal {V}}(K)$
, is dense in
$V\in {\mathcal {V}}(K)$
, is dense in
![]() $H({\mathbb {D}})$
. Similarly, if the sets
$H({\mathbb {D}})$
. Similarly, if the sets
![]() $\Gamma (l,n,m)$
,
$\Gamma (l,n,m)$
,
![]() $l,n,m\in {\mathbb {N}}$
, are instead given by point (4), then Proposition 6.1 gives us that the set
$l,n,m\in {\mathbb {N}}$
, are instead given by point (4), then Proposition 6.1 gives us that the set
![]() $\mathcal {FU}^{u=1}_A(\mathbb {D})$
consisting of those
$\mathcal {FU}^{u=1}_A(\mathbb {D})$
consisting of those
![]() $f\in H({\mathbb {D}})$
such that
$f\in H({\mathbb {D}})$
such that
![]() $\overline {d_u}(N_f(V,K))=1$
for any compact set
$\overline {d_u}(N_f(V,K))=1$
for any compact set
![]() $K\subset {\mathbb {T}}$
different from
$K\subset {\mathbb {T}}$
different from
![]() ${\mathbb {T}}$
and any
${\mathbb {T}}$
and any
![]() $V\in {\mathcal {V}}(K)$
, is dense in
$V\in {\mathcal {V}}(K)$
, is dense in
![]() $H({\mathbb {D}})$
.
$H({\mathbb {D}})$
.
Moreover, in the same way, Proposition 6.1 and points (1) and (3) of Lemma 6.4 immediately tell us that the sets
![]() $\mathcal {FU}_A(\mathbb {D},\varrho )$
and
$\mathcal {FU}_A(\mathbb {D},\varrho )$
and
![]() $\mathcal {FU}_A(\mathbb {D})$
are dense in
$\mathcal {FU}_A(\mathbb {D})$
are dense in
![]() $H({\mathbb {D}})$
. Since
$H({\mathbb {D}})$
. Since
![]() $\underline {d}(E)=1-\overline {d}({\mathbb {N}}\setminus E)$
,
$\underline {d}(E)=1-\overline {d}({\mathbb {N}}\setminus E)$
,
![]() $E\in {\mathbb {N}}$
(resp.
$E\in {\mathbb {N}}$
(resp.
![]() $\underline {d_u}(\Gamma )=1-\overline {d_u}([0,1)\setminus \Gamma )$
,
$\underline {d_u}(\Gamma )=1-\overline {d_u}([0,1)\setminus \Gamma )$
,
![]() $\Gamma \subset [0,1)$
), the corollary is proved once we have shown that the sets
$\Gamma \subset [0,1)$
), the corollary is proved once we have shown that the sets
![]() $\mathcal {FU}^{u=1}_A(\mathbb {D},\varrho )$
and
$\mathcal {FU}^{u=1}_A(\mathbb {D},\varrho )$
and
![]() $\mathcal {FU}^{u=1}_A(\mathbb {D})$
are
$\mathcal {FU}^{u=1}_A(\mathbb {D})$
are
![]() $G_{\delta }$
in
$G_{\delta }$
in
![]() $H({\mathbb {D}})$
. The proof for both sets being very similar, we only deal with
$H({\mathbb {D}})$
. The proof for both sets being very similar, we only deal with
![]() $\mathcal {FU}^{u=1}_A(\mathbb {D})$
.
$\mathcal {FU}^{u=1}_A(\mathbb {D})$
.
To do so, note that
 $$ \begin{align*} \begin{array}{l}\displaystyle\mathcal{F{\kern1pt}U}^{u=1}_A(\mathbb{D})=\\ \displaystyle\bigcap_{l\in {\mathbb{N}}}\bigcap_{n\in {\mathbb{N}}}\bigcap_{m\geq 1}\bigcap_{k\geq 1}\bigcup_{N\geq k}\left\{f\in H({\mathbb{D}}):\,\left|N_f(V_n(l),K_l)\cap [1-1/N,1)]\right|> \left(1-\frac{1}{m}\right)N\right\}\!.\end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{l}\displaystyle\mathcal{F{\kern1pt}U}^{u=1}_A(\mathbb{D})=\\ \displaystyle\bigcap_{l\in {\mathbb{N}}}\bigcap_{n\in {\mathbb{N}}}\bigcap_{m\geq 1}\bigcap_{k\geq 1}\bigcup_{N\geq k}\left\{f\in H({\mathbb{D}}):\,\left|N_f(V_n(l),K_l)\cap [1-1/N,1)]\right|> \left(1-\frac{1}{m}\right)N\right\}\!.\end{array} \end{align*} $$
Since each set
![]() $\left \{f\in H({\mathbb {D}}):\,\left |N_f(V_n(l),K_l)\cap [1-1/N,1)]\right |> \left (1-\frac {1}{m}\right )N\right \}$
is easily seen to be open, the proof is complete.
$\left \{f\in H({\mathbb {D}}):\,\left |N_f(V_n(l),K_l)\cap [1-1/N,1)]\right |> \left (1-\frac {1}{m}\right )N\right \}$
is easily seen to be open, the proof is complete.
Remark 6.7 The previous proof shows that the sets
![]() $\mathcal {FU}^{u=1}_A(\mathbb {D},\varrho )$
and
$\mathcal {FU}^{u=1}_A(\mathbb {D},\varrho )$
and
![]() $\mathcal {FU}^{u=1}_A(\mathbb {D})$
are
$\mathcal {FU}^{u=1}_A(\mathbb {D})$
are
![]() $G_{\delta }$
subsets of
$G_{\delta }$
subsets of
![]() $H({\mathbb {D}})$
, a conclusion which is stronger than that stated in point (1) of Corollary 6.6. We mention that it was shown in [Reference Mouze and Munnier38] that all universal Taylor series are upper frequently universal, with upper densities of the relevant sets equal to
$H({\mathbb {D}})$
, a conclusion which is stronger than that stated in point (1) of Corollary 6.6. We mention that it was shown in [Reference Mouze and Munnier38] that all universal Taylor series are upper frequently universal, with upper densities of the relevant sets equal to
![]() $1$
.
$1$
.
Since
![]() $\mathcal {FU}^{u=1}_A(\mathbb {D},\varrho )$
and
$\mathcal {FU}^{u=1}_A(\mathbb {D},\varrho )$
and
![]() $\mathcal {FU}^{u=1}_A(\mathbb {D})$
are residual in
$\mathcal {FU}^{u=1}_A(\mathbb {D})$
are residual in
![]() $H({\mathbb {D}})$
(see the proof of Corollary 6.6 for the definition of these sets), it is not difficult to check that
$H({\mathbb {D}})$
(see the proof of Corollary 6.6 for the definition of these sets), it is not difficult to check that
 $$ \begin{align*} H({\mathbb{D}}) & = \mathcal{F{\kern1pt}U}^{u=1}_A(\mathbb{D},\varrho) + \mathcal{F{\kern1pt}U}^{u=1}_A(\mathbb{D},\varrho)\\ & = \mathcal{F{\kern1pt}U}^u_A(\mathbb{D}) + \mathcal{F{\kern1pt}U}^u_A(\mathbb{D}). \end{align*} $$
$$ \begin{align*} H({\mathbb{D}}) & = \mathcal{F{\kern1pt}U}^{u=1}_A(\mathbb{D},\varrho) + \mathcal{F{\kern1pt}U}^{u=1}_A(\mathbb{D},\varrho)\\ & = \mathcal{F{\kern1pt}U}^u_A(\mathbb{D}) + \mathcal{F{\kern1pt}U}^u_A(\mathbb{D}). \end{align*} $$
In fact, it is also true that any function in
![]() $H({\mathbb {D}})$
can be written as the sum of two functions in
$H({\mathbb {D}})$
can be written as the sum of two functions in
![]() $\mathcal {FU}_A(\mathbb {D})$
or in
$\mathcal {FU}_A(\mathbb {D})$
or in
![]() $\mathcal {FU}_A(\mathbb {D},\varrho )$
, even if the latter sets are first category. This is contained in the next proposition.
$\mathcal {FU}_A(\mathbb {D},\varrho )$
, even if the latter sets are first category. This is contained in the next proposition.
Proposition 6.8 We have
 $$ \begin{align*} H({\mathbb{D}}) & = \mathcal{F{\kern1pt}U}_A(\mathbb{D},\varrho) + \mathcal{F{\kern1pt}U}_A(\mathbb{D},\varrho)\\ & = \mathcal{F{\kern1pt}U}_A(\mathbb{D}) + \mathcal{F{\kern1pt}U}_A(\mathbb{D}). \end{align*} $$
$$ \begin{align*} H({\mathbb{D}}) & = \mathcal{F{\kern1pt}U}_A(\mathbb{D},\varrho) + \mathcal{F{\kern1pt}U}_A(\mathbb{D},\varrho)\\ & = \mathcal{F{\kern1pt}U}_A(\mathbb{D}) + \mathcal{F{\kern1pt}U}_A(\mathbb{D}). \end{align*} $$
Proof The proofs of the two equalities being analogous to that of [Reference Bonilla and Grosse-Erdmann9, Theorem 5.9], we only sketch the proof of the first equality. Let h be in
![]() $H(\mathbb {D})$
, and let
$H(\mathbb {D})$
, and let
![]() $A(l,n)$
,
$A(l,n)$
,
![]() $l,n\in {\mathbb {N}}$
, be given by point (1) of Lemma 6.4. We split each
$l,n\in {\mathbb {N}}$
, be given by point (1) of Lemma 6.4. We split each
![]() $A(l,n)$
into two disjoint sets
$A(l,n)$
into two disjoint sets
![]() $A^1(l,n),A^2(l,n)$
with positive lower density. Proceeding as in the proof of Theorem 6.1, we build
$A^1(l,n),A^2(l,n)$
with positive lower density. Proceeding as in the proof of Theorem 6.1, we build
![]() $f\in H({\mathbb {D}})$
such that for any
$f\in H({\mathbb {D}})$
such that for any
![]() $k\in A^1(l,n)$
,
$k\in A^1(l,n)$
,
![]() $f\circ \phi _{r_k}\in V_n(l)$
and for any
$f\circ \phi _{r_k}\in V_n(l)$
and for any
![]() $k\in A^2(l,n)$
,
$k\in A^2(l,n)$
,
![]() $f\circ \phi _{r_k} \in h\circ \phi ^{-1}_{r_k}- V_n(l)$
, where
$f\circ \phi _{r_k} \in h\circ \phi ^{-1}_{r_k}- V_n(l)$
, where
![]() $h\circ \phi ^{-1}_{r_k}- V_n(l):=\{h\circ \phi ^{-1}_{r_k} - g:\,g\in V_n(l)\}$
. Then f and
$h\circ \phi ^{-1}_{r_k}- V_n(l):=\{h\circ \phi ^{-1}_{r_k} - g:\,g\in V_n(l)\}$
. Then f and
![]() $h-f$
belong to
$h-f$
belong to
![]() $\mathcal {FU}_A(\mathbb {D},\varrho )$
and we obviously have
$\mathcal {FU}_A(\mathbb {D},\varrho )$
and we obviously have
![]() $h=f+(h-f)$
.
$h=f+(h-f)$
.
We shall now continue our illustration of how flexible the notion of Abel universal functions is. It is usually difficult to prove results of common frequent universality (see [Reference Bayart4, Reference Charpentier, Ernst, Mestiri and Mouze13]). In the next two results, we are interested in common (frequent)
![]() $\varrho (\lambda )$
-Abel universality with respect to general sequences
$\varrho (\lambda )$
-Abel universality with respect to general sequences
![]() $(\rho (\lambda ))_{\lambda \in \Lambda }$
,
$(\rho (\lambda ))_{\lambda \in \Lambda }$
,
![]() $\Lambda \subset {\mathbb {R}}$
. First, we state a result for common universality inspired by [Reference Grosse-Erdmann and Peris Manguillot29, Theorem 11.5]. We shall say that a set is
$\Lambda \subset {\mathbb {R}}$
. First, we state a result for common universality inspired by [Reference Grosse-Erdmann and Peris Manguillot29, Theorem 11.5]. We shall say that a set is
![]() $\sigma $
-compact if it is a countable union of compact sets.
$\sigma $
-compact if it is a countable union of compact sets.
Proposition 6.9 Let
![]() $\Lambda \subset \mathbb {R}$
be a
$\Lambda \subset \mathbb {R}$
be a
![]() $\sigma $
-compact set, and let
$\sigma $
-compact set, and let
![]() $(\rho (\lambda ))_{\lambda \in \Lambda }$
be a family of increasing sequences
$(\rho (\lambda ))_{\lambda \in \Lambda }$
be a family of increasing sequences
![]() $(r_n(\lambda ))_n$
. We assume that
$(r_n(\lambda ))_n$
. We assume that
![]() $r_n(\lambda ) \to 1$
for any
$r_n(\lambda ) \to 1$
for any
![]() $\lambda \in \Lambda $
and that the map
$\lambda \in \Lambda $
and that the map
![]() $\lambda \mapsto r_n(\lambda )$
is continuous on
$\lambda \mapsto r_n(\lambda )$
is continuous on
![]() $\Lambda $
for any
$\Lambda $
for any
![]() $n\in {\mathbb {N}}$
. Then
$n\in {\mathbb {N}}$
. Then
Proof Let
![]() $(I_m)_m$
be a sequence of compact sets whose union is
$(I_m)_m$
be a sequence of compact sets whose union is
![]() $\Lambda $
. Clearly, we have
$\Lambda $
. Clearly, we have
where
 $$ \begin{align*} E(j,l,m,s)= \left\{f\in H(\mathbb{D}):\,\forall\lambda\in I_m,\, \exists n\geq 0,\, \sup_{\zeta\in K_l}\vert f(r_{n}(\lambda)\zeta)-\varphi_j(\zeta)\vert<1/s\right\}\!. \end{align*} $$
$$ \begin{align*} E(j,l,m,s)= \left\{f\in H(\mathbb{D}):\,\forall\lambda\in I_m,\, \exists n\geq 0,\, \sup_{\zeta\in K_l}\vert f(r_{n}(\lambda)\zeta)-\varphi_j(\zeta)\vert<1/s\right\}\!. \end{align*} $$
By compactness of
![]() $I_m$
and continuity of
$I_m$
and continuity of
![]() $\lambda \mapsto r_n(\lambda )$
on
$\lambda \mapsto r_n(\lambda )$
on
![]() $\Lambda $
,
$\Lambda $
,
![]() $n\in {\mathbb {N}}$
, each set
$n\in {\mathbb {N}}$
, each set
![]() $E(j,l,m,s)$
,
$E(j,l,m,s)$
,
![]() $j,l,m,s\geq 1$
, is open. By the Baire Category Theorem, it is enough to prove that
$j,l,m,s\geq 1$
, is open. By the Baire Category Theorem, it is enough to prove that
![]() $E(j,l,m,s)$
is dense in
$E(j,l,m,s)$
is dense in
![]() $H(\mathbb {D})$
for any
$H(\mathbb {D})$
for any
![]() $j,l,m,s\geq 1$
. Let us then fix
$j,l,m,s\geq 1$
. Let us then fix
![]() $j,l,m,s\geq 1$
and
$j,l,m,s\geq 1$
and
![]() $g\in H(\mathbb {D})$
,
$g\in H(\mathbb {D})$
,
![]() $0<r<1$
and
$0<r<1$
and
![]() $\varepsilon>0$
. Let us set
$\varepsilon>0$
. Let us set
![]() $r<\tilde {r}<1$
. Now, observe that the assumptions and Dini’s theorem imply that
$r<\tilde {r}<1$
. Now, observe that the assumptions and Dini’s theorem imply that
![]() $(r_n(\cdot ))_n$
tends to
$(r_n(\cdot ))_n$
tends to
![]() $1$
uniformly on each compact set
$1$
uniformly on each compact set
![]() $I_m$
. Therefore, there exists
$I_m$
. Therefore, there exists
![]() $c_{n,I_m}>0$
with
$c_{n,I_m}>0$
with
![]() $c_{n,I_m}\rightarrow 0$
as
$c_{n,I_m}\rightarrow 0$
as
![]() $n\rightarrow +\infty $
so that
$n\rightarrow +\infty $
so that
![]() $\vert r_n(\lambda )-1\vert \leq c_{n,I_m}$
for any
$\vert r_n(\lambda )-1\vert \leq c_{n,I_m}$
for any
![]() $\lambda \in I_m$
, whence one can find
$\lambda \in I_m$
, whence one can find
![]() $N_1\geq 1$
such that
$N_1\geq 1$
such that
By Mergelyan’s theorem, there exists a polynomial f such that
We get, for any
![]() $\lambda \in I_m$
and any
$\lambda \in I_m$
and any
![]() $n\geq N_1$
,
$n\geq N_1$
,
 $$ \begin{align*} \displaystyle\sup_{\zeta\in K_l}\vert f(r_{n}(\lambda)\zeta)-\varphi_j(\zeta)\vert&\leq \displaystyle \sup_{\zeta\in K_l}\vert f(r_{n}(\lambda)\zeta)-\varphi_j(r_{n}(\lambda)\zeta)\vert+\sup_{\zeta\in K_l}\vert \varphi_j(r_{n}(\lambda)\zeta)-\varphi_j(\zeta)\vert\\&\leq\displaystyle \frac{1}{2s}+\sup_{\zeta\in K_l}\vert \varphi_j(r_{n}(\lambda)\zeta)-\varphi_j(\zeta)\vert. \end{align*} $$
$$ \begin{align*} \displaystyle\sup_{\zeta\in K_l}\vert f(r_{n}(\lambda)\zeta)-\varphi_j(\zeta)\vert&\leq \displaystyle \sup_{\zeta\in K_l}\vert f(r_{n}(\lambda)\zeta)-\varphi_j(r_{n}(\lambda)\zeta)\vert+\sup_{\zeta\in K_l}\vert \varphi_j(r_{n}(\lambda)\zeta)-\varphi_j(\zeta)\vert\\&\leq\displaystyle \frac{1}{2s}+\sup_{\zeta\in K_l}\vert \varphi_j(r_{n}(\lambda)\zeta)-\varphi_j(\zeta)\vert. \end{align*} $$
Using again the property
![]() $\vert r_n(\lambda )-1\vert \leq c_{n,I_m}$
with
$\vert r_n(\lambda )-1\vert \leq c_{n,I_m}$
with
![]() $c_{n,I_m}\rightarrow 0$
, one can find
$c_{n,I_m}\rightarrow 0$
, one can find
![]() $N_2\geq N_1$
such that for all
$N_2\geq N_1$
such that for all
![]() $\lambda \in I_m$
and
$\lambda \in I_m$
and
![]() $n\geq N_2$
,
$n\geq N_2$
,
![]() $\sup _{\zeta \in K_l}\vert \varphi _j(r_{n}(\lambda )\zeta )-\varphi _j(\zeta )\vert <1/2s.$
This completes the proof.
$\sup _{\zeta \in K_l}\vert \varphi _j(r_{n}(\lambda )\zeta )-\varphi _j(\zeta )\vert <1/2s.$
This completes the proof.
We saw that Proposition 6.1 allows to exhibit
![]() $\varrho $
-frequently Abel universal functions for any sequence
$\varrho $
-frequently Abel universal functions for any sequence
![]() $\varrho =(r_n)_n$
(with
$\varrho =(r_n)_n$
(with
![]() $r_n\to 1$
as
$r_n\to 1$
as
![]() $n\to \infty $
). Actually, it can similarly allow us to prove the existence of functions
$n\to \infty $
). Actually, it can similarly allow us to prove the existence of functions
![]() $f\in H({\mathbb {D}})$
that are
$f\in H({\mathbb {D}})$
that are
![]() $\varrho (l)$
-frequently Abel universal simultaneously for countably many sequences
$\varrho (l)$
-frequently Abel universal simultaneously for countably many sequences
![]() $\varrho (l)$
,
$\varrho (l)$
,
![]() $l\in {\mathbb {N}}$
, up to some assumptions. This is the content of the next proposition, whose proof is left to the reader.
$l\in {\mathbb {N}}$
, up to some assumptions. This is the content of the next proposition, whose proof is left to the reader.
Proposition 6.10 For
![]() $l\in {\mathbb {N}}$
, let
$l\in {\mathbb {N}}$
, let
![]() $\varrho (l)=(r_n^l)_n$
be increasing sequences in
$\varrho (l)=(r_n^l)_n$
be increasing sequences in
![]() $(0,1)$
such that
$(0,1)$
such that
![]() $r_n^l\to 1$
as
$r_n^l\to 1$
as
![]() $n\to \infty $
. We assume that for any
$n\to \infty $
. We assume that for any
![]() $l\neq l'$
,
$l\neq l'$
,
![]() $\{r_n^l:\,n\in {\mathbb {N}}\}\cap \{r_n^{l'}:\,n\in {\mathbb {N}}\}=\emptyset $
. Then
$\{r_n^l:\,n\in {\mathbb {N}}\}\cap \{r_n^{l'}:\,n\in {\mathbb {N}}\}=\emptyset $
. Then
So far, we know no general result of common
![]() $\varrho (\lambda )$
-frequent Abel universality, where
$\varrho (\lambda )$
-frequent Abel universality, where
![]() $\lambda $
belongs to some uncountable families of sequences. This seems to us to be an interesting problem.
$\lambda $
belongs to some uncountable families of sequences. This seems to us to be an interesting problem.
We shall end the paper by pointing out, however, that frequently Abel universal functions are easily seen to be automatically frequently universal for some uncountable families of composition operators. This result will come from a more general statement for universal families. More precisely, let us consider
![]() $T_r:X\rightarrow Y$
,
$T_r:X\rightarrow Y$
,
![]() $r\in [0,1)$
, be continuous mappings between topological spaces X and Y. For
$r\in [0,1)$
, be continuous mappings between topological spaces X and Y. For
![]() $x\in X$
and a nonempty open set
$x\in X$
and a nonempty open set
![]() $V\subset Y$
, define
$V\subset Y$
, define
Then we will say that
![]() $x\in X$
is universal for
$x\in X$
is universal for
![]() $(T_r)$
if, for any nonempty open set
$(T_r)$
if, for any nonempty open set
![]() $V\subset Y$
and any
$V\subset Y$
and any
![]() $n\geq 1$
,
$n\geq 1$
,
Moreover, we will say that
![]() $x\in X$
is frequently universal (resp. upper frequently universal) for
$x\in X$
is frequently universal (resp. upper frequently universal) for
![]() $(T_r)$
if, for any nonempty open set
$(T_r)$
if, for any nonempty open set
![]() $V\subset Y$
,
$V\subset Y$
,
The following result holds.
Proposition 6.11 Let
![]() $h:[0,1)\rightarrow \mathbb [0,1)$
be any increasing continuous function with
$h:[0,1)\rightarrow \mathbb [0,1)$
be any increasing continuous function with
![]() $h(r)\rightarrow 1$
as
$h(r)\rightarrow 1$
as
![]() $r\rightarrow 1$
.
$r\rightarrow 1$
.
-
(1) A vector x in X is universal for
 $(T_r)_r$
if and only if it is universal for
$(T_r)_r$
if and only if it is universal for
 $(T_{h(r)})_r$
.
$(T_{h(r)})_r$
. -
(2) If we assume in addition that h is differentiable and
 $c\leq \liminf \limits _{r\rightarrow 1} h'(r)\leq \limsup \limits _{r\rightarrow 1} h'(r) \leq C$
for some
$c\leq \liminf \limits _{r\rightarrow 1} h'(r)\leq \limsup \limits _{r\rightarrow 1} h'(r) \leq C$
for some
 $C\geq c>0$
, then a vector x in X is frequently universal (resp. upper frequently universal) for
$C\geq c>0$
, then a vector x in X is frequently universal (resp. upper frequently universal) for
 $(T_r)_r$
if and only if it is frequently universal (resp. upper frequently universal) for
$(T_r)_r$
if and only if it is frequently universal (resp. upper frequently universal) for
 $(T_{h(r)})_r$
.
$(T_{h(r)})_r$
.
Proof By assumptions, it is sufficient in both cases to deal with only one implication.
For any nonempty open set
![]() $V\subset Y$
, we set
$V\subset Y$
, we set
![]() $N_x^0((T_r)_r,V):=N_x((T_r)_r,V)\cap (h(0),1)$
. We note that
$N_x^0((T_r)_r,V):=N_x((T_r)_r,V)\cap (h(0),1)$
. We note that
and that
![]() $N_x^0((T_r)_r,V)$
is infinite whenever
$N_x^0((T_r)_r,V)$
is infinite whenever
![]() $N_x((T_r)_r,V)$
is infinite. This proves that if x is universal for
$N_x((T_r)_r,V)$
is infinite. This proves that if x is universal for
![]() $(T_r)_r$
, then it is also universal for
$(T_r)_r$
, then it is also universal for
![]() $(T_{h(r)})_r$
. Observe also that if
$(T_{h(r)})_r$
. Observe also that if
![]() $N_x((T_r)_r,V)$
has positive lower (resp. upper) density, so has
$N_x((T_r)_r,V)$
has positive lower (resp. upper) density, so has
![]() $N_x^0((T_r)_r,V)$
. To finish the proof, it is thus enough to check that if
$N_x^0((T_r)_r,V)$
. To finish the proof, it is thus enough to check that if
![]() $N_x^0((T_r)_r,V)$
has positive lower (resp. upper) density, then
$N_x^0((T_r)_r,V)$
has positive lower (resp. upper) density, then
![]() $h^{-1}\left (N_x^0((T_r)_r,V)\right )$
also has positive lower (resp. upper) density. This may be a consequence of a known general result about densities, but we have not found it in the literature. So let us give the details. This is essentially a change of variable. Indeed, by assumption, there exist two positive constants
$h^{-1}\left (N_x^0((T_r)_r,V)\right )$
also has positive lower (resp. upper) density. This may be a consequence of a known general result about densities, but we have not found it in the literature. So let us give the details. This is essentially a change of variable. Indeed, by assumption, there exist two positive constants
![]() $0<c\leq C$
such that
$0<c\leq C$
such that
![]() $c\leq h'(r) \leq C$
for any
$c\leq h'(r) \leq C$
for any
![]() $r\in (0,1)$
large enough. Then the change of variable formula gives for any such r,
$r\in (0,1)$
large enough. Then the change of variable formula gives for any such r,
Choosing
![]() $r=1-1/N$
(resp.
$r=1-1/N$
(resp.
![]() $r=r_N=h^{-1}(1-1/N)$
), we get from (6.3) and N large enough,
$r=r_N=h^{-1}(1-1/N)$
), we get from (6.3) and N large enough,
(resp.
If we set
![]() $t_N:=(1-h(1-1/N))^{-1}$
, from (6.4), we obtain
$t_N:=(1-h(1-1/N))^{-1}$
, from (6.4), we obtain
 $$ \begin{align*} &N\left|h^{-1}\left(N_x^0((T_r)_r,V)\right)\cap \left(1-\displaystyle\frac{1}{N},1\right)\right| \geq \frac{N}{C}\left|N_x^0((T_r)_r,V)\cap \displaystyle\left(1-\frac{1}{\lfloor t_N \rfloor+1},1\right)\right|\\ &\quad= \displaystyle\frac{N}{C(\lfloor t_N \rfloor+1)}\displaystyle \left(\lfloor t_N \rfloor+1\right)\left|N_x^0((T_r)_r,V)\cap \left(1-\frac{1}{\lfloor t_N \rfloor+1},1\right)\right|. \end{align*} $$
$$ \begin{align*} &N\left|h^{-1}\left(N_x^0((T_r)_r,V)\right)\cap \left(1-\displaystyle\frac{1}{N},1\right)\right| \geq \frac{N}{C}\left|N_x^0((T_r)_r,V)\cap \displaystyle\left(1-\frac{1}{\lfloor t_N \rfloor+1},1\right)\right|\\ &\quad= \displaystyle\frac{N}{C(\lfloor t_N \rfloor+1)}\displaystyle \left(\lfloor t_N \rfloor+1\right)\left|N_x^0((T_r)_r,V)\cap \left(1-\frac{1}{\lfloor t_N \rfloor+1},1\right)\right|. \end{align*} $$
Since by assumptions
![]() $\liminf \limits _{N\to \infty }\frac {N}{\lfloor t_N \rfloor +1}\geq c>0$
, we deduce that
$\liminf \limits _{N\to \infty }\frac {N}{\lfloor t_N \rfloor +1}\geq c>0$
, we deduce that
and hence that x is frequently universal for
![]() $(T_{h(r)})_r$
whenever x is frequently universal for
$(T_{h(r)})_r$
whenever x is frequently universal for
![]() $(T_r)_r$
.
$(T_r)_r$
.
Similarly, from (6.5) (with
![]() $r_N=h^{-1}(1-1/N)$
), we obtain, if we set this time
$r_N=h^{-1}(1-1/N)$
), we obtain, if we set this time
![]() $t_N:=(1-r_N)^{-1}$
,
$t_N:=(1-r_N)^{-1}$
,
Since
![]() $\limsup \limits _{N\to \infty }\frac {\lfloor t_N \rfloor +1}{N}\geq c>0$
, we deduce that
$\limsup \limits _{N\to \infty }\frac {\lfloor t_N \rfloor +1}{N}\geq c>0$
, we deduce that
and hence that x is upper frequently universal for
![]() $(T_{h(r)})_r$
whenever x is upper frequently universal for
$(T_{h(r)})_r$
whenever x is upper frequently universal for
![]() $(T_r)_r$
.
$(T_r)_r$
.
Applying this proposition in the context of Abel universal series, we obtain the following corollary. Let us say that a function f in
![]() $H({\mathbb {D}})$
is universal (resp. frequently universal, resp. upper frequently universal) for the family
$H({\mathbb {D}})$
is universal (resp. frequently universal, resp. upper frequently universal) for the family
![]() $\{\phi _{h(r)}:\,r\in [0,1)\}$
, if for every compact set
$\{\phi _{h(r)}:\,r\in [0,1)\}$
, if for every compact set
![]() $K\subset {\mathbb {T}}$
different from
$K\subset {\mathbb {T}}$
different from
![]() ${\mathbb {T}}$
, and any
${\mathbb {T}}$
, and any
![]() $V\in {\mathcal {V}}(K)$
, the set
$V\in {\mathcal {V}}(K)$
, the set
![]() $N_f(V,K):=\{r\in [0,1):\,f\circ \phi _{h(r)}\in V\}$
is nonempty (resp. has positive uniform lower density, resp. has positive uniform upper density).
$N_f(V,K):=\{r\in [0,1):\,f\circ \phi _{h(r)}\in V\}$
is nonempty (resp. has positive uniform lower density, resp. has positive uniform upper density).
Corollary 6.12 For every h satisfying the assumptions of Proposition 6.11, a function f is in
![]() ${\mathcal {U}}_A({\mathbb {D}})$
(resp. any f in
${\mathcal {U}}_A({\mathbb {D}})$
(resp. any f in
![]() $\mathcal {FU}_A({\mathbb {D}})$
, resp. any f in
$\mathcal {FU}_A({\mathbb {D}})$
, resp. any f in
![]() $\mathcal {FU}^u_A({\mathbb {D}})$
) if and only if f is simultaneously universal (resp. frequently universal, resp. upper frequently universal) for
$\mathcal {FU}^u_A({\mathbb {D}})$
) if and only if f is simultaneously universal (resp. frequently universal, resp. upper frequently universal) for
![]() $\{\phi _{h(r)}:\,0<r<1\}$
.
$\{\phi _{h(r)}:\,0<r<1\}$
.
Acknowledgment
We would like to thank the anonymous referee for her/his useful suggestions and comments that greatly improved the quality of the manuscript.