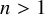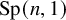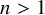1 Introduction
1.1 The problem
The purpose of this article is to determine the lattices in the Lie group
![]() $G = \operatorname {\mathrm {PSp}}(n,1)$
of minimal covolume for any integer
$G = \operatorname {\mathrm {PSp}}(n,1)$
of minimal covolume for any integer
![]() $n> 1$
. For other rank one real simple Lie groups (namely
$n> 1$
. For other rank one real simple Lie groups (namely
![]() $G = \operatorname {\mathrm {PO}}(n,1)$
, and
$G = \operatorname {\mathrm {PO}}(n,1)$
, and
![]() $G = \operatorname {\mathrm {PU}}(n,1)$
), this problem has been addressed in several different papers (see, for instance, [Reference Gehring and Martin12, Reference Hild14, Reference Belolipetsky and Emery3, Reference Emery and Stover11]). The result in the case
$G = \operatorname {\mathrm {PU}}(n,1)$
), this problem has been addressed in several different papers (see, for instance, [Reference Gehring and Martin12, Reference Hild14, Reference Belolipetsky and Emery3, Reference Emery and Stover11]). The result in the case
![]() $G=\operatorname {\mathrm {PGL}}_2(\mathbb R)$
is a classical theorem of Siegel [Reference Siegel34]. Many of the results mentioned above are restricted to the class of arithmetic lattices: This allows the use of Prasad’s volume formula [Reference Prasad28] along with techniques from Borel–Prasad [Reference Borel and Prasad4] as the main ingredient in the proof, and we shall adopt the same strategy in this paper. A significant advantage when treating the case
$G=\operatorname {\mathrm {PGL}}_2(\mathbb R)$
is a classical theorem of Siegel [Reference Siegel34]. Many of the results mentioned above are restricted to the class of arithmetic lattices: This allows the use of Prasad’s volume formula [Reference Prasad28] along with techniques from Borel–Prasad [Reference Borel and Prasad4] as the main ingredient in the proof, and we shall adopt the same strategy in this paper. A significant advantage when treating the case
![]() $G= \operatorname {\mathrm {PSp}}(n,1)$
is that all lattices are arithmetic (since superrigidity holds) so that the results obtained below solve the problem in this Lie group.
$G= \operatorname {\mathrm {PSp}}(n,1)$
is that all lattices are arithmetic (since superrigidity holds) so that the results obtained below solve the problem in this Lie group.
It will be more convenient to work with lattices in the group
![]() $\operatorname {\mathrm {Sp}}(n,1)$
, which is a double cover of
$\operatorname {\mathrm {Sp}}(n,1)$
, which is a double cover of
![]() $\operatorname {\mathrm {PSp}}(n,1) = \operatorname {\mathrm {Sp}}(n,1)/\left \{ \pm I \right \}$
. Let
$\operatorname {\mathrm {PSp}}(n,1) = \operatorname {\mathrm {Sp}}(n,1)/\left \{ \pm I \right \}$
. Let
![]() $\mathbb H$
denote the Hamiltonian quaternions. By definition,
$\mathbb H$
denote the Hamiltonian quaternions. By definition,
![]() $\operatorname {\mathrm {Sp}}(n,1)$
is the unitary group
$\operatorname {\mathrm {Sp}}(n,1)$
is the unitary group
![]() $\operatorname {\mathrm {\mathbf {U}}}(V_{\mathbb R}, h)$
of
$\operatorname {\mathrm {\mathbf {U}}}(V_{\mathbb R}, h)$
of
![]() $\mathbb H$
-linear automorphisms of
$\mathbb H$
-linear automorphisms of
![]() $V_{\mathbb R} = \mathbb H^{n+1}$
preserving the Hermitian form
$V_{\mathbb R} = \mathbb H^{n+1}$
preserving the Hermitian form
In Section 1.5, we explain how our results translate back into the original problem in
![]() $\operatorname {\mathrm {PSp}}(n,1)$
, and we discuss their geometric meaning in terms of quaternionic hyperbolic orbifolds.
$\operatorname {\mathrm {PSp}}(n,1)$
, and we discuss their geometric meaning in terms of quaternionic hyperbolic orbifolds.
We will use the Euler–Poincaré characteristic
![]() $\chi $
(defined in the sense of C.T.C. Wall) as a measure of the covolume: There exists a normalization
$\chi $
(defined in the sense of C.T.C. Wall) as a measure of the covolume: There exists a normalization
![]() $\mu ^{\mathrm {EP}}$
of the Haar measure on
$\mu ^{\mathrm {EP}}$
of the Haar measure on
![]() $\operatorname {\mathrm {Sp}}(n,1)$
such that
$\operatorname {\mathrm {Sp}}(n,1)$
such that
![]() $\mu ^{\mathrm {EP}}(\Gamma \backslash \operatorname {\mathrm {Sp}}(n,1)) = \chi (\Gamma )$
for any lattice
$\mu ^{\mathrm {EP}}(\Gamma \backslash \operatorname {\mathrm {Sp}}(n,1)) = \chi (\Gamma )$
for any lattice
![]() $\Gamma \subset \operatorname {\mathrm {Sp}}(n,1)$
; see Section 4.2. The problem is then to find the lattices
$\Gamma \subset \operatorname {\mathrm {Sp}}(n,1)$
; see Section 4.2. The problem is then to find the lattices
![]() $\Gamma \subset \operatorname {\mathrm {Sp}}(n,1)$
with minimal value for
$\Gamma \subset \operatorname {\mathrm {Sp}}(n,1)$
with minimal value for
![]() $\chi (\Gamma )$
. It is usual (and natural) to separate the problem into the subcases of
$\chi (\Gamma )$
. It is usual (and natural) to separate the problem into the subcases of
![]() $\Gamma $
uniform (i.e., the quotient
$\Gamma $
uniform (i.e., the quotient
![]() $\Gamma \backslash \operatorname {\mathrm {Sp}}(n,1)$
being compact), respectively,
$\Gamma \backslash \operatorname {\mathrm {Sp}}(n,1)$
being compact), respectively,
![]() $\Gamma $
nonuniform.
$\Gamma $
nonuniform.
1.2 The nonuniform case
Denote by
![]() $\mathscr H \subset \mathbb H$
the ring of Hurwitz integers, which consists of elements of the form
$\mathscr H \subset \mathbb H$
the ring of Hurwitz integers, which consists of elements of the form
![]() $\alpha _0 + \alpha _1 i + \alpha _2 j +\alpha _3 k \in \mathbb H$
with either all
$\alpha _0 + \alpha _1 i + \alpha _2 j +\alpha _3 k \in \mathbb H$
with either all
![]() $\alpha _i \in \mathbb Z$
or all
$\alpha _i \in \mathbb Z$
or all
![]() $\alpha _i \in \mathbb Z +\frac {1}{2}$
. Let
$\alpha _i \in \mathbb Z +\frac {1}{2}$
. Let
![]() $\operatorname {\mathrm {Sp}}(n,1, \mathscr H)$
be the subgroup
$\operatorname {\mathrm {Sp}}(n,1, \mathscr H)$
be the subgroup
![]() $\operatorname {\mathrm {\mathbf {U}}}(L, h) \subset \operatorname {\mathrm {\mathbf {U}}}(V_{\mathbb R}, h)$
stabilizing the lattice
$\operatorname {\mathrm {\mathbf {U}}}(L, h) \subset \operatorname {\mathrm {\mathbf {U}}}(V_{\mathbb R}, h)$
stabilizing the lattice
![]() $L = \mathscr H^{n+1} \subset V_{\mathbb R}$
. In matrix notation, it corresponds to the set of elements of
$L = \mathscr H^{n+1} \subset V_{\mathbb R}$
. In matrix notation, it corresponds to the set of elements of
![]() $\operatorname {\mathrm {Sp}}(n,1)$
with coefficients in
$\operatorname {\mathrm {Sp}}(n,1)$
with coefficients in
![]() $\mathscr H$
, whence the notation. The group
$\mathscr H$
, whence the notation. The group
![]() $\operatorname {\mathrm {Sp}}(n,1, \mathscr H)$
is a nonuniform lattice of
$\operatorname {\mathrm {Sp}}(n,1, \mathscr H)$
is a nonuniform lattice of
![]() $\operatorname {\mathrm {Sp}}(n,1)$
(see Section 2.3). It is easily checked that it is normalized by the scalar matrix
$\operatorname {\mathrm {Sp}}(n,1)$
(see Section 2.3). It is easily checked that it is normalized by the scalar matrix
![]() $g= I (1+ i)/\sqrt {2}$
, for which
$g= I (1+ i)/\sqrt {2}$
, for which
![]() $g^2 \in \operatorname {\mathrm {Sp}}(n,1, \mathscr H)$
holds. We denote by
$g^2 \in \operatorname {\mathrm {Sp}}(n,1, \mathscr H)$
holds. We denote by
![]() $\Gamma ^0_n$
the subgroup extension of
$\Gamma ^0_n$
the subgroup extension of
![]() $\operatorname {\mathrm {Sp}}(n,1, \mathscr H)$
by g. Thus,
$\operatorname {\mathrm {Sp}}(n,1, \mathscr H)$
by g. Thus,
![]() $\Gamma ^0_n$
contains
$\Gamma ^0_n$
contains
![]() $\operatorname {\mathrm {Sp}}(n,1, \mathscr H)$
as a subgroup of index
$\operatorname {\mathrm {Sp}}(n,1, \mathscr H)$
as a subgroup of index
![]() $2$
. For
$2$
. For
![]() $n=2$
, this lattice has been considered in [Reference Kim and Parker15, Prop. 5.8]. We will compute the following (see Corollary 5.8):
$n=2$
, this lattice has been considered in [Reference Kim and Parker15, Prop. 5.8]. We will compute the following (see Corollary 5.8):
 $$ \begin{align} \chi(\Gamma^0_n) = \frac{(n+1)}{2} \prod_{j=1}^{n+1} \frac{2^j + (-1)^j}{4j} |B_{2j}|, \end{align} $$
$$ \begin{align} \chi(\Gamma^0_n) = \frac{(n+1)}{2} \prod_{j=1}^{n+1} \frac{2^j + (-1)^j}{4j} |B_{2j}|, \end{align} $$
where
![]() $B_m$
is the m-th Bernoulli number. For the reader’s convenience, we list the first few values for
$B_m$
is the m-th Bernoulli number. For the reader’s convenience, we list the first few values for
![]() $\chi (\Gamma ^0_n)$
in Table 1. Note the few distinct prime factors (namely,
$\chi (\Gamma ^0_n)$
in Table 1. Note the few distinct prime factors (namely,
![]() $p=2,3$
) appearing for
$p=2,3$
) appearing for
![]() $n=2$
; this compares with
$n=2$
; this compares with
![]() $\chi (\operatorname {\mathrm {SL}}_2(\mathbb Z)) = -1/12$
.
$\chi (\operatorname {\mathrm {SL}}_2(\mathbb Z)) = -1/12$
.
Table 1 Some explicit values for
![]() $n \le 5$
.
$n \le 5$
.

Theorem 1. For any n even, the lattice
![]() $\Gamma ^0_n$
realizes the smallest covolume among nonuniform lattices in
$\Gamma ^0_n$
realizes the smallest covolume among nonuniform lattices in
![]() $\operatorname {\mathrm {Sp}}(n,1)$
. Up to conjugacy, it is the unique lattice with this property.
$\operatorname {\mathrm {Sp}}(n,1)$
. Up to conjugacy, it is the unique lattice with this property.
At this point, we would like to stress the relative simplicity of the description of the lattice
![]() $\Gamma ^0_n$
. In comparison, the results of [Reference Belolipetsky2, Reference Belolipetsky and Emery3, Reference Emery and Stover11] concerning
$\Gamma ^0_n$
. In comparison, the results of [Reference Belolipetsky2, Reference Belolipetsky and Emery3, Reference Emery and Stover11] concerning
![]() $\operatorname {\mathrm {PO}}(n,1)$
and
$\operatorname {\mathrm {PO}}(n,1)$
and
![]() $\operatorname {\mathrm {PU}}(n,1)$
describe the minimal covolume lattices as normalizers of principal arithmetic subgroups, i.e., by using a local-to-global (adelic) description that heavily depends on Bruhat–Tits theory (see Section 4). A more concrete description in those cases is only available in low dimensions (in the form of Coxeter groups) or in a few special cases (see, for instance, [Reference Emery, Parkkonen and Paulin8, Reference Emery9]). Another situation where satisfactory descriptions are available is the case of a split Lie group G (see, for instance, [Reference Thilmany35] and [Reference Lubotzky18, 31] in the positive characteristic case).
$\operatorname {\mathrm {PU}}(n,1)$
describe the minimal covolume lattices as normalizers of principal arithmetic subgroups, i.e., by using a local-to-global (adelic) description that heavily depends on Bruhat–Tits theory (see Section 4). A more concrete description in those cases is only available in low dimensions (in the form of Coxeter groups) or in a few special cases (see, for instance, [Reference Emery, Parkkonen and Paulin8, Reference Emery9]). Another situation where satisfactory descriptions are available is the case of a split Lie group G (see, for instance, [Reference Thilmany35] and [Reference Lubotzky18, 31] in the positive characteristic case).
The adelic description of arithmetic subgroups is the setting needed to apply Prasad’s formula, and in this respect, the proof of Theorem 1 (and Theorem 3 below) follows the same strategy as in those previous articles. The improvement in the present case is stated in Theorem 5.7, where we have been able to express a large class of stabilizers of Hermitian lattices—including
![]() $\operatorname {\mathrm {Sp}}(n,1, \mathscr H)$
—as principal arithmetic subgroups, in particular permitting the computation of their covolumes. This makes these subgroups more tractable to geometric or algebraic investigation; for instance, the reflectivity of
$\operatorname {\mathrm {Sp}}(n,1, \mathscr H)$
—as principal arithmetic subgroups, in particular permitting the computation of their covolumes. This makes these subgroups more tractable to geometric or algebraic investigation; for instance, the reflectivity of
![]() $\operatorname {\mathrm {Sp}}(n,1, \mathscr H)$
has already been studied by Allcock in [Reference Allcock1].
$\operatorname {\mathrm {Sp}}(n,1, \mathscr H)$
has already been studied by Allcock in [Reference Allcock1].
For n odd, there is a nonuniform lattice of covolume smaller than
![]() $\Gamma _n^0$
:
$\Gamma _n^0$
:
Theorem 2. Let
![]() $n>1$
be odd. There exists a unique (up to conjugacy) nonuniform lattice
$n>1$
be odd. There exists a unique (up to conjugacy) nonuniform lattice
![]() $\Gamma ^1_n \subset \operatorname {\mathrm {Sp}}(n,1)$
of minimal covolume. It is commensurable with
$\Gamma ^1_n \subset \operatorname {\mathrm {Sp}}(n,1)$
of minimal covolume. It is commensurable with
![]() $\Gamma ^0_n$
, and
$\Gamma ^0_n$
, and
 $$ \begin{align} \chi(\Gamma^1_n) = \frac{(n+1)}{2} \prod_{j=1}^{n+1} \frac{2^{2j} - 1}{4j} |B_{2j}| \prod_{j=1}^{\frac{n+1}{2}} \frac{1}{2^{4j} -1}. \end{align} $$
$$ \begin{align} \chi(\Gamma^1_n) = \frac{(n+1)}{2} \prod_{j=1}^{n+1} \frac{2^{2j} - 1}{4j} |B_{2j}| \prod_{j=1}^{\frac{n+1}{2}} \frac{1}{2^{4j} -1}. \end{align} $$
For the lattice
![]() $\Gamma _n^1$
, we did not manage to find an alternative to the construction relying on principal arithmetic subgroups. Thus, a possible improvement of our result would be to obtain a more concrete description for it.
$\Gamma _n^1$
, we did not manage to find an alternative to the construction relying on principal arithmetic subgroups. Thus, a possible improvement of our result would be to obtain a more concrete description for it.
Remark 1.1. The notation has been chosen so that
![]() $\Gamma ^s_n$
denotes the nonuniform lattice of the smallest covolume for any n when setting
$\Gamma ^s_n$
denotes the nonuniform lattice of the smallest covolume for any n when setting
![]() $s = (n \mod 2) \in \left \{ 0,1 \right \}$
.
$s = (n \mod 2) \in \left \{ 0,1 \right \}$
.
1.3 The uniform case
Let
![]() $k = \mathbb Q(\sqrt {5})$
, and let
$k = \mathbb Q(\sqrt {5})$
, and let
![]() $\mathscr I$
denote the icosian ring, i.e.,
$\mathscr I$
denote the icosian ring, i.e.,
![]() $\mathscr I$
is the unique (up to conjugacy) maximal order in the quaternion k-algebra
$\mathscr I$
is the unique (up to conjugacy) maximal order in the quaternion k-algebra
![]() $\left ( \frac {-1, -1}{k} \right )$
(see [Reference Conway and Sloane5, Sect. 8.2] or [Reference Vignéras38, p.141]). We have an inclusion
$\left ( \frac {-1, -1}{k} \right )$
(see [Reference Conway and Sloane5, Sect. 8.2] or [Reference Vignéras38, p.141]). We have an inclusion
![]() $\mathscr I \subset \mathbb H$
. The following Hermitian form restricts to the standard
$\mathscr I \subset \mathbb H$
. The following Hermitian form restricts to the standard
![]() $\mathscr I$
-lattice
$\mathscr I$
-lattice
![]() $\mathscr I^{n+1}$
in
$\mathscr I^{n+1}$
in
![]() $V_{\mathbb R} = \mathbb H^{n+1}$
:
$V_{\mathbb R} = \mathbb H^{n+1}$
:
The stabilizer
![]() $\operatorname {\mathrm {\mathbf {U}}}(\mathscr I^{n+1}, h)$
is a uniform lattice in
$\operatorname {\mathrm {\mathbf {U}}}(\mathscr I^{n+1}, h)$
is a uniform lattice in
![]() $\operatorname {\mathrm {Sp}}(n,1)$
(see Section 2.3), which we will denote by the symbol
$\operatorname {\mathrm {Sp}}(n,1)$
(see Section 2.3), which we will denote by the symbol
![]() $\Delta _n$
in the following.
$\Delta _n$
in the following.
Theorem 3. For any
![]() $n> 1$
, the lattice
$n> 1$
, the lattice
![]() $\Delta _n$
realizes the smallest covolume among uniform lattices in
$\Delta _n$
realizes the smallest covolume among uniform lattices in
![]() $\operatorname {\mathrm {Sp}}(n,1)$
. Up to conjugacy, it is the unique lattice with this property. Its Euler characteristic is given by
$\operatorname {\mathrm {Sp}}(n,1)$
. Up to conjugacy, it is the unique lattice with this property. Its Euler characteristic is given by
 $$ \begin{align} \chi(\Delta_n) = (n+1) \prod_{j=1}^{n+1} \frac{\zeta_k(1-2j)}{4}, \end{align} $$
$$ \begin{align} \chi(\Delta_n) = (n+1) \prod_{j=1}^{n+1} \frac{\zeta_k(1-2j)}{4}, \end{align} $$
where
![]() $\zeta _k$
denotes the Dedekind zeta function of
$\zeta _k$
denotes the Dedekind zeta function of
![]() $k=\mathbb Q(\sqrt {5})$
.
$k=\mathbb Q(\sqrt {5})$
.
Remark 1.2. The special values
![]() $\zeta _k(1-2j)$
appearing in equation (1.5) are known to be rational by the Klingen–Siegel theorem (more generally, for any totally real k), and they can be precisely evaluated (see [Reference Serre33, Sect. 3.7]). A list for
$\zeta _k(1-2j)$
appearing in equation (1.5) are known to be rational by the Klingen–Siegel theorem (more generally, for any totally real k), and they can be precisely evaluated (see [Reference Serre33, Sect. 3.7]). A list for
![]() $j=1,\ldots ,5$
is given, for instance, in [Reference Emery10, Table 2], from which we obtain the explicit values for
$j=1,\ldots ,5$
is given, for instance, in [Reference Emery10, Table 2], from which we obtain the explicit values for
![]() $\chi (\Delta _n)$
listed in Table 1. We omit
$\chi (\Delta _n)$
listed in Table 1. We omit
![]() $n=5$
for reason of space.
$n=5$
for reason of space.
1.4 Numerical values, growth
We can now compare the nonuniform and uniform lattices and study the asymptotic of their covolumes with respect to the dimension. We give a few numerical values in Table 2. One sees that
![]() $\chi (\Gamma ^s_n)$
and
$\chi (\Gamma ^s_n)$
and
![]() $\chi (\Delta _n)$
are very close for
$\chi (\Delta _n)$
are very close for
![]() $n=2$
, but then
$n=2$
, but then
![]() $\chi (\Delta _n)$
starts growing much faster than
$\chi (\Delta _n)$
starts growing much faster than
![]() $\chi (\Gamma ^s_n)$
(which also grows with
$\chi (\Gamma ^s_n)$
(which also grows with
![]() $n>5$
). More precisely, we can state the following result, which essentially follows from Theorems 1–3; see Section 6.5 for the discussion of the proof.
$n>5$
). More precisely, we can state the following result, which essentially follows from Theorems 1–3; see Section 6.5 for the discussion of the proof.
Table 2 Some approximate values.

Corollary 1. Each of the sequences
![]() $\chi (\Gamma ^s_n)$
,
$\chi (\Gamma ^s_n)$
,
![]() $\chi (\Delta _n)$
, and
$\chi (\Delta _n)$
, and
![]() $\chi (\Delta _n)/\chi (\Gamma ^s_n)$
grows superexponentially as
$\chi (\Delta _n)/\chi (\Gamma ^s_n)$
grows superexponentially as
![]() $n \to \infty $
.
$n \to \infty $
.
Geometric lower bounds—by means of embedded balls—for the volume of quaternionic hyperbolic manifolds have been obtained by Philippe in her thesis (see [Reference Philippe26, Cor. 5.2]), and in [Reference Kim and Parker15, Cor. 5.3] for noncompact manifolds. In contrast to Corollary 1, these bounds decrease fast with the dimension.
It is clear from Corollary 1 that the proof of the next result now follows by inspecting a finite number of values.
Corollary 2. For
![]() $n=2$
, the lattice of the smallest covolume in
$n=2$
, the lattice of the smallest covolume in
![]() $\operatorname {\mathrm {Sp}}(n,1)$
is uniform. For any
$\operatorname {\mathrm {Sp}}(n,1)$
is uniform. For any
![]() $n>2$
, this lattice is nonuniform. The smallest Euler characteristic of a lattice in
$n>2$
, this lattice is nonuniform. The smallest Euler characteristic of a lattice in
![]() $\operatorname {\mathrm {Sp}}(n,1)$
(with
$\operatorname {\mathrm {Sp}}(n,1)$
(with
![]() $n>1$
arbitrary) is given by
$n>1$
arbitrary) is given by
![]() $\chi (\Gamma ^1_5)$
.
$\chi (\Gamma ^1_5)$
.
1.5 Quaternionic hyperbolic orbifolds
Let
![]() $\pi : \operatorname {\mathrm {Sp}}(n,1) \to \operatorname {\mathrm {PSp}}(n,1)$
denote the projection. Any lattice
$\pi : \operatorname {\mathrm {Sp}}(n,1) \to \operatorname {\mathrm {PSp}}(n,1)$
denote the projection. Any lattice
![]() $\Gamma ' \subset \operatorname {\mathrm {PSp}}(n,1)$
is the image of a lattice
$\Gamma ' \subset \operatorname {\mathrm {PSp}}(n,1)$
is the image of a lattice
![]() $\Gamma = \pi ^{-1}(\Gamma ')$
that contains the center
$\Gamma = \pi ^{-1}(\Gamma ')$
that contains the center
![]() $\left \{ \pm I \right \}$
. Then we have
$\left \{ \pm I \right \}$
. Then we have
![]() $\chi (\Gamma ') = 2 \chi (\Gamma )$
. It follows that
$\chi (\Gamma ') = 2 \chi (\Gamma )$
. It follows that
![]() $\Gamma '$
is of minimal covolume in
$\Gamma '$
is of minimal covolume in
![]() $\operatorname {\mathrm {PSp}}(n,1)$
if and only if so is
$\operatorname {\mathrm {PSp}}(n,1)$
if and only if so is
![]() $\Gamma $
in
$\Gamma $
in
![]() $\operatorname {\mathrm {Sp}}(n,1)$
(note that a lattice of minimal covolume in
$\operatorname {\mathrm {Sp}}(n,1)$
(note that a lattice of minimal covolume in
![]() $\operatorname {\mathrm {Sp}}(n,1)$
necessarily contains the center
$\operatorname {\mathrm {Sp}}(n,1)$
necessarily contains the center
![]() $\left \{ \pm I \right \}$
).
$\left \{ \pm I \right \}$
).
The group
![]() $\operatorname {\mathrm {PSp}}(n,1)$
identifies with the isometries of the quaternionic hyperbolic n-space
$\operatorname {\mathrm {PSp}}(n,1)$
identifies with the isometries of the quaternionic hyperbolic n-space
![]() $\mathbf H_{\mathbb H}^n$
. For any lattice
$\mathbf H_{\mathbb H}^n$
. For any lattice
![]() $\Gamma ' \subset \operatorname {\mathrm {PSp}}(n,1)$
, we consider the finite-volume quaternionic hyperbolic orbifold
$\Gamma ' \subset \operatorname {\mathrm {PSp}}(n,1)$
, we consider the finite-volume quaternionic hyperbolic orbifold
![]() $M = \Gamma '\backslash \mathbf H_{\mathbb H}^n$
. Alternatively, we may write M as the quotient
$M = \Gamma '\backslash \mathbf H_{\mathbb H}^n$
. Alternatively, we may write M as the quotient
![]() $M = \Gamma \backslash \mathbf H_{\mathbb H}^n$
, where
$M = \Gamma \backslash \mathbf H_{\mathbb H}^n$
, where
![]() $\Gamma = \pi ^{-1}(\Gamma ')$
. Then the orbifold Euler–Poincaré characteristic of M is given by
$\Gamma = \pi ^{-1}(\Gamma ')$
. Then the orbifold Euler–Poincaré characteristic of M is given by
![]() $\chi (M) = \chi (\Gamma ') = 2 \chi (\Gamma )$
. In case
$\chi (M) = \chi (\Gamma ') = 2 \chi (\Gamma )$
. In case
![]() $\Gamma '$
is torsion-free, M is a quaternionic hyperbolic manifold, and
$\Gamma '$
is torsion-free, M is a quaternionic hyperbolic manifold, and
![]() $\chi (M)$
corresponds to the usual (i.e., topological) Euler characteristic. The volume of the orbifold M is proportional to
$\chi (M)$
corresponds to the usual (i.e., topological) Euler characteristic. The volume of the orbifold M is proportional to
![]() $\chi (M)$
(see below). Thus, Theorems 1–3 determine the quaternionic hyperbolic orbifolds (compact or noncompact) of the smallest volume.
$\chi (M)$
(see below). Thus, Theorems 1–3 determine the quaternionic hyperbolic orbifolds (compact or noncompact) of the smallest volume.
The choice of a normalization of the volume form on
![]() $\mathbf H^n_{\mathbb H}$
induces a volume form on its compact dual, i.e., on the quaternionic projective space
$\mathbf H^n_{\mathbb H}$
induces a volume form on its compact dual, i.e., on the quaternionic projective space
![]() $\mathbb H P^n$
. For the induced volume on a quotient
$\mathbb H P^n$
. For the induced volume on a quotient
![]() $M = \Gamma '\backslash \mathbf H^n_{\mathbb H}$
, we have
$M = \Gamma '\backslash \mathbf H^n_{\mathbb H}$
, we have
where
![]() $n+1$
appears as the Euler characteristic of
$n+1$
appears as the Euler characteristic of
![]() $\mathbb H P^n$
.
$\mathbb H P^n$
.
1.6 Outline
The classification of arithmetic subgroups in
![]() $\operatorname {\mathrm {Sp}}(n,1)$
is discussed in Section 2. In Section 3, we recall some materials from Bruhat–Tits theory, in particular to prepare the discussion of Prasad’s volume formula in Section 4. Section 5 deals with lattices that are defined as stabilizers of Hermitian modules. The proofs of the results stated in the introduction are contained in Section 6, with the exception of the uniqueness, which is proved in Section 7.
$\operatorname {\mathrm {Sp}}(n,1)$
is discussed in Section 2. In Section 3, we recall some materials from Bruhat–Tits theory, in particular to prepare the discussion of Prasad’s volume formula in Section 4. Section 5 deals with lattices that are defined as stabilizers of Hermitian modules. The proofs of the results stated in the introduction are contained in Section 6, with the exception of the uniqueness, which is proved in Section 7.
2 Arithmetic subgroups in
 $\operatorname {\mathrm {Sp}}(n,1)$
$\operatorname {\mathrm {Sp}}(n,1)$
2.1 Admissible groups
Let k be a number field, and consider an absolutely simple algebraic k-group
![]() $\mathbf G$
such that
$\mathbf G$
such that
for some compact group K. Then
![]() $\mathbf G$
is simply connected of type
$\mathbf G$
is simply connected of type
![]() $\mathrm {C}_{n+1}$
, and k is totally real. Moreover, we can fix an embedding
$\mathrm {C}_{n+1}$
, and k is totally real. Moreover, we can fix an embedding
![]() $k \subset \mathbb R$
so that
$k \subset \mathbb R$
so that
![]() $\mathbf G(\mathbb R)$
identifies with
$\mathbf G(\mathbb R)$
identifies with
![]() $\operatorname {\mathrm {Sp}}(n,1)$
. It follows from the classification of simple algebraic group (see [Reference Tits36] and Remark 2.2 below) that
$\operatorname {\mathrm {Sp}}(n,1)$
. It follows from the classification of simple algebraic group (see [Reference Tits36] and Remark 2.2 below) that
![]() $\mathbf G$
is isomorphic over k to some unitary group
$\mathbf G$
is isomorphic over k to some unitary group
![]() $\operatorname {\mathrm {\mathbf {U}}}(V, h)$
, where
$\operatorname {\mathrm {\mathbf {U}}}(V, h)$
, where
-
○ D is a quaternion algebra over k, with the standard involution
 $x \mapsto \overline {x}$
.
$x \mapsto \overline {x}$
. -
○ V is a right D-vector space.
-
○ h is a nondegenerate hermitian form on V (sesquilinear with respect to the standard involution).
Such a k-group
![]() $\mathbf G = \operatorname {\mathrm {\mathbf {U}}}(V, h)$
satisfying equation (2.1) will be called admissible, and in this case, we shall use the same terminology for the Hermitian space
$\mathbf G = \operatorname {\mathrm {\mathbf {U}}}(V, h)$
satisfying equation (2.1) will be called admissible, and in this case, we shall use the same terminology for the Hermitian space
![]() $(V, h)$
. We call D the defining algebra of
$(V, h)$
. We call D the defining algebra of
![]() $\mathbf G$
. Facts concerning quaternion algebras will be recalled along the lines; we refer to [Reference Vignéras38] or [Reference Maclachlan and Reid19, Ch. 2 and 6].
$\mathbf G$
. Facts concerning quaternion algebras will be recalled along the lines; we refer to [Reference Vignéras38] or [Reference Maclachlan and Reid19, Ch. 2 and 6].
Remark 2.1. For any field extension
![]() $K/k$
, we have by definition
$K/k$
, we have by definition
![]() $\mathbf G(K) = \operatorname {\mathrm {\mathbf {U}}}(V_K, h)$
, where
$\mathbf G(K) = \operatorname {\mathrm {\mathbf {U}}}(V_K, h)$
, where
![]() $V_K = V \otimes _k K$
. The latter is seen as a
$V_K = V \otimes _k K$
. The latter is seen as a
![]() $D_K$
-module for
$D_K$
-module for
![]() $D_K = D \otimes _k K$
. In particular, we can use the notation
$D_K = D \otimes _k K$
. In particular, we can use the notation
![]() $\operatorname {\mathrm {\mathbf {U}}}(V_k, h)$
to denote the k-points
$\operatorname {\mathrm {\mathbf {U}}}(V_k, h)$
to denote the k-points
![]() $\mathbf G(k)$
.
$\mathbf G(k)$
.
Remark 2.2. In [Reference Tits36, p. 56] Tits describes the classification in terms of the special unitary group
![]() $\operatorname {\mathrm {\mathbf {SU}}}$
; however, in our case
$\operatorname {\mathrm {\mathbf {SU}}}$
; however, in our case
![]() $\operatorname {\mathrm {\mathbf {SU}}} = \operatorname {\mathrm {\mathbf {U}}}$
since symplectic transformations have determinant
$\operatorname {\mathrm {\mathbf {SU}}} = \operatorname {\mathrm {\mathbf {U}}}$
since symplectic transformations have determinant
![]() $1$
.
$1$
.
2.2 Admissible defining algebras
We denote by
![]() $\mathcal {V}_k = \mathcal {V}_k^{\infty } \cup \mathcal {V}_k^{\mathrm {f}}$
the set of (infinite or finite) places of k, and, for any
$\mathcal {V}_k = \mathcal {V}_k^{\infty } \cup \mathcal {V}_k^{\mathrm {f}}$
the set of (infinite or finite) places of k, and, for any
![]() $v \in \mathcal {V}_k$
, by
$v \in \mathcal {V}_k$
, by
![]() $D_v$
the quaternion algebra
$D_v$
the quaternion algebra
![]() $D_{k_v} = D \otimes _k k_v$
. The algebra D is completely determined by the set of places
$D_{k_v} = D \otimes _k k_v$
. The algebra D is completely determined by the set of places
![]() $v \in \mathcal {V}_k$
where it ramifies (i.e., for which
$v \in \mathcal {V}_k$
where it ramifies (i.e., for which
![]() $D_v$
is a division algebra), and the set of such places is of even (finite) cardinality. There is no other obstruction to the existence of a quaternion algebra D with prescribed localizations
$D_v$
is a division algebra), and the set of such places is of even (finite) cardinality. There is no other obstruction to the existence of a quaternion algebra D with prescribed localizations
![]() $\left \{ D_v \, |\, v \in V \right \}$
; see [Reference Maclachlan and Reid19, Sect. 7.3].
$\left \{ D_v \, |\, v \in V \right \}$
; see [Reference Maclachlan and Reid19, Sect. 7.3].
Let
![]() $\mathbf G = \operatorname {\mathrm {\mathbf {U}}}(V, h)$
as above, with V over D. The following (well-known) result appears as a special case of Lemma 5.2 below. Recall that
$\mathbf G = \operatorname {\mathrm {\mathbf {U}}}(V, h)$
as above, with V over D. The following (well-known) result appears as a special case of Lemma 5.2 below. Recall that
![]() $D_v$
is said split if it is isomorphic to
$D_v$
is said split if it is isomorphic to
![]() $M_2(k_v)$
, and this happens exactly when
$M_2(k_v)$
, and this happens exactly when
![]() $D_v$
is not ramified.
$D_v$
is not ramified.
Lemma 2.3. Let
![]() $v \in \mathcal {V}_k$
. The algebraic group
$v \in \mathcal {V}_k$
. The algebraic group
![]() $\mathbf G_{k_v}$
(obtained by scalars extension) splits if and only if
$\mathbf G_{k_v}$
(obtained by scalars extension) splits if and only if
![]() $D_v$
splits (i.e., is not ramified).
$D_v$
splits (i.e., is not ramified).
Proof. It follows from the classification in [Reference Tits36, p. 56] that
![]() $\mathbf G_{k_v}$
has relative rank less than
$\mathbf G_{k_v}$
has relative rank less than
![]() $n+1$
if
$n+1$
if
![]() $D_v$
is a division algebra; thus, in this case,
$D_v$
is a division algebra; thus, in this case,
![]() $\mathbf G_{k_v}$
is not split. If
$\mathbf G_{k_v}$
is not split. If
![]() $D_v$
splits the fact that
$D_v$
splits the fact that
![]() $\mathbf G_{k_v}$
splits will follow from Lemma 5.2 below with
$\mathbf G_{k_v}$
splits will follow from Lemma 5.2 below with
![]() $R = k_v$
.
$R = k_v$
.
Corollary 2.4. The k-isomorphism class of
![]() $\mathbf G$
determines its defining algebra D uniquely up to k-isomorphism.
$\mathbf G$
determines its defining algebra D uniquely up to k-isomorphism.
Proof. This is now clear since D is determined by the set of places where it splits.
Corollary 2.5. In order for the Hermitian space
![]() $(V, h)$
over D to be admissible, it is necessary that D ramifies at any
$(V, h)$
over D to be admissible, it is necessary that D ramifies at any
![]() $v \in \mathcal {V}_k^{\infty }$
, i.e.,
$v \in \mathcal {V}_k^{\infty }$
, i.e.,
![]() $D_v \cong \mathbb H$
for any
$D_v \cong \mathbb H$
for any
![]() $v \in \mathcal {V}_k^{\infty }$
.
$v \in \mathcal {V}_k^{\infty }$
.
Proof. By the admissibility condition, for any
![]() $v \in \mathcal {V}_k^{\infty }$
the group
$v \in \mathcal {V}_k^{\infty }$
the group
![]() $\mathbf G(k_v)$
is either
$\mathbf G(k_v)$
is either
![]() $\operatorname {\mathrm {Sp}}(n,1)$
or
$\operatorname {\mathrm {Sp}}(n,1)$
or
![]() $\operatorname {\mathrm {Sp}}(n+1)=\operatorname {\mathrm {Sp}}(n+1,0)$
. For
$\operatorname {\mathrm {Sp}}(n+1)=\operatorname {\mathrm {Sp}}(n+1,0)$
. For
![]() $n>1$
, these groups are not split. It follows from Lemma 2.3 that D ramifies at each
$n>1$
, these groups are not split. It follows from Lemma 2.3 that D ramifies at each
![]() $v \in \mathcal {V}_k^{\infty }$
so that
$v \in \mathcal {V}_k^{\infty }$
so that
![]() $D_v \cong \mathbb H$
(see [Reference Maclachlan and Reid19, Sect. 2.5]).
$D_v \cong \mathbb H$
(see [Reference Maclachlan and Reid19, Sect. 2.5]).
A pair
![]() $(k, D)$
with
$(k, D)$
with
![]() $k \subset \mathbb R$
a totally real number field and D a quaternion algebra over k will be called admissible if D satisfies the necessary condition of Corollary 2.5. More simply, we say that ‘D is admissible’.
$k \subset \mathbb R$
a totally real number field and D a quaternion algebra over k will be called admissible if D satisfies the necessary condition of Corollary 2.5. More simply, we say that ‘D is admissible’.
Proposition 2.6. Let
![]() $(V, h)$
and
$(V, h)$
and
![]() $(V', h')$
be two admissible Hermitian spaces of the same dimension over the same quaternion k-algebra D. Then
$(V', h')$
be two admissible Hermitian spaces of the same dimension over the same quaternion k-algebra D. Then
![]() $\operatorname {\mathrm {\mathbf {U}}}(V, h)$
is k-isomorphic to
$\operatorname {\mathrm {\mathbf {U}}}(V, h)$
is k-isomorphic to
![]() $\operatorname {\mathrm {\mathbf {U}}}(V', h')$
.
$\operatorname {\mathrm {\mathbf {U}}}(V', h')$
.
Proof. Being admissible, the two Hermitian spaces
![]() $(V,h)$
and
$(V,h)$
and
![]() $(V',h')$
have the same signature over
$(V',h')$
have the same signature over
![]() $k_v$
for any
$k_v$
for any
![]() $v \in \mathcal {V}_k^{\infty }$
, and it follows from [Reference Scharlau32, 10.1.8 (iii)] that
$v \in \mathcal {V}_k^{\infty }$
, and it follows from [Reference Scharlau32, 10.1.8 (iii)] that
![]() $(V, h) \cong (V', h')$
.
$(V, h) \cong (V', h')$
.
Remark 2.7. There is actually a bijection between the set of admissible pairs
![]() $(k, D)$
for
$(k, D)$
for
![]() $k\subset \mathbb R$
totally real and the set of algebraic groups that are admissible for
$k\subset \mathbb R$
totally real and the set of algebraic groups that are admissible for
![]() $\operatorname {\mathrm {Sp}}(n,1)$
; see [Reference Meyer21, Sect. 4]. We will not need this fact in its full generality.
$\operatorname {\mathrm {Sp}}(n,1)$
; see [Reference Meyer21, Sect. 4]. We will not need this fact in its full generality.
2.3 The classification of lattices
Let
![]() $\mathbf G$
be an admissible k-group, and let
$\mathbf G$
be an admissible k-group, and let
![]() $\mathcal O_k$
denote the ring of integers in k. By the Theorem of Borel and Harish-Chandra, any subgroup
$\mathcal O_k$
denote the ring of integers in k. By the Theorem of Borel and Harish-Chandra, any subgroup
![]() $\Gamma \subset \mathbf G(\mathbb R)$
that is commensurable with
$\Gamma \subset \mathbf G(\mathbb R)$
that is commensurable with
![]() $\mathbf G(\mathcal O_k)$
(for some embedding
$\mathbf G(\mathcal O_k)$
(for some embedding
![]() $\mathbf G \subset \operatorname {\mathrm {GL}}_N$
) is a lattice in
$\mathbf G \subset \operatorname {\mathrm {GL}}_N$
) is a lattice in
![]() $\operatorname {\mathrm {Sp}}(n,1)$
. Such a subgroup is called arithmetic. The work of Margulis [Reference Margulis20] has shown that superrigidity for
$\operatorname {\mathrm {Sp}}(n,1)$
. Such a subgroup is called arithmetic. The work of Margulis [Reference Margulis20] has shown that superrigidity for
![]() $\operatorname {\mathrm {Sp}}(n,1)$
(later proved by Gromov and Schoen [Reference Gromov and Schoen13] in the non-Archimedean case and Corlette [Reference Corlette6] in the Archimedean) implies the arithmeticity of any lattice in
$\operatorname {\mathrm {Sp}}(n,1)$
(later proved by Gromov and Schoen [Reference Gromov and Schoen13] in the non-Archimedean case and Corlette [Reference Corlette6] in the Archimedean) implies the arithmeticity of any lattice in
![]() $\operatorname {\mathrm {Sp}}(n,1)$
, i.e., any lattice in
$\operatorname {\mathrm {Sp}}(n,1)$
, i.e., any lattice in
![]() $\operatorname {\mathrm {Sp}}(n,1)$
can be constructed as an arithmetic subgroup, as above. A pair
$\operatorname {\mathrm {Sp}}(n,1)$
can be constructed as an arithmetic subgroup, as above. A pair
![]() $(k, \mathbf G)$
with
$(k, \mathbf G)$
with
![]() $\mathbf G$
admissible determines exactly one commensurability class of lattices in
$\mathbf G$
admissible determines exactly one commensurability class of lattices in
![]() $\operatorname {\mathrm {Sp}}(n,1)$
(up to conjugacy); see [Reference Prasad and Rapinchuk29, Prop. 2.5]. We will say that the lattices
$\operatorname {\mathrm {Sp}}(n,1)$
(up to conjugacy); see [Reference Prasad and Rapinchuk29, Prop. 2.5]. We will say that the lattices
![]() $\Gamma $
in such a commensurability class are defined over k. Moreover, with Corollary 2.4, we see that the defining k-algebra D of
$\Gamma $
in such a commensurability class are defined over k. Moreover, with Corollary 2.4, we see that the defining k-algebra D of
![]() $\mathbf G$
is an invariant of the commensurability class. We take over the terminology and say that that D is the defining algebra of
$\mathbf G$
is an invariant of the commensurability class. We take over the terminology and say that that D is the defining algebra of
![]() $\Gamma $
. Conversely, by Proposition 2.6, the pair
$\Gamma $
. Conversely, by Proposition 2.6, the pair
![]() $(k,D)$
uniquely determines the commensurability class.
$(k,D)$
uniquely determines the commensurability class.
Proposition 2.8 (Compactness criterion)
A lattice
![]() $\Gamma \subset \operatorname {\mathrm {Sp}}(n,1)$
is nonuniform if and only if it is defined over
$\Gamma \subset \operatorname {\mathrm {Sp}}(n,1)$
is nonuniform if and only if it is defined over
![]() $\mathbb Q$
.
$\mathbb Q$
.
Proof. This is specialization of Godement’s compactness criterion, which asserts that an arithmetic subgroup of
![]() $\mathbf G$
semisimple is nonuniform in
$\mathbf G$
semisimple is nonuniform in
![]() $\mathbf G(k\otimes _{\mathbb Q} \mathbb R)$
if and only if
$\mathbf G(k\otimes _{\mathbb Q} \mathbb R)$
if and only if
![]() $\mathbf G$
is k-isotropic. If
$\mathbf G$
is k-isotropic. If
![]() $k \neq \mathbb Q$
, an admissible k-group
$k \neq \mathbb Q$
, an admissible k-group
![]() $\mathbf G$
has a compact factor
$\mathbf G$
has a compact factor
![]() $\mathbf G(k_v)$
for some
$\mathbf G(k_v)$
for some
![]() $v \in \mathcal {V}_k^{\infty }$
so that
$v \in \mathcal {V}_k^{\infty }$
so that
![]() $\mathbf G$
cannot be isotropic. Let
$\mathbf G$
cannot be isotropic. Let
![]() $k=\mathbb Q$
, and let
$k=\mathbb Q$
, and let
![]() $\mathbf G = \operatorname {\mathrm {\mathbf {U}}}(V, h)$
admissible defined over
$\mathbf G = \operatorname {\mathrm {\mathbf {U}}}(V, h)$
admissible defined over
![]() $\mathbb Q$
. Then
$\mathbb Q$
. Then
![]() $\mathbf G$
is isotropic when
$\mathbf G$
is isotropic when
![]() $(V, h)$
is, and by [Reference Scharlau32, Theorem 10.1.1], this happens exactly when its trace form
$(V, h)$
is, and by [Reference Scharlau32, Theorem 10.1.1], this happens exactly when its trace form
![]() $q_h$
(which is a quadratic form over
$q_h$
(which is a quadratic form over
![]() $\mathbb Q$
in
$\mathbb Q$
in
![]() $4(n+1)$
variables) is isotropic. Then
$4(n+1)$
variables) is isotropic. Then
![]() $\mathbf G$
is isotropic by [Reference Scharlau32, Cor. 5.7.3 (iii)].
$\mathbf G$
is isotropic by [Reference Scharlau32, Cor. 5.7.3 (iii)].
We will describe in Section 5 a concrete way to construct arithmetic subgroups in
![]() $\operatorname {\mathrm {Sp}}(n,1)$
.
$\operatorname {\mathrm {Sp}}(n,1)$
.
3 Parahoric subgroups and Galois cohomology
We collect in this section some notions of the Bruhat–Tits theory; we refer to [Reference Tits37]. Section 3.1 and 3.2 are needed for the volume computation in Section 4. The content of Section 3.3 will appear later, in Section 6.3, and the reader might want to skip it until they reach this point.
In this section,
![]() $\mathbf G$
denotes an admissible k-group. For any finite place
$\mathbf G$
denotes an admissible k-group. For any finite place
![]() $v \in \mathcal {V}_k^{\mathrm {f}}$
, we denote by
$v \in \mathcal {V}_k^{\mathrm {f}}$
, we denote by
![]() $\mathfrak o_v$
the valuation ring in
$\mathfrak o_v$
the valuation ring in
![]() $k_v$
.
$k_v$
.
3.1 Parahoric subgroups
For any
![]() $v \in \mathcal {V}_k^{\mathrm {f}}$
, the group
$v \in \mathcal {V}_k^{\mathrm {f}}$
, the group
![]() $\mathbf G(k_v)$
acts on its associated Bruhat–Tits building
$\mathbf G(k_v)$
acts on its associated Bruhat–Tits building
![]() $X_v$
. A parahoric subgroup
$X_v$
. A parahoric subgroup
![]() $P_v \subset \mathbf G(k_v)$
is by definition a stabilizer of a facet of
$P_v \subset \mathbf G(k_v)$
is by definition a stabilizer of a facet of
![]() $X_v$
(note that we are working with
$X_v$
(note that we are working with
![]() $\mathbf G$
simply connected). Maximal parahoric subgroups correspond to stabilizers of vertices on
$\mathbf G$
simply connected). Maximal parahoric subgroups correspond to stabilizers of vertices on
![]() $X_v$
. If
$X_v$
. If
![]() $\Delta _v$
denotes the affine root system of
$\Delta _v$
denotes the affine root system of
![]() $\mathbf G(k_v)$
, then the conjugacy classes of parahoric subgroups
$\mathbf G(k_v)$
, then the conjugacy classes of parahoric subgroups
![]() $P_v \subset \mathbf G(k_v)$
are in correspondence with the subsets
$P_v \subset \mathbf G(k_v)$
are in correspondence with the subsets
![]() $\Theta _v \subsetneq \Delta _v$
; then
$\Theta _v \subsetneq \Delta _v$
; then
![]() $\Theta _v$
is called the type of
$\Theta _v$
is called the type of
![]() $P_v$
. The correspondence preserves the inclusion, and thus, maximal subgroups have types that omit exactly one element in
$P_v$
. The correspondence preserves the inclusion, and thus, maximal subgroups have types that omit exactly one element in
![]() $\Delta _v$
.
$\Delta _v$
.
Assume first that
![]() $\mathbf G_{k_v}$
is split. Then its affine root system is given by the following local Dynkin diagram:
$\mathbf G_{k_v}$
is split. Then its affine root system is given by the following local Dynkin diagram:
The parahoric subgroups of maximal volume in
![]() $\mathbf G(k_v)$
are those that are hyperspecial, i.e., of type
$\mathbf G(k_v)$
are those that are hyperspecial, i.e., of type
![]() $\Delta _v \smallsetminus \left \{\alpha \right \}$
, where
$\Delta _v \smallsetminus \left \{\alpha \right \}$
, where
![]() $\alpha $
is any of the two hyperspecial vertices (labelled ‘hs’ in equation (3.1)).
$\alpha $
is any of the two hyperspecial vertices (labelled ‘hs’ in equation (3.1)).
There is exactly one nonsplit form of
![]() $\mathbf G_{k_v}$
of type
$\mathbf G_{k_v}$
of type
![]() $\mathrm {C}_{n+1}$
, and it splits over the maximal unramified extension
$\mathrm {C}_{n+1}$
, and it splits over the maximal unramified extension
![]() $\widehat {k}_v/k_v$
. If
$\widehat {k}_v/k_v$
. If
![]() $\mathbf G_{k_v}$
is not split, it corresponds to the local type named
$\mathbf G_{k_v}$
is not split, it corresponds to the local type named
![]() $^2\mathrm {C}_{n+1}$
in [Reference Tits37, Sect. 4.3]; we have reproduced in Table 3 the corresponding local indices (their description depends on the parity of n). It is a general fact, proved in [Reference Borel and Prasad4, App. A], that parahoric subgroups of maximal volume in
$^2\mathrm {C}_{n+1}$
in [Reference Tits37, Sect. 4.3]; we have reproduced in Table 3 the corresponding local indices (their description depends on the parity of n). It is a general fact, proved in [Reference Borel and Prasad4, App. A], that parahoric subgroups of maximal volume in
![]() $\mathbf G(k_v)$
are those of type
$\mathbf G(k_v)$
are those of type
![]() $\Delta _v \smallsetminus \left \{ \alpha \right \}$
, where
$\Delta _v \smallsetminus \left \{ \alpha \right \}$
, where
![]() $\alpha $
is very special (see loc. cit. for the definition). In our case, the very special vertex in
$\alpha $
is very special (see loc. cit. for the definition). In our case, the very special vertex in
![]() $\Delta _v$
is
$\Delta _v$
is
![]() $\alpha _0$
for n even, respectively,
$\alpha _0$
for n even, respectively,
![]() $\alpha _1$
for n odd (as shown in Table 3; note that
$\alpha _1$
for n odd (as shown in Table 3; note that
![]() $\alpha _1$
is defined only for n odd). Thus, for
$\alpha _1$
is defined only for n odd). Thus, for
![]() $s = n \mod 2$
, a parahoric subgroup of
$s = n \mod 2$
, a parahoric subgroup of
![]() $\mathbf G(k_v)$
is of maximal volume exactly when it is of type
$\mathbf G(k_v)$
is of maximal volume exactly when it is of type
![]() $\Theta _v = \Delta _v \smallsetminus \left \{ \alpha _s \right \}$
.
$\Theta _v = \Delta _v \smallsetminus \left \{ \alpha _s \right \}$
.
Table 3 Local indices for the type
![]() $^2\mathrm {C}_{n+1}$
.
$^2\mathrm {C}_{n+1}$
.

3.2 The group scheme structure
Let
![]() $\mathbf G(k_v)$
as above, split or not. Each parahoric subgroup
$\mathbf G(k_v)$
as above, split or not. Each parahoric subgroup
![]() $P_v \subset \mathbf G(k_v)$
can be written as
$P_v \subset \mathbf G(k_v)$
can be written as
![]() $P_v = \mathscr G(\mathfrak o_v)$
for some canonical smooth group scheme
$P_v = \mathscr G(\mathfrak o_v)$
for some canonical smooth group scheme
![]() $\mathscr G$
over
$\mathscr G$
over
![]() $\mathfrak o_v$
. Let
$\mathfrak o_v$
. Let
![]() $\mathfrak f_v$
be the residue field of
$\mathfrak f_v$
be the residue field of
![]() $k_v$
. For a fixed
$k_v$
. For a fixed
![]() $P_v$
, following the notation of [Reference Prasad28], we denote by
$P_v$
, following the notation of [Reference Prasad28], we denote by
![]() $\overline {\mathrm M}_{v}$
the maximal reductive quotient of the
$\overline {\mathrm M}_{v}$
the maximal reductive quotient of the
![]() $\mathfrak f_v$
-group
$\mathfrak f_v$
-group
![]() $\mathscr G_{f_v}$
obtained from
$\mathscr G_{f_v}$
obtained from
![]() $\mathscr G$
by base change;
$\mathscr G$
by base change;
![]() $\overline {\mathrm M}_{v}$
is connected. The structure of
$\overline {\mathrm M}_{v}$
is connected. The structure of
![]() $\overline {\mathrm M}_{v}$
can be obtained from the type of
$\overline {\mathrm M}_{v}$
can be obtained from the type of
![]() $P_v$
by using the procedure explained in [Reference Tits37, Sect. 3.5.2]. If
$P_v$
by using the procedure explained in [Reference Tits37, Sect. 3.5.2]. If
![]() $\mathbf G_{k_v}$
is split, then
$\mathbf G_{k_v}$
is split, then
![]() $P_v$
is hyperspecial if and only if
$P_v$
is hyperspecial if and only if
![]() $\overline {\mathrm M}_{v}$
is simple of type
$\overline {\mathrm M}_{v}$
is simple of type
![]() $\mathrm {C}_{n+1}$
(i.e., of the same type as
$\mathrm {C}_{n+1}$
(i.e., of the same type as
![]() $\mathbf G_{k_v}$
). In this case, we will write
$\mathbf G_{k_v}$
). In this case, we will write
![]() $\overline {\mathrm M}_{v} = \overline {\mathscr M}_{\!\! v}$
.
$\overline {\mathrm M}_{v} = \overline {\mathscr M}_{\!\! v}$
.
3.3 The Galois cohomology action
For
![]() $\mathbf G$
admissible over k, we let
$\mathbf G$
admissible over k, we let
![]() $\mathbf C$
denote its center and
$\mathbf C$
denote its center and
![]() $\overline {\mathbf G} = \mathbf G/\mathbf C$
its adjoint quotient. For any field extension
$\overline {\mathbf G} = \mathbf G/\mathbf C$
its adjoint quotient. For any field extension
![]() $K/k$
, the group
$K/k$
, the group
![]() $\overline {\mathbf G}(K)$
identifies with the group of inner K-automorphisms of
$\overline {\mathbf G}(K)$
identifies with the group of inner K-automorphisms of
![]() $\mathbf G$
. We denote by
$\mathbf G$
. We denote by
![]() $\delta $
the connecting map in the Galois cohomology exact sequence:
$\delta $
the connecting map in the Galois cohomology exact sequence:
For
![]() $K = k_v$
non-Archimedean, this provides an action of
$K = k_v$
non-Archimedean, this provides an action of
![]() $H^1(k_v, \mathbf C)$
on the local Dynkin diagram
$H^1(k_v, \mathbf C)$
on the local Dynkin diagram
![]() $\Delta _v$
(see [Reference Borel and Prasad4, Sect. 2.8]); the action respects the symmetries of
$\Delta _v$
(see [Reference Borel and Prasad4, Sect. 2.8]); the action respects the symmetries of
![]() $\Delta _v$
so that
$\Delta _v$
so that
![]() $H^1(k_v, \mathbf C) \to \operatorname {\mathrm {Aut}}(\Delta _v)$
. Note in particular that, for
$H^1(k_v, \mathbf C) \to \operatorname {\mathrm {Aut}}(\Delta _v)$
. Note in particular that, for
![]() $\mathbf G_{k_v}$
nonsplit of type
$\mathbf G_{k_v}$
nonsplit of type
![]() $\mathrm {C}_{n+1}$
, we have
$\mathrm {C}_{n+1}$
, we have
![]() $\operatorname {\mathrm {Aut}}(\Delta _v) = 1$
. In the split case, there is exactly one nontrivial symmetry. We denote by
$\operatorname {\mathrm {Aut}}(\Delta _v) = 1$
. In the split case, there is exactly one nontrivial symmetry. We denote by
![]() $\xi $
the induced ‘global’ map
$\xi $
the induced ‘global’ map
![]() $H^1(k, \mathbf C) \to \prod _{v\in \mathcal {V}_k^{\mathrm {f}}} \operatorname {\mathrm {Aut}}(\Delta _v)$
(the image actually lies in the direct product).
$H^1(k, \mathbf C) \to \prod _{v\in \mathcal {V}_k^{\mathrm {f}}} \operatorname {\mathrm {Aut}}(\Delta _v)$
(the image actually lies in the direct product).
Of particular interest to us is the subgroup
![]() $\delta (\overline {\mathbf G}(k))' = \delta (\overline {\mathbf G}(k) \cap \pi (\mathbf G(\mathbb R)))$
(the notation follows [Reference Borel and Prasad4, Sect. 2.8]; recall that we have fixed an inclusion
$\delta (\overline {\mathbf G}(k))' = \delta (\overline {\mathbf G}(k) \cap \pi (\mathbf G(\mathbb R)))$
(the notation follows [Reference Borel and Prasad4, Sect. 2.8]; recall that we have fixed an inclusion
![]() $k \subset \mathbb R$
). We will make use of the following alternative description.
$k \subset \mathbb R$
). We will make use of the following alternative description.
Lemma 3.1. The group
![]() $\delta (\overline {\mathbf G}(k))'$
coincides with the kernel of the diagonal map
$\delta (\overline {\mathbf G}(k))'$
coincides with the kernel of the diagonal map
 $$ \begin{align*} H^1(k, \mathbf C) \to \prod_{v \in \mathcal{V}_k^{\infty}} H^1(k_v, \mathbf C). \end{align*} $$
$$ \begin{align*} H^1(k, \mathbf C) \to \prod_{v \in \mathcal{V}_k^{\infty}} H^1(k_v, \mathbf C). \end{align*} $$
Proof. For
![]() $x \in H^1(k, \mathbf C)$
, we denote by
$x \in H^1(k, \mathbf C)$
, we denote by
![]() $(x_v)_{v\in \mathcal {V}_k^{\infty }}$
its image in
$(x_v)_{v\in \mathcal {V}_k^{\infty }}$
its image in
![]() $\prod _{v\in \mathcal {V}_k^{\infty }} H^1(k_v, \mathbf C)$
. Let us first assume
$\prod _{v\in \mathcal {V}_k^{\infty }} H^1(k_v, \mathbf C)$
. Let us first assume
![]() $x \in \delta (\overline {\mathbf G}(k))'$
. Then for the place
$x \in \delta (\overline {\mathbf G}(k))'$
. Then for the place
![]() $v = \mathrm {id}$
corresponding to the inclusion
$v = \mathrm {id}$
corresponding to the inclusion
![]() $k \subset \mathbb R$
, we have
$k \subset \mathbb R$
, we have
![]() $x_v \in (\delta \circ \pi )(\mathbf G(\mathbb R))$
, which by exactness of equation (3.2) (with
$x_v \in (\delta \circ \pi )(\mathbf G(\mathbb R))$
, which by exactness of equation (3.2) (with
![]() $K = \mathbb R$
) is equivalent to
$K = \mathbb R$
) is equivalent to
![]() $x_v = 1$
. For
$x_v = 1$
. For
![]() $v \neq \mathrm {id}$
, the group
$v \neq \mathrm {id}$
, the group
![]() $\mathbf G(k_v)$
is compact, and in this case, it is known that
$\mathbf G(k_v)$
is compact, and in this case, it is known that
![]() $\pi : \mathbf G(k_v) \to \overline {\mathbf G}(k_v)$
is surjective (see [Reference Platonov and Rapinchuck27, Sect. 3.2: Cor. 3]). Since
$\pi : \mathbf G(k_v) \to \overline {\mathbf G}(k_v)$
is surjective (see [Reference Platonov and Rapinchuck27, Sect. 3.2: Cor. 3]). Since
![]() $x_v \in \delta (\overline {\mathbf G}(k_v))$
, we thus have
$x_v \in \delta (\overline {\mathbf G}(k_v))$
, we thus have
![]() $x_v = 1$
again by the exactness of equation (3.2). Conversely, suppose that x has trivial image in
$x_v = 1$
again by the exactness of equation (3.2). Conversely, suppose that x has trivial image in
![]() $\prod _{v\in \mathcal {V}_k^{\infty }}H^1(k_v, \mathbf C)$
. Then
$\prod _{v\in \mathcal {V}_k^{\infty }}H^1(k_v, \mathbf C)$
. Then
![]() $(x_v)$
has certainly trivial image in
$(x_v)$
has certainly trivial image in
![]() $\prod _{v \in \mathcal {V}_k^{\infty }} H^1(k_v, \mathbf G)$
. But for
$\prod _{v \in \mathcal {V}_k^{\infty }} H^1(k_v, \mathbf G)$
. But for
![]() $\mathbf G$
simply connected the latter identifies with
$\mathbf G$
simply connected the latter identifies with
![]() $H^1(k, \mathbf G)$
by the Hasse principle (see [Reference Platonov and Rapinchuck27, Theorem 6.6]). By exactness of equation (3.2) with
$H^1(k, \mathbf G)$
by the Hasse principle (see [Reference Platonov and Rapinchuck27, Theorem 6.6]). By exactness of equation (3.2) with
![]() $K = k$
, it follows that
$K = k$
, it follows that
![]() $x \in \delta (\overline {\mathbf G}(k))'$
.
$x \in \delta (\overline {\mathbf G}(k))'$
.
Remark 3.2. We will see in Lemma 7.1 that actually
![]() $\mathbf G(k_v) \to \overline {\mathbf G}(k_v)$
is surjective for
$\mathbf G(k_v) \to \overline {\mathbf G}(k_v)$
is surjective for
![]() $v = \mathrm {id}$
as well, which slightly simplifies the proof. We have preferred giving the above proof, which works quite generally when
$v = \mathrm {id}$
as well, which slightly simplifies the proof. We have preferred giving the above proof, which works quite generally when
![]() $\mathbf G$
is simply connected; it appears in [Reference Emery7, Sect. 12.2].
$\mathbf G$
is simply connected; it appears in [Reference Emery7, Sect. 12.2].
4 Principal arithmetic subgroups and volumes
4.1 Principal arithmetic subgroups
For
![]() $\mathbf G$
an admissible k-group, we will denote by
$\mathbf G$
an admissible k-group, we will denote by
![]() $P = (P_v)_{v \in \mathcal {V}_k^{\mathrm {f}}}$
a collection of parahoric subgroups
$P = (P_v)_{v \in \mathcal {V}_k^{\mathrm {f}}}$
a collection of parahoric subgroups
![]() $P_v \subset \mathbf G(k_v)$
(
$P_v \subset \mathbf G(k_v)$
(
![]() $v \in \mathcal {V}_k^{\mathrm {f}}$
). Such a collection is called coherent if the product
$v \in \mathcal {V}_k^{\mathrm {f}}$
). Such a collection is called coherent if the product
![]() $\prod _{v\in \mathcal {V}_k^{\mathrm {f}}} P_v$
is open in the group
$\prod _{v\in \mathcal {V}_k^{\mathrm {f}}} P_v$
is open in the group
![]() $\mathbf G(\mathbb A_{\mathrm {f}})$
, where
$\mathbf G(\mathbb A_{\mathrm {f}})$
, where
![]() $\mathbb A_{\mathrm {f}}$
denotes the finite adèles of k. This condition implies that
$\mathbb A_{\mathrm {f}}$
denotes the finite adèles of k. This condition implies that
![]() $P_v$
is hyperspecial for all but finitely many
$P_v$
is hyperspecial for all but finitely many
![]() $v \in \mathcal {V}_k^{\mathrm {f}}$
. Moreover, one has that the subgroup
$v \in \mathcal {V}_k^{\mathrm {f}}$
. Moreover, one has that the subgroup
![]() $\Lambda _P = \mathbf G(k) \cap \prod _{v \in \mathcal {V}_k^{\mathrm {f}}} P_v$
is an arithmetic subgroup of
$\Lambda _P = \mathbf G(k) \cap \prod _{v \in \mathcal {V}_k^{\mathrm {f}}} P_v$
is an arithmetic subgroup of
![]() $\mathbf G(k)$
, called principal.
$\mathbf G(k)$
, called principal.
4.2 The normalized Haar measure
The covolume of the principal arithmetic subgroup
![]() $\Lambda _P \subset \mathbf G(k)$
can be computed with Prasad’s volume formula [Reference Prasad28] in terms of the volumes of the parahoric subgroups
$\Lambda _P \subset \mathbf G(k)$
can be computed with Prasad’s volume formula [Reference Prasad28] in terms of the volumes of the parahoric subgroups
![]() $P_v$
(
$P_v$
(
![]() $v\in \mathcal {V}_k^{\mathrm {f}}$
). In the notation of loc. cit., our situation corresponds to the case
$v\in \mathcal {V}_k^{\mathrm {f}}$
). In the notation of loc. cit., our situation corresponds to the case
![]() $\mathbf G_S = \mathbf G(\mathbb R)$
(i.e., S contains a single infinite place corresponding to the inclusion
$\mathbf G_S = \mathbf G(\mathbb R)$
(i.e., S contains a single infinite place corresponding to the inclusion
![]() $k \subset \mathbb R$
). We write
$k \subset \mathbb R$
). We write
![]() $\mu = \mu _S$
for the normalization of the Haar measure on
$\mu = \mu _S$
for the normalization of the Haar measure on
![]() $\mathbf G(\mathbb R)$
used in [Reference Prasad28, Sect. 3.6]. Then for the Euler–Poincaré characteristic (in the sense of C.T.C. Wall) of
$\mathbf G(\mathbb R)$
used in [Reference Prasad28, Sect. 3.6]. Then for the Euler–Poincaré characteristic (in the sense of C.T.C. Wall) of
![]() $\Gamma \subset \mathbf G(\mathbb R)$
, one has
$\Gamma \subset \mathbf G(\mathbb R)$
, one has
![]() $|\chi (\Gamma )| = |\chi (X_u)|\, \mu (\Gamma \backslash \mathbf G(\mathbb R))$
, where
$|\chi (\Gamma )| = |\chi (X_u)|\, \mu (\Gamma \backslash \mathbf G(\mathbb R))$
, where
![]() $X_u$
is the compact dual symmetric space associated with
$X_u$
is the compact dual symmetric space associated with
![]() $\mathbf H^n_{\mathbb H}$
(see [Reference Borel and Prasad4, §4]). Explicitly,
$\mathbf H^n_{\mathbb H}$
(see [Reference Borel and Prasad4, §4]). Explicitly,
![]() $X_u = \operatorname {\mathrm {Sp}}(n+1)/(\operatorname {\mathrm {Sp}}(n) \times \operatorname {\mathrm {Sp}}(1))$
is the quaternionic projective space
$X_u = \operatorname {\mathrm {Sp}}(n+1)/(\operatorname {\mathrm {Sp}}(n) \times \operatorname {\mathrm {Sp}}(1))$
is the quaternionic projective space
![]() $\mathbb H P^n$
, for which
$\mathbb H P^n$
, for which
![]() $\chi (X_u) = n+1$
. Moreover, since the symmetric space of
$\chi (X_u) = n+1$
. Moreover, since the symmetric space of
![]() $\operatorname {\mathrm {Sp}}(n,1)$
has dimension
$\operatorname {\mathrm {Sp}}(n,1)$
has dimension
![]() $4n$
, it follows from [Reference Serre33, Prop. 23] that
$4n$
, it follows from [Reference Serre33, Prop. 23] that
![]() $\chi (\Gamma )$
is positive. Thus,
$\chi (\Gamma )$
is positive. Thus,
4.3 Prasad’s volume formula
To state the volume formula for
![]() $\Lambda _P \subset \mathbf G(k)$
in an explicit way, we need to introduce some notation; we mostly follow [Reference Prasad28]. The symbol
$\Lambda _P \subset \mathbf G(k)$
in an explicit way, we need to introduce some notation; we mostly follow [Reference Prasad28]. The symbol
![]() $\mathscr D_k$
denotes the absolute value of the discriminant of k, and we write
$\mathscr D_k$
denotes the absolute value of the discriminant of k, and we write
![]() $d = [k:\mathbb Q]$
for the degree. For each
$d = [k:\mathbb Q]$
for the degree. For each
![]() $v \in \mathcal {V}_k^{\mathrm {f}}$
, let
$v \in \mathcal {V}_k^{\mathrm {f}}$
, let
![]() $\mathfrak f_v$
be the residue field of
$\mathfrak f_v$
be the residue field of
![]() $k_v$
, and let
$k_v$
, and let
![]() $q_v$
be the cardinality of
$q_v$
be the cardinality of
![]() $\mathfrak f_v$
. For each parahoric subgroup
$\mathfrak f_v$
. For each parahoric subgroup
![]() $P_v$
, the reductive
$P_v$
, the reductive
![]() $\mathfrak f_v$
-group
$\mathfrak f_v$
-group
![]() $\overline {\mathrm M}_{v}$
is defined in Section 3.2. The reductive
$\overline {\mathrm M}_{v}$
is defined in Section 3.2. The reductive
![]() $\mathfrak f_v$
-group corresponding to a hyperspecial parahoric subgroup in the split form of
$\mathfrak f_v$
-group corresponding to a hyperspecial parahoric subgroup in the split form of
![]() $\mathbf G$
is denoted by
$\mathbf G$
is denoted by
![]() $\overline {\mathscr M}_{\!\! v}$
. For all but finitely many
$\overline {\mathscr M}_{\!\! v}$
. For all but finitely many
![]() $v \in \mathcal {V}_k^{\mathrm {f}}$
, we have that
$v \in \mathcal {V}_k^{\mathrm {f}}$
, we have that
![]() $P_v$
is hyperspecial and thus
$P_v$
is hyperspecial and thus
![]() $\overline {\mathrm M}_{v} \cong \overline {\mathscr M}_{\!\! v}$
. In our situation, Prasad’s volume formula [Reference Prasad28, Theorem 3.7] takes the following form (note that in our case
$\overline {\mathrm M}_{v} \cong \overline {\mathscr M}_{\!\! v}$
. In our situation, Prasad’s volume formula [Reference Prasad28, Theorem 3.7] takes the following form (note that in our case
![]() $\ell = k$
since
$\ell = k$
since
![]() $\mathbf G$
is of type
$\mathbf G$
is of type
![]() $\mathrm {C}$
and thus has no outer symmetries):
$\mathrm {C}$
and thus has no outer symmetries):
 $$ \begin{align} \mu(\Lambda_P\backslash \mathbf G(\mathbb R)) &= \mathscr D_k^{\dim \mathbf G /2} \left( \prod_{j = 1}^{n+1} \frac{(2j-1)!}{(2 \pi)^{2j}} \right)^d \mathscr{E}(P), \end{align} $$
$$ \begin{align} \mu(\Lambda_P\backslash \mathbf G(\mathbb R)) &= \mathscr D_k^{\dim \mathbf G /2} \left( \prod_{j = 1}^{n+1} \frac{(2j-1)!}{(2 \pi)^{2j}} \right)^d \mathscr{E}(P), \end{align} $$
where the ‘Euler product’
![]() $\mathscr {E}(P)$
is given by
$\mathscr {E}(P)$
is given by
 $$ \begin{align} \mathscr{E}(P) &= \prod_{v\in\mathcal{V}_k^{\mathrm{f}}} \frac{q_v^{(\dim \overline{\mathrm M}_{v} + \dim \overline{\mathscr M}_{\!\! v})/2}}{|\overline{\mathrm M}_{v}(\mathfrak f_v)|}. \end{align} $$
$$ \begin{align} \mathscr{E}(P) &= \prod_{v\in\mathcal{V}_k^{\mathrm{f}}} \frac{q_v^{(\dim \overline{\mathrm M}_{v} + \dim \overline{\mathscr M}_{\!\! v})/2}}{|\overline{\mathrm M}_{v}(\mathfrak f_v)|}. \end{align} $$
4.4 The Euler product and zeta functions
Let T be the finite set of places
![]() $v \in \mathcal {V}_k^{\mathrm {f}}$
such that
$v \in \mathcal {V}_k^{\mathrm {f}}$
such that
![]() $P_v$
is not hyperspecial. For
$P_v$
is not hyperspecial. For
![]() $v \not \in T$
, we have that
$v \not \in T$
, we have that
![]() $\overline {\mathrm M}_{v} \cong \overline {\mathscr M}_{\!\! v}$
, which is an
$\overline {\mathrm M}_{v} \cong \overline {\mathscr M}_{\!\! v}$
, which is an
![]() $\mathfrak f_v$
-split simple group of type
$\mathfrak f_v$
-split simple group of type
![]() $\mathrm {C}_{n+1}$
, for which
$\mathrm {C}_{n+1}$
, for which
![]() $|\overline {\mathscr M}_{\!\! v}(\mathfrak f_v)| = q_v^{(n+1)^2} \prod _{j=1}^{n+1}(q_v^{2j} -1)$
(see [Reference Ono24, Tab. 1]), and
$|\overline {\mathscr M}_{\!\! v}(\mathfrak f_v)| = q_v^{(n+1)^2} \prod _{j=1}^{n+1}(q_v^{2j} -1)$
(see [Reference Ono24, Tab. 1]), and
![]() $\dim \overline {\mathscr M}_{\!\! v} = \dim \mathbf G = (n+1)(2n+3)$
. By a direct computation, we may rewrite
$\dim \overline {\mathscr M}_{\!\! v} = \dim \mathbf G = (n+1)(2n+3)$
. By a direct computation, we may rewrite
![]() $\mathscr {E}(P)$
as the following:
$\mathscr {E}(P)$
as the following:
 $$ \begin{align} \mathscr{E}(P) &= \prod_{v \in T} e'(P_v) \prod_{v \in \mathcal{V}_k^{\mathrm{f}}} \nonumber \frac{q_v^{\dim \overline{\mathscr M}_{\!\! v}}}{|\overline{\mathscr M}_{\!\! v}(\mathfrak f_v)|}\\ &= \prod_{v \in T} e'(P_v) \prod_{v \in \mathcal{V}_k^{\mathrm{f}}} \prod_{j=1}^{n+1} \frac{1}{1 - q_v^{-2j}} \nonumber \\ &= \prod_{v \in T} e'(P_v) \prod_{j=1}^{n+1} \zeta_k(2j), \end{align} $$
$$ \begin{align} \mathscr{E}(P) &= \prod_{v \in T} e'(P_v) \prod_{v \in \mathcal{V}_k^{\mathrm{f}}} \nonumber \frac{q_v^{\dim \overline{\mathscr M}_{\!\! v}}}{|\overline{\mathscr M}_{\!\! v}(\mathfrak f_v)|}\\ &= \prod_{v \in T} e'(P_v) \prod_{v \in \mathcal{V}_k^{\mathrm{f}}} \prod_{j=1}^{n+1} \frac{1}{1 - q_v^{-2j}} \nonumber \\ &= \prod_{v \in T} e'(P_v) \prod_{j=1}^{n+1} \zeta_k(2j), \end{align} $$
where
![]() $\zeta _k$
is the Dedekind zeta function of k, and the correcting factors
$\zeta _k$
is the Dedekind zeta function of k, and the correcting factors
![]() $e'(P_v)$
(so called ‘lambda factors’ in [Reference Belolipetsky and Emery3]) are given by
$e'(P_v)$
(so called ‘lambda factors’ in [Reference Belolipetsky and Emery3]) are given by
 $$ \begin{align} e'(P_v) &= q_v^{(\dim \overline{\mathrm M}_{v} - \dim \overline{\mathscr M}_{\!\! v})/2} \frac{|\overline{\mathscr M}_{\!\! v}(\mathfrak f_v)|}{|\overline{\mathrm M}_{v}(\mathfrak f_v)|}. \end{align} $$
$$ \begin{align} e'(P_v) &= q_v^{(\dim \overline{\mathrm M}_{v} - \dim \overline{\mathscr M}_{\!\! v})/2} \frac{|\overline{\mathscr M}_{\!\! v}(\mathfrak f_v)|}{|\overline{\mathrm M}_{v}(\mathfrak f_v)|}. \end{align} $$
Putting together equations (4.1), (4.2) and (4.4), we can finally write (where the second line is obtained from the functional equation of
![]() $\zeta _k$
; see [Reference Neukirch22, Ch.VII (5.11)]):
$\zeta _k$
; see [Reference Neukirch22, Ch.VII (5.11)]):
 $$ \begin{align} \chi(\Lambda_P) &= (n+1) \mathscr D_k^{\dim \mathbf G /2} \prod_{v \in T} e'(P_v) \prod_{j=1}^{n+1} \left(\frac{(2j-1)!}{(2 \pi)^{2j}}\right)^d \zeta_k(2j) \end{align} $$
$$ \begin{align} \chi(\Lambda_P) &= (n+1) \mathscr D_k^{\dim \mathbf G /2} \prod_{v \in T} e'(P_v) \prod_{j=1}^{n+1} \left(\frac{(2j-1)!}{(2 \pi)^{2j}}\right)^d \zeta_k(2j) \end{align} $$
 $$ \begin{align} &= (n+1) \prod_{v \in T} e'(P_v) \prod_{j=1}^{n+1} 2^{-d} |\zeta_k(1-2j)|.\qquad\end{align} $$
$$ \begin{align} &= (n+1) \prod_{v \in T} e'(P_v) \prod_{j=1}^{n+1} 2^{-d} |\zeta_k(1-2j)|.\qquad\end{align} $$
4.5 The nonsplit local factors
We compute in the following lemma the local factors
![]() $e'(P_v)$
of interest to us.
$e'(P_v)$
of interest to us.
Lemma 4.1. Suppose that
![]() $\mathbf G_{k_v}$
is nonsplit, and let
$\mathbf G_{k_v}$
is nonsplit, and let
![]() $P^t_v \subset \mathbf G(k_v)$
be a special parahoric subgroup of type
$P^t_v \subset \mathbf G(k_v)$
be a special parahoric subgroup of type
![]() $\Delta _v \smallsetminus \left \{ \alpha _t \right \}$
(assuming n odd if
$\Delta _v \smallsetminus \left \{ \alpha _t \right \}$
(assuming n odd if
![]() $t=1$
). Then
$t=1$
). Then
 $$ \begin{align} e'(P^0_v) &= \prod_{j=1}^{n+1} (q_v^j + (-1)^j); \end{align} $$
$$ \begin{align} e'(P^0_v) &= \prod_{j=1}^{n+1} (q_v^j + (-1)^j); \end{align} $$
 $$ \begin{align} e'(P^1_v) &= \frac{\prod_{j=1}^{2m} (q_v^{2j}-1)}{\prod_{j=1}^m(q_v^{4j} -1)}, \end{align} $$
$$ \begin{align} e'(P^1_v) &= \frac{\prod_{j=1}^{2m} (q_v^{2j}-1)}{\prod_{j=1}^m(q_v^{4j} -1)}, \end{align} $$
where
![]() $n+1 = 2m$
in the latter.
$n+1 = 2m$
in the latter.
Remark 4.2. Note that
![]() $e'(P_v^1)$
is clearly an integer. The fact that
$e'(P_v^1)$
is clearly an integer. The fact that
![]() $P^1_v$
has larger volume than
$P^1_v$
has larger volume than
![]() $P^0_v$
(see Section 3.1) is reflected by the fact that
$P^0_v$
(see Section 3.1) is reflected by the fact that
![]() $e'(P^1_v)$
is smaller than
$e'(P^1_v)$
is smaller than
![]() $e'(P^0_v)$
; this inequality can be checked empirically (and probably rigorously with some effort) from the formulas in Lemma 4.1. One may notice that, as polynomials in
$e'(P^0_v)$
; this inequality can be checked empirically (and probably rigorously with some effort) from the formulas in Lemma 4.1. One may notice that, as polynomials in
![]() $q_v$
, these two local factors have quite similar order of magnitude though.
$q_v$
, these two local factors have quite similar order of magnitude though.
Proof. The definition of
![]() $e'(P^t_v)$
is given in equation (4.5). The dimension and order for
$e'(P^t_v)$
is given in equation (4.5). The dimension and order for
![]() $\overline {\mathscr M}_{\!\! v}$
are given in Section 4.4. We obtain the description of
$\overline {\mathscr M}_{\!\! v}$
are given in Section 4.4. We obtain the description of
![]() $\overline {\mathrm M}_{v}$
(see Section 3.2) in each case by [Reference Tits37, Sec. 3.5.2]. We refer to [Reference Ono24, Tab. 1] for the order of the classical finite simple groups. For
$\overline {\mathrm M}_{v}$
(see Section 3.2) in each case by [Reference Tits37, Sec. 3.5.2]. We refer to [Reference Ono24, Tab. 1] for the order of the classical finite simple groups. For
![]() $P_v^0$
, we have that
$P_v^0$
, we have that
![]() $\overline {\mathrm M}_{v}$
is given as an almost direct product
$\overline {\mathrm M}_{v}$
is given as an almost direct product
![]() $\overline {\mathrm M}_{v} = T \cdot H$
, where T is a nonsplit one-dimensional torus, and H is a simple of type
$\overline {\mathrm M}_{v} = T \cdot H$
, where T is a nonsplit one-dimensional torus, and H is a simple of type
![]() $^2\mathrm {A}_n$
. In particular,
$^2\mathrm {A}_n$
. In particular,
![]() $\dim \overline {\mathrm M}_{v} = (n+1)^2$
, and
$\dim \overline {\mathrm M}_{v} = (n+1)^2$
, and
![]() $|T(\mathfrak f_v)| =q_v+1$
. By Lang’s isogeny theorem, we have
$|T(\mathfrak f_v)| =q_v+1$
. By Lang’s isogeny theorem, we have
![]() $|\overline {\mathrm M}_{v}(\mathfrak f_v)| = (q_v + 1) |H(\mathfrak f_v)|$
, and the formula for
$|\overline {\mathrm M}_{v}(\mathfrak f_v)| = (q_v + 1) |H(\mathfrak f_v)|$
, and the formula for
![]() $e'(P_v^0)$
now follows from a straightforward computation. Note that, for
$e'(P_v^0)$
now follows from a straightforward computation. Note that, for
![]() $n = 2$
, the local index
$n = 2$
, the local index
![]() $^2\mathrm {C}_3$
needs to be listed separately (see [Reference Tits37, p.63]); however, the description for
$^2\mathrm {C}_3$
needs to be listed separately (see [Reference Tits37, p.63]); however, the description for
![]() $\overline {\mathrm M}_{v}$
is similar, and the formula remains the same.
$\overline {\mathrm M}_{v}$
is similar, and the formula remains the same.
For
![]() $P_v^1$
with
$P_v^1$
with
![]() $n+1 = 2m$
, we have that
$n+1 = 2m$
, we have that
![]() $\overline {\mathrm M}_{v}$
is obtained by Weil restriction of scalars as
$\overline {\mathrm M}_{v}$
is obtained by Weil restriction of scalars as
![]() $\overline {\mathrm M}_{v} = \mathrm {Res}_{\mathfrak {k}_v/\mathfrak f_v}(H)$
, where H is simple of type
$\overline {\mathrm M}_{v} = \mathrm {Res}_{\mathfrak {k}_v/\mathfrak f_v}(H)$
, where H is simple of type
![]() $\mathrm {C}_m$
and
$\mathrm {C}_m$
and
![]() $\mathfrak {k}_v/\mathfrak f_v$
is quadratic (i.e.,
$\mathfrak {k}_v/\mathfrak f_v$
is quadratic (i.e.,
![]() $\mathfrak {k}_v$
has cardinality
$\mathfrak {k}_v$
has cardinality
![]() $q_v^2$
). Thus,
$q_v^2$
). Thus,
![]() $\overline {\mathrm M}_{v}$
has twice the dimension of H, which is
$\overline {\mathrm M}_{v}$
has twice the dimension of H, which is
![]() $m(2m+1)$
, and
$m(2m+1)$
, and
![]() $|\overline {\mathrm M}_{v}(\mathfrak f_v)| = |H(\mathfrak {k}_v)|$
. The result for
$|\overline {\mathrm M}_{v}(\mathfrak f_v)| = |H(\mathfrak {k}_v)|$
. The result for
![]() $e'(P_v^1)$
follows directly.
$e'(P_v^1)$
follows directly.
5 Stabilizers of Hermitian lattices
In this section, we obtain the covolume of the lattices
![]() $\Gamma ^0_n$
and
$\Gamma ^0_n$
and
![]() $\Delta _n$
in
$\Delta _n$
in
![]() $\operatorname {\mathrm {Sp}}(n,1)$
as a consequence of Theorem 5.4. To prove the latter, we first need to study the structure of the stabilizers of Hermitian lattices; this is done in Section 5.1 and 5.2. In those sections, R will denote an integral domain containing the ring of integers
$\operatorname {\mathrm {Sp}}(n,1)$
as a consequence of Theorem 5.4. To prove the latter, we first need to study the structure of the stabilizers of Hermitian lattices; this is done in Section 5.1 and 5.2. In those sections, R will denote an integral domain containing the ring of integers
![]() $\mathcal O_k$
, and K will be the field of fractions of R.
$\mathcal O_k$
, and K will be the field of fractions of R.
5.1 Hermitian lattices over orders
Let us fix an order
![]() $\mathcal O_D$
in an admissible quaternion k-algebra D, and consider the right
$\mathcal O_D$
in an admissible quaternion k-algebra D, and consider the right
![]() $\mathcal O_D$
-module
$\mathcal O_D$
-module
![]() $L = \mathcal O_D^{n+1}$
. We set
$L = \mathcal O_D^{n+1}$
. We set
![]() $\mathcal O_{D, R} = \mathcal O_D \otimes _{\mathcal O_k} R$
. Then
$\mathcal O_{D, R} = \mathcal O_D \otimes _{\mathcal O_k} R$
. Then
![]() $L_R = L \otimes _{\mathcal O_k} R$
is a right
$L_R = L \otimes _{\mathcal O_k} R$
is a right
![]() $\mathcal O_{D,R}$
-module. Consider a Hermitian form h on L, described as follows:
$\mathcal O_{D,R}$
-module. Consider a Hermitian form h on L, described as follows:
 $$ \begin{align} h(x, y) &= \sum_{i=0}^n a_i \overline{x}_i y_i, \end{align} $$
$$ \begin{align} h(x, y) &= \sum_{i=0}^n a_i \overline{x}_i y_i, \end{align} $$
where the coefficients
![]() $a_i$
are taken in
$a_i$
are taken in
![]() $\mathcal O_k$
. Note that the standard involution on D restricts to
$\mathcal O_k$
. Note that the standard involution on D restricts to
![]() $\mathcal O_D$
(use the trace) so that
$\mathcal O_D$
(use the trace) so that
![]() $(L, h)$
is indeed a Hermitian module in the sense of [Reference Scharlau32, Ch. 7] (and so is
$(L, h)$
is indeed a Hermitian module in the sense of [Reference Scharlau32, Ch. 7] (and so is
![]() $(L_R, h)$
for any ring extension R of
$(L_R, h)$
for any ring extension R of
![]() $\mathcal O_k$
). We write
$\mathcal O_k$
). We write
![]() $V = L_k = D^{n+1}$
, and we will assume that
$V = L_k = D^{n+1}$
, and we will assume that
![]() $(V, h)$
is admissible. We say in this case that the module
$(V, h)$
is admissible. We say in this case that the module
![]() $(L, h)$
itself is admissible.
$(L, h)$
itself is admissible.
Recall that by definition the Hermitian module
![]() $(L_R, h)$
is regular (or nonsingular) if the map
$(L_R, h)$
is regular (or nonsingular) if the map
![]() $\phi _h: x \mapsto h(x, \cdot )$
induces an isomorphism of
$\phi _h: x \mapsto h(x, \cdot )$
induces an isomorphism of
![]() $\mathcal O_{D,R}$
-modules from
$\mathcal O_{D,R}$
-modules from
![]() $L_R$
onto its dual module
$L_R$
onto its dual module
![]() $(L_R)^*$
, seen as a right module via
$(L_R)^*$
, seen as a right module via
![]() $f \alpha = \overline {\alpha } f$
(see [Reference Scharlau32, Sect. 7.1]). When R is a field this is equivalent to
$f \alpha = \overline {\alpha } f$
(see [Reference Scharlau32, Sect. 7.1]). When R is a field this is equivalent to
![]() $(L_R, h)$
being nondegenerate, i.e.,
$(L_R, h)$
being nondegenerate, i.e.,
![]() $(L_R)^{\perp } = 0$
. For more general R, we will need the following result.
$(L_R)^{\perp } = 0$
. For more general R, we will need the following result.
Lemma 5.1. If the coefficients of h are invertible in R (i.e.,
![]() $a_i \in R^{\times }$
for
$a_i \in R^{\times }$
for
![]() $i = 0,\dots , n$
), then the Hermitian module
$i = 0,\dots , n$
), then the Hermitian module
![]() $(L_R, h)$
is regular.
$(L_R, h)$
is regular.
Proof. Let
![]() $\left \{ \mathbf {e}_i \right \}$
be the standard basis of
$\left \{ \mathbf {e}_i \right \}$
be the standard basis of
![]() $L_R = \mathcal O_{D,R}^{n+1}$
, and let
$L_R = \mathcal O_{D,R}^{n+1}$
, and let
![]() $\left \{ \mathbf {e}_i^* \right \} \subset (L_R)^*$
be the associated dual basis. We have
$\left \{ \mathbf {e}_i^* \right \} \subset (L_R)^*$
be the associated dual basis. We have
![]() $\phi _h(\mathbf {e}_i) = a_i \mathbf {e}^*_i = \mathbf {e}^*_i a_i$
(note that
$\phi _h(\mathbf {e}_i) = a_i \mathbf {e}^*_i = \mathbf {e}^*_i a_i$
(note that
![]() $a_i = \overline {a}_i$
since
$a_i = \overline {a}_i$
since
![]() $a_i \in \mathcal O_k$
). The map
$a_i \in \mathcal O_k$
). The map
![]() $\mathbf {e}_i^* \mapsto \mathbf {e}_i a_i^{-1}$
from
$\mathbf {e}_i^* \mapsto \mathbf {e}_i a_i^{-1}$
from
![]() $(L_R)^*$
to
$(L_R)^*$
to
![]() $L_R$
is then inverse to
$L_R$
is then inverse to
![]() $\phi _h$
.
$\phi _h$
.
5.2 A key lemma
For
![]() $(L, h)$
and
$(L, h)$
and
![]() $(V, h)$
as above, consider the stabilizer of L in
$(V, h)$
as above, consider the stabilizer of L in
![]() $\mathbf G(k) = \operatorname {\mathrm {\mathbf {U}}}(V, h)$
, i.e., the subgroup
$\mathbf G(k) = \operatorname {\mathrm {\mathbf {U}}}(V, h)$
, i.e., the subgroup
This is an arithmetic subgroup of
![]() $\mathbf G(k)$
. More generally, we will denote by
$\mathbf G(k)$
. More generally, we will denote by
![]() $\operatorname {\mathrm {\mathbf {U}}}(L_R, h) \subset \mathbf G(K)$
the stabilizer of
$\operatorname {\mathrm {\mathbf {U}}}(L_R, h) \subset \mathbf G(K)$
the stabilizer of
![]() $L_R \subset V_K$
. The following lemma is the key result that will be used in Section 5.3.
$L_R \subset V_K$
. The following lemma is the key result that will be used in Section 5.3.
Lemma 5.2. Assume that the following conditions hold:
-
1. R is a principal ideal domain;
-
2.
 $\mathcal O_{D,R}$
splits, i.e.,
$\mathcal O_{D,R}$
splits, i.e.,
 $\mathcal O_{D,R} \cong M_2(R)$
;
$\mathcal O_{D,R} \cong M_2(R)$
; -
3. the hermitian module
 $(L_R, h)$
is regular.
$(L_R, h)$
is regular.
Then there is an isomorphism
![]() $\phi : \operatorname {\mathrm {\mathbf {U}}}(V_K, h) \to \operatorname {\mathrm {Sp}}_{2n+2}(K)$
such that
$\phi : \operatorname {\mathrm {\mathbf {U}}}(V_K, h) \to \operatorname {\mathrm {Sp}}_{2n+2}(K)$
such that
![]() $\phi (\operatorname {\mathrm {\mathbf {U}}}(L_R, h)) = \operatorname {\mathrm {Sp}}_{2n+2}(R)$
.
$\phi (\operatorname {\mathrm {\mathbf {U}}}(L_R, h)) = \operatorname {\mathrm {Sp}}_{2n+2}(R)$
.
Proof. We adapt the discussion from [Reference Scharlau32, pp. 361-362] (which considers skew-Hermitian spaces, only over fields) to our setting. First, we may fix an identification
![]() $\mathcal O_{D, R} = M_2(R)$
; the standard involution is then given by
$\mathcal O_{D, R} = M_2(R)$
; the standard involution is then given by
 $$ \begin{align} \overline{\left(\begin{array}{cc}a & b \\ c & d \end{array}\right)} &= \left(\begin{array}{cc}d & -b \\ -c & a \end{array}\right). \end{align} $$
$$ \begin{align} \overline{\left(\begin{array}{cc}a & b \\ c & d \end{array}\right)} &= \left(\begin{array}{cc}d & -b \\ -c & a \end{array}\right). \end{align} $$
Let
 $e_1 = \left (\begin {array}{cc}1 & 0 \\ 0 & 0 \end {array}\right )$
and
$e_1 = \left (\begin {array}{cc}1 & 0 \\ 0 & 0 \end {array}\right )$
and
 $e_2 = \left (\begin {array}{cc}0 & 0 \\ 0 & 1 \end {array}\right )$
so that
$e_2 = \left (\begin {array}{cc}0 & 0 \\ 0 & 1 \end {array}\right )$
so that
![]() $V_K$
has the following splitting:
$V_K$
has the following splitting:
![]() $V_K = V_K e_1 \oplus V_K e_2$
. We set
$V_K = V_K e_1 \oplus V_K e_2$
. We set
![]() $V_1 = V_K e_1$
. As for loc. cit., we obtain from h a bilinear form
$V_1 = V_K e_1$
. As for loc. cit., we obtain from h a bilinear form
![]() $b_h$
on
$b_h$
on
![]() $V_1$
determined by
$V_1$
determined by
 $$ \begin{align} h(x e_1, y e_1) = \left(\begin{array}{cc}0 & 0 \\ b_h(x e_1, y e_1) & 0 \end{array}\right), \end{align} $$
$$ \begin{align} h(x e_1, y e_1) = \left(\begin{array}{cc}0 & 0 \\ b_h(x e_1, y e_1) & 0 \end{array}\right), \end{align} $$
and in our case,
![]() $b_h$
is easily seen to be antisymmetric. Since
$b_h$
is easily seen to be antisymmetric. Since
![]() $(L_R, h)$
is a Hermitian module, the form
$(L_R, h)$
is a Hermitian module, the form
![]() $b_h$
actually restricts to a bilinear (antisymmetric) form on the R-lattice
$b_h$
actually restricts to a bilinear (antisymmetric) form on the R-lattice
![]() $L_1 = L_R e_1$
of
$L_1 = L_R e_1$
of
![]() $V_1$
. Note that
$V_1$
. Note that
![]() $L_1$
is free over R of rank
$L_1$
is free over R of rank
![]() $2n+2$
. If
$2n+2$
. If
![]() $f \in L_1^*$
, then we can extend f to
$f \in L_1^*$
, then we can extend f to
![]() $L_R$
by setting for any
$L_R$
by setting for any
![]() $x \in L_R$
:
$x \in L_R$
:
where
 $e = \left (\begin {array}{cc}0 & 1 \\ 1 & 0 \end {array}\right )$
. One computes that this is indeed an extension, which is actually
$e = \left (\begin {array}{cc}0 & 1 \\ 1 & 0 \end {array}\right )$
. One computes that this is indeed an extension, which is actually
![]() $\mathcal O_{D,R}$
-linear, i.e.,
$\mathcal O_{D,R}$
-linear, i.e.,
![]() $\tilde {f} \in (L_R)^*$
. In particular, we have that the symplectic module
$\tilde {f} \in (L_R)^*$
. In particular, we have that the symplectic module
![]() $(L_1, b_h)$
is regular, as
$(L_1, b_h)$
is regular, as
![]() $(L_R, h)$
itself is assumed to be regular. Since by assumption R is a principal ideal domain (PID), we can now deduce that
$(L_R, h)$
itself is assumed to be regular. Since by assumption R is a principal ideal domain (PID), we can now deduce that
![]() $(L_1, h)$
is a orthogonal sum of hyperbolic modules (see, for instance, [Reference Kirkwood and McDonald16, Prop. 2.1]), and thus, its isometry group is isomorphic to
$(L_1, h)$
is a orthogonal sum of hyperbolic modules (see, for instance, [Reference Kirkwood and McDonald16, Prop. 2.1]), and thus, its isometry group is isomorphic to
![]() $\operatorname {\mathrm {Sp}}_{2n+2}(R)$
.
$\operatorname {\mathrm {Sp}}_{2n+2}(R)$
.
An analogous formula to equation (5.5) can be used to extend any isometry
![]() $\sigma $
of
$\sigma $
of
![]() $(L_1, h)$
to an isometry
$(L_1, h)$
to an isometry
![]() $\tilde {\sigma } \in \operatorname {\mathrm {\mathbf {U}}}(L_R, h)$
(see [Reference Scharlau32, p.362]). This shows that
$\tilde {\sigma } \in \operatorname {\mathrm {\mathbf {U}}}(L_R, h)$
(see [Reference Scharlau32, p.362]). This shows that
![]() $g \mapsto g|_{L_1}$
yields an isomorphism from
$g \mapsto g|_{L_1}$
yields an isomorphism from
![]() $\operatorname {\mathrm {\mathbf {U}}}(L_R, h)$
to
$\operatorname {\mathrm {\mathbf {U}}}(L_R, h)$
to
![]() $\operatorname {\mathrm {Sp}}_{2n+2}(R)$
. The same construction with
$\operatorname {\mathrm {Sp}}_{2n+2}(R)$
. The same construction with
![]() $R = K$
thus provides the isomorphism
$R = K$
thus provides the isomorphism
![]() $\phi $
in the statement.
$\phi $
in the statement.
5.3 The local structure of lattice stabilizers
Let again
![]() $(L, h)$
denote an admissible lattice over
$(L, h)$
denote an admissible lattice over
![]() $\mathcal O_D$
, with D defined over the number field k and
$\mathcal O_D$
, with D defined over the number field k and
![]() $\mathcal O_D \subset D$
an order. The following (nonstandard) terminology will be convenient for us.
$\mathcal O_D \subset D$
an order. The following (nonstandard) terminology will be convenient for us.
Definition 5.3. We say that
![]() $(L, h)$
is of maximal type if
$(L, h)$
is of maximal type if
![]() $\mathcal O_D$
is maximal and
$\mathcal O_D$
is maximal and
![]() $(L, h)$
is regular.
$(L, h)$
is regular.
Remark 5.4. Given D, the existence of an admissible
![]() $(L, h)$
of maximal type does not seem to be obvious (and we believe that it is wrong in general).
$(L, h)$
of maximal type does not seem to be obvious (and we believe that it is wrong in general).
For each finite place
![]() $v \in \mathcal {V}_k^{\mathrm {f}}$
, we shall abbreviate the notation from Section 5.1 (with
$v \in \mathcal {V}_k^{\mathrm {f}}$
, we shall abbreviate the notation from Section 5.1 (with
![]() $R = \mathfrak o_v$
) as follows:
$R = \mathfrak o_v$
) as follows:
![]() $L_v = L_{\mathfrak o_v}$
. As above,
$L_v = L_{\mathfrak o_v}$
. As above,
![]() $\mathcal {R}$
denotes the set of finite places
$\mathcal {R}$
denotes the set of finite places
![]() $v \in \mathcal {V}_k^{\mathrm {f}}$
, where
$v \in \mathcal {V}_k^{\mathrm {f}}$
, where
![]() $D_v$
ramifies, and
$D_v$
ramifies, and
![]() $\mathbf G = \operatorname {\mathrm {\mathbf {U}}}(V, h)$
.
$\mathbf G = \operatorname {\mathrm {\mathbf {U}}}(V, h)$
.
Lemma 5.5. Assume that
![]() $(L, h)$
is of maximal type, and let
$(L, h)$
is of maximal type, and let
![]() $v \in \mathcal {V}_k^{\mathrm {f}}$
be a finite place with
$v \in \mathcal {V}_k^{\mathrm {f}}$
be a finite place with
![]() $v \notin \mathcal {R}$
. Then
$v \notin \mathcal {R}$
. Then
![]() $\operatorname {\mathrm {\mathbf {U}}}(L_v, h)$
is a hyperspecial parahoric subgroup in
$\operatorname {\mathrm {\mathbf {U}}}(L_v, h)$
is a hyperspecial parahoric subgroup in
![]() $\mathbf G(k_v) \cong \operatorname {\mathrm {Sp}}_{2n+2}(k_v)$
.
$\mathbf G(k_v) \cong \operatorname {\mathrm {Sp}}_{2n+2}(k_v)$
.
Proof. The order
![]() $\mathcal O_{D, \mathfrak o_v}$
, being maximal in
$\mathcal O_{D, \mathfrak o_v}$
, being maximal in
![]() $D_v \cong M_2(k_v)$
, must be conjugate to
$D_v \cong M_2(k_v)$
, must be conjugate to
![]() $M_2(\mathfrak o_v)$
(see [Reference Maclachlan and Reid19, Ch. 6]). Thus, we can apply Lemma 5.2: It implies that
$M_2(\mathfrak o_v)$
(see [Reference Maclachlan and Reid19, Ch. 6]). Thus, we can apply Lemma 5.2: It implies that
![]() $\operatorname {\mathrm {\mathbf {U}}}(L_v, h)$
identifies with
$\operatorname {\mathrm {\mathbf {U}}}(L_v, h)$
identifies with
![]() $\operatorname {\mathrm {Sp}}_{2n+2}(\mathfrak o_v)$
, which is hyperspecial parahoric by [Reference Tits37, Sect. 3.4.2].
$\operatorname {\mathrm {Sp}}_{2n+2}(\mathfrak o_v)$
, which is hyperspecial parahoric by [Reference Tits37, Sect. 3.4.2].
We now turn our attention to the case of places where D ramifies.
Lemma 5.6. For
![]() $(L, h)$
of maximal type and
$(L, h)$
of maximal type and
![]() $v \in \mathcal {R}$
, the subgroup
$v \in \mathcal {R}$
, the subgroup
![]() $\operatorname {\mathrm {\mathbf {U}}}(L_v, h)$
is a special parahoric subgroup in
$\operatorname {\mathrm {\mathbf {U}}}(L_v, h)$
is a special parahoric subgroup in
![]() $\mathbf G(k_v)$
of type
$\mathbf G(k_v)$
of type
![]() $\Delta _v \smallsetminus \left \{ \alpha _0 \right \}$
.
$\Delta _v \smallsetminus \left \{ \alpha _0 \right \}$
.
Proof. Let
![]() $\widehat {k}_v$
be the maximal unramified extension of
$\widehat {k}_v$
be the maximal unramified extension of
![]() $k_v$
, with ring of integers
$k_v$
, with ring of integers
![]() $\widehat {\mathfrak o}_v$
. Let
$\widehat {\mathfrak o}_v$
. Let
![]() $\mathcal O_{D,v} = \mathcal O_{D, \mathfrak o_v}$
and
$\mathcal O_{D,v} = \mathcal O_{D, \mathfrak o_v}$
and
![]() $\widehat {\mathcal O} = \mathcal O_{D,v} \otimes _{\mathfrak o_v} \widehat {\mathfrak o}_v$
. The latter in an order in
$\widehat {\mathcal O} = \mathcal O_{D,v} \otimes _{\mathfrak o_v} \widehat {\mathfrak o}_v$
. The latter in an order in
![]() $\widehat {D}_v = D_v \otimes \widehat {k}_v$
, and we consider a maximal order
$\widehat {D}_v = D_v \otimes \widehat {k}_v$
, and we consider a maximal order
![]() $\mathcal O' \subset \widehat {D}_v$
containing
$\mathcal O' \subset \widehat {D}_v$
containing
![]() $\widehat {\mathcal O}$
. That is,
$\widehat {\mathcal O}$
. That is,
Thus
![]() $\mathcal O' \cap D_v$
is an order in
$\mathcal O' \cap D_v$
is an order in
![]() $D_v$
, which equals
$D_v$
, which equals
![]() $\mathcal O_{D,v}$
since the latter is maximal. Note that
$\mathcal O_{D,v}$
since the latter is maximal. Note that
![]() $\widehat {D}_v$
is split (see [Reference Maclachlan and Reid19, Theorem 2.6.5]).
$\widehat {D}_v$
is split (see [Reference Maclachlan and Reid19, Theorem 2.6.5]).
From the inclusions (5.6), we may interpret the subgroup
![]() $P_v = \operatorname {\mathrm {\mathbf {U}}}(L_v, h) \cong \operatorname {\mathrm {\mathbf {U}}}(\mathcal O_{D,v}^{n+1}, h)$
of
$P_v = \operatorname {\mathrm {\mathbf {U}}}(L_v, h) \cong \operatorname {\mathrm {\mathbf {U}}}(\mathcal O_{D,v}^{n+1}, h)$
of
![]() $\mathbf G(k_v)$
as a subgroup of the matrix group
$\mathbf G(k_v)$
as a subgroup of the matrix group
![]() $P_v' = \operatorname {\mathrm {\mathbf {U}}}((\mathcal O')^{n+1}, h)$
. The latter is a hyperspecial parahoric of
$P_v' = \operatorname {\mathrm {\mathbf {U}}}((\mathcal O')^{n+1}, h)$
. The latter is a hyperspecial parahoric of
![]() $\mathbf G(\widehat {k}_v)$
by Lemma 5.5. From the equality
$\mathbf G(\widehat {k}_v)$
by Lemma 5.5. From the equality
![]() $\mathcal O' \cap D_v = \mathcal O_{D,v}$
, we deduce
$\mathcal O' \cap D_v = \mathcal O_{D,v}$
, we deduce
![]() $P_v' \cap \mathbf G(k_v) = P_v$
. But in view of the local indices in Table 3, this means that
$P_v' \cap \mathbf G(k_v) = P_v$
. But in view of the local indices in Table 3, this means that
![]() $P_v$
is a special parahoric subgroup of type
$P_v$
is a special parahoric subgroup of type
![]() $\Delta _v \smallsetminus \left \{ \alpha _0 \right \}$
(since
$\Delta _v \smallsetminus \left \{ \alpha _0 \right \}$
(since
![]() $\alpha _0$
is the unique affine root in
$\alpha _0$
is the unique affine root in
![]() $\Delta _v$
that appears as the restriction of hyperspecial roots of
$\Delta _v$
that appears as the restriction of hyperspecial roots of
![]() $\mathbf G(\widehat {k}_v)$
).
$\mathbf G(\widehat {k}_v)$
).
5.4 The volume formula for the maximal type
Lattices of maximal type are particularly interesting because of the following result. Recall that
![]() $q_v$
denotes the cardinality of the residue field of
$q_v$
denotes the cardinality of the residue field of
![]() $k_v$
(for
$k_v$
(for
![]() $v \in \mathcal {V}_k^{\mathrm {f}}$
). See Definition 5.3 for ‘maximal type’.
$v \in \mathcal {V}_k^{\mathrm {f}}$
). See Definition 5.3 for ‘maximal type’.
Theorem 5.7. Let
![]() $(L, h)$
be an admissible Hermitian
$(L, h)$
be an admissible Hermitian
![]() $\mathcal O_D$
-lattice of maximal type. Then
$\mathcal O_D$
-lattice of maximal type. Then
![]() $\operatorname {\mathrm {\mathbf {U}}}(L, h)$
is a principal arithmetic subgroup of
$\operatorname {\mathrm {\mathbf {U}}}(L, h)$
is a principal arithmetic subgroup of
![]() $\mathbf G(k) = \operatorname {\mathrm {\mathbf {U}}}(V, h)$
, and
$\mathbf G(k) = \operatorname {\mathrm {\mathbf {U}}}(V, h)$
, and
 $$ \begin{align} \chi(\operatorname{\mathrm{\mathbf{U}}}(L, h)) &= (n+1) \prod_{j=1}^{n+1} \left( \frac{\zeta_k(1-2j)}{2^{\scriptscriptstyle [k:\mathbb Q]}} \prod_{v \in \mathcal{R}} q_v^j + (-1)^j \right), \end{align} $$
$$ \begin{align} \chi(\operatorname{\mathrm{\mathbf{U}}}(L, h)) &= (n+1) \prod_{j=1}^{n+1} \left( \frac{\zeta_k(1-2j)}{2^{\scriptscriptstyle [k:\mathbb Q]}} \prod_{v \in \mathcal{R}} q_v^j + (-1)^j \right), \end{align} $$
where
![]() $\mathcal {R}$
is the set of finite places where D ramifies.
$\mathcal {R}$
is the set of finite places where D ramifies.
Proof. We can write
![]() $L = V_k \cap \prod _{v \in \mathcal {V}_k^{\mathrm {f}}} L_v$
, from which we obtain (for
$L = V_k \cap \prod _{v \in \mathcal {V}_k^{\mathrm {f}}} L_v$
, from which we obtain (for
![]() $\mathbf G(k)$
diagonally embedded in
$\mathbf G(k)$
diagonally embedded in
![]() $\prod _v \mathbf G(k_v)$
):
$\prod _v \mathbf G(k_v)$
):
 $$ \begin{align*} \operatorname{\mathrm{\mathbf{U}}}(L, h) &= \mathbf G(k) \cap \prod_{v \in \mathcal{V}_k^{\mathrm{f}}} \operatorname{\mathrm{\mathbf{U}}}(L_v, h). \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{\mathbf{U}}}(L, h) &= \mathbf G(k) \cap \prod_{v \in \mathcal{V}_k^{\mathrm{f}}} \operatorname{\mathrm{\mathbf{U}}}(L_v, h). \end{align*} $$
With Lemmas 5.5 and 5.6, this shows that
![]() $\operatorname {\mathrm {\mathbf {U}}}(L, h)$
is principal, and the formula for
$\operatorname {\mathrm {\mathbf {U}}}(L, h)$
is principal, and the formula for
![]() $\chi (\operatorname {\mathrm {\mathbf {U}}}(L, h))$
is deduced from equation (4.7) and Lemma 4.1.
$\chi (\operatorname {\mathrm {\mathbf {U}}}(L, h))$
is deduced from equation (4.7) and Lemma 4.1.
We emphasize the special case of the standard Hermitian form over the Hurwitz integers in the next corollary. It implies the formula in equation (1.2) since we have
![]() $\chi (\Gamma ^0_n) = \chi (\operatorname {\mathrm {Sp}}(n,1, \mathscr H)) / 2$
by construction.
$\chi (\Gamma ^0_n) = \chi (\operatorname {\mathrm {Sp}}(n,1, \mathscr H)) / 2$
by construction.
Corollary 5.8. The arithmetic subgroup
![]() $\operatorname {\mathrm {Sp}}(n,1, \mathscr H)$
is principal, and
$\operatorname {\mathrm {Sp}}(n,1, \mathscr H)$
is principal, and
 $$ \begin{align} \chi(\operatorname{\mathrm{Sp}}(n,1, \mathscr H)) &= (n+1) \prod_{j=1}^{n+1} \frac{2^j + (-1)^j}{4j} |B_{2j}|, \end{align} $$
$$ \begin{align} \chi(\operatorname{\mathrm{Sp}}(n,1, \mathscr H)) &= (n+1) \prod_{j=1}^{n+1} \frac{2^j + (-1)^j}{4j} |B_{2j}|, \end{align} $$
where
![]() $B_m$
is the m-th Bernoulli number.
$B_m$
is the m-th Bernoulli number.
Proof. We have that
![]() $\mathscr H$
is a maximal order in
$\mathscr H$
is a maximal order in
![]() $D = \mathscr H \otimes \mathbb Q = \left ( \frac {-1, -1}{\mathbb Q} \right )$
, and the latter is the quaternion
$D = \mathscr H \otimes \mathbb Q = \left ( \frac {-1, -1}{\mathbb Q} \right )$
, and the latter is the quaternion
![]() $\mathbb Q$
-algebra that ramifies exactly at
$\mathbb Q$
-algebra that ramifies exactly at
![]() $p = 2$
and
$p = 2$
and
![]() $p = \infty $
(see [Reference Vignéras38, p.79]). By Lemma 5.1, it is clear that
$p = \infty $
(see [Reference Vignéras38, p.79]). By Lemma 5.1, it is clear that
![]() $(\mathscr H^{n+1}, h)$
, with h given in equation (1.1), is of maximal type. Thus, we can apply the theorem, and the formula in equation (5.8) follows immediately from the known expression:
$(\mathscr H^{n+1}, h)$
, with h given in equation (1.1), is of maximal type. Thus, we can apply the theorem, and the formula in equation (5.8) follows immediately from the known expression:
5.5 The covolume of
 $\Delta _n$
$\Delta _n$
Let
![]() $L = \mathscr I^{n+1}$
, where
$L = \mathscr I^{n+1}$
, where
![]() $\mathscr I$
is the icosian ring. The Hermitian form equation (1.4) has been chosen so that
$\mathscr I$
is the icosian ring. The Hermitian form equation (1.4) has been chosen so that
![]() $(L, h)$
is of maximal type. By definition,
$(L, h)$
is of maximal type. By definition,
![]() $\Delta _n = \operatorname {\mathrm {\mathbf {U}}}(L, h)$
. The formula in equation (1.5) for
$\Delta _n = \operatorname {\mathrm {\mathbf {U}}}(L, h)$
. The formula in equation (1.5) for
![]() $\chi (\Delta _n)$
is thus an immediate consequence of Theorem 5.7 since in this case
$\chi (\Delta _n)$
is thus an immediate consequence of Theorem 5.7 since in this case
![]() $\mathcal {R} = \emptyset $
(see [Reference Vignéras38, p.150]).
$\mathcal {R} = \emptyset $
(see [Reference Vignéras38, p.150]).
6 The minimality of
 $\chi (\Gamma ^s_n)$
and
$\chi (\Gamma ^s_n)$
and
 $\chi (\Delta _n)$
$\chi (\Delta _n)$
6.1 Normalizers of minimal covolume
Let
![]() $\Gamma \subset \operatorname {\mathrm {Sp}}(n,1)$
be a maximal lattice, i.e., maximal with respect to inclusion as in Section 2.3. We have
$\Gamma \subset \operatorname {\mathrm {Sp}}(n,1)$
be a maximal lattice, i.e., maximal with respect to inclusion as in Section 2.3. We have
![]() $\Gamma \subset \mathbf G(\overline {k} \cap \mathbb R)$
for some admissible k-group
$\Gamma \subset \mathbf G(\overline {k} \cap \mathbb R)$
for some admissible k-group
![]() $\mathbf G$
, but the stricter inclusion
$\mathbf G$
, but the stricter inclusion
![]() $\Gamma \subset \mathbf G(k)$
does not hold in general. By [Reference Borel and Prasad4, Prop. 1.4], we have that
$\Gamma \subset \mathbf G(k)$
does not hold in general. By [Reference Borel and Prasad4, Prop. 1.4], we have that
![]() $\Gamma $
is a normalizer
$\Gamma $
is a normalizer
![]() $N_{\mathbf G(\mathbb R)}(\Lambda _P)$
, where
$N_{\mathbf G(\mathbb R)}(\Lambda _P)$
, where
![]() $\Lambda _P \subset \mathbf G(k)$
is a principal arithmetic subgroup.
$\Lambda _P \subset \mathbf G(k)$
is a principal arithmetic subgroup.
Let
![]() $P = (P_v)$
be a coherent collection such that any parahoric subgroup
$P = (P_v)$
be a coherent collection such that any parahoric subgroup
![]() $P_v$
is of maximal volume. Then
$P_v$
is of maximal volume. Then
![]() $\Lambda _P$
is of minimal covolume among arithmetic lattices contained in
$\Lambda _P$
is of minimal covolume among arithmetic lattices contained in
![]() $\mathbf G(k)$
. It is a priori not clear—but turns out to be true—that the normalizer
$\mathbf G(k)$
. It is a priori not clear—but turns out to be true—that the normalizer
![]() $N_{\mathbf G(\mathbb R)}(\Lambda _P)$
for such a choice of P is of minimal covolume in its commensurability class in
$N_{\mathbf G(\mathbb R)}(\Lambda _P)$
for such a choice of P is of minimal covolume in its commensurability class in
![]() $\mathbf G(\mathbb R)$
. This can be proved in the same way as in [Reference Belolipetsky and Emery3, Sect. 4.3] (see also [Reference Emery7, Sect. 12.3] for a more detailed exposition). We state the result in the following lemma. In the rest of this section,
$\mathbf G(\mathbb R)$
. This can be proved in the same way as in [Reference Belolipetsky and Emery3, Sect. 4.3] (see also [Reference Emery7, Sect. 12.3] for a more detailed exposition). We state the result in the following lemma. In the rest of this section,
![]() $\mathcal {R}$
denotes the set of finite places where
$\mathcal {R}$
denotes the set of finite places where
![]() $\mathbf G$
does not split (equivalently, where its defining algebra ramifies).
$\mathbf G$
does not split (equivalently, where its defining algebra ramifies).
Lemma 6.1. The lattice
![]() $\Gamma = N_{\mathbf G(\mathbb R)}(\Lambda _P)$
is of minimal covolume in its commensurability class if and only if the coherent collection
$\Gamma = N_{\mathbf G(\mathbb R)}(\Lambda _P)$
is of minimal covolume in its commensurability class if and only if the coherent collection
![]() $P= (P_v)$
satisfies
$P= (P_v)$
satisfies
-
1.
 $P_v$
is hyperspecial for each
$P_v$
is hyperspecial for each
 $v\notin \mathcal {R}$
; and
$v\notin \mathcal {R}$
; and -
2.
 $P_v$
is special of maximal volume for
$P_v$
is special of maximal volume for
 $v \in \mathcal {R}$
.
$v \in \mathcal {R}$
.
Recall that for
![]() $v \in \mathcal {R}$
a parahoric subgroup
$v \in \mathcal {R}$
a parahoric subgroup
![]() $P_v \subset \mathbf G(k_v)$
is special of maximal volume exactly when it has type
$P_v \subset \mathbf G(k_v)$
is special of maximal volume exactly when it has type
![]() $\Delta _v \smallsetminus \left \{ \alpha _s \right \}$
, where
$\Delta _v \smallsetminus \left \{ \alpha _s \right \}$
, where
![]() $s = n \mod 2$
. Using Lemmas 5.5 and 5.6, we thus have:
$s = n \mod 2$
. Using Lemmas 5.5 and 5.6, we thus have:
Corollary 6.2. Let
![]() $(L, h)$
be an admissible
$(L, h)$
be an admissible
![]() $\mathcal O_D$
-lattice of maximal type. If n is even or
$\mathcal O_D$
-lattice of maximal type. If n is even or
![]() $\mathcal {R} =\emptyset $
, then the lattice
$\mathcal {R} =\emptyset $
, then the lattice
![]() $N_{\operatorname {\mathrm {Sp}}(n,1)}(\operatorname {\mathrm {\mathbf {U}}}(L, h))$
is of minimal covolume in its commensurability class.
$N_{\operatorname {\mathrm {Sp}}(n,1)}(\operatorname {\mathrm {\mathbf {U}}}(L, h))$
is of minimal covolume in its commensurability class.
6.2 The index computation
We will need to estimate the index
![]() $[\Gamma : \Lambda _P]$
for
$[\Gamma : \Lambda _P]$
for
![]() $\Gamma = N_{\mathbf G(\mathbb R)}(\Lambda _P)$
of minimal covolume in its commensurability class. For this, we state the following lemma, which considers a slightly more general situation. The symbol
$\Gamma = N_{\mathbf G(\mathbb R)}(\Lambda _P)$
of minimal covolume in its commensurability class. For this, we state the following lemma, which considers a slightly more general situation. The symbol
![]() $h_k$
denotes the class number of k, and
$h_k$
denotes the class number of k, and
![]() $U_k$
(respectively,
$U_k$
(respectively,
![]() $U_k^+$
) are the units (respectively, totally positive units) in
$U_k^+$
) are the units (respectively, totally positive units) in
![]() $\mathcal O_k$
.
$\mathcal O_k$
.
Lemma 6.3. Let
![]() $P = (P_v)$
such that
$P = (P_v)$
such that
![]() $P_v$
is hyperspecial for any
$P_v$
is hyperspecial for any
![]() $v \in \mathcal {V}_k^{\mathrm {f}} \smallsetminus \mathcal {R}$
. Then
$v \in \mathcal {V}_k^{\mathrm {f}} \smallsetminus \mathcal {R}$
. Then
Proof. We assume the notation of Section 3.3; in particular,
![]() $\mathbf C$
is the center of
$\mathbf C$
is the center of
![]() $\mathbf G$
. We set
$\mathbf G$
. We set
![]() $A = \delta (\overline {\mathbf G}(k))'$
. Let
$A = \delta (\overline {\mathbf G}(k))'$
. Let
![]() $\Theta = (\Theta _v)_{v\in \mathcal {V}_k^{\mathrm {f}}}$
be the type of the coherent collection P. From the assumption, it follows that none of the types
$\Theta = (\Theta _v)_{v\in \mathcal {V}_k^{\mathrm {f}}}$
be the type of the coherent collection P. From the assumption, it follows that none of the types
![]() $\Theta _v$
has symmetries, and thus, the stabilizer of
$\Theta _v$
has symmetries, and thus, the stabilizer of
![]() $\Theta $
in A equals the kernel
$\Theta $
in A equals the kernel
![]() $A_{\xi }$
of
$A_{\xi }$
of
![]() $\xi $
. By [Reference Borel and Prasad4, Prop. 2.9], we thus have the exact sequence
$\xi $
. By [Reference Borel and Prasad4, Prop. 2.9], we thus have the exact sequence
In our case,
![]() $\mathbf C = \mu _2$
, and it follows that the left part vanishes. Hence,
$\mathbf C = \mu _2$
, and it follows that the left part vanishes. Hence,
![]() $[\Gamma :\Lambda _P] = |A_{\xi }|$
. We now use the identification
$[\Gamma :\Lambda _P] = |A_{\xi }|$
. We now use the identification
![]() $H^1(k, \mu _2) = k^{\times }/(k^{\times })^2$
. For
$H^1(k, \mu _2) = k^{\times }/(k^{\times })^2$
. For
![]() $S \subset \mathcal {V}_k^{\mathrm {f}}$
any finite set of places, we define
$S \subset \mathcal {V}_k^{\mathrm {f}}$
any finite set of places, we define
and
![]() $k_2 = k_{2, \emptyset }$
. Since
$k_2 = k_{2, \emptyset }$
. Since
![]() $\operatorname {\mathrm {Aut}}(\Delta _v)$
is trivial for any
$\operatorname {\mathrm {Aut}}(\Delta _v)$
is trivial for any
![]() $v \in \mathcal {R}$
, it follows from [Reference Borel and Prasad4, Prop. 2.7] that
$v \in \mathcal {R}$
, it follows from [Reference Borel and Prasad4, Prop. 2.7] that
![]() $H^1(k, \mathbf C)_{\xi } = k_{2, \mathcal {R}}/(k^{\times })^2$
. See [Reference Borel and Prasad4] for the definitions. For
$H^1(k, \mathbf C)_{\xi } = k_{2, \mathcal {R}}/(k^{\times })^2$
. See [Reference Borel and Prasad4] for the definitions. For
![]() $k_{2, S}^+ \subset k_{2, S}$
denoting the subgroup consisting of totally positive elements, we conclude from Lemma 3.1 that
$k_{2, S}^+ \subset k_{2, S}$
denoting the subgroup consisting of totally positive elements, we conclude from Lemma 3.1 that
![]() $A_{\xi } = k_{2, \mathcal {R}}^+/(k^{\times })^2$
. This group contains
$A_{\xi } = k_{2, \mathcal {R}}^+/(k^{\times })^2$
. This group contains
![]() $k_2^+/(k^{\times })^2$
with index at most
$k_2^+/(k^{\times })^2$
with index at most
![]() $2^{\#\mathcal {R}}$
, and the order of the latter can be bounded by
$2^{\#\mathcal {R}}$
, and the order of the latter can be bounded by
![]() $h_k \cdot |U^+_{k}/U_k^2|$
by using the same argument as in the proof of [Reference Borel and Prasad4, Prop. 0.12].
$h_k \cdot |U^+_{k}/U_k^2|$
by using the same argument as in the proof of [Reference Borel and Prasad4, Prop. 0.12].
The following is obtained as a corollary of the proof.
Corollary 6.4. Let
![]() $k = \mathbb Q$
and
$k = \mathbb Q$
and
![]() $\#\mathcal {R} = 1$
, and assume P as above. Then
$\#\mathcal {R} = 1$
, and assume P as above. Then
![]() $[\Gamma : \Lambda _P] = 2$
.
$[\Gamma : \Lambda _P] = 2$
.
Proof. Let
![]() $\mathcal {R} = \left \{ p \right \}$
, with
$\mathcal {R} = \left \{ p \right \}$
, with
![]() $p>0$
. Lemma 6.3 shows
$p>0$
. Lemma 6.3 shows
![]() $[\Gamma :\Lambda _P] \le 2$
, but on the other hand, p provides a nontrivial element in
$[\Gamma :\Lambda _P] \le 2$
, but on the other hand, p provides a nontrivial element in
![]() $\mathbb Q^+_{2, \mathcal {R}}/(\mathbb Q^{\times })^2$
.
$\mathbb Q^+_{2, \mathcal {R}}/(\mathbb Q^{\times })^2$
.
6.3 The nonuniform lattices
 $\Gamma _n^s$
$\Gamma _n^s$
By definition,
![]() $\Gamma ^0_n = \left < g, \operatorname {\mathrm {Sp}}(n,1, \mathscr H) \right>$
with g of order
$\Gamma ^0_n = \left < g, \operatorname {\mathrm {Sp}}(n,1, \mathscr H) \right>$
with g of order
![]() $2$
that normalizes
$2$
that normalizes
![]() $\operatorname {\mathrm {Sp}}(n,1, \mathscr H)$
. Let D be the defining algebra of
$\operatorname {\mathrm {Sp}}(n,1, \mathscr H)$
. Let D be the defining algebra of
![]() $\Gamma _n^0$
(i.e.,
$\Gamma _n^0$
(i.e.,
![]() $D = \mathscr H \otimes \mathbb Q$
). It ramifies precisely at
$D = \mathscr H \otimes \mathbb Q$
). It ramifies precisely at
![]() $p=2$
and
$p=2$
and
![]() $p=\infty $
. Thus, we can apply Corollary 6.4, and it follows that
$p=\infty $
. Thus, we can apply Corollary 6.4, and it follows that
![]() $\Gamma _n^0$
coincides with the normalizer of
$\Gamma _n^0$
coincides with the normalizer of
![]() $\operatorname {\mathrm {Sp}}(n,1, \mathscr H)$
in
$\operatorname {\mathrm {Sp}}(n,1, \mathscr H)$
in
![]() $\operatorname {\mathrm {Sp}}(n,1)$
. For n even, Corollary 6.2 then shows that
$\operatorname {\mathrm {Sp}}(n,1)$
. For n even, Corollary 6.2 then shows that
![]() $\Gamma ^0_n$
is of minimal covolume in its commensurability class. On the other hand, Rohlfs’ criterion [Reference Rohlfs30, Satz 3.5] shows that
$\Gamma ^0_n$
is of minimal covolume in its commensurability class. On the other hand, Rohlfs’ criterion [Reference Rohlfs30, Satz 3.5] shows that
![]() $\Gamma _n^0$
is maximal (w.r.t. inclusion) for any
$\Gamma _n^0$
is maximal (w.r.t. inclusion) for any
![]() $n>1$
.
$n>1$
.
For
![]() $n>1$
odd, we construct
$n>1$
odd, we construct
![]() $\Gamma _n^1$
as follows. Let
$\Gamma _n^1$
as follows. Let
![]() $\mathbf G$
be the
$\mathbf G$
be the
![]() $\mathbb Q$
-group that contains
$\mathbb Q$
-group that contains
![]() $\operatorname {\mathrm {Sp}}(n,1, \mathscr H)$
. We choose a coherent collection
$\operatorname {\mathrm {Sp}}(n,1, \mathscr H)$
. We choose a coherent collection
![]() $P = (P_v)$
with
$P = (P_v)$
with
![]() $P_v$
hyperspecial for
$P_v$
hyperspecial for
![]() $v \neq 2$
, and
$v \neq 2$
, and
![]() $P_v = P^1_v$
of type
$P_v = P^1_v$
of type
![]() $\Delta _v \smallsetminus \left \{ \alpha _1 \right \}$
for
$\Delta _v \smallsetminus \left \{ \alpha _1 \right \}$
for
![]() $v = 2$
. Let
$v = 2$
. Let
![]() $\Gamma _n^1 = N_{\mathbf G(\mathbb R)}(\Lambda _P)$
. By Lemma 6.1, it is of minimal covolume in its commensurability class. Moreover, by Corollary 6.4, we have
$\Gamma _n^1 = N_{\mathbf G(\mathbb R)}(\Lambda _P)$
. By Lemma 6.1, it is of minimal covolume in its commensurability class. Moreover, by Corollary 6.4, we have
![]() $[\Gamma _n^1:\Lambda _P] = 2$
. In particular,
$[\Gamma _n^1:\Lambda _P] = 2$
. In particular,
 $$ \begin{align} \chi(\Gamma_n^1) &= \frac{e'(P^1_2)}{e'(P^0_2)} \chi(\Gamma_n^0), \end{align} $$
$$ \begin{align} \chi(\Gamma_n^1) &= \frac{e'(P^1_2)}{e'(P^0_2)} \chi(\Gamma_n^0), \end{align} $$
from which we obtain the formula in equation (1.3) with Lemma 4.1.
The following proposition now implies—up to the uniqueness—Theorems 1 and 2.
Proposition 6.5. Let
![]() $\Gamma \subset \operatorname {\mathrm {Sp}}(n,1)$
be a nonuniform lattice of minimal covolume, and let
$\Gamma \subset \operatorname {\mathrm {Sp}}(n,1)$
be a nonuniform lattice of minimal covolume, and let
![]() $s= (n \mod 2)$
. Then
$s= (n \mod 2)$
. Then
![]() $\Gamma $
is commensurable to
$\Gamma $
is commensurable to
![]() $\Gamma ^s_n$
, and they have the same covolume.
$\Gamma ^s_n$
, and they have the same covolume.
Proof. We have seen that
![]() $\Gamma ^s_n$
is of minimal covolume in its commensurability class, so it suffices to prove the commensurability. By Section 2,
$\Gamma ^s_n$
is of minimal covolume in its commensurability class, so it suffices to prove the commensurability. By Section 2,
![]() $\Gamma $
nonuniform is constructed as an arithmetic subgroup of
$\Gamma $
nonuniform is constructed as an arithmetic subgroup of
![]() $\mathbf G = \operatorname {\mathrm {\mathbf {U}}}(V, h)$
for
$\mathbf G = \operatorname {\mathrm {\mathbf {U}}}(V, h)$
for
![]() $(V, h)$
admissible, and V a vector space over a quaternion
$(V, h)$
admissible, and V a vector space over a quaternion
![]() $\mathbb Q$
-algebra D. Let
$\mathbb Q$
-algebra D. Let
![]() $\mathcal {R}$
be the set of places v such that
$\mathcal {R}$
be the set of places v such that
![]() $D_v$
ramifies. Being of minimal covolume, we may write
$D_v$
ramifies. Being of minimal covolume, we may write
![]() $\Gamma = N_{\mathbf G(\mathbb R)}(\Lambda _P)$
, with
$\Gamma = N_{\mathbf G(\mathbb R)}(\Lambda _P)$
, with
![]() $P_v$
hyperspecial unless
$P_v$
hyperspecial unless
![]() $v \in \mathcal {R}$
(by Lemma 6.1). Moreover, for
$v \in \mathcal {R}$
(by Lemma 6.1). Moreover, for
![]() $v \in \mathcal {R}$
the subgroup
$v \in \mathcal {R}$
the subgroup
![]() $P_v$
is of maximal volume and thus of type
$P_v$
is of maximal volume and thus of type
![]() $\Delta \smallsetminus \left \{ \alpha _s \right \}$
by Section 3.1. By Lemma 6.3 (with
$\Delta \smallsetminus \left \{ \alpha _s \right \}$
by Section 3.1. By Lemma 6.3 (with
![]() $k=\mathbb Q$
), we have
$k=\mathbb Q$
), we have
![]() $[\Gamma :\Lambda _P] \le 2^{\#\mathcal {R}}$
. Together with equation (4.7), this gives
$[\Gamma :\Lambda _P] \le 2^{\#\mathcal {R}}$
. Together with equation (4.7), this gives
 $$ \begin{align} \chi(\Gamma) &\ge \frac{\chi(\Lambda_P)}{[\Gamma : \Lambda_P]} \nonumber\\ &\ge (n+1) \prod_{v \in \mathcal{R}} \frac{e'(P_v)}{2} \prod_{j=1}^{n+1} \frac{\zeta(1-2j)}{2}. \end{align} $$
$$ \begin{align} \chi(\Gamma) &\ge \frac{\chi(\Lambda_P)}{[\Gamma : \Lambda_P]} \nonumber\\ &\ge (n+1) \prod_{v \in \mathcal{R}} \frac{e'(P_v)}{2} \prod_{j=1}^{n+1} \frac{\zeta(1-2j)}{2}. \end{align} $$
Only the middle factor in equation (6.3) depends on the choice of
![]() $\Lambda _P$
, and it takes the smallest possible value for
$\Lambda _P$
, and it takes the smallest possible value for
![]() $\mathcal {R} = \left \{ 2 \right \}$
(note that
$\mathcal {R} = \left \{ 2 \right \}$
(note that
![]() $\mathcal {R} = \emptyset $
cannot appear here; see Section 2.2). But in that case, this lower bound is precisely
$\mathcal {R} = \emptyset $
cannot appear here; see Section 2.2). But in that case, this lower bound is precisely
![]() $\chi (\Gamma ^s_n)$
, whence
$\chi (\Gamma ^s_n)$
, whence
![]() $\chi (\Gamma ) = \chi (\Gamma ^s_n)$
(by minimality of
$\chi (\Gamma ) = \chi (\Gamma ^s_n)$
(by minimality of
![]() $\chi (\Gamma ))$
. Since D is now ramified exactly at
$\chi (\Gamma ))$
. Since D is now ramified exactly at
![]() $p = 2$
and
$p = 2$
and
![]() $p=\infty $
, it has same defining algebra as
$p=\infty $
, it has same defining algebra as
![]() $\Gamma ^0_n$
, and the commensurability follows from Section 2.3.
$\Gamma ^0_n$
, and the commensurability follows from Section 2.3.
6.4 The minimality of
 $\chi (\Delta _n)$
$\chi (\Delta _n)$
We now discuss the uniform case. Recall that the covolume of
![]() $\Delta _n$
has been discussed in Section 5.5. Lemma 6.3 (with
$\Delta _n$
has been discussed in Section 5.5. Lemma 6.3 (with
![]() $k = \mathbb Q(\sqrt {5})$
and
$k = \mathbb Q(\sqrt {5})$
and
![]() $\mathcal {R} = \emptyset $
) implies that
$\mathcal {R} = \emptyset $
) implies that
![]() $\Delta _n$
coincides with its own normalizer in
$\Delta _n$
coincides with its own normalizer in
![]() $\operatorname {\mathrm {Sp}}(n,1)$
. Corollary 6.2 thus implies that
$\operatorname {\mathrm {Sp}}(n,1)$
. Corollary 6.2 thus implies that
![]() $\Delta _n$
is of minimal covolume in its commensurability class. The following proposition proves the first statement in Theorem 3. In the proof, we omit details that should be clear from the proof of Proposition 6.5.
$\Delta _n$
is of minimal covolume in its commensurability class. The following proposition proves the first statement in Theorem 3. In the proof, we omit details that should be clear from the proof of Proposition 6.5.
Proposition 6.6. Let
![]() $\Gamma \subset \operatorname {\mathrm {Sp}}(n,1)$
be a uniform lattice of minimal covolume. Then
$\Gamma \subset \operatorname {\mathrm {Sp}}(n,1)$
be a uniform lattice of minimal covolume. Then
![]() $\Gamma $
is commensurable to
$\Gamma $
is commensurable to
![]() $\Delta _n$
, and they have the same covolume.
$\Delta _n$
, and they have the same covolume.
Proof. Let
![]() $\Gamma $
be a uniform lattice of minimal covolume, and let k be its field of definition. Then k is totally real, of degree
$\Gamma $
be a uniform lattice of minimal covolume, and let k be its field of definition. Then k is totally real, of degree
![]() $d \ge 2$
. Assume first that
$d \ge 2$
. Assume first that
![]() $k= \mathbb Q(\sqrt {5})$
, and let D be the defining algebra of
$k= \mathbb Q(\sqrt {5})$
, and let D be the defining algebra of
![]() $\Gamma $
. It is clear that any nontrivial local factor
$\Gamma $
. It is clear that any nontrivial local factor
![]() $e'(P_v)$
would contribute to increase the volume formula, and this shows that D does not ramify at any finite place; this implies that
$e'(P_v)$
would contribute to increase the volume formula, and this shows that D does not ramify at any finite place; this implies that
![]() $\Gamma $
is commensurable to
$\Gamma $
is commensurable to
![]() $\Delta _n$
. Thus, it suffices to prove that
$\Delta _n$
. Thus, it suffices to prove that
![]() $k = \mathbb Q(\sqrt {5})$
, i.e., that
$k = \mathbb Q(\sqrt {5})$
, i.e., that
![]() $d = 2$
and
$d = 2$
and
![]() $\mathscr D_k = 5$
(recall that
$\mathscr D_k = 5$
(recall that
![]() $\mathscr D_k$
denotes the discriminant in absolute value).
$\mathscr D_k$
denotes the discriminant in absolute value).
Let
![]() $\mathbf G$
be the algebraic k-group used to construct the arithmetic subgroup
$\mathbf G$
be the algebraic k-group used to construct the arithmetic subgroup
![]() $\Gamma $
, and let us write
$\Gamma $
, and let us write
![]() $\Gamma = N_{\mathbf G(\mathbb R)}(\Lambda _P)$
with
$\Gamma = N_{\mathbf G(\mathbb R)}(\Lambda _P)$
with
![]() $P = (P_v)$
a coherent collection of parahoric subgroups
$P = (P_v)$
a coherent collection of parahoric subgroups
![]() $P_v \subset \mathbf G(k_v)$
(of maximal volume). Combining equation (4.6) and Lemma 6.3, we find
$P_v \subset \mathbf G(k_v)$
(of maximal volume). Combining equation (4.6) and Lemma 6.3, we find
 $$ \begin{align*} \chi(\Gamma) &\ge \frac{(n+1) \mathscr D_k^{\dim\mathbf G/2}}{2^{\#\mathcal{R}}\; h_k \; |U_k^+/U_k^2|} \; C(n)^d \; \prod_{v \in \mathcal{R}} e'(P_v) \prod_{j=1}^{n+1} \zeta_k(2j), \end{align*} $$
$$ \begin{align*} \chi(\Gamma) &\ge \frac{(n+1) \mathscr D_k^{\dim\mathbf G/2}}{2^{\#\mathcal{R}}\; h_k \; |U_k^+/U_k^2|} \; C(n)^d \; \prod_{v \in \mathcal{R}} e'(P_v) \prod_{j=1}^{n+1} \zeta_k(2j), \end{align*} $$
with
 $$ \begin{align} C(n) &= \prod_{j=1}^{n+1} \frac{(2j-1)!}{(2\pi)^{2j}}. \end{align} $$
$$ \begin{align} C(n) &= \prod_{j=1}^{n+1} \frac{(2j-1)!}{(2\pi)^{2j}}. \end{align} $$
We clearly have
![]() $\zeta _k(2j)> 1$
, and
$\zeta _k(2j)> 1$
, and
![]() $|U_k^+/U_k^2| \le 2^{d-1}$
(by Dirichlet’s unit theorem). Moreover,
$|U_k^+/U_k^2| \le 2^{d-1}$
(by Dirichlet’s unit theorem). Moreover,
![]() $e'(P_v)> 2$
for any
$e'(P_v)> 2$
for any
![]() $v \in \mathcal {R}$
, so that the factor
$v \in \mathcal {R}$
, so that the factor
![]() $2^{-\#\mathcal {R}}$
is compensated by the product of those local factors. We can use the bound
$2^{-\#\mathcal {R}}$
is compensated by the product of those local factors. We can use the bound
![]() $h_k \le 16 \left ( \pi /12 \right )^d \mathscr D_k$
(see [Reference Belolipetsky and Emery3, Sect. 7.2]: the argument given there for a non-totally real field
$h_k \le 16 \left ( \pi /12 \right )^d \mathscr D_k$
(see [Reference Belolipetsky and Emery3, Sect. 7.2]: the argument given there for a non-totally real field
![]() $\ell $
provides the same bound for k; see [Reference Emery7, Sect. 15.2] for details). This gives
$\ell $
provides the same bound for k; see [Reference Emery7, Sect. 15.2] for details). This gives
 $$ \begin{align*} \chi(\Gamma) &\ge \frac{(n+1)}{16\; \mathscr D_k\; 2^{d-1}}\; \left( \frac{12}{\pi} \right)^d \mathscr D_k^{\dim\mathbf G/2} \; C(n)^d. \end{align*} $$
$$ \begin{align*} \chi(\Gamma) &\ge \frac{(n+1)}{16\; \mathscr D_k\; 2^{d-1}}\; \left( \frac{12}{\pi} \right)^d \mathscr D_k^{\dim\mathbf G/2} \; C(n)^d. \end{align*} $$
On the other hand, we have
 $$ \begin{align*} \chi(\Delta_n) &= (n+1)\, 5^{\dim\mathbf G/2}\, C(n)^2 \prod_{j=1}^{n+1} \zeta_{\mathbb Q(\sqrt{5})}(2j) \\ &< 1.2 \cdot (n+1)\, 5^{\dim\mathbf G/2}\, C(n)^2. \end{align*} $$
$$ \begin{align*} \chi(\Delta_n) &= (n+1)\, 5^{\dim\mathbf G/2}\, C(n)^2 \prod_{j=1}^{n+1} \zeta_{\mathbb Q(\sqrt{5})}(2j) \\ &< 1.2 \cdot (n+1)\, 5^{\dim\mathbf G/2}\, C(n)^2. \end{align*} $$
Here we bound the product of zeta functions by the value
![]() $1.2$
by adapting the proof in [Reference Belolipetsky2, p.760: proof of (
$1.2$
by adapting the proof in [Reference Belolipetsky2, p.760: proof of (
![]() $\ast$
)] as follows (see loc. cit. for details):
$\ast$
)] as follows (see loc. cit. for details):
 $$ \begin{align*} \prod_{j=1}^{n+1} \zeta_{\mathbb Q(\sqrt{5})}(2j) &< \zeta_{\mathbb Q(\sqrt{5})}(2)\, \zeta_{\mathbb Q(\sqrt{5})}(4)\, \zeta_{\mathbb Q(\sqrt{5})}(6)\, \prod_{j=4}^{\infty} \left(1 + \frac{2}{2^{2j}}\right)^2 \\ &< \zeta_{\mathbb Q(\sqrt{5})}(2) \,\zeta_{\mathbb Q(\sqrt{5})}(4) \,\zeta_{\mathbb Q(\sqrt{5})}(6) \,e^{1/48}, \end{align*} $$
$$ \begin{align*} \prod_{j=1}^{n+1} \zeta_{\mathbb Q(\sqrt{5})}(2j) &< \zeta_{\mathbb Q(\sqrt{5})}(2)\, \zeta_{\mathbb Q(\sqrt{5})}(4)\, \zeta_{\mathbb Q(\sqrt{5})}(6)\, \prod_{j=4}^{\infty} \left(1 + \frac{2}{2^{2j}}\right)^2 \\ &< \zeta_{\mathbb Q(\sqrt{5})}(2) \,\zeta_{\mathbb Q(\sqrt{5})}(4) \,\zeta_{\mathbb Q(\sqrt{5})}(6) \,e^{1/48}, \end{align*} $$
and we evaluate this last bound with Pari/GP [25].
For the quotient, this gives
 $$ \begin{align} \frac{\chi(\Gamma)}{\chi(\Delta_n)} &> \frac{1}{39\, \mathscr D_k} \left( \frac{12}{\pi} \right)^d \left( \frac{\mathscr D_k}{5} \right)^{\frac{(n+1)(2n+3)}{2}} \left(\frac{C(n)}{2} \right)^{d-2}. \end{align} $$
$$ \begin{align} \frac{\chi(\Gamma)}{\chi(\Delta_n)} &> \frac{1}{39\, \mathscr D_k} \left( \frac{12}{\pi} \right)^d \left( \frac{\mathscr D_k}{5} \right)^{\frac{(n+1)(2n+3)}{2}} \left(\frac{C(n)}{2} \right)^{d-2}. \end{align} $$
Let us write
![]() $f(n, d, \mathscr D_k)$
for the bound on the right-hand side. We have to show that
$f(n, d, \mathscr D_k)$
for the bound on the right-hand side. We have to show that
![]() $f(n, d, \mathscr D_k) \ge 1$
unless
$f(n, d, \mathscr D_k) \ge 1$
unless
![]() $d=2$
and
$d=2$
and
![]() $\mathscr D_k=5$
.
$\mathscr D_k=5$
.
The constant
![]() $C(n)/2$
is larger than
$C(n)/2$
is larger than
![]() $1$
for
$1$
for
![]() $n\ge 13$
, and grows monotone from that point. Thus,
$n\ge 13$
, and grows monotone from that point. Thus,
![]() $f(n, d, \mathscr D_k) \ge f(13, d, \mathscr D_k)$
, and it suffices to consider the range
$f(n, d, \mathscr D_k) \ge f(13, d, \mathscr D_k)$
, and it suffices to consider the range
![]() $n \in \left \{ 2, \dots , 13 \right \}$
. For
$n \in \left \{ 2, \dots , 13 \right \}$
. For
![]() $d=2$
, the smallest discriminant after
$d=2$
, the smallest discriminant after
![]() $5$
is
$5$
is
![]() $\mathscr D_k = 8$
, and numerical evaluation shows that
$\mathscr D_k = 8$
, and numerical evaluation shows that
![]() $f(n, 2, 8)> 1$
for all
$f(n, 2, 8)> 1$
for all
![]() $n \le 13$
. This shows
$n \le 13$
. This shows
![]() $d> 2$
. For k totally real of degree
$d> 2$
. For k totally real of degree
![]() $d = 3$
, the lowest discriminant is
$d = 3$
, the lowest discriminant is
![]() $\mathscr D_k = 49$
. Again, we check that
$\mathscr D_k = 49$
. Again, we check that
![]() $f(n, 3, 49)> 1$
. And similarly with
$f(n, 3, 49)> 1$
. And similarly with
![]() $d = 4$
and
$d = 4$
and
![]() $\mathscr D_k \ge 725$
.
$\mathscr D_k \ge 725$
.
It remains to exclude
![]() $d \ge 5$
. In that case, we use the following bound due to Odlyzko (see [Reference Odlyzko23, Tab. 4]):
$d \ge 5$
. In that case, we use the following bound due to Odlyzko (see [Reference Odlyzko23, Tab. 4]):
![]() $\mathscr D_k> (6.5)^d$
. Then equation (6.5) transforms into
$\mathscr D_k> (6.5)^d$
. Then equation (6.5) transforms into
 $$ \begin{align} \frac{\chi(\Gamma)}{\chi(\Delta_n)} &> \frac{1}{39 \cdot 5} \left( \frac{12}{\pi} \right)^2 \left( \frac{(6.5)^2}{5} \right)^{\delta(n)} a(n)^{d-2}, \end{align} $$
$$ \begin{align} \frac{\chi(\Gamma)}{\chi(\Delta_n)} &> \frac{1}{39 \cdot 5} \left( \frac{12}{\pi} \right)^2 \left( \frac{(6.5)^2}{5} \right)^{\delta(n)} a(n)^{d-2}, \end{align} $$
where
![]() $a(n) = (6/\pi ) C(n) (6.5)^{\delta (n)}$
and
$a(n) = (6/\pi ) C(n) (6.5)^{\delta (n)}$
and
![]() $\delta (n) = \dim \mathbf G/2 -1$
. We check that
$\delta (n) = \dim \mathbf G/2 -1$
. We check that
![]() $a(n)> 1$
for all
$a(n)> 1$
for all
![]() $n \in \left \{ 2, \dots , 13 \right \}$
. The product preceding
$n \in \left \{ 2, \dots , 13 \right \}$
. The product preceding
![]() $a(n)$
in equation (6.6) is also easily seen to be (much) larger than
$a(n)$
in equation (6.6) is also easily seen to be (much) larger than
![]() $1$
. This finishes the proof.
$1$
. This finishes the proof.
6.5 The proof of Corollary 1
We have that each of
![]() $\chi (\Delta _n)$
,
$\chi (\Delta _n)$
,
![]() $\chi (\Gamma ^s_n)$
and their quotients contains a factor
$\chi (\Gamma ^s_n)$
and their quotients contains a factor
![]() $C(n)$
(which is given in (6.4)); see equation (4.6). For n large enough, it is easily seen that this factor grows faster than (say)
$C(n)$
(which is given in (6.4)); see equation (4.6). For n large enough, it is easily seen that this factor grows faster than (say)
![]() $(2n+1)!$
, i.e., it grows superexponentially. This implies immediately that
$(2n+1)!$
, i.e., it grows superexponentially. This implies immediately that
![]() $\chi (\Delta _n)$
and
$\chi (\Delta _n)$
and
![]() $\chi (\Gamma ^s_n)$
grow superexponentially, as their remaining factors also increase with n. Moreover, the other factors appearing in
$\chi (\Gamma ^s_n)$
grow superexponentially, as their remaining factors also increase with n. Moreover, the other factors appearing in
![]() $\chi (\Gamma ^s_n)$
grow at most exponentially so that the
$\chi (\Gamma ^s_n)$
grow at most exponentially so that the
![]() $\chi (\Delta _n)/\chi (\Gamma ^s_n)$
has a superexponentially growth as well.
$\chi (\Delta _n)/\chi (\Gamma ^s_n)$
has a superexponentially growth as well.
7 Proof of the uniqueness
In this section, we complete the proof of Theorems 1–3 by showing the uniqueness statements.
7.1 The surjectivity of the adjoint map
We start by proving the following auxiliary result.
Lemma 7.1. For
![]() $n>1$
and
$n>1$
and
![]() $\mathbf G$
admissible for
$\mathbf G$
admissible for
![]() $\operatorname {\mathrm {Sp}}(n,1)$
, the map
$\operatorname {\mathrm {Sp}}(n,1)$
, the map
![]() $\pi : \mathbf G(\mathbb R) \to \overline {\mathbf G}(\mathbb R)$
is surjective.
$\pi : \mathbf G(\mathbb R) \to \overline {\mathbf G}(\mathbb R)$
is surjective.
Proof. We have to show that
![]() $\delta : \overline {\mathbf G}(\mathbb R) \to H^1(\mathbb R, \mathbf C)$
has trivial image; see (3.2). Recall that
$\delta : \overline {\mathbf G}(\mathbb R) \to H^1(\mathbb R, \mathbf C)$
has trivial image; see (3.2). Recall that
![]() $H^1(\mathbb R, \mathbf C) = \mathbb R^{\times }/(\mathbb R^{\times })^2$
. Let
$H^1(\mathbb R, \mathbf C) = \mathbb R^{\times }/(\mathbb R^{\times })^2$
. Let
![]() $\mathbf G = \operatorname {\mathrm {\mathbf {U}}}(V, h)$
. By [Reference Knus, Merkurjev, Rost and Tignol17, Prop. 12.20 and Sect. 31.A], the image of
$\mathbf G = \operatorname {\mathrm {\mathbf {U}}}(V, h)$
. By [Reference Knus, Merkurjev, Rost and Tignol17, Prop. 12.20 and Sect. 31.A], the image of
![]() $\delta $
corresponds (modulo squares) to elements
$\delta $
corresponds (modulo squares) to elements
![]() $\alpha \in \mathbb R^{\times }$
such that
$\alpha \in \mathbb R^{\times }$
such that
![]() $(V, \alpha h)$
is isomorphic to
$(V, \alpha h)$
is isomorphic to
![]() $(V, h)$
. For h of signature
$(V, h)$
. For h of signature
![]() $(n,1)$
with
$(n,1)$
with
![]() $n>1$
, this requires
$n>1$
, this requires
![]() $\alpha> 0$
, whence the result.
$\alpha> 0$
, whence the result.
7.2 Counting the conjugacy classes
Let
![]() $\Gamma \subset \operatorname {\mathrm {Sp}}(n,1)$
be a nonuniform (respectively, uniform) lattice that realizes the smallest covolume. Then by Section 6, we have
$\Gamma \subset \operatorname {\mathrm {Sp}}(n,1)$
be a nonuniform (respectively, uniform) lattice that realizes the smallest covolume. Then by Section 6, we have
![]() $\Gamma = N_{\operatorname {\mathrm {Sp}}(n,1)}(\Lambda _P)$
, where
$\Gamma = N_{\operatorname {\mathrm {Sp}}(n,1)}(\Lambda _P)$
, where
![]() $P = (P_v)$
is a coherent collection of parahoric subgroups
$P = (P_v)$
is a coherent collection of parahoric subgroups
![]() $P_v \subset \mathbf G(k_v)$
of maximal volume for each
$P_v \subset \mathbf G(k_v)$
of maximal volume for each
![]() $v \in \mathcal {V}_k^{\mathrm {f}}$
, and
$v \in \mathcal {V}_k^{\mathrm {f}}$
, and
![]() $\mathbf G$
is precisely the admissible k-group that determines
$\mathbf G$
is precisely the admissible k-group that determines
![]() $\Gamma ^s_n$
(resp.
$\Gamma ^s_n$
(resp.
![]() $\Delta _n$
). For
$\Delta _n$
). For
![]() $v \in \mathcal {R}$
, this determines the type
$v \in \mathcal {R}$
, this determines the type
![]() $\Theta _v$
of
$\Theta _v$
of
![]() $P_v$
uniquely (see Lemma 6.1), and for
$P_v$
uniquely (see Lemma 6.1), and for
![]() $v \notin \mathcal {R}$
we have that
$v \notin \mathcal {R}$
we have that
![]() $\Theta _v$
is one of the two conjugate hyperspecial types. These two hyperspecial types are conjugate by
$\Theta _v$
is one of the two conjugate hyperspecial types. These two hyperspecial types are conjugate by
![]() $\overline {\mathbf G}(k_v)$
. Up to
$\overline {\mathbf G}(k_v)$
. Up to
![]() $\overline {\mathbf G}(k)$
-conjugacy, the number of principal arithmetic subgroups
$\overline {\mathbf G}(k)$
-conjugacy, the number of principal arithmetic subgroups
![]() $\Lambda _P$
with such a type
$\Lambda _P$
with such a type
![]() $\Theta = (\Theta _v)$
is given by the order of following class group (see, for instance, [Reference Belolipetsky and Emery3, Sect. 6.2]):
$\Theta = (\Theta _v)$
is given by the order of following class group (see, for instance, [Reference Belolipetsky and Emery3, Sect. 6.2]):
 $$ \begin{align} \mathfrak{C}_P = \frac{\prod'_{v\in\mathcal{V}_k^{\mathrm{f}}} H^1(k_v, \mathbf C)}{\delta(\overline{\mathbf G}(k)) \prod_{v \in \mathcal{V}_k^{\mathrm{f}}} \delta(\overline{P}_v)}, \end{align} $$
$$ \begin{align} \mathfrak{C}_P = \frac{\prod'_{v\in\mathcal{V}_k^{\mathrm{f}}} H^1(k_v, \mathbf C)}{\delta(\overline{\mathbf G}(k)) \prod_{v \in \mathcal{V}_k^{\mathrm{f}}} \delta(\overline{P}_v)}, \end{align} $$
where
![]() $\overline {P}_v \subset \overline {\mathbf G}(k_v)$
is the stabilizer of
$\overline {P}_v \subset \overline {\mathbf G}(k_v)$
is the stabilizer of
![]() $P_v$
, and in the numerator,
$P_v$
, and in the numerator,
![]() $\prod '$
denotes the restricted product with respect to the collection of subgroups
$\prod '$
denotes the restricted product with respect to the collection of subgroups
![]() $\delta (\overline {P}_v)$
.
$\delta (\overline {P}_v)$
.
By Lemma 7.1, this order also gives an upper bound on the number of
![]() $\mathbf G(\mathbb R)$
-conjugacy classes of
$\mathbf G(\mathbb R)$
-conjugacy classes of
![]() $\Lambda _P$
(note that
$\Lambda _P$
(note that
![]() $k \subset \mathbb R$
). Thus, the uniqueness in Theorems 1–3 follows immediately from the following.
$k \subset \mathbb R$
). Thus, the uniqueness in Theorems 1–3 follows immediately from the following.
Proposition 7.2. For
![]() $k= \mathbb Q(\sqrt {5})$
(respectively,
$k= \mathbb Q(\sqrt {5})$
(respectively,
![]() $k = \mathbb Q$
), we have
$k = \mathbb Q$
), we have
![]() $\mathfrak {C}_P = 1$
.
$\mathfrak {C}_P = 1$
.
Proof. We have
![]() $H^1(k_v, \mathbf C) = k_v^{\times }/(k_v^{\times })^2$
. The subgroup
$H^1(k_v, \mathbf C) = k_v^{\times }/(k_v^{\times })^2$
. The subgroup
![]() $\delta (\overline {P}_v) \subset H^1(k_v, \mathbf C)$
equals the type stabilizer
$\delta (\overline {P}_v) \subset H^1(k_v, \mathbf C)$
equals the type stabilizer
![]() $H^1(k_v, \mathbf C)_{\Theta _v}$
. If
$H^1(k_v, \mathbf C)_{\Theta _v}$
. If
![]() $v \in \mathcal {R}$
, then
$v \in \mathcal {R}$
, then
![]() $\operatorname {\mathrm {Aut}}(\Delta _v) = 1$
(see Table 3) so that this stabilizer is trivially the whole
$\operatorname {\mathrm {Aut}}(\Delta _v) = 1$
(see Table 3) so that this stabilizer is trivially the whole
![]() $H^1(k_v, \mathbf C)$
. For
$H^1(k_v, \mathbf C)$
. For
![]() $v \notin \mathcal {R}$
, we have
$v \notin \mathcal {R}$
, we have
![]() $\delta (\overline {P}_v) = \mathfrak o^{\times }_v (k_v^{\times })^2/(k_v^{\times })^2$
by [Reference Borel and Prasad4, Prop. 2.7]. Thus,
$\delta (\overline {P}_v) = \mathfrak o^{\times }_v (k_v^{\times })^2/(k_v^{\times })^2$
by [Reference Borel and Prasad4, Prop. 2.7]. Thus,
![]() $\mathfrak {C}_P$
is a quotient of
$\mathfrak {C}_P$
is a quotient of
 $$ \begin{align} \mathfrak{C}_P' &= \frac{\prod'_{v\in\mathcal{V}_k^{\mathrm{f}}}k_v^{\times}/(k_v^{\times})^2}{\delta(\overline{\mathbf G}(k)) \prod_{v \in \mathcal{V}_k^{\mathrm{f}}} \mathfrak o^{\times}_v (k_v^{\times})^2/(k_v^{\times})^2}. \end{align} $$
$$ \begin{align} \mathfrak{C}_P' &= \frac{\prod'_{v\in\mathcal{V}_k^{\mathrm{f}}}k_v^{\times}/(k_v^{\times})^2}{\delta(\overline{\mathbf G}(k)) \prod_{v \in \mathcal{V}_k^{\mathrm{f}}} \mathfrak o^{\times}_v (k_v^{\times})^2/(k_v^{\times})^2}. \end{align} $$
Now by Lemma 7.1 and the proof of Lemma 3.1, we have that
![]() $\delta (\overline {\mathbf G}(k)) = \delta (\overline {\mathbf G}(k))' = k^{(+)}/(k^{\times })^2$
, where
$\delta (\overline {\mathbf G}(k)) = \delta (\overline {\mathbf G}(k))' = k^{(+)}/(k^{\times })^2$
, where
From equation (7.2), we obtain an isomorphism
where
![]() $\mathcal {J}_k$
is the group of finite idèles of k, and
$\mathcal {J}_k$
is the group of finite idèles of k, and
![]() $\mathcal {J}_k^{\infty } \subset \mathcal {J}_k$
its subgroup consisting of integral idèles. For both
$\mathcal {J}_k^{\infty } \subset \mathcal {J}_k$
its subgroup consisting of integral idèles. For both
![]() $k = \mathbb Q$
and
$k = \mathbb Q$
and
![]() $k = \mathbb Q(\sqrt {5})$
, the unit group
$k = \mathbb Q(\sqrt {5})$
, the unit group
![]() $U_k$
contains a representative of each class of
$U_k$
contains a representative of each class of
![]() $k^{\times }/k^{(+)}$
. Thus,
$k^{\times }/k^{(+)}$
. Thus,
 $$ \begin{align*} k^{(+)} \mathcal{J}_k^{\infty} &= k^{(+)} U_k \mathcal{J}_k^{\infty} \\ &= k^{\times} \mathcal{J}_k^{\infty} \end{align*} $$
$$ \begin{align*} k^{(+)} \mathcal{J}_k^{\infty} &= k^{(+)} U_k \mathcal{J}_k^{\infty} \\ &= k^{\times} \mathcal{J}_k^{\infty} \end{align*} $$
so that
But the latter is a quotient of the class group of k (see [Reference Platonov and Rapinchuck27, Sect. 1.2.1]), which is trivial here.
Acknowledgement
We would like to thank Jeff Meyer for helpful correspondence concerning the classification of arithmetic subgroups in
![]() $\operatorname {\mathrm {Sp}}(n,1)$
, and Ruben Bär for his help with the icosian ring. The first author thanks the KIAS for hospitality and financial support during two short stays in Korea, and the HIM in Bonn and the organizers of the program ‘Periods in Number Theory, Algebraic Geometry and Physics’ for providing a nice working atmosphere. We also thank the referee for a careful reading and many useful remarks.The first author is supported by the Swiss National Science Foundation, Project number PP00P2_157583. The Second author gratefully acknowledges the partial support of Grant NRF-2019R1A2C1083865 and KIAS Individual Grant (MG031408).
$\operatorname {\mathrm {Sp}}(n,1)$
, and Ruben Bär for his help with the icosian ring. The first author thanks the KIAS for hospitality and financial support during two short stays in Korea, and the HIM in Bonn and the organizers of the program ‘Periods in Number Theory, Algebraic Geometry and Physics’ for providing a nice working atmosphere. We also thank the referee for a careful reading and many useful remarks.The first author is supported by the Swiss National Science Foundation, Project number PP00P2_157583. The Second author gratefully acknowledges the partial support of Grant NRF-2019R1A2C1083865 and KIAS Individual Grant (MG031408).
Conflicts of Interest
none