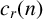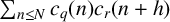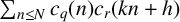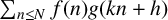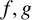1 Introduction
Let us write
![]() $e(x)=\exp (2\pi i x)$
and let
$e(x)=\exp (2\pi i x)$
and let
![]() $\mathbb {N}$
be the set of positive integers. In [Reference Ramanujan11], Ramanujan introduced the following sums for
$\mathbb {N}$
be the set of positive integers. In [Reference Ramanujan11], Ramanujan introduced the following sums for
![]() $r\in \mathbb {N}$
and
$r\in \mathbb {N}$
and
![]() $n\in \mathbb {Z}$
, now known as Ramanujan sums:
$n\in \mathbb {Z}$
, now known as Ramanujan sums:
 $$ \begin{align*}c_{r}(n) = \sum_{\substack{a=1\\(a,r)=1}}^r e(an/r), \end{align*} $$
$$ \begin{align*}c_{r}(n) = \sum_{\substack{a=1\\(a,r)=1}}^r e(an/r), \end{align*} $$
where
![]() $(a,r)$
denotes the greatest common divisor (gcd) of a and r. An important feature of Ramanujan sums is that they satisfy certain orthogonality relations, first noticed by Carmichael [Reference Carmichael1].
$(a,r)$
denotes the greatest common divisor (gcd) of a and r. An important feature of Ramanujan sums is that they satisfy certain orthogonality relations, first noticed by Carmichael [Reference Carmichael1].
Theorem 1.1 (Shifted orthogonality relations)
Let
![]() $h\in \mathbb {Z}$
and let
$h\in \mathbb {Z}$
and let
![]() $q,r\in \mathbb {N}$
. Then,
$q,r\in \mathbb {N}$
. Then,
 $$ \begin{align*} \lim_{N\to \infty}\frac{1}{N}\sum_{n=1}^N c_q(n)c_r(n+h)=\begin{cases} c_r(h) & \mbox{ if }r=q,\\ 0 & \mbox{ otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} \lim_{N\to \infty}\frac{1}{N}\sum_{n=1}^N c_q(n)c_r(n+h)=\begin{cases} c_r(h) & \mbox{ if }r=q,\\ 0 & \mbox{ otherwise.} \end{cases} \end{align*} $$
That is, the orthogonality relations give an asymptotic formula for the shifted convolution of Ramanujan sums. Our first result is a generalisation for affine convolutions.
Theorem 1.2 (Affine orthogonality relations)
Let
![]() $h\in \mathbb {Z}$
and let
$h\in \mathbb {Z}$
and let
![]() $k,q,r\in \mathbb {N}$
. Then,
$k,q,r\in \mathbb {N}$
. Then,
 $$ \begin{align*} &\sum_{n=1}^N c_q(n)c_r(kn+h)\\ &\quad=\begin{cases} c_r(h) N + O(q^2r^2) & \mbox{if there is}\ d\mid k\ \mbox{with}\ r=dq\ \mbox{and}\ (k/d, q)=1,\\ O(q^2r^2) & \mbox{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} &\sum_{n=1}^N c_q(n)c_r(kn+h)\\ &\quad=\begin{cases} c_r(h) N + O(q^2r^2) & \mbox{if there is}\ d\mid k\ \mbox{with}\ r=dq\ \mbox{and}\ (k/d, q)=1,\\ O(q^2r^2) & \mbox{otherwise.} \end{cases} \end{align*} $$
Here and in the rest of this article, the term affine refers to the fact that the arguments used in the convolutions are n and
![]() $kn+h$
; thus, they are related by an affine transformation.
$kn+h$
; thus, they are related by an affine transformation.
A Ramanujan–Fourier expansion for an arithmetical function
![]() $f:\mathbb {N}\to \mathbb {C}$
is a series representation of the form
$f:\mathbb {N}\to \mathbb {C}$
is a series representation of the form
 $$ \begin{align*} f(n)= \sum_{r=1}^\infty \hat{f}(r) c_r(n), \end{align*} $$
$$ \begin{align*} f(n)= \sum_{r=1}^\infty \hat{f}(r) c_r(n), \end{align*} $$
where the series converges for each positive integer n. The coefficients
![]() $\hat {f}(r)$
are called Ramanujan–Fourier coefficients for f. In [Reference Ramanujan11], Ramanujan obtained Ramanujan–Fourier expansions for several classical arithmetical functions. The literature on Ramanujan–Fourier expansions is vast, and we refer the reader to [Reference Murty9] for a survey.
$\hat {f}(r)$
are called Ramanujan–Fourier coefficients for f. In [Reference Ramanujan11], Ramanujan obtained Ramanujan–Fourier expansions for several classical arithmetical functions. The literature on Ramanujan–Fourier expansions is vast, and we refer the reader to [Reference Murty9] for a survey.
For example, we have the following result due to Ramanujan [Reference Ramanujan11]:
 $$ \begin{align} \frac{\sigma_s(n)}{n^s}=\zeta(s+1) \sum_{q=1}^\infty \frac{c_q(n)}{q^{s+1}} \end{align} $$
$$ \begin{align} \frac{\sigma_s(n)}{n^s}=\zeta(s+1) \sum_{q=1}^\infty \frac{c_q(n)}{q^{s+1}} \end{align} $$
for
![]() $s>0$
, where
$s>0$
, where
![]() $\sigma _s(n)=\sum _{d\mid n}d^s$
and
$\sigma _s(n)=\sum _{d\mid n}d^s$
and
![]() $\zeta (z)$
is the Riemann-zeta function. In this case, the series is absolutely convergent.
$\zeta (z)$
is the Riemann-zeta function. In this case, the series is absolutely convergent.
A more delicate example due to Hardy [Reference Hardy7] is a Ramanujan–Fourier expansion for (essentially) the von Mangoldt function
![]() $\Lambda (n)$
:
$\Lambda (n)$
:
 $$ \begin{align} \frac{\varphi(n)}{n}\Lambda(n)=\sum_{r=1}^\infty\frac{\mu(r)}{\varphi(r)}c_r(n), \end{align} $$
$$ \begin{align} \frac{\varphi(n)}{n}\Lambda(n)=\sum_{r=1}^\infty\frac{\mu(r)}{\varphi(r)}c_r(n), \end{align} $$
where
![]() $\varphi (n)$
is the Euler totient function and
$\varphi (n)$
is the Euler totient function and
![]() $\mu (n)$
is the Möbius function. In this case, the series converges for each n but not absolutely.
$\mu (n)$
is the Möbius function. In this case, the series converges for each n but not absolutely.
A topic that has captured considerable attention is that of shifted convolutions of arithmetical functions admitting a Ramanujan–Fourier expansion (see, for instance, [Reference Coppola and Murty2–Reference Gadiyar, Murty and Padma5, Reference Murty and Saha10, Reference Saha12]). Namely, given
![]() $f(n)=\sum _{r} \hat {f}(r)c_r(n)$
and
$f(n)=\sum _{r} \hat {f}(r)c_r(n)$
and
![]() $g(n)=\sum _{r} \hat {g}(r)c_r(n)$
, two arithmetical functions admitting Ramanujan–Fourier expansions, the orthogonality relations for Ramanujan sums heuristically suggest
$g(n)=\sum _{r} \hat {g}(r)c_r(n)$
, two arithmetical functions admitting Ramanujan–Fourier expansions, the orthogonality relations for Ramanujan sums heuristically suggest
 $$ \begin{align} \lim_{n\le N}\frac{1}{N} \sum_{n\le N} f(n)g(n+h) = \sum_{r=1}^\infty\hat{f}(r)\hat{g}(r)c_r(h), \end{align} $$
$$ \begin{align} \lim_{n\le N}\frac{1}{N} \sum_{n\le N} f(n)g(n+h) = \sum_{r=1}^\infty\hat{f}(r)\hat{g}(r)c_r(h), \end{align} $$
in analogy with the Wiener–Khintchine formula from the theory of Fourier series. In fact, such a formula has been proved in several cases, as in the examples just cited.
Under suitable convergence conditions, we use Theorem 1.2 to prove an analogous formula for affine convolutions.
Theorem 1.3. Let
![]() $f(n)=\sum _{r} \hat {f}(r)c_r(n)$
and
$f(n)=\sum _{r} \hat {f}(r)c_r(n)$
and
![]() $g(n)=\sum _{r} \hat {g}(r)c_r(n)$
be arithmetical functions admitting Ramanujan–Fourier expansions. Suppose that
$g(n)=\sum _{r} \hat {g}(r)c_r(n)$
be arithmetical functions admitting Ramanujan–Fourier expansions. Suppose that
 $$ \begin{align*} \sum_{r=1}^\infty |\hat{f}(r)|r^2 \quad\mbox{and}\quad \sum_{r=1}^\infty |\hat{g}(r)|r^2 \end{align*} $$
$$ \begin{align*} \sum_{r=1}^\infty |\hat{f}(r)|r^2 \quad\mbox{and}\quad \sum_{r=1}^\infty |\hat{g}(r)|r^2 \end{align*} $$
converge. Let
![]() $k\in \mathbb {N}$
and
$k\in \mathbb {N}$
and
![]() $h\in \mathbb {Z}$
. Then,
$h\in \mathbb {Z}$
. Then,
where
 $$ \begin{align*} \kappa(f,g,k,h) = \sum_{q=1}^\infty \sum_{\substack{d\mid k \\ (k/d,q)=1}} \hat{f}(q)\hat{g}(dq)c_{dq}(h). \end{align*} $$
$$ \begin{align*} \kappa(f,g,k,h) = \sum_{q=1}^\infty \sum_{\substack{d\mid k \\ (k/d,q)=1}} \hat{f}(q)\hat{g}(dq)c_{dq}(h). \end{align*} $$
This result is applicable, for instance, to sums of powers of divisors.
Corollary 1.4. Let
![]() $s\in \mathbb {R}$
with
$s\in \mathbb {R}$
with
![]() $s>2$
, let
$s>2$
, let
![]() $h\in \mathbb {Z}$
and let
$h\in \mathbb {Z}$
and let
![]() $k\in \mathbb {N}$
. Then,
$k\in \mathbb {N}$
. Then,
 $$ \begin{align*} \sum_{n\le N} \frac{\sigma_s(n)}{n^s} \cdot \frac{\sigma_s(kn+h)}{(kn+h)^s} = C(s,k,h)\cdot N + O(1), \end{align*} $$
$$ \begin{align*} \sum_{n\le N} \frac{\sigma_s(n)}{n^s} \cdot \frac{\sigma_s(kn+h)}{(kn+h)^s} = C(s,k,h)\cdot N + O(1), \end{align*} $$
where
![]() $C(s,k,h)>0$
is a constant depending only on s, k and h.
$C(s,k,h)>0$
is a constant depending only on s, k and h.
Corollary 1.4 gives a variation of a result of Ingham [Reference Gadiyar, Murty and Padma5, Reference Ingham8]. Theorem 1.3 motivates the following question.
Question 1.5. Let
![]() $f(n)=\sum _{r} \hat {f}(r)c_r(n)$
and
$f(n)=\sum _{r} \hat {f}(r)c_r(n)$
and
![]() $g(n)=\sum _{r} \hat {g}(r)c_r(n)$
be arithmetical functions admitting Ramanujan–Fourier expansions and let
$g(n)=\sum _{r} \hat {g}(r)c_r(n)$
be arithmetical functions admitting Ramanujan–Fourier expansions and let
![]() $k\ge 1$
and h be integers. Does the asymptotic formula
$k\ge 1$
and h be integers. Does the asymptotic formula
hold with
 $$ \begin{align*} \kappa(f,g,k,h) = \sum_{q=1}^\infty \sum_{\substack{d\mid k \\ (k/d,q)=1}} \hat{f}(q)\hat{g}(dq)c_{dq}(h)? \end{align*} $$
$$ \begin{align*} \kappa(f,g,k,h) = \sum_{q=1}^\infty \sum_{\substack{d\mid k \\ (k/d,q)=1}} \hat{f}(q)\hat{g}(dq)c_{dq}(h)? \end{align*} $$
A motivation to study shifted convolutions via Ramanujan–Fourier expansions comes from [Reference Gadiyar and Padma6], where it is shown that if (1.3) holds for
![]() $f(n)=g(n)=\varphi (n)\Lambda (n)/n$
with the Ramanujan–Fourier expansion (1.2), then the twin prime conjecture would hold in the following strong form conjectured by Hardy and Littlewood.
$f(n)=g(n)=\varphi (n)\Lambda (n)/n$
with the Ramanujan–Fourier expansion (1.2), then the twin prime conjecture would hold in the following strong form conjectured by Hardy and Littlewood.
Conjecture 1.6 (Twin prime conjecture)
Let
![]() $\pi _2(x)=\#\{p<x : p, p+2$
are primes} and let
$\pi _2(x)=\#\{p<x : p, p+2$
are primes} and let
 $$ \begin{align*} C_2=2\prod_{p>2}\bigg(1-\frac{1}{(p-1)^2}\bigg). \end{align*} $$
$$ \begin{align*} C_2=2\prod_{p>2}\bigg(1-\frac{1}{(p-1)^2}\bigg). \end{align*} $$
Then we have the asymptotic formula
Arguing as in [Reference Gadiyar and Padma6] but using affine convolutions instead of shifted convolutions, one can study prime pairs of the form p,
![]() $kp+h$
. In particular, let
$kp+h$
. In particular, let
be the counting function of Sophie Germain primes.
Theorem 1.7 (Heuristic for Sophie Germain primes)
If Question 1.5 has a positive answer for
![]() $f(n)=g(n)=\varphi (n)\Lambda (n)/n$
with the Ramanujan–Fourier expansion (1.2) and
$f(n)=g(n)=\varphi (n)\Lambda (n)/n$
with the Ramanujan–Fourier expansion (1.2) and
![]() $k=2$
,
$k=2$
,
![]() $h=1$
, then there are infinitely many Sophie Germain primes and, moreover,
$h=1$
, then there are infinitely many Sophie Germain primes and, moreover,
where
![]() $C_2$
is the same constant appearing in the twin prime conjecture.
$C_2$
is the same constant appearing in the twin prime conjecture.
It will be clear from the proof that our argument works, more generally, for prime pairs of the form
![]() $p, kp+h$
. We restrict our attention to the case of Sophie Germain primes for the sake of exposition.
$p, kp+h$
. We restrict our attention to the case of Sophie Germain primes for the sake of exposition.
2 Orthogonality relations
We need the following simple estimate.
Lemma 2.1 (Trigonometric sums)
Let
![]() $\alpha $
be a nonintegral rational number and let
$\alpha $
be a nonintegral rational number and let
![]() $D>0$
be an integer with
$D>0$
be an integer with
![]() $\alpha D\in \mathbb {Z}$
. Let
$\alpha D\in \mathbb {Z}$
. Let
![]() $P<Q$
be positive integers. Then,
$P<Q$
be positive integers. Then,
 $$ \begin{align*} \bigg|\sum_{n=P}^Q e(n\alpha)\bigg|\le D/2. \end{align*} $$
$$ \begin{align*} \bigg|\sum_{n=P}^Q e(n\alpha)\bigg|\le D/2. \end{align*} $$
Proof. Using the elementary formula for a geometric sum, one finds
 $$ \begin{align*} \bigg|\sum_{n=P}^Q e(n\alpha)\bigg|\le \frac{2}{e(\alpha)-1} = \frac{1}{\sin(\pi\alpha)} \end{align*} $$
$$ \begin{align*} \bigg|\sum_{n=P}^Q e(n\alpha)\bigg|\le \frac{2}{e(\alpha)-1} = \frac{1}{\sin(\pi\alpha)} \end{align*} $$
and the result follows.
Proof of Theorem 1.2
Let
![]() $S=\sum _{n=1}^N c_q(n)c_r(kn+h)$
and note that
$S=\sum _{n=1}^N c_q(n)c_r(kn+h)$
and note that
 $$ \begin{align*} S= \sum_{\substack{b=1 \\ (b,r)=1}}^r e(bh/r) \sum_{\substack{a=1 \\ (a,q)=1}}^q E(a,b), \end{align*} $$
$$ \begin{align*} S= \sum_{\substack{b=1 \\ (b,r)=1}}^r e(bh/r) \sum_{\substack{a=1 \\ (a,q)=1}}^q E(a,b), \end{align*} $$
where
 $$ \begin{align*}E(a,b)=\sum_{n=1}^Ne\bigg(n\bigg(\frac{a}{q} + \frac{kb}{r}\bigg)\bigg). \end{align*} $$
$$ \begin{align*}E(a,b)=\sum_{n=1}^Ne\bigg(n\bigg(\frac{a}{q} + \frac{kb}{r}\bigg)\bigg). \end{align*} $$
We consider three cases.
Case 1:
![]() $dq\ne r$
for every
$dq\ne r$
for every
![]() $d\mid k$
. We claim that for
$d\mid k$
. We claim that for
![]() $a,b$
as in S, the number
$a,b$
as in S, the number
![]() $a/q + kb/r$
is not an integer. For otherwise, let m be this integer and note that
$a/q + kb/r$
is not an integer. For otherwise, let m be this integer and note that
![]() $ar+kbq=mqr$
. Since
$ar+kbq=mqr$
. Since
![]() $(a,q)=1$
, this implies
$(a,q)=1$
, this implies
![]() $q\mid r$
, say
$q\mid r$
, say
![]() $r=dq$
, which in turn gives
$r=dq$
, which in turn gives
![]() $ad+kb=mdq$
. As
$ad+kb=mdq$
. As
![]() $(b,dq)=(b,r)=1$
, we have
$(b,dq)=(b,r)=1$
, we have
![]() $(b,d)=1$
, and hence
$(b,d)=1$
, and hence
![]() $d\mid k$
, which is a contradiction.
$d\mid k$
, which is a contradiction.
By Lemma 2.1,
![]() $|E(a,b)|\le qr/2$
, and hence
$|E(a,b)|\le qr/2$
, and hence
![]() $|S|\le \varphi (r)\varphi (q) qr/2 < (qr)^2$
.
$|S|\le \varphi (r)\varphi (q) qr/2 < (qr)^2$
.
Case 2:
![]() $dq= r$
for some
$dq= r$
for some
![]() $d\mid k$
with
$d\mid k$
with
![]() $(k/d,q)>1$
. We claim that for
$(k/d,q)>1$
. We claim that for
![]() $a,b$
as in S, the number
$a,b$
as in S, the number
![]() $a/q + kb/r$
is not an integer. Indeed, let
$a/q + kb/r$
is not an integer. Indeed, let
![]() $s=k/d$
and note that
$s=k/d$
and note that
![]() $a/q + kb/r = (a+sb)/q$
, which is not an integer because
$a/q + kb/r = (a+sb)/q$
, which is not an integer because
![]() $(a,q)=1$
, while
$(a,q)=1$
, while
![]() $(sb,q)\ge (s,q)>1$
.
$(sb,q)\ge (s,q)>1$
.
As in the previous case, we apply Lemma 2.1 to deduce
![]() $|S|< (qr)^2$
.
$|S|< (qr)^2$
.
Case 3:
![]() $dq= r$
for some
$dq= r$
for some
![]() $d\mid k$
with
$d\mid k$
with
![]() $(k/d,q)=1$
. Let
$(k/d,q)=1$
. Let
![]() $s=k/d$
so that
$s=k/d$
so that
![]() $(s,q)=1$
. Let a and b be as in S. Note that
$(s,q)=1$
. Let a and b be as in S. Note that
![]() $(b,q)=1$
because
$(b,q)=1$
because
![]() $(b,dq)=(b,r)=1$
. Thus, for each b, there is a unique
$(b,dq)=(b,r)=1$
. Thus, for each b, there is a unique
![]() $a\in (\mathbb {Z}/q\mathbb {Z})^\times $
satisfying
$a\in (\mathbb {Z}/q\mathbb {Z})^\times $
satisfying
![]() $a\equiv -sb \bmod q$
, which is equivalent to
$a\equiv -sb \bmod q$
, which is equivalent to
![]() $a/q+kb/r = (a+sb)/q\in \mathbb {Z}$
.
$a/q+kb/r = (a+sb)/q\in \mathbb {Z}$
.
Consequently,
![]() $E(a,b)=N$
if
$E(a,b)=N$
if
![]() $a\equiv -sb \bmod q$
(which, for a given b, occurs exactly for one a), while
$a\equiv -sb \bmod q$
(which, for a given b, occurs exactly for one a), while
![]() $|E(a,b)|\le qr/2$
otherwise (by Lemma 2.1). It follows that
$|E(a,b)|\le qr/2$
otherwise (by Lemma 2.1). It follows that
 $$ \begin{align*} S&=\sum_{\substack{b=1 \\ (b,r)=1}}^r e(bh/r) \sum_{\substack{a=1 \\ (a,q)=1}}^q E(a,b)\\ &= N\sum_{\substack{b=1 \\ (b,r)=1}}^r e(bh/r) + O(\varphi(r)(\varphi(q)-1)qr)\\ &=N\cdot c_r((h) + O((qr)^2).\\[-3.2pc] \end{align*} $$
$$ \begin{align*} S&=\sum_{\substack{b=1 \\ (b,r)=1}}^r e(bh/r) \sum_{\substack{a=1 \\ (a,q)=1}}^q E(a,b)\\ &= N\sum_{\substack{b=1 \\ (b,r)=1}}^r e(bh/r) + O(\varphi(r)(\varphi(q)-1)qr)\\ &=N\cdot c_r((h) + O((qr)^2).\\[-3.2pc] \end{align*} $$
3 Convolutions
Proof of Theorem 1.3
Since
![]() $|c_r(n)|\le \phi (r)\le r$
, the convergence hypothesis implies that the Ramanujan–Fourier expansions
$|c_r(n)|\le \phi (r)\le r$
, the convergence hypothesis implies that the Ramanujan–Fourier expansions
![]() $f(n)=\sum _r \hat {f}(r)c_r(n)$
and
$f(n)=\sum _r \hat {f}(r)c_r(n)$
and
![]() $g(n)=\sum _r \hat {g}(r)c_r(n)$
are absolutely convergent, which justifies the following computation:
$g(n)=\sum _r \hat {g}(r)c_r(n)$
are absolutely convergent, which justifies the following computation:
 $$ \begin{align*} \sum_{n\le N} f(n)g(kn+h) &= \sum_{n\le N} \bigg(\sum_q \hat{f}(q)c_q(n)\bigg)\bigg(\sum_r \hat{g}(r)c_r(kn+h)\bigg)\\ &= \sum_{q,r\ge 1} \hat{f}(q)\hat{g}(r)\sum_{n\le N} c_q(n)c_r(kn+h). \end{align*} $$
$$ \begin{align*} \sum_{n\le N} f(n)g(kn+h) &= \sum_{n\le N} \bigg(\sum_q \hat{f}(q)c_q(n)\bigg)\bigg(\sum_r \hat{g}(r)c_r(kn+h)\bigg)\\ &= \sum_{q,r\ge 1} \hat{f}(q)\hat{g}(r)\sum_{n\le N} c_q(n)c_r(kn+h). \end{align*} $$
By Theorem 1.2, this last expression is
 $$ \begin{align*} N\sum_{q\ge 1} \sum_{\substack{d\mid k \\ (k/d,q)=1}} \hat{f}(q)\hat{g}(dq)c_{dq}(h) + O\bigg(\sum_{q,r} | \hat{f}(q)\hat{g}(r)|q^2r^2\bigg). \end{align*} $$
$$ \begin{align*} N\sum_{q\ge 1} \sum_{\substack{d\mid k \\ (k/d,q)=1}} \hat{f}(q)\hat{g}(dq)c_{dq}(h) + O\bigg(\sum_{q,r} | \hat{f}(q)\hat{g}(r)|q^2r^2\bigg). \end{align*} $$
Finally, by the convergence hypothesis, the error term is
![]() $O(1)$
.
$O(1)$
.
4 Sophie Germain primes
Before proving Theorem 1.7, we need the following lemma.
Lemma 4.1. We have
 $$ \begin{align*} \frac{1}{(\log N)^2}\sum_{n\le N} \Lambda(n)\Lambda(2n+1) = (1 + O((\log N ) ^{-1/2}))\cdot \pi_{G}(N) + O((\log N)^{-5/2}). \end{align*} $$
$$ \begin{align*} \frac{1}{(\log N)^2}\sum_{n\le N} \Lambda(n)\Lambda(2n+1) = (1 + O((\log N ) ^{-1/2}))\cdot \pi_{G}(N) + O((\log N)^{-5/2}). \end{align*} $$
Proof. Let
 $$ \begin{align*} L(N) = \sum_{\substack{p\le N \\ p, 2p+1 {\mathrm{\, are\, primes}}}} \log(p)\log(2p+1). \end{align*} $$
$$ \begin{align*} L(N) = \sum_{\substack{p\le N \\ p, 2p+1 {\mathrm{\, are\, primes}}}} \log(p)\log(2p+1). \end{align*} $$
First we note that
 $$ \begin{align*} \sum_{n\le N} \Lambda(n)\Lambda(2n+1) = L(N) + O\bigg(\log N\sum_{\alpha=2}^{ 2 \log N} \sum_{p\le 2 N^{1/\alpha}}\log p\bigg). \end{align*} $$
$$ \begin{align*} \sum_{n\le N} \Lambda(n)\Lambda(2n+1) = L(N) + O\bigg(\log N\sum_{\alpha=2}^{ 2 \log N} \sum_{p\le 2 N^{1/\alpha}}\log p\bigg). \end{align*} $$
By Chebyshev’s bounds, the sum inside the error term is
![]() $O( N^{1/2}\log N )$
from which
$O( N^{1/2}\log N )$
from which
We observe that
 $$ \begin{align} L(N)=\sum_{\substack{p\le N \\ p, 2p+1 {\mathrm{\, are\, primes}}}} \log^2(p) + O(\pi_G(N) \log N). \end{align} $$
$$ \begin{align} L(N)=\sum_{\substack{p\le N \\ p, 2p+1 {\mathrm{\, are\, primes}}}} \log^2(p) + O(\pi_G(N) \log N). \end{align} $$
By partial summation,
 $$ \begin{align} \sum_{\substack{p\le N \\ p, 2p+1 {\mathrm{\, are\, primes}}}} \log^2(p) = \pi_G(N) \log^2(N) + O\bigg(\int_{2}^N \frac{\pi_G(t) \log(t)}{t}\,dt\bigg). \end{align} $$
$$ \begin{align} \sum_{\substack{p\le N \\ p, 2p+1 {\mathrm{\, are\, primes}}}} \log^2(p) = \pi_G(N) \log^2(N) + O\bigg(\int_{2}^N \frac{\pi_G(t) \log(t)}{t}\,dt\bigg). \end{align} $$
At this point, we could use an unconditional upper bound for
![]() $\pi _G(t)$
coming from sieve theory, but let us proceed in a more elementary way. We split the integral at
$\pi _G(t)$
coming from sieve theory, but let us proceed in a more elementary way. We split the integral at
![]() $T=N/\sqrt {\log N}$
and use Chebyshev’s bound
$T=N/\sqrt {\log N}$
and use Chebyshev’s bound
![]() $\pi _G(t)\le \pi (t) = O(t/\log t)$
to find
$\pi _G(t)\le \pi (t) = O(t/\log t)$
to find
 $$ \begin{align*} \int_{2}^N \frac{\pi_G(t) \log(t)}{t}\,dt &= \int_{2}^T \frac{\pi_G(t) \log(t)}{t}\,dt + \int_{T}^N \frac{\pi_G(t) \log(t)}{t}\,dt\\[4pt] &\le \int_{2}^T \,dt + \pi_G(N)\int_{T}^N \frac{ \log(t)}{t}\,dt\\[4pt] &=O(T) + O(\pi_G(N) \cdot N \cdot (\log T)/T)\\[4pt] & = O(N/(\log N)^{1/2} + \pi_G(N) (\log N)^{3/2}). \end{align*} $$
$$ \begin{align*} \int_{2}^N \frac{\pi_G(t) \log(t)}{t}\,dt &= \int_{2}^T \frac{\pi_G(t) \log(t)}{t}\,dt + \int_{T}^N \frac{\pi_G(t) \log(t)}{t}\,dt\\[4pt] &\le \int_{2}^T \,dt + \pi_G(N)\int_{T}^N \frac{ \log(t)}{t}\,dt\\[4pt] &=O(T) + O(\pi_G(N) \cdot N \cdot (\log T)/T)\\[4pt] & = O(N/(\log N)^{1/2} + \pi_G(N) (\log N)^{3/2}). \end{align*} $$
Proof of Theorem 1.7
Under the given assumptions,
 $$ \begin{align*} \sum_{n\le N} \frac{\varphi(n)}{n}\Lambda(n)\cdot \frac{\varphi(2n+1)}{2n+1}\Lambda(2n+1)\sim \kappa \cdot N, \end{align*} $$
$$ \begin{align*} \sum_{n\le N} \frac{\varphi(n)}{n}\Lambda(n)\cdot \frac{\varphi(2n+1)}{2n+1}\Lambda(2n+1)\sim \kappa \cdot N, \end{align*} $$
where
 $$ \begin{align*} \kappa = \sum_{q=1}^\infty \sum_{\substack{d\mid2\\ (2/d, q)=1}} \frac{\mu(q)\mu(dq)}{\varphi(q)\varphi(dq)}c_{dq}(1). \end{align*} $$
$$ \begin{align*} \kappa = \sum_{q=1}^\infty \sum_{\substack{d\mid2\\ (2/d, q)=1}} \frac{\mu(q)\mu(dq)}{\varphi(q)\varphi(dq)}c_{dq}(1). \end{align*} $$
By a computation similar to (14) in [Reference Gadiyar and Padma6], we deduce
By Lemma 4.1, we obtain
 $$ \begin{align*} \pi_G(N)\sim \kappa \cdot\frac{N}{(\log N)^2}. \end{align*} $$
$$ \begin{align*} \pi_G(N)\sim \kappa \cdot\frac{N}{(\log N)^2}. \end{align*} $$
It only remains to show
![]() $\kappa = C_2$
. Since
$\kappa = C_2$
. Since
![]() $c_r(1)=\mu (r)$
and the only divisors of
$c_r(1)=\mu (r)$
and the only divisors of
![]() $2$
are
$2$
are
![]() $d=1$
and
$d=1$
and
![]() $d=2$
, we find
$d=2$
, we find
 $$ \begin{align*} \kappa &= \sum_{q=1}^\infty \sum_{\substack{d\mid2\\ (2/d, q)=1}} \frac{\mu(q)\mu(dq)^2}{\varphi(q)\varphi(dq)}\\[4pt] &= \sum_{q\ge 1 \, \mathrm{odd}} \frac{\mu(q)^3}{\varphi(q)^2} +\sum_{q\ge 1} \frac{\mu(q)\mu(2q)^2}{\varphi(q)\varphi(2q)}\\[4pt] &= \sum_{q\ge 1\, \mathrm{odd}} \frac{\mu(q)}{\varphi(q)^2} +\sum_{q\ge 1\, \mathrm{odd}} \frac{\mu(q)\mu(2q)^2}{\varphi(q)\varphi(2q)}\\ &= \sum_{q\ge 1 \, \mathrm{odd}} \frac{\mu(q)}{\varphi(q)^2} +\sum_{q\ge 1\, \mathrm{odd}} \frac{\mu(q)\mu(2)^2}{\varphi(q)^2\varphi(2)}\\[4pt] &= 2\sum_{q\ge 1 \, \mathrm{odd}} \frac{\mu(q)}{\varphi(q)^2}=C_2.\\[-3.2pc] \end{align*} $$
$$ \begin{align*} \kappa &= \sum_{q=1}^\infty \sum_{\substack{d\mid2\\ (2/d, q)=1}} \frac{\mu(q)\mu(dq)^2}{\varphi(q)\varphi(dq)}\\[4pt] &= \sum_{q\ge 1 \, \mathrm{odd}} \frac{\mu(q)^3}{\varphi(q)^2} +\sum_{q\ge 1} \frac{\mu(q)\mu(2q)^2}{\varphi(q)\varphi(2q)}\\[4pt] &= \sum_{q\ge 1\, \mathrm{odd}} \frac{\mu(q)}{\varphi(q)^2} +\sum_{q\ge 1\, \mathrm{odd}} \frac{\mu(q)\mu(2q)^2}{\varphi(q)\varphi(2q)}\\ &= \sum_{q\ge 1 \, \mathrm{odd}} \frac{\mu(q)}{\varphi(q)^2} +\sum_{q\ge 1\, \mathrm{odd}} \frac{\mu(q)\mu(2)^2}{\varphi(q)^2\varphi(2)}\\[4pt] &= 2\sum_{q\ge 1 \, \mathrm{odd}} \frac{\mu(q)}{\varphi(q)^2}=C_2.\\[-3.2pc] \end{align*} $$
Acknowledgement
This research was conducted while the author was an MSc student at Pontificia Universidad Católica de Chile under the supervision of Hector Pasten. The author wishes to thank Professor Pasten for suggesting the topic and for his help in writing up the results.