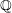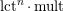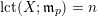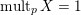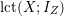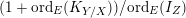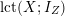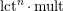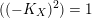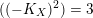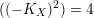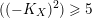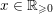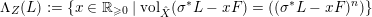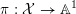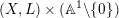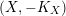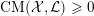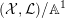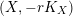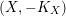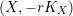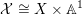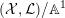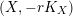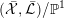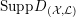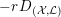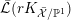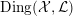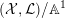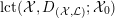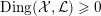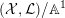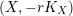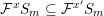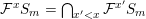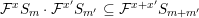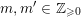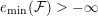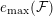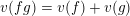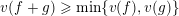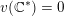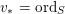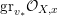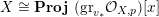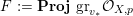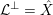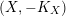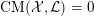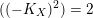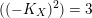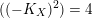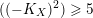1 Introduction
An
![]() $n$
-dimensional complex projective variety
$n$
-dimensional complex projective variety
![]() $X$
is said to be a
$X$
is said to be a
![]() $\mathbb{Q}$
-Fano variety if
$\mathbb{Q}$
-Fano variety if
![]() $X$
has klt singularities and
$X$
has klt singularities and
![]() $-K_{X}$
is an ample
$-K_{X}$
is an ample
![]() $\mathbb{Q}$
-Cartier divisor. When
$\mathbb{Q}$
-Cartier divisor. When
![]() $n\geqslant 2$
, the (anti-canonical) volume
$n\geqslant 2$
, the (anti-canonical) volume
 $((-K_{X})^{n})$
of a
$((-K_{X})^{n})$
of a
![]() $\mathbb{Q}$
-Fano variety
$\mathbb{Q}$
-Fano variety
![]() $X$
can be arbitrarily large, such as volumes of weighted projective spaces (see [Reference DolgachevDol82]). In the smooth case, Kollár et al. [Reference Kollár, Miyaoka and MoriKMM92] and Campana [Reference CampanaCam92] showed that there exists a uniform volume upper bound
$X$
can be arbitrarily large, such as volumes of weighted projective spaces (see [Reference DolgachevDol82]). In the smooth case, Kollár et al. [Reference Kollár, Miyaoka and MoriKMM92] and Campana [Reference CampanaCam92] showed that there exists a uniform volume upper bound
![]() $C_{n}$
for
$C_{n}$
for
![]() $n$
-dimensional Fano manifolds. If
$n$
-dimensional Fano manifolds. If
![]() $n\leqslant 3$
, then
$n\leqslant 3$
, then
![]() $\mathbb{P}^{n}$
has the largest volume among all
$\mathbb{P}^{n}$
has the largest volume among all
![]() $n$
-dimensional Fano manifolds. This fails immediately when
$n$
-dimensional Fano manifolds. This fails immediately when
![]() $n\geqslant 4$
by examples of Batyrev [Reference BatyrevBat81]. However, if a
$n\geqslant 4$
by examples of Batyrev [Reference BatyrevBat81]. However, if a
![]() $\mathbb{Q}$
-Fano variety
$\mathbb{Q}$
-Fano variety
![]() $X$
admits a Kähler–Einstein metric (in the sense of [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ11]), then it is expected that
$X$
admits a Kähler–Einstein metric (in the sense of [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ11]), then it is expected that
![]() $\mathbb{P}^{n}$
has the largest volume (see [Reference TianTia90, Reference Odaka, Spotti and SunOSS16] for
$\mathbb{P}^{n}$
has the largest volume (see [Reference TianTia90, Reference Odaka, Spotti and SunOSS16] for
![]() $n=2$
, and [Reference Berman and BerndtssonBB11, Reference Berman and BerndtssonBB17] for smooth cases). Recently, Fujita [Reference FujitaFuj15] showed that if
$n=2$
, and [Reference Berman and BerndtssonBB11, Reference Berman and BerndtssonBB17] for smooth cases). Recently, Fujita [Reference FujitaFuj15] showed that if
![]() $X$
is a
$X$
is a
![]() $n$
-dimensional
$n$
-dimensional
![]() $\mathbb{Q}$
-Fano variety admitting a Kähler–Einstein metric, then the anti-canonical volume
$\mathbb{Q}$
-Fano variety admitting a Kähler–Einstein metric, then the anti-canonical volume
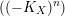 $((-K_{X})^{n})$
is less than or equal to
$((-K_{X})^{n})$
is less than or equal to
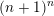 $(n+1)^{n}$
(
$(n+1)^{n}$
(
![]() $=$
the volume of
$=$
the volume of
![]() $\mathbb{P}^{n}$
).
$\mathbb{P}^{n}$
).
In this paper, we refine the result [Reference FujitaFuj15] by looking at invariants of the local singularities. Our first main result is as follows.
Theorem 1. Let
![]() $X$
be a Kähler–Einstein
$X$
be a Kähler–Einstein
![]() $\mathbb{Q}$
-Fano variety. Let
$\mathbb{Q}$
-Fano variety. Let
![]() $p\in X$
be a closed point. Let
$p\in X$
be a closed point. Let
![]() $Z$
be a closed subscheme of
$Z$
be a closed subscheme of
![]() $X$
with
$X$
with
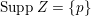 $\text{Supp}\,Z=\{p\}$
. Then we have
$\text{Supp}\,Z=\{p\}$
. Then we have
 $$\begin{eqnarray}((-K_{X})^{n})\leqslant \biggl(1+\frac{1}{n}\biggr)^{n}\operatorname{lct}(X;I_{Z})^{n}\operatorname{mult}_{Z}X,\end{eqnarray}$$
$$\begin{eqnarray}((-K_{X})^{n})\leqslant \biggl(1+\frac{1}{n}\biggr)^{n}\operatorname{lct}(X;I_{Z})^{n}\operatorname{mult}_{Z}X,\end{eqnarray}$$
where
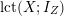 $\operatorname{lct}(X;I_{Z})$
is the log canonical threshold of the ideal sheaf
$\operatorname{lct}(X;I_{Z})$
is the log canonical threshold of the ideal sheaf
![]() $I_{Z}$
, and
$I_{Z}$
, and
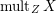 $\operatorname{mult}_{Z}X$
is the Hilbert–Samuel multiplicity of
$\operatorname{mult}_{Z}X$
is the Hilbert–Samuel multiplicity of
![]() $X$
along
$X$
along
![]() $Z$
.
$Z$
.
Note that the invariant
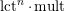 $\operatorname{lct}^{n}\cdot \operatorname{mult}$
has been studied by de Fernex, Ein and Mustaţă in [Reference MustaţăMus02, Reference de Fernex, Ein and MustaţădFEM03, Reference de Fernex, Ein and MustaţădFEM04, Reference de Fernex and MustaţădFM15].
$\operatorname{lct}^{n}\cdot \operatorname{mult}$
has been studied by de Fernex, Ein and Mustaţă in [Reference MustaţăMus02, Reference de Fernex, Ein and MustaţădFEM03, Reference de Fernex, Ein and MustaţădFEM04, Reference de Fernex and MustaţădFM15].
There are three major aspects of Theorem 1:
– If we take
 $Z=p$
to be a smooth point on
$Z=p$
to be a smooth point on
 $X$
, then
$X$
, then
 $\operatorname{lct}(X;\mathfrak{m}_{p})=n$
and
$\operatorname{lct}(X;\mathfrak{m}_{p})=n$
and
 $\operatorname{mult}_{p}X=1$
. In particular, we recover Fujita’s result [Reference FujitaFuj15, Corollary 1.3].
$\operatorname{mult}_{p}X=1$
. In particular, we recover Fujita’s result [Reference FujitaFuj15, Corollary 1.3].– By definition,
 $\operatorname{lct}(X;I_{Z})$
is the infimum of
$\operatorname{lct}(X;I_{Z})$
is the infimum of
 $(1+\text{ord}_{E}(K_{Y/X}))/\text{ord}_{E}(I_{Z})$
among all prime divisors
$(1+\text{ord}_{E}(K_{Y/X}))/\text{ord}_{E}(I_{Z})$
among all prime divisors
 $E$
on a resolution
$E$
on a resolution
 $Y$
of
$Y$
of
 $X$
. Although
$X$
. Although
 $\operatorname{lct}(X;I_{Z})$
is not easy to compute in general, we can always get a volume upper bound by considering one divisor
$\operatorname{lct}(X;I_{Z})$
is not easy to compute in general, we can always get a volume upper bound by considering one divisor
 $E$
, e.g. Theorems 3 and 25.
$E$
, e.g. Theorems 3 and 25.– On the other hand, if we fix a singularity
 $p$
on a Kähler–Einstein
$p$
on a Kähler–Einstein
 $\mathbb{Q}$
-Fano variety
$\mathbb{Q}$
-Fano variety
 $X$
, we get a lower bound of
$X$
, we get a lower bound of
 $\operatorname{lct}^{n}\cdot \operatorname{mult}$
among all thickenings of
$\operatorname{lct}^{n}\cdot \operatorname{mult}$
among all thickenings of
 $p$
. For example, if
$p$
. For example, if
 $X=\mathbb{P}^{n}$
then the inequality (1.1) recovers the main result in [Reference de Fernex, Ein and MustaţădFEM04] (see Theorem 22). More generally, we get de Fernex–Ein–Mustaţă type inequalities for all cone singularities with K-semistable base using a logarithmic version of Theorem 1 (see Theorem 7).
$X=\mathbb{P}^{n}$
then the inequality (1.1) recovers the main result in [Reference de Fernex, Ein and MustaţădFEM04] (see Theorem 22). More generally, we get de Fernex–Ein–Mustaţă type inequalities for all cone singularities with K-semistable base using a logarithmic version of Theorem 1 (see Theorem 7).
For a real valuation
![]() $v$
on
$v$
on
![]() $\mathbb{C}(X)$
centered at a closed point
$\mathbb{C}(X)$
centered at a closed point
![]() $p$
, the normalized volume function
$p$
, the normalized volume function
![]() $\widehat{\operatorname{vol}}$
, introduced by C. Li in [Reference LiLi15], is defined as
$\widehat{\operatorname{vol}}$
, introduced by C. Li in [Reference LiLi15], is defined as
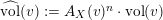 $\widehat{\operatorname{vol}}(v):=A_{X}(v)^{n}\cdot \operatorname{vol}(v)$
, where
$\widehat{\operatorname{vol}}(v):=A_{X}(v)^{n}\cdot \operatorname{vol}(v)$
, where
![]() $A_{X}(v)$
is the log discrepancy of
$A_{X}(v)$
is the log discrepancy of
![]() $v$
and
$v$
and
![]() $\operatorname{vol}(v)$
is the volume of
$\operatorname{vol}(v)$
is the volume of
![]() $v$
. The following theorem gives an upper bound for the anti-canonical volume of
$v$
. The following theorem gives an upper bound for the anti-canonical volume of
![]() $X$
in terms of the normalized volume of a real valuation.
$X$
in terms of the normalized volume of a real valuation.
Theorem 2. Let
![]() $X$
be a Kähler–Einstein
$X$
be a Kähler–Einstein
![]() $\mathbb{Q}$
-Fano variety. Let
$\mathbb{Q}$
-Fano variety. Let
![]() $p\in X$
be a closed point. Let
$p\in X$
be a closed point. Let
![]() $v$
be a real valuation on
$v$
be a real valuation on
![]() $\mathbb{C}(X)$
centered at
$\mathbb{C}(X)$
centered at
![]() $p$
. Then we have
$p$
. Then we have
 $$\begin{eqnarray}((-K_{X})^{n})\leqslant \biggl(1+\frac{1}{n}\biggr)^{n}\,\widehat{\operatorname{vol}}(v).\end{eqnarray}$$
$$\begin{eqnarray}((-K_{X})^{n})\leqslant \biggl(1+\frac{1}{n}\biggr)^{n}\,\widehat{\operatorname{vol}}(v).\end{eqnarray}$$
Minimizing the normalized volume function,
![]() $\widehat{\operatorname{vol}}$
has been studied by Li, Xu, Blum and the author in [Reference LiLi15, Reference LiLi17, Reference Li and LiuLL16, Reference Li and XuLX16, Reference BlumBlu18]. In [Reference Li and LiuLL16], a logarithmic version of Theorem 2 was developed to obtain the sharp lower bound of the normalized volume function for cone singularities over Kähler–Einstein
$\widehat{\operatorname{vol}}$
has been studied by Li, Xu, Blum and the author in [Reference LiLi15, Reference LiLi17, Reference Li and LiuLL16, Reference Li and XuLX16, Reference BlumBlu18]. In [Reference Li and LiuLL16], a logarithmic version of Theorem 2 was developed to obtain the sharp lower bound of the normalized volume function for cone singularities over Kähler–Einstein
![]() $\mathbb{Q}$
-Fano varieties.
$\mathbb{Q}$
-Fano varieties.
To compare Theorems 1 and 2, we know from [Reference MustaţăMus02, Reference LiLi15] that the infimum of
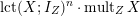 $\operatorname{lct}(X;I_{Z})^{n}\cdot \operatorname{mult}_{Z}X$
among all thickenings
$\operatorname{lct}(X;I_{Z})^{n}\cdot \operatorname{mult}_{Z}X$
among all thickenings
![]() $Z$
of
$Z$
of
![]() $p$
is no bigger than the infimum of
$p$
is no bigger than the infimum of
![]() $\widehat{\operatorname{vol}}(v)$
among all real valuations centered at
$\widehat{\operatorname{vol}}(v)$
among all real valuations centered at
![]() $p$
. In fact, we show that these two infimums are the same (see Theorem 27). In particular, this means that Theorems 1 and 2 are actually equivalent.
$p$
. In fact, we show that these two infimums are the same (see Theorem 27). In particular, this means that Theorems 1 and 2 are actually equivalent.
As an application of Theorems 1 and 2, we get sharp volume upper bounds for Kähler–Einstein
![]() $\mathbb{Q}$
-Fano varieties with quotient singularities.
$\mathbb{Q}$
-Fano varieties with quotient singularities.
Theorem 3. Let
![]() $X$
be a Kähler–Einstein
$X$
be a Kähler–Einstein
![]() $\mathbb{Q}$
-Fano variety of dimension
$\mathbb{Q}$
-Fano variety of dimension
![]() $n$
. Let
$n$
. Let
![]() $p\in X$
be a closed point. Suppose
$p\in X$
be a closed point. Suppose
![]() $(X,p)$
is a quotient singularity with local analytic model
$(X,p)$
is a quotient singularity with local analytic model
![]() $\mathbb{C}^{n}/G$
where
$\mathbb{C}^{n}/G$
where
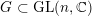 $G\subset \text{GL}(n,\mathbb{C})$
acts freely in codimension
$G\subset \text{GL}(n,\mathbb{C})$
acts freely in codimension
![]() $1$
. Then
$1$
. Then
 $$\begin{eqnarray}((-K_{X})^{n})\leqslant \frac{(n+1)^{n}}{|G|},\end{eqnarray}$$
$$\begin{eqnarray}((-K_{X})^{n})\leqslant \frac{(n+1)^{n}}{|G|},\end{eqnarray}$$
with equality if and only if
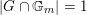 $|G\cap \mathbb{G}_{m}|=1$
and
$|G\cap \mathbb{G}_{m}|=1$
and
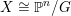 $X\cong \mathbb{P}^{n}/G$
, where
$X\cong \mathbb{P}^{n}/G$
, where
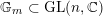 $\mathbb{G}_{m}\subset \text{GL}(n,\mathbb{C})$
is the subgroup consisting of non-zero scalar matrices.
$\mathbb{G}_{m}\subset \text{GL}(n,\mathbb{C})$
is the subgroup consisting of non-zero scalar matrices.
It is well known that for algebraic surfaces, klt singularities are the same as quotient singularities. In [Reference TianTia90], Tian showed that the anti-canonical volume of a Kähler–Einstein log Del Pezzo surface is bounded from above by
![]() $48/|G|$
where
$48/|G|$
where
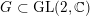 $G\subset \text{GL}(2,\mathbb{C})$
is the orbifold group at a closed point. In [Reference Odaka, Spotti and SunOSS16], Odaka, Spotti and Sun improved the volume upper bounds to
$G\subset \text{GL}(2,\mathbb{C})$
is the orbifold group at a closed point. In [Reference Odaka, Spotti and SunOSS16], Odaka, Spotti and Sun improved the volume upper bounds to
![]() $12/|G|$
.
$12/|G|$
.
As a direct consequence of Theorem 3, we get the sharp volume upper bounds
![]() $9/|G|$
for Kähler–Einstein log Del Pezzo surfaces.
$9/|G|$
for Kähler–Einstein log Del Pezzo surfaces.
Corollary 4. Let
![]() $X$
be a Kähler–Einstein log Del Pezzo surface. Let
$X$
be a Kähler–Einstein log Del Pezzo surface. Let
![]() $p\in X$
be a closed point with local analytic model
$p\in X$
be a closed point with local analytic model
![]() $\mathbb{C}^{2}/G$
, where
$\mathbb{C}^{2}/G$
, where
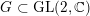 $G\subset \text{GL}(2,\mathbb{C})$
acts freely in codimension
$G\subset \text{GL}(2,\mathbb{C})$
acts freely in codimension
![]() $1$
. Then
$1$
. Then
 $$\begin{eqnarray}((-K_{X})^{2})\leqslant \frac{9}{|G|},\end{eqnarray}$$
$$\begin{eqnarray}((-K_{X})^{2})\leqslant \frac{9}{|G|},\end{eqnarray}$$
with equality if and only if
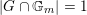 $|G\cap \mathbb{G}_{m}|=1$
and
$|G\cap \mathbb{G}_{m}|=1$
and
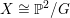 $X\cong \mathbb{P}^{2}/G$
.
$X\cong \mathbb{P}^{2}/G$
.
Remark 5. The author was informed by Kento Fujita that he independently obtained cases of Corollary 4 when
![]() $(X,p)$
is Du Val.
$(X,p)$
is Du Val.
It was conjectured by Cheltsov and Kosta in [Reference Cheltsov and KostaCK14, Conjecture 1.18] that a Gorenstein Del Pezzo surface admits Kähler–Einstein metrics if and only if the singularities are of certain types depending on the anti-canonical volume. This conjecture was proved by Odaka et al. in [Reference Odaka, Spotti and SunOSS16, p. 165] where
![]() $\mathbb{Q}$
-Gorenstein smoothable Kähler–Einstein log Del Pezzo surfaces are classified. As a quick application of Corollary 4, we give an alternative proof of the ‘only if’ part of this conjecture. We remark that partial results are known before [Reference Odaka, Spotti and SunOSS16], e.g. [Reference Ding and TianDT92, Reference JeffresJef97, Reference WonWon13] on the ‘only if’ part and [Reference Mabuchi and MukaiMM93, Reference Ghigi and KollárGK07, Reference CheltsovChe08, Reference ShiShi10, Reference Cheltsov and KostaCK14] on the ‘if’ part.
$\mathbb{Q}$
-Gorenstein smoothable Kähler–Einstein log Del Pezzo surfaces are classified. As a quick application of Corollary 4, we give an alternative proof of the ‘only if’ part of this conjecture. We remark that partial results are known before [Reference Odaka, Spotti and SunOSS16], e.g. [Reference Ding and TianDT92, Reference JeffresJef97, Reference WonWon13] on the ‘only if’ part and [Reference Mabuchi and MukaiMM93, Reference Ghigi and KollárGK07, Reference CheltsovChe08, Reference ShiShi10, Reference Cheltsov and KostaCK14] on the ‘if’ part.
Corollary 6. Let
![]() $X$
be a Kähler–Einstein log Del Pezzo surface with at most Du Val singularities.
$X$
be a Kähler–Einstein log Del Pezzo surface with at most Du Val singularities.
(i) If
 $((-K_{X})^{2})=1$
, then
$((-K_{X})^{2})=1$
, then
 $X$
has at most singularities of type
$X$
has at most singularities of type
 $\mathbb{A}_{1}$
,
$\mathbb{A}_{1}$
,
 $\mathbb{A}_{2}$
,
$\mathbb{A}_{2}$
,
 $\mathbb{A}_{3}$
,
$\mathbb{A}_{3}$
,
 $\mathbb{A}_{4}$
,
$\mathbb{A}_{4}$
,
 $\mathbb{A}_{5}$
,
$\mathbb{A}_{5}$
,
 $\mathbb{A}_{6}$
,
$\mathbb{A}_{6}$
,
 $\mathbb{A}_{7}$
or
$\mathbb{A}_{7}$
or
 $\mathbb{D}_{4}$
.
$\mathbb{D}_{4}$
.(ii) If
 $((-K_{X})^{2})=2$
, then
$((-K_{X})^{2})=2$
, then
 $X$
has at most singularities of type
$X$
has at most singularities of type
 $\mathbb{A}_{1}$
,
$\mathbb{A}_{1}$
,
 $\mathbb{A}_{2}$
or
$\mathbb{A}_{2}$
or
 $\mathbb{A}_{3}$
.
$\mathbb{A}_{3}$
.(iii) If
 $((-K_{X})^{2})=3$
, then
$((-K_{X})^{2})=3$
, then
 $X$
has at most singularities of type
$X$
has at most singularities of type
 $\mathbb{A}_{1}$
or
$\mathbb{A}_{1}$
or
 $\mathbb{A}_{2}$
.
$\mathbb{A}_{2}$
.(iv) If
 $((-K_{X})^{2})=4$
, then
$((-K_{X})^{2})=4$
, then
 $X$
has at most singularities of type
$X$
has at most singularities of type
 $\mathbb{A}_{1}$
.
$\mathbb{A}_{1}$
.(v) If
 $((-K_{X})^{2})\geqslant 5$
, then
$((-K_{X})^{2})\geqslant 5$
, then
 $X$
is smooth.
$X$
is smooth.
The comparison between Theorems 1 and 2 also allows us to rephrase the results from [Reference LiLi17, Reference Li and LiuLL16] in terms of
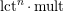 $\operatorname{lct}^{n}\cdot \operatorname{mult}$
. The following theorem gives a necessary and sufficient condition for a Fano manifold to be K-semistable.
$\operatorname{lct}^{n}\cdot \operatorname{mult}$
. The following theorem gives a necessary and sufficient condition for a Fano manifold to be K-semistable.
Theorem 7. Let
![]() $V$
be a Fano manifold of dimension
$V$
be a Fano manifold of dimension
![]() $n-1$
. Assume
$n-1$
. Assume
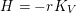 $H=-rK_{V}$
is an ample Cartier divisor for some
$H=-rK_{V}$
is an ample Cartier divisor for some
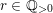 $r\in \mathbb{Q}_{{>}0}$
. Let
$r\in \mathbb{Q}_{{>}0}$
. Let
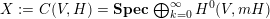 $X:=C(V,H)=\mathbf{Spec}\,\bigoplus _{k=0}^{\infty }H^{0}(V,mH)$
be the affine cone with cone vertex
$X:=C(V,H)=\mathbf{Spec}\,\bigoplus _{k=0}^{\infty }H^{0}(V,mH)$
be the affine cone with cone vertex
![]() $o$
. Then
$o$
. Then
![]() $V$
is K-semistable if and only if for any closed subscheme
$V$
is K-semistable if and only if for any closed subscheme
![]() $Z$
of
$Z$
of
![]() $X$
supported at
$X$
supported at
![]() $o$
, the following inequality holds:
$o$
, the following inequality holds:
 $$\begin{eqnarray}\operatorname{lct}(X;I_{Z})^{n}\cdot \operatorname{mult}_{Z}X\geqslant \frac{1}{r}((-K_{V})^{n-1}).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{lct}(X;I_{Z})^{n}\cdot \operatorname{mult}_{Z}X\geqslant \frac{1}{r}((-K_{V})^{n-1}).\end{eqnarray}$$
In particular, from the ‘only if’ part of Theorem 7 we get de Fernex–Ein–Mustaţă type inequalities (1.3) on cone singularities with K-semistable bases (see [Reference de Fernex, Ein and MustaţădFEM04] or Theorem 22 for the smooth case). Note that the ‘if’ part is a straight-forward consequence after [Reference LiLi17] using the relations between
 $\operatorname{lct}^{n}\cdot \operatorname{mult}$
and
$\operatorname{lct}^{n}\cdot \operatorname{mult}$
and
![]() $\widehat{\operatorname{vol}}$
from [Reference MustaţăMus02, Reference LiLi15].
$\widehat{\operatorname{vol}}$
from [Reference MustaţăMus02, Reference LiLi15].
The proofs of Theorems 1 and 2 rely on the recent result [Reference FujitaFuj15] where Fujita settled the optimal volume upper bounds for Ding-semistable
![]() $\mathbb{Q}$
-Fano varieties. Recall that a
$\mathbb{Q}$
-Fano varieties. Recall that a
![]() $\mathbb{Q}$
-Fano variety
$\mathbb{Q}$
-Fano variety
![]() $X$
is said to be Ding-semistable if the Ding invariant
$X$
is said to be Ding-semistable if the Ding invariant
 $\text{Ding}({\mathcal{X}},{\mathcal{L}})$
is non-negative for any normal test configuration
$\text{Ding}({\mathcal{X}},{\mathcal{L}})$
is non-negative for any normal test configuration
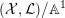 $({\mathcal{X}},{\mathcal{L}})/\mathbb{A}^{1}$
of
$({\mathcal{X}},{\mathcal{L}})/\mathbb{A}^{1}$
of
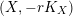 $(X,-rK_{X})$
. The results in [Reference BermanBer16, § 3] show that, if a
$(X,-rK_{X})$
. The results in [Reference BermanBer16, § 3] show that, if a
![]() $\mathbb{Q}$
-Fano variety
$\mathbb{Q}$
-Fano variety
![]() $X$
admits a Kähler–Einstein metric, then
$X$
admits a Kähler–Einstein metric, then
![]() $X$
is Ding-semistable (see also [Reference FujitaFuj15, Theorem 3.2]). This allows us to prove Theorems 1 and 2 under the weaker assumption that
$X$
is Ding-semistable (see also [Reference FujitaFuj15, Theorem 3.2]). This allows us to prove Theorems 1 and 2 under the weaker assumption that
![]() $X$
is Ding-semistable (see Theorems 16 and 21). To prove the equality case of Theorem 3, we blow up a flag ideal associated to the
$X$
is Ding-semistable (see Theorems 16 and 21). To prove the equality case of Theorem 3, we blow up a flag ideal associated to the
![]() $\widehat{\operatorname{vol}}$
-minimizing valuation to obtain a test configuration with zero
$\widehat{\operatorname{vol}}$
-minimizing valuation to obtain a test configuration with zero
![]() $\text{CM}$
weight. Then K-polystability is enough to characterize the
$\text{CM}$
weight. Then K-polystability is enough to characterize the
![]() $\mathbb{Q}$
-Fano variety with maximal volume (see Lemma 33 for details).
$\mathbb{Q}$
-Fano variety with maximal volume (see Lemma 33 for details).
The paper is organized as follows. In § 2, we recall the notions of Seshadri constants, Ding-semistability, filtrations and normalized volume of real valuations. As a generalization of [Reference FujitaFuj15, Theorem 2.3], we characterize the Seshadri constant of an arbitrary thickening of a close point in terms of the volume function in Lemma 10. In § 3.1, we prove Theorems 1 and 2. The proof of Theorem 1 is a quick application of [Reference FujitaFuj15, Theorem 1.2] and Lemma 10. To prove Theorem 2, we apply [Reference FujitaFuj15, Theorem 4.9] to the filtration associated to any real valuation. In § 3.2, we give some applications of Theorems 1 and 2. We recover the main result from [Reference de Fernex, Ein and MustaţădFEM04]. We prove the inequality part of Theorem 3. We also get a volume upper bound for a Ding-semistable
![]() $\mathbb{Q}$
-Fano variety with an isolated singularity that is not terminal (see Theorem 25). Section 4 is devoted to comparing the two invariants occurred in the volume upper bounds, i.e.
$\mathbb{Q}$
-Fano variety with an isolated singularity that is not terminal (see Theorem 25). Section 4 is devoted to comparing the two invariants occurred in the volume upper bounds, i.e.
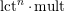 $\operatorname{lct}^{n}\cdot \operatorname{mult}$
and
$\operatorname{lct}^{n}\cdot \operatorname{mult}$
and
![]() $\widehat{\operatorname{vol}}$
. In Theorem 27, we show that these two invariants have the same infimums among ideals supported (respectively valuations centered) at a klt point. This implies that Theorems 1 and 2 are equivalent to each other. We prove Theorem 7 using Theorem 27 and results from [Reference LiLi17, Reference Li and LiuLL16]. In § 4.2, we study the existence of minimizers of
$\widehat{\operatorname{vol}}$
. In Theorem 27, we show that these two invariants have the same infimums among ideals supported (respectively valuations centered) at a klt point. This implies that Theorems 1 and 2 are equivalent to each other. We prove Theorem 7 using Theorem 27 and results from [Reference LiLi17, Reference Li and LiuLL16]. In § 4.2, we study the existence of minimizers of
 $\operatorname{lct}^{n}\cdot \operatorname{mult}$
and
$\operatorname{lct}^{n}\cdot \operatorname{mult}$
and
![]() $\widehat{\operatorname{vol}}$
. In § 5, we study the equality case of Theorems 1 and 2. Lemma 33 characterizes the equality case of Theorem 2 when
$\widehat{\operatorname{vol}}$
. In § 5, we study the equality case of Theorems 1 and 2. Lemma 33 characterizes the equality case of Theorem 2 when
![]() $X$
is K-polystable with extra conditions on the real valuation. Applying this lemma, we prove the equality case of Theorem 3 and Corollary 6. We also prove that
$X$
is K-polystable with extra conditions on the real valuation. Applying this lemma, we prove the equality case of Theorem 3 and Corollary 6. We also prove that
![]() $\mathbb{P}^{n}$
is the only Ding-semistable
$\mathbb{P}^{n}$
is the only Ding-semistable
![]() $\mathbb{Q}$
-Fano variety of volume at least
$\mathbb{Q}$
-Fano variety of volume at least
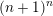 $(n+1)^{n}$
(see Theorem 36). This theorem improves the equality case of [Reference FujitaFuj15, Theorem 1.1] where Fujita proved for Ding-semistable Fano manifolds.
$(n+1)^{n}$
(see Theorem 36). This theorem improves the equality case of [Reference FujitaFuj15, Theorem 1.1] where Fujita proved for Ding-semistable Fano manifolds.
Notation
Throughout this paper, we work over the complex numbers
![]() $\mathbb{C}$
. Let
$\mathbb{C}$
. Let
![]() $X$
be an
$X$
be an
![]() $n$
-dimensional normal variety. Let
$n$
-dimensional normal variety. Let
![]() $\unicode[STIX]{x1D6E5}$
be an effective
$\unicode[STIX]{x1D6E5}$
be an effective
![]() $\mathbb{Q}$
-divisor on
$\mathbb{Q}$
-divisor on
![]() $X$
such that
$X$
such that
![]() $(X,\unicode[STIX]{x1D6E5})$
is a klt pair. For a closed subscheme
$(X,\unicode[STIX]{x1D6E5})$
is a klt pair. For a closed subscheme
![]() $Z$
of
$Z$
of
![]() $X$
, the log canonical threshold of its ideal sheaf
$X$
, the log canonical threshold of its ideal sheaf
![]() $I_{Z}$
with respect to
$I_{Z}$
with respect to
![]() $(X,\unicode[STIX]{x1D6E5})$
is defined as
$(X,\unicode[STIX]{x1D6E5})$
is defined as
 $$\begin{eqnarray}\operatorname{lct}(X,\unicode[STIX]{x1D6E5};I_{Z}):=\inf _{E}\frac{1+\text{ord}_{E}(K_{Y}-f^{\ast }(K_{X}+\unicode[STIX]{x1D6E5}))}{\text{ord}_{E}(I_{Z})},\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{lct}(X,\unicode[STIX]{x1D6E5};I_{Z}):=\inf _{E}\frac{1+\text{ord}_{E}(K_{Y}-f^{\ast }(K_{X}+\unicode[STIX]{x1D6E5}))}{\text{ord}_{E}(I_{Z})},\end{eqnarray}$$
where the infimum is taken over all prime divisors
![]() $E$
on a log resolution
$E$
on a log resolution
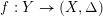 $f:Y\rightarrow (X,\unicode[STIX]{x1D6E5})$
. We also denote by
$f:Y\rightarrow (X,\unicode[STIX]{x1D6E5})$
. We also denote by
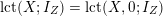 $\operatorname{lct}(X;I_{Z})=\operatorname{lct}(X,0;I_{Z})$
when
$\operatorname{lct}(X;I_{Z})=\operatorname{lct}(X,0;I_{Z})$
when
![]() $\unicode[STIX]{x1D6E5}=0$
. If
$\unicode[STIX]{x1D6E5}=0$
. If
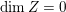 $\dim Z=0$
, the Hilbert–Samuel multiplicity of
$\dim Z=0$
, the Hilbert–Samuel multiplicity of
![]() $X$
along
$X$
along
![]() $Z$
is defined as
$Z$
is defined as
 $$\begin{eqnarray}\operatorname{mult}_{Z}(X):=\lim _{k\rightarrow \infty }\frac{\ell ({\mathcal{O}}_{X}/I_{Z}^{k})}{k^{n}/n!}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{mult}_{Z}(X):=\lim _{k\rightarrow \infty }\frac{\ell ({\mathcal{O}}_{X}/I_{Z}^{k})}{k^{n}/n!}.\end{eqnarray}$$
We will also use the notation
![]() $\operatorname{lct}(\mathfrak{a})$
(and
$\operatorname{lct}(\mathfrak{a})$
(and
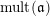 $\operatorname{mult}(\mathfrak{a})$
) as abbreviation of
$\operatorname{mult}(\mathfrak{a})$
) as abbreviation of
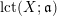 $\operatorname{lct}(X;\mathfrak{a})$
(and
$\operatorname{lct}(X;\mathfrak{a})$
(and
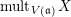 $\operatorname{mult}_{V(\mathfrak{a})}X$
) for a coherent ideal sheaf
$\operatorname{mult}_{V(\mathfrak{a})}X$
) for a coherent ideal sheaf
![]() $\mathfrak{a}$
(of dimension
$\mathfrak{a}$
(of dimension
![]() $0$
) once the variety
$0$
) once the variety
![]() $X$
is specified.
$X$
is specified.
Following [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ11, Reference BermanBer16], on an
![]() $n$
-dimensional
$n$
-dimensional
![]() $\mathbb{Q}$
-Fano variety
$\mathbb{Q}$
-Fano variety
![]() $X$
, a Kähler metric
$X$
, a Kähler metric
![]() $\unicode[STIX]{x1D714}$
on the smooth locus
$\unicode[STIX]{x1D714}$
on the smooth locus
![]() $X_{\text{reg}}$
is said to be a Kähler–Einstein metric on
$X_{\text{reg}}$
is said to be a Kähler–Einstein metric on
![]() $X$
if it has constant Ricci curvature, i.e.
$X$
if it has constant Ricci curvature, i.e.
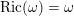 $\text{Ric}(\unicode[STIX]{x1D714})=\unicode[STIX]{x1D714}$
on
$\text{Ric}(\unicode[STIX]{x1D714})=\unicode[STIX]{x1D714}$
on
![]() $X_{\text{reg}}$
, and
$X_{\text{reg}}$
, and
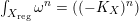 $\int _{X_{\text{reg}}}\unicode[STIX]{x1D714}^{n}=((-K_{X})^{n})$
. By [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ11, Definition 3.5 and Proposition 3.8], this is equivalent to saying that
$\int _{X_{\text{reg}}}\unicode[STIX]{x1D714}^{n}=((-K_{X})^{n})$
. By [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ11, Definition 3.5 and Proposition 3.8], this is equivalent to saying that
![]() $\unicode[STIX]{x1D714}$
is a closed positive
$\unicode[STIX]{x1D714}$
is a closed positive
![]() $(1,1)$
-current with full Monge–Ampère mass on
$(1,1)$
-current with full Monge–Ampère mass on
![]() $X$
satisfying
$X$
satisfying
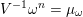 $V^{-1}\unicode[STIX]{x1D714}^{n}=\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D714}}$
(see [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ11, § 3] for details).
$V^{-1}\unicode[STIX]{x1D714}^{n}=\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D714}}$
(see [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ11, § 3] for details).
Given a normal variety
![]() $X$
and a (not necessarily effective)
$X$
and a (not necessarily effective)
![]() $\mathbb{Q}$
-divisor
$\mathbb{Q}$
-divisor
![]() $\unicode[STIX]{x1D6E5}$
, we say that
$\unicode[STIX]{x1D6E5}$
, we say that
![]() $(X,\unicode[STIX]{x1D6E5})$
is a sub pair if
$(X,\unicode[STIX]{x1D6E5})$
is a sub pair if
 $K_{X}+\unicode[STIX]{x1D6E5}$
is
$K_{X}+\unicode[STIX]{x1D6E5}$
is
![]() $\mathbb{Q}$
-Cartier. Let
$\mathbb{Q}$
-Cartier. Let
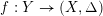 $f:Y\rightarrow (X,\unicode[STIX]{x1D6E5})$
be a log resolution, then we have the following equality
$f:Y\rightarrow (X,\unicode[STIX]{x1D6E5})$
be a log resolution, then we have the following equality
 $$\begin{eqnarray}K_{Y}=f^{\ast }(K_{X}+\unicode[STIX]{x1D6E5})+\mathop{\sum }_{i}a_{i}E_{i},\end{eqnarray}$$
$$\begin{eqnarray}K_{Y}=f^{\ast }(K_{X}+\unicode[STIX]{x1D6E5})+\mathop{\sum }_{i}a_{i}E_{i},\end{eqnarray}$$
where
![]() $E_{i}$
are distinct prime divisors on
$E_{i}$
are distinct prime divisors on
![]() $Y$
. We say that
$Y$
. We say that
![]() $(X,\unicode[STIX]{x1D6E5})$
is sub log canonical if
$(X,\unicode[STIX]{x1D6E5})$
is sub log canonical if
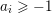 $a_{i}\geqslant -1$
for all
$a_{i}\geqslant -1$
for all
![]() $i$
. If
$i$
. If
![]() $D$
is a
$D$
is a
![]() $\mathbb{Q}$
-Cartier
$\mathbb{Q}$
-Cartier
![]() $\mathbb{Q}$
-divisor on
$\mathbb{Q}$
-divisor on
![]() $X$
, then the log canonical threshold of
$X$
, then the log canonical threshold of
![]() $D$
with respect to a sub pair
$D$
with respect to a sub pair
![]() $(X,\unicode[STIX]{x1D6E5})$
is defined as
$(X,\unicode[STIX]{x1D6E5})$
is defined as
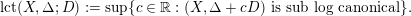 $$\begin{eqnarray}\operatorname{lct}(X,\unicode[STIX]{x1D6E5};D):=\sup \{c\in \mathbb{R}:(X,\unicode[STIX]{x1D6E5}+cD)\text{ is sub log canonical}\}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{lct}(X,\unicode[STIX]{x1D6E5};D):=\sup \{c\in \mathbb{R}:(X,\unicode[STIX]{x1D6E5}+cD)\text{ is sub log canonical}\}.\end{eqnarray}$$
2 Preliminaries
2.1 Seshadri constants
Definition 8 [Reference LazarsfeldLaz04].
Let
![]() $X$
be a projective variety of dimension
$X$
be a projective variety of dimension
![]() $n$
. For a
$n$
. For a
![]() $\mathbb{Q}$
-Cartier
$\mathbb{Q}$
-Cartier
![]() $\mathbb{Q}$
-divisor
$\mathbb{Q}$
-divisor
![]() $L$
on
$L$
on
![]() $X$
, we define the volume of
$X$
, we define the volume of
![]() $L$
on
$L$
on
![]() $X$
to be
$X$
to be
 $$\begin{eqnarray}\operatorname{vol}_{X}(L):=\limsup _{k\rightarrow \infty ,kL\text{ Cartier}}\frac{h^{0}(X,{\mathcal{O}}_{X}(kL))}{k^{n}/n!}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{vol}_{X}(L):=\limsup _{k\rightarrow \infty ,kL\text{ Cartier}}\frac{h^{0}(X,{\mathcal{O}}_{X}(kL))}{k^{n}/n!}.\end{eqnarray}$$
We know that the lim sup computing
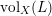 $\operatorname{vol}_{X}(L)$
is actually a limit. If
$\operatorname{vol}_{X}(L)$
is actually a limit. If
![]() $L\equiv L^{\prime }$
, then
$L\equiv L^{\prime }$
, then
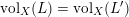 $\operatorname{vol}_{X}(L)=\operatorname{vol}_{X}(L^{\prime })$
. Moreover, we can extend it uniquely to a continuous function
$\operatorname{vol}_{X}(L)=\operatorname{vol}_{X}(L^{\prime })$
. Moreover, we can extend it uniquely to a continuous function
 $$\begin{eqnarray}\operatorname{vol}_{X}:N^{1}(X)_{\mathbb{ R}}\rightarrow \mathbb{R}_{{\geqslant}0}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{vol}_{X}:N^{1}(X)_{\mathbb{ R}}\rightarrow \mathbb{R}_{{\geqslant}0}.\end{eqnarray}$$
Definition 9. Let
![]() $X$
be a projective variety,
$X$
be a projective variety,
![]() $L$
be an ample
$L$
be an ample
![]() $\mathbb{Q}$
-Cartier divisor on
$\mathbb{Q}$
-Cartier divisor on
![]() $X$
. Let
$X$
. Let
![]() $Z$
be a non-empty proper closed subscheme of
$Z$
be a non-empty proper closed subscheme of
![]() $X$
with ideal sheaf
$X$
with ideal sheaf
![]() $I_{Z}$
. Denote by
$I_{Z}$
. Denote by
 $\unicode[STIX]{x1D70E}:\hat{X}\rightarrow X$
the blow up of
$\unicode[STIX]{x1D70E}:\hat{X}\rightarrow X$
the blow up of
![]() $X$
along
$X$
along
![]() $Z$
. Let
$Z$
. Let
![]() $F$
be the Cartier divisor on
$F$
be the Cartier divisor on
![]() $\hat{X}$
given by
$\hat{X}$
given by
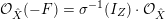 ${\mathcal{O}}_{\hat{X}}(-F)=\unicode[STIX]{x1D70E}^{-1}(I_{Z})\cdot {\mathcal{O}}_{\hat{X}}$
. The Seshadri constant of
${\mathcal{O}}_{\hat{X}}(-F)=\unicode[STIX]{x1D70E}^{-1}(I_{Z})\cdot {\mathcal{O}}_{\hat{X}}$
. The Seshadri constant of
![]() $L$
along
$L$
along
![]() $Z$
, denoted by
$Z$
, denoted by
![]() $\unicode[STIX]{x1D716}_{Z}(L)$
, is defined as
$\unicode[STIX]{x1D716}_{Z}(L)$
, is defined as
 $$\begin{eqnarray}\unicode[STIX]{x1D716}_{Z}(L):=\sup \{x\in \mathbb{R}_{{>}0}\mid \unicode[STIX]{x1D70E}^{\ast }L-xF\text{ is ample}\}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D716}_{Z}(L):=\sup \{x\in \mathbb{R}_{{>}0}\mid \unicode[STIX]{x1D70E}^{\ast }L-xF\text{ is ample}\}.\end{eqnarray}$$
Lemma 10. Let
![]() $X$
be an
$X$
be an
![]() $n$
-dimensional normal projective variety with
$n$
-dimensional normal projective variety with
![]() $n\geqslant 2$
,
$n\geqslant 2$
,
![]() $L$
be an ample
$L$
be an ample
![]() $\mathbb{Q}$
-divisor on
$\mathbb{Q}$
-divisor on
![]() $X$
,
$X$
,
![]() $p\in X$
be a closed point. Let
$p\in X$
be a closed point. Let
![]() $Z$
be a closed subscheme of
$Z$
be a closed subscheme of
![]() $X$
with
$X$
with
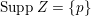 $\text{Supp}\,Z=\{p\}$
. Let
$\text{Supp}\,Z=\{p\}$
. Let
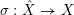 $\unicode[STIX]{x1D70E}:\hat{X}\rightarrow X$
be the blow up along
$\unicode[STIX]{x1D70E}:\hat{X}\rightarrow X$
be the blow up along
![]() $Z$
, and
$Z$
, and
![]() $F\subset \hat{X}$
be the Cartier divisor defined by the equation
$F\subset \hat{X}$
be the Cartier divisor defined by the equation
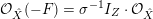 ${\mathcal{O}}_{\hat{X}}(-F)=\unicode[STIX]{x1D70E}^{-1}I_{Z}\cdot {\mathcal{O}}_{\hat{X}}$
.
${\mathcal{O}}_{\hat{X}}(-F)=\unicode[STIX]{x1D70E}^{-1}I_{Z}\cdot {\mathcal{O}}_{\hat{X}}$
.
(i) For any
 $x\in \mathbb{R}_{{\geqslant}0}$
, we have
$x\in \mathbb{R}_{{\geqslant}0}$
, we have  $$\begin{eqnarray}\operatorname{vol}_{\hat{X}}(\unicode[STIX]{x1D70E}^{\ast }L-xF)\geqslant ((\unicode[STIX]{x1D70E}^{\ast }L-xF)^{n})=(L^{n})-\operatorname{mult}_{Z}X\cdot x^{n}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{vol}_{\hat{X}}(\unicode[STIX]{x1D70E}^{\ast }L-xF)\geqslant ((\unicode[STIX]{x1D70E}^{\ast }L-xF)^{n})=(L^{n})-\operatorname{mult}_{Z}X\cdot x^{n}.\end{eqnarray}$$
(ii) Set
 $\unicode[STIX]{x1D6EC}_{Z}(L):=\{x\in \mathbb{R}_{{\geqslant}0}\mid \operatorname{vol}_{\hat{X}}(\unicode[STIX]{x1D70E}^{\ast }L-xF)=((\unicode[STIX]{x1D70E}^{\ast }L-xF)^{n})\}$
. Then we have
$\unicode[STIX]{x1D6EC}_{Z}(L):=\{x\in \mathbb{R}_{{\geqslant}0}\mid \operatorname{vol}_{\hat{X}}(\unicode[STIX]{x1D70E}^{\ast }L-xF)=((\unicode[STIX]{x1D70E}^{\ast }L-xF)^{n})\}$
. Then we have  $$\begin{eqnarray}\unicode[STIX]{x1D716}_{Z}(L)=\max \{x\in \mathbb{R}_{{\geqslant}0}\mid y\in \unicode[STIX]{x1D6EC}_{Z}(L)\text{ for all }y\in [0,x]\}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D716}_{Z}(L)=\max \{x\in \mathbb{R}_{{\geqslant}0}\mid y\in \unicode[STIX]{x1D6EC}_{Z}(L)\text{ for all }y\in [0,x]\}.\end{eqnarray}$$
Proof. The proof goes along the same line as [Reference FujitaFuj15, Theorem 2.3].
(i) The equality
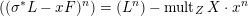 $((\unicode[STIX]{x1D70E}^{\ast }L-xF)^{n})=(L^{n})-\operatorname{mult}_{Z}X\cdot x^{n}$
follows from the fact that
$((\unicode[STIX]{x1D70E}^{\ast }L-xF)^{n})=(L^{n})-\operatorname{mult}_{Z}X\cdot x^{n}$
follows from the fact that
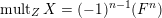 $\operatorname{mult}_{Z}X=(-1)^{n-1}(F^{n})$
(see [Reference RamanujamRam73]).
$\operatorname{mult}_{Z}X=(-1)^{n-1}(F^{n})$
(see [Reference RamanujamRam73]).
For the inequality part, we can assume that
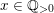 $x\in \mathbb{Q}_{{>}0}$
since the function
$x\in \mathbb{Q}_{{>}0}$
since the function
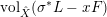 $\operatorname{vol}_{\hat{X}}(\unicode[STIX]{x1D70E}^{\ast }L-xF)$
is continuous. Take any sufficiently large
$\operatorname{vol}_{\hat{X}}(\unicode[STIX]{x1D70E}^{\ast }L-xF)$
is continuous. Take any sufficiently large
 $k\in \mathbb{Z}_{{>}0}$
with
$k\in \mathbb{Z}_{{>}0}$
with
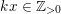 $kx\in \mathbb{Z}_{{>}0}$
and
$kx\in \mathbb{Z}_{{>}0}$
and
![]() $kL$
Cartier. Notice that we have the long exact sequence
$kL$
Cartier. Notice that we have the long exact sequence
 $$\begin{eqnarray}\displaystyle 0\rightarrow H^{0}(\hat{X},\unicode[STIX]{x1D70E}^{\ast }(kL)-kxF)\rightarrow H^{0}(\hat{X},\unicode[STIX]{x1D70E}^{\ast }(kL))\rightarrow H^{0}(kxF,\unicode[STIX]{x1D70E}^{\ast }(kL)|_{kxF})\rightarrow \cdots & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0\rightarrow H^{0}(\hat{X},\unicode[STIX]{x1D70E}^{\ast }(kL)-kxF)\rightarrow H^{0}(\hat{X},\unicode[STIX]{x1D70E}^{\ast }(kL))\rightarrow H^{0}(kxF,\unicode[STIX]{x1D70E}^{\ast }(kL)|_{kxF})\rightarrow \cdots & & \displaystyle\end{eqnarray}$$
Thus
 $$\begin{eqnarray}\displaystyle h^{0}(\hat{X},\unicode[STIX]{x1D70E}^{\ast }(kL)-kxF) & {\geqslant} & \displaystyle h^{0}(\hat{X},\unicode[STIX]{x1D70E}^{\ast }(kL))-h^{0}(kxF,\unicode[STIX]{x1D70E}^{\ast }(kL)|_{kxF})\nonumber\\ \displaystyle & = & \displaystyle h^{0}(X,kL)-h^{0}(kxF,{\mathcal{O}}_{kxF}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle h^{0}(\hat{X},\unicode[STIX]{x1D70E}^{\ast }(kL)-kxF) & {\geqslant} & \displaystyle h^{0}(\hat{X},\unicode[STIX]{x1D70E}^{\ast }(kL))-h^{0}(kxF,\unicode[STIX]{x1D70E}^{\ast }(kL)|_{kxF})\nonumber\\ \displaystyle & = & \displaystyle h^{0}(X,kL)-h^{0}(kxF,{\mathcal{O}}_{kxF}).\nonumber\end{eqnarray}$$
Consequently,
 $$\begin{eqnarray}\operatorname{vol}_{\hat{X}}(\unicode[STIX]{x1D70E}^{\ast }L-xF)\geqslant \operatorname{vol}_{X}(L)-\lim _{k\rightarrow \infty }\frac{h^{0}(kxF,{\mathcal{O}}_{kxF})}{(kx)^{n}/n!}x^{n}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{vol}_{\hat{X}}(\unicode[STIX]{x1D70E}^{\ast }L-xF)\geqslant \operatorname{vol}_{X}(L)-\lim _{k\rightarrow \infty }\frac{h^{0}(kxF,{\mathcal{O}}_{kxF})}{(kx)^{n}/n!}x^{n}.\end{eqnarray}$$
Hence it suffices to show that
 $$\begin{eqnarray}\lim _{j\rightarrow \infty }\frac{h^{0}(jF,{\mathcal{O}}_{jF})}{j^{n}/n!}=\operatorname{mult}_{Z}X.\end{eqnarray}$$
$$\begin{eqnarray}\lim _{j\rightarrow \infty }\frac{h^{0}(jF,{\mathcal{O}}_{jF})}{j^{n}/n!}=\operatorname{mult}_{Z}X.\end{eqnarray}$$
We look at the exact sequence
 $$\begin{eqnarray}\displaystyle 0\rightarrow {\mathcal{O}}_{\hat{X}}(-jF)|_{F}\rightarrow {\mathcal{O}}_{(j+1)F}\rightarrow {\mathcal{O}}_{jF}\rightarrow 0. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0\rightarrow {\mathcal{O}}_{\hat{X}}(-jF)|_{F}\rightarrow {\mathcal{O}}_{(j+1)F}\rightarrow {\mathcal{O}}_{jF}\rightarrow 0. & & \displaystyle\end{eqnarray}$$
The isomorphism
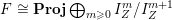 $F\cong \mathbf{Proj}\bigoplus _{m\geqslant 0}I_{Z}^{m}/I_{Z}^{m+1}$
yields
$F\cong \mathbf{Proj}\bigoplus _{m\geqslant 0}I_{Z}^{m}/I_{Z}^{m+1}$
yields
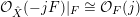 ${\mathcal{O}}_{\hat{X}}(-jF)|_{F}\cong {\mathcal{O}}_{F}(j)$
. Since
${\mathcal{O}}_{\hat{X}}(-jF)|_{F}\cong {\mathcal{O}}_{F}(j)$
. Since
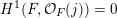 $H^{1}(F,{\mathcal{O}}_{F}(j))=0$
for
$H^{1}(F,{\mathcal{O}}_{F}(j))=0$
for
![]() $j\gg 0$
, we have an exact sequence
$j\gg 0$
, we have an exact sequence
 $$\begin{eqnarray}0\rightarrow H^{0}(F,{\mathcal{O}}_{F}(j))\rightarrow H^{0}((j+1)F,{\mathcal{O}}_{(j+1)F})\rightarrow H^{0}(jF,{\mathcal{O}}_{jF})\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow H^{0}(F,{\mathcal{O}}_{F}(j))\rightarrow H^{0}((j+1)F,{\mathcal{O}}_{(j+1)F})\rightarrow H^{0}(jF,{\mathcal{O}}_{jF})\rightarrow 0.\end{eqnarray}$$
Hence
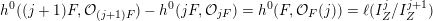 $h^{0}((j+1)F,{\mathcal{O}}_{(j+1)F})-h^{0}(jF,{\mathcal{O}}_{jF})=h^{0}(F,{\mathcal{O}}_{F}(j))=\ell (I_{Z}^{j}/I_{Z}^{j+1})$
for
$h^{0}((j+1)F,{\mathcal{O}}_{(j+1)F})-h^{0}(jF,{\mathcal{O}}_{jF})=h^{0}(F,{\mathcal{O}}_{F}(j))=\ell (I_{Z}^{j}/I_{Z}^{j+1})$
for
![]() $j\gg 0$
. As a result,
$j\gg 0$
. As a result,
 $$\begin{eqnarray}h^{0}(jF,{\mathcal{O}}_{jF})=\ell ({\mathcal{O}}_{X}/I_{Z}^{j})+\text{const}.\end{eqnarray}$$
$$\begin{eqnarray}h^{0}(jF,{\mathcal{O}}_{jF})=\ell ({\mathcal{O}}_{X}/I_{Z}^{j})+\text{const}.\end{eqnarray}$$
for
![]() $j\gg 0$
. Hence we prove (i).
$j\gg 0$
. Hence we prove (i).
(ii) Assume
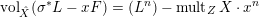 $\operatorname{vol}_{\hat{X}}(\unicode[STIX]{x1D70E}^{\ast }L-xF)=(L^{n})-\operatorname{mult}_{Z}X\cdot x^{n}$
for some
$\operatorname{vol}_{\hat{X}}(\unicode[STIX]{x1D70E}^{\ast }L-xF)=(L^{n})-\operatorname{mult}_{Z}X\cdot x^{n}$
for some
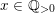 $x\in \mathbb{Q}_{{>}0}$
. We will show that
$x\in \mathbb{Q}_{{>}0}$
. We will show that
 $$\begin{eqnarray}h^{i}(\hat{X},\unicode[STIX]{x1D70E}^{\ast }(kL)-kxF)=o(k^{n})\quad \text{for }i\geqslant 1,k\gg 0\text{ with }kx\in \mathbb{Z}_{{>}0}.\end{eqnarray}$$
$$\begin{eqnarray}h^{i}(\hat{X},\unicode[STIX]{x1D70E}^{\ast }(kL)-kxF)=o(k^{n})\quad \text{for }i\geqslant 1,k\gg 0\text{ with }kx\in \mathbb{Z}_{{>}0}.\end{eqnarray}$$
For
![]() $i\geqslant 2$
, the long exact sequence (2.1) yields
$i\geqslant 2$
, the long exact sequence (2.1) yields
 $$\begin{eqnarray}h^{i}(\hat{X},\unicode[STIX]{x1D70E}^{\ast }(kL)-kxF)\leqslant h^{i-1}(kxF,{\mathcal{O}}_{kxF})+h^{i}(\hat{X},\unicode[STIX]{x1D70E}^{\ast }(kL)).\end{eqnarray}$$
$$\begin{eqnarray}h^{i}(\hat{X},\unicode[STIX]{x1D70E}^{\ast }(kL)-kxF)\leqslant h^{i-1}(kxF,{\mathcal{O}}_{kxF})+h^{i}(\hat{X},\unicode[STIX]{x1D70E}^{\ast }(kL)).\end{eqnarray}$$
Since
![]() $\unicode[STIX]{x1D70E}^{\ast }(kL)$
is nef, we know that
$\unicode[STIX]{x1D70E}^{\ast }(kL)$
is nef, we know that
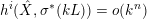 $h^{i}(\hat{X},\unicode[STIX]{x1D70E}^{\ast }(kL))=o(k^{n})$
. Serre vanishing theorem implies that
$h^{i}(\hat{X},\unicode[STIX]{x1D70E}^{\ast }(kL))=o(k^{n})$
. Serre vanishing theorem implies that
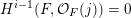 $H^{i-1}(F,{\mathcal{O}}_{F}(j))=0$
for
$H^{i-1}(F,{\mathcal{O}}_{F}(j))=0$
for
![]() $i\geqslant 2$
,
$i\geqslant 2$
,
![]() $j\gg 0$
. Then the exact sequence (2.2) implies that
$j\gg 0$
. Then the exact sequence (2.2) implies that
 $$\begin{eqnarray}H^{i-1}((j+1)F,{\mathcal{O}}_{(j+1)F})\cong H^{i-1}(jF,{\mathcal{O}}_{jF})\end{eqnarray}$$
$$\begin{eqnarray}H^{i-1}((j+1)F,{\mathcal{O}}_{(j+1)F})\cong H^{i-1}(jF,{\mathcal{O}}_{jF})\end{eqnarray}$$
for
![]() $i\geqslant 2$
,
$i\geqslant 2$
,
![]() $j\gg 0$
. As a result,
$j\gg 0$
. As a result,
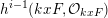 $h^{i-1}(kxF,{\mathcal{O}}_{kxF})$
is constant for
$h^{i-1}(kxF,{\mathcal{O}}_{kxF})$
is constant for
![]() $k\gg 0$
. Therefore,
$k\gg 0$
. Therefore,
 $h^{i}(\hat{X},\unicode[STIX]{x1D70E}^{\ast }(kL)-kxF)=o(k^{n})$
for any
$h^{i}(\hat{X},\unicode[STIX]{x1D70E}^{\ast }(kL)-kxF)=o(k^{n})$
for any
![]() $i\geqslant 2$
.
$i\geqslant 2$
.
By the asymptotic Riemann–Roch theorem we know that
 $$\begin{eqnarray}\displaystyle \lim _{k\rightarrow \infty }\frac{\unicode[STIX]{x1D712}(\hat{X},\unicode[STIX]{x1D70E}^{\ast }(kL)-kxF)}{k^{n}/n!} & = & \displaystyle ((\unicode[STIX]{x1D70E}^{\ast }L-xF)^{n})\nonumber\\ \displaystyle & = & \displaystyle (L^{n})-\operatorname{mult}_{Z}X\cdot x^{n}\nonumber\\ \displaystyle & = & \displaystyle \operatorname{vol}_{\hat{X}}(\unicode[STIX]{x1D70E}^{\ast }L-xF).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \lim _{k\rightarrow \infty }\frac{\unicode[STIX]{x1D712}(\hat{X},\unicode[STIX]{x1D70E}^{\ast }(kL)-kxF)}{k^{n}/n!} & = & \displaystyle ((\unicode[STIX]{x1D70E}^{\ast }L-xF)^{n})\nonumber\\ \displaystyle & = & \displaystyle (L^{n})-\operatorname{mult}_{Z}X\cdot x^{n}\nonumber\\ \displaystyle & = & \displaystyle \operatorname{vol}_{\hat{X}}(\unicode[STIX]{x1D70E}^{\ast }L-xF).\nonumber\end{eqnarray}$$
Hence we have
 $$\begin{eqnarray}\lim _{k\rightarrow \infty }\frac{1}{k^{n}}\mathop{\sum }_{i=1}^{n}(-1)^{i}h^{i}(\hat{X},\unicode[STIX]{x1D70E}^{\ast }(kL)-kxF)=0.\end{eqnarray}$$
$$\begin{eqnarray}\lim _{k\rightarrow \infty }\frac{1}{k^{n}}\mathop{\sum }_{i=1}^{n}(-1)^{i}h^{i}(\hat{X},\unicode[STIX]{x1D70E}^{\ast }(kL)-kxF)=0.\end{eqnarray}$$
Since
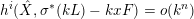 $h^{i}(\hat{X},\unicode[STIX]{x1D70E}^{\ast }(kL)-kxF)=o(k^{n})$
for
$h^{i}(\hat{X},\unicode[STIX]{x1D70E}^{\ast }(kL)-kxF)=o(k^{n})$
for
![]() $i\geqslant 2$
, we conclude that
$i\geqslant 2$
, we conclude that
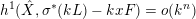 $h^{1}(\hat{X},\unicode[STIX]{x1D70E}^{\ast }(kL)-kxF)=o(k^{n})$
as well.
$h^{1}(\hat{X},\unicode[STIX]{x1D70E}^{\ast }(kL)-kxF)=o(k^{n})$
as well.
Now let us prove (ii). Denote by
![]() $a$
the right-hand side of the equation in (ii). For any nef divisor, its volume is equal to its self intersection number. Hence it is obvious that
$a$
the right-hand side of the equation in (ii). For any nef divisor, its volume is equal to its self intersection number. Hence it is obvious that
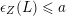 $\unicode[STIX]{x1D716}_{Z}(L)\leqslant a$
. Then it suffices to show that
$\unicode[STIX]{x1D716}_{Z}(L)\leqslant a$
. Then it suffices to show that
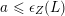 $a\leqslant \unicode[STIX]{x1D716}_{Z}(L)$
. Equivalently, we only need to show that for
$a\leqslant \unicode[STIX]{x1D716}_{Z}(L)$
. Equivalently, we only need to show that for
![]() $\unicode[STIX]{x1D716}>0$
sufficiently small with
$\unicode[STIX]{x1D716}>0$
sufficiently small with
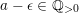 $a-\unicode[STIX]{x1D716}\in \mathbb{Q}_{{>}0}$
,
$a-\unicode[STIX]{x1D716}\in \mathbb{Q}_{{>}0}$
,
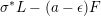 $\unicode[STIX]{x1D70E}^{\ast }L-(a-\unicode[STIX]{x1D716})F$
is ample. Fix
$\unicode[STIX]{x1D70E}^{\ast }L-(a-\unicode[STIX]{x1D716})F$
is ample. Fix
 $\unicode[STIX]{x1D6FF}\in \mathbb{Q}_{{>}0}$
such that
$\unicode[STIX]{x1D6FF}\in \mathbb{Q}_{{>}0}$
such that
 $\unicode[STIX]{x1D6FF}<\unicode[STIX]{x1D716}_{Z}(L)$
, that is,
$\unicode[STIX]{x1D6FF}<\unicode[STIX]{x1D716}_{Z}(L)$
, that is,
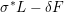 $\unicode[STIX]{x1D70E}^{\ast }L-\unicode[STIX]{x1D6FF}F$
is ample. By [Reference de Fernex, Küronya and LazarsfelddFKL07, Theorem A], we only need to show that
$\unicode[STIX]{x1D70E}^{\ast }L-\unicode[STIX]{x1D6FF}F$
is ample. By [Reference de Fernex, Küronya and LazarsfelddFKL07, Theorem A], we only need to show that
 $$\begin{eqnarray}h^{i}(\hat{X},m((\unicode[STIX]{x1D70E}^{\ast }L-(a-\unicode[STIX]{x1D716})F)-t(\unicode[STIX]{x1D70E}^{\ast }L-\unicode[STIX]{x1D6FF}F)))=o(m^{n})\end{eqnarray}$$
$$\begin{eqnarray}h^{i}(\hat{X},m((\unicode[STIX]{x1D70E}^{\ast }L-(a-\unicode[STIX]{x1D716})F)-t(\unicode[STIX]{x1D70E}^{\ast }L-\unicode[STIX]{x1D6FF}F)))=o(m^{n})\end{eqnarray}$$
for any
![]() $i>0$
, any sufficiently small
$i>0$
, any sufficiently small
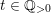 $t\in \mathbb{Q}_{{>}0}$
and suitably divisible
$t\in \mathbb{Q}_{{>}0}$
and suitably divisible
![]() $m$
. Denote
$m$
. Denote
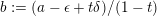 $b:=(a-\unicode[STIX]{x1D716}+t\unicode[STIX]{x1D6FF})/(1-t)$
. Notice that
$b:=(a-\unicode[STIX]{x1D716}+t\unicode[STIX]{x1D6FF})/(1-t)$
. Notice that
 $$\begin{eqnarray}\frac{1}{1-t}((\unicode[STIX]{x1D70E}^{\ast }L-(a-\unicode[STIX]{x1D716})F)-t(\unicode[STIX]{x1D70E}^{\ast }L-\unicode[STIX]{x1D6FF}F))=\unicode[STIX]{x1D70E}^{\ast }L-\frac{a-\unicode[STIX]{x1D716}+t\unicode[STIX]{x1D6FF}}{1-t}F=\unicode[STIX]{x1D70E}^{\ast }L-bF.\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{1-t}((\unicode[STIX]{x1D70E}^{\ast }L-(a-\unicode[STIX]{x1D716})F)-t(\unicode[STIX]{x1D70E}^{\ast }L-\unicode[STIX]{x1D6FF}F))=\unicode[STIX]{x1D70E}^{\ast }L-\frac{a-\unicode[STIX]{x1D716}+t\unicode[STIX]{x1D6FF}}{1-t}F=\unicode[STIX]{x1D70E}^{\ast }L-bF.\end{eqnarray}$$
It is clear that
![]() $b<a$
for
$b<a$
for
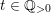 $t\in \mathbb{Q}_{{>}0}$
sufficiently small. Hence from the description of
$t\in \mathbb{Q}_{{>}0}$
sufficiently small. Hence from the description of
![]() $a$
we get:
$a$
we get:
 $$\begin{eqnarray}\operatorname{vol}_{\hat{X}}(\unicode[STIX]{x1D70E}^{\ast }L-bF)=(L^{n})-\operatorname{mult}_{Z}X\cdot b^{n}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{vol}_{\hat{X}}(\unicode[STIX]{x1D70E}^{\ast }L-bF)=(L^{n})-\operatorname{mult}_{Z}X\cdot b^{n}.\end{eqnarray}$$
Then applying (2.3) yields that
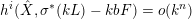 $h^{i}(\hat{X},\unicode[STIX]{x1D70E}^{\ast }(kL)-kbF)=o(k^{n})$
for
$h^{i}(\hat{X},\unicode[STIX]{x1D70E}^{\ast }(kL)-kbF)=o(k^{n})$
for
![]() $i>0$
, sufficiently small
$i>0$
, sufficiently small
 $t\in \mathbb{Q}_{{>}0}$
and suitably divisible
$t\in \mathbb{Q}_{{>}0}$
and suitably divisible
![]() $k$
. In other words, (2.4) is true under the same condition for
$k$
. In other words, (2.4) is true under the same condition for
![]() $i$
,
$i$
,
![]() $t$
and
$t$
and
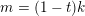 $m=(1-t)k$
. Hence we prove the lemma.◻
$m=(1-t)k$
. Hence we prove the lemma.◻
2.2 K-semistability and Ding-semistability
In this section we recall the definition of K-semistability, and its recent equivalence Ding-semistability.
Definition 11 ([Reference TianTia97, Reference DonaldsonDon02], see also [Reference Li and XuLX14]).
Let
![]() $X$
be an
$X$
be an
![]() $n$
-dimensional
$n$
-dimensional
![]() $\mathbb{Q}$
-Fano variety.
$\mathbb{Q}$
-Fano variety.
(a) Let
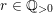 $r\in \mathbb{Q}_{{>}0}$
such that
$r\in \mathbb{Q}_{{>}0}$
such that
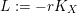 $L:=-rK_{X}$
is Cartier. A test configuration (respectively a semi test configuration) of
$L:=-rK_{X}$
is Cartier. A test configuration (respectively a semi test configuration) of
![]() $(X,L)$
consists of the following data:
$(X,L)$
consists of the following data:
– a variety
 ${\mathcal{X}}$
admitting a
${\mathcal{X}}$
admitting a
 $\mathbb{G}_{m}$
-action and a
$\mathbb{G}_{m}$
-action and a
 $\mathbb{G}_{m}$
-equivariant morphism
$\mathbb{G}_{m}$
-equivariant morphism
 $\unicode[STIX]{x1D70B}:{\mathcal{X}}\rightarrow \mathbb{A}^{1}$
, where the action of
$\unicode[STIX]{x1D70B}:{\mathcal{X}}\rightarrow \mathbb{A}^{1}$
, where the action of
 $\mathbb{G}_{m}$
on
$\mathbb{G}_{m}$
on
 $\mathbb{A}^{1}$
is given by the standard multiplication;
$\mathbb{A}^{1}$
is given by the standard multiplication;– a
 $\mathbb{G}_{m}$
-equivariant
$\mathbb{G}_{m}$
-equivariant
 $\unicode[STIX]{x1D70B}$
-ample (respectively
$\unicode[STIX]{x1D70B}$
-ample (respectively
 $\unicode[STIX]{x1D70B}$
-semiample) line bundle
$\unicode[STIX]{x1D70B}$
-semiample) line bundle
 ${\mathcal{L}}$
on
${\mathcal{L}}$
on
 ${\mathcal{X}}$
such that
${\mathcal{X}}$
such that
 $({\mathcal{X}},{\mathcal{L}})|_{\unicode[STIX]{x1D70B}^{-1}(\mathbb{A}^{1}\setminus \{0\})}$
is equivariantly isomorphic to
$({\mathcal{X}},{\mathcal{L}})|_{\unicode[STIX]{x1D70B}^{-1}(\mathbb{A}^{1}\setminus \{0\})}$
is equivariantly isomorphic to
 $(X,L)\times (\mathbb{A}^{1}\setminus \{0\})$
with the natural
$(X,L)\times (\mathbb{A}^{1}\setminus \{0\})$
with the natural
 $\mathbb{G}_{m}$
-action.
$\mathbb{G}_{m}$
-action.
Moreover, if
![]() ${\mathcal{X}}$
is normal in addition, then we say that
${\mathcal{X}}$
is normal in addition, then we say that
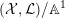 $({\mathcal{X}},{\mathcal{L}})/\mathbb{A}^{1}$
is a normal test configuration (respectively a normal semi test configuration) of
$({\mathcal{X}},{\mathcal{L}})/\mathbb{A}^{1}$
is a normal test configuration (respectively a normal semi test configuration) of
![]() $(X,L)$
.
$(X,L)$
.
(b) Assume that
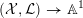 $({\mathcal{X}},{\mathcal{L}})\rightarrow \mathbb{A}^{1}$
is a normal test configuration. Let
$({\mathcal{X}},{\mathcal{L}})\rightarrow \mathbb{A}^{1}$
is a normal test configuration. Let
 $\bar{\unicode[STIX]{x1D70B}}:(\bar{{\mathcal{X}}},\bar{{\mathcal{L}}})\rightarrow \mathbb{P}^{1}$
be the natural equivariant compactification of
$\bar{\unicode[STIX]{x1D70B}}:(\bar{{\mathcal{X}}},\bar{{\mathcal{L}}})\rightarrow \mathbb{P}^{1}$
be the natural equivariant compactification of
 $({\mathcal{X}},{\mathcal{L}})\rightarrow \mathbb{A}^{1}$
. The CM weight (equivalently, Donaldson–Futaki invariant) of
$({\mathcal{X}},{\mathcal{L}})\rightarrow \mathbb{A}^{1}$
. The CM weight (equivalently, Donaldson–Futaki invariant) of
![]() $({\mathcal{X}},{\mathcal{L}})$
is defined by the intersection formula:
$({\mathcal{X}},{\mathcal{L}})$
is defined by the intersection formula:
 $$\begin{eqnarray}\text{CM}({\mathcal{X}},{\mathcal{L}}):=\frac{1}{(n+1)((-K_{X})^{n})}\biggl(\frac{n}{r^{n+1}}(\bar{{\mathcal{L}}}^{n+1})+\frac{n+1}{r^{n}}(\bar{{\mathcal{L}}}^{n}\cdot K_{\bar{{\mathcal{X}}}/\mathbb{P}^{1}})\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\text{CM}({\mathcal{X}},{\mathcal{L}}):=\frac{1}{(n+1)((-K_{X})^{n})}\biggl(\frac{n}{r^{n+1}}(\bar{{\mathcal{L}}}^{n+1})+\frac{n+1}{r^{n}}(\bar{{\mathcal{L}}}^{n}\cdot K_{\bar{{\mathcal{X}}}/\mathbb{P}^{1}})\biggr).\end{eqnarray}$$
(c)
– The pair
 $(X,-K_{X})$
is called K-semistable if
$(X,-K_{X})$
is called K-semistable if
 $\text{CM}({\mathcal{X}},{\mathcal{L}})\geqslant 0$
for any normal test configuration
$\text{CM}({\mathcal{X}},{\mathcal{L}})\geqslant 0$
for any normal test configuration
 $({\mathcal{X}},{\mathcal{L}})/\mathbb{A}^{1}$
of
$({\mathcal{X}},{\mathcal{L}})/\mathbb{A}^{1}$
of
 $(X,-rK_{X})$
.
$(X,-rK_{X})$
.– The pair
 $(X,-K_{X})$
is called K-polystable if
$(X,-K_{X})$
is called K-polystable if
 $\text{CM}({\mathcal{X}},{\mathcal{L}})\geqslant 0$
for any normal test configuration
$\text{CM}({\mathcal{X}},{\mathcal{L}})\geqslant 0$
for any normal test configuration
 $({\mathcal{X}},{\mathcal{L}})/\mathbb{A}^{1}$
of
$({\mathcal{X}},{\mathcal{L}})/\mathbb{A}^{1}$
of
 $(X,-rK_{X})$
, and the equality holds if and only if
$(X,-rK_{X})$
, and the equality holds if and only if
 ${\mathcal{X}}\cong X\times \mathbb{A}^{1}$
.
${\mathcal{X}}\cong X\times \mathbb{A}^{1}$
.
In [Reference DingDin88], Ding introduced the so-called Ding functional on the space of Kähler metrics on Fano manifolds and showed that Kähler–Einstein metrics are critical points of the Ding functional. Recently, Berman [Reference BermanBer16] established a formula expressing CM-weights in terms of the slope of Ding functional along a geodesic ray in the space of all bounded positively curved metrics on the anti-canonical
![]() $\mathbb{Q}$
-line bundle of a
$\mathbb{Q}$
-line bundle of a
![]() $\mathbb{Q}$
-Fano variety. Later on, this slope was called Ding invariant by Fujita [Reference FujitaFuj15] in order to define the concept of Ding-semistability. Next we will recall the recent work by Berman [Reference BermanBer16] and Fujita [Reference FujitaFuj15].
$\mathbb{Q}$
-Fano variety. Later on, this slope was called Ding invariant by Fujita [Reference FujitaFuj15] in order to define the concept of Ding-semistability. Next we will recall the recent work by Berman [Reference BermanBer16] and Fujita [Reference FujitaFuj15].
Definition 12 [Reference BermanBer16, Reference FujitaFuj15].
Let
![]() $X$
be an
$X$
be an
![]() $n$
-dimensional
$n$
-dimensional
![]() $\mathbb{Q}$
-Fano variety.
$\mathbb{Q}$
-Fano variety.
(a) Let
 $({\mathcal{X}},{\mathcal{L}})/\mathbb{A}^{1}$
be a normal semi test configuration of
$({\mathcal{X}},{\mathcal{L}})/\mathbb{A}^{1}$
be a normal semi test configuration of
 $(X,-rK_{X})$
and
$(X,-rK_{X})$
and
 $(\bar{{\mathcal{X}}},\bar{{\mathcal{L}}})/\mathbb{P}^{1}$
be its natural compactification. Let
$(\bar{{\mathcal{X}}},\bar{{\mathcal{L}}})/\mathbb{P}^{1}$
be its natural compactification. Let
 $D_{({\mathcal{X}},{\mathcal{L}})}$
be the
$D_{({\mathcal{X}},{\mathcal{L}})}$
be the
 $\mathbb{Q}$
-divisor on
$\mathbb{Q}$
-divisor on
 ${\mathcal{X}}$
satisfying the following conditions:
${\mathcal{X}}$
satisfying the following conditions:– the support
 $\text{Supp}D_{({\mathcal{X}},{\mathcal{L}})}$
is contained in
$\text{Supp}D_{({\mathcal{X}},{\mathcal{L}})}$
is contained in
 ${\mathcal{X}}_{0}$
;
${\mathcal{X}}_{0}$
;– the divisor
 $-rD_{({\mathcal{X}},{\mathcal{L}})}$
is a
$-rD_{({\mathcal{X}},{\mathcal{L}})}$
is a
 $\mathbb{Z}$
-divisor corresponding to the divisorial sheaf
$\mathbb{Z}$
-divisor corresponding to the divisorial sheaf
 $\bar{{\mathcal{L}}}(rK_{\bar{{\mathcal{X}}}/\mathbb{P}^{1}})$
.
$\bar{{\mathcal{L}}}(rK_{\bar{{\mathcal{X}}}/\mathbb{P}^{1}})$
.
(b) The Ding invariant
 $\text{Ding}({\mathcal{X}},{\mathcal{L}})$
of
$\text{Ding}({\mathcal{X}},{\mathcal{L}})$
of
 $({\mathcal{X}},{\mathcal{L}})/\mathbb{A}^{1}$
is defined as Here
$({\mathcal{X}},{\mathcal{L}})/\mathbb{A}^{1}$
is defined as Here $$\begin{eqnarray}\text{Ding}({\mathcal{X}},{\mathcal{L}}):=\frac{-(\bar{{\mathcal{L}}}^{n+1})}{(n+1)r^{n+1}((-K_{X})^{n})}-(1-\operatorname{lct}({\mathcal{X}},D_{({\mathcal{X}},{\mathcal{L}})};{\mathcal{X}}_{0})).\end{eqnarray}$$
$$\begin{eqnarray}\text{Ding}({\mathcal{X}},{\mathcal{L}}):=\frac{-(\bar{{\mathcal{L}}}^{n+1})}{(n+1)r^{n+1}((-K_{X})^{n})}-(1-\operatorname{lct}({\mathcal{X}},D_{({\mathcal{X}},{\mathcal{L}})};{\mathcal{X}}_{0})).\end{eqnarray}$$
 $\operatorname{lct}({\mathcal{X}},D_{({\mathcal{X}},{\mathcal{L}})};{\mathcal{X}}_{0})$
is defined in the sense of (1.4).
$\operatorname{lct}({\mathcal{X}},D_{({\mathcal{X}},{\mathcal{L}})};{\mathcal{X}}_{0})$
is defined in the sense of (1.4).(c)
 $X$
is called Ding-semistable if
$X$
is called Ding-semistable if
 $\text{Ding}({\mathcal{X}},{\mathcal{L}})\geqslant 0$
for any normal test configuration
$\text{Ding}({\mathcal{X}},{\mathcal{L}})\geqslant 0$
for any normal test configuration
 $({\mathcal{X}},{\mathcal{L}})/\mathbb{A}^{1}$
of
$({\mathcal{X}},{\mathcal{L}})/\mathbb{A}^{1}$
of
 $(X,-rK_{X})$
.
$(X,-rK_{X})$
.
The following theorem illustrates relations among the existence of Kähler–Einstein metrics, K-semistability and Ding-semistability of
![]() $\mathbb{Q}$
-Fano varieties.
$\mathbb{Q}$
-Fano varieties.
Theorem 13. (i) If a
![]() $\mathbb{Q}$
-Fano variety
$\mathbb{Q}$
-Fano variety
![]() $X$
admits a Kähler–Einstein metric, then
$X$
admits a Kähler–Einstein metric, then
![]() $X$
is Ding-semistable.
$X$
is Ding-semistable.
(ii) A
![]() $\mathbb{Q}$
-Fano variety is K-semistable if and only if it is Ding-semistable.
$\mathbb{Q}$
-Fano variety is K-semistable if and only if it is Ding-semistable.
Proof. Part (i) is proved by Berman in [Reference BermanBer16] (see also [Reference FujitaFuj15, Theorem 3.2]).
In (ii), the direction that Ding-semistability implies K-semistability is proved by Berman in [Reference BermanBer16] using the inequality that
 $\text{Ding}({\mathcal{X}},{\mathcal{L}})\geqslant \text{CM}({\mathcal{X}},{\mathcal{L}})$
for any normal test configuration
$\text{Ding}({\mathcal{X}},{\mathcal{L}})\geqslant \text{CM}({\mathcal{X}},{\mathcal{L}})$
for any normal test configuration
![]() $({\mathcal{X}},{\mathcal{L}})$
(see also [Reference FujitaFuj15, Theorem 3.2.2]). The direction that K-semistability implies Ding-semistability is proved in [Reference Berman, Boucksom and JonssonBBJ15] based on [Reference Li and XuLX14] (see also [Reference FujitaFuj16, § 3]).◻
$({\mathcal{X}},{\mathcal{L}})$
(see also [Reference FujitaFuj15, Theorem 3.2.2]). The direction that K-semistability implies Ding-semistability is proved in [Reference Berman, Boucksom and JonssonBBJ15] based on [Reference Li and XuLX14] (see also [Reference FujitaFuj16, § 3]).◻
2.3 Filtrations
The use of filtrations to study stability notions was initiated by Witt Nyström in [Reference Witt NyströmWN12]. We recall the relevant definitions about filtrations after [Reference Boucksom and ChenBC11, Reference Witt NyströmWN12] (see also [Reference Boucksom, Hisamoto and JonssonBHJ17] and [Reference FujitaFuj15, § 4.1]).
Definition 14. A good filtration of a graded
![]() $\mathbb{C}$
-algebra
$\mathbb{C}$
-algebra
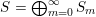 $S=\bigoplus _{m=0}^{\infty }S_{m}$
is a decreasing, left continuous, multiplicative and linearly bounded
$S=\bigoplus _{m=0}^{\infty }S_{m}$
is a decreasing, left continuous, multiplicative and linearly bounded
![]() $\mathbb{R}$
-filtrations of
$\mathbb{R}$
-filtrations of
![]() $S$
. In other words, for each
$S$
. In other words, for each
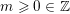 $m\geqslant 0\in \mathbb{Z}$
, there is a family of subspaces
$m\geqslant 0\in \mathbb{Z}$
, there is a family of subspaces
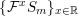 $\{{\mathcal{F}}^{x}S_{m}\}_{x\in \mathbb{R}}$
of
$\{{\mathcal{F}}^{x}S_{m}\}_{x\in \mathbb{R}}$
of
![]() $S_{m}$
such that:
$S_{m}$
such that:
–
 ${\mathcal{F}}^{x}S_{m}\subseteq {\mathcal{F}}^{x^{\prime }}S_{m}$
, if
${\mathcal{F}}^{x}S_{m}\subseteq {\mathcal{F}}^{x^{\prime }}S_{m}$
, if
 $x\geqslant x^{\prime }$
;
$x\geqslant x^{\prime }$
;–
 ${\mathcal{F}}^{x}S_{m}=\bigcap _{x^{\prime }<x}{\mathcal{F}}^{x^{\prime }}S_{m}$
;
${\mathcal{F}}^{x}S_{m}=\bigcap _{x^{\prime }<x}{\mathcal{F}}^{x^{\prime }}S_{m}$
;–
 ${\mathcal{F}}^{x}S_{m}\cdot {\mathcal{F}}^{x^{\prime }}S_{m^{\prime }}\subseteq {\mathcal{F}}^{x+x^{\prime }}S_{m+m^{\prime }}$
, for any
${\mathcal{F}}^{x}S_{m}\cdot {\mathcal{F}}^{x^{\prime }}S_{m^{\prime }}\subseteq {\mathcal{F}}^{x+x^{\prime }}S_{m+m^{\prime }}$
, for any
 $x,x^{\prime }\in \mathbb{R}$
and
$x,x^{\prime }\in \mathbb{R}$
and
 $m,m^{\prime }\in \mathbb{Z}_{{\geqslant}0}$
;
$m,m^{\prime }\in \mathbb{Z}_{{\geqslant}0}$
;–
 $e_{\min }({\mathcal{F}})>-\infty$
and
$e_{\min }({\mathcal{F}})>-\infty$
and
 $e_{\max }({\mathcal{F}})<+\infty$
, where
$e_{\max }({\mathcal{F}})<+\infty$
, where
 $e_{\min }({\mathcal{F}})$
and
$e_{\min }({\mathcal{F}})$
and
 $e_{\max }({\mathcal{F}})$
are defined by the following operations: (2.5)
$e_{\max }({\mathcal{F}})$
are defined by the following operations: (2.5) $$\begin{eqnarray}\begin{array}{@{}c@{}}e_{\min }(S_{m},{\mathcal{F}}):=\inf \{t\in \mathbb{R}:{\mathcal{F}}^{t}S_{m}\neq S_{m}\};\\ e_{\max }(S_{m},{\mathcal{F}}):=\sup \{t\in \mathbb{R}:{\mathcal{F}}^{t}S_{m}\neq 0\};\\ \displaystyle e_{\min }({\mathcal{F}})=e_{\min }(S_{\bullet },{\mathcal{F}}):=\liminf _{m\rightarrow \infty }\frac{e_{\min }(S_{m},{\mathcal{F}})}{m};\\ \displaystyle e_{\max }({\mathcal{F}})=e_{\max }(S_{\bullet },{\mathcal{F}}):=\limsup _{i\rightarrow \infty }\frac{e_{\max }(S_{m},{\mathcal{F}})}{m}.\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}c@{}}e_{\min }(S_{m},{\mathcal{F}}):=\inf \{t\in \mathbb{R}:{\mathcal{F}}^{t}S_{m}\neq S_{m}\};\\ e_{\max }(S_{m},{\mathcal{F}}):=\sup \{t\in \mathbb{R}:{\mathcal{F}}^{t}S_{m}\neq 0\};\\ \displaystyle e_{\min }({\mathcal{F}})=e_{\min }(S_{\bullet },{\mathcal{F}}):=\liminf _{m\rightarrow \infty }\frac{e_{\min }(S_{m},{\mathcal{F}})}{m};\\ \displaystyle e_{\max }({\mathcal{F}})=e_{\max }(S_{\bullet },{\mathcal{F}}):=\limsup _{i\rightarrow \infty }\frac{e_{\max }(S_{m},{\mathcal{F}})}{m}.\end{array}\end{eqnarray}$$
Define
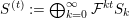 $S^{(t)}:=\bigoplus _{k=0}^{\infty }{\mathcal{F}}^{kt}S_{k}$
. When we want to emphasize the dependence of
$S^{(t)}:=\bigoplus _{k=0}^{\infty }{\mathcal{F}}^{kt}S_{k}$
. When we want to emphasize the dependence of
![]() $S^{(t)}$
on the filtration
$S^{(t)}$
on the filtration
![]() ${\mathcal{F}}$
, we also denote
${\mathcal{F}}$
, we also denote
![]() $S^{(t)}$
by
$S^{(t)}$
by
![]() ${\mathcal{F}}S^{(t)}$
. The following concept of volume will be important for us:
${\mathcal{F}}S^{(t)}$
. The following concept of volume will be important for us:
 $$\begin{eqnarray}\operatorname{vol}(S^{(t)})=\operatorname{vol}({\mathcal{F}}S^{(t)}):=\limsup _{k\rightarrow \infty }\frac{\dim _{\mathbb{C}}{\mathcal{F}}^{mt}S_{m}}{m^{n}/n!}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{vol}(S^{(t)})=\operatorname{vol}({\mathcal{F}}S^{(t)}):=\limsup _{k\rightarrow \infty }\frac{\dim _{\mathbb{C}}{\mathcal{F}}^{mt}S_{m}}{m^{n}/n!}.\end{eqnarray}$$
Now assume
![]() $L$
is an ample line bundle over
$L$
is an ample line bundle over
![]() $X$
and
$X$
and
 $S=\bigoplus _{m=0}^{\infty }H^{0}(X,L^{m})=\bigoplus _{m=0}^{\infty }S_{m}$
is the section ring of
$S=\bigoplus _{m=0}^{\infty }H^{0}(X,L^{m})=\bigoplus _{m=0}^{\infty }S_{m}$
is the section ring of
![]() $(X,L)$
. Then following [Reference FujitaFuj15], we can define a sequence of ideal sheaves on
$(X,L)$
. Then following [Reference FujitaFuj15], we can define a sequence of ideal sheaves on
![]() $X$
:
$X$
:
 $$\begin{eqnarray}I_{(m,x)}^{{\mathcal{F}}}=\text{Image}({\mathcal{F}}^{x}S_{m}\otimes L^{-m}\rightarrow {\mathcal{O}}_{X}),\end{eqnarray}$$
$$\begin{eqnarray}I_{(m,x)}^{{\mathcal{F}}}=\text{Image}({\mathcal{F}}^{x}S_{m}\otimes L^{-m}\rightarrow {\mathcal{O}}_{X}),\end{eqnarray}$$
and define
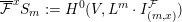 $\overline{{\mathcal{F}}}^{x}S_{m}:=H^{0}(V,L^{m}\cdot I_{(m,x)}^{{\mathcal{F}}})$
to be the saturation of
$\overline{{\mathcal{F}}}^{x}S_{m}:=H^{0}(V,L^{m}\cdot I_{(m,x)}^{{\mathcal{F}}})$
to be the saturation of
![]() ${\mathcal{F}}^{x}S_{m}$
such that
${\mathcal{F}}^{x}S_{m}$
such that
 ${\mathcal{F}}^{x}S^{m}\subseteq \overline{{\mathcal{F}}}^{x}S_{m}$
.
${\mathcal{F}}^{x}S^{m}\subseteq \overline{{\mathcal{F}}}^{x}S_{m}$
.
![]() ${\mathcal{F}}$
is called saturated if
${\mathcal{F}}$
is called saturated if
 $\overline{{\mathcal{F}}}^{x}S_{m}={\mathcal{F}}^{x}S_{m}$
for any
$\overline{{\mathcal{F}}}^{x}S_{m}={\mathcal{F}}^{x}S_{m}$
for any
![]() $x\in \mathbb{R}$
and
$x\in \mathbb{R}$
and
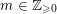 $m\in \mathbb{Z}_{{\geqslant}0}$
. Notice that with the notation above we have:
$m\in \mathbb{Z}_{{\geqslant}0}$
. Notice that with the notation above we have:
 $$\begin{eqnarray}\operatorname{vol}(\overline{{\mathcal{F}}}S^{(t)}):=\limsup _{k\rightarrow \infty }\frac{\dim _{\mathbb{C}}\overline{{\mathcal{F}}}^{kt}H^{0}(X,kL)}{k^{n}/n!}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{vol}(\overline{{\mathcal{F}}}S^{(t)}):=\limsup _{k\rightarrow \infty }\frac{\dim _{\mathbb{C}}\overline{{\mathcal{F}}}^{kt}H^{0}(X,kL)}{k^{n}/n!}.\end{eqnarray}$$
2.4 Normalized volume of real valuations
Let
![]() $(X,p)$
be a normal
$(X,p)$
be a normal
![]() $\mathbb{Q}$
-Gorenstein singularity with
$\mathbb{Q}$
-Gorenstein singularity with
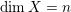 $\dim X=n$
. A real valuation
$\dim X=n$
. A real valuation
![]() $v$
on the function field
$v$
on the function field
![]() $\mathbb{C}(X)$
is a map
$\mathbb{C}(X)$
is a map
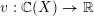 $v:\mathbb{C}(X)\rightarrow \mathbb{R}$
, satisfying:
$v:\mathbb{C}(X)\rightarrow \mathbb{R}$
, satisfying:
–
 $v(fg)=v(f)+v(g)$
;
$v(fg)=v(f)+v(g)$
;–
 $v(f+g)\geqslant \min \{v(f),v(g)\}$
;
$v(f+g)\geqslant \min \{v(f),v(g)\}$
;–
 $v(\mathbb{C}^{\ast })=0$
.
$v(\mathbb{C}^{\ast })=0$
.
Denote by
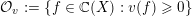 ${\mathcal{O}}_{v}:=\{f\in \mathbb{C}(X):v(f)\geqslant 0\}$
the valuation ring of
${\mathcal{O}}_{v}:=\{f\in \mathbb{C}(X):v(f)\geqslant 0\}$
the valuation ring of
![]() $v$
. Denote by
$v$
. Denote by
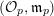 $({\mathcal{O}}_{p},\mathfrak{m}_{p})$
the local ring of
$({\mathcal{O}}_{p},\mathfrak{m}_{p})$
the local ring of
![]() $X$
at
$X$
at
![]() $p$
. We say that a real valuation
$p$
. We say that a real valuation
![]() $v$
on
$v$
on
![]() $\mathbb{C}(X)$
is centered at
$\mathbb{C}(X)$
is centered at
![]() $p$
if the local ring
$p$
if the local ring
![]() ${\mathcal{O}}_{p}$
is dominated by
${\mathcal{O}}_{p}$
is dominated by
![]() ${\mathcal{O}}_{v}$
. In other words,
${\mathcal{O}}_{v}$
. In other words,
![]() $v$
is non-negative on
$v$
is non-negative on
![]() ${\mathcal{O}}_{p}$
and strictly positive on
${\mathcal{O}}_{p}$
and strictly positive on
![]() $\mathfrak{m}_{p}$
. Denote by
$\mathfrak{m}_{p}$
. Denote by
![]() $\text{Val}_{X,p}$
the set of real valuations centered at
$\text{Val}_{X,p}$
the set of real valuations centered at
![]() $p$
. Given a valuation
$p$
. Given a valuation
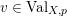 $v\in \text{Val}_{X,p}$
, define the valuation ideals for any
$v\in \text{Val}_{X,p}$
, define the valuation ideals for any
![]() $x\in \mathbb{R}$
as follows:
$x\in \mathbb{R}$
as follows:
 $$\begin{eqnarray}\mathfrak{a}_{x}(v):=\{f\in {\mathcal{O}}_{X}:v(f)\geqslant x\}.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{a}_{x}(v):=\{f\in {\mathcal{O}}_{X}:v(f)\geqslant x\}.\end{eqnarray}$$
The volume of the valuation
![]() $v$
is defined as
$v$
is defined as
 $$\begin{eqnarray}\operatorname{vol}(v):=\lim _{x\rightarrow +\infty }\frac{\ell ({\mathcal{O}}_{X}/\mathfrak{a}_{x}(v))}{x^{n}/n!}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{vol}(v):=\lim _{x\rightarrow +\infty }\frac{\ell ({\mathcal{O}}_{X}/\mathfrak{a}_{x}(v))}{x^{n}/n!}.\end{eqnarray}$$
By [Reference Ein, Lazarsfeld and SmithELS03, Reference MustaţăMus02, Reference CutkoskyCut13], the limit on the right-hand side exists and is equal to the multiplicity of the graded family of ideals
![]() $\mathfrak{a}_{\bullet }(v)$
:
$\mathfrak{a}_{\bullet }(v)$
:
 $$\begin{eqnarray}\operatorname{vol}(v)=\lim _{m\rightarrow \infty }\frac{\operatorname{mult}(\mathfrak{a}_{m}(v))}{m^{n}}=:\operatorname{mult}(\mathfrak{a}_{\bullet }(v)).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{vol}(v)=\lim _{m\rightarrow \infty }\frac{\operatorname{mult}(\mathfrak{a}_{m}(v))}{m^{n}}=:\operatorname{mult}(\mathfrak{a}_{\bullet }(v)).\end{eqnarray}$$
Following [Reference Jonsson and MustaţăJM12, Reference Boucksom, de Fernex, Favre and UrbinatiBdFFU15], we can define the log discrepancy for any valuation
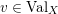 $v\in \text{Val}_{X}$
. This is achieved in three steps in [Reference Jonsson and MustaţăJM12, Reference Boucksom, de Fernex, Favre and UrbinatiBdFFU15]. Firstly, for a divisorial valuation
$v\in \text{Val}_{X}$
. This is achieved in three steps in [Reference Jonsson and MustaţăJM12, Reference Boucksom, de Fernex, Favre and UrbinatiBdFFU15]. Firstly, for a divisorial valuation
![]() $\text{ord}_{E}$
associated to a prime divisor
$\text{ord}_{E}$
associated to a prime divisor
![]() $E$
over
$E$
over
![]() $X$
, define
$X$
, define
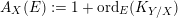 $A_{X}(E):=1+\text{ord}_{E}(K_{Y/X})$
, where
$A_{X}(E):=1+\text{ord}_{E}(K_{Y/X})$
, where
 $\unicode[STIX]{x1D70B}:Y\rightarrow X$
is a resolution of
$\unicode[STIX]{x1D70B}:Y\rightarrow X$
is a resolution of
![]() $X$
containing
$X$
containing
![]() $E$
. Next we define the log discrepancy of a quasi-monomial valuation (also called Abhyankar valuation). For a resolution
$E$
. Next we define the log discrepancy of a quasi-monomial valuation (also called Abhyankar valuation). For a resolution
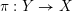 $\unicode[STIX]{x1D70B}:Y\rightarrow X$
, let
$\unicode[STIX]{x1D70B}:Y\rightarrow X$
, let
 $\text{}\underline{y}:=(y_{1},\ldots ,y_{r})$
be a system of algebraic coordinate of a point
$\text{}\underline{y}:=(y_{1},\ldots ,y_{r})$
be a system of algebraic coordinate of a point
![]() $\unicode[STIX]{x1D702}\in Y$
. By [Reference Jonsson and MustaţăJM12, Proposition 3.1], for every
$\unicode[STIX]{x1D702}\in Y$
. By [Reference Jonsson and MustaţăJM12, Proposition 3.1], for every
 $\unicode[STIX]{x1D6FC}=(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{r})\in \mathbb{R}_{{\geqslant}0}^{n}$
one can associate a unique valuation
$\unicode[STIX]{x1D6FC}=(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{r})\in \mathbb{R}_{{\geqslant}0}^{n}$
one can associate a unique valuation
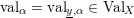 $\text{val}_{\unicode[STIX]{x1D6FC}}=\text{val}_{\text{}\underline{y},\unicode[STIX]{x1D6FC}}\in \text{Val}_{X}$
with the following property: whenever
$\text{val}_{\unicode[STIX]{x1D6FC}}=\text{val}_{\text{}\underline{y},\unicode[STIX]{x1D6FC}}\in \text{Val}_{X}$
with the following property: whenever
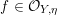 $f\in {\mathcal{O}}_{Y,\unicode[STIX]{x1D702}}$
is written in
$f\in {\mathcal{O}}_{Y,\unicode[STIX]{x1D702}}$
is written in
![]() $\widehat{{\mathcal{O}}_{Y,\unicode[STIX]{x1D702}}}$
as
$\widehat{{\mathcal{O}}_{Y,\unicode[STIX]{x1D702}}}$
as
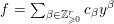 $f=\sum _{\unicode[STIX]{x1D6FD}\in \mathbb{Z}_{{\geqslant}0}^{r}}c_{\unicode[STIX]{x1D6FD}}y^{\unicode[STIX]{x1D6FD}}$
, with each
$f=\sum _{\unicode[STIX]{x1D6FD}\in \mathbb{Z}_{{\geqslant}0}^{r}}c_{\unicode[STIX]{x1D6FD}}y^{\unicode[STIX]{x1D6FD}}$
, with each
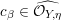 $c_{\unicode[STIX]{x1D6FD}}\in \widehat{{\mathcal{O}}_{Y,\unicode[STIX]{x1D702}}}$
either zero or a unit, we have
$c_{\unicode[STIX]{x1D6FD}}\in \widehat{{\mathcal{O}}_{Y,\unicode[STIX]{x1D702}}}$
either zero or a unit, we have
 $$\begin{eqnarray}\text{val}_{\unicode[STIX]{x1D6FC}}(f)=\min \{\langle \unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\rangle \mid c_{\unicode[STIX]{x1D6FD}}\neq 0\}.\end{eqnarray}$$
$$\begin{eqnarray}\text{val}_{\unicode[STIX]{x1D6FC}}(f)=\min \{\langle \unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\rangle \mid c_{\unicode[STIX]{x1D6FD}}\neq 0\}.\end{eqnarray}$$
Such valuations are called quasi-monomial valuations (or equivalently, Abhyankar valuations by [Reference Ein, Lazarsfeld and SmithELS03]). Let
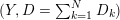 $(Y,D=\sum _{k=1}^{N}D_{k})$
be a log smooth model of
$(Y,D=\sum _{k=1}^{N}D_{k})$
be a log smooth model of
![]() $X$
, i.e.
$X$
, i.e.
 $\unicode[STIX]{x1D70B}:Y\rightarrow X$
is an isomorphism outside of the support of
$\unicode[STIX]{x1D70B}:Y\rightarrow X$
is an isomorphism outside of the support of
![]() $D$
. We denote by
$D$
. We denote by
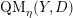 $\text{QM}_{\unicode[STIX]{x1D702}}(Y,D)$
the set of all quasi-monomial valuations
$\text{QM}_{\unicode[STIX]{x1D702}}(Y,D)$
the set of all quasi-monomial valuations
![]() $v$
that can be described at the point
$v$
that can be described at the point
![]() $\unicode[STIX]{x1D702}\in Y$
with respect to coordinates
$\unicode[STIX]{x1D702}\in Y$
with respect to coordinates
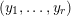 $(y_{1},\ldots ,y_{r})$
such that each
$(y_{1},\ldots ,y_{r})$
such that each
![]() $y_{i}$
defines at
$y_{i}$
defines at
![]() $\unicode[STIX]{x1D702}$
an irreducible component of
$\unicode[STIX]{x1D702}$
an irreducible component of
![]() $D$
(hence
$D$
(hence
![]() $\unicode[STIX]{x1D702}$
is the generic point of a connected component of the intersection of some of the divisors
$\unicode[STIX]{x1D702}$
is the generic point of a connected component of the intersection of some of the divisors
![]() $D_{i}$
). We put
$D_{i}$
). We put
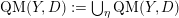 $\text{QM}(Y,D):=\bigcup _{\unicode[STIX]{x1D702}}\text{QM}(Y,D)$
. Suppose
$\text{QM}(Y,D):=\bigcup _{\unicode[STIX]{x1D702}}\text{QM}(Y,D)$
. Suppose
![]() $\unicode[STIX]{x1D702}$
is a generic point of a connected component of
$\unicode[STIX]{x1D702}$
is a generic point of a connected component of
 $D_{i_{1}}\cap \cdots \cap \,D_{i_{r}}$
, then the log discrepancy of
$D_{i_{1}}\cap \cdots \cap \,D_{i_{r}}$
, then the log discrepancy of
![]() $\text{val}_{\unicode[STIX]{x1D6FC}}$
is defined as
$\text{val}_{\unicode[STIX]{x1D6FC}}$
is defined as
 $$\begin{eqnarray}A_{X}(\text{val}_{\unicode[STIX]{x1D6FC}}):=\mathop{\sum }_{j=1}^{r}\unicode[STIX]{x1D6FC}_{j}\cdot A_{X}(\text{ord}_{D_{i_{j}}})=\mathop{\sum }_{j=1}^{r}\unicode[STIX]{x1D6FC}_{j}\cdot (1+\text{ord}_{D_{i_{j}}}(K_{Y/X})).\end{eqnarray}$$
$$\begin{eqnarray}A_{X}(\text{val}_{\unicode[STIX]{x1D6FC}}):=\mathop{\sum }_{j=1}^{r}\unicode[STIX]{x1D6FC}_{j}\cdot A_{X}(\text{ord}_{D_{i_{j}}})=\mathop{\sum }_{j=1}^{r}\unicode[STIX]{x1D6FC}_{j}\cdot (1+\text{ord}_{D_{i_{j}}}(K_{Y/X})).\end{eqnarray}$$
Finally, in [Reference Jonsson and MustaţăJM12] Jonsson and Mustaţă showed that there exists a retraction map
 $r_{Y,D}:\text{Val}_{X}\rightarrow \text{QM}(Y,D)$
for any log smooth model
$r_{Y,D}:\text{Val}_{X}\rightarrow \text{QM}(Y,D)$
for any log smooth model
![]() $(Y,D)$
over
$(Y,D)$
over
![]() $X$
, such that it induces a homeomorphism
$X$
, such that it induces a homeomorphism
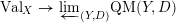 $\text{Val}_{X}\rightarrow \mathop{\varprojlim }\nolimits_{(Y,D)}\text{QM}(Y,D)$
. For any real valuation
$\text{Val}_{X}\rightarrow \mathop{\varprojlim }\nolimits_{(Y,D)}\text{QM}(Y,D)$
. For any real valuation
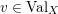 $v\in \text{Val}_{X}$
, we define
$v\in \text{Val}_{X}$
, we define
 $$\begin{eqnarray}A_{X}(v)=\sup _{(Y,D)}A_{X}(r_{(Y,D)}(v)),\end{eqnarray}$$
$$\begin{eqnarray}A_{X}(v)=\sup _{(Y,D)}A_{X}(r_{(Y,D)}(v)),\end{eqnarray}$$
where
![]() $(Y,D)$
ranges over all log smooth models over
$(Y,D)$
ranges over all log smooth models over
![]() $X$
. For details, see [Reference Jonsson and MustaţăJM12] and [Reference Boucksom, de Fernex, Favre and UrbinatiBdFFU15, Theorem 3.1]. It is possible that
$X$
. For details, see [Reference Jonsson and MustaţăJM12] and [Reference Boucksom, de Fernex, Favre and UrbinatiBdFFU15, Theorem 3.1]. It is possible that
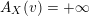 $A_{X}(v)=+\infty$
for some
$A_{X}(v)=+\infty$
for some
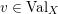 $v\in \text{Val}_{X}$
, see e.g. [Reference Jonsson and MustaţăJM12, Remark 5.12].
$v\in \text{Val}_{X}$
, see e.g. [Reference Jonsson and MustaţăJM12, Remark 5.12].
Following [Reference LiLi15], the normalized volume function
![]() $\widehat{\operatorname{vol}}(v)$
for any
$\widehat{\operatorname{vol}}(v)$
for any
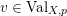 $v\in \text{Val}_{X,p}$
is defined as
$v\in \text{Val}_{X,p}$
is defined as
 $$\begin{eqnarray}\widehat{\operatorname{vol}}(v):=\left\{\begin{array}{@{}ll@{}}A_{X}(v)^{n}\cdot \operatorname{vol}(v)\quad & \text{if }A_{X}(v)<+\infty ,\\ +\infty \quad & \text{if }A_{X}(v)=+\infty .\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\widehat{\operatorname{vol}}(v):=\left\{\begin{array}{@{}ll@{}}A_{X}(v)^{n}\cdot \operatorname{vol}(v)\quad & \text{if }A_{X}(v)<+\infty ,\\ +\infty \quad & \text{if }A_{X}(v)=+\infty .\end{array}\right.\end{eqnarray}$$
Notice that
![]() $\widehat{\operatorname{vol}}(v)$
is rescaling invariant:
$\widehat{\operatorname{vol}}(v)$
is rescaling invariant:
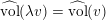 $\widehat{\operatorname{vol}}(\unicode[STIX]{x1D706}v)=\widehat{\operatorname{vol}}(v)$
for any
$\widehat{\operatorname{vol}}(\unicode[STIX]{x1D706}v)=\widehat{\operatorname{vol}}(v)$
for any
![]() $\unicode[STIX]{x1D706}>0$
. By Izumi’s theorem (see [Reference IzumiIzu85, Reference ReesRee89, Reference Ein, Lazarsfeld and SmithELS03, Reference Jonsson and MustaţăJM12, Reference Boucksom, Favre and JonssonBFJ14, Reference LiLi15]), one can show that
$\unicode[STIX]{x1D706}>0$
. By Izumi’s theorem (see [Reference IzumiIzu85, Reference ReesRee89, Reference Ein, Lazarsfeld and SmithELS03, Reference Jonsson and MustaţăJM12, Reference Boucksom, Favre and JonssonBFJ14, Reference LiLi15]), one can show that
![]() $\widehat{\operatorname{vol}}$
is uniformly bounded from below by a positive number on
$\widehat{\operatorname{vol}}$
is uniformly bounded from below by a positive number on
![]() $\text{Val}_{X,p}$
.
$\text{Val}_{X,p}$
.
3 Proofs of main theorems
3.1 Proofs
It was proved by Berman [Reference BermanBer16] that the existence of a Kähler–Einstein metric on a
![]() $\mathbb{Q}$
-Fano variety implies Ding-semistability (see Theorem 13). In this section, we will prove Theorem 1 and 2 with the weaker assumption that
$\mathbb{Q}$
-Fano variety implies Ding-semistability (see Theorem 13). In this section, we will prove Theorem 1 and 2 with the weaker assumption that
![]() $X$
is Ding-semistable.
$X$
is Ding-semistable.
The following result by Fujita is crucial for proving Theorem 1.
Theorem 15 [Reference FujitaFuj15, Theorem 1.2].
Let
![]() $X$
be a
$X$
be a
![]() $\mathbb{Q}$
-Fano variety. Assume that
$\mathbb{Q}$
-Fano variety. Assume that
![]() $X$
is Ding-semistable. Take any non-empty proper closed subscheme
$X$
is Ding-semistable. Take any non-empty proper closed subscheme
 $\emptyset \neq Z\subsetneq X$
corresponds to an ideal sheaf
$\emptyset \neq Z\subsetneq X$
corresponds to an ideal sheaf
 $0\neq I_{Z}\subsetneq {\mathcal{O}}_{X}$
. Let
$0\neq I_{Z}\subsetneq {\mathcal{O}}_{X}$
. Let
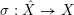 $\unicode[STIX]{x1D70E}:\hat{X}\rightarrow X$
be the blow up along
$\unicode[STIX]{x1D70E}:\hat{X}\rightarrow X$
be the blow up along
![]() $Z$
, let
$Z$
, let
![]() $F\subset \hat{X}$
be the Cartier divisor defined by the equation
$F\subset \hat{X}$
be the Cartier divisor defined by the equation
 ${\mathcal{O}}_{\hat{X}}(-F)=\unicode[STIX]{x1D70E}^{-1}I_{Z}\cdot {\mathcal{O}}_{\hat{X}}$
. Then we have
${\mathcal{O}}_{\hat{X}}(-F)=\unicode[STIX]{x1D70E}^{-1}I_{Z}\cdot {\mathcal{O}}_{\hat{X}}$
. Then we have
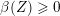 $\unicode[STIX]{x1D6FD}(Z)\geqslant 0$
, where
$\unicode[STIX]{x1D6FD}(Z)\geqslant 0$
, where
 $$\begin{eqnarray}\unicode[STIX]{x1D6FD}(Z):=\operatorname{lct}(X;I_{Z})\cdot \operatorname{vol}_{X}(-K_{X})-\int _{0}^{+\infty }\operatorname{vol}_{\hat{X}}(\unicode[STIX]{x1D70E}^{\ast }(-K_{X})-xF)\,dx.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FD}(Z):=\operatorname{lct}(X;I_{Z})\cdot \operatorname{vol}_{X}(-K_{X})-\int _{0}^{+\infty }\operatorname{vol}_{\hat{X}}(\unicode[STIX]{x1D70E}^{\ast }(-K_{X})-xF)\,dx.\end{eqnarray}$$
We will prove the following theorem, a stronger result that implies Theorem 1.
Theorem 16. Let
![]() $X$
be a Ding-semistable
$X$
be a Ding-semistable
![]() $\mathbb{Q}$
-Fano variety. Let
$\mathbb{Q}$
-Fano variety. Let
![]() $p\in X$
be a closed point. Let
$p\in X$
be a closed point. Let
![]() $Z$
be a closed subscheme of
$Z$
be a closed subscheme of
![]() $X$
with
$X$
with
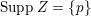 $\text{Supp}\,Z=\{p\}$
. Then we have
$\text{Supp}\,Z=\{p\}$
. Then we have
 $$\begin{eqnarray}((-K_{X})^{n})\leqslant \biggl(1+\frac{1}{n}\biggr)^{n}\operatorname{lct}(X;I_{Z})^{n}\operatorname{mult}_{Z}X.\end{eqnarray}$$
$$\begin{eqnarray}((-K_{X})^{n})\leqslant \biggl(1+\frac{1}{n}\biggr)^{n}\operatorname{lct}(X;I_{Z})^{n}\operatorname{mult}_{Z}X.\end{eqnarray}$$
Proof. Let
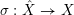 $\unicode[STIX]{x1D70E}:\hat{X}\rightarrow X$
be the blow up along
$\unicode[STIX]{x1D70E}:\hat{X}\rightarrow X$
be the blow up along
![]() $Z$
, and let
$Z$
, and let
![]() $F\subset \hat{X}$
be the Cartier divisor defined by the equation
$F\subset \hat{X}$
be the Cartier divisor defined by the equation
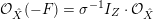 ${\mathcal{O}}_{\hat{X}}(-F)=\unicode[STIX]{x1D70E}^{-1}I_{Z}\cdot {\mathcal{O}}_{\hat{X}}$
. By Theorem 15, we have
${\mathcal{O}}_{\hat{X}}(-F)=\unicode[STIX]{x1D70E}^{-1}I_{Z}\cdot {\mathcal{O}}_{\hat{X}}$
. By Theorem 15, we have
 $$\begin{eqnarray}\operatorname{lct}(X;I_{Z})\cdot ((-K_{X})^{n})\geqslant \int _{0}^{+\infty }\operatorname{vol}_{\hat{X}}(\unicode[STIX]{x1D70E}^{\ast }(-K_{X})-xF)\,dx.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{lct}(X;I_{Z})\cdot ((-K_{X})^{n})\geqslant \int _{0}^{+\infty }\operatorname{vol}_{\hat{X}}(\unicode[STIX]{x1D70E}^{\ast }(-K_{X})-xF)\,dx.\end{eqnarray}$$
On the other hand, by Lemma 10, we have
 $$\begin{eqnarray}\displaystyle \int _{0}^{+\infty }\operatorname{vol}_{\hat{X}}(\unicode[STIX]{x1D70E}^{\ast }(-K_{X})-xF)\,dx & {\geqslant} & \displaystyle \int _{0}^{\sqrt[n]{((-K_{X})^{n})/\operatorname{mult}_{Z}X}}(((-K_{X})^{n})-\operatorname{mult}_{Z}X\cdot x^{n})\,dx\nonumber\\ \displaystyle & = & \displaystyle \frac{n}{n+1}((-K_{X}))^{n}\cdot \sqrt[n]{((-K_{X})^{n})/\operatorname{mult}_{Z}X}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{0}^{+\infty }\operatorname{vol}_{\hat{X}}(\unicode[STIX]{x1D70E}^{\ast }(-K_{X})-xF)\,dx & {\geqslant} & \displaystyle \int _{0}^{\sqrt[n]{((-K_{X})^{n})/\operatorname{mult}_{Z}X}}(((-K_{X})^{n})-\operatorname{mult}_{Z}X\cdot x^{n})\,dx\nonumber\\ \displaystyle & = & \displaystyle \frac{n}{n+1}((-K_{X}))^{n}\cdot \sqrt[n]{((-K_{X})^{n})/\operatorname{mult}_{Z}X}.\nonumber\end{eqnarray}$$
Hence we get the desired inequality
 $$\begin{eqnarray}((-K_{X})^{n})\leqslant \biggl(1+\frac{1}{n}\biggr)^{n}\operatorname{lct}(X;I_{Z})^{n}\operatorname{mult}_{Z}X.\Box\end{eqnarray}$$
$$\begin{eqnarray}((-K_{X})^{n})\leqslant \biggl(1+\frac{1}{n}\biggr)^{n}\operatorname{lct}(X;I_{Z})^{n}\operatorname{mult}_{Z}X.\Box\end{eqnarray}$$
Remark 17. As we see in the proof above, if the equality of (3.1) holds, then
 $$\begin{eqnarray}\operatorname{vol}_{\hat{X}}(\unicode[STIX]{x1D70E}_{\ast }(-K_{X})-xF)=\max \{((-K_{X})^{n})-\operatorname{mult}_{Z}X\cdot x^{n},0\}\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{vol}_{\hat{X}}(\unicode[STIX]{x1D70E}_{\ast }(-K_{X})-xF)=\max \{((-K_{X})^{n})-\operatorname{mult}_{Z}X\cdot x^{n},0\}\end{eqnarray}$$
for any
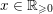 $x\in \mathbb{R}_{{\geqslant}0}$
. Then by Lemma 10 (ii) we have that
$x\in \mathbb{R}_{{\geqslant}0}$
. Then by Lemma 10 (ii) we have that
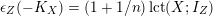 $\unicode[STIX]{x1D716}_{Z}(-K_{X})=(1+1/n)\operatorname{lct}(X;I_{Z})$
.
$\unicode[STIX]{x1D716}_{Z}(-K_{X})=(1+1/n)\operatorname{lct}(X;I_{Z})$
.
The following result by Fujita is the main tool to prove Theorem 2.
Theorem 18 [Reference FujitaFuj15, Theorem 4.9].
Let
![]() $X$
be a
$X$
be a
![]() $\mathbb{Q}$
-Fano variety of dimension
$\mathbb{Q}$
-Fano variety of dimension
![]() $n$
. Assume that
$n$
. Assume that
![]() $X$
is Ding-semistable. Let
$X$
is Ding-semistable. Let
![]() ${\mathcal{F}}$
be a good graded filtration of
${\mathcal{F}}$
be a good graded filtration of
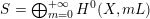 $S=\bigoplus _{m=0}^{+\infty }H^{0}(X,mL)$
where
$S=\bigoplus _{m=0}^{+\infty }H^{0}(X,mL)$
where
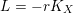 $L=-rK_{X}$
is Cartier. Then the pair
$L=-rK_{X}$
is Cartier. Then the pair
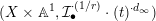 $(X\times \mathbb{A}^{1},{\mathcal{I}}_{\bullet }^{\cdot (1/r)}\cdot (t)^{\cdot d_{\infty }})$
is sub log canonical in the sense of [Reference FujitaFuj15, Definition 2.4], where
$(X\times \mathbb{A}^{1},{\mathcal{I}}_{\bullet }^{\cdot (1/r)}\cdot (t)^{\cdot d_{\infty }})$
is sub log canonical in the sense of [Reference FujitaFuj15, Definition 2.4], where
 $$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{I}}_{m}=I_{(m,me_{+})}^{{\mathcal{F}}}+I_{(m,me_{+}-1)}^{{\mathcal{F}}}t^{1}+\cdots +I_{(m,me_{-}+1)}^{{\mathcal{F}}}t^{m(e_{+}-e_{-})-1}+(t^{m(e_{+}-e_{-})}), & \displaystyle \nonumber\\ \displaystyle & \displaystyle d_{\infty }=1-\frac{e_{+}-e_{-}}{r}+\frac{1}{r^{n+1}((-K_{X})^{n})}\int _{e_{-}}^{e_{+}}\operatorname{vol}(\overline{{\mathcal{F}}}S^{(t)})\,dt, & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{I}}_{m}=I_{(m,me_{+})}^{{\mathcal{F}}}+I_{(m,me_{+}-1)}^{{\mathcal{F}}}t^{1}+\cdots +I_{(m,me_{-}+1)}^{{\mathcal{F}}}t^{m(e_{+}-e_{-})-1}+(t^{m(e_{+}-e_{-})}), & \displaystyle \nonumber\\ \displaystyle & \displaystyle d_{\infty }=1-\frac{e_{+}-e_{-}}{r}+\frac{1}{r^{n+1}((-K_{X})^{n})}\int _{e_{-}}^{e_{+}}\operatorname{vol}(\overline{{\mathcal{F}}}S^{(t)})\,dt, & \displaystyle \nonumber\end{eqnarray}$$
and
 $e_{+},e_{-}\in \mathbb{Z}$
with
$e_{+},e_{-}\in \mathbb{Z}$
with
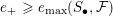 $e_{+}\geqslant e_{\max }(S_{\bullet },{\mathcal{F}})$
and
$e_{+}\geqslant e_{\max }(S_{\bullet },{\mathcal{F}})$
and
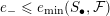 $e_{-}\leqslant e_{\min }(S_{\bullet },{\mathcal{F}})$
.
$e_{-}\leqslant e_{\min }(S_{\bullet },{\mathcal{F}})$
.
We will follow the notation of Theorem 18. Let
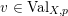 $v\in \text{Val}_{X,p}$
be a real valuation centered at
$v\in \text{Val}_{X,p}$
be a real valuation centered at
![]() $p$
. Define an
$p$
. Define an
![]() $\mathbb{R}$
-filtration
$\mathbb{R}$
-filtration
![]() ${\mathcal{F}}_{v}$
of
${\mathcal{F}}_{v}$
of
![]() $S$
as
$S$
as
 $$\begin{eqnarray}{\mathcal{F}}_{v}^{x}S_{m}:=H^{0}(X,L^{m}\cdot \mathfrak{a}_{x}(v)).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{F}}_{v}^{x}S_{m}:=H^{0}(X,L^{m}\cdot \mathfrak{a}_{x}(v)).\end{eqnarray}$$
Lemma 19. The
![]() $\mathbb{R}$
-filtration
$\mathbb{R}$
-filtration
![]() ${\mathcal{F}}_{v}$
of
${\mathcal{F}}_{v}$
of
![]() $S$
is decreasing, left-continuous, multiplicative and saturated. Moreover, if
$S$
is decreasing, left-continuous, multiplicative and saturated. Moreover, if
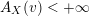 $A_{X}(v)<+\infty$
then
$A_{X}(v)<+\infty$
then
![]() ${\mathcal{F}}_{v}$
is also linearly bounded.
${\mathcal{F}}_{v}$
is also linearly bounded.
Proof. The decreasing, left-continuous and multiplicative properties of
![]() ${\mathcal{F}}_{v}$
follows from the corresponding properties of
${\mathcal{F}}_{v}$
follows from the corresponding properties of
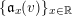 $\{\mathfrak{a}_{x}(v)\}_{x\in \mathbb{R}}$
. To prove that
$\{\mathfrak{a}_{x}(v)\}_{x\in \mathbb{R}}$
. To prove that
![]() ${\mathcal{F}}_{v}$
is saturated, notice that the homomorphism
${\mathcal{F}}_{v}$
is saturated, notice that the homomorphism
 $$\begin{eqnarray}{\mathcal{F}}_{v}^{x}S_{m}\otimes _{\mathbb{C}}L^{-m}{\twoheadrightarrow}I_{(m,x)}^{{\mathcal{F}}_{v}}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{F}}_{v}^{x}S_{m}\otimes _{\mathbb{C}}L^{-m}{\twoheadrightarrow}I_{(m,x)}^{{\mathcal{F}}_{v}}\end{eqnarray}$$
induces the inclusion
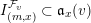 $I_{(m,x)}^{{\mathcal{F}}_{v}}\subset \mathfrak{a}_{x}(v)$
for any
$I_{(m,x)}^{{\mathcal{F}}_{v}}\subset \mathfrak{a}_{x}(v)$
for any
![]() $x\in \mathbb{R}$
. Thus
$x\in \mathbb{R}$
. Thus
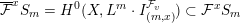 $\overline{{\mathcal{F}}}^{x}S_{m}=H^{0}(X,L^{m}\cdot I_{(m,x)}^{{\mathcal{F}}_{v}})\subset {\mathcal{F}}^{x}S_{m}$
, which implies that
$\overline{{\mathcal{F}}}^{x}S_{m}=H^{0}(X,L^{m}\cdot I_{(m,x)}^{{\mathcal{F}}_{v}})\subset {\mathcal{F}}^{x}S_{m}$
, which implies that
![]() ${\mathcal{F}}_{v}$
is saturated.
${\mathcal{F}}_{v}$
is saturated.
If
 $A_{X}(v)<+\infty$
, then by [Reference LiLi15, Theorem 3.1] there exists a constant
$A_{X}(v)<+\infty$
, then by [Reference LiLi15, Theorem 3.1] there exists a constant
 $c=c(X,p)$
such that
$c=c(X,p)$
such that
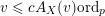 $v\leqslant cA_{X}(v)\text{ord}_{p}$
. So it is easy to see that
$v\leqslant cA_{X}(v)\text{ord}_{p}$
. So it is easy to see that
 $$\begin{eqnarray}e_{\max }(S_{\bullet },{\mathcal{F}}_{v})\leqslant cA_{X}(v)\cdot e_{\max }(S_{\bullet },{\mathcal{F}}_{\text{ord}_{p}})<+\infty .\end{eqnarray}$$
$$\begin{eqnarray}e_{\max }(S_{\bullet },{\mathcal{F}}_{v})\leqslant cA_{X}(v)\cdot e_{\max }(S_{\bullet },{\mathcal{F}}_{\text{ord}_{p}})<+\infty .\end{eqnarray}$$
The second inequality follows from the work in [Reference Boucksom, Küronya, Maclean and SzembergBKMS15]. Next, it is clear that
 $\mathfrak{a}_{x}(v)={\mathcal{O}}_{X}$
for
$\mathfrak{a}_{x}(v)={\mathcal{O}}_{X}$
for
![]() $x\leqslant 0$
. Hence
$x\leqslant 0$
. Hence
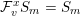 ${\mathcal{F}}_{v}^{x}S_{m}=S_{m}$
for
${\mathcal{F}}_{v}^{x}S_{m}=S_{m}$
for
![]() $x\leqslant 0$
, which implies
$x\leqslant 0$
, which implies
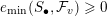 $e_{\min }(S_{\bullet },{\mathcal{F}}_{v})\geqslant 0$
. Hence
$e_{\min }(S_{\bullet },{\mathcal{F}}_{v})\geqslant 0$
. Hence
![]() ${\mathcal{F}}_{v}$
is linearly bounded.◻
${\mathcal{F}}_{v}$
is linearly bounded.◻
It is clear that
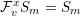 ${\mathcal{F}}_{v}^{x}S_{m}=S_{m}$
for
${\mathcal{F}}_{v}^{x}S_{m}=S_{m}$
for
![]() $x\leqslant 0$
. Hence we may choose
$x\leqslant 0$
. Hence we may choose
![]() $e_{-}=0$
. The graded sequence of ideal sheaves
$e_{-}=0$
. The graded sequence of ideal sheaves
![]() ${\mathcal{I}}_{\bullet }$
on
${\mathcal{I}}_{\bullet }$
on
![]() $X\times \mathbb{A}^{1}$
becomes:
$X\times \mathbb{A}^{1}$
becomes:
 $$\begin{eqnarray}{\mathcal{I}}_{m}=I_{(m,me_{+})}^{{\mathcal{F}}_{v}}+I_{(m,me_{+}-1)}^{{\mathcal{F}}_{v}}t^{1}+\cdots +I_{(m,1)}^{{\mathcal{F}}_{v}}t^{me_{+}-1}+(t^{me_{+}}).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{I}}_{m}=I_{(m,me_{+})}^{{\mathcal{F}}_{v}}+I_{(m,me_{+}-1)}^{{\mathcal{F}}_{v}}t^{1}+\cdots +I_{(m,1)}^{{\mathcal{F}}_{v}}t^{me_{+}-1}+(t^{me_{+}}).\end{eqnarray}$$
We also have that
 $$\begin{eqnarray}d_{\infty }=1-\frac{e_{+}}{r}+\frac{1}{r^{n+1}((-K_{X})^{n})}\int _{0}^{+\infty }\operatorname{vol}({\mathcal{F}}_{v}S^{(t)})\,dt.\end{eqnarray}$$
$$\begin{eqnarray}d_{\infty }=1-\frac{e_{+}}{r}+\frac{1}{r^{n+1}((-K_{X})^{n})}\int _{0}^{+\infty }\operatorname{vol}({\mathcal{F}}_{v}S^{(t)})\,dt.\end{eqnarray}$$
The valuation
![]() $v$
extends to a
$v$
extends to a
![]() $\mathbb{G}_{m}$
-invariant valuation
$\mathbb{G}_{m}$
-invariant valuation
![]() $\bar{v}$
on
$\bar{v}$
on
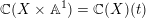 $\mathbb{C}(X\times \mathbb{A}^{1})=\mathbb{C}(X)(t)$
, such that for any
$\mathbb{C}(X\times \mathbb{A}^{1})=\mathbb{C}(X)(t)$
, such that for any
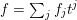 $f=\sum _{j}f_{j}t^{j}$
we have
$f=\sum _{j}f_{j}t^{j}$
we have
 $$\begin{eqnarray}\bar{v}(f)=\min _{j}\{v(f_{j})+j\}.\end{eqnarray}$$
$$\begin{eqnarray}\bar{v}(f)=\min _{j}\{v(f_{j})+j\}.\end{eqnarray}$$
Proposition 20. Let
![]() $X$
be a
$X$
be a
![]() $\mathbb{Q}$
-Fano variety of dimension
$\mathbb{Q}$
-Fano variety of dimension
![]() $n$
. Assume that
$n$
. Assume that
![]() $X$
is Ding-semistable. Let
$X$
is Ding-semistable. Let
![]() $p\in X$
be a closed point. Let
$p\in X$
be a closed point. Let
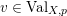 $v\in \text{Val}_{X,p}$
be a real valuation centered at
$v\in \text{Val}_{X,p}$
be a real valuation centered at
![]() $p$
. Then we have
$p$
. Then we have
 $$\begin{eqnarray}A_{X}(v)\geqslant \frac{1}{r^{n+1}((-K_{X})^{n})}\int _{0}^{+\infty }\operatorname{vol}({\mathcal{F}}_{v}S^{(t)})\,dt.\end{eqnarray}$$
$$\begin{eqnarray}A_{X}(v)\geqslant \frac{1}{r^{n+1}((-K_{X})^{n})}\int _{0}^{+\infty }\operatorname{vol}({\mathcal{F}}_{v}S^{(t)})\,dt.\end{eqnarray}$$
Proof. We may assume that
 $A_{X}(v)<+\infty$
, since otherwise the inequality holds automatically. Hence Lemma 19 implies that
$A_{X}(v)<+\infty$
, since otherwise the inequality holds automatically. Hence Lemma 19 implies that
![]() ${\mathcal{F}}_{v}$
is good and saturated.
${\mathcal{F}}_{v}$
is good and saturated.
By Theorem 18, we know that
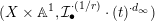 $(X\times \mathbb{A}^{1},{\mathcal{I}}_{\bullet }^{\cdot (1/r)}\cdot (t)^{\cdot d_{\infty }})$
is sub log canonical. Since
$(X\times \mathbb{A}^{1},{\mathcal{I}}_{\bullet }^{\cdot (1/r)}\cdot (t)^{\cdot d_{\infty }})$
is sub log canonical. Since
![]() $X\times \mathbb{A}^{1}$
has klt singularities, for any
$X\times \mathbb{A}^{1}$
has klt singularities, for any
 $0<\unicode[STIX]{x1D716}\ll 1$
there exists
$0<\unicode[STIX]{x1D716}\ll 1$
there exists
 $m=m(\unicode[STIX]{x1D716})$
such that
$m=m(\unicode[STIX]{x1D716})$
such that
 $$\begin{eqnarray}{\mathcal{O}}_{X\times \mathbb{A}^{1}}\subset {\mathcal{J}}(X\times \mathbb{A}^{1},{\mathcal{I}}_{m}^{\cdot (1-\unicode[STIX]{x1D716})/(rm)}\cdot (t)^{\cdot (1-\unicode[STIX]{x1D716})d_{\infty }}),\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{O}}_{X\times \mathbb{A}^{1}}\subset {\mathcal{J}}(X\times \mathbb{A}^{1},{\mathcal{I}}_{m}^{\cdot (1-\unicode[STIX]{x1D716})/(rm)}\cdot (t)^{\cdot (1-\unicode[STIX]{x1D716})d_{\infty }}),\end{eqnarray}$$
where the right-hand side is the multiplier ideal sheaf. By [Reference Boucksom, de Fernex, Favre and UrbinatiBdFFU15, Theorem 1.2] we know that the following inequality holds for any real valuation
![]() $u$
on
$u$
on
![]() $X\times \mathbb{A}^{1}$
:
$X\times \mathbb{A}^{1}$
:
 $$\begin{eqnarray}A_{X\times \mathbb{A}^{1}}(u)>\frac{(1-\unicode[STIX]{x1D716})}{rm}u({\mathcal{I}}_{m})+(1-\unicode[STIX]{x1D716})d_{\infty }u(t).\end{eqnarray}$$
$$\begin{eqnarray}A_{X\times \mathbb{A}^{1}}(u)>\frac{(1-\unicode[STIX]{x1D716})}{rm}u({\mathcal{I}}_{m})+(1-\unicode[STIX]{x1D716})d_{\infty }u(t).\end{eqnarray}$$
Let us choose a sequence of quasi-monomial real valuations
![]() $\{v_{n}\}$
on
$\{v_{n}\}$
on
![]() $X$
such that
$X$
such that
![]() $v_{n}\rightarrow v$
and
$v_{n}\rightarrow v$
and
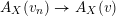 $A_{X}(v_{n})\rightarrow A_{X}(v)$
when
$A_{X}(v_{n})\rightarrow A_{X}(v)$
when
![]() $n\rightarrow \infty$
. It is easy to see that
$n\rightarrow \infty$
. It is easy to see that
![]() $\{\bar{v}_{n}\}$
is a sequence of quasi-monomial valuations on
$\{\bar{v}_{n}\}$
is a sequence of quasi-monomial valuations on
![]() $X\times \mathbb{A}^{1}$
satisfying
$X\times \mathbb{A}^{1}$
satisfying
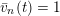 $\bar{v}_{n}(t)=1$
and
$\bar{v}_{n}(t)=1$
and
 $$\begin{eqnarray}A_{X\times \mathbb{A}^{1}}(\bar{v}_{n})=A_{X}(v_{n})+1.\end{eqnarray}$$
$$\begin{eqnarray}A_{X\times \mathbb{A}^{1}}(\bar{v}_{n})=A_{X}(v_{n})+1.\end{eqnarray}$$
Hence we have
 $$\begin{eqnarray}\displaystyle A_{X}(v)+1 & = & \displaystyle \lim _{n\rightarrow \infty }A_{X}(\bar{v}_{n})\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \frac{(1-\unicode[STIX]{x1D716})}{rm}\lim _{n\rightarrow \infty }\bar{v}_{n}({\mathcal{I}}_{m})+(1-\unicode[STIX]{x1D716})d_{\infty }.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle A_{X}(v)+1 & = & \displaystyle \lim _{n\rightarrow \infty }A_{X}(\bar{v}_{n})\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \frac{(1-\unicode[STIX]{x1D716})}{rm}\lim _{n\rightarrow \infty }\bar{v}_{n}({\mathcal{I}}_{m})+(1-\unicode[STIX]{x1D716})d_{\infty }.\nonumber\end{eqnarray}$$
From the definition of
![]() ${\mathcal{F}}_{v}^{x}S_{m}$
we get:
${\mathcal{F}}_{v}^{x}S_{m}$
we get:
 $$\begin{eqnarray}v(I_{(m,x)}^{{\mathcal{F}}_{v}})\geqslant x.\end{eqnarray}$$
$$\begin{eqnarray}v(I_{(m,x)}^{{\mathcal{F}}_{v}})\geqslant x.\end{eqnarray}$$
Therefore,
 $$\begin{eqnarray}\displaystyle \lim _{n\rightarrow \infty }\bar{v}_{n}({\mathcal{I}}_{m}) & = & \displaystyle \lim _{n\rightarrow \infty }\min _{0\leqslant j\leqslant re_{+}}\{v_{n}(I_{(m,j)}^{{\mathcal{F}}_{v}})+me_{+}-j\}\nonumber\\ \displaystyle & = & \displaystyle \min _{0\leqslant j\leqslant re_{+}}\{\lim _{n\rightarrow \infty }v_{n}(I_{(m,j)}^{{\mathcal{F}}_{v}})+me_{+}-j\}\nonumber\\ \displaystyle & = & \displaystyle \min _{0\leqslant j\leqslant re_{+}}\{v(I_{(m,j)}^{{\mathcal{F}}_{v}})+me_{+}-j\}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle me_{+}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \lim _{n\rightarrow \infty }\bar{v}_{n}({\mathcal{I}}_{m}) & = & \displaystyle \lim _{n\rightarrow \infty }\min _{0\leqslant j\leqslant re_{+}}\{v_{n}(I_{(m,j)}^{{\mathcal{F}}_{v}})+me_{+}-j\}\nonumber\\ \displaystyle & = & \displaystyle \min _{0\leqslant j\leqslant re_{+}}\{\lim _{n\rightarrow \infty }v_{n}(I_{(m,j)}^{{\mathcal{F}}_{v}})+me_{+}-j\}\nonumber\\ \displaystyle & = & \displaystyle \min _{0\leqslant j\leqslant re_{+}}\{v(I_{(m,j)}^{{\mathcal{F}}_{v}})+me_{+}-j\}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle me_{+}.\nonumber\end{eqnarray}$$
Hence when
 $\unicode[STIX]{x1D716}\rightarrow 0+$
we get:
$\unicode[STIX]{x1D716}\rightarrow 0+$
we get:
 $$\begin{eqnarray}A_{X}(v)+1\geqslant \frac{e_{+}}{r}+d_{\infty }.\end{eqnarray}$$
$$\begin{eqnarray}A_{X}(v)+1\geqslant \frac{e_{+}}{r}+d_{\infty }.\end{eqnarray}$$
Therefore,
 $$\begin{eqnarray}A_{X}(v)\geqslant -1+\frac{e_{+}}{r}+d_{\infty }=\frac{1}{r^{n+1}((-K_{X})^{n})}\int _{0}^{+\infty }\operatorname{vol}({\mathcal{F}}_{v}S^{(t)})\,dt.\end{eqnarray}$$
$$\begin{eqnarray}A_{X}(v)\geqslant -1+\frac{e_{+}}{r}+d_{\infty }=\frac{1}{r^{n+1}((-K_{X})^{n})}\int _{0}^{+\infty }\operatorname{vol}({\mathcal{F}}_{v}S^{(t)})\,dt.\end{eqnarray}$$
Hence we get the desired inequality. ◻
The following theorem is a stronger result that implies Theorem 2.
Theorem 21. Let
![]() $X$
be a Ding-semistable
$X$
be a Ding-semistable
![]() $\mathbb{Q}$
-Fano variety. Let
$\mathbb{Q}$
-Fano variety. Let
![]() $p\in X$
be a closed point. Let
$p\in X$
be a closed point. Let
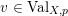 $v\in \text{Val}_{X,p}$
be a real valuation centered at
$v\in \text{Val}_{X,p}$
be a real valuation centered at
![]() $p$
. Then we have
$p$
. Then we have
 $$\begin{eqnarray}((-K_{X})^{n})\leqslant \biggl(1+\frac{1}{n}\biggr)^{n}\,\widehat{\operatorname{vol}}(v).\end{eqnarray}$$
$$\begin{eqnarray}((-K_{X})^{n})\leqslant \biggl(1+\frac{1}{n}\biggr)^{n}\,\widehat{\operatorname{vol}}(v).\end{eqnarray}$$
Proof. We may assume
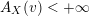 $A_{X}(v)<+\infty$
, since otherwise the inequality holds automatically. Since
$A_{X}(v)<+\infty$
, since otherwise the inequality holds automatically. Since
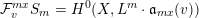 ${\mathcal{F}}_{v}^{mx}S_{m}=H^{0}(X,L^{m}\cdot \mathfrak{a}_{mx}(v))$
, we have the exact sequence
${\mathcal{F}}_{v}^{mx}S_{m}=H^{0}(X,L^{m}\cdot \mathfrak{a}_{mx}(v))$
, we have the exact sequence
 $$\begin{eqnarray}0\rightarrow {\mathcal{F}}_{v}^{mx}S_{m}\rightarrow H^{0}(X,L^{m})\rightarrow H^{0}(X,L^{m}\otimes ({\mathcal{O}}_{X}/\mathfrak{a}_{mx}(v))).\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow {\mathcal{F}}_{v}^{mx}S_{m}\rightarrow H^{0}(X,L^{m})\rightarrow H^{0}(X,L^{m}\otimes ({\mathcal{O}}_{X}/\mathfrak{a}_{mx}(v))).\end{eqnarray}$$
Hence we have
 $$\begin{eqnarray}\dim {\mathcal{F}}_{v}^{mx}S_{m}\geqslant h^{0}(X,L^{m})-\ell ({\mathcal{O}}_{X}/\mathfrak{a}_{mx}(v)).\end{eqnarray}$$
$$\begin{eqnarray}\dim {\mathcal{F}}_{v}^{mx}S_{m}\geqslant h^{0}(X,L^{m})-\ell ({\mathcal{O}}_{X}/\mathfrak{a}_{mx}(v)).\end{eqnarray}$$
This implies
 $$\begin{eqnarray}\operatorname{vol}({\mathcal{F}}_{v}S^{(x)})\geqslant (L^{n})-\operatorname{vol}(v)x^{n}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{vol}({\mathcal{F}}_{v}S^{(x)})\geqslant (L^{n})-\operatorname{vol}(v)x^{n}.\end{eqnarray}$$
So we have the estimate:
 $$\begin{eqnarray}\displaystyle \int _{0}^{+\infty }\operatorname{vol}({\mathcal{F}}_{v}S^{(x)})\,dx & {\geqslant} & \displaystyle \int _{0}^{\sqrt[n]{(L^{n})/\operatorname{vol}(v)}}((L^{n})-\operatorname{vol}(v)x^{n})\,dx\nonumber\\ \displaystyle & = & \displaystyle \frac{n}{n+1}(L^{n})\cdot \sqrt[n]{(L^{n})/\operatorname{vol}(v)}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{0}^{+\infty }\operatorname{vol}({\mathcal{F}}_{v}S^{(x)})\,dx & {\geqslant} & \displaystyle \int _{0}^{\sqrt[n]{(L^{n})/\operatorname{vol}(v)}}((L^{n})-\operatorname{vol}(v)x^{n})\,dx\nonumber\\ \displaystyle & = & \displaystyle \frac{n}{n+1}(L^{n})\cdot \sqrt[n]{(L^{n})/\operatorname{vol}(v)}.\nonumber\end{eqnarray}$$
Applying (3.3) we get the inequality:
 $$\begin{eqnarray}\displaystyle A_{X}(v) & {\geqslant} & \displaystyle \frac{1}{r(L^{n})}\int _{0}^{+\infty }\operatorname{vol}({\mathcal{F}}_{v}S^{(t)})\,dt\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \frac{1}{r(L^{n})}\frac{n}{n+1}(L^{n})\sqrt[n]{(L^{n})/\operatorname{vol}(v)}=\frac{n}{n+1}\sqrt[n]{((-K_{X})^{n})/\operatorname{vol}(v)}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle A_{X}(v) & {\geqslant} & \displaystyle \frac{1}{r(L^{n})}\int _{0}^{+\infty }\operatorname{vol}({\mathcal{F}}_{v}S^{(t)})\,dt\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \frac{1}{r(L^{n})}\frac{n}{n+1}(L^{n})\sqrt[n]{(L^{n})/\operatorname{vol}(v)}=\frac{n}{n+1}\sqrt[n]{((-K_{X})^{n})/\operatorname{vol}(v)}.\nonumber\end{eqnarray}$$
This is exactly equivalent to
 $$\begin{eqnarray}((-K_{X})^{n})\leqslant \biggl(1+\frac{1}{n}\biggr)^{n}A_{X}(v)^{n}\operatorname{vol}(v)=\biggl(1+\frac{1}{n}\biggr)^{n}\,\widehat{\operatorname{vol}}(v).\Box\end{eqnarray}$$
$$\begin{eqnarray}((-K_{X})^{n})\leqslant \biggl(1+\frac{1}{n}\biggr)^{n}A_{X}(v)^{n}\operatorname{vol}(v)=\biggl(1+\frac{1}{n}\biggr)^{n}\,\widehat{\operatorname{vol}}(v).\Box\end{eqnarray}$$
3.2 Applications
The following result is an easy consequence of Theorem 1.
Theorem 22 [Reference de Fernex, Ein and MustaţădFEM04].
Let
![]() $X$
be a variety of dimension
$X$
be a variety of dimension
![]() $n$
. Let
$n$
. Let
![]() $Z$
be a closed subscheme of
$Z$
be a closed subscheme of
![]() $X$
supported at a single smooth closed point. Then
$X$
supported at a single smooth closed point. Then
 $$\begin{eqnarray}\biggl(\frac{\operatorname{lct}(X;I_{Z})}{n}\biggr)^{n}\operatorname{mult}_{Z}X\geqslant 1.\end{eqnarray}$$
$$\begin{eqnarray}\biggl(\frac{\operatorname{lct}(X;I_{Z})}{n}\biggr)^{n}\operatorname{mult}_{Z}X\geqslant 1.\end{eqnarray}$$
Proof. It is clear that the multiplicity is preserved under completion. Next, [Reference de Fernex, Ein and MustaţădFEM11, Proposition 2.11] implies that
![]() $\operatorname{lct}$
is also preserved under completion. Hence it suffices to prove the theorem for
$\operatorname{lct}$
is also preserved under completion. Hence it suffices to prove the theorem for
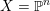 $X=\mathbb{P}^{n}$
. This follows directly by applying Theorem 1 to the case
$X=\mathbb{P}^{n}$
. This follows directly by applying Theorem 1 to the case
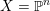 $X=\mathbb{P}^{n}$
.◻
$X=\mathbb{P}^{n}$
.◻
Now we will illustrate some volume bounds for singular
![]() $X$
.
$X$
.
Theorem 23. Let
![]() $X$
be a Ding-semistable
$X$
be a Ding-semistable
![]() $\mathbb{Q}$
-Fano variety. Let
$\mathbb{Q}$
-Fano variety. Let
![]() $p\in X$
be a closed point. Suppose
$p\in X$
be a closed point. Suppose
![]() $(X,p)$
is a quotient singularity with local analytic model
$(X,p)$
is a quotient singularity with local analytic model
![]() $\mathbb{C}^{2}/G$
where
$\mathbb{C}^{2}/G$
where
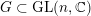 $G\subset \text{GL}(n,\mathbb{C})$
acts freely in codimension
$G\subset \text{GL}(n,\mathbb{C})$
acts freely in codimension
![]() $1$
. Then
$1$
. Then
 $$\begin{eqnarray}((-K_{X})^{n})\leqslant \frac{(n+1)^{n}}{|G|}.\end{eqnarray}$$
$$\begin{eqnarray}((-K_{X})^{n})\leqslant \frac{(n+1)^{n}}{|G|}.\end{eqnarray}$$
Proof. Let
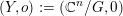 $(Y,o):=(\mathbb{C}^{n}/G,0)$
be the local analytic model of the quotient singularity
$(Y,o):=(\mathbb{C}^{n}/G,0)$
be the local analytic model of the quotient singularity
![]() $(X,p)$
. Let
$(X,p)$
. Let
 $H:=G\cap \mathbb{G}_{m}$
with
$H:=G\cap \mathbb{G}_{m}$
with
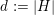 $d:=|H|$
. Define the real valuation
$d:=|H|$
. Define the real valuation
![]() $u_{0}$
on
$u_{0}$
on
![]() $Y$
to be the pushforward of the valuation
$Y$
to be the pushforward of the valuation
![]() $\text{ord}_{0}$
on
$\text{ord}_{0}$
on
![]() $\mathbb{C}^{n}$
under the quotient map
$\mathbb{C}^{n}$
under the quotient map
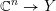 $\mathbb{C}^{n}\rightarrow Y$
.
$\mathbb{C}^{n}\rightarrow Y$
.
We first show that
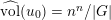 $\widehat{\operatorname{vol}}(u_{0})=n^{n}/|G|$
. Let
$\widehat{\operatorname{vol}}(u_{0})=n^{n}/|G|$
. Let
![]() $\widehat{\mathbb{C}^{n}}$
be the blow up of
$\widehat{\mathbb{C}^{n}}$
be the blow up of
![]() $\mathbb{C}^{n}$
at the origin
$\mathbb{C}^{n}$
at the origin
![]() $0$
with exceptional divisor
$0$
with exceptional divisor
![]() $E$
. Denote by
$E$
. Denote by
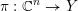 $\unicode[STIX]{x1D70B}:\mathbb{C}^{n}\rightarrow Y$
the quotient map. Then
$\unicode[STIX]{x1D70B}:\mathbb{C}^{n}\rightarrow Y$
the quotient map. Then
![]() $\unicode[STIX]{x1D70B}$
lifts to
$\unicode[STIX]{x1D70B}$
lifts to
![]() $\widehat{\mathbb{C}^{n}}$
as
$\widehat{\mathbb{C}^{n}}$
as
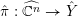 $\hat{\unicode[STIX]{x1D70B}}:\widehat{\mathbb{C}^{n}}\rightarrow {\hat{Y}}$
, where
$\hat{\unicode[STIX]{x1D70B}}:\widehat{\mathbb{C}^{n}}\rightarrow {\hat{Y}}$
, where
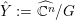 ${\hat{Y}}:=\widehat{\mathbb{C}^{n}}/G$
. We have the following commutative diagram:
${\hat{Y}}:=\widehat{\mathbb{C}^{n}}/G$
. We have the following commutative diagram:

Let
![]() $F\subset {\hat{Y}}$
be the exceptional divisor of
$F\subset {\hat{Y}}$
be the exceptional divisor of
![]() $h$
. For a general point on
$h$
. For a general point on
![]() $F$
, its stabilizer under the
$F$
, its stabilizer under the
![]() $G$
-action is exactly
$G$
-action is exactly
![]() $H$
. So
$H$
. So
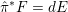 $\hat{\unicode[STIX]{x1D70B}}^{\ast }F=dE$
, which implies that
$\hat{\unicode[STIX]{x1D70B}}^{\ast }F=dE$
, which implies that
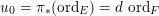 $u_{0}=\unicode[STIX]{x1D70B}_{\ast }(\text{ord}_{E})=d~\text{ord}_{F}$
. It is clear that
$u_{0}=\unicode[STIX]{x1D70B}_{\ast }(\text{ord}_{E})=d~\text{ord}_{F}$
. It is clear that
 $$\begin{eqnarray}K_{\widehat{\mathbb{C}^{n}}}=\hat{\unicode[STIX]{x1D70B}}^{\ast }\biggl(K_{{\hat{Y}}}+\biggl(1-\frac{1}{d}\biggr)F\biggr).\end{eqnarray}$$
$$\begin{eqnarray}K_{\widehat{\mathbb{C}^{n}}}=\hat{\unicode[STIX]{x1D70B}}^{\ast }\biggl(K_{{\hat{Y}}}+\biggl(1-\frac{1}{d}\biggr)F\biggr).\end{eqnarray}$$
Then combining these equalities with
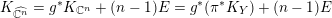 $K_{\widehat{\mathbb{C}^{n}}}=g^{\ast }K_{\mathbb{C}^{n}}+(n-1)E=g^{\ast }(\unicode[STIX]{x1D70B}^{\ast }K_{Y})+(n-1)E$
, we get
$K_{\widehat{\mathbb{C}^{n}}}=g^{\ast }K_{\mathbb{C}^{n}}+(n-1)E=g^{\ast }(\unicode[STIX]{x1D70B}^{\ast }K_{Y})+(n-1)E$
, we get
 $$\begin{eqnarray}K_{{\hat{Y}}}=h^{\ast }K_{Y}+\biggl(\frac{n}{d}-1\biggr)F.\end{eqnarray}$$
$$\begin{eqnarray}K_{{\hat{Y}}}=h^{\ast }K_{Y}+\biggl(\frac{n}{d}-1\biggr)F.\end{eqnarray}$$
Hence
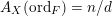 $A_{X}(\text{ord}_{F})=n/d$
and
$A_{X}(\text{ord}_{F})=n/d$
and
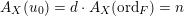 $A_{X}(u_{0})=d\cdot A_{X}(\text{ord}_{F})=n$
. Lemma 24 implies that
$A_{X}(u_{0})=d\cdot A_{X}(\text{ord}_{F})=n$
. Lemma 24 implies that
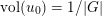 $\operatorname{vol}(u_{0})=1/|G|$
. Therefore,
$\operatorname{vol}(u_{0})=1/|G|$
. Therefore,
 $\widehat{\operatorname{vol}}(u_{0})=n^{n}/|G|$
.
$\widehat{\operatorname{vol}}(u_{0})=n^{n}/|G|$
.
Since
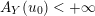 $A_{Y}(u_{0})<+\infty$
, a singular version of [Reference Jonsson and MustaţăJM12, Corollary 5.11] for klt singularities (such a statement is true thanks to the Izumi inequality for klt singularities [Reference LiLi15, Proposition 3.1]) implies that
$A_{Y}(u_{0})<+\infty$
, a singular version of [Reference Jonsson and MustaţăJM12, Corollary 5.11] for klt singularities (such a statement is true thanks to the Izumi inequality for klt singularities [Reference LiLi15, Proposition 3.1]) implies that
![]() $u_{0}$
has a unique extension, say
$u_{0}$
has a unique extension, say
![]() $\hat{u} _{0}$
, as a valuation on
$\hat{u} _{0}$
, as a valuation on
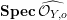 $\mathbf{Spec}\,\widehat{{\mathcal{O}}_{Y,o}}$
that centered at the closed point. By assumption we have an isomorphism
$\mathbf{Spec}\,\widehat{{\mathcal{O}}_{Y,o}}$
that centered at the closed point. By assumption we have an isomorphism
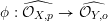 $\unicode[STIX]{x1D719}:\widehat{{\mathcal{O}}_{X,p}}\rightarrow \widehat{{\mathcal{O}}_{Y,o}}$
. Let
$\unicode[STIX]{x1D719}:\widehat{{\mathcal{O}}_{X,p}}\rightarrow \widehat{{\mathcal{O}}_{Y,o}}$
. Let
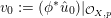 $v_{0}:=(\unicode[STIX]{x1D719}^{\ast }\hat{u} _{0})|_{{\mathcal{O}}_{X,p}}$
, then
$v_{0}:=(\unicode[STIX]{x1D719}^{\ast }\hat{u} _{0})|_{{\mathcal{O}}_{X,p}}$
, then
 $v_{0}\in \text{Val}_{X,p}$
. By a singular version of [Reference Jonsson and MustaţăJM12, Proposition 5.13], we know that
$v_{0}\in \text{Val}_{X,p}$
. By a singular version of [Reference Jonsson and MustaţăJM12, Proposition 5.13], we know that
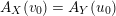 $A_{X}(v_{0})=A_{Y}(u_{0})$
. On the other hand, since the colength of any
$A_{X}(v_{0})=A_{Y}(u_{0})$
. On the other hand, since the colength of any
![]() $\mathfrak{m}$
-primary ideal does not change under completion, we have
$\mathfrak{m}$
-primary ideal does not change under completion, we have
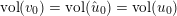 $\operatorname{vol}(v_{0})=\operatorname{vol}(\hat{u} _{0})=\operatorname{vol}(u_{0})$
. As a result, we have
$\operatorname{vol}(v_{0})=\operatorname{vol}(\hat{u} _{0})=\operatorname{vol}(u_{0})$
. As a result, we have
 $$\begin{eqnarray}\widehat{\operatorname{vol}}(v_{0})=\widehat{\operatorname{vol}}(u_{0})=\frac{n^{n}}{|G|}.\end{eqnarray}$$
$$\begin{eqnarray}\widehat{\operatorname{vol}}(v_{0})=\widehat{\operatorname{vol}}(u_{0})=\frac{n^{n}}{|G|}.\end{eqnarray}$$
Hence the theorem follows as a direct application of Theorem 2 to
![]() $v=v_{0}$
.◻
$v=v_{0}$
.◻
Lemma 24. Let
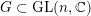 $G\subset \text{GL}(n,\mathbb{C})$
be a finite group acting on
$G\subset \text{GL}(n,\mathbb{C})$
be a finite group acting on
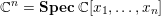 $\mathbb{C}^{n}=\mathbf{Spec}\,\mathbb{C}[x_{1},\ldots ,x_{n}]$
. Then we have
$\mathbb{C}^{n}=\mathbf{Spec}\,\mathbb{C}[x_{1},\ldots ,x_{n}]$
. Then we have
 $$\begin{eqnarray}\lim _{m\rightarrow \infty }\frac{\dim _{\mathbb{C}}\mathbb{C}[x_{1},\ldots ,x_{n}]_{{<}m}^{G}}{m^{n}/n!}=\frac{1}{|G|}.\end{eqnarray}$$
$$\begin{eqnarray}\lim _{m\rightarrow \infty }\frac{\dim _{\mathbb{C}}\mathbb{C}[x_{1},\ldots ,x_{n}]_{{<}m}^{G}}{m^{n}/n!}=\frac{1}{|G|}.\end{eqnarray}$$
Proof. Denote
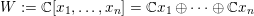 $W:=\mathbb{C}[x_{1},\ldots ,x_{n}]=\mathbb{C}x_{1}\oplus \cdots \oplus \mathbb{C}x_{n}$
. Then we have that
$W:=\mathbb{C}[x_{1},\ldots ,x_{n}]=\mathbb{C}x_{1}\oplus \cdots \oplus \mathbb{C}x_{n}$
. Then we have that
 $$\begin{eqnarray}\mathbb{C}[x_{1},\ldots ,x_{n}]\cong \bigoplus _{m\geqslant 0}\text{Sym}^{m}W.\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{C}[x_{1},\ldots ,x_{n}]\cong \bigoplus _{m\geqslant 0}\text{Sym}^{m}W.\end{eqnarray}$$
Denote by
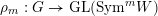 $\unicode[STIX]{x1D70C}_{m}:G\rightarrow \text{GL}(\text{Sym}^{m}W)$
the induced representation of
$\unicode[STIX]{x1D70C}_{m}:G\rightarrow \text{GL}(\text{Sym}^{m}W)$
the induced representation of
![]() $G$
on
$G$
on
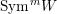 $\text{Sym}^{m}W$
. Since
$\text{Sym}^{m}W$
. Since
![]() $G$
is finite,
$G$
is finite,
![]() $\unicode[STIX]{x1D70C}_{m}(g)$
is diagonalizable for any
$\unicode[STIX]{x1D70C}_{m}(g)$
is diagonalizable for any
![]() $m\geqslant 0$
and
$m\geqslant 0$
and
![]() $g\in G$
. Denote the
$g\in G$
. Denote the
![]() $n$
eigenvalues of
$n$
eigenvalues of
![]() $\unicode[STIX]{x1D70C}_{1}(g)$
by
$\unicode[STIX]{x1D70C}_{1}(g)$
by
 $\unicode[STIX]{x1D706}_{g,1},\ldots ,\unicode[STIX]{x1D706}_{g,n}$
. Then the eigenvalues of
$\unicode[STIX]{x1D706}_{g,1},\ldots ,\unicode[STIX]{x1D706}_{g,n}$
. Then the eigenvalues of
![]() $\unicode[STIX]{x1D70C}_{m}(g)$
are exactly all monomials in
$\unicode[STIX]{x1D70C}_{m}(g)$
are exactly all monomials in
![]() $\unicode[STIX]{x1D706}_{g,i}$
of degree
$\unicode[STIX]{x1D706}_{g,i}$
of degree
![]() $m$
. Let
$m$
. Let
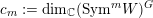 $c_{m}:=\dim _{\mathbb{C}}(\text{Sym}^{m}W)^{G}$
and
$c_{m}:=\dim _{\mathbb{C}}(\text{Sym}^{m}W)^{G}$
and
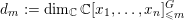 $d_{m}:=\dim _{\mathbb{C}}\mathbb{C}[x_{1},\ldots ,x_{n}]_{{\leqslant}m}^{G}$
. From representation theory we know that
$d_{m}:=\dim _{\mathbb{C}}\mathbb{C}[x_{1},\ldots ,x_{n}]_{{\leqslant}m}^{G}$
. From representation theory we know that
 $$\begin{eqnarray}c_{m}=\frac{1}{|G|}\mathop{\sum }_{g\in G}\text{tr}(\unicode[STIX]{x1D70C}_{m}(g)).\end{eqnarray}$$
$$\begin{eqnarray}c_{m}=\frac{1}{|G|}\mathop{\sum }_{g\in G}\text{tr}(\unicode[STIX]{x1D70C}_{m}(g)).\end{eqnarray}$$
Hence
 $$\begin{eqnarray}c(t):=\mathop{\sum }_{m=0}^{\infty }c_{m}t^{m}=\frac{1}{|G|}\mathop{\sum }_{g\in G}\frac{1}{(1-\unicode[STIX]{x1D706}_{g,1}t)\cdots (1-\unicode[STIX]{x1D706}_{g,n}t)}.\end{eqnarray}$$
$$\begin{eqnarray}c(t):=\mathop{\sum }_{m=0}^{\infty }c_{m}t^{m}=\frac{1}{|G|}\mathop{\sum }_{g\in G}\frac{1}{(1-\unicode[STIX]{x1D706}_{g,1}t)\cdots (1-\unicode[STIX]{x1D706}_{g,n}t)}.\end{eqnarray}$$
This is also known as Molien’s theorem [Reference MolienMol97]. Since
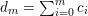 $d_{m}=\sum _{i=0}^{m}c_{i}$
, we have
$d_{m}=\sum _{i=0}^{m}c_{i}$
, we have
 $$\begin{eqnarray}\displaystyle d(t) & := & \displaystyle \mathop{\sum }_{m=0}^{\infty }d_{m}t^{m}=\frac{c(t)}{1-t}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{|G|}\mathop{\sum }_{g\in G}\frac{1}{(1-t)(1-\unicode[STIX]{x1D706}_{g,1}t)\cdots (1-\unicode[STIX]{x1D706}_{g,n}t)}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle d(t) & := & \displaystyle \mathop{\sum }_{m=0}^{\infty }d_{m}t^{m}=\frac{c(t)}{1-t}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{|G|}\mathop{\sum }_{g\in G}\frac{1}{(1-t)(1-\unicode[STIX]{x1D706}_{g,1}t)\cdots (1-\unicode[STIX]{x1D706}_{g,n}t)}.\nonumber\end{eqnarray}$$
Here all eigenvalues
![]() $\unicode[STIX]{x1D706}_{g,i}$
are roots of unity. Using partial fraction decomposition, for any
$\unicode[STIX]{x1D706}_{g,i}$
are roots of unity. Using partial fraction decomposition, for any
![]() $g\neq id$
we have
$g\neq id$
we have
 $$\begin{eqnarray}\frac{1}{(1-t)(1-\unicode[STIX]{x1D706}_{g,1}t)\cdots (1-\unicode[STIX]{x1D706}_{g,n}t)}=\mathop{\sum }_{m=0}^{\infty }o(m^{n})t^{m}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{(1-t)(1-\unicode[STIX]{x1D706}_{g,1}t)\cdots (1-\unicode[STIX]{x1D706}_{g,n}t)}=\mathop{\sum }_{m=0}^{\infty }o(m^{n})t^{m}.\end{eqnarray}$$
Hence
 $$\begin{eqnarray}\displaystyle d(t) & = & \displaystyle \frac{1}{|G|}\cdot \frac{1}{(1-t)^{n+1}}+\mathop{\sum }_{m=0}^{\infty }o(m^{n})t^{m}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{m=0}^{\infty }\biggl(\frac{1}{|G|}\binom{n+m}{n}+o(m^{n})\biggr)t^{m}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle d(t) & = & \displaystyle \frac{1}{|G|}\cdot \frac{1}{(1-t)^{n+1}}+\mathop{\sum }_{m=0}^{\infty }o(m^{n})t^{m}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{m=0}^{\infty }\biggl(\frac{1}{|G|}\binom{n+m}{n}+o(m^{n})\biggr)t^{m}.\nonumber\end{eqnarray}$$
As a result,
 $$\begin{eqnarray}\lim _{m\rightarrow \infty }\frac{d_{m-1}}{m^{n}/n!}=\lim _{m\rightarrow \infty }\frac{1/|G|\binom{n+m-1}{n}}{m^{n}/n!}=\frac{1}{|G|}.\Box\end{eqnarray}$$
$$\begin{eqnarray}\lim _{m\rightarrow \infty }\frac{d_{m-1}}{m^{n}/n!}=\lim _{m\rightarrow \infty }\frac{1/|G|\binom{n+m-1}{n}}{m^{n}/n!}=\frac{1}{|G|}.\Box\end{eqnarray}$$
Theorem 25. Let
![]() $X$
be a Ding-semistable
$X$
be a Ding-semistable
![]() $\mathbb{Q}$
-Fano variety. Let
$\mathbb{Q}$
-Fano variety. Let
![]() $p\in X$
be an isolated singularity. If
$p\in X$
be an isolated singularity. If
![]() $X$
is not terminal at
$X$
is not terminal at
![]() $p$
, then
$p$
, then
 $$\begin{eqnarray}((-K_{X})^{n})\leqslant \biggl(1+\frac{1}{n}\biggr)^{n}\operatorname{mult}_{p}X<e~\operatorname{mult}_{p}X.\end{eqnarray}$$
$$\begin{eqnarray}((-K_{X})^{n})\leqslant \biggl(1+\frac{1}{n}\biggr)^{n}\operatorname{mult}_{p}X<e~\operatorname{mult}_{p}X.\end{eqnarray}$$
Proof. Denote by
![]() $\mathfrak{m}_{p}$
the maximal ideal at
$\mathfrak{m}_{p}$
the maximal ideal at
![]() $p$
. We first show that
$p$
. We first show that
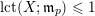 $\operatorname{lct}(X;\mathfrak{m}_{p})\leqslant 1$
. Since
$\operatorname{lct}(X;\mathfrak{m}_{p})\leqslant 1$
. Since
![]() $p$
is an isolated singularity, we may take a log resolution of
$p$
is an isolated singularity, we may take a log resolution of
![]() $(X,\mathfrak{m}_{p})$
, namely
$(X,\mathfrak{m}_{p})$
, namely
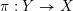 $\unicode[STIX]{x1D70B}:Y\rightarrow X$
such that
$\unicode[STIX]{x1D70B}:Y\rightarrow X$
such that
![]() $\unicode[STIX]{x1D70B}$
is an isomorphism away from
$\unicode[STIX]{x1D70B}$
is an isomorphism away from
![]() $p$
and
$p$
and
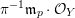 $\unicode[STIX]{x1D70B}^{-1}\mathfrak{m}_{p}\cdot {\mathcal{O}}_{Y}$
is an invertible ideal sheaf on
$\unicode[STIX]{x1D70B}^{-1}\mathfrak{m}_{p}\cdot {\mathcal{O}}_{Y}$
is an invertible ideal sheaf on
![]() $Y$
. Let
$Y$
. Let
![]() $E_{i}$
be the exceptional divisors of
$E_{i}$
be the exceptional divisors of
![]() $\unicode[STIX]{x1D70B}$
. We define the numbers
$\unicode[STIX]{x1D70B}$
. We define the numbers
![]() $a_{i}$
and
$a_{i}$
and
![]() $b_{i}$
by
$b_{i}$
by
 $$\begin{eqnarray}K_{Y}=\unicode[STIX]{x1D70B}^{\ast }K_{X}+\mathop{\sum }_{i}a_{i}E_{i}\quad \text{and}\quad \unicode[STIX]{x1D70B}^{-1}\mathfrak{m}_{p}\cdot {\mathcal{O}}_{Y}={\mathcal{O}}_{Y}\biggl(\!-\!\mathop{\sum }_{i}b_{i}E_{i}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}K_{Y}=\unicode[STIX]{x1D70B}^{\ast }K_{X}+\mathop{\sum }_{i}a_{i}E_{i}\quad \text{and}\quad \unicode[STIX]{x1D70B}^{-1}\mathfrak{m}_{p}\cdot {\mathcal{O}}_{Y}={\mathcal{O}}_{Y}\biggl(\!-\!\mathop{\sum }_{i}b_{i}E_{i}\biggr).\end{eqnarray}$$
It is clear that
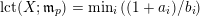 $\operatorname{lct}(X;\mathfrak{m}_{p})=\min _{i}((1+a_{i})/b_{i})$
. Since
$\operatorname{lct}(X;\mathfrak{m}_{p})=\min _{i}((1+a_{i})/b_{i})$
. Since
![]() $\unicode[STIX]{x1D70B}$
is an isomorphism away from
$\unicode[STIX]{x1D70B}$
is an isomorphism away from
![]() $p$
, we have
$p$
, we have
![]() $b_{i}\geqslant 1$
for any
$b_{i}\geqslant 1$
for any
![]() $i$
. Since
$i$
. Since
![]() $X$
is not terminal at
$X$
is not terminal at
![]() $p$
, there exists an index
$p$
, there exists an index
![]() $i_{0}$
such that
$i_{0}$
such that
![]() $a_{i_{0}}\leqslant 0$
. Hence
$a_{i_{0}}\leqslant 0$
. Hence
 $$\begin{eqnarray}\operatorname{lct}(X;\mathfrak{m}_{p})\leqslant \frac{1+a_{i_{0}}}{b_{i_{0}}}\leqslant 1.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{lct}(X;\mathfrak{m}_{p})\leqslant \frac{1+a_{i_{0}}}{b_{i_{0}}}\leqslant 1.\end{eqnarray}$$
So we finish the proof by applying Theorem 1 to
![]() $Z=p$
.◻
$Z=p$
.◻
4 Comparing invariants for ideals and valuations
In this section, we will always assume that
![]() $(X,p)$
is a normal
$(X,p)$
is a normal
![]() $\mathbb{Q}$
-Gorenstein klt singularity of dimension
$\mathbb{Q}$
-Gorenstein klt singularity of dimension
![]() $n$
with
$n$
with
![]() $p\in X$
a closed point.
$p\in X$
a closed point.
4.1 The infimums of invariants
Lemma 26. Let
![]() $\mathfrak{a}$
be an ideal sheaf on
$\mathfrak{a}$
be an ideal sheaf on
![]() $X$
supported at
$X$
supported at
![]() $p$
. Let
$p$
. Let
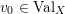 $v_{0}\in \text{Val}_{X}$
be a divisorial valuation that computes
$v_{0}\in \text{Val}_{X}$
be a divisorial valuation that computes
![]() $\operatorname{lct}(\mathfrak{a})$
. Then
$\operatorname{lct}(\mathfrak{a})$
. Then
![]() $v_{0}$
is centered at
$v_{0}$
is centered at
![]() $p$
, and we have
$p$
, and we have
 $$\begin{eqnarray}\operatorname{lct}(\mathfrak{a})^{n}\cdot \operatorname{mult}(\mathfrak{a})\geqslant \widehat{\operatorname{vol}}(v_{0}).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{lct}(\mathfrak{a})^{n}\cdot \operatorname{mult}(\mathfrak{a})\geqslant \widehat{\operatorname{vol}}(v_{0}).\end{eqnarray}$$
Proof. Since
![]() $v_{0}$
computes
$v_{0}$
computes
![]() $\operatorname{lct}(\mathfrak{a})$
, we have that
$\operatorname{lct}(\mathfrak{a})$
, we have that
 $\operatorname{lct}(\mathfrak{a})=A_{X}(v_{0})/v_{0}(\mathfrak{a})$
. Denote
$\operatorname{lct}(\mathfrak{a})=A_{X}(v_{0})/v_{0}(\mathfrak{a})$
. Denote
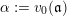 $\unicode[STIX]{x1D6FC}:=v_{0}(\mathfrak{a})$
. Then
$\unicode[STIX]{x1D6FC}:=v_{0}(\mathfrak{a})$
. Then
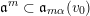 $\mathfrak{a}^{m}\subset \mathfrak{a}_{m\unicode[STIX]{x1D6FC}}(v_{0})$
since
$\mathfrak{a}^{m}\subset \mathfrak{a}_{m\unicode[STIX]{x1D6FC}}(v_{0})$
since
 $v_{0}(\mathfrak{a}^{m})=m\unicode[STIX]{x1D6FC}$
. Therefore,
$v_{0}(\mathfrak{a}^{m})=m\unicode[STIX]{x1D6FC}$
. Therefore,
 $$\begin{eqnarray}\displaystyle \operatorname{mult}(\mathfrak{a}) & = & \displaystyle \lim _{m\rightarrow \infty }\frac{\ell ({\mathcal{O}}_{X}/\mathfrak{a}^{m})}{m^{n}/n!}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \lim _{m\rightarrow \infty }\frac{\ell ({\mathcal{O}}_{X}/\mathfrak{a}_{m\unicode[STIX]{x1D6FC}}(v_{0}))}{m^{n}/n!}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FC}\,\operatorname{vol}(v_{0}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{mult}(\mathfrak{a}) & = & \displaystyle \lim _{m\rightarrow \infty }\frac{\ell ({\mathcal{O}}_{X}/\mathfrak{a}^{m})}{m^{n}/n!}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \lim _{m\rightarrow \infty }\frac{\ell ({\mathcal{O}}_{X}/\mathfrak{a}_{m\unicode[STIX]{x1D6FC}}(v_{0}))}{m^{n}/n!}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FC}\,\operatorname{vol}(v_{0}).\nonumber\end{eqnarray}$$
Hence we prove the lemma. ◻
Following [Reference Ein, Lazarsfeld and SmithELS03], for a graded sequence of ideals
![]() $\mathfrak{a}_{\bullet }$
supported at
$\mathfrak{a}_{\bullet }$
supported at
![]() $p$
, the volume of
$p$
, the volume of
![]() $\mathfrak{a}_{\bullet }$
is defined as
$\mathfrak{a}_{\bullet }$
is defined as
 $$\begin{eqnarray}\operatorname{vol}(\mathfrak{a}_{\bullet }):=\limsup _{m\rightarrow \infty }\frac{\ell (R/\mathfrak{a}_{m})}{m^{n}/n!},\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{vol}(\mathfrak{a}_{\bullet }):=\limsup _{m\rightarrow \infty }\frac{\ell (R/\mathfrak{a}_{m})}{m^{n}/n!},\end{eqnarray}$$
while the multiplicity of
![]() $\mathfrak{a}_{\bullet }$
is defined as
$\mathfrak{a}_{\bullet }$
is defined as
 $$\begin{eqnarray}\operatorname{mult}(\mathfrak{a}_{\bullet }):=\lim _{m\rightarrow \infty }\frac{\operatorname{mult}(\mathfrak{a}_{m})}{m^{n}}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{mult}(\mathfrak{a}_{\bullet }):=\lim _{m\rightarrow \infty }\frac{\operatorname{mult}(\mathfrak{a}_{m})}{m^{n}}.\end{eqnarray}$$
By [Reference Lazarsfeld and MustaţăLM09, Reference CutkoskyCut13], we know that
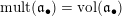 $\operatorname{mult}(\mathfrak{a}_{\bullet })=\operatorname{vol}(\mathfrak{a}_{\bullet })$
when
$\operatorname{mult}(\mathfrak{a}_{\bullet })=\operatorname{vol}(\mathfrak{a}_{\bullet })$
when
![]() $X$
is normal.
$X$
is normal.
Theorem 27. We have
 $$\begin{eqnarray}\inf _{\mathfrak{a}}(\operatorname{lct}(\mathfrak{a})^{n}\cdot \operatorname{mult}(\mathfrak{a}))=\inf _{\mathfrak{ a}_{\bullet }}(\operatorname{lct}(\mathfrak{a}_{\bullet })^{n}\cdot \operatorname{vol}(\mathfrak{a}_{\bullet }))=\inf _{v}\widehat{\operatorname{vol}}(v),\end{eqnarray}$$
$$\begin{eqnarray}\inf _{\mathfrak{a}}(\operatorname{lct}(\mathfrak{a})^{n}\cdot \operatorname{mult}(\mathfrak{a}))=\inf _{\mathfrak{ a}_{\bullet }}(\operatorname{lct}(\mathfrak{a}_{\bullet })^{n}\cdot \operatorname{vol}(\mathfrak{a}_{\bullet }))=\inf _{v}\widehat{\operatorname{vol}}(v),\end{eqnarray}$$
where the infimums are taken over all ideals
![]() $\mathfrak{a}$
supported at
$\mathfrak{a}$
supported at
![]() $p$
, all graded sequences of ideals
$p$
, all graded sequences of ideals
![]() $\mathfrak{a}_{\bullet }$
supported at
$\mathfrak{a}_{\bullet }$
supported at
![]() $p$
and all real valuations
$p$
and all real valuations
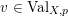 $v\in \text{Val}_{X,p}$
, respectively. We also set
$v\in \text{Val}_{X,p}$
, respectively. We also set
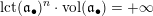 $\operatorname{lct}(\mathfrak{a}_{\bullet })^{n}\cdot \operatorname{vol}(\mathfrak{a}_{\bullet })=+\infty$
if
$\operatorname{lct}(\mathfrak{a}_{\bullet })^{n}\cdot \operatorname{vol}(\mathfrak{a}_{\bullet })=+\infty$
if
 $\operatorname{lct}(\mathfrak{a}_{\bullet })=+\infty$
.
$\operatorname{lct}(\mathfrak{a}_{\bullet })=+\infty$
.
Proof. Let
![]() $\mathfrak{a}_{\bullet }$
be a graded sequence of ideal sheaves supported at
$\mathfrak{a}_{\bullet }$
be a graded sequence of ideal sheaves supported at
![]() $p$
. By [Reference Jonsson and MustaţăJM12, Reference Boucksom, de Fernex, Favre and UrbinatiBdFFU15], we have
$p$
. By [Reference Jonsson and MustaţăJM12, Reference Boucksom, de Fernex, Favre and UrbinatiBdFFU15], we have
 $$\begin{eqnarray}\lim _{m\rightarrow \infty }m~\operatorname{lct}(\mathfrak{a}_{m})=\operatorname{lct}(\mathfrak{a}_{\bullet }).\end{eqnarray}$$
$$\begin{eqnarray}\lim _{m\rightarrow \infty }m~\operatorname{lct}(\mathfrak{a}_{m})=\operatorname{lct}(\mathfrak{a}_{\bullet }).\end{eqnarray}$$
Since
 $\operatorname{mult}(\mathfrak{a}_{\bullet })=\operatorname{vol}(\mathfrak{a}_{\bullet })$
, if
$\operatorname{mult}(\mathfrak{a}_{\bullet })=\operatorname{vol}(\mathfrak{a}_{\bullet })$
, if
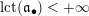 $\operatorname{lct}(\mathfrak{a}_{\bullet })<+\infty$
then
$\operatorname{lct}(\mathfrak{a}_{\bullet })<+\infty$
then
 $$\begin{eqnarray}\lim _{m\rightarrow \infty }\operatorname{lct}(\mathfrak{a}_{m})^{n}\cdot \operatorname{mult}(\mathfrak{a}_{m})=\operatorname{lct}(\mathfrak{a}_{\bullet })^{n}\cdot \operatorname{vol}(\mathfrak{a}_{\bullet }).\end{eqnarray}$$
$$\begin{eqnarray}\lim _{m\rightarrow \infty }\operatorname{lct}(\mathfrak{a}_{m})^{n}\cdot \operatorname{mult}(\mathfrak{a}_{m})=\operatorname{lct}(\mathfrak{a}_{\bullet })^{n}\cdot \operatorname{vol}(\mathfrak{a}_{\bullet }).\end{eqnarray}$$
Thus we have
 $$\begin{eqnarray}\inf _{\mathfrak{a}}(\operatorname{lct}(\mathfrak{a})^{n}\cdot \operatorname{mult}(\mathfrak{a}))\leqslant \inf _{\mathfrak{ a}_{\bullet }}(\operatorname{lct}(\mathfrak{a}_{\bullet })^{n}\cdot \operatorname{vol}(\mathfrak{a}_{\bullet })).\end{eqnarray}$$
$$\begin{eqnarray}\inf _{\mathfrak{a}}(\operatorname{lct}(\mathfrak{a})^{n}\cdot \operatorname{mult}(\mathfrak{a}))\leqslant \inf _{\mathfrak{ a}_{\bullet }}(\operatorname{lct}(\mathfrak{a}_{\bullet })^{n}\cdot \operatorname{vol}(\mathfrak{a}_{\bullet })).\end{eqnarray}$$
Next, Lemma 26 implies that
 $$\begin{eqnarray}\inf _{\mathfrak{a}}(\operatorname{lct}(\mathfrak{a})^{n}\cdot \operatorname{mult}(\mathfrak{a}))\geqslant \inf _{v}\widehat{\operatorname{vol}}(v).\end{eqnarray}$$
$$\begin{eqnarray}\inf _{\mathfrak{a}}(\operatorname{lct}(\mathfrak{a})^{n}\cdot \operatorname{mult}(\mathfrak{a}))\geqslant \inf _{v}\widehat{\operatorname{vol}}(v).\end{eqnarray}$$
Finally, for any real valuation
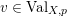 $v\in \text{Val}_{X,p}$
with
$v\in \text{Val}_{X,p}$
with
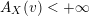 $A_{X}(v)<+\infty$
, by [Reference Boucksom, de Fernex, Favre and UrbinatiBdFFU15, Theorem 1.2] we have
$A_{X}(v)<+\infty$
, by [Reference Boucksom, de Fernex, Favre and UrbinatiBdFFU15, Theorem 1.2] we have
 $$\begin{eqnarray}\operatorname{lct}(\mathfrak{a}_{\bullet }(v))\leqslant \frac{A_{X}(v)}{v(\mathfrak{a}_{\bullet }(v))}=A_{X}(v)<+\infty .\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{lct}(\mathfrak{a}_{\bullet }(v))\leqslant \frac{A_{X}(v)}{v(\mathfrak{a}_{\bullet }(v))}=A_{X}(v)<+\infty .\end{eqnarray}$$
By definition we have
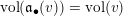 $\operatorname{vol}(\mathfrak{a}_{\bullet }(v))=\operatorname{vol}(v)$
. Therefore,
$\operatorname{vol}(\mathfrak{a}_{\bullet }(v))=\operatorname{vol}(v)$
. Therefore,
 $$\begin{eqnarray}\operatorname{lct}(\mathfrak{a}_{\bullet }(v))^{n}\cdot \operatorname{vol}(\mathfrak{a}_{\bullet }(v))\leqslant A_{X}(v)^{n}\cdot \operatorname{vol}(v)=\widehat{\operatorname{vol}}(v).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{lct}(\mathfrak{a}_{\bullet }(v))^{n}\cdot \operatorname{vol}(\mathfrak{a}_{\bullet }(v))\leqslant A_{X}(v)^{n}\cdot \operatorname{vol}(v)=\widehat{\operatorname{vol}}(v).\end{eqnarray}$$
Hence we have
 $$\begin{eqnarray}\inf _{\mathfrak{a}_{\bullet }}(\operatorname{lct}(\mathfrak{a}_{\bullet })^{n}\cdot \operatorname{vol}(\mathfrak{a}_{\bullet }))\leqslant \inf _{v}\widehat{\operatorname{vol}}(v).\end{eqnarray}$$
$$\begin{eqnarray}\inf _{\mathfrak{a}_{\bullet }}(\operatorname{lct}(\mathfrak{a}_{\bullet })^{n}\cdot \operatorname{vol}(\mathfrak{a}_{\bullet }))\leqslant \inf _{v}\widehat{\operatorname{vol}}(v).\end{eqnarray}$$
Combining (4.2), (4.3) and (4.5) together, we finish the proof. ◻
Remark 28. (a) The first equality in (4.1) was observed by Mustaţă in [Reference MustaţăMus02] where he showed that
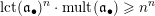 $\operatorname{lct}(\mathfrak{a}_{\bullet })^{n}\cdot \operatorname{mult}(\mathfrak{a}_{\bullet })\geqslant n^{n}$
for any graded sequence of
$\operatorname{lct}(\mathfrak{a}_{\bullet })^{n}\cdot \operatorname{mult}(\mathfrak{a}_{\bullet })\geqslant n^{n}$
for any graded sequence of
![]() $\mathfrak{m}$
-primary ideals
$\mathfrak{m}$
-primary ideals
![]() $\mathfrak{a}_{\bullet }$
of a regular local ring of dimension
$\mathfrak{a}_{\bullet }$
of a regular local ring of dimension
![]() $n$
. The inequality (4.4) was essentially realized by Li in [Reference LiLi15, Remark 2.8] where he considered the smooth case.
$n$
. The inequality (4.4) was essentially realized by Li in [Reference LiLi15, Remark 2.8] where he considered the smooth case.
(b) By Izumi’s theorem, the infimums in Theorem 27 are always positive (see § 2.4).
We will use Theorem 27 to prove Theorem 7 based on [Reference LiLi17, Reference Li and LiuLL16].
Theorem 29 (= Theorem 7).
Let
![]() $V$
be a Fano manifold of dimension
$V$
be a Fano manifold of dimension
![]() $n-1$
. Assume
$n-1$
. Assume
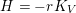 $H=-rK_{V}$
is an ample Cartier divisor for some
$H=-rK_{V}$
is an ample Cartier divisor for some
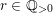 $r\in \mathbb{Q}_{{>}0}$
. Let
$r\in \mathbb{Q}_{{>}0}$
. Let
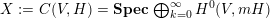 $X:=C(V,H)=\mathbf{Spec}\,\bigoplus _{k=0}^{\infty }H^{0}(V,mH)$
be the affine cone with cone vertex
$X:=C(V,H)=\mathbf{Spec}\,\bigoplus _{k=0}^{\infty }H^{0}(V,mH)$
be the affine cone with cone vertex
![]() $o$
. Then
$o$
. Then
![]() $V$
is K-semistable if and only if for any closed subscheme
$V$
is K-semistable if and only if for any closed subscheme
![]() $Z$
of
$Z$
of
![]() $X$
supported at
$X$
supported at
![]() $o$
, the following inequality holds:
$o$
, the following inequality holds:
 $$\begin{eqnarray}\operatorname{lct}(X;I_{Z})^{n}\cdot \operatorname{mult}_{Z}X\geqslant \frac{1}{r}((-K_{V})^{n-1}).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{lct}(X;I_{Z})^{n}\cdot \operatorname{mult}_{Z}X\geqslant \frac{1}{r}((-K_{V})^{n-1}).\end{eqnarray}$$
Proof. It is clear that
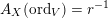 $A_{X}(\text{ord}_{V})=r^{-1}$
and
$A_{X}(\text{ord}_{V})=r^{-1}$
and
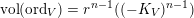 $\operatorname{vol}(\text{ord}_{V})=r^{n-1}((-K_{V})^{n-1})$
. Hence the right-hand side of (4.6) is equal to
$\operatorname{vol}(\text{ord}_{V})=r^{n-1}((-K_{V})^{n-1})$
. Hence the right-hand side of (4.6) is equal to
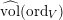 $\widehat{\operatorname{vol}}(\text{ord}_{V})$
. From Theorem 27 we know that (4.6) is equivalent to saying that the normalized volume
$\widehat{\operatorname{vol}}(\text{ord}_{V})$
. From Theorem 27 we know that (4.6) is equivalent to saying that the normalized volume
![]() $\widehat{\operatorname{vol}}$
is minimized at
$\widehat{\operatorname{vol}}$
is minimized at
![]() $\text{ord}_{V}$
over
$\text{ord}_{V}$
over
![]() $(X,o)$
. This is equivalent to
$(X,o)$
. This is equivalent to
![]() $V$
being K-semistable by [Reference Li and LiuLL16, Corollary 1.5].◻
$V$
being K-semistable by [Reference Li and LiuLL16, Corollary 1.5].◻
4.2 Finding minimizers
Assume that the infimum of
 $\operatorname{lct}^{n}(\mathfrak{a})\cdot \operatorname{mult}(\mathfrak{a})$
is attained by some ideal
$\operatorname{lct}^{n}(\mathfrak{a})\cdot \operatorname{mult}(\mathfrak{a})$
is attained by some ideal
![]() $\mathfrak{a}=\mathfrak{a}_{0}$
. Then Lemma 26 and Theorem 27 together imply that the divisorial valuation
$\mathfrak{a}=\mathfrak{a}_{0}$
. Then Lemma 26 and Theorem 27 together imply that the divisorial valuation
![]() $v_{0}$
that computes
$v_{0}$
that computes
![]() $\operatorname{lct}(\mathfrak{a}_{0})$
is a minimizer of
$\operatorname{lct}(\mathfrak{a}_{0})$
is a minimizer of
![]() $\widehat{\operatorname{vol}}$
. In this subsection, we will study the converse problem, i.e. assume there exists a minimizer
$\widehat{\operatorname{vol}}$
. In this subsection, we will study the converse problem, i.e. assume there exists a minimizer
![]() $v_{\ast }$
of
$v_{\ast }$
of
![]() $\widehat{\operatorname{vol}}$
that is divisorial, can the infimum of
$\widehat{\operatorname{vol}}$
that is divisorial, can the infimum of
 $\operatorname{lct}^{n}\cdot \operatorname{mult}$
for ideals be achieved? In Proposition 31, we give an affirmative answer to this problem assuming an extra condition on
$\operatorname{lct}^{n}\cdot \operatorname{mult}$
for ideals be achieved? In Proposition 31, we give an affirmative answer to this problem assuming an extra condition on
![]() $v_{\ast }$
.
$v_{\ast }$
.
Definition 30. Let
![]() $R$
be a Noetherian local domain. For a real valuation
$R$
be a Noetherian local domain. For a real valuation
![]() $v$
of
$v$
of
![]() $K(R)$
dominating
$K(R)$
dominating
![]() $R$
, we define the associate graded algebra of
$R$
, we define the associate graded algebra of
![]() $v$
as
$v$
as
 $$\begin{eqnarray}\text{gr}_{v}R:=\bigoplus _{m\in \unicode[STIX]{x1D6F7}}\mathfrak{a}_{m}(v)/\mathfrak{a}_{{>}m}(v),\end{eqnarray}$$
$$\begin{eqnarray}\text{gr}_{v}R:=\bigoplus _{m\in \unicode[STIX]{x1D6F7}}\mathfrak{a}_{m}(v)/\mathfrak{a}_{{>}m}(v),\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6F7}$
is the valuation semigroup of
$\unicode[STIX]{x1D6F7}$
is the valuation semigroup of
![]() $v$
.
$v$
.
Proposition 31. Assume that
![]() $\widehat{\operatorname{vol}}(\cdot )$
is minimized at a divisorial valuation
$\widehat{\operatorname{vol}}(\cdot )$
is minimized at a divisorial valuation
![]() $v_{\ast }$
. If the graded algebra
$v_{\ast }$
. If the graded algebra
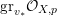 $\text{gr}_{v_{\ast }}{\mathcal{O}}_{X,p}$
is a finitely generated
$\text{gr}_{v_{\ast }}{\mathcal{O}}_{X,p}$
is a finitely generated
![]() $\mathbb{C}$
-algebra, then for any sufficiently divisible
$\mathbb{C}$
-algebra, then for any sufficiently divisible
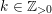 $k\in \mathbb{Z}_{{>}0}$
we have
$k\in \mathbb{Z}_{{>}0}$
we have
 $$\begin{eqnarray}\operatorname{lct}(\mathfrak{a}_{k}(v_{\ast }))^{n}\cdot \operatorname{mult}(\mathfrak{a}_{k}(v_{\ast }))=\widehat{\operatorname{vol}}(v_{\ast }).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{lct}(\mathfrak{a}_{k}(v_{\ast }))^{n}\cdot \operatorname{mult}(\mathfrak{a}_{k}(v_{\ast }))=\widehat{\operatorname{vol}}(v_{\ast }).\end{eqnarray}$$
In particular, the function
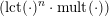 $(\operatorname{lct}(\cdot )^{n}\cdot \operatorname{mult}(\cdot ))$
attains its minimum at
$(\operatorname{lct}(\cdot )^{n}\cdot \operatorname{mult}(\cdot ))$
attains its minimum at
![]() $\mathfrak{a}_{k}(v_{\ast })$
.
$\mathfrak{a}_{k}(v_{\ast })$
.
Proof. By Izumi’s theorem we know that the filtration
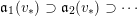 $\mathfrak{a}_{1}(v_{\ast })\supset \mathfrak{a}_{2}(v_{\ast })\supset \cdots \,$
defines the same topology on
$\mathfrak{a}_{1}(v_{\ast })\supset \mathfrak{a}_{2}(v_{\ast })\supset \cdots \,$
defines the same topology on
![]() ${\mathcal{O}}_{X,p}$
as the
${\mathcal{O}}_{X,p}$
as the
![]() $\mathfrak{m}_{p}$
-adic topology on
$\mathfrak{m}_{p}$
-adic topology on
![]() ${\mathcal{O}}_{X,p}$
. Then Lemma 32 implies
${\mathcal{O}}_{X,p}$
. Then Lemma 32 implies
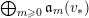 $\bigoplus _{m\geqslant 0}\mathfrak{a}_{m}(v_{\ast })$
is a finitely generated
$\bigoplus _{m\geqslant 0}\mathfrak{a}_{m}(v_{\ast })$
is a finitely generated
![]() ${\mathcal{O}}_{X,p}$
-algebra. Therefore, the degree
${\mathcal{O}}_{X,p}$
-algebra. Therefore, the degree
![]() $k$
Veronese subalgebra
$k$
Veronese subalgebra
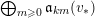 $\bigoplus _{m\geqslant 0}\mathfrak{a}_{km}(v_{\ast })$
is generated in degree
$\bigoplus _{m\geqslant 0}\mathfrak{a}_{km}(v_{\ast })$
is generated in degree
![]() $1$
for
$1$
for
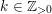 $k\in \mathbb{Z}_{{>}0}$
sufficiently divisible. This means
$k\in \mathbb{Z}_{{>}0}$
sufficiently divisible. This means
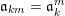 $\mathfrak{a}_{km}=\mathfrak{a}_{k}^{m}$
for any
$\mathfrak{a}_{km}=\mathfrak{a}_{k}^{m}$
for any
![]() $m\geqslant 0$
. From inequality (4.4) we have
$m\geqslant 0$
. From inequality (4.4) we have
 $$\begin{eqnarray}\displaystyle \widehat{\operatorname{vol}}(v_{\ast }) & {\geqslant} & \displaystyle \operatorname{lct}(\mathfrak{a}_{\bullet }(v_{\ast }))^{n}\cdot \operatorname{vol}(\mathfrak{a}_{\bullet }(v_{\ast }))\nonumber\\ \displaystyle & = & \displaystyle \operatorname{lct}(\mathfrak{a}_{k\bullet }(v_{\ast }))^{n}\cdot \operatorname{vol}(\mathfrak{a}_{k\bullet }(v_{\ast }))\nonumber\\ \displaystyle & = & \displaystyle \operatorname{lct}(\mathfrak{a}_{k}(v_{\ast }))^{n}\cdot \operatorname{mult}(\mathfrak{a}_{k}(v_{\ast })).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{\operatorname{vol}}(v_{\ast }) & {\geqslant} & \displaystyle \operatorname{lct}(\mathfrak{a}_{\bullet }(v_{\ast }))^{n}\cdot \operatorname{vol}(\mathfrak{a}_{\bullet }(v_{\ast }))\nonumber\\ \displaystyle & = & \displaystyle \operatorname{lct}(\mathfrak{a}_{k\bullet }(v_{\ast }))^{n}\cdot \operatorname{vol}(\mathfrak{a}_{k\bullet }(v_{\ast }))\nonumber\\ \displaystyle & = & \displaystyle \operatorname{lct}(\mathfrak{a}_{k}(v_{\ast }))^{n}\cdot \operatorname{mult}(\mathfrak{a}_{k}(v_{\ast })).\nonumber\end{eqnarray}$$
On the other hand, Theorem 27 also implies that
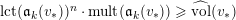 $\operatorname{lct}(\mathfrak{a}_{k}(v_{\ast }))^{n}\cdot \operatorname{mult}(\mathfrak{a}_{k}(v_{\ast }))\geqslant \widehat{\operatorname{vol}}(v_{\ast })$
because
$\operatorname{lct}(\mathfrak{a}_{k}(v_{\ast }))^{n}\cdot \operatorname{mult}(\mathfrak{a}_{k}(v_{\ast }))\geqslant \widehat{\operatorname{vol}}(v_{\ast })$
because
![]() $v_{\ast }$
is a minimizer of
$v_{\ast }$
is a minimizer of
![]() $\widehat{\operatorname{vol}}(\cdot )$
. So we prove the proposition.◻
$\widehat{\operatorname{vol}}(\cdot )$
. So we prove the proposition.◻
Lemma 32. Let
![]() $(R,\mathfrak{m})$
be a Noetherian local ring. Let
$(R,\mathfrak{m})$
be a Noetherian local ring. Let
![]() $\mathfrak{a}_{\bullet }$
be a graded sequence of
$\mathfrak{a}_{\bullet }$
be a graded sequence of
![]() $\mathfrak{m}$
-primary ideals. Assume that the linear topology on
$\mathfrak{m}$
-primary ideals. Assume that the linear topology on
![]() $R$
defined by the filtration
$R$
defined by the filtration
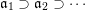 $\mathfrak{a}_{1}\supset \mathfrak{a}_{2}\supset \cdots \,$
is the same as the
$\mathfrak{a}_{1}\supset \mathfrak{a}_{2}\supset \cdots \,$
is the same as the
![]() $\mathfrak{m}$
-adic topology on
$\mathfrak{m}$
-adic topology on
![]() $R$
. Assume that
$R$
. Assume that
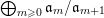 $\bigoplus _{m\geqslant 0}\mathfrak{a}_{m}/\mathfrak{a}_{m+1}$
is a finitely generated
$\bigoplus _{m\geqslant 0}\mathfrak{a}_{m}/\mathfrak{a}_{m+1}$
is a finitely generated
![]() $R/\mathfrak{a}_{1}$
-algebra. Then
$R/\mathfrak{a}_{1}$
-algebra. Then
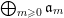 $\bigoplus _{m\geqslant 0}\mathfrak{a}_{m}$
is a finitely generated
$\bigoplus _{m\geqslant 0}\mathfrak{a}_{m}$
is a finitely generated
![]() $R$
-algebra.
$R$
-algebra.
Proof. We take a set of homogeneous generators of
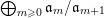 $\bigoplus _{m\geqslant 0}\mathfrak{a}_{m}/\mathfrak{a}_{m+1}$
, say
$\bigoplus _{m\geqslant 0}\mathfrak{a}_{m}/\mathfrak{a}_{m+1}$
, say
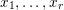 $x_{1},\ldots ,x_{r}$
. Let
$x_{1},\ldots ,x_{r}$
. Let
![]() $d_{i}$
be the degree of
$d_{i}$
be the degree of
![]() $x_{i}$
, i.e.
$x_{i}$
, i.e.
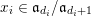 $x_{i}\in \mathfrak{a}_{d_{i}}/\mathfrak{a}_{d_{i}+1}$
. Take
$x_{i}\in \mathfrak{a}_{d_{i}}/\mathfrak{a}_{d_{i}+1}$
. Take
![]() $y_{i}\in \mathfrak{a}_{d_{i}}$
such that
$y_{i}\in \mathfrak{a}_{d_{i}}$
such that
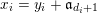 $x_{i}=y_{i}+\mathfrak{a}_{d_{i}+1}$
. Denote by
$x_{i}=y_{i}+\mathfrak{a}_{d_{i}+1}$
. Denote by
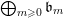 $\bigoplus _{m\geqslant 0}\mathfrak{b}_{m}$
the graded
$\bigoplus _{m\geqslant 0}\mathfrak{b}_{m}$
the graded
![]() $R$
-subalgebra of
$R$
-subalgebra of
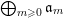 $\bigoplus _{m\geqslant 0}\mathfrak{a}_{m}$
generated by
$\bigoplus _{m\geqslant 0}\mathfrak{a}_{m}$
generated by
 $y_{1},\ldots ,y_{r}$
.
$y_{1},\ldots ,y_{r}$
.
Since
![]() $\{x_{i}\}$
generates
$\{x_{i}\}$
generates
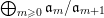 $\bigoplus _{m\geqslant 0}\mathfrak{a}_{m}/\mathfrak{a}_{m+1}$
, we have
$\bigoplus _{m\geqslant 0}\mathfrak{a}_{m}/\mathfrak{a}_{m+1}$
, we have
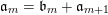 $\mathfrak{a}_{m}=\mathfrak{b}_{m}+\mathfrak{a}_{m+1}$
. Hence for any
$\mathfrak{a}_{m}=\mathfrak{b}_{m}+\mathfrak{a}_{m+1}$
. Hence for any
![]() $l>0$
the induction yields
$l>0$
the induction yields
 $$\begin{eqnarray}\mathfrak{a}_{m}=(\mathfrak{b}_{m}+\mathfrak{b}_{m+1}+\cdots +\mathfrak{b}_{m+l-1})+\mathfrak{a}_{m+l}.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{a}_{m}=(\mathfrak{b}_{m}+\mathfrak{b}_{m+1}+\cdots +\mathfrak{b}_{m+l-1})+\mathfrak{a}_{m+l}.\end{eqnarray}$$
Because
![]() $R$
is Noetherian, the ideals
$R$
is Noetherian, the ideals
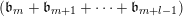 $(\mathfrak{b}_{m}+\mathfrak{b}_{m+1}+\cdots +\mathfrak{b}_{m+l-1})$
stabilize for
$(\mathfrak{b}_{m}+\mathfrak{b}_{m+1}+\cdots +\mathfrak{b}_{m+l-1})$
stabilize for
![]() $l$
sufficiently large. Denote the stabilized ideal by
$l$
sufficiently large. Denote the stabilized ideal by
![]() $\mathfrak{c}_{m}$
, then we have
$\mathfrak{c}_{m}$
, then we have
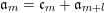 $\mathfrak{a}_{m}=\mathfrak{c}_{m}+\mathfrak{a}_{m+l}$
for
$\mathfrak{a}_{m}=\mathfrak{c}_{m}+\mathfrak{a}_{m+l}$
for
![]() $l$
sufficiently large. Since the filtration
$l$
sufficiently large. Since the filtration
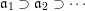 $\mathfrak{a}_{1}\supset \mathfrak{a}_{2}\supset \cdots \,$
defines the same topology as the
$\mathfrak{a}_{1}\supset \mathfrak{a}_{2}\supset \cdots \,$
defines the same topology as the
![]() $\mathfrak{m}$
-adic topology, we may take
$\mathfrak{m}$
-adic topology, we may take
![]() $l$
sufficiently large such that
$l$
sufficiently large such that
 $\mathfrak{a}_{m+l}\subset \mathfrak{m}\mathfrak{a}_{m}$
. As a result, we have
$\mathfrak{a}_{m+l}\subset \mathfrak{m}\mathfrak{a}_{m}$
. As a result, we have
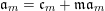 $\mathfrak{a}_{m}=\mathfrak{c}_{m}+\mathfrak{m}\mathfrak{a}_{m}$
which implies that
$\mathfrak{a}_{m}=\mathfrak{c}_{m}+\mathfrak{m}\mathfrak{a}_{m}$
which implies that
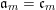 $\mathfrak{a}_{m}=\mathfrak{c}_{m}$
by Nakayama’s lemma.
$\mathfrak{a}_{m}=\mathfrak{c}_{m}$
by Nakayama’s lemma.
Now it suffices to show that
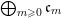 $\bigoplus _{m\geqslant 0}\mathfrak{c}_{m}$
is a finitely generated graded
$\bigoplus _{m\geqslant 0}\mathfrak{c}_{m}$
is a finitely generated graded
![]() $R$
-algebra. By definition,
$R$
-algebra. By definition,
![]() $\mathfrak{c}_{m}$
is generated by monomials in
$\mathfrak{c}_{m}$
is generated by monomials in
![]() $\{y_{i}\}$
of weighted degree at least
$\{y_{i}\}$
of weighted degree at least
![]() $m$
. For any
$m$
. For any
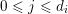 $0\leqslant j\leqslant d_{i}$
, denote by
$0\leqslant j\leqslant d_{i}$
, denote by
![]() $y_{i,j}$
the homogeneous element
$y_{i,j}$
the homogeneous element
![]() $y_{i}\in \mathfrak{a}_{j}$
of degree
$y_{i}\in \mathfrak{a}_{j}$
of degree
![]() $j$
. Then any monomial in
$j$
. Then any monomial in
![]() $\{y_{i}\}$
of weighted degree at least
$\{y_{i}\}$
of weighted degree at least
![]() $m$
is equal to a monomial in
$m$
is equal to a monomial in
![]() $\{y_{i,j}\}$
of weighted degree
$\{y_{i,j}\}$
of weighted degree
![]() $m$
. Hence
$m$
. Hence
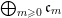 $\bigoplus _{m\geqslant 0}\mathfrak{c}_{m}$
is generated by
$\bigoplus _{m\geqslant 0}\mathfrak{c}_{m}$
is generated by
![]() $\{y_{i,j}\}$
as a graded
$\{y_{i,j}\}$
as a graded
![]() $R$
-algebra, which finishes the proof.◻
$R$
-algebra, which finishes the proof.◻
Postscript remark.
Since the first version of this article was posted on the arXiv, there has been a lot of progresses studying properties of the minimizer of
![]() $\widehat{\operatorname{vol}}$
. Here we mention two of them which are useful in our presentation.
$\widehat{\operatorname{vol}}$
. Here we mention two of them which are useful in our presentation.
– Blum [Reference BlumBlu18] proved that there always exists a minimizer of
 $\widehat{\operatorname{vol}}$
for any klt singularity
$\widehat{\operatorname{vol}}$
for any klt singularity
 $x\in X$
;
$x\in X$
;– If a divisorial valuation
 $v_{\ast }=\text{ord}_{S}$
minimizes
$v_{\ast }=\text{ord}_{S}$
minimizes
 $\widehat{\operatorname{vol}}$
in
$\widehat{\operatorname{vol}}$
in
 $\text{Val}_{X,x}$
, then
$\text{Val}_{X,x}$
, then
 $S$
is necessarily a Kollár component (see [Reference Li and XuLX16] for a definition). In particular,
$S$
is necessarily a Kollár component (see [Reference Li and XuLX16] for a definition). In particular,
 $\text{gr}_{v_{\ast }}{\mathcal{O}}_{X,x}$
is finitely generated. This was proved by Blum [Reference BlumBlu18] and Li and Xu [Reference Li and XuLX16] independently.
$\text{gr}_{v_{\ast }}{\mathcal{O}}_{X,x}$
is finitely generated. This was proved by Blum [Reference BlumBlu18] and Li and Xu [Reference Li and XuLX16] independently.
5 Maximal volume cases
5.1 K-polystable varieties of maximal volume
The following lemma is the main technical tool to prove the equality case of Theorem 3 and Corollary 6.
Lemma 33. Let
![]() $X$
be a K-polystable
$X$
be a K-polystable
![]() $\mathbb{Q}$
-Fano variety of dimension
$\mathbb{Q}$
-Fano variety of dimension
![]() $n$
. Let
$n$
. Let
![]() $p\in X$
be a closed point. Assume that there exists a divisorial valuation
$p\in X$
be a closed point. Assume that there exists a divisorial valuation
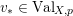 $v_{\ast }\in \text{Val}_{X,p}$
satisfying
$v_{\ast }\in \text{Val}_{X,p}$
satisfying
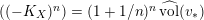 $((-K_{X})^{n})=(1+1/n)^{n}\,\widehat{\operatorname{vol}}(v_{\ast })$
. Then we have:
$((-K_{X})^{n})=(1+1/n)^{n}\,\widehat{\operatorname{vol}}(v_{\ast })$
. Then we have:
(i)
 $v_{\ast }$
is a minimizer of the normalized volume function
$v_{\ast }$
is a minimizer of the normalized volume function
 $\widehat{\operatorname{vol}}$
on
$\widehat{\operatorname{vol}}$
on
 $\text{Val}_{X,p}$
;
$\text{Val}_{X,p}$
;(ii)
 $X\cong \mathbf{Proj}~(\text{gr}_{v_{\ast }}{\mathcal{O}}_{X,p})[x]$
, where
$X\cong \mathbf{Proj}~(\text{gr}_{v_{\ast }}{\mathcal{O}}_{X,p})[x]$
, where
 $x$
is a homogeneous element of degree
$x$
is a homogeneous element of degree
 $1$
(we may view
$1$
(we may view
 $X$
as an orbifold projective cone over
$X$
as an orbifold projective cone over
 $F:=\mathbf{Proj}~\text{gr}_{v_{\ast }}{\mathcal{O}}_{X,p}$
).
$F:=\mathbf{Proj}~\text{gr}_{v_{\ast }}{\mathcal{O}}_{X,p}$
).
Proof. Part (i) is a direct consequence of Theorem 2.
We need some preparation to prove part (ii). Since
![]() $v_{\ast }$
is a divisorial minimizer of
$v_{\ast }$
is a divisorial minimizer of
![]() $\widehat{\operatorname{vol}}$
by (i), it is induced by a Kollár component by [Reference BlumBlu18, Proposition 4.9] and [Reference Li and XuLX16, Theorem 1.2]. In particular,
$\widehat{\operatorname{vol}}$
by (i), it is induced by a Kollár component by [Reference BlumBlu18, Proposition 4.9] and [Reference Li and XuLX16, Theorem 1.2]. In particular,
 $\text{gr}_{v_{\ast }}{\mathcal{O}}_{X,p}$
is a finitely generated
$\text{gr}_{v_{\ast }}{\mathcal{O}}_{X,p}$
is a finitely generated
![]() $\mathbb{C}$
-algebra. Let
$\mathbb{C}$
-algebra. Let
![]() $\bar{v}_{\ast }$
be the corresponding divisorial valuation on
$\bar{v}_{\ast }$
be the corresponding divisorial valuation on
![]() $X\times \mathbb{A}^{1}$
(see (3.2)). Let
$X\times \mathbb{A}^{1}$
(see (3.2)). Let
![]() $t$
be the parameter of
$t$
be the parameter of
![]() $\mathbb{A}^{1}$
. Let
$\mathbb{A}^{1}$
. Let
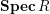 $\mathbf{Spec}\,R$
be an affine Zariski open subset of
$\mathbf{Spec}\,R$
be an affine Zariski open subset of
![]() $X$
. By Lemma 32,
$X$
. By Lemma 32,
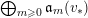 $\bigoplus _{m\geqslant 0}\mathfrak{a}_{m}(v_{\ast })$
is a finitely generated
$\bigoplus _{m\geqslant 0}\mathfrak{a}_{m}(v_{\ast })$
is a finitely generated
![]() $R$
-algebra. Then
$R$
-algebra. Then
 $$\begin{eqnarray}\mathfrak{a}_{m}(\bar{v}_{\ast })=\mathfrak{a}_{m}(v_{\ast })+\mathfrak{a}_{m-1}(v_{\ast })t+\cdots +\mathfrak{a}_{1}(v_{\ast })t^{m-1}+(t^{m}).\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{a}_{m}(\bar{v}_{\ast })=\mathfrak{a}_{m}(v_{\ast })+\mathfrak{a}_{m-1}(v_{\ast })t+\cdots +\mathfrak{a}_{1}(v_{\ast })t^{m-1}+(t^{m}).\end{eqnarray}$$
In order to keep track of the degree of the graded ring
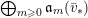 $\bigoplus _{m\geqslant 0}\mathfrak{a}_{m}(\bar{v}_{\ast })$
, denote by
$\bigoplus _{m\geqslant 0}\mathfrak{a}_{m}(\bar{v}_{\ast })$
, denote by
![]() $s$
the element
$s$
the element
![]() $t$
in
$t$
in
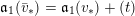 $\mathfrak{a}_{1}(\bar{v}_{\ast })=\mathfrak{a}_{1}(v_{\ast })+(t)$
. Hence
$\mathfrak{a}_{1}(\bar{v}_{\ast })=\mathfrak{a}_{1}(v_{\ast })+(t)$
. Hence
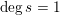 $\deg s=1$
,
$\deg s=1$
,
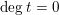 $\deg t=0$
and we have
$\deg t=0$
and we have
 $$\begin{eqnarray}\mathfrak{a}_{m}(\bar{v}_{\ast })=\mathfrak{a}_{m}(v_{\ast })+\mathfrak{a}_{m-1}(v_{\ast })s+\cdots +\mathfrak{a}_{1}(v_{\ast })s^{m-1}+s^{m}R[t],\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{a}_{m}(\bar{v}_{\ast })=\mathfrak{a}_{m}(v_{\ast })+\mathfrak{a}_{m-1}(v_{\ast })s+\cdots +\mathfrak{a}_{1}(v_{\ast })s^{m-1}+s^{m}R[t],\end{eqnarray}$$
where
 $\deg \mathfrak{a}_{i}(v_{\ast })=i$
. As an
$\deg \mathfrak{a}_{i}(v_{\ast })=i$
. As an
![]() $R[t]$
-algebra,
$R[t]$
-algebra,
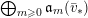 $\bigoplus _{m\geqslant 0}\mathfrak{a}_{m}(\bar{v}_{\ast })$
is generated by
$\bigoplus _{m\geqslant 0}\mathfrak{a}_{m}(\bar{v}_{\ast })$
is generated by
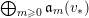 $\bigoplus _{m\geqslant 0}\mathfrak{a}_{m}(v_{\ast })$
and
$\bigoplus _{m\geqslant 0}\mathfrak{a}_{m}(v_{\ast })$
and
![]() $s$
. Since
$s$
. Since
 $\bigoplus _{m\geqslant 0}\mathfrak{a}_{m}(v_{\ast })$
is a finitely generated
$\bigoplus _{m\geqslant 0}\mathfrak{a}_{m}(v_{\ast })$
is a finitely generated
![]() $R$
-algebra, we have that
$R$
-algebra, we have that
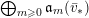 $\bigoplus _{m\geqslant 0}\mathfrak{a}_{m}(\bar{v}_{\ast })$
is of finite type over
$\bigoplus _{m\geqslant 0}\mathfrak{a}_{m}(\bar{v}_{\ast })$
is of finite type over
![]() ${\mathcal{O}}_{X\times \mathbb{A}^{1}}$
.
${\mathcal{O}}_{X\times \mathbb{A}^{1}}$
.
Let
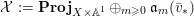 ${\mathcal{X}}:={\mathbf{Proj}_{X\times \mathbb{A}^{1}}\oplus }_{m\geqslant 0}\mathfrak{a}_{m}(\bar{v}_{\ast })$
, hence
${\mathcal{X}}:={\mathbf{Proj}_{X\times \mathbb{A}^{1}}\oplus }_{m\geqslant 0}\mathfrak{a}_{m}(\bar{v}_{\ast })$
, hence
![]() ${\mathcal{X}}$
is normal by Lemma 34. Denote by
${\mathcal{X}}$
is normal by Lemma 34. Denote by
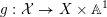 $g:{\mathcal{X}}\rightarrow X\times \mathbb{A}^{1}$
the projection. Denote the composite map by
$g:{\mathcal{X}}\rightarrow X\times \mathbb{A}^{1}$
the projection. Denote the composite map by
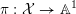 $\unicode[STIX]{x1D70B}:{\mathcal{X}}\rightarrow \mathbb{A}^{1}$
. The
$\unicode[STIX]{x1D70B}:{\mathcal{X}}\rightarrow \mathbb{A}^{1}$
. The
![]() $\mathbb{Q}$
-line bundle
$\mathbb{Q}$
-line bundle
![]() ${\mathcal{L}}$
on
${\mathcal{L}}$
on
![]() ${\mathcal{X}}$
is defined as
${\mathcal{X}}$
is defined as
 $$\begin{eqnarray}{\mathcal{L}}:=g^{\ast }(-K_{X\times \mathbb{A}^{1}/\mathbb{A}^{1}})+\biggl(1+\frac{1}{n}\biggr)A_{X}(v_{\ast }){\mathcal{O}}_{{\mathcal{X}}}(1),\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{L}}:=g^{\ast }(-K_{X\times \mathbb{A}^{1}/\mathbb{A}^{1}})+\biggl(1+\frac{1}{n}\biggr)A_{X}(v_{\ast }){\mathcal{O}}_{{\mathcal{X}}}(1),\end{eqnarray}$$
where we treat
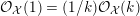 ${\mathcal{O}}_{{\mathcal{X}}}(1)=(1/k){\mathcal{O}}_{{\mathcal{X}}}(k)$
as a
${\mathcal{O}}_{{\mathcal{X}}}(1)=(1/k){\mathcal{O}}_{{\mathcal{X}}}(k)$
as a
![]() $\mathbb{Q}$
-line bundle for sufficiently divisible
$\mathbb{Q}$
-line bundle for sufficiently divisible
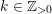 $k\in \mathbb{Z}_{{>}0}$
. Let
$k\in \mathbb{Z}_{{>}0}$
. Let
 $\hat{X}:=g_{\ast }^{-1}(X\times \{0\})$
and
$\hat{X}:=g_{\ast }^{-1}(X\times \{0\})$
and
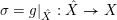 $\unicode[STIX]{x1D70E}=g|_{\hat{X}}:\hat{X}\rightarrow X$
. Let
$\unicode[STIX]{x1D70E}=g|_{\hat{X}}:\hat{X}\rightarrow X$
. Let
![]() $E$
be the exceptional divisor of
$E$
be the exceptional divisor of
![]() $g$
given by
$g$
given by
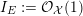 $I_{E}:={\mathcal{O}}_{{\mathcal{X}}}(1)$
. Hence
$I_{E}:={\mathcal{O}}_{{\mathcal{X}}}(1)$
. Hence
 $$\begin{eqnarray}E\cong \mathbf{Proj}~\bigoplus _{m\geqslant 0}\mathfrak{a}_{m}(\bar{v}_{\ast })/\mathfrak{a}_{m+1}(\bar{v}_{\ast })=\mathbf{Proj}(\text{gr}_{v_{\ast }}{\mathcal{O}}_{X,p})[s],\end{eqnarray}$$
$$\begin{eqnarray}E\cong \mathbf{Proj}~\bigoplus _{m\geqslant 0}\mathfrak{a}_{m}(\bar{v}_{\ast })/\mathfrak{a}_{m+1}(\bar{v}_{\ast })=\mathbf{Proj}(\text{gr}_{v_{\ast }}{\mathcal{O}}_{X,p})[s],\end{eqnarray}$$
where
![]() $s$
is a homogeneous element of degree
$s$
is a homogeneous element of degree
![]() $1$
. Since
$1$
. Since
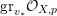 $\text{gr}_{v_{\ast }}{\mathcal{O}}_{X,p}$
is an integral domain,
$\text{gr}_{v_{\ast }}{\mathcal{O}}_{X,p}$
is an integral domain,
![]() $E$
is irreducible and reduced.
$E$
is irreducible and reduced.
We will show the following statements:
(a)
 ${\mathcal{L}}$
is
${\mathcal{L}}$
is
 $\unicode[STIX]{x1D70B}$
-nef with
$\unicode[STIX]{x1D70B}$
-nef with
 ${\mathcal{L}}^{\bot }=\hat{X}$
;
${\mathcal{L}}^{\bot }=\hat{X}$
;(b)
 ${\mathcal{L}}$
is
${\mathcal{L}}$
is
 $\unicode[STIX]{x1D70B}$
-semiample, hence
$\unicode[STIX]{x1D70B}$
-semiample, hence
 $({\mathcal{X}},{\mathcal{L}})$
is a semi
$({\mathcal{X}},{\mathcal{L}})$
is a semi
 $\mathbb{Q}$
-test configuration of
$\mathbb{Q}$
-test configuration of
 $(X,-K_{X})$
;
$(X,-K_{X})$
;(c)
 $\text{CM}({\mathcal{X}},{\mathcal{L}})=0$
.
$\text{CM}({\mathcal{X}},{\mathcal{L}})=0$
.
For (a), we see that
 ${\mathcal{L}}_{t}\cong -K_{{\mathcal{X}}_{t}}$
is ample whenever
${\mathcal{L}}_{t}\cong -K_{{\mathcal{X}}_{t}}$
is ample whenever
![]() $t\neq 0$
. From the definition we know that
$t\neq 0$
. From the definition we know that
![]() ${\mathcal{L}}$
is
${\mathcal{L}}$
is
![]() $g$
-ample, hence
$g$
-ample, hence
![]() ${\mathcal{L}}|_{E}$
is ample. On
${\mathcal{L}}|_{E}$
is ample. On
![]() $\hat{X}$
, we have that
$\hat{X}$
, we have that
 $$\begin{eqnarray}{\mathcal{L}}|_{\hat{X}}\cong \unicode[STIX]{x1D70E}^{\ast }(-K_{X})+\biggl(1+\frac{1}{n}\biggr)A_{X}(v_{\ast }){\mathcal{O}}_{\hat{X}}(1).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{L}}|_{\hat{X}}\cong \unicode[STIX]{x1D70E}^{\ast }(-K_{X})+\biggl(1+\frac{1}{n}\biggr)A_{X}(v_{\ast }){\mathcal{O}}_{\hat{X}}(1).\end{eqnarray}$$
For
 $k\in \mathbb{Z}_{{>}0}$
sufficiently divisible, let
$k\in \mathbb{Z}_{{>}0}$
sufficiently divisible, let
![]() $Z$
be the thickening of
$Z$
be the thickening of
![]() $p$
in
$p$
in
![]() $X$
such that
$X$
such that
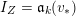 $I_{Z}=\mathfrak{a}_{k}(v_{\ast })$
. From (i) we know that
$I_{Z}=\mathfrak{a}_{k}(v_{\ast })$
. From (i) we know that
![]() $v_{\ast }$
minimizes
$v_{\ast }$
minimizes
![]() $\widehat{\operatorname{vol}}$
, hence
$\widehat{\operatorname{vol}}$
, hence
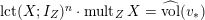 $\operatorname{lct}(X;I_{Z})^{n}\cdot \operatorname{mult}_{Z}X=\widehat{\operatorname{vol}}(v_{\ast })$
by Proposition 31. Since
$\operatorname{lct}(X;I_{Z})^{n}\cdot \operatorname{mult}_{Z}X=\widehat{\operatorname{vol}}(v_{\ast })$
by Proposition 31. Since
 $$\begin{eqnarray}((-K_{X})^{n})=\biggl(1+\frac{1}{n}\biggr)^{n}\,\widehat{\operatorname{vol}}(v_{\ast })=\biggl(1+\frac{1}{n}\biggr)^{n}\operatorname{lct}(X;I_{Z})^{n}\cdot \operatorname{mult}_{Z}X,\end{eqnarray}$$
$$\begin{eqnarray}((-K_{X})^{n})=\biggl(1+\frac{1}{n}\biggr)^{n}\,\widehat{\operatorname{vol}}(v_{\ast })=\biggl(1+\frac{1}{n}\biggr)^{n}\operatorname{lct}(X;I_{Z})^{n}\cdot \operatorname{mult}_{Z}X,\end{eqnarray}$$
by Lemma 10 and Remark 17 we have that
![]() ${\mathcal{L}}|_{\hat{X}}$
is nef with zero top self intersection number. In addition,
${\mathcal{L}}|_{\hat{X}}$
is nef with zero top self intersection number. In addition,
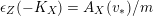 $\unicode[STIX]{x1D716}_{Z}(-K_{X})=A_{X}(v_{\ast })/m$
. As a result,
$\unicode[STIX]{x1D716}_{Z}(-K_{X})=A_{X}(v_{\ast })/m$
. As a result,
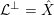 ${\mathcal{L}}^{\bot }=\hat{X}$
.
${\mathcal{L}}^{\bot }=\hat{X}$
.
For (b), we first show that
![]() ${\mathcal{X}}$
is normal
${\mathcal{X}}$
is normal
![]() $\mathbb{Q}$
-Gorenstein with klt singularities. By Lemma 34 we have that
$\mathbb{Q}$
-Gorenstein with klt singularities. By Lemma 34 we have that
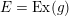 $E=\text{Ex}(g)$
is a
$E=\text{Ex}(g)$
is a
![]() $\mathbb{Q}$
-Cartier prime divisor on
$\mathbb{Q}$
-Cartier prime divisor on
![]() ${\mathcal{X}}$
. Hence
${\mathcal{X}}$
. Hence
 $$\begin{eqnarray}K_{{\mathcal{X}}}=g^{\ast }K_{X\times \mathbb{A}^{1}}+(A_{{\mathcal{X}}}(\text{ord}_{E})-1)E\end{eqnarray}$$
$$\begin{eqnarray}K_{{\mathcal{X}}}=g^{\ast }K_{X\times \mathbb{A}^{1}}+(A_{{\mathcal{X}}}(\text{ord}_{E})-1)E\end{eqnarray}$$
is
![]() $\mathbb{Q}$
-Cartier. To show that
$\mathbb{Q}$
-Cartier. To show that
![]() ${\mathcal{X}}$
has klt singularities, it suffices to show that
${\mathcal{X}}$
has klt singularities, it suffices to show that
![]() $({\mathcal{X}},\hat{X})$
is plt. By Lemma 34, we have
$({\mathcal{X}},\hat{X})$
is plt. By Lemma 34, we have
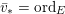 $\bar{v}_{\ast }=\text{ord}_{E}$
. Hence
$\bar{v}_{\ast }=\text{ord}_{E}$
. Hence
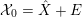 ${\mathcal{X}}_{0}=\hat{X}+E$
as Weil divisors since
${\mathcal{X}}_{0}=\hat{X}+E$
as Weil divisors since
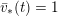 $\bar{v}_{\ast }(t)=1$
. In particular,
$\bar{v}_{\ast }(t)=1$
. In particular,
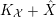 $K_{{\mathcal{X}}}+\hat{X}$
is
$K_{{\mathcal{X}}}+\hat{X}$
is
![]() $\mathbb{Q}$
-Cartier.
$\mathbb{Q}$
-Cartier.
It is clear that
 $$\begin{eqnarray}I_{E}/(I_{E}\cdot I_{\hat{X}})=I_{E}|_{\hat{X}}={\mathcal{O}}_{{\mathcal{X}}}(1)|_{\hat{X}}={\mathcal{O}}_{\hat{X}}(1)\subset {\mathcal{O}}_{\hat{X}}.\end{eqnarray}$$
$$\begin{eqnarray}I_{E}/(I_{E}\cdot I_{\hat{X}})=I_{E}|_{\hat{X}}={\mathcal{O}}_{{\mathcal{X}}}(1)|_{\hat{X}}={\mathcal{O}}_{\hat{X}}(1)\subset {\mathcal{O}}_{\hat{X}}.\end{eqnarray}$$
Since the kernel of
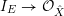 $I_{E}\rightarrow {\mathcal{O}}_{\hat{X}}$
is
$I_{E}\rightarrow {\mathcal{O}}_{\hat{X}}$
is
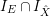 $I_{E}\cap I_{\hat{X}}$
, we have that
$I_{E}\cap I_{\hat{X}}$
, we have that
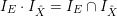 $I_{E}\cdot I_{\hat{X}}=I_{E}\cap I_{\hat{X}}$
. On the other hand, by computing graded ideals we know that
$I_{E}\cdot I_{\hat{X}}=I_{E}\cap I_{\hat{X}}$
. On the other hand, by computing graded ideals we know that
 $I_{E}+I_{\hat{X}}=I_{F}$
. Denote by
$I_{E}+I_{\hat{X}}=I_{F}$
. Denote by
![]() $\unicode[STIX]{x1D702}$
the generic point of
$\unicode[STIX]{x1D702}$
the generic point of
![]() $F$
, then
$F$
, then
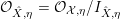 ${\mathcal{O}}_{\hat{X},\unicode[STIX]{x1D702}}={\mathcal{O}}_{{\mathcal{X}},\unicode[STIX]{x1D702}}/I_{\hat{X},\unicode[STIX]{x1D702}}$
is a DVR since
${\mathcal{O}}_{\hat{X},\unicode[STIX]{x1D702}}={\mathcal{O}}_{{\mathcal{X}},\unicode[STIX]{x1D702}}/I_{\hat{X},\unicode[STIX]{x1D702}}$
is a DVR since
![]() $\hat{X}$
is normal. Applying Lemma 35 to
$\hat{X}$
is normal. Applying Lemma 35 to
 $(R,\mathfrak{p},\mathfrak{q})=({\mathcal{O}}_{{\mathcal{X}},\unicode[STIX]{x1D702}},I_{E,\unicode[STIX]{x1D702}},I_{\hat{X},\unicode[STIX]{x1D702}})$
yields that
$(R,\mathfrak{p},\mathfrak{q})=({\mathcal{O}}_{{\mathcal{X}},\unicode[STIX]{x1D702}},I_{E,\unicode[STIX]{x1D702}},I_{\hat{X},\unicode[STIX]{x1D702}})$
yields that
![]() $E$
is Cartier at
$E$
is Cartier at
![]() $\unicode[STIX]{x1D702}$
. Since
$\unicode[STIX]{x1D702}$
. Since
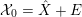 ${\mathcal{X}}_{0}=\hat{X}+E$
is Cartier and
${\mathcal{X}}_{0}=\hat{X}+E$
is Cartier and
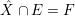 $\hat{X}\cap E=F$
, we have that
$\hat{X}\cap E=F$
, we have that
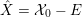 $\hat{X}={\mathcal{X}}_{0}-E$
is Cartier in codimension
$\hat{X}={\mathcal{X}}_{0}-E$
is Cartier in codimension
![]() $2$
. Next we notice that
$2$
. Next we notice that
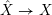 $\hat{X}\rightarrow X$
produces a Kollár component, hence
$\hat{X}\rightarrow X$
produces a Kollár component, hence
![]() $\hat{X}$
has klt singularities. Thus
$\hat{X}$
has klt singularities. Thus
![]() $({\mathcal{X}},\hat{X})$
is plt by inverse of adjunction [Reference Kollár and MoriKM98, Theorem 5.50].
$({\mathcal{X}},\hat{X})$
is plt by inverse of adjunction [Reference Kollár and MoriKM98, Theorem 5.50].
By Shokurov’s base-point-free theorem, to show
![]() ${\mathcal{L}}$
is
${\mathcal{L}}$
is
![]() $\unicode[STIX]{x1D70B}$
-semiample we only need to show that
$\unicode[STIX]{x1D70B}$
-semiample we only need to show that
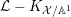 ${\mathcal{L}}-K_{{\mathcal{X}}/\mathbb{A}^{1}}$
is
${\mathcal{L}}-K_{{\mathcal{X}}/\mathbb{A}^{1}}$
is
![]() $\unicode[STIX]{x1D70B}$
-ample. It follows from Lemma 34 that
$\unicode[STIX]{x1D70B}$
-ample. It follows from Lemma 34 that
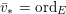 $\bar{v}_{\ast }=\text{ord}_{E}$
and
$\bar{v}_{\ast }=\text{ord}_{E}$
and
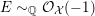 $E{\sim}_{\mathbb{Q}}{\mathcal{O}}_{{\mathcal{X}}}(-1)$
. Hence we have
$E{\sim}_{\mathbb{Q}}{\mathcal{O}}_{{\mathcal{X}}}(-1)$
. Hence we have
 $$\begin{eqnarray}\displaystyle -K_{{\mathcal{X}}/\mathbb{A}^{1}} & = & \displaystyle g^{\ast }(-K_{X\times \mathbb{A}^{1}/\mathbb{A}^{1}})-(A_{X\times \mathbb{A}^{1}}(\bar{v}_{\ast })-1)E\nonumber\\ \displaystyle & = & \displaystyle g^{\ast }(-K_{X\times \mathbb{A}^{1}/\mathbb{A}^{1}})+A_{X}(v_{\ast }){\mathcal{O}}_{{\mathcal{X}}}(1).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle -K_{{\mathcal{X}}/\mathbb{A}^{1}} & = & \displaystyle g^{\ast }(-K_{X\times \mathbb{A}^{1}/\mathbb{A}^{1}})-(A_{X\times \mathbb{A}^{1}}(\bar{v}_{\ast })-1)E\nonumber\\ \displaystyle & = & \displaystyle g^{\ast }(-K_{X\times \mathbb{A}^{1}/\mathbb{A}^{1}})+A_{X}(v_{\ast }){\mathcal{O}}_{{\mathcal{X}}}(1).\nonumber\end{eqnarray}$$
Since
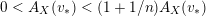 $0<A_{X}(v_{\ast })<(1+1/n)A_{X}(v_{\ast })$
, we see that
$0<A_{X}(v_{\ast })<(1+1/n)A_{X}(v_{\ast })$
, we see that
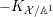 $-K_{{\mathcal{X}}/\mathbb{A}^{1}}$
is
$-K_{{\mathcal{X}}/\mathbb{A}^{1}}$
is
![]() $\unicode[STIX]{x1D70B}$
-ample. Hence
$\unicode[STIX]{x1D70B}$
-ample. Hence
 ${\mathcal{L}}-K_{{\mathcal{X}}/\mathbb{A}^{1}}$
is
${\mathcal{L}}-K_{{\mathcal{X}}/\mathbb{A}^{1}}$
is
![]() $\unicode[STIX]{x1D70B}$
-ample.
$\unicode[STIX]{x1D70B}$
-ample.
For (c), we know that
 $$\begin{eqnarray}\text{CM}({\mathcal{X}},{\mathcal{L}})=\frac{1}{(n+1)((-K_{X})^{n})}(n(\bar{{\mathcal{L}}}^{n+1})+(n+1)(\bar{{\mathcal{L}}}^{n}\cdot K_{\bar{{\mathcal{X}}}/\mathbb{P}^{1}})).\end{eqnarray}$$
$$\begin{eqnarray}\text{CM}({\mathcal{X}},{\mathcal{L}})=\frac{1}{(n+1)((-K_{X})^{n})}(n(\bar{{\mathcal{L}}}^{n+1})+(n+1)(\bar{{\mathcal{L}}}^{n}\cdot K_{\bar{{\mathcal{X}}}/\mathbb{P}^{1}})).\end{eqnarray}$$
By definition of
![]() ${\mathcal{L}}$
we know that
${\mathcal{L}}$
we know that
 $$\begin{eqnarray}\displaystyle & \displaystyle \bar{{\mathcal{L}}}=\bar{g}^{\ast }(-K_{X\times \mathbb{P}^{1}/\mathbb{P}^{1}})+\biggl(1+\frac{1}{n}\biggr)A_{X}(v_{\ast }){\mathcal{O}}_{\bar{{\mathcal{X}}}}(1), & \displaystyle \nonumber\\ \displaystyle & \displaystyle K_{\bar{{\mathcal{X}}}/\mathbb{P}^{1}}=\bar{g}^{\ast }K_{X\times \mathbb{P}^{1}/\mathbb{P}^{1}}-A_{X}(v_{\ast }){\mathcal{O}}_{\bar{{\mathcal{X}}}}(1). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \bar{{\mathcal{L}}}=\bar{g}^{\ast }(-K_{X\times \mathbb{P}^{1}/\mathbb{P}^{1}})+\biggl(1+\frac{1}{n}\biggr)A_{X}(v_{\ast }){\mathcal{O}}_{\bar{{\mathcal{X}}}}(1), & \displaystyle \nonumber\\ \displaystyle & \displaystyle K_{\bar{{\mathcal{X}}}/\mathbb{P}^{1}}=\bar{g}^{\ast }K_{X\times \mathbb{P}^{1}/\mathbb{P}^{1}}-A_{X}(v_{\ast }){\mathcal{O}}_{\bar{{\mathcal{X}}}}(1). & \displaystyle \nonumber\end{eqnarray}$$
Since
![]() ${\mathcal{O}}_{\bar{{\mathcal{X}}}}(1)$
is supported in
${\mathcal{O}}_{\bar{{\mathcal{X}}}}(1)$
is supported in
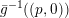 $\bar{g}^{-1}((p,0))$
, we have
$\bar{g}^{-1}((p,0))$
, we have
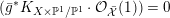 $(\bar{g}^{\ast }K_{X\times \mathbb{P}^{1}/\mathbb{P}^{1}}\cdot {\mathcal{O}}_{\bar{{\mathcal{X}}}}(1))=0$
as a cycle. Next, it is clear that
$(\bar{g}^{\ast }K_{X\times \mathbb{P}^{1}/\mathbb{P}^{1}}\cdot {\mathcal{O}}_{\bar{{\mathcal{X}}}}(1))=0$
as a cycle. Next, it is clear that
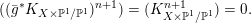 $((\bar{g}^{\ast }K_{X\times \mathbb{P}^{1}/\mathbb{P}^{1}})^{n+1})=(K_{X\times \mathbb{P}^{1}/\mathbb{P}^{1}}^{n+1})=0.$
Hence we have
$((\bar{g}^{\ast }K_{X\times \mathbb{P}^{1}/\mathbb{P}^{1}})^{n+1})=(K_{X\times \mathbb{P}^{1}/\mathbb{P}^{1}}^{n+1})=0.$
Hence we have
 $$\begin{eqnarray}\displaystyle & \displaystyle (\bar{{\mathcal{L}}}^{n+1})=\biggl(1+\frac{1}{n}\biggr)^{n+1}A_{X}(v_{\ast })^{n+1}({\mathcal{O}}_{\bar{{\mathcal{X}}}}(1)^{n+1}), & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\bar{{\mathcal{L}}}^{n}\cdot K_{\bar{{\mathcal{X}}}/\mathbb{P}^{1}})=-\biggl(1+\frac{1}{n}\biggr)^{n}A_{X}(v_{\ast })^{n+1}({\mathcal{O}}_{\bar{{\mathcal{X}}}}(1)^{n+1}). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle (\bar{{\mathcal{L}}}^{n+1})=\biggl(1+\frac{1}{n}\biggr)^{n+1}A_{X}(v_{\ast })^{n+1}({\mathcal{O}}_{\bar{{\mathcal{X}}}}(1)^{n+1}), & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\bar{{\mathcal{L}}}^{n}\cdot K_{\bar{{\mathcal{X}}}/\mathbb{P}^{1}})=-\biggl(1+\frac{1}{n}\biggr)^{n}A_{X}(v_{\ast })^{n+1}({\mathcal{O}}_{\bar{{\mathcal{X}}}}(1)^{n+1}). & \displaystyle \nonumber\end{eqnarray}$$
Thus
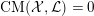 $\text{CM}({\mathcal{X}},{\mathcal{L}})=0$
.
$\text{CM}({\mathcal{X}},{\mathcal{L}})=0$
.
Now we are ready to prove part (ii). By (b) we know that
![]() ${\mathcal{L}}$
is semiample. Denote the ample model of
${\mathcal{L}}$
is semiample. Denote the ample model of
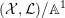 $({\mathcal{X}},{\mathcal{L}})/\mathbb{A}^{1}$
by
$({\mathcal{X}},{\mathcal{L}})/\mathbb{A}^{1}$
by
![]() $({\mathcal{Y}},{\mathcal{M}})$
, with
$({\mathcal{Y}},{\mathcal{M}})$
, with
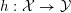 $h:{\mathcal{X}}\rightarrow {\mathcal{Y}}$
and
$h:{\mathcal{X}}\rightarrow {\mathcal{Y}}$
and
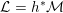 ${\mathcal{L}}=h^{\ast }{\mathcal{M}}$
. Then
${\mathcal{L}}=h^{\ast }{\mathcal{M}}$
. Then
![]() $({\mathcal{Y}},{\mathcal{M}})$
is a normal
$({\mathcal{Y}},{\mathcal{M}})$
is a normal
![]() $\mathbb{Q}$
-test configuration of
$\mathbb{Q}$
-test configuration of
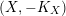 $(X,-K_{X})$
. Since
$(X,-K_{X})$
. Since
 $\bar{h}_{\ast }K_{\bar{{\mathcal{X}}}/\mathbb{P}^{1}}=K_{\bar{{\mathcal{Y}}}/\mathbb{P}^{1}}$
, we have
$\bar{h}_{\ast }K_{\bar{{\mathcal{X}}}/\mathbb{P}^{1}}=K_{\bar{{\mathcal{Y}}}/\mathbb{P}^{1}}$
, we have
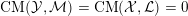 $\text{CM}({\mathcal{Y}},{\mathcal{M}})=\text{CM}({\mathcal{X}},{\mathcal{L}})=0$
. From (a) we know that
$\text{CM}({\mathcal{Y}},{\mathcal{M}})=\text{CM}({\mathcal{X}},{\mathcal{L}})=0$
. From (a) we know that
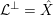 ${\mathcal{L}}^{\bot }=\hat{X}$
, so
${\mathcal{L}}^{\bot }=\hat{X}$
, so
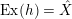 $\text{Ex}(h)=\hat{X}$
. Hence
$\text{Ex}(h)=\hat{X}$
. Hence
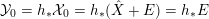 ${\mathcal{Y}}_{0}=h_{\ast }{\mathcal{X}}_{0}=h_{\ast }(\hat{X}+E)=h_{\ast }E$
. In particular,
${\mathcal{Y}}_{0}=h_{\ast }{\mathcal{X}}_{0}=h_{\ast }(\hat{X}+E)=h_{\ast }E$
. In particular,
![]() ${\mathcal{Y}}_{0}$
is a prime divisor on
${\mathcal{Y}}_{0}$
is a prime divisor on
![]() ${\mathcal{Y}}$
. It is clear that
${\mathcal{Y}}$
. It is clear that
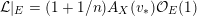 ${\mathcal{L}}|_{E}=(1+1/n)A_{X}(v_{\ast }){\mathcal{O}}_{E}(1)$
is ample, hence
${\mathcal{L}}|_{E}=(1+1/n)A_{X}(v_{\ast }){\mathcal{O}}_{E}(1)$
is ample, hence
 $h|_{E}:E\rightarrow {\mathcal{Y}}_{0}$
is a finite birational morphism. Since
$h|_{E}:E\rightarrow {\mathcal{Y}}_{0}$
is a finite birational morphism. Since
![]() $X$
is K-polystable by assumption, hence
$X$
is K-polystable by assumption, hence
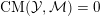 $\text{CM}({\mathcal{Y}},{\mathcal{M}})=0$
yields that
$\text{CM}({\mathcal{Y}},{\mathcal{M}})=0$
yields that
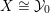 $X\cong {\mathcal{Y}}_{0}$
. Then
$X\cong {\mathcal{Y}}_{0}$
. Then
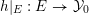 $h|_{E}:E\rightarrow {\mathcal{Y}}_{0}$
has to be an isomorphism because
$h|_{E}:E\rightarrow {\mathcal{Y}}_{0}$
has to be an isomorphism because
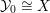 ${\mathcal{Y}}_{0}\cong X$
is normal. Hence
${\mathcal{Y}}_{0}\cong X$
is normal. Hence
 $X\cong E\cong \mathbf{Proj}~(\text{gr}_{v_{\ast }}{\mathcal{O}}_{X,p})[s]$
.◻
$X\cong E\cong \mathbf{Proj}~(\text{gr}_{v_{\ast }}{\mathcal{O}}_{X,p})[s]$
.◻
Lemma 34. Let
![]() $(X,p)$
be a normal singularity. Let
$(X,p)$
be a normal singularity. Let
![]() $v_{\ast }$
be a divisorial valuation on
$v_{\ast }$
be a divisorial valuation on
![]() $X$
centered at
$X$
centered at
![]() $p$
. Assume that
$p$
. Assume that
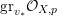 $\text{gr}_{v_{\ast }}{\mathcal{O}}_{X,p}$
is a finitely generated
$\text{gr}_{v_{\ast }}{\mathcal{O}}_{X,p}$
is a finitely generated
![]() $\mathbb{C}$
-algebra. Let
$\mathbb{C}$
-algebra. Let
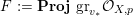 $F:=\mathbf{Proj}~\text{gr}_{v_{\ast }}{\mathcal{O}}_{X,p}$
. Define
$F:=\mathbf{Proj}~\text{gr}_{v_{\ast }}{\mathcal{O}}_{X,p}$
. Define
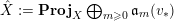 $\hat{X}:={\mathbf{Proj}_{X}\bigoplus }_{m\geqslant 0}\mathfrak{a}_{m}(v_{\ast })$
with the projection
$\hat{X}:={\mathbf{Proj}_{X}\bigoplus }_{m\geqslant 0}\mathfrak{a}_{m}(v_{\ast })$
with the projection
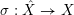 $\unicode[STIX]{x1D70E}:\hat{X}\rightarrow X$
. Then
$\unicode[STIX]{x1D70E}:\hat{X}\rightarrow X$
. Then
![]() $\hat{X}$
is normal,
$\hat{X}$
is normal,
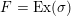 $F=\text{Ex}(\unicode[STIX]{x1D70E})$
is a
$F=\text{Ex}(\unicode[STIX]{x1D70E})$
is a
![]() $\mathbb{Q}$
-Cartier prime divisor on
$\mathbb{Q}$
-Cartier prime divisor on
![]() $\hat{X}$
, and
$\hat{X}$
, and
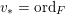 $v_{\ast }=\text{ord}_{F}$
. (Note that
$v_{\ast }=\text{ord}_{F}$
. (Note that
![]() $\unicode[STIX]{x1D70E}$
is called a prime blow-up in [Reference IshiiIsh04].)
$\unicode[STIX]{x1D70E}$
is called a prime blow-up in [Reference IshiiIsh04].)
Proof. By Lemma 32, we know that
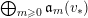 $\bigoplus _{m\geqslant 0}\mathfrak{a}_{m}(v_{\ast })$
is a finitely generated
$\bigoplus _{m\geqslant 0}\mathfrak{a}_{m}(v_{\ast })$
is a finitely generated
![]() ${\mathcal{O}}_{X}$
-algebra. Since the valuation ideals
${\mathcal{O}}_{X}$
-algebra. Since the valuation ideals
![]() $\mathfrak{a}_{m}(v_{\ast })$
are always integrally closed,
$\mathfrak{a}_{m}(v_{\ast })$
are always integrally closed,
![]() $\hat{X}$
is normal. By definition of
$\hat{X}$
is normal. By definition of
![]() $F$
we know that the ideal sheaf
$F$
we know that the ideal sheaf
![]() $I_{F}$
is the same as the coherent sheaf
$I_{F}$
is the same as the coherent sheaf
![]() ${\mathcal{O}}_{\hat{X}}(1)$
. Let
${\mathcal{O}}_{\hat{X}}(1)$
. Let
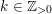 $k\in \mathbb{Z}_{{>}0}$
be sufficiently divisible so that
$k\in \mathbb{Z}_{{>}0}$
be sufficiently divisible so that
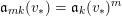 $\mathfrak{a}_{mk}(v_{\ast })=\mathfrak{a}_{k}(v_{\ast })^{m}$
for any positive integer
$\mathfrak{a}_{mk}(v_{\ast })=\mathfrak{a}_{k}(v_{\ast })^{m}$
for any positive integer
![]() $m$
. Thus
$m$
. Thus
![]() $\hat{X}$
is naturally isomorphic to the blow up of
$\hat{X}$
is naturally isomorphic to the blow up of
![]() $X$
along the ideal sheaf
$X$
along the ideal sheaf
![]() $\mathfrak{a}_{k}(v_{\ast })$
. In particular,
$\mathfrak{a}_{k}(v_{\ast })$
. In particular,
 ${\mathcal{O}}_{\hat{X}}(k)=\unicode[STIX]{x1D70E}^{-1}\mathfrak{a}_{k}(v_{\ast })\cdot {\mathcal{O}}_{\hat{X}}$
is an invertible ideal sheaf. Next,
${\mathcal{O}}_{\hat{X}}(k)=\unicode[STIX]{x1D70E}^{-1}\mathfrak{a}_{k}(v_{\ast })\cdot {\mathcal{O}}_{\hat{X}}$
is an invertible ideal sheaf. Next,
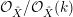 ${\mathcal{O}}_{\hat{X}}/{\mathcal{O}}_{\hat{X}}(k)$
is supported at the exceptional locus of
${\mathcal{O}}_{\hat{X}}/{\mathcal{O}}_{\hat{X}}(k)$
is supported at the exceptional locus of
![]() $\unicode[STIX]{x1D70E}$
. As ideal sheaves on
$\unicode[STIX]{x1D70E}$
. As ideal sheaves on
![]() $\hat{X}$
, we know that
$\hat{X}$
, we know that
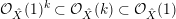 ${\mathcal{O}}_{\hat{X}}(1)^{k}\subset {\mathcal{O}}_{\hat{X}}(k)\subset {\mathcal{O}}_{\hat{X}}(1)$
. Hence
${\mathcal{O}}_{\hat{X}}(1)^{k}\subset {\mathcal{O}}_{\hat{X}}(k)\subset {\mathcal{O}}_{\hat{X}}(1)$
. Hence
![]() ${\mathcal{O}}_{\hat{X}}(1)$
and
${\mathcal{O}}_{\hat{X}}(1)$
and
![]() ${\mathcal{O}}_{\hat{X}}(k)$
have the same nilradical as ideal sheaves, and
${\mathcal{O}}_{\hat{X}}(k)$
have the same nilradical as ideal sheaves, and
 $$\begin{eqnarray}F_{\text{red}}=\text{Supp}({\mathcal{O}}_{\hat{X}}/{\mathcal{O}}_{\hat{X}}(1))=\text{Supp}({\mathcal{O}}_{\hat{X}}/{\mathcal{O}}_{\hat{X}}(k))\end{eqnarray}$$
$$\begin{eqnarray}F_{\text{red}}=\text{Supp}({\mathcal{O}}_{\hat{X}}/{\mathcal{O}}_{\hat{X}}(1))=\text{Supp}({\mathcal{O}}_{\hat{X}}/{\mathcal{O}}_{\hat{X}}(k))\end{eqnarray}$$
which is the reduced exceptional locus of
![]() $\unicode[STIX]{x1D70E}$
. On the other hand, it is easy to see that
$\unicode[STIX]{x1D70E}$
. On the other hand, it is easy to see that
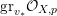 $\text{gr}_{v_{\ast }}{\mathcal{O}}_{X,p}$
is an integral domain, so
$\text{gr}_{v_{\ast }}{\mathcal{O}}_{X,p}$
is an integral domain, so
![]() $F$
is an integral scheme.
$F$
is an integral scheme.
For
![]() $k$
sufficiently divisible, we have that
$k$
sufficiently divisible, we have that
![]() ${\mathcal{O}}_{\hat{X}}(k)$
is invertible and
${\mathcal{O}}_{\hat{X}}(k)$
is invertible and
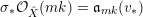 $\unicode[STIX]{x1D70E}_{\ast }{\mathcal{O}}_{\hat{X}}(mk)=\mathfrak{a}_{mk}(v_{\ast })$
for any
$\unicode[STIX]{x1D70E}_{\ast }{\mathcal{O}}_{\hat{X}}(mk)=\mathfrak{a}_{mk}(v_{\ast })$
for any
 $m\in \mathbb{Z}_{{\geqslant}0}$
. Thus
$m\in \mathbb{Z}_{{\geqslant}0}$
. Thus
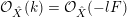 ${\mathcal{O}}_{\hat{X}}(k)={\mathcal{O}}_{\hat{X}}(-lF)$
for some positive integer
${\mathcal{O}}_{\hat{X}}(k)={\mathcal{O}}_{\hat{X}}(-lF)$
for some positive integer
![]() $l$
(so
$l$
(so
![]() $F$
is
$F$
is
![]() $\mathbb{Q}$
-Cartier). Then for any
$\mathbb{Q}$
-Cartier). Then for any
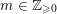 $m\in \mathbb{Z}_{{\geqslant}0}$
we have the following equivalences:
$m\in \mathbb{Z}_{{\geqslant}0}$
we have the following equivalences:
 $$\begin{eqnarray}\displaystyle v_{\ast }(f)\geqslant m & \Leftrightarrow & \displaystyle v_{\ast }(f^{k})\geqslant mk\Leftrightarrow f^{k}\in \mathfrak{a}_{mk}(v_{\ast })\Leftrightarrow \unicode[STIX]{x1D70E}^{\ast }f^{k}\in {\mathcal{O}}_{\hat{X}}(mk)\nonumber\\ \displaystyle & \Leftrightarrow & \displaystyle \text{ord}_{F}(\unicode[STIX]{x1D70E}^{\ast }f^{k})\geqslant ml\Leftrightarrow \text{ord}_{F}(f)\geqslant \frac{ml}{k}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle v_{\ast }(f)\geqslant m & \Leftrightarrow & \displaystyle v_{\ast }(f^{k})\geqslant mk\Leftrightarrow f^{k}\in \mathfrak{a}_{mk}(v_{\ast })\Leftrightarrow \unicode[STIX]{x1D70E}^{\ast }f^{k}\in {\mathcal{O}}_{\hat{X}}(mk)\nonumber\\ \displaystyle & \Leftrightarrow & \displaystyle \text{ord}_{F}(\unicode[STIX]{x1D70E}^{\ast }f^{k})\geqslant ml\Leftrightarrow \text{ord}_{F}(f)\geqslant \frac{ml}{k}.\nonumber\end{eqnarray}$$
Assume
 $v_{\ast }(f)=m$
. If
$v_{\ast }(f)=m$
. If
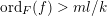 $\text{ord}_{F}(f)>ml/k$
, then we have
$\text{ord}_{F}(f)>ml/k$
, then we have
 $\text{ord}_{F}(f)\geqslant (ml+1)/k$
. Hence
$\text{ord}_{F}(f)\geqslant (ml+1)/k$
. Hence
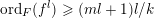 $\text{ord}_{F}(f^{l})\geqslant (ml+1)l/k$
which implies that
$\text{ord}_{F}(f^{l})\geqslant (ml+1)l/k$
which implies that
 $v_{\ast }(f^{l})\geqslant ml+1$
, a contradiction! Hence we have
$v_{\ast }(f^{l})\geqslant ml+1$
, a contradiction! Hence we have
 $\text{ord}_{F}=(l/k)v_{\ast }$
. Therefore,
$\text{ord}_{F}=(l/k)v_{\ast }$
. Therefore,
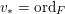 $v_{\ast }=\text{ord}_{F}$
since both
$v_{\ast }=\text{ord}_{F}$
since both
![]() $v_{\ast }$
and
$v_{\ast }$
and
![]() $\text{ord}_{F}$
are divisorial.◻
$\text{ord}_{F}$
are divisorial.◻
Lemma 35. Let
![]() $(R,\mathfrak{m})$
be a Noetherian local ring. Let
$(R,\mathfrak{m})$
be a Noetherian local ring. Let
![]() $\mathfrak{p},\mathfrak{q}$
be two prime ideals in
$\mathfrak{p},\mathfrak{q}$
be two prime ideals in
![]() $R$
satisfying that
$R$
satisfying that
 $\mathfrak{p}+\mathfrak{q}=\mathfrak{m}$
,
$\mathfrak{p}+\mathfrak{q}=\mathfrak{m}$
,
 $\mathfrak{p}\cap \mathfrak{q}=\mathfrak{p}\mathfrak{q}$
and
$\mathfrak{p}\cap \mathfrak{q}=\mathfrak{p}\mathfrak{q}$
and
![]() $R/\mathfrak{q}$
is a DVR. Then
$R/\mathfrak{q}$
is a DVR. Then
![]() $\mathfrak{p}$
is principal.
$\mathfrak{p}$
is principal.
Proof. Let
![]() $x+\mathfrak{q}$
be a uniformizer of
$x+\mathfrak{q}$
be a uniformizer of
![]() $R/\mathfrak{q}$
. Since
$R/\mathfrak{q}$
. Since
 $\mathfrak{m}=\mathfrak{p}+\mathfrak{q}$
, we may choose
$\mathfrak{m}=\mathfrak{p}+\mathfrak{q}$
, we may choose
![]() $x$
so that
$x$
so that
![]() $x\in \mathfrak{p}$
. Hence we have
$x\in \mathfrak{p}$
. Hence we have
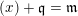 $(x)+\mathfrak{q}=\mathfrak{m}$
. As a result,
$(x)+\mathfrak{q}=\mathfrak{m}$
. As a result,
 $$\begin{eqnarray}\mathfrak{p}=(x)+\mathfrak{p}\cap \mathfrak{q}=(x)+\mathfrak{p}\mathfrak{q}.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{p}=(x)+\mathfrak{p}\cap \mathfrak{q}=(x)+\mathfrak{p}\mathfrak{q}.\end{eqnarray}$$
So
![]() $\mathfrak{p}=(x)$
by Nakayama lemma.◻
$\mathfrak{p}=(x)$
by Nakayama lemma.◻
5.2 Applications
The following theorem improves Fujita’s result on the equality case in [Reference FujitaFuj15, Theorem 5.1].
Theorem 36. Let
![]() $X$
be a Ding-semistable
$X$
be a Ding-semistable
![]() $\mathbb{Q}$
-Fano variety of dimension
$\mathbb{Q}$
-Fano variety of dimension
![]() $n$
. If
$n$
. If
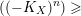 $((-K_{X})^{n})\geqslant$
$((-K_{X})^{n})\geqslant$
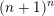 $(n+1)^{n}$
, then
$(n+1)^{n}$
, then
 $X\cong \mathbb{P}^{n}$
.
$X\cong \mathbb{P}^{n}$
.
Proof 1.
Notice that
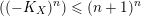 $((-K_{X})^{n})\leqslant (n+1)^{n}$
by [Reference FujitaFuj15, Corollary 1.3]. Thus we have
$((-K_{X})^{n})\leqslant (n+1)^{n}$
by [Reference FujitaFuj15, Corollary 1.3]. Thus we have
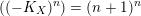 $((-K_{X})^{n})=(n+1)^{n}$
. Let
$((-K_{X})^{n})=(n+1)^{n}$
. Let
![]() $p\in X$
be a smooth point. From [Reference FujitaFuj15, Proof of Theorem 5.1] or Remark 17, we see that
$p\in X$
be a smooth point. From [Reference FujitaFuj15, Proof of Theorem 5.1] or Remark 17, we see that
 $\unicode[STIX]{x1D716}_{p}(-K_{X})=n+1$
. Then the theorem is a consequence of the forthcoming paper [Reference Liu and ZhuangLZ16] (joint with Ziquan Zhuang), where we show that if an
$\unicode[STIX]{x1D716}_{p}(-K_{X})=n+1$
. Then the theorem is a consequence of the forthcoming paper [Reference Liu and ZhuangLZ16] (joint with Ziquan Zhuang), where we show that if an
![]() $n$
-dimensional
$n$
-dimensional
![]() $\mathbb{Q}$
-Fano variety
$\mathbb{Q}$
-Fano variety
![]() $X$
satisfies
$X$
satisfies
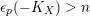 $\unicode[STIX]{x1D716}_{p}(-K_{X})>n$
for some smooth point
$\unicode[STIX]{x1D716}_{p}(-K_{X})>n$
for some smooth point
![]() $p\in X$
, then
$p\in X$
, then
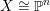 $X\cong \mathbb{P}^{n}$
.◻
$X\cong \mathbb{P}^{n}$
.◻
Proof 2.
We follow the strategy and notation of the proof of Lemma 33. Let
 $v_{\ast }:=\text{ord}_{p}$
for a smooth point
$v_{\ast }:=\text{ord}_{p}$
for a smooth point
![]() $p\in X$
. As argued in the first proof, the assumptions of Lemma 33 are fulfilled except that
$p\in X$
. As argued in the first proof, the assumptions of Lemma 33 are fulfilled except that
![]() $X$
is only Ding-semistable rather than K-polystable. Nevertheless, we still have a semi
$X$
is only Ding-semistable rather than K-polystable. Nevertheless, we still have a semi
![]() $\mathbb{Q}$
-test configuration
$\mathbb{Q}$
-test configuration
![]() $({\mathcal{X}},{\mathcal{L}})$
of
$({\mathcal{X}},{\mathcal{L}})$
of
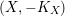 $(X,-K_{X})$
such that
$(X,-K_{X})$
such that
 ${\mathcal{L}}^{\bot }=\hat{X}$
and
${\mathcal{L}}^{\bot }=\hat{X}$
and
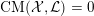 $\text{CM}({\mathcal{X}},{\mathcal{L}})=0$
. Let
$\text{CM}({\mathcal{X}},{\mathcal{L}})=0$
. Let
![]() $({\mathcal{Y}},{\mathcal{M}})$
be the ample model of
$({\mathcal{Y}},{\mathcal{M}})$
be the ample model of
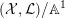 $({\mathcal{X}},{\mathcal{L}})/\mathbb{A}^{1}$
, with
$({\mathcal{X}},{\mathcal{L}})/\mathbb{A}^{1}$
, with
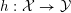 $h:{\mathcal{X}}\rightarrow {\mathcal{Y}}$
and
$h:{\mathcal{X}}\rightarrow {\mathcal{Y}}$
and
 ${\mathcal{L}}=h^{\ast }{\mathcal{M}}$
. We will show that
${\mathcal{L}}=h^{\ast }{\mathcal{M}}$
. We will show that
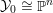 ${\mathcal{Y}}_{0}\cong \mathbb{P}^{n}$
.
${\mathcal{Y}}_{0}\cong \mathbb{P}^{n}$
.
Following the proof of Lemma 33, we know that
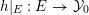 $h|_{E}:E\rightarrow {\mathcal{Y}}_{0}$
is a finite birational morphism. Since
$h|_{E}:E\rightarrow {\mathcal{Y}}_{0}$
is a finite birational morphism. Since
 $v_{\ast }=\text{ord}_{p}$
and
$v_{\ast }=\text{ord}_{p}$
and
![]() $p\in X$
is a smooth point, we have that
$p\in X$
is a smooth point, we have that
![]() $E\cong \mathbb{P}^{n}$
. Therefore,
$E\cong \mathbb{P}^{n}$
. Therefore,
![]() $E$
is the normalization of
$E$
is the normalization of
![]() ${\mathcal{Y}}_{0}$
. Consider the short exact sequence
${\mathcal{Y}}_{0}$
. Consider the short exact sequence
 $$\begin{eqnarray}0\rightarrow {\mathcal{O}}_{{\mathcal{X}}}(-E)\rightarrow {\mathcal{O}}_{{\mathcal{X}}}\rightarrow {\mathcal{O}}_{E}\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow {\mathcal{O}}_{{\mathcal{X}}}(-E)\rightarrow {\mathcal{O}}_{{\mathcal{X}}}\rightarrow {\mathcal{O}}_{E}\rightarrow 0.\end{eqnarray}$$
By taking
![]() $h_{\ast }$
, we get a long exact sequence
$h_{\ast }$
, we get a long exact sequence
 $$\begin{eqnarray}0\rightarrow h_{\ast }{\mathcal{O}}_{{\mathcal{X}}}(-E)\rightarrow {\mathcal{O}}_{{\mathcal{Y}}}\rightarrow h_{\ast }{\mathcal{O}}_{E}\rightarrow R^{1}h_{\ast }{\mathcal{O}}_{{\mathcal{X}}}(-E)\rightarrow \cdots \,.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow h_{\ast }{\mathcal{O}}_{{\mathcal{X}}}(-E)\rightarrow {\mathcal{O}}_{{\mathcal{Y}}}\rightarrow h_{\ast }{\mathcal{O}}_{E}\rightarrow R^{1}h_{\ast }{\mathcal{O}}_{{\mathcal{X}}}(-E)\rightarrow \cdots \,.\end{eqnarray}$$
Since
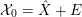 ${\mathcal{X}}_{0}=\hat{X}+E$
, we have that
${\mathcal{X}}_{0}=\hat{X}+E$
, we have that
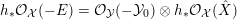 $h_{\ast }{\mathcal{O}}_{{\mathcal{X}}}(-E)={\mathcal{O}}_{{\mathcal{Y}}}(-{\mathcal{Y}}_{0})\otimes h_{\ast }{\mathcal{O}}_{{\mathcal{X}}}(\hat{X})$
. Notice that
$h_{\ast }{\mathcal{O}}_{{\mathcal{X}}}(-E)={\mathcal{O}}_{{\mathcal{Y}}}(-{\mathcal{Y}}_{0})\otimes h_{\ast }{\mathcal{O}}_{{\mathcal{X}}}(\hat{X})$
. Notice that
![]() $\hat{X}$
is
$\hat{X}$
is
![]() $h$
-exceptional, hence
$h$
-exceptional, hence
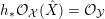 $h_{\ast }{\mathcal{O}}_{{\mathcal{X}}}(\hat{X})={\mathcal{O}}_{{\mathcal{Y}}}$
. As a result,
$h_{\ast }{\mathcal{O}}_{{\mathcal{X}}}(\hat{X})={\mathcal{O}}_{{\mathcal{Y}}}$
. As a result,
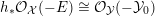 $h_{\ast }{\mathcal{O}}_{{\mathcal{X}}}(-E)\cong {\mathcal{O}}_{{\mathcal{Y}}}(-{\mathcal{Y}}_{0})$
. On the other hand, we have
$h_{\ast }{\mathcal{O}}_{{\mathcal{X}}}(-E)\cong {\mathcal{O}}_{{\mathcal{Y}}}(-{\mathcal{Y}}_{0})$
. On the other hand, we have
 $$\begin{eqnarray}h^{\ast }{\mathcal{M}}={\mathcal{L}}=g^{\ast }(-K_{X\times \mathbb{A}^{1}/\mathbb{A}^{1}})-(n+1)E=-K_{{\mathcal{X}}/\mathbb{A}^{1}}-E.\end{eqnarray}$$
$$\begin{eqnarray}h^{\ast }{\mathcal{M}}={\mathcal{L}}=g^{\ast }(-K_{X\times \mathbb{A}^{1}/\mathbb{A}^{1}})-(n+1)E=-K_{{\mathcal{X}}/\mathbb{A}^{1}}-E.\end{eqnarray}$$
So
 $-E=K_{{\mathcal{X}}/\mathbb{A}^{1}}+h^{\ast }{\mathcal{M}}{\sim}_{\mathbb{Q},h}K_{{\mathcal{X}}}$
. Since
$-E=K_{{\mathcal{X}}/\mathbb{A}^{1}}+h^{\ast }{\mathcal{M}}{\sim}_{\mathbb{Q},h}K_{{\mathcal{X}}}$
. Since
![]() ${\mathcal{X}}$
has klt singularities, we have that
${\mathcal{X}}$
has klt singularities, we have that
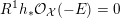 $R^{1}h_{\ast }{\mathcal{O}}_{{\mathcal{X}}}(-E)=0$
by the generalized Kodaira vanishing theorem [Reference KollárKol95, Theorem 10.19.4]. Thus the exact sequence (5.1) yields that
$R^{1}h_{\ast }{\mathcal{O}}_{{\mathcal{X}}}(-E)=0$
by the generalized Kodaira vanishing theorem [Reference KollárKol95, Theorem 10.19.4]. Thus the exact sequence (5.1) yields that
 $h_{\ast }{\mathcal{O}}_{E}={\mathcal{O}}_{{\mathcal{Y}}_{0}}$
, which implies
$h_{\ast }{\mathcal{O}}_{E}={\mathcal{O}}_{{\mathcal{Y}}_{0}}$
, which implies
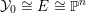 ${\mathcal{Y}}_{0}\cong E\cong \mathbb{P}^{n}$
.
${\mathcal{Y}}_{0}\cong E\cong \mathbb{P}^{n}$
.
Since
![]() $\mathbb{P}^{n}$
is rigid under smooth deformation (cf. [Reference KollárKol96, Exercise V.1.11.12.2]), we conclude that
$\mathbb{P}^{n}$
is rigid under smooth deformation (cf. [Reference KollárKol96, Exercise V.1.11.12.2]), we conclude that
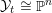 ${\mathcal{Y}}_{t}\cong \mathbb{P}^{n}$
for general
${\mathcal{Y}}_{t}\cong \mathbb{P}^{n}$
for general
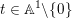 $t\in \mathbb{A}^{1}\setminus \{0\}$
, hence
$t\in \mathbb{A}^{1}\setminus \{0\}$
, hence
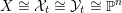 $X\cong {\mathcal{X}}_{t}\cong {\mathcal{Y}}_{t}\cong \mathbb{P}^{n}$
.◻
$X\cong {\mathcal{X}}_{t}\cong {\mathcal{Y}}_{t}\cong \mathbb{P}^{n}$
.◻
In the following theorem, we show the equality case of Theorem 3.
Theorem 37. Let
![]() $X$
be a Kähler–Einstein
$X$
be a Kähler–Einstein
![]() $\mathbb{Q}$
-Fano variety. Let
$\mathbb{Q}$
-Fano variety. Let
![]() $p\in X$
be a closed point. Suppose
$p\in X$
be a closed point. Suppose
![]() $(X,p)$
is a quotient singularity with local analytic model
$(X,p)$
is a quotient singularity with local analytic model
![]() $\mathbb{C}^{n}/G$
, where
$\mathbb{C}^{n}/G$
, where
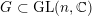 $G\subset \text{GL}(n,\mathbb{C})$
acts freely in codimension
$G\subset \text{GL}(n,\mathbb{C})$
acts freely in codimension
![]() $1$
. Then
$1$
. Then
 $((-K_{X})^{n})=(n+1)^{n}/|G|$
if and only if
$((-K_{X})^{n})=(n+1)^{n}/|G|$
if and only if
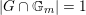 $|G\cap \mathbb{G}_{m}|=1$
and
$|G\cap \mathbb{G}_{m}|=1$
and
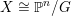 $X\cong \mathbb{P}^{n}/G$
.
$X\cong \mathbb{P}^{n}/G$
.
Proof. For the ‘if’ part, we may assume that
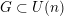 $G\subset U(n)$
. Hence
$G\subset U(n)$
. Hence
![]() $G$
preserves the Fubini–Study metric
$G$
preserves the Fubini–Study metric
![]() $\unicode[STIX]{x1D714}_{FS}$
on
$\unicode[STIX]{x1D714}_{FS}$
on
![]() $\mathbb{P}^{n}$
. Since
$\mathbb{P}^{n}$
. Since
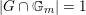 $|G\cap \mathbb{G}_{m}|=1$
, the
$|G\cap \mathbb{G}_{m}|=1$
, the
![]() $G$
-action on
$G$
-action on
![]() $\mathbb{P}^{n}$
is free in codimension
$\mathbb{P}^{n}$
is free in codimension
![]() $1$
. This implies that the quotient metric of
$1$
. This implies that the quotient metric of
![]() $\unicode[STIX]{x1D714}_{FS}$
on
$\unicode[STIX]{x1D714}_{FS}$
on
![]() $\mathbb{P}^{n}/G$
is Kähler–Einstein and
$\mathbb{P}^{n}/G$
is Kähler–Einstein and
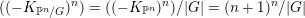 $((-K_{\mathbb{P}^{n}/G})^{n})=((-K_{\mathbb{P}^{n}})^{n})/|G|=(n+1)^{n}/|G|$
.
$((-K_{\mathbb{P}^{n}/G})^{n})=((-K_{\mathbb{P}^{n}})^{n})/|G|=(n+1)^{n}/|G|$
.
For the ‘only if’ part, let
 $(Y,o):=(\mathbb{C}^{n}/G,0)$
be the local analytic model of
$(Y,o):=(\mathbb{C}^{n}/G,0)$
be the local analytic model of
![]() $(X,p)$
. Let
$(X,p)$
. Let
 $d:=|G\cap \mathbb{G}_{m}|$
. Following the proof of Theorem 23, we have a partial resolution
$d:=|G\cap \mathbb{G}_{m}|$
. Following the proof of Theorem 23, we have a partial resolution
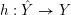 $h:{\hat{Y}}\rightarrow Y$
of
$h:{\hat{Y}}\rightarrow Y$
of
![]() $Y$
that is the quotient of the blow up
$Y$
that is the quotient of the blow up
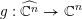 $g:\widehat{\mathbb{C}^{n}}\rightarrow \mathbb{C}^{n}$
. Since
$g:\widehat{\mathbb{C}^{n}}\rightarrow \mathbb{C}^{n}$
. Since
![]() ${\hat{Y}}$
is the quotient of
${\hat{Y}}$
is the quotient of
![]() $\widehat{\mathbb{C}^{n}}$
, it has klt singularities. Denote by
$\widehat{\mathbb{C}^{n}}$
, it has klt singularities. Denote by
![]() $F$
the exceptional divisor of
$F$
the exceptional divisor of
![]() $h$
, then we have
$h$
, then we have
 $F\cong \mathbb{P}^{n-1}/G$
. Let
$F\cong \mathbb{P}^{n-1}/G$
. Let
 $u_{\ast }:=\text{ord}_{F}$
be the divisorial on
$u_{\ast }:=\text{ord}_{F}$
be the divisorial on
![]() $Y$
centered at
$Y$
centered at
![]() $o$
, then we have
$o$
, then we have
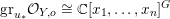 $\text{gr}_{u_{\ast }}{\mathcal{O}}_{Y,o}\cong \mathbb{C}[x_{1},\ldots ,x_{n}]^{G}$
is a finitely generated
$\text{gr}_{u_{\ast }}{\mathcal{O}}_{Y,o}\cong \mathbb{C}[x_{1},\ldots ,x_{n}]^{G}$
is a finitely generated
![]() $\mathbb{C}$
-algebra. (Here we assume
$\mathbb{C}$
-algebra. (Here we assume
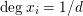 $\deg x_{i}=1/d$
so that the grading is preserved under the isomorphism.) Theorem 23 also implies
$\deg x_{i}=1/d$
so that the grading is preserved under the isomorphism.) Theorem 23 also implies
 $\widehat{\operatorname{vol}}(u_{\ast })=n^{n}/|G|$
.
$\widehat{\operatorname{vol}}(u_{\ast })=n^{n}/|G|$
.
Since
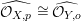 $\widehat{{\mathcal{O}}_{X,p}}\cong \widehat{{\mathcal{O}}_{Y,o}}$
, the divisorial valuation
$\widehat{{\mathcal{O}}_{X,p}}\cong \widehat{{\mathcal{O}}_{Y,o}}$
, the divisorial valuation
![]() $u_{\ast }$
induces a divisorial valuation
$u_{\ast }$
induces a divisorial valuation
![]() $v_{\ast }$
on
$v_{\ast }$
on
![]() $X$
centered at
$X$
centered at
![]() $p$
as in the proof of Theorem 23. Thus
$p$
as in the proof of Theorem 23. Thus
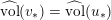 $\widehat{\operatorname{vol}}(v_{\ast })=\widehat{\operatorname{vol}}(u_{\ast })$
,
$\widehat{\operatorname{vol}}(v_{\ast })=\widehat{\operatorname{vol}}(u_{\ast })$
,
 $\text{gr}_{v_{\ast }}({\mathcal{O}}_{X,p})\cong \text{gr}_{u_{\ast }}({\mathcal{O}}_{Y,o})$
is a finitely generated
$\text{gr}_{v_{\ast }}({\mathcal{O}}_{X,p})\cong \text{gr}_{u_{\ast }}({\mathcal{O}}_{Y,o})$
is a finitely generated
![]() $\mathbb{C}$
-algebra,
$\mathbb{C}$
-algebra,
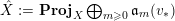 $\hat{X}:={\mathbf{Proj}_{X}\bigoplus }_{m\geqslant 0}\mathfrak{a}_{m}(v_{\ast })$
has klt singularities, and
$\hat{X}:={\mathbf{Proj}_{X}\bigoplus }_{m\geqslant 0}\mathfrak{a}_{m}(v_{\ast })$
has klt singularities, and
 $$\begin{eqnarray}((-K_{X})^{n})=\frac{(n+1)^{n}}{|G|}=\biggl(1+\frac{1}{n}\biggr)^{n}\,\widehat{\operatorname{vol}}(v_{\ast }).\end{eqnarray}$$
$$\begin{eqnarray}((-K_{X})^{n})=\frac{(n+1)^{n}}{|G|}=\biggl(1+\frac{1}{n}\biggr)^{n}\,\widehat{\operatorname{vol}}(v_{\ast }).\end{eqnarray}$$
By [Reference BermanBer16] we have that
![]() $X$
is K-polystable. Hence applying Lemma 33 yields
$X$
is K-polystable. Hence applying Lemma 33 yields
 $$\begin{eqnarray}X\cong \mathbf{Proj}~\text{gr}_{v_{\ast }}{\mathcal{O}}_{X,p}[x]\cong \mathbf{Proj}~\mathbb{C}[x_{1},\ldots ,x_{n}]^{G}[x],\end{eqnarray}$$
$$\begin{eqnarray}X\cong \mathbf{Proj}~\text{gr}_{v_{\ast }}{\mathcal{O}}_{X,p}[x]\cong \mathbf{Proj}~\mathbb{C}[x_{1},\ldots ,x_{n}]^{G}[x],\end{eqnarray}$$
where
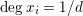 $\deg x_{i}=1/d$
and
$\deg x_{i}=1/d$
and
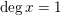 $\deg x=1$
. Denote
$\deg x=1$
. Denote
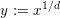 $y:=x^{1/d}$
, then
$y:=x^{1/d}$
, then
 $\mathbb{C}[x_{1},\ldots ,x_{n}]^{G}[x]$
is the Veronese subalgebra of
$\mathbb{C}[x_{1},\ldots ,x_{n}]^{G}[x]$
is the Veronese subalgebra of
 $\mathbb{C}[x_{1},\ldots ,x_{n}]^{G}[y]$
where
$\mathbb{C}[x_{1},\ldots ,x_{n}]^{G}[y]$
where
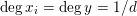 $\deg x_{i}=\deg y=1/d$
. As a result,
$\deg x_{i}=\deg y=1/d$
. As a result,
 $$\begin{eqnarray}X\cong \mathbf{Proj}~\mathbb{C}[x_{1},\ldots ,x_{n}]^{G}[y]=\mathbb{P}^{n}/G.\end{eqnarray}$$
$$\begin{eqnarray}X\cong \mathbf{Proj}~\mathbb{C}[x_{1},\ldots ,x_{n}]^{G}[y]=\mathbb{P}^{n}/G.\end{eqnarray}$$
Denote by
![]() $H_{\infty }$
the hyperplane at infinity in
$H_{\infty }$
the hyperplane at infinity in
![]() $\mathbb{P}^{n}$
. Let
$\mathbb{P}^{n}$
. Let
![]() $D$
be the prime divisor in
$D$
be the prime divisor in
![]() $X$
corresponding to
$X$
corresponding to
![]() $H_{\infty }/G$
in
$H_{\infty }/G$
in
![]() $\mathbb{P}^{n}/G$
. It is clear that
$\mathbb{P}^{n}/G$
. It is clear that
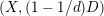 $(X,(1-1/d)D)$
is an orbifold as a global quotient of
$(X,(1-1/d)D)$
is an orbifold as a global quotient of
![]() $\mathbb{P}^{n}$
. Denote by
$\mathbb{P}^{n}$
. Denote by
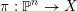 $\unicode[STIX]{x1D70B}:\mathbb{P}^{n}\rightarrow X$
the quotient map, then we have
$\unicode[STIX]{x1D70B}:\mathbb{P}^{n}\rightarrow X$
the quotient map, then we have
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}^{\ast }\biggl(K_{X}+\biggl(1-\frac{1}{d}\biggr)D\biggr)=K_{\mathbb{P}^{n}},\quad \unicode[STIX]{x1D70B}^{\ast }D=dH_{\infty }.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}^{\ast }\biggl(K_{X}+\biggl(1-\frac{1}{d}\biggr)D\biggr)=K_{\mathbb{P}^{n}},\quad \unicode[STIX]{x1D70B}^{\ast }D=dH_{\infty }.\end{eqnarray}$$
Hence
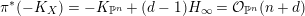 $\unicode[STIX]{x1D70B}^{\ast }(-K_{X})=-K_{\mathbb{P}^{n}}+(d-1)H_{\infty }={\mathcal{O}}_{\mathbb{P}^{n}}(n+d)$
. This implies
$\unicode[STIX]{x1D70B}^{\ast }(-K_{X})=-K_{\mathbb{P}^{n}}+(d-1)H_{\infty }={\mathcal{O}}_{\mathbb{P}^{n}}(n+d)$
. This implies
 $((-K_{X})^{n})=(n+d)^{n}/|G|$
, so
$((-K_{X})^{n})=(n+d)^{n}/|G|$
, so
![]() $d=1$
.◻
$d=1$
.◻
Remark 38. (i) The restriction on
![]() $G$
in Theorem 37 can be dropped in its logarithmic version as follows: suppose
$G$
in Theorem 37 can be dropped in its logarithmic version as follows: suppose
![]() $(X,D)$
is a conical Kähler–Einstein log Fano pair,
$(X,D)$
is a conical Kähler–Einstein log Fano pair,
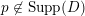 $p\not \in \text{Supp}(D)$
,
$p\not \in \text{Supp}(D)$
,
![]() $(X,p)$
is analytically isomorphic to
$(X,p)$
is analytically isomorphic to
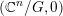 $(\mathbb{C}^{n}/G,0)$
and
$(\mathbb{C}^{n}/G,0)$
and
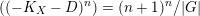 $((-K_{X}-D)^{n})=(n+1)^{n}/|G|$
, then
$((-K_{X}-D)^{n})=(n+1)^{n}/|G|$
, then
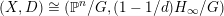 $(X,D)\cong (\mathbb{P}^{n}/G,(1-1/d)H_{\infty }/G)$
where
$(X,D)\cong (\mathbb{P}^{n}/G,(1-1/d)H_{\infty }/G)$
where
 $d=|G\cap \mathbb{G}_{m}|$
.
$d=|G\cap \mathbb{G}_{m}|$
.
(ii) The K-polystable condition in Lemma 33 and Kähler–Einstein condition in Theorem 3 cannot be dropped since any cubic surface in
![]() $\mathbb{P}^{3}$
with only one or two
$\mathbb{P}^{3}$
with only one or two
![]() $\mathbb{A}_{2}$
singularities is K-semistable but not K-polystable (hence not Kähler–Einstein) according to [Reference Odaka, Spotti and SunOSS16, § 4.2], but all global quotients of
$\mathbb{A}_{2}$
singularities is K-semistable but not K-polystable (hence not Kähler–Einstein) according to [Reference Odaka, Spotti and SunOSS16, § 4.2], but all global quotients of
![]() $\mathbb{P}^{2}$
are Kähler–Einstein (hence K-polystable).
$\mathbb{P}^{2}$
are Kähler–Einstein (hence K-polystable).
Corollary 39 (= Corollary 6).
Let
![]() $X$
be a Kähler–Einstein log Del Pezzo surface with at most Du Val singularities.
$X$
be a Kähler–Einstein log Del Pezzo surface with at most Du Val singularities.
(i) If
 $((-K_{X})^{2})=1$
, then
$((-K_{X})^{2})=1$
, then
 $X$
has at most singularities of type
$X$
has at most singularities of type
 $\mathbb{A}_{1}$
,
$\mathbb{A}_{1}$
,
 $\mathbb{A}_{2}$
,
$\mathbb{A}_{2}$
,
 $\mathbb{A}_{3}$
,
$\mathbb{A}_{3}$
,
 $\mathbb{A}_{4}$
,
$\mathbb{A}_{4}$
,
 $\mathbb{A}_{5}$
,
$\mathbb{A}_{5}$
,
 $\mathbb{A}_{6}$
,
$\mathbb{A}_{6}$
,
 $\mathbb{A}_{7}$
or
$\mathbb{A}_{7}$
or
 $\mathbb{D}_{4}$
.
$\mathbb{D}_{4}$
.(ii) If
 $((-K_{X})^{2})=2$
, then
$((-K_{X})^{2})=2$
, then
 $X$
has at most singularities of type
$X$
has at most singularities of type
 $\mathbb{A}_{1}$
,
$\mathbb{A}_{1}$
,
 $\mathbb{A}_{2}$
or
$\mathbb{A}_{2}$
or
 $\mathbb{A}_{3}$
.
$\mathbb{A}_{3}$
.(iii) If
 $((-K_{X})^{2})=3$
, then
$((-K_{X})^{2})=3$
, then
 $X$
has at most singularities of type
$X$
has at most singularities of type
 $\mathbb{A}_{1}$
or
$\mathbb{A}_{1}$
or
 $\mathbb{A}_{2}$
.
$\mathbb{A}_{2}$
.(iv) If
 $((-K_{X})^{2})=4$
, then
$((-K_{X})^{2})=4$
, then
 $X$
has at most singularities of type
$X$
has at most singularities of type
 $\mathbb{A}_{1}$
.
$\mathbb{A}_{1}$
.(v) If
 $((-K_{X})^{2})\geqslant 5$
, then
$((-K_{X})^{2})\geqslant 5$
, then
 $X$
is smooth.
$X$
is smooth.
Proof. Let
![]() $\mathbb{C}^{2}/G$
be the local analytic model of
$\mathbb{C}^{2}/G$
be the local analytic model of
![]() $(X,p)$
for any closed point
$(X,p)$
for any closed point
![]() $p\in X$
. By Corollary 4, we know that
$p\in X$
. By Corollary 4, we know that
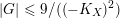 $|G|\leqslant 9/((-K_{X})^{2})$
.
$|G|\leqslant 9/((-K_{X})^{2})$
.
Recall that the order of orbifold group at an
![]() $\mathbb{A}_{k}$
singularity is
$\mathbb{A}_{k}$
singularity is
![]() $k+1$
, a
$k+1$
, a
![]() $\mathbb{D}_{k}$
singularity is
$\mathbb{D}_{k}$
singularity is
 $4(k-2)$
, an
$4(k-2)$
, an
![]() $\mathbb{E}_{6}$
singularity is
$\mathbb{E}_{6}$
singularity is
![]() $24$
, an
$24$
, an
![]() $\mathbb{E}_{7}$
singularity is
$\mathbb{E}_{7}$
singularity is
![]() $48$
, and an
$48$
, and an
![]() $\mathbb{E}_{8}$
singularity is
$\mathbb{E}_{8}$
singularity is
![]() $120$
. Hence the inequality
$120$
. Hence the inequality
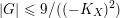 $|G|\leqslant 9/((-K_{X})^{2})$
implies (ii)–(v). For part (i), the same argument yields that
$|G|\leqslant 9/((-K_{X})^{2})$
implies (ii)–(v). For part (i), the same argument yields that
![]() $X$
has at most singularities type of
$X$
has at most singularities type of
![]() $\mathbb{A}_{k}$
with
$\mathbb{A}_{k}$
with
![]() $k\leqslant 8$
, or of type
$k\leqslant 8$
, or of type
![]() $\mathbb{D}_{4}$
. Hence we only need to rule out
$\mathbb{D}_{4}$
. Hence we only need to rule out
![]() $\mathbb{A}_{8}$
cases.
$\mathbb{A}_{8}$
cases.
Assume to the contrary that
![]() $(X,p)$
is of type
$(X,p)$
is of type
![]() $\mathbb{A}_{8}$
. Since
$\mathbb{A}_{8}$
. Since
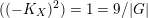 $((-K_{X})^{2})=1=9/|G|$
, Theorem 37 implies that
$((-K_{X})^{2})=1=9/|G|$
, Theorem 37 implies that
 $X\cong \mathbb{P}^{2}/G$
, where
$X\cong \mathbb{P}^{2}/G$
, where
 $G=\mathbb{Z}/9\mathbb{Z}$
acts on
$G=\mathbb{Z}/9\mathbb{Z}$
acts on
![]() $\mathbb{P}^{2}$
as follows:
$\mathbb{P}^{2}$
as follows:
 $$\begin{eqnarray}[x,y,z]\mapsto [\unicode[STIX]{x1D701}^{i}x,\unicode[STIX]{x1D701}^{-i}y,z]\quad \text{for }i\in \mathbb{Z}/9\mathbb{Z},\end{eqnarray}$$
$$\begin{eqnarray}[x,y,z]\mapsto [\unicode[STIX]{x1D701}^{i}x,\unicode[STIX]{x1D701}^{-i}y,z]\quad \text{for }i\in \mathbb{Z}/9\mathbb{Z},\end{eqnarray}$$
where
 $\unicode[STIX]{x1D701}:=e^{2\unicode[STIX]{x1D70B}i/9}$
is the ninth root of unity. The point
$\unicode[STIX]{x1D701}:=e^{2\unicode[STIX]{x1D70B}i/9}$
is the ninth root of unity. The point
![]() $p$
is the quotient of
$p$
is the quotient of
![]() $[0,0,1]$
under this action, which is of type
$[0,0,1]$
under this action, which is of type
 $\frac{1}{9}(1,-1)$
as a cyclic quotient singularity. However, the quotient singularities at
$\frac{1}{9}(1,-1)$
as a cyclic quotient singularity. However, the quotient singularities at
![]() $[1,0,0]$
and
$[1,0,0]$
and
![]() $[0,1,0]$
are both of type
$[0,1,0]$
are both of type
![]() $\frac{1}{9}(1,2)$
which are not Du Val, contradiction!◻
$\frac{1}{9}(1,2)$
which are not Du Val, contradiction!◻
Acknowledgements
I would like to thank my advisor János Kollár for his constant support, encouragement and numerous inspiring conversations. I wish to thank Chi Li and Chenyang Xu for fruitful discussions and encouragement. I also wish to thank Charles Stibitz, Yury Ustinovskiy, Xiaowei Wang and Ziquan Zhuang for many useful discussions, Lue Pan for providing an argument for Lemma 24, and Harold Blum, Kento Fujita and Song Sun for helpful comments and suggestions through e-mails.
The author is partially supported by NSF grant DMS-0968337 and DMS-1362960.