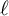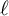1 Introduction
Towers of moduli spaces of p-divisible groups with additional structure as defined by Drinfeld [Reference Drinfeld35] and Rapoport and Zink [Reference Rapoport and Zink80] have become a central topic in the study of the geometric realisation of local Langlands correspondences. These towers consist of covering spaces of the generic fibre of moduli spaces of p-divisible groups with EL or PEL structure. They carry a Hecke action and an action of an associated automorphism group of the defining p-divisible group with extra structure and possess a period morphism to a p-adic period space. Recently, generalisations of these moduli spaces to groups of unramified Hodge type (instead of PEL type) have been defined by Kim [Reference Kim69] and Howard and Pappas [Reference Howard and Pappas62]. Conjecturally, in all of these cases, the cohomology of the tower realises local Langlands correspondences. Several cases of these conjectures have been shown so far; compare, for example, [Reference Fargues36], [Reference Chen27]. However, in general, still very little is known.
In the present article we define the analogous towers, cohomology groups and period spaces in the function field case and study their basic properties. This generalises Drinfeld’s work [Reference Drinfeld35]. We thus provide the foundations for a theory similar to the one initiated by Drinfeld, Rapoport and Zink. It is conceivable that the cohomology of our towers likewise realises local Langlands correspondences. For Drinfeld’s towers [Reference Drinfeld35] this was conjectured by Carayol [Reference Carayol26] and proved by Boyer [Reference Boyer23] and Hausberger [Reference Hausberger59], building on work of Laumon, Rapoport and Stuhler [Reference Laumon, Rapoport and Stuhler73]. One major difference in our context is that instead of being restricted to groups of PEL or Hodge type, there is a natural and group-theoretic way to define moduli spaces of local G-shtukas for any reductive group G. Furthermore, one can define more general boundedness conditions than minuscule bounds which would be the direct analogue of the number field situation.
To give an overview of their definition, let
![]() ${\mathbb {F}}_q$
be a finite field with q elements, let
${\mathbb {F}}_q$
be a finite field with q elements, let
![]() ${\mathbb {F}}$
be a fixed algebraic closure of
${\mathbb {F}}$
be a fixed algebraic closure of
![]() ${\mathbb {F}}_q$
and let
${\mathbb {F}}_q$
and let
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}z\mathrm {]}\kern-0.15em\mathrm {]}$
and
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}z\mathrm {]}\kern-0.15em\mathrm {]}$
and
![]() ${\mathbb {F}}_q\mathrm{[}\kern-0.15em\mathrm{[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
be the power series rings over
${\mathbb {F}}_q\mathrm{[}\kern-0.15em\mathrm{[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
be the power series rings over
![]() ${\mathbb {F}}_q$
in the (independent) variables z, respectively
${\mathbb {F}}_q$
in the (independent) variables z, respectively
![]() $\zeta $
. As base schemes we will consider the category
$\zeta $
. As base schemes we will consider the category
![]() ${{\mathcal {N}}\!\mathit {ilp}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}}$
consisting of schemes over
${{\mathcal {N}}\!\mathit {ilp}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}}$
consisting of schemes over
![]() $\operatorname {\mathrm {Spec}}{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
on which
$\operatorname {\mathrm {Spec}}{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
on which
![]() $\zeta $
is locally nilpotent. Let G be a parahoric group scheme over
$\zeta $
is locally nilpotent. Let G be a parahoric group scheme over
![]() $\operatorname {\mathrm {Spec}}{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
in the sense of [Reference Bruhat and Tits25, Définition 5.2.6] and [Reference Haines and Rapoport48] with connected reductive generic fibre. (One may ask whether the assumptions on G can be relaxed, but we crucially use the ind-projectivity of
$\operatorname {\mathrm {Spec}}{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
in the sense of [Reference Bruhat and Tits25, Définition 5.2.6] and [Reference Haines and Rapoport48] with connected reductive generic fibre. (One may ask whether the assumptions on G can be relaxed, but we crucially use the ind-projectivity of
![]() ${\mathcal {F}}\ell _G$
in the central Propositions 2.6 and 7.8; see the beginning of Section 2 for more explanations.)
${\mathcal {F}}\ell _G$
in the central Propositions 2.6 and 7.8; see the beginning of Section 2 for more explanations.)
Let
![]() $S\in {{\mathcal {N}}\!\mathit {ilp}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}}$
and let H be a sheaf of groups on S for the fpqc topology. By a (right) H-torsor on S we mean a sheaf
$S\in {{\mathcal {N}}\!\mathit {ilp}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}}$
and let H be a sheaf of groups on S for the fpqc topology. By a (right) H-torsor on S we mean a sheaf
![]() ${\mathcal {H}}$
for the fpqc topology on S together with a (right) action of the sheaf H such that
${\mathcal {H}}$
for the fpqc topology on S together with a (right) action of the sheaf H such that
![]() ${\mathcal {H}}$
is isomorphic to H on an fpqc covering of S. Here H is viewed as an H-torsor by right multiplication. Let
${\mathcal {H}}$
is isomorphic to H on an fpqc covering of S. Here H is viewed as an H-torsor by right multiplication. Let
![]() $LG$
and
$LG$
and
![]() $L^+G$
be the loop group and the group of positive loops associated with G; compare Section 2. Let
$L^+G$
be the loop group and the group of positive loops associated with G; compare Section 2. Let
![]() ${\mathcal {G}}$
be an
${\mathcal {G}}$
be an
![]() $L^+G$
-torsor on S. Via the inclusion of sheaves
$L^+G$
-torsor on S. Via the inclusion of sheaves
![]() $L^+G\subset LG$
we can associate an
$L^+G\subset LG$
we can associate an
![]() $LG$
-torsor
$LG$
-torsor
![]() $L{\mathcal {G}}$
with
$L{\mathcal {G}}$
with
![]() ${\mathcal {G}}$
. Also, for an
${\mathcal {G}}$
. Also, for an
![]() $LG$
-torsor
$LG$
-torsor
![]() ${\mathcal {G}}$
on S we denote by
${\mathcal {G}}$
on S we denote by
![]() $\sigma ^\ast {\mathcal {G}}$
the pullback of
$\sigma ^\ast {\mathcal {G}}$
the pullback of
![]() ${\mathcal {G}}$
under the q-Frobenius morphism
${\mathcal {G}}$
under the q-Frobenius morphism
![]() $\sigma :=\operatorname {\mathrm {Frob}}_q\colon S\to S$
.
$\sigma :=\operatorname {\mathrm {Frob}}_q\colon S\to S$
.
Definition 1.1. A local G-shtuka over some
![]() $S\in {{\mathcal {N}}\!\mathit {ilp}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}}$
is a pair
$S\in {{\mathcal {N}}\!\mathit {ilp}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}}$
is a pair
![]() ${\underline {{\mathcal {G}}}} = ({\mathcal {G}},\tau _{\mathcal {G}})$
consisting of an
${\underline {{\mathcal {G}}}} = ({\mathcal {G}},\tau _{\mathcal {G}})$
consisting of an
![]() $L^+G$
-torsor
$L^+G$
-torsor
![]() ${\mathcal {G}}$
on S and an isomorphism of the associated
${\mathcal {G}}$
on S and an isomorphism of the associated
![]() $LG$
-torsors
$LG$
-torsors
![]() .
.
A quasi-isogeny
![]() $g\colon ({\mathcal {G}}^{\prime }\!,\tau _{{\mathcal {G}}^{\prime }})\to ({\mathcal {G}},\tau _{\mathcal {G}})$
between local G-shtukas over S is an isomorphism
$g\colon ({\mathcal {G}}^{\prime }\!,\tau _{{\mathcal {G}}^{\prime }})\to ({\mathcal {G}},\tau _{\mathcal {G}})$
between local G-shtukas over S is an isomorphism
![]() of the associated
of the associated
![]() $LG$
-torsors with
$LG$
-torsors with
![]() $g\circ \tau _{{\mathcal {G}}^{\prime }}=\tau _{\mathcal {G}}\circ \sigma ^\ast g$
.
$g\circ \tau _{{\mathcal {G}}^{\prime }}=\tau _{\mathcal {G}}\circ \sigma ^\ast g$
.
Local G-shtukas were introduced and studied in [Reference Hartl and Viehmann56], [Reference Hartl and Viehmann57] in the case where G is a constant split reductive group over
![]() ${\mathbb {F}}_q$
and in [Reference Genestier and Lafforgue41], [Reference Hartl50] for
${\mathbb {F}}_q$
and in [Reference Genestier and Lafforgue41], [Reference Hartl50] for
![]() $G=\operatorname {\mathrm {GL}}_r$
. The general case was considered in [Reference Arasteh Rad and Hartl4]. For a local G-shtuka
$G=\operatorname {\mathrm {GL}}_r$
. The general case was considered in [Reference Arasteh Rad and Hartl4]. For a local G-shtuka
![]() ${\underline {{\mathcal {G}}}}$
over S there exists an étale covering
${\underline {{\mathcal {G}}}}$
over S there exists an étale covering
![]() $S^{\prime }\to S$
and a trivialisation
$S^{\prime }\to S$
and a trivialisation
![]() ${\underline {{\mathcal {G}}}}\times _S S^{\prime }\cong \big ((L^+G)_{S^{\prime }},b\sigma ^\ast \big )$
with
${\underline {{\mathcal {G}}}}\times _S S^{\prime }\cong \big ((L^+G)_{S^{\prime }},b\sigma ^\ast \big )$
with
![]() $b\in LG(S^{\prime })$
; see [Reference Hartl and Viehmann56, Proposition 2.2(c)] and [Reference Arasteh Rad and Hartl4, Proposition 2.4].
$b\in LG(S^{\prime })$
; see [Reference Hartl and Viehmann56, Proposition 2.2(c)] and [Reference Arasteh Rad and Hartl4, Proposition 2.4].
Note that we may view
![]() $\operatorname {\mathrm {Spf}}{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
as an ind-scheme. By
$\operatorname {\mathrm {Spf}}{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
as an ind-scheme. By
![]() ${\mathcal {F}}\ell _G$
we denote the affine flag variety of G over
${\mathcal {F}}\ell _G$
we denote the affine flag variety of G over
![]() ${\mathbb {F}}_q$
; compare Section 2. We may form the fibre product
${\mathbb {F}}_q$
; compare Section 2. We may form the fibre product
![]() ${\widehat {{\mathcal {F}}\ell }}_G:={\mathcal {F}}\ell _G\widehat {\displaystyle \times }_{{\mathbb {F}}_q}\operatorname {\mathrm {Spf}}{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
in the category of ind-schemes. By [Reference Arasteh Rad and Hartl4, Theorem 4.4] it represents the functor on
${\widehat {{\mathcal {F}}\ell }}_G:={\mathcal {F}}\ell _G\widehat {\displaystyle \times }_{{\mathbb {F}}_q}\operatorname {\mathrm {Spf}}{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
in the category of ind-schemes. By [Reference Arasteh Rad and Hartl4, Theorem 4.4] it represents the functor on
![]() ${{\mathcal {N}}\!\mathit {ilp}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}}$
with
${{\mathcal {N}}\!\mathit {ilp}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}}$
with

We consider local G-shtukas that satisfy an additional boundedness condition. Similar to [Reference Arasteh Rad and Hartl4, § 4.2], we introduce the notion of a bound
![]() $\hat Z$
and its reflex ring
$\hat Z$
and its reflex ring
![]() $R_{\hat Z}$
, which is a finite extension of
$R_{\hat Z}$
, which is a finite extension of
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
. Our bounds are defined as closed ind-subschemes
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
. Our bounds are defined as closed ind-subschemes
![]() $\hat Z\subset {\widehat {{\mathcal {F}}\ell }}_{G,R}={\mathcal {F}}\ell _G\widehat {\displaystyle \times }_{{\mathbb {F}}_q}\operatorname {\mathrm {Spf}} R$
satisfying certain additional properties. Here R is a finite extension of
$\hat Z\subset {\widehat {{\mathcal {F}}\ell }}_{G,R}={\mathcal {F}}\ell _G\widehat {\displaystyle \times }_{{\mathbb {F}}_q}\operatorname {\mathrm {Spf}} R$
satisfying certain additional properties. Here R is a finite extension of
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
. In particular, we allow more general bounds than usual, in the sense that they do not have to correspond directly to some coweight
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
. In particular, we allow more general bounds than usual, in the sense that they do not have to correspond directly to some coweight
![]() $\mu $
(which in the classical context even had to be minuscule). We consider local G-shtukas
$\mu $
(which in the classical context even had to be minuscule). We consider local G-shtukas
![]() ${\underline {{\mathcal {G}}}}=({\mathcal {G}},\tau _{\mathcal {G}})$
over schemes in
${\underline {{\mathcal {G}}}}=({\mathcal {G}},\tau _{\mathcal {G}})$
over schemes in
![]() ${{\mathcal {N}}\!\mathit {ilp}}_{R_{\hat Z}}$
such that the singularities of the morphism
${{\mathcal {N}}\!\mathit {ilp}}_{R_{\hat Z}}$
such that the singularities of the morphism
![]() $\tau _{\mathcal {G}}^{-1}$
are bounded by
$\tau _{\mathcal {G}}^{-1}$
are bounded by
![]() $\hat Z$
; compare Definition 2.2. In this case we say that
$\hat Z$
; compare Definition 2.2. In this case we say that
![]() ${\underline {{\mathcal {G}}}}$
is bounded by
${\underline {{\mathcal {G}}}}$
is bounded by
![]() $\hat {Z}^{-1}$
; see Remark 2.3(a) for a comment on this terminology. These bounded local G-shtukas can be seen as the function field analogues of p-divisible groups with extra structure. We write
$\hat {Z}^{-1}$
; see Remark 2.3(a) for a comment on this terminology. These bounded local G-shtukas can be seen as the function field analogues of p-divisible groups with extra structure. We write
![]() $R_{\hat Z}=\kappa \mathrm {[}\kern-0.15em\mathrm {[}\xi \mathrm {]}\kern-0.15em\mathrm {]}$
, let
$R_{\hat Z}=\kappa \mathrm {[}\kern-0.15em\mathrm {[}\xi \mathrm {]}\kern-0.15em\mathrm {]}$
, let
![]() $E:=E_{\hat Z}:=\kappa (\kern-0.15em(\xi )\kern-0.15em)$
be its fraction field and let
$E:=E_{\hat Z}:=\kappa (\kern-0.15em(\xi )\kern-0.15em)$
be its fraction field and let
![]() $\breve R_{\hat Z}={\mathbb {F}}\mathrm {[}\kern-0.15em\mathrm {[}\xi \mathrm {]}\kern-0.15em\mathrm {]}$
and
$\breve R_{\hat Z}={\mathbb {F}}\mathrm {[}\kern-0.15em\mathrm {[}\xi \mathrm {]}\kern-0.15em\mathrm {]}$
and
![]() $\breve E:=\breve E_{\hat Z}:={\mathbb {F}}(\kern-0.15em(\xi )\kern-0.15em)$
be the completions of the maximal unramified extensions.
$\breve E:=\breve E_{\hat Z}:={\mathbb {F}}(\kern-0.15em(\xi )\kern-0.15em)$
be the completions of the maximal unramified extensions.
One can then consider the usual Rapoport-Zink type moduli space representing the following functor: Let
![]() ${\underline {{\mathbb {G}}}}_0$
be a local G-shtuka over
${\underline {{\mathbb {G}}}}_0$
be a local G-shtuka over
![]() ${\mathbb {F}}$
and consider the functor
${\mathbb {F}}$
and consider the functor
![]() ${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}\colon ({{\mathcal {N}}\!\mathit {ilp}}_{\breve R_{\hat Z}})^o \;\longrightarrow \; {{\mathcal {S}} \!\mathit {ets}}$
,
${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}\colon ({{\mathcal {N}}\!\mathit {ilp}}_{\breve R_{\hat Z}})^o \;\longrightarrow \; {{\mathcal {S}} \!\mathit {ets}}$
,
 $$ \begin{align*} S&\longmapsto \Big\{\,\text{Isomorphism classes of }({\underline{{\mathcal{G}}}},\bar\delta)\colon\text{ where }{\underline{{\mathcal{G}}}}\text{ is a local } G\text{-shtuka over} S \\ &~~~~ \text{bounded by } \hat{Z}^{-1} \text{ and }\bar{\delta}\colon {\underline{{\mathcal{G}}}}_{\bar{S}}\to {\underline{{\mathbb{G}}}}_{0,\bar{S}}~\text{is a quasi-isogeny over } \bar{S} \Big\}. \end{align*} $$
$$ \begin{align*} S&\longmapsto \Big\{\,\text{Isomorphism classes of }({\underline{{\mathcal{G}}}},\bar\delta)\colon\text{ where }{\underline{{\mathcal{G}}}}\text{ is a local } G\text{-shtuka over} S \\ &~~~~ \text{bounded by } \hat{Z}^{-1} \text{ and }\bar{\delta}\colon {\underline{{\mathcal{G}}}}_{\bar{S}}\to {\underline{{\mathbb{G}}}}_{0,\bar{S}}~\text{is a quasi-isogeny over } \bar{S} \Big\}. \end{align*} $$
Here
![]() $\bar {S}:=\operatorname {\mathrm {V}}_S(\zeta )$
is the zero locus of
$\bar {S}:=\operatorname {\mathrm {V}}_S(\zeta )$
is the zero locus of
![]() $\zeta $
in S. The functor
$\zeta $
in S. The functor
![]() ${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
is ind-representable by a formal scheme over
${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
is ind-representable by a formal scheme over
![]() $\operatorname {\mathrm {Spf}}\breve R_{\hat Z}$
that is locally formally of finite type and separated; see [Reference Arasteh Rad and Hartl4, Theorem 4.18]. The group
$\operatorname {\mathrm {Spf}}\breve R_{\hat Z}$
that is locally formally of finite type and separated; see [Reference Arasteh Rad and Hartl4, Theorem 4.18]. The group
![]() $J=\operatorname {\mathrm {QIsog}}_{{\mathbb {F}}}({\underline {{\mathbb {G}}}}_0)$
of self-quasi-isogenies of
$J=\operatorname {\mathrm {QIsog}}_{{\mathbb {F}}}({\underline {{\mathbb {G}}}}_0)$
of self-quasi-isogenies of
![]() ${\underline {{\mathbb {G}}}}_0$
acts on
${\underline {{\mathbb {G}}}}_0$
acts on
![]() ${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
via
${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
via
![]() $g\colon ({\underline {{\mathcal {G}}}},\bar \delta )\mapsto ({\underline {{\mathcal {G}}}},g\circ \bar \delta )$
for
$g\colon ({\underline {{\mathcal {G}}}},\bar \delta )\mapsto ({\underline {{\mathcal {G}}}},g\circ \bar \delta )$
for
![]() $g\in \operatorname {\mathrm {QIsog}}_{{\mathbb {F}}}({\underline {{\mathbb {G}}}}_0)$
.
$g\in \operatorname {\mathrm {QIsog}}_{{\mathbb {F}}}({\underline {{\mathbb {G}}}}_0)$
.
We consider the generic fibre
![]() $({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\textrm {an}}$
of this moduli space as a strictly
$({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\textrm {an}}$
of this moduli space as a strictly
![]() $\breve E$
-analytic space in the sense of Berkovich [Reference Berkovich7], [Reference Berkovich8]. Using the fully faithful functors [Reference Berkovich8, § 1.6] and [Reference Huber63, (1.1.11)] from strictly
$\breve E$
-analytic space in the sense of Berkovich [Reference Berkovich7], [Reference Berkovich8]. Using the fully faithful functors [Reference Berkovich8, § 1.6] and [Reference Huber63, (1.1.11)] from strictly
![]() $\breve E$
-analytic spaces to rigid analytic spaces over
$\breve E$
-analytic spaces to rigid analytic spaces over
![]() $\breve E$
, respectively from rigid analytic spaces to Huber’s analytic adic spaces, many of the results below can be formulated likewise in terms of rigid analytic, respectively analytic adic spaces. However, because we want to use étale fundamental groups and local systems on these spaces, we prefer in this work the Berkovich point of view for which such a theory exists in the literature.
$\breve E$
, respectively from rigid analytic spaces to Huber’s analytic adic spaces, many of the results below can be formulated likewise in terms of rigid analytic, respectively analytic adic spaces. However, because we want to use étale fundamental groups and local systems on these spaces, we prefer in this work the Berkovich point of view for which such a theory exists in the literature.
As in [Reference Arasteh Rad and Hartl4, Definition 3.5], we consider the rational (dual) Tate module of the universal local G-shtuka over each connected component Y of
![]() $({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\textrm {an}}$
; see Section 7. It is a tensor functor
$({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\textrm {an}}$
; see Section 7. It is a tensor functor
Here
![]() $\operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G$
denotes the Tannakian category of
$\operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G$
denotes the Tannakian category of
![]() ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em) $
-rational representations of G, and
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em) $
-rational representations of G, and
![]() $\operatorname {\mathrm {Rep}}^{\textrm {cont}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em) }\big (\pi _1^{\mathrm {\acute {e}t}}(Y,\bar s)\big )$
denotes the category of finite-dimensional
$\operatorname {\mathrm {Rep}}^{\textrm {cont}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em) }\big (\pi _1^{\mathrm {\acute {e}t}}(Y,\bar s)\big )$
denotes the category of finite-dimensional
![]() ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em) $
-vector spaces with a continuous action of de Jong’s [Reference de Jong31, § 2] étale fundamental group
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em) $
-vector spaces with a continuous action of de Jong’s [Reference de Jong31, § 2] étale fundamental group
![]() $\pi _1^{\mathrm {\acute {e}t}}(Y,\bar s)$
, where
$\pi _1^{\mathrm {\acute {e}t}}(Y,\bar s)$
, where
![]() $\bar s$
is a fixed base point in the given component.
$\bar s$
is a fixed base point in the given component.
Trivialising the rational Tate module up to the action of K for each compact open subgroup
![]() $K\subset G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
, we obtain a tower
$K\subset G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
, we obtain a tower
![]() $({\breve {\mathcal {M}}}^K)_K$
of analytic spaces. Each of the spaces is equipped with an action of the group
$({\breve {\mathcal {M}}}^K)_K$
of analytic spaces. Each of the spaces is equipped with an action of the group
![]() $J=\operatorname {\mathrm {QIsog}}_{{\mathbb {F}}}({\underline {{\mathbb {G}}}}_0)$
that is induced by the action on the moduli space
$J=\operatorname {\mathrm {QIsog}}_{{\mathbb {F}}}({\underline {{\mathbb {G}}}}_0)$
that is induced by the action on the moduli space
![]() ${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
itself. Furthermore, the group
${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
itself. Furthermore, the group
![]() $G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
acts vertically on the tower via Hecke operators; that is, for
$G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
acts vertically on the tower via Hecke operators; that is, for
![]() $g\in G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
we have compatible isomorphisms
$g\in G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
we have compatible isomorphisms
![]() .
.
In the last section we consider the
![]() $\ell $
-adic cohomology with compact support of the spaces
$\ell $
-adic cohomology with compact support of the spaces
![]() ${\breve {\mathcal {M}}}^K$
and their limit over K together with induced actions of J, of
${\breve {\mathcal {M}}}^K$
and their limit over K together with induced actions of J, of
![]() $G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
and of the Weil group
$G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
and of the Weil group
![]() $W_E$
. We provide basic finiteness properties of these cohomology groups and representations. Note that Tate modules, towers of moduli spaces of local G-shtukas and their cohomology are also considered in a similar but slightly different context by Neupert in [Reference Neupert76]. There, the relation to moduli spaces of global G-shtukas and their cohomology is studied.
$W_E$
. We provide basic finiteness properties of these cohomology groups and representations. Note that Tate modules, towers of moduli spaces of local G-shtukas and their cohomology are also considered in a similar but slightly different context by Neupert in [Reference Neupert76]. There, the relation to moduli spaces of global G-shtukas and their cohomology is studied.
Besides this construction of the tower of moduli spaces, our second main topic is the definition of the associated period space and the properties of the period morphism. Period spaces are strictly
![]() ${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
-analytic spaces in the sense of Berkovich [Reference Berkovich7], [Reference Berkovich8]. Because we allow more general bounds than those associated with minuscule coweights, these period spaces have to be defined as subspaces of an affine Grassmannian instead of a (classical) flag variety. To define them, we consider the group scheme
${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
-analytic spaces in the sense of Berkovich [Reference Berkovich7], [Reference Berkovich8]. Because we allow more general bounds than those associated with minuscule coweights, these period spaces have to be defined as subspaces of an affine Grassmannian instead of a (classical) flag variety. To define them, we consider the group scheme
![]() $G\times _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}\operatorname {\mathrm {Spec}} {\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
under the homomorphism
$G\times _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}\operatorname {\mathrm {Spec}} {\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
under the homomorphism
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\to {\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]},\,z\mapsto z=\zeta +(z-\zeta )$
. Note that because this induces an inclusion
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\to {\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]},\,z\mapsto z=\zeta +(z-\zeta )$
. Note that because this induces an inclusion
![]() ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\to {\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
, this group is reductive. The associated affine Grassmannian
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\to {\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
, this group is reductive. The associated affine Grassmannian
![]() $\operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}}$
is the sheaf of sets for the fpqc topology on
$\operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}}$
is the sheaf of sets for the fpqc topology on
![]() $\operatorname {\mathrm {Spec}} {\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
associated with the presheaf
$\operatorname {\mathrm {Spec}} {\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
associated with the presheaf
![]() $\operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}}$
is an ind-scheme over
$\operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}}$
is an ind-scheme over
![]() $\operatorname {\mathrm {Spec}}{\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
which is ind-projective by [Reference Pappas and Rapoport77, Theorem 1.4] and [Reference Richarz84, Theorem A]. Here, the notation
$\operatorname {\mathrm {Spec}}{\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
which is ind-projective by [Reference Pappas and Rapoport77, Theorem 1.4] and [Reference Richarz84, Theorem A]. Here, the notation
![]() ${\mathbf {B}}_{\textrm {dR}}$
refers to the fact that if C is the completion of an algebraic closure of
${\mathbf {B}}_{\textrm {dR}}$
refers to the fact that if C is the completion of an algebraic closure of
![]() ${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
, then
${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
, then
![]() $C(\kern-0.15em( z-\zeta )\kern-0.15em)$
is the function field analogue of Fontaine’s p-adic period field
$C(\kern-0.15em( z-\zeta )\kern-0.15em)$
is the function field analogue of Fontaine’s p-adic period field
![]() ${\mathbf {B}}_{\textrm {dR}}$
; compare [Reference Hartl49, \S2.9].
${\mathbf {B}}_{\textrm {dR}}$
; compare [Reference Hartl49, \S2.9].
For our fixed bound
![]() $\hat Z$
we call the associated E-analytic space
$\hat Z$
we call the associated E-analytic space
![]() ${\mathcal {H}}_{G,\hat Z}^{\textrm {an}}:=\hat Z^{\textrm {an}}$
the space of Hodge-Pink G-structures bounded by
${\mathcal {H}}_{G,\hat Z}^{\textrm {an}}:=\hat Z^{\textrm {an}}$
the space of Hodge-Pink G-structures bounded by
![]() $\hat Z$
. It is the E-analytic space associated with a projective variety
$\hat Z$
. It is the E-analytic space associated with a projective variety
![]() ${\mathcal {H}}_{G,\hat Z}$
over
${\mathcal {H}}_{G,\hat Z}$
over
![]() $E=E_{\hat Z}$
by Proposition 2.6(d) and is a closed subscheme of
$E=E_{\hat Z}$
by Proposition 2.6(d) and is a closed subscheme of
![]() $\operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}}\otimes _{{\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)} E$
. Let
$\operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}}\otimes _{{\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)} E$
. Let
![]() ${\underline {{\mathbb {G}}}}_0$
be the local G-shtuka over
${\underline {{\mathbb {G}}}}_0$
be the local G-shtuka over
![]() ${\mathbb {F}}$
from above and fix a trivialisation
${\mathbb {F}}$
from above and fix a trivialisation
![]() ${\underline {{\mathbb {G}}}}_0\cong (L^+G_{\mathbb {F}},b\sigma ^\ast )$
, where
${\underline {{\mathbb {G}}}}_0\cong (L^+G_{\mathbb {F}},b\sigma ^\ast )$
, where
![]() $b\in LG({\mathbb {F}})$
represents the Frobenius morphism. The period space
$b\in LG({\mathbb {F}})$
represents the Frobenius morphism. The period space
![]() $\breve {\mathcal {H}}_{G,\hat Z,b}^{wa}$
is then defined as the set of all
$\breve {\mathcal {H}}_{G,\hat Z,b}^{wa}$
is then defined as the set of all
![]() $\gamma \in \breve {\mathcal {H}}_{G,\hat Z}^{\textrm {an}}:={\mathcal {H}}_{G,\hat Z}^{\textrm {an}}\widehat \otimes _{E}\breve E$
such that
$\gamma \in \breve {\mathcal {H}}_{G,\hat Z}^{\textrm {an}}:={\mathcal {H}}_{G,\hat Z}^{\textrm {an}}\widehat \otimes _{E}\breve E$
such that
![]() $(b,\gamma )$
is weakly admissible. For the usual condition of weak admissibility (checked on all representations of G) we refer to Definition 4.3. Likewise, one defines the admissible locus
$(b,\gamma )$
is weakly admissible. For the usual condition of weak admissibility (checked on all representations of G) we refer to Definition 4.3. Likewise, one defines the admissible locus
![]() $\breve {\mathcal {H}}_{G,\hat Z,b}^{a}$
in
$\breve {\mathcal {H}}_{G,\hat Z,b}^{a}$
in
![]() $\breve {\mathcal {H}}_{G,\hat Z}^{\textrm {an}}$
as the subset over which the universal
$\breve {\mathcal {H}}_{G,\hat Z}^{\textrm {an}}$
as the subset over which the universal
![]() $\sigma $
-bundle has slope zero. In Theorem 4.20 we show that
$\sigma $
-bundle has slope zero. In Theorem 4.20 we show that
![]() $\breve {\mathcal {H}}_{G,\hat Z,b}^{wa}$
and
$\breve {\mathcal {H}}_{G,\hat Z,b}^{wa}$
and
![]() $\breve {\mathcal {H}}_{G,\hat Z,b}^{a}$
are open paracompact strictly
$\breve {\mathcal {H}}_{G,\hat Z,b}^{a}$
are open paracompact strictly
![]() $\breve E$
-analytic subspaces of
$\breve E$
-analytic subspaces of
![]() $\breve {\mathcal {H}}_{G,\hat Z}^{\textrm {an}}$
.
$\breve {\mathcal {H}}_{G,\hat Z}^{\textrm {an}}$
.
We prove that there is an étale period morphism
Very roughly, it is defined as follows: Consider the filtration on the universal local G-shtuka on
![]() $({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\textrm {an}}$
induced by the image of the inverse of the universal Frobenius morphism
$({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\textrm {an}}$
induced by the image of the inverse of the universal Frobenius morphism
![]() $\tau _{{\underline {\mathcal {G}}}^{\textrm {univ}}}$
. This filtration is the function field analogue of the Hodge filtration on the de Rham cohomology and is bounded by
$\tau _{{\underline {\mathcal {G}}}^{\textrm {univ}}}$
. This filtration is the function field analogue of the Hodge filtration on the de Rham cohomology and is bounded by
![]() $\hat Z$
. Using the universal quasi-isogeny, one can associate with it a natural filtration on the base change of
$\hat Z$
. Using the universal quasi-isogeny, one can associate with it a natural filtration on the base change of
![]() ${\underline {{\mathbb {G}}}}_0$
, which is bounded by
${\underline {{\mathbb {G}}}}_0$
, which is bounded by
![]() $\hat Z$
. Strictly speaking, we carry out this construction with the Hodge-Pink G-structure instead of the filtration; see Definition 4.1 and Remark 4.4(a). The reason for this is again that as we allow nonminuscule bounds, the Hodge-Pink G-structure contains more information than just the Hodge filtration. The former yields a point of
$\hat Z$
. Strictly speaking, we carry out this construction with the Hodge-Pink G-structure instead of the filtration; see Definition 4.1 and Remark 4.4(a). The reason for this is again that as we allow nonminuscule bounds, the Hodge-Pink G-structure contains more information than just the Hodge filtration. The former yields a point of
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^a$
. This period morphism also induces compatible period morphisms for all elements
$\breve {\mathcal {H}}_{G,\hat {Z},b}^a$
. This period morphism also induces compatible period morphisms for all elements
![]() ${\breve {\mathcal {M}}}^K$
of the tower of coverings. In Theorem 8.1(a) we show that the image of the period morphism is equal to a suitable union of connected components of
${\breve {\mathcal {M}}}^K$
of the tower of coverings. In Theorem 8.1(a) we show that the image of the period morphism is equal to a suitable union of connected components of
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^a$
.
$\breve {\mathcal {H}}_{G,\hat {Z},b}^a$
.
There is an analogy between the theory of local G-shtukas and the theory of p-divisible groups [Reference Hartl49, § 3.9]. In this sense, our results have natural counterparts in the theory of p-divisible groups, for particular cases by [Reference Hartl51] and in general by Scholze and Weinstein [Reference Scholze and Weinstein89, [Reference Scholze and Weinstein90] using the Fargues-Fontaine curve [Reference Fargues and Fontaine37]. One main difference is that in the function field case, the flag variety
![]() ${\mathcal {F}}\ell _G$
is an honest ind-scheme. In addition, the Fargues-Fontaine curve is replaced by its role model, the Hartl-Pink curve [Reference Hartl and Pink55]. This allows us to consider nonminuscule Hodge-Pink structures and to work without Scholze’s theory of diamonds. One feature of our theory is the group-theoretic approach, which makes the results automatically functorial in the group G; see Remarks 3.7, 4.21 and 7.19. Interestingly, the proofs for local G-shtukas in this work had to be largely different from the techniques used for p-divisible groups and are technically quite involved.
${\mathcal {F}}\ell _G$
is an honest ind-scheme. In addition, the Fargues-Fontaine curve is replaced by its role model, the Hartl-Pink curve [Reference Hartl and Pink55]. This allows us to consider nonminuscule Hodge-Pink structures and to work without Scholze’s theory of diamonds. One feature of our theory is the group-theoretic approach, which makes the results automatically functorial in the group G; see Remarks 3.7, 4.21 and 7.19. Interestingly, the proofs for local G-shtukas in this work had to be largely different from the techniques used for p-divisible groups and are technically quite involved.
2 Bounded local G-shtukas
Recall that we fixed a parahoric group scheme G over
![]() $\operatorname {\mathrm {Spec}} {\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
.
$\operatorname {\mathrm {Spec}} {\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
.
For an
![]() ${\mathbb {F}}_q$
-scheme S we let
${\mathbb {F}}_q$
-scheme S we let
![]() ${\mathcal {O}}_S\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
be the sheaf of
${\mathcal {O}}_S\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
be the sheaf of
![]() ${\mathcal {O}}_S$
-algebras on S for the fpqc topology whose ring of sections on an S-scheme Y is the ring of power series
${\mathcal {O}}_S$
-algebras on S for the fpqc topology whose ring of sections on an S-scheme Y is the ring of power series
![]() ${\mathcal {O}}_S\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}(Y):=\Gamma (Y,{\mathcal {O}}_Y)\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
. This is indeed a sheaf being the countable direct product of
${\mathcal {O}}_S\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}(Y):=\Gamma (Y,{\mathcal {O}}_Y)\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
. This is indeed a sheaf being the countable direct product of
![]() ${\mathcal {O}}_S$
. A sheaf M of
${\mathcal {O}}_S$
. A sheaf M of
![]() ${\mathcal {O}}_S\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-modules on S that is finite free fpqc-locally on S is already finite free Zariski-locally on S by [Reference Hartl and Viehmann56, Proposition 2.3]. We call those modules locally free sheaves of
${\mathcal {O}}_S\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-modules on S that is finite free fpqc-locally on S is already finite free Zariski-locally on S by [Reference Hartl and Viehmann56, Proposition 2.3]. We call those modules locally free sheaves of
![]() ${\mathcal {O}}_S\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-modules. Let
${\mathcal {O}}_S\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-modules. Let
![]() ${\mathcal {O}}_S(\kern-0.15em( z)\kern-0.15em)$
be the fpqc sheaf of
${\mathcal {O}}_S(\kern-0.15em( z)\kern-0.15em)$
be the fpqc sheaf of
![]() ${\mathcal {O}}_S$
-algebras on S associated with the presheaf
${\mathcal {O}}_S$
-algebras on S associated with the presheaf
![]() $Y\mapsto \Gamma (Y,{\mathcal {O}}_Y)\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\frac {1}{z}]$
. If Y is quasi-compact, then
$Y\mapsto \Gamma (Y,{\mathcal {O}}_Y)\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\frac {1}{z}]$
. If Y is quasi-compact, then
![]() ${\mathcal {O}}_S(\kern-0.15em( z)\kern-0.15em)(Y)=\Gamma (Y,{\mathcal {O}}_Y)\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\frac {1}{z}]$
by [Reference de Jong32, Tag 009F]. The group of positive loops associated with G is the infinite-dimensional affine group scheme
${\mathcal {O}}_S(\kern-0.15em( z)\kern-0.15em)(Y)=\Gamma (Y,{\mathcal {O}}_Y)\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\frac {1}{z}]$
by [Reference de Jong32, Tag 009F]. The group of positive loops associated with G is the infinite-dimensional affine group scheme
![]() $L^+G$
over
$L^+G$
over
![]() ${\mathbb {F}}_q$
whose S-valued points are
${\mathbb {F}}_q$
whose S-valued points are
![]() $L^+G(S):=G\big ({\mathcal {O}}_S\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}(S)\big )=G\big (\Gamma (S,{\mathcal {O}}_S)\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
. The group of loops associated with G is the ind-group-scheme
$L^+G(S):=G\big ({\mathcal {O}}_S\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}(S)\big )=G\big (\Gamma (S,{\mathcal {O}}_S)\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
. The group of loops associated with G is the ind-group-scheme
![]() $LG$
over
$LG$
over
![]() ${\mathbb {F}}_q$
that represents the fpqc sheaf of groups
${\mathbb {F}}_q$
that represents the fpqc sheaf of groups
![]() $S\longmapsto LG(S):=G\big ({\mathcal {O}}_S(\kern-0.15em( z)\kern-0.15em)(S)\big )$
. A good reference for the theory of ind-schemes is [Reference Beilinson and Drinfeld6, § 7.11]. The affine flag variety
$S\longmapsto LG(S):=G\big ({\mathcal {O}}_S(\kern-0.15em( z)\kern-0.15em)(S)\big )$
. A good reference for the theory of ind-schemes is [Reference Beilinson and Drinfeld6, § 7.11]. The affine flag variety
![]() ${\mathcal {F}}\ell _G$
associated with G is the fpqc sheaf associated with the presheaf
${\mathcal {F}}\ell _G$
associated with G is the fpqc sheaf associated with the presheaf
on the category of
![]() ${\mathbb {F}}_q$
-schemes. Pappas and Rapoport [Reference Pappas and Rapoport77, Theorem 1.4] and Richarz [Reference Richarz84, Theorem A] showed that
${\mathbb {F}}_q$
-schemes. Pappas and Rapoport [Reference Pappas and Rapoport77, Theorem 1.4] and Richarz [Reference Richarz84, Theorem A] showed that
![]() ${\mathcal {F}}\ell _G$
is represented by an ind-scheme that is ind-projective over
${\mathcal {F}}\ell _G$
is represented by an ind-scheme that is ind-projective over
![]() ${\mathbb {F}}_q$
and that the natural morphism
${\mathbb {F}}_q$
and that the natural morphism
![]() $LG\to {\mathcal {F}}\ell _G$
admits sections locally for the étale topology. We crucially use the ind-projectivity of
$LG\to {\mathcal {F}}\ell _G$
admits sections locally for the étale topology. We crucially use the ind-projectivity of
![]() ${\mathcal {F}}\ell _G$
in Propositions 2.6 and 7.8. By [Reference Pappas and Rapoport77, Theorem 0.1], after base change to
${\mathcal {F}}\ell _G$
in Propositions 2.6 and 7.8. By [Reference Pappas and Rapoport77, Theorem 0.1], after base change to
![]() ${\mathbb {F}}$
the connected components of
${\mathbb {F}}$
the connected components of
![]() $LG{\widehat {\otimes }}_{{\mathbb {F}}_q}{\mathbb {F}}$
and
$LG{\widehat {\otimes }}_{{\mathbb {F}}_q}{\mathbb {F}}$
and
![]() ${\mathcal {F}}\ell _G{\widehat {\otimes }}_{{\mathbb {F}}_q}{\mathbb {F}}$
are in canonical bijection to the coinvariants
${\mathcal {F}}\ell _G{\widehat {\otimes }}_{{\mathbb {F}}_q}{\mathbb {F}}$
are in canonical bijection to the coinvariants
![]() $\pi _1(G)_I$
. Here
$\pi _1(G)_I$
. Here
![]() $\pi _1(G)$
is Borovoi’s fundamental group [Reference Borovoi16, Chapter 1], defined as
$\pi _1(G)$
is Borovoi’s fundamental group [Reference Borovoi16, Chapter 1], defined as
![]() $\pi _1(G):=X_*(T)/\mathrm {(coroot\ lattice)}$
for a maximal torus T of
$\pi _1(G):=X_*(T)/\mathrm {(coroot\ lattice)}$
for a maximal torus T of
![]() $G_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)^{\textrm {sep}}}$
. Moreover,
$G_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)^{\textrm {sep}}}$
. Moreover,
![]() $\pi _1(G)_{I}$
denotes the group of coinvariants under the inertia subgroup I of
$\pi _1(G)_{I}$
denotes the group of coinvariants under the inertia subgroup I of
![]() $\Gamma =\operatorname {\mathrm {Gal}}\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)^{\textrm {sep}}\!/{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
. The bijection
$\Gamma =\operatorname {\mathrm {Gal}}\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)^{\textrm {sep}}\!/{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
. The bijection
![]() $\pi _0({\mathcal {F}}\ell _G{\widehat {\otimes }}_{{\mathbb {F}}_q}{\mathbb {F}})=\pi _0(LG{\widehat {\otimes }}_{{\mathbb {F}}_q}{\mathbb {F}})\cong \pi _1(G)_I$
is induced by the Kottwitz homomorphism
$\pi _0({\mathcal {F}}\ell _G{\widehat {\otimes }}_{{\mathbb {F}}_q}{\mathbb {F}})=\pi _0(LG{\widehat {\otimes }}_{{\mathbb {F}}_q}{\mathbb {F}})\cong \pi _1(G)_I$
is induced by the Kottwitz homomorphism
![]() $\kappa _G\colon LG({\mathbb {F}})=G({\mathbb {F}}(\kern-0.15em( z)\kern-0.15em))\rightarrow \pi _1(G)_{I}$
(introduced by Kottwitz in [Reference Kottwitz71]; for the reformulation used here, compare [Reference Pappas and Rapoport77, 2.a.2]). It induces a bijection between the set
$\kappa _G\colon LG({\mathbb {F}})=G({\mathbb {F}}(\kern-0.15em( z)\kern-0.15em))\rightarrow \pi _1(G)_{I}$
(introduced by Kottwitz in [Reference Kottwitz71]; for the reformulation used here, compare [Reference Pappas and Rapoport77, 2.a.2]). It induces a bijection between the set
![]() $\pi _0(LG)=\pi _0({\mathcal {F}}\ell _G)$
and the set of
$\pi _0(LG)=\pi _0({\mathcal {F}}\ell _G)$
and the set of
![]() $\langle \sigma \rangle $
-orbits in
$\langle \sigma \rangle $
-orbits in
![]() $\pi _1(G)_I$
by [Reference Neupert76, Lemma 2.2.6], a set that is in general no longer a group.
$\pi _1(G)_I$
by [Reference Neupert76, Lemma 2.2.6], a set that is in general no longer a group.
Remark 2.1. We will define bounds on local G-shtukas as (equivalence classes of) certain ind-subschemes of
![]() ${\widehat {{\mathcal {F}}\ell }}_{G,R}:={\mathcal {F}}\ell _G\widehat {\displaystyle \times }_{{\mathbb {F}}_q}\operatorname {\mathrm {Spf}} R$
where R is a finite extension of
${\widehat {{\mathcal {F}}\ell }}_{G,R}:={\mathcal {F}}\ell _G\widehat {\displaystyle \times }_{{\mathbb {F}}_q}\operatorname {\mathrm {Spf}} R$
where R is a finite extension of
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
. In order to define and consider also the generic fibre of the associated moduli spaces, one needs to bound the singularities with respect to
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
. In order to define and consider also the generic fibre of the associated moduli spaces, one needs to bound the singularities with respect to
![]() $z-\zeta $
of the local G-shtukas. In particular, our definition is more restrictive than the one in [Reference Arasteh Rad and Hartl4, Definitions 4.5 and 4.8]. To encode this condition in our notion of bounds, we have to compare
$z-\zeta $
of the local G-shtukas. In particular, our definition is more restrictive than the one in [Reference Arasteh Rad and Hartl4, Definitions 4.5 and 4.8]. To encode this condition in our notion of bounds, we have to compare
![]() ${\widehat {{\mathcal {F}}\ell }}_{G,R}$
to the following closed ind-subschemes associated with a representation of G.
${\widehat {{\mathcal {F}}\ell }}_{G,R}$
to the following closed ind-subschemes associated with a representation of G.
If
![]() $A={\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
or
$A={\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
or
![]() $A={\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
, we let
$A={\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
, we let
![]() $\operatorname {\mathrm {Rep}}_{A}G$
denote the category of (algebraic) representations of G on finite free A-modules. Here, we consider representations
$\operatorname {\mathrm {Rep}}_{A}G$
denote the category of (algebraic) representations of G on finite free A-modules. Here, we consider representations
![]() $\rho \colon G\to \operatorname {\mathrm {SL}}_r$
over
$\rho \colon G\to \operatorname {\mathrm {SL}}_r$
over
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
and the induced functor
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
and the induced functor
![]() ${\mathcal {G}}\mapsto \rho _*{\mathcal {G}}$
from
${\mathcal {G}}\mapsto \rho _*{\mathcal {G}}$
from
![]() $L^+G$
-torsors to
$L^+G$
-torsors to
![]() $L^+\operatorname {\mathrm {SL}}_r$
-torsors, which in turn yields a morphism
$L^+\operatorname {\mathrm {SL}}_r$
-torsors, which in turn yields a morphism
![]() $\rho _*\colon {\widehat {{\mathcal {F}}\ell }}_G\to {\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {SL}}_r}$
. Here,
$\rho _*\colon {\widehat {{\mathcal {F}}\ell }}_G\to {\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {SL}}_r}$
. Here,
![]() ${\widehat {{\mathcal {F}}\ell }}_{G}:={\mathcal {F}}\ell _{G,{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}}$
. The category of
${\widehat {{\mathcal {F}}\ell }}_{G}:={\mathcal {F}}\ell _{G,{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}}$
. The category of
![]() $L^+\operatorname {\mathrm {SL}}_r$
-torsors on S is equivalent to the category of pairs
$L^+\operatorname {\mathrm {SL}}_r$
-torsors on S is equivalent to the category of pairs
![]() $(M,\alpha )$
, where M is a finite locally free
$(M,\alpha )$
, where M is a finite locally free
![]() ${\mathcal {O}}_S\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-module of rank r on S and
${\mathcal {O}}_S\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-module of rank r on S and
![]() is an isomorphism of
is an isomorphism of
![]() ${\mathcal {O}}_S\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-modules, with isomorphisms as morphisms. We denote the
${\mathcal {O}}_S\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-modules, with isomorphisms as morphisms. We denote the
![]() ${\mathcal {O}}_S\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-module associated with an
${\mathcal {O}}_S\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-module associated with an
![]() $L^+\operatorname {\mathrm {SL}}_r$
-torsor
$L^+\operatorname {\mathrm {SL}}_r$
-torsor
![]() ${\mathcal {S}}$
by
${\mathcal {S}}$
by
![]() $M({\mathcal {S}})$
. For example,
$M({\mathcal {S}})$
. For example,
![]() $M\big ((L^+\operatorname {\mathrm {SL}}_r)_S\big )={\mathcal {O}}_S\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}^{\oplus r}$
. For a positive integer n we consider the closed ind-subscheme of
$M\big ((L^+\operatorname {\mathrm {SL}}_r)_S\big )={\mathcal {O}}_S\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}^{\oplus r}$
. For a positive integer n we consider the closed ind-subscheme of
![]() ${\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {SL}}_r}$
given by
${\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {SL}}_r}$
given by

It is a
![]() $\zeta $
-adic formal scheme over
$\zeta $
-adic formal scheme over
![]() $\operatorname {\mathrm {Spf}}{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
by [Reference Hartl and Viehmann56, Proposition 5.5]; see Example 2.8 for more explanations. Note that the compatibility with the isomorphism
$\operatorname {\mathrm {Spf}}{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
by [Reference Hartl and Viehmann56, Proposition 5.5]; see Example 2.8 for more explanations. Note that the compatibility with the isomorphism
![]() is equivalent to the assertion that the inclusion of the exterior powers in (2.1) is an equality for
is equivalent to the assertion that the inclusion of the exterior powers in (2.1) is an equality for
![]() $j=r$
, because
$j=r$
, because
![]() $\big ({\mathcal {S}},\,\delta \big )\in {\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {SL}}_r}(S)$
implies
$\big ({\mathcal {S}},\,\delta \big )\in {\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {SL}}_r}(S)$
implies
![]() $\wedge ^r M(\delta )=\alpha $
. We then require the bounds to factor through some
$\wedge ^r M(\delta )=\alpha $
. We then require the bounds to factor through some
![]() ${\widehat {{\mathcal {F}}\ell }}^{(n)}_{\operatorname {\mathrm {SL}}_r}$
; cf. Condition (b)(iv).
${\widehat {{\mathcal {F}}\ell }}^{(n)}_{\operatorname {\mathrm {SL}}_r}$
; cf. Condition (b)(iv).
A different way to formulate such a condition would be to use the isomorphism
where the right-hand side is the BD-Grassmannian associated with G of [Reference Richarz84, Definition 3.3]. Here we use that G extends by [Reference Richarz84, Lemma 3.1] to a smooth affine group scheme
![]() $G_X$
on a smooth connected curve X over
$G_X$
on a smooth connected curve X over
![]() ${\mathbb {F}}_q$
on which
${\mathbb {F}}_q$
on which
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
is identified with the completion of the local ring at a point
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
is identified with the completion of the local ring at a point
![]() $x\in X$
. The map
$x\in X$
. The map
![]() $\operatorname {\mathrm {Spec}} R\to X$
comes from the inclusion
$\operatorname {\mathrm {Spec}} R\to X$
comes from the inclusion
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\hookrightarrow R, z\mapsto \zeta $
. The isomorphism (2.2) also induces a comparison between specific bounds with global Schubert varieties of [Reference Richarz84]; compare Example 2.7.
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\hookrightarrow R, z\mapsto \zeta $
. The isomorphism (2.2) also induces a comparison between specific bounds with global Schubert varieties of [Reference Richarz84]; compare Example 2.7.
We now define bounds by requiring minimal conditions needed to obtain the results of this article. In Remark 2.11 we will discuss further conditions that seem reasonable to impose but that we do not need to assume in this article. We will then also describe more explicitly which bounds can arise, and in Examples 2.7 and 2.8 we will give a more specific class of bounds that depend on cocharacters of the generic fibre of G.
Definition 2.2.
-
(a) We fix an algebraic closure
 ${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)^{\textrm {alg}}$
of
${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)^{\textrm {alg}}$
of
 ${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
and consider pairs
${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
and consider pairs
 $(R,\hat Z_R)$
, where
$(R,\hat Z_R)$
, where
 $R/{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
is a finite extension of discrete valuation rings such that
$R/{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
is a finite extension of discrete valuation rings such that
 $R\subset {\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)^{\textrm {alg}}$
and where
$R\subset {\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)^{\textrm {alg}}$
and where
 $\hat Z_R\subset {\widehat {{\mathcal {F}}\ell }}_{G,R}:={\mathcal {F}}\ell _G\widehat {\displaystyle \times }_{{\mathbb {F}}_q}\operatorname {\mathrm {Spf}} R$
is a closed ind-subscheme. Two such pairs
$\hat Z_R\subset {\widehat {{\mathcal {F}}\ell }}_{G,R}:={\mathcal {F}}\ell _G\widehat {\displaystyle \times }_{{\mathbb {F}}_q}\operatorname {\mathrm {Spf}} R$
is a closed ind-subscheme. Two such pairs
 $(R,\hat Z_R)$
and
$(R,\hat Z_R)$
and
 $(R^{\prime }\!,\hat Z^{\prime }_{R^{\prime }})$
are equivalent if for some finite extension of discrete valuation rings
$(R^{\prime }\!,\hat Z^{\prime }_{R^{\prime }})$
are equivalent if for some finite extension of discrete valuation rings
 ${\widetilde {R}}/{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
with
${\widetilde {R}}/{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
with
 $R,R^{\prime }\subset {\widetilde {R}}$
the two closed ind-subschemes
$R,R^{\prime }\subset {\widetilde {R}}$
the two closed ind-subschemes
 $\hat {Z}_R\widehat {\displaystyle \times }_{\operatorname {\mathrm {Spf}} R}\operatorname {\mathrm {Spf}}{\widetilde {R}}$
and
$\hat {Z}_R\widehat {\displaystyle \times }_{\operatorname {\mathrm {Spf}} R}\operatorname {\mathrm {Spf}}{\widetilde {R}}$
and
 $\hat {Z}^{\prime }_{R^{\prime }}\widehat {\displaystyle \times }_{\operatorname {\mathrm {Spf}} R^{\prime }}\operatorname {\mathrm {Spf}}{\widetilde {R}}$
of
$\hat {Z}^{\prime }_{R^{\prime }}\widehat {\displaystyle \times }_{\operatorname {\mathrm {Spf}} R^{\prime }}\operatorname {\mathrm {Spf}}{\widetilde {R}}$
of
 ${\widehat {{\mathcal {F}}\ell }}_{G,{\widetilde {R}}}$
are equal. By [Reference Arasteh Rad and Hartl4, Remark 4.6], this then holds for all such rings
${\widehat {{\mathcal {F}}\ell }}_{G,{\widetilde {R}}}$
are equal. By [Reference Arasteh Rad and Hartl4, Remark 4.6], this then holds for all such rings
 ${\widetilde {R}}$
.
${\widetilde {R}}$
. -
(b) A bound is an equivalence class
 $\hat Z:=[(R,\hat Z_R)]$
of pairs
$\hat Z:=[(R,\hat Z_R)]$
of pairs
 $(R,\hat Z_R)$
as above satisfying the following properties:
$(R,\hat Z_R)$
as above satisfying the following properties:-
(i) All
 $\hat {Z}_R\subset {\widehat {{\mathcal {F}}\ell }}_{G,R}$
are stable under the left
$\hat {Z}_R\subset {\widehat {{\mathcal {F}}\ell }}_{G,R}$
are stable under the left
 $L^+G$
-action.
$L^+G$
-action. -
(ii) The special fibre
 $Z_R:=\hat {Z}_R\widehat {\displaystyle \times }_{\operatorname {\mathrm {Spf}} R}\operatorname {\mathrm {Spec}} \kappa _R$
is a quasi-compact subscheme of
$Z_R:=\hat {Z}_R\widehat {\displaystyle \times }_{\operatorname {\mathrm {Spf}} R}\operatorname {\mathrm {Spec}} \kappa _R$
is a quasi-compact subscheme of
 ${\mathcal {F}}\ell _G\widehat {\displaystyle \times }_{{\mathbb {F}}_q}\kappa _R$
where
${\mathcal {F}}\ell _G\widehat {\displaystyle \times }_{{\mathbb {F}}_q}\kappa _R$
where
 $\kappa _R$
is the residue field of R. (By [Reference Arasteh Rad and Hartl4, Remark 4.10] this implies that the
$\kappa _R$
is the residue field of R. (By [Reference Arasteh Rad and Hartl4, Remark 4.10] this implies that the
 $\hat Z_R$
are formal schemes in the sense of [Reference Grothendieck44,
$\hat Z_R$
are formal schemes in the sense of [Reference Grothendieck44,
 $\mathrm{I}_{\mathrm{new}}$
, § 10].)
$\mathrm{I}_{\mathrm{new}}$
, § 10].) -
(iii)
 $\hat Z_R$
is a
$\hat Z_R$
is a
 $\zeta $
-adic formal scheme over
$\zeta $
-adic formal scheme over
 $\operatorname {\mathrm {Spf}} R$
.
$\operatorname {\mathrm {Spf}} R$
. -
(iv) There is a faithful representation
 $\rho \colon G\hookrightarrow \operatorname {\mathrm {SL}}_r$
over
$\rho \colon G\hookrightarrow \operatorname {\mathrm {SL}}_r$
over
 ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
and a positive integer n such that all of the induced morphisms
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
and a positive integer n such that all of the induced morphisms
 $\rho _*\colon \hat {Z}_R\to {\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {SL}}_r,R}$
factor through
$\rho _*\colon \hat {Z}_R\to {\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {SL}}_r,R}$
factor through
 ${\widehat {{\mathcal {F}}\ell }}^{(n)}_{\operatorname {\mathrm {SL}}_r,R}$
.
${\widehat {{\mathcal {F}}\ell }}^{(n)}_{\operatorname {\mathrm {SL}}_r,R}$
. -
(v) Let
 $\hat {Z}_R^{\textrm {an}}$
be the strictly
$\hat {Z}_R^{\textrm {an}}$
be the strictly
 $R[\tfrac {1}{\zeta }]$
-analytic space associated with
$R[\tfrac {1}{\zeta }]$
-analytic space associated with
 $\hat {Z}_R$
. By Proposition 2.6(d) there is a closed subscheme
$\hat {Z}_R$
. By Proposition 2.6(d) there is a closed subscheme
 $\hat Z_E$
of the affine Grassmannian
$\hat Z_E$
of the affine Grassmannian
 $\operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}}\times _{{\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)}\operatorname {\mathrm {Spec}} E_{\hat Z}$
from (1.2) such that
$\operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}}\times _{{\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)}\operatorname {\mathrm {Spec}} E_{\hat Z}$
from (1.2) such that
 $\hat {Z}_R^{\textrm {an}}$
arises by base change to
$\hat {Z}_R^{\textrm {an}}$
arises by base change to
 $R[\tfrac {1}{\zeta }]$
from the strictly
$R[\tfrac {1}{\zeta }]$
from the strictly
 $E_{\hat Z}$
-analytic space
$E_{\hat Z}$
-analytic space
 $(\hat Z_E)^{\textrm {an}}$
associated with
$(\hat Z_E)^{\textrm {an}}$
associated with
 $\hat Z_E$
. Then we require that
$\hat Z_E$
. Then we require that
 $\hat Z_E$
, and hence also all of the
$\hat Z_E$
, and hence also all of the
 $\hat {Z}_R^{\textrm {an}}$
are invariant under the left multiplication of
$\hat {Z}_R^{\textrm {an}}$
are invariant under the left multiplication of
 $G\big ({\,{\scriptscriptstyle \bullet }\,}\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )$
on
$G\big ({\,{\scriptscriptstyle \bullet }\,}\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )$
on
 $\operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}}$
.
$\operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}}$
.
-
-
(c) The reflex ring
 $R_{\hat Z}$
of a bound
$R_{\hat Z}$
of a bound
 $\hat Z=[(R,\hat Z_R)]$
is the intersection of the fixed field of
$\hat Z=[(R,\hat Z_R)]$
is the intersection of the fixed field of
 $\{\gamma \in \operatorname {\mathrm {Aut}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}}({\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)^{\textrm {alg}})\colon \gamma (\hat {Z})=\hat {Z}\,\}$
in
$\{\gamma \in \operatorname {\mathrm {Aut}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}}({\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)^{\textrm {alg}})\colon \gamma (\hat {Z})=\hat {Z}\,\}$
in
 ${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)^{\textrm {alg}}$
with all of the finite extensions
${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)^{\textrm {alg}}$
with all of the finite extensions
 $R\subset {\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)^{\textrm {alg}}$
of
$R\subset {\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)^{\textrm {alg}}$
of
 ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
over which a representative
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
over which a representative
 $\hat {Z}_R$
of
$\hat {Z}_R$
of
 $\hat {Z}$
exists. We write
$\hat {Z}$
exists. We write
 $R_{\hat Z}=\kappa \mathrm {[}\kern-0.15em\mathrm {[}\xi \mathrm {]}\kern-0.15em\mathrm {]}$
and call its fraction field
$R_{\hat Z}=\kappa \mathrm {[}\kern-0.15em\mathrm {[}\xi \mathrm {]}\kern-0.15em\mathrm {]}$
and call its fraction field
 $E:=E_{\hat Z}=\kappa (\kern-0.15em(\xi )\kern-0.15em)$
the reflex field of
$E:=E_{\hat Z}=\kappa (\kern-0.15em(\xi )\kern-0.15em)$
the reflex field of
 $\hat {Z}$
. We let
$\hat {Z}$
. We let
 $\breve R_{\hat Z}:={\mathbb {F}}\mathrm {[}\kern-0.15em\mathrm {[}\xi \mathrm {]}\kern-0.15em\mathrm {]}$
and
$\breve R_{\hat Z}:={\mathbb {F}}\mathrm {[}\kern-0.15em\mathrm {[}\xi \mathrm {]}\kern-0.15em\mathrm {]}$
and
 $\breve E:=\breve E_{\hat Z}:={\mathbb {F}}(\kern-0.15em(\xi )\kern-0.15em)$
be the completions of their maximal unramified extensions, where
$\breve E:=\breve E_{\hat Z}:={\mathbb {F}}(\kern-0.15em(\xi )\kern-0.15em)$
be the completions of their maximal unramified extensions, where
 ${\mathbb {F}}$
is an algebraic closure of the finite field
${\mathbb {F}}$
is an algebraic closure of the finite field
 $\kappa $
.
$\kappa $
. -
(d) Let
 $\hat Z=[(R,\hat Z_R)]$
be a bound with reflex ring
$\hat Z=[(R,\hat Z_R)]$
be a bound with reflex ring
 $R_{\hat Z}$
. Let
$R_{\hat Z}$
. Let
 ${\mathcal {G}}$
and
${\mathcal {G}}$
and
 ${\mathcal {G}}^{\prime }$
be
${\mathcal {G}}^{\prime }$
be
 $L^+G$
-torsors over a scheme
$L^+G$
-torsors over a scheme
 $S\in {{\mathcal {N}}\!\mathit {ilp}}_{R_{\hat Z}}$
and let
$S\in {{\mathcal {N}}\!\mathit {ilp}}_{R_{\hat Z}}$
and let
 be an isomorphism of the associated
be an isomorphism of the associated
 $LG$
-torsors. We consider an étale covering
$LG$
-torsors. We consider an étale covering
 $S^{\prime }\to S$
over which trivialisations
$S^{\prime }\to S$
over which trivialisations
 and
and
 exist. Then the automorphism
exist. Then the automorphism
 $\alpha ^{\prime }\circ \delta \circ \alpha ^{-1}$
of
$\alpha ^{\prime }\circ \delta \circ \alpha ^{-1}$
of
 $(LG)_{S^{\prime }}$
corresponds to a morphism
$(LG)_{S^{\prime }}$
corresponds to a morphism
 $S^{\prime }\to LG\widehat {\displaystyle \times }_{{\mathbb {F}}_q}\operatorname {\mathrm {Spf}} R_{\hat Z}$
. We say that
$S^{\prime }\to LG\widehat {\displaystyle \times }_{{\mathbb {F}}_q}\operatorname {\mathrm {Spf}} R_{\hat Z}$
. We say that
 $\delta $
is bounded by
$\delta $
is bounded by
 $\hat {Z}$
if for every such trivialisation and for every finite extension R of
$\hat {Z}$
if for every such trivialisation and for every finite extension R of
 ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
over which a representative
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
over which a representative
 $\hat Z_R$
of
$\hat Z_R$
of
 $\hat Z$
exists the induced morphism factors through
$\hat Z$
exists the induced morphism factors through $$ \begin{align*} S^{\prime}\widehat{\displaystyle\times}_{R_{\hat Z}}\operatorname{\mathrm{Spf}} R\longrightarrow LG\widehat{\displaystyle\times}_{{\mathbb{F}}_q}\operatorname{\mathrm{Spf}} R\longrightarrow {\widehat{{\mathcal{F}}\ell}}_{G,R} \end{align*} $$
$$ \begin{align*} S^{\prime}\widehat{\displaystyle\times}_{R_{\hat Z}}\operatorname{\mathrm{Spf}} R\longrightarrow LG\widehat{\displaystyle\times}_{{\mathbb{F}}_q}\operatorname{\mathrm{Spf}} R\longrightarrow {\widehat{{\mathcal{F}}\ell}}_{G,R} \end{align*} $$
 $\hat {Z}_R$
. Furthermore, we say that a local G-shtuka
$\hat {Z}_R$
. Furthermore, we say that a local G-shtuka
 ${\underline {{\mathcal {G}}}}=({\mathcal {G}}, \tau _{\mathcal {G}})$
is bounded by
${\underline {{\mathcal {G}}}}=({\mathcal {G}}, \tau _{\mathcal {G}})$
is bounded by
 $\hat {Z}$
if
$\hat {Z}$
if
 $\tau _{\mathcal {G}}$
is bounded by
$\tau _{\mathcal {G}}$
is bounded by
 $\hat {Z}$
and, even more important, that
$\hat {Z}$
and, even more important, that
 ${\underline {{\mathcal {G}}}}$
is bounded by
${\underline {{\mathcal {G}}}}$
is bounded by
 $\hat {Z}^{-1}$
if the inverse
$\hat {Z}^{-1}$
if the inverse
 $\tau _{\mathcal {G}}^{-1}$
of its Frobenius is bounded by
$\tau _{\mathcal {G}}^{-1}$
of its Frobenius is bounded by
 $\hat {Z}$
; compare the remark below.
$\hat {Z}$
; compare the remark below.
Let us explain the conditions of this definition in more detail.
Remark 2.3. (a) The definition of a bound in Definition 2.2(b) is more restrictive than the one in [Reference Arasteh Rad and Hartl4, Definition 4.8] where only conditions (b)(i) and (b)(ii) were required. The reason is that in [Reference Arasteh Rad and Hartl4] the content of Proposition 2.6 was not needed and the
![]() $R[\tfrac {1}{\zeta }]$
-analytic spaces
$R[\tfrac {1}{\zeta }]$
-analytic spaces
![]() $(\hat {Z}_R)^{\textrm {an}}$
were not considered.
$(\hat {Z}_R)^{\textrm {an}}$
were not considered.
In this article we will mainly consider local G-shtukas that are bounded by
![]() $\hat {Z}^{-1}$
. This definition coincides with the notion of boundedness from [Reference Arasteh Rad and Hartl4, Definition 4.8(b)] in the following way. If
$\hat {Z}^{-1}$
. This definition coincides with the notion of boundedness from [Reference Arasteh Rad and Hartl4, Definition 4.8(b)] in the following way. If
![]() $\hat {Z}$
is a bound in the sense of [Reference Arasteh Rad and Hartl4, Definition 4.8], like, for example, our bound
$\hat {Z}$
is a bound in the sense of [Reference Arasteh Rad and Hartl4, Definition 4.8], like, for example, our bound
![]() $\hat Z$
, then by Lemma 2.12 there is a bound
$\hat Z$
, then by Lemma 2.12 there is a bound
![]() $\hat {Z}^{-1}$
in the sense of [Reference Arasteh Rad and Hartl4, Definition 4.8] and
$\hat {Z}^{-1}$
in the sense of [Reference Arasteh Rad and Hartl4, Definition 4.8] and
![]() $\tau _{\mathcal {G}}^{-1}$
is bounded by
$\tau _{\mathcal {G}}^{-1}$
is bounded by
![]() $\hat {Z}$
if and only if
$\hat {Z}$
if and only if
![]() $\tau _{\mathcal {G}}$
is bounded by
$\tau _{\mathcal {G}}$
is bounded by
![]() $\hat {Z}^{-1}$
.
$\hat {Z}^{-1}$
.
(b) The reflex ring in Definition 2.2(c) is always the ring of integers of a finite extension of
![]() ${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
. For a detailed explanation of the definition of the reflex ring and a comparison with the number field case, see [Reference Arasteh Rad and Hartl4, Remark 4.7]. We do not know whether in general
${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
. For a detailed explanation of the definition of the reflex ring and a comparison with the number field case, see [Reference Arasteh Rad and Hartl4, Remark 4.7]. We do not know whether in general
![]() $\hat Z$
has a representative over the reflex ring. In contrast, the equivalence class of the
$\hat Z$
has a representative over the reflex ring. In contrast, the equivalence class of the
![]() $Z_R:=\hat {Z}_R\widehat {\displaystyle \times }_{\operatorname {\mathrm {Spf}} R}\operatorname {\mathrm {Spec}} \kappa _R$
always has a representative
$Z_R:=\hat {Z}_R\widehat {\displaystyle \times }_{\operatorname {\mathrm {Spf}} R}\operatorname {\mathrm {Spec}} \kappa _R$
always has a representative
![]() $Z\subset {\mathcal {F}}\ell _G\widehat {\displaystyle \times }_{{\mathbb {F}}_q}\operatorname {\mathrm {Spec}}\kappa $
over the residue field
$Z\subset {\mathcal {F}}\ell _G\widehat {\displaystyle \times }_{{\mathbb {F}}_q}\operatorname {\mathrm {Spec}}\kappa $
over the residue field
![]() $\kappa $
of the reflex ring
$\kappa $
of the reflex ring
![]() $R_{\hat Z}$
, because the Galois descent for closed ind-subschemes of
$R_{\hat Z}$
, because the Galois descent for closed ind-subschemes of
![]() ${\mathcal {F}}\ell _G$
is effective. We call Z the special fibre of
${\mathcal {F}}\ell _G$
is effective. We call Z the special fibre of
![]() $\hat Z$
. It is a projective scheme over
$\hat Z$
. It is a projective scheme over
![]() $\kappa $
by [Reference Hartl and Viehmann56, Lemma 5.4] because
$\kappa $
by [Reference Hartl and Viehmann56, Lemma 5.4] because
![]() ${\mathcal {F}}\ell _G$
is ind-projective.
${\mathcal {F}}\ell _G$
is ind-projective.
(c) The condition of Definition 2.2(d) is satisfied for all trivialisations
![]() $\alpha $
and
$\alpha $
and
![]() $\alpha ^{\prime }$
and for all such finite extensions R of
$\alpha ^{\prime }$
and for all such finite extensions R of
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
if and only if it is satisfied for one trivialisation and for one such finite extension. Indeed, by the
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
if and only if it is satisfied for one trivialisation and for one such finite extension. Indeed, by the
![]() $L^+G$
-invariance of
$L^+G$
-invariance of
![]() $\hat Z$
, the definition is independent of the trivialisations. That one finite extension suffices follows from [Reference Arasteh Rad and Hartl4, Remark 4.6].
$\hat Z$
, the definition is independent of the trivialisations. That one finite extension suffices follows from [Reference Arasteh Rad and Hartl4, Remark 4.6].
(d) At first glance one might think that conditions (b)(i) and (b)(v) of Definition 2.2 are related. However, in Example 2.9 we show that we really need to impose both of them.
Before we discuss properties of bounds, we recall the following well-known lemma.
Lemma 2.4. Let
![]() $f\colon X\to Y$
be a morphism of locally Noetherian adic formal schemes. Then f is a closed immersion in the sense of [Reference Grothendieck44,
$f\colon X\to Y$
be a morphism of locally Noetherian adic formal schemes. Then f is a closed immersion in the sense of [Reference Grothendieck44,
![]() $\mathrm{I}_{\mathrm{new}}$
, Definition 10.14.2] if and only if f is adic and an ind-closed immersion of ind-schemes.
$\mathrm{I}_{\mathrm{new}}$
, Definition 10.14.2] if and only if f is adic and an ind-closed immersion of ind-schemes.
Proof. By definition f is a closed immersion if and only if there is a covering of Y by open affine formal subschemes
![]() $\operatorname {\mathrm {Spf}} B$
such that
$\operatorname {\mathrm {Spf}} B$
such that
![]() $X\times _Y\operatorname {\mathrm {Spf}} B\cong \operatorname {\mathrm {Spf}} B/{\mathfrak {a}}$
for an ideal
$X\times _Y\operatorname {\mathrm {Spf}} B\cong \operatorname {\mathrm {Spf}} B/{\mathfrak {a}}$
for an ideal
![]() ${\mathfrak {a}}\subset B$
. In particular, if
${\mathfrak {a}}\subset B$
. In particular, if
![]() $I\subset B$
is a finitely generated ideal of definition of
$I\subset B$
is a finitely generated ideal of definition of
![]() $\operatorname {\mathrm {Spf}} B$
, then
$\operatorname {\mathrm {Spf}} B$
, then
![]() $I\cdot B/{\mathfrak {a}}$
is an ideal of definition of
$I\cdot B/{\mathfrak {a}}$
is an ideal of definition of
![]() $\operatorname {\mathrm {Spf}} B/{\mathfrak {a}}$
and so f is adic. Moreover,
$\operatorname {\mathrm {Spf}} B/{\mathfrak {a}}$
and so f is adic. Moreover,
![]() $\operatorname {\mathrm {Spf}} B={\displaystyle \lim _{\longleftarrow }}\operatorname {\mathrm {Spec}} B/I^n$
and
$\operatorname {\mathrm {Spf}} B={\displaystyle \lim _{\longleftarrow }}\operatorname {\mathrm {Spec}} B/I^n$
and
![]() $\operatorname {\mathrm {Spf}} B/{\mathfrak {a}}={\displaystyle \lim _{\longleftarrow }}\operatorname {\mathrm {Spec}} B/({\mathfrak {a}}+I^n)$
and so f is an ind-closed immersion of ind-schemes.
$\operatorname {\mathrm {Spf}} B/{\mathfrak {a}}={\displaystyle \lim _{\longleftarrow }}\operatorname {\mathrm {Spec}} B/({\mathfrak {a}}+I^n)$
and so f is an ind-closed immersion of ind-schemes.
To prove the converse, let
![]() ${\mathcal {I}}\subset {\mathcal {O}}_Y$
be an ideal sheaf of definition. Because f is adic,
${\mathcal {I}}\subset {\mathcal {O}}_Y$
be an ideal sheaf of definition. Because f is adic,
![]() ${\mathcal {I}}\cdot {\mathcal {O}}_X$
is an ideal sheaf of definition of X. That f is an ind-closed immersion means that
${\mathcal {I}}\cdot {\mathcal {O}}_X$
is an ideal sheaf of definition of X. That f is an ind-closed immersion means that
![]() $X_n:=(X,{\mathcal {O}}_X/{\mathcal {I}}^n)\hookrightarrow Y_n:=(Y,{\mathcal {O}}_Y/{\mathcal {I}}^n)$
is a closed immersion of schemes. So there is a sheaf of ideals
$X_n:=(X,{\mathcal {O}}_X/{\mathcal {I}}^n)\hookrightarrow Y_n:=(Y,{\mathcal {O}}_Y/{\mathcal {I}}^n)$
is a closed immersion of schemes. So there is a sheaf of ideals
![]() ${\mathfrak {a}}_n\subset {\mathcal {O}}_Y/{\mathcal {I}}^n$
defining
${\mathfrak {a}}_n\subset {\mathcal {O}}_Y/{\mathcal {I}}^n$
defining
![]() $X_n$
. Moreover,
$X_n$
. Moreover,
![]() ${\mathfrak {a}}_n={\mathfrak {a}}_{n+1}\cdot {\mathcal {O}}_Y/{\mathcal {I}}^n$
, because
${\mathfrak {a}}_n={\mathfrak {a}}_{n+1}\cdot {\mathcal {O}}_Y/{\mathcal {I}}^n$
, because
![]() $X_n=X_{n+1}\times _{Y_{n+1}}Y_n$
. Let
$X_n=X_{n+1}\times _{Y_{n+1}}Y_n$
. Let
![]() ${\mathfrak {a}}:={\displaystyle \lim _{\longleftarrow }} {\mathfrak {a}}_n\subset {\displaystyle \lim _{\longleftarrow }} {\mathcal {O}}_Y/{\mathcal {I}}^n={\mathcal {O}}_Y$
. Because Y is locally Noetherian,
${\mathfrak {a}}:={\displaystyle \lim _{\longleftarrow }} {\mathfrak {a}}_n\subset {\displaystyle \lim _{\longleftarrow }} {\mathcal {O}}_Y/{\mathcal {I}}^n={\mathcal {O}}_Y$
. Because Y is locally Noetherian,
![]() ${\mathfrak {a}}$
is a coherent sheaf of
${\mathfrak {a}}$
is a coherent sheaf of
![]() ${\mathcal {O}}_Y$
-modules by [Reference Grothendieck44,
${\mathcal {O}}_Y$
-modules by [Reference Grothendieck44,
![]() $\hbox{I}_{\mathrm{new}}$
, Theorem 10.10.2]. Then
$\hbox{I}_{\mathrm{new}}$
, Theorem 10.10.2]. Then
![]() $X_n=(X,\big ({\mathcal {O}}_Y/({\mathfrak {a}}+{\mathcal {I}}^n)\big )|_X)$
and
$X_n=(X,\big ({\mathcal {O}}_Y/({\mathfrak {a}}+{\mathcal {I}}^n)\big )|_X)$
and
![]() $X=\big (X,({\mathcal {O}}_Y/{\mathfrak {a}})|_X\big )$
. This proves that f is a closed immersion in the sense of [Reference Grothendieck44,
$X=\big (X,({\mathcal {O}}_Y/{\mathfrak {a}})|_X\big )$
. This proves that f is a closed immersion in the sense of [Reference Grothendieck44,
![]() $\mathrm{I}_{\mathrm{new}}$
, Definition 10.14.2].
$\mathrm{I}_{\mathrm{new}}$
, Definition 10.14.2].
Remark 2.5. Without the assumption that f is adic, the conclusion of the lemma is false, as the following example shows. Let
![]() $Y={\displaystyle \lim _{\longrightarrow }} Y_n$
with
$Y={\displaystyle \lim _{\longrightarrow }} Y_n$
with
![]() $Y_n=\operatorname {\mathrm {Spec}}{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}[x]/(\zeta ^n)$
and
$Y_n=\operatorname {\mathrm {Spec}}{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}[x]/(\zeta ^n)$
and
![]() $X={\displaystyle \lim _{\longrightarrow }} X_n$
with
$X={\displaystyle \lim _{\longrightarrow }} X_n$
with
![]() $X_n=\operatorname {\mathrm {Spec}}{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}[x]/(\zeta ,x)^n$
. Then
$X_n=\operatorname {\mathrm {Spec}}{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}[x]/(\zeta ,x)^n$
. Then
![]() $X=\operatorname {\mathrm {Spf}}{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta ,x\mathrm {]}\kern-0.15em\mathrm {]}\to Y=\operatorname {\mathrm {Spf}}{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}\langle x\rangle $
, with the notation of (6.3), is an ind-closed immersion of ind-schemes but not a closed immersion of formal schemes.
$X=\operatorname {\mathrm {Spf}}{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta ,x\mathrm {]}\kern-0.15em\mathrm {]}\to Y=\operatorname {\mathrm {Spf}}{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}\langle x\rangle $
, with the notation of (6.3), is an ind-closed immersion of ind-schemes but not a closed immersion of formal schemes.
In the next proposition we associate with a bound
![]() $\hat Z$
a strictly
$\hat Z$
a strictly
![]() ${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
-analytic space in the sense of Berkovich [Reference Berkovich7], [Reference Berkovich8]. On the category of
${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
-analytic space in the sense of Berkovich [Reference Berkovich7], [Reference Berkovich8]. On the category of
![]() ${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
-analytic spaces we consider the étale topology; see [Reference Berkovich8, § 4.1].
${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
-analytic spaces we consider the étale topology; see [Reference Berkovich8, § 4.1].
Proposition 2.6. Let
![]() $\hat Z=[(R,\hat Z_R)]$
be a bound with reflex ring
$\hat Z=[(R,\hat Z_R)]$
be a bound with reflex ring
![]() $R_{\hat {Z}}$
, and let
$R_{\hat {Z}}$
, and let
![]() $E:=E_{\hat Z}:=R_{\hat Z}[\tfrac {1}{\zeta }]$
be its field of fractions. We only assume that Z satisfies conditions (b)(i)–(b)(iv) from Definition 2.2 but not condition (b)(v), whose formulation uses the results of the present proposition.
$E:=E_{\hat Z}:=R_{\hat Z}[\tfrac {1}{\zeta }]$
be its field of fractions. We only assume that Z satisfies conditions (b)(i)–(b)(iv) from Definition 2.2 but not condition (b)(v), whose formulation uses the results of the present proposition.
-
(a) Then for every representation
 $\rho \colon G\to \operatorname {\mathrm {SL}}_{r}$
over
$\rho \colon G\to \operatorname {\mathrm {SL}}_{r}$
over
 ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
there is a positive integer n such that all of the induced morphisms
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
there is a positive integer n such that all of the induced morphisms
 $\rho _*\colon \hat {Z}_R\hookrightarrow {\widehat {{\mathcal {F}}\ell }}_{G,R}\to {\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {SL}}_{r},R}$
factor through
$\rho _*\colon \hat {Z}_R\hookrightarrow {\widehat {{\mathcal {F}}\ell }}_{G,R}\to {\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {SL}}_{r},R}$
factor through
 ${\widehat {{\mathcal {F}}\ell }}^{(n)}_{\operatorname {\mathrm {SL}}_{r},R}$
.
${\widehat {{\mathcal {F}}\ell }}^{(n)}_{\operatorname {\mathrm {SL}}_{r},R}$
. -
(b)
 ${\widehat {{\mathcal {F}}\ell }}^{(n)}_{\operatorname {\mathrm {SL}}_{r}}$
is a
${\widehat {{\mathcal {F}}\ell }}^{(n)}_{\operatorname {\mathrm {SL}}_{r}}$
is a
 $\zeta $
-adic formal scheme over
$\zeta $
-adic formal scheme over
 $\operatorname {\mathrm {Spf}}{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
. It is the
$\operatorname {\mathrm {Spf}}{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
. It is the
 $\zeta $
-adic completion of a projective scheme over
$\zeta $
-adic completion of a projective scheme over
 $\operatorname {\mathrm {Spec}}{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
that we also denote by
$\operatorname {\mathrm {Spec}}{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
that we also denote by
 ${\widehat {{\mathcal {F}}\ell }}^{(n)}_{\operatorname {\mathrm {SL}}_{r}}$
. The corresponding strictly
${\widehat {{\mathcal {F}}\ell }}^{(n)}_{\operatorname {\mathrm {SL}}_{r}}$
. The corresponding strictly
 ${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
-analytic space
${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
-analytic space
 $\big ({\widehat {{\mathcal {F}}\ell }}^{(n)}_{\operatorname {\mathrm {SL}}_{r}}\big )^{\textrm {an}}$
is the analytification of the projective scheme
$\big ({\widehat {{\mathcal {F}}\ell }}^{(n)}_{\operatorname {\mathrm {SL}}_{r}}\big )^{\textrm {an}}$
is the analytification of the projective scheme
 ${\widehat {{\mathcal {F}}\ell }}^{(n)}_{\operatorname {\mathrm {SL}}_{r}}\times _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}}\operatorname {\mathrm {Spec}}{\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
over
${\widehat {{\mathcal {F}}\ell }}^{(n)}_{\operatorname {\mathrm {SL}}_{r}}\times _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}}\operatorname {\mathrm {Spec}}{\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
over
 $\operatorname {\mathrm {Spec}}{\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
that represents the sheaf of sets for the étale topology associated with the presheaf (2.3)The scheme
$\operatorname {\mathrm {Spec}}{\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
that represents the sheaf of sets for the étale topology associated with the presheaf (2.3)The scheme
 ${\widehat {{\mathcal {F}}\ell }}^{(n)}_{\operatorname {\mathrm {SL}}_{r}}\times _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}}\operatorname {\mathrm {Spec}}{\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
is a closed subscheme of the affine Grassmannian
${\widehat {{\mathcal {F}}\ell }}^{(n)}_{\operatorname {\mathrm {SL}}_{r}}\times _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}}\operatorname {\mathrm {Spec}}{\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
is a closed subscheme of the affine Grassmannian
 $\operatorname {\mathrm {Gr}}_{\operatorname {\mathrm {SL}}_r}^{{\mathbf {B}}_{\textrm {dR}}}$
from (1.2).
$\operatorname {\mathrm {Gr}}_{\operatorname {\mathrm {SL}}_r}^{{\mathbf {B}}_{\textrm {dR}}}$
from (1.2).
-
(c) If n and
 $\rho $
are as in (a) such that
$\rho $
are as in (a) such that
 $\rho $
is faithful with quasi-affine quotient
$\rho $
is faithful with quasi-affine quotient
 $\operatorname {\mathrm {SL}}_{r}/G$
, then all
$\operatorname {\mathrm {SL}}_{r}/G$
, then all
 $\rho _*\colon \hat {Z}_R\hookrightarrow {\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {SL}}_{r},R}^{(n)}$
are closed immersions of formal schemes over
$\rho _*\colon \hat {Z}_R\hookrightarrow {\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {SL}}_{r},R}^{(n)}$
are closed immersions of formal schemes over
 $\operatorname {\mathrm {Spf}} R$
in the sense of [Reference Grothendieck44,
$\operatorname {\mathrm {Spf}} R$
in the sense of [Reference Grothendieck44,
 $\mathrm{I}_{\mathrm{new}}$
, Definition 10.14.2].
$\mathrm{I}_{\mathrm{new}}$
, Definition 10.14.2]. -
(d) All
 $\hat {Z}_R$
are
$\hat {Z}_R$
are
 $\zeta $
-adic formal schemes, projective over
$\zeta $
-adic formal schemes, projective over
 $\operatorname {\mathrm {Spf}} R$
. All of their associated
$\operatorname {\mathrm {Spf}} R$
. All of their associated
 $R[\tfrac {1}{\zeta }]$
-analytic spaces
$R[\tfrac {1}{\zeta }]$
-analytic spaces
 $(\hat {Z}_R)^{\textrm {an}}$
arise by base change to
$(\hat {Z}_R)^{\textrm {an}}$
arise by base change to
 $R[\tfrac {1}{\zeta }]$
from one strictly
$R[\tfrac {1}{\zeta }]$
from one strictly
 $E_{\hat Z}$
-analytic space
$E_{\hat Z}$
-analytic space
 $\hat Z^{\textrm {an}}:=(\hat Z_E)^{\textrm {an}}$
associated with a projective scheme
$\hat Z^{\textrm {an}}:=(\hat Z_E)^{\textrm {an}}$
associated with a projective scheme
 $\hat Z_E$
over
$\hat Z_E$
over
 $\operatorname {\mathrm {Spec}} E_{\hat Z}$
. The latter is a closed subscheme of the affine Grassmannian
$\operatorname {\mathrm {Spec}} E_{\hat Z}$
. The latter is a closed subscheme of the affine Grassmannian
 $\operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}}\times _{{\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)}\operatorname {\mathrm {Spec}} E_{\hat Z}$
from (1.2).
$\operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}}\times _{{\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)}\operatorname {\mathrm {Spec}} E_{\hat Z}$
from (1.2).
Remark. The proof of statements (c) and (d) uses the ind-projectivity of the affine flag variety
![]() ${\mathcal {F}}\ell _G$
. If G is not parahoric, it is not clear to us whether
${\mathcal {F}}\ell _G$
. If G is not parahoric, it is not clear to us whether
![]() $\rho _*\colon \hat {Z}_R\hookrightarrow {\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {SL}}_{r},R}^{(n)}$
is a locally closed immersion of
$\rho _*\colon \hat {Z}_R\hookrightarrow {\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {SL}}_{r},R}^{(n)}$
is a locally closed immersion of
![]() $\zeta $
-adic formal schemes.
$\zeta $
-adic formal schemes.
Proof. Proof of Proposition 2.6
(a) Let
![]() $\rho ^{\prime }\colon G\hookrightarrow \operatorname {\mathrm {SL}}_{r^{\prime }}$
and
$\rho ^{\prime }\colon G\hookrightarrow \operatorname {\mathrm {SL}}_{r^{\prime }}$
and
![]() $n^{\prime }$
be the representation and the integer from Definition 2.2(b) for which all
$n^{\prime }$
be the representation and the integer from Definition 2.2(b) for which all
![]() $\rho ^{\prime }_*\colon \hat {Z}_R\to {\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {SL}}_{r^{\prime }},R}$
factor through
$\rho ^{\prime }_*\colon \hat {Z}_R\to {\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {SL}}_{r^{\prime }},R}$
factor through
![]() ${\widehat {{\mathcal {F}}\ell }}^{(n^{\prime })}_{\operatorname {\mathrm {SL}}_{r^{\prime }},R}$
. Let
${\widehat {{\mathcal {F}}\ell }}^{(n^{\prime })}_{\operatorname {\mathrm {SL}}_{r^{\prime }},R}$
. Let
![]() ${\widehat {L\operatorname {\mathrm {SL}}}}_{r^{\prime }\!,R}:=L\operatorname {\mathrm {SL}}_{r^{\prime }}\widehat {\displaystyle \times }_{{\mathbb {F}}_q}\operatorname {\mathrm {Spf}} R$
and define
${\widehat {L\operatorname {\mathrm {SL}}}}_{r^{\prime }\!,R}:=L\operatorname {\mathrm {SL}}_{r^{\prime }}\widehat {\displaystyle \times }_{{\mathbb {F}}_q}\operatorname {\mathrm {Spf}} R$
and define
![]() ${\widehat {L\operatorname {\mathrm {SL}}}}_{r^{\prime }\!,R}^{(n^{\prime })}:={\widehat {L\operatorname {\mathrm {SL}}}}_{r^{\prime }\!,R}\widehat {\displaystyle \times }_{{\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {SL}}_{r^{\prime }},R}}{\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {SL}}_{r^{\prime }},R}^{(n^{\prime })}$
. Then
${\widehat {L\operatorname {\mathrm {SL}}}}_{r^{\prime }\!,R}^{(n^{\prime })}:={\widehat {L\operatorname {\mathrm {SL}}}}_{r^{\prime }\!,R}\widehat {\displaystyle \times }_{{\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {SL}}_{r^{\prime }},R}}{\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {SL}}_{r^{\prime }},R}^{(n^{\prime })}$
. Then
![]() ${\widehat {L\operatorname {\mathrm {SL}}}}_{r^{\prime }\!,R}^{(n^{\prime })}(S)\;=\;$
${\widehat {L\operatorname {\mathrm {SL}}}}_{r^{\prime }\!,R}^{(n^{\prime })}(S)\;=\;$
This implies that
![]() ${\widehat {L\operatorname {\mathrm {SL}}}}_{r^{\prime }\!,R}^{(n^{\prime })}$
is an infinite-dimensional affine formal scheme over
${\widehat {L\operatorname {\mathrm {SL}}}}_{r^{\prime }\!,R}^{(n^{\prime })}$
is an infinite-dimensional affine formal scheme over
![]() $\operatorname {\mathrm {Spf}} R$
. Thus, its closed subscheme
$\operatorname {\mathrm {Spf}} R$
. Thus, its closed subscheme
![]() ${\widehat {LG}}^{(n^{\prime })}_R:=(LG\widehat {\displaystyle \times }_{{\mathbb {F}}_q}\operatorname {\mathrm {Spf}} R)\widehat {\displaystyle \times }_{{\widehat {L\operatorname {\mathrm {SL}}}}_{r^{\prime }\!,R}}{\widehat {L\operatorname {\mathrm {SL}}}}_{r^{\prime }\!,R}^{(n^{\prime })}$
is also affine. By [Reference Arasteh Rad and Hartl4, Remark 4.10], the ind-schemes
${\widehat {LG}}^{(n^{\prime })}_R:=(LG\widehat {\displaystyle \times }_{{\mathbb {F}}_q}\operatorname {\mathrm {Spf}} R)\widehat {\displaystyle \times }_{{\widehat {L\operatorname {\mathrm {SL}}}}_{r^{\prime }\!,R}}{\widehat {L\operatorname {\mathrm {SL}}}}_{r^{\prime }\!,R}^{(n^{\prime })}$
is also affine. By [Reference Arasteh Rad and Hartl4, Remark 4.10], the ind-schemes
![]() $\hat {Z}_R$
are in fact formal schemes over
$\hat {Z}_R$
are in fact formal schemes over
![]() $\operatorname {\mathrm {Spf}} R$
in the sense of [Reference Grothendieck44,
$\operatorname {\mathrm {Spf}} R$
in the sense of [Reference Grothendieck44,
![]() $\mathrm{I}_{\mathrm{new}}$
]. Because the morphism
$\mathrm{I}_{\mathrm{new}}$
]. Because the morphism
![]() $LG\to {\mathcal {F}}\ell _G$
has sections étale locally, there is an étale covering of formal schemes
$LG\to {\mathcal {F}}\ell _G$
has sections étale locally, there is an étale covering of formal schemes
![]() $\hat {Z}_R^{\prime }\to \hat {Z}_R$
such that the morphism
$\hat {Z}_R^{\prime }\to \hat {Z}_R$
such that the morphism
![]() $\hat {Z}_R^{\prime }\to {\widehat {{\mathcal {F}}\ell }}_{G,R}$
factors through
$\hat {Z}_R^{\prime }\to {\widehat {{\mathcal {F}}\ell }}_{G,R}$
factors through
![]() ${\widehat {LG}}^{(n^{\prime })}_R$
. Let
${\widehat {LG}}^{(n^{\prime })}_R$
. Let
![]() $\operatorname {\mathrm {Spf}} A\subset \hat {Z}_R^{\prime }$
be an affine open formal subscheme with
$\operatorname {\mathrm {Spf}} A\subset \hat {Z}_R^{\prime }$
be an affine open formal subscheme with
![]() $\operatorname {\mathrm {Spf}} A={\displaystyle \lim _{\longrightarrow }} \operatorname {\mathrm {Spec}} A_i$
for some
$\operatorname {\mathrm {Spf}} A={\displaystyle \lim _{\longrightarrow }} \operatorname {\mathrm {Spec}} A_i$
for some
![]() $A_i$
. The induced compatible collection of morphisms
$A_i$
. The induced compatible collection of morphisms
![]() $\operatorname {\mathrm {Spec}} A_i\to {\widehat {LG}}^{(n^{\prime })}_R\hookrightarrow {\widehat {L\operatorname {\mathrm {SL}}}}_{r^{\prime }\!,R}^{(n^{\prime })}$
corresponds to a compatible collection of ring homomorphisms
$\operatorname {\mathrm {Spec}} A_i\to {\widehat {LG}}^{(n^{\prime })}_R\hookrightarrow {\widehat {L\operatorname {\mathrm {SL}}}}_{r^{\prime }\!,R}^{(n^{\prime })}$
corresponds to a compatible collection of ring homomorphisms
![]() ${\mathcal {O}}({\widehat {L\operatorname {\mathrm {SL}}}}_{r^{\prime }\!,R}^{(n^{\prime })})\twoheadrightarrow {\mathcal {O}}({\widehat {LG}}^{(n^{\prime })}_R)\to A_i$
and thus to a homomorphism
${\mathcal {O}}({\widehat {L\operatorname {\mathrm {SL}}}}_{r^{\prime }\!,R}^{(n^{\prime })})\twoheadrightarrow {\mathcal {O}}({\widehat {LG}}^{(n^{\prime })}_R)\to A_i$
and thus to a homomorphism
![]() ${\mathcal {O}}({\widehat {L\operatorname {\mathrm {SL}}}}_{r^{\prime }\!,R}^{(n^{\prime })})\twoheadrightarrow {\mathcal {O}}({\widehat {LG}}^{(n^{\prime })}_R)\to A$
. We view the latter as an element
${\mathcal {O}}({\widehat {L\operatorname {\mathrm {SL}}}}_{r^{\prime }\!,R}^{(n^{\prime })})\twoheadrightarrow {\mathcal {O}}({\widehat {LG}}^{(n^{\prime })}_R)\to A$
. We view the latter as an element
![]() $b\in \operatorname {\mathrm {SL}}_{r^{\prime }}\big (A\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z-\zeta }]\big )\cap \big ((z-\zeta )^{-n^{\prime }({r^{\prime }}-1)}A\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\big )^{r^{\prime }\times r^{\prime }}$
. It actually lies in
$b\in \operatorname {\mathrm {SL}}_{r^{\prime }}\big (A\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z-\zeta }]\big )\cap \big ((z-\zeta )^{-n^{\prime }({r^{\prime }}-1)}A\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\big )^{r^{\prime }\times r^{\prime }}$
. It actually lies in
![]() $G\big (A\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z-\zeta }]\big )$
, because the closed ind-subscheme
$G\big (A\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z-\zeta }]\big )$
, because the closed ind-subscheme
![]() $LG\hookrightarrow L\operatorname {\mathrm {SL}}_{r^{\prime }}$
is defined by the equations that, applied to the entries of a matrix in
$LG\hookrightarrow L\operatorname {\mathrm {SL}}_{r^{\prime }}$
is defined by the equations that, applied to the entries of a matrix in
![]() $\operatorname {\mathrm {SL}}_{r^{\prime }}$
, cut out the closed subgroup
$\operatorname {\mathrm {SL}}_{r^{\prime }}$
, cut out the closed subgroup
![]() $\rho ^{\prime }\colon G\hookrightarrow \operatorname {\mathrm {SL}}_{r^{\prime }}$
.
$\rho ^{\prime }\colon G\hookrightarrow \operatorname {\mathrm {SL}}_{r^{\prime }}$
.
If now
![]() $\rho \colon G\to \operatorname {\mathrm {SL}}_{r}$
is any representation over
$\rho \colon G\to \operatorname {\mathrm {SL}}_{r}$
is any representation over
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
, then we claim that there is a positive integer n that only depends on
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
, then we claim that there is a positive integer n that only depends on
![]() $\rho $
and
$\rho $
and
![]() $n^{\prime }$
such that
$n^{\prime }$
such that
![]() $\rho (b)\in \operatorname {\mathrm {SL}}_{r}\big (A\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z-\zeta }]\big )$
and all
$\rho (b)\in \operatorname {\mathrm {SL}}_{r}\big (A\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z-\zeta }]\big )$
and all
![]() $j\times j$
minors of
$j\times j$
minors of
![]() $\rho (b)$
lie in
$\rho (b)$
lie in
![]() $(z-\zeta )^{n(j^2-jr)}A\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
for all j. Indeed, equality for
$(z-\zeta )^{n(j^2-jr)}A\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
for all j. Indeed, equality for
![]() $j=r$
always holds because the image of
$j=r$
always holds because the image of
![]() $\rho $
is in
$\rho $
is in
![]() $\operatorname {\mathrm {SL}}_{r}$
. For the other j we realise
$\operatorname {\mathrm {SL}}_{r}$
. For the other j we realise
![]() $\rho $
as a subquotient of
$\rho $
as a subquotient of
![]() $\bigoplus _{i=1}^{i_0} (\rho ^{\prime })^{\otimes l_i}\otimes (\rho ^{\prime }{}^{\scriptscriptstyle \lor })^{\otimes m_i}$
for suitable
$\bigoplus _{i=1}^{i_0} (\rho ^{\prime })^{\otimes l_i}\otimes (\rho ^{\prime }{}^{\scriptscriptstyle \lor })^{\otimes m_i}$
for suitable
![]() $i_0$
,
$i_0$
,
![]() $l_i$
and
$l_i$
and
![]() $m_i$
. Then it is enough to show the claim for this direct sum. Here we can bound all minors by bounds only depending on
$m_i$
. Then it is enough to show the claim for this direct sum. Here we can bound all minors by bounds only depending on
![]() $n^{\prime }$
,
$n^{\prime }$
,
![]() $i_0$
and the
$i_0$
and the
![]() $l_i$
and
$l_i$
and
![]() $m_i$
. The claim follows. Thus,
$m_i$
. The claim follows. Thus,
![]() $\rho _*\colon \hat {Z}_R\to {\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {SL}}_{r},R}$
factors through
$\rho _*\colon \hat {Z}_R\to {\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {SL}}_{r},R}$
factors through
![]() ${\widehat {{\mathcal {F}}\ell }}^{(n)}_{\operatorname {\mathrm {SL}}_{r},R}$
because the equations defining the closed ind-subscheme
${\widehat {{\mathcal {F}}\ell }}^{(n)}_{\operatorname {\mathrm {SL}}_{r},R}$
because the equations defining the closed ind-subscheme
![]() ${\widehat {{\mathcal {F}}\ell }}^{(n)}_{\operatorname {\mathrm {SL}}_{r},R}\subset {\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {SL}}_{r},R}$
vanish on the étale covering
${\widehat {{\mathcal {F}}\ell }}^{(n)}_{\operatorname {\mathrm {SL}}_{r},R}\subset {\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {SL}}_{r},R}$
vanish on the étale covering
![]() $\hat {Z}^{\prime }_R\to \hat {Z}_R$
.
$\hat {Z}^{\prime }_R\to \hat {Z}_R$
.
(b) To show that
![]() ${\widehat {{\mathcal {F}}\ell }}^{(n)}_{\operatorname {\mathrm {SL}}_r}(S)$
is projective over
${\widehat {{\mathcal {F}}\ell }}^{(n)}_{\operatorname {\mathrm {SL}}_r}(S)$
is projective over
![]() $\operatorname {\mathrm {Spf}}{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
, we use the equivalence between
$\operatorname {\mathrm {Spf}}{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
, we use the equivalence between
![]() $L^+\operatorname {\mathrm {SL}}_r$
-torsors over S and pairs
$L^+\operatorname {\mathrm {SL}}_r$
-torsors over S and pairs
![]() $(M,\alpha )$
where M is a locally free
$(M,\alpha )$
where M is a locally free
![]() ${\mathcal {O}}_S\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-module on S and
${\mathcal {O}}_S\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-module on S and
![]() is an isomorphism of
is an isomorphism of
![]() ${\mathcal {O}}_S\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-modules. Under this equivalence and using that
${\mathcal {O}}_S\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-modules. Under this equivalence and using that
![]() ${\mathcal {O}}_S\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}={\mathcal {O}}_S\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
for all
${\mathcal {O}}_S\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}={\mathcal {O}}_S\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
for all
![]() $S\in {{\mathcal {N}}\!\mathit {ilp}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}}$
, we may identify
$S\in {{\mathcal {N}}\!\mathit {ilp}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}}$
, we may identify
![]() ${\widehat {{\mathcal {F}}\ell }}^{(n)}_{\operatorname {\mathrm {SL}}_r}(S)$
with the set
${\widehat {{\mathcal {F}}\ell }}^{(n)}_{\operatorname {\mathrm {SL}}_r}(S)$
with the set
 $$ \begin{align} & \Big\{\text{ locally free } {\mathcal{O}}_S\text{[}\kern-0.15em\text{[} z-\zeta\text{]}\kern-0.15em\text{]}\text{-submodules } M\subset(z-\zeta)^{-n(r-1)}{\mathcal{O}}_S\text{[}\kern-0.15em\text{[} z-\zeta\text{]}\kern-0.15em\text{]}^{\oplus r} \text{such that for all} \nonumber \\&j=1,\ldots,r \text{ we have the inclusion }\textstyle\bigwedge^j_{{\mathcal{O}}_S\text{[}\kern-0.15em\text{[} z-\zeta\text{]}\kern-0.15em\text{]}}M\;\subset\;(z-\zeta)^{n(j^2-jr)} \cdot\bigwedge^j_{{\mathcal{O}}_S\text{[}\kern-0.15em\text{[} z-\zeta\text{]}\kern-0.15em\text{]}} {\mathcal{O}}_S\text{[}\kern-0.15em\text{[} z-\zeta\text{]}\kern-0.15em\text{]}^{\oplus r} \nonumber \\&\text{with equality for }j=r \Big\}\,. \end{align} $$
$$ \begin{align} & \Big\{\text{ locally free } {\mathcal{O}}_S\text{[}\kern-0.15em\text{[} z-\zeta\text{]}\kern-0.15em\text{]}\text{-submodules } M\subset(z-\zeta)^{-n(r-1)}{\mathcal{O}}_S\text{[}\kern-0.15em\text{[} z-\zeta\text{]}\kern-0.15em\text{]}^{\oplus r} \text{such that for all} \nonumber \\&j=1,\ldots,r \text{ we have the inclusion }\textstyle\bigwedge^j_{{\mathcal{O}}_S\text{[}\kern-0.15em\text{[} z-\zeta\text{]}\kern-0.15em\text{]}}M\;\subset\;(z-\zeta)^{n(j^2-jr)} \cdot\bigwedge^j_{{\mathcal{O}}_S\text{[}\kern-0.15em\text{[} z-\zeta\text{]}\kern-0.15em\text{]}} {\mathcal{O}}_S\text{[}\kern-0.15em\text{[} z-\zeta\text{]}\kern-0.15em\text{]}^{\oplus r} \nonumber \\&\text{with equality for }j=r \Big\}\,. \end{align} $$
Note that the quotient
![]() $(z-\zeta )^{-n(r-1)}{\mathcal {O}}_S\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}^{\oplus r}/M$
is finite locally free as
$(z-\zeta )^{-n(r-1)}{\mathcal {O}}_S\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}^{\oplus r}/M$
is finite locally free as
![]() ${\mathcal {O}}_S$
-module by [Reference Hartl and Viehmann56, Lemma 4.3]. From Cramer’s rule (e.g., [Reference Bourbaki22, III.8.6, Formulas (21) and (22)]), one sees that the above condition for
${\mathcal {O}}_S$
-module by [Reference Hartl and Viehmann56, Lemma 4.3]. From Cramer’s rule (e.g., [Reference Bourbaki22, III.8.6, Formulas (21) and (22)]), one sees that the above condition for
![]() $j=r-1$
implies that
$j=r-1$
implies that
![]() $M\supset (z-\zeta )^{n(r-1)}{\mathcal {O}}_S\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}^{\oplus r}$
. By considering the image
$M\supset (z-\zeta )^{n(r-1)}{\mathcal {O}}_S\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}^{\oplus r}$
. By considering the image
![]() ${\,\overline {\!M}}$
of
${\,\overline {\!M}}$
of
![]() $(z-\zeta )^{n(r-1)}M$
in
$(z-\zeta )^{n(r-1)}M$
in
![]() $\big ({\mathcal {O}}_S\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}/(z-\zeta )^{2n(r-1)}\big )^{\oplus r}$
and using arguments similar to [Reference Hartl and Hellmann52, Lemma 2.7] (see also [Reference Schauch87, Proposition 2.4.6]), we obtain a closed embedding of
$\big ({\mathcal {O}}_S\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}/(z-\zeta )^{2n(r-1)}\big )^{\oplus r}$
and using arguments similar to [Reference Hartl and Hellmann52, Lemma 2.7] (see also [Reference Schauch87, Proposition 2.4.6]), we obtain a closed embedding of
![]() ${\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {SL}}_r}^{(n)}$
into the formal
${\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {SL}}_r}^{(n)}$
into the formal
![]() $\zeta $
-adic completion
$\zeta $
-adic completion
of Grothendieck’s Quot-scheme whose points over a
![]() $\operatorname {\mathrm {Spec}}{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
-scheme S are
$\operatorname {\mathrm {Spec}}{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
-scheme S are
 $$ \begin{align*} & (\textrm{Quot}_{{\mathcal{O}}^r\,|\,\operatorname{\mathrm{Spec}}{\mathbb{F}}_q\text{[}\kern-0.15em\text{[}\zeta\text{]}\kern-0.15em\text{]}[z]/(z-\zeta)^{2n(r-1)}\,|\,\operatorname{\mathrm{Spec}}{\mathbb{F}}_q \text{[}\kern-0.15em\text{[}\zeta\text{]}\kern-0.15em\text{]}})(S)= \\[2mm] & \Big\{\text{finitely presented } {\mathcal{O}}_S[z]/(z-\zeta)^{2n(r-1)}\text{-submodules } {\,\overline{\!M}}\subset\big({\mathcal{O}}_S[z]/(z-\zeta)^{2n(r-1)}\big)^{\oplus r} \\ & \qquad\qquad\qquad\qquad \text{ whose quotient is finite locally free over } {\mathcal{O}}_S\Big\}\,; \end{align*} $$
$$ \begin{align*} & (\textrm{Quot}_{{\mathcal{O}}^r\,|\,\operatorname{\mathrm{Spec}}{\mathbb{F}}_q\text{[}\kern-0.15em\text{[}\zeta\text{]}\kern-0.15em\text{]}[z]/(z-\zeta)^{2n(r-1)}\,|\,\operatorname{\mathrm{Spec}}{\mathbb{F}}_q \text{[}\kern-0.15em\text{[}\zeta\text{]}\kern-0.15em\text{]}})(S)= \\[2mm] & \Big\{\text{finitely presented } {\mathcal{O}}_S[z]/(z-\zeta)^{2n(r-1)}\text{-submodules } {\,\overline{\!M}}\subset\big({\mathcal{O}}_S[z]/(z-\zeta)^{2n(r-1)}\big)^{\oplus r} \\ & \qquad\qquad\qquad\qquad \text{ whose quotient is finite locally free over } {\mathcal{O}}_S\Big\}\,; \end{align*} $$
see [Reference Grothendieck43,
![]() $\mathrm{n}^{\circ}221$
, Theorem 3.1] or [Reference Altman and Kleiman2, Theorem 2.6]. By the projectivity of the Quot-scheme,
$\mathrm{n}^{\circ}221$
, Theorem 3.1] or [Reference Altman and Kleiman2, Theorem 2.6]. By the projectivity of the Quot-scheme,
![]() ${\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {SL}}_r}^{(n)}$
is projective over
${\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {SL}}_r}^{(n)}$
is projective over
![]() $\operatorname {\mathrm {Spf}}{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
. From (2.4) also the description of the sheaf represented by
$\operatorname {\mathrm {Spf}}{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
. From (2.4) also the description of the sheaf represented by
![]() $\big ({\widehat {{\mathcal {F}}\ell }}^{(n)}_{\operatorname {\mathrm {SL}}_r}\big )^{\textrm {an}}$
follows.
$\big ({\widehat {{\mathcal {F}}\ell }}^{(n)}_{\operatorname {\mathrm {SL}}_r}\big )^{\textrm {an}}$
follows.
(c) If
![]() $\rho \colon G\hookrightarrow \operatorname {\mathrm {SL}}_{r}$
is a faithful representation with quasi-affine quotient
$\rho \colon G\hookrightarrow \operatorname {\mathrm {SL}}_{r}$
is a faithful representation with quasi-affine quotient
![]() $\operatorname {\mathrm {SL}}_{r}/\rho (G)$
, then Pappas and Rapoport [Reference Pappas and Rapoport77, Theorem 1.4] showed that the induced morphism
$\operatorname {\mathrm {SL}}_{r}/\rho (G)$
, then Pappas and Rapoport [Reference Pappas and Rapoport77, Theorem 1.4] showed that the induced morphism
![]() $\rho _*\colon {\mathcal {F}}\ell _G\hookrightarrow {\mathcal {F}}\ell _{\operatorname {\mathrm {SL}}_{r}}$
is a locally ind-closed immersion of ind-schemes. Because
$\rho _*\colon {\mathcal {F}}\ell _G\hookrightarrow {\mathcal {F}}\ell _{\operatorname {\mathrm {SL}}_{r}}$
is a locally ind-closed immersion of ind-schemes. Because
![]() ${\mathcal {F}}\ell _G$
is ind-proper by [Reference Richarz84, Theorem A], this is even an ind-closed immersion. Because
${\mathcal {F}}\ell _G$
is ind-proper by [Reference Richarz84, Theorem A], this is even an ind-closed immersion. Because
![]() $\hat Z_R$
is a
$\hat Z_R$
is a
![]() $\zeta $
-adic formal scheme by Definition 2.2(b)(iii), all
$\zeta $
-adic formal scheme by Definition 2.2(b)(iii), all
![]() $\rho _*\colon \hat {Z}_R\hookrightarrow {\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {SL}}_{r},R}^{(n)}$
are adic ind-closed immersions of formal schemes over
$\rho _*\colon \hat {Z}_R\hookrightarrow {\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {SL}}_{r},R}^{(n)}$
are adic ind-closed immersions of formal schemes over
![]() $\operatorname {\mathrm {Spf}} R$
and hence closed immersions by Lemma 2.4.
$\operatorname {\mathrm {Spf}} R$
and hence closed immersions by Lemma 2.4.
(d) By [Reference Pappas and Rapoport77, Proposition 1.3] there is a faithful representation
![]() $\rho \colon G\hookrightarrow \operatorname {\mathrm {SL}}_{r}$
as in (a) with quasi-affine quotient
$\rho \colon G\hookrightarrow \operatorname {\mathrm {SL}}_{r}$
as in (a) with quasi-affine quotient
![]() $\operatorname {\mathrm {SL}}_{r}/\rho (G)$
. Therefore, all
$\operatorname {\mathrm {SL}}_{r}/\rho (G)$
. Therefore, all
![]() $\hat Z_R$
are projective over
$\hat Z_R$
are projective over
![]() $\operatorname {\mathrm {Spf}} R$
by (b) and (c), and the associated strictly
$\operatorname {\mathrm {Spf}} R$
by (b) and (c), and the associated strictly
![]() $R[\tfrac {1}{\zeta }]$
-analytic space
$R[\tfrac {1}{\zeta }]$
-analytic space
![]() $(\hat Z_R)^{\textrm {an}}$
is Zariski-closed in the projective
$(\hat Z_R)^{\textrm {an}}$
is Zariski-closed in the projective
![]() $R[\tfrac {1}{\zeta }]$
-analytic space
$R[\tfrac {1}{\zeta }]$
-analytic space
![]() $({\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {SL}}_{r},R}^{(n)})^{\textrm {an}}$
. By analytic GAGA [Reference Lütkebohmert75, Theorem 2.8],
$({\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {SL}}_{r},R}^{(n)})^{\textrm {an}}$
. By analytic GAGA [Reference Lütkebohmert75, Theorem 2.8],
![]() $(\hat Z_R)^{\textrm {an}}$
is the analytification of a closed subscheme
$(\hat Z_R)^{\textrm {an}}$
is the analytification of a closed subscheme
![]() $\hat Z_{R[\frac {1}{\zeta }]}$
of the projective scheme
$\hat Z_{R[\frac {1}{\zeta }]}$
of the projective scheme
![]() ${\widehat {{\mathcal {F}}\ell }}^{(n)}_{\operatorname {\mathrm {SL}}_{r}}\times _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}}\operatorname {\mathrm {Spec}} R[\tfrac {1}{\zeta }]$
. By [Reference Arasteh Rad and Hartl4, Remark 4.7(f)] there is an R over which a representative
${\widehat {{\mathcal {F}}\ell }}^{(n)}_{\operatorname {\mathrm {SL}}_{r}}\times _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}}\operatorname {\mathrm {Spec}} R[\tfrac {1}{\zeta }]$
. By [Reference Arasteh Rad and Hartl4, Remark 4.7(f)] there is an R over which a representative
![]() $\hat Z_R$
exists, such that
$\hat Z_R$
exists, such that
![]() $R[\tfrac {1}{\zeta }]$
is Galois over
$R[\tfrac {1}{\zeta }]$
is Galois over
![]() $E_{\hat Z}$
and
$E_{\hat Z}$
and
![]() $\hat Z_R$
is invariant under
$\hat Z_R$
is invariant under
![]() $\operatorname {\mathrm {Gal}}(R[\tfrac {1}{\zeta }]/E_{\hat Z})$
. Because the Galois descent for projective
$\operatorname {\mathrm {Gal}}(R[\tfrac {1}{\zeta }]/E_{\hat Z})$
. Because the Galois descent for projective
![]() $E_{\hat Z}$
-schemes is effective by [Reference Grothendieck45, Chapitre VIII, Corollaire 7.7], the scheme
$E_{\hat Z}$
-schemes is effective by [Reference Grothendieck45, Chapitre VIII, Corollaire 7.7], the scheme
![]() $\hat Z_{R[\frac {1}{\zeta }]}$
and its analytification
$\hat Z_{R[\frac {1}{\zeta }]}$
and its analytification
![]() $(\hat Z_R)^{\textrm {an}}$
descend to a projective scheme
$(\hat Z_R)^{\textrm {an}}$
descend to a projective scheme
![]() $\hat Z_E$
over
$\hat Z_E$
over
![]() $\operatorname {\mathrm {Spec}} E_{\hat Z}$
and its associated strictly
$\operatorname {\mathrm {Spec}} E_{\hat Z}$
and its associated strictly
![]() $E_{\hat Z}$
-analytic space
$E_{\hat Z}$
-analytic space
![]() $(\hat Z_E)^{\textrm {an}}$
.
$(\hat Z_E)^{\textrm {an}}$
.
By our proof of (a), there is an étale covering of
![]() $\hat {Z}_R$
formed by formal schemes
$\hat {Z}_R$
formed by formal schemes
![]() $\operatorname {\mathrm {Spf}} A$
on which a lift of the inclusion
$\operatorname {\mathrm {Spf}} A$
on which a lift of the inclusion
![]() $\hat Z_R\hookrightarrow {\widehat {{\mathcal {F}}\ell }}_{G,R}$
to a point in
$\hat Z_R\hookrightarrow {\widehat {{\mathcal {F}}\ell }}_{G,R}$
to a point in
![]() $G\big (A\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z-\zeta }]\big )$
exists, which is unique up to multiplication by
$G\big (A\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z-\zeta }]\big )$
exists, which is unique up to multiplication by
![]() $G(A\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
on the right. Under the map
$G(A\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
on the right. Under the map
![]() $A\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\hookrightarrow A[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
,
$A\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\hookrightarrow A[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
,
![]() $z\mapsto z=\zeta +(z-\zeta )$
, this point gives rise to a point in
$z\mapsto z=\zeta +(z-\zeta )$
, this point gives rise to a point in
![]() $G\big (A[\tfrac {1}{\zeta }](\kern-0.15em( z-\zeta )\kern-0.15em)\big )$
. The latter induces a morphism
$G\big (A[\tfrac {1}{\zeta }](\kern-0.15em( z-\zeta )\kern-0.15em)\big )$
. The latter induces a morphism
![]() $\operatorname {\mathrm {Spec}} A[\tfrac {1}{\zeta }]\to \operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}}\times _{{\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)}\operatorname {\mathrm {Spec}} R[\tfrac {1}{\zeta }]$
and we consider its analytification
$\operatorname {\mathrm {Spec}} A[\tfrac {1}{\zeta }]\to \operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}}\times _{{\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)}\operatorname {\mathrm {Spec}} R[\tfrac {1}{\zeta }]$
and we consider its analytification
![]() $(\operatorname {\mathrm {Spf}} A)^{\textrm {an}}\to \big (\operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}}\times _{{\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)}\operatorname {\mathrm {Spec}} R[\tfrac {1}{\zeta }]\big )^{\textrm {an}}$
, which now descends to a morphism
$(\operatorname {\mathrm {Spf}} A)^{\textrm {an}}\to \big (\operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}}\times _{{\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)}\operatorname {\mathrm {Spec}} R[\tfrac {1}{\zeta }]\big )^{\textrm {an}}$
, which now descends to a morphism
![]() $(\hat {Z}_R)^{\textrm {an}}\to \big (\operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}}\times _{{\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)}\operatorname {\mathrm {Spec}} R[\tfrac {1}{\zeta }]\big )^{\textrm {an}}$
. By Galois descent it descends further to
$(\hat {Z}_R)^{\textrm {an}}\to \big (\operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}}\times _{{\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)}\operatorname {\mathrm {Spec}} R[\tfrac {1}{\zeta }]\big )^{\textrm {an}}$
. By Galois descent it descends further to
![]() $(\hat Z_E)^{\textrm {an}}$
and provides the closed immersion into
$(\hat Z_E)^{\textrm {an}}$
and provides the closed immersion into
![]() $\operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}}\times _{{\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)}\operatorname {\mathrm {Spec}} E_{\hat Z}$
.
$\operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}}\times _{{\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)}\operatorname {\mathrm {Spec}} E_{\hat Z}$
.
Example 2.7. We describe bounds that arise from a conjugacy class of coweights. Let
![]() $E_0$
be a finite field extension of
$E_0$
be a finite field extension of
![]() $\mathbb {F}_q(\kern-0.15em(\zeta )\kern-0.15em)$
and let
$\mathbb {F}_q(\kern-0.15em(\zeta )\kern-0.15em)$
and let
![]() $\mu \colon {\mathbb {G}}_{m,E_0}\to G_{E_0}:=G\times _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]},z\mapsto \zeta }{E_0}$
be a coweight over
$\mu \colon {\mathbb {G}}_{m,E_0}\to G_{E_0}:=G\times _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]},z\mapsto \zeta }{E_0}$
be a coweight over
![]() ${E_0}$
of the generic fibre of G. Because the following construction only depends on the conjugacy class of
${E_0}$
of the generic fibre of G. Because the following construction only depends on the conjugacy class of
![]() $\mu $
, we may assume that
$\mu $
, we may assume that
![]() ${E_0}$
is separable over
${E_0}$
is separable over
![]() ${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
by [Reference Borel14, § 8.11, Corollary 1]. Recall the affine Grassmannian
${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
by [Reference Borel14, § 8.11, Corollary 1]. Recall the affine Grassmannian
![]() $\operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}}$
from (1.2). We first define
$\operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}}$
from (1.2). We first define
![]() $\hat {Z}_{\preceq \mu ,{E_0}}$
as the scheme-theoretic closure in
$\hat {Z}_{\preceq \mu ,{E_0}}$
as the scheme-theoretic closure in
![]() $\operatorname {\mathrm {Gr}}_{G,{E_0}}^{{\mathbf {B}}_{\textrm {dR}}}:=\operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}}\times _{{\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)}\operatorname {\mathrm {Spec}} {E_0}$
of
$\operatorname {\mathrm {Gr}}_{G,{E_0}}^{{\mathbf {B}}_{\textrm {dR}}}:=\operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}}\times _{{\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)}\operatorname {\mathrm {Spec}} {E_0}$
of
That is,
![]() $\hat {Z}_{\preceq \mu ,{E_0}}$
is the (reduced) closed Schubert variety associated with
$\hat {Z}_{\preceq \mu ,{E_0}}$
is the (reduced) closed Schubert variety associated with
![]() $\mu $
. Choose a faithful representation
$\mu $
. Choose a faithful representation
![]() $\rho \colon G\hookrightarrow \operatorname {\mathrm {SL}}_{r}$
over
$\rho \colon G\hookrightarrow \operatorname {\mathrm {SL}}_{r}$
over
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
. Then there is a positive integer n such that the induced morphisms
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
. Then there is a positive integer n such that the induced morphisms
![]() $\rho _*\colon \hat {Z}_{\preceq \mu ,{E_0}}\hookrightarrow \operatorname {\mathrm {Gr}}_{G,{E_0}}^{{\mathbf {B}}_{\textrm {dR}}}\hookrightarrow \operatorname {\mathrm {Gr}}_{\operatorname {\mathrm {SL}}_r,{E_0}}^{{\mathbf {B}}_{\textrm {dR}}}$
factors through the closed subscheme
$\rho _*\colon \hat {Z}_{\preceq \mu ,{E_0}}\hookrightarrow \operatorname {\mathrm {Gr}}_{G,{E_0}}^{{\mathbf {B}}_{\textrm {dR}}}\hookrightarrow \operatorname {\mathrm {Gr}}_{\operatorname {\mathrm {SL}}_r,{E_0}}^{{\mathbf {B}}_{\textrm {dR}}}$
factors through the closed subscheme
![]() ${\widehat {{\mathcal {F}}\ell }}^{(n)}_{\operatorname {\mathrm {SL}}_{r},{E_0}}:={\widehat {{\mathcal {F}}\ell }}^{(n)}_{\operatorname {\mathrm {SL}}_{r}}\times _{{\mathbb {F}}_q \mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}}\operatorname {\mathrm {Spec}} {E_0}\subset \operatorname {\mathrm {Gr}}_{\operatorname {\mathrm {SL}}_r,{E_0}}^{{\mathbf {B}}_{\textrm {dR}}}$
from (2.3), which is projective over
${\widehat {{\mathcal {F}}\ell }}^{(n)}_{\operatorname {\mathrm {SL}}_{r},{E_0}}:={\widehat {{\mathcal {F}}\ell }}^{(n)}_{\operatorname {\mathrm {SL}}_{r}}\times _{{\mathbb {F}}_q \mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}}\operatorname {\mathrm {Spec}} {E_0}\subset \operatorname {\mathrm {Gr}}_{\operatorname {\mathrm {SL}}_r,{E_0}}^{{\mathbf {B}}_{\textrm {dR}}}$
from (2.3), which is projective over
![]() $\operatorname {\mathrm {Spec}} {E_0}$
. We let R be the integral closure of
$\operatorname {\mathrm {Spec}} {E_0}$
. We let R be the integral closure of
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
in
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
in
![]() ${E_0}$
and we let
${E_0}$
and we let
![]() $\hat {Z}_R$
be a closed subscheme of the projective R-scheme
$\hat {Z}_R$
be a closed subscheme of the projective R-scheme
 $$ \begin{align} {\widehat{{\mathcal{F}}\ell}}_{G,R}\underset{{\widehat{{\mathcal{F}}\ell}}_{\operatorname{\mathrm{SL}}_r,R}}{\times} ({\widehat{{\mathcal{F}}\ell}}^{(n)}_{\operatorname{\mathrm{SL}}_{r}}\times_{{\mathbb{F}}_q\text{[}\kern-0.15em\text{[}\zeta\text{]}\kern-0.15em\text{]}}\operatorname{\mathrm{Spec}} R) \end{align} $$
$$ \begin{align} {\widehat{{\mathcal{F}}\ell}}_{G,R}\underset{{\widehat{{\mathcal{F}}\ell}}_{\operatorname{\mathrm{SL}}_r,R}}{\times} ({\widehat{{\mathcal{F}}\ell}}^{(n)}_{\operatorname{\mathrm{SL}}_{r}}\times_{{\mathbb{F}}_q\text{[}\kern-0.15em\text{[}\zeta\text{]}\kern-0.15em\text{]}}\operatorname{\mathrm{Spec}} R) \end{align} $$
with
![]() $\hat {Z}_R\times _R\operatorname {\mathrm {Spec}} {E_0}=\hat {Z}_{\preceq \mu ,{E_0}}$
. For example, one could take
$\hat {Z}_R\times _R\operatorname {\mathrm {Spec}} {E_0}=\hat {Z}_{\preceq \mu ,{E_0}}$
. For example, one could take
![]() $\hat {Z}_R$
as the reduced closure of
$\hat {Z}_R$
as the reduced closure of
![]() $\hat {Z}_{\preceq \mu ,{E_0}}$
, which is flat over
$\hat {Z}_{\preceq \mu ,{E_0}}$
, which is flat over
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
and which we call
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
and which we call
![]() $\hat {Z}_{\preceq \mu ,R}$
. In this case, it coincides with the global Schubert variety of [Reference Richarz84, Definition 3.5]; compare Remark 2.1. However, this is not the only possible choice for
$\hat {Z}_{\preceq \mu ,R}$
. In this case, it coincides with the global Schubert variety of [Reference Richarz84, Definition 3.5]; compare Remark 2.1. However, this is not the only possible choice for
![]() $\hat {Z}_R$
.
$\hat {Z}_R$
.
By our assumption that G is parahoric,
![]() ${\widehat {{\mathcal {F}}\ell }}_{G,R}$
is ind-projective by [Reference Richarz84, Theorem A] and the schemes (2.5) and
${\widehat {{\mathcal {F}}\ell }}_{G,R}$
is ind-projective by [Reference Richarz84, Theorem A] and the schemes (2.5) and
![]() $\hat {Z}_R$
are indeed projective over
$\hat {Z}_R$
are indeed projective over
![]() $\operatorname {\mathrm {Spec}} R$
. Therefore, the formal
$\operatorname {\mathrm {Spec}} R$
. Therefore, the formal
![]() $\zeta $
-adic completion of
$\zeta $
-adic completion of
![]() $\hat {Z}_R$
defines a bound
$\hat {Z}_R$
defines a bound
![]() $\hat {Z}$
whose associated strictly
$\hat {Z}$
whose associated strictly
![]() ${E_0}$
-analytic space
${E_0}$
-analytic space
![]() $(\hat {Z}_R)^{\textrm {an}}$
arises as the analytification of
$(\hat {Z}_R)^{\textrm {an}}$
arises as the analytification of
![]() $\hat {Z}_{E_0}$
. If
$\hat {Z}_{E_0}$
. If
![]() $\hat {Z}_R=\hat {Z}_{\preceq \mu ,R}$
, we denote the associated bound by
$\hat {Z}_R=\hat {Z}_{\preceq \mu ,R}$
, we denote the associated bound by
![]() $\hat {Z}_{\preceq \mu }$
.
$\hat {Z}_{\preceq \mu }$
.
Claim. The reflex field
![]() $E_{\hat {Z}_{\preceq \mu }}$
of
$E_{\hat {Z}_{\preceq \mu }}$
of
![]() $\hat {Z}_{\preceq \mu }$
is equal to the reflex field
$\hat {Z}_{\preceq \mu }$
is equal to the reflex field
![]() $E_\mu $
of the conjugacy class of
$E_\mu $
of the conjugacy class of
![]() $\mu $
and is, in particular, separable over
$\mu $
and is, in particular, separable over
![]() ${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
.
${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
.
Indeed, the field
![]() $E_\mu $
is defined as the fixed field in a separable closure
$E_\mu $
is defined as the fixed field in a separable closure
![]() ${E_0}^{\textrm {sep}}$
of the group
${E_0}^{\textrm {sep}}$
of the group
The field
![]() $E_\mu $
is contained in
$E_\mu $
is contained in
![]() ${E_0}$
and, more generally, in every field over which a representative of the conjugacy class of
${E_0}$
and, more generally, in every field over which a representative of the conjugacy class of
![]() $\mu $
exists, but these inclusions may be strict. To show that
$\mu $
exists, but these inclusions may be strict. To show that
![]() $E_{\hat {Z}_{\preceq \mu }}\subset E_\mu $
, we note that
$E_{\hat {Z}_{\preceq \mu }}\subset E_\mu $
, we note that
![]() $E_{\hat {Z}_{\preceq \mu }}\subset {E_0}\subset {E_0}^{\textrm {sep}}$
and that every element of the group (2.6) satisfies
$E_{\hat {Z}_{\preceq \mu }}\subset {E_0}\subset {E_0}^{\textrm {sep}}$
and that every element of the group (2.6) satisfies
![]() $\gamma (\hat {Z}_{\preceq \mu })=\hat {Z}_{\preceq \mu }$
, because
$\gamma (\hat {Z}_{\preceq \mu })=\hat {Z}_{\preceq \mu }$
, because
![]() $\hat {Z}_{\preceq \mu }$
is defined as the closure of
$\hat {Z}_{\preceq \mu }$
is defined as the closure of
![]() $\hat {Z}_{\preceq \mu ,{E_0}}$
and
$\hat {Z}_{\preceq \mu ,{E_0}}$
and
![]() ${}^\gamma \!\mu (z-\zeta )=g\cdot \mu (z-\zeta )\cdot g^{-1}$
implies
${}^\gamma \!\mu (z-\zeta )=g\cdot \mu (z-\zeta )\cdot g^{-1}$
implies
![]() $\gamma (\hat {Z}_{\preceq \mu ,{E_0}})=\hat {Z}_{\preceq \mu ,{E_0}}$
. For the opposite inclusion
$\gamma (\hat {Z}_{\preceq \mu ,{E_0}})=\hat {Z}_{\preceq \mu ,{E_0}}$
. For the opposite inclusion
![]() $E_\mu \subset E_{\hat {Z}_{\preceq \mu }}$
, note that every
$E_\mu \subset E_{\hat {Z}_{\preceq \mu }}$
, note that every
![]() $\gamma \in \operatorname {\mathrm {Gal}}\big ({E_0}^{\textrm {sep}}\!/{\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)\big )$
with
$\gamma \in \operatorname {\mathrm {Gal}}\big ({E_0}^{\textrm {sep}}\!/{\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)\big )$
with
![]() $\gamma (\hat {Z}_{\preceq \mu })=\hat {Z}_{\preceq \mu }$
satisfies
$\gamma (\hat {Z}_{\preceq \mu })=\hat {Z}_{\preceq \mu }$
satisfies
![]() $\hat {Z}_{\preceq {}^\gamma \!\mu ,{E_0}}=\gamma (\hat {Z}_{\preceq \mu ,{E_0}})=\hat {Z}_{\preceq \mu ,{E_0}}$
. Because the Schubert varieties in
$\hat {Z}_{\preceq {}^\gamma \!\mu ,{E_0}}=\gamma (\hat {Z}_{\preceq \mu ,{E_0}})=\hat {Z}_{\preceq \mu ,{E_0}}$
. Because the Schubert varieties in
![]() $\operatorname {\mathrm {Gr}}_{G,{E_0}^{\textrm {sep}}}^{{\mathbf {B}}_{\textrm {dR}}}$
are in bijection with the
$\operatorname {\mathrm {Gr}}_{G,{E_0}^{\textrm {sep}}}^{{\mathbf {B}}_{\textrm {dR}}}$
are in bijection with the
![]() $G({E_0}^{\textrm {sep}})$
-conjugacy classes of cocharacters
$G({E_0}^{\textrm {sep}})$
-conjugacy classes of cocharacters
![]() ${\mathbb {G}}_{m,{E_0}^{\textrm {sep}}}\to G_{{E_0}^{\textrm {sep}}}$
, we conclude that
${\mathbb {G}}_{m,{E_0}^{\textrm {sep}}}\to G_{{E_0}^{\textrm {sep}}}$
, we conclude that
![]() ${}^\gamma \!\mu $
is conjugate to
${}^\gamma \!\mu $
is conjugate to
![]() $\mu $
and
$\mu $
and
![]() $\gamma $
lies in the group (2.6). Therefore,
$\gamma $
lies in the group (2.6). Therefore,
![]() $E_\mu \subset E_{\hat {Z}_{\preceq \mu }}$
, and our claim is proved.
$E_\mu \subset E_{\hat {Z}_{\preceq \mu }}$
, and our claim is proved.
We describe the generic fibre of
![]() $\hat {Z}$
. Let L be the completion of an algebraic closure of
$\hat {Z}$
. Let L be the completion of an algebraic closure of
![]() ${E_0}$
. Choose a maximal torus T of
${E_0}$
. Choose a maximal torus T of
![]() $G_L$
through which
$G_L$
through which
![]() $\mu $
factors, a Borel subgroup
$\mu $
factors, a Borel subgroup
![]() $B\supset T$
with respect to which
$B\supset T$
with respect to which
![]() $\mu $
is dominant, and consider all dominant
$\mu $
is dominant, and consider all dominant
![]() $\mu ^{\prime }\in X_*(T)_{\textrm {dom}}$
with
$\mu ^{\prime }\in X_*(T)_{\textrm {dom}}$
with
![]() $\mu ^{\prime }\preceq \mu $
in the Bruhat order. Then the L-valued points of
$\mu ^{\prime }\preceq \mu $
in the Bruhat order. Then the L-valued points of
![]() $\hat Z^{\textrm {an}}$
lie in the union of the
$\hat Z^{\textrm {an}}$
lie in the union of the
![]() $G(L\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]})$
-cosets
$G(L\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]})$
-cosets
The special fibre of
![]() $\hat {Z}_{\preceq \mu }$
is discussed in [Reference Richarz84, p. 3739 ff.] as a certain union of Schubert varieties.
$\hat {Z}_{\preceq \mu }$
is discussed in [Reference Richarz84, p. 3739 ff.] as a certain union of Schubert varieties.
Finally, because
![]() $\hat {Z}_{\preceq \mu }$
is defined as the closure of
$\hat {Z}_{\preceq \mu }$
is defined as the closure of
![]() $\hat {Z}_{\preceq \mu ,{E_0}}$
, the bound
$\hat {Z}_{\preceq \mu ,{E_0}}$
, the bound
![]() $(\hat {Z}_{\preceq \mu })^{-1}$
from Lemma 2.12 equals
$(\hat {Z}_{\preceq \mu })^{-1}$
from Lemma 2.12 equals
![]() $\hat {Z}_{\preceq (-\mu )}$
where the cocharacter
$\hat {Z}_{\preceq (-\mu )}$
where the cocharacter
![]() $-\mu \colon {\mathbb {G}}_{m,{E_0}}\to G_{E_0}$
is obtained from
$-\mu \colon {\mathbb {G}}_{m,{E_0}}\to G_{E_0}$
is obtained from
![]() $\mu $
by precomposing with the inversion on
$\mu $
by precomposing with the inversion on
![]() ${\mathbb {G}}_{m,{E_0}}$
.
${\mathbb {G}}_{m,{E_0}}$
.
Example 2.8. We explain the relation of boundedness in Definition 2.2 to the definition from [Reference Hartl and Viehmann56]. Consider a split reductive group
![]() $G_0$
over
$G_0$
over
![]() ${\mathbb {F}}_q$
, and set
${\mathbb {F}}_q$
, and set
![]() $G:=G_0\times _{{\mathbb {F}}_q}\operatorname {\mathrm {Spec}}{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
. Let
$G:=G_0\times _{{\mathbb {F}}_q}\operatorname {\mathrm {Spec}}{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
. Let
![]() $T\subset G_0$
be a maximal split torus over
$T\subset G_0$
be a maximal split torus over
![]() ${\mathbb {F}}_q$
. Let B be a Borel subgroup containing T and
${\mathbb {F}}_q$
. Let B be a Borel subgroup containing T and
![]() ${\,\overline {\!B}}$
its opposite Borel. Let
${\,\overline {\!B}}$
its opposite Borel. Let
![]() $\mu \in X_*(T)_{\textrm {dom}}$
be a coweight that is dominant with respect to B. In [Reference Hartl and Viehmann56, Definition 3.5], we define ‘boundedness by
$\mu \in X_*(T)_{\textrm {dom}}$
be a coweight that is dominant with respect to B. In [Reference Hartl and Viehmann56, Definition 3.5], we define ‘boundedness by
![]() $(\mu ,z-\zeta )$
’ as follows. We consider a finite generating system
$(\mu ,z-\zeta )$
’ as follows. We consider a finite generating system
![]() $\Lambda $
of the monoid of dominant weights
$\Lambda $
of the monoid of dominant weights
![]() $X^*(T)_{\textrm {dom}}$
, and for all
$X^*(T)_{\textrm {dom}}$
, and for all
![]() $\lambda \in \Lambda $
the Weyl module
$\lambda \in \Lambda $
the Weyl module
![]() $V_\lambda :=\big (\operatorname {\mathrm {Ind}}_{\,\overline {\!B}}^{G_0}(-\lambda )_{\textrm {dom}}\big )^{\scriptscriptstyle \lor }$
. Here
$V_\lambda :=\big (\operatorname {\mathrm {Ind}}_{\,\overline {\!B}}^{G_0}(-\lambda )_{\textrm {dom}}\big )^{\scriptscriptstyle \lor }$
. Here
![]() $(-\lambda )_{\textrm {dom}}$
is the dominant representative in the Weyl group orbit of
$(-\lambda )_{\textrm {dom}}$
is the dominant representative in the Weyl group orbit of
![]() $-\lambda $
. Let
$-\lambda $
. Let
![]() ${\mathcal {G}}$
and
${\mathcal {G}}$
and
![]() ${\mathcal {G}}^{\prime }$
be
${\mathcal {G}}^{\prime }$
be
![]() $L^+G$
-torsors over a scheme
$L^+G$
-torsors over a scheme
![]() $S\in {{\mathcal {N}}\!\mathit {ilp}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}}$
and let
$S\in {{\mathcal {N}}\!\mathit {ilp}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}}$
and let
![]() be an isomorphism of the associated
be an isomorphism of the associated
![]() $LG$
-torsors. For the representation
$LG$
-torsors. For the representation
![]() $\rho _\lambda \colon G\to \operatorname {\mathrm {GL}}(V_\lambda )$
in
$\rho _\lambda \colon G\to \operatorname {\mathrm {GL}}(V_\lambda )$
in
![]() $\operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}G$
, we consider the sheaves of
$\operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}G$
, we consider the sheaves of
![]() ${\mathcal {O}}_{S}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-modules
${\mathcal {O}}_{S}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-modules
![]() $\rho _{\lambda *}{\mathcal {G}}$
and
$\rho _{\lambda *}{\mathcal {G}}$
and
![]() $\rho _{\lambda *}{\mathcal {G}}^{\prime }$
associated with the
$\rho _{\lambda *}{\mathcal {G}}^{\prime }$
associated with the
![]() $L^+G$
-torsors
$L^+G$
-torsors
![]() ${\mathcal {G}}$
and
${\mathcal {G}}$
and
![]() ${\mathcal {G}}^{\prime }$
over S. The isomorphism
${\mathcal {G}}^{\prime }$
over S. The isomorphism
![]() $\delta $
induces an isomorphism
$\delta $
induces an isomorphism
![]() . After choosing trivialisations of
. After choosing trivialisations of
![]() ${\mathcal {G}}$
and
${\mathcal {G}}$
and
![]() ${\mathcal {G}}^{\prime }$
over an étale covering
${\mathcal {G}}^{\prime }$
over an étale covering
![]() $S^{\prime }\to S$
, the isomorphism
$S^{\prime }\to S$
, the isomorphism
![]() $\delta $
is given by multiplication with an element
$\delta $
is given by multiplication with an element
![]() $\delta _{S^{\prime }}\in LG(S^{\prime })$
. The latter corresponds to a morphism
$\delta _{S^{\prime }}\in LG(S^{\prime })$
. The latter corresponds to a morphism
![]() $S^{\prime }\to LG$
. Let
$S^{\prime }\to LG$
. Let
![]() $LG_{\mu ^\#}\subset LG$
and
$LG_{\mu ^\#}\subset LG$
and
![]() ${\mathcal {F}}_{\mu ^\#}\subset {\widehat {{\mathcal {F}}\ell }}_G$
be the connected components corresponding to the image
${\mathcal {F}}_{\mu ^\#}\subset {\widehat {{\mathcal {F}}\ell }}_G$
be the connected components corresponding to the image
![]() $\mu ^{\#}\in \pi _1(G)_I=\pi _1(G)=\pi _1(G_0)=\pi _0({\widehat {{\mathcal {F}}\ell }}_G)=\pi _0(LG)$
of
$\mu ^{\#}\in \pi _1(G)_I=\pi _1(G)=\pi _1(G_0)=\pi _0({\widehat {{\mathcal {F}}\ell }}_G)=\pi _0(LG)$
of
![]() $\mu $
. According to [Reference Hartl and Viehmann56, Definition 3.5], ‘
$\mu $
. According to [Reference Hartl and Viehmann56, Definition 3.5], ‘
![]() $\delta $
is bounded by
$\delta $
is bounded by
![]() $(\mu ,z-\zeta )$
’ if
$(\mu ,z-\zeta )$
’ if
-
• the morphism
 $S^{\prime }\to LG$
factors through
$S^{\prime }\to LG$
factors through
 $LG_{\mu ^\#}$
and
$LG_{\mu ^\#}$
and -
•
 $\rho _{\lambda *}\delta \,(\rho _{\lambda *}{\mathcal {G}})\;\subset \;(z-\zeta )\;^{-\langle \,(-\lambda )_{\textrm {dom}},\mu \rangle }\cdot \rho _{\lambda *}{\mathcal {G}}^{\prime }$
for all
$\rho _{\lambda *}\delta \,(\rho _{\lambda *}{\mathcal {G}})\;\subset \;(z-\zeta )\;^{-\langle \,(-\lambda )_{\textrm {dom}},\mu \rangle }\cdot \rho _{\lambda *}{\mathcal {G}}^{\prime }$
for all
 $\lambda \in \Lambda $
.
$\lambda \in \Lambda $
.
In terms of Definition 2.2, this can be described as follows. Consider the ind-scheme
and let
![]() $M_\lambda \in L\operatorname {\mathrm {GL}}(V_\lambda )(Y_\lambda )$
be the universal element over
$M_\lambda \in L\operatorname {\mathrm {GL}}(V_\lambda )(Y_\lambda )$
be the universal element over
![]() $Y_{\lambda }$
. Because
$Y_{\lambda }$
. Because
![]() ${\mathcal {O}}_{Y_{\lambda ,m}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[z^{-1}]={\mathcal {O}}_{Y_{\lambda ,m}}\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z-\zeta }]$
, we can write
${\mathcal {O}}_{Y_{\lambda ,m}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[z^{-1}]={\mathcal {O}}_{Y_{\lambda ,m}}\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z-\zeta }]$
, we can write
![]() $M_\lambda =(M_{\lambda ,m})_m$
with
$M_\lambda =(M_{\lambda ,m})_m$
with
Let
![]() ${\overline {Y}}_\lambda \subset Y_{\lambda }$
be the closed ind-subscheme where the matrix
${\overline {Y}}_\lambda \subset Y_{\lambda }$
be the closed ind-subscheme where the matrix
![]() $(z-\zeta )^{\langle \,(-\lambda )_{\textrm {dom}},\mu \rangle }M_\lambda $
has entries in
$(z-\zeta )^{\langle \,(-\lambda )_{\textrm {dom}},\mu \rangle }M_\lambda $
has entries in
![]() ${\mathcal {O}}_{Y_\lambda }\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}={\mathcal {O}}_{Y_{\lambda ,m}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
for all m, and let
${\mathcal {O}}_{Y_\lambda }\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}={\mathcal {O}}_{Y_{\lambda ,m}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
for all m, and let
![]() ${\overline {Y}}^{\prime }_\lambda \subset Y_{\lambda }$
be the closed ind-subscheme where the matrix
${\overline {Y}}^{\prime }_\lambda \subset Y_{\lambda }$
be the closed ind-subscheme where the matrix
![]() $(z-\zeta )^{\langle \,(-\lambda )_{\textrm {dom}},\mu \rangle }M_\lambda ^{-1}$
has entries in
$(z-\zeta )^{\langle \,(-\lambda )_{\textrm {dom}},\mu \rangle }M_\lambda ^{-1}$
has entries in
![]() ${\mathcal {O}}_{Y_{\lambda ,m}}\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}={\mathcal {O}}_{Y_{\lambda ,m}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
for all m. Set
${\mathcal {O}}_{Y_{\lambda ,m}}\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}={\mathcal {O}}_{Y_{\lambda ,m}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
for all m. Set
 $$ \begin{align*}\hat Z^{\scriptscriptstyle\textrm{Weyl}}_{\preceq\mu,\lambda} & := {\overline{Y}}_\lambda/(L^+\operatorname{\mathrm{GL}}(V_\lambda)\widehat{\displaystyle\times}_{{\mathbb{F}}_q}\operatorname{\mathrm{Spf}}{\mathbb{F}}_q\text{[}\kern-0.15em\text{[}\zeta\text{]}\kern-0.15em\text{]})\;\subset\;{\widehat{{\mathcal{F}}\ell}}_{\operatorname{\mathrm{GL}}(V_\lambda)} \quad\text{and} \\[2mm]\hat Z^{\scriptscriptstyle\textrm{Weyl},-1}_{\preceq\mu,\lambda} &:= {\overline{Y}}^{\prime}_\lambda/(L^+\operatorname{\mathrm{GL}}(V_\lambda)\widehat{\displaystyle\times}_{{\mathbb{F}}_q}\operatorname{\mathrm{Spf}}{\mathbb{F}}_q\text{[}\kern-0.15em\text{[}\zeta\text{]}\kern-0.15em\text{]})\;\subset\;{\widehat{{\mathcal{F}}\ell}}_{\operatorname{\mathrm{GL}}(V_\lambda)}.\end{align*} $$
$$ \begin{align*}\hat Z^{\scriptscriptstyle\textrm{Weyl}}_{\preceq\mu,\lambda} & := {\overline{Y}}_\lambda/(L^+\operatorname{\mathrm{GL}}(V_\lambda)\widehat{\displaystyle\times}_{{\mathbb{F}}_q}\operatorname{\mathrm{Spf}}{\mathbb{F}}_q\text{[}\kern-0.15em\text{[}\zeta\text{]}\kern-0.15em\text{]})\;\subset\;{\widehat{{\mathcal{F}}\ell}}_{\operatorname{\mathrm{GL}}(V_\lambda)} \quad\text{and} \\[2mm]\hat Z^{\scriptscriptstyle\textrm{Weyl},-1}_{\preceq\mu,\lambda} &:= {\overline{Y}}^{\prime}_\lambda/(L^+\operatorname{\mathrm{GL}}(V_\lambda)\widehat{\displaystyle\times}_{{\mathbb{F}}_q}\operatorname{\mathrm{Spf}}{\mathbb{F}}_q\text{[}\kern-0.15em\text{[}\zeta\text{]}\kern-0.15em\text{]})\;\subset\;{\widehat{{\mathcal{F}}\ell}}_{\operatorname{\mathrm{GL}}(V_\lambda)}.\end{align*} $$
Write
![]() $\Lambda =\{\lambda _1,\ldots ,\lambda _m\}$
and for each
$\Lambda =\{\lambda _1,\ldots ,\lambda _m\}$
and for each
![]() $\lambda _i$
consider the morphism
$\lambda _i$
consider the morphism
![]() $\rho _{\lambda _i*}\colon {\widehat {{\mathcal {F}}\ell }}_G\to {\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {GL}}(V_{\lambda _i})}$
induced from
$\rho _{\lambda _i*}\colon {\widehat {{\mathcal {F}}\ell }}_G\to {\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {GL}}(V_{\lambda _i})}$
induced from
![]() $\rho _{\lambda _i}$
. Let
$\rho _{\lambda _i}$
. Let
![]() $\hat Z^{\scriptscriptstyle \textrm {Weyl}}_{G_0,\preceq \mu }\subset {\mathcal {F}}_{\mu ^\#}$
be the base change of the closed ind-subscheme
$\hat Z^{\scriptscriptstyle \textrm {Weyl}}_{G_0,\preceq \mu }\subset {\mathcal {F}}_{\mu ^\#}$
be the base change of the closed ind-subscheme
under the morphism
![]() $\prod _i\rho _{\lambda _i*}\colon {\mathcal {F}}_{\mu ^\#}\to {\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {GL}}(V_{\lambda _1})}\widehat {\displaystyle \times }_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}}\ldots \widehat {\displaystyle \times }_{{\mathbb {F}}_q \mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}}{\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {GL}}(V_{\lambda _m})}$
. Likewise, let
$\prod _i\rho _{\lambda _i*}\colon {\mathcal {F}}_{\mu ^\#}\to {\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {GL}}(V_{\lambda _1})}\widehat {\displaystyle \times }_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}}\ldots \widehat {\displaystyle \times }_{{\mathbb {F}}_q \mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}}{\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {GL}}(V_{\lambda _m})}$
. Likewise, let
![]() $\hat Z^{\scriptscriptstyle \textrm {Weyl},-1}_{G_0,\preceq \mu }\subset {\mathcal {F}}_{-\mu ^\#}$
be the base change of the closed ind-subscheme
$\hat Z^{\scriptscriptstyle \textrm {Weyl},-1}_{G_0,\preceq \mu }\subset {\mathcal {F}}_{-\mu ^\#}$
be the base change of the closed ind-subscheme
under the morphism
![]() $\prod _i\rho _{\lambda _i*}\colon {\mathcal {F}}_{-\mu ^\#}\to {\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {GL}}(V_{\lambda _1})}\widehat {\displaystyle \times }_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}}\ldots \widehat {\displaystyle \times }_{{\mathbb {F}}_q \mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}}{\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {GL}}(V_{\lambda _m})}$
. The ind-subscheme
$\prod _i\rho _{\lambda _i*}\colon {\mathcal {F}}_{-\mu ^\#}\to {\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {GL}}(V_{\lambda _1})}\widehat {\displaystyle \times }_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}}\ldots \widehat {\displaystyle \times }_{{\mathbb {F}}_q \mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}}{\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {GL}}(V_{\lambda _m})}$
. The ind-subscheme
![]() $\hat Z^{\scriptscriptstyle \textrm {Weyl},-1}_{G_0,\preceq \mu }\subset {\mathcal {F}}_{-\mu ^\#}$
was denoted
$\hat Z^{\scriptscriptstyle \textrm {Weyl},-1}_{G_0,\preceq \mu }\subset {\mathcal {F}}_{-\mu ^\#}$
was denoted
![]() ${\widehat {\operatorname {\mathrm {Gr}}}}^{\preceq (\mu ,z-\zeta )}$
in [Reference Hartl and Viehmann56, Definition 5.5]. We will show that both
${\widehat {\operatorname {\mathrm {Gr}}}}^{\preceq (\mu ,z-\zeta )}$
in [Reference Hartl and Viehmann56, Definition 5.5]. We will show that both
![]() $\hat Z^{\scriptscriptstyle \textrm {Weyl}}_{G_0,\preceq \mu }$
and
$\hat Z^{\scriptscriptstyle \textrm {Weyl}}_{G_0,\preceq \mu }$
and
![]() $\hat Z^{\scriptscriptstyle \textrm {Weyl},-1}_{G_0,\preceq \mu }$
define bounds in the sense of Definition 2.2(b) with reflex ring
$\hat Z^{\scriptscriptstyle \textrm {Weyl},-1}_{G_0,\preceq \mu }$
define bounds in the sense of Definition 2.2(b) with reflex ring
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
and are representatives defined over the reflex ring. In terms of Lemma 2.12, they satisfy
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
and are representatives defined over the reflex ring. In terms of Lemma 2.12, they satisfy
![]() $\hat Z^{\scriptscriptstyle \textrm {Weyl},-1}_{G_0,\preceq \mu }=\big (\hat Z^{\scriptscriptstyle \textrm {Weyl}}_{G_0,\preceq \mu }\big )^{-1}$
and
$\hat Z^{\scriptscriptstyle \textrm {Weyl},-1}_{G_0,\preceq \mu }=\big (\hat Z^{\scriptscriptstyle \textrm {Weyl}}_{G_0,\preceq \mu }\big )^{-1}$
and
![]() $\hat Z^{\scriptscriptstyle \textrm {Weyl}}_{G_0,\preceq \mu }=\big (\hat Z^{\scriptscriptstyle \textrm {Weyl},-1}_{G_0,\preceq \mu }\big )^{-1}$
. Conditions (b)(i), respectively (b)(v), are satisfied because all of the
$\hat Z^{\scriptscriptstyle \textrm {Weyl}}_{G_0,\preceq \mu }=\big (\hat Z^{\scriptscriptstyle \textrm {Weyl},-1}_{G_0,\preceq \mu }\big )^{-1}$
. Conditions (b)(i), respectively (b)(v), are satisfied because all of the
![]() $\hat Z^{\scriptscriptstyle \textrm {Weyl}}_{\preceq \mu ,\lambda }$
and
$\hat Z^{\scriptscriptstyle \textrm {Weyl}}_{\preceq \mu ,\lambda }$
and
![]() $\hat Z^{\scriptscriptstyle \textrm {Weyl},-1}_{\preceq \mu ,\lambda }$
are invariant by multiplication on the left with
$\hat Z^{\scriptscriptstyle \textrm {Weyl},-1}_{\preceq \mu ,\lambda }$
are invariant by multiplication on the left with
![]() $L^+G$
, respectively with
$L^+G$
, respectively with
![]() $G\big ({\,{\scriptscriptstyle \bullet }\,}\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )$
. Conditions (b)(ii) and (b)(iii) for
$G\big ({\,{\scriptscriptstyle \bullet }\,}\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )$
. Conditions (b)(ii) and (b)(iii) for
![]() $\hat Z^{\scriptscriptstyle \textrm {Weyl},-1}_{G_0,\preceq \mu }$
follow from [Reference Hartl and Viehmann56, Proposition 5.5] and for
$\hat Z^{\scriptscriptstyle \textrm {Weyl},-1}_{G_0,\preceq \mu }$
follow from [Reference Hartl and Viehmann56, Proposition 5.5] and for
![]() $\hat Z^{\scriptscriptstyle \textrm {Weyl}}_{G_0,\preceq \mu }$
from Lemma 2.12. This proposition also says that the underlying reduced subscheme of
$\hat Z^{\scriptscriptstyle \textrm {Weyl}}_{G_0,\preceq \mu }$
from Lemma 2.12. This proposition also says that the underlying reduced subscheme of
![]() $\hat Z^{\scriptscriptstyle \textrm {Weyl},-1}_{G_0,\preceq \mu }$
is the closed Schubert variety associated with
$\hat Z^{\scriptscriptstyle \textrm {Weyl},-1}_{G_0,\preceq \mu }$
is the closed Schubert variety associated with
![]() $(-\mu )_{\textrm {dom}}$
in
$(-\mu )_{\textrm {dom}}$
in
![]() ${\mathcal {F}}\ell _G$
and the underlying reduced subscheme of
${\mathcal {F}}\ell _G$
and the underlying reduced subscheme of
![]() $\hat Z^{\scriptscriptstyle \textrm {Weyl}}_{G_0,\preceq \mu }$
is the closed Schubert variety associated with
$\hat Z^{\scriptscriptstyle \textrm {Weyl}}_{G_0,\preceq \mu }$
is the closed Schubert variety associated with
![]() $\mu $
. If
$\mu $
. If
![]() $V:=\bigoplus _{\lambda \in \Lambda }V_\lambda $
and
$V:=\bigoplus _{\lambda \in \Lambda }V_\lambda $
and
![]() $\rho $
is the representation of
$\rho $
is the representation of
![]() $G_0$
on
$G_0$
on
![]() $V\oplus (\det V)^{\scriptscriptstyle \lor }$
which is faithful by [Reference Hartl and Viehmann56, Proposition 3.14] and factors through
$V\oplus (\det V)^{\scriptscriptstyle \lor }$
which is faithful by [Reference Hartl and Viehmann56, Proposition 3.14] and factors through
![]() $\operatorname {\mathrm {SL}}_{1+\dim V}$
, then
$\operatorname {\mathrm {SL}}_{1+\dim V}$
, then
![]() $\hat Z^{\scriptscriptstyle \textrm {Weyl}}_{G_0,\preceq \mu }$
is contained in
$\hat Z^{\scriptscriptstyle \textrm {Weyl}}_{G_0,\preceq \mu }$
is contained in
![]() ${\widehat {{\mathcal {F}}\ell }}^{(n)}_{\operatorname {\mathrm {SL}}_{1+\dim V}}$
for
${\widehat {{\mathcal {F}}\ell }}^{(n)}_{\operatorname {\mathrm {SL}}_{1+\dim V}}$
for
![]() $n=\max \big \{\langle (-\lambda )_{\textrm {dom}},\mu \rangle \colon \lambda \in \Lambda \big \}$
; that is, Condition (b)(iv) holds for
$n=\max \big \{\langle (-\lambda )_{\textrm {dom}},\mu \rangle \colon \lambda \in \Lambda \big \}$
; that is, Condition (b)(iv) holds for
![]() $\hat Z^{\scriptscriptstyle \textrm {Weyl}}_{G_0,\preceq \mu }$
. Then it also holds for
$\hat Z^{\scriptscriptstyle \textrm {Weyl}}_{G_0,\preceq \mu }$
. Then it also holds for
![]() $\hat Z^{\scriptscriptstyle \textrm {Weyl},-1}_{G_0,\preceq \mu }$
by Lemma 2.12.
$\hat Z^{\scriptscriptstyle \textrm {Weyl},-1}_{G_0,\preceq \mu }$
by Lemma 2.12.
Now
![]() $\delta $
‘is bounded by
$\delta $
‘is bounded by
![]() $(\mu ,z-\zeta )$
’ in the sense of [Reference Hartl and Viehmann56, Definition 3.5] if and only if the morphism
$(\mu ,z-\zeta )$
’ in the sense of [Reference Hartl and Viehmann56, Definition 3.5] if and only if the morphism
![]() $S^{\prime }\to LG\widehat {\displaystyle \times }_{{\mathbb {F}}_q}\operatorname {\mathrm {Spf}}{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}\twoheadrightarrow {\widehat {{\mathcal {F}}\ell }}_G$
given by
$S^{\prime }\to LG\widehat {\displaystyle \times }_{{\mathbb {F}}_q}\operatorname {\mathrm {Spf}}{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}\twoheadrightarrow {\widehat {{\mathcal {F}}\ell }}_G$
given by
![]() $\delta _{S^{\prime }}\in LG(S^{\prime })$
factors through
$\delta _{S^{\prime }}\in LG(S^{\prime })$
factors through
![]() $\hat Z^{\scriptscriptstyle \textrm {Weyl}}_{G_0,\preceq \mu }$
; that is, if and only if
$\hat Z^{\scriptscriptstyle \textrm {Weyl}}_{G_0,\preceq \mu }$
; that is, if and only if
![]() $\delta $
is bounded by
$\delta $
is bounded by
![]() $\hat Z^{\scriptscriptstyle \textrm {Weyl}}_{G_0,\preceq \mu }$
in the sense of Definition 2.2(d). This is the case if and only if the morphism
$\hat Z^{\scriptscriptstyle \textrm {Weyl}}_{G_0,\preceq \mu }$
in the sense of Definition 2.2(d). This is the case if and only if the morphism
![]() $S^{\prime }\to LG\widehat {\displaystyle \times }_{{\mathbb {F}}_q}\operatorname {\mathrm {Spf}}{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}\twoheadrightarrow {\widehat {{\mathcal {F}}\ell }}_G$
given by
$S^{\prime }\to LG\widehat {\displaystyle \times }_{{\mathbb {F}}_q}\operatorname {\mathrm {Spf}}{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}\twoheadrightarrow {\widehat {{\mathcal {F}}\ell }}_G$
given by
![]() $\delta _{S^{\prime }}^{-1}\in LG(S^{\prime })$
factors through
$\delta _{S^{\prime }}^{-1}\in LG(S^{\prime })$
factors through
![]() $\hat Z^{\scriptscriptstyle \textrm {Weyl},-1}_{G_0,\preceq \mu }$
; that is, if and only if
$\hat Z^{\scriptscriptstyle \textrm {Weyl},-1}_{G_0,\preceq \mu }$
; that is, if and only if
![]() $\delta ^{-1}$
is bounded by
$\delta ^{-1}$
is bounded by
![]() $\hat Z^{\scriptscriptstyle \textrm {Weyl},-1}_{G_0,\preceq \mu }$
. In particular, a local G-shtuka is bounded by
$\hat Z^{\scriptscriptstyle \textrm {Weyl},-1}_{G_0,\preceq \mu }$
. In particular, a local G-shtuka is bounded by
![]() $\hat Z^{\scriptscriptstyle \textrm {Weyl}}_{G_0,\preceq \mu }$
in the sense of Definition 2.2(d) if and only if it is ‘bounded by
$\hat Z^{\scriptscriptstyle \textrm {Weyl}}_{G_0,\preceq \mu }$
in the sense of Definition 2.2(d) if and only if it is ‘bounded by
![]() $(\mu ,z-\zeta )$
’.
$(\mu ,z-\zeta )$
’.
For the constant split group
![]() $G=G_0\times _{{\mathbb {F}}_q}\operatorname {\mathrm {Spec}}{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
, the double cosets occurring in the description of the sets of closed points of the generic and of the special fibre of bounds are both parametrised by the set
$G=G_0\times _{{\mathbb {F}}_q}\operatorname {\mathrm {Spec}}{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
, the double cosets occurring in the description of the sets of closed points of the generic and of the special fibre of bounds are both parametrised by the set
![]() $X_*(T)_{\textrm {dom}}$
, and for our bound
$X_*(T)_{\textrm {dom}}$
, and for our bound
![]() $\hat Z^{\scriptscriptstyle \textrm {Weyl}}_{G_0,\preceq \mu }$
, both the generic fibre and the special fibre correspond to the union of all double cosets for
$\hat Z^{\scriptscriptstyle \textrm {Weyl}}_{G_0,\preceq \mu }$
, both the generic fibre and the special fibre correspond to the union of all double cosets for
![]() $\mu ^{\prime }\preceq \mu $
. That is, the reduced generic, respectively the reduced special fibre of
$\mu ^{\prime }\preceq \mu $
. That is, the reduced generic, respectively the reduced special fibre of
![]() $\hat Z^{\scriptscriptstyle \textrm {Weyl}}_{G_0,\preceq \mu }$
, equals the closed Schubert variety associated with
$\hat Z^{\scriptscriptstyle \textrm {Weyl}}_{G_0,\preceq \mu }$
, equals the closed Schubert variety associated with
![]() $\mu $
in
$\mu $
in
![]() $\operatorname {\mathrm {Gr}}_{G}^{{\mathbf {B}}_{\textrm {dR}}}$
, respectively in
$\operatorname {\mathrm {Gr}}_{G}^{{\mathbf {B}}_{\textrm {dR}}}$
, respectively in
![]() ${\mathcal {F}}\ell _G$
. So the underlying reduced structure of
${\mathcal {F}}\ell _G$
. So the underlying reduced structure of
![]() $\hat Z^{\scriptscriptstyle \textrm {Weyl}}_{G_0,\preceq \mu }$
coincides with the bound
$\hat Z^{\scriptscriptstyle \textrm {Weyl}}_{G_0,\preceq \mu }$
coincides with the bound
![]() $\hat Z_{\preceq \mu }$
defined in Example 2.7, and in terms of Remark 2.11 condition (a) and
$\hat Z_{\preceq \mu }$
defined in Example 2.7, and in terms of Remark 2.11 condition (a) and
![]() $N_0=N_{\textrm {an}}$
from (b) are satisfied. The nilpotent structure as discussed in Remark 2.11(c) is in general not so clear in this case. For example, if
$N_0=N_{\textrm {an}}$
from (b) are satisfied. The nilpotent structure as discussed in Remark 2.11(c) is in general not so clear in this case. For example, if
![]() $G_0=\operatorname {\mathrm {GL}}_r$
and
$G_0=\operatorname {\mathrm {GL}}_r$
and
![]() $\mu =2n\rho ^{\scriptscriptstyle \lor }$
where
$\mu =2n\rho ^{\scriptscriptstyle \lor }$
where
![]() $2\rho ^{\scriptscriptstyle \lor }=(r-1,\ldots ,1-r)$
is the sum of the positive coroots of
$2\rho ^{\scriptscriptstyle \lor }=(r-1,\ldots ,1-r)$
is the sum of the positive coroots of
![]() $G_0$
, then
$G_0$
, then
![]() $(-\mu )_{\textrm {dom}}=\mu $
and all bounds
$(-\mu )_{\textrm {dom}}=\mu $
and all bounds
![]() $\hat Z^{\scriptscriptstyle \textrm {Weyl}}_{\operatorname {\mathrm {GL}}_r,\preceq \mu }, \hat Z^{\scriptscriptstyle \textrm {Weyl},-1}_{\operatorname {\mathrm {GL}}_r,\preceq \mu },\hat Z^{\scriptscriptstyle \textrm {Weyl}}_{\operatorname {\mathrm {GL}}_r,\preceq (-\mu )_{\textrm {dom}}}\subset {\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {GL}}_r}$
are equal to
$\hat Z^{\scriptscriptstyle \textrm {Weyl}}_{\operatorname {\mathrm {GL}}_r,\preceq \mu }, \hat Z^{\scriptscriptstyle \textrm {Weyl},-1}_{\operatorname {\mathrm {GL}}_r,\preceq \mu },\hat Z^{\scriptscriptstyle \textrm {Weyl}}_{\operatorname {\mathrm {GL}}_r,\preceq (-\mu )_{\textrm {dom}}}\subset {\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {GL}}_r}$
are equal to
![]() ${\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {SL}}_r}^{(n)}\subset {\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {SL}}_r}\subset {\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {GL}}_r}$
by [Reference Hartl and Viehmann56, Lemma 4.3]. Note, however, that in general
${\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {SL}}_r}^{(n)}\subset {\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {SL}}_r}\subset {\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {GL}}_r}$
by [Reference Hartl and Viehmann56, Lemma 4.3]. Note, however, that in general
![]() $\big (\hat Z^{\scriptscriptstyle \textrm {Weyl}}_{G_0,\preceq \mu }\big )^{-1}=\hat Z^{\scriptscriptstyle \textrm {Weyl},-1}_{G_0,\preceq \mu }$
coincides with
$\big (\hat Z^{\scriptscriptstyle \textrm {Weyl}}_{G_0,\preceq \mu }\big )^{-1}=\hat Z^{\scriptscriptstyle \textrm {Weyl},-1}_{G_0,\preceq \mu }$
coincides with
![]() $\hat Z^{\scriptscriptstyle \textrm {Weyl}}_{G_0,\preceq (-\mu )_{\textrm {dom}}}$
only on the underlying reduced structure but not in the nilpotent structure; see Example 2.13.
$\hat Z^{\scriptscriptstyle \textrm {Weyl}}_{G_0,\preceq (-\mu )_{\textrm {dom}}}$
only on the underlying reduced structure but not in the nilpotent structure; see Example 2.13.
Example 2.9. We give an example of an ind-scheme
![]() $\hat Z$
satisfying all properties of a bound in Definition 2.2 except for (b)(v) to show that this condition is not implied by (b)(i). Let
$\hat Z$
satisfying all properties of a bound in Definition 2.2 except for (b)(v) to show that this condition is not implied by (b)(i). Let
![]() $\hat Z\subset {\widehat {{\mathcal {F}}\ell }}^{(1)}_{\operatorname {\mathrm {SL}}_2}$
be the ind-closure of
$\hat Z\subset {\widehat {{\mathcal {F}}\ell }}^{(1)}_{\operatorname {\mathrm {SL}}_2}$
be the ind-closure of
![]() $\hat Y\subset {\widehat {{\mathcal {F}}\ell }}^{(1)}_{\operatorname {\mathrm {SL}}_2}$
given by
$\hat Y\subset {\widehat {{\mathcal {F}}\ell }}^{(1)}_{\operatorname {\mathrm {SL}}_2}$
given by
 $$ \begin{align*}\hat Y(B):=L^+\operatorname{\mathrm{SL}}_2(B)\cdot\big\{\left(\begin{smallmatrix} a & b \\c & d \end{smallmatrix}\right)\in L\operatorname{\mathrm{SL}}_2(B)\colon a,b,d\in B\text{[}\kern-0.15em\text{[} z\text{]}\kern-0.15em\text{]}, c\in \tfrac{\zeta}{z-\zeta}B\text{[}\kern-0.15em\text{[} z\text{]}\kern-0.15em\text{]}\,\big\}&\\\cdot L^+\operatorname{\mathrm{SL}}_2(B)/L^+\operatorname{\mathrm{SL}}_2(B)&\end{align*} $$
$$ \begin{align*}\hat Y(B):=L^+\operatorname{\mathrm{SL}}_2(B)\cdot\big\{\left(\begin{smallmatrix} a & b \\c & d \end{smallmatrix}\right)\in L\operatorname{\mathrm{SL}}_2(B)\colon a,b,d\in B\text{[}\kern-0.15em\text{[} z\text{]}\kern-0.15em\text{]}, c\in \tfrac{\zeta}{z-\zeta}B\text{[}\kern-0.15em\text{[} z\text{]}\kern-0.15em\text{]}\,\big\}&\\\cdot L^+\operatorname{\mathrm{SL}}_2(B)/L^+\operatorname{\mathrm{SL}}_2(B)&\end{align*} $$
for any
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
-algebra B. This satisfies all conditions in the definition of bounds except for possibly (b)(v). Notice further that the special fibre of
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
-algebra B. This satisfies all conditions in the definition of bounds except for possibly (b)(v). Notice further that the special fibre of
![]() $\hat Z$
consists just of the one point
$\hat Z$
consists just of the one point
![]() $L^+\operatorname {\mathrm {SL}}_2/L^+\operatorname {\mathrm {SL}}_2$
.
$L^+\operatorname {\mathrm {SL}}_2/L^+\operatorname {\mathrm {SL}}_2$
.
We have that
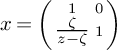 $x=\left (\begin {smallmatrix} 1 & 0 \\ \tfrac {\zeta }{z-\zeta } & 1 \end {smallmatrix}\right )$
and
$x=\left (\begin {smallmatrix} 1 & 0 \\ \tfrac {\zeta }{z-\zeta } & 1 \end {smallmatrix}\right )$
and
 $y=\left (\begin {smallmatrix} z-\zeta & 0 \\ 0 & \tfrac {1}{z-\zeta } \end {smallmatrix}\right )$
are elements of
$y=\left (\begin {smallmatrix} z-\zeta & 0 \\ 0 & \tfrac {1}{z-\zeta } \end {smallmatrix}\right )$
are elements of
![]() $L\operatorname {\mathrm {SL}}_2(B)$
for all B such that
$L\operatorname {\mathrm {SL}}_2(B)$
for all B such that
![]() $\zeta $
is nilpotent in B. Therefore,
$\zeta $
is nilpotent in B. Therefore,
![]() $x\in \hat Z(\operatorname {\mathrm {Spf}} {\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]})$
as one can see by reducing modulo
$x\in \hat Z(\operatorname {\mathrm {Spf}} {\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]})$
as one can see by reducing modulo
![]() $(\zeta ^i)$
for all i. However, already considering the reduction modulo
$(\zeta ^i)$
for all i. However, already considering the reduction modulo
![]() $\zeta $
shows that y is not an element of
$\zeta $
shows that y is not an element of
![]() $\hat Z({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]})$
. On the other hand,
$\hat Z({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]})$
. On the other hand,
This shows that
![]() $\hat Z^{\textrm {an}}$
is not invariant under multiplication with
$\hat Z^{\textrm {an}}$
is not invariant under multiplication with
![]() $\operatorname {\mathrm {SL}}_2({\,{\scriptscriptstyle \bullet }\,}\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]})$
on the left.
$\operatorname {\mathrm {SL}}_2({\,{\scriptscriptstyle \bullet }\,}\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]})$
on the left.
We need condition (b)(v) of Definition 2.2 mainly in form of the following lemma.
Lemma 2.10. Let
![]() $\hat Z$
be a bound. Then
$\hat Z$
be a bound. Then
![]() $\hat Z^{\textrm {an}}\otimes _{E_{\hat Z}}\breve E_{\hat Z}$
is invariant under left and right multiplication with
$\hat Z^{\textrm {an}}\otimes _{E_{\hat Z}}\breve E_{\hat Z}$
is invariant under left and right multiplication with
![]() $LG({\mathbb {F}})$
.
$LG({\mathbb {F}})$
.
Here, as always, we use the morphism
![]() ${\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)\to {\mathcal {O}}_X\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]},\,z\mapsto z=\zeta +(z-\zeta )$
for an
${\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)\to {\mathcal {O}}_X\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]},\,z\mapsto z=\zeta +(z-\zeta )$
for an
![]() $\breve E_{\hat Z}$
-scheme X and the induced homomorphism
$\breve E_{\hat Z}$
-scheme X and the induced homomorphism
![]() $LG({\mathbb {F}})=G\big ({\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)\big )\to G\big ({\mathcal {O}}_X\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )$
to define the actions.
$LG({\mathbb {F}})=G\big ({\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)\big )\to G\big ({\mathcal {O}}_X\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )$
to define the actions.
Proof. This follows directly from the right invariance of
![]() $\hat Z^{\textrm {an}}$
as a subscheme of the affine Grassmannian and the left invariance imposed in condition (b)(v) of Definition 2.2.
$\hat Z^{\textrm {an}}$
as a subscheme of the affine Grassmannian and the left invariance imposed in condition (b)(v) of Definition 2.2.
Remark 2.11. We discuss some possible additional assumptions on bounds.
-
(a) The set
 $\pi _0({\widehat {{\mathcal {F}}\ell }}_{G,R})$
coincides with the set of
$\pi _0({\widehat {{\mathcal {F}}\ell }}_{G,R})$
coincides with the set of
 $\Gamma $
-orbits in
$\Gamma $
-orbits in
 $\pi _1(G)_I$
by [Reference Neupert76, Lemma 2.2.6]. Every bound is a disjoint union of its intersections with the various connected components of
$\pi _1(G)_I$
by [Reference Neupert76, Lemma 2.2.6]. Every bound is a disjoint union of its intersections with the various connected components of
 ${\widehat {{\mathcal {F}}\ell }}_{G,R}$
, and thus we also obtain similar decompositions of base schemes for bounded local G-shtukas and later of the corresponding moduli spaces. If one wants to consider only one of these disjoint parts at a time, one has to assume that there is a
${\widehat {{\mathcal {F}}\ell }}_{G,R}$
, and thus we also obtain similar decompositions of base schemes for bounded local G-shtukas and later of the corresponding moduli spaces. If one wants to consider only one of these disjoint parts at a time, one has to assume that there is a
 $\Gamma $
-orbit of elements
$\Gamma $
-orbit of elements
 $\xi \in \pi _1(G)_I$
such that the
$\xi \in \pi _1(G)_I$
such that the
 $\hat Z_R$
are contained in the corresponding connected component of
$\hat Z_R$
are contained in the corresponding connected component of
 ${\widehat {{\mathcal {F}}\ell }}_{G,R}$
.
${\widehat {{\mathcal {F}}\ell }}_{G,R}$
.Also compare the nonemptiness condition of Theorem 4.20, which is in terms of
 $\pi _1(G)_{\Gamma }$
instead of
$\pi _1(G)_{\Gamma }$
instead of
 $\pi _1(G)_{I}/\Gamma $
. The natural projection map
$\pi _1(G)_{I}/\Gamma $
. The natural projection map
 $\pi _1(G)_{I}/\Gamma \rightarrow \pi _1(G)_{\Gamma }$
is surjective but in general not injective. Thus, there may be several connected components of a given bound that lead to nonempty parts of the period domain.
$\pi _1(G)_{I}/\Gamma \rightarrow \pi _1(G)_{\Gamma }$
is surjective but in general not injective. Thus, there may be several connected components of a given bound that lead to nonempty parts of the period domain. -
(b) If one wants to compare properties of the generic and the special fibre of a moduli space of local G-shtukas bounded by
 $\hat Z^{-1}$
(as defined in Section 3), it might be useful to consider bounds
$\hat Z^{-1}$
(as defined in Section 3), it might be useful to consider bounds
 $\hat Z$
satisfying certain flatness or extension properties.
$\hat Z$
satisfying certain flatness or extension properties.Assumptions (b)(i) and (b)(v) of Definition 2.2 imply that the closed points of the special fibre Z from Remark 2.3(b), respectively of the analytic space
 $\hat Z^{\textrm {an}}$
of
$\hat Z^{\textrm {an}}$
of
 $\hat Z$
from Proposition 2.6(d), consist of the points of a finite set
$\hat Z$
from Proposition 2.6(d), consist of the points of a finite set
 $N_0$
of
$N_0$
of
 $L^+G$
-cosets, respectively a finite set
$L^+G$
-cosets, respectively a finite set
 $N_{\textrm {an}}$
of
$N_{\textrm {an}}$
of
 $G\big ({\,{\scriptscriptstyle \bullet }\,}\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )$
-cosets. The former cosets are parametrised by some quotient
$G\big ({\,{\scriptscriptstyle \bullet }\,}\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )$
-cosets. The former cosets are parametrised by some quotient
 $\bar W$
of the extended affine Weyl group
$\bar W$
of the extended affine Weyl group
 $\widetilde W$
of G with respect to a chosen maximal torus T of
$\widetilde W$
of G with respect to a chosen maximal torus T of
 $G_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}$
. Let
$G_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}$
. Let
 $L_0\supset {\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
be a finite separable field extension over which
$L_0\supset {\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
be a finite separable field extension over which
 $T_{L_0}:=T\times _{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em),z\mapsto \zeta }\operatorname {\mathrm {Spec}} L_0$
(and therefore also
$T_{L_0}:=T\times _{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em),z\mapsto \zeta }\operatorname {\mathrm {Spec}} L_0$
(and therefore also
 $G_{L_0}$
) splits. Because
$G_{L_0}$
) splits. Because
 $G\big (L_0\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )\subset G\big (L_0(\kern-0.15em( z-\zeta )\kern-0.15em)\big )$
is a hyperspecial maximal bounded open subgroup, every
$G\big (L_0\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )\subset G\big (L_0(\kern-0.15em( z-\zeta )\kern-0.15em)\big )$
is a hyperspecial maximal bounded open subgroup, every
 $G\big (L_0\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )$
-coset is of the form
$G\big (L_0\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )$
-coset is of the form
 $G\big (L_0\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )\mu (z-\zeta )G\big (L_0\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )\big / G\big (L_0\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )$
for a uniquely determined determined
$G\big (L_0\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )\mu (z-\zeta )G\big (L_0\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )\big / G\big (L_0\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )$
for a uniquely determined determined
 $\mu \in X_*(T_{L_0})_{\textrm {dom}}= X_*(T)_{\textrm {dom}}$
where dominance is with respect to some chosen Borel subgroup. It would thus be interesting to see whether such flatness conditions can be formulated in terms of the associated sets
$\mu \in X_*(T_{L_0})_{\textrm {dom}}= X_*(T)_{\textrm {dom}}$
where dominance is with respect to some chosen Borel subgroup. It would thus be interesting to see whether such flatness conditions can be formulated in terms of the associated sets
 $N_0\subset \bar W$
and
$N_0\subset \bar W$
and
 $N_{\textrm {an}}\subset X_*(T)_{\textrm {dom}}$
. However, for the present article we do not need any such condition.
$N_{\textrm {an}}\subset X_*(T)_{\textrm {dom}}$
. However, for the present article we do not need any such condition. -
(c) Given the discussion above, one might ask whether bounds should just be defined by the corresponding sets of double cosets of their geometric points. Even under assumptions as discussed above, our definition gives some more freedom in the sense that the nilpotent structure of the bound may still vary.
For the sake of completeness, we want to add the following lemma that was used in Remark 2.3(a).
Lemma 2.12. Let
![]() $\hat {Z}=[(R,\hat Z_R)]$
be a bound in the sense of [Reference Arasteh Rad and Hartl4, Definition 4.8]; that is, satisfying conditions (b)(i) and (b)(ii) from Definition 2.2. Consider the subsheaves
$\hat {Z}=[(R,\hat Z_R)]$
be a bound in the sense of [Reference Arasteh Rad and Hartl4, Definition 4.8]; that is, satisfying conditions (b)(i) and (b)(ii) from Definition 2.2. Consider the subsheaves
![]() $\hat {Z}_R^{-1}\subset {\widehat {{\mathcal {F}}\ell }}_{G,R}$
defined on schemes S in
$\hat {Z}_R^{-1}\subset {\widehat {{\mathcal {F}}\ell }}_{G,R}$
defined on schemes S in
![]() ${{\mathcal {N}}\!\mathit {ilp}}_R$
as the subset
${{\mathcal {N}}\!\mathit {ilp}}_R$
as the subset
![]() $\hat {Z}_R^{-1}(S)$
of
$\hat {Z}_R^{-1}(S)$
of
![]() ${\widehat {{\mathcal {F}}\ell }}_{G,R}(S)$
given by
${\widehat {{\mathcal {F}}\ell }}_{G,R}(S)$
given by
 $$ \begin{align*} &\Big\{\;x\in{\widehat{{\mathcal{F}}\ell}}_{G,R}(S)\colon\text{ there is an \'etale covering } f\colon S^{\prime}\to S \text{ and an element } g\in LG(S^{\prime}) \\ & \quad \text{ such that }f^*x = g\cdot L^+G(S^{\prime})\text{ in }{\widehat{{\mathcal{F}}\ell}}_{G,R}(S^{\prime})\text{ and } g^{-1}\cdot L^+G(S^{\prime})\in\hat{Z}_R(S^{\prime})\;\Big\}\,. \end{align*} $$
$$ \begin{align*} &\Big\{\;x\in{\widehat{{\mathcal{F}}\ell}}_{G,R}(S)\colon\text{ there is an \'etale covering } f\colon S^{\prime}\to S \text{ and an element } g\in LG(S^{\prime}) \\ & \quad \text{ such that }f^*x = g\cdot L^+G(S^{\prime})\text{ in }{\widehat{{\mathcal{F}}\ell}}_{G,R}(S^{\prime})\text{ and } g^{-1}\cdot L^+G(S^{\prime})\in\hat{Z}_R(S^{\prime})\;\Big\}\,. \end{align*} $$
Then
![]() $\hat Z^{-1}=[(R,\hat Z_R^{-1})]$
is a bound in the sense of [Reference Arasteh Rad and Hartl4, Definition 4.8] with the same reflex ring
$\hat Z^{-1}=[(R,\hat Z_R^{-1})]$
is a bound in the sense of [Reference Arasteh Rad and Hartl4, Definition 4.8] with the same reflex ring
![]() $R_{\hat Z}$
as
$R_{\hat Z}$
as
![]() $\hat {Z}$
. If, in addition,
$\hat {Z}$
. If, in addition,
![]() $\hat {Z}$
satisfies condition (b)(iii) and (b)(iv) from Definition 2.2, then the same is true for
$\hat {Z}$
satisfies condition (b)(iii) and (b)(iv) from Definition 2.2, then the same is true for
![]() $\hat {Z}^{-1}$
. Moreover, for two
$\hat {Z}^{-1}$
. Moreover, for two
![]() $L^+G$
-torsors
$L^+G$
-torsors
![]() ${\mathcal {G}}$
and
${\mathcal {G}}$
and
![]() ${\mathcal {G}}^{\prime }$
over a scheme
${\mathcal {G}}^{\prime }$
over a scheme
![]() $S\in {{\mathcal {N}}\!\mathit {ilp}}_{R_{\hat Z}}$
, an isomorphism
$S\in {{\mathcal {N}}\!\mathit {ilp}}_{R_{\hat Z}}$
, an isomorphism
![]() between the associated
between the associated
![]() $LG$
-torsors is bounded by
$LG$
-torsors is bounded by
![]() $\hat {Z}$
if and only if
$\hat {Z}$
if and only if
![]() $\delta ^{-1}$
is bounded by
$\delta ^{-1}$
is bounded by
![]() $\hat {Z}^{-1}$
.
$\hat {Z}^{-1}$
.
We do not know whether the same is true for condition (b)(v) from Definition 2.2 in general. It is true, however, for the bounds in Example 2.7.
Proof of Lemma 2.12
The subset is well defined, because
![]() $\hat {Z}_R$
is by Definition 2.2(b)(i) invariant under multiplication with
$\hat {Z}_R$
is by Definition 2.2(b)(i) invariant under multiplication with
![]() $L^+G$
on the left. We fix a faithful representation
$L^+G$
on the left. We fix a faithful representation
![]() $\rho \colon G\hookrightarrow \operatorname {\mathrm {SL}}_r$
and consider the induced morphism
$\rho \colon G\hookrightarrow \operatorname {\mathrm {SL}}_r$
and consider the induced morphism
![]() $\rho _*\colon {\mathcal {F}}\ell _G\hookrightarrow {\mathcal {F}}\ell _{\operatorname {\mathrm {SL}}_r}$
. The ind-scheme structure on
$\rho _*\colon {\mathcal {F}}\ell _G\hookrightarrow {\mathcal {F}}\ell _{\operatorname {\mathrm {SL}}_r}$
. The ind-scheme structure on
![]() ${\mathcal {F}}\ell _{G,R}$
is given as the inductive limit of the schemes
${\mathcal {F}}\ell _{G,R}$
is given as the inductive limit of the schemes
where
![]() ${\widehat {{\mathcal {F}}\ell }}^{(n)}_{\operatorname {\mathrm {SL}}_r}$
was defined in (2.1). We must show that
${\widehat {{\mathcal {F}}\ell }}^{(n)}_{\operatorname {\mathrm {SL}}_r}$
was defined in (2.1). We must show that
![]() $\hat {Z}_R^{-1}\times _{{\widehat {{\mathcal {F}}\ell }}_{G,R}}X_n$
is representable by a closed subscheme of
$\hat {Z}_R^{-1}\times _{{\widehat {{\mathcal {F}}\ell }}_{G,R}}X_n$
is representable by a closed subscheme of
![]() $X_n$
. Let
$X_n$
. Let
![]() $Y_n:=X_n\widehat {\displaystyle \times }_{{\widehat {{\mathcal {F}}\ell }}_{G,R}}\big (LG\widehat {\displaystyle \times }_{{\mathbb {F}}_q}\operatorname {\mathrm {Spec}} R/(\zeta ^n)\big )$
. Because
$Y_n:=X_n\widehat {\displaystyle \times }_{{\widehat {{\mathcal {F}}\ell }}_{G,R}}\big (LG\widehat {\displaystyle \times }_{{\mathbb {F}}_q}\operatorname {\mathrm {Spec}} R/(\zeta ^n)\big )$
. Because
![]() $X_n\widehat {\displaystyle \times }_{{\widehat {{\mathcal {F}}\ell }}_{G,R}}\hat {Z}_R\subset X_n$
is a closed subscheme, the base change
$X_n\widehat {\displaystyle \times }_{{\widehat {{\mathcal {F}}\ell }}_{G,R}}\hat {Z}_R\subset X_n$
is a closed subscheme, the base change
![]() $Z_n:=Y_n\widehat {\displaystyle \times }_{X_n}X_n\widehat {\displaystyle \times }_{{\widehat {{\mathcal {F}}\ell }}_{G,R}}\hat {Z}_R$
is a closed subscheme of
$Z_n:=Y_n\widehat {\displaystyle \times }_{X_n}X_n\widehat {\displaystyle \times }_{{\widehat {{\mathcal {F}}\ell }}_{G,R}}\hat {Z}_R$
is a closed subscheme of
![]() $Y_n$
, on which
$Y_n$
, on which
![]() $L^+G_{R/(\zeta ^n)}:=L^+G\widehat {\displaystyle \times }_{{\mathbb {F}}_q}\operatorname {\mathrm {Spec}} R/(\zeta ^n)$
acts by multiplication on the left. By Cramer’s rule (e.g., [Reference Bourbaki22, III.8.6, Formulas (21) and (22)]), the inversion
$L^+G_{R/(\zeta ^n)}:=L^+G\widehat {\displaystyle \times }_{{\mathbb {F}}_q}\operatorname {\mathrm {Spec}} R/(\zeta ^n)$
acts by multiplication on the left. By Cramer’s rule (e.g., [Reference Bourbaki22, III.8.6, Formulas (21) and (22)]), the inversion
![]() $g\mapsto g^{-1}$
on
$g\mapsto g^{-1}$
on
![]() $LG$
induces isomorphisms of
$LG$
induces isomorphisms of
![]() $X_n$
with the quotient sheaf
$X_n$
with the quotient sheaf
![]() $L^+G_{R/(\zeta ^n)}\backslash Y_n$
and of
$L^+G_{R/(\zeta ^n)}\backslash Y_n$
and of
![]() $\hat {Z}_R^{-1}\times _{{\widehat {{\mathcal {F}}\ell }}_{G,R}}X_n$
with
$\hat {Z}_R^{-1}\times _{{\widehat {{\mathcal {F}}\ell }}_{G,R}}X_n$
with
![]() $L^+G_{R/(\zeta ^n)}\backslash Z_n$
. Therefore, it suffices to show that the morphism
$L^+G_{R/(\zeta ^n)}\backslash Z_n$
. Therefore, it suffices to show that the morphism
![]() $L^+G_{R/(\zeta ^n)}\backslash Z_n\to L^+G_{R/(\zeta ^n)}\backslash Y_n$
of sheaves is representable by a closed immersion. The latter follows by fpqc descent [Reference Bosch, Lütkebohmert and Raynaud20, § 6.1, Theorem 6] and [Reference Grothendieck44, IV
$L^+G_{R/(\zeta ^n)}\backslash Z_n\to L^+G_{R/(\zeta ^n)}\backslash Y_n$
of sheaves is representable by a closed immersion. The latter follows by fpqc descent [Reference Bosch, Lütkebohmert and Raynaud20, § 6.1, Theorem 6] and [Reference Grothendieck44, IV
![]() ${}_2$
, Proposition 2.7.1] from the fact that the diagram
${}_2$
, Proposition 2.7.1] from the fact that the diagram

is Cartesian and the right vertical arrow is an affine faithfully flat morphism of schemes. This proves that
![]() $\hat {Z}^{-1}_R\subset {\widehat {{\mathcal {F}}\ell }}_{G,R}$
is representable by a closed ind-subscheme. By construction it satisfies the invariance under left multiplication by
$\hat {Z}^{-1}_R\subset {\widehat {{\mathcal {F}}\ell }}_{G,R}$
is representable by a closed ind-subscheme. By construction it satisfies the invariance under left multiplication by
![]() $L^+G$
from Definition 2.2(b)(i).
$L^+G$
from Definition 2.2(b)(i).
To show that
![]() $\hat {Z}^{-1}_R$
satisfies Definition 2.2(b)(ii), let
$\hat {Z}^{-1}_R$
satisfies Definition 2.2(b)(ii), let
![]() $S^{\prime }$
be an étale covering of the special fibre
$S^{\prime }$
be an étale covering of the special fibre
![]() $Z_R$
of
$Z_R$
of
![]() $\hat {Z}_R$
, such that the closed immersion
$\hat {Z}_R$
, such that the closed immersion
![]() $Z_R\hookrightarrow {\widehat {{\mathcal {F}}\ell }}_{G,R}\widehat {\displaystyle \times }_R\operatorname {\mathrm {Spec}}\kappa _R$
lifts to a morphism
$Z_R\hookrightarrow {\widehat {{\mathcal {F}}\ell }}_{G,R}\widehat {\displaystyle \times }_R\operatorname {\mathrm {Spec}}\kappa _R$
lifts to a morphism
![]() $S^{\prime }\to LG\widehat {\displaystyle \times }_{{\mathbb {F}}_q}\operatorname {\mathrm {Spec}}\kappa _R$
, which we view as an element
$S^{\prime }\to LG\widehat {\displaystyle \times }_{{\mathbb {F}}_q}\operatorname {\mathrm {Spec}}\kappa _R$
, which we view as an element
![]() $g^{-1}\in LG(S^{\prime })$
. Because
$g^{-1}\in LG(S^{\prime })$
. Because
![]() $Z_R$
is quasi-compact, we may choose
$Z_R$
is quasi-compact, we may choose
![]() $S^{\prime }$
to be quasi-compact. Then the element
$S^{\prime }$
to be quasi-compact. Then the element
![]() $g\cdot L^+G(S^{\prime })$
in
$g\cdot L^+G(S^{\prime })$
in
![]() ${\widehat {{\mathcal {F}}\ell }}_{G,R}(S^{\prime })$
corresponds to a morphism
${\widehat {{\mathcal {F}}\ell }}_{G,R}(S^{\prime })$
corresponds to a morphism
![]() $S^{\prime }\to {\widehat {{\mathcal {F}}\ell }}_{G,R}\widehat {\displaystyle \times }_R\operatorname {\mathrm {Spec}}\kappa _R$
that factors through
$S^{\prime }\to {\widehat {{\mathcal {F}}\ell }}_{G,R}\widehat {\displaystyle \times }_R\operatorname {\mathrm {Spec}}\kappa _R$
that factors through
![]() $Z_R^{-1}$
. The morphism
$Z_R^{-1}$
. The morphism
![]() $L^+G\widehat {\displaystyle \times }_{{\mathbb {F}}_q}S^{\prime }\twoheadrightarrow Z_R^{-1}$
,
$L^+G\widehat {\displaystyle \times }_{{\mathbb {F}}_q}S^{\prime }\twoheadrightarrow Z_R^{-1}$
,
![]() $(h,g)\mapsto hg\cdot L^+G$
is a surjective morphism of ind-schemes. Therefore,
$(h,g)\mapsto hg\cdot L^+G$
is a surjective morphism of ind-schemes. Therefore,
![]() $Z_R^{-1}$
is a quasi-compact scheme.
$Z_R^{-1}$
is a quasi-compact scheme.
If
![]() $\hat {Z}$
satisfies conditions (b)(iii) and (b)(iv) from Definition 2.2 for some
$\hat {Z}$
satisfies conditions (b)(iii) and (b)(iv) from Definition 2.2 for some
![]() $\rho \colon G\hookrightarrow \operatorname {\mathrm {SL}}_r$
and some n, then
$\rho \colon G\hookrightarrow \operatorname {\mathrm {SL}}_r$
and some n, then
![]() $\hat {Z}^{-1}$
also satisfies (b)(iv) for the same
$\hat {Z}^{-1}$
also satisfies (b)(iv) for the same
![]() $\rho $
and n by Cramer’s rule (e.g., [Reference Bourbaki22, III.8.6, Formulas (21) and (22)]). Then
$\rho $
and n by Cramer’s rule (e.g., [Reference Bourbaki22, III.8.6, Formulas (21) and (22)]). Then
![]() $\hat {Z}_R^{-1}=\lim \limits _{\longrightarrow m} \hat {Z}_R^{-1}\times _{{\widehat {{\mathcal {F}}\ell }}_{G,R}}X_{n,m}$
for constant n and variable m. In particular,
$\hat {Z}_R^{-1}=\lim \limits _{\longrightarrow m} \hat {Z}_R^{-1}\times _{{\widehat {{\mathcal {F}}\ell }}_{G,R}}X_{n,m}$
for constant n and variable m. In particular,
![]() $\hat {Z}_R^{-1}=\lim \limits _{\longrightarrow m} \hat {Z}_R^{-1}\times _R\operatorname {\mathrm {Spec}} R/(\zeta ^m)$
is
$\hat {Z}_R^{-1}=\lim \limits _{\longrightarrow m} \hat {Z}_R^{-1}\times _R\operatorname {\mathrm {Spec}} R/(\zeta ^m)$
is
![]() $\zeta $
-adic; that is, satisfies condition (b)(iii)
$\zeta $
-adic; that is, satisfies condition (b)(iii)
The equality of reflex rings follows from the fact that
![]() $\gamma (\hat {Z})=\hat {Z}$
if and only if
$\gamma (\hat {Z})=\hat {Z}$
if and only if
![]() $\gamma (\hat {Z}^{-1})=\hat {Z}^{-1}$
for
$\gamma (\hat {Z}^{-1})=\hat {Z}^{-1}$
for
![]() $\gamma \in \operatorname {\mathrm {Aut}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}}({\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)^{\textrm {alg}})$
. Finally, the statement about the boundedness of
$\gamma \in \operatorname {\mathrm {Aut}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}}({\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)^{\textrm {alg}})$
. Finally, the statement about the boundedness of
![]() $\delta $
and
$\delta $
and
![]() $\delta ^{-1}$
is clear from the definition of the
$\delta ^{-1}$
is clear from the definition of the
![]() $\hat {Z}_R^{-1}$
.
$\hat {Z}_R^{-1}$
.
Example 2.13. We revert to Example 2.8. If
![]() $G_0=\operatorname {\mathrm {GL}}_r$
or
$G_0=\operatorname {\mathrm {GL}}_r$
or
![]() $G_0=\operatorname {\mathrm {SL}}_r$
, then
$G_0=\operatorname {\mathrm {SL}}_r$
, then
by Cramer’s rule (e.g., [Reference Bourbaki22, III.8.6, Formulas (21) and (22)]). However, this is not true for general
![]() $G_0$
. For example, let
$G_0$
. For example, let
![]() $G_0=\operatorname {\mathrm {PGL}}_2$
and
$G_0=\operatorname {\mathrm {PGL}}_2$
and
![]() $\operatorname {\mathrm {char}}({\mathbb {F}}_q)=2$
. We choose
$\operatorname {\mathrm {char}}({\mathbb {F}}_q)=2$
. We choose
![]() $\Lambda $
to consist of the only positive root
$\Lambda $
to consist of the only positive root
![]() $\alpha $
. The corresponding Weyl module
$\alpha $
. The corresponding Weyl module
![]() $V_\alpha $
is the dual of the adjoint representation. With respect to the decomposition
$V_\alpha $
is the dual of the adjoint representation. With respect to the decomposition
![]() $V_\alpha =(\operatorname {\mathrm {Lie}} T\oplus \operatorname {\mathrm {Lie}} U_\alpha \oplus \operatorname {\mathrm {Lie}} U_{-\alpha })^{\scriptscriptstyle \lor }$
it is given by
$V_\alpha =(\operatorname {\mathrm {Lie}} T\oplus \operatorname {\mathrm {Lie}} U_\alpha \oplus \operatorname {\mathrm {Lie}} U_{-\alpha })^{\scriptscriptstyle \lor }$
it is given by
 $$ \begin{align*} \rho_\alpha\colon\operatorname{\mathrm{PGL}}_2\to\operatorname{\mathrm{GL}}(V_\alpha)\;,\quad g=\left(\begin{matrix}a&b\\c&d\end{matrix}\right)\mapsto\left(\begin{array}{ccc} 1&\frac{ac}{\det g}&\frac{bd}{\det g}\\[1mm] 0&\frac{a^2}{\det g}&\frac{b^2}{\det g}\\[1mm] 0&\frac{c^2}{\det g}&\frac{d^2}{\det g}\end{array}\right). \end{align*} $$
$$ \begin{align*} \rho_\alpha\colon\operatorname{\mathrm{PGL}}_2\to\operatorname{\mathrm{GL}}(V_\alpha)\;,\quad g=\left(\begin{matrix}a&b\\c&d\end{matrix}\right)\mapsto\left(\begin{array}{ccc} 1&\frac{ac}{\det g}&\frac{bd}{\det g}\\[1mm] 0&\frac{a^2}{\det g}&\frac{b^2}{\det g}\\[1mm] 0&\frac{c^2}{\det g}&\frac{d^2}{\det g}\end{array}\right). \end{align*} $$
We let
![]() $\mu \in X_*(T)_{\textrm {dom}}$
be the dominant coweight with
$\mu \in X_*(T)_{\textrm {dom}}$
be the dominant coweight with
![]() $\mu (a)=\left (\begin {smallmatrix} a & 0 \\ 0 & 1 \end {smallmatrix}\right )$
. Then
$\mu (a)=\left (\begin {smallmatrix} a & 0 \\ 0 & 1 \end {smallmatrix}\right )$
. Then
![]() $(-\mu )_{\textrm {dom}}=\mu $
and
$(-\mu )_{\textrm {dom}}=\mu $
and
![]() $\langle \mu ,\alpha \rangle =1$
. Over the
$\langle \mu ,\alpha \rangle =1$
. Over the
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}/(\zeta )$
-algebra
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}/(\zeta )$
-algebra
![]() $B={\mathbb {F}}_q[\varepsilon ]/(\varepsilon ^2)$
the element
$B={\mathbb {F}}_q[\varepsilon ]/(\varepsilon ^2)$
the element
![]() $g=\left (\begin {smallmatrix} 1 & \frac {\varepsilon }{z} \\ 0 & z \end {smallmatrix}\right )\in LG(B)=\operatorname {\mathrm {PGL}}_2\big (B(\kern-0.15em( z)\kern-0.15em)\big )$
lies in
$g=\left (\begin {smallmatrix} 1 & \frac {\varepsilon }{z} \\ 0 & z \end {smallmatrix}\right )\in LG(B)=\operatorname {\mathrm {PGL}}_2\big (B(\kern-0.15em( z)\kern-0.15em)\big )$
lies in
![]() $\hat {Z}^{\scriptscriptstyle \textrm {Weyl},-1}_{\operatorname {\mathrm {PGL}}_2,\,\preceq \mu }$
, but
$\hat {Z}^{\scriptscriptstyle \textrm {Weyl},-1}_{\operatorname {\mathrm {PGL}}_2,\,\preceq \mu }$
, but
![]() $g^{-1}=\left (\begin {smallmatrix} z & -\frac {\varepsilon }{z} \\ 0 & 1 \end {smallmatrix}\right )$
does not belong to
$g^{-1}=\left (\begin {smallmatrix} z & -\frac {\varepsilon }{z} \\ 0 & 1 \end {smallmatrix}\right )$
does not belong to
![]() $\hat {Z}^{\scriptscriptstyle \textrm {Weyl},-1}_{\operatorname {\mathrm {PGL}}_2,\,\preceq \mu }$
because
$\hat {Z}^{\scriptscriptstyle \textrm {Weyl},-1}_{\operatorname {\mathrm {PGL}}_2,\,\preceq \mu }$
because
 $$ \begin{align*} \rho_\alpha(g)= \left(\begin{array}{ccc} 1&0&\frac{\varepsilon}{z}\\[1mm] 0&\frac{1}{z}&0\\[1mm] 0&0&z\end{array}\right) \qquad\text{and}\qquad \rho_\alpha(g^{-1})= \left(\begin{array}{ccc} 1&0&-\frac{\varepsilon}{z^2}\\[1mm] 0&z&0\\[1mm] 0&0&\frac{1}{z}\end{array}\right). \end{align*} $$
$$ \begin{align*} \rho_\alpha(g)= \left(\begin{array}{ccc} 1&0&\frac{\varepsilon}{z}\\[1mm] 0&\frac{1}{z}&0\\[1mm] 0&0&z\end{array}\right) \qquad\text{and}\qquad \rho_\alpha(g^{-1})= \left(\begin{array}{ccc} 1&0&-\frac{\varepsilon}{z^2}\\[1mm] 0&z&0\\[1mm] 0&0&\frac{1}{z}\end{array}\right). \end{align*} $$
So
![]() $\hat {Z}^{\scriptscriptstyle \textrm {Weyl}}_{\operatorname {\mathrm {PGL}}_2,\,\preceq \mu }\ne \hat {Z}^{\scriptscriptstyle \textrm {Weyl},-1}_{\operatorname {\mathrm {PGL}}_2,\preceq (-\mu )_{\textrm {dom}}}$
in this case. Note that, nevertheless, the underlying topological spaces of these two bounds coincide by Remark 2.11(b). So the difference lies in the nilpotent structure.
$\hat {Z}^{\scriptscriptstyle \textrm {Weyl}}_{\operatorname {\mathrm {PGL}}_2,\,\preceq \mu }\ne \hat {Z}^{\scriptscriptstyle \textrm {Weyl},-1}_{\operatorname {\mathrm {PGL}}_2,\preceq (-\mu )_{\textrm {dom}}}$
in this case. Note that, nevertheless, the underlying topological spaces of these two bounds coincide by Remark 2.11(b). So the difference lies in the nilpotent structure.
3 Rapoport-Zink spaces for bounded local G-shtukas
To recall the definition of Rapoport-Zink spaces for local G-shtukas, let
![]() ${\underline {{\mathbb {G}}}}_0$
be a local G-shtuka over
${\underline {{\mathbb {G}}}}_0$
be a local G-shtuka over
![]() ${\mathbb {F}}$
. Because
${\mathbb {F}}$
. Because
![]() ${\mathbb {F}}$
has no nontrivial étale coverings, we may fix a trivialisation
${\mathbb {F}}$
has no nontrivial étale coverings, we may fix a trivialisation
![]() ${\underline {{\mathbb {G}}}}_0\cong \big ((L^+G)_{\mathbb {F}},b\sigma ^\ast \big )$
where
${\underline {{\mathbb {G}}}}_0\cong \big ((L^+G)_{\mathbb {F}},b\sigma ^\ast \big )$
where
![]() $b\in LG({\mathbb {F}})$
represents the Frobenius morphism. In all that follows we may replace
$b\in LG({\mathbb {F}})$
represents the Frobenius morphism. In all that follows we may replace
![]() ${\underline {{\mathbb {G}}}}_0$
by a quasi-isogenous local G-shtuka
${\underline {{\mathbb {G}}}}_0$
by a quasi-isogenous local G-shtuka
![]() ${\underline {{\mathbb {G}}}}^{\prime }_0\cong \big ((L^+G)_{\mathbb {F}},b^{\prime }\sigma ^\ast \big )$
. In terms of the trivialisations, this means that there is an
${\underline {{\mathbb {G}}}}^{\prime }_0\cong \big ((L^+G)_{\mathbb {F}},b^{\prime }\sigma ^\ast \big )$
. In terms of the trivialisations, this means that there is an
![]() $h\in LG({\mathbb {F}})$
with
$h\in LG({\mathbb {F}})$
with
![]() $b^{\prime }=h^{-1}b\sigma ^\ast (h)$
. In this case we say that b and
$b^{\prime }=h^{-1}b\sigma ^\ast (h)$
. In this case we say that b and
![]() $b^{\prime }$
are
$b^{\prime }$
are
![]() $\sigma $
-conjugate under
$\sigma $
-conjugate under
![]() $LG({\mathbb {F}})$
or
$LG({\mathbb {F}})$
or
![]() $LG({\mathbb {F}})$
-
$LG({\mathbb {F}})$
-
![]() $\sigma $
-conjugate. We write
$\sigma $
-conjugate. We write
![]() $[b]$
for the
$[b]$
for the
![]() $LG({\mathbb {F}})$
-
$LG({\mathbb {F}})$
-
![]() $\sigma $
-conjugacy class of b.
$\sigma $
-conjugacy class of b.
Definition 3.1. Let
![]() $\hat {Z}=[(R,\hat Z_R)]$
be a bound with reflex ring
$\hat {Z}=[(R,\hat Z_R)]$
be a bound with reflex ring
![]() $R_{\hat Z}=\kappa \mathrm {[}\kern-0.15em\mathrm {[}\xi \mathrm {]}\kern-0.15em\mathrm {]}$
, set
$R_{\hat Z}=\kappa \mathrm {[}\kern-0.15em\mathrm {[}\xi \mathrm {]}\kern-0.15em\mathrm {]}$
, set
![]() $\breve R_{\hat Z}:={\mathbb {F}}\mathrm {[}\kern-0.15em\mathrm {[}\xi \mathrm {]}\kern-0.15em\mathrm {]}$
and consider the functor
$\breve R_{\hat Z}:={\mathbb {F}}\mathrm {[}\kern-0.15em\mathrm {[}\xi \mathrm {]}\kern-0.15em\mathrm {]}$
and consider the functor
![]() ${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}\colon ({{\mathcal {N}}\!\mathit {ilp}}_{\breve R_{\hat Z}})^o \;\longrightarrow \;{{\mathcal {S}} \!\mathit {ets}}$
${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}\colon ({{\mathcal {N}}\!\mathit {ilp}}_{\breve R_{\hat Z}})^o \;\longrightarrow \;{{\mathcal {S}} \!\mathit {ets}}$
 $$ \begin{align*} S&\longmapsto \bigg\{\,\text{Isomorphism classes of }({\underline{{\mathcal{G}}}},\bar\delta)\colon\text{ where }{\underline{{\mathcal{G}}}}\text{ is a local } G\text{-shtuka over } S \\ &~~~~ \text{bounded by } \hat{Z}^{-1} \text{ and }\bar{\delta}\colon {\underline{{\mathcal{G}}}}_{\bar{S}}\to {\underline{{\mathbb{G}}}}_{0,\bar{S}}~\text{is a quasi-isogeny over } \bar{S}\bigg\}. \end{align*} $$
$$ \begin{align*} S&\longmapsto \bigg\{\,\text{Isomorphism classes of }({\underline{{\mathcal{G}}}},\bar\delta)\colon\text{ where }{\underline{{\mathcal{G}}}}\text{ is a local } G\text{-shtuka over } S \\ &~~~~ \text{bounded by } \hat{Z}^{-1} \text{ and }\bar{\delta}\colon {\underline{{\mathcal{G}}}}_{\bar{S}}\to {\underline{{\mathbb{G}}}}_{0,\bar{S}}~\text{is a quasi-isogeny over } \bar{S}\bigg\}. \end{align*} $$
Here
![]() $\bar {S}:=\operatorname {\mathrm {V}}_S(\zeta )$
is the zero locus of
$\bar {S}:=\operatorname {\mathrm {V}}_S(\zeta )$
is the zero locus of
![]() $\zeta $
in S.
$\zeta $
in S.
The group
![]() $\operatorname {\mathrm {QIsog}}_{{\mathbb {F}}}({\underline {{\mathbb {G}}}}_0)$
of quasi-isogenies of
$\operatorname {\mathrm {QIsog}}_{{\mathbb {F}}}({\underline {{\mathbb {G}}}}_0)$
of quasi-isogenies of
![]() ${\underline {{\mathbb {G}}}}_0$
acts on the functor
${\underline {{\mathbb {G}}}}_0$
acts on the functor
![]() ${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
via
${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
via
![]() $j\colon ({\underline {{\mathcal {G}}}},\bar \delta )\mapsto ({\underline {{\mathcal {G}}}},j\circ \bar \delta )$
for
$j\colon ({\underline {{\mathcal {G}}}},\bar \delta )\mapsto ({\underline {{\mathcal {G}}}},j\circ \bar \delta )$
for
![]() $j\in \operatorname {\mathrm {QIsog}}_{{\mathbb {F}}}({\underline {{\mathbb {G}}}}_0)$
.
$j\in \operatorname {\mathrm {QIsog}}_{{\mathbb {F}}}({\underline {{\mathbb {G}}}}_0)$
.
Remark 3.2. Because
![]() ${\underline {{\mathbb {G}}}}_0\cong \big ((L^+G)_{\mathbb {F}},b\sigma ^\ast \big )$
, we can identify
${\underline {{\mathbb {G}}}}_0\cong \big ((L^+G)_{\mathbb {F}},b\sigma ^\ast \big )$
, we can identify
![]() $\operatorname {\mathrm {QIsog}}_{\mathbb {F}}({\underline {{\mathbb {G}}}}_0)\cong J_b\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
where
$\operatorname {\mathrm {QIsog}}_{\mathbb {F}}({\underline {{\mathbb {G}}}}_0)\cong J_b\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
where
![]() $J_b$
is the connected algebraic group over
$J_b$
is the connected algebraic group over
![]() ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
that is defined by its functor of points that assigns to an
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
that is defined by its functor of points that assigns to an
![]() ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-algebra A the group
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-algebra A the group
see [Reference Arasteh Rad and Hartl4, Remark 4.16].
Remark 3.3. As in the arithmetic case (compare [Reference Rapoport and Zink80, 3.48]), we have a Weil descent datum
![]() $\alpha $
on the functor
$\alpha $
on the functor
![]() ${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
. To define it, let
${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
. To define it, let
![]() $S\in {{\mathcal {N}}\!\mathit {ilp}}_{\breve R_{\hat Z}}$
and let
$S\in {{\mathcal {N}}\!\mathit {ilp}}_{\breve R_{\hat Z}}$
and let
![]() $f\colon S\rightarrow \operatorname {\mathrm {Spf}}\breve R_{\hat Z}$
and
$f\colon S\rightarrow \operatorname {\mathrm {Spf}}\breve R_{\hat Z}$
and
![]() $\bar f\colon \bar S\rightarrow \operatorname {\mathrm {Spec}}\breve R_{\hat Z}/(\zeta )$
be the structure morphisms. Let
$\bar f\colon \bar S\rightarrow \operatorname {\mathrm {Spec}}\breve R_{\hat Z}/(\zeta )$
be the structure morphisms. Let
![]() $\varphi $
be the Frobenius of
$\varphi $
be the Frobenius of
![]() $\breve R_{\hat Z}={\mathbb {F}}\mathrm {[}\kern-0.15em\mathrm {[}\xi \mathrm {]}\kern-0.15em\mathrm {]}$
over
$\breve R_{\hat Z}={\mathbb {F}}\mathrm {[}\kern-0.15em\mathrm {[}\xi \mathrm {]}\kern-0.15em\mathrm {]}$
over
![]() $R_{\hat Z}=\kappa \mathrm {[}\kern-0.15em\mathrm {[}\xi \mathrm {]}\kern-0.15em\mathrm {]}$
and let
$R_{\hat Z}=\kappa \mathrm {[}\kern-0.15em\mathrm {[}\xi \mathrm {]}\kern-0.15em\mathrm {]}$
and let
![]() $S_\varphi $
be the scheme S together with the structure morphism
$S_\varphi $
be the scheme S together with the structure morphism
![]() $\varphi \circ f\colon S\rightarrow \operatorname {\mathrm {Spf}}\breve R_{\hat Z}$
. If
$\varphi \circ f\colon S\rightarrow \operatorname {\mathrm {Spf}}\breve R_{\hat Z}$
. If
![]() $\#\kappa =q^e$
, the inclusion
$\#\kappa =q^e$
, the inclusion
![]() ${\mathbb {F}}\hookrightarrow \breve R_{\hat Z}$
is equivariant for the action of
${\mathbb {F}}\hookrightarrow \breve R_{\hat Z}$
is equivariant for the action of
![]() $\varphi $
on
$\varphi $
on
![]() $\breve R_{\hat Z}$
and the action of
$\breve R_{\hat Z}$
and the action of
![]() $\sigma ^e$
on
$\sigma ^e$
on
![]() ${\mathbb {F}}$
. To define
${\mathbb {F}}$
. To define
![]() , let
, let
![]() $({\underline {{\mathcal {G}}}},\bar \delta )$
be a point in the first set. To make the definition more clear, we write
$({\underline {{\mathcal {G}}}},\bar \delta )$
be a point in the first set. To make the definition more clear, we write
![]() ${\underline {{\mathbb {G}}}}_{0,\bar {S}}=\bar f^*({\underline {{\mathbb {G}}}}_0)$
. Then we set
${\underline {{\mathbb {G}}}}_{0,\bar {S}}=\bar f^*({\underline {{\mathbb {G}}}}_0)$
. Then we set
![]() $\alpha ({\underline {{\mathcal {G}}}},\bar \delta )=({\underline {{\mathcal {G}}}},\bar f^*(\tau _{{\mathbb {G}}_0}^e)^{-1}\circ \bar \delta )$
; that is, we replace the quasi-isogeny
$\alpha ({\underline {{\mathcal {G}}}},\bar \delta )=({\underline {{\mathcal {G}}}},\bar f^*(\tau _{{\mathbb {G}}_0}^e)^{-1}\circ \bar \delta )$
; that is, we replace the quasi-isogeny
![]() $\bar \delta $
by the composite
$\bar \delta $
by the composite
![]() ${\underline {{\mathcal {G}}}}_{\bar {S}}\to \bar f^*({\underline {{\mathbb {G}}}}_0)\to \bar f^*\sigma ^{e*}({\underline {{\mathbb {G}}}}_0)=(\bar \varphi \bar f)^*({\underline {{\mathbb {G}}}}_0)$
. Although this Weil descent datum is in general not effective,
${\underline {{\mathcal {G}}}}_{\bar {S}}\to \bar f^*({\underline {{\mathbb {G}}}}_0)\to \bar f^*\sigma ^{e*}({\underline {{\mathbb {G}}}}_0)=(\bar \varphi \bar f)^*({\underline {{\mathbb {G}}}}_0)$
. Although this Weil descent datum is in general not effective,
![]() ${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
always descends to a finite unramified extension of
${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
always descends to a finite unramified extension of
![]() $\breve R_{\hat Z}$
; see Remark 3.6(b).
$\breve R_{\hat Z}$
; see Remark 3.6(b).
Remark 3.4. By its definition,
![]() ${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
only depends on the triple
${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
only depends on the triple
![]() $(G,[b],\hat {Z})$
, where
$(G,[b],\hat {Z})$
, where
![]() $[b]$
is the
$[b]$
is the
![]() $LG({\mathbb {F}})$
-
$LG({\mathbb {F}})$
-
![]() $\sigma $
-conjugacy class of b corresponding to the isogeny class of
$\sigma $
-conjugacy class of b corresponding to the isogeny class of
![]() ${\underline {{\mathbb {G}}}}_0\cong \big ((L^+G)_{\mathbb {F}},b\sigma ^\ast \big )$
. In the arithmetic analogue, the corresponding independence of the Rapoport-Zink spaces on additional choices made in their definition is far from obvious. It was conjectured in [Reference Rapoport and Viehmann79, Conjecture 4.16] and proved in [Reference Scholze and Weinstein90, Corollary 23.4.3 and thereafter].
${\underline {{\mathbb {G}}}}_0\cong \big ((L^+G)_{\mathbb {F}},b\sigma ^\ast \big )$
. In the arithmetic analogue, the corresponding independence of the Rapoport-Zink spaces on additional choices made in their definition is far from obvious. It was conjectured in [Reference Rapoport and Viehmann79, Conjecture 4.16] and proved in [Reference Scholze and Weinstein90, Corollary 23.4.3 and thereafter].
As in Remark 2.3(a) and (b), we let
![]() $\hat Z^{-1}$
be the bound from Lemma 2.12, and we let
$\hat Z^{-1}$
be the bound from Lemma 2.12, and we let
![]() $Z^{-1}$
be the special fibre of
$Z^{-1}$
be the special fibre of
![]() $\hat Z^{-1}$
over
$\hat Z^{-1}$
over
![]() $\kappa $
. We define the associated affine Deligne-Lusztig variety as the reduced closed ind-subscheme
$\kappa $
. We define the associated affine Deligne-Lusztig variety as the reduced closed ind-subscheme
![]() $X_{Z^{-1}}(b)\subset {\mathcal {F}}\ell _G$
whose K-valued points (for any field extension K of
$X_{Z^{-1}}(b)\subset {\mathcal {F}}\ell _G$
whose K-valued points (for any field extension K of
![]() ${\mathbb {F}}$
) are given by
${\mathbb {F}}$
) are given by
In [Reference Arasteh Rad and Hartl4, Theorem 4.18 and Corollary 4.26], the following theorem was proved.
Theorem 3.5. The functor
![]() ${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}\colon ({{\mathcal {N}}\!\mathit {ilp}}_{\breve R_{\hat Z}})^o\to {{\mathcal {S}} \!\mathit {ets}}$
from Definition 3.1 is ind-representable by a formal scheme over
${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}\colon ({{\mathcal {N}}\!\mathit {ilp}}_{\breve R_{\hat Z}})^o\to {{\mathcal {S}} \!\mathit {ets}}$
from Definition 3.1 is ind-representable by a formal scheme over
![]() $\operatorname {\mathrm {Spf}} \breve R_{\hat Z}$
which is locally formally of finite type and separated. It is an ind-closed ind-subscheme of
$\operatorname {\mathrm {Spf}} \breve R_{\hat Z}$
which is locally formally of finite type and separated. It is an ind-closed ind-subscheme of
![]() ${\mathcal {F}}\ell _G\widehat {\displaystyle \times }_{{\mathbb {F}}_q}\operatorname {\mathrm {Spf}}\breve R_{\hat Z}$
. Its underlying reduced subscheme equals
${\mathcal {F}}\ell _G\widehat {\displaystyle \times }_{{\mathbb {F}}_q}\operatorname {\mathrm {Spf}}\breve R_{\hat Z}$
. Its underlying reduced subscheme equals
![]() $X_{Z^{-1}}(b)$
, which is a scheme locally of finite type and separated over
$X_{Z^{-1}}(b)$
, which is a scheme locally of finite type and separated over
![]() ${\mathbb {F}}$
, all of whose irreducible components are projective.
${\mathbb {F}}$
, all of whose irreducible components are projective.
The formal scheme representing
![]() ${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
is called a Rapoport-Zink space for bounded local G-shtukas. Recall that a formal scheme over
${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
is called a Rapoport-Zink space for bounded local G-shtukas. Recall that a formal scheme over
![]() $\breve R_{\hat Z}$
in the sense of [Reference Grothendieck44,
$\breve R_{\hat Z}$
in the sense of [Reference Grothendieck44,
![]() $\mathrm{I}_{\mathrm{new}}$
, 10] is called locally formally of finite type if it is locally Noetherian and adic and its reduced subscheme is locally of finite type over
$\mathrm{I}_{\mathrm{new}}$
, 10] is called locally formally of finite type if it is locally Noetherian and adic and its reduced subscheme is locally of finite type over
![]() ${\mathbb {F}}$
.
${\mathbb {F}}$
.
Remark 3.6. (a)
![]() $LG({\mathbb {F}})$
-
$LG({\mathbb {F}})$
-
![]() $\sigma $
-conjugacy classes in
$\sigma $
-conjugacy classes in
![]() $LG({\mathbb {F}})$
are in bijection to isogeny classes of local G-shtukas over
$LG({\mathbb {F}})$
are in bijection to isogeny classes of local G-shtukas over
![]() ${\mathbb {F}}$
. To classify them, Kottwitz associated with every element
${\mathbb {F}}$
. To classify them, Kottwitz associated with every element
![]() $b\in LG({\mathbb {F}})$
a slope homomorphism
$b\in LG({\mathbb {F}})$
a slope homomorphism
![]() $\nu _b\colon {\mathbb {D}}_{{\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)}\to G_{{\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)}$
, called Newton point (or Newton polygon) of b; see [Reference Kottwitz70, 4.2]. Here
$\nu _b\colon {\mathbb {D}}_{{\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)}\to G_{{\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)}$
, called Newton point (or Newton polygon) of b; see [Reference Kottwitz70, 4.2]. Here
![]() ${\mathbb {D}}$
is the diagonalisable pro-algebraic group over
${\mathbb {D}}$
is the diagonalisable pro-algebraic group over
![]() ${\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)$
with character group
${\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)$
with character group
![]() ${\mathbb {Q}}$
. The slope homomorphism is characterised by assigning the slope filtration of
${\mathbb {Q}}$
. The slope homomorphism is characterised by assigning the slope filtration of
to any
![]() $(V,\rho )$
in
$(V,\rho )$
in
![]() $\operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G$
; see [Reference Kottwitz70, Section 4]. Furthermore, he showed that
$\operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G$
; see [Reference Kottwitz70, Section 4]. Furthermore, he showed that
![]() $\sigma $
-conjugating b amounts to conjugating
$\sigma $
-conjugating b amounts to conjugating
![]() $\nu _b$
by the corresponding element. One can thus associate with the
$\nu _b$
by the corresponding element. One can thus associate with the
![]() $LG({\mathbb {F}})$
-
$LG({\mathbb {F}})$
-
![]() $\sigma $
-conjugacy class
$\sigma $
-conjugacy class
![]() $[b]$
a well-defined
$[b]$
a well-defined
![]() $G\big ({\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)\big )$
-conjugacy class
$G\big ({\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)\big )$
-conjugacy class
![]() $\{\nu _b\}$
in
$\{\nu _b\}$
in
![]() $\operatorname {\mathrm {Hom}}({\mathbb {D}}_{{\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)},G_{{\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)})$
, which moreover is invariant under
$\operatorname {\mathrm {Hom}}({\mathbb {D}}_{{\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)},G_{{\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)})$
, which moreover is invariant under
![]() $\sigma $
by [Reference Kottwitz70, 4.4].
$\sigma $
by [Reference Kottwitz70, 4.4].
The second important invariant of
![]() $[b]$
is defined as follows. Consider again the Kottwitz homomorphism
$[b]$
is defined as follows. Consider again the Kottwitz homomorphism
![]() $\kappa _G\colon LG({\mathbb {F}})\rightarrow \pi _1(G)_{I}$
as explained in [Reference Pappas and Rapoport77, 2.a.2]. We compose
$\kappa _G\colon LG({\mathbb {F}})\rightarrow \pi _1(G)_{I}$
as explained in [Reference Pappas and Rapoport77, 2.a.2]. We compose
![]() $\kappa _G$
with the projection to
$\kappa _G$
with the projection to
![]() $\pi _1(G)_{\Gamma }$
. This then yields a well-defined map (again denoted
$\pi _1(G)_{\Gamma }$
. This then yields a well-defined map (again denoted
![]() $\kappa _G$
) from the set of
$\kappa _G$
) from the set of
![]() $\sigma $
-conjugacy classes
$\sigma $
-conjugacy classes
![]() $B(G)$
to
$B(G)$
to
![]() $\pi _1(G)_{\Gamma }$
(see [Reference Kottwitz71]). Together,
$\pi _1(G)_{\Gamma }$
(see [Reference Kottwitz71]). Together,
![]() $\{\nu _b\}$
and
$\{\nu _b\}$
and
![]() $\kappa _G([b])$
determine
$\kappa _G([b])$
determine
![]() $[b]$
uniquely. We denote by
$[b]$
uniquely. We denote by
![]() $[b]^{\#}$
the images of
$[b]^{\#}$
the images of
![]() $\kappa _G(b)$
in
$\kappa _G(b)$
in
![]() $\pi _1(G)_{\Gamma }$
and in
$\pi _1(G)_{\Gamma }$
and in
![]() $\pi _1(G)_{\Gamma ,{\mathbb {Q}}}:=\pi _1(G)_{\Gamma }\otimes _{\mathbb {Z}}{\mathbb {Q}}$
. The latter equals the image of the conjugacy class
$\pi _1(G)_{\Gamma ,{\mathbb {Q}}}:=\pi _1(G)_{\Gamma }\otimes _{\mathbb {Z}}{\mathbb {Q}}$
. The latter equals the image of the conjugacy class
![]() $\{\nu _b\}$
in
$\{\nu _b\}$
in
![]() $\pi _1(G)_{\Gamma ,{\mathbb {Q}}}$
; see [Reference Rapoport and Richartz78, Theorem 1.15(iii)].
$\pi _1(G)_{\Gamma ,{\mathbb {Q}}}$
; see [Reference Rapoport and Richartz78, Theorem 1.15(iii)].
(b) Because
![]() ${\mathbb {F}}$
is algebraically closed and the generic fibre of G is connected reductive, we may replace b by
${\mathbb {F}}$
is algebraically closed and the generic fibre of G is connected reductive, we may replace b by
![]() $h^{-1}b\sigma ^\ast (h)$
and assume that
$h^{-1}b\sigma ^\ast (h)$
and assume that
![]() $b\in LG({\mathbb {F}})$
satisfies a decency equation for a positive integer s; that is,
$b\in LG({\mathbb {F}})$
satisfies a decency equation for a positive integer s; that is,
![]() $s\nu _b:{\mathbb {D}}_{{\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)}\to G_{{\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)}$
factors through
$s\nu _b:{\mathbb {D}}_{{\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)}\to G_{{\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)}$
factors through
![]() ${\mathbb {G}}_m$
, and
${\mathbb {G}}_m$
, and
see [Reference Kottwitz70, Section 4]. Let
![]() ${\mathbb {F}}_{q^s}\subset {\mathbb {F}}$
be the finite field extension of
${\mathbb {F}}_{q^s}\subset {\mathbb {F}}$
be the finite field extension of
![]() ${\mathbb {F}}_q$
of degree s. Then
${\mathbb {F}}_q$
of degree s. Then
![]() $b\in LG({\mathbb {F}}_{q^s})$
,
$b\in LG({\mathbb {F}}_{q^s})$
,
![]() $\nu _b$
is defined over
$\nu _b$
is defined over
![]() ${\mathbb {F}}_{q^s}(\kern-0.15em( z)\kern-0.15em)$
([Reference Rapoport and Zink80, Corollary 1.9]) and
${\mathbb {F}}_{q^s}(\kern-0.15em( z)\kern-0.15em)$
([Reference Rapoport and Zink80, Corollary 1.9]) and
![]() $J_b\times _{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}{\mathbb {F}}_{q^s}(\kern-0.15em( z)\kern-0.15em)$
is an inner form of the centraliser of the 1-parameter subgroup
$J_b\times _{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}{\mathbb {F}}_{q^s}(\kern-0.15em( z)\kern-0.15em)$
is an inner form of the centraliser of the 1-parameter subgroup
![]() $s\nu _b$
of G, a Levi subgroup of
$s\nu _b$
of G, a Levi subgroup of
![]() $G_{{\mathbb {F}}_{q^s}(\kern-0.15em( z)\kern-0.15em)}$
; see [Reference Rapoport and Zink80, Corollary 1.14]. In particular,
$G_{{\mathbb {F}}_{q^s}(\kern-0.15em( z)\kern-0.15em)}$
; see [Reference Rapoport and Zink80, Corollary 1.14]. In particular,
![]() $J_b\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )\subset G\big ({\mathbb {F}}_{q^s}(\kern-0.15em( z)\kern-0.15em)\big )= LG({\mathbb {F}}_{q^s})$
. Moreover, in this case
$J_b\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )\subset G\big ({\mathbb {F}}_{q^s}(\kern-0.15em( z)\kern-0.15em)\big )= LG({\mathbb {F}}_{q^s})$
. Moreover, in this case
![]() ${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
descends by [Reference Arasteh Rad and Hartl4, Theorem 4.18] to a formal scheme locally formally of finite type over
${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
descends by [Reference Arasteh Rad and Hartl4, Theorem 4.18] to a formal scheme locally formally of finite type over
![]() $({\mathbb {F}}_{q^s}\cdot \kappa )\mathrm {[}\kern-0.15em\mathrm {[}\xi \mathrm {]}\kern-0.15em\mathrm {]}$
where
$({\mathbb {F}}_{q^s}\cdot \kappa )\mathrm {[}\kern-0.15em\mathrm {[}\xi \mathrm {]}\kern-0.15em\mathrm {]}$
where
![]() ${\mathbb {F}}_{q^s}\cdot \kappa $
is the compositum inside
${\mathbb {F}}_{q^s}\cdot \kappa $
is the compositum inside
![]() ${\mathbb {F}}$
.
${\mathbb {F}}$
.
(c) If more generally we start with a local G-shtuka
![]() ${\underline {{\mathbb {G}}}}_0$
over any field k in
${\underline {{\mathbb {G}}}}_0$
over any field k in
![]() ${{\mathcal {N}}\!\mathit {ilp}}_{ R_{\hat Z}}$
, we can define the Rapoport-Zink functor
${{\mathcal {N}}\!\mathit {ilp}}_{ R_{\hat Z}}$
, we can define the Rapoport-Zink functor
![]() ${{\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
as in Definition 3.1 on the category
${{\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
as in Definition 3.1 on the category
![]() ${{\mathcal {N}}\!\mathit {ilp}}_{k\mathrm {[}\kern-0.15em\mathrm {[}\xi \mathrm {]}\kern-0.15em\mathrm {]}}$
. Then
${{\mathcal {N}}\!\mathit {ilp}}_{k\mathrm {[}\kern-0.15em\mathrm {[}\xi \mathrm {]}\kern-0.15em\mathrm {]}}$
. Then
![]() ${\underline {{\mathbb {G}}}}_0\otimes _k k^{\textrm {alg}}$
is trivial and decent and hence
${\underline {{\mathbb {G}}}}_0\otimes _k k^{\textrm {alg}}$
is trivial and decent and hence
![]() ${{\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}\otimes _k k^{\textrm {alg}}$
is ind-representable by a formal scheme locally formally of finite type over
${{\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}\otimes _k k^{\textrm {alg}}$
is ind-representable by a formal scheme locally formally of finite type over
![]() $k^{\textrm {alg}}\mathrm {[}\kern-0.15em\mathrm {[}\xi \mathrm {]}\kern-0.15em\mathrm {]}$
. By an unpublished result of Eike Lau on Galois descent of formal schemes locally formally of finite type, already
$k^{\textrm {alg}}\mathrm {[}\kern-0.15em\mathrm {[}\xi \mathrm {]}\kern-0.15em\mathrm {]}$
. By an unpublished result of Eike Lau on Galois descent of formal schemes locally formally of finite type, already
![]() ${{\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
is ind-representable by a formal scheme locally formally of finite type over
${{\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
is ind-representable by a formal scheme locally formally of finite type over
![]() $k\mathrm {[}\kern-0.15em\mathrm {[}\xi \mathrm {]}\kern-0.15em\mathrm {]}$
. However, we will not use this in the rest of this work.
$k\mathrm {[}\kern-0.15em\mathrm {[}\xi \mathrm {]}\kern-0.15em\mathrm {]}$
. However, we will not use this in the rest of this work.
Remark 3.7. The constructions described above are functorial with respect to the group scheme G. To explain this, let
![]() $\varepsilon \colon G\to G^{\prime }$
be a morphism of parahoric group schemes over
$\varepsilon \colon G\to G^{\prime }$
be a morphism of parahoric group schemes over
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
. Important examples are closed immersions, epimorphisms or the change of the parahoric model, that is, morphisms that are generically isomorphisms. Then
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
. Important examples are closed immersions, epimorphisms or the change of the parahoric model, that is, morphisms that are generically isomorphisms. Then
![]() $\varepsilon $
induces a functor
$\varepsilon $
induces a functor
The morphism
![]() $\varepsilon $
also induces morphisms
$\varepsilon $
also induces morphisms
![]() $\varepsilon \colon L^+G\to L^+G^{\prime }$
and
$\varepsilon \colon L^+G\to L^+G^{\prime }$
and
![]() $\varepsilon \colon LG\to LG^{\prime }$
and
$\varepsilon \colon LG\to LG^{\prime }$
and
![]() $\varepsilon \colon {\mathcal {F}}\ell _G\to {\mathcal {F}}\ell _{G^{\prime }}$
. We say that
$\varepsilon \colon {\mathcal {F}}\ell _G\to {\mathcal {F}}\ell _{G^{\prime }}$
. We say that
![]() $\varepsilon $
is compatible with two given bounds
$\varepsilon $
is compatible with two given bounds
![]() $\hat {Z}=[(R,\hat {Z}_R)]$
and
$\hat {Z}=[(R,\hat {Z}_R)]$
and
![]() $\hat {Z}^{\prime }=[(R,\hat {Z}^{\prime }_R)]$
with
$\hat {Z}^{\prime }=[(R,\hat {Z}^{\prime }_R)]$
with
![]() $\hat {Z}_R\subset {\widehat {{\mathcal {F}}\ell }}_{G,R}$
and
$\hat {Z}_R\subset {\widehat {{\mathcal {F}}\ell }}_{G,R}$
and
![]() $\hat {Z}^{\prime }_R\subset {\widehat {{\mathcal {F}}\ell }}_{G^{\prime }\!,R}$
if
$\hat {Z}^{\prime }_R\subset {\widehat {{\mathcal {F}}\ell }}_{G^{\prime }\!,R}$
if
![]() $\varepsilon (\hat {Z}_R)\subset \hat {Z}^{\prime }_R$
for all suitable R. If
$\varepsilon (\hat {Z}_R)\subset \hat {Z}^{\prime }_R$
for all suitable R. If
![]() $\varepsilon $
is compatible with
$\varepsilon $
is compatible with
![]() $\hat {Z}$
and
$\hat {Z}$
and
![]() $\hat {Z}^{\prime }$
and
$\hat {Z}^{\prime }$
and
![]() ${\underline {{\mathcal {G}}}}$
is bounded by
${\underline {{\mathcal {G}}}}$
is bounded by
![]() $\hat {Z}^{-1}$
, then
$\hat {Z}^{-1}$
, then
![]() $\varepsilon _*{\underline {{\mathcal {G}}}}$
is bounded by
$\varepsilon _*{\underline {{\mathcal {G}}}}$
is bounded by
![]() $(\hat {Z}^{\prime })^{-1}$
.
$(\hat {Z}^{\prime })^{-1}$
.
Let
![]() ${\underline {{\mathbb {G}}}}_0\cong \big ((L^+G)_{\mathbb {F}},b\sigma ^\ast \big )$
be a local G-shtuka over
${\underline {{\mathbb {G}}}}_0\cong \big ((L^+G)_{\mathbb {F}},b\sigma ^\ast \big )$
be a local G-shtuka over
![]() ${\mathbb {F}}$
with
${\mathbb {F}}$
with
![]() $b\in LG({\mathbb {F}})$
. Then
$b\in LG({\mathbb {F}})$
. Then
![]() ${\underline {{\mathbb {G}}}}^{\prime }_0:=\varepsilon _*{\underline {{\mathbb {G}}}}_0\cong \big ((L^+G^{\prime })_{\mathbb {F}},b^{\prime }\sigma ^\ast \big )$
with
${\underline {{\mathbb {G}}}}^{\prime }_0:=\varepsilon _*{\underline {{\mathbb {G}}}}_0\cong \big ((L^+G^{\prime })_{\mathbb {F}},b^{\prime }\sigma ^\ast \big )$
with
![]() $b^{\prime }=\varepsilon (b)$
. Kottwitz’s classification of isogeny classes is functorial in the sense that
$b^{\prime }=\varepsilon (b)$
. Kottwitz’s classification of isogeny classes is functorial in the sense that
![]() $\nu _{b^{\prime }}=\varepsilon \circ \nu _b$
and
$\nu _{b^{\prime }}=\varepsilon \circ \nu _b$
and
![]() $\varepsilon \circ \kappa _G=\kappa _{G^{\prime }}\circ \varepsilon $
for the induced
$\varepsilon \circ \kappa _G=\kappa _{G^{\prime }}\circ \varepsilon $
for the induced
![]() $\Gamma $
-equivariant morphism
$\Gamma $
-equivariant morphism
![]() $\varepsilon \colon \pi _1(G)\to \pi _1(G^{\prime })$
. We also obtain a morphism of Rapoport-Zink spaces
$\varepsilon \colon \pi _1(G)\to \pi _1(G^{\prime })$
. We also obtain a morphism of Rapoport-Zink spaces
which is equivariant for the group
![]() $J_b^G$
that acts on the target via the morphism of algebraic groups over
$J_b^G$
that acts on the target via the morphism of algebraic groups over
![]() ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
,
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
,
4 Period spaces for bounded local G-shtukas
In this section we construct period spaces. These will be strictly
![]() ${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
-analytic spaces in the sense of Berkovich [Reference Berkovich7], [Reference Berkovich8]. We equip the category of
${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
-analytic spaces in the sense of Berkovich [Reference Berkovich7], [Reference Berkovich8]. We equip the category of
![]() ${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
-schemes and the category of
${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
-schemes and the category of
![]() ${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
-analytic spaces with the étale topology; see [Reference Berkovich8, § 4.1]. Recall the group scheme
${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
-analytic spaces with the étale topology; see [Reference Berkovich8, § 4.1]. Recall the group scheme
![]() $G\times _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}\operatorname {\mathrm {Spec}} {\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
, which is reductive because
$G\times _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}\operatorname {\mathrm {Spec}} {\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
, which is reductive because
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\to {\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]},\,z\mapsto z=\zeta +(z-\zeta )$
factors through
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\to {\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]},\,z\mapsto z=\zeta +(z-\zeta )$
factors through
![]() ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
, and recall its affine Grassmannian
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
, and recall its affine Grassmannian
![]() $\operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}}$
from (1.2). For
$\operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}}$
from (1.2). For
![]() $G=\operatorname {\mathrm {GL}}_r$
, Hilbert 90 for loop groups [Reference Hartl and Viehmann56, Proposition 2.3] shows that
$G=\operatorname {\mathrm {GL}}_r$
, Hilbert 90 for loop groups [Reference Hartl and Viehmann56, Proposition 2.3] shows that
for any field extension
![]() $L/{\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
.
$L/{\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
.
Again, for all G as above, the morphism of sheaves of sets on
![]() $\operatorname {\mathrm {Spec}} {\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
,
$\operatorname {\mathrm {Spec}} {\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
,
admits local sections for the étale topology. By [Reference Springer93, Proposition 13.1.1] there is a finite separable field extension
![]() $L_0\supset {\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
such that
$L_0\supset {\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
such that
![]() $G_{L_0}:=G\otimes _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]},z\mapsto \zeta }L_0$
splits. Therefore, the group
$G_{L_0}:=G\otimes _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]},z\mapsto \zeta }L_0$
splits. Therefore, the group
![]() $G\otimes _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}{\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)(\kern-0.15em( z-\zeta )\kern-0.15em)$
over
$G\otimes _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}{\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)(\kern-0.15em( z-\zeta )\kern-0.15em)$
over
![]() ${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)(\kern-0.15em( z-\zeta )\kern-0.15em)$
is unramified. Thus, the inertia group of
${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)(\kern-0.15em( z-\zeta )\kern-0.15em)$
is unramified. Thus, the inertia group of
![]() $\operatorname {\mathrm {Gal}}\big ({\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)(\kern-0.15em( z-\zeta )\kern-0.15em)^{\textrm {sep}}\!/{\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)(\kern-0.15em( z-\zeta )\kern-0.15em)\big )$
acts trivially on
$\operatorname {\mathrm {Gal}}\big ({\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)(\kern-0.15em( z-\zeta )\kern-0.15em)^{\textrm {sep}}\!/{\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)(\kern-0.15em( z-\zeta )\kern-0.15em)\big )$
acts trivially on
![]() $\pi _1(G)$
and the connected components of
$\pi _1(G)$
and the connected components of
![]() $\operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}}{\widehat {\otimes }}_{{\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)}{\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)^{\textrm {alg}}$
are in canonical bijection with
$\operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}}{\widehat {\otimes }}_{{\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)}{\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)^{\textrm {alg}}$
are in canonical bijection with
![]() $\pi _1(G)$
by [Reference Pappas and Rapoport77, Theorem 5.1]. For every field extension
$\pi _1(G)$
by [Reference Pappas and Rapoport77, Theorem 5.1]. For every field extension
![]() $L\subset {\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)^{\textrm {alg}}$
of
$L\subset {\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)^{\textrm {alg}}$
of
![]() ${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
we then obtain from [Reference Neupert76, Lemma 2.2.6] that
${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
we then obtain from [Reference Neupert76, Lemma 2.2.6] that
where the quotient is the set of
![]() $\operatorname {\mathrm {Gal}}(L^{\textrm {sep}}\!/L)$
-orbits. It has a natural projection to the group of coinvariants
$\operatorname {\mathrm {Gal}}(L^{\textrm {sep}}\!/L)$
-orbits. It has a natural projection to the group of coinvariants
![]() $\pi _1(G)_{\Gamma _L}$
. In particular,
$\pi _1(G)_{\Gamma _L}$
. In particular,
![]() $\pi _0\big (\operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}}{\widehat {\otimes }}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)} L_0\big )=\pi _1(G)$
.
$\pi _0\big (\operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}}{\widehat {\otimes }}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)} L_0\big )=\pi _1(G)$
.
Definition 4.1. Let X be an
![]() ${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
-scheme or a strictly
${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
-scheme or a strictly
![]() ${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
-analytic space. A Hodge-Pink G-structure over X is an element
${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
-analytic space. A Hodge-Pink G-structure over X is an element
![]() $\gamma $
in
$\gamma $
in
![]() $\operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}}(X)$
. For a Hodge-Pink G-structure
$\operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}}(X)$
. For a Hodge-Pink G-structure
![]() $\gamma \in \operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}}(L)$
with values in a field L, we let
$\gamma \in \operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}}(L)$
with values in a field L, we let
![]() $\gamma ^\#\in \pi _1(G)_\Gamma $
be its image under the projection
$\gamma ^\#\in \pi _1(G)_\Gamma $
be its image under the projection
![]() $\pi _0(\operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}})\twoheadrightarrow \pi _1(G)_\Gamma $
induced by (4.1).
$\pi _0(\operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}})\twoheadrightarrow \pi _1(G)_\Gamma $
induced by (4.1).
A Hodge-Pink structure of rank r over X is a sheaf
![]() ${\mathfrak {q}}$
on X of
${\mathfrak {q}}$
on X of
![]() ${\mathcal {O}}_X\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
-submodules of
${\mathcal {O}}_X\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
-submodules of
![]() ${\mathcal {O}}_X(\kern-0.15em( z-\zeta )\kern-0.15em)^r$
that is finitely generated as
${\mathcal {O}}_X(\kern-0.15em( z-\zeta )\kern-0.15em)^r$
that is finitely generated as
![]() ${\mathcal {O}}_X\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
-module, is a direct summand as
${\mathcal {O}}_X\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
-module, is a direct summand as
![]() ${\mathcal {O}}_X$
-module and satisfies
${\mathcal {O}}_X$
-module and satisfies
![]() ${\mathcal {O}}_X(\kern-0.15em( z-\zeta )\kern-0.15em)\cdot {\mathfrak {q}}={\mathcal {O}}_X(\kern-0.15em( z-\zeta )\kern-0.15em)^r$
.
${\mathcal {O}}_X(\kern-0.15em( z-\zeta )\kern-0.15em)\cdot {\mathfrak {q}}={\mathcal {O}}_X(\kern-0.15em( z-\zeta )\kern-0.15em)^r$
.
Remark 4.2. By [Reference Schauch87, Proposition 2.2.5], a Hodge-Pink structure
![]() ${\mathfrak {q}}$
of rank r over X is Zariski-locally on X free of rank r as
${\mathfrak {q}}$
of rank r over X is Zariski-locally on X free of rank r as
![]() ${\mathcal {O}}_X\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
-module. In particular, it is of the form
${\mathcal {O}}_X\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
-module. In particular, it is of the form
![]() ${\mathfrak {q}}=\gamma \cdot {\mathcal {O}}_X\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}^r\subset {\mathcal {O}}_X(\kern-0.15em( z-\zeta )\kern-0.15em)^r$
for a uniquely determined Hodge-Pink
${\mathfrak {q}}=\gamma \cdot {\mathcal {O}}_X\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}^r\subset {\mathcal {O}}_X(\kern-0.15em( z-\zeta )\kern-0.15em)^r$
for a uniquely determined Hodge-Pink
![]() $\operatorname {\mathrm {GL}}_r$
-structure
$\operatorname {\mathrm {GL}}_r$
-structure
![]() $\gamma \in \operatorname {\mathrm {Gr}}_{\operatorname {\mathrm {GL}}_r}^{{\mathbf {B}}_{\textrm {dR}}}(X)$
over X. This yields an equivalence between Hodge-Pink
$\gamma \in \operatorname {\mathrm {Gr}}_{\operatorname {\mathrm {GL}}_r}^{{\mathbf {B}}_{\textrm {dR}}}(X)$
over X. This yields an equivalence between Hodge-Pink
![]() $\operatorname {\mathrm {GL}}_r$
-structures and Hodge-Pink structures of rank r over X.
$\operatorname {\mathrm {GL}}_r$
-structures and Hodge-Pink structures of rank r over X.
To define the notion of weak admissibility, recall from [Reference Hartl, Kim, Böckle, Goss, Hartl and Papanikolas54, Definitions 3.5.1 and 3.5.2] that a z-isocrystal over
![]() ${\mathbb {F}}$
is a pair
${\mathbb {F}}$
is a pair
![]() $(D,\tau _D)$
consisting of a finite-dimensional
$(D,\tau _D)$
consisting of a finite-dimensional
![]() ${\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)$
-vector space D and an
${\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)$
-vector space D and an
![]() ${\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)$
-isomorphism
${\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)$
-isomorphism
![]() . A Hodge-Pink structure on
. A Hodge-Pink structure on
![]() $(D,\tau _D)$
over a field extension L of
$(D,\tau _D)$
over a field extension L of
![]() ${\mathbb {F}}(\kern-0.15em(\zeta )\kern-0.15em)$
is a free
${\mathbb {F}}(\kern-0.15em(\zeta )\kern-0.15em)$
is a free
![]() $L\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
-submodule
$L\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
-submodule
![]() ${\mathfrak {q}}_D\subset D\otimes _{{\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)}L(\kern-0.15em( z-\zeta )\kern-0.15em)$
of full rank. Here, as always, we use the homomorphism
${\mathfrak {q}}_D\subset D\otimes _{{\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)}L(\kern-0.15em( z-\zeta )\kern-0.15em)$
of full rank. Here, as always, we use the homomorphism
![]() ${\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)\hookrightarrow {\mathbb {F}}(\kern-0.15em(\zeta )\kern-0.15em)\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]},\,z\mapsto z=\zeta +(z-\zeta )$
.
${\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)\hookrightarrow {\mathbb {F}}(\kern-0.15em(\zeta )\kern-0.15em)\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]},\,z\mapsto z=\zeta +(z-\zeta )$
.
Definition 4.3. Assume that
![]() ${\mathbb {F}}(\kern-0.15em(\zeta )\kern-0.15em)\subset L$
and let
${\mathbb {F}}(\kern-0.15em(\zeta )\kern-0.15em)\subset L$
and let
![]() $b\in LG({\mathbb {F}})$
and
$b\in LG({\mathbb {F}})$
and
![]() $\gamma \in \operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}}(L)$
.
$\gamma \in \operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}}(L)$
.
-
(a) Let
 $\rho \colon G_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}\to \operatorname {\mathrm {GL}}_{r,{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}$
be in
$\rho \colon G_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}\to \operatorname {\mathrm {GL}}_{r,{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}$
be in
 $\operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G$
and set
$\operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G$
and set
 $V={\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)^{\oplus r}$
, the representation space. We consider the elements
$V={\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)^{\oplus r}$
, the representation space. We consider the elements
 $\rho (b)\in \operatorname {\mathrm {GL}}_r({\mathbb {F}}(\kern-0.15em( z)\kern-0.15em))$
and
$\rho (b)\in \operatorname {\mathrm {GL}}_r({\mathbb {F}}(\kern-0.15em( z)\kern-0.15em))$
and
 $\rho (\gamma )\in \operatorname {\mathrm {Gr}}_{\operatorname {\mathrm {GL}}_r}^{{\mathbf {B}}_{\textrm {dR}}}(L)=\operatorname {\mathrm {GL}}_r\big (L(\kern-0.15em( z-\zeta )\kern-0.15em)\big )/\operatorname {\mathrm {GL}}_r\big (L\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )$
. Then we define the z -isocrystal over
$\rho (\gamma )\in \operatorname {\mathrm {Gr}}_{\operatorname {\mathrm {GL}}_r}^{{\mathbf {B}}_{\textrm {dR}}}(L)=\operatorname {\mathrm {GL}}_r\big (L(\kern-0.15em( z-\zeta )\kern-0.15em)\big )/\operatorname {\mathrm {GL}}_r\big (L\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )$
. Then we define the z -isocrystal over $$ \begin{align*} {\underline{D\!}\,}_b(V,\rho)\;:=\;(D,\tau_D)\;:=\;\big(V\otimes_{{\mathbb{F}}_q(\kern-0.15em( z )\kern-0.15em)}{\mathbb{F}}(\kern-0.15em( z )\kern-0.15em),\,\rho(\sigma^\ast b)\sigma^\ast\big) \end{align*} $$
$$ \begin{align*} {\underline{D\!}\,}_b(V,\rho)\;:=\;(D,\tau_D)\;:=\;\big(V\otimes_{{\mathbb{F}}_q(\kern-0.15em( z )\kern-0.15em)}{\mathbb{F}}(\kern-0.15em( z )\kern-0.15em),\,\rho(\sigma^\ast b)\sigma^\ast\big) \end{align*} $$
 ${\mathbb {F}}$
and the Hodge-Pink structure on it over L. We set
${\mathbb {F}}$
and the Hodge-Pink structure on it over L. We set $$ \begin{align*} {\mathfrak{q}}_D(V)\;:=\;\rho(\gamma)\cdot V\otimes_{{\mathbb{F}}_q(\kern-0.15em( z )\kern-0.15em)}L\text{[}\kern-0.15em\text{[} z-\zeta\text{]}\kern-0.15em\text{]}\;\subset\; V\otimes_{{\mathbb{F}}_q(\kern-0.15em( z )\kern-0.15em)}L(\kern-0.15em( z -\zeta)\kern-0.15em)\;=\;D\otimes_{{\mathbb{F}}(\kern-0.15em( z )\kern-0.15em)}L(\kern-0.15em( z -\zeta)\kern-0.15em) \end{align*} $$
$$ \begin{align*} {\mathfrak{q}}_D(V)\;:=\;\rho(\gamma)\cdot V\otimes_{{\mathbb{F}}_q(\kern-0.15em( z )\kern-0.15em)}L\text{[}\kern-0.15em\text{[} z-\zeta\text{]}\kern-0.15em\text{]}\;\subset\; V\otimes_{{\mathbb{F}}_q(\kern-0.15em( z )\kern-0.15em)}L(\kern-0.15em( z -\zeta)\kern-0.15em)\;=\;D\otimes_{{\mathbb{F}}(\kern-0.15em( z )\kern-0.15em)}L(\kern-0.15em( z -\zeta)\kern-0.15em) \end{align*} $$
 ${\underline {D\!}\,}_{b,\gamma }(V):=\big (V\otimes _{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}{\mathbb {F}}(\kern-0.15em( z)\kern-0.15em),\,\rho (\sigma ^\ast b)\sigma ^\ast ,\,{\mathfrak {q}}_D(V)\big )$
.
${\underline {D\!}\,}_{b,\gamma }(V):=\big (V\otimes _{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}{\mathbb {F}}(\kern-0.15em( z)\kern-0.15em),\,\rho (\sigma ^\ast b)\sigma ^\ast ,\,{\mathfrak {q}}_D(V)\big )$
.
-
(b) Let
 ${\underline {D\!}\,}=(D,\tau _D,{\mathfrak {q}}_D)$
be a z-isocrystal over
${\underline {D\!}\,}=(D,\tau _D,{\mathfrak {q}}_D)$
be a z-isocrystal over
 ${\mathbb {F}}$
with Hodge-Pink structure over L and let
${\mathbb {F}}$
with Hodge-Pink structure over L and let
 $\det \tau _D$
be the determinant of the matrix representing
$\det \tau _D$
be the determinant of the matrix representing
 $\tau _D$
with respect to an
$\tau _D$
with respect to an
 ${\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)$
-basis of D. The z-adic valuation
${\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)$
-basis of D. The z-adic valuation
 $t_N({\underline {D\!}\,}):=\operatorname {\mathrm {ord}}_z(\det \tau _D)$
is independent of this basis and is called the Newton degree of
$t_N({\underline {D\!}\,}):=\operatorname {\mathrm {ord}}_z(\det \tau _D)$
is independent of this basis and is called the Newton degree of
 ${\underline {D\!}\,}$
. The integer
${\underline {D\!}\,}$
. The integer
 $t_H({\underline {D\!}\,})$
with
$t_H({\underline {D\!}\,})$
with
 $\wedge ^r{\mathfrak {q}}_D=(z-\zeta )^{-t_H({\underline {D\!}\,})}\wedge ^r{\mathfrak {p}}_D$
is called the Hodge degree of
$\wedge ^r{\mathfrak {q}}_D=(z-\zeta )^{-t_H({\underline {D\!}\,})}\wedge ^r{\mathfrak {p}}_D$
is called the Hodge degree of
 ${\underline {D\!}\,}$
, where
${\underline {D\!}\,}$
, where
 ${\mathfrak {p}}_D:=D\otimes _{{\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)}L\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
.
${\mathfrak {p}}_D:=D\otimes _{{\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)}L\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
.In particular, we have
 $t_N({\underline {D\!}\,}_{b,\gamma }(V))=\operatorname {\mathrm {ord}}_z(\det \rho (\sigma ^\ast b))=\operatorname {\mathrm {ord}}_z(\det \rho (b))$
and
$t_N({\underline {D\!}\,}_{b,\gamma }(V))=\operatorname {\mathrm {ord}}_z(\det \rho (\sigma ^\ast b))=\operatorname {\mathrm {ord}}_z(\det \rho (b))$
and
 $t_H({\underline {D\!}\,}_{b,\gamma }(V))=-\operatorname {\mathrm {ord}}_{z-\zeta }(\det \rho (\gamma ))$
.
$t_H({\underline {D\!}\,}_{b,\gamma }(V))=-\operatorname {\mathrm {ord}}_{z-\zeta }(\det \rho (\gamma ))$
. -
(c) We say that
 ${\underline {D\!}\,}$
is weakly admissible if
${\underline {D\!}\,}$
is weakly admissible if
 $t_H({\underline {D\!}\,})=t_N({\underline {D\!}\,})$
and the following equivalent conditions are satisfied (compare [Reference Hartl50, Definition 2.2.4]):
$t_H({\underline {D\!}\,})=t_N({\underline {D\!}\,})$
and the following equivalent conditions are satisfied (compare [Reference Hartl50, Definition 2.2.4]):-
•
 $t_H({\underline {D\!}\,}^{\prime })\leq t_N({\underline {D\!}\,}^{\prime })$
for every strict subobject (4.2)of
$t_H({\underline {D\!}\,}^{\prime })\leq t_N({\underline {D\!}\,}^{\prime })$
for every strict subobject (4.2)of $$ \begin{align} {\underline{D\!}\,}^{\prime}\,=\,\big(D^{\prime}\!,\,\tau_D|_{\sigma^\ast D^{\prime}},\,{\mathfrak{q}}_D\cap D^{\prime}\otimes_{{\mathbb{F}}(\kern-0.15em( z )\kern-0.15em)}L(\kern-0.15em( z -\zeta)\kern-0.15em)\big) \end{align} $$
$$ \begin{align} {\underline{D\!}\,}^{\prime}\,=\,\big(D^{\prime}\!,\,\tau_D|_{\sigma^\ast D^{\prime}},\,{\mathfrak{q}}_D\cap D^{\prime}\otimes_{{\mathbb{F}}(\kern-0.15em( z )\kern-0.15em)}L(\kern-0.15em( z -\zeta)\kern-0.15em)\big) \end{align} $$
 ${\underline {D\!}\,}$
, where
${\underline {D\!}\,}$
, where
 $D^{\prime }\subset D$
is a
$D^{\prime }\subset D$
is a
 $\tau _D$
-stable
$\tau _D$
-stable
 ${\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)$
-subspace,
${\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)$
-subspace,
-
•
 $t_H({\underline {D\!}\,}^{\prime \prime })\geq t_N({\underline {D\!}\,}^{\prime \prime })$
for every strict quotient object
$t_H({\underline {D\!}\,}^{\prime \prime })\geq t_N({\underline {D\!}\,}^{\prime \prime })$
for every strict quotient object
 ${\underline {D\!}\,}^{\prime \prime }=(D^{\prime \prime }\!,\tau _{D^{\prime \prime }},{\mathfrak {q}}_{D^{\prime \prime }})$
of
${\underline {D\!}\,}^{\prime \prime }=(D^{\prime \prime }\!,\tau _{D^{\prime \prime }},{\mathfrak {q}}_{D^{\prime \prime }})$
of
 ${\underline {D\!}\,}$
, where
${\underline {D\!}\,}$
, where
 $f\colon D\twoheadrightarrow D^{\prime \prime }$
is a
$f\colon D\twoheadrightarrow D^{\prime \prime }$
is a
 $\tau _D$
-stable
$\tau _D$
-stable
 ${\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)$
-quotient space and
${\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)$
-quotient space and
 ${\mathfrak {q}}_{D^{\prime \prime }}=(f\otimes \operatorname {\mbox { id}})({\mathfrak {q}}_D)$
.
${\mathfrak {q}}_{D^{\prime \prime }}=(f\otimes \operatorname {\mbox { id}})({\mathfrak {q}}_D)$
.
-
Remark 4.4. (a) The Hodge-Pink structure
![]() ${\mathfrak {q}}_D$
on
${\mathfrak {q}}_D$
on
![]() $(D,\tau _D)$
induces a decreasing Hodge-Pink filtration on
$(D,\tau _D)$
induces a decreasing Hodge-Pink filtration on
![]() $D_L:=D\otimes _{{\mathbb {F}}(\kern-0.15em( z)\kern-0.15em),z\mapsto \zeta }L={\mathfrak {p}}_D/(z-\zeta ){\mathfrak {p}}_D$
given by
$D_L:=D\otimes _{{\mathbb {F}}(\kern-0.15em( z)\kern-0.15em),z\mapsto \zeta }L={\mathfrak {p}}_D/(z-\zeta ){\mathfrak {p}}_D$
given by
If
![]() $(D,\tau _D,Fil^\bullet D_L)$
is weakly admissible in the sense of Fontaine (see [Reference Fontaine38, Définition 4.1.4]), then
$(D,\tau _D,Fil^\bullet D_L)$
is weakly admissible in the sense of Fontaine (see [Reference Fontaine38, Définition 4.1.4]), then
![]() $(D,\tau _D,{\mathfrak {q}}_D)$
is weakly admissible, but the converse is false in general. An example is
$(D,\tau _D,{\mathfrak {q}}_D)$
is weakly admissible, but the converse is false in general. An example is
![]() $D={\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)^2$
,
$D={\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)^2$
,
![]() $\tau _D=z^{-1}$
,
$\tau _D=z^{-1}$
,
![]() ${\mathfrak {q}}_D=\binom {z-\zeta }{1}L\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}+(z-\zeta )^2{\mathfrak {p}}_D$
and
${\mathfrak {q}}_D=\binom {z-\zeta }{1}L\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}+(z-\zeta )^2{\mathfrak {p}}_D$
and
![]() $D^{\prime }=\binom {0}{1}{\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)$
. This is due to the fact that our Hodge slope
$D^{\prime }=\binom {0}{1}{\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)$
. This is due to the fact that our Hodge slope
![]() $t_H(D,\tau _D,{\mathfrak {q}}_D)$
equals Fontaine’s Hodge slope
$t_H(D,\tau _D,{\mathfrak {q}}_D)$
equals Fontaine’s Hodge slope
![]() $t_H(D,\tau _D,Fil^\bullet D_L):= \sum _{i\in {\mathbb {Z}}}i\cdot \dim _L Fil^i D_L/Fil^{i+1}D_L$
, see [Reference Hartl50, p. 1290 before Definition 2.2.4] and that the subspace
$t_H(D,\tau _D,Fil^\bullet D_L):= \sum _{i\in {\mathbb {Z}}}i\cdot \dim _L Fil^i D_L/Fil^{i+1}D_L$
, see [Reference Hartl50, p. 1290 before Definition 2.2.4] and that the subspace
![]() $Fil^iD^{\prime }_L$
of
$Fil^iD^{\prime }_L$
of
![]() $D^{\prime }_L$
induced by
$D^{\prime }_L$
induced by
![]() ${\underline {D\!}\,}^{\prime }$
from (4.2) is (in general strictly) contained in
${\underline {D\!}\,}^{\prime }$
from (4.2) is (in general strictly) contained in
![]() $D^{\prime }_L\cap Fil^iD_L$
.
$D^{\prime }_L\cap Fil^iD_L$
.
(b) We obtain an
![]() ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-linear tensor functor
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-linear tensor functor
![]() ${\underline {D\!}\,}_{b,\gamma }\colon V\mapsto {\underline {D\!}\,}_{b,\gamma }(V)$
. Namely, if
${\underline {D\!}\,}_{b,\gamma }\colon V\mapsto {\underline {D\!}\,}_{b,\gamma }(V)$
. Namely, if
![]() $f\colon (V,\rho )\to (V^{\prime }\!,\rho ^{\prime })$
is a morphism in
$f\colon (V,\rho )\to (V^{\prime }\!,\rho ^{\prime })$
is a morphism in
![]() $\operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G$
and
$\operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G$
and
![]() $(D,\tau _D,{\mathfrak {q}}_D)={\underline {D\!}\,}_{b,\gamma }(V)$
and
$(D,\tau _D,{\mathfrak {q}}_D)={\underline {D\!}\,}_{b,\gamma }(V)$
and
![]() $(D^{\prime }\!,\tau _{D^{\prime }},{\mathfrak {q}}_{D^{\prime }})={\underline {D\!}\,}_{b,\gamma }(V^{\prime })$
, then
$(D^{\prime }\!,\tau _{D^{\prime }},{\mathfrak {q}}_{D^{\prime }})={\underline {D\!}\,}_{b,\gamma }(V^{\prime })$
, then
![]() $\sigma ^*f=f$
and so
$\sigma ^*f=f$
and so
![]() $f\circ \tau _D=(f\circ \rho (\sigma ^\ast b))\sigma ^\ast =(\rho ^{\prime }(\sigma ^\ast b)\circ f)\sigma ^\ast =(\rho ^{\prime }(\sigma ^\ast b)\circ \sigma ^\ast f)\sigma ^\ast =\tau _{D^{\prime }}\circ \sigma ^*f$
and
$f\circ \tau _D=(f\circ \rho (\sigma ^\ast b))\sigma ^\ast =(\rho ^{\prime }(\sigma ^\ast b)\circ f)\sigma ^\ast =(\rho ^{\prime }(\sigma ^\ast b)\circ \sigma ^\ast f)\sigma ^\ast =\tau _{D^{\prime }}\circ \sigma ^*f$
and
![]() $f({\mathfrak {q}}_D)\subset {\mathfrak {q}}_{D^{\prime }}$
. Furthermore, the compatibility with tensor products
$f({\mathfrak {q}}_D)\subset {\mathfrak {q}}_{D^{\prime }}$
. Furthermore, the compatibility with tensor products
is clear.
If L is a finite field extension of
![]() ${\mathbb {F}}(\kern-0.15em(\zeta )\kern-0.15em)$
, then ‘weakly admissible implies admissible’ by the analogue [Reference Hartl50, Theorem 2.5.3] of the theorem of Colmez and Fontaine [Reference Colmez and Fontaine28, Théorème A]. More precisely, when
${\mathbb {F}}(\kern-0.15em(\zeta )\kern-0.15em)$
, then ‘weakly admissible implies admissible’ by the analogue [Reference Hartl50, Theorem 2.5.3] of the theorem of Colmez and Fontaine [Reference Colmez and Fontaine28, Théorème A]. More precisely, when
![]() ${\underline {D\!}\,}_{b,\gamma }(V)$
is weakly admissible, it is even admissible; that is, it arises from a local shtuka over
${\underline {D\!}\,}_{b,\gamma }(V)$
is weakly admissible, it is even admissible; that is, it arises from a local shtuka over
![]() ${\mathcal {O}}_L$
via the analogue
${\mathcal {O}}_L$
via the analogue
![]() ${\mathbb {H}}$
of Fontaine’s mysterious functor; see [Reference Hartl50, § 2.3] or Theorem 8.1. In contrast, if L is algebraically closed, weakly admissible does not imply admissible. In general, there is a criterion for admissibility in terms of
${\mathbb {H}}$
of Fontaine’s mysterious functor; see [Reference Hartl50, § 2.3] or Theorem 8.1. In contrast, if L is algebraically closed, weakly admissible does not imply admissible. In general, there is a criterion for admissibility in terms of
![]() $\sigma $
-bundles over the analogue of the Robba ring as follows.
$\sigma $
-bundles over the analogue of the Robba ring as follows.
We consider field extensions L of
![]() ${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
equipped with an absolute value
${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
equipped with an absolute value
![]() $|\,.\,|\colon L\to {\mathbb {R}}_{\ge 0}$
extending the
$|\,.\,|\colon L\to {\mathbb {R}}_{\ge 0}$
extending the
![]() $\zeta $
-adic absolute value on
$\zeta $
-adic absolute value on
![]() ${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
such that L is complete with respect to
${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
such that L is complete with respect to
![]() $|\,.\,|$
. We call such an L a complete valued field extension of
$|\,.\,|$
. We call such an L a complete valued field extension of
![]() ${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
, and we let
${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
, and we let
![]() ${\overline {L}}:={\widehat {L^{\textrm {alg}}}}$
be the completion of an algebraic closure of L. For a rational number
${\overline {L}}:={\widehat {L^{\textrm {alg}}}}$
be the completion of an algebraic closure of L. For a rational number
![]() $s>0$
, we define the ring
$s>0$
, we define the ring
 $$ \begin{align*} L{\textstyle\langle\frac{z}{\zeta^{s}},z^{-1}\}}\;:=\;\left\{\;{\textstyle\sum\limits_{i=-\infty}^\infty} b_i z^i\colon b_i\in L,\, |b_i|\,|\zeta|^{s^{\prime}i}\to0\enspace(i\to\pm\infty)\text{ for all }s^{\prime}\ge s\;\right\}. \end{align*} $$
$$ \begin{align*} L{\textstyle\langle\frac{z}{\zeta^{s}},z^{-1}\}}\;:=\;\left\{\;{\textstyle\sum\limits_{i=-\infty}^\infty} b_i z^i\colon b_i\in L,\, |b_i|\,|\zeta|^{s^{\prime}i}\to0\enspace(i\to\pm\infty)\text{ for all }s^{\prime}\ge s\;\right\}. \end{align*} $$
It equals the ring of rigid analytic functions on the punctured disc
![]() $\{0<|z|\le |\zeta |^s\}$
over L of radius
$\{0<|z|\le |\zeta |^s\}$
over L of radius
![]() $|\zeta |^s$
. The ring
$|\zeta |^s$
. The ring
![]() $L{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}$
is the function field analogue of the Robba ring; see [Reference Hartl49, § 2.8]. It contains the element
$L{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}$
is the function field analogue of the Robba ring; see [Reference Hartl49, § 2.8]. It contains the element
Definition 4.5. Let
![]() $s\in {\mathbb {Q}}$
satisfy
$s\in {\mathbb {Q}}$
satisfy
![]() $1>s>\frac {1}{q}$
. A
$1>s>\frac {1}{q}$
. A
![]() $\sigma $
-bundle (on
$\sigma $
-bundle (on
![]() $\{0<|z|\le |\zeta |^s\}$
) over L is a pair
$\{0<|z|\le |\zeta |^s\}$
) over L is a pair
![]() ${\underline {{\mathcal {F}}\!}\,}=({\mathcal {F}},\tau _{\mathcal {F}})$
consisting of a locally free
${\underline {{\mathcal {F}}\!}\,}=({\mathcal {F}},\tau _{\mathcal {F}})$
consisting of a locally free
![]() $L{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}$
-module
$L{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}$
-module
![]() ${\mathcal {F}}$
of finite rank together with an isomorphism
${\mathcal {F}}$
of finite rank together with an isomorphism
![]() of
of
![]() $L{\textstyle \langle \frac {z}{\zeta ^{qs}},z^{-1}\}}$
-modules, where
$L{\textstyle \langle \frac {z}{\zeta ^{qs}},z^{-1}\}}$
-modules, where
![]() $\sigma ^*{\mathcal {F}}:={\mathcal {F}}\otimes _{L{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}},\,\sigma }\,L{\textstyle \langle \frac {z}{\zeta ^{qs}},z^{-1}\}}$
and
$\sigma ^*{\mathcal {F}}:={\mathcal {F}}\otimes _{L{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}},\,\sigma }\,L{\textstyle \langle \frac {z}{\zeta ^{qs}},z^{-1}\}}$
and
![]() $\iota ^*{\mathcal {F}}:={\mathcal {F}}\otimes _{L{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}},\,\iota }\,L{\textstyle \langle \frac {z}{\zeta ^{qs}},z^{-1}\}}$
for the natural inclusion
$\iota ^*{\mathcal {F}}:={\mathcal {F}}\otimes _{L{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}},\,\iota }\,L{\textstyle \langle \frac {z}{\zeta ^{qs}},z^{-1}\}}$
for the natural inclusion
![]() $\iota \colon L{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}\hookrightarrow L{\textstyle \langle \frac {z}{\zeta ^{qs}},z^{-1}\}},\,\sum _ib_iz^i\mapsto \sum _ib_iz^i$
. The abelian group
$\iota \colon L{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}\hookrightarrow L{\textstyle \langle \frac {z}{\zeta ^{qs}},z^{-1}\}},\,\sum _ib_iz^i\mapsto \sum _ib_iz^i$
. The abelian group
![]() $\operatorname {\mathrm {Hom}}_\sigma ({\underline {{\mathcal {F}}\!}\,},{\underline {{\mathcal {F}}\!}\,}^{\prime })$
of morphisms between two
$\operatorname {\mathrm {Hom}}_\sigma ({\underline {{\mathcal {F}}\!}\,},{\underline {{\mathcal {F}}\!}\,}^{\prime })$
of morphisms between two
![]() $\sigma $
-bundles
$\sigma $
-bundles
![]() ${\underline {{\mathcal {F}}\!}\,}=({\mathcal {F}},\tau _{\mathcal {F}})$
and
${\underline {{\mathcal {F}}\!}\,}=({\mathcal {F}},\tau _{\mathcal {F}})$
and
![]() ${\underline {{\mathcal {F}}\!}\,}^{\prime }=({\mathcal {F}}^{\prime }\!,\tau _{{\mathcal {F}}^{\prime }})$
consists of all
${\underline {{\mathcal {F}}\!}\,}^{\prime }=({\mathcal {F}}^{\prime }\!,\tau _{{\mathcal {F}}^{\prime }})$
consists of all
![]() $L{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}$
-homomorphisms
$L{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}$
-homomorphisms
![]() $f\colon {\mathcal {F}}\to {\mathcal {F}}^{\prime }$
that satisfy
$f\colon {\mathcal {F}}\to {\mathcal {F}}^{\prime }$
that satisfy
![]() $\tau _{{\mathcal {F}}^{\prime }}\circ \sigma ^\ast f=\iota ^\ast f\circ \tau _{\mathcal {F}}$
.
$\tau _{{\mathcal {F}}^{\prime }}\circ \sigma ^\ast f=\iota ^\ast f\circ \tau _{\mathcal {F}}$
.
The category of
![]() $\sigma $
-bundles over L is an
$\sigma $
-bundles over L is an
![]() ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-linear rigid additive tensor category with unit object
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-linear rigid additive tensor category with unit object
![]() ${\underline {{\mathcal {O}}}}(0):=(L{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}},\tau _{{\mathcal {O}}(0)}=\operatorname {\mbox { id}})$
.
${\underline {{\mathcal {O}}}}(0):=(L{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}},\tau _{{\mathcal {O}}(0)}=\operatorname {\mbox { id}})$
.
Example 4.6. For
![]() $d\in {\mathbb {Z}}$
we define the
$d\in {\mathbb {Z}}$
we define the
![]() $\sigma $
-bundle
$\sigma $
-bundle
![]() ${\underline {{\mathcal {O}}}}(d)$
over L as the pair
${\underline {{\mathcal {O}}}}(d)$
over L as the pair
![]() $(L{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}},\tau _{{\mathcal {O}}(d)}=z^{-d}\cdot \operatorname {\mbox { id}})$
. For more examples, let d and n be relatively prime integers with
$(L{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}},\tau _{{\mathcal {O}}(d)}=z^{-d}\cdot \operatorname {\mbox { id}})$
. For more examples, let d and n be relatively prime integers with
![]() $n>0$
. Consider the matrix
$n>0$
. Consider the matrix

Let
![]() ${\underline {{\mathcal {F}}\!}\,}_{d,n}=\big (L{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}^n,\tau _{{\mathcal {F}}_{d,n}}=A_{d,n}\big )$
. It is a
${\underline {{\mathcal {F}}\!}\,}_{d,n}=\big (L{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}^n,\tau _{{\mathcal {F}}_{d,n}}=A_{d,n}\big )$
. It is a
![]() $\sigma $
-bundle of rank n over L. As a special case if
$\sigma $
-bundle of rank n over L. As a special case if
![]() $n=1$
, we obtain
$n=1$
, we obtain
![]() ${\underline {{\mathcal {F}}\!}\,}_{d,1}={\underline {{\mathcal {O}}}}(d)$
.
${\underline {{\mathcal {F}}\!}\,}_{d,1}={\underline {{\mathcal {O}}}}(d)$
.
Proposition 4.7 [Reference Hartl and Pink55, Theorem 11.1 and Corollary 11.8]
If L is algebraically closed (and complete), every
![]() $\sigma $
-bundle
$\sigma $
-bundle
![]() ${\underline {{\mathcal {F}}\!}\,}$
is isomorphic to a direct sum
${\underline {{\mathcal {F}}\!}\,}$
is isomorphic to a direct sum
![]() $\bigoplus _{i}{\underline {{\mathcal {F}}\!}\,}_{d_i,n_i}$
for uniquely determined pairs
$\bigoplus _{i}{\underline {{\mathcal {F}}\!}\,}_{d_i,n_i}$
for uniquely determined pairs
![]() $(d_i,n_i)$
up to permutation with
$(d_i,n_i)$
up to permutation with
![]() $\gcd (d_i,n_i)=1$
. One has
$\gcd (d_i,n_i)=1$
. One has
![]() $\wedge ^n{\underline {{\mathcal {F}}\!}\,}\cong {\underline {{\mathcal {F}}\!}\,}_{d,1}={\underline {{\mathcal {O}}}}(d)$
where
$\wedge ^n{\underline {{\mathcal {F}}\!}\,}\cong {\underline {{\mathcal {F}}\!}\,}_{d,1}={\underline {{\mathcal {O}}}}(d)$
where
![]() $n=\operatorname {\mathrm {rk}}{\underline {{\mathcal {F}}\!}\,}=\sum _i n_i$
and
$n=\operatorname {\mathrm {rk}}{\underline {{\mathcal {F}}\!}\,}=\sum _i n_i$
and
![]() $d=\sum _i d_i$
. One calls d the degree of
$d=\sum _i d_i$
. One calls d the degree of
![]() ${\underline {{\mathcal {F}}\!}\,}$
.
${\underline {{\mathcal {F}}\!}\,}$
.
Proposition 4.8 [Reference Hartl and Pink55, Proposition 8.5]
If L is algebraically closed (and complete), then
![]() $\operatorname {\mathrm {Hom}}_\sigma ({\underline {{\mathcal {F}}\!}\,}_{d,n},\,{\underline {{\mathcal {F}}\!}\,}_{d^{\prime }\!,n^{\prime }})\ne (0)$
if and only if
$\operatorname {\mathrm {Hom}}_\sigma ({\underline {{\mathcal {F}}\!}\,}_{d,n},\,{\underline {{\mathcal {F}}\!}\,}_{d^{\prime }\!,n^{\prime }})\ne (0)$
if and only if
![]() $d/n\le d^{\prime }/n^{\prime }$
.
$d/n\le d^{\prime }/n^{\prime }$
.
Let
![]() ${\underline {D\!}\,}=(D,\tau _D,{\mathfrak {q}}_D)$
be a z-isocrystal over
${\underline {D\!}\,}=(D,\tau _D,{\mathfrak {q}}_D)$
be a z-isocrystal over
![]() ${\mathbb {F}}$
with a Hodge-Pink structure over a complete valued field extension L of
${\mathbb {F}}$
with a Hodge-Pink structure over a complete valued field extension L of
![]() ${\mathbb {F}}(\kern-0.15em(\zeta )\kern-0.15em)$
. To define the
${\mathbb {F}}(\kern-0.15em(\zeta )\kern-0.15em)$
. To define the
![]() $\sigma $
-bundles associated with
$\sigma $
-bundles associated with
![]() ${\underline {D\!}\,}$
, we first define the
${\underline {D\!}\,}$
, we first define the
![]() $\sigma $
-bundle
$\sigma $
-bundle
over L. Then
![]() ${\mathcal {E}}({\underline {D\!}\,})\otimes L\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}={\mathfrak {p}}_D:=D\otimes _{{\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)}L\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
and the Hodge-Pink structure
${\mathcal {E}}({\underline {D\!}\,})\otimes L\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}={\mathfrak {p}}_D:=D\otimes _{{\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)}L\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
and the Hodge-Pink structure
![]() ${\mathfrak {q}}_D\subset {\mathcal {E}}\otimes L\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}[\frac {1}{z-\zeta }]$
defines a
${\mathfrak {q}}_D\subset {\mathcal {E}}\otimes L\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}[\frac {1}{z-\zeta }]$
defines a
![]() $\sigma $
-bundle
$\sigma $
-bundle
![]() ${\underline {{\mathcal {F}}\!}\,}({\underline {D\!}\,})$
over L that is a modification of
${\underline {{\mathcal {F}}\!}\,}({\underline {D\!}\,})$
over L that is a modification of
![]() ${\underline {{\mathcal {E}}\!}\,}({\underline {D\!}\,})$
at
${\underline {{\mathcal {E}}\!}\,}({\underline {D\!}\,})$
at
![]() $z=\zeta ^{q^i}$
for
$z=\zeta ^{q^i}$
for
![]() $i\in {\mathbb {N}}_0$
as follows. Consider the isomorphism
$i\in {\mathbb {N}}_0$
as follows. Consider the isomorphism
![]() $\eta _i:=\big (\tau _{\mathcal {E}}\circ \ldots \circ (\sigma ^{i-1})^\ast \tau _{\mathcal {E}}\big )\otimes \operatorname {\mbox { id}}$
$\eta _i:=\big (\tau _{\mathcal {E}}\circ \ldots \circ (\sigma ^{i-1})^\ast \tau _{\mathcal {E}}\big )\otimes \operatorname {\mbox { id}}$
We define
![]() ${\mathcal {F}}={\mathcal {F}}({\underline {D\!}\,})$
as the
${\mathcal {F}}={\mathcal {F}}({\underline {D\!}\,})$
as the
![]() $L{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}$
-submodule of
$L{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}$
-submodule of
![]() ${\mathcal {E}}[\tfrac {1}{t_{\scriptscriptstyle -}}]$
that coincides with
${\mathcal {E}}[\tfrac {1}{t_{\scriptscriptstyle -}}]$
that coincides with
![]() ${\mathcal {E}}$
outside
${\mathcal {E}}$
outside
![]() $z=\zeta ^{q^i}$
for
$z=\zeta ^{q^i}$
for
![]() $i\in {\mathbb {N}}_0$
and at
$i\in {\mathbb {N}}_0$
and at
![]() $z=\zeta ^{q^i}$
satisfies
$z=\zeta ^{q^i}$
satisfies
![]() ${\mathcal {F}}\otimes L\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta ^{q^i}\mathrm {]}\kern-0.15em\mathrm {]}\;=\;\eta _i(\sigma ^{i\ast }{\mathfrak {q}}_D)$
; that is,
${\mathcal {F}}\otimes L\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta ^{q^i}\mathrm {]}\kern-0.15em\mathrm {]}\;=\;\eta _i(\sigma ^{i\ast }{\mathfrak {q}}_D)$
; that is,
This can equivalently be viewed as the global sections over
![]() $\{0<|z|\le |\zeta |^s\}$
of the sheaf
$\{0<|z|\le |\zeta |^s\}$
of the sheaf
![]() ${\widetilde {{\mathcal {F}}}}$
obtained as the modification of the sheaf associated with
${\widetilde {{\mathcal {F}}}}$
obtained as the modification of the sheaf associated with
![]() ${\mathcal {E}}$
at the discrete set
${\mathcal {E}}$
at the discrete set
![]() $\{z=\zeta ^{q^i}:i\in {\mathbb {N}}_0\}$
according to the rule given in (4.4).
$\{z=\zeta ^{q^i}:i\in {\mathbb {N}}_0\}$
according to the rule given in (4.4).
By construction,
![]() $\tau _{\mathcal {E}}$
induces on
$\tau _{\mathcal {E}}$
induces on
![]() ${\mathcal {F}}$
the structure of a
${\mathcal {F}}$
the structure of a
![]() $\sigma $
-bundle
$\sigma $
-bundle
![]() ${\underline {{\mathcal {F}}\!}\,}({\underline {D\!}\,})=({\mathcal {F}},\tau _{\mathcal {F}})$
over L, and
${\underline {{\mathcal {F}}\!}\,}({\underline {D\!}\,})=({\mathcal {F}},\tau _{\mathcal {F}})$
over L, and
![]() ${\underline {{\mathcal {F}}\!}\,}({\underline {D\!}\,})$
is the unique
${\underline {{\mathcal {F}}\!}\,}({\underline {D\!}\,})$
is the unique
![]() $\sigma $
-subbundle of
$\sigma $
-subbundle of
![]() ${\underline {{\mathcal {E}}\!}\,}[\tfrac {1}{t_{\scriptscriptstyle -}}]$
that coincides with
${\underline {{\mathcal {E}}\!}\,}[\tfrac {1}{t_{\scriptscriptstyle -}}]$
that coincides with
![]() ${\underline {{\mathcal {E}}\!}\,}$
outside
${\underline {{\mathcal {E}}\!}\,}$
outside
![]() $z=\zeta ^{q^i}$
for
$z=\zeta ^{q^i}$
for
![]() $i\in {\mathbb {N}}_0$
and satisfies
$i\in {\mathbb {N}}_0$
and satisfies
![]() ${\mathcal {F}}\otimes L\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\;=\;{\mathfrak {q}}_D$
. This characterisation implies that the assignment
${\mathcal {F}}\otimes L\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\;=\;{\mathfrak {q}}_D$
. This characterisation implies that the assignment
![]() ${\underline {D\!}\,}\mapsto \big ({\underline {{\mathcal {E}}\!}\,}({\underline {D\!}\,}),\,{\underline {{\mathcal {F}}\!}\,}({\underline {D\!}\,})\big )$
is an
${\underline {D\!}\,}\mapsto \big ({\underline {{\mathcal {E}}\!}\,}({\underline {D\!}\,}),\,{\underline {{\mathcal {F}}\!}\,}({\underline {D\!}\,})\big )$
is an
![]() ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-linear tensor functor.
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-linear tensor functor.
Definition 4.9. The pair of
![]() $\sigma $
-bundles associated with
$\sigma $
-bundles associated with
![]() ${\underline {D\!}\,}$
is the pair
${\underline {D\!}\,}$
is the pair
![]() $\big ({\underline {{\mathcal {E}}\!}\,}({\underline {D\!}\,}),\,{\underline {{\mathcal {F}}\!}\,}({\underline {D\!}\,})\big )$
constructed above.
$\big ({\underline {{\mathcal {E}}\!}\,}({\underline {D\!}\,}),\,{\underline {{\mathcal {F}}\!}\,}({\underline {D\!}\,})\big )$
constructed above.
The z-isocrystal with Hodge-Pink structure
![]() ${\underline {D\!}\,}$
is said to be admissible if
${\underline {D\!}\,}$
is said to be admissible if
![]() ${\underline {{\mathcal {F}}\!}\,}({\underline {D\!}\,})\otimes _{L{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}}{\overline {L}}{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}\cong ({\underline {{\mathcal {F}}\!}\,}_{0,1})^{\oplus \dim D}\otimes _{L{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}}{\overline {L}}{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}$
.
${\underline {{\mathcal {F}}\!}\,}({\underline {D\!}\,})\otimes _{L{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}}{\overline {L}}{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}\cong ({\underline {{\mathcal {F}}\!}\,}_{0,1})^{\oplus \dim D}\otimes _{L{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}}{\overline {L}}{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}$
.
In the notation of Definition 4.3, let
![]() ${\underline {D\!}\,}={\underline {D\!}\,}_{b,\gamma }(V)$
for a representation
${\underline {D\!}\,}={\underline {D\!}\,}_{b,\gamma }(V)$
for a representation
![]() $\rho \colon G\to \operatorname {\mathrm {GL}}(V)$
in
$\rho \colon G\to \operatorname {\mathrm {GL}}(V)$
in
![]() $\operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G$
and write
$\operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G$
and write
![]() $\big ({\underline {{\mathcal {E}}\!}\,}_{b,\gamma }(V),\,{\underline {{\mathcal {F}}\!}\,}_{b,\gamma }(V)\big ):=\big ({\underline {{\mathcal {E}}\!}\,}({\underline {D\!}\,}),\,{\underline {{\mathcal {F}}\!}\,}({\underline {D\!}\,})\big )$
.
$\big ({\underline {{\mathcal {E}}\!}\,}_{b,\gamma }(V),\,{\underline {{\mathcal {F}}\!}\,}_{b,\gamma }(V)\big ):=\big ({\underline {{\mathcal {E}}\!}\,}({\underline {D\!}\,}),\,{\underline {{\mathcal {F}}\!}\,}({\underline {D\!}\,})\big )$
.
As a motivation for this definition, note that
![]() ${\underline {D\!}\,}$
is admissible if and only if it arises from a local
${\underline {D\!}\,}$
is admissible if and only if it arises from a local
![]() $\operatorname {\mathrm {GL}}_r$
-shtuka over
$\operatorname {\mathrm {GL}}_r$
-shtuka over
![]() ${\mathcal {O}}_L$
by [Reference Hartl50, Theorem 2.4.7 and Definition 2.3.3].
${\mathcal {O}}_L$
by [Reference Hartl50, Theorem 2.4.7 and Definition 2.3.3].
Proposition 4.10 [Reference Hartl50, Lemma 2.4.5]
For every z-isocrystal with Hodge-Pink structure
![]() ${\underline {D\!}\,}$
over L, the degree (defined in Proposition 4.7) satisfies
${\underline {D\!}\,}$
over L, the degree (defined in Proposition 4.7) satisfies
![]() $\deg {\underline {{\mathcal {F}}\!}\,}({\underline {D\!}\,})\;=\;t_H({\underline {D\!}\,})-t_N({\underline {D\!}\,})$
and
$\deg {\underline {{\mathcal {F}}\!}\,}({\underline {D\!}\,})\;=\;t_H({\underline {D\!}\,})-t_N({\underline {D\!}\,})$
and
![]() $\deg {\underline {{\mathcal {E}}\!}\,}({\underline {D\!}\,})\;=\;-t_N({\underline {D\!}\,})$
.
$\deg {\underline {{\mathcal {E}}\!}\,}({\underline {D\!}\,})\;=\;-t_N({\underline {D\!}\,})$
.
Corollary 4.11. If
![]() ${\underline {D\!}\,}_{b,\gamma }(V)$
is admissible, then
${\underline {D\!}\,}_{b,\gamma }(V)$
is admissible, then
![]() ${\underline {D\!}\,}_{b,\gamma }(V)$
is weakly admissible.
${\underline {D\!}\,}_{b,\gamma }(V)$
is weakly admissible.
Proof. If
![]() ${\underline {D\!}\,}:={\underline {D\!}\,}_{b,\gamma }(V)$
is admissible, then
${\underline {D\!}\,}:={\underline {D\!}\,}_{b,\gamma }(V)$
is admissible, then
![]() ${\underline {{\mathcal {F}}\!}\,}({\underline {D\!}\,})\otimes _{L{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}}{\overline {L}}{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}\cong ({\underline {{\mathcal {F}}\!}\,}_{0,1})^{\oplus \dim V}$
and therefore
${\underline {{\mathcal {F}}\!}\,}({\underline {D\!}\,})\otimes _{L{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}}{\overline {L}}{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}\cong ({\underline {{\mathcal {F}}\!}\,}_{0,1})^{\oplus \dim V}$
and therefore
![]() $t_H({\underline {D\!}\,})-t_N({\underline {D\!}\,})=\deg ({\underline {{\mathcal {F}}\!}\,}({\underline {D\!}\,}))=0$
. If
$t_H({\underline {D\!}\,})-t_N({\underline {D\!}\,})=\deg ({\underline {{\mathcal {F}}\!}\,}({\underline {D\!}\,}))=0$
. If
![]() ${\underline {D\!}\,}^{\prime }\subset {\underline {D\!}\,}$
is a strict subobject, then
${\underline {D\!}\,}^{\prime }\subset {\underline {D\!}\,}$
is a strict subobject, then
![]() ${\underline {{\mathcal {F}}\!}\,}({\underline {D\!}\,}^{\prime })\subset {\underline {{\mathcal {F}}\!}\,}({\underline {D\!}\,})$
is a
${\underline {{\mathcal {F}}\!}\,}({\underline {D\!}\,}^{\prime })\subset {\underline {{\mathcal {F}}\!}\,}({\underline {D\!}\,})$
is a
![]() $\sigma $
-subbundle. It satisfies
$\sigma $
-subbundle. It satisfies
![]() ${\underline {{\mathcal {F}}\!}\,}({\underline {D\!}\,}^{\prime })\otimes _{L{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}}{\overline {L}}{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}} \cong \bigoplus _i{\underline {{\mathcal {F}}\!}\,}_{d_i,n_i}$
for some
${\underline {{\mathcal {F}}\!}\,}({\underline {D\!}\,}^{\prime })\otimes _{L{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}}{\overline {L}}{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}} \cong \bigoplus _i{\underline {{\mathcal {F}}\!}\,}_{d_i,n_i}$
for some
![]() $d_i,n_i$
by Proposition 4.7. By Proposition 4.8, all
$d_i,n_i$
by Proposition 4.7. By Proposition 4.8, all
![]() $d_i\le 0$
and hence
$d_i\le 0$
and hence
![]() $t_H({\underline {D\!}\,}^{\prime })-t_N({\underline {D\!}\,}^{\prime })\;=\;\deg {\underline {{\mathcal {F}}\!}\,}({\underline {D\!}\,}^{\prime })\;=\;\sum _i d_i\le 0$
.
$t_H({\underline {D\!}\,}^{\prime })-t_N({\underline {D\!}\,}^{\prime })\;=\;\deg {\underline {{\mathcal {F}}\!}\,}({\underline {D\!}\,}^{\prime })\;=\;\sum _i d_i\le 0$
.
Lemma 4.12. Let
![]() $\nu _b\colon {\mathbb {D}}_{{\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)}\to G_{{\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)}$
be the Newton point associated with b; see Remark 3.6(a). Let
$\nu _b\colon {\mathbb {D}}_{{\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)}\to G_{{\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)}$
be the Newton point associated with b; see Remark 3.6(a). Let
![]() $\rho \colon G\to \operatorname {\mathrm {GL}}(V)$
be a representation in
$\rho \colon G\to \operatorname {\mathrm {GL}}(V)$
be a representation in
![]() $\operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G$
. Then under the canonical identifications
$\operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G$
. Then under the canonical identifications
![]() $\pi _1\big (\operatorname {\mathrm {GL}}(V)\big )_\Gamma =\pi _1\big (\operatorname {\mathrm {GL}}(V)\big )={\mathbb {Z}}$
and
$\pi _1\big (\operatorname {\mathrm {GL}}(V)\big )_\Gamma =\pi _1\big (\operatorname {\mathrm {GL}}(V)\big )={\mathbb {Z}}$
and
![]() $\operatorname {\mathrm {Hom}}({\mathbb {D}}_{{\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)},{\mathbb {G}}_m)={\mathbb {Q}}$
, we have
$\operatorname {\mathrm {Hom}}({\mathbb {D}}_{{\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)},{\mathbb {G}}_m)={\mathbb {Q}}$
, we have
In particular, the images
![]() $[b]^{\#}$
and
$[b]^{\#}$
and
![]() $\gamma ^{\#}$
of
$\gamma ^{\#}$
of
![]() $\nu _b$
and
$\nu _b$
and
![]() $\gamma $
in
$\gamma $
in
![]() $\pi _1(G)_{{\Gamma },{\mathbb {Q}}}:=\pi _1(G)_{\Gamma }\otimes _{\mathbb {Z}}{\mathbb {Q}}$
coincide if and only if
$\pi _1(G)_{{\Gamma },{\mathbb {Q}}}:=\pi _1(G)_{\Gamma }\otimes _{\mathbb {Z}}{\mathbb {Q}}$
coincide if and only if
![]() $t_N\big ({\underline {D\!}\,}_{b,\gamma }(V)\big )=t_H\big ({\underline {D\!}\,}_{b,\gamma }(V)\big )$
for all
$t_N\big ({\underline {D\!}\,}_{b,\gamma }(V)\big )=t_H\big ({\underline {D\!}\,}_{b,\gamma }(V)\big )$
for all
![]() $V\in \operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G$
.
$V\in \operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G$
.
Proof. Because
![]() $\sigma ^\ast b=b(\sigma ^\ast b) \sigma ^\ast b^{-1}$
– that is,
$\sigma ^\ast b=b(\sigma ^\ast b) \sigma ^\ast b^{-1}$
– that is,
![]() $\sigma ^\ast b$
and b are
$\sigma ^\ast b$
and b are
![]() $\sigma $
-conjugate via b – their Newton points
$\sigma $
-conjugate via b – their Newton points
![]() $\nu _{\sigma ^\ast b}$
and
$\nu _{\sigma ^\ast b}$
and
![]() $\nu _b$
are conjugate via b. So it suffices to show that
$\nu _b$
are conjugate via b. So it suffices to show that
![]() $\det _V\circ \rho \circ \nu _{\sigma ^\ast b}=t_N\big ({\underline {D\!}\,}_{b,\gamma }(V)\big )$
. The latter follows from the construction of
$\det _V\circ \rho \circ \nu _{\sigma ^\ast b}=t_N\big ({\underline {D\!}\,}_{b,\gamma }(V)\big )$
. The latter follows from the construction of
![]() $\nu _{\sigma ^\ast b}$
in [Reference Kottwitz70, § 4.2]. The statement about
$\nu _{\sigma ^\ast b}$
in [Reference Kottwitz70, § 4.2]. The statement about
![]() $t_H$
follows from the fact that
$t_H$
follows from the fact that
![]() $\rho _*(\gamma ^\#)=\rho (\gamma )^\#=-\operatorname {\mathrm {ord}}_{z-\zeta }\big (\det \rho (\gamma ))$
under the identification
$\rho _*(\gamma ^\#)=\rho (\gamma )^\#=-\operatorname {\mathrm {ord}}_{z-\zeta }\big (\det \rho (\gamma ))$
under the identification
![]() $\pi _0(\operatorname {\mathrm {Gr}}_{\operatorname {\mathrm {GL}}(V)}^{{\mathbf {B}}_{\textrm {dR}}})=\pi _1(\operatorname {\mathrm {GL}}(V))_{\Gamma }\cong {\mathbb {Z}}$
. If
$\pi _0(\operatorname {\mathrm {Gr}}_{\operatorname {\mathrm {GL}}(V)}^{{\mathbf {B}}_{\textrm {dR}}})=\pi _1(\operatorname {\mathrm {GL}}(V))_{\Gamma }\cong {\mathbb {Z}}$
. If
![]() $[b]^{\#}=\gamma ^{\#}$
holds in
$[b]^{\#}=\gamma ^{\#}$
holds in
![]() $\pi _1(G)_{\Gamma ,{\mathbb {Q}}}$
, then
$\pi _1(G)_{\Gamma ,{\mathbb {Q}}}$
, then
![]() $\rho _*([b]^\#)=\rho _*(\gamma ^\#)$
in
$\rho _*([b]^\#)=\rho _*(\gamma ^\#)$
in
![]() $\pi _1(\operatorname {\mathrm {GL}}(V))_{\Gamma ,{\mathbb {Q}}}\cong {\mathbb {Q}}$
. Under the last isomorphism we have
$\pi _1(\operatorname {\mathrm {GL}}(V))_{\Gamma ,{\mathbb {Q}}}\cong {\mathbb {Q}}$
. Under the last isomorphism we have
![]() $\rho _*([b]^\#)=(\rho \circ \nu _b)^\#=\det _V\circ \rho \circ \nu _b$
. This proves one direction of the last assertion. For the other direction we use the isomorphism
$\rho _*([b]^\#)=(\rho \circ \nu _b)^\#=\det _V\circ \rho \circ \nu _b$
. This proves one direction of the last assertion. For the other direction we use the isomorphism
![]() $\pi _1(G)_{\Gamma ,{\mathbb {Q}}}\cong \pi _1(G_{\textrm {ab}})_{\Gamma ,{\mathbb {Q}}}\cong X_*(G_{\textrm {ab}})_{\Gamma ,{\mathbb {Q}}}$
, where
$\pi _1(G)_{\Gamma ,{\mathbb {Q}}}\cong \pi _1(G_{\textrm {ab}})_{\Gamma ,{\mathbb {Q}}}\cong X_*(G_{\textrm {ab}})_{\Gamma ,{\mathbb {Q}}}$
, where
![]() $G_{\textrm {ab}}$
denotes the maximal abelian quotient of G (compare [Reference Rapoport and Richartz78, Theorem 1.15(ii)]). Now assume that
$G_{\textrm {ab}}$
denotes the maximal abelian quotient of G (compare [Reference Rapoport and Richartz78, Theorem 1.15(ii)]). Now assume that
![]() $[b]^{\#}\neq \gamma ^{\#}$
. Then there is a homomorphism
$[b]^{\#}\neq \gamma ^{\#}$
. Then there is a homomorphism
![]() $\varphi \colon \pi _1(G)_{{\Gamma },{\mathbb {Q}}}\rightarrow {\mathbb {Q}}$
of
$\varphi \colon \pi _1(G)_{{\Gamma },{\mathbb {Q}}}\rightarrow {\mathbb {Q}}$
of
![]() ${\mathbb {Q}}$
-vector spaces such that
${\mathbb {Q}}$
-vector spaces such that
![]() $\varphi ([b]^{\#})\neq \varphi (\gamma ^{\#})$
. We have
$\varphi ([b]^{\#})\neq \varphi (\gamma ^{\#})$
. We have
![]() $\textrm {Hom}(\pi _1(G)_{{\Gamma },{\mathbb {Q}}}, {\mathbb {Q}})\cong X^*(G_{\textrm {ab}})^{\Gamma }_{{\mathbb {Q}}}$
; thus, a nonzero integral multiple of
$\textrm {Hom}(\pi _1(G)_{{\Gamma },{\mathbb {Q}}}, {\mathbb {Q}})\cong X^*(G_{\textrm {ab}})^{\Gamma }_{{\mathbb {Q}}}$
; thus, a nonzero integral multiple of
![]() $\varphi $
induces a morphism
$\varphi $
induces a morphism
![]() $\rho \colon G\rightarrow G_{\textrm {ab}}\rightarrow {\mathbb {G}}_m$
over
$\rho \colon G\rightarrow G_{\textrm {ab}}\rightarrow {\mathbb {G}}_m$
over
![]() ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)^{\textrm {sep}}$
that is
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)^{\textrm {sep}}$
that is
![]() ${\Gamma }$
-invariant and therefore defined over
${\Gamma }$
-invariant and therefore defined over
![]() ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
. For this representation
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
. For this representation
![]() $\rho $
, we then have
$\rho $
, we then have
![]() $t_N\big ({\underline {D\!}\,}_{b,\gamma }(V)\big )\neq t_H\big ({\underline {D\!}\,}_{b,\gamma }(V)\big )$
.
$t_N\big ({\underline {D\!}\,}_{b,\gamma }(V)\big )\neq t_H\big ({\underline {D\!}\,}_{b,\gamma }(V)\big )$
.
Definition 4.13. We say that the pair
![]() $(b,\gamma )\in LG({\mathbb {F}})\times \operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}}(L)$
is (weakly) admissible if
$(b,\gamma )\in LG({\mathbb {F}})\times \operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}}(L)$
is (weakly) admissible if
![]() $[b]^{\#}=\gamma ^{\#}$
in
$[b]^{\#}=\gamma ^{\#}$
in
![]() $\pi _1(G)_{\Gamma ,{\mathbb {Q}}}$
and one of the following equivalent conditions holds:
$\pi _1(G)_{\Gamma ,{\mathbb {Q}}}$
and one of the following equivalent conditions holds:
-
(a)
 ${\underline {D\!}\,}_{b,\gamma }(V)$
is (weakly) admissible for every representation V in
${\underline {D\!}\,}_{b,\gamma }(V)$
is (weakly) admissible for every representation V in
 $\operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G$
,
$\operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G$
, -
(b)
 ${\underline {D\!}\,}_{b,\gamma }(V)$
is (weakly) admissible for some faithful representation V in
${\underline {D\!}\,}_{b,\gamma }(V)$
is (weakly) admissible for some faithful representation V in
 $\operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G$
.
$\operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G$
.
In addition,
![]() $(b,\gamma )$
is neutral if
$(b,\gamma )$
is neutral if
![]() $[b]^{\#}=\gamma ^{\#}$
in
$[b]^{\#}=\gamma ^{\#}$
in
![]() $\pi _1(G)_\Gamma $
already without tensoring with
$\pi _1(G)_\Gamma $
already without tensoring with
![]() ${\mathbb {Q}}$
.
${\mathbb {Q}}$
.
Remark 4.14. If
![]() ${\underline {D\!}\,}_{b,\gamma }(V)$
is (weakly) admissible for every representation V in
${\underline {D\!}\,}_{b,\gamma }(V)$
is (weakly) admissible for every representation V in
![]() $\operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G$
, then
$\operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G$
, then
![]() $[b]^{\#}=\gamma ^{\#}$
automatically holds in
$[b]^{\#}=\gamma ^{\#}$
automatically holds in
![]() $\pi _1(G)_{\Gamma ,{\mathbb {Q}}}$
by Lemma 4.12.
$\pi _1(G)_{\Gamma ,{\mathbb {Q}}}$
by Lemma 4.12.
In the analogous situation in mixed characteristic, the condition
![]() $[b]^{\#}=\gamma ^{\#}$
also follows from (b), due to the fact that in that case every W as in the beginning of the following proof is even a direct summand of U.
$[b]^{\#}=\gamma ^{\#}$
also follows from (b), due to the fact that in that case every W as in the beginning of the following proof is even a direct summand of U.
Proof. Proof of the equivalence in Definition 4.13
Clearly, (a) implies (b). For the converse, fix a faithful representation V. Then every
![]() ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-rational representation W of
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-rational representation W of
![]() $G_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}$
is a subquotient of
$G_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}$
is a subquotient of
![]() $U:=\bigoplus _{i=1}^r V^{\otimes l_i}\otimes (V^{\scriptscriptstyle \lor })^{\otimes m_i}$
for suitable r,
$U:=\bigoplus _{i=1}^r V^{\otimes l_i}\otimes (V^{\scriptscriptstyle \lor })^{\otimes m_i}$
for suitable r,
![]() $l_i$
and
$l_i$
and
![]() $m_i$
. If
$m_i$
. If
![]() ${\underline {D\!}\,}_{b,\gamma }(V)$
is weakly admissible, then this also holds for
${\underline {D\!}\,}_{b,\gamma }(V)$
is weakly admissible, then this also holds for
![]() ${\underline {D\!}\,}_{b,\gamma }(U)$
by [Reference Hartl50, Theorem 2.2.5]. Likewise, if
${\underline {D\!}\,}_{b,\gamma }(U)$
by [Reference Hartl50, Theorem 2.2.5]. Likewise, if
![]() ${\underline {D\!}\,}_{b,\gamma }(V)$
is admissible, we use the compatibility of the functor
${\underline {D\!}\,}_{b,\gamma }(V)$
is admissible, we use the compatibility of the functor
![]() $V\mapsto {\underline {{\mathcal {F}}\!}\,}_{b,\gamma }(V)$
with direct sums, tensor products and duals to compute
$V\mapsto {\underline {{\mathcal {F}}\!}\,}_{b,\gamma }(V)$
with direct sums, tensor products and duals to compute
 $$ \begin{align*}&{\underline{{\mathcal{F}}\!}\,}_{b,\gamma}(U)\otimes_{L{\textstyle\langle\frac{z}{\zeta^{s}},z^{-1}\}}}{\overline{L}}{\textstyle \langle\frac{z}{\zeta^{s}},z^{-1}\}}\\&\quad \cong \bigoplus_{i=1}^r {\underline{{\mathcal{F}}\!}\,}_{b,\gamma}(V)^{\otimes l_i}\otimes ({\underline{{\mathcal{F}}\!}\,}_{b,\gamma}(V)^{\scriptscriptstyle\lor})^{\otimes m_i}\otimes_{L{\textstyle\langle\frac{z}{\zeta^{s}},z^{-1}\}}}{\overline{L}}{\textstyle\langle\frac{z}{\zeta^{s}},z^{-1}\}} \\&\quad \cong \bigoplus_{i=1}^r ({\underline{{\mathcal{F}}\!}\,}_{0,1}{}^{\oplus\dim V})^{\otimes l_i}\otimes (({\underline{{\mathcal{F}}\!}\,}_{0,1}{}^{\oplus\dim V})^{\scriptscriptstyle\lor})^{\otimes m_i}\otimes_{L{\textstyle\langle\frac{z}{\zeta^{s}},z^{-1}\}}}{\overline{L}}{\textstyle\langle\frac{z}{\zeta^{s}},z^{-1}\}} \\&\quad \cong {\underline{{\mathcal{F}}\!}\,}_{0,1}{}^{\oplus\dim U}\otimes_{L{\textstyle\langle\frac{z}{\zeta^{s}},z^{-1}\}}}{\overline{L}}{\textstyle\langle\frac{z}{\zeta^{s}},z^{-1}\}}. \end{align*} $$
$$ \begin{align*}&{\underline{{\mathcal{F}}\!}\,}_{b,\gamma}(U)\otimes_{L{\textstyle\langle\frac{z}{\zeta^{s}},z^{-1}\}}}{\overline{L}}{\textstyle \langle\frac{z}{\zeta^{s}},z^{-1}\}}\\&\quad \cong \bigoplus_{i=1}^r {\underline{{\mathcal{F}}\!}\,}_{b,\gamma}(V)^{\otimes l_i}\otimes ({\underline{{\mathcal{F}}\!}\,}_{b,\gamma}(V)^{\scriptscriptstyle\lor})^{\otimes m_i}\otimes_{L{\textstyle\langle\frac{z}{\zeta^{s}},z^{-1}\}}}{\overline{L}}{\textstyle\langle\frac{z}{\zeta^{s}},z^{-1}\}} \\&\quad \cong \bigoplus_{i=1}^r ({\underline{{\mathcal{F}}\!}\,}_{0,1}{}^{\oplus\dim V})^{\otimes l_i}\otimes (({\underline{{\mathcal{F}}\!}\,}_{0,1}{}^{\oplus\dim V})^{\scriptscriptstyle\lor})^{\otimes m_i}\otimes_{L{\textstyle\langle\frac{z}{\zeta^{s}},z^{-1}\}}}{\overline{L}}{\textstyle\langle\frac{z}{\zeta^{s}},z^{-1}\}} \\&\quad \cong {\underline{{\mathcal{F}}\!}\,}_{0,1}{}^{\oplus\dim U}\otimes_{L{\textstyle\langle\frac{z}{\zeta^{s}},z^{-1}\}}}{\overline{L}}{\textstyle\langle\frac{z}{\zeta^{s}},z^{-1}\}}. \end{align*} $$
So if
![]() ${\underline {D\!}\,}_{b,\gamma }(V)$
is admissible,
${\underline {D\!}\,}_{b,\gamma }(V)$
is admissible,
![]() ${\underline {D\!}\,}_{b,\gamma }(U)$
also is. Therefore, it suffices to show that (weak) admissibility is preserved under passage to subrepresentations and quotient representations.
${\underline {D\!}\,}_{b,\gamma }(U)$
also is. Therefore, it suffices to show that (weak) admissibility is preserved under passage to subrepresentations and quotient representations.
By Lemma 4.12, the condition
![]() $[b]^{\#}=\gamma ^{\#}$
in
$[b]^{\#}=\gamma ^{\#}$
in
![]() $\pi _1(G)_{\Gamma ,{\mathbb {Q}}}$
implies
$\pi _1(G)_{\Gamma ,{\mathbb {Q}}}$
implies
![]() $t_N\big ({\underline {D\!}\,}_{b,\gamma }(W)\big )\,=\,t_H\big ({\underline {D\!}\,}_{b,\gamma }(W)\big )$
for all representations W. Now let U be a representation such that
$t_N\big ({\underline {D\!}\,}_{b,\gamma }(W)\big )\,=\,t_H\big ({\underline {D\!}\,}_{b,\gamma }(W)\big )$
for all representations W. Now let U be a representation such that
![]() ${\underline {D\!}\,}_{b,\gamma }(U)$
is weakly admissible. Then the equivalent conditions from Definition 4.3(c) show that for every subrepresentation or quotient representation W of
${\underline {D\!}\,}_{b,\gamma }(U)$
is weakly admissible. Then the equivalent conditions from Definition 4.3(c) show that for every subrepresentation or quotient representation W of
![]() $U$
the
$U$
the
![]() $z$
-isocrystal with Hodge-Pink structure
$z$
-isocrystal with Hodge-Pink structure
![]() ${\underline {D\!}\,}_{b,\gamma }(W)$
is also weakly admissible.
${\underline {D\!}\,}_{b,\gamma }(W)$
is also weakly admissible.
If
![]() ${\underline {D\!}\,}_{b,\gamma }(U)$
is actually admissible, then
${\underline {D\!}\,}_{b,\gamma }(U)$
is actually admissible, then
![]() ${\underline {{\mathcal {F}}\!}\,}_{b,\gamma }(U)\otimes _{L{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}}{\overline {L}}{\textstyle \langle \frac {z}{\zeta ^{s}}, z^{-1}\}}\cong {\underline {{\mathcal {F}}\!}\,}_{0,1}{}^{\oplus \dim U}$
. If
${\underline {{\mathcal {F}}\!}\,}_{b,\gamma }(U)\otimes _{L{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}}{\overline {L}}{\textstyle \langle \frac {z}{\zeta ^{s}}, z^{-1}\}}\cong {\underline {{\mathcal {F}}\!}\,}_{0,1}{}^{\oplus \dim U}$
. If
![]() $W\subset U$
is a subrepresentation, then the
$W\subset U$
is a subrepresentation, then the
![]() $\sigma $
-subbundle
$\sigma $
-subbundle
![]() ${\underline {{\mathcal {F}}\!}\,}_{b,\gamma }(W)\subset {\underline {{\mathcal {F}}\!}\,}_{b,\gamma }(U)$
satisfies
${\underline {{\mathcal {F}}\!}\,}_{b,\gamma }(W)\subset {\underline {{\mathcal {F}}\!}\,}_{b,\gamma }(U)$
satisfies
![]() ${\underline {{\mathcal {F}}\!}\,}_{b,\gamma }(W)\otimes _{L{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}}{\overline {L}}{\textstyle \langle \frac {z}{\zeta ^{s}}, z^{-1}\}}\cong \bigoplus _i{\underline {{\mathcal {F}}\!}\,}_{d_i,n_i}$
for some
${\underline {{\mathcal {F}}\!}\,}_{b,\gamma }(W)\otimes _{L{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}}{\overline {L}}{\textstyle \langle \frac {z}{\zeta ^{s}}, z^{-1}\}}\cong \bigoplus _i{\underline {{\mathcal {F}}\!}\,}_{d_i,n_i}$
for some
![]() $d_i,n_i$
by Proposition 4.7. By Proposition 4.8, all
$d_i,n_i$
by Proposition 4.7. By Proposition 4.8, all
![]() $d_i\leq 0$
. Because
$d_i\leq 0$
. Because
by Proposition 4.10, all
![]() $d_i$
must be zero and
$d_i$
must be zero and
![]() ${\underline {{\mathcal {F}}\!}\,}_{b,\gamma }(W)$
is admissible. Dually, if W is a quotient representation of U, the
${\underline {{\mathcal {F}}\!}\,}_{b,\gamma }(W)$
is admissible. Dually, if W is a quotient representation of U, the
![]() $\sigma $
-quotient-bundle
$\sigma $
-quotient-bundle
![]() ${\underline {{\mathcal {F}}\!}\,}_{b,\gamma }(W)$
of
${\underline {{\mathcal {F}}\!}\,}_{b,\gamma }(W)$
of
![]() ${\underline {{\mathcal {F}}\!}\,}_{b,\gamma }(U)$
satisfies
${\underline {{\mathcal {F}}\!}\,}_{b,\gamma }(U)$
satisfies
![]() ${\underline {{\mathcal {F}}\!}\,}_{b,\gamma }(W)\otimes _{L{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}}{\overline {L}}{\textstyle \langle \frac {z}{\zeta ^{s}}, z^{-1}\}}\cong \bigoplus _i{\underline {{\mathcal {F}}\!}\,}_{d_i,n_i}$
for some
${\underline {{\mathcal {F}}\!}\,}_{b,\gamma }(W)\otimes _{L{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}}{\overline {L}}{\textstyle \langle \frac {z}{\zeta ^{s}}, z^{-1}\}}\cong \bigoplus _i{\underline {{\mathcal {F}}\!}\,}_{d_i,n_i}$
for some
![]() $d_i,n_i$
with
$d_i,n_i$
with
![]() $d_i\ge 0$
by Proposition 4.8. Again,
$d_i\ge 0$
by Proposition 4.8. Again,
![]() $\deg {\underline {{\mathcal {F}}\!}\,}_{b,\gamma }(W)=0$
implies
$\deg {\underline {{\mathcal {F}}\!}\,}_{b,\gamma }(W)=0$
implies
![]() $d_i=0$
and
$d_i=0$
and
![]() ${\underline {{\mathcal {F}}\!}\,}_{b,\gamma }(W)$
is admissible.
${\underline {{\mathcal {F}}\!}\,}_{b,\gamma }(W)$
is admissible.
Remark 4.15. Let
![]() $b\in LG({\mathbb {F}})$
. Let
$b\in LG({\mathbb {F}})$
. Let
![]() $L_0$
be a finite field extension of
$L_0$
be a finite field extension of
![]() ${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
for which
${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
for which
![]() $G_{L_0}:=G\times _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]},z\mapsto \zeta }L_0$
is split. Let T be a maximal split torus of
$G_{L_0}:=G\times _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]},z\mapsto \zeta }L_0$
is split. Let T be a maximal split torus of
![]() $G_{L_0}$
that contains the image of the Newton point
$G_{L_0}$
that contains the image of the Newton point
![]() $\nu _b\colon {\mathbb {D}}_{{\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)}\to G_{{\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)}$
; see Remark 3.6(a). We may view
$\nu _b\colon {\mathbb {D}}_{{\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)}\to G_{{\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)}$
; see Remark 3.6(a). We may view
![]() $\nu _b$
as an element of
$\nu _b$
as an element of
![]() $X_*(T)_{\mathbb {Q}}:=X_*(T)\otimes _{\mathbb {Z}} {\mathbb {Q}}$
. Let L be a complete valued field extension of the completion of the maximal unramified extension
$X_*(T)_{\mathbb {Q}}:=X_*(T)\otimes _{\mathbb {Z}} {\mathbb {Q}}$
. Let L be a complete valued field extension of the completion of the maximal unramified extension
![]() $\breve L_0$
of
$\breve L_0$
of
![]() $L_0$
and let
$L_0$
and let
![]() $\gamma \in \operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}}(L)$
. By the Cartan decomposition there is a unique dominant cocharacter
$\gamma \in \operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}}(L)$
. By the Cartan decomposition there is a unique dominant cocharacter
![]() $\mu _{\gamma }\in X_*(T)$
called the Hodge point of
$\mu _{\gamma }\in X_*(T)$
called the Hodge point of
![]() $\gamma $
such that
$\gamma $
such that
If
![]() $(b,\gamma )$
is weakly admissible, then
$(b,\gamma )$
is weakly admissible, then
![]() $\nu _b\preceq \mu _{\gamma }$
(see [Reference Dat, Orlik and Rapoport30, Theorem 9.5.10], which is for the arithmetic context but gives a proof that can directly be translated to our situation); in other words,
$\nu _b\preceq \mu _{\gamma }$
(see [Reference Dat, Orlik and Rapoport30, Theorem 9.5.10], which is for the arithmetic context but gives a proof that can directly be translated to our situation); in other words,
![]() $([b],\{\mu _\gamma \})$
is acceptable in the sense of [Reference Rapoport and Viehmann79, Definition 2.5]. The converse of this is not true. However, if
$([b],\{\mu _\gamma \})$
is acceptable in the sense of [Reference Rapoport and Viehmann79, Definition 2.5]. The converse of this is not true. However, if
![]() $\mu \in X_*(T)$
is dominant with
$\mu \in X_*(T)$
is dominant with
![]() $\nu _b\preceq \mu $
, then one can show that there exists a cocharacter
$\nu _b\preceq \mu $
, then one can show that there exists a cocharacter
![]() $\operatorname {\mathrm {Int}}_g\circ \mu \colon {\mathbb {G}}_{m,L}\to G_L$
with
$\operatorname {\mathrm {Int}}_g\circ \mu \colon {\mathbb {G}}_{m,L}\to G_L$
with
![]() $g\in G(L)$
for a finite extension
$g\in G(L)$
for a finite extension
![]() $L\supset \breve L_0$
, which induces a weakly admissible Hodge-Pink filtration on
$L\supset \breve L_0$
, which induces a weakly admissible Hodge-Pink filtration on
![]() ${\underline {D\!}\,}_b(V)$
for all V. Indeed, this can be shown in the same way as the arithmetic counterpart; compare [Reference Dat, Orlik and Rapoport30, Theorem 9.5.10]. Then by Remark 4.4(a),
${\underline {D\!}\,}_b(V)$
for all V. Indeed, this can be shown in the same way as the arithmetic counterpart; compare [Reference Dat, Orlik and Rapoport30, Theorem 9.5.10]. Then by Remark 4.4(a),
![]() ${\underline {D\!}\,}_{b,\gamma }(V)$
is weakly admissible (and even admissible) for every Hodge-Pink G-structure
${\underline {D\!}\,}_{b,\gamma }(V)$
is weakly admissible (and even admissible) for every Hodge-Pink G-structure
![]() $\gamma \in \operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}}(L)$
that induces
$\gamma \in \operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}}(L)$
that induces
![]() $\operatorname {\mathrm {Int}}_g\circ \mu $
, like, for example,
$\operatorname {\mathrm {Int}}_g\circ \mu $
, like, for example,
![]() $\gamma =g\cdot \mu (z-\zeta )$
. For more details and references in the arithmetic context, compare also the discussion in [Reference Rapoport and Viehmann79, Section 2.2 and Proposition 3.1].
$\gamma =g\cdot \mu (z-\zeta )$
. For more details and references in the arithmetic context, compare also the discussion in [Reference Rapoport and Viehmann79, Section 2.2 and Proposition 3.1].
We next want to define period spaces in the bounded situation. Let
![]() $\hat {Z}=[(R,\hat Z_R)]$
be a bound as in Definition 2.2 with reflex ring
$\hat {Z}=[(R,\hat Z_R)]$
be a bound as in Definition 2.2 with reflex ring
![]() $R_{\hat Z}=\kappa \mathrm {[}\kern-0.15em\mathrm {[}\xi \mathrm {]}\kern-0.15em\mathrm {]}$
and set
$R_{\hat Z}=\kappa \mathrm {[}\kern-0.15em\mathrm {[}\xi \mathrm {]}\kern-0.15em\mathrm {]}$
and set
![]() $E:=E_{\hat Z}=\kappa (\kern-0.15em( \xi )\kern-0.15em)$
and
$E:=E_{\hat Z}=\kappa (\kern-0.15em( \xi )\kern-0.15em)$
and
![]() $\breve E:={\mathbb {F}}(\kern-0.15em( \xi )\kern-0.15em)$
. By Proposition 2.6(d), the associated strictly
$\breve E:={\mathbb {F}}(\kern-0.15em( \xi )\kern-0.15em)$
. By Proposition 2.6(d), the associated strictly
![]() $R[\tfrac {1}{\zeta }]$
-analytic spaces
$R[\tfrac {1}{\zeta }]$
-analytic spaces
![]() $\hat {Z}_R^{\textrm {an}}$
arise by base change to
$\hat {Z}_R^{\textrm {an}}$
arise by base change to
![]() $R[\tfrac {1}{\zeta }]$
from a strictly
$R[\tfrac {1}{\zeta }]$
from a strictly
![]() $E_{\hat Z}$
-analytic space
$E_{\hat Z}$
-analytic space
![]() $\hat Z^{\textrm {an}}$
associated with a projective scheme
$\hat Z^{\textrm {an}}$
associated with a projective scheme
![]() $\hat {Z}_E$
over
$\hat {Z}_E$
over
![]() $\operatorname {\mathrm {Spec}} E_{\hat Z}$
, which is a closed subscheme of the affine Grassmannian
$\operatorname {\mathrm {Spec}} E_{\hat Z}$
, which is a closed subscheme of the affine Grassmannian
![]() $\operatorname {\mathrm {Gr}}_{G,E}^{{\mathbf {B}}_{\textrm {dR}}}:=\operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}}\times _{{\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)}\operatorname {\mathrm {Spec}} E_{\hat Z}$
.
$\operatorname {\mathrm {Gr}}_{G,E}^{{\mathbf {B}}_{\textrm {dR}}}:=\operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}}\times _{{\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)}\operatorname {\mathrm {Spec}} E_{\hat Z}$
.
Definition 4.16. We call
![]() ${\mathcal {H}}_{G,\hat {Z}}:=\hat {Z}_E$
the space of Hodge-Pink G-structures bounded by
${\mathcal {H}}_{G,\hat {Z}}:=\hat {Z}_E$
the space of Hodge-Pink G-structures bounded by
![]() $\hat {Z}$
and set
$\hat {Z}$
and set
![]() $\breve {\mathcal {H}}_{G,\hat {Z}}:={\mathcal {H}}_{G,\hat {Z}}\times _{E_{\hat Z}}\operatorname {\mathrm {Spec}}\breve E$
. Let
$\breve {\mathcal {H}}_{G,\hat {Z}}:={\mathcal {H}}_{G,\hat {Z}}\times _{E_{\hat Z}}\operatorname {\mathrm {Spec}}\breve E$
. Let
![]() ${\underline {{\mathbb {G}}}}_0=\big ((L^+G)_{\mathbb {F}},b\sigma ^\ast \big )$
be a local G-shtuka over
${\underline {{\mathbb {G}}}}_0=\big ((L^+G)_{\mathbb {F}},b\sigma ^\ast \big )$
be a local G-shtuka over
![]() ${\mathbb {F}}$
. We define the period spaces of (weakly) admissible Hodge-Pink G-structures on
${\mathbb {F}}$
. We define the period spaces of (weakly) admissible Hodge-Pink G-structures on
![]() ${\underline {{\mathbb {G}}}}_0$
bounded by
${\underline {{\mathbb {G}}}}_0$
bounded by
![]() $\hat {Z}$
as
$\hat {Z}$
as
 $$ \begin{align*} \breve{\mathcal{H}}_{G,\hat{Z},b}^{wa} & := \big\{\,\gamma\in\breve{\mathcal{H}}_{G,\hat{Z}}^{\textrm{an}}\colon\text{ the pair } (b,\gamma) \text{ is weakly admissible} \big\},\\[2mm]\breve{\mathcal{H}}_{G,\hat{Z},b}^{a} & := \big\{\,\gamma\in\breve{\mathcal{H}}_{G,\hat{Z}}^{\textrm{an}}\colon\text{ the pair } (b,\gamma) \text{ is admissible}\big\}\quad\text{and}\\[2mm]\breve{\mathcal{H}}_{G,\hat{Z},b}^{na} & := \big\{\,\gamma\in\breve{\mathcal{H}}_{G,\hat{Z}}^{\textrm{an}}\colon\text{ the pair } (b,\gamma) \text{ is admissible and neutral}\big\}\,. \end{align*} $$
$$ \begin{align*} \breve{\mathcal{H}}_{G,\hat{Z},b}^{wa} & := \big\{\,\gamma\in\breve{\mathcal{H}}_{G,\hat{Z}}^{\textrm{an}}\colon\text{ the pair } (b,\gamma) \text{ is weakly admissible} \big\},\\[2mm]\breve{\mathcal{H}}_{G,\hat{Z},b}^{a} & := \big\{\,\gamma\in\breve{\mathcal{H}}_{G,\hat{Z}}^{\textrm{an}}\colon\text{ the pair } (b,\gamma) \text{ is admissible}\big\}\quad\text{and}\\[2mm]\breve{\mathcal{H}}_{G,\hat{Z},b}^{na} & := \big\{\,\gamma\in\breve{\mathcal{H}}_{G,\hat{Z}}^{\textrm{an}}\colon\text{ the pair } (b,\gamma) \text{ is admissible and neutral}\big\}\,. \end{align*} $$
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^{na}$
equals the intersection of
$\breve {\mathcal {H}}_{G,\hat {Z},b}^{na}$
equals the intersection of
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^{a}$
with the union of those connected components of
$\breve {\mathcal {H}}_{G,\hat {Z},b}^{a}$
with the union of those connected components of
![]() $\breve {\mathcal {H}}_{G,\hat Z}$
that map to
$\breve {\mathcal {H}}_{G,\hat Z}$
that map to
![]() $[b]^\#\in \pi _1(G)_\Gamma $
under the map
$[b]^\#\in \pi _1(G)_\Gamma $
under the map
![]() $\pi _0(\breve {\mathcal {H}}_{G,\hat Z})\to \pi _0(\operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}})\twoheadrightarrow \pi _1(G)_\Gamma $
induced by (4.1). In particular,
$\pi _0(\breve {\mathcal {H}}_{G,\hat Z})\to \pi _0(\operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}})\twoheadrightarrow \pi _1(G)_\Gamma $
induced by (4.1). In particular,
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^{na}$
is a union of connected components of
$\breve {\mathcal {H}}_{G,\hat {Z},b}^{na}$
is a union of connected components of
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^{a}$
. The period spaces only depend on b and on the generic fibres
$\breve {\mathcal {H}}_{G,\hat {Z},b}^{a}$
. The period spaces only depend on b and on the generic fibres
![]() $G_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}$
and
$G_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}$
and
![]() $\hat {Z}_E$
of G and
$\hat {Z}_E$
of G and
![]() $\hat {Z}$
.
$\hat {Z}$
.
Remark 4.17. If
![]() $\breve E\subset L$
, then the homomorphism
$\breve E\subset L$
, then the homomorphism
![]() ${\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)\to L\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]},\,z\mapsto z=\zeta +(z-\zeta )$
induces a homomorphism
${\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)\to L\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]},\,z\mapsto z=\zeta +(z-\zeta )$
induces a homomorphism
![]() $LG({\mathbb {F}})=G\big ({\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)\big )\to G\big (L\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )$
. Thus, if
$LG({\mathbb {F}})=G\big ({\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)\big )\to G\big (L\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )$
. Thus, if
![]() $b^{\prime }=g\,b\,\sigma ^\ast (g^{-1})$
for some
$b^{\prime }=g\,b\,\sigma ^\ast (g^{-1})$
for some
![]() $g\in LG({\mathbb {F}})$
, one can check that
$g\in LG({\mathbb {F}})$
, one can check that
![]() $\gamma \mapsto \sigma ^\ast (g)\cdot \gamma =:\gamma ^{\prime }$
maps
$\gamma \mapsto \sigma ^\ast (g)\cdot \gamma =:\gamma ^{\prime }$
maps
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^{wa}$
isomorphically onto
$\breve {\mathcal {H}}_{G,\hat {Z},b}^{wa}$
isomorphically onto
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b^{\prime }}^{wa}$
(and likewise for
$\breve {\mathcal {H}}_{G,\hat {Z},b^{\prime }}^{wa}$
(and likewise for
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b^{\prime }}^{a}$
and
$\breve {\mathcal {H}}_{G,\hat {Z},b^{\prime }}^{a}$
and
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b^{\prime }}^{na}$
), because
$\breve {\mathcal {H}}_{G,\hat {Z},b^{\prime }}^{na}$
), because
![]() $\sigma ^\ast (g)$
maps
$\sigma ^\ast (g)$
maps
![]() $\breve {\mathcal {H}}_{G,\hat Z}^{\textrm {an}}$
to itself by Lemma 2.10 and induces isomorphisms
$\breve {\mathcal {H}}_{G,\hat Z}^{\textrm {an}}$
to itself by Lemma 2.10 and induces isomorphisms
![]() ${\underline {D\!}\,}_{b^{\prime }\!,\gamma ^{\prime }}(V)\cong {\underline {D\!}\,}_{b,\gamma }(V)$
and
${\underline {D\!}\,}_{b^{\prime }\!,\gamma ^{\prime }}(V)\cong {\underline {D\!}\,}_{b,\gamma }(V)$
and
![]() ${\underline {{\mathcal {F}}\!}\,}_{b^{\prime }\!,\gamma ^{\prime }}(V)\cong {\underline {{\mathcal {F}}\!}\,}_{b,\gamma }(V)$
. In particular,
${\underline {{\mathcal {F}}\!}\,}_{b^{\prime }\!,\gamma ^{\prime }}(V)\cong {\underline {{\mathcal {F}}\!}\,}_{b,\gamma }(V)$
. In particular,
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^{wa}$
,
$\breve {\mathcal {H}}_{G,\hat {Z},b}^{wa}$
,
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^{a}$
and
$\breve {\mathcal {H}}_{G,\hat {Z},b}^{a}$
and
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^{na}$
are invariant under the group
$\breve {\mathcal {H}}_{G,\hat {Z},b}^{na}$
are invariant under the group
![]() $J_b\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )\;=\;\operatorname {\mathrm {QIsog}}_{\mathbb {F}}\big ((L^+G)_{\mathbb {F}},b\sigma ^\ast \big )$
from (3.1).
$J_b\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )\;=\;\operatorname {\mathrm {QIsog}}_{\mathbb {F}}\big ((L^+G)_{\mathbb {F}},b\sigma ^\ast \big )$
from (3.1).
Proposition 4.18. The space
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^{a}$
is contained in
$\breve {\mathcal {H}}_{G,\hat {Z},b}^{a}$
is contained in
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^{wa}$
with
$\breve {\mathcal {H}}_{G,\hat {Z},b}^{wa}$
with
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^{a}(L)=\breve {\mathcal {H}}_{G,\hat {Z},b}^{wa}(L)$
for all complete valued field extensions
$\breve {\mathcal {H}}_{G,\hat {Z},b}^{a}(L)=\breve {\mathcal {H}}_{G,\hat {Z},b}^{wa}(L)$
for all complete valued field extensions
![]() $L/\breve E$
satisfying the following condition: Let
$L/\breve E$
satisfying the following condition: Let
![]() ${\overline {L}}$
be the completion of an algebraic closure of L, let
${\overline {L}}$
be the completion of an algebraic closure of L, let
![]() $\bar \ell \subset {\overline {L}}$
be a subfield isomorphic to the residue field of
$\bar \ell \subset {\overline {L}}$
be a subfield isomorphic to the residue field of
![]() ${\overline {L}}$
under the residue map
${\overline {L}}$
under the residue map
![]() ${\mathcal {O}}_{{\overline {L}}}\twoheadrightarrow {\mathcal {O}}_{{\overline {L}}}/{\mathfrak {m}}_{{\overline {L}}}$
and let
${\mathcal {O}}_{{\overline {L}}}\twoheadrightarrow {\mathcal {O}}_{{\overline {L}}}/{\mathfrak {m}}_{{\overline {L}}}$
and let
![]() ${\widetilde {L}}$
be the closure of the compositum
${\widetilde {L}}$
be the closure of the compositum
![]() $\bar \ell L$
inside
$\bar \ell L$
inside
![]() ${\overline {L}}$
. (In particular, if the residue field of L is perfect, then
${\overline {L}}$
. (In particular, if the residue field of L is perfect, then
![]() ${\widetilde {L}}$
is the completion of the maximal unramified extension of L.) The condition is that
${\widetilde {L}}$
is the completion of the maximal unramified extension of L.) The condition is that
![]() ${\widetilde {L}}$
does not contain an element a with
${\widetilde {L}}$
does not contain an element a with
![]() $0<|a|<1$
such that all of the q-power roots of a also lie in
$0<|a|<1$
such that all of the q-power roots of a also lie in
![]() ${\widetilde {L}}$
.
${\widetilde {L}}$
.
Proof. The inclusion
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^{a}\subset \breve {\mathcal {H}}_{G,\hat {Z},b}^{wa}$
follows from Corollary 4.11. The equality
$\breve {\mathcal {H}}_{G,\hat {Z},b}^{a}\subset \breve {\mathcal {H}}_{G,\hat {Z},b}^{wa}$
follows from Corollary 4.11. The equality
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^{a}(L)=\breve {\mathcal {H}}_{G,\hat {Z},b}^{wa}(L)$
for the mentioned fields was proved in [Reference Hartl50, Theorem 2.5.3].
$\breve {\mathcal {H}}_{G,\hat {Z},b}^{a}(L)=\breve {\mathcal {H}}_{G,\hat {Z},b}^{wa}(L)$
for the mentioned fields was proved in [Reference Hartl50, Theorem 2.5.3].
Remark 4.19.
-
(a) The condition of the proposition, and hence
 $\breve {\mathcal {H}}_{G,\hat {Z},b}^{a}(L)=\breve {\mathcal {H}}_{G,\hat {Z},b}^{wa}(L)$
, holds if the value group of L does not contain a nonzero element that is arbitrarily often divisible by q. This is due to the fact that the value groups of L and
$\breve {\mathcal {H}}_{G,\hat {Z},b}^{a}(L)=\breve {\mathcal {H}}_{G,\hat {Z},b}^{wa}(L)$
, holds if the value group of L does not contain a nonzero element that is arbitrarily often divisible by q. This is due to the fact that the value groups of L and
 ${\widetilde {L}}$
coincide. In particular, this is the case if L is a finite field extension of
${\widetilde {L}}$
coincide. In particular, this is the case if L is a finite field extension of
 $\breve E$
or, more generally, if L is discretely valued or even if the value group of L is finitely generated. See [Reference Hartl50, Condition (2.3) on page 1294] for further discussion of this condition.
$\breve E$
or, more generally, if L is discretely valued or even if the value group of L is finitely generated. See [Reference Hartl50, Condition (2.3) on page 1294] for further discussion of this condition. -
(b) If L violates the condition – for example, if L is algebraically closed and complete – it can happen that
 $\breve {\mathcal {H}}_{G,\hat {Z},b}^{a}(L)\subsetneq \breve {\mathcal {H}}_{G,\hat {Z},b}^{wa}(L)$
. Examples in the case
$\breve {\mathcal {H}}_{G,\hat {Z},b}^{a}(L)\subsetneq \breve {\mathcal {H}}_{G,\hat {Z},b}^{wa}(L)$
. Examples in the case
 $G=\operatorname {\mathrm {GL}}_r$
were given in [Reference Hartl50, Example 3.3.2].
$G=\operatorname {\mathrm {GL}}_r$
were given in [Reference Hartl50, Example 3.3.2].
Theorem 4.20. The period space
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^{wa}$
and the admissible locus
$\breve {\mathcal {H}}_{G,\hat {Z},b}^{wa}$
and the admissible locus
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^a$
are open paracompact strictly
$\breve {\mathcal {H}}_{G,\hat {Z},b}^a$
are open paracompact strictly
![]() $\breve E$
-analytic subspaces of
$\breve E$
-analytic subspaces of
![]() $\breve {\mathcal {H}}_{G,\hat {Z}}^{\textrm {an}}$
. The intersections of any connected component of
$\breve {\mathcal {H}}_{G,\hat {Z}}^{\textrm {an}}$
. The intersections of any connected component of
![]() $\breve {\mathcal {H}}_{G,\hat {Z}}^{\textrm {an}}$
with
$\breve {\mathcal {H}}_{G,\hat {Z}}^{\textrm {an}}$
with
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^{wa}$
and
$\breve {\mathcal {H}}_{G,\hat {Z},b}^{wa}$
and
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^a$
are arcwise connected. In the terminology of Remarks 2.11(b) and 4.15, the spaces
$\breve {\mathcal {H}}_{G,\hat {Z},b}^a$
are arcwise connected. In the terminology of Remarks 2.11(b) and 4.15, the spaces
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^{wa}$
and
$\breve {\mathcal {H}}_{G,\hat {Z},b}^{wa}$
and
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^a$
intersect after base change to
$\breve {\mathcal {H}}_{G,\hat {Z},b}^a$
intersect after base change to
![]() $\breve L_0$
precisely those connected components of
$\breve L_0$
precisely those connected components of
![]() $\operatorname {\mathrm {Gr}}_{G,\breve L_0}^{{\mathbf {B}}_{\textrm {dR}}}$
whose image in
$\operatorname {\mathrm {Gr}}_{G,\breve L_0}^{{\mathbf {B}}_{\textrm {dR}}}$
whose image in
![]() $\pi _1(G)=\pi _0(\operatorname {\mathrm {Gr}}_{G,\breve L_0}^{{\mathbf {B}}_{\textrm {dR}}})$
(using (4.1)) is of the form
$\pi _1(G)=\pi _0(\operatorname {\mathrm {Gr}}_{G,\breve L_0}^{{\mathbf {B}}_{\textrm {dR}}})$
(using (4.1)) is of the form
![]() $\mu ^{\#}\in \pi _1(G)$
for a
$\mu ^{\#}\in \pi _1(G)$
for a
![]() $\mu \in N_{\textrm {an}}$
with
$\mu \in N_{\textrm {an}}$
with
![]() $\nu _b\preceq \mu $
.
$\nu _b\preceq \mu $
.
Proof. Choose a faithful representation
![]() $\rho \colon G\hookrightarrow \operatorname {\mathrm {GL}}_r$
in
$\rho \colon G\hookrightarrow \operatorname {\mathrm {GL}}_r$
in
![]() $\operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G$
that factors through
$\operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G$
that factors through
![]() $\operatorname {\mathrm {SL}}_r$
, and let n be an integer as in Proposition 2.6(a) for which
$\operatorname {\mathrm {SL}}_r$
, and let n be an integer as in Proposition 2.6(a) for which
![]() $\rho _*\colon \hat {Z}\to {\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {SL}}_r}$
factors through
$\rho _*\colon \hat {Z}\to {\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {SL}}_r}$
factors through
![]() ${\widehat {{\mathcal {F}}\ell }}^{(n)}_{\operatorname {\mathrm {SL}}_r}=\hat Z_{\operatorname {\mathrm {GL}}_r,2n\rho ^{\scriptscriptstyle \lor }}$
; see Examples 2.8 and 2.13. By Proposition 2.6, the
${\widehat {{\mathcal {F}}\ell }}^{(n)}_{\operatorname {\mathrm {SL}}_r}=\hat Z_{\operatorname {\mathrm {GL}}_r,2n\rho ^{\scriptscriptstyle \lor }}$
; see Examples 2.8 and 2.13. By Proposition 2.6, the
![]() $\breve E$
-analytic space
$\breve E$
-analytic space
![]() $\breve {\mathcal {H}}_{G,\hat {Z}}^{\textrm {an}}$
is a subspace of
$\breve {\mathcal {H}}_{G,\hat {Z}}^{\textrm {an}}$
is a subspace of
![]() ${\mathcal {H}}_{\operatorname {\mathrm {GL}}_r,2n\rho ^{\scriptscriptstyle \lor }}^{\textrm {an}}{\widehat {\otimes }}_{{\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)}\breve E$
, where
${\mathcal {H}}_{\operatorname {\mathrm {GL}}_r,2n\rho ^{\scriptscriptstyle \lor }}^{\textrm {an}}{\widehat {\otimes }}_{{\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)}\breve E$
, where
![]() ${\mathcal {H}}_{\operatorname {\mathrm {GL}}_r,2n\rho ^{\scriptscriptstyle \lor }}^{\textrm {an}}:=(\hat {Z}_{\operatorname {\mathrm {GL}}_r,2n\rho ^{\scriptscriptstyle \lor }})^{\textrm {an}}$
. On the connected components of
${\mathcal {H}}_{\operatorname {\mathrm {GL}}_r,2n\rho ^{\scriptscriptstyle \lor }}^{\textrm {an}}:=(\hat {Z}_{\operatorname {\mathrm {GL}}_r,2n\rho ^{\scriptscriptstyle \lor }})^{\textrm {an}}$
. On the connected components of
![]() $\breve {\mathcal {H}}_{G,\hat {Z}}^{\textrm {an}}$
where
$\breve {\mathcal {H}}_{G,\hat {Z}}^{\textrm {an}}$
where
![]() $[b]^{\#}=\gamma ^{\#}$
in
$[b]^{\#}=\gamma ^{\#}$
in
![]() $\pi _1(G)_{\Gamma ,{\mathbb {Q}}}$
, we have by Definition 4.13
$\pi _1(G)_{\Gamma ,{\mathbb {Q}}}$
, we have by Definition 4.13
 $$ \begin{align*} \breve{\mathcal{H}}_{G,\hat{Z},b}^{wa} & = \breve{\mathcal{H}}_{G,\hat{Z}}^{\textrm{an}}\;\cap\; \breve{\mathcal{H}}_{\operatorname{\mathrm{GL}}_r,2n\rho^{\scriptscriptstyle\lor}\!,\rho(b)}^{wa}{\widehat{\otimes}}_{{\mathbb{F}}(\kern-0.15em( \zeta )\kern-0.15em)}\breve E\qquad \text{and}\\[2mm] \breve{\mathcal{H}}_{G,\hat{Z},b}^a & = \breve{\mathcal{H}}_{G,\hat{Z}}^{\textrm{an}}\;\cap\;\breve{\mathcal{H}}_{\operatorname{\mathrm{GL}}_r,2n \rho^{\scriptscriptstyle\lor}\!,\rho(b)}^a{\widehat{\otimes}}_{{\mathbb{F}}(\kern-0.15em( \zeta )\kern-0.15em)}\breve E. \end{align*} $$
$$ \begin{align*} \breve{\mathcal{H}}_{G,\hat{Z},b}^{wa} & = \breve{\mathcal{H}}_{G,\hat{Z}}^{\textrm{an}}\;\cap\; \breve{\mathcal{H}}_{\operatorname{\mathrm{GL}}_r,2n\rho^{\scriptscriptstyle\lor}\!,\rho(b)}^{wa}{\widehat{\otimes}}_{{\mathbb{F}}(\kern-0.15em( \zeta )\kern-0.15em)}\breve E\qquad \text{and}\\[2mm] \breve{\mathcal{H}}_{G,\hat{Z},b}^a & = \breve{\mathcal{H}}_{G,\hat{Z}}^{\textrm{an}}\;\cap\;\breve{\mathcal{H}}_{\operatorname{\mathrm{GL}}_r,2n \rho^{\scriptscriptstyle\lor}\!,\rho(b)}^a{\widehat{\otimes}}_{{\mathbb{F}}(\kern-0.15em( \zeta )\kern-0.15em)}\breve E. \end{align*} $$
The intersections of the other components with
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^{wa}$
and
$\breve {\mathcal {H}}_{G,\hat {Z},b}^{wa}$
and
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^a$
are empty. Because every open subspace of the compact
$\breve {\mathcal {H}}_{G,\hat {Z},b}^a$
are empty. Because every open subspace of the compact
![]() $\breve E$
-analytic space
$\breve E$
-analytic space
![]() $\breve {\mathcal {H}}_{G,\hat {Z}}^{\textrm {an}}$
is paracompact by [Reference Hartl50, Lemma A.2.6], it suffices to show that
$\breve {\mathcal {H}}_{G,\hat {Z}}^{\textrm {an}}$
is paracompact by [Reference Hartl50, Lemma A.2.6], it suffices to show that
![]() $\breve {\mathcal {H}}_{\operatorname {\mathrm {GL}}_r,2n\rho ^{\scriptscriptstyle \lor }\!,\rho (b)}^{wa}$
and
$\breve {\mathcal {H}}_{\operatorname {\mathrm {GL}}_r,2n\rho ^{\scriptscriptstyle \lor }\!,\rho (b)}^{wa}$
and
![]() $\breve {\mathcal {H}}_{\operatorname {\mathrm {GL}}_r,2n\rho ^{\scriptscriptstyle \lor }\!,\rho (b)}^a$
are open in
$\breve {\mathcal {H}}_{\operatorname {\mathrm {GL}}_r,2n\rho ^{\scriptscriptstyle \lor }\!,\rho (b)}^a$
are open in
![]() $\breve {\mathcal {H}}_{\operatorname {\mathrm {GL}}_r,2n\rho ^{\scriptscriptstyle \lor }}^{\textrm {an}}{\widehat {\otimes }}_{{\mathbb {F}}(\kern-0.15em(\zeta )\kern-0.15em)}\breve E$
. An analogous statement was proved in [Reference Hartl50, Theorems 3.2.2 and 3.2.4] for the quasi-projective Schubert cell
$\breve {\mathcal {H}}_{\operatorname {\mathrm {GL}}_r,2n\rho ^{\scriptscriptstyle \lor }}^{\textrm {an}}{\widehat {\otimes }}_{{\mathbb {F}}(\kern-0.15em(\zeta )\kern-0.15em)}\breve E$
. An analogous statement was proved in [Reference Hartl50, Theorems 3.2.2 and 3.2.4] for the quasi-projective Schubert cell
from [Reference Hartl50, Definition 3.1.6], which is open and dense in the Schubert variety
![]() $\breve {\mathcal {H}}_{\operatorname {\mathrm {GL}}_r,2n\rho ^{\scriptscriptstyle \lor }}$
. Let us explain how to modify that proof to obtain a proof of the assertion above. The Schubert cell is a homogeneous space
$\breve {\mathcal {H}}_{\operatorname {\mathrm {GL}}_r,2n\rho ^{\scriptscriptstyle \lor }}$
. Let us explain how to modify that proof to obtain a proof of the assertion above. The Schubert cell is a homogeneous space
![]() $\breve {\mathcal {C}}={\widetilde {G}}/S$
; see [Reference Hartl50, p. 1318]. The properties that were needed in the proofs of [Reference Hartl50, Theorems 3.2.2 and 3.2.4] were the following two. The morphism
$\breve {\mathcal {C}}={\widetilde {G}}/S$
; see [Reference Hartl50, p. 1318]. The properties that were needed in the proofs of [Reference Hartl50, Theorems 3.2.2 and 3.2.4] were the following two. The morphism
![]() ${\widetilde {G}}^{\textrm {an}}\to \breve {\mathcal {C}}^{\textrm {an}}$
is smooth, and therefore
${\widetilde {G}}^{\textrm {an}}\to \breve {\mathcal {C}}^{\textrm {an}}$
is smooth, and therefore
![]() $\breve {\mathcal {C}}^{\textrm {an}}$
carries the quotient topology under the morphism
$\breve {\mathcal {C}}^{\textrm {an}}$
carries the quotient topology under the morphism
![]() ${\widetilde {G}}^{\textrm {an}}\to \breve {\mathcal {C}}^{\textrm {an}}$
. Secondly, the universal Hodge-Pink structure on
${\widetilde {G}}^{\textrm {an}}\to \breve {\mathcal {C}}^{\textrm {an}}$
. Secondly, the universal Hodge-Pink structure on
![]() $\breve {\mathcal {C}}$
is given on
$\breve {\mathcal {C}}$
is given on
![]() ${\widetilde {G}}$
by a universal matrix g in
${\widetilde {G}}$
by a universal matrix g in
![]() $\operatorname {\mathrm {GL}}_r\big ({\mathcal {O}}_{{\widetilde {G}}}\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}/(z-\zeta )^{2n(r-1)}\big )$
.
$\operatorname {\mathrm {GL}}_r\big ({\mathcal {O}}_{{\widetilde {G}}}\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}/(z-\zeta )^{2n(r-1)}\big )$
.
For our purpose here we modify this as follows. Because
![]() $LG\to {\mathcal {F}}\ell _G$
has local sections for the étale topology, there is an étale covering X of
$LG\to {\mathcal {F}}\ell _G$
has local sections for the étale topology, there is an étale covering X of
![]() $\breve {\mathcal {H}}_{\operatorname {\mathrm {GL}}_r,2n\rho ^{\scriptscriptstyle \lor }}^{\textrm {an}}$
on which the universal Hodge-Pink G-structure is given by a universal element h in
$\breve {\mathcal {H}}_{\operatorname {\mathrm {GL}}_r,2n\rho ^{\scriptscriptstyle \lor }}^{\textrm {an}}$
on which the universal Hodge-Pink G-structure is given by a universal element h in
![]() $G\big ({\mathcal {O}}_X(\kern-0.15em( z-\zeta )\kern-0.15em)\big )$
that satisfies
$G\big ({\mathcal {O}}_X(\kern-0.15em( z-\zeta )\kern-0.15em)\big )$
that satisfies
![]() $\rho (h)\in M_r\big ((z-\zeta )^{-n(r-1)}{\mathcal {O}}_X\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )$
. We replace g by
$\rho (h)\in M_r\big ((z-\zeta )^{-n(r-1)}{\mathcal {O}}_X\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )$
. We replace g by
![]() $(z-\zeta )^{n(r-1)}\rho (h)\;\textrm {mod}\; (z-\zeta )^{2n(r-1)}$
and use that
$(z-\zeta )^{n(r-1)}\rho (h)\;\textrm {mod}\; (z-\zeta )^{2n(r-1)}$
and use that
![]() $\breve {\mathcal {H}}_{\operatorname {\mathrm {GL}}_r,2n\rho ^{\scriptscriptstyle \lor }}^{\textrm {an}}$
carries the quotient topology under the morphism
$\breve {\mathcal {H}}_{\operatorname {\mathrm {GL}}_r,2n\rho ^{\scriptscriptstyle \lor }}^{\textrm {an}}$
carries the quotient topology under the morphism
![]() $X\to \breve {\mathcal {H}}_{\operatorname {\mathrm {GL}}_r,2n\rho ^{\scriptscriptstyle \lor }}^{\textrm {an}}$
by [Reference Berkovich8, Corollary 3.7.4]. With these modifications the proofs of [Reference Hartl50, Theorems 3.2.2 and 3.2.4] carry over to our situation.
$X\to \breve {\mathcal {H}}_{\operatorname {\mathrm {GL}}_r,2n\rho ^{\scriptscriptstyle \lor }}^{\textrm {an}}$
by [Reference Berkovich8, Corollary 3.7.4]. With these modifications the proofs of [Reference Hartl50, Theorems 3.2.2 and 3.2.4] carry over to our situation.
The connectedness of
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^{wa}$
and
$\breve {\mathcal {H}}_{G,\hat {Z},b}^{wa}$
and
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^a$
can be proved by the same arguments as in [Reference Hartl50, Theorem 3.2.5].
$\breve {\mathcal {H}}_{G,\hat {Z},b}^a$
can be proved by the same arguments as in [Reference Hartl50, Theorem 3.2.5].
It remains to compute which connected components of
![]() $\operatorname {\mathrm {Gr}}_{G,\breve L_0}^{{\mathbf {B}}_{\textrm {dR}}}$
meet
$\operatorname {\mathrm {Gr}}_{G,\breve L_0}^{{\mathbf {B}}_{\textrm {dR}}}$
meet
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^a$
and
$\breve {\mathcal {H}}_{G,\hat {Z},b}^a$
and
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^{wa}$
. By Remark 4.15, for every point
$\breve {\mathcal {H}}_{G,\hat {Z},b}^{wa}$
. By Remark 4.15, for every point
![]() $\gamma \in \breve {\mathcal {H}}_{G,\hat {Z},b}^{wa}{\widehat {\otimes }}_{\breve E}\breve L_0$
the Hodge point
$\gamma \in \breve {\mathcal {H}}_{G,\hat {Z},b}^{wa}{\widehat {\otimes }}_{\breve E}\breve L_0$
the Hodge point
![]() $\mu _\gamma \in X_*(T)$
lies in
$\mu _\gamma \in X_*(T)$
lies in
![]() $N_{\textrm {an}}$
and
$N_{\textrm {an}}$
and
![]() $\nu _b\preceq \mu _\gamma $
. In particular,
$\nu _b\preceq \mu _\gamma $
. In particular,
![]() $\gamma $
lies in the component with image
$\gamma $
lies in the component with image
![]() $\mu _\gamma ^\#\in \pi _1(G)$
. Conversely, let
$\mu _\gamma ^\#\in \pi _1(G)$
. Conversely, let
![]() $\mu \in N_{\textrm {an}}$
with
$\mu \in N_{\textrm {an}}$
with
![]() $\nu _b\preceq \mu $
. Then Remark 4.15 implies that there is a point
$\nu _b\preceq \mu $
. Then Remark 4.15 implies that there is a point
![]() $\gamma \in \operatorname {\mathrm {Gr}}_{G,\breve L_0}^{{\mathbf {B}}_{\textrm {dR}}}$
with Hodge point
$\gamma \in \operatorname {\mathrm {Gr}}_{G,\breve L_0}^{{\mathbf {B}}_{\textrm {dR}}}$
with Hodge point
![]() $\mu $
such that
$\mu $
such that
![]() $(b,\gamma )$
is weakly admissible. By Remark 2.11(b), the point
$(b,\gamma )$
is weakly admissible. By Remark 2.11(b), the point
![]() $\gamma $
lies in
$\gamma $
lies in
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^a$
and
$\breve {\mathcal {H}}_{G,\hat {Z},b}^a$
and
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^{wa}$
and, moreover, it lies in the connected component of
$\breve {\mathcal {H}}_{G,\hat {Z},b}^{wa}$
and, moreover, it lies in the connected component of
![]() $\operatorname {\mathrm {Gr}}_{G,\breve L_0}^{{\mathbf {B}}_{\textrm {dR}}}$
with image
$\operatorname {\mathrm {Gr}}_{G,\breve L_0}^{{\mathbf {B}}_{\textrm {dR}}}$
with image
![]() $\mu ^\#$
in
$\mu ^\#$
in
![]() $\pi _0(\operatorname {\mathrm {Gr}}_{G,\breve L_0}^{{\mathbf {B}}_{\textrm {dR}}})=\pi _1(G)$
.
$\pi _0(\operatorname {\mathrm {Gr}}_{G,\breve L_0}^{{\mathbf {B}}_{\textrm {dR}}})=\pi _1(G)$
.
Remark 4.21. We keep the notation of Remark 3.7. The morphism
![]() $\varepsilon \colon G\to G^{\prime }$
of parahoric group schemes over
$\varepsilon \colon G\to G^{\prime }$
of parahoric group schemes over
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
induces a morphism
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
induces a morphism
![]() $\varepsilon \colon \operatorname {\mathrm {Gr}}_{G}^{{\mathbf {B}}_{\textrm {dR}}}\to \operatorname {\mathrm {Gr}}_{G^{\prime }}^{{\mathbf {B}}_{\textrm {dR}}}$
of the affine Grassmannians from (1.2). It maps Hodge-Pink G-structures
$\varepsilon \colon \operatorname {\mathrm {Gr}}_{G}^{{\mathbf {B}}_{\textrm {dR}}}\to \operatorname {\mathrm {Gr}}_{G^{\prime }}^{{\mathbf {B}}_{\textrm {dR}}}$
of the affine Grassmannians from (1.2). It maps Hodge-Pink G-structures
![]() $\gamma \in \operatorname {\mathrm {Gr}}_{G}^{{\mathbf {B}}_{\textrm {dR}}}$
to Hodge-Pink
$\gamma \in \operatorname {\mathrm {Gr}}_{G}^{{\mathbf {B}}_{\textrm {dR}}}$
to Hodge-Pink
![]() $G^{\prime }$
-structures
$G^{\prime }$
-structures
![]() $\gamma ^{\prime }:=\varepsilon (\gamma )\in \operatorname {\mathrm {Gr}}_{G^{\prime }}^{{\mathbf {B}}_{\textrm {dR}}}$
and the corresponding element
$\gamma ^{\prime }:=\varepsilon (\gamma )\in \operatorname {\mathrm {Gr}}_{G^{\prime }}^{{\mathbf {B}}_{\textrm {dR}}}$
and the corresponding element
![]() $\gamma ^\#\in \pi _1(G)_\Gamma $
to
$\gamma ^\#\in \pi _1(G)_\Gamma $
to
![]() $(\gamma ^{\prime })^\#=\varepsilon (\gamma ^\#)\in \pi _1(G^{\prime })_\Gamma $
.
$(\gamma ^{\prime })^\#=\varepsilon (\gamma ^\#)\in \pi _1(G^{\prime })_\Gamma $
.
The morphism
![]() $\varepsilon $
also induces a tensor functor
$\varepsilon $
also induces a tensor functor
![]() $\varepsilon ^*\colon \operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G^{\prime }\to \operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G$
, given by
$\varepsilon ^*\colon \operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G^{\prime }\to \operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G$
, given by
![]() $(V^{\prime }\!,\rho ^{\prime })\mapsto \varepsilon ^*(V^{\prime }\!,\rho ^{\prime }):=(V^{\prime }\!,\rho ^{\prime }\circ \varepsilon )$
. It satisfies
$(V^{\prime }\!,\rho ^{\prime })\mapsto \varepsilon ^*(V^{\prime }\!,\rho ^{\prime }):=(V^{\prime }\!,\rho ^{\prime }\circ \varepsilon )$
. It satisfies
![]() ${\underline {D\!}\,}_{b,\gamma }(\varepsilon ^*(V^{\prime }\!,\rho ^{\prime }))={\underline {D\!}\,}_{b^{\prime }\!,\gamma ^{\prime }}(V^{\prime }\!,\rho ^{\prime })$
for
${\underline {D\!}\,}_{b,\gamma }(\varepsilon ^*(V^{\prime }\!,\rho ^{\prime }))={\underline {D\!}\,}_{b^{\prime }\!,\gamma ^{\prime }}(V^{\prime }\!,\rho ^{\prime })$
for
![]() $b^{\prime }=\varepsilon (b)$
. Therefore,
$b^{\prime }=\varepsilon (b)$
. Therefore,
![]() ${\underline {{\mathcal {E}}\!}\,}_{b,\gamma }(\varepsilon ^*(V^{\prime }\!,\rho ^{\prime }))={\underline {{\mathcal {E}}\!}\,}_{b^{\prime }\!,\gamma ^{\prime }}(V^{\prime }\!,\rho ^{\prime })$
and
${\underline {{\mathcal {E}}\!}\,}_{b,\gamma }(\varepsilon ^*(V^{\prime }\!,\rho ^{\prime }))={\underline {{\mathcal {E}}\!}\,}_{b^{\prime }\!,\gamma ^{\prime }}(V^{\prime }\!,\rho ^{\prime })$
and
![]() ${\underline {{\mathcal {F}}\!}\,}_{b,\gamma }(\varepsilon ^*(V^{\prime }\!,\rho ^{\prime }))={\underline {{\mathcal {F}}\!}\,}_{b^{\prime }\!,\gamma ^{\prime }}(V^{\prime }\!,\rho ^{\prime })$
. It follows that
${\underline {{\mathcal {F}}\!}\,}_{b,\gamma }(\varepsilon ^*(V^{\prime }\!,\rho ^{\prime }))={\underline {{\mathcal {F}}\!}\,}_{b^{\prime }\!,\gamma ^{\prime }}(V^{\prime }\!,\rho ^{\prime })$
. It follows that
![]() $(b,\gamma )$
is (weakly) admissible for G if and only if
$(b,\gamma )$
is (weakly) admissible for G if and only if
![]() $(b^{\prime }\!,\gamma ^{\prime })$
is for
$(b^{\prime }\!,\gamma ^{\prime })$
is for
![]() $G^{\prime }$
. Moreover, if
$G^{\prime }$
. Moreover, if
![]() $(b,\gamma )$
is neutral, then
$(b,\gamma )$
is neutral, then
![]() $(b^{\prime }\!,\gamma ^{\prime })$
is also neutral. In other words, if
$(b^{\prime }\!,\gamma ^{\prime })$
is also neutral. In other words, if
![]() $\varepsilon (\hat {Z})\subset \hat {Z}^{\prime }$
, then
$\varepsilon (\hat {Z})\subset \hat {Z}^{\prime }$
, then
![]() $\varepsilon $
induces morphisms
$\varepsilon $
induces morphisms
for
![]() $\bullet \in \{wa, a, na\}$
.
$\bullet \in \{wa, a, na\}$
.
5 Local systems of
 ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-vector spaces
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-vector spaces
Definition 5.1. For a ring A we let
![]() $\textrm {FMod}_A$
denote the category of finite locally free A-modules. If the ring A is either
$\textrm {FMod}_A$
denote the category of finite locally free A-modules. If the ring A is either
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
or
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
or
![]() ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
and
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
and
![]() $\Pi $
is a topological group, we denote by
$\Pi $
is a topological group, we denote by
![]() $\operatorname {\mathrm {Rep}}^{\textrm {cont}}_A(\Pi )$
the category of continuous representations in finite free A-modules and by
$\operatorname {\mathrm {Rep}}^{\textrm {cont}}_A(\Pi )$
the category of continuous representations in finite free A-modules and by
the forgetful fibre functor. Moreover, we let
be the forgetful fibre functor. We also write
![]() $\omega ^\circ :=\omega ^\circ _{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}$
. Then
$\omega ^\circ :=\omega ^\circ _{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}$
. Then
![]() $\operatorname {\mathrm {Aut}}^\otimes (\omega ^\circ )=G_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}$
by [Reference Deligne and Milne33, Theorem 2.11] and
$\operatorname {\mathrm {Aut}}^\otimes (\omega ^\circ )=G_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}$
by [Reference Deligne and Milne33, Theorem 2.11] and
![]() $\operatorname {\mathrm {Aut}}^\otimes (\omega ^\circ _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}})=G$
by [Reference Wedhorn96, Corollary 5.20].
$\operatorname {\mathrm {Aut}}^\otimes (\omega ^\circ _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}})=G$
by [Reference Wedhorn96, Corollary 5.20].
Let X be a strictly L-analytic space, where L is a field extensions of
![]() ${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
that is complete with respect to an absolute value
${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
that is complete with respect to an absolute value
![]() $|\,.\,|\colon L\to {\mathbb {R}}_{\ge 0}$
extending the
$|\,.\,|\colon L\to {\mathbb {R}}_{\ge 0}$
extending the
![]() $\zeta $
-adic absolute value on
$\zeta $
-adic absolute value on
![]() ${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
. For any group or ring A we denote by
${\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
. For any group or ring A we denote by
![]() ${\underline {A}}$
the locally constant sheaf on the étale site
${\underline {A}}$
the locally constant sheaf on the étale site
![]() $X_{\mathrm {\acute {e}t}}$
of X.
$X_{\mathrm {\acute {e}t}}$
of X.
We recall de Jong’s [Reference de Jong31, § 2] definition of the étale fundamental group of X. De Jong calls a morphism
![]() $f\colon Y\to X$
of L-analytic spaces an étale covering space of X if for every analytic point x of X there exists an open neighbourhood
$f\colon Y\to X$
of L-analytic spaces an étale covering space of X if for every analytic point x of X there exists an open neighbourhood
![]() $U\subset X$
such that
$U\subset X$
such that
![]() $Y\times _XU$
is a disjoint union of L-analytic spaces
$Y\times _XU$
is a disjoint union of L-analytic spaces
![]() $V_i$
each mapping finite étale to U. The étale covering spaces of X form a category
$V_i$
each mapping finite étale to U. The étale covering spaces of X form a category
![]() ${\underline {\operatorname {\mathrm {Cov}}}}_X^{\mathrm {\acute {e}t}}$
. It contains the full subcategory
${\underline {\operatorname {\mathrm {Cov}}}}_X^{\mathrm {\acute {e}t}}$
. It contains the full subcategory
![]() ${\underline {\operatorname {\mathrm {Cov}}}}_X^{\textrm {alg}}$
of finite étale covering spaces.
${\underline {\operatorname {\mathrm {Cov}}}}_X^{\textrm {alg}}$
of finite étale covering spaces.
A geometric base point
![]() $\bar x$
of X is a morphism
$\bar x$
of X is a morphism
![]() $\bar x\colon {\mathtt {BSpec}}({\overline {L}})\to X$
where we denote by
$\bar x\colon {\mathtt {BSpec}}({\overline {L}})\to X$
where we denote by
![]() ${\mathtt {BSpec}}({\overline {L}})$
the Berkovich spectrum of an algebraically closed complete extension
${\mathtt {BSpec}}({\overline {L}})$
the Berkovich spectrum of an algebraically closed complete extension
![]() ${\overline {L}}$
of L. For a geometric base point
${\overline {L}}$
of L. For a geometric base point
![]() $\bar x$
of X, define the fibre functors at
$\bar x$
of X, define the fibre functors at
![]() $\bar x$
$\bar x$
 $$ \begin{align} F_{\bar x}^{\mathrm{\acute{e}t}} := &\; F_{X,\bar x}^{\mathrm{\acute{e}t}}\colon \!{\underline{\operatorname{\mathrm{Cov}}}}_X^{\mathrm{\acute{e}t}} \;\longrightarrow \;{\underline{\textrm{Sets}}}\;,\quad F_{\bar x}^{\mathrm{\acute{e}t}}\big(f\colon Y\to X\big) \;:=\;\{\,\bar{y}\colon{\mathtt{BSpec}}({\overline{L}})\to Y \;\text{with} \; f\circ\bar{y} = \bar{x}\,\} \nonumber\\[2mm]F_{\bar x}^{\textrm{alg}} := &\; F_{X,\bar x}^{\textrm{alg}}\colon \!{\underline{\operatorname{\mathrm{Cov}}}}_X^{\textrm{alg}} \;\longrightarrow \;{\underline{\textrm{Sets}}}\;,\quad F_{\bar x}^{\textrm{alg}}:=F_{\bar x}^{\mathrm{\acute{e}t}}|_{{\underline{\operatorname{\mathrm{Cov}}}}_X^{\textrm{alg}}}\;. \end{align} $$
$$ \begin{align} F_{\bar x}^{\mathrm{\acute{e}t}} := &\; F_{X,\bar x}^{\mathrm{\acute{e}t}}\colon \!{\underline{\operatorname{\mathrm{Cov}}}}_X^{\mathrm{\acute{e}t}} \;\longrightarrow \;{\underline{\textrm{Sets}}}\;,\quad F_{\bar x}^{\mathrm{\acute{e}t}}\big(f\colon Y\to X\big) \;:=\;\{\,\bar{y}\colon{\mathtt{BSpec}}({\overline{L}})\to Y \;\text{with} \; f\circ\bar{y} = \bar{x}\,\} \nonumber\\[2mm]F_{\bar x}^{\textrm{alg}} := &\; F_{X,\bar x}^{\textrm{alg}}\colon \!{\underline{\operatorname{\mathrm{Cov}}}}_X^{\textrm{alg}} \;\longrightarrow \;{\underline{\textrm{Sets}}}\;,\quad F_{\bar x}^{\textrm{alg}}:=F_{\bar x}^{\mathrm{\acute{e}t}}|_{{\underline{\operatorname{\mathrm{Cov}}}}_X^{\textrm{alg}}}\;. \end{align} $$
The étale fundamental group
![]() $\pi _1^{\mathrm {\acute {e}t}}(X,\bar {x})$
and the algebraic fundamental group
$\pi _1^{\mathrm {\acute {e}t}}(X,\bar {x})$
and the algebraic fundamental group
![]() $\pi _1^{\textrm {alg}}(X,\bar {x})$
of X are the automorphism groups
$\pi _1^{\textrm {alg}}(X,\bar {x})$
of X are the automorphism groups
These fundamental groups classify (finite) étale covering spaces in the sense that
![]() $F_{\bar x}^{\mathrm {\acute {e}t}}$
induces an equivalence
$F_{\bar x}^{\mathrm {\acute {e}t}}$
induces an equivalence
Connected coverings correspond to
![]() $\pi _1^{\mathrm {\acute {e}t}}(X,\bar {x})$
-orbits and similarly for
$\pi _1^{\mathrm {\acute {e}t}}(X,\bar {x})$
-orbits and similarly for
![]() $F_{\bar x}^{\textrm {alg}}$
; see [Reference de Jong31, Theorem 2.10]. Here
$F_{\bar x}^{\textrm {alg}}$
; see [Reference de Jong31, Theorem 2.10]. Here
![]() $\pi _1^{\mathrm {\acute {e}t}}(X,\bar {x})\text{-}\underline{\text{Sets}}$
(respectively
$\pi _1^{\mathrm {\acute {e}t}}(X,\bar {x})\text{-}\underline{\text{Sets}}$
(respectively
![]() $\pi _1^{\textrm {alg}}(X,\bar {x})\text{-}\underline{\text{Sets}}$
is the category of discrete (respectively finite) sets endowed with a continuous left action of
$\pi _1^{\textrm {alg}}(X,\bar {x})\text{-}\underline{\text{Sets}}$
is the category of discrete (respectively finite) sets endowed with a continuous left action of
![]() $\pi _1^{\mathrm {\acute {e}t}}(X,\bar {x})$
(respectively
$\pi _1^{\mathrm {\acute {e}t}}(X,\bar {x})$
(respectively
![]() $\pi _1^{\textrm {alg}}(X,\bar {x})$
).
$\pi _1^{\textrm {alg}}(X,\bar {x})$
).
The natural continuous group homomorphism
![]() $\pi _1^{\mathrm {\acute {e}t}}(X,\bar {x}) \to \pi _1^{\textrm {alg}}(X,\bar {x})$
has dense image. The étale fundamental group
$\pi _1^{\mathrm {\acute {e}t}}(X,\bar {x}) \to \pi _1^{\textrm {alg}}(X,\bar {x})$
has dense image. The étale fundamental group
![]() $\pi _1^{\mathrm {\acute {e}t}}(X,\bar {x})$
is Hausdorff and pro-discrete,
$\pi _1^{\mathrm {\acute {e}t}}(X,\bar {x})$
is Hausdorff and pro-discrete,
![]() $\pi _1^{\textrm {alg}}(X,\bar {x})$
is pro-finite and every continuous homomorphism from
$\pi _1^{\textrm {alg}}(X,\bar {x})$
is pro-finite and every continuous homomorphism from
![]() $\pi _1^{\mathrm {\acute {e}t}}(X,\bar {x})$
to a pro-finite group factors through
$\pi _1^{\mathrm {\acute {e}t}}(X,\bar {x})$
to a pro-finite group factors through
![]() $\pi _1^{\textrm {alg}}(X,\bar {x})$
; see [Reference de Jong31, Lemma 2.7 and Theorem 2.10]. In particular,
$\pi _1^{\textrm {alg}}(X,\bar {x})$
; see [Reference de Jong31, Lemma 2.7 and Theorem 2.10]. In particular,
![]() $\operatorname {\mathrm {Rep}}^{\textrm {cont}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}\big (\pi _1^{\mathrm {\acute {e}t}}(X,\bar x)\big )=\operatorname {\mathrm {Rep}}^{\textrm {cont}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}\big (\pi _1^{\textrm {alg}}(X,\bar x)\big )$
, but this is not true for representations on
$\operatorname {\mathrm {Rep}}^{\textrm {cont}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}\big (\pi _1^{\mathrm {\acute {e}t}}(X,\bar x)\big )=\operatorname {\mathrm {Rep}}^{\textrm {cont}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}\big (\pi _1^{\textrm {alg}}(X,\bar x)\big )$
, but this is not true for representations on
![]() ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-vector spaces.
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-vector spaces.
For the following overview we follow [Reference Hartl50, Definition A4.4].
Definition 5.2. A local system of
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-lattices on X is a projective system
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-lattices on X is a projective system
![]() ${\mathcal {F}}=({\mathcal {F}}_n,i_n)$
of sheaves
${\mathcal {F}}=({\mathcal {F}}_n,i_n)$
of sheaves
![]() ${\mathcal {F}}_n$
of
${\mathcal {F}}_n$
of
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}/(z^n)$
-modules on
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}/(z^n)$
-modules on
![]() $X_{\mathrm {\acute {e}t}}$
, such that
$X_{\mathrm {\acute {e}t}}$
, such that
-
(a)
 ${\mathcal {F}}_n$
is étale locally a constant free
${\mathcal {F}}_n$
is étale locally a constant free
 ${\underline {{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z \mathrm {]}\kern-0.15em\mathrm {]}/(z^n)}}$
-module of finite rank,
${\underline {{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z \mathrm {]}\kern-0.15em\mathrm {]}/(z^n)}}$
-module of finite rank, -
(b)
 is an isomorphism of sheaves of
is an isomorphism of sheaves of
 ${\underline {{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z \mathrm {]}\kern-0.15em\mathrm {]}/(z^{n-1})}}$
-modules.
${\underline {{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z \mathrm {]}\kern-0.15em\mathrm {]}/(z^{n-1})}}$
-modules.
The category
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\mbox {-}{\underline {\mathrm {Loc}}}_X$
of local systems of
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\mbox {-}{\underline {\mathrm {Loc}}}_X$
of local systems of
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-lattices with the obvious morphisms is an additive
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-lattices with the obvious morphisms is an additive
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-linear rigid tensor category. If
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-linear rigid tensor category. If
![]() $\bar x$
is a geometric point of X,
$\bar x$
is a geometric point of X,
is the stalk
![]() ${\mathcal {F}}_{\bar x}$
of
${\mathcal {F}}_{\bar x}$
of
![]() ${\mathcal {F}}$
at
${\mathcal {F}}$
at
![]() $\bar x$
. It is a finite free
$\bar x$
. It is a finite free
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-module. Starting from
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-module. Starting from
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-lattices one defines local systems of
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-lattices one defines local systems of
![]() ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-vector spaces and their stalks as in [Reference de Jong31, § 4] or [Reference Hartl50, Definition A4.4].
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-vector spaces and their stalks as in [Reference de Jong31, § 4] or [Reference Hartl50, Definition A4.4].
Local systems of
![]() ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-vector spaces form a category
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-vector spaces form a category
![]() ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\mbox {-}{\underline {\mathrm {Loc}}}_X$
. It is an abelian
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\mbox {-}{\underline {\mathrm {Loc}}}_X$
. It is an abelian
![]() ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-linear rigid tensor category. The theory of these local systems parallels the theory of local systems of
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-linear rigid tensor category. The theory of these local systems parallels the theory of local systems of
![]() ${\mathbb {Q}}_\ell $
-vector spaces developed in [Reference de Jong31]. In particular, there is the following description.
${\mathbb {Q}}_\ell $
-vector spaces developed in [Reference de Jong31]. In particular, there is the following description.
Proposition 5.3 Compare [Reference de Jong31, Corollary 4.2]
For any geometric point
![]() $\bar x$
of X there is a natural
$\bar x$
of X there is a natural
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-linear tensor functor
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-linear tensor functor
and a natural
![]() ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-linear tensor functor
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-linear tensor functor
that assigns to a local system
![]() ${\mathcal {F}}\in {\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\mbox {-}{\underline {\mathrm {Loc}}}_X$
, respectively
${\mathcal {F}}\in {\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\mbox {-}{\underline {\mathrm {Loc}}}_X$
, respectively
![]() ${\mathcal {V}}\in {\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\mbox {-}{\underline {\mathrm {Loc}}}_X$
, the representation of
${\mathcal {V}}\in {\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\mbox {-}{\underline {\mathrm {Loc}}}_X$
, the representation of
![]() $\pi _1^{\mathrm {alg}}(X,\bar x)$
on
$\pi _1^{\mathrm {alg}}(X,\bar x)$
on
![]() ${\mathcal {F}}_{\bar x}$
, respectively of
${\mathcal {F}}_{\bar x}$
, respectively of
![]() $\pi _1^{\mathrm {\acute {e}t}}(X,\bar x)$
on
$\pi _1^{\mathrm {\acute {e}t}}(X,\bar x)$
on
![]() ${\mathcal {V}}_{\bar x}$
. These tensor functors are equivalences if X is connected.
${\mathcal {V}}_{\bar x}$
. These tensor functors are equivalences if X is connected.
Proof. De Jong [Reference de Jong31, Corollary 4.2] proved this for
![]() ${\mathbb {Q}}_\ell $
and the statement for
${\mathbb {Q}}_\ell $
and the statement for
![]() ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
is proved verbatim. We indicate the (easier) argument for
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
is proved verbatim. We indicate the (easier) argument for
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
. Let
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
. Let
![]() ${\mathcal {F}}=({\mathcal {F}}_n,i_n)\in {\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\mbox {-}{\underline {\mathrm {Loc}}}_X$
. Then the
${\mathcal {F}}=({\mathcal {F}}_n,i_n)\in {\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\mbox {-}{\underline {\mathrm {Loc}}}_X$
. Then the
![]() ${\mathcal {F}}_n$
are represented by finite étale covering spaces
${\mathcal {F}}_n$
are represented by finite étale covering spaces
![]() $Y_n$
of X. This yields an action of
$Y_n$
of X. This yields an action of
![]() $\pi _1^{\textrm {alg}}(X,\bar x)$
on
$\pi _1^{\textrm {alg}}(X,\bar x)$
on
![]() $F^{\textrm {alg}}_{\bar x}(Y_n)={\mathcal {F}}_{n,\bar x}$
and on
$F^{\textrm {alg}}_{\bar x}(Y_n)={\mathcal {F}}_{n,\bar x}$
and on
![]() ${\mathcal {F}}_{\bar x}:={\displaystyle \lim _{\longleftarrow }}({\mathcal {F}}_{n,\bar x},\,i_n)$
.
${\mathcal {F}}_{\bar x}:={\displaystyle \lim _{\longleftarrow }}({\mathcal {F}}_{n,\bar x},\,i_n)$
.
Let
![]() $A={\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
or
$A={\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
or
![]() $A={\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
and recall the forgetful fibre functor
$A={\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
and recall the forgetful fibre functor
![]() $\omega ^\circ _A\colon \operatorname {\mathrm {Rep}}_{A}G\to \textrm {FMod}_A$
from Definition 5.1. If
$\omega ^\circ _A\colon \operatorname {\mathrm {Rep}}_{A}G\to \textrm {FMod}_A$
from Definition 5.1. If
![]() $A={\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
, we let in addition
$A={\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
, we let in addition
![]() ${\widetilde {\omega }}\colon \operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G\to \textrm {FMod}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}$
be another fibre functor, and we let
${\widetilde {\omega }}\colon \operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G\to \textrm {FMod}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}$
be another fibre functor, and we let
![]() ${\widetilde {G}}:=\operatorname {\mathrm {Aut}}^\otimes ({\widetilde {\omega }})$
be the group scheme over
${\widetilde {G}}:=\operatorname {\mathrm {Aut}}^\otimes ({\widetilde {\omega }})$
be the group scheme over
![]() ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
of tensor automorphisms of
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
of tensor automorphisms of
![]() ${\widetilde {\omega }}$
; see [Reference Deligne and Milne33, Theorem 2.11]. Then
${\widetilde {\omega }}$
; see [Reference Deligne and Milne33, Theorem 2.11]. Then
![]() $\operatorname {\mathrm {Isom}}^\otimes (\omega ^\circ ,{\widetilde {\omega }})$
is a left G-torsor and a right
$\operatorname {\mathrm {Isom}}^\otimes (\omega ^\circ ,{\widetilde {\omega }})$
is a left G-torsor and a right
![]() ${\widetilde {G}}$
-torsor over
${\widetilde {G}}$
-torsor over
![]() ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
and corresponds to a cohomology class
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
and corresponds to a cohomology class
![]() $cl(\omega ^\circ ,{\widetilde {\omega }})\in \operatorname {\mathrm {H}}^1({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em),G)$
by [Reference Deligne and Milne33, Theorem 3.2]. The group
$cl(\omega ^\circ ,{\widetilde {\omega }})\in \operatorname {\mathrm {H}}^1({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em),G)$
by [Reference Deligne and Milne33, Theorem 3.2]. The group
![]() ${\widetilde {G}}$
is isomorphic to the inner form of G defined by the image of
${\widetilde {G}}$
is isomorphic to the inner form of G defined by the image of
![]() $cl(\omega ^\circ ,{\widetilde {\omega }})$
in
$cl(\omega ^\circ ,{\widetilde {\omega }})$
in
![]() $\operatorname {\mathrm {H}}^1({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em),G^{\textrm {ad}})$
, where
$\operatorname {\mathrm {H}}^1({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em),G^{\textrm {ad}})$
, where
![]() $G\twoheadrightarrow G^{\textrm {ad}}$
is the adjoint quotient. If
$G\twoheadrightarrow G^{\textrm {ad}}$
is the adjoint quotient. If
![]() $A={\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
, we set
$A={\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
, we set
![]() ${\widetilde {\omega }}:=\omega ^\circ _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}$
and
${\widetilde {\omega }}:=\omega ^\circ _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}$
and
![]() ${\widetilde {G}}:=G$
. This is no restriction because Lang’s theorem [Reference Lang72, Theorem 2], stating
${\widetilde {G}}:=G$
. This is no restriction because Lang’s theorem [Reference Lang72, Theorem 2], stating
![]() $\operatorname {\mathrm {H}}^1({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]},G)=\operatorname {\mathrm {H}}^1({\mathbb {F}}_q,G)=(1)$
, implies that all fibre functors
$\operatorname {\mathrm {H}}^1({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]},G)=\operatorname {\mathrm {H}}^1({\mathbb {F}}_q,G)=(1)$
, implies that all fibre functors
![]() $\operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}G\to \textrm {FMod}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}$
are isomorphic to
$\operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}G\to \textrm {FMod}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}$
are isomorphic to
![]() $\omega ^\circ _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}$
.
$\omega ^\circ _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}$
.
Let X be connected, let
![]() $\bar x$
be a geometric base point of X and recall the forgetful fibre functor
$\bar x$
be a geometric base point of X and recall the forgetful fibre functor
![]() $\mathit {forget}\colon \operatorname {\mathrm {Rep}}^{\textrm {cont}}_{A}\big (\pi _1^{\mathrm {\acute {e}t}}(X,\bar x)\big )\to \textrm {FMod}_A$
from (5.1).
$\mathit {forget}\colon \operatorname {\mathrm {Rep}}^{\textrm {cont}}_{A}\big (\pi _1^{\mathrm {\acute {e}t}}(X,\bar x)\big )\to \textrm {FMod}_A$
from (5.1).
Corollary 5.4. In the situation above, consider the set
![]() ${\mathcal {T}}_A$
of isomorphism classes of pairs
${\mathcal {T}}_A$
of isomorphism classes of pairs
![]() $({\underline {{\mathcal {V}}\!}\,},\beta )$
where
$({\underline {{\mathcal {V}}\!}\,},\beta )$
where
![]() ${\underline {{\mathcal {V}}\!}\,}\colon \operatorname {\mathrm {Rep}}_{A}G\to A\mbox {-}{\underline {\mathrm {Loc}}}_X$
is a tensor functor and
${\underline {{\mathcal {V}}\!}\,}\colon \operatorname {\mathrm {Rep}}_{A}G\to A\mbox {-}{\underline {\mathrm {Loc}}}_X$
is a tensor functor and
![]() $\beta \in \operatorname {\mathrm {Isom}}^\otimes ({\widetilde {\omega }},\,\mathit {forget}\circ \omega _{\bar x}\circ {\underline {{\mathcal {V}}\!}\,})(A)$
is an isomorphism of tensor functors. There is a canonical bijection between
$\beta \in \operatorname {\mathrm {Isom}}^\otimes ({\widetilde {\omega }},\,\mathit {forget}\circ \omega _{\bar x}\circ {\underline {{\mathcal {V}}\!}\,})(A)$
is an isomorphism of tensor functors. There is a canonical bijection between
![]() ${\mathcal {T}}_A$
and the set of continuous group homomorphisms
${\mathcal {T}}_A$
and the set of continuous group homomorphisms
Proof. Let
![]() $({\underline {{\mathcal {V}}\!}\,},\beta )\in {\mathcal {T}}_A$
. By Proposition 5.3, any element of
$({\underline {{\mathcal {V}}\!}\,},\beta )\in {\mathcal {T}}_A$
. By Proposition 5.3, any element of
![]() $\pi _1^{\mathrm {\acute {e}t}}(X,\bar x)$
yields a tensor automorphism of the fibre functor
$\pi _1^{\mathrm {\acute {e}t}}(X,\bar x)$
yields a tensor automorphism of the fibre functor
![]() $\mathit {forget}\circ \omega _{\bar x}\circ {\underline {{\mathcal {V}}\!}\,}$
. By
$\mathit {forget}\circ \omega _{\bar x}\circ {\underline {{\mathcal {V}}\!}\,}$
. By
![]() $\beta $
it is transported to a tensor automorphism of
$\beta $
it is transported to a tensor automorphism of
![]() ${\widetilde {\omega }}$
; that is, an element of
${\widetilde {\omega }}$
; that is, an element of
![]() ${\widetilde {G}}(A)$
. This defines a group homomorphism
${\widetilde {G}}(A)$
. This defines a group homomorphism
![]() $f:=f_{({\underline {{\mathcal {V}}\!}\,},\beta )}\colon \pi _1^{\mathrm {\acute {e}t}}(X,\bar x)\to {\widetilde {G}}(A)$
. Because for all
$f:=f_{({\underline {{\mathcal {V}}\!}\,},\beta )}\colon \pi _1^{\mathrm {\acute {e}t}}(X,\bar x)\to {\widetilde {G}}(A)$
. Because for all
![]() $V\in \operatorname {\mathrm {Rep}}_{A}G$
the induced homomorphism
$V\in \operatorname {\mathrm {Rep}}_{A}G$
the induced homomorphism
![]() $\pi _1^{\mathrm {\acute {e}t}}(X,\bar x)\to {\widetilde {G}}(A)\to \operatorname {\mathrm {GL}}\big ({\widetilde {\omega }}(V)\big )(A)$
is continuous, f is also continuous.
$\pi _1^{\mathrm {\acute {e}t}}(X,\bar x)\to {\widetilde {G}}(A)\to \operatorname {\mathrm {GL}}\big ({\widetilde {\omega }}(V)\big )(A)$
is continuous, f is also continuous.
Conversely, let
![]() $f\colon \pi _1^{\mathrm {\acute {e}t}}(X,\bar x)\to {\widetilde {G}}(A)$
be a continuous group homomorphism. Then we define a tensor functor
$f\colon \pi _1^{\mathrm {\acute {e}t}}(X,\bar x)\to {\widetilde {G}}(A)$
be a continuous group homomorphism. Then we define a tensor functor
![]() $\operatorname {\mathrm {Rep}}_{A}G \to \operatorname {\mathrm {Rep}}^{\textrm {cont}}_{A}\big (\pi _1^{\mathrm {\acute {e}t}}(X,\bar x)\big )$
by sending a representation V in
$\operatorname {\mathrm {Rep}}_{A}G \to \operatorname {\mathrm {Rep}}^{\textrm {cont}}_{A}\big (\pi _1^{\mathrm {\acute {e}t}}(X,\bar x)\big )$
by sending a representation V in
![]() $\operatorname {\mathrm {Rep}}_{A}G$
to the representation
$\operatorname {\mathrm {Rep}}_{A}G$
to the representation
![]() $\big ({\widetilde {\omega }}(V),\rho ^{\prime }_V\big )$
given by
$\big ({\widetilde {\omega }}(V),\rho ^{\prime }_V\big )$
given by
Here
![]() ${\widetilde {\omega }}(V)(f(g))$
is the automorphism by which
${\widetilde {\omega }}(V)(f(g))$
is the automorphism by which
![]() $f(g)\in {\widetilde {G}}(A)=\operatorname {\mathrm {Aut}}^\otimes ({\widetilde {\omega }})(A)$
acts on the A-module
$f(g)\in {\widetilde {G}}(A)=\operatorname {\mathrm {Aut}}^\otimes ({\widetilde {\omega }})(A)$
acts on the A-module
![]() ${\widetilde {\omega }}(V)$
. Note that
${\widetilde {\omega }}(V)$
. Note that
![]() $\rho ^{\prime }_V$
is continuous because
$\rho ^{\prime }_V$
is continuous because
![]() ${\widetilde {G}}(A)\to \operatorname {\mathrm {GL}}\big ({\widetilde {\omega }}(V)\big )(A)$
is continuous. Let
${\widetilde {G}}(A)\to \operatorname {\mathrm {GL}}\big ({\widetilde {\omega }}(V)\big )(A)$
is continuous. Let
![]() ${\underline {{\mathcal {V}}\!}\,}_f(V)\in A\mbox {-}{\underline {\mathrm {Loc}}}_X$
be the local system on X induced from
${\underline {{\mathcal {V}}\!}\,}_f(V)\in A\mbox {-}{\underline {\mathrm {Loc}}}_X$
be the local system on X induced from
![]() $\rho ^{\prime }_V$
via Proposition 5.3. This defines a tensor functor
$\rho ^{\prime }_V$
via Proposition 5.3. This defines a tensor functor
![]() ${\underline {{\mathcal {V}}\!}\,}_f\colon \operatorname {\mathrm {Rep}}_{A}G \to A\mbox {-}{\underline {\mathrm { Loc}}}_{X}$
for which
${\underline {{\mathcal {V}}\!}\,}_f\colon \operatorname {\mathrm {Rep}}_{A}G \to A\mbox {-}{\underline {\mathrm { Loc}}}_{X}$
for which
![]() $\textit {forget}\circ \omega _{\bar x}\circ {\underline {{\mathcal {V}}\!}\,}$
is identified with
$\textit {forget}\circ \omega _{\bar x}\circ {\underline {{\mathcal {V}}\!}\,}$
is identified with
![]() ${\widetilde {\omega }}$
. We let
${\widetilde {\omega }}$
. We let
![]() $\beta _f\in \operatorname {\mathrm {Isom}}^\otimes ({\widetilde {\omega }},\mathit {forget}\circ \omega _{\bar x}\circ {\underline {{\mathcal {V}}\!}\,})(A)$
be this identification.
$\beta _f\in \operatorname {\mathrm {Isom}}^\otimes ({\widetilde {\omega }},\mathit {forget}\circ \omega _{\bar x}\circ {\underline {{\mathcal {V}}\!}\,})(A)$
be this identification.
Clearly, the assignments
![]() $({\underline {{\mathcal {V}}\!}\,},\beta )\mapsto f_{({\underline {{\mathcal {V}}\!}\,},\beta )}$
and
$({\underline {{\mathcal {V}}\!}\,},\beta )\mapsto f_{({\underline {{\mathcal {V}}\!}\,},\beta )}$
and
![]() $f\mapsto ({\underline {{\mathcal {V}}\!}\,}_f,\beta _f)$
satisfy
$f\mapsto ({\underline {{\mathcal {V}}\!}\,}_f,\beta _f)$
satisfy
![]() $f=f_{({\underline {{\mathcal {V}}\!}\,}_f,\beta _f)}$
. Conversely, if
$f=f_{({\underline {{\mathcal {V}}\!}\,}_f,\beta _f)}$
. Conversely, if
![]() $({\underline {{\mathcal {V}}\!}\,},\beta )\in {\mathcal {T}}_A$
and
$({\underline {{\mathcal {V}}\!}\,},\beta )\in {\mathcal {T}}_A$
and
![]() $f=f_{({\underline {{\mathcal {V}}\!}\,},\beta )}$
, then
$f=f_{({\underline {{\mathcal {V}}\!}\,},\beta )}$
, then
![]() $\beta $
provides an isomorphism
$\beta $
provides an isomorphism
![]() , and so
, and so
![]() $({\underline {{\mathcal {V}}\!}\,},\beta )$
and
$({\underline {{\mathcal {V}}\!}\,},\beta )$
and
![]() $({\underline {{\mathcal {V}}\!}\,}_f,\beta _f)$
coincide in
$({\underline {{\mathcal {V}}\!}\,}_f,\beta _f)$
coincide in
![]() ${\mathcal {T}}_A$
.
${\mathcal {T}}_A$
.
Remark 5.5. (a) In the situation of Corollary 5.4, any tensor functor
![]() ${\underline {{\mathcal {V}}\!}\,}\colon \operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G \to {\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\mbox {-}{\underline {\mathrm {Loc}}}_{X}$
induces a tower of étale covering spaces of X with Hecke action, as described in [Reference Hartl51, Remark 2.7(a)]. To recall the construction, assume that
${\underline {{\mathcal {V}}\!}\,}\colon \operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G \to {\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\mbox {-}{\underline {\mathrm {Loc}}}_{X}$
induces a tower of étale covering spaces of X with Hecke action, as described in [Reference Hartl51, Remark 2.7(a)]. To recall the construction, assume that
![]() $\operatorname {\mathrm {Isom}}^\otimes ({\widetilde {\omega }},\mathit {forget}\circ \omega _{\bar x}\circ {\underline {{\mathcal {V}}\!}\,})\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
is nonempty. The whole construction does not depend on the choice of the base point
$\operatorname {\mathrm {Isom}}^\otimes ({\widetilde {\omega }},\mathit {forget}\circ \omega _{\bar x}\circ {\underline {{\mathcal {V}}\!}\,})\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
is nonempty. The whole construction does not depend on the choice of the base point
![]() $\bar x$
by [Reference de Jong31, Theorem 2.9] and hence also applies if X is not connected. Let
$\bar x$
by [Reference de Jong31, Theorem 2.9] and hence also applies if X is not connected. Let
![]() ${\widetilde {K}}\subset {\widetilde {G}}\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
be a compact open subgroup. For a strictly L-analytic space S over X and a lift of
${\widetilde {K}}\subset {\widetilde {G}}\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
be a compact open subgroup. For a strictly L-analytic space S over X and a lift of
![]() $\bar x$
to a geometric base point
$\bar x$
to a geometric base point
![]() $\bar s$
of S, a rational
$\bar s$
of S, a rational
![]() ${\widetilde {K}}$
-level structure on
${\widetilde {K}}$
-level structure on
![]() ${\underline {{\mathcal {V}}\!}\,}$
over S is a residue class modulo
${\underline {{\mathcal {V}}\!}\,}$
over S is a residue class modulo
![]() ${\widetilde {K}}$
of
${\widetilde {K}}$
of
![]() ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-rational tensor isomorphisms
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-rational tensor isomorphisms
such that the class
![]() $\beta {\widetilde {K}}$
is invariant under the étale fundamental group
$\beta {\widetilde {K}}$
is invariant under the étale fundamental group
![]() $\pi _1^{\mathrm {\acute {e}t}}(S,\bar s)$
. Here
$\pi _1^{\mathrm {\acute {e}t}}(S,\bar s)$
. Here
![]() $\operatorname {\mathrm {Isom}}^\otimes ({\widetilde {\omega }},\mathit {forget}\circ \omega _{\bar x}\circ {\underline {{\mathcal {V}}\!}\,})\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
carries an action of
$\operatorname {\mathrm {Isom}}^\otimes ({\widetilde {\omega }},\mathit {forget}\circ \omega _{\bar x}\circ {\underline {{\mathcal {V}}\!}\,})\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
carries an action of
![]() ${\widetilde {K}}$
through the action of
${\widetilde {K}}$
through the action of
![]() ${\widetilde {G}}$
on
${\widetilde {G}}$
on
![]() ${\widetilde {\omega }}$
and an action of
${\widetilde {\omega }}$
and an action of
![]() $\pi _1^{\mathrm {\acute {e}t}}(S,\bar s)$
through its action on
$\pi _1^{\mathrm {\acute {e}t}}(S,\bar s)$
through its action on
![]() $\omega _{\bar x}\circ {\underline {{\mathcal {V}}\!}\,}$
via the map
$\omega _{\bar x}\circ {\underline {{\mathcal {V}}\!}\,}$
via the map
![]() $\pi _1^{\mathrm {\acute {e}t}}(S,\bar s)\to \pi _1^{\mathrm {\acute {e}t}}(X,\bar x)$
and Proposition 5.3.
$\pi _1^{\mathrm {\acute {e}t}}(S,\bar s)\to \pi _1^{\mathrm {\acute {e}t}}(X,\bar x)$
and Proposition 5.3.
Let
![]() ${\breve {\mathcal {E}}}_{{\widetilde {K}}}$
be the étale covering space of X corresponding to the discrete
${\breve {\mathcal {E}}}_{{\widetilde {K}}}$
be the étale covering space of X corresponding to the discrete
![]() $\pi _{1}^{\mathrm {\acute {e}t}} (X,\bar {x})$
-set
$\pi _{1}^{\mathrm {\acute {e}t}} (X,\bar {x})$
-set
![]() $\operatorname {\mathrm {Isom}}^{\otimes }({\widetilde {\omega }}, \mathit {forget}\circ \omega _{\bar {x}} \circ {\underline {{\mathcal {V}}\!}\,}) \big ({\mathbb {F}}_q(\kern-0.15em( z )\kern-0.15em)\big )/{\widetilde {K}}$
. Then
$\operatorname {\mathrm {Isom}}^{\otimes }({\widetilde {\omega }}, \mathit {forget}\circ \omega _{\bar {x}} \circ {\underline {{\mathcal {V}}\!}\,}) \big ({\mathbb {F}}_q(\kern-0.15em( z )\kern-0.15em)\big )/{\widetilde {K}}$
. Then
![]() ${\breve {\mathcal {E}}}_{{\widetilde {K}}}$
represents the rational
${\breve {\mathcal {E}}}_{{\widetilde {K}}}$
represents the rational
![]() ${\widetilde {K}}$
-level structures on
${\widetilde {K}}$
-level structures on
![]() ${\underline {{\mathcal {V}}\!}\,}$
. Any choice of a fixed tensor isomorphism
${\underline {{\mathcal {V}}\!}\,}$
. Any choice of a fixed tensor isomorphism
![]() $\beta _0\in \operatorname {\mathrm {Isom}}^{\otimes }({\widetilde {\omega }},\mathit {forget}\circ \omega _{\bar {x}} \circ {\underline {{\mathcal {V}}\!}\,}) \big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
associates with
$\beta _0\in \operatorname {\mathrm {Isom}}^{\otimes }({\widetilde {\omega }},\mathit {forget}\circ \omega _{\bar {x}} \circ {\underline {{\mathcal {V}}\!}\,}) \big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
associates with
![]() ${\underline {{\mathcal {V}}\!}\,}$
a representation
${\underline {{\mathcal {V}}\!}\,}$
a representation
![]() $\pi _{1}^{\mathrm {\acute {e}t}}(X,\bar {x})\to {\widetilde {G}}\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
as in Corollary 5.4 and induces an identification of the
$\pi _{1}^{\mathrm {\acute {e}t}}(X,\bar {x})\to {\widetilde {G}}\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
as in Corollary 5.4 and induces an identification of the
![]() $\pi _1^{\mathrm {\acute {e}t}}(X,\bar x)$
-sets
$\pi _1^{\mathrm {\acute {e}t}}(X,\bar x)$
-sets
![]() $\operatorname {\mathrm {Isom}}^{\otimes }({\widetilde {\omega }},\mathit {forget}\circ \omega _{\bar {x}} \circ {\underline {{\mathcal {V}}\!}\,})\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )/{\widetilde {K}}$
and
$\operatorname {\mathrm {Isom}}^{\otimes }({\widetilde {\omega }},\mathit {forget}\circ \omega _{\bar {x}} \circ {\underline {{\mathcal {V}}\!}\,})\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )/{\widetilde {K}}$
and
![]() ${\widetilde {G}}\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )/{\widetilde {K}}$
. Moreover, if
${\widetilde {G}}\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )/{\widetilde {K}}$
. Moreover, if
![]() $\widetilde{K}^{\prime} \subset \widetilde{K} \subset \widetilde{G} \big( \mathbb{F}_q((z)) \big)$
are compact open subgroups, there is a natural projection morphism
$\widetilde{K}^{\prime} \subset \widetilde{K} \subset \widetilde{G} \big( \mathbb{F}_q((z)) \big)$
are compact open subgroups, there is a natural projection morphism
![]() ${\breve {\pi }}_{{\widetilde {K}}, {\widetilde {K}}^{\prime }} \colon {\breve {\mathcal {E}}}_{{\widetilde {K}}^{\prime }} \to {\breve {\mathcal {E}}}_{{\widetilde {K}}}$
,
${\breve {\pi }}_{{\widetilde {K}}, {\widetilde {K}}^{\prime }} \colon {\breve {\mathcal {E}}}_{{\widetilde {K}}^{\prime }} \to {\breve {\mathcal {E}}}_{{\widetilde {K}}}$
,
![]() $\beta {\widetilde {K}}^{\prime }\mapsto \beta {\widetilde {K}}$
.
$\beta {\widetilde {K}}^{\prime }\mapsto \beta {\widetilde {K}}$
.
On the tower
![]() $({\breve {\mathcal {E}}}_{{\widetilde {K}}})_{{\widetilde {K}}\subset {\widetilde {G}}({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em))}$
the group
$({\breve {\mathcal {E}}}_{{\widetilde {K}}})_{{\widetilde {K}}\subset {\widetilde {G}}({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em))}$
the group
![]() ${\widetilde {G}}\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
acts via Hecke correspondences: Let
${\widetilde {G}}\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
acts via Hecke correspondences: Let
![]() $g\in {\widetilde {G}}\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
and let
$g\in {\widetilde {G}}\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
and let
![]() ${\widetilde {K}}\subset {\widetilde {G}}\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
be a compact open subgroup. Then g induces an isomorphism
${\widetilde {K}}\subset {\widetilde {G}}\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
be a compact open subgroup. Then g induces an isomorphism
(b) Assume, moreover, that a group J acts on X and let
![]() ${\underline {{\mathcal {V}}\!}\,}\colon \operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G \to {\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\mbox {-}{\underline {\mathrm {Loc}}}_{X}$
be a tensor functor that carries a J -linearisation; that is, for every
${\underline {{\mathcal {V}}\!}\,}\colon \operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G \to {\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\mbox {-}{\underline {\mathrm {Loc}}}_{X}$
be a tensor functor that carries a J -linearisation; that is, for every
![]() $j\in J$
an isomorphism
$j\in J$
an isomorphism
![]() of tensor functors (where
of tensor functors (where
![]() $j^*{\underline {{\mathcal {V}}\!}\,}$
is the pullback of
$j^*{\underline {{\mathcal {V}}\!}\,}$
is the pullback of
![]() ${\underline {{\mathcal {V}}\!}\,}$
under the morphism
${\underline {{\mathcal {V}}\!}\,}$
under the morphism
![]() $j\colon X\to X$
), satisfying a cocycle condition. Then the tower of étale covering spaces
$j\colon X\to X$
), satisfying a cocycle condition. Then the tower of étale covering spaces
![]() ${\breve {\mathcal {E}}}_{{\widetilde {K}}}$
inherits an action of J over X as in [Reference Hartl51, Remark 2.7(b)].
${\breve {\mathcal {E}}}_{{\widetilde {K}}}$
inherits an action of J over X as in [Reference Hartl51, Remark 2.7(b)].
We now apply these considerations to the period spaces of Hodge-Pink G-structures.
Remark 5.6. The construction of the
![]() $\sigma $
-bundle
$\sigma $
-bundle
![]() ${\underline {{\mathcal {F}}\!}\,}_{b,\gamma }(V)$
from Definition 4.9 works not only over a field extension L of
${\underline {{\mathcal {F}}\!}\,}_{b,\gamma }(V)$
from Definition 4.9 works not only over a field extension L of
![]() $\breve E$
but more generally over the entire
$\breve E$
but more generally over the entire
![]() $\breve E$
-analytic space
$\breve E$
-analytic space
![]() $\breve {\mathcal {H}}_{G,\hat {Z}}^{\textrm {an}}$
from Definition 4.16. There it produces a
$\breve {\mathcal {H}}_{G,\hat {Z}}^{\textrm {an}}$
from Definition 4.16. There it produces a
![]() $\sigma $
-bundle
$\sigma $
-bundle
![]() ${\underline {{\mathcal {F}}\!}\,}_b(V)$
over
${\underline {{\mathcal {F}}\!}\,}_b(V)$
over
![]() $\breve {\mathcal {H}}_{G,\hat {Z}}^{\textrm {an}}$
whose fibre at each point
$\breve {\mathcal {H}}_{G,\hat {Z}}^{\textrm {an}}$
whose fibre at each point
![]() $\gamma $
is
$\gamma $
is
![]() ${\underline {{\mathcal {F}}\!}\,}_{b,\gamma }(V)$
; see [Reference Hartl50, § 2.4].
${\underline {{\mathcal {F}}\!}\,}_{b,\gamma }(V)$
; see [Reference Hartl50, § 2.4].
The restriction of
![]() ${\underline {{\mathcal {F}}\!}\,}_b(V)$
to
${\underline {{\mathcal {F}}\!}\,}_b(V)$
to
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^a$
induces by Theorem [Reference Hartl50, Theorem 3.4.1] a canonical local system
$\breve {\mathcal {H}}_{G,\hat {Z},b}^a$
induces by Theorem [Reference Hartl50, Theorem 3.4.1] a canonical local system
![]() ${\underline {{\mathcal {V}}\!}\,}_b(V)$
of
${\underline {{\mathcal {V}}\!}\,}_b(V)$
of
![]() ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-vector spaces on
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-vector spaces on
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^a$
. It can be described as follows. On every connected component Y of
$\breve {\mathcal {H}}_{G,\hat {Z},b}^a$
. It can be described as follows. On every connected component Y of
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^a$
we choose a geometric base point
$\breve {\mathcal {H}}_{G,\hat {Z},b}^a$
we choose a geometric base point
![]() $\bar \gamma \colon {\mathtt {BSpec}}({\overline {L}})\to Y$
. We consider the pullback
$\bar \gamma \colon {\mathtt {BSpec}}({\overline {L}})\to Y$
. We consider the pullback
![]() $\bar \gamma ^*{\underline {{\mathcal {F}}\!}\,}_b(V)$
and its
$\bar \gamma ^*{\underline {{\mathcal {F}}\!}\,}_b(V)$
and its
![]() $\tau $
-invariants
$\tau $
-invariants
Because
![]() $\bar \gamma ^*{\underline {{\mathcal {F}}\!}\,}_b(V)\cong {\underline {{\mathcal {F}}\!}\,}_{0,1}{}^{\oplus \dim V}$
, the
$\bar \gamma ^*{\underline {{\mathcal {F}}\!}\,}_b(V)\cong {\underline {{\mathcal {F}}\!}\,}_{0,1}{}^{\oplus \dim V}$
, the
![]() $\tau $
-invariants
$\tau $
-invariants
![]() $\bar \gamma ^*{\underline {{\mathcal {F}}\!}\,}_b(V)^\tau $
form an
$\bar \gamma ^*{\underline {{\mathcal {F}}\!}\,}_b(V)^\tau $
form an
![]() ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-vector space of dimension equal to
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-vector space of dimension equal to
![]() $\dim V$
, which is equipped with a continuous action of the étale fundamental group
$\dim V$
, which is equipped with a continuous action of the étale fundamental group
![]() $\pi _1^{\mathrm {\acute {e}t}}(Y,\bar \gamma )$
. This defines the local system
$\pi _1^{\mathrm {\acute {e}t}}(Y,\bar \gamma )$
. This defines the local system
![]() ${\underline {{\mathcal {V}}\!}\,}_b(V)$
of
${\underline {{\mathcal {V}}\!}\,}_b(V)$
of
![]() ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-vector spaces on Y under the correspondence of Proposition 5.3. It satisfies
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-vector spaces on Y under the correspondence of Proposition 5.3. It satisfies
![]() ${\underline {{\mathcal {V}}\!}\,}_b(V)_{\bar \gamma }=\bar \gamma ^*{\underline {{\mathcal {F}}\!}\,}_b(V)^\tau $
and
${\underline {{\mathcal {V}}\!}\,}_b(V)_{\bar \gamma }=\bar \gamma ^*{\underline {{\mathcal {F}}\!}\,}_b(V)^\tau $
and
![]() ${\underline {{\mathcal {V}}\!}\,}_b(V)_{\bar \gamma }\otimes _{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}{\overline {L}}{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}=\bar \gamma ^*{\underline {{\mathcal {F}}\!}\,}_b(V)^\tau \otimes _{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}{\overline {L}}{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}=\bar \gamma ^*{\underline {{\mathcal {F}}\!}\,}_b(V)={\underline {{\mathcal {F}}\!}\,}_{b,\bar \gamma }(V)$
.
${\underline {{\mathcal {V}}\!}\,}_b(V)_{\bar \gamma }\otimes _{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}{\overline {L}}{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}=\bar \gamma ^*{\underline {{\mathcal {F}}\!}\,}_b(V)^\tau \otimes _{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}{\overline {L}}{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}=\bar \gamma ^*{\underline {{\mathcal {F}}\!}\,}_b(V)={\underline {{\mathcal {F}}\!}\,}_{b,\bar \gamma }(V)$
.
If
![]() $\gamma \in \breve {\mathcal {H}}_{G,\hat {Z},b}^a$
is the image of the geometric point
$\gamma \in \breve {\mathcal {H}}_{G,\hat {Z},b}^a$
is the image of the geometric point
![]() $\bar \gamma $
and L is the residue field of
$\bar \gamma $
and L is the residue field of
![]() $\gamma $
, then the fibre
$\gamma $
, then the fibre
![]() ${\underline {{\mathcal {V}}\!}\,}_b(V)_\gamma $
of
${\underline {{\mathcal {V}}\!}\,}_b(V)_\gamma $
of
![]() ${\underline {{\mathcal {V}}\!}\,}_b(V)$
at
${\underline {{\mathcal {V}}\!}\,}_b(V)$
at
![]() $\gamma $
is a continuous representation of
$\gamma $
is a continuous representation of
![]() $\operatorname {\mathrm {Gal}}(L^{\textrm {sep}}\!/L)$
on the finite-dimensional
$\operatorname {\mathrm {Gal}}(L^{\textrm {sep}}\!/L)$
on the finite-dimensional
![]() ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-vector space
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-vector space
![]() $\bar \gamma ^*{\underline {{\mathcal {F}}\!}\,}_b(V)$
. By [Reference Hartl, Kim, Böckle, Goss, Hartl and Papanikolas54, Remark 3.6.17] and with the notation from (6.1), this Galois-representation can be described as
$\bar \gamma ^*{\underline {{\mathcal {F}}\!}\,}_b(V)$
. By [Reference Hartl, Kim, Böckle, Goss, Hartl and Papanikolas54, Remark 3.6.17] and with the notation from (6.1), this Galois-representation can be described as
for
![]() ${\underline {D\!}\,}_{b,\gamma }(V)={\underline {D\!}\,}=(D,\tau _D,{\mathfrak {q}}_D)$
. Here we use the notation from (6.1) and in addition we let
${\underline {D\!}\,}_{b,\gamma }(V)={\underline {D\!}\,}=(D,\tau _D,{\mathfrak {q}}_D)$
. Here we use the notation from (6.1) and in addition we let
![]() $t_i\in {\mathcal {O}}_{{\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)^{\textrm {sep}}}$
be solutions of the equations
$t_i\in {\mathcal {O}}_{{\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)^{\textrm {sep}}}$
be solutions of the equations
![]() $t_0^{q-1}=-\zeta $
and
$t_0^{q-1}=-\zeta $
and
![]() $t_i^q+\zeta t_i=t_{i-1}$
and set
$t_i^q+\zeta t_i=t_{i-1}$
and set
![]() $t_{\scriptscriptstyle +}:=\sum _{i=0}^\infty t_iz^i\in {\mathcal {O}}_{{\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)^{\textrm {sep}}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
and
$t_{\scriptscriptstyle +}:=\sum _{i=0}^\infty t_iz^i\in {\mathcal {O}}_{{\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)^{\textrm {sep}}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
and
![]() $t:=t_{\scriptscriptstyle +}t_{\scriptscriptstyle -}\in {\mathcal {O}}_{{\overline {L}}}\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}$
, where
$t:=t_{\scriptscriptstyle +}t_{\scriptscriptstyle -}\in {\mathcal {O}}_{{\overline {L}}}\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}$
, where
![]() $t_{\scriptscriptstyle -}$
was defined in (4.3). In particular, if L is discretely valued, then
$t_{\scriptscriptstyle -}$
was defined in (4.3). In particular, if L is discretely valued, then
![]() ${\underline {{\mathcal {V}}\!}\,}_b(V)_\gamma $
is the (equal characteristic) crystalline Galois representation associated with the (weakly) admissible z-isocrystal with Hodge-Pink structure
${\underline {{\mathcal {V}}\!}\,}_b(V)_\gamma $
is the (equal characteristic) crystalline Galois representation associated with the (weakly) admissible z-isocrystal with Hodge-Pink structure
![]() ${\underline {D\!}\,}_{b,\gamma }(V)$
in the sense of [Reference Hartl, Kim, Böckle, Goss, Hartl and Papanikolas54, Definition 3.4.21 and Remark 3.6.17].
${\underline {D\!}\,}_{b,\gamma }(V)$
in the sense of [Reference Hartl, Kim, Böckle, Goss, Hartl and Papanikolas54, Definition 3.4.21 and Remark 3.6.17].
Theorem 5.7. Let
![]() $b\in LG({\mathbb {F}})$
and let
$b\in LG({\mathbb {F}})$
and let
![]() $\hat {Z}=[(R,\hat Z_R)]$
be a bound as in Definition 2.2 with reflex ring
$\hat {Z}=[(R,\hat Z_R)]$
be a bound as in Definition 2.2 with reflex ring
![]() $R_{\hat Z}=\kappa \mathrm {[}\kern-0.15em\mathrm {[}\xi \mathrm {]}\kern-0.15em\mathrm {]}$
. Then the assignments
$R_{\hat Z}=\kappa \mathrm {[}\kern-0.15em\mathrm {[}\xi \mathrm {]}\kern-0.15em\mathrm {]}$
. Then the assignments
![]() $V\mapsto {\underline {{\mathcal {F}}\!}\,}_b(V)\mapsto \bar \gamma ^*{\underline {{\mathcal {F}}\!}\,}_b(V)^\tau \mapsto {\underline {{\mathcal {V}}\!}\,}_b(V)$
define an
$V\mapsto {\underline {{\mathcal {F}}\!}\,}_b(V)\mapsto \bar \gamma ^*{\underline {{\mathcal {F}}\!}\,}_b(V)^\tau \mapsto {\underline {{\mathcal {V}}\!}\,}_b(V)$
define an
![]() ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-linear tensor functor
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-linear tensor functor
![]() ${\underline {{\mathcal {V}}\!}\,}_b$
from
${\underline {{\mathcal {V}}\!}\,}_b$
from
![]() $\operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G$
to the category
$\operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G$
to the category
![]() ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\mbox {-}{\underline {\mathrm {Loc}}}_{\breve {\mathcal {H}}_{G,\hat {Z},b}^{a}}$
of local systems of
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\mbox {-}{\underline {\mathrm {Loc}}}_{\breve {\mathcal {H}}_{G,\hat {Z},b}^{a}}$
of local systems of
![]() ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-vector spaces on
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-vector spaces on
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^{a}$
. There is a canonical
$\breve {\mathcal {H}}_{G,\hat {Z},b}^{a}$
. There is a canonical
![]() $J_b\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
-linearisation on
$J_b\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
-linearisation on
![]() ${\underline {{\mathcal {V}}\!}\,}_b$
.
${\underline {{\mathcal {V}}\!}\,}_b$
.
Proof. First of all, the functors
![]() $V\mapsto {\underline {D\!}\,}_{b,\gamma }(V)$
from Remark 4.4 and
$V\mapsto {\underline {D\!}\,}_{b,\gamma }(V)$
from Remark 4.4 and
![]() ${\underline {D\!}\,}\mapsto \big ({\underline {{\mathcal {E}}\!}\,}({\underline {D\!}\,}),\,{\underline {{\mathcal {F}}\!}\,}({\underline {D\!}\,})\big )$
from Definition 4.9 are
${\underline {D\!}\,}\mapsto \big ({\underline {{\mathcal {E}}\!}\,}({\underline {D\!}\,}),\,{\underline {{\mathcal {F}}\!}\,}({\underline {D\!}\,})\big )$
from Definition 4.9 are
![]() ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-linear tensor functors, and this works equally for the entire families over
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-linear tensor functors, and this works equally for the entire families over
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^{a}$
. In particular,
$\breve {\mathcal {H}}_{G,\hat {Z},b}^{a}$
. In particular,
![]() $V\mapsto {\underline {{\mathcal {F}}\!}\,}_b(V)$
is a tensor functor from
$V\mapsto {\underline {{\mathcal {F}}\!}\,}_b(V)$
is a tensor functor from
![]() $\operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G$
to the category of
$\operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G$
to the category of
![]() $\sigma $
-bundles over
$\sigma $
-bundles over
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^{a}$
. Next, taking
$\breve {\mathcal {H}}_{G,\hat {Z},b}^{a}$
. Next, taking
![]() $\tau $
-invariants is obviously compatible with morphisms. It is in general not compatible with tensor products, but because
$\tau $
-invariants is obviously compatible with morphisms. It is in general not compatible with tensor products, but because
![]() $\bar \gamma ^*{\underline {{\mathcal {F}}\!}\,}_b(V)\cong {\underline {{\mathcal {F}}\!}\,}_{0,1}{}^{\oplus \dim V}$
, we have
$\bar \gamma ^*{\underline {{\mathcal {F}}\!}\,}_b(V)\cong {\underline {{\mathcal {F}}\!}\,}_{0,1}{}^{\oplus \dim V}$
, we have
![]() $\bar \gamma ^*{\underline {{\mathcal {F}}\!}\,}_b(V)\cong \big (\bar \gamma ^*{\underline {{\mathcal {F}}\!}\,}_b(V)^\tau \big )\otimes _{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}{\overline {L}}{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}$
. Therefore,
$\bar \gamma ^*{\underline {{\mathcal {F}}\!}\,}_b(V)\cong \big (\bar \gamma ^*{\underline {{\mathcal {F}}\!}\,}_b(V)^\tau \big )\otimes _{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}{\overline {L}}{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}$
. Therefore,
 $$ \begin{align*} \bar\gamma^*{\underline{{\mathcal{F}}\!}\,}_b(V\otimes V^{\prime}) & \cong \bar\gamma^*{\underline{{\mathcal{F}}\!}\,}_b(V)\otimes_{{\overline{L}}{\textstyle\langle \frac{z}{\zeta^{s}},z^{-1}\}}}\bar\gamma^*{\underline{{\mathcal{F}}\!}\,}_b(V^{\prime}) \\[2mm] & \cong \big(\bar\gamma^*{\underline{{\mathcal{F}}\!}\,}_b(V)^\tau\otimes_{{\mathbb{F}}_q(\kern-0.15em( z )\kern-0.15em)}\bar\gamma^*{\underline{{\mathcal{F}}\!}\,}_b(V)^\tau\big)\otimes_{{\mathbb{F}}_q(\kern-0.15em( z )\kern-0.15em)}{\overline{L}}{\textstyle\langle\frac{z}{\zeta^{s}},z^{-1}\}}, \end{align*} $$
$$ \begin{align*} \bar\gamma^*{\underline{{\mathcal{F}}\!}\,}_b(V\otimes V^{\prime}) & \cong \bar\gamma^*{\underline{{\mathcal{F}}\!}\,}_b(V)\otimes_{{\overline{L}}{\textstyle\langle \frac{z}{\zeta^{s}},z^{-1}\}}}\bar\gamma^*{\underline{{\mathcal{F}}\!}\,}_b(V^{\prime}) \\[2mm] & \cong \big(\bar\gamma^*{\underline{{\mathcal{F}}\!}\,}_b(V)^\tau\otimes_{{\mathbb{F}}_q(\kern-0.15em( z )\kern-0.15em)}\bar\gamma^*{\underline{{\mathcal{F}}\!}\,}_b(V)^\tau\big)\otimes_{{\mathbb{F}}_q(\kern-0.15em( z )\kern-0.15em)}{\overline{L}}{\textstyle\langle\frac{z}{\zeta^{s}},z^{-1}\}}, \end{align*} $$
and hence
![]() $\bar \gamma ^*{\underline {{\mathcal {F}}\!}\,}_b(V\otimes V^{\prime })^\tau \cong \bar \gamma ^*{\underline {{\mathcal {F}}\!}\,}_b(V)^\tau \otimes _{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}\bar \gamma ^*{\underline {{\mathcal {F}}\!}\,}_b(V)^\tau $
. We now use Proposition 5.3 to conclude that
$\bar \gamma ^*{\underline {{\mathcal {F}}\!}\,}_b(V\otimes V^{\prime })^\tau \cong \bar \gamma ^*{\underline {{\mathcal {F}}\!}\,}_b(V)^\tau \otimes _{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}\bar \gamma ^*{\underline {{\mathcal {F}}\!}\,}_b(V)^\tau $
. We now use Proposition 5.3 to conclude that
![]() ${\underline {{\mathcal {V}}\!}\,}_b$
is an
${\underline {{\mathcal {V}}\!}\,}_b$
is an
![]() ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-linear tensor functor.
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-linear tensor functor.
If
![]() $j\in J_b\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
the isomorphism
$j\in J_b\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
the isomorphism
from Remark 4.17 yields
![]() $J_b\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
-linearisations
$J_b\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
-linearisations
![]() and
and
![]() .
.
Let us end this section by stating the significance of Theorem 5.7 in terms of the étale fundamental group and in terms of étale covering spaces. Let
![]() $\bar \gamma $
be a geometric base point of
$\bar \gamma $
be a geometric base point of
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^{a}$
.
$\breve {\mathcal {H}}_{G,\hat {Z},b}^{a}$
.
Remark 5.8. Let
![]() $\omega ^\circ $
and
$\omega ^\circ $
and
![]() $\omega _{b,\bar \gamma }:=\mathit {forget}\circ \omega _{\bar \gamma }\circ {\underline {{\mathcal {V}}\!}\,}_b$
be the fibre functors from
$\omega _{b,\bar \gamma }:=\mathit {forget}\circ \omega _{\bar \gamma }\circ {\underline {{\mathcal {V}}\!}\,}_b$
be the fibre functors from
![]() $\operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G$
to
$\operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G$
to
![]() $\textrm {FMod}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}$
with
$\textrm {FMod}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}$
with
![]() $\omega ^\circ (V):=V$
and
$\omega ^\circ (V):=V$
and
![]() $\omega _{b,\bar \gamma }(V):={\underline {{\mathcal {V}}\!}\,}_b(V)_{\bar \gamma }=\bar \gamma ^*{\underline {{\mathcal {F}}\!}\,}_b(V)^\tau $
. By [Reference de Jong31, Theorem 2.9], the fibre functors
$\omega _{b,\bar \gamma }(V):={\underline {{\mathcal {V}}\!}\,}_b(V)_{\bar \gamma }=\bar \gamma ^*{\underline {{\mathcal {F}}\!}\,}_b(V)^\tau $
. By [Reference de Jong31, Theorem 2.9], the fibre functors
![]() $\omega _{b,\bar \gamma }$
and
$\omega _{b,\bar \gamma }$
and
![]() $\omega _{b,\bar \gamma ^{\prime }}$
are isomorphic for any two geometric base points
$\omega _{b,\bar \gamma ^{\prime }}$
are isomorphic for any two geometric base points
![]() $\bar \gamma $
and
$\bar \gamma $
and
![]() $\bar \gamma ^{\prime }$
that lie in the same connected component of
$\bar \gamma ^{\prime }$
that lie in the same connected component of
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^{a}$
. Let
$\breve {\mathcal {H}}_{G,\hat {Z},b}^{a}$
. Let
![]() ${\widetilde {G}}:=\operatorname {\mathrm {Aut}}^\otimes (\omega _{b,\bar \gamma })$
. Then
${\widetilde {G}}:=\operatorname {\mathrm {Aut}}^\otimes (\omega _{b,\bar \gamma })$
. Then
![]() $\operatorname {\mathrm {Isom}}^\otimes (\omega ^\circ ,\omega _{b,\bar \gamma })$
is a left G-torsor and a right
$\operatorname {\mathrm {Isom}}^\otimes (\omega ^\circ ,\omega _{b,\bar \gamma })$
is a left G-torsor and a right
![]() ${\widetilde {G}}$
-torsor over
${\widetilde {G}}$
-torsor over
![]() ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
and corresponds to a cohomology class
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
and corresponds to a cohomology class
![]() $cl(b,\bar \gamma )\in \operatorname {\mathrm {H}}^1({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em),G)$
by [Reference Deligne and Milne33, Theorem 3.2].
$cl(b,\bar \gamma )\in \operatorname {\mathrm {H}}^1({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em),G)$
by [Reference Deligne and Milne33, Theorem 3.2].
![]() ${\widetilde {G}}$
is the inner form of G defined by the image
${\widetilde {G}}$
is the inner form of G defined by the image
![]() $cl(b,\bar \gamma )\in \operatorname {\mathrm {H}}^1({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em),G^{\textrm {ad}})$
.
$cl(b,\bar \gamma )\in \operatorname {\mathrm {H}}^1({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em),G^{\textrm {ad}})$
.
In the analogous situation over
![]() ${\mathbb {Q}}_p$
, the torsor between the crystalline and the étale fibre functor is given by the cohomology class
${\mathbb {Q}}_p$
, the torsor between the crystalline and the étale fibre functor is given by the cohomology class
This was proved by Rapoport and Zink [Reference Rapoport and Zink80, 1.20] if
![]() $G_{\textrm {der}}$
is simply connected and in general by Wintenberger [Reference Wintenberger97, Corollary to Proposition 4.5.3]; see also [Reference Colmez and Fontaine28, Proposition on page 4].
$G_{\textrm {der}}$
is simply connected and in general by Wintenberger [Reference Wintenberger97, Corollary to Proposition 4.5.3]; see also [Reference Colmez and Fontaine28, Proposition on page 4].
The analogue of Wintenberger’s theorem in our situation (which has not been proved yet) is the statement that the torsor
![]() $\operatorname {\mathrm {Isom}}^\otimes (\omega ^\circ ,\omega _{b,\bar \gamma })$
is given by the cohomology class
$\operatorname {\mathrm {Isom}}^\otimes (\omega ^\circ ,\omega _{b,\bar \gamma })$
is given by the cohomology class
Note that also in the function field case considered here, the weak admissibility of the pair
![]() $(b,\bar \gamma )$
implies that the difference
$(b,\bar \gamma )$
implies that the difference
![]() $[b]^\#-\bar \gamma ^\#$
lies in
$[b]^\#-\bar \gamma ^\#$
lies in
![]() $(\pi _1(G)_\Gamma )_{\textrm {tors}}$
, which is identified with
$(\pi _1(G)_\Gamma )_{\textrm {tors}}$
, which is identified with
![]() $\operatorname {\mathrm {H}}^1({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em),G)$
; see [Reference Rapoport and Richartz78, Theorem 1.15] (and use [Reference Borel and Springer15, 8.6] instead of Steinberg’s theorem). In particular, if
$\operatorname {\mathrm {H}}^1({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em),G)$
; see [Reference Rapoport and Richartz78, Theorem 1.15] (and use [Reference Borel and Springer15, 8.6] instead of Steinberg’s theorem). In particular, if
![]() $\bar \gamma \in \breve {\mathcal {H}}_{G,\hat {Z},b}^{na}$
and the analogue (5.6) of Wintenberger’s theorem is established, then there is an
$\bar \gamma \in \breve {\mathcal {H}}_{G,\hat {Z},b}^{na}$
and the analogue (5.6) of Wintenberger’s theorem is established, then there is an
![]() ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-rational tensor isomorphism
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-rational tensor isomorphism
![]() and
and
![]() ${\widetilde {G}}:=\operatorname {\mathrm {Aut}}^\otimes (\omega _{b,\bar \gamma })\cong G$
.
${\widetilde {G}}:=\operatorname {\mathrm {Aut}}^\otimes (\omega _{b,\bar \gamma })\cong G$
.
Remark 5.9. By Corollary 5.4, the restriction of the tensor functor
![]() ${\underline {{\mathcal {V}}\!}\,}_b$
from Theorem 5.7 to the connected component Y of
${\underline {{\mathcal {V}}\!}\,}_b$
from Theorem 5.7 to the connected component Y of
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^{a}$
containing the geometric base point
$\breve {\mathcal {H}}_{G,\hat {Z},b}^{a}$
containing the geometric base point
![]() $\bar \gamma $
corresponds to a continuous group homomorphism
$\bar \gamma $
corresponds to a continuous group homomorphism
(under the choice of
![]() $\beta :=\operatorname {\mbox { id}}_{{\widetilde {\omega }}}$
for
$\beta :=\operatorname {\mbox { id}}_{{\widetilde {\omega }}}$
for
![]() ${\widetilde {\omega }}:={\widetilde {\omega }}_{b,\bar \gamma }$
).
${\widetilde {\omega }}:={\widetilde {\omega }}_{b,\bar \gamma }$
).
By Remark 5.5, the tensor functor
![]() ${\underline {{\mathcal {V}}\!}\,}_b$
defines a tower
${\underline {{\mathcal {V}}\!}\,}_b$
defines a tower
![]() $({\breve {\mathcal {E}}}_{{\widetilde {K}}})_{{\widetilde {K}}\subset {\widetilde {G}}({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em))}$
of étale covering spaces of
$({\breve {\mathcal {E}}}_{{\widetilde {K}}})_{{\widetilde {K}}\subset {\widetilde {G}}({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em))}$
of étale covering spaces of
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^{a}$
. However, the group
$\breve {\mathcal {H}}_{G,\hat {Z},b}^{a}$
. However, the group
![]() ${\widetilde {G}}$
might vary on the different connected components of
${\widetilde {G}}$
might vary on the different connected components of
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^{a}$
. It is therefore more useful to fix a base point
$\breve {\mathcal {H}}_{G,\hat {Z},b}^{a}$
. It is therefore more useful to fix a base point
![]() $\bar \gamma $
and to define
$\bar \gamma $
and to define
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^{a,\bar \gamma }$
as the union of those connected components consisting of elements
$\breve {\mathcal {H}}_{G,\hat {Z},b}^{a,\bar \gamma }$
as the union of those connected components consisting of elements
![]() $\bar \gamma ^{\prime }$
with
$\bar \gamma ^{\prime }$
with
![]() ${\widetilde {\omega }}_{b,\bar \gamma ^{\prime }}\cong {\widetilde {\omega }}_{b,\bar \gamma }$
. Then we obtain a tower
${\widetilde {\omega }}_{b,\bar \gamma ^{\prime }}\cong {\widetilde {\omega }}_{b,\bar \gamma }$
. Then we obtain a tower
![]() $({\breve {\mathcal {E}}}_{{\widetilde {K}}}^{\bar \gamma })_{{\widetilde {K}}\subset {\widetilde {G}}({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em))}$
of étale covering spaces of
$({\breve {\mathcal {E}}}_{{\widetilde {K}}}^{\bar \gamma })_{{\widetilde {K}}\subset {\widetilde {G}}({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em))}$
of étale covering spaces of
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^{a,\bar \gamma }$
with commuting actions of
$\breve {\mathcal {H}}_{G,\hat {Z},b}^{a,\bar \gamma }$
with commuting actions of
![]() ${\widetilde {G}}\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
by Hecke correspondences and of the quasi-isogeny group
${\widetilde {G}}\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
by Hecke correspondences and of the quasi-isogeny group
![]() $J_b\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
of
$J_b\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
of
![]() ${\underline {{\mathbb {G}}}}_0=\big ((L^+G)_{\mathbb {F}},b\sigma ^\ast \big )$
from (3.1).
${\underline {{\mathbb {G}}}}_0=\big ((L^+G)_{\mathbb {F}},b\sigma ^\ast \big )$
from (3.1).
Note that for
![]() $A={\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
it can happen that
$A={\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
it can happen that
![]() ${\widetilde {\omega }}\not \cong \omega ^\circ $
but
${\widetilde {\omega }}\not \cong \omega ^\circ $
but
![]() ${\widetilde {G}}\cong G$
, namely, if
${\widetilde {G}}\cong G$
, namely, if
![]() $cl(\omega ^\circ ,{\widetilde {\omega }})\in \operatorname {\mathrm {H}}^1({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em),G)$
is nontrivial and lies in the image of
$cl(\omega ^\circ ,{\widetilde {\omega }})\in \operatorname {\mathrm {H}}^1({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em),G)$
is nontrivial and lies in the image of
![]() $\operatorname {\mathrm {H}}^1({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em),Z)$
, where
$\operatorname {\mathrm {H}}^1({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em),Z)$
, where
![]() $Z\subset G_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}$
is the center. In this case, Corollary 5.4 could be applied to a continuous group homomorphism
$Z\subset G_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}$
is the center. In this case, Corollary 5.4 could be applied to a continuous group homomorphism
![]() $\pi _1^{\mathrm {\acute {e}t}}(X,\bar x)\to G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
using both
$\pi _1^{\mathrm {\acute {e}t}}(X,\bar x)\to G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
using both
![]() $\omega ^\circ $
and
$\omega ^\circ $
and
![]() ${\widetilde {\omega }}$
. One obtains two tensor functors
${\widetilde {\omega }}$
. One obtains two tensor functors
![]() ${\underline {{\mathcal {V}}\!}\,},{\widetilde {{\underline {{\mathcal {V}}\!}\,}}}\colon \operatorname {\mathrm {Rep}}_{A}G\to A\mbox {-}{\underline {\mathrm {Loc}}}_X$
and tensor isomorphisms
${\underline {{\mathcal {V}}\!}\,},{\widetilde {{\underline {{\mathcal {V}}\!}\,}}}\colon \operatorname {\mathrm {Rep}}_{A}G\to A\mbox {-}{\underline {\mathrm {Loc}}}_X$
and tensor isomorphisms
and
Because
![]() $cl(\omega ^\circ ,{\widetilde {\omega }})$
is trivialised by a finite unramified extension
$cl(\omega ^\circ ,{\widetilde {\omega }})$
is trivialised by a finite unramified extension
![]() ${\mathbb {F}}_{q^n}(\kern-0.15em( z)\kern-0.15em)$
of
${\mathbb {F}}_{q^n}(\kern-0.15em( z)\kern-0.15em)$
of
![]() ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
by [Reference Borel and Springer15, 8.6], the pairs
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
by [Reference Borel and Springer15, 8.6], the pairs
![]() $({\underline {{\mathcal {V}}\!}\,},\beta )$
and
$({\underline {{\mathcal {V}}\!}\,},\beta )$
and
![]() $({\widetilde {{\underline {{\mathcal {V}}\!}\,}}},\tilde \beta )$
become isomorphic after tensoring with
$({\widetilde {{\underline {{\mathcal {V}}\!}\,}}},\tilde \beta )$
become isomorphic after tensoring with
![]() ${\mathbb {F}}_{q^n}(\kern-0.15em( z)\kern-0.15em)$
.
${\mathbb {F}}_{q^n}(\kern-0.15em( z)\kern-0.15em)$
.
6 The period morphisms
In this section we fix a local G-shtuka
![]() ${\underline {{\mathbb {G}}}}_0=\big ((L^+G)_{\mathbb {F}},b\sigma ^\ast \big )$
over
${\underline {{\mathbb {G}}}}_0=\big ((L^+G)_{\mathbb {F}},b\sigma ^\ast \big )$
over
![]() ${\mathbb {F}}$
and a bound
${\mathbb {F}}$
and a bound
![]() $\hat {Z}$
with reflex ring
$\hat {Z}$
with reflex ring
![]() $R_{\hat Z}=\kappa \mathrm {[}\kern-0.15em\mathrm {[}\xi \mathrm {]}\kern-0.15em\mathrm {]}$
. We set
$R_{\hat Z}=\kappa \mathrm {[}\kern-0.15em\mathrm {[}\xi \mathrm {]}\kern-0.15em\mathrm {]}$
. We set
![]() $E_{\hat Z}=\kappa (\kern-0.15em( \xi )\kern-0.15em)$
and
$E_{\hat Z}=\kappa (\kern-0.15em( \xi )\kern-0.15em)$
and
![]() $\breve E:={\mathbb {F}}(\kern-0.15em( \xi )\kern-0.15em)$
. For any point
$\breve E:={\mathbb {F}}(\kern-0.15em( \xi )\kern-0.15em)$
. For any point
![]() $({\underline {{\mathcal {G}}}},\bar \delta )\in {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}(S)$
with values in
$({\underline {{\mathcal {G}}}},\bar \delta )\in {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}(S)$
with values in
![]() $S\in {{\mathcal {N}}\!\mathit {ilp}}_{\breve R_{\hat Z}}$
, the quasi-isogeny
$S\in {{\mathcal {N}}\!\mathit {ilp}}_{\breve R_{\hat Z}}$
, the quasi-isogeny
![]() $\bar \delta \colon {\underline {{\mathcal {G}}}}_{\,\overline {\!S}}\to {\underline {{\mathbb {G}}}}_{0,{\,\overline {\!S}}}$
lifts to a quasi-isogeny
$\bar \delta \colon {\underline {{\mathcal {G}}}}_{\,\overline {\!S}}\to {\underline {{\mathbb {G}}}}_{0,{\,\overline {\!S}}}$
lifts to a quasi-isogeny
![]() $\delta \colon {\underline {{\mathcal {G}}}}\to {\underline {{\mathbb {G}}}}_{0,S}$
by rigidity [Reference Arasteh Rad and Hartl4, Proposition 2.11]. To construct period morphisms for local G-shtukas we need to lift the universal
$\delta \colon {\underline {{\mathcal {G}}}}\to {\underline {{\mathbb {G}}}}_{0,S}$
by rigidity [Reference Arasteh Rad and Hartl4, Proposition 2.11]. To construct period morphisms for local G-shtukas we need to lift the universal
![]() $\bar \delta $
, which is defined over the zero locus
$\bar \delta $
, which is defined over the zero locus
![]() $\operatorname {\mathrm {V}}(\zeta )$
of
$\operatorname {\mathrm {V}}(\zeta )$
of
![]() $\zeta $
in
$\zeta $
in
![]() ${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
, to the entire formal scheme
${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
, to the entire formal scheme
![]() ${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
. This lift will no longer be a quasi-isogeny, because it acquires larger and larger powers of z in the denominators by lifting successively modulo
${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
. This lift will no longer be a quasi-isogeny, because it acquires larger and larger powers of z in the denominators by lifting successively modulo
![]() $\zeta ^{q^n}$
. To describe what the limit of this lifting procedure is, we need the following generalisation of [Reference Hartl50, Lemma 2.3.1] and [Reference Genestier and Lafforgue41, Lemmas 2.8 and 6.4]. For an
$\zeta ^{q^n}$
. To describe what the limit of this lifting procedure is, we need the following generalisation of [Reference Hartl50, Lemma 2.3.1] and [Reference Genestier and Lafforgue41, Lemmas 2.8 and 6.4]. For an
![]() ${\mathbb {F}}\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
-algebra B that is complete and separated with respect to a bounded norm
${\mathbb {F}}\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
-algebra B that is complete and separated with respect to a bounded norm
![]() $|\,.\,|\colon B\to \{x\in {\mathbb {R}}\colon 0\le x\le 1\}$
with
$|\,.\,|\colon B\to \{x\in {\mathbb {R}}\colon 0\le x\le 1\}$
with
![]() $0<|\zeta |<1$
, we define the
$0<|\zeta |<1$
, we define the
![]() ${\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)$
-algebra
${\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)$
-algebra
 $$ \begin{align} B\text{[}\kern-0.15em\text{[} z,z^{-1}\}\;:=\;\left\{\,\sum_{i\in{\mathbb{Z}}} b_iz^i\colon b_i\in B\,{,}\,|b_i|\,|\zeta|^{ri}\to0\;(i\to-\infty) \text{ for all }r>0\,\right\}. \end{align} $$
$$ \begin{align} B\text{[}\kern-0.15em\text{[} z,z^{-1}\}\;:=\;\left\{\,\sum_{i\in{\mathbb{Z}}} b_iz^i\colon b_i\in B\,{,}\,|b_i|\,|\zeta|^{ri}\to0\;(i\to-\infty) \text{ for all }r>0\,\right\}. \end{align} $$
Note that the convergence
![]() $|b_i|\,|\zeta |^{ri}\to 0$
for
$|b_i|\,|\zeta |^{ri}\to 0$
for
![]() $i\to -\infty $
implies that
$i\to -\infty $
implies that
![]() $|b_i|<1$
for
$|b_i|<1$
for
![]() $i\gg 0$
. The element
$i\gg 0$
. The element
![]() $t_{\scriptscriptstyle -}:=\prod _{i\in {\mathbb {N}}_0}\big (1-{\tfrac {\zeta ^{q^i}}{z}}\big )$
lies in
$t_{\scriptscriptstyle -}:=\prod _{i\in {\mathbb {N}}_0}\big (1-{\tfrac {\zeta ^{q^i}}{z}}\big )$
lies in
![]() $B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}$
and satisfies
$B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}$
and satisfies
![]() $z\,t_{\scriptscriptstyle -}=(z-\zeta )\sigma ^\ast (t_{\scriptscriptstyle -})$
; see (4.3). Note that
$z\,t_{\scriptscriptstyle -}=(z-\zeta )\sigma ^\ast (t_{\scriptscriptstyle -})$
; see (4.3). Note that
![]() $B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}$
contains
$B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}$
contains
![]() $B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
and
$B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
and
![]() $z^{-1}$
and that
$z^{-1}$
and that
![]() $B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}/(\zeta )={\,\overline {\!B}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z}]=:{\,\overline {\!B}}(\kern-0.15em( z)\kern-0.15em)$
, for
$B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}/(\zeta )={\,\overline {\!B}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z}]=:{\,\overline {\!B}}(\kern-0.15em( z)\kern-0.15em)$
, for
![]() ${\,\overline {\!B}}:=B/\zeta B$
. Moreover, note that
${\,\overline {\!B}}:=B/\zeta B$
. Moreover, note that
![]() $\sigma ^*(t_{\scriptscriptstyle -})\in B[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}^{\scriptscriptstyle \times }$
, and
$\sigma ^*(t_{\scriptscriptstyle -})\in B[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}^{\scriptscriptstyle \times }$
, and
![]() $B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}\subset B[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
by
$B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}\subset B[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
by
![]() $\sum _i b_i z^i=\sum _i b_i \big (\zeta +(z-\zeta )\big )^i=\sum _{n\ge 0}\sum _i b_i\binom {i}{n}\zeta ^{i-n}(z-\zeta )^n$
. Therefore,
$\sum _i b_i z^i=\sum _i b_i \big (\zeta +(z-\zeta )\big )^i=\sum _{n\ge 0}\sum _i b_i\binom {i}{n}\zeta ^{i-n}(z-\zeta )^n$
. Therefore,
Lemma 6.1. Let B be an
![]() ${\mathbb {F}}\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
-algebra as above. Let
${\mathbb {F}}\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
-algebra as above. Let
![]() $b\in LG({\mathbb {F}})=G\big ({\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)\big )$
,
$b\in LG({\mathbb {F}})=G\big ({\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)\big )$
,
![]() $A\in G\big (B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z-\zeta }]\big )$
and
$A\in G\big (B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z-\zeta }]\big )$
and
![]() ${\,\overline {\!\Delta \!}\,}\in LG({\,\overline {\!B}})=G\big ({\,\overline {\!B}}(\kern-0.15em( z)\kern-0.15em)\big )$
such that
${\,\overline {\!\Delta \!}\,}\in LG({\,\overline {\!B}})=G\big ({\,\overline {\!B}}(\kern-0.15em( z)\kern-0.15em)\big )$
such that
![]() ${\,\overline {\!\Delta \!}\,}\cdot (A\;\textrm {mod}\;\zeta )=b\cdot \sigma ^\ast ({\,\overline {\!\Delta \!}\,})$
in
${\,\overline {\!\Delta \!}\,}\cdot (A\;\textrm {mod}\;\zeta )=b\cdot \sigma ^\ast ({\,\overline {\!\Delta \!}\,})$
in
![]() $G\big ({\,\overline {\!B}}(\kern-0.15em( z)\kern-0.15em)\big )$
. Then there is a unique
$G\big ({\,\overline {\!B}}(\kern-0.15em( z)\kern-0.15em)\big )$
. Then there is a unique
![]() $\Delta \in G\big (B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{t_{\scriptscriptstyle -}}]\big )$
with
$\Delta \in G\big (B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{t_{\scriptscriptstyle -}}]\big )$
with
![]() $\Delta \;\textrm {mod}\;\zeta ={\,\overline {\!\Delta \!}\,}$
and
$\Delta \;\textrm {mod}\;\zeta ={\,\overline {\!\Delta \!}\,}$
and
![]() $\Delta \cdot A=b\cdot \sigma ^\ast (\Delta )$
in
$\Delta \cdot A=b\cdot \sigma ^\ast (\Delta )$
in
![]() $G\big (B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{t_{\scriptscriptstyle -}}]\big )$
.
$G\big (B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{t_{\scriptscriptstyle -}}]\big )$
.
Proof. We choose a faithful representation
![]() $\rho \colon G\hookrightarrow \operatorname {\mathrm {GL}}_{r,{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}$
over
$\rho \colon G\hookrightarrow \operatorname {\mathrm {GL}}_{r,{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}$
over
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
. There is a positive integer N such that
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
. There is a positive integer N such that
![]() $\rho (b),\rho (b^{-1})\in M_r\big (z^{-N}{\mathbb {F}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\big )$
, as well as
$\rho (b),\rho (b^{-1})\in M_r\big (z^{-N}{\mathbb {F}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\big )$
, as well as
![]() $\rho (A),\rho (A^{-1})\in M_r\big ((z-\zeta )^{-N}B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\big )$
, and
$\rho (A),\rho (A^{-1})\in M_r\big ((z-\zeta )^{-N}B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\big )$
, and
![]() $\rho ({\,\overline {\!\Delta \!}\,}),\rho ({\,\overline {\!\Delta \!}\,}^{-1})\in M_r\big (z^{-2N}{\,\overline {\!B}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\big )$
. We choose
$\rho ({\,\overline {\!\Delta \!}\,}),\rho ({\,\overline {\!\Delta \!}\,}^{-1})\in M_r\big (z^{-2N}{\,\overline {\!B}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\big )$
. We choose
![]() $C_0,D_0\in M_r\big (z^{-2N}B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\big )$
with
$C_0,D_0\in M_r\big (z^{-2N}B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\big )$
with
![]() $C_0\equiv \rho ({\,\overline {\!\Delta \!}\,})\ \pmod {\zeta }$
and
$C_0\equiv \rho ({\,\overline {\!\Delta \!}\,})\ \pmod {\zeta }$
and
![]() $D_0\equiv \rho ({\,\overline {\!\Delta \!}\,}^{-1})\ \pmod {\zeta }$
. For
$D_0\equiv \rho ({\,\overline {\!\Delta \!}\,}^{-1})\ \pmod {\zeta }$
. For
![]() $m>0$
we inductively define
$m>0$
we inductively define
 $$ \begin{align*} C_m&:=(z^{-N}\rho(b))\sigma^{*}C_{m-1}((z-\zeta)^N\rho(A^{-1}))\\[2mm] D_m&:=((z-\zeta)^N\rho(A))\sigma^{*}D_{m-1}( z^{-N}\rho(b^{-1})) \end{align*} $$
$$ \begin{align*} C_m&:=(z^{-N}\rho(b))\sigma^{*}C_{m-1}((z-\zeta)^N\rho(A^{-1}))\\[2mm] D_m&:=((z-\zeta)^N\rho(A))\sigma^{*}D_{m-1}( z^{-N}\rho(b^{-1})) \end{align*} $$
in
![]() $M_r\big (z^{-2N(m+1)}B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\big )$
. The assumption on
$M_r\big (z^{-2N(m+1)}B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\big )$
. The assumption on
![]() $\bar \Delta $
implies
$\bar \Delta $
implies
By induction on m, we obtain that
 $$ \begin{align*} C_{m+1}- C_m & = (z^{-N}\rho(b))\sigma^{*}(C_m-C_{m-1})((z-\zeta)^N\rho(A^{-1})) \\[2mm] & \equiv 0 \ \pmod{\sigma^*(\sigma^{m-1})^{*}(\zeta)} \\[2mm] & \equiv 0 \ \pmod{(\sigma^{m})^{*}(\zeta)}\,. \end{align*} $$
$$ \begin{align*} C_{m+1}- C_m & = (z^{-N}\rho(b))\sigma^{*}(C_m-C_{m-1})((z-\zeta)^N\rho(A^{-1})) \\[2mm] & \equiv 0 \ \pmod{\sigma^*(\sigma^{m-1})^{*}(\zeta)} \\[2mm] & \equiv 0 \ \pmod{(\sigma^{m})^{*}(\zeta)}\,. \end{align*} $$
Therefore, the sequence
![]() $(C_m)_m$
converges to a matrix
$(C_m)_m$
converges to a matrix
![]() $C\in M_r\big (B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}\big )$
and the sequence
$C\in M_r\big (B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}\big )$
and the sequence
![]() $\big (\prod _{i=0}^m(1-\tfrac {\zeta ^{q^i}}{z})^{-N}\cdot C_m\big )_m$
converges to the matrix
$\big (\prod _{i=0}^m(1-\tfrac {\zeta ^{q^i}}{z})^{-N}\cdot C_m\big )_m$
converges to the matrix
![]() $t_{\scriptscriptstyle -}^{-N}\cdot C\in M_r\big (B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{t_{\scriptscriptstyle -}}]\big )$
with
$t_{\scriptscriptstyle -}^{-N}\cdot C\in M_r\big (B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{t_{\scriptscriptstyle -}}]\big )$
with
![]() $(t_{\scriptscriptstyle -}^{-N}C)\equiv C\equiv \rho ({\,\overline {\!\Delta \!}\,})\ \pmod {\zeta }$
. The equation
$(t_{\scriptscriptstyle -}^{-N}C)\equiv C\equiv \rho ({\,\overline {\!\Delta \!}\,})\ \pmod {\zeta }$
. The equation
 $$ \begin{align*} \prod_{i=0}^m(1-\tfrac{\zeta^{q^i}}{z})^{-N}\cdot C_m\cdot \rho(A) \;=\; \rho(b)\cdot\sigma^\ast\left(\prod_{i=0}^{m-1}(1-\tfrac{\zeta^{q^i}}{z})^{-N}\cdot C_{m-1}\right) \end{align*} $$
$$ \begin{align*} \prod_{i=0}^m(1-\tfrac{\zeta^{q^i}}{z})^{-N}\cdot C_m\cdot \rho(A) \;=\; \rho(b)\cdot\sigma^\ast\left(\prod_{i=0}^{m-1}(1-\tfrac{\zeta^{q^i}}{z})^{-N}\cdot C_{m-1}\right) \end{align*} $$
implies
![]() $(t_{\scriptscriptstyle -}^{-N}C)\rho (A)=\rho (b)\sigma ^\ast (t_{\scriptscriptstyle -}^{-N}C)$
in
$(t_{\scriptscriptstyle -}^{-N}C)\rho (A)=\rho (b)\sigma ^\ast (t_{\scriptscriptstyle -}^{-N}C)$
in
![]() $M_r\big (B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{t_{\scriptscriptstyle -}}]\big )$
. In the same way, one sees that
$M_r\big (B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{t_{\scriptscriptstyle -}}]\big )$
. In the same way, one sees that
![]() $(D_m)_m$
converges to a matrix
$(D_m)_m$
converges to a matrix
![]() $D\in M_r\big (B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}\big )$
with
$D\in M_r\big (B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}\big )$
with
![]() $(t_{\scriptscriptstyle -}^{-N}D)\rho (b)=\rho (A)\sigma ^\ast (t_{\scriptscriptstyle -}^{-N}D)$
in
$(t_{\scriptscriptstyle -}^{-N}D)\rho (b)=\rho (A)\sigma ^\ast (t_{\scriptscriptstyle -}^{-N}D)$
in
![]() $M_r\big (B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{t_{\scriptscriptstyle -}}]\big )$
and
$M_r\big (B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{t_{\scriptscriptstyle -}}]\big )$
and
![]() $(t_{\scriptscriptstyle -}^{-N}D)\;\textrm {mod}\;\zeta =\rho ({\,\overline {\!\Delta \!}\,}^{-1})$
. We obtain the congruences
$(t_{\scriptscriptstyle -}^{-N}D)\;\textrm {mod}\;\zeta =\rho ({\,\overline {\!\Delta \!}\,}^{-1})$
. We obtain the congruences
 $$ \begin{align*} \operatorname{\mathrm{Id}}_r-t_{\scriptscriptstyle -}^{-2N}CD & \equiv 0\ \pmod{\zeta}\quad \text{and by induction}\\[2mm] \operatorname{\mathrm{Id}}_r-t_{\scriptscriptstyle -}^{-2N}CD & = \rho(b)\cdot\sigma^\ast(\operatorname{\mathrm{Id}}_r-t_{\scriptscriptstyle -}^{-2N}CD)\rho(b)^{-1} \enspace\equiv\enspace 0\ \pmod{\zeta^{q^m}} \quad\text{for all } m\,. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Id}}_r-t_{\scriptscriptstyle -}^{-2N}CD & \equiv 0\ \pmod{\zeta}\quad \text{and by induction}\\[2mm] \operatorname{\mathrm{Id}}_r-t_{\scriptscriptstyle -}^{-2N}CD & = \rho(b)\cdot\sigma^\ast(\operatorname{\mathrm{Id}}_r-t_{\scriptscriptstyle -}^{-2N}CD)\rho(b)^{-1} \enspace\equiv\enspace 0\ \pmod{\zeta^{q^m}} \quad\text{for all } m\,. \end{align*} $$
By looking at power series expansions in z of the matrix coefficients, these congruences imply by the separatedness of the norm
![]() $|\,.\,|$
that
$|\,.\,|$
that
![]() $(t_{\scriptscriptstyle -}^{-N}C)(t_{\scriptscriptstyle -}^{-N}D)=\operatorname {\mathrm {Id}}_r$
; that is,
$(t_{\scriptscriptstyle -}^{-N}C)(t_{\scriptscriptstyle -}^{-N}D)=\operatorname {\mathrm {Id}}_r$
; that is,
![]() $t_{\scriptscriptstyle -}^{-N}C\in \operatorname {\mathrm {GL}}_r\big (B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{t_{\scriptscriptstyle -}}]\big )$
. Because
$t_{\scriptscriptstyle -}^{-N}C\in \operatorname {\mathrm {GL}}_r\big (B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{t_{\scriptscriptstyle -}}]\big )$
. Because
![]() $(\sigma ^{m*}C)\;\textrm {mod}\;\zeta ^{q^m}=\sigma ^{m*}(C\;\textrm {mod}\;\zeta )=\rho (\sigma ^{m*}{\,\overline {\!\Delta \!}\,})$
, it follows that
$(\sigma ^{m*}C)\;\textrm {mod}\;\zeta ^{q^m}=\sigma ^{m*}(C\;\textrm {mod}\;\zeta )=\rho (\sigma ^{m*}{\,\overline {\!\Delta \!}\,})$
, it follows that
 $$ \begin{align*} (t_{\scriptscriptstyle -}^{-N}C)\;\textrm{mod}\;\zeta^{q^m} & = \left(\prod_{i=0}^{m-1}(1-\tfrac{\zeta^{q^i}}{z})^{-N}\cdot C_{m-1}\right)\;\textrm{mod}\;\zeta^{q^m}\\[2mm] & = \rho\Big(b\cdot\ldots\cdot\sigma^{(m-1)*}(b)\cdot\sigma^{m*}({\,\overline{\!\Delta\!}\,})\cdot\sigma^{(m-1)*}(A^{-1})\cdot\ldots\cdot A^{-1}\Big)\;\textrm{mod}\;\zeta^{q^m} \end{align*} $$
$$ \begin{align*} (t_{\scriptscriptstyle -}^{-N}C)\;\textrm{mod}\;\zeta^{q^m} & = \left(\prod_{i=0}^{m-1}(1-\tfrac{\zeta^{q^i}}{z})^{-N}\cdot C_{m-1}\right)\;\textrm{mod}\;\zeta^{q^m}\\[2mm] & = \rho\Big(b\cdot\ldots\cdot\sigma^{(m-1)*}(b)\cdot\sigma^{m*}({\,\overline{\!\Delta\!}\,})\cdot\sigma^{(m-1)*}(A^{-1})\cdot\ldots\cdot A^{-1}\Big)\;\textrm{mod}\;\zeta^{q^m} \end{align*} $$
satisfies the equations that cut out the closed subgroup scheme
![]() $\rho (G)$
of
$\rho (G)$
of
![]() $\operatorname {\mathrm {GL}}_r$
. Because B is separated with respect to the norm
$\operatorname {\mathrm {GL}}_r$
. Because B is separated with respect to the norm
![]() $|\,.\,|$
, we must have
$|\,.\,|$
, we must have
![]() $t_{\scriptscriptstyle -}^{-N}C=\rho (\Delta )$
for a matrix
$t_{\scriptscriptstyle -}^{-N}C=\rho (\Delta )$
for a matrix
![]() $\Delta \in G\big (B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{t_{\scriptscriptstyle -}}]\big )$
.
$\Delta \in G\big (B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{t_{\scriptscriptstyle -}}]\big )$
.
Finally, to prove the uniqueness of
![]() $\Delta $
, we assume that
$\Delta $
, we assume that
![]() $\Delta ^{\prime }$
also satisfies the assertions of the lemma. Then
$\Delta ^{\prime }$
also satisfies the assertions of the lemma. Then
![]() $U:=\rho (\Delta )-\rho (\Delta ^{\prime })$
satisfies
$U:=\rho (\Delta )-\rho (\Delta ^{\prime })$
satisfies
![]() $U\in M_r(\zeta \cdot B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{t_{\scriptscriptstyle -}}]\big )$
and
$U\in M_r(\zeta \cdot B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{t_{\scriptscriptstyle -}}]\big )$
and
![]() $U=\rho (b)\cdot \sigma ^\ast (U)\cdot \rho (A^{-1})$
. Because B is separated with respect to the norm
$U=\rho (b)\cdot \sigma ^\ast (U)\cdot \rho (A^{-1})$
. Because B is separated with respect to the norm
![]() $|\,.\,|$
, it follows that
$|\,.\,|$
, it follows that
![]() $U=0$
and
$U=0$
and
![]() $\Delta ^{\prime }=\Delta $
.
$\Delta ^{\prime }=\Delta $
.
We can now define the period morphism as a morphism of
![]() $\breve E$
-analytic spaces
$\breve E$
-analytic spaces
as follows. Let S be an affinoid, strictly
![]() $\breve E$
-analytic space and let
$\breve E$
-analytic space and let
![]() $S\to ({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\textrm {an}}$
be a morphism of
$S\to ({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\textrm {an}}$
be a morphism of
![]() $\breve E$
-analytic spaces. With it we have to associate a uniquely determined morphism
$\breve E$
-analytic spaces. With it we have to associate a uniquely determined morphism
![]() $S\to \breve {\mathcal {H}}_{G,\hat {Z}}^{\textrm {an}}$
. Then the period morphism is obtained by glueing when S runs through an affinoid covering of
$S\to \breve {\mathcal {H}}_{G,\hat {Z}}^{\textrm {an}}$
. Then the period morphism is obtained by glueing when S runs through an affinoid covering of
![]() $({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\textrm {an}}$
.
$({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\textrm {an}}$
.
Before we proceed, we recall that an algebra B over
![]() $\breve R_{\hat Z}={\mathbb {F}}\mathrm {[}\kern-0.15em\mathrm {[}\xi \mathrm {]}\kern-0.15em\mathrm {]}$
is admissible in the sense of Raynaud [Reference Raynaud82] if it has no
$\breve R_{\hat Z}={\mathbb {F}}\mathrm {[}\kern-0.15em\mathrm {[}\xi \mathrm {]}\kern-0.15em\mathrm {]}$
is admissible in the sense of Raynaud [Reference Raynaud82] if it has no
![]() $\xi $
-torsion and is a quotient of an
$\xi $
-torsion and is a quotient of an
![]() $\breve R_{\hat Z}$
-algebra of the form
$\breve R_{\hat Z}$
-algebra of the form
 $$ \begin{align} \breve R_{\hat Z}\langle X_1,\ldots,X_s\rangle \;:=\;\left\{\,\sum_{{\underline{n}}\in{\mathbb{N}}_0^s}b_{{\underline{n}}}X_1^{n_1}\cdot\ldots\cdot X_s^{n_s}\colon b_{{\underline{n}}}\in\breve R_{\hat Z},\enspace \lim_{|{\underline{n}}|\to\infty}b_{{\underline{n}}}=0\,\right\}, \end{align} $$
$$ \begin{align} \breve R_{\hat Z}\langle X_1,\ldots,X_s\rangle \;:=\;\left\{\,\sum_{{\underline{n}}\in{\mathbb{N}}_0^s}b_{{\underline{n}}}X_1^{n_1}\cdot\ldots\cdot X_s^{n_s}\colon b_{{\underline{n}}}\in\breve R_{\hat Z},\enspace \lim_{|{\underline{n}}|\to\infty}b_{{\underline{n}}}=0\,\right\}, \end{align} $$
where
![]() ${\underline {n}}=(n_1,\ldots ,n_s)$
and
${\underline {n}}=(n_1,\ldots ,n_s)$
and
![]() $|{\underline {n}}|:=n_1+\ldots +n_s$
. A formal
$|{\underline {n}}|:=n_1+\ldots +n_s$
. A formal
![]() $\breve R_{\hat Z}$
-scheme
$\breve R_{\hat Z}$
-scheme
![]() ${\mathscr {S}}$
is admissible if it is locally
${\mathscr {S}}$
is admissible if it is locally
![]() $\breve R_{\hat Z}$
-isomorphic to
$\breve R_{\hat Z}$
-isomorphic to
![]() $\operatorname {\mathrm {Spf}} B$
for admissible
$\operatorname {\mathrm {Spf}} B$
for admissible
![]() $\breve R_{\hat Z}$
-algebras B; see [Reference Bosch and Lütkebohmert18, § 1].
$\breve R_{\hat Z}$
-algebras B; see [Reference Bosch and Lütkebohmert18, § 1].
Recall that
![]() $({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\textrm {an}}$
is constructed as the union of the strictly
$({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\textrm {an}}$
is constructed as the union of the strictly
![]() $\breve E$
-analytic spaces associated with a family of admissible formal
$\breve E$
-analytic spaces associated with a family of admissible formal
![]() $\breve R_{\hat Z}$
-schemes, which are obtained by admissible formal blowing-ups of
$\breve R_{\hat Z}$
-schemes, which are obtained by admissible formal blowing-ups of
![]() ${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
in closed ideals; see [Reference Rapoport and Zink80, Chapter 5] or [Reference Berthelot13, § 0.2]. By Raynaud’s theorem, the morphism
${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
in closed ideals; see [Reference Rapoport and Zink80, Chapter 5] or [Reference Berthelot13, § 0.2]. By Raynaud’s theorem, the morphism
![]() $S\to ({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\textrm {an}}$
is induced by a morphism from a quasi-compact admissible formal
$S\to ({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\textrm {an}}$
is induced by a morphism from a quasi-compact admissible formal
![]() $\breve R_{\hat Z}$
-scheme
$\breve R_{\hat Z}$
-scheme
![]() ${\mathscr {S}}$
with
${\mathscr {S}}$
with
![]() ${\mathscr {S}}^{\textrm {an}}=S$
to one of these admissible formal
${\mathscr {S}}^{\textrm {an}}=S$
to one of these admissible formal
![]() $\breve R_{\hat Z}$
-schemes; see [Reference Bosch and Lütkebohmert18, Theorem 4.1] or, for example, [Reference Hartl50, Theorem A.2.5] for a formulation with Berkovich spaces. Composing with the map to
$\breve R_{\hat Z}$
-schemes; see [Reference Bosch and Lütkebohmert18, Theorem 4.1] or, for example, [Reference Hartl50, Theorem A.2.5] for a formulation with Berkovich spaces. Composing with the map to
![]() ${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
yields a morphism of formal schemes
${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
yields a morphism of formal schemes
![]() ${\mathscr {S}}\to {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
. The latter corresponds to
${\mathscr {S}}\to {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
. The latter corresponds to
![]() $({\underline {{\mathcal {G}}}},\bar \delta )\in {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}({\mathscr {S}})$
.
$({\underline {{\mathcal {G}}}},\bar \delta )\in {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}({\mathscr {S}})$
.
Lemma 6.2. There is an étale covering
![]() ${\mathscr {S}}^{\prime }=\operatorname {\mathrm {Spf}} B^{\prime }\to {\mathscr {S}}$
of admissible formal
${\mathscr {S}}^{\prime }=\operatorname {\mathrm {Spf}} B^{\prime }\to {\mathscr {S}}$
of admissible formal
![]() $\breve R_{\hat Z}$
-schemes such that there is a trivialisation
$\breve R_{\hat Z}$
-schemes such that there is a trivialisation
![]() for some
for some
![]() $A\in G\big (B^{\prime }\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z-\zeta }]\big )$
.
$A\in G\big (B^{\prime }\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z-\zeta }]\big )$
.
Proof. We may choose an étale covering
![]() ${\,\overline {\!{\mathscr {S}}}}^{\prime }$
of
${\,\overline {\!{\mathscr {S}}}}^{\prime }$
of
![]() ${\,\overline {\!{\mathscr {S}}}}:=\operatorname {\mathrm {V}}_{\mathscr {S}}(\zeta )$
together with a trivialisation
${\,\overline {\!{\mathscr {S}}}}:=\operatorname {\mathrm {V}}_{\mathscr {S}}(\zeta )$
together with a trivialisation
![]() . After refining the covering
. After refining the covering
![]() ${\,\overline {\!{\mathscr {S}}}}^{\prime }$
, there is by [Reference Bosch and Lütkebohmert19, Lemma 1.4(a)] an étale morphism
${\,\overline {\!{\mathscr {S}}}}^{\prime }$
, there is by [Reference Bosch and Lütkebohmert19, Lemma 1.4(a)] an étale morphism
![]() ${\mathscr {S}}^{\prime }\to {\mathscr {S}}$
of admissible formal
${\mathscr {S}}^{\prime }\to {\mathscr {S}}$
of admissible formal
![]() $\breve R_{\hat Z}$
-schemes lifting
$\breve R_{\hat Z}$
-schemes lifting
![]() ${\,\overline {\!{\mathscr {S}}}}^{\prime }\to {\,\overline {\!{\mathscr {S}}}}$
. Because
${\,\overline {\!{\mathscr {S}}}}^{\prime }\to {\,\overline {\!{\mathscr {S}}}}$
. Because
![]() ${\mathscr {S}}$
is quasi-compact, we may further assume that
${\mathscr {S}}$
is quasi-compact, we may further assume that
![]() ${\mathscr {S}}^{\prime }=\operatorname {\mathrm {Spf}} B^{\prime }$
is affine. By [Reference Hartl and Viehmann56, Proposition 2.2(c)], there is a lift
${\mathscr {S}}^{\prime }=\operatorname {\mathrm {Spf}} B^{\prime }$
is affine. By [Reference Hartl and Viehmann56, Proposition 2.2(c)], there is a lift
![]() of the trivialisation
of the trivialisation
![]() $\bar \alpha $
. Because
$\bar \alpha $
. Because
![]() ${\underline {{\mathcal {G}}}}$
is bounded by
${\underline {{\mathcal {G}}}}$
is bounded by
![]() $\hat {Z}^{-1}$
, this lift induces an isomorphism
$\hat {Z}^{-1}$
, this lift induces an isomorphism
![]() for
for
![]() $A\in G\big (B^{\prime }\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z-\zeta }]\big )$
; compare the proof of Proposition 2.6(a).
$A\in G\big (B^{\prime }\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z-\zeta }]\big )$
; compare the proof of Proposition 2.6(a).
In addition, the quasi-isogeny
![]() $\bar \delta \colon {\underline {{\mathcal {G}}}}_{{\,\overline {\!{\mathscr {S}}}}^{\prime }}\to {\underline {{\mathbb {G}}}}_{0,{\,\overline {\!{\mathscr {S}}}}^{\prime }}$
corresponds under
$\bar \delta \colon {\underline {{\mathcal {G}}}}_{{\,\overline {\!{\mathscr {S}}}}^{\prime }}\to {\underline {{\mathbb {G}}}}_{0,{\,\overline {\!{\mathscr {S}}}}^{\prime }}$
corresponds under
![]() $\bar \alpha $
to an element
$\bar \alpha $
to an element
![]() ${\,\overline {\!\Delta \!}\,}\in LG({\,\overline {\!B}}^{\prime })$
. We apply Lemma 6.1 to obtain a uniquely determined element
${\,\overline {\!\Delta \!}\,}\in LG({\,\overline {\!B}}^{\prime })$
. We apply Lemma 6.1 to obtain a uniquely determined element
![]() $\Delta \in G\big (B^{\prime }\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{t_{\scriptscriptstyle -}}]\big )$
lifting
$\Delta \in G\big (B^{\prime }\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{t_{\scriptscriptstyle -}}]\big )$
lifting
![]() ${\,\overline {\!\Delta \!}\,}$
with
${\,\overline {\!\Delta \!}\,}$
with
![]() $\Delta A=b\,\sigma ^\ast (\Delta )$
for A as in Lemma 6.2. We set
$\Delta A=b\,\sigma ^\ast (\Delta )$
for A as in Lemma 6.2. We set
 $$ \begin{align} \gamma & := \sigma^\ast(\Delta)A^{-1}\cdot G\big(B^{\prime}[\tfrac{1}{\zeta}]\text{[}\kern-0.15em\text{[} z-\zeta\text{]}\kern-0.15em\text{]}\big)= b^{-1}\Delta\cdot G\big(B^{\prime}[\tfrac{1}{\zeta}]\text{[}\kern-0.15em\text{[} z-\zeta\text{]}\kern-0.15em\text{]}\big)\\[2mm] & \in G\big(B^{\prime}[\tfrac{1}{\zeta}](\kern-0.15em( z -\zeta)\kern-0.15em)\big)\big/G\big(B^{\prime}[\tfrac{1}{\zeta}]\text{[}\kern-0.15em\text{[} z-\zeta\text{]}\kern-0.15em\text{]}\big)\,.\nonumber \end{align} $$
$$ \begin{align} \gamma & := \sigma^\ast(\Delta)A^{-1}\cdot G\big(B^{\prime}[\tfrac{1}{\zeta}]\text{[}\kern-0.15em\text{[} z-\zeta\text{]}\kern-0.15em\text{]}\big)= b^{-1}\Delta\cdot G\big(B^{\prime}[\tfrac{1}{\zeta}]\text{[}\kern-0.15em\text{[} z-\zeta\text{]}\kern-0.15em\text{]}\big)\\[2mm] & \in G\big(B^{\prime}[\tfrac{1}{\zeta}](\kern-0.15em( z -\zeta)\kern-0.15em)\big)\big/G\big(B^{\prime}[\tfrac{1}{\zeta}]\text{[}\kern-0.15em\text{[} z-\zeta\text{]}\kern-0.15em\text{]}\big)\,.\nonumber \end{align} $$
Because
![]() ${\underline {{\mathcal {G}}}}$
is bounded by
${\underline {{\mathcal {G}}}}$
is bounded by
![]() $\hat {Z}^{-1}$
, the inverse
$\hat {Z}^{-1}$
, the inverse
![]() $A^{-1}$
yields a point of
$A^{-1}$
yields a point of
![]() $\hat Z^{\textrm {an}}({\mathscr {S}}^{\prime }{}^{\textrm {an}})=\breve {\mathcal {H}}_{G,\hat {Z}}^{\textrm {an}}({\mathscr {S}}^{\prime }{}^{\textrm {an}})$
. Because
$\hat Z^{\textrm {an}}({\mathscr {S}}^{\prime }{}^{\textrm {an}})=\breve {\mathcal {H}}_{G,\hat {Z}}^{\textrm {an}}({\mathscr {S}}^{\prime }{}^{\textrm {an}})$
. Because
![]() $\sigma ^\ast (\Delta )\in G\big (B^{\prime }\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{\sigma ^\ast t_{\scriptscriptstyle -}}]\big )$
and
$\sigma ^\ast (\Delta )\in G\big (B^{\prime }\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{\sigma ^\ast t_{\scriptscriptstyle -}}]\big )$
and
![]() $\sigma ^\ast t_{\scriptscriptstyle -}\in B^{\prime }[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}^{\scriptscriptstyle \times }$
, we have
$\sigma ^\ast t_{\scriptscriptstyle -}\in B^{\prime }[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}^{\scriptscriptstyle \times }$
, we have
using (6.2) and Definition 2.2(b)(v). If we replace our trivialisation
![]() $\alpha $
by a different trivialisation
$\alpha $
by a different trivialisation
![]() , there is an
, there is an
![]() $h\in L^+G(B^{\prime })=G\big (B^{\prime }\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\big )\subset G(B^{\prime }[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]})$
with
$h\in L^+G(B^{\prime })=G\big (B^{\prime }\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\big )\subset G(B^{\prime }[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]})$
with
![]() $\alpha ^{\prime }=h\cdot \alpha $
and
$\alpha ^{\prime }=h\cdot \alpha $
and
![]() $A^{\prime }=hA\,\sigma ^\ast (h)^{-1}$
. Then the quasi-isogeny
$A^{\prime }=hA\,\sigma ^\ast (h)^{-1}$
. Then the quasi-isogeny
![]() $\bar \delta $
corresponds to
$\bar \delta $
corresponds to
![]() ${\,\overline {\!\Delta \!}\,}^{\prime }={\,\overline {\!\Delta \!}\,} h^{-1}\in LG({\,\overline {\!B}}^{\prime })$
and
${\,\overline {\!\Delta \!}\,}^{\prime }={\,\overline {\!\Delta \!}\,} h^{-1}\in LG({\,\overline {\!B}}^{\prime })$
and
![]() $\Delta ^{\prime }=\Delta h^{-1}$
is the lift of
$\Delta ^{\prime }=\Delta h^{-1}$
is the lift of
![]() ${\,\overline {\!\Delta \!}\,}^{\prime }$
from Lemma 6.1. This yields
${\,\overline {\!\Delta \!}\,}^{\prime }$
from Lemma 6.1. This yields
Therefore,
![]() $\gamma $
descends to an element
$\gamma $
descends to an element
![]() $\gamma \in \breve {\mathcal {H}}_{G,\hat {Z}}^{\textrm {an}}(S)$
giving the desired morphism
$\gamma \in \breve {\mathcal {H}}_{G,\hat {Z}}^{\textrm {an}}(S)$
giving the desired morphism
![]() $S\to \breve {\mathcal {H}}_{G,\hat {Z}}^{\textrm {an}}$
. This completes the construction of the period morphism.
$S\to \breve {\mathcal {H}}_{G,\hat {Z}}^{\textrm {an}}$
. This completes the construction of the period morphism.
Definition 6.3. The morphism
![]() $\breve \pi \colon ({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\textrm {an}}\to \breve {\mathcal {H}}_{G,\hat {Z}}^{\textrm {an}}$
of
$\breve \pi \colon ({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\textrm {an}}\to \breve {\mathcal {H}}_{G,\hat {Z}}^{\textrm {an}}$
of
![]() $\breve E$
-analytic spaces constructed above is called the period morphism associated with
$\breve E$
-analytic spaces constructed above is called the period morphism associated with
![]() ${\underline {{\mathbb {G}}}}_0$
and
${\underline {{\mathbb {G}}}}_0$
and
![]() $\hat Z$
.
$\hat Z$
.
Remark 6.4. If
![]() $G=\operatorname {\mathrm {GL}}_r$
and B is an admissible
$G=\operatorname {\mathrm {GL}}_r$
and B is an admissible
![]() ${\mathbb {F}}\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
-algebra in the sense of Raynaud, there is an equivalence [Reference Hartl and Viehmann56, § 4] between local
${\mathbb {F}}\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
-algebra in the sense of Raynaud, there is an equivalence [Reference Hartl and Viehmann56, § 4] between local
![]() $\operatorname {\mathrm {GL}}_r$
-shtukas and local shtukas
$\operatorname {\mathrm {GL}}_r$
-shtukas and local shtukas
![]() ${\underline {M\!}\,}=(M,\tau _M)$
over
${\underline {M\!}\,}=(M,\tau _M)$
over
![]() ${\mathscr {S}}=\operatorname {\mathrm {Spf}} B$
consisting of a locally free
${\mathscr {S}}=\operatorname {\mathrm {Spf}} B$
consisting of a locally free
![]() $B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-module M of rank r and an isomorphism
$B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-module M of rank r and an isomorphism
. The de Rham cohomology
of
![]() ${\underline {M\!}\,}$
over
${\underline {M\!}\,}$
over
![]() ${\mathscr {S}}^{\textrm {an}}$
carries a natural Hodge-Pink structure
${\mathscr {S}}^{\textrm {an}}$
carries a natural Hodge-Pink structure
see [Reference Hartl, Kim, Böckle, Goss, Hartl and Papanikolas54, Definition 3.4.13]. If, moreover, there is a fixed local
![]() $\operatorname {\mathrm {GL}}_r$
-shtuka
$\operatorname {\mathrm {GL}}_r$
-shtuka
![]() ${\underline {{\mathbb {G}}}}_0$
over
${\underline {{\mathbb {G}}}}_0$
over
![]() ${\mathbb {F}}$
with associated local shtuka
${\mathbb {F}}$
with associated local shtuka
![]() $({\mathbb {M}},\tau _{\mathbb {M}})=({\mathbb {F}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}^r,b\sigma ^\ast )$
and a quasi-isogeny
$({\mathbb {M}},\tau _{\mathbb {M}})=({\mathbb {F}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}^r,b\sigma ^\ast )$
and a quasi-isogeny
![]() $\bar \delta \colon {\underline {{\mathcal {G}}}}_{\operatorname {\mathrm {Spec}} B/(\zeta )}\to {\underline {{\mathbb {G}}}}_{0,\operatorname {\mathrm {Spec}} B/(\zeta )}$
given by
$\bar \delta \colon {\underline {{\mathcal {G}}}}_{\operatorname {\mathrm {Spec}} B/(\zeta )}\to {\underline {{\mathbb {G}}}}_{0,\operatorname {\mathrm {Spec}} B/(\zeta )}$
given by
![]() ${\,\overline {\!\Delta \!}\,}\in LG\big (B/(\zeta )\big )$
, then the lift
${\,\overline {\!\Delta \!}\,}\in LG\big (B/(\zeta )\big )$
, then the lift
![]() $\Delta $
from Lemma 6.1 provides an isomorphism
$\Delta $
from Lemma 6.1 provides an isomorphism
that transports the Hodge-Pink structure
![]() ${\mathfrak {q}}^{\underline {M\!}\,}$
to the family
${\mathfrak {q}}^{\underline {M\!}\,}$
to the family
of Hodge-Pink structures on the constant z-isocrystal
![]() $\operatorname {\mathrm {H}}^1_{\textrm {cris}}\big ({\underline {{\mathbb {M}}}},{\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)\big )\,:=\,\sigma ^\ast {\underline {{\mathbb {M}}}}\otimes _{{\mathbb {F}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}{\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)$
; see [Reference Hartl, Kim, Böckle, Goss, Hartl and Papanikolas54, Definition 3.5.14]. Our period morphism
$\operatorname {\mathrm {H}}^1_{\textrm {cris}}\big ({\underline {{\mathbb {M}}}},{\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)\big )\,:=\,\sigma ^\ast {\underline {{\mathbb {M}}}}\otimes _{{\mathbb {F}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}{\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)$
; see [Reference Hartl, Kim, Böckle, Goss, Hartl and Papanikolas54, Definition 3.5.14]. Our period morphism
![]() $\breve \pi $
associates this family of Hodge-Pink structures with the universal local
$\breve \pi $
associates this family of Hodge-Pink structures with the universal local
![]() $\operatorname {\mathrm {GL}}_r$
-shtuka over
$\operatorname {\mathrm {GL}}_r$
-shtuka over
![]() ${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
. More precisely, this family equals
${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
. More precisely, this family equals
![]() $\gamma \cdot B[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}^r$
where the element
$\gamma \cdot B[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}^r$
where the element
![]() $\gamma $
from (6.4) is the image under
$\gamma $
from (6.4) is the image under
![]() $\breve \pi $
of the local
$\breve \pi $
of the local
![]() $\operatorname {\mathrm {GL}}_r$
-shtuka
$\operatorname {\mathrm {GL}}_r$
-shtuka
![]() $({\underline {M\!}\,},\bar \delta )\in {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}(\operatorname {\mathrm {Spf}} B)$
.
$({\underline {M\!}\,},\bar \delta )\in {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}(\operatorname {\mathrm {Spf}} B)$
.
Remark 6.5. The period morphism
![]() $\breve \pi $
is equivariant for the action of
$\breve \pi $
is equivariant for the action of
![]() $J:=J_b\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
. Indeed,
$J:=J_b\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
. Indeed,
![]() $j\in J$
acts on
$j\in J$
acts on
![]() ${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
by
${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
by
![]() $j\colon ({\underline {{\mathcal {G}}}},\bar \delta )\mapsto ({\underline {{\mathcal {G}}}},j\circ \bar \delta )$
. In terms of (6.4) this means that
$j\colon ({\underline {{\mathcal {G}}}},\bar \delta )\mapsto ({\underline {{\mathcal {G}}}},j\circ \bar \delta )$
. In terms of (6.4) this means that
![]() $j\in J\subset G\big ({\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)\big )$
sends
$j\in J\subset G\big ({\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)\big )$
sends
![]() $\Delta $
to
$\Delta $
to
![]() $j\cdot \Delta $
and
$j\cdot \Delta $
and
![]() $\gamma $
to
$\gamma $
to
![]() $\sigma ^\ast (j)\cdot \gamma $
. Thus, it coincides with the action on
$\sigma ^\ast (j)\cdot \gamma $
. Thus, it coincides with the action on
![]() $\breve {\mathcal {H}}_{G,\hat {Z}}^{\textrm {an}}$
defined in Remark 4.17.
$\breve {\mathcal {H}}_{G,\hat {Z}}^{\textrm {an}}$
defined in Remark 4.17.
Remark 6.6. As in the arithmetic case, these period morphisms are not compatible with Weil descent data of source and target. Here the source is equipped with the Weil descent datum induced by the one in Remark 3.3. On the target we have the natural Weil descent datum given by the fact that
![]() ${\mathcal {H}}_{G,\hat {Z}}^{\textrm {an}}$
is defined over
${\mathcal {H}}_{G,\hat {Z}}^{\textrm {an}}$
is defined over
![]() $E_{\hat {Z}}$
. In order to ensure such a compatibility, one has to extend the period morphism by a second component mapping to
$E_{\hat {Z}}$
. In order to ensure such a compatibility, one has to extend the period morphism by a second component mapping to
![]() $\pi _1(G)_{\Gamma }$
. For a more detailed discussion we refer to [Reference Rapoport and Zink80] or [Reference Rapoport and Viehmann79, Properties 4.27(iv)].
$\pi _1(G)_{\Gamma }$
. For a more detailed discussion we refer to [Reference Rapoport and Zink80] or [Reference Rapoport and Viehmann79, Properties 4.27(iv)].
Remark 6.7. In the above construction the bounded local G-shtuka
![]() $\big ((L^+G)_{{\mathscr {S}}^{\prime }},A\sigma ^\ast \big )$
over
$\big ((L^+G)_{{\mathscr {S}}^{\prime }},A\sigma ^\ast \big )$
over
![]() ${\mathscr {S}}^{\prime }$
with
${\mathscr {S}}^{\prime }$
with
![]() $A\in G\big (B^{\prime }\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z-\zeta }]\big )$
induces an étale local G-shtuka
$A\in G\big (B^{\prime }\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z-\zeta }]\big )$
induces an étale local G-shtuka
![]() $\big ((L^+G)_{S^{\prime }},A\sigma ^\ast \big )$
over
$\big ((L^+G)_{S^{\prime }},A\sigma ^\ast \big )$
over
![]() $S^{\prime }:=({\mathscr {S}}^{\prime })^{\textrm {an}}$
in the sense of Definition 6.8, because
$S^{\prime }:=({\mathscr {S}}^{\prime })^{\textrm {an}}$
in the sense of Definition 6.8, because
![]() $(z-\zeta )^{-1}=-\sum _{i=0}^\infty \zeta ^{-i-1}z^i\in {\mathcal {O}}_{S^{\prime }}(S^{\prime })\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
implies
$(z-\zeta )^{-1}=-\sum _{i=0}^\infty \zeta ^{-i-1}z^i\in {\mathcal {O}}_{S^{\prime }}(S^{\prime })\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
implies
![]() $B^{\prime }\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z-\zeta }]\subset {\mathcal {O}}_{S^{\prime }}(S^{\prime })\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
. The isomorphism
$B^{\prime }\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z-\zeta }]\subset {\mathcal {O}}_{S^{\prime }}(S^{\prime })\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
. The isomorphism
![]() yields a descent datum
yields a descent datum
![]() $g:=pr_2^*\alpha \circ pr_1^*\alpha ^{-1}\in L^+G({\mathscr {S}}^{\prime \prime })$
with
$g:=pr_2^*\alpha \circ pr_1^*\alpha ^{-1}\in L^+G({\mathscr {S}}^{\prime \prime })$
with
![]() $pr_2^*A\cdot \sigma ^\ast (g)=g\cdot pr_1^*A$
, where
$pr_2^*A\cdot \sigma ^\ast (g)=g\cdot pr_1^*A$
, where
![]() ${\mathscr {S}}^{\prime \prime }:={\mathscr {S}}^{\prime }\times _{\mathscr {S}}{\mathscr {S}}^{\prime }$
and
${\mathscr {S}}^{\prime \prime }:={\mathscr {S}}^{\prime }\times _{\mathscr {S}}{\mathscr {S}}^{\prime }$
and
![]() $pr_i\colon {\mathscr {S}}^{\prime \prime }\to {\mathscr {S}}^{\prime }$
is the projection onto the ith factor. Viewing
$pr_i\colon {\mathscr {S}}^{\prime \prime }\to {\mathscr {S}}^{\prime }$
is the projection onto the ith factor. Viewing
![]() $g\in L^+G(S^{\prime \prime })$
where
$g\in L^+G(S^{\prime \prime })$
where
![]() $S^{\prime \prime }:=({\mathscr {S}}^{\prime \prime })^{\textrm {an}}=S^{\prime }\times _S S^{\prime }$
provides a descent datum
$S^{\prime \prime }:=({\mathscr {S}}^{\prime \prime })^{\textrm {an}}=S^{\prime }\times _S S^{\prime }$
provides a descent datum
![]() on the
on the
![]() $L^+G$
-torsor
$L^+G$
-torsor
![]() $(L^+G)_{S^{\prime }}$
via multiplication by g on the right. This allows to descend
$(L^+G)_{S^{\prime }}$
via multiplication by g on the right. This allows to descend
![]() $\big ((L^+G)_{S^{\prime }},A\sigma ^\ast \big )$
to an étale local G-shtuka over
$\big ((L^+G)_{S^{\prime }},A\sigma ^\ast \big )$
to an étale local G-shtuka over
![]() $S={\mathscr {S}}^{\textrm {an}}$
, which by abuse of notation we denote again by
$S={\mathscr {S}}^{\textrm {an}}$
, which by abuse of notation we denote again by
![]() ${\underline {{\mathcal {G}}}}$
. In this way we obtain the universal family of étale local G-shtukas over
${\underline {{\mathcal {G}}}}$
. In this way we obtain the universal family of étale local G-shtukas over
![]() $({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\textrm {an}}$
.
$({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\textrm {an}}$
.
Definition 6.8. Let S be an
![]() ${\mathbb {F}}(\kern-0.15em(\zeta )\kern-0.15em)$
-scheme or a strictly
${\mathbb {F}}(\kern-0.15em(\zeta )\kern-0.15em)$
-scheme or a strictly
![]() ${\mathbb {F}}(\kern-0.15em(\zeta )\kern-0.15em)$
-analytic space. An étale local G-shtuka over S is a pair
${\mathbb {F}}(\kern-0.15em(\zeta )\kern-0.15em)$
-analytic space. An étale local G-shtuka over S is a pair
![]() ${\underline {{\mathcal {G}}}}=({\mathcal {G}},\tau _{\mathcal {G}})$
consisting of an
${\underline {{\mathcal {G}}}}=({\mathcal {G}},\tau _{\mathcal {G}})$
consisting of an
![]() $L^+G$
-torsor
$L^+G$
-torsor
![]() ${\mathcal {G}}$
on S and an isomorphism
${\mathcal {G}}$
on S and an isomorphism
![]() of
of
![]() $L^+G$
-torsors.
$L^+G$
-torsors.
Proposition 6.9. The period morphism factors through the open
![]() $\breve E$
-analytic subspace
$\breve E$
-analytic subspace
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^a$
.
$\breve {\mathcal {H}}_{G,\hat {Z},b}^a$
.
Proof. Let x be a point of
![]() $({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\textrm {an}}$
with values in a complete field extension L of
$({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\textrm {an}}$
with values in a complete field extension L of
![]() $\breve E$
and let
$\breve E$
and let
![]() $\gamma :=\breve \pi (x)\in \breve {\mathcal {H}}_{G,\hat {Z}}^{\textrm {an}}$
be its image under the period morphism. Then x corresponds to a pair
$\gamma :=\breve \pi (x)\in \breve {\mathcal {H}}_{G,\hat {Z}}^{\textrm {an}}$
be its image under the period morphism. Then x corresponds to a pair
![]() $({\underline {{\mathcal {G}}}},\bar \delta )\in {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}\!(\operatorname {\mathrm {Spf}}{\mathcal {O}}_L)$
where
$({\underline {{\mathcal {G}}}},\bar \delta )\in {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}\!(\operatorname {\mathrm {Spf}}{\mathcal {O}}_L)$
where
![]() ${\underline {{\mathcal {G}}}}$
is a local G-shtuka over the valuation ring
${\underline {{\mathcal {G}}}}$
is a local G-shtuka over the valuation ring
![]() ${\mathcal {O}}_L$
of L. Choose a faithful
${\mathcal {O}}_L$
of L. Choose a faithful
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-rational representation
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-rational representation
![]() $(\rho ,V)$
of G, and under the equivalence between local
$(\rho ,V)$
of G, and under the equivalence between local
![]() $\operatorname {\mathrm {GL}}(V)$
-shtukas and local shtukas from Remark 6.4 let
$\operatorname {\mathrm {GL}}(V)$
-shtukas and local shtukas from Remark 6.4 let
![]() ${\underline {M\!}\,}:=M(\rho _*{\underline {{\mathcal {G}}}})$
be the associated local shtuka over
${\underline {M\!}\,}:=M(\rho _*{\underline {{\mathcal {G}}}})$
be the associated local shtuka over
![]() ${\mathcal {O}}_L$
, and let
${\mathcal {O}}_L$
, and let
![]() $M(\rho _*\bar \delta )$
be the associated quasi-isogeny. By [Reference Hartl50, Proposition 2.4.4] the
$M(\rho _*\bar \delta )$
be the associated quasi-isogeny. By [Reference Hartl50, Proposition 2.4.4] the
![]() $\sigma $
-bundle
$\sigma $
-bundle
![]() ${\underline {{\mathcal {F}}\!}\,}_{b,\gamma }(V)$
is isomorphic to
${\underline {{\mathcal {F}}\!}\,}_{b,\gamma }(V)$
is isomorphic to
![]() ${\underline {M\!}\,}\otimes _{{\mathcal {O}}_L\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}L{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}$
and hence
${\underline {M\!}\,}\otimes _{{\mathcal {O}}_L\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}L{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}$
and hence
![]() ${\underline {{\mathcal {F}}\!}\,}_{b,\gamma }(V)\otimes _{L{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}}{\overline {L}}{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}\cong {\underline {{\mathcal {F}}\!}\,}_{0,1}{}^{\oplus \dim \rho }$
; see [Reference Hartl50, (Proof of) Theorem 2.4.7]. In other words,
${\underline {{\mathcal {F}}\!}\,}_{b,\gamma }(V)\otimes _{L{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}}{\overline {L}}{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}\cong {\underline {{\mathcal {F}}\!}\,}_{0,1}{}^{\oplus \dim \rho }$
; see [Reference Hartl50, (Proof of) Theorem 2.4.7]. In other words,
![]() $\gamma \in \breve {\mathcal {H}}_{G,\hat {Z},b}^a$
.
$\gamma \in \breve {\mathcal {H}}_{G,\hat {Z},b}^a$
.
Proposition 6.10. The period morphism
![]() $\breve \pi \colon ({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\textrm {an}}\to \breve {\mathcal {H}}_{G,\hat {Z},b}^a$
is étale.
$\breve \pi \colon ({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\textrm {an}}\to \breve {\mathcal {H}}_{G,\hat {Z},b}^a$
is étale.
For later use, we formulate one smaller step in the proof as a separate lemma.
Lemma 6.11.
![]() $({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\textrm {ad}}$
is separated and partially proper over
$({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\textrm {ad}}$
is separated and partially proper over
![]() $\breve E$
.
$\breve E$
.
Proof. The irreducible components of its special fibre are proper by Theorem 3.5. Thus, the lemma follows from [Reference Huber63, Remark 1.3.18].
Proof. Proof of Proposition 6.10
Let
![]() $\breve \pi ^{\textrm {rig}}\colon ({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\textrm {rig}}\rightarrow (\breve {\mathcal {H}}_{G,\hat {Z},b}^a)^{\textrm {rig}}$
be the associated morphism of rigid analytic spaces and let
$\breve \pi ^{\textrm {rig}}\colon ({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\textrm {rig}}\rightarrow (\breve {\mathcal {H}}_{G,\hat {Z},b}^a)^{\textrm {rig}}$
be the associated morphism of rigid analytic spaces and let
![]() $\breve \pi ^{\textrm {ad}}\colon ({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\textrm {ad}}\rightarrow (\breve {\mathcal {H}}_{G,\hat {Z},b}^a)^{\textrm {ad}}$
be the associated morphism of adic spaces in the sense of Huber [Reference Huber63]. By [Reference Huber63, Assertion (a) on p. 427], the morphism
$\breve \pi ^{\textrm {ad}}\colon ({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\textrm {ad}}\rightarrow (\breve {\mathcal {H}}_{G,\hat {Z},b}^a)^{\textrm {ad}}$
be the associated morphism of adic spaces in the sense of Huber [Reference Huber63]. By [Reference Huber63, Assertion (a) on p. 427], the morphism
![]() $\breve \pi $
is étale if and only if
$\breve \pi $
is étale if and only if
![]() $\breve \pi ^{\textrm {ad}}$
is étale and partially proper. The subspace
$\breve \pi ^{\textrm {ad}}$
is étale and partially proper. The subspace
![]() $(\breve {\mathcal {H}}_{G,\hat {Z},b}^a)^{\textrm {ad}}\subset (\breve {\mathcal {H}}_{G,\hat {Z}})^{\textrm {ad}}$
is open by Theorem 4.20 and [Reference Huber63, Assertion (1) on p. 431]. Therefore,
$(\breve {\mathcal {H}}_{G,\hat {Z},b}^a)^{\textrm {ad}}\subset (\breve {\mathcal {H}}_{G,\hat {Z}})^{\textrm {ad}}$
is open by Theorem 4.20 and [Reference Huber63, Assertion (1) on p. 431]. Therefore,
![]() $(\breve {\mathcal {H}}_{G,\hat {Z},b}^a)^{\textrm {ad}}$
is separated over
$(\breve {\mathcal {H}}_{G,\hat {Z},b}^a)^{\textrm {ad}}$
is separated over
![]() $\breve E$
by [Reference Huber63, Lemma 1.10.17]. So by [Reference Huber63, Lemma 1.10.17(vi)] and the above lemma,
$\breve E$
by [Reference Huber63, Lemma 1.10.17]. So by [Reference Huber63, Lemma 1.10.17(vi)] and the above lemma,
![]() $\breve \pi ^{\textrm {ad}}$
is partially proper.
$\breve \pi ^{\textrm {ad}}$
is partially proper.
It remains to show that
![]() $\breve \pi ^{\textrm {ad}}$
is étale. By [Reference Huber63, Proposition 1.7.11], this is equivalent to
$\breve \pi ^{\textrm {ad}}$
is étale. By [Reference Huber63, Proposition 1.7.11], this is equivalent to
![]() $\breve \pi ^{\textrm {rig}}$
being étale. So by [Reference Bosch, Lütkebohmert and Raynaud21, Proposition 2.4] we must show that for any admissible
$\breve \pi ^{\textrm {rig}}$
being étale. So by [Reference Bosch, Lütkebohmert and Raynaud21, Proposition 2.4] we must show that for any admissible
![]() $\breve R_{\hat Z}$
-algebra B in the sense of Raynaud and for any ideal
$\breve R_{\hat Z}$
-algebra B in the sense of Raynaud and for any ideal
![]() $I\subset B$
with
$I\subset B$
with
![]() $I^2=0$
and any commutative diagram with solid arrows
$I^2=0$
and any commutative diagram with solid arrows

there is a unique dashed arrow f making the diagram commutative. We set
![]() ${\mathscr {S}}:=\operatorname {\mathrm {Spf}} B$
, as well as
${\mathscr {S}}:=\operatorname {\mathrm {Spf}} B$
, as well as
![]() $B_0:=B/I$
and
$B_0:=B/I$
and
![]() ${\mathscr {S}}_0:=\operatorname {\mathrm {Spf}} B_0$
. We will construct f as a morphism
${\mathscr {S}}_0:=\operatorname {\mathrm {Spf}} B_0$
. We will construct f as a morphism
![]() ${\mathscr {S}}\to {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
after replacing
${\mathscr {S}}\to {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
after replacing
![]() ${\mathscr {S}}$
by an admissible blowing-up. Note that every admissible blowing-up of
${\mathscr {S}}$
by an admissible blowing-up. Note that every admissible blowing-up of
![]() ${\mathscr {S}}_0$
is induced by an admissible blowing-up of
${\mathscr {S}}_0$
is induced by an admissible blowing-up of
![]() ${\mathscr {S}}$
. Moreover, in the course of the proof we may replace S by a quasi-compact, quasi-separated, étale covering
${\mathscr {S}}$
. Moreover, in the course of the proof we may replace S by a quasi-compact, quasi-separated, étale covering
![]() $S^{\prime }\to S$
. Namely, by [Reference Bosch and Lütkebohmert19, Corollaries 5.10 and 5.4], every such covering is obtained from a quasi-compact morphism
$S^{\prime }\to S$
. Namely, by [Reference Bosch and Lütkebohmert19, Corollaries 5.10 and 5.4], every such covering is obtained from a quasi-compact morphism
![]() ${\mathscr {S}}^{\prime }\to {\mathscr {S}}$
of formal schemes that is faithfully flat after replacing
${\mathscr {S}}^{\prime }\to {\mathscr {S}}$
of formal schemes that is faithfully flat after replacing
![]() ${\mathscr {S}}$
by an admissible blowing-up. By the uniqueness assertion for f it suffices to construct f over
${\mathscr {S}}$
by an admissible blowing-up. By the uniqueness assertion for f it suffices to construct f over
![]() ${\mathscr {S}}^{\prime }$
and descend it back to
${\mathscr {S}}^{\prime }$
and descend it back to
![]() ${\mathscr {S}}$
.
${\mathscr {S}}$
.
After replacing
![]() ${\mathscr {S}}$
by an admissible blowing-up, the morphism
${\mathscr {S}}$
by an admissible blowing-up, the morphism
![]() $f_0$
extends to
$f_0$
extends to
![]() $f_0\colon {\mathscr {S}}_0\to {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
and corresponds to a pair
$f_0\colon {\mathscr {S}}_0\to {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
and corresponds to a pair
![]() $({\underline {{\mathcal {G}}}}_0,\bar \delta _0)\in {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}({\mathscr {S}}_0)$
where
$({\underline {{\mathcal {G}}}}_0,\bar \delta _0)\in {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}({\mathscr {S}}_0)$
where
![]() ${\underline {{\mathcal {G}}}}_0$
is a local G-shtuka over
${\underline {{\mathcal {G}}}}_0$
is a local G-shtuka over
![]() ${\mathscr {S}}_0$
. By Lemma 6.2 we may replace
${\mathscr {S}}_0$
. By Lemma 6.2 we may replace
![]() ${\mathscr {S}}_0$
by an étale covering such that
${\mathscr {S}}_0$
by an étale covering such that
![]() ${\underline {{\mathcal {G}}}}_0\cong \big ((L^+G)_{{\mathscr {S}}_0},A_0\sigma ^\ast \big )$
for some
${\underline {{\mathcal {G}}}}_0\cong \big ((L^+G)_{{\mathscr {S}}_0},A_0\sigma ^\ast \big )$
for some
![]() $A_0\in G\big (B_0\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z-\zeta }]\big )$
. By [Reference Grothendieck45, Théorème I.8.3], this étale covering lifts uniquely to an étale covering of
$A_0\in G\big (B_0\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z-\zeta }]\big )$
. By [Reference Grothendieck45, Théorème I.8.3], this étale covering lifts uniquely to an étale covering of
![]() ${\mathscr {S}}$
. The quasi-isogeny
${\mathscr {S}}$
. The quasi-isogeny
![]() $\bar \delta _0\colon {\underline {{\mathcal {G}}}}_{0,{\,\overline {\!{\mathscr {S}}}}_0}\to {\underline {{\mathbb {G}}}}_{0,{\,\overline {\!{\mathscr {S}}}}_0}$
over
$\bar \delta _0\colon {\underline {{\mathcal {G}}}}_{0,{\,\overline {\!{\mathscr {S}}}}_0}\to {\underline {{\mathbb {G}}}}_{0,{\,\overline {\!{\mathscr {S}}}}_0}$
over
![]() ${\,\overline {\!{\mathscr {S}}}}_0:=\operatorname {\mathrm {Spec}} B_0/(\zeta )$
corresponds to an element
${\,\overline {\!{\mathscr {S}}}}_0:=\operatorname {\mathrm {Spec}} B_0/(\zeta )$
corresponds to an element
![]() ${\,\overline {\!\Delta \!}\,}_0\in LG\big (B_0/(\zeta )\big )$
that lifts by Lemma 6.1 to a unique
${\,\overline {\!\Delta \!}\,}_0\in LG\big (B_0/(\zeta )\big )$
that lifts by Lemma 6.1 to a unique
![]() $\Delta _0\in G\big (B_0\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{t_{\scriptscriptstyle -}}]\big )$
with
$\Delta _0\in G\big (B_0\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{t_{\scriptscriptstyle -}}]\big )$
with
![]() $\Delta _0\;\textrm {mod}\;\zeta ={\,\overline {\!\Delta \!}\,}_0$
and
$\Delta _0\;\textrm {mod}\;\zeta ={\,\overline {\!\Delta \!}\,}_0$
and
![]() $\Delta _0\cdot A_0=b\cdot \sigma ^\ast (\Delta _0)$
. If we let
$\Delta _0\cdot A_0=b\cdot \sigma ^\ast (\Delta _0)$
. If we let
![]() $\gamma _0\in \breve {\mathcal {H}}_{G,\hat {Z},b}^a(S_0)$
be the pullback of
$\gamma _0\in \breve {\mathcal {H}}_{G,\hat {Z},b}^a(S_0)$
be the pullback of
![]() $\gamma \in \breve {\mathcal {H}}_{G,\hat {Z},b}^a(S)$
, then
$\gamma \in \breve {\mathcal {H}}_{G,\hat {Z},b}^a(S)$
, then
![]() $\gamma _0=\sigma ^\ast (\Delta _0)A_0^{-1}\cdot G\big (B_0[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )$
and
$\gamma _0=\sigma ^\ast (\Delta _0)A_0^{-1}\cdot G\big (B_0[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )$
and
![]() $\sigma ^\ast (\Delta _0)^{-1}\gamma _0=A_0^{-1}\cdot G\big (B_0[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )$
.
$\sigma ^\ast (\Delta _0)^{-1}\gamma _0=A_0^{-1}\cdot G\big (B_0[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )$
.
We claim that
![]() $\sigma ^\ast (\Delta _0)$
lifts to a uniquely determined element of
$\sigma ^\ast (\Delta _0)$
lifts to a uniquely determined element of
![]() $G\big (B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{\sigma ^\ast t_{\scriptscriptstyle -}}]\big )$
. Indeed, after choosing a faithful
$G\big (B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{\sigma ^\ast t_{\scriptscriptstyle -}}]\big )$
. Indeed, after choosing a faithful
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-rational representation
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-rational representation
![]() $\rho \colon G\hookrightarrow \operatorname {\mathrm {SL}}_r$
there is an integer e such that the matrix
$\rho \colon G\hookrightarrow \operatorname {\mathrm {SL}}_r$
there is an integer e such that the matrix
![]() $t_{\scriptscriptstyle -}^e\cdot \rho (\Delta _0)\in B_0\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}^{r\times r}$
. Because
$t_{\scriptscriptstyle -}^e\cdot \rho (\Delta _0)\in B_0\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}^{r\times r}$
. Because
![]() $\sigma ^\ast (I)=0$
, the morphism
$\sigma ^\ast (I)=0$
, the morphism
![]() $\sigma ^\ast \colon B\to B$
,
$\sigma ^\ast \colon B\to B$
,
![]() $x\mapsto x^q$
factors over
$x\mapsto x^q$
factors over
![]() $B\twoheadrightarrow B_0\to B$
, and so
$B\twoheadrightarrow B_0\to B$
, and so
![]() $(\sigma ^\ast t_{\scriptscriptstyle -})^e\cdot \rho (\sigma ^\ast \Delta _0)=\sigma ^\ast \big (t_{\scriptscriptstyle -}^e\cdot \rho (\Delta _0)\big )\in B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}^{r\times r}$
. This implies
$(\sigma ^\ast t_{\scriptscriptstyle -})^e\cdot \rho (\sigma ^\ast \Delta _0)=\sigma ^\ast \big (t_{\scriptscriptstyle -}^e\cdot \rho (\Delta _0)\big )\in B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}^{r\times r}$
. This implies
![]() $\rho (\sigma ^\ast \Delta _0)\in \operatorname {\mathrm {SL}}_r\big (B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{\sigma ^\ast t_{\scriptscriptstyle -}}]\big )$
and
$\rho (\sigma ^\ast \Delta _0)\in \operatorname {\mathrm {SL}}_r\big (B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{\sigma ^\ast t_{\scriptscriptstyle -}}]\big )$
and
![]() $\sigma ^\ast (\Delta _0)\in G\big (B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{\sigma ^\ast t_{\scriptscriptstyle -}}]\big )$
. By (6.2) it follows, moreover, that
$\sigma ^\ast (\Delta _0)\in G\big (B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{\sigma ^\ast t_{\scriptscriptstyle -}}]\big )$
. By (6.2) it follows, moreover, that
![]() $\sigma ^\ast (\Delta _0)\in G\big (B[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )$
.
$\sigma ^\ast (\Delta _0)\in G\big (B[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )$
.
We now replace S by a quasi-compact, quasi-separated, étale covering over which
![]() $\sigma ^\ast (\Delta _0)^{-1}\gamma $
is induced from an element
$\sigma ^\ast (\Delta _0)^{-1}\gamma $
is induced from an element
![]() $g\in G\big (B[\tfrac {1}{\zeta }](\kern-0.15em( z-\zeta )\kern-0.15em)\big )$
. Consider the element
$g\in G\big (B[\tfrac {1}{\zeta }](\kern-0.15em( z-\zeta )\kern-0.15em)\big )$
. Consider the element
![]() $c_0:=(g\;\textrm {mod}\; I)^{-1}A_0^{-1}\in G(B_0[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]})$
. Because the kernel of
$c_0:=(g\;\textrm {mod}\; I)^{-1}A_0^{-1}\in G(B_0[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]})$
. Because the kernel of
![]() $B[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\to B_0[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
is a nilpotent ideal and G is smooth,
$B[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\to B_0[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
is a nilpotent ideal and G is smooth,
![]() $c_0$
lifts to an element
$c_0$
lifts to an element
![]() $c\in G(B[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]})$
and replacing g by
$c\in G(B[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]})$
and replacing g by
![]() $gc$
yields
$gc$
yields
![]() $g\;\textrm {mod}\; I=A_0^{-1}$
. Also,
$g\;\textrm {mod}\; I=A_0^{-1}$
. Also,
![]() $\sigma ^\ast (\Delta _0)^{-1}\gamma \in (\breve {\mathcal {H}}_{G,\hat Z})^{\textrm {rig}}(S)$
by Definition 2.2(b)(v), whence
$\sigma ^\ast (\Delta _0)^{-1}\gamma \in (\breve {\mathcal {H}}_{G,\hat Z})^{\textrm {rig}}(S)$
by Definition 2.2(b)(v), whence
![]() $g\cdot G(B[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]})\;\in \;(\hat Z_E{\widehat {\otimes }}_E\breve E)^{\textrm {rig}}(S)$
. We denote the corresponding morphism of rigid analytic spaces by
$g\cdot G(B[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]})\;\in \;(\hat Z_E{\widehat {\otimes }}_E\breve E)^{\textrm {rig}}(S)$
. We denote the corresponding morphism of rigid analytic spaces by
![]() $\alpha \colon S\to (\hat Z_E{\widehat {\otimes }}_E\breve E)^{\textrm {rig}}$
. Let R be an extension of
$\alpha \colon S\to (\hat Z_E{\widehat {\otimes }}_E\breve E)^{\textrm {rig}}$
. Let R be an extension of
![]() $R_{\hat Z}$
over which a representative
$R_{\hat Z}$
over which a representative
![]() $\hat Z_R$
of
$\hat Z_R$
of
![]() $\hat Z$
exists and such that
$\hat Z$
exists and such that
![]() $\operatorname {\mathrm {Frac}}(R)$
is a finite Galois extension of
$\operatorname {\mathrm {Frac}}(R)$
is a finite Galois extension of
![]() $E_{\hat Z}$
. We let
$E_{\hat Z}$
. We let
![]() $\breve R$
be the ring of integers in the completion of the maximal unramified extension of
$\breve R$
be the ring of integers in the completion of the maximal unramified extension of
![]() $\operatorname {\mathrm {Frac}}(R)$
, and we set
$\operatorname {\mathrm {Frac}}(R)$
, and we set
![]() $\hat {Z}_{\breve R}:=\hat {Z}_R\widehat {\displaystyle \times }_R\operatorname {\mathrm {Spf}}\breve R$
. By applying Galois descent with respect to the field extension
$\hat {Z}_{\breve R}:=\hat {Z}_R\widehat {\displaystyle \times }_R\operatorname {\mathrm {Spf}}\breve R$
. By applying Galois descent with respect to the field extension
![]() $\operatorname {\mathrm {Frac}}(\breve R)/\breve E$
in the end, we may restrict to the case where
$\operatorname {\mathrm {Frac}}(\breve R)/\breve E$
in the end, we may restrict to the case where
![]() ${\mathscr {S}}$
is a formal scheme over
${\mathscr {S}}$
is a formal scheme over
![]() $\operatorname {\mathrm {Spf}}\breve R$
and not just over
$\operatorname {\mathrm {Spf}}\breve R$
and not just over
![]() $\operatorname {\mathrm {Spf}}\breve R_{\hat Z}$
. Let
$\operatorname {\mathrm {Spf}}\breve R_{\hat Z}$
. Let
![]() ${\mathscr {S}}^{\prime }\subset \hat Z_{\breve R}\widehat {\displaystyle \times }_{\breve R}{\mathscr {S}}$
be the
${\mathscr {S}}^{\prime }\subset \hat Z_{\breve R}\widehat {\displaystyle \times }_{\breve R}{\mathscr {S}}$
be the
![]() $\zeta $
-adic completion of the scheme theoretic closure of the graph of
$\zeta $
-adic completion of the scheme theoretic closure of the graph of
![]() $\alpha $
. It is projective over
$\alpha $
. It is projective over
![]() ${\mathscr {S}}$
by Proposition 2.6(d) and therefore
${\mathscr {S}}$
by Proposition 2.6(d) and therefore
![]() $({\mathscr {S}}^{\prime })^{\textrm {rig}}={\mathscr {S}}^{\textrm {rig}}$
. So
$({\mathscr {S}}^{\prime })^{\textrm {rig}}={\mathscr {S}}^{\textrm {rig}}$
. So
![]() ${\mathscr {S}}^{\prime }\to {\mathscr {S}}$
is an admissible blowing-up by [Reference Bosch and Lütkebohmert19, Corollary 5.4] and we replace
${\mathscr {S}}^{\prime }\to {\mathscr {S}}$
is an admissible blowing-up by [Reference Bosch and Lütkebohmert19, Corollary 5.4] and we replace
![]() ${\mathscr {S}}$
by
${\mathscr {S}}$
by
![]() ${\mathscr {S}}^{\prime }$
to obtain an extension
${\mathscr {S}}^{\prime }$
to obtain an extension
![]() $\alpha \colon {\mathscr {S}}\to \hat Z_{\breve R}$
. After replacing
$\alpha \colon {\mathscr {S}}\to \hat Z_{\breve R}$
. After replacing
![]() ${\mathscr {S}}$
by an étale covering, this morphism
${\mathscr {S}}$
by an étale covering, this morphism
![]() $\alpha $
is of the form
$\alpha $
is of the form
![]() $A^{-1}\cdot G(B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})\in \hat Z_{\breve R}({\mathscr {S}})$
for an element
$A^{-1}\cdot G(B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})\in \hat Z_{\breve R}({\mathscr {S}})$
for an element
![]() $A^{-1}\in G(B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z-\zeta }])$
; compare the proof of Proposition 2.6. Because g and
$A^{-1}\in G(B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z-\zeta }])$
; compare the proof of Proposition 2.6. Because g and
![]() $A^{-1}$
both correspond to the morphism
$A^{-1}$
both correspond to the morphism
![]() $\alpha \colon S\to (\breve {\mathcal {H}}_{G,\hat Z})^{\textrm {rig}}$
, we have
$\alpha \colon S\to (\breve {\mathcal {H}}_{G,\hat Z})^{\textrm {rig}}$
, we have
![]() $g\cdot G(B[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]})=A^{-1}\cdot G(B[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]})$
in
$g\cdot G(B[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]})=A^{-1}\cdot G(B[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]})$
in
![]() $(\breve {\mathcal {H}}_{G,\hat Z})^{\textrm {rig}}(S)$
. We consider the element
$(\breve {\mathcal {H}}_{G,\hat Z})^{\textrm {rig}}(S)$
. We consider the element
![]() $a_0:=A_0(A^{-1}\;\textrm {mod}\; I)\in G(B_0\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z-\zeta }])$
. Its image in
$a_0:=A_0(A^{-1}\;\textrm {mod}\; I)\in G(B_0\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z-\zeta }])$
. Its image in
![]() $(\breve {\mathcal {H}}_{G,\hat Z})^{\textrm {rig}}(S_0)$
equals
$(\breve {\mathcal {H}}_{G,\hat Z})^{\textrm {rig}}(S_0)$
equals
 $$ \begin{align*}(g^{-1}\;\textrm{mod}\; I)(A^{-1}\;\textrm{mod}\; I)\cdot G(B_0[\tfrac{1}{\zeta}]\text{[}\kern-0.15em\text{[} z-\zeta\text{]}\kern-0.15em\text{]})&=(g^{-1}g\;\textrm{mod}\; I)\cdot G(B_0[\tfrac{1}{\zeta}]\text{[}\kern-0.15em\text{[} z-\zeta\text{]}\kern-0.15em\text{]})\\&=1\cdot G(B_0[\tfrac{1}{\zeta}]\text{[}\kern-0.15em\text{[} z-\zeta\text{]}\kern-0.15em\text{]}); \end{align*} $$
$$ \begin{align*}(g^{-1}\;\textrm{mod}\; I)(A^{-1}\;\textrm{mod}\; I)\cdot G(B_0[\tfrac{1}{\zeta}]\text{[}\kern-0.15em\text{[} z-\zeta\text{]}\kern-0.15em\text{]})&=(g^{-1}g\;\textrm{mod}\; I)\cdot G(B_0[\tfrac{1}{\zeta}]\text{[}\kern-0.15em\text{[} z-\zeta\text{]}\kern-0.15em\text{]})\\&=1\cdot G(B_0[\tfrac{1}{\zeta}]\text{[}\kern-0.15em\text{[} z-\zeta\text{]}\kern-0.15em\text{]}); \end{align*} $$
that is,
![]() $a_0\in G(B_0[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]})$
. By the following Lemma 6.13, this implies that
$a_0\in G(B_0[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]})$
. By the following Lemma 6.13, this implies that
![]() $a_0\in G(B_0\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
. Again, because the kernel of
$a_0\in G(B_0\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
. Again, because the kernel of
![]() $B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\to B_0\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
is nilpotent and G is smooth,
$B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\to B_0\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
is nilpotent and G is smooth,
![]() $a_0$
lifts to an element
$a_0$
lifts to an element
![]() $a\in G(B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
, and replacing
$a\in G(B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
, and replacing
![]() $A^{-1}$
by
$A^{-1}$
by
![]() $A^{-1}a^{-1}$
yields
$A^{-1}a^{-1}$
yields
![]() $A\;\textrm {mod}\; I=A_0$
. We consider the local G-shtuka
$A\;\textrm {mod}\; I=A_0$
. We consider the local G-shtuka
![]() ${\underline {{\mathcal {G}}}}:=\big ((L^+G)_{{\mathscr {S}}},A\sigma ^\ast \big )$
with
${\underline {{\mathcal {G}}}}:=\big ((L^+G)_{{\mathscr {S}}},A\sigma ^\ast \big )$
with
![]() ${\underline {{\mathcal {G}}}}_{{\mathscr {S}}_0}={\underline {{\mathcal {G}}}}_0$
. Then
${\underline {{\mathcal {G}}}}_{{\mathscr {S}}_0}={\underline {{\mathcal {G}}}}_0$
. Then
![]() $\Delta _0$
lifts to
$\Delta _0$
lifts to
![]() $\Delta :=b\,\sigma ^\ast (\Delta _0)\,A^{-1}\in G\big (B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{t_{\scriptscriptstyle -}}]\big )$
and
$\Delta :=b\,\sigma ^\ast (\Delta _0)\,A^{-1}\in G\big (B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{t_{\scriptscriptstyle -}}]\big )$
and
![]() ${\,\overline {\!\Delta \!}\,}:=\Delta \;\textrm {mod}\;(\zeta )\colon {\underline {{\mathcal {G}}}}_{{\,\overline {\!{\mathscr {S}}}}}\to {\underline {{\mathbb {G}}}}_{0,{\,\overline {\!{\mathscr {S}}}}}$
is the unique lift of the quasi-isogeny
${\,\overline {\!\Delta \!}\,}:=\Delta \;\textrm {mod}\;(\zeta )\colon {\underline {{\mathcal {G}}}}_{{\,\overline {\!{\mathscr {S}}}}}\to {\underline {{\mathbb {G}}}}_{0,{\,\overline {\!{\mathscr {S}}}}}$
is the unique lift of the quasi-isogeny
![]() $\bar \delta _0={\,\overline {\!\Delta \!}\,}_0$
by rigidity. We let
$\bar \delta _0={\,\overline {\!\Delta \!}\,}_0$
by rigidity. We let
![]() $f\colon {\mathscr {S}}\to {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
be the morphism given by
$f\colon {\mathscr {S}}\to {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
be the morphism given by
![]() $({\underline {{\mathcal {G}}}},{\,\overline {\!\Delta \!}\,})\in {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}({\mathscr {S}})$
. It makes the diagram (6.5) commutative, because
$({\underline {{\mathcal {G}}}},{\,\overline {\!\Delta \!}\,})\in {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}({\mathscr {S}})$
. It makes the diagram (6.5) commutative, because
![]() $\sigma ^\ast (\Delta )A^{-1}\cdot G\big (B[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )\;=\; \sigma ^\ast (\Delta _0)g\cdot G\big (B[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )\;=\;\gamma $
.
$\sigma ^\ast (\Delta )A^{-1}\cdot G\big (B[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )\;=\; \sigma ^\ast (\Delta _0)g\cdot G\big (B[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )\;=\;\gamma $
.
To prove that f is uniquely determined, let
![]() $f^{\prime }\colon {\mathscr {S}}\to {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
be a second morphism making the diagram (6.5) commutative. The corresponding point
$f^{\prime }\colon {\mathscr {S}}\to {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
be a second morphism making the diagram (6.5) commutative. The corresponding point
![]() $({\underline {{\mathcal {G}}}}^{\prime }\!,\bar \delta ^{\prime })\in {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}({\mathscr {S}})$
is of the form
$({\underline {{\mathcal {G}}}}^{\prime }\!,\bar \delta ^{\prime })\in {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}({\mathscr {S}})$
is of the form
![]() ${\underline {{\mathcal {G}}}}^{\prime }=\big ((L^+G)_{{\mathscr {S}}},A^{\prime }\sigma ^\ast \big )$
with
${\underline {{\mathcal {G}}}}^{\prime }=\big ((L^+G)_{{\mathscr {S}}},A^{\prime }\sigma ^\ast \big )$
with
![]() $A^{\prime }\;\textrm {mod}\; I=A_0$
and
$A^{\prime }\;\textrm {mod}\; I=A_0$
and
![]() $\Delta ^{\prime }=b\,\sigma ^\ast (\Delta _0)\,A^{\prime }{}^{-1}\in G\big (B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{t_{\scriptscriptstyle -}}]\big )$
. We assume that it is mapped under
$\Delta ^{\prime }=b\,\sigma ^\ast (\Delta _0)\,A^{\prime }{}^{-1}\in G\big (B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{t_{\scriptscriptstyle -}}]\big )$
. We assume that it is mapped under
![]() $\breve \pi ^{\textrm {rig}}$
also to
$\breve \pi ^{\textrm {rig}}$
also to
![]() $\gamma $
. This means
$\gamma $
. This means
![]() $\sigma ^\ast (\Delta _0)A^{-1}\cdot G\big (B[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )\;=\;\gamma \;=\;\sigma ^\ast (\Delta _0)A^{\prime }{}^{-1}\cdot G\big (B[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )$
, whence
$\sigma ^\ast (\Delta _0)A^{-1}\cdot G\big (B[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )\;=\;\gamma \;=\;\sigma ^\ast (\Delta _0)A^{\prime }{}^{-1}\cdot G\big (B[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )$
, whence
![]() $\Phi :=A^{\prime }A^{-1}\in G(B[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]})\subset G(B[\tfrac {1}{\zeta }](\kern-0.15em( z-\zeta )\kern-0.15em))$
. From Lemma 6.13 it follows that
$\Phi :=A^{\prime }A^{-1}\in G(B[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]})\subset G(B[\tfrac {1}{\zeta }](\kern-0.15em( z-\zeta )\kern-0.15em))$
. From Lemma 6.13 it follows that
![]() $\Phi \in G(B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
. Also,
$\Phi \in G(B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
. Also,
![]() $\sigma ^\ast (\Phi )=\sigma ^\ast (A^{\prime }A^{-1}\;\textrm {mod}\; I)=\sigma ^\ast (1)=1$
implies
$\sigma ^\ast (\Phi )=\sigma ^\ast (A^{\prime }A^{-1}\;\textrm {mod}\; I)=\sigma ^\ast (1)=1$
implies
![]() $\Phi A=A^{\prime }\sigma ^\ast (\Phi )$
and
$\Phi A=A^{\prime }\sigma ^\ast (\Phi )$
and
![]() $\Phi =\Delta ^{\prime }{}^{-1}\Delta $
. We conclude that
$\Phi =\Delta ^{\prime }{}^{-1}\Delta $
. We conclude that
![]() $\Phi $
is an isomorphism
$\Phi $
is an isomorphism
![]() . This means
. This means
![]() $f=f^{\prime }$
and finishes the proof.
$f=f^{\prime }$
and finishes the proof.
Remark 6.12. When
![]() $G=\operatorname {\mathrm {GL}}_r$
, the proof starts in terms of Remark 6.4 with a local shtuka
$G=\operatorname {\mathrm {GL}}_r$
, the proof starts in terms of Remark 6.4 with a local shtuka
![]() ${\underline {M\!}\,}_0$
over
${\underline {M\!}\,}_0$
over
![]() ${\mathscr {S}}_0$
. Then it considers the de Rham cohomology of
${\mathscr {S}}_0$
. Then it considers the de Rham cohomology of
![]() ${\underline {M\!}\,}_0$
, which lifts to
${\underline {M\!}\,}_0$
, which lifts to
![]() ${\mathscr {S}}$
by its crystalline nature. Next it produces from the Hodge-Pink structure
${\mathscr {S}}$
by its crystalline nature. Next it produces from the Hodge-Pink structure
![]() $\gamma $
a Hodge-Pink structure on the de Rham cohomology of
$\gamma $
a Hodge-Pink structure on the de Rham cohomology of
![]() ${\underline {M\!}\,}_0$
over
${\underline {M\!}\,}_0$
over
![]() ${\mathscr {S}}$
that lifts the Hodge-Pink structure of
${\mathscr {S}}$
that lifts the Hodge-Pink structure of
![]() ${\underline {M\!}\,}_0$
. This lift of the Hodge-Pink structure corresponds to a unique lift of
${\underline {M\!}\,}_0$
. This lift of the Hodge-Pink structure corresponds to a unique lift of
![]() ${\underline {M\!}\,}_0$
to a local shtuka
${\underline {M\!}\,}_0$
to a local shtuka
![]() ${\underline {M\!}\,}$
over
${\underline {M\!}\,}$
over
![]() ${\mathscr {S}}$
by [Reference Genestier and Lafforgue41, Proposition 6.3]. In that sense, our proof is a direct translation of [Reference Rapoport and Zink80, Proposition 5.17].
${\mathscr {S}}$
by [Reference Genestier and Lafforgue41, Proposition 6.3]. In that sense, our proof is a direct translation of [Reference Rapoport and Zink80, Proposition 5.17].
Lemma 6.13. Let B be an
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
-algebra without
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
-algebra without
![]() $\zeta $
-torsion that is
$\zeta $
-torsion that is
![]() $\zeta $
-adically complete, and let
$\zeta $
-adically complete, and let
![]() $a\in G(B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z-\zeta }])$
such that the image of a in
$a\in G(B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z-\zeta }])$
such that the image of a in
![]() $G(B[\tfrac {1}{\zeta }](\kern-0.15em( z-\zeta )\kern-0.15em))$
lies in
$G(B[\tfrac {1}{\zeta }](\kern-0.15em( z-\zeta )\kern-0.15em))$
lies in
![]() $G(B[\tfrac {1}{\zeta }] \mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]})$
. Then
$G(B[\tfrac {1}{\zeta }] \mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]})$
. Then
![]() $a\in G(B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
.
$a\in G(B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
.
Proof. Note that
![]() $B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
has no
$B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
has no
![]() $(z-\zeta )$
-torsion, because B has no
$(z-\zeta )$
-torsion, because B has no
![]() $\zeta $
-torsion. Let
$\zeta $
-torsion. Let
![]() $\rho \colon G\hookrightarrow \operatorname {\mathrm {SL}}_r$
be a faithful representation over
$\rho \colon G\hookrightarrow \operatorname {\mathrm {SL}}_r$
be a faithful representation over
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
and consider the matrix
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
and consider the matrix
![]() $\rho (a)\in \operatorname {\mathrm {SL}}_r(B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z-\zeta }])\subset B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z-\zeta }]^{r\times r}$
.
$\rho (a)\in \operatorname {\mathrm {SL}}_r(B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z-\zeta }])\subset B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z-\zeta }]^{r\times r}$
.
It is enough to show that this matrix is in
![]() $B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}^{r\times r}$
as
$B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}^{r\times r}$
as
![]() $\operatorname {\mathrm {SL}}_r(B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z-\zeta }])\cap B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}^{r\times r}= \operatorname {\mathrm {SL}}_r(B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
and
$\operatorname {\mathrm {SL}}_r(B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z-\zeta }])\cap B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}^{r\times r}= \operatorname {\mathrm {SL}}_r(B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
and
![]() $\operatorname {\mathrm {SL}}_r(B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})\cap \rho (G(B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z-\zeta }]))= \rho (G(B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}))$
as
$\operatorname {\mathrm {SL}}_r(B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})\cap \rho (G(B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z-\zeta }]))= \rho (G(B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}))$
as
![]() $\rho $
is defined over
$\rho $
is defined over
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}.$
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}.$
After multiplying
![]() $\rho (a)$
by
$\rho (a)$
by
![]() $(z-\zeta )^n$
for sufficiently large n, its denominators disappear and its image in
$(z-\zeta )^n$
for sufficiently large n, its denominators disappear and its image in
![]() $B[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}^{r\times r}$
is divisible by
$B[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}^{r\times r}$
is divisible by
![]() $(z-\zeta )^n$
. Thus, it suffices to show that an element f of
$(z-\zeta )^n$
. Thus, it suffices to show that an element f of
![]() $B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
whose image in
$B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
whose image in
![]() $B[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
is divisible by
$B[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
is divisible by
![]() $z-\zeta $
is already divisible by
$z-\zeta $
is already divisible by
![]() $z-\zeta $
in
$z-\zeta $
in
![]() $B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
. This follows as in Lemma 7.6.
$B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
. This follows as in Lemma 7.6.
We end this section with some examples.
Example 6.14 The Drinfeld period morphism
This example is due to Drinfeld [Reference Drinfeld35]. A good account is given by Genestier and Lafforgue [Reference Genestier39], [Reference Genestier and Lafforgue40]. Let d be a positive integer and let D be the central division algebra over
![]() ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
of Hasse invariant
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
of Hasse invariant
![]() $1/d$
. Let
$1/d$
. Let
![]() ${\mathcal {O}}_D$
be its maximal order. We may identify
${\mathcal {O}}_D$
be its maximal order. We may identify
![]() $D\cong \bigoplus _{i=0}^{d-1}{\mathbb {F}}_{q^d}(\kern-0.15em( z)\kern-0.15em)\Pi ^i$
and
$D\cong \bigoplus _{i=0}^{d-1}{\mathbb {F}}_{q^d}(\kern-0.15em( z)\kern-0.15em)\Pi ^i$
and
![]() ${\mathcal {O}}_D\cong \bigoplus _{i=0}^{d-1}{\mathbb {F}}_{q^d}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\Pi ^i$
with
${\mathcal {O}}_D\cong \bigoplus _{i=0}^{d-1}{\mathbb {F}}_{q^d}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\Pi ^i$
with
![]() $\Pi ^d=z$
and
$\Pi ^d=z$
and
![]() $\Pi a=\sigma (a)\Pi $
for
$\Pi a=\sigma (a)\Pi $
for
![]() $a\in {\mathbb {F}}_{q^d}(\kern-0.15em( z)\kern-0.15em)$
. We let
$a\in {\mathbb {F}}_{q^d}(\kern-0.15em( z)\kern-0.15em)$
. We let
![]() $G:={\mathcal {O}}_D^{\scriptscriptstyle \times }$
be the group scheme over
$G:={\mathcal {O}}_D^{\scriptscriptstyle \times }$
be the group scheme over
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
with
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
with
![]() $G(A)=({\mathcal {O}}_D\otimes _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}A)^{\scriptscriptstyle \times }$
for
$G(A)=({\mathcal {O}}_D\otimes _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}A)^{\scriptscriptstyle \times }$
for
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-algebras A. Consider the matrices
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-algebras A. Consider the matrices

The field extension
![]() ${\mathbb {F}}_{q^d}$
of
${\mathbb {F}}_{q^d}$
of
![]() ${\mathbb {F}}_q$
splits the division algebra D by the isomorphisms
${\mathbb {F}}_q$
splits the division algebra D by the isomorphisms
![]() $D\otimes _{{\mathbb {F}}_q}{\mathbb {F}}_{q^d}\cong {\mathbb {F}}_{q^d}(\kern-0.15em( z)\kern-0.15em)^{d\times d}$
and
$D\otimes _{{\mathbb {F}}_q}{\mathbb {F}}_{q^d}\cong {\mathbb {F}}_{q^d}(\kern-0.15em( z)\kern-0.15em)^{d\times d}$
and
![]() ${\mathcal {O}}_D\otimes _{{\mathbb {F}}_q}{\mathbb {F}}_{q^d}\cong \{g\in {\mathbb {F}}_{q^d}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}^{d\times d}\colon g\;\textrm {mod}\; z\mathrm { is lower triangular}\}$
sending
${\mathcal {O}}_D\otimes _{{\mathbb {F}}_q}{\mathbb {F}}_{q^d}\cong \{g\in {\mathbb {F}}_{q^d}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}^{d\times d}\colon g\;\textrm {mod}\; z\mathrm { is lower triangular}\}$
sending
![]() $\Pi \otimes 1$
to
$\Pi \otimes 1$
to
![]() ${\,\overline {\!T}}$
and
${\,\overline {\!T}}$
and
![]() $a\otimes 1$
to
$a\otimes 1$
to
![]() $\operatorname {\mathrm {diag}}\big (\sigma ^{d-1}(a),\sigma ^{d-2}(a),\ldots ,a\big )$
for
$\operatorname {\mathrm {diag}}\big (\sigma ^{d-1}(a),\sigma ^{d-2}(a),\ldots ,a\big )$
for
![]() $a\in {\mathbb {F}}_{q^d}(\kern-0.15em( z)\kern-0.15em)\subset D$
. So
$a\in {\mathbb {F}}_{q^d}(\kern-0.15em( z)\kern-0.15em)\subset D$
. So
![]() $G\otimes _{{\mathbb {F}}_q}{\mathbb {F}}_{q^d}$
is the Iwahori group scheme
$G\otimes _{{\mathbb {F}}_q}{\mathbb {F}}_{q^d}$
is the Iwahori group scheme
![]() $I:=\{g\in \operatorname {\mathrm {GL}}_d\colon g\;\textrm {mod}\; z\mathrm { is lower triangular}\}$
. Let
$I:=\{g\in \operatorname {\mathrm {GL}}_d\colon g\;\textrm {mod}\; z\mathrm { is lower triangular}\}$
. Let
![]() $b=\Pi \in LG({\mathbb {F}}_q)=D^{\scriptscriptstyle \times }$
and let the bound
$b=\Pi \in LG({\mathbb {F}}_q)=D^{\scriptscriptstyle \times }$
and let the bound
![]() $\hat Z$
be represented over
$\hat Z$
be represented over
![]() $R={\mathbb {F}}_{q^d}\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
by
$R={\mathbb {F}}_{q^d}\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
by
Its reflex ring is
![]() $R_{\hat Z}={\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
and
$R_{\hat Z}={\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
and
![]() $\breve {\mathcal {H}}_{G,\hat Z}={\mathbb {P}}^{d-1}_{{\mathbb {F}}(\kern-0.15em(\zeta )\kern-0.15em)}$
. The quasi-isogeny group
$\breve {\mathcal {H}}_{G,\hat Z}={\mathbb {P}}^{d-1}_{{\mathbb {F}}(\kern-0.15em(\zeta )\kern-0.15em)}$
. The quasi-isogeny group
![]() $J_b$
equals
$J_b$
equals
![]() $\operatorname {\mathrm {GL}}_d$
. We are going to describe
$\operatorname {\mathrm {GL}}_d$
. We are going to describe
![]() ${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
.
${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
.
The category of
![]() $L^+G$
-torsors over a scheme
$L^+G$
-torsors over a scheme
![]() $S\in {{\mathcal {N}}\!\mathit {ilp}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}}$
is equivalent to the category of
$S\in {{\mathcal {N}}\!\mathit {ilp}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}}$
is equivalent to the category of
![]() ${\mathcal {O}}_S\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-modules with
${\mathcal {O}}_S\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-modules with
![]() ${\mathcal {O}}_{D^{\textrm {opp}}}{\widehat {\otimes }}_{{\mathbb {F}}_q}{\mathcal {O}}_S$
-action, which are Zariski locally on S of the form
${\mathcal {O}}_{D^{\textrm {opp}}}{\widehat {\otimes }}_{{\mathbb {F}}_q}{\mathcal {O}}_S$
-action, which are Zariski locally on S of the form
![]() ${\mathcal {O}}_D{\widehat {\otimes }}_{{\mathbb {F}}_q}{\mathcal {O}}_S$
, where
${\mathcal {O}}_D{\widehat {\otimes }}_{{\mathbb {F}}_q}{\mathcal {O}}_S$
, where
![]() ${\mathcal {O}}_{D^{\textrm {opp}}}{\widehat {\otimes }}_{{\mathbb {F}}_q}{\mathcal {O}}_S$
acts by multiplication on the right. This equivalence sends an
${\mathcal {O}}_{D^{\textrm {opp}}}{\widehat {\otimes }}_{{\mathbb {F}}_q}{\mathcal {O}}_S$
acts by multiplication on the right. This equivalence sends an
![]() $L^+G$
-torsor
$L^+G$
-torsor
![]() ${\mathcal {G}}$
that is trivialised over an étale covering
${\mathcal {G}}$
that is trivialised over an étale covering
![]() $S^{\prime }\to S$
by
$S^{\prime }\to S$
by
![]() with
with
![]() $h:=p_1^*\alpha \circ p_2^*\alpha ^{-1}\in L^+G(S^{\prime \prime })=\big ({\mathcal {O}}_D\otimes _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}\Gamma (S^{\prime \prime }\!,{\mathcal {O}}_{S^{\prime \prime }})\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\big )^{\scriptscriptstyle \times }$
, where
$h:=p_1^*\alpha \circ p_2^*\alpha ^{-1}\in L^+G(S^{\prime \prime })=\big ({\mathcal {O}}_D\otimes _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}\Gamma (S^{\prime \prime }\!,{\mathcal {O}}_{S^{\prime \prime }})\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\big )^{\scriptscriptstyle \times }$
, where
![]() $p_i\colon S^{\prime \prime }:=S^{\prime }\times _SS^{\prime }\to S^{\prime }$
is the projection onto the ith factor, to the
$p_i\colon S^{\prime \prime }:=S^{\prime }\times _SS^{\prime }\to S^{\prime }$
is the projection onto the ith factor, to the
![]() ${\mathcal {O}}_S\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-module M obtained by descent from
${\mathcal {O}}_S\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-module M obtained by descent from
![]() $M^{\prime }:={\mathcal {O}}_D{\widehat {\otimes }}_{{\mathbb {F}}_q}{\mathcal {O}}_{S^{\prime }}$
with the descent datum
$M^{\prime }:={\mathcal {O}}_D{\widehat {\otimes }}_{{\mathbb {F}}_q}{\mathcal {O}}_{S^{\prime }}$
with the descent datum
![]() ,
,
![]() $m\mapsto hm$
. Then M is Zariski locally trivial by Hilbert 90; see [Reference Hartl and Viehmann56, Proposition 2.3]. If
$m\mapsto hm$
. Then M is Zariski locally trivial by Hilbert 90; see [Reference Hartl and Viehmann56, Proposition 2.3]. If
![]() $S^{\prime }\in {{\mathcal {N}}\!\mathit {ilp}}_{{\mathbb {F}}_{q^d}\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}}$
, then
$S^{\prime }\in {{\mathcal {N}}\!\mathit {ilp}}_{{\mathbb {F}}_{q^d}\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}}$
, then
![]() $M^{\prime }={\mathcal {O}}_D{\widehat {\otimes }}_{{\mathbb {F}}_q}{\mathcal {O}}_{S^{\prime }}$
decomposes as a direct sum of eigenspaces
$M^{\prime }={\mathcal {O}}_D{\widehat {\otimes }}_{{\mathbb {F}}_q}{\mathcal {O}}_{S^{\prime }}$
decomposes as a direct sum of eigenspaces
![]() $M^{\prime }_i$
on which
$M^{\prime }_i$
on which
![]() $a\in {\mathbb {F}}_{q^d}\subset {\mathcal {O}}_D$
acts as
$a\in {\mathbb {F}}_{q^d}\subset {\mathcal {O}}_D$
acts as
![]() $a^{q^i}\in {\mathcal {O}}_{S^{\prime }}$
for
$a^{q^i}\in {\mathcal {O}}_{S^{\prime }}$
for
![]() $i\in {\mathbb {Z}}/d{\mathbb {Z}}$
. Under the isomorphism
$i\in {\mathbb {Z}}/d{\mathbb {Z}}$
. Under the isomorphism
![]() ${\mathcal {O}}_D{\widehat {\otimes }}_{{\mathbb {F}}_q}{\mathcal {O}}_{S^{\prime }}\cong \{g\in {\mathcal {O}}_{S^{\prime }}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}^{d\times d}\colon g\;\textrm {mod}\; z\mathrm { is lower triangular}\}$
the ith eigenspace
${\mathcal {O}}_D{\widehat {\otimes }}_{{\mathbb {F}}_q}{\mathcal {O}}_{S^{\prime }}\cong \{g\in {\mathcal {O}}_{S^{\prime }}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}^{d\times d}\colon g\;\textrm {mod}\; z\mathrm { is lower triangular}\}$
the ith eigenspace
![]() $M^{\prime }_i$
is mapped to the
$M^{\prime }_i$
is mapped to the
![]() $(d-i)$
th column in the matrix space (for
$(d-i)$
th column in the matrix space (for
![]() $0\le i<d$
). Multiplication with
$0\le i<d$
). Multiplication with
![]() $\Pi $
on the right defines morphisms
$\Pi $
on the right defines morphisms
![]() $\Pi \colon M^{\prime }_i\to M^{\prime }_{i+1}$
. If
$\Pi \colon M^{\prime }_i\to M^{\prime }_{i+1}$
. If
![]() ${\underline {{\mathcal {G}}}}$
is a local G-shtuka over such an
${\underline {{\mathcal {G}}}}$
is a local G-shtuka over such an
![]() $S^{\prime }$
, then
$S^{\prime }$
, then
![]() $\tau _{\mathcal {G}}$
maps
$\tau _{\mathcal {G}}$
maps
![]() $\sigma ^*M^{\prime }_i$
to
$\sigma ^*M^{\prime }_i$
to
![]() $M^{\prime }_{i+1}[\tfrac {1}{z}]$
. It is bounded by
$M^{\prime }_{i+1}[\tfrac {1}{z}]$
. It is bounded by
![]() $\hat Z^{-1}$
if and only if for all i the map
$\hat Z^{-1}$
if and only if for all i the map
![]() $\tau _{\mathcal {G}}$
is a morphism
$\tau _{\mathcal {G}}$
is a morphism
![]() $\sigma ^*M^{\prime }_i\to M^{\prime }_{i+1}$
with cokernel locally free of rank
$\sigma ^*M^{\prime }_i\to M^{\prime }_{i+1}$
with cokernel locally free of rank
![]() $1$
over
$1$
over
![]() $S^{\prime }$
. This means that M is the local shtuka (called ‘module de coordonnées’ in [Reference Genestier39], [Reference Genestier and Lafforgue40]) of a special formal
$S^{\prime }$
. This means that M is the local shtuka (called ‘module de coordonnées’ in [Reference Genestier39], [Reference Genestier and Lafforgue40]) of a special formal
![]() ${\mathcal {O}}_D$
-module of dimension d and height
${\mathcal {O}}_D$
-module of dimension d and height
![]() $d^2$
in the sense of Drinfeld [Reference Drinfeld35].
$d^2$
in the sense of Drinfeld [Reference Drinfeld35].
The formal scheme
![]() ${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}=\coprod _{\mathbb {Z}}{\widehat {\Omega }}^d$
and the space
${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}=\coprod _{\mathbb {Z}}{\widehat {\Omega }}^d$
and the space
![]() $({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\textrm {an}}=\coprod _{\mathbb {Z}}\Omega ^d$
are the disjoint unions indexed by the height of the quasi-isogeny
$({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\textrm {an}}=\coprod _{\mathbb {Z}}\Omega ^d$
are the disjoint unions indexed by the height of the quasi-isogeny
![]() $\bar \delta $
, where
$\bar \delta $
, where
is Drinfeld’s upper halfspace over
![]() $\breve E={\mathbb {F}}(\kern-0.15em(\zeta )\kern-0.15em)$
and
$\breve E={\mathbb {F}}(\kern-0.15em(\zeta )\kern-0.15em)$
and
![]() ${\widehat {\Omega }}^d$
is its formal model over
${\widehat {\Omega }}^d$
is its formal model over
![]() ${\mathbb {F}}\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
constructed by Drinfeld, Deligne and Mumford. The representability and structure of
${\mathbb {F}}\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
constructed by Drinfeld, Deligne and Mumford. The representability and structure of
![]() ${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
is described in detail in [Reference Genestier39, Chapitre II]. The period space
${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
is described in detail in [Reference Genestier39, Chapitre II]. The period space
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^{na}=\breve {\mathcal {H}}_{G,\hat {Z},b}^{wa}$
also equals
$\breve {\mathcal {H}}_{G,\hat {Z},b}^{na}=\breve {\mathcal {H}}_{G,\hat {Z},b}^{wa}$
also equals
![]() $\Omega ^d$
and on each connected component of
$\Omega ^d$
and on each connected component of
![]() $({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\textrm {an}}$
the period morphism is the identity of
$({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\textrm {an}}$
the period morphism is the identity of
![]() $\Omega ^d$
. The fibres of
$\Omega ^d$
. The fibres of
![]() $\breve \pi $
are in bijection with
$\breve \pi $
are in bijection with
![]() ${\mathbb {Z}}=D^{\scriptscriptstyle \times }/{\mathcal {O}}_D^{\scriptscriptstyle \times }$
; compare Proposition 7.16 and Theorem 8.1(a). Note that this example has a
${\mathbb {Z}}=D^{\scriptscriptstyle \times }/{\mathcal {O}}_D^{\scriptscriptstyle \times }$
; compare Proposition 7.16 and Theorem 8.1(a). Note that this example has a
![]() ${\mathbb {Q}}_p$
-analogue also going back to Drinfeld, which is discussed by [Reference Rapoport and Zink80, 1.44–1.46, 3.54–3.77 and 5.48–5.49]. Our exposition differs from [Reference Rapoport and Zink80] because they take covariant Dieudonné modules of formal
${\mathbb {Q}}_p$
-analogue also going back to Drinfeld, which is discussed by [Reference Rapoport and Zink80, 1.44–1.46, 3.54–3.77 and 5.48–5.49]. Our exposition differs from [Reference Rapoport and Zink80] because they take covariant Dieudonné modules of formal
![]() ${\mathcal {O}}_D$
-modules, whereas the local shtuka functor [Reference Genestier and Lafforgue40, § 2.1] is contravariant.
${\mathcal {O}}_D$
-modules, whereas the local shtuka functor [Reference Genestier and Lafforgue40, § 2.1] is contravariant.
Example 6.15 The Gross-Hopkins period morphism
This example is also discussed in [Reference Genestier and Lafforgue40]. Gross and Hopkins [Reference Hopkins and Gross60], [Reference Hopkins and Gross61] take
![]() $G=\operatorname {\mathrm {GL}}_r$
, with the upper triangular Borel subgroup and the diagonal torus. Let
$G=\operatorname {\mathrm {GL}}_r$
, with the upper triangular Borel subgroup and the diagonal torus. Let
![]() $b\in LG({\mathbb {F}}_q)$
be the matrix
$b\in LG({\mathbb {F}}_q)$
be the matrix
![]() ${\,\overline {\!T}}$
from (6.6), and let the bound
${\,\overline {\!T}}$
from (6.6), and let the bound
![]() $\hat Z=\hat Z_{\preceq \mu }$
be as in Example 2.7 for
$\hat Z=\hat Z_{\preceq \mu }$
be as in Example 2.7 for
![]() $\mu =(0,\ldots ,0,-1) \in {\mathbb {Z}}^r\cong X_*(T)$
and with reflex field
$\mu =(0,\ldots ,0,-1) \in {\mathbb {Z}}^r\cong X_*(T)$
and with reflex field
![]() $E:=E_{\hat Z}={\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
. Then
$E:=E_{\hat Z}={\mathbb {F}}_q(\kern-0.15em(\zeta )\kern-0.15em)$
. Then
![]() $\hat Z^{-1}=\hat Z_{\preceq (-\mu )_{\textrm {dom}}}$
with
$\hat Z^{-1}=\hat Z_{\preceq (-\mu )_{\textrm {dom}}}$
with
![]() $(-\mu )_{\textrm {dom}}=(1,0,\ldots ,0)$
; compare Example 2.7. The quasi-isogeny group
$(-\mu )_{\textrm {dom}}=(1,0,\ldots ,0)$
; compare Example 2.7. The quasi-isogeny group
![]() $J_b$
is the unit group of the central skew field over
$J_b$
is the unit group of the central skew field over
![]() ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
with Hasse invariant
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
with Hasse invariant
![]() $1/r$
. The Rapoport-Zink space is the Lubin-Tate space
$1/r$
. The Rapoport-Zink space is the Lubin-Tate space
of
![]() $1$
-dimensional formal
$1$
-dimensional formal
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-modules of height r. Its connected components are indexed by the height of the quasi-isogeny
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-modules of height r. Its connected components are indexed by the height of the quasi-isogeny
![]() $\bar \delta $
; that is, the image of
$\bar \delta $
; that is, the image of
![]() $\bar \delta \in {\mathcal {F}}\ell _{\operatorname {\mathrm {GL}}_r}$
under the map
$\bar \delta \in {\mathcal {F}}\ell _{\operatorname {\mathrm {GL}}_r}$
under the map
![]() ${\mathcal {F}}\ell _{\operatorname {\mathrm {GL}}_r}\to \pi _0({\mathcal {F}}\ell _{\operatorname {\mathrm {GL}}_r})=\pi _1(\operatorname {\mathrm {GL}}_r)={\mathbb {Z}}$
. The period space is
${\mathcal {F}}\ell _{\operatorname {\mathrm {GL}}_r}\to \pi _0({\mathcal {F}}\ell _{\operatorname {\mathrm {GL}}_r})=\pi _1(\operatorname {\mathrm {GL}}_r)={\mathbb {Z}}$
. The period space is
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^{na}=\breve {\mathcal {H}}_{G,\hat {Z}}^{\textrm {an}}={\mathbb {P}}^{r-1}_{{\mathbb {F}}(\kern-0.15em(\zeta )\kern-0.15em)}$
; compare [Reference Hartl50, Example 3.3.1]. To define the Hodge-Pink structure on the universal formal
$\breve {\mathcal {H}}_{G,\hat {Z},b}^{na}=\breve {\mathcal {H}}_{G,\hat {Z}}^{\textrm {an}}={\mathbb {P}}^{r-1}_{{\mathbb {F}}(\kern-0.15em(\zeta )\kern-0.15em)}$
; compare [Reference Hartl50, Example 3.3.1]. To define the Hodge-Pink structure on the universal formal
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-module, Gross and Hopkins [Reference Hopkins and Gross61, § 11] used the universal additive extension. See [Reference Hartl, Juschka, Böckle, Goss, Hartl and Papanikolas53, Remark 2.5.43] for a comparison of this definition with our definition of the Hodge-Pink structure in Remark 6.4. In [Reference Hopkins and Gross61, § 23] they constructed the period morphism
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-module, Gross and Hopkins [Reference Hopkins and Gross61, § 11] used the universal additive extension. See [Reference Hartl, Juschka, Böckle, Goss, Hartl and Papanikolas53, Remark 2.5.43] for a comparison of this definition with our definition of the Hodge-Pink structure in Remark 6.4. In [Reference Hopkins and Gross61, § 23] they constructed the period morphism
![]() $\breve \pi $
and showed that its image is
$\breve \pi $
and showed that its image is
![]() $({\mathbb {P}}^{r-1}_{\breve E})^{\textrm {an}}$
; compare Theorem 8.1(a). Note that Gross and Hopkins treated the
$({\mathbb {P}}^{r-1}_{\breve E})^{\textrm {an}}$
; compare Theorem 8.1(a). Note that Gross and Hopkins treated the
![]() ${\mathbb {Q}}_p$
-analogue simultaneously; see also [Reference Rapoport and Zink80, 5.50].
${\mathbb {Q}}_p$
-analogue simultaneously; see also [Reference Rapoport and Zink80, 5.50].
Example 6.16 The
 $\boldsymbol {\zeta }$
-adic Carlitz logarithm
$\boldsymbol {\zeta }$
-adic Carlitz logarithm
The following example was computed by Breutmann [Reference Breutmann24]. Let
![]() $G=\operatorname {\mathrm {GL}}_2$
, and let the Borel, the maximal torus, the bound
$G=\operatorname {\mathrm {GL}}_2$
, and let the Borel, the maximal torus, the bound
![]() $\hat Z=\hat Z_{\preceq \mu }$
and
$\hat Z=\hat Z_{\preceq \mu }$
and
![]() $\mu $
be as in the previous example. Let
$\mu $
be as in the previous example. Let
![]() $b=\left (\begin {smallmatrix} z & 0 \\ 0 & 1 \end {smallmatrix}\right )$
. Then
$b=\left (\begin {smallmatrix} z & 0 \\ 0 & 1 \end {smallmatrix}\right )$
. Then
![]() $J_b$
is the diagonal torus in
$J_b$
is the diagonal torus in
![]() $\operatorname {\mathrm {GL}}_2$
. The Rapoport-Zink space descends to
$\operatorname {\mathrm {GL}}_2$
. The Rapoport-Zink space descends to
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
as the formal scheme
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
as the formal scheme
 $$ \begin{align*} {\mathcal{M}}_{\underline{{\mathbb{G}}}_{0}}^{\hat{Z}^{-1}} \;=\; \coprod_{(i,j)\in{\mathbb{Z}}^2}\operatorname{\mathrm{Spf}} {\mathbb{F}}_q \text{[}\kern-0.15em\text{[}\zeta,h\text{]}\kern-0.15em\text{]}\,{,} \end{align*} $$
$$ \begin{align*} {\mathcal{M}}_{\underline{{\mathbb{G}}}_{0}}^{\hat{Z}^{-1}} \;=\; \coprod_{(i,j)\in{\mathbb{Z}}^2}\operatorname{\mathrm{Spf}} {\mathbb{F}}_q \text{[}\kern-0.15em\text{[}\zeta,h\text{]}\kern-0.15em\text{]}\,{,} \end{align*} $$
whose underlying affine Deligne-Lusztig variety
![]() $X_{Z^{-1}}(b)=\coprod _{{\mathbb {Z}}^2}\operatorname {\mathrm {Spec}}{\mathbb {F}}_q$
is
$X_{Z^{-1}}(b)=\coprod _{{\mathbb {Z}}^2}\operatorname {\mathrm {Spec}}{\mathbb {F}}_q$
is
![]() $0$
-dimensional. Over the component
$0$
-dimensional. Over the component
![]() $(i,j)\in {\mathbb {Z}}^i$
, the universal local
$(i,j)\in {\mathbb {Z}}^i$
, the universal local
![]() $\operatorname {\mathrm {GL}}_2$
-shtuka
$\operatorname {\mathrm {GL}}_2$
-shtuka
![]() ${\underline {{\mathcal {G}}}}$
is given by the local shtuka
${\underline {{\mathcal {G}}}}$
is given by the local shtuka
![]() ${\underline {M\!}\,}({\underline {{\mathcal {G}}}})=({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta ,h\mathrm {]}\kern-0.15em\mathrm {]}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}^2,\tau _M)$
with
${\underline {M\!}\,}({\underline {{\mathcal {G}}}})=({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta ,h\mathrm {]}\kern-0.15em\mathrm {]}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}^2,\tau _M)$
with
![]() $\tau _M=\left (\begin {smallmatrix} z-\zeta & 0 \\ h & 1 \end {smallmatrix}\right )$
; see Remark 6.4. The universal quasi-isogeny
$\tau _M=\left (\begin {smallmatrix} z-\zeta & 0 \\ h & 1 \end {smallmatrix}\right )$
; see Remark 6.4. The universal quasi-isogeny
 $$ \begin{align*} \bar\delta=\left(\begin{matrix} z^i & 0 \\[2mm] -z^j\sum_{\nu=0}^\infty h^{q^\nu}\!\!/z^{\nu+1}\; & z^j \end{matrix}\right) \end{align*} $$
$$ \begin{align*} \bar\delta=\left(\begin{matrix} z^i & 0 \\[2mm] -z^j\sum_{\nu=0}^\infty h^{q^\nu}\!\!/z^{\nu+1}\; & z^j \end{matrix}\right) \end{align*} $$
lifts to
 $$ \begin{align*} \Delta\;=\;\left(\begin{array}{c@{\qquad}c} z^i\prod\limits_{\nu=0}^\infty\dfrac{z}{z-\zeta^{q^\nu}} & 0 \\[4mm] -z^j\sum\limits_{\nu=0}^\infty \dfrac{h^{q^\nu}}{(z-\zeta)\cdots(z-\zeta^{q^\nu})} & z^j \end{array}\right). \end{align*} $$
$$ \begin{align*} \Delta\;=\;\left(\begin{array}{c@{\qquad}c} z^i\prod\limits_{\nu=0}^\infty\dfrac{z}{z-\zeta^{q^\nu}} & 0 \\[4mm] -z^j\sum\limits_{\nu=0}^\infty \dfrac{h^{q^\nu}}{(z-\zeta)\cdots(z-\zeta^{q^\nu})} & z^j \end{array}\right). \end{align*} $$
The E-analytic space
![]() $({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\textrm {an}}$
is the disjoint union indexed by
$({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\textrm {an}}$
is the disjoint union indexed by
![]() $(i,j)\in {\mathbb {Z}}^2$
of the open unit discs with coordinate h and
$(i,j)\in {\mathbb {Z}}^2$
of the open unit discs with coordinate h and
![]() ${\mathcal {H}}_{G,\hat {Z},b}^{na}={\mathcal {H}}_{G,\hat {Z},b}^{wa}={\mathbb {A}}^1_E={\mathbb {P}}^1_E\setminus \{(0:1)\}\subset {\mathcal {H}}_{G,\hat {Z}}^{\textrm {an}}={\mathbb {P}}^1_E$
; compare [Reference Hartl50, Example 3.3.3]. On the component
${\mathcal {H}}_{G,\hat {Z},b}^{na}={\mathcal {H}}_{G,\hat {Z},b}^{wa}={\mathbb {A}}^1_E={\mathbb {P}}^1_E\setminus \{(0:1)\}\subset {\mathcal {H}}_{G,\hat {Z}}^{\textrm {an}}={\mathbb {P}}^1_E$
; compare [Reference Hartl50, Example 3.3.3]. On the component
![]() $(i,j)$
the period morphism
$(i,j)$
the period morphism
![]() $\breve \pi $
is given by
$\breve \pi $
is given by
![]() $h\mapsto \zeta ^{j-i}(\sigma ^\ast t_{\scriptscriptstyle -})|_{z=\zeta }\log _{\mathrm {Carlitz}}(h)$
, where
$h\mapsto \zeta ^{j-i}(\sigma ^\ast t_{\scriptscriptstyle -})|_{z=\zeta }\log _{\mathrm {Carlitz}}(h)$
, where
![]() $t_{\scriptscriptstyle -}$
was defined in (4.3) and
$t_{\scriptscriptstyle -}$
was defined in (4.3) and
![]() $\log _{\mathrm {Carlitz}}(h):=\sum _{\nu =0}^\infty \tfrac {h^{q^\nu }}{(\zeta -\zeta ^q)\cdots (\zeta -\zeta ^{q^\nu })}$
is the
$\log _{\mathrm {Carlitz}}(h):=\sum _{\nu =0}^\infty \tfrac {h^{q^\nu }}{(\zeta -\zeta ^q)\cdots (\zeta -\zeta ^{q^\nu })}$
is the
![]() $\zeta $
-adic Carlitz logarithm; see [Reference Goss42, § 3.4]. In particular,
$\zeta $
-adic Carlitz logarithm; see [Reference Goss42, § 3.4]. In particular,
![]() $\breve \pi $
is surjective onto
$\breve \pi $
is surjective onto
![]() ${\mathcal {H}}_{G,\hat {Z},b}^{na}$
; compare Theorem 8.1(a). This example is analogous to the period morphism for p-divisible groups [Reference Rapoport and Zink80, 5.51, 5.52] given by the p-adic logarithm, which was constructed by Dwork; compare [Reference Katz66, §§ 7,8].
${\mathcal {H}}_{G,\hat {Z},b}^{na}$
; compare Theorem 8.1(a). This example is analogous to the period morphism for p-divisible groups [Reference Rapoport and Zink80, 5.51, 5.52] given by the p-adic logarithm, which was constructed by Dwork; compare [Reference Katz66, §§ 7,8].
7 The tower of étale coverings
In this section we fix a local G-shtuka
![]() ${\underline {{\mathbb {G}}}}_0$
over
${\underline {{\mathbb {G}}}}_0$
over
![]() ${\mathbb {F}}$
and a bound
${\mathbb {F}}$
and a bound
![]() $\hat Z$
with reflex ring
$\hat Z$
with reflex ring
![]() $R_{\hat Z}=\kappa \mathrm {[}\kern-0.15em\mathrm {[}\xi \mathrm {]}\kern-0.15em\mathrm {]}$
. Let again
$R_{\hat Z}=\kappa \mathrm {[}\kern-0.15em\mathrm {[}\xi \mathrm {]}\kern-0.15em\mathrm {]}$
. Let again
![]() $E_{\hat Z}=\kappa (\kern-0.15em( \xi )\kern-0.15em)$
and
$E_{\hat Z}=\kappa (\kern-0.15em( \xi )\kern-0.15em)$
and
![]() $\breve E={\mathbb {F}}(\kern-0.15em( \xi )\kern-0.15em)$
and
$\breve E={\mathbb {F}}(\kern-0.15em( \xi )\kern-0.15em)$
and
![]() $\breve R_{\hat Z}={\mathbb {F}}\mathrm {[}\kern-0.15em\mathrm {[}\xi \mathrm {]}\kern-0.15em\mathrm {]}$
. We write
$\breve R_{\hat Z}={\mathbb {F}}\mathrm {[}\kern-0.15em\mathrm {[}\xi \mathrm {]}\kern-0.15em\mathrm {]}$
. We write
![]() ${\breve {\mathcal {M}}}$
for the strictly
${\breve {\mathcal {M}}}$
for the strictly
![]() $\breve E$
-analytic space
$\breve E$
-analytic space
![]() $({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\textrm {an}}$
. We shall construct a tower of finite étale coverings of
$({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\textrm {an}}$
. We shall construct a tower of finite étale coverings of
![]() ${\breve {\mathcal {M}}}$
obtained by trivialising the Tate module of the universal étale local G-shtuka
${\breve {\mathcal {M}}}$
obtained by trivialising the Tate module of the universal étale local G-shtuka
![]() ${\underline {{\mathcal {G}}}}$
over
${\underline {{\mathcal {G}}}}$
over
![]() ${\breve {\mathcal {M}}}$
from Remark 6.7.
${\breve {\mathcal {M}}}$
from Remark 6.7.
We start more generally with a field extension
![]() $L/\breve E$
that is complete with respect to an absolute value extending the absolute value on
$L/\breve E$
that is complete with respect to an absolute value extending the absolute value on
![]() $\breve E$
and with an étale local G-shtuka
$\breve E$
and with an étale local G-shtuka
![]() ${\underline {{\mathcal {G}}}}$
over a connected strictly L-analytic space X as in Definition 6.8. We choose a geometric base point
${\underline {{\mathcal {G}}}}$
over a connected strictly L-analytic space X as in Definition 6.8. We choose a geometric base point
![]() $\bar x$
of X.
$\bar x$
of X.
Definition 7.1. Let
![]() $\rho :G\rightarrow \operatorname {\mathrm {GL}}_r$
be in
$\rho :G\rightarrow \operatorname {\mathrm {GL}}_r$
be in
![]() $\operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}G$
. Let
$\operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}G$
. Let
![]() ${\underline {M\!}\,}=(M,\tau _M)$
be the étale local shtuka of rank r associated with the étale local
${\underline {M\!}\,}=(M,\tau _M)$
be the étale local shtuka of rank r associated with the étale local
![]() $\operatorname {\mathrm {GL}}_r$
-shtuka
$\operatorname {\mathrm {GL}}_r$
-shtuka
![]() $\rho _*{\underline {{\mathcal {G}}}}$
obtained from
$\rho _*{\underline {{\mathcal {G}}}}$
obtained from
![]() ${\underline {{\mathcal {G}}}}$
via
${\underline {{\mathcal {G}}}}$
via
![]() $\rho $
, see [Reference Arasteh Rad and Hartl4, § 3], and let
$\rho $
, see [Reference Arasteh Rad and Hartl4, § 3], and let
![]() ${\underline {M\!}\,}_{\bar x}$
denote its fibre over
${\underline {M\!}\,}_{\bar x}$
denote its fibre over
![]() $\bar x$
. Then the (dual) Tate module
$\bar x$
. Then the (dual) Tate module
![]() $\check T_{{\underline {{\mathcal {G}}}},\bar x}(\rho )$
of
$\check T_{{\underline {{\mathcal {G}}}},\bar x}(\rho )$
of
![]() ${\underline {{\mathcal {G}}}}$
with respect to
${\underline {{\mathcal {G}}}}$
with respect to
![]() $\rho $
is defined as the (dual) Tate module of
$\rho $
is defined as the (dual) Tate module of
![]() ${\underline {M\!}\,}_{\bar x}$
,
${\underline {M\!}\,}_{\bar x}$
,
By [Reference Taguchi and Wan94, Proposition 6.1] it is a free
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]} $
-module of rank r with a continuous monodromy action of
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]} $
-module of rank r with a continuous monodromy action of
![]() $\pi _1^{\mathrm {\acute {e}t}}(X,\bar x)$
. This action factors through
$\pi _1^{\mathrm {\acute {e}t}}(X,\bar x)$
. This action factors through
![]() $\pi _1^{\textrm {alg}}(X,\bar x)$
.
$\pi _1^{\textrm {alg}}(X,\bar x)$
.
Let now
![]() $\rho :G\rightarrow \operatorname {\mathrm {GL}}_r$
be in
$\rho :G\rightarrow \operatorname {\mathrm {GL}}_r$
be in
![]() $\operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G$
. Let
$\operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G$
. Let
![]() ${\underline {N\!}\,}=(N,\tau _N)$
be the locally free
${\underline {N\!}\,}=(N,\tau _N)$
be the locally free
![]() ${\mathcal {O}}_X(\kern-0.15em( z)\kern-0.15em)$
-module of rank r and the
${\mathcal {O}}_X(\kern-0.15em( z)\kern-0.15em)$
-module of rank r and the
![]() $\sigma $
-linear isomorphism associated with
$\sigma $
-linear isomorphism associated with
![]() $\rho _*L{\underline {{\mathcal {G}}}}$
obtained from
$\rho _*L{\underline {{\mathcal {G}}}}$
obtained from
![]() $L{\underline {{\mathcal {G}}}}$
via
$L{\underline {{\mathcal {G}}}}$
via
![]() $\rho $
. Let
$\rho $
. Let
![]() ${\underline {N\!}\,}_{\bar x}$
denote its fibre over
${\underline {N\!}\,}_{\bar x}$
denote its fibre over
![]() $\bar x$
. The rational (dual) Tate module
$\bar x$
. The rational (dual) Tate module
![]() $\check V_{{\underline {{\mathcal {G}}}},\bar x}(\rho )$
of
$\check V_{{\underline {{\mathcal {G}}}},\bar x}(\rho )$
of
![]() ${\underline {{\mathcal {G}}}}$
with respect to
${\underline {{\mathcal {G}}}}$
with respect to
![]() $\rho $
is
$\rho $
is
a finite-dimensional
![]() ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em) $
-vector space with a continuous monodromy action of
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em) $
-vector space with a continuous monodromy action of
![]() $\pi _1^{\mathrm {\acute {e}t}}(X,\bar x)$
.
$\pi _1^{\mathrm {\acute {e}t}}(X,\bar x)$
.
Remark 7.2. As was pointed out to us by S. Neupert (see also [Reference Neupert76, 2.6]), one can also use the following direct way to define the Tate module of an étale local G-shtuka that does not use tensor functors. Let
![]() ${\underline {{\mathcal {G}}}}=({\mathcal {G}}, \tau _{\mathcal {G}})$
be an étale local G-shtuka over a base scheme or a strictly
${\underline {{\mathcal {G}}}}=({\mathcal {G}}, \tau _{\mathcal {G}})$
be an étale local G-shtuka over a base scheme or a strictly
![]() ${\mathbb {F}}(\kern-0.15em(\zeta )\kern-0.15em)$
-analytic space S; in other words,
${\mathbb {F}}(\kern-0.15em(\zeta )\kern-0.15em)$
-analytic space S; in other words,
![]() $\tau _{\mathcal {G}}$
induces an isomorphism
$\tau _{\mathcal {G}}$
induces an isomorphism
![]() . Consider for each
. Consider for each
![]() $n\in {\mathbb {N}}$
the
$n\in {\mathbb {N}}$
the
![]() $\tau $
-invariants of the induced map
$\tau $
-invariants of the induced map
![]() $\sigma ^*{\mathcal {G}}_n\rightarrow {\mathcal {G}}_n$
. Here
$\sigma ^*{\mathcal {G}}_n\rightarrow {\mathcal {G}}_n$
. Here
![]() ${\mathcal {G}}_n$
is the
${\mathcal {G}}_n$
is the
![]() $G/G_n$
-torsor induced by
$G/G_n$
-torsor induced by
![]() ${\mathcal {G}}$
where
${\mathcal {G}}$
where
![]() $G_n$
is the kernel of the projection
$G_n$
is the kernel of the projection
![]() $G({\mathbb {F}}_q[[z]])\rightarrow G({\mathbb {F}}_q[[z]]/(z^n))$
. These
$G({\mathbb {F}}_q[[z]])\rightarrow G({\mathbb {F}}_q[[z]]/(z^n))$
. These
![]() $\tau $
-invariants form a
$\tau $
-invariants form a
![]() $G({\mathbb {F}}_q[[z]]/(z^n))$
-torsor that is trivialised by a finite étale covering. One can then define the Tate module of
$G({\mathbb {F}}_q[[z]]/(z^n))$
-torsor that is trivialised by a finite étale covering. One can then define the Tate module of
![]() ${\underline {{\mathcal {G}}}}$
as the inverse limit over n of these torsors.
${\underline {{\mathcal {G}}}}$
as the inverse limit over n of these torsors.
Remark 7.3.
-
(a) Let
 $(\rho ^{\prime }\!,V)\in \operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G$
. Let
$(\rho ^{\prime }\!,V)\in \operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G$
. Let
 $\Lambda _0$
be any
$\Lambda _0$
be any
 ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-lattice in V. Then the stabiliser in
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-lattice in V. Then the stabiliser in
 $G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
of
$G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
of
 $\Lambda _0$
is open and, in particular, of finite index in the compact group
$\Lambda _0$
is open and, in particular, of finite index in the compact group
 $G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
. Therefore, is an intersection of finitely many translations of
$G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
. Therefore, is an intersection of finitely many translations of $$ \begin{align*}\Lambda:=\bigcap_{g\in G({\mathbb{F}}_q\text{[}\kern-0.15em\text{[} z\text{]}\kern-0.15em\text{]})}\rho^{\prime}(g)(\Lambda_0) \end{align*} $$
$$ \begin{align*}\Lambda:=\bigcap_{g\in G({\mathbb{F}}_q\text{[}\kern-0.15em\text{[} z\text{]}\kern-0.15em\text{]})}\rho^{\prime}(g)(\Lambda_0) \end{align*} $$
 $\Lambda _0$
and hence a lattice in V. By definition,
$\Lambda _0$
and hence a lattice in V. By definition,
 $\Lambda $
is
$\Lambda $
is
 $G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
-invariant. Thus,
$G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
-invariant. Thus,
 $\rho ^{\prime }$
is induced by
$\rho ^{\prime }$
is induced by
 $(\rho ,\Lambda ):=(\rho ^{\prime }|_{\Lambda },\Lambda )\in \operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}G$
. From the definition above, we obtain In particular, the vector space
$(\rho ,\Lambda ):=(\rho ^{\prime }|_{\Lambda },\Lambda )\in \operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}G$
. From the definition above, we obtain In particular, the vector space $$ \begin{align*}\check V_{{\underline{{\mathcal{G}}}},\bar x}(\rho^{\prime})=\check T_{{\underline{{\mathcal{G}}}},\bar x}(\rho)\otimes_{{\mathbb{F}}_q\text{[}\kern-0.15em\text{[} z\text{]}\kern-0.15em\text{]} }{\mathbb{F}}_q(\kern-0.15em( z )\kern-0.15em). \end{align*} $$
$$ \begin{align*}\check V_{{\underline{{\mathcal{G}}}},\bar x}(\rho^{\prime})=\check T_{{\underline{{\mathcal{G}}}},\bar x}(\rho)\otimes_{{\mathbb{F}}_q\text{[}\kern-0.15em\text{[} z\text{]}\kern-0.15em\text{]} }{\mathbb{F}}_q(\kern-0.15em( z )\kern-0.15em). \end{align*} $$
 $\check V_{{\underline {{\mathcal {G}}}},\bar x}(\rho ^{\prime })$
is of dimension
$\check V_{{\underline {{\mathcal {G}}}},\bar x}(\rho ^{\prime })$
is of dimension
 $\dim V$
.
$\dim V$
.
-
(b) These definitions are independent of the chosen base point
 $\bar x$
, because for any other geometric base point
$\bar x$
, because for any other geometric base point
 $\bar x^{\prime }$
of X there is an isomorphism of fibre functors
$\bar x^{\prime }$
of X there is an isomorphism of fibre functors
 $\check T_{{\underline {{\mathcal {G}}}},\bar x}\cong \check T_{{\underline {{\mathcal {G}}}},\bar x^{\prime }}$
and
$\check T_{{\underline {{\mathcal {G}}}},\bar x}\cong \check T_{{\underline {{\mathcal {G}}}},\bar x^{\prime }}$
and
 $\check V_{{\underline {{\mathcal {G}}}},\bar x}\cong \check V_{{\underline {{\mathcal {G}}}},\bar x^{\prime }}$
by [Reference de Jong31, Theorem 2.9] and Remark 7.2.
$\check V_{{\underline {{\mathcal {G}}}},\bar x}\cong \check V_{{\underline {{\mathcal {G}}}},\bar x^{\prime }}$
by [Reference de Jong31, Theorem 2.9] and Remark 7.2. -
(c) From the definition one obtains that the Tate module and the rational Tate module are tensor functors
In terms of Definition 5.2, we may view $$ \begin{align*} & \check T_{{\underline{{\mathcal{G}}}},\bar x}\colon\operatorname{\mathrm{Rep}}_{{\mathbb{F}}_q\text{[}\kern-0.15em\text{[} z\text{]}\kern-0.15em\text{]}}G\;\longrightarrow\; \operatorname{\mathrm{Rep}}^{\textrm{cont}}_{{\mathbb{F}}_q\text{[}\kern-0.15em\text{[} z\text{]}\kern-0.15em\text{]} }\big(\pi_1^{\mathrm{\acute{e}t}}(X,\bar x)\big)\;=\;\operatorname{\mathrm{Rep}}^{\textrm{cont}}_{{\mathbb{F}}_q\text{[}\kern-0.15em\text{[} z\text{]}\kern-0.15em\text{]} }\big(\pi_1^{\textrm{alg}}(X,\bar x)\big)\qquad\text{and}\\[2mm] & \check V_{{\underline{{\mathcal{G}}}},\bar x}\colon\operatorname{\mathrm{Rep}}_{{\mathbb{F}}_q(\kern-0.15em( z )\kern-0.15em)}G\;\longrightarrow\; \operatorname{\mathrm{Rep}}^{\textrm{cont}}_{{\mathbb{F}}_q(\kern-0.15em( z )\kern-0.15em) }\big(\pi_1^{\mathrm{\acute{e}t}}(X,\bar x)\big)\,. \end{align*} $$
$$ \begin{align*} & \check T_{{\underline{{\mathcal{G}}}},\bar x}\colon\operatorname{\mathrm{Rep}}_{{\mathbb{F}}_q\text{[}\kern-0.15em\text{[} z\text{]}\kern-0.15em\text{]}}G\;\longrightarrow\; \operatorname{\mathrm{Rep}}^{\textrm{cont}}_{{\mathbb{F}}_q\text{[}\kern-0.15em\text{[} z\text{]}\kern-0.15em\text{]} }\big(\pi_1^{\mathrm{\acute{e}t}}(X,\bar x)\big)\;=\;\operatorname{\mathrm{Rep}}^{\textrm{cont}}_{{\mathbb{F}}_q\text{[}\kern-0.15em\text{[} z\text{]}\kern-0.15em\text{]} }\big(\pi_1^{\textrm{alg}}(X,\bar x)\big)\qquad\text{and}\\[2mm] & \check V_{{\underline{{\mathcal{G}}}},\bar x}\colon\operatorname{\mathrm{Rep}}_{{\mathbb{F}}_q(\kern-0.15em( z )\kern-0.15em)}G\;\longrightarrow\; \operatorname{\mathrm{Rep}}^{\textrm{cont}}_{{\mathbb{F}}_q(\kern-0.15em( z )\kern-0.15em) }\big(\pi_1^{\mathrm{\acute{e}t}}(X,\bar x)\big)\,. \end{align*} $$
 $\check T_{{\underline {{\mathcal {G}}}},\bar x}$
and
$\check T_{{\underline {{\mathcal {G}}}},\bar x}$
and
 $\check V_{{\underline {{\mathcal {G}}}},\bar x}$
as tensor functors (7.1)
$\check V_{{\underline {{\mathcal {G}}}},\bar x}$
as tensor functors (7.1) $$ \begin{align} & \check T_{{\underline{{\mathcal{G}}}}}\colon\operatorname{\mathrm{Rep}}_{{\mathbb{F}}_q\text{[}\kern-0.15em\text{[} z\text{]}\kern-0.15em\text{]}}G\;\longrightarrow\; {\mathbb{F}}_q\text{[}\kern-0.15em\text{[} z\text{]}\kern-0.15em\text{]}\mbox{-}{\underline{\text{Loc}}}_X\qquad\text{and} \end{align} $$
(7.2)with
$$ \begin{align} & \check T_{{\underline{{\mathcal{G}}}}}\colon\operatorname{\mathrm{Rep}}_{{\mathbb{F}}_q\text{[}\kern-0.15em\text{[} z\text{]}\kern-0.15em\text{]}}G\;\longrightarrow\; {\mathbb{F}}_q\text{[}\kern-0.15em\text{[} z\text{]}\kern-0.15em\text{]}\mbox{-}{\underline{\text{Loc}}}_X\qquad\text{and} \end{align} $$
(7.2)with $$ \begin{align}& \check V_{{\underline{{\mathcal{G}}}}}\colon\operatorname{\mathrm{Rep}}_{{\mathbb{F}}_q(\kern-0.15em( z )\kern-0.15em)}G\;\longrightarrow\; {\mathbb{F}}_q(\kern-0.15em( z )\kern-0.15em)\mbox{-}{\underline{\text{Loc}}}_X\,{,} \end{align} $$
$$ \begin{align}& \check V_{{\underline{{\mathcal{G}}}}}\colon\operatorname{\mathrm{Rep}}_{{\mathbb{F}}_q(\kern-0.15em( z )\kern-0.15em)}G\;\longrightarrow\; {\mathbb{F}}_q(\kern-0.15em( z )\kern-0.15em)\mbox{-}{\underline{\text{Loc}}}_X\,{,} \end{align} $$
 $\check T_{{\underline {{\mathcal {G}}}},\bar x}=F_{\bar x}^{\mathrm {\acute {e}t}}\circ \check T_{{\underline {{\mathcal {G}}}}}$
and
$\check T_{{\underline {{\mathcal {G}}}},\bar x}=F_{\bar x}^{\mathrm {\acute {e}t}}\circ \check T_{{\underline {{\mathcal {G}}}}}$
and
 $\check V_{{\underline {{\mathcal {G}}}},\bar x}=F_{\bar x}^{\mathrm {\acute {e}t}}\circ \check V_{{\underline {{\mathcal {G}}}}}$
. The tensor functors (7.1) and (7.2) also exist if X is not connected.
$\check V_{{\underline {{\mathcal {G}}}},\bar x}=F_{\bar x}^{\mathrm {\acute {e}t}}\circ \check V_{{\underline {{\mathcal {G}}}}}$
. The tensor functors (7.1) and (7.2) also exist if X is not connected.
Furthermore,
 $\check T_{{\underline {{\mathcal {G}}}},\bar x}$
and
$\check T_{{\underline {{\mathcal {G}}}},\bar x}$
and
 $\check T_{{\underline {{\mathcal {G}}}}}$
are functorial on the category of étale local G-shtukas
$\check T_{{\underline {{\mathcal {G}}}}}$
are functorial on the category of étale local G-shtukas
 ${\underline {{\mathcal {G}}}}$
with isomorphisms as morphisms, and
${\underline {{\mathcal {G}}}}$
with isomorphisms as morphisms, and
 $\check V_{{\underline {{\mathcal {G}}}},\bar x}$
and
$\check V_{{\underline {{\mathcal {G}}}},\bar x}$
and
 $\check V_{{\underline {{\mathcal {G}}}}}$
are functorial on the category of étale local G-shtukas
$\check V_{{\underline {{\mathcal {G}}}}}$
are functorial on the category of étale local G-shtukas
 ${\underline {{\mathcal {G}}}}$
with isogenies as morphisms. Indeed, an isomorphism, respectively an isogeny, of étale local G-shtukas canonically induces an isomorphism between the corresponding
${\underline {{\mathcal {G}}}}$
with isogenies as morphisms. Indeed, an isomorphism, respectively an isogeny, of étale local G-shtukas canonically induces an isomorphism between the corresponding
 ${\underline {M\!}\,}$
, respectively
${\underline {M\!}\,}$
, respectively
 ${\underline {N\!}\,}$
.
${\underline {N\!}\,}$
.
Recall the forgetful functors
![]() $\omega ^{\circ }_A:\operatorname {\mathrm {Rep}}_A G\to \textrm {FMod}_A$
and
$\omega ^{\circ }_A:\operatorname {\mathrm {Rep}}_A G\to \textrm {FMod}_A$
and
![]() $\mathit {forget}\colon \operatorname {\mathrm {Rep}}^{\textrm {cont}}_{A}\big (\pi _1^{\mathrm {\acute {e}t}}(X,\bar x)\big )\to \textrm {FMod}_A$
from Definition 5.1. For an étale local G-shtuka
$\mathit {forget}\colon \operatorname {\mathrm {Rep}}^{\textrm {cont}}_{A}\big (\pi _1^{\mathrm {\acute {e}t}}(X,\bar x)\big )\to \textrm {FMod}_A$
from Definition 5.1. For an étale local G-shtuka
![]() ${\underline {{\mathcal {G}}}}$
over X, the sets
${\underline {{\mathcal {G}}}}$
over X, the sets
 $$ \begin{align} \operatorname{\mathrm{Triv}}_{{\underline{{\mathcal{G}}}},\bar x}({\mathbb{F}}_q\text{[}\kern-0.15em\text{[} z\text{]}\kern-0.15em\text{]}) & := \operatorname{\mathrm{Isom}}^{\otimes}(\omega^{\circ}_{{\mathbb{F}}_q\text{[}\kern-0.15em\text{[} z\text{]}\kern-0.15em\text{]} },\mathit{forget}\circ\check T_{{\underline{{\mathcal{G}}}},\bar x})({\mathbb{F}}_q\text{[}\kern-0.15em\text{[} z\text{]}\kern-0.15em\text{]})\qquad\text{and}\\[2mm] \operatorname{\mathrm{Triv}}_{{\underline{{\mathcal{G}}}},\bar x}\big({\mathbb{F}}_q(\kern-0.15em( z )\kern-0.15em)\big) & := \operatorname{\mathrm{Isom}}^{\otimes}(\omega^{\circ},\mathit{ forget}\circ\check V_{{\underline{{\mathcal{G}}}},\bar x})\big({\mathbb{F}}_q(\kern-0.15em( z )\kern-0.15em)\big) \nonumber \end{align} $$
$$ \begin{align} \operatorname{\mathrm{Triv}}_{{\underline{{\mathcal{G}}}},\bar x}({\mathbb{F}}_q\text{[}\kern-0.15em\text{[} z\text{]}\kern-0.15em\text{]}) & := \operatorname{\mathrm{Isom}}^{\otimes}(\omega^{\circ}_{{\mathbb{F}}_q\text{[}\kern-0.15em\text{[} z\text{]}\kern-0.15em\text{]} },\mathit{forget}\circ\check T_{{\underline{{\mathcal{G}}}},\bar x})({\mathbb{F}}_q\text{[}\kern-0.15em\text{[} z\text{]}\kern-0.15em\text{]})\qquad\text{and}\\[2mm] \operatorname{\mathrm{Triv}}_{{\underline{{\mathcal{G}}}},\bar x}\big({\mathbb{F}}_q(\kern-0.15em( z )\kern-0.15em)\big) & := \operatorname{\mathrm{Isom}}^{\otimes}(\omega^{\circ},\mathit{ forget}\circ\check V_{{\underline{{\mathcal{G}}}},\bar x})\big({\mathbb{F}}_q(\kern-0.15em( z )\kern-0.15em)\big) \nonumber \end{align} $$
are nonempty; see [Reference Arasteh Rad and Hartl4, after Definition 3.5]. This is due to the fact that we assumed G to have connected fibres. In [Reference Rapoport and Zink80, 5.32], where nonconnected orthogonal groups are also allowed, the isomorphism class of the étale fibre functor analogous to
![]() $\mathit {forget}\circ \check T_{{\underline {{\mathcal {G}}}},\bar x}$
can vary. By the definition of the Tate functor,
$\mathit {forget}\circ \check T_{{\underline {{\mathcal {G}}}},\bar x}$
can vary. By the definition of the Tate functor,
![]() $\operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}},\bar x}({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
carries an action of
$\operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}},\bar x}({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
carries an action of
![]() $G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]} )\times \pi _1^{\textrm {alg}}(X,\bar x)$
where the first factor acts through
$G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]} )\times \pi _1^{\textrm {alg}}(X,\bar x)$
where the first factor acts through
![]() $\omega ^{\circ }_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]} }$
and the action of
$\omega ^{\circ }_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]} }$
and the action of
![]() $\pi _1^{\textrm {alg}}(X,\bar x)$
is induced by the action on the Tate functor. Similarly,
$\pi _1^{\textrm {alg}}(X,\bar x)$
is induced by the action on the Tate functor. Similarly,
![]() $\operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}},\bar x}\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
admits an action of
$\operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}},\bar x}\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
admits an action of
![]() $G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )\times \pi _1^{\mathrm {\acute {e}t}}(X,\bar x)$
. For every choice of an element
$G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )\times \pi _1^{\mathrm {\acute {e}t}}(X,\bar x)$
. For every choice of an element
![]() $\eta \in \operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}},\bar x}({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
, we obtain a
$\eta \in \operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}},\bar x}({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
, we obtain a
![]() $G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]} )$
-equivariant bijection
$G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]} )$
-equivariant bijection
where
![]() $G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]} )$
acts on itself by multiplication on the right. Under this bijection, the action of
$G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]} )$
acts on itself by multiplication on the right. Under this bijection, the action of
![]() $\pi _1^{\textrm {alg}}(X,\bar x)$
corresponds to a group homomorphism
$\pi _1^{\textrm {alg}}(X,\bar x)$
corresponds to a group homomorphism
that is independent of
![]() $\eta $
up to conjugation by elements of
$\eta $
up to conjugation by elements of
![]() $G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]} )$
. Similar statements hold for
$G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]} )$
. Similar statements hold for
![]() $\operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}},\bar x}\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
with
$\operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}},\bar x}\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
with
![]() $G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]} )$
and
$G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]} )$
and
![]() $\pi _1^{\textrm {alg}}(X,\bar x)$
replaced by
$\pi _1^{\textrm {alg}}(X,\bar x)$
replaced by
![]() $G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
and
$G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
and
![]() $\pi _1^{\mathrm {\acute {e}t}}(X,\bar x)$
.
$\pi _1^{\mathrm {\acute {e}t}}(X,\bar x)$
.
Definition 7.4. Let
![]() ${\underline {{\mathcal {G}}}}$
be an étale local G-shtuka over a connected
${\underline {{\mathcal {G}}}}$
be an étale local G-shtuka over a connected
![]() ${\mathbb {F}}(\kern-0.15em(\zeta )\kern-0.15em)$
-analytic space X, and let
${\mathbb {F}}(\kern-0.15em(\zeta )\kern-0.15em)$
-analytic space X, and let
![]() $K\subset G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
be an open subgroup. Then an integral K-level structure on
$K\subset G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
be an open subgroup. Then an integral K-level structure on
![]() ${\underline {{\mathcal {G}}}}$
is a
${\underline {{\mathcal {G}}}}$
is a
![]() $\pi _1^{\textrm {alg}}(X,\bar x)$
-invariant K-orbit in
$\pi _1^{\textrm {alg}}(X,\bar x)$
-invariant K-orbit in
![]() $\operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}},\bar x}({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
.
$\operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}},\bar x}({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
.
If
![]() $K\subset G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
is an open compact subgroup, a rational K-level structure on
$K\subset G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
is an open compact subgroup, a rational K-level structure on
![]() ${\underline {{\mathcal {G}}}}$
is a
${\underline {{\mathcal {G}}}}$
is a
![]() $\pi _1^{\mathrm {\acute {e}t}}(X,\bar x)$
-invariant K-orbit in
$\pi _1^{\mathrm {\acute {e}t}}(X,\bar x)$
-invariant K-orbit in
![]() $\operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}},\bar x}\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
. For nonconnected X we make a similar definition choosing a base point on each connected component and an integral, respectively rational K-level structure on the restriction to each connected component separately. Note that every integral K-level structure on
$\operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}},\bar x}\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
. For nonconnected X we make a similar definition choosing a base point on each connected component and an integral, respectively rational K-level structure on the restriction to each connected component separately. Note that every integral K-level structure on
![]() ${\underline {{\mathcal {G}}}}$
defines a rational K-level structure but not conversely.
${\underline {{\mathcal {G}}}}$
defines a rational K-level structure but not conversely.
For an open subgroup
![]() $K\subset G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
, let
$K\subset G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
, let
![]() $X^K$
be the functor on the category of L-analytic spaces over X parametrising integral K-level structures on the étale local G-shtuka
$X^K$
be the functor on the category of L-analytic spaces over X parametrising integral K-level structures on the étale local G-shtuka
![]() ${\underline {{\mathcal {G}}}}$
over X.
${\underline {{\mathcal {G}}}}$
over X.
Proposition 7.5.
-
(a)
 $X^K$
is represented by the finite étale covering space of X that corresponds to the finite
$X^K$
is represented by the finite étale covering space of X that corresponds to the finite
 $\pi _1^{\textrm {alg}}(X,\bar x)$
-set
$\pi _1^{\textrm {alg}}(X,\bar x)$
-set
 $\operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}},\bar x}({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})/K$
under the equivalence (5.4). In particular
$\operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}},\bar x}({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})/K$
under the equivalence (5.4). In particular
 $X^K$
is a strictly L-analytic space.
$X^K$
is a strictly L-analytic space. -
(b) For
 $K_0=G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]} )$
, the morphism assigning to
$K_0=G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]} )$
, the morphism assigning to
 ${\underline {{\mathcal {G}}}}$
the
${\underline {{\mathcal {G}}}}$
the
 $K_0$
-orbit of all elements of
$K_0$
-orbit of all elements of
 $\operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}},\bar x}({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
induces an isomorphism
$\operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}},\bar x}({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
induces an isomorphism
 $X\cong X^{K_0}$
.
$X\cong X^{K_0}$
. -
(c) For any inclusion of open subgroups
 $K^{\prime }\subset K\subset G\big ({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\big )\big )$
, forgetting part of the level structure induces compatible finite étale surjective morphisms which are Galois with Galois group
$K^{\prime }\subset K\subset G\big ({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\big )\big )$
, forgetting part of the level structure induces compatible finite étale surjective morphisms which are Galois with Galois group $$ \begin{align*} {\breve{\pi}}_{K,K^{\prime}}:X^{K^{\prime}}\rightarrow X^K, \end{align*} $$
$$ \begin{align*} {\breve{\pi}}_{K,K^{\prime}}:X^{K^{\prime}}\rightarrow X^K, \end{align*} $$
 $K/K^{\prime }$
if
$K/K^{\prime }$
if
 $K^{\prime }$
is normal in K.
$K^{\prime }$
is normal in K.
Proof. Denote by
![]() ${\widetilde {X}}^K$
the finite étale covering space of X from (a). Let
${\widetilde {X}}^K$
the finite étale covering space of X from (a). Let
![]() $f\colon Y\to X$
be a connected L-analytic space over X and let
$f\colon Y\to X$
be a connected L-analytic space over X and let
![]() $\eta K$
be an integral K-level structure on
$\eta K$
be an integral K-level structure on
![]() $f^*{\underline {{\mathcal {G}}}}$
; that is,
$f^*{\underline {{\mathcal {G}}}}$
; that is,
![]() $\eta \in \operatorname {\mathrm {Triv}}_{f^*{\underline {{\mathcal {G}}}},\bar y}({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]} )$
and the K-orbit
$\eta \in \operatorname {\mathrm {Triv}}_{f^*{\underline {{\mathcal {G}}}},\bar y}({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]} )$
and the K-orbit
![]() $\eta K$
is
$\eta K$
is
![]() $\pi _1^{\textrm {alg}}(Y,\bar y)$
-invariant where
$\pi _1^{\textrm {alg}}(Y,\bar y)$
-invariant where
![]() $\bar y$
is a geometric base point of Y. We must show that
$\bar y$
is a geometric base point of Y. We must show that
![]() $\eta K$
arises from a uniquely determined X-morphism
$\eta K$
arises from a uniquely determined X-morphism
![]() $Y\to {\widetilde {X}}^K$
. Moving
$Y\to {\widetilde {X}}^K$
. Moving
![]() $\bar x$
by Remark 7.3(b), we may assume that
$\bar x$
by Remark 7.3(b), we may assume that
![]() $f(\bar y)=\bar x$
, and hence
$f(\bar y)=\bar x$
, and hence
![]() $\check T_{f^*{\underline {{\mathcal {G}}}},\bar y}=\check T_{{\underline {{\mathcal {G}}}},\bar x}$
. Consider the finite étale covering space
$\check T_{f^*{\underline {{\mathcal {G}}}},\bar y}=\check T_{{\underline {{\mathcal {G}}}},\bar x}$
. Consider the finite étale covering space
![]() ${\widetilde {X}}^K\times _X Y\to Y$
. Then
${\widetilde {X}}^K\times _X Y\to Y$
. Then
![]() $F^{\mathrm {\acute {e}t}}_{Y,\bar y}({\widetilde {X}}^K\times _X Y)=F^{\mathrm {\acute {e}t}}_{X,\bar x}({\widetilde {X}}^K)=\operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}},\bar x}({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})/K$
for the étale fibre functors from (5.3). In particular, the element
$F^{\mathrm {\acute {e}t}}_{Y,\bar y}({\widetilde {X}}^K\times _X Y)=F^{\mathrm {\acute {e}t}}_{X,\bar x}({\widetilde {X}}^K)=\operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}},\bar x}({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})/K$
for the étale fibre functors from (5.3). In particular, the element
![]() $\eta K$
defines a
$\eta K$
defines a
![]() $\pi _1^{\textrm {alg}}(Y,\bar y)$
-equivariant map from the one-element set
$\pi _1^{\textrm {alg}}(Y,\bar y)$
-equivariant map from the one-element set
![]() $\{\bar y\}=F^{\mathrm {\acute {e}t}}_{Y,\bar y}(Y)$
to
$\{\bar y\}=F^{\mathrm {\acute {e}t}}_{Y,\bar y}(Y)$
to
![]() $F^{\mathrm {\acute {e}t}}_{Y,\bar y}({\widetilde {X}}^K\times _X Y)$
. By [Reference de Jong31, Theorem 2.10], this map corresponds to a uniquely determined Y-morphism
$F^{\mathrm {\acute {e}t}}_{Y,\bar y}({\widetilde {X}}^K\times _X Y)$
. By [Reference de Jong31, Theorem 2.10], this map corresponds to a uniquely determined Y-morphism
![]() $Y\to {\widetilde {X}}^K\times _X Y$
. The projection
$Y\to {\widetilde {X}}^K\times _X Y$
. The projection
![]() $Y\to {\widetilde {X}}^K$
onto the first component is the desired X-morphism that induces the integral K-level structure
$Y\to {\widetilde {X}}^K$
onto the first component is the desired X-morphism that induces the integral K-level structure
![]() $\eta K$
over Y.
$\eta K$
over Y.
For arbitrary X and
![]() ${\underline {{\mathcal {G}}}}$
, Proposition 7.5 is the best one can hope for. However, if
${\underline {{\mathcal {G}}}}$
, Proposition 7.5 is the best one can hope for. However, if
![]() $X=({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\textrm {an}}$
, one can even replace
$X=({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\textrm {an}}$
, one can even replace
![]() $\check T_{{\underline {{\mathcal {G}}}},\bar x}$
and
$\check T_{{\underline {{\mathcal {G}}}},\bar x}$
and
![]() $\operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}},\bar x}({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
by
$\operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}},\bar x}({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
by
![]() $\check V_{{\underline {{\mathcal {G}}}},\bar x}$
and
$\check V_{{\underline {{\mathcal {G}}}},\bar x}$
and
![]() $\operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}},\bar x}\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
and allow compact open subgroups
$\operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}},\bar x}\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
and allow compact open subgroups
![]() $K\subset G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
; see Corollaries 7.11 and 7.13. To explain this (also as a preparation to define rational level structures in Definition 7.10), we keep the field L introduced at the beginning of this section and consider in the following an admissible
$K\subset G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
; see Corollaries 7.11 and 7.13. To explain this (also as a preparation to define rational level structures in Definition 7.10), we keep the field L introduced at the beginning of this section and consider in the following an admissible
![]() ${\mathcal {O}}_L$
-algebra B in the sense of Raynaud; that is, B is a quotient
${\mathcal {O}}_L$
-algebra B in the sense of Raynaud; that is, B is a quotient
![]() $\beta \colon {\mathcal {O}}_L\langle X_1,\ldots ,X_s\rangle \twoheadrightarrow B$
that is
$\beta \colon {\mathcal {O}}_L\langle X_1,\ldots ,X_s\rangle \twoheadrightarrow B$
that is
![]() $\zeta $
-torsion free; see (6.3) and [Reference Bosch and Lütkebohmert18, p. 293]. Then
$\zeta $
-torsion free; see (6.3) and [Reference Bosch and Lütkebohmert18, p. 293]. Then
![]() ${\mathcal {X}}:=\operatorname {\mathrm {Spf}} B$
is an admissible formal
${\mathcal {X}}:=\operatorname {\mathrm {Spf}} B$
is an admissible formal
![]() ${\mathcal {O}}_L$
-scheme. Let
${\mathcal {O}}_L$
-scheme. Let
![]() $B[\tfrac {1}{\zeta }]$
be the associated strictly affinoid L-algebra. We equip
$B[\tfrac {1}{\zeta }]$
be the associated strictly affinoid L-algebra. We equip
![]() $B[\tfrac {1}{\zeta }]$
with the quotient map
$B[\tfrac {1}{\zeta }]$
with the quotient map
![]() $\beta \colon L\langle X_1,\ldots ,X_s\rangle \twoheadrightarrow B[\tfrac {1}{\zeta }]$
and the L-Banach norm
$\beta \colon L\langle X_1,\ldots ,X_s\rangle \twoheadrightarrow B[\tfrac {1}{\zeta }]$
and the L-Banach norm
![]() $|b|:=\inf \{ |f|_{\sup } \colon f\in \beta ^{-1}(b)\}$
, where
$|b|:=\inf \{ |f|_{\sup } \colon f\in \beta ^{-1}(b)\}$
, where
![]() $|f|_{\sup }$
denotes the Gauß norm on the Tate algebra
$|f|_{\sup }$
denotes the Gauß norm on the Tate algebra
![]() $L\langle X_1,\ldots ,X_s\rangle $
. Then
$L\langle X_1,\ldots ,X_s\rangle $
. Then
![]() $B=\{b\in B[\tfrac {1}{\zeta }]\colon |b|\le 1\}$
. The Berkovich spectrum
$B=\{b\in B[\tfrac {1}{\zeta }]\colon |b|\le 1\}$
. The Berkovich spectrum
![]() $X={\mathtt {BSpec}} B[\tfrac {1}{\zeta }]$
is the L-analytic space
$X={\mathtt {BSpec}} B[\tfrac {1}{\zeta }]$
is the L-analytic space
![]() ${\mathcal {X}}^{\textrm {an}}$
associated with the formal scheme
${\mathcal {X}}^{\textrm {an}}$
associated with the formal scheme
![]() ${\mathcal {X}}$
.
${\mathcal {X}}$
.
Lemma 7.6. Recall the notation from (6.1). Let
![]() $f=\sum \limits _{i\in {\mathbb {Z}}}b_i z^i\in B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}$
and
$f=\sum \limits _{i\in {\mathbb {Z}}}b_i z^i\in B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}$
and
![]() $a\in B$
with
$a\in B$
with
![]() $|a|<1$
and assume that
$|a|<1$
and assume that
![]() $f\in B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
or
$f\in B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
or
![]() $a\in {\mathcal {O}}_L\setminus \{0\}$
. If
$a\in {\mathcal {O}}_L\setminus \{0\}$
. If
![]() $f(a)=\sum \limits _{i\in {\mathbb {Z}}}b_i a^i=0$
in
$f(a)=\sum \limits _{i\in {\mathbb {Z}}}b_i a^i=0$
in
![]() $B[\tfrac {1}{\zeta }]$
, then
$B[\tfrac {1}{\zeta }]$
, then
![]() $f=(z-a)\cdot g$
for a uniquely determined
$f=(z-a)\cdot g$
for a uniquely determined
![]() $g=\sum \limits _{n\in {\mathbb {Z}}}c_n z^n\in B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}$
with
$g=\sum \limits _{n\in {\mathbb {Z}}}c_n z^n\in B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}$
with
![]() $c_n=\sum _{i>n} b_i a^{i-n-1}\in B$
. Moreover, if
$c_n=\sum _{i>n} b_i a^{i-n-1}\in B$
. Moreover, if
![]() $f\in B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
then also
$f\in B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
then also
![]() $g\in B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
.
$g\in B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
.
Proof. First of all,
![]() $b_i\in B$
and
$b_i\in B$
and
![]() $|a|<1$
implies that the series
$|a|<1$
implies that the series
![]() $c_n:=\sum _{i>n} b_i a^{i-n-1}$
converge in B for all
$c_n:=\sum _{i>n} b_i a^{i-n-1}$
converge in B for all
![]() $n\in {\mathbb {Z}}$
. One easily computes that
$n\in {\mathbb {Z}}$
. One easily computes that
![]() $f=(z-a)\cdot g$
for
$f=(z-a)\cdot g$
for
![]() $g:=\sum _{n\in {\mathbb {Z}}}c_n z^n$
. To prove uniqueness, let
$g:=\sum _{n\in {\mathbb {Z}}}c_n z^n$
. To prove uniqueness, let
![]() $\tilde g=\sum _{n\in {\mathbb {Z}}}\tilde c_n z^n\in B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}$
also satisfy
$\tilde g=\sum _{n\in {\mathbb {Z}}}\tilde c_n z^n\in B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}$
also satisfy
![]() $f=(z-a)\cdot \tilde g$
. Setting
$f=(z-a)\cdot \tilde g$
. Setting
![]() $c^{\prime }_n:=c_n-\tilde c_n$
yields
$c^{\prime }_n:=c_n-\tilde c_n$
yields
![]() $c^{\prime }_{n-1}=ac^{\prime }_n$
, whence
$c^{\prime }_{n-1}=ac^{\prime }_n$
, whence
![]() $c^{\prime }_n=a^{m-n}c^{\prime }_m$
for all
$c^{\prime }_n=a^{m-n}c^{\prime }_m$
for all
![]() $m\ge n$
. Letting m go to
$m\ge n$
. Letting m go to
![]() $\infty $
and using
$\infty $
and using
![]() $c^{\prime }_m\in B$
shows that
$c^{\prime }_m\in B$
shows that
![]() $|c^{\prime }_n|$
is arbitrarily small, and therefore
$|c^{\prime }_n|$
is arbitrarily small, and therefore
![]() $c^{\prime }_n=0$
for all n. This proves the uniqueness of g.
$c^{\prime }_n=0$
for all n. This proves the uniqueness of g.
If
![]() $f\in B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
and
$f\in B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
and
![]() $n<0$
, then
$n<0$
, then
![]() $c_n=a^{-n-1}\cdot f(a)=0$
and therefore
$c_n=a^{-n-1}\cdot f(a)=0$
and therefore
![]() $g\in B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
. If
$g\in B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
. If
![]() $a\in {\mathcal {O}}_L\setminus \{0\}$
, we must verify the convergence condition
$a\in {\mathcal {O}}_L\setminus \{0\}$
, we must verify the convergence condition
![]() $\lim _{n\to -\infty }|c_n|\,|a|^{rn}=0$
for all
$\lim _{n\to -\infty }|c_n|\,|a|^{rn}=0$
for all
![]() $r\ge 1$
. We compute
$r\ge 1$
. We compute
![]() $c_n=-\sum _{i\le n} b_i a^{i-n-1}$
. If
$c_n=-\sum _{i\le n} b_i a^{i-n-1}$
. If
![]() $i\le n$
, then
$i\le n$
, then
![]() $|a|^{(r-1)n}\le |a|^{(r-1)i}$
, and hence
$|a|^{(r-1)n}\le |a|^{(r-1)i}$
, and hence
The latter goes to zero for
![]() $n\to -\infty $
because
$n\to -\infty $
because
![]() $f\in B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}$
. Therefore,
$f\in B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}$
. Therefore,
![]() $g\in B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}$
.
$g\in B\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}$
.
Remark 7.7. In addition to the loop group
![]() $LG$
, we consider over
$LG$
, we consider over
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
the loop groups defined as the fppf-sheaves on
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
the loop groups defined as the fppf-sheaves on
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
-algebras R by
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
-algebras R by
and the canonical maps of groups
![]() $L^+G\to LG\to L_{z(z-\zeta )}G$
and
$L^+G\to LG\to L_{z(z-\zeta )}G$
and
![]() $L^+G\to L_{z-\zeta }G\to L_{z(z-\zeta )}G$
that coincide as homomorphisms
$L^+G\to L_{z-\zeta }G\to L_{z(z-\zeta )}G$
that coincide as homomorphisms
![]() $L^+G\to L_{z(z-\zeta )}G$
. If
$L^+G\to L_{z(z-\zeta )}G$
. If
![]() $\zeta \in R^{\scriptscriptstyle \times }$
is a unit, note that
$\zeta \in R^{\scriptscriptstyle \times }$
is a unit, note that
![]() $z-\zeta \in R\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}^{\scriptscriptstyle \times }$
, and hence
$z-\zeta \in R\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}^{\scriptscriptstyle \times }$
, and hence
![]() $L_{z-\zeta }G=L^+G$
and
$L_{z-\zeta }G=L^+G$
and
![]() $L_{z(z-\zeta )}G=LG$
. On the other hand, if
$L_{z(z-\zeta )}G=LG$
. On the other hand, if
![]() $\zeta $
is nilpotent in R, then
$\zeta $
is nilpotent in R, then
![]() $L_{z-\zeta }G=L_{z(z-\zeta )}G=LG$
.
$L_{z-\zeta }G=L_{z(z-\zeta )}G=LG$
.
Recall from [Reference Arasteh Rad and Hartl4, Definition 4.22] that a local G-shtuka over an admissible formal
![]() ${\mathcal {O}}_L$
-scheme
${\mathcal {O}}_L$
-scheme
![]() ${\mathcal {X}}$
can be viewed as a projective system
${\mathcal {X}}$
can be viewed as a projective system
![]() $({\underline {{\mathcal {G}}}}_m)_{m\in {\mathbb {N}}}$
of local G-shtukas
$({\underline {{\mathcal {G}}}}_m)_{m\in {\mathbb {N}}}$
of local G-shtukas
![]() ${\underline {{\mathcal {G}}}}_m$
over
${\underline {{\mathcal {G}}}}_m$
over
![]() ${\mathcal {X}}_m=\operatorname {\mathrm {V}}(\zeta ^m)\subset {\mathcal {X}}$
with
${\mathcal {X}}_m=\operatorname {\mathrm {V}}(\zeta ^m)\subset {\mathcal {X}}$
with
![]() ${\underline {{\mathcal {G}}}}_{m-1}\cong {\underline {{\mathcal {G}}}}_m\otimes _{{\mathcal {X}}_m}{\mathcal {X}}_{m-1}$
. On
${\underline {{\mathcal {G}}}}_{m-1}\cong {\underline {{\mathcal {G}}}}_m\otimes _{{\mathcal {X}}_m}{\mathcal {X}}_{m-1}$
. On
![]() ${\mathcal {X}}_m$
the element
${\mathcal {X}}_m$
the element
![]() $\zeta $
is nilpotent.
$\zeta $
is nilpotent.
Now let B and
![]() $B[\tfrac {1}{\zeta }]$
be as before. If
$B[\tfrac {1}{\zeta }]$
be as before. If
![]() $({\underline {{\mathcal {G}}}},\bar \delta )$
is an
$({\underline {{\mathcal {G}}}},\bar \delta )$
is an
![]() $\operatorname {\mathrm {Spf}} B$
-valued point in
$\operatorname {\mathrm {Spf}} B$
-valued point in
![]() ${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}(\operatorname {\mathrm {Spf}} B)$
, then the étale covering
${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}(\operatorname {\mathrm {Spf}} B)$
, then the étale covering
![]() $\operatorname {\mathrm {Spf}} B^{\prime }\to \operatorname {\mathrm {Spf}} B$
from Lemma 6.2 is given by a faithfully flat ring homomorphism
$\operatorname {\mathrm {Spf}} B^{\prime }\to \operatorname {\mathrm {Spf}} B$
from Lemma 6.2 is given by a faithfully flat ring homomorphism
![]() $B\to B^{\prime }$
by [Reference Bosch and Lütkebohmert18, Lemma 1.6], and this implies that
$B\to B^{\prime }$
by [Reference Bosch and Lütkebohmert18, Lemma 1.6], and this implies that
![]() ${\underline {{\mathcal {G}}}}$
comes from an
${\underline {{\mathcal {G}}}}$
comes from an
![]() $L^+G$
-torsor
$L^+G$
-torsor
![]() ${\mathcal {G}}$
over
${\mathcal {G}}$
over
![]() $\operatorname {\mathrm {Spec}} B$
together with an isomorphism of the associated
$\operatorname {\mathrm {Spec}} B$
together with an isomorphism of the associated
![]() $L_{z-\zeta }G$
-torsors
$L_{z-\zeta }G$
-torsors
![]() . We view
. We view
![]() $({\mathcal {G}},\tau _{\mathcal {G}})$
as the bounded local G-shtuka over
$({\mathcal {G}},\tau _{\mathcal {G}})$
as the bounded local G-shtuka over
![]() $\operatorname {\mathrm {Spec}} B$
induced from the bounded local G-shtuka
$\operatorname {\mathrm {Spec}} B$
induced from the bounded local G-shtuka
![]() ${\underline {{\mathcal {G}}}}$
over
${\underline {{\mathcal {G}}}}$
over
![]() $\operatorname {\mathrm {Spf}} B$
. A quasi-isogeny
$\operatorname {\mathrm {Spf}} B$
. A quasi-isogeny
![]() $u\colon ({\mathcal {G}}^{\prime }\!,\tau _{{\mathcal {G}}^{\prime }})\to ({\mathcal {G}},\tau _{\mathcal {G}})$
between two such bounded local G-shtukas
$u\colon ({\mathcal {G}}^{\prime }\!,\tau _{{\mathcal {G}}^{\prime }})\to ({\mathcal {G}},\tau _{\mathcal {G}})$
between two such bounded local G-shtukas
![]() $({\mathcal {G}}^{\prime }\!,\tau _{{\mathcal {G}}^{\prime }})$
and
$({\mathcal {G}}^{\prime }\!,\tau _{{\mathcal {G}}^{\prime }})$
and
![]() $({\mathcal {G}},\tau _{\mathcal {G}})$
over
$({\mathcal {G}},\tau _{\mathcal {G}})$
over
![]() $\operatorname {\mathrm {Spec}} B$
is an isomorphism of the associated
$\operatorname {\mathrm {Spec}} B$
is an isomorphism of the associated
![]() $LG$
-torsors
$LG$
-torsors
![]() that satisfies
that satisfies
![]() $u\circ \tau _{{\mathcal {G}}^{\prime }}=\tau _{\mathcal {G}}\circ \sigma ^\ast u$
as isomorphism of the associated
$u\circ \tau _{{\mathcal {G}}^{\prime }}=\tau _{\mathcal {G}}\circ \sigma ^\ast u$
as isomorphism of the associated
![]() $L_{z(z-\zeta )}G$
-torsors.
$L_{z(z-\zeta )}G$
-torsors.
In particular,
![]() $({\mathcal {G}},\tau _{\mathcal {G}})$
induces an étale local G-shtuka on the L-analytic space
$({\mathcal {G}},\tau _{\mathcal {G}})$
induces an étale local G-shtuka on the L-analytic space
![]() $X=(\operatorname {\mathrm {Spf}} B)^{\textrm {an}}={\mathtt {BSpec}}(B[\tfrac {1}{\zeta }])$
.
$X=(\operatorname {\mathrm {Spf}} B)^{\textrm {an}}={\mathtt {BSpec}}(B[\tfrac {1}{\zeta }])$
.
The following proposition is a weaker analogue of the fact that lifts of p-divisible groups and morphisms between them correspond uniquely to lifts of the Hodge-filtrations on the associated crystals (respectively morphisms between them). We do not dispose of the full analogue of this assertion because in our (in general nonminuscule) context Griffiths transversality does not hold; compare the discussion of Genestier and Lafforgue in [Reference Genestier and Lafforgue41, § 11].
Proposition 7.8. Let
![]() ${\mathcal {X}}=\operatorname {\mathrm {Spf}} B$
be an admissible formal
${\mathcal {X}}=\operatorname {\mathrm {Spf}} B$
be an admissible formal
![]() ${\mathcal {O}}_L$
-scheme and let
${\mathcal {O}}_L$
-scheme and let
![]() $X:={\mathcal {X}}^{\mathrm {an}}$
be its associated L-analytic space. Assume that X is connected and choose a geometric base point
$X:={\mathcal {X}}^{\mathrm {an}}$
be its associated L-analytic space. Assume that X is connected and choose a geometric base point
![]() $\bar x$
of X. Let
$\bar x$
of X. Let
![]() $({\underline {{\mathcal {G}}}},\bar \delta )$
and
$({\underline {{\mathcal {G}}}},\bar \delta )$
and
![]() $({\underline {{\mathcal {G}}}}^{\prime }\!,\bar \delta ^{\prime })$
be (representatives of) points in
$({\underline {{\mathcal {G}}}}^{\prime }\!,\bar \delta ^{\prime })$
be (representatives of) points in
![]() ${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}({\mathcal {X}})$
. Then
${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}({\mathcal {X}})$
. Then
![]() $\breve \pi ({\underline {{\mathcal {G}}}},\bar \delta )=\breve \pi ({\underline {{\mathcal {G}}}}^{\prime }\!,\bar \delta ^{\prime })$
in
$\breve \pi ({\underline {{\mathcal {G}}}},\bar \delta )=\breve \pi ({\underline {{\mathcal {G}}}}^{\prime }\!,\bar \delta ^{\prime })$
in
![]() $\breve {\mathcal {H}}_{G,\hat {Z}}^{\textrm {an}}(X)$
if and only if the unique lift of the quasi-isogeny
$\breve {\mathcal {H}}_{G,\hat {Z}}^{\textrm {an}}(X)$
if and only if the unique lift of the quasi-isogeny
![]() $\bar \delta ^{-1}\circ \bar \delta ^{\prime }$
by rigidity [Reference Arasteh Rad and Hartl4, Proposition 2.11] is a quasi-isogeny
$\bar \delta ^{-1}\circ \bar \delta ^{\prime }$
by rigidity [Reference Arasteh Rad and Hartl4, Proposition 2.11] is a quasi-isogeny
![]() $u\colon {\underline {{\mathcal {G}}}}^{\prime }\to {\underline {{\mathcal {G}}}}$
over
$u\colon {\underline {{\mathcal {G}}}}^{\prime }\to {\underline {{\mathcal {G}}}}$
over
![]() $\operatorname {\mathrm {Spec}} B$
in the sense of Remark 7.7. In this case, u induces an isomorphism of the rational Tate module functors
$\operatorname {\mathrm {Spec}} B$
in the sense of Remark 7.7. In this case, u induces an isomorphism of the rational Tate module functors
![]() over X and the following assertions are equivalent:
over X and the following assertions are equivalent:
-
(a)
 $u\colon {\underline {{\mathcal {G}}}}^{\prime }\to {\underline {{\mathcal {G}}}}$
is an isomorphism of local G-shtukas, that is
$u\colon {\underline {{\mathcal {G}}}}^{\prime }\to {\underline {{\mathcal {G}}}}$
is an isomorphism of local G-shtukas, that is
 $({\underline {{\mathcal {G}}}},\bar \delta )=({\underline {{\mathcal {G}}}}^{\prime }\!,\bar \delta ^{\prime })$
in
$({\underline {{\mathcal {G}}}},\bar \delta )=({\underline {{\mathcal {G}}}}^{\prime }\!,\bar \delta ^{\prime })$
in
 ${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}({\mathcal {X}})$
,
${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}({\mathcal {X}})$
, -
(b)
 $\check V_{u,\bar x}$
is an isomorphism
$\check V_{u,\bar x}$
is an isomorphism
 of the integral Tate module functors,
of the integral Tate module functors, -
(c)
 $\check V_{u,\bar x}(\rho )$
is an isomorphism
$\check V_{u,\bar x}(\rho )$
is an isomorphism
 for some faithful
for some faithful
 $\rho \in \operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}G$
.
$\rho \in \operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}G$
.
Moreover, for every rational
![]() $G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
-level structure
$G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
-level structure
![]() $\eta G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
on
$\eta G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
on
![]() ${\underline {{\mathcal {G}}}}$
with
${\underline {{\mathcal {G}}}}$
with
![]() $\eta \in \operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}},\bar x}\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
there is an admissible formal blowing-up
$\eta \in \operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}},\bar x}\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
there is an admissible formal blowing-up
![]() ${\mathcal {Y}}\to {\mathcal {X}}$
and a
${\mathcal {Y}}\to {\mathcal {X}}$
and a
![]() $({\underline {{\mathcal {G}}}}^{\prime \prime }\!,\bar \delta ^{\prime \prime })\in {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}({\mathcal {Y}})$
with
$({\underline {{\mathcal {G}}}}^{\prime \prime }\!,\bar \delta ^{\prime \prime })\in {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}({\mathcal {Y}})$
with
![]() $\breve \pi ({\underline {{\mathcal {G}}}},\bar \delta )=\breve \pi ({\underline {{\mathcal {G}}}}^{\prime \prime }\!,\bar \delta ^{\prime \prime })$
and
$\breve \pi ({\underline {{\mathcal {G}}}},\bar \delta )=\breve \pi ({\underline {{\mathcal {G}}}}^{\prime \prime }\!,\bar \delta ^{\prime \prime })$
and
![]() $(\check V_{u^{\prime \prime }\!,\bar x})^{-1}\circ \eta \in \operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}}^{\prime \prime }\!,\bar x}({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
, where
$(\check V_{u^{\prime \prime }\!,\bar x})^{-1}\circ \eta \in \operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}}^{\prime \prime }\!,\bar x}({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
, where
![]() $u^{\prime \prime }\colon {\underline {{\mathcal {G}}}}^{\prime \prime }\to {\underline {{\mathcal {G}}}}$
is the unique lift of
$u^{\prime \prime }\colon {\underline {{\mathcal {G}}}}^{\prime \prime }\to {\underline {{\mathcal {G}}}}$
is the unique lift of
![]() $\bar \delta ^{-1}\circ \bar \delta ^{\prime \prime }$
.
$\bar \delta ^{-1}\circ \bar \delta ^{\prime \prime }$
.
Remark. The last assertion uses the ind-projectivity of the affine flag variety
![]() ${\mathcal {F}}\ell _G$
and is in general false if G is not parahoric; see Example 8.6.
${\mathcal {F}}\ell _G$
and is in general false if G is not parahoric; see Example 8.6.
Proof. Proof of Proposition 7.8
By Lemma 6.2 there is an étale covering
![]() ${\widetilde {{\mathcal {X}}}}=\operatorname {\mathrm {Spf}} {\widetilde {B}}\to {\mathcal {X}}$
of admissible formal
${\widetilde {{\mathcal {X}}}}=\operatorname {\mathrm {Spf}} {\widetilde {B}}\to {\mathcal {X}}$
of admissible formal
![]() ${\mathcal {O}}_L$
-schemes and trivialisations
${\mathcal {O}}_L$
-schemes and trivialisations
![]() and
and
![]() with
with
![]() $A,A^{\prime }\in G\big ({\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z-\zeta }]\big )$
. Note that
$A,A^{\prime }\in G\big ({\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z-\zeta }]\big )$
. Note that
![]() ${\widetilde {B}}\subset {\widetilde {B}}[\tfrac {1}{\zeta }]$
because
${\widetilde {B}}\subset {\widetilde {B}}[\tfrac {1}{\zeta }]$
because
![]() ${\widetilde {B}}$
has no
${\widetilde {B}}$
has no
![]() $\zeta $
-torsion. In addition, the quasi-isogenies
$\zeta $
-torsion. In addition, the quasi-isogenies
![]() $\bar \delta $
and
$\bar \delta $
and
![]() $\bar \delta ^{\prime }$
correspond under
$\bar \delta ^{\prime }$
correspond under
![]() $\alpha $
and
$\alpha $
and
![]() $\alpha ^{\prime }$
to elements
$\alpha ^{\prime }$
to elements
![]() ${\,\overline {\!\Delta \!}\,},{\,\overline {\!\Delta \!}\,}^{\prime }\in LG\big ({\widetilde {B}}/(\zeta )\big )$
, which lift by Lemma 6.1 to uniquely determined elements
${\,\overline {\!\Delta \!}\,},{\,\overline {\!\Delta \!}\,}^{\prime }\in LG\big ({\widetilde {B}}/(\zeta )\big )$
, which lift by Lemma 6.1 to uniquely determined elements
![]() $\Delta ,\Delta ^{\prime }\in G\big ({\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{t_{\scriptscriptstyle -}}]\big )$
with
$\Delta ,\Delta ^{\prime }\in G\big ({\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{t_{\scriptscriptstyle -}}]\big )$
with
![]() $\Delta A=b\,\sigma ^\ast (\Delta )$
and
$\Delta A=b\,\sigma ^\ast (\Delta )$
and
![]() $\Delta ^{\prime } A^{\prime }=b\,\sigma ^\ast (\Delta ^{\prime })$
. In particular, the quasi-isogeny
$\Delta ^{\prime } A^{\prime }=b\,\sigma ^\ast (\Delta ^{\prime })$
. In particular, the quasi-isogeny
![]() $\bar \delta ^{-1}\circ \bar \delta ^{\prime }\colon {\underline {{\mathcal {G}}}}\to {\underline {{\mathcal {G}}}}^{\prime }$
over
$\bar \delta ^{-1}\circ \bar \delta ^{\prime }\colon {\underline {{\mathcal {G}}}}\to {\underline {{\mathcal {G}}}}^{\prime }$
over
![]() $\operatorname {\mathrm {Spec}} B/(\zeta )$
lifts to
$\operatorname {\mathrm {Spec}} B/(\zeta )$
lifts to
![]() $U=\Delta ^{-1}\Delta ^{\prime }\in G\big ({\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{t_{\scriptscriptstyle -}}]\big )$
with
$U=\Delta ^{-1}\Delta ^{\prime }\in G\big ({\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{t_{\scriptscriptstyle -}}]\big )$
with
![]() $UA^{\prime }=A\sigma ^\ast (U)$
. The morphism
$UA^{\prime }=A\sigma ^\ast (U)$
. The morphism
![]() $\breve \pi $
sends
$\breve \pi $
sends
![]() $({\underline {{\mathcal {G}}}},\bar \delta )$
and
$({\underline {{\mathcal {G}}}},\bar \delta )$
and
![]() $({\underline {{\mathcal {G}}}}^{\prime }\!,\bar \delta ^{\prime })$
to
$({\underline {{\mathcal {G}}}}^{\prime }\!,\bar \delta ^{\prime })$
to
 $$ \begin{align*} \gamma & := \sigma^\ast(\Delta)A^{-1}\cdot G\big({\widetilde{B}}[\tfrac{1}{\zeta}]\text{[}\kern-0.15em\text{[} z-\zeta\text{]}\kern-0.15em\text{]}\big)\qquad\text{and}\\[2mm] \gamma^{\prime} & := \sigma^\ast(\Delta^{\prime})(A^{\prime})^{-1}\cdot G\big({\widetilde{B}}[\tfrac{1}{\zeta}]\text{[}\kern-0.15em\text{[} z-\zeta\text{]}\kern-0.15em\text{]}\big)\\[2mm] & = \sigma^\ast(\Delta)A^{-1}U\cdot G\big({\widetilde{B}}[\tfrac{1}{\zeta}]\text{[}\kern-0.15em\text{[} z-\zeta\text{]}\kern-0.15em\text{]}\big). \end{align*} $$
$$ \begin{align*} \gamma & := \sigma^\ast(\Delta)A^{-1}\cdot G\big({\widetilde{B}}[\tfrac{1}{\zeta}]\text{[}\kern-0.15em\text{[} z-\zeta\text{]}\kern-0.15em\text{]}\big)\qquad\text{and}\\[2mm] \gamma^{\prime} & := \sigma^\ast(\Delta^{\prime})(A^{\prime})^{-1}\cdot G\big({\widetilde{B}}[\tfrac{1}{\zeta}]\text{[}\kern-0.15em\text{[} z-\zeta\text{]}\kern-0.15em\text{]}\big)\\[2mm] & = \sigma^\ast(\Delta)A^{-1}U\cdot G\big({\widetilde{B}}[\tfrac{1}{\zeta}]\text{[}\kern-0.15em\text{[} z-\zeta\text{]}\kern-0.15em\text{]}\big). \end{align*} $$
If u is a quasi-isogeny over
![]() $\operatorname {\mathrm {Spec}} B$
, then
$\operatorname {\mathrm {Spec}} B$
, then
![]() $U\in G({\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z}])\subset G\big ({\widetilde {B}}[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )$
and hence
$U\in G({\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z}])\subset G\big ({\widetilde {B}}[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )$
and hence
![]() $\breve \pi ({\underline {{\mathcal {G}}}},\bar \delta )=\gamma =\gamma ^{\prime }=\breve \pi ({\underline {{\mathcal {G}}}}^{\prime }\!,\bar \delta ^{\prime })$
in
$\breve \pi ({\underline {{\mathcal {G}}}},\bar \delta )=\gamma =\gamma ^{\prime }=\breve \pi ({\underline {{\mathcal {G}}}}^{\prime }\!,\bar \delta ^{\prime })$
in
![]() $\breve {\mathcal {H}}_{G,\hat Z}^{\textrm {an}}$
.
$\breve {\mathcal {H}}_{G,\hat Z}^{\textrm {an}}$
.
Conversely, the condition
![]() $\breve \pi ({\underline {{\mathcal {G}}}},\bar \delta )=\breve \pi ({\underline {{\mathcal {G}}}}^{\prime }\!,\bar \delta ^{\prime })$
yields
$\breve \pi ({\underline {{\mathcal {G}}}},\bar \delta )=\breve \pi ({\underline {{\mathcal {G}}}}^{\prime }\!,\bar \delta ^{\prime })$
yields
![]() $U\in G\big ({\widetilde {B}}[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )$
. We claim that this implies
$U\in G\big ({\widetilde {B}}[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )$
. We claim that this implies
![]() $U\in G\big ({\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{\sigma ^\ast (t_{\scriptscriptstyle -})}]\big )$
. To prove the claim, let
$U\in G\big ({\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{\sigma ^\ast (t_{\scriptscriptstyle -})}]\big )$
. To prove the claim, let
![]() $\rho \colon G\hookrightarrow \operatorname {\mathrm {GL}}_r$
be a faithful representation. Then the entries of
$\rho \colon G\hookrightarrow \operatorname {\mathrm {GL}}_r$
be a faithful representation. Then the entries of
![]() $\rho (U)$
and
$\rho (U)$
and
![]() $\rho (U)^{-1}$
are of the form
$\rho (U)^{-1}$
are of the form
![]() $t_{\scriptscriptstyle -}^{-e}f$
with
$t_{\scriptscriptstyle -}^{-e}f$
with
![]() $e\in {\mathbb {N}}_0$
and
$e\in {\mathbb {N}}_0$
and
![]() $f\in {\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}$
. We must show that there is a
$f\in {\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}$
. We must show that there is a
![]() $g\in {\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}$
with
$g\in {\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}$
with
![]() $t_{\scriptscriptstyle -}^{-e}f=\sigma ^\ast (t_{\scriptscriptstyle -})^{-e}g$
. Recall from (4.3) that
$t_{\scriptscriptstyle -}^{-e}f=\sigma ^\ast (t_{\scriptscriptstyle -})^{-e}g$
. Recall from (4.3) that
![]() $t_{\scriptscriptstyle -}^{-e}f=(1-\tfrac {\zeta }{z})^{-e}\sigma ^\ast (t_{\scriptscriptstyle -})^{-e}f$
. If
$t_{\scriptscriptstyle -}^{-e}f=(1-\tfrac {\zeta }{z})^{-e}\sigma ^\ast (t_{\scriptscriptstyle -})^{-e}f$
. If
![]() $e>0$
, then
$e>0$
, then
![]() $U\in G\big ({\widetilde {B}}[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )$
, respectively
$U\in G\big ({\widetilde {B}}[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )$
, respectively
![]() $U^{-1}\in G\big ({\widetilde {B}}[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )$
, implies that
$U^{-1}\in G\big ({\widetilde {B}}[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )$
, implies that
![]() $f(\zeta )=0$
in
$f(\zeta )=0$
in
![]() ${\widetilde {B}}[\tfrac {1}{\zeta }]$
. By Lemma 7.6 we find
${\widetilde {B}}[\tfrac {1}{\zeta }]$
. By Lemma 7.6 we find
![]() $f=(z-\zeta )g_1=(1-\tfrac {\zeta }{z})zg_1$
with
$f=(z-\zeta )g_1=(1-\tfrac {\zeta }{z})zg_1$
with
![]() $g_1\in {\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}$
, and hence
$g_1\in {\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}$
, and hence
![]() $t_{\scriptscriptstyle -}^{-e}f=(1-\tfrac {\zeta }{z})^{1-e}\sigma ^\ast (t_{\scriptscriptstyle -})^{-e}zg_1$
. Continuing in this way for
$t_{\scriptscriptstyle -}^{-e}f=(1-\tfrac {\zeta }{z})^{1-e}\sigma ^\ast (t_{\scriptscriptstyle -})^{-e}zg_1$
. Continuing in this way for
![]() $\rho (U)$
and
$\rho (U)$
and
![]() $\rho (U)^{-1}$
, we obtain that
$\rho (U)^{-1}$
, we obtain that
![]() $\rho (U)\in \operatorname {\mathrm {GL}}_r\big ({\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{\sigma ^\ast (t_{\scriptscriptstyle -})}]\big )$
. The claim follows.
$\rho (U)\in \operatorname {\mathrm {GL}}_r\big ({\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{\sigma ^\ast (t_{\scriptscriptstyle -})}]\big )$
. The claim follows.
This shows that
![]() $\sigma ^\ast (U)\in G\big ({\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{\sigma ^{2*}(t_{\scriptscriptstyle -})}]\big )\subset G\big ({\widetilde {B}}[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta ^q\mathrm {]}\kern-0.15em\mathrm {]}\big )$
, where we use (6.2). Because
$\sigma ^\ast (U)\in G\big ({\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{\sigma ^{2*}(t_{\scriptscriptstyle -})}]\big )\subset G\big ({\widetilde {B}}[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta ^q\mathrm {]}\kern-0.15em\mathrm {]}\big )$
, where we use (6.2). Because
![]() $A,\; A^{\prime }\in G\big ({\widetilde {B}}[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta ^{q^i}\mathrm {]}\kern-0.15em\mathrm {]}\big )$
for all
$A,\; A^{\prime }\in G\big ({\widetilde {B}}[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta ^{q^i}\mathrm {]}\kern-0.15em\mathrm {]}\big )$
for all
![]() $i>0$
, we obtain
$i>0$
, we obtain
Analogous to the previous paragraph, this implies that
![]() $U\in G\big ({\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{\sigma ^{2*}(t_{\scriptscriptstyle -})}]\big )$
and iteratively
$U\in G\big ({\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{\sigma ^{2*}(t_{\scriptscriptstyle -})}]\big )$
and iteratively
![]() $U\in G\big ({\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{\sigma ^{i*}(t_{\scriptscriptstyle -})}]\big )$
for all
$U\in G\big ({\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{\sigma ^{i*}(t_{\scriptscriptstyle -})}]\big )$
for all
![]() $i>0$
. It follows that the entries of
$i>0$
. It follows that the entries of
![]() $\rho (U)$
converge on all of
$\rho (U)$
converge on all of
![]() $\{0<|z|<1\}$
, whence lie in
$\{0<|z|<1\}$
, whence lie in
![]() ${\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}$
, and so
${\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}$
, and so
![]() $U\in G\big ({\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}\big )$
.
$U\in G\big ({\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}\big )$
.
Now let
![]() ${\mathfrak {p}}\subset {\widetilde {B}}[\tfrac {1}{\zeta }]$
be a minimal prime ideal and let
${\mathfrak {p}}\subset {\widetilde {B}}[\tfrac {1}{\zeta }]$
be a minimal prime ideal and let
![]() $x\in {\widetilde {{\mathcal {X}}}}^{\textrm {an}}={\mathtt {BSpec}}({\widetilde {B}}[\tfrac {1}{\zeta }])$
be a point given by a multiplicative semi-norm
$x\in {\widetilde {{\mathcal {X}}}}^{\textrm {an}}={\mathtt {BSpec}}({\widetilde {B}}[\tfrac {1}{\zeta }])$
be a point given by a multiplicative semi-norm
![]() $|\,.\,|_x\colon {\widetilde {B}}[\tfrac {1}{\zeta }]\to {\mathbb {R}}_{\ge 0}$
such that
$|\,.\,|_x\colon {\widetilde {B}}[\tfrac {1}{\zeta }]\to {\mathbb {R}}_{\ge 0}$
such that
![]() $\{b\in {\widetilde {B}}[\tfrac {1}{\zeta }]\colon |b|_x=0\}={\mathfrak {p}}$
. Note that
$\{b\in {\widetilde {B}}[\tfrac {1}{\zeta }]\colon |b|_x=0\}={\mathfrak {p}}$
. Note that
![]() $|\,.\,|_x$
exists by [Reference Berkovich7, Corollary 2.1.16], for example as the preimage of the multiplicative Gauß norm on
$|\,.\,|_x$
exists by [Reference Berkovich7, Corollary 2.1.16], for example as the preimage of the multiplicative Gauß norm on
![]() $L\langle X_1,\ldots ,X_d\rangle $
under a Noether normalisation map
$L\langle X_1,\ldots ,X_d\rangle $
under a Noether normalisation map
![]() $L\langle X_1,\ldots ,X_d\rangle \hookrightarrow {\widetilde {B}}[\tfrac {1}{\zeta }]/{\mathfrak {p}}$
; see [Reference Bosch, Güntzer and Remmert17, § 6.1.2, Theorem 1]. Let
$L\langle X_1,\ldots ,X_d\rangle \hookrightarrow {\widetilde {B}}[\tfrac {1}{\zeta }]/{\mathfrak {p}}$
; see [Reference Bosch, Güntzer and Remmert17, § 6.1.2, Theorem 1]. Let
![]() $\Omega $
be the completion with respect to
$\Omega $
be the completion with respect to
![]() $|\,.\,|_x$
of an algebraic closure of
$|\,.\,|_x$
of an algebraic closure of
![]() ${\widetilde {B}}[\tfrac {1}{\zeta }]/{\mathfrak {p}}$
and let
${\widetilde {B}}[\tfrac {1}{\zeta }]/{\mathfrak {p}}$
and let
![]() ${\mathcal {O}}_{\Omega }$
be the valuation ring of
${\mathcal {O}}_{\Omega }$
be the valuation ring of
![]() $\Omega $
. Then the image of
$\Omega $
. Then the image of
![]() ${\widetilde {B}}$
in
${\widetilde {B}}$
in
![]() $\Omega $
lies in
$\Omega $
lies in
![]() ${\mathcal {O}}_{\Omega }$
. We denote the image of U in
${\mathcal {O}}_{\Omega }$
. We denote the image of U in
![]() $G\big ({\mathcal {O}}_{\Omega }\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}\big )$
by
$G\big ({\mathcal {O}}_{\Omega }\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}\big )$
by
![]() $U_{\mathfrak {p}}$
. By [Reference Arasteh Rad and Hartl4, Lemma 2.8] there are elements
$U_{\mathfrak {p}}$
. By [Reference Arasteh Rad and Hartl4, Lemma 2.8] there are elements
![]() $H_{\mathfrak {p}},H_{\mathfrak {p}}^{\prime }\in G(\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
with
$H_{\mathfrak {p}},H_{\mathfrak {p}}^{\prime }\in G(\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
with
![]() $A\sigma ^\ast (H_{\mathfrak {p}})=H_{\mathfrak {p}}$
and
$A\sigma ^\ast (H_{\mathfrak {p}})=H_{\mathfrak {p}}$
and
![]() $A^{\prime }\sigma ^\ast (H_{\mathfrak {p}}^{\prime })=H_{\mathfrak {p}}^{\prime }$
that provide a trivialisation of the Tate module functors. By [Reference Hartl, Kim, Böckle, Goss, Hartl and Papanikolas54, Remark 3.4.3], we even have
$A^{\prime }\sigma ^\ast (H_{\mathfrak {p}}^{\prime })=H_{\mathfrak {p}}^{\prime }$
that provide a trivialisation of the Tate module functors. By [Reference Hartl, Kim, Böckle, Goss, Hartl and Papanikolas54, Remark 3.4.3], we even have
![]() $\rho (H_{\mathfrak {p}}),\rho (H_{\mathfrak {p}}^{\prime })\in \operatorname {\mathrm {GL}}_r(\Omega \langle \tfrac {z}{\zeta ^s}\rangle )$
for every
$\rho (H_{\mathfrak {p}}),\rho (H_{\mathfrak {p}}^{\prime })\in \operatorname {\mathrm {GL}}_r(\Omega \langle \tfrac {z}{\zeta ^s}\rangle )$
for every
![]() $s>\frac {1}{q}$
. We compute
$s>\frac {1}{q}$
. We compute
![]() $\rho (H_{\mathfrak {p}}^{-1}U_{\mathfrak {p}} H_{\mathfrak {p}}^{\prime })=\rho (\sigma ^\ast (H_{\mathfrak {p}}^{-1})A^{-1}U_{\mathfrak {p}} A^{\prime }\sigma ^\ast (H_{\mathfrak {p}}^{\prime }))=\sigma ^\ast \rho (H_{\mathfrak {p}}^{-1}U_{\mathfrak {p}} H_{\mathfrak {p}}^{\prime })\in \operatorname {\mathrm {GL}}_r(\Omega {\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}})$
, and this implies
$\rho (H_{\mathfrak {p}}^{-1}U_{\mathfrak {p}} H_{\mathfrak {p}}^{\prime })=\rho (\sigma ^\ast (H_{\mathfrak {p}}^{-1})A^{-1}U_{\mathfrak {p}} A^{\prime }\sigma ^\ast (H_{\mathfrak {p}}^{\prime }))=\sigma ^\ast \rho (H_{\mathfrak {p}}^{-1}U_{\mathfrak {p}} H_{\mathfrak {p}}^{\prime })\in \operatorname {\mathrm {GL}}_r(\Omega {\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}})$
, and this implies
![]() $\rho (H_{\mathfrak {p}}^{-1}U_{\mathfrak {p}} H_{\mathfrak {p}}^{\prime })\in \operatorname {\mathrm {GL}}_r\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
because
$\rho (H_{\mathfrak {p}}^{-1}U_{\mathfrak {p}} H_{\mathfrak {p}}^{\prime })\in \operatorname {\mathrm {GL}}_r\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
because
![]() $\Omega {\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}^\sigma ={\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
. Let
$\Omega {\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}^\sigma ={\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
. Let
![]() $N_{\mathfrak {p}}\in {\mathbb {N}}_0$
be minimal such that
$N_{\mathfrak {p}}\in {\mathbb {N}}_0$
be minimal such that
![]() $z^{N_{\mathfrak {p}}}\rho (H_{\mathfrak {p}}^{-1}U_{\mathfrak {p}} H_{\mathfrak {p}}^{\prime }),\,z^{N_{\mathfrak {p}}}\rho (H_{\mathfrak {p}}^{-1}U_{\mathfrak {p}} H_{\mathfrak {p}}^{\prime })^{-1}\,\in \,{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}^{r\times r}$
. Then
$z^{N_{\mathfrak {p}}}\rho (H_{\mathfrak {p}}^{-1}U_{\mathfrak {p}} H_{\mathfrak {p}}^{\prime }),\,z^{N_{\mathfrak {p}}}\rho (H_{\mathfrak {p}}^{-1}U_{\mathfrak {p}} H_{\mathfrak {p}}^{\prime })^{-1}\,\in \,{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}^{r\times r}$
. Then
![]() $N_{\mathfrak {p}}=0$
if and only if
$N_{\mathfrak {p}}=0$
if and only if
![]() $\rho (H_{\mathfrak {p}}^{-1}U_{\mathfrak {p}} H_{\mathfrak {p}}^{\prime })\in \operatorname {\mathrm {GL}}_r({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
; that is,
$\rho (H_{\mathfrak {p}}^{-1}U_{\mathfrak {p}} H_{\mathfrak {p}}^{\prime })\in \operatorname {\mathrm {GL}}_r({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
; that is,
![]() $H_{\mathfrak {p}}^{-1}U_{\mathfrak {p}} H_{\mathfrak {p}}^{\prime }\in G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
. Moreover,
$H_{\mathfrak {p}}^{-1}U_{\mathfrak {p}} H_{\mathfrak {p}}^{\prime }\in G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
. Moreover,
![]() $z^{N_{\mathfrak {p}}}\rho (U_{\mathfrak {p}}),\,z^{N_{\mathfrak {p}}}\rho (U_{\mathfrak {p}})^{-1}\in \Omega \langle \tfrac {z}{\zeta ^s}\rangle ^{r\times r}\cap {\mathcal {O}}_{\Omega }\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}^{r\times r}={\mathcal {O}}_{\Omega }\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}^{r\times r}$
. Because this holds for all of the finitely many minimal prime ideals of
$z^{N_{\mathfrak {p}}}\rho (U_{\mathfrak {p}}),\,z^{N_{\mathfrak {p}}}\rho (U_{\mathfrak {p}})^{-1}\in \Omega \langle \tfrac {z}{\zeta ^s}\rangle ^{r\times r}\cap {\mathcal {O}}_{\Omega }\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}^{r\times r}={\mathcal {O}}_{\Omega }\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}^{r\times r}$
. Because this holds for all of the finitely many minimal prime ideals of
![]() ${\widetilde {B}}[\tfrac {1}{\zeta }]$
and the intersection of these is the nil-radical
${\widetilde {B}}[\tfrac {1}{\zeta }]$
and the intersection of these is the nil-radical
![]() ${\mathcal {N}}$
of
${\mathcal {N}}$
of
![]() ${\widetilde {B}}[\tfrac {1}{\zeta }]$
, we see that
${\widetilde {B}}[\tfrac {1}{\zeta }]$
, we see that
![]() $U\in G\big ({\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}\big )$
implies
$U\in G\big ({\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}\big )$
implies
![]() $z^N\rho (U),z^N\rho (U^{-1})\in {\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}^{r\times r}+{\mathcal {N}}\mathrm {[}\kern-0.15em\mathrm {[} z^{-1}\mathrm {]}\kern-0.15em\mathrm {]}^{r\times r}$
for
$z^N\rho (U),z^N\rho (U^{-1})\in {\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}^{r\times r}+{\mathcal {N}}\mathrm {[}\kern-0.15em\mathrm {[} z^{-1}\mathrm {]}\kern-0.15em\mathrm {]}^{r\times r}$
for
![]() $N:=\max \{N_{\mathfrak {p}}\colon {\mathfrak {p}}\ \mathrm{minimal}\}$
. Because
$N:=\max \{N_{\mathfrak {p}}\colon {\mathfrak {p}}\ \mathrm{minimal}\}$
. Because
![]() ${\widetilde {B}}[\tfrac {1}{\zeta }]$
is Noetherian, the nil-radical is nilpotent and there is an integer m such that
${\widetilde {B}}[\tfrac {1}{\zeta }]$
is Noetherian, the nil-radical is nilpotent and there is an integer m such that
![]() ${\mathcal {N}}^{q^m}=(0)$
. In particular,
${\mathcal {N}}^{q^m}=(0)$
. In particular,
![]() $z^N\rho (\sigma ^{m*}(U))\in {\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}^{r\times r}$
. Let n be such that
$z^N\rho (\sigma ^{m*}(U))\in {\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}^{r\times r}$
. Let n be such that
![]() $(z-\zeta )^n\rho (A),(z-\zeta )^n\rho (A^{\prime })^{-1}\in {\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}^{r\times r}$
. Then
$(z-\zeta )^n\rho (A),(z-\zeta )^n\rho (A^{\prime })^{-1}\in {\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}^{r\times r}$
. Then
 $$ \begin{align*}\left(\prod_{i=0}^{m-1}(z-\zeta^{q^i})^{2n}\right)\cdot z^N\rho(U) & = (z-\zeta)^n\rho(A)\cdot\ldots\cdot\sigma^{(m-1)*}\big((z-\zeta)^n\rho(A)\big)\cdot z^N\rho(\sigma^{m*}(U))\cdot\\[-3mm]& \quad \cdot\,\sigma^{(m-1)*}\big((z-\zeta)^n\rho(A^{\prime})^{-1}\big)\cdot\ldots\cdot(z-\zeta)^n\rho(A^{\prime})^{-1}\\&\quad \in {\widetilde{B}}\text{[}\kern-0.15em\text{[} z\text{]}\kern-0.15em\text{]}^{r\times r} \end{align*} $$
$$ \begin{align*}\left(\prod_{i=0}^{m-1}(z-\zeta^{q^i})^{2n}\right)\cdot z^N\rho(U) & = (z-\zeta)^n\rho(A)\cdot\ldots\cdot\sigma^{(m-1)*}\big((z-\zeta)^n\rho(A)\big)\cdot z^N\rho(\sigma^{m*}(U))\cdot\\[-3mm]& \quad \cdot\,\sigma^{(m-1)*}\big((z-\zeta)^n\rho(A^{\prime})^{-1}\big)\cdot\ldots\cdot(z-\zeta)^n\rho(A^{\prime})^{-1}\\&\quad \in {\widetilde{B}}\text{[}\kern-0.15em\text{[} z\text{]}\kern-0.15em\text{]}^{r\times r} \end{align*} $$
and applying Lemma 7.6 with
![]() $a=\zeta ^{q^i}$
for
$a=\zeta ^{q^i}$
for
![]() $i=0,\ldots ,m-1$
to the entries of this matrix yields
$i=0,\ldots ,m-1$
to the entries of this matrix yields
![]() $z^N\rho (U)\in {\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}^{r\times r}$
. In the same way, we see that
$z^N\rho (U)\in {\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}^{r\times r}$
. In the same way, we see that
![]() $z^N\rho (U^{-1})\in {\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}^{r\times r}$
. This implies
$z^N\rho (U^{-1})\in {\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}^{r\times r}$
. This implies
![]() $\rho (U)\in \operatorname {\mathrm {GL}}_r\big ({\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z}]\big )$
and
$\rho (U)\in \operatorname {\mathrm {GL}}_r\big ({\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z}]\big )$
and
![]() $U\in G\big ({\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z}]\big )=LG({\widetilde {B}})$
. We conclude that U defines a quasi-isogeny
$U\in G\big ({\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z}]\big )=LG({\widetilde {B}})$
. We conclude that U defines a quasi-isogeny
![]() $U\colon {\underline {{\mathcal {G}}}}_{{\widetilde {B}}}\to {\underline {{\mathcal {G}}}}^{\prime }_{{\widetilde {B}}}$
which induces the isomorphism of the rational Tate module functors
$U\colon {\underline {{\mathcal {G}}}}_{{\widetilde {B}}}\to {\underline {{\mathcal {G}}}}^{\prime }_{{\widetilde {B}}}$
which induces the isomorphism of the rational Tate module functors
![]() for the geometric base point
for the geometric base point
![]() $\bar x\colon {\mathtt {BSpec}}(\Omega )\to X$
. By uniqueness U descends to a quasi-isogeny
$\bar x\colon {\mathtt {BSpec}}(\Omega )\to X$
. By uniqueness U descends to a quasi-isogeny
![]() $u\colon {\underline {{\mathcal {G}}}}^{\prime }\to {\underline {{\mathcal {G}}}}$
over
$u\colon {\underline {{\mathcal {G}}}}^{\prime }\to {\underline {{\mathcal {G}}}}$
over
![]() $\operatorname {\mathrm {Spec}} B$
as desired.
$\operatorname {\mathrm {Spec}} B$
as desired.
In this situation, clearly (a) implies (b) and (b) implies (c). We further see that (c) for our representation
![]() $\rho $
implies
$\rho $
implies
![]() $\rho (H_{\mathfrak {p}}^{-1}U_{\mathfrak {p}} H_{\mathfrak {p}}^{\prime })\in \operatorname {\mathrm {GL}}_r\big ({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\big )$
for all minimal
$\rho (H_{\mathfrak {p}}^{-1}U_{\mathfrak {p}} H_{\mathfrak {p}}^{\prime })\in \operatorname {\mathrm {GL}}_r\big ({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\big )$
for all minimal
![]() ${\mathfrak {p}}\subset {\widetilde {B}}[\tfrac {1}{\zeta }]$
, and hence the integer N defined above is zero and
${\mathfrak {p}}\subset {\widetilde {B}}[\tfrac {1}{\zeta }]$
, and hence the integer N defined above is zero and
![]() $U\in G\big ({\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\big )$
. In particular, (c) implies (a), because
$U\in G\big ({\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\big )$
. In particular, (c) implies (a), because
![]() is an isomorphism of local G-shtukas if and only if
is an isomorphism of local G-shtukas if and only if
![]() $U\in G\big ({\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\big )$
.
$U\in G\big ({\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\big )$
.
It remains to prove the last assertion about the rational
![]() $G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
-level structure
$G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
-level structure
![]() $\eta G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
on
$\eta G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
on
![]() ${\underline {{\mathcal {G}}}}$
where
${\underline {{\mathcal {G}}}}$
where
![]() $\eta \in \operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}},\bar x}\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
. Let
$\eta \in \operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}},\bar x}\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
. Let
![]() $\rho ^{\prime \prime }\colon \pi _1^{\mathrm {\acute {e}t}}(X,\bar x)\to G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
be the homomorphism by which the fundamental group acts on
$\rho ^{\prime \prime }\colon \pi _1^{\mathrm {\acute {e}t}}(X,\bar x)\to G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
be the homomorphism by which the fundamental group acts on
![]() $\eta $
; that is,
$\eta $
; that is,
![]() $g(\eta )=\eta \cdot \rho ^{\prime \prime }(g)$
for
$g(\eta )=\eta \cdot \rho ^{\prime \prime }(g)$
for
![]() $g\in \pi _1^{\mathrm {\acute {e}t}}(X,\bar x)$
. Note that
$g\in \pi _1^{\mathrm {\acute {e}t}}(X,\bar x)$
. Note that
![]() $\rho ^{\prime \prime }(g)$
indeed lies in
$\rho ^{\prime \prime }(g)$
indeed lies in
![]() $G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
because g fixes
$G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
because g fixes
![]() $\eta G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
. In particular,
$\eta G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
. In particular,
![]() $\rho ^{\prime \prime }$
factors through a representation
$\rho ^{\prime \prime }$
factors through a representation
![]() $\pi _1^{\textrm {alg}}(X,\bar x)\to G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
. By Corollary 5.4, Proposition 5.3 and [Reference Arasteh Rad and Hartl4, Proposition 3.6],
$\pi _1^{\textrm {alg}}(X,\bar x)\to G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
. By Corollary 5.4, Proposition 5.3 and [Reference Arasteh Rad and Hartl4, Proposition 3.6],
![]() $\rho ^{\prime \prime }$
comes from an étale local G-shtuka
$\rho ^{\prime \prime }$
comes from an étale local G-shtuka
![]() ${\underline {{\mathcal {G}}}}^{\prime \prime }_L$
over
${\underline {{\mathcal {G}}}}^{\prime \prime }_L$
over
![]() $\operatorname {\mathrm {Spec}} B[\tfrac {1}{\zeta }]$
together with a tensor isomorphism
$\operatorname {\mathrm {Spec}} B[\tfrac {1}{\zeta }]$
together with a tensor isomorphism
![]() $\beta \in \operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}}^{\prime \prime }\!,\bar x}({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
, and the tensor isomorphism
$\beta \in \operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}}^{\prime \prime }\!,\bar x}({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
, and the tensor isomorphism
![]() is of the form
is of the form
![]() $\check V_{u^{\prime \prime }_L,\bar x}$
for a quasi-isogeny
$\check V_{u^{\prime \prime }_L,\bar x}$
for a quasi-isogeny
![]() $u^{\prime \prime }_L\colon {\underline {{\mathcal {G}}}}^{\prime \prime }_L\to {\underline {{\mathcal {G}}}}_{B[\frac {1}{\zeta }]}$
over
$u^{\prime \prime }_L\colon {\underline {{\mathcal {G}}}}^{\prime \prime }_L\to {\underline {{\mathcal {G}}}}_{B[\frac {1}{\zeta }]}$
over
![]() $\operatorname {\mathrm {Spec}} B[\tfrac {1}{\zeta }]$
. This means that
$\operatorname {\mathrm {Spec}} B[\tfrac {1}{\zeta }]$
. This means that
![]() ${\underline {{\mathcal {G}}}}^{\prime \prime }_L=({\mathcal {G}}^{\prime \prime }_L,\tau ^{\prime \prime })$
, where
${\underline {{\mathcal {G}}}}^{\prime \prime }_L=({\mathcal {G}}^{\prime \prime }_L,\tau ^{\prime \prime })$
, where
![]() ${\mathcal {G}}^{\prime \prime }_L$
is an
${\mathcal {G}}^{\prime \prime }_L$
is an
![]() $L^+G$
-torsor over
$L^+G$
-torsor over
![]() $\operatorname {\mathrm {Spec}} B[\tfrac {1}{\zeta }]$
and
$\operatorname {\mathrm {Spec}} B[\tfrac {1}{\zeta }]$
and
![]() is an isomorphism of
is an isomorphism of
![]() $L^+G$
-torsors. Also,
$L^+G$
-torsors. Also,
![]() is an isomorphism of the associated
is an isomorphism of the associated
![]() $LG$
-torsors with
$LG$
-torsors with
![]() $u^{\prime \prime }_L\circ \tau ^{\prime \prime }=\tau _{\mathcal {G}}\circ \sigma ^\ast u^{\prime \prime }_L$
. Note that the assumption on the nilpotence of
$u^{\prime \prime }_L\circ \tau ^{\prime \prime }=\tau _{\mathcal {G}}\circ \sigma ^\ast u^{\prime \prime }_L$
. Note that the assumption on the nilpotence of
![]() $\zeta $
in [Reference Arasteh Rad and Hartl4, Proposition 3.6] is not satisfied for
$\zeta $
in [Reference Arasteh Rad and Hartl4, Proposition 3.6] is not satisfied for
![]() $\operatorname {\mathrm {Spec}} B[\tfrac {1}{\zeta }]$
, but is also not used in the proof of [Reference Arasteh Rad and Hartl4, Proposition 3.6]
$\operatorname {\mathrm {Spec}} B[\tfrac {1}{\zeta }]$
, but is also not used in the proof of [Reference Arasteh Rad and Hartl4, Proposition 3.6]
We may thus apply the following Lemma 7.9 by taking the
![]() $LG$
-torsor associated with
$LG$
-torsor associated with
![]() ${\mathcal {G}}$
as the
${\mathcal {G}}$
as the
![]() $LG$
-torsor
$LG$
-torsor
![]() ${\mathcal {G}}$
in Lemma 7.9. It provides an extension of the pair
${\mathcal {G}}$
in Lemma 7.9. It provides an extension of the pair
![]() $({\underline {{\mathcal {G}}}}^{\prime \prime }_L,u^{\prime \prime }_L)$
to a local G-shtuka
$({\underline {{\mathcal {G}}}}^{\prime \prime }_L,u^{\prime \prime }_L)$
to a local G-shtuka
![]() ${\underline {{\mathcal {G}}}}^{\prime \prime }$
bounded by
${\underline {{\mathcal {G}}}}^{\prime \prime }$
bounded by
![]() $\hat {Z}^{-1}$
and a quasi-isogeny
$\hat {Z}^{-1}$
and a quasi-isogeny
![]() $u^{\prime \prime }\colon {\underline {{\mathcal {G}}}}^{\prime \prime }\to {\underline {{\mathcal {G}}}}$
over a blowing-up Y of
$u^{\prime \prime }\colon {\underline {{\mathcal {G}}}}^{\prime \prime }\to {\underline {{\mathcal {G}}}}$
over a blowing-up Y of
![]() $\operatorname {\mathrm {Spec}} B$
in a finitely generated ideal
$\operatorname {\mathrm {Spec}} B$
in a finitely generated ideal
![]() ${\mathfrak {b}}\subset B$
containing a power of
${\mathfrak {b}}\subset B$
containing a power of
![]() $\zeta $
. By [Reference Bosch and Lütkebohmert18, Propositions 2.1 and 1.3] the
$\zeta $
. By [Reference Bosch and Lütkebohmert18, Propositions 2.1 and 1.3] the
![]() $\zeta $
-adic completion
$\zeta $
-adic completion
![]() ${\mathcal {Y}}$
of Y is the admissible formal blowing-up of
${\mathcal {Y}}$
of Y is the admissible formal blowing-up of
![]() ${\mathcal {X}}=\operatorname {\mathrm {Spf}} B$
in the ideal
${\mathcal {X}}=\operatorname {\mathrm {Spf}} B$
in the ideal
![]() ${\mathfrak {b}}$
. In particular,
${\mathfrak {b}}$
. In particular,
![]() ${\mathcal {Y}}^{\textrm {an}}\to X$
is an isomorphism. We set
${\mathcal {Y}}^{\textrm {an}}\to X$
is an isomorphism. We set
![]() $\bar \delta ^{\prime \prime }:=\bar \delta \circ (u^{\prime \prime }\;\textrm {mod}\;\zeta )$
. Then
$\bar \delta ^{\prime \prime }:=\bar \delta \circ (u^{\prime \prime }\;\textrm {mod}\;\zeta )$
. Then
![]() $({\underline {{\mathcal {G}}}}^{\prime \prime }\!,\bar \delta ^{\prime \prime })\in {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}({\mathcal {Y}})$
, and
$({\underline {{\mathcal {G}}}}^{\prime \prime }\!,\bar \delta ^{\prime \prime })\in {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}({\mathcal {Y}})$
, and
![]() $\breve \pi ({\underline {{\mathcal {G}}}},\bar \delta )=\breve \pi ({\underline {{\mathcal {G}}}}^{\prime \prime }\!,\bar \delta ^{\prime \prime })$
by the first part of the proposition, and
$\breve \pi ({\underline {{\mathcal {G}}}},\bar \delta )=\breve \pi ({\underline {{\mathcal {G}}}}^{\prime \prime }\!,\bar \delta ^{\prime \prime })$
by the first part of the proposition, and
![]() $(\check V_{u^{\prime \prime }\!,\bar x})^{-1}\circ \eta =\beta \in \operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}}^{\prime \prime }\!,\bar x}({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
by construction.
$(\check V_{u^{\prime \prime }\!,\bar x})^{-1}\circ \eta =\beta \in \operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}}^{\prime \prime }\!,\bar x}({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
by construction.
Lemma 7.9. Let B be an admissible formal
![]() ${\mathcal {O}}_L$
-algebra. Let
${\mathcal {O}}_L$
-algebra. Let
![]() ${\mathcal {G}}$
be an
${\mathcal {G}}$
be an
![]() $LG$
-torsor over
$LG$
-torsor over
![]() $\operatorname {\mathrm {Spec}} B$
and assume that there is an étale covering
$\operatorname {\mathrm {Spec}} B$
and assume that there is an étale covering
![]() $\operatorname {\mathrm {Spf}}{\widetilde {B}}\to \operatorname {\mathrm {Spf}} B$
of admissible formal
$\operatorname {\mathrm {Spf}}{\widetilde {B}}\to \operatorname {\mathrm {Spf}} B$
of admissible formal
![]() ${\mathcal {O}}_L$
-schemes such that
${\mathcal {O}}_L$
-schemes such that
![]() ${\mathcal {G}}$
admits a trivialisation
${\mathcal {G}}$
admits a trivialisation
![]() . Let
. Let
![]() be an isomorphism of the associated
be an isomorphism of the associated
![]() $L_{z(z-\zeta )}G$
-torsors. Furthermore, let
$L_{z(z-\zeta )}G$
-torsors. Furthermore, let
![]() ${\mathcal {G}}^{\prime \prime }_L$
be an
${\mathcal {G}}^{\prime \prime }_L$
be an
![]() $L^+G$
-torsor over
$L^+G$
-torsor over
![]() $\operatorname {\mathrm {Spec}} B[\tfrac {1}{\zeta }]$
, let
$\operatorname {\mathrm {Spec}} B[\tfrac {1}{\zeta }]$
, let
![]() be an isomorphism of
be an isomorphism of
![]() $L^+G$
-torsors and let
$L^+G$
-torsors and let
![]() be an isomorphism of
be an isomorphism of
![]() $LG$
-torsors over
$LG$
-torsors over
![]() $\operatorname {\mathrm {Spec}} B[\frac {1}{\zeta }]$
satisfying
$\operatorname {\mathrm {Spec}} B[\frac {1}{\zeta }]$
satisfying
![]() $u^{\prime \prime }_L\circ \tau ^{\prime \prime }=\tau _{\mathcal {G}}\circ \sigma ^\ast u^{\prime \prime }_L$
.
$u^{\prime \prime }_L\circ \tau ^{\prime \prime }=\tau _{\mathcal {G}}\circ \sigma ^\ast u^{\prime \prime }_L$
.
Then there is a blowing-up Y of
![]() $\operatorname {\mathrm {Spec}} B$
in a finitely generated ideal
$\operatorname {\mathrm {Spec}} B$
in a finitely generated ideal
![]() ${\mathfrak {b}}\subset B$
containing a power of
${\mathfrak {b}}\subset B$
containing a power of
![]() $\zeta $
, an
$\zeta $
, an
![]() $L^+G$
-torsor
$L^+G$
-torsor
![]() ${\mathcal {G}}^{\prime \prime }$
over Y, an isomorphism
${\mathcal {G}}^{\prime \prime }$
over Y, an isomorphism
![]() of the associated
of the associated
![]() $L_{z-\zeta }G$
-torsors over Y and an isomorphism
$L_{z-\zeta }G$
-torsors over Y and an isomorphism
![]() of
of
![]() $LG$
-torsors satisfying
$LG$
-torsors satisfying
![]() $u^{\prime \prime }\circ \tau _{{\mathcal {G}}^{\prime \prime }}=\tau _{\mathcal {G}}\circ \sigma ^\ast u^{\prime \prime }$
, such that the pullback of
$u^{\prime \prime }\circ \tau _{{\mathcal {G}}^{\prime \prime }}=\tau _{\mathcal {G}}\circ \sigma ^\ast u^{\prime \prime }$
, such that the pullback of
![]() $({\mathcal {G}}^{\prime \prime }\!,\tau _{{\mathcal {G}}^{\prime \prime }},u^{\prime \prime })$
to
$({\mathcal {G}}^{\prime \prime }\!,\tau _{{\mathcal {G}}^{\prime \prime }},u^{\prime \prime })$
to
![]() $Y\times _B\operatorname {\mathrm {Spec}} B[\tfrac {1}{\zeta }]=\operatorname {\mathrm {Spec}} B[\tfrac {1}{\zeta }]$
is isomorphic to
$Y\times _B\operatorname {\mathrm {Spec}} B[\tfrac {1}{\zeta }]=\operatorname {\mathrm {Spec}} B[\tfrac {1}{\zeta }]$
is isomorphic to
![]() $({\mathcal {G}}^{\prime \prime }_L,\tau ^{\prime \prime }\!,u^{\prime \prime }_L)$
via an isomorphism of
$({\mathcal {G}}^{\prime \prime }_L,\tau ^{\prime \prime }\!,u^{\prime \prime }_L)$
via an isomorphism of
![]() $L^+G$
-torsors
$L^+G$
-torsors
![]() satisfying
satisfying
![]() $h\circ \tau _{{\mathcal {G}}^{\prime \prime }}=\tau ^{\prime \prime }\circ \sigma ^\ast h$
and
$h\circ \tau _{{\mathcal {G}}^{\prime \prime }}=\tau ^{\prime \prime }\circ \sigma ^\ast h$
and
![]() $u^{\prime \prime }=u^{\prime \prime }_L\circ h$
.
$u^{\prime \prime }=u^{\prime \prime }_L\circ h$
.
Moreover, if the element
![]() $\sigma ^\ast \alpha \circ \tau _{\mathcal {G}}^{-1}\circ \alpha ^{-1}\in G\big ({\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z(z-\zeta )}]\big )\subset G\big ({\widetilde {B}}[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z-\zeta }]\big )$
maps to a point in
$\sigma ^\ast \alpha \circ \tau _{\mathcal {G}}^{-1}\circ \alpha ^{-1}\in G\big ({\widetilde {B}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z(z-\zeta )}]\big )\subset G\big ({\widetilde {B}}[\tfrac {1}{\zeta }]\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z-\zeta }]\big )$
maps to a point in
![]() $\hat {Z}^{\textrm {an}}({\mathtt {BSpec}}{\widetilde {B}}[\tfrac {1}{\zeta }])$
, then
$\hat {Z}^{\textrm {an}}({\mathtt {BSpec}}{\widetilde {B}}[\tfrac {1}{\zeta }])$
, then
![]() $\tau _{{\mathcal {G}}^{\prime \prime }}$
is bounded by
$\tau _{{\mathcal {G}}^{\prime \prime }}$
is bounded by
![]() $\hat {Z}^{-1}$
and
$\hat {Z}^{-1}$
and
![]() ${\underline {{\mathcal {G}}}}^{\prime \prime }=({\mathcal {G}}^{\prime \prime }\!,\tau _{{\mathcal {G}}^{\prime \prime }})$
is a local shtuka over Y bounded by
${\underline {{\mathcal {G}}}}^{\prime \prime }=({\mathcal {G}}^{\prime \prime }\!,\tau _{{\mathcal {G}}^{\prime \prime }})$
is a local shtuka over Y bounded by
![]() $\hat {Z}^{-1}$
in the sense of Remark 7.7.
$\hat {Z}^{-1}$
in the sense of Remark 7.7.
Proof. We consider the functor
![]() ${\underline {{\mathcal {M}}}}_{{\underline {{\mathcal {G}}}}}$
on
${\underline {{\mathcal {M}}}}_{{\underline {{\mathcal {G}}}}}$
on
![]() $\operatorname {\mathrm {Spec}} B$
-schemes classifying quasi-isogenies of (unbounded) local
$\operatorname {\mathrm {Spec}} B$
-schemes classifying quasi-isogenies of (unbounded) local
![]() ${\mathcal {G}}$
-shtukas to
${\mathcal {G}}$
-shtukas to
![]() ${\underline {{\mathcal {G}}}}:=({\mathcal {G}},\tau _{\mathcal {G}})$
, which on affine B-schemes
${\underline {{\mathcal {G}}}}:=({\mathcal {G}},\tau _{\mathcal {G}})$
, which on affine B-schemes
![]() $S=\operatorname {\mathrm {Spec}} R$
is defined by
$S=\operatorname {\mathrm {Spec}} R$
is defined by

Here
![]() $({\mathcal {G}}^{\prime \prime }\!,\tau _{{\mathcal {G}}^{\prime \prime }},u^{\prime \prime })$
and
$({\mathcal {G}}^{\prime \prime }\!,\tau _{{\mathcal {G}}^{\prime \prime }},u^{\prime \prime })$
and
![]() $({\mathcal {G}}^{\prime }\!,\tau _{{\mathcal {G}}^{\prime }},u^{\prime })$
are isomorphic if there is an isomorphism
$({\mathcal {G}}^{\prime }\!,\tau _{{\mathcal {G}}^{\prime }},u^{\prime })$
are isomorphic if there is an isomorphism
of
![]() $L^+G$
-torsors satisfying
$L^+G$
-torsors satisfying
![]() $h\circ \tau _{{\mathcal {G}}^{\prime \prime }}=\tau _{{\mathcal {G}}^{\prime }}\circ \sigma ^\ast h$
and
$h\circ \tau _{{\mathcal {G}}^{\prime \prime }}=\tau _{{\mathcal {G}}^{\prime }}\circ \sigma ^\ast h$
and
![]() $u^{\prime \prime }=u^{\prime }\circ h$
.
$u^{\prime \prime }=u^{\prime }\circ h$
.
The functor
![]() ${\underline {{\mathcal {M}}}}_{{\underline {{\mathcal {G}}}}}$
is representable by an ind-projective ind-scheme over
${\underline {{\mathcal {M}}}}_{{\underline {{\mathcal {G}}}}}$
is representable by an ind-projective ind-scheme over
![]() $\operatorname {\mathrm {Spec}} B$
as follows. We consider its base change
$\operatorname {\mathrm {Spec}} B$
as follows. We consider its base change
![]() ${\underline {{\mathcal {M}}}}_{{\underline {{\mathcal {G}}}}}\otimes _B{\widetilde {B}}$
and fix a trivialisation
${\underline {{\mathcal {M}}}}_{{\underline {{\mathcal {G}}}}}\otimes _B{\widetilde {B}}$
and fix a trivialisation
![]() . Over a
. Over a
![]() ${\widetilde {B}}$
-algebra R the data
${\widetilde {B}}$
-algebra R the data
![]() $({\mathcal {G}}^{\prime \prime }\!,\alpha \circ u^{\prime \prime })$
are represented by the ind-projective ind-scheme
$({\mathcal {G}}^{\prime \prime }\!,\alpha \circ u^{\prime \prime })$
are represented by the ind-projective ind-scheme
![]() ${\mathcal {F}}\ell _G\widehat {\displaystyle \times }_{{\mathbb {F}}_q}\operatorname {\mathrm {Spec}}{\widetilde {B}}$
over
${\mathcal {F}}\ell _G\widehat {\displaystyle \times }_{{\mathbb {F}}_q}\operatorname {\mathrm {Spec}}{\widetilde {B}}$
over
![]() $\operatorname {\mathrm {Spec}}{\widetilde {B}}$
. Indeed, over an étale covering
$\operatorname {\mathrm {Spec}}{\widetilde {B}}$
. Indeed, over an étale covering
![]() $\operatorname {\mathrm {Spec}} {\widetilde {R}}$
of
$\operatorname {\mathrm {Spec}} {\widetilde {R}}$
of
![]() $\operatorname {\mathrm {Spec}} R$
the
$\operatorname {\mathrm {Spec}} R$
the
![]() $L^+G$
-torsor
$L^+G$
-torsor
![]() ${\mathcal {G}}^{\prime \prime }$
can be trivialised by an isomorphism
${\mathcal {G}}^{\prime \prime }$
can be trivialised by an isomorphism
![]() and then
and then
![]() $\alpha \circ u^{\prime \prime }\circ \beta ^{-1}$
yields an
$\alpha \circ u^{\prime \prime }\circ \beta ^{-1}$
yields an
![]() ${\widetilde {R}}$
-valued point of
${\widetilde {R}}$
-valued point of
![]() ${\mathcal {F}}\ell _G$
that is independent of all choices and descends to an R-valued point of
${\mathcal {F}}\ell _G$
that is independent of all choices and descends to an R-valued point of
![]() ${\mathcal {F}}\ell _G$
; see [Reference Hartl and Viehmann56, Theorem 6.2] or [Reference Arasteh Rad and Hartl4, Theorem 4.4] for more details and for the inverse construction. Over
${\mathcal {F}}\ell _G$
; see [Reference Hartl and Viehmann56, Theorem 6.2] or [Reference Arasteh Rad and Hartl4, Theorem 4.4] for more details and for the inverse construction. Over
![]() $\operatorname {\mathrm {Spec}}{\widetilde {R}}$
, also
$\operatorname {\mathrm {Spec}}{\widetilde {R}}$
, also
is uniquely determined by
![]() $u^{\prime \prime }$
. This shows that
$u^{\prime \prime }$
. This shows that
![]() is an ind-projective ind-scheme over
is an ind-projective ind-scheme over
![]() $\operatorname {\mathrm {Spec}}{\widetilde {B}}$
. It descends to an ind-projective ind-scheme
$\operatorname {\mathrm {Spec}}{\widetilde {B}}$
. It descends to an ind-projective ind-scheme
![]() ${\underline {{\mathcal {M}}}}_{{\underline {{\mathcal {G}}}}}$
over
${\underline {{\mathcal {M}}}}_{{\underline {{\mathcal {G}}}}}$
over
![]() $\operatorname {\mathrm {Spec}} B$
, because
$\operatorname {\mathrm {Spec}} B$
, because
![]() $B\to {\widetilde {B}}$
is faithfully flat by [Reference Bosch and Lütkebohmert18, Lemma 1.6]; see [Reference Arasteh Rad and Hartl4, Theorem 4.4] for details.
$B\to {\widetilde {B}}$
is faithfully flat by [Reference Bosch and Lütkebohmert18, Lemma 1.6]; see [Reference Arasteh Rad and Hartl4, Theorem 4.4] for details.
The triple
![]() $({\mathcal {G}}^{\prime \prime }_L,\tau ^{\prime \prime }\!,u^{\prime \prime }_L)$
corresponds to a morphism
$({\mathcal {G}}^{\prime \prime }_L,\tau ^{\prime \prime }\!,u^{\prime \prime }_L)$
corresponds to a morphism
![]() $f\colon \operatorname {\mathrm {Spec}} B[\tfrac {1}{\zeta }]\to {\underline {{\mathcal {M}}}}_{{\underline {{\mathcal {G}}}}}$
. Because its source is quasi-compact, f factors through a subscheme
$f\colon \operatorname {\mathrm {Spec}} B[\tfrac {1}{\zeta }]\to {\underline {{\mathcal {M}}}}_{{\underline {{\mathcal {G}}}}}$
. Because its source is quasi-compact, f factors through a subscheme
![]() ${\underline {{\mathcal {M}}}}_{{\underline {{\mathcal {G}}}}}^{(N)}$
that is projective over
${\underline {{\mathcal {M}}}}_{{\underline {{\mathcal {G}}}}}^{(N)}$
that is projective over
![]() $\operatorname {\mathrm {Spec}} B$
; see [Reference Hartl and Viehmann56, Lemma 5.4]. The scheme-theoretic closure
$\operatorname {\mathrm {Spec}} B$
; see [Reference Hartl and Viehmann56, Lemma 5.4]. The scheme-theoretic closure
![]() $\Gamma $
of the graph of f in
$\Gamma $
of the graph of f in
![]() ${\underline {{\mathcal {M}}}}_{{\underline {{\mathcal {G}}}}}^{(N)}$
is a projective scheme over
${\underline {{\mathcal {M}}}}_{{\underline {{\mathcal {G}}}}}^{(N)}$
is a projective scheme over
![]() $\operatorname {\mathrm {Spec}} B$
and the projection
$\operatorname {\mathrm {Spec}} B$
and the projection
![]() $\Gamma \to \operatorname {\mathrm {Spec}} B$
is an isomorphism over
$\Gamma \to \operatorname {\mathrm {Spec}} B$
is an isomorphism over
![]() $\operatorname {\mathrm {Spec}} B[\tfrac {1}{\zeta }]$
. By the flattening technique of Raynaud and Gruson [Reference Raynaud and Gruson83, Corollaire 5.7.12], there is a blowing-up Y of
$\operatorname {\mathrm {Spec}} B[\tfrac {1}{\zeta }]$
. By the flattening technique of Raynaud and Gruson [Reference Raynaud and Gruson83, Corollaire 5.7.12], there is a blowing-up Y of
![]() $\operatorname {\mathrm {Spec}} B$
in a finitely generated ideal
$\operatorname {\mathrm {Spec}} B$
in a finitely generated ideal
![]() ${\mathfrak {b}}\subset B$
containing a power of
${\mathfrak {b}}\subset B$
containing a power of
![]() $\zeta $
, such that the strict transform of
$\zeta $
, such that the strict transform of
![]() $\Gamma $
– that is, the closed subscheme of
$\Gamma $
– that is, the closed subscheme of
![]() $\Gamma \times _B Y$
defined by the sheaf of ideals of
$\Gamma \times _B Y$
defined by the sheaf of ideals of
![]() $\zeta $
-torsion – is isomorphic to Y. The morphism
$\zeta $
-torsion – is isomorphic to Y. The morphism
![]() $Y\to \Gamma \to {\underline {{\mathcal {M}}}}_{{\underline {{\mathcal {G}}}}}^{(N)}$
corresponds to an extension over Y of the triple
$Y\to \Gamma \to {\underline {{\mathcal {M}}}}_{{\underline {{\mathcal {G}}}}}^{(N)}$
corresponds to an extension over Y of the triple
![]() $({\mathcal {G}}^{\prime \prime }_L,\tau ^{\prime \prime }\!,u^{\prime \prime }_L)$
from
$({\mathcal {G}}^{\prime \prime }_L,\tau ^{\prime \prime }\!,u^{\prime \prime }_L)$
from
![]() $\operatorname {\mathrm {Spec}} B[\tfrac {1}{\zeta }]$
. This means that over Y there is an
$\operatorname {\mathrm {Spec}} B[\tfrac {1}{\zeta }]$
. This means that over Y there is an
![]() $L^+G$
-torsor
$L^+G$
-torsor
![]() ${\mathcal {G}}^{\prime \prime }$
, an isomorphism of the associated
${\mathcal {G}}^{\prime \prime }$
, an isomorphism of the associated
![]() $L_{z(z-\zeta )}G$
-torsors
$L_{z(z-\zeta )}G$
-torsors
![]() and an isomorphism of the associated
and an isomorphism of the associated
![]() $LG$
-torsors
$LG$
-torsors
![]() with
with
![]() $\tau _{\mathcal {G}}\circ \sigma ^\ast u^{\prime \prime }=u^{\prime \prime }\circ \tau _{{\mathcal {G}}^{\prime \prime }}$
and over
$\tau _{\mathcal {G}}\circ \sigma ^\ast u^{\prime \prime }=u^{\prime \prime }\circ \tau _{{\mathcal {G}}^{\prime \prime }}$
and over
![]() $Y\times _B\operatorname {\mathrm {Spec}} B[\tfrac {1}{\zeta }]=\operatorname {\mathrm {Spec}} B[\tfrac {1}{\zeta }]$
an isomorphism of
$Y\times _B\operatorname {\mathrm {Spec}} B[\tfrac {1}{\zeta }]=\operatorname {\mathrm {Spec}} B[\tfrac {1}{\zeta }]$
an isomorphism of
![]() $L^+G$
-torsors
$L^+G$
-torsors
![]() satisfying
satisfying
![]() $h\circ \tau _{{\mathcal {G}}^{\prime \prime }}=\tau ^{\prime \prime }\circ \sigma ^\ast h$
and
$h\circ \tau _{{\mathcal {G}}^{\prime \prime }}=\tau ^{\prime \prime }\circ \sigma ^\ast h$
and
![]() $u^{\prime \prime }=u^{\prime \prime }_L\circ h$
.
$u^{\prime \prime }=u^{\prime \prime }_L\circ h$
.
We claim that
![]() $\tau _{{\mathcal {G}}^{\prime \prime }}$
comes from an isomorphism of
$\tau _{{\mathcal {G}}^{\prime \prime }}$
comes from an isomorphism of
![]() $L_{z-\zeta }G$
-torsors
$L_{z-\zeta }G$
-torsors
![]() . We choose a trivialisation of
. We choose a trivialisation of
![]() ${\underline {{\mathcal {G}}}}^{\prime \prime }$
over an étale covering
${\underline {{\mathcal {G}}}}^{\prime \prime }$
over an étale covering
![]() ${\widetilde {Y}}$
of
${\widetilde {Y}}$
of
![]() $Y\times _{\operatorname {\mathrm {Spec}} B}\operatorname {\mathrm {Spec}}{\widetilde {B}}$
and write the Frobenius
$Y\times _{\operatorname {\mathrm {Spec}} B}\operatorname {\mathrm {Spec}}{\widetilde {B}}$
and write the Frobenius
![]() $\tau _{{\mathcal {G}}^{\prime \prime }}$
of
$\tau _{{\mathcal {G}}^{\prime \prime }}$
of
![]() ${\underline {{\mathcal {G}}}}^{\prime \prime }$
as an element
${\underline {{\mathcal {G}}}}^{\prime \prime }$
as an element
![]() $\tau _{{\mathcal {G}}^{\prime \prime }}\in G\big ({\mathcal {O}}_{{\widetilde {Y}}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z(z-\zeta )}]\big )$
. Our claim means that
$\tau _{{\mathcal {G}}^{\prime \prime }}\in G\big ({\mathcal {O}}_{{\widetilde {Y}}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z(z-\zeta )}]\big )$
. Our claim means that
![]() $\tau _{{\mathcal {G}}^{\prime \prime }}$
actually lies in
$\tau _{{\mathcal {G}}^{\prime \prime }}$
actually lies in
![]() $G\big ({\mathcal {O}}_{{\widetilde {Y}}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z-\zeta }]\big )$
. To prove the claim, we choose a faithful representation
$G\big ({\mathcal {O}}_{{\widetilde {Y}}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z-\zeta }]\big )$
. To prove the claim, we choose a faithful representation
![]() $\rho \colon G\hookrightarrow \operatorname {\mathrm {SL}}_r$
and we consider the matrix entries
$\rho \colon G\hookrightarrow \operatorname {\mathrm {SL}}_r$
and we consider the matrix entries
![]() $g_{ij}$
of
$g_{ij}$
of
![]() $\rho (\tau _{{\mathcal {G}}^{\prime \prime }})$
that satisfy
$\rho (\tau _{{\mathcal {G}}^{\prime \prime }})$
that satisfy
![]() $(z-\zeta )^mg_{ij}\in {\mathcal {O}}_{{\widetilde {Y}}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z}]$
for an appropriate power m. Because
$(z-\zeta )^mg_{ij}\in {\mathcal {O}}_{{\widetilde {Y}}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z}]$
for an appropriate power m. Because
![]() $\tau _{{\mathcal {G}}^{\prime \prime }}$
differs from
$\tau _{{\mathcal {G}}^{\prime \prime }}$
differs from
![]() $\tau ^{\prime \prime }$
over
$\tau ^{\prime \prime }$
over
![]() ${\widetilde {Y}}_L:={\widetilde {Y}}\otimes _{{\mathcal {O}}_L}L$
by the isomorphism h of
${\widetilde {Y}}_L:={\widetilde {Y}}\otimes _{{\mathcal {O}}_L}L$
by the isomorphism h of
![]() $L^+G$
-torsors, we see that
$L^+G$
-torsors, we see that
![]() $(z-\zeta )^mg_{ij}\in {\mathcal {O}}_{{\widetilde {Y}}_L}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
. Because the intersection of
$(z-\zeta )^mg_{ij}\in {\mathcal {O}}_{{\widetilde {Y}}_L}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
. Because the intersection of
![]() ${\mathcal {O}}_{{\widetilde {Y}}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z}]$
and
${\mathcal {O}}_{{\widetilde {Y}}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z}]$
and
![]() ${\mathcal {O}}_{{\widetilde {Y}}_L}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
in
${\mathcal {O}}_{{\widetilde {Y}}_L}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
in
![]() ${\mathcal {O}}_{{\widetilde {Y}}_L}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z}]$
equals
${\mathcal {O}}_{{\widetilde {Y}}_L}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z}]$
equals
![]() ${\mathcal {O}}_{{\widetilde {Y}}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
, this shows that
${\mathcal {O}}_{{\widetilde {Y}}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
, this shows that
![]() $(z-\zeta )^mg_{ij}\in {\mathcal {O}}_{{\widetilde {Y}}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
. In particular,
$(z-\zeta )^mg_{ij}\in {\mathcal {O}}_{{\widetilde {Y}}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
. In particular,
![]() $g_{ij}\in {\mathcal {O}}_{{\widetilde {Y}}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z-\zeta }]$
, and this proves our claim.
$g_{ij}\in {\mathcal {O}}_{{\widetilde {Y}}}\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z-\zeta }]$
, and this proves our claim.
It remains to show that
![]() ${\underline {{\mathcal {G}}}}^{\prime \prime }$
is bounded by
${\underline {{\mathcal {G}}}}^{\prime \prime }$
is bounded by
![]() $\hat Z^{-1}$
under the additional assumptions on
$\hat Z^{-1}$
under the additional assumptions on
![]() $\tau _{\mathcal {G}}$
. By [Reference Bosch and Lütkebohmert18, Propositions 2.1 and 1.3], the
$\tau _{\mathcal {G}}$
. By [Reference Bosch and Lütkebohmert18, Propositions 2.1 and 1.3], the
![]() $\zeta $
-adic completion
$\zeta $
-adic completion
![]() ${\mathcal {Y}}$
of Y is the admissible formal blowing-up of
${\mathcal {Y}}$
of Y is the admissible formal blowing-up of
![]() $\operatorname {\mathrm {Spf}} B$
in the ideal
$\operatorname {\mathrm {Spf}} B$
in the ideal
![]() ${\mathfrak {b}}$
. By Proposition 2.6(a), there is an integer n such that for all representatives
${\mathfrak {b}}$
. By Proposition 2.6(a), there is an integer n such that for all representatives
![]() $(R,\hat Z_R)$
of
$(R,\hat Z_R)$
of
![]() $\hat Z$
the morphism
$\hat Z$
the morphism
![]() $\hat {Z}_R\to {\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {SL}}_r,R}$
factors through
$\hat {Z}_R\to {\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {SL}}_r,R}$
factors through
![]() ${\widehat {{\mathcal {F}}\ell }}^{(n)}_{\operatorname {\mathrm {SL}}_r,R}$
. By enlarging n, we may assume that the morphism
${\widehat {{\mathcal {F}}\ell }}^{(n)}_{\operatorname {\mathrm {SL}}_r,R}$
. By enlarging n, we may assume that the morphism
![]() $\tilde f\colon {\widetilde {{\mathcal {Y}}}}\to {\widehat {{\mathcal {F}}\ell }}_{G,R_{\hat Z}}\to {\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {SL}}_r,R_{\hat Z}}$
defined by
$\tilde f\colon {\widetilde {{\mathcal {Y}}}}\to {\widehat {{\mathcal {F}}\ell }}_{G,R_{\hat Z}}\to {\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {SL}}_r,R_{\hat Z}}$
defined by
![]() $\tau _{{\mathcal {G}}^{\prime \prime }}^{-1}$
factors through
$\tau _{{\mathcal {G}}^{\prime \prime }}^{-1}$
factors through
![]() ${\widehat {{\mathcal {F}}\ell }}^{(n)}_{\operatorname {\mathrm {SL}}_r,R_{\hat Z}}$
. Let
${\widehat {{\mathcal {F}}\ell }}^{(n)}_{\operatorname {\mathrm {SL}}_r,R_{\hat Z}}$
. Let
![]() $(R,\hat Z_R)$
be such a representative and set
$(R,\hat Z_R)$
be such a representative and set
![]() ${\widetilde {{\mathcal {Y}}}}_R:={\widetilde {{\mathcal {Y}}}}\widehat {\displaystyle \times }_{R_{\hat Z}}\operatorname {\mathrm {Spf}} R$
. Thus,
${\widetilde {{\mathcal {Y}}}}_R:={\widetilde {{\mathcal {Y}}}}\widehat {\displaystyle \times }_{R_{\hat Z}}\operatorname {\mathrm {Spf}} R$
. Thus,
![]() $\tilde f{\widehat {\otimes }}\operatorname {\mbox { id}}_R\colon {\widetilde {{\mathcal {Y}}}}_R\to {\widehat {{\mathcal {F}}\ell }}^{(n)}_{G,R}:={\widehat {{\mathcal {F}}\ell }}_{G,R}\widehat {\displaystyle \times }_{{\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {SL}}_r,R}}{\widehat {{\mathcal {F}}\ell }}^{(n)}_{\operatorname {\mathrm {SL}}_r,R}$
and
$\tilde f{\widehat {\otimes }}\operatorname {\mbox { id}}_R\colon {\widetilde {{\mathcal {Y}}}}_R\to {\widehat {{\mathcal {F}}\ell }}^{(n)}_{G,R}:={\widehat {{\mathcal {F}}\ell }}_{G,R}\widehat {\displaystyle \times }_{{\widehat {{\mathcal {F}}\ell }}_{\operatorname {\mathrm {SL}}_r,R}}{\widehat {{\mathcal {F}}\ell }}^{(n)}_{\operatorname {\mathrm {SL}}_r,R}$
and
![]() $\hat Z_R$
is a closed formal subscheme of
$\hat Z_R$
is a closed formal subscheme of
![]() ${\widehat {{\mathcal {F}}\ell }}^{(n)}_{G,R}$
, defined by a sheaf of ideals
${\widehat {{\mathcal {F}}\ell }}^{(n)}_{G,R}$
, defined by a sheaf of ideals
![]() ${\mathfrak {a}}$
on
${\mathfrak {a}}$
on
![]() ${\widehat {{\mathcal {F}}\ell }}^{(n)}_{G,R}$
. We must show that
${\widehat {{\mathcal {F}}\ell }}^{(n)}_{G,R}$
. We must show that
![]() $(\tilde f{\widehat {\otimes }}\operatorname {\mbox { id}}_R)^*{\mathfrak {a}}=(0)$
. The associated morphism of
$(\tilde f{\widehat {\otimes }}\operatorname {\mbox { id}}_R)^*{\mathfrak {a}}=(0)$
. The associated morphism of
![]() $\operatorname {\mathrm {Frac}}(R)$
-analytic spaces
$\operatorname {\mathrm {Frac}}(R)$
-analytic spaces
![]() $(\tilde f{\widehat {\otimes }}\operatorname {\mbox { id}}_R)^{\mathrm {an}}\colon ({\widetilde {{\mathcal {Y}}}}_R)^{\mathrm {an}}\to ({\widehat {{\mathcal {F}}\ell }}^{(n)}_{G,R})^{\mathrm {an}}$
is given by
$(\tilde f{\widehat {\otimes }}\operatorname {\mbox { id}}_R)^{\mathrm {an}}\colon ({\widetilde {{\mathcal {Y}}}}_R)^{\mathrm {an}}\to ({\widehat {{\mathcal {F}}\ell }}^{(n)}_{G,R})^{\mathrm {an}}$
is given by
![]() $\tau _{{\mathcal {G}}^{\prime \prime }}^{-1}=(\sigma ^\ast u^{\prime \prime })^{-1}\circ \tau _{\mathcal {G}}^{-1}\circ u^{\prime \prime }$
and factors through
$\tau _{{\mathcal {G}}^{\prime \prime }}^{-1}=(\sigma ^\ast u^{\prime \prime })^{-1}\circ \tau _{\mathcal {G}}^{-1}\circ u^{\prime \prime }$
and factors through
![]() $\hat Z_R^{\mathrm {an}}$
, because
$\hat Z_R^{\mathrm {an}}$
, because
![]() $\sigma ^\ast \alpha \circ \tau _{\mathcal {G}}^{-1}\circ \alpha ^{-1}\in \hat Z_R^{\mathrm {an}}({\widetilde {{\mathcal {Y}}}}^{\mathrm {an}})$
, as well as
$\sigma ^\ast \alpha \circ \tau _{\mathcal {G}}^{-1}\circ \alpha ^{-1}\in \hat Z_R^{\mathrm {an}}({\widetilde {{\mathcal {Y}}}}^{\mathrm {an}})$
, as well as
![]() $\alpha \circ u^{\prime \prime }\!,\sigma ^\ast (\alpha \circ u^{\prime \prime })^{-1}\in G({\mathcal {O}}_{{\widetilde {{\mathcal {Y}}}}^{\mathrm {an}}}\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]})$
, and
$\alpha \circ u^{\prime \prime }\!,\sigma ^\ast (\alpha \circ u^{\prime \prime })^{-1}\in G({\mathcal {O}}_{{\widetilde {{\mathcal {Y}}}}^{\mathrm {an}}}\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]})$
, and
![]() $\hat Z_R^{\mathrm {an}}$
is invariant under multiplication with
$\hat Z_R^{\mathrm {an}}$
is invariant under multiplication with
![]() $G({\mathcal {O}}_{{\widetilde {{\mathcal {Y}}}}^{\mathrm {an}}}\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]})$
on the left. This implies
$G({\mathcal {O}}_{{\widetilde {{\mathcal {Y}}}}^{\mathrm {an}}}\mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]})$
on the left. This implies
![]() $(\tilde f{\widehat {\otimes }}\operatorname {\mbox { id}}_R)^{\mathrm {an}*}{\mathfrak {a}}=(0)$
on
$(\tilde f{\widehat {\otimes }}\operatorname {\mbox { id}}_R)^{\mathrm {an}*}{\mathfrak {a}}=(0)$
on
![]() $({\widetilde {{\mathcal {Y}}}}_R)^{\mathrm {an}}$
and because
$({\widetilde {{\mathcal {Y}}}}_R)^{\mathrm {an}}$
and because
![]() ${\mathcal {O}}_{{\widetilde {{\mathcal {Y}}}}_R}\subset {\mathcal {O}}_{({\widetilde {{\mathcal {Y}}}}_R)^{\mathrm {an}}}$
, we obtain
${\mathcal {O}}_{{\widetilde {{\mathcal {Y}}}}_R}\subset {\mathcal {O}}_{({\widetilde {{\mathcal {Y}}}}_R)^{\mathrm {an}}}$
, we obtain
![]() $(\tilde f{\widehat {\otimes }}\operatorname {\mbox { id}}_R)^*{\mathfrak {a}}=(0)$
on
$(\tilde f{\widehat {\otimes }}\operatorname {\mbox { id}}_R)^*{\mathfrak {a}}=(0)$
on
![]() ${\widetilde {{\mathcal {Y}}}}_R$
. Therefore, the morphism
${\widetilde {{\mathcal {Y}}}}_R$
. Therefore, the morphism
![]() ${\widetilde {{\mathcal {Y}}}}_R\to {\widehat {{\mathcal {F}}\ell }}^{(n)}_{G,R}$
given by
${\widetilde {{\mathcal {Y}}}}_R\to {\widehat {{\mathcal {F}}\ell }}^{(n)}_{G,R}$
given by
![]() $\tau _{{\mathcal {G}}^{\prime \prime }}^{-1}$
factors through the closed formal subscheme
$\tau _{{\mathcal {G}}^{\prime \prime }}^{-1}$
factors through the closed formal subscheme
![]() $\hat Z_R$
. By Definition 2.2(d) and Remark 2.3(c), this means that
$\hat Z_R$
. By Definition 2.2(d) and Remark 2.3(c), this means that
![]() $\tau _{{\mathcal {G}}^{\prime \prime }}^{-1}$
is bounded by
$\tau _{{\mathcal {G}}^{\prime \prime }}^{-1}$
is bounded by
![]() $\hat Z$
and
$\hat Z$
and
![]() ${\underline {{\mathcal {G}}}}^{\prime \prime }$
is bounded by
${\underline {{\mathcal {G}}}}^{\prime \prime }$
is bounded by
![]() $\hat {Z}^{-1}$
.
$\hat {Z}^{-1}$
.
To define
![]() ${\breve {\mathcal {M}}}^K$
for all compact open subgroups
${\breve {\mathcal {M}}}^K$
for all compact open subgroups
![]() $K\subset G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
, we proceed slightly differently than Rapoport and Zink [Reference Rapoport and Zink80, 5.34] and instead use the following definition and corollary. For a comparison with [Reference Rapoport and Zink80, 5.34], see Remark 7.14.
$K\subset G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
, we proceed slightly differently than Rapoport and Zink [Reference Rapoport and Zink80, 5.34] and instead use the following definition and corollary. For a comparison with [Reference Rapoport and Zink80, 5.34], see Remark 7.14.
Definition 7.10. Let X be a connected affinoid strictly L-analytic space with geometric base point
![]() $\bar x$
, and let
$\bar x$
, and let
![]() $K\subset G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
be a compact open subgroup. Consider the category of triples
$K\subset G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
be a compact open subgroup. Consider the category of triples
![]() $({\underline {{\mathcal {G}}}},\bar \delta ,\eta K)$
where
$({\underline {{\mathcal {G}}}},\bar \delta ,\eta K)$
where
![]() $({\underline {{\mathcal {G}}}},\bar \delta )\in {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}({\mathcal {X}})$
for an admissible formal model
$({\underline {{\mathcal {G}}}},\bar \delta )\in {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}({\mathcal {X}})$
for an admissible formal model
![]() ${\mathcal {X}}$
of X and
${\mathcal {X}}$
of X and
![]() $\eta K\in \operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}},\bar x}\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )/K$
is a rational K-level structure on
$\eta K\in \operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}},\bar x}\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )/K$
is a rational K-level structure on
![]() ${\underline {{\mathcal {G}}}}$
over X. Morphisms between two such triples
${\underline {{\mathcal {G}}}}$
over X. Morphisms between two such triples
![]() $({\underline {{\mathcal {G}}}}_1,\bar \delta _1,\eta _1 K)$
and
$({\underline {{\mathcal {G}}}}_1,\bar \delta _1,\eta _1 K)$
and
![]() $({\underline {{\mathcal {G}}}}_2,\bar \delta _2,\eta _2 K)$
over admissible formal models
$({\underline {{\mathcal {G}}}}_2,\bar \delta _2,\eta _2 K)$
over admissible formal models
![]() ${\mathcal {X}}_1$
, respectively
${\mathcal {X}}_1$
, respectively
![]() ${\mathcal {X}}_2$
, are quasi-isogenies
${\mathcal {X}}_2$
, are quasi-isogenies
![]() $u\colon {\underline {{\mathcal {G}}}}_1\to {\underline {{\mathcal {G}}}}_2$
as in Remark 7.7 over a model
$u\colon {\underline {{\mathcal {G}}}}_1\to {\underline {{\mathcal {G}}}}_2$
as in Remark 7.7 over a model
![]() ${\widetilde {{\mathcal {X}}}}$
dominating both
${\widetilde {{\mathcal {X}}}}$
dominating both
![]() ${\mathcal {X}}_i$
with
${\mathcal {X}}_i$
with
![]() $\bar \delta _2\circ (u\;\textrm {mod}\;\zeta ) =\bar \delta _1$
such that
$\bar \delta _2\circ (u\;\textrm {mod}\;\zeta ) =\bar \delta _1$
such that
![]() $\check V_{u,\bar x}\circ \eta _1 K=\eta _2 K$
. In particular, all morphisms are isomorphisms and by rigidity of quasi-isogenies [Reference Arasteh Rad and Hartl4, Proposition 2.11], all Hom sets contain at most one element.
$\check V_{u,\bar x}\circ \eta _1 K=\eta _2 K$
. In particular, all morphisms are isomorphisms and by rigidity of quasi-isogenies [Reference Arasteh Rad and Hartl4, Proposition 2.11], all Hom sets contain at most one element.
For
![]() $K\subset G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
we consider over
$K\subset G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
we consider over
![]() ${\breve {\mathcal {M}}}^K$
the triple
${\breve {\mathcal {M}}}^K$
the triple
![]() $({\underline {{\mathcal {G}}}}^{\textrm {univ}},\bar \delta ^{\textrm {univ}},\eta ^{\textrm {univ}} K)$
, where
$({\underline {{\mathcal {G}}}}^{\textrm {univ}},\bar \delta ^{\textrm {univ}},\eta ^{\textrm {univ}} K)$
, where
![]() $\eta ^{\textrm {univ}} K$
is the rational K-level structure on
$\eta ^{\textrm {univ}} K$
is the rational K-level structure on
![]() ${\underline {{\mathcal {G}}}}^{\textrm {univ}}$
induced from the universal integral K-level structure on
${\underline {{\mathcal {G}}}}^{\textrm {univ}}$
induced from the universal integral K-level structure on
![]() ${\underline {{\mathcal {G}}}}^{\textrm {univ}}$
via the inclusion
${\underline {{\mathcal {G}}}}^{\textrm {univ}}$
via the inclusion
![]() $\operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}},\bar x}({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})\to \operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}},\bar x}\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
.
$\operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}},\bar x}({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})\to \operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}},\bar x}\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
.
Corollary 7.11. Let
![]() ${\breve {\mathcal {M}}}=({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\mathrm {an}}$
and for every open subgroup
${\breve {\mathcal {M}}}=({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\mathrm {an}}$
and for every open subgroup
![]() $K\subset G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
let
$K\subset G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
let
![]() ${\breve {\mathcal {M}}}^K$
be the finite étale covering space from Definition 7.4 parametrising integral K-level structures on the universal local G-shtuka
${\breve {\mathcal {M}}}^K$
be the finite étale covering space from Definition 7.4 parametrising integral K-level structures on the universal local G-shtuka
![]() ${\underline {{\mathcal {G}}}}^{\textrm {univ}}$
over
${\underline {{\mathcal {G}}}}^{\textrm {univ}}$
over
![]() ${\breve {\mathcal {M}}}$
from Remark 7.7. Then
${\breve {\mathcal {M}}}$
from Remark 7.7. Then
![]() ${\breve {\mathcal {M}}}^K$
also parametrises isomorphism classes of triples
${\breve {\mathcal {M}}}^K$
also parametrises isomorphism classes of triples
![]() $({\underline {{\mathcal {G}}}},\bar \delta ,\eta K)$
in the sense of Definition 7.10.
$({\underline {{\mathcal {G}}}},\bar \delta ,\eta K)$
in the sense of Definition 7.10.
Proof. Let X be a connected affinoid strictly L-analytic space with geometric base point
![]() $\bar x$
, and let
$\bar x$
, and let
![]() $({\underline {{\mathcal {G}}}},\bar \delta ,\eta K)$
be a triple over X, where
$({\underline {{\mathcal {G}}}},\bar \delta ,\eta K)$
be a triple over X, where
![]() $({\underline {{\mathcal {G}}}},\bar \delta )\in {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}({\mathcal {X}})$
for an admissible formal model
$({\underline {{\mathcal {G}}}},\bar \delta )\in {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}({\mathcal {X}})$
for an admissible formal model
![]() ${\mathcal {X}}$
of X, and
${\mathcal {X}}$
of X, and
![]() $\eta K$
is a rational K-level structure on
$\eta K$
is a rational K-level structure on
![]() ${\underline {{\mathcal {G}}}}$
over X. We may assume that
${\underline {{\mathcal {G}}}}$
over X. We may assume that
![]() ${\mathcal {X}}=\operatorname {\mathrm {Spf}} B$
is affine. By Proposition 7.8 there is an admissible formal blowing-up
${\mathcal {X}}=\operatorname {\mathrm {Spf}} B$
is affine. By Proposition 7.8 there is an admissible formal blowing-up
![]() ${\mathcal {Y}}\to {\mathcal {X}}$
and a
${\mathcal {Y}}\to {\mathcal {X}}$
and a
![]() $({\underline {{\mathcal {G}}}}^{\prime \prime }\!,\bar \delta ^{\prime \prime })\in {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}({\mathcal {Y}})$
with
$({\underline {{\mathcal {G}}}}^{\prime \prime }\!,\bar \delta ^{\prime \prime })\in {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}({\mathcal {Y}})$
with
![]() $\breve \pi ({\underline {{\mathcal {G}}}},\bar \delta )=\breve \pi ({\underline {{\mathcal {G}}}}^{\prime \prime }\!,\bar \delta ^{\prime \prime })$
and an isogeny
$\breve \pi ({\underline {{\mathcal {G}}}},\bar \delta )=\breve \pi ({\underline {{\mathcal {G}}}}^{\prime \prime }\!,\bar \delta ^{\prime \prime })$
and an isogeny
![]() $u^{\prime \prime }\colon {\underline {{\mathcal {G}}}}\to {\underline {{\mathcal {G}}}}^{\prime \prime }$
over
$u^{\prime \prime }\colon {\underline {{\mathcal {G}}}}\to {\underline {{\mathcal {G}}}}^{\prime \prime }$
over
![]() ${\mathcal {Y}}$
lifting
${\mathcal {Y}}$
lifting
![]() $(\bar \delta ^{\prime \prime })^{-1}\circ \bar \delta $
such that
$(\bar \delta ^{\prime \prime })^{-1}\circ \bar \delta $
such that
![]() $\check V_{u^{\prime \prime }\!,\bar x}\circ \eta \in \operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}}^{\prime \prime }\!,\bar x}({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
. The pair
$\check V_{u^{\prime \prime }\!,\bar x}\circ \eta \in \operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}}^{\prime \prime }\!,\bar x}({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
. The pair
![]() $({\underline {{\mathcal {G}}}}^{\prime \prime }\!,\bar \delta ^{\prime \prime })$
induces a morphism of
$({\underline {{\mathcal {G}}}}^{\prime \prime }\!,\bar \delta ^{\prime \prime })$
induces a morphism of
![]() $\breve E$
-analytic spaces
$\breve E$
-analytic spaces
![]() $X={\mathcal {Y}}^{\mathrm {an}}\to {\breve {\mathcal {M}}}$
that is independent of the admissible formal blowing-up
$X={\mathcal {Y}}^{\mathrm {an}}\to {\breve {\mathcal {M}}}$
that is independent of the admissible formal blowing-up
![]() ${\mathcal {Y}}$
. By Proposition 7.5(a) the integral K-level structure
${\mathcal {Y}}$
. By Proposition 7.5(a) the integral K-level structure
![]() $(\check V_{u^{\prime \prime }\!,\bar x}\circ \eta )K$
on
$(\check V_{u^{\prime \prime }\!,\bar x}\circ \eta )K$
on
![]() ${\underline {{\mathcal {G}}}}^{\prime \prime }$
defines a uniquely determined
${\underline {{\mathcal {G}}}}^{\prime \prime }$
defines a uniquely determined
![]() ${\breve {\mathcal {M}}}$
-morphism
${\breve {\mathcal {M}}}$
-morphism
![]() $f\colon X\to {\breve {\mathcal {M}}}^K$
such that
$f\colon X\to {\breve {\mathcal {M}}}^K$
such that
![]() $(f^*{\underline {{\mathcal {G}}}}^{\textrm {univ}},f^*\bar \delta ^{\textrm {univ}},f^*\eta ^{\textrm {univ}} K)=\big ({\underline {{\mathcal {G}}}}^{\prime \prime }\!,\bar \delta ^{\prime \prime }\!,(\check V_{u^{\prime \prime }\!,\bar x}\circ \eta )K\big )\cong ({\underline {{\mathcal {G}}}},\bar \delta ,\eta K)$
.
$(f^*{\underline {{\mathcal {G}}}}^{\textrm {univ}},f^*\bar \delta ^{\textrm {univ}},f^*\eta ^{\textrm {univ}} K)=\big ({\underline {{\mathcal {G}}}}^{\prime \prime }\!,\bar \delta ^{\prime \prime }\!,(\check V_{u^{\prime \prime }\!,\bar x}\circ \eta )K\big )\cong ({\underline {{\mathcal {G}}}},\bar \delta ,\eta K)$
.
Definition 7.12. Let
![]() $K\subset G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
be a compact open subgroup. Let
$K\subset G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
be a compact open subgroup. Let
![]() $K^{\prime }\subset K$
be a normal subgroup of finite index with
$K^{\prime }\subset K$
be a normal subgroup of finite index with
![]() $K^{\prime }\subset G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
. (Such a subgroup exists because
$K^{\prime }\subset G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
. (Such a subgroup exists because
![]() $K\cap G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})\subset K$
is of finite index due to the openness of
$K\cap G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})\subset K$
is of finite index due to the openness of
![]() $G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
and the compactness of K.) Then we define
$G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
and the compactness of K.) Then we define
![]() ${\breve {\mathcal {M}}}^K$
as the
${\breve {\mathcal {M}}}^K$
as the
![]() $\breve E$
-analytic space that is the quotient of
$\breve E$
-analytic space that is the quotient of
![]() ${\breve {\mathcal {M}}}^{K^{\prime }}$
by the finite group
${\breve {\mathcal {M}}}^{K^{\prime }}$
by the finite group
![]() $K/K^{\prime }$
; see [Reference Berkovich7, Proposition 2.1.14(ii)] and [Reference Berkovich10, Lemma 4]. Here
$K/K^{\prime }$
; see [Reference Berkovich7, Proposition 2.1.14(ii)] and [Reference Berkovich10, Lemma 4]. Here
![]() $gK^{\prime }\in K/K^{\prime }$
acts on
$gK^{\prime }\in K/K^{\prime }$
acts on
![]() ${\breve {\mathcal {M}}}^{K^{\prime }}$
by sending the universal triple
${\breve {\mathcal {M}}}^{K^{\prime }}$
by sending the universal triple
![]() $({\underline {{\mathcal {G}}}}^{\textrm {univ}},\bar \delta ^{\textrm {univ}},\eta ^{\textrm {univ}} K^{\prime })$
over
$({\underline {{\mathcal {G}}}}^{\textrm {univ}},\bar \delta ^{\textrm {univ}},\eta ^{\textrm {univ}} K^{\prime })$
over
![]() ${\breve {\mathcal {M}}}^{K^{\prime }}$
from Corollary 7.11 to the triple
${\breve {\mathcal {M}}}^{K^{\prime }}$
from Corollary 7.11 to the triple
![]() $({\underline {{\mathcal {G}}}}^{\textrm {univ}},\bar \delta ^{\textrm {univ}},\eta ^{\textrm {univ}} gK^{\prime })$
. By Remark 7.14, this means that
$({\underline {{\mathcal {G}}}}^{\textrm {univ}},\bar \delta ^{\textrm {univ}},\eta ^{\textrm {univ}} gK^{\prime })$
. By Remark 7.14, this means that
![]() $gK^{\prime }\in K/K^{\prime }$
acts on
$gK^{\prime }\in K/K^{\prime }$
acts on
![]() ${\breve {\mathcal {M}}}^{K^{\prime }}$
as the Hecke correspondence
${\breve {\mathcal {M}}}^{K^{\prime }}$
as the Hecke correspondence
![]() $\iota (g)_{K^{\prime }}$
. In particular,
$\iota (g)_{K^{\prime }}$
. In particular,
![]() $\breve {\mathcal {M}}^{K_0}=({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\mathrm {an}}$
for
$\breve {\mathcal {M}}^{K_0}=({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\mathrm {an}}$
for
![]() $K_0=G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
. We denote by
$K_0=G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
. We denote by
![]() $({\underline {{\mathcal {G}}}}^{\textrm {univ}},\bar \delta ^{\textrm {univ}},\eta ^{\textrm {univ}} K)$
the triple over
$({\underline {{\mathcal {G}}}}^{\textrm {univ}},\bar \delta ^{\textrm {univ}},\eta ^{\textrm {univ}} K)$
the triple over
![]() ${\breve {\mathcal {M}}}^K$
induced by the universal triple
${\breve {\mathcal {M}}}^K$
induced by the universal triple
![]() $({\underline {{\mathcal {G}}}}^{\textrm {univ}},\bar \delta ^{\textrm {univ}},\eta ^{\textrm {univ}} K^{\prime })$
over
$({\underline {{\mathcal {G}}}}^{\textrm {univ}},\bar \delta ^{\textrm {univ}},\eta ^{\textrm {univ}} K^{\prime })$
over
![]() ${\breve {\mathcal {M}}}^{K^{\prime }}$
. It is universal by the following corollary.
${\breve {\mathcal {M}}}^{K^{\prime }}$
. It is universal by the following corollary.
By Proposition 7.5(c), the definition of
![]() ${\breve {\mathcal {M}}}^K$
is independent of the normal subgroup
${\breve {\mathcal {M}}}^K$
is independent of the normal subgroup
![]() $K^{\prime }\subset K$
and Proposition 7.5(c) continues to hold in this more general setting. We will see in Theorem 8.1 that
$K^{\prime }\subset K$
and Proposition 7.5(c) continues to hold in this more general setting. We will see in Theorem 8.1 that
![]() ${\breve {\mathcal {M}}}^K$
always is a strictly
${\breve {\mathcal {M}}}^K$
always is a strictly
![]() $\breve E$
-analytic space.
$\breve E$
-analytic space.
Corollary 7.13. If
![]() $K\subset G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
is any compact open subgroup then
$K\subset G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
is any compact open subgroup then
![]() ${\breve {\mathcal {M}}}^K$
is an
${\breve {\mathcal {M}}}^K$
is an
![]() $\breve E$
-analytic space that is separated and partially proper over
$\breve E$
-analytic space that is separated and partially proper over
![]() $\breve E$
and parametrises isomorphism classes of triples
$\breve E$
and parametrises isomorphism classes of triples
![]() $({\underline {{\mathcal {G}}}},\bar \delta ,\eta K)$
in the sense of Definition 7.10.
$({\underline {{\mathcal {G}}}},\bar \delta ,\eta K)$
in the sense of Definition 7.10.
Proof. That
![]() ${\breve {\mathcal {M}}}^K$
is separated and partially proper over
${\breve {\mathcal {M}}}^K$
is separated and partially proper over
![]() $\breve E$
follows from Lemma 6.11 and [Reference Huber63, Lemma 1.10.17 (iv), (vii)]. Let X be a connected affinoid strictly L-analytic space with geometric base point
$\breve E$
follows from Lemma 6.11 and [Reference Huber63, Lemma 1.10.17 (iv), (vii)]. Let X be a connected affinoid strictly L-analytic space with geometric base point
![]() $\bar x$
, and let
$\bar x$
, and let
![]() $({\underline {{\mathcal {G}}}},\bar \delta ,\eta K)$
be a triple over X where
$({\underline {{\mathcal {G}}}},\bar \delta ,\eta K)$
be a triple over X where
![]() $({\underline {{\mathcal {G}}}},\bar \delta )\in {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}({\mathcal {X}})$
for an admissible formal model
$({\underline {{\mathcal {G}}}},\bar \delta )\in {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}({\mathcal {X}})$
for an admissible formal model
![]() ${\mathcal {X}}$
of X and where
${\mathcal {X}}$
of X and where
![]() $\eta K\in \operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}},\bar x}\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )/K$
is a rational K-level structure on
$\eta K\in \operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}},\bar x}\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )/K$
is a rational K-level structure on
![]() ${\underline {{\mathcal {G}}}}$
over X. Let
${\underline {{\mathcal {G}}}}$
over X. Let
![]() $K^{\prime }\subset K$
be a normal subgroup of finite index with
$K^{\prime }\subset K$
be a normal subgroup of finite index with
![]() $K^{\prime }\subset G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
. Consider the étale covering space
$K^{\prime }\subset G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
. Consider the étale covering space
![]() $X^{\prime }\to X$
corresponding to the
$X^{\prime }\to X$
corresponding to the
![]() $\pi _1^{\mathrm {\acute {e}t}}(X,\bar x)$
-set
$\pi _1^{\mathrm {\acute {e}t}}(X,\bar x)$
-set
![]() $\{\eta ^{\prime }K^{\prime }\in \operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}},\bar x}\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )/K^{\prime }\colon \eta ^{\prime }K=\eta K\}$
that is isomorphic to
$\{\eta ^{\prime }K^{\prime }\in \operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}},\bar x}\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )/K^{\prime }\colon \eta ^{\prime }K=\eta K\}$
that is isomorphic to
![]() $K/K^{\prime }$
under the maps
$K/K^{\prime }$
under the maps
![]() $\eta ^{\prime }K^{\prime }\mapsto \eta ^{-1}\eta ^{\prime }K^{\prime }$
and
$\eta ^{\prime }K^{\prime }\mapsto \eta ^{-1}\eta ^{\prime }K^{\prime }$
and
![]() . In particular,
. In particular,
![]() $X^{\prime }\to X$
is a
$X^{\prime }\to X$
is a
![]() $K/K^{\prime }$
-torsor. By Corollary 7.11 there is a uniquely determined
$K/K^{\prime }$
-torsor. By Corollary 7.11 there is a uniquely determined
![]() $\breve E$
-morphism
$\breve E$
-morphism
![]() $X^{\prime }\to {\breve {\mathcal {M}}}^{K^{\prime }}$
which is equivariant for the action of
$X^{\prime }\to {\breve {\mathcal {M}}}^{K^{\prime }}$
which is equivariant for the action of
![]() $K/K^{\prime }$
and therefore descends to a uniquely determined
$K/K^{\prime }$
and therefore descends to a uniquely determined
![]() $\breve E$
-morphism
$\breve E$
-morphism
![]() $X\to {\breve {\mathcal {M}}}^K$
.
$X\to {\breve {\mathcal {M}}}^K$
.
Remark 7.14. We have an action of
![]() $G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
on the tower
$G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
on the tower
![]() $({\breve {\mathcal {M}}}^K)_{K\subset G({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em))}$
by Hecke correspondences defined as follows. Let
$({\breve {\mathcal {M}}}^K)_{K\subset G({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em))}$
by Hecke correspondences defined as follows. Let
![]() $g\in G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
and let K be a compact open subgroup of
$g\in G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
and let K be a compact open subgroup of
![]() $G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
. Then g induces an isomorphism
$G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
. Then g induces an isomorphism
by sending the universal triple
![]() $({\underline {{\mathcal {G}}}}^{\textrm {univ}},\bar \delta ^{\textrm {univ}},\eta ^{\textrm {univ}} K)$
over
$({\underline {{\mathcal {G}}}}^{\textrm {univ}},\bar \delta ^{\textrm {univ}},\eta ^{\textrm {univ}} K)$
over
![]() ${\breve {\mathcal {M}}}^K$
from Definition 7.12 to the triple
${\breve {\mathcal {M}}}^K$
from Definition 7.12 to the triple
![]() $\big ({\underline {{\mathcal {G}}}}^{\textrm {univ}},\bar \delta ^{\textrm {univ}},\eta ^{\textrm {univ}} Kg=\eta ^{\textrm {univ}} g(g^{-1}Kg)\big )$
. The morphisms
$\big ({\underline {{\mathcal {G}}}}^{\textrm {univ}},\bar \delta ^{\textrm {univ}},\eta ^{\textrm {univ}} Kg=\eta ^{\textrm {univ}} g(g^{-1}Kg)\big )$
. The morphisms
![]() $\iota (g)$
are compatible with the group structure on
$\iota (g)$
are compatible with the group structure on
![]() $G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
; that is, they satisfy
$G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
; that is, they satisfy
![]() $\iota (gh)_K=\iota (g)_{h^{-1}Kh}\circ \iota (h)_K$
for all
$\iota (gh)_K=\iota (g)_{h^{-1}Kh}\circ \iota (h)_K$
for all
![]() $g,h\in G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
and all K. They are also compatible with the projection maps
$g,h\in G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
and all K. They are also compatible with the projection maps
![]() $\breve \pi _{K,K^{\prime }}$
; that is,
$\breve \pi _{K,K^{\prime }}$
; that is,
![]() $\iota (g)_K\circ \breve \pi _{K,K^{\prime }}=\breve \pi _{g^{-1}Kg,\,g^{-1}K^{\prime }g}\circ \iota (g)_{K^{\prime }}$
.
$\iota (g)_K\circ \breve \pi _{K,K^{\prime }}=\breve \pi _{g^{-1}Kg,\,g^{-1}K^{\prime }g}\circ \iota (g)_{K^{\prime }}$
.
If both K and
![]() $g^{-1}Kg$
are contained in
$g^{-1}Kg$
are contained in
![]() $G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
, we can translate the definition of
$G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
, we can translate the definition of
![]() $\iota (g)_K$
in terms of integral K-level structures by inspecting the proof of Corollary 7.11. Namely, we start with the universal integral K-level structure
$\iota (g)_K$
in terms of integral K-level structures by inspecting the proof of Corollary 7.11. Namely, we start with the universal integral K-level structure
![]() $\eta ^{\textrm {univ}} K\in \operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}}^{\textrm {univ}},\bar x}({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})/K$
on
$\eta ^{\textrm {univ}} K\in \operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}}^{\textrm {univ}},\bar x}({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})/K$
on
![]() ${\underline {{\mathcal {G}}}}^{\textrm {univ}}$
over
${\underline {{\mathcal {G}}}}^{\textrm {univ}}$
over
![]() ${\breve {\mathcal {M}}}^K$
. The rational
${\breve {\mathcal {M}}}^K$
. The rational
![]() $g^{-1}Kg$
-level structure
$g^{-1}Kg$
-level structure
![]() $\eta ^{\textrm {univ}} Kg=\eta ^{\textrm {univ}} g(g^{-1}Kg)$
yields a pair
$\eta ^{\textrm {univ}} Kg=\eta ^{\textrm {univ}} g(g^{-1}Kg)$
yields a pair
![]() $({\underline {{\mathcal {G}}}}^{\prime \prime }\!,\bar \delta ^{\prime \prime })\in {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}({\mathcal {Y}})$
for an admissible formal blowing-up
$({\underline {{\mathcal {G}}}}^{\prime \prime }\!,\bar \delta ^{\prime \prime })\in {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}({\mathcal {Y}})$
for an admissible formal blowing-up
![]() ${\mathcal {Y}}\to {\mathcal {X}}$
with
${\mathcal {Y}}\to {\mathcal {X}}$
with
![]() $\breve \pi ({\underline {{\mathcal {G}}}}^{\textrm {univ}},\bar \delta ^{\textrm {univ}})=\breve \pi ({\underline {{\mathcal {G}}}}^{\prime \prime }\!,\bar \delta ^{\prime \prime })$
and
$\breve \pi ({\underline {{\mathcal {G}}}}^{\textrm {univ}},\bar \delta ^{\textrm {univ}})=\breve \pi ({\underline {{\mathcal {G}}}}^{\prime \prime }\!,\bar \delta ^{\prime \prime })$
and
![]() $\check V_{u^{\prime \prime }\!,\bar x}\circ \eta ^{\textrm {univ}} g\in \operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}}^{\prime \prime }\!,\bar x}({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
, where
$\check V_{u^{\prime \prime }\!,\bar x}\circ \eta ^{\textrm {univ}} g\in \operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}}^{\prime \prime }\!,\bar x}({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
, where
![]() $u^{\prime \prime }$
is the unique lift of
$u^{\prime \prime }$
is the unique lift of
![]() $(\bar \delta ^{\prime \prime })^{-1}\circ \bar \delta ^{\textrm {univ}}$
. Then the morphism
$(\bar \delta ^{\prime \prime })^{-1}\circ \bar \delta ^{\textrm {univ}}$
. Then the morphism
![]() $\iota (g)_K$
is given by
$\iota (g)_K$
is given by
This shows that the definition of
![]() $\iota (g)_K$
in this case and therefore the definitions of
$\iota (g)_K$
in this case and therefore the definitions of
![]() ${\breve {\mathcal {M}}}^K$
,
${\breve {\mathcal {M}}}^K$
,
![]() $\breve \pi _{K,K^{\prime }}$
and
$\breve \pi _{K,K^{\prime }}$
and
![]() $\iota (g)_K$
for all K coincide with the definitions analogous to [Reference Rapoport and Zink80, 5.34].
$\iota (g)_K$
for all K coincide with the definitions analogous to [Reference Rapoport and Zink80, 5.34].
Although it is not explicitly stated in [Reference Rapoport and Zink80], the analogue of Corollary 7.13 also holds in their setup, because it can be deduced from the existence of the
![]() $\iota (g)_K$
as follows. If
$\iota (g)_K$
as follows. If
![]() $({\underline {{\mathcal {G}}}},\bar \delta )\in {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}({\mathcal {X}})$
and
$({\underline {{\mathcal {G}}}},\bar \delta )\in {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}({\mathcal {X}})$
and
![]() $\eta K$
with
$\eta K$
with
![]() $\eta \in \operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}},\bar x}\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
is a rational K-level structure on
$\eta \in \operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}},\bar x}\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
is a rational K-level structure on
![]() ${\underline {{\mathcal {G}}}}$
over
${\underline {{\mathcal {G}}}}$
over
![]() $X={\mathcal {X}}^{\mathrm {an}}$
, we can choose an element
$X={\mathcal {X}}^{\mathrm {an}}$
, we can choose an element
![]() $\eta _0\in \operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}},\bar x}({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
and set
$\eta _0\in \operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}},\bar x}({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
and set
![]() $g:=\eta _0^{-1}\eta \in \operatorname {\mathrm {Aut}}^\otimes (\omega ^\circ )=G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
. Then
$g:=\eta _0^{-1}\eta \in \operatorname {\mathrm {Aut}}^\otimes (\omega ^\circ )=G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
. Then
![]() $\eta K g^{-1}=\eta _0(gKg^{-1})$
is an integral
$\eta K g^{-1}=\eta _0(gKg^{-1})$
is an integral
![]() $gKg^{-1}$
-level structure on
$gKg^{-1}$
-level structure on
![]() ${\underline {{\mathcal {G}}}}$
and defines a uniquely determined
${\underline {{\mathcal {G}}}}$
and defines a uniquely determined
![]() $\breve E$
-morphism
$\breve E$
-morphism
![]() $X\to {\breve {\mathcal {M}}}^{gKg^{-1}}$
. Composing with
$X\to {\breve {\mathcal {M}}}^{gKg^{-1}}$
. Composing with
![]() $\iota (g)_{gKg^{-1}}$
produces the desired
$\iota (g)_{gKg^{-1}}$
produces the desired
![]() $\breve E$
-morphism
$\breve E$
-morphism
![]() $X\to {\breve {\mathcal {M}}}^K$
.
$X\to {\breve {\mathcal {M}}}^K$
.
Proposition 7.15. The period morphism
![]() $\breve \pi $
induces compatible morphisms
$\breve \pi $
induces compatible morphisms
![]() $\breve \pi _K\colon {\breve {\mathcal {M}}}^K\to \breve {\mathcal {H}}_{G,\hat Z}^{\mathrm {an}}$
for all compact open subgroups
$\breve \pi _K\colon {\breve {\mathcal {M}}}^K\to \breve {\mathcal {H}}_{G,\hat Z}^{\mathrm {an}}$
for all compact open subgroups
![]() $K\subset G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
. In terms of Corollary 7.13, it has the form
$K\subset G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
. In terms of Corollary 7.13, it has the form
![]() $\breve \pi _K\colon ({\underline {{\mathcal {G}}}}^{\textrm {univ}},\bar \delta ^{\textrm {univ}},\eta ^{\textrm {univ}} K)\mapsto \breve \pi ({\underline {{\mathcal {G}}}}^{\textrm {univ}},\bar \delta ^{\textrm {univ}})$
where
$\breve \pi _K\colon ({\underline {{\mathcal {G}}}}^{\textrm {univ}},\bar \delta ^{\textrm {univ}},\eta ^{\textrm {univ}} K)\mapsto \breve \pi ({\underline {{\mathcal {G}}}}^{\textrm {univ}},\bar \delta ^{\textrm {univ}})$
where
![]() $\eta ^{\textrm {univ}} K$
is the universal (integral or) rational K-level structure on
$\eta ^{\textrm {univ}} K$
is the universal (integral or) rational K-level structure on
![]() ${\underline {{\mathcal {G}}}}^{\textrm {univ}}$
. These morphisms commute with the Hecke correspondences in the sense that
${\underline {{\mathcal {G}}}}^{\textrm {univ}}$
. These morphisms commute with the Hecke correspondences in the sense that
![]() $\breve \pi _{g^{-1}Kg}\circ \iota (g)_K=\breve \pi _K$
for all g and K.
$\breve \pi _{g^{-1}Kg}\circ \iota (g)_K=\breve \pi _K$
for all g and K.
Proof. To construct
![]() $\breve \pi _K$
, we choose a normal subgroup
$\breve \pi _K$
, we choose a normal subgroup
![]() $K^{\prime }\subset K$
of finite index with
$K^{\prime }\subset K$
of finite index with
![]() $K^{\prime }\subset G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
. We let
$K^{\prime }\subset G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
. We let
![]() $\breve \pi _{K^{\prime }}:=\breve \pi \circ \breve \pi _{G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}),K^{\prime }}\colon {\breve {\mathcal {M}}}^{K^{\prime }}\to \breve {\mathcal {H}}_{G,\hat Z}^{\mathrm {an}}$
. It has the given form. If
$\breve \pi _{K^{\prime }}:=\breve \pi \circ \breve \pi _{G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}),K^{\prime }}\colon {\breve {\mathcal {M}}}^{K^{\prime }}\to \breve {\mathcal {H}}_{G,\hat Z}^{\mathrm {an}}$
. It has the given form. If
![]() $g\in G({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em))$
satisfies
$g\in G({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em))$
satisfies
![]() $g^{-1}K^{\prime }g\subset G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
, we see from the description of
$g^{-1}K^{\prime }g\subset G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
, we see from the description of
![]() $\iota (g)_{K^{\prime }}$
in (7.6) that
$\iota (g)_{K^{\prime }}$
in (7.6) that
![]() $\breve \pi _{g^{-1}K^{\prime }g}\circ \iota (g)_{K^{\prime }}=\breve \pi _{K^{\prime }}$
. In particular, if
$\breve \pi _{g^{-1}K^{\prime }g}\circ \iota (g)_{K^{\prime }}=\breve \pi _{K^{\prime }}$
. In particular, if
![]() $g\in K$
, then
$g\in K$
, then
![]() $\breve \pi _{K^{\prime }}$
is
$\breve \pi _{K^{\prime }}$
is
![]() $K/K^{\prime }$
-invariant. Therefore,
$K/K^{\prime }$
-invariant. Therefore,
![]() $\breve \pi _{K^{\prime }}$
descends to a morphism
$\breve \pi _{K^{\prime }}$
descends to a morphism
![]() $\breve \pi _K\colon {\breve {\mathcal {M}}}^K\to \breve {\mathcal {H}}_{G,\hat Z}^{\mathrm {an}}$
that has the given form. By Proposition 7.5(c), the definition of
$\breve \pi _K\colon {\breve {\mathcal {M}}}^K\to \breve {\mathcal {H}}_{G,\hat Z}^{\mathrm {an}}$
that has the given form. By Proposition 7.5(c), the definition of
![]() $\breve \pi _K$
is independent of the chosen
$\breve \pi _K$
is independent of the chosen
![]() $K^{\prime }$
and satisfies
$K^{\prime }$
and satisfies
![]() $\breve \pi _K\circ \breve \pi _{K,{\widetilde {K}}}=\breve \pi _{{\widetilde {K}}}$
for all compact open subgroups
$\breve \pi _K\circ \breve \pi _{K,{\widetilde {K}}}=\breve \pi _{{\widetilde {K}}}$
for all compact open subgroups
![]() ${\widetilde {K}}\subset K\subset G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
. From this
${\widetilde {K}}\subset K\subset G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
. From this
![]() $\breve \pi _{g^{-1}Kg}\circ \iota (g)_K=\breve \pi _K$
also follows.
$\breve \pi _{g^{-1}Kg}\circ \iota (g)_K=\breve \pi _K$
also follows.
The following result is the analogue of [Reference Rapoport and Zink80, Proposition 5.37] and can be proved in the same way. However, we give a different proof using Corollary 7.13.
Proposition 7.16. Let
![]() $K_1,K_2\subset G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
be compact open subgroups and let
$K_1,K_2\subset G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
be compact open subgroups and let
![]() $\Omega $
be an algebraically closed complete extension of
$\Omega $
be an algebraically closed complete extension of
![]() $\breve E$
. Then two points
$\breve E$
. Then two points
![]() $x_1\in {\breve {\mathcal {M}}}^{K_1}(\Omega )$
and
$x_1\in {\breve {\mathcal {M}}}^{K_1}(\Omega )$
and
![]() $x_2\in {\breve {\mathcal {M}}}^{K_2}(\Omega )$
satisfy
$x_2\in {\breve {\mathcal {M}}}^{K_2}(\Omega )$
satisfy
![]() $\breve \pi _{K_1}(x_1)=\breve \pi _{K_2}(x_2)$
if and only if they are mapped to each other under a Hecke correspondence; that is, if there is a
$\breve \pi _{K_1}(x_1)=\breve \pi _{K_2}(x_2)$
if and only if they are mapped to each other under a Hecke correspondence; that is, if there is a
![]() $g\in G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
and a
$g\in G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
and a
![]() $y\in {\breve {\mathcal {M}}}^{K_1\cap gK_2g^{-1}}(\Omega )$
with
$y\in {\breve {\mathcal {M}}}^{K_1\cap gK_2g^{-1}}(\Omega )$
with
![]() $\breve \pi _{K_1,\,K_1\cap gK_2g^{-1}}(y)=x_1$
and
$\breve \pi _{K_1,\,K_1\cap gK_2g^{-1}}(y)=x_1$
and
![]() $\breve \pi _{K_2,\,g^{-1}K_1g\cap K_2}\circ \iota (g)_{K_1\cap gK_2g^{-1}}(y)=x_2$
. In particular, the geometric fibres of
$\breve \pi _{K_2,\,g^{-1}K_1g\cap K_2}\circ \iota (g)_{K_1\cap gK_2g^{-1}}(y)=x_2$
. In particular, the geometric fibres of
![]() $\breve \pi _K$
are (noncanonically) isomorphic to
$\breve \pi _K$
are (noncanonically) isomorphic to
![]() $G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )/K$
.
$G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )/K$
.
Proof. Because one direction was proved in Proposition 7.15, we now assume
![]() $\breve \pi _{K_1}(x_1)=\breve \pi _{K_2}(x_2)$
. In terms of Corollary 7.13, let
$\breve \pi _{K_1}(x_1)=\breve \pi _{K_2}(x_2)$
. In terms of Corollary 7.13, let
![]() $x_i$
correspond to the triple
$x_i$
correspond to the triple
![]() $({\underline {{\mathcal {G}}}}_i,\bar \delta _i,\eta _iK_i)$
. Because
$({\underline {{\mathcal {G}}}}_i,\bar \delta _i,\eta _iK_i)$
. Because
![]() $\Omega $
is algebraically closed, we may choose representatives
$\Omega $
is algebraically closed, we may choose representatives
![]() $\eta _i\in \operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}}_i,{\mathtt {BSpec}}(\Omega )}\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
of
$\eta _i\in \operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}}_i,{\mathtt {BSpec}}(\Omega )}\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
of
![]() $\eta _iK_i$
. By the description of
$\eta _iK_i$
. By the description of
![]() $\breve \pi _K$
in Proposition 7.15, we have
$\breve \pi _K$
in Proposition 7.15, we have
![]() $\breve \pi ({\underline {{\mathcal {G}}}}_1,\bar \delta _1)=\breve \pi ({\underline {{\mathcal {G}}}}_2,\bar \delta _2)$
and so Proposition 7.8 yields a quasi-isogeny
$\breve \pi ({\underline {{\mathcal {G}}}}_1,\bar \delta _1)=\breve \pi ({\underline {{\mathcal {G}}}}_2,\bar \delta _2)$
and so Proposition 7.8 yields a quasi-isogeny
![]() $u\colon {\underline {{\mathcal {G}}}}_2\to {\underline {{\mathcal {G}}}}_1$
over
$u\colon {\underline {{\mathcal {G}}}}_2\to {\underline {{\mathcal {G}}}}_1$
over
![]() $\operatorname {\mathrm {Spec}}{\mathcal {O}}_\Omega $
with
$\operatorname {\mathrm {Spec}}{\mathcal {O}}_\Omega $
with
![]() $\bar \delta _1\circ (u\;\textrm {mod}\;\zeta ) =\bar \delta _2$
. We set
$\bar \delta _1\circ (u\;\textrm {mod}\;\zeta ) =\bar \delta _2$
. We set
![]() $\eta ^{\prime }_1:=\check V_{u,{\mathtt {BSpec}}(\Omega )}\circ \eta _2\in \operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}}_1,{\mathtt {BSpec}}(\Omega )}\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
. Then
$\eta ^{\prime }_1:=\check V_{u,{\mathtt {BSpec}}(\Omega )}\circ \eta _2\in \operatorname {\mathrm {Triv}}_{{\underline {{\mathcal {G}}}}_1,{\mathtt {BSpec}}(\Omega )}\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
. Then
![]() $x_2=({\underline {{\mathcal {G}}}}_2,\bar \delta _2,\eta _2K_2)\cong ({\underline {{\mathcal {G}}}}_1,\bar \delta _1,\eta ^{\prime }_1K_2)$
. Therefore,
$x_2=({\underline {{\mathcal {G}}}}_2,\bar \delta _2,\eta _2K_2)\cong ({\underline {{\mathcal {G}}}}_1,\bar \delta _1,\eta ^{\prime }_1K_2)$
. Therefore,
![]() $g:=\eta _1^{-1}\eta _1^{\prime }\in \operatorname {\mathrm {Aut}}^\otimes (\omega ^\circ )=G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
and
$g:=\eta _1^{-1}\eta _1^{\prime }\in \operatorname {\mathrm {Aut}}^\otimes (\omega ^\circ )=G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
and
![]() $y=({\underline {{\mathcal {G}}}}_1,\bar \delta _1,\eta _1(K_1\cap gK_2g^{-1})\big )\in {\breve {\mathcal {M}}}^{K_1\cap gK_2g^{-1}}(\Omega )$
solve the problem.
$y=({\underline {{\mathcal {G}}}}_1,\bar \delta _1,\eta _1(K_1\cap gK_2g^{-1})\big )\in {\breve {\mathcal {M}}}^{K_1\cap gK_2g^{-1}}(\Omega )$
solve the problem.
Thus, after the choice of the representative
![]() $\eta _1$
of
$\eta _1$
of
![]() $\eta _1K_1$
, the bijection between
$\eta _1K_1$
, the bijection between
![]() $G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )/K_1$
and the fibre of
$G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )/K_1$
and the fibre of
![]() $\breve \pi _{K_1}$
over
$\breve \pi _{K_1}$
over
![]() $\breve \pi _{K_1}(x_1)$
is given by
$\breve \pi _{K_1}(x_1)$
is given by
![]() $gK_1\mapsto ({\underline {{\mathcal {G}}}}_1,\bar \delta _1,\eta _1gK_1)$
with inverse
$gK_1\mapsto ({\underline {{\mathcal {G}}}}_1,\bar \delta _1,\eta _1gK_1)$
with inverse
![]() .
.
Remark 7.17. Finally, the action of
![]() $j\in J_b\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
on
$j\in J_b\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
on
![]() ${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
from Definition 3.1 induces actions on each of the spaces
${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
from Definition 3.1 induces actions on each of the spaces
![]() ${\breve {\mathcal {M}}}^K$
individually by
${\breve {\mathcal {M}}}^K$
individually by
In other words, the pullback
![]() $j^*({\underline {{\mathcal {G}}}}^{\textrm {univ}},\bar \delta ^{\textrm {univ}},\eta ^{\textrm {univ}} K)$
of the universal triple over
$j^*({\underline {{\mathcal {G}}}}^{\textrm {univ}},\bar \delta ^{\textrm {univ}},\eta ^{\textrm {univ}} K)$
of the universal triple over
![]() $\breve {\mathcal {M}}^K$
is isomorphic to
$\breve {\mathcal {M}}^K$
is isomorphic to
![]() $({\underline {{\mathcal {G}}}}^{\textrm {univ}},j\circ \bar \delta ^{\textrm {univ}},\eta ^{\textrm {univ}} K)$
in the category of triples from Definition 7.10. Using the universal property of
$({\underline {{\mathcal {G}}}}^{\textrm {univ}},j\circ \bar \delta ^{\textrm {univ}},\eta ^{\textrm {univ}} K)$
in the category of triples from Definition 7.10. Using the universal property of
![]() ${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
, the condition
${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
, the condition
![]() $j^*({\underline {{\mathcal {G}}}}^{\textrm {univ}},\bar \delta ^{\textrm {univ}})\cong ({\underline {{\mathcal {G}}}}^{\textrm {univ}},j\circ \bar \delta ^{\textrm {univ}})$
shows that there is an isomorphism
$j^*({\underline {{\mathcal {G}}}}^{\textrm {univ}},\bar \delta ^{\textrm {univ}})\cong ({\underline {{\mathcal {G}}}}^{\textrm {univ}},j\circ \bar \delta ^{\textrm {univ}})$
shows that there is an isomorphism
![]() of local G-shtukas with
of local G-shtukas with
![]() $j^\ast \bar \delta ^{\textrm {univ}}=j\circ \bar \delta ^{\textrm {univ}}\circ (\Phi _j\;\textrm {mod}\;\zeta )$
. By rigidity of quasi-isogenies [Reference Arasteh Rad and Hartl4, Proposition 2.11], the isomorphism
$j^\ast \bar \delta ^{\textrm {univ}}=j\circ \bar \delta ^{\textrm {univ}}\circ (\Phi _j\;\textrm {mod}\;\zeta )$
. By rigidity of quasi-isogenies [Reference Arasteh Rad and Hartl4, Proposition 2.11], the isomorphism
![]() $\Phi _j$
is uniquely determined and a straightforward calculation shows that
$\Phi _j$
is uniquely determined and a straightforward calculation shows that
![]() $\Phi _j\circ j^\ast \Phi _{j^{\prime }}=\Phi _{j^{\prime }j}$
. It follows from Definition 7.10 that
$\Phi _j\circ j^\ast \Phi _{j^{\prime }}=\Phi _{j^{\prime }j}$
. It follows from Definition 7.10 that
![]() $j^*\eta ^{\textrm {univ}} K=(\check V_{\Phi _j,\bar x}^{-1}\circ \eta ^{\textrm {univ}}) K$
. The
$j^*\eta ^{\textrm {univ}} K=(\check V_{\Phi _j,\bar x}^{-1}\circ \eta ^{\textrm {univ}}) K$
. The
![]() $J_b\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
-action on
$J_b\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
-action on
![]() $\breve {\mathcal {M}}^K$
is compatible with the projection maps
$\breve {\mathcal {M}}^K$
is compatible with the projection maps
![]() $\breve \pi _{K,K^{\prime }}$
and the Hecke action.
$\breve \pi _{K,K^{\prime }}$
and the Hecke action.
Lemma 7.18. The action of
![]() $J:=J_b\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
on
$J:=J_b\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
on
![]() ${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
and the induced actions on each
${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
and the induced actions on each
![]() ${\breve {\mathcal {M}}}^K$
are continuous.
${\breve {\mathcal {M}}}^K$
are continuous.
Proof. For the first assertion we have to show the following claim. Let
![]() $S\in {{\mathcal {N}}\!\mathit {ilp}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\xi \mathrm {]}\kern-0.15em\mathrm {]}}$
be a quasi-compact scheme and
$S\in {{\mathcal {N}}\!\mathit {ilp}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[}\xi \mathrm {]}\kern-0.15em\mathrm {]}}$
be a quasi-compact scheme and
![]() $({\underline {{\mathcal {G}}}},\bar \delta )\in {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}(S)$
. We must show that there is a neighbourhood U of
$({\underline {{\mathcal {G}}}},\bar \delta )\in {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}(S)$
. We must show that there is a neighbourhood U of
![]() $1\in J$
such that for
$1\in J$
such that for
![]() $j\in U$
we have
$j\in U$
we have
![]() $j({\underline {{\mathcal {G}}}},\bar \delta )\cong ({\underline {{\mathcal {G}}}},\bar \delta )$
; that is,
$j({\underline {{\mathcal {G}}}},\bar \delta )\cong ({\underline {{\mathcal {G}}}},\bar \delta )$
; that is,
![]() ${\overline {\delta }}^{-1}\circ j\circ {\overline {\delta }}$
lifts to an automorphism of
${\overline {\delta }}^{-1}\circ j\circ {\overline {\delta }}$
lifts to an automorphism of
![]() ${\underline {{\mathcal {G}}}}$
over S.
${\underline {{\mathcal {G}}}}$
over S.
To prove this claim, let
![]() $\delta \colon {\underline {{\mathcal {G}}}}\to {\underline {{\mathbb {G}}}}_{0,S}$
be the quasi-isogeny that lifts
$\delta \colon {\underline {{\mathcal {G}}}}\to {\underline {{\mathbb {G}}}}_{0,S}$
be the quasi-isogeny that lifts
![]() $\bar \delta $
by rigidity of quasi-isogenies [Reference Arasteh Rad and Hartl4, Proposition 2.11]. Let
$\bar \delta $
by rigidity of quasi-isogenies [Reference Arasteh Rad and Hartl4, Proposition 2.11]. Let
![]() $S^{\prime }\to S$
be an étale covering that trivialises
$S^{\prime }\to S$
be an étale covering that trivialises
![]() ${\underline {{\mathcal {G}}}}\cong \big ((L^+G)_{S^{\prime }},A\sigma ^\ast \big )$
. Because S is quasi-compact, there is a refinement of this covering such that
${\underline {{\mathcal {G}}}}\cong \big ((L^+G)_{S^{\prime }},A\sigma ^\ast \big )$
. Because S is quasi-compact, there is a refinement of this covering such that
![]() $S^{\prime }=\operatorname {\mathrm {Spec}} B$
is affine. Then
$S^{\prime }=\operatorname {\mathrm {Spec}} B$
is affine. Then
![]() $\delta $
corresponds to an element
$\delta $
corresponds to an element
![]() $\Delta \in LG(B)$
. We fix a faithful representation
$\Delta \in LG(B)$
. We fix a faithful representation
![]() $\rho \colon G\hookrightarrow \operatorname {\mathrm {SL}}_r$
and consider the elements
$\rho \colon G\hookrightarrow \operatorname {\mathrm {SL}}_r$
and consider the elements
![]() $\rho (\Delta )$
and
$\rho (\Delta )$
and
![]() $\rho (\Delta ^{-1})$
of
$\rho (\Delta ^{-1})$
of
![]() $L\operatorname {\mathrm {SL}}_r(B)=\operatorname {\mathrm {SL}}_r(B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z}])$
. Let
$L\operatorname {\mathrm {SL}}_r(B)=\operatorname {\mathrm {SL}}_r(B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z}])$
. Let
![]() $N\in {\mathbb {N}}_0$
be such that the matrices
$N\in {\mathbb {N}}_0$
be such that the matrices
![]() $z^N\cdot \rho (\Delta )$
and
$z^N\cdot \rho (\Delta )$
and
![]() $z^N\cdot \rho (\Delta ^{-1})$
have their entries in
$z^N\cdot \rho (\Delta ^{-1})$
have their entries in
![]() $B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
. If
$B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
. If
![]() $\rho (j)\equiv 1\;\textrm {mod}\; z^{2N}$
, then
$\rho (j)\equiv 1\;\textrm {mod}\; z^{2N}$
, then
![]() $\rho (\Delta ^{-1}\cdot j\cdot \Delta )\in \operatorname {\mathrm {SL}}_r(B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
, and hence
$\rho (\Delta ^{-1}\cdot j\cdot \Delta )\in \operatorname {\mathrm {SL}}_r(B\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
, and hence
![]() $\Delta ^{-1}\cdot j\cdot \Delta \in L^+G(B)$
and
$\Delta ^{-1}\cdot j\cdot \Delta \in L^+G(B)$
and
![]() $\delta ^{-1}\circ j\circ \delta \in \operatorname {\mathrm {Aut}}({\underline {{\mathcal {G}}}})$
. Because the map
$\delta ^{-1}\circ j\circ \delta \in \operatorname {\mathrm {Aut}}({\underline {{\mathcal {G}}}})$
. Because the map
![]() $J\subset LG({\mathbb {F}})\xrightarrow {\;\rho \,}L\operatorname {\mathrm {SL}}_r({\mathbb {F}})$
is continuous with respect to the z-adic topology, the claim follows.
$J\subset LG({\mathbb {F}})\xrightarrow {\;\rho \,}L\operatorname {\mathrm {SL}}_r({\mathbb {F}})$
is continuous with respect to the z-adic topology, the claim follows.
Because the action on
![]() ${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
is continuous, the same holds for each
${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
is continuous, the same holds for each
![]() ${\breve {\mathcal {M}}}^K$
by [Reference Berkovich9, Lemma 8.4]. Note that continuity of the J-action is defined as continuity of the homomorphism
${\breve {\mathcal {M}}}^K$
by [Reference Berkovich9, Lemma 8.4]. Note that continuity of the J-action is defined as continuity of the homomorphism
![]() $J\to {\mathscr {G}}({\breve {\mathcal {M}}}^K)$
, where
$J\to {\mathscr {G}}({\breve {\mathcal {M}}}^K)$
, where
![]() ${\mathscr {G}}({\breve {\mathcal {M}}}^K)$
is the topological automorphism group defined by Berkovich [Reference Berkovich9, § 6]. The topology of
${\mathscr {G}}({\breve {\mathcal {M}}}^K)$
is the topological automorphism group defined by Berkovich [Reference Berkovich9, § 6]. The topology of
![]() ${\mathscr {G}}({\breve {\mathcal {M}}}^K)$
is defined via compact subspaces of
${\mathscr {G}}({\breve {\mathcal {M}}}^K)$
is defined via compact subspaces of
![]() ${\breve {\mathcal {M}}}^K$
. Therefore, the continuity of the J-action on
${\breve {\mathcal {M}}}^K$
. Therefore, the continuity of the J-action on
![]() ${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
we proved above and [Reference Berkovich9, Lemma 8.4] are applicable although
${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
we proved above and [Reference Berkovich9, Lemma 8.4] are applicable although
![]() ${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
is not quasi-compact.
${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
is not quasi-compact.
Remark 7.19. We keep the notation from Remarks 3.7 and 4.21 and let
![]() $\varepsilon \colon G\to G^{\prime }$
be a morphism of parahoric group schemes over
$\varepsilon \colon G\to G^{\prime }$
be a morphism of parahoric group schemes over
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
. If
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
. If
![]() $\varepsilon (\hat {Z})\subset \hat {Z}^{\prime }$
and
$\varepsilon (\hat {Z})\subset \hat {Z}^{\prime }$
and
![]() ${\underline {{\mathbb {G}}}}^{\prime }_0=\varepsilon _*{\underline {{\mathbb {G}}}}_0\cong \big ((L^+G^{\prime })_{\mathbb {F}},b^{\prime }\sigma ^\ast \big )$
where
${\underline {{\mathbb {G}}}}^{\prime }_0=\varepsilon _*{\underline {{\mathbb {G}}}}_0\cong \big ((L^+G^{\prime })_{\mathbb {F}},b^{\prime }\sigma ^\ast \big )$
where
![]() ${\underline {{\mathbb {G}}}}_0\cong \big ((L^+G)_{\mathbb {F}},b\sigma ^\ast \big )$
and
${\underline {{\mathbb {G}}}}_0\cong \big ((L^+G)_{\mathbb {F}},b\sigma ^\ast \big )$
and
![]() $b^{\prime }=\varepsilon (b)$
, then there is a commutative diagram of
$b^{\prime }=\varepsilon (b)$
, then there is a commutative diagram of
![]() $\breve E$
-analytic spaces
$\breve E$
-analytic spaces

where
![]() $\breve \pi $
and
$\breve \pi $
and
![]() $\breve \pi ^{\prime }$
are the period morphisms from Definition 6.3 for
$\breve \pi ^{\prime }$
are the period morphisms from Definition 6.3 for
![]() ${\underline {{\mathbb {G}}}}_0$
and
${\underline {{\mathbb {G}}}}_0$
and
![]() $\hat {Z}$
, respectively for
$\hat {Z}$
, respectively for
![]() ${\underline {{\mathbb {G}}}}^{\prime }_0$
and
${\underline {{\mathbb {G}}}}^{\prime }_0$
and
![]() $\hat {Z}^{\prime }$
, and where the horizontal morphisms
$\hat {Z}^{\prime }$
, and where the horizontal morphisms
![]() $\varepsilon _*$
and
$\varepsilon _*$
and
![]() $\varepsilon $
were described in (3.4) and (4.5). This diagram is equivariant for the action of
$\varepsilon $
were described in (3.4) and (4.5). This diagram is equivariant for the action of
![]() $J^G_b$
that acts on the right column via the morphism
$J^G_b$
that acts on the right column via the morphism
![]() $J_b^G\to J_{b^{\prime }}^{G^{\prime }}$
from (3.5). The diagram is indeed commutative, because in the notation of Lemma 6.2 and equation (6.4), the left morphism
$J_b^G\to J_{b^{\prime }}^{G^{\prime }}$
from (3.5). The diagram is indeed commutative, because in the notation of Lemma 6.2 and equation (6.4), the left morphism
![]() $\breve \pi $
sends
$\breve \pi $
sends
![]() ${\underline {{\mathcal {G}}}}_{{\mathscr {S}}^{\prime }}\cong \big ((L^+G)_{{\mathscr {S}}^{\prime }},A\sigma ^\ast \big )$
to
${\underline {{\mathcal {G}}}}_{{\mathscr {S}}^{\prime }}\cong \big ((L^+G)_{{\mathscr {S}}^{\prime }},A\sigma ^\ast \big )$
to
![]() $\gamma :=\sigma ^*(\Delta ) A^{-1}=b^{-1}\Delta $
and the right morphism
$\gamma :=\sigma ^*(\Delta ) A^{-1}=b^{-1}\Delta $
and the right morphism
![]() $\breve \pi ^{\prime }$
sends
$\breve \pi ^{\prime }$
sends
![]() $\varepsilon _*({\underline {{\mathcal {G}}}})_{{\mathscr {S}}^{\prime }}\cong \big ((L^+G^{\prime })_{{\mathscr {S}}^{\prime }},\varepsilon (A)\sigma ^\ast \big )$
to
$\varepsilon _*({\underline {{\mathcal {G}}}})_{{\mathscr {S}}^{\prime }}\cong \big ((L^+G^{\prime })_{{\mathscr {S}}^{\prime }},\varepsilon (A)\sigma ^\ast \big )$
to
![]() $\gamma ^{\prime }:=\sigma ^*(\varepsilon (\Delta )) \varepsilon (A)^{-1}=\varepsilon (b)^{-1}\varepsilon (\Delta )=\varepsilon (\gamma )$
.
$\gamma ^{\prime }:=\sigma ^*(\varepsilon (\Delta )) \varepsilon (A)^{-1}=\varepsilon (b)^{-1}\varepsilon (\Delta )=\varepsilon (\gamma )$
.
The tensor functors
![]() ${\underline {{\mathcal {V}}\!}\,}_b$
and
${\underline {{\mathcal {V}}\!}\,}_b$
and
![]() ${\underline {{\mathcal {V}}\!}\,}_{b^{\prime }}$
from Theorem 5.7 are part of a commutative diagram of tensor functors
${\underline {{\mathcal {V}}\!}\,}_{b^{\prime }}$
from Theorem 5.7 are part of a commutative diagram of tensor functors

where the right vertical arrow denotes pullback of local systems of
![]() ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-vector spaces along the morphism
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-vector spaces along the morphism
![]() $\varepsilon \colon \breve {\mathcal {H}}_{G,\hat Z,b}^{a}\to \breve {\mathcal {H}}_{G^{\prime }\!,\hat Z^{\prime }\!,b^{\prime }}^{a}$
from (4.5), and the left vertical functor sends
$\varepsilon \colon \breve {\mathcal {H}}_{G,\hat Z,b}^{a}\to \breve {\mathcal {H}}_{G^{\prime }\!,\hat Z^{\prime }\!,b^{\prime }}^{a}$
from (4.5), and the left vertical functor sends
![]() $(V^{\prime },\rho ^{\prime })$
to
$(V^{\prime },\rho ^{\prime })$
to
![]() $(V^{\prime },\rho ^{\prime }\circ \varepsilon )$
; see Remark 4.21.
$(V^{\prime },\rho ^{\prime }\circ \varepsilon )$
; see Remark 4.21.
Moreover, the Tate module functor
![]() $\check {T}_{{\underline {{\mathcal {G}}}}}$
from (7.1) satisfies
$\check {T}_{{\underline {{\mathcal {G}}}}}$
from (7.1) satisfies
![]() $\check {T}_{\varepsilon _*{\underline {{\mathcal {G}}}}}(\rho ^{\prime })=\check {T}_{{\underline {{\mathcal {G}}}}}(\rho ^{\prime }\circ \varepsilon )$
; that is,
$\check {T}_{\varepsilon _*{\underline {{\mathcal {G}}}}}(\rho ^{\prime })=\check {T}_{{\underline {{\mathcal {G}}}}}(\rho ^{\prime }\circ \varepsilon )$
; that is,
![]() $\check {T}_{\varepsilon _*{\underline {{\mathcal {G}}}}}=\check {T}_{{\underline {{\mathcal {G}}}}}\circ \varepsilon ^*$
, and likewise
$\check {T}_{\varepsilon _*{\underline {{\mathcal {G}}}}}=\check {T}_{{\underline {{\mathcal {G}}}}}\circ \varepsilon ^*$
, and likewise
![]() $\check {V}_{\varepsilon _*{\underline {{\mathcal {G}}}}}=\check {V}_{{\underline {{\mathcal {G}}}}}\circ \varepsilon ^*$
. This defines a map of the sets from (7.3)
$\check {V}_{\varepsilon _*{\underline {{\mathcal {G}}}}}=\check {V}_{{\underline {{\mathcal {G}}}}}\circ \varepsilon ^*$
. This defines a map of the sets from (7.3)
for both arguments
![]() $A={\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
and
$A={\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
and
![]() $A={\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
. In particular, if
$A={\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
. In particular, if
![]() $K\subset G(A)$
and
$K\subset G(A)$
and
![]() $K^{\prime }\subset G^{\prime }(A)$
are compact open subgroups with
$K^{\prime }\subset G^{\prime }(A)$
are compact open subgroups with
![]() $\varepsilon (K)\subset K^{\prime }$
, then the map
$\varepsilon (K)\subset K^{\prime }$
, then the map
![]() $\varepsilon _*\colon \eta K\mapsto \varepsilon _*(\eta )K^{\prime }$
sends K-level structures on
$\varepsilon _*\colon \eta K\mapsto \varepsilon _*(\eta )K^{\prime }$
sends K-level structures on
![]() ${\underline {{\mathcal {G}}}}$
to
${\underline {{\mathcal {G}}}}$
to
![]() $K^{\prime }$
-level structures on
$K^{\prime }$
-level structures on
![]() $\varepsilon _*{\underline {{\mathcal {G}}}}$
. This yields a commutative diagram of
$\varepsilon _*{\underline {{\mathcal {G}}}}$
. This yields a commutative diagram of
![]() $\breve E$
-analytic spaces
$\breve E$
-analytic spaces

which is again
![]() $J^G_b$
-equivariant. It is further equivariant for the action of
$J^G_b$
-equivariant. It is further equivariant for the action of
![]() $g\in G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
that acts on the left column by the Hecke correspondence
$g\in G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
that acts on the left column by the Hecke correspondence
![]() $\iota (g)_K$
from Remark 7.14 and on the right column by the Hecke correspondence
$\iota (g)_K$
from Remark 7.14 and on the right column by the Hecke correspondence
![]() $\iota \big (\varepsilon (g)\big )_{K^{\prime }}$
.
$\iota \big (\varepsilon (g)\big )_{K^{\prime }}$
.
8 The image of the period morphism
In this section we fix a local G-shtuka
![]() ${\underline {{\mathbb {G}}}}_0=\big ((L^+G)_{\mathbb {F}},b\sigma ^\ast \big )$
over
${\underline {{\mathbb {G}}}}_0=\big ((L^+G)_{\mathbb {F}},b\sigma ^\ast \big )$
over
![]() ${\mathbb {F}}$
and a bound
${\mathbb {F}}$
and a bound
![]() $\hat {Z}$
with reflex ring
$\hat {Z}$
with reflex ring
![]() $R_{\hat Z}=\kappa \mathrm {[}\kern-0.15em\mathrm {[}\xi \mathrm {]}\kern-0.15em\mathrm {]}$
. We set
$R_{\hat Z}=\kappa \mathrm {[}\kern-0.15em\mathrm {[}\xi \mathrm {]}\kern-0.15em\mathrm {]}$
. We set
![]() $E_{\hat Z}=\kappa (\kern-0.15em( \xi )\kern-0.15em)$
and
$E_{\hat Z}=\kappa (\kern-0.15em( \xi )\kern-0.15em)$
and
![]() $\breve E:={\mathbb {F}}(\kern-0.15em( \xi )\kern-0.15em)$
.
$\breve E:={\mathbb {F}}(\kern-0.15em( \xi )\kern-0.15em)$
.
We will determine the image of the period morphism
![]() $\breve \pi $
from Definition 6.3. This is the function field analogue of [Reference Hartl51, Theorem 8.4], where the situation of PEL-Rapoport-Zink spaces for p-divisible groups was treated. Note, however, that our proof here is entirely different from [Reference Hartl51, Theorem 8.4], because here we already constructed a tensor functor to the category of local systems in Theorem 5.7 and will use this to determine the image of
$\breve \pi $
from Definition 6.3. This is the function field analogue of [Reference Hartl51, Theorem 8.4], where the situation of PEL-Rapoport-Zink spaces for p-divisible groups was treated. Note, however, that our proof here is entirely different from [Reference Hartl51, Theorem 8.4], because here we already constructed a tensor functor to the category of local systems in Theorem 5.7 and will use this to determine the image of
![]() $\breve \pi $
. In [Reference Hartl51, Theorem 8.4], the proof proceeds in the opposite direction and first determines the image of the period morphism and then constructs the local systems.
$\breve \pi $
. In [Reference Hartl51, Theorem 8.4], the proof proceeds in the opposite direction and first determines the image of the period morphism and then constructs the local systems.
Theorem 8.1.
-
(a) The image
 $\breve \pi \big (({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\mathrm {an}}\big )$
of the period morphism
$\breve \pi \big (({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\mathrm {an}}\big )$
of the period morphism
 $\breve \pi $
equals the union of the connected components of
$\breve \pi $
equals the union of the connected components of
 $\breve {\mathcal {H}}_{G,\hat {Z},b}^{a}$
on which there is an
$\breve {\mathcal {H}}_{G,\hat {Z},b}^{a}$
on which there is an
 ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-rational isomorphism
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-rational isomorphism
 between the tensor functors
between the tensor functors
 $\omega ^\circ $
and
$\omega ^\circ $
and
 $\omega _{b,\bar \gamma }$
from Remark 5.8.
$\omega _{b,\bar \gamma }$
from Remark 5.8. -
(b) The rational dual Tate module
 $\check V_{{\underline {{\mathcal {G}}}}}$
of the universal local G-shtuka
$\check V_{{\underline {{\mathcal {G}}}}}$
of the universal local G-shtuka
 ${\underline {{\mathcal {G}}}}$
over
${\underline {{\mathcal {G}}}}$
over
 $({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\mathrm {an}}$
descends to a tensor functor
$({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\mathrm {an}}$
descends to a tensor functor
 $\check V_{{\underline {{\mathcal {G}}}}}$
from
$\check V_{{\underline {{\mathcal {G}}}}}$
from
 $\operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G$
to the category of local systems of
$\operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G$
to the category of local systems of
 ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-vector spaces on
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-vector spaces on
 $\breve \pi \big (({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\mathrm {an}}\big )$
. It carries a canonical
$\breve \pi \big (({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\mathrm {an}}\big )$
. It carries a canonical
 $J_b\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
-linearisation and is canonically
$J_b\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
-linearisation and is canonically
 $J_b\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
-equivariantly isomorphic to the tensor functor
$J_b\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
-equivariantly isomorphic to the tensor functor
 ${\underline {{\mathcal {V}}\!}\,}_b$
from Theorem 5.7.
${\underline {{\mathcal {V}}\!}\,}_b$
from Theorem 5.7. -
(c) The tower of strictly
 $\breve E$
-analytic spaces
$\breve E$
-analytic spaces
 $({\breve {\mathcal {M}}}^K)_{K\subset G({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em))}$
is canonically isomorphic over
$({\breve {\mathcal {M}}}^K)_{K\subset G({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em))}$
is canonically isomorphic over
 $\breve \pi \big (({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\mathrm {an}}\big )$
in a Hecke and
$\breve \pi \big (({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\mathrm {an}}\big )$
in a Hecke and
 $J_b\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
-equivariant way to the tower of étale covering spaces
$J_b\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
-equivariant way to the tower of étale covering spaces
 $({\breve {\mathcal {E}}}_K)_{K\subset G({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em))}$
of
$({\breve {\mathcal {E}}}_K)_{K\subset G({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em))}$
of
 $\breve \pi \big (({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\mathrm {an}}\big )$
associated with the tensor functor
$\breve \pi \big (({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\mathrm {an}}\big )$
associated with the tensor functor
 ${\underline {{\mathcal {V}}\!}\,}_b$
in Remark 5.9.
${\underline {{\mathcal {V}}\!}\,}_b$
in Remark 5.9.
Remark 8.2. (a) Note that if the analogue of Wintenberger’s theorem (5.6) is established, the union of connected components in (a) is simply
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^{na}$
. In particular, this would imply that
$\breve {\mathcal {H}}_{G,\hat {Z},b}^{na}$
. In particular, this would imply that
![]() $\breve {\mathcal {M}}^K\ne \emptyset $
if and only if
$\breve {\mathcal {M}}^K\ne \emptyset $
if and only if
![]() $[b]\in B(G,\hat {Z}_E)$
. This is the analogue of [Reference Rapoport and Viehmann79, Conjecture 4.21].
$[b]\in B(G,\hat {Z}_E)$
. This is the analogue of [Reference Rapoport and Viehmann79, Conjecture 4.21].
(b) By Theorem 8.1(c), the tower
![]() $({\breve {\mathcal {M}}}^K)_{K\subset G({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em))}$
only depends on the triple
$({\breve {\mathcal {M}}}^K)_{K\subset G({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em))}$
only depends on the triple
![]() $(G_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)},[b],\hat {Z}_E)$
, where
$(G_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)},[b],\hat {Z}_E)$
, where
![]() $[b]$
is the
$[b]$
is the
![]() $\sigma $
-conjugacy class of b under
$\sigma $
-conjugacy class of b under
![]() $LG({\mathbb {F}})$
. Indeed, the tower
$LG({\mathbb {F}})$
. Indeed, the tower
![]() $({\breve {\mathcal {E}}}_K)_{K\subset G({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em))}$
only depends on this triple; see Definition 4.16 and Remark 5.9. In the arithmetic situation, the analogues of the tower
$({\breve {\mathcal {E}}}_K)_{K\subset G({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em))}$
only depends on this triple; see Definition 4.16 and Remark 5.9. In the arithmetic situation, the analogues of the tower
![]() $({\breve {\mathcal {M}}}^K)_{K\subset G({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em))}$
are called local Shimura varieties; see [Reference Rapoport and Viehmann79, § 5.2] and [Reference Scholze and Weinstein90, § 24]. For the same reason they also only depend on the group scheme over
$({\breve {\mathcal {M}}}^K)_{K\subset G({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em))}$
are called local Shimura varieties; see [Reference Rapoport and Viehmann79, § 5.2] and [Reference Scholze and Weinstein90, § 24]. For the same reason they also only depend on the group scheme over
![]() ${\mathbb {Q}}_p$
, the bounding cocharacter
${\mathbb {Q}}_p$
, the bounding cocharacter
![]() $\mu $
and the
$\mu $
and the
![]() $\sigma $
-conjugacy class
$\sigma $
-conjugacy class
![]() $[b]$
; see [Reference Scholze and Weinstein90, Proposition 23.2.1 and thereafter].
$[b]$
; see [Reference Scholze and Weinstein90, Proposition 23.2.1 and thereafter].
To prove Theorem 8.1, we will take a Tannakian approach and make use of the following proposition.
Proposition 8.3. Let G be a faithfully flat affine group scheme over a Dedekind domain A and let B be an A-algebra. Let
![]() $\operatorname {\mathrm {Rep}}_AG$
be the Tannakian category of representations of G on finite projective A-modules and let
$\operatorname {\mathrm {Rep}}_AG$
be the Tannakian category of representations of G on finite projective A-modules and let
![]() $\omega ^\circ \colon \operatorname {\mathrm {Rep}}_AG\to \textrm {FMod}_A$
be the forgetful fibre functor. Let
$\omega ^\circ \colon \operatorname {\mathrm {Rep}}_AG\to \textrm {FMod}_A$
be the forgetful fibre functor. Let
![]() $\omega \colon \operatorname {\mathrm {Rep}}_AG\to \textrm {FMod}_B$
be a tensor functor to the category
$\omega \colon \operatorname {\mathrm {Rep}}_AG\to \textrm {FMod}_B$
be a tensor functor to the category
![]() $\textrm {FMod}_B$
of finite projective B-modules, which sends morphisms in
$\textrm {FMod}_B$
of finite projective B-modules, which sends morphisms in
![]() $\operatorname {\mathrm {Rep}}_AG$
that are epimorphisms on the underlying A-modules to epimorphisms in
$\operatorname {\mathrm {Rep}}_AG$
that are epimorphisms on the underlying A-modules to epimorphisms in
![]() $\textrm {FMod}_B$
. Then
$\textrm {FMod}_B$
. Then
![]() $\operatorname {\mathrm {Isom}}^\otimes (\omega ^\circ \otimes _AB,\omega )$
is representable by a G-torsor over B (for the fpqc topology).
$\operatorname {\mathrm {Isom}}^\otimes (\omega ^\circ \otimes _AB,\omega )$
is representable by a G-torsor over B (for the fpqc topology).
Proof. Let
![]() $BG=[\operatorname {\mathrm {Spec}} A/G]$
be the classifying stack of G that parametrises G-torsors over A-schemes. By [Reference de Jong32, Tags 0443 and 06WS], the category of linear representations of G on (arbitrary) A-modules is tensor equivalent to the category
$BG=[\operatorname {\mathrm {Spec}} A/G]$
be the classifying stack of G that parametrises G-torsors over A-schemes. By [Reference de Jong32, Tags 0443 and 06WS], the category of linear representations of G on (arbitrary) A-modules is tensor equivalent to the category
![]() $\textrm {Mod}_{BG}$
of quasi-coherent sheaves on (the big fppf-site of)
$\textrm {Mod}_{BG}$
of quasi-coherent sheaves on (the big fppf-site of)
![]() $BG$
; see [Reference de Jong32, Tags 06NT and 03DL]. This equivalence is given by the functor that sends a quasi-coherent sheaf
$BG$
; see [Reference de Jong32, Tags 06NT and 03DL]. This equivalence is given by the functor that sends a quasi-coherent sheaf
![]() ${\mathcal {F}}$
on
${\mathcal {F}}$
on
![]() $BG$
to its pullback under the morphism
$BG$
to its pullback under the morphism
![]() $p_0\colon \operatorname {\mathrm {Spec}} A\to BG$
. The quasi-inverse functor sends a representation of G on an A-module F to its faithfully flat descent on
$p_0\colon \operatorname {\mathrm {Spec}} A\to BG$
. The quasi-inverse functor sends a representation of G on an A-module F to its faithfully flat descent on
![]() $BG$
. By faithfully flat descent [Reference Grothendieck44, IV
$BG$
. By faithfully flat descent [Reference Grothendieck44, IV
![]() ${}_2$
, Proposition 2.5.2],
${}_2$
, Proposition 2.5.2],
![]() ${\mathcal {F}}$
is finite locally free if and only if the representation is a finite locally free A-module. In particular, the category
${\mathcal {F}}$
is finite locally free if and only if the representation is a finite locally free A-module. In particular, the category
![]() $\operatorname {\mathrm {Rep}}_AG$
is tensor equivalent to the category
$\operatorname {\mathrm {Rep}}_AG$
is tensor equivalent to the category
![]() $\textrm {FMod}_{BG}$
of finite locally free sheaves on
$\textrm {FMod}_{BG}$
of finite locally free sheaves on
![]() $BG$
.
$BG$
.
If we write
![]() $G=\operatorname {\mathrm {Spec}}\Gamma $
, the multiplication of G makes
$G=\operatorname {\mathrm {Spec}}\Gamma $
, the multiplication of G makes
![]() $\Gamma $
into a comodule, which is the filtered union of its finitely generated subcomodules by [Reference Serre91, § 1.5, Corollaire]. Because
$\Gamma $
into a comodule, which is the filtered union of its finitely generated subcomodules by [Reference Serre91, § 1.5, Corollaire]. Because
![]() $\Gamma $
is a flat A-module and A is Dedekind, these finitely generated subcomodules are torsion free and hence finite projective and dualisable. The Hopf algebroid
$\Gamma $
is a flat A-module and A is Dedekind, these finitely generated subcomodules are torsion free and hence finite projective and dualisable. The Hopf algebroid
![]() $(A,\Gamma )$
is therefore an Adams Hopf algebroid and the stack
$(A,\Gamma )$
is therefore an Adams Hopf algebroid and the stack
![]() $BG$
is an Adams stack; see [Reference Schäppi85, § 1.3]. Due to our assumption, the tensor functor
$BG$
is an Adams stack; see [Reference Schäppi85, § 1.3]. Due to our assumption, the tensor functor
![]() $\omega $
defines a tensor functor from
$\omega $
defines a tensor functor from
![]() $\textrm {FMod}_{BG}$
to
$\textrm {FMod}_{BG}$
to
![]() $\textrm {Mod}_B$
that sends locally split epimorphisms
$\textrm {Mod}_B$
that sends locally split epimorphisms
![]() $\varphi $
to epimorphisms. Indeed, if U is a scheme and
$\varphi $
to epimorphisms. Indeed, if U is a scheme and
![]() $u\colon U\to BG$
is an fpqc covering over which
$u\colon U\to BG$
is an fpqc covering over which
![]() $u^*\varphi $
splits, then
$u^*\varphi $
splits, then
![]() $u^*\varphi $
is an epimorphism of quasi-coherent sheaves on U. Because
$u^*\varphi $
is an epimorphism of quasi-coherent sheaves on U. Because
![]() $U\times _{BG}\operatorname {\mathrm {Spec}} A\to \operatorname {\mathrm {Spec}} A$
is an fpqc covering, fpqc descent [Reference Grothendieck44, IV
$U\times _{BG}\operatorname {\mathrm {Spec}} A\to \operatorname {\mathrm {Spec}} A$
is an fpqc covering, fpqc descent [Reference Grothendieck44, IV
![]() ${}_2$
, Proposition 2.2.7] shows that
${}_2$
, Proposition 2.2.7] shows that
![]() $p_0^*\varphi $
is an epimorphism on the underlying A-modules, and our assumption applies. Thus, by [Reference Schäppi86, Corollary 3.4.3] and [Reference Schäppi85, Theorems 1.3.2 and 1.2.1], the functor
$p_0^*\varphi $
is an epimorphism on the underlying A-modules, and our assumption applies. Thus, by [Reference Schäppi86, Corollary 3.4.3] and [Reference Schäppi85, Theorems 1.3.2 and 1.2.1], the functor
![]() $\omega $
corresponds to a morphism
$\omega $
corresponds to a morphism
![]() $f\colon \operatorname {\mathrm {Spec}} B\to BG$
and an isomorphism of tensor functors
$f\colon \operatorname {\mathrm {Spec}} B\to BG$
and an isomorphism of tensor functors
![]() .
.
By definition of
![]() $BG$
, this morphism corresponds to a G-torsor
$BG$
, this morphism corresponds to a G-torsor
![]() $p\colon X\to \operatorname {\mathrm {Spec}} B$
, which is obtained as the base change
$p\colon X\to \operatorname {\mathrm {Spec}} B$
, which is obtained as the base change

We will show that X represents
![]() $\operatorname {\mathrm {Isom}}^\otimes (\omega ^\circ \otimes _AB,\omega )$
. Because
$\operatorname {\mathrm {Isom}}^\otimes (\omega ^\circ \otimes _AB,\omega )$
. Because
![]() $p_0^*$
is an equivalence between
$p_0^*$
is an equivalence between
![]() $\textrm {FMod}_{BG}$
and
$\textrm {FMod}_{BG}$
and
![]() $\operatorname {\mathrm {Rep}}_AG$
, the tensor functor
$\operatorname {\mathrm {Rep}}_AG$
, the tensor functor
induces a tensor isomorphism
over X and hence a morphism
![]() $X\to \operatorname {\mathrm {Isom}}^\otimes (\omega ^\circ \otimes _AB,\omega )$
. To prove that the latter is an isomorphism, let
$X\to \operatorname {\mathrm {Isom}}^\otimes (\omega ^\circ \otimes _AB,\omega )$
. To prove that the latter is an isomorphism, let
![]() $s\colon S=\operatorname {\mathrm {Spec}} R\to \operatorname {\mathrm {Spec}} B$
and let
$s\colon S=\operatorname {\mathrm {Spec}} R\to \operatorname {\mathrm {Spec}} B$
and let
![]() $\beta \in \operatorname {\mathrm {Isom}}^\otimes (\omega ^\circ \otimes _AB,\omega )(S)$
, which we view as a tensor isomorphism
$\beta \in \operatorname {\mathrm {Isom}}^\otimes (\omega ^\circ \otimes _AB,\omega )(S)$
, which we view as a tensor isomorphism
. Let
![]() $r\colon \operatorname {\mathrm {Spec}} B\to \operatorname {\mathrm {Spec}} A$
be the structure morphism. The two morphisms
$r\colon \operatorname {\mathrm {Spec}} B\to \operatorname {\mathrm {Spec}} A$
be the structure morphism. The two morphisms
![]() $f\circ s$
and
$f\circ s$
and
![]() $p_0\circ r\circ s$
from S to
$p_0\circ r\circ s$
from S to
![]() $BG$
induce the pullback functors
$BG$
induce the pullback functors
![]() $s^*\circ f^*$
and
$s^*\circ f^*$
and
![]() $s^*\circ r^*\circ p_0^*=s^*\circ (\omega ^\circ \otimes _AB)\circ p_0^*$
, which are isomorphic by
$s^*\circ r^*\circ p_0^*=s^*\circ (\omega ^\circ \otimes _AB)\circ p_0^*$
, which are isomorphic by
Again by [Reference Schäppi86, Corollary 3.4.3] and [Reference Schäppi85, Theorems 1.3.2 and 1.2.1], the latter isomorphism corresponds to an isomorphism
![]() $\eta $
between the morphisms
$\eta $
between the morphisms
![]() $f\circ s$
and
$f\circ s$
and
![]() $p_0\circ r\circ s$
from S to
$p_0\circ r\circ s$
from S to
![]() $BG$
. The data
$BG$
. The data
![]() $(s,r\circ s,\eta )$
define a morphism
$(s,r\circ s,\eta )$
define a morphism
![]() $S\to X$
and this proves that
$S\to X$
and this proves that
as desired.
We also need the following easy lemma.
Lemma 8.4. Let
![]() $\Omega $
be an algebraically closed field, which is complete with respect to an absolute value
$\Omega $
be an algebraically closed field, which is complete with respect to an absolute value
![]() $|\,.\,|\colon \Omega \to {\mathbb {R}}_{\ge 0}$
, and let
$|\,.\,|\colon \Omega \to {\mathbb {R}}_{\ge 0}$
, and let
![]() ${\mathcal {O}}_\Omega $
be its valuation ring. Let
${\mathcal {O}}_\Omega $
be its valuation ring. Let
![]() ${\mathfrak {m}}_\Omega \subset {\mathcal {O}}_\Omega $
be the maximal ideal and
${\mathfrak {m}}_\Omega \subset {\mathcal {O}}_\Omega $
be the maximal ideal and
![]() $\kappa _\Omega ={\mathcal {O}}_\Omega /{\mathfrak {m}}_\Omega $
.
$\kappa _\Omega ={\mathcal {O}}_\Omega /{\mathfrak {m}}_\Omega $
.
-
(a) If
 ${\mathfrak {p}}\subset {\mathcal {O}}_\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
is a prime ideal then one of the following assertions holds:
${\mathfrak {p}}\subset {\mathcal {O}}_\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
is a prime ideal then one of the following assertions holds:-
(i)
 ${\mathfrak {p}}$
is contained in
${\mathfrak {p}}$
is contained in
 ${\mathfrak {p}}_0\,:=\,\{\,\sum _{i=0}^\infty b_i z^i\colon b_i\in {\mathfrak {m}}_\Omega \,\}\,=\,\ker ({\mathcal {O}}_\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\twoheadrightarrow \kappa _\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
,
${\mathfrak {p}}_0\,:=\,\{\,\sum _{i=0}^\infty b_i z^i\colon b_i\in {\mathfrak {m}}_\Omega \,\}\,=\,\ker ({\mathcal {O}}_\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\twoheadrightarrow \kappa _\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
, -
(ii)
 ${\mathfrak {p}}=(z-\alpha )$
for an
${\mathfrak {p}}=(z-\alpha )$
for an
 $\alpha \in {\mathfrak {m}}_\Omega $
or
$\alpha \in {\mathfrak {m}}_\Omega $
or -
(iii)
 ${\mathfrak {p}}=(z)+{\mathfrak {m}}_\Omega $
is the maximal ideal of
${\mathfrak {p}}=(z)+{\mathfrak {m}}_\Omega $
is the maximal ideal of
 ${\mathcal {O}}_\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
.
${\mathcal {O}}_\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
.
-
-
(b) The maximal ideals
 ${\mathfrak {m}}$
of the ring
${\mathfrak {m}}$
of the ring
 ${\mathcal {O}}_\Omega (\kern-0.15em( z)\kern-0.15em):={\mathcal {O}}_\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z}]$
are all of the following form:
${\mathcal {O}}_\Omega (\kern-0.15em( z)\kern-0.15em):={\mathcal {O}}_\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z}]$
are all of the following form:
 ${\mathfrak {m}}=(z-\alpha )$
for
${\mathfrak {m}}=(z-\alpha )$
for
 $\alpha \in {\mathfrak {m}}_\Omega \setminus \{0\}$
with
$\alpha \in {\mathfrak {m}}_\Omega \setminus \{0\}$
with
 ${\mathcal {O}}_\Omega (\kern-0.15em( z)\kern-0.15em)/{\mathfrak {m}}=\Omega $
or
${\mathcal {O}}_\Omega (\kern-0.15em( z)\kern-0.15em)/{\mathfrak {m}}=\Omega $
or
 ${\mathfrak {m}}\,=\,{\mathfrak {m}}_0\,:=\,\{\,\sum _i b_i z^i\colon b_i\in {\mathfrak {m}}_\Omega \,\}\,=\,\ker \big ({\mathcal {O}}_\Omega (\kern-0.15em( z)\kern-0.15em)\twoheadrightarrow \kappa _\Omega (\kern-0.15em( z)\kern-0.15em)\big )$
with
${\mathfrak {m}}\,=\,{\mathfrak {m}}_0\,:=\,\{\,\sum _i b_i z^i\colon b_i\in {\mathfrak {m}}_\Omega \,\}\,=\,\ker \big ({\mathcal {O}}_\Omega (\kern-0.15em( z)\kern-0.15em)\twoheadrightarrow \kappa _\Omega (\kern-0.15em( z)\kern-0.15em)\big )$
with
 ${\mathcal {O}}_\Omega (\kern-0.15em( z)\kern-0.15em)/{\mathfrak {m}}=\kappa _\Omega (\kern-0.15em( z)\kern-0.15em)$
.
${\mathcal {O}}_\Omega (\kern-0.15em( z)\kern-0.15em)/{\mathfrak {m}}=\kappa _\Omega (\kern-0.15em( z)\kern-0.15em)$
.
Proof. (a) If (i) fails – that is, if
![]() ${\mathfrak {p}}\not \subset {\mathfrak {p}}_0$
– then there is an element
${\mathfrak {p}}\not \subset {\mathfrak {p}}_0$
– then there is an element
![]() $f=\sum _{i=0}^\infty b_i z^i\in {\mathfrak {p}}$
with
$f=\sum _{i=0}^\infty b_i z^i\in {\mathfrak {p}}$
with
![]() $b_n\in {\mathcal {O}}_\Omega ^{\scriptscriptstyle \times }$
for some n. We may assume that
$b_n\in {\mathcal {O}}_\Omega ^{\scriptscriptstyle \times }$
for some n. We may assume that
![]() $b_i\in {\mathfrak {m}}_\Omega $
for all
$b_i\in {\mathfrak {m}}_\Omega $
for all
![]() $i<n$
, and hence the image
$i<n$
, and hence the image
![]() $\bar f$
of f in
$\bar f$
of f in
![]() $\kappa _\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
has
$\kappa _\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
has
![]() $\operatorname {\mathrm {ord}}_z(\bar f)=n$
, where
$\operatorname {\mathrm {ord}}_z(\bar f)=n$
, where
![]() $\operatorname {\mathrm {ord}}_z$
is the valuation of the discrete valuation ring
$\operatorname {\mathrm {ord}}_z$
is the valuation of the discrete valuation ring
![]() $\kappa _\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
. If
$\kappa _\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
. If
![]() $n=0$
, then f would be a unit, which is not the case. So
$n=0$
, then f would be a unit, which is not the case. So
![]() $|b_0|<|b_n|=1$
and the Newton polygon of f has a negative slope. By [Reference Lazard74, Proposition 2] there is an element
$|b_0|<|b_n|=1$
and the Newton polygon of f has a negative slope. By [Reference Lazard74, Proposition 2] there is an element
![]() $\alpha \in {\mathfrak {m}}_\Omega $
and a power series
$\alpha \in {\mathfrak {m}}_\Omega $
and a power series
![]() $g=\sum _{i=0}^\infty c_i z^i\in \Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
with
$g=\sum _{i=0}^\infty c_i z^i\in \Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
with
![]() $f=(z-\alpha )\cdot g$
; that is,
$f=(z-\alpha )\cdot g$
; that is,
![]() $b_i=c_{i-1}-\alpha c_i$
, such that the region of convergence of f is contained in the one of g. In particular, g converges for all z in
$b_i=c_{i-1}-\alpha c_i$
, such that the region of convergence of f is contained in the one of g. In particular, g converges for all z in
![]() ${\mathfrak {m}}_\Omega $
.
${\mathfrak {m}}_\Omega $
.
We claim that
![]() $g\in {\mathcal {O}}_\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
; that is,
$g\in {\mathcal {O}}_\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
; that is,
![]() $|c_i|\le 1$
for all i. Assume contrarily that there exists an
$|c_i|\le 1$
for all i. Assume contrarily that there exists an
![]() $m>0$
with
$m>0$
with
![]() $|c_{m-1}|>1\ge |b_m|$
. Then
$|c_{m-1}|>1\ge |b_m|$
. Then
![]() $\alpha c_m=c_{m-1}-b_m$
implies
$\alpha c_m=c_{m-1}-b_m$
implies
![]() $|c_m|=|\alpha ^{-1} c_{m-1}|>|c_{m-1}|$
and by induction
$|c_m|=|\alpha ^{-1} c_{m-1}|>|c_{m-1}|$
and by induction
![]() $|c_i|=|\alpha |^{m-1-i}|c_{m-1}|$
for all
$|c_i|=|\alpha |^{m-1-i}|c_{m-1}|$
for all
![]() $i\ge m-1$
. This implies that g does not converge at
$i\ge m-1$
. This implies that g does not converge at
![]() $z=\alpha $
. So we obtain a contradiction and the claim is proved.
$z=\alpha $
. So we obtain a contradiction and the claim is proved.
For the images in
![]() $\kappa _\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
we obtain
$\kappa _\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
we obtain
![]() $\bar f=z\cdot \bar g$
and
$\bar f=z\cdot \bar g$
and
![]() $\operatorname {\mathrm {ord}}_z(\bar g)=\operatorname {\mathrm {ord}}_z(\bar f)-1$
. Continuing in this way, we find that
$\operatorname {\mathrm {ord}}_z(\bar g)=\operatorname {\mathrm {ord}}_z(\bar f)-1$
. Continuing in this way, we find that
![]() $f=(z-\alpha _1)\cdot \ldots \cdot (z-\alpha _n)\cdot h$
for
$f=(z-\alpha _1)\cdot \ldots \cdot (z-\alpha _n)\cdot h$
for
![]() $\alpha _i\in {\mathfrak {m}}_\Omega $
and a unit
$\alpha _i\in {\mathfrak {m}}_\Omega $
and a unit
![]() $h\in {\mathcal {O}}_\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}^{\scriptscriptstyle \times }$
. Because
$h\in {\mathcal {O}}_\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}^{\scriptscriptstyle \times }$
. Because
![]() ${\mathfrak {p}}$
is prime, it contains
${\mathfrak {p}}$
is prime, it contains
![]() $z-\alpha _i$
for some i. Under the isomorphism
$z-\alpha _i$
for some i. Under the isomorphism
![]() ,
,
![]() $z\mapsto \alpha _i$
, the quotient
$z\mapsto \alpha _i$
, the quotient
![]() ${\mathfrak {p}}/(z-\alpha _i)$
is a prime ideal in
${\mathfrak {p}}/(z-\alpha _i)$
is a prime ideal in
![]() ${\mathcal {O}}_\Omega $
. If
${\mathcal {O}}_\Omega $
. If
![]() ${\mathfrak {p}}/(z-\alpha _i)=(0)$
, then
${\mathfrak {p}}/(z-\alpha _i)=(0)$
, then
![]() ${\mathfrak {p}}=(z-\alpha _i)$
and we are in case (ii). If
${\mathfrak {p}}=(z-\alpha _i)$
and we are in case (ii). If
![]() ${\mathfrak {p}}/(z-\alpha _i)={\mathfrak {m}}_\Omega $
, then
${\mathfrak {p}}/(z-\alpha _i)={\mathfrak {m}}_\Omega $
, then
![]() ${\mathfrak {p}}=(z-\alpha _i)+{\mathfrak {m}}_\Omega =(z)+{\mathfrak {m}}_\Omega $
and we are in case (iii).
${\mathfrak {p}}=(z-\alpha _i)+{\mathfrak {m}}_\Omega =(z)+{\mathfrak {m}}_\Omega $
and we are in case (iii).
(b) follows from (a) via the identification of the prime ideals in
![]() ${\mathcal {O}}_\Omega (\kern-0.15em( z)\kern-0.15em)$
with the prime ideals in
${\mathcal {O}}_\Omega (\kern-0.15em( z)\kern-0.15em)$
with the prime ideals in
![]() ${\mathcal {O}}_\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
not containing z.
${\mathcal {O}}_\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
not containing z.
Proof. Proof of Theorem 8.1
(a) Because the proof is quite long and involved, let us give a summary first. By [Reference de Jong31, Theorem 2.9], the subset of points
![]() $\bar \gamma $
admitting an
$\bar \gamma $
admitting an
![]() ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-rational isomorphism
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-rational isomorphism
![]() between the tensor functors
between the tensor functors
![]() $\omega ^\circ $
and
$\omega ^\circ $
and
![]() $\omega _{b,\bar \gamma }$
is a union of connected components. Thus, the task is to prove that it agrees with the image of the period morphism.
$\omega _{b,\bar \gamma }$
is a union of connected components. Thus, the task is to prove that it agrees with the image of the period morphism.
We start with a point
![]() $\bar \gamma \in \breve {\mathcal {H}}_{G,\hat Z,b}^{a}(\Omega )$
with values in an algebraically closed, complete field
$\bar \gamma \in \breve {\mathcal {H}}_{G,\hat Z,b}^{a}(\Omega )$
with values in an algebraically closed, complete field
![]() $\Omega $
and a tensor isomorphism
$\Omega $
and a tensor isomorphism
![]() $\beta $
. In Step 1 we construct from these data a tensor functor
$\beta $
. In Step 1 we construct from these data a tensor functor
![]() ${\underline {{\mathcal {T}}\!}\,}_b\colon \operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}G\to {\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\mbox {-}{\underline {\mathrm {Loc}}}_{{\breve {\mathcal {E}}}_{K_0}}$
over an étale covering space
${\underline {{\mathcal {T}}\!}\,}_b\colon \operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}G\to {\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\mbox {-}{\underline {\mathrm {Loc}}}_{{\breve {\mathcal {E}}}_{K_0}}$
over an étale covering space
![]() ${\breve {\mathcal {E}}}_{K_0}$
of
${\breve {\mathcal {E}}}_{K_0}$
of
![]() $\breve {\mathcal {H}}_{G,\hat Z,b}^{a}$
. By the admissibility of
$\breve {\mathcal {H}}_{G,\hat Z,b}^{a}$
. By the admissibility of
![]() $\bar \gamma $
, in Step 2 this tensor functor will induce a tensor functor
$\bar \gamma $
, in Step 2 this tensor functor will induce a tensor functor
![]() $M\colon \operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}G\to \textrm {FMod}_{{\mathcal {O}}_{\Omega }\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}},\,V\mapsto M_V$
, which gives the underlying module
$M\colon \operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}G\to \textrm {FMod}_{{\mathcal {O}}_{\Omega }\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}},\,V\mapsto M_V$
, which gives the underlying module
![]() $M_V$
of a local shtuka
$M_V$
of a local shtuka
![]() ${\underline {M\!}\,}_V$
. Unfortunately, it is not clear that the functor
${\underline {M\!}\,}_V$
. Unfortunately, it is not clear that the functor
![]() $V\mapsto M_V$
is exact without using the hypothesis that G is parahoric. This might even be false for groups G with nonreductive generic fibre, as Example 8.6 shows. Nevertheless, we show in Step 3 that
$V\mapsto M_V$
is exact without using the hypothesis that G is parahoric. This might even be false for groups G with nonreductive generic fibre, as Example 8.6 shows. Nevertheless, we show in Step 3 that
![]() $V\mapsto M_V\otimes _{{\mathcal {O}}_\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}{\mathcal {O}}_\Omega (\kern-0.15em( z)\kern-0.15em)$
is exact and corresponds to a G-torsor
$V\mapsto M_V\otimes _{{\mathcal {O}}_\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}{\mathcal {O}}_\Omega (\kern-0.15em( z)\kern-0.15em)$
is exact and corresponds to a G-torsor
![]() ${\mathcal {G}}$
over
${\mathcal {G}}$
over
![]() ${\mathcal {O}}_\Omega (\kern-0.15em( z)\kern-0.15em)$
. From [Reference Anschütz3, Proposition 11.5], we obtain that
${\mathcal {O}}_\Omega (\kern-0.15em( z)\kern-0.15em)$
. From [Reference Anschütz3, Proposition 11.5], we obtain that
![]() ${\mathcal {G}}\cong G\otimes _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}{\mathcal {O}}_\Omega (\kern-0.15em( z)\kern-0.15em)$
is trivial. This allows us in Step 4 to apply Lemma 7.9 to produce a local G-shtuka
${\mathcal {G}}\cong G\otimes _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}{\mathcal {O}}_\Omega (\kern-0.15em( z)\kern-0.15em)$
is trivial. This allows us in Step 4 to apply Lemma 7.9 to produce a local G-shtuka
![]() $({\underline {{\mathcal {G}}}}^{\prime \prime }\!,\bar \Delta ^{\prime \prime })\in {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}({\mathcal {O}}_\Omega )$
with
$({\underline {{\mathcal {G}}}}^{\prime \prime }\!,\bar \Delta ^{\prime \prime })\in {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}({\mathcal {O}}_\Omega )$
with
![]() $\breve \pi ({\underline {{\mathcal {G}}}}^{\prime \prime }\!,\bar \Delta ^{\prime \prime })=\bar \gamma $
.
$\breve \pi ({\underline {{\mathcal {G}}}}^{\prime \prime }\!,\bar \Delta ^{\prime \prime })=\bar \gamma $
.
1. Let
![]() $\gamma \in \breve {\mathcal {H}}_{G,\hat Z,b}^{a}$
and let
$\gamma \in \breve {\mathcal {H}}_{G,\hat Z,b}^{a}$
and let
![]() $\bar \gamma $
be a geometric point lying above
$\bar \gamma $
be a geometric point lying above
![]() $\gamma $
with algebraically closed, complete residue field
$\gamma $
with algebraically closed, complete residue field
![]() $\Omega $
. We consider the tensor functor
$\Omega $
. We consider the tensor functor
![]() ${\underline {{\mathcal {V}}\!}\,}_b\colon \operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G\to {\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\mbox {-}{\underline {\mathrm {Loc}}}_{\breve {\mathcal {H}}_{G,\hat Z,b}^{a}}$
from Theorem 5.7 and the two fibre functors
${\underline {{\mathcal {V}}\!}\,}_b\colon \operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G\to {\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\mbox {-}{\underline {\mathrm {Loc}}}_{\breve {\mathcal {H}}_{G,\hat Z,b}^{a}}$
from Theorem 5.7 and the two fibre functors
![]() $\omega _{b,\bar \gamma }:=\mathit { forget}\circ \omega _{\bar \gamma }\circ {\underline {{\mathcal {V}}\!}\,}_b$
and
$\omega _{b,\bar \gamma }:=\mathit { forget}\circ \omega _{\bar \gamma }\circ {\underline {{\mathcal {V}}\!}\,}_b$
and
![]() $\omega ^\circ \colon \operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G\to \textrm {FMod}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}$
from Remark 5.8 and assume that there is an
$\omega ^\circ \colon \operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G\to \textrm {FMod}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}$
from Remark 5.8 and assume that there is an
![]() ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-rational isomorphism
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-rational isomorphism
of tensor functors that we fix. It induces an isomorphism of group schemes
![]() over
over
![]() ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
. Consider the compact open subgroup
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
. Consider the compact open subgroup
![]() $K_0:=G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})\subset G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
and the étale covering space
$K_0:=G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})\subset G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
and the étale covering space
![]() ${\breve {\mathcal {E}}}_{K_0}$
of
${\breve {\mathcal {E}}}_{K_0}$
of
![]() $\breve {\mathcal {H}}_{G,\hat Z,b}^{a}$
from Remark 5.5 associated with the local system
$\breve {\mathcal {H}}_{G,\hat Z,b}^{a}$
from Remark 5.5 associated with the local system
![]() ${\underline {{\mathcal {V}}\!}\,}_b$
on
${\underline {{\mathcal {V}}\!}\,}_b$
on
![]() $\breve {\mathcal {H}}_{G,\hat Z,b}^{a}$
. The point
$\breve {\mathcal {H}}_{G,\hat Z,b}^{a}$
. The point
![]() $\beta K_0\in \operatorname {\mathrm {Isom}}^\otimes (\omega ^\circ ,\omega _{b,\bar \gamma })\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )/K_0=F_{\bar \gamma }^{\mathrm {\acute {e}t}}({\breve {\mathcal {E}}}_{K_0})$
corresponds to a lift of the base point
$\beta K_0\in \operatorname {\mathrm {Isom}}^\otimes (\omega ^\circ ,\omega _{b,\bar \gamma })\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )/K_0=F_{\bar \gamma }^{\mathrm {\acute {e}t}}({\breve {\mathcal {E}}}_{K_0})$
corresponds to a lift of the base point
![]() $\bar \gamma $
to a geometric base point
$\bar \gamma $
to a geometric base point
![]() $\bar \gamma $
of
$\bar \gamma $
of
![]() ${\breve {\mathcal {E}}}_{K_0}$
such that the morphism
${\breve {\mathcal {E}}}_{K_0}$
such that the morphism
![]() $\pi _1^{\mathrm {\acute {e}t}}({\breve {\mathcal {E}}}_{K_0},\bar \gamma )\to \pi _1^{\mathrm {\acute {e}t}}(\breve {\mathcal {H}}_{G,\hat Z,b}^{a},\bar \gamma )\to G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
from (5.7) factors through
$\pi _1^{\mathrm {\acute {e}t}}({\breve {\mathcal {E}}}_{K_0},\bar \gamma )\to \pi _1^{\mathrm {\acute {e}t}}(\breve {\mathcal {H}}_{G,\hat Z,b}^{a},\bar \gamma )\to G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
from (5.7) factors through
![]() $K_0$
. By Corollary 5.4 the induced morphism
$K_0$
. By Corollary 5.4 the induced morphism
![]() $\pi _1^{\mathrm {\acute {e}t}}({\breve {\mathcal {E}}}_{K_0},\bar \gamma )\to K_0$
yields a tensor functor
$\pi _1^{\mathrm {\acute {e}t}}({\breve {\mathcal {E}}}_{K_0},\bar \gamma )\to K_0$
yields a tensor functor
![]() ${\underline {{\mathcal {T}}\!}\,}_b\colon \operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}G\to {\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\mbox {-}{\underline {\mathrm {Loc}}}_{{\breve {\mathcal {E}}}_{K_0}}$
and an isomorphism
${\underline {{\mathcal {T}}\!}\,}_b\colon \operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}G\to {\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\mbox {-}{\underline {\mathrm {Loc}}}_{{\breve {\mathcal {E}}}_{K_0}}$
and an isomorphism
![]() , which equals the restriction of
, which equals the restriction of
![]() $\beta $
by construction. In particular, for each
$\beta $
by construction. In particular, for each
![]() $V\in \operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}G$
, the fibre
$V\in \operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}G$
, the fibre
![]() ${\underline {{\mathcal {T}}\!}\,}_b(V)_{\bar \gamma }$
is a free
${\underline {{\mathcal {T}}\!}\,}_b(V)_{\bar \gamma }$
is a free
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-module of rank equal to the rank of V.
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-module of rank equal to the rank of V.
2. Let
![]() $(\rho _V,V)\in \operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}G$
. Then the z-isocrystal with Hodge-Pink structure
$(\rho _V,V)\in \operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}G$
. Then the z-isocrystal with Hodge-Pink structure
over
![]() $\Omega $
is admissible and comes from a pair
$\Omega $
is admissible and comes from a pair
![]() $({\underline {M\!}\,}_V,\delta _V)$
where
$({\underline {M\!}\,}_V,\delta _V)$
where
![]() ${\underline {M\!}\,}_V=(M_V,\tau _{M_V})$
is a local shtuka over
${\underline {M\!}\,}_V=(M_V,\tau _{M_V})$
is a local shtuka over
![]() ${\mathcal {O}}_{\Omega }$
with
${\mathcal {O}}_{\Omega }$
with
![]() $M_V\cong {\mathcal {O}}_{\Omega }\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}^r$
and
$M_V\cong {\mathcal {O}}_{\Omega }\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}^r$
and
![]() and with the notation (6.1),
and with the notation (6.1),
is an isomorphism satisfying
![]() $\delta _V\circ \tau _{M_V}=\rho _V(b)\circ \sigma ^\ast \delta _V$
, such that
$\delta _V\circ \tau _{M_V}=\rho _V(b)\circ \sigma ^\ast \delta _V$
, such that
and so
This follows from [Reference Hartl50, Proposition 2.4.9] with
![]() $X_L=\operatorname {\mathrm {Sp}}\Omega $
and
$X_L=\operatorname {\mathrm {Sp}}\Omega $
and
![]() $X=\operatorname {\mathrm {Spf}}{\mathcal {O}}_{\Omega }$
, where our pair
$X=\operatorname {\mathrm {Spf}}{\mathcal {O}}_{\Omega }$
, where our pair
![]() $({\underline {M\!}\,}_V,\delta _V)$
is the rigidified local shtuka of [Reference Hartl50, Proposition 2.4.9] We may apply this proposition by taking
$({\underline {M\!}\,}_V,\delta _V)$
is the rigidified local shtuka of [Reference Hartl50, Proposition 2.4.9] We may apply this proposition by taking
![]() ${\mathcal {Q}}^{\prime }:={\underline {{\mathcal {T}}\!}\,}_b(V)_{\bar \gamma }\otimes _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}\Omega \langle \tfrac {z}{\zeta ^s}\rangle $
inside
${\mathcal {Q}}^{\prime }:={\underline {{\mathcal {T}}\!}\,}_b(V)_{\bar \gamma }\otimes _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}\Omega \langle \tfrac {z}{\zeta ^s}\rangle $
inside
![]() ${\mathcal {Q}}:={\underline {{\mathcal {F}}\!}\,}_{b,\bar \gamma }(V)={\mathcal {Q}}^{\prime }\otimes _{\Omega \langle \frac {z}{\zeta ^s}\rangle }\Omega {\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}$
for an s with
${\mathcal {Q}}:={\underline {{\mathcal {F}}\!}\,}_{b,\bar \gamma }(V)={\mathcal {Q}}^{\prime }\otimes _{\Omega \langle \frac {z}{\zeta ^s}\rangle }\Omega {\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}$
for an s with
![]() $1>s>\frac {1}{q}$
; see Remark 5.6. Note that our notation here of the underlying z-isocrystal deviates from [Reference Hartl50]. Namely, our
$1>s>\frac {1}{q}$
; see Remark 5.6. Note that our notation here of the underlying z-isocrystal deviates from [Reference Hartl50]. Namely, our
![]() ${\underline {D\!}\,}_{b}(V)=\big (V\otimes _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}{\mathbb {F}}(\kern-0.15em( z)\kern-0.15em),\rho _V(\sigma ^\ast b)\sigma ^*\big )$
was called
${\underline {D\!}\,}_{b}(V)=\big (V\otimes _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}{\mathbb {F}}(\kern-0.15em( z)\kern-0.15em),\rho _V(\sigma ^\ast b)\sigma ^*\big )$
was called
![]() $\sigma ^*(D,F_D)$
in [Reference Hartl50, Proposition 2.4.9]. So the
$\sigma ^*(D,F_D)$
in [Reference Hartl50, Proposition 2.4.9]. So the
![]() $(D,F_D)$
from [Reference Hartl50, Proposition 2.4.9] is equal to our
$(D,F_D)$
from [Reference Hartl50, Proposition 2.4.9] is equal to our
![]() $\big (V\otimes _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}{\mathbb {F}}(\kern-0.15em( z)\kern-0.15em),\rho _V(b)\sigma ^*\big )$
. The latter equals the z-isocrystal associated with the local
$\big (V\otimes _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}{\mathbb {F}}(\kern-0.15em( z)\kern-0.15em),\rho _V(b)\sigma ^*\big )$
. The latter equals the z-isocrystal associated with the local
![]() $\operatorname {\mathrm {GL}}(V)$
-shtuka
$\operatorname {\mathrm {GL}}(V)$
-shtuka
![]() $\rho _{V,*}{\underline {{\mathbb {G}}}}_0$
over
$\rho _{V,*}{\underline {{\mathbb {G}}}}_0$
over
![]() ${\mathbb {F}}$
that was used in (the proof of) Lemma 6.1.
${\mathbb {F}}$
that was used in (the proof of) Lemma 6.1.
As can be seen from the proof of [Reference Hartl50, Proposition 2.4.9], there is an isomorphism
![]() yielding
yielding
![]() $\check T_z{\underline {M\!}\,}_V\cong ({\mathcal {Q}}^{\prime })^\tau ={\underline {{\mathcal {T}}\!}\,}_b(V)_{\bar \gamma }$
. Alternatively, [Reference Hartl50, Proposition 2.4.4] provides an isomorphism
$\check T_z{\underline {M\!}\,}_V\cong ({\mathcal {Q}}^{\prime })^\tau ={\underline {{\mathcal {T}}\!}\,}_b(V)_{\bar \gamma }$
. Alternatively, [Reference Hartl50, Proposition 2.4.4] provides an isomorphism
![]() yielding
yielding
![]() $\check T_z{\underline {M\!}\,}_V\otimes _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\cong ({\underline {{\mathcal {F}}\!}\,}_{b,\bar \gamma }(V))^\tau ={\underline {{\mathcal {T}}\!}\,}_b(V)_{\bar \gamma }\otimes _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)={\underline {{\mathcal {V}}\!}\,}_b(V)_{\bar \gamma }$
. Now the existence of a uniquely determined pair
$\check T_z{\underline {M\!}\,}_V\otimes _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\cong ({\underline {{\mathcal {F}}\!}\,}_{b,\bar \gamma }(V))^\tau ={\underline {{\mathcal {T}}\!}\,}_b(V)_{\bar \gamma }\otimes _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)={\underline {{\mathcal {V}}\!}\,}_b(V)_{\bar \gamma }$
. Now the existence of a uniquely determined pair
![]() $({\underline {M\!}\,}_V,\delta _V)$
with
$({\underline {M\!}\,}_V,\delta _V)$
with
![]() $\varepsilon _V(\check T_z{\underline {M\!}\,}_V)={\underline {{\mathcal {T}}\!}\,}_b(V)_{\bar \gamma }$
follows from Proposition 7.8.
$\varepsilon _V(\check T_z{\underline {M\!}\,}_V)={\underline {{\mathcal {T}}\!}\,}_b(V)_{\bar \gamma }$
follows from Proposition 7.8.
We claim that the underlying free
![]() ${\mathcal {O}}_{\Omega }\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-module
${\mathcal {O}}_{\Omega }\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-module
![]() $M_V$
of the local shtuka
$M_V$
of the local shtuka
![]() ${\underline {M\!}\,}_V$
defines a tensor functor
${\underline {M\!}\,}_V$
defines a tensor functor
![]() $M\colon \operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}G\to \textrm {FMod}_{{\mathcal {O}}_{\Omega }\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}},\,V\mapsto M_V$
. We use the isomorphisms
$M\colon \operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}G\to \textrm {FMod}_{{\mathcal {O}}_{\Omega }\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}},\,V\mapsto M_V$
. We use the isomorphisms
where
is induced from the isomorphism
![]() $\beta $
from (8.1). Consider the identification
$\beta $
from (8.1). Consider the identification
Then the isomorphisms
![]() $\sigma ^\ast \delta _V\circ \tau _{M_V}^{-1}$
and
$\sigma ^\ast \delta _V\circ \tau _{M_V}^{-1}$
and
![]() $(\beta _V\otimes \operatorname {\mbox { id}}_{\Omega \langle \frac {z}{\zeta ^s}\rangle })^{-1}\circ \varepsilon _V$
satisfy
$(\beta _V\otimes \operatorname {\mbox { id}}_{\Omega \langle \frac {z}{\zeta ^s}\rangle })^{-1}\circ \varepsilon _V$
satisfy

and
![]() $M_V$
is obtained from the intersection
$M_V$
is obtained from the intersection
inside
![]() $V\otimes _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}\Omega {\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}{}[\tfrac {1}{t_{\scriptscriptstyle -}}]$
.
$V\otimes _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}\Omega {\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}{}[\tfrac {1}{t_{\scriptscriptstyle -}}]$
.
To prove compatibility with morphisms
![]() $f\colon V\to V^{\prime }$
in
$f\colon V\to V^{\prime }$
in
![]() $\operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}G$
, we consider the induced morphisms
$\operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}G$
, we consider the induced morphisms
![]() ${\mathcal {E}}_{b,\bar \gamma }(f):=f\otimes \operatorname {\mbox { id}}_{\Omega {\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}{}[\frac {1}{t_{\scriptscriptstyle -}}]}\colon {\mathcal {E}}_{b,\bar \gamma }(V)\to {\mathcal {E}}_{b,\bar \gamma }(V^{\prime })$
and
${\mathcal {E}}_{b,\bar \gamma }(f):=f\otimes \operatorname {\mbox { id}}_{\Omega {\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}{}[\frac {1}{t_{\scriptscriptstyle -}}]}\colon {\mathcal {E}}_{b,\bar \gamma }(V)\to {\mathcal {E}}_{b,\bar \gamma }(V^{\prime })$
and
![]() ${\underline {{\mathcal {T}}\!}\,}_b(f)_{\bar \gamma }\colon {\underline {{\mathcal {T}}\!}\,}_b(V)_{\bar \gamma }\to {\underline {{\mathcal {T}}\!}\,}_b(V^{\prime })_{\bar \gamma }$
. Because
${\underline {{\mathcal {T}}\!}\,}_b(f)_{\bar \gamma }\colon {\underline {{\mathcal {T}}\!}\,}_b(V)_{\bar \gamma }\to {\underline {{\mathcal {T}}\!}\,}_b(V^{\prime })_{\bar \gamma }$
. Because
![]() $h_{V^{\prime }}\circ {\underline {{\mathcal {T}}\!}\,}_b(f)_{\bar \gamma }={\mathcal {E}}_{b,\bar \gamma }(f)\circ h_V$
and
$h_{V^{\prime }}\circ {\underline {{\mathcal {T}}\!}\,}_b(f)_{\bar \gamma }={\mathcal {E}}_{b,\bar \gamma }(f)\circ h_V$
and
![]() ${\underline {{\mathcal {T}}\!}\,}_b(f)_{\bar \gamma }\circ \beta _V=\beta _{V^{\prime }}\circ f$
, the morphism f induces via (8.6) a morphism
${\underline {{\mathcal {T}}\!}\,}_b(f)_{\bar \gamma }\circ \beta _V=\beta _{V^{\prime }}\circ f$
, the morphism f induces via (8.6) a morphism
![]() $M_f\colon M_V\to M_{V^{\prime }}$
.
$M_f\colon M_V\to M_{V^{\prime }}$
.
Finally, if
![]() $V,V^{\prime }\in \operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}G$
then
$V,V^{\prime }\in \operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}G$
then
![]() $({\underline {M\!}\,}_V,\delta _V)\otimes ({\underline {M\!}\,}_{V^{\prime }},\delta _{V^{\prime }})$
has
$({\underline {M\!}\,}_V,\delta _V)\otimes ({\underline {M\!}\,}_{V^{\prime }},\delta _{V^{\prime }})$
has
![]() ${\underline {D\!}\,}_{b,\bar \gamma }(V)\otimes {\underline {D\!}\,}_{b,\bar \gamma }(V^{\prime })={\underline {D\!}\,}_{b,\bar \gamma }(V\otimes V^{\prime })$
as z-isocrystal with Hodge-Pink structure and
${\underline {D\!}\,}_{b,\bar \gamma }(V)\otimes {\underline {D\!}\,}_{b,\bar \gamma }(V^{\prime })={\underline {D\!}\,}_{b,\bar \gamma }(V\otimes V^{\prime })$
as z-isocrystal with Hodge-Pink structure and
![]() $\check T_z{\underline {M\!}\,}_V\otimes \check T_z{\underline {M\!}\,}_{V^{\prime }}\cong {\underline {{\mathcal {T}}\!}\,}_b(V)_{\bar \gamma }\otimes {\underline {{\mathcal {T}}\!}\,}_b(V^{\prime })_{\bar \gamma }={\underline {{\mathcal {T}}\!}\,}_b(V\otimes V^{\prime })_{\bar \gamma }$
as Tate-module. This implies that
$\check T_z{\underline {M\!}\,}_V\otimes \check T_z{\underline {M\!}\,}_{V^{\prime }}\cong {\underline {{\mathcal {T}}\!}\,}_b(V)_{\bar \gamma }\otimes {\underline {{\mathcal {T}}\!}\,}_b(V^{\prime })_{\bar \gamma }={\underline {{\mathcal {T}}\!}\,}_b(V\otimes V^{\prime })_{\bar \gamma }$
as Tate-module. This implies that
![]() $({\underline {M\!}\,}_{V\otimes V^{\prime }},\delta _{V\otimes V^{\prime }})=({\underline {M\!}\,}_V,\delta _V)\otimes ({\underline {M\!}\,}_{V^{\prime }},\delta _{V^{\prime }})$
and so M is indeed a tensor functor.
$({\underline {M\!}\,}_{V\otimes V^{\prime }},\delta _{V\otimes V^{\prime }})=({\underline {M\!}\,}_V,\delta _V)\otimes ({\underline {M\!}\,}_{V^{\prime }},\delta _{V^{\prime }})$
and so M is indeed a tensor functor.
Unfortunately, it is not a priori clear that this tensor functor comes from a G-torsor over
![]() ${\mathcal {O}}_\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
. Namely, a necessary (and by Proposition 8.3 also sufficient) condition is that for every sequence
${\mathcal {O}}_\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
. Namely, a necessary (and by Proposition 8.3 also sufficient) condition is that for every sequence
![]() $0\to V^{\prime }\to V\to V^{\prime \prime }\to 0$
in
$0\to V^{\prime }\to V\to V^{\prime \prime }\to 0$
in
![]() $\operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}G$
, which is exact on the underlying free
$\operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}G$
, which is exact on the underlying free
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-modules; also, the sequence
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-modules; also, the sequence
![]() $0\to M_{V^{\prime }}\to M_V\to M_{V^{\prime \prime }}\to 0$
of free
$0\to M_{V^{\prime }}\to M_V\to M_{V^{\prime \prime }}\to 0$
of free
![]() ${\mathcal {O}}_\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-modules is exact. This is not obvious without using the hypothesis that G is parahoric and may even be false if the generic fibre of G is not reductive as Example 8.6 below shows.
${\mathcal {O}}_\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-modules is exact. This is not obvious without using the hypothesis that G is parahoric and may even be false if the generic fibre of G is not reductive as Example 8.6 below shows.
3. We first claim that the sequence of
![]() ${\mathcal {O}}_\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-modules
${\mathcal {O}}_\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-modules
![]() $0\to M_{V^{\prime }}\to M_V\to M_{V^{\prime \prime }}\to 0$
becomes exact after tensoring with
$0\to M_{V^{\prime }}\to M_V\to M_{V^{\prime \prime }}\to 0$
becomes exact after tensoring with
![]() ${\mathcal {O}}_\Omega (\kern-0.15em( z)\kern-0.15em):={\mathcal {O}}_\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z}]$
. Namely, because the cokernel C of
${\mathcal {O}}_\Omega (\kern-0.15em( z)\kern-0.15em):={\mathcal {O}}_\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z}]$
. Namely, because the cokernel C of
![]() $M_V[\tfrac {1}{z}]\to M_{V^{\prime \prime }}[\tfrac {1}{z}]$
is finitely generated, it suffices by Nakayama’s lemma to prove that
$M_V[\tfrac {1}{z}]\to M_{V^{\prime \prime }}[\tfrac {1}{z}]$
is finitely generated, it suffices by Nakayama’s lemma to prove that
![]() $C/{\mathfrak {m}} C=(0)$
for every maximal ideal
$C/{\mathfrak {m}} C=(0)$
for every maximal ideal
![]() ${\mathfrak {m}}\subset {\mathcal {O}}_\Omega (\kern-0.15em( z)\kern-0.15em)$
. By Lemma 8.4(b) there are two cases, namely,
${\mathfrak {m}}\subset {\mathcal {O}}_\Omega (\kern-0.15em( z)\kern-0.15em)$
. By Lemma 8.4(b) there are two cases, namely,
![]() ${\mathfrak {m}}={\mathfrak {m}}_0=\ker \big ({\mathcal {O}}_\Omega (\kern-0.15em( z)\kern-0.15em)\twoheadrightarrow \kappa _\Omega (\kern-0.15em( z)\kern-0.15em)\big )$
and
${\mathfrak {m}}={\mathfrak {m}}_0=\ker \big ({\mathcal {O}}_\Omega (\kern-0.15em( z)\kern-0.15em)\twoheadrightarrow \kappa _\Omega (\kern-0.15em( z)\kern-0.15em)\big )$
and
![]() ${\mathfrak {m}}=(z-\alpha )$
for
${\mathfrak {m}}=(z-\alpha )$
for
![]() $\alpha \in {\mathfrak {m}}_\Omega \setminus \{0\}$
. In the first case, the morphism
$\alpha \in {\mathfrak {m}}_\Omega \setminus \{0\}$
. In the first case, the morphism
![]() ${\mathcal {O}}_\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\to {\mathcal {O}}_\Omega (\kern-0.15em( z)\kern-0.15em)/{\mathfrak {m}}_0=\kappa _\Omega (\kern-0.15em( z)\kern-0.15em)$
factors through
${\mathcal {O}}_\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\to {\mathcal {O}}_\Omega (\kern-0.15em( z)\kern-0.15em)/{\mathfrak {m}}_0=\kappa _\Omega (\kern-0.15em( z)\kern-0.15em)$
factors through
![]() ${\mathcal {O}}_\Omega \mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{t_{\scriptscriptstyle -}}]$
, because
${\mathcal {O}}_\Omega \mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{t_{\scriptscriptstyle -}}]$
, because
![]() $t_{\scriptscriptstyle -}\equiv 1\ \pmod {{\mathfrak {m}}_0}$
, and hence
$t_{\scriptscriptstyle -}\equiv 1\ \pmod {{\mathfrak {m}}_0}$
, and hence
![]() $C/{\mathfrak {m}}_0 C\cong \operatorname {\mathrm {coker}}(V\twoheadrightarrow V^{\prime \prime })\otimes _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}\kappa _\Omega (\kern-0.15em( z)\kern-0.15em)=(0)$
by using the isomorphism (8.4). In the second case, if
$C/{\mathfrak {m}}_0 C\cong \operatorname {\mathrm {coker}}(V\twoheadrightarrow V^{\prime \prime })\otimes _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}\kappa _\Omega (\kern-0.15em( z)\kern-0.15em)=(0)$
by using the isomorphism (8.4). In the second case, if
![]() $|\alpha |>|\zeta |^s$
, the morphism
$|\alpha |>|\zeta |^s$
, the morphism
![]() ${\mathcal {O}}_\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\to {\mathcal {O}}_\Omega (\kern-0.15em( z)\kern-0.15em)/{\mathfrak {m}}=\Omega $
,
${\mathcal {O}}_\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\to {\mathcal {O}}_\Omega (\kern-0.15em( z)\kern-0.15em)/{\mathfrak {m}}=\Omega $
,
![]() $z\mapsto \alpha $
likewise factors through
$z\mapsto \alpha $
likewise factors through
![]() ${\mathcal {O}}_\Omega \mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{t_{\scriptscriptstyle -}}]$
, because
${\mathcal {O}}_\Omega \mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{t_{\scriptscriptstyle -}}]$
, because
![]() $t_{\scriptscriptstyle -}(\alpha )=\prod _{i\in {\mathbb {N}}_0}\big (1-{\tfrac {\zeta ^{q^i}}{\alpha }}\big )\ne 0$
, and hence
$t_{\scriptscriptstyle -}(\alpha )=\prod _{i\in {\mathbb {N}}_0}\big (1-{\tfrac {\zeta ^{q^i}}{\alpha }}\big )\ne 0$
, and hence
![]() $C/{\mathfrak {m}}_0 C\cong \operatorname {\mathrm {coker}}(V\twoheadrightarrow V^{\prime \prime })\otimes _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}\Omega =(0)$
by using the isomorphism (8.4) again. Finally, in the second case, if
$C/{\mathfrak {m}}_0 C\cong \operatorname {\mathrm {coker}}(V\twoheadrightarrow V^{\prime \prime })\otimes _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}\Omega =(0)$
by using the isomorphism (8.4) again. Finally, in the second case, if
![]() $|\alpha |\le |\zeta |^s$
, the morphism
$|\alpha |\le |\zeta |^s$
, the morphism
![]() ${\mathcal {O}}_\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\to {\mathcal {O}}_\Omega (\kern-0.15em( z)\kern-0.15em)/{\mathfrak {m}}=\Omega $
factors through
${\mathcal {O}}_\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\to {\mathcal {O}}_\Omega (\kern-0.15em( z)\kern-0.15em)/{\mathfrak {m}}=\Omega $
factors through
![]() $\Omega \langle \frac {z}{\zeta ^s}\rangle $
, and hence
$\Omega \langle \frac {z}{\zeta ^s}\rangle $
, and hence
![]() $C/{\mathfrak {m}}_0 C\cong \operatorname {\mathrm {coker}}(V\twoheadrightarrow V^{\prime \prime })\otimes _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}\Omega =(0)$
by using the isomorphism (8.5).
$C/{\mathfrak {m}}_0 C\cong \operatorname {\mathrm {coker}}(V\twoheadrightarrow V^{\prime \prime })\otimes _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}\Omega =(0)$
by using the isomorphism (8.5).
Now Proposition 8.3 shows that
![]() ${\mathcal {G}}:=\operatorname {\mathrm {Isom}}^\otimes \big (\omega ^\circ \otimes _{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}{\mathcal {O}}_\Omega (\kern-0.15em( z)\kern-0.15em),\,M\otimes _{{\mathcal {O}}_\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}{\mathcal {O}}_\Omega (\kern-0.15em( z)\kern-0.15em)\big )$
is a G-torsor over
${\mathcal {G}}:=\operatorname {\mathrm {Isom}}^\otimes \big (\omega ^\circ \otimes _{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}{\mathcal {O}}_\Omega (\kern-0.15em( z)\kern-0.15em),\,M\otimes _{{\mathcal {O}}_\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}{\mathcal {O}}_\Omega (\kern-0.15em( z)\kern-0.15em)\big )$
is a G-torsor over
![]() ${\mathcal {O}}_\Omega (\kern-0.15em( z)\kern-0.15em)$
for the fpqc-topology, and hence for the étale topology, because G is smooth. By [Reference Anschütz3, Proposition 11.5], the G-torsor
${\mathcal {O}}_\Omega (\kern-0.15em( z)\kern-0.15em)$
for the fpqc-topology, and hence for the étale topology, because G is smooth. By [Reference Anschütz3, Proposition 11.5], the G-torsor
![]() ${\mathcal {G}}$
over
${\mathcal {G}}$
over
![]() ${\mathcal {O}}_\Omega (\kern-0.15em( z)\kern-0.15em)$
is trivial.
${\mathcal {O}}_\Omega (\kern-0.15em( z)\kern-0.15em)$
is trivial.
4. From the triviality of
![]() ${\mathcal {G}}$
and from the isomorphism (8.5) we obtain an
${\mathcal {G}}$
and from the isomorphism (8.5) we obtain an
![]() ${\mathcal {O}}_\Omega (\kern-0.15em( z)\kern-0.15em)$
-rational, respectively
${\mathcal {O}}_\Omega (\kern-0.15em( z)\kern-0.15em)$
-rational, respectively
![]() $\Omega \langle \tfrac {z}{\zeta ^s}\rangle $
-rational, tensor isomorphism
$\Omega \langle \tfrac {z}{\zeta ^s}\rangle $
-rational, tensor isomorphism
, respectively
, which we fix in the sequel. Over
![]() $\Omega \langle \tfrac {z}{\zeta ^s}\rangle [z^{-1}]$
the composition
$\Omega \langle \tfrac {z}{\zeta ^s}\rangle [z^{-1}]$
the composition
![]() $u^{\prime \prime }_\Omega :=\theta ^{-1}\circ \theta _2$
corresponds to an element
$u^{\prime \prime }_\Omega :=\theta ^{-1}\circ \theta _2$
corresponds to an element
![]() $u^{\prime \prime }_\Omega \in G\big (\Omega \langle \tfrac {z}{\zeta ^s}\rangle [z^{-1}]\big )\subset G\big (\Omega (\kern-0.15em( z)\kern-0.15em)\big )=LG(\Omega )$
. The isomorphisms
$u^{\prime \prime }_\Omega \in G\big (\Omega \langle \tfrac {z}{\zeta ^s}\rangle [z^{-1}]\big )\subset G\big (\Omega (\kern-0.15em( z)\kern-0.15em)\big )=LG(\Omega )$
. The isomorphisms

provide an automorphism of the tensor functor
![]() $\omega ^\circ \otimes _{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}{\mathcal {O}}_{\Omega }\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z(z-\zeta )}]$
; that is, an element
$\omega ^\circ \otimes _{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}{\mathcal {O}}_{\Omega }\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z(z-\zeta )}]$
; that is, an element
![]() $A\in G\big ({\mathcal {O}}_{\Omega }\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z(z-\zeta )}]\big )=L_{z(z-\zeta )}G({\mathcal {O}}_\Omega )$
. We consider A as an isomorphism
$A\in G\big ({\mathcal {O}}_{\Omega }\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}[\tfrac {1}{z(z-\zeta )}]\big )=L_{z(z-\zeta )}G({\mathcal {O}}_\Omega )$
. We consider A as an isomorphism
of trivial
![]() $L_{z(z-\zeta )}G$
-torsors. Likewise, the isomorphisms
$L_{z(z-\zeta )}G$
-torsors. Likewise, the isomorphisms
provide an automorphism of the tensor functor
![]() $\omega ^\circ \otimes _{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}{\mathcal {O}}_{\Omega }\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{t_{\scriptscriptstyle -}}]$
; that is, an element
$\omega ^\circ \otimes _{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}{\mathcal {O}}_{\Omega }\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{t_{\scriptscriptstyle -}}]$
; that is, an element
![]() $\Delta \in G\big ({\mathcal {O}}_{\Omega }\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{t_{\scriptscriptstyle -}}]\big )$
. The equalities
$\Delta \in G\big ({\mathcal {O}}_{\Omega }\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{t_{\scriptscriptstyle -}}]\big )$
. The equalities
![]() $\rho _V(b)\circ \sigma ^\ast \delta _V=\delta _V\circ \tau _{M_V}$
yield the equality
$\rho _V(b)\circ \sigma ^\ast \delta _V=\delta _V\circ \tau _{M_V}$
yield the equality
![]() $b\cdot \sigma ^\ast \Delta =\Delta \cdot A$
in
$b\cdot \sigma ^\ast \Delta =\Delta \cdot A$
in
![]() $G\big ({\mathcal {O}}_{\Omega }\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{t_{\scriptscriptstyle -}}]\big )$
. Finally, the isomorphisms
$G\big ({\mathcal {O}}_{\Omega }\mathrm {[}\kern-0.15em\mathrm {[} z,z^{-1}\}[\tfrac {1}{t_{\scriptscriptstyle -}}]\big )$
. Finally, the isomorphisms
provide an automorphism of the tensor functor
![]() $\omega ^\circ _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}\otimes _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}\Omega \langle \tfrac {z}{\zeta ^{qs}}\rangle $
; that is, an element
$\omega ^\circ _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}\otimes _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}\Omega \langle \tfrac {z}{\zeta ^{qs}}\rangle $
; that is, an element
![]() $A^{\prime \prime }\in G\big (\Omega \langle \tfrac {z}{\zeta ^{qs}}\rangle \big )\subset G\big (\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\big )=L^+G(\Omega )$
. It satisfies
$A^{\prime \prime }\in G\big (\Omega \langle \tfrac {z}{\zeta ^{qs}}\rangle \big )\subset G\big (\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\big )=L^+G(\Omega )$
. It satisfies
![]() $u^{\prime \prime }_\Omega \cdot A^{\prime \prime }=A\cdot \sigma ^\ast u^{\prime \prime }_\Omega $
. We view
$u^{\prime \prime }_\Omega \cdot A^{\prime \prime }=A\cdot \sigma ^\ast u^{\prime \prime }_\Omega $
. We view
![]() $A^{\prime \prime }$
as an isomorphism
$A^{\prime \prime }$
as an isomorphism
of trivial
![]() $L^+G$
-torsors satisfying
$L^+G$
-torsors satisfying
![]() $u^{\prime \prime }_\Omega \circ \tau ^{\prime \prime }=\tau _{\mathcal {G}}\circ \sigma ^\ast u^{\prime \prime }_\Omega $
.
$u^{\prime \prime }_\Omega \circ \tau ^{\prime \prime }=\tau _{\mathcal {G}}\circ \sigma ^\ast u^{\prime \prime }_\Omega $
.
Moreover, choose a representative
![]() $\bar \gamma \in G\big (\Omega (\kern-0.15em( z-\zeta )\kern-0.15em)\big )$
of
$\bar \gamma \in G\big (\Omega (\kern-0.15em( z-\zeta )\kern-0.15em)\big )$
of
![]() $\bar \gamma \in {\mathcal {H}}_{G,\hat Z}^{\mathrm {an}}(\Omega )\subset \operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}}(\Omega )$
. Then the element
$\bar \gamma \in {\mathcal {H}}_{G,\hat Z}^{\mathrm {an}}(\Omega )\subset \operatorname {\mathrm {Gr}}_G^{{\mathbf {B}}_{\textrm {dR}}}(\Omega )$
. Then the element
![]() $h:=A\cdot \sigma ^*\Delta ^{-1}\cdot \bar \gamma \in G\big (\Omega (\kern-0.15em( z-\zeta )\kern-0.15em)\big )$
satisfies
$h:=A\cdot \sigma ^*\Delta ^{-1}\cdot \bar \gamma \in G\big (\Omega (\kern-0.15em( z-\zeta )\kern-0.15em)\big )$
satisfies
![]() $\rho _V(h)=\theta _V^{-1}\circ \tau _{M_V}\circ \sigma ^\ast \delta _V^{-1}\circ \rho _V(\bar \gamma )$
. In formula (8.3) we computed that this is an automorphism of
$\rho _V(h)=\theta _V^{-1}\circ \tau _{M_V}\circ \sigma ^\ast \delta _V^{-1}\circ \rho _V(\bar \gamma )$
. In formula (8.3) we computed that this is an automorphism of
![]() $V\otimes _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}\Omega \mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
. Thus,
$V\otimes _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}\Omega \mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}$
. Thus,
![]() $h\in G(\Omega \mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]})$
, and hence
$h\in G(\Omega \mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]})$
, and hence
![]() $A^{-1}=\sigma ^*\Delta ^{-1}\cdot \bar \gamma \cdot h^{-1}$
lies in
$A^{-1}=\sigma ^*\Delta ^{-1}\cdot \bar \gamma \cdot h^{-1}$
lies in
![]() $\hat {Z}^{\mathrm {an}}(\Omega )$
, because
$\hat {Z}^{\mathrm {an}}(\Omega )$
, because
![]() $\sigma ^*\Delta \in G(\Omega \mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]})$
. Therefore, the pair
$\sigma ^*\Delta \in G(\Omega \mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]})$
. Therefore, the pair
![]() $(LG_{{\mathcal {O}}_\Omega },\tau _{\mathcal {G}})$
consisting of the trivial
$(LG_{{\mathcal {O}}_\Omega },\tau _{\mathcal {G}})$
consisting of the trivial
![]() $LG$
-torsor over
$LG$
-torsor over
![]() ${\mathcal {O}}_\Omega $
associated with
${\mathcal {O}}_\Omega $
associated with
![]() ${\mathcal {G}}$
and
${\mathcal {G}}$
and
![]() $\tau _{\mathcal {G}}:=A\sigma ^\ast $
, as well as the pair
$\tau _{\mathcal {G}}:=A\sigma ^\ast $
, as well as the pair
![]() $({\mathcal {G}}^{\prime \prime }_\Omega ,\tau ^{\prime \prime })$
consisting of the trivial
$({\mathcal {G}}^{\prime \prime }_\Omega ,\tau ^{\prime \prime })$
consisting of the trivial
![]() $L^+G$
-torsor
$L^+G$
-torsor
![]() ${\mathcal {G}}^{\prime \prime }_\Omega :=L^+G_\Omega $
over
${\mathcal {G}}^{\prime \prime }_\Omega :=L^+G_\Omega $
over
![]() $\Omega $
with
$\Omega $
with
![]() $\tau ^{\prime \prime }:=A^{\prime \prime }\sigma ^\ast $
, together with
$\tau ^{\prime \prime }:=A^{\prime \prime }\sigma ^\ast $
, together with
![]() $u^{\prime \prime }_\Omega $
satisfy the hypothesis of Lemma 7.9 with
$u^{\prime \prime }_\Omega $
satisfy the hypothesis of Lemma 7.9 with
![]() $B={\mathcal {O}}_\Omega $
and
$B={\mathcal {O}}_\Omega $
and
![]() $L=\Omega $
. We apply this lemma. Because every finitely generated ideal of
$L=\Omega $
. We apply this lemma. Because every finitely generated ideal of
![]() ${\mathcal {O}}_\Omega $
is principal,
${\mathcal {O}}_\Omega $
is principal,
![]() $Y=\operatorname {\mathrm {Spec}}{\mathcal {O}}_\Omega $
. We obtain a local G-shtuka
$Y=\operatorname {\mathrm {Spec}}{\mathcal {O}}_\Omega $
. We obtain a local G-shtuka
![]() ${\underline {{\mathcal {G}}}}^{\prime \prime }=({\mathcal {G}}^{\prime \prime }\!,\tau _{{\mathcal {G}}^{\prime \prime }})$
over
${\underline {{\mathcal {G}}}}^{\prime \prime }=({\mathcal {G}}^{\prime \prime }\!,\tau _{{\mathcal {G}}^{\prime \prime }})$
over
![]() ${\mathcal {O}}_\Omega $
bounded by
${\mathcal {O}}_\Omega $
bounded by
![]() $\hat {Z}^{-1}$
and an isomorphism
$\hat {Z}^{-1}$
and an isomorphism
![]() of
of
![]() $LG$
-torsors over
$LG$
-torsors over
![]() ${\mathcal {O}}_\Omega $
satisfying
${\mathcal {O}}_\Omega $
satisfying
![]() $u^{\prime \prime }\circ \tau _{{\mathcal {G}}^{\prime \prime }}=\tau _{\mathcal {G}}\circ \sigma ^\ast u^{\prime \prime }$
. The reduction modulo
$u^{\prime \prime }\circ \tau _{{\mathcal {G}}^{\prime \prime }}=\tau _{\mathcal {G}}\circ \sigma ^\ast u^{\prime \prime }$
. The reduction modulo
![]() $\zeta $
of
$\zeta $
of
![]() $\Delta ^{\prime \prime }:=\Delta \circ u^{\prime \prime }$
provides a quasi-isogeny
$\Delta ^{\prime \prime }:=\Delta \circ u^{\prime \prime }$
provides a quasi-isogeny
![]() ${\underline {{\mathcal {G}}}}^{\prime \prime }_{{\mathcal {O}}_\Omega /(\zeta )}\to {\underline {{\mathbb {G}}}}_{0,{\mathcal {O}}_\Omega /(\zeta )}$
, because
${\underline {{\mathcal {G}}}}^{\prime \prime }_{{\mathcal {O}}_\Omega /(\zeta )}\to {\underline {{\mathbb {G}}}}_{0,{\mathcal {O}}_\Omega /(\zeta )}$
, because
![]() $\Delta \circ u^{\prime \prime }\circ \tau _{{\mathcal {G}}^{\prime \prime }}=\Delta \cdot A\circ \sigma ^\ast u^{\prime \prime }=b\circ \sigma ^\ast (\Delta \circ u^{\prime \prime })$
. This yields an
$\Delta \circ u^{\prime \prime }\circ \tau _{{\mathcal {G}}^{\prime \prime }}=\Delta \cdot A\circ \sigma ^\ast u^{\prime \prime }=b\circ \sigma ^\ast (\Delta \circ u^{\prime \prime })$
. This yields an
![]() ${\mathcal {O}}_\Omega $
-valued point
${\mathcal {O}}_\Omega $
-valued point
![]() $({\underline {{\mathcal {G}}}}^{\prime \prime }\!,\bar \Delta ^{\prime \prime })\in {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}({\mathcal {O}}_\Omega )$
. Its image under
$({\underline {{\mathcal {G}}}}^{\prime \prime }\!,\bar \Delta ^{\prime \prime })\in {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}({\mathcal {O}}_\Omega )$
. Its image under
![]() $\breve \pi $
is computed as
$\breve \pi $
is computed as
![]() $\breve \pi ({\underline {{\mathcal {G}}}}^{\prime \prime }\!,\bar \Delta ^{\prime \prime })=b^{-1}\Delta ^{\prime \prime }\cdot G\big (\Omega \mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )$
with
$\breve \pi ({\underline {{\mathcal {G}}}}^{\prime \prime }\!,\bar \Delta ^{\prime \prime })=b^{-1}\Delta ^{\prime \prime }\cdot G\big (\Omega \mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )$
with
![]() $b^{-1}\Delta ^{\prime \prime }=b^{-1}\Delta \circ u^{\prime \prime }=\sigma ^\ast \Delta \cdot A^{-1}\cdot u^{\prime \prime }=\bar \gamma \cdot h^{-1}u^{\prime \prime }$
. Because
$b^{-1}\Delta ^{\prime \prime }=b^{-1}\Delta \circ u^{\prime \prime }=\sigma ^\ast \Delta \cdot A^{-1}\cdot u^{\prime \prime }=\bar \gamma \cdot h^{-1}u^{\prime \prime }$
. Because
![]() $h,u^{\prime \prime }\in G\big (\Omega \mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )$
, this shows that
$h,u^{\prime \prime }\in G\big (\Omega \mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )$
, this shows that
![]() $\breve \pi ({\underline {{\mathcal {G}}}}^{\prime \prime }\!,\bar \Delta ^{\prime \prime })=\bar \gamma $
and finally (a) is proved.
$\breve \pi ({\underline {{\mathcal {G}}}}^{\prime \prime }\!,\bar \Delta ^{\prime \prime })=\bar \gamma $
and finally (a) is proved.
To prove (b), fix a representation
![]() $\rho \in \operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G$
. By Remark 7.3, the rational Tate module
$\rho \in \operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)}G$
. By Remark 7.3, the rational Tate module
![]() $\check V_{{\underline {{\mathcal {G}}}}}(\rho )$
is a local system of
$\check V_{{\underline {{\mathcal {G}}}}}(\rho )$
is a local system of
![]() ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-vector spaces on
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-vector spaces on
![]() ${\breve {\mathcal {M}}}:=({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\mathrm {an}}$
. In order that it descends to a local system on
${\breve {\mathcal {M}}}:=({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\mathrm {an}}$
. In order that it descends to a local system on
![]() $\breve \pi \big (({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\mathrm {an}}\big )=:\operatorname {\mathrm {im}}(\breve \pi )$
, it suffices by [Reference de Jong31, Definition 4.1] to show that
$\breve \pi \big (({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\mathrm {an}}\big )=:\operatorname {\mathrm {im}}(\breve \pi )$
, it suffices by [Reference de Jong31, Definition 4.1] to show that
-
(i)
 $\breve \pi \colon {\breve {\mathcal {M}}}\to \operatorname {\mathrm {im}}(\breve \pi )$
is a covering for the étale topology and
$\breve \pi \colon {\breve {\mathcal {M}}}\to \operatorname {\mathrm {im}}(\breve \pi )$
is a covering for the étale topology and -
(ii) there is a descent datum
 over
over
 ${\breve {\mathcal {M}}}\times _{\operatorname {\mathrm {im}}(\breve \pi )}{\breve {\mathcal {M}}}$
where
${\breve {\mathcal {M}}}\times _{\operatorname {\mathrm {im}}(\breve \pi )}{\breve {\mathcal {M}}}$
where
 $pr_i:{\breve {\mathcal {M}}}\times _{\operatorname {\mathrm {im}}(\breve \pi )}{\breve {\mathcal {M}}}\to {\breve {\mathcal {M}}}$
is the projection onto the ith factor, such that
$pr_i:{\breve {\mathcal {M}}}\times _{\operatorname {\mathrm {im}}(\breve \pi )}{\breve {\mathcal {M}}}\to {\breve {\mathcal {M}}}$
is the projection onto the ith factor, such that
 $\psi $
satisfies the cocycle condition on
$\psi $
satisfies the cocycle condition on
 ${\breve {\mathcal {M}}}\times _{\operatorname {\mathrm {im}}(\breve \pi )}{\breve {\mathcal {M}}}\times _{\operatorname {\mathrm {im}}(\breve \pi )}{\breve {\mathcal {M}}}$
.
${\breve {\mathcal {M}}}\times _{\operatorname {\mathrm {im}}(\breve \pi )}{\breve {\mathcal {M}}}\times _{\operatorname {\mathrm {im}}(\breve \pi )}{\breve {\mathcal {M}}}$
.
Statement (i) follows from Proposition 6.10. To prove (ii), let L and B be as introduced before Lemma 7.6 and let
![]() ${\mathcal {X}}=\operatorname {\mathrm {Spf}} B$
and
${\mathcal {X}}=\operatorname {\mathrm {Spf}} B$
and
![]() $X={\mathcal {X}}^{\mathrm {an}}={\mathtt {BSpec}}(B[\tfrac {1}{\zeta }])$
. Consider an X-valued point of
$X={\mathcal {X}}^{\mathrm {an}}={\mathtt {BSpec}}(B[\tfrac {1}{\zeta }])$
. Consider an X-valued point of
![]() ${\breve {\mathcal {M}}}\times _{\operatorname {\mathrm {im}}(\breve \pi )}{\breve {\mathcal {M}}}$
and its image in
${\breve {\mathcal {M}}}\times _{\operatorname {\mathrm {im}}(\breve \pi )}{\breve {\mathcal {M}}}$
and its image in
![]() ${\breve {\mathcal {M}}}\times _{\breve E}{\breve {\mathcal {M}}}$
. By [Reference Bosch and Lütkebohmert18, Theorem 4.1], this X-valued point is induced by two
${\breve {\mathcal {M}}}\times _{\breve E}{\breve {\mathcal {M}}}$
. By [Reference Bosch and Lütkebohmert18, Theorem 4.1], this X-valued point is induced by two
![]() $\operatorname {\mathrm {Spf}} B$
-valued points
$\operatorname {\mathrm {Spf}} B$
-valued points
![]() $({\underline {{\mathcal {G}}}},\bar \delta )$
and
$({\underline {{\mathcal {G}}}},\bar \delta )$
and
![]() $({\underline {{\mathcal {G}}}}^{\prime }\!,\bar \delta ^{\prime })$
of
$({\underline {{\mathcal {G}}}}^{\prime }\!,\bar \delta ^{\prime })$
of
![]() ${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
with
${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
with
![]() $\breve \pi ({\underline {{\mathcal {G}}}},\bar \delta )=\breve \pi ({\underline {{\mathcal {G}}}}^{\prime }\!,\bar \delta ^{\prime })$
in
$\breve \pi ({\underline {{\mathcal {G}}}},\bar \delta )=\breve \pi ({\underline {{\mathcal {G}}}}^{\prime }\!,\bar \delta ^{\prime })$
in
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^{a}(X)$
possibly after replacing
$\breve {\mathcal {H}}_{G,\hat {Z},b}^{a}(X)$
possibly after replacing
![]() $\operatorname {\mathrm {Spf}} B$
by an affine covering of an admissible formal blowing-up; see the explanations before Lemma 6.2 for more details. Now Proposition 7.8 (together with Proposition 5.3) yields a canonical isomorphism
$\operatorname {\mathrm {Spf}} B$
by an affine covering of an admissible formal blowing-up; see the explanations before Lemma 6.2 for more details. Now Proposition 7.8 (together with Proposition 5.3) yields a canonical isomorphism
![]() of local systems of
of local systems of
![]() ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-vector spaces over X which is functorial in
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-vector spaces over X which is functorial in
![]() $\rho $
and satisfies the cocycle condition by canonicity. Therefore,
$\rho $
and satisfies the cocycle condition by canonicity. Therefore,
![]() $\check V_{{\underline {{\mathcal {G}}}}}(\rho )$
descends to a local system of
$\check V_{{\underline {{\mathcal {G}}}}}(\rho )$
descends to a local system of
![]() ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-vector spaces on
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
-vector spaces on
![]() $\breve \pi \big (({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\mathrm {an}}\big )$
. Clearly,
$\breve \pi \big (({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\mathrm {an}}\big )$
. Clearly,
![]() $\check V_{{\underline {{\mathcal {G}}}}}\colon \rho \mapsto \check V_{{\underline {{\mathcal {G}}}}}(\rho )$
is a tensor functor. The isomorphism
$\check V_{{\underline {{\mathcal {G}}}}}\colon \rho \mapsto \check V_{{\underline {{\mathcal {G}}}}}(\rho )$
is a tensor functor. The isomorphism
![]() from Remark 7.17 yields a canonical
from Remark 7.17 yields a canonical
![]() $J_b\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
-linearisation
$J_b\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
-linearisation
![]() on
on
![]() $\check V_{{\underline {{\mathcal {G}}}}}$
over
$\check V_{{\underline {{\mathcal {G}}}}}$
over
![]() ${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
that descends to
${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
that descends to
![]() $\breve \pi \big (({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\mathrm {an}}\big )$
because the period morphism
$\breve \pi \big (({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\mathrm {an}}\big )$
because the period morphism
![]() $\breve \pi $
is
$\breve \pi $
is
![]() $J_b\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
-equivariant by Remark 6.5.
$J_b\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
-equivariant by Remark 6.5.
Let
![]() $\rho \colon G\to \operatorname {\mathrm {GL}}_r$
be in
$\rho \colon G\to \operatorname {\mathrm {GL}}_r$
be in
![]() $\operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}G$
. By [Reference Hartl50, Proposition 2.4.4] the pullback to
$\operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}G$
. By [Reference Hartl50, Proposition 2.4.4] the pullback to
![]() ${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
under
${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
under
![]() $\breve \pi $
of the
$\breve \pi $
of the
![]() $\sigma $
-bundle
$\sigma $
-bundle
![]() ${\underline {{\mathcal {F}}\!}\,}_b(\rho )$
over
${\underline {{\mathcal {F}}\!}\,}_b(\rho )$
over
![]() $\breve \pi \big (({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\mathrm {an}}\big )$
from Remark 5.6 is canonically isomorphic to
$\breve \pi \big (({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\mathrm {an}}\big )$
from Remark 5.6 is canonically isomorphic to
![]() ${\underline {M\!}\,}_\rho \otimes {\mathcal {O}}_{{\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}}{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}$
where
${\underline {M\!}\,}_\rho \otimes {\mathcal {O}}_{{\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}}{\textstyle \langle \frac {z}{\zeta ^{s}},z^{-1}\}}$
where
![]() ${\underline {M\!}\,}_\rho $
is the local shtuka over
${\underline {M\!}\,}_\rho $
is the local shtuka over
![]() ${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
associated with the local
${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
associated with the local
![]() $\operatorname {\mathrm {GL}}_r$
-shtuka
$\operatorname {\mathrm {GL}}_r$
-shtuka
![]() $\rho _*{\underline {{\mathcal {G}}}}^{\textrm {univ}}$
obtained from the universal local G-shtuka
$\rho _*{\underline {{\mathcal {G}}}}^{\textrm {univ}}$
obtained from the universal local G-shtuka
![]() ${\underline {{\mathcal {G}}}}^{\textrm {univ}}$
over
${\underline {{\mathcal {G}}}}^{\textrm {univ}}$
over
![]() ${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
. This isomorphism is functorial in
${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
. This isomorphism is functorial in
![]() $\rho $
and compatible with tensor products and pullback under the action of
$\rho $
and compatible with tensor products and pullback under the action of
![]() $j\in J_b\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
because the period morphism
$j\in J_b\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
because the period morphism
![]() $\breve \pi $
is
$\breve \pi $
is
![]() $J_b\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
-equivariant. Descending it to
$J_b\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
-equivariant. Descending it to
![]() $\breve \pi \big (({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\mathrm {an}}\big )$
and taking
$\breve \pi \big (({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\mathrm {an}}\big )$
and taking
![]() $\tau $
-invariants yields a canonical isomorphism of tensor functors
$\tau $
-invariants yields a canonical isomorphism of tensor functors
![]() , which satisfies
, which satisfies
![]() $\alpha \circ \varphi _j=\check V_{\Phi _j}\circ j^*\alpha $
where
$\alpha \circ \varphi _j=\check V_{\Phi _j}\circ j^*\alpha $
where
![]() is the linearisation from Theorem 5.7.
is the linearisation from Theorem 5.7.
(c) We fix a geometric base point
![]() $\bar \gamma $
of
$\bar \gamma $
of
![]() $\breve \pi \big (({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\mathrm {an}}\big )$
and consider the canonical family of morphisms
$\breve \pi \big (({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\mathrm {an}}\big )$
and consider the canonical family of morphisms
![]() $(f_K\colon {\breve {\mathcal {M}}}^K\to {\breve {\mathcal {E}}}_K)_{K\subset G({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em))}$
that sends an X-valued triple
$(f_K\colon {\breve {\mathcal {M}}}^K\to {\breve {\mathcal {E}}}_K)_{K\subset G({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em))}$
that sends an X-valued triple
![]() $({\underline {{\mathcal {G}}}},\bar \delta ,\eta K)$
over
$({\underline {{\mathcal {G}}}},\bar \delta ,\eta K)$
over
![]() ${\breve {\mathcal {M}}}^K$
from Corollary 7.13 with
${\breve {\mathcal {M}}}^K$
from Corollary 7.13 with
to the X-valued point of
![]() ${\breve {\mathcal {E}}}_K$
given by the K-orbit
${\breve {\mathcal {E}}}_K$
given by the K-orbit
![]() $\beta K\in \operatorname {\mathrm {Isom}}^\otimes (\omega ^\circ ,\mathit { forget}\circ \omega _{\bar \gamma }\circ {\underline {{\mathcal {V}}\!}\,}_b)\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )/K$
of tensor isomorphisms where
$\beta K\in \operatorname {\mathrm {Isom}}^\otimes (\omega ^\circ ,\mathit { forget}\circ \omega _{\bar \gamma }\circ {\underline {{\mathcal {V}}\!}\,}_b)\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )/K$
of tensor isomorphisms where
![]() $\beta :=(\mathit {forget}\circ \omega _{\bar \gamma })(\alpha )^{-1}\circ \eta $
; see Remarks 5.8 and 5.5(a). The map
$\beta :=(\mathit {forget}\circ \omega _{\bar \gamma })(\alpha )^{-1}\circ \eta $
; see Remarks 5.8 and 5.5(a). The map
![]() $f_K$
does not depend on the chosen base point
$f_K$
does not depend on the chosen base point
![]() $\bar \gamma $
by [Reference de Jong31, Theorem 2.9] and is thus defined on all connected components of the
$\bar \gamma $
by [Reference de Jong31, Theorem 2.9] and is thus defined on all connected components of the
![]() ${\breve {\mathcal {M}}}^K$
. The family
${\breve {\mathcal {M}}}^K$
. The family
![]() $(f_K)_K$
is equivariant for the Hecke action of
$(f_K)_K$
is equivariant for the Hecke action of
![]() $G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
on both towers defined in (5.5) and (7.5). For any algebraically closed complete extension
$G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
on both towers defined in (5.5) and (7.5). For any algebraically closed complete extension
![]() $\Omega $
of
$\Omega $
of
![]() $\breve E$
, the morphism
$\breve E$
, the morphism
![]() $f_K$
is bijective on
$f_K$
is bijective on
![]() $\Omega $
-valued points because the fibres of
$\Omega $
-valued points because the fibres of
![]() ${\breve {\mathcal {M}}}^K(\Omega )$
and
${\breve {\mathcal {M}}}^K(\Omega )$
and
![]() ${\breve {\mathcal {E}}}_K(\Omega )$
over a fixed
${\breve {\mathcal {E}}}_K(\Omega )$
over a fixed
![]() $\Omega $
-valued point of
$\Omega $
-valued point of
![]() $\breve \pi \big (({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\mathrm {an}}\big )$
are both isomorphic to the quotient
$\breve \pi \big (({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\mathrm {an}}\big )$
are both isomorphic to the quotient
![]() $G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )/K$
by Remark 5.5(a) and Proposition 7.16. Hence,
$G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )/K$
by Remark 5.5(a) and Proposition 7.16. Hence,
![]() $f_K$
is quasi-finite by [Reference Berkovich8, Proposition 3.1.4]. Because
$f_K$
is quasi-finite by [Reference Berkovich8, Proposition 3.1.4]. Because
![]() ${\breve {\mathcal {M}}}^K$
and
${\breve {\mathcal {M}}}^K$
and
![]() ${\breve {\mathcal {E}}}_K$
are étale over
${\breve {\mathcal {E}}}_K$
are étale over
![]() $\breve \pi \big (({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\mathrm {an}}\big )$
, the morphisms
$\breve \pi \big (({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\mathrm {an}}\big )$
, the morphisms
![]() $f_K$
are étale by [Reference Berkovich8, Corollary 3.3.9] and hence isomorphisms by [Reference Hartl51, Proposition A.4].
$f_K$
are étale by [Reference Berkovich8, Corollary 3.3.9] and hence isomorphisms by [Reference Hartl51, Proposition A.4].
To prove that the
![]() $f_K$
are
$f_K$
are
![]() $J_b\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
-equivariant, we must show that the upper ‘rectangle’ in the diagram
$J_b\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
-equivariant, we must show that the upper ‘rectangle’ in the diagram

is commutative; that is,
![]() $f_K\circ j_{\breve {\mathcal {M}}^K}=j_{{\breve {\mathcal {E}}}_K}\circ f_K$
holds. Recall from Remark 7.17 that the action
$f_K\circ j_{\breve {\mathcal {M}}^K}=j_{{\breve {\mathcal {E}}}_K}\circ f_K$
holds. Recall from Remark 7.17 that the action
![]() $j_{\breve {\mathcal {M}}^K}\colon \breve {\mathcal {M}}^K\to \breve {\mathcal {M}}^K$
of
$j_{\breve {\mathcal {M}}^K}\colon \breve {\mathcal {M}}^K\to \breve {\mathcal {M}}^K$
of
![]() $j\in J_b\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
is defined on the universal objects by
$j\in J_b\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
is defined on the universal objects by
This triple on the source of the morphism
![]() $j_{\breve {\mathcal {M}}^K}\colon \breve {\mathcal {M}}^K\to \breve {\mathcal {M}}^K$
is mapped under the dashed arrow f to
$j_{\breve {\mathcal {M}}^K}\colon \breve {\mathcal {M}}^K\to \breve {\mathcal {M}}^K$
is mapped under the dashed arrow f to
![]() $(\mathit {forget}\circ \omega _{\bar \gamma })(j^*\alpha )^{-1}\circ \mathit {forget}(\check V_{\Phi _j,\bar x}^{-1})\circ \eta K\;=\;(\mathit { forget}\circ \omega _{\bar \gamma })(\varphi _j^{-1}\circ \alpha ^{-1})\circ \eta K$
. Likewise, the image
$(\mathit {forget}\circ \omega _{\bar \gamma })(j^*\alpha )^{-1}\circ \mathit {forget}(\check V_{\Phi _j,\bar x}^{-1})\circ \eta K\;=\;(\mathit { forget}\circ \omega _{\bar \gamma })(\varphi _j^{-1}\circ \alpha ^{-1})\circ \eta K$
. Likewise, the image
![]() $f_K({\underline {{\mathcal {G}}}}^{\textrm {univ}},\bar \delta ^{\textrm {univ}},\eta ^{\textrm {univ}} K)= (\mathit {forget}\circ \omega _{\bar \gamma })(\alpha )^{-1}\circ \eta K$
on
$f_K({\underline {{\mathcal {G}}}}^{\textrm {univ}},\bar \delta ^{\textrm {univ}},\eta ^{\textrm {univ}} K)= (\mathit {forget}\circ \omega _{\bar \gamma })(\alpha )^{-1}\circ \eta K$
on
![]() ${\breve {\mathcal {E}}}_K$
of the universal object on
${\breve {\mathcal {E}}}_K$
of the universal object on
![]() $\breve {\mathcal {M}}^K$
is mapped by [Reference Hartl51, Formula (2.11)] to
$\breve {\mathcal {M}}^K$
is mapped by [Reference Hartl51, Formula (2.11)] to
![]() $(\mathit { forget}\circ \omega _{\bar \gamma })(\varphi _j^{-1})\circ (\mathit {forget}\circ \omega _{\bar \gamma })(\alpha )^{-1}\circ \eta K$
on
$(\mathit { forget}\circ \omega _{\bar \gamma })(\varphi _j^{-1})\circ (\mathit {forget}\circ \omega _{\bar \gamma })(\alpha )^{-1}\circ \eta K$
on
![]() $j^*{\breve {\mathcal {E}}}_K$
. This proves the commutativity of the upper ‘rectangle’ and the
$j^*{\breve {\mathcal {E}}}_K$
. This proves the commutativity of the upper ‘rectangle’ and the
![]() $J_b\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
-equivariance of the isomorphism
$J_b\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
-equivariance of the isomorphism
![]() $f_K$
.
$f_K$
.
Corollary 8.5. Every point
![]() $x\in \breve {\mathcal {M}}^K$
has an affinoid neighbourhood U that is finite étale over its image
$x\in \breve {\mathcal {M}}^K$
has an affinoid neighbourhood U that is finite étale over its image
![]() $\breve \pi (U)$
in
$\breve \pi (U)$
in
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^{a}$
. This image
$\breve {\mathcal {H}}_{G,\hat {Z},b}^{a}$
. This image
![]() $\breve \pi (U)$
is an affinoid subspace of the projective variety
$\breve \pi (U)$
is an affinoid subspace of the projective variety
![]() $\breve {\mathcal {H}}_{G,\hat {Z}}$
. In particular,
$\breve {\mathcal {H}}_{G,\hat {Z}}$
. In particular,
![]() $\breve {\mathcal {M}}^K$
is quasi-algebraic over
$\breve {\mathcal {M}}^K$
is quasi-algebraic over
![]() $\breve E$
; compare [Reference Fargues36, Définition 4.1.11].
$\breve E$
; compare [Reference Fargues36, Définition 4.1.11].
Proof. Note that the affinoid neighbourhoods of
![]() $\breve \pi (x)$
in
$\breve \pi (x)$
in
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^{a}$
form a basis of neighbourhoods of
$\breve {\mathcal {H}}_{G,\hat {Z},b}^{a}$
form a basis of neighbourhoods of
![]() $\breve \pi (x)$
by [Reference Berkovich7, p. 48]. By Theorem 8.1(c) and by the definition of an étale covering space, the point
$\breve \pi (x)$
by [Reference Berkovich7, p. 48]. By Theorem 8.1(c) and by the definition of an étale covering space, the point
![]() $\breve \pi (x)$
therefore has an affinoid neighbourhood V in
$\breve \pi (x)$
therefore has an affinoid neighbourhood V in
![]() $\breve {\mathcal {H}}_{G,\hat {Z},b}^{a}$
such that
$\breve {\mathcal {H}}_{G,\hat {Z},b}^{a}$
such that
![]() $\breve \pi ^{-1}(V)$
is a disjoint union of
$\breve \pi ^{-1}(V)$
is a disjoint union of
![]() $\breve E$
-analytic spaces, each of which is mapping finitely étale to V. We can thus take U as the connected component of
$\breve E$
-analytic spaces, each of which is mapping finitely étale to V. We can thus take U as the connected component of
![]() $\breve \pi ^{-1}(V)$
containing x.
$\breve \pi ^{-1}(V)$
containing x.
Example 8.6. We exhibit a case in which the tensor functor
![]() $M\colon \operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}G\to \textrm {FMod}_{{\mathcal {O}}_{\Omega }\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}},\,V\mapsto M_V$
used in the proof of Theorem 8.1(a) does not come from a G-torsor over
$M\colon \operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}G\to \textrm {FMod}_{{\mathcal {O}}_{\Omega }\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}},\,V\mapsto M_V$
used in the proof of Theorem 8.1(a) does not come from a G-torsor over
![]() ${\mathcal {O}}_\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
. This is also the function field analogue of [Reference Scholze and Weinstein89, Remark 5.2.9]. Consider the nonreductive group scheme
${\mathcal {O}}_\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
. This is also the function field analogue of [Reference Scholze and Weinstein89, Remark 5.2.9]. Consider the nonreductive group scheme
![]() $G={\mathbb {G}}_a\rtimes {\mathbb {G}}_m$
over
$G={\mathbb {G}}_a\rtimes {\mathbb {G}}_m$
over
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
and its representations
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
and its representations
![]() on
on
![]() $V={\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}^2$
and
$V={\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}^2$
and
![]() $\rho ^{\prime }\colon G \twoheadrightarrow {\mathbb {G}}_m$
on
$\rho ^{\prime }\colon G \twoheadrightarrow {\mathbb {G}}_m$
on
![]() $V^{\prime }={\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
. They sit in an exact sequence in
$V^{\prime }={\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
. They sit in an exact sequence in
![]() $\operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}G$
$\operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}G$
where
![]() ${\mathrm {1\kern -2.7pt l\kern .9pt}}\colon G\to \{1\}\subset {\mathbb {G}}_m$
is the trivial representation on
${\mathrm {1\kern -2.7pt l\kern .9pt}}\colon G\to \{1\}\subset {\mathbb {G}}_m$
is the trivial representation on
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
. Let
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
. Let
![]() $b = \left (\begin {smallmatrix} 1 & 0 \\ 0 & -z \end {smallmatrix}\right )\in G\big ({\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)\big )$
and
$b = \left (\begin {smallmatrix} 1 & 0 \\ 0 & -z \end {smallmatrix}\right )\in G\big ({\mathbb {F}}(\kern-0.15em( z)\kern-0.15em)\big )$
and
![]() $\bar \gamma = \left (\begin {smallmatrix} 1 & 0 \\ 0 & (z-\zeta )^{-1} \end {smallmatrix}\right )\in G\big (\Omega (\kern-0.15em( z-\zeta )\kern-0.15em)\big )\big /G\big (\Omega \mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )$
.
$\bar \gamma = \left (\begin {smallmatrix} 1 & 0 \\ 0 & (z-\zeta )^{-1} \end {smallmatrix}\right )\in G\big (\Omega (\kern-0.15em( z-\zeta )\kern-0.15em)\big )\big /G\big (\Omega \mathrm {[}\kern-0.15em\mathrm {[} z-\zeta \mathrm {]}\kern-0.15em\mathrm {]}\big )$
.
Consider the local G-shtuka
![]() ${\widetilde {{\underline {{\mathcal {G}}}}}}=\big ((L^+G)_{{\mathcal {O}}_\Omega },\tau _{\mathcal {G}}=\left (\begin {smallmatrix} 1 & 0 \\ 0 & \zeta -z \end {smallmatrix}\right )\big )$
over
${\widetilde {{\underline {{\mathcal {G}}}}}}=\big ((L^+G)_{{\mathcal {O}}_\Omega },\tau _{\mathcal {G}}=\left (\begin {smallmatrix} 1 & 0 \\ 0 & \zeta -z \end {smallmatrix}\right )\big )$
over
![]() ${\mathcal {O}}_\Omega $
. Recall the functor from
${\mathcal {O}}_\Omega $
. Recall the functor from
![]() $\operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}G$
to the category of local shtukas that assigns to
$\operatorname {\mathrm {Rep}}_{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}G$
to the category of local shtukas that assigns to
![]() $(V,\rho )$
the local shtuka
$(V,\rho )$
the local shtuka
![]() ${\underline {M\!}\,}_V$
associated with the local
${\underline {M\!}\,}_V$
associated with the local
![]() $\operatorname {\mathrm {GL}}(V)$
-shtuka
$\operatorname {\mathrm {GL}}(V)$
-shtuka
![]() $\rho _*{\widetilde {{\underline {{\mathcal {G}}}}}}$
from Remark 6.4. The underlying
$\rho _*{\widetilde {{\underline {{\mathcal {G}}}}}}$
from Remark 6.4. The underlying
![]() ${\mathcal {O}}_\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-module of
${\mathcal {O}}_\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
-module of
![]() ${\underline {M\!}\,}_V$
equals
${\underline {M\!}\,}_V$
equals
![]() $V\otimes _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}{\mathcal {O}}_\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
. Applied to
$V\otimes _{{\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}}{\mathcal {O}}_\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
. Applied to
![]() ${\widetilde {{\underline {{\mathcal {G}}}}}}$
this functor yields the exact sequence of local shtukas
${\widetilde {{\underline {{\mathcal {G}}}}}}$
this functor yields the exact sequence of local shtukas
Let
![]() $f:=\sqrt [q-1]{-1}\cdot t_{\scriptscriptstyle +}$
. Then the rational Tate module
$f:=\sqrt [q-1]{-1}\cdot t_{\scriptscriptstyle +}$
. Then the rational Tate module
![]() ${\mathcal {V}}_{b,\bar \gamma }=\check {V}_z{\widetilde {{\underline {{\mathcal {G}}}}}}$
is ‘generated by’
${\mathcal {V}}_{b,\bar \gamma }=\check {V}_z{\widetilde {{\underline {{\mathcal {G}}}}}}$
is ‘generated by’
![]() $\left (\begin {smallmatrix} 1 & 0 \\ 0 & f \end {smallmatrix}\right )=\left (\begin {smallmatrix} 1 & 0 \\ 0 & \zeta -z \end {smallmatrix}\right )\cdot \sigma ^*\left (\begin {smallmatrix} 1 & 0 \\ 0 & f \end {smallmatrix}\right )$
; that is, the tensor isomorphism
$\left (\begin {smallmatrix} 1 & 0 \\ 0 & f \end {smallmatrix}\right )=\left (\begin {smallmatrix} 1 & 0 \\ 0 & \zeta -z \end {smallmatrix}\right )\cdot \sigma ^*\left (\begin {smallmatrix} 1 & 0 \\ 0 & f \end {smallmatrix}\right )$
; that is, the tensor isomorphism
is given by multiplication with
Now we let
![]() $\pi \in {\mathcal {O}}_\Omega $
satisfy
$\pi \in {\mathcal {O}}_\Omega $
satisfy
![]() $\pi ^{q-1}=\zeta $
and we choose a different tensor isomorphism
$\pi ^{q-1}=\zeta $
and we choose a different tensor isomorphism
which is given by multiplication with
![]() $\rho \left (\begin {smallmatrix} 1 & 0 \\ f & zf \end {smallmatrix}\right )=\rho (\left (\begin {smallmatrix} 1 & 0 \\ 0 & f \end {smallmatrix}\right )\cdot \left (\begin {smallmatrix} 1 & 0 \\ 1 & z \end {smallmatrix}\right ))$
, where
$\rho \left (\begin {smallmatrix} 1 & 0 \\ f & zf \end {smallmatrix}\right )=\rho (\left (\begin {smallmatrix} 1 & 0 \\ 0 & f \end {smallmatrix}\right )\cdot \left (\begin {smallmatrix} 1 & 0 \\ 1 & z \end {smallmatrix}\right ))$
, where
![]() $\left (\begin {smallmatrix} 1 & 0 \\ 1 & z \end {smallmatrix}\right )\in G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
. The construction in step 2 of the proof of Theorem 8.1(a) with
$\left (\begin {smallmatrix} 1 & 0 \\ 1 & z \end {smallmatrix}\right )\in G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
. The construction in step 2 of the proof of Theorem 8.1(a) with
![]() $\beta $
instead of
$\beta $
instead of
![]() $\tilde \beta $
replaces every
$\tilde \beta $
replaces every
![]() ${\underline {M\!}\,}_V$
by a quasi-isogenous one. We claim that for the sequence (8.7) it yields the upper row in the commutative diagram of local shtukas
${\underline {M\!}\,}_V$
by a quasi-isogenous one. We claim that for the sequence (8.7) it yields the upper row in the commutative diagram of local shtukas

To prove our claim, we note that (8.8) yields over
![]() $R:={\mathcal {O}}_\Omega /(\zeta )$
the diagram
$R:={\mathcal {O}}_\Omega /(\zeta )$
the diagram

Also, when we consider the element
the upper row of (8.8) is right exact on Tate modules, because it induces the following commutative diagram:

Finally, the vertical quasi-isogeny in the middle of (8.8) induces the following commutative diagram on Tate modules:

This proves the claim.
Now, in diagram (8.8), the map
![]() $(z,\pi )$
in the upper row is not surjective, and this provides an example where the tensor functor
$(z,\pi )$
in the upper row is not surjective, and this provides an example where the tensor functor
![]() $(V,\rho )\mapsto M_V$
is not exact and hence does not come from a G-torsor
$(V,\rho )\mapsto M_V$
is not exact and hence does not come from a G-torsor
![]() ${\mathcal {G}}$
over
${\mathcal {G}}$
over
![]() ${\mathcal {O}}_\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
. One can also check, although
${\mathcal {O}}_\Omega \mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
. One can also check, although
 $$ \begin{align*} \left(\begin{matrix} 1 & 0 \\ 0 & f \end{matrix}\right)\cdot\left(\begin{matrix} 1 & 0 \\ 1 & z \end{matrix}\right) \;=\; \left(\begin{matrix} 1 & 0 \\ f & zf \end{matrix}\right) \;=\; \left(\begin{matrix} z & \pi \\ 0 & 1 \end{matrix}\right) \cdot \left(\begin{matrix} y & \,-\pi f \\ f & zf \end{matrix}\right) \;\in\;\operatorname{\mathrm{GL}}_2\big({\mathcal{O}}_\Omega(\kern-0.15em( z )\kern-0.15em)\big)\cdot\operatorname{\mathrm{GL}}_2(\Omega\langle\tfrac{z}{\zeta}\rangle)\,{,} \end{align*} $$
$$ \begin{align*} \left(\begin{matrix} 1 & 0 \\ 0 & f \end{matrix}\right)\cdot\left(\begin{matrix} 1 & 0 \\ 1 & z \end{matrix}\right) \;=\; \left(\begin{matrix} 1 & 0 \\ f & zf \end{matrix}\right) \;=\; \left(\begin{matrix} z & \pi \\ 0 & 1 \end{matrix}\right) \cdot \left(\begin{matrix} y & \,-\pi f \\ f & zf \end{matrix}\right) \;\in\;\operatorname{\mathrm{GL}}_2\big({\mathcal{O}}_\Omega(\kern-0.15em( z )\kern-0.15em)\big)\cdot\operatorname{\mathrm{GL}}_2(\Omega\langle\tfrac{z}{\zeta}\rangle)\,{,} \end{align*} $$
it is not possible to write it as a product in
![]() $G\big ({\mathcal {O}}_\Omega (\kern-0.15em( z)\kern-0.15em)\big )\cdot G(\Omega \langle \tfrac {z}{\zeta }\rangle )$
. This corresponds to the fact that the quasi-isogeny
$G\big ({\mathcal {O}}_\Omega (\kern-0.15em( z)\kern-0.15em)\big )\cdot G(\Omega \langle \tfrac {z}{\zeta }\rangle )$
. This corresponds to the fact that the quasi-isogeny
![]() ${\underline {M\!}\,}\to {\underline {M\!}\,}^{\prime \prime }\oplus {\underline {M\!}\,}^{\prime }$
does not come from a quasi-isogeny
${\underline {M\!}\,}\to {\underline {M\!}\,}^{\prime \prime }\oplus {\underline {M\!}\,}^{\prime }$
does not come from a quasi-isogeny
![]() ${\underline {{\mathcal {G}}}}\to {\widetilde {{\underline {{\mathcal {G}}}}}}$
of local G-shtukas over
${\underline {{\mathcal {G}}}}\to {\widetilde {{\underline {{\mathcal {G}}}}}}$
of local G-shtukas over
![]() ${\mathcal {O}}_\Omega $
, because
${\mathcal {O}}_\Omega $
, because
![]() ${\underline {{\mathcal {G}}}}$
does not exist. Note also that in terms of the proofs of Proposition 7.8 and Lemma 7.9, it is not possible to extend the étale local G-shtuka
${\underline {{\mathcal {G}}}}$
does not exist. Note also that in terms of the proofs of Proposition 7.8 and Lemma 7.9, it is not possible to extend the étale local G-shtuka
![]() ${\underline {{\mathcal {G}}}}^{\prime \prime }$
over
${\underline {{\mathcal {G}}}}^{\prime \prime }$
over
![]() $\Omega $
to
$\Omega $
to
![]() ${\mathcal {O}}_\Omega $
, because G is not parahoric and
${\mathcal {O}}_\Omega $
, because G is not parahoric and
![]() ${\mathcal {F}}\ell _G$
and
${\mathcal {F}}\ell _G$
and
![]() ${\underline {{\mathcal {M}}}}_{{\widetilde {{\underline {{\mathcal {G}}}}}}}$
are not ind-projective.
${\underline {{\mathcal {M}}}}_{{\widetilde {{\underline {{\mathcal {G}}}}}}}$
are not ind-projective.
9 Cohomology
In this section we provide basic properties of the cohomology of the towers of moduli spaces. This theory and all of the proofs parallel the one for Rapoport-Zink spaces in [Reference Fargues36] to which we also refer for some arguments that go over to our case without modification. Note that instead of the
![]() $\breve E$
-analytic space
$\breve E$
-analytic space
![]() $\breve {\mathcal {M}}^K$
in the sense of Berkovich, we may work with the associated adic space in the sense of Huber by [Reference Huber63, Proposition 8.2.12 and Theorem 8.3.5].
$\breve {\mathcal {M}}^K$
in the sense of Berkovich, we may work with the associated adic space in the sense of Huber by [Reference Huber63, Proposition 8.2.12 and Theorem 8.3.5].
Let
![]() $\ell $
be a prime different from the characteristic of
$\ell $
be a prime different from the characteristic of
![]() ${\mathbb {F}}_q$
and let
${\mathbb {F}}_q$
and let
![]() ${\,\overline {\!E}}$
be the completion of an algebraic closure of
${\,\overline {\!E}}$
be the completion of an algebraic closure of
![]() $\breve E$
.
$\breve E$
.
Definition 9.1. We denote by
![]() $H_c^{\bullet }({\breve {\mathcal {M}}}^K\hat {\otimes }_{\breve E}{\,\overline {\!E}},{\mathbb {Q}}_{\ell })$
the
$H_c^{\bullet }({\breve {\mathcal {M}}}^K\hat {\otimes }_{\breve E}{\,\overline {\!E}},{\mathbb {Q}}_{\ell })$
the
![]() $\ell $
-adic cohomology with compact support of the analytic space
$\ell $
-adic cohomology with compact support of the analytic space
![]() ${\breve {\mathcal {M}}}^K$
. For short, we denote it by
${\breve {\mathcal {M}}}^K$
. For short, we denote it by
![]() $H_c^{\bullet }({\breve {\mathcal {M}}}^K,{\mathbb {Q}}_{\ell })$
and write
$H_c^{\bullet }({\breve {\mathcal {M}}}^K,{\mathbb {Q}}_{\ell })$
and write
![]() $H_c^{\bullet }({\breve {\mathcal {M}}}^K,\overline {{\mathbb {Q}}}_{\ell }):=H_c^{\bullet }({\breve {\mathcal {M}}}^K,{\mathbb {Q}}_{\ell })\otimes _{{\mathbb {Q}}_\ell } \overline {{\mathbb {Q}}}_{\ell }$
.
$H_c^{\bullet }({\breve {\mathcal {M}}}^K,\overline {{\mathbb {Q}}}_{\ell }):=H_c^{\bullet }({\breve {\mathcal {M}}}^K,{\mathbb {Q}}_{\ell })\otimes _{{\mathbb {Q}}_\ell } \overline {{\mathbb {Q}}}_{\ell }$
.
Because the spaces
![]() ${\breve {\mathcal {M}}}^K$
are in general only quasi-algebraic, the definition of the cohomology needs some explanation, for which we refer to Fargues [Reference Fargues36, § 4.1].
${\breve {\mathcal {M}}}^K$
are in general only quasi-algebraic, the definition of the cohomology needs some explanation, for which we refer to Fargues [Reference Fargues36, § 4.1].
These cohomology groups are equipped with the following group actions. The action of
![]() $J:=J_b\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
on
$J:=J_b\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
on
![]() ${\breve {\mathcal {M}}}^K$
induces an action on
${\breve {\mathcal {M}}}^K$
induces an action on
![]() $H_c^{\bullet }({\breve {\mathcal {M}}}^K,{\mathbb {Q}}_{\ell })$
for each K. Furthermore, we obtain an action of the Weil group
$H_c^{\bullet }({\breve {\mathcal {M}}}^K,{\mathbb {Q}}_{\ell })$
for each K. Furthermore, we obtain an action of the Weil group
![]() $W_E$
of E. Indeed, the inertia subgroup
$W_E$
of E. Indeed, the inertia subgroup
![]() $\operatorname {\mathrm {Gal}}(\breve E^{\textrm {sep}}\!/\breve E)$
acts on the coefficients
$\operatorname {\mathrm {Gal}}(\breve E^{\textrm {sep}}\!/\breve E)$
acts on the coefficients
![]() ${\,\overline {\!E}}$
inducing an action on the cohomology. The action of Frobenius
${\,\overline {\!E}}$
inducing an action on the cohomology. The action of Frobenius
![]() $\sigma \in W_E$
is induced by the Weil descent datum of Remark 3.3. As in [Reference Fargues36, Remarque 4.4.3], one can show that the induced morphism on cohomology is invertible and thus induces an action of
$\sigma \in W_E$
is induced by the Weil descent datum of Remark 3.3. As in [Reference Fargues36, Remarque 4.4.3], one can show that the induced morphism on cohomology is invertible and thus induces an action of
![]() $W_E$
. Furthermore, for varying K the action by Hecke correspondences induces an action of
$W_E$
. Furthermore, for varying K the action by Hecke correspondences induces an action of
![]() $G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em) \big )$
on the cohomology groups of the whole tower.
$G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em) \big )$
on the cohomology groups of the whole tower.
If
![]() $\varepsilon \colon G\to G^{\prime }$
is a morphism of parahoric group schemes over
$\varepsilon \colon G\to G^{\prime }$
is a morphism of parahoric group schemes over
![]() ${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
as in Remarks 3.7, 4.21 and 7.19 with
${\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}$
as in Remarks 3.7, 4.21 and 7.19 with
![]() $\varepsilon (K)\subset K^{\prime }$
, we obtain a morphism
$\varepsilon (K)\subset K^{\prime }$
, we obtain a morphism
that is compatible with the actions of the Weil group
![]() $W_E$
, the Hecke action of
$W_E$
, the Hecke action of
![]() $G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
that acts on the source via the morphism
$G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
that acts on the source via the morphism
![]() $G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )\to G^{\prime }\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
and the action of the group
$G\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )\to G^{\prime }\big ({\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)\big )$
and the action of the group
![]() $J^G_b$
that acts on the source via the morphism
$J^G_b$
that acts on the source via the morphism
![]() $J^G_b\to J^{G^{\prime }}_{\varepsilon (b)}$
.
$J^G_b\to J^{G^{\prime }}_{\varepsilon (b)}$
.
Lemma 9.2. For each K, the
![]() $J\times W_E$
-representation
$J\times W_E$
-representation
![]() $H_c^{\bullet }({\breve {\mathcal {M}}}^K,{\mathbb {Q}}_{\ell })$
is smooth for the action of J and continuous for the action of
$H_c^{\bullet }({\breve {\mathcal {M}}}^K,{\mathbb {Q}}_{\ell })$
is smooth for the action of J and continuous for the action of
![]() $W_E$
.
$W_E$
.
Proof. As in the arithmetic context (compare [Reference Fargues36, Corollaire 4.4.7]), this follows from the fact that the
![]() ${\breve {\mathcal {M}}}^K$
are quasi-algebraic by Corollary 8.5 and that J acts continuously on
${\breve {\mathcal {M}}}^K$
are quasi-algebraic by Corollary 8.5 and that J acts continuously on
![]() ${\breve {\mathcal {M}}}^K$
by Lemma 7.18, using [Reference Fargues36, Corollaires 4.1.19, 4.1.20], two general assertions on the cohomology of Berkovich spaces. Note for this that J has an open pro-p subgroup, namely,
${\breve {\mathcal {M}}}^K$
by Lemma 7.18, using [Reference Fargues36, Corollaires 4.1.19, 4.1.20], two general assertions on the cohomology of Berkovich spaces. Note for this that J has an open pro-p subgroup, namely,
![]() $\{j\in J\cap L^+G({\mathbb {F}})\colon j\equiv 1\;\textrm {mod}\; z\}$
.
$\{j\in J\cap L^+G({\mathbb {F}})\colon j\equiv 1\;\textrm {mod}\; z\}$
.
Next we are interested in finiteness and vanishing properties of cohomology groups. We need the following finiteness statement for the set of irreducible components.
Lemma 9.3. The action of J on the set of irreducible components of
![]() ${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
has only finitely many orbits.
${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
has only finitely many orbits.
Proof. This is a statement about the underlying reduced subscheme; that is, on the set of irreducible components of the affine Deligne-Lusztig variety
![]() $X_{Z^{-1}}(b)$
from (3.2). By [Reference Rapoport and Zink81, Theorem 1.4 and Subsection 2.1] there is a closed subscheme
$X_{Z^{-1}}(b)$
from (3.2). By [Reference Rapoport and Zink81, Theorem 1.4 and Subsection 2.1] there is a closed subscheme
![]() $Y\subset {\mathcal {F}}\ell _G$
of finite type such that for each
$Y\subset {\mathcal {F}}\ell _G$
of finite type such that for each
![]() $g\in X_{Z^{-1}}(b)$
there is a
$g\in X_{Z^{-1}}(b)$
there is a
![]() $j\in J$
with
$j\in J$
with
![]() $j^{-1}g\in Y$
. In other words, g has a representative satisfying
$j^{-1}g\in Y$
. In other words, g has a representative satisfying
![]() $g^{-1}b\sigma ^\ast (g)=h^{-1}b\sigma ^\ast (h)$
for some (representative of an element)
$g^{-1}b\sigma ^\ast (g)=h^{-1}b\sigma ^\ast (h)$
for some (representative of an element)
![]() $h=j^{-1}g\in Y\cap X_{Z^{-1}}(b)$
. In particular, it is enough to show that
$h=j^{-1}g\in Y\cap X_{Z^{-1}}(b)$
. In particular, it is enough to show that
![]() $Y\cap X_{Z^{-1}}(b)$
has only finitely many irreducible components. This follows because
$Y\cap X_{Z^{-1}}(b)$
has only finitely many irreducible components. This follows because
![]() $Y\cap X_{Z^{-1}}(b)$
is of finite type.
$Y\cap X_{Z^{-1}}(b)$
is of finite type.
Proposition 9.4. For each compact open subgroup
![]() $K\subset G\big ({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\big )$
, the J-representation
$K\subset G\big ({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]}\big )$
, the J-representation
![]() $H_c^{\bullet }({\breve {\mathcal {M}}}^K,{\mathbb {Q}}_{\ell })$
is of finite type.
$H_c^{\bullet }({\breve {\mathcal {M}}}^K,{\mathbb {Q}}_{\ell })$
is of finite type.
Proof. Let
![]() $X_1,\dotsc ,X_t$
be representatives of the finitely many orbits of the action of J on the set of irreducible components of
$X_1,\dotsc ,X_t$
be representatives of the finitely many orbits of the action of J on the set of irreducible components of
![]() ${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
(compare Lemma 9.3). Let
${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
(compare Lemma 9.3). Let
![]() $K_0=G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
and let
$K_0=G({\mathbb {F}}_q\mathrm {[}\kern-0.15em\mathrm {[} z\mathrm {]}\kern-0.15em\mathrm {]})$
and let
![]() $U\subset({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\mathrm {an}}=\breve {\mathcal {M}}={\breve {\mathcal {M}}}^{K_0}$
be the tube over
$U\subset({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\mathrm {an}}=\breve {\mathcal {M}}={\breve {\mathcal {M}}}^{K_0}$
be the tube over
![]() $X:=X_1\cup \ldots \cup X_t$
; that is, the preimage of X under the specialisation map
$X:=X_1\cup \ldots \cup X_t$
; that is, the preimage of X under the specialisation map
![]() $sp$
from
$sp$
from
![]() $({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\mathrm {an}}$
to the underlying topological space of
$({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\mathrm {an}}$
to the underlying topological space of
![]() ${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
; see [Reference Berkovich11, § 1]. If
${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
; see [Reference Berkovich11, § 1]. If
![]() $V_0$
is a quasi-compact open subset of
$V_0$
is a quasi-compact open subset of
![]() ${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
containing X, then the complement
${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
containing X, then the complement
![]() $Y:=V_0\setminus X$
is open and quasi-compact, because
$Y:=V_0\setminus X$
is open and quasi-compact, because
![]() $V_0$
is Noetherian. Therefore,
$V_0$
is Noetherian. Therefore,
![]() $V:=sp^{-1}(V_0)\subset \breve {\mathcal {M}}^{K_0}$
is a compact neighbourhood of U and
$V:=sp^{-1}(V_0)\subset \breve {\mathcal {M}}^{K_0}$
is a compact neighbourhood of U and
![]() $V\setminus U=sp^{-1}(Y)$
is compact, whence U is open in
$V\setminus U=sp^{-1}(Y)$
is compact, whence U is open in
![]() ${\breve {\mathcal {M}}}^{K_0}$
. Let
${\breve {\mathcal {M}}}^{K_0}$
. Let
![]() $U_K:=\breve \pi _{K_0,K}^{-1}(U)\subset {\breve {\mathcal {M}}}^K$
.
$U_K:=\breve \pi _{K_0,K}^{-1}(U)\subset {\breve {\mathcal {M}}}^K$
.
Under the fully faithful functor [Reference Berkovich8, § 1.6] from strictly
![]() $\breve E$
-analytic spaces to rigid analytic spaces, U and
$\breve E$
-analytic spaces to rigid analytic spaces, U and
![]() $U_K$
correspond to
$U_K$
correspond to
![]() $U^{\textrm {rig}}=sp^{-1}(X)$
and
$U^{\textrm {rig}}=sp^{-1}(X)$
and
![]() $U_K^{\textrm {rig}}=(\breve \pi _{K_0,K}^{\textrm {rig}})^{-1}(U^{\textrm {rig}})$
, where
$U_K^{\textrm {rig}}=(\breve \pi _{K_0,K}^{\textrm {rig}})^{-1}(U^{\textrm {rig}})$
, where
![]() $sp\colon ({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\textrm {rig}}\to {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
is the specialisation map [Reference Berthelot13, (0.2.2.1)]. These are admissible open subspaces of
$sp\colon ({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\textrm {rig}}\to {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
is the specialisation map [Reference Berthelot13, (0.2.2.1)]. These are admissible open subspaces of
![]() $({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\textrm {rig}}$
and
$({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\textrm {rig}}$
and
![]() $(\breve {\mathcal {M}}^K)^{\textrm {rig}}$
. Under the fully faithful functor [Reference Huber63, (1.1.11)] from rigid analytic spaces over
$(\breve {\mathcal {M}}^K)^{\textrm {rig}}$
. Under the fully faithful functor [Reference Huber63, (1.1.11)] from rigid analytic spaces over
![]() $\breve E$
to Huber’s adic spaces,
$\breve E$
to Huber’s adic spaces,
![]() $U^{\textrm {rig}}$
and
$U^{\textrm {rig}}$
and
![]() $U_K^{\textrm {rig}}$
correspond to
$U_K^{\textrm {rig}}$
correspond to
![]() $U^{\textrm {ad}}=sp^{-1}(X)^\circ $
and
$U^{\textrm {ad}}=sp^{-1}(X)^\circ $
and
![]() $U_K^{\textrm {ad}}=(\breve \pi _{K_0,K}^{\textrm {ad}})^{-1}(U^{\textrm {ad}})$
, where
$U_K^{\textrm {ad}}=(\breve \pi _{K_0,K}^{\textrm {ad}})^{-1}(U^{\textrm {ad}})$
, where
![]() $sp\colon ({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\textrm {ad}}\to {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
is the specialisation map [Reference Huber63, Proposition 1.9.1] and
$sp\colon ({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\textrm {ad}}\to {\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
is the specialisation map [Reference Huber63, Proposition 1.9.1] and
![]() $sp^{-1}(X)^\circ $
denotes the open interior. These are open subspaces of
$sp^{-1}(X)^\circ $
denotes the open interior. These are open subspaces of
![]() $({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\textrm {ad}}$
and
$({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\textrm {ad}}$
and
![]() $(\breve {\mathcal {M}}^K)^{\textrm {ad}}$
. By definition [Reference Huber63, formula (*) on p. 315],
$(\breve {\mathcal {M}}^K)^{\textrm {ad}}$
. By definition [Reference Huber63, formula (*) on p. 315],
and this is a finite-dimensional
![]() ${\mathbb {Q}}_\ell $
-vector space by [Reference Huber65, Corollaries 5.8 and 5.4]. Because X is proper over
${\mathbb {Q}}_\ell $
-vector space by [Reference Huber65, Corollaries 5.8 and 5.4]. Because X is proper over
![]() ${\mathbb {F}}$
by Theorem 3.5,
${\mathbb {F}}$
by Theorem 3.5,
![]() $U_K^{\textrm {rig}}$
is partially proper over
$U_K^{\textrm {rig}}$
is partially proper over
![]() $\breve E$
by [Reference Huber63, Remark 1.3.18]. So
$\breve E$
by [Reference Huber63, Remark 1.3.18]. So
![]() $H^q_c(U_K,{\mathbb {Q}}_{\ell })=H^q_c(U_K^{\textrm {rig}},{\mathbb {Q}}_{\ell })$
by [Reference Huber64, Proposition 1.5]. Note that the proof of [Reference Huber64, Proposition 1.5] only uses that
$H^q_c(U_K,{\mathbb {Q}}_{\ell })=H^q_c(U_K^{\textrm {rig}},{\mathbb {Q}}_{\ell })$
by [Reference Huber64, Proposition 1.5]. Note that the proof of [Reference Huber64, Proposition 1.5] only uses that
![]() $U_K^{\textrm {rig}}$
is partially proper over
$U_K^{\textrm {rig}}$
is partially proper over
![]() $\breve E$
and not the stated assumption that
$\breve E$
and not the stated assumption that
![]() $U_K$
is closed. (We thank Roland Huber for explaining these arguments to us.)
$U_K$
is closed. (We thank Roland Huber for explaining these arguments to us.)
Let
![]() $J^{\prime }\subset J$
be the stabiliser of
$J^{\prime }\subset J$
be the stabiliser of
![]() $U_K$
, a compact open subgroup. Then the
$U_K$
, a compact open subgroup. Then the
![]() $g\cdot U_K$
for
$g\cdot U_K$
for
![]() $\bar g\in J/J^{\prime }$
are a covering of
$\bar g\in J/J^{\prime }$
are a covering of
![]() ${\breve {\mathcal {M}}}^K$
. We consider the associated spectral sequence for Cech cohomology of [Reference Fargues36, Proposition 4.2.2],
${\breve {\mathcal {M}}}^K$
. We consider the associated spectral sequence for Cech cohomology of [Reference Fargues36, Proposition 4.2.2],
 $$ \begin{align*}E_1^{pq}=\bigoplus_{\alpha\subset J/J^{\prime}}H^q_c(U_K(\alpha),{\mathbb{Q}}_{\ell})\;\Longrightarrow\; H_c^{p+q}({\breve{\mathcal{M}}}^K,{\mathbb{Q}}_{\ell}), \end{align*} $$
$$ \begin{align*}E_1^{pq}=\bigoplus_{\alpha\subset J/J^{\prime}}H^q_c(U_K(\alpha),{\mathbb{Q}}_{\ell})\;\Longrightarrow\; H_c^{p+q}({\breve{\mathcal{M}}}^K,{\mathbb{Q}}_{\ell}), \end{align*} $$
with the sum being over subsets
![]() $\alpha $
with
$\alpha $
with
![]() $-p+1$
elements and where
$-p+1$
elements and where
![]() $U_K(\alpha )=\bigcap _{\bar g\in \alpha }g\cdot U_K$
. It is concentrated in degrees
$U_K(\alpha )=\bigcap _{\bar g\in \alpha }g\cdot U_K$
. It is concentrated in degrees
![]() $p\leq 0$
and
$p\leq 0$
and
![]() $0\leq q\leq \dim ({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\mathrm {an}}$
. Furthermore, it is J-equivariant where
$0\leq q\leq \dim ({\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}})^{\mathrm {an}}$
. Furthermore, it is J-equivariant where
![]() $g\in J$
acts via
$g\in J$
acts via
For
![]() $\alpha \subset J/J^{\prime }$
, let
$\alpha \subset J/J^{\prime }$
, let
![]() $J^{\prime }_{\alpha }=\bigcap _{\bar g\in \alpha }gJ^{\prime }g^{-1}$
. By Lemma 7.18,
$J^{\prime }_{\alpha }=\bigcap _{\bar g\in \alpha }gJ^{\prime }g^{-1}$
. By Lemma 7.18,
![]() $J^{\prime }_{\alpha }\subset J$
acts continuously on
$J^{\prime }_{\alpha }\subset J$
acts continuously on
![]() $U_K(\alpha )$
. Hence, the
$U_K(\alpha )$
. Hence, the
![]() $H_c^q(U_K(\alpha ),{\mathbb {Q}}_{\ell })$
are smooth
$H_c^q(U_K(\alpha ),{\mathbb {Q}}_{\ell })$
are smooth
![]() $J^{\prime }_{\alpha }$
-modules. We can rewrite
$J^{\prime }_{\alpha }$
-modules. We can rewrite
![]() $E_1^{pq}$
as compact induction
$E_1^{pq}$
as compact induction
where the sum is now over equivalence classes
![]() $\bar \alpha $
of subsets
$\bar \alpha $
of subsets
![]() $\alpha \subset J/J^{\prime }$
with
$\alpha \subset J/J^{\prime }$
with
![]() $-p+1$
elements up to the action of J diagonally on
$-p+1$
elements up to the action of J diagonally on
![]() $(J/J^{\prime })^{-p+1}$
. We claim that there are only finitely many such
$(J/J^{\prime })^{-p+1}$
. We claim that there are only finitely many such
![]() $\bar \alpha $
with
$\bar \alpha $
with
![]() $U_K(\alpha )\neq \emptyset $
.
$U_K(\alpha )\neq \emptyset $
.
To show this claim, note that if A is a finite union of irreducible components of
![]() ${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
, then the set
${\breve {\mathcal {M}}}_{{\underline {{\mathbb {G}}}}_0}^{\hat {Z}^{-1}}$
, then the set
![]() $\{g\in J\colon g\cdot A\cap A\neq \emptyset \}$
is compact. In particular,
$\{g\in J\colon g\cdot A\cap A\neq \emptyset \}$
is compact. In particular,
![]() $J^{\prime \prime }=\{g\in J\colon g\cdot U_K\cap U_K\neq \emptyset \}$
is compact and contains
$J^{\prime \prime }=\{g\in J\colon g\cdot U_K\cap U_K\neq \emptyset \}$
is compact and contains
![]() $J^{\prime }$
. Thus, if
$J^{\prime }$
. Thus, if
![]() $\bar \alpha =\{g_1,\dotsc ,g_{-p+1}\}$
is as above with
$\bar \alpha =\{g_1,\dotsc ,g_{-p+1}\}$
is as above with
![]() $U_K(\alpha )\neq \emptyset $
, then for
$U_K(\alpha )\neq \emptyset $
, then for
![]() $i\neq j$
we have
$i\neq j$
we have
![]() $g_i^{-1}g_j\in J^{\prime \prime }$
. Modulo the left action of J on the index set we may assume that
$g_i^{-1}g_j\in J^{\prime \prime }$
. Modulo the left action of J on the index set we may assume that
![]() $g_{-p+1}\in J^{\prime \prime }/J^{\prime }$
; hence, all
$g_{-p+1}\in J^{\prime \prime }/J^{\prime }$
; hence, all
![]() $g_i$
are in
$g_i$
are in
![]() $J^{\prime \prime }/J^{\prime }$
, a finite set. In particular, the index set is finite.
$J^{\prime \prime }/J^{\prime }$
, a finite set. In particular, the index set is finite.
Altogether we obtain that
![]() $E_1^{pq}$
is a finite sum of compact inductions of finite-dimensional representations and hence a representation of J of finite type. By [Reference Bernstein and Deligne12, Remarque 3.12], the category of smooth J-modules is locally Noetherian. Because
$E_1^{pq}$
is a finite sum of compact inductions of finite-dimensional representations and hence a representation of J of finite type. By [Reference Bernstein and Deligne12, Remarque 3.12], the category of smooth J-modules is locally Noetherian. Because
![]() $H_c^{p+q}({\breve {\mathcal {M}}}^K,{\mathbb {Q}}_{\ell })$
has a finite filtration with all subquotients of finite type, it is itself of finite type.
$H_c^{p+q}({\breve {\mathcal {M}}}^K,{\mathbb {Q}}_{\ell })$
has a finite filtration with all subquotients of finite type, it is itself of finite type.
Corollary 9.5. Let
![]() $\Pi $
be an admissible representation of J. Then for all K, p and q
$\Pi $
be an admissible representation of J. Then for all K, p and q
Proof. This follows from the preceding proposition together with the following fact. Let H be a reductive group over
![]() ${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
and let
${\mathbb {F}}_q(\kern-0.15em( z)\kern-0.15em)$
and let
![]() $\Pi _1$
be a smooth representation of H of finite type and
$\Pi _1$
be a smooth representation of H of finite type and
![]() $\Pi _2$
an admissible representation. Then
$\Pi _2$
an admissible representation. Then
![]() $\dim (\textrm {Ext}_{H\mathrm {-smooth}}^i(\Pi _1,\Pi _2))<\infty $
. This fact can be shown in the same way as for p-adic groups; compare [Reference Fargues36, Lemme 4.4.15].
$\dim (\textrm {Ext}_{H\mathrm {-smooth}}^i(\Pi _1,\Pi _2))<\infty $
. This fact can be shown in the same way as for p-adic groups; compare [Reference Fargues36, Lemme 4.4.15].
Acknowledgments
We thank the anonymous referee for careful reading and many good comments. We further thank Johannes Anschütz, Bhargav Bhatt, Ofer Gabber, Tom Haines, Jack Hall, Jochen Heinloth, Roland Huber, Eike Lau, Brandon Levin, Stephan Neupert, Timo Richarz, Daniel Schäppi, Peter Scholze and Torsten Wedhorn for helpful discussions and Johannes Anschütz for pointing out an error in an earlier proof of Theorem 8.1(a). The first author acknowledges support of the DFG (German Research Foundation) in the form of SFB 878, Project-ID 427320536 – SFB 1442, and Germany’s Excellence Strategy EXC 2044–390685587 ‘Mathematics Münster: Dynamics–Geometry–Structure’. The second author was partially supported by ERC starting grant 277889 ‘Moduli spaces of local G-shtukas’.