1 results
Further properties of fractional stochastic dominance
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 28 March 2022, pp. 202-223
- Print publication:
- March 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
A continuum of stochastic dominance rules, also referred to as fractional stochastic dominance (SD), was introduced by Müller, Scarsini, Tsetlin, and Winkler (2017) to cover preferences from first- to second-order SD. Fractional SD can be used to explain many individual behaviors in economics. In this paper we introduce the concept of fractional pure SD, a special case of fractional SD. We investigate further properties of fractional SD, for example the generating processes of fractional pure SD via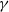
$\gamma$
-transfers of probability, Yaari’s dual characterization by utilizing the special class of distortion functions, the separation theorem in terms of first-order SD and fractional pure SD, Strassen’s representation, and bivariate characterization. We also establish several closure properties of fractional SD under quantile truncation, under comonotonic sums, and under distortion, as well as its equivalence characterization. Examples of distributions ordered in the sense of fractional SD are provided.
