1 results
Towards a Weighted Version of the Hajnal–Szemerédi Theorem
-
- Journal:
- Combinatorics, Probability and Computing / Volume 22 / Issue 3 / May 2013
- Published online by Cambridge University Press:
- 28 February 2013, pp. 346-350
-
- Article
- Export citation
-
For a positive integer r ≥ 2, a Kr-factor of a graph is a collection vertex-disjoint copies of Kr which covers all the vertices of the given graph. The celebrated theorem of Hajnal and Szemerédi asserts that every graph on n vertices with minimum degree at least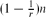
$(1-\frac{1}{r})n contains a Kr-factor. In this note, we propose investigating the relation between minimum degree and existence of perfect Kr-packing for edge-weighted graphs. The main question we study is the following. Suppose that a positive integer r ≥ 2 and a real t ∈ [0, 1] is given. What is the minimum weighted degree of Kn that guarantees the existence of a Kr-factor such that every factor has total edge weight at least 
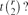$$t\binom{r}{2}$?$ We provide some lower and upper bounds and make a conjecture on the asymptotics of the threshold as n goes to infinity.
