In general, the tensor product, 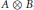 $A\otimes B$, of the lattices
$A\otimes B$, of the lattices  $A$ and
$A$ and  $B$ with zero is not a lattice (it is only a join-semilattice with zero). If
$B$ with zero is not a lattice (it is only a join-semilattice with zero). If 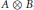 $A\otimes B$ is a capped tensor product, then
$A\otimes B$ is a capped tensor product, then 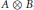 $A\otimes B$ is a lattice (the converse is not known). In this paper, we investigate lattices
$A\otimes B$ is a lattice (the converse is not known). In this paper, we investigate lattices  $A$ with zero enjoying the property that
$A$ with zero enjoying the property that 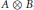 $A\otimes B$ is a capped tensor product, for every lattice
$A\otimes B$ is a capped tensor product, for every lattice  $B$ with zero; we shall call such lattices amenable.
$B$ with zero; we shall call such lattices amenable.
The first author introduced in 1966 the concept of a sharply transferable lattice. In 1972, H. Gaskill defined, similarly, sharply transferable semilattices, and characterized them by a very effective condition 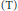 $\left( \text{T} \right)$.
$\left( \text{T} \right)$.
We prove that a finite lattice  $A$ is amenable iff it is sharply transferable as a join-semilattice.
$A$ is amenable iff it is sharply transferable as a join-semilattice.
For a general lattice  $A$ with zero, we obtain the result:
$A$ with zero, we obtain the result:  $A$ is amenable iff
$A$ is amenable iff  $A$ is locally finite and every finite sublattice of
$A$ is locally finite and every finite sublattice of  $A$ is transferable as a join-semilattice.
$A$ is transferable as a join-semilattice.
This yields, for example, that a finite lattice  $A$ is amenable iff
$A$ is amenable iff 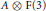 $A\otimes \text{F}\left( 3 \right)$ is a lattice iff
$A\otimes \text{F}\left( 3 \right)$ is a lattice iff  $A$ satisfies
$A$ satisfies 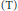 $\left( \text{T} \right)$, with respect to join. In particular,
$\left( \text{T} \right)$, with respect to join. In particular, 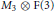 ${{M}_{3}}\,\otimes \,\text{F}\left( 3 \right)$ is not a lattice. This solves a problem raised by R. W. Quackenbush in 1985 whether the tensor product of lattices with zero is always a lattice.
${{M}_{3}}\,\otimes \,\text{F}\left( 3 \right)$ is not a lattice. This solves a problem raised by R. W. Quackenbush in 1985 whether the tensor product of lattices with zero is always a lattice.
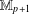 $\mathbb{M}_{p+1}$
$\mathbb{M}_{p+1}$