We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let d(n;l,k) denote the number of divisors of the positive integer n which are congruent to I modulo k. The objective of the present paper is to prove that (for some exponent θ<⅓)
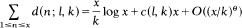
holds uniformly in l, k and x satisfying 1≤l≤k≤x. This improves a recent result due to R. A. Smith and M. V. Subbarao [3].
