For the superelliptic curves of the form

$$\begin{eqnarray}(x+1)\cdots (x+i-1)(x+i+1)\cdots (x+k)=y^{\ell }\end{eqnarray}$$

$y\neq 0$

$k\geqslant 3$

$\ell \geqslant 2,$

$i\in [2,k]\setminus \unicode[STIX]{x1D6FA}$

$\ell <\text{e}^{3^{k}}.$

$\unicode[STIX]{x1D6FA}$

$[p_{\unicode[STIX]{x1D703}},(k-p_{\unicode[STIX]{x1D703}}))$

$p_{\unicode[STIX]{x1D703}}$

$k/2$

$i=1$

Euler noted the relation 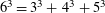$6^{3}\,=\,3^{3}+4^{3}+5^{3}$ and asked for other instances of cubes that are sums of consecutive cubes. Similar problems have been studied by Cunningham, Catalan, Gennochi, Lucas, Pagliani, Cassels, Uchiyama, Stroeker and Zhongfeng Zhang. In particular, Stroeker determined all squares that can be written as a sum of at most 50 consecutive cubes. We generalize Stroeker’s work by determining all perfect powers that are sums of at most 50 consecutive cubes. Our methods include descent, linear forms in two logarithms and Frey–Hellegouarch curves.

Given $k\geqslant 2$ , we show that there are at most finitely many rational numbers $x$ and $y\neq 0$ and integers $\ell \geqslant 2$ (with $(k,\ell )\neq (2,2)$ ) for which

$$\begin{eqnarray}x(x+1)\cdots (x+k-1)=y^{\ell }.\end{eqnarray}$$

$\ell$

$(x,y,\ell )$

$y=0$

$\ell <\exp (3^{k})$

We explicitly solve a collection of binomial Thue equations with unknown degree and unknown $S$-unit coefficients, for a number of sets $S$ of small cardinality. Equivalently, we characterize integers $x$ such that the polynomial $x^2+x$ assumes perfect power values, modulo $S$-units. These results are proved through a combination of techniques, including Frey curves and associated modular forms, lower bounds for linear forms in logarithms, the hypergeometric method of Thue and Siegel, local methods, and computational approaches to Thue equations of low degree. Along the way, we derive some new results on Fermat-type ternary equations, combining classical cyclotomy with Frey curve techniques.