Let  $F$ be a
$F$ be a  $p$-adic local field and let
$p$-adic local field and let  $A_{i}^{\times }$ be the unit group of a central simple
$A_{i}^{\times }$ be the unit group of a central simple  $F$-algebra
$F$-algebra  ${{A}_{i}}$ of reduced degree
${{A}_{i}}$ of reduced degree  $n\,>\,1\,(i\,=\,1,\,2)$. Let
$n\,>\,1\,(i\,=\,1,\,2)$. Let  ${{\mathcal{R}}^{2}}\left( A_{i}^{\times } \right)$ denote the set of irreducible discrete series representations of
${{\mathcal{R}}^{2}}\left( A_{i}^{\times } \right)$ denote the set of irreducible discrete series representations of  $A_{i}^{\times }$. The “Abstract Matching Theorem” asserts the existence of a bijection, the “Jacquet-Langlands” map,
$A_{i}^{\times }$. The “Abstract Matching Theorem” asserts the existence of a bijection, the “Jacquet-Langlands” map,  $J{{L}_{{{A}_{2}},{{A}_{1}}}}\,:\,{{R}^{2}}\left( A_{1}^{\times } \right)\,\to \,{{R}^{2}}\left( A_{2}^{\times } \right)$ which, up to known sign, preserves character values for regular elliptic elements. This paper addresses the question of explicitly describing the map 𝒥ℒ, but only for “level zero” representations. We prove that the restriction
$J{{L}_{{{A}_{2}},{{A}_{1}}}}\,:\,{{R}^{2}}\left( A_{1}^{\times } \right)\,\to \,{{R}^{2}}\left( A_{2}^{\times } \right)$ which, up to known sign, preserves character values for regular elliptic elements. This paper addresses the question of explicitly describing the map 𝒥ℒ, but only for “level zero” representations. We prove that the restriction  $J{{L}_{{{A}_{2}},{{A}_{1}}}}\,:\,R_{0}^{2}\left( A_{1}^{\times } \right)\,\to \,R_{0}^{2}\left( A_{2}^{\times } \right)$ is a bijection of level zero discrete series (Proposition 3.2) and we give a parameterization of the set of unramified twist classes of level zero discrete series which does not depend upon the algebra
$J{{L}_{{{A}_{2}},{{A}_{1}}}}\,:\,R_{0}^{2}\left( A_{1}^{\times } \right)\,\to \,R_{0}^{2}\left( A_{2}^{\times } \right)$ is a bijection of level zero discrete series (Proposition 3.2) and we give a parameterization of the set of unramified twist classes of level zero discrete series which does not depend upon the algebra  ${{A}_{i}}$ and is invariant under
${{A}_{i}}$ and is invariant under  $J{{L}_{{{A}_{2}},{{A}_{1}}}}$ (Theorem 4.1).
$J{{L}_{{{A}_{2}},{{A}_{1}}}}$ (Theorem 4.1).
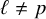 $\ell \neq p$
$\ell \neq p$
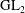 ${\rm GL}_2$ over
${\rm GL}_2$ over 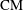 ${\rm CM}$ fields
${\rm CM}$ fields
 $\mathfrak{p}$-Adic Simple Algebras
$\mathfrak{p}$-Adic Simple Algebras