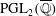New simple functional equations of zeta functions of the prehomogeneous vector spaces consisting of symmetric matrices are obtained, using explicit forms of zeta functions in the previous paper, Part I, and real analytic Eisenstein series of half-integral weight. When the matrix size is 2, our functional equations are identical with the ones by Shintani, but we give here an alternative proof. The special values of the zeta functions at nonpositive integers and the residues are also explicitly obtained. These special values, written by products of Bernoulli numbers, are used to give the contribution of “central” unipotent elements in the dimension formula of Siegel cusp forms of any degree. These results lead us to a conjecture on explicit values of dimensions of Siegel cusp forms of any torsion-free principal congruence subgroups of the symplectic groups of general degree.
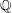 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{Q}$
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{Q}$