If $K$ is an algebraic function field of one variable over an algebraically closed field $k$ and $F$ is a finite extension of $K$, then any element $a$ of $K$ can be written as a norm of some $b$ in $F$ by Tsen's theorem. All zeros and poles of $a$ lead to zeros and poles of $b$, but in general additional zeros and poles occur. The paper shows how this number of additional zeros and poles of $b$ can be restricted in terms of the genus of $K$, respectively $F$. If $k$ is the field of all complex numbers, then we use Abel's theorem concerning the existence of meromorphic functions on a compact Riemann surface. From this, the general case of characteristic 0 can be derived by means of principles from model theory, since the theory of algebraically closed fields is model-complete. Some of these results also carry over to the case of characteristic $p>0$ using standard arguments from valuation theory.

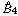 . A consequence is to represent a matrix specialization of the ‘equianharmonic’ parameter in terms of special values of the adelic beta function introduced and studied by Anderson and Ihara.
. A consequence is to represent a matrix specialization of the ‘equianharmonic’ parameter in terms of special values of the adelic beta function introduced and studied by Anderson and Ihara.