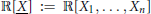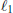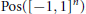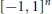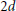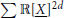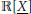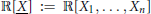In a paper from 1976, Berg, Christensen, and Ressel prove that the closure of the cone of sums of squares $\sum{\mathbb{R}{{\left[ \underline{X} \right]}^{2}}}$ in the polynomial ring $\mathbb{R}\left[ \underline{X} \right]\,:=\,\mathbb{R}\left[ {{X}_{1}},\,.\,.\,.\,,\,{{X}_{n}} \right]$ in the topology induced by the 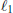$~{{\ell }_{1}}$-norm is equal to 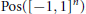$\text{Pos}\left( {{\left[ -1,\,1 \right]}^{n}} \right)$, the cone consisting of all polynomials that are non-negative on the hypercube 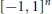${{\left[ -1,\,1 \right]}^{n}}$. The result is deduced as a corollary of a general result, established in the same paper, which is valid for any commutative semigroup. In later work, Berg and Maserick and Berg, Christensen, and Ressel establish an even more general result, for a commutative semigroup with involution, for the closure of the cone of sums of squares of symmetric elements in the weighted 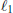$~{{\ell }_{1}}$-seminorm topology associated with an absolute value. In this paper we give a new proof of these results, which is based on Jacobi’s representation theorem from 2001. At the same time, we use Jacobi’s representation theorem to extend these results from sums of squares to sums of 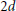$2d$-powers, proving, in particular, that for any integer $d\,\ge \,1$, the closure of the cone of sums of 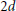$2d$-powers 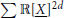$\sum \mathbb{R}{{\left[ \underline{X} \right]}^{2d}}$ in the 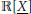$\mathbb{R}\left[ \underline{X} \right]$ topology induced by the 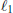$~{{\ell }_{1}}$-norm is equal to 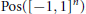$\text{Pos}\left( {{\left[ -1,\,1 \right]}^{n}} \right)$.

Dimension groups (not countable) that are also real ordered vector spaces can be obtained as direct limits (over directed sets) of simplicial real vector spaces (finite dimensional vector spaces with the coordinatewise ordering), but the directed set is not as interesting as one would like; for instance, it is not true that a countable-dimensional real vector space that has interpolation can be represented as such a direct limit over a countable directed set. It turns out this is the case when the group is additionally simple, and it is shown that the latter have an ordered tensor product decomposition. In an appendix, we provide a huge class of polynomial rings that, with a pointwise ordering, are shown to satisfy interpolation, extending a result outlined by Fuchs.

The results obtained extend Madden’s result for Dedekind domains to more general types of 1-dimensional Noetherian rings. In particular, these results apply to piecewise polynomial functions t:C → R where R is a real closed field and C ⊆ Rn is a closed 1-dimensional semi-algebraic set, and also to the associated “relative” case where t, C are defined over some subfield K ⊆ R.