Let
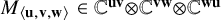 $M_{\langle \mathbf {u},\mathbf {v},\mathbf {w}\rangle }\in \mathbb C^{\mathbf {u}\mathbf {v}}{\mathord { \otimes } } \mathbb C^{\mathbf {v}\mathbf {w}}{\mathord { \otimes } } \mathbb C^{\mathbf {w}\mathbf {u}}$
denote the matrix multiplication tensor (and write
$M_{\langle \mathbf {u},\mathbf {v},\mathbf {w}\rangle }\in \mathbb C^{\mathbf {u}\mathbf {v}}{\mathord { \otimes } } \mathbb C^{\mathbf {v}\mathbf {w}}{\mathord { \otimes } } \mathbb C^{\mathbf {w}\mathbf {u}}$
denote the matrix multiplication tensor (and write
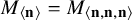 $M_{\langle \mathbf {n} \rangle }=M_{\langle \mathbf {n},\mathbf {n},\mathbf {n}\rangle }$
), and let
$M_{\langle \mathbf {n} \rangle }=M_{\langle \mathbf {n},\mathbf {n},\mathbf {n}\rangle }$
), and let
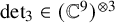 $\operatorname {det}_3\in (\mathbb C^9)^{{\mathord { \otimes } } 3}$
denote the determinant polynomial considered as a tensor. For a tensor T, let
$\operatorname {det}_3\in (\mathbb C^9)^{{\mathord { \otimes } } 3}$
denote the determinant polynomial considered as a tensor. For a tensor T, let
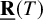 $\underline {\mathbf {R}}(T)$
denote its border rank. We (i) give the first hand-checkable algebraic proof that
$\underline {\mathbf {R}}(T)$
denote its border rank. We (i) give the first hand-checkable algebraic proof that
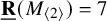 $\underline {\mathbf {R}}(M_{\langle 2\rangle })=7$
, (ii) prove
$\underline {\mathbf {R}}(M_{\langle 2\rangle })=7$
, (ii) prove
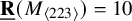 $\underline {\mathbf {R}}(M_{\langle 223\rangle })=10$
and
$\underline {\mathbf {R}}(M_{\langle 223\rangle })=10$
and
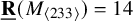 $\underline {\mathbf {R}}(M_{\langle 233\rangle })=14$
, where previously the only nontrivial matrix multiplication tensor whose border rank had been determined was
$\underline {\mathbf {R}}(M_{\langle 233\rangle })=14$
, where previously the only nontrivial matrix multiplication tensor whose border rank had been determined was
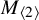 $M_{\langle 2\rangle }$
, (iii) prove
$M_{\langle 2\rangle }$
, (iii) prove
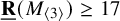 $\underline {\mathbf {R}}( M_{\langle 3\rangle })\geq 17$
, (iv) prove
$\underline {\mathbf {R}}( M_{\langle 3\rangle })\geq 17$
, (iv) prove
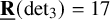 $\underline {\mathbf {R}}(\operatorname {det}_3)=17$
, improving the previous lower bound of
$\underline {\mathbf {R}}(\operatorname {det}_3)=17$
, improving the previous lower bound of
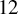 $12$
, (v) prove
$12$
, (v) prove
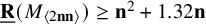 $\underline {\mathbf {R}}(M_{\langle 2\mathbf {n}\mathbf {n}\rangle })\geq \mathbf {n}^2+1.32\mathbf {n}$
for all
$\underline {\mathbf {R}}(M_{\langle 2\mathbf {n}\mathbf {n}\rangle })\geq \mathbf {n}^2+1.32\mathbf {n}$
for all
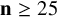 $\mathbf {n}\geq 25$
, where previously only
$\mathbf {n}\geq 25$
, where previously only
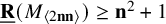 $\underline {\mathbf {R}}(M_{\langle 2\mathbf {n}\mathbf {n}\rangle })\geq \mathbf {n}^2+1$
was known, as well as lower bounds for
$\underline {\mathbf {R}}(M_{\langle 2\mathbf {n}\mathbf {n}\rangle })\geq \mathbf {n}^2+1$
was known, as well as lower bounds for
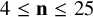 $4\leq \mathbf {n}\leq 25$
, and (vi) prove
$4\leq \mathbf {n}\leq 25$
, and (vi) prove
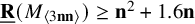 $\underline {\mathbf {R}}(M_{\langle 3\mathbf {n}\mathbf {n}\rangle })\geq \mathbf {n}^2+1.6\mathbf {n}$
for all
$\underline {\mathbf {R}}(M_{\langle 3\mathbf {n}\mathbf {n}\rangle })\geq \mathbf {n}^2+1.6\mathbf {n}$
for all
 $\mathbf {n} \ge 18$
, where previously only
$\mathbf {n} \ge 18$
, where previously only
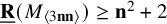 $\underline {\mathbf {R}}(M_{\langle 3\mathbf {n}\mathbf {n}\rangle })\geq \mathbf {n}^2+2$
was known. The last two results are significant for two reasons: (i) they are essentially the first nontrivial lower bounds for tensors in an “unbalanced” ambient space and (ii) they demonstrate that the methods we use (border apolarity) may be applied to sequences of tensors.
$\underline {\mathbf {R}}(M_{\langle 3\mathbf {n}\mathbf {n}\rangle })\geq \mathbf {n}^2+2$
was known. The last two results are significant for two reasons: (i) they are essentially the first nontrivial lower bounds for tensors in an “unbalanced” ambient space and (ii) they demonstrate that the methods we use (border apolarity) may be applied to sequences of tensors.
The methods used to obtain the results are new and “nonnatural” in the sense of Razborov and Rudich, in that the results are obtained via an algorithm that cannot be effectively applied to generic tensors. We utilize a new technique, called border apolarity developed by Buczyńska and Buczyński in the general context of toric varieties. We apply this technique to develop an algorithm that, given a tensor T and an integer r, in a finite number of steps, either outputs that there is no border rank r decomposition for T or produces a list of all normalized ideals which could potentially result from a border rank decomposition. The algorithm is effectively implementable when T has a large symmetry group, in which case it outputs potential decompositions in a natural normal form. The algorithm is based on algebraic geometry and representation theory.
 $(p,k)$-norms of tensor products of matrices
$(p,k)$-norms of tensor products of matrices
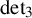 $\operatorname {det}_3$
$\operatorname {det}_3$